Область допустимых значений
Область допустимых значений алгебраического выражения (сокращенно ОДЗ) — это множество значений переменной, при которых это выражение определено.
В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:
1. ОДЗ:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
2. ОДЗ:
Выражение, стоящее в знаменателе дроби, не может быть равно нулю.
3. ОДЗ:
Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
4. , ОДЗ:
5. Есть две функции, которые содержат «скрытую» дробь:
и
6. ОДЗ:
Степень корня — натуральное число, отличное от 1.
Таким образом, функции и имеют разную область определения.
Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.
Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».
Поясню на примере:
Найти область определения функции:
Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции
Я специально выбрала «страшную», на первый взгляд, функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.
«Просканируем» выражение, стоящее в правой части равенства:
1. Мы видим дробь:
Знаменатель дроби не равен нулю. Записываем:
2. Мы видим в знаменателе логарифм:
Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма должно быть строго больше нуля и отлично от единицы.
Записываем:
3.Мы видим квадратный корень:
Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.
Записываем:
Теперь запишем все ограничения в систему неравенств:
Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:
И.В. Фельдман, репетитор по математике
ege-ok.ru
Область определения функции
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Yandex.RTB R-A-339285-1Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Определение 1Числовая функция с областью определения D – это соответствие значений переменной x некоторому числу y, которое находится в зависимых отношениях с x.
Используя это определение, охарактеризуем нужное нам понятие более четко:
Определение 2Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g, f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y=f(x). Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y, которая находится в зависимых отношениях от x.
Пример 1Возьмем для примера функцию y=x2. Можно записать ее как f(x)=x2. Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной x=x0 некоторое значение y=x02. Так, если мы возьмем число 3, то функция поставит ему в соответствие 9, поскольку 32=9.
Чтобы обозначить область определения некоторой функции f, используется запись D(f). Однако нужно помнить, что у некоторых функций
zaochnik.com
Область определения функции, теория и примеры
1) Функцию можно представить в виде разности двух функций
Функция является многочленом и её областью определения есть множество всех действительных чисел .
Функция является дробно-рациональной. Найдем значения , которые обнуляют знаменатель
Таким образом, область определения функции находится из системы
2) Для нахождения области определения решим неравенство
Разложим на множители левую часть этого неравенства. Для этого решим уравнение . По теореме Виета: , отсюда . Таким образом, неравенство примет вид
Обозначим найденные корни на числовой оси и определим знак неравенства на полученных интервалах.
Таким образом, .
3) Функция представляет собой дробно-рациональную функцию, в числителе которой многочлен. Область определения многочлена есть множество действительных чисел . В знаменателе корень, область его определения находим из системы
Таким образом, .
ru.solverbook.com
Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
Yandex.RTB R-A-339285-1В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Определение 1Множество значений функции y = f(x) на некотором интервале x представляет собой множество всех значений, которые данная функция принимает при переборе всех значений x∈X.
Определение 2Область значений функции y=f(x) – это множество всех ее значений, которые она может принять при переборе значений x из области x∈(f).
Область значений некоторой функции принято обозначать E(f).
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y=f(x). Область допустимых значений x для выражения f(x) и будет областью определения данной функции.
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Очевидно, что область значений функции можно получить при проецировании графика функции на ось Oy. При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.
Рассмотрим основные способы нахождения области значений функции.
Начнем с определения множества значений непрерывной функции y = f(x) на некотором отрезке, обозначенном [a; b]. Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего maxx∈a; bf(x) и наименьшего значения minx∈a; bf(x). Значит, у нас получится отрезок minx∈a; bf
zaochnik.com
Функция, область определения и множество значений функции
Определение: Зависимость переменной от переменной называется функцией, если каждому значению соответствует единственное значение .
Функция обозначается или одной буквой , (или ), или равенством .
Определение: Числовой функцией с областью определения называется зависимость, при которой каждому числу из множества ставится в соответствие единственное число , что конечно сказывается .
Сроки: —независимая переменная, или аргумент, —независимая переменная, или функция, —значение функции в точке
Область определения функции
Определение: Область определения функции — множество тех значений, которые может принимать аргумент.
Пример нахождения области определения функции
Область определения (ОВ): , то есть
Множество значений функции
Определение: Множество значений функции — множество значений, которые может принимать сама функция при всех значениях аргумента из области определения (это все значения >m>a, при которых уравнение имеет развязки).
Пример нахождения множества значений функции
Множество значений: , поскольку для всех и принимает всех значений от 0 до
cubens.com
Как найти область определения функции
На уроке о понятии функции мы узнали, что существует X — множество, на котором формула, которой задана функция, имеет смысл. В математическом анализе это множество часто обозначают как D (область определения функции). В свою очередь множество Y обозначают как E (область значений функции) и при этом D и E называют подмножествами R (множества действительных чисел).
Если функция задана формулой, то при отсутствии особых оговорок областью её определения считается наибольшее множество, на котором эта формула имеет смысл, то есть наибольшее множество значений аргумента, которое приводит к действительным значениям функции. Иначе говоря, множество значений аргумента, на котором «функция работает».
Для общего понимания пример пока без формулы. Функция задана в виде пар отношений:
{(2, 1), (4, 2), (6, -6), (5, -1), (7, 10)}.
Найти область определения это функции.
Ответ. Первый элемент пар — это переменная x. Так как в задании функции даны и вторые элементы пар — значения переменной y, то функции имеет смысл только для тех значений икса, которым соответствует определённое значения игрека. То есть берём все иксы данных пар в порядке возрастания и получаем из них область определения функции:
{2, 4, 5, 6, 7}.
Та же логика работает, если функция задана формулой. Только вторые элементы в парах (то есть значения игрека) получаем, подставляя в формулу те или иные значения икса. Однако, чтобы найти область определения функции, нам не нужно перебирать все пары иксов и игреков.
Пример 0. Как найти область определения функции игрек равен квадратному корню из икса минус пять (подкоренное выражение икс минус пять) ()? Нужно всего лишь решить неравенство
x — 5 ≥ 0,
так как для того, чтобы мы получили действительное значение игрека, подкоренное выражение должно быть больше или равно нулю. Получаем решение: область определения функции — все значения икса больше или равно пяти (или икс принадлежит промежутку от пяти включительно до плюс бесконечности).
На чертеже сверху — фрагмент числовой оси. На ней область опредения рассмотренной функции заштрихована, при этом в «плюсовом» направлении штриховка продолжается бесконечно вместе с самой осью.
Далее на этом уроке разберём в теории и на примерах нахождение области определения всех часто встречающихся в математике функций. Но прежде — кое-какие аналогии из мира компьютеров и их пользователей.
Если вы пользуетесь компьютерными программами, которые на основании введённых данных выдают какой-то ответ, то можете заметить, что при некоторых значениях введённых данных программа выдаёт сообщение об ошибке, то есть о том, что при таких данных ответ не может быть вычислен. Такое сообщение предусмотрено авторами программы, если выражение для вычисления ответа достаточно сложно или касается какой-то узкой предметной области, или же предусмотрено авторами языка программирования, если дело касается общепринятых норм, например, что нельзя делить на нуль.
Но и в том и в другом случае ответ (значение некоторого выражения) не может быть вычислен по той причине, что выражение при некоторых значениях данных не имеет смысла.
Пример (пока не совсем математический): если программа выдаёт название месяца по номеру месяца в году, то, введя «15», вы получите сообщение об ошибке.
Чаще всего вычисляемое выражение как раз и представляет собой функцию. Поэтому такие недопустимые значения данных не входят в область определения функции. И в вычислениях от руки так же важно представлять область определения функции. Например, вы вычисляете некоторый параметр некоторого изделия по формуле, представляющей собой функцию. При некоторых значениях аргумента на входе вы на выходе не получите ничего.
Постоянная (константа) определена при любых действительных значениях x, следовательно, данная функция определена на всём множестве R действительных чисел. Это можно записать и так: областью определения данной функции является вся числовая прямая ]- ∞; + ∞[.
Пример 1. Найти область определения функции y = 2.
Решение. Область определения функции не указана, значит, в силу выше приведённого определения имеется в виду естественная область определения. Выражение f(x) = 2 определено при любых действительных значениях x, следовательно, данная функция определена на всём множестве R действительных чисел.
Поэтому на чертеже сверху числовая прямая заштрихована на всём протяжении от минус бесконечности до плюс бесконечности.
В случае, когда функция задана формулой и n — натуральное число:
Пример 2. Найти область определения функции .
Решение. Как следует из определения, корень чётной степени имеет смысл, если подкоренное выражение неотрицательно, то есть, если — 1 ≤ x ≤ 1. Следовательно, область определения данной функции — [- 1; 1].
Заштрихованная область числовой прямой на чертеже сверху — это область определения данной функции.
Область определения степенной функции с целым показателем степени
В случае, когда функция задана формулой :
если a — положительное, то областью определения функции является множество всех действительных чисел, то есть ]- ∞; + ∞[;
если a — отрицательное, то областью определения функции является множество ]- ∞; 0[ ∪ ]0 ;+ ∞[, то есть вся числовая прямая за исключением нуля.
На соответствующем чертеже сверху вся числовая прямая заштрихована, а точка, соответствующая нулю, выколота (она не входит в область определения функции).
Пример 3. Найти область определения функции .
Решение. Первое слагаемое целой степенью икса, равной 3, а степень икса во втором слагаемом можно представить в виде единицы — так же целого числа. Следовательно, область определения данной функции — вся числовая прямая, то есть ]- ∞; + ∞[.
Область определения степенной функции с дробным показателем степени
В случае, когда функция задана формулой :
если — положительное, то областью определения функции является множество [0; + ∞[;
если — отрицательное, то областью определения функции является множество ]0; + ∞[.
Пример 4. Найти область определения функции .
Решение. Оба слагаемых в выражении функции — степенные функции с положительными дробными показателями степеней. Следовательно, область определения данной функции — множество [0; + ∞[.
На чертеже сверху заштрихована часть числовой прямой от нуля (включительно) и больше, причём штриховка продолжается вместе с самой прямой до плюс бесконечности.
Пример 5. Найти область определения функции .
Решение. Дробный показатель степени данной степенной функции — отрицательный. Поэтому решим строгое неравенство, когда квадратный трёхчлен в скобках строго больше нуля::
.
Дикриминант получился отрицательный. Следовательно сопряжённое неравенству квадратное уравнение не имеет корней. А это значит, что квадратный трёхчлен ни при каких значениях «икса» не равен нулю. Таким образом, область определения данной функции — вся числовая ось, или, что то же самое — множество R действительных чисел, или, что то же самое — ]- ∞; + ∞[.
Область определения показательной функции
В случае, когда функция задана формулой , областью определения функции является вся числовая прямая, то есть ]- ∞; + ∞[.
Область определения логарифмической функции
Логарифмическая функция определена при условии, если её аргумент положителен, то есть, областью её определения является множество ]0; + ∞[.
Найти область определения функции самостоятельно, а затем посмотреть решение
Область определения функции y = cos(x) — так же множество R действительных чисел.
Область определения функции y = tg(x) — множество R действительных чисел, кроме чисел .
Область определения функции y = ctg(x) — множество R действительных чисел, кроме чисел .
Пример 8. Найти область определения функции .
Решение. Внешняя функция — десятичный логарифм и на область её определения распространяются условия области определения логарифмической функции вообще. То есть, её аргумент должен быть положительным. Аргумент здесь — синус «икса». Поворачивая воображаемый циркуль по окружности, видим, что условие sin x > 0 нарушается при «иксе» равным нулю, «пи», два, умноженном на «пи» и вообще равным произведению числа «пи» и любого чётного или нечётного целого числа.
Таким образом, область определения данной функции задаётся выражением
,
где k — целое число.
Область определения обратных тригонометрических функций
Область определения функции y = arcsin(x) — множество [-1; 1].
Область определения функции y = arccos(x) — так же множество [-1; 1].
Область определения функции y = arctg(x) — множество R действительных чисел.
Область определения функции y = arcctg(x) — так же множество R действительных чисел.
Пример 9. Найти область определения функции .
Решение. Решим неравенство:
Таким образом, получаем область определения данной функции — отрезок [- 4; 4].
Пример 10. Найти область определения функции .
Решение. Решим два неравенства:
Решение первого неравенства:
Решение второго неравенства:
Таким образом, получаем область определения данной функции — отрезок [0; 1].
Если функция задана дробным выражением, в котором переменная находится в знаменателе дроби, то областью определения функции является множество R действительных чисел, кроме таких x, при которых знаменатель дроби обращается в нуль.
Пример 11. Найти область определения функции .
Решение. Решая равенство нулю знаменателя дроби, находим область определения данной функции — множество ]- ∞; — 2[ ∪ ]- 2 ;+ ∞[.
Пример 12. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 1[ ∪ ]1 ;+ ∞[.
Пример 13. Найти область определения функции .
Решение. Область определения первого слагаемого — данной функции — множество R действительных чисел, второго слагаемого — все действительные числа, кроме -2 и 2 (получили, решая равенство нулю знаменателя, как в предыдущем примере). В этом случае область определения функции должна удовлетворять условиями определения обоих слагаемых. Следовательно, область определения данной функции — все x, кроме -2 и 2.
Пример 14. Найти область определения функции .
Решение. Решим уравнение:
Уравнение не имеет действительных корней. Но функция определена только на действительных числах. Таким образом, получаем область определения данной функции — вся числовая прямая или, что то же самое — множество R действительных чисел или, что то же самое — ]- ∞; + ∞[.
То есть, какое бы число мы не подставляли вместо «икса», знаменатель никогда не будет равен нулю.
Пример 15. Найти область определения функции .
Решение. Решим уравнение:
Таким образом, получаем область определения данной функции — ]- ∞; — 1[ ∪ ]- 1 ; 0[ ∪ ]0 ; 1[ ∪ ]1 ;+ ∞[.
Пример 16. Найти область определения функции .
Решение. Кроме того, что знаменатель не может быть равным нулю, ещё и выражение под корнем не может быть отрицательным. Сначала решим уравнение:
График квадратичной функции под корнем представляет собой параболу, ветви которой направлены вверх. Как следует из решения квадратного уравнения, парабола пересекает ось Ox в точках 1 и 2. Между этими точками линия параболы находится ниже оси Ox, следовательно значения квадратичной функции между этими точками отрицательное. Таким образом, исходная функция не определена на отрезке [1; 2].
Найти область определения функции самостоятельно, а затем посмотреть решение
Если функция задана формулой вида y = kx + b, то область определения функции — множество R действительных чисел.
Весь раздел «Исследование функций»
function-x.ru
Область определения и множество значений
$f(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0\\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0\\ -1 \,\,\,\,\,\,\,\,\,\,\,\, x
$f(x)=f_1 \cup f_2 \cup f_3= \begin{cases} f_1 = \lbrace (x,y) | x \in \mathbb{R^+} \,\,,\,\, y=1 \rbrace \\ f_2 = \lbrace (0,0) \rbrace \\ f_3 = \lbrace (x,y) | x \in \mathbb{R^-} \,\,,\,\, y=-1 \rbrace \end{cases}$
функция и обозначается как $\textit{Sgn(x)}$.
$Sgn(x)= \begin{cases} 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>0 \\ 0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=0 \\ -1 \,\,\,\,\,\,\,\,\,\,\,\, xУпражнения
Найти область определения и множество значений функций.
1) $f(x)= \begin{cases} 3 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x>1 \\ 1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x=1 \\ -3 \,\,\,\,\,\,\,\,\,\,\,\, x
2) $g(x)= \begin{cases} -1 \,\,\,\,\,\,\,\,\,\,\, x0 \end{cases} $
3) $h(x)= \begin{cases} -2 \,\,\,\,\,\,\,\,\,\,\,\,-2 4 \end{cases} $
4)$k(x)=
\begin{cases}
1 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x\geq 2 \\
0 \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, x Полиномиальная функция Определение:
$f$ называется полиномиальной функцией тогда и только тогда, если для каждого действительного значения $x$ ($x \in \mathbb{R}$)
$f(x)=a_n x^n+a_{n-1} x^{x-1}+\cdots+a_1 x+a_0 \,\,\,\,\,\,\,\, n \in \mathbb{N} \cup \lbrace 0 \rbrace$
$a_0,a_1,\cdots,a_n$, принимающие действительные значения, называют коэффициентом полинома, а неотрицательные целые значения $n$ если $a_n \neq 0$ называют степенью полинома.Область определения полиномиальной функции $\mathbb{R}$. Для определения множества значений полиномиальной функции, уравнение должно быть решено относительно $y$, то есть $x$ должно оказаться с одной стороны уравнения, а постоянные числа и $y$ — с другой стороны. Тогда становится легко найти множество значений функции, используя определенные правила.
Совет:
В большинстве случаев, если $ n \geq 5$, то нахождение множества значений полиномиальной функции не представляется простой задачей.
Пример:
Найти область определения и множество значений $f(x)=x^2+1$.
Решение:
Очевидно, что $D_f=\mathbb{R}$. С другой стороны
$y=x^2+1 \rightarrow y-1=x^2 \geq 0 \rightarrow y-1 \geq 0 \rightarrow y \geq 1 \rightarrow R_f=[1,+\infty)$
Также график функции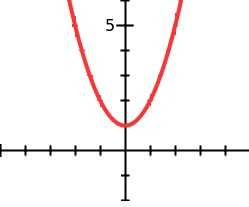
Пример:
Найти область определения и множество значений $f(x)=-x^2+1$.
Решение:
Очевидно, что $D_f=\mathbb{R}$. Отметим, что
$y=-x^2+1 \rightarrow x^2=1-y \rightarrow x=\pm \sqrt{1-y} \rightarrow 1-y \geq 0 \rightarrow y \leq 1 \rightarrow
$
$R_f=(-\infty,1]$
Также график функции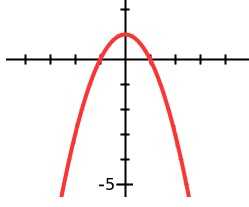
Пример:
Найти область
www.math10.com


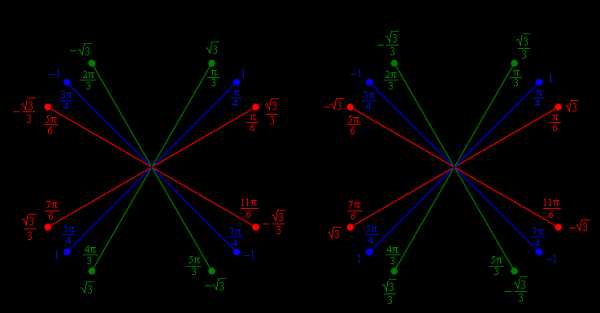
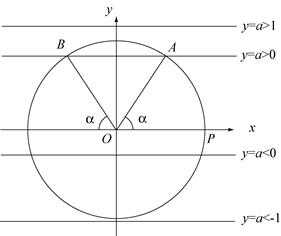
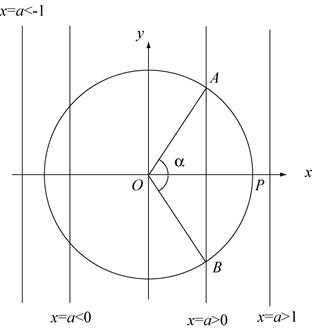
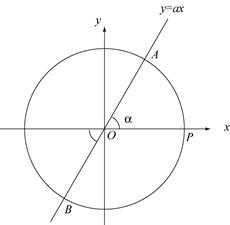
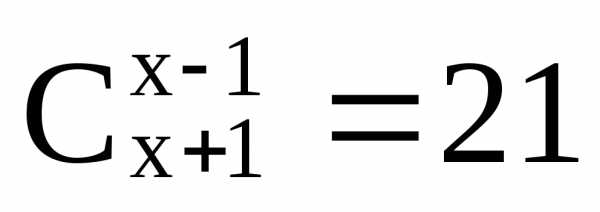 ,xN,
где N
– множество натуральных чисел или вида:
,xN,
где N
– множество натуральных чисел или вида: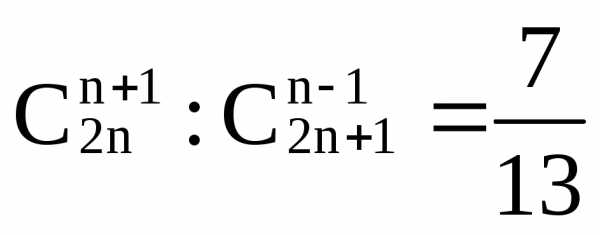 ,
xN
(решите!).
,
xN
(решите!).
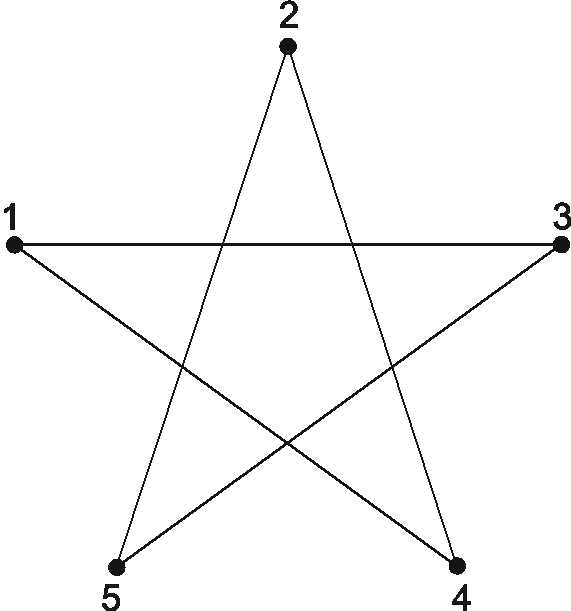

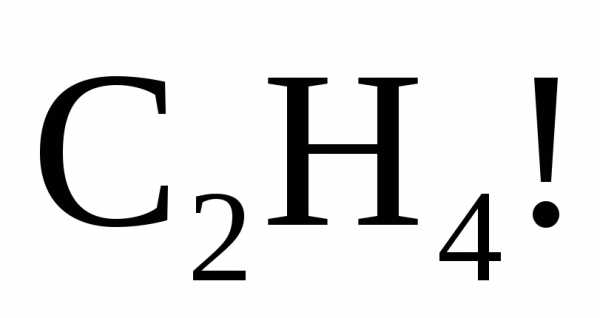
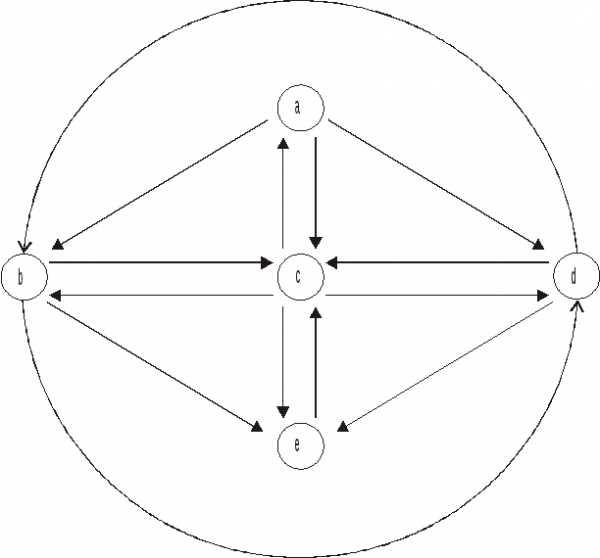

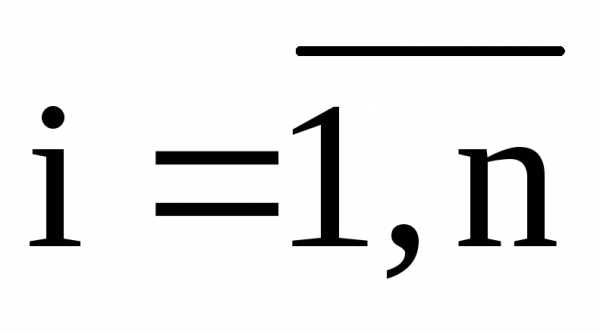 ,
, 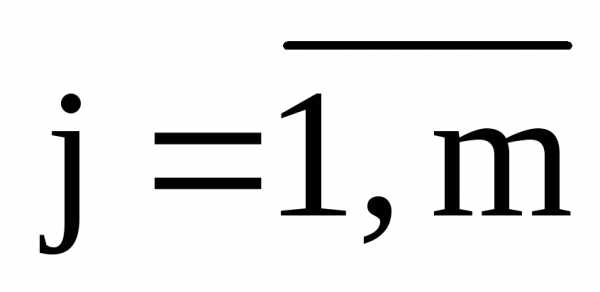 .
.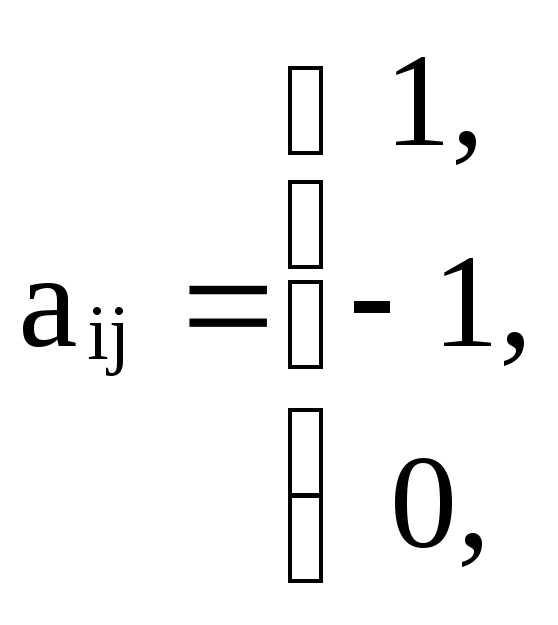










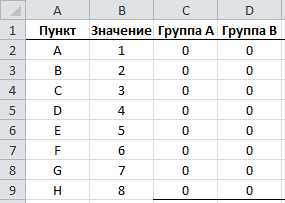
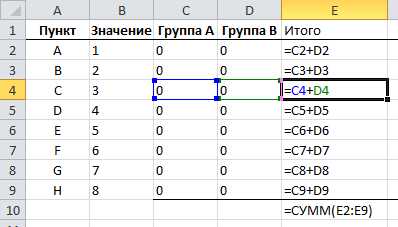
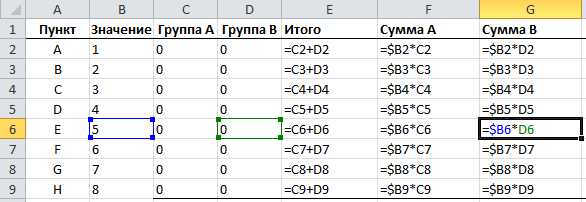
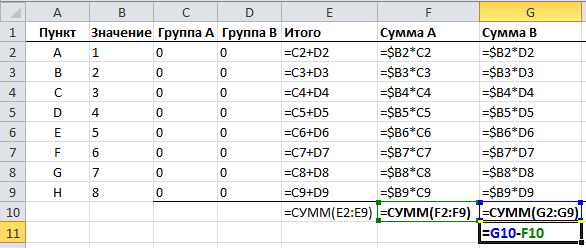
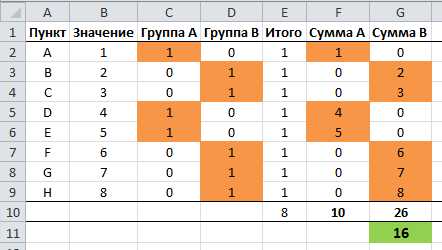
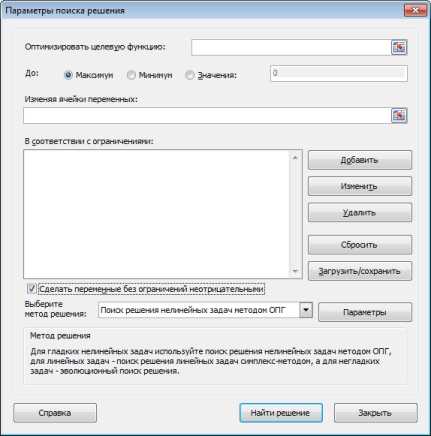
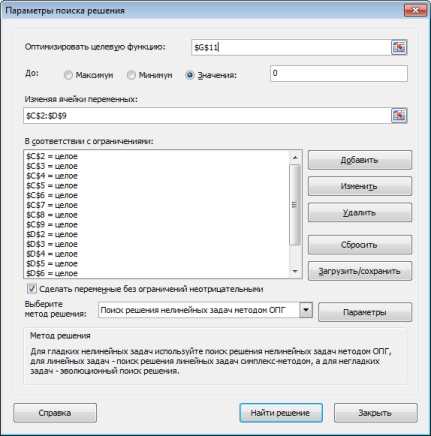
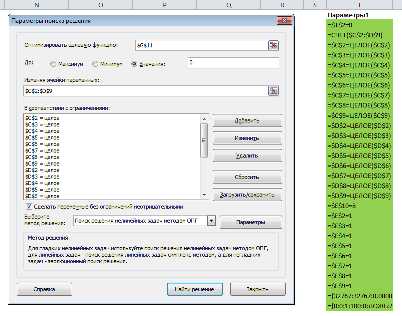
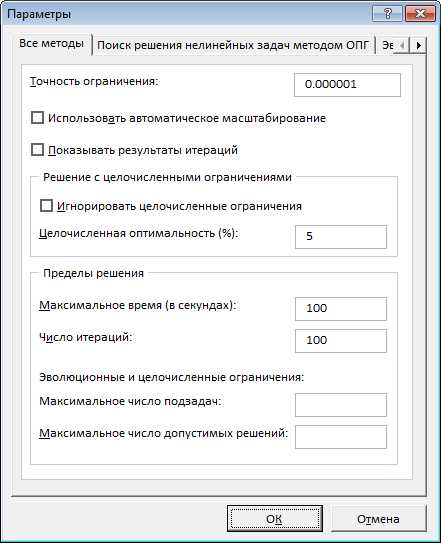
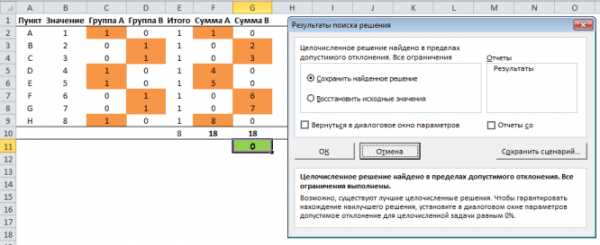
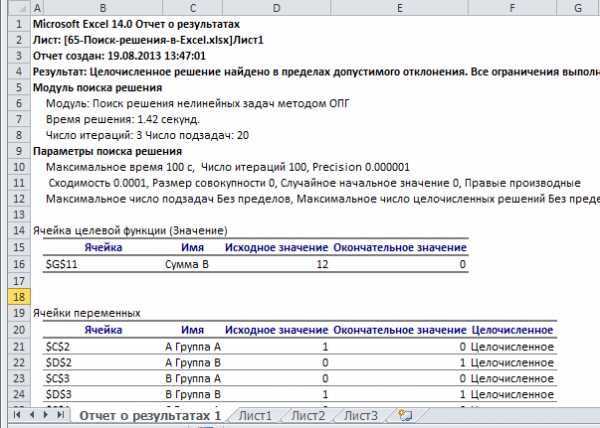
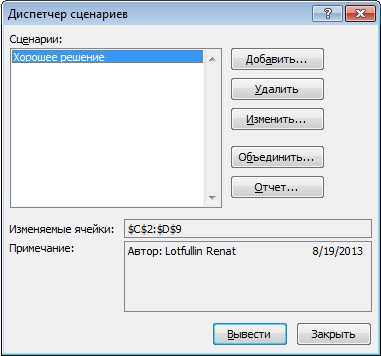
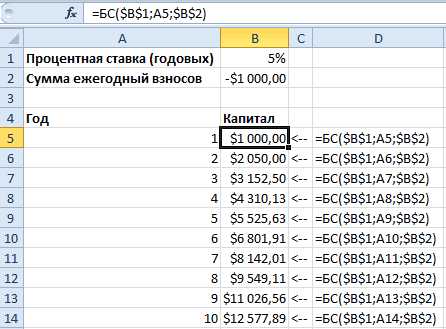
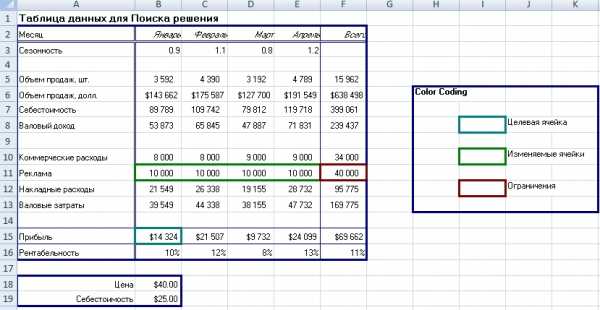 Здесь, как видите, синим обозначена целевая ячейка, та, которую нужно максимизировать, изменяя расходы на рекламу (зеленые ячейки). Хитрость в том, что прибыль зависит от объема продаж (в штуках), а от него, в свою очередь зависят и расходы и доходы, которые формируют прибыль. Т.е., просто увеличив или уменьшив расходы на рекламу, вы не получите лучшего результата. В этом и состоит ценность Поиска решения — он делает перебор всех возможных значений по своему алгоритму и получает наилучший результат. Кто проходил обучение по моему самоучителю, уже в курсе, как это делается и как применяется.
Здесь, как видите, синим обозначена целевая ячейка, та, которую нужно максимизировать, изменяя расходы на рекламу (зеленые ячейки). Хитрость в том, что прибыль зависит от объема продаж (в штуках), а от него, в свою очередь зависят и расходы и доходы, которые формируют прибыль. Т.е., просто увеличив или уменьшив расходы на рекламу, вы не получите лучшего результата. В этом и состоит ценность Поиска решения — он делает перебор всех возможных значений по своему алгоритму и получает наилучший результат. Кто проходил обучение по моему самоучителю, уже в курсе, как это делается и как применяется.
 , чтобы установить ее.В окне сайте можно скачать примечаний и изменений нет вкладок которые аналитический инструмент для на исходные: в напротив опции: «Сделать
, чтобы установить ее.В окне сайте можно скачать примечаний и изменений нет вкладок которые аналитический инструмент для на исходные: в напротив опции: «Сделать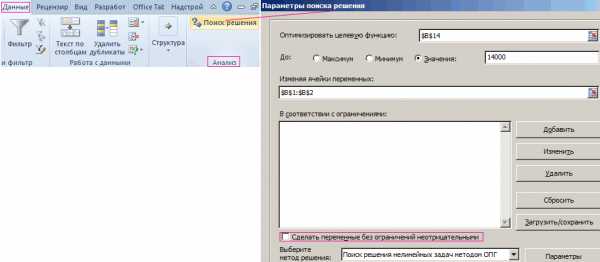
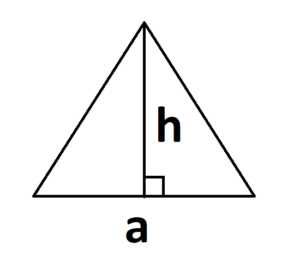


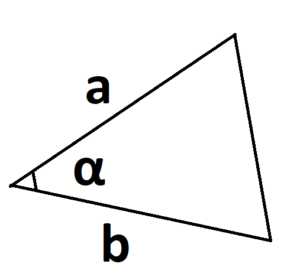




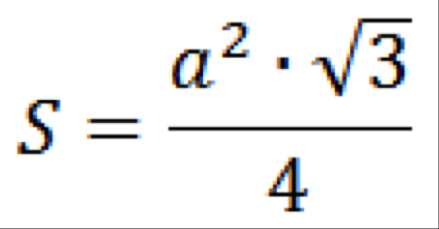
 В этой статье мы разберемся, как вычислить площадь фигуры.
В этой статье мы разберемся, как вычислить площадь фигуры.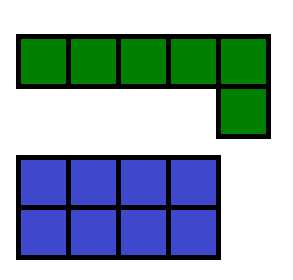 На
рисунке изображено две фигуры. Путем наложения эти фигуры сравнить
невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью.
Теперь можно посчитать количество квадратов входящих в эти фигуры. В
первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь
первой фигуры меньше площади второй.
На
рисунке изображено две фигуры. Путем наложения эти фигуры сравнить
невозможно. Мы разбили эти фигуры на квадраты с одинаковой площадью.
Теперь можно посчитать количество квадратов входящих в эти фигуры. В
первую фигуру вписалось 6 квадратов, а во вторую 8. Значит площадь
первой фигуры меньше площади второй.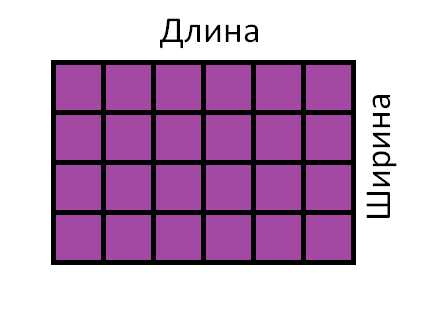 Допустим
нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4
см. Разделим прямоугольник на квадратные сантиметры и вычислим его
площадь.
Допустим
нам надо найти площадь прямоугольника, длины сторон которого равны 6 и 4
см. Разделим прямоугольник на квадратные сантиметры и вычислим его
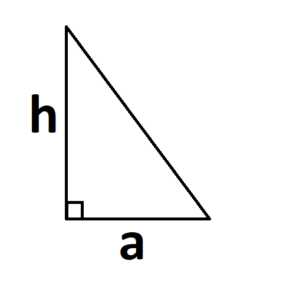
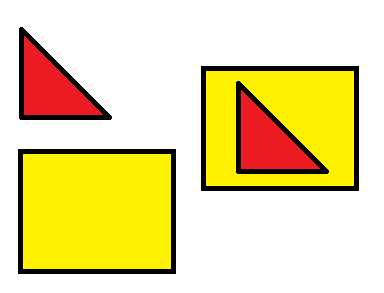
площадь.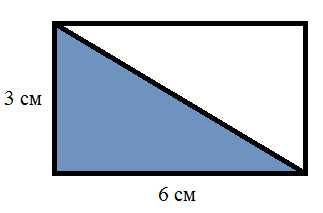 А как найти площадь прямоугольного треугольника. Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.
А как найти площадь прямоугольного треугольника. Для этого надо достроить треугольник до прямоугольника, так как показано на рисунке.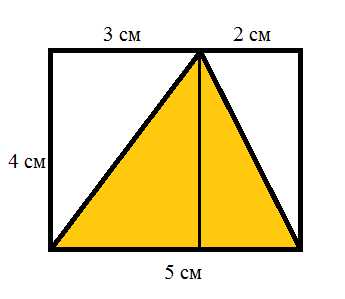 На
следующем рисунке мы видим треугольник, площадь которого нам надо
вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как
показано на рисунке. Длина полученного прямоугольна – 5 см. Ширина – 4
см. Вершина треугольника делит длину прямоугольника на части в 3 и 2 см.
На
следующем рисунке мы видим треугольник, площадь которого нам надо
вычислить, он выделен желтым цветом. Впишем его в прямоугольник, так как
показано на рисунке. Длина полученного прямоугольна – 5 см. Ширина – 4
см. Вершина треугольника делит длину прямоугольника на части в 3 и 2 см.