Тест с ответами: «Рынок труда»
1. Отметьте понятия, относящиеся к рынку труда:
а) Ликвидность
б) +Средства производства
в) +Рабочая сила
г) +Труд
2. Чем является цена реализации труда или цена реализации рабочей силы?
а) Оптовой ценой
б) Ценой без НДС
в) +Заработная плата
3. Отметьте элементы, которые включает в себя современная структура рынка труда?
а) Производственную систему
б) +Систему найма
в) +Систему подготовки кадров
г) +Систему переподготовки и переквалификации
4. От чего зависит спрос на труд и предложение труда?
а) Цен на продукты питания
б) Мировых цен
в) +Цены реализации труда
5. Отметьте основные подходы к анализу механизма функционирования рынка труда:
а) Ленинизм
б) +Монетаристская модель
в) +Неоклассический
г) +Марксизм
6. К какому понятию относятся «трудовые ресурсы»??
а) «Финансовые ресурсы»
б) «Материальные ресурсы»
в) «Сырьевые ресурсы»
г) +«Человеческие ресурсы»
7. Что характеризует трудовой потенциал?
а) Количество и структуру труда
б) +Качество и потенциальные возможности труда
8. Что входит в качественную характеристику трудового потенциала?
а) Психическую составляющую
б) +Социальную составляющую
в) +Интеллектуальную составляющую
г) +Физическую составляющую
9. Какие составляющие включает в себя экономически активное население?
а) Все население страны
б) Безработных, не ищущих работу
в) +Безработных, активно ищущих работу и готовых приступить к ней
г) +Занятых общественно-полезной деятельностью, приносящей доход
10. Главная составная часть трудовых ресурсов:
а) работники
б) предприниматели
в) +наемная рабочая сила
г) все население страны
11. Дайте определение понятия «Рынок труда» –
а) Статическая система, включающая в себя комплекс социально-трудовых отношений по поводу условий найма, использования и обмена рабочей силы на жизненные средства
б) +Механизм спроса и предложения, функционирующий на основе информации, поступающей в виде изменений цены труда (заработной платы)
в) +Динамическая система, включающая в себя комплекс социально-трудовых отношений по поводу условий найма, использования и обмена рабочей силы на жизненные средства
12. Что входит в структуру трудового рынка?
а) Объекты рынка труда
б) +Рыночный механизм
в) +Конкуренцию
г) +Субъекты рынка труда
13. Что входить в структуру механизма трудового рынка?
а) Сотрудничество
б) +Конкуренция
в) +Предложение труда
г) +Цена труда
д) +Спрос на труд
14. Рынком труда являются товарно-денежные отношения, связанные:
а) Со временем формирования рабочей силы
б) +Со временем использования рабочей силы
в) +Со спросом на рабочую силу, определяемым спросом на товар в обществе
г) +С использованием профессиональных востребованных способностей и их вознаграждением
15. Является ли механизм рынка труда взаимодействием и согласованием разнообразных интересов работодателей и трудоспособного населения, которое желает работать по найму на основе информации, получаемой в виде изменений цены труда?
а) Нет
б) +Да
16. Отметьте существующие модели рынка труда:
а) Африканская
б) +Шведская
в) +Американская
г) +Японская
17. Отметьте название новых тенденций в развитии экономики, придавших новое качество рынку труда:
а) «жесткий рынок труда»
б) «эластичный рынок труда»
в) +«гибкий рынок труда»
18. Что такое гибкость?
а) Способность экономической системы отвечать на внутренние воздействия, ее способность сохранять управляемость и функциональное равновесие при изменении внутренних условий
б) +Способность экономической системы отвечать на внешние воздействия, ее способность сохранять управляемость и функциональное равновесие при изменении внешних условий
19. К какому рынку ближе российская модель рынка труда?
а) К внешнему рынку труда
б) +К внутреннему рынку труда
20. Чем является подвижное использование рабочего времени и функциональная смена рабочих мест?
а) Стандартные режимы использования полного рабочего времени
б) Режимы использования полного рабочего времени
+в) Нестандартные режимы использования полного рабочего времени
21. Чем принято определять удовлетворенный спрос на рабочую силу?
а) Числом работников, ищущих работу в течение определенного периода времени
б) +Числом работников, нанятых предприятиями в течение определенного периода времени
22. Чем принято определять неудовлетворенный спрос на рабочую силу?
а) Числом работников, ищущих работу
б) +Количеством рабочих мест, остающихся свободными
23. Отметьте основные группы, которые в себя включает структура спроса на рабочую силу?
а) Спрос на профессиональную рабочую силу
б) +Спрос на неквалифицированную рабочую силу
в) +Спрос на рабочую силу низкой квалификации
г) +Спрос на высококвалифицированную рабочую силу
24. Отметьте звенья, из которых состоит совокупный спрос на рабочую силу: Индивидуальный спрос отдельно взятого покупателя
а) +Индивидуальный спрос отдельно взятой фирмы
б) +Суммарный спрос индивидуальных фирм данной отрасли
25. Будет ли совокупный объем предложения рабочей силы на рынке труда кроме занятых лиц, которые имеют работу, включать и незанятых лиц, ищущих работу?
а) Нет
б) +Да
26. Что такое предложение рабочей силы?
а) Спрос на товары и услуги
б) Спрос на рабочую силу
в) +Спрос на рабочие места
27. К чему приведет внедрение новой техники и технологии?
а) к значительному увеличению рабочей силы, вовлечению ее в сферу производства
б) +к значительному сокращению рабочей силы, высвобождению ее из сферы производства
28. Когда наемными работниками, занятыми на предприятиях фирмы Х, продают свою рабочую силу на внутрифирменном рынке труда?
а) ежедневно
б) непрерывно
в) +лишь с наступлением срока заключения нового коллективного договора (соглашения) между профсоюзом, объединяющим данный трудовой коллектив, и хозяевами фирмы — работодателями, покупателями рабочей силы
29. В случае если работник стремится получить максимум дохода, и готов посветить свое свободное сверхурочную работу, то эта ситуация увеличивает предложение труда и имеет название:
а) «Эффект доход»
б) +«Замещающий эффект»
30. Отметьте слово, которое является лишним:
а) +Труд,
б) безработица,
в) предпринимательские способности,
г) капитал,
д) земля.
31. Как был сформирован ряд слов в предыдущем вопросе?
а) Указаны экономические издержки
б) +Указаны факторы производства
в) Указаны источники финансирования бизнеса
г) Указаны механизмы государственного регулирования рыночной экономики
32. Что можно приобрести на рынке труда?
а) Оборудование, необходимое рабочим для трудовой деятельности
б) Право на использование способностей работника
в) Способности человека, необходимые для создания материальных ценностей
г) +Работника, обладающего необходимыми трудовыми навыками
33. Главный участник рынка труда:
а) Продавец и посетитель
б) Покупатель и работник
в) +Работодатель и работник
г) Работодатель и продавец
34. Как реализуются взаимодействия на рынке труда?
а) +посредством обмена на основе спроса и предложения
б) за счёт эффективного использования рабочей силы
в) за счёт ограниченности экономических ресурсов
г) посредством вложения капиталов с целью последующего получения прибыли
35. Отметьте аргумент при построении функции спроса на труд:
а) заработная плата;
б) +цена;
в) ставка процента;
г) доход.
36. Отметьте то, что не относится к основным механизмам рынка труда:
а) Предложение
б) +Профессиональная переподготовка
в) Спрос
г) Рыночная цена трудовых услуг
37. Что из представленного в ответах будет являться формой материального вознаграждения?
а) Рента
б) Процент по вкладу
в) +Заработная плата
г) Ставка заработной платы
38. От чего будет зависеть величина спроса на рынке труда?
а) Качества труда
б) Потребностей работника в деньгах
в) Спроса потребителей на выпускаемые работодателем товары и услуги
г) +Цен на товары и услуги
39. Отметьте те понятия, которые относятся к видам безработицы:
а) естественная
+б) структурная
+в) циклическая
г) сезонная
40. Чем является занятость населения?
а) отсутствие свободного времени
+б) деятельность граждан, необходимая для своих и общественных потребностей
в) отсутствие экономической свободы
г) безработица
41. Что такое рынок труда:
а) продажа трудовых вакансий
б) спрос фирм на работников
+в) система социально – трудовых отношений
г) аукцион трудовых затрат
42. Отметьте виды заработной платы:
а) посменная
+б) повременная
в) посезонная
+г) сдельная
43. Отметьте то, что не будет являться причиной возникновения безработицы:
а) низкая мобильность работника
б) применение современных технологий
+в) тяжелые климатические условия
г) международная конкуренция
44. Что произойдет с гражданином без работы?
а)подвергнется большому риску заболеваемости
+б) потеряет квалификацию
в) будет изгнан из общества
г) снизится жизненный уровень+
45. Государственной формой регулирования безработицы является:
а) + инвестиции в предприятия для сохранения рабочих мест
б) полный запрет на иностранную рабочую силу
в) +поддержка частного предпринимательства
г) уменьшение работникам заработной платы
46. Откуда происходит финансирование программы занятости граждан РФ?
а) из средств работодателя
б) из средств работника
в) + из федерального бюджета
г) +из местного бюджета
47. Основными участниками рынка труда является:
а) +работодатель
б) государство
в) + работник
г) организация, предприятие
48. Что такое прожиточный минимум?
а) пособие по безработице
б) минимальная заработная плата
в) + доход необходимый для основных жизненных потребностей человека
г) затраты человека на свои потребности
49. Что будет компенсировать работнику компенсационная заработная плата?
а)затраты на получение образования
б)затраты на командировочные расходы
+в)вредные условия труда
г)отсутствие квартальных премий в течение последнего год
50. Формированием чего будет обеспечено участие предприятий в регулировании рынка руда?
а) структуры предложения на рынке труда
+б) структуры спроса на рабочую силу
в) объема найма работников
г) характеристик найма работников
51. Сопоставив заработную плату с динамикой … можно выяснить изменение в уровне реальной заработной платы.
а) нормы прибыли;
+б) уровня цен на товары и услуги;
в) ставки налогообложения;
г) продолжительности рабочей недели
52. При помощи чего принято учитывать количество труда при его оплате?
+а) нормирования труда;
б) тарифной системы оплаты труда;
в) форм и систем оплаты труда.
53. При помощи чего устанавливают размер оплаты труда за каждую единицу рабочего времени?
а) нормирования труда;
+б) тарифной системы;
в) форм и систем оплаты труда.
54. Отметьте не существующие формы оплаты труда:
+а) сдельно-премиальная;
б) повременная;
в) сдельная.
55. Отметьте факторы, не вызывающие сдвига кривой спроса:
а) изменения в доходе;
+б) изменения цены данного товара;
в) изменения цен товаров- комплиментов и заменителей;
г) ожидание роста цен.
56. Что произойдет в случае, если рыночная цена ниже равновесной?
а)формируется рынок покупателя
+б)возникает дефицит товаров
в)появляются избытки товаров
г)падает цена ресурсов
57. Отметьте термин, отражающий способность и желание людей платить за что-либо:
а) потребность
+б) спрос
в) необходимость
г) желание
liketest.ru
Рынок труда Тесты с ответами Темы 1-6
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 1. Рынок труда в системе рыночной экономики
Какие из перечисленных понятий относятся к рынку труда?
Ликвидность
+Средства производства
+Рабочая сила
+Труд
Цена реализации труда или цена реализации рабочей силы – это:
Оптовая цена
Цена без НДС
+Заработная плата
Какие элементы включает в себя современная структура рынка труда?
Производственную систему
+Систему найма
+Систему подготовки кадров
+Систему переподготовки и переквалификации
Спрос на труд, и предложение труда прежде всего зависят от:
Цен на продукты питания
Мировых цен
+Цены реализации труда
Укажите основные подходы к анализу механизма функционирования рынка труда:
Ленинизм
+Монетаристская модель
+Неоклассический
+Марксизм
Друзья, более 600 собак Воронежского приюта Дора https://vk.com/priyt_dora очень нуждаются в поддержке! Приют бедствует, не хватает средств на корм и лечение. Не откладывайте добрые дела, перечислите прямо сейчас любую сумму на «Голодный телефон» +7 960 111 77 23 или карту сбербанка 4276 8130 1703 0573. По всем вопросам обращаться +7 903 857 05 77 (Шамарин Юрий Иванович)
Тема 2. Труд как фактор производства и объект рыночных отношений
Трудовые ресурсы — одна из форм выражения понятия:
«Финансовые ресурсы»
«Материальные ресурсы»
«Сырьевые ресурсы»
+«Человеческие ресурсы»
Трудовой потенциал характеризует:
Количество и структуру труда
+Качество и потенциальные возможности труда
Качественная характеристика трудового потенциала включает:
Психическую составляющую
+Социальную составляющую
+Интеллектуальную составляющую
+Физическую составляющую
Экономически активное население включает:
Все население страны
Безработных, не ищущих работу
+Безработных, активно ищущих работу и готовых приступить к ней
+Занятых общественно-полезной деятельностью, приносящей доход
Главной составной частью трудовых ресурсов является:
работники
предприниматели
+наемная рабочая сила
все население страны
Тема 3. Сущность, структура, механизм функционирования и особенности рынка труда
Рынок труда — это:
Статическая система, включающая в себя комплекс социально-трудовых отношений по поводу условий найма, использования и обмена рабочей силы на жизненные средства
+Механизм спроса и предложения, функционирующий на основе информации, поступающей в виде изменений цены труда (заработной платы)
+Динамическая система, включающая в себя комплекс социально-трудовых отношений по поводу условий найма, использования и обмена рабочей силы на жизненные средства
Структура рынка труда включает:
Объекты рынка труда
+Рыночный механизм
+Конкуренцию
+Субъекты рынка труда
Структура механизма рынка труда включает:
Сотрудничество
+Конкуренцию
+Предложение труда
+Цену труда
+Спрос на труд
Рынок труда — это только те товарно-денежные отношения, которые связаны:
Со временем формирования рабочей силы
+Со временем использования рабочей силы
+Со спросом на рабочую силу, определяемым спросом на товар в обществе
+С использованием профессиональных востребованных способностей и их вознаграждением
Верно ли, что механизм рынка труда — это взаимодействие и согласование разнообразных интересов работодателей и трудоспособного населения, желающего работать по найму на основе информации, получаемой в виде изменений цены труда?
Нет
+Да
Тема 4. Виды, сегменты и гибкость рынка труда
Существуют следующие модели рынка труда:
Африканская
+Шведская
+Американская
+Японская
Новые тенденции в развитии экономики придали новое качество рынку труда, получившее название:
«жесткий рынок труда»
«эластичный рынок труда»
+«гибкий рынок труда»
Гибкость — это:
Способность экономической системы отвечать на внутренние воздействия, ее способность сохранять управляемость и функциональное равновесие при изменении внутренних условий
+Способность экономической системы отвечать на внешние воздействия, ее способность сохранять управляемость и функциональное равновесие при изменении внешних условий
Российская модель рынка труда ближе:
К внешнему рынку труда
+К внутреннему рынку труда
Подвижное использование рабочего времени и функциональная смена рабочих мест — это:
Стандартные режимы использования полного рабочего времени
Режимы использования полного рабочего времени
+Нестандартные режимы использования полного рабочего времени
Тема 5. Рабочая сила на рынке труда: факторы спроса
Удовлетворенный спрос на рабочую силу определяется:
Числом работников, ищущих работу в течение определенного периода времени
+Числом работников, нанятых предприятиями в течение определенного периода времени
Неудовлетворенный спрос на рабочую силу определяется:
Числом работников, ищущих работу
+Количеством рабочих мест, остающихся свободными
Структура спроса на рабочую силу включает следующие основные группы:
Спрос на профессиональную рабочую силу
+Спрос на неквалифицированную рабочую силу
+Спрос на рабочую силу низкой квалификации
+Спрос на высококвалифицированную рабочую силу
Совокупного спроса на рабочую силу слагается из следующих звеньев:
Индивидуальный спрос отдельно взятого покупателя
+Индивидуальный спрос отдельно взятой фирмы
+Суммарный спрос индивидуальных фирм данной отрасли
Возможности расширения спроса на рабочую силу благодаря … существенно ограничиваются факторами экономического, социального и правового характера.
перерасчету заработной платы
повышению заработной платы
изменению заработной платы
+понижению заработной платы
Тема 6. Рабочая сила на рынке труда: факторы предложения
Верно ли утверждение, что совокупный объем предложения рабочей силы на рынке труда кроме занятых лиц, имеющих работу, включает и незанятых лиц, ищущих работу?
Нет
+Да
Предложение рабочей силы — это:
Спрос на товары и услуги
Спрос на рабочую силу
+Спрос на рабочие места
Внедрение новой техники и технологии ведет …
к значительному увеличению рабочей силы, вовлечению ее в сферу производства
+к значительному сокращению рабочей силы, высвобождению ее из сферы производства
Наемные работники, занятые на предприятиях данной фирмы, продают свою рабочую силу на внутрифирменном рынке труда…
ежедневно
непрерывно
+лишь с наступлением срока заключения нового коллективного договора (соглашения) между профсоюзом, объединяющим данный трудовой коллектив, и хозяевами фирмы — работодателями, покупателями рабочей силы
Если работник, в стремление получить максимум дохода, свободное время тратит на сверхурочную работу, то эта ситуация увеличивает предложение труда и именуется:
«Эффектом дохода»
+«Замещающим эффектом»
test-for-you.ru
Тест с ответами: Рынок труда
- Лизинг персонала необходим для:
а) Привлечение новых работников н предприятие на постоянной основе.
б) Покрытия краткосрочной временной потребности в персонале (через болезнь, через серьезные колебания в деятельности предприятия и т.д.). +
в) Повышение квалификации работников предприятия.
г) Возможности получения предприятием дополнительного дохода.
- При выборе предприятием формы привлечения персонала исследуется рынок труда, который подразделяется на:
а) Специализированный.
б) Внутрифирменый.
в) Внешний.
г) Верны ответы “б” и “в”. +
- При исследовании внутрифирменного (внутреннего) рынка труда анализируется:
а) Социально-демографическая ситуация.
б) Кадровая ситуация.
в) Политическая ситуация.
г) Верными являются ответы “а” и “б”. +
- При исследовании внешнего рынка труда анализируется:
а) Уровень конкуренции на выбранном сегменте рынка труда.
б) Местонахождение предприятия, его преимущества и недостатки для потенциальных сотрудников.
в) Наличие или отсутствие возможности помощи со стороны других организаций по привлечению персонала.
г) Все ответы верны. +
- Налаживание контакта с потенциальными работниками предприятия с целью побудить их подать заявление о приеме на работу имеет название:
а) Маркетинг персонала.
б) Тестирование персонал
в) Вербовка персонала. +
г) Аттестация персонала.
- Опосредованное вербовка персонала — это:
а) Привлечения персонала на имеющиеся вакантные должности в текущем периоде.
б) Формирование положительного имиджа предприятия на рынке труда. +
в) Представление предприятием информации о необходимости привлечения персонала в текущем периоде.
г) Представление предприятием информации о необходимости привлечения персонала в будущем периоде.
- К вербовочной структуры объявления входит информация о:
а) Описание особенностей организации.
б) Характеристика вакантной должности.
в) Требования, предъявляемые к соискателю.
г) Все ответы верны. +
- К методам оценки способностей претендентов входят:
а) Тесты.
б) Интерактивные методы.
в) Документы претендентов.
г) Все ответы верны. +
- Профессиональный опыт соискателя можно оценить с помощью:
а) Документов претендента (трудовой биографии).
б) Собеседования.
в) Тестов с проверки сенсорных способностей.
г) Верны ответы “а” и “б”. +
- Сокращение персонала означает целенаправленное снижение его численности в случае:
а) В случае, когда фактическое наличие персонала превышает необходимую численность.
б) В случае, когда фактическое наличие персонала является недостаточной.
в) В случае несоответствия требованиям к занимаемой должности или требованиям выполняемой работы (квалификационная несоответствие, несоответствие по состоянию здоровья).
г) Верны ответы “а” и “в”. +
- Освобождение считаются массовыми, когда высвобождают:
а) 50% от общей численности работников предприятия.
б) 100% от общей численности работников предприятия.
в) 10% от общей численности работников предприятия. +
г) 25% от общей численности работников предприятия.
- К внешним факторам, которые могут быть причинами высвобождения относят:
а) Падение спроса, технический прогресс, который ведет к ликвидации ряда профессий, необходимость сокращения затрат труда. +
б) Ошибки в подборе персонала, расстановке кадров, а также усиление конкуренции на внутреннем рынке труда.
в) Профессиональная несоответствие большинства работников предприятия.
г) Все ответы не верны.
- внутренних факторов, которые могут быть причинами высвобождения относят:
а) Падение спроса, технический прогресс, который ведет к ликвидации ряда профессий, необходимость сокращения затрат труда.
б) Ошибки в подборе персонала и в расстановке кадров.
в) Усиление конкуренции на внутреннем рынке труда.
г) Верны ответы “б” и “в”. +
- С экономической точки зрения высвобождение персонала означает:
а) Устранение излишней численности и качественное совершенствование требований, предъявляемых к работнику, чтобы обеспечить баланс между качественными и количественными параметрами рабочего места и характеристиками работника. +
б) Ухудшение морально-психологического климата в коллективе.
в) Возможность судебных разбирательств по вопросу трудовых конфликтов между собственником и работником.
г) Верны ответы “а” и “б”.
- С социальной точки зрения высвобождение персонала означает:
а) Устранение излишней численности и качественное совершенствование требований, предъявляемых к работнику, чтобы обеспечить баланс между качественными и количественными параметрами рабочего места и характеристиками работника.
б) Ухудшение морально-психологического климата в коллективе.
в) Возможность судебных разбирательств по вопросу трудовых конфликтов между собственником и работником.
г) Верны ответы “б” и “в”. +
- До вариантов высвобождения персонала относят:
а) Прекращение найма.
б) Переводы и перемещения на предприятии.
в) Сокращение нормальной продолжительности рабочего дня и введение укороченного рабочего недели.
г) Все ответы верны. +
- Первой реакцией на излишнюю численность должна быть:
а) Переводы и перемещения на предприятии.
б) Прекращение найма. +
в) Сокращение нормальной продолжительности рабочего дня и введение укороченного рабочего недели.
г) Прекращение выдачи заказов на сторону.
- За счет естественной текучести можно обеспечить:
а) 5-% сокращение численности персонала. +
б) 10-% сокращение численности персонала.
в) 15-% сокращение численности персонала.
г) 20-% сокращение численности персонала.
- Прекращение найма может привести к:
а) Ухудшение морально-психологического климата в коллективе.
б) Ухудшение квалификационной структуры персонала.
в) Ухудшение возрастной структуры персонала. +
г) Все ответы не верны.
- Какие из условий трудового соглашения могут измениться при переводах работников:
а) Размер заработной платы.
б) Условия труда.
в) Режимы рабочего времени.
г) Все ответы верны. +
- Согласие работника является важным при:
а) Перемещениях.
б) Переводах. +
в) В обоих случаях.
г) ни в одном из случаев.
- Введение сокращенного рабочего дня нельзя применять для:
а) Основного персонала.
б) Дополнительного персонала.
в) Руководителей. +
г) ни в одном из случаев.
- Отмена (сокращение) сверхурочной работы — это реакция на:
а) Увеличение государством размера минимальной заработной платы.
б) Недостаточное загрузки определенного количества работников. +
в) Снижение численности персонала предприятия.
г) Все варианты верны.
- Введение сокращенного рабочего дня возможно в случае, когда:
а) Эту форму высвобождения персонала оговорено в коллективном договоре.
б) Эту форму высвобождения персонала оговорено в индивидуальном трудовом соглашении.
в) Эту форму высвобождения персонала используют предприятия отрасли, к которой относится предприятие.
г) Верны ответы “а” и “б”. +
- Нормальной продолжительностью рабочей недели согласно Законодательству в Украине считается:
а) 40 часов. +
б) 37 часов.
в) 35 часов.
г) 32 часа.
- За неоднократное совершение дисциплинарных проступков отдельным работником руководитель:
а) Обязан расторгнуть трудовой договор.
б) вправе, но не обязан расторгнуть трудовой договор. +
в) Не имеет права разрывать трудовое соглашение.
г) Обязан пересмотреть условия трудового соглашения.
- При массовых увольнениях руководство предприятия должно:
а) Объяснить работникам причины предстоящего сокращения численности персонала.
б) Обосновать масштабы сокращения.
в) Установить контакт с центром занятости и представить туда соответствующую информацию.
г) Все ответы верны. +
- В случае массового сокращения в центр занятости предоставляется информация о:
а) Общую численность персонала предприятия.
б) Количество и сроки запланированных увольнений.
в) Возраст, опыт и квалификацию работников, освобождаются.
г) Все ответы верны. +
- Форм гибкой занятости относятся:
а) Сменная работа.
б) Счета рабочего времени.
в) 4-х дневную рабочую неделю.
г) Все ответы верны. +
- Какие два этапа включает профессиональное образование:
а) Повышение квалификации и освоение смежной профессии.
б) Первичную профессиональную подготовку и повышение квалификации. +
в) Школьное образование и первичную профессиональную подготовку.
г) Все ответы не верны.
testdoc.ru
Тест по теме «Особенности рынка труда»
1)Компенсационная
заработная плата призвана компенсировать
работнику:
а)затраты на
получение образования б)затраты на командировочные
расходы
+в)вредные
условия труда г)отсутствие
квартальных премий в течение последнего
год
2) Участие
предприятий в регулировании рынка руда
обеспечивается формированием:
а)
структуры предложения на рынке труда
+б)
структуры спроса на рабочую силу
в)
объема найма работников
г) характеристик
найма работников
3) Главными
участниками рынка труда являются:
а)Продавец и
посетитель
б)Покупатель и
работник
+в)Работодатель
и работник
г)Работодатель и
продавец
4)
Изменения в уровне реальной заработной
платы можно определить путем сопоставления
номинальной заработной платы с динамикой
одного из следующих показателей:
а)
нормы прибыли;
+б)
уровня цен на товары и услуги;
в)
ставки налогообложения;
г)
продолжительности рабочей недели
5)
Количество труда при его оплате
учитывается с помощью:
+а)
нормирования труда;
б)
тарифной системы оплаты труда;
в)
форм и систем оплаты труда.
6)
. Размер
оплаты труда за каждую единицу рабочего
времени устанавливается с помощью:
а)
нормирования труда;
+б)
тарифной системы;
в)
форм и систем оплаты труда.
7) Какие не существуют формы оплаты труда:
+а) сдельно-премиальная;
б) повременная;
в) сдельная.
8) Какие
из следующих факторов не вызывают сдвига
кривой спроса?
а)
изменения в доходе;
+б)
изменения цены данного товара;
в)
изменения цен товаров- комплиментов и
заменителей;
г)
ожидание роста цен.
9)
Если рыночная цена ниже равновесной,
то: а)формируется рынок покупателя
+б)возникает
дефицит товаров
в)появляются
избытки товаров
г)падает цена ресурсов
10) Какой термин
отражает способность и желание людей
платить за что-либо: а)потребность
+б)спрос в)необходимость
г)желание
Лекция №2
Социальные
проблемы труда. Государственное
регулирование
трудовых отношений .
В настоящее время
в странах развиты профсоюзы.
Профсоюзы –
добровольная организация, объединение
наемных работников для защиты своих
социальных, экономических прав и
интересов.
Социальное
партнерство –это система взаимоотношений между
работниками, работодателями, организациями,
государственной власти и власть местного
самоуправления, направленная на
обеспечивание согласования интересов
работников и работодателей по вопросам
трудовых отношений.
Социальное
партнерство является важным элементом
смешанной рыночной экономики.
Она обеспечивает
взаимодействие государства, работодателя
и работника. Его объективной основой
является рост экономического потенциала
и распределения его результатов между
предпринимателями и работодателями.
Социальное
партнерство осуществляется формами:
1) коллективных
переговоров
2) взаимных
консультаций по вопросам регулирования
трудовых отношений и обеспечения
гарантии трудовых прав работника.
3) участие работников
и их представителей в управлении.
Сделки на рынке
труда оформляются в виде добровольных
трудовых договоров (контрактов), в
которых на основе компромиссов увязываются
противоположные интересы работодателей
и работника.
Трудовой договор
(контракт) –это соглашение между работником и
работодателем, по которому работник
обязуется выполнять работу по определенной
специальности, квалификации или
должности, с подчинением внутреннему
трудовому распорядку, а работодатель
обязуется выплачивать ему зарплату и
обеспечивать условия труда.
Основным документом,
регламентирующим трудовые отношения,
является Трудовой Кодекс, введенный с
1 февраля 2002 года.
Основные положения
ТК РФ касаются:
1) Трудовые права
и обязанности работника и работодателя.
2) Социальное
партнерство в сфере труда, трудовых
договоров (заключений), норм рабочего
времени и времени отдыха, условия оплаты
труда, соблюдение трудовой дисциплины.
Кодексом запрещается
снижение оплаты труда работнику. В
России действует закон «О коллективных
договорах и соглашениях»
Соглашение –это правовой акт, регулирующий
социальный трудовые отношения между
работником и работодателем, заключенных
на уровне РФ, ее субъектов, территории
, отрасли или профессии.
Коллективный
договор –правовой акт, регулирующий социальные
трудовые отношения между работником
предприятия с работодателем.
Регулирование
зарплаты осуществляется следующей
формой :
установление
размеров минимальной зарплаты.
регламентация
ряда надбавок к зарплате.
изменении зарплаты
в связи с инфляцией.(ее увеличения по
мере роста цен)
studfiles.net
Тест по курсу дисциплины Эффективное поведение на рынке труда
Тест по дисциплине «Эффективное поведение на рынке труда»
Безработица – это …
а. социально-экономическое явление, при котором часть трудоспособного населения не может найти работу;
б. экономическая ситуация, при которой часть трудоспособного населения не хочет работать;
в. социально-экономическое явление, при котором часть экономически-активного населения не занята в производстве товаров и услуг
К основным правам работника не относится …
а. право иметь рабочее место, отвечающее нормам и стандартам, установленным законом;
б. право на отдых;
в. право на компенсацию расходов на проезд
К экономически-неактивному населению не относятся …
а. пенсионеры;
б. инвалиды;
в. предприниматели
Специально разработанная система, которая реализует материальное обеспечение граждан в старости – это …
а. пенсионное страхование;
б. медицинское страхование;
в. социальное страхование
К обязательным пунктам в резюме не относится …
а. сведения об образовании;
б. сведения о путешествиях за границу;
в. сведения о месте жительства
Перечислите правильную последовательность этапов профессиональной карьеры:
а. предварительный этап, этап становления, этап продвижения, этап сохранения, этап завершения
б. предварительный этап, этап продвижения, этап становления, этап сохранения, этап завершения
в. предварительный этап, этап продвижения, этап сохранения, этап становления, этап завершения
Какие документы необходимы в первую очередь для заключения трудового договора?
а. справка о заработной плате с предыдущего места работы;
б. СНИЛС;
в. медицинское заключение на право управления транспортным средством
Профессиональная деятельность – это …
а. уровень профессионального мастерства;
б. система знаний, основанная на опыте её применения;
в. ограниченная стандартами область деятельности, которая предполагает определенный объем, уровень знаний и навыков их практического применения
9. К какому виду пенсионного страхования относится пенсия за выслугу лет?
а. обязательное пенсионное страхование
б. государственное пенсионное обеспечение
в. негосударственное пенсионное обеспечение
10. Что не подходит к классификации профессий по объекту труда (по Климову Е.А.):
а. человек-человек
б. человек-живая природа
в. человек-наука
11. Приведите пример гностической профессии:
а. судебно-медицинский эксперт
б. бухгалтер
в. инженер-конструктор
12. Приведите пример изыскательной профессии:
а. зооинженер
б. дизайнер
в. искусствовед
13. Что относится к активной форме профориентации:
а. проведение викторин на знание профессий
б. беседы о профессиях
в. занятия в учебно-производственных комбинатах
14. Профессиональная консультация – это …
а. оказание помощи человеку в профессиональном самоопределении с целью принятия осознанного решения о выборе профессионального пути
б. определение степени профессиональной пригодности человека к конкретной профессии
в. система мер, способствующих профессиональному становлению работника, формированию у него соответствующих социальных и профессиональных качеств
Отношения, основанные на соглашении между работником и работодателем о личном выполнении работником за плату трудовой функции – это …
а. трудовые отношения
б. деловые отношения
в. личные отношения
Выберите правильный вариант условий заключения трудового договора:
а. трудовой договор заключается на неопределенный срок, в трех экземплярах
б. трудовой договор заключается на срок не более пяти лет, в двух экземплярах
в. трудовой договор заключается на неопределенный срок либо на срок не более пяти лет, в двух экземплярах
Профессиональная квалификация бывает:
а. формальная и реальная
б. формальная и неформальная
в. формальная и возможная
Обязательное медицинское страхование делится на:
а. денежные выплаты и дополнительное финансирование
б. денежные выплаты и компенсации расходов
в. компенсацию расходов и дополнительные платные услуги
Основная характеристика этапа продвижения в профессиональной карьере:
а. 45-60 лет, наступление пика карьеры, передача знаний и опыта молодым специалистам
б. 25-30 лет, адаптация на рабочем месте, приобретение знаний, умений и навыков, повышение квалификации
в. 30-45 лет, продвижение по служебной лестнице, накопление профессионального опыта
Что недопустимо на самопрезентации при трудоустройстве:
а. наличие сумки
б. яркий макияж
в. отсутствие пиджака
Культура делового общения – это…
а. это уровень речевого, письменного и неречевого взаимодействия, который позволяет устанавливать точное межличностное восприятие, понимание и взаимодействие людей в процессе трудовой деятельности
б. процесс взаимосвязи и взаимодействия людей с целью передачи друг другу разнообразной информации, обмена мнениями, суждениями, знаниями
в. взаимодействие двух и более людей, состоящее в обмене информацией познавательного или эмоционально-оценочного характера
Приведите пример невербального общения:
а. крик
б. словосочетание
в. мимика
Письменная форма опроса, осуществляемая при помощи специально составленных анкет и происходящая без непосредственного контакта исследователя с респондентом – это …
а. интеллектуальный тест
б. анкетирование
в. наблюдение
Какие бывают вопросы в анкетировании:
а. открытые и закрытые
б. открытые, закрытые и полузакрытые
в. открытые, прямые и полупрямые
Профессиональная адаптация – это …
а. система мер и мероприятий, которые способствуют профессиональному становлению работника и формируют у него соответствующие профессиональные качества
б. повторная социализация, связанная с переходом на новую должность или на другое место работы с сохранением прежней должности
в. перестраивание своего организма, привычек к новому режиму труда и отдыха
Перечислите виды адаптации:
а. психологическая, профессиональная, социальная, структурная
б. психологическая, профессиональная, социально-психологическая, функциональная
в. психофизическая, профессиональная, социально-психологическая, организационная
Перечислите правильную структуру резюме:
а. анкетные данные, сведения об образовании, качества личности, дополнительные сведения (увлечения, хобби)
б. анкетные данные, сведения об образовании, опыт работы, качества личности, дополнительные сведения (увлечения, хобби)
в. сведения об образовании, опыт работы, анкетные данные, качества личности, дополнительные сведения (увлечения, хобби)
Перечислите правильный список документов, необходимых для заключения трудового договора:
а. СНИЛС, ИНН, трудовая книжка, санитарная книжка
б. паспорт, ИНН, трудовая книжка
в. паспорт, СНИЛС, ИНН, трудовая книжка
Перечислите правильные принципы непрерывного образования:
а. принципы гуманизма, демократизма, мобильности, опережения, открытости, непрерывности
б. принципы гуманизма, демократизма, мобильности, ответственности, открытости, непрерывности
в. принципы гуманизма, демократизма, мобильности, опережения, открытости, незаконченности
Назовите правильную характеристику принципа гуманизма:
а. реализуется через создание благоприятных возможностей для развития творческой индивидуальности каждого человека
б. выражается в многообразии средств, способов, организационных форм системы непрерывного образования
в. предполагает доступность образования в любом возрасте благодаря многообразию форм обучения, в соответствии с интересами, возможностями и потребностями человека
31. Что не является основной характеристикой потребности?
а. периодичность
б. способ удовлетворения
в. скорость удовлетворения
32. По условиям проведения наблюдение делится на:
а. лабораторное и полевое
б. лабораторное и естественное
в. естественное и неестественное
33. Профессиональный подбор – это …
а. предоставление рекомендаций человеку о возможных направлениях профессиональной деятельности, наиболее соответствующих его психологическим, психофизиологическим, физиологическим особенностям, на основе результатов психологической, психофизиологической и медицинской диагностики
б. определение степени профессиональной пригодности человека к конкретной профессии (рабочему месту, должности) в соответствии с нормативными требованиями
в. система мер, способствующих профессиональному становлению работника, формированию у него соответствующих социальных и профессиональных качеств, установок и потребностей к активному творческому труду, достижению высшего уровня профессионализма
34. Перечислите правильную последовательность потребностей по Маслоу:
а. физиологические потребности, потребность в безопасности, потребность в принадлежности, потребность в уважении, самоактуализация
б. физиологические потребности, потребность в принадлежности, потребность в безопасности, потребность в уважении, самоактуализация
в. физиологические потребности, потребность в безопасности, потребность в уважении, потребность в принадлежности, самоактуализация
35. Устная форма ответов на вопросы, осуществляемая при помощи непосредственного контакта исследователя с респондентом – это …
а. опрос
б. анкетирование
в. наблюдение
36. В зависимости от масштаба проведения анкетирование бывает:
а. по месту учебы/работы, по месту жительства
б. почтовые анкеты, раздаточные анкеты
в. сплошное, выборочное
37. Назовите функции мотивов …
а. побуждение, направление, смыслообразование
б. побуждение, направление, анализ
в. побуждение, решение, смыслообразование
38. Оказание помощи человеку в профессиональном самоопределении с целью принятия осознанного решения о выборе профессионального пути с учетом его психологических особенностей и возможностей, а также потребностей общества – это …
а. профессиональная консультация
б. профессиональная адаптация
в. профессиональный подбор
39. Обобщенное понятие одного из компонентов общечеловеческой культуры, проявляющегося в форме заботы общества о профессиональном становлении подрастающего поколения, проведения комплекса специальных мер содействия человеку в профессиональном самоопределении с учетом его потребностей и возможностей, социально — экономической ситуации на рынке труда – это …
а. профессиональная консультация
б. профессиональная ориентация
в. профессиональный отбор
40. По адресату тестового материала психологические диагностики делятся на:
а. прямые и косвенные
б. сознательные и бессознательные
в. направленные и бесцельные
41. На рынке труда можно купить:
а. работника, обладающего необходимыми трудовыми навыками
б. право на использование способностей работника
в. способности человека, необходимые для создания материальных ценностей
42. Главными участниками рынка труда являются
а. продавец и посетитель
б. покупатель и работник
в. работодатель и работник
43. Взаимодействие на рынке труда осуществляется
а. посредством обмена на основе спроса и предложения
б. за счёт эффективного использования рабочей силы
в. за счёт ограниченности экономических ресурсов
44. При построении функции спроса на труд аргументом выступает:
а. заработная плата
б. цена
в. доход в виде прибыли
45. Выберите неверный вариант: основные механизмы рынка труда:
а. спрос и предложение
б. профессиональная переподготовка
в. рыночная цена трудовых услуг
46. Формой материального вознаграждения за труд является:
а. рента
б. процент по вкладу
в. заработная плата
47. Величина спроса на рабочую силу не зависит от:
а. от заработной платы
б. потребностей работника в деньгах
в. спроса потребителей на выпускаемые работодателем товары и услуги
48. Оцените утверждения. Какое из них верно?
а. спрос на рынке труда, как и предложение, находится в обратной зависимости от ставки заработной платы
б. предложение на рынке труда, в отличие от спроса, находится в прямой зависимости от ставки заработной платы
в. спрос и предложение на рынке труда не зависит от величины заработной платы
49. Под рынком труда понимают:
а. куплю и продажу товаров и услуг
б. общественные отношения, связанные с наймом и предложением рабочей силы
в. рынок сырья, материалов, товаров и услуг, ценных бумаг
50. Цена рабочей силы это:
а. процент по вкладу
б. форма материального вознаграждения за труд
в. доход от продажи товаров и услуг
51. Вертикальная карьера характеризуется:
а. расширением круга полномочий без смены должности
б. подъемом на более высокую ступень в должности
в. дружескими отношениями с начальством
52. Горизонтальная карьера означает:
а. повышение в должности
б. выстраиваемый человеком жизненный путь
в. расширение функциональных обязанностей на той же должности
53. Приведите пример невербального средства общения:
а. крик
б. словосочетание
в. предложение
54. К невербальным средствам общения не относятся:
а. движения рук, головы, ног, туловища, походка, жесты, прикосновение, пожатие руки
б. речь
в. организация пространства (дистанция) и времени
55. Способствуют созданию благоприятной атмосферы для деловой беседы:
a. подробный рассказ автобиографии
б. обращения к собеседнику по имени-отчеству
в. долгое обдумывание над ответом
56. Какие типичные ошибки допускаются при написании резюме?
а. последовательный характер описания
б. краткость и структурированность
в. большой объем текста
57. Что повышает привлекательность резюме?
а. красочное оформление с использованием множества шрифтов и стилей
б. энергичные глаголы, указывающие на активность соискателя: сделал, получил, освоил рабочее место
в. конкретность (указание точных и конкретных целей)
Дайте правильную характеристику фазе развития профессионала – фаза интернала…
а. человек стоит перед проблемой выбора профессии или вынужденной переменой профессии и осуществляет свой выбор
б. профессионал приобретает значительный профессиональный опыт, имеет профессиональную направленность, способен самостоятельно выполнять основные профессиональные функции на данном трудовом посту
в. по мере многолетней профессиональной подготовки у субъекта учебно–профессиональной деятельности происходят существенные изменения в самосознании, в направленности, информированности, умелости
59. По форме представления тестового материала психологические диагностики делятся на:
а. бланковые, технические, сенсорные
б. бланковые, устные
в. бланковые, технические, устные
60. Профессиональное самоопределение это:
а. получение должностных привилегий
б. осознание человеком культуры
в. выбор профессии
Ключ к тесту по дисциплине «Эффективное поведение на рынке труда»
В
В
В
А
Б
А
Б
Б
Б
В
А
Б
В
А
А
В
А
Б
В
Б
А
В
Б
Б
А
В
Б
В
А
А
В
А
А
А
А
В
А
А
Б
Б
В
В
Б
А
Б
В
В
А
Б
Б
Б
В
А
Б
Б
В
В
Б
А
В
Критерии оценки:
5 «отлично» — правильный ответ на 53-60 вопросов
4 «хорошо» — правильный ответ на 42-52 вопросов
3 «удовлетворительно» — правильный ответ на 35-41 вопросов
2 «неуд» — менее 35 правильных ответов
infourok.ru
Тест по обществознанию на тему «Рынок труда и безработица»
Группа №______ Дата__________
Студент_______________________________
1. Какие понятия относятся к видам безработицы?
а) естественная
б) структурная
в) циклическая
г) сезонная
2. Занятость населения:
а) отсутствие свободного времени
б) деятельность граждан, необходимая для своих и общественных потребностей
в) отсутствие экономической свободы
г) безработица
3. Рынок труда:
а) продажа трудовых вакансий
б) спрос фирм на работников
в) система социально – трудовых отношений
г) аукцион трудовых затрат
4. Виды заработной платы:
а) посменная
б) повременная
в) посезонная
г) сдельная
5. Что не относится к причинам возникновения безработицы:
а) низкая мобильность работника
б) применение современных технологий
в) тяжелые климатические условия
г) международная конкуренция
6. Что грозит безработному гражданину?
а) большой риск заболеваемости
б) потеря квалификации
в) изгнание из общества
г) снижение жизненного уровня
7. Что относится к государственным формам регулирования безработицы?
а) инвестиции в предприятия для сохранения рабочих мест
б) полный запрет на иностранную рабочую силу
в) поддержка частного предпринимательства
г) уменьшение работникам заработной платы
8. Из каких средств финансируется программа занятости граждан РФ
а) из средств работодателя
б) из средств работника
в) из федерального бюджета
г) из местного бюджета
9. Основные участники рынка труда?
а) работодатель
б) государство
в) работник
г) организация, предприятие
10 . Прожиточный минимум:
а) пособие по безработице
б) минимальная заработная плата
в) доход необходимый для основных жизненных потребностей человека
г) затраты человека на свои потребности
ОТВЕТЫ:
1 – б, в
2 – б
3 – в
4 – б, г
5 – в
6 – б, г
7 – а, в
8 – в, г
9 – а, в
10 – в
infourok.ru
Материал для подготовки к ЕГЭ (ГИА) по экономике (10 класс) на тему: тест по теме «Рынок труда»
Тема «Рынок труда»
А1. Кто из приведенных ниже граждан является циклическим безработным?
- Банкир, уволившийся из-за ссоры с начальством
- Строитель, уволенный в связи с остановленным строительством фабрики
- Программист, уволившийся из-за поиска более высоко оплачиваемой работы
- президент корпорации, обанкротившейся во время финансово-экономического кризиса
А 2. Что способствует снижению уровня безработицы?
1) повышение минимальной зарплаты
2) создание программ профессиональной переподготовки
3) выплата пособий по безработице
4) уменьшение таможенной пошлины
А3. Верны ли следующие суждения о безработице?
А. Безработица ведет к снижению трудовой мотивации у работающих
Б. Безработица создает социальную напряженность в обществе.
1) верно только А 3) верны оба ответа
2) верно только Б 4) оба ответа неверны
А4. Рабочие, занятые в частной фирме переведены на неполный рабочий день. К какой категории населения относятся эти работники?
1) частично безработные 3) нетрудоспособные
2) занятые 4) бюджетники
А5. Недостаточная осведомленность граждан о свободных местах может быть одной из причин
- фрикционной безработицы 3) сезонной безработицы
- структурной безработицы 4) циклической безработицы.
А 6. Какой вид безработицы чаще всего возникает в курортных городах
- фрикционная безработица 3) сезонная безработица
- структурная безработица 4) циклическая безработица.
А7. К неэкономическим последствиям безработицы относятся
- повышение конкуренции на рынке труда
- рост числа правонарушений
- недополученный выпуск продукции
- уменьшение шансов найти высокооплачиваемую работу в будущем.
А8. Верны ли следующие суждения о трудовом договоре?
А. Трудовой договор заключается в письменной форме, составляется в двух экземплярах, каждый из которых подписывается сторонами.
Б. Условия договора могут быть изменены в одностороннем порядке.
1) верно только А 3) верны оба суждения
2) верно только Б 4) оба суждения неверны
А9. Верны ли следующие утверждения о факторах увеличения предложения труда
А. Фактором увеличения предложения на рынке труда является увеличение заработной платы.
Б. Фактором снижения предложения является тягость труда.
1) верно только А 3) верны оба суждения
2) верно только Б 4) оба суждения неверны
А10. Терпящая убытки фирма, привлекла талантливого кризис-менеджера, который за год смог вывести ее из кризисного состояния. Какой фактор производства был использован фирмой в первую очередь?
1) информация
2) предпринимательские способности
3)земля и природные ресурсы
4) капитал.
В1. В государстве З. высокий уровень безработицы. Какие категории населения могут быть отнесены к фрикционным безработным? Выберите нужные позиции и запишите их номера.
- уволившиеся по собственному желанию
- нашедшие работу, но не приступившие к ней
- уволенные в связи с падением спроса на их услуги
- уволенные в результате общего спада производства в стране
- занятые неполный рабочий день
- вновь появившиеся на рынке труда и имеющие требуемую квалификацию
В-2 Установите соответствие между примерами и соответствующими им видами безработицы.
Признаки виды безработицы
А) в связи с изменениями спроса на энергоносители 1) сезонная
многие шахты закрылись, а шахтеры остались без 2) циклическая
работы 3) структурная
Б) выпускники вузов ищут работу по специальности 4) фрикционная
В) жители приморского города обслуживают туристов
летом, а в остальное время большинство не могут
найти работу.
Г) Безработные отказываются от предложенных вакансий
в центре занятости и просят подобрать им работу
менеджеров
Д) произошло сокращение персонала фирмы в связи с
экономическим кризисом.
В-3
Запиши слово, пропущенное в схеме
Виды оплаты труда![]()
![]()
Повременная оплата труда ?……оплата труда
В 4. Найдите понятие, которое является обобщающим для всех остальных понятий представленного ниже ряда, и запишите цифру, под которой оно указано.
1) рабочая сила 4) трудоспособное население
2) безработные 5) менеджеры
3) занятые
В-5. Прочитайте приведенный ниже текст, в котором пропущен ряд слов. Выберите из приведенного ниже списка слова, которые необходимо вставить на место пропусков.
« Уровень заработной платы работника связан с его личными качествами, так называемым____________(А): ценность работника определяется его природными способностями, уровнем его _________(Б), квалификацией, опытом работы, здоровьем, духовным богатством. Есть еще ряд факторов, определяющих уровень зарплаты: особенности региона, специфика отрасли, условия___________(В) и др. Судить о размере заработка можно по __________(Г) заработной плате, которая учитывает уровень инфляции в стране. Если в стране высокая инфляция, то покупательная способность ________(Д) падает, и даже при высокой_________(Е) зарплате доступным становится все меньшее количество благ.
- труд 6) реальная
- деньги 7) номинальная
- человеческий капитал 8) фирма
- товар 9) государство
- образование
Блок С.
С-1. Какой смысл вкладывают экономисты в понятие «безработица»? Составьте два предложения, содержащие информацию о безработице.
Ключ
Вариант-1
А-1 | А-2 | А-3 | А-4 | А-5 | А-6 | А-7 | А-8 | А- 9 | А-10 | В-1 | В-2 | В-3 | В-4 | В-5 |
4 | 2 | 3 | 1 | 1 | 3 | 2 | 1 | 3 | 2 | 1, 2, 6 | 3 4 1 4 2 | сдельная | 4 | А-3 Б-5 В-1 Г-6 Д-2 Е-7 |
КЭС | | | | | | | | | | | | | | |
| | | | | | | | | | | | | | |
nsportal.ru
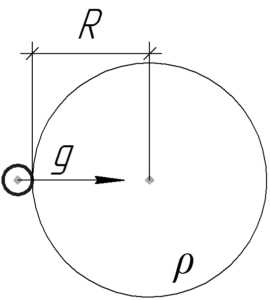Давайте узнаем как зависит ускорение свободного падения на поверхности некоторой планеты от её средней плотности и радиуса, для этого запишем формулу его определения:
,
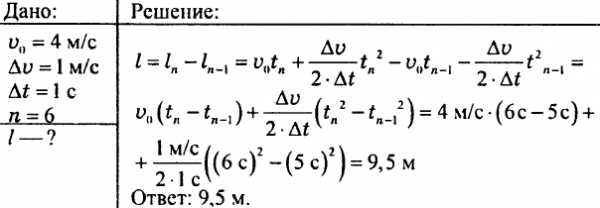
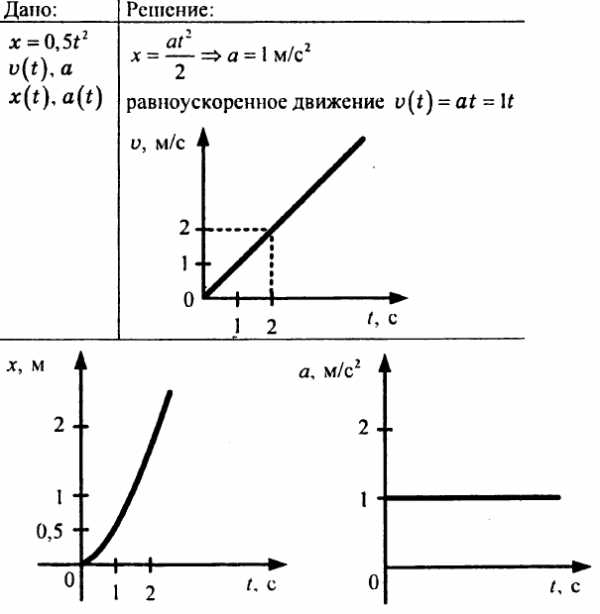
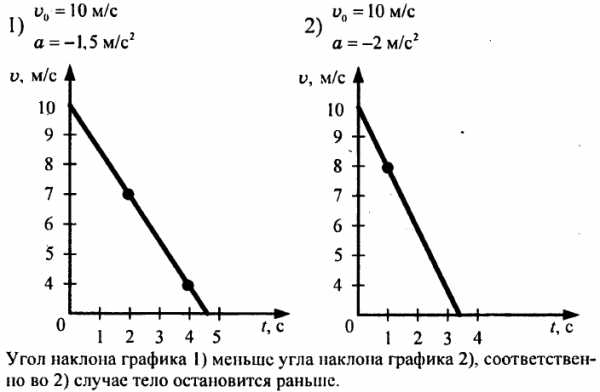
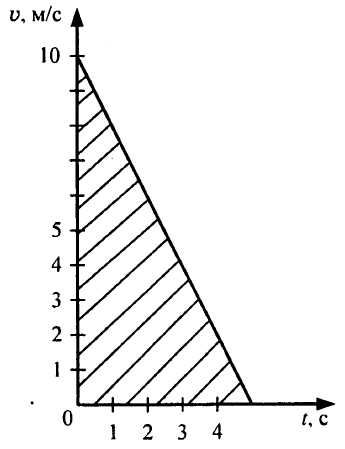
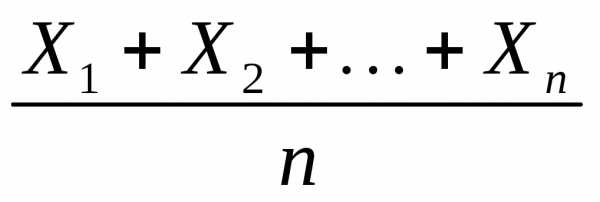равная их среднему арифметическому, с
большой вероятностью примет значение,
близкое к фиксированному числу
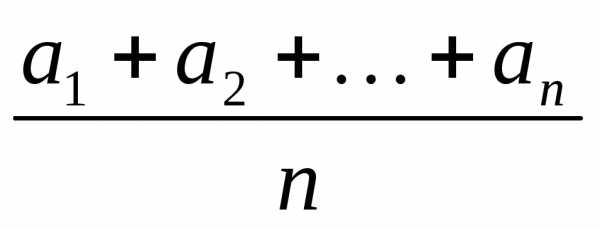(это среднее всех математических
ожиданий). Это означает следующее. Пусть
в результате испытания независимые
случайные величиныХ1,
Х2,
… , Хn (их много!) приняли значения соответственно х1,
х2,
… , хn соответственно. Тогда если сами эти
значения могут оказаться далекими от
средних значений соответствующих
случайных величин, их среднее значение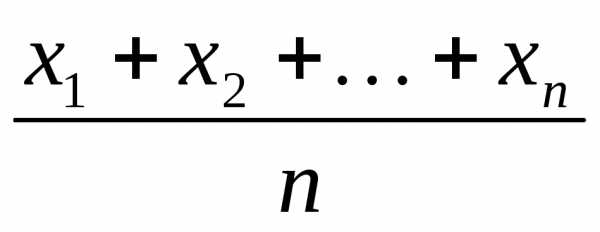 
с большой вероятностью окажется близким
к числу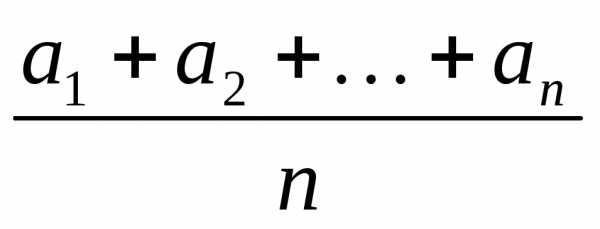
.
Таким образом, среднее арифметическое
большого числа случайных величин уже
теряет случайный характер и может быть
предсказано с большой точностью. Это
можно объяснить тем, что случайные
отклонения значенийХi от ai могут быть разных знаков, а потому в в
сумме эти отклонения с большой вероятностью
компенсируются.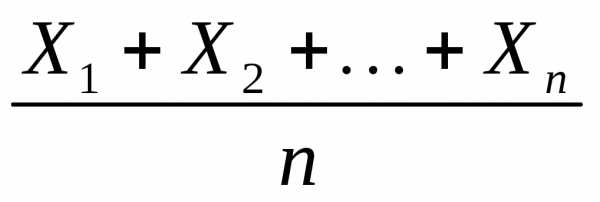
в нашем эксперименте (заключающемся в
проведении серии изn измерений), т.е.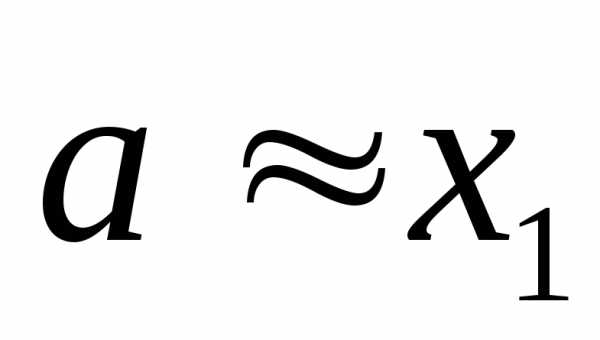
,
а затем среднее арифметическое всех
измерений.
Точность измерения прибора такова, что
среднее квадратическое отклонение
измерения σ не более 1 (потому дисперсияD=σ2 тоже не превосходит 1). Для каждого из
способов измерения оценить вероятность,
что ошибка измерения не превзойдет 2.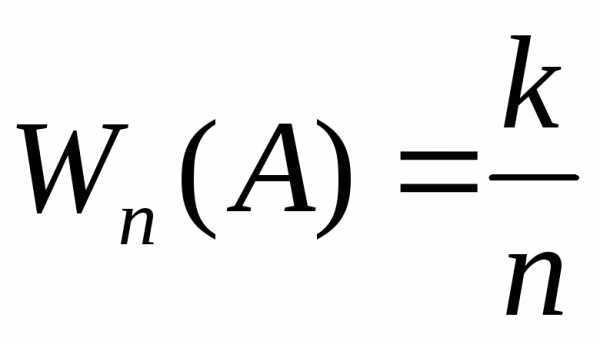
,
равная отношению числа появлений событияА в n независимых испытаниях, к общему числу
испытаний , ранее была названа относительной
частотой события А в n испытаниях . Поэтому имеет место
неравенство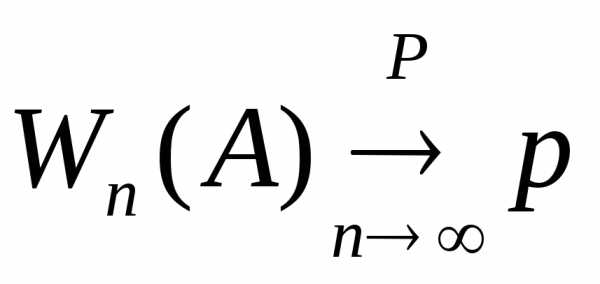
(по вероятности). Это составляет содержание
закона больших чисел в форме Бернулли.
Из него следует, что при достаточно
большом числе испытанийn сколь угодно малые отклонения относительной
частоты 
события от его вероятностир − почти достоверные события, а большие
отклонения − почти невозможные.
Полученный вывод о такой устойчивости
относительных частот (о которой мы ранее
говорили как об экспериментальном факте) оправдывает введенное ранее
статистическое определение вероятности
события как числа, около которого
колеблется относительная частота
события.
на интервале изменения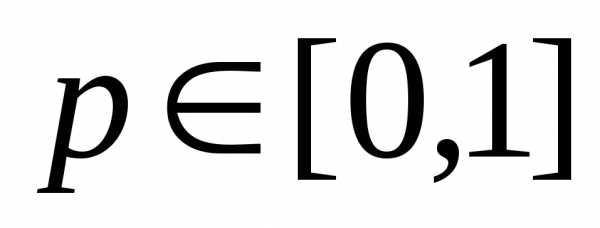
(в этом легко убедиться, найдя минимум
этой функции на этом отрезке), из
приведенного выше неравенствалегко получить, что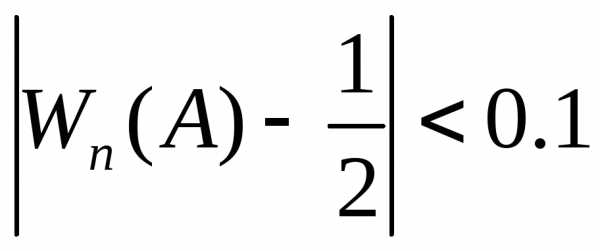
.
Как мы только что убедились из предыдущего
примера, вероятность такого события не
менее0.975.
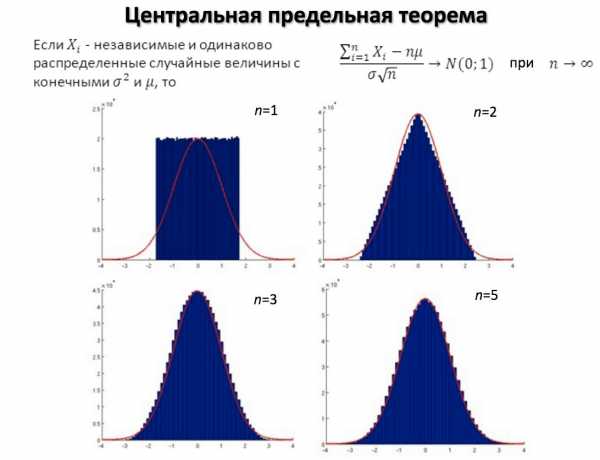
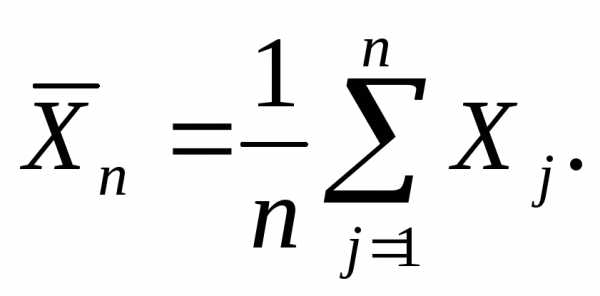
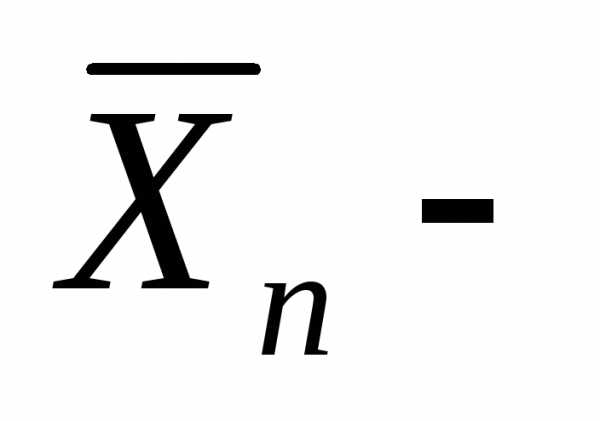случайная,
а значить, она имеет некоторый закон
распределения. Оказывается этот
замечательный факт, составляет содержание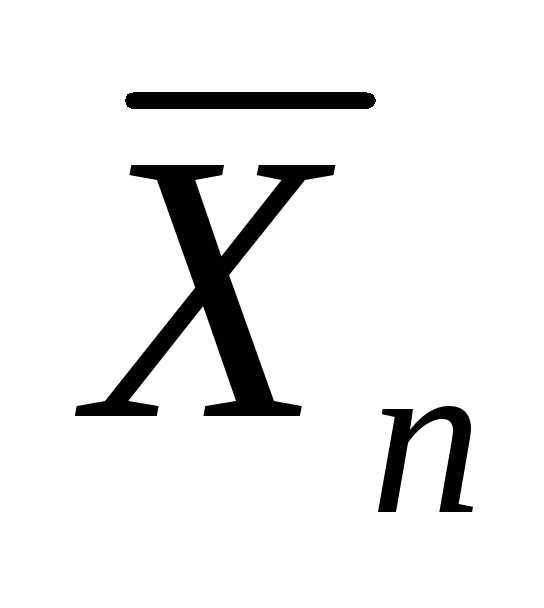
близок к нормальному закону.
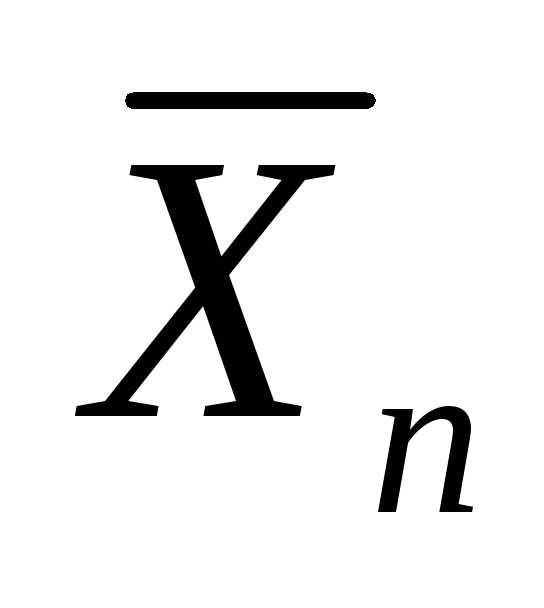отличается
от суммы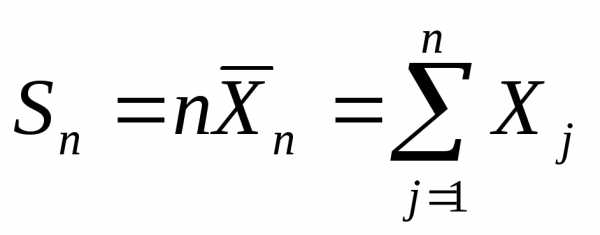
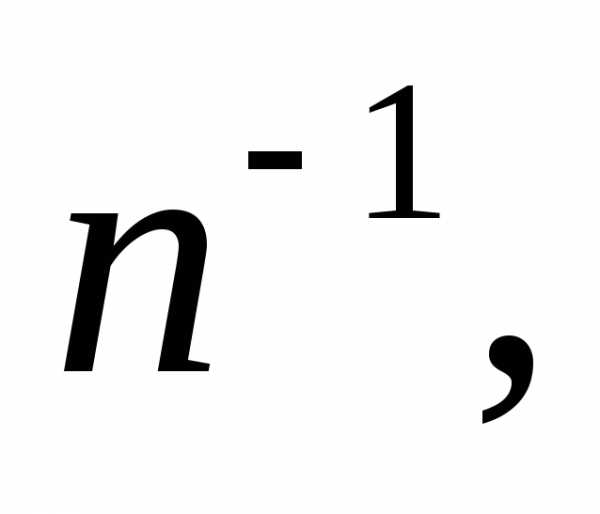то
в общих чертах содержание ЦПТ может
быть сформулировано следующим образом.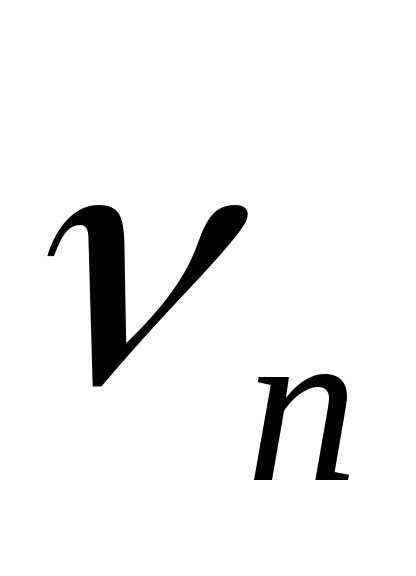
«близка» к нормальному закону?».
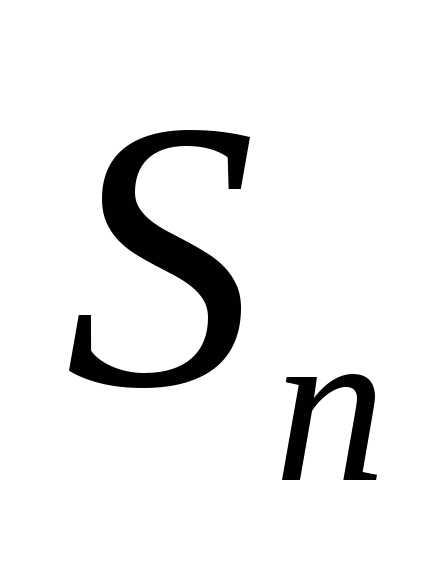перейдём к «нормированной» случайной
величине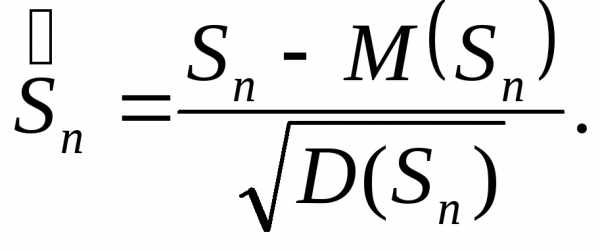
,
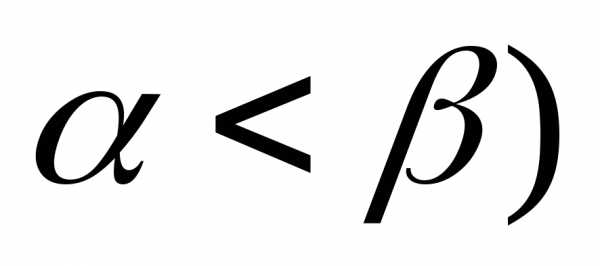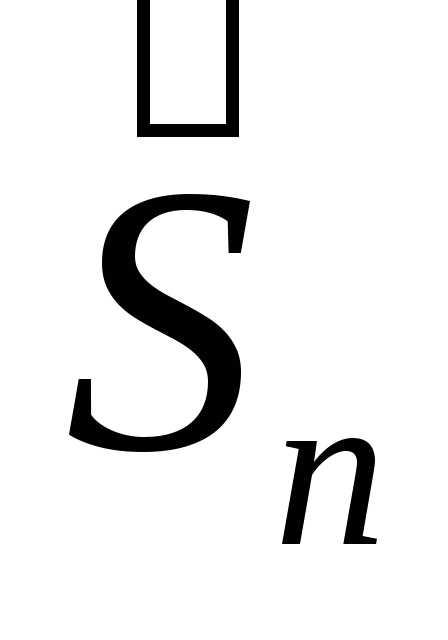с ростом
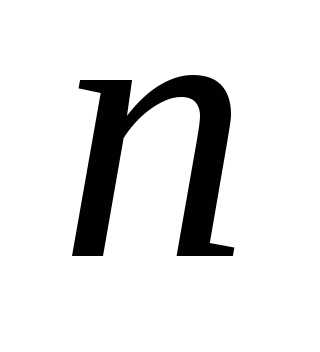приближается к нормальному закону с.
Разумеется, из того факта, что величина
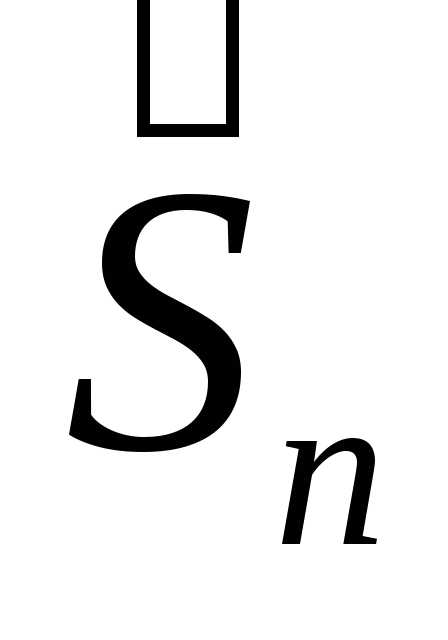имеет приближенно нормальное
распределение, следует, что и величина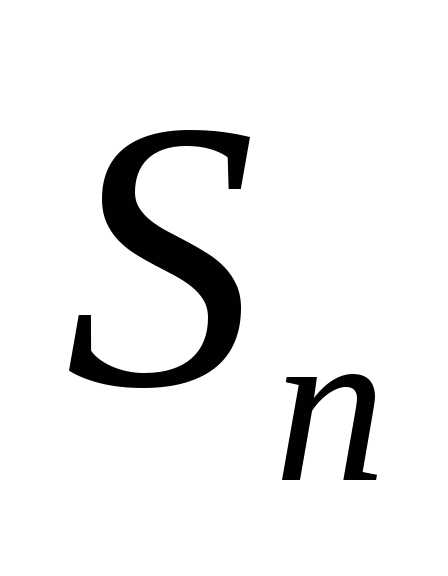
распределена приближенно нормально,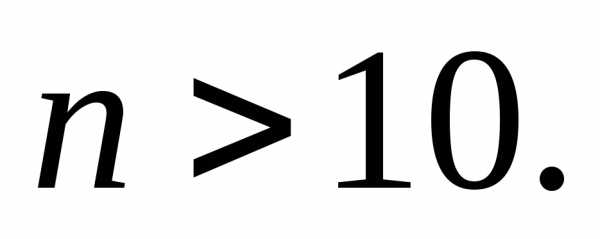
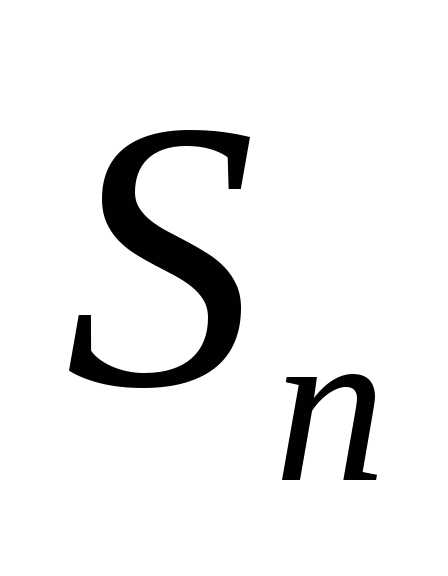от её математического ожидания. Общий
смысл накладываемых условий, на величинызаключается в том, что отдельные
отклонениядолжны быть равномерно малы по сравнению
с суммарным отклонениемТочную формулировку этих условий, при
которых справедливо предельное
соотношение дал М.А. Ляпунов в 1901 году.
Она заключается в следующем.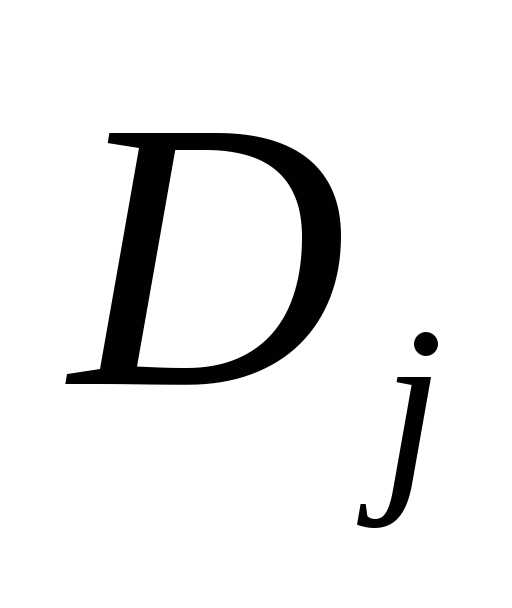
есть дисперсия с.в.
—
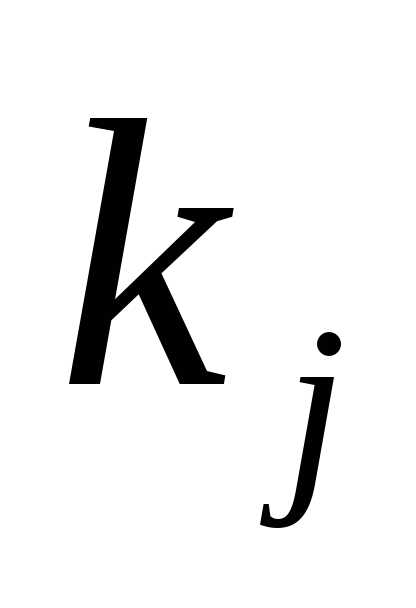«центральный момент третьего порядка»).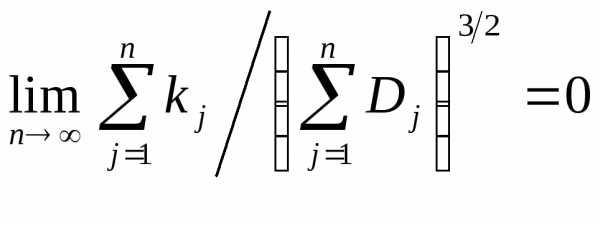
,
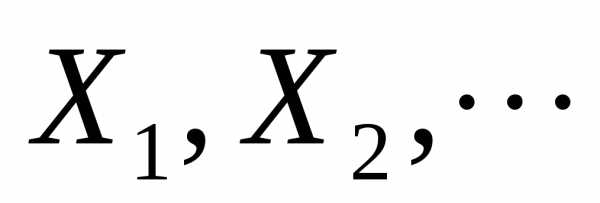удовлетворяетусловию Ляпунова.
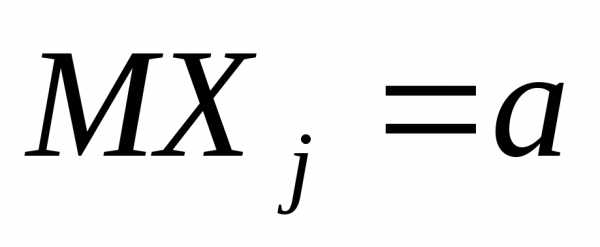и дисперсию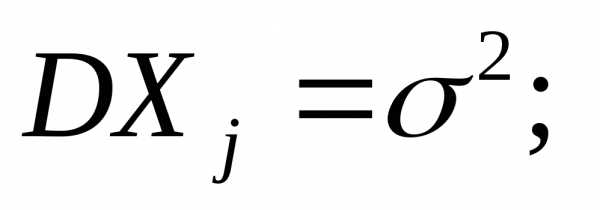
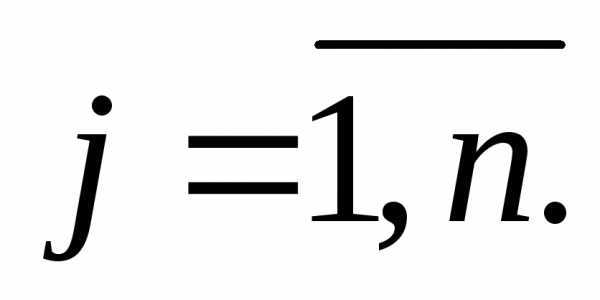
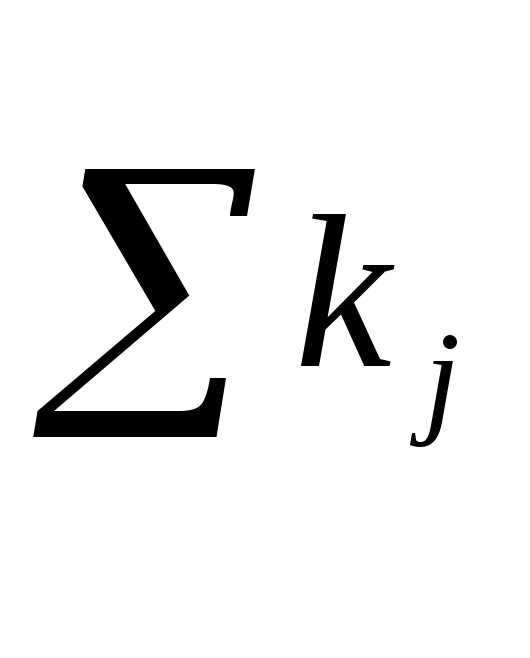имеет
порядок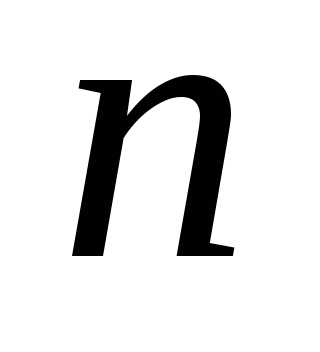
,
а величина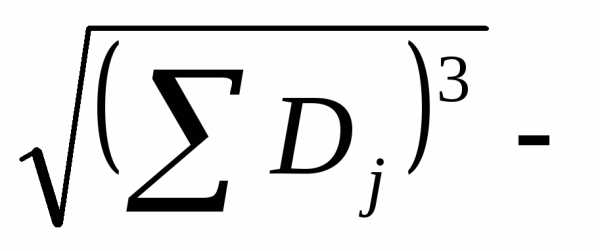
порядок
,
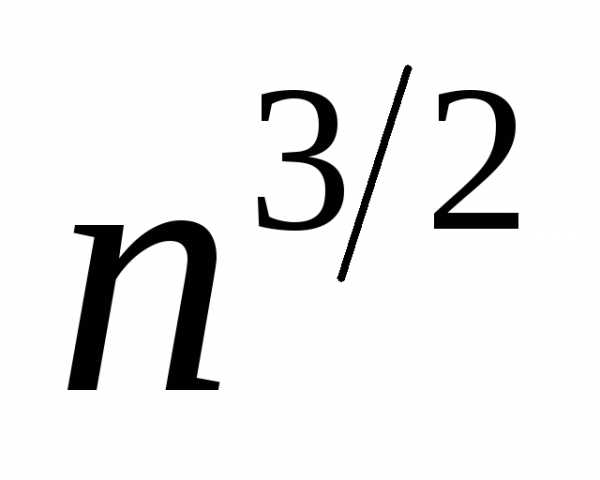тем самым отношение первой величины
ко второй стремится, к 0.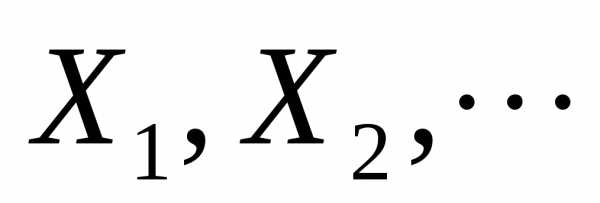
независимых случайных величин
удовлетворяет условию Ляпунова, то
справедливо предельное соотношение 
и
,
при этом (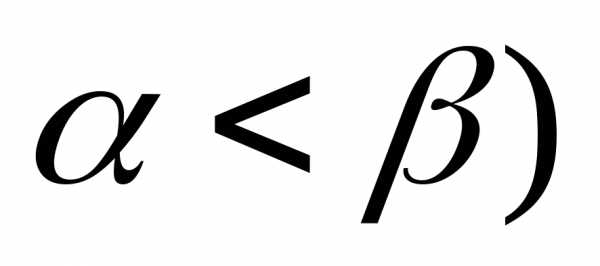
.
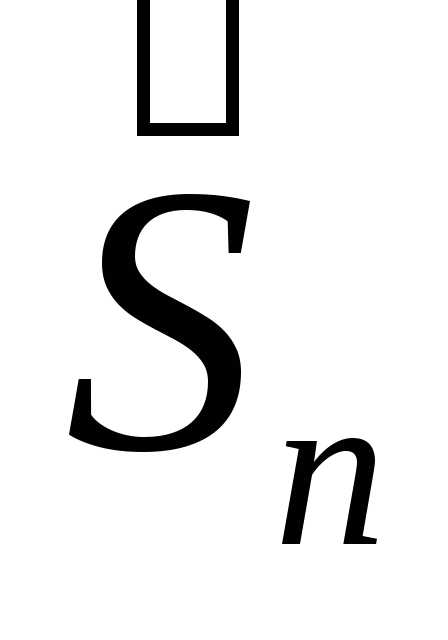сходится к нормальному закону с
параметрами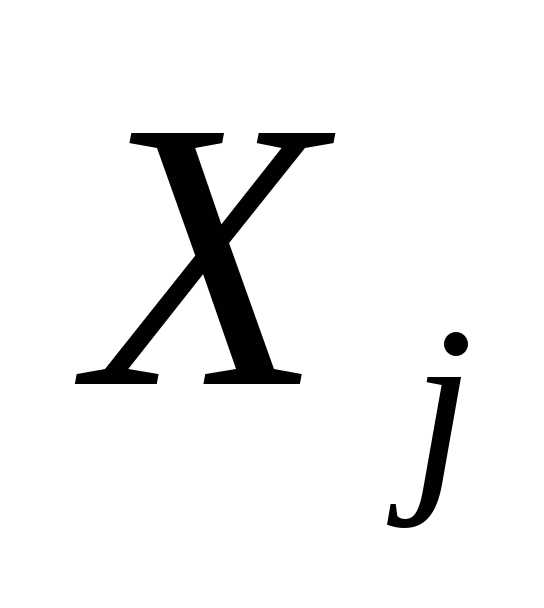 
распределены
равномерно на отрезке [0,1]. Найти закон
распределения с.в.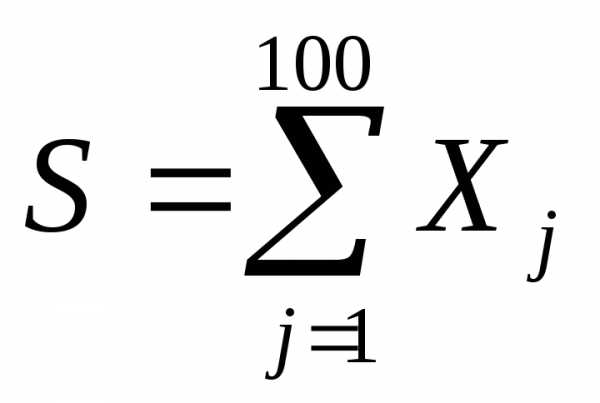
,
а также вероятность того, что
имеет приближенно плотность распределения
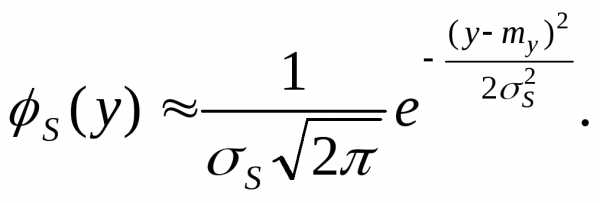
– π/3 ≤ π/2.
