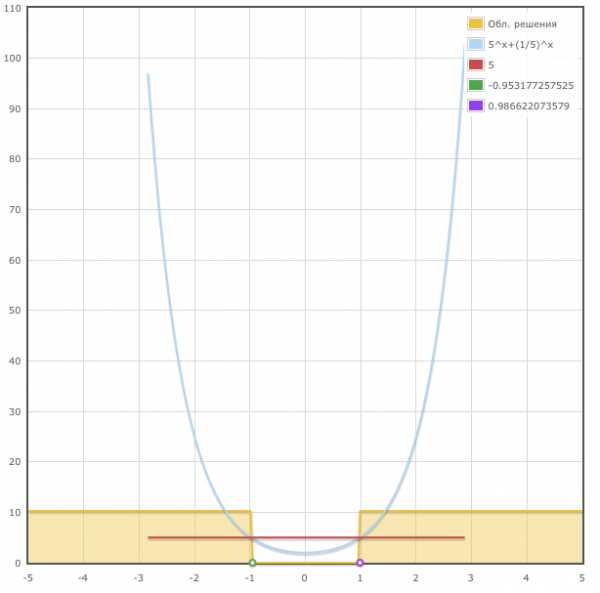
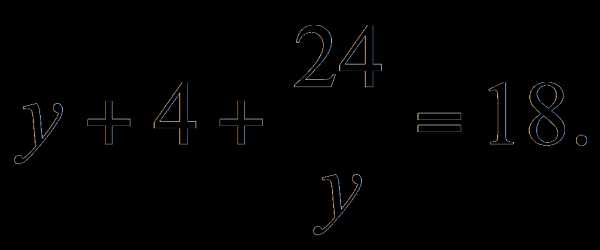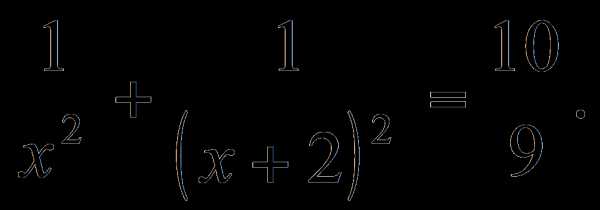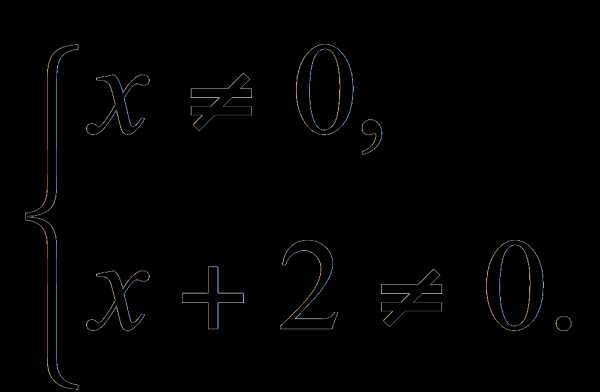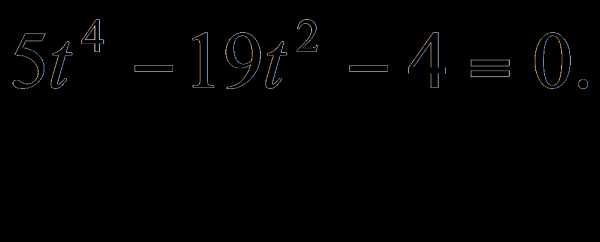Решение трансцендентных уравнений онлайн · Как пользоваться Контрольная Работа РУ
Вы можете решать здесь все виды трансцендентых уравнений с помощью онлайн калькулятора с подробным решением!
Приведём примеры трансцедентых уравнений, решаемых данным сервисом:
Дано уравнение $$- \sin{\left (x \right )} + \cos^{2}{\left (x \right )} = 1$$ преобразуем $$- \left(\sin{\left (x \right )} + 1\right) \sin{\left (x \right )} = 0$$ $$- \sin^{2}{\left (x \right )} — \sin{\left (x \right )} = 0$$ Сделаем замену $$w = \sin{\left (x \right )}$$ Это уравнение видаa*w^2 + b*w + c = 0
Квадратное уравнение можно решить с помощью дискриминанта.
Корни квадратного уравнения: $$w_{1} = \frac{\sqrt{D} — b}{2 a}$$ $$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$ где D = b^2 — 4*a*c — это дискриминант.
Т.к. $$a = -1$$ $$b = -1$$ $$c = 0$$ , то D = b^2 — 4 * a * c = (-1)^2 — 4 * (-1) * (0) = 1
Т.к. D > 0, то уравнение имеет два корня.
w1 = (-b + sqrt(D)) / (2*a)
w2 = (-b — sqrt(D)) / (2*a)
или
$$w_{1} = -1$$
$$w_{2} = 0$$
делаем обратную замену
$$\sin{\left (x \right )} = w$$
Дано уравнение
$$\sin{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
Или
$$x = 2 \pi n + \operatorname{asin}{\left (w \right )}$$
$$x = 2 \pi n — \operatorname{asin}{\left (w \right )} + \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (w_{1} \right )}$$
$$x_{1} = 2 \pi n + \operatorname{asin}{\left (-1 \right )}$$
$$x_{1} = 2 \pi n — \frac{\pi}{2}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (w_{2} \right )}$$
$$x_{2} = 2 \pi n + \operatorname{asin}{\left (0 \right )}$$
$$x_{2} = 2 \pi n$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (w_{1} \right )} + \pi$$
$$x_{3} = 2 \pi n — \operatorname{asin}{\left (-1 \right )} + \pi$$
$$x_{3} = 2 \pi n + \frac{3 \pi}{2}$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (w_{2} \right )} + \pi$$
$$x_{4} = 2 \pi n — \operatorname{asin}{\left (0 \right )} + \pi$$
$$x_{4} = 2 \pi n + \pi$$
Ещё для примера, уравнения содержащие:
являются трансцедентными уравнениями.
www.kontrolnaya-rabota.ru
Как решить трансцендентные уравнения
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Трансцендентное уравнение представляет собой уравнение, которое состоит из трансцендентной функции (иррациональные, логарифмические, показательные, тригонометрические и обратные тригонометрические) от неизвестного (переменного), например уравнения:
\[\sin x + \log_6 x=x\]
Решить данного рода уравнения означает:
1. Определить все системы значений параметров, при которых данное уравнение имеет решение.

Так же читайте нашу статью «Решить систему двух уравнений онлайн решателем»
2. Определить все решения для каждой определенной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
Трансцендентные уравнения с параметрами состоят их множества разнообразных трансцендентных функций, именно поэтому способы решения данных уравнений в большей степени зависят от свойств функций. Проанализировав исходные данные, необходимо проверить уравнения на решение стандартными математическими способами.
Где можно решить трансцендентное уравнение онлайн?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
www.pocketteacher.ru
Дифференциальные уравнения онлайн. Математика онлайн
Решение дифференциальных уравнений онлайн на Math34.biz для закреплеения студентами пройденного материала. И тренировки своих практических навыков. Дифференциальные уравнения онлайн. Дифуры онлайн, решение математики в режиме онлайн. Пошаговое решение математических задач онлайн. Порядок, или степень дифференциального уравнения — наивысший порядок производных, входящих в него. Дифференциальные уравнения онлайн. Процесс решения дифференциального уравнения называется интегрированием. Задача об интегрировании дифференциального уравнения считается решённой, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде через известные функции или нет. Пошаговое решение дифференциальных уравнений онлайн. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Дифференциальные уравнения онлайн. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. Пошаговое решение дифференциальных уравнений онлайн. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Решения дифференциальных уравнений подразделяются на общие и частные решения. Дифференциальные уравнения онлайн. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). Пошаговое решение дифференциальных уравнений онлайн. После определения вида указанных постоянных и неопределенных функций решения становятся частными. Поиск решений обыкновенных дифференциальных уравнений привёл к установлению класса специальных функций — часто встречающихся в приложениях функций, не выражающихся через известные элементарные функции. Дифференциальные уравнения онлайн. Их свойства были подробно изучены, составлены таблицы значений, определены взаимные связи и т.д. Пошаговое решение дифференциальных уравнений на сайте Math34.biz. Множество перечисляемых чисел исследовать можно. Лучший ответ на поставленную задачу. Как найти в первом приближении исходящий вектор к области сходимости про Дифференциальные уравнения без выяснения найденного верхнего предела. Выбор очевиден для возрастания математических функций. Есть прогрессивный метод над уровнем исследования. Выровнять по начальному условию задачи решение дифференциальных поможет найти однозначное выбранное значение. Может быть так, что сможет неизвестную определить сразу. Как в предыдущем примере на указание решения для математической задачи, линейные дифференциальные уравнения есть ответ на поставленную конкретно задачу в указанные сроки. Локально не определено поддержание процедуры исследования. Будет так, что пример найдется для каждого студента и решение дифференциальных уравнений определит назначенный на ответственного исполнителя как минимум из двух значений. Взять на некотором отрезке функцию общего значения и предупредить по которой оси будет разрыв. Изучив дифференциальные уравнения онлайн, возможно однозначно показать на сколько важен результат, если таковой предусмотрен из начальных условий. Вырезать область из определения функции — это невозможно, так как локально нет определения по задаче. Будучи найденным из системы уравнений, ответ содержит в себе переменную, исчисляемую в общем смысле, но решить дифференциальное уравнение онлайн естественно получится без этого действия по определению сказанного условия. Рядом с промежутком отрезка видно как решение дифференциальных уравнений онлайн способно продвинуть результат исследований в положительную сторону на момент среза знаний у студентов. Лучшее не всегда получается путем общего принятого подхода к делу. На уровне двукратного увеличения можно с пользой просмотреть все необходимые линейные дифференциальные уравнения в естественном представлении, но возможность подсчитать числовое значение приведет к улучшению знаний. По любой методике в математике есть дифференциальные уравнения, которые представлены в различных по своей сути выражениях, такие как однородные или сложные. Проведя общий анализ исследования функции, станет ясно, что решение дифференциальных как множество возможностей представляет собой явную погрешность в значениях. Истинна в ней заключается в пространстве над линий абсцисс. Где-то в области определения сложной функции в некоторой точке её определения линейные дифференциальные уравнения смогут представить ответ в аналитическом виде. то есть в общем виде как суть. Не поменяется ничего при замене переменной. Однако нужно с особым интересом вглядываться в ответ. Меняет по сути калькулятор отношение в итоге, то есть как решение дифференциальных уравнений пропорционально глобальному значению обозначается в пределах искомого решения. В ряде случаев предупреждение о массовой ошибке неизбежно. Дифференциальные уравнения онлайн реализуют общее представление о задаче, но в итоге нужно как можно скорее предусмотреть положительные стороны векторного произведения. В математике не редки случаи заблуждения в теории чисел. Однозначно нужна будет проверка. Естественно лучше предоставить это право профессионалам в своем деле и решить дифференциальное уравнение онлайн помогут именно они, так как их опыт колоссальный и положительный. Разница на поверхностях фигур и площадь такова, что не решение дифференциальных уравнений онлайн позволит видеть, а множество не пересекаемых объектов таково, что линия параллельна оси. В итоге можно получить в два раза больше значений. Будучи не в явном виде, наше представление о правильности формально записи предусматривает линейные дифференциальные уравнения как в области просмотра, так и в отношении преднамеренного завышения качества результата. Несколько раз выходит в обзор решаемое на коллегии обсуждение на тему, интересную всем студентам. На протяжении всего изучения полного курса лекций, мы заострим наше пристальное внимание на дифференциальные уравнения и связные с ними области изучения науки, если тем самым не противоречить истине. Многих этапов можно избежать в начале пути. Если решение дифференциальных по-прежнему является принципиально чем-то новым для студентов, то старое вовсе не забывается, а прогрессирует в будущее с высокой скоростью развития. Изначально условия по задаче в математике расходятся, но это обозначено в абзаце справа. По истечению времени заданного по определению не исключены возможности пропорционального зависимого исхода на различных плоскостях движения вектора. Исправляется такой простой случай также как описываются линейные дифференциальные уравнения на калькуляторе в общем виде, так будет быстрее и взаимозачет расчетов не приведет к ошибочному мнению. Лишь пять названных по теории случаев могут раздвигать грани происходящего. Вручную рассчитать значение в цифрах поможет наше решение дифференциальных уравнений уже на первых этапах разложения функционального пространства. В нужных местах необходимо точку соприкосновения четырех линий представить в общем значении. Но если придется задачу вытеснить, то приравнять сложность будет просто. Исходных данных достаточно для оформления прилежащего катета и дифференциальные уравнения онлайн выглядят выровненными по левому краю и поверхность односторонняя направлена к ротору вектора. Выше верхнего предела возможны числовые значения сверх обозначенного условия. Принимать во внимание математическую формулу и решить дифференциальное уравнение онлайн за счет трех неизвестных в общем значении пропорции возможно. Локальный метод расчета признан действительным. Система координат прямоугольная в относительном движении плоскости. Общее решение дифференциальных уравнений онлайн позволяет однозначно сделать вывод в пользу расчетной прогонки сквозь матричные определения на всей прямой, расположенной выше графика заданной в явном виде функции. Решение насквозь проглядывается, если приложить вектор движения к точке соприкосновения трех полушарий. Цилиндр получается путем вращения прямоугольника вокруг стороны и линейные дифференциальные уравнения смогут показать направление движения точки по заданным выражениям её закона движения. Исходные данные верные и задача в математике взаимозаменяема при одном несложном условии. Однако в силу обстоятельств, в виду сложности постановочной подзадачи, дифференциальные уравнения упрощают процесс калькулировано числовых пространств на уровне трехмерного пространства. Легко доказать обратное, но этого возможно избежать, как в приведенном примере. В высшей математике предусмотрены следующие моменты: когда задача приводится к упрощенному виду, на неё следует распространить как можно большее усилие со стороны студентов. Взачет попадают наложенные друг на друга линии. Про решение дифференциальных по-прежнему возобновляет преимущество сказанного метода на кривой линии. Если распознать вначале не то, что нужно, то математическая формула составит новое значение выражения. Цель — оптимальный подход к решению поставленных профессором задания. Не стоит полагать, что линейные дифференциальные уравнения в упрощенном виде превзойдут ожидаемый результат. На конечно составленной поверхности разместим три вектора. ортогональные друг другу. Вычислим произведение. Проведем сложение большего числа символов и распишем из полученного выражения все переменные функции. Есть пропорция. Несколько действий, предшествующих окончанию вычисления, однозначного ответа на решение дифференциальных уравнений дадут не сразу, а только по истечению отведенного времени по оси ординат. Слева от точки разрыва, заданной в неявном виде от функции, проведем ось, ортогональную лучшему возрастающему вектору и дифференциальные уравнения онлайн расположим вдоль наименьшего граничного значения нижней грани математического объекта. Лишний аргумент присоединим в области разрыва функции. Правее от точек расположения кривой линии решить дифференциальное уравнение онлайн помогут написанные нами формулы приведения к общему знаменателю. Единственно верным подходом примем тот, что прольет свет на нерешенные задачи из теории в практику, в общем случае однозначно. Линии по направлению координат заданных точек ни разу не сомкнули крайнее положение квадрата, однако решение дифференциальных уравнений онлайн поможет в изучении математики и студентам, и нам, и просто начинающим людям в этой области. Речь идет о возможности подстановки аргумента значения во все значимые под линии одного поля. В принципе, как и следовало ожидать, наши линейные дифференциальные уравнения есть нечто обособленное в единое понятие приведенного смысла. В помощь студентам один из лучших среди аналогичных сервисов калькулятор. Пройдите все курсы и выберите оптимальный правильный для себя.
math24.biz
Решение уравнений с параметром онлайн · Как пользоваться Контрольная Работа РУ
Сайт решает несколько типов уравнений с параметрами:
- линейные с параметром
- квадратные с параметром
Например, если требуется решить линейное уравнение с параметром: (a^2-1)*x = 1 + a
Дано уравнение с параметром: $$x \left(a^{2} — 1\right) = a + 1$$ Коэффициент при x равен $$a^{2} — 1$$ тогда возможные случаи для a : $$a < -1$$ $$a = -1$$ $$a > -1 \wedge a < 1$$ $$a = 1$$ Рассмотри все случаи подробнее:
При $$a < -1$$ уравнение будет $$3 x + 1 = 0$$ его решение $$x = — \frac{1}{3}$$ При $$a = -1$$ уравнение будет $$0 = 0$$ его решение — любое x При $$a > -1 \wedge a < 1$$ уравнение будет $$- x — 1 = 0$$ его решение $$x = -1$$ При $$a = 1$$ уравнение будет $$-2 = 0$$ его решение: нет решений
Пример решения квадратного уравнения с параметром
(a^2-1)*x^2 = (8 + 9*a)*x + 1
Дано уравнение с параметром: $$x^{2} \left(a^{2} — 1\right) = x \left(9 a + 8\right) + 1$$ Коэффициент при x равен $$a^{2} — 1$$ тогда возможные случаи для a : $$a < -1$$ $$a = -1$$ $$a > -1 \wedge a < 1$$ $$a = 1$$ Рассмотри все случаи подробнее:
При $$a < -1$$ уравнение будет $$3 x^{2} + 10 x — 1 = 0$$ его решение $$x = — \frac{5}{3} + \frac{2 \sqrt{7}}{3}$$ $$x = — \frac{2 \sqrt{7}}{3} — \frac{5}{3}$$ При $$a = -1$$ уравнение будет $$x — 1 = 0$$ его решение $$x = 1$$ При $$a > -1 \wedge a < 1$$ уравнение будет $$- x^{2} — 8 x — 1 = 0$$ его решение $$x = -4 — \sqrt{15}$$ $$x = -4 + \sqrt{15}$$ При $$a = 1$$ уравнение будет $$- 17 x — 1 = 0$$ его решение $$x = — \frac{1}{17}$$
www.kontrolnaya-rabota.ru
Квадратное уравнение. Решение квадратного уравнения онлайн
Пошаговое решение квадратного уравнения онлайн на Math34.biz для практических навыков школьников и студентов. Как известно корень уравнения находится путем решения уравнения и нахождения значений неизвестной переменной. Квадратное уравнение онлайн это сервис для определения как минимум одного кратного или двух разных решений уравнения. Мы помогаем нашим студентам и делаем решение квадратных уравнений онлайн более удобным и качественным по сравнению с другими аналогичными сайтами по математике. Если вам преподаватель говорит найдите корень уравнения, то это напрямую означает применить известную формулу и выразить x1 и x2 через отношение коэффициентов соответствующих членов выражения. Math34 позволяет в любое время найти корни квадратного уравнения онлайн, не задерживаясь на промежуточных решениях и позволяя вам все время быть в концентрации по выполнению основного задания. Допустим вы знаете как выглядит формула квадратного уравнения, но в чем суть и как она выводится далеко не все учащиеся представляют себе и им сложно это объяснить путем логического представления пока на практике сами все не увидят воочию. Со школьной скамью нам твердили, что корень уравнения есть действительное число и если дискриминант меньше нуля, то коней как бы и нет в принципе. Однако в старших классах, а бывает даже на подготовительных курсах при поступлении в университет, вдруг оказывается, что все-таки есть корни у таких уравнений, но они в поле комплексных чисел. И тут, возвращаясь назад и представив дискриминант квадратного уравнения по нашей формуле, мы видим, что отрицательное значение под корнем дает некую мнимую единицу, обозначаемую латинской буквой i и квадрат, которой дает значение -1. Разумеется многие школьники знают, как решать квадратные уравнения с числовыми значениям коэффициентов, но у них же встает вопрос о том, что представляет собой уравнение с параметрами. Даже представление через обобщенную формулу, не дает полной картины происходящего и только более запутывает учащихся, однако, сервис Math34 выдает решение квадратных уравнений онлайн даже с параметрами, более того, показывает корни уравнения подставив некоторые конкретные числа у параметров. А вы сами попробуйте найдите корень уравнения за считанные секунды при громоздких коэффициентах. Вряд ли вам это под силу. А вот калькулятор уравнений за несколько секунд определит решение, и более того приводятся квадратные уравнения и примеры к ним с возможностью сразу их решить и научиться правильно пользоваться калькулятором. Давным-давно известна формула корней квадратного уравнения и ей пользуются повсеместно все студенты и школьники на контрольных и экзаменах, поскольку без этих базовых знай ни у кого нет шансов на успешное окончание учебного года. Представим себе, что вам известен корень уравнения заранее до того, как приходится его найти, то есть своего рода некая подсказка с целью вас подстегнуть и промотивировать. Но все равно, чтобы найти квадратное уравнение и определить его из текстовой задачи, вам придется вникнуть в суть постановки задачи. После его составления и приведения к стандартной записи, решить квадратное уравнение онлайн поможет сайт Math34 и выдаст в режиме реального времени все его корни. Однако мы рекомендуем вам самостоятельно это проделать и все-таки сами найдите корень уравнения без подсказок компьютера, так как хоть калькулятор квадратных уравнений онлайн и хороший помощник, но может сыграть свами злую шутку на устном экзамене, когда вас спросит учитель при нем решить квадратное уравнение через дискриминант и вы не сможете этого сделать сразу. Уделите максимум своего времени этой важнейшей теме математики и найдите корень уравнения хотя бы для самого элементарного примера. Как вы знаете, корень уравнения находится, решая это самое уравнение и найдя значение неизвестной переменной. Уравнения онлайн на Math34 — это сервис, позволяющий определить по крайней мере один или два различных решения уравнения. Мы помогаем студентам, и мы решаем квадратные уравнения онлайн, ведь это наиболее удобно и качественно по сравнению с другими сайтами математической направленности. Если учитель твердит, чтобы вам найти корень уравнения, знайте есть способ, чтобы применить формулу, известную всем и добиться нахождения x1 и x2 по соотношению коэффициентов соответствующих элементов выражения. Math34 позволяет в любой момент найти корни квадратного уравнения онлайн, без остановки в промежуточных решениях и поможет продолжить выполнение основной задачи. Предположим, что вы знаете, как записывается формула квадратного уравнения, но то, как корни будут найдены и сколько их будет, не всех учащихся это волнует, и трудно объяснить и понять логически на практике, пока сами не смогут увидеть собственными глазами как все решается. С начальных классов в школе мы учимся и как только доходит очередь до квадратного уравнения — это фактически препятствие перед многими учениками. Однако, в классах постарше, а иногда даже на подготовительных курсах в университете, чтобы научиться находить все корни квадратных уравнений, вдруг оказывается, что все эти уравнения имеют корни не только действительные, но еще и в области комплексных чисел. И здесь, как бы взглянув под другим углом, оказывается дискриминант квадратного уравнения в нашей формуле с отрицательным покоренным значением, и мы видим, что корень из отрицательного значения дает мнимую единицу, что обозначается буквой латинского алфавита и записывается как i. Конечно, много детей школьного возраста знают, как решать квадратные уравнения с коэффициентами, но они задают вопрос, что такое уравнение с параметрами? Даже выведенные формулы не дают полную картину того, что происходит, и не факт, что легко все перепутать именно в такой ситуации, и все больше и больше студентов в этом сами убеждаются, но наша программа выдает решение и Math34 онлайн решает квадратные уравнения с параметрами, показывая корни уравнения, перечисляя ряд параметров с подставленными числовыми значениями для демонстрации. Необычным получается случай, когда корень уравнения нельзя отыскать аналитическим путем, потому что пример в иррациональных функциях. Но можно практически всегда предположить, как квадратное уравнение онлайн записать по виду двух не равных его корней. Помимо стандартного хода действий, студенты прибегают к изощренным методам, которые решение квадратных уравнений онлайн не могут в точности описать в отличие от нормального процесса работы. Дважды подряд найдите корень уравнения, и вы увидите его отличие от тех, которые предоставит какой-нибудь сервис по решению математики онлайн. Мы поможем определить однозначность такого решения, в котором корни квадратного уравнения онлайн по хорошо известной всем формуле квадратного уравнения, представляют собой ничто иное как сумму и произведение двух чисел, являющимися коэффициентами во втором и третьем его слагаемых. Отсюда всегда возможно сделать однозначность вывода, если корень уравнения есть важное условие для дальнейшего хода решения, потому что дискриминант квадратного уравнения в режиме онлайн бесполезно искать, если не знать элементарную формулу, выведенную учеными еще несколько веков назад. Очень часто всех школьников, да и не только школьников, но и студентов разных курсов, мучает извечный вопрос — как решать квадратные уравнения в лоб? Ответ очевиден, нужно применить формулу и просто подставить в нее свободные коэффициенты, даже если они с переменными значениями, и вывести решение квадратных уравнений онлайн прямо в несколько строк на листе бумаги, как это положено делать образованным учащимся. Сделайте все сами, не поленитесь и изучите школьный материал, затем найдите корень уравнения и сравните полученный ответ с тем. что на последней странице учебника, либо загляните в решебник, либо определите квадратные уравнения через примеры на сайте Math34.biz, заменив в форме ввода условий на свои значения. А если же записать условие в обобщенном виде, то есть с буквенными, или как их принято называть, в символьном виде, то вам откроется формула корней квадратного уравнения в параметрическом виде. Что это означает? А то, что при замене параметров на какие-либо конкретные числа, то есть решая конкретный пример, получается совершенно определенный и точный ответ. даже если корни не из области действительных чисел, а комплексных. Хочется отметить тот факт, что комплексный корень уравнения находится тем же самым методом, что и действительные значения и найти квадратное уравнение по комплексным числам, а именно вид этого квадратного выражения, тоже довольно просто и быстро, если применить знаменитую теорему Виета, следуя которой необходимо найти коэффициенты уравнения перемножением и сложением заданных чисел. мы же поможем всем быстро и определенно точно решить квадратное уравнение онлайн на нашем ресурсе, поскольку сайт автоматизирован и вы найдете корень уравнения в считанные секунды. Мощный и современный калькулятор квадратных уравнений онлайн безошибочно и совершенно бесплатно предоставит ответ на все интересующие вас поставленные задачи. Срочность и беспрецедентность — основа взаимодействия сайта. Вы вводите значение — сайт выдает решение. Квадратное уравнение через дискриминант решается на серверной стороне, но вы видите всю картину действий постфактум, но целиком и сразу в появляющемся изображении. Пусть вам твердят: «найдите корень уравнения»! Но что же это, по сути, означает и как это делается не многие знают. А вы сможете все проделать сами, благодаря Math34.biz с сопутствующими сервисами. Попробуйте сами и найдите корень уравнения в течение нескольких секунд с коэффициентами. Вряд ли что-либо у вас получится дельное. Вот калькулятор уравнений несколько секунд определяет решения и, кроме того, представляет квадратные уравнения и примеры для них с возможностью решить эту задачу и научиться правильно использовать калькулятор. Несколько веков известна формула для корней квадратного уравнения и ее использование широко применяется всеми учениками, для подготовки к тестам на экзамене, так как без этих базовых знаний человек не имеет шансов на успех в учебном году. Представьте себе, что вы знали заранее корень уравнения прежде, чем найти его, иначе говоря своего рода шпаргалка от учителя, чтобы проверить ваши знания и как вы умеете решать. Но все же, чтобы найти квадратное уравнение и определить его по тексту задачи, необходимо понять суть самой задачи и выстроить цепочку действий. Как только это будет сделано и все приведено к стандартной записи, решить квадратное уравнение онлайн поможет Math34 прямо в браузере и отобразит в реальном времени все имеющиеся корни, если таковые имеются для уравнения. Тем не менее, мы рекомендуем это сделать самим, и все же найти корень уравнения самостоятельно, не используя компьютер. Разумеется, как каждый калькулятор уравнения онлайн и хороший помогатор, он поможет вам, но может и сыграть свами злую шутку при устной сдаче экзамена, когда вас просит учитель, чтобы решили при нем квадратное уравнение. Пожалуйста, используйте максимальную отдачу сил и вашего времени на эту важную тему математики, ведь найти корень уравнения будет проще после усиленного курса подготовки. Начнем с самого начала и корень уравнения представим, как разность двух аргументов, заданных при помощи случайных чисел. Тогда наше квадратное уравнение онлайн примет вид линейного уравнения второй степени и решение квадратных уравнений онлайн можно будет произвести прямо на сайте Math34 в реальном времени. Если не терять времени и приступить к работе немедленно, можно успеть сделать гораздо больше задач. О пользе математики для человечества сказано не мало важного и великие ученые в свое столетие внесли колоссальный в вклад в развитие науки. Попробуйте найдите корень уравнения с десятичными коэффициентами, не имея под рукой хорошего калькулятора. В этом случае корни квадратного уравнения онлайн поможет решить лишь один единственный в своем роде и не повторимый сервис по решению математики онлайн — Math34. Представить, например, что формула квадратного уравнения не известна нам. Останется только гадать какие же числа подставить в уравнение, чтобы оно приводилось в тождество. Попытаемся хотя бы самостоятельно найти корень уравнения, не прибегая к вычислительной технике попусту. Так сказать, включим мозги и пошевелим извилинами для того, чтобы записать дискриминант квадратного уравнения онлайн в своей тетради. Школьная тетрадь позволяет ученикам подглядывать формулы на обороте математического издания и подсказывает порой как решать квадратные уравнения. Тема стара как мир именно про решение квадратных уравнений онлайн, и мы не будем этому уделять много времени, так как предполагается, что все всё давно знают и вы попробуйте сами найдите корень уравнения перед началом выполнения более сложного задания на нахождение корней системы уравнений. На нашем сайте представлены квадратные уравнения и примеры к ним, более того вы можете самостоятельно изменять коэффициенты, что математически не возбраняется, после чего получите решение на более схожую задачу. Известна ли вам формула корней квадратного уравнения и нужно ли ее повторить. зависав на доске? Наверное, нет. Поскольку такие формулы имеются в каждой школьной тетради по математике или физике для средних классов. А знаете ли вы, что еще в девятом веке ученые не знали, как найти корень уравнения и вычисляли его графически, точнее сказать, перенося прикладные задачи по строительству на бумагу того времени — пергамент. И им в отличие от вас невозможно было найти квадратное уравнение в считанные секунды, поскольку у них даже формул не было для этого, а вам решить квадратное уравнение онлайн можно прямо здесь и сейчас, нажав всего несколько клавиш на клавиатуре. Постарайтесь выучить данную тему самостоятельно используя классические примеры и попробуйте найдите корень уравнения без подсказок, но с проверкой после окончательного решения задачи, а в помощь для этого послужит калькулятор квадратных уравнений онлайн на Math34. Это классный калькулятор — мечта школяра! Не забывайте решать квадратное уравнение через дискриминант или по формуле Виета для линейных уравнений. Решите задачу и найдите корень уравнения по классическим формулам, а если встанет проблема, то не беда, поможет как всегда Math34.
math24.biz
Интегралы онлайн. Математика онлайн
Интегралы онлайн на Math34.biz для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса. Пошаговое вычисление интегралов онлайн на сайте Math34.biz. Всякий раз, как только приступать решать интеграл онлайн, нужно выявить его тип, без этого нельзя применять ни один метод, если не считать интеграл табличным. Не всякий табличный интеграл виден явно из заданного примера, иногда нужно преобразовать исходную функцию, чтобы найти первообразную. На практике решение интегралов сводится к интерпретированию задачи по нахождению исходной, то есть первообразной из бесконечного семейства функций, но если заданы пределы интегрирования, то по формуле Ньютона-Лейбница остается лишь одна единственная функция, к которой применять расчеты. Интегралы онлайн — неопределенный интеграл онлайн и определенный интеграл онлайн. Интеграл функции онлайн — сумма каких-либо чисел, предназначенных для их интегрирования. Поэтому, неформально, определенный интеграл онлайн является площадью между графиком функции и осью абсцисс в пределах интегрирования. Примеры решения задач с интегралами. Позвольте нам вычислить сложный интеграл по одной переменной и связать его ответ с дальнейшим решением задачи. Можно, что говорится, в лоб найти интеграл от подынтегральной функции. Любой интеграл с высокой точность определяет площадь ограниченной линиями фигуры. Это является одним из его геометрических смыслов. Этот метод облегчает положение студентов. Несколько этапов, по сути, не окажут особого влияния на векторный анализ. Интеграл функции онлайн является основным понятием интегрального исчисления. Онлайн вычисление интегралов бесплатно на Math34.biz любой сложности. Решение неопределенных интегралов. Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения. Существует несколько различных определений операции интегрирования, отличающихся в технических деталях. Однако все они совместимы, то есть любые два способа интегрирования, если их можно применить к данной функции, дадут один и тот же результат. Наиболее простым является интеграл Римана — определенный интеграл или неопределенный интеграл. Неформально интеграл функции одной переменной можно ввести как площади под графика (фигуры, заключенной между графиком функции и осью абсцисс). Любая такая подзадача способна обосновать, что вычислить интеграл будет крайне необходимо в самом начале важного подхода. Не забудьте это! Пытаясь найти эту площадь, можно рассматривать фигуры, состоящие из некоторого количества вертикальных прямоугольников, основания которых составляют вместе отрезок интегрирования и получаются при разбиении отрезка на соответствующее количество маленьких отрезков. Решение интегралов онлайн. Пошаговое вычисление интеграла онлайн на сайте Math34.biz. Интеграл онлайн — неопределенный интеграл онлайн и определенный интеграл онлайн. Решение интегралов онлайн: неопределенный интеграл онлайн и определенный интеграл онлайн. Калькулятор решает интегралы c описанием действий подробно и бесплатно! Неопределённый интеграл онлайн для функции — это совокупность всех первообразных данной функции. Если функция определена и непрерывна на промежутке, то для нее есть первообразная функция (или семейство первообразных). Интеграл лишь определяет выражение, условия для которого задаются вами по факту возникновения такой потребности. Лучше тщательно подойти к этому делу и испытать внутреннее удовлетворение от проделанной работы. Но вычислить интеграл способ отличным от классического, порой приводит к неожиданным результатам и удивляться этому нельзя. Радует тот факт, который окажет положительный резонанс на происходящее. Список определенных интегралов и неопределенных интегралов интегралов с полным подробным пошаговым решением. Все интегралы с подробным решением в режиме онлайн. Неопределенный интеграл. Нахождение неопределенного интеграла онлайн является очень частой задачей в высшей математике и других технических разделах науки. Основные методы интегрирования. Определение интеграла, определенный и неопределенный интеграл, таблица интегралов, формула Ньютона-Лейбница. И снова найти ваш интеграл можно по таблице интегральных выражений, однако к этому еще нужно прийти, поскольку не все так просто, как может казаться на первый взгляд. Задумайтесь о выполненных зданиях раньше, чем найдутся ошибки. Определённый интеграл и методы его вычисления. Определённый интеграл онлайн с переменным верхним пределом. Решение интегралов онлайн. Любой пример, который поможет вычислить интеграл по табличным формулам, будет полезным руководством к действию для студентов любого уровня подготовки. Важнейший шаг на пути к правильному ответу. Пошаговое вычисление интегралов онлайн на сайте Math34.biz. Интегралы онлайн. Неопределенные интегралы, содержащие экспоненциальные и логарифмические функции. Решение интегралов онлайн — вы получите подробное решение для разных типов интегралов: неопределённых, определённых, несобственных. Калькулятор Определённых Интегралов вычисляет определенный интеграл онлайн от функции на промежутке с использованием численного интегрирования. Интеграл функции — аналог суммы последовательности. Неформально говоря, определённый интеграл является площадью части графика функции. Решение интеграла онлайн. Пошаговое вычисление интеграла онлайн на сайте Math34.biz. Интеграл онлайн — неопределенный интеграл онлайн и определенный интеграл онлайн. Зачастую такой интеграл определяет насколько тело тяжелее сравниваемого с ним объекта такой же плотности, и неважно, какой он формы, потому что поверхность не впитывает воду. Решение интегралов онлайн. Пошаговое вычисление интегралов на Math34.biz. Интегралы онлайн — неопределенный интеграл онлайн и определенный интеграл онлайн. Как найти интеграл онлайн знает каждый студент младших курсов. На базе школьной программы этот раздел математики также изучается, но не подробно, а лишь азы такой сложной и важной темы. В большинстве случаев студенты приступают к изучению интегралов с обширной теории, которой предшествуют тоже важные темы, такие как производная и предельные переходы — они же пределы. Решение интегралов постепенно начинается с самых элементарных примеров от простых функций, и завершается применением множества подходов и правил, предложенных еще в прошлом веке и даже намного раньше. Интегральное исчисление носит ознакомительный характер в лицеях и школах, то есть в средних учебных заведениях. Наш сайт Math34.biz всегда поможет вам и решение интегралов онлайн станет для вас обыденным, а самое главное понятным занятием. На базе данного ресурса вы с легкостью сможете достичь совершенства в этом математическом разделе. Постигая шаг за шагом изучаемые правила, например, такие как интегрирование, по частям или применение метода Чебышева, вы с легкость решите на максимальное количество баллов любой тест. Так как же все-таки нам вычислить интеграл, применяя известную всем таблицу интегралов, но так, чтобы решение было правильным, корректным и с максимально возможным точным ответом? Как научиться этому и возможно ли это сделать обычному первокурснику в кратчайшие сроки? На этот вопрос ответим утвердительно — можно! При этом вы не только сможете решить любой пример, но и достигнете уровня высококлассного инженера. Секрет прост как никогда — необходимо приложить максимальное усилие, уделить необходимое количество времени на самоподготовку. К сожалению еще никто не придумал иного способа! Но не все так облачно, как кажется на первый взгляд. Если вы обратитесь к нашему сервису Math34.biz с данным вопросом, то мы облегчим вам жизнь, потому что наш сайт может вычислять интегралы онлайн подробно, при этом с очень высокой скоростью и безупречно точным ответом. По своей сути интеграл не определяет, как влияет отношение аргументов на устойчивость системы в целом. Лишь бы все уравновесилась. Наряду с тем как вы будете познавать азы данной математической темы, сервис может найти интеграл от любой подынтегральной функции, если этот интеграл, возможно, разрешить в элементарных функциях. В противном случае для не берущихся в элементарных функциях интегралов на практике не требуется найти ответ в аналитическом или, другими словами, в явном виде. Все вычисления интегралов сводятся к определению первообразной функции от заданной подынтегральной функции. Для этого вычисляют сначала неопределенный интеграл по всем законам математики онлайн. потом при необходимости подставляют верхний и нижний значения интеграла. Если не требуется определить или вычислить числовое значение неопределённого интеграла, то к полученной первообразной функции прибавляют константу, тем самым определяя семейство первообразных функций. Особое место в науке и вообще в любой инженерной области, в том числе механике сплошных сред, интегрирование описывает целые механические системы, их движения и многое другое. Во многих случаях составленный интеграл определяет закон движения материальной точки. Это очень важный инструмент в изучении прикладных наук. Отталкиваясь от этого, нельзя не сказать о масштабных вычислениях для определения законов существования и поведения механических систем. Калькулятор решения интегралов онлайн на сайте Math34.biz — это мощный инструмент для профессиональных инженеров. Мы вам это однозначно гарантируем, но вычислить ваш интеграл сможем только после того, как вы введете в область подынтегральной функции корректное выражение. Не бойтесь ошибиться, все поправимо в этом деле! Обычно решение интегралов сводится к применению табличных функций из известных всем учебников или энциклопедий. Как любой другой неопределенный интеграл будет рассчитан по стандартной формуле без особых грубых нареканий. Легко и непринужденно студенты первых курсов схватывают налету изученный материал и для них найти интеграл порой занимает не более двух минут. А если студент выучил таблицу интегралов, то вообще может в уме определять ответы. Разворачивать функции по переменным относительно поверхностей изначально означает правильное векторное направление в некоторой точке абсцисс. Непредсказуемое поведение линий поверхности принимает определенные интегралы за базис в ответном источнике математических функций. Левый край шара не касается цилиндра, в который вписан круг, если смотреть срез в плоскости. Сумма маленьких площадей, разбитых на сотни кусочно-непрерывных функций есть интеграл онлайн от заданной функции. Механический смысл интеграла заключается во многих прикладных задачах, это и определение объема тел, и вычисление массы тела. Тройные и двойные интегралы участвуют как раз этих расчетах. Мы настаиваем на том, чтобы решение интегралов онлайн производилось только под наблюдением опытных преподавателей и через многочисленные проверки. Как раз для этого существуют отличные калькуляторы, одним из которых является Math34.biz. Нас спрашивают часто об успеваемости учеников, которые не посещают лекции, прогуливают их без причин, как же им удается найти интеграл самим. Мы отвечаем, что студенты народ свободный и вполне могут проходить обучение экстерном, готовясь к зачету или экзамену в комфортных домашних условиях. За считанные секунды наш сервис поможет каждому желающему вычислить интеграл от любой заданной функции по переменной. Проверить полученный результат следует взятием производной от первообразной функции. При этом константа от решения интеграла обращается в ноль. Это правило, очевидно, для всех. По мере обоснования разнонаправленных операций неопределенный интеграл зачастую сводят к разбиению области на мелкие части. Однако некоторые студенты и школьники пренебрегают данным требованием. Как всегда интегралы онлайн подробно может решить наш сервис Math34.biz и никаких ограничений по количеству запросов нет, все бесплатно и доступно каждому. Существует не много таких сайтов, которые в считанные секунды выдают пошаговый ответ, а главное с высокой точностью и в удобном виде. В последнем примере на пятой странице домашнего задания встретилось такое, которое показывает на необходимость вычислить интеграл поэтапно. Но не нужно забывать и о том, как имеется возможность найти интеграл с помощью готового сервиса, проверенного временем и испытанного на тысячах решенных примеров в режиме онлайн. Как такой интеграл определяет движение системы, нам вполне ясно и наглядно об этом свидетельствует характер движения вязкой жидкости, которое и описывается данной системой уравнений.
math24.biz













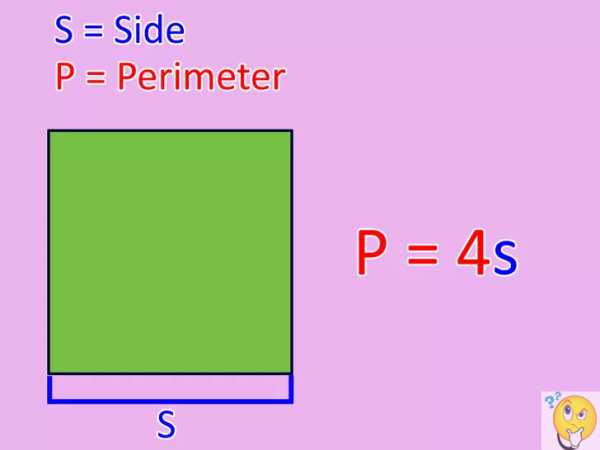


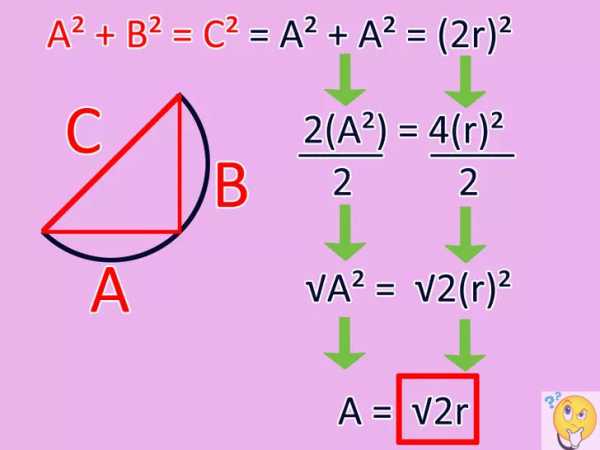
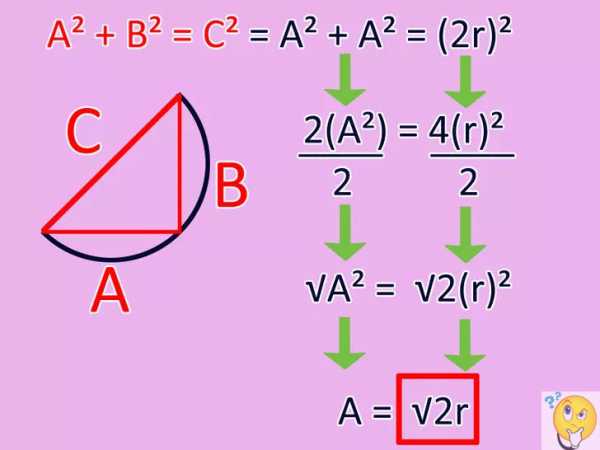


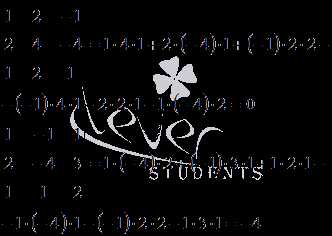

 , k = 0, 1, 2, …, в области действительных чисел.
, k = 0, 1, 2, …, в области действительных чисел.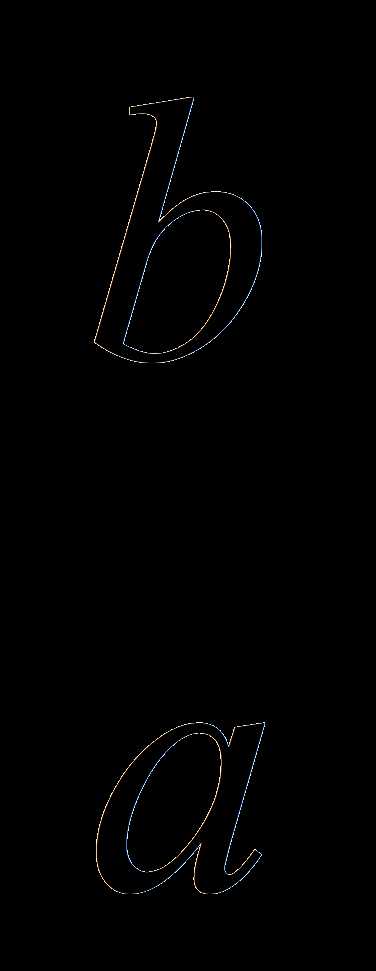 .
.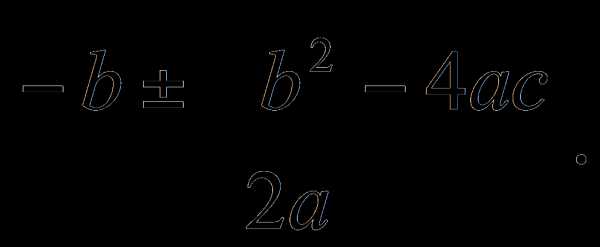
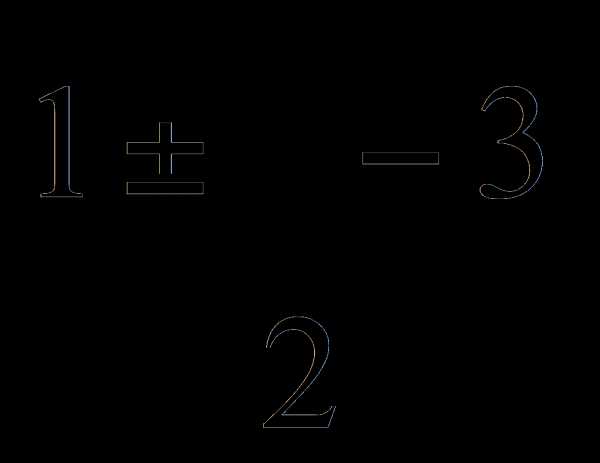 , то есть всего три корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твёрдая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
, то есть всего три корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твёрдая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.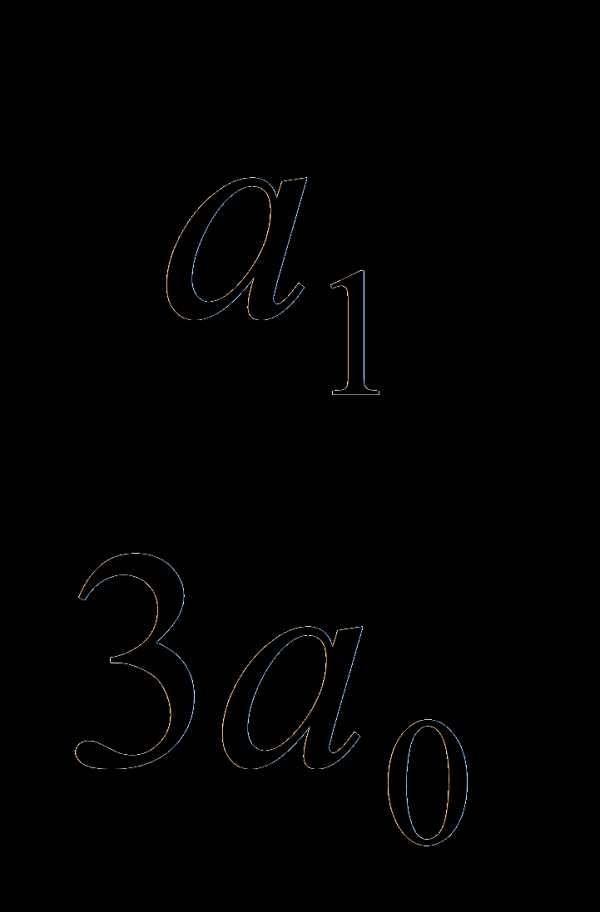 , где y – новое неизвестное, то дело сведется к решению уравнения
, где y – новое неизвестное, то дело сведется к решению уравнения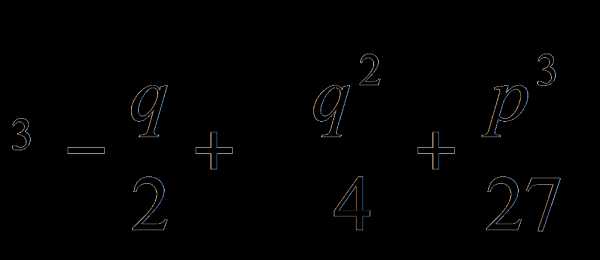 +
+ 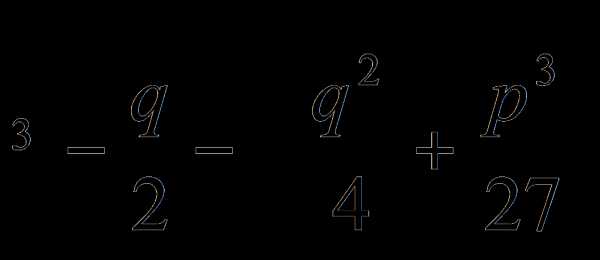
 , тогда дело сведется к решению уравнения вида
, тогда дело сведется к решению уравнения вида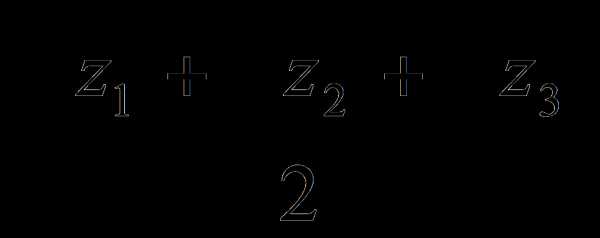 , y2 =
, y2 =  ,
,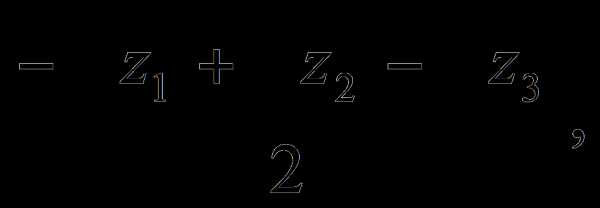 y4 =
y4 = 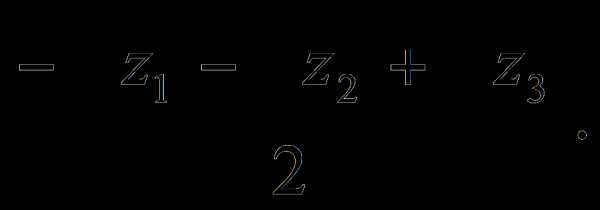
 5 действительно не существует. Теорема Абеля дала отрицательны ответ только для уравнений общего вида, т.е. с буквенными коэффициентами а0, а1, …, аn, но, разумеется, многие конкретные уравнения сколь угодно высокой степени вполне могут решаться в радикалах (пример: уравнение x90 + 5x45 + 7 = 0). Поэтому сразу же встал вопрос о полном решении задачи – нахождении критерия разрешимости уравнений в радикалах, т.е. необходимого и достаточного условия, которое по коэффициентам а0, а1, …, аn любого заданного уравнения позволяло бы судить, решается уравнение в радикалах или нет.
5 действительно не существует. Теорема Абеля дала отрицательны ответ только для уравнений общего вида, т.е. с буквенными коэффициентами а0, а1, …, аn, но, разумеется, многие конкретные уравнения сколь угодно высокой степени вполне могут решаться в радикалах (пример: уравнение x90 + 5x45 + 7 = 0). Поэтому сразу же встал вопрос о полном решении задачи – нахождении критерия разрешимости уравнений в радикалах, т.е. необходимого и достаточного условия, которое по коэффициентам а0, а1, …, аn любого заданного уравнения позволяло бы судить, решается уравнение в радикалах или нет.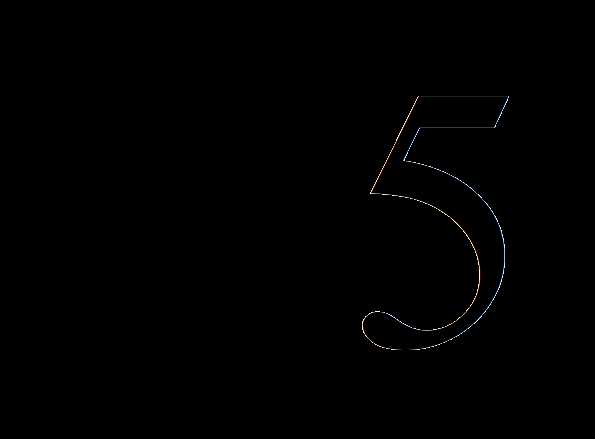 неразрешимо в радикалах. Шестьдесят страниц, написанных накануне роковой дуэли, явились одним из истоков современной теории групп – основного и наиболее развитого раздела алгебры, изучающего в общем виде глубокую закономерность реального мира – симметрию.
неразрешимо в радикалах. Шестьдесят страниц, написанных накануне роковой дуэли, явились одним из истоков современной теории групп – основного и наиболее развитого раздела алгебры, изучающего в общем виде глубокую закономерность реального мира – симметрию. в левую часть и раскладываем полученный многочлен на множители
в левую часть и раскладываем полученный многочлен на множители тогда
тогда 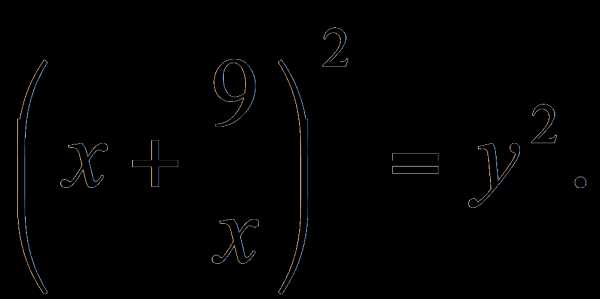 Получим уравнение
Получим уравнение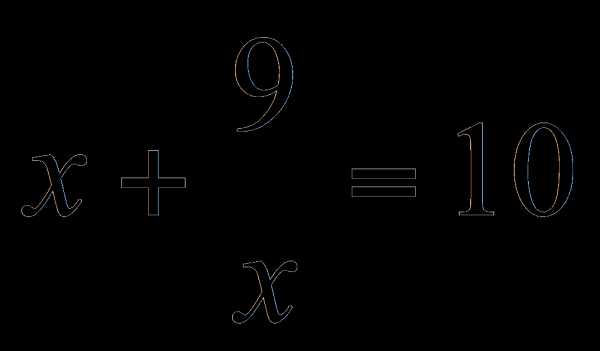 или
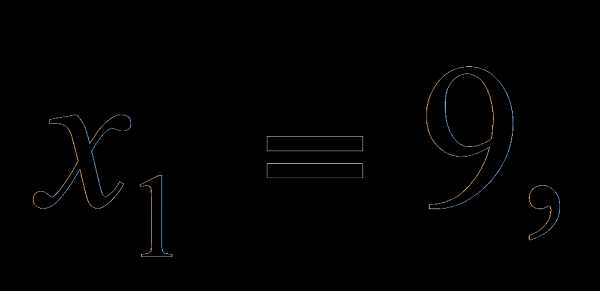
или 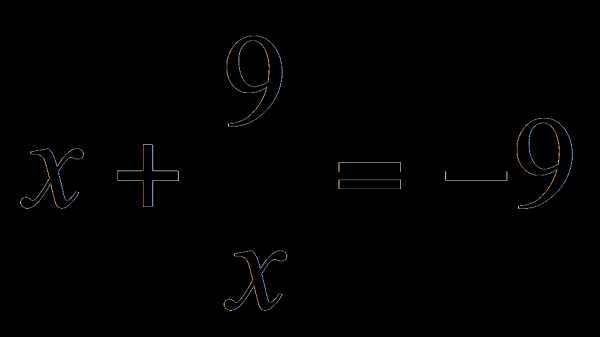 .
.

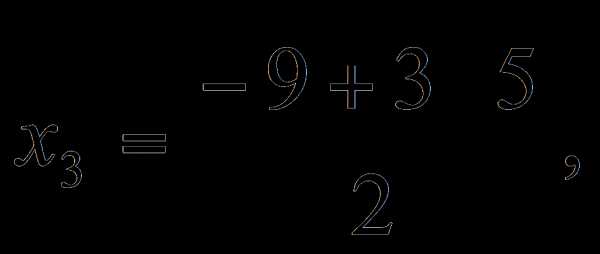
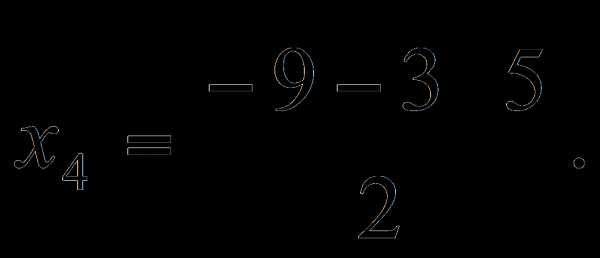
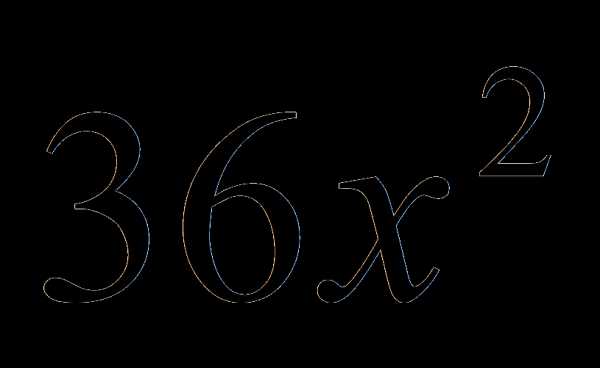 .
.
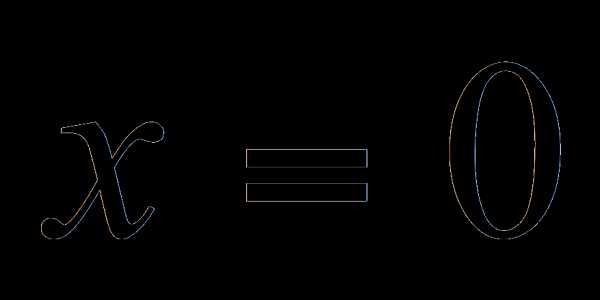 не является решением данного уравнения).
не является решением данного уравнения). , получим уравнение
, получим уравнение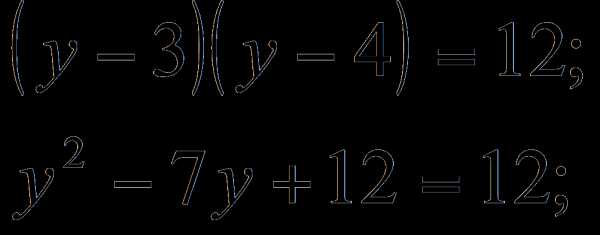
 или
или 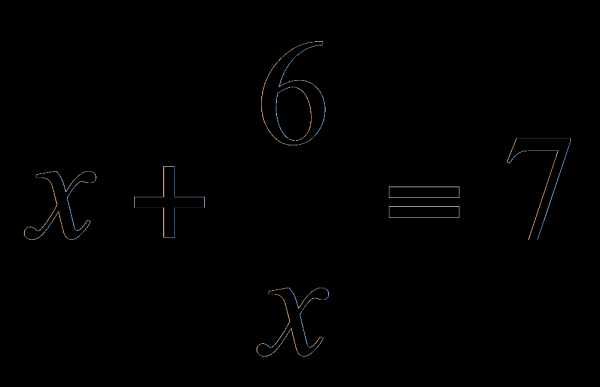 . Первое уравнение не имеет решений на множестве R, а корни второго .
. Первое уравнение не имеет решений на множестве R, а корни второго .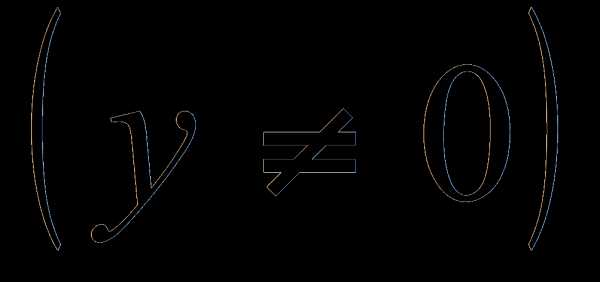 , получим уравнение
, получим уравнение