Экономическая теория Тесты с ответами Тема 1-10
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 1. Предмет и метод экономической теории
Термин «политическая экономия» впервые в своей книге использовал :
Т. Мэнкью
+Антуан Монкретьен де Ваттевиль
П. Сэмуэльсон
_____________ метод, являясь одним из системных методов исследования, позволяет в формализованном виде определить причины изменений экономических явлений, закономерности этих изменений, их последствия, возможности и издержки влияния на ход изменений, а также делает реальным прогнозирование экономических процессов
+экономико-математический
исторический
логический
систематический
Мысленное расчленение изучаемого явления на составные части и исследование каждой из этих частей отдельно. Это:
Индукция
+Анализ
дедукция
Анализ, дающий возможность увидеть экономические явления и процессы такими, какие они есть на самом деле, что было или может быть – это ______
+Позитивный анализ
Системный анализ
Нормативный анализ
Объектом экономической теории выступает:
общественные институты
+экономическая жизнь обществах
права человека
Друзья, более 600 собак Воронежского приюта Дора https://vk.com/priyt_dora очень нуждаются в поддержке! Приют бедствует, не хватает средств на корм и лечение. Не откладывайте добрые дела, перечислите прямо сейчас любую сумму на «Голодный телефон» +7 960 111 77 23 или карту сбербанка 4276 8130 1703 0573. По всем вопросам обращаться +7 903 857 05 77 (Шамарин Юрий Иванович)
Тема 2. Основные этапы развития экономической теории
Теоретическую работу «Экономическая таблица» (1758) написал:
А. Смит
У. Пети
+Ф. Кэне
Теория человеческого капитала разработана:
Р. Коузом
К.Менгером
+Г. Беккером+
Первый этап развития маржинализма (1870-1880) связан с именами:
У. Пети
+К. Менгера
+А. Вальраса
Зарождение и формирование основ экономической теории в качестве политической экономии – разработки рекомендаций государственного устройства для эффективного ведения хозяйства («ойкос») — происходило уже __________
В 19 веке
В Средние века
+В Древнем мире
В Древней Руси
Для анализа экономических законов и закономерностей __________ предложили использовать «предельные», т.е. приростные величины
кейнсианцы
+маржиналисты
меркантилисты
Тема 3. Зарождение и основные этапы развития экономической теории
«Кое-что о деньгах» (1682 г.) – это работа…
+У. Петти
Т. Мана
Ф. Энгельса
Он вошел в историю экономической мысли как основоположник классической политической экономии:
Д. Рикардо
Т. Веблен
+А. Смит
Это направление экономической теории, служит важнейшим теоретическим обоснованием государственного регулирования развитой рыночной экономики путем увеличения или сокращения спроса через изменение наличной и безналичной денежной массы.
меркантилизм
+кейнсианство
институциализм
Теория стабилизации экономики, в которой главенствующую роль играют денежные факторы — это …
+монетаризм
институциализм
кейнсианство
неолиберализм
«Этика» и «Политика» — это работы…
+Аристотеля
А. Смита
А. Маршалла
Дж. Кейнса
Тема 4. Производство и его роль в экономике
К материальному виду производства относятся:
+промышленность
+личное подсобное хозяйство
+торговля
здравоохранение
+коммунальное хозяйство
__________ выделяют производство средств производства, производство предметов потребления, потребительских товаров и услуг, используемых конечными потребителями
в территориальной структуре производства
в отраслевой структуре производства
+в зависимости от назначения производимой продукции
Термин __________ применяют к продукции, товарам, производимым в количествах, измеряемых многими тысячами и даже миллионами единиц в течении месяца, года.
«серийное производство»
+«массовое производство»
«индивидуальное производство»
Есть ли связь между материальным и нематериальным видами производства?
есть, несущественная
+да, это два взаимосвязанных вида производства
нет
К факторам производства относят:
Х-фактор
+труд
+земля
+предпринимательство
+капитал
Тема 5. Организация предпринимательской деятельности
__________ – это самостоятельный хозяйствующий субъект, созданный в порядке, установленном действующем законодательством, и производящий продукцию, товары, выполняющий работы, оказывающий услуги в целях удовлетворения общественных потребностей и получения прибыли
предприниматель
отрасль
личное подсобное хозяйство
промышленность
+предприятие (фирма, организация)
____________ учитывает иерархию и соподчинение целей и может быть представлено многообразными вторичными, третичными и еще менее значимыми производственными целями.
+«дерево целей»
миссия предприятия
«целевое дерево»
организационная структура предприятия
Общество, уставный капитал которого разделен на определенное число акций – это _________
+закрытое акционерное общество
товарищество
+открытое акционерное общество
кооператив
общество с ограниченной ответственностью
Общество с ограниченной ответственностью, открытое акционерное общество, закрытое акционерное общество, товарищество – это __________
название предприятий
классификация обществ
основные формы собственности
+основные организационно-правовые формы предприятий
Основная цель создания предприятий всех форм собственности – это __________
оказание услуг
+максимизация прибыли
производство продукции
минимизация затрат
Тема 6. Введение в макроэкономику
Номинальный ВНП возрос на 7%, а инфляционный прирост цен составил 10%. Реальный ВНП:
увеличился на 3%
увеличился на 17%
уменьшился на 17%
+уменьшился на 3%
При расчете этого индекса не принимаются во внимание изменения в структуре потребления в текущем периоде, связанные как с изменением доходов субъектов рынка, так и заменой одних благ другими (дорогих более дешевыми) в условиях роста цен. Это __________
Индекс Пааше
+индекс Ласпейреса
индекс Фишера
__________ представляет собой совокупность всех фирм, зарегистрированных внутри страны.
+сектор предпринимательства
сектор государства
сектор домашних хозяйств
заграница
В соответствии с законом Вальраса о национальном хозяйстве:
спрос сам создает соответствующую себе по объему величину спроса
+на одном из рынков не может существовать неравновесие, если на всех других рынках достигнуто равновесие
сумма избыточного спроса на всех рынках всегда равно нулю
__________ — это стоимость конечных продуктов, созданных за определенный период времени производителями, ведущими производство на территории данной страны с помощью факторов производства, находящихся на территории названной страны.
Чистый национальный продукт (ЧНП)
+Валовой внутренний продукт (ВВП)
Валовой национальный продукт (ВНП)
Национальный доход (НД)
Тема 7. Макроэкономическое равновесие на товарном рынке
Кривая ,которая показывает количество товаров и услуг, которое потребители готовы приобрести при каждом возможном уровне цен.
+кривая совокупного спроса
кривая спроса
кривая совокупного предложения
Действие неценовых факторов совокупного предложения выражается :
+сдвигом кривой AS
сдвигом кривой AD
скольжением вдоль кривой AS
скольжением вдоль кривой AD
__________ это общее количество конечных товаров и услуг, произведенных в экономике (в стоимостном выражении).
объем производства
+совокупное предложение
совокупный спрос
Неценовыми факторами совокупного предложения являются:
+изменение цен на ресурсы
+изменение в технологии
предпочтения потребителей
Изменение цен на этом участке кривой AS вызывает рост цен при неизменном реальном объеме производства:
кейнсианский
промежуточный
+классический
Тема 8. Совместное равновесие товарного и денежного рынков
Из модели IS—LM следует, что процентная ставка определяется в результате взаимодействия:
товарного рынка с рынком труда
спроса и предложения на денежном рынке
денежного рынка с рынком ценных бумаг
спроса и предложения на товарном рынке
+денежного рынка с товарным рынком
Модель IS—LM основана на предположении, что:
+уровень цен в экономике не меняется
объем потребления определяется только текущим доходом
объем инвестиций зависит от величины национального дохода
сбережения являются функцией процентной ставки
В ситуации ликвидной ловушки эффективной является:
кредитно-денежная политика
политика протекционизма
антиинфляционная политика
+бюджетно-налоговая политика
политика невмешательства в экономику
Сдвиг кривой LM вправо наблюдается при:
сокращении потребительских расходов
+снижении уровня цен
снижении уровня государственных расходов
сокращении предложения денег
снижении процентной ставки
В состоянии инвестиционной ловушки:
кривая IS пересекает кривую LM на вертикальном ее участке
+инвестиционный спрос не эластичен по процентной ставке
инвестиции чрезмерно реагируют на любые изменения процентных ставок
линия LM перпендикулярна оси абсцисс
рост автономных инвестиций не увеличивает совокупный спрос
Сдвиг кривой IS влево наблюдается при:
росте процентной ставки
снижении процентной ставки
снижении подоходного налога
увеличении уровня государственных расходов
+сокращении потребительских расходов
Тема 9.Макроэкономическая нестабильность: безработица, инфляция
В теории экономического цикла изучается:
+причины колебаний реального объема национального производства
механизм согласования планов фирм, потребителей, государства
структура ВВП страны
перспективы развития государства
Кто из названных людей является безработным:
+человек, который потерял работу 4 месяца назад и до сих пор продолжает поиски новой
женщина, находящаяся в декретном отпуске
студент, который хотел бы работать, но пока не приступил к поиску работы
человек, который потерял работу 5 лет назад и уже давно ее не ищет
Продолжительность экономического цикла составляет:
десять лет
один год
пять лет
+нельзя дать однозначного ответа
Что из ниже перечисленного можно отнести к последствиям безработицы:
+отставание реального ВВП от потенциально возможного уровня
снижение производительности труда
+снижение уровня жизни
рост реального ВВП
Инфляция проявляется
в росте реальных и номинальных доходов населения
в снижении общего уровня цен и номинальных доходов
+в росте общего уровня цен и падении реальных доходов населения
только в росте общего уровня цен без изменения реальных доходов
К антиинфляционным мерам относятся следующие:
увеличение денежной массы
рост государственных расходов
+ограничение денежной массы
+сокращение государственных расходов
Тема 10. Экономический рост
К прямым факторам экономического роста относятся:
степень монополизации рынка
эффективность кредитно-банковской системы
+ количество и качество трудовых ресурсов
действующая система распределения доходов
К экстенсивным факторам экономического роста относятся
+вовлечение в хозяйственный оборот новых земель
улучшение организации производства
увеличение производительности труда
+увеличение отработанного времени
Наиболее существенной причиной экономического роста развитых стран является
применение государством стимулирующей фискальной политики
+ технологические изменения в производстве
увеличение объема применяемого капитала
увеличение количества рабочей сипы
Показателем экономического и социального прогресса в обществе является
увеличение доли рабочего времени в совокупном времени общества
+увеличение доли свободного времени в совокупном времени общества
сокращение потерь рабочего времени
уменьшение доли свободного времени в совокупном времени общества
К косвенным факторам экономического роста относятся:
+степень монополизации рынка
количество и качество трудовых ресурсов
объем основного капитала
+эффективность кредитно-банковской системы
test-for-you.ru
Тест экономика. Введение в экономическую теорию
Экономика и экономическая теория
Тесты по экономике, для тестирования знаний по разделу «Введение в экономическую теорию». 22 тестовых вопроса — правильные варианты, выделены красным цветом.
1. Фундаментальная проблема, с которой сталкиваются все экономические системы это…
- инвестиции
- производство
- инфляция
- ограниченность ресурсов
2. Теория экономики ограничивается исследованием явлений и процессов, связанных с:
- наращиванием материального богатства
- наращиванием духовного богатства
- жизнедеятельностью человека и общества
- развитием производительных сил и производственных отношений
- развитием и совершенствованием орудий труда
3. Положения, относящиеся к предмету экономической теории:
- экономическое благо
- неограниченность ресурсов
- максимизация удовлетворения потребностей
- эффективное использование ресурсов
- правовые отношения
4. Экономические модели предназначены для:
- раскрытия экономических принципов и законов
- описания экономических явлений и процессов
- определения количественных параметров и качественного уровня развития экономики, к которому следует стремиться
- объяснения того, как функционирует национальная экономика и отдельные ее сферы
- выявления сущности экономических отношений
5. Историчность экономических категорий и законов определяется их … .
- временным характером
- неподвластностью времени
- неизменностью в условиях видоизменения экономических отношений
- появлением и отмиранием под воздействием смены социально-экономических отношений
- сохранностью при любых формах хозяйствования
6. Экономические законы отражают:
- необходимые и устойчивые взаимозависимости экономических отношений
- случайные и неповторяющиеся экономические взаимосвязи
- количественные оценки экономических явлений и процессов
- содержание экономических взаимосвязей
- переходные состояния экономических отношений
7. Экономические категории представляют собой:
- взаимосвязи между понятиями
- научные абстракции, выражающие экономические отношения
- доказательства о наличии или отсутствии тех или иных явлений
единичные случаи проявления тех или иных событий - обобщения, раскрывающие экономические явления и процессы или их содержание
8. Законы обращения денежных единиц изучаются в рамках:
- микроэкономики
- мезоэкономики
- региональной экономики
- макроэкономики
- мегаэкономики
9. Высказывание, относящееся к микроэкономике…
- предприятие в связи с сокращением производства увольняет 10 работников
- рост производства в России планируется в следующем году 8%.
- банк снизил ставку по вкладам на 1%.
- дефицит госбюджета ведет к инфляции
10. Основные причины, по которым экономисты разрабатывают модели…
- модель нужна для проверки гипотезы
- модель позволяет учесть и систематизировать решения проблемы
- модель необходима при определении индекса
- в модели используются только фактические переменные
11. Основным методом исследования экономической теории является…
- статистический
- исторический
- научная абстракция
- математический
12. Для экономикса характерны:
- поверхностный эмпиризм
- феноменально-математизированный анализ
- качественно-эволюционный анализ
- экономический инженеризм
- эвристический метод
13. Политическая экономия рассматривает человека в качестве:
- создателя материального богатства
- носителя духовных ценностей
- носителя прав и обязанностей
- созидателя своего мира и бытия
- главной производительной силы
14. Экономика – это наука о том, как общество решает:
- что производить
- как производить
- кому производить
- для кого
15. Объектами исследования в политической экономии и в экономике является поведение:
- естественного человека
- экономического человека
- человека в хозяйстве и на рынке
- человека, руководствующегося этическими ценностями
- человека в обществе
16. Микроэкономика изучает:
- валовый национальный продукт
- принятие решений, поведение отдельных экономических субъектов в условиях экономического выбора
- количество денег в обращении
- роль государства в регулировании экономики
- численность занятых в национальном хозяйстве
17. Национальная экономическая теория занимается:
- разработкой общетеоретических принципов и моделей социально-экономического развития
- сопоставлением моделей социально-экономического развития
- адаптацией общетеоретических принципов и моделей развития к специфике развития национальной экономики
- выявлением преимуществ различных моделей развития экономики
- выявлением специфики общественных отношений
18. Наиболее полно соответствует определению предмета экономической теории:
- хозяйственная жизнь общества
- средства производства
- человек и средства производства
- производительные силы и научно-технический прогресс
- взаимодействие производительных сил и производственных отношений
19. Производственные отношения – это:
- использование ресурсов
- этические, морально-нравственные взаимосвязи и отношения между людьми
- отношения производства, распределения, обмена и потребления
- взаимодействие человека со средствами производства
- отношения, возникающие в процессе общественного воспроизводства
20. Позитивная экономика занимается:
- определением имеющихся ресурсов
- раскрытием законов и закономерностей развития экономики
- поисками путей выхода из кризиса
- выявлением содержательной стороны экономических процессов и явлений, взаимосвязей как внутри их, так и между ними
- принятием решений по тем или иным социально-экономическим вопросам
21. Нормативная экономика занимается:
- исследованием фактов, процессов, явлений с целью выявления их сущности
- выявлением взаимосвязей между экономическими процессами и явлениями
- определением взаимосвязей между природой и обществом
- использованием экономических законов и принципов при решении определенных социально-экономических задач
- процессом реализации экономической политики
22. Экономика рассматривает человека, прежде всего как:
- создатель и носитель духовных ценностей
- естественный носитель всех общественных отношений
- потребитель благ
- творческая личность
- экономический человек
info-stadiya.ru
Тесты по экономической теории с ответами
Правильный ответ отмечен +
1. Общая полезность растет, когда предельная полезность:
а. Увеличивается
+ б. Уменьшается
в. Увеличивается или уменьшается, оставаясь при этом положительной величиной
2. Рынок товаров и услуг находится в равновесном состоянии, если:
+ а. Объем спроса и предложения одинаковы
б. Доходы покупателей непрерывно растут
в. Объем предложения превышает объем спроса
3. Общие издержки производства представляют собой:
а. Затраты, переносимые на стоимость готового изделия в полном объеме
б. Совокупные затраты предприятия, понесенные им за один производственный цикл
+ в. Совокупные затраты предприятия, понесенные им на одной стадии производства
4. Увеличение дохода потребителя графически выражается в:
+ а. Параллельном сдвиге бюджетной линии вправо
б. Параллельном сдвиге бюджетной линии влево
в. Параллельном сдвиге бюджетной линии вверх и вправо
5. Вещество природы является экономическим благом, если:
а. Его можно использовать в общественном производстве
б. Его можно продать за определенную стоимость, и есть покупатель, готовый его приобрести
+ в. Процессу его потребления предшествует процесс переработки
6.Тест. Экономические категории представляют собой:
+ а. Теоретические выражения, т. е. сформулированные мысли, выражающие суть экономических отношений, явлений и процессов, которые реально существуют
б. Научно доказанные тезисы
в. Научные тезисы, которые следует принимать верными без доказательств
7. Потребитель стремится максимизировать:
а. Экономический эффект
б. Среднюю полезность
+ в. Общую полезность
8. Кривая абсолютно неэластичного спроса представляет собой:
+ а. Вертикальную линию
б. Горизонтальную линию
в. Гиперболу
9. Кривая рыночного спроса показывает:
+ а. Количество блага, которое потребители желают и могут купить в единицу времени при различных ценах
б. Какие товары покупатели более склонны покупать в данный момент времени
в. Как будет снижаться цена блага при снижении реальных доходов населения
10. Если два товара взаимозаменяемы, то рост цены на первый вызовет:
а. Снижение цены на второй товар
+ б. Рост цены на второй товар
в. Рост цен на взаимно дополняемые товары
11. Сдельная оплата труда целесообразна, если:
+ а. Выработка напрямую зависит от квалификации и заинтересованности рабочего
б. Рабочий хочет иметь свободный график
в. Рабочий выполняет слаботочные работы
12. Назначение классификации по калькуляционным статьям расходов:
а. Служит основой для составления сметы затрат на производство
б. Помогает рассчитать отдельно постоянные и переменные расходы
+ в. Представляет собой расчет себестоимости единицы конкретного вида продукции
13. Нормативная экономика занимается:
а. Познанием и действием экономических законов
+ б. Использованием экономических законов
в. Познанием и действием экономических законов для дальнейшего их использования.
14. Экономические законы отражают:
+ а. Необходимые, причинно-обусловленные взаимосвязи и взаимозависимости между экономическими явлениями и процессами
б. Объективные закономерности функционирования экономики
в. Общепринятые обществом правила функционирования экономики
15. Олигополия сформируется скорее всего на рынке:
а. Яблок
+ б. Медицинской техники
в. Детской косметики
16. Складочный капитал формируется при создании:
а. Открытого акционерного общества
б. Закрытого акционерного общества
+ в. Полного товарищества
17. Отличительной чертой кредитных денег является:
а. Обязательная возвратность
б. Срочность обращения
+ в. Выпуск их в обращение посредством кредитных операций
18. Закон предложения «Если цены растут, а прочие условия неизменны» проявляется:
+ а. В росте объема предложения
б. В снижении объема предложения
в. В росте объема спроса
19. Эффект дохода имеет место в случае, если:
а. Доходы людей падают, они покупают меньше данного продукта
б. Объем покупок некоторых товаров сокращается по мере сокращения доходов людей
+ в. Удешевление товаров приводит к тому, что потребитель может купить больше данного товара, не сокращая объема приобретения других товаров
20. Явные издержки:
+ а. Обязательно находят место в расчетах с контрагентами и отражаются в бухгалтерской отчетности
б. Могут быть дополнительно вменены контрагентами в расчетах с ними
в. Отражают основные затраты на весь производственный цикл
21. Неявные издержки:
а. Обязательно находят место в расчетах с контрагентами и отражаются в бухгалтерской отчетности
+ б. Представляют собой издержки упущенных возможностей и необязательно фиксируются в бухгалтерской отчетности
в. Рассчитываются по завершению основного производственного цикла, т. е. представляют собой дополнительные производственные затраты.
22. Постоянные издержки фирмы — это:
+ а. Расходы фирмы, остающиеся неизменными и не зависящие от структуры и объемов производства
б. Расходы фирмы, связанные с внедрением новых производственных технологий
в. Расходы фирмы, величина которых зависит от структуры и объемов производства
23. Закон убывающей предельной полезности гласит, что:
а. Ни одно благо не может быть для человека абсолютно полезным, т. е. не иметь заменителей
+ б. С ростом потребления блага общая полезность, получаемая потребителем, будет возрастать, но с каждым разом все медленнее и медленнее
в. Рост потребления вызывает рост потребности в том или ином благе
24. Хозяйственным товариществом является:
+ а. Коммандитное товарищество
б. Полное товарищество
в. Товарищество собственников
25. Потребительское равновесие на карте безразличия – это:
а. Точка пересечения бюджетной линии и кривой безразличия
б. Любая точка на кривой безразличия
+ в. Точка, в которой наклон бюджетной линии равен наклону касательной к ней кривой безразличия
26. К фондам обращения относятся:
а. Материальные запасы и готовая продукция на складе предприятия
б. Сырье, расходные материалы, располагаемая рабочая сила и денежные средства, размещенные на банковских счетах предприятия;
+ в. Средства предприятия, вложенные в запасы готовой продукции, отгруженные, но неоплаченные товары, а также денежные средства в кассе и на банковских счетах предприятия
27. Совершенствование технологии сдвигает:
+ а. Кривую предложения вниз и вправо
б. Кривую предложения вверх и вправо
в. Кривую предложения вверх и влево
28. Эффективность использования оборотных средств характеризуют:
а. Коэффициент оборачиваемости оборотных средств
б. Время оборота
+ в. Коэффициент оборачиваемости оборотных средств и время их оборота
29. По классификации затрат по экономическим элементам выделяют:
+ а. Основное и вспомогательное сырье и материалы, ТЭР, основную и дополнительную заработную плату и отчисления с нее, амортизационные отчисления
б. Накладные расходы и плановые накопления
в. Себестоимость, прибыль, налоговое бремя, прочие затраты
30. Валовые частные инвестиции учитываются при расчете:
а. ВВП методом конечного использования
б. ВНП методом потока доходов
+ в. ВНП методом потока расходов
31. Рыночный спрос не испытывает влияния:
— Уровня реальных доходов потребителей
+ Цен на ресурсы
— Цен на взаимозаменяемые товары
32. Тест. Что обладает более высокой ликвидностью?
+ Наличные деньги и деньги, размещенные на банковских счетах
— Автомобиль
— Участок земли
33. Рынок совершенной конкуренции характеризуется:
— Наличием нескольких продавцов и множеством потребителей; невозможностью попасть на рынок новому производителю; жестким контролем цен со стороны государства
— Относительно большим количеством продавцов и разнородной продукцией; возможностью устанавливать цену на товар по собственному усмотрению; невысокими барьерами для входа на рынок
+ Однородностью продукции; отсутствием входных барьеров на рынок; бесконечным числом продавцов и потребителей; высокой мобильностью факторов производства
34. Перевозка грузов является … благом
— Общественным, материальным, кратковременным
+ Экономическим, нематериальным, кратковременным
— Социальным, материальным, долговременным
35. Циклический характер развития экономики проявляется:
— В колебаниях числа занятого населения
— В колебаниях курса национальной валюты по отношению к иностранным валютам
+ В колебаниях конъюнктуры экономики, которые имеют периодический характер
Тест. 36. Термин «операции на открытом рынке» означает:
+ Деятельность, которую ведет Центробанк по купле-продаже ценных бумаг
— Свободную торговлю факторами производства
— Установление равновесных цен на государственные ценные бумаги
37. Экономическая теория – это наука:
— Изучающая экономические взаимосвязи количественного и качественного характера при помощи математических методов
+ Изучающая проблему выбора в условиях ограниченности ресурсов для максимального удовлетворения потребностей общества
— Изучающая активность отдельных экономических агентов в ходе их производственной, потребительской, обменной и распределительной деятельности
38. Экономическая теория выполняет … функции
— Предупредительную, защитную, планирующую, контрольную
— Теоретическую, практическую, направляющую, контрольную, защитную
+ Теоретическую, мировоззренческую, критическую, методологическую, прогностическую
39. Экономическая теория изучает экономическое поведение людей:
+ В условиях какой-либо экономической системы
— В условиях безграничного выбора благ
— В условиях экономических кризисов
40. Кейнсианство как экономическая теория утверждает, что:
— Полная загрузка производственных мощностей способна обеспечить полное удовлетворение потребностей общества
+ Рыночная экономика не способна самостоятельно обеспечить полное использование своих ресурсов
— Общественные блага не подлежат государственному контролю
41.Основные положения экономической теории:
— Потребности общества колеблются и имеют сезонный характер; распределение производственных ресурсов в разных странах неодинаково
— Имеющиеся на сегодняшний день производственные ресурсы способны удовлетворить все потребности общества
+ Потребности общества постоянны и не имеют границ; ресурсы, способные удовлетворить потребности общества, ограничены
42. Расположите этапы развития экономической теории в правильной последовательности:
+ Меркантилизм, классическая политическая экономия, марксистская политическая экономия, экономикс
— Экономикс, меркантилизм, классическая политическая экономия, марксистская политическая экономия
— Классическая политическая экономия, марксистская политическая экономия, меркантилизм, экономикс
Тесты по экономической теории с правильным ответом:
1. Экономическая теория как наука зародилась:
Б) Древний Риме
2. Термин политическая экономика в научный оборот ввел:
В) Антуан де Монкретье
3. Экономическая теория, выражающая интересы торговой буржуазий эпохи первоначального накопления капитала – это:
Г) Меркантилизм
4. Предметом изучения экономической теорий является:
Б) Экономическое отношение и законы
7. Общественное производство состоит из следующих фаз:
Б) Производство, распределение, обмен и потребление
8. Конечный общественный продукт — это:
А) Масса всей произведенной в течение года готовой продукции
9. Триада отношений собственности — это:
Б) Владение, распоряжение, пользование
10. Собственность экономическая реализуется, если:
А) Приносит доход ее владельцу
12 — Тест. Национальное богатство — это:
А) Сумма материальных и духовных благ, накопленных в стране
14. Товар — это:
В) Вещь, произведенная для удовлетворения потребностей общества
15. Величина стоимости товара определяется:
Г) Затраты труда на производство товара
Тест по экономической теории №21. Если номинальная стоимость денег не изменяется, а цена на товары и услуги увеличится в 2 раза, то покупательская способность
А) Возрастет в 2 раза
22. Если в определенной стране объем экономических ресурсов увеличился, то:
В) Технология производства стала более совершенной
23. Показателем эффективности использования средств труда является:
А) Фондоотдача
25. Что не относится к основным признакам предприятия:
Б) Первичное звено сферы материального производства
26. Производство максимального количества товаров и услуг для удовлетворения потребностей общества при минимальных затрат на их производство является:
Г) Основной функций предприятия
27. По своему характеру предпринимательство делится:
А) Коммерческое и некоммерческое
28. Какая черта не характерна для предпринимательства?
В) Ориентация на прошлый опыт
29. В каких из перечисленных организационно — правовых формах хозяйствования физическое лицо рискует своим капиталом в наименьшей мере?
Г) Акционерное общество
32. Держатель одной акций АО является его:
В) Совладельцем
33. Непрерывный и последовательный процесс смены одной стадий и формы капитала в другую — это:
Б) Кругооборот капитала
34. Часть производственного капитала, стоимость которого входит в продукт целиком и полностью возвращается предприятию в денежном форме — это:
В) Оборотный капитал
35. Амортизация — это:
Г) Отчисления на потребления капитала
37. К числу переменных затрат(издержек) можно отвести:
Г) Процент по кредиту
39. Если норма амортизаций комбайна составляет 5%, то его стоимость должна возмещена за:
Г) 20 лет
40. Рынок — это способ организаций общественного производства, характерным признаком которого является:
В) Формирования цен на основе спроса и предложения
41. Какой термин отражается способность и желаний людей платить за какие-либо нужные им товары или услуги?
А) Спрос
42. Что не входит в рыночный механизм?
Г) Рыночная инфраструктура
43. Закон предложения при прочих равных условиях устанавливает:
Б) Прямая связь между ценой и количеством прилагаемого товара
44. Рынок товара находится в равновесном состояний, если:
В) При данной цене намерения покупателей купить данное количество товаров
48 — Тест. Олигополия — это рыночная структура, где действует:
А) небольшое количество конкурирующих фирм
49. Необходимость государственного регулирование рыночной экономики теорий обосновал:
В) Джон Кейс
59. Для характеристики российской экономики 90-х годов 20-го столетия наиболее точно подходит прилагательное:
В) Переходная
60 Оптимальной целью экономического роста является:
Б) Повешения жизненного уровня населения
61. Если увеличение национального продукта осуществляется за счет привлечения дополнительных факторов производства, то это
А) Экстенсивный тип экономического роста
65. Величина стоимости товара определяется:
Г) Затратами труда на производства товара
66. Какая из функций не относится к закону стоимости:
А) Закон стоимости определять полезности товара
67. «Деньги-это то, что деньги делают» — утверждение
В) Функция денег
69. Распространение ложных или порочащих товар сведений
В) Недобросовестная конкуренция
Тест № 70 по экономической теории. Отмена таможенной пошлины на импортируемый товар
В) К снижению производства данного товара
testua.ru
Тест с ответами на тему Введение в экономику
Экономика наиболее всего раскрывает:
a) то, как прибыль распределяется на всех уровнях государства
b) всевозможные уровни подготовки торговли
c) государственный контроль в ведении бизнеса
+d) то, как лучше удовлетворить неограниченные потребности ограниченным количеством ресурсов.
Вопрос 2
Что является предметом изучения макроэкономики?
a) возрастания величины продаж скутеров по причине повышения прибыли покупателей.
+b) появление нехватки на рынке жилья по причине появления государственного верхнего предела арендной платы за аренду жилья.
c) повышение цен в России из-за смены сезона на покупку зарубежной одежды.
d) повышение уровня заработной платы в Рязанской области по причине изменения налогового кодекса.
Вопрос 3
Какие направления стоят перед любыми экономическими системами? Как…
a) увеличить объём экспорта и импорта
b) увеличить объём государственного бюджета
+ c) наиболее эффективно израсходовать ограниченные ресурсы
d) максимально уменьшить государственную задолженность.
Вопрос 4
Альтернативная стоимость строительства здания новейшей общеобразовательной школы:
a) денежные средства на зарплату педагогам;
b) расходы на строительство здания в сегодняшних ценах;
c) количество налоговых сборов на добавленную стоимость;
+ d) другие товары и услуги, от которых нужно было отказаться в пользу строительства данной общеобразовательной школы.
Вопрос 5
Что из представленного ниже является предметом изучения микроэкономики?
+a) повышение налоговых сборов уменьшило продажу товаров в Иваново
b) возмещение таможенных сборов помогло к многочиленному открытию предприятий в лёгкой промышленности
c) покупатель пожелал приобрести автомобиль или квартиру, приобрёл яхту
d) падение сбора урожая в Беларусии привело к увеличению объёмов производства на фермах Соединённых Штатов Америки.
Вопрос 6
Экономика наиболее эффективна, если в ней достигнута:
a) нулевая безработица
+ b) полное использование производственных ресурсов
c) эффективное и максимальное использование других ресурсов
d) максимальная и эффективная использование внутренних ресурсов.
Вопрос 7
Товарное хозяйство представляет собой:
a) хозяйство с наименьшим количеством производимых продуктов
+ b) производство товаров и услуг для продажи
c) производство дешёвых товаров для удовлетвореня потребностей покупателя
d) хозяйство, в котором используются продвинутые технологии
e) все предствленные ответы верны.
Вопрос 8
Из-за не большого количества денежных средств вы должны приобрести несколько дорогих, но красивых кружек и несколько кружек не дорогих. Вы столкнулись…
a) с недостатком нужных ресурсов
b) с недостатком нужных ресурсов и возможностью не возможного выбора
+ c) с проблемой ограниченности ресурсов, необходимостью компромиссного выбора и оценкой альтернативной стоимости
d) с возможностью не возможного выбора и переоценкой цены товаров.
Вопрос 9
Дефицит бюджета появляется, как только…
a) повышаются государственные затраты
b) снижаютя цены
c) общие издержки превышают общую прибыль
+ d) государственные расходы превышают государственные доходы
Вопрос 10
Собственность, представляет собой:
a) принадлежность объекта субъекту, право пользования объектом
b) умение владения и распоряжения собственностью
+ c) совокупность экономических отношений, связанных с присвоением условий производства и его результатов;
d) все предствленные ответы верны.
Вопрос 11
Какой из представленных терминов показывает возможность и пожелание покупателей тратить на что-либо?
a) нужда
+ b) спрос
c) возможность
d) потребность.
Вопрос 12
Что нельзя отнести к экономическими ресурсами:
a) капитал
+ b) денежные средства
c) земля
d) труд
Вопрос 13
Если государство пользуется всеми человеческими и материальными ресурсами, то наибольшее количество какого-либо товара…
a) изготовлено одним индивидуальным предпринимателем
+b) может быть произведено только при сокращении производства каких-либо товаров
c) может быть изготовлено при условии обобщённым снижением стоимости
d) не может быть произведено.
Вопрос 14
Экономический закон, говорящий, что с повышением цены падает количество покупаемых продуктов, называется закон…
+ a) спроса
b) падения стоимости
c) эффективности вложений
d) кривых показателей
Вопрос 15
Если стоимость велосипедов повыселась по пречине повышения спроса на велосипеды, то результатом этого станет:
+ a) рост спроса на покрышки
b) увеличения спроса на мороженное
c) рост предложения насососов
d) снижение величины спроса на мороженное при неизменном спросе на покрышки.
Вопрос 16
Чего, отсутсвует в командной экономике:
a) анализ финансов;
b) не рациональное использование ресурсов;
c) назначаемых чиновниками цен;
+ d) ориентации производителей в основном на платежеспособный спрос;
e) все предствленные ответы верны.
Вопрос 17
К какому пункту имеет отношение термин экономики под названием «предложение»?
a) объём произведённой продукции
b) цена произведённой продукции
+ c) зависимость между количеством товара, представленного на рынке и его ценой
d) объём произведённой продукции, которую нужно реализовать для получения прибыли.
Вопрос 18
Рынок как система экономики представляет собой:
a) совокупность беспорядоченности и неоднозначенности;
+ b) сложный механизм координации, действующий через систему рынков, цен, прибылей, убытков, конкуренции;
c) совокупность торговых взаимотношений продавцов и покупателей;
d) все предыдущие ответы неверны
Вопрос 19
Что может быть основой во время выбора решений в условиях неопределенности?
+ a) риск
b) сверхзатраты
c) повышение специализации рабочего персонала
d) недостаток рабочего контроля.
Вопрос 20
Каково основное требование хозяйственного решения:
+ a)соответствовие действующему законодательству и уставным документам предприятия;
b) хорошая эффективность использования;
c) прибыль хозяйственного решения должна быть прогнозируемой;
d) все предыдущие ответы верны
testdoc.ru
ТЕСТЫ ПО ЭКОНОМИЧЕСКОЙ ТЕОРИИ
Стр 1 из 5Следующая ⇒
ТЕСТЫ ПО ЭКОНОМИЧЕСКОЙ ТЕОРИИ
ТЕМА 1. ЭКОНОМИЧЕСКАЯ ТЕОРИЯ: ИСТОРИЯ РАЗВИТИЯ,
ПРЕДМЕТ И МЕТОДЫ
1. Экономические отношения на уровне предприятий, фирм изучает:
1) макроэкономика;
2) микроэкономика;
3) мегаэкономика;
4) мезоэкономика;
2. Первым ввел в оборот термин «экономия»:
1) Маркс; 2) Платон; 3) Ксенофонт;4) Самуэльсон.
3. Обобщение экономического опыта и практики хозяйственной деятельности человечества, совокупность понятий и положений, характеризующих экономическую жизнь — это:
1) социология;
2) политология;
3) психология;
Экономическая теория.
4. Первым широко распространённым экономическим учением становится:
1) монетаризм;
2) марксизм;
3) меркантилизм;
4) маржинализм.
5. Экономическое учение о необходимости и значимости государственного регулирования развития экономики – это:
1) кейнсианство;
2) меркантилизм;
3) монетаризм;
4) марксизм;
5) маржинализм.
6. Экономическая школа, сторонники которой в научном анализе экономических явлений используют предельные величины, — это:
1) меркантилизм;
2) теория общего равновесия;
3) теория частичного равновесия;
4) маржинализм;
5) монетаризм.
7. Представитель английской школы классической политэкономии, которому принадлежит идея разумного эгоизма — это:
1) П. Самуэльсон;
2) А. Смит;
3) Ф. Кенэ;
4) Т. Веблен;
5) А. Маршалл.
8. Теория, в соответствии с которой денежная масса, находящаяся в обращении, играет определяющую роль в стабилизации и развитии экономики, называется:
1) монетаризм;
2) марксизм;
3) меркантилизм;
4) маржинализм
9. Течение экономической мысли, которое в качестве движущей силы экономики кроме материальных факторов выдвигает моральные, духовные, правовые и др., рассматриваемые в историческом плане – это:
1) либерализм;
2) институционализм;
3) монетаризм;
4) марксизм.
10. Устойчивые, существенные, постоянно повторяющиеся причинно-следственные связи и взаимосвязи экономических явлений и процессов — это:
1) экономические категории;
2) экономические законы;
3) экономические функции;
4) экономические показатели.
11. Макроэкономика изучает:
1) спрос и предложение на определенные товары;
2) законы и закономерности развития национальной экономики в целом;
3) экономические издержки и пути их сокращения;
4) систему показателей эффективного использования ресурсов на предприятии.
12. Объективность экономических законов означает, что:
1) они издаются законодательными органами страны;
2) люди бессильны в их познании и использовании;
3) они действуют независимо от воли и сознания людей;
4) они зависят от воли и сознания человека.
ТЕМА 2. ПОТРЕБНОСТИ И РЕСУРСЫ.
ПРОБЛЕМА ВЫБОРА В ЭКОНОМИКЕ
13. Исходным побудительным мотивом экономической деятельности людей являются:
1) интересы;
2) запросы;
3) блага;
4) ресурсы;
Потребности.
14. Нужда, принявшая специфическую форму в соответствии с культурным уровнем и личностью индивида, – это:
1) выгода;
2) потребность;
3) спрос;
4) мотив.
15. Наличие потребностей и желание их удовлетворить является главным стимулом:
1) циклического развития экономики;
2) технического прогресса;
3) производства экономических благ;
4) централизации производства.
16. Целенаправленная деятельность людей, в процессе которой они изготавливают все то, что служит удовлетворению их материальных и духовных потребностей, – это:
1) потребление; 2) выбор; 3) бизнес; 4) производство;5) распределение.
17. Производство, в котором величина конечного результата превышает величину затраченных ресурсов, – это:
1) неэффективное производство;
2) эффективное производство;
3) перспективное производство;
4) расширенное производство;
18. Процесс воспроизводства как постоянно повторяющийся процесс производства включает следующие фазы:
1) производство, распределение, обмен, потребление;
2) распределение, обмен, потребление;
3) производство, распределение, обмен;
4) производство, выбор, обмен, потребление;
5) производство, обмен, потребление.
19. Процесс удовлетворения потребностей как фаза в воспроизводственном цикле – это:
1) производство;
2) обмен;
3) потребление;
4) распределение.
20. Базовыми ресурсами, которые образуют обязательное условие любого даже самого простого производства, являются:
1) финансовые, трудовые и материальные ресурсы;
2) информационные, природные, трудовые ресурсы;
3) природные, трудовые и материальные ресурсы;
4) природные, трудовые и время как ресурс;
5) трудовые, финансовые и информационные ресурсы.
21. Совокупность созданных человеком средств производства, имеющая материально-вещественную форму, – это:
1) финансовые ресурсы;
2) природные ресурсы;
3) материальные ресурсы;
4) трудовые ресурсы;
5) информационные ресурсы.
22. Ресурс, имеющий нематериальный характер, – это:
1) финансы; 2) природные ресурсы; 3) информация;4) капитал.
23. Та часть ресурсов, которая непосредственно вовлекается в процесс производства и используется в качестве его условий, принято называть:
1) технологическими факторами;
2) факторами производства;
3) материальными факторами;
4) производственными ресурсами.
24. В современной экономической теории выделяют следующие факторы производства:
1) земля; 2) труд; 3) капитал; 4) предпринимательство;5) инвестиции.
25. Ограниченность ресурсов – это проблема, которая существует:
1) в развивающихся странах;
2) в странах с переходной экономикой;
3) во всех странах;
4) в развитых и богатых странах;
5) в слабо развитых странах.
26. Экономическая ситуация, при которой для удовлетворения каких-то конкретных потребностей людей ресурсов достаточно, – это:
1) ограниченность ресурсов;
2) предельная ограниченность ресурсов;
3) относительная ограниченность ресурсов;
4) неограниченность ресурсов;
5) абсолютная ограниченность ресурсов.
27. Определение наилучшего результата использования ограниченных ресурсов достигается посредством:
1) анализа;
2) расчета;
3) калькуляции;
4) выбора.
28. Решая проблему выбора, на какие главные вопросы должна ответить каждая экономическая система?
1) что производить;
2) как производить;
3) для кого производить;
4) зачем производить.
29. Каждая точка на кривой производственных возможностей показывает:
1) точное количество двух видов продуктов, которое предприятие планирует производить;
2) лучшие из возможностей сочетания двух благ;
3) предельные возможности совместного производства двух товаров;
Максимальный объем производства двух товаров при полном использовании всех ресурсов.
30. Для получения каждой дополнительной единицы одного товара приходится расплачиваться потерей определенного количества другого товара. Это явление в рыночной экономике получило название:
1) издержек производства;
2) издержек распределения;
3) альтернативных издержек;
4) предельных издержек.
31. Максимальное удовлетворение потребностей населения при минимальных затратах факторов производства – это:
1) высший принцип экономики;
2) объективный закон производства;
3) золотое правило экономики;
4) требование общества.
ТЕМА 3. ЭКОНОМИЧЕСКИЕ СИСТЕМЫ
32. Совокупность материальных и духовных средств экономической деятельности, а также традиций, норм, привычек людей, регулирующих экономическую жизнь, – это:
1) хозяйственный механизм;
2) экономическая система;
3) экономическая культура;
33. Укажите тип собственности, когда исключительное право на владение, распоряжение и пользование объектов собственности и получение доходов имеет частное лицо:
1) коллективная собственность;
2) общественная собственность;
3) кооперативная собственность;
4) акционерная собственность;
Частная собственность.
34. Совокупность форм и методов организации общественного производства – это:
1) экономическая система;
2) хозяйственный механизм;
3) общественная собственность.
35. Экономист, который предложил теорию стадий экономического роста, – это:
1) К. Р. Макконнел; 2) Дж. Дебре; 3) У. Ростоу.
36. Укажите одну из особенностей американской экономической модели:
1) всемерное поощрение предпринимательской активности;
2) сильная социальная политика;
3) высокая степень социальной защищенности населения от негативных последствий рынка.
37. Основной отличительный признак (свойство) экономической системы – это:
1) целостность;
2) иерархичность;
3) самовоспроизведение;
4) целесообразность.
38. Важнейшей категорией классификации экономических систем с позиций формационного подхода является:
1) индустриальное общество;
2) технологический способ производства;
3) общественно-экономическая формация;
39. Белорусская национальная модель экономики – это:
1) социально ориентированная экономика;
2) экологически ответственная смешанная экономика;
3) социально ориентированная рыночная экономика;
4) социально ориентированная смешанная экономика;
5) смешанная экономика.
40. Экономика, которая находится в процессе изменения, перехода из одного состояния в другое, – это:
1) античная;
2) постиндустриальная;
3) социалистическая;
4) переходная.
41. Для экономически отсталых стран характерна:
1) экономика переходного периода;
2) экономика классического капитализма;
3) плановая экономика;
4) экономика индустриального общества;
Традиционная экономика.
42. Исторически изменяющиеся отношения между людьми по поводу владения, использования, распоряжения факторами, условиями и результатами производства – это:
1) распределение;
2) иерархия;
3) собственность;
4) экономика;
43. Определите 3-х субъектов собственности:
1) предприятия;
2) государство;
3) денежные средства;
4) население.
44. Определите две формы частной собственности:
1) трудовая;
2) арендная;
3) кооперативная;
4) нетрудовая.
45. Если субъект собственности реализует отношения владения, распоряжения и пользования, то это собственность:
1) номинальная; 2) временная; 3) постоянная; 4) полная;5) частичная.
Средства платежа.
54. Выделите товар-эквивалент, который был распространен на территории Беларуси: ракушки; соль; куны;овцы; коровы.
55. Впервые стали выпускать бумажные деньги в:
1) Германии;
2) России;
3) США;
4) Китае;
5) Греции.
56. По закону денежного обращения между количеством денег в обращении и объемом производства продукции:
1) существует обратная связь;
2) прямая связь;
3) переменная связь;
4) такой связи нет вообще.
Верно 1,2,3,4.
75. При росте доходов населения спрос на дешевые товары низкого качества:
1) увеличивается;
2) стабилизируется;
3) не меняется;
4) снижается;
5) дифференцируется.
76. Найдите два верных утверждения:
1) количество предложенных товаров и услуг находятся в обратной зависимости от цены;
2) предложение возрастает с увеличением цены;
3) предложение не изменяется с уменьшением цены;
4) спрос возрастает со снижением цены;
5) спрос уменьшается с уменьшением цены.
77. Если рыночная цена ниже равновесной, то:
1) появляются избытки товаров;
2) возникает дефицит товаров;
3) формируется рынок покупателя;
4) падает цена ресурсов.
78. Предложение – это:
1) прямой, непосредственный обмен товара на товар;
2) желание и способность продавцов предоставлять товары для продажи на рынке;
3) способ общественного выражения экономической ценности блага;
4) любой вид инициативной хозяйственной деятельности, направленной на поучение не только прибыли, но и сверхприбыли;
5) потребность и возможность (платёжеспособность) людей покупать товары и оплачивать услуги.
79. Зависимость предложения от цены товара выражается:
1) законом спроса;
2) законом убывающей доходности;
3) законом цен;
4) законом денежного обращения;
5) законом предложения.
80. Что происходит с кривой предложения под воздействием различных неценовых факторов?
1) кривая предложения смещается вправо;
2) кривая предложения смещается влево;
3) кривая предложения не смещается;
4) имеет место перемещение вдоль кривой предложения;
Верны позиции 1) и 2).
81. Показатель степени реагирования величины предложения на изменение цены – это:
1) опцион; 2) лизинг; 3) демпинг; 4) девальвация; 5) эластичность.
82. Как называется ситуация, при которой рыночная цена устанавливается выше равновесной и предложение превышает спрос:
1) дефицит товара;
2) издержки обращения;
3) избыточный спрос;
4) избыток товара;
5) стагнация.
83. Рыночное равновесие стабильно, когда:
1) нарушенное равновесие не восстанавливается;
2) нарушенное равновесие быстро восстанавливается вновь;
3) нарушенное равновесие сохраняется;
4) равновесие не устанавливается;
5) оно жестко зафиксировано.
84. Цена – это:
1) способ общественного выражения экономической ценности блага;
2) часть личного располагаемого дохода, не используемая на потребление;
3) долговое обязательство в виде расписки, в которой покупатель указывает сумму и срок его выплаты;
4) воплощённые в товаре общественно полезные затраты труда, соответствующие средним условиям, умелости и интенсивности труда;
В РЫНОЧНОЙ ЭКОНОМИКЕ
86. Цель рационального потребителя состоит в том, чтобы:
1) купить товар по меньшей цене;
2) на определенную сумму денег купить максимально возможное количество товаров;
3) на определенную сумму денег приобрести максимально полезный набор товаров и услуг;
4) такую цель невозможно определить.
87. Согласно правилу полезности потребляемого однородного блага:
1) полезность каждой единицы однородных потребляемых благ не зависит от их количества;
2) полезность каждого последующего потребляемого однородного блага для потребителя уменьшается;
3) полезность каждого последующего потребляемого однородного блага для потребителя возрастает;
4) полезность суммы потребляемых однородных благ для потребителя должна быть неизменной по величине.
88. По теории полезности цена партии однородного товара определяется:
1) средней полезностью;
2) общей полезностью;
3) полезностью последней единицы товара;
4)наибольшей полезностью.
89. Уменьшение предельной полезности товара с увеличением его потребляемого количества называется:
1) законом предельной полезности;
2) законом максимизации полезности;
3) законом возрастающей предельной полезности;
4) законом выигрыша потребителя;
ТЕМА 8. ТЕОРИЯ ФИРМЫ
99. Основной формой хозяйствования на микроуровне является:
1) домашнее хозяйство; 2) индивидуальная деятельность; 3) предприятие;
4) национальная экономика; 5) глобальная экономика.
100. Характерными чертами предприятия являются:
1) организационное единство;
2) технико-производственное единство;
3) экономическая обособленность;
4) экономическая самостоятельность;
5) организационное многообразие.
101. Основной целью предприятия является:
1) выпуск продукции для удовлетворения личных и общественных потребностей;
2) максимизация выпуска продукции для удовлетворения личных и общественных потребностей;
3) максимизация прибыли путем выпуска продукции для удовлетворения личных и общественных потребностей;
4) максимизация прибыли путем продажи продукции;
5) удовлетворение личных и общественных потребностей.
102. В зависимости от формы собственности предприятия подразделяются на:
1) акционерные; 2) хозяйственные товарищества; 3) коммерческие;
Система национальных счетов
3) системы макроэкономических показателей
4) системы балансов активов и пассивов
116. Республиканская Система национальных счетов была разработана на основе обновленного варианта СНС ООН 1992:
1) в 1992 году 2) в 1993 году3) в 1994 году 4) в 1995 году
117. Основные три направления использования национального дохода – это:
1) потребление;
2) торговля;
3) рефинансирование;
4) сбережения;
Инвестиции.
118. Совокупная стоимость всех товаров и услуг, произведенных в течении года всеми предприятиями, расположенными на территории данной страны, независимо от их национальной принадлежности – это:
1) ВНД;
2) ВВП;
3) ЧНП;
4) РЛД;
119. ВВП по расходам включает:
1) потребительские расходы и государственные закупки;
2) валовые внутренние инвестиции;
3) чистый экспорт;
4) заработную плату работников.
120. ВВП, выраженный в текущих ценах, – это:
1) суммарный ВВП;
2) номинальный ВВП;
3) реальный ВВП;
4) активный ВВП;
5) пассивный ВВП.
121. В период инфляции:
1) реальный ВВП растет быстрее номинального;
2) номинальный ВВП растет быстрее реального;
3)номинальный и реальный ВВП увеличиваются одинаковыми темпами.
122. Чистый национальный доход равен разнице между:
1) валовым национальным доходом и амортизацией;
2) ЧНП и амортизационными отчислениями;
3) ЧНП и косвенными налогами.
123. Основными тремя субъектами макроэкономики являются:
1) домашние хозяйства;
2) учреждения МВД;
3) предприятия, фирмы;
4) государство, правительственные учреждения.
124. Количественное и качественное совершенствование производства и увеличение общественного продукта, способствующие решению проблемы ограниченности ресурсов и повышению уровня жизни – это:
1) эффективное производство; 2) расширенное воспроизводство
3) экономический рост;4) реструктуризация экономики
125. Выделяют три типа экономического роста:
1) экстенсивный; 2) интенсивный; 3) смешенный;
4) прогрессивный; 5) регрессивный
126. К экстенсивным факторам экономического роста относится:
1) увеличение производительности труда;
2) улучшение организации производства;
Верно 2,3,4.
142. Безработица, связанная с неправильным распределением трудовых ресурсов по регионам – это:
1) добровольная безработица; 2) скрытая безработица; 3) застойная безработица; 4) региональная безработица;
5) циклическая безработица.
143. Если число работников на производстве превышает объективно необходимое, то это:
1) скрытая безработица; 2) добровольная безработица;
3) сезонная безработица; 4) структурная безработица;
5) технологическая безработица.
144. Состояние национальной экономики, которое сопровождается обесцениванием денег вследствие их избытка в обращении и ростом цен на товары и услуги:
1) дефляция;
2) нуллификация;
3) инфляция;
4) стагнация;
5) девальвация.
145. Инфляция, характеризующаяся продолжительным ростом цен:
1) открытая инфляция;
2) подавленная инфляция;
3) ожидаемая инфляция;
4) неожидаемая инфляция;
5) инфляция издержек.
146. Инфляция по масштабу охвата:
1) локальная и мировая;
2) открытая и подавленная;
3) спроса и предложения;
4) издержек и доходов;
5) ожидаемая и неожидаемая.
147. Форма инфляции, при которой рост цен от 10% до 200% в год:
1) умеренная;
2) галопирующая;
3) гиперинфляция,
148. Каких типов инфляции не существует в экономике:
1) умеренная; 2) галопирующая; 3) мегаинфляция; 4) интеринфляция;
5) гиперинфляция.
Верно 2, 3,4.
161. Основным условием макроэкономического равновесия является:
1) сбалансированность денежного и товарного потоков;
2) устойчивое, сбалансированное и пропорциональное экономическое развитие;
3) наличие в экономике страны специального механизма регулирования;
4) равенство совокупного спроса и совокупного предложения.
162. На каких рынках обеспечивается общее макроэкономическое равновесие:
1) на товарных рынках;
2) на рынках факторов производства;
3) на рынках денежного капитала;
4) на рынках ценных бумаг;
5) на всех рынках.
И РАСХОДОВ
163. Если предельная склонность к потреблению снижается, то в экономике будет иметь место:
1) снижение предельной склонности к инвестированию;
2) рост предельной склонности к сбережению;
3) усиление макроэкономической нестабильности;
4) макроэкономическая стабильность;
5) рост предельной склонности к инвестированию.
164. Какие из перечисленных факторов влияют на инвестиционный спрос?
1) процентная ставка;
2) ожидаемая прибыль;
3) оптимизм или пессимизм предпринимателей;
4) все ответы неверны.
165. Как определяется макроэкономическое равновесие в кейнсианской модели?
1) Пересечением линии потребления и сбережений;
2) пересечением линии потребления и инвестиций;
3) пересечением линии совокупных расходов с линией «нулевого сбережения»;
4) пересечением кривой сбережений и биссектрисой.
166. Мультипликатор равен:
1) отношению прироста дохода к приросту потребления;
2) отношению прироста ВВП к приросту инвестиций;
3) отношению прироста потребления к приросту инвестиций;
4) величине, обратной предельной склонности к потреблению.
167. Предельная склонность к сбережению равна отношению:
1) сбережений к доходу;
2) дохода к приросту сбережений;
3) прироста сбережений к приросту дохода;
4) сбережений к потреблению.
168. Предельная склонность к потреблению равна:
1) отношению прироста дохода к приросту сбережений;
2) отношению сбережений к доходу;
3) приросту потребления при увеличении дохода на 1%;
Их сумма равна 1.
175. В кейнсианской модели экономики равновесный уровень ВВП – это уровень, при котором:
1) сбережения равны планируемым инвестициям;
2) сбережения равны фактическим инвестициям;
3) фактические расходы равны произведенному доходу.
176. Вложения государственного или частного капитала в различные отрасли экономики как внутри страны, так и за ее пределами с целью получения прибыли – это:
1) инфляция; 2) инновации; 3) отчисления; 4) депонирование; 5) инвестиции.
Общественные объединения.
214. Стратегическими целями социальной политики являются:
1) улучшение материального положения и условий жизни людей;
2) обеспечение прав и социальных гарантий, предоставляемых семье;
3) стимулирование экспортно-импортных операций;
4) обеспечение эффективной занятости работников и повышение их конкурентоспособности на рынке труда;
5) стимулирование инвестиций.
215. Регулирующими инструментами социальной политики являются:
1) купля-продажа государственных ценных бумаг;
2) изменение резервной нормы коммерческих банков;
3) адресная система социальной защиты;
4) трансфертные платежи;
Прибыли (предприниматели),
ТЕСТЫ ПО ЭКОНОМИЧЕСКОЙ ТЕОРИИ
Рекомендуемые страницы:
lektsia.com
Тест по экономике на тему Введение в экономическую теорию
Тестовые задания Тема: Введение в экономическую теорию Тест.
1. Выберите наиболее полное определение предмета экономической теории:
1) Экономика изучает производство и занятость;
2) Экономика изучает деньги, кредит, банковскую и финансовую деятельность;
3) Экономика изучает рациональное использование ограниченных ресурсов для удовлетворения потребностей;
4) экономика изучает цены, ценообразование, рынок.
2. Какое из положений не имеет отношения к определению предмета экономической теории?
1) анализ рыночного хозяйства;
2) неограниченные производственные ресурсы;
3) потребности людей;
4) редкость блага.
3. Изучение экономической теории позволит:
1) улучшить свое материальное положение;
2) научить студентов «уметь жить»;
3) расширить удовлетворение своих потребностей;
4) сознательно участвовать в экономической жизни.
4. Что из перечисленного является объектом микроэкономического анализа?
1) трудовые ресурсы и занятость;
2) причины, закономерности и последствия функционирования отдельных экономических субъектов;
3) функционирование смешанной экономической системы;
4) потребности и вкусы покупателей.
5. Позитивная экономическая теория изучает:
1) реальное положение;
2) что должно быть;
3) прогрессивные тенденции;
4)негативные тенденции.
6. Нормативная экономическая теория изучает:
1) реальное положение;
2) что должно быть;
3) прогрессивные тенденции;
4) негативные тенденции.
7. Необходимость государственного регулирования рыночного хозяйствования следует из теории:
А.Смита,
А. Маршалла,
Д.Кейнса,
П.Саммуэльсона.
8. Что из перечисленного не изучает макроэкономика:
безработица и занятость,
сбережения и инвестиции,
экономический рост и цикличность развития.
ценообразование на рынках отдельных товаров.
9. Что изучает экономическая теория:
производственные отношения,
классовые отношения,
отношения, складывающиеся в надстройке,
анализирует рыночное хозяйство.
10. Что из перечисленного изучает микроэкономика:
национальное производство,
общий уровень цен и инфляцию,
поведение фирмы на рынке,
занятость и безработицу.
infourok.ru
Тест с ответами по экономической теории для 1 курса
1. Средства, необходимые для удовлетворения потребностей людей и имеющиеся в распоряжении общества в ограниченном количестве.
1) деньги
2) экономические блага +
3) свободные блага
4) нет правильного ответа
2. Что включает в себя произведенные человеком средства производства?
1) ресурсы
2) рента
3) капитал +
4) труд
3. Это люди, обладающие физическими и интеллектуальными способностями, благодаря которым они могут производить товары и услуги.
1) трудовые ресурсы +
2) рабочая сила
3) экономически неактивное население
4) персонал
4. Рациональность предполагает целесообразную деятельность, подразумевает постановку …
1) цели +
2) задач
3) актуальности
4) темы
5. Это наука, которая изучает, каким образом в обществе, располагающем ограниченными ресурсами, решаются проблемы, что, как и для кого надо производить
1) экономика +
2) политология
3) психология
4) культурология
6. Первый уровень экономики
1) микроэкономика +
2) макроэкономика
3) все ответы неверны
7. Имеет дело с экономикой в целом, а не с отдельными субъектами
1) микроэкономика
2) макроэкономика +
3) все ответы неверны
8. Это упрощенное описание экономики, которое выражает функциональную зависимость между двумя или несколькими переменными
1) экономическая модель +
2) экономический тип
3) экономическая стратегия
4) экономический вид
9. Это факты, выраженные, как правило, в виде цифр, несущие информацию об экономических переменных
1) экономическая модель
2) экономические данные +
3) экономическая стратегия
4) экономический вид
10. Экономические величины, выраженные в текущих ценах, называются
1) реальными
2) номинальными +
3) все ответы верны
11. Экономические величины, выраженные в неизменных ценах, называются
1) реальными +
2) номинальными
3) все ответы верны
12. Для определения уровня и динамики многих экономических показателей используются…
1) индексы +
2) коэффициенты
3) стратегии
4) нет верного ответа
13. Это форма контактов между продавцами и покупателями товаров и услуг, недвижимости, ценных бумаг и валюты
1) базар
2) рынок +
3) магазин
4) улица
14. Экономика не дает ответа на вопрос
1) что произвести
2) какую использовать технологию
3) кто будет потребителем
4) какую социальную значимость имеет данный продукт. +
15. Тип экономической системы определяется
1) формой государственной власти
2) собственностью и способами управления +
3) количеством населения страны
4) запасами полезных ископаемых.
16. Натуральное хозяйство характерно:
1) для традиционного общества +
2) для социалистического общества
3) только для первобытного строя
4) для индустриальной эпохи.
17. Признаком плановой экономической системы не является
1) государственная собственность на средства производства
2) централизованное управление экономикой
3) свободное ценообразование +
4) нормированное распределение
18. Признаком рыночной экономики является
1) прямой продуктообмен
2) распределение труда по полу и возрасту
3) прямой государственный контроль над ценами
4) целью производства является получение прибыли. +
19. Смешанная экономическая система
1) существовала в первобытном обществе
2) начала развиваться в период феодализма
3) была основой социалистического хозяйства
4) возникла в ХХ веке в развитых странах. +
20. Целью участия государства в рыночных отношениях является
1) получение большей прибыли
2) смягчение негативных последствий действия рыночного механизма+
3) обогащение властной элиты
4) усиление контроля над обществом
21. Об уровне экономики любой страны судят
1) по количеству фабрик и заводов
2) по запасам минерального сырья
3) по производству продуктов питания
4) во валовому внутреннему продукту+
22. Организация производства – это
1) покупка орудий труда
2) закупка сырья
3) найм рабочей силы
4) приведение в соответствие человеческого и вещественного факторов производства. +
23. Производительность труда – это
1) скорость выполнения работы
2) качество произведенной продукции
3) количество продукции в единицу времени +
4) уровень развития технологии.
24. Плата за использование земли называется
1) предпринимательский доход
2) цена земли
3) рента +
4) прибыль
25. Основным показателем эффективности производства на данном предприятии является
1) доход его акционеров
2) заработная плата рабочих
3) величина налогов, отчисляемых государству
4) прибыль +
26. Степень эффективности использования собственных ресурсов предприятия показывает
1) прибыль
2) рентабельность +
3) дивиденды
4) бухгалтерский учет
27. В процессе производства между людьми скидываются отношения
1) деловые
2) доверительные
3) рабочие
4) производственные +
28. Акция – это ценная бумага
1) на которую выплачивается часть прибыли +
2) выдаваемая в качестве поощрения за доблестный труд
3) являющаяся одной из форм заработной платы
4) удостоверяющая личность владельца предприятия
29. Разновидностью смешанной формы собственности не является собственность
1) акционерного общества
2) совместного предприятия
3) кооператива
4) фермера +
30. В рыночной экономике продукт труда называется
1) простым продуктом
2) прибавочной стоимостью
3) товаром +
4) изделием
testdoc.ru

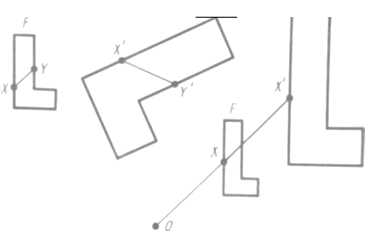
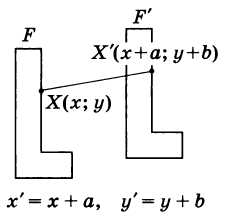



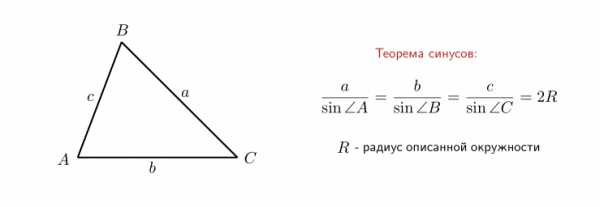

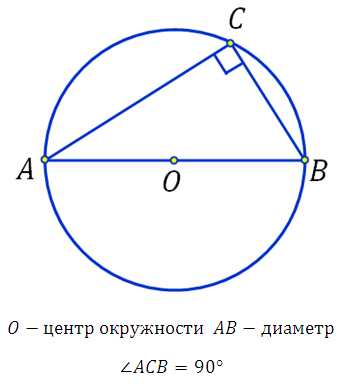
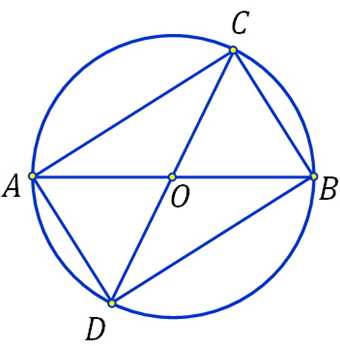 Получили четырёхугольник. Треугольник АОD равен треугольнику СОВ по двум сторонам и углу между ними:
Получили четырёхугольник. Треугольник АОD равен треугольнику СОВ по двум сторонам и углу между ними:


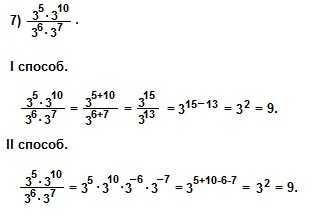 При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .

