Свойства пределов функции. Вычисление пределов. — КиберПедия
Свойства пределов функции
1) Предел постоянной величины
Предел постоянной величины равен самой постоянной величине:
2) Предел суммы
Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций.
Расширенное свойство предела суммы:
Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций.
3) Предел произведения функции на постоянную величину
Постоянный коэффициэнт можно выносить за знак предела:
4) Предел произведения
Предел произведения двух функций равен произведению пределов этих функций:
Расширенное свойство предела произведения
Предел произведения нескольких функций равен произведению пределов этих функций:
5) Предел частного
Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ НА ОСНОВЕ ОПРЕДЕЛЕНИЯ ПРЕДЕЛА
Пример 1. Докажем, что
Пусть задано произвольное e>0. Тогда для того чтобы выполнялось неравенство
|f(x)-a|<e, необходимо выполнение неравенства |x-a|<e, которое, очевидно, выполняется, если |x-a|<d, где d=e. Таким образом, согласно определению предела функции, число a, действительно, является пределом функции x при x стремящемся к a.
Пример 2. Докажем, что
Нужно доказать, что при произвольном e>0 найдется такое положительное d, что неравенство
будет выполняться, если |x-1|<d. Но, если x не равно 1, то (1) эквивалентно неравенству
или
При произвольном e неравенство (1) будет выполняться, если будет справедливо (2), а последнее справедливо, если |x-1|<d, где d=e. Поэтому в соответствии с определением предела функции данная функция при x стремящемся к 1 имеет пределом число 2.
Определение числового ряда.
Сумма числового ряда определяется как предел, к которому стремятся суммы первых nслагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится. Элементы ряда представляют собой либо вещественные, либо комплексные числа.
Определение
Пусть — числовой ряд. Число называется -ой частичной суммойряда .
Сумма (числового) ряда — это предел частичных сумм , если он существует и конечен. Таким образом, если существует число , то в этом случае пишут . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то говорят, что ряд расходится.
Сходимость числовых рядов
Свойство 1. Если ряд
(1.1)
сходится и его сумма равна S, то ряд
(1.2)
где c — произвольное число, также сходится и его сумма равна cS. Если же ряд (1.1) расходится и с ≠ 0, то ряд расходится.
Свойство 2. Если сходится ряд (1.1) и сходится ряд
,
а их суммы равны и соответственно, то сходятся и ряды
,
причём сумма каждого равна соответственно .
Необходимый признак сходимости ряда
Ряд может сходиться лишь в том случае, когда член (общий член ряда) стремится к нулю:
Это необходимый признак сходимости ряда (но не достаточный!). Если же общий член ряда не стремится к нулю — это достаточный признак расходимости.
cyberpedia.su
Свойства пределов функций
Разделы: Математика
Цели урока:
— научиться решать основные типы пределов
функций, раскрывать неопределённости;
— совершенствование мыслительных умений
учащихся сравнивать, анализировать и обобщать;
— формирование образовательных,
коммуникативных и информационных
компетентностей для продолжения
математического образования в вузах;
— формирование навыков самостоятельной работы,
чувства ответственности, познавательного
интереса к обучению.
Задачи урока:
— изучить свойства пределов функций;
— отработать навыки применения данных знаний
при решении примеров различной сложности,
раскрытия неопределённостей;
— отработать навыки самостоятельной работы;
— отработать навыки тестирования в режиме online;
— способствовать развитию алгоритмического
мышления учащихся;
— воспитывать уважение к интеллектуальному
труду.
Тип урока: урок изучения и первичного
закрепления новых знаний.
Оборудование: персональные ПК (подключены к
сети Интернет), МП, раздаточный материал.
Учебник: Алгебра и начала математического
анализа. 11 класс: учебник для
общеобразовательных учреждений: базовый и
профильный уровни / [С.М.Никольский, М.К.Потапов,
Н.Н.Решетников, А.В.Шевкин]. — 10-е изд. –
М.:Просвещение, 2011. -464 с.: ил. – (МГУ – школе).
Эпиграф:
“В математике следует помнить не
формулы, а процессы мышления”.
В. П. Ермаков
Ход урока
1. Оргмомент. Постановка цели урока.
2. Актуализация знаний. Подготовка к ЕГЭ.
Тестирование on-line на сервисе проверки знаний
учащихся http://www.diagtest.ru/ по теме “Основы
тригонометрии”. Итог тестирования (Приложение
1).
3. Изучение нового материала.
Мотивирование. На первом курсе университета
студенты часто сталкиваются с вопросом как
решить предел функции? Решение пределов — это
довольно трудный этап математического обучения
который сразу встает перед Вами высокой и
непробиваемой стеной, поскольку первокурсники
еще не научились как следует преодолевать
сложные теории. А теория пределов — это серьезная
и сложная теория, без четкого понимания которой
нельзя полноценно научиться решать задачи по
вычислению пределов.
Лекция учителя и первичное закрепление новых
знаний. (Приложение 2 – МП, Приложение 3 – раздаточный материал).
а) Свойства пределов:
Закрепление. Устно № 2.15 а), б). (с. 59)
б) Для решения пределов вспомним первый и
второй замечательные пределы:
Закрепление. Доказательство (фронтально, с
помощью учителя) № 2.16. а), б). (с.59)
Решение (использование подсказки – слайд № 6 ):
— самостоятельно: 1 вариант — № 2.17г), 2 вариант №
2.17и),
— у доски: 2.18 в) с. 59.
Рекомендация: если в пределе (практически
любого типа) можно вынести число за скобку, то
всегда это делаем.
в) раскрытие неопределённостей:
Неопреде-
лённость |
Алгебраические
преобразования |
|
В числителе и знаменателе
сложные степенные или показательные функции. Для
степенных функций – вынести за скобку в
числителе и знаменателе х с наибольшим
показателем степени;
для показательных функций – вынести за
скобку в числителе и знаменателе наиболее быстро
возрастающее слагаемое.
После сокращения дроби неопределённость
устраняется.
Пример №1.
.
Старшая степень числителя и знаменателя равна
2.
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если
она есть.
Во-вторых, желательно прервать решение для
промежуточных объяснений. Можно использовать
знак (*), он не несет никакого математического
смысла, а обозначает, что решение прервано для
промежуточного объяснения.
В-третьих, в пределе желательно помечать, что и
куда стремится. Когда работа оформляется от руки,
удобнее это сделать так:
Для пометок лучше использовать простой карандаш.
Закрепление.
Пример №2.
|
|
Если в числителе и знаменателе
находятся многочлены, и имеется
неопределенности вида , то для ее раскрытия нужно
разложить числитель и знаменатель на множители,
затем сократить и вычислить предел. Для этого
чаще всего нужно решить квадратное уравнение и
(или) использовать формулы сокращенного
умножения. В тригонометрических выражениях
необходимо упростить выражение, чтобы привести к
первому замечательному пределу. Пример №3. , разложив
квадратный трёхчлен на множители и сократив,
получим
Рекомендация: если в пределе (практически
любого типа) можно вынести число за скобку, то
всегда это делаем.
Пример №4.
|
|
Если функция представляет собой
алгебраическую сумму дробей, то
неопределённость устраняется или приводится к
типу
после приведения дробей к общему знаменателю.
Если функция представляет собой алгебраическую
сумму иррациональных выражений (корней), то
неопределённость устраняется или приводится к
типу
путём домножения и деления функции на одно и то
же (сопряжённое) выражение, приводящее к
формулам сокращённого умножения. |
|
xn--i1abbnckbmcl9fb.xn--p1ai
Предел функции в точке. Свойства предела — Мегаобучалка
По Гейне:
Число А называется пределом функции f(x) в точке x0, если для любой последовательность значений аргумента ({xn}→x0) соответствующая последовательность значений функции f(x) стремится к числу А.
По Коши:
Число А называется пределом функции f(x) в точке x0 если для любого e>0, найдется такое число d>0, что при всех x из условия будет выполняться неравенство (значение функции попадает в d окрестность точки А)
Свойства пределов.
1)Если функция имеет предел, то только один.
2) lim C=C, где С – постоянная величина
3) предел произведения равен произведению пределов
4) константы можно выносить за знак предела
5)
Предел функции на бесконечности. Бесконечно большие и бесконечно малые функции, их свойства.
Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю.
Пусть задана числовая функция с неограниченной сверху областью определения, то есть и Число называется пределом функции f при x стремящемся к бесконечности, если
Пишут:
Бесконечно большие функции.
Ранее мы рассмотрели случаи, когда функция f(x) стремилась к некоторому конечному пределу b при x → a или x → ∞.
Рассмотрим теперь случай, когда функция y=f(x) стремится к бесконечности при некотором способе изменения аргумента.
Функция f(x) стремится к бесконечности при x → a, т.е. является бесконечно большой величиной, если для любого числа М, как бы велико оно ни было, можно найти такое δ > 0, что для всех значений х≠a, удовлетворяющих условию |x-a| < δ, имеет место неравенство |f(x)| > M.
Если f(x) стремится к бесконечности при x→a, то пишут или f(x)→∞ при x→a.
Если f(x) стремится к бесконечности при x→a и при этом принимает только положительные или только отрицательные значения, соответственно пишут или .
Бесконечно малые функции.
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.
Свойства.
1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.
2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.
3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.
Соотношение между бесконечно большими и бесконечно малыми функциями.
Теорема Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a. Две функции называются эквивалентными, если . Если , то бесконечно малая f(x) есть функция большего порядка малости.
megaobuchalka.ru
Свойства предела функции
существует предела функции f в точке a.
Пример 2.15. Показать, что функция sin x не имеет предела при стремлении x к +∞ (или к −∞).
Для последовательности {xn} : xn =π2 + nπ, n N, sin xn = (−1)n, и потому последовательность {sin xn} не имеет предела.
Теорема 2.32. Пустьf : X R → R,a — предельная точка
множества X, Ua — некоторая окрестность точки а,ϕ = f U◦ a∩X . Для того чтобы функцияf имела в точкеa предел, необходимо и
достаточно, чтобы функция ϕ имела предел в точкеa. В случае
существования предела lim f = lim ϕ.
a a
Утверждение сразу следует из определения предела функции.
Теорема 2.33. Функция не может иметь в точке двух различных пределов.
Предположим, что функция f : X → R имеет в точке a два предела
lim f = A | , lim f = A | , A | = A | . По теореме Гейне для любой фиксиро- |
a | 1 | a | 2 | | 1 6 2 | |
ванной последовательности {xn} : xn X \{a}, n N, xn → a получим,
что lim f(xn) = A1, | lim f(xn) = A2, чего быть не может. |
n→∞ | n→∞ |
Определение 2.25. Функцияf : X → R называется локально
ограниченной в точке a (a — предельная точкаX), если существует
◦
такая окрестность Ua точкиa, что множество{f(x) | x Ua ∩X} ограничено. Учитывая определение ограниченного числового множества, заключаем, что локальная ограниченность функцииf в точкеa означает:
◦ \
Ua M > 0 : |f(x)| ≤ M , x Ua X
Теорема 2.34. Если функцияf имеет в точкеa конечный предел, то она локально ограничена в точкеa.
| | Пусть lim f = A, A | | R | . По определению 2.22 предела функции |
| a | | | ◦ | T | |
| найдется такая окрестность Ua точки a, что в каждой точке x | | X |
| ◦ |
| | Ua | |
выполняется неравенство |f(x) − A| < 1. Следовательно, для x Ua T X
|f(x)| ≤ |f(x) − A| + |A| < 1 + |A|,
что означает локальную ограниченность функции f в точке a.
studfiles.net
1. Последовательность называется постоянной, если все её члены равны постоянному числу , т. е. , при всех . Предел постоянной последовательности равен постоянному числу , т. е. если , то .
2. Если , то , где – бесконечно малая последовательность.
3. Если последовательность имеет предел, то она ограничена, т. е. если , то , где – некоторое положительное число.
4. Если последовательность имеет предел, то он один.
5. Предел суммы двух последовательностей равен сумму их пределов, если предел каждого слагаемого существует, т. е.
,
Если пределы справа существуют.
Следствие. Предел суммы конечного числа последовательностей, имеющих предел, равен сумме их пределов.
6. Предел произведения двух сходящихся последовательностей равен произведению их пределов, т. е.
,
Если пределы справа существуют.
Следствие 1. Постоянный множитель можно выносить за знак предела, т. е.
.
Следствие 2. Предел произведения конечного числа сходящихся последовательностей равен произведению пределов сомножителей.
Следствие 3. Предел степени последовательности, имеющей предел, равен степени предела последовательности, т. е.
,
Если существует и – конечное число.
Следствие 4. Предел корня из сходящейся последовательности равен корню той же степени из предела последовательности, т. е.
,
Если предел справа существует (предполагается также, что корни слева и справа существуют, т. е. если корни являются корнями четной степени, то подкоренные выражения неотрицательны).
7. Предел частного двух сходящихся последовательностей равен частному их пределов, если предел делителя не равен нулю, т. е.
,
Если пределы справа существуют и .
В тех случаях, когда пределы отдельных последовательностей, над которыми производятся действия, не существуют, то это еще не означает, что не существует общий предел (предел результата действий). Последний может существовать, только он не может быть найден с помощью указанных свойств пределов; его следует находить в каждом отдельном случае особыми приемами.
То же самое можно сказать и о пределе частного, когда пределы делимого и делителя равны нулю.
Рассмотрим примеры на нахождение пределов последовательностей.
Пример 7. Дана последовательность . Доказать, что .
Доказательство. Пусть задано . Найдём разность
.
По определению предела должно выполняться неравенство
,
Откуда
.
Следовательно, , если . Поэтому .
Находить пределы последовательностей, пользуясь непосредственно определением предела, нецелесообразно. Рассмотренный предел можно найти, применяя свойства пределов:
.
Обычно все промежуточные выкладки опускают, и решение выглядит так:
.
Пример 8. Найти предел .
Решение. Рассмотрим отдельно три случая:
.
а) Пусть ; тогда
.
б) Пусть ; тогда
.
в) Пусть ; тогда
.
Ответ:
Пример 9. Найти предел .
Решение. Вынося старшие степени числителя и знаменателя за скобки, имеем:
.
Пример 10. Найти предел .
Решение. Применить непосредственно свойства пределов здесь нельзя. Чтобы найти данный предел, умножим и разделим выражение, стоящее под знаком предела, на сопряженное ему, тогда
(второй предел равен нулю).
Следовательно, числитель есть общий член бесконечно малой последовательности. Так как знаменатель – общий член бесконечно большой последовательности, то последовательность бесконечно мала, а ее предел равен нулю.
Ответ: .
Пример 11. Найти предел .
Решение. Частное от деления ограниченной последовательности на бесконечно большую есть бесконечно малая последовательность (свойство 6 бесконечно малых последовательностей). Поэтому предел равен нулю.
Ответ: .
Иногда при нахождении пределов формальные преобразования не достигают цели и нужно рассмотрение по существу. Например, при изучении выражений, содержащих , при , надо иметь в виду, что при значение при , а при значение неограниченно растет.
Пример 12. Найти .
Решение. Рассмотрим отдельно три случая:
.
а) Пусть ; тогда
.
б) Пусть ; тогда
.
в) Пусть ; тогда
.
Ответ:
matica.org.ua
свойства пределов — ПриМат
Будем рассматривать функции $f: X \to \mathbb R$, где $X \subset \mathbb R.$Окрестностью радиуса $\delta > 0$ (или $\delta$-окрестностью) точки $a \in \mathbb R$ мы называли множество таких $x ∈ \mathbb R$, что $a − \delta < x < a + \delta$, или, что то же самое, $\left | x − a \right | < \delta.$ Проколотой $\delta$-окрестностью точки $a$ называем $\delta$-окрестность точки $a \in \mathbb R$, из которой удалена сама точка $a$. Другими словами, проколотая $\delta$-окрестность точки $a$ – это множество всех точек $x \in \mathbb R$, таких, что $a−\delta < x < a$ или $a < x < a + \delta$. Это можно записать так: $0 < \left | x − a \right | < \delta$.
Определение предела функции по Коши. Пусть функция $f$ определена в некоторой проколотой окрестности точки $a$. Число $A$ называется пределом функции $f$ в точке $a$, если для любого $\varepsilon > 0$ найдется такое $\delta > 0$, зависящее, вообще говоря, от $\varepsilon$, что для всех $x$, удовлетворяющих условию $0 < \left | x − a \right | < \delta$, справедливо неравенство от $\left | f \left ( x \right ) − A \right | < \varepsilon$. Если число $A$ является пределом функции $x$ в точке $a$, то говорят, что функция $f$ стремится к $A$ при $x$, стремящемся к $a$, и пишут: $\lim \limits_{x \to a} f \left ( x \right ) = A$, или $f \left (x \right ) \to A$ при $x \to a$.
Пример 1.
Пусть $f \left ( x \right ) = x \cdot \sin \frac{1}{x}, x\neq 0, a = 0.$
Данная функция определена в проколотой окрестности точки $a = 0.$ Покажем, что: $\lim \limits_{x \to 0} f \left (x \right ) = 0$. Зададим $\varepsilon > 0.$ Тогда для $x\neq 0$ неравенство $$\left | f \left (x \right ) — 0 \right | = \left | x \cdot \sin \frac{1}{x} \right |\leqslant \left | x \right | \leqslant \varepsilon$$ справедливо, если только $0 < \left | x − 0 \right | = \left | x \right | < \delta$, где в качестве $\delta$ мы выбираем $\varepsilon$, т.е. $\delta = \varepsilon.$ Так как $\varepsilon > 0$ произвольно, то для любого $\varepsilon > 0$ найдется такое $\delta \left ( \delta = \varepsilon \right )$, что для всех $x$, удовлетворяющих условию $0 < \left | x − 0 \right | < \delta$, справедливо неравенство $\displaystyle \left | x \cdot \sin \frac{1}{x} — 0 \right | < \varepsilon$. По определению, это и означает, что $\displaystyle \lim \limits_{x \to 0} x \cdot \sin \frac{1}{x} = 0$.
Пример 2.
Пусть $f \left (x \right) = \operatorname {sgn} x = \left\{\begin{matrix}
1, x > 0, & \\
0, x = 0, & \\
-1, x < 0. &
\end{matrix}\right.$
Покажем, что функция $f$ не имеет предела в точке $a = 0$, т.е. для любого $A ∈ \mathbb R$ найдется такое $\varepsilon_{0} > 0$, что для каждого $\delta > 0$, найдется такое $x$, удовлетворяющее условию $0 < \left | x − 0 \right | < \delta$, при котором $\left | f \left (x \right ) − A \right | \leqslant \varepsilon_{0}.$
Пусть $A \in \mathbb R$. Покажем, что $\varepsilon_{0} = 1$ обладает требуемым свойством. В самом деле, зададим произвольное $\delta > 0$. Если $A \leqslant 0$, то выберем такое $x$, что $−\delta < x < 0$, например, $\displaystyle x = \frac{−\delta}{2}$. Тогда $0 < \left | x − 0 \right | < \delta$, и $\left | f \left (x \right ) − A \right | = \left | − 1 − A \right | = 1 + A \leqslant 1 = \varepsilon_{0}$. Если же $A < 0$, то выберем такое $x$, что $0 < x < \delta$, например, $\displaystyle x = \frac{δ}{2}$. Тогда снова получим, что $0< \left | x − 0 \right | < δ$, и $\left | f \left( x \right) − A \right | = \left | 1 − A \right | = 1 − A \leqslant 1 = \varepsilon_{0}$. Итак, никакое $A ∈ \mathbb R$ не является пределом функции $f \left (x \right ) = \operatorname {sign} x $ в точке $a = 0$.
Пример 3.
Пусть $f \left ( x \right ) = |\operatorname {sign} x |= \left\{\begin{matrix}
1, x\neq 0, & \\
0, x = 0. &
\end{matrix}\right.$
Покажем, что $\lim \limits_{x \to 0} f \left ( x \right ) = 1$.
Действительно, зададим $\varepsilon > 0$ и в качестве $\delta$ выберем любое положительное число, например, $\delta = 1$. Тогда из неравенства $0 < \left | x − 0 \right | = \left | x \right | < \delta$ вытекает $\left |f \left ( x \right) − 1 \right | = \left |1 − 1 \right | = 0 < \varepsilon$. Следует обратить внимание на то, что неравенство $\left | f \left( x \right) − 1 \right | < \varepsilon$ может и не выполняться при $x = 0$ (оно действительно не выполняется, если $\varepsilon \leqslant 1$. Но мы и не требуем, чтобы оно выполнялось при $x = 0$, т.к. рассматриваются лишь такие значения $x$, для которых $\left | x \right | > 0$.
Пример 4.
Докажем, что $\displaystyle \lim \limits_{x \to 1} \frac{x^{2}-1}{x-1} = 2$.
В самом деле, если $x \neq 1$, то $\displaystyle \frac{x^{2}-1}{x-1} = x + 1$, и тогда $\left | f \left (x \right) – 2 \right | = \left | \left( x+1 \right ) – 2 \right | = \left | x-1 \right | < \varepsilon$, если только $0 < \left | x-1 \right | < \delta$, где $\delta = \varepsilon$.
Пример 5.
Докажем, что $\lim \limits_{x \to a} \sqrt{x} = \sqrt{a}$ при любом $a > 0$.
Зададим $\varepsilon > 0$.Тогда для $x > 0$ неравенство $\displaystyle |\sqrt{x} — \sqrt{a}|= \frac{|x — a|}{\sqrt{x} + \sqrt{a}} \leqslant \frac{1}{\sqrt{a}} < \varepsilon$ будет иметь место, если только $0 < |x — a| < \sqrt{a} \cdot \varepsilon = \delta$.
Теорема 1(единственность предела)
Если функция $f$ имеет предел в точке $a$, то он единственный.
Пусть $\lim \limits_{x \to a} f \left (x \right ) = A$ и $\lim \limits_{x \to a} f \left ( x \right ) = B$. Зададим $\varepsilon > 0$ и найдем $\delta _{1} > 0$, такое, что из неравенства $0 < \left |x − a \right | < \delta_{1}$ следует $\displaystyle \left |f \left ( x \right ) − A \right | < \frac{\varepsilon}{2}$. Далее, найдем $\delta_{2} > 0$, такое, что из неравенства $0 < \left |x−a \right | < \delta_{2}$ следует $\displaystyle \left |f \left ( x \right )−B \right | < \frac{\varepsilon}{2}$. Положим $\delta = min \left ( \delta_{1}, \delta_{2} \right)$ и выберем такое $x$, что $0 < \left |x − a \right | < \delta$. Тогда $\displaystyle \left |B − A \right | \leqslant \left | f \left ( x \right ) − A \right | + \left | f \left ( x \right ) − B \right | < \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon$.
Поскольку $\varepsilon > 0$ произвольное и $\left |B − A \right | < \varepsilon$, то это означает, что $A = B$.
Локальная ограниченность функции, имеющей предел.
Функция $f$ называется ограниченной сверху (снизу) на множестве $E$, если существует такое число $M(m)$, что для всех $x \in E$ справедливо неравенство $f \left( x \right) \leqslant M \left ( f \left (x \right ) \leqslant m \right )$. Функция $f$ называется ограниченной на множестве $E$, если она ограничена на этом множестве сверху и снизу.
Другое эквивалентное определение ограниченности функции можно дать, используя понятие модуля. Именно, функция $f$ называется ограниченной на множестве $E$, если существует такое число $A$, что для всех $x \in E$ справедливо неравенство $\left |f \left (x \right ) \right | \leqslant A$.
Доказательство равносильности этих двух определений ограниченности элементарно и мы его опускаем.
Выше мы установили, что сходящаяся последовательность ограничена. Рассмотрим аналогичный вопрос для функций. Именно, следует ли из существования предела функции ее ограниченность? Отрицательный ответ на этот вопрос дает, например, функция $\displaystyle f \left ( x \right) = \frac{1}{x}, 0 < x < +\infty$. Действительно, легко видеть, что функция $f$ неограничена на $\left ( 0, +\infty \right )$. В то же время $\displaystyle \lim \limits_{x \to 1} \frac{1}{x} = 1$. В самом деле, $\begin{vmatrix}
\frac{1}{x} – 1
\end{vmatrix} = \left |x − 1 \right | x \leqslant 2 \left| x − 1 \right | < \varepsilon,$ если только $\displaystyle \left |x − 1 \right | < \delta = min \left\{ \frac{1}{2}, \frac{\varepsilon}{2} \right\}.$ Тем не менее, справедлива.
Теорема 2
Пусть функция $f$ определена в проколотой окрестности $U$ точки $a$ и имеет предел в этой точке. Тогда существует такая проколотая окрестность $V \subset U$, на которой функция $f$ ограничена.
Пусть $\lim \limits_{x \to a}f \left (x \right) = A$. Зададим $\varepsilon = 1$ и найдем такое $\delta > 0$, что для всех $x \in U$, удовлетворяющих условию $0 < \left | x − a \right | < \delta$, справедливо неравенство $\left | f \left( x \right) − A \right | < 1$. Обозначим $V = U \cap {x : 0 < \left |x − a \right | < \delta}$. Тогда для всех $x ∈ V$ справедливо неравенство $\left | f(x) \right | \leqslant \left | f \left( x \right) − A \right | + \left |A \right | \leqslant \left |A \right | + 1$, которое и означает, что функция $f$ ограничена на $V$
Определение предела функции по Гейне.
Мы хотим связать определения предела функции и предела последовательности. Пусть функция $f$ определена в некоторой проколотой окрестности $U$ точки $a$. Возьмем произвольную последовательность аргументов $\begin{Bmatrix}
{x_{n}}
\end{Bmatrix}_{n=1}^{\infty}$, т.е. $x_{n} \in U \left( x_{n} \neq a, n = 1, 2, \cdots \right )$. Эта последовательность аргументов порождает последовательность значений функции $f$ в точках $x_{n}$, т.е. мы получаем последовательность $\begin{Bmatrix}
{f \left (x_{n} \right )}
\end{Bmatrix}_{n=1}^{\infty}$.
Определение. Пусть функция $f$ определена в проколотой окрестности $U$ точки $a$. Число $A$ называется пределом функции $f$ в точке $a,$ если каждая последовательность аргументов $\left\{f \left ( x_{n} \right ) \right\}$, стремящаяся к $a \left (т.е. x_{n} \in U, x_{n} \neq a, n = 1, 2, \cdots \right)$ порождает соответствующую последовательность значений функции $\begin{Bmatrix}
{f \left ( x_{n} \right )}
\end{Bmatrix}$, стремящуюся к $A$.
Итак, мы имеем два определения предела функции: по Коши и по Гейне. Покажем, что эти определения эквивалентны.
Эквивалентность двух определений предела функции в точке.
Пусть $\lim \limits_{x \to a} f \left (x \right) = A$ в смысле определения по Коши. Возьмем произвольную последовательность $\begin{Bmatrix}
{x_{n}}
\end{Bmatrix}, x_{n} \to a \left( n \to \infty \right), x_{n} \neq a$ и покажем, что $f \left( x_{n} \right) \to A \left( n \to \infty \right )$. Зададим $\varepsilon > 0$ и найдем $\delta > 0$, такое, что из неравенства $0 < \left |x − a \right | < \delta$ следует $\left |f \left ( x \right ) − A \right | < \varepsilon$. Пользуясь тем, что $x_{n} \to a \left ( n \to \infty \right )$, для найденного $\delta$ найдем номер $N$, такой, что при каждом $n \leqslant N$ справедливо неравенство $\left |x_{n} − a \right | < \delta$. Но тогда при каждом $n \leqslant N$ будет выполнено неравенство $|f \left( x_{n} \right ) − a| < \varepsilon$. Итак, для заданного $\varepsilon > 0$ найдется такой номер $N$, что для всех $n \leqslant N$ справедливо неравенство $|f \left( x_{n} \right ) − A| < \varepsilon$. Так как $\varepsilon > 0$ произвольно, то это означает, что $\lim \limits_{n \to \infty} f \left( x_{n} \right ) = A$.
Обратно, пусть число $A$ является пределом функции $f$ при $x \to a$ в смысле Гейне, т.е. для любой последовательности $\begin{Bmatrix}
{x_{n}}
\end{Bmatrix}\left ( x_{n} \to a, x_{n} \neq a \right )$ соответствующая последовательность значений функции $\begin{Bmatrix}
{f \left ( x_{n} \right )}
\end{Bmatrix}$ стремится к $A$. Предположим, что $A$ не является пределом функции $f$ в точке $a$ в смысле Коши. Это означает, что найдется такое $\varepsilon_{0} > 0$, что для любого $\delta > 0$ существует такое $x$, что $0 < \left |x − a \right | < \delta$, но $\left |f \left ( x \right ) − A \right | \leqslant \varepsilon_{0}$. Возьмем $\delta = 1$ и найдем такое $x_{1}$, что $0 < \left |x_{1} − a \right | < 1$ и $\left |f \left ( x_{1} \right ) − A \right | \leqslant \varepsilon_{0}$. Далее, для $ \displaystyle \delta = \frac{1}{2}$ найдем такое $x_{2}$, что $\displaystyle 0 < \left |x_{2} − a \right | < \frac{1}{2}$ и $\left | f \left( x_{2} \right) − A \right | \leqslant \varepsilon_{0}$. Полагая $\displaystyle \delta = \frac{1}{n}$, найдем такое $x_{n}$, что $\displaystyle 0 < \left | x_{n} − a \right | < \frac{1}{n}$ и $\left |f \left( x_{n} \right ) − A \right | \leqslant \varepsilon_{0}$. В результате получим последовательность $\begin{Bmatrix}
{x_{n}}
\end{Bmatrix}$. Из условия $\displaystyle \left|x_{n} − a \right| < \frac{1}{n}$ следует, что $x_{n} \to a \left (n \to \infty \right )$, а поскольку $\left |x_{n} − a \right| > 0$, то $x_{n} \neq a \left (n = 1, 2, \cdots \right)$. Кроме того, $\left |f(x_{n}) − A \right | \leqslant \varepsilon_{0}$. Это неравенство означает, что соответствующая последовательность значений функции $\left\{f \left (x_{n} \right ) \right\}$ не стремится к $A$. Окончательно, мы построили такую последовательность аргументов $\left\{x_{n}\right\}, x_{n} \to a, x_{n} \neq a$, что соответствующая последовательность значений функции $\left\{f \left( x_{n} \right ) \right\}$ не стремится к $A$. Это противоречит условию.
Итак, мы показали, что определения предела по Коши и по Гейне эквивалентны. Часто на практике определение предела по Гейне используется для доказательства того, что у функции нет предела в точке $a$. Именно, отрицание определения предела в смысле Гейне выглядит следующим образом. Число $A$ не является пределом функции $f$ в точке $a$, если существует последовательность аргументов $\begin{Bmatrix}
{x_{n}}
\end{Bmatrix} \left (x_{n} \to a, x_{n} \neq a \right )$, такая, что $f \left (x_{n} \right)$ не стремится к $A$.
Предположим, что найдется такая последовательность аргументов, что соответствующая последовательность значений функции $\begin{Bmatrix}
{f \left( x_{n} \right )}
\end{Bmatrix}$ расходится. Тогда ясно, что никакое число не является пределом функции $f$ в точке $a$, т. е. $f$ не имеет предела при $x \to a$. Итак, для того чтобы показать, что функция $f$ не имеет предела в точке $a$, достаточно построить последовательность $\begin{Bmatrix}
{x_{n}}
\end{Bmatrix} \left(x_{n} \to a, x_{n} \neq a \right)$, такую, что $\begin{Bmatrix}
{f \left (x_{n} \right)}
\end{Bmatrix}$ не имеет предела.
Упражнение.
Доказать, что справедливо и обратное утверждение. Именно, если функция $f$ не имеет предела в точке $a$, то существует такая последовательность $\left\{x_{n} \right\} \left( x_{n} \to a, x_{n} \neq a \right)$, что $\left\{f \left (x_{n} \right ) \right\}$ расходится.
Пример.
Пусть $\displaystyle f(x) = \sin \frac{1}{x} \left(x \neq 0 \right )$. Выберем две последовательности $\displaystyle {x}’_{k} = \frac{1}{2\pi k}$ и $\displaystyle {x}^{\prime\prime}_{k} = \frac{1}{2\pi \left(\frac{k+1}{4} \right)} \left(k = 1, 2,\cdots \right).$
Тогда ${x}’_{k} \to 0, {x}^{\prime\prime}_{k} \to 0 \left(k \to \infty \right)и f \left({x}’_{k} \right) = 0, f \left({x}^{\prime\prime}_{k} \right) = 1$. Составим последовательность аргументов ${x}’_{1}, {x}^{\prime\prime}_{1}, {x}’_{2}, {x}^{\prime\prime}_{2}, \cdots$. Тогда соответствующая им последовательность значений функции будет иметь вид $0, 1, 0, 1,…$ , которая, очевидно, расходится. Итак, мы построили стремящуюся к нулю последовательность отличных от нуля аргументов, такую, что соответствующая последовательность значений функции не имеет предела. Значит, на основании определения предела функции, функция $\displaystyle f \left(x \right) = sin \frac{1}{x}$ не имеет предела при $x \to 0$.
Идея решения этого примера часто используется и при решении других задач. Именно, для того чтобы показать, что функция $f$ не имеет предела при $x \to a$, достаточно построить две последовательности $\left\{{x}’_{n} \right\}$ и $\left\{{x}^{\prime\prime}_{n}\right\}$, стремящиеся к $a \left({x}’_{n} \neq a, {x}^{\prime\prime}_{n} \neq a \right)$, такие, что $\left\{f \left({x}’_{n} \right) \right\} $ и $\left\{f \left({x}^{\prime\prime}_{n} \right)\right\}$ аргументов ${x}’_{1}, {x}^{\prime\prime}_{1}, {x}’_{2}, {x}^{\prime\prime}_{2}, \cdots$ соответствующая последовательность значений функции $f \left({x}’_{1} \right), f \left( {x}^{\prime\prime}_{1} \right), f \left({x}’_{2} \right), f \left({x}^{\prime\prime}_{2} \right), \cdots$ будет расходящейся, так как у нее есть два различных частичных предела (не выполнено условие критерия сходимости в терминах верхнего и нижнего пределов последовательности).
Теорема (арифметические свойства пределов).
Пусть функции $f$ и $g$ заданы в проколотой окрестности $U$ точки $a$ $\lim \limits_{x \to a} f \left(x \right) = A$ и $\lim \limits_{x \to a} g \left( x \right) = B$. Тогда
1) $\lim{x \to a} \left( f \left(x \right) + g \left(x \right) \right) = A + B$;
2) $\lim{x \to a} \left(f \left(x \right) \cdot g \left(x \right) \right)= A \cdot B$;
3) если $ g \left(x \right) \neq 0 \left(x \in U \right)$ и $ B \neq 0, $ то $\displaystyle \lim \limits_{x \to a} \frac{f \left(x \right)}{g \left(x \right)} = \frac{A}{B}.$
Эта теорема мгновенно может быть получена как следствие соответствующей теоремы об арифметических свойствах пределов последовательностей. Достаточно применить определение предела в смысле Гейне.
Теорема (предельный переход и неравенства).
Пусть функции $f$ и $g$ заданы в проколотой окрестности $U$ точки $a$, $\lim \limits_{x \to a}f \left(x \right) = A$ и $\lim \limits_{x \to a}g \left(x \right) = B$, причем $B > A$. Тогда найдется проколотая окрестность $\Delta ⊂ U$ точки $a$, такая, что $f \left(x \right) < g \left(x \right)$ для всех $x ∈ \Delta$.
Зададим $\varepsilon = \frac{B-A}{2} > 0$ и найдем такое ${\delta}’ > 0$, что для всех $x$, удовлетворяющих условию $0 < \left|x − a \right| < {\delta}’$, справедливо неравенство $ \left|f(x) − A \right| < \varepsilon$, т. е. $A − \varepsilon < f \left(x \right) < A + \varepsilon$. Далее, найдем такое ${\delta}^{\prime\prime} > 0$, что если только $0 < \left|x − a \right| < {\delta}$ , то $ \left|g \left(x \right) − A \right| < \varepsilon$, т. е. $B − \varepsilon < g \left(x \right) < B + \varepsilon$. Положим $\delta = min \left({\delta}’, {\delta}^{\prime\prime} \right) > 0$. Тогда для всех $x$, удовлетворяющих условию $0 < \left|x − a \right| < \delta$, справедливы неравенства $\displaystyle f \left(x \right) < A + \varepsilon = \frac{A+B}{2} = B − \varepsilon < g \left(x \right)$, из которых следует, что $f \left(x \right) < g \left(x \right) \left( x \in \Delta = {x : 0 < \left |x − a \right| < \delta} \right)$
Следствие. Если $f \left(x \right) \leqslant g \left(x \right)$ для всех $x$, принадлежащих проколотой окрестности $U$ точки $a$, то $\lim \limits_{x \to a} f \left(x \right) \leqslant \lim \limits_{x \to a} g \left(x \right)$, если эти пределы существуют. Действительно, если предположить, что $\lim \limits_{x \to a} f \left(x \right) < \lim \limits_{x \to a} g \left(x \right)$, то, в силу предыдущей теоремы, в некоторой проколотой окрестности точки $a$ будет справедливо неравенство $f \left(x \right) < g \left(x \right)$, что противоречит условию.
Теорема (о трех пределах). Пусть функции $f, g, h$ определены в проколотой окрестности $U$ точки $a$ и такие, что $f \left(x \right) \leqslant g \left(x \right) \leqslant h \left(x \right)$ для всех $x \in U$. Если $\lim \limits_{x \to a} f \left(x \right) = \lim \limits_{x \to a} h \left(x \right) = A$, то существует $\lim \limits_{x \to a} g \left(x \right) = A$.
Для доказательства этой теоремы достаточно применить определение предела функции по Гейне и соответствующую теорему о трех пределах для последовательностей.
Примеры решения задач
Рассмотрим примеры задач, в которых могут использоваться предел функции и его элементарные свойства. Читателю с целью самопроверки предлагается решить данные примеры самому, а затем сверить свое решение с приведенным.
- Пользуясь определением предела функции по Гейне, доказать, что $f \left(x \right) = \cos x$ не имеет предела при $x \to \infty $.
РешениеВыберем две последовательности точек $\left \{ {x}’_{n} \right \}$, $ {x}’_{n} = \left \left( \frac{\pi}{2} + 2 \pi n \right \right), n \in \mathbb{N}$ и $\left \{ {x}^{\prime\prime}_{n} \right \}$, ${x}^{\prime\prime}_{n} = \left(2 \pi n \right), n \in \mathbb{N}.$ Обе эти последовательности стремятся к $+\infty$. Им соответствуют последовательности значений функций: $\left \{ f \left({x}’_{n} \right) \right \}$, $f \left({x}’_{n}) = \cos \left ( \frac{\pi}{2} + 2 \pi n \right ) = 0$ и $\left \{ f \left({x}^{\prime\prime}_{n} \right) \right \}$, $f \left({x}^{\prime\prime}_{n} \right) = \cos\left ( 2 \pi n \right ) = 1$. Последовательности значений функции $\left \{ f \left({x}’_{n} \right) \right \}$ и $\left \{ f \left({x}^{\prime\prime}_{n} \right) \right \}$ — стационарные, сходятся к числам $A = 0$ и $B = 1$ соответственно. Так как $A \neq B$, то ни число $A$, ни число $B$, ни какое-либо другое число не могут быть пределом функции $f \left(x \right)$ при $x \to +\infty$, т.е. функция $f \left( x \right)$ не имеет предела при $x \to +\infty$.
- Доказать, что $\lim \limits_{x \to a} f \left(x \right) = A$ (указать $\delta_{\varepsilon}$).$$\lim \limits_{x \to -1}\frac{7x^{2} + 8x + 1}{x + 1} = -6.$$
РешениеПоложим $f \left(x \right) = \frac{7x^{2} + 8x + 1}{x + 1} = -6.$ Надо показать, что для любого $\varepsilon > 0$ найдется такое положительное число $\delta$ , что для всех $\left|x — 1 \right| < \delta$ выполняется условие $\left|f \left(x \right) + 6 \right| < \varepsilon.$
Запишем этот модуль разности: $$\left |\frac{7x^{2} + 8x + 1}{x + 1} + 6 \right | < \varepsilon$$ $$\left |\frac{7x^{2} + 8x + 1}{x + 1} + 6 \right | = \left|7x + 1 + 6 \right| = 7 \left|x+1 \right| < \varepsilon,$$ $$\left|x + 1 \right| < \frac{\varepsilon}{7}.$$
Если выбрать $\delta = \frac{\varepsilon}{7}$ , то для любых $\left|x + 1 \right| < \delta$ искомое неравенство будет выполнено, что и означает, что $$ \displastyle\lim \limits_{x \to -1}\frac{7x^{2} + 8x + 1}{x + 1} = -6$$
- Пользуясь определением пределов функции по Коши и другими определениями предела функции в точке, показать, что $$\lim \limits_{x \to 2} \left(4x — 5 \right) = 3$$
РешениеНадо показать, что для любого $\varepsilon > 0$ существует такое $\delta = \delta_{\varepsilon} > 0$, что для всех $х$ (область определения функции $f\left(x \right) = 4x — 5$ – вся числовая ось), удовлетворяющих неравенству $0 < \left|x — 2 \right| <\delta$, будет выполняться неравенство $ \left|f \left(x \right) — 3 \right| < \varepsilon$. Последнее неравенство равносильно неравенствам: $\left|4x — 5 — 3 \right| < \varepsilon;$ $\left|4x- 8 \right| < \varepsilon;$ $4 \left|x-2 \right| < \varepsilon;$ $\left|x-2 \right| < \frac{\varepsilon}{4}.$
Принимая $\delta = \frac{\varepsilon}{4}$, получаем, что из неравенства $\left|x-2 \right| < \delta = \frac{\varepsilon}{4}$ следует неравенство $\left| \left(4x — 5 \right) — 3 \right| < \varepsilon$, следовательно, $\lim \limits_{x \to 2} \left(4x — 5 \right) = 3.$
Предел функции и его элементарные свойства
Лимит времени: 0
Информация
Пройдите этот тест, чтобы проверить свои знания по только что прочитанной теме
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 6
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат | |
| Ваш результат | |
Рубрики
- Нет рубрики
0%
- Математический анализ
0%
максимум из 6 баллов| Место | Имя | Записано | Баллы | Результат |
|---|
| Таблица загружается |
| Нет данных |
| | | | |
Ваш результат был записан в таблицу лидеров
- С ответом
- С отметкой о просмотре
Смотрите также
- Коляда В. И., Кореновский А. А. Курс лекций по математическому анализу, т.1. — Одесса: Астропринт, 2009, с. 53-60
- Кудрявцев Л.Д. Курс математического анализа, т.1. — М.: Дрофа; — 2003, с. 162-172, 177-184
- Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления Т.I. — М.: ФМЛ, 1962, с. 115-117
- Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа, 3-е изд., испр. — М.: 2001, с. 73-77
Поделиться ссылкой:
ib.mazurok.com
Свойства пределов функции
Поиск Лекций
1° Предел суммы/разности двух функций равен сумме/разности их пределов:
Пример
Задание. Вычислить предел
Решение. Воспользуемся первым свойство, разложим функцию на несколько более простых и отдельно найдем их пределы.
Ответ.
2° Предел произведения двух функций равен произведению их пределов:
Пример
Задание. Вычислить предел
Решение. Воспользуемся вторым свойство, разложим функцию на несколько более простых и отдельно найдем их пределы.
Ответ.
3° Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:
Пример
Задание. Вычислить предел
Решение. Воспользуемся третьим свойство, сделаем числитель и знаменатель функции отдельными пределами и независимо найдем их.
Ответ.
4° Константу можно выносить за знак предела:
Пример
Задание. Вычислить предел
Решение. Воспользуемся первым и четвертым свойствами, разложим функцию на несколько более простых и отдельно найдем их пределы.
Ответ.
5° Предел степени с натуральным показателем равен степени предела:
Пример
Задание. Вычислить предел
Решение. Воспользуемся пятым свойством, внесем предел под третью степень. Сначала найдем предел более простой функции, а затем возведем его в третью степень.
Ответ.
Первый замечательный предел:
Определение
Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю.
Применение первого замечательного предела на практике
Пример
Задание. Найти предел
Решение. Воспользуемся заменой и первым замечательным пределом.
Ответ.
Пример
Задание. Найти предел
Решение. Разложим тангенс на синус и косинус и воспользуемся свойствами пределов.
Ответ.
Второй замечательный предел:
здесь е — число Эйлера.
Пример
Задание. Найти предел
Решение. Подставим , получим неопределенность и для решения предела воспользуемся вторым замечательным пределом.
Ответ.
Следствия из второго замечательного предела
1°
2°
3°
4°
5°
6°
Понятие непрерывности функции в точке
Основные понятия и определения
Функция называется непрерывной в точке , если:
1. функция определена в точке и ее окрестности;
2. существует конечный предел функции в точке ;
3. это предел равен значению функции в точке , т.е.
Пример
Задание. Вычислить предел
Решение.
Ответ.
Приращение аргумента и функции
Рассмотрим функцию , которая определена в некотором интервале и рассмотрим произвольную точку из этого интервала: .
Определение
Приращением аргумента в точке называется разность
Замечание. Из последнего равенства легко увидеть, что .
Приращением функции в точке называется разность соответствующих значений функции или, используя равенство из выше приведенного замечания, будем иметь:
Теорема
Функция непрерывна в точке тогда и только тогда, когда бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции :
Теорема
Если функции и непрерывны в точке , то функции , , также непрерывны в точке .
Пусть функция задана на множестве , а — множество значений этой функции. Пусть на множестве задана функция . Тогда говорят, что на множестве задана композиция функций (или сложная функция) .
Теорема
Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда композиция функций непрерывна в точке .
Теорема
Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru




 Тестирование:
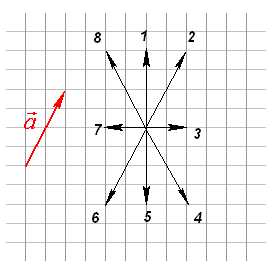
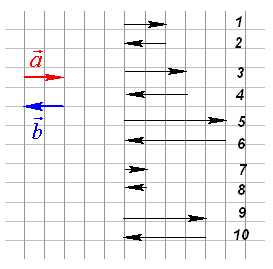
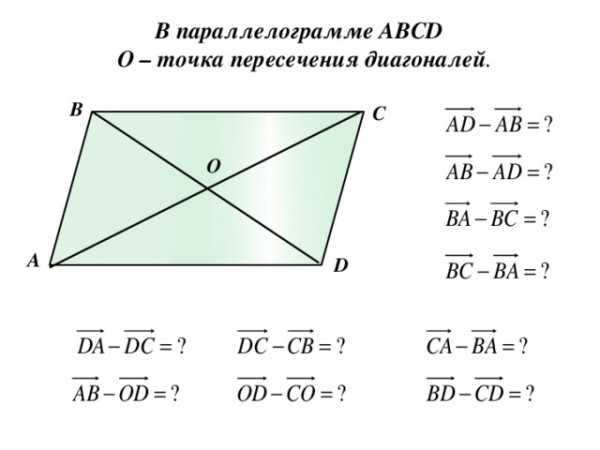
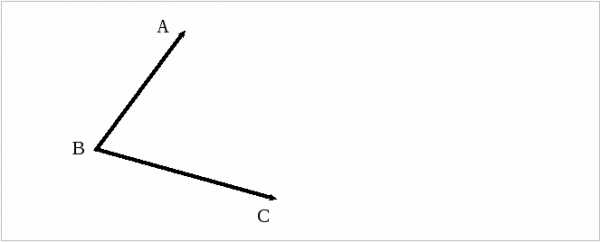
Тестирование: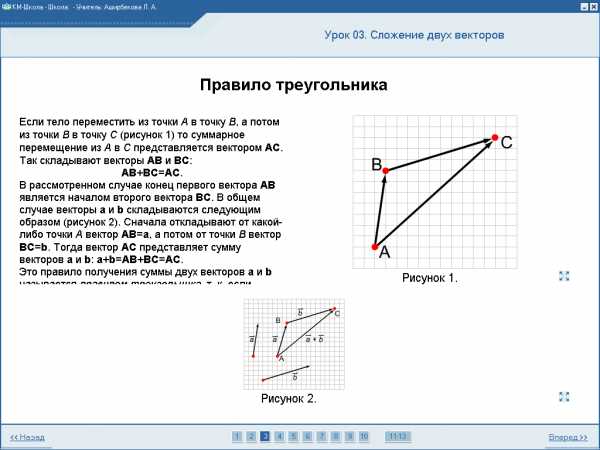 . Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?
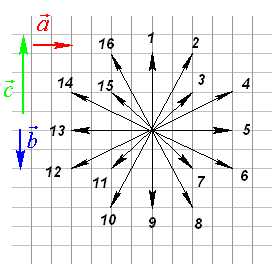
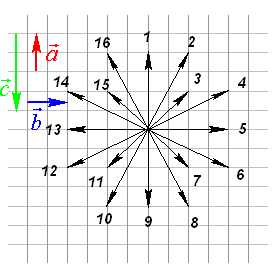
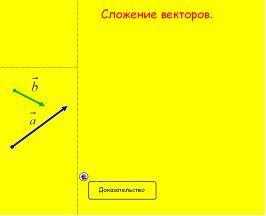
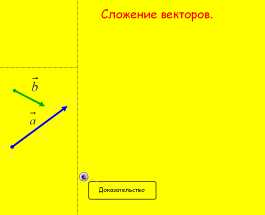
. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?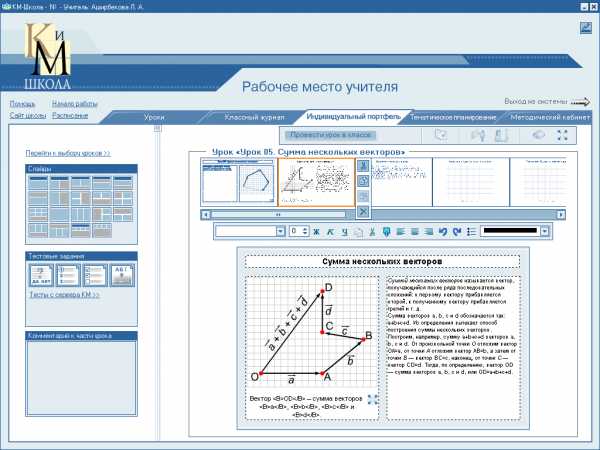 5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом…
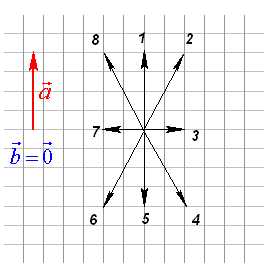
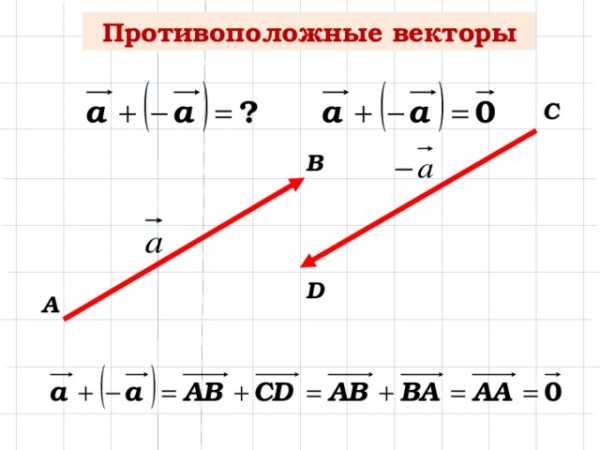
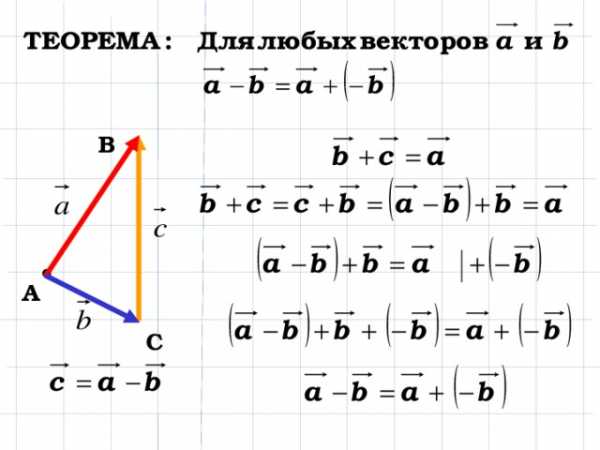
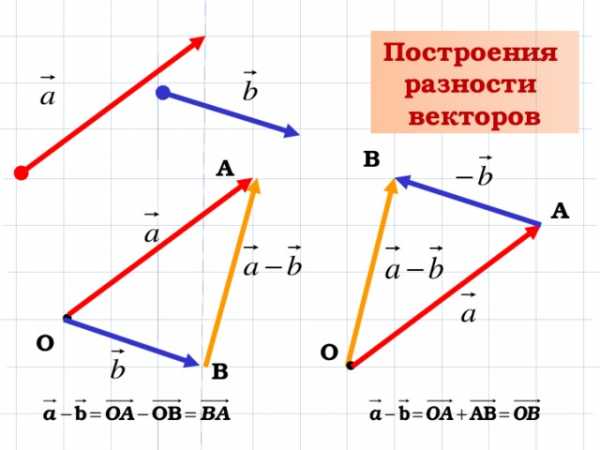
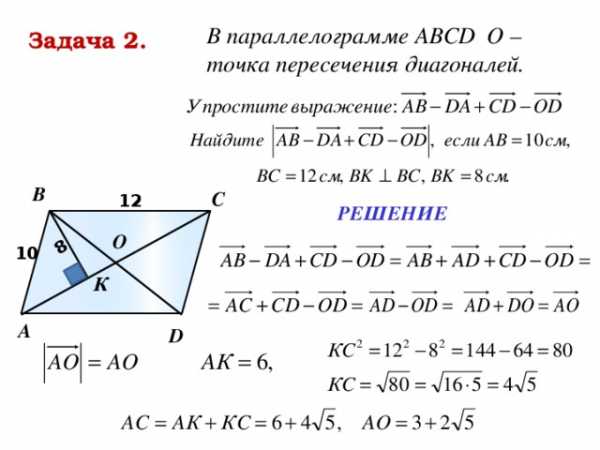
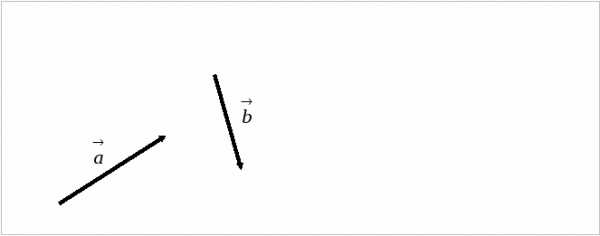
5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом… ычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку
ычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку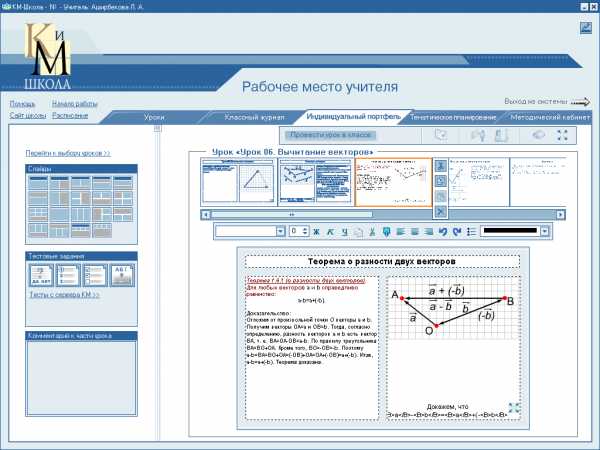

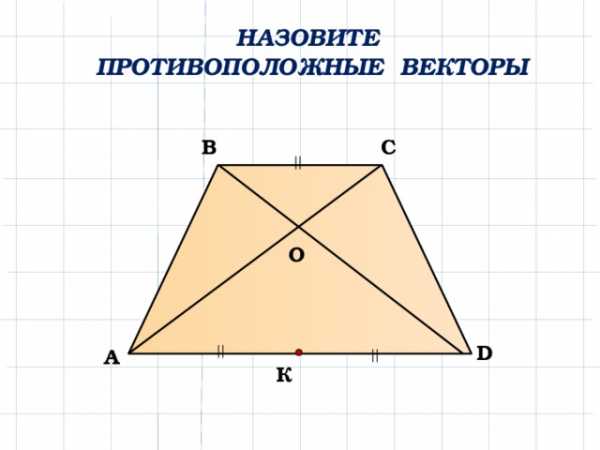
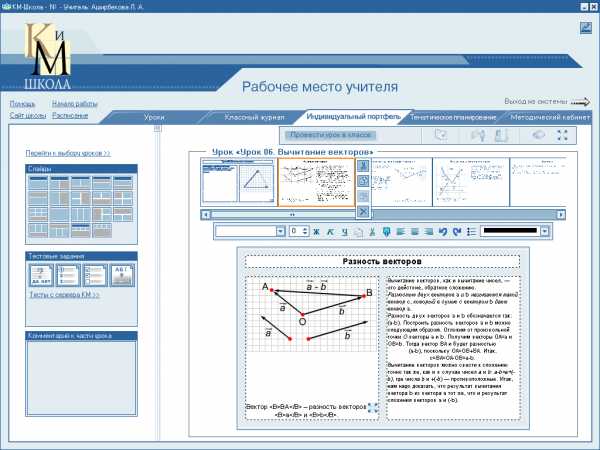 Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений
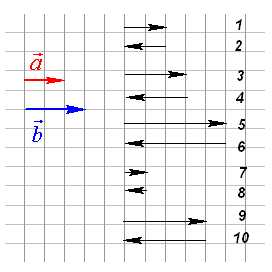
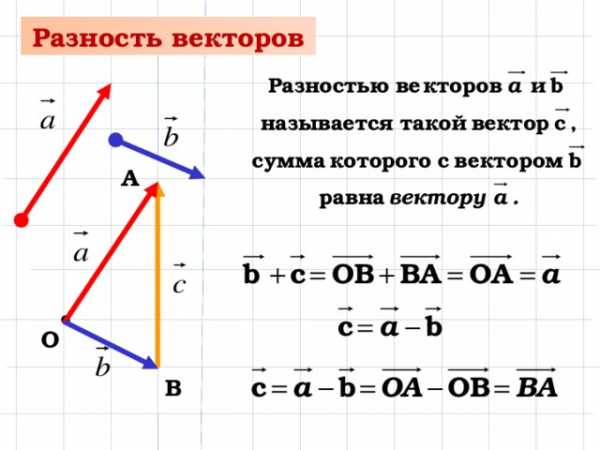
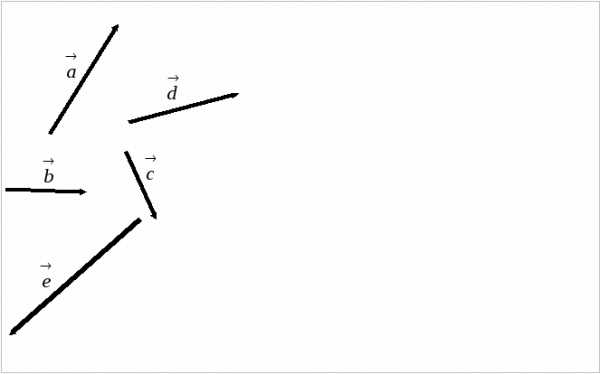
Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений . Какой вектор, изображенный на рисунке, является разностью векторов и ?
. Какой вектор, изображенный на рисунке, является разностью векторов и ?







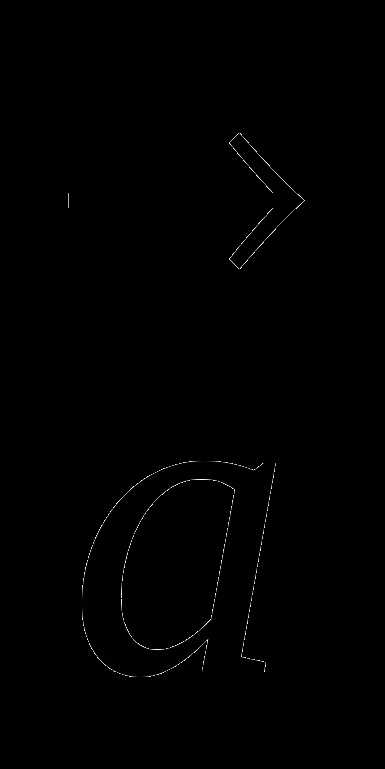 и
и 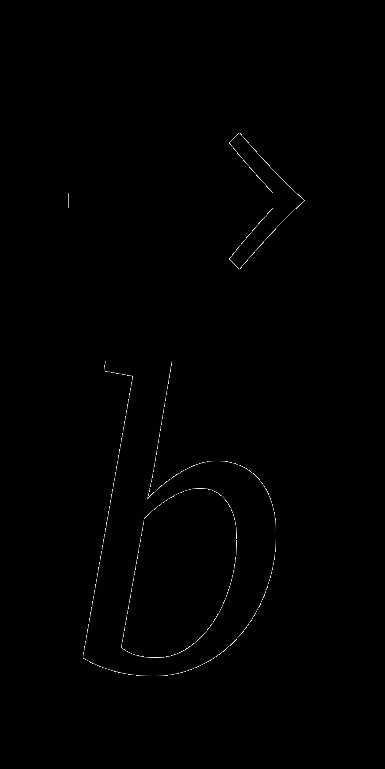 .
. и
и  .
.
 и
и  .
.
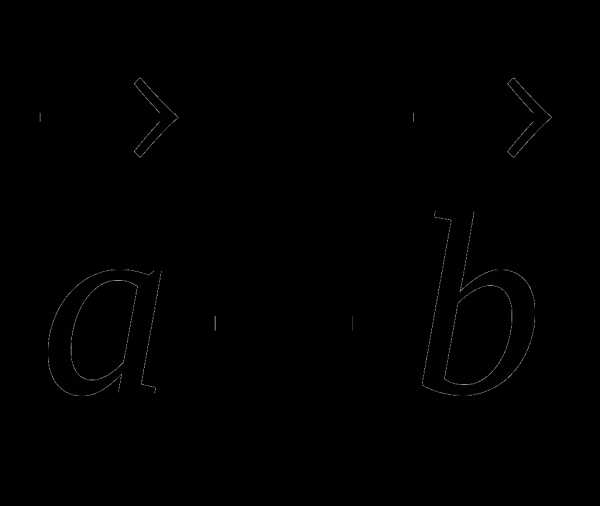 .
.















 Востребованность в наборе римских цифр в Word достаточно велика. Римские цифры применяют в рефератах и контрольных работах как по латинскому языку, так и по другим учебным предметам. Как набрать римские цифры в Word? Можно выделить два способа набора римских цифр в Word 2007.I.
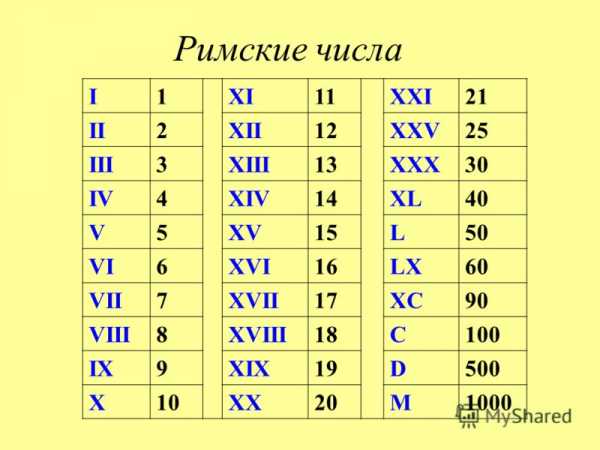
Востребованность в наборе римских цифр в Word достаточно велика. Римские цифры применяют в рефератах и контрольных работах как по латинскому языку, так и по другим учебным предметам. Как набрать римские цифры в Word? Можно выделить два способа набора римских цифр в Word 2007.I.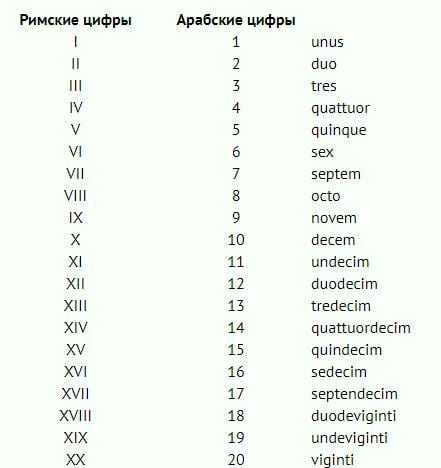 Римские цифры от 1 до 20
Римские цифры от 1 до 20 Таблица записи римских цифр
Таблица записи римских цифр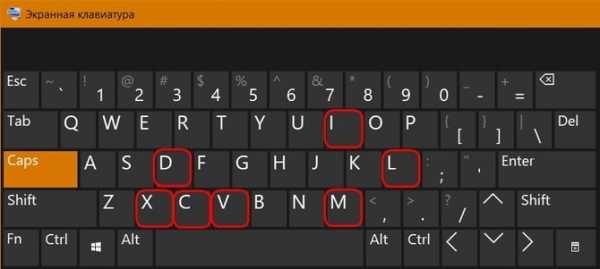 Основные римские цифры на клавиатуре
Основные римские цифры на клавиатуре