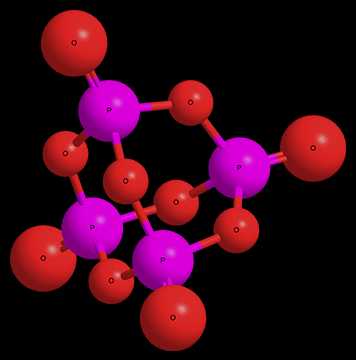
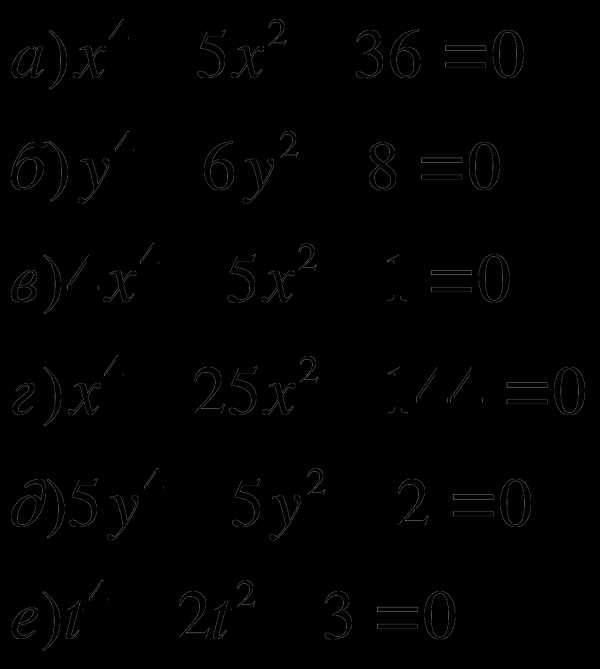Оксид фосфора (V) | справочник Пестициды.ru
Информация
Традиционно содержание Фосфора в удбрениях выражают содержанием Оксида фосфора.
Все свойства Фосфора, как питательного элемента описаны в статье Фосфор.
Подробнее >>>
Химические и физические свойства
Оксид фосфора – бесцветное аморфное или стекловидное вещество, существующеев трех кристаллических, двух аморфных и двух жидких формах.[1]
Токсичное вещество. Вызывает ожоги кожи и раздражение слизистой оболочки.
Пентаоксид фосфора очень гигроскопичен. Реагирует со спиртами эфирами, фенолами, кислотами и прочими веществами. В процессе реакции с органическими веществами происходит разрыв связей фосфора с кислородом, и образуются фосфорорганические соединения. Вступает в химические реакции с аммиаком (NH3) и галогеноводородами с образованием фосфатов аммония и оксигалогенидов фосфора. С основными оксидами образует фосфаты.[3]
Трехмерная модель молекулыТрехмерная модель молекулы
Содержание пентаоксида фосфора в почве и удобрениях
Фактически в почве имеются только соли ортофосфорной кислоты H3PO4, но в сложных удобрениях могут быть и соли мета-, пиро- и полифосфорных кислот.[4]
Основой для образования ортофосфорной кислоты является пентаоксида фосфора. Именно поэтому, а так же в связи с тем, что растения не поглощают элементарный фосфор, условлено обозначать концентрацию фосфора через содержание пентаоксида фосфора.[2]
P2O5 + 3H2O → 2H3PO4
Все встречающиеся в почве соли ортофосфорной кислоты и одновалентных катионов (NH4+, Na+, K+) и однозамещенные соли двухвалентных катионов (Ca(H2PO4)2 и Mg(H2PO4)2) растворимы в воде.
Двузамещенные соли двухвалентных катионов в воде не растворимы, но легко растворяются в слабокислых кислотах корневых выделений и органических кислотах жизнедеятельности микроорганизмов. В этой связи они так же являются хорошим источником P2O5 для растений.[4]
Поглощение пентаоксида фосфора растениями
Как указывалось выше, в природе основной источник фосфора – это соли ортофосфорнонй кислоты H3PO4. Однако после гидролиза пиро-, поли- и метафосфаты так же используются практически всеми культурами.
Гидролиз пирофосфата натрия:
Na4P2O7 + H2O + 2H+ → 2NaH2PO4 +2Na+
Гидролиз триполифосфата натрия:
Na5P3O10 + 2H2O + 2H+ → 3NaH2PO4 +2Na+
Гидролиз метафосфат иона (в кислой среде):
(PO3)66- + 3H2O → H2P3O103- + H2P2O72- + H2PO4—
Ортофосфорная кислота, будучи трехосновной отдиссоциирует три аниона H2PO—4, HPO42-, PO4 3- . В условиях слабокислой реакции среды, именно в них возделываются растения, наиболее распространен и доступен первый ион, в меньшей степени второй и практически недоступен третий. Однако люпин, гречиха, горчица, горох, донник, конопля и другие растения способны усваивать фосфор из трехзамещенных фосфатов.[4]
Некоторые растения приспособились усваивать фосфат-ион из фосфорорганических соединений (фитин, глицефосфаты и прочее). Корни данных растений выделяют особый фермент (фотофтазу), который и отщипляет анион фосфорной кислоты от органических соединений, а затем растения поглощают этот анион. К подобного рода растениям относятся горох, бобы, кукуруза. Причем фосфатазная активность возрастает в условиях фосфорного голода.
Многие растения могут питаться фосфором из очень разбавленных растворов, вплоть до 0,01 мг /л P2O5 . Естественно, что удовлетворить потребность в фосфоре растения могут только при условии постоянного возобновления в нем концентрации хотя бы такого же низкого уровня.
Опытным путем установлено, что поглощаемый корнями фосфор прежде всего идет на синтез нуклеотидов, а для дальнейшего продвижения в наземную часть фосфаты вновь поступают в проводящие сосуды корня в виде минеральных соединений.[4]
Рерасчет содержения фосфора в удобрениях
В некоторых случаях требуется рассчитать процентное содержание фосфора в удобрении, если дано содержание по P2O5. Расчет производится по формуле:
y = x,% × 30,974 (молярная масса P) × 2 / 30,974 (молярная масса P) × 2 + 15,999 (молярная масса O) × 5
где:
х – содержание P2O5 в удобрении, %;
y – содержание P в удобрении, %
Или:
y = x, % × 0,43643
Например:
в удобрении содержится 40% оксида фосфора
для пересчета процентного содержания элемента фосфор в удобрении нужно умножить массовую долю оксида в удобрении на массовую долю элемента в оксиде (для P2O5 – 0,43643): 40 * 0,43643 = 17,4572 %
Статья составлена с использованием следующих материалов:
Литературные источники:
1.Ван Везер «Фосфор и его соединения». Монография. т. 1.: Изд-во иностранной литературы, М., 1962.
2.Калинский А.А., Вильдфлуш И.Р., Ионас В.А. и др. – Агрохимия в вопросах и ответах – Мн.: Урожай,1991. – 240 с.: ил.
3.Химическая энциклопедия: в пяти томах: т.1: А-Дарзана/Редкол.: Кнунянц И.Л. (гл. ред.) и др. – М.: Советская энциклопедия, 1988. – 623.: ил
4.Ягодин Б.А., Жуков Ю.П., Кобзаренко В.И. Агрохимия / Под редакцией Б.А. Ягодина.– М.: Колос, 2002.– 584 с.: ил (Учебники и учебные пособия для студентов высших учебных заведений).
Свернуть Список всех источниковwww.pesticidy.ru
Химия фосфора и его соединений
1. Положение фосфора в периодической системе химических элементов
2. Строение атома фосфора
3. Физические свойства и нахождение в природе
4. Строение молекулы
5. Соединения фосфора
6. Способы получения
7. Химические свойства
7.1. Взаимодействие с простыми веществами
7.1.1. Взаимодействие с кислородом
7.1.2. Взаимодействие с галогенами
7.1.3. Взаимодействие с серой
7.1.4. Взаимодействие с металлами
7.1.5. Взаимодействие с активными металлами
7.1.6. Взаимодействие с водородом
7.2. Взаимодействие со сложными веществами
7.2.1. Взаимодействие с окислителями
7.2.2. Взаимодействие с щелочами
Фосфин
1. Строение молекулы и физические свойства
2. Способы получения
3. Химические свойства
3.1. Основные свойства
3.2. Взаимодействие с кислородом
3.3. Восстановительные свойства
Фосфиды
Способы получения фосфидов
Химические свойства фосфидов
Оксиды фосфора
1. Оксид фосфора (III)
2. Оксид фосфора (V)
Фосфорная кислота
1. Строение молекулы и физические свойства
2. Способы получения
3. Химические свойства
3.1. Диссоциация фосфорной кислоты
3.2. Кислотные свойства фосфорной кислоты
3.3. Взаимодействие с солями более слабых кислот
3.4. Разложение при нагревании
3.5. Взаимодействие с металлами
3.6. Качественная реакция на фосфат-ионы
Фосфористая кислота
Соли фосфорной кислоты
Фосфор
Положение в периодической системе химических элементов
Фосфор расположен в главной подгруппе V группы (или в 15 группе в современной форме ПСХЭ) и в третьем периоде периодической системы химических элементов Д.И. Менделеева.
Электронное строение фосфора
Электронная конфигурация фосфора в основном состоянии:
Атом фосфора содержит на внешнем энергетическом уровне 3 неспаренных электрона и одну неподеленную электронную пару в основном энергетическом состоянии. Следовательно, атом фосфора может образовывать 3 связи по обменному механизму. Однако, в отличие от азота, за счет вакантной 3d орбитали атом фосфора может переходить в возбужденное энергетическое состояние.
Электронная конфигурация фосфора в возбужденном состоянии:
При этом один электрон из неподеленной электронной пары на 3s-орбитали переходит на переходит на 3d-орбиталь. Для атома фосфора в возбужденном энергетическом состоянии характерна валентность V.
Таким образом, максимальная валентность фосфора в соединениях равна V (в отличие от азота). Также характерная валентность фосфора в соединениях — III.
Степени окисления атома фосфора – от -3 до +5. Характерные степени окисления -3, 0, +1, +3, +5.
Физические свойства и нахождение в природе
Фосфор образует различные простые вещества (аллотропные модификации).
Белый фосфор — это вещество состава P4. Мягкий, бесцветный, ядовитый, имеет характерный чесночный запах. Молекулярная кристаллическая решетка, а следовательно, невысокая температура плавления (44°С), высокая летучесть. Очень реакционноспособен, самовоспламеняется на воздухе.
Красный фосфор – это модификация с атомной кристаллической решеткой. Формула красного фосфора Pn, это полимер со сложной структурой. Твердое вещество без запаха, красно-бурого цвета, не ядовитое. Это гораздо более устойчивая модификация, чем белый фосфор. В темноте не светится. Образуется из белого фосфора при t=250-300оС без доступа воздуха.
Черный фосфор – то наиболее стабильная термодинамически и химически наименее активная форма элементарного фосфора. Чёрный фосфор — это чёрное вещество с металлическим блеском, жирное на ощупь и весьма похожее на графит, полностью нерастворимое в воде или органических растворителях.
Известны также такие модификации, как желтый фосфор и металлический фосфор. Желтый фосфор – это неочищенный белый фосфор. При очень высоком давлении фосфор переходит в новую модификацию – металлический фосфор, который очень хорошо проводит электрический ток.

В природе фосфор встречается только в виде соединений. В основном это апатиты (например, Ca3(PO4)2), фосфориты и др. Фосфор входит в состав важнейших биологических соединений —фосфолипидов.
Соединения фосфора
Типичные соединения фосфора:
| Степень окисления | Типичные соединения |
| +5 | оксид фосфора (V) P2O5 ортофосфорная кислота H3PO4 метафосфорная кислота HPO3 пирофосфорная кислота H4P2O7 фосфаты MePO4 Гидрофосфаты MeНРО4 Дигидрофосфаты MeН2РО4 Галогенангидриды: PОCl3, PCl5 |
| +3 | Оксид фосфора (III) P2O3 Фосфористая кислота H3PO3 Фосфиты MeHPO3 Галогенангидриды: PCl3 |
| +1 | Фосфорноватистая кислота H3PO2 Соли фосфорноватистой кислоты — гипофосфиты: MeH2PO2 |
| -3 | Фосфин PH3 Фосфиды металлов MeP |
Способы получения фосфора
1. Белый фосфор получают из природных фосфатов, прокаливая их с коксом и песком в электрической печи:
Ca3(PO4)2 + 3SiO2 + 5C → 3CaSiO3 + 5CO + 2P
2. Вместо фосфатов можно использовать другие неорганические соединения фосфора, например, метафосфорную кислоту.
4HPO3 + 10C → P4 + 2H2O + 10 CO
3. Красный и черный фосфор получают из белого фосфора.
Химические свойства фосфора
При нормальных условиях фосфор довольно химически активен.
1. Фосфор проявляет свойства окислителя (с элементами, которые расположены ниже и левее в Периодической системе) и свойства восстановителя (с элементами, расположенными выше и правее). Поэтому фосфор реагирует с металлами и неметаллами.
1.1. При взаимодействии с кислородом воздуха образуются оксиды – ангидриды соответствующих кислот:
4P + 3O2 → 2P2O3
4P + 5O2 → 2P2O5
1.2. При взаимодействии фосфора с галогенами образуются галогениды с общей формулой PHal3 и PHal5:
2P + 3Cl2 → 2PCl3
2P + 5Cl2 → 2PCl5
1.3. При взаимодействии фосфора с серой образуются сульфиды:
2P + 3S → P2S3
2P + 5S → P2S5
1.4. При взаимодействии с металлами фосфор проявляет свойства окислителя, продукты реакции называют фосфидами.
Например, кальций и магний реагируют с фосфором с образованием фосфидов кальция и магния:
2P + 3Ca → Ca3P2
2P + 3Mg → Mg3P2
Еще пример: натрий взаимодействует с фосфором с образованием фосфида натрия:
P + 3Na → Na3P
1.5. С водородом фосфор непосредственно не взаимодействует.
2. Со сложными веществами фосфор реагирует, проявляя окислительные и восстановительные свойства. Фосфор диспропорционирует при взаимодействии с некоторыми веществами.
2.1. При взаимодействии с окислителями фосфор окисляется до оксида фосфора (V) или до фосфорной кислоты.
Например, азотная кислота окисляет фосфор до фосфорной кислоты:
5HNO3 + P → H3PO4 + 5NO2↑ + H2O
5HNO3 + 3P + 2H2O → 3H3PO4 + 5NO↑
Серная кислота также окисляет фосфор:
2P + 3H2SO4 → 2H3PO4 + 3SO2
Соединения хлора, например, бертолетова соль, также окисляют фосфор:
6P + 5KClO3 → 3P2O5 + 5KCl
Некоторые металлы-сильные окислители также окисляют фосфор. Например, оксид серебра (I):
2P + 5Ag2O → P2O5 + 10Ag
2.2. При растворении в щелочах фосфор диспропорционирует до гипофосфита и фосфина.
Например, фосфор реагирует с гидроксидом калия:
4P + 3KOH + 3H2O → 3KH2PO2 + PH3↑ или
P4 + 3KOH + 3H2O → 3KH2PO2 + PH3↑
Или с гидроксидом кальция:
8P + 3Ca(OH)2 + 6H2O → 3Ca(H2PO2)2 + 2PH3↑
Фосфин
Строение молекулы и физические свойства
Фосфин PH3 – это бинарное соединение водорода с фосфором, относится к летучим водородным соединениям. Следовательно, фосфин газ, с неприятным запахом, бесцветный, мало растворимый в воде, химически нестойкий и ядовитый. Водородные связи между молекулами фосфина не образуются. В твердом состоянии имеет молекулярную кристаллическую решетку.
Геометрическая форма молекулы фосфина похожа на структуру аммиака — правильная треугольная пирамида. Но валентный угол H-P-H меньше, чем угол H-N-H в аммиаке и составляет 93,5о.
У атома фосфора в фосфине на внешнем энергетическом уровне остается неподеленная электронная пара. Эта электронная пара оказывает значительное влиение на свойства фосфина, а также на его структуру. Электронная структура фосфина — тетраэдр , с атомом фосфора в центре.
Способы получения фосфина
В лаборатории фосфин получают водным или кислотным гидролизом фосфидов – бинарных соединений фосфора и металлов.
Например, фосфин образуется при водном гидролизе фосфида кальция:
Ca3P2 + 6H2O → 3Са(ОН)2 + 2PH3
Или при кислотном гидролизе, например, фосфида магния в соляной кислоте:
Mg3P2 + 6HCl → 3MgCl2 + 2PH3↑
Еще один лабораторный способ получения фосфина – диспропорционирование фосфора в щелочах.
Например, фосфор реагирует с гидроксидом калия с образованием гипофосфита калия и фосфина:
4P + 3KOH + 3H2O → 3KH2PO2 + PH3↑
Химические свойства фосфина
1. В водном растворе фосфин проявляет очень слабые основные свойства (за счет неподеленной электронной пары). Принимая протон (ион H+), он превращается в ион фосфония. Основные свойства фосфина гораздо слабее основных свойств аммиака. Проявляются при взаимодействии с безводными кислотами.
Например, фосфин реагирует с йодоводородной кислотой:
PH3 + HI → PH4I
Соли фосфония неустойчивые, легко гидролизуются.
2. Фосфин PH3 – сильный восстановитель за счет фосфора в степени окисления -3. На воздухе самопроизвольно самовоспламеняетя:
2PH3 + 4O2 → P2O5 + 3H2O
PH3 + 2O2 → H3PO4
3. Как сильный восстановитель, фосфин легко окисляется под действием окислителей.
Например, азотная кислота окисляет фосфин. При этом фосфор переходит в сетпень окисления +5 и образует фосфорную кислоту.
PH3 + 8HNO3 → H3PO4 + 8NO2 + 4H2O
Серная кислота также окисляет фосфин:
PH3 + 3H2SO4 → H3PO4 + 3SO2 + 3H2O
С фосфином также реагируют другие соединения фосфора, с более высокими степенями окисления фосфора.
Например, хлорид фосфора (III) окисляет фосфин:
2PH3 + 2PCl3 → 4P + 6HCl
Фосфиды
Фосфиды – это бинарные соединения фосфора и металлов или некоторых неметаллов.
Способы получения фосфидов
Фосфиды получают при взаимодействии фосфора с металлами. При этом фосфор проявляет свойства окислителя.
Например, фосфор взаимодействует с магнием и кальцием:
2P + 3Mg → Mg3P2
2P + 3Ca → Ca3P2
Фосфор взаимодействует с натрием:
P + 3Na → Na3P
Химические свойства фосфидов
1. Фосфиды легко разлагаются водой или кислотами с образованием фосфина.
Например, фосфид кальция разлагается водой:
Ca3P2 + 6H2O → 3Са(ОН)2 + 2PH3↑
Фосфид магния разлагается соляной кислотой:
Mg3P2 + 6HCl → 3MgCl2 + 2PH3↑
2. Фосфиды металлов проявляют сильные восстановительные свойства за счет фосфора в степени окисления -3.
Оксиды фосфора
| Оксиды азота | Цвет | Фаза | Характер оксида |
| P2O3 Оксид фосфора (III), фосфористый ангидрид | белый | твердый | кислотный |
| P2O5 Оксид фосфора(V), фосфорный ангидрид | белый | твердый | кислотный |
Оксид фосфора (III)
Оксид фосфора (III) – это кислотный оксид. Белые кристаллы при обычных условиях. Пары состоят из молекул P4O6.
Получить оксид фосфора (III) можно окислением фосфора при недостатке кислорода:
4P + 3O2 → 2P2O3
Химические свойства оксида фосфора (III):
Оксид фосфора (III) очень ядовит и неустойчив. Для P2O3 (P4O6) характерны два типа реакций.
1. Поскольку фосфор в оксиде фосфора (III) проявляет промежуточную степень окисления, то он принимает участие в окислительно-восстановительных процессах, повышая либо понижая степень окисления атома фосфора. Характерны для P2O3 реакции диспропорционирования.
Например, оксид фосфора (III) диспропорционирует в горячей воде:
2Р2О3 + 6Н2О (гор.) → РН3 + 3Н3РО4
2. При взаимодействии с окислителями P2O3 проявяет свойства восстановителя.
Например, N2O окисляется кислородом:
Р2О3 + О2 → Р2О5
3. С другой стороны Р2О3 проявляет свойства кислотного оксида (ангидрид фосфористой кислоты), взаимодействуя с водой с образованием фосфористой кислоты:
Р2О3 + 3Н2О → 2Н3РО3
а со щелочами – с образованием солей (фосфитов):
Р2О3 + 4KOH → 2K2HРО3 + H2O
Оксид фосфора (V)
Оксид фосфора (V) – это кислотный оксид. В нормальных условиях образует белые кристаллы. В парах состоит из молекул P4H10. Очень гигроскопичен (используется как осушитель газов и жидкостей).
Способы получения. Оксид фосфора (V) получают сжиганием фосфора в избытке кислорода.
4P + 5O2 → 2P2O5
Химические свойства.
1. Оксид фосфора (V) – очень гигроскопичное вещество, которое используется для осушения газов. Обладая высоким сродством к воде, оксид фосфора (V) дегидратирует до ангидридов неорганические и органические кислоты.
Например, оксид фосфора (V) дегидратирует серную, азотную и уксусную кислоты:
P2O5 + H2SO4 → 2HPO3 + SO3
P2O5 + 2HNO3 → 2HPO3 + N2O5
P2O5 + 2CH3COOH → 2HPO3 + (CH3CO)2O
2. Фосфорный ангидрид является типичным кислотным оксидом, взаимодействует с водой с образованием фосфорных кислот:
P2O5 + 3H2O → 2H3PO4
В зависимости от количества воды и от других условий образуются мета-фосфорная, орто-фосфорная или пиро-фосфорная кислота:
P2O5 + 2H2O → 2H4P2O7
P2O5 + H2O → HPO3
Видеоопыт взаимодействия оксида фосфора с водой можно посмотреть здесь.
3. Как кислотный оксид, оксид фосфора (V) взаимодействует с основными оксидами и основаниями.
Например, оксид фосфора (V) взаимодействует с гидроксидом натрия. При этом образуются средние или кислые соли:
P2O5 + 6NaOH → 2Na3PO4 + 3H2O
P2O5 + 2NaOH + H2O → 2NaH2PO4
P2O5 + 4NaOH → 2Na2HPO4 + H2O
Еще пример: оксид фосфора взаимодействует с оксидом бария (при сплавлении):
P2O5 + 3BaO → Ba3(PO4)2
Фосфорная кислота
Строение молекулы и физические свойства
Фосфор в степени окисления +5 образует несколько кислот: орто-фосфорную H3PO4, мета-фосфорную HPO3, пиро-фосфорную H4P2O7.
Фосфорная кислота H3PO4 – это кислота средней силы, трехосновная, прочная и нелетучая. При обычных условиях фосфорная кислота – твердое вещество, хорошо растворимое в воде и гигроскопичное.
Валентность фосфора в фосфорной кислоте равна V.
При температуре выше +213 °C орто-фосфорная кислота переходит в пирофосфорную H4P2O7.
При взаимодействии высшего оксида фосфора с водой на холоде образуется метафосфорная кислота HPO3, представляющая собой прозрачную стекловидную массу.
Способы получения
Наибольшее практическое значение из фосфорных кислот имеет орто-фосфорная кислота.
1. Получить орто-фосфорную кислоту можно взаимодействием оксида фосфора (V) с водой:
P2O5 + 3H2O → 2H3PO4
2. Еще один способ получения фосфорной кислоты — вытеснение фосфорной кислоты из солей (фосфатов, гидрофосфатов и дигидрофосфатов) под действием более сильных кислот (серной, азотной, соляной и др.).
Промышленный способ получения фосфорной кислоты обработка фосфорита концентрированной серной кислотой:
Ca3(PO4)2(тв) + 3H2SO4(конц) → 2H3PO4 + 3CaSO4
3. Фосфорную кислоту также можно получить жестким окислением соединений фосфора в водном растворе в присутствии кислот.
Например, концентрированная азотная кислота окисляет фосфор до фосфорной кислоты:
5HNO3 + P → H3PO4 + 5NO2↑ + H2O
Химические свойства
Фосфорная кислота – это кислота средней силы (по второй и третьей ступени слабая).
1. Фосфорная кислота частично и ступенчато диссоциирует в водном растворе.
H3PO4 ⇄ H+ + H2PO4–
H2PO4– ⇄ H+ + HPO42–
HPO42– ⇄ H+ + PO43–
2. Фосфорная кислота реагирует с основными оксидами, основаниями, амфотерными оксидами и амфотерными гидроксидами.
Например, фосфорная кислота взаимодействует с оксидом магния:
2H3PO4 + 3MgO → Mg3(PO4)2 + 3H2O
Еще пример: при взаимодействии фосфорной кислоты с гидроксидом калия образуются фосфаты, гидрофосфаты или дигидрофосфаты:
H3PO4 + КОН → KH2РО4 + H2O
H3PO4 + 2КОН → К2НРО4 + 2H2O
H3PO4 + 3КОН → К3РО4 + 3H2O
3. Фосфорная кислота вытесняет более слабые кислоты из их солей (карбонатов, сульфидов и др.). Также фосфорная кислота вступает в обменные реакции с солями.
Например, фосфорная кислота взаимодействует с гидрокарбонатом натрия:
Н3PO4 + 3NaHCO3 → Na3PO4 + CO2 + 3H2O
4. При нагревании H3PO4 до 200°С происходит отщепление от нее молекулы воды с образованием пирофосфорной кислоты H2P2O7:
2H3PO4 → H2P2O7 + H2O
5. Фосфорная кислота взаимодествует с металлами, которые расположены в ряду активности металлов до водорода. При этом образуются соль и водород.
Например, фосфорная кислота реагирует с магнием:
2H3PO4 + 3Mg → Mg3(PO4)2 + 3H2
Фосфорная кислота взаимодействует также с аммиаком с образованием солей аммония:
2H3PO4 + 3NH3 → NH4H2PO4 + (NH4)2HPO4
7. Качественная реакция на фосфат-ионы и фосфорную кислоту — взаимодействие с нитратом серебра. При этом образуется ярко-желтый осадок фосфата серебра:
Н3PO4 + 3AgNO3 → Ag3PO4↓ + 3НNO3
Видеоопыт взаимодействия фосфата натрия и нитрата серебра в растворе (качественная реакция на фосфат-ион) можно посмотреть здесь.
Фосфористая кислота
Фосфористая кислота H3PO3 — это двухосновная кислородсодержащая кислота. При нормальных условиях бесцветное кристаллическое вещество, хорошо растворимое в воде.
Валентность фосфора в фосфористой кислота равна V, а степень окисления +3.
Получение фосфористой кислоты.
Фосфористую кислоту можно получить гидролизом галогенидов фосфора (III).
Например, гидролизом хлорида фосора (III):
PCl3 + 3H2O → H3PO3 + 3HCl
Фосфористую кислоту можно получить также взаимодействием оксида фосфора (III) с водой:
Р2О3 + 3Н2О → 2Н3РО3
Химические свойства.
1. Фосфористая кислота H3PO3 в водном растворе — двухосновная кислота средней силы. Взаимодействует с основаниями с образованием солей-фосфитов.
Например, при взаимодействии с гидроксидом натрия фосфористая кислота образует фосфит натрия:
H3PO3 + 2NaOH → Na2HPO3 + 2H2O
2. При нагревании фосфористая кислота разлагается на фосфин (Р-3) и фосфорную кислоту (Р+5):
4H3PO3 → 3H3PO4 + PH3
3. За счет фосфора в степени окисления +3 фосфористая кислота проявляет восстановительные свойства.
Например, H3PO3 окисляется перманганатом калия в кислой среде:
5H3PO3 + 2KMnO4 + 3H2SO4 → 5H3PO4 + K2SO4 + 2MnSO4 + 3H2O
Еще пример: фосфористая кислота окисляется соединениями ртути (II):
H3PO3 + HgCl2 + H2O → H3PO4 + Hg + 2HCl
Соли фосфорной кислоты — фосфаты
Фосфорная кислота образует разные типы солей: средние – фосфаты, кислые – гидрофосфаты, дигидрофосфаты.
1. Качественная реакция на фосфаты — взаимодействие с нитратом серебра. При этом образуется желтый осадок фосфата серебра.
K3PO4 + 3AgNO3 → Ag3PO4↓ + 3KNO3
2. Нерастворимые фосфаты растворяются под действием сильных кислот, либо под действием фосфорной кислоты.
Например, фосфат кальция реагирует с фосфорной кислотой с образованием дигидрофосфата кальция:
Ca3(PO4)2 + 4H3PO4 → 3Ca(H2PO4)2
Фосфат кальция растворяется под действием серной кислоты:
Ca3(PO4)2 + 2H2SO4 → Ca(H2PO4)2 + 2CaSO4
3. За счет фосфора со степенью окисления +5 фосфаты проявляют слабые окислительные свойства и могут взаимодействовать с восстановителями.
Например, фосфат кальция при сплавлении реагирует с углеродом с образованием фосфида кальция и угарного газа:
Ca3(PO4)2 + 8C → Ca3P2 + 8CO
Фосфат кальция также восстанавливается алюминием при сплавлении:
3Ca3(PO4)2 + 16Al → 3Ca3P2 + 8Al2O3
4. Гидрофосфаты могут взаимодействовать и с более сильными кислотами, и с щелочами. Под действием фосфорной кислоты гидрофосфаты переходят в дигидрофосфаты.
Например, гидрофосфат калия взаимодействует с фосфорной кислотой с образованием дигидрофосфата калия:
K2HPO4 + H3PO4 → 2KH2PO4
Под действием едкого кали гидрофосфат калия образует более среднюю соль — фосфат калия:
K2HPO4 + KOH → K3PO4 + H2O
5. Дигидрофосфаты могут взаимодействовать с более сильными кислотами и щелочами, но не реагируют с фосфорной кислотой.
Например, дигидрофосфат натрия взаимодействует с избытком гидроксида натрия с образованием фосфата:
NaH2PO4 + 2NaOH → Na3PO4 + 2H2O
Поделиться ссылкой:
chemege.ru
P2O5 какой это оксид
Оксид фосфора (V) (фосфорный ангидрид) представляет собой очень гигроскопичное вещество белого цвета. Является сильнейшим дегидратирующим агентом. Существует в аморфном (в виде хлопьев), стеклообразном и кристаллическом состояниях. При нагревании кристаллический оксид фосфора (V) возгоняется. Плавится только под избыточным давлением, переходя при этом в легкоподвижную жидкость. При дальнейшем нагревании полимеризуется, при охлаждении жидкости образуется стеклообразный продукт состава .
Оксид фосфора (V) проявляет кислотные свойства (P2O5 какой это оксид). Энергично реагирует с водой, щелочами. Легко галогенируется. Восстанавливается фосфором. Образует пероксосоединения.
Оксид фосфора (V) в промышленных масштабах получают сжиганием фосфора в избытке кислорода или воздуха:
ru.solverbook.com
P + O2 = P2O5 расставить коэффициенты
Реакция протекает по схеме:
P + O2 = P2O5.
В ходе реакции степень окисления фосфора повышается от 0 до (+5) (фосфор окисляется), а кислорода – понижается от 0 до (-2) (кислород восстанавливается).
Уравнение полуреакции окисления фосфора:
Уравнение полуреакции восстановления кислорода:
Поскольку отношение чисел электронов, принятых при восстановлении кислорода и отданных при окислении фосфора, равно 2:5, то, складывая уравнения полуреакций восстановления и окисления, первое из них нужно домножить на 2, а второе – на 5:
В молекулярной форме полученное уравнение имеет следующий вид:
Оксид фосфора (V) (фосфорный ангидрид) представляет собой очень гигроскопичное вещество белого цвета. Является сильнейшим дегидратирующим агентом. Существует в аморфном (в виде хлопьев), стеклообразном и кристаллическом состояниях. При нагревании кристаллический оксид фосфора (V) возгоняется. Плавится только под избыточным давлением, переходя при этом в легкоподвижную жидкость. При дальнейшем нагревании полимеризуется, при охлаждении жидкости образуется стеклообразный продукт состава .
Оксид фосфора (V) проявляет кислотные свойства. Энергично реагирует с водой, щелочами. Легко галогенируется. Восстанавливается фосфором. Образует пероксосоединения.
Оксид фосфора (V) в промышленных масштабах получают сжиганием фосфора в избытке кислорода или воздуха:
ru.solverbook.com
P2O5+h3O=? уравнение реакции
Реакция взаимодействия между оксидом фосфора (V) и водой (P2O5 + h3O = ?) приводит к образованию сложного соединения – ортофосфорной кислоты, формула которой имеет вид . Молекулярное уравнение реакции имеет вид:
Теперь переходим к решению задачи. Первоначально рассчитаем количество молей веществ, вступивших в реакцию (, ():
Это означает, что вода находится в избытке и дальнейшие расчеты производим по оксиду фосфора (V).
Согласно уравнению реакции , значит . Тогда масса ортофосфорной кислоты будет равна (молярная масса – 98 g/mole):
ru.solverbook.com
BaO + P2O5 = ? уравнение реакции
Реакция взаимодействия между оксидом фосфора (V) и оксидом бария (BaO + P2O5 = ?) позволяет получить среднюю соль – фосфат бария (соединение). Молекулярное уравнение реакции имеет вид:
Записать уравнение в ионном виде в данном случае не предоставляется возможным, поскольку реакция протекает в твердой фазе, а не в растворе.
Оксид фосфора (V) (фосфорный ангидрид) представляет собой очень гигроскопичное вещество белого цвета. Является сильнейшим дегидратирующим агентом. Существует в аморфном (в виде хлопьев), стеклообразном и кристаллическом состояниях. При нагревании кристаллический оксид фосфора (V) возгоняется. Плавится только под избыточным давлением, переходя при этом в легкоподвижную жидкость. При дальнейшем нагревании полимеризуется, при охлаждении жидкости образуется стеклообразный продукт состава .
Оксид фосфора (V) проявляет кислотные свойства. Энергично реагирует с водой, щелочами. Легко галогенируется. Восстанавливается фосфором. Образует пероксосоединения.
Оксид фосфора (V) в промышленных масштабах получают сжиганием фосфора в избытке кислорода или воздуха:
ru.solverbook.com
P2O5 + MgO = ? уравнение реакции
Реакция взаимодействия между оксидом фосфора (V) и оксидом магния (P2O5 + MgO = ?) позволяет получить среднюю соль – фосфат магния (соединение). Молекулярное уравнение реакции имеет вид:
Записать уравнение в ионном виде в данном случае не предоставляется возможным, поскольку реакция протекает в твердой фазе, а не в растворе.
Оксид фосфора (V) (фосфорный ангидрид) представляет собой очень гигроскопичное вещество белого цвета. Является сильнейшим дегидратирующим агентом. Существует в аморфном (в виде хлопьев), стеклообразном и кристаллическом состояниях. При нагревании кристаллический оксид фосфора (V) возгоняется. Плавится только под избыточным давлением, переходя при этом в легкоподвижную жидкость. При дальнейшем нагревании полимеризуется, при охлаждении жидкости образуется стеклообразный продукт состава .
Оксид фосфора (V) проявляет кислотные свойства. Энергично реагирует с водой, щелочами. Легко галогенируется. Восстанавливается фосфором. Образует пероксосоединения.
Оксид фосфора (V) в промышленных масштабах получают сжиганием фосфора в избытке кислорода или воздуха:
ru.solverbook.com

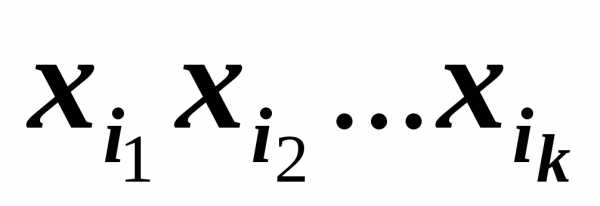 ),
где суммирование ведётся по некоторому
множеству различных наборов (i1, i2,
…, ik),
в которых все ij также различны.
),
где суммирование ведётся по некоторому
множеству различных наборов (i1, i2,
…, ik),
в которых все ij также различны. &
&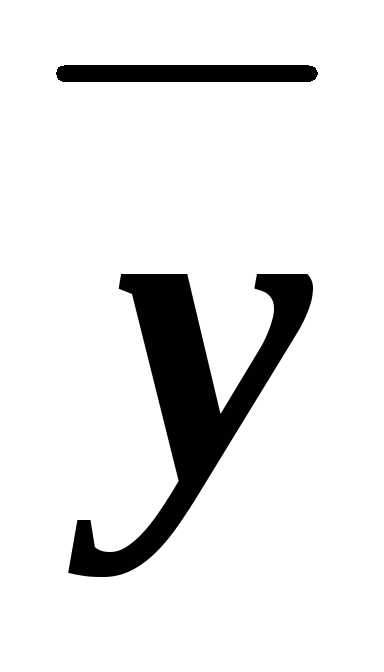 )
имеем
)
имеем &
&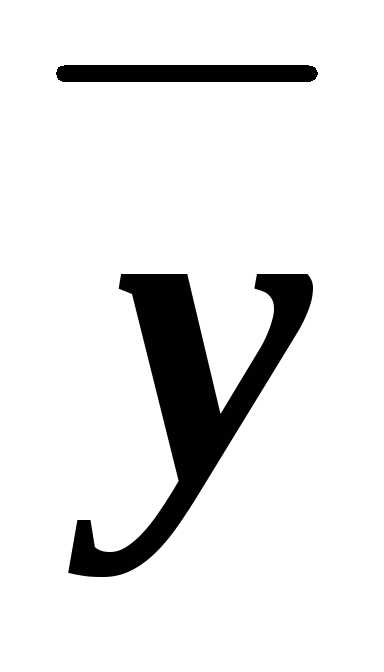 )=ху
)=ху
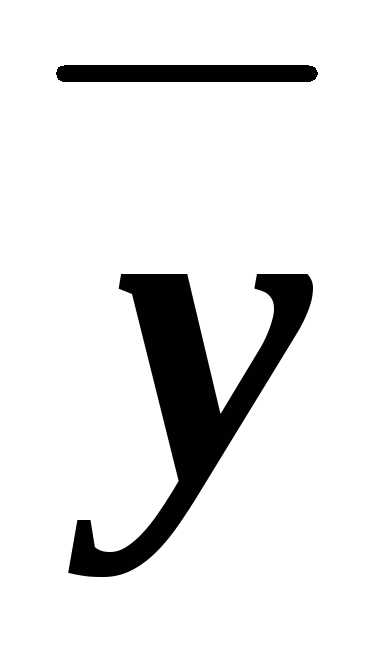 ху
ху
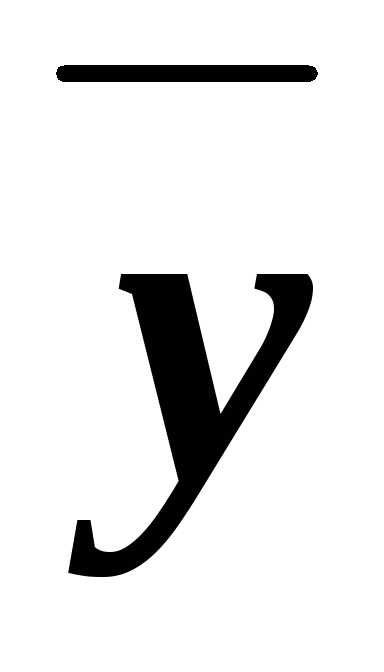 =ху
=ху
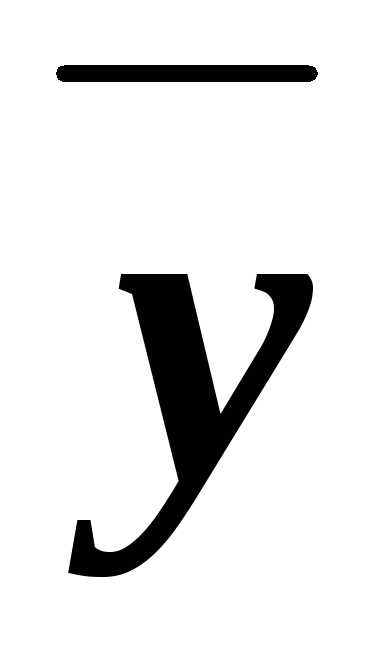 =
= &
&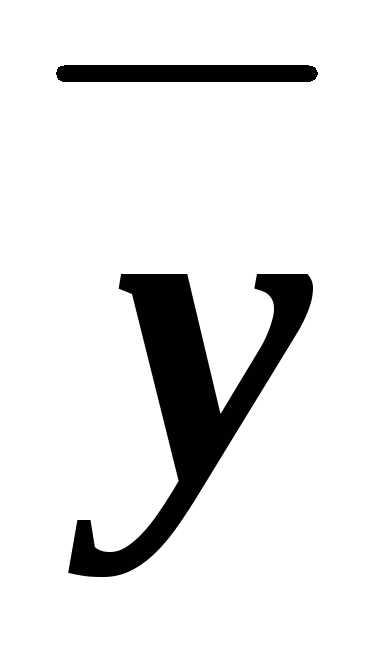 )=1ху (в чём мы уже убеждались). Для функции х
)=1ху (в чём мы уже убеждались). Для функции х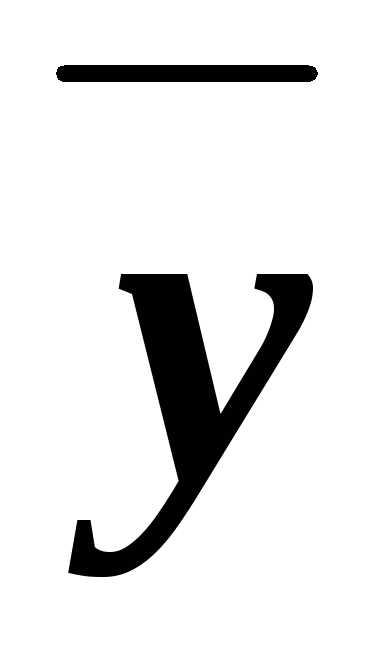 имеемх
имеемх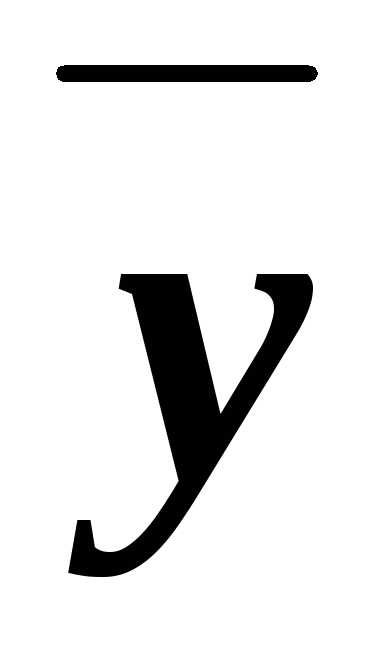 =х(1у)=хху,
то есть х
=х(1у)=хху,
то есть х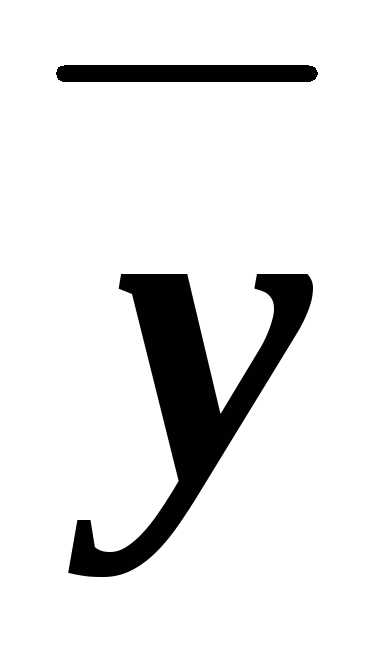 =хху.
=хху.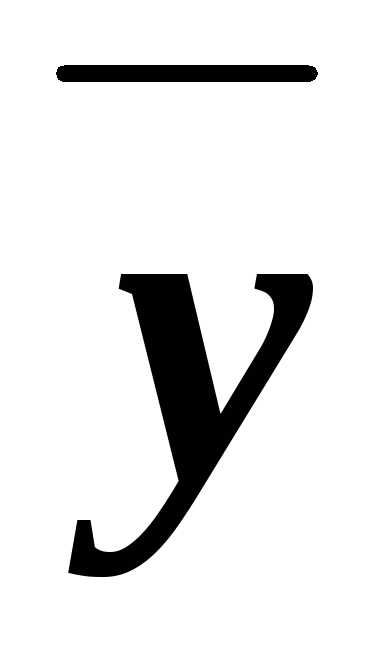 полином Жегалкина содержит произведения
переменных. Такие полиномы называютсянелинейными.
Полиномы Жегалкина вида c0c1x1c2x2…cnxn называются линейными.
Таким образом, линейная функция
представима в виде линейного полинома
Жегалкина.
полином Жегалкина содержит произведения
переменных. Такие полиномы называютсянелинейными.
Полиномы Жегалкина вида c0c1x1c2x2…cnxn называются линейными.
Таким образом, линейная функция
представима в виде линейного полинома
Жегалкина.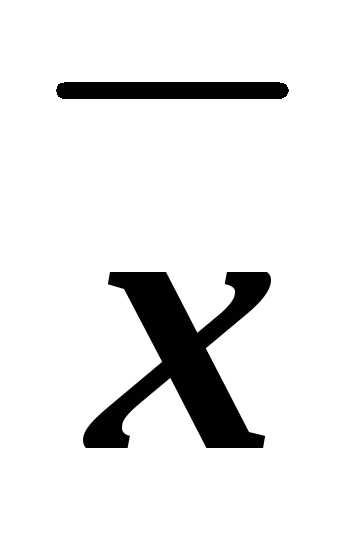
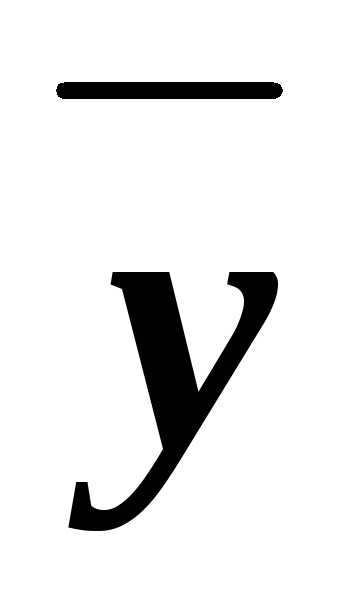 z
z y
y x
x z(см. решение упражнения 5.1, а)). Учитывая,
что
z(см. решение упражнения 5.1, а)). Учитывая,
что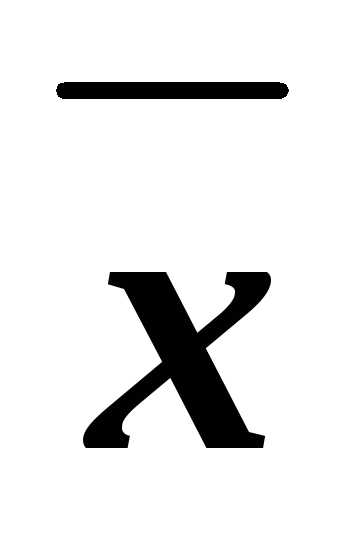 =1х,
=1х, 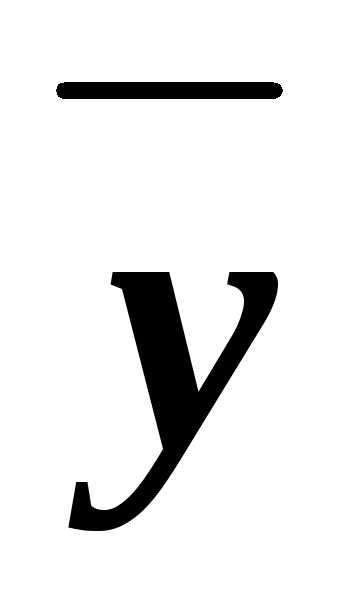 =1у,
=1у, =1 zи раскрывая
скобки, получаем
=1 zи раскрывая
скобки, получаем
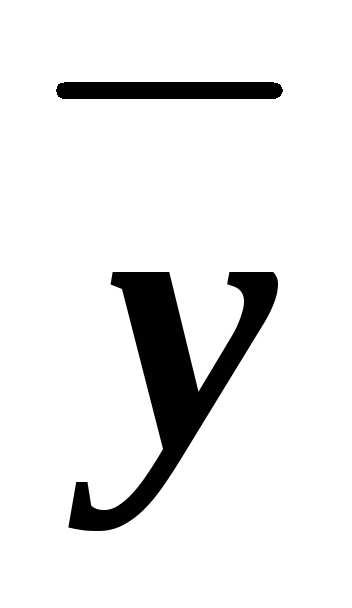 z
z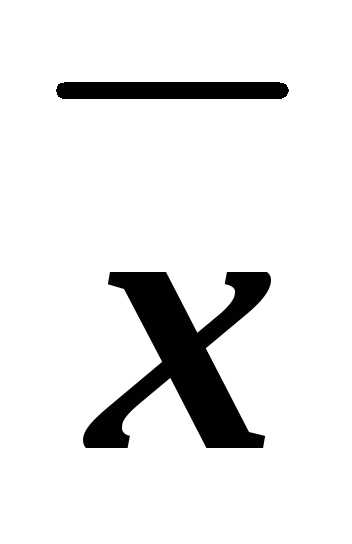 y
y x
x z=
z=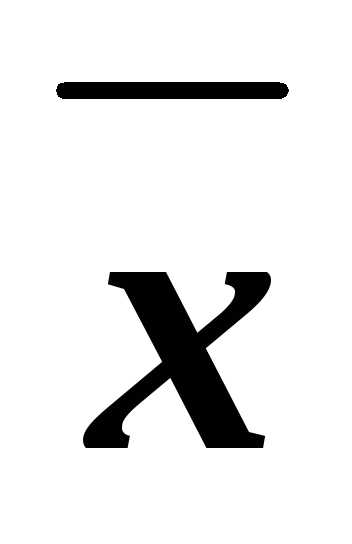
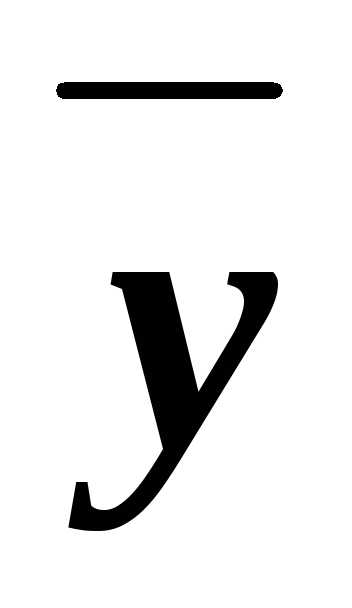 z
z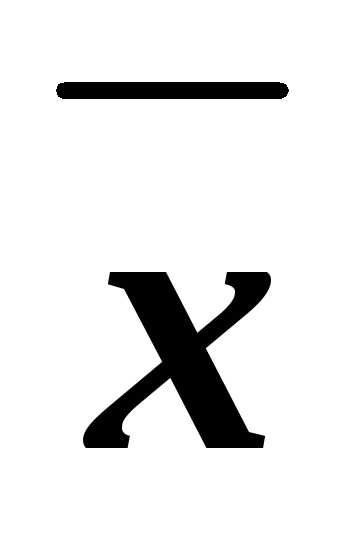 y
y x
x z=(1х)(1у)z(1х)y(1 z)x(1у)z=
z=(1х)(1у)z(1х)y(1 z)x(1у)z=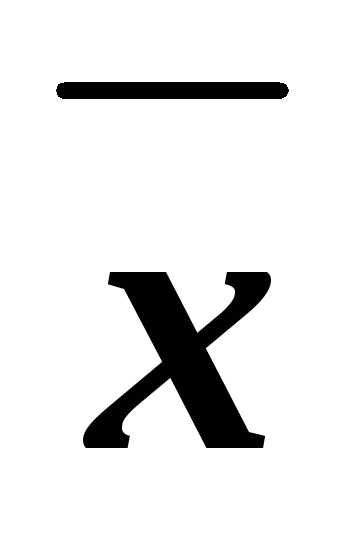
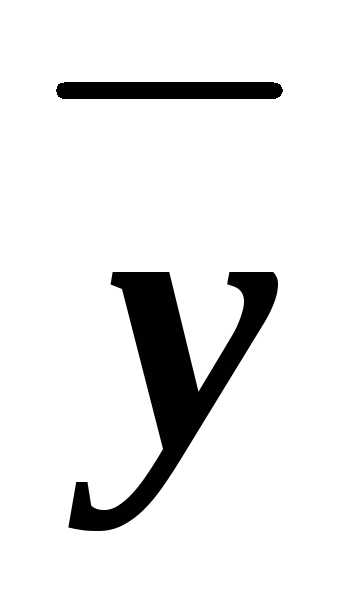 z
z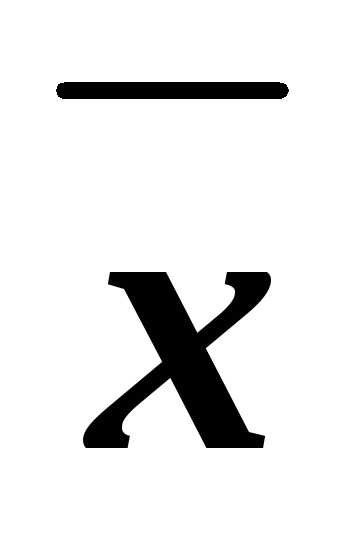 y
y x
x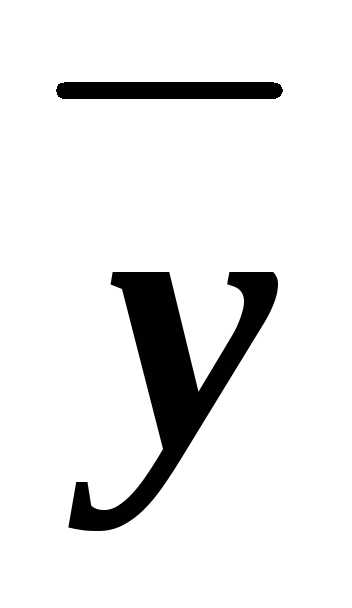 z=yzxyхyz.
В частности, функция не является линейной.
z=yzxyхyz.
В частности, функция не является линейной.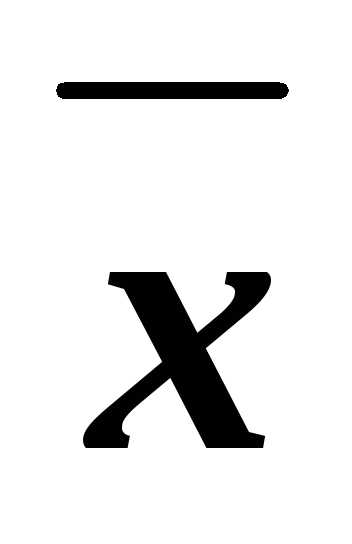

 В
В С где А, В, С — пересекающиеся множества. Тогда
разбиение множества М на классы можно представить
в следующем виде:
С где А, В, С — пересекающиеся множества. Тогда
разбиение множества М на классы можно представить
в следующем виде: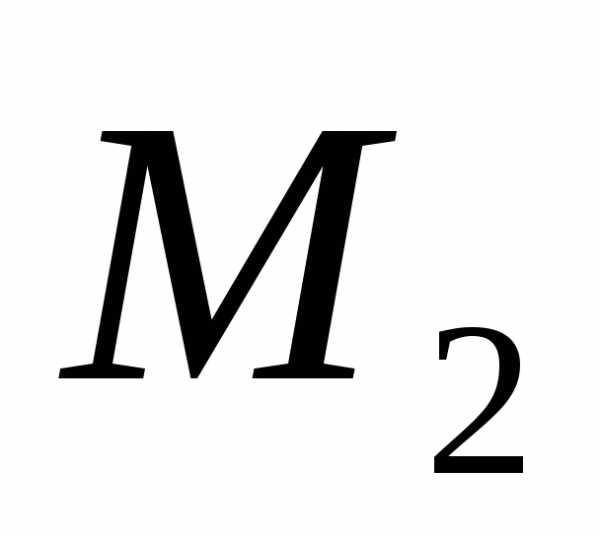 +
+ 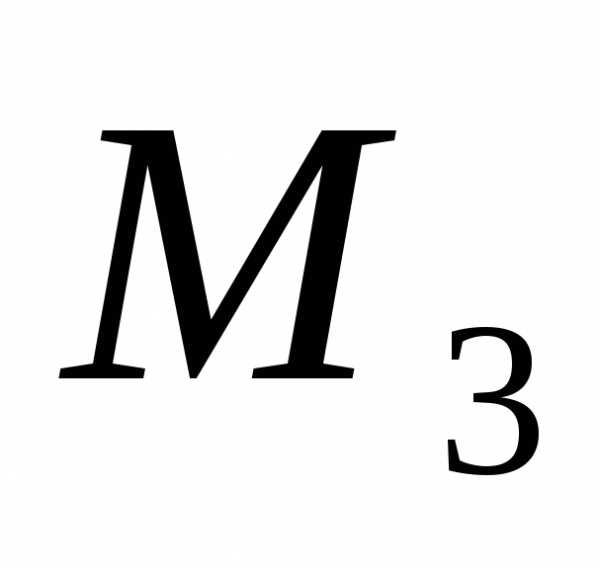 +
+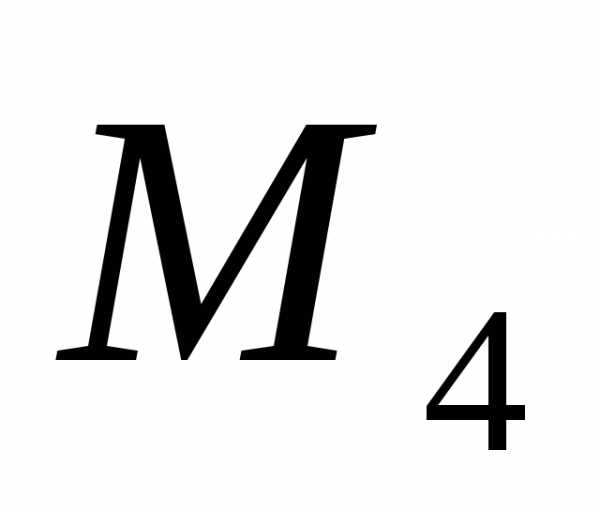 = 20 +15 +35 = 70
= 20 +15 +35 = 70
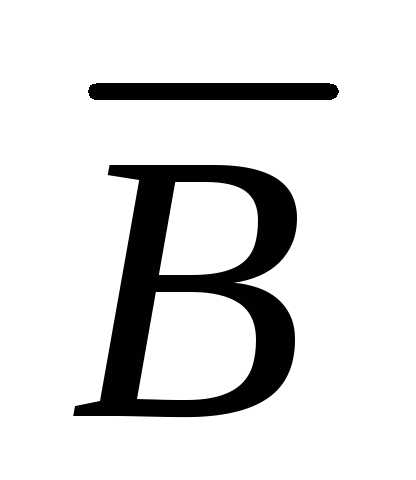
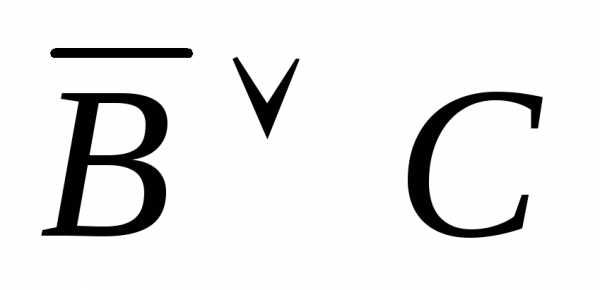
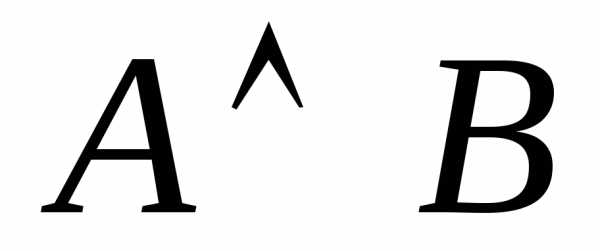
 )
)
 =
=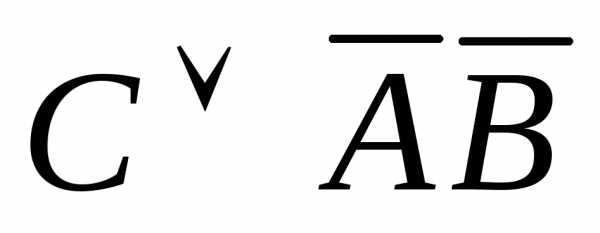 =
= =
=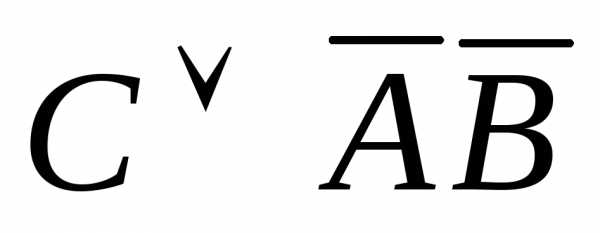 =
=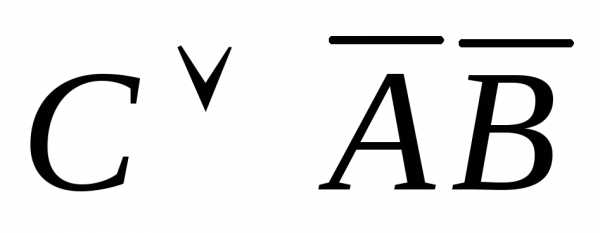 ,КНФ
=
,КНФ
=
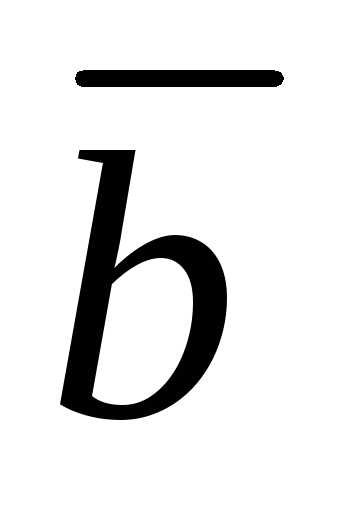
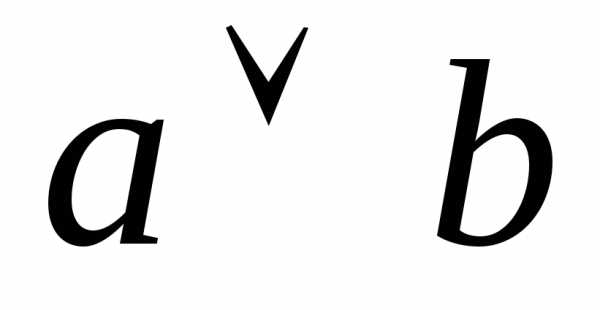
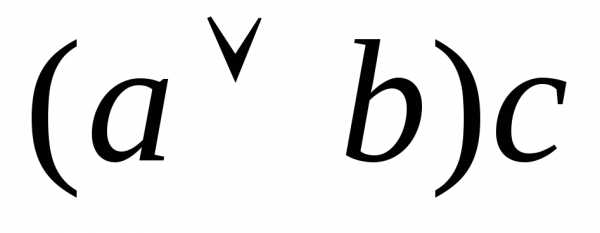

 )
)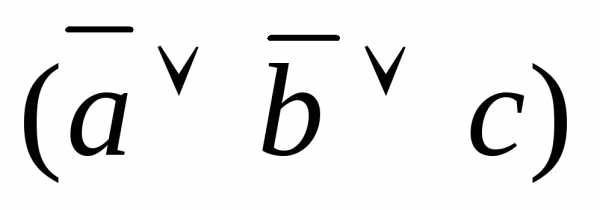

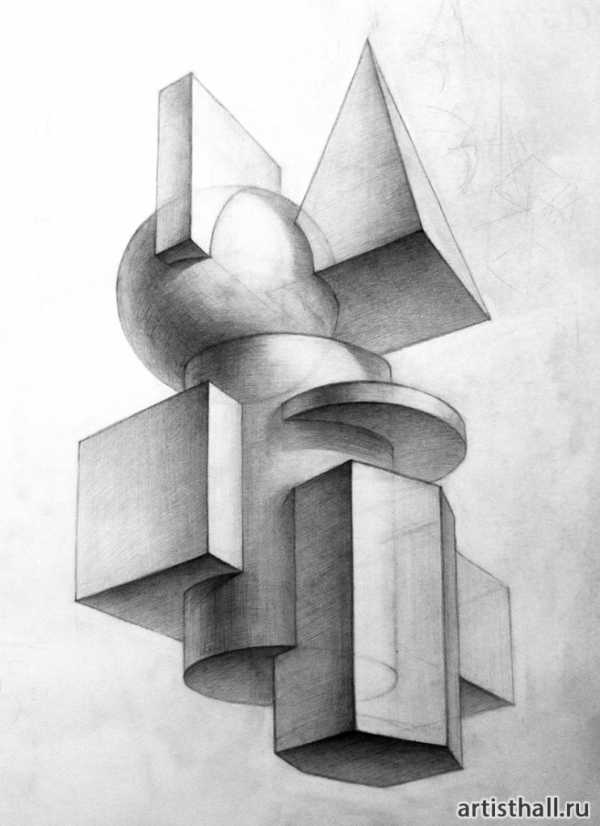
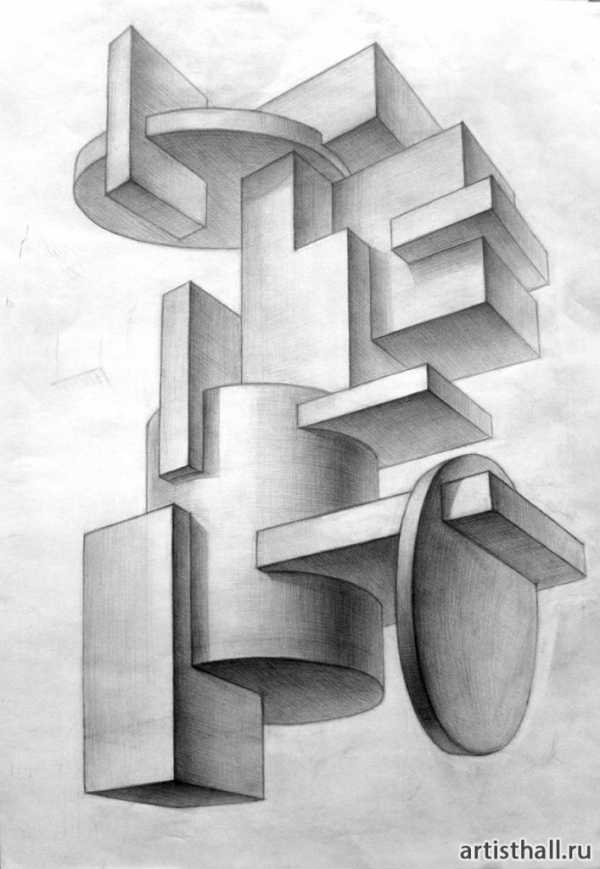
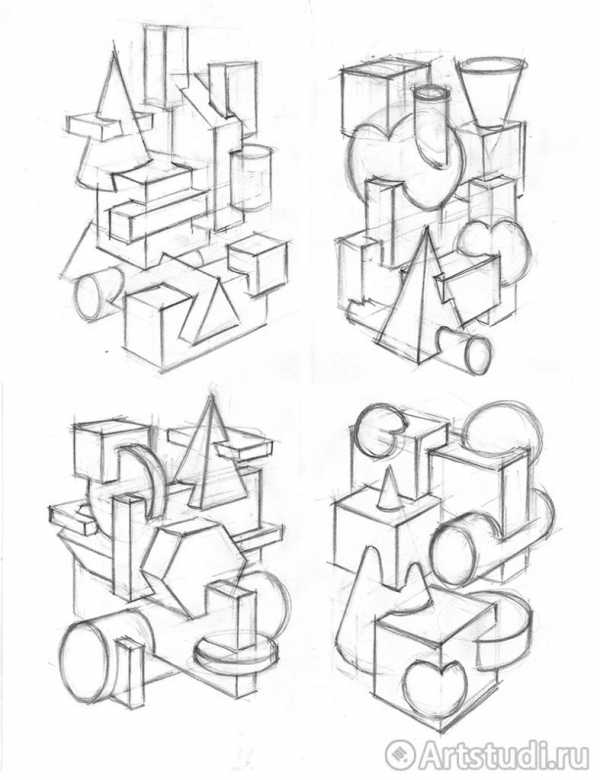
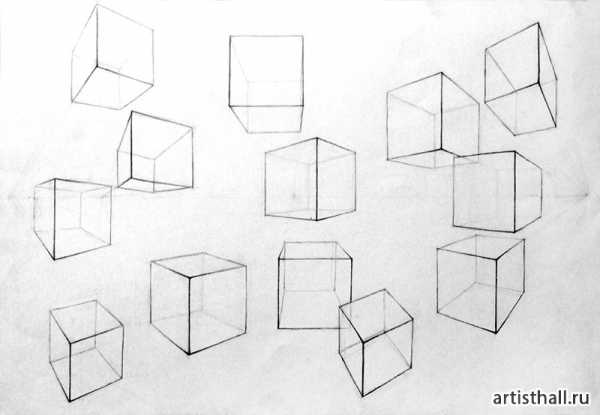
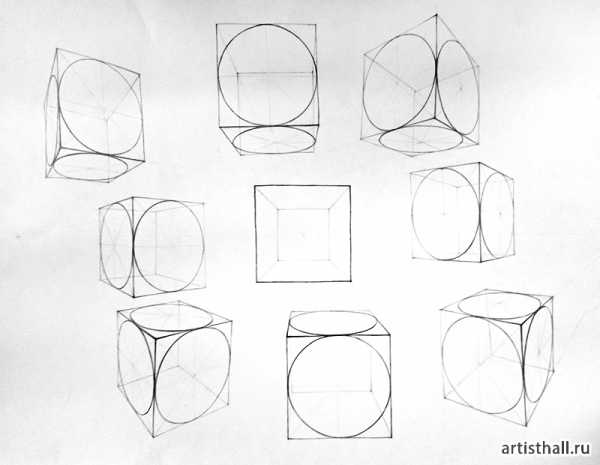
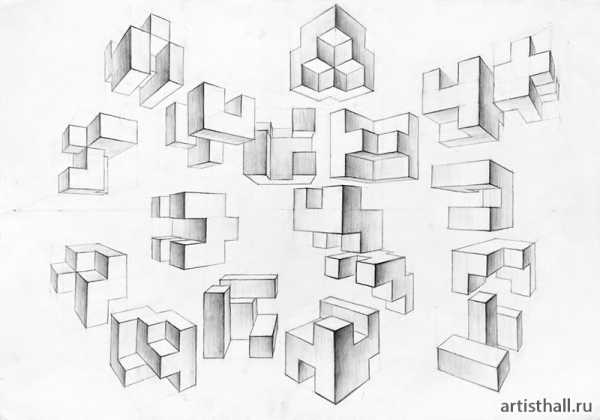
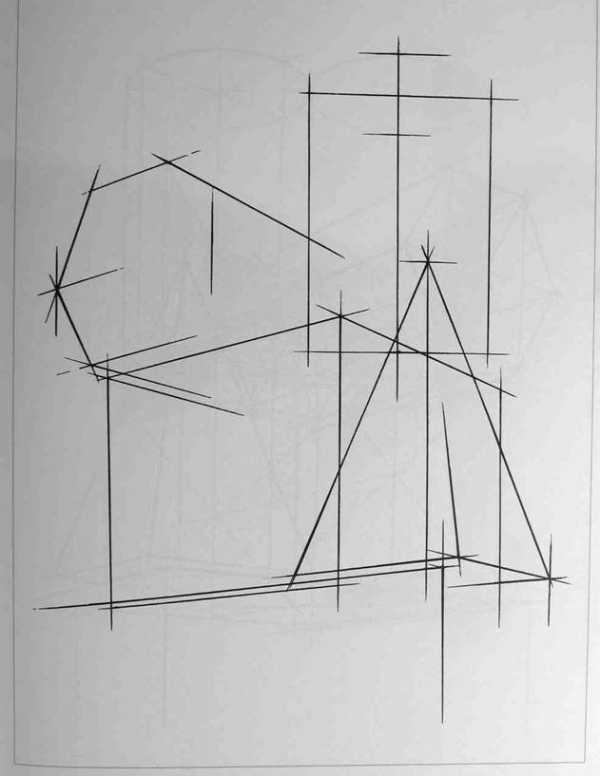
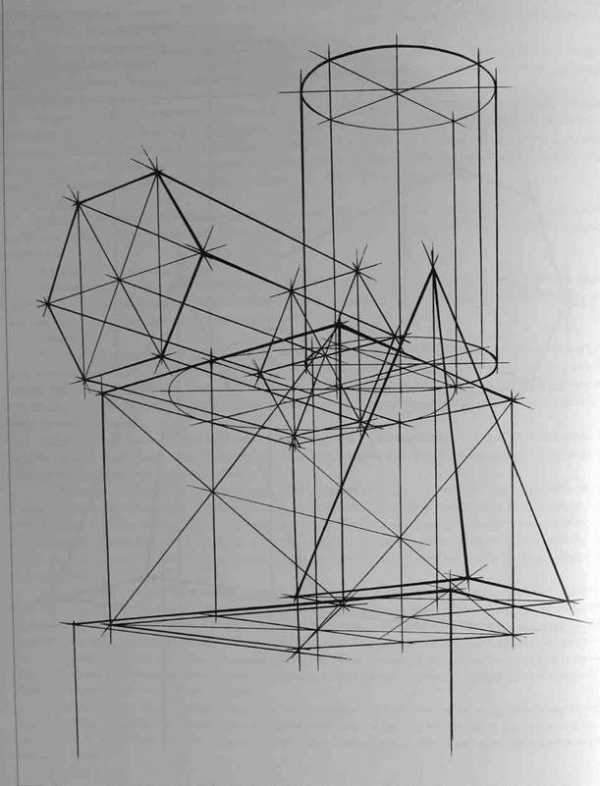
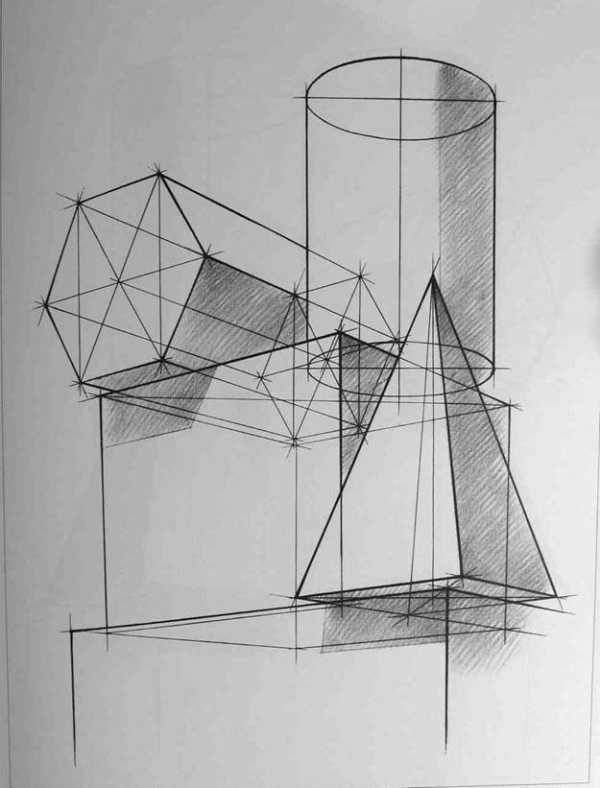
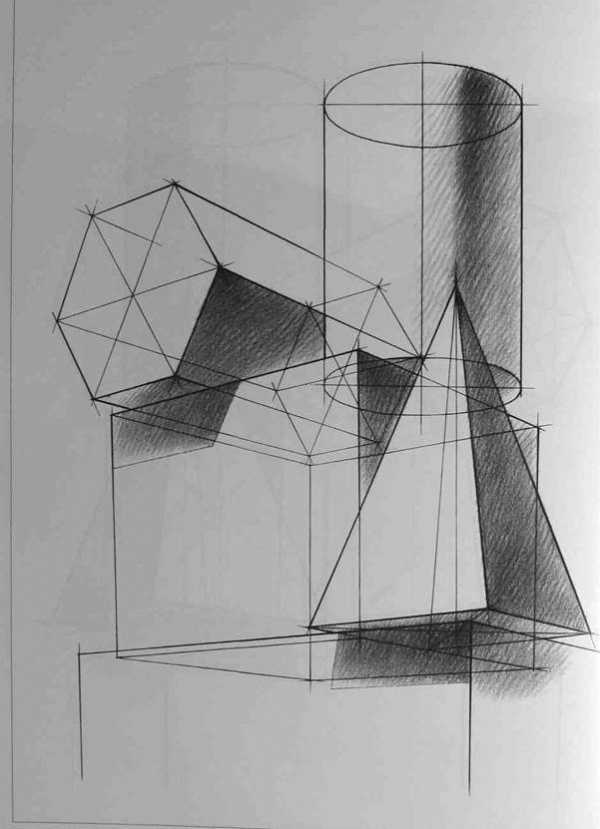
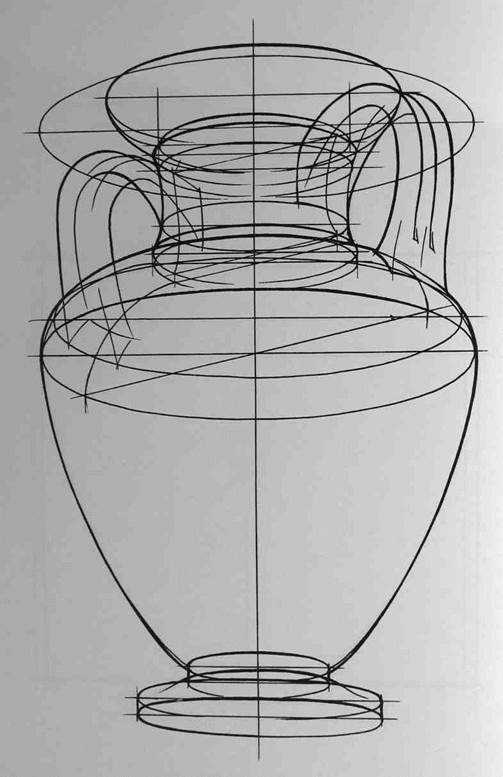
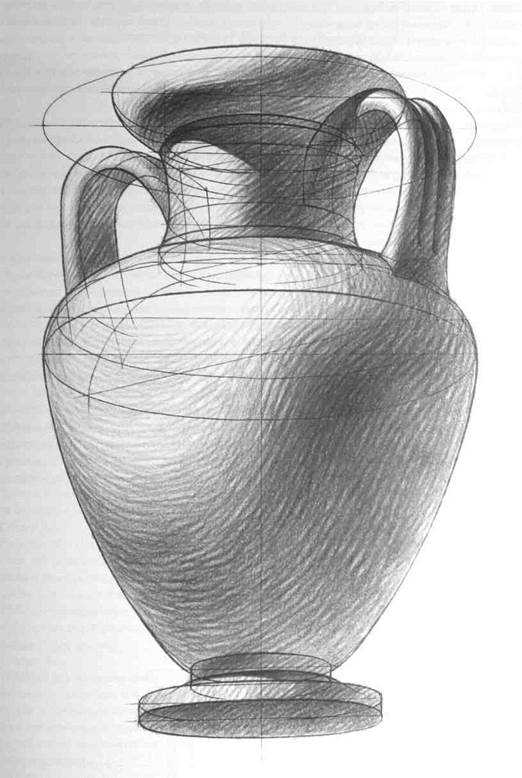
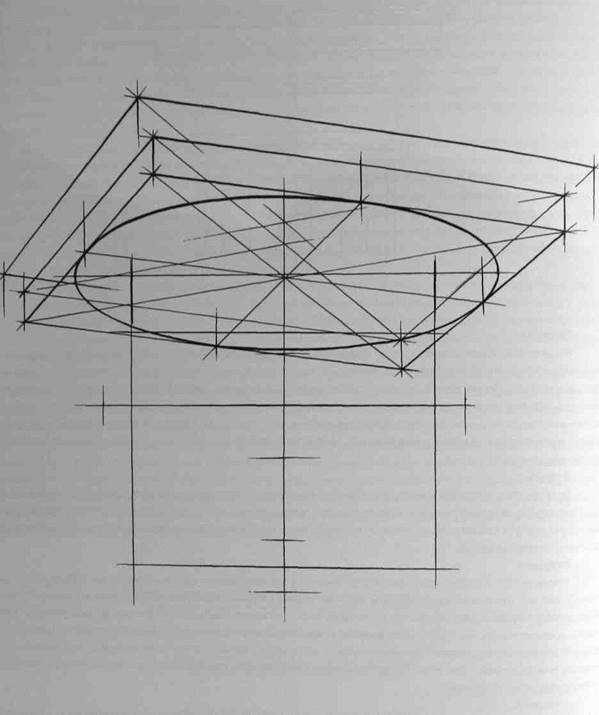
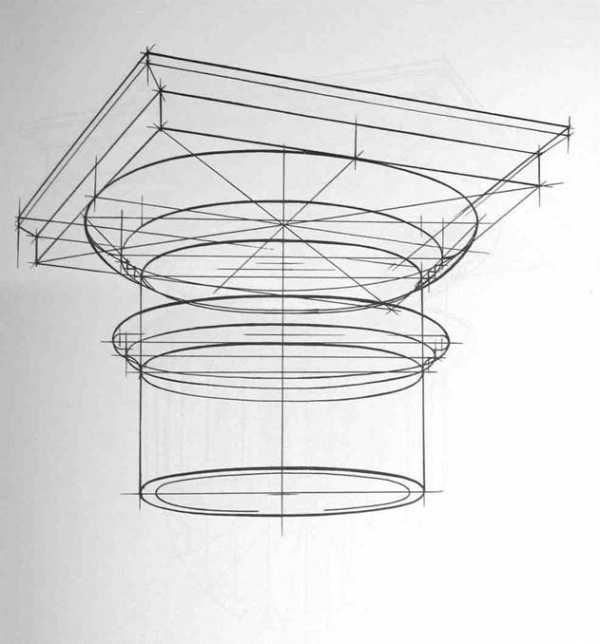
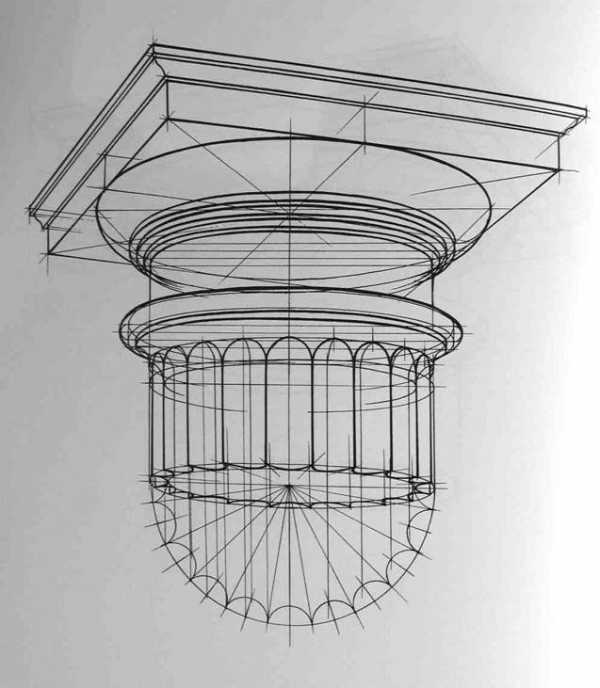
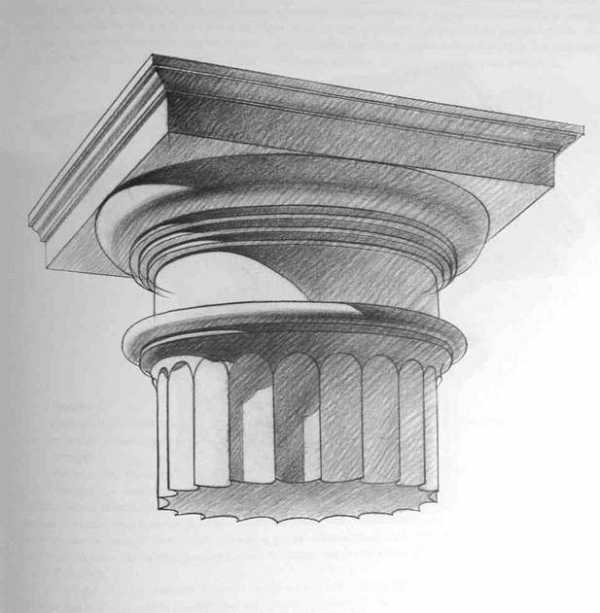
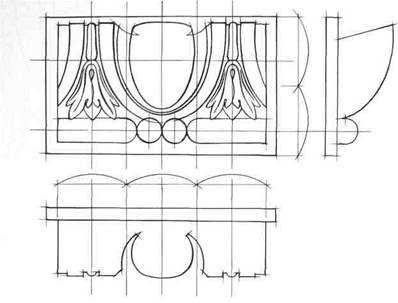
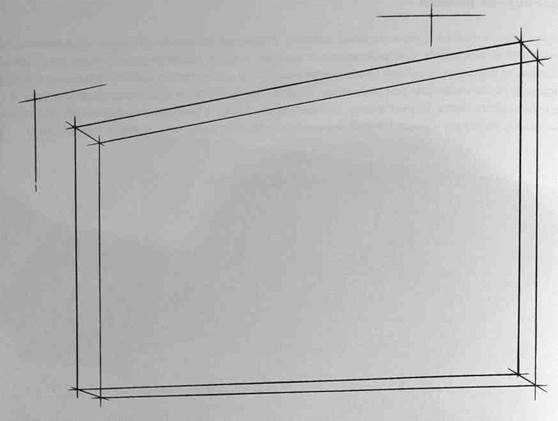
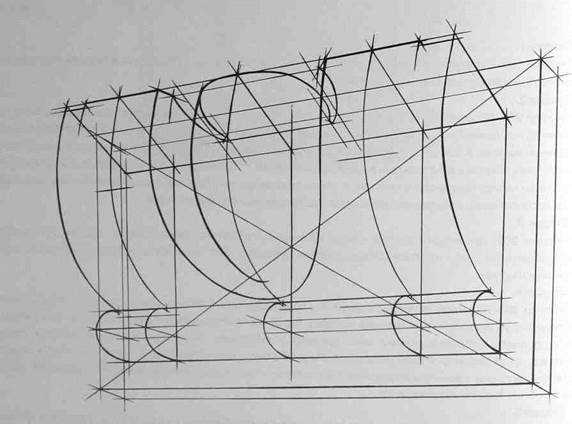
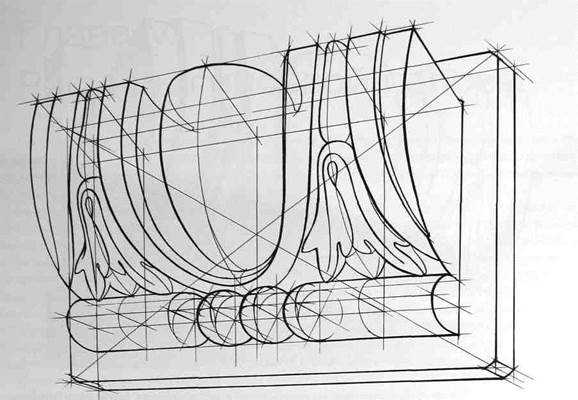
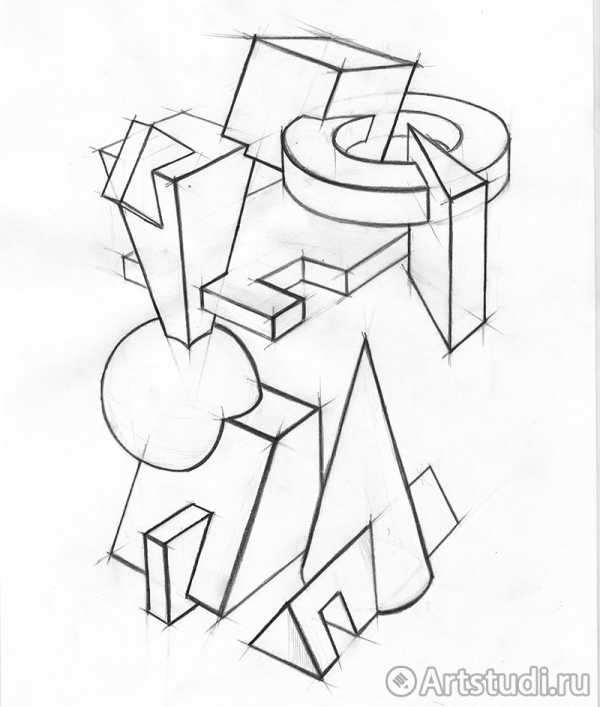 После определения положения точки осмотра начинается конструктивная разработка группы и создание пластического образа. Для этого можно использовать следующие удобные приемы:
После определения положения точки осмотра начинается конструктивная разработка группы и создание пластического образа. Для этого можно использовать следующие удобные приемы: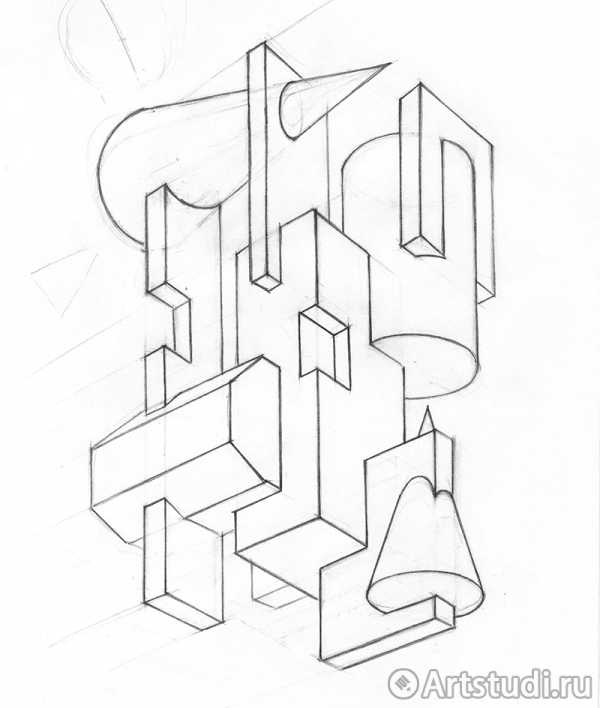
































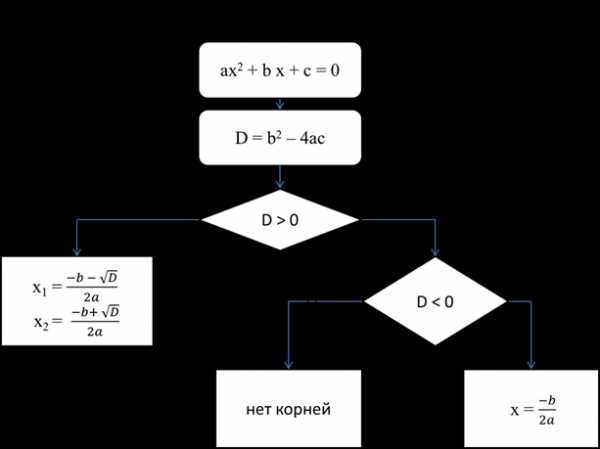

 для квадратного уравнения? (дискриминант)
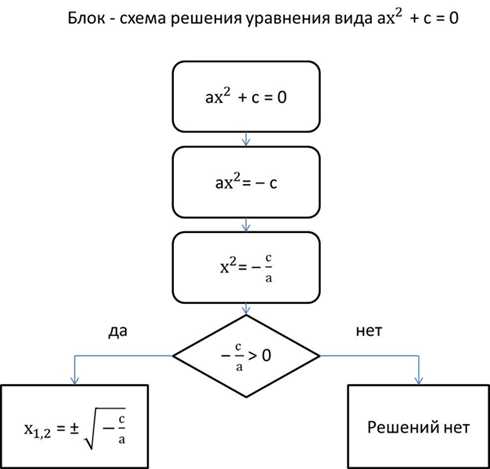
для квадратного уравнения? (дискриминант) . (биквадратное)
. (биквадратное)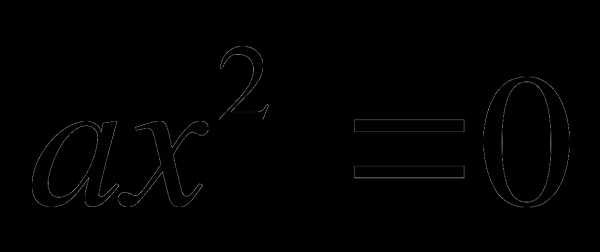 . (ноль)
. (ноль) .
.