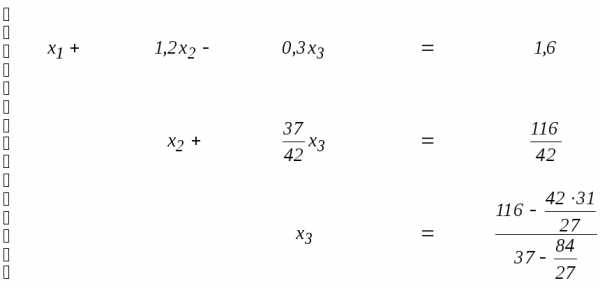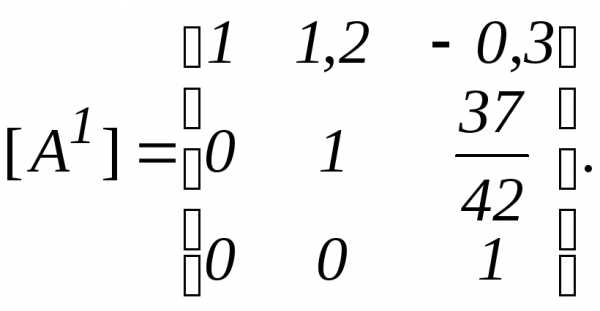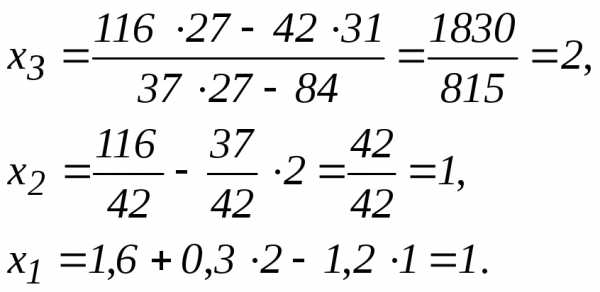Решение простых задач с недостающими данными — Мегаобучалка
Пример:
а) В вазе стояли красные и желтые тюльпаны. Красных было 5. Сколько всего тюльпанов стояло в вазе?
б) На лыжах катались мальчики и 3 девочек. Сколько всего детей катались на лыжах?
После чтения таких задач учитель спрашивает, можно ли узнать, сколько всего тюльпанов стояло в вазе (сколько детей катались на лыжах), и почему нельзя (неизвестно, сколько было желтых тюльпанов, или неизвестно, сколько было мальчиков). Далее дети подбирают числа и решают задачу.
При выполнении таких упражнений, ученики убеждаются, что не всегда можно сразу ответить на вопрос задачи, так как может не хватать числовых данных, их надо получить (в данном случае подобрать числа, а при решении составных задач найти, выполнив соответствующее действие).
2)Решение задач с двумя вопросами.Пример. На первой полке было 5 книг, а на второй на 2 книги больше.
Сколько книг на второй полке? Сколько книг на двух полках вместе?
3) Решение пар простых задач, в которых число, полученное в ответ< на вопрос первой задачи, является однимиз данных во второй задаче.
Пример:
а) На первой полке было 5 книг, а на второй на 2 книги больше. Сколько книг на второй попке?
б) На первой попке было 5 книг, а на второй 7 книг. Сколько книг на двух полках вместе?
Учитель объясняет, что такие две задачи можно заменить одной: «На первой полке было 5 книг, а на второй на 2 книги больше. Сколько книг на двух полках вместе?»
4)Постановка вопроса к данному условию. Детям предлагаете условие «В вазе стояли 5 красных и 2 желтых тюльпана» и выясняете, какой вопрос можно поставить к этому условию? (Сколько всего тюльпанов в вазе? На сколько красных тюльпанов больше, чем желтых»?) Показывается, что от смены вопроса меняется решение задачи.
5)Выработка умений решать простые задачи, входящих в составную.Следует помнить, что необходимым условием для решения составной задачи является твердое умение детей решать простые задачи и умение обосновать выбор арифметического действия при решении простых задач. Следовательно, до введения составных задач определенной структуры надо сформировать у детей умение решать соответствующие простые задачи.
Все эти упражнения надо включать при работе над простыми задачами до введения составных задач.
При знакомстве с составными задачами учитель должен иметь ввиду, что первыми решаются составные задачи только в два действия. Эти дачи могут различаться:
а) количеством данных в них;
6) сочетанием действий, которыми они решаются.
Пример.
1. Миша нашел 9 грибов, а Коля на 2 гриба меньше. Сколько грибов нашли Миша и Копя вместе?
Решение:
1) 9 – 2 = 7 (гр.)
2) 9 + 7 = 16 (гр.)
(9 — 2) + 9 = 16 (гр.)
В этой задаче два числовых данных, она решается двумя разными действиями.
2. Миша нашел 9 грибов, а Коля на 2 гриба больше. Сколько грибов Миша и Копя вместе?
Решение:
1) 9 + 2 = 11 (гр.)
2) 9 + 11 = 20 (гр.)
(9 + 2) + 9 = 20 (гр.)
В этой задаче два числовых данных, она решается двумя одинаковыми действиями.
3. Оля купила 5 тетрадей в линейку и 7 тетрадей в клетку. Три из них она отдала брату. Сколько тетрадей осталось у Оли?
Решение:
1) 5 + 7 = 12 (т.)
2) 12 – 3 = 7 (т.)
(5 + 7) – 3 = 7 (т.)
В этой задаче три числовых данных, она решается двумя разными действиями.
Эти различия между составными задачами в 2 действия могут помочь увидеть детям различия между простыми и составными задачами.
Для первоначального знакомства с составными задачами рекомендуется отбирать задачи, при решении которых надо выполнить два различных арифметических действия: сложение и вычитание. При этом необходимо взять такую задачу, которая понятна детям по содержанию, и ее легко проиллюстрировать.
Можно начать с решения задач в два действия, включающих простые задачи на нахождение суммы и на нахождение остатка, например: «В одной вазе лежало 6 яблок, а во второй — 5 яблок. 4 яблока съели. Сколько яблок осталось?» Такая задача явно отличается от простой — в ее условии три числа, т. е. здесь обе простые задачи как бы лежат на поверхности. Это должно быстрее привести детей к уяснению существенного признака составной задачи — ее нельзя решить сразу, выполнив одно действие. Здесь содержание задачи помогает правильному установлению связей. В этом случае детям легче составить по задаче выражение.
Можно начать с задач в два действия, которые включают простые задачи на уменьшение числа на несколько единиц и на нахождение суммы, например: «У Оли 7 тетрадей, в у Сережи на 4 тетради меньше. Сколько тетрадей у них вместе?» В условии этой задачи два числа, что делает ее сходной с простой задачей, а поэтому учащиеся склонны решать такие задачи, выполнив одно действие. Кроме того, простая задача на уменьшение числа на несколько единиц, входящая в эту составную, труднее задачи на нахождение остатка, которая входит в первую составную задачу. Решение этих задач на первых порах сопряжено у детей с целым рядом трудностей. Поэтому лучше начинать с решения составных задач, включающих три числовых данных, а затем включать задачи другой математической структуры. Покажем, как это можно сделать.
Учитель читает задачу: «Витя нашел сначала 4 гриба, а потом еще 5 грибов. 6 грибов он отдал Саше. Сколько грибов осталось у Вити?»
О чем задача? (О грибах)
Что известно о грибах? (Витя нашел сначала 4 гриба, а потом еще 5 грибов.)
Запишем это кратко, выделяя главные слова.
Еще что известно? (6 грибов он отдал Саше.) Запишем.
Что надо узнать? (Сколько грибов осталось у Вити.)
Запишем.
Получается запись:
Нашел — 4 гр. и 5 гр.
Отдал — 6 гр.
Осталось — ?
Объясните, что показывает каждое число в этой записи. (Объясняют.)
Назовите вопрос задачи. (Сколько грибов осталось у Вити?)
У доски выполняется иллюстрация: в корзинку кладут сначала 4 гриба, затем 5 грибов, затем вынимают 6 грибов. Оставшиеся грибы скрыты, их нельзя сосчитать.
Можно ли сразу узнать, сколько грибов осталось у Вити? (Нет.)
Почему? (Не знаем, сколько всего грибов нашел Витя.).
Можно ли сразу узнать, сколько всего грибов нашел Витя? (Можно.)
Как? (К 4 прибавим 5.)
Запишем сумму, но вычислять не будем. (Запись: 4+5.)
Что обозначает эта сумма?
Что узнаем, когда вычислим? (Сколько всего грибов нашел Витя.)
Сколько грибов он отдала Саше? (6.)
Можно ли узнать, сколько грибов осталось у Вити? (Можно.)
Как? (Из суммы вычесть 6.)
На доске и в тетрадях записывается выражение: (4 + 5) — 6.
Далее на этом и на следующих уроках решаются аналогичные задачи, но с большей долей самостоятельного участия детей.
Позже вводятся составные задачи, в условии которых даны два числа, включающие такие простые: одну на уменьшение числа на несколько единиц, а другую на нахождение суммы, например: «У Тани было 10 карандашей, а у Светы на 2 карандаша меньше. Сколько карандашей было у Тани и Светы вместе?»
Работа над задачами этого вида ведется примерно в том же плане, как и над рассмотренными ранее задачами. Однако перед их введением следует уделить внимание решению задач с двумя вопросами.
В период ознакомлением с составными задачами очень важно добиться различения детьми простых и составных задач. С этой целью надо чаще включать составные задачи в противопоставлении с простыми, выясняя каждый раз, почему одна из них решается одним действием, а другая — двумя. Целесообразно также предлагать детям упражнения по преобразованию простых задач в составные и обратно.
Пример. Учащиеся решают задачу: «На лыжах катались 7 мальчиков, а девочек на 2 меньше. Сколько девочек каталось на лыжах?»
После решения учитель предлагает изменить вопрос задачи так, чтобы задача решалась двумя действиями. (Сколько всего детей каталось на лыжах?).
Полезно включать также упражнения на составление задач:
— аналогичных решенной;
— по данному ее решению;
— по краткой записи и др.
megaobuchalka.ru
Задачи с недостающими данными
3 «В» класс
Тема: «Задачи с недостающими данными»
Задачи уроков:
— формирование умения распознавать задачу с неполными данными, осуществлять
правильную (полную) формулировку задачи, дополняя ее недостающими данными;
— формирование УУД: использование таблиц и схем при решении задач, анализ
условий задач на основе выделения существенных признаков.
Пропедевтика: решение сюжетных задач в несколько действий.
Повторение: решение сюжетной арифметической задачи.
Методы и приемы организации деятельности учащихся: беседа по вопросам учебника,
организация самостоятельной работы учащихся по заданиям учебника.
Учебно-методическое обеспечение: У-2, Т-2, презентация
Вводная часть урока
В школьной библиотеке за день выдаётся 10 книг. Сколько книг будет выдано за неделю?
Школьная библиотека содержит 1 200 книг, а домашняя на 1 000 книг меньше. Сколько книг в домашней библиотеке?
В сельской библиотеке книг в 1 000 раз больше, чем в домашней. Сколько книг в сельской библиотеке?
— Решите задачи устно.
— Какую задачу вы не смогли решить? Почему? (не хватает данных)
— Определите тему и задачи урока
• Учащиеся про себя читают тему урока и формулируют задачи урока
(слайд 2)
Продолжение урока
Задание № 217 (У-2, с. 75)
На доске проиллюстрирована незаполненная таблица:
• Просим учеников прочитать текст задачи и составить краткую запись задачи с недостающими данными в виде таблицы. (слайд 3)
• Предлагаем еще раз назвать условие задачи («Во второй коробке лежало в 2 раза больше конфет, чем в первой») и ее требование («Сколько конфет лежало во второй коробке?»).
• Выясняем, что решить данную задачу невозможно, так как мы не знаем, сколько конфет лежало в первой коробке.
• Предлагаем учащимся самостоятельно дополнить условие задачи. Слушаем ответы учеников (20 конфет, 15 конфет, 30 конфет).
Делаем вывод: ответ задачи будет зависеть от того числа, которое мы зададим, но решение будет одним и тем же. Это задача на кратное сравнение, решение которой находится действием умножения.
• Просим дополнить задачу недостающим данным, заполнив таблицу числом 20.
• Далее учащиеся находят ответ задачи (20 • 2 = (40 к.) — во второй коробке).
• Спрашиваем: почему задачу относят к задачам с недостающими данными?
Ожидаемый ответ: потому что невозможно выполнить требование такой задачи из-за отсутствия необходимых данных.
• Делаем вывод, что задачу, требование которой невозможно выполнить из-за отсутствия необходимых данных, будем называть задачей с недостающими данными, а данные, которыми нужно дополнить условие задачи, будем называть дополнительными данными.
Задание № 218 (У-2, с. 75–76)
• Предлагаем учащимся самостоятельно прочитать три предложенные задачи и выбрать ту, которая будет относиться к задачам с недостающими данными.
Ожидаемый ответ: Миша поймал 15 карасей, а Костя больше. Сколько карасей они поймали вместе?
• Предлагаем доказать, что эта задача с недостающими данными.
Ожидаемый ответ: невозможно выполнить требование этой задачи, так как неизвестно, на сколько или во сколько раз больше поймал карасей Костя.
• Спрашиваем: можно ли дополнить условие задачи недостающим данным? (Да.)
• Слушаем ответы учеников. Останавливаемся на том, что Костя мог поймать на 3 карася больше, чем Миша, или в 2 раза больше, чем Миша.
• Просим учащихся выполнить краткую запись в виде таблицы к полной задаче:
Миша поймал 15 карасей, а Костя — на 3 больше, чем Миша. Сколько карасей они поймали вместе?
Проверяем правильность заполнения таблицы и предлагаем самостоятельно решить задачу по действиям.
Устно проверяем решение задачи с пояснением.
1) 15 + 3 = 18 (к.) — поймал Костя
2) 15 + 18 = 33 (к.) — всего
Ответ: 33 карася.
Задание № 219 (У-2, с. 76)
• Организуем выполнение задания в условиях парной работы.
• Сначала предлагаем учащимся самостоятельно сформулировать задачу с недостающими данными и сделать краткую запись в виде таблицы, а затем дополнить задачу недостающим данным, решить ее и записать ответ.
• Обращаем внимание учащихся на то, что составление задачи можно выполнить по аналогии с заданиями № 217 или 218.
• Учащиеся самостоятельно выполняют задание, а учитель оказывает педагогическую поддержку тем, кому она необходима.
81
Тема: «Задачи с недостающими данными» (2 урока)
Задание № 220 (У-2, с. 76)
• Учащиеся самостоятельно читают задание и объясняют, почему данная задача относится к задачам с недостающими данными.
• Предлагаем ученикам дополнить условие задачи недостающими данными и решить полученную задачу.
• Слушаем ответы учеников и спрашиваем: какие числа нельзя использовать в этой задаче в качестве дополнительного данного?
Ожидаемый ответ: нельзя использовать те числа, которые невозможно разделитьна 2, так как число учащихся студии бального танца в 2 раза меньше, чем в хоровой студии. Кроме того, нельзя брать «нереальные» числа, то есть числа, которые не будут соответствовать действительности. В хоровой студии, как правило, занимается не больше 30–50 человек. Поэтому, если мы придумаем такое дополнительное данное,
как 1000 человек, то найти решение и получить ответ можно. Но ответ не будет соответствовать реальной жизни.
— Приведите пример числа, которое нельзя использовать в этой задаче в качестве числового данного об учащихся хоровой студии. (23, 25, 27, 29 и т. д.)Напоминаем учащимся, что числа, которые не делятся на два без остатка, например 3, 5, 7, 9, 11, 13 и т.д., называются нечетными числами. А числа, которые делятся на два без остатка, например 2, 4, 6, 8, 10, 12 и т.д., называются четными.
Таблица:
Задание № 221 (У-2, с. 76–77) или № 115 (Т-2, с. 50)
• Учащиеся самостоятельно читают задание.
• Выясняем, что значит дополнить запись реально возможными недостающими данными?
Ожидаемый ответ, к которому мы придем в результате совместных поисков: дополнить запись задачи реально возможными недостающими данными означает, что надо подобрать такие данные, которые соответствуют действительности. Например, пешеход за один день не может пройти столько, сколько он может проехать на машине. Но исходя из того что во 2-й день туристы прошли 20 км, в другие дни они могут пройти примерно столько же.
• Даем время на выполнение задания. Слушаем ответы учеников, записываем один из вариантов в таблицу.
Резервные задания
Задание № 222 (У-2, с. 77)
• Учащиеся самостоятельно читают задание и устно выполняют его.
• Слушаем ответы учащихся и одобряем правильные. Предлагаем свой вариант задачи: в школьную столовую привезли 50 кг яблок, а груш — в 3 раза больше. Сколько килограммов яблок и груш привезли в школьную столовую?
– Далее ученики самостоятельно в тетрадях оформляют решение, вычисление и ответ задачи.
Задание № 223 (У-2, с. 77), задание № 116 (Т-2, с. 50)
• Предлагаем учащимся рассмотреть круговую схему и дополнить задачу недостающими данными, обращая внимание на величину «метр».
• Слушаем ответы. Спрашиваем: почему данные должны быть меньше 500 м?
Ожидаемый ответ: решение предусматривает действие вычитания. Поскольку уменьшаемое 500, вычитаемое должно быть меньше 500 м. Останавливаемся на величине 300 м и вычисляем значение разности (200 м).
• Исходя из того что 200 м — это данные второй круговой схемы, дополняем вторую схему еще одной величиной, например, 400 м.
Иллюстрируем схему на доске.
• Просим учащихся по этим данным сформулировать текст возможной задачи.
• Примерный текст задачи: на складе было 500 м проволоки. Продали 300 м проволоки. На следующий день на склад привезли еще 400 м проволоки. Сколько метров проволоки стало на складе?
• Предлагаем ученикам решить задачу по схеме и записать ответ.
Рефлексия Итог урока
— Как вы поняли тему? Оцените свою работу на уроке.
Домашняя работа
Задание № 117 (Т-2, с. 50)
• Обращаем внимание учеников на то, что недостающее данное в этой задаче может быть только четным числом
Задание № 118 (Т-2, с. 51)
83
Тема: «Как получить недостающие данные» (1 урок)
• Далее можно предложить учащимся самостоятельно оформить решение задачи.
Учитель оказывает педагогическую поддержку тем учащимся, кому она необходима.
Задание на дом: № 119–120 (Т-2, с. 51) — после первого урока; № 230, 293 (У-2, с. 80,
101) — после второго урока.
Задания, которые не были выполнены на уроке:
infourok.ru
Решение задач с недостающими данными
Тема урока: Задачи с недостающими данными. 3 класс
Цель
формирование умений распознавать задачи с недостающими данными, преобразовывать их условие; Знакомство, получать недостающие данные из различных источников.
Задачи
совершенствовать вычислительные навыки, знания таблицы умножения
закреплять умение решать текстовые задачи;
учить работать с текстами, получать недостающие данные из различных источников
формировать коммуникативные способности;
формировать чувство дружбы, ответственности;
развивать навыки самостоятельной работы;
развивать информационную культуру учащихся;
развивать познавательный интерес к предмету
Личностные: Учить уважать и принимать чужое мнение, если оно обосновано, находить решение и обосновывать его, способность принимать самостоятельные решения
Познавательные: познакомить учащихся с новым видом задач: задачи с недостающими данными;
учить дополнять условие задачи с недостающими данными; Регулятивные: формировать умение формулировать и удерживать учебную задачу при работе с учебником;
формировать умение выделять и формулировать то, что усвоено, определять качество и степень усвоения
Коммуникативные: формировать умение формулировать собственное мнение и позицию; строить понятные для других высказывания;
Ход урока
I Организационный этап.
Какое у вас настроение перед уроком? Поздоровайтесь и поделитесь улыбкой с гостями. Я хочу, чтобы в такой доброй и приятной атмосфере проходил наш урок.
Вам нравится математика? Чем? И не забываем, что математика
Очень строгая наука
Очень точная наука
Интересная наука
И так начнём.
II Актуализация знаний
а) (запись на доске)
42 | 32 | 17 | 9 | 23 | 12 | 41 | 13 | 21 | 28 | 19 | 34 |
А | Ч | М | З | Р | А | И | С | Д | А | И | Р |
-Выпишите в тетрадь только те числа, которые есть среди ответов в «Таблице умножения»
(Дети выписывают числа 42,32,9,12,21,28)
б) – На следующей строке расположите выписанные числа в порядке возрастания, расшифруйте слово, которое есть в теме нашего урока.
(В тетрадях запись)
9 | 12 | 21 | 28 | 32 | 42 |
З | А | Д | А | Ч | А |
в) — Вспомните, из каких частей состоит задача. Выберите таблички с нужными словами, расположите их по порядку.
(На доске таблички со словами: ответ, высказывание, условие, текст, заголовок, решение, вопрос (требование). Дети выстраивают на доске схему)
задача
условие |
вопрос |
решение |
ответ |
г) – Что значит «решить задачу?» (Выполнив необходимые действия, дать ответ на поставленный вопрос)
Хоть ты смейся, хоть ты плачь,
Не люблю решать задач.
Потому что нет удачи
На проклятые задачи.
Может быть, учебник скверный
Может быть, таланта нет?
Не могу открыть секрет:
Как задаче дать ответ…
Вы умеете решать задачи? Решите задачи на карточках (работа в парах).
III Постановка цели и задач урока.
— Какая пара решила все задачи? Какая задача не получается? Почему?
— А задача ли это? (Да, в ней есть части задачи) Почему же вы не можете её решить?
— Чему же мы должны сегодня научиться? (Как узнавать такие задачи, как их называть, как их решать)
Тема урока и задачи
IV Первичное усвоение новых знаний.
С.68 №142
— Кто нашёл название этих задач? (зачитывается тема урока «Задачи с недостающими данными»)
— На какое слово следует обратить внимание? («с недостающими») Как вы его понимаете?
— Какие рекомендации даёт вам учебник? (составить краткую запись) Можно ли это сделать?
V Первичная проверка понимания. (работа в группах)
Работа по распознаванию и преобразованию задач с недостающими данными
а) Через 45 дней будет Новый год.
б) У одной кормушки 25 воробьёв, у другой – на 6 меньше. Сколько воробьёв у второй кормушки?
в) Сколько тебе лет?
г) Бабушка испекла пирожков с капустой на 4 больше, чем с мясом. Сколько всего пирожков испекла бабушка?
д) На ёлке висят 10 красных, 7 синих и 4 жёлтых шара. Сколько красных и синих шаров висит на ёлке?
Найдите среди текстов задачи. Среди задач – задачу с недостающими данными. Преобразуйте, то есть дополните её в группе, самостоятельно решите, сверьте.
IV Первичное закрепление (разные способы добавления данных)
Данные добавляем коллективно, решаем самостоятельно
Длина нашего класса 9 метров.
Чему равна площадь нашего класса?
В нашем классе 15 мальчиков. Кого больше в классе, девочек или мальчиков и на сколько?
Индийский или африканский слон тяжелее и на сколько?
VI Д/З с.70 №146 (1,2)
VII Рефлексия.
Итог.
Закончите предложения на карточках:
«1.У любой задачи есть _____________ , _____________, решение и ответ. (условие, вопрос или требование). 2. Если при составлении краткой записи в виде таблицы хотя бы один из столбцов остаётся незаполненным, то это задача с _____________________данными. (недостающими) 3.Чтобы решить задачу с недостающими данными, следует эти данные _____________ (дополнить)». |
Я не понял…
Мне было интересно…
Я узнал…
Самооценка. ( красный, жёлтый, зелёный)
videouroki.net
ПНШ 3 класс. Математика. Учебник № 2, с. 97
Задачи с избыточными данными
Ответы к с. 97
287. Реши задачу. Вычисли и запиши ответ.
Маша нашла 30 белых грибов. Это оказалось на 10 больше, чем нашёл Миша, но на 10 меньше, чем нашёл папа. Втроём они нашли белых грибов в 3 раза больше, чем нашла Маша.
Сколько белых грибов они нашли втроём?
Все ли данные будут использованы при решении данной задачи? Назови данные, которые будут лишними.
Почему данная задача относится к ЗАДАЧАМ С ИЗБЫТОЧНЫМИ ДАННЫМИ?
При решении задачи можно использовать данные, насколько Маша нашла грибов больше и меньше, чем Миша и папа, или данные, что втроём они нашли в 3 раза больше грибов, чем Маша. В зависимости от решения одни из этих данных не будут использованы и будут являться избыточными, то есть не нужными при решении задачи. Задачи с данными, которые не используются при решении, но соответствуют условию задачи, называются задачами с избыточными данными.
а) 1) 30 — 10 = 20 (г.) — нашёл Миша
2) 30 + 10 = 40 (г.) — нашёл папа
3) 30 + 20 + 40 = 90 (г.)
О т в е т: втроём они нашли 90 грибов.
При этом решении не учитываются данные о том, что втроём они нашли в 3 раза больше грибов, чем Маша.
б) 30 • 3 = 90 (г.)
О т в е т: втроём они нашли 90 грибов.
При этом решении не учитываются данные о том, что Маша нашла грибов больше и меньше, чем Миша и папа. Как видно, это решение задачи наиболее рациональное — задача решается в одно действие.
288. Сформулируй условие, в котором будут присутствовать все данные из следующей таблицы:
| Грузовые автомашины | Легковые автомашины | Всего | |
| В гараже | 15 | 17 | 32 |
| На стоянке | 10 | 8 | 18 |
Какое требование нужно добавить к твоему условию, чтобы получить задачу с избыточными данными?
Реши задачу со следующим требованием: «Сколько всего автомашин стояло в гараже и на стоянке?». Можно ли решить эту задачу, используя только два данных числа из таблицы? Реши задачу, не используя данные из последнего столбика таблицы.
В гараже было 15 грузовых и 17 легковых автомашин — всего 32 машины, а на стоянке находилось 10 грузовых и 8 легковых автомашин — всего 18 машин. Сколько всего автомашин находилось в гараже и на стоянке?
(15 + 17) + (10 + 8) = 50 (а.)
О т в е т: всего было 50 автомашин.
Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.
Математика. 3 класс. Чекин А.Л.
ПНШ 3 класс. Математика. Учебник № 2, с. 97
5 (100%) от 3 голосующихe-razumniki.ru
Математика. Решение задач с недостающими данными
Тема: «Решение задач. Как получить недостающие данные»
Цель: знакомство с возможностями получения недостающих данных из различных источников при решении задач
Задачи
Образовательная:
совершенствовать вычислительные навыки;
закреплять умение решать текстовые задачи;
повторить нумерацию чисел;
учить работать с текстами, таблицами, получать недостающие данные из различных источников
Воспитательная:
прививать любовь к родному краю;
воспитывать бережное отношение к природе;
формировать коммуникативные способности;
формировать чувство дружбы, ответственности;
Развивающая:
развивать навыки самостоятельной работы;
развивать информационную культуру учащихся;
развивать познавательный интерес к предмету
Оборудование: ПК, компьютерная презентация, карточки с названиями районов Кемеровской области, тексты для работы в группах, измерительная линейка, атлас Кемеровской области
ХОД УРОКА
1. Организационный момент урока.
Уч.- Здравствуйте, ребята! Настроены ли Вы на работу? Все ли принадлежности приготовлены к уроку? Тогда в добрый путь! Я думаю, что урок у нас будет интересным и плодотворным.
2. Актуализация знаний
Уч.- Мы продолжаем работать над решением задач. Определите, где записаны задачи, а где просто текст? (слайд 2)
а) В одной коробке лежало 12 конфет, а во второй в 2 раза больше конфет, чем в первой. Сколько конфет лежало во второй коробке?
б) В одной коробке лежало 12 конфет. А в другой 24 конфеты.
в) Во второй коробке лежало в 2 раза больше конфет, чем в первой. Сколько конфет лежало во второй коробке?
Д.- Под буквой б)
Уч.- Почему?
Д.- Нет вопроса.
Уч.- А какую задачу мы не сможем решить? Почему?
Д.- Под буквой в) Мы не знаем, сколько конфет лежало в первой коробке.
Уч. – Дополните условие задачи так, чтобы ее можно было решить.
( Работа в парах. Взаимопроверка.)
3. Работа над новым материалом
Уч.- Представьте, что перед нами стоит задача узнать, сколько линолеума потребовалось при ремонте нашего класса. Как нам это сделать?
Д.- Мы должны вычислить площадь пола в классе.
Уч. — Какие данные мы должны знать?
Д.- Длину и ширину класса.
Уч. А как мы можем их получить?
Д.- Измерить, спросить у кого-нибудь.
Уч.- Давайте произведем необходимые замеры. Итак, длина класса 8 м., ширина – 5 м. Можем сейчас вычислить площадь? Запишите решение в тетрадь.
(Проверка полученного результата)
Уч.- А если нам нужно сравнить площади Кемеровской области и Новокузнецкого района? Можем ли мы получить данные при помощи измерения?
Д.- Нет. Можно воспользоваться данными из атласа Кемеровской области. Площадь Кемеровской области 95 600 кв.км, площадь Новокузнецкого района 13 290 кв.км
Уч. – Вычислите, на сколько кв.км площадь Новокузнецкого района меньше?
Д.- на 82 310 кв.км
Уч. — Кроме Новокузнецкого района в состав Кемеровской области входит еще 18 районов. Все они примечательны уникальными природными ландшафтами — горный рельеф с порожистыми реками, тайга (слайд 3), сменяются равнинным пейзажем в центральной части области. (слайд 4)
4. Динамическая игра (слайд 5)
Уч. — Расположите карточки с названиями районов в порядке возрастания их площади. Какой рациональный способ выполнения этой работы вы можете предложить?
(Выслушать все ответы детей. Один из возможных вариантов: упорядочить величины сначала по классу тысяч, а потом по классу единиц)
Гурьевский — 2 390 кв.км (п)
Ленинск-Кузнецкий — 2 400 кв.км (р)
Юргинский — 2 520 кв.км (и)
Топкинский — 2 690 кв.км (р)
Яйский — 2 760 кв.км (о)
Промышленновский — 3 080 кв.км (д)
Беловский — 3 300 кв.км (н)
Яшкинский — 3 480 кв.км (о)
Прокопьевский — 3 500 кв.км (е)
Тяжинский — 3 540 кв.км (б)
Ижморский — 3 580 кв.км (о)
Чебулинский — 3780 кв.км (г)
Кемеровский — 4 391.кв. км (а)
Мариинский — 5 580 кв.км (т)
Крапивинский — 6 930 кв.км (с)
Междуреченский – 7 250 кв.км (т)
Тисульский — 8 060 кв.км (в)
Таштагольский — 11 320 кв.км (о)
Новокузнецкий — 13 290 кв.км (уголь)
(Дети по очереди выходят к доске и выставляют карточки с названиями районов в порядке возрастания величин.. Для проверки переворачивают карточки – у них должно получиться предложение: «Природное богатство — уголь.»
5. Работа с задачами
Уч. — Природа щедро наградила своими богатствами Кузнецкую землю. Основное природное богатство Кузбасса — уголь — добывается в 6 районах.
На территории Новокузнецкого района располагаются более 30 месторождений каменного и бурого угля, 5 месторождений железа, 4 месторождения глин, 14 – подземных пресных вод, 1 — подземной минеральной воды. (слайд 6)
Уч.- Составьте задачу на кратное сравнение и решите ее.
Д.- На территории Новокузнецкого района располагаются более 30 месторождений каменного и бурого угля, и 5 месторождений железа. Во сколько раз больше (меньше) месторождений угля, чем железа?
Уч. – Все ли данные вы использовали в таблице? Почему?
Д.- Нет, для составления задачи на кратное сравнения нам потребовались не все данные
Уч. — Запишите решение задачи.
(Проверка результата)
Уч. — Но не только полезными богатствами славится наш край. Разнообразен также растительный и животный мир. В Кемеровской области водится около 450 видов позвоночных животных, в том числе 68 видов млекопитающих (слайд 7), более 300 видов птиц (слайд 8), 6 рептилий (слайд 9), 5 амфибий (слайд 10) и 42 вида рыб (слайд 11). Большинство из них издревле обитали здесь. Но за последние десятилетия в районах крупных промышленных центров Кузбасса значительно сократился видовой состав фауны, значительно сократилась плотность расселения птиц, млекопитающих. Некоторые виды птиц полностью покинули прежние гнездовья. Как вы думаете, чем это вызвано?
Д.- Неразумная деятельность человека, загрязнение окружающей среды, вспашка земель, браконьерство, вырубка лесов, осушение болот.
6. Работа в группах
Уч . — Я предлагаю разделиться на группы. Каждая группа получит листочек с текстом. Это статья из газеты «Кузнецкий рабочий» Вам нужно узнать, на сколько сократилась, а может быть и увеличилась численность того или иного вида животных по сравнению с 1994 годом. Все недостающие данные вы найдете в предложенной статье (Приложение 1)
(Дети заполняют таблицы. (Приложение 2) Производят необходимые вычисления. Результаты вывешиваются на доске).
Уч. – Какой можно сделать вывод?
Д. – Уменьшилось число зайцев и рысей, зато увеличилось число лосей и соболей.
Уч. — А с чем это связано?
Д. – Человек стал заботиться о животных, оберегать их
Уч. – К сожалению, время нашего урока подходит к концу. Мы с вами решили много задач, но ни разу не открыли учебник. Вспомните, где мы находили данные для вычислений?
Д. — Измеряли длину и ширину класса, искали в атласе Кемеровской области, находили данные в статье, для первой задачи придумали сами.
7. Домашнее задание
Уч.- Я хочу добавить, что данные можно найти, просто наблюдая за тем, что происходит вокруг. Поэтому дома решите задачу № 228 на с.79 и составьте похожую по своим наблюдениям. А на следующем уроке самые интересные мы попробуем решить.
Рефлексия.
Уч. — Посмотрите на слайд. Вспомните все этапы нашего урока и закончите предложения:
сегодня я узнал…
было интересно…
было трудно…
я понял, что…
теперь я могу…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
ПРИЛОЖЕНИЕ 1
В Кемеровской области идёт «перепись» охотничьих животных
Среда, 18 января 2012 «Кузнецкий рабочий»
Сейчас на территории Кемеровской области, по данным учёта 2010 года, числится около 3 000 лосей, около 4 000 сибирских косуль, более 2 200 медведей, 3 500 красных лисиц, 28 000 зайцев, 242 рыси, 7 500 соболей, более 80 000 глухарей и тетеревов.
Существует несколько методик оценки численности животных, но, по словам специалистов, самая надёжная из них – работа со следами животных. Поэтому и проводится учёт зимой: по пересечению следов выбранного маршрута на снегу высчитываются все необходимые данные. В это время года легче определить видовой состав животных, а также их количество в связи с тем, что все они собираются у мест кормления.
Проходя по намеченному маршруту, наблюдатели отметят в учётной карточке или на схеме маршрута все появившиеся следы, с указанием вида и количества представителей животного мира, их оставивших. Кстати, специалист может по следам определить не только вид и количество зверя, но и то, как именно животное существовало в этот момент – охотилось или, наоборот, пыталось спастись от опасных хищников.
ПРИЛОЖЕНИЕ 2
1994 год
2010 год
Лоси
2 700
_________________________________________________
1994 год
2010 год
Зайцы
40 000
_________________________________________________
1994 год
2010 год
Рыси
250
_________________________________________________
1994 год
2010 год
Соболи
6 8000
_________________________________________________
ЛИТЕРАТУРА
ЧекинА.Л., Математика: 3 кл.: Учебник: В 2 ч. – М., Академкнига/Учебник, 2009 — 160с.
Чекин А.Л. Математика: 3 кл.: Методическое пособие – М., Академкнига/Учебник, 2009 – 240 с.
Кемеровская область. Атлас для школьников. / Под ред. В.Н. Гнатишина и др. – Новосибирск: Просвещение-регион, 2002. – 30 с.
Кузнецкий рабочий. 2012. 18 янв.
Мониторинг охотничье-промысловых млекопитающих [Электронный ресурс]: http://www.biodat.ru, (дата обращения: 18.04.2012).
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Учащиеся знакомятся с различными способами получения недостающих знаний, которые позволяют сделать формулировку задачи полной, т.е. такой, из которой можно получить ответ на поставленное требование. В качестве таких способов рассмотрено два основных.
К первому способу отнесены такие действия, которые связаны с непосредственным получением недостающих данных путем счета или измерения (например, подсчетом ящиков, которые привезли на склад — задача № 228, или измерение длины и ширины пола классной комнаты).
Ко второму способу отнесены все действия, которые заключены в получении необходимой информации из дополнительных источников (в данном случае из справочной литературы, средств массовой информации, от знающих эту информацию людей и т.д.).
Это направление работы над задачей очень тесно связано с формированием умения правильно формулировать задачи на основе анализа некоторой реальной ситуации. Овладение именно этим умением позволяет говорить о практической направленности данного урока: в реальной жизни постоянно приходится сталкиваться с ситуациями, которые требуют преобразования их в сюжетные арифметические задачи с последующим решением. В виде готового текста задачи существуют лишь в учебниках, но не в реальной жизни.
Другое направление работ над задачей связано с формированием умения производить отбор необходимых данных из их избыточного перечня.
Выбор рационального способа решения — это еще одно из направлений, отрабатываемых на уроке. Рационализм выбранного пути решения может проявляться в минимализации числа выполняемых для получения ответа действий.
Работа по обучению решению задач проводится практически на каждом уроке. [2[
infourok.ru
ПНШ 3 класс. Математика. Учебник № 2, с. 76
Задачи с недостающими данными
Ответы к с. 76
219. Сформулируй задачу с недостающими данными. Сделай для неё краткую запись в виде таблицы. Предложи соседу по парте дополнить её недостающими данными, решить задачу, вычислить и записать ответ.
Проверь, правильно ли выполнены твои указания.
В зоомагазине волнистых попугайчиков в 2 раза меньше, чем ара, а неразлучников на 10 больше, чем ара. Сколько всего попугаев в зоомагазине?
| Волнистые | Ара | Неразлучники | Всего | |
| Количество попугаев | ? В 2 раза меньше → | ? ← На 10 п. больше | ? |
Дополнительное условие задачи: а ара — 30 попугаев.
| Волнистые | Ара | Неразлучники | Всего | |
| Количество попугаев | ? В 2 раза меньше → | 30 | ? ← На 10 п. больше | ? |
1) 30 : 2 = 15 (п.) — волнистых
2) 30 + 10 = 40 (п.) — неразлучников
3) 15 + 30 + 40 = 85 (п.)
О т в е т: всего 85 попугаев.
220. Объясни, почему следующая задача относится к задачам с недостающими данными.
В студии бального танца занималось в 2 раза меньше учащихся, чем в хоровой студии. Сколько учащихся занималось в студии бального танца?
Дополни задачу недостающими данными о числе учащихся хоровой студии.
Реши полученную задачу. Вычисли ответ.
Приведи пример числа, которое нельзя использовать в этой задаче в качестве числового данного об учащихся хоровой студии.
Данную задачу решить нельзя. Не хватает данных для составления выражения. Неизвестно сколько учащихся занималось в хоровой студии.
В хоровой студии занималось 40 учащихся.
40 : 2 = 20 (у.)
О т в е т: в студии бального танца занималось 20 учащихся.
Нельзя использовать число 1 и любое другое нечётное число.
221. Дополни в тетради краткую запись реально возможными недостающими данными.
| В 1-й день | Во 2-й день | В 3-й день | Всего | |
| Прошли туристы | ? На 6 км меньше → | 20 км | ? ← На 16 км больше | ? |
Ответы к заданиям. Математика. Учебник. Часть 2. Чекин А.Л. 2013 г.
Математика. 3 класс. Чекин А.Л.
ПНШ 3 класс. Математика. Учебник № 2, с. 76
5 (100%) от 1 голосующихe-razumniki.ru
Урок математики на тему «Задачи с избыточными данными»
МБОУ« Цивильская средняя общеобразовательная школа № 1 им. М. В.Силантьева»
Открытый урок математики
«Задачи с избыточными данными»
(программа ПНШ, 3-В класс)
Учитель начальных классов
Викторова Елена Борисовна
г. Цивильск, 2017
Тема урока: «Задачи с избыточными данными»
Задачи урока:
— формирование умения распознавать избыточные данные в формулировке задачи;
— формирование понимания того, что избыточные данные позволяют выбрать оптимальный вариант решения задачи;
— формирование УУД : поиск рациональных путей решения задач практического содержания
Ход урока:
1.Организационный момент
Чтоб урок наш стал светлее,
Мы поделимся добром.
Вы ладони протяните,
В них любовь свою вложите,
И с друзьями поделитесь
Вы друг другу улыбнитесь.
2. Слайд 1
Наши герои Маша и Миша предлагают начать наш урок с геометрической разминки. Назовите фигуры, которые вы видите на доске. Назовите лишнюю фигуру. (параллелепипед, круг)
— Какие величины мы можем измерить у оставшихся фигур? (длину и ширину сторон, периметр, площадь)
— Как найти периметры фигур? Соедините фигуру с подходящей формулой
— Из 3 фигур назовите лишнюю. (четырёхугольник)
Слайд 2
— Как найти площадь оставшихся фигур – квадрата, прямоугольника?
3. – А теперь Маша и Миша предлагают вам решить некоторые задачи
Слайд 3 Длина стороны квадрата 8 см. Найдите площадь и периметр квадрата.
(Самостоятельное решение).
Р = 8 · 4 = 32 (см)
S= 8 · 8 = 64 (см2)
Ответ: 32 см, 64 см2
Длина стороны прямоугольника 8 см. Найдите площадь и периметр прямоугольника. (Нельзя решить. Задача с недостающими данными)
(Подбор данных и решение. 1 ученик решает задачу у доски.
Например: Р = (8 + 5) · 2 = 26 (см)
S= 8 · 5 = 4 0(см2)
Ответ: 26 см, 40 см2
Слайд 4
Площадь прямоугольника 36 кв. см Длина прямоугольника 9 см, ширина 4 см. Найдите периметр данного прямоугольника. (Задача с избыточными данными)
— Все ли данные будут использованы при решении задачи ? Какие данные необходимы для вычисления периметра прямоугольника? (длина и ширина прямоугольника)
(Работа с задачей – удаляем по очереди разные данные и решаем задачи с помощью выражений.)
Р = (9 + 4) · 2 = 26 (см)
— Возможно ли удалить другое данное и решить задачу? Попробуйте это сделать.
Дети читают получившуюся задачу:
Площадь прямоугольника 36 кв. см Длина прямоугольника 9 см. Найдите периметр данного прямоугольника
(36 : 9 + 9) · 2 = 26 (см)
Можно записать решение по действиям:
36 : 9 = 4 (см) – ширина прямоугольника
4 * 2+ 9 * 2 = 26 см
4. Сформулируйте тему нашего урока: Задачи с избыточными данными
— Как вы понимаете слово «Избыточные»? ( такие данные , которые не используются при решении задач)
а) Найдите значение выражения и узнаете страницу учебника , по которой мы будем работать.
(180 · 5 + 35 · 2) : 10 = 97 (выражение записано на доске).
б) Работа с задачей, её решение. Учебник с. 97 № 287
— Прочитайте задачу. Все ли данные будут использованы при решении данной задачи? ( Для решения задачи достаточно знать, что Маша собрала 30 белых грибов, а втроём они нашли нашли в 3 раза больше, то есть 90 грибов).
— Назовите ЛИШНИЕ данные.
Запись выражением:
1 вариант: 30 · 3 = 90
Ответ: 90 грибов.
— А если удалить эти данные, и оставить другие (Отношения « на 10 грибов меньше и на 10 грибов больше»), то как можно решить эту задачу?
2 вариант решения:
30 -10 = 20 (гр.) — нашёл Миша
30 + 10 = 40 (гр.) – нашёл папа
30 + 20 + 40 = 90 (гр.) –всего
Ответ: 90 грибов всего.
— Как проверить данное решение?
в) Применение избыточных данных при решении практических задач
— Как вы думаете, пригодятся ли нам эти знания в жизни ? Откройте учебник на с.101, № 294
— Рассмотрите таблицу. Какие данные в ней представлены? Нам нужно купить только хлеб и молоко. Данные о стоимости сметаны для нас избыточные.
— В магазинах, железнодорожных кассах очень много данных о цене товаров и билетов, но мы выбираем только те, которые нам нужны для решения определённой конкретной задачи.
г) Работа в группах
 — Рассмотрите таблицу. Обсудите в группе – какая информация, представленная в данной таблице, является избыточной для нахождения искомого?
— Рассмотрите таблицу. Обсудите в группе – какая информация, представленная в данной таблице, является избыточной для нахождения искомого?
— Исключите избыточные данные. Сделайте два-три варианта такой таблицы. По каждой таблице сформулируйте задачу.
( Каждая группа вывешивает на доску варианты таблицы)
— Сформулируйте задачу по каждой таблице.
Проверка.
Решение одной задачи двумя способами.
1 сп. 1) Сколько книг во 2 шкафу?
250 + 25 = 275 (к)
2) Сколько книг в 3 шкафу?
250 + 15 = 265 (к)
3) Сколько книг в 3 шкафах?
250 + 275 + 265 = 790 (к)
Ответ: 790 книг.
— Как проверить данное решение?
2 сп. 1) Сколько книг в 3 шкафах, если в них книг поровну?
250 · 3 = 750 (к)
2) Сколько всего книг в 3 шкафах?
750 + 25 + 15 = 790 (к)
Ответ: 790 книг.
— Как проверить данное решение?
5. Итог урока. Рефлексия.
— С каким видом задач вы познакомились сегодня на уроке?
Я предлагаю закончить предложения:
— На уроке я узнал(а)…
— Мне было интересно …
— Сегодня я похвалил(а) бы себя за …
— Сегодня я сумел(а) …
— Мне было трудно …
— У меня пока не получилось…
— Заполните лесенку успеха (слайд 7)
Домашнее задание: № 288 –с.97 учебника
infourok.ru





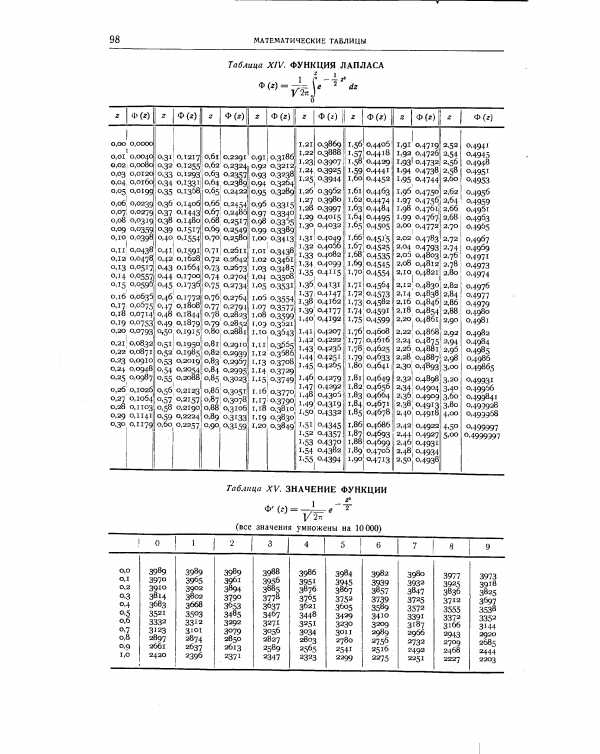
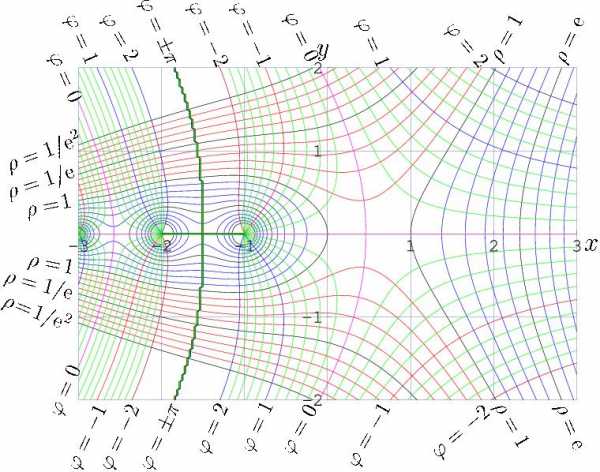 Амплитуда и фаза факториала комплексного аргумента.
Амплитуда и фаза факториала комплексного аргумента. Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом. Начнем с определения: факториалом числа n называется произведение всех натуральных чисел от 1 до числа n включительно. Формула для вычисления факториала записывается так: $$n!=1\cdot 2\cdot 3\cdot …\cdot n$$ Надо еще знать соглашение: 0!=1. Почему факториал нуля равен единице можно спорить до бесконечности. Часто приводится и Гамма функция для объяснений и выражение типа: n!=(n-1)!n, в которое подставляют n=1 и радостно доказывают потом, что: из выражения 1!=(1-1)!1 следует 1=0!. Но на самом деле, это последнее выражение только доказывает, что правильно таки математики договорились считать, что 0!=1 для того, чтобы не нарушались правила вычисления факториала и в формулах не появлялось противоречие. А больше нигде это равенство 0!=1 и не используется. Поэтому и можно было договориться, чтобы не морочить себе голову в будущем. Но не об этом сейчас речь. Нас будет интересовать способ, как быстро (в домашних условиях) и правильно вычислить факториал большого числа. Проблема в том, что для вычисления факториалов больших чисел часто не хватает или памяти или числа знаков, поддерживаемых или калькулятором или компьютером. Ведь результат получается огромным, если число большое. Посмотрите на картинку (кликабельно) — на ней результат вычисления значения 500!. Но, теперь проблема решена — вы можете вычислять факториал от огромных чисел. Зачем только вам это может понадобиться не очень понятно. Ну, например, чтобы удивить вашего учителя или получить оригинальную заставку для вашего телефона. Правда иногда, программистам предлагают такую задачку решить, чтобы они помучились. Теперь все просто — вводите в строку ваше число, набираете восклицательный знак и жмете кнопку «Решить». Пример ввода приведен ниже.
Начнем с определения: факториалом числа n называется произведение всех натуральных чисел от 1 до числа n включительно. Формула для вычисления факториала записывается так: $$n!=1\cdot 2\cdot 3\cdot …\cdot n$$ Надо еще знать соглашение: 0!=1. Почему факториал нуля равен единице можно спорить до бесконечности. Часто приводится и Гамма функция для объяснений и выражение типа: n!=(n-1)!n, в которое подставляют n=1 и радостно доказывают потом, что: из выражения 1!=(1-1)!1 следует 1=0!. Но на самом деле, это последнее выражение только доказывает, что правильно таки математики договорились считать, что 0!=1 для того, чтобы не нарушались правила вычисления факториала и в формулах не появлялось противоречие. А больше нигде это равенство 0!=1 и не используется. Поэтому и можно было договориться, чтобы не морочить себе голову в будущем. Но не об этом сейчас речь. Нас будет интересовать способ, как быстро (в домашних условиях) и правильно вычислить факториал большого числа. Проблема в том, что для вычисления факториалов больших чисел часто не хватает или памяти или числа знаков, поддерживаемых или калькулятором или компьютером. Ведь результат получается огромным, если число большое. Посмотрите на картинку (кликабельно) — на ней результат вычисления значения 500!. Но, теперь проблема решена — вы можете вычислять факториал от огромных чисел. Зачем только вам это может понадобиться не очень понятно. Ну, например, чтобы удивить вашего учителя или получить оригинальную заставку для вашего телефона. Правда иногда, программистам предлагают такую задачку решить, чтобы они помучились. Теперь все просто — вводите в строку ваше число, набираете восклицательный знак и жмете кнопку «Решить». Пример ввода приведен ниже.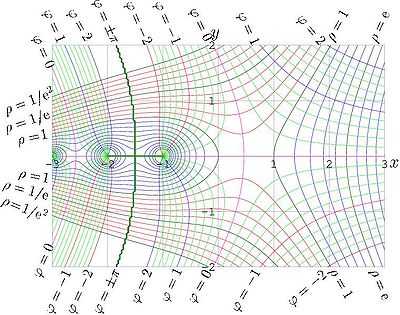









 (1)
(1)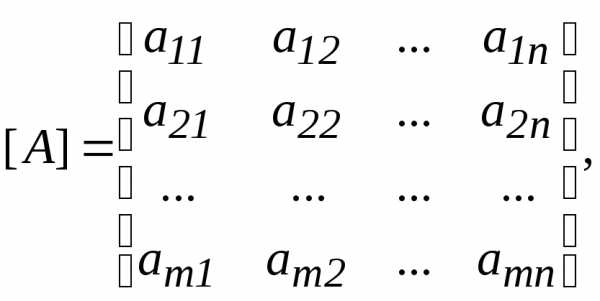
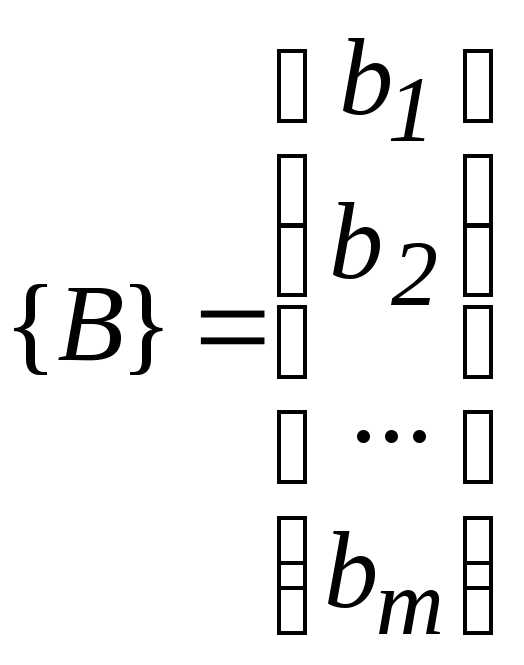 .
.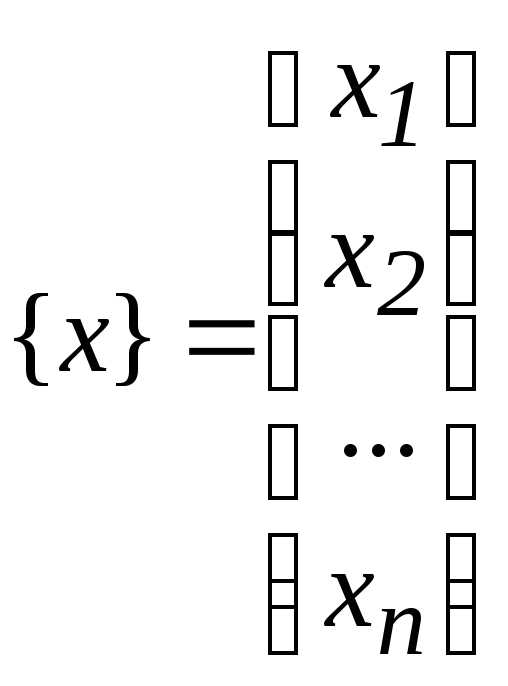 — столбец неизвестных.
— столбец неизвестных. .
. .
.
 .
.
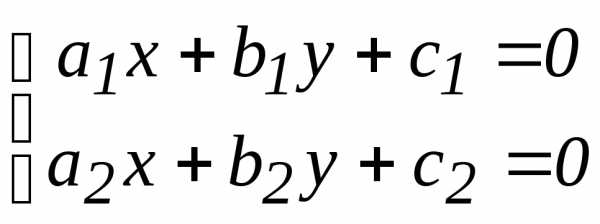 .
.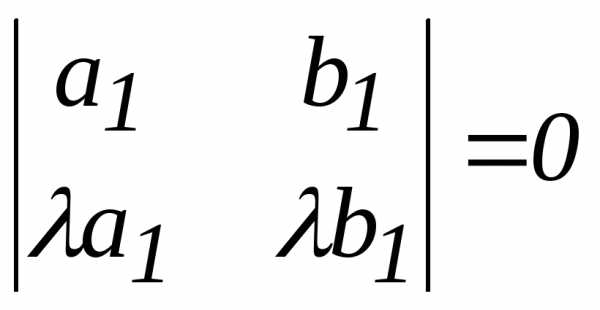 ,
,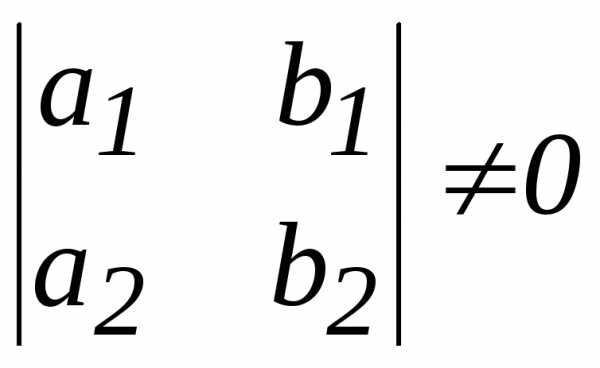 .
Решением этой системы являются координаты
точки пересечения прямых
.
Решением этой системы являются координаты
точки пересечения прямых — определитель
матрицы, получаемой из [A]
заменой i-ого
столбца на столбец свободных
членов:
— определитель
матрицы, получаемой из [A]
заменой i-ого
столбца на столбец свободных
членов: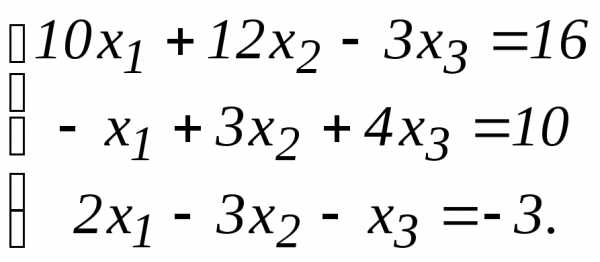

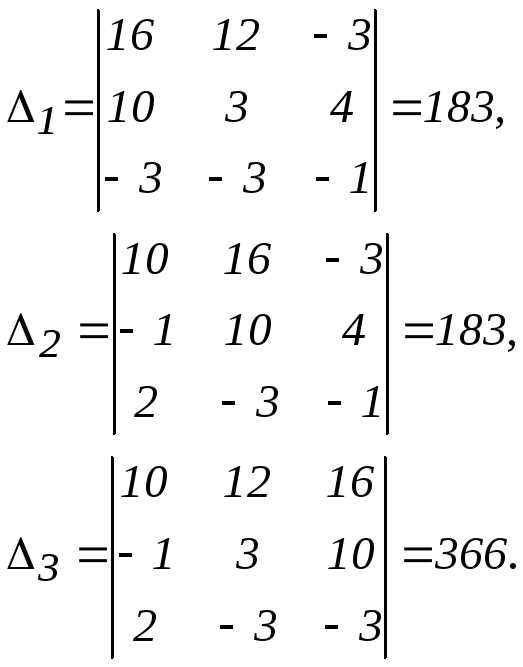
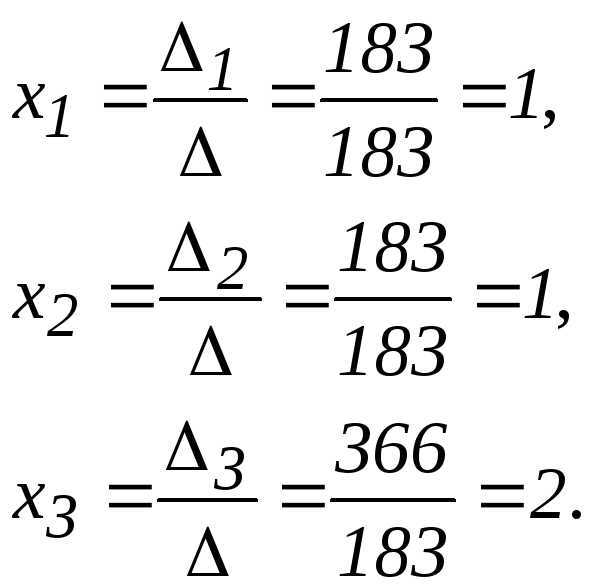
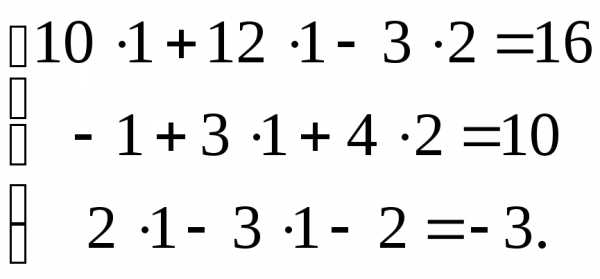
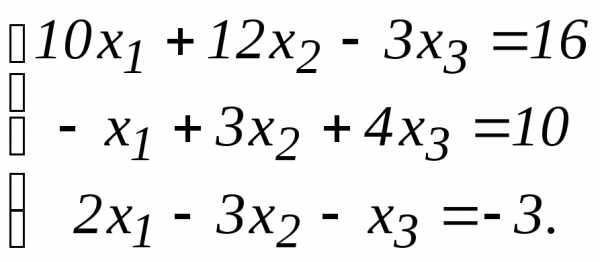
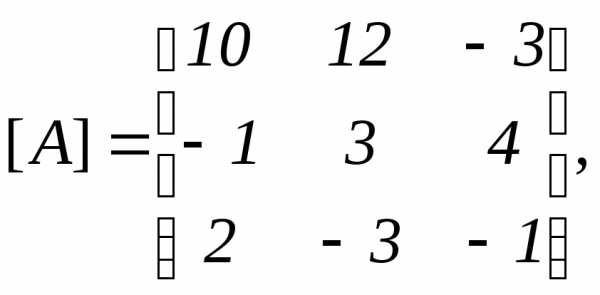 ее определитель detA==183.
ее определитель detA==183.
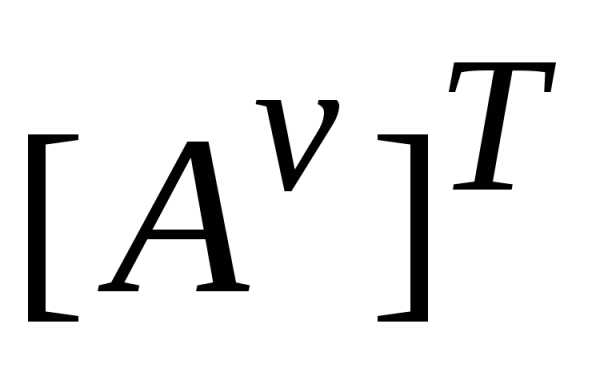 ,
тогда
,
тогда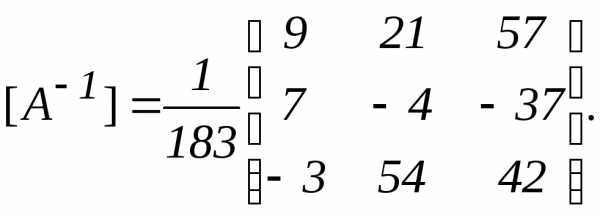
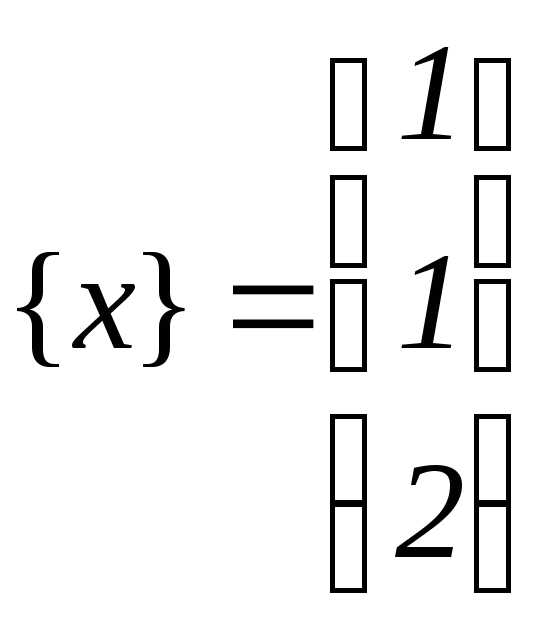 .
.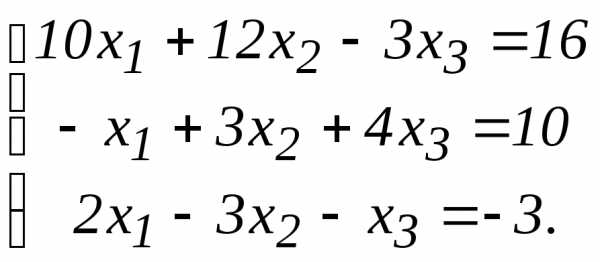
 преобразованной системы стал равен 1,
а коэффициенты
преобразованной системы стал равен 1,
а коэффициенты 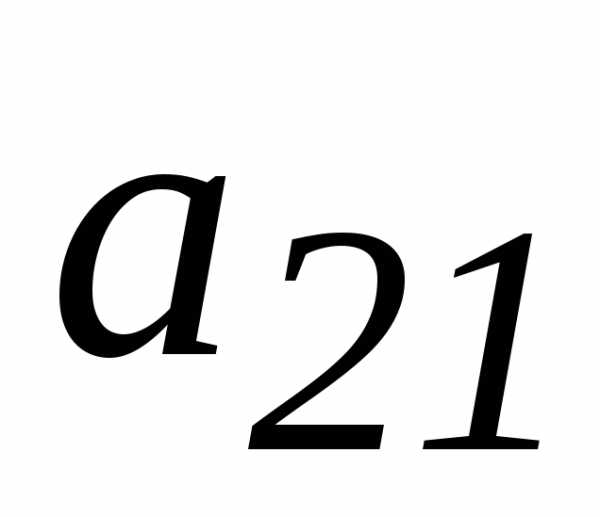 и
и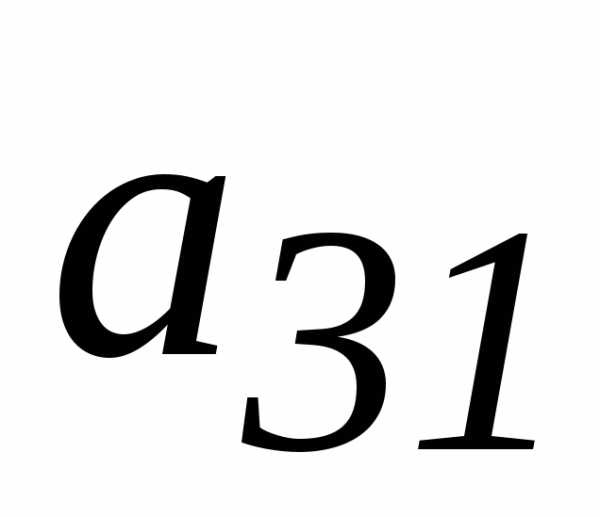 обратились в ноль. Для этого первое
уравнение умножим на1/10,
второе уравнение умножим на 10 и сложим с первым, третье уравнение
умножим на -10/2 и сложим с первым. После этих преобразований
получим
обратились в ноль. Для этого первое
уравнение умножим на1/10,
второе уравнение умножим на 10 и сложим с первым, третье уравнение
умножим на -10/2 и сложим с первым. После этих преобразований
получим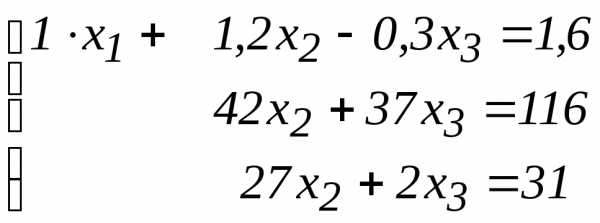
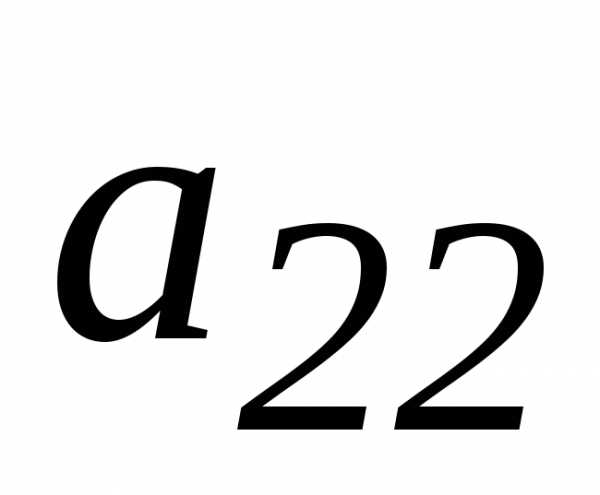 стал равным1,
а коэффициент
стал равным1,
а коэффициент  .
Для этого второе уравнение разделим на 42,
а третье уравнение умножим на -42/27 и сложим со
вторым. Получим систему уравнений
.
Для этого второе уравнение разделим на 42,
а третье уравнение умножим на -42/27 и сложим со
вторым. Получим систему уравнений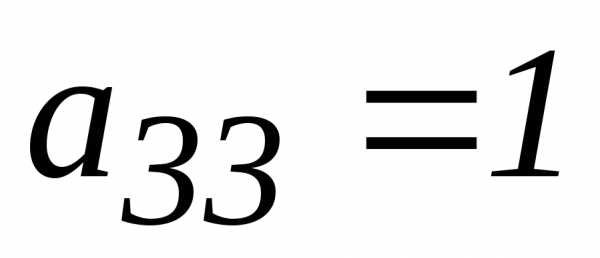 .
Для этого третье уравнение разделим на(37 — 84/27);
получим
.
Для этого третье уравнение разделим на(37 — 84/27);
получим