урок по теме «Тригонометрические тождества»
Урок по теме:
Тригонометрические тождества, 10 класс.
Цели урока:
Деятельностная цель: формирование у учащихся способностей к рефлексии коррекционно-контрольного типа при преобразовании тригонометрических тождеств и реализации коррекционной нормы (фиксирование собственных затруднений в применении основных тригонометрических формул, выявление их причин, поиск выхода из затруднения).
Образовательная цель: коррекция и тренинг изученных понятий.
Задачи урока:
повторить определение синуса, косинуса, тангенса, котангенса числа ;
повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
научить применять полученные знания при упрощении тригонометрических выражений, доказательстве тождеств.
Тип урока: урок рефлексии.
Оборудование: учебники, компьютер, мультимедийный проектор
Ход урока:
Организационный момент, вступительная беседа.
Математический диктант.
Это интересно.
Самостоятельная работа.
Проверка самостоятельной работы
Закрепление знаний и умений.
Подведение итогов урока.
Домашнее задание.
1. Организационный момент.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные тригонометрические формулы. Каждый раз выводить нужную формулу, например, для преобразования тригонометрического уравнения время уйдет достаточно много. Поэтому круг формул, которые необходимо знать, должен быть достаточно широким.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. “Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.
Так вот, давайте сегодня на уроке работать активно, внимательно, будем поглощать знания с большим желанием, ведь они вам пригодятся.
2 Математический диктант ( самопроверка с помощью проектора)
Вариант 1
Синусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
tg α =
sin2 α +cos2 α=
1+ tg2 α=
=
Вариант 2.
1.Косинусом угла α называется _____ точки, полученной поворотом точки______ вокруг начала координат на угол α
ctg α=
tg α∙ ctg α=
1+ ctg2 α=
=
Ответы :
Вариант 1.
Синусом угла α называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
tg α =
sin2 α +cos2 α = 1
1+ tg2 α =
= 1+ ctg2 α
Вариант 2.
Косинусом угла α называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол α
ctg α=
tg α∙ ctg α = 1
1+ ctg2 α=
=1+ tg2 α
Проверка проводится на уроке с выставлением оценок. (правильный ответ – 1 балл).
3. Это интересно. Презентация ученика « Тригонометрия на ладошке»
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.
Тригонометрия на ладошке
Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30° и 45° и приложим вершину нужного угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных пальцев)
Смотрите, я прикладываю угол в 30°; оказывается, это угол
— между мизинцем и безымянным пальцем;
— между мизинцем и средним пальцем — 45°;
— между мизинцем и указательным пальцем — 60°;
— между мизинцем и большим пальцем — 90°;
И это у всех людей без исключения.
Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:
№0 — Мизинец №0 Мизинец 0°
№1 — Безымянный №1 Безымянный
№2 — Средний №2 Средний 45°
№3 -Указательный №3 Указательный 60°
№4 — Большой №4 Большой 90°
n — номер пальца sin a =
Значения синуса и косинуса угла по “ладони” приведено в таблице.
Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки.
Значения синуса № пальца Угол
0 0
1 30°
2 45°
3 60°
4 90°
Значения косинуса № пальца Угол
4 0°
3 30°
2 45°
1 60°
0 90°
4. Самостоятельная работа с взаимопроверкой
1 вариант.
1) 1 — sin α cos α ctg α
2) 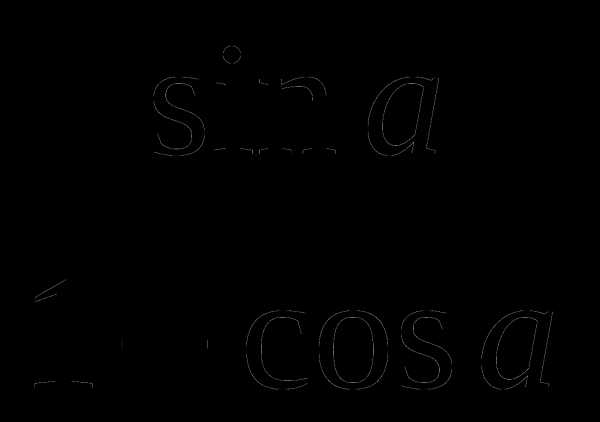 +
+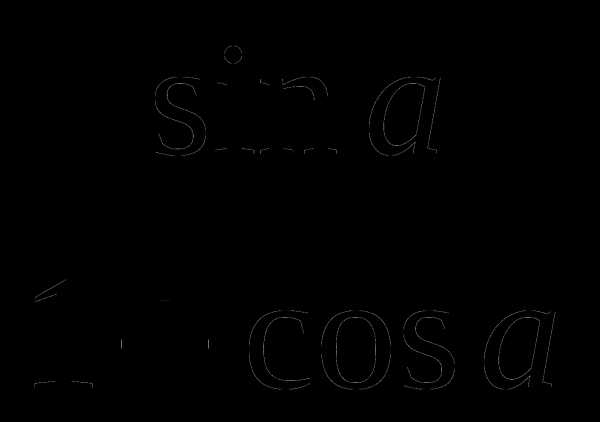
3) (sin a + cos a) 2 — 2 sin a cos a
4) 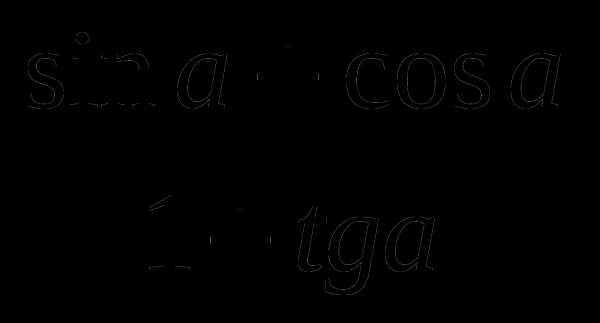
5) +
+ 
2 вариант
1) 1 — sin a cos a tg a
2)  +
+
3) sin4a + cos4a + 2sin2a cos2a
4) 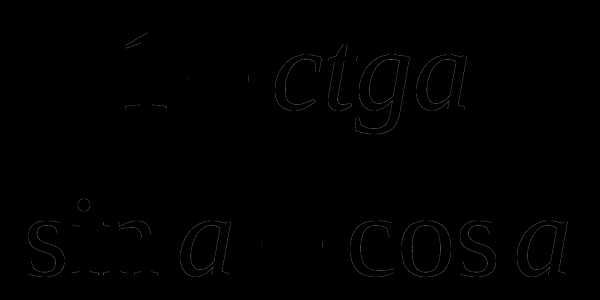
5) 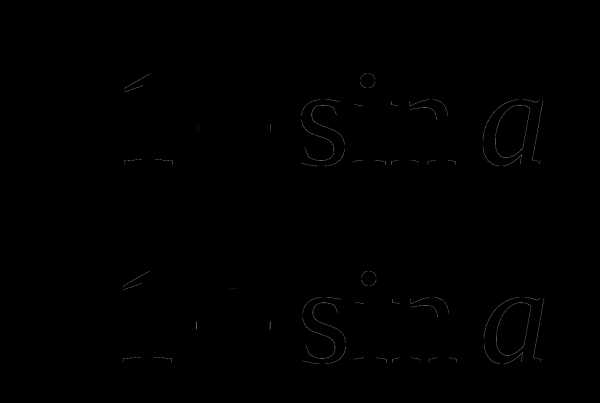 +
+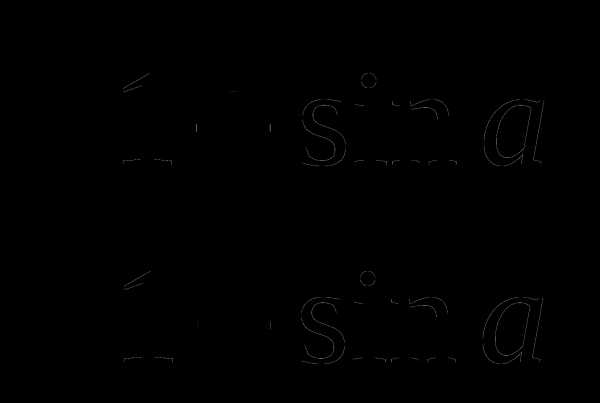
5.Проверка самостоятельной работы (проверка проводится на уроке, оценки выставляются выборочно).
6. Закрепление знаний и умений.
Работа по учебнику № 85(1), 86 (профильный уровень), 88,89 (для интересующихся математикой) с.280
7. Итоги урока.
8. Домашнее задание на доске
стр. 280 № 85 (2), стр.305 №198, стр.280 № 89
Спасибо, урок окончен!
Используемая литература
Колягин Ю.М., Ткачев М.В. и др. Алгебра и начала анализа: учеб. Для общеобразовательных учреждений: базовый и профильный уровни – 4-е изд. – М.: Просвещение, 2008.
МИОО Сборник тестовых заданий для тематического и итогового контроля. Алгебра и начала анализа 10-11 классы. «Интеллект-центр» Москва 2009
Алгебры и начал анализа 10-11: Методические рекомендации к учеб.; кн. для учителя / Г.И.Григорьева- Волгоград: Учитель, 2004.
Дидактические материалы по алгебре и началам анализа для 10 класс/М.И. Шабунин, М.В. Ткачева и др. -2-е изд. — М.: Просвещение, 2007.
Сборники заданий к ЕГЭ 2006, 2013.
infourok.ru
|
| ||||||||||||||||
|
| ||||||||||||||||
| ]2 вариант
|
nsportal.ru
Самостоятельная работа по теме Основное тригонометрическое тождество ВАРИАНТ 1 | Самостоятельная работа по теме Основное тригонометрическое тождество ВАРИАНТ 2 | ||
1 | Вычислить значение выражения 12∙cosα -4,5 . если sinα= | 1 | Вычислить значение выражения 3,5∙sinα-1,5 , если cosα = . |
2 | Вычислить значение выражения 3cos2α- 6 +3sin2α при cosα=-0.3. | 2 | Вычислить значение выражения 5sin2α +0,61 +5 cos2α при sinα= -0.4. |
3 | Вычислить значение выражения 2cos2 α+ 1, при tgα=. | 3 | Вычислить значение выражения 26cos2 α – 1, при tgα=. |
4 | .Упростите: cos2α ∙ tg2α : ( 1- cos2α ) . | 4 | Упростите: sin2α ∙ ctg2α : ( 1- sin2α ) |
5 | Упростите: ( 2+ cosα )∙ ( 2 — cosα) + +( 2- sinα )∙ ( 2+ sinα ) . | 5 | Упростите: ( 3+ cosα )∙ ( 3 — cosα) + +( 3- sinα )∙ ( 3+ sinα ) . |
6 | Упростите: . | 6 | Упростите: . |
7 | Упростите: – . | 7 | Упростите: – . |
8 | Упростите: ( sin α — 2 cos α )2 + 4 sin α cos α | 8 | Упростите: ( 3sinα + 2 cosα)2 — 12sinαcosα |
Самостоятельная работа по теме Основное тригонометрическое тождество ВАРИАНТ 1 | Самостоятельная работа по теме Основное тригонометрическое тождество ВАРИАНТ 2 | ||
1 | Вычислить значение выражения 12∙cosα -4,5 . если sinα= | 1 | Вычислить значение выражения 3,5∙sinα-1,5 , если cosα = . |
2 | Вычислить значение выражения 3cos2α- 6 +3sin2α при cosα=-0.3. | 2 | Вычислить значение выражения 5sin2α +0,61 +5 cos2α при sinα= -0.4. |
3 | Вычислить значение выражения 2cos2 α+ 1, при tgα=. | 3 | Вычислить значение выражения 26cos2 α – 1, при tgα=. |
4 | .Упростите: cos2α ∙ tg2α : ( 1- cos2α ) . | 4 | Упростите: sin2α ∙ ctg2α : ( 1- sin2α ) |
5 | Упростите: ( 2+ cosα )∙ ( 2 — cosα) + +( 2- sinα )∙ ( 2+ sinα ) . | 5 | Упростите: ( 3+ cosα )∙ ( 3 — cosα) + +( 3- sinα )∙ ( 3+ sinα ) . |
6 | Упростите: . | 6 | Упростите: . |
7 | Упростите: – . | 7 | Упростите: – . |
8 | Упростите: ( sin α — 2 cos α )2 + 4 sin α cos α | 8 | Упростите: ( 3sinα + 2 cosα)2 — 12sinαcosα |
www.prodlenka.org
Самостоятельная работа по теме «Тригонометрические тождества» 10 класс.
Самостоятельная работа по теме
«Тригонометрические тождества»
Вариант 1.
1. Вычислить: .
2.Дано:. Найти: 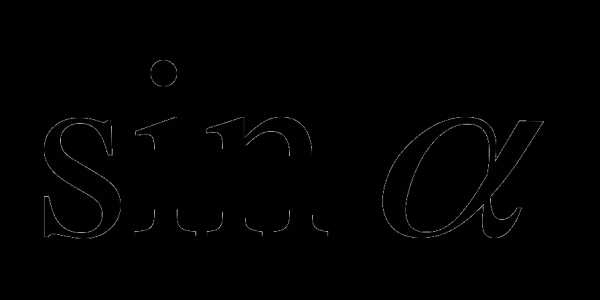 ,
, 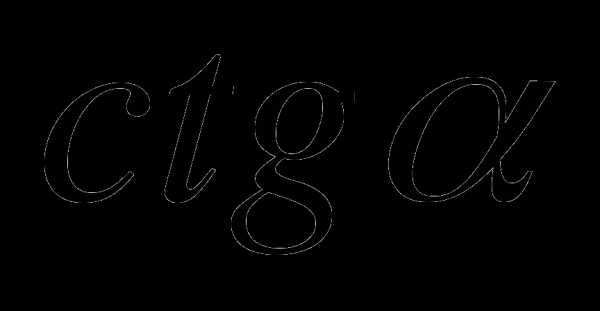 .
.
3.Упростить выражение:  .
.
2. Доказать тождество: .
4. Доказать тождество: 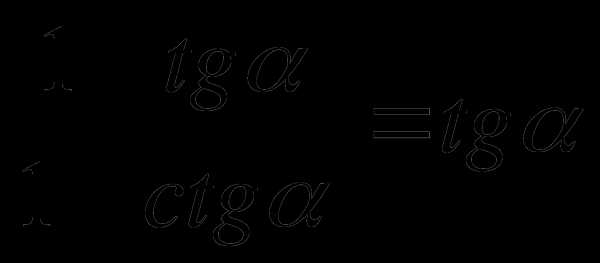 .
.
Вариант 2.
1. Вычислить: .
2. Дано:. Найти:  ,
, 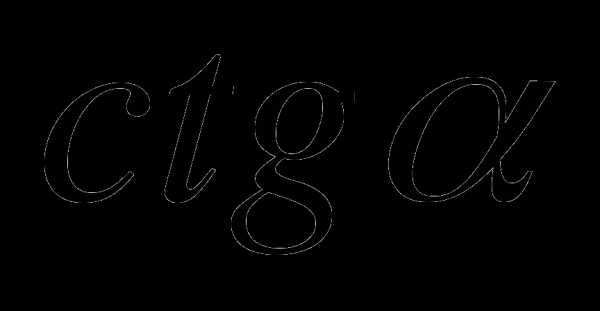 .
.
3.Упростить выражение: .
4. Доказать тождество: .
5. Доказать тождество: .
Самостоятельная работа по теме
«Тригонометрические тождества»
Вариант 1.
1. Вычислить: .
2.Дано:. Найти: 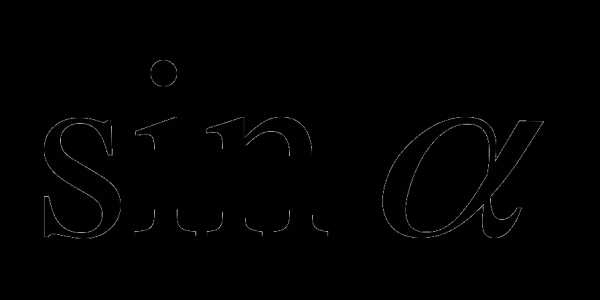 ,
, 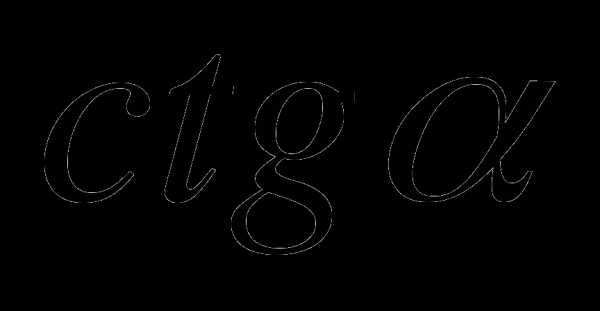 .
.
3.Упростить выражение:  .
.
2. Доказать тождество: .
4. Доказать тождество: 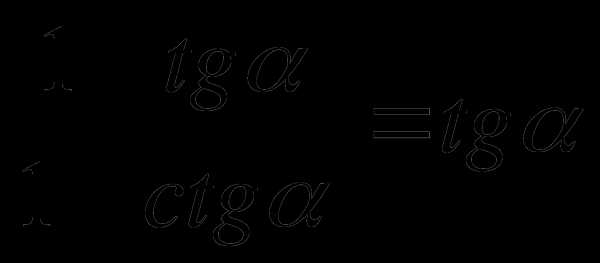 .
.
Вариант 2.
1. Вычислить: .
2. Дано:. Найти: 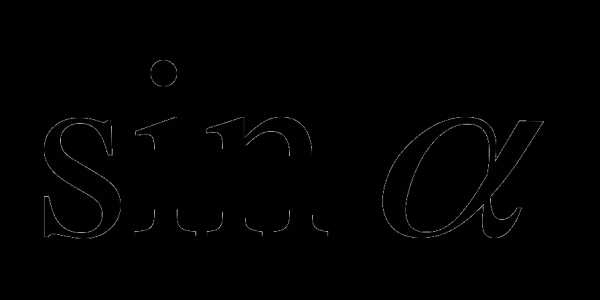 ,
, 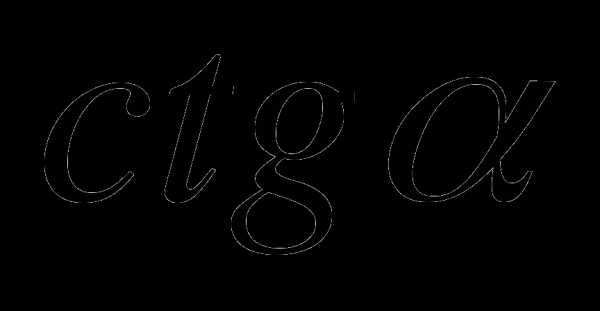 .
.
3.Упростить выражение: .
4. Доказать тождество: .
5. Доказать тождество: .
infourok.ru
Проверочная самостоятельная работа по теме»Основное тригонометрическое тождество»
Проверочная самостоятельная работа
по теме
« Основное тригонометрическое тождество
и следствия из него»
ВАРИАНТ 1
№
ВАРИАНТ 2
1
Вычислить значение выражения
12∙ cos α -4,5 . если
sin α=
1
Вычислить значение выражения
3,5∙ sin α-1,5 , если
cos α = .
2
Вычислить значение выражения
3cos2 α- 6 +3sin2 α
при cos α=-0.3.
2
Вычислить значение выражения
5sin2 α +0,61 +5 cos2 α
при sin α= -0.4.
3
Вычислить значение выражения
2 cos2 α+ 1
при tg α= .
3
Вычислить значение выражения
26 cos2 α — 1
при tg α= .
4
.Упростите:
cos2 α ∙ tg2 α : ( 1- cos2 α ) .
4
Упростите:
sin2 α ∙ ctg2 α : ( 1- sin2 α )
5
Упростите:
( 2+ cos α )∙ ( 2 — cos α) +
+( 2- sin α )∙ ( 2+ sin α ) .
5
Упростите:
( 3+ cos α )∙ ( 3 — cos α) +
+( 3- sin α )∙ ( 3+ sin α ) .
6
Упростите:
.
6
Упростите:
.
7
Упростите:
– .
7
Упростите:
– .
8
Упростите:
( sin α — 2 cos α )2 + 4 sin α cos α
8
Упростите:
( 3sin α + 2 cos α)2 — 12sin α cos α
Проверочная самостоятельная работа предназначена для промежуточного контроля знаний и умений учащихся по указанной теме, для совершенствования полученных навыков. Работа состоит из двух вариантов и содержит разно-уровневые задания.
САМОСТОЯТЕЛЬНАЯ РАБОТА
infourok.ru
Самостоятельная работа по теме «Тригонометрические уравнения» (10 класс)
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
sinx = 0;
2tg3x = 0;
2cosx = 1;
2sin(2x – 4π) =;
cos22x = 2;
1 – sin2x = 0;
2cos2x -5cosx – 3 = 0;
3sin2x + 7cosx – 3 = 0;
2tg23x – 3tg3x + 1 = 0;
(1 – cos2x)(сtg(-2x) +
 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
cosx = 0;
3ctg2x = 0;
2sinx =
2cos(2x – 4 π) = ;
sin4x = 1;
1 – cos2x = 0;
2 + cos2 x — 3 cos x = 0;
2cos2x + 5sinx – 4 = 0;
tg 2 2x – 9 tg 2x + 8 = 0;
(sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 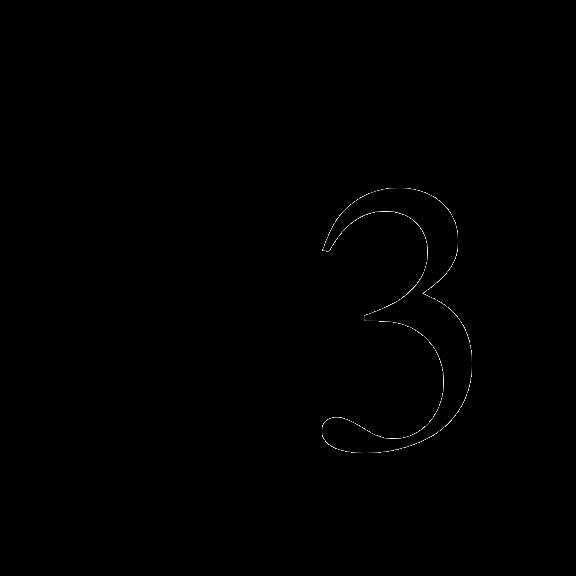 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
3ctg2x = 0;
2sinx =
2cos(2x – 4 π) = ;
sin4x = 1;
1 – cos2x = 0;
2 + cos2 x — 3 cos x = 0;
2cos2x + 5sinx – 4 = 0;
tg 2 2x – 9 tg 2x + 8 = 0;
(sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 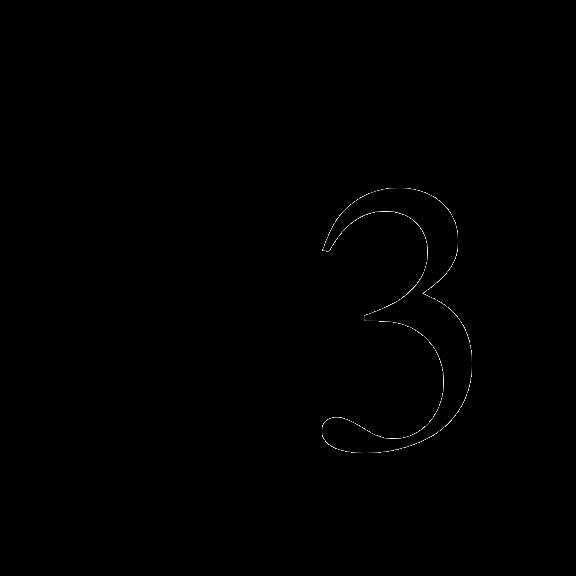 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 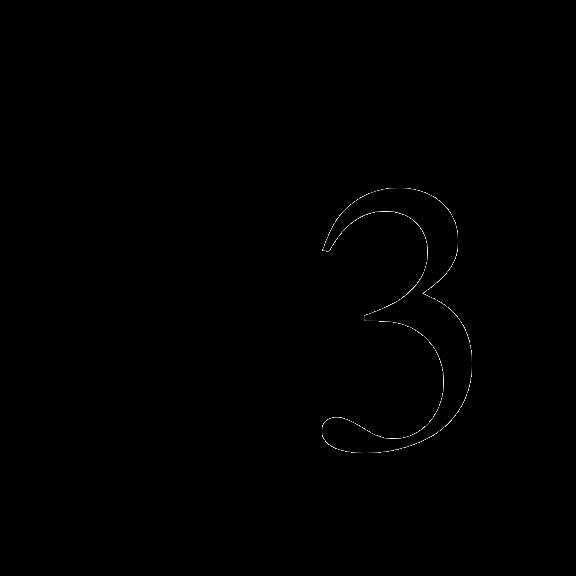 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10.(1 – cos2x)(сtg(-2x) + 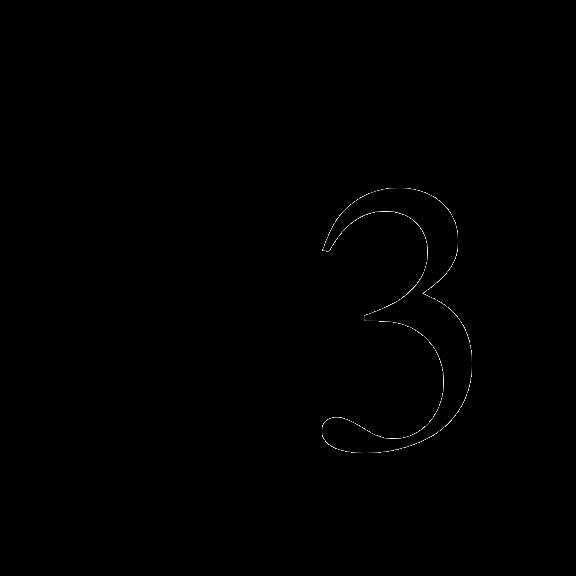 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
1 вариант
1. sinx = 0;
2. 2tg3x = 0;
3. 2cosx = 1;
4. 2sin(2x – 4π) =;
5. cos22x = 2;
6. 1 – sin2x = 0;
7. 2cos2x -5cosx – 3 = 0;
8. 3sin2x + 7cosx – 3 = 0;
9. 2tg23x – 3tg3x + 1 = 0;
10. (1 – cos2x)(сtg(-2x) + 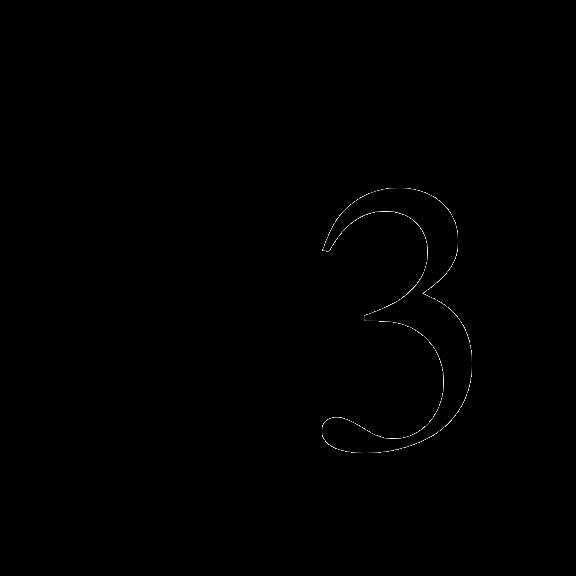 ) = 0.
) = 0.
Самостоятельная работа по теме «Тригонометрические уравнения»
2 вариант
1. cosx = 0;
2. 3ctg2x = 0;
3. 2sinx =
4. 2cos(2x – 4 π) = ;
5. sin4x = 1;
6. 1 – cos2x = 0;
7. 2 + cos2 x — 3 cos x = 0;
8. 2cos2x + 5sinx – 4 = 0;
9. tg 2 2x – 9 tg 2x + 8 = 0;
10. (sinx + 1)(ctg(-2x)–) = 0.
infourok.ru
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
Самостоятельная работа. В.1 | Самостоятельная работа. В.2 |
№1.Найти | №1. Найти |
№2. Найти | №2.Найти |
№3.Найти , если | №3.Найти , если |
videouroki.net



 Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.
Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.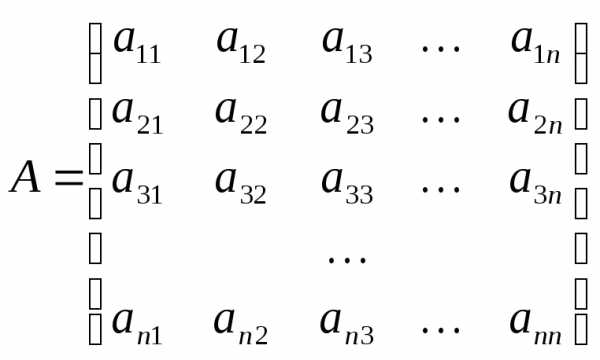
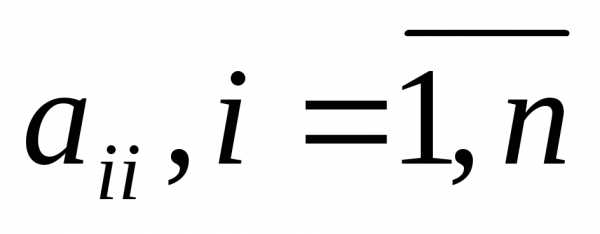

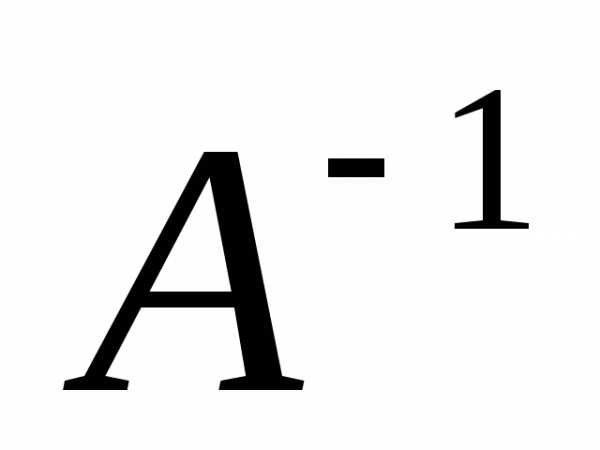
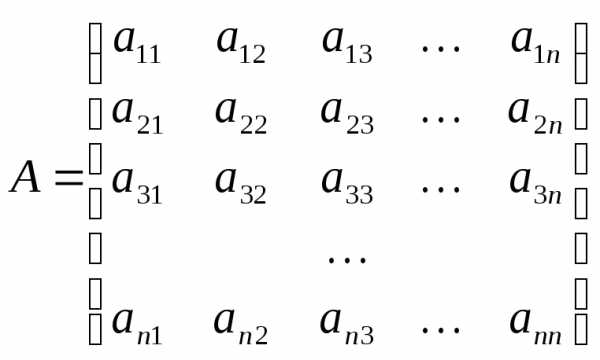 .
.
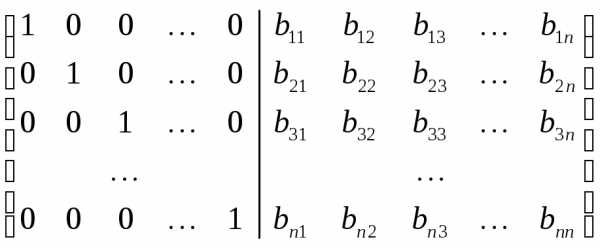
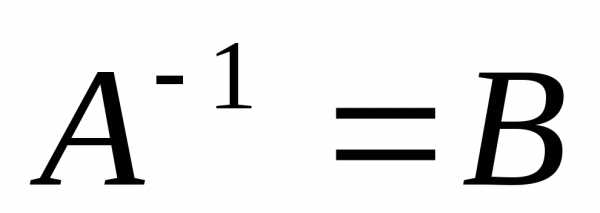 .
.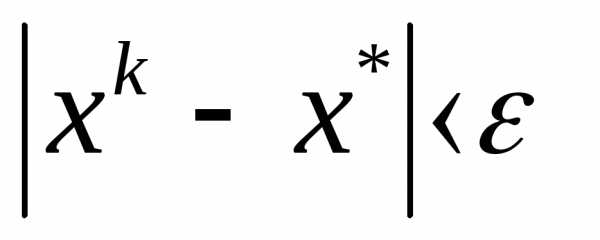 ,где
,где -точные
решения.
-точные
решения.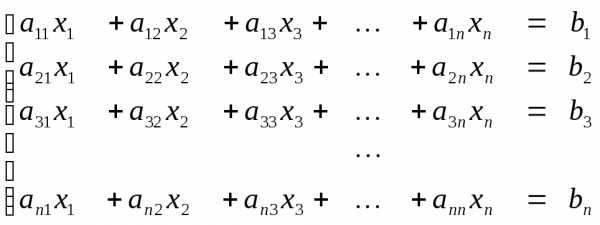
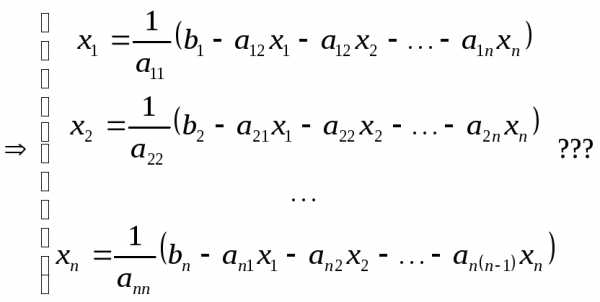
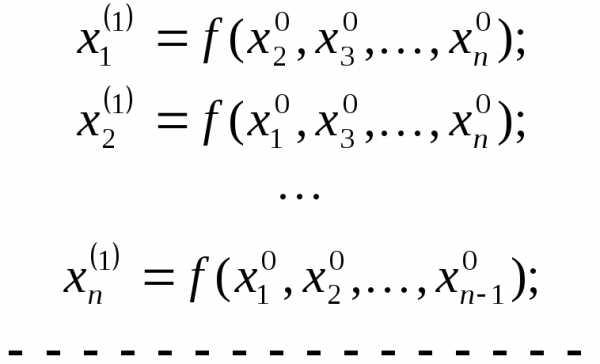
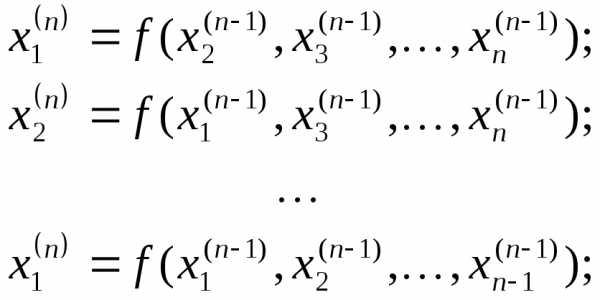
 ,
тогда по схеме Зайделя
,
тогда по схеме Зайделя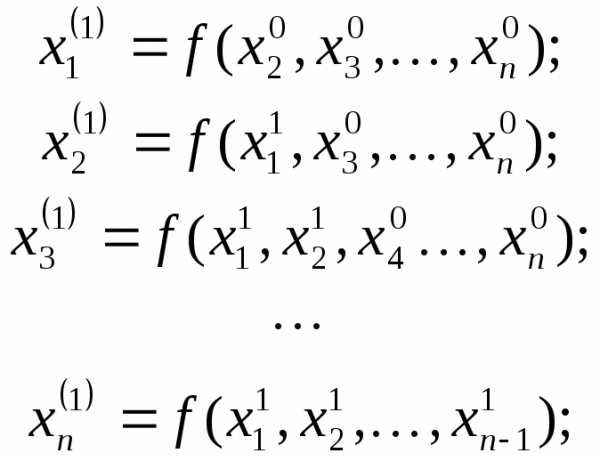
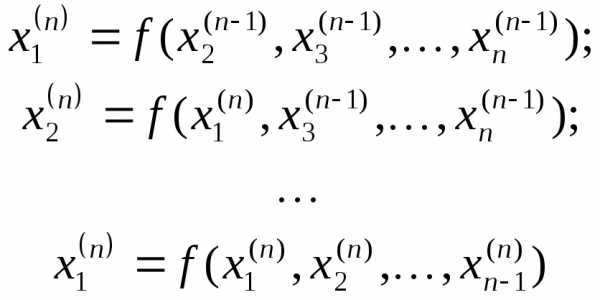

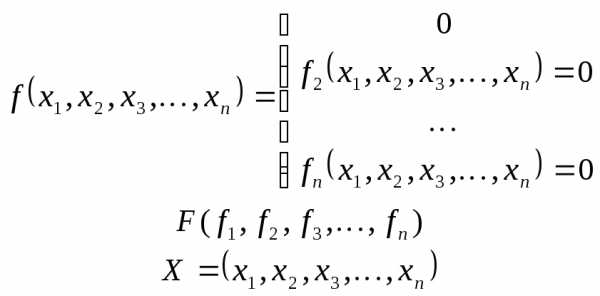
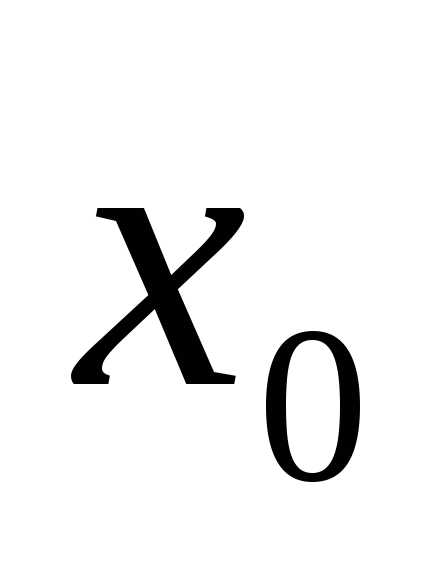
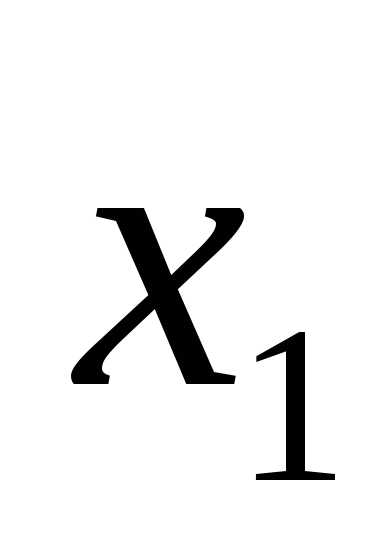
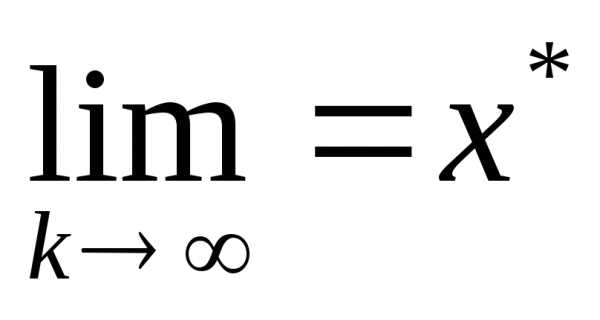

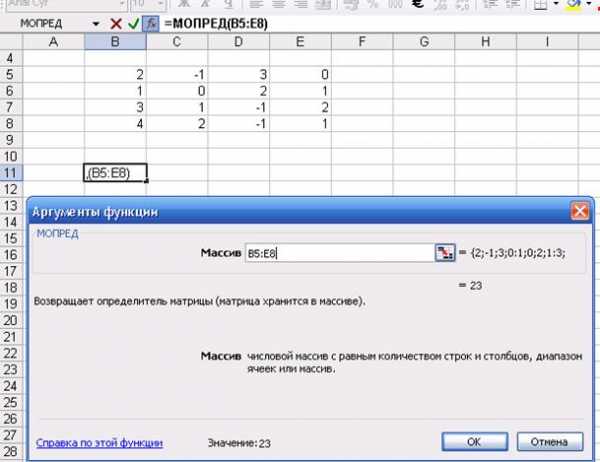
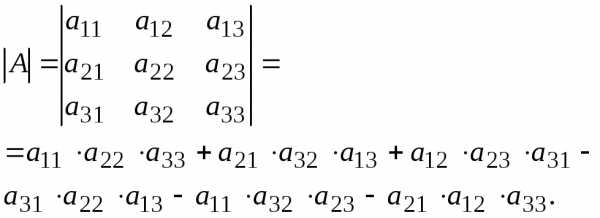

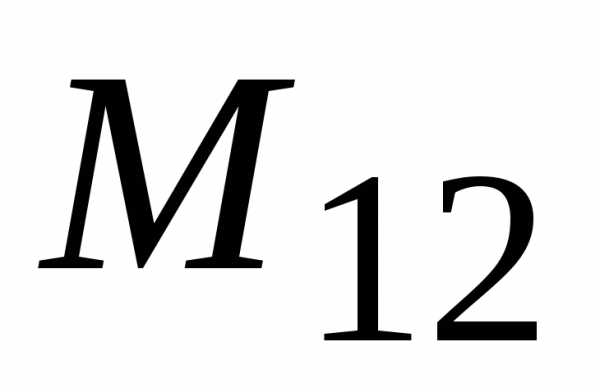 определителя
определителя 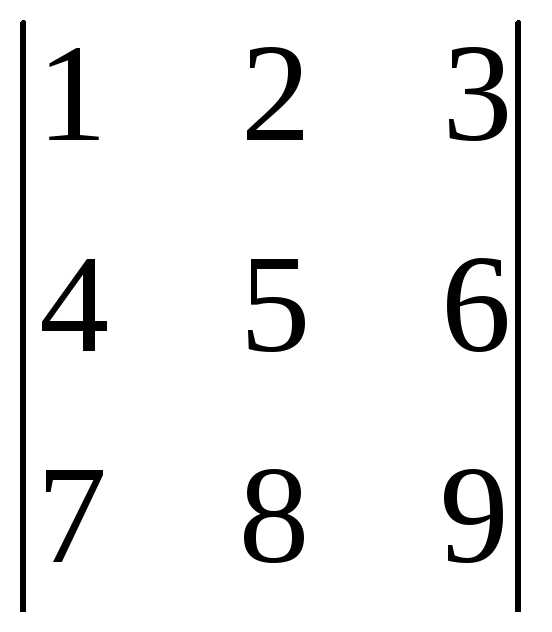 есть.
есть.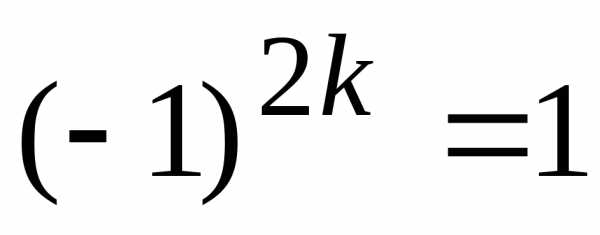 и.
и.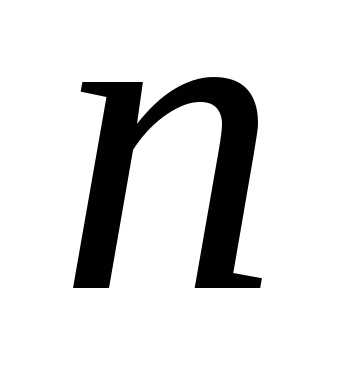 -го
порядка можно свести к вычислению
определителей порядка
-го
порядка можно свести к вычислению
определителей порядка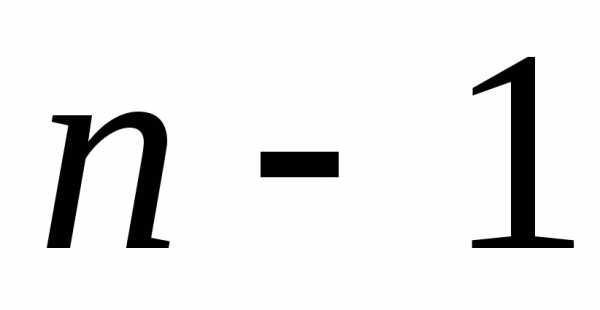 ,
используя следующие формулы.
,
используя следующие формулы.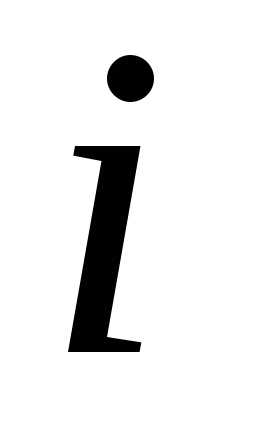 -й
строке:
-й
строке: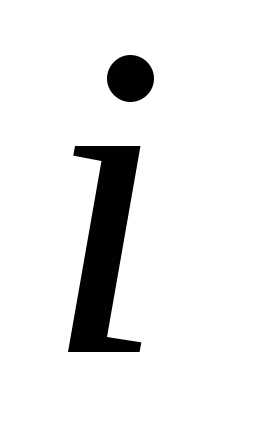 -йстроки на их алгебраические
дополнения.
-йстроки на их алгебраические
дополнения. разложением по первой строке.
разложением по первой строке. -му
столбцу:
-му
столбцу: -го
столбца на их алгебраические дополнения.
-го
столбца на их алгебраические дополнения.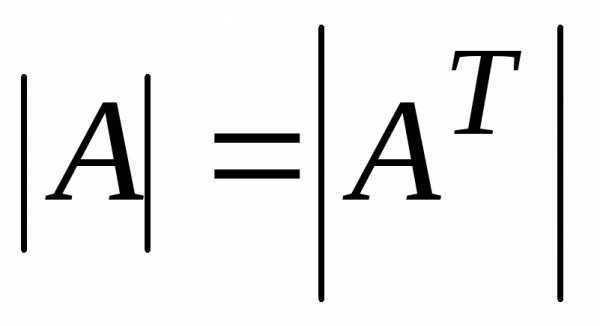 .
.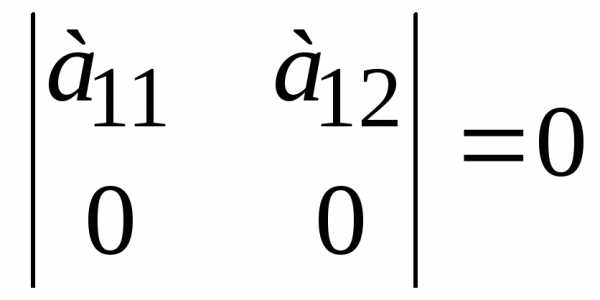 ;
;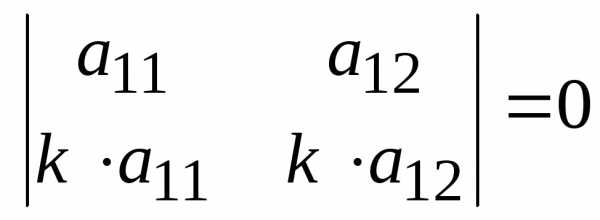 .
.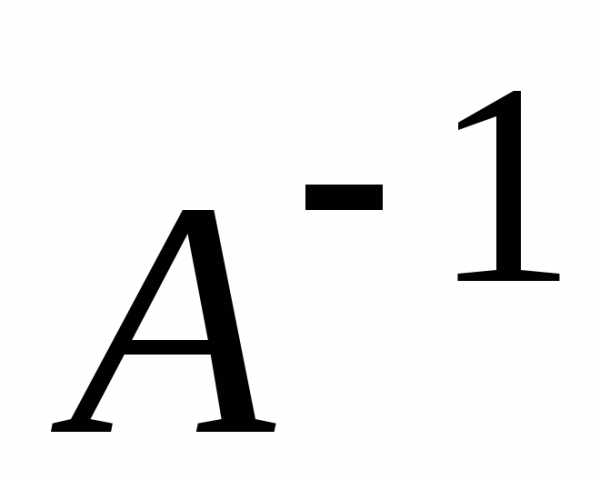 , то
есть .
, то
есть .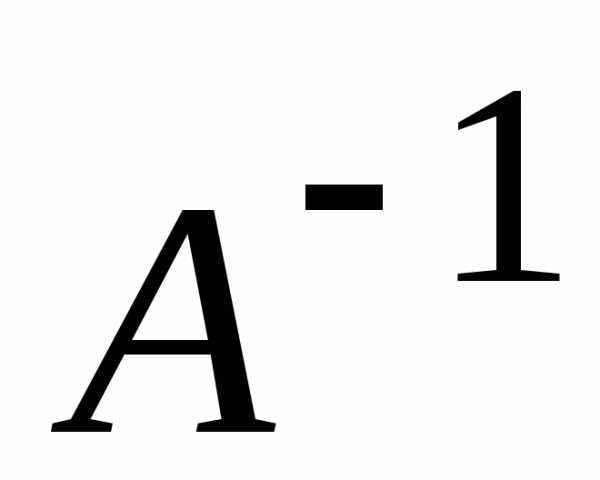 .
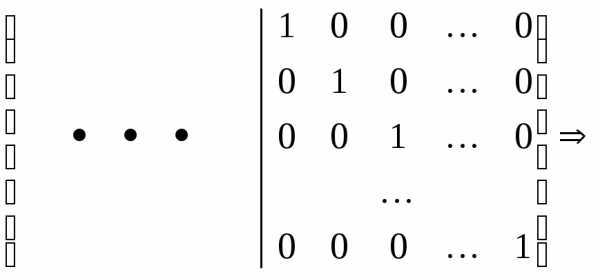
. имела обратную матрицу
имела обратную матрицу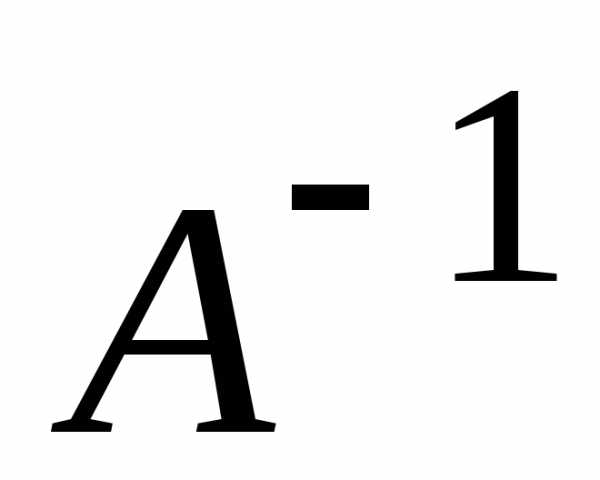 ,
необходимо и достаточно, чтобы определитель
матрицы
,
необходимо и достаточно, чтобы определитель
матрицы был не равен нулю.
был не равен нулю.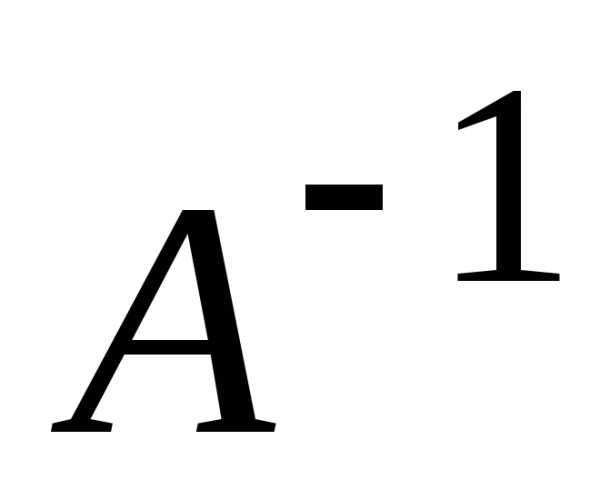
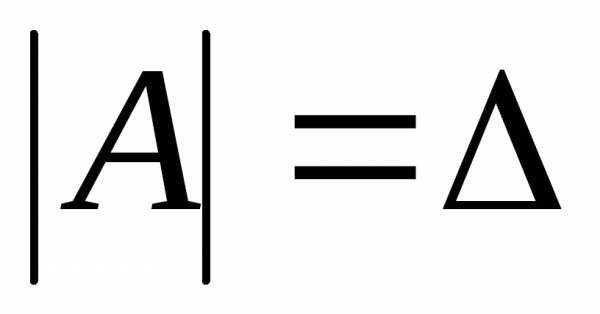 :
если он не равен нулю, то обратная матрица
существует:;
:
если он не равен нулю, то обратная матрица
существует:;  если
равен нулю, то обратной матрицы нет.
если
равен нулю, то обратной матрицы нет. вычисляем его алгебраическое дополнение
вычисляем его алгебраическое дополнение .
.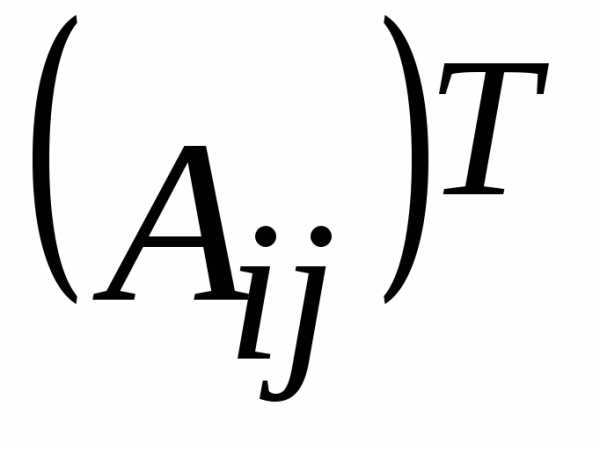 делим на определитель
делим на определитель :
: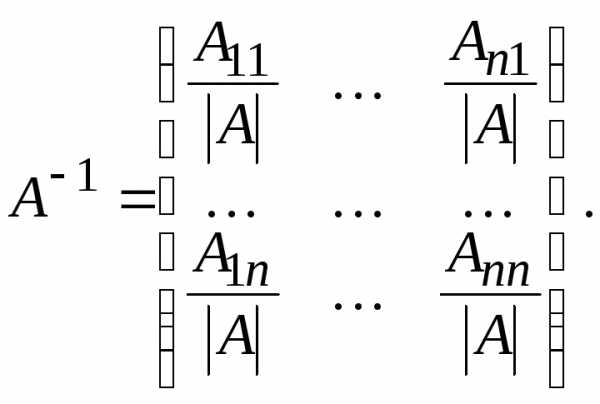 Получаем матрицу, обратную данной.
Получаем матрицу, обратную данной.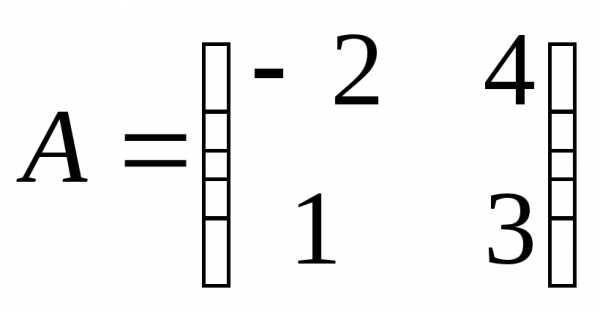 .
Найти обратную матрицу.
.
Найти обратную матрицу.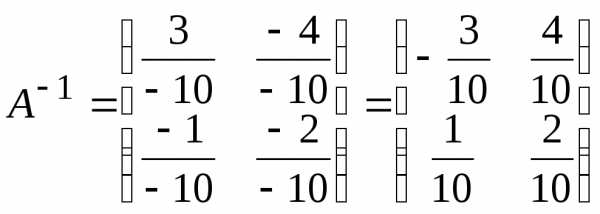
 и
и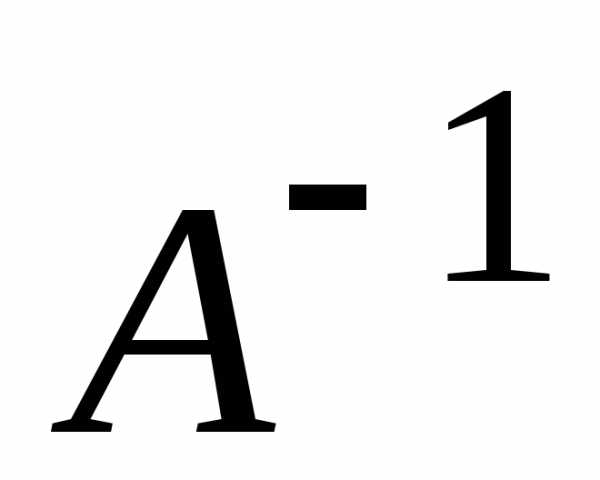 .
.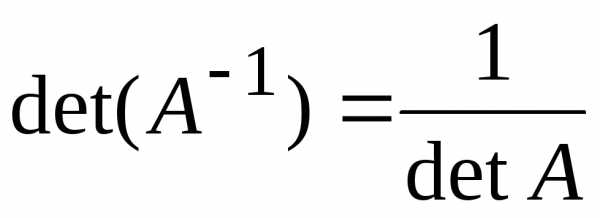 .
.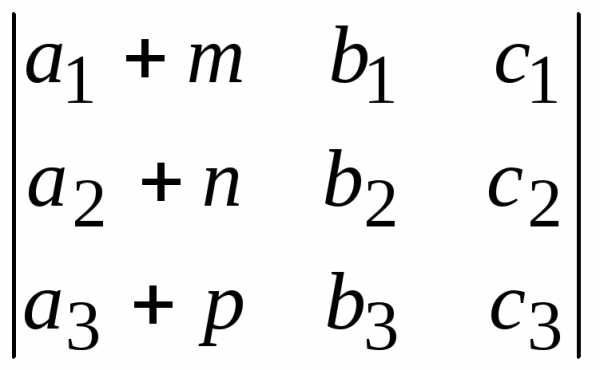 в виде суммы двух определителей.
в виде суммы двух определителей.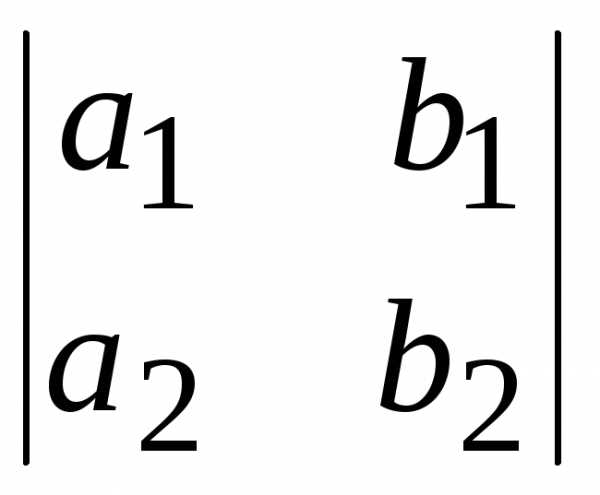 и
и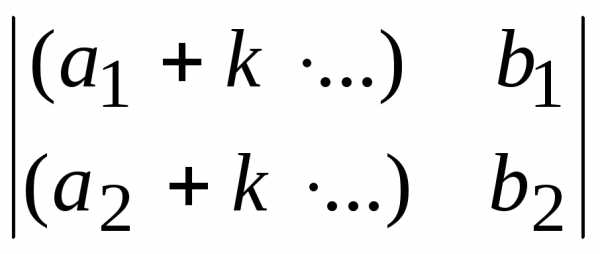 .
. и
и взаимно обратными?
взаимно обратными?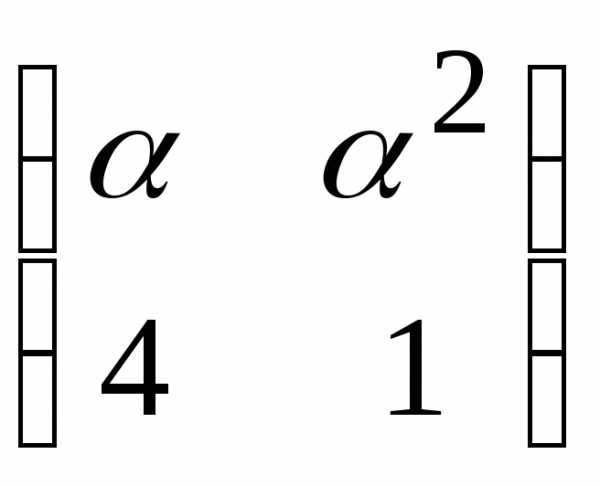 ?
?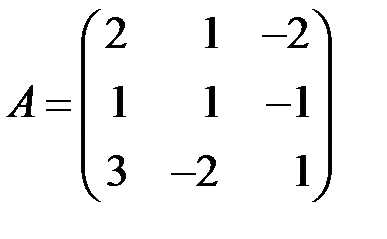 .
. .
.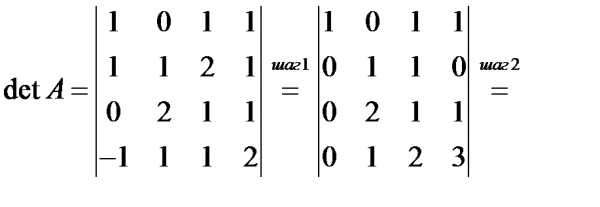
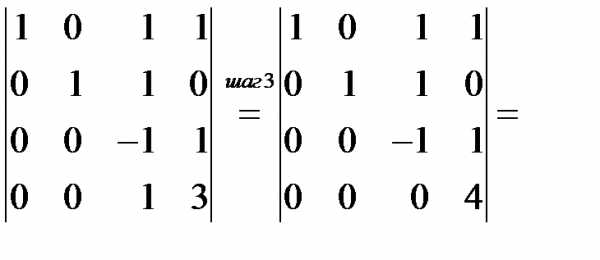
 соответствует элементу
соответствует элементу ,элементу
,элементу .
.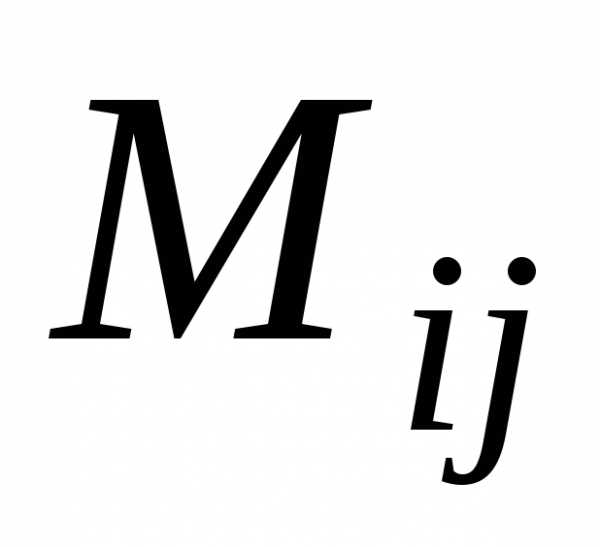 — минор, также соответствующий элементу.
— минор, также соответствующий элементу.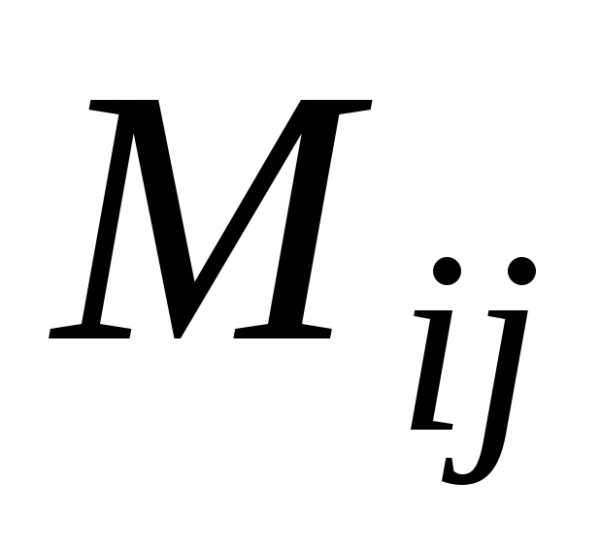 элемента
элемента называется определитель
называется определитель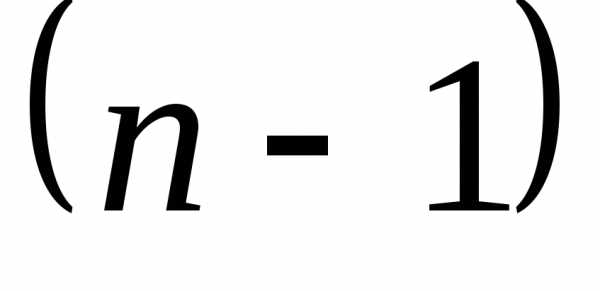 -го
порядка
-го
порядка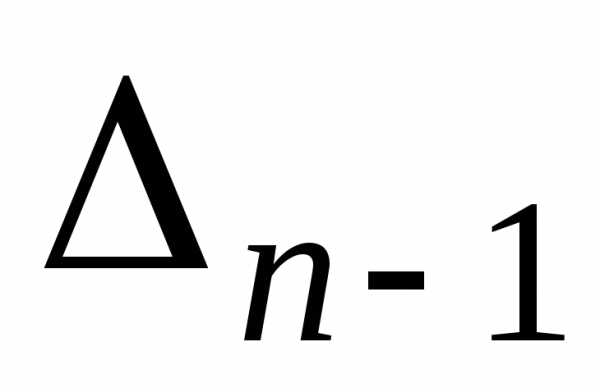 ,
полученный из определителя
,
полученный из определителя -го
порядка
-го
порядка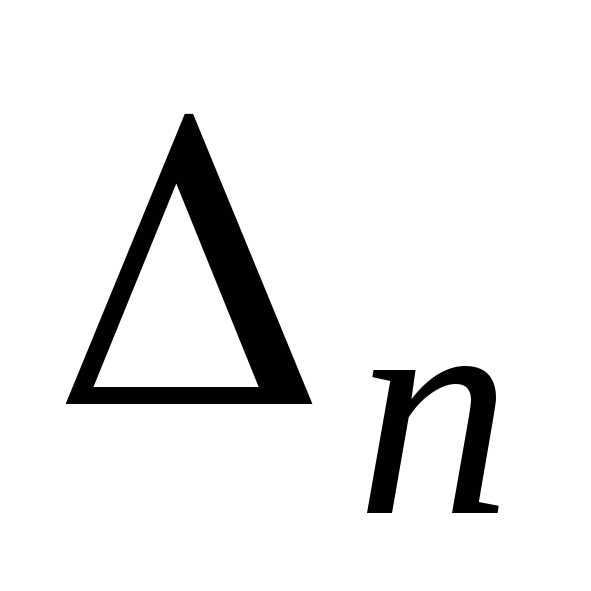 вычеркиванием
вычеркиванием -й
строки и
-й
строки и -го
столбца (на пересечении которых стоит
элемент).
-го
столбца (на пересечении которых стоит
элемент).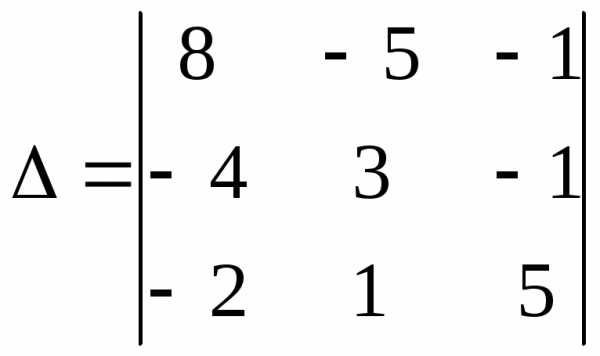
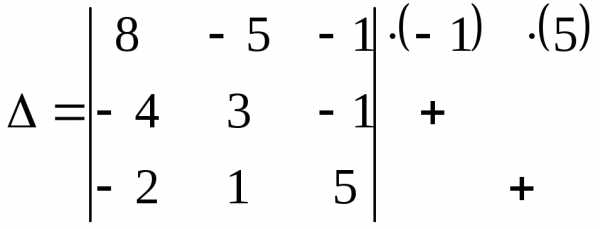
 и сложим с соответствующими элементами
второй строки, затем элементы первой
строки умножим на 5 и сложим с
соответствующими элементами третьей
строки.
и сложим с соответствующими элементами
второй строки, затем элементы первой
строки умножим на 5 и сложим с
соответствующими элементами третьей
строки.
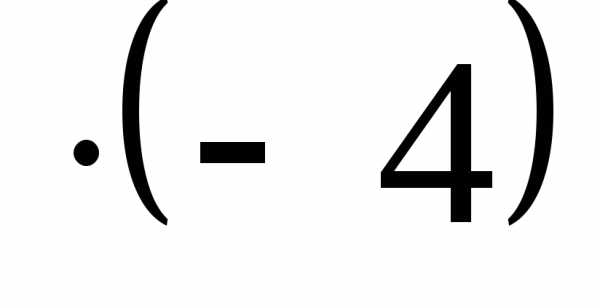
 .
. +
+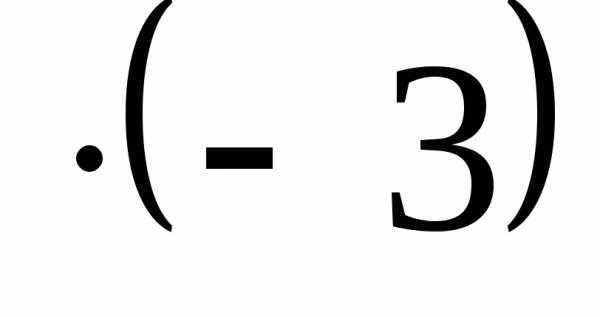 +
+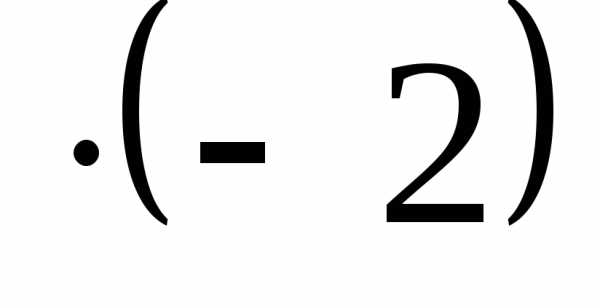 +
+ .
. ==
==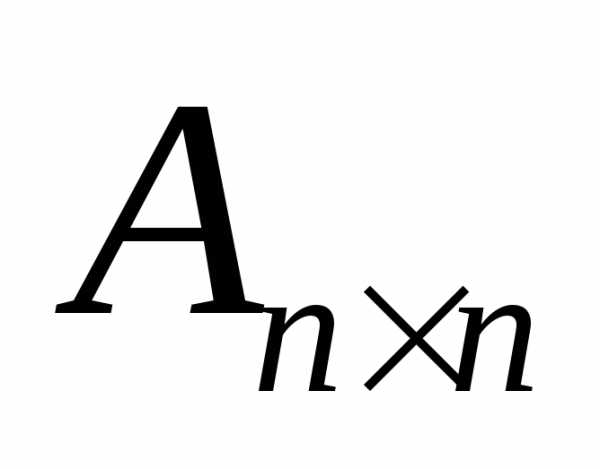 — квадратная матрица порядка n. Представим ее как систему n арифметических
векторов-строк:
— квадратная матрица порядка n. Представим ее как систему n арифметических
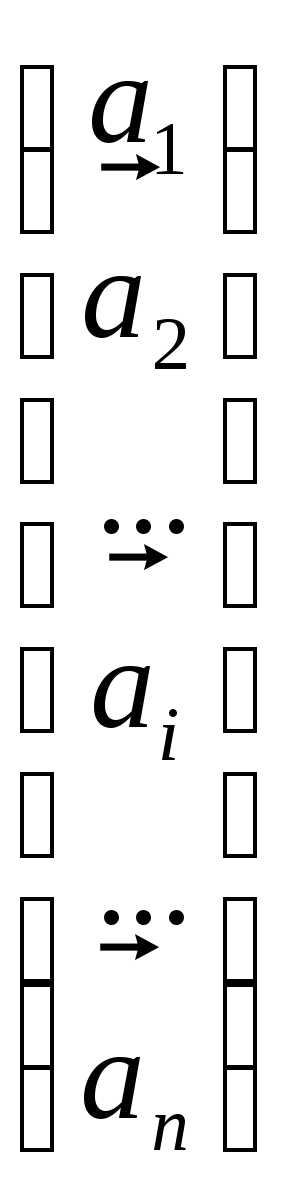
векторов-строк: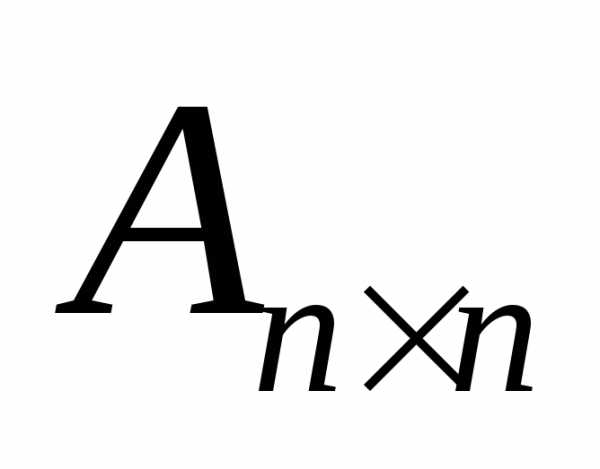 =
= =
=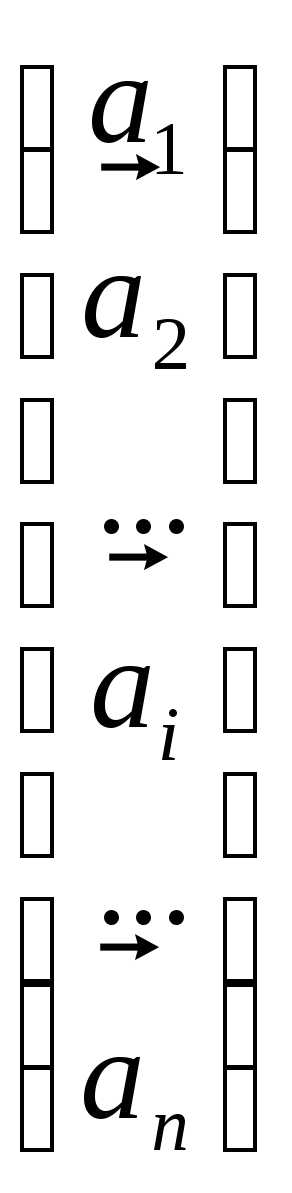 .
.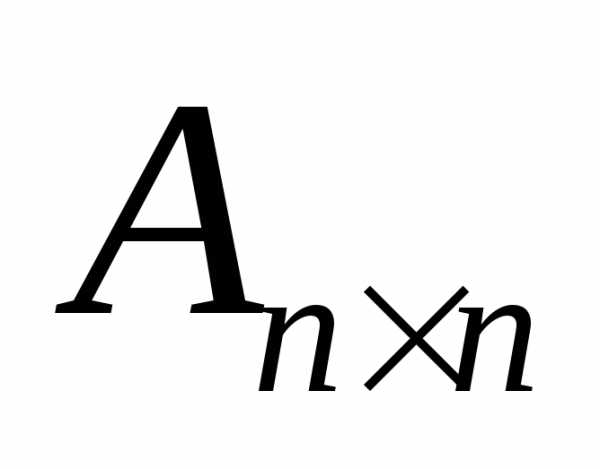 =
= =
=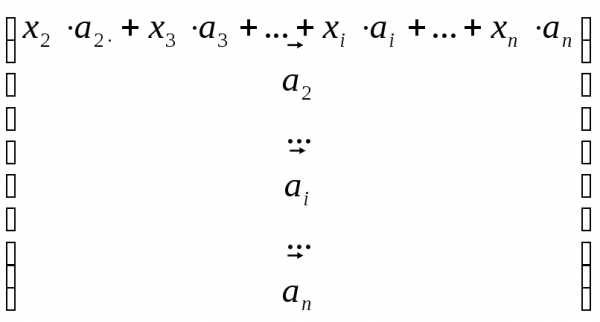

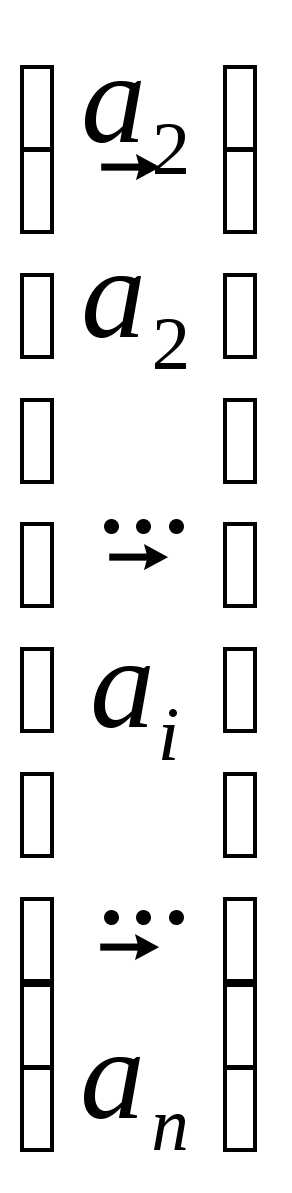 +
+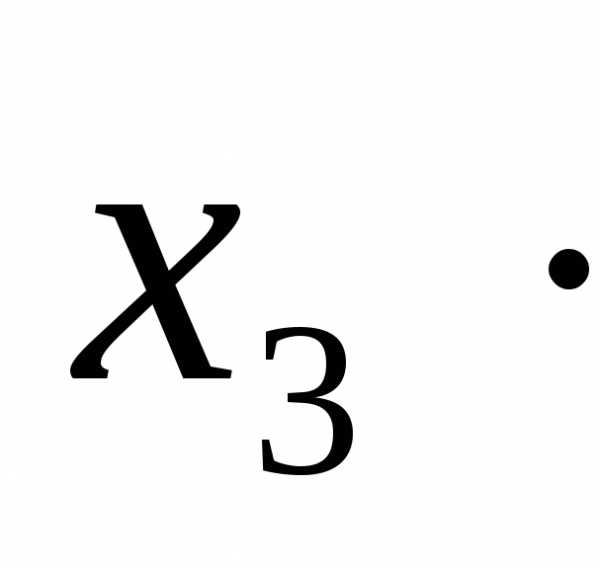

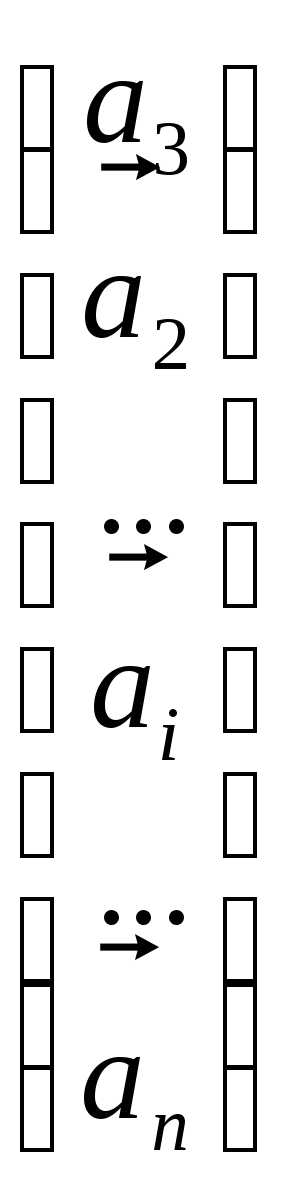 +….+
+….+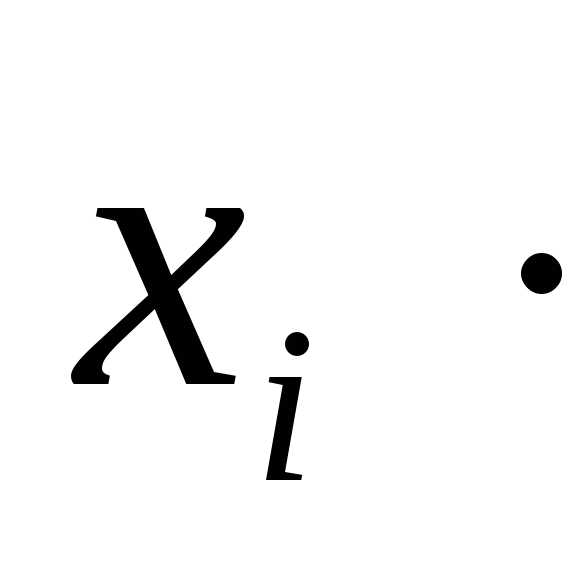

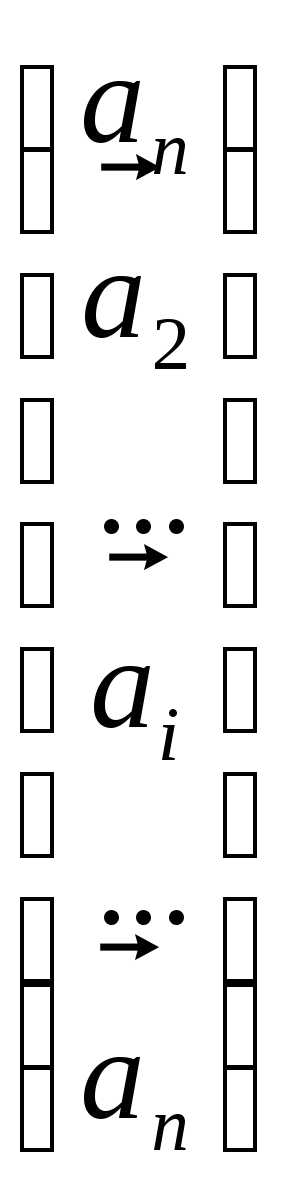
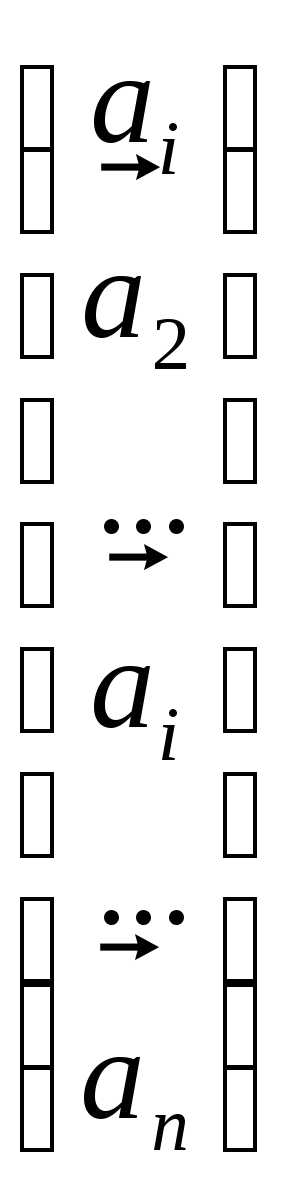
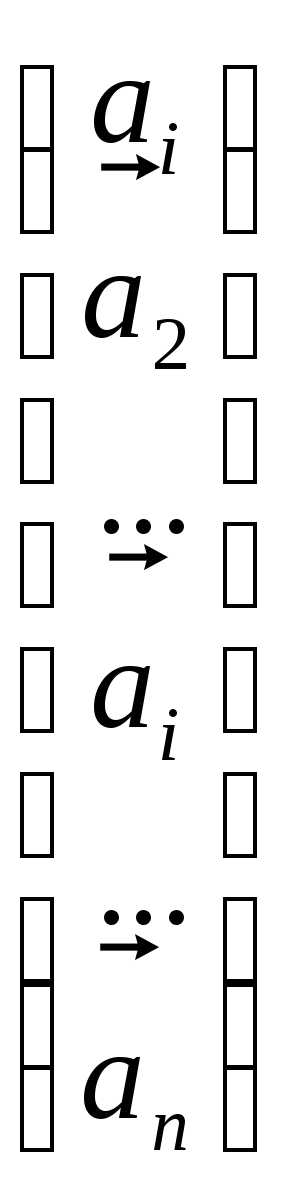 +….+
+….+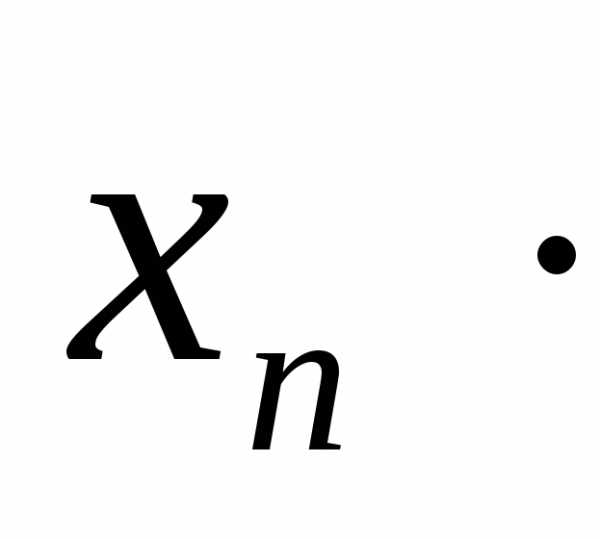

 (*)
(*) Ai=
Ai=
 .
Если поменять местами первую иi-тую
строку в этом определителе, то он не
изменится, так как эти строки состоят
из одинаковых чисел. Но согласно свойству
антикоммутативности, определитель при
этом должен сменить знак:
.
Если поменять местами первую иi-тую
строку в этом определителе, то он не
изменится, так как эти строки состоят
из одинаковых чисел. Но согласно свойству
антикоммутативности, определитель при
этом должен сменить знак: Ai = —
Ai = —  Ai.
Ai. Ai=0.
Но тогда и все остальные определители
в правой части равенства (*) равны нулю.
Из этого вытекает, что
Ai=0.
Но тогда и все остальные определители
в правой части равенства (*) равны нулю.
Из этого вытекает, что 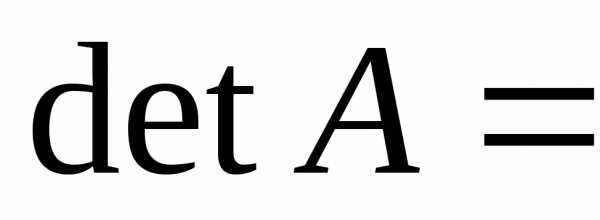 0.
0.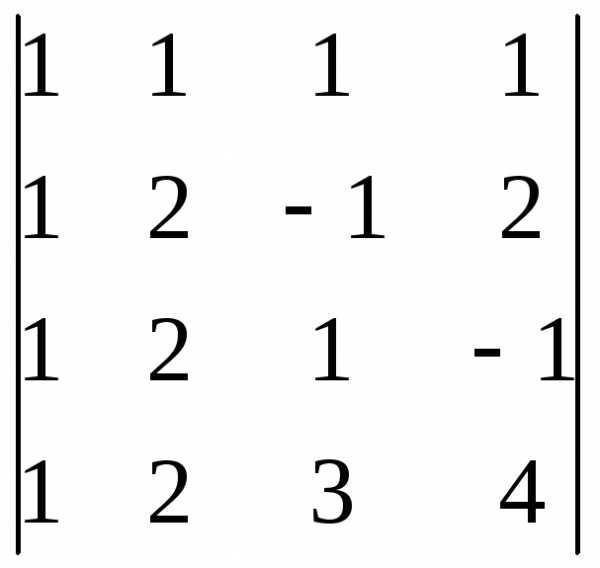 =
=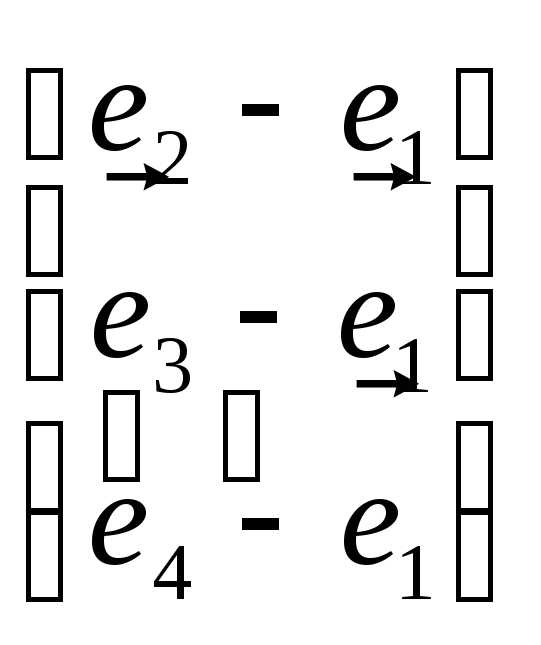 =
= =
=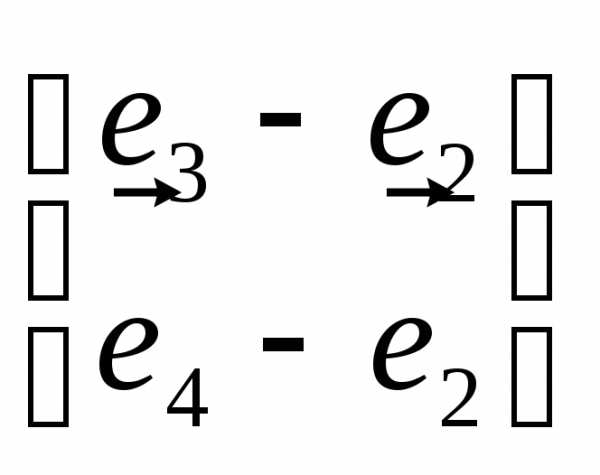 =
= =
=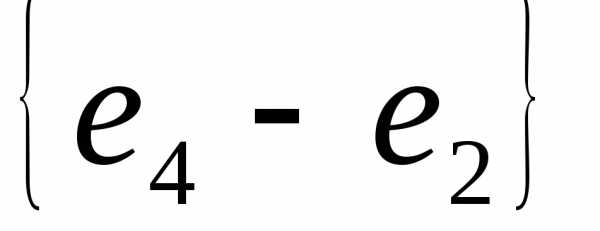 =
= =.
=.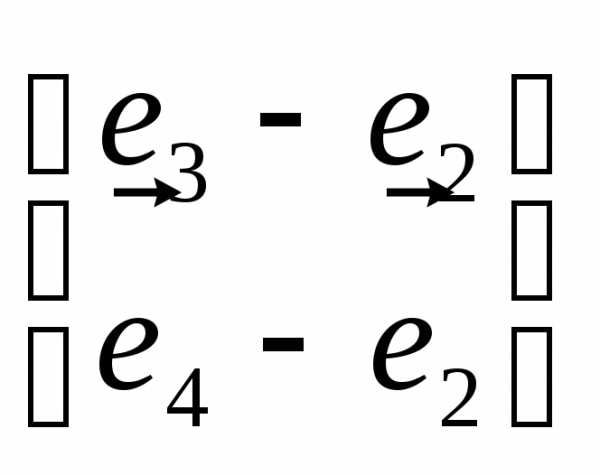 означает: из третьей и четвертой строк
вычли вторую строку.
означает: из третьей и четвертой строк
вычли вторую строку.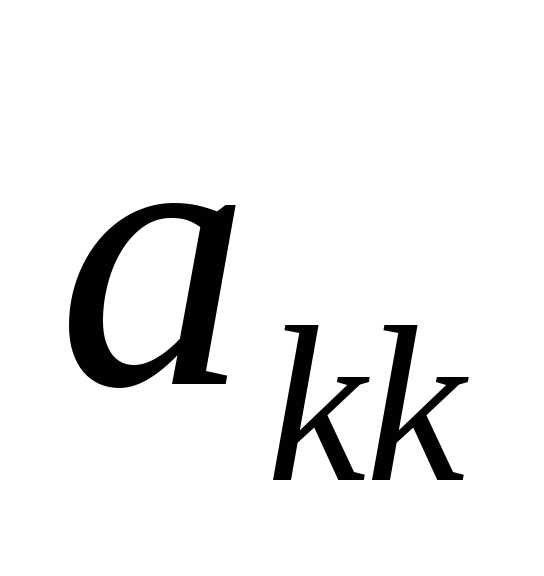 .
.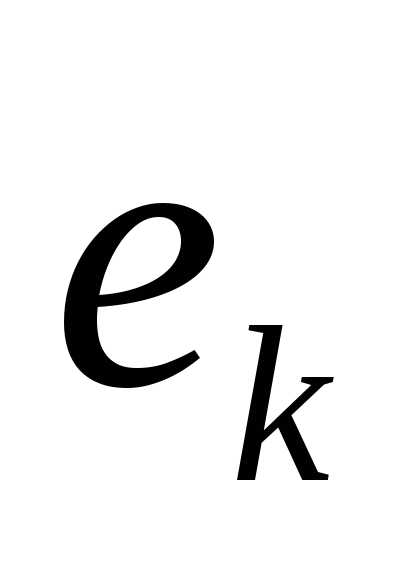 ).
).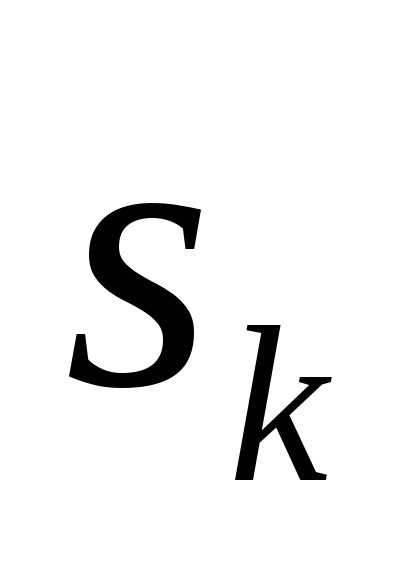 )
записать нули.
)
записать нули.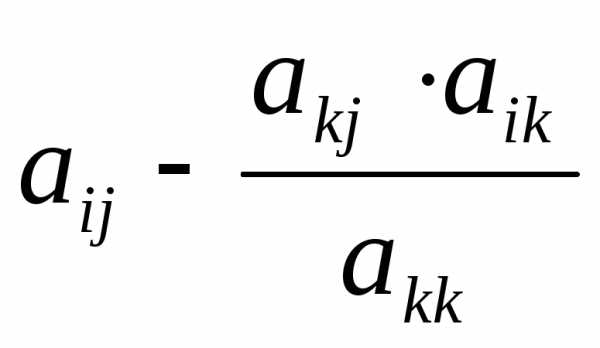 ,
(),
которую легко запомнить какправило
прямоугольника:
,
(),
которую легко запомнить какправило
прямоугольника:

 ,
на втором —
,
на втором — и т.д., на шаге (n—1)
—
и т.д., на шаге (n—1)
—  .
.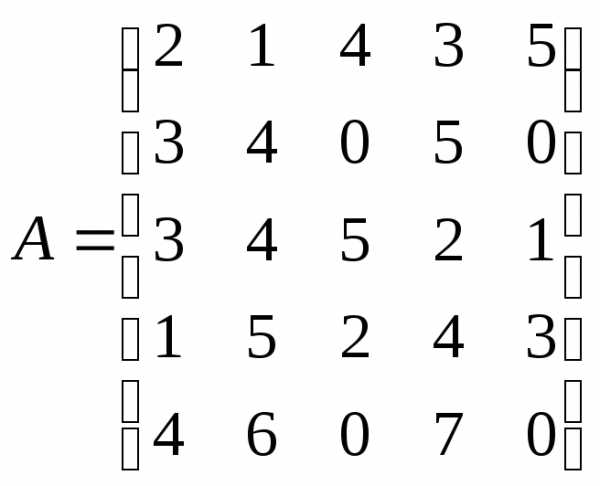
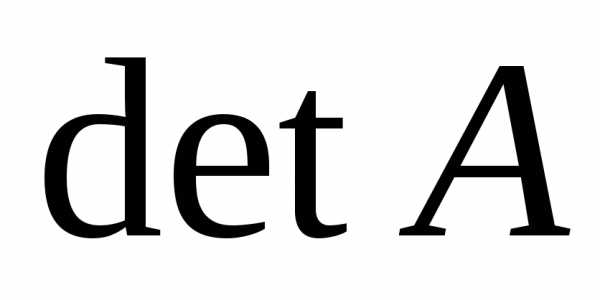 =
=
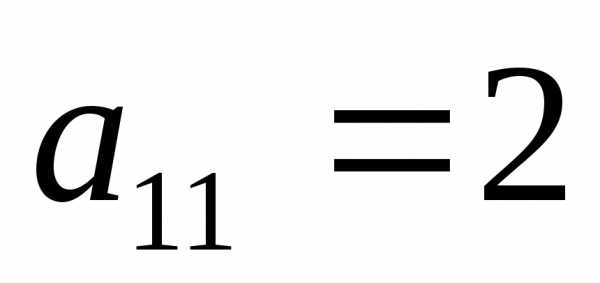 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4: =
= 
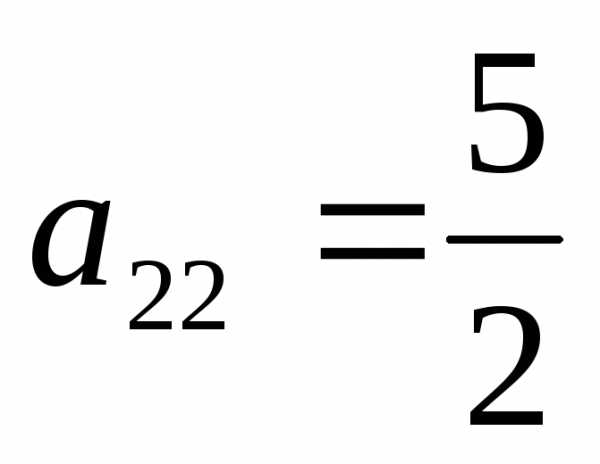 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4: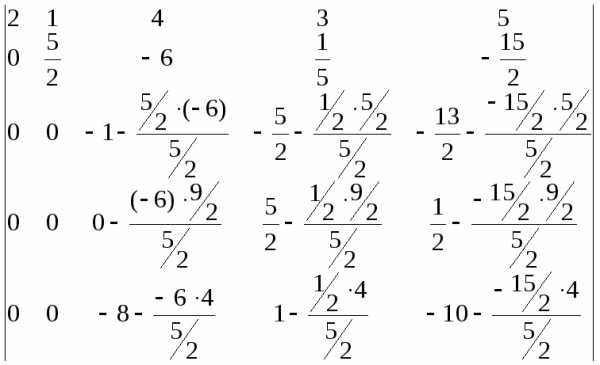 =
= 
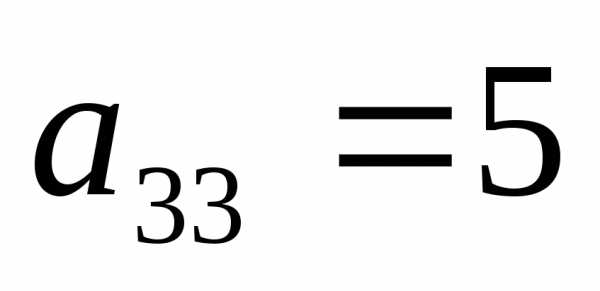 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
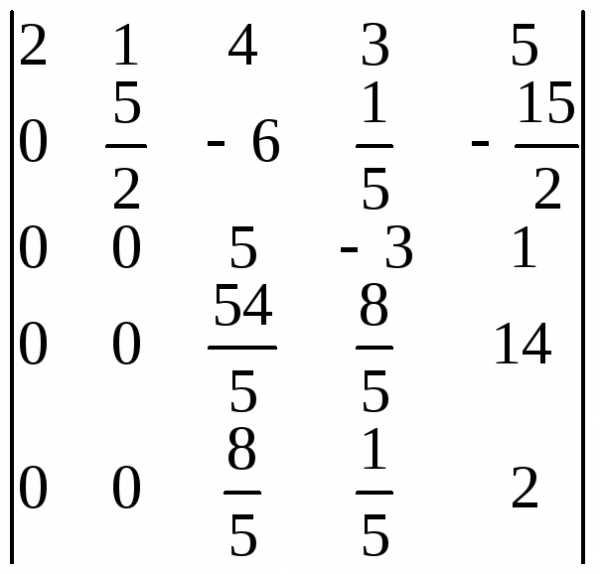
1-4: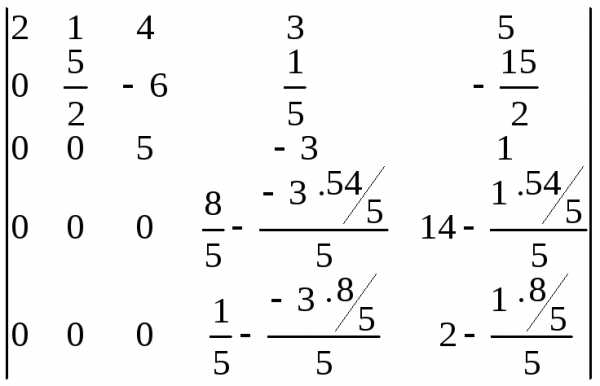 =
= 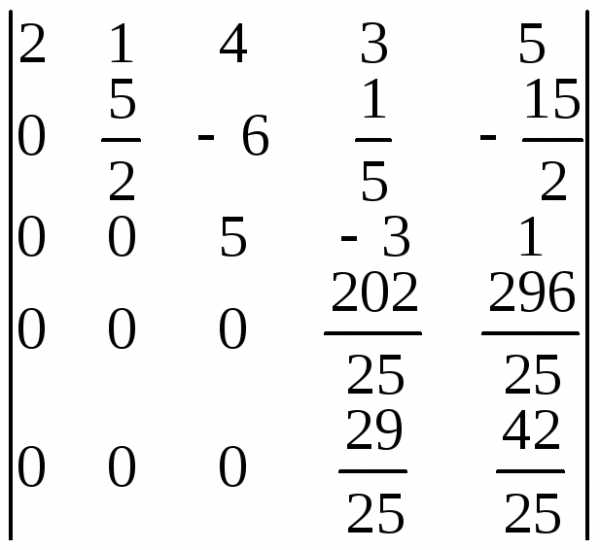
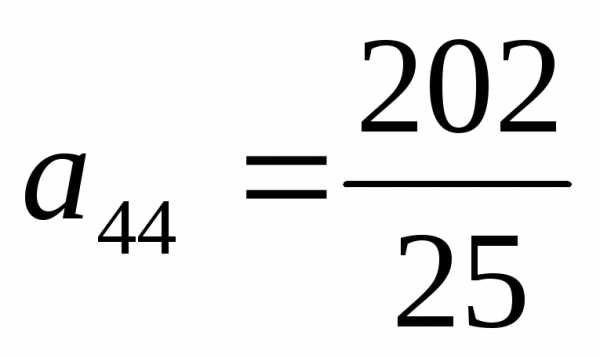 .
Выполняем последовательность действий
1-4:
.
Выполняем последовательность действий
1-4: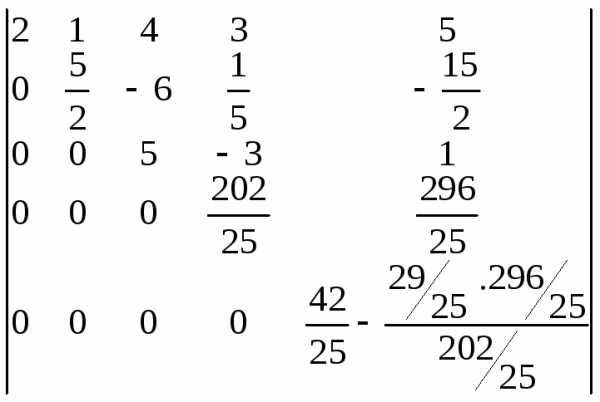 =
=  .
. =
=

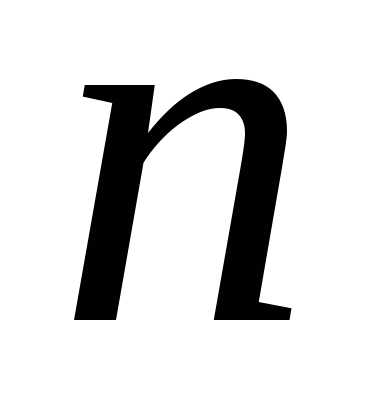 -го
порядка было введено понятие минора
-го
порядка было введено понятие минора элемента
элемента .
Напомним, что так был назван определитель
порядка
.
Напомним, что так был назван определитель
порядка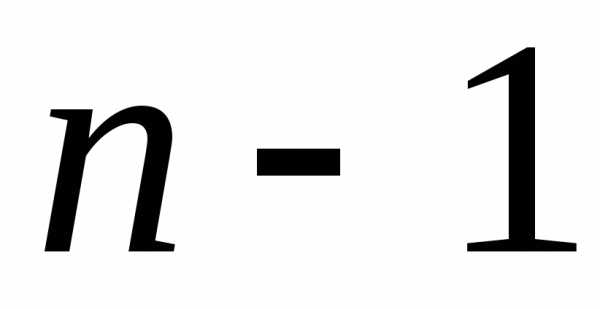 ,
полученный из определителя
,
полученный из определителя вычеркиванием
вычеркиванием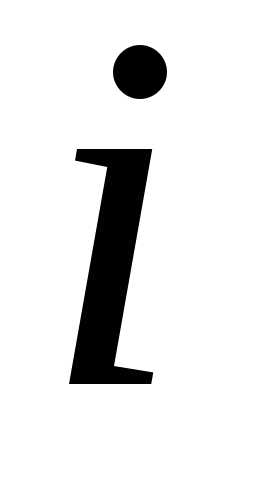 -й
строки и
-й
строки и -го
столбца.
-го
столбца. .
Выберем какие-нибудь
.
Выберем какие-нибудь номеров строки
номеров строки номеров столбцов.
номеров столбцов. матрицы
матрицы  (соответствующим выбранным строкам и
столбцам) называется определитель
порядка
(соответствующим выбранным строкам и
столбцам) называется определитель
порядка ,
образованный элементами, стоящими на
пересечении выбранных строк и столбцов,
т.е. число
,
образованный элементами, стоящими на
пересечении выбранных строк и столбцов,
т.е. число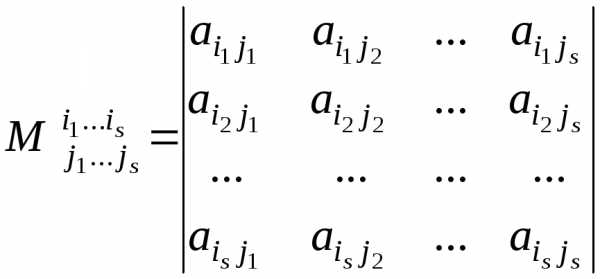 .
. ,
сколькими способами можно выбрать
номера строк
,
сколькими способами можно выбрать
номера строк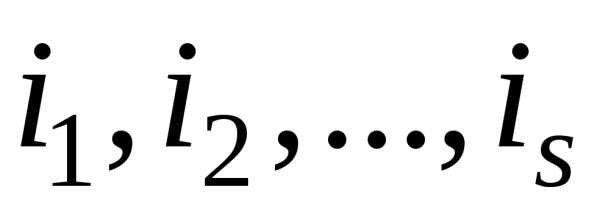 и столбцов.
и столбцов. размеров
размеров минор порядка
минор порядка называетсябазисным,
если он отличен от нуля, а все миноры
порядка
называетсябазисным,
если он отличен от нуля, а все миноры
порядка 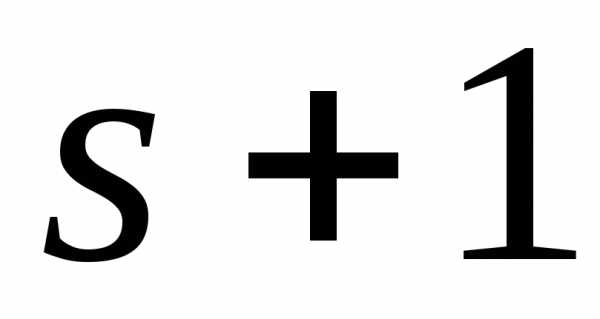 равны нулю или миноров порядка
равны нулю или миноров порядка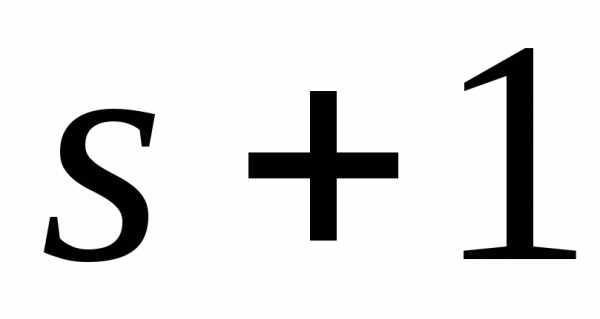 у матрицы
у матрицы вообще нет.
вообще нет.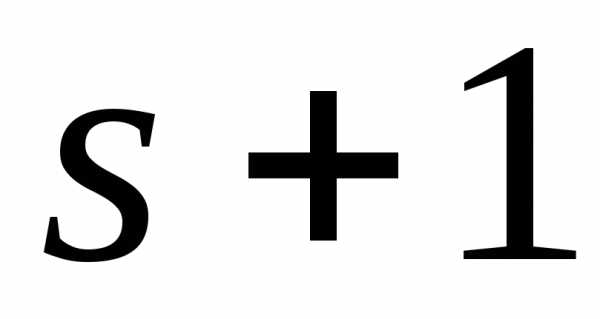 равны нулю, то равны нулю и все миноры
порядка
равны нулю, то равны нулю и все миноры
порядка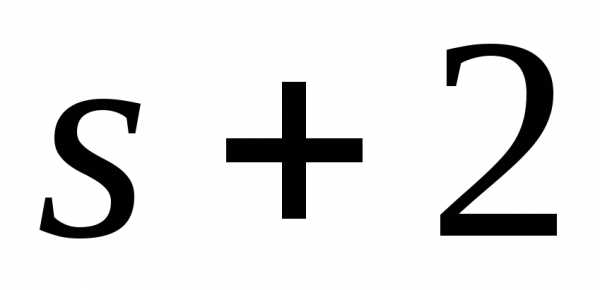 ,
а, следовательно, и всех бόльших порядков.
,
а, следовательно, и всех бόльших порядков. будем обозначать символом
будем обозначать символом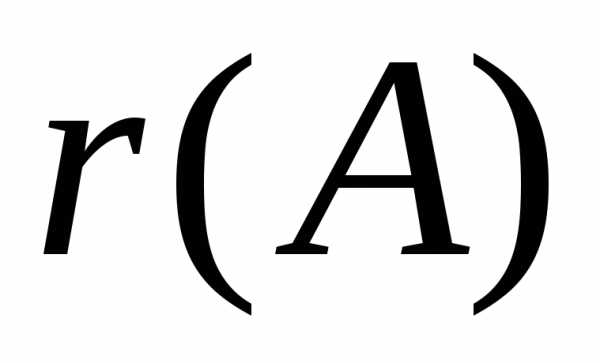 .
Из определения ранга следует, что для
матрицы
.
Из определения ранга следует, что для
матрицы размеров
размеров справедливо соотношение.
справедливо соотношение.
 -го
порядка, отличный от нуля. Рассмотрим
лишь те миноры
-го
порядка, отличный от нуля. Рассмотрим
лишь те миноры -го
порядка, которые содержат в себе
(окаймляют) минор
-го
порядка, которые содержат в себе
(окаймляют) минор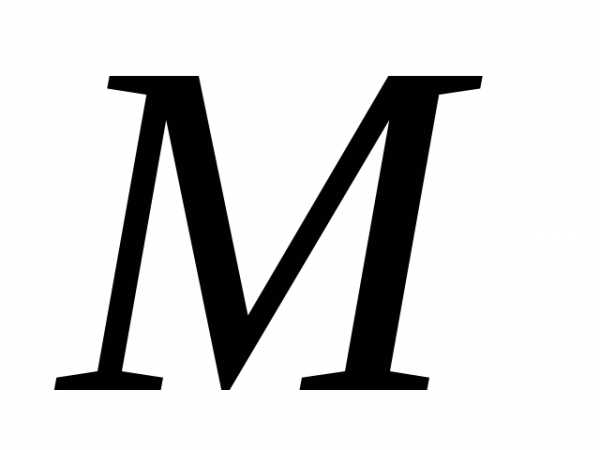 :
если все они равны нулю, то ранг матрицы
равен
:
если все они равны нулю, то ранг матрицы
равен .
В противном случае среди окаймляющих
миноров найдется ненулевой минор
.
В противном случае среди окаймляющих
миноров найдется ненулевой минор -го
порядка, и вся процедура повторяется.
-го
порядка, и вся процедура повторяется. методом окаймляющих миноров.
методом окаймляющих миноров.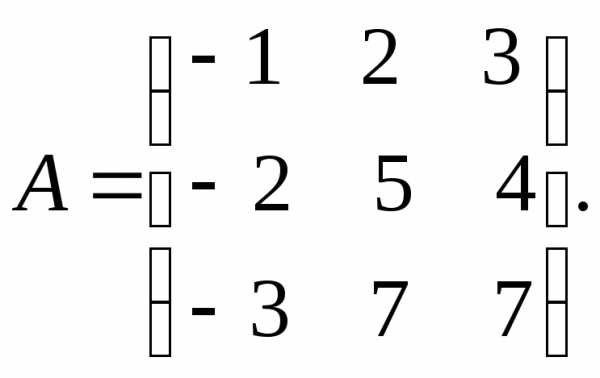
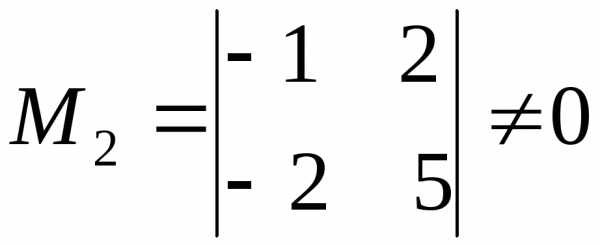 .
Существует только один минор третьего
порядка, окаймляющий выбранный минор
.
Существует только один минор третьего
порядка, окаймляющий выбранный минор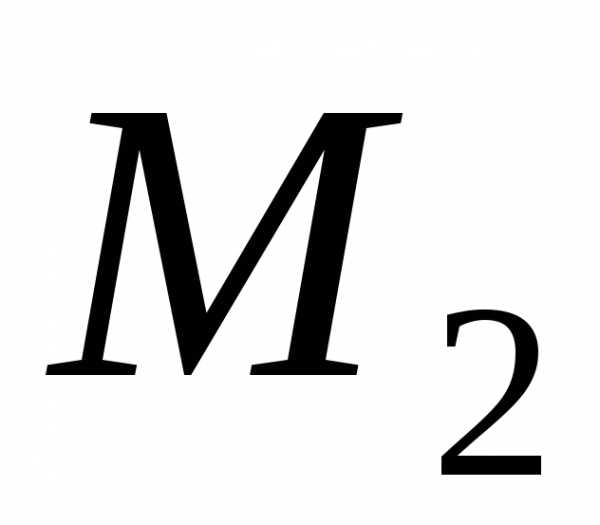 .
Вычислим его.
.
Вычислим его.
 приводят к виду
приводят к виду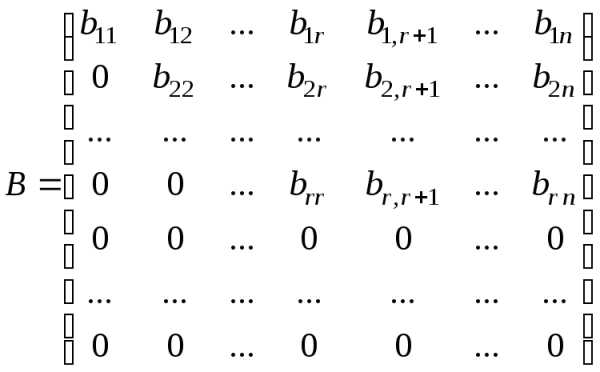 ,
(5)
,
(5) такого вида треугольной (иначе, ее
называют диагональной, трапециевидной
или лестничной). После приведения матрицы
такого вида треугольной (иначе, ее
называют диагональной, трапециевидной
или лестничной). После приведения матрицы к треугольному виду можно сразу записать,
что
к треугольному виду можно сразу записать,
что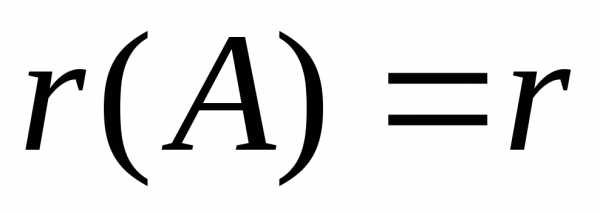 .
. существует отличный от нуля минор
порядка
существует отличный от нуля минор
порядка :
: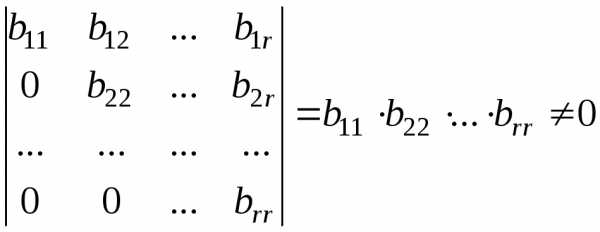 ,
,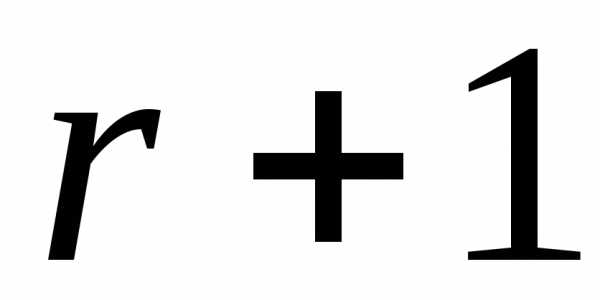 содержит нулевую строку и поэтому равен
нулю.
содержит нулевую строку и поэтому равен
нулю. с помощью элементарных преобразований:
для нахождения ранга матрицы
с помощью элементарных преобразований:
для нахождения ранга матрицы следует с помощью элементарных
преобразований привести ее к треугольному
виду
следует с помощью элементарных
преобразований привести ее к треугольному
виду .
Тогда ранг матрицы
.
Тогда ранг матрицы будет равен числу ненулевых строк в
полученной матрице
будет равен числу ненулевых строк в
полученной матрице .
. методом
элементарных преобразований
методом
элементарных преобразований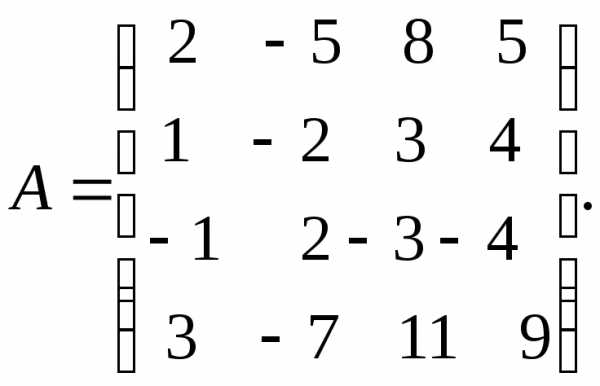

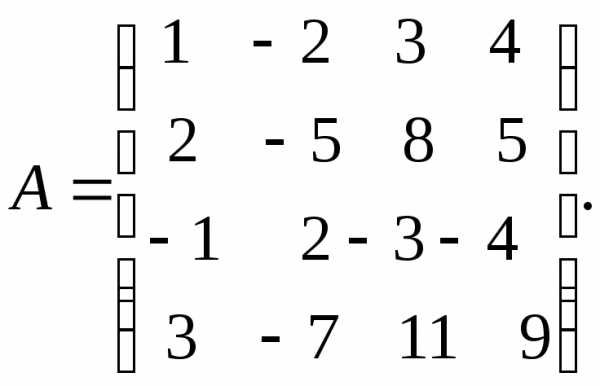
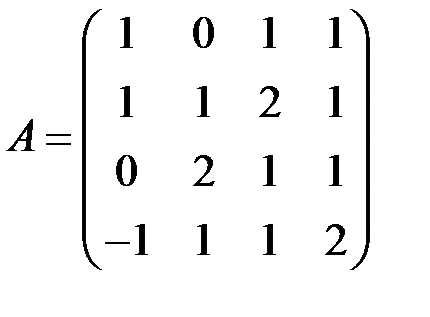
 -тую
строку матрицы –
-тую
строку матрицы – .
Нам необходимо привести исходную матрицу
к треугольному виду. Первую строку будем
считать ведущей, она будет участвовать
во всех преобразованиях, но сама остается
без изменений.
.
Нам необходимо привести исходную матрицу
к треугольному виду. Первую строку будем
считать ведущей, она будет участвовать
во всех преобразованиях, но сама остается
без изменений. ,
а из третьей вычтем первую, умноженную
на 3Получаем матрицу, ранг которой совпадает
с рангом данной матрицы. Обозначим ее
той же буквой
,
а из третьей вычтем первую, умноженную
на 3Получаем матрицу, ранг которой совпадает
с рангом данной матрицы. Обозначим ее
той же буквой :
: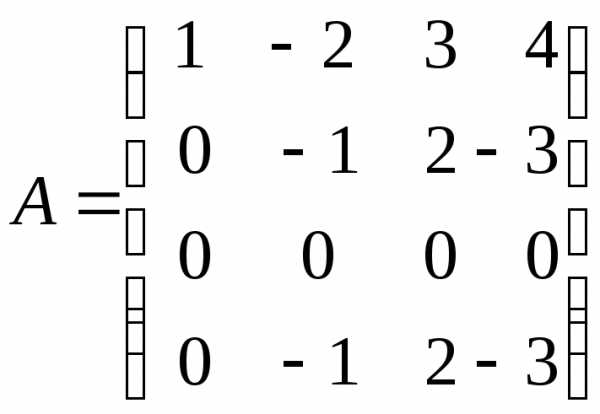 .
.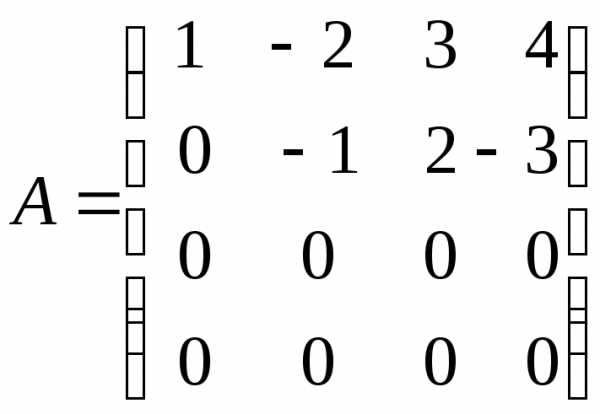 .
.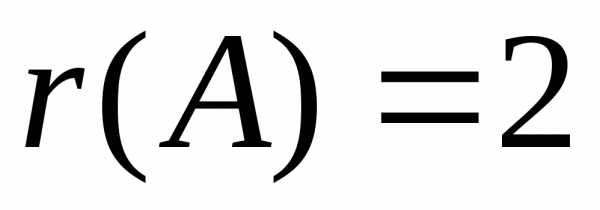 ,
т. е. числу ненулевых строк. Коротко
решение задачи можно записать следующим
образом:
,
т. е. числу ненулевых строк. Коротко
решение задачи можно записать следующим
образом: :
: .
. произвольных строк и
произвольных строк и произвольных столбцов.
Тогда определитель
произвольных столбцов.
Тогда определитель -го
порядка, составленный из элементов
матрицы
-го
порядка, составленный из элементов
матрицы ,
расположенных на пересечении выделенных
строк и столбцов, называется минором
,
расположенных на пересечении выделенных
строк и столбцов, называется минором -го
порядка матрицы
-го
порядка матрицы .
. называется наибольший порядок минора
этой матрицы, отличного от нуля.
называется наибольший порядок минора
этой матрицы, отличного от нуля. .
.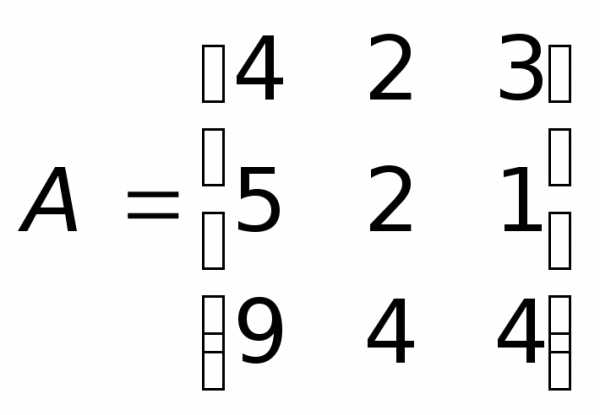 .
.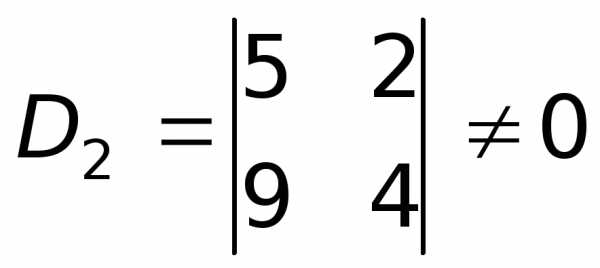 .
.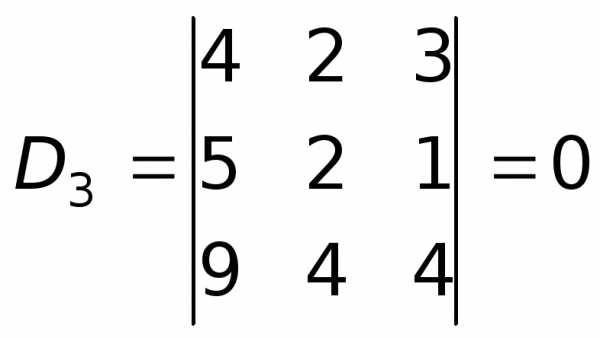 .
.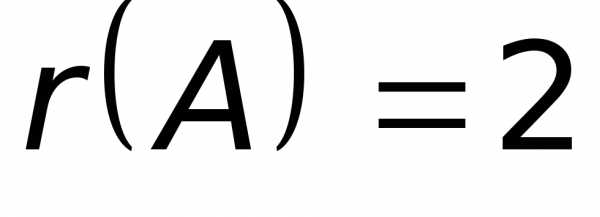 .
.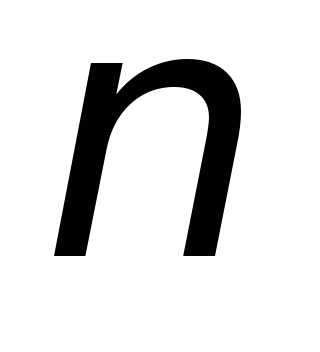 -го
порядкабыл равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы.
-го
порядкабыл равен нулю, необходимо и достаточно,
чтобы его строки (столбцы) были линейно
зависимы. и
и называются эквивалентными, если их
ранги равны, т.е..
называются эквивалентными, если их
ранги равны, т.е.. и
и эквивалентны, то отмечают
эквивалентны, то отмечают
 .
. любые из следующих действий над матрицей:
любые из следующих действий над матрицей: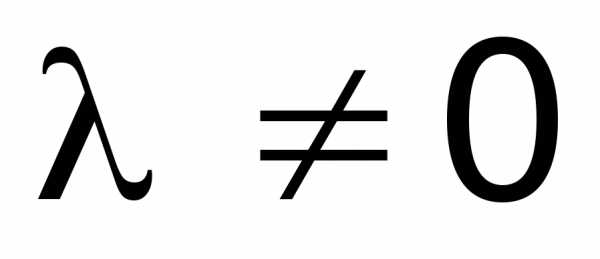 .
. получена из матрицы
получена из матрицы при помощи конечного числа элементарных
преобразований, то матрицы
при помощи конечного числа элементарных
преобразований, то матрицы и
и эквивалентны.
эквивалентны.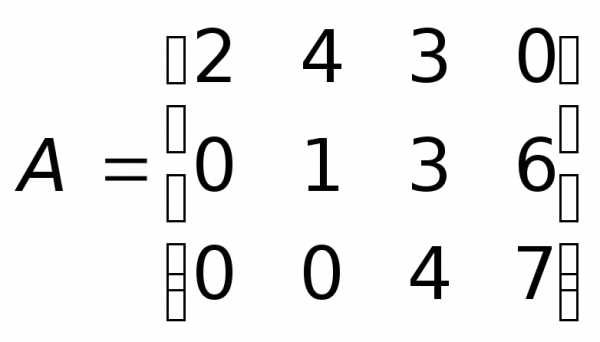 .
.
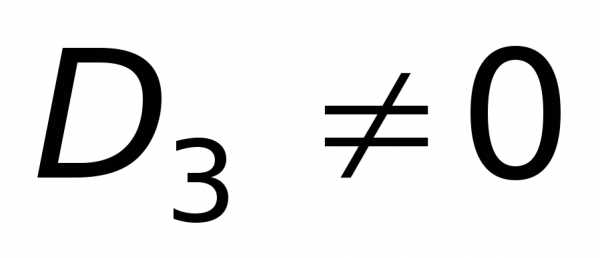 ,
элементы матрицыобращаются в нуль. Тогда форма представления
такой матрицы будет трапециевидной.
,
элементы матрицыобращаются в нуль. Тогда форма представления
такой матрицы будет трапециевидной.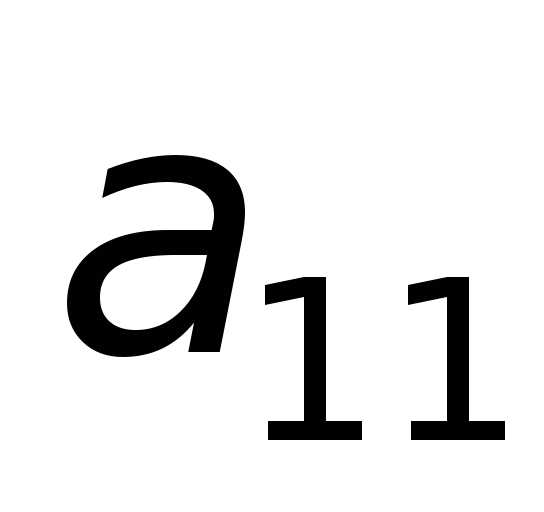 ,
превращались бы в нуль. Затем, умножая
элементы второго столбца на соответствующие
множители, добиваются, чтобы все элементы
второго столбца, расположенные ниже
элемента,
превращались бы в нуль. Далее поступают
аналогично.
,
превращались бы в нуль. Затем, умножая
элементы второго столбца на соответствующие
множители, добиваются, чтобы все элементы
второго столбца, расположенные ниже
элемента,
превращались бы в нуль. Далее поступают
аналогично. .
.



 .
.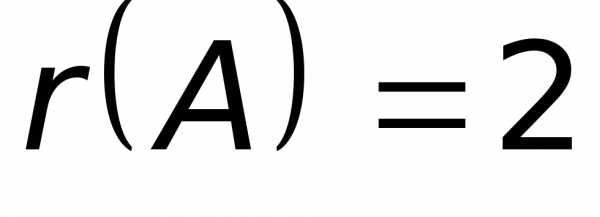 .
Однако, для приведения результата к
более изящному виду можно далее продолжить
преобразования над столбцами.
.
Однако, для приведения результата к
более изящному виду можно далее продолжить
преобразования над столбцами.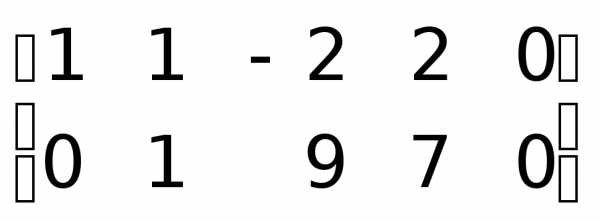
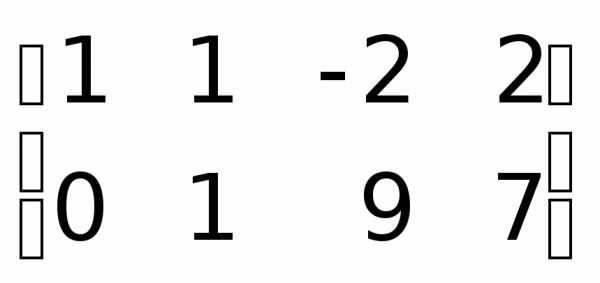
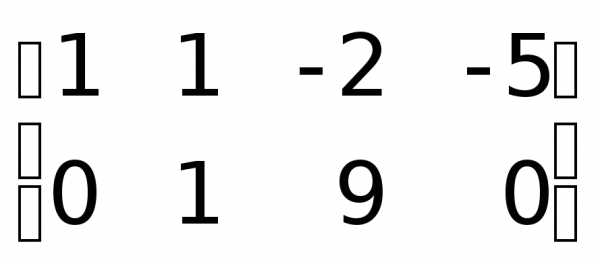

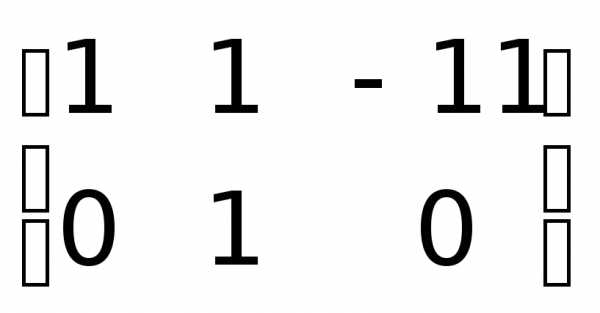

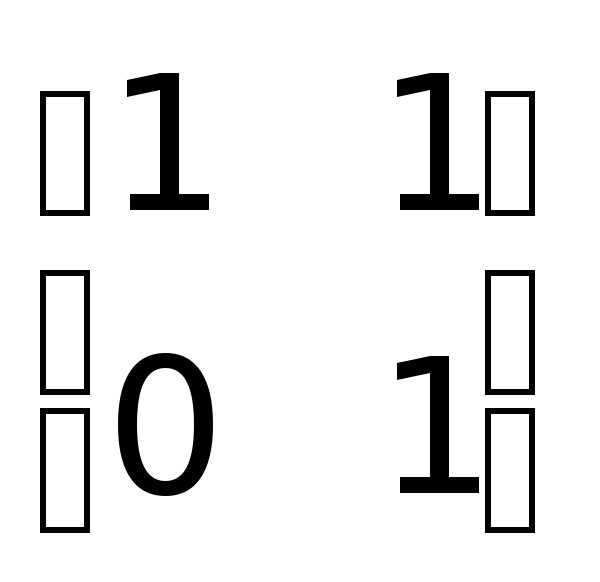 .
.