Рубрика: Школьная жизнь

Квадратные уравнения — примеры с решением, особенности и формулы

В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители

Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.

Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax² (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax², оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.

Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax² и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.

Пример

8x² — 3x = 0

x(8x – 3) = 0

Далее действуем согласно только что описанному правилу.

x=0 или 8х – 3 = 0

В результате получаем два корня уравнения: 0 и 0,375.

Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v₀t + gt²/2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители

Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.

X² – 33x + 200 = 0

Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.

Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.

Например: 2x³ + 2x² – 18x – 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).

В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.

Извлечение квадратного корня

Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax² и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.

3x²— 48 = 0

3x² = 48

В данном случае корнями уравнения окажутся числа -4 и 4.

Вычисление пощади земельного участка

Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.

Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м².

Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.

Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.

Дискриминант

Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x² + 16x – 612 = 0. Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.

Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b² – 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D<0, никаких шансов для решения у уравнения вообще не имеется.

О корнях и их формуле

В нашем случае дискриминант равен: 256 – 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к примеру, дискриминант, решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.

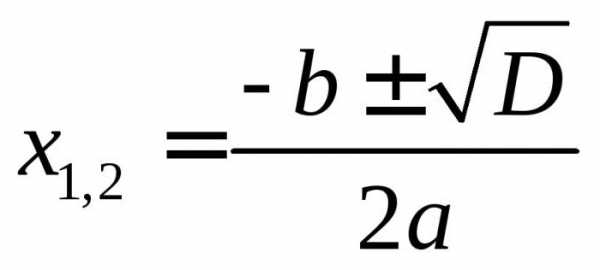
Это значит, что в представленном случае: x₁=18, x₂=-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м²).

Примеры и задачи

Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.

1) 15x² + 20x + 5 = 12x² + 27x + 1

Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.

15x² + 20x + 5 – 12x² – 27x – 1 = 0

Сложив подобные, определим дискриминант: D = 49 – 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.

2) Теперь раскроем загадки другого рода.

Выясним, есть ли вообще здесь корни x² – 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 – 20 = -4, а значит, корней действительно нет.

Теорема Виета

Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь Франсуа Виета, который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.

Теперь рассмотрим конкретные задачи.

3x² + 21x – 54 = 0

Для простоты преобразуем выражение:

x² + 7x – 18 = 0

Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.

График и уравнение параболы

Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

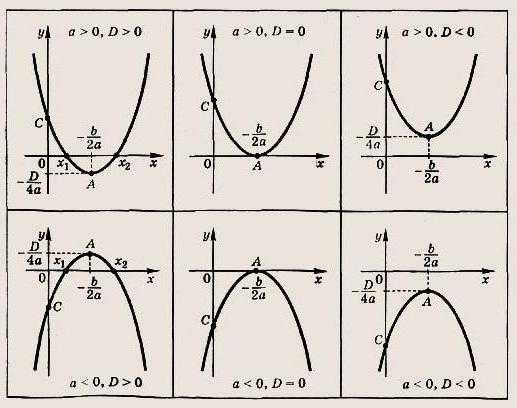
Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a<0, они рисуются вниз. Простейшим примером подобной зависимости является функция y = x². В данном случае в уравнении x²=0 неизвестное может принимать только одно значение, то есть х=0, а значит существует только один корень. Это неудивительно, ведь здесь D=0, потому что a=1, b=0, c=0. Выходит формула корней (точнее одного корня) квадратного уравнения запишется так: x = -b/2a.

Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x₀ = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y₀, то есть вторую координату вершины параболы, принадлежащую оси ординат.

Пересечение ветвей параболы с осью абсцисс

Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у₀ принимает отрицательные значения. А для a<0 координата у₀ должна быть положительна. Для указанных вариантов D>0. В противном случае D<0. А когда D=0, вершина параболы расположена непосредственно на оси 0х.

По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

Из истории

С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.

Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.

fb.ru

Квадратные уравнения: выделение полного квадрата

Квадратные уравнения можно решать еще до изучения темы «Квадратный корень»: выделение полного квадрата позволяет разложить квадратный трёхчлен на множители.

Рассмотрим на примерах, как можно использовать выделение квадрата двучлена для решения квадратных уравнений.

Выделим полный квадрат из трёхчлена, стоящего в левой части уравнения:

64 представим как квадрат 8:

Левую часть уравнения расложи на множители по формуле разности квадратов:

Получили уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:

Ответ: -6; 10.

Выделяем полный квадрат:

то есть быть раной нулю левая часть уравнения быть не может. Следовательно, данное уравнение не имеет корней.

Ответ: корней нет.

Разделим обе части уравнения почленно на число, стоящее перед x ²:

Выделим полный квадрат

Ответ: -1,5; -1.

С помощью выделения полного квадрата можно решать квадратные уравнения даже в курсе алгебры 7 класса при условии, что корни — рациональные числа.

Если корни — иррациональные числа, решить квадратное уравнение выделением квадрата двучлена также можно, но уже после введения понятия квадратного корня.

Пример.

Выделяем полный квадрат двучлена

Так как

Ответ:

Хотя выделение полного квадрата для решения квадратных уравнений в курсе алгебры используют редко, не стоит пренебрегать возможностью выработать соответствующий навык, который пригодится в будущем (например, в курсе математического анализа).

www.algebraclass.ru

Как решать неполные квадратные уравнения

Как решать неполные квадратные уравнения

Квадратное уравнение имеет вид , где . Если или , то уравнение называется неполным и допускает решение без использования дискриминанта (подробнее о дискриминанте в статье Как решать квадратные уравнения). Рассмотрим каждый случай на примерах.

а) случай

Неполное квадратное уравнение имеет вид , где .

Пример 1. .

В этом уравнении корней нет, так как левая часть при любых значениях  положительна, в то время как правая часть равна нулю. Следовательно, равенство невозможно. Ответ: нет корней.

Пример 2. .

Правая часть уравнения отрицательна (-4<0), а левая часть при любых таковой не является, ведь любое число в квадрате неотрицательно. Ответ: нет корней.

Пример 3. .

Уравнение имеет единственный корень, равный нулю. Ответ: 0.

Пример 4. .

Типичной ошибкой является ответ . На самом деле . То есть уравнение имеет два корня. Ответ:

Пример 5. .

Перенесем число в правую часть. При этом слагаемое поменяет знак. Тогда . Откуда . Остается немного упростить полученное выражение. Ответ: .

Пример 6. .

Важно не забыть проанализировать знак правой части. Число , так как , поэтому уравнение не имеет корней. Ошибкой было бы считать, что , ведь квадратный корень из отрицательного числа не существует.

Таким образом, в случае сначала упрощаем уравнение к виду , затем определяем знак числа . Если , то корней нет. Если , то . И если , то уравнение имеет два корня .

б) случай

Уравнение имеет вид , где .

Пример 7. .

Наша цель применить метод разложения на множители. Для этого в правой части должен быть 0, а в левой части — произведение. Вынесем за скобки, тогда . Произведение равно нулю, значит, хотя бы один из множителей равен нулю. Поэтому или , откуда или . То есть уравнение распалось на два более простых (линейных) уравнения. Ответ: .

Пример 8.

Раскроем скобки и приведем подобные слагаемые:

Далее разложим левую часть на множители.

Получим два линейных уравнения.

или , откуда или .

Ответ:

Таким образом, в случае неполное квадратное уравнение решается методом разложения на множители.

Если у вас трудности с арифметическими вычислениями, потренироваться можно здесь.

Задачи для самостоятельного решения

Ответы

1. 0; -3/7
2. 0; 5/4
3. -2; 2
4. -4; 4

еще задачи здесь (номера 1-4, 29-34, ответы в комментариях)

еще статья Как решать квадратные уравнения

все статьи по школьной математике

умножение матрицы на вектор | C++ для приматов

Даны квадратная матрица [latex]A[/latex] порядка [latex]n[/latex], векторы [latex]x[/latex] и [latex]y[/latex] с [latex]n[/latex] элементами. Получить вектор [latex]A(x+y)[/latex].

Примеры:

Алгоритм решения: Вводим матрицу [latex]A[/latex] порядка [latex]n[/latex]. Вводим векторы [latex]x[/latex] и [latex]y[/latex], прибавляем векторы [latex]x[/latex] и [latex]y[/latex]. После умножаем матрицу [latex]A[/latex] на вектор [latex]x + y[/latex] и получаем вектор [latex]A(x + y)[/latex]. С помощью цикла выводим результирующий вектор.

Код программы :

Оригинал кода можно увидеть перейдя по ссылке

cpp.mazurok.com

Умножение комплексного вектора на матрицу

Результат умножения вектора-строки на матрицу с*A

Результат умножения матрицы на вектор-столбец A*b

Каждый вектор можно рассматривать как одностолбцовую или однострочную матрицу. Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.

Если A-матрица размера m*n, то вектор столбец b имеет размер n, а вектор строка b имеет размер m.

Таким образом, что бы умножить матрицу на вектор, надо рассматривать вектор как вектор-столбец. При умножении вектора на матрицу, его нужно рассматривать как вектор -строку.

Пример.

Умножить матрицу

на комплексный вектор

Получаем результат

Как видите при неизменной размерности вектора, у нас могут существовать два решения.

Хотелось бы обратить Ваше внимание на то что матрица в первом и втором варианте, несмотря на одинаковые значения, совершенно разные (имеют различную размерность)

В первом случае вектор считается как столбец и тогда необходимо  умножать матрицу на вектор, а во втором случае у нас вектор-строка и тогда у нас произведение вектора на матрицу.

Свойства умножения матрицы на вектор

1. Произведение матрицы на сумму векторов-столбцов равна сумме произведений матрицы на каждый из векторов

2. Произведение суммы векторов-строк на матрицу  равна сумме произведений векторов на матрицу

3. Общий множитель вектора  можно вынести за пределы произведения матрицы на вектор/вектора на матрицу

4.Произведение вектора-строки на произведение матрицы и вектора столбца, равноценно произведению произведения вектора-строки на матрицу и вектора-столбца.

Удачных расчетов!!

• Умножение матриц с комплексными значениями онлайн >>

abakbot.ru

Умножение матрицы на вектор

Блок реализует процедуру умножения квадратной матрицы на вектор соответствующей размерности:

Входы

• matrix — порт для ввода матрицы A, представляемой в виде вектора коэффициентов при распаковке матрицы по строкам. Размерность векторного сигнала на 1-ом входном порте должна быть равна n×n, где n – размерность матрицы;
• vector — порт для ввода вектора u(t). Размерность вектора равна n.

Выходы

• output — порт для вывода вектора y(t). Размерность вектора равна n.

Свойства:

нет

Параметры

нет

Пример

Требуется умножить матрицу A на вектор u, если:

Примечание: блок выполняет процедуру умножения квадратной матрицы на вектор после каждого успешного шага интегрирования.

simintech.ru

Умножение вектора на матрицу: ilynva

module Main where

-- | Л.р. №6. Операции ввода-вывода в языке Haskell. Часть 2. Задача 20.
--   Программа считывает из одного файла матрицу, а из другого — вектор и 
--   записывает в третий файл результат умножения матрицы на вектор. 

import IO
import System.Environment
main = do
   [fileMatrix, fileVector, fileResult] <- getArgs  
   fileSource1 <- readFile fileMatrix     
   -- | Форма вектора в лабораторной не оговаривается,  будем иметь в виду вектор-столбец.
   fileSource2 <- readFile fileVector
   let fm1 = map (\x ->  map (\i -> (read i) :: Double) $ words x) $ lines fileSource1
   print fm1    
   let fm2 = (map (\x ->  (read x) :: Double) $ words fileSource2)    
   print fm2    
   if ((length fm2) == (length $ head fm1))
      then
         writeFile fileResult (mulMatVec fileSource1 fileSource2)
      else
         error "mulMatVec *** The vector x can be multiplied by matrix A of suitable dimension!!!"
   return () 

-- | Если размерность вектора J, а размерность матрицы I×J то в результате получится вектор размерности I.  
--   Умножение вектора на матрицу
mulMatVec :: String -> String -> String
mulMatVec sm sv = res where
  fm1 = map (\x ->  map (\i -> (read i) :: Double) $ words x) $ lines sm
  -- Вектор считаем как список вещественных чисел
  fm2 = (map (\x ->  (read x) :: Double) $ words sv)
  -- | Вектор x можно умножать на матрицу A подходящей размерности.  
  -- | Перемножаем.  
  mul = map (\x -> sum x) (map (\x  -> zipWith (*) x fm2) fm1)
  res = unlines (map (\x -> show x) mul)
   
{-|
Тест. Исходные файлы:

1.2	-3.5	1.8	-2.2	-5.3
10.2	-2.8	3.2	-2.8	1.5
2.3	-6.5	-9.2	6.5	-1.2

1.2
0.5
0.8
2.1
-1.4

>r6220 mf.dat vf.dat m.res

3.929999999999998
5.419999999999999
7.48

Результат совпадает 

Links:
 http://pv.bstu.ru/flp/flplabs.htm
 http://www.chemometrics.ru/materials/textbooks/matrix.htm#ch216
 http://oldunesco.kemsu.ru/mps/html/node5_33.htm
 http://vts.math.kubsu.ru/pascal/matrvect.htm
 http://u3d.agava.ru/doc/theory/matrix_ops.shtml
Tags: 
  Haskell, Roganova, Roganova6, Операции ввода-вывода, Interactive programs, Command line arguments, Input and Output, Матрицы и Векоторы, matrix haskell 
-}

ilynva.livejournal.com

Умножение матрицы на вектор — Энциклопедия по машиностроению XXL

При помощи матрицы А можно представить квадратичную форму кинетической Энергии (3) в более компактном виде. Введем обычную операцию умножения матрицы на вектор (матрицу-столбец) и скалярное произведение двух векторов х и у в п-мерном пространстве  [c.55]

Точка в условии означает операцию скалярного умножения тензора модулей упругости на вектор и справа (в компонентах — умножение матрицы на вектор — столбец справа) двойная точка в уравнении (5) означает двойное скалярное произведение (свертку) пары тензоров.  [c.479]

Составление такой матрицы имеет регулярный характер и может рассматриваться как операция умножения матрицы на вектор. Рассмотрим подробно операцию расчета матрицы коэффициентов Ку = I I, определяющих относительное увеличение выпуска в предшествующих по маршруту цехах, необходимое для восполнения потерь в последующих цехах. Заметим, что в каждой строке матрицы х.. ненулевые элементы встречаются один раз и только там, где пересечение / -й строки с / -М столбцом определяет передачу детали из /-го цеха в / -й. Последо-  [c.59]

Операции умножения матрицы на вектор или матрицу и умножения многомерных объектов (многомерных матриц и тензоров). Анализ выполним на примере операции умножения двухмерных матриц, рассматривая общий случай, когда ни один из операндов и результат не размещаются целиком в ОЗУ. Операнды будем обозначать А л В, з результат — С. Будем исходить из того, что операнды вначале упорядочены нужным образом, а упорядоченностью результата интересоваться не будем. Представим схему умножения так, как показано на рис. 2.3. В надписях на рисунке под порцией понимается строка одной исходной матрицы и столбец другой, а для результата — либо строка, либо столбец. Будем считать, что каждая порция целиком размещается в ОЗУ. Тогда вся операция выполняется за п этапов. Каждый из этапов аналогичен поэлементной операции, выполняемой над одной порцией однократно обмениваемого файла (назовем его 4). На протяжении всего этапа порция находится в ОЗУ и поэлементная операция выполняется над ней и всеми порциями многократно обмениваемого файла (назовем его В). Файл В порциями поступает в ОЗУ. Над поступающими порциями выполняются операции АЛУ, и получается порция результирующего файла, выводимая после получения во внешний накопитель.  [c.67]

Рассмотрим теперь частные случаи умножения двухмерных матриц, а также умножение матрицы на вектор.  [c.68]

Если операция есть умножение матрицы на вектор, то для вектора назначаем  [c.88]

Ниже представлены примеры выполнения свертки каждым из типов архитектур, рассмотренных для одной и той же задачи. Для большей убедительности взят случай умножения матрицы на вектор. Задача выглядит следующим образом.  [c.192]

В табл. 7.1 приведена скорость выполнения операции умножения матрицы на вектор. В первой колонке представлены выражения для числа тактовых циклов, необходимых для завершения одной операции умножения. Умножение матрицы тХп на вектор /гХ1 требует 2тп операций сложения и умножения. Если предположить, что биты данных проходят в системе с частотой 10 МГц (величина 0,1 мкс/бит является достаточно обоснованной для существующих электронных устройств), то можно вычислить скорость выполнения операций. Представлены два случая. Первый из них соответствует п = т = 32, при /=16 (I эквивалентно точности вычислений), а второй случай относится к п = т=128, / = 32. В табл. 7.2 представлены аналогичные данные для умножителей, выполняющих умножение матрицы на матрицу с точностью I цифр. В третьем столбце показаны результаты для /=16, п = т = к = 32, а четвертый столбец соответствует / = 32, п = т = к= 28. Во всех случаях результаты даны для операций с фиксированной запятой, выполняемых в одну секунду. Ни один цифровой процессор (оптический или элект-  [c.207]

На рис. 11.9, а изображен граф для процедуры вычисления внутреннего произведения ряда векторов с образцовым вектором Ь во временной области посредством рекурсивного удвоения. При умножении матрицы на вектор вектора могут рассматриваться как строки матрицы А. В то время как один вектор умножается в процессорах с 1 по 8, результаты предшествующего умножения суммируются в процессорах с 9 по 12. Величина выходного вектора для умножения матрицы на вектор получается в каждом тактовом цикле, или шаге выполнения расчетов.  [c.387]

Элементная база интегральной оптики достаточно просто позволяет реализовать практически все элементарные арифметические операции, однако двухмерная природа ОИС несколько ограничивает возможности проектирования по сравнению с объемными оптическими процессорами. В настоящий момент реализация таких операций, как умножения матрицы на вектор, матрицы на матрицу, активно исследуется. В схеме параллельного умножения матрицы на вектор однородная плоская волна попадает на N элементов электрооптического дифракционного модулятора. Затем световой поток проходит через ряд дифракционных решеток, разделяющих его на N пучков, каждый из которых попадает на следующий дифракционный модулятор, где пучки модулируются пропорционально соответствующим элементам матрицы М. Умножение производится по елочной схеме, а произведения, соответствующие компонентам результирующего вектора, суммируются с помощью линейки линз.  [c.155]

Для получения неизвестных [Су j требуется лишь умножение матрицы на вектор. Следовательно, явный метод значительно быстрее неявного. Однако при достаточно больших значениях временных шагов At явные методы могут быть численно неустойчивы.  [c.312]

Умножение матрицы на вектор является частным случаем перемножения прямоугольных матриц. Умножение производится в порядке, определяемом уравнением (1). В этом случае векторы записываются в виде матрицы-столбца  [c.156]

При расчете характеристик АР с различными амплитудно-фазовыми распределениями волн [Л], падающих на входы согласованных излучателей, использование модели (3.4) значительно сокращает время вычислений. Это обусловлено тем, что матрица [ >] рассчитывается только один раз и запоминается в ОП ЭВМ, а расчет вектор-столбца [/] заключается в простом умножении матрицы [/)] на вектор-столбцы [С]=[/ ] [Л], соответствующие различным амплитудно-фазовым распределениям сигналов, возбуждающих АФАР.  [c.90]

Умножение матрицы на вектор-столбец Произвольное и периодическое  [c.108]

Полагая, что читателю известен способ умножения матрицы на вектор, приведем метод получения грубой оценки согласованности.  [c.33]

При нахождении суммы тензоров одинакового ранга элементы, занимающие одно и то же место в матрице, суммируются. Для умножения диады на вектор нужно выполнять операцию умножения только тех векторов, между которыми стоит соответствующий знак умножения (скалярного или векторного).  [c.39]

При вычислении вектора Р в соответствии с (19.26) приходится вычислять а — 1 произведений матрицы на вектор, что потребует 4 (а — 1)/г операций умножения, так как матрицы могут быть вычислены при вычислении матрицы Н.  [c.140]

При умножении матриц и матриц на вектор в каждой отдельно взятой операции прямой доступ к файлам не дает преимуществ по сравнению с последовательным. Однако преимущество появляется при реализации комплекса операций, в котором данные используются в различной упорядоченности. В этом случае прямой доступ исключает операции пере-упорядочивания (транспонирования), которые пришлось бы выполнять при последовательной организации файлов.  [c.75]

Нетрудно убедиться в том, что умножение М-матрицы на вектор напряжений ребер Up= U u U 2, Ua, U i, Uni, Ur2, Ue, Ue2, Уез) b соответствии с (3.6a) приводит к получению уравнений ЗНК  [c.78]

В символьных вычислениях центральное место занимает операция вычисления внутреннего произведения, эквивалентная умножению составляющих элементов на вектор (векторное умножение), на матрицу (умножение матрицы на матрицу) или на корреляционную функцию. В предыдущих разделах была установлена общность процедур вычисления внутреннего произведения для большого числа алгоритмов из области цифровых вычислений. В одном типичном представлении символьных вычислений отношения знаний выражаются в терминах логического сопоставления с образцом, процедура которого определяется поиском соглашения по предпосылке-условию (с левой стороны) соотношения если [А], тогда [В] (см. разд. 10.3.5). Здесь [А] является подпространством Л -мерного векторного пространства  [c.354]

Эти выражения поясняют понятия матрицы и матричного умножения. Матрицы определяются как массивы чисел указанного в (А 1.2) типа. Массив в виде одного столбца чисел часто называется вектором или матрицей-столбцом. Умножение матрицы на матрицу-столбец записывается в виде (А1.1) или (А1.1а).  [c.526]

Заметим, что матрица вырождена после умножения ее на вектор (1, 1, 1) получается нуль. Вектор до = 1, дч2 = 1. горизонтальную прямую = 1, так что ее производная равна нулю. Вырождение  [c.71]

Таким образом, дополнительные затраты на вычисление отношения Релея здесь с лихвой окупаются. Отметим, что вычисление (5.23) эквивалентно умножению двух разреженных матриц на векторы.  [c.123]

Умножение матрицы на вектор. Данная операция всегда может быть выполнена при однократном обмене, даже когда ни один из операндов (или результат) не размещается в ОЗУ. Пусть вектор4 = а. упорядо-68  [c.68]

Линейно-алгебраические операции, рассмотренные в предыдущем параграфе, можно отнести к трем типам, исходя из принципов организации реализующих их вычислительных процессов. К типу коротких отнесем операции, для реализации которых принципиально достаточен однократный обмен файлов, содержащих операнды и результат сложение матриц и векторов, умножение на скаляр и т. п. К типу длинных отнесем операции, для реализации которых принципиально требуется многократный обмен одного файла, содержащего операнд или результат транспонирование, обращение матрицы, умножение двух матриц и т. п., в случае когда операнды и результат не размещаются целиком в ОЗУ. К типу условнокоротких отнесем операции, для реализации которых при некоторых дополнительных условиях достаточен однократный обмен файлов. В основном, это весьма распространенная в АСУ операция умножения матрицы на вектор, когда операнды и результат не размещаются в ОЗУ. В общем случае эта операция выполнима по алгоритму умножения двух матриц. Однако, если матрица упорядочена так, что старший индекс ее элементов является индексом, различающим элементы вектора, то эта операция реализуется однократным обменом. Таким образом, при дополнительном условии — при совпадении упорядоченностей элементов матрицы и вектора — эта операция является короткой. Без этого дополнительного условия операция является длинной, так как в этом случае она выполняется либо как умножение двух матриц, либо (что короче) в две стадии сначала выполняется транспонирование матрицы, затем собственно умножение, но при однократном обмене.  [c.77]

Рассмотрение данного примера было вызвано необходимостью обеспечить высокую скорость при выполнении операции внутреннего произведения в линейной алгебре (например, для умножения матрицы на вектор или матрицы на матрицу), в противном случае эти операции становятся бессысленными. Операции внутреннего произведения включают умножение двух чисел и сложение результата с третьим числом. Например, 2-разрядный умножитель-сумматор умножает два 2-раз-рядных числа М ц Ы, прибавляет результат к 5-разрядному входному числу X и выводит результаты в виде 5-разрядного числа У. В синхронизированном режиме работы выходной сигнал У мог бы подаваться по цепи обратной связи на вход X для того, чтобы достичь эффекта многократного накопления результата (если имеется возможность накопления до трех произведений и при этом не возникает переполнение).  [c.155]

Одна из целей цифровых оптических вычислений состоит в достижении большей гибкости системы, чем у их аналоговых предшественников. Особенность оптических компьютеров состоит в том, что они скорее выполняют не монолитные операции, а ряд простых операций, которые можно объединить для выполнения широкого круга задач. Однако в данном случае это не так плохо, поскольку при построении оптических процессоров, осуществляющих функции регистра, их возможности поднимутся на качественно новый уровень. С этой точки зрения матричное умножение (под которым подразумевают либо умножение матрицы на вектор, либо матрицы на матрицу), возможно, является наиболее полезной операцией среднего уровня из числа тех, которые только можно придумать. Многие сложные проблемы, например калмановское фильтрование,  [c.183]

Два основных блока умножителей, показанные на рис. 7.3, могз т использоваться в различных сочетаниях при формировании систолических процессоров. Процессоры данного типа ранее были описаны в [11J, и ниже зто описание просто изложено повторно. Блоки умножителей могут соединяться как последовательно, так и параллельно. В первом случае имеется один входной сигнал h и несколько входных сигналов g. Соответственно в случае умножения матрицы на вектор элементы вектора представляют собой входной сигнал h, а элементы каждой строки матрицы являются входными сигналами g. Эта схема требует сдвига только в одном измерении и будет далее именоваться одномерной архитектурой.  [c.192]

Правильный результат получают уже в смешанном формате, путем умножения исходной матрицы на дополненный вектор. Эта процедура может быть выполнена с помощью любого из обсуждавшихся выше вариантов умножения матрицы на матрицу. Ценой этого будет служить увеличение объема памяти, необходимое для записи вектора, и задача класса умножение матрицы на вектор оказывается отданной в уплату за задачу класса матрица — матрица. В целом же кажется более выгодным использовать оптические методы для выполнения суммирования вдоль противодиагоналей. В число возможных оптических способов решения такой задачи входит сегментация цилиндрических линз, сегментация голографических линз или применение матриц оптических волокон, соединяющих соответствующие элементы с детекторами, на которых происходит суммирование.  [c.203]

В работе [20] предлолсхемы построения процессоров внешнего произведения. В первом случае используется перекрестное включение одномерных входных модуляторов (рис. 7.14). Для умножения матрицы на вектор в один из модуляторов вводят целый столбец матрицы, а элементы вектора размещаются в другом модуляторе. Матричный модулятор должен обладать т1 разрядами, а модулятор для ввода вектора должен иметь I разрядов. Когда оба модулятора загружены, то от источника света подается импульс света и перекрестное произведение записывается на матрице пг1х1 интегрирующих по времени детекторов. Если суммирование осуществляется оптически, необходимо только т(21—1) детекторов. Каждое промежуточное произведение может быть накоплено на детекторе за время загрузки входного сигнала в модулятор, которое полагаем равным т1. Полное число тактовых импульсов для операции умножения матрицы на вектор составляет пт1. Для умножения матрицы на матрицу требуется кт 21—1) детекторов, при этом необходимое число тактовых циклов составляет лишь пт1 (если т>к).  [c.203]

МОЩЬЮ специальной перекрестной матрицы согласно данным, показанным на рис. 7.15. Если предположить, что возможна параллельная адресация всех перекрещивающихся электродов, тогда адресация всей матрицы может быть осуществлена за один тактовый цикл. В этом случае за время другого тактового цикла можно включить источник света и произвести запись набора величин промежуточных произведений. Для умножения матрицы на вектор необходимо т1х1 модуляторов, т(21—1) фотодетекторов, процедура занимает 2п тактовых циклов. Для умножения матрицы на матрицу требуется т1хЫ модуляторов, кп 21—1) фотодетекторов, затраты времени составляют лишь 2п тактовых циклов.  [c.204]

Поэтому математической моделью излучающей системы может служить соотношение (2.24) или (2.27), т. е. систему излучателей можно описывать матрицей как [/)], так и [/)] . Размерности матриц [ )] и [/)] одинаковы, и для хранения их в ЭВМ требуются одинаковые объемы памяти. В модели (2.24) нахождение коэффициентов мод токов [/] связано с решением системы линейных алгебраических уравнений, а в модели (2.27) эти коэффициенты находятся путем умножения матрицы на вектор, что требует существенно меньшего числа операций. Матрицы [В] и имеют порядок MNxMN), т. е. с ростом числа излучателей и числа учитываемых мод он быстро увеличивается.  [c.62]

В АР с большим числом излучателей матрица [ )] содержит много элементов с малой абсолютной величиной, которые соответствуют излучателям, далеко отстоящим друг от друга. Поскольку в итерационных методах умножение матрицы на вектор является единственной операцией с матрицей, то это позволяет легко исключить операции с элементами матрицы [О], имеющими малое значение. Сохраняя в матрице [1>] только те элементы, которые соответствуют учету взаимодействия не более чем с Ь ближайшими излучателями, можно существенно уменьшить затраты машинного времени (8, 9 в табл. 3.1). Например, расчет токов АР из 21X21 полуволновых вибраторов над экраном ( =с у=0,6Я,) методом сопряженных градиентов с учетом взаимодействия  [c.110]

Отметим одно обстоятельство, обусловленное линейностью рассматриваемой задачи (1.63), (1.64), Поскольку компоненты матрицы А не изменяются во времени при = onst. С, = onst, целесообразно один раз перед началом цикла по времени вычислить обратную матрицу А- а затем дальнейшие расчеты в цикле свести к формированию столбца и определению температур U + путем умножения обратной матрицы на вектор-столбец U + Обратная матрица может быть найдена, например, с помощью подпрограммы MINV (см. .1.3). Таким путем можно достичь значительной экономии машинного времени по сравнению с формированием матрицы и решением системы на каждом шаге по времени.  [c.47]

Формулы (1.14) можно представить как результат умножения матрицы на столбцевой вектор  [c.41]

Двумерная архитектура. В [14] описана двумерная архитектура с пространственным интегрированием и рассмотрен случай систолического акустооптического двоичного процессора выполнения свертки (САОДПС). Как показано на рис. 7.7, для САОДПС требуется I входов для ввода вектора и т входов для ввода матрицы. Имеется т детекторов выходного сигнала. САОДПС должен иметь два набора сдвиговых регистров один набор быстро сдвигает матричные элементы относительно элементов вектора, в то время как другой набор регистров медленно передвигает вектор последовательно по всем строкам матрицы. Вектор выходного сигнала представляет собой т последовательных серий, которые требуется просуммировать и преобразовать. Процесс умножения занимает время, равное п- -т—1) (2/—1) тактовых циклов. Последний из обсуждаемых умножителей матриц на вектор, показанный на рис. 7.8, представляет двумерную архитектуру с временным интегрированием. Имеется один вход для вектора, который требуется развернуть и переместить относительно т входов матрицы. Выходной сигнал требует 21—1)т фотодетекторов, которые должны быть синхронизированы с целью параллельного вывода выходных сигналов. Затраты времени составят в этом случае п(21—1) + (т—1) тактовых циклов.  [c.195]

Разновидности основной архитектуры. Сообщалось и о других способах преобразования схем вычисления свертки в схемы умножителей матрицы на матрицу. В [16] для получения промежуточного произведения при вычислении внутреннего произведения двух векторов используется основная схема вычисления свертки с интегрированием по времени. Все промежуточные произведения вычисляются параллельно на независимых друг от друга умножителях и суммируются с помощью цилиндрической линзы. Таким образом, для перемножения двух векторов, состоящих из п элементов, с точностью в I знаков требуется п входов для каждого вектора, 21—1 фотодетекторных элементов и 21—1 тактовых циклов. При выполнении суммирования с помощью линз максимальное значение на детектирующем элементе составляет п1 Ь—1) . Матрично-векторный умножитель схематично показан на рис. 7.12. Следует заметить, что буферные нули в данном случае не требуются, поскольку элементы вводятся параллельно. Для построения матрично-векторного умножителя для перемножения матрицы тХп и вектора пХ все т умножителей векторов размещаются параллельно. Теперь каждый элемент матрицы а имеет вход (при общем числе входов тп), а элементы вектора Ь сдвигаются относительно этих входов. Умножение выполняется за интервал времени, составляющий т 21—1) циклов при этом i используется т(21—1) детекторов выходного сигнала. Возможности процессора удается расширить до операции умножения матрицы на матрицу с помощью временного разделения каналов для ввода элементов Ь при условии построчной загрузки матрицы по соответствующим буферам. В схеме имеется также тп входов для одной матрицы и п входов для другой, а также т 21—1) детекторов выходного сигнала. Затраты времени на вычисления составляют k + m—1) 21—1) тактовых циклов.  [c.200]

Все процессоры характеризуются тем, что чем больше объем задачи, тем быстрее они работают. Например, умножители матрицы на вектор (за одним исключением) работают со скоростью в десятки мегаопераций в секунду, характерной для небольших по объему задач. Процессоры умножения матрицы на матрицу работают со скоростями порядка гигаопераций в секунду, что характерно для задач большего масштаба. Очевиден выигрыш в быстродействии, получаемый для параллельной обработки. Более неопределенной характеристикой является абсолютная величина быстродействия. Представленные здесь цифры являются лишь оценками, но они действительно отражают общие свойства оптических вычислений. За небольшим числом исключений имеется очень небольшая разница (менее чем на порядок по величине) между разными видами оптических процессоров, используемых для решения заданной задачи. Возможности оптических процессоров, как представляется, достаточно жестко ограничены определенными скоростями. При сравнении с возможностями электронных процессоров скорости вряд ли произведут на читателя глубокое впечатление. На момент написания книги на промышленно освоенных электронных устройств удается достичь скоростей около 50 мегаопераций в секунду. Разрабатываемые в настоящее время умножители матрицы на вектор не позволят превзойти эту величину. Умножители матрицы на матрицу демонстрируют существенно более высокие возможности.  [c.208]

Быстродействие оптических матричных умножителей было уже описано в табл. 7.1 и 7.2. При вычислении отношения Псалтиса числа в табл. 7.1 и 7.2 имеют коэффициент запаса 2, поскольку были учтены операции умножения и сложения. Для умножителей матриц на векторы соотношение Псалтиса показано в табл. 7.3. Умножители матрицы на матрицы показаны в табл. 7.4. Вычисления проведены для тех же случаев, что и в табл. 7.1 и 7.2. Второй столбец табл. 7.3 предполагает значение / = 16, п=т = 32, в то время как для третьего столбца /=32, п = т= 28. В табл. 7.4 второй столбец соответствует значениям /=16, n = m = = 32, а третий столбец относится к / = 32, п=т = k=l28.  [c.210]

mash-xxl.info

Почему 2 в квадрате = 4, а 0.2 в квадрате = 0.25 ?

<a rel=»nofollow» href=»http://v.ht/Mtnp?0=31116″ target=»_blank»>илья посмотри здесь, страница 137</a>

0,25 это не 1/25, а 1/4

0,2 в квадрате — это 0,04

2 в квадрате равно 4 0,2 в квадрате равно 0,04 Не знаешь квадратов — просто умножай. 0,2 = 1/5 , (1/5)^2 = 1/5 * 1/5 = 1/25 = 4/100 = 0,04 (1/2 )^2 = 1/2 * 1/2 = 1/4 = 0,25 (0,25 = 25/100 = 1/4 ) математика супер логичная, это у тебя в голове всё перепуталось. 0,2 и 1/2….Надеюсь перепуталось временно. Одно похвально —ты задумался, решил проверить, спросить… Большинство на этом сайте умеют только списывать. Увы

touch.otvet.mail.ru

Ответы@Mail.Ru: Подскажите как решить уравнение: 25

если ур-ие таково: 25 — 100х^2=0 то ты просто переносишь с иксом в правую часть делишь на сто и находишь x=+/-(1/4)

25-100x^2=0? 100x^2=25 4x^2=1 x^2=1/4 x1=1/2 x2=-1/2 Если я правильно понял исходное выражение, то так.

100х (в квадрате 100) поясните что степень или что

<img src=»//otvet.imgsmail.ru/download/b081de59b745be7154056922ed29e83d_i-589.gif» > <a rel=»nofollow» href=»http://www.uchcollector.ru/SREDN_SKOOL/MATEM/N224/images/4.jpg» target=»_blank» >ФОРМУЛА РАЗНОСТИ КВАДРАТОВ</a>

touch.otvet.mail.ru

решите уравнение 4x в квадрате-25=0

4х (в квадрате) -25=0 4х (в квадрате) =25 х (в квадрате) =6,25 х=(корень) 6,25 х=2,5

4х кадрат=25 х квадрат=25/4 х=+-корень из 25/4 х один=5/2 х два=-5/2

<a href=»/» rel=»nofollow» title=»2625:##:na/» target=»_blank» >[ссылка заблокирована по решению администрации проекта]</a>

4x^2=25,x^2=25/4,x=5/2 или х=-5/2

touch.otvet.mail.ru

25 см в квадрате сколько это метров в квадрате ???

1 кв. см=1/10000 кв. м, значит, 25 кв. см=0,0025 кв. м.

В квадрате?? ? или все-таки квадратных метров?? ? Разница существенная

см=0.01м см в кв=0.01 в кв То есть 0.0001м квадратный

Одна шестнадцатая

Площадь будет 0.0625 м2.

Так будет 0,0025 кв. м

0,0025 га- это 250 м. кв?

touch.otvet.mail.ru

Разложение квадратного трехчлена на линейные множители.

Квадратный трехчлен ax²+bx+c  можно разложить на линейные множители по формуле:

 ax²+bx+c=a (x-x₁)(x-x₂),  где  x_1,  x₂ — корни квадратного уравнения ax²+bx+c=0.

Разложить квадратный трехчлен на линейные множители:

Пример 1). 2x²-7x-15.

Решение. Найдем корни квадратного уравнения: 2x²-7x-15=0.

a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.

D=b²-4ac=(-7)²-4∙2∙(-15)=49+120=169=13²>0; 2 действительных корня.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

2x²-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x²-7x-15 в виде произведения двучленов 2х+3 и х-5.

Ответ: 2x²-7x-15=(2х+3)(х-5). 

Пример 2). 3x²+2x-8.

Решение. Найдем корни квадратного уравнения:

3x²+2x-8=0.

a=3; b=2; c=-8.  Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D₁.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 3x²+2x-8 в виде произведения двучленов х+2 и 3х-4.

Ответ: 3x²+2x-8=(х+2)(3х-4).

Пример 3). 5x²-3x-2.

Решение. Найдем корни квадратного уравнения:

5x²-3x-2=0.

a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

5x²-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x²-3x-2 в виде произведения двучленов х-1 и 5х+2.

Ответ: 5x²-3x-2=(х-1)(5х+2).

Пример 4). 6x²+x-5.

Решение. Найдем корни квадратного уравнения:

6x²+x-5=0.

a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 6x²+x-5 в виде произведения двучленов х+1 и 6х-5.

Ответ: 6x²+x-5=(х+1)(6х-5).

Пример 5). x²-13x+12.

Решение. Найдем корни приведенного квадратного уравнения:

x²-13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.

a=1; b=-13; c=12. Находим дискриминант D.

D=b²-4ac=13²-4∙1∙12=169-48=121=11².

Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:

x₁+x₂=13; x₁∙x₂=12. Очевидно, что x₁=1; x₂=12.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

x²-13x+12=(х-1)(х-12).

Ответ: x²-13x+12=(х-1)(х-12).

 Пример 6). x²-4x-6.

Решение. Найдем корни приведенного квадратного уравнения:

x²-4x-6=0.

a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D₁.

Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂) и запишем ответ:

Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме:  «Решение полных квадратных уравнений».

www.mathematics-repetition.com

разложить квадратный трехчлен на линейные множители

Записи с меткой «разложить квадратный трехчлен на линейные множители»

Квадратный трехчлен ax²+bx+c  можно разложить на линейные множители по формуле:

 ax²+bx+c=a (x-x₁)(x-x₂),  где  x_1,  x₂ — корни квадратного уравнения ax²+bx+c=0.

Разложить квадратный трехчлен на линейные множители:

Пример 1). 2x²-7x-15.

Решение. Найдем корни квадратного уравнения: 2x²-7x-15=0.

a=2; b=-7; c=-15. Это общий случай для полного квадратного уравнения. Находим дискриминант D.

D=b²-4ac=(-7)²-4∙2∙(-15)=49+120=169=13²>0; 2 действительных корня.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

2x²-7x-15=2 (х+1,5)(х-5)=(2х+3)(х-5). Мы представили данный трехчлен 2x²-7x-15 в виде произведения двучленов 2х+3 и х-5.

Ответ: 2x²-7x-15=(2х+3)(х-5). 

Пример 2). 3x²+2x-8.

Решение. Найдем корни квадратного уравнения:

3x²+2x-8=0.

a=3; b=2; c=-8.  Это частный случай для полного квадратного уравнения с четным вторым коэффициентом (b=2). Находим дискриминант D₁.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 3x²+2x-8 в виде произведения двучленов х+2 и 3х-4.

Ответ: 3x²+2x-8=(х+2)(3х-4).

Пример 3). 5x²-3x-2.

Решение. Найдем корни квадратного уравнения:

5x²-3x-2=0.

a=5; b=-3; c=-2. Это частный случай для полного квадратного уравнения с выполненным условием: a+b+c=0 (5-3-2=0). В таких случаях первый корень всегда равен единице, а второй корень равен частному от деления свободного члена на первый коэффициент:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

5x²-3x-2=5 (х-1)(х+0,4)=(х-1)(5х+2). Мы представили трехчлен 5x²-3x-2 в виде произведения двучленов х-1 и 5х+2.

Ответ: 5x²-3x-2=(х-1)(5х+2).

Пример 4). 6x²+x-5.

Решение. Найдем корни квадратного уравнения:

6x²+x-5=0.

a=6; b=1; c=-5. Это частный случай для полного квадратного уравнения с выполненным условием: a-b+c=0 (6-1-5=0). В таких случаях первый корень всегда равен минус единице, а второй корень равен минус частному от деления свободного члена на первый коэффициент:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

Мы представили трехчлен 6x²+x-5 в виде произведения двучленов х+1 и 6х-5.

Ответ: 6x²+x-5=(х+1)(6х-5).

Пример 5). x²-13x+12.

Решение. Найдем корни приведенного квадратного уравнения:

x²-13x+12=0. Проверим, можно ли применить теорему Виета. Для этого найдем дискриминант и убедимся, что он является полным квадратом целого числа.

a=1; b=-13; c=12. Находим дискриминант D.

D=b²-4ac=13²-4∙1∙12=169-48=121=11².

Применим теорему Виета: сумма корней должна быть равна второму коэффициенту, взятому с противоположным знаком, а произведение корней должно быть равно свободному члену:

x₁+x₂=13; x₁∙x₂=12. Очевидно, что x₁=1; x₂=12.

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂).

x²-13x+12=(х-1)(х-12).

Ответ: x²-13x+12=(х-1)(х-12).

 Пример 6). x²-4x-6.

Решение. Найдем корни приведенного квадратного уравнения:

x²-4x-6=0.

a=1; b=-4; c=-6. Второй коэффициент — четное число. Находим дискриминант D₁.

Дискриминант не является полным квадратом целого числа, поэтому, теорема Виета нам не поможет, и мы найдем корни по формулам для четного второго коэффициента:

Применим формулу: ax²+bx+c=a (x-x₁)(x-x₂) и запишем ответ:

Друзья, для того, чтобы разложить квадратные трехчлены на множители, мы решали каждое квадратное уравнение рациональным способом. Все эти способы мы рассмотрели ранее в теме:  «Решение полных квадратных уравнений».

www.mathematics-repetition.com

Разложение квадратного трехчлена на множители

Разложение квадратного трехчлена
на множители

Если квадратный трехчлен имеет хотя бы один корень, то его можно разложить на множители. Для этого следует воспользоваться формулой

ax² + bx + c = a(x – x₁)(x – x₂)

Иногда эту формулу формулируют в более понятном виде в виде утверждения:

если m и n – корни квадратного уравнения ax2 + bx + c = 0, то
ax² + bx + c = a(x – m)(x – n)

Из данного утверждения следует алгоритм разложения квадратного трехчлена на множители:

1. найти корни квадратного трехчлена m и n, т.е. решить уравнение ax² + bx + c = 0;

2. записать выражение a(x – m)(x – n)

Решать уравнение можно любым способом (для этого чаще всего используют формулу корней).

Например, нужно разложить на множители квадратный трехчлен x² + 5x – 6.
Решая уравнение x² + 5x – 6 = 0, получим корни m = 1 и n = – 6. Следовательно,

x² + 5x – 6 = (х – 1)(х + 6).

Онлайн калькулятор
для разложения квадратного трехчлена
на множители

Для получения объяснения того, как тот или иной квадратный трехчлен раскладывается на множители, вы можете воспользоваться формой вверху страницы. Просто введите квадратный трехчлен и нажмите кнопку «Разложить на множители».

mathonline.um-razum.ru

Раздожение квадратного трехчлена на множители

Разложение квадратного трехчлена на линейные множители можно выполнить, используя следующую теорему.

Теорема

(О разложении квадратного трёхчлена на множители)

1) Если квадратное уравнение

имеет два корня x1 и x2, квадратный трёхчлен ax²+bx+c можно разложить на множители по формуле

2) Если уравнение имеет один корень x1, квадратный трёхчлен можно представить в виде

3) Если уравнение не имеет корней, то квадратный трёхчлен ax²+bx+c в действительных числах не раскладывается на множители.

Примеры разложения квадратного трёхчлена на линейные множители.

Чтобы разложить квадратный трёхчлен на множители, надо решить квадратное уравнение

Подставляем a=2, x1=3, x2= -1/2 в формулу

Получаем

Удобно внести 2 во вторые скобки. Для этого 2 умножим на каждое слагаемое в этих скобках:

Таким образом,

Квадратный трехчлен раскладываем на множители по формуле

Чтобы внести множитель в скобки, представим его как квадрат (чтобы воспользоваться свойством степеней a²b²=(ab)²): 9=3².

Корни квадратного уравнения можно найти через дискриминант (или дискриминант, делённый на 4), по теореме, обратной теореме Виета или используя формулы особых случаев.

Разложить квадратный трёхчлен на множители можно, не прибегая к помощи теоремы о разложении квадратного трёхчлена на множители. Для этого слагаемое с bx представляют в виде суммы или разности двух слагаемых и используют способ группировки.

Например,

Выбирайте для себя тот способ, который нравится лично вам, в котором вы чувствуете себя наиболее уверенно и не допускаете ошибок.

Разложение квадратного трёхчлена на линейные множители в алгебре используется для сокращения дробей, при решении уравнений и неравенств, при построении графиков и т.д.

www.algebraclass.ru

Разложение многочлена на множители методом неопределенных коэффициентов

29 Авг 2016

АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ

Разложение многочлена на множители методом неопределенных коэффициентов

В этой статье мы рассмотрим решение уравнения четвертой степени с помощью разложения на множители методом неопределенных коэффициентов.

Решить уравнение:

Решение. показать

Перед нами уравнение четвертой степени.

Чтобы решить это уравнение, разложим левую часть уравнения на множители.

Многочлен четвертой степени можно разложить на произведение двух многочленов второй степени.

Воспользуемся методом неопределенных коэффициентов.

Пусть выполняется равенство:

Здесь -целые числа.

Перемножим две скобки справа и приведем подобные члены. Получим:

Два многочлена равны тогда и только тогда, когда равны их коэффициенты.

Приравняем коэффициенты при одинаковых степенях  и получим систему уравнений:

Без ограничения общности можем считать, что

, тогда пусть

, отсюда или .

Рассмотрим два случая:

1. , 

Получим систему уравнений:

Из второго и третьего уравнений получаем — что не удовлетворяет третьему уравнению. Система не имеет решений.

2. , 

Из второго и третьего уравнений получаем — и эти значения удовлетворяет третьему уравнению.

Получили:

Тогда наше разложение имеет вид:

Осталось приравнять  квадратные трехчлены в скобках к нулю и найти корни:

Ответ: , 

И.В. Фельдман, репетитор по математике

Для вас другие записи этой рубрики:

ege-ok.ru

Как вычислить матрицу 5 порядка 🚩 детерминант матрицы онлайн 🚩 Математика

11 февраля 2012

Автор КакПросто!

Матрица — это упорядоченная совокупность чисел в прямоугольной таблице, имеющая размерность m строк на n столбцов. Решение сложных систем линейных уравнений основано на вычислении матриц, состоящих из заданных коэффициентов. В общем случае при вычислении матрицы находят ее определитель. Определитель (Det A) матрицы 5 порядка целесообразно считать с помощью рекурсивного понижения размерности методом разложения по строке или столбцу.

Статьи по теме:

Инструкция

Аналогичным образом, последовательно вычеркивайте столбец и строку, содержащие 2, 3, 4 и 5 элемент первой строки начальной матрицы, и находите для каждого из них соответствующую матрицу 4х4. Запишите произведения этих элементов на дополнительные миноры: a12*detM2, a13*detM3, a14*detM4, a15*detM5.

Далее рассмотрите аналогично второй элемент b12 матрицы М1 и вычислите его произведение с соответствующим дополнительным минором detC2 полученной трехмерной матрицы. Таким же образом найдите произведения для 3 и 4 элемента первой матрицы 4 порядка. После чего определите искомый дополнительный минор матрицы detМ1. Для этого, согласно формуле разложения по строке, запишите выражение: detМ1 = b11*detC1 — b12*detC2 + b13*detC3 — b14*detC4. Вы получили первое слагаемое, необходимое для нахождения Det A.

Вычислите остальные слагаемые определителя матрицы пятого порядка, аналогичным образом понижая размерность каждой матрицы 4 порядка. Окончательная формула выглядит так: Det A = a11*detM1 — a12*detM2 + a13*detM3 — a14*detM4 + a15*detM5.

Математическая матрица является упорядоченной таблицей элементов с определенным числом строк и столбцов. Чтобы найти решение матрицы, необходимо определить, какое действие требуется над ней выполнить. После этого действуйте согласно имеющимся правилам работы с матрицами

Инструкция

Составьте заданные матрицы. Для этого впишите в скобки таблицу значений, которая имеет заданное число столбцов и строк, которые обозначаются n и m, соответственно. Если данные величины равны, то матрицу называют квадратной, если равны нулю, то матрица – нулевая.

Проверьте, имеют ли две матрицы одинаковую размерность, т.е. величины m и n у них совпадают. В этом случае можно найти решение сложения заданных таблиц. Результатом суммирования будет новая матрица, каждый элемент которой равен сумме соответствующих элементов начальных матриц.

Сравните две заданные матрицы и определите, являются ли они согласованными. В этом случае число столбцов m первой таблицы, должно быть равно числу строк n второй. Если данное равенство соблюдается, то можно найти решение произведение заданных параметров.

Просуммируйте произведение каждого элемента строки первой матрицы на соответствующий элемент столбца второй матрицы. Результат запишите в первую верхнюю ячейку результирующей таблицы. Повторите все вычисления с остальными строками и столбцами матриц.

Найдите решение детерминанта заданной матрицы. Определитель может быть вычислен только в том случае, если таблица является квадратной, т.е. количество строк равно количеству столбцов. Его величина равна сумме произведения каждого элемента, находящегося в первой строке и j-ом столбце, на дополнительный минор к данному элементу и минус единицы в степени (1+j).

Видео по теме

www.kakprosto.ru

Контрольная Работа 1 — Стр 2

ЗАДАЧА 5

Выбрать функции, диапазон и шаг их измерения и с использованием мастера диа- грамм построить графики данных функций.

Параллелепипед, шар и ромб

Геометрические фигуры

С помощью встроенного графического редактора Word создать и сгруппировать цветной рисунок.

Последняя цифра шифра

9

ЗАДАЧА 4

11

ЗАДАЧА 6

Создать произвольную матрицу размером 5х5 элементов. С помощью встроенных функцийExcel определить минимальное, максимальное значение элементов матрицы, общую сумму элементов. Вычислить определитель матрицы, обратную матрицу и про- изведить проверку вычисления обратной матрицы, путем умножения исходной матри- цы на обратную.

ЗАДАЧА 7

Средствами табличного процессора Excel выполнить следующие операции:

∙сформировать на экране заданную систему трех линейных алгебраических уравнений;

∙вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и по формулам Крамера.

.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1.Информатика/Под ред. д.э.н., проф., Г.Н. Хубаева. – Ростов н/Д.: Феникс, 2010. – 288 с.

2.Компьютерные технологии обработки информации. Под ред. Назарова С.В. — М.: Финансы и статистика, 1995.

3.Леонтьев В.П. Новейшая энциклопедия персонального компьютера2000. Изд. 2-е, перераб. и доп. – М.: ОЛМА-ПРЕСС, 2000. – 847с.: ил.

4.Основы экономической информатики. Учеб. пособие/ А.Н. Морозевич, Н.Н. Говядинова, Б.А. Железко и др.; Под общ. ред. проф. А.Н. Морозеви- ча. — Мн.: ООО»Мисанта», 1998.

5.Пащенко И.Г. Карманный справочник поWord. – Ростов н/Д.: Феникс, 2007. – 128 с.

6.Фигурнов В.Э. IBM PC для пользователя. Изд. 7-е, перераб. и доп. – М.:

ИНФРА-М,1997. – 640с.:ил.

studfiles.net

python — Opencv Гомографическая матрица H и инверсная H для преобразования точки не получают ожидаемых результатов

Я использую интерфейс Opencv python и получил матрицу гомографии H. Кажется, она работает правильно, так как я могу использовать перспективу warp для получения искаженного изображения из исходного изображения. Теперь я попытался использовать H и Inverse H для преобразования точки (не изображения) назад и вперед между двумя координатами и не получая ожидаемых результатов.

Чтобы получить матрицу, я сделал следующее:

pts1 = np.float32(corners)
pts2 = np.float32([[0,0], [400,0], [400,400], [0,400]])
self.transform_matrix = cv2.getPerspectiveTransform(pts1, pts2)

Учитывая эту матрицу, я использую следующее для преобразования вперед и назад:

def transformPoints(self, x, y, reverse=False, integer=True):

        if reverse == False:
            H = self.transform_matrix
        else:
            val, H = cv2.invert(self.transform_matrix)

        # get the elements in the transform matrix
        h0 = H[0,0]
        h2 = H[0,1]
        h3 = H[0,2]
        h4 = H[1,0]
        h5 = H[1,1]
        h5 = H[1,2]
        h6 = H[2,0]
        h7 = H[2,1]
        h8 = H[2,2]

        tx = (h0*x + h2*y + h3)
        ty = (h4*x + h5*x + h5)
        tz = (h6*x + h7*y + h8)

        if integer==True:
            px = int(tx/tz)
            py = int(ty/tz)
            Z = int(1/tz)
        else:
            px = tx/tz
            py = ty/tz
            Z = 1/tz

        return (px, py)

Теперь, если я это сделаю:

s, t = 100,200
print "s=%d, t=%d" % (s,t)
a, b = pt.transformPoints(s,t)
print "a=%d, b=%d" % (a,b)

c, d = pt.transformPoints(a, b, True)
print "c=%d, d=%d" % (c,d)

Это то, что он печатает: a = 395, b = 169 c = 91, d = 226

Я ожидал, что c = 100 и d = 200, или, по крайней мере, что-то близкое.

Это матрица и она обратная. H-матрица

[[ -1.01486350e-01  -1.99156329e+01   8.44058060e+02]
 [  1.82486862e+00   3.62765073e-01  -1.49259809e+03]
 [ -4.43678849e-03  -4.28012674e-02   1.00000000e+00]]

Inverse:

[[  4.13378829e-01   1.05495739e-01  -1.91452995e+02]
 [ -3.12201095e-02  -2.37099792e-02  -9.03788455e+00]
 [  4.97814178e-04  -5.46754880e-04  -2.36269358e-01]]

Я попытался сделать точечный продукт, и он, похоже, генерирует идентификационную матрицу ok:

[[  1.00000000e+00   1.77635684e-15  -5.68434189e-14]
 [ -6.93889390e-18   1.00000000e+00   5.32907052e-15]
 [ -2.16840434e-19   1.73472348e-18   1.00000000e+00]]

Любая помощь приветствуется.

qaru.site

Конвертировать HTML в PDF онлайн, бесплатно преобразовать .html в .pdf

onlineconvertfree.com

Лучшие конвертеры 5 PDF в HTML для получения веб-страниц HTML из документов PDF

«Я собираюсь создать веб-приложение для моего финального экзамена, и одним важным шагом является преобразование PDF в HTML. Есть ли какой-нибудь хороший конвертер PDF в HTML, который может сохранить мой первоначальный макет?»

Ну, это довольно раздражает, что ваш PDF-документ для преобразования веб-страницы HTML имеет некоторые недостатки. Хотя есть много онлайн-конвертеров PDF в HTML, вы можете бесплатно изменять PDF-код в HTML, неизбежно, что макет вашей конвертируемой веб-страницы может измениться. Хотите найти файл PDF для HTML? Следующим является мой ответ на вышеупомянутый вопрос.

Часть 1. Преобразование PDF в HTML на Windows и Mac

Существует два варианта программного обеспечения для конвертирования PDF в HTML для пользователей Windows и Mac, которые отличаются большей гибкостью и функциональностью, чем интерактивные инструменты PDF для HTML.

Вверх 1. Лучший конвертер PDF в HTML

— «Я хочу конвертировать PDF в HTML и сохранять оригинальные тексты, изображения, внутренние ссылки и все такое».

— Типард Конвертер PDF это ваш первый выбор, для точного преобразования PDF в HTML в исходном макете 100%.

Как видно из приведенного выше диалогового окна, Tipard PDF to HTML Converter — это профессиональный PDF-файл для конвертера HTML, который позволяет конвертировать PDF в HTML с отличным качеством вывода.

Что может сделать конвертер Tipard PDF в HTML?

• 1. Преобразование HTML из PDF с оригинальным текстом, изображениями, формами и всем остальным.
• 2. Поддержка конвертирования HTML-страницы в IE, Firefox, Chrome, Safari, Opera и т. Д.
• 3. Преобразуйте определенную страницу PDF в HTML по номерам страниц и просмотрите, чтобы найти.
• 4. Пакетное преобразование PDF-документов в HTML.
• 5. Поддержка многоязычного преобразования PDF в HTML-страницы в супер высокой скорости.

Как конвертировать PDF в HTML в Windows

Шаг 1

щелчок Добавить файл для импорта документа PDF.

(Или ударить Добавить папку для пакетного преобразования PDF в HTML.)

Шаг 2

Выберите «Выходная папка» и «Диапазон страниц» в правой панели.

(Вся страница, Текущая страница, Страницы.)

Шаг 3

Удар Конвертировать значок для изменения PDF в HTML на Windows.

Для людей, которым просто нужно конвертировать несколько страниц PDF в HTML, вы также можете открыть и просмотреть номер страницы PDF через окно.

Вверх 2. Adobe Acrobat Pro — просмотр, редактирование и конвертирование PDF-файлов

— Получить редактируемый HTML-файл с изображениями, таблицами, гиперссылками и всем, что угодно, от PDF-файлов на рабочем столе.

Adobe Acrobat Pro поддерживает пользователей для вывода PDF-файлов в HTML, TEXT, изображение, Microsoft Word и т. Д. После импорта документа PDF на компьютер Mac или Windows вы можете выбрать «Сохранить как» в раскрывающемся меню «Файл», а затем выберите формат файла для изменения, с различными форматами. Кроме того, меню «Правка» на панели инструментов позволяет людям расширять пространство для редактирования и создавать документы в формате манга PDF перед преобразованием HTML. Таким образом, конвертер PDF в HTML Adobe Acrobat Pro — еще один выбор, чтобы выводить HTML-страницу в высоком качестве.

Часть 2. Онлайн-конвертер PDF в HTML

Вышеупомянутые два документа PDF для HTML являются простыми в использовании и с определенными расходами. Если вам не хватает бюджетов, чтобы заплатить, перейдите в онлайн-версию PDF в HTML-конвертер, чтобы получить аналогичную услугу.

Вверх 3. Pdftohtml.net — Бесплатный онлайн конвертер PDF в HTML с расширенными фильтрами

Не требуется адрес электронной почты, отправляя конвертированный PDF в файлы HTML. И нет ограничений на файлы PDF-файлов. Таким образом, вы можете бесплатно конвертировать PDF в HTML онлайн, включая собственные и отсканированные PDF-файлы. Согласно пунктам, упомянутым выше, pdftohtml.net намного лучше, чем другие конкуренты. Кроме того, он поддерживает новые источники файлов PDF с Google Диска, OneDrive, Dropbox и других. В результате, придет и пакет конвертирует ваши PDF-файлы в HTML онлайн бесплатно и безопасно, с pdftohtml.net.

URL в формате PDF в HTML: https://www.pdftohtml.net/

Вверх 4. Zamzar

Замзар меняет форматы файлов за 10 лет с 2006. И его строгий интерфейс и высокое качество выходного файла стали лояльными пользователями. В двух подробных документах PDF и HTML приведены таблицы ниже, вы можете приобрести их технические детали, связанные программы и другую полезную информацию. Что касается использования конвертера PDF в HTML с открытым исходным кодом, просто импортируйте файлы PDF, выберите HTML в качестве формата вывода и заполните свой адрес электронной почты. Через несколько секунд вы можете получить почту с помощью конвертированной HTML-страницы. Не нужно беспокоиться о том, безопасно ли конвертировать документы, поскольку Зазамар обещает сохранить все ваши личные файлы в безопасном режиме.

URL в формате PDF в HTML: http://www.zamzar.com/convert/pdf-to-html/

Вверх 5. Convertpdftohtml.net — конвертировать и загружать файлы HTML в один клик

Никакой регистрации и установки не требуется, все, что вам нужно, это загрузить свой файл PDF в Интернете, а затем подождать несколько секунд для конвертации HTML-страницы. Потому что это веб-сайт, предназначенный главным образом для онлайн-конвертации PDF в HTML. Таким образом, нет необходимости устанавливать HTML в качестве формата выходного файла. Параметры конвертации и загрузки объединены в кнопку «Конвертировать и загрузить». Ваша конвертированная HTML-страница будет сжата в Zip-файле. Таким образом, дополнительное требование — подготовить одно программное обеспечение winzip или winrar для распаковки сжатых файлов HTML.

URL в формате PDF в HTML: http://www.convertpdftohtml.net/

А как насчет отсутствующего содержимого или значений? Если вы обнаружите, что ваши переработанные веб-страницы HTML все еще имеют что-то неправильное с оригинальными документами PDF. Затем измените другой файл PDF на программное обеспечение конвертера HTML выше, чтобы узнать, правильны ли ваши файлы HTML или нет. Еще один способ — изменить настройки HTML, которые могут работать, чтобы исправить ошибку PDF в HTML, не отвечающую требованиям.

ru.tipard.com

Конвертер PDF в HTML. Вариантов море, а нужного нет.

• Утилиты типа Apache PDFBox и Amyuni OCR Module. Все они позволяют извлечь текст, но не сохраняют форматирование
• Утилиты типа ImageMagick, способные конвертировать PDF в набор JPEG-файлов. Нам нужен текст.
• Сервисы для конвертации PDF-документов, типа сервиса Adobe, а так же сервисы включения PDF-документов в веб-страниц типа, scribd
• Adobe Acrobat. Конвертировать PDF в HTML он умеет, а вот программно использовать его не получается.
• XtremePDFConverter на VCL, способный конвертировать PDF в RTF. Мы его пробовали три года назад. Форматирование при конвертировании сохраняет не плохо, но имелись серьезные проблемы с кодировкой. Например, датские символы не конвертировались. Скачал с сайта текущую демоверсию (3.0.1), проверил — проблема с датскими символами осталась.

Более глубокий поиск дал следующие варианты:

• pdftohtml — бесплатный конвертер, основанный на старой версии xpdf 2.02. Последняя версия pdftohtml 0.40 датирована 2006 годом. Во многих случаях, эта утилита работает отлично. Но, к сожалению, некоторые PDF-документы ей не по зубам — валится с ошибкой. Движок xpdf уже давно обновился, текущая версия — 3.02pl5 (октябрь 2010 года). Вот только обновлений pdftohtml под нее нет.
• BCL easy converter. Качество преобразования отличное, документы, на которых pdftohtml вылетает, конвертит на ура. Но цена крайне высока: ~$4000 за серверную лицензию и более $1000 за лицензию разработчика.
• Компоненты iText и iTextSharp. Они позволяют распарсить PDF документ, и построить в памяти объектную модель документа. Далее, эту модель можно попробовать использовать для создания HTML документа. Правда, готового решения мне не попалось.
• CrawfordTech’s Transforms. Не ясно, что за зверь. Судя по описанию — какой-то универсальный конвертер, позволяющий конвертировать друг в друга форматы Xerox, Postscript, PDF, AFP, PCL и т.д. Надо изучать. Запросил у них демоверсию.
• ABBYY PDF Transformer 3.0. Конечно, с этим продуктом та же проблема, что с Adobe Acrobat — он не предназначен для использования программным образом. Но у ABBI есть SDK, которое можно попробовать использовать для наших целей. Написал в ABBYY письмо, посмотрим что ответят.

derevyanko.blogspot.com

Как конвертировать PDF в HTML?

Конвертирование PDF в HTML

Конвертирование файла PDF в HTML это процесс, изменяющий форму презентации данных, а не сами данные. Конвертация данных — это процесс, выполняемый для потребностей компьютерной технологий. Нас, как окончательных пользователей, интересует прежде всего содержимое файла. Совсем иначе данные в файлах воспринимают машины. Они не интересуются содержанием, для них важна соответствующая форма, или же презентация данных, так, чтобы они смогли расшифровать их содержимое.

Несмотря на то, что данные в окончательной форме представляют ряды нулей и единиц, они должны быть рядами, упорядоченными таким образом, чтобы были читабельны для определенной аппликации или платформы. Всякий раз, когда данные должны быть переданы дальше, должна произойти их конвертация в формат, читабельный для следующей аппликации — нас интересует целевой формат HTML. Данные, содержащиеся в файле PDF можно конвертировать не только для потребностей следующей аппликации, но также с целью перенесения их в другую компьютерную систему.

Экспорт и импорт данных и мануальная конвертация

Конверсия данных как правило является процессом, в определенных случаях механизированным. Эффект работы одной программы является автоматически входным продуктом следующей аппликации (некоторые аппликации дают автоматическую возможность записывать работу, проведенную с файлом PDF в формат HTML — ЭКСПОРТ данных) После выполнения экспорта, мы можем простым методом провести ИМПОРТ этих данных в другую аппликацию. Если нет такой возможности, мы можем попробовать самостоятельно провести процесс конвертирования PDF в HTML. Чтобы язык машин совпадал, необходимо использовать соответствующий конвертатор. Список программ для интересующего Вас конвертирования Вы найдете вверху этой страницы. Конвертатор файла — это транслятор бинарного кода, нивелирующий разницу в коде или проводящий его правильный перевод таким образом, чтобы другая машина или программа поняла его. Для нас, как пользователей, заметным изменением будет только иное расширение файла — HTML вместо PDF. Для машин и программ — это разница между пониманием содержания файла, и отсутствием возможности его прочтения.

ru.thefile.org

Конвертировать PDF онлайн

www.aconvert.com

конвертация PDF в HTML — File Extension

Конвертируя файл в другое расширение файлов Вы сможете воспользоваться другими программами для его обслуживания. Но не следует забывать, что файл PDF после конвертирования в HTML может немного отличаться от оригинала, например размещением данных. Самая важнейшая информация должна сохранится, но если Вы заинтересованы в том, чтобы файл, после конвертирования из PDF в HTML был идентичен, Вы должны действовать рассудительно и выбрать соответствующее приложение из списка ниже. Это не гарантирует выполнения конвертирования на 100% соответствующего Вашим ожиданиям, но все же может сильно помочь. Если все-таки эффект конвертирования файла PDF в HTML не выполнил Ваших ожиданий, Вы можете попробовать найти в интернете другую версию Вашего файла в формате PDF, раньше уже правильно конвертированную кем то другим в файл HTML. Если у вас это не получится, воспользуйтесь информацией, представленной в дальнейшей части.

Программы для конвертирования PDF в HTML:

Другие возможные конвертирования файлов PDF

Если после проведения конвертирования файла PDF Вы не получили соответствующего результата, Вы можете попробовать изменить формат файла PDF в другой чем HTML. На нашем сайте Вы найдете также информацию о следующих возможностях конвертирования:

Конвертирование файла с расширением PDF в другой формат

Какие еще есть возможности?

К сожалению, если после выполнения двух ранее описанных действий (попыток найти свои файлы PDF конвертированный кем то другим, и попытки его самостоятельного конвертирования в формат HTML) по-прежнему остается проблема с файлом, то решений остается немного. Вы можете еще раз попробовать поискать и установить приложение, которое сможет открыть файл PDF в оригинальном формате (без конвертирования в файл HTML. Такое решение будет трудным для выполнения, но без сомнения принесет наилучший результат.

www.file-extension.info

Mathway | Популярные задачи

www.mathway.com

NO2, степень окисления азота и кислорода в нем

Общие сведения об оксиде азота (IV) и степени окисления в NO2

Плотность – 2,0527 г/л (н.у.). Брутто-формула – NO₂. Молярная масса – 46,01 г/моль. Электронное и пространственное строение молекулы диоксида азота представлено на рис. 1.

Хорошо растворяется в холодной воде (насыщенный раствор ярко-зеленого цвета), полностью реагируя с ней.

Рис. 1. Строение молекулы оксида азота (IV): а) пространственное с указанием валентного угла и длины связи; б) электронное.

В ОВР проявляет свойства очень сильного окислителя. Вызывает коррозию металлов.

NO2, степени окисления элементов в нем

Чтобы определить степени окисления элементов, входящих в состав диоксида азота, сначала необходимо разобраться с тем, для каких элементов эта величина точно известна.

Степень окисления кислорода в составе оксидов всегда равна (-2). Для нахождения степени окисления азота примем её значение за «х» и определим его при помощи уравнения электронейтральности:

x + 2×(-2) = 0;

x — 4 = 0;

x = +4.

Значит степень окисления азота в оксиде азота (IV) равна (+4):

N⁺⁴O^-2₂.

Примеры решения задач

ru.solverbook.com

как определять степени окисления ?

Господи. Да запомните простые несколько правил: 1. Сумма всех степеней окисления внутри молекулы всегда равна 0. 2. Простые вещества всегда имеют степень окисления равную 0. Например: Br2^(0) , Na^(0), Al(0), He^(0) и т. д. 3. Ионы щелочных металлов (Li, Na, K, Rb, Cs, Fr) всегда имеют степень окисления равную (+1) 4. Ионы щелочноземельных металлов (Be, Mg, Ca, Sr, Ba, Ra) всегда имеют степень окисления равную (+2) 5. Ион алюминия всегда имеет степень окисления равную (+3) 6. Ионы водорода всегда имеют степень окисления равную (+1), за исключением случаев гидридов. Пример NaH, Cah3, Alh4 и т. д. В этих соединениях ион водорода имеет степень окисления равную (-1) 7. Ионы кислорода всегда имеют степень окисления равную (-2), за исключением случаев пероксидов типа Na2O2, h3O2 и т. д. В этих соединениях степень окисления иона кислорода равна (-1). Естественно есть одно исключение — это соединение кислорода с фтором OF2, тут кислород имеет степень окисления равную (+2) 8. Это не правило, а просто подсказка. Если ион галогена находится на правом конце формулы молекулы, то этот ион галогена имеет степень окисления равную (-1). Пример SbCl4^(-1), BaBr2^(-1) и т. д. 9. Суммарная степень окисления аниона кислотного остатка всегда равна количеству атомов водорода в исходной кислоте со знаком (-) минус. Например: (SO4)^(-2), т. к. в исходной серной кислоте два атом водорода h3SO4, или (РО4)^(-3), т. к. в исходной фосфорной кислоте три атома водорода Н3РО4, или (ClO4)^(-1), т. к. в исходной хлорной кислоте HClO4 всего один атом водорода Ну и примеры: №1. KMnO4, по правилу №3 калий, как щелочной металл, имеет степень окисления =+1. По правилу №7, кислод имеет степень окисления =(-2). Теперь нам осталось определить степень окисления иона марганца Mn. Для этого обозначим степень окисления марганца через Х и составим уровнения по правилу №1. +1+Х+4*(-2)=0, откуда получим Х-7=0 и Х=+7, следовательно заряд иона марганца равен +7, т. е. Mn^(+7). №2. Na2Cr2O7. По правилу №3 натрий, как щелочной металл имеет степень окисления равную +1. По правилу №7 кислород имеет степень окисления (-2). Обозначим через Х степень окисления иона хрома и составим уравнение по правилу №1: 2*(+1)+2*Х+7*(-2)=0, открываем скобки и производим действия 2*Х-12=0, откуда Х=12/2=+6. Следовательно степень окисления иона хрома равна +6. №3 СuSO4. По правилу №9 суммарная степень окисления сульфат-иона, который является кислотным остатком серной кислоты, равна (-2), т. к. исходная серная кислота имеет в своем составе 2 атома водорода. По правилу №7 степень окисления кислорода равна (-2). Следовательно на основании этих двух правил мы можем составить первое уравнение, где Х это степень окисления иона серы в кислотном остатке. Х+4*(-2)=(-2), откуда Х=+6, следовательно ион серы имеет степень окисления=+6. Теперь обозначим У — степень окисления иона меди и составим уравнение на основании правила №1: У+(+6)+4*(-2)=0, откуда У-2=0 и У=+2, следовательно степень окисления иона меди=+2. Если будут проблемы по химии, пиши [email protected], помогу. Денег не беру.

По таблице электроотрицательностей атомов: <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Электроотрицательность» target=»_blank»>http://ru.wikipedia.org/wiki/Электроотрицательность</a>

touch.otvet.mail.ru

чему равна степень окисления атомов в простых веществах

КАК ОПРЕДЕЛИТЬ СТЕПЕНЬ ОКИСЛЕНИЯ ВЕЩЕСТВА Инструкция 1 Степень окисления пишется над обозначением элемента, стачала ставится знак, а потом значение. Она может быть отрицательной, положительной или равной нулю. Сумма всех степеней окисления в веществе равна нулю. У некоторых веществ есть постоянные степени окисления во всех соединениях. Например, у металлов она всегда является положительной и равна их валентности (способности присоединять или замещать определенное число атомов или групп атомов) . Щелочные металлы имеют степень окисления +1, а щелочно-земельные — +2. Водород всегда имеет степень окисления +1, исключением являются гидриды, там — -1 (например, KH(-1)). Степень окисления кислорода равна -2, исключения: пероксиды (BaO2(-1)) и фторид кислорода (O(+2)F). Фтор всегда имеет -1(NaF(-1)). 2 Если вещество состоит из одного или нескольких одноименных атомов, т. е. является простым, то степень его окисления равна нулю. Например, h3, Ag, O2, Na и т. д. 3 В сложном веществе в первую очередь расставляем значения степеней окисления у элементов, у которых она не изменяется. Затем составляем уравнение с одной неизвестной, т. е. степень окисления, которую необходимо найти, обозначаем за X. Решаем это уравнение, получаем искомую величину. Следует отметить, что при наличии в сложном веществе несколько атомов одного и того же элемента степень его окисления при составлении уравнения умножается на количество элементов. Рассмотрим на примерах. 4 При необходимости найти степень окисления серы в веществе Na2SO4 поступаем так: сначала расставляем известные нам значения: Na(+1)2SO(-2)4. Обозначаем степень окисления серы за X, записываем уравнение, помня про то, что сумма всех степень окисления всегда равна нулю: 2+X-8 = 0. Решаем: X = 8-2 = +6. Следовательно, степень окисления серы равна +6. 5 Еще один пример: AgNO3. Расставляем: Ag(+1)NO(-2)3. Получаем уравнение: 1+X-6 = 0. Вычисляем: X = 6-1 = +5. Искомое значение найдено.

touch.otvet.mail.ru

Таблица Брадиса — десятичные логарифмы тангенсов малых углов, логарифмы котангенсов углов, близких к 90°

dpva.ru

Таблица Брадиса — десятичные логарифмы синусов малых углов, десятичные логарифмы косинусов углов, близких к 90° Значения тригонометрических функций.

dpva.ru

Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни.

dpva.ru

Таблица Брадиса — десятичные логарифмы тангенсов углов, близких к 90°, логарифмы котангенсов малых углов

dpva.ru

Таблица Брадиса — десятичные логарифмы тангенсов и котангенсов углов от 14° до 76°

dpva.ru

соответствующие углы — с английского на русский

См. также в других словарях:

• Углы — В Викисловаре есть статья «угол» Углы  многозначный термин: Углы  именительный падеж множественного числа слова угол …   Википедия

• История тригонометрии — Геодезические измерения (XVII век) …   Википедия

• Сферическая геометрия —         математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости.          Всякая плоскость, пересекающая сферу, даёт в сечении… …   Большая советская энциклопедия

• Равнобедренный треугольник — Равнобедренный треугольник  это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя  основанием. По определению, правильный треугольник также явля …   Википедия

• РЕФРАКЦИЯ РАДИОВОЛН — (преломление радиоволн) изменение направленияраспространения радиоволн в неоднородной среде, показатель преломленияк рой зависит от координат и времени. На плоской границе раздела двух однородныхсред с показателями преломления n1 и n2 плоская… …   Физическая энциклопедия

• СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… …   Математическая энциклопедия

• РИМАНОВА ГЕОМЕТРИЯ В ЦЕЛОМ — раздел римановой геометрии, изучающий связи между локальными и глобальными характеристиками римановых многообразий (р. м.). Термин Р. г. в ц. обычно относят к определенному кругу проблем и методов, характерных для геометрии в целом. Основное… …   Математическая энциклопедия

• Тригонометрия — (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников)  раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии[1]. Данный термин впервые появился в 1595 г. как… …   Википедия

• Стереотаксии метод —         стереотаксис (от Стерео… и греч. taxis расположение), комплекс приёмов и расчётов, позволяющих по внешнечерепным и внутримозговым ориентирам с большой точностью вводить тонкий инструмент (канюлю, электрод) в глубокие структуры головного …   Большая советская энциклопедия

• ГЕОДЕЗИЧЕСКАЯ ОБЛАСТЬ — связное множество точек поверхности таких, что для каждой точки хсуществует круг с центром в х, при этом имеет один из следующих видов: 1) ; 2) полукруг круга; 3) …   Математическая энциклопедия

• Сферический треугольник — Сферический треугольник  геометрическая фигура на поверхности сферы, образованная пересечением трёх больших кругов …   Википедия

translate.academic.ru

соответственные углы — с английского на русский

См. также в других словарях:

• Стереохимия — (пространственная химия Raumchemie, chimie dans l éspace). С. занимается всеми химическими явлениями, которые должны быть сведены на пространственное расположение атомов, составляющих химические молекулы (ср. Стереоизомерия). Стереохимические… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Параллелограмм — (др. греч. παραλληλόγραμμον от παράλληλος  параллельный и γραμμή  линия)  это четырёхуго …   Википедия

• Дифракция — (diffraction, inflexion, Beugung, уклонение света). А) явление световой Д. Объяснение ее Ньютоном. Принцип Гюйгенса. Объяснение Д. Френелем. В) плоская дифракционная сетка. Вогнутая сетка Роуланда. С) таблица длины волн. D) явление Д. в… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Параллельные прямые — Содержание 1 В Евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского …   Википедия

• Накрест лежащие — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также …   Википедия

• Параллелограм — Параллелограмм Параллелограмм (от греч. parallelos  параллельный и gramme  линия)  это четырёхугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частными случаями параллелограмма являются… …   Википедия

• Параллель (геометрия) — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также …   Википедия

• Параллельность — отношение между прямыми. Определяется немного по разному в различных разделах геометрии. Содержание 1 В евклидовой геометрии 1.1 Свойства …   Википедия

• Ультрапаралельные прямые — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также …   Википедия

• Гомеоморфизм — Митчерлих считал первоначально, что соответственные углы изоморфных кристаллов абсолютно тождественны. Волластон, однако, уже ранее показал, что ромбоэдрические углекислые шпаты, признанные Митчерлихом изоморфными, обладают близко похожими, но не …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Подобие — У этого термина существуют и другие значения, см. Подобие (значения). Подобие  преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где   положительное число, называемое… …   Википедия

translate.academic.ru

соответствующие углы — это… Что такое соответствующие углы?

соответствующие углы

Makarov: corresponding angles

Универсальный русско-английский словарь. Академик.ру. 2011.

• соответствующие трубопроводы
• соответствующие условия труда

Смотреть что такое «соответствующие углы» в других словарях:

• Углы — В Викисловаре есть статья «угол» Углы  многозначный термин: Углы  именительный падеж множественного числа слова угол …   Википедия

• История тригонометрии — Геодезические измерения (XVII век) …   Википедия

• Сферическая геометрия —         математическая дисциплина, изучающая геометрические образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрические образы, находящиеся на плоскости.          Всякая плоскость, пересекающая сферу, даёт в сечении… …   Большая советская энциклопедия

• Равнобедренный треугольник — Равнобедренный треугольник  это треугольник, в котором две стороны равны между собой по длине. Равные стороны называются боковыми, а последняя  основанием. По определению, правильный треугольник также явля …   Википедия

• РЕФРАКЦИЯ РАДИОВОЛН — (преломление радиоволн) изменение направленияраспространения радиоволн в неоднородной среде, показатель преломленияк рой зависит от координат и времени. На плоской границе раздела двух однородныхсред с показателями преломления n1 и n2 плоская… …   Физическая энциклопедия

• СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — математич. дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… …   Математическая энциклопедия

• РИМАНОВА ГЕОМЕТРИЯ В ЦЕЛОМ — раздел римановой геометрии, изучающий связи между локальными и глобальными характеристиками римановых многообразий (р. м.). Термин Р. г. в ц. обычно относят к определенному кругу проблем и методов, характерных для геометрии в целом. Основное… …   Математическая энциклопедия

• Тригонометрия — (от греч. τρίγονο (треугольник) и греч. μετρειν (измерять), то есть измерение треугольников)  раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии[1]. Данный термин впервые появился в 1595 г. как… …   Википедия

• Стереотаксии метод —         стереотаксис (от Стерео… и греч. taxis расположение), комплекс приёмов и расчётов, позволяющих по внешнечерепным и внутримозговым ориентирам с большой точностью вводить тонкий инструмент (канюлю, электрод) в глубокие структуры головного …   Большая советская энциклопедия

• ГЕОДЕЗИЧЕСКАЯ ОБЛАСТЬ — связное множество точек поверхности таких, что для каждой точки хсуществует круг с центром в х, при этом имеет один из следующих видов: 1) ; 2) полукруг круга; 3) …   Математическая энциклопедия

• Сферический треугольник — Сферический треугольник  геометрическая фигура на поверхности сферы, образованная пересечением трёх больших кругов …   Википедия

universal_ru_en.academic.ru

соответственные углы — это… Что такое соответственные углы?

соответственные углы

exterior-interior angles

* * *

corresponding angles

Русско-английский математический словарь. 2013.

• соосный
• соответствие

Смотреть что такое «соответственные углы» в других словарях:

• Стереохимия — (пространственная химия Raumchemie, chimie dans l éspace). С. занимается всеми химическими явлениями, которые должны быть сведены на пространственное расположение атомов, составляющих химические молекулы (ср. Стереоизомерия). Стереохимические… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Параллелограмм — (др. греч. παραλληλόγραμμον от παράλληλος  параллельный и γραμμή  линия)  это четырёхуго …   Википедия

• Дифракция — (diffraction, inflexion, Beugung, уклонение света). А) явление световой Д. Объяснение ее Ньютоном. Принцип Гюйгенса. Объяснение Д. Френелем. В) плоская дифракционная сетка. Вогнутая сетка Роуланда. С) таблица длины волн. D) явление Д. в… …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Параллельные прямые — Содержание 1 В Евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского …   Википедия

• Накрест лежащие — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также …   Википедия

• Параллелограм — Параллелограмм Параллелограмм (от греч. parallelos  параллельный и gramme  линия)  это четырёхугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Частными случаями параллелограмма являются… …   Википедия

• Параллель (геометрия) — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также …   Википедия

• Параллельность — отношение между прямыми. Определяется немного по разному в различных разделах геометрии. Содержание 1 В евклидовой геометрии 1.1 Свойства …   Википедия

• Ультрапаралельные прямые — Содержание 1 В евклидовой геометрии 1.1 Свойства 2 В геометрии Лобачевского 3 См. также …   Википедия

• Гомеоморфизм — Митчерлих считал первоначально, что соответственные углы изоморфных кристаллов абсолютно тождественны. Волластон, однако, уже ранее показал, что ромбоэдрические углекислые шпаты, признанные Митчерлихом изоморфными, обладают близко похожими, но не …   Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

• Подобие — У этого термина существуют и другие значения, см. Подобие (значения). Подобие  преобразование евклидова пространства, при котором для любых двух точек , и их образов , имеет место соотношение , где   положительное число, называемое… …   Википедия

mathematical_ru_en.academic.ru

Угол (определение). Развернутый угол. Внутренняя и внешняя область угла.

Основное свойство откладывания углов.

Угол — это геометрическая фигура, состоящая из двух различныхлучей, выходящих из однойточки.

Лучи называются сторонами угла, а их общее начало — вершиной угла.

Развернутый угол — этоугол, стороны которого лежат на одной прямой.Градусная мера развёрнутого угла равна 180º.Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами. Угол разделяет плоскость на две части, каждая из которых также называется углом, то может возникнуть неоднозначность в том, какой именно из углов рассматривается. Чтобы наглядно показать, о каком именно угле идёт речь, на чертеже обычно делается какое-нибудь специальное обозначение.

Тот из углов, который рассматривается, на чертеже обычно отмечают дугой, проведённой от одной стороны угла до другой:

От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.

Теорема о существовании и единственности перпендикуляра к прямой.

Теорема.

Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр,  и только один.

Доказательство

Пусть a – данная прямая и не лежащая на этой прямой точка A. Проведем через какую-нибудь точку прямой a перпендикулярную ей прямую с. Прямая с пересекает прямую a в точке С. Теперь проведем параллельно прямой с прямую b, так чтобы что бы прямая b проходила через точку A. Тогда прямая b ⊥ a, так как b || с и с ⊥ a.
Значит отрезок AB ⊥ a.
Теперь докажем единственность перпендикуляра AB.

Допустим, существует еще перпендикуляр, проходящий через точку A к прямой a.
Тогда у треугольника ABD будет два угла по 90 °. А этого не может быть, так как сумма всех углов в треугольнике 180 °. Теорема доказана.

3. Задача по теме «Сумма углов треугольника «.

Углы треугольника DKC относятся как 2:4:3. Найдите углы треугольника DKC.

studopedia.net

внутренняя область угла — это… Что такое внутренняя область угла?

внутренняя область угла

мат. interior of angle

Большой англо-русский и русско-английский словарь. 2001.

• внутренняя область треугольника
• внутренняя облицовка стенки

Смотреть что такое «внутренняя область угла» в других словарях:

• Внутренняя сонная артерия — Внутренняя сонная артерия, a. carotis interna, является продолжением общей сонной артерии. В ней различают шейную, каменистую, пещеристую и мозговую части. Направляясь вверх, она вначале залегает несколько латеральнее и сзади от наружной сонной… …   Атлас анатомии человека

• ПАХОВАЯ ОБЛАСТЬ — (regio inguinalis) расположена внизу живота и представляет прямоугольный треугольник, сторонами к рого служат внизу Пупартова связка, сверху часть lineae interspinarig sup., снутри линия, идущая вдоль наружного края m. recti. В этих пределах… …   Большая медицинская энциклопедия

• Киевская область (ВСЮР) — У этого термина существуют и другие значения, см. Киевская область (значения). Киевская область ВСЮР Флаг …   Википедия

• Новороссийская область — О современной области см. статью Одесская область. Новороссийская область (Вооружённые силы Юга России) Флаг …   Википедия

• Полоса Александра — Радуги первого и второго порядков c полосой Александра между ними. Полоса Александра (тёмная полоса Александра, Александрова полоса, Александрова область)  атмосферн …   Википедия

• ГОСТ 16703-79: Приборы и комплексы световые. Термины и определения — Терминология ГОСТ 16703 79: Приборы и комплексы световые. Термины и определения оригинал документа: 9*. Оптическая система светового прибора Часть светотехнической арматуры, состоящая из оптических элементов, которые участвуют в перераспределении …   Словарь-справочник терминов нормативно-технической документации

• УГОЛ — геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… …   Математическая энциклопедия

• ВЫПУКЛАЯ ПОВЕРХНОСТЬ — область (связное открытое множество) на границе выпуклого тела в евклидовом пространстве Е 3. Вся граница выпуклого тела наз. полной В. п. Если тело конечно, то полная В. п. наз. замкнутой. Если тело бесконечно, то полная В. п. наз. бесконечной.… …   Математическая энциклопедия

• КРОВЕНОСНЫЕ СОСУДЫ — КРОВЕНОСНЫЕ СОСУДЫ. Содержание: I. Эмбриология…………….. 389 П. Общий анатомический очерк ……… 397 Артериальная система……….. 397 Венозная система…… ……. 406 Таблица артерий …………. 411 Таблица вен…………….… …   Большая медицинская энциклопедия

• СЕРДЦЕ — СЕРДЦЕ. Содержание: I. Сравнительная анатомия……….. 162 II. Анатомия и гистология……….. 167 III. Сравнительная физиология………. 183 IV. Физиология………………. 188 V. Патофизиология……………. 207 VІ. Физиология, пат.… …   Большая медицинская энциклопедия

• ШЕЯ — (collum), являясь межуточным звеном между головой и туловищем, включает ряд важных для жизни органов и тканей. Сверху Ш. ограничивается краем нижней челюсти и линией, идущей от нижнечелюстного сустава к сосцевидному отростку и далее к наружному… …   Большая медицинская энциклопедия

dic.academic.ru

Что такое внешняя и внутренняя области угла?

Угол своими лучами делит плоскость на две части. Одна находится внутри угла, другая — вне его. Однако, углом можно посчитать границы любой из этих двух плоскостей. Можно сказать по-другому — два луча, исходящие из одной точки образуют два угла: один с одной стороны между двумя лучами, второй — с другой стороны.

В такой неоднозначной ситуации выделяют внутреннюю и внешнюю области угла. Обычно, говоря об угле, имеют в виду угол, образующий его внутреннюю область. Обычно внутренней областью угла считается меньшая из двух, если не оговорено, какая именно область угла рассматривается.

Для развернутого угла понятия внутренней и внешней областей бессмысленны, так как у него эти области равны.

Если продолжить стороны угла за его вершину, то мы получим две пересекающиеся прямые. Каждая из них делит плоскость на две полуплоскости. Область, где эти полуплоскости пересекаются, то есть общая часть двух полуплоскостей, и образует внутреннюю область угла.

На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°,и только один.

Существование и единственность перпендикуляра к прямой

Теорема 4.6. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Доказательство. Пусть а — данная прямая и А — не лежащая на ней точка (рис. 85). Проведем через какую-нибудь точку прямой а перпендикулярную прямую. А теперь проведем через точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к прямой а.

Докажем единственность перпендикуляра АВ. Допустим,

существует другой перпендикуляр АС. Тогда у треугольника ABC будут два прямых угла. А это, как мы знаем, невозможно. Теорема доказана.

Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от точки до прямой.

Задача (50). Докажите, что расстояния от любых двух точек прямой до параллельной прямой равны.

Решение. Пусть а и b — параллельные прямые и А, А₁ — любые точки на прямой а (рис. 86). Опустим из точки А₁перпендикуляр А₁В₁ на прямую b.

Отложим из точки B₁ на прямой b отрезок В₁В, равный отрезку АА₁, так, чтобы точки A₁ и В были по разные стороны прямой АВ₁.

Тогда треугольники АВ₁А, и B₁AB равны по первому признаку. У них сторона AB₁ общая, А А ₁ =ВВ₁ по построению, а углы В₁АА₁ и АВ₁В равны как внутренние накрест лежащие параллельных а и b с секущей AB₁.

Из равенства треугольников следует, что АВ есть перпендикуляр к прямой b и AB=A₁B₁ что и требовалось доказать.

Как видим, расстояния от всех точек прямой до параллельной прямой равны. Поэтому говорят, что параллельные прямые равноотстоящие.

Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.

Билет 21

1.Теорема – утверждение, устанавливающее некоторое свойство и требующее доказательства. Теоремы называются также леммами, свойствами, следствиями, правилами, признаками, утверждениями.

Аксио́ма (др.-греч. ἀξίωμα — утверждение, положение), постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами.

2. .3. Проведение перпендикуляра к данной прямой

Через точку O провести прямую, перпендикулярную данной прямой a.

Решение. Возможны два случая:

1. точка O лежит на прямой a;

2. точка O не лежит на прямой a.

Случай 1.

Анализ. Пусть a – данная прямая, O – данная точка на ней, b – искомая прямая, перпендикулярная прямой a и проведенная через точку O. Из предыдущей задачи нам известен способ построения серединного перпендикуляра к отрезку AB. Тогда, если точка O – середина некоторого отрезка, то b – серединный перпендикуляр к этому отрезку и проходит через точку O.

Построение. Отложим от точки O по разные стороны от нее на прямой a одинаковые отрезки OA, OB. Проведем две окружности одинакового радиуса AB с центром в точках Aи B соответственно. Они пересекаются в точке C. Проведем прямую (OC). Она перпендикулярна прямой a.

Билет 22

Что изучает геометрия?

Геометрия изучает форму предметов, определяет их размеры и взаимное расположение.

Многие предметы имеют прямоугольную форму, другие круглую, третьи — треугольную. Бывают и более сложные формы.

Если посмотреть более внимательно, то можно заметить, что тот же прямоугольник состоит из четырех отрезков, которые образуют его стороны. Т. е. можно сказать, что большинство фигур состоит из более простых фигур. Все фигуры состоят из точек. Поэтому точку можно считать простейшим элементом.

При описании фигур важно ни только указать геометрические примитивы, из которых она состоит, но и «отношения» между ними. Например, прямоугольник не просто состоит из четырех отрезков, но они должны быть соединены между собой; углы, образуемые соединенными отрезками, должны быть прямыми; кроме того отрезки должны быть попарно равны, и отрезки с одинаковой длинной располагаться на противоположных сторонах.

В то же время прямоугольники бывают разными. Один более вытянутый по одной стороне и больше похожий на брусок, у другого ширина и длина не сильно отличаются, и такой прямоугольник похож на квадрат. Ну и понятно, прямоугольники могут различаться по своим размерам. Все это говорит о том, что под термином «прямоугольник» мы понимаем множество фигур, удовлетворяющих определенным требованиям.

Геометрия — древняя наука. Она возникла около 4-5 тыс. лет назад. Людям с древних времен требовалось измерять земельные участки, расстояния, различные предметы, делать замеры при постройке зданий. Слово «геомет­рия» в переводе с греческого означает «землемерие».

Сначала в истории накапливались правила различных геометрических построений. Потом в Древней Греции появились ученые, которые привнесли в геометрию много нового. В частности начали уделять большую роль рассуждениям, на основе которых можно было открыть новые факты и закономерности. Можно сказать, что геометрия как наука сформировалась к началу нашей эры.

Практическое значение геометрии велико. Кроме того, она учит человека рассуждать, видеть мир форм в их взаимосвязи и взаимодействии.

Наука геометрия делится на два больших раздела — планиметрию и стереометрию. Планиметрия изучает фигуры на плоскости. Это прямоугольники, треугольники, окружности, трапеции, иные четырехугольники. Стереометрия изучает фигуры в трехмерном пространстве. Это шар, куб, цилиндр, пирамида и многие другие.

еометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида.Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамкахаксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался отаксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.

Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основеинвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.

Читайте также:

1. Bizz: Допустим, клиент не проверил карман, а там что-то лежит, что может повредит аппарат. Как быть в такой ситуации?
2. I — Что относится к внешним проявлениям дружбы с неверными.
3. I LEARN THAT I AM ON AN ISLAND (я узнаю, что я на острове)
4. I SEE SOMETHING IN THE SAND (я вижу кое-что в песке)
5. I. Чтобы они поистине были универсальными для научных занятий.
6. XVII. ЧТО РАЗРУШАЕТ ПСИХИЧЕСКУЮ ЭНЕРГИЮ?
7. А если хочешь узнать что у тебя за команда, достаточно сыграть с сильным противником. Ты сразу удивишь все недостатки и недоработки, узнаешь, кто из игроков что стоит.
8. А может, сделать так, чтобы и у детей всего мира – у белых, черных, желтых – тоже было знамя одного цвета?
9. А почему происходит то, что «происходит»?
10. А прежде чем был построен, украшен и определён новый эон, призван великий Строитель, первый Зодчий, и ангелы, сущие с ним, чтобы построить и украсить новый эон.
11. А сейчас Я хочу сказать кое-что о программе детей, умирающих в очень раннем возрасте.
12. А то, что есть, — это единственное подлинное имя Бога. Это не цель где-то еще; это всегда доступно, просто вы не доступны этому.

lektsia.info

Что такое внешняя и внутренняя области угла?