МАГИЧЕСКИЕ ТРЕУГОЛЬНИКИ | sibac.info
МАГИЧЕСКИЕ ТРЕУГОЛЬНИКИ
Долгоруков Михаил
класс 4 «В», лицей им. М.В. Ломоносова, РФ, г. Йошкар-Ола
Салихова Лилия Марсельевна
научный руководитель, ст. преп. кафедры Прикладной математики, ФГБОУ ВПО «ПГТУ», РФ, г. Йошкар-Ола
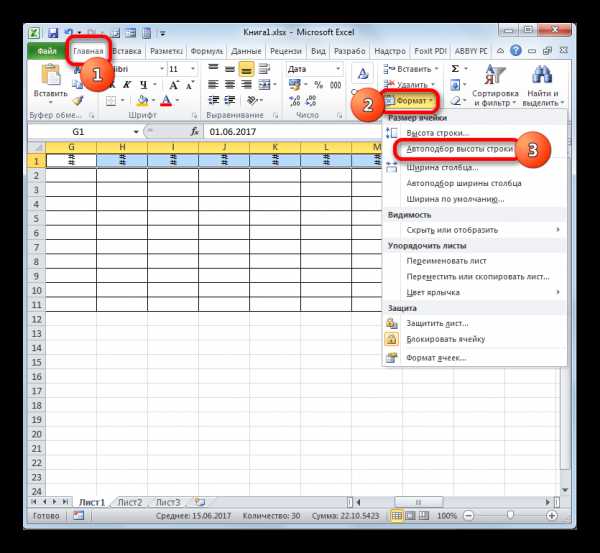
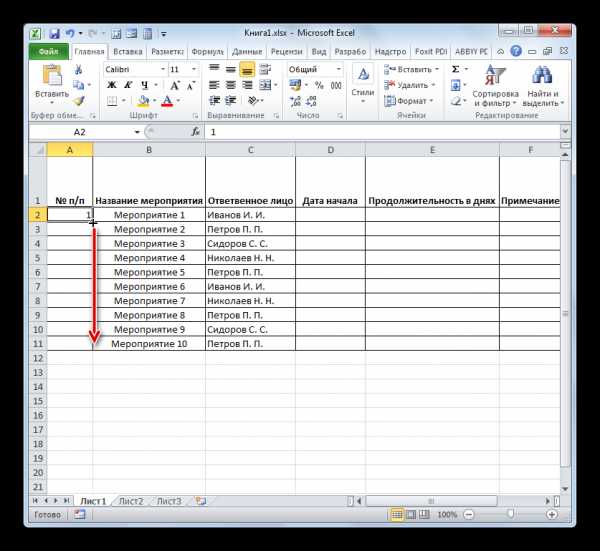
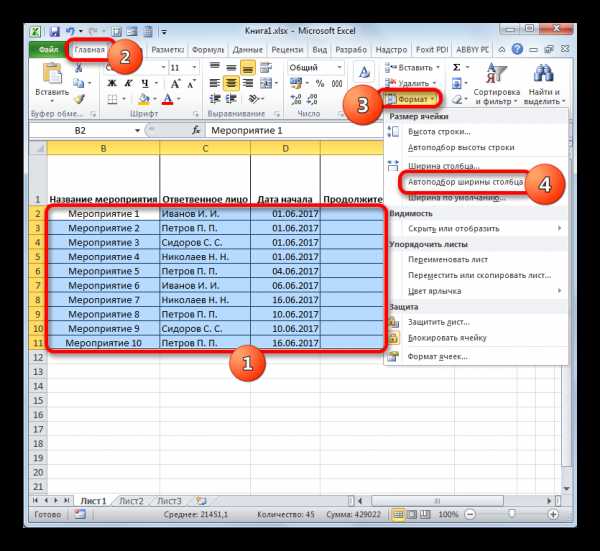
Цель работы:
1. Познакомиться с магическими треугольникамими.
2. Узнать историю возникновения треугольников.
3. Научиться правильно и быстро заполнять магические треугольники.
4. Узнать, знакомы ли мои одноклассники с чудесными треугольниками.
5. Познакомиться с учёными, которые приложили немного труда для изучения математики.
Геометрия — это одна из древнейших наук. Ее история насчитывает не одно тысячелетие. Исследовать различные пространственные формы издавна побуждало людей их практическая деятельность. Древнегреческий ученый Эвдем Родосский в IV веке до нашей эры писал: «Геометрия была открыта египтянами, и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшей границы». Как наука, геометрия впервые сформировалась в Древней Греции. Треугольник является незаменимой фигурой во всей геометрии, так как именно он лежит в основе этой науки.
Простейший из многоугольников, треугольник, играет в геометрии важнейшую роль. Треугольник был сначала обычной геометрической фигурой на плоскости, которую маглы использовали в разных целях. Одна из таких целей — земледелие. Например, в древности участки делили таким образом: выбирали три произвольные точки и соединяли их линиями. Так и появились первые треугольники.
Треугольник является также одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов. В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека. Перевернутый треугольник у многих народов был символом сердца, символом жертвенной чаши — в Индии, символом внутреннего мира человека — в древней Руси, На Древнем Востоке треугольник с вершиной, соединенной с такой же геометрической фигурой, использовали в качестве эмблемы временного цикла.
Фигуры называют магическими, если числа, нужные для их заполнения размещены так, что в каждом горизонтальном, вертикальном и диагональном ряду получается одна и та же сумма.
Магические фигуры делятся на плоские и пространственные, так как существуют магические квадраты, треугольники, прямоугольники, многоугольники и круги, а также и магические кубы.
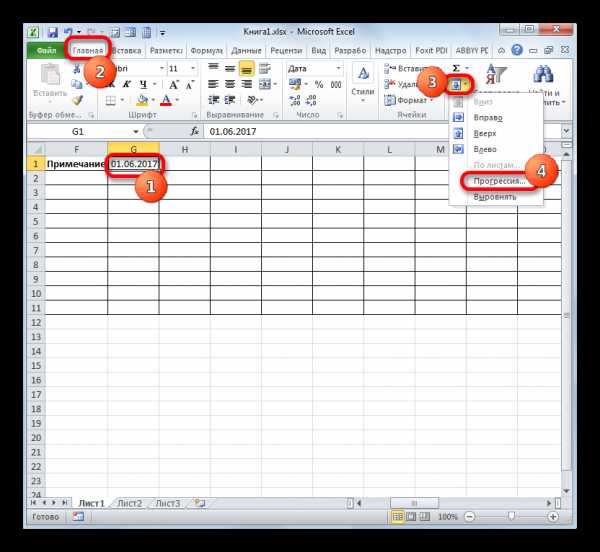
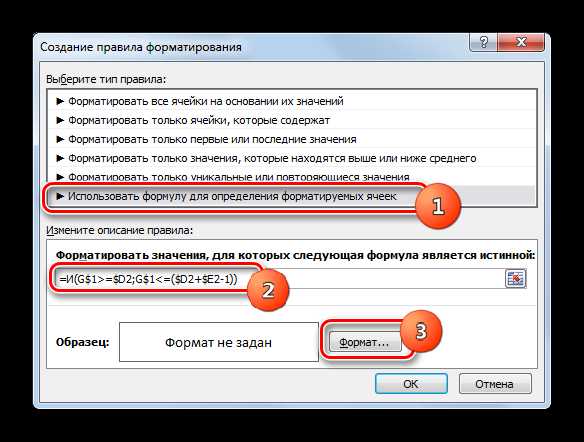
Магическим треугольником называется такое размещение шести натуральных чисел в вершинах и серединах сторон треугольника, при котором суммы чисел на каждой из сторон равны между собой. Пример магического треугольника приведен на рисунке 1.
Рисунок 1. Пример магического треугольника
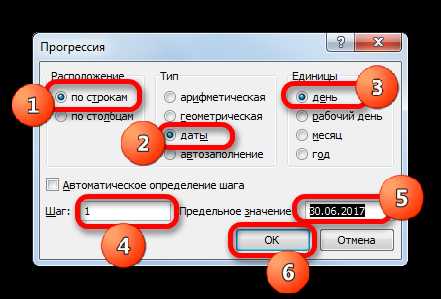
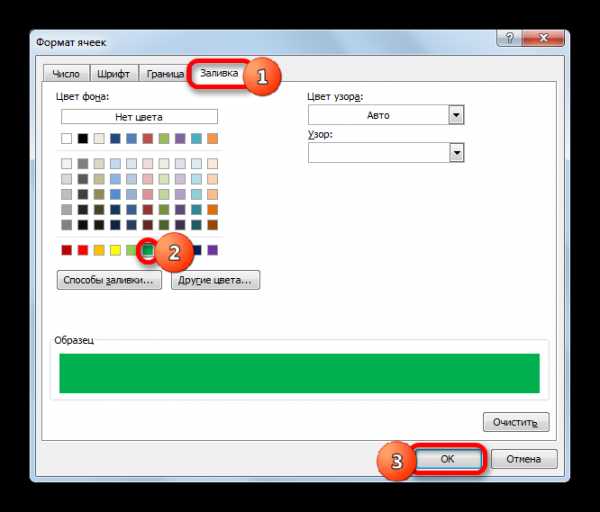
После того, как все цифры в треугольнике будут расставлены на свои места, получается следующий вид (см. рис 2).
Рисунок 2. Решенный магический треугольник
Существуют различные классификации магических треугольников. Изучив особенности и обобщив научные сведения об этих магических фигурах, можно сказать, что именно они являются основным составляющим головоломок и задач на сообразительность.
Для тех, кто заинтересовался данными треугольниками ниже приведены задачи для решения.
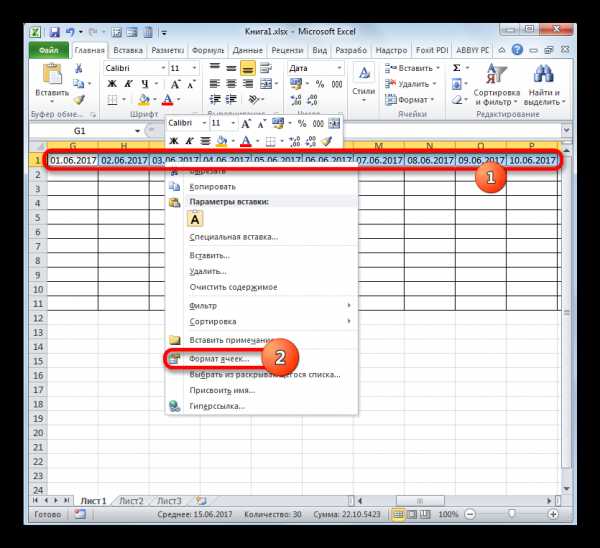
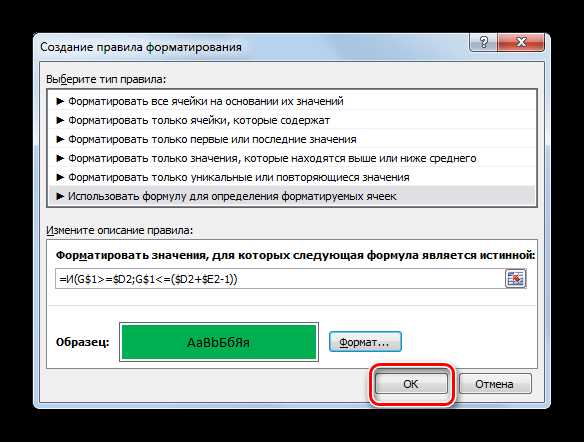
1. Реши магический треугольник. Сумма цифр вдоль каждой стороны треугольника должна быть равна 12. Используй цифры внизу рисунка. Повторяться они не должны.
Рисунок 3. Рисунок к задаче 1
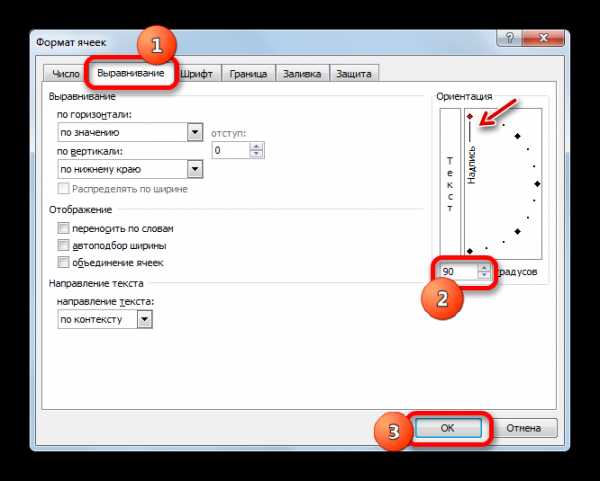
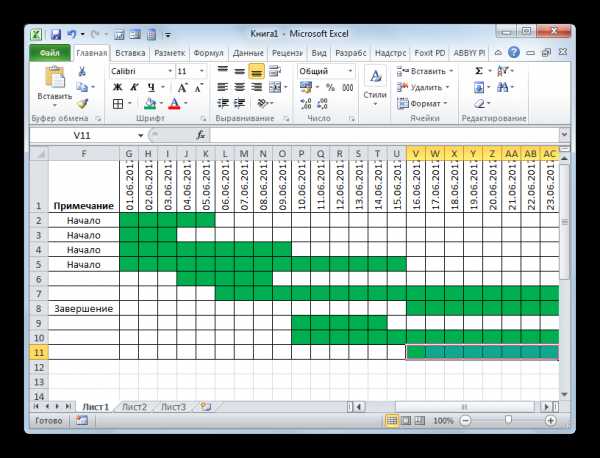
2. Реши магический треугольник. Сумма цифр вдоль каждой стороны треугольника должна быть равна числу в середине. Используй цифры внизу рисунка. Повторяться они не должны.
Рисунок 4. Рисунок к задаче 2
3. В данном треугольнике имеются з треугольника поменьше, содержащие каждый по 4 маленьких. Если большой треугольник является магическим, то сумма чисел в треугольниках поменьше равна какому-то одному числу. Расставьте числа 0,2,3,4,5,6,8,9,12 в соответствии с правилами магического треугольника так, чтобы сумма чисел в каждом треугольнике поменьше была равна 18.
Рисунок 5. Рисунок к задаче 3
Список литературы:
1.Волина З.В. «Веселая математика» М., 1999 г.
2.Перельман Я.И. Живая математика. Математические рассказы и головоломки. М.: Мир энциклопедий Аванта+, Астрель, 2008. — 271 с.
sibac.info
Стратегия форекс «Волшебный треугольник»: +273% за 12 мес
Стратегия форекс «Волшебный треугольник» довольно необычная и даже странная торговая система. Несмотря на довольно спорный способ торговли, мы все же решили познакомить вас и с этим торговым методом. Для применения этой стратегии трейдеру не нужны какие-то особые знания и навыки анализа, достаточно лишь уметь пользовать торговым терминалом.
К минусам системы можно отнести только торговое время: сигнал ожидается с 00:00 часов по 10:00 терминального времени АЛЬПАРИ (EST).
Статистика:
С апреля 2018 года по апрель 2019 года торговая система показала положительный результат в районе +273% при риске на сделку в 3%. Максимальная просадка – 15%.
Временной интервал – Н1.
Валютная пара – GBP/AUD.
Индикаторы не требуются.
Условия для покупки торговой системы «Волшебный треугольник»:

1) На открытии нового торгового дня следует определить максимум и минимум закрытого дня.
2) Так же по цене открытия нового дня проводим горизонтальную линию.
3) По уровню будущей 9-ти часовой свечи проводим вертикальную линию.
4) Точку пересечения этих двух линий далее будем называть точкой «0».
5) Максимум и минимум предыдущего торгового дня следует соединить линиями с точкой «0».
6) Таким образом формируется своеобразный треугольник.
7) Если очередная свеча закрывается выше верхней линии этого треугольника (интересует именно цена закрытия), то на открытии следующей свечи заключается сделка на покупку.
8 ) Стоп-лосс устанавливается на 5 пунктов ниже точки «0». Минимальный размер стопа 30, а максимальный – 60 пунктов.
9) После прохождения 50 пунктов в положительной зоне сделка переводится в безубыток.
10) Тейк-профит в три раза больше стоп-лосс ордера.
11) Если на закрытии дня сделка все еще активна, то её следует закрыть по рыночной цене.
12) Если треугольник строится так, что обе его линии восходящие или нисходящие, то в этот день не торгуем.
13) Если первая цена закрытия вне зоны треугольника расположена от треугольника на расстоянии более 40 пунктов, то в этот день так же не торгуем.
Условия для сделок на продажу:

1) На открытии нового торгового дня следует определить MAX и MIN уже закрытого дня.
2) По цене открытия нового дня проводим горизонтальную линию (на рисунке выше — фиолетовая).
3) По уровню будущей 9-ти часовой свечи проводим вертикальную линию (на рисунке — синяя пунктирная).
4) Точку, где пересекаются эти 2 линии будем называть точкой «0».
5) MAX и MIN предыдущего дня следует соединить линиями с «0».
6) В итоге получаем своеобразный треугольник.
7) Если следующая h2 свеча закрывается ниже нижней линии получившегося треугольника (интересует именно цена закрытия), то на открытии следующей h2 свечи открывается сделка на продажу.
8 ) Страховочный стоп-лосс нужно установить на 5 пунктов выше точки «0». Минимальный размер стопа — 30 пунктов, а максимальный – 60.
9) После того, как цена пройдет 50 пунктов в «+» зоне, сделка переводится в точку безубыточности.
10) Ордер фиксации прибыли — тейк-профит в 3 раза больше установленного стоп-лосса.
11) Если на закрытии дня сделка все еще не закрыта, то её нужно все-таки закрыть по текущей рыночной цене.
12) Если полученный треугольник построен так, что 2 его линии восходящие или нисходящие, то в этот день торговать не нужно.
13) Если 1-я цена закрытия свечи вне зоны треугольника расположена от его линий на расстоянии более 40 пунктов, то в этот день так же торговать не нужно.
Видео версия стратегии форекс «Волшебный треугольник»:
Индикаторов нет, поэтому и шаблона для МТ4 тоже нет.
strategy4you.ru
Магический треугольник.
Как выйти из этой игры?
Я считаю, что самое плохое, что может случиться в судьбе, кроме смерти любимых, — это попадание в магический треугольник. Я так называю магическую войну, силы в которой с обеих сторон примерно равны или хотя бы сопоставимы.
За что разгорается магическая война? Как и любая схватка – за деньги, собственность, сексуального партнёра. Ещё частая причина магического треугольника – месть.
В треугольнике противники связаны не только с предметом своей войны, но и между собой. И с каждым днём войны эта связь только крепнет. А может быть хуже, чем быть связанным неразрывно со злейшим врагом? Но люди так вовлекаются в противостояние, что иногда уже не могут жить, не зная, как там на «другой стороне». В моей практике был случай, когда после смерти врага человек не смог жить дальше, покончил с собой. Просто силы кончились у обоих – они ведь и были почти равны. И один ушёл раньше, а второй – за ним….
Скажете «странно»? И лишь те, кто живёт или жил в этом аду, меня поймут. Только представьте: все силы, деньги, здоровье, радости жизни утекает в чёрную дыру схватки. Цикл выглядит обычно так: нападение со стороны — чистка-защита- собственная атака-пауза, когда противник выполняет предыдущий цикл… Противник так или иначе пробивает защиту, и снова чистка-защита-атака…. И так по кругу годами. Даже если человек не тратит деньги на мастера, а делает всё сам, как умеет, другие сферы жизни неминуемо страдают от недостатка сил. К тому же, непрофессиональная магия неминуемо разрушает здоровье, физическое и психическое….
Так что же делать?
Разумеется, я предлагаю моим клиентам самые высокие степени защиты из возможных. Руны – это боевая магия викингов, и они созданы для войны. Однако, и Руны не всесильны, и с другой стороны может оказаться такой же сильный противник.
Если человек ввязался в магическую войну и циклы повторяются более года, то ясно, что силы соизмеримы и надо правильно выходить из игры.
Как я уже сказала, магическая война, повторяя цикл раз за разом, разрушает всё в человеке, и тело, и судьбу и душу. И в любом случае из неё надо выходить, если не чтобы победить, то хотя бы чтобы выжить и сберечь душу. Конечно, лучше воспользоваться помощью профессионала и он подскажет, как поступить….
Однако магия услуга платная всегда, а у человека в результате магической войны может не остаться ни денег, ни здоровья. И всё же есть способ, даже когда платить уже нечем.
Именно он описан в Великой Книге как «подставь вторую щёку» обидчику. Я не толкую Книгу, не возьму на себя смелости. Однако я считаю, и это уже моё право, что там описан именно выход из закольцованной магической войны.
Да, надо набраться решимости и мудрости, собрать остаток воли и сил, набраться смирения перед Миром и – отойти от схватки, оставить поле боя за противником, подчинившись Судьбе.
Если Вы правы перед Миром (а правота эта не подвластна пониманию человека, это не правота перед законом, церковью или даже Родом, здесь другое), то Ваш противник неминуемо останется один на один с Высшими силами. И вот тогда на Вашем месте встанет ТОТ, кто не проиграет. И, что самое парадоксальное, сыграет ЗА Вас!
Но сначала должно пройти время, и в это время Вы не должны ни жалеть об отступлении, ни вспоминать о проигранном, ни сокрушаться о «несправедливости» судьбы, ни желать ничего противнику….
Собственно, единственное, что можно делать в это время, это работать над собой и с собой. Выстраивать вновь по кирпичику свою жизнь, пусть медленно и трудно, следя не за результатом, а за процессом.
И при этом Вы должны понимать, что возможно уже всё проиграли. Ведь Вы не можете знать, кто из вас «на белой стороне». Возможно, это не Вы!
Однако, когда нет выхода, то этот – единственный. Даже, если Вы не «за белых», то хотя бы сохраните, что осталось.
А вот если всё же «за белых» и ушли из схватки «без оглядки», смирив гордыню и доверившись Миру и своей судьбе, тогда противнику, и так истощённому войной, придёт конец. И такому концу не позавидуешь….
Так что шансы есть всегда: 50 на 50 – это совсем не плохо!
Кстати, и об этом тоже есть в Книге.
Всем, кому нужно разобраться в проблеме, подобрать ключи к решению какой-то загадке, выйти из тупика или просто получить совет, — обращайтесь к Рунам, я постараюсь помочь.
С пожеланием успехов моим читателям,
Инга
runmagic.ru
Факультативное занятие по математике «Магический треугольник»
Разделы: Начальная школа, Внеклассная работа
Цели:
- Познакомить с понятием «магический треугольник», сформировать умение решать магический треугольник.
- Развитие зрительной памяти на цифровом материале, концентрации и объёма внимания, мышления, речи.
- Повторить сложения и вычитания в пределах 100.
Оборудование: презентация.
Ход занятия
I. Разминка.
Ответьте на вопросы
- Титул самого «правдивого» человека на свете. (Барон Мюнхаузен)
- Ребёнок лошади. (Жеребёнок)
- Страна, где жил великий сказочник Андерсен. (Дания)
- Северная ездовая охотничья собака. (Лайка)
- Полосатая африканская лошадь. (Зебра)
- Часть одежды, куда кладут деньги. (Карман)
- Дедов сын. (Отец)
- Метательное оружие, возвращающееся к охотнику. (Бумеранг)
II. а) Упражнения на развитие зрительной памяти на цифровом материале.
Посмотрите внимательно (20 сек. ) на предлагаемые вашему вниманию ряды чисел.
Постарайтесь запомнить их взаимное расположение, порядок следования.
7, 12, 3, 24, 10, 9.
- Каких чисел в ряду больше – однозначных или двузначных?
- Каким по счёту стоит наименьшее двузначное число?
- Чему равна сумма третьего и последнего чисел?
- Каким по счёту идёт число, в котором меньше букв?
- Какое число по счёту соответствует количеству гласных букв в русском алфавите?
- Правда ли , что разность между вторым и последним числами является 3?
- Сколько раз в ряду повторяется цифра 2?
- Правда ли, что сумма первого и третьего чисел равна круглому числу?
- В каких сказках встречается второе число ряда?
б)Упражнения на развитие зрительной памяти.
Внимательно прочитайте три раза слова, попытайтесь их запомнить, а затем напишите
| ключ | арбуз | ведро | дерево |
| груша | книга | птица | чашка |
в) Упражнения на развитие концентрации и объёма внимания.
Назовите в обратном порядке.
4 – 23
6 – 1 – 15
61 – 7 – 43 – 8
97 – 4 – 6 – 9 – 31
6 – 1 – 6 – 93 – 4 – 23
III. Магический треугольник.
Магический треугольник составлен из девяти маленьких треугольников, в которые вписали числа. В каждом магическом треугольнике можно найти 3 треугольника, которые составлены из четырёх маленьких треугольников.
– Найдите суммы в этих треугольниках.
7 + 1 + 6 + 3 = 17
2 + 1 + 5 + 9 = 17
3 + 2 + 4 + 8 = 17
– Суммы одинаковы, значит треугольник магический
Посчитайте ещё один треугольник.
1.
6 + 12 + 13 + 7 = 38
12 + 15 + 9 + 2 = 38
13 + 9 + 10 + 6 = 38
Суммы одинаковы, значит треугольник магический
2.
11 + 5 + 4 + 10 = 30
5 + 2 + 7 + 16 = 30
4 + 7 + 6 + 13 = 30
Суммы одинаковы, значит треугольник магический
3.
13+16+3+10=42
16+11+13+2=42
10+13+15+4=42
Суммы одинаковы, значит треугольник магический
4.
7 + 8 + 9 + 5 = 29
2 + 8 + 6 + 1 = 17
3 + 1 + 4 + 9 = 17
Суммы не одинаковы, значит треугольник не магический
5.
5 + 2+1 + 16 = 24
2 + 13 + 6 + 3 = 24
3 + 1 + 6 + 14 =24
IV. Итог урока.
18.01.2013
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Магический треугольник: математический пазл для детей
Готовы ли вы дать своим детям веселую математическую головоломку и отличный тренажер для развития логического мышления? Делимся с вами простой и отличной идеей — мы называем его волшебный треугольник!
Оба моих сына 7-летний и 11-летний действительно с большим удовольствием пытались решить эту головоломку. Мой 11-летний взял меньший треугольник, но моментально решил его, а вот треугольник большего размера оказался идеальной задачей. Младший сын долго и упорно пытался, сражался и через ряд ошибок победил — О, как он был горд собой, когда нашел верное решение!
Итак, приступим!
Есть несколько различных видов волшебных треугольников, и я делюсь 2 из них с вами. Каждая головоломка имеет несколько решений, так что удовольствие может длиться и длиться…плюс, вы можете выбрать головоломку в зависимости от возраста и способностей вашего ребенка.
Что вам нужно:
— Ребенок! (Один или более)
— Карандаш, линейка, ножницы и цветная бумага.
Советую привлечь ребенка к изготовлению, ведь известно, что приготовленная собственноручно и еда вкуснее, и игра увлекательнее).
На фото образцы головоломки. На первой картинке, та что попроще, на второй — для более взрослых деток.

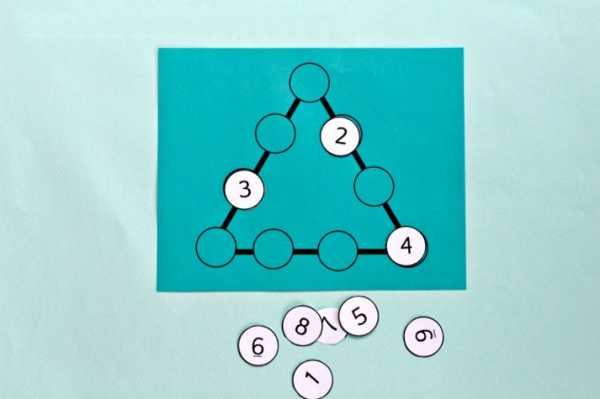
А теперь собственно инструкции:
Расположить цифры для каждого треугольника (1-6 для маленького и 1-9 для большого треугольника) так, чтобы сумма чисел на каждой стороне была равна сумме чисел на любой другой боковой стороне.
Для небольшого треугольника, расставить числа таким образом, чтобы сумма каждой стороны была равна 9. Существуют также решения, чтобы сумма на каждой стороне составляла 10, 11 и 12.
Для большого треугольника расположить числа так, чтобы сумма каждой стороны была равна 17. Вы также можете найти решения для 19, 20, 21 и 23.
Для продвинутых молодых математиков:
Не говорите детям сумму для каждой волшебной стороны треугольника. Просто дайте задание, упорядочить числа так, чтобы сумма на каждой стороне была равна остальным. Пусть самостоятельно попытается выяснить сумму и найти свое собственное решение!
Почему именно магический треугольник?
Решение упражнений с магическими треугольниками развивают не только базовые навыки сложения у детей, но и критическое мышление, устный счет и логическое мышление!Решение
Я настоятельно рекомендую, чтобы дети находили решение сами! Не может ребенок решить магический треугольник сегодня? Пусть снова попробует завтра. Ваши дети получат гораздо больше удовлетворения, если они сумеют покорить «магический треугольник» самостоятельно!
Готова поспорить, даже взрослый не сразу найдет решение, поэтому по секрету делюсь с вами решением магического треугольника…Только детям не подсказываем…ну ладно — самую малость!
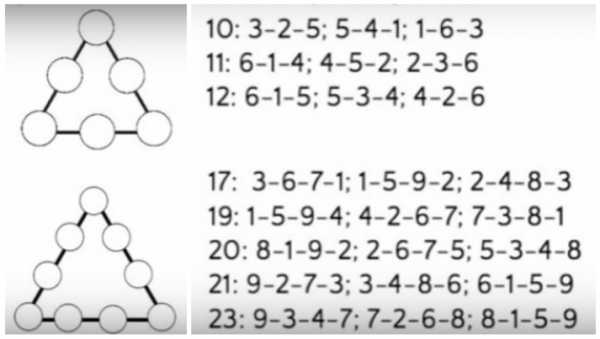
Метки: задачи для детей, игры и головоломки.
Читать также:
deniska.kharkov.ua
Амулет треугольник: значение, магические свойства
Издавна символ треугольника использовали, как оберег на товар или имущество, потому что геометричная форма является мощнейшим защитным символом. Современные практики советуют приобретать треугольные амулеты, если нужно развить магические способности, уберечься от врагов и потусторонних сущностей. Сакральный символ присутствует в культурах всех древних народов и в различных верованиях, а потому его может использовать каждый. Следует учитывать, что эффект от амулета меняется в зависимости от вида и количества геометрических фигур.

Магические свойства оберегов
Общее сакральное значение
Амулет в виде пирамиды, смотрящей вершиной вверх, практики рекомендуют заряжать солнечной энергией, а перевернутый — лунной. При этом первый лучше изготавливать из желтых металлов, а второй из серебра.
Треугольные талисманы обладают наибольшей магической силой, так как заостренная форма позволяет эффективно аккумулировать энергию и четко направлять ее на решение конкретной цели. Сакральное значение таким амулетам придает количество сторон геометрической фигуры, потому что тройкой в магии описываются фазы жизни человека, а еще единство различных миров — божеств, людей и потусторонних сущностей.
Владелец оберега может наладить контакт с высшими силами и заручиться их поддержкой. Главное предназначение треугольных амулетов — это исполнение заветных желаний. Лучше заговаривать один символ на достижение единичной цели. Дополнительный плюс заключается в обретении везения, которое поможет реализовать все намеченные планы и не испытывать при этом трудностей.
Вернуться к оглавлениюЗначение треугольной формы в разных культурах
 Древние славяне трактовали значение треугольника как явь, где идет жизнь людей и их мир.
Древние славяне трактовали значение треугольника как явь, где идет жизнь людей и их мир.Геометрическая фигура имела сакральный смысл у следующих древних народов:
- В Поднебесной считается, что треугольник олицетворяет женскую энергетику, а потому зачастую его использовали для гармонизации энергии Инь.
- Древние славяне, проживающие на территории Киевской Руси, считали, что фигура олицетворяет 3 мира:
- Правь, где обитает языческий пантеон богов;
- Явь — мир людей;
- Навь, из которой приходят потусторонние сущности.
- Тибетские монахи чаще использовали пересечение треугольных форм, чтобы изобразить единение мужского и женского.
- Восточные мудрецы считали, что треугольником описывается все материальные и нематериальные объекты.
- В христианстве треугольная форма считается олицетворение Троицы — Отца, Сына и Святого Духа, которые едины.
- В Древней Греции треугольные амулеты олицетворяли саму жизнь, а еще женщин и плодородие. Такой талисман зачастую использовали представительницы женского пола, чтобы принести гармонию в семью. При этом пифагорейцы использовали геометрическую фигуру с равными сторонами для изображения мудрой Афины.
- Племена ацтеков рисовали соединенные вершинами фигуры, чтобы обозначить циклы времени.
- Древние египтяне считали, что пирамидальная форма накапливает могущественную космическую энергию, позволяющую развить духовность и обрести мудрость.
- В текстах алхимиков, проживающих на территории средневековой Европы, треугольная форма с крестиком служило обозначением химического соединения — серы. Если же рисунок был перевернут, то это обозначало завершение какого-то великого события.
Магические амулеты треугольной формы
Виды треугольных символов
В зависимости от направления и вида фигуры практики используют амулеты для защиты или установления связи со стихиями. Наиболее распространенные виды представлены в таблице:
| Вид | Магические свойства амулета |
| Вершина направлена вверх | Впитывание солярной энергетики |
| Использование стихии огня | |
| Очищение от негатива | |
| Обрезанная верхушка смотрит вниз | Обретение стабильности |
| Управление силой земли | |
| Перевернутый | Усиление женственности и красоты |
| Лечение женских заболеваний | |
| Продолжение рода | |
| Управление водной стихией | |
| Обрезанная вершина направлена вверх | Использование энергии ветра |
| Помощник в путешествиях | |
| Пересеченная троица | Защитный символ от негатива и магического воздействия |
| Горизонтально расположенная пара с прикасающимися вершинами | Впитывание лунной энергетики |
| Обретение молодости | |
| Развитие духовности | |
| Усиление интуиции и дара предвидения | |
| Пересечение фигур, направленных в разные стороны | Обретение полной гармонии |
| Защита от магического воздействия |
Наиболее известный амулет — печать Соломона
 Печать Соломона применяется в качестве помощи в поиске своего пути, ограждая от агрессии.
Печать Соломона применяется в качестве помощи в поиске своего пути, ограждая от агрессии.Талисман создан, благодаря наложению пары равносторонних треугольников, смотрящих в противоположные стороны. Считается, что великий царь заманил в такую магическую ловушку армию демонов и заставил подчиниться себе. Обладать амулета сможет защититься от магической атаки и потусторонней агрессивной сущности, обретет тайные знания и найдет собственный путь в жизни. Символ можно начертить самостоятельно, но требуется соблюдение точность линий и пропорций.
В зависимости от предназначения амулета выбирается определенный день недели для изготовления или покупки.
Зачастую украшение носится в виде подвески или кольца, а изготавливается из благородных металлов. Воспользоваться амулетов, в котором заключена сила треугольников, может каждый вне зависимости от пола и возраста. Однако для правильной работы магического украшения следует предварительно зарядить материал, положив под солнечные или лунные лучи. Другой эффективный способ зарядки — использование сил стихий.
protalismany.ru
Талисман на деньги «Магический треугольник богатства»
На страницах нашего сайта мы не раз говорили о таких мистических предметах, как амулеты, обереги и талисманы, помогающие привлекать удачу и притягивать деньги к своему владельцу. Мы писали об известных фен-шуй талисманах на деньги, рунических талисманах, о талисманах на деньги от астролога Павла Глобы, о знаменитых амулетах на деньги, и том, как их сделать своими руками.
Узнать в чем принципиальное отличие амулета от талисмана вы можете в этой статье.
В данном материале мы расскажем о мощном древнем талисмане на деньги, который вы сможете сделать самостоятельно — это «Магический треугольник богатства».

Безусловно, вы можете купить талисман на деньги в специализированных магазинах, но подобные вещицы, как мы уже ни раз говорили, не несут в себе магической программы и энергетической зарядки, а скорее являются стилизованными пустышками. А ведь зарядка талисмана — это значимая составляющая любого магического предмета, будь то амулет, талисман или оберег. Лучший вариант приобретения настоящего талисмана на деньги — это заказать его у профессионального мага, который сделает ваш персональный магический инструмент и вложит в него магическую программу, соответствущую вашим индивидуальным предпочтениям. Но если возможности заказать или купить талисман нет, его можно сделать самому.
О том, как сделать и зарядить амулет или талисман для другого человека вы можете прочитать здесь.
Прежде чем приступить к созданию талисмана на деньги, помните, что изготавливать подобные магические предметы нужно только на растущую луну. А лучший день недели для создания конкретно этого талисмана на деньги — четверг.
Итак, для создания талисмана на деньги «Магический треугольник богатства» вам понадобится:
— 12 монет одинакового достоинства;
— Зеленая нить;
— Непосредственно сам магический треугольник;
banner_ydacha_dengi_old
Первый этап создания талисмана:
Вам понадобится лишь одна из 12-ти монет и ее следует выбрать, проделав следующий обряд:

— Возьмите все 12 монет и перемешайте их в ладонях.
— После этого высыпьте все монеты на стол и отберите из них только те, которые выпали решкой.
— С монетами, выпавшими решкой проделайте ту же самую процедуру: встряхните в руках, высыпьте и отберите только те, что выпали решкой.
— Проделайте этот ритуал до тех пор, пока не останется одна (последняя), выпавшая решкой монета. Именно эта монета и будет помогать привлекать деньги в вашем будущем талисмане.
Второй этап:
Обратите внимание на рисунок магического треугольника, который изображен ниже.
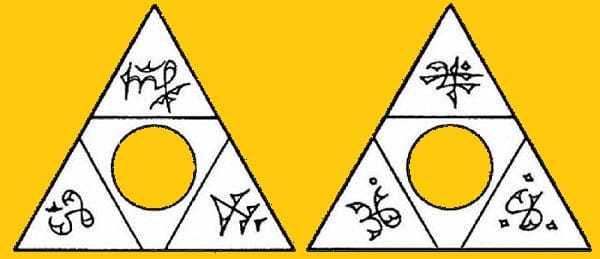
Это основная заготовка будущего талисмана на деньги. Рекомендуем самостоятельно нарисовать два идентичных треугольника. Лучше всего это делать на плотном листе картона золотого цвета (цвет богатства), а если вы обладаете навыками работы по дереву, то лучше выжечь или нарисовать его изображение на деревянной доске. Но если ни один из способов вам не подходит, просто распечатайте это изображение.
После того, как вы нарисовали/распечатали изображение треугольников, необходимо их вырезать по контуру, а также вырезать круг, изображенный в его середине.
Внимание: круг должен быть меньше по диаметру, чем выбранная монета.
— Теперь поместите монету между двумя сторонами треугольника, так, чтобы она была видна в отверстии круга.
— Склейте эти две стороны.
— К вершине магического треугольника привяжите петельку из зеленой нити. Талисман на деньги готов!
— Разместите этот талисман в том месте где храните свои сбережения или в кошельке.
Сила талисмана «Магический треугольник богатства»:
— Действие этого талисмана на деньги заключается в силе древних таинственных формул на удачу и богатство указанных с двух сторон на трех вершинах треугольника. Эти формулы помогают проявиться магической программе, вложенной вами в талисман на деньги. Расположенные в определенном порядке они образуют мощный заговор-заклинание, концентрируя и направляя действие талисмана.
banner_masson_428x60
— Круг, который находится в центре талисмана на деньги особенно важен. Он играет роль некой точки сборки энергетической программы и работы всего талисмана. Не зря в самый центр, «сердцевину», помещается монета, как ядро и основной пункт концентрации и посыла денежной энергии извне. Этот центр будет генерировать денежную энергию, привлекать и направлять ее в ваш кошелек.
— Сама фигура треугольника тоже неслучайна. Во многих народах эта геометрическая фигура считается сакральной и воплощает в себе триединую природу Вселенной, состоящую из трех различных основополагающих понятий мироздания.
Если вы все сделали правильно, согласно приведенным инструкциям, и главное — вложили душу и веру в эту вещь, то талисман на деньги «Магический треугольник богатства» принесет вам удачу во всех сферах, так или иначе, касающихся прибыли и заработка. Почаще контактируйте со своим талисманом и заряжайте его энергией своей веры и надежды.
whitekarma.ru


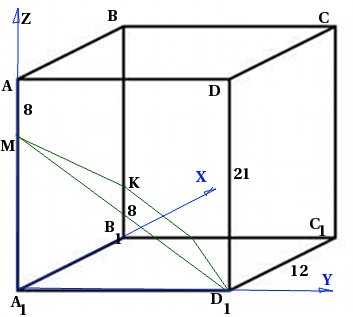
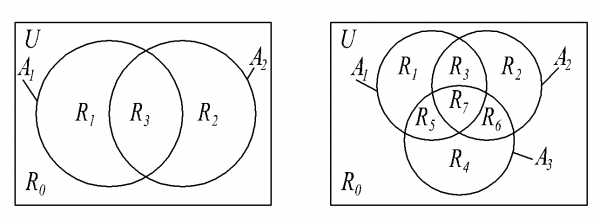
 .
. >,
в которой истинны все предложения из
множества S.
>,
в которой истинны все предложения из
множества S. A,
то есть S
├ (A&
A,
то есть S
├ (A& )
) ,
то это рассуждение естественно считать
не правильным. Если рассуждение не
противоречиво, естественно его считать
правильным.
,
то это рассуждение естественно считать
не правильным. Если рассуждение не
противоречиво, естественно его считать
правильным. )
) -правило,
-правило, -правило,
примененные к истинным формулам, снова
дают истинные формулы (*).
-правило,
примененные к истинным формулам, снова
дают истинные формулы (*). )
)  И
И счетно, то множество всех формул
счетно, то множество всех формул  также счетно.
также счетно. S1
S1 S2
S2 …
предложения вложены, тогда множество
T
вида:
…
предложения вложены, тогда множество
T
вида: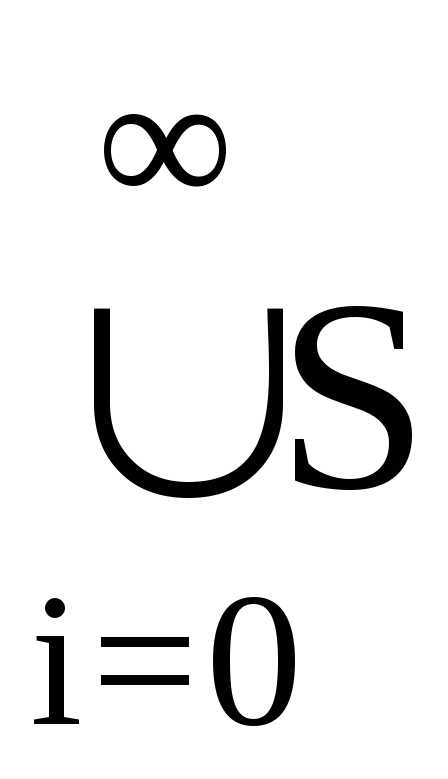 i также непротиворечиво.
i также непротиворечиво. )
) представляет собой конечный набор
формул и поэтому использует лишь конечное
число гипотез из Т.
представляет собой конечный набор
формул и поэтому использует лишь конечное
число гипотез из Т. ,
то есть
,
то есть )
) }
является непротиворечивым.
}
является непротиворечивым. }
– противоречивы, тогда существуют такие
предложенияB
и C,
что S,
A
├ (B&
}
– противоречивы, тогда существуют такие
предложенияB
и C,
что S,
A
├ (B& )
и S,
)
и S,  ├ (C&
├ (C& )
) )
├ (C&
)
├ (C& )
либо (C&
)
либо (C& )
├ (B&
)
├ (B& )
) ├ (C&
├ (C& )
) )
правило удаления
)
правило удаления  :S(A
:S(A
 )
├ (C&
)
├ (C& )
)
 )
является доказуемой в ИП. Следовательно,
исходное множествоS
обеспечивает выводимость(*):
)
является доказуемой в ИП. Следовательно,
исходное множествоS
обеспечивает выводимость(*):
 )
) (C&
(C& )
(*)
)
(*) называется полным в сигнатуре
называется полным в сигнатуре  ,
если для каждого предложения A
сигнатуры
,
если для каждого предложения A
сигнатуры  выполняется:
выполняется:
 не выводимо из T,
то тогда, очевидно, что из Т выводится
его отрицание. Но тогда, очевидно, T
не выводимо из T,
то тогда, очевидно, что из Т выводится
его отрицание. Но тогда, очевидно, T {A}
будет противоречивым.
{A}
будет противоречивым. .
Пронумеруем все предложения данной
сигнатуры A1,…,An,
An+1,…
(1)
.
Пронумеруем все предложения данной
сигнатуры A1,…,An,
An+1,…
(1)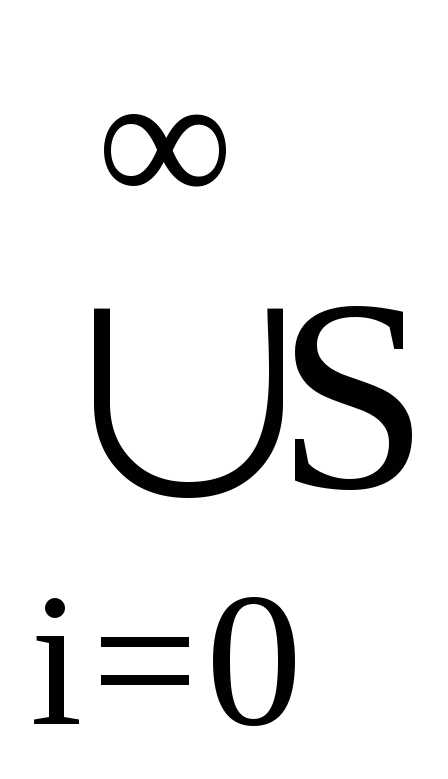 i
i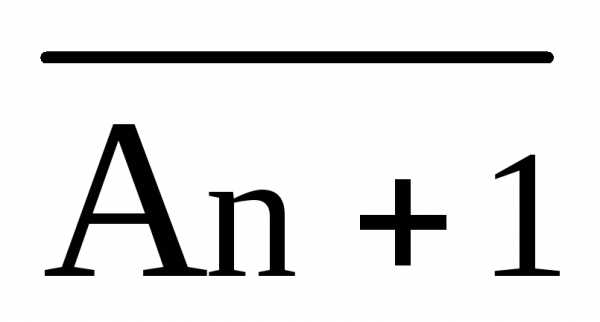 },
в противном случае
},
в противном случае S1
S1 S2
S2 …
… Sn
Sn Sn+1
Sn+1 …,
…,  n
(An
n
(An Sn)
или
(
Sn)
или
( n
n Sn)
Sn)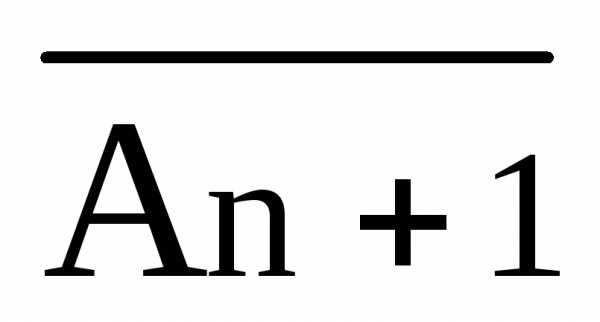 }-является
непротиворечивым.
}-является
непротиворечивым.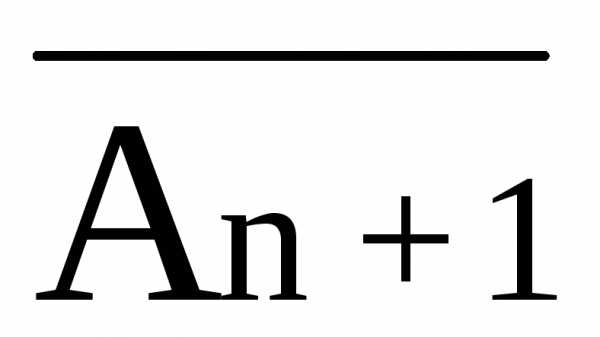 },
то выражение (4) удовлетворяет лемме 2 и
множество T=
},
то выражение (4) удовлетворяет лемме 2 и
множество T=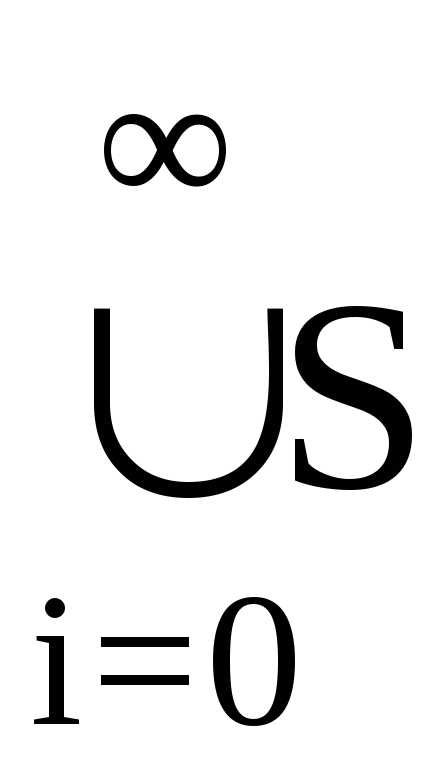 n является искомым.
n является искомым. совпадает с некоторым предложением An
из выражения (3): (A
совпадает с некоторым предложением An
из выражения (3): (A Sn)
или (
Sn)
или (
 Sn)
Sn) .
На основании этого, можем утверждать:
Т – полное множество сигнатуры
.
На основании этого, можем утверждать:
Т – полное множество сигнатуры  .
.
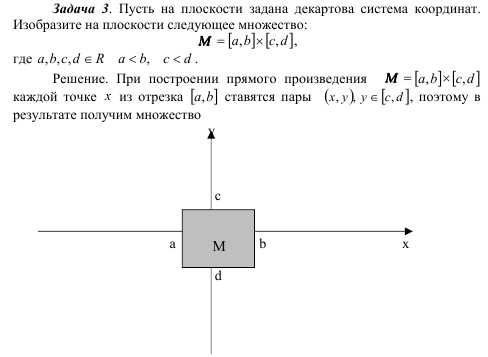
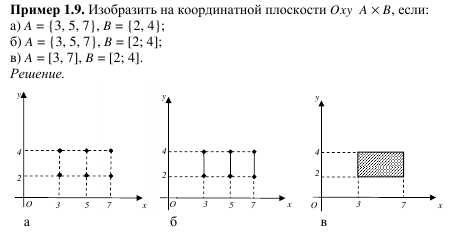
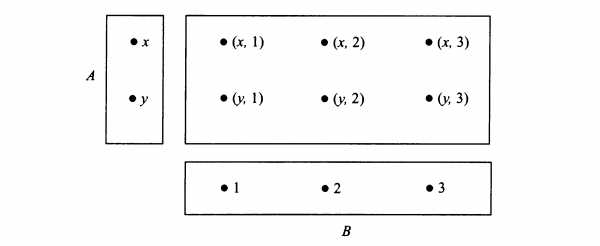
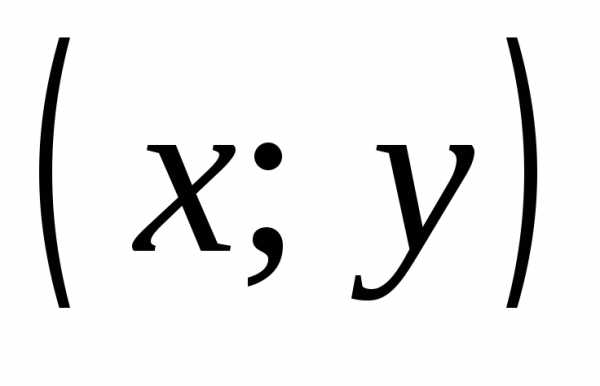 определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары
определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары 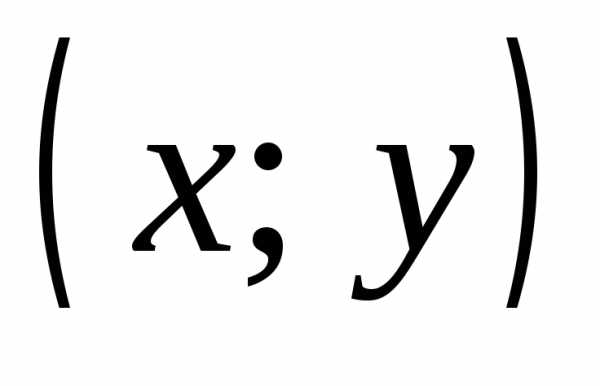 и
и 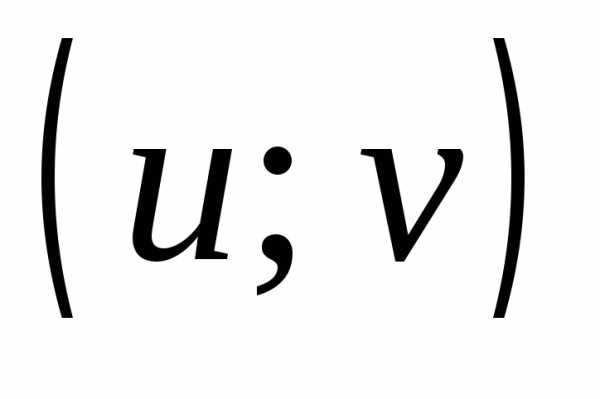 считаются равными тогда и только тогда,
когда x=u и y=v.
считаются равными тогда и только тогда,
когда x=u и y=v.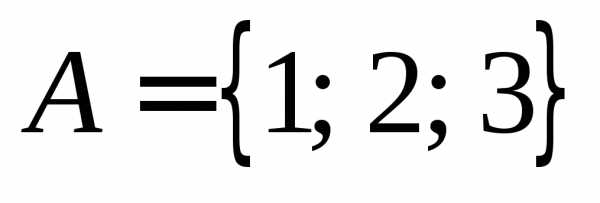 и
и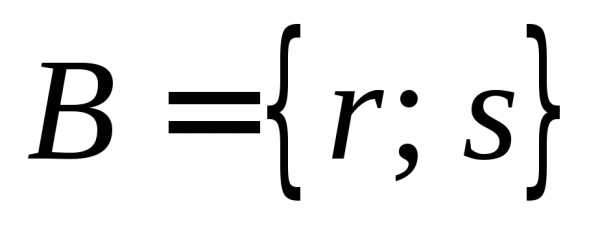 .
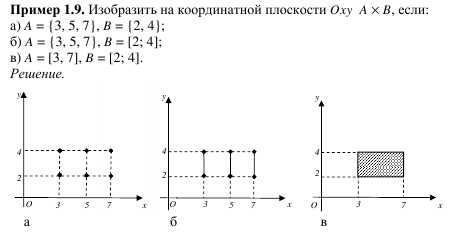
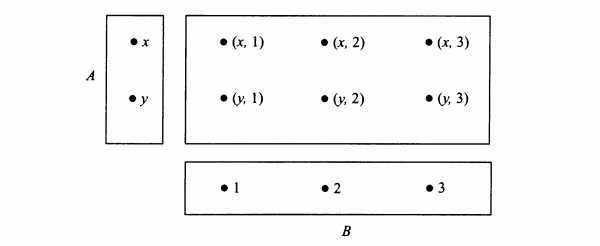
Тогда
.
Тогда



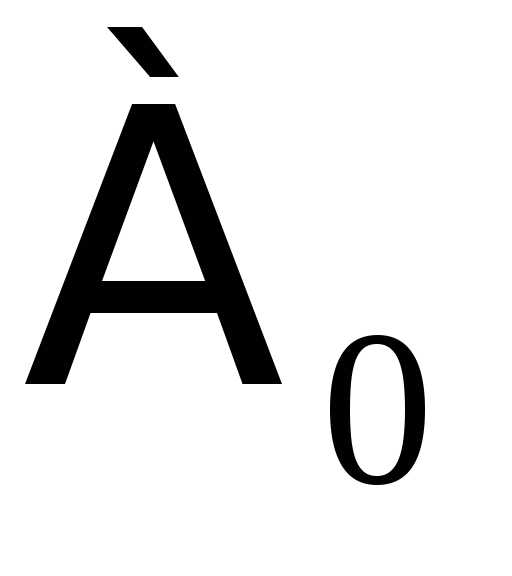 (
( – первая буква древнееврейского
алфавита, называемая «алеф», символ
– первая буква древнееврейского
алфавита, называемая «алеф», символ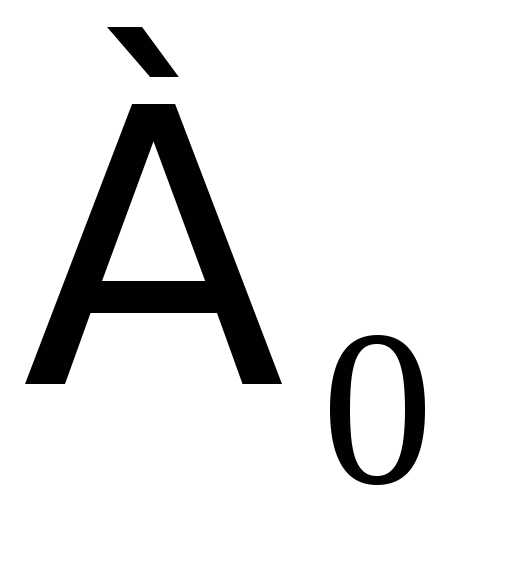 читается: «алеф-нуль»).
читается: «алеф-нуль»).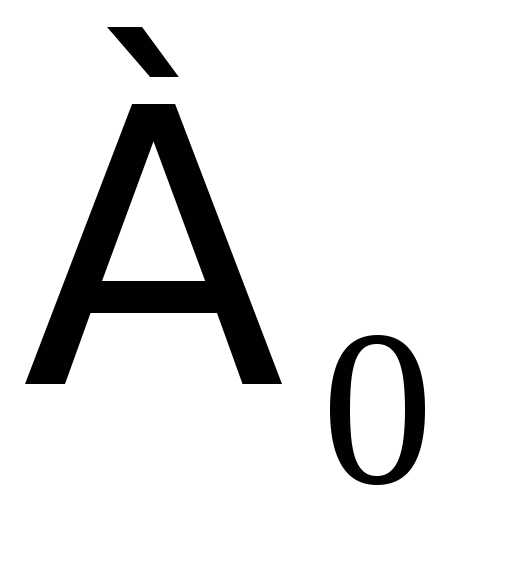 .
.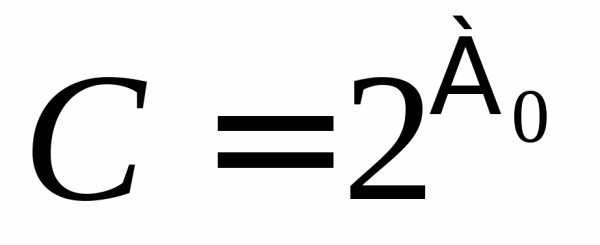 .
Следующую теорему примем без доказательства.
.
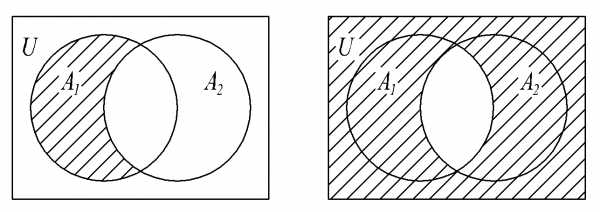
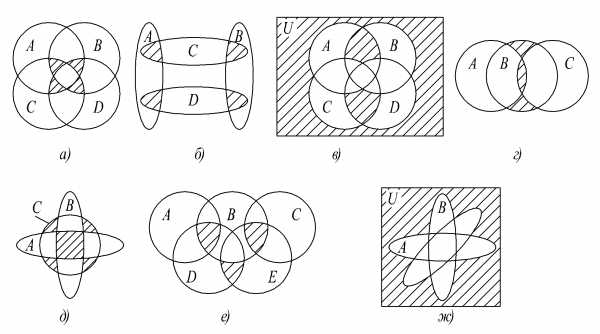
Следующую теорему примем без доказательства.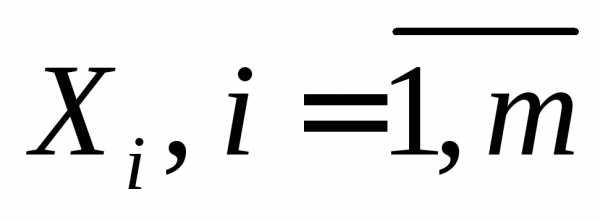 ,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.
,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
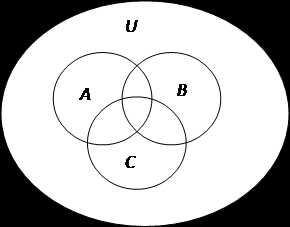
не разбиением.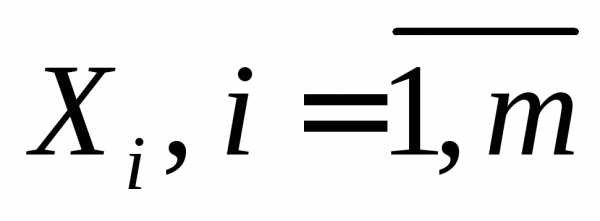 ,
справедлива формулавключений
и исключений.
,
справедлива формулавключений
и исключений.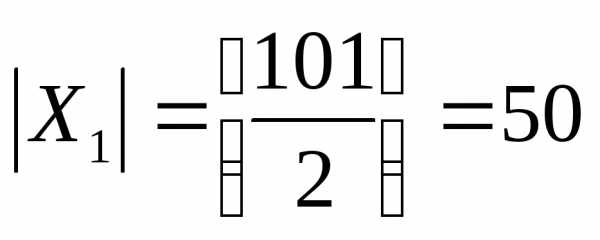 .
.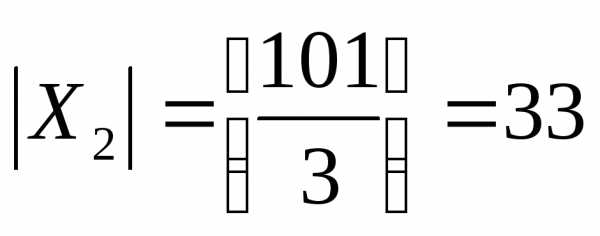 .
.
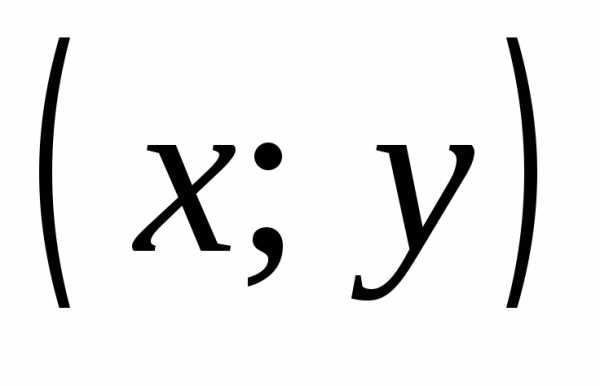 определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары
определяется как совокупность, состоящая
из двух элементов x и y,
расположенных в определенном порядке.
Две пары 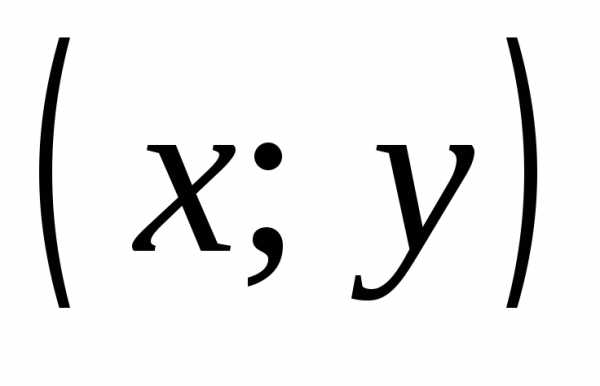 и
и 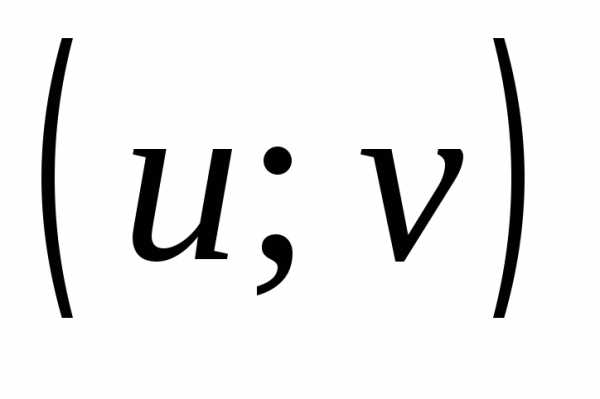 считаются равными тогда и только тогда,
когда x=u и y=v.
считаются равными тогда и только тогда,
когда x=u и y=v.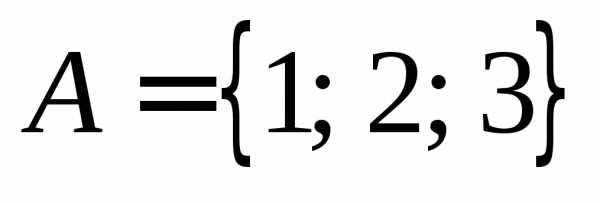 и
и .
Тогда
.
Тогда


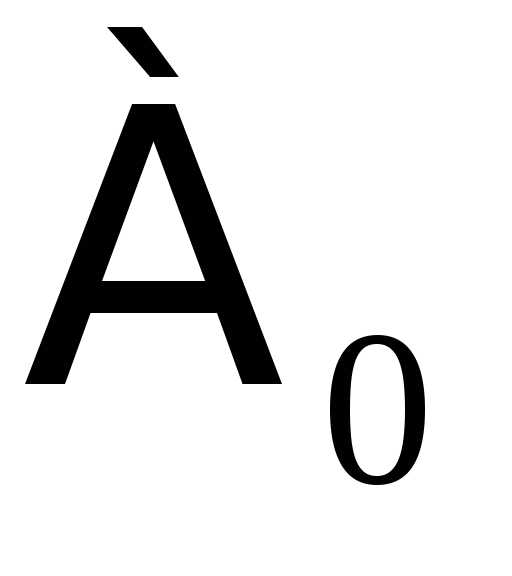 (
( – первая буква древнееврейского
алфавита, называемая «алеф», символ
– первая буква древнееврейского
алфавита, называемая «алеф», символ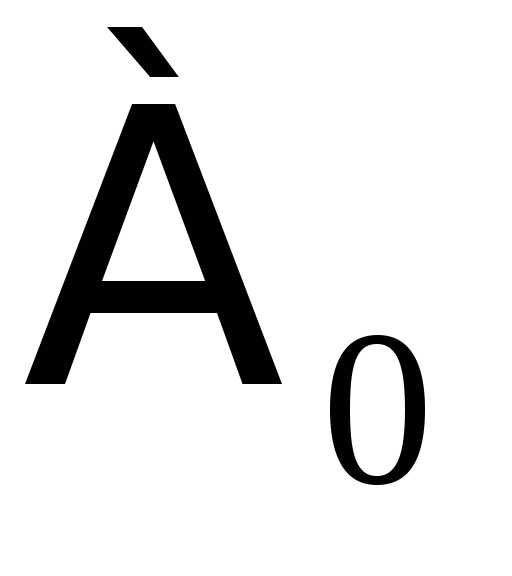 читается: «алеф-нуль»).
читается: «алеф-нуль»).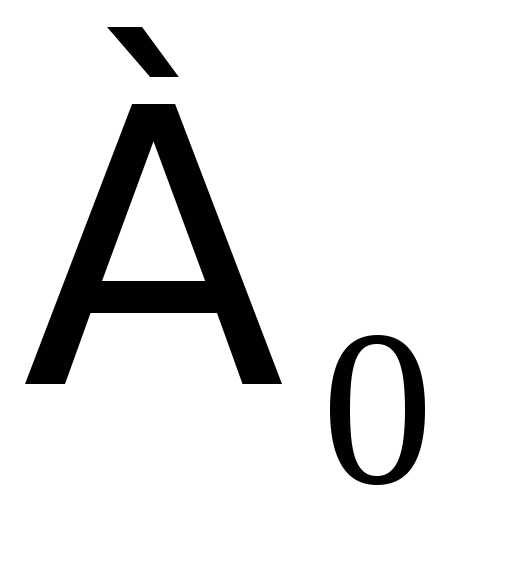 .
.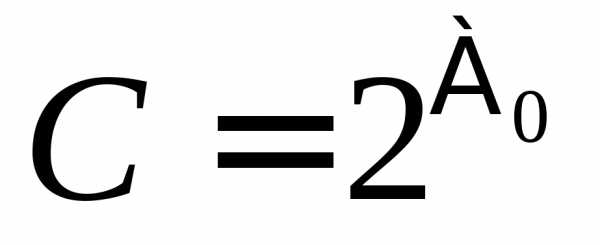 .
Следующую теорему примем без доказательства.
.
Следующую теорему примем без доказательства.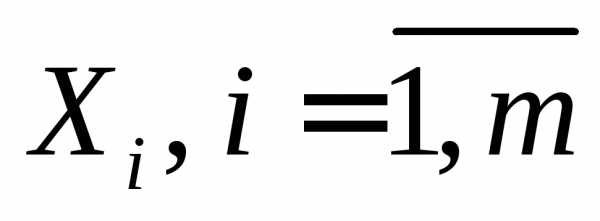 ,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.
,
которые могут иметь непустые пересечения
между собой, т.е. объединение может быть
не разбиением.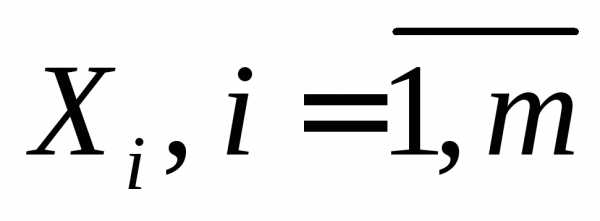 ,
справедлива формулавключений
и исключений.
,
справедлива формулавключений
и исключений.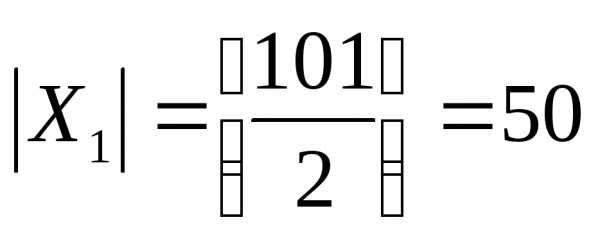 .
.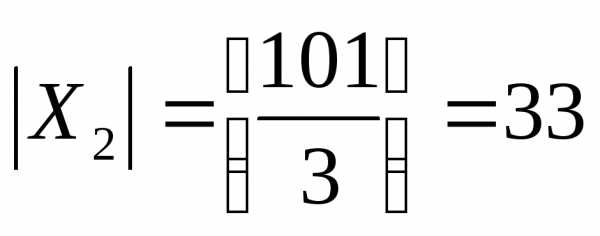 .
.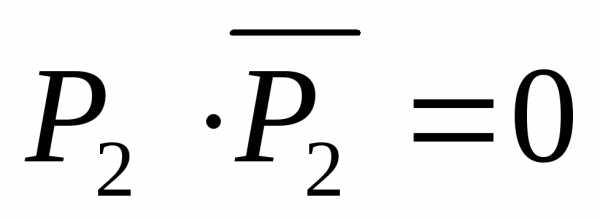 (согласно
(11)), а, следовательно, ложно и высказывание
(согласно
(11)), а, следовательно, ложно и высказывание  .
Поэтому должно быть истинным высказывание
.
Поэтому должно быть истинным высказывание 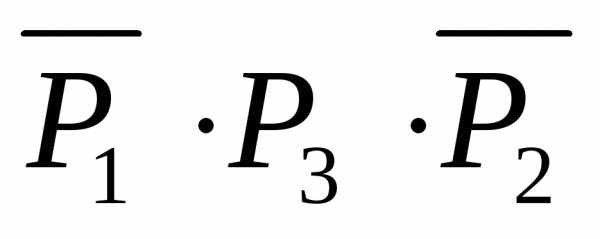 .
.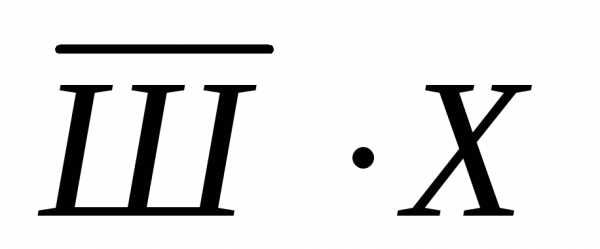 ,Ник:
,Ник: 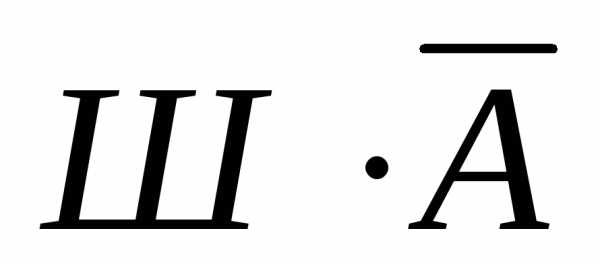 ,
Питер:
,
Питер: 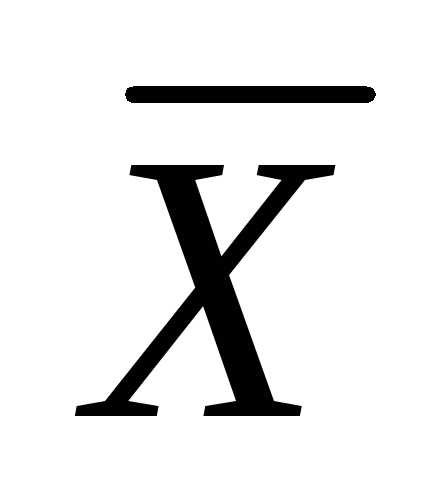 .
.
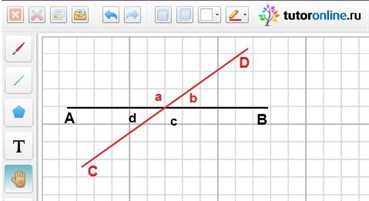 На рисунке углы a и b являются смежными, смежные и углы b и c, и углы c и d, и углы a и d.
На рисунке углы a и b являются смежными, смежные и углы b и c, и углы c и d, и углы a и d.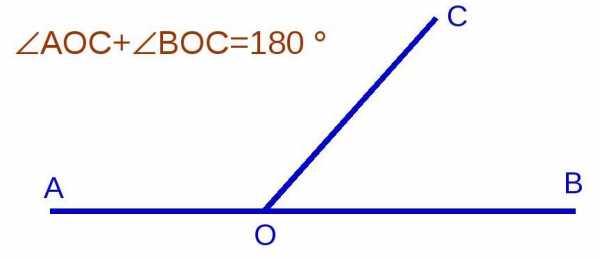

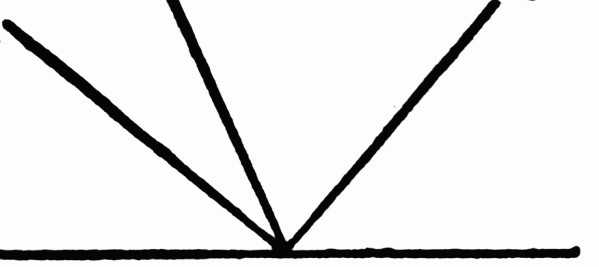 Смежные и вертикальные углы – это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
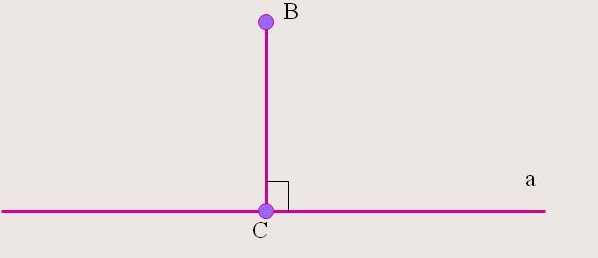
Смежные и вертикальные углы – это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве. Острым называется угол, мера которого не превышает 90 градусов.
Острым называется угол, мера которого не превышает 90 градусов.


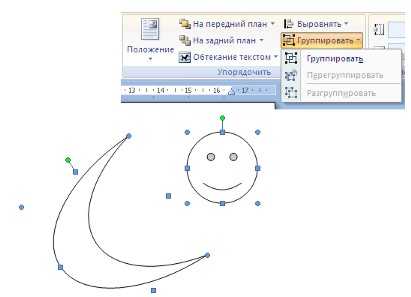

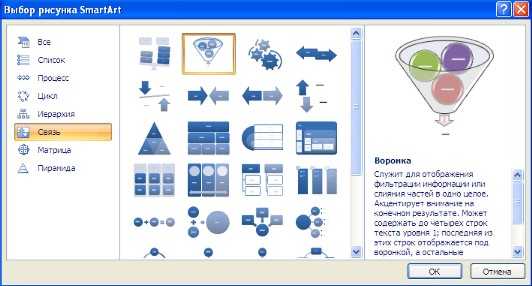
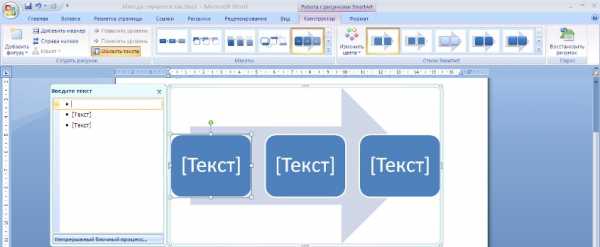
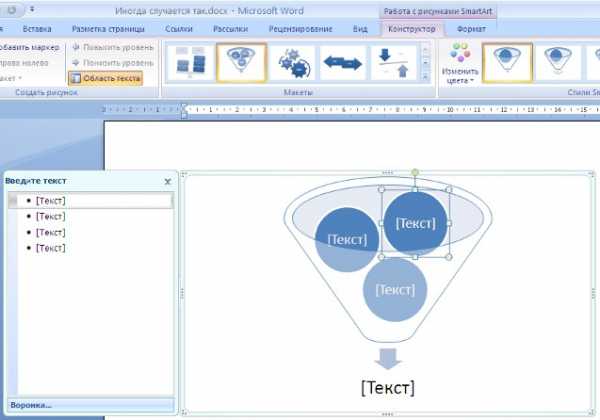

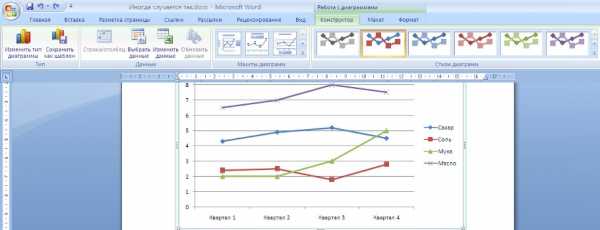
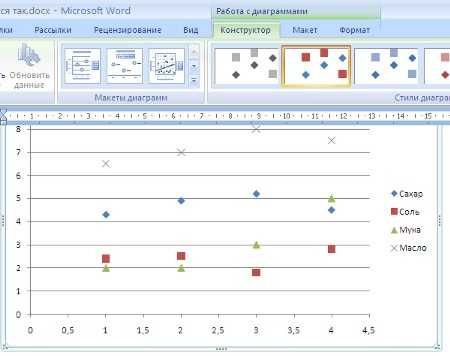
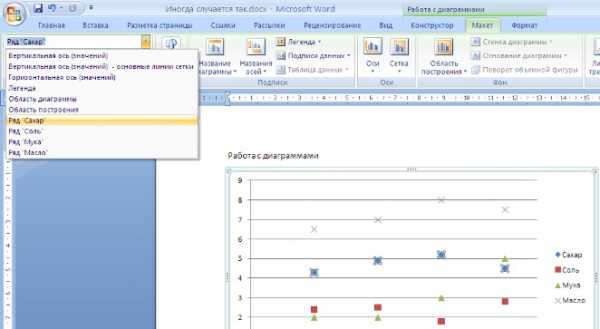

 рактическая работа №1
рактическая работа №1 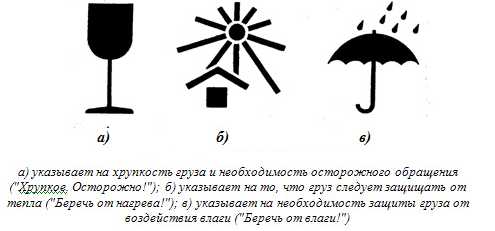




 окупатель — человек, который платит нам зарплату. Без него нам пришлось бы закрыться.
окупатель — человек, который платит нам зарплату. Без него нам пришлось бы закрыться.


 адание 2:
адание 2: рактическая работа № 6
рактическая работа № 6
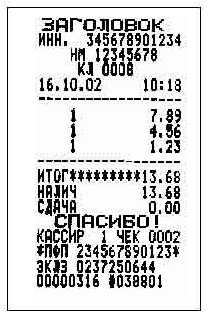 что обозначает каждая строчка кассового чека.
что обозначает каждая строчка кассового чека.
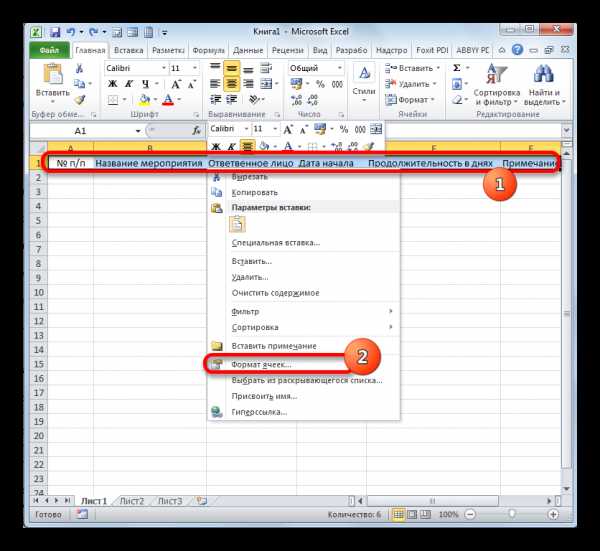
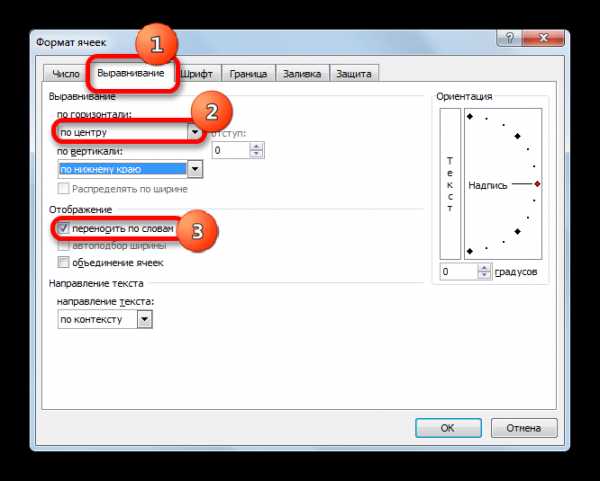
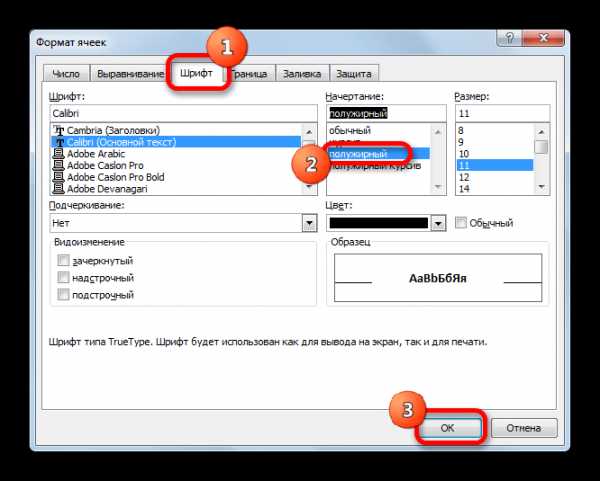
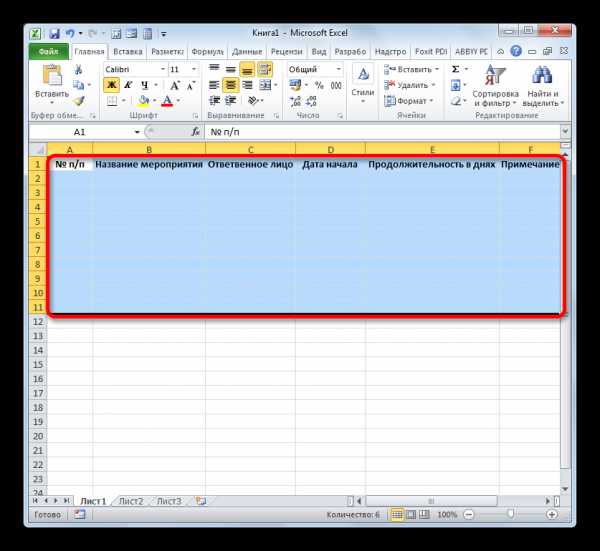
 Выполните форматирование текста:
Выполните форматирование текста: аголовок и слоган – фигурный текст
аголовок и слоган – фигурный текст