КАЛЬКУЛЯТОР — Орфографический словарь — Русский язык
Смотрите еще толкования, синонимы, значения слова и что такое КАЛЬКУЛЯТОР в русском языке в словарях, энциклопедиях и справочниках:
- КАЛЬКУЛЯТОР в Справочнике Секретов игр, программ, оборудования, кино, пасхальных яйцах.
- КАЛЬКУЛЯТОР в Большом энциклопедическом словаре:
(лат. calculator — счетчик) портативное вычислительное устройство. В отличие от предшествующих ему арифмометра с ручным приводом или электромеханических счетных машин … - КАЛЬКУЛЯТОР в Энциклопедическом словарике:
1) счетный работник, составляющий калькуляцию; 2) вычислительное … - КАЛЬКУЛЯТОР в Энциклопедическом словарике:
а, м. 1. одуш. Специалист по калькуляции. Калькуляторский — относящийся к калькулятору, калькуляторам. 2. Электрический или электронный прибор для быстрого … - КАЛЬКУЛЯТОР в Энциклопедическом словаре:
, -а, м. 1. Специалист, производящий калькуляцию. 2. Прибор для автоматических вычислений. II прил. калькуляторский, -ая, -ое (к 1 знач.) … - КАЛЬКУЛЯТОР в Большом российском энциклопедическом словаре:
КАЛЬКУЛ́ЯТОР ЭКСПОЗИЦИИ, простейший тип экспонометра в виде … - КАЛЬКУЛЯТОР в Большом российском энциклопедическом словаре:
КАЛЬКУЛ́ЯТОР (лат. calculator — счётчик), портативное вычислит. устройство. В отличие от предшествующих ему арифмометра с ручным приводом или эл.-механич. счётных … - КАЛЬКУЛЯТОР в Полной акцентуированной парадигме по Зализняку:
калькуля’тор, калькуля’торы, калькуля’тора, калькуля’торов, калькуля’тору, калькуля’торам, калькуля’тора, калькуля’торов, калькуля’тором, калькуля’торами, калькуля’торе, … - КАЛЬКУЛЯТОР в Словаре великорусского языка делового общения:
экономист низшего звена, не принимающий самостоятельных управленческих … - КАЛЬКУЛЯТОР в Тезаурусе русской деловой лексики:
‘прибор’ Syn: вычислитель, … - КАЛЬКУЛЯТОР в Новом словаре иностранных слов:
1) специалист по калькуляции; 2) вычислительное устройство для выполнения элементарных операций над числами, требующее ручного ввода данных и обычно ручного … - КАЛЬКУЛЯТОР в Словаре иностранных выражений:
1. специалист по калькуляции; 2. вычислительное устройство для выполнения элементарных операций над числами, требующее ручного ввода данных и обычно ручного … - КАЛЬКУЛЯТОР в Тезаурусе русского языка:
‘прибор’ Syn: вычислитель, … - КАЛЬКУЛЯТОР в словаре Синонимов русского языка:
прибор Syn: вычислитель, … - КАЛЬКУЛЯТОР в Новом толково-словообразовательном словаре русского языка Ефремовой:
м. 1) Тот, кто составляет калькуляцию. 2) Портативное вычислительное … - КАЛЬКУЛЯТОР в Словаре русского языка Лопатина:
калькул`ятор, … - КАЛЬКУЛЯТОР в Полном орфографическом словаре русского языка:
калькулятор, … - КАЛЬКУЛЯТОР в Словаре русского языка Ожегова:
специалист, производящий калькуляцию калькулятор прибор для автоматических … - КАЛЬКУЛЯТОР в Современном толковом словаре, БСЭ:
(лат. calculator — счетчик), портативное вычислительное устройство. В отличие от предшествующих ему арифмометра с ручным приводом или электромеханических счетных машин … - КАЛЬКУЛЯТОР в Толковом словаре русского языка Ушакова:
калькулятора, м. (торг.). Человек, занимающийся калькуляцией, специалист по … - КАЛЬКУЛЯТОР в Толковом словаре Ефремовой:
калькулятор м. 1) Тот, кто составляет калькуляцию. 2) Портативное вычислительное … - КАЛЬКУЛЯТОР в Новом словаре русского языка Ефремовой:
м. 1. Тот, кто составляет калькуляцию. 2. Портативное вычислительное … - КАЛЬКУЛЯТОР в Большом современном толковом словаре русского языка:
I м. Тот, кто составляет калькуляцию. II м. Портативное электронно-вычислительное устройство индивидуального пользования на основе микропроцессора; … - КАЛЬКУЛЯТОР KENKO в Справочнике Секретов игр, программ, оборудования, кино, пасхальных яйцах:
Мало кто знает если на калькуляторах Kenko набрать комбинацию клавиш, то он выключится. калькуляторы: Kennko модель KK-803LA Kennko модель KK-568A … - ПЕРВЫЕ КОМПЬЮТЕРЫ С ПРОГРАММНЫМОБЕСПЕЧЕНИЕМ;»АВТОМАТИЧЕСКИЙ КАЛЬКУЛЯТОР С ЭЛЕКТРОННОЙ ПАМЯТЬЮ» в Книге рекордов Гиннеса 1998 года:
Первымпрактическим полномасштабным компьютером с программным обеспечением,несмотря на свое название, был Автоматический калькулятор с электроннойпамятью (EDSAC), созданный в Кембриджском университете, Великобритания,группой … - GOOGLE.COM в Справочнике Секретов игр, программ, оборудования, кино, пасхальных яйцах:
1.) Поисковик военных сайтов. http://www.google.com.ua/unclesam/ 2.) Пасхальная игра http://www.google.com/Easter/feature_easter.html . 3.) Поисковик Google — предоставляет интерфейсы не только на национальных … - ПЕРВЫЙ ЭЛЕКТРОННЫЙ КОМПЬЮТЕР;»АТАНАСОФФ-БЕРРИ» в Книге рекордов Гиннеса 1998 года:
Атанасофф-Берри, разработанный в 1942 г. в УниверситетеАйовы, США, Джоном Атанасофф и Клиффордом Берри, стал считаться первымэлектронным компьютером, когда суд США … - МИКРОКАЛЬКУЛЯТОР в Большом энциклопедическом словаре:
(от микро… и калькулятор) (электронный калькулятор) портативная микро-ЭВМ индивидуального … - МИКРОКАЛЬКУЛЯТОР в Большом российском энциклопедическом словаре:
МИКРОКАЛЬКУЛ́ЯТОР (от микро … и калькулятор ) (электронный калькулятор), портативная микроЭВМ индивид. пользования. Предназначены преим. для выполнения арифметич. операций и … - ОРГТЕХНИКА — А. КАЛЬКУЛЯТОРЫ в Словаре Кольера:
К статье ОРГТЕХНИКА И КАНЦЕЛЯРСКОЕ ОБОРУДОВАНИЕ Калькулятор представляет собой электронное устройство, выполняющее арифметические операции. Он может быть печатающим и выполняет … - МИКРОКАЛЬКУЛЯТОР в Современном толковом словаре, БСЭ:
(от микро … и калькулятор) (электронный калькулятор), портативная микро-ЭВМ индивидуального …
slovar.cc
Кредитный калькулятор Русский Стандарт
Процедура оформления кредита сегодня сродни покупки продуктов в супермаркете. Банки предлагают многообразие программ, разрабатывают выгодные условия и бонусы – все, чтобы привлечь внимание потенциальных клиентов.Нередко небольшой заработок, желание приобрести крупную бытовую технику, транспортное средство или же улучшить жилищные условия заставляют людей взять ссуду в банке. Как же понять, под силу ли займ? В этом поможет кредитный калькулятор.
Сделать это правильно и без последствий можно. Главное – быть внимательными, просчитать все достоинства и недостатки, а также подобрать идеальную программу кредитования и рассчитать ее на кредитном калькуляторе.
Кредитный калькулятор банка «Русский Стандарт»:
На сегодняшний день банк «Русский Стандарт» — одно из популярных финансовых учреждений Российской Федерации. Он предлагает своим партнерам и клиентам широкий спектр услуг: от кредитования различной категории до открытия депозитных линий, в том числе и расчет займа на кредитном калькуляторе.
Кстати, кредитный калькулятор есть не только на сайте «Русского Стандарта», но и на нашем сайте.
[/butt_callcul]Воспользоваться кредитным калькулятором онлайн![/butt_callcul]
В банке можно получить заем на покупку жилья, нецелевой потребительский кредит или ссуду на автомобиль. Многообразие разработанных программ позволяет подобрать оптимальные условия, которые будут по плечу заемщику и рассчитать их на кредитном калькуляторе.
• Как оформить рефинансирование в банке «Русский Стандарт»?
Чтобы определиться с конечной программой кредита, «Русский Стандарт» предлагает воспользоваться услугами специального сервиса – кредитного калькулятора, который поможет сделать первичный расчет платежей, что в дальнейшем отразится на выборе программы.
Кредитный калькулятор доступен абсолютно всем клиентам банка «Русский Стандарт». Чтобы применить его, необходимо зайти на страницу, где расположена форма и заполнить необходимые графы. В классической формуле кредитного калькулятора потребительского кредита от «Русского Стандарта» потребуется отразить:
• Сумму, на которую будет оформляться ссуда;
• Процентную ставку;
• Срок кредитования;
• Способ оплаты.
Нажав на кнопку кредитного калькулятора «Рассчитать», клиент получает предварительные данные, а точнее – сумму ежемесячных выплат. Помимо этого, на кредитном калькуляторе можно рассчитать график выплат, узнать какую сумму будет составлять погашение кредита от «Русского Стандарта», а какую – переплата.
Кредитный калькулятор позволяет без труда оценить свой финансовый доход и актуальность обращения в «Русский Стандарт» за кредитом наличными. Он имеет простой и понятный каждому интерфейс. Кредитный калькулятор – отличный помощник для всех. Используя его, можно узнать все интересующие данные не только по потребительским ссудам, но и прочим.
Удобный способ получить денежную поддержку:
Работая на благо клиентов и партнеров, «Русский Стандарт» предлагает не только рассчитать кредит на кредитном калькуляторе, но и подать заявку в режиме реального времени (см. онлайн заявка в «Русский Стандарт»).
Теперь не требуется посещать офис учреждения – необходимо лишь заполнить анкету на сайте и рассчитать ссуду на кредитном калькуляторе. Отметим, что данные, которые выдаст кредитный калькулятор, примерные. Тем не менее это позволит понять общую картину.
По условиям кредитно-финансового учреждения, стать кредиторами могут резиденты Российской Федерации, отвечающие следующим параметрам:
• Возраст от 25 до 65 лет;
• Наличие постоянной работы, а также фиксированной заработной платы;
• Наличие прописки по месту, где будет оформляться заем;
• Представление двух контактных номеров.
Подобные рамки делают получение денежных средств оперативным. Рассмотрение заявок происходит в течение 3-14 дней с момента подачи. В большинстве случаев «Русский Стандарт» дает положительное решение. А рассчитать займ на кредитном калькуляторе можно за считанные минуты. Для этого не нужно переходить на сайт кредитной организации. Ведь калькулятор есть на нашем портале.
После расчета на кредитном калькуляторе и получения разрешения на открытие кредитной линии потребуется отправиться в офис банка. С собой необходимо иметь пакет документов:
• Паспорт;
• Трудовую книжку, которая будет заверена в отделе кадров;
• Справку НДФЛ-2.
Подписывая контракт, стоит внимательно изучить все тонкости и обратить внимание на условия, прописанные мелким шрифтом. Именно в договоре будут прописаны точные данные. Они могут немного отличаться от тех, которые после расчета выдал калькулятор.
Сделав расчет на кредитном калькуляторе, можно будет избежать неприятных недоразумений и стать надежным партнером для финансового учреждения, которое сможет поддержать в сложную минуту. Ведь кредитный калькулятор отражает общую переплату, а также размер ежемесячных платежей. Следовательно, условия займа не будут неожиданностью. Благодаря калькулятору, оформление займа будет обдуманным и взвешенным.
infapronet.ru
Онлайн калькулятор: Старинные русские деньги
Калькулятор сделан по запросу Перевод алтын и деньги в рубли и копейки
Собственно, он переводит из заданных старинных денежных единиц в более привычные нам рубли и копейки.
Некоторый ликбез по старинным русским денежным единицам, как водится, после калькулятора.
Сохранить share extension
Итак, пару слов об истории. Я не специалист, конечно, поэтому верю тому, что нашел в интернете.
Начнем с седой старины, когда, как известно, денег не было. В качестве средства платежа использовали пушнину или скот (смотря у кого что было) — цену назначали в количествах шкур или головах скота. Думаю, эти денежные единицы затруднительно перевести в рубли и копейки. В общем, не деньги были, а товарный эквивалент.
Но товар использовать в качестве денег не очень удобно, и постепенно он стал мигрировать в эквиваленты, у которых номинальная стоимость была выше природной, то есть служить прообразом денег, как посредника при обмене. Например, головы белок.
Дальнейшее развитие, как и во всем мире, пришло к тому, что товарными эквивалентами стали выступать металлы. Сначала это были изделия из металла, потом слитки, а потом и монеты.
Первые монеты стали проникать на территорию Древней Руси из Арабского Халифата, примерно с восьмого века нашей эры. Первой, так сказать, национальной денежной единицей стала гривна кун — слиток серебра весом примерно 68,22 г. — это 9-10 век нашей эры. Википедия подсказывает нам, что эта гривна менялась на ходившие по Руси арабские монеты по определенному курсу, привязанному к куньим шкурам. Она как бы являла собой эквивалент определенного количества куньих шкур.
Дальше, в связи с феодальной раздробленностью, нашествием татаро-монгол и тому подобными неприятностями долгое время был бардак. Пытались иногда чеканить монеты, но как-то неудачно, а в обращении были арабские дирхемы. Этот период (с середины двенадцатого века и до середины четырнадцатого) называют безмонетным. В этот период появляется серебряная гривна, даже несколько ее разновидностей, типа киевская гривна, новгородская, черниговская и т. п. Все это были слитки серебра.
Новгородские гривны в какой-то момент времени стали называться рублями (и это название позже перешло на основную денежную единицу).
Наконец, с середины четырнадцатого века, стали чеканить и монеты, но чеканили их все, кому не лень, и как придется — В Москве, в Рязани, в Пскове, в Новгороде. Чеканили из серебра, и такую мелкую серебряную монету называли денгой. Кроме денег чеканились и полуденьги, или полушки.
Потом, как известно, Москва всех под себя подмяла, и денежные системы Москвы и Новгорода, как наиболее крупные, объединились и образовали общую денежную систему. Чтобы удобнее было считать, была введена «счетная денежная единица» — счетный рубль, который равнялся 100 новгородкам (новгородским денгам), 200 московкам (московским денгам, которые были примерно в два раза легче по весу, чем новгородские) или 400 полушкам. Ну то есть монеты такой не было, а скажешь «рубль», все понимают, что отдашь 100 новгородок.
Еще одной счетной денежной единицей стал алтын. Алтын равнялся 6 московкам или 3 новгородкам. А нужен он был для удобства расчетов с Золотой Ордой. Слово это происходит от тюркского «шесть». Дело в том, что монголо-татарская денежная система была двенадцатеричной, в отличие от русской — десятичной, ну и использование алтынов в расчетах облегчало переход из одной системы в другую. Например, 3 рубля = 100 алтынов.
Елена Глинская, вторая жена великого князя Василия III, которая правила Великим княжеством Московским после его смерти, и до тех пор, пока ее не отравили Шуйские (с 1533 по 1538), провела первую денежную реформу, которая унифицировала денежные единицы, бывшие в обращении. Вызвано это было экономическими причинами, а также расплодившимися фальшивомонетчиками. Ну, углубляться не будем, желающие сами могут погуглить и почитать.
Была начата чеканка копеек (0.68 г серебра), денег (0.34 г) и полушек (0.17 г). Копейка, по сути, бывшая новгородская денга, денга суть московка, ну а полушка — полденги или четверть копейки. Рубли и алтыны не чеканились, а использовались для счета. В документах денежные суммы обычно выражались в рублях, алтынах и денгах.
Дальше все это каким-то образом жило, пока денег в обращении не перестало хватать, да и номиналов было мало и слишком мелкие. Тогда Алексей Михайлович решил провести еще одну денежную реформу. Было это в 1654-1663 годах. Попытались расширить набор номиналов монет, в частности, начать чеканить серебряный рубль, полуполтину, алтын и грош (2 копейки), а также использовать для монет медь, наряду с серебром (медные полтины).
Серебряные рублевые монеты, известные под названием рублевые ефимки (от Йоахимсталер (Joachimsthaler) — названия первых талеров, чеканившихся в Йоахимстале), как следует из названия, перечеканивали из талеров. Талеры по весу были примерно на треть меньше 100 серебряных копеек, поэтому копейки люди стали придерживать, как более качественные, что вызвало отток из обращения мелкой серебряной монеты. Выпуск рублевых ефимок прекратили, и стали выпускать новую монету, получившую название ефимок с признаком — у него было дополнительное клеймо и он имел курс 64 копейки.
Было не очень удобно, и в 1659 году ефимки с признаком были изъяты из обращения. Как мы видим, с рублем у реформаторов как-то не задалось, да и медные монеты, которые изначально должны были идти один к одному с серебряными, стали обесцениваться.
В общем, в итоге после Медного бунта (к этому моменту за одну серебряную копейку давали пятнадцать медных) постепенно откатили все назад, и опять стали чеканить только копейки, денги и полушки и только из серебра. Остальные номиналы по прежнему были счетными денежными единицами: рубль (100 копеек), полтина или полтинник (50 копеек), полуполтина (25 копеек), гривна или гривенник (10 копеек) и алтын (3 копейки).
Потом за дело взялся Петр Первый и провел еще одну денежную реформу. Первым делом выпустили в обращение медные монеты достоинством ниже копейки — полполушку, полушку и денгу. 8 полполушек, 4 полушки или 2 денги меняли на одну серебряную копейку. Потом серебряную копейку заменили медной. Ввели счет на рубли и копейки, запретили счет на денги и алтыны. Стали чеканить серебряный рубль, другие номиналы — грош (2 копейки), алтын (3 копейки), двухгрошевик, пятак, гривенник, 15 и 30 копеек, полуполтиник и полтинник. Чеканили их не все время, в разные периоды, когда из серебра, когда из меди, но чеканили.
Большинство из названий, как я думаю, большинству из читающих этот текст уже должны быть знакомы. На этом я заканчиваю экскурс в историю, дальше смотри Википедию, раздел Монеты России.
planetcalc.ru
Русский Стандарт Банк — Кредитный калькулятор 2019
Кредитный калькулятор Русский Стандарт может рассчитать кредит, узнать процентную ставку и условия кредитования на сегодня для физических лиц. Хотите взять потребительский кредит в Русский Стандарт в 2019 году? Воспользуйтесь для расчета кредита бесплатным калькулятором с официального сайта! Кредиты наличными доступны через сеть филиалов банка. Выберите один из вариантов потребительских кредитов и оцените, насколько это выгодно и удобно.
Калькулятор погашения кредита поможет рассчитать онлайн:
- сумму платежа с процентами,
- сумму платежа для кредитов с досрочным погашением,
- сумму платежа для кредитов с частичным досрочным погашением.
Также можно посмотреть, скачать и распечатать результат расчета с графиком платежей помесячно.
Условия кредитования
- Цель кредита на цели личного потребления
- Валюта кредита Рубли РФ
- Мин. сумма кредита 30 000
- Макс. сумма кредита 5 000 000, если получаете зарплату на счет в банке
- Срок кредита от 3 месяцев до 5 лет
- Комиссия за выдачу кредита отсутствует
- Обеспечение по кредиту не требуется
Процентные ставки
- Специальные условия — если вы получаете зарплату или пенсию на счёт в банке от 12,9% до 18,9%
- Общие условия от 13,9% до 19,9%
Раздел процентных ставок на ипотеку еженедельно обновляется.
Предприятия и организации являются участниками зарплатных проектов, а их сотрудники — владельцами зарплатных карт, что упрощает оформление кредита.
Калькулятор кредитного займа произведет расчет:
- для держателей зарплатных карт,
- для физических (частных) лиц,
- для пенсионеров,
- для юридических лиц,
- для ИП.
Условия предоставления кредита зависят от назначения кредита, целей заемщика и определяют необходимый пакет документов заемщика.
Заём можно взять:
- наличными,
- на развитие малого бизнеса,
- на покупку автомобиля (на машину),
- на покупку жилья,
- на строительство дома,
- на рефинансирование,
Желаем вам приятного расчёта и максимально выгодных условий.
Они отличаются гибкостью условий, легкой доступностью и в то же время высокой процентной ставкой.
Кредитные программы банка популярны, так как максимально приближены к потребителю: оформить кредит можно как в отделениях банка, так и в офисах партнёров — торговых сетей «М-Видео», «Белый Ветер цифровой», «Техносила» и других.
www.kreditnyi-kalkulyator.com

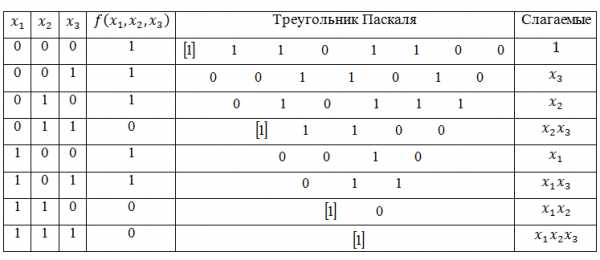
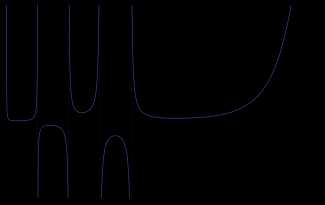 Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом. Аннотация: Тишин В. В. Дискретная математика в примерах и задачах. —
СПб.: БХВ-Петербург, 2008. — 352 с: ил. — (Учебная литература для вузов)
Аннотация: Тишин В. В. Дискретная математика в примерах и задачах. —
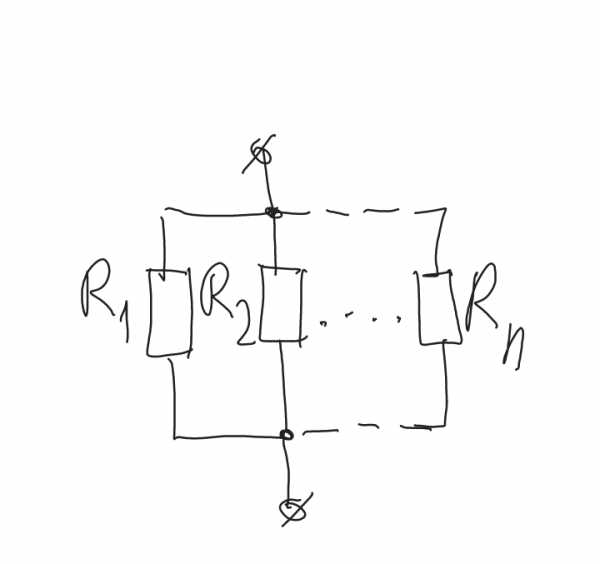
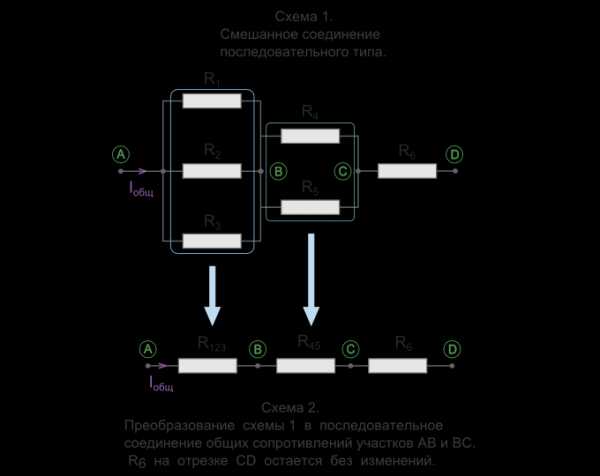
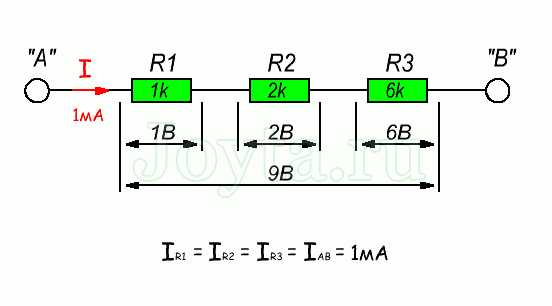
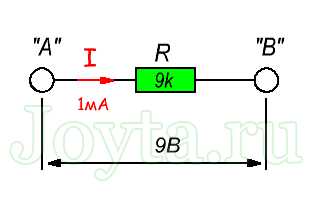
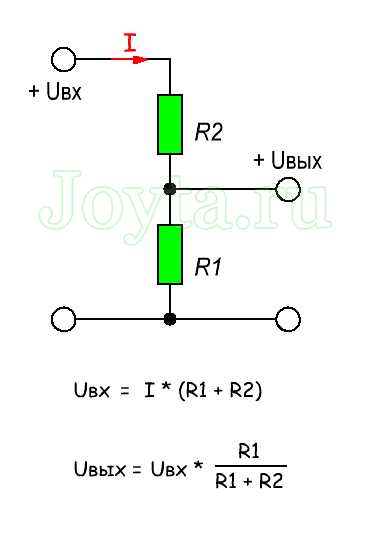
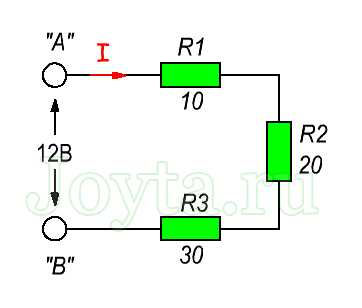
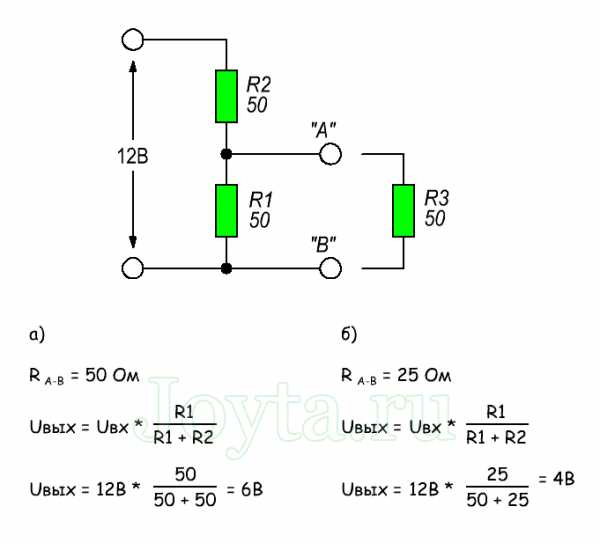
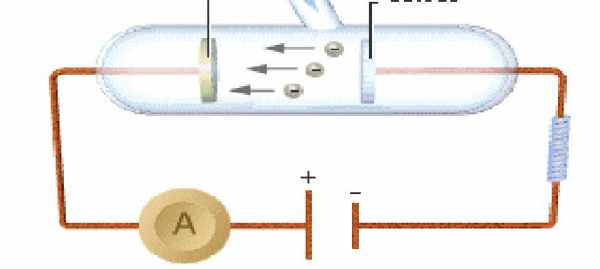
СПб.: БХВ-Петербург, 2008. — 352 с: ил. — (Учебная литература для вузов)  Параллельное соединение резисторов
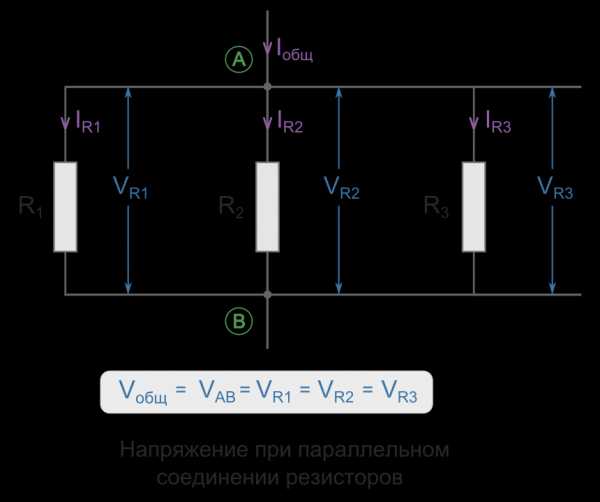
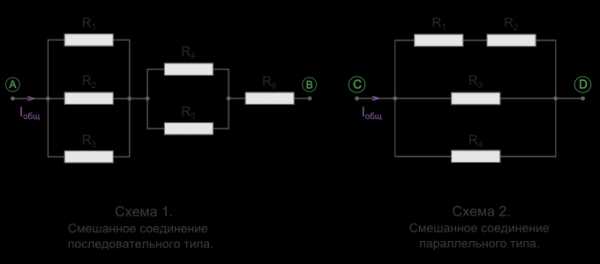
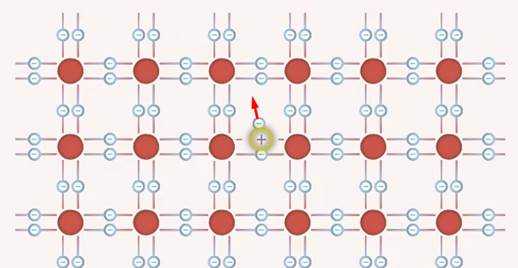
Параллельное соединение резисторов



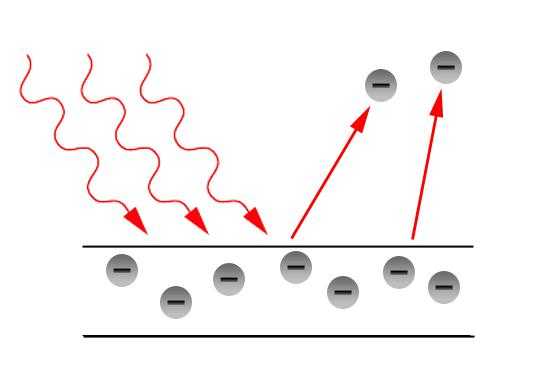
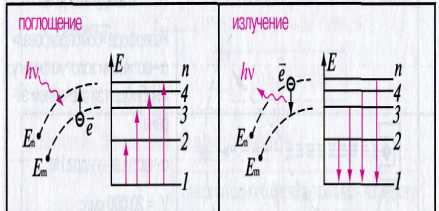 поглощение
поглощение
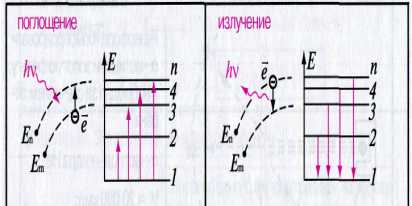 излучение
излучение

























 Дядя Валера сильный шахматист, мастер спорта времен СССР.
Дядя Валера сильный шахматист, мастер спорта времен СССР. Дядя Паша является не только автором этого сайта, но еще и моим тренером по шахматам.
Дядя Паша является не только автором этого сайта, но еще и моим тренером по шахматам.