Таблица менделеева — Электронный учебник K-tree
Электронный учебник
Периодический закон, открытый Д. И. Менделеевым был выражен в таблице. Периодическая таблица химических элементов, или таблица менделеева.
1
H
1.008
2
He
4.003
3
Li
6.938
4
Be
9.012
5
B
10.806
6
C
12.01
7
N
14.006
8
O
15.999
9
F
18.998
10
Ne
20.18
11
Na
22.99
12
Mg
24.304
13
Al
26.982
14
Si
28.084
15
P
30.974
16
S
32.059
17
Cl
35.446
18
Ar
39.948
19
K
39.098
20
Ca
40.078
21
Sc
44.956
22
Ti
47.867
23
V
50.942
24
Cr
51. 996
996
25
Mn
54.938
26
Fe
55.845
27
Co
58.933
28
Ni
58.693
29
Cu
63.546
30
Zn
65.38
31
Ga
69.723
32
Ge
72.63
33
As
74.922
34
Se
78.971
35
Br
79.901
36
Kr
83.798
37
Rb
85.468
38
Sr
87.62
39
Y
88.906
40
Zr
91.224
41
Nb
92.906
42
Mo
95.95
44
Ru
101.07
45
Rh
102.906
46
Pd
106.42
47
Ag
107.868
48
Cd
112.414
49
In
114.818
50
Sn
118.71
51
Sb
121.76
52
Te
127.6
53
I
126.904
54
Xe
131.293
55
Cs
132.905
56
Ba
137.327
57
La
138.905
72
Hf
178. 49
49
73
Ta
180.948
74
W
183.84
75
Re
186.207
76
Os
190.23
77
Ir
192.217
78
Pt
195.084
79
Au
196.967
80
Hg
200.592
81
Tl
204.382
82
Pb
207.2
83
Bi
208.98
58
Ce
140.116
59
Pr
140.908
60
Nd
144.242
62
Sm
150.36
63
Eu
151.964
64
Gd
157.25
65
Tb
158.925
66
Dy
162.5
67
Ho
164.93
68
Er
167.259
69
Tm
168.934
70
Yb
173.045
71
Lu
174.967
90
Th
232.038
91
Pa
231.036
92
U
238.029
В таблице менделеева колонки называются группами, строки называются периодами. Элементы в группах как правило имеют
одинаковые электронные конфигурации внешних оболочек, например, благородные газы — последняя группа, имеют законченную
электронную конфигурацию.
Как заполняется электронная конфигурация элементов подробно описано в статье
Скачать таблицу менделеева в хорошем качестве
© 2015-2022 — K-Tree.ru • Электронный учебник
По любым вопросам Вы можете связаться по почте [email protected]
Копия материалов, размещённых на данном сайте, допускается только по письменному разрешению владельцев сайта.
Дидактический материал Тренировочные тесты ЕГЭ по химии Электроотрицательность. Степень окисления и валентность химических элементов. 1. Электроотрицательность атома – это 1) отрицательный заряд атома в молекуле 2) способность атома переходить в возбужденное состояние 3) способность атома, участвующего в химической связи, смещать к себе электронную пару, участвующую в образовании химической связи 4) потенциал ионизации атома
2. 1) O, H, Br, Te 2) C, I, B, P 3) Sn, Se, Br, F 4) H, Br, C, B
3. Степень окисления атома – это 1) условный заряд, вычисленный из предположения, что все полярные ковалентные связи являются ионными 2) число отданных в ходе химической реакции электронов 3) отрицательный заряд, сосредоточенный на какой-либо части молекулы 4) заряд иона в нерастворимом веществе
4. Степень окисления элемента в простом веществе равна 1) нулю 2) числу электронов во внешнем электронном слое 3) числу неспаренных электронов 4) номеру группы 5. Высшую степень окисления марганец проявляет в соединении 1) КМnО4 2) МnО2 3) К2MnО4 4) MnSO4
6. Наибольшую степень окисления марганец проявляет в соединении 7. 1) MnSO4 2) МnО2 3) К2МnО4 4) Мn2Оз
8. Степень окисления — 3 фосфор проявляет в соединении 1) РН3 2) Р2Оз 3) NaH2PO4 4) Н3РО4
9. Наименьшую степень окисления сера проявляет в соединении 1) Na2S 2) Na2SO3 3) Na2SO4 4) SO3
10. Степень окисления — 3 фосфор проявляет в соединении 1) РН3 2) Р2Оз 3) NaH2PO4 4) НзРО4
11. Наибольшую степень окисления сера проявляет в соединении I ) Na2S 2) Na2SO3 3) Na2SO4 4) SO2
12. 1) N2O5, HNO3, NaNO3 2) NО2, HNO3, KNO3 3) NO, NO2, N2O3 4) HNO3,HNO2,NO2 13. В порядке увеличения электроотрицательности элементы расположены в ряду: 1) O-N-C-B 2) Si-Ge-Sn-Pb 3) Li-Na-K-Rb 4) Sb-P-S-Cl
14. Степень окисления азота увеличивается в ряду веществ: 1) NH3,NO,HNO3 2) NO,NO2,NH3 3) NH3,HNO3,NO2 4) KNO3, KNO2, NO2
15. Электроотрицательность химических элементов увеличивается в ряду: 1) Be,Mg,Ca 2) F,Cl,Br 3) P,S,C1 4) Cl.S.P
16. В порядке возрастания относительной электроотрицательности элементы расположены в ряду: 1) Na, Mg,Al 2) N,P,As 3) O,N,C 4) Cl, Br, I
17.
18. Степень окисления хлора в Са(С1О)2 равна 1)+1 2) +3 3) +5 4) +7
19. Степень окисления хлора в Ва(СlOз)2 равна 1) + 1 2) + 3 3) +5 4) + 7
20. Минимальную степень окисления хлор проявляет в соединении 1) NH4Cl 2) Сl2 3) Ca(OCl)2 4} NaCIO
21. Степень окисления + 3 азот проявляет в каждом из двух соединений: 1) HNO2 и NH3 2) NH4C1 и N203 3) NaNO2 и NF3 4) HNO3 и N2
22. В каком соединении степень окисления серы равна +4? 1) H2SO4 2) FeS 3) H2SO3 4) SO3
23. 1) кремний 2) свинец 3) олово 4) углерод
24. Азот проявляет степень окисления +3 в каждом соединении, указанном в ряду: 1) N203, HNO2, NH3 2) NH4C1, N20, NF3 3) HNO2,N2H4,N2 4) NaNO2, NF3, N2O3
25. Наиболее электроотрицательным элементом является I) кремний 2) азот 3) фосфор 4) селен
26. В порядке возрастания электроотрицательности элементы расположены в ряду 1) H-Se-S-O-F 2) F-O-C1-S-H 3) H-CI-S-O-F 4) H-S-C1-F-O
27. Хлор проявляет положительную степень окисления в соединении с 1) серой 2) водородом 3) кислородом 4) железом
28. Степень окисления + 3 азот проявляет в соединении 1) NН4С1 2) NaNO3 3) N2O4 4) KNO2
29. 1) СrО 2) Сr2О3 3) СrО3 4) Н2СrО4
30. Степень окисления азота в сульфате аммония равна 1) — 3 2) — 1 3) + 1 4) + 3
Ответы: 1-3, 2-3, 3-1, 4-1, 5-1, 6-3, 7-3, 8-1, 9-1, 10-1, 11-3, 12-1, 13-4, 14-1, 15-3, 16-1, 17-4, 18-1, 19-3, 20-1, 21-3, 22-3, 23-4, 24-4, 25-2, 26-1, 27-3, 28-4, 29-2, 30-1 |
Назначьте степень окисления каждому атому в каждом элементе, ионе или com…
Последние каналы
- Общая химия
Химия
- Общая химия
- Органическая химия
- Аналитическая химия
- GOB Химия
- Биохимия
Биология
- Общая биология
- Микробиология
- Анатомия и физиология
- Генетика
- Биология клетки
Математика
- Алгебра колледжа
- Тригонометрия
- Предварительный анализ
Физика
- Физика 9 0008
Бизнес
- Микроэкономика
- Макроэкономика
- Финансовый учет
Общественные науки
- Психология
Начните вводить текст, затем используйте стрелки вверх и вниз, чтобы выбрать вариант из списка.
Общая химия6. Химические количества и водные реакцииРасчет степеней окисления
6:23
минуты
Задача 94
Вопрос из учебника
Проверенное решение
Наши преподаватели рекомендовали это видео-решение как полезное для описанной выше задачи.
Было ли это полезно?
Смотреть дальше
Master Расчет чисел окисления с небольшим видео-объяснением от Жюля Бруно
Начать обучение
Похожие видео номер
Leah5sci MCAT
Как рассчитать число окисления или степень окисления? Easy Trick
Академия Najam
Вычисление степени окисления
Не думайте слишком много! с Praxis Academic
Расчет степеней окисления
Жюль Брюно
Как рассчитать степень окисления переходных металлов в координационных соединениях
Полное руководство ко всему
Как рассчитать степени окисления — Основы введения — Dr K
ChemSimplified
Присвоение чисел окисления — Учебное пособие по химии
TheChemistrySolution
Как рассчитать числа окисления Практические задачи
Тайлер ДеВитт
Как найти O Числа окисления (правила и примеры)
Wayne Breslyn
Расчет чисел окисления Пример 1
Jules Bruno
Расчет степеней окисления
Jules Bruno
Расчет степеней окисления Пример 2
9Пример 3 Жюль БрюноРасчет числа окисления Пример 4
Жюль Брюно
Окисление и восстановление
Окисление и сокращение Самый ранний взгляд на окисление и восстановление заключается в добавлении кислорода с образованием оксида (окисление) или удалении кислорода (восстановление). водород окисляется, а кислород восстанавливается. Сочетание азота и кислорода, возникающее при высоких температурах, происходит по той же схеме. Это образование оксида азота окисляет азот и восстанавливает кислород. В некоторых реакциях наиболее заметно окисление. Например, при сжигании метана и углерод, и водород окисляются (приобретают кислород). Сопутствующее восстановление кислорода, возможно, легче увидеть, когда вы описываете восстановление как получение водорода. С другой стороны, реакция двуокиси свинца при высоких температурах представляется просто восстановительной. Восстановление двуокиси свинца понятно, но связанное с ним окисление кислорода легче увидеть, когда вы описываете окисление как потерю электронов. | Индекс Окисление/ Ссылка | ||
| Назад |
Первоначальный взгляд на окисление и восстановление заключается в добавлении или удалении кислорода. Альтернативный подход состоит в том, чтобы описывать окисление как потерю водорода, а восстановление как приобретение водорода. Это имеет преимущество при описании сжигания метана. При таком подходе ясно, что углерод окисляется (теряет все четыре атома водорода), а часть кислорода восстанавливается (приобретает водород). Еще одна реакция, в которой водородный подход проясняет ситуацию, — это пропускание метанола через горячую медную сетку с образованием формальдегида и газообразного водорода (Хилл и Колб): . Обе углеродсодержащие молекулы имеют одинаковое содержание кислорода, но образование формальдегида рассматривается как окисление, поскольку теряется водород. Образование H 2 представляет собой процесс восстановления, когда два высвобождающихся атома водорода объединяются. Образование метанола в результате реакции монооксида углерода с водородом сочетает окисление и восстановление в единый молекулярный продукт. CO восстанавливается, потому что он получает водород, а водород окисляется в результате его ассоциации с кислородом. | Индекс Окисление/ Ссылка | ||
| Назад |
Первоначальный взгляд на окисление и восстановление заключается в добавлении или удалении кислорода. В этой реакции атомы свинца получают электрон (восстановление), а кислород теряет электроны (окисление). Этот электронный взгляд на окисление и восстановление поможет вам понять тот факт, что «окисление» может происходить даже при отсутствии кислорода! Определение окислительно-восстановительных реакций расширено и включает другие реакции с неметаллами, такими как хлор и бром. Например, реакция Магний теряет электроны и поэтому называется «окисленным», тогда как хлор приобретает электроны и считается восстановленным. Другой способ судить о восстановлении хлора состоит в том, что заряд атомов становится более отрицательным или уменьшается. Взгляд на окисление и восстановление как на потерю и приобретение электронов соответственно особенно подходит для обсуждения реакций в электрохимических элементах. Например, в цинково-медном элементе полуреакции окисления и восстановления составляют
| Индекс Окисление/ Ссылка | ||||||
| Назад |
Первоначальный взгляд на окисление и восстановление заключается в добавлении или удалении кислорода. Альтернативная точка зрения, полезная при работе с ионами, заключается в определении степени окисления, равной суммарному заряду продукта реакции. Затем окисление рассматривается как реакция, которая увеличивает степень окисления, а восстановление — как реакция, которая уменьшает степень окисления.
Этот взгляд на окисление и восстановление поможет вам справиться с тем фактом, что «окисление» может происходить даже при отсутствии кислорода! Определение окислительно-восстановительных реакций расширено и включает другие реакции с неметаллами, такими как хлор и бром. 24.09.2015 11:10 Учитель решила, что пользоваться нельзя. Автора это не устраивает. Она хочет свои правила установить. Anonymous 24.09.2015 11:11 Так мож пусть тогда автор и преподает. Creambird F 24.09.2015 11:36 Ошибаетесь. Я не собираюсь свои правила устанавливать. Я хочу знать общие правила, которые должны действовать для всех. Zehir F 24.09.2015 13:30 Нет общих правил для всех. Даже учебники разные могут быть. Использование калькулятора регламентируется учителем. Anonymous 24.09.2015 11:13 » temur kvaratskheliya Я, как педагог, категорический запрещаю использование калькулятора. Šedevr KF* 25.09.2015 10:08 Золотые слова! Тезисы распечатаю повешу дочке. Ануля F* Калькулятор и математический решатель — это совершенный математический инструмент, в котором есть все, что вам нужно для выполнения основных расчетов, выполнения домашних заданий или заданий, подготовки к экзаменам и даже управления расходами. Приложение, которому доверяют уже более 10 лет, его загрузили более 210 миллионов раз, охватывает множество тем, таких как базовая математика, АЛГЕБРА, ПРЕДВЫЧИСЛЕНИЕ, ВЫЧИСЛЕНИЕ и ТРИГОНОМЕТРИЯ. ПРИЛОЖЕНИЕ №1 ДЛЯ КАЛЬКУЛЯТОРА И МАТЕМАТИЧЕСКОГО РЕШАТЕЛЯ БАЗОВЫЙ И НАУЧНЫЙ ФУНКЦИЯ ИСТОРИИ РАЗДЕЛЬНЫЙ ПРОСМОТР МНОГОЗАДАЧНОСТЬ ТЕМЫ ЧТО ДЕЛАЕТ ЭТО ПРИЛОЖЕНИЕ ДЛЯ МАТЕМАТИКА? Нравится приложение? Покажите свою поддержку, оценив нас. ПОВЫШЕНИЕ ДО ПРЕМИУМ-ЧЛЕНСТВА Подписки автоматически продлеваются каждый месяц за 24 часа до окончания текущего периода, и с вашей учетной записи iTunes будет взиматься плата, если автоматическое продление не будет отключено по крайней мере за 24 часа до окончания текущего периода. Вы можете отключить автоматическое продление в любое время из приложения. Любая неиспользованная часть бесплатной пробной версии будет аннулирована, если вы приобретете подписку. *Решение математических задач и пошаговые объяснения доступны только на английском языке. Если у вас есть какие-либо предложения или вы не можете найти ответы на какие-либо из ваших вопросов, наша служба поддержки готова и рада помочь. Условия и положения: https://impalastudios.com/terms Политика конфиденциальности: https://impalastudios.com/privacy Калькулятор (C) 2000 Impala Studios. Версия 7.4.2 В этом последнем обновлении вы найдете: Нравится приложение? Тогда не забудьте оценить нас! 1,5 млн оценок : я копирую и вставляю свое уравнение и результат, и получается другое число, чем я вычислил. В этом калькуляторе есть все, что нужно трудолюбивым официантам и работникам, принимающим чаевые, чтобы быстро и правильно сбалансировать свой повседневный заработок без ручки и бумаги. Калькулятор просто работает и не зависает во время использования. Просто нужно, чтобы он заменил тупой калькулятор Apple, который просто вычисляет, а не помогает с историческими расчетами или ошибками. Двойной палец вверх! Спасибо, что обратились к нам по этому вопросу. Приносим извинения за неудобства. Мне очень нравится это приложение, так как я использую его в школе, и оно очень простое в использовании, а также позволяет использовать более сложные уравнения! Моя единственная проблема заключается в том, что я должен платить ежемесячную плату только за то, чтобы использовать другие функции калькулятора, которые есть в обычных калькуляторах, это просто смешно! Я понимаю, что вы, ребята, хотите зарабатывать деньги, но вам действительно нужно заставить людей платить ежемесячную плату только за то, чтобы они могли считать дроби! Я был бы абсолютно в порядке, если бы это была разовая плата, но почему ежемесячная плата!? Это одно из самых загружаемых приложений-калькуляторов в App Store, если не самое лучшее, не говоря уже о небольших дополнениях внизу (совсем не отвлекающих), на которых вы зарабатываете деньги, что показывает, что вы уже зарабатываете немало. Я определенно рекомендую это приложение людям, которые хотели бы настроить свой калькулятор таким образом, чтобы сделать его более ✨декоративным✨ и, кроме того, вы можете использовать его как обычный калькулятор. Просто с рекламой внизу экрана, но это не полноэкранная реклама, которая появляется из ниоткуда, так что это хорошо, по крайней мере, для меня. Математический решатель/Полный доступ/Без рекламы Помощник по выполнению домашних заданий по математике Бесплатная пробная версия Неограниченные математические вычисления Фракция и конвертер Calc 1yr. Бесплатная пробная версия Разработчик, компания International Travel Weather Calculator, указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика. Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям: Следующие данные могут быть собраны и связаны с вашей личностью: Могут быть собраны следующие данные, но они не связаны с вашей личностью: Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Математические калькуляторы — это фантастический инструмент, который может помочь вам в математических вычислениях. Вы можете использовать математические калькуляторы для решения сумм на основе различных тем, таких как преобразования, квадратные уравнения, арифметические операции, такие как деление в длинную, процентное соотношение, площадь различных фигур, объем трехмерных фигур и так далее. Для вашего удобства доступные тематические математические калькуляторы расположены в алфавитном порядке. Для вашего удобства ссылки на список математических калькуляторов, доступных по разным темам, расположены в алфавитном порядке. Ниже приведен список всех возможных математических калькуляторов, которые могут потребоваться учащимся в зависимости от того, к какому классу они относятся. Используйте эти калькуляторы, чтобы помочь вам в решении вопросов и убедиться, что вы получаете точные ответы. Лучшие математические онлайн-калькуляторы — это те, которые обеспечивают простой интерфейс для пользователей и отображают результаты в форме, которую можно быстро интерпретировать. Они не должны быть сложными в использовании и должны объяснять, как они пришли к окончательному ответу. Калькуляторы Cuemath — одни из лучших математических онлайн-калькуляторов, которые соответствуют пунктам, упомянутым выше. Кроме того, они предоставляют калькуляторы по всем темам, которые требуются студентам. Математические калькуляторы очень важны для детей, так как помогают им в школьной программе. Есть несколько мифов, связанных с математическими калькуляторами, например, что они являются костылями, они недостаточно бросают вызов учащимся или, может быть, особый образ мышления, который рассматривает математические калькуляторы как порок, а не благо. Математический калькулятор — это инструмент решения, который используется для выполнения вычислений. Их можно использовать для различных приложений, таких как простые арифметические вычисления, преобразование единиц и решение сложных алгебраических выражений. Математические калькуляторы — одно из лучших доступных устройств для выполнения трудоемких вычислений за считанные секунды, чтобы дети могли направить свои усилия на реальное понимание темы. Все дети должны научиться выполнять базовые вычисления в раннем возрасте. Таким образом, дети никогда не будут зависеть от математического калькулятора, поскольку они уже знают, какие вычисления выполнять при решении вопроса. Однако математические калькуляторы — это инструменты, которые помогают учащимся решать задачи и позволяют им сосредоточиться на более важных аспектах математики. Чтобы прийти к разумному выводу, дети должны знать основные шаги, необходимые для получения конечного результата. Математический калькулятор просто ускоряет процесс, чтобы у детей было больше времени, чтобы сосредоточиться на понимании концепций, лежащих в основе шагов, вместо того, чтобы тратить больше времени на механическое заучивание формул. Как только у ребенка появятся кристально чистые понятия, он автоматически узнает, как подходить к вопросу и правильно его решать. Математические онлайн-калькуляторы разработаны таким образом, что ими могут пользоваться люди всех возрастов, независимо от их технических знаний. Пользовательский интерфейс прост: все, что вам нужно сделать, это выбрать функцию, ввести выражение и нажать кнопку, чтобы получить результат. Большинство калькуляторов также предоставляют пошаговое решение для получения ответа, поэтому, если дети столкнутся с препятствием, у них будет справочный материал. Вы искали калькулятор онлайн решить систему уравнений с помощью обратной матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор решений систем уравнений матричным методом, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «калькулятор онлайн решить систему уравнений с помощью обратной матрицы». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Решить задачу калькулятор онлайн решить систему уравнений с помощью обратной матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Добрый день! Как и обещал в первой своей статье, я хочу ознакомить Вас с одним из методов решения системы диофантовых уравнений. Цель статьи ознакомить остальных читателей с этой методикой и донести её в более или менее понятном виде. Рассмотрим систему из двух диофантовых уравнений Найдем все возможные решения первого уравнения. Как, спросите Вы? Наверняка есть разные методики, но я поделюсь в одной из следующих статей, как бы я решал подобную задачу. А сейчас просто примем что общее решение имеет вид Как проверить что я не лгу? Достаточно вспомнить матричное исчисление и умножить вектор значений нашего первого диофантового уравнения(без свободного члена) на матрицу всех коэффициентов. получили в результате значение свободного члена, а следовательно вычисления правильные Следующим этапом мы подставим наше общее решение во второе уравнение Процедура такая же: умножаем вектор из коэффициентов второго уравнения на общее решение первого получаем вот такой результат то есть мы получили уравнение вида С правой стороны второго диофантового уравнения как был свободный член равный -335, так и остался, то есть наше окончательное решение на этом этапе имеет вид Или перенеся свободные члены в правую сторону получим Итак, мы получили очередное диофантовое уравнение. то есть общее решение имеет вид А теперь делаем обратное преобразование(пусть так называется). То есть в систему Мы вместо неизвестных x подставляем то, что получилось на последнем этапе В матричном исчислении это решается умножением одной матрицы на другую. Результат умножения двух матриц порождает матрицу Последний столбец это свободные члены этой системы. наш окончательный ответ в виде матрицы Проверим? Векторное произведение коэффициентов первого уравнения и матрицы а векторное произведение коэффициентов второго уравнения и матрицы Как видим, результат совпадает с свободным членом каждого из уравнений. где m,p,q — могут принимать любые целые значения Таким незамысловатым способом можно решать и более сложные линейные диофантовые уравнения. По следам этого алгоритма создан калькулятор правда, этот калькулятор очень не любит когда вместо значений в коэффициентах первого уравнения начальной системы встречаются нули. Но это проблема конкретной моей реализации этого алгоритма. В следующей теме я расскажу как создавать диофантовые уравнения по матрице общего решения. Задача в общем то банальна и делается в одно действие, но вдруг кто то не знает. Буду благодарен за замечания, отзывы и предложения. Учеба Математика Алгебра линейная алгебра Матричная триангуляция с использованием методов Гаусса. Ниже приведены два калькулятора для матричной триангуляции. 3 2 3 4
4 4 3 2
1 4 4 3
2 3 1 1 Матрица Точность вычисления Разряды после запятой: 4 Треугольная матрица (метод Гаусса) Треугольная матрица (метод Гаусса с максимальным выбором в столбце): 1 9002 угловая матрица (метод Гаусса с максимальным выбором по всей матрице): 3 2 3 4
4 4 3 2
1 4 4 3
2 3 1 1 Матрица Точность вычислений Знаки после запятой: 4 Треугольная матрица (метод Барейса) Треугольная матрица (метод Барейса с максимальным выбором в столбце) Треугольная матрица с максимальным выбором во всем методе Барейса матрица) Сначала дадим понятие треугольной или ступенчатой матрице строк: Пример эшелонированной матрицы строк: Пример верхней треугольной матрицы: Вы спросите, что интересного в этих ступенчатых (и треугольных) матрицах? Что ж, у них есть удивительное свойство — любую прямоугольную матрицу можно свести к ступенчатой матрице с помощью элементарных преобразований. Итак, что же такое элементарные преобразования, спросите вы? Что теперь? Путем триангуляции матрицы линейного уравнения AX=B к A’X = B’, т.е. с соответствующим преобразованием столбца B, вы можете сделать так называемую «обратную подстановку». Для объяснения воспользуемся приведенной выше треугольной матрицей и перепишем систему уравнений в более общем виде (я составил столбец B): Понятно, что сначала найдем , а потом подставим в предыдущее уравнение, найти и так далее – переход от последнего уравнения к первому. Это то, что называется обратной заменой. Теперь немного мыслей об этом методе. Нуль в первом уравнении Во втором уравнении нет где N – размерность строки, – i-я строка, Однако существует радикальная модификация метода Гаусса – метод Барейса. Барейс предложил разделить приведенное выше выражение на и показал, что если исходными элементами матрицы являются целые числа, то и результирующее число будет целым. Также предполагается, что для нулевой строки . Кстати, тот факт, что алгоритм Барейса сводит целые элементы исходной матрицы к треугольной матрице с целыми элементами, т.е. без накопления отклонений, является весьма важной особенностью с точки зрения машинной арифметики. Алгоритм Барейса можно представить в виде: Этот алгоритм можно модернизировать, аналогично Гауссу, с максимальной выборкой в столбце (вся матрица) и перестановкой соответствующих строк (строк и столбцов). URL скопирован в буфер обмена Барейс треугольная матрица Барейса метод Барейса метод Гаусса линейная алгебра математическая матрица треугольная матрица PLANETCALC, Калькуляторы матричной триангуляции Тимур 2020-12-04 10:52:19 9000 онлайн калькулятор обратных матриц 9001 1 Для любой невырожденной матрицы (т. А∙А −1 = А -1 ∙А
= Е Наш онлайн-калькулятор поддерживает два различных метода вычисления обратной матрицы: с помощью метода Гаусса-Жордана и с помощью композиций алгебраических дополнений к исходной матрице. Чтобы найти обратную матрицу с помощью метода Гаусса-Жордана, нужно прикрепить единичную матрицу справа от исходной матрицы: ( А | Е ) Затем с помощью элементарных преобразований преобразовать исходную матрицу в единичную, применяя те же преобразования к единичной матрице, выписанной справа. Следовательно, исходная матрица будет преобразована в единичную, а выписанная справа единичная матрица — в обратную: ( А | Е ) → ( Е | А −1 ) Этот способ легкий, удобный и не такой трудоемкий. Чтобы найти обратную матрицу с помощью алгебраического метода дополнений, можно использовать следующую формулу: где
| А |
— определитель матрицы
А, По определению A i j = (-1) i+j M i j где
М и — минор элемента и матрицы
А. По определению — минор элемента и матрицы
А
– определитель, полученный удалением
я
ряд,
Дж
столбец матрицы
А. Итак, алгебраический адъюнктный метод нахождения матрицы, обратной исходной матрице порядка
н
очень трудоемко, так как нужно вычислять не только определитель исходной матрицы, но и
п 2 детерминанты порядка
п-1
. Бесплатная программа ЛовиОтвет — функциональный калькулятор для решения примеров и уравнений. В программе Лови Ответ происходит автоматическое решение математических примеров и уравнений с выводом действий и этапов их решения. Для чего нужна такая программа? Программа Лови Ответ — это своего рода математический решебник, который выводит ответ, с пошаговым решением выполненного задания. Содержание: Программа Лови Ответ будет интересна школьникам и их родителям. С помощью этой программы родители могут проверять домашние задания, которые выполнил учащийся. Также школьники и студенты могут решать примеры и уравнения при помощи этого математического калькулятора. Взрослые, которые уже не помнят многого из школьного курса, а также учащиеся смогут при помощи данной программы, быстро решить математический пример любой степени сложности. В программе ЛовиОтвет можно будет выполнять такие математические действия: Примеры и уравнения будут решены в программе Лови Ответ пошагово, с последовательными действиями. Визуально, в окне программы, вы увидите решение примера или уравнения. Ответ и пошаговые действия для его решения, будут записаны на своеобразном тетрадном листе. Все этапы решения можно будет записывать в программе в столбик. Скачать программу ЛовиОтвет можно с официального сайта производителя. Программа доступна для работы на компьютерах с операционной системой Windows. Есть версии программы для устройств на операционной системе Android, для Aplle устройств (iPad, iPhone/iPod), для мобильных телефонов (java, java-mini). Лови Ответ скачать После загрузки, вам можно будет установить программу на свой компьютер. Запустите процесс установки программы LoviOtvet на своем компьютере. При установке программы будьте внимательны! Снимите флажки в тех пунктах, где вам предложат установить дополнительные программы, для того, чтобы не устанавливать на свой компьютер постороннее программное обеспечение. По завершению установки программы на компьютер, будет открыто главное окно программы ЛовиОтвет. В верхней части окна программы расположены кнопки меню для управления программой. С помощью кнопки меню «Правка» вы можете скопировать решение на свой компьютер, выбрав необходимый вариант копирования из контекстного меню. Из меню «Настройки» вы можете выбрать размер листа, клеток, очистить историю. Здесь вы можете изменить цвет отображения окна программы, передвинув в нужное место ползунок, по шкале цвета. Под панелью меню расположено поле, в которое вводится задание. В левой части окна расположены кнопки и переключатели для ввода данных. Дополнительную панель можно будет скрыть с помощью кнопки «Скрыть дополнительную панель». Отсюда, в случае необходимости, вы можете изменить размер листа и размер клеток в рабочей области. Остальную часть окна программы занимает рабочая область, в которой будет отображено решение задания. Для решения примера, с помощью соответствующих кнопок введите выражение, а затем нажмите на кнопку «Ответ». Решение можно будет выводить в нескольких вариантах: стандартное решение, обыкновенные дроби, решение «в столбик». После клика по треугольнику в крайней правой части поля, в котором вводится пример или уравнение, откроется дополнительное поле, в котором будут отображена история расчетов. В этом поле можно будет очистить историю расчетов. Подробнее о том, как пользоваться математическим калькулятором, можно будет прочитать на официальном сайте производителя программы ЛовиОтвет, на странице сайта «Как пользоваться». Производитель запустил онлайн версию программы ЛовиОтвет, которая доступна по такому адресу: По заявлению производителя, версия Лови Ответ онлайн менее функциональна, чем программа, которая устанавливается на компьютер или мобильное устройство. Но, все равно, онлайн калькулятор может быть полезен в некоторых случаях, для выполнения решения поставленных задач. Бесплатная программа Лови Ответ — математический решебник и калькулятор, который помогает школьникам, студентам и родителям выполнять или проверять решение примеров и уравнений любой степени сложности. ЛовиОтвет — программа для решения примеров и уравнений (видео) Нажимая на кнопку, я даю согласие на обработку персональных данных и принимаю политику конфиденциальности Меньше года до ОГЭ и ЕГЭ — что делать? Конечно, готовиться! Это можно делать увлекательнее, чем просто корпеть над учебниками. 1. ФИПИ занимается разработкой заданий для ЕГЭ и ОГЭ. Сайт пригодится каждому выпускнику, чтобы найти и скачать демоверсии, спецификации и кодификаторы по выбранным предметам и получить всю актуальную информацию об экзаменах. 2. Калькулятор баллов ЕГЭ пригодится, когда экзамены будут сданы. На основе набранных баллов сайт поможет узнать, каковы шансы абитуриента поступить в тот или иной вуз на бюджетное или платное отделение. 3. Информационный портал ЕГЭ — вся официальная информация об экзаменах. Расписание, подача апелляций, демонстрационные задания, результаты экзаменов. 4. Сайт Александра Ларина — один из самых популярных сайтов для подготовки к ЕГЭ по математике. Тут регулярно публикуют материалы для экзамена, есть генератор вариантов ЕГЭ, а на форуме отвечают на вопросы. 5. 6. Photomath (Android, iOS) — пожалуй, лучший калькулятор с камерой и возможностью распознавания рукописного текста. Выдаёт не только готовый ответ, но и подробное пошаговое решение. 7. Мои достижения — бесплатный онлайн-сервис, где можно тренироваться выполнять задания на конкретные темы, решать тригонометрические или иррациональные уравнения, а также ознакомиться и решить варианты ЕГЭ предыдущих годов. 8. Math Games — тренажёр, который требует минимальное знания английского. На личной страничке отображается вся статистика о проделанной работе: время, затраченное на каждое задание, начало и конец занятий, результаты по каждой теме. Удобно использовать, так как выдаёт списки заданий либо по классу, либо по темам. Подходит для средних классов, но и помогает повторить, так как в ЕГЭ включаются темы с седьмого класса. 9. 10. Buzzmath — тренажёр на английском с интересной подачей заданий. На сайте указано, что задания рассчитаны на шестой-девятый классы. Сайт платный, но если заходить как «визитор», то можно заниматься бесплатно. Единственный минус — ваши результаты сохраняться не будут. 11. Учительский портал — тренажеры на русском языке (предварительно скачать по указанным ссылкам). 12. А+клик: Математические Задачи — тесты на русском языке с 1 по 11 класс. 13. Вся элементарная математика — много теории, по каждой теме есть задания. 14. Matific — математические игры и материалы. 15. www.problems.ru— сайт для продвинутых математиков — разобранные решения олимпиад и прочее. 16. Задачи на логику и смекалку — много интересных задач по разным разделам математики. 17. nazva.net— отличная копилка задач для тех, кто любит думать. 18. Знания — русскоязычный сайт, на котором вы можете задать любой интересующий вопрос и получить ответ онлайн от помощника. Есть возможность и для повторения других предметов. 19. Школьная математика — охватывает всего несколько тем как онлайн-решатель, но зато довольно доступно подаётся теория. 20. Лови Ответ — помогает решать примеры и уравнения с отображением этапов решения. 21. Видеоуроки математики — канал с видеоуроками по математике. 22. Сдам ГИА: решу ЕГЭ — лучший онлайн-тренажёр с решениями заданий. 23. Яндекс.Репетитор — тренировочные варианты онлайн. 188480, Ленинградская область, г. Кингисепп, ул. Иванова, дом 26 телефоны: секретарь (81375) 2-58-72, директор (81375) 2-58-75 факс (81375) 2-58-75 e-mail: [email protected] БЕСПЛАТНАЯ ВЕРСИЯ IM K–12 MATH Мы понимаем, что учителям сложно найти ресурсы, которые помогут учащимся сформировать прочное понимание математики. Помогите учащимся научиться математике на всю жизнь. Превью ИМ К–12 Матем. Готовы начать работу с сертификацией IM? Уже пользуетесь мгновенными сообщениями, но хотите узнать больше? Все зеленые на всех шлюзах EdReports Математическое мышление моих учеников поражает меня! Каждый ученик в моем классе может объяснить свой ответ. Табита Э. Учитель 3 класса, Миссури Учебная программа помогает нашим учащимся вести продуктивную борьбу, и учителя были рады перейти от роли «мудреца на сцене» к роли «проводника на стороне» 9.0003 Коррин Уильямс, специалист по математике средней школы, Evergreen Public Schools, WA IM 9–12 Математика привела к быстрому изменению моего подхода к преподаванию и изучению математики. Кроме того, мои студенты развили более глубокое понимание математических концепций, придавая смысл своим разговорам друг с другом и со мной по обсуждаемой теме. Джозеф Дзюба, учитель математики, Государственные школы Нью-Брансуика, Нью-Джерси Мы считаем, что клеймо инструктора «IM Certified™» означает качество и опыт как в области математики, так и в обеспечении наилучшего профессионального опыта для учителей и тренеров. Кэти Мартин, ведущий учитель математики в средних школах округа Нью-Ганновер, Северная Каролина Несмотря на все исследования, доказывающие, что математики становятся , а не рождаются , я не виню вас за то, что вы думаете, что у вас просто плохо с математикой, потому что математика чертовски жесткий . Чтобы построить свой математический «дом», вы должны убедиться, что каждый фрагмент знаний подходит идеально, чтобы вы могли строить поверх него, не опасаясь, что позже все это рухнет. И если вы промедлите хотя бы с одной фундаментальной темой, ваши знания рухнут перед лицом скрежещущих ночей над наборами задач и учащенного сердцебиения на важном экзамене. Итак, вопрос о деньгах таков: Как улучшить математику? Чтобы стать лучше в математике, вам нужно решать все более сложные математические задачи, применяя стратегию, которую психолог Андерс Эрикссон называет 9. Он определяет это как «целенаправленную практику, которая знает, куда она идет и как туда добраться». Это означает, что вы должны намеренно находить проблемы, которые ставят вас в тупик, и работать над ними. И если проблема слишком сложна, сначала найдите более легкую для решения. Это один из самых важных первых принципов, который нужно помнить при изучении математики. В этом посте я поделюсь некоторыми советами о том, как вы можете это сделать. «Если вы не можете решить проблему, то есть более простая проблема, которую вы можете решить: найти ее». — Джордж Полиа , Как решить Чтобы разобраться в сути каждой проблемы, вы должны определить концепции, выделить их и попрактиковаться. Возьмем, к примеру, такую задачу на суммирование: Это относительно простая задача, которую должен уметь решать старшеклассник. Для решения этой задачи необходимо знание суммирования и дробных показателей. Итак, прежде чем погрузиться в задачу, вы должны сначала убедиться, что понимаете суммирование и дробные показатели степени сами по себе. Например, вы можете взять дробный показатель и решить начальную задачу без него: В результате вы получите следующее решение: Затем вы можете убрать дробный показатель из задачи и работать над его освоением: И поймите, что это не так сложно решить самостоятельно: Как только вы разобрались с этими двумя понятиями сами по себе, вы можете соединить их вместе, чтобы решить исходное уравнение. Посмотрите, как они сочетаются друг с другом: Поздравляем! Теперь вы нашли решение: Если вы еще раз посмотрите на мой пример, то заметите, что в нем используются простые числа и низкий предел: Точно так же, когда вы учитесь, сначала работайте над задачами с простыми числами. Однако иногда ваше понимание проблемы слишком шатко. (Хорошо, давайте будем честными: так бывает в большинстве случаев.) В таком случае пора порыться в учебнике и просмотреть свои заметки с урока. (Я предполагаю, что вы делаете заметки A+. Если нет, узнайте, как делать заметки лучше, здесь.) Если вы все еще не поняли, есть много видео на YouTube и статей с пояснениями, которые помогут вам. Часто в них есть пошаговые решения, которые показывают, как другие люди приходят к своим ответам: Наконец, обратитесь за помощью к своему профессору или учителю. Эрикссон говорит: «Хороший учитель математики… будет смотреть не только на решение задачи; он будет смотреть на то, как именно ученик получил ответ, чтобы понять, какие ментальные репрезентации он использовал. Если нужно, он даст совет, как эффективнее думать о проблеме». Квалифицированные учителя часто могут перефразировать или переформулировать понятия. Иногда все, что нужно, — это немного другой выбор слов, чтобы сложная концепция встала на свое место. Иногда полезно увидеть пошаговое решение проблемы, над которой вы работаете, если вы сначала попытаетесь разобраться в ней самостоятельно. Есть три отличных инструмента для решения проблем, с которыми вы сталкиваетесь: Wolfram Alpha — это инструмент, который может решить практически любую математическую задачу, а также предоставить вам подробные решения (хотя вам понадобится премиум-версия, чтобы увидеть все шаги): Напротив, хотя пользовательский интерфейс Symbolab более громоздкий и менее интуитивным, его пошаговые решения бесплатны: Наконец, если вам нужны решения конкретных задач в вашем учебнике, вы можете проверить Chegg Study. Независимо от того, что вы выберете, убедитесь, что после этого вы сами решаете проблемы, не глядя на решения. Это поможет вам избежать того, что Джеффри Карпик, исследователь, специализирующийся на стратегиях обучения студентов, называет иллюзией компетентности . Это когда вы чувствуете, что понимаете концепцию, потому что прочитали абзац несколько раз и можете быстрее обработать его Вместо перечитывания Карпик обнаружил, что пытается извлечь информацию из памяти — самая эффективная форма обучения. Он выступал за такие методы, как метод Фейнмана, чтобы помочь вам вспомнить и запомнить концепции глубоко. Точно так же честно спросите себя: Довел ли я свой мозг до предела, пытаясь сначала решить эту проблему? Если у вас есть, но вы все равно не можете его получить, можно поискать ответ. Опять же, весь смысл математики в освойте концепции , с которыми вы работаете, чтобы вы могли опираться на них, а не только для выполнения домашнего задания. «Простое понимание того, как была решена проблема, не обязательно создает кусок, который вы можете легко вспомнить позже. Не , а не путают «ага!» прорыва в понимании с солидным опытом!» – Барбара Окли Очень заманчиво решить домашние задания как можно быстрее, чтобы вы могли вернуться к игре Цивилизация VI или Ведьмак 3 . Но технические предметы, такие как математика и естественные науки, требуют, чтобы вы не торопились. Для начала, в книге профессора инженерии Барбары Окли « Разум для чисел » Окли предлагает применять интервальных повторений . Этот вид медленного, преднамеренного обучения позволяет вашему мозгу получить четкое представление о каждой концепции и, что более важно, о связях между ними. Чтобы по-настоящему овладеть своими инструментами, вам нужно научиться приспосабливать их к различным ситуациям. Точно так же, чтобы действительно сказать, что вы освоили часть математики, вам нужно видеть сквозь проблемы и знать, какую формулу или процесс использовать в мгновение ока. «Я не верю в то, что есть несколько особенных людей, способных понимать математику, а остальной мир нормальный. Математика — это человеческое открытие, и она не сложнее, чем люди могут понять». – Ричард Фейнман, Omni Magazine Улучшить математику просто, но не легко. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособие. В 10 т. Т. II. Теория поля.— 7-е изд., испр.— М.: Наука. Гл. ред. физ.-мат. лит., 1988. 512 с.
Предлагаемая книга представляет собой новое издание (6-е изд. выходило в 1973 г.) второго тома курса теоретической физики, заслужившего широкую известность в нашей стране и за рубежом. Том посвящен классической теории электромагнитных и гравитационных полей. В нем излагаются основы специальной теории относительности, вывод уравнений электродинамики из принципа наименьшего действия, вопросы распространения и излучения электромагнитных волн. Последние главы книги посвящены общей теории относительности. Параллельно с развитием этой теории излагаются основы тензорного анализа. Для студентов университетов, студентов физических специальностей вузов, а также для аспирантов соответствующих специальностей.
%PDF-1.6
%
1 0 obj
>
endobj
50 0 obj
>stream
application/pdf Fm )8亗،H
O[oDC»m8W}%Az\ht)q晴:IE#@7ܑ
WtسeWJ- )»TZQr)##`Dh,AÚ{k%KS@+$rXD(j狈Ѹ!ԦQ03:Bƍ@j]MY8X5_%JpaHs!Z4+BZeWo.Ax@ùǯV3uOhˎ;jRg-MFEiBl$
bxxcYCefRY=jAޒ=M2ԙWK»`G{ N~ն[5ʃ?c0)(L+%:39,ݵ\KKPgJkEXkڝؤ
ZўY|(Qw/
ky߃(G,+(B+uioF1(]6nWk
HdDRMҏfE»>j
YEGܝ ŽZbӨ.F>X;I($GAlv@fm+nKBs)9ΝIykyV8q’OA{
‘8/㗯&)śOK-#
U Excel для Microsoft 365 Excel для Интернета Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Дополнительно. Вы можете преобразовать содержимое ячейки, содержащей формулу, чтобы вычисляемое значение заменяло формулу. Если вы хотите заморозить только часть формулы, вы можете заменить только ту часть, которую не хотите пересчитывать. Замена формулы ее результатом может быть полезна, если в книге много или сложные формулы и вы хотите повысить производительность за счет создания статических данных. Вы можете преобразовывать формулы в их значения либо по ячейкам, либо преобразовывать весь диапазон сразу. Важно: Убедитесь, что вы изучили влияние замены формулы ее результатами, особенно если формулы ссылаются на другие ячейки, содержащие формулы. Рекомендуется сделать копию рабочей книги, прежде чем заменять формулу ее результатами. В этой статье не рассматриваются параметры и методы расчета. Чтобы узнать, как включить или отключить автоматический пересчет для рабочего листа, см. статью Изменение пересчета формулы, итерации или точности. При замене формул их значениями Excel безвозвратно удаляет формулы. Если вы случайно заменили формулу значением и хотите восстановить формулу, нажмите Отменить сразу после ввода или вставки значения. Выберите ячейку или диапазон ячеек, содержащих формулы. Если формула является формулой массива, выберите диапазон, содержащий формулу массива. Как выбрать диапазон, содержащий формулу массива Щелкните ячейку в формуле массива. На вкладке Главная в группе Редактирование щелкните Найти и выбрать , а затем щелкните Перейти к . Нажмите Специальный . Нажмите Текущий массив . Щелкните Копировать . Щелкните Вставьте . Щелкните стрелку рядом с Параметры вставки , а затем щелкните Только значения . В следующем примере показана формула в ячейке D2, которая умножает ячейки A2, B2 и скидку, полученную из C2, для расчета суммы счета-фактуры для продажи. Чтобы скопировать фактическое значение вместо формулы из ячейки на другой лист или книгу, вы можете преобразовать формулу в своей ячейке в ее значение, выполнив следующие действия: Нажмите F2, чтобы отредактировать ячейку. Нажмите F9, а затем нажмите клавишу ВВОД. После преобразования ячейки из формулы в значение значение отображается как 1932,322 в строке формул. Обратите внимание, что 1932,322 — это фактическое расчетное значение, а 1932,32 — это значение, отображаемое в ячейке в денежном формате. Совет: При редактировании ячейки, содержащей формулу, можно нажать F9, чтобы навсегда заменить формулу ее вычисленным значением. В некоторых случаях может потребоваться заменить только часть формулы ее вычисляемым значением. При замене части формулы ее значением эта часть формулы не может быть восстановлена. Щелкните ячейку, содержащую формулу. В строке формул выберите часть формулы, которую вы хотите заменить вычисленным значением. Когда вы выбираете часть формулы, которую хотите заменить, убедитесь, что вы включили весь операнд. Чтобы рассчитать выбранную часть, нажмите F9. Чтобы заменить выбранную часть формулы ее расчетным значением, нажмите клавишу ВВОД. В Excel для Интернета результаты уже отображаются в ячейке книги, а формула отображается только в строке формул. Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов. Главная // Блог и советы по Excel // Отрицательные числа Excel в скобках Без категории Один из наиболее распространенных запросов на форматирование – как получить отрицательные числа Excel в квадратных скобках (и красного цвета) вместо простого знака минуса (-) перед числом. Фактическая проблема не в Excel, а скорее на уровне Windows, но вы можете внести изменения либо на уровне Windows (в этом случае изменятся все программы, использующие числа), либо на уровне Excel. Это необходимо изменить на уровне Windows. Одно предостережение: у вас могут быть программы, которым нужен альтернативный формат. Поэтому, если вы вносите это изменение, протестируйте другие свои программы или, по крайней мере, запомните это изменение, если у вас вдруг возникнут проблемы в других программах. В Windows: Когда вы вернетесь в Excel, вы увидите, что отрицательные числа теперь заключены в скобки, а в поле «Формат ячеек» в разделе «Числа» у вас теперь есть опция для красного цвета и в скобках (если это не выглядит так, может потребоваться перезагрузка компьютера). Отныне Excel и другие ваши программы должны иметь эту возможность. В качестве альтернативы вы можете изменить формат ячейки, чтобы показать отрицательные числа в скобках, но вам нужно будет перейти к параметру пользовательских форматов (поскольку Excel использует региональные настройки по умолчанию, если только сказано иначе). Самый простой способ сделать это — создать пользовательский формат. Как показано ниже, вы можете УчебаМатематикаАлгебра Калькулятор раскладывает дробь из двух многочленов на простейшие методом неопределенных коэффициентов. Следующий калькулятор раскладывает полиномиальную дробь на сумму более простых дробей методом неопределенных коэффициентов. Числитель дроби — многочлен, который задается набором коэффициентов (коэффициенты задаются через пробел, начиная с коэффициента старшей степени). Знаменатель представляет собой произведение многочленов 1-й или 2-й степени, возведенных в некоторую степень (>=1). Многочлены-множители знаменателя задаются в виде таблицы коэффициентов, аналогично многочлену в числителе. Разделенные пробелом коэффициенты многочлена. Данные Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: 1 2 3 4;50 Загрузить данные из csv файла Задача Решение Файл очень большой, при загрузке и создании может наблюдаться торможение браузера. Файл очень большой, при загрузке и создании может наблюдаться торможение браузера. Еще один калькулятор, вычисляет то же самое, но он позволяет задать знаменатель в виде многочлена и сам пытается найти его разложение на множители. Если при разложении знаменателя окажется неразлагаемый множитель выше 2-й степени, то метод неопределенных коэффициентов не сработает. Разделенные пробелом коэффициенты многочлена. Коэффициенты многочлена, разделенные пробелом. Задача Решение Файл очень большой, при загрузке и создании может наблюдаться торможение браузера. Файл очень большой, при загрузке и создании может наблюдаться торможение браузера. Метод неопределенных коэффициентов для разложения полиномиальной дроби P(x)/Q(x), где P(x) и Q(x) — полиномы одно переменной в общем случае сводится к такой последовательности шагов: , где , где ajk, bjk,cjk — вещественные числа. Эти шаги будут отображены в деталях со ссылками на простейшие действия, если в калькуляторе включить галочку «Детали». В.А.Зорич Математический анализ том.1 ↩ Ссылка скопирована в буфер обмена Алгебра дробь Матанализ Математика математический анализ метод неопределенных коэффициентов Многочлены разложение Anton2020-11-03 14:19:38 Примеры ↑ Введите нижнюю границу интеграла и верхнюю границу интеграла b, подинтегральную функцию f(x) — смотрите пример { кусочно-заданную функцию ввести здесь. Неопределенные коэффициенты — это метод, который можно использовать для нахождения общего решения неоднородного дифференциального уравнения второго (или более высокого) порядка. Привет! Я Криста. Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. Помните, что однородные дифференциальные уравнения имеют ???0??? в правой части, где неоднородные дифференциальные уравнения имеют ненулевую функцию в правой части. Общее решение ???Y(x)??? неоднородному дифференциальному уравнению всегда будет суммой дополнительного решения ???y_c(x)??? и конкретное решение ???y_p(x)???. ???Y(x)=y_c(x)+y_p(x)??? Начнем с поиска дополнительного решения, предположив, что неоднородное уравнение на самом деле является однородным уравнением. Другими словами, мы просто заменяем ???g(x)??? с ???0??? а затем решить для значений ???x??? которые являются решениями однородного уравнения. В зависимости от значений ???x??? которое мы найдем, мы сгенерируем дополнительное решение дифференциального уравнения. Как только мы нашли дополнительное решение, пришло время сделать предположение о конкретном решении, используя правую часть дифференциального уравнения. Требуется практика, чтобы хорошо угадывать конкретное решение, но вот некоторые общие рекомендации. Для полиномиальной функции, такой как ???x^2+1???, угадайте ???Ax^2+Bx+C???, убедившись, что включены все члены более низкой степени, чем члены высшей степени в многочлен. Получив окончательное предположение для конкретного решения, возьмите производную и вторую производную вашего предположения, затем подставьте предположение в исходное дифференциальное уравнение для ???y(x)???, подставьте его производную для ??? y'(x)???, и подставьте вторую производную вместо ???y»(x)???. Затем вы сможете комбинировать одинаковые члены и приравнивать коэффициенты с обеих сторон, чтобы найти константы, и в конечном итоге получить частное решение, которое вы можете комбинировать с дополнительным решением, чтобы получить общее решение дифференциального уравнения. . Пример 9{-2x}??? Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, дифференциальные уравнения, второй порядок, уравнения второго порядка, дифференциальные уравнения второго порядка, неизвестные коэффициенты, неоднородные уравнения, неоднородные уравнения второго порядка, неоднородные дифференциальные уравнения , дополнительное решение, частное решение, общее решение Для линейного неоднородного обыкновенного дифференциального уравнения с постоянными коэффициентами где все константы и , неоднородный член иногда содержит только линейные комбинации или кратные некоторые простые функции, производные которых более предсказуемы или хорошо известны. Пробные функции в методе неопределенных коэффициентов : Некоторые частные случаи и их пробные решения перечислены ниже: Содержание: Содержание Определение
Площадь параллелограмма, построенного на векторах, определяется как произведение их длин на синус угла между ними. Если по условию задачи даны длины этих векторов, то вычисление площади параллелограмм не вызывает затруднений. Для этого необходимо воспользоваться формулой: \( S=\left|a\right|\times\left|b\right|\times\sin\beta\) Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут. Векторным произведением некоторых векторов m и n является третий вектор p. \(\overline p\;=\left|\overline m\right|\times\left|\overline n\right|\\\) Определение
Модуль векторного произведения, то есть скаляр вектора p определяется как произведение модулей векторов m и n, на синус лежащего между ними угла α. Это определение записывается математическим языком так: \(\left|p\right|=\left|m\right|\times\left|n\right|\times\sin\alpha\\\) Все три эти вектора образуют правую тройку. Допустим, вектора заданы координатами: \(\overline m=\left\{x_1;y_1;z_1\right\}\\\) \(\overline n=\left\{x_2;y_2;z_2\right\}\\\) В декартовой системе координат их произведение можно будет вычислить по формуле: \(\left[m\times n\right]=\left\{y_1\times z_2-y_2\times z_1;z\times x_2-z_2\times x_1;x_2\times y_2-x_2\times y_1\right\}\\\) Примечание
В этом виде запомнить формулу достаточно сложно. Значительно проще представить ее в другой форме: \(\left[m\times n\right]=\begin{vmatrix}i&j&k\\x_1&y_1&z_1\\x_2&y_2&z_2\end{vmatrix}\\\\\\\) Пример Рассмотрим еще один пример. Дан параллелограмм с длиной сторон a – 5 см, b – 6 см и углом между ними равным 30^0\\\\\\. Таким образом, площадь данного параллелограмма равна 15 квадратным сантиметрам. Пример Даны два вектора, а и b, имеющие в декартовой системе следующие координаты: \(\left\{4,\;2,\;6\right\}\\\\\\\) \(\left\{4,\;8,\;11\right\}\\\\\\\) Требуется найти площадь, образуемого ими параллелограмма. Для решения требуется найти векторное произведение заданных векторов: \(\left[a\times b\right]=\begin{vmatrix}i&j&k\\4&2&6\\4&8&11\end{vmatrix}=i\begin{vmatrix}2&6\\8&11\end{vmatrix}-j\begin{vmatrix}4&6\\4&11\end{vmatrix}+k\begin{vmatrix}4&2\\4&8\end{vmatrix}=i\left(2\times11-48\right)-j\left(44-24\right)+k\left(32-8\right)=-26i-20j+24k=\left\{-26;-20;24\right\}\\\\\\\) Для полученного отрезка, имеющего направление, найдем модульное значение. Оно и будет площадью параллелограмма, построенного на векторах а и b. После извлечения квадратного корня получаем, что площадь параллелограмма равна 40,64. Пример Вычислить площадь параллелограмма, заданного векторами a и b. Их координаты: \(\left\{4;\;5\right\}\\\\\\\) \(\left\{-7;\;8\right\}\\\\\\\) Оба эти вектора лежат в одной плоскости. Поэтому третью их координату принимаем за 0. Тогда площадь данного параллелограмма будет равна: \(S=\sqrt{32+35}=\sqrt{67}\approx8.2\\\\\\\) Насколько полезной была для вас статья? У этой статьи пока нет оценок. Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter» Вы искали векторы площадь параллелограмма? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выразить площадь проекции параллелограмма на векторах, не
исключение. Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как векторы площадь параллелограмма,выразить площадь проекции параллелограмма на векторах,вычислите площадь параллелограмма построенного на векторах,вычислить диагонали и площадь параллелограмма построенного на векторах,вычислить площадь параллелограмма построенного на векторах,вычислить площадь параллелограмма построенного на векторах a и b,вычислить площадь параллелограмма построенного на векторах a и b онлайн,вычислить площадь параллелограмма построенного на векторах а и b,вычислить площадь параллелограмма построенного на векторах а и в,вычислить площадь параллелограмма построенного на векторах и,как вычислить площадь параллелограмма построенного на векторах,как найти площадь параллелограмма построенного на векторах,как найти площадь параллелограмма построенного на векторах а и в,найдите площадь параллелограмма построенного на векторах,найти высоту параллелограмма построенного на векторах,найти площадь параллелограмма диагоналями которого служат векторы,найти площадь параллелограмма построенного на векторах,найти площадь параллелограмма построенного на векторах онлайн,обчислити площу паралелограма побудованого на векторах,онлайн калькулятор площадь параллелограмма построенного на векторах,онлайн найти площадь параллелограмма построенного на векторах,параллелограмм построен на векторах a и b,площадь параллелограмма векторы,площадь параллелограмма на векторах,площадь параллелограмма по векторам,площадь параллелограмма построенного на векторах,площадь параллелограмма построенного на векторах найти онлайн,площадь параллелограмма построенного на векторах онлайн калькулятор,площадь параллелограмма через вектора,площадь параллелограмма через векторы,пользуясь параллелограммом построенным на векторах a и b,построить параллелограмм на векторах. Решить задачу векторы площадь параллелограмма вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Даны два вектора u и v с общим
начальная точка, множество конечных точек векторов s u + t v для 0 £ s , t £ 1 определяется как параллелограмм охватывает u и против . Рассмотрим два приложения теоремы 3.3. Во-первых, если и и v параллельны, тогда q = 0 и u × v = 0. Таким образом, площадь параллелограмма, образованного и и и , равна || и |||| против || грех(q) . Последний результат следует из того, что и — и делят пополам
параллелограмм, образованный и и и . ПРИМЕР 5 Найдите площадь треугольника с вершинами P 1 ( 2,2) , P 2 ( 4,4) , и P 3 ( 6, Решение: Легко видеть, что u =
б2,2
с и v =
б 4,-1
с . Как
векторов в R 3 , имеем u =
б2,2,0
с и v =
а 4,-1,0
с .
Таким образом, их векторное произведение равно Решение: Для этого сначала построим векторы u и против : П 1 П 2 Р 1 Р 3 Рисунок Maple/Javaview Есть два способа получить произведение пары векторов. Перекрестное произведение определено только для трехмерных векторов. Если $\vc{a}$ и $\vc{b}$ — два трехмерных вектора, то их векторное произведение, записанное как $\vc{a} \times \vc{b}$ и произносимое как «a cross b , — еще один трехмерный вектор. Мы определяем этот вектор перекрестного произведения $\vc{a} \times \vc{b}$ следующими тремя требованиями: На приведенном ниже рисунке показано, как с помощью тригонометрии мы можем вычислить, что площадь
параллелограмм, натянутый на $\vc{a}$ и $\vc{b}$, является
\начать{выравнивать*}
\|\vc{а}\| ~ \|\vc{b}\| \sin\тета,
\конец{выравнивание*}
где $\тета$
угол между $\vc{a}$ и $\vc{b}$. На рисунке показан параллелограмм с основанием длиной $\|\vc{b}\|$ и
перпендикулярная высота $\|\vc{a}\| \sin\тета$. Эта формула показывает, что величина векторного произведения равна
наибольшее, когда $\vc{a}$ и $\vc{b}$ перпендикулярны. С другой
стороны, если $\vc{a}$ и $\vc{b}$ параллельны или любой из векторов является
нулевой вектор, то векторное произведение является нулевым вектором. (Это хороший
Дело в том, что в этих случаях мы получаем нулевой вектор, так что приведенное выше
определение по-прежнему имеет смысл. Ниже приведен апплет, который помогает проиллюстрировать, как перекрестное произведение
работает. Хотя, по общему признанию, трудно манипулировать точным
образом, вы можете убедиться, что перечисленные выше свойства
перекрестное произведение удовлетворяется вектором перекрестного произведения, показанным на
апплет. Перекрестное произведение. Вектор $\color{red}{\vc{c}}$ (красный) является векторным произведением векторов $\color{blue}{\vc{a}}$ (синим) и
$\color{green}{\vc{b}}$ (зеленым цветом), $\color{red}{\vc{c}} = \color{blue}{\vc{a}} \times \color{ зеленый}{\vc{b}}$. Параллелограмм, образованный параллелограммом $\color{blue}{\vc{a}}$ и $\color{green}{\vc{b}}$, розовый на той стороне, где перекрестное произведение $\color{red}{\ точки vc{c}}$ и фиолетовый цвет на противоположной стороне. Дополнительная информация об апплете. Обратите внимание, что площадь параллелограмма (и, следовательно, величина
векторного произведения) стремятся к нулю при приближении $\vc{a}$ и $\vc{b}$
параллельный (где термин «параллельный» также включает то, что вы
может считаться антипараллельным). Вы также можете убедиться, что апплет
демонстрирует $\vc{b} \times \vc{a} = — \vc{a} \times \vc{b}$ и $\vc{a}
\times \vc{a} = \vc{0}$, которые являются важными свойствами креста.
продукт. Геометрическое определение перекрестного произведения полезно для понимания его свойств. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Оценить | квадратный корень из 12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Оценить | квадратный корень из 20 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Оценить | квадратный корень из 50 | 94 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Оценить | квадратный корень из 45 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Оценить | квадратный корень из 32 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Оценить | квадратный корень из 18 | 92 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | ||||||||||||||||||||||||||||||||||||
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | ||||||||||||||||||||||||||||||||||||
| 3 | Оценка | 5+5 | ||||||||||||||||||||||||||||||||||||
| 4 | Оценить | 7*7 | ||||||||||||||||||||||||||||||||||||
| 5 | Найти простую факторизацию | 24 | ||||||||||||||||||||||||||||||||||||
| 6 | Преобразование в смешанный номер | 52/6 | ||||||||||||||||||||||||||||||||||||
| 7 | Преобразование в смешанный номер | 93/8 | ||||||||||||||||||||||||||||||||||||
| 8 | Преобразование в смешанный номер | 34/5 | ||||||||||||||||||||||||||||||||||||
| 9 | График | у=х+1 | ||||||||||||||||||||||||||||||||||||
| 10 | Оценить, используя заданное значение | квадратный корень из 128 | ||||||||||||||||||||||||||||||||||||
| 11 | Найдите площадь поверхности | сфера (3) | | |||||||||||||||||||||||||||||||||||
| 12 | Оценить | 54-6÷2+6 | ||||||||||||||||||||||||||||||||||||
| 13 | График | г=-2x | ||||||||||||||||||||||||||||||||||||
| 14 | Оценить | 8*8 | ||||||||||||||||||||||||||||||||||||
| 15 | Преобразование в десятичное число | 5/9 | ||||||||||||||||||||||||||||||||||||
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | ||||||||||||||||||||||||||||||||||||
| 17 | График | у=2 | ||||||||||||||||||||||||||||||||||||
| 18 | Преобразование в смешанный номер | 7/8 | ||||||||||||||||||||||||||||||||||||
| 19 | Оценить | 9*9 | ||||||||||||||||||||||||||||||||||||
| 20 | Решите для C | С=5/9*(Ф-32) | ||||||||||||||||||||||||||||||||||||
| 21 | Упростить | 1/3+1 1/12 | ||||||||||||||||||||||||||||||||||||
| 22 | График | у=х+4 | ||||||||||||||||||||||||||||||||||||
| 23 | График | г=-3 | ||||||||||||||||||||||||||||||||||||
| 24 | График | х+у=3 | ||||||||||||||||||||||||||||||||||||
| 25 | График | х=5 | ||||||||||||||||||||||||||||||||||||
| 26 | Оценить | 6*6 | ||||||||||||||||||||||||||||||||||||
| 27 | Оценка | 2*2 | ||||||||||||||||||||||||||||||||||||
| 28 | Оценить | 4*4 | ||||||||||||||||||||||||||||||||||||
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | ||||||||||||||||||||||||||||||||||||
| 30 | Оценить | 1/3+13/12 | ||||||||||||||||||||||||||||||||||||
| 31 | Оценить | 5*5 | ||||||||||||||||||||||||||||||||||||
| 32 | Решить для d | 2д=5в(о)-вр | ||||||||||||||||||||||||||||||||||||
| 33 | Преобразование в смешанный номер | 3/7 | ||||||||||||||||||||||||||||||||||||
| 34 | График | г=-2 | ||||||||||||||||||||||||||||||||||||
| 35 | Найдите склон | у=6 | ||||||||||||||||||||||||||||||||||||
| 36 | Преобразование в проценты | 9 | ||||||||||||||||||||||||||||||||||||
| 37 | График | у=2х+2 | 92+5х+6=0||||||||||||||||||||||||||||||||||||
| 41 | Преобразование в смешанный номер | 1/6 | ||||||||||||||||||||||||||||||||||||
| 42 | Преобразование в десятичное число | 9% | ||||||||||||||||||||||||||||||||||||
| 43 | Найти n | 12н-24=14н+28 | ||||||||||||||||||||||||||||||||||||
| 44 | Оценить | 16*4 | ||||||||||||||||||||||||||||||||||||
| 45 | Упростить | кубический корень из 125 | ||||||||||||||||||||||||||||||||||||
| 46 | Преобразование в упрощенную дробь | 43% | ||||||||||||||||||||||||||||||||||||
| 47 | График | х=1 | ||||||||||||||||||||||||||||||||||||
| 48 | График | у=6 | ||||||||||||||||||||||||||||||||||||
| 49 | График | г=-7 | ||||||||||||||||||||||||||||||||||||
| 50 | График | у=4х+2 | ||||||||||||||||||||||||||||||||||||
| 51 | Найдите склон | у=7 | ||||||||||||||||||||||||||||||||||||
| 52 | График | у=3х+4 | ||||||||||||||||||||||||||||||||||||
| 53 | График | у=х+5 | ||||||||||||||||||||||||||||||||||||
| 54 | График | 92-9=0|||||||||||||||||||||||||||||||||||||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | ||||||||||||||||||||||||||||||||||||
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | ||||||||||||||||||||||||||||||||||||
| 60 | Найти простую факторизацию | 14 | ||||||||||||||||||||||||||||||||||||
| 61 | Преобразование в смешанный номер | 7/10 | ||||||||||||||||||||||||||||||||||||
| 62 | Решите для | (-5а)/2=75 | ||||||||||||||||||||||||||||||||||||
| 63 | Упростить | х | ||||||||||||||||||||||||||||||||||||
| 64 | Оценить | 6*4 | ||||||||||||||||||||||||||||||||||||
| 65 | Оценить | 6+6 | ||||||||||||||||||||||||||||||||||||
| 66 | Оценить | -3-5 | ||||||||||||||||||||||||||||||||||||
| 67 | Оценить | -2-2 | ||||||||||||||||||||||||||||||||||||
| 68 | Упростить | квадратный корень из 1 | ||||||||||||||||||||||||||||||||||||
| 69 | Упростить | квадратный корень из 4 | ||||||||||||||||||||||||||||||||||||
| 70 | Найди обратное | 1/3 | ||||||||||||||||||||||||||||||||||||
| 71 | Преобразование в смешанный номер | 20. Интеграл как считать: Как решать интегралы для чайников, примеры решенийНесвойственные интегралы 1-го и 2-го родаНесвойственный интеграл I родаЕсли функция f(x) интегрирована за Риманом на каждом конечном промежутке [a;b], тогда несвойственный интеграл находят через предельный переход за формулой Несвойственный интеграл ІІ родаЕсли функция f(x) неограничена в околе точки B и интегрирована за Риманом на каждом конечном промежутке , тогда несвойственный интеграл ІІ рода вычисляют по формуле І. Вычислить интегралыНачнем рассмотрение готовых ответов к несвойственным интегралам от простых к сложным заданиям. Пример 2.147 (2334) Найти несвойственный интеграл
Пример 2.148 ( 2335) Найти интеграл
Пример 2.149 (2336) Вычислить интеграл
Пример 2.
Пример 2.151 ( 2338) Найти интеграл
Пример 2.152 (2339) Найти интеграл В конечной формуле можно еще избавиться от иррациональности в знаменателе, но это уже проделайте самостоятельно.
Пример 2.153 ( 2340)Найти интеграл Подставим их в расписание и найдем неопределенный интеграл
Пример 2. І способ: расписание методом неопределенных коэффициентов: Чему равен арктангенс в нуле, единице и бесконечности Вы должны знать на память при решении подобных заданий.
Пример 2.155 (2342) Найти интеграл
Пример 2.156 (2343) Найти интеграл
Пример 2.158 (2345) Вычислить интеграл
Пример 2.159 (2346) Найти интеграл
Пример 2.160 ( 2347) Найти интеграл Из нее найти интеграл достаточно просто:
Пример 2.161 Найти интеграл
Пример 2.162 Найти интеграл
Пример 2.163 Вычислить интеграл
Пример 2.164 Найти интеграл
Пример 2.165 Найти интеграл
Пример 2.166 Найти интеграл
Пример 2.167 Найти интеграл
Пример 2.168 Найти интеграл
Пример 2.169 Найти интеграл
Пример 2.170 Найти интеграл
Пример 2.171 Найти интеграл
Пример 2.172 Найти интеграл
Пример 2.173 Вычислить интеграл
Пример 2.174 Найти интеграл В подобных примерах нужно дважды применять интегрирование частями.
Пример 2.175 Найти интеграл Пример 2.176 Найти интеграл Пример 2.177 Найти интеграл
Пример 2.178 Найти интеграл Найденный интеграл не что другое как площадь фигуры между функцией и осью ординат. За исключением особенности в нуле графики функции имеет вид верхней линии, а значение интеграла — заштрихованной на рисунке поверхности. Пример 2.179 Найти интеграл Пример 2.180 Найти интеграл Пример 2.181 Найти интеграл Пример 2.182 Найти интеграл
Пример 2.183 Найти интеграл Пример 2.184 (2348) Найти интеграл Дальше интегрированием частями находим значение для номера n На этом ознакомление с основными приемами нахождения несвойственных интегралов подходит к концу. Обзор методов вычисления интегралов по времени и пространствуИнтегрирование — один из важнейших математических инструментов, особенно в численном моделировании. Например, дифференциальные уравнения в частных производных обычно выводятся из интегральных уравнений сохранения. Когда возникает необходимость численного решения уравнения в частных производных, интегрирование также играет важную роль. Важность интеграловВ COMSOL используется метод конечных элементов, который преобразует описывающее некоторый процесс уравнение в частных производных в интегральное уравнение — другими словами, в слабую форму (weak form). При детальном и глубоком изучении формулировок, используемых в интерфейсах COMSOL, вы обнаружите, что множество граничных условий реализованы через интегралы. В качестве наиболее характерных примеров можно привести условия Total heat flux (Общий тепловой поток) или Floating potential (Плавающий потенциал). Вычисление интегралов также играет ключевую роль в процессе постобработки результатов, поскольку COMSOL рассчитывает большое количество вспомогательных величин через интегралы, например энергию электрического поля, скорость потока или общий тепловой поток. Разумеется, пользователи вольны использовать интегрирование в COMSOL в своих целях, и в этой статье мы объясним вам, как это делать максимально эффективно. где [t_0,t_1] — это временной интервал, \Omega — это пространственная область, а F(u) — это произвольное выражение, включающее зависимую переменную u и произвольные функции от нее, в том числе производные по пространству, времени, а также любой другой величине. Наиболее удобный способ вычисления интегралов — использование узла Derived Values (Расчет выражений) в разделе Results (Результаты) ленты Ribbon или дерева модели (Лента Ribbon отсутствует в том случае, если ваш компьютер работает не под управлением ОС Windows®). Вы можете обратиться к любому доступному решению, выбрав соответствующий набор данных (data set). В поле Expression (Выражение) вводится подынтегральная функция, включающая зависимые или производные переменные. Для данных расчета во временной области пространственный интеграл вычисляется на каждом временном шаге. Оператор Average (Усреднение) — еще одна операция в разделе Derived Values, связанная с вычислением интегралов. Оператор вычисляет интеграл и делит его на объем, площадь или длину выбранной области. Операция Averageв узле Data Series Operations аналогично вводит деление на продолжительность временного диапазона. Операторы узла Derived Values — важный инструмент, однако их можно использовать только во время постобработки, а значит с их помощью можно рассчитать далеко не любой интеграл. Именно поэтому в COMSOL представлены другие более мощные и гибкие инструменты для вычисления интегралов. Стационарное решение, нажмите на изображение для увеличения. Нестационарное решение (для момента времени 100 секунд), нажмите на изображение для увеличения. Вычисление пространственного интеграла с использованием операторов узла Component CouplingОператоры узла Component Coupling (Сопряжение компонентов) используются в тех случаях, когда, например, в одном выражении объединяются несколько интегралов, или интегралы требуются в процессе вычислений, или требуется множество контурных интегралов. Операторы данного узла определяются в разделе Definitions (Определения). На этом этапе режультат использования оператора не просчитывается, а указываются только их название и выборки областей.
В нашем примере мы для начала хотим вычислить пространственный интеграл для стационарного распределения температуры, равный \int_{\Omega}T(x,y)\ \mathrm{d}x\mathrm{d}y = 301. В пакете COMSOL оператор вычисления интеграла по умолчанию получает имя intop1. Окно настроек оператора интегрирования. Расчет результата интегрирования через оператор. Теперь давайте рассмотрим, как оператор интегрирования может использоваться непосредственно в процессе расчета модели. С его помощью мы могли бы, например, выяснить, какая нагревательная мощность потребуется для получения средней температуры 303.15 К, то есть температуры, на 10 К превышающей температуру окружающей среды. Прежде всего нам необходимо вычислить разницу между требуемым и действительным средними значениями. Среднее значение вычисляется путем деления интеграла от T на интеграл от постоянной функции 1, который равен площади области. Нетрудно догадаться, что вычисление подобного вида легко выполнить с помощью представленного в COMSOL оператора Average (Усреднение), см. комментарии выше. По умолчанию данный оператор получает название aveop1. Вычисление неопределенного интеграла посредством оператора интегрированияВ своих обращениях в службу поддержки пользователи часто задают один и тот же вопрос: как рассчитать неопределенный пространственный интеграл? Для этой цели нам также пригодится оператор интегрирования, задаваемый через Component Couplings. Нахождение неопределенного интеграла — операция, обратная дифференцированию. Неопределенный интеграл позволяет вычислять площади произвольных областей, ограниченных графиками функций. Одна из самых важных прикладных задач — вычисление вероятностей в статистическом анализе. Для того чтобы это продемонстрировать, мы зафиксируем y=0 и обозначим неопределенный интеграл от T(x,0) как u(x). Это значит, что \frac{\partial u}{\partial x}=T(x,0). Тогда неопределенный интеграл имеет вид u(\bar x) = \int_0^{\bar x}T(x,0)\mathrm{d} x Здесь мы используем \bar x, чтобы отличать переменную интегрирования от внешней переменной. Во-вторых, нам понадобится оператор вычисления интеграла, который будет действовать на нижней границе области из примера. Давайте обозначим его как intop2. В-третьих, мы должны отличать переменную интегрирования от внешней переменной. Принятые обозначения для такого случая: x называется источником (source), а \bar x — точкой назначения (destination). При использовании операторов интегрирования доступен встроенный оператор dest, который позволяет явно оглашать, что соответствующее выражение не относится к переменным интегрирования. Точнее, это значит, что в COMSOL \bar x=dest(x). Объединив логическое выражение с оператором dest, мы получим выражение вида T*(x<=dest(x)), которое является именно тем входным выражением, которое требуется для intop2. Объединив все вместе, мы можем вычислить неопределенный интеграл, воспользовавшись выражением intop2(T*(x<=dest(x))).
В пакете COMSOL дополнительно доступны еще два оператора вычисления интеграла, а именно общая проекция (general projection) и линейная проекция (linear projection). Эти операторы можно использовать для получения множества контурных интегралов в любом направлении в области. Другими словами, вычисление интеграла производится только вдоль одного измерения. В результате мы получаем функцию размерности на единицу меньше, чем размерность области. Для двухмерного примера результатом будет одномерная функция, которая может быть рассчитана на любой границе. Более подробная информация об использовании данных операторов будет представлена в одной из следующих публикаций в нашем компоративном блоге. Вычисление пространственного интеграла посредством дополнительного физического интерфейсаНаиболее гибким способом вычисления пространственных интегралов является техника с добавлением дополнительного PDE-интерфейса. \frac{\partial u}{\partial x}=T(x,y) с граничным условием типа Дирихле u=0 на левой границе. Расчет такого уравнения проще всего реализовать в физическом (математическом) интерфейсе Coefficient Form PDE (Дифференциальное уравнение в частных производных, коэффициентная форма записи), который потребует следующих настроек:
Зависимая переменная u представляет собой неопределенный интеграл по x и доступна в процессе расчета модели и в постобработке. Помимо гибкости, дополнительным преимуществом данного подхода является точность, так как интеграл рассчитывается не вспомогательными инструментами на основе уже определенного распределения переменной, а непосредственно в процессе расчета с учетом алгоритмов оценки погрешностей и т. На поверхностном графике ниже представлен результирующий интеграл, являющийся функцией пространственных переменных (x,y):
Схожие операторы существуют для вычисления интегралов на сферических зонах, а именно ballint, circint, diskint и sphint. Вычисление временного интеграла посредством дополнительного физического интерфейсаВ случае если временные интегралы нужно использовать непосредственно в модели в процессе расчета, вам будет необходимо задать их как дополнительные зависимые переменные. Аналогично представленному выше примеру с интерфейсом Coefficient Form PDE, это можно сделать, добавив ODE-интерфейс из раздела Mathematics. Предположим, например, что на каждом временном шаге требуется вычислять интеграл от величины общего теплового потока на промежутке от старта до текущего момента, который показывает накопленную энергию.
В чем польза подобной техники? Полученный интеграл можно повторно использовать в других физических интерфейсах, поля в которых могут зависеть от накопленной в системе энергии. Более того, полученный резултат будет мгноменно доступен для всех видов постобработки, что удобнее и быстрее, чем использование встроенных операторов. Рекомендуем ознакомится с моделью Carbon Deposition in Hetereogeneous Catalysis (Образование сажевых отложений при гетерогенном катализе), в которой ОДЕ в области используется для вычисления пористости катализатора при наличии химических реакций в виде нестационарной полевой переменной. Вычисление интеграла от аналитических функций и выраженийДо сих пор мы демонстрировали, каким образом вычислять интеграл от искомых переменных в процессе расчета или при постобработке. Но не касались случая взятия интегралов от аналитических функций или выражений. Для этой операции в среде COMSOL доступен встроенный оператор integrate(expression, integration variable, lower bound, upper bound). Выражение может представлять собой любую одномерную функцию, например sin(x). При этом допускается включение дополнительных переменных, например sin(x*y). Второй параметр определяет, по какой переменной вычисляется интеграл. Например, integrate(sin(x*y),y,0,1) выдает функцию переменной x, потому что интегрирование выполняется только по переменной y. Обратите внимание, что данный оператор также может использоваться для работы с аналитическими функциями, заданными в узле Definitions (Определения) текущего компонента. Добавление аналитической функции. Вычисление интеграла от аналитической функции. Материалы для дальнейшего изучения
Как находить интегральные выраженияВсе ресурсы исчисления 110 Диагностические тесты 438 практических тестов Вопрос дня Карточки Learn by Concept ← Предыдущая 1 2 3 4 5 6 7 8 9 … 18 19 Следующая → Исчисление 1 Помощь » Функции » Уравнения » Написание уравнений » Интегральные выражения » Как найти интегральные выражения Какова площадь под кривой для ? Возможные ответы: Правильный ответ: Объяснение: По нормальным правилам экспоненты , поэтому мы устанавливаем определенный интеграл , , который интегрируется с: Сообщить об ошибке Интегральная формула Гаусса утверждает, что . Чему равен интеграл от ? Возможные ответы: Правильный ответ: Пояснение: Интегрируя по частям с , , , получаем: Сообщить об ошибке Определить, учитывая, что Определить. Возможные ответы: Правильный ответ: Пояснение: В этой задаче требуется вычислить неопределенный интеграл от заданной функции f’(x). Интегрируя каждый член функции по x, мы просто делим каждый коэффициент на (n+1), где n — значение показателя степени x для этого конкретного члена, а затем добавляем 1 к значению показателя степени каждого члена. Икс. Это дает нам: Правильный ответ должен включать константу C, так как исходная функция могла иметь константу, которая не отражена в уравнении для ее производной.
Сообщить об ошибке Каково значение следующего определенного интеграла? Возможные ответы: Правильный ответ: Объяснение: Начнем с интегрирования функции в скобках по x, а затем вычтем оценку нижнего предела из оценки верхнего предела: Сообщить об ошибке. Правильный ответ: Пояснение: Эта задача призвана продемонстрировать одно из возможных приложений исчисления в области физики. Уравнение для работы, данное в физике, выглядит следующим образом: Используя это уравнение, мы просто устанавливаем определенный интеграл с нашими границами, заданными интересующим нас интервалом в задаче: Чтобы толкнуть коробку с x=2 метра на x=5 метров, требуется 39,8 джоуля. Сообщить об ошибке Вычислить определенный интеграл в интервале . Возможные ответы: Правильный ответ: Объяснение: Чтобы решить эту задачу, мы должны знать, что В этом случае у нас есть: Наш первый шаг — интегрировать: наши значения
Сообщить об ошибке Запишите выражение площади под следующей кривой от до . Возможные ответы: Правильный ответ:
Объяснение: Просто используйте интегральное выражение с заданными значениями x в качестве границ. Не забудьте добавить dx! Сообщить об ошибке Вычислить определенный интеграл в интервале . Возможные ответы: Правильный ответ: Объяснение: Чтобы решить эту задачу, мы должны помнить, что: В этом случае у нас есть:
Наш первый шаг состоит в интеграции: в наших значениях Сообщить об ошибке Вычислить определенный интеграл в интервале Возможные ответы: Правильный ответ: Объяснение: Чтобы решить эту задачу, мы должны помнить, что: В этом случае у нас есть: Наш первый шаг — интегрировать: Затем мы приходим к нашему решению, подключая значения Сообщить об ошибке Вычислить неопределенный интеграл. Возможные ответы: Правильный ответ: Объяснение: Нас просят интегрировать функцию. Для этого нам нужно запомнить правило степени интегралов, Используя это правило, мы можем вычислить следующий интеграл: Сообщить об ошибке ← Предыдущий 1 5 6 3 7 4 8 9 … 18 19 Далее → Уведомление об авторских правах Все ресурсы исчисления 110 диагностических тестов 438 практических тестов Вопрос дня Карточки Learn by Concept Интегральное исчисление в Python В этом посте показано, как выполнить интегральное исчисление непрерывных и ограниченных реальных функций реальных переменных в Python.
за счет использования общих библиотек Python, часто используемых в научных приложениях. Для всех различных фрагментов кода, описанных в этом посте, требуется Python версии 3 и библиотека NumPy, в то время как по отдельности они требуют дополнительной библиотеки (и ее зависимостей, если таковые имеются) между SciPy и SymPy. Мы благодарим профессора Фаусту Д’Акунцо из Preparazione 2.0 за теоретическую поддержку, оказанную в области интегрального исчисления с несколькими переменными. Чтобы получить код, см. параграф «Полная загрузка кода» внизу этого поста. Интеграция через SciPyИнтеграл функции одной переменной (с конечными экстремумами) В интегральном исчислении определенный интеграл — это оператор, который для вещественнозначной функции вещественнозначной переменной и интервала $[a,b]$ (подмножества области определения)
сопоставляет функции площадь, стягиваемую ее графиком в интервале $[a,b]$. Вычисление интеграла с трапецией Функция трапеции 6624352673Вот ссылка на код на GitHub. Вычисление интеграла с помощьюcumulative_trapezoid Функция 6624352677Вот ссылка на код на GitHub. Вычисление интеграла с помощьюСимпсона Функция Расчет длины дуги плоской кривой Как известно, интегралы от функции одной переменной можно использовать и для вычисления длины дуги плоской кривой.
Если кривая представлена в виде $y=f(x)$ и является непрерывной и выводимой
формула для расчета длины дуги кривой между $x=a$ и $x=b$ выглядит следующим образом:
$$ \int_{a}^{b} \sqrt{1 + \left(\frac{\,dy}{\,dx}\right)^2} \,dx $$
92} \, дх $$
аналитическое решение которого
$\около 2. Двойной интеграл функции двух переменных В интегральном исчислении определенный двойной интеграл — это оператор, который для заданной вещественной функции двух вещественных переменных и множества, включенного в область определения,
связывает с функцией объем твердого тела (называемого цилиндроидом) между поверхностью, описываемой функцией, и плоскостью, содержащей данный набор. 9{-x y} \,dx dy $$
аналитическое решение которого
$\около 1.0273$
проверяется онлайн через Wolfram Alpha. Интеграция через SymPyИнтеграл функции одной переменной (с конечными экстремумами) В интегральном исчислении определенный интеграл — это оператор, который для вещественнозначной функции вещественнозначной переменной и интервала $[a,b]$ (подмножества области определения)
сопоставляет функции площадь, стягиваемую ее графиком в интервале $[a,b]$. Вот ссылка на код на GitHub. Двойной интеграл функции двух переменных В интегральном исчислении определенный двойной интеграл — это оператор, который для заданной вещественной функции двух вещественных переменных и множества, включенного в область определения,
связывает с функцией объем твердого тела (называемого цилиндроидом) между поверхностью, описываемой функцией, и плоскостью, содержащей данный набор. Конвертировать doc в txt: Конвертировать DOC (WORD) в TXT онлайн — ConvertioWord в TXT | ZamzarКонвертировать DOC в TXT — онлайн и бесплатноШаг 1. Выберите файлы для конвертации. Перетащите сюда файлы Шаг 2. Преобразуйте файлы вConvert To Или выберите новый формат Шаг 3 — Начать преобразованиеИ согласиться с нашими Условиями Эл. адрес? You are attempting to upload a file that exceeds our 50MB free limit. You will need to create a paid Zamzar account to be able to download your converted file. Would you like to continue to upload your file for conversion? * Links must be prefixed with http or https, e. Ваши файлы. Ваши данные. Вы в контроле.
Вы в хорошей компании:Zamzar конвертировал около 510 миллионов файлов начиная с 2006 года DOC (Document)
TXT (Document)
Преобразование файлов DOCИспользуя Zamzar можно конвертировать файлы DOC во множество других форматов
DOC to TXT — Convert file now Available Translations: English | Français | Español | Italiano | Pyccĸий | Deutsch Конвертировать DOC В ТЕКСТ БесплатноDOC в текст
Разработано на базе программных решений от
aspose. Выберите DOC файлы или перетащите DOC файлы мышью Google Drive Dropbox Использовать пароль Этот пароль будет применяться ко всем документам Использовать распознавание текста Использовать распознавание текста АнглийскийАрабскийИспанскийИтальянскийКитайский упрощенныйНемецкийПерсидскийПольскийПортугальскийРусскийФранцузский Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности. Сохранить как TXTDOCXDOCDOTDOCMDOTXDOTMRTFODTOTT КОНВЕРТИРОВАТЬ Ваши файлы были успешно сконвертированы СКАЧАТЬ Загрузить в Google Загрузить в Dropbox
Конвертация других документов
Отправить на электронную почту
Хотите сообщить об этой ошибке на форуме Aspose, чтобы мы могли изучить и решить проблему? Когда ошибка будет исправлена, вы получите уведомление на email. Форма отчета
Google Sheets Конвертировать DOC в текст онлайнИспользуйте конвертер DOC в текст для экспорта файлов DOC в текст формат онлайн. Вы можете использовать конвертер из DOC в текст совершенно бесплатно, в любое время и с любого устройства. Онлайн Конвертер DOC в текстКонвертация DOC файлов в текст формат — одна из самых распространенных операций. Нам часто нужны обе функции, предоставляемые форматами DOC и текст. DOC и текст в определённых случаях дополняют друг друга. Конвертировать файл DOC в текст онлайнЧтобы конвертировать DOC в текст формат, просто перетащите DOC файл в область загрузки данных, укажите параметры преобразования, нажмите кнопку ‘Конвертировать’ и получите выходной текст файл за считанные секунды. Бесплатный онлайн конвертер DOC в текст основан на продуктах компании Aspose, которые широко используются во всем мире для программной обработки DOC и текст с высокой скоростью и профессиональным качеством результата. Как преобразовать DOC в текст
Вопросы-ОтветыКак конвертировать DOC в текст бесплатно?Просто используйте наш DOC в текст Converter. Вы получите выходные файлы текст одним кликом мыши. Сколько DOC файлов я могу конвертировать в текст формат за раз?Вы можете конвертировать до 10 DOC файлов за раз. Каков максимально допустимый размер DOC файла?Размер каждого DOC файла не должен превышать 10 МБ. Какие есть способы получить результат в текст формате?После завершения преобразования DOC в текст вы получите ссылку для скачивания. Вы можете скачать результат сразу или отправить ссылку на скачивание текст на свой e-mail позже. Как долго мои файлы будут храниться на ваших серверах?Все пользовательские файлы хранятся на серверах Aspose в течение 24 часов. По истечении этого времени они автоматически удаляются. Можете ли вы гарантировать сохранность моих файлов? Все безопасно?Aspose уделяет первостепенное внимание безопасности и защите пользовательских данных. Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа. Почему конвертация DOC в текст занимает немного больше времени, чем я ожидал?Конвертация больших DOC файлов в текст формат может занять некоторое время, поскольку эта операция включает перекодирование и повторное сжатие данных. Word в TXT — конвертируйте DOC в TXT бесплатно онлайнКонвертируйте DOC в TXT онлайн и бесплатно Шаг 1. Выберите файлы для конвертации Перетаскивание файлов Шаг 2. Конвертируйте ваши файлы вКонвертируйте в Или выберите другой формат Шаг 3. Начните конвертировать(и примите наши Условия) Электронная почта, когда закончите? Вы пытаетесь загрузить файл, размер которого превышает наш свободный лимит в 50 МБ. Вам нужно будет создать платную учетную запись Zamzar, чтобы иметь возможность скачать преобразованный файл. Хотите продолжить загрузку файла для конвертации? * Ссылки должны иметь префикс http или https , например. http://48ers.com/magnacarta.pdf Частные лица и компании доверяют Zamzar с 2006 года. Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов.
Попробовала и сразу влюбилась! Это было так легко использовать! После пары преобразований я купил ребятам чашку кофе. Еще пара и решил, что это слишком хорошо, чтобы злоупотреблять! Я присоеденился! Моя жизнь намного проще! Тилли У меня был огромный проблемный файл для преобразования, который не мог пройти обычный процесс автоматического преобразования. Команда Zamzar быстро отреагировала на мою просьбу о помощи и предприняла дополнительные шаги, необходимые для того, чтобы сделать это вручную. ПДинСФ Использовал его более года для преобразования моих банковских выписок в файлы csv. Агата Вежбицкая Я использовал этот продукт в течение многих лет. И обслуживание клиентов отличное. Только что возникла проблема, когда мне предъявили обвинение, и я не согласился с обвинением, и они позаботились об этом, хотя в этом не было необходимости. JH Очень полезный и профессиональный сайт. Сервис прост в использовании, а администраторы услужливы и вежливы. Дэвид Шелтон Я впервые им пользуюсь. У меня были некоторые сложности. Я не очень хорош в этом. Но я написал в компанию, и мне очень помогли. Я доволен обслуживанием клиентов и приложением. Ана Суарес Я использую Zamar всякий раз, когда мне нужно преобразовать аудио- и видеофайлы из нескольких отправителей в единый формат файла для редактирования аудио и видео. Кристофер Би Отлично подходит, когда вам нужно много конверсий за короткое время. Вы имеете прямой доступ и даже можете оформить подписку всего на месяц. Сабина Калис Я чувствую, что Замзар — активный член команды, особенно в проектах, над которыми я работаю, где я являюсь рабочей лошадкой, и это экономит так много времени и нервов. Я избалован Zamzar, потому что они установили очень высокую планку для преобразования файлов и обслуживания клиентов. Дебора Герман Фантастический сервис! Компьютер моей мамы умер, и у нее есть более 1000 файлов Word Perfect, которые она по какой-то причине хочет сохранить. Поскольку Word Perfect практически мертв, я решил конвертировать все ее файлы. Преобразователь Замзара был идеальным. Арон Бойетт Нам доверяют сотрудники этих брендов Сотрудники некоторых из самых известных мировых брендов полагаются на Zamzar для безопасного и эффективного преобразования своих файлов, гарантируя, что у них есть форматы, необходимые для работы. Ваши файлы в надежных рукахОт вашего личного рабочего стола до ваших бизнес-файлов, мы обеспечим васМы предлагаем ряд инструментов, которые помогут вам конвертировать ваши файлы наиболее удобным для вас способом. Помимо нашей онлайн-службы преобразования файлов, мы также предлагаем настольное приложение для преобразования файлов прямо с вашего рабочего стола и API для автоматического преобразования файлов для разработчиков. Какой инструмент вы используете, зависит от вас! Хотите конвертировать файлы прямо с рабочего стола?Получить приложение Полностью интегрирован в ваш рабочий стол Преобразование более 150 различных форматов файлов Конвертируйте документы, видео, аудио файлы в один клик Нужна функциональность преобразования в вашем приложении?Изучите API Один простой API для преобразования файлов 100 форматов на ваш выбор Документы, видео, аудио, изображения и многое другое. Почему выбирают Замзар?С Zamzar конвертация файлов проста, надежна и удобна, поэтому вы можете быстро конвертировать документы, изображения, видео и многое другое в нужные вам форматы. Благодаря более быстрой загрузке преобразованных файлов и дружелюбной и полезной поддержке, когда вам это нужно, у вас будет все необходимое для работы с вашими файлами. Несколько форматов файловМы поддерживаем более 1100 различных типов преобразования и постоянно добавляем новые! Любое устройствоМы знаем, что вам может понадобиться конвертировать файлы в пути, поэтому наш инструмент конвертации работает как на телефоне, так и на планшете. Доступен круглосуточно и без выходныхВы можете не только преобразовать файл в любое время, но и обратиться в нашу специализированную службу поддержки, которая работает круглый год. Новые типы преобразованияПримеры некоторых новых типов преобразования, которые мы недавно добавили, включают преобразование отсканированного PDF в TXT и преобразование GIF в MP4! Инструменты, соответствующие вашим потребностям в преобразовании и сжатии файлов В Zamzar вы найдете все необходимые инструменты для преобразования и сжатия в одном месте. Формат документа DOC DOC-конвертерDOC и DOCX являются наиболее распространенными форматами файлов для обработки текстов. DOC в основном использовался Microsoft для своей программы Word до 2003 года. С 2007 года Word использует DOCX в качестве стандарта, хотя вы по-прежнему можете открывать файлы DOC и сохранять их в более старом формате. DOC и DOCX используются для форматированных текстовых документов, таких как отчеты, письма или резюме. Они могут включать изображения, диаграммы и графики, а также обычный или форматированный текст, а также могут содержать редактируемый шаблон. Word является частью Microsoft Office, который доступен в виде платного программного приложения или доступен в Интернете по подписке Microsoft 365. Связанные инструменты
Формат документа TXT TXT-конвертер Файл TXT также называется обычным текстовым файлом и широко используется. Частично их привлекательность заключается в том, что их можно открыть практически на любом устройстве и в любой ОС. У Microsoft и Apple есть встроенные приложения для текстового редактора, называемые Notepad и TextEdit соответственно, которые часто используются для создания файлов TXT. Они широко используются не только обычным уличным пользователем, который может решить вести протоколы совещаний, заметки и т. п., но и более технически подкованными ИТ-специалистами, которые могут использовать их при написании кода. Файлы TXT не имеют тех же функций, что и файлы DOC, поскольку вы не можете выбрать шрифт, выделить слово жирным шрифтом или добавить такие элементы, как таблицы, поэтому, если пользователю нужны эти типы функций, он часто использует текстовый процессор. как Word, чтобы сделать это вместо использования обычного текстового файла. Связанные инструменты
Как преобразовать DOC в файл TXT?
Преобразование из DOCИспользуя Zamzar, можно конвертировать файлы DOC во множество других форматов: DOC в AZW3 DOC в BMP DOC в DOCX DOC в EPUB DOC в FB2 DOC в GIF DOC в HTML DOC в HTML4 DOC в HTML5 DOC в JPG DOC в LIT DOC в LRF DOC в MOBI DOC в MP3 DOC в ODT DOC в OEB DOC на СТРАНИЦЫ DOC на СТРАНИЦЫ09DOC в PCX DOC в PDF DOC в PML DOC в PNG DOC в PS DOC в РБ DOC в TCR DOC в TIFF DOC в THUMBNAIL DOC в TXT Преобразовать в DOCИспользуя Zamzar, можно конвертировать в файлы DOC множество других форматов: BMP в DOC
CSV в DOC
DOCX в DOC
EML в DOC
GIF в DOC
JPG в DOC
MDI в DOC
MSG в DOC
ODG в DOC
ODS в DOC
ODT в DOC
СТРАНИЦ в DOC
PAGES. Часто задаваемые вопросыЕсли у вас есть какие-либо вопросы о преобразовании или сжатии файлов с помощью Zamzar, мы будем рады помочь! Ниже мы ответили на несколько часто задаваемых вопросов, чтобы вы могли начать работу, а дополнительную информацию о преобразовании и сжатии файлов с помощью Zamzar вы можете найти в нашем Справочном центре. Если у вас есть доступ к Microsoft Word, вы можете открыть файл DOC, а затем использовать функцию «Сохранить как», чтобы сохранить его как файл . Если вы можете открыть документ в Word, вы можете сохранить его как файл TXT, выбрав «Сохранить как» в меню «Файл», а затем выбрав «Обычный текст (*.txt)» в раскрывающемся списке. Если у вас нет Microsoft Office, все равно легко преобразовать документ Word в TXT с помощью инструмента преобразования, такого как Zamzar. Просто загрузите документ Word, выберите его для преобразования в формат TXT, а затем загрузите текстовый файл. Вы можете создать новый файл . Существует несколько способов преобразования Word в текст, включая бесплатный онлайн-инструмент преобразования на веб-сайте Zamzar. Вы можете конвертировать сразу несколько файлов без доступа к Microsoft Word — просто загрузите файлы DOC в трехэтапный инструмент, выберите, чтобы преобразовать их в TXT, а затем загрузите новые документы. Если у вас есть только один документ для преобразования, вы также можете сохранить его как файл *. DOC и TXT — это форматы текстовых файлов, но они разные. DOC — это исходный формат Microsoft Word, и документы могут включать форматирование, шрифты, текстовые рисунки, диаграммы и изображения. Файлы TXT предназначены только для обычного текста, но их можно открывать в других программах, не требуя доступа к Microsoft Office. Файлы DOC легко преобразовать в TXT, сохранив файлы как .txt в Word или используя онлайн-инструмент преобразования, такой как Zamzar. Вы можете конвертировать несколько файлов в режиме реального времени с помощью веб-сайта Zamzar — просто загрузите свои файлы DOC, нажмите, чтобы преобразовать их в TXT, а затем загрузите преобразованные файлы. Преобразовать СЛОВО в текст | Онлайн и бесплатноПреобразование документов WORD в текстовые документыРаботает на aspose.com и aspose.cloudПеретащите или загрузите свои файлы* Выбрать файл Выбрать с Google Диска Выбрать из Drop поле Введите URL-адрес *Загружая файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности0003 Ваши файлы успешно обработаны СКАЧАТЬОтправить результат по адресу: ПОСМОТРЕТЬ РЕЗУЛЬТАТЫПОСМОТРЕТЬ РЕЗУЛЬТАТЫ Лучший бесплатный онлайн конвертер слов в текст  Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство. Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.Быстро и просто Преобразователь Word в текст — это онлайн-сервис для преобразования файлов из одного типа в другой. Мы поддерживаем множество популярных форматов для работы, все возможные форматы изображений, форматы мультимедийных файлов и т. Безопасность гарантирована Мы гарантируем безопасность и конфиденциальность. Мы не получаем права на ваш файл и ручной проверки не будет. Мы заботимся о вашей конфиденциальности и ваших файлах. В связи с этим мы также не будем передавать ваши данные другим сторонам. Крайне важно, чтобы у вас была возможность немедленно удалить загруженные вами файлы с нашего сервера. Если вы забудете это сделать, они будут автоматически удалены с нашего сервера через 24 часа. Мы полностью защищаем вашу информацию. Универсальное преобразование Вы можете конвертировать файлы Word в текст из любой ОС или устройства с подключением к Интернету. Наш сервис работает на любой ОС, включая Windows, Mac и Linux. Самые популярные варианты конвертации Мы поддерживаем самые распространенные варианты конвертации для работы и учебы. Используйте наше бесплатное приложение, чтобы уменьшить нагрузку при работе как с документами, так и с файлами изображений. Книги о том, как преобразовать Word в текст
Как преобразовать Word в текст
Часто задаваемые вопросы
|

 Элементы расположены в порядке возрастания электроотрицательности в ряду
Элементы расположены в порядке возрастания электроотрицательности в ряду Наибольшую степень окисления марганец имеет в соединении
Наибольшую степень окисления марганец имеет в соединении Одинаковую степень окисления азот проявляет в веществах, указанных в РЯДУ:
Одинаковую степень окисления азот проявляет в веществах, указанных в РЯДУ: Из перечисленных элементов наиболее электроотрицательным является
Из перечисленных элементов наиболее электроотрицательным является Наиболее электроотрицательным элементом является
Наиболее электроотрицательным элементом является Степень окисления + 3 хром имеет в соединении
Степень окисления + 3 хром имеет в соединении Они всегда происходят вместе. Например, при сжигании водорода
Они всегда происходят вместе. Например, при сжигании водорода
 Альтернативная точка зрения состоит в том, чтобы описывать окисление как потерю электронов и восстановление как приобретение электронов. Одним из примеров, в котором этот подход имеет значение, является высокотемпературная реакция двуокиси свинца.
Альтернативная точка зрения состоит в том, чтобы описывать окисление как потерю электронов и восстановление как приобретение электронов. Одним из примеров, в котором этот подход имеет значение, является высокотемпературная реакция двуокиси свинца. Обработка этого заряда как «степени окисления» — еще один способ охарактеризовать окисление и восстановление.
Обработка этого заряда как «степени окисления» — еще один способ охарактеризовать окисление и восстановление. Для аккумулятора это плюсовая клемма.
Для аккумулятора это плюсовая клемма.
 В этом смысле полученный калькулятором результат никакой пользы не приносит, но возможен вред — неумение оценивать величины, недополученные некоего вычислительного опыта, а значит той гимнастики, которая впредь обеспечит развитие интуитивного понимания величин, поможет абстрагировать числа до более сложных объектов. Калькулятор облегчает некие действия, но в то же время в таковых действиях смысл гимнастики и улучшения работоспособности. Ведь обучаясь музыке, мы не просим других исполнить за нас отдельные, нам уже неинтересные фрагменты. Поэтому: нет калькуляторам, «решебникам», стремлению получить результат-ответ без процесса его достижения. Любое математическое обучение, любая помощь должна подразумевать увеличение мыслительного процесса, его эффективности. А не наоборот. » http://postnauka.ru/talks/31178
В этом смысле полученный калькулятором результат никакой пользы не приносит, но возможен вред — неумение оценивать величины, недополученные некоего вычислительного опыта, а значит той гимнастики, которая впредь обеспечит развитие интуитивного понимания величин, поможет абстрагировать числа до более сложных объектов. Калькулятор облегчает некие действия, но в то же время в таковых действиях смысл гимнастики и улучшения работоспособности. Ведь обучаясь музыке, мы не просим других исполнить за нас отдельные, нам уже неинтересные фрагменты. Поэтому: нет калькуляторам, «решебникам», стремлению получить результат-ответ без процесса его достижения. Любое математическое обучение, любая помощь должна подразумевать увеличение мыслительного процесса, его эффективности. А не наоборот. » http://postnauka.ru/talks/31178 Тоже иногда спрашивает калькулятор.
Тоже иногда спрашивает калькулятор. Онлайн калькулятор
Онлайн калькулятор Теория чисел
Теория чисел Решение задач линейного программирования
Решение задач линейного программирования Многочлены и их корни
Многочлены и их корни Онлайн калькулятор
Онлайн калькулятор Аналитическая геометрия
Аналитическая геометрия Онлайн калькулятор
Онлайн калькулятор Онлайн калькулятор
Онлайн калькулятор Простой в использовании и обладающий интуитивно понятным дизайном, это все равно, что иметь своего личного репетитора по математике на ладони!
Простой в использовании и обладающий интуитивно понятным дизайном, это все равно, что иметь своего личного репетитора по математике на ладони! Или, если вы предпочитаете вычисления в портретном режиме, просто проведите пальцем влево.
Или, если вы предпочитаете вычисления в портретном режиме, просто проведите пальцем влево. Это поможет нам создать еще лучший продукт!
Это поможет нам создать еще лучший продукт! Недостаток в копировании и вставке на обоих вариантах. Это сделало меня немного более разочарованным в получении правильного результата. Странные функции и полноэкранная реклама. К счастью, я купил это приложение не из-за рекламы, я удалил его и повторил попытку в неопределенном будущем. Это было хорошо, пока мне не пришлось ждать еще пару секунд, пока кнопка X не появится в рекламе, довольно навязчиво, чтобы подсчитать мои чаевые от каждой отдельной официантки, которая давала мне чаевые. Хороший чистый макет, но я думаю, что пока останусь со своим вторым телефонным калькулятором Samsung S5.
Недостаток в копировании и вставке на обоих вариантах. Это сделало меня немного более разочарованным в получении правильного результата. Странные функции и полноэкранная реклама. К счастью, я купил это приложение не из-за рекламы, я удалил его и повторил попытку в неопределенном будущем. Это было хорошо, пока мне не пришлось ждать еще пару секунд, пока кнопка X не появится в рекламе, довольно навязчиво, чтобы подсчитать мои чаевые от каждой отдельной официантки, которая давала мне чаевые. Хороший чистый макет, но я думаю, что пока останусь со своим вторым телефонным калькулятором Samsung S5. К счастью, мы уже знаем об этой проблеме и планируем исправить ее как можно скорее. Я не могу обещать, когда это исправление будет готово, но мы сделаем все возможное, чтобы решить эту проблему как можно быстрее.
К счастью, мы уже знаем об этой проблеме и планируем исправить ее как можно скорее. Я не могу обещать, когда это исправление будет готово, но мы сделаем все возможное, чтобы решить эту проблему как можно быстрее. Просто чтобы напомнить людям, читающим это, если вы посмотрите на другие обзоры, они могли бы сказать, что вам нужно платить, чтобы делать определенные вещи, что действительно необходимо, я только что получил это приложение неделю назад, так что я не много знаю. Когда вы используете это приложение, вы должны заплатить, чтобы иметь возможность использовать функцию валюты и дроби, но если вы не планируете ничего платить, они позволят вам попробовать его 3 раза, после чего вы больше не сможете его использовать. В целом это приложение очень хорошее! Я просто убрал одну звезду, потому что мне хотелось бы, чтобы они добавили больше попыток, чтобы использовать функцию дроби и валюты, или каким-то образом напомнить нам, что у нас даже ЕСТЬ ограниченное количество попыток, когда я впервые использовал это приложение, я понятия не имел, что у нас были попытки, когда я использовал функцию валюты, поэтому, когда он сказал, что вы должны заплатить, я был так сбит с толку. Я ЕЩЕ РАЗ ПОКАЖУ ЭТО, в целом приложение очень хорошее!
Просто чтобы напомнить людям, читающим это, если вы посмотрите на другие обзоры, они могли бы сказать, что вам нужно платить, чтобы делать определенные вещи, что действительно необходимо, я только что получил это приложение неделю назад, так что я не много знаю. Когда вы используете это приложение, вы должны заплатить, чтобы иметь возможность использовать функцию валюты и дроби, но если вы не планируете ничего платить, они позволят вам попробовать его 3 раза, после чего вы больше не сможете его использовать. В целом это приложение очень хорошее! Я просто убрал одну звезду, потому что мне хотелось бы, чтобы они добавили больше попыток, чтобы использовать функцию дроби и валюты, или каким-то образом напомнить нам, что у нас даже ЕСТЬ ограниченное количество попыток, когда я впервые использовал это приложение, я понятия не имел, что у нас были попытки, когда я использовал функцию валюты, поэтому, когда он сказал, что вы должны заплатить, я был так сбит с толку. Я ЕЩЕ РАЗ ПОКАЖУ ЭТО, в целом приложение очень хорошее! Узнать больше
Узнать больше Математика может быть сложным предметом, особенно когда речь идет о решении сложных вычислений. Математический калькулятор является решением этой проблемы. Вы можете использовать этот инструмент для решения математических задач, чтобы выполнять сложные вычисления за считанные секунды. Начиная от простых арифметических операций и заканчивая сложными задачами по решению уравнений, этот простой инструмент поможет вам быстрее выполнить свою работу и перепроверить свои ответы.
Математика может быть сложным предметом, особенно когда речь идет о решении сложных вычислений. Математический калькулятор является решением этой проблемы. Вы можете использовать этот инструмент для решения математических задач, чтобы выполнять сложные вычисления за считанные секунды. Начиная от простых арифметических операций и заканчивая сложными задачами по решению уравнений, этот простой инструмент поможет вам быстрее выполнить свою работу и перепроверить свои ответы. Так что выбирайте тему и начинайте работать с нашим бесплатным калькулятором.
Так что выбирайте тему и начинайте работать с нашим бесплатным калькулятором. Однако калькуляторы улучшают математические навыки ребенка не одним, а несколькими способами.
Однако калькуляторы улучшают математические навыки ребенка не одним, а несколькими способами.

 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор онлайн решить систему уравнений с помощью обратной матрицы. Просто введите задачу в окошко и нажмите
«решить» здесь (например, матричный калькулятор матричный метод).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и калькулятор онлайн решить систему уравнений с помощью обратной матрицы. Просто введите задачу в окошко и нажмите
«решить» здесь (например, матричный калькулятор матричный метод).
 Давайте найдем его общее решение и проверим его на истинность.
Давайте найдем его общее решение и проверим его на истинность.
 Описание методов и их теории ниже.
Описание методов и их теории ниже. Это выглядит так: треугольная матрица — это квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
Это выглядит так: треугольная матрица — это квадратная матрица, в которой все элементы ниже главной диагонали равны нулю. А если вспомнить, что системы линейных алгебраических уравнений записываются только в матричной форме, то это означает, что элементарные матричные преобразования не меняют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.
А если вспомнить, что системы линейных алгебраических уравнений записываются только в матричной форме, то это означает, что элементарные матричные преобразования не меняют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

 е. определитель не равен нулю) существует обратная матрица ,
например, его произведение на исходную матрицу дает единичную матрицу:
е. определитель не равен нулю) существует обратная матрица ,
например, его произведение на исходную матрицу дает единичную матрицу:


 Здесь находится основная и дополнительная панель.
Здесь находится основная и дополнительная панель.
 Мы сделали подборку 23 сайтов, тренажеров, приложений, YouTube-каналов, игр и платформ для подготовки к экзаменам.
Мы сделали подборку 23 сайтов, тренажеров, приложений, YouTube-каналов, игр и платформ для подготовки к экзаменам.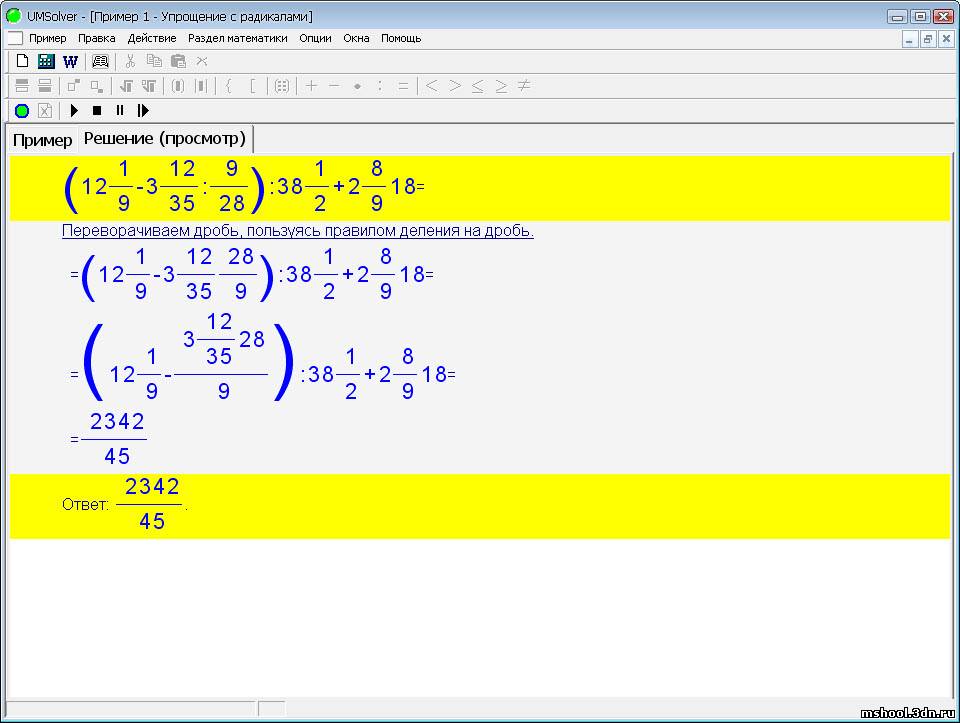 YouTube-канал «GetAClass — Просто математика» — красивые видеоуроки по математике.
YouTube-канал «GetAClass — Просто математика» — красивые видеоуроки по математике. CK-12 — ещё один тренажёр на английском.
CK-12 — ещё один тренажёр на английском.
 Только IM Certified Experience помогает учителям активизировать математические навыки с помощью увлекательного и инклюзивного подхода, который помогает учащимся овладеть навыками, пониманием и практикой, которые останутся с ними на всю жизнь. IM K–12 Math предоставляет вам эксклюзивный доступ к увлекательному контенту и профессиональному обучению, а также к инклюзивному сообществу.
Только IM Certified Experience помогает учителям активизировать математические навыки с помощью увлекательного и инклюзивного подхода, который помогает учащимся овладеть навыками, пониманием и практикой, которые останутся с ними на всю жизнь. IM K–12 Math предоставляет вам эксклюзивный доступ к увлекательному контенту и профессиональному обучению, а также к инклюзивному сообществу. Скоро будут отчеты K–5.
Скоро будут отчеты K–5. Их стратегии выглядят по-разному, потому что все они подходят к задачам и решают их по-разному, но они могут использовать слова, диаграммы и уравнения, чтобы объяснить свой ответ.
Их стратегии выглядят по-разному, потому что все они подходят к задачам и решают их по-разному, но они могут использовать слова, диаграммы и уравнения, чтобы объяснить свой ответ.
 0006 преднамеренная практика в его книге Пик: секреты новой науки экспертизы .
0006 преднамеренная практика в его книге Пик: секреты новой науки экспертизы . Но есть часть уравнения, которая все усложняет:
Но есть часть уравнения, которая все усложняет: Вместо сложности проблемы работа с задачами, которые имеют небольшие целые числа, позволяет сосредоточиться на концепциях и принципах.
Вместо сложности проблемы работа с задачами, которые имеют небольшие целые числа, позволяет сосредоточиться на концепциях и принципах.
 Он покажет вам пошаговые решения всех задач из учебника, который используется в вашем классе по математике:
Он покажет вам пошаговые решения всех задач из учебника, который используется в вашем классе по математике: Но после этого бросьте себе вызов вернуться назад и решить проблему, не заглядывая в свои заметки и ссылки.
Но после этого бросьте себе вызов вернуться назад и решить проблему, не заглядывая в свои заметки и ссылки. Вместо того, чтобы проводить долгие часы в библиотеке, она советует проводить более короткие и частые учебные занятия, растянутые на недели, а не дни.
Вместо того, чтобы проводить долгие часы в библиотеке, она советует проводить более короткие и частые учебные занятия, растянутые на недели, а не дни.
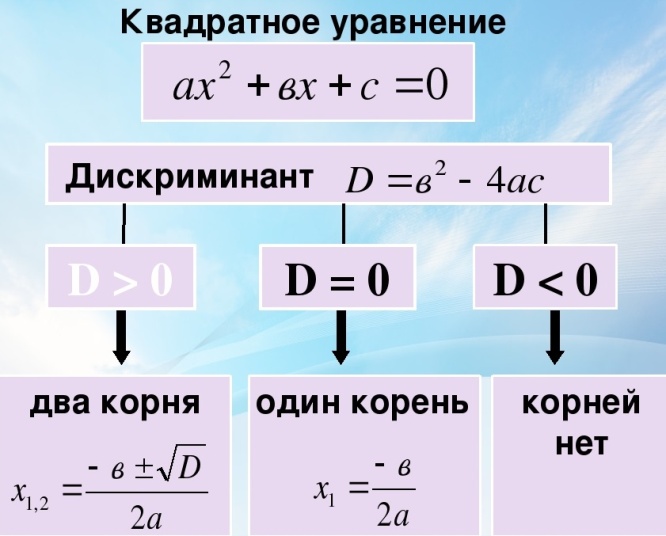 Четырехмерный потенциал поля
Четырехмерный потенциал поля Поле равномерно движущегося заряда
Поле равномерно движущегося заряда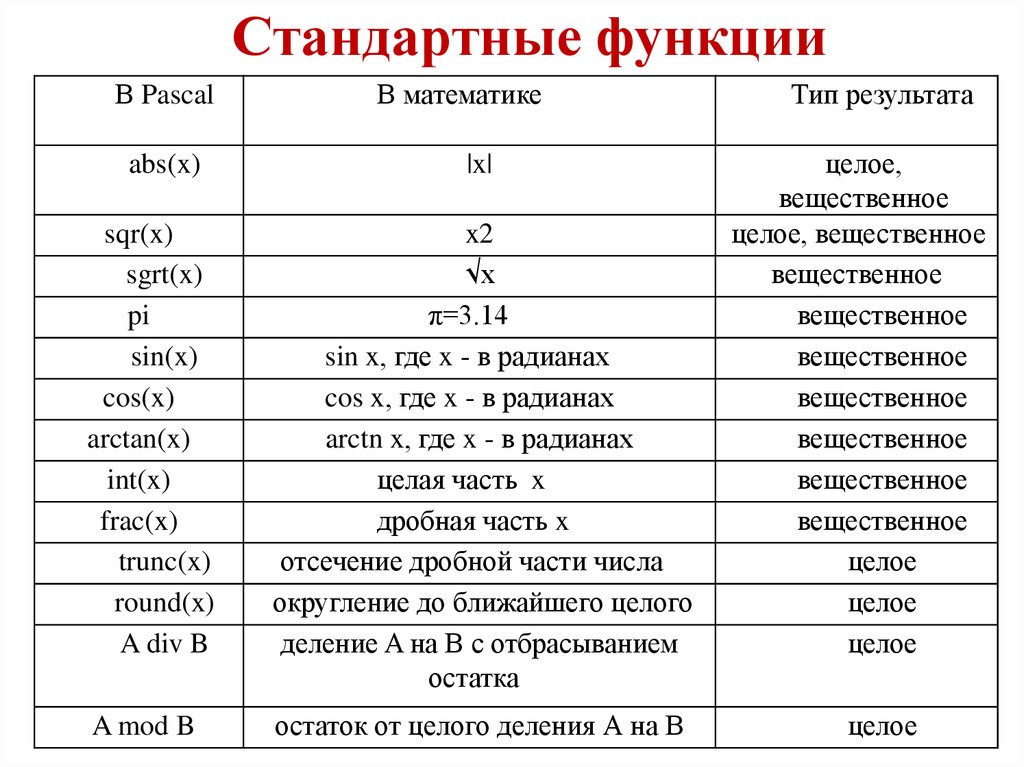 Функция Лагранжа с точностью до членов второго порядка
Функция Лагранжа с точностью до членов второго порядка Расстояния и промежутки времени
Расстояния и промежутки времени Гравитационное поле вдали от тел
Гравитационное поле вдали от тел cdr
cdr 205 0.0 853.228 566.929]/Type/Page>>
endobj
54 0 obj
>/Type/Page>>
endobj
55 0 obj
>
endobj
6 0 obj
>/Resources>/ProcSet[/PDF/ImageC/Text/ImageB/ImageI]/Shading>/XObject>>>/TrimBox[0.0 0.0 411.024 566.929]/Type/Page>>
endobj
64 0 obj
>stream
HtMo$
+@jDsrqCAc`fyITVvc}P$>sA[oi{ҷ}J$Yu 7o̼_{{Kod\ʞs3/$Z[cj=ŏG»M8yDZKx|oaЯ3ߟ+kvwѤfHd7NBqֻL|g)D3F\9Jh fKiYꮽkӗmP>#6YfKl6BU#pXLicQ
[jNR+a-B
c2Vv6`T*Hhc|cw,0.{Hؙ!MG$!ln$qNxƅ6Z9XBWK~j`HVp&1$E9yvʺM6u0$boJjRH.A*!.::g!\f쮊T`L/vL9fp,
205 0.0 853.228 566.929]/Type/Page>>
endobj
54 0 obj
>/Type/Page>>
endobj
55 0 obj
>
endobj
6 0 obj
>/Resources>/ProcSet[/PDF/ImageC/Text/ImageB/ImageI]/Shading>/XObject>>>/TrimBox[0.0 0.0 411.024 566.929]/Type/Page>>
endobj
64 0 obj
>stream
HtMo$
+@jDsrqCAc`fyITVvc}P$>sA[oi{ҷ}J$Yu 7o̼_{{Kod\ʞs3/$Z[cj=ŏG»M8yDZKx|oaЯ3ߟ+kvwѤfHd7NBqֻL|g)D3F\9Jh fKiYꮽkӗmP>#6YfKl6BU#pXLicQ
[jNR+a-B
c2Vv6`T*Hhc|cw,0.{Hؙ!MG$!ln$qNxƅ6Z9XBWK~j`HVp&1$E9yvʺM6u0$boJjRH.A*!.::g!\f쮊T`L/vL9fp, .. Меньше
.. Меньше

 Например, вы хотите зафиксировать значение, которое используется в качестве первоначального взноса для автокредита. Этот первоначальный взнос был рассчитан на основе процента от годового дохода заемщика. В настоящее время эта сумма дохода не изменится, поэтому вы хотите зафиксировать авансовый платеж в формуле, которая вычисляет платеж на основе различных сумм кредита.
Например, вы хотите зафиксировать значение, которое используется в качестве первоначального взноса для автокредита. Этот первоначальный взнос был рассчитан на основе процента от годового дохода заемщика. В настоящее время эта сумма дохода не изменится, поэтому вы хотите зафиксировать авансовый платеж в формуле, которая вычисляет платеж на основе различных сумм кредита. Например, если вы выбираете функцию, вы должны выбрать полное имя функции, открывающую скобку, аргументы и закрывающую скобку.
Например, если вы выбираете функцию, вы должны выбрать полное имя функции, открывающую скобку, аргументы и закрывающую скобку. co.za
co.za

 1
1 2
2 3
3 14159..
14159..
 {5x}??? не.
{5x}??? не. Понимая эти простые функции и их производные, мы можем угадать пробное решение с неопределенными коэффициентами , подставить в уравнение, а затем найти неизвестные коэффициенты, чтобы получить конкретное решение. Этот метод называется метод неопределенных коэффициентов .
Понимая эти простые функции и их производные, мы можем угадать пробное решение с неопределенными коэффициентами , подставить в уравнение, а затем найти неизвестные коэффициенты, чтобы получить конкретное решение. Этот метод называется метод неопределенных коэффициентов .
 Это значит, что если привести их к общему началу из конца третьего вектора (р), то кратчайший поворот от первого вектора (m) ко второму вектору (n) будет совершаться против часовой стрелки.
Это значит, что если привести их к общему началу из конца третьего вектора (р), то кратчайший поворот от первого вектора (m) ко второму вектору (n) будет совершаться против часовой стрелки. 0=30\times\frac12=15\\\\\\\)
0=30\times\frac12=15\\\\\\\) 2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\)
2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\) Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «векторы площадь параллелограмма».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «векторы площадь параллелограмма».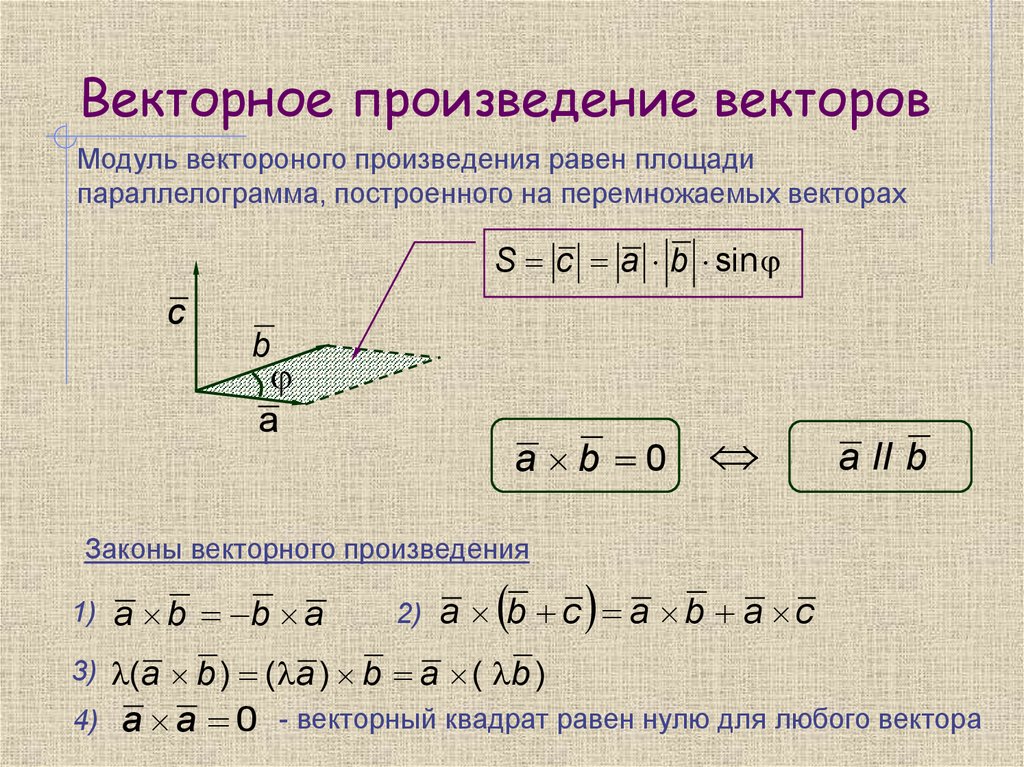 На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и векторы площадь параллелограмма. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислите площадь параллелограмма построенного на векторах).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и векторы площадь параллелограмма. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислите площадь параллелограмма построенного на векторах).
 3: Если q — угол, образованный u и v , то
3: Если q — угол, образованный u и v , то Действительно, имеем следующее:
Действительно, имеем следующее:
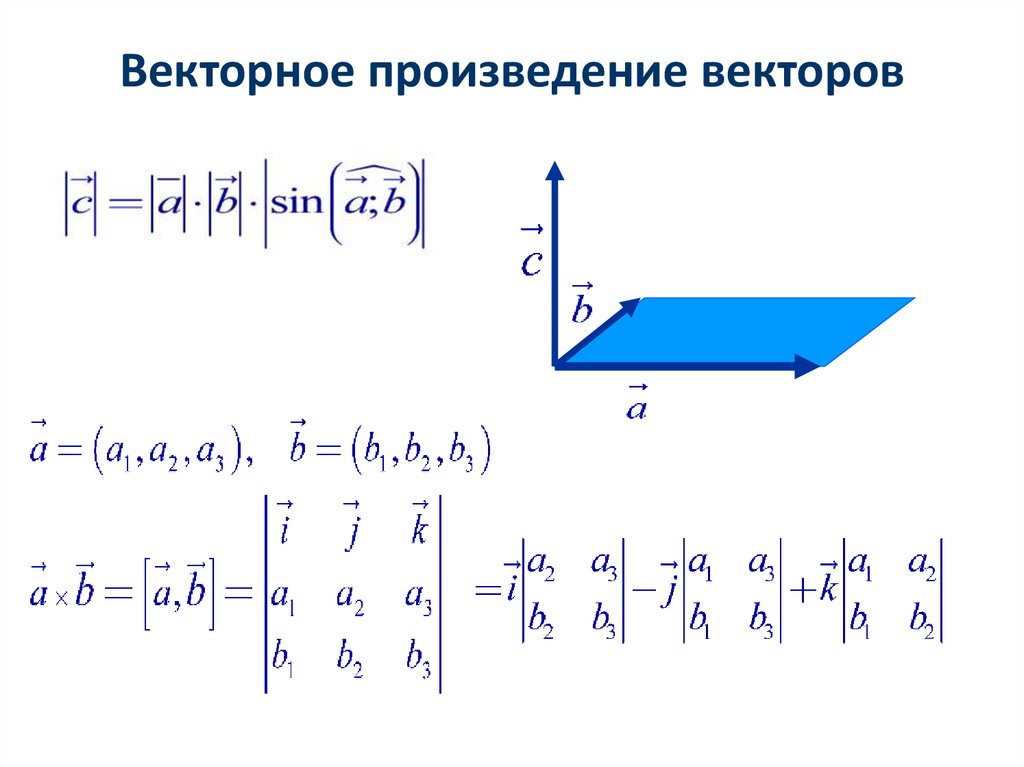 Таким образом, их векторное произведение равно
Таким образом, их векторное произведение равно Одним из таких методов умножения является перекрестное произведение на , которому посвящена эта страница. Другое умножение — скалярное произведение, которое мы обсуждаем на другой странице.
Одним из таких методов умножения является перекрестное произведение на , которому посвящена эта страница. Другое умножение — скалярное произведение, которое мы обсуждаем на другой странице. (Это означает, что если мы согнем пальцы
правой рукой от $\vc{a}$ до $\vc{b}$, затем большой палец указывает на
направление $\vc{a} \times \vc{b}$.)
(Это означает, что если мы согнем пальцы
правой рукой от $\vc{a}$ до $\vc{b}$, затем большой палец указывает на
направление $\vc{a} \times \vc{b}$.) Если векторы параллельны или один
вектор является нулевым вектором, тогда не существует уникальной линии
перпендикулярно обоим $\vc{a}$ и $\vc{b}$. Но так как есть только
один вектор нулевой длины, определение по-прежнему однозначно определяет
перекрестное произведение.)
Если векторы параллельны или один
вектор является нулевым вектором, тогда не существует уникальной линии
перпендикулярно обоим $\vc{a}$ и $\vc{b}$. Но так как есть только
один вектор нулевой длины, определение по-прежнему однозначно определяет
перекрестное произведение.) Используя мышь, вы можете перетаскивать кончики стрелок векторов $\color{blue}{\vc{a}}$ и $\color{green}{\vc{b}}$, чтобы изменить эти векторы. Посмотрите, как векторное произведение $\color{red}{\vc{c}}$ и параллелограмм изменяются в ответ. (Вы не можете изменить вектор красного перекрестного произведения $\color{red}{\vc{c}}$ напрямую.) Трехмерную перспективу этого графика будет легче воспринимать, если вы будете вращать фигуру, перетаскивая ее рукой. мышь.
Используя мышь, вы можете перетаскивать кончики стрелок векторов $\color{blue}{\vc{a}}$ и $\color{green}{\vc{b}}$, чтобы изменить эти векторы. Посмотрите, как векторное произведение $\color{red}{\vc{c}}$ и параллелограмм изменяются в ответ. (Вы не можете изменить вектор красного перекрестного произведения $\color{red}{\vc{c}}$ напрямую.) Трехмерную перспективу этого графика будет легче воспринимать, если вы будете вращать фигуру, перетаскивая ее рукой. мышь.
 150 (2337 ) Найти интеграл
150 (2337 ) Найти интеграл
 154 ( 2341)Вычислить интеграл
154 ( 2341)Вычислить интеграл
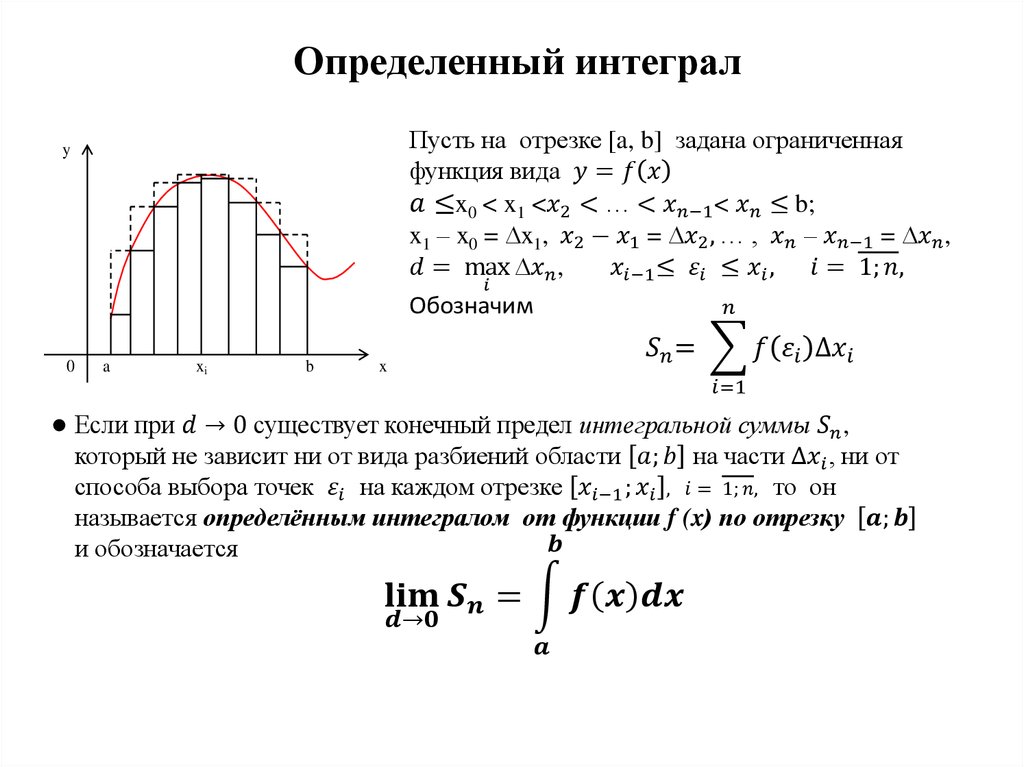



 В результате приходим к логарифму, который расписываем к самому простому виду
В результате приходим к логарифму, который расписываем к самому простому виду



 Такие функции интегрируемые и по схеме выше находим предел в нуле.
Такие функции интегрируемые и по схеме выше находим предел в нуле. В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования.
В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования. {t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t
{t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл.
В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл. 2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже.
2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже. 65
65 2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К.
2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К. 1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x
1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x Результат данной операции можно проиллюстрировать следующим графиком:
Результат данной операции можно проиллюстрировать следующим графиком: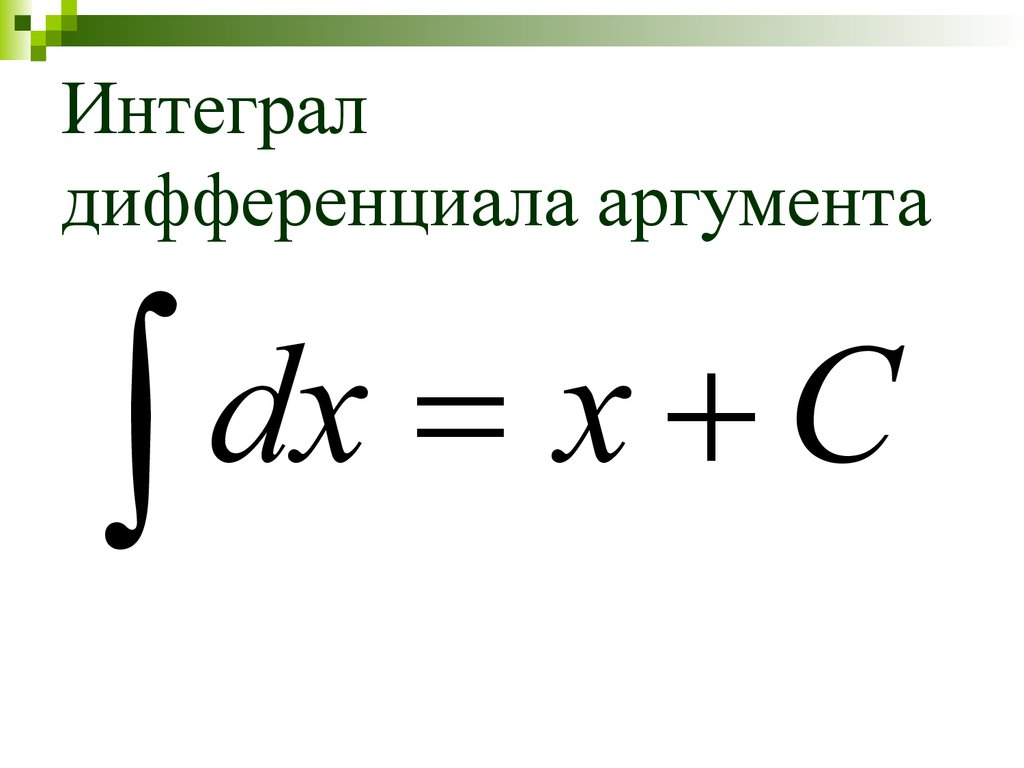 Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных
Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных {100}T(x,y,t)\ \mathrm{d} t
{100}T(x,y,t)\ \mathrm{d} t Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.
Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.
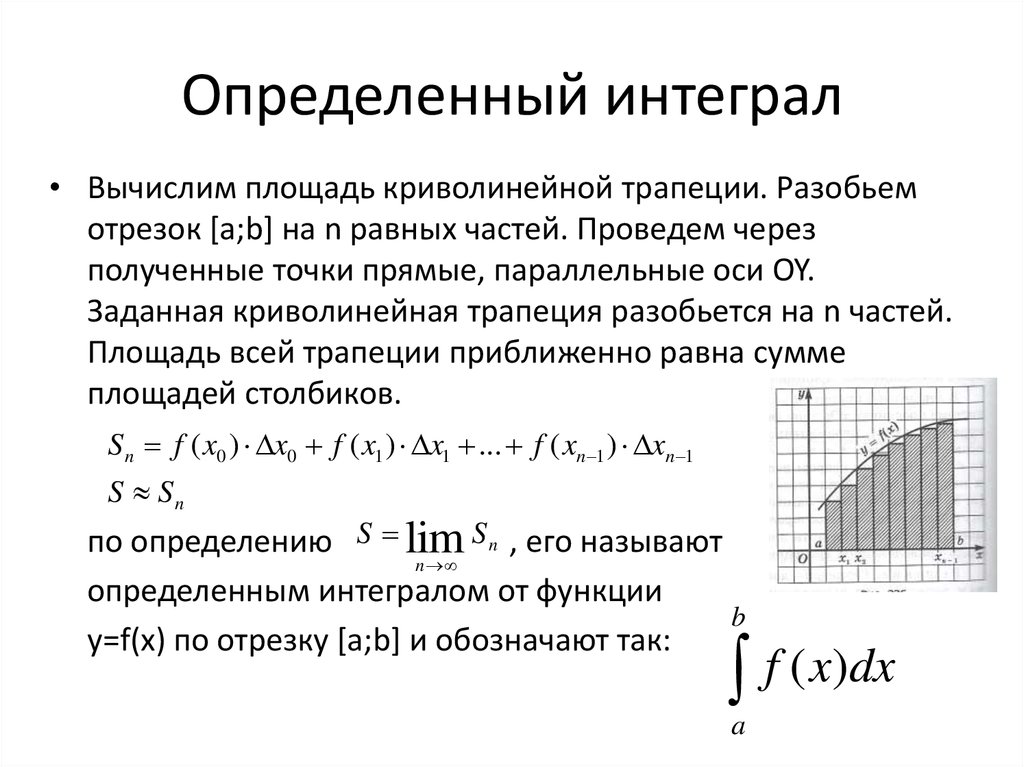





 Интегральные методы расчета здесь в основном численные, поскольку этот сайт посвящен вычислениям,
однако также показаны некоторые аналитические методы.
Интегральные методы расчета здесь в основном численные, поскольку этот сайт посвящен вычислениям,
однако также показаны некоторые аналитические методы.  -x от x=1 до x=5′)
подынтегральная функция = лямбда x: 2 * x * np.exp(-x)
а = 1.
б = 5.
результат = spi.romberg (интегральное выражение, a, b)
print(‘Результат ‘, результат)
9-x от х=1 до х=5
Результат 1.3
-x от x=1 до x=5′)
подынтегральная функция = лямбда x: 2 * x * np.exp(-x)
а = 1.
б = 5.
результат = spi.romberg (интегральное выражение, a, b)
print(‘Результат ‘, результат)
9-x от х=1 до х=5
Результат 1.3
 3(t) от t=0 до t=2pi’)
x = лямбда t : anp.cos(t) ** 3
y = лямбда t : anp.sin(t) ** 3
dx_dt = аг.град(х)
dy_dt = ag.grad(y)
подынтегральное выражение = лямбда t : anp.sqrt (dx_dt (t) ** 2 + dy_dt (t) ** 2)
а = 0.
б = 2 * отн.пи
результат, ошибка = spi.quad (интегральное выражение, a, b)
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
93(t) от t=0 до t=2pi
Результат 6.0 с ошибкой 6.616929226765933e-14 Вот ссылка на код на GitHub.
3(t) от t=0 до t=2pi’)
x = лямбда t : anp.cos(t) ** 3
y = лямбда t : anp.sin(t) ** 3
dx_dt = аг.град(х)
dy_dt = ag.grad(y)
подынтегральное выражение = лямбда t : anp.sqrt (dx_dt (t) ** 2 + dy_dt (t) ** 2)
а = 0.
б = 2 * отн.пи
результат, ошибка = spi.quad (интегральное выражение, a, b)
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
93(t) от t=0 до t=2pi
Результат 6.0 с ошибкой 6.616929226765933e-14 Вот ссылка на код на GitHub. 2 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)’)
подынтегральная функция = лямбда x, y, z : x + y * z ** 2
bounds_z = лямбда: [1., 2.]
bounds_y = лямбда z : [z+1, z+2]
bounds_x = лямбда z, y : [y+z, 2 * (y+z)]
ya=лямбда z: z + 1
yb=лямбда z: z + 2
ха = лямбда z, y : y + z
xb=лямбда z, y : 2 * (y + z)
результат, ошибка = spi.nquad (интегральное выражение, [bounds_x, bounds_y, bounds_z])
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
92 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)
Результат 65.71944444444445 с ошибкой 1.659412309590769e-12 Вот ссылка на код на GitHub.
2 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)’)
подынтегральная функция = лямбда x, y, z : x + y * z ** 2
bounds_z = лямбда: [1., 2.]
bounds_y = лямбда z : [z+1, z+2]
bounds_x = лямбда z, y : [y+z, 2 * (y+z)]
ya=лямбда z: z + 1
yb=лямбда z: z + 2
ха = лямбда z, y : y + z
xb=лямбда z, y : 2 * (y + z)
результат, ошибка = spi.nquad (интегральное выражение, [bounds_x, bounds_y, bounds_z])
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
92 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)
Результат 65.71944444444445 с ошибкой 1.659412309590769e-12 Вот ссылка на код на GitHub. -x от x=1 до x=5′)
х = sp.Symbol(‘x’)
f = 2 * x * sp.exp(-x)
примитив = sp.integrate(f, x)
print(‘Примитив есть’, примитив)
примитив_лямбда = sp.lambdify(x, примитив)
а = 1.
б = 5.
интеграл = примитивная_лямбда(б) — примитивная_лямбда(а)
print(‘Результат равен’, целое число)
9-x от х=1 до х=5
Примитив (-2*x — 2)*exp(-x)
Результат 1.3
-x от x=1 до x=5′)
х = sp.Symbol(‘x’)
f = 2 * x * sp.exp(-x)
примитив = sp.integrate(f, x)
print(‘Примитив есть’, примитив)
примитив_лямбда = sp.lambdify(x, примитив)
а = 1.
б = 5.
интеграл = примитивная_лямбда(б) — примитивная_лямбда(а)
print(‘Результат равен’, целое число)
9-x от х=1 до х=5
Примитив (-2*x — 2)*exp(-x)
Результат 1.3
 Почти все использовали формат файла DOC каждый раз, при написании письма, при работе или вообще при написании чего-либо на компьютере вы бы использовали формат файла DOC. В 1990-х годах Microsoft выбрала расширение DOC для обработки своих файлов программы Microsoft Word. По мере развития и роста технологий ПК, первоначальное использование расширения стало менее важным и в значительной степени исчезло из мира ПК.
Почти все использовали формат файла DOC каждый раз, при написании письма, при работе или вообще при написании чего-либо на компьютере вы бы использовали формат файла DOC. В 1990-х годах Microsoft выбрала расширение DOC для обработки своих файлов программы Microsoft Word. По мере развития и роста технологий ПК, первоначальное использование расширения стало менее важным и в значительной степени исчезло из мира ПК.
 txt
txt Unicode является соперничающим форматом для текстовых файлов. Простой текстовый файл должен содержать только несколько непечатных символов, таких как новые строки, табуляция и перевод страницы
Unicode является соперничающим форматом для текстовых файлов. Простой текстовый файл должен содержать только несколько непечатных символов, таких как новые строки, табуляция и перевод страницы 0 File)
0 File) com
а также
aspose.cloud
com
а также
aspose.cloud
 Наш конвертер файлов проанализирует содержимое исходного DOC файла до мельчайших деталей и воссоздаст содержимое в целевом текст формате.
Наш конвертер файлов проанализирует содержимое исходного DOC файла до мельчайших деталей и воссоздаст содержимое в целевом текст формате.

 размер файла 50MB (хотите больше?)
Как мои файлы защищены?
размер файла 50MB (хотите больше?)
Как мои файлы защищены?
 Отличное быстрое приложение, значительно увеличило мою производительность. Также замечательная поддержка — всегда быстро помогали!
Отличное быстрое приложение, значительно увеличило мою производительность. Также замечательная поддержка — всегда быстро помогали! Я могу сделать несколько больших файлов за короткий промежуток времени.
Я могу сделать несколько больших файлов за короткий промежуток времени. Сотрудники этих организаций, от глобальных корпораций и медиа-компаний до уважаемых учебных заведений и газетных изданий, доверяют Zamzar предоставление точных и надежных услуг по конвертации, в которых они нуждаются.
Сотрудники этих организаций, от глобальных корпораций и медиа-компаний до уважаемых учебных заведений и газетных изданий, доверяют Zamzar предоставление точных и надежных услуг по конвертации, в которых они нуждаются. ..
.. С поддержкой более 1100 типов преобразования файлов, независимо от того, нужно ли вам конвертировать видео, аудио, документы или изображения, вы легко найдете то, что вам нужно, и вскоре ваши файлы будут в форматах и размерах, которые вам подходят.
С поддержкой более 1100 типов преобразования файлов, независимо от того, нужно ли вам конвертировать видео, аудио, документы или изображения, вы легко найдете то, что вам нужно, и вскоре ваши файлы будут в форматах и размерах, которые вам подходят. Microsoft Office был разработан для операционной системы Windows, но вы также можете установить приложения Office в других операционных системах, таких как macOS от Apple и ChromeOS от Google. Базовая бесплатная программа «Word для Интернета» также доступна в Интернете для владельцев учетных записей Microsoft. Файлы DOC легко передавать и распечатывать, и их можно открыть в большинстве программ обработки текстов, включая LibreOffice, Apple Pages и Google Docs, а также в Microsoft Word.
Microsoft Office был разработан для операционной системы Windows, но вы также можете установить приложения Office в других операционных системах, таких как macOS от Apple и ChromeOS от Google. Базовая бесплатная программа «Word для Интернета» также доступна в Интернете для владельцев учетных записей Microsoft. Файлы DOC легко передавать и распечатывать, и их можно открыть в большинстве программ обработки текстов, включая LibreOffice, Apple Pages и Google Docs, а также в Microsoft Word. Файлы TXT содержат только текст и, в отличие от других типов файлов документов, таких как DOC, не содержат изображений или другого мультимедиа.
Файлы TXT содержат только текст и, в отличие от других типов файлов документов, таких как DOC, не содержат изображений или другого мультимедиа.
 ZIP в DOC
PDF в DOC
PNG в DOC
PPS в DOC
PPSX в DOC
PPT в DOC
PPTX в DOC
PSD в DOC
PUB в DOC
RTF в DOC
TIFF в DOC
WKS в DOC
WPD в DOC
WPS в DOC
ZIP в DOC
PDF в DOC
PNG в DOC
PPS в DOC
PPSX в DOC
PPT в DOC
PPTX в DOC
PSD в DOC
PUB в DOC
RTF в DOC
TIFF в DOC
WKS в DOC
WPD в DOC
WPS в DOC txt. Однако, если у вас нет Microsoft Office или нужно преобразовать много файлов, вам может быть проще использовать инструмент преобразования, такой как Zamzar. Просто загрузите файлы DOC на сайт Zamzar, конвертируйте их и загрузите файлы TXT.
txt. Однако, если у вас нет Microsoft Office или нужно преобразовать много файлов, вам может быть проще использовать инструмент преобразования, такой как Zamzar. Просто загрузите файлы DOC на сайт Zamzar, конвертируйте их и загрузите файлы TXT.  TXT, открыв приложение для заметок, такое как Блокнот Microsoft, и сохранив новый документ в виде файла .txt. Вы можете печатать прямо в приложении или использовать скопированный и вставленный текст. Вы также можете открывать электронные письма или документы Word и сохранять их в виде файлов .txt. Если у вас есть целый документ, который вы хотите преобразовать, и у вас нет Microsoft Office, также легко преобразовать весь документ Word в TXT с помощью веб-сайтов преобразования файлов, таких как Zamzar. Просто загрузите документ Word, нажмите, чтобы преобразовать, а затем загрузите новый файл TXT.
TXT, открыв приложение для заметок, такое как Блокнот Microsoft, и сохранив новый документ в виде файла .txt. Вы можете печатать прямо в приложении или использовать скопированный и вставленный текст. Вы также можете открывать электронные письма или документы Word и сохранять их в виде файлов .txt. Если у вас есть целый документ, который вы хотите преобразовать, и у вас нет Microsoft Office, также легко преобразовать весь документ Word в TXT с помощью веб-сайтов преобразования файлов, таких как Zamzar. Просто загрузите документ Word, нажмите, чтобы преобразовать, а затем загрузите новый файл TXT. txt, открыв его в Word и используя параметр «Сохранить как» в меню «Файл».
txt, открыв его в Word и используя параметр «Сохранить как» в меню «Файл». д. Наш инструмент преобразования Word в текст прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
д. Наш инструмент преобразования Word в текст прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
 Вы можете получить результат в течение нескольких секунд.
Вы можете получить результат в течение нескольких секунд.