Интерфейс «Таблица» · Loginom Help
Интерфейс представлен таблицей со следующими столбцами:
Значения ячеек столбца «Входные» редактируются. Редактирование ячейки осуществляется путем выбора из списка полей/переменных входного набора порта.
Панель инструментов таблицы содержит следующие команды:
При необходимости настроить несколько позиций одновременно, их можно выделить следующими способами:
Оба способа можно применять последовательно: например, сначала выбрать список через SHIFT, а потом зажать CTRL и убрать некоторые поля из списка или выделить другие. |
Возможности редактора кода — Visual Studio (Windows)
- Статья
Применимо к: Visual Studio Visual Studio для Mac Visual Studio Code
Редактор Visual Studio предоставляет множество возможностей, облегчающих написание кода и текста, а также управление им. Используя структуру, вы можете разворачивать и сворачивать различные блоки кода. Получить дополнительные сведения о коде можно с помощью технологии IntelliSense, окна Обозреватель объектов и иерархии вызовов. Для поиска в коде можно использовать такие функции, как Перейти, Перейти к определению и Найти все ссылки. Вставлять блоки кода можно с помощью фрагментов кода. Код также можно создавать с помощью функций, таких как Создание в результате использования. Если вы ранее не работали в редакторе Visual Studio, см. статью со сведениями об использовании редактора кода.
Для поиска в коде можно использовать такие функции, как Перейти, Перейти к определению и Найти все ссылки. Вставлять блоки кода можно с помощью фрагментов кода. Код также можно создавать с помощью функций, таких как Создание в результате использования. Если вы ранее не работали в редакторе Visual Studio, см. статью со сведениями об использовании редактора кода.
Примечание
Этот раздел относится к Visual Studio в Windows. Информацию о Visual Studio для Mac см. в статье Редактор исходного кода (Visual Studio для Mac).
Код можно просматривать различными способами. По умолчанию в обозревателе решений код упорядочен по файлам. Чтобы просмотреть код, упорядоченный по классам, можно выбрать вкладку Представление классов в нижней части окна.
Можно выполнять поиск и замену текста в одном или нескольких файлах. Дополнительные сведения см. в статье Поиск и замена текста. Регулярные выражения платформы используются для поиска и замены текста. Дополнительные сведения см. в статье Использование регулярных выражений в Visual Studio.
Дополнительные сведения см. в статье Использование регулярных выражений в Visual Studio.
Разные языки Visual Studio предоставляют разные наборы функций, а в некоторых случаях одни и те же функции ведут себя по-разному в разных языках. Многие из этих отличий указаны в описаниях функций. Дополнительные сведения можно найти в разделах, посвященных конкретным языкам Visual Studio.
Возможности редактора
| Функция | Описание |
|---|---|
| Цветовая раскраска синтаксических конструкций | Некоторые элементы синтаксиса кода и файлов разметки для наглядности выделяются разными цветами. Например, ключевые слова (такие как using в C# и Imports в Visual Basic) выделены одним цветом, а типы (такие как Console и Uri) — другим. Другие элементы синтаксиса (например, строковые литералы и комментарии) также выделены цветом. Язык C++ использует цвета для различения типов, перечислений и макросов среди других токенов. Вы можете узнать, какой цвет задан по умолчанию для каждого типа, и изменить цвет для любого элемента синтаксиса в диалоговом окне Fonts and Colors, Environment, Options Dialog Box, которое можно открыть с помощью меню Сервис. |
| Маркеры ошибок и предупреждений | В процессе добавления кода и сборки решения вы можете увидеть в коде (а) волнистые линии различного цвета (знак «тильда») или (б) лампочки. Красные волнистые линии обозначают ошибки синтаксиса, синие обозначают ошибку компилятора, зеленые — предупреждения, а фиолетовые — другие типы ошибок. Быстрые действия предлагают способы решения проблем и помогают легко применить их. Вы можете узнать, какой цвет задан по умолчанию для каждой пометки ошибки и предупреждения, в диалоговом окне Сервис>Параметры>Среда>Шрифты и цвета. Посмотрите пункты: Синтаксическая ошибка, Ошибка компилятора, Предупреждениеи Другие ошибки. |
| Согласование скобок | Если курсор мыши поместить на открывающую фигурную скобку в файле кода, выделяются обе скобки — открывающая и закрывающая. Эта функция позволяет оперативно реагировать на неправильно поставленную или отсутствующую фигурную скобку. Парные фигурные скобки можно включить или отключить с помощью параметра Автоматически выделять разделители (Сервис>Параметры>Текстовый редактор). Цвет выделения можно изменить в разделе Шрифты и цвета (Сервис>Параметры>Среда). Используйте параметр Парные фигурные скобки (выделение) или Парные фигурные скобки (прямоугольник) . |
| Визуализатор структуры | Парные фигурные скобки в файлах кода соединяются пунктирными линиями, что делает работу с кодом более наглядной. Это поможет вам быстрее находить код в базе. Чтобы включить или отключить эти линии, используйте параметр Показать направляющие структуры в разделе Отображение на странице Сервис>Параметры>Текстовый редактор>Общие. |
| Номера строк | Номера строк могут отображаться в левом поле окна кода. По умолчанию они не отображаются. Этот режим можно включить в разделе Текстовый редактор > Все языки (Сервис>Параметры>Текстовый редактор>Все языки). Номера строк для отдельных языков программирования можно отобразить, изменив параметры для этих языков (язык> текстового редактора<>параметров>инструментов>). Чтобы номера строк выводились на печать, нужно установить флажок Включить номера строк в диалоговом окне Печать. |
| Отслеживание изменений | С помощью цвета левого поля окна можно отслеживать изменения, внесенные в файл. Если с момента открытия файла были внесены изменения и они не были сохранены, в левом поле окна (поле выделения) появляется желтая полоска. Если изменения сохранить, но оставить файл открытым, полоска станет зеленой. Если отменить изменения после сохранения файла, полоска станет оранжевой. Включить или отключить эту функцию можно с помощью параметра Отслеживать изменения в настройках текстового редактора (Сервис>Параметры>Текстовый редактор). Если отменить изменения после сохранения файла, полоска станет оранжевой. Включить или отключить эту функцию можно с помощью параметра Отслеживать изменения в настройках текстового редактора (Сервис>Параметры>Текстовый редактор). |
| Выбор кода и текста | Текст можно выбрать в стандартном режиме в виде непрерывного потока или в режиме блока, когда выбирается прямоугольный фрагмент текста, а не набор строк. Чтобы сделать выделение в режиме поля, нажмите клавиши ALT при наведении указателя мыши на выделение (или клавиши ALT+SHIFT+<>). В выделение попадают все символы внутри прямоугольника, определяемого первым и последним символами выделенной области. Текст, введенный или вставленный в выделенной области, помещается в одну и ту же точку в каждой строке. |
| Масштаб | Вы можете увеличить или уменьшить масштаб в любом окне кода, нажав и удерживая клавишу CTRL , и переместив колесико прокрутки мыши (или CTRL+SHIFT+, чтобы увеличить и ctrl+SHIFT+, чтобы уменьшить). Кроме того, можно указать конкретное значение масштаба в процентах в поле Масштаб, расположенном в левом нижнем углу окна кода. Функция масштабирования не работает в окнах инструментов. Кроме того, можно указать конкретное значение масштаба в процентах в поле Масштаб, расположенном в левом нижнем углу окна кода. Функция масштабирования не работает в окнах инструментов. |
| Виртуальное пространство | По умолчанию строки в редакторах Visual Studio заканчиваются после последнего символа. Это означает, что при нажатии клавиши СТРЕЛКА ВПРАВО в конце строки происходит перемещение курсора в начало следующей строки. В некоторых других редакторах строка не заканчивается после последнего символа и вы можете поместить курсор в любое место в строке. Разрешить виртуальное пространство в редакторе можно, выбрав Сервис>Параметры>Текстовый редактор>Все языки. Обратите внимание, что вы можете включить только какой-либо один из режимов: Виртуальное пространство или Перенос по словам. |
| Печать | Используя параметры в диалоговом окне Печать , можно включить номера строк или скрыть свернутые области кода при печати файла. В диалоговом окне Параметры страницы вы можете также задать печать полного пути и имени файла, выбрав вариант Верхний колонтитул страницы. В диалоговом окне Параметры страницы вы можете также задать печать полного пути и имени файла, выбрав вариант Верхний колонтитул страницы.Параметры цветной печати можно задать в диалоговом окне Сервис>Параметры>Среда>Шрифты и цвета. Выберите пункт Принтер в списке Показать параметры для , чтобы настроить цветную печать. Для печати файла можно указать не такие цвета, как для редактирования файла. |
| Глобальные действия отмены и повтора | Команды Отменить последнее глобальное действие и Повторить последнее глобальное действие в меню Правка позволяют отменить или повторить глобальные действия, выполняемые над множеством файлов. К глобальным действиям относятся: переименование класса или пространства имен, выполнение операции поиска и замены по всему решению, рефакторинг базы данных или любое другое действие, приводящее к изменению множества файлов. Вы можете применить глобальные команды отмены и повтора для действий в текущем сеансе Visual Studio даже после закрытия решения, в котором применялись эти действия. Вы можете применить глобальные команды отмены и повтора для действий в текущем сеансе Visual Studio даже после закрытия решения, в котором применялись эти действия. |
Дополнительные возможности редактирования
В меню Правка>Дополнительно на панели инструментов есть набор дополнительных функций. Не все они доступны для каждого типа файлов кода.
| Функция | Описание |
|---|---|
| Форматировать документ | Установка правильного отступа строк кода и перемещение фигурных скобок для разделения строк в документе. |
| Форматировать выделенный фрагмент | Установка правильного отступа строк кода и перемещение фигурных скобок для разделения строк в выделенном фрагменте. |
| Преобразовать пробелы в знаки табуляции в выделенных строках | Замена начальных пробелов на знаки табуляции там, где это уместно. |
| Преобразовать знаки табуляции в пробелы в выделенных строках | Замена начальных знаков табуляции на пробелы. Если требуется преобразовать все пробелы в знаки табуляции в файле (или все знаки табуляции в пробелы), можно использовать команды Если требуется преобразовать все пробелы в знаки табуляции в файле (или все знаки табуляции в пробелы), можно использовать команды Edit.ConvertSpacesToTabs и Edit.ConvertTabsToSpaces . Эти команды не включены в меню Visual Studio, но их можно вызывать из окна быстрого доступа или окна командной строки. |
| Все прописные | Перевод всех символов в выделенном фрагменте в верхний регистр или, если ничего не выбрано, перевод символа в позиции курсора в верхний регистр. Ярлык. CTRL+SHIFT+U. |
| Все строчные | Перевод всех символов в выделенном фрагменте в нижний регистр или, если ничего не выбрано, перевод символа в позиции курсора в нижний регистр. Ярлык. CTRL+U. |
| Переместить выбранные строки вверх | Перемещение выбранной строки вверх на одну строку. Ярлык. ALT+СТРЕЛКА ВВЕРХ. |
| Переместить выбранные строки вниз | Перемещение выбранной строки вниз на одну строку. Ярлык. ALT+ВНИЗ. |
| Удалить пустое пространство по горизонтали | Удаление символов табуляции и пробелов в конце текущей строки. Ярлык. CTRL+K, CTRL+\ |
| Показать пустое пространство | Отображение пробелов в виде приподнятых точек, а символов табуляции — в виде стрелок. Конец файла отображается как прямоугольный глиф. Если с помощью меню выбран вариант Сервис>Параметры>Текстовый редактор>Все языки>Перенос по словам>Показывать графические метки в местах переноса слов, этот глиф также будет отображаться. |
| Перенос по словам | В этом режиме все строки документа отображаются полностью в окне кода. Перенос по словам можно включить или отключить в разделе Все языки для текстового редактора (Сервис>Параметры>Текстовый редактор>Все языки). |
| Закомментировать выделенный фрагмент | Добавление символов комментария к выбранному фрагменту или текущей строке. Ярлык. CTRL+K, CTRL+C |
| Раскомментировать выделенный фрагмент | Удаление символов комментария из выбранного фрагмента или текущей строки. Ярлык. CTRL+K, CTRL+U |
| Увеличить отступ строки | Добавление символа табуляции (или эквивалентных пробелов) к выбранным строкам или текущей строке. |
| Уменьшить отступ строки | Удаление символа табуляции (или эквивалентных пробелов) из выбранных строк или текущей строки. |
| Выбрать тег | Выбор тега в документе, содержащем теги (например, XML или HTML). |
| Выделить содержимое тега | Выбор содержимого в документе, содержащем теги (например, XML или HTML). |
Перемещение по коду и поиск
Перемещаться по редактору кода можно несколькими способами, включая переход назад и вперед к точкам вставки, просмотр определения типа или члена и переход к определенному методу с помощью панели навигации. Дополнительные сведения см. в статье Навигация по коду.
Дополнительные сведения см. в статье Навигация по коду.
Поиск ссылок в базе коде
Чтобы найти, где именно в базе кода используются ссылки на элементы кода, можно использовать команду Найти все ссылки или нажать SHIFT+F12. Кроме того, когда вы щелкаете тип или член, функция выделения ссылок автоматически выделяет все ссылки на него. Дополнительные сведения см. в разделе Поиск ссылок в коде.
Создание, исправление или рефакторинг кода
Visual Studio помогает создавать, исправлять код и выполнять его рефакторинг самыми разными способами.
Вы можете использовать фрагменты кода для вставки шаблона, такого как блок switch или объявление enum.
Вы можете использовать быстрые действия для создания кода, например классов и свойств, или для введения локальной переменной. Кроме того, быстрые действия можно использовать для улучшения кода, например для удаления ненужных приведений и переменных либо для добавления проверок значений NULL перед обращением к переменным.

Вы можете выполнять рефакторинг кода, например чтобы переименовывать переменные, изменять порядок параметров метода или синхронизировать тип с его именем файла.
Настройка редактора
Вы можете использовать свои параметры Visual Studio совместно с другим разработчиком, привести параметры в соответствие со стандартом или вернуться к настройкам, заданным по умолчанию в Visual Studio, с помощью команды Мастер импорта и экспорта параметров в меню Сервис. В мастере импорта и экспорта параметров можно изменить выбранные общие параметры, а также зависящие от языка и проекта параметры.
Чтобы определить новые или переопределить существующие сочетания клавиш, выберите Сервис>Параметры>Среда>Клавиатура. Дополнительные сведения о сочетаниях клавиш см. в статье Сочетания клавиш по умолчанию в Visual Studio.
Параметры редактора для JavaScript см.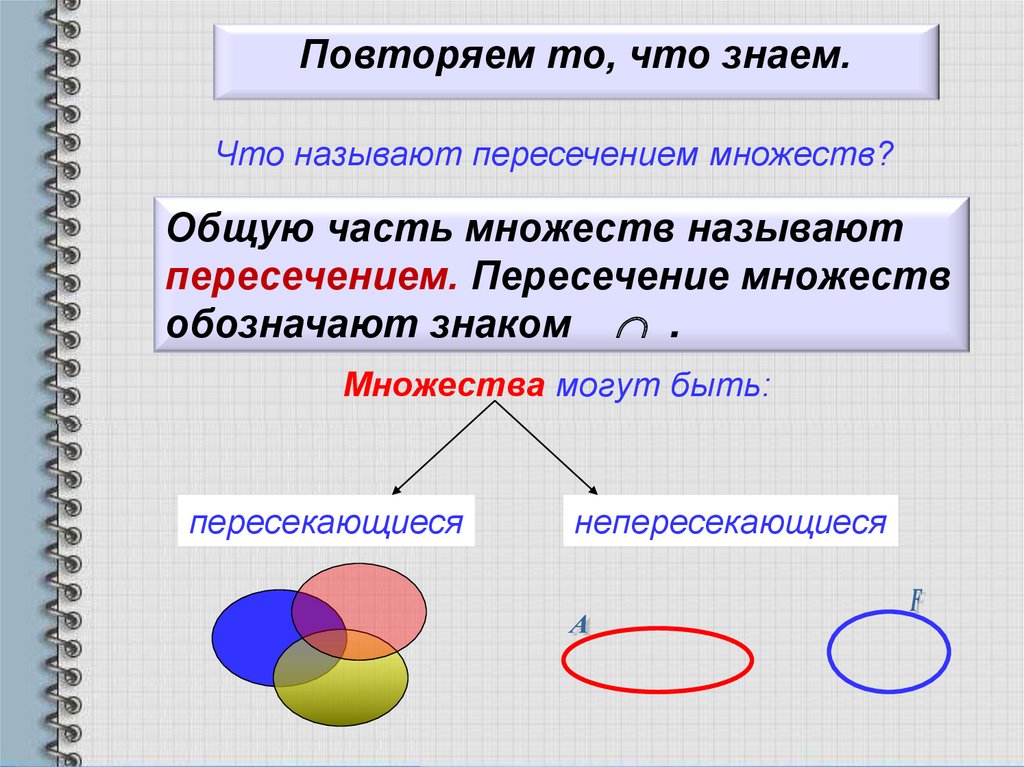 в статье о параметрах редактора JavaScript.
в статье о параметрах редактора JavaScript.
См. также
- Редактор исходного кода (Visual Studio для Mac)
- Интегрированная среда разработки Visual Studio
- Начало работы с C++ в Visual Studio
- Начало работы с C# и ASP.NET в Visual Studio
- Начало работы с Python в Visual Studio
этикеток и селекторов | Kubernetes
Метки — это пары ключ/значение, прикрепленные к объектам, например к модулям. Метки предназначены для указания идентифицирующих атрибутов объектов. значимые и релевантные для пользователей, но не подразумевающие непосредственно семантику к основной системе. Метки можно использовать для организации и выбора подмножеств объекты. Метки могут быть прикреплены к объектам во время создания и впоследствии добавлены и изменены в любое время. Каждый объект может иметь набор меток ключ/значение определенный. Каждый ключ должен быть уникальным для данного объекта.
"метаданные": {
"метки": {
"ключ1": "значение1",
"ключ2": "значение2"
}
}
Метки обеспечивают эффективные запросы и наблюдения и идеально подходят для использования в пользовательских интерфейсах. и CLI. Неидентифицирующая информация должна быть записана с использованием
аннотации.
и CLI. Неидентифицирующая информация должна быть записана с использованием
аннотации.
Мотивация
Метки позволяют пользователям сопоставлять свои собственные организационные структуры с системными объектами слабосвязанным образом, не требуя, чтобы клиенты сохраняли эти сопоставления.
Развертывания служб и конвейеры пакетной обработки часто являются многомерными объектами (например, несколько разделов или развертываний, несколько версий выпуска, несколько уровней, несколько микросервисов на уровне). Менеджмент часто требует сквозных операций, что нарушает инкапсуляцию строго иерархических представлений, особенно жестких иерархии, определяемые инфраструктурой, а не пользователями.
Примеры меток:
-
«релиз»: «стабильный»,«релиз»: «канареечный» -
«среда»: «dev», 9021«среда» 20 «среда»: «производство» -
«уровень»: «внешняя часть»,«уровень»: «внутренняя часть»,«уровень»: «кеш» -
«раздел»: «» ,"раздел" : "customerB" -
"трек" : "ежедневно","след" : "еженедельно"
Это примеры
часто используемые этикетки;
вы вольны разрабатывать свои собственные соглашения. Имейте в виду, что метка Key должна быть уникальной для данного объекта.
Имейте в виду, что метка Key должна быть уникальной для данного объекта.
Синтаксис и набор символов
Метки представляют собой пары ключ/значение. Действительные ключи меток имеют два сегмента: необязательный
префикс и имя, разделенные косой чертой ( / ). Сегмент имени является обязательным и
должно быть не более 63 символов, начиная и заканчивая буквенно-цифровым
персонаж ( [a-z0-9A-Z] ) с тире ( - ), подчеркиванием ( _ ), точками ( . ),
и буквенно-цифровые символы между ними. Префикс является необязательным. Если указано, префикс
должен быть поддоменом DNS: серия меток DNS, разделенных точками ( . ),
не более 253 символов, за которыми следует косая черта ( / ).
Если префикс опущен, предполагается, что ключ метки является личным для пользователя.
Компоненты автоматизированной системы (например, kube-scheduler , куб-контроллер-менеджер , kube-apiserver , kubectl или другая сторонняя автоматизация) которые добавляют метки
для объектов конечного пользователя необходимо указать префикс.
Префиксы kubernetes.io/ и k8s.io/ зарезервировано для основных компонентов Kubernetes.
Допустимое значение метки:
- должно содержать не более 63 символов (может быть пустым),
- , если оно не пусто, должно начинаться и заканчиваться буквенно-цифровым символом (
[a-z0-9A-Z]), - может содержать дефисы (
-), символы подчеркивания (_), точки (.) и буквенно-цифровые символы между ними.
Например, вот манифест для модуля с двумя метками
Среда : производство и приложение : nginx :
apiVersion: v1
вид: стручок
метаданные:
название: лейбл-демо
этикетки:
среда: производство
приложение: nginx
спецификация:
контейнеры:
- имя: nginx
изображение: nginx:1.14.2
порты:
- контейнерПорт: 80
Селекторы меток
В отличие от имен и UID, метки
не обеспечивают уникальности. Как правило, мы ожидаем, что многие объекты будут иметь одинаковые метки.
Как правило, мы ожидаем, что многие объекты будут иметь одинаковые метки.
С помощью селектора меток клиент/пользователь может идентифицировать набор объектов. Селектор меток — это основной примитив группировки в Kubernetes.
В настоящее время API поддерживает два типа селекторов: на основе равенства и на основе набора .
Селектор меток может состоять из нескольких требований , которые разделены запятыми.
В случае нескольких требований все должны быть удовлетворены, поэтому разделитель запятой
действует как логический оператор И ( && ).
Семантика пустых или неуказанных селекторов зависит от контекста, и типы API, которые используют селекторы, должны документировать достоверность и значение их.
Примечание. Для некоторых типов API, таких как наборы реплик, селекторы меток двух экземпляров должны
не перекрываются внутри пространства имен, иначе контроллер увидит конфликтующие
инструкции и не могут определить, сколько реплик должно присутствовать.
Предупреждение: Как для условий, основанных на равенстве, так и для условий, основанных на множестве, нет логического оператора ИЛИ ( || ).
Убедитесь, что операторы фильтра структурированы соответствующим образом.
Требование , основанное на равенстве, или , основанное на неравенстве, позволяет выполнять фильтрацию по ключам и значениям меток.
Соответствующие объекты должны удовлетворять всем указанным ограничениям меток, хотя они могут
также иметь дополнительные метки. Допускаются три вида операторов = , == , != .
Первые два представляют равенство (и являются синонимами), а последний представляет неравенство .
Например:
среда = производство уровень != внешний интерфейс
Первый выбирает все ресурсы с ключом равным environment и значением равным production . Последний выбирает все ресурсы с ключом равным
Последний выбирает все ресурсы с ключом равным tier и значением отличным от frontend ,
и все ресурсы без меток с 9Ключ уровня 0020 . Можно фильтровать ресурсы в производстве исключая внешний интерфейс с использованием оператора запятой: environment=production,tier!=frontend
Один из сценариев использования требования к метке на основе равенства должен указывать поды
Критерии выбора узлов. Например, пример пода ниже выбирает узлы с
метка « ускоритель=nvidia-tesla-p100 «.
APIВерсия: v1
вид: стручок
метаданные:
имя: cuda-тест
спецификация:
контейнеры:
- имя: cuda-тест
изображение: "registry.k8s.io/cuda-vector-add:v0.1"
Ресурсы:
пределы:
nvidia.com/gpu: 1
селектор узлов:
ускоритель: nvidia-tesla-p100
Требование на основе набора Требования метки на основе набора позволяют фильтровать ключи в соответствии с набором значений.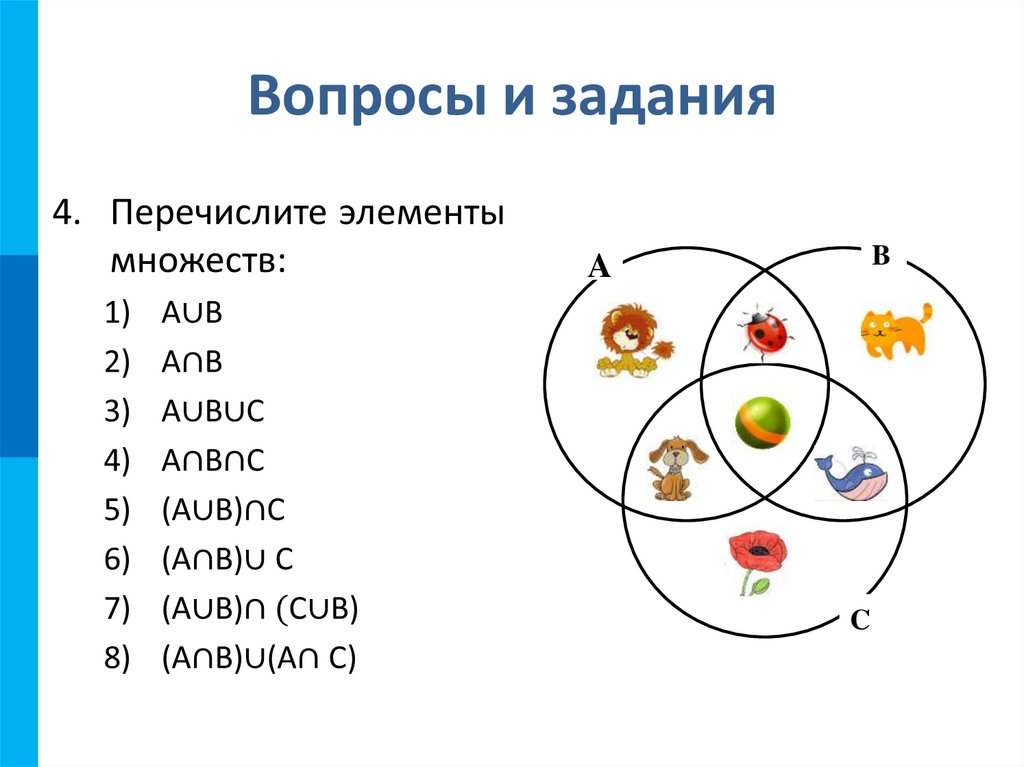 Поддерживаются три вида операторов:
Поддерживаются три вида операторов: в , не в и существует (только идентификатор ключа).
Например:
среда в (производство, качество) уровень notin (интерфейс, бэкэнд) раздел !раздел
- В первом примере выбираются все ресурсы с ключом, равным
, средаи значение равнопроизводствоилиqa. - Во втором примере выбираются все ресурсы с ключом равным
tierи другими значениями чемfrontendиbackend, и все ресурсы без меток с ключом уровня. - В третьем примере выбираются все ресурсы, включая метку с ключом
, раздел; никакие значения не проверяются. - В четвертом примере выбираются все ресурсы без метки с ключом
раздел; никакие значения не проверяются.
Точно так же разделитель-запятая действует как оператор И . Итак, фильтрация ресурсов
с разделом ключ (независимо от значения) и со средой отличается
чем qa , может быть достигнуто с использованием раздела , среды notin (qa) . Селектор меток на основе набора является общей формой равенства, поскольку
Селектор меток на основе набора является общей формой равенства, поскольку environment=production эквивалентно environment в (production) ;
аналогично для != и , а не .
Требования , основанные на множестве, можно смешивать с требованиями , основанными на равенстве.
Например: раздел в (customerA, customerB),environment!=qa .
API
Фильтрация LIST и WATCH
Операции LIST и WATCH могут указывать селекторы меток для фильтрации наборов объектов возвращается с использованием параметра запроса. Оба требования разрешены (представлены здесь так, как они будут отображаться в строке запроса URL):
- на основе равенства требования:
?labelSelector=environment%3Dproduction,tier%3Dfrontend - на основе множества требования:
?labelSelector=environment%2Ctier%9%28production2%2 конец %29
Оба стиля селектора меток можно использовать для отображения или просмотра ресурсов через клиент REST. Например, нацеливаясь на
Например, нацеливаясь на apiserver с kubectl и используя на основе равенства , можно написать:
kubectl get pods -l environment=production,tier=frontend
или с использованием на основе набора требований :
kubectl get pods -l 'среда в (производстве), уровень в (внешнем интерфейсе)'
Как уже упоминалось, на основе набора требования более выразительны. Например, они могут реализовать оператор ИЛИ для значений:
kubectl get pods -l 'среда в (производство, качество)'
или ограничение отрицательного совпадения через notin 9Оператор 0004:
kubectl get pods -l 'среда, среда не в (внешнем интерфейсе)'
Установить ссылки в объектах API
Некоторые объекты Kubernetes, например, службы и контроллеров репликации ,
также используйте селекторы меток для указания наборов других ресурсов, таких как
стручки.
Служба и контроллер репликации
Набор модулей, на которые нацелена служба , определяется с помощью селектора меток.
Точно так же популяция стручков, которые контроллер репликации должен
управление также определяется с помощью селектора меток.
Селекторы меток для обоих объектов определены в файлах json или yaml с использованием карт,
и поддерживаются только селектора требований на основе равенства:
"селектор": {
«компонент»: «редис»,
}
или
селектор: компонент: редис
Этот селектор (соответственно в формате json или yaml ) эквивалентен
9Компонент 0020=redis или компонент в (redis) .
Ресурсы, поддерживающие требования на основе набора
Более новые ресурсы, такие как Job , Развертывание , набор реплик и Набор Демонов ,
также поддерживает требования , основанные на наборе .
селектор:
метки соответствия:
компонент: редис
matchExpressions:
- {ключ: уровень, оператор: In, значения: [кеш]}
- {ключ: среда, оператор: NotIn, значения: [dev]}
matchLabels — это карта из {ключ, значение} пары. Один {ключ, значение} в
Карта matchLabels эквивалентна элементу matchExpressions , чей ключ поле является «ключевым», оператор — «В», а массив значений содержит только «значение». matchExpressions — это список требований к селектору модулей. Допустимые операторы включают
In, NotIn, Exists и DoesNotExist. Набор значений должен быть непустым в случае
В и Не В. Все требования, начиная с matchLabels и matchExpressions объединяются по И вместе — все они должны быть удовлетворены, чтобы соответствовать.
Выбор наборов узлов
Одним из вариантов использования выбора над метками является ограничение набора узлов, на которые
модуль может планировать. См. документацию на
выбор узла для получения дополнительной информации.
См. документацию на
выбор узла для получения дополнительной информации.
Что дальше
- Узнайте, как добавить метку к узлу
- Найдите известные метки, аннотации и пометки
- См. Рекомендуемые метки
- Обеспечьте соблюдение стандартов безопасности Pod с помощью меток пространства имен
- Эффективно используйте метки для управления развертываниями.
- Прочтите блог о написании контроллера для меток модулей
Последнее изменение: 19 февраля 2023 г., 16:30 по тихоокеанскому времени: аккуратные страницы концепций в метках и аннотациях (3ca95d6c88)
Добавление или удаление меток данных на диаграмме
Чтобы быстро определить ряд данных на диаграмме, вы можете добавить метки данных к точкам данных диаграммы. По умолчанию метки данных связаны со значениями на листе и автоматически обновляются при внесении изменений в эти значения.
Метки данных упрощают понимание диаграммы, поскольку они отображают сведения о ряде данных или отдельных точках данных. Например, на круговой диаграмме ниже без меток данных было бы трудно сказать, что кофе составил 38% от общего объема продаж. В зависимости от того, что вы хотите выделить на диаграмме, вы можете добавить метки к одной серии, ко всем сериям (всей диаграмме) или к одной точке данных.
Например, на круговой диаграмме ниже без меток данных было бы трудно сказать, что кофе составил 38% от общего объема продаж. В зависимости от того, что вы хотите выделить на диаграмме, вы можете добавить метки к одной серии, ко всем сериям (всей диаграмме) или к одной точке данных.
Примечание. Следующие процедуры применимы к Office 2013 и более поздним версиям. Ищете шаги для Office 2010?
Добавить метки данных на диаграмму
Щелкните ряд данных или диаграмму. Чтобы пометить одну точку данных, после щелчка по ряду щелкните эту точку данных.
В правом верхнем углу рядом с диаграммой нажмите Добавить элемент диаграммы > Метки данных .

Чтобы изменить местоположение, щелкните стрелку и выберите один из вариантов.
Если вы хотите, чтобы метка данных отображалась внутри текстового пузыря, щелкните Выноска данных .
Чтобы метки данных было легче читать, их можно переместить внутрь точек данных или даже за пределы диаграммы. Чтобы переместить метку данных, перетащите ее в нужное место.
Если вы решите, что метки делают вашу диаграмму слишком загроможденной, вы можете удалить некоторые или все из них, щелкнув метки данных и нажав Удалить.
Совет: Если текст внутри меток данных слишком трудно прочитать, измените размер меток данных, нажав на них, а затем перетащив их до нужного размера.
Изменение внешнего вида меток данных
Щелкните правой кнопкой мыши ряд данных или метку данных, чтобы отобразить дополнительные данные, а затем щелкните Формат меток данных .
Щелкните Параметры метки и в разделе Ярлык содержит выберите нужные параметры.
Использовать значения ячеек в качестве меток данных
Вы можете использовать значения ячеек в качестве меток данных для диаграммы.
Щелкните правой кнопкой мыши ряд данных или метку данных, чтобы отобразить дополнительные данные, а затем щелкните Формат меток данных .
Щелкните Параметры метки и в разделе Метка содержит установите флажок Значения из ячеек .
Когда появится диалоговое окно Диапазон меток данных , вернитесь к электронной таблице и выберите диапазон, для которого вы хотите, чтобы значения ячеек отображались как метки данных. Когда вы это сделаете, выбранный диапазон появится в диалоговом окне Data Label Range . Затем нажмите OK .
Затем нажмите OK .
Значения ячеек теперь будут отображаться в виде меток данных на диаграмме.
Изменение текста, отображаемого в метках данных
Щелкните метку данных с текстом, который необходимо изменить, а затем щелкните ее еще раз, чтобы выбрать только эту метку данных.
Выберите существующий текст и введите текст замены.
Щелкните в любом месте за пределами метки данных.

Совет: Если вы хотите добавить комментарий к диаграмме или иметь только одну метку данных, вы можете использовать текстовое поле.
Удалить метки данных с диаграммы
Щелкните диаграмму, из которой вы хотите удалить метки данных.
Отображает Инструменты диаграммы , добавляя вкладки Дизайн и Формат .
Выполните одно из следующих действий:
- org/ListItem»>
На вкладке Design в Макетах диаграмм , щелкните Добавить элемент диаграммы , выберите Метки данных , а затем щелкните Нет .
Щелкните метку данных один раз, чтобы выбрать все метки данных в ряду данных, или два раза, чтобы выбрать только одну метку данных, которую вы хотите удалить, а затем нажмите клавишу DELETE.
Щелкните правой кнопкой мыши метку данных и выберите Удалить .
Примечание. При этом удаляются все метки данных из серии данных.
org/ListItem»>
Вы также можете удалить метки данных сразу после их добавления, нажав Отменить на Панели быстрого доступа или нажав CTRL+Z.
Добавление или удаление меток данных на диаграмме в Office 2010
На графике выполните одно из следующих действий:
Чтобы добавить метку данных ко всем точкам данных всех рядов данных, щелкните область диаграммы.
org/ListItem»>
Чтобы добавить метку данных ко всем точкам данных ряда данных, щелкните один раз, чтобы выбрать ряд данных, который вы хотите пометить.
Чтобы добавить метку данных к одной точке данных в ряду данных, щелкните ряд данных, содержащий точку данных, которую вы хотите пометить, а затем снова щелкните точку данных.
Отображает Инструменты диаграммы , добавляя вкладки Дизайн , Макет и Формат .
На вкладке Макет в группе Этикетки щелкните Метки данных , а затем выберите нужный вариант отображения.

В зависимости от используемого типа диаграммы будут доступны различные параметры меток данных.
На графике выполните одно из следующих действий:
Чтобы отобразить дополнительные записи меток для всех точек данных ряда, щелкните метку данных один раз, чтобы выбрать все метки данных ряда данных.
Чтобы отобразить дополнительные записи метки для одной точки данных, щелкните метку данных в точке данных, которую вы хотите изменить, а затем снова щелкните метку данных.

Отображает Инструменты диаграммы , добавляя вкладки Дизайн , Макет и Формат .
На вкладке Формат в группе Текущий выбор щелкните Формат выбора .
Можно также щелкнуть правой кнопкой мыши выбранную метку или метки на диаграмме, а затем щелкнуть Форматировать метку данных или Форматировать метки данных .
Щелкните Параметры метки , если он не выбран, а затем в разделе Метка содержит установите флажок для записей метки, которые вы хотите добавить.

Доступные параметры метки зависят от типа диаграммы. Например, в круговой диаграмме метки данных могут содержать проценты и линии выноски.
Чтобы изменить разделитель между записями меток данных, выберите нужный разделитель или введите пользовательский разделитель в поле Разделитель .
Чтобы настроить положение метки для лучшего представления дополнительного текста, выберите нужный параметр в разделе 9.0433 Позиция метки .
Если вы ввели текст пользовательской метки, но хотите снова отобразить записи метки данных, связанные со значениями рабочего листа, вы можете нажать Сбросить текст метки .
На диаграмме щелкните метку данных в точке данных, которую вы хотите изменить, а затем щелкните метку данных еще раз, чтобы выбрать только эту метку.
Щелкните внутри поля метки данных, чтобы перейти в режим редактирования.
Выполните одно из следующих действий:
Чтобы ввести новый текст, перетащите его, чтобы выбрать текст, который вы хотите изменить, а затем введите нужный текст.

Чтобы связать метку данных с текстом или значениями на листе, перетащите мышью, чтобы выбрать текст, который вы хотите изменить, а затем выполните следующие действия:
На рабочем листе щелкните строку формул и введите знак равенства (=).
Выберите ячейку рабочего листа, содержащую данные или текст, которые вы хотите отобразить на диаграмме.
Вы также можете ввести ссылку на ячейку рабочего листа в строке формул.
 Включите знак равенства, имя листа, за которым следует восклицательный знак; например, =Лист1!F2
Включите знак равенства, имя листа, за которым следует восклицательный знак; например, =Лист1!F2 Нажмите ВВОД.
Совет: Вы можете использовать любой метод для ввода процентов — вручную, если вы знаете, что это такое, или путем ссылки на проценты на листе. Проценты не рассчитываются на диаграмме, но вы можете рассчитать проценты на рабочем листе, используя уравнение количество / итог = процент . Например, если вы вычислите 10/100 = 0,1 , а затем отформатируете 0.1 в процентах, число будет правильно отображаться как 10% . Дополнительные сведения о вычислении процентов см. в разделе Вычисление процентов.
Размер поля метки данных подстраивается под размер текста. Вы не можете изменить размер окна метки данных, и текст может стать обрезанным, если он не соответствует максимальному размеру. Чтобы вместить больше текста, вы можете вместо этого использовать текстовое поле. Дополнительные сведения см. в разделе Добавление текстового поля на диаграмму.
Вы не можете изменить размер окна метки данных, и текст может стать обрезанным, если он не соответствует максимальному размеру. Чтобы вместить больше текста, вы можете вместо этого использовать текстовое поле. Дополнительные сведения см. в разделе Добавление текстового поля на диаграмму.
Положение одной метки данных можно изменить, перетащив ее. Вы также можете размещать метки данных в стандартном положении относительно их маркеров данных. В зависимости от типа диаграммы вы можете выбрать один из множества вариантов позиционирования.
На графике выполните одно из следующих действий:
Чтобы переместить все метки данных для всего ряда данных, щелкните метку данных один раз, чтобы выбрать ряд данных.

Чтобы изменить положение определенной метки данных, дважды щелкните эту метку данных, чтобы выбрать ее.
Отображает Инструменты диаграммы , добавляя вкладки Дизайн , Макет и Формат .
На вкладке Макет в группе Этикетки щелкните Метки данных , а затем выберите нужный вариант.
Для получения дополнительных параметров метки данных щелкните Дополнительные параметры метки данных , щелкните Параметры метки , если он не выбран, а затем выберите нужные параметры.

Щелкните диаграмму, из которой вы хотите удалить метки данных.
Отображает Инструменты диаграммы , добавляя вкладки Дизайн , Макет и Формат .
Выполните одно из следующих действий:
На вкладке Макет в группе Этикетки щелкните Метки данных , а затем щелкните Нет .
org/ListItem»>
Щелкните метку данных один раз, чтобы выбрать все метки данных в ряду данных, или два раза, чтобы выбрать только одну метку данных, которую вы хотите удалить, а затем нажмите клавишу DELETE.
Щелкните правой кнопкой мыши метку данных и выберите Удалить .
Примечание. При этом удаляются все метки данных из серии данных.
Вы также можете удалить метки данных сразу после их добавления, нажав Отменить на панели быстрого доступа или нажав CTRL+Z.
Метки данных упрощают понимание диаграммы, поскольку они отображают сведения о ряде данных или отдельных точках данных. Например, на круговой диаграмме ниже без меток данных было бы трудно сказать, что кофе составил 38% от общего объема продаж. В зависимости от того, что вы хотите выделить на диаграмме, вы можете добавить метки к одной серии, ко всем сериям (всей диаграмме) или к одной точке данных.
Например, на круговой диаграмме ниже без меток данных было бы трудно сказать, что кофе составил 38% от общего объема продаж. В зависимости от того, что вы хотите выделить на диаграмме, вы можете добавить метки к одной серии, ко всем сериям (всей диаграмме) или к одной точке данных.
Добавить метки данных
Вы можете добавить метки данных, чтобы показать значения точек данных из листа Excel на диаграмме.
Этот шаг относится только к Word для Mac: в меню Вид щелкните Макет печати .
Щелкните диаграмму, а затем щелкните значок 9.0433 Дизайн диаграммы вкладка.

Щелкните Добавить элемент диаграммы и выберите Метки данных , а затем выберите расположение для параметра метки данных.
Примечание. Параметры будут различаться в зависимости от типа диаграммы.
Если вы хотите, чтобы метка данных отображалась внутри текстового пузыря, нажмите Выноска данных .
Чтобы метки данных было легче читать, их можно переместить внутрь точек данных или даже за пределы диаграммы. Чтобы переместить метку данных, перетащите ее в нужное место.
Примечание. Если текст внутри меток данных слишком трудно прочитать, измените размер меток данных, щелкнув их, а затем перетащив до нужного размера.

Щелкните Дополнительные параметры меток данных , чтобы изменить внешний вид меток данных.
Измените внешний вид меток данных
Щелкните правой кнопкой мыши любую метку данных и выберите Формат меток данных .
Нажмите Параметры этикетки и ниже Этикетка содержит , выберите нужные параметры.
Изменение текста, отображаемого в метках данных
Щелкните метку данных с текстом, который необходимо изменить, а затем щелкните ее еще раз, чтобы выбрать только эту метку данных.
Выберите существующий текст и введите замещающий текст.
Щелкните в любом месте за пределами метки данных.
Совет: Если вы хотите добавить комментарий к диаграмме или иметь только одну метку данных, вы можете использовать текстовое поле.
Удалить метки данных
Если вы решите, что метки делают вашу диаграмму слишком загроможденной, вы можете удалить некоторые или все из них, щелкнув метки данных и нажав Удалить .
Примечание. При этом удаляются все метки данных из серии данных.
Использовать значения ячеек в качестве меток данных
Вы можете использовать значения ячеек в качестве меток данных для диаграммы.
Щелкните правой кнопкой мыши ряд данных или метку данных, чтобы отобразить дополнительные данные, а затем щелкните Формат меток данных .
Щелкните Параметры метки и в разделе Метка содержит установите флажок Значения из ячеек .






 Включите знак равенства, имя листа, за которым следует восклицательный знак; например, =Лист1!F2
Включите знак равенства, имя листа, за которым следует восклицательный знак; например, =Лист1!F2 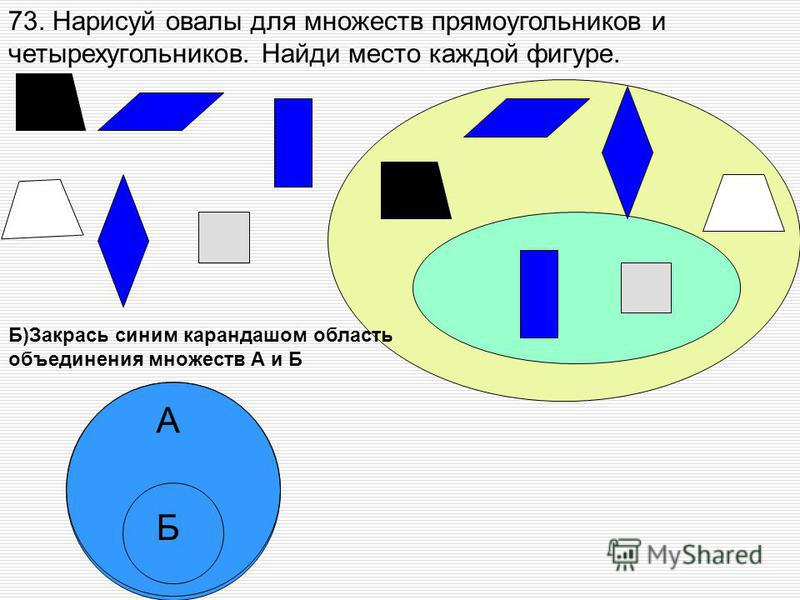
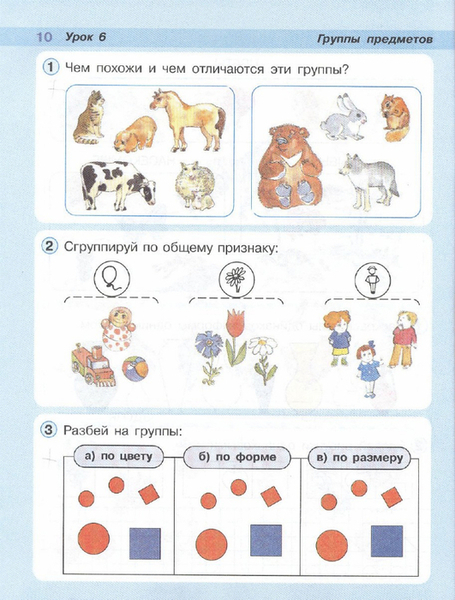

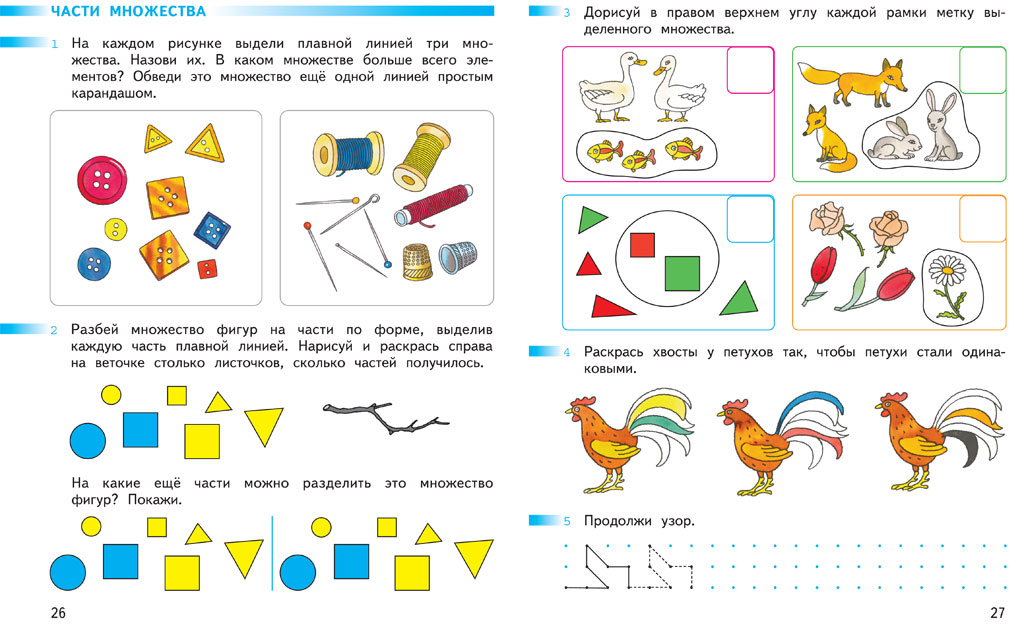
 Простые проценты обычно начисляются, когда период кредитования короткий и часто меньше года. Когда деньги ссужаются или берутся взаймы на более длительный период времени, если проценты выплачиваются (или начисляются) не только на основную сумму, но и на прошлые проценты, тогда мы говорим, что проценты равны 9.0046 составной.
Простые проценты обычно начисляются, когда период кредитования короткий и часто меньше года. Когда деньги ссужаются или берутся взаймы на более длительный период времени, если проценты выплачиваются (или начисляются) не только на основную сумму, но и на прошлые проценты, тогда мы говорим, что проценты равны 9.0046 составной.  2=\$ 233. 28 \nonumber \] 9{5}=\$ 293,87 \номер\]
2=\$ 233. 28 \nonumber \] 9{5}=\$ 293,87 \номер\] {t}\), когда \(n = 1\). 9{t}
{t}\), когда \(n = 1\). 9{t} 

 {n}\) 9{0,07}-1 \\
{n}\) 9{0,07}-1 \\  Это приближение, оно не является точным и исходит из нашего предыдущего решения. Мы подсчитали, что
Это приближение, оно не является точным и исходит из нашего предыдущего решения. Мы подсчитали, что

 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать [latex]\frac{3%}{12}[/latex]= 0,25% в месяц.
Поскольку проценты выплачиваются ежемесячно, каждый месяц мы будем зарабатывать [latex]\frac{3%}{12}[/latex]= 0,25% в месяц. Это ключевое преимущество составляет проценты дают нам.
Это ключевое преимущество составляет проценты дают нам. 18
18 [латекс]г[/латекс]. 9{m+n}[/латекс].
[латекс]г[/латекс]. 9{m+n}[/латекс]. Если проценты по вашему депозиту начисляются ежемесячно, то [latex]k = 12[/latex]. Если оставить депозит на [latex]1[/latex] год, то [latex]m = 12[/latex]. Но если [latex]k = 12[/latex] и вы оставляете залог на [latex]2[/latex] лет, тогда [latex]m = 2*12 = 24[/latex]. Если посмотреть на это с другой стороны, [латекс]м = N\текст{ лет} * к[/латекс].
Если проценты по вашему депозиту начисляются ежемесячно, то [latex]k = 12[/latex]. Если оставить депозит на [latex]1[/latex] год, то [latex]m = 12[/latex]. Но если [latex]k = 12[/latex] и вы оставляете залог на [latex]2[/latex] лет, тогда [latex]m = 2*12 = 24[/latex]. Если посмотреть на это с другой стороны, [латекс]м = N\текст{ лет} * к[/латекс].
 Ставка [latex]r[/latex] в формулах процентов должна быть преобразована из процентов в десятичную форму перед использованием формулы.
Ставка [latex]r[/latex] в формулах процентов должна быть преобразована из процентов в десятичную форму перед использованием формулы.

 Округление 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр.
Округление 0,00012345 до 0,000123 обычно дает «достаточно близкий» ответ, но всегда лучше оставить больше цифр. Для наших целей ответ, который мы получили, округлив до 0,00417, трех значащих цифр, достаточно близок — скидка 5 долларов с 4500 долларов не так уж и плоха. Конечно, сохранение этого четвертого знака после запятой не помешало бы.
Для наших целей ответ, который мы получили, округлив до 0,00417, трех значащих цифр, достаточно близок — скидка 5 долларов с 4500 долларов не так уж и плоха. Конечно, сохранение этого четвертого знака после запятой не помешало бы.




 Например, американский пенни сделан из цинка, покрытого слоем гальванической меди.
Например, американский пенни сделан из цинка, покрытого слоем гальванической меди.
 Ржавление — это непрерывный процесс, который постепенно разрушает предметы и делает их бесполезными. Различные факторы, такие как кислотная среда и соленая вода, могут ускорить процесс ржавления железа.
Ржавление — это непрерывный процесс, который постепенно разрушает предметы и делает их бесполезными. Различные факторы, такие как кислотная среда и соленая вода, могут ускорить процесс ржавления железа.
 Они используют фотосинтез для преобразования солнечного света, воды, углекислого газа в кислород и простой сахар.
Они используют фотосинтез для преобразования солнечного света, воды, углекислого газа в кислород и простой сахар. Хорошим примером может служить закалка стали для изготовления лезвия ножа.
Хорошим примером может служить закалка стали для изготовления лезвия ножа. Это означает, что вы не можете превратить элемент в другой элемент или разложить его обычными химическими средствами, такими как электролиз, нагревание или реакция. Кислород, азот, золото и серебро являются примерами чистых веществ.
Это означает, что вы не можете превратить элемент в другой элемент или разложить его обычными химическими средствами, такими как электролиз, нагревание или реакция. Кислород, азот, золото и серебро являются примерами чистых веществ.
 Ваши мышечные клетки выполняют анаэробное дыхание всякий раз, когда вы исчерпываете поступающий к ним кислород, например, во время интенсивных или длительных упражнений. Анаэробное дыхание дрожжами и бактериями используется для брожения с получением этанола, углекислого газа и других химических веществ, которые делают сыр, вино, пиво, йогурт, хлеб и многие другие распространенные продукты.
Ваши мышечные клетки выполняют анаэробное дыхание всякий раз, когда вы исчерпываете поступающий к ним кислород, например, во время интенсивных или длительных упражнений. Анаэробное дыхание дрожжами и бактериями используется для брожения с получением этанола, углекислого газа и других химических веществ, которые делают сыр, вино, пиво, йогурт, хлеб и многие другие распространенные продукты. Это пример реакции окисления . Другие повседневные примеры включают образование зелени на меди и потускнение серебра.
Это пример реакции окисления . Другие повседневные примеры включают образование зелени на меди и потускнение серебра. Спонтанные окислительно — восстановительные реакции протекают в гальванических элементах , в то время как неспонтанные химические реакции принимают место в электролизерах .
Спонтанные окислительно — восстановительные реакции протекают в гальванических элементах , в то время как неспонтанные химические реакции принимают место в электролизерах .
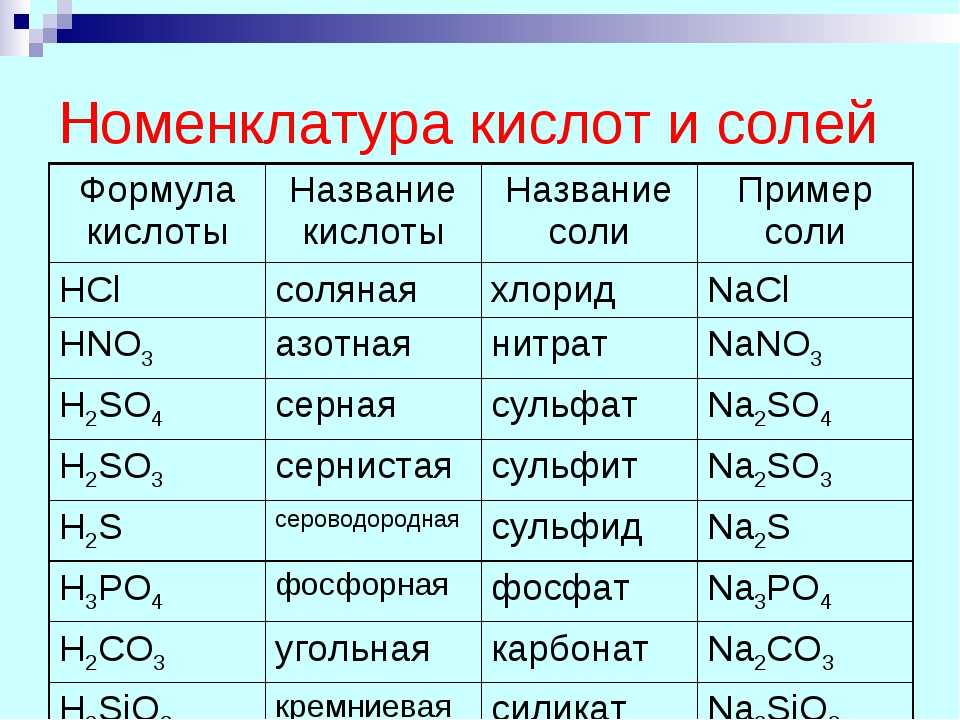 Когда вы обжариваете мясо или выпечку, реакция Майяра между аминокислотами и сахарами дает коричневый цвет и желательный вкус.
Когда вы обжариваете мясо или выпечку, реакция Майяра между аминокислотами и сахарами дает коричневый цвет и желательный вкус. Представьте, что вы способны сжаться в миллиард раз, как человек-муравей, что позволяет вам увидеть то, что в противном случае осталось бы невидимым. Химия сложна, потому что вы должны соединить макро и микро миры в общую концепцию и посмотреть, как они связаны. VR делает это очень визуально. Интерактивные эксперименты с атомами и молекулами Мы не подражаем классической лаборатории, а предоставляем интерактивные ур
Представьте, что вы способны сжаться в миллиард раз, как человек-муравей, что позволяет вам увидеть то, что в противном случае осталось бы невидимым. Химия сложна, потому что вы должны соединить макро и микро миры в общую концепцию и посмотреть, как они связаны. VR делает это очень визуально. Интерактивные эксперименты с атомами и молекулами Мы не подражаем классической лаборатории, а предоставляем интерактивные ур


 Все, что мы слышим, видим, обоняем, пробуем на вкус и осязаем, связано с химией и химическими веществами (материей). Слух, зрение, вкус и осязание включают в себя сложную серию химических реакций и взаимодействий в нашем теле. Многие изменения, которые мы наблюдаем в окружающем мире, вызваны химическими реакциями. Химия не ограничивается стаканами и лабораториями. Он окружает нас повсюду, и чем лучше мы знаем химию, тем лучше мы познаем наш мир. Химия присутствует во всех аспектах жизни, и несколько примеров химии в повседневной жизни:0004
Все, что мы слышим, видим, обоняем, пробуем на вкус и осязаем, связано с химией и химическими веществами (материей). Слух, зрение, вкус и осязание включают в себя сложную серию химических реакций и взаимодействий в нашем теле. Многие изменения, которые мы наблюдаем в окружающем мире, вызваны химическими реакциями. Химия не ограничивается стаканами и лабораториями. Он окружает нас повсюду, и чем лучше мы знаем химию, тем лучше мы познаем наш мир. Химия присутствует во всех аспектах жизни, и несколько примеров химии в повседневной жизни:0004
 Это означает роль химии в нашей повседневной жизни.
Это означает роль химии в нашей повседневной жизни.

 {1-k}}{1-k}+C, k=2,3,4,…
\end{array} \right.
\]
{1-k}}{1-k}+C, k=2,3,4,…
\end{array} \right.
\]
 4-1}.
\]
4-1}.
\]



 Необходимо доопределить функцию
и найти её значение в каждой
токе-иррациональное число.
Необходимо доопределить функцию
и найти её значение в каждой
токе-иррациональное число.
 Логарифмической называют функцию,
заданную формулой
Логарифмической называют функцию,
заданную формулой


 Теорема
Вейерштрасса. Для y=f (x) достигает в каких-то точках
отрезка [a, b] своего наименьшего значения
A и своего наибольшего значения B, где
максимальное значение функции равно B
и минимальное равно A, значения аргумента
функции в этих точках принадлежат
данному отрезку.
Теорема
Вейерштрасса. Для y=f (x) достигает в каких-то точках
отрезка [a, b] своего наименьшего значения
A и своего наибольшего значения B, где
максимальное значение функции равно B
и минимальное равно A, значения аргумента
функции в этих точках принадлежат
данному отрезку.

 х, где а> 0 и отлично от 1,
является трансцендентной функцией.
х, где а> 0 и отлично от 1,
является трансцендентной функцией. Значит, одно и тоже значение c
эти функции принимают в бесконечном
ряде различных точек. Предположим, что
эти функции алгебраические, то есть
каждая из них в некотором промежутке
(область определения функции) удовлетворяет
некотооому алгебраическому уравнению
P (x, y)=0. Степень алгебраического уравнения
относительно переменной у определяется
степенью вхождения переменной у в запись
уравнения — это конкретное целое число.
Значит, одно и тоже значение c
эти функции принимают в бесконечном
ряде различных точек. Предположим, что
эти функции алгебраические, то есть
каждая из них в некотором промежутке
(область определения функции) удовлетворяет
некотооому алгебраическому уравнению
P (x, y)=0. Степень алгебраического уравнения
относительно переменной у определяется
степенью вхождения переменной у в запись
уравнения — это конкретное целое число.
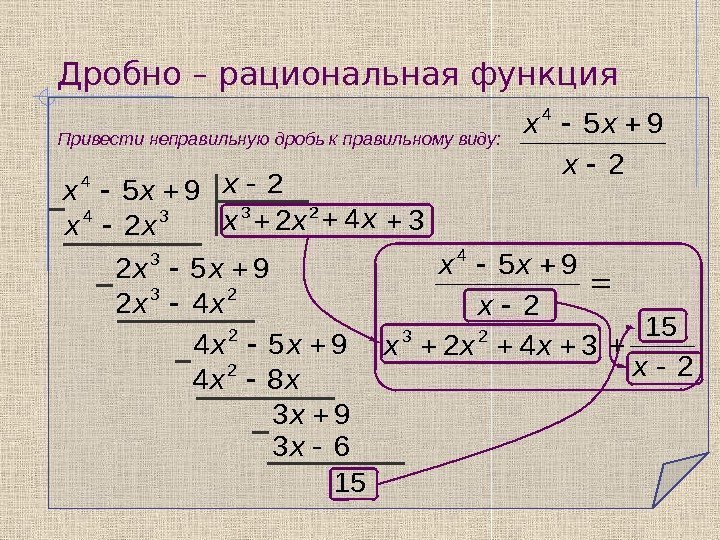


 достигается за исключением нуля: по мере того, как 𝑥 становится все больше в
величина, выход становится все меньше; однако выход никогда не может достичь
нуль. Следовательно, диапазон функции равен ℝ−{0}.
достигается за исключением нуля: по мере того, как 𝑥 становится все больше в
величина, выход становится все меньше; однако выход никогда не может достичь
нуль. Следовательно, диапазон функции равен ℝ−{0}. Однако мы должны также проверить это алгебраически.
Однако мы должны также проверить это алгебраически.

 Чтобы упростить этот процесс, полезно разделить верхнюю и нижнюю часть
используйте 𝑥, чтобы получить
𝑓(𝑥)=2+4+.
Чтобы упростить этот процесс, полезно разделить верхнюю и нижнюю часть
используйте 𝑥, чтобы получить
𝑓(𝑥)=2+4+. Из
функции, записанной в таком виде, мы можем видеть, что есть две точки, в которых функция
не определено: когда 𝑥−3=0 и когда 𝑥+4=0. Это означает
что функция не определена, когда 𝑥=−4 и 𝑥=3. Следовательно, область определения функции — это все действительные числа, кроме −4 и 3,
обозначается ℝ−{−4,3}.
Из
функции, записанной в таком виде, мы можем видеть, что есть две точки, в которых функция
не определено: когда 𝑥−3=0 и когда 𝑥+4=0. Это означает
что функция не определена, когда 𝑥=−4 и 𝑥=3. Следовательно, область определения функции — это все действительные числа, кроме −4 и 3,
обозначается ℝ−{−4,3}. Следовательно, для нахождения области необходимо найти нули уравнения
10𝑥+70𝑥=0. Чтобы решить это, мы можем факторизовать
из 𝑥 получить 𝑥10𝑥+70=0.
Следовательно, для нахождения области необходимо найти нули уравнения
10𝑥+70𝑥=0. Чтобы решить это, мы можем факторизовать
из 𝑥 получить 𝑥10𝑥+70=0.

 д.
д. 
 д.)
д.)  Это дает единственное решение x = 0.
Это дает единственное решение x = 0. Для (x + 3)(x – 3) = 0 два решения равны x = -3 и x = 3.
Для (x + 3)(x – 3) = 0 два решения равны x = -3 и x = 3. Мы замечаем, что мы можем выделить GCF (наибольший общий множитель) x, а затем перейти от этого:
Мы замечаем, что мы можем выделить GCF (наибольший общий множитель) x, а затем перейти от этого:
 Для x (x + 1) (x – 1) (x + 2) = 0 четыре решения: x = -2, x = -1, x = 0 , и x = 1.
Для x (x + 1) (x – 1) (x + 2) = 0 четыре решения: x = -2, x = -1, x = 0 , и x = 1.

 Обратите внимание, что знаменатель подкоренной дроби не может быть равен нулю. Итак, х не равен нулю.
Обратите внимание, что знаменатель подкоренной дроби не может быть равен нулю. Итак, х не равен нулю. Мы используем стандартные шаги, чтобы найти обратную функцию:
Мы используем стандартные шаги, чтобы найти обратную функцию:
 kz — уникальные вещи с доставкой на дом
kz — уникальные вещи с доставкой на дом Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
Это может показаться фантастическим, но мы объясним это без жаргона! Давай сделаем это.
 com/calculator/exponent/what-is-3-to-the-12th-power/.
com/calculator/exponent/what-is-3-to-the-12th-power/. для расчета тока, мощности, сопротивления или напряжения.
*Обновлено 8 января 2011 г., чтобы принять/изменить запятые на точки для тех, кто использует запятые в качестве десятичных разделителей.
для расчета тока, мощности, сопротивления или напряжения.
*Обновлено 8 января 2011 г., чтобы принять/изменить запятые на точки для тех, кто использует запятые в качестве десятичных разделителей.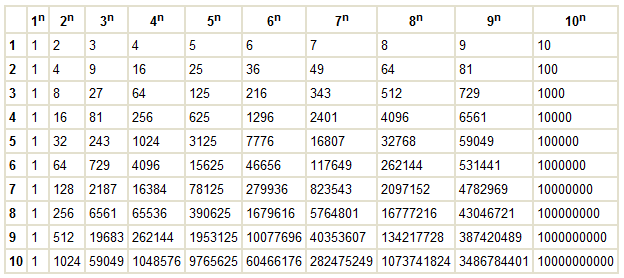

 По сути, монетка является очень важным атрибутом каждого судьи. Зачастую наличие эффективного подкидывания монетки является хорошим фундаментом для победы команды, которая угадает правильную сторону.
По сути, монетка является очень важным атрибутом каждого судьи. Зачастую наличие эффективного подкидывания монетки является хорошим фундаментом для победы команды, которая угадает правильную сторону.
 То есть, если, например, 5 раз подряд выпала решка, то создается впечатление, что вероятность выпадения орла в 6 раз выше, хотя на самом деле она равна 50%, так как сами события между собой совершенно независимы.
То есть, если, например, 5 раз подряд выпала решка, то создается впечатление, что вероятность выпадения орла в 6 раз выше, хотя на самом деле она равна 50%, так как сами события между собой совершенно независимы.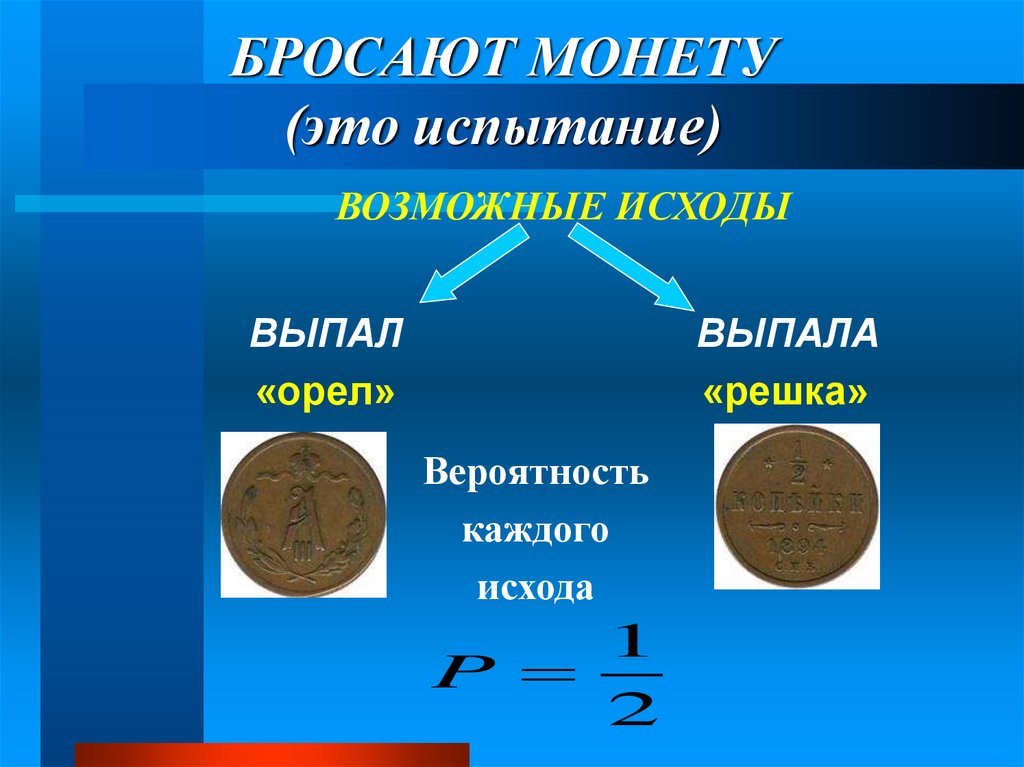

 Бесплатный онлайн сервис бросить монетку решит вашу дилемму в онлайн режиме.
Бесплатный онлайн сервис бросить монетку решит вашу дилемму в онлайн режиме. Все кажется неопределенным до момента подкидывания монетки в воздух или гадание на да или нет. В туже секунду вы начнете мысленно надеяться на выпадение определенной стороны, которая будет верной. После осознания собственного внутреннего выбора смотреть результат гадания на да нет не обязательно, ведь для себя вы уже все решили.
Все кажется неопределенным до момента подкидывания монетки в воздух или гадание на да или нет. В туже секунду вы начнете мысленно надеяться на выпадение определенной стороны, которая будет верной. После осознания собственного внутреннего выбора смотреть результат гадания на да нет не обязательно, ведь для себя вы уже все решили.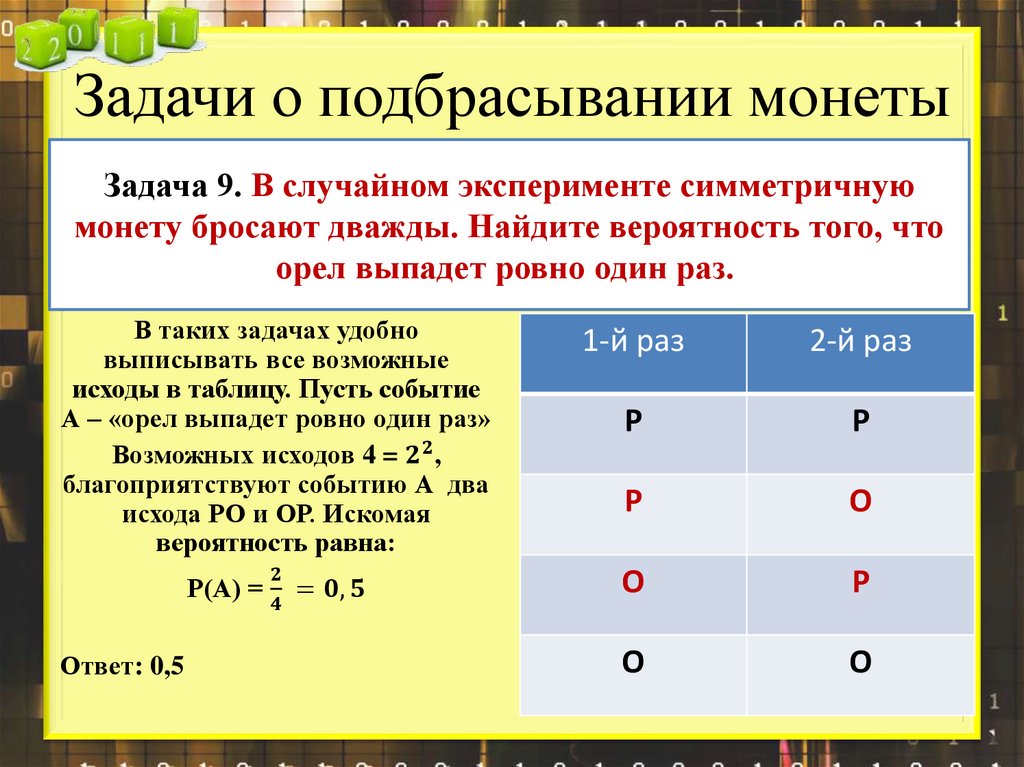
 com. Наш онлайн генератор бросить монетку бесплатно поможет взять верх над ситуацией и выбрать только один исход, правильный. Созданный нами рандом да нет точно поможет вам!
com. Наш онлайн генератор бросить монетку бесплатно поможет взять верх над ситуацией и выбрать только один исход, правильный. Созданный нами рандом да нет точно поможет вам!
 Затем будет показан результат подбрасывания монеты.
Затем будет показан результат подбрасывания монеты. Чем больше вы сможете сделать одинаковых бросков, тем выше будет ваш показатель удачи.
Чем больше вы сможете сделать одинаковых бросков, тем выше будет ваш показатель удачи.



 ..
.. Найди правильный ответ.
Найди правильный ответ. Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов
 Представим целое число в виде обратной дроби7 это 1/7. Умножим дроби 15/4 и 1/7. Перемножим числители 15*1 = 15, перемножим знаменатели4*7 = 28
Представим целое число в виде обратной дроби7 это 1/7. Умножим дроби 15/4 и 1/7. Перемножим числители 15*1 = 15, перемножим знаменатели4*7 = 28 8
8


 Перезаписывание этих входов.
Перезаписывание этих входов.


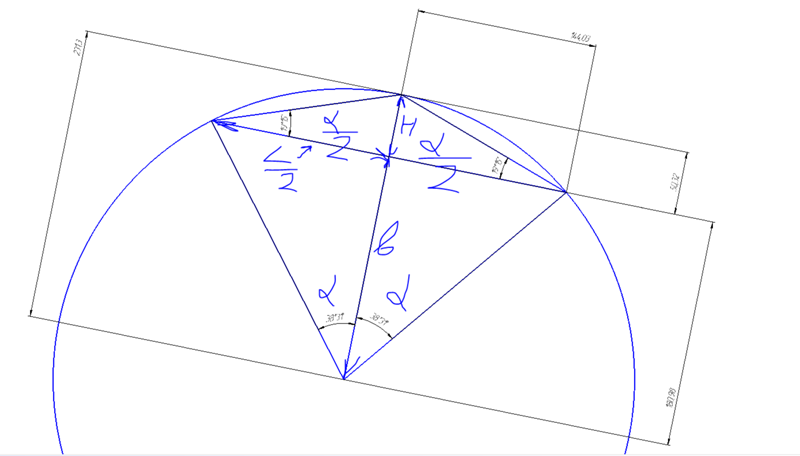
 Полная дуга полукруга всегда равна 180 ° (эквивалентно π радиан или пол-оборота).
Полная дуга полукруга всегда равна 180 ° (эквивалентно π радиан или пол-оборота).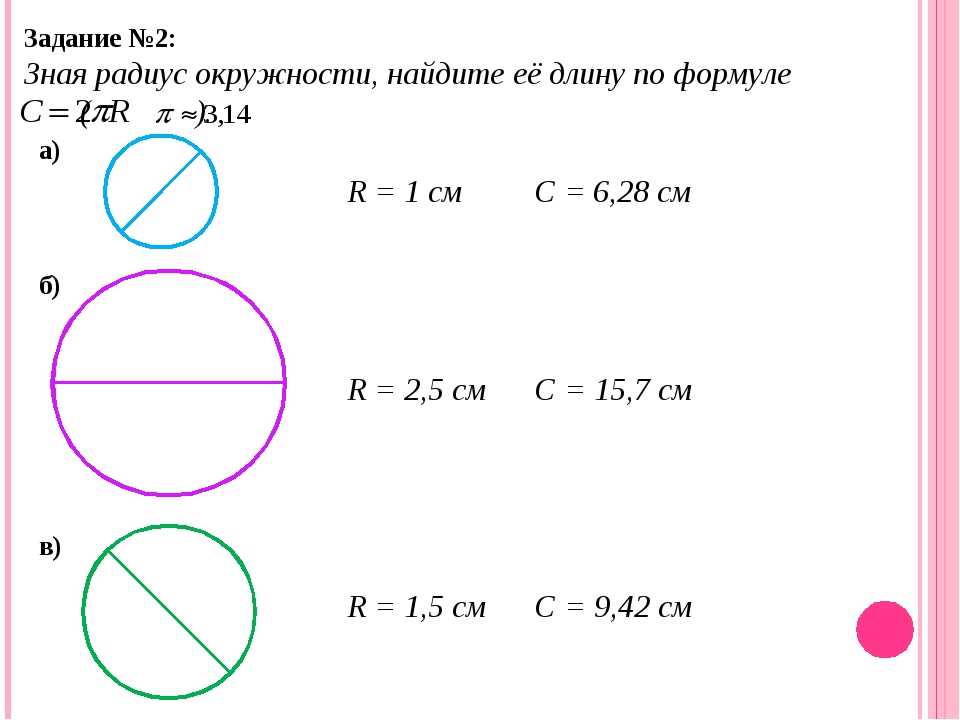 ⓘ Радиус кривой [RC]
ⓘ Радиус кривой [RC]
 Преобразование входов в базовый блок
Преобразование входов в базовый блок 578/Радиус кривой)*(pi/180)
578/Радиус кривой)*(pi/180)
 578/(Степень изгиба*(180/pi))
578/(Степень изгиба*(180/pi))
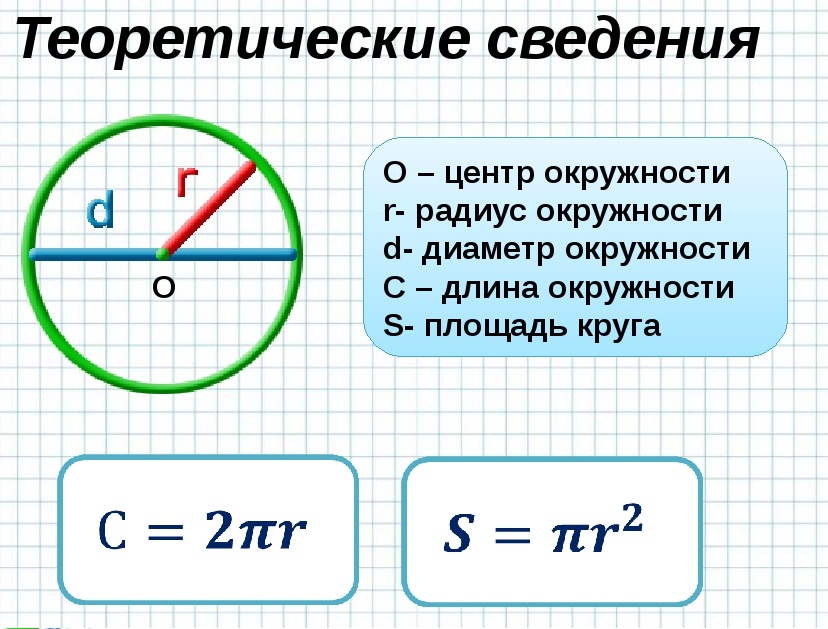
 Если вы можете точно измерить время, вы можете вычислить
угол точно.
Используйте следующую пропорцию:
Если вы можете точно измерить время, вы можете вычислить
угол точно.
Используйте следующую пропорцию:.jpg)

 У меня нет линейки с десятыми долями дюйма, поэтому я использовал 16 38/64 (16,594″). Я отрегулировал свой трамблер по радиусу и начертил круг на нижней стороне стола (вы можете видеть это на картинке выше).
У меня нет линейки с десятыми долями дюйма, поэтому я использовал 16 38/64 (16,594″). Я отрегулировал свой трамблер по радиусу и начертил круг на нижней стороне стола (вы можете видеть это на картинке выше).
 д. Ноль тоже относится к четным числам.
д. Ноль тоже относится к четным числам.


 Признаки делимости.
Признаки делимости.
 Это и есть признаки делимости натуральных чисел
Это и есть признаки делимости натуральных чисел
 То есть, если натуральное число не делится нацело ни на что, кроме как на единицу и на само это число, то такое число – простое.
То есть, если натуральное число не делится нацело ни на что, кроме как на единицу и на само это число, то такое число – простое. В этом вам помогут признаки делимости чисел.
В этом вам помогут признаки делимости чисел.


 k — 1,\), где \(k \ge 1,\) всегда делится на \(9\) и, следовательно, сумма цифр числа в этом случае должна делиться на \(9\), так что само число делится на \(9\), тем самым доказывая признак делимости \(9\) .
k — 1,\), где \(k \ge 1,\) всегда делится на \(9\) и, следовательно, сумма цифр числа в этом случае должна делиться на \(9\), так что само число делится на \(9\), тем самым доказывая признак делимости \(9\) .  \(_\квадрат\)
\(_\квадрат\) k,\) где \(k \ge 3,\) всегда делится на \(125\) и, следовательно, если разряды сотен, десятков и единиц числа, взятые в таком порядке, делятся на \(125\), то число также делится на \(125\). 9k \equiv -1 \bmod{11} \text{ если } k \text{ нечетное}\big)\]
k,\) где \(k \ge 3,\) всегда делится на \(125\) и, следовательно, если разряды сотен, десятков и единиц числа, взятые в таком порядке, делятся на \(125\), то число также делится на \(125\). 9k \equiv -1 \bmod{11} \text{ если } k \text{ нечетное}\big)\] \конец{выравнивание}\]
Следовательно, \(N \equiv 0 \pmod{11}\), если \(\left( a_{n-1} + a_{n-3} + \cdots + a_2 + a_0 \right) — \left( a_n + a_{n-2} + \cdots + a_3 + a_1 \right) \equiv 0 \pmod{11},\) при условии, что \(n\) нечетно.
\конец{выравнивание}\]
Следовательно, \(N \equiv 0 \pmod{11}\), если \(\left( a_{n-1} + a_{n-3} + \cdots + a_2 + a_0 \right) — \left( a_n + a_{n-2} + \cdots + a_3 + a_1 \right) \equiv 0 \pmod{11},\) при условии, что \(n\) нечетно. \(_\квадрат\)
\(_\квадрат\)

 Например, возьмем число 753.
Например, возьмем число 753. , который делится на 7. Следовательно, 343 также делится на 7.
, который делится на 7. Следовательно, 343 также делится на 7.
 е. оканчивается на 0, оно является четным числом и делится на 2.
е. оканчивается на 0, оно является четным числом и делится на 2.


