| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.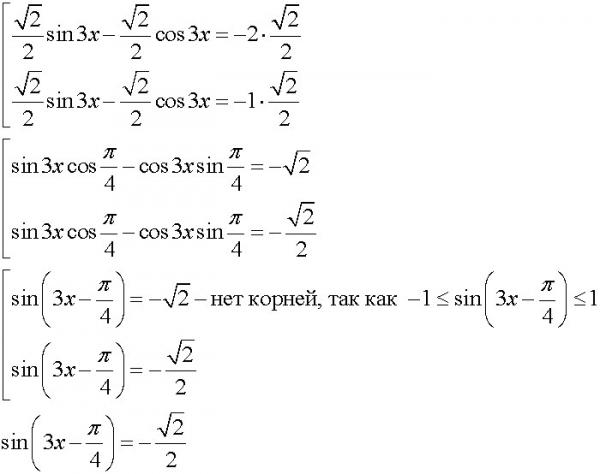 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.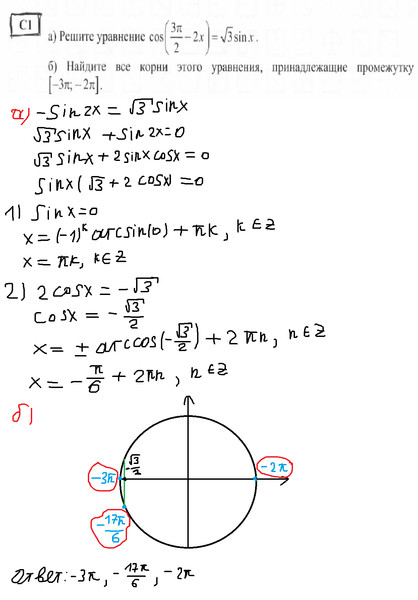 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град.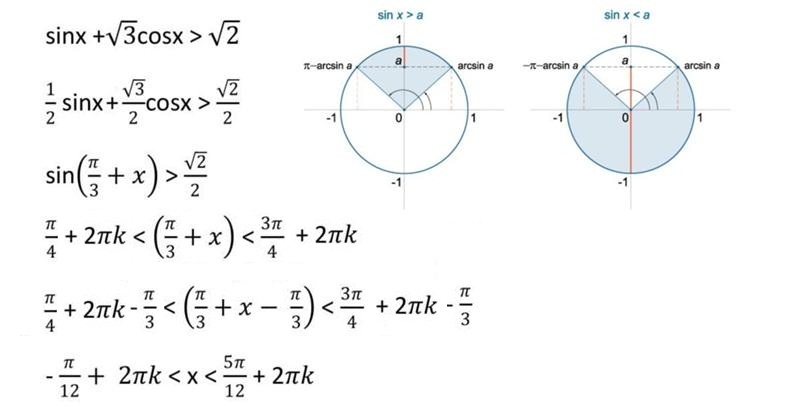 ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.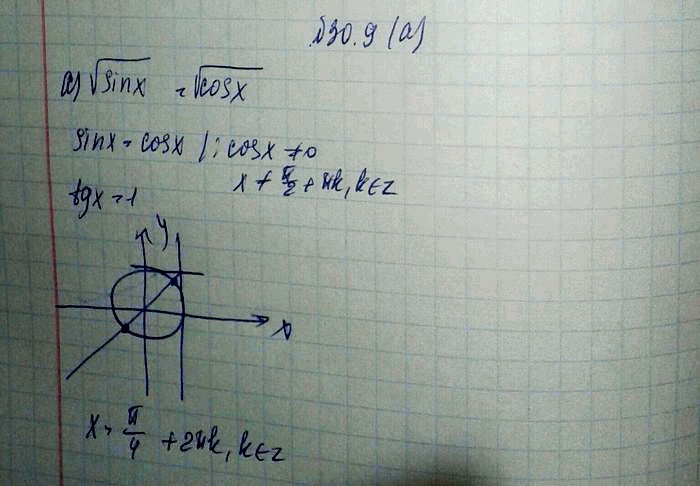 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.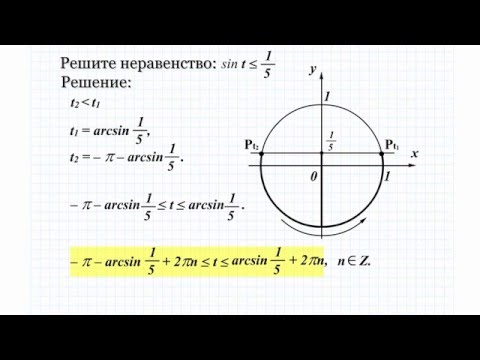 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найти точное значение | грех(45) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти точное значение | грех(30 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найти точное значение | грех(60 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найти точное значение | загар (30 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найти точное значение | угловой синус(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти точное значение | грех(пи/6) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Найти точное значение | cos(pi/4) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найти точное значение | грех(45 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти точное значение | грех(пи/3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти точное значение | арктан(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найти точное значение | cos(45 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найти точное значение | cos(30 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найти точное значение | желтовато-коричневый(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найти точное значение | csc(45 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | загар (60 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найти точное значение | сек(30 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найти точное значение | cos(60 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найти точное значение | соз(150) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найти точное значение | грех(60) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найти точное значение | cos(pi/2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти точное значение | загар (45 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найти точное значение | csc(60 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найти точное значение | сек(45 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найти точное значение | csc(30 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найти точное значение | грех(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найти точное значение | грех(120) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найти точное значение | соз(90) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Преобразовать из радианов в градусы | пи/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найти точное значение | желтовато-коричневый(30) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Преобразование градусов в радианы 92 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Преобразовать из радианов в градусы | пи/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найти точное значение | детская кроватка(30 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найти точное значение | арккос(-1) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | арктан(0) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найти точное значение | детская кроватка(60 градусов) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразование градусов в радианы | 30 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Преобразовать из радианов в градусы | (2 шт.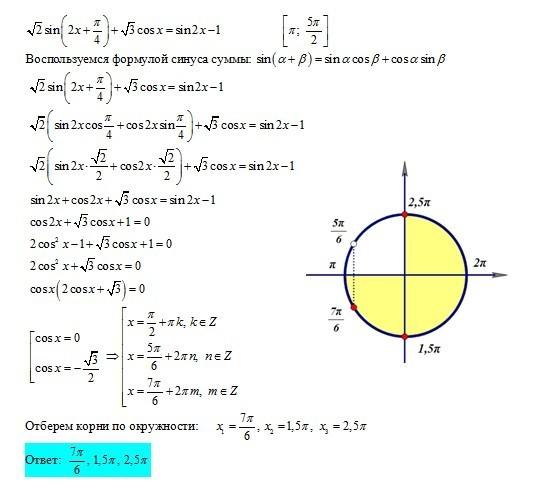 Первообразная cos 2x sin 2x: Mathway | Популярные задачи 2x. — вопрос №1650981 — Учеба и наука Ответы
|
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . Дослідити на парність функцію: Приклади на парність та непарність функційПриклади на парність та непарність функційПродовжуємо цикл публікацій із ЗНО підготовки на властивості елементарних функцій. Сьогодні розберемо приклади на парність та непарність функцій, формули перевірки парності та непарності, далі вивчатимемо періодичність тригонометричних функцій. Завдання досить прості, тому Ви швидко зможете засвоїти основні властивості функцій та алгоритми обчислень подібних завдань. Розділ 22. Елементарні функції та їх властивості Приклад 22.12 Указати парну функцію.
Приклад 22.13 Яка з наведених функцій є непарною?
Приклад 22.14 Функція f(x) — парна, а функція g(x) — непарна. f(7)=-11, g(5)=-2. Обчислити 2f(-7)-3g(-5).
Приклад 22.15 На рисунку зображено графік функції y=f(x), визначеної на проміжку [-4;4].
Приклад 22.16 За ескізом графіка y=ax+b вказати знаки параметрів a і b.
Приклад 22.39 Установити відповідність між функціями (1–4) та їх парністю (А–Д).
Розв’язування: Функція y=y(x) парна, якщо y(-x)=y(x) (графік симетричний відносно осі Oy). 2. y(x)=x3+tg(x). 3. y(x)=x4-sin(x). 4. y(x)=x5·sin(x).
Приклад 22.52 За якого найбільшого значення параметра a функція буде непарною? Знання властивостей функцій потрібні для швидкого їх дослідження, що перевіряється в шкільній практиці та продовжують вивчати у ВУЗах. Вступні тести є перехідним етапом, але через обмеженість часу Ви маєте вивчити великий об’єм матеріалу, тому починайти готуватися завчасно.
Числові функції. Їх властивості та графіки Їх властивості та графікиПри вивченні множин ми бачили, що можна задати зв’язок між множинами, тобто поставити відповідність між елементами двох множин. Така залежність, при якій кожному елементу з однієї множини (множини Х) ставиться у відповідність єдиний елемент з другої множини (множини Y), називається функцією. Зазначимо, що функція не є взаємно однозначною відповідністю: деякому елементу з множини Y може відповідати декілька елементів з множини X. Найчастіше позначається функція записом f, f(x),y, y(x). Існує декілька способів задання функції. Формульний. Наприклад, y=2x+4. Перевагою такого способу є те, що можна знайти значення функції в кожній точці. Недоліком є те, що потрібно час на обчислення, відсутня наочність. Табличний. Задається таблицею, де прописується пара x,y.Перевагою такого способу є те, що дуже швидко знаходиться значення функції в певних точках. Недоліком є те, що не для всіх чисел задано значення.
Графічний. Словесний. Застосовується тоді, коли функцію важко задати іншими способами. Чим характеризується кожна функція? По-перше, можна вказати відповідні множини Х та У. Множина Х називається областю визначення функції і позначається D(y), множина Y називається областю значень функції і позначається E(Y). Приклад 1. Задано функцію y=4+x2. Знайти область визначення та область значень функції. Розв’язання. Оскільки замість х ми можемо поставити будь-яке дійсне число, то областю визначення функції є всі дійсні числа. Тобто D(y): x∈R (або x∈(-∞;+∞). Оскільки x2 може приймати значення від 0 до +∞, то 4+x2 може приймати значення від 4 до +∞. Тобто E(y): y∈[4;+∞). Щоб отримати значення функції в певній точці, достатньо підставити у рівняння функції замість невідомої значення
абсциси (х) точки. Приклад 2. Знайти значення функції y=3x2+4x-2 в точці 5. Розв’язання. у(5)= 3⋅52+4⋅5-2=3⋅25+20-2=75+20-2=93. Приклад 3. Перевірити, чи належать точки (2;12),(3;38) графіку функції y=4x2+2x-4. Розв’язання. 1) Підставимо замість х число 2, замість у число 12. Отримаємо 12=4⋅22+2⋅2-4, тобто 12=16. Рівність не вірна,
тому точка (2;12) не належить графіку функції. Одним зі способів задання функції є графічний, коли показано залежність між множинами. Властивості функції. Якщо більшому значенню аргументу відповідає більше значення функції (якщо x1<x2, то y1<y2), то така функція називається зростаючою. Якщо ж навпаки, більшому значенню аргументу відповідає менше значення функції (якщо x1<x2, то y1>y2), то така функція називається спадною. Графік зростаючої функції виглядає як підйом у гору, а спадної — як спуск з гори. Функція називається парною, якщо для будь-якого х з її області визначення f(-x)=f(x).
Якщо значення функції при протилежних значення аргументу співпадає, то така функція називається парною. Прикладом парної функції є y=x2 (y(-x)=(-x)2=x2=y(x)). Якщо ж протилежним значенням аргумента відповідають протилежні значення функції, тобто f(-x)=-f(x), то така функція називається непарною. Функція називається непарною, якщо для будь-якого х з її області визначення f(-x)=-f(x) Прикладом непарної функції є y=x3 (y(-x)=(-x)3=-x3=-y(x)). Графік непарної функції симетричний відносно початку координат. Зверніть увагу, що є також функції, які не є ні парними, ні непарними. Прикладом такої функції є y=x2+4х (y(-x)=(-x)2+4⋅(-х)=x2-4х. Таке значення не співпадає ні з y(x), ні з -y(x). Приклад 4. Дослідити функції на парність та непарність. 1) y=x4+3x2+5; 2) y=x3-2x; 3) y=x2+4x. Розв’язання. 1) y(-x)=(-x)4+3(-x)2+5=x4+3x2+5=y(x). Функція парна. Приклад 5. Дослідити функції на парність та непарність за її графіком. Розв’язання. 1) Оскільки графік функції симетричний відносно осі ОУ, то функція парна. 2) Оскільки графік функції не симетричний ні відносно осі ОУ, ні відносно початку координат, то функція ні парна, ні непарна. 3) Оскільки графік функції симетричний відносно початку координат, то функція непарна. Определение функции четности и интуиция, характеристическая функция множества.Мы определяем $\tilde x\in\mathbb{Z}$ и $\tilde x_i\in\mathbb{Z_2}$ (это битовое значение), и $\tilde x_i = 1-2x_i$ ясно представлена следующая функция: \begin{align*} f(x) = \begin{случаи} 1 &\text{если $x$ = 0}\\ -1 &\text{если $x$ = 1} \end{cases}\end{align*} Когда $x$ (входной бит) равен $0$, функция возвращает $1$, иначе, если $x$ равно $1$, функция возвращает $-1$ . Заглавная буква «пи» обозначает умножение последовательных значений. Следовательно, мы перемножаем вместе все четности. А поскольку $f(x)$ возвращает либо $1$, либо $-1$, то $P(\tilde x)$ возвращает либо значение $-1$, либо значение $1$. Процесс $P$ является итеративным, и значение $-1$ никогда не изменяется, если последующая четность также не равна $-1$ (тогда она меняет свой знак), эта четность будет переворачиваться столько раз, сколько единиц в таблице. бинарное расширение ($\tilde x$) и сохранение конечного состояния при $i=N-1$. Конечное состояние в основном зависит от количества $1$ в двоичном расширении. Короче говоря, каждый раз, когда $\tilde x_i=1$, произведение будет менять свой знак, но когда $\tilde x_i=0$, произведение никак не повлияет на результат. Эти два ряда действий легко понять, когда $x\cdot -1=-x$ и $x\cdot 1=x$. то есть: $$+\cdot+ = +$$ $$+\cdot- = -$$ $$-\cdot+ = -$$ $$-\cdot- = +$$ Из приведенных выше рассуждений мы можем вывести некоторые факты:
Примеры: $$P(2_{10}) = P(10_2) = -1$$ $$P(13_{10}) = P(1101_2) = -1$$ $$P(27_{10}) = P(11011_2) = 1$$ $$P(60_{10}) = P(111100_2) = 1$$ Другие факты: Длина бита сама по себе не влияет на четность. Ответы: 1) Функция, которая возвращает младший (самый правый) бит аргумента. $$P(00_2) = 1$$ $$P(01_2) = -1$$ $$P(10_2) = -1$$ $$P(11_2) = 1$$ Есть два возможных входа, при которых возвращается $1$: $0$ и $3_{10}$. 2) Функция, возвращающая k-нумерованный бит аргумента, где k меньше n. Я не уверен, что вы имеете в виду под k-нумерованным битом аргумента. Предполагая, что вы имеете в виду битовую длину аргумента, это не влияет на выходную четность. 3) const f(x) = 1 Функция является четной только тогда, когда $\tilde x = 0$ или в двоичном представлении $\tilde x$ есть четное число $1$. 4) const f(x) = 0 $0=$ паритет $1$ 5) «Характеристическая функция множества мощности 5» Предположим, вы имеете в виду, что паритет $1$ четный, тогда $5$ четный. 6) f(x)=1, только если x имеет нечетное количество единиц при записи в двоичном формате False, $P(\tilde x)=-1$, если число единиц нечетное. 7) f(x)=1, только если x имеет четное число единиц при записи в двоичном формате Верно, $P(\tilde x)=1$, если число единиц четное. Определение, формула, принцип работы и примерыЧто такое паритет пут-колл? Термин «паритет пут-колл» относится к принципу, определяющему взаимосвязь между ценой европейских опционов пут и колл одного и того же класса. Проще говоря, эта концепция подчеркивает согласованность этих же классов. Опционы пут и колл должны иметь одинаковый базовый актив, цену исполнения и дату экспирации, чтобы быть в одном классе. Основные выводы
Паритет пут-коллПонимание четности пут-колл Как отмечалось выше, паритет пут-колл — это концепция, применимая к европейским опционам. Эти опционы относятся к одному классу, то есть у них есть базовый актив, цена исполнения и дата экспирации. Паритет пут-колл утверждает, что одновременное владение коротким европейским путом и длинным европейским коллом того же класса принесет такую же прибыль, как и владение одним форвардным контрактом на тот же базовый актив с тем же сроком действия и форвардной ценой, равной страйку опциона. цена. Если цены опционов пут и колл расходятся так, что это соотношение не сохраняется, существует возможность арбитража. Это означает, что опытные трейдеры теоретически могут получать безрисковую прибыль. Такие возможности редки и недолговечны на ликвидных рынках. Уравнение, выражающее паритет пут-колл: С + п В ( Икс ) «=» п + С где: С «=» Цена европейского колл-опциона п В ( Икс ) «=» Текущая стоимость цены исполнения (x), со скидкой от стоимости по истечении срока действия дата по безрисковой ставке п «=» Цена европейского пута С «=» Спотовая цена или текущая рыночная стоимость базового актива \begin{aligned}&C + PV(x) = P + S \\&\textbf{где:} \\&C = \text{Цена европейского колл-опциона} \\&PV(x) = \text{Текущая стоимость от цены исполнения (x),} \\&\text{дисконтировано от значения на момент экспирации} \\&\text{дата по безрисковой ставке} \\ &P = \text{Цена европейского пут} \\&S = \text{Спотовая цена или текущая рыночная стоимость} \\&\text{базового актива} \\\end{aligned} C+PV(x)=P+S, где:C=Цена европейского колл-опционаPV(x)=Текущая стоимость цены исполнения (x), дисконтированная от стоимости на дату экспирации по безрисковой ставкеP=Цена европейский пут=цена спот или текущая рыночная стоимость базового актива Концепция паритета пут-колл была введена экономистом Хансом Р. Особые указанияКогда одна сторона уравнения паритета пут-колл больше другой, это представляет собой возможность арбитража. Вы можете продать более дорогую часть уравнения и купить более дешевую, чтобы получить во всех смыслах безрисковую прибыль. На практике это означает продажу пут, короткую продажу акций, покупку колла и покупку безрискового актива (например, TIPS). На самом деле возможности для арбитража недолговечны и их трудно найти. Кроме того, маржа, которую они предлагают, может быть настолько незначительной, что для того, чтобы воспользоваться ими, потребуется огромный капитал. Паритет пут-колл и арбитраж На двух графиках выше ось y- представляет стоимость портфеля, а не прибыль или убыток, потому что мы предполагаем, что трейдеры раздают опционы. Но это не так, и цены европейских опционов пут и колл в конечном итоге регулируются паритетом пут-колл. С + п В ( Икс ) «=» п + С \begin{выровнено}&C + PV(x) = P + S \\\end{выровнено} C+PV(x)=P+S Предположим, что безрисковая ставка составляет 4%, а акции TCKR торгуются по 10 долларов. Давайте продолжим игнорировать комиссии за транзакции и предположим, что TCKR не выплачивает дивиденды. Для опционов TCKR со сроком действия один год и ценой исполнения 15 долларов мы имеем: С + ( 15 ÷ 1,04 ) «=» п + 10 4,42 «=» п − С \begin{выровнено}&C + ( 15 \div 1.04 ) = P + 10 \\&4.42 = P — C \\\end{выровнено}
С+(15÷1,04)=Р+104,42=Р-С На этом гипотетическом рынке путы TCKR должны торговаться с премией в 4,42 доллара к соответствующим коллам. Поскольку TCKR торгуется по цене всего 67% от цены исполнения, бычий колл, кажется, имеет более высокие шансы, что интуитивно понятно. Допустим, это не так, хотя по какой-то причине путы торгуются по 12 долларов, а коллы по 7 долларов. Допустим, вы покупаете европейский колл-опцион на акции TCKR. Дата экспирации — через год, цена исполнения — 15 долларов, а покупка колла стоит 5 долларов. Этот контракт дает вам право, но не обязательство, купить акции TCKR по истечении срока действия за 15 долларов, какой бы ни была рыночная цена. Если через год TCKR будет торговаться по 10 долларов, вы не воспользуетесь опционом. Если, с другой стороны, TCKR торгуется по 20 долларов за акцию, вы воспользуетесь опционом, купите TCKR по 15 долларов и безубыточности, поскольку изначально вы заплатили 5 долларов за опцион. Любая сумма TCKR, превышающая 20 долларов США, является чистой прибылью при нулевой комиссии за транзакцию. 7 + 14.42 < 12 + 10 21.42 доверительный звонок < 22 защищенный пут \begin{выровнено}&7 + 14.42 < 12 + 10 \\&21.42 \ \text{фидуциарное требование} < 22 \ \text{защищенное размещение} \\\end{выровнено}
7+14.42<12+1021.42 фидуциарный вызов<22 защищенный пут Защитный слой Еще один способ представить паритет пут-колл — сравнить производительность защитного пут-опциона и фидуциарного колл-опциона одного и того же класса. Фидуциарный звонокФидуциарный колл — это длинный колл в сочетании с денежными средствами, равными приведенной стоимости (с поправкой на ставку дисконтирования) цены реализации; это гарантирует, что у инвестора будет достаточно денежных средств для исполнения опциона в дату истечения срока действия. Ранее мы говорили, что опционы пут и колл TCKR со страйком $15 и сроком действия в один год торгуются по $5, но давайте на секунду предположим, что они торгуются бесплатно. Пример паритета пут-колл Допустим, вы также продаете (или «выписываете» или «коротко») европейский пут-опцион на акции TCKR. Дата экспирации, цена исполнения и стоимость опциона одинаковы. Вы получаете 5 долларов за продажу опциона, и вам не решать, использовать ли опцион или нет, поскольку вы им не владеете. Покупатель приобретает право, но не обязательство, продать вам акции TCKR по цене исполнения. Таким образом, если TCKR торгуется по 10 долларов через год, покупатель продает вам акции по 15 долларов. Вы оба безубыточны — вы уже заработали 5 долларов на продаже опциона пут, восполнив свой дефицит, в то время как покупатель уже потратил 5 долларов на его покупку, поглотив свою прибыль. Если TCKR торгуется по цене 15 долларов или выше, вы зарабатываете 5 долларов и только 5 долларов, поскольку другая сторона не использует опцион. Если TCKR торгуется ниже 10 долларов, вы теряете деньги — до 10 долларов, если TCKR падает до нуля. Прибыль или убыток по этим позициям для разных цен на акции TCKR выделены на графике непосредственно над этим разделом. Обратите внимание, что если вы добавите прибыль или убыток от длинного колла к короткому путу, вы заработаете или потеряете ровно столько, сколько получили бы, если бы просто подписали форвардный контракт на акции TCKR по цене 15 долларов, срок действия которого истекает через год. Еще один способ представить паритет пут-колл — сравнить производительность защитного пут-опциона и фидуциарного колл-опциона одного и того же класса. Защитный пут — это длинная позиция по акциям в сочетании с длинным путом, который ограничивает отрицательную сторону владения акциями. Фидуциарный колл — это длинный колл в сочетании с денежными средствами, равными приведенной стоимости (с поправкой на ставку дисконтирования) цены реализации; это гарантирует, что у инвестора будет достаточно денежных средств для исполнения опциона в дату истечения срока действия. Ранее мы говорили, что опционы пут и колл TCKR со страйком $15 и сроком действия в один год торгуются по $5, но давайте на секунду предположим, что они торгуются бесплатно. Почему важен паритет пут-колл? Паритет пут-колл позволяет рассчитать приблизительную стоимость пут-колла по отношению к другим его компонентам. Какова формула паритета пут-колл?Паритет пут-колл утверждает, что одновременная покупка и продажа европейского колл-опциона и пут-опциона одного и того же класса (тот же базовый актив, цена исполнения и дата экспирации) идентична покупке базового актива прямо сейчас. Обратное этому соотношению также было бы верно. Цена опциона «колл» + PV(x) = цена опциона «пут» + текущая цена базового актива -или- Текущая цена базового актива = цена опциона «колл» — цена опциона «пут» + PV(x) где: PV(x) = текущая стоимость цены исполнения (x), дисконтированная от стоимости на дату экспирации по безрисковой ставке Как оцениваются опционы? Цена опциона представляет собой сумму его внутренней стоимости, которая представляет собой разницу между текущей ценой базового актива и ценой исполнения опциона, и временной стоимости, которая напрямую связана со временем, оставшимся до истечения срока действия опциона. Деление комплексных чисел формула: Деление комплексных чисел | МатематикаКак найти частное двух комплексных чисел: формула, примерыSign in Password recovery Восстановите свой пароль Ваш адрес электронной почты MicroExcel.ru Математика Алгебра Деление комплексных чисел В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.
Деление в алгебраической формеРезультатом деления (т.е. частное) двух комплексных чисел x = a1 + b1i и y = a2 + b2i также является комплексное число z: Порядок действий следующий:
Пример 1: Решение: Деление в геометрической формеЕсли комплексные числа заданы в тригонометрической форме, например, x = |x| ⋅ (cos φ1 + i ⋅ sin φ1) и y = |y| ⋅ (cos φ2 + i ⋅ sin φ2), то разделить их можно по формуле ниже: Пример 2 Решение: ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТТаблица знаков зодиака Нахождение площади трапеции: формула и примеры Нахождение длины окружности: формула и задачи Римские цифры: таблицы Таблица синусов Тригонометрическая функция: Тангенс угла (tg) Нахождение площади ромба: формула и примеры Нахождение объема цилиндра: формула и задачи Тригонометрическая функция: Синус угла (sin) Геометрическая фигура: треугольник Нахождение объема шара: формула и задачи Тригонометрическая функция: Косинус угла (cos) Нахождение объема конуса: формула и задачи Таблица сложения чисел Нахождение площади квадрата: формула и примеры Что такое тетраэдр: определение, виды, формулы площади и объема Нахождение объема пирамиды: формула и задачи Признаки подобия треугольников Нахождение периметра прямоугольника: формула и задачи Формула Герона для треугольника Что такое средняя линия треугольника Нахождение площади треугольника: формула и примеры Нахождение площади поверхности конуса: формула и задачи Что такое прямоугольник: определение, свойства, признаки, формулы Разность кубов: формула и примеры Степени натуральных чисел Нахождение площади правильного шестиугольника: формула и примеры Тригонометрические значения углов: sin, cos, tg, ctg Нахождение периметра квадрата: формула и задачи Теорема Фалеса: формулировка и пример решения задачи Сумма кубов: формула и примеры Нахождение объема куба: формула и задачи Куб разности: формула и примеры Нахождение площади шарового сегмента Что такое окружность: определение, свойства, формулы как делать в алгебраической, показательной и тригонометрической формеСодержание:
Содержание
Деление комплексных чисел — основные правилаОпределение 1 Частным двух комплексных чисел \(z_{1}=a_{1}+b_{1} i\) и \(z_{2}=a_{2}+b_{2} \)i называют число z, заданное соотношением: \(z=\frac{z_{1}}{z_{2}}=\frac{a_{1} a_{2}+b_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}}+\frac{a_{2} b_{1}-a_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}} i\) Общий алгоритм для деления комплексных чисел на практике: Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).
В каких формах это можно делатьКомплексные числа делят разными методами, подтвержденными доказательствами. Существуют алгебраическая, тригонометрическая и показательная формы для подобных операций. В каждом перечисленном случае необходимо использовать определенную формулу. Формула деления в алгебраической формеКогда требуется выполнить деление комплексных чисел в алгебраической форме, в первую очередь числитель и знаменатель умножают на число, сопряженное к знаменателю. Таким образом, удается исключить комплексность в знаменателе: \(\frac{z_1}{z_2} = \frac{a_1 + b_1 i}{a_2 + b_2 i} = \frac{(a_1+b_1 i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)} = \frac{a_1 \cdot a_2 + b_1 \cdot b_2}{a_2 ^2 + b_2 ^2} + i\frac{a_2 \cdot b_1 — a_1 \cdot b_2}{a_2 ^2 + b_2 ^2}\) Формула деления в тригонометрической формеДеление в тригонометрической форме подразумевает деление модулей комплексных чисел. Примеры решения задачЗадача 1 Задача Необходимо найти частное пары комплексных чисел: \(z_1 = 3+i\) и \(z_2 = 2-3i\) Решение: Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу. \(\frac{z_1}{z_2} = \frac{3+i}{2-3i} =\) Сопряженное комплексное число к знаменателю: \(\overline{z_2} = 2+3i\) Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе: \(= \frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = \frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =\) Далее следует привести подобные слагаемые и записать вывод с ответом: \(= \frac{3 + 11i}{13} = \frac{3}{13} + \frac{11}{13}i\) Ответ: \(\frac{z_1}{z_2} = \frac{3}{13} + \frac{11}{13}i\) Задача 2 Задача Требуется выполнить деление комплексных чисел: \(z_1 = 2(\cos \frac{\pi}{3} + i\sin \frac{\pi}{6})\) \(z_2 = 4(\cos \frac{\pi}{6} + i\sin \frac{\pi}{6})\) Решение: Комплексные числа в условии задачи записаны в тригонометрической форме. \(=\frac{-3-i}{1-(-1)}=\frac{-3-i}{2}=-\frac{3}{2}-\frac{i}{2}\) Ответ:\( \frac{-2+i}{1-i}=-\frac{3}{2}-\frac{i}{2}\) Задача 5 Задача Необходимо найти частное: \(\frac{z_{1}}{z_{2}}\) При условии, что: \(z_{1}=2 \cdot\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)\) \(z_{2}=\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\) Решение: Искомое частное: \(\frac{z_{1}}{z_{2}}=\frac{2 \cdot\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)}{\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}}=\) \(=\frac{2}{1} \cdot\left[\cos \left(\frac{3 \pi}{4}-\frac{\pi}{4}\right)+i \sin \left(\frac{3 \pi}{4}-\frac{\pi}{4}\right)\right]=\) \(=2 \cdot\left[\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right]=2 \cdot(0+i)=2 i\) Ответ: \(\frac{z_{1}}{z_{2}}=2 \cdot\left(\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right)=2 i\) Задача 6 Задача Необходимо разделить два комплексных числа: \(z_{1}=-1+3i\) \(z_{2}=1+2i\) Решение: С помощью соответствующей формулы можно записать уравнение: \(z_{1} \div z_{2} = \frac{-1+3i}{1+2i} = \frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = \frac{-1 \cdot 1 + 3 \cdot 2}{1^{2}+2^{2}} + i \frac{3 \cdot 1 + (-1) \cdot (-2)}{1^{2}+2^{2}} =\) \(= \frac{5}{5} + i \frac{5}{5}=1+i\) Ответ: \( z_{1} \div z_{2} = 1+i\) Задача 7 Задача Необходимо вычислить частное комплексных чисел: \(z_{1}=\sqrt{2} \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right)\) \(z_{2}=\sqrt{2} \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right)\) Решение: Используя соответствующую формулу, запишем: \(z_{1} \div z_{2} = \frac{r_{1}}{r_{2}} (\cos ( \varphi _{1} — \varphi _{2}) + i \sin ( \varphi _{1} — \varphi _{2})) = \frac{\sqrt{2}}{\sqrt{2}} \left( \cos \left( \frac{\pi}{2}-\frac{\pi}{4} \right) + i \sin \left( \frac{\pi}{2}-\frac{\pi}{4} \right) \right) =\) \(= 1 \cdot \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right) = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}\) Ответ:\( z_{1} \div z_{2} = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}\) Задача 8 Задача Требуется разделить два комплексных числа: \(z_{1} = \sqrt{2} e^{-\frac{\pi}{2}i}\) \(z_{2} = 2 e^{-\frac{\pi}{4}i}\) Решение: Используя соответствующую формулу деления комплексных чисел, можно решить уравнение: \(z_{1} \div z_{2} = \frac{r_{1}}{r_{2}} \cdot e^{i ( \varphi _{1} — \varphi _{2})} = \frac{\sqrt{2}}{2} \cdot e^{i \left( -\frac{\pi}{2} +\frac{\pi}{4} \right) } = \frac{\sqrt{2}}{2} \cdot e^{-\frac{\pi}{4}i}\) Ответ: \(z_{1} \div z_{2} = \frac{\sqrt{2}}{2} \cdot e^{-\frac{\pi}{4}i}\)
Насколько полезной была для вас статья? У этой статьи пока нет оценок. Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter» Поиск по содержимомуОбъяснение урока: Деление комплексных чиселВ этом объяснении мы научимся выполнять деление комплексных чисел. Когда учащийся впервые сталкивается с комплексными числами, такие выражения, как 3−6𝑖1−5𝑖 может показаться немного загадочным или, по крайней мере, может показаться трудно понять, как можно вычислить результат. Этот объяснитель свяжет это идея к более знакомым областям математики и поможет вам понять, как вычислять выражения так. Прежде чем мы займемся делением комплексных чисел вообще, рассмотрим два более простых случая деления на действительное число и деление на чисто мнимое число. Пример 1: Деление комплексного числа на вещественное числоУчитывая 𝑧=5+3𝑖, выразить 𝑧2 в виде 𝑎+𝑏𝑖. Ответ Подставляя значение 𝑧, получаем 𝑧2=5+3𝑖2. Мы можем распределить 12 по комплексному числу, чтобы получить 𝑧2=52+32𝑖. Во многих отношениях деление комплексного числа на действительное число является довольно тривиальным упражнением. Однако деление комплексного числа на мнимое не так тривиально, как следующее пример продемонстрирует. Пример 2. Деление комплексного числа на мнимое числоУпростить 2+4𝑖𝑖. ОтветЧтобы упростить эту дробь, нам нужно как-то преобразовать знаменатель в действительное число. Этого можно добиться, используя тот факт, что 𝑖=−1. Следовательно, если мы умножаем и числитель и знаменатель на 𝑖, получим вещественное числа в знаменателе, что позволит нам упростить дробь. Следовательно, 2+4𝑖𝑖=2+4𝑖𝑖×𝑖𝑖=(2+4𝑖)𝑖𝑖. Распределяя по скобкам в числителе, имеем 2+4𝑖𝑖=2𝑖+4𝑖𝑖. Используя 𝑖=−1, получаем 2+4𝑖𝑖=−4+2𝑖−1=4−2𝑖. Метод, который мы использовали выше, можно обобщить, чтобы помочь нам понять, как разделить любые два
комплексные числа. В этом случае мы умножаем числитель и знаменатель на сопряженное число
знаменатель. Этот прием часто называют рационализацией знаменателя. Теперь давайте рассмотрим пример, где нам нужно упростить деление двух комплексные числа, подобно тому, как мы рационализируем знаменатель с помощью радикалы. Пример 3: Деление комплексных чиселУпростить 3−6𝑖1−5𝑖. ОтветНачнем с определения комплексного числа, которое при умножении на знаменатель дает в реальном числе. Обычно мы используем комплексное сопряжение знаменателя: 1+5𝑖. Теперь умножаем и числитель, и знаменатель на это числа следующим образом: 3−6𝑖1−5𝑖=3−6𝑖1−5𝑖×1+5𝑖1+5𝑖=(3−6𝑖)(1+5𝑖)(1−5𝑖)(1+5𝑖). Раскрывая скобки в числителе и знаменателе, имеем 3−6𝑖1−5𝑖=3+15𝑖−6𝑖−30𝑖1+5𝑖−5𝑖−25𝑖. Используя 𝑖=−1 и собирая подобные термины, мы получаем 3−6𝑖1−5𝑖=33+9𝑖26. Наконец, мы выражаем это в форме 𝑎+𝑏𝑖 следующим образом:
3−6𝑖1−5𝑖=3326+926𝑖. Практическое руководство. Деление комплексных чиселЧтобы разделить комплексные числа, мы используем следующую технику (иногда называемую «реализуя» знаменатель):
Используя эту технику, мы можем получить общую форму для деления сложных числа, как продемонстрирует следующий пример. Пример 4: Общая форма сложного деления
ОтветЧасть 1 Раскрывая скобки с помощью FOIL или любого другого метода, мы имеем
(𝑝+𝑞𝑖)(𝑝−𝑞𝑖)=𝑝−𝑝𝑞𝑖+𝑝𝑞𝑖−𝑞𝑖. Используя 𝑖=−1 и упрощая, имеем (𝑝+𝑞 𝑖)(𝑝−𝑞𝑖)=𝑝+𝑞. Часть 2 Аналогично, раскрывая скобки, получаем 𝑏𝑞𝑖. Сбор похожих терминов и использование 𝑖=−1 , имеем (𝑎+𝑏𝑖)(𝑝−𝑞𝑖)=(𝑎𝑝+𝑏𝑞)+(𝑏𝑝−𝑎𝑞)𝑖. Часть 3 Чтобы выразить эту дробь действительным знаменателем, мы умножаем числитель и знаменателя на комплексное сопряжение знаменателя следующим образом: Подставляя наши ответы из части 1 и части 2, мы имеем Несмотря на то, что мы вывели общую формулу для сложных разделение, желательно знакомиться с техникой, а не просто запоминать формулу. Пример 5: Свойства комплексного деленияЕсли 𝑎+𝑏𝑖=−3−5𝑖−3+5𝑖, верно ли, что 𝑎+𝑏=1? ОтветЧтобы выразить −3−5𝑖−3+5𝑖 в виде 𝑎+𝑏𝑖, умножаем числитель и знаменатель на комплексное сопряжение знаменателя следующим образом: −3−5𝑖−3+5𝑖=(−3−5𝑖)(−3−5𝑖)(−3+5𝑖)(−3−5𝑖). Расширение скобки, мы имеем −3–5𝑖 — 3+5𝑖 = 9+15𝑖+15𝑖+25𝑖9+15𝑖 — 15𝑖 — 25𝑖. Используя 𝑖 = −1 и собирая, как термины, у нас есть -3 −5𝑖−3+5𝑖=−16+30𝑖34. Упрощая, имеем −3−5𝑖−3+5𝑖=−817+1517𝑖. Следовательно, 𝑎=−817 и 𝑏=1517. Сейчас мы можем рассмотреть сумму их квадратов: Следовательно, верно, что 𝑎+𝑏=1. Тот факт, что 𝑎+𝑏=1 в предыдущем вопросе, не случаен. В на самом деле, это пример общего правила: если 𝑎+𝑏𝑖=𝑧𝑧 для некоторого комплексного числа 𝑧, то 𝑎+𝑏=1. Это можно доказать, работая с алгеброй. Однако это не очень поучительно. Наоборот, такие результаты лучше всего понять, когда мы узнать о модуле и аргументе. Пример 6. Решение сложных уравнений деленияРешите уравнение 𝑧(2+𝑖)=3−𝑖 относительно 𝑧. ОтветМы начинаем с деления обеих частей уравнения на 2+𝑖, что приводит к следующее уравнение: 𝑧=3−𝑖2+𝑖. Теперь упростим дробь, выполнив сложное деление. Следовательно, умножая оба
числителя и знаменателя комплексно-сопряженным знаменателю, получаем
𝑧=(3−𝑖)(2−𝑖)(2+𝑖)(2−𝑖). Раскрыв скобки, мы имеем 𝑧=6−3𝑖−2𝑖+𝑖4+2𝑖−2𝑖−𝑖. Используя 𝑖=−1 и собрав подобные термины, мы можем переписать это как 𝑧=5−5𝑖5=1−𝑖. В связи с тем, что умножать и делить комплексные числа таким способом можно довольно долго потребляя, полезно рассмотреть, какой подход будет наиболее эффективным. Это часто включает в себя использование свойств комплексных чисел или замечание факторов, которые мы можем быстро отменить. Следующие два примера продемонстрируют, как мы можем упростить наши вычисления. Пример 7: комплексный разделУпростить (−3+2𝑖)(3+3𝑖)(4+𝑖)(4+4𝑖). Ответ При представлении такого выражения хорошо сначала подумать, какой подход
мы должны взяться за ее решение. Мы могли бы расширить скобки в числителе и
знаменатель, а затем умножить числитель и знаменатель на комплекс
сопряжение знаменателя. В качестве альтернативы мы могли бы разделить дробь на две части и попытаться
упростите каждую часть, затем умножьте полученные комплексные числа. Теперь мы можем умножить и числитель, и знаменатель на комплексно-сопряженное число знаменатель следующим образом: 34(−3+2𝑖)(4+𝑖)=34(−3+2𝑖)(4−𝑖)(4+𝑖)(4−𝑖). Раскрывая скобки в числителе и знаменателе, имеем 34(−3+2𝑖)(4−𝑖)(4+𝑖)(4−𝑖)=34(−12+3𝑖+8𝑖−2𝑖)(16+4𝑖−4𝑖−𝑖). Используя 𝑖 =−1 и собирая подобные термины, мы можем переписать это как 34−12+3𝑖+8𝑖−2𝑖(16+4𝑖−4𝑖−𝑖)=34(−10+11𝑖)17. Наконец, мы можем упростить, чтобы получить 34−12+3𝑖+8𝑖− 2𝑖(16+4𝑖−4𝑖−𝑖)=−1534+3368𝑖. В ответ на следующий вопрос мы снова рассмотрим пример, в котором применяются свойства
комплексные числа могут упростить вычисления. Пример 8: Сложные выражения, включающие делениеУпростить 3−4𝑖2+2𝑖+3−4𝑖2−2𝑖. ОтветЭту задачу можно решить, выполнив сложное деление на обоих дроби, а затем сложение их результатов. Однако мы можем упростить наши вычисления, сначала заметив, что мы можем вынести 3−4𝑖 из обоих членов. Следовательно, мы можем переписать выражение как
Теперь рассмотрим выражение в скобках; обратите внимание, что знаменатели две дроби представляют собой комплексно-сопряженную пару; то есть выражение имеет вид 1𝑧+1𝑧. Если мы представим это как одну дробь над общим знаменателем, мы получим 1𝑧+1𝑧=𝑧+𝑧𝑧𝑧. Используя свойства комплексных сопряженных, мы знаем, что если 𝑧=𝑎+𝑏𝑖, 𝑧𝑧=𝑎+𝑏 и 𝑧+𝑧=2(𝑧)=2𝑎Re. Следовательно, 1𝑧+1𝑧=2𝑎𝑎+𝑏. Следовательно, 12+2𝑖+12−2𝑖=2×22+2=12. Подставив это в (1), мы получим 3−4𝑖2+2𝑖+3−4𝑖2−2𝑖=12(3 −4𝑖)=32−2𝑖. Наконец, давайте рассмотрим пример, в котором нам нужно найти пропущенные значения в уравнение путем деления комплексных чисел. Пример 9. Решение линейного уравнения с двумя переменными и комплексными коэффициентамиУчитывая, что 𝑦 — действительные числа, определите значение 𝑥 и значение из 𝑦. ОтветВ этом примере мы хотим определить недостающие значения 𝑥 и 𝑦 в линейном уравнении с двумя переменными с комплексным коэффициенты. Данное уравнение содержит 3 отдельных сложных деления, два слева и одно справа сторону уравнения. Начнем с упрощения каждого члена, выполнив сложное деление. Это достигается путем умножения числителя и знаменателя на комплексно-сопряженное число знаменателя, что приводит к действительное число в знаменателе после распределения по скобкам. Для первого члена 𝑥+𝑖𝑦1−3𝑖 мы умножаем
знаменатель и числитель на 1+3𝑖, что является комплексно-сопряженным
знаменателя:
𝑥+𝑖𝑦1−3𝑖=𝑥+𝑖𝑦1−3𝑖×1+3𝑖1+3𝑖=(𝑥+𝑖𝑦)(1+3𝑖)(1−3𝑖)(1+3𝑖). Распределяя по скобкам в числителе и знаменателе, имеем 𝑥+𝑖𝑦1−3𝑖=𝑥+3𝑥𝑖+𝑦𝑖+3𝑖𝑦1+3𝑖−3𝑖−9𝑖=𝑥+3𝑥𝑖+𝑦𝑖−3𝑦1+9=(𝑥−3𝑦)+ 𝑖(3𝑥+𝑦)10. Повторение этого процесс для второго члена, 9𝑥−𝑖𝑦1+3𝑖, на этот раз умножив числитель и знаменатель на 1−3𝑖, получаем 9𝑥−𝑖𝑦1+3𝑖=9𝑥−𝑖𝑦1+3𝑖×1−3𝑖1−3𝑖=(9𝑥−𝑖𝑦)(1−3𝑖)(1+3𝑖)(1−3𝑖)=9𝑥−27𝑥𝑖− 𝑦𝑖+3𝑖𝑦1+3𝑖−3𝑖 −9𝑖=9𝑥−27𝑥𝑖−𝑦𝑖−3𝑦1+9=(9𝑥−3𝑦)+𝑖(−27𝑥−𝑦)10. Наконец, для последнего члена 6+5𝑖4−8𝑖, с правой стороны, умножив знаменатель и числитель на 4+8𝑖, 6+5𝑖4–8𝑖 = 6+5𝑖4–8𝑖 × 4+8𝑖4+8𝑖 = (6+5𝑖) (4+8𝑖) (4–8𝑖) (4+8𝑖) = 24+48𝑖+20𝑖+40𝑖16+32𝑖 — 32𝑖 −64𝑖=24+48𝑖+20𝑖−4016+64=−16+68𝑖80. Таким образом, данное уравнение принимает вид 𝑥+𝑖𝑦1−3𝑖−9𝑥−𝑖𝑦1+3𝑖=6+5𝑖4−8𝑖(𝑥−3𝑦)+𝑖(3𝑥+𝑦)10−(9𝑥−3𝑦)+𝑖(−27𝑥−𝑦) 10=−16+68𝑖80 (𝑥−3𝑦)−(9𝑥−3𝑦)+𝑖(3𝑥+𝑦)+𝑖(27𝑥+𝑦)10=−16+68𝑖80−8𝑥+𝑖(30𝑥+2𝑦)10=−16+68𝑖80−8𝑥+𝑖(30𝑥+2 𝑦)=− 16+68𝑖8. Действительные значения 𝑥 и 𝑦 можно найти, приравняв действительную и мнимую части обеих сторон. Теперь мнимые части, 30𝑥+2𝑦=688𝑦=6816−15𝑥=6816−154=12. Подводя итог, можно сказать, что реальными решениями данного уравнения являются 𝑥=14,𝑦=12. Давайте резюмируем некоторые ключевые моменты, которые мы рассмотрели в этом объяснении. Ключевые моменты
Разделить комплексные числа | Колледж АлгебраРезультаты обучения
Деление комплексных чиселДеление двух комплексных чисел сложнее, чем сложение, вычитание и умножение, потому что мы не можем делить на мнимое число, а это означает, что у любой дроби должен быть действительный знаменатель. Нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в качестве знаменателя. Этот термин называется комплексное сопряжение знаменателя, которое находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение [латекс]а+би[/латекс] есть [латекс]а-би[/латекс]. Обратите внимание, что комплексные сопряжения имеют обратную связь: комплексное сопряжение [латекс]а+би[/латекс] равно [латекс]а-би[/латекс], а комплексное сопряжение [латекс]а-би[/ латекс] это [латекс]а+би[/латекс]. Важно отметить, что комплексно-сопряженные пары обладают особым свойством. Предположим, мы хотим разделить [latex]c+di[/latex] на [latex]a+bi[/latex], где ни [latex]a[/latex], ни [латекс]b[/латекс] равно нулю. Сначала запишем деление в виде дроби, затем найдем комплексно-сопряженную часть знаменателя и умножим. [латекс]\dfrac{c+di}{a+bi}[/latex], где [латекс]a\ne 0[/латекс] и [латекс]b\ne 0[/латекс]. Умножить числитель и знаменатель на комплексное сопряжение знаменателя. [латекс]\dfrac{\left(c+di\right)}{\left(a+bi\right)}\cdot \dfrac{\left(a-bi\right)}{\left(a- би \ вправо)} = \ dfrac {\ влево (с + ди \ вправо) \ влево (а-би \ вправо)} {\ влево (а + би \ вправо) \ влево (а-би \ вправо)} [/ латекс] 9{2}}\end{align}[/latex] A Общее примечание: комплексное сопряжение Комплексное сопряжение комплексного числа [latex]a+bi[/latex] равно [latex]a-bi [/латекс]. Его находят изменением знака мнимой части комплексного числа. Действительная часть числа остается неизменной.
Пример: нахождение комплексно-сопряженных чиселНайдите комплексно-сопряженные числа каждого числа.
Показать решение Как: Даны два комплексных числа, разделить одно на другое.
Бесплатно математика: Бесплатные уроки по математикеБесплатные уроки по математикеМы дарим вам более сотни бесплатных уроков по математике в виде обучающих статей от репетиторов tutoronline.ru. Изучив данные уроки, вы как минимум улучшите знания в области математики, а применив многие из них на практике, можно самому подготовиться к ЕГЭ! Выберите нужный раздел и устраните пробелы в знаниях самого удивительного школьного предмета!
Сравнение
Проценты
Числа
Графики
Системы уравнений
Числовые последовательности
Многочлены
Тригонометрия
Иррациональные цифры и уравнения
Модули
Логарифмы
Производные
Показательная функция
Интегралы
Треугольники
Параллелограмм
Ромб
Трапеция
Окружность
Координаты и Векторы
Периметр
Площадь
Стереометрия
Математика с нуля. Пошаговое изучение математики«Математика с нуля. Пошаговое изучение математики для начинающих» – это новый проект, предназначенный для людей, которые хотят изучить математику самостоятельно с нуля. Сразу скажем, здесь нет лёгких решений и подобных заявлений как «Купи эту книгу и сдай математику на 5» или «Освой математику за 12 часов» вы тут не увидите. Математика большая наука, которую следует осваивать последовательно и очень медленно. Сайт представляет собой уроки по математике, которые упорядочены по принципу «от простого к сложному». Каждый урок затрагивает одну или несколько тем из математики. Уроки разбиты на шаги. Начинать изучение следует с первого шага и далее по возрастанию. Каждый пройденный урок обязательно должен быть усвоен. Поэтому, не поняв одного урока, нельзя переходить к следующему, поскольку каждый урок в математике основан на понимании предыдущего. Математика хорошо усваивается, когда человек самостоятельно открыв учебник, учит самогó себя. При этом вырабатывается определенная дисциплина, которая очень помогает в будущем. Если Вы будете придерживаться принципа «от простого к сложному», то с удивлением обнаружите, что математика не так уж и сложна. Возможно даже она покажется вам интересной и увлекательной. Что даст вам знание математики? Во-первых, уверенность. Математику знает не каждый, поэтому осознание того, что вы знаете хоть какую-то часть этой серьёзной науки, делает вас особенным. Во-вторых, освоив математику, вы с лёгкостью освоите другие науки и сможете мыслить гораздо шире. Знание математики позволяет овладеть такими профессиями как программист, бухгалтер, экономист. Никто не станет спорить, что эти профессии сегодня очень востребованы. В общем, дерзай друг! Желаем тебе удачи в изучении математики!
Новые уроки будут скоро. Оставайся с нами! Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках Free Math — собирайте, систематизируйте и просматривайте домашнее задание по цифровой математикеУчебное пособие для студентов Демо-оценка учителя Запустить бесплатную математику Учащиеся демонстрируют пошаговую работуУчащиеся могут начать с чистого документа Free Math, копируя и решая задачи так же, как в бумажных тетрадях. Учащиеся сохраняют свою работу в виде файла и отправляют его через LMS в ответ на задание. Одновременно просмотреть все заданияПоказаны полные решения, сгруппированные по сходному окончательному ответу. Вы можете присудить частичный балл и оставить отзыв учащимся, которым нужна помощь. Вам не нужно вводить ключ ответа, Free Math просто обеспечивает систематизированное представление всей работы учащихся. Роланд Смокер Free Math App — отличный инструмент для беспрепятственной оценки работы учащихся без предварительной подготовки. Учащиеся могут получить доступ к любому математическому символу, которого нет во многих текстовых редакторах, что позволяет им точно и быстро отображать свою математическую работу. Хосе Я просто хотел бы поблагодарить вас, ребята, за работу, которую вы проделали с веб-сайтом. Кристина Вуд Благодаря вашему сайту учителям стало намного легче справляться с трудными временами дистанционного обучения. Я в восторге от вашего сайта нескольким учителям, и мы используем его на всех наших средних и старших классах. Используйте все имеющиеся у вас материалыВы можете назначать задачи из любого места, включая учебник, рабочий лист или цифровой документ, такой как Google Doc, файл Microsoft Word или PDF. Гибкий подход к сортировке означает, что вам не нужно конвертировать ваши материалы.
Студенты просто ссылаются на проблемы из любого места и создают цифровую работу
которые можно просмотреть в Free Math сразу, без предварительной настройки. Embrace Visual LearningУчащиеся могут добавлять цифровые рисунки и графики к своим заданиям или вставьте изображение с другого сайта, например Desmos или Geogebra. Когда некоторым учащимся лучше писать на бумаге, они могут быстро сфотографировать свои ноутбуки с помощью веб-камеры. Учетная запись или загрузка не требуютсяВесь опыт работает прямо в вашем веб-браузере. Предусмотрена прямая интеграция для Google Диска и Класса, включая интеграцию с журналом оценок. Для других LMS и поставщиков облачных хранилищ задания и сеансы оценивания сохраняются напрямую из браузера в файлы в папке загрузок, а оттуда их можно загрузить в любой сервис, который вы используете для своего класса. Файлы можно собрать в любой LMS, скачать все вместе и загрузить для оценивания.
После оценки ваша LMS также легко предоставляет каждому учащемуся индивидуальный файл обратной связи. Начало работыИзбранное наЧасы работы Есть вопросы о том, как начать работу с Free Math? Запланируйте время встречи с нашей командой, используя ссылку ниже. Назначить встречуПримите участие Free Math имеет открытый исходный код, что означает, что исходный код сайта доступен для
просматривать, изменять и распространять в соответствии с условиями публичной лицензии GNU. Помогите нам построить нашу революцию, Free Math уже используется десятками тысяч учеников и учителей чтобы помочь улучшить обратную связь и обсуждение в своих классах. Сообщить об ошибке или запросить функцию Распространяйте информациюПомогите нам сделать простые математические задания в произвольной форме доступными для школьников по всему миру. Отлично подходит для многих областей математики 92-16}=\frac{3}{x+4}x−41+x2−162=x+431x−4+2(x−4)(x+4)=3x+4 \frac{1}{x-4}+\frac{2}{\left(x-4\right)\left(x+4\right)}=\frac{3}{x+4}x−41 +(x−4)(x+4)2=x+43 1x−4⋅(x+4x+4)+2(x−4)(x+4)=3x+4⋅( x−4x−4)\frac{1}{x-4}\cdot\left(\frac{x+4}{x+4}\right)+\frac{2}{\left(x-4\ вправо)\влево(x+4\вправо)}=\frac{3}{x+4}\cdot\left(\frac{x-4}{x-4}\right)x−41⋅(x +4x+4)+(x−4)(x+4)2=x+43⋅(x−4x−4) 1(x+4)(x−4)(x+4 )+2(x−4)(x+4)=3(x−4)(x+4)(x−4)\frac{1\left(x+4\right)}{\left(x- 4 \ вправо) \ влево (х + 4 \ вправо)} + \ гидроразрыва {2} {\ влево (х-4 \ вправо) \ влево (х + 4 \ вправо)} = \ гидроразрыва {3 \ влево (х- 4\вправо)}{\влево(х+4\вправо)\влево(х-4\вправо)}(х-4)(х+4)1(х+4)+(х-4)(х +4)2=(x+4)(x−4)3(x−4) 92+c2x2lnx−41x2+c Физика Мяч бросают с высоты 1 м над землей. Начальная скорость 20 м/с\text{Начальная скорость 20 м/с} Начальная скорость 20 м/с Под углом 40 градусов над горизонталью \text{Под углом 40 градусов к горизонту}Под углом 40 градусов к горизонту 92y(t)=1+12,9t−4,9t2vy(t)=vsin(θ)−9,8tv_y\left(t\right)=v\sin\left(\theta\right)-9,8tvy (t)=vsin(θ)−9,8t vy(t)=12,9−9,8tv_y\left(t\right)=12,9-9,8tvy(t)=12,9−9,8t max высота на vy (t)=0\max\ высота\ at\ v_y\left(t\right)=0max высота at vy(t)=0 12,9−9,8t=012,9-9,8t=012,9−9,8t=0 -9,8t=-12,9-9,8t=-12,9-9,8t=-12,9 =1,3 y(1,3)=1+12,9(1,3)−4,9(1,3)2y\влево(1,3\вправо)=1+12,92y(1.3)=1+12.9(1.3)−4.9(1.3)2 y(1.3)=9.5my\left(1.3\right)=9.5\ my(1.3)=9.5m y составляющая скорости 0 при наибольшем pty\ компоненте\ скорости\ равно\ 0\ при\ наибольшем\ pty компоненте скорости равно 0 при наибольшем pt общая скорость =vx=15,3 мсобщая\ скорость\ =v_x=15,3\ \frac{m} {s}общая скорость =vx=15,3 см политика конфиденциальности Creative Commons Media и открытый исходный код, используемые на этом сайте Free Math — это бесплатное программное обеспечение: вы можете распространять его и/или модифицировать. Бесплатные математические рабочие листы от Math-Drills Math-Drills.com содержит более 58 тысяч бесплатных математических рабочих листов , которые могут быть использованы учащимися для изучения математики. Сайт Math-Drills.com был запущен в 2005 году и содержит около 400 математических листов. С тех пор были добавлены еще десятки тысяч математических листов. Веб-сайт и контент продолжают улучшаться на основе отзывов и предложений наших пользователей, а также наших собственных знаний об эффективных математических методах. Большинство пользователей Math-Drills являются классными учителями или родителями. Классные руководители используют наши рабочие листы по математике, чтобы оценить усвоение учащимися основных математических фактов, дать учащимся дополнительную математическую практику, научить новым математическим стратегиям и сэкономить драгоценное время на планирование. Родители используют наши рабочие листы по математике, чтобы дать своим детям дополнительную математическую практику во время школьных каникул и улучшить их математическое образование. Тур по Math-Drills.com на YouTube. Самые популярные бесплатные задания по математике на этой неделе Плюс сложение двухзначных чисел с некоторой перегруппировкой (25 вопросов) (1313 просмотров на этой неделе )100 вопросов сложения однозначных чисел с некоторой перегруппировкой ( 1203 просмотров на этой неделе ) Умножение двухзначных чисел на однозначные числа ( 1044 просмотров на этой неделе )Поддержка обучения учащихся с помощью бесплатных математических заданий от Math-Drills Math-Drills считает, что образование должно быть доступным для всех детей, независимо от их социально-экономического положения или любых других факторов. С момента своего появления в 2005 году все математические рабочие листы на Math-Drills были бесплатными для учащихся, изучающих математику. Рабочие листы Math-Drills также используются в специальном образовании, обучении взрослых, репетиторстве, колледжах, средних школах, тюрьмах и во множестве других ситуаций. Учителям специального образования особенно нравится, что мы разбиваем математические навыки и предоставляем варианты с крупным шрифтом. Взрослые учащиеся ценят простой лаконичный формат, предлагаемый нашими рабочими листами. Репетиторы используют наши рабочие листы по математике, чтобы сократить свои расходы и сосредоточиться на обучении учащихся. Преподаватели средних школ, колледжей и университетов иногда нуждаются в коррекционных ресурсах для учащихся, чтобы они могли продолжить изучение более сложных тем. Учащиеся, которые тренируют свои математические навыки с нашими математическими таблицами во время школьных каникул, сохраняют свои математические навыки на уровне предстоящих школьных семестров. Разложить на комплексные множители: Mathway | Популярные задачи 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ ГЛАВА I.  ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ ЧИСЛО. ПЕРЕМЕННАЯ. ФУНКЦИЯ§ 1. Действительные числа. § 2. Абсолютная величина действительного числа § 3. Переменные и постоянные величины § 4. Область изменения переменной величины § 5. Упорядоченная переменная величина. Возрастающая и убывающая переменные величины Ограниченная переменная величина § 6. Функция § 7. Способы задания функции § 8. Основные элементарные функции. Элементарные функции § 9. Алгебраические функции § 10. Полярная система координат Упражнения к главе I ГЛАВА II. ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ § 1. Предел переменной величины. Бесконечно большая переменная величина § 2. Предел функции § 3. Функция, стремящаяся к бесконечности. Ограниченные функции § 4. Бесконечно малые и их основные свойства § 5. Основные теоремы о пределах § 6. Предел функции (sin x)/x при x->0 § 7. Число e § 8. Натуральные логарифмы § 9. Непрерывность функций § 10. Некоторые свойства непрерывных функций § 11.  n при n целом и положительном n при n целом и положительном§ 6. Производные от функций y = sinx; y = cosx § 7. Производные постоянной, произведения постоянной на функцию, суммы, произведения, частного § 8. Производная логарифмической функции § 9. Производная от сложной функции § 10. Производные функций y = tgx, y = ctgx, y = ln|x| § 11. Неявная функция и ее дифференцирование § 12. Производные степенной функции при любом действительном показателе, показательной функции, сложной показательной функции § 13. Обратная функция и ее дифференцирование § 14. Обратные тригонометрические функции и их дифференцирование § 15. Таблица основных формул дифференцирования § 16. Параметрическое задание функции § 17. Уравнения некоторых кривых в параметрической форме § 18. Производная функции, заданной параметрически § 19. Гиперболические функции § 20. Дифференциал § 21. Геометрическое значение дифференциала Рассмотрим функцию § 22. Производные различных порядков § 23.  x, sin x, cos x x, sin x, cos xУпражнения к главе IV ГЛАВА V. ИССЛЕДОВАНИЕ ПОВЕДЕНИЯ ФУНКЦИЙ § 2. Возрастание и убывание функции § 3. Максимум и минимум функций § 4. Схема исследования дифференцируемой функции на максимум и минимум с помощью первой производной § 5. Исследование функции на максимум и минимум с помощью второй производной § 6. Наибольшее и наименьшее значения функции на отрезке § 7. Применение теории максимума и минимума функций к решению задач § 8. Исследование функции на максимум и минимум с помощью формулы Тейлора § 9. Выпуклость и вогнутость кривой. Точки перегиба § 10. Асимптоты § 11. Общий план исследования функций и построения графиков § 12. Исследование кривых, заданных параметрически Упражнения к главе V ГЛАВА VI. КРИВИЗНА КРИВОЙ § 1. Длина дуги и ее производная § 2. Кривизна § 3. Вычисление кривизны § 4. Вычисление кривизны линии, заданной параметрически § 5. Вычисление кривизны линии, заданной уравнением в полярных координатах § 6.  Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента§ 7. Свойства эволюты § 8. Приближенное вычисление действительных корней уравнения Упражнения к главе VI ГЛАВА VII. КОМПЛЕКСНЫЕ ЧИСЛА, МНОГОЧЛЕНЫ § 1. Комплексные числа. Исходные определения § 2. Основные действия над комплексными числами § 3. Возведение комплексного числа в степень и извлечение корня из комплексного числа § 4. Показательная функция с комплексным показателем и ее свойства § 5. Формула Эйлера. Показательная форма комплексного числа § 6. Разложение многочлена на множители § 7. О кратных корнях многочлена § 8. Разложение многочлена на множители в случае комплексных корней § 9. Интерполирование. Интерполяционная формула Лагранжа § 10. Интерполяционная формула Ньютона § 11. Численное дифференцирование § 12. О наилучшем приближении функций многочленами. Теория Чебышева Упражнения к главе VII ГЛАВА VIII. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. Определение функции нескольких переменных § 2.  Геометрическое изображение функции двух переменных Геометрическое изображение функции двух переменных§ 3. Частное и полное приращение функции § 4. Непрерывность функции нескольких переменных § 5. Частные производные функции нескольких переменных § 6. Геометрическая интерпретация частных производных функции двух переменных § 7. Полное приращение и полный дифференциал § 8. Применение полного дифференциала в приближенных вычислениях § 9. Приложение дифференциала к оценке погрешности при вычислениях § 10. Производная сложной функции. Полная производная. Полный дифференциал сложной функции § 11. Производная от функции, заданной неявно § 12. Частные производные различных порядков § 13. Поверхности уровня § 14. Производная по направлению § 15. Градиент § 16. Формула Тейлора для функции двух переменных § 17. Максимум и минимум функции нескольких переменных § 18. Максимум и минимум функции нескольких переменных, связанных данными уравнениями (условные максимумы и минимумы) § 19.  Получение функции на основании экспериментальных данных по методу наименьших квадратов Получение функции на основании экспериментальных данных по методу наименьших квадратов§ 20. Особые точки кривой Упражнения к главе VIII ГЛАВА IX. ПРИЛОЖЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ К ГЕОМЕТРИИ В ПРОСТРАНСТВЕ § 1. Уравнения кривой в пространстве § 2. Предел и производная векторной функции скалярного аргумента. Уравнение касательной к кривой. Уравнение нормальной плоскости § 3. Правила дифференцирования векторов (векторных функций) § 4. Первая и вторая производные вектора по длине дуги. Кривизна кривой. Главная нормаль. Скорость и ускорение точки в криволинейном движении § 5. Соприкасающаяся плоскость. Бинормаль. Кручение. § 6. Касательная плоскость и нормаль к поверхности Упражнения к главе IX ГЛАВА X. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Первообразная и неопределенный интеграл § 2. Таблица интегралов § 3. Некоторые свойства неопределенного интеграла § 4. Интегрирование методом замены переменной или способом подстановки § 5. Интегралы от некоторых функций, содержащих квадратный трехчлен § 6.  Интегрирование по частям Интегрирование по частям§ 7. Рациональные дроби. Простейшие рациональные дроби и их интегрирование § 8. Разложение рациональной дроби на простейшие § 9. Интегрирование рациональных дробей § 10. Интегралы от иррациональных функций § 11. Интегралы вида … § 12. Интегрирование некоторых классов тригонометрических функций § 13. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок § 14. О функциях, интегралы от которых не выражаются через элементарные функции Упражнения к главе X ГЛАВА XI. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. Постановка задачи. Нижняя и верхняя интегральные суммы § 2. Определенный интеграл. Теорема о существовании определенного интеграла § 3. Основные свойства определенного интеграла § 4. Вычисление определенного интеграла. Формула Ньютона — Лейбница § 5. Замена переменной в определенном интеграле § 6. Интегрирование по частям § 7. Несобственные интегралы § 8. Приближенное вычисление определенных интегралов § 9.  Формула Чебышева Формула Чебышева§ 10. Интегралы, зависящие от параметра. Гамма-функция § 11. Интегрирование комплексной функции действительной переменной Упражнения кглаве XI ГЛАВА XII. ГЕОМЕТРИЧЕСКИЕ И МЕХАНИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА § 1. Вычисление площадей в прямоугольных координатах § 2. Площадь криволинейного сектора в полярных координатах § 3. Длина дуги кривой § 4. Вычисление объема тела по площадям параллельных сечений § 5. Объем тела вращения § 6. Площадь поверхности тела вращения § 7. Вычисление работы с помощью определенного интеграла § 8. Координаты центра масс § 9. Вычисление момента инерции линии, круга и цилиндра с помощью определенного интеграла Упражнения к главе XII |
Факторизация комплексных чисел
Факторизация комплексных чиселТеперь вы увидите математиков за работой: усложняя простые вещи, чтобы сделать их проще!
Дедушка всех примеров.
 Рассмотрим многочлен . Его нельзя разложить на действительные числа, так как его график не имеет x -перехватов. (График представляет собой просто стандартную параболу, сдвинутую вверх на единицу!)
Рассмотрим многочлен . Его нельзя разложить на действительные числа, так как его график не имеет x -перехватов. (График представляет собой просто стандартную параболу, сдвинутую вверх на единицу!)Как мы можем сказать, что многочлен неприводим, когда мы выполняем заполнение квадрата или используем квадратичную формулу? Давайте попробуем квадратное завершение: Здесь не так много, чтобы завершить, передача постоянного члена — это все, что нам нужно сделать, чтобы увидеть, в чем проблема:
Теперь мы не можем извлекать квадратные корни, так как квадрат каждого действительного числа неотрицательен!
Здесь в дело вступает математик: она (или он) воображает , что существуют корни из -1 (хотя и не настоящие числа), и называет их i и — i . Таким образом, определяющим свойством этого воображаемого числа и является то, что
Теперь полином внезапно стал приводимым , мы можем написать
Комплексные числа.
 Давайте организуем: число вида , где a и b — действительные числа, называется комплексным числом . Вот некоторые примеры:
Давайте организуем: число вида , где a и b — действительные числа, называется комплексным числом . Вот некоторые примеры:Число a называется действительной частью числа a + bi , число b называется мнимой частью числа a + bi 900 13 .
К счастью, алгебра с комплексными числами работает очень предсказуемо, вот несколько примеров:
В общем, умножение работает с методом FOIL:
Два комплексных числа a + bi и a — bi называются комплексно-сопряженной парой . Замечательным свойством комплексно-сопряженной пары является то, что их произведение всегда является неотрицательным действительным числом:
Используя это свойство, мы можем увидеть, как разделить два комплексных числа. Давайте посмотрим на пример
Фокус в том, чтобы умножить числитель и знаменатель на комплексно-сопряженный спутник знаменателя, в нашем примере мы умножаем на 1+ i :
Так как (1+ i )(1- i )=2 и (2+3 i )(1+ i )=-1+5 i , мы получаем
и готово!
Вы можете найти больше информации в нашем разделе «Комплексные числа».
Квадратичные многочлены с комплексными корнями.
Рассмотрим многочленИспользуя квадратичную формулу, корни вычисляются как
Нетрудно увидеть из формы квадратичной формулы, что если квадратный многочлен имеет комплексные корни, то они всегда будут комплексно-сопряженной парой !
Вот еще один пример. Рассмотрим многочлен
Его корни даны
Дискриминант.
Из графика многочлена видно, имеет ли он действительные корни или неприводим к действительным числам. Как мы можем сказать алгебраически , имеет ли квадратичный многочлен вещественные или комплексные корни? Символ i появляется на картинке именно тогда, когда член под квадратным корнем в квадратной формуле равен отрицательному. Этот терминназывается дискриминантом .
Рассмотрим дискриминант квадратичного многочлена .
- Если дискриминант положительный, многочлен имеет 2 различных действительных корня.

- Если дискриминант отрицательный, многочлен имеет 2 комплексных корня, которые образуют комплексно-сопряженную пару.
- Если дискриминант равен нулю, многочлен имеет один действительный корень кратности 2.
Основная теорема алгебры, дубль два.
Мы уже знаем, что любой многочлен можно разложить по действительным числам в произведение линейных множителей и неприводимых квадратичных многочленов. Но теперь мы также заметили, что каждый квадратный многочлен можно разложить на 2 линейных множителя, если мы допускаем комплексные числа. Следовательно, комплексная версия Основной теоремы алгебры выглядит следующим образом:
| В комплексных числах любой многочлен (с действительными коэффициентами) можно разложить на множители. |
Мы можем сказать это также на корневом языке:
Над комплексными числами каждый многочлен степени n (с действительными коэффициентами) имеет n корней, считая по их кратности. |
Использование комплексных чисел делает операторы более простыми и «красивыми»!
Упражнение 1.
Найдите все (действительные или комплексные) корни многочлена .Ответ.
Упражнение 2.
Разложите многочлен полностью (a) по действительным числам, (b) по комплексным числам.Ответ.
Упражнение 3.
При каких значениях c многочлен имеет два комплексно-сопряженных корня?Ответ.
Упражнение 4.
При каких значениях и полином имеет два различных действительных корня?Ответ.
Упражнение 5.
Каждый квадратичный многочлен имеет либо 2 различных действительных корня, либо один действительный корень кратности 2, либо 2 комплексных корня. Какие случаи могут иметь место для многочлена степени 3? Приведите пример для каждого из этих случаев.Ответ.
Упражнение 6.
(a) Покажите, что каждый многочлен степени 3 имеет хотя бы один х — перехват.
(b) Приведите пример многочлена степени 4 без каких-либо x -пересечений.
Ответ.
Упражнение 7.
Приведите пример многочлена степени 5, единственными действительными корнями которого являются х = 2 с кратностью 2 и х = -1 с кратностью 1.Ответ.
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
Многочлены с комплексными корнями
Горячая математика Основная теорема алгебры
уверяет нас, что любой
многочлен
с
настоящий номер
коэффициенты можно полностью разложить по полю
комплексные числа
.
В случае квадратичные многочлены , корни комплексные, когда дискриминант отрицательный.
Пример 1:
Фактор полностью, используя комплексные числа.
Икс 3 + 10 Икс 2 + 169 Икс
Во-первых, Икс .
Икс 3 + 10 Икс 2 + 169Икс «=» Икс ( Икс 2 + 10 Икс + 169 )
Теперь используйте
квадратичная формула
для выражения в скобках, чтобы найти значения
Икс
для которого
Икс
2
+
10
Икс
+
169
«=»
0
.
Здесь а «=» 1 , б «=» 10 и с «=» 169 .
Икс «=» − б ± б 2 − 4 а с 2 а
Икс «=» − 10 ± 10 2 − 4 ( 1 ) ( 169 ) 2 ( 1 ) «=» − 10 ± 100 − 676 2 «=» − 10 ± − 576 2
Запишите квадратный корень, используя мнимые числа.
Икс «=» − 10 ± 24 я 2 «=» − 5 ± 12 я
Теперь мы знаем, что значения Икс для которого выражение
Икс 2 + 10 Икс + 169
равно 0 являются Икс «=» − 5 + 12 я и Икс «=» − 5 − 12 я .
Таким образом, исходный многочлен можно представить как
Икс 3 + 10 Икс 2 + 169Икс «=» Икс ( Икс − [ − 5 + 12 я ] ) ( Икс − [ − 5 − 12 я ] )
Вы можете убедиться в этом, используя
ФОЛЬГА
.
Иногда вы можете разложить многочлен на множители, используя комплексные числа, не используя квадратную формулу. Например, разница квадратов правило:
Икс 2 − а 2 «=» ( Икс + а ) ( Икс − а )
Это также может быть использовано с комплексными числами, когда а 2 отрицательно, следующим образом:
Икс 2 + 25 «=» ( Икс + 5 я ) ( Икс − 5 я )
Пример 2:
Фактор полностью, используя комплексные числа.
9 Икс 2 у + 64 у
Во-первых, исключить
у
.

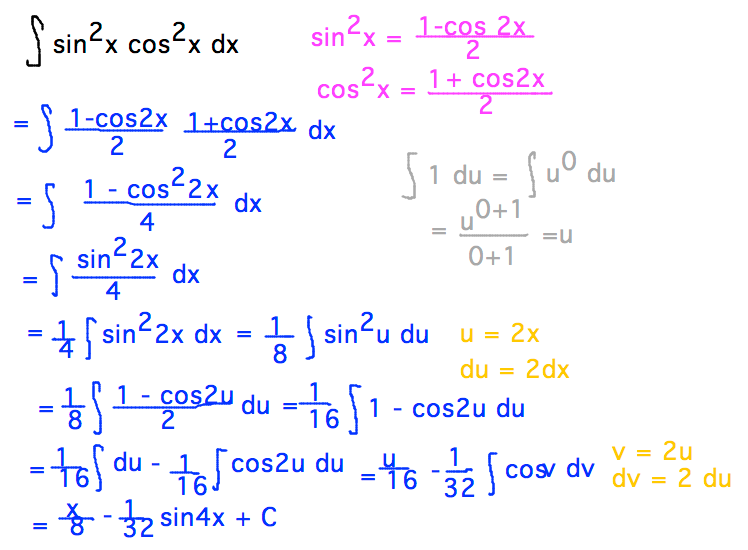

 Ні парна, ні непарна
Ні парна, ні непарна 
 Перевагою цього способу є те, що наочно видно залежність між х та у, видно зміну значень. Недоліком є те, що неможливо встановити точного значення функції в певній точці.
Перевагою цього способу є те, що наочно видно залежність між х та у, видно зміну значень. Недоліком є те, що неможливо встановити точного значення функції в певній точці. Відповідно, для того, щоб перевірити, чи належить точка графіку функції, достатньо підставити відповідні
значення абсциси та ординати у рівняння. Якщо отримаємо рівність, то точка належить графіку функції, якщо ні — то не належить.
Відповідно, для того, щоб перевірити, чи належить точка графіку функції, достатньо підставити відповідні
значення абсциси та ординати у рівняння. Якщо отримаємо рівність, то точка належить графіку функції, якщо ні — то не належить.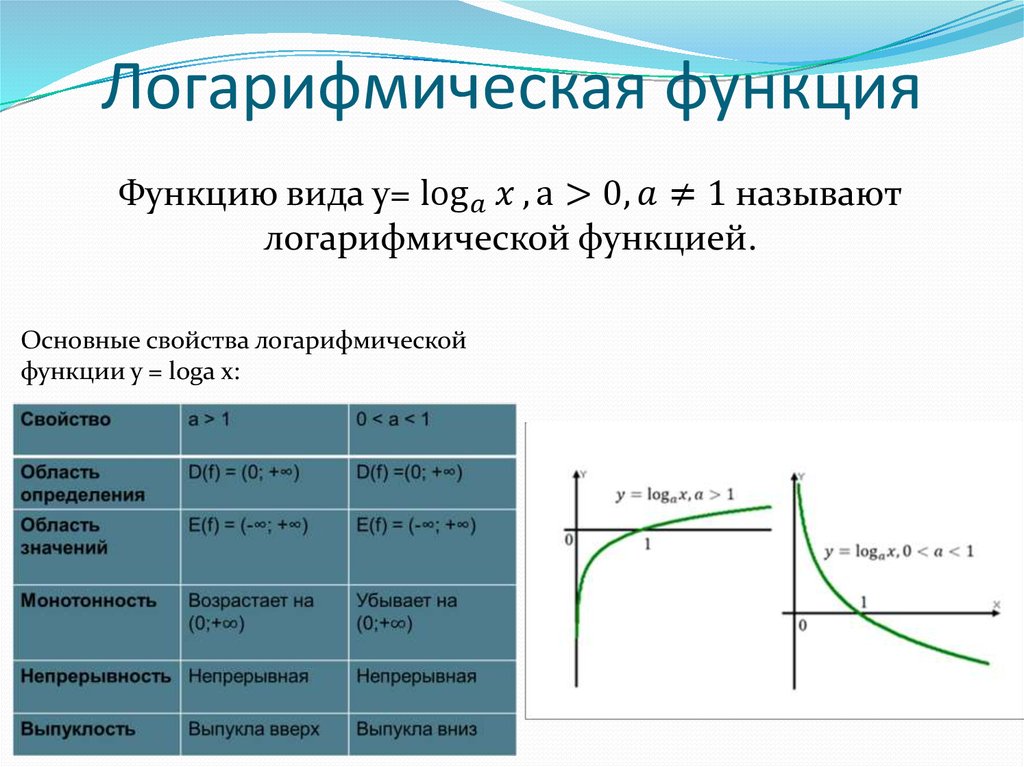 Це дозволяє швидко охопити картину поведінки функції. Тому доцільно для функції будувати її графік. Отже, графік функції y(x) — множина точок координатної площини з координатами (х,у), де х∈D(y), y — відповідне значення функції при даному значенні х.
Це дозволяє швидко охопити картину поведінки функції. Тому доцільно для функції будувати її графік. Отже, графік функції y(x) — множина точок координатної площини з координатами (х,у), де х∈D(y), y — відповідне значення функції при даному значенні х. Графік парної функції симетричний відносно осі ординат.
Графік парної функції симетричний відносно осі ординат. 2) y(-x)=(-x)3-2(-x)=-x3+2x=-(x3-2x)=-y(x). Функція непарна.
3) y(-x)=(-x)2+4(-x)=x2-4x. y(-x) не дорівнює y(x), y(-x) не дорівнює -y(x). Функція ні парна, ні непарна.
2) y(-x)=(-x)3-2(-x)=-x3+2x=-(x3-2x)=-y(x). Функція непарна.
3) y(-x)=(-x)2+4(-x)=x2-4x. y(-x) не дорівнює y(x), y(-x) не дорівнює -y(x). Функція ні парна, ні непарна. 9{N-1} е (\ тильда x_i),
\end{align*}
9{N-1} е (\ тильда x_i),
\end{align*}

 Паритет пут-колл, применимый только к европейским опционам, можно определить с помощью уравнения.
Паритет пут-колл, применимый только к европейским опционам, можно определить с помощью уравнения. Таким образом, этот принцип не применяется к американским опционам, которые могут быть исполнены в любое время до истечения срока действия.
Таким образом, этот принцип не применяется к американским опционам, которые могут быть исполнены в любое время до истечения срока действия. Столлом в его статье «Взаимосвязь между ценами опционов пут и колл» в декабре 1969 года, которая была опубликована в The Journal of Finance .
Столлом в его статье «Взаимосвязь между ценами опционов пут и колл» в декабре 1969 года, которая была опубликована в The Journal of Finance . На теоретическом, совершенно эффективном рынке цены на европейские опционы пут и колл будут регулироваться уравнением, которое мы отметили выше:
На теоретическом, совершенно эффективном рынке цены на европейские опционы пут и колл будут регулироваться уравнением, которое мы отметили выше:
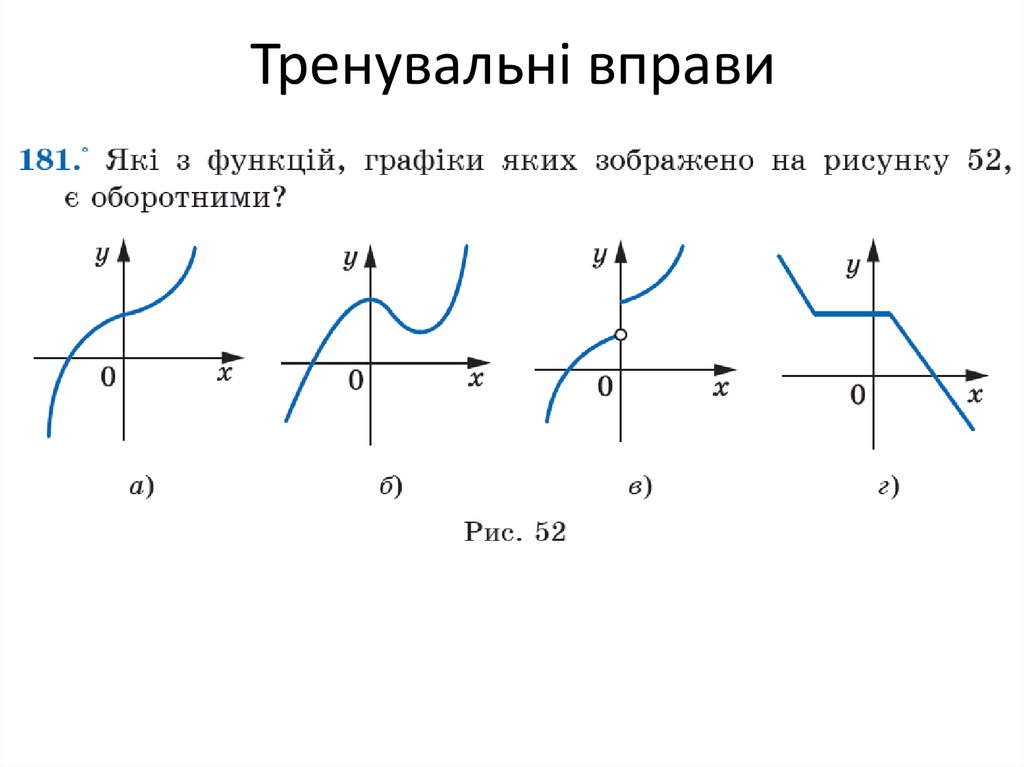 Защитный пут — это длинная позиция по акциям в сочетании с длинным путом, который ограничивает отрицательную сторону владения акциями.
Защитный пут — это длинная позиция по акциям в сочетании с длинным путом, который ограничивает отрицательную сторону владения акциями. Это означает, что вы обязаны заключить эту сделку, какой бы ни была рыночная цена акций TCKR.
Это означает, что вы обязаны заключить эту сделку, какой бы ни была рыночная цена акций TCKR.  Если акции продаются менее чем за 15 долларов, вы теряете деньги. Если они пойдут на большее, вы выиграете. Опять же, этот сценарий игнорирует все комиссии за транзакции.
Если акции продаются менее чем за 15 долларов, вы теряете деньги. Если они пойдут на большее, вы выиграете. Опять же, этот сценарий игнорирует все комиссии за транзакции. Если соотношение пут-колл нарушается, что означает, что цены опционов пут и колл расходятся, так что это соотношение не сохраняется, существует возможность арбитража. Хотя такие возможности редки и краткосрочны на ликвидных рынках, опытные трейдеры теоретически могут получать безрисковую прибыль. Кроме того, он предлагает гибкость для создания синтетических позиций.
Если соотношение пут-колл нарушается, что означает, что цены опционов пут и колл расходятся, так что это соотношение не сохраняется, существует возможность арбитража. Хотя такие возможности редки и краткосрочны на ликвидных рынках, опытные трейдеры теоретически могут получать безрисковую прибыль. Кроме того, он предлагает гибкость для создания синтетических позиций.

 Если нет возможности написать самому, закажите тут.
Если нет возможности написать самому, закажите тут. {(\varphi_1 — \varphi_2)i}\)
{(\varphi_1 — \varphi_2)i}\)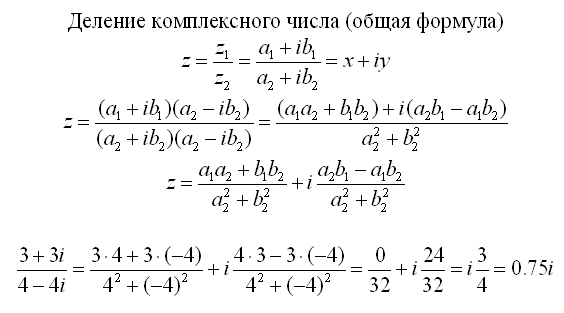 {2}}=\)
{2}}=\)

 Первое, что нам нужно сделать, это определить комплексное число, которое, когда
умножение на знаменатель дает действительное число. Тогда мы можем умножить оба числителя
и знаменатель на это число и упростить. Вопрос в том, что задано комплексное число
𝑧, какое число при умножении на 𝑧 дает действительное
число? Это тот момент, когда мы должны вспомнить свойства комплексного сопряжения, в
в частности, что для комплексного числа 𝑧=𝑎+𝑏𝑖, 𝑧𝑧=𝑎+𝑏, является действительным числом. Следовательно, умножая
числитель и знаменатель комплексным сопряжением знаменателя, мы можем
исключить мнимую часть из знаменателя, а затем упростить результат. Эта техника
не должно быть новым для большинства людей. Узнавая о радикалах, мы сталкиваемся с похожей проблемой.
пытаясь упростить выражения вида 𝑎+𝑏√𝑐𝑑+𝑒√𝑓.
Первое, что нам нужно сделать, это определить комплексное число, которое, когда
умножение на знаменатель дает действительное число. Тогда мы можем умножить оба числителя
и знаменатель на это число и упростить. Вопрос в том, что задано комплексное число
𝑧, какое число при умножении на 𝑧 дает действительное
число? Это тот момент, когда мы должны вспомнить свойства комплексного сопряжения, в
в частности, что для комплексного числа 𝑧=𝑎+𝑏𝑖, 𝑧𝑧=𝑎+𝑏, является действительным числом. Следовательно, умножая
числитель и знаменатель комплексным сопряжением знаменателя, мы можем
исключить мнимую часть из знаменателя, а затем упростить результат. Эта техника
не должно быть новым для большинства людей. Узнавая о радикалах, мы сталкиваемся с похожей проблемой.
пытаясь упростить выражения вида 𝑎+𝑏√𝑐𝑑+𝑒√𝑓. С комплексом
чисел, во многом мы используем ту же технику в особом случае, когда
𝑓 — отрицательное число.
С комплексом
чисел, во многом мы используем ту же технику в особом случае, когда
𝑓 — отрицательное число.



 Принятый подход будет
обычно зависят от конкретного данного выражения; однако хорошо поискать
особенности выражения, которые могут упростить вычисление. В этом случае хорошо
заметить, что у нас есть общий множитель (1+𝑖) в обоих числителях
и знаменатель. Отменив сначала этот фактор, мы можем упростить наши вычисления. Следовательно, (−3+2𝑖)(3+3𝑖)(4+𝑖)(4+4𝑖)=3(−3+2𝑖)(1+𝑖)4(4+𝑖)(1+𝑖)=34( −3+2𝑖)(4+𝑖).
Принятый подход будет
обычно зависят от конкретного данного выражения; однако хорошо поискать
особенности выражения, которые могут упростить вычисление. В этом случае хорошо
заметить, что у нас есть общий множитель (1+𝑖) в обоих числителях
и знаменатель. Отменив сначала этот фактор, мы можем упростить наши вычисления. Следовательно, (−3+2𝑖)(3+3𝑖)(4+𝑖)(4+4𝑖)=3(−3+2𝑖)(1+𝑖)4(4+𝑖)(1+𝑖)=34( −3+2𝑖)(4+𝑖).


 Первое приравнивание
настоящие детали у нас есть
−8𝑥=−168𝑥=14.
Первое приравнивание
настоящие детали у нас есть
−8𝑥=−168𝑥=14.
 Их продукт всегда реален. 92\end{align}[/latex]
Их продукт всегда реален. 92\end{align}[/latex]

 Площадь круга
Площадь круга Как перепроверить решение
Как перепроверить решение  Если Вы с первого раза урок не поняли – не расстраивайтесь. Знайте, что некоторые люди потратили месяцы и годы, чтобы понять хотя бы одну единственную тему. Отчаяние и уныние точно не ваш путь. Читайте, изучайте, пробуйте и снова пробуйте.
Если Вы с первого раза урок не поняли – не расстраивайтесь. Знайте, что некоторые люди потратили месяцы и годы, чтобы понять хотя бы одну единственную тему. Отчаяние и уныние точно не ваш путь. Читайте, изучайте, пробуйте и снова пробуйте.
 Проценты
Проценты Общие сведения о неравенствах
Общие сведения о неравенствах Неравенства с модулем
Неравенства с модулем
 Это спасло жизнь. Все мои классы используют это, и некоторым ученикам пришлось поместить в карантин, но они все еще могут работать над HW и отправлять его.
Это спасло жизнь. Все мои классы используют это, и некоторым ученикам пришлось поместить в карантин, но они все еще могут работать над HW и отправлять его.


 \text{Мяч бросают с высоты 1 м над землей.} Мяч бросают с высоты 1 м земля.
\text{Мяч бросают с высоты 1 м над землей.} Мяч бросают с высоты 1 м земля. на условиях Стандартной общественной лицензии GNU, опубликованной
Free Software Foundation, либо версию 3 Лицензии, либо
(на ваш выбор) любую более позднюю версию.
Free Math распространяется в надежде, что она будет полезна,
но БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ; даже без подразумеваемой гарантии
КОММЕРЧЕСКАЯ ПРИГОДНОСТЬ или ПРИГОДНОСТЬ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ. См.
Стандартная общественная лицензия GNU для более подробной информации.
Вы должны были получить копию Стандартной общественной лицензии GNU.
вместе со свободной математикой. Если нет, см.
на условиях Стандартной общественной лицензии GNU, опубликованной
Free Software Foundation, либо версию 3 Лицензии, либо
(на ваш выбор) любую более позднюю версию.
Free Math распространяется в надежде, что она будет полезна,
но БЕЗ КАКИХ-ЛИБО ГАРАНТИЙ; даже без подразумеваемой гарантии
КОММЕРЧЕСКАЯ ПРИГОДНОСТЬ или ПРИГОДНОСТЬ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ. См.
Стандартная общественная лицензия GNU для более подробной информации.
Вы должны были получить копию Стандартной общественной лицензии GNU.
вместе со свободной математикой. Если нет, см.  Наши математические рабочие листы доступны по широкому кругу тем, включая смысл чисел, арифметику, предварительную алгебру, геометрию, измерения, денежные понятия и многое другое. Есть две интерактивные математические функции: математические карточки и математическая игра в точки.
Наши математические рабочие листы доступны по широкому кругу тем, включая смысл чисел, арифметику, предварительную алгебру, геометрию, измерения, денежные понятия и многое другое. Есть две интерактивные математические функции: математические карточки и математическая игра в точки. Домашние школы используют наши рабочие листы по математике в своих программах для развития и укрепления математических навыков у своих детей.
Домашние школы используют наши рабочие листы по математике в своих программах для развития и укрепления математических навыков у своих детей. Веб-сайт Math-Drills хорошо работает на любом устройстве, а рабочие листы можно распечатать или использовать на экране.
Веб-сайт Math-Drills хорошо работает на любом устройстве, а рабочие листы можно распечатать или использовать на экране.





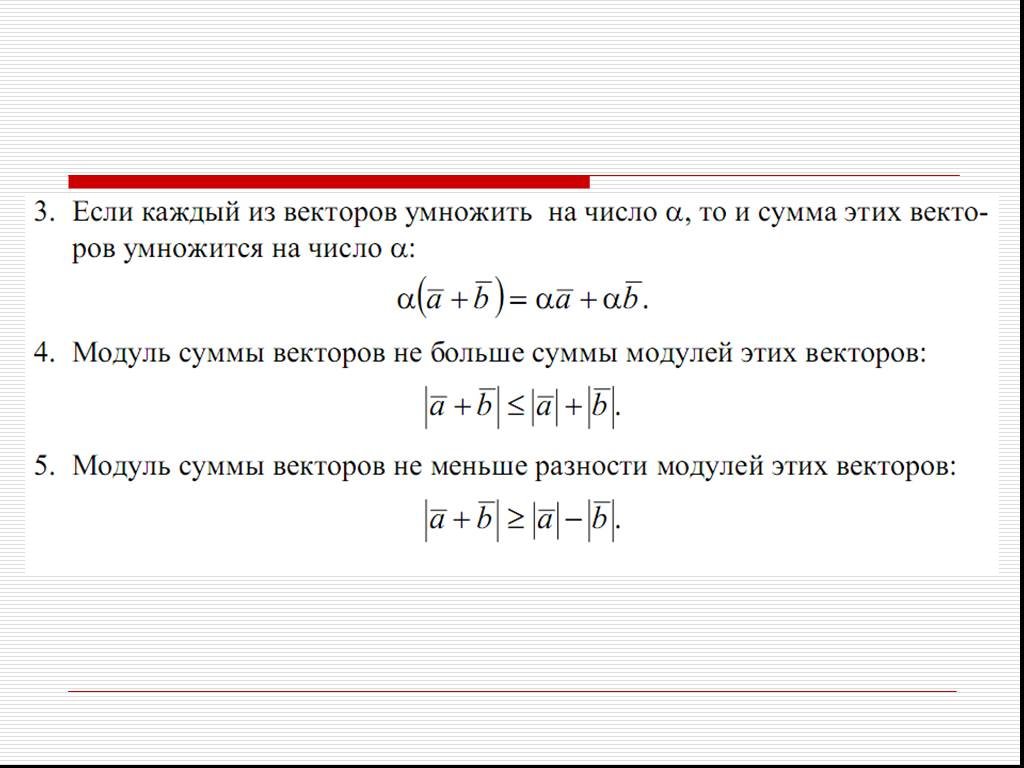 Нормальные подгруппы и факторгруппы
Нормальные подгруппы и факторгруппы
 Модули над кольцом главных идеалов.
Модули над кольцом главных идеалов. Действия над тензорами
Действия над тензорами Следовательно, и модуль не может быть меньше нуля.
Следовательно, и модуль не может быть меньше нуля. Мне любопытно, потому что это кажется очень интересным результатом. Полное утверждение:
Мне любопытно, потому что это кажется очень интересным результатом. Полное утверждение: Вуаля. Ваше комплексное число выставляется как сумма комплексных чисел по модулю единицы.
Вуаля. Ваше комплексное число выставляется как сумма комплексных чисел по модулю единицы.



 Вам необходимо конвертировать JPG в Word таким образом, чтобы извлечь текстовое содержимое из изображения для вставки в документ Word. Затем распознанный текст вы отредактируете по своему усмотрению.
Вам необходимо конвертировать JPG в Word таким образом, чтобы извлечь текстовое содержимое из изображения для вставки в документ Word. Затем распознанный текст вы отредактируете по своему усмотрению.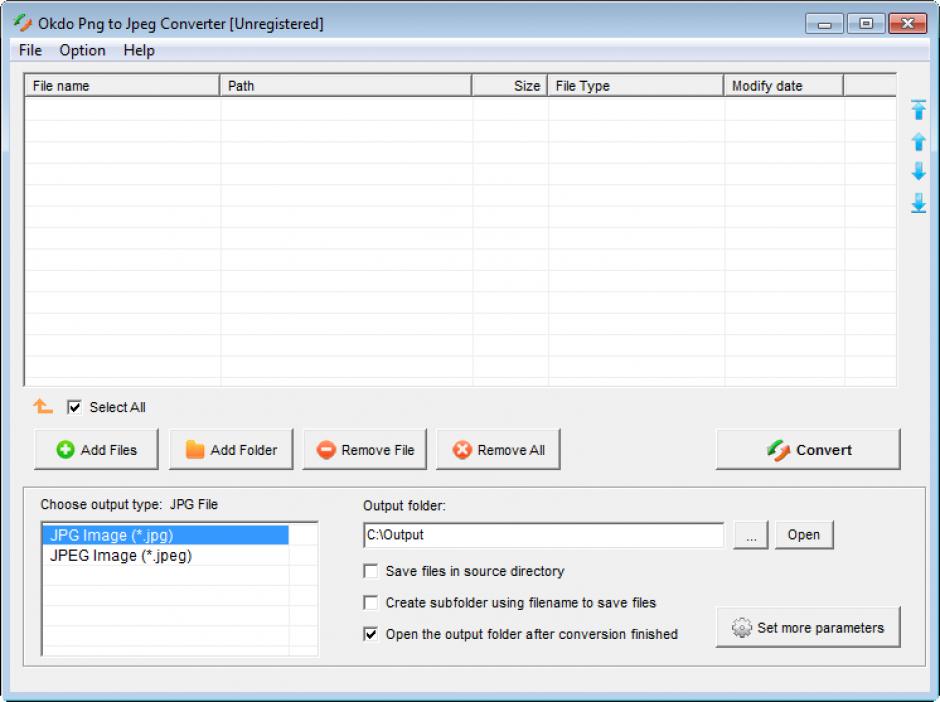



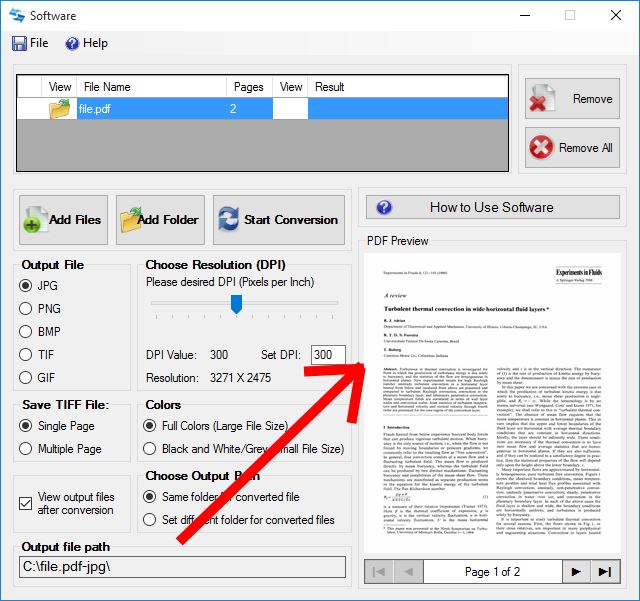


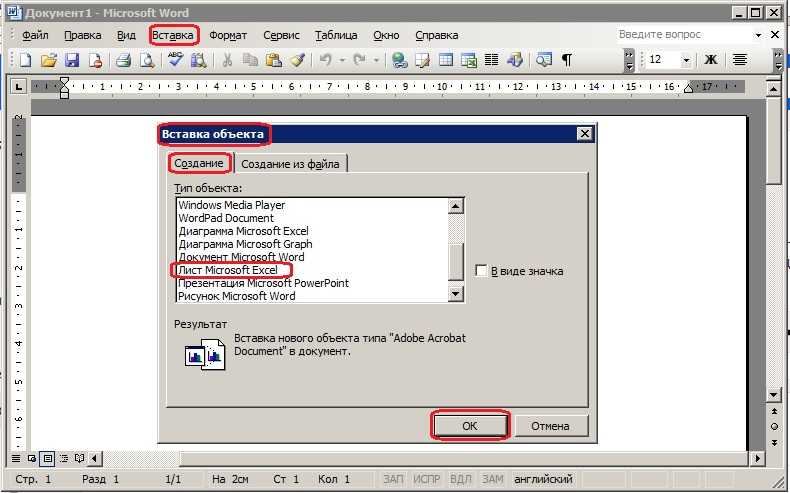 Мгновенно изменить файл изображения на документ Word:
Мгновенно изменить файл изображения на документ Word: Однако, если вы хотите просмотреть некоторые полезные и продуктивные приложения, мы хотели бы, чтобы вы установили и изучили наше мобильное приложение из магазина Google Play, чтобы получить доступ к аналогичным инструментам, программам для чтения и конвертации.
Однако, если вы хотите просмотреть некоторые полезные и продуктивные приложения, мы хотели бы, чтобы вы установили и изучили наше мобильное приложение из магазина Google Play, чтобы получить доступ к аналогичным инструментам, программам для чтения и конвертации. 0°, шаг 180°. После обработки OCR у вас есть несколько вариантов отображения и обработки полученного текста, включая загрузку в виде файла, редактирование в Google Docs, перевод с помощью Google Translate или Bing Translator, публикацию в Интернете, копирование в буфер обмена и многое другое. Наш сервис способен обрабатывать даже плохо отсканированные и сфотографированные страницы и изображения с низким разрешением.
0°, шаг 180°. После обработки OCR у вас есть несколько вариантов отображения и обработки полученного текста, включая загрузку в виде файла, редактирование в Google Docs, перевод с помощью Google Translate или Bing Translator, публикацию в Интернете, копирование в буфер обмена и многое другое. Наш сервис способен обрабатывать даже плохо отсканированные и сфотографированные страницы и изображения с низким разрешением.

 )
) )
) )
) )
) )
) )
) )
)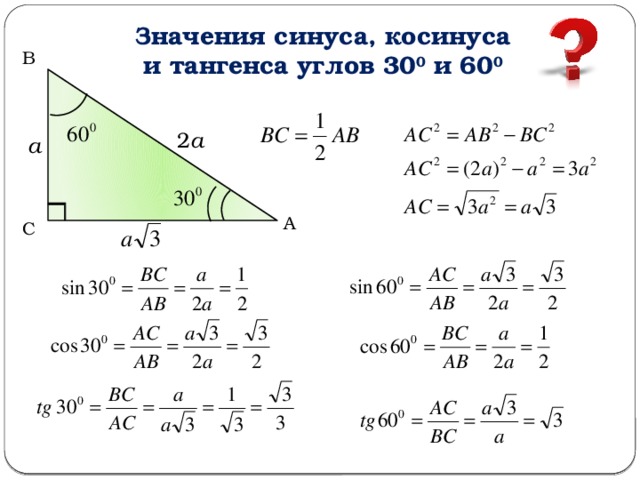 )
) 2-е изд., перераб. и доп., М.: 1974г. — 592с.
2-е изд., перераб. и доп., М.: 1974г. — 592с.
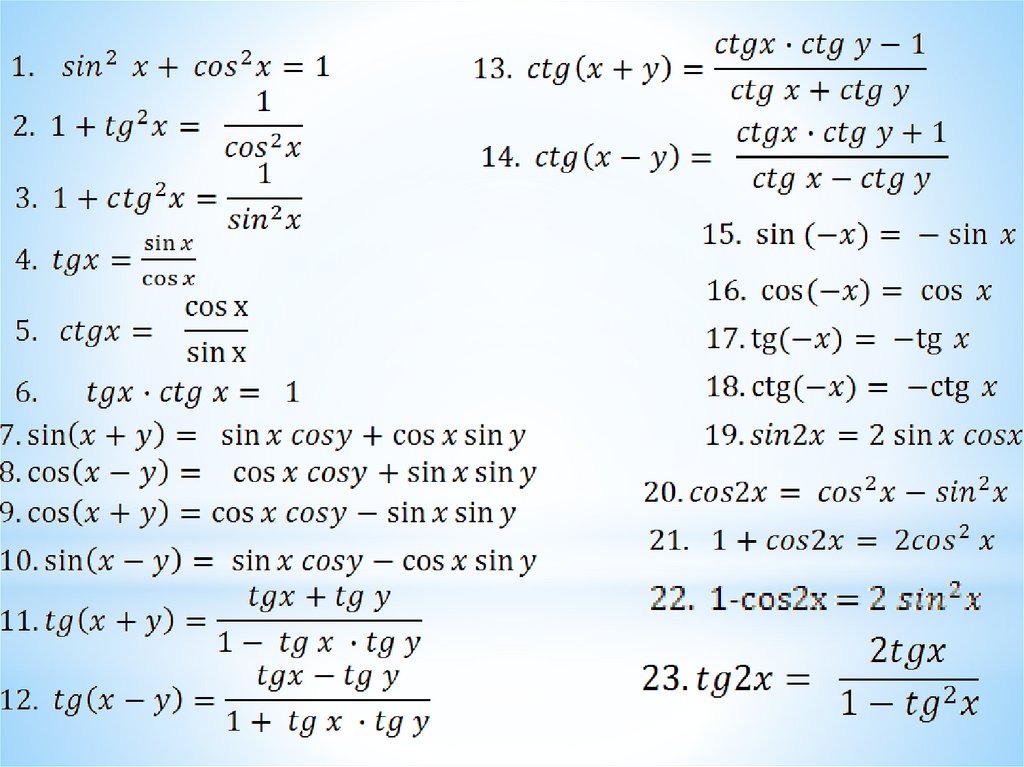
 n.
n.
 Равносильные неравенства.
Равносильные неравенства.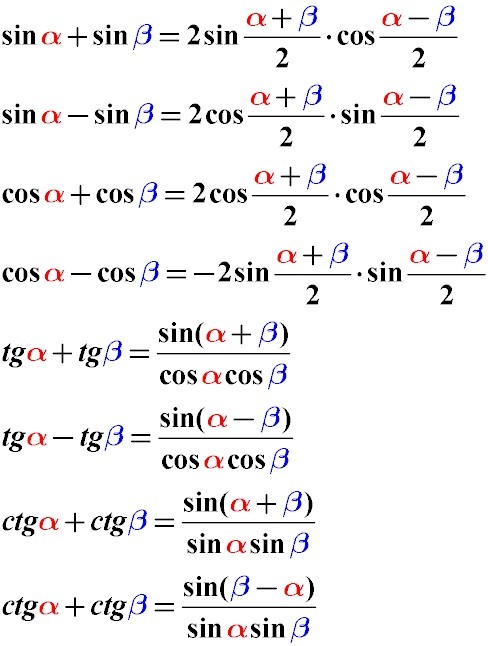
 Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента
 Функция у = arcsin (sin x).
Функция у = arcsin (sin x).


 Теорема Пифагора.
Теорема Пифагора.


 1 секунда, международное название – sec, состоит из 1000 миллисекунд.
1 секунда, международное название – sec, состоит из 1000 миллисекунд.
 io/ru/date/how-many-until/3-november-2024
io/ru/date/how-many-until/3-november-2024 Это означает, что до этого момента осталось 28,0 недель, 4704,0 часа и 7,0 месяцев. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 3 ноября для вас особенное событие, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
Это означает, что до этого момента осталось 28,0 недель, 4704,0 часа и 7,0 месяцев. Мы используем этот расчет довольно часто в календаре, даже если
мы этого не осознаем. Обратный отсчет чьего-то дня рождения, юбилея или особой даты важен, чтобы вовремя заказать подарки!
Если 3 ноября для вас особенное событие, сделайте одолжение себе в будущем и установите напоминание в календаре на день раньше и
сделай это повторяющимся. Пожалуйста.
 и 10,0% в течение ноября.
и 10,0% в течение ноября. ?
? день недели 700019 70019 пятница ()
день недели 700019 70019 пятница ()