Вычислить пример онлайн с решением
В Интернете столько различных программ, что возникает вопрос: можно ли вычислять примеры для их решения в режиме онлайн. Такие приложение уже существуют. Они самостоятельно ищут ответ на ваши задачи и показывают на экране ответ. Это очень удобно и практично. О них и пойдёт речь далее.
Содержание
- «Математический сканер по фото» — поможет вычислить любой пример
- Порядок действий для проведения вычислений онлайн:
- Решение задач онлайн через камеру телефона
- Mathway — онлайн-сервис для вычисления примеров
- «Контрольная работа» — быстрое решение сложных задач онлайн
- Pocket Teacher — поможет вычислить уравнения по математике
- Видео-инструкция
«Математический сканер по фото» — поможет вычислить любой пример
Задание по разным предметам иногда заставляет нас с любой успеваемости зайти в тупик. Пример может сильно отличаться от тех, которые были рассмотрены в школе. Чтобы решить его, придется искать решение в Интернете вручную. Или просить более опытных людей помочь с этим заданием. Есть ещё один вариант выхода с этого положения — воспользоваться онлайн сканером «Математический сканер по фото» на Андроид.
Или просить более опытных людей помочь с этим заданием. Есть ещё один вариант выхода с этого положения — воспользоваться онлайн сканером «Математический сканер по фото» на Андроид.
Он устанавливается на мобильный телефон в виде приложения и способен решать ваши задания при помощи фотографии.
Порядок действий для проведения вычислений онлайн:
- Работать сканер может в двух режимах: по фотографии и при вводе условий вручную;
- Чтобы сфотографировать пример, наведите камеру на условие и нажмите кнопку создания фото;
- На следующем экране появится решение этой задачи с несколькими действиями. Чтобы больше узнать о данном примере, просмотрите внимательно все его этапы решения. И попробуйте разобраться самостоятельно.
Если не выходит понять задачу, в меню приложение «Онлайн» сканер можно найти статьи по теме. В нём множество учебного материала на разные темы по математике и другим предметам. Для этой программы не требуется подключение к Интернету. Она может решать любые примеры оффлайн без доступа к базе данным или поисковым системам. В приложение встроен умный калькулятор, который может быть вызван одной кнопкой на панели в меню. Сканер легко справляется с задачами по математике для начинающих и выпускных классов.
Она может решать любые примеры оффлайн без доступа к базе данным или поисковым системам. В приложение встроен умный калькулятор, который может быть вызван одной кнопкой на панели в меню. Сканер легко справляется с задачами по математике для начинающих и выпускных классов.
Это может быть полезным: решение задач по физике по фото.
Решение задач онлайн через камеру телефона
С каждым учебным годом математика усложняет задачи для учащихся. Становится всё труднее решать примеры быстро и практически не задумываясь. Появляются новые темы, функции, уравнения и прочее. Чтобы со всем этим справиться при вычислении примеров с верным решением, используйте «Камеру Калькулятор» на Андроид.
Это один из лучших способов решать примеры автоматически, применяя лишь камеру мобильного телефона. Пользователю нужно сфотографировать пример, чтобы решить его.
Возможности приложения:
- В приложении есть умный и удобный калькулятор для решения любых задач по предмету;
- Встроен научный калькулятор со всеми инструментами, которые есть в классической версии;
- Отдельно реализован калькулятор уравнений.

Мобильное приложение «Камера Калькулятор» способно справляться с решением интегралов, интеграций, производных, дифференцирования, пределов и многое другое. Для тех пользователей, которым необходимы простые функции, он является таковым. Более сложные инструменты находятся в меню и могут быть запущены при необходимости. Поэтому вычислить любой пример онлайн и получить его подробное решение не составим труда. Программа будет полезна школьникам старших классов, которые сталкиваются со сложными заданиями на самостоятельных работах и контрольных.
Также «Камера Калькулятор» станет незаменимым помощником для студентов разных профессий. Приложение не займёт много памяти в мобильном телефоне и может работать беззвучно.
Читайте также: решение задач по геометрии по фото.
Mathway — онлайн-сервис для вычисления примеров
С вычислением сложных примеров и их вычислением в Интернете поможет онлайн-приложение Mathway. Без надобности устанавливать какие-либо программы на телефон. Откройте в браузере ссылку на сайт Mathway.com.
Без надобности устанавливать какие-либо программы на телефон. Откройте в браузере ссылку на сайт Mathway.com.
При нажатии на кнопку с фотоаппаратом на экране появится виртуальная клавиатура со всеми подходящими символами для решения математических уравнений. Если к вашему устройству подключена веб-камера или вы используете сайт с мобильного устройства, то появится возможность сфотографировать условия задачи.
Также его можно записать в пустой строке, которая выше виртуальной клавиатуры приглашает: «Введите задачу». Чтобы выбрать другой предмет в онлайн-сервисе, нажмите на кнопку меню вверху.
Среди них можно выбрать:
- Решение задач по элементарной математике;
- Тригонометрии;
- Статистике,
- Алгебре;
- Линейной алгебре;
- Химии;
- Создание графиков;
- Основа математического анализа.
В меню онлайн-программы доступны примеры по разным предметам. Чтобы их открыть, нажмите на кнопку с тремя точками вверху. И выберите пункт «Примеры». Появится новый раздел, где вы сможете выбрать примеры по алгебре. Для того, чтобы рассмотреть один из них, выберите его курсором мыши или тапом по экране мобильного. Когда пример будет выбран, его условия и решение развернется на экране. Дополнительно появится возможность открыть каждый шаг в решении. Или показать график из этого примера на экране. Ссылки для этого в конце примера.
И выберите пункт «Примеры». Появится новый раздел, где вы сможете выбрать примеры по алгебре. Для того, чтобы рассмотреть один из них, выберите его курсором мыши или тапом по экране мобильного. Когда пример будет выбран, его условия и решение развернется на экране. Дополнительно появится возможность открыть каждый шаг в решении. Или показать график из этого примера на экране. Ссылки для этого в конце примера.
«Контрольная работа» — быстрое решение сложных задач онлайн
Быстро и точно примеры может решать сервис «Контрольная работа» www.kontrolnaya-rabota.ru/s. Всё что нужно пользователю — это ввести условие в пустую строку. Сервис удобно использовать на мобильном телефоне через браузер или на компьютере во время выполнения задания. Чтобы получить большой список калькуляторов для разных условий, на главной странице необходимо выбрать кнопку «Начать сейчас».
Из перечня перед вами можно выбрать:
- Решение уравнений и упрощённых выражений онлайн с возможностью вводить условия;
- Калькулятор для решения неравенств с отображением графиков решения на экране;
- Поиск пределов в сервисе — найдите его для любой функции.
 Применяются решения по Лопиталю;
Применяются решения по Лопиталю; - На сайте есть производные функций, графики. Вы сможете построить свой график в пространстве;
- Калькулятор для решения неравенств;
- Доступны практически любые действия с неравенствами: умножение, возведение в степень, ранг матрицы, обратные матрицы и другое;
- На сайте есть возможность решить со своими условиями комплексные числа, геометрическую интерпретацию.
Кроме этого на сайте ещё множество возможностей, связанных с решением математических задач и условий по другим предметам. Можно найти таблицы интегралов, Брадиса, таблицы производных. Примеры из высшей математики и полезные и интересные калькуляторы. Если у вас возникнут трудности, в нижней части списка с возможностями находится подробная инструкция, как пользоваться тем или иным инструментом. Представлено множество текстов, описывающих не только работу калькуляторов и таблиц, но и с рассмотрением конкретных примеров.
Pocket Teacher — поможет вычислить уравнения по математике
Рассмотрим ещё один интересный онлайн-сервис с решениями для математики. Называется он Pocket Teacher.
Называется он Pocket Teacher.
Ссылка: https://www.pocketteacher.ru/solve-page. Сайт является большим и всесторонним инструментом, для решения практически любых математических условий заданий. На главной странице пользователю предлагается выбрать один из трёх основных разделов сайта: алгебра, геометрия, высшая математика и текстовая задача. На экране отображается клавиатура с математическими знаками.
- Начните вводить символы условия своей задачи;
- Возле примера находятся кнопки для управления вводом. Нажмите «Очистить» или «Удалить», если допустили ошибку при вводе;
- Чтобы пример решить, нажмите на соответствующую кнопку справа и выберите пункт «Решение».
Каждое решение на время сохраняется на сайте. Его можно вернуть при помощи кнопок на панели. Это приложение можно скачать на мобильный телефон с Android или с IOS. Ссылки расположены на главной странице сайта.
Видео-инструкция
Рассмотренные инструменты помогут вычислить любой сложный пример в режиме онлайн с подробным решением. Посмотрите о дополнительных приложениях в видео.
Посмотрите о дополнительных приложениях в видео.
App Store: Калькулятор лимита с шагами
Описание
Решатель предельных калькуляторов — это подарок всем, кто изучает математику, и тем, кто преподает математический анализ. Потому что этот калькулятор рассчитывает лимиты и показывает пошаговые результаты.
Этот онлайн-калькулятор пределов позволяет сразу найти предел любой сложной дифференцируемой функции. Вы можете получить подробное решение любой функции, заключенной в определенные границы, используя этот искатель пределов.
Что такое предел?
«Предел говорит нам о поведении конкретной функции вблизи точки, но не точно в этой точке».
Эта операция обеспечивает надежную поддержку при решении различных числовых задач. Воспользуйтесь этим приложением калькулятора пределов, чтобы выполнить ряд математических вычислений в кратчайшие сроки. Этот искатель пределов не только вычисляет границы, но и отображает разложение данной функции в ряд Тейлора.
Правило Лопиталя:
Это специальное правило предлагается для нахождения пределов точно так же, как 0/0 или ∞/∞. Наш калькулятор лимитов сразу же упрощает такие лимиты и предоставляет вам правильный способ выполнения расчетов.
Как найти предел сложных функций с помощью калькулятора пределов?
Поскольку пределы широко используются в математике, вы можете найти границы функции, в которых она сохраняет свою непрерывность. Что вам нужно сделать, так это ввести функцию в наш лимитный калькулятор с шагами, и он быстро определит характер функции. Найдем как!
Запишите функцию в указанное поле
Теперь выберите переменную, для которой вы хотите найти предел
Затем выберите точку, вблизи которой должен быть определен предел.
Из следующего выпадающего списка выберите направление предела, которое может быть как положительным, так и отрицательным.
Нажмите кнопку расчета, и калькулятор пределов предоставит пошаговый шаг решения на экране вашего устройства.
Возможности многопараметрического решателя:
Дружественный интерфейс
100% точные результаты
Пошаговые расчеты
Легко загружаемый PDF-файл всего решения для лучшего понимания проблемы
Простота в использовании
Удобная клавиатура для ввода любой сложной функции без каких-либо препятствий
Итак, используйте это приложение-калькулятор пределов, чтобы получить четкое представление о задачах исчисления, связанных с ограничениями.
»
Версия 1.0.2
— Исправление ошибки
— Добавление дополнительных функций
— Улучшение взаимодействия с пользователем
Разработчик Асад Ахсан указал, что политика конфиденциальности приложения может включать обработку данных, как описано ниже. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Для получения дополнительной информации см. политику конфиденциальности разработчика.
Данные, используемые для отслеживания вас
Следующие данные могут использоваться для отслеживания вас в приложениях и на веб-сайтах, принадлежащих другим компаниям:
Данные, связанные с вами
Следующие данные могут быть собраны и связаны с вашей личностью:
Методы обеспечения конфиденциальности могут различаться, например, в зависимости от используемых вами функций или вашего возраста. Узнать больше
Информация
- Продавец
- Асад Ахсан
- Размер
- 36,2 МБ
- Категория
- Образование
- Возрастной рейтинг
- 4+
- Авторское право
- © 2022 eClixTech.

- Цена
- Бесплатно
- Сайт разработчика
- Тех. поддержка
- политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Счетчик символов и инструмент предварительного просмотра текста
Калькулятор длины SMS: счетчик символов и инструмент предварительного просмотра текстаПодсчет символов в сообщении, расчет стоимости отправки и предварительный просмотр текстовых сообщений на различных мобильных устройствах
Калькулятор длины текстового сообщения — это простой инструмент, который может многое рассказать о текстовом сообщении, например, количество символов, тип используемых символов, стоимость текстового сообщения и многое другое.
Вот как его использовать:
Шаг № 1: Скопируйте и вставьте или напишите текстовое сообщение. Вы также можете выбрать один из доступных шаблонов.
Шаг #2: Выберите один из доступных вариантов для поля «От», чтобы увидеть, как SMS-сообщение будет выглядеть на телефоне клиента.
Шаг №3: В правой части экрана выберите страну назначения для вашего SMS-сообщения, чтобы рассчитать стоимость текстового сообщения.
Почему вам следует использовать калькулятор длины SMS
Есть несколько причин, по которым вам следует использовать наш инструмент подсчета символов текстовых сообщений:
Подсчитайте количество символов в вашем текстовом сообщении. Это может показаться излишним, учитывая название инструмента, но не все символы одинаковы. Как вы знаете, стандартная длина текстовых сообщений составляет 160 символов, но использование кодировки Unicode уменьшит эту длину до 70 символов. Кроме того, для некоторых символов из набора символов GSM 03.
 38 требуются «экранирующие символы». Эти escape-символы занимают два символа (14 бит) для кодирования. Таким образом, даже если у вас есть 160 символов GSM, сообщение может быть разделено, если оно содержит один такой символ.
38 требуются «экранирующие символы». Эти escape-символы занимают два символа (14 бит) для кодирования. Таким образом, даже если у вас есть 160 символов GSM, сообщение может быть разделено, если оно содержит один такой символ.Приблизительная стоимость текстового сообщения. В правой части экрана вы также увидите инструмент «Стоимость текстового сообщения», который позволяет вам выбрать страну, в которую будет отправлено SMS. Это автоматически рассчитает стоимость вашего текстового сообщения.
Предварительный просмотр вашего текстового сообщения на разных мобильных устройствах. Инструмент счетчика символов также имеет опцию предварительного просмотра, которая покажет вам, как текстовое сообщение будет отображаться на устройствах Apple, устройствах Android и обычных сотовых телефонах.
Изучите «детальный вид» вашего текстового сообщения. С помощью подробного просмотра вы можете исследовать характер используемых символов. Обычные символы GSM отображаются серым цветом, символы, отличные от GSM, которые переводят текст в кодировку Unicode, выделяются красным, а символы GSM, закодированные как символы Unicode, выделяются желтым цветом.
 Подробный вид дает вам больше контроля над текстовыми сообщениями, а также возможность изменять или редактировать символы, которые увеличивают количество ваших символов.
Подробный вид дает вам больше контроля над текстовыми сообщениями, а также возможность изменять или редактировать символы, которые увеличивают количество ваших символов.
Зачем мы создали этот инструмент
Мы считаем, что форматирование чрезвычайно важно при обмене текстовыми сообщениями. Разделенное, неполное или неправильно отформатированное SMS-сообщение может оттолкнуть клиента от принятия мер. Мы создали инструмент счетчика текстовых символов, чтобы помочь нашим посетителям проверять не только длину их текстовых сообщений, но также типы используемых символов и способ отображения текста на разных мобильных устройствах.
Преимущества использования калькулятора длины SMS
Инструмент подсчета символов SMS даст вам больше контроля над вашими текстовыми сообщениями. Вот основные преимущества использования нашего инструмента:
Быстро определяйте количество символов в ваших текстовых сообщениях.
Узнайте, на сколько частей будет разбито текстовое сообщение.

Идентификация символов GSM, символов Unicode и символов GSM, использующих кодировку Unicode.
Предварительный просмотр вашего текстового сообщения, как оно будет выглядеть на Apple, Android и обычных мобильных устройствах.
Оцените стоимость отправки текстового сообщения в разные страны.
Отредактируйте символы, которые занимают место, чтобы избежать сегментации SMS.
Как уменьшить длину текстового сообщения?
Используя подробное представление нашего онлайн-инструмента подсчета символов, вы можете определить символы, которые занимают слишком много места в вашем текстовом сообщении. Лучший способ уменьшить длину SMS-сообщения — заменить такие символы (обычно символы Unicode, символы GSM, для которых требуется кодировка Unicode, или escape-символы) их эквивалентом GSM.
ГЛОССАРИЙ
Кодировка GSM: Кодировка GSM 03.38 является стандартным набором символов для обмена текстовыми сообщениями на сотовых телефонах с поддержкой GSM. Все телефоны GSM и сетевые элементы поддерживают 7-битный алфавит GSM. Базовая кодировка GSM содержит буквы от A до Z (прописные и строчные), цифры, специальные символы и несколько символов греческого алфавита.
Все телефоны GSM и сетевые элементы поддерживают 7-битный алфавит GSM. Базовая кодировка GSM содержит буквы от A до Z (прописные и строчные), цифры, специальные символы и несколько символов греческого алфавита.
@ Δ SP 0 ¡ P ¿ p
£ _ ! 1 A Q a Q
$ Φ " 2 B R b r
¥ Γ # 3 C S c s
è Λ ¤ 4 D T d t
é Ω % 5 E U e u
ù Π & 6 F V f v
ì Ψ ' 7 G W g w
ò Σ ( 8 H X h x
Ç Θ ) 9, {, }, €, [ ~, ] и \. Символы Unicode: Unicode — это стандарт для кодирования, обработки и представления текста, выраженного во многих мировых системах письма. Последний список символов Unicode содержит более 120 000 символов из нескольких наборов символов и 129 исторических и современных шрифтов.
Кодировка Unicode: По сравнению с кодировкой GSM кодировка Unicode поддерживает огромное количество языков и символов. Однако, если ваше текстовое сообщение содержит символ, который не входит в 7-битный алфавит, необходимо использовать кодировку UCS-2. Этот тип кодирования занимает много места, поэтому допустимое количество символов в сообщении сокращается до 70.


 Применяются решения по Лопиталю;
Применяются решения по Лопиталю;
 38 требуются «экранирующие символы». Эти escape-символы занимают два символа (14 бит) для кодирования. Таким образом, даже если у вас есть 160 символов GSM, сообщение может быть разделено, если оно содержит один такой символ.
38 требуются «экранирующие символы». Эти escape-символы занимают два символа (14 бит) для кодирования. Таким образом, даже если у вас есть 160 символов GSM, сообщение может быть разделено, если оно содержит один такой символ. Подробный вид дает вам больше контроля над текстовыми сообщениями, а также возможность изменять или редактировать символы, которые увеличивают количество ваших символов.
Подробный вид дает вам больше контроля над текстовыми сообщениями, а также возможность изменять или редактировать символы, которые увеличивают количество ваших символов.


 э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.
э., он использовал для этого геометрический способ доказательства формулы, так как буквами для обозначения чисел не пользовались и учёные древней Эллады. Ими повсеместно употреблялись не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник , заключенный между отрезками a и b”.




 Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства). В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².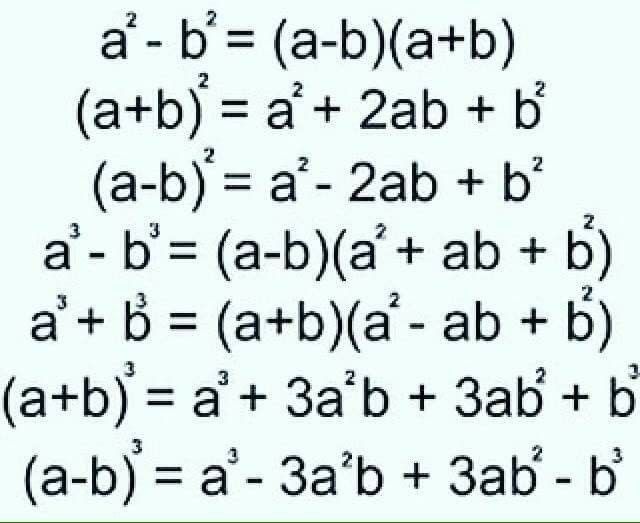 Известны лишь величины их сторон.
Известны лишь величины их сторон. Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба.
Необходимо вычислить объем фигуры, которая останется после вычитания из объема синего куба объемной фигуры желтого цвета, которая также является кубом. Известна лишь величина стороны маленького и большого куба. (a+b)(a-b)=a 2 -b 2
(a+b)(a-b)=a 2 -b 2
 Формулы сокращённого умножения нужно знать наизусть:
Формулы сокращённого умножения нужно знать наизусть: Формула, позволяющая выписывать разложение алгебраической
суммы двух слагаемых произвольной степени, впервые была предложена Ньютоном в
1664–1665 г. и получила название бинома Ньютона. Коэффициенты
формулы называются биномиальными коэффициентами. Если n – положительное
целое число, то коэффициенты обращаются в нуль при любом k > n,
поэтому разложение содержит лишь конечное число членов. Во всех остальных
случаях разложение представляет собой бесконечный (биномиальный) ряд.
(Условия сходимости биномиального ряда впервые были установлены в начале
19 в. Н.Абелем.) Такие частные случаи, как
Формула, позволяющая выписывать разложение алгебраической
суммы двух слагаемых произвольной степени, впервые была предложена Ньютоном в
1664–1665 г. и получила название бинома Ньютона. Коэффициенты
формулы называются биномиальными коэффициентами. Если n – положительное
целое число, то коэффициенты обращаются в нуль при любом k > n,
поэтому разложение содержит лишь конечное число членов. Во всех остальных
случаях разложение представляет собой бесконечный (биномиальный) ряд.
(Условия сходимости биномиального ряда впервые были установлены в начале
19 в. Н.Абелем.) Такие частные случаи, как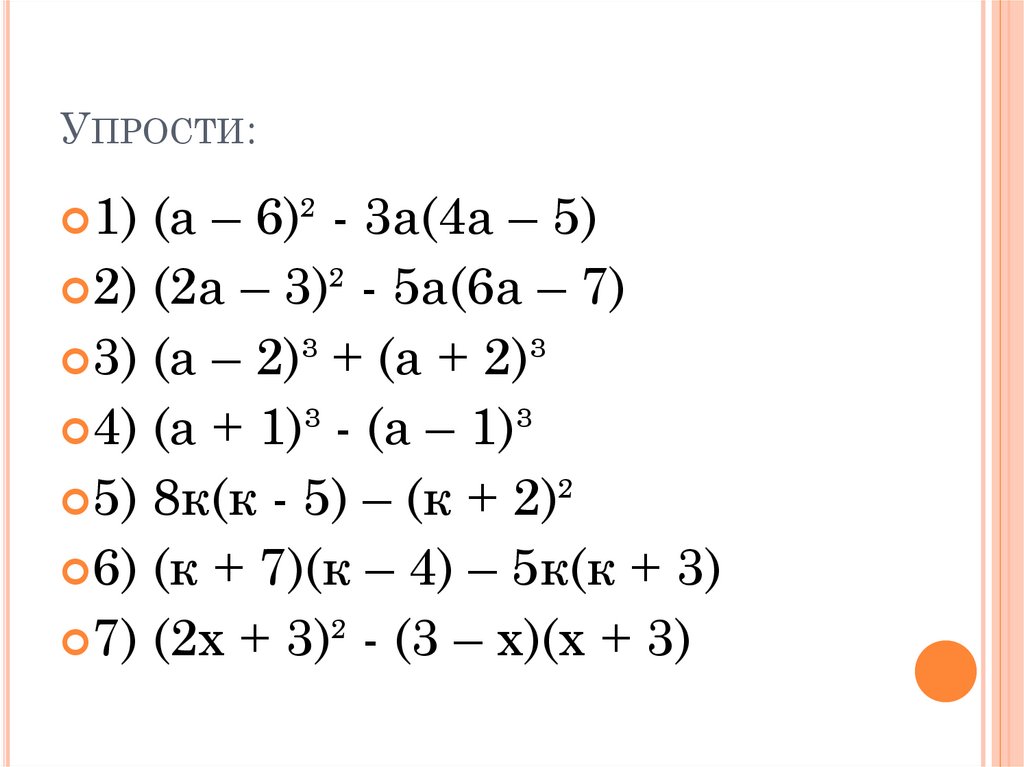 Для данного n соответствующая
(n-я) строка треугольника Паскаля дает по порядку коэффициенты биномиального
разложения n-й степени, в чем нетрудно убедиться при n = 2 и n = 3.
Для данного n соответствующая
(n-я) строка треугольника Паскаля дает по порядку коэффициенты биномиального
разложения n-й степени, в чем нетрудно убедиться при n = 2 и n = 3.
 Убедитесь, что у вашего ученика нет проблем с умножением двучленов.
Убедитесь, что у вашего ученика нет проблем с умножением двучленов. Это покажет связь между алгеброй и геометрией и закрепит понимание справедливости ФСУ.
Это покажет связь между алгеброй и геометрией и закрепит понимание справедливости ФСУ. Благодаря им можно легко возводить в квадрат двузначные числа.
Благодаря им можно легко возводить в квадрат двузначные числа. Последний скандал касался этого, казалось бы, простого вопроса:
Последний скандал касался этого, казалось бы, простого вопроса: 
 Затем вы имеете дело с любыми показателями. Далее следуют умножение и деление, которые, как я уже сказал, имеют равный приоритет, а двусмысленность устраняется за счет работы слева направо. Наконец, идут сложение и вычитание, которые также имеют одинаковый приоритет, с двусмысленностью, снова устраняемой за счет работы слева направо.
Затем вы имеете дело с любыми показателями. Далее следуют умножение и деление, которые, как я уже сказал, имеют равный приоритет, а двусмысленность устраняется за счет работы слева направо. Наконец, идут сложение и вычитание, которые также имеют одинаковый приоритет, с двусмысленностью, снова устраняемой за счет работы слева направо.  В этом смысле PEMDAS является произвольным. Кроме того, по моему опыту математика, выражения вроде 8÷2×4 выглядят абсурдно надуманными. Ни один профессиональный математик никогда не напишет что-то столь явно двусмысленное. Мы вставляли круглые скобки, чтобы указать наше значение и сигнализировать о том, следует ли сначала выполнить деление или умножение.
В этом смысле PEMDAS является произвольным. Кроме того, по моему опыту математика, выражения вроде 8÷2×4 выглядят абсурдно надуманными. Ни один профессиональный математик никогда не напишет что-то столь явно двусмысленное. Мы вставляли круглые скобки, чтобы указать наше значение и сигнализировать о том, следует ли сначала выполнить деление или умножение. 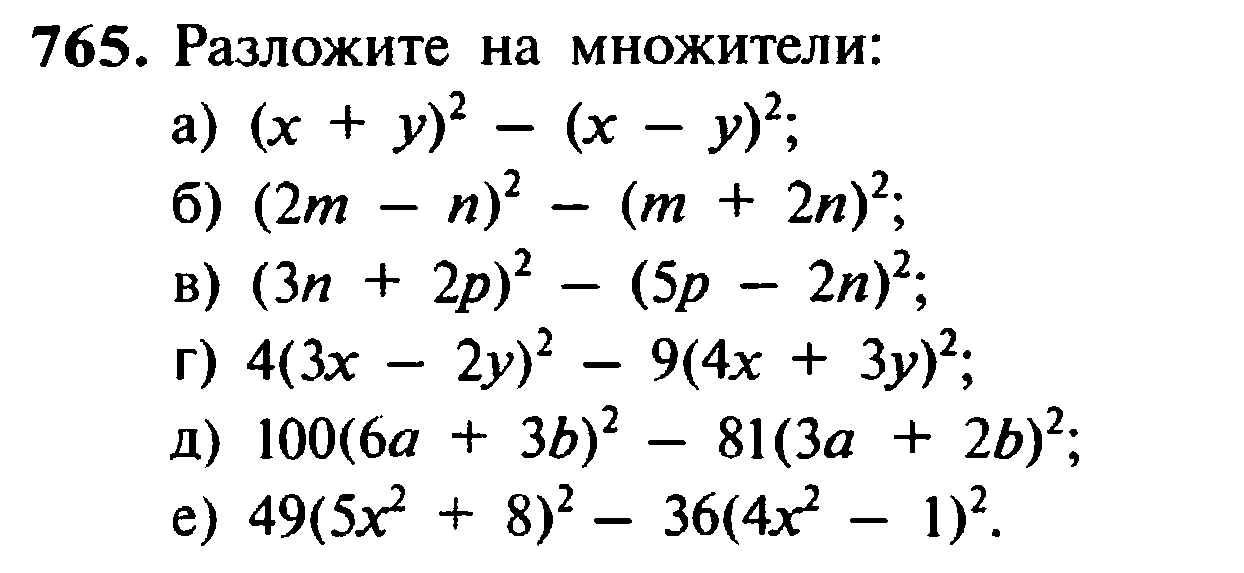
 Ясно, что если этот последний приступ путаницы в Интернете является каким-либо признаком того, что многие студенты не в состоянии усвоить более глубокий и важный урок. Возможно, пришло время перестать извинять дорогую тетю Салли и вместо этого обнять ее.
Ясно, что если этот последний приступ путаницы в Интернете является каким-либо признаком того, что многие студенты не в состоянии усвоить более глубокий и важный урок. Возможно, пришло время перестать извинять дорогую тетю Салли и вместо этого обнять ее.  .. Меньше
.. Меньше 


 2\over4}}$$
2\over4}}$$
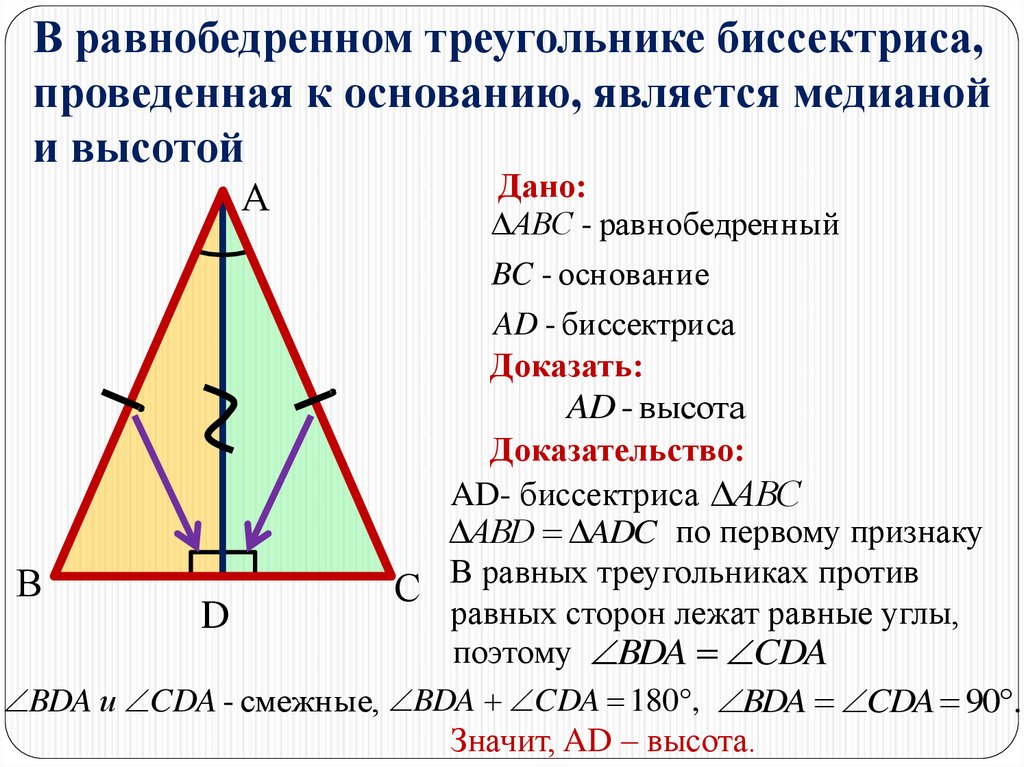
 Выразим ее через формулу медианы равностороннего треугольника.
Выразим ее через формулу медианы равностороннего треугольника.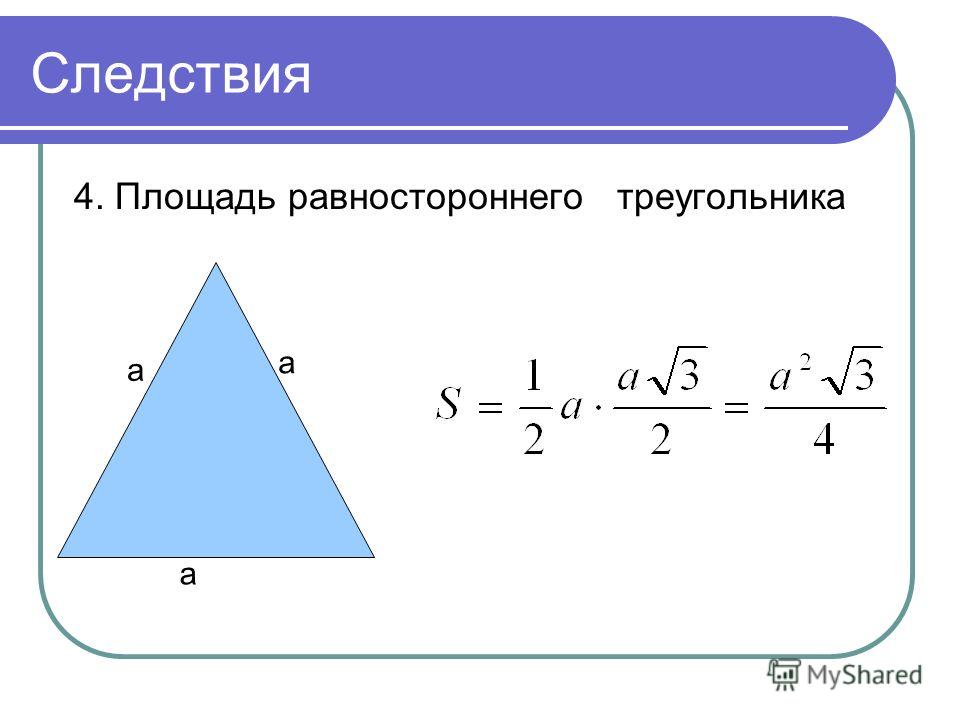 11.21
11.21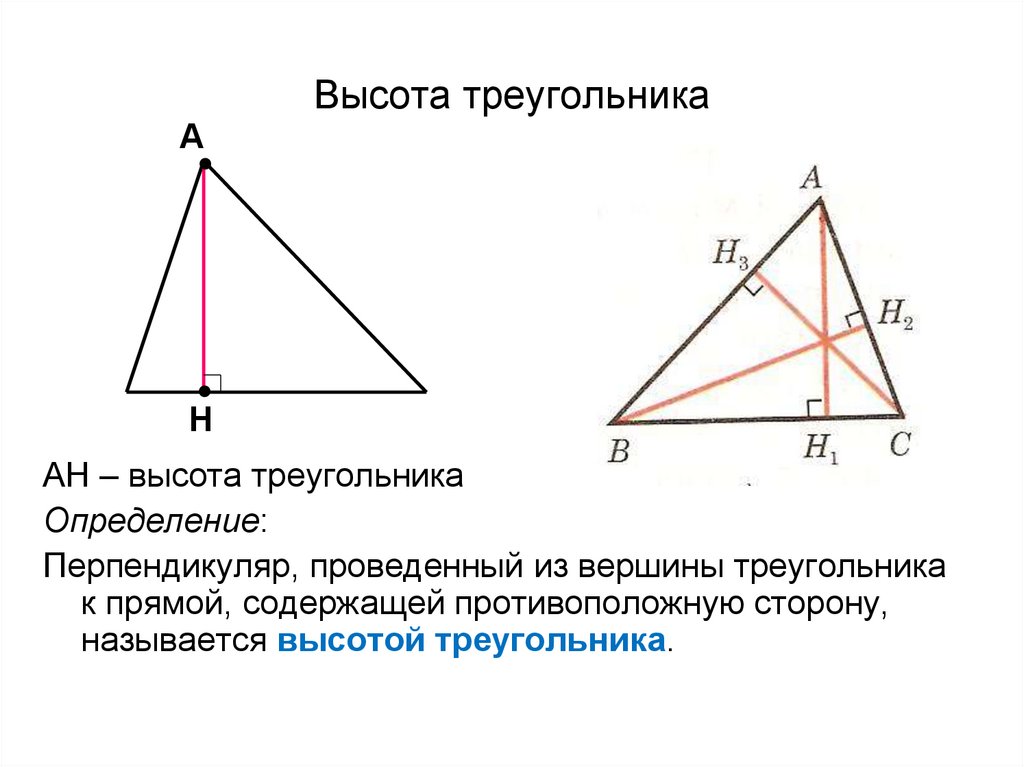
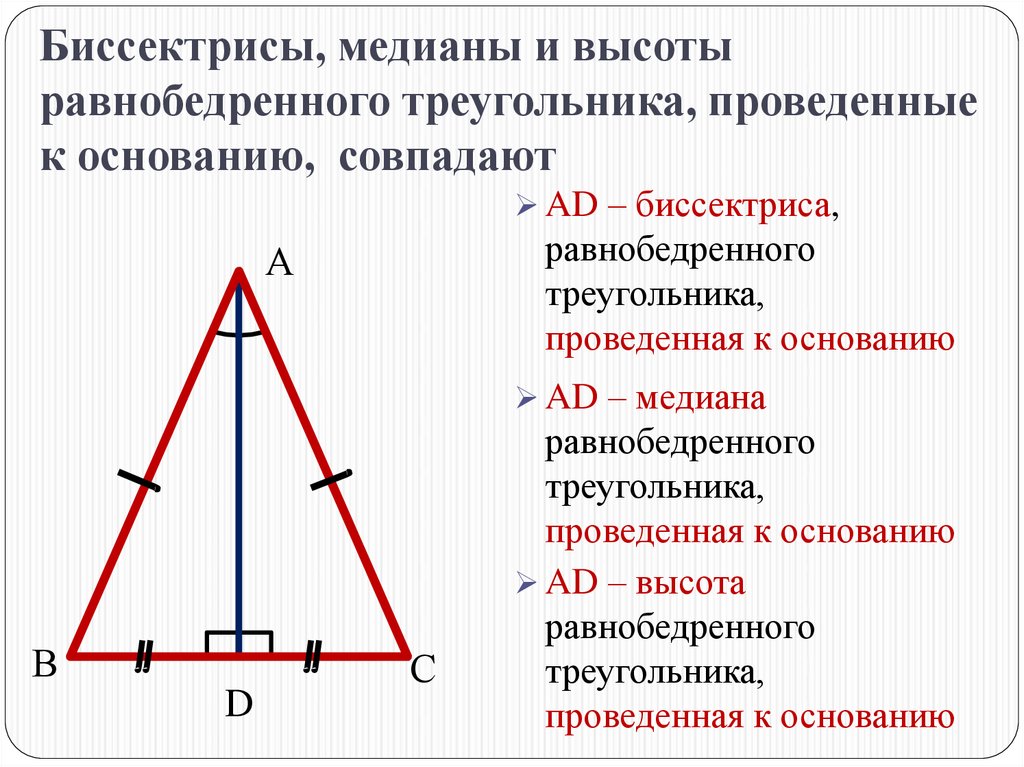 Точку, в которой она соприкасается с прямой, называют основанием медианы. Существуют свойства, характерные только для рассматриваемой прямой. Так, можно, зная медиану, найти сторону треугольника, его площадь или угол вершины.
Точку, в которой она соприкасается с прямой, называют основанием медианы. Существуют свойства, характерные только для рассматриваемой прямой. Так, можно, зная медиану, найти сторону треугольника, его площадь или угол вершины.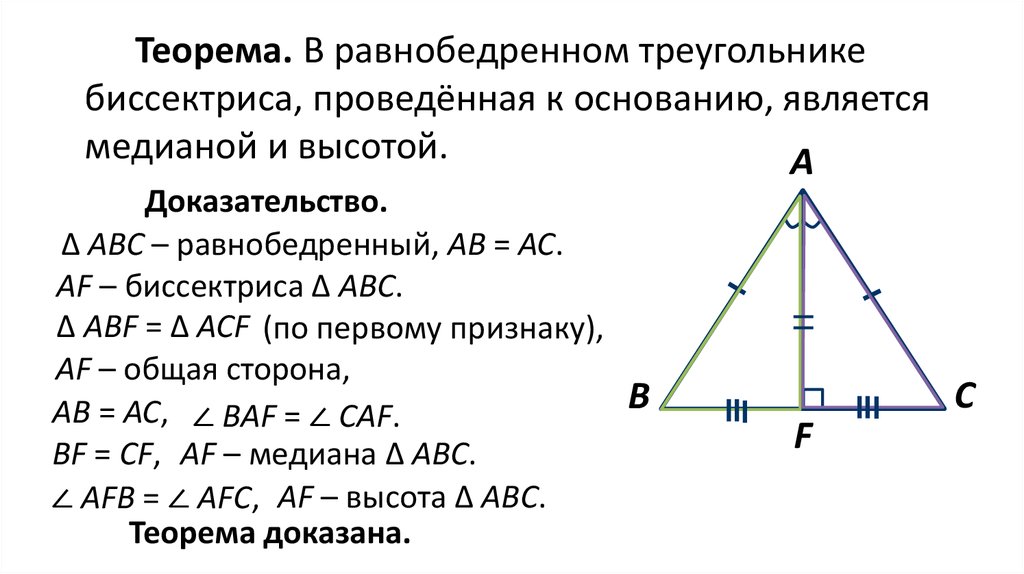 Так как ограниченная прямая — это медиана, то AD = DC. Отсюда следует, что фигура делится на 2 равные части. Значит, S1 = S2, что и нужно было доказать.
Так как ограниченная прямая — это медиана, то AD = DC. Отсюда следует, что фигура делится на 2 равные части. Значит, S1 = S2, что и нужно было доказать.
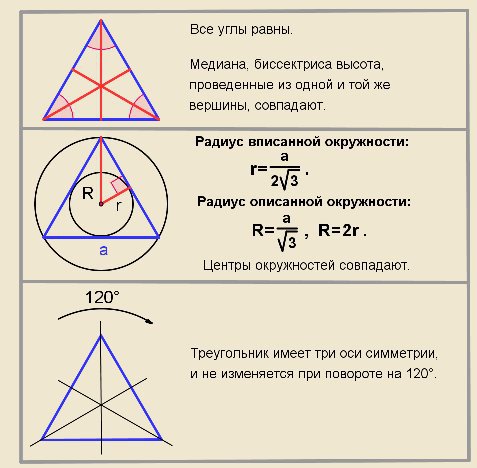
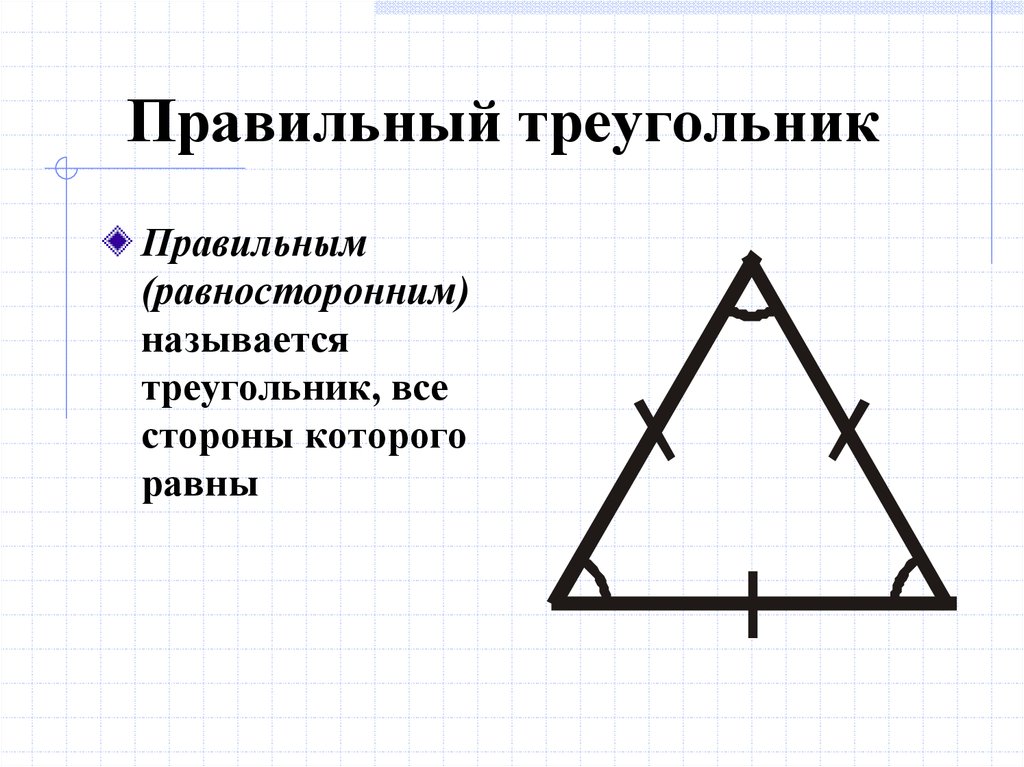
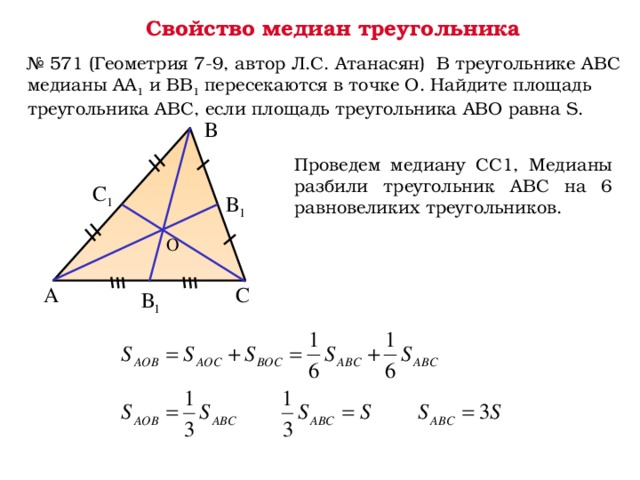 При этом все остальные углы равны 60 градусам.
При этом все остальные углы равны 60 градусам.
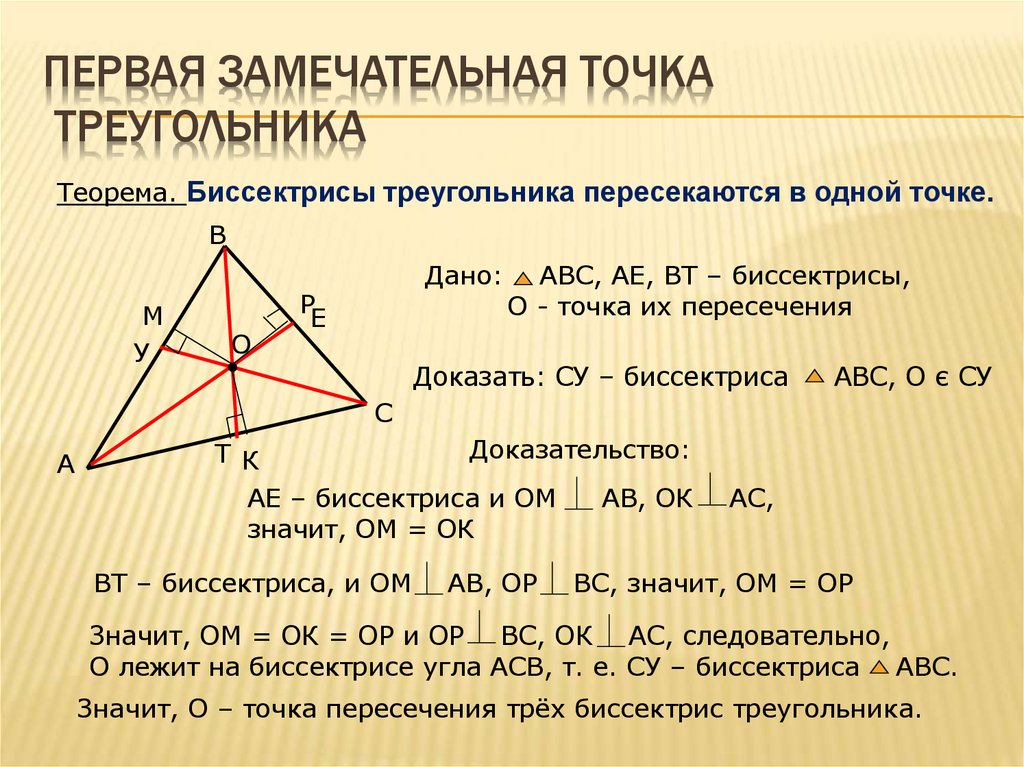 При этом существует риск допустить оплошность, приводящую к неправильному ответу.
При этом существует риск допустить оплошность, приводящую к неправильному ответу.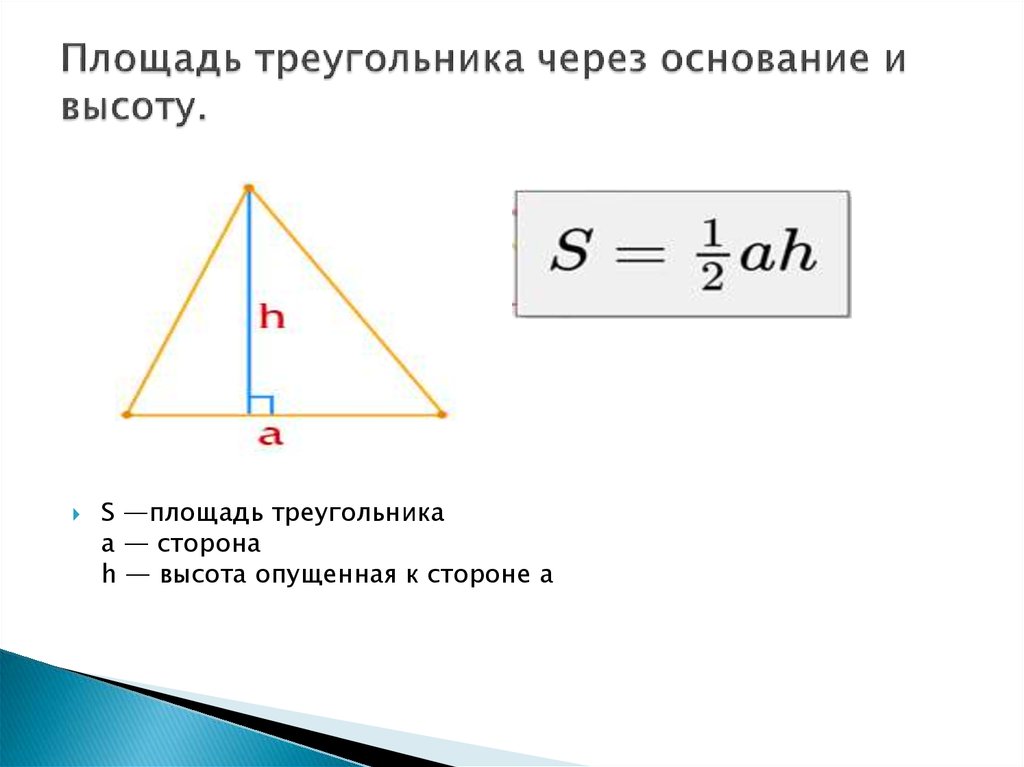
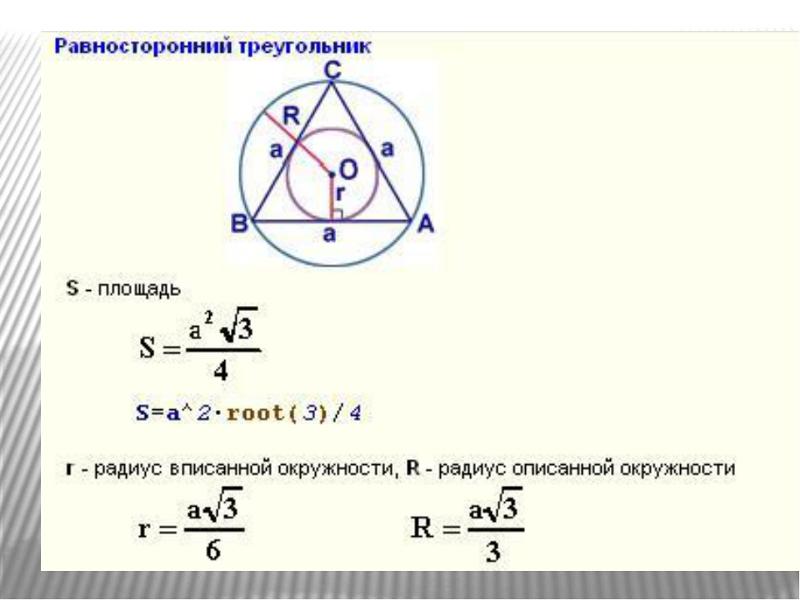 )
) 

 Сокращенные
Сокращенные  02 Уравнения прямоугольного треугольника
02 Уравнения прямоугольного треугольника 
 Если есть необходимость, то вынести "знак минус" в одном из знаменателей.
Если есть необходимость, то вынести "знак минус" в одном из знаменателей.

 Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так: Например:
Например: При сложении десятичных дробей нужно отдельно сложить каждую часть.
При сложении десятичных дробей нужно отдельно сложить каждую часть. Запишем тройку в десятой части ответа:
Запишем тройку в десятой части ответа: От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
От нуля невозможно вычесть число 2. Поэтому займем единицу у соседнего разряда. Таким образом 0 превращается в число 10. Вычисляем десятые части: 10 − 2 = 8. Запишем восьмерку в десятой части ответа:
 Я не знаю, какие травмирующие события вы пережили в детстве, но мне жаль, что они были такими болезненными.
Я не знаю, какие травмирующие события вы пережили в детстве, но мне жаль, что они были такими болезненными. 
 По сути, мы делим дроби на части меньшего размера, пока они не станут одинакового размера. Это называется найти общий знаменатель.
По сути, мы делим дроби на части меньшего размера, пока они не станут одинакового размера. Это называется найти общий знаменатель. 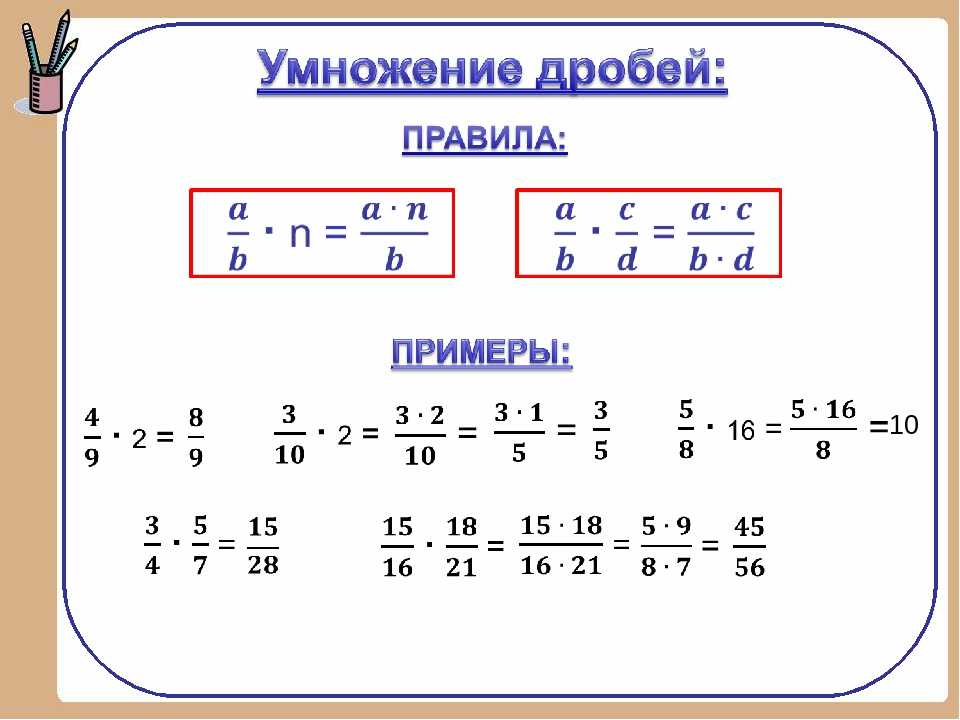
 Например, 5 входит в число 14 два раза (поскольку 5 x 2 = 10), и остается 4 части.
Например, 5 входит в число 14 два раза (поскольку 5 x 2 = 10), и остается 4 части. Что делает их быстрыми и легкими в управлении.
Что делает их быстрыми и легкими в управлении.

 Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…



 {x+2}-1}
{x+2}-1} x). \] Каково значение \( a + b? \) 92-x-4=0 \ подразумевает x=\frac{1 \pm \sqrt{17}}{2}\). Только \(\frac{1-\sqrt{17}}{2} \in [ -2, 1 ] \), так что это единственное решение в этом подслучае.
x). \] Каково значение \( a + b? \) 92-x-4=0 \ подразумевает x=\frac{1 \pm \sqrt{17}}{2}\). Только \(\frac{1-\sqrt{17}}{2} \in [ -2, 1 ] \), так что это единственное решение в этом подслучае. } \\ x \ln(2) & = & \ln(129) & \mbox{степенное правило} \\[4pt] x & = &\dfrac{\ln(129)}{\ln(2)} & \\ \end{массив}\nonumber\]
} \\ x \ln(2) & = & \ln(129) & \mbox{степенное правило} \\[4pt] x & = &\dfrac{\ln(129)}{\ln(2)} & \\ \end{массив}\nonumber\] 9{2x}\справа)\). Правило мощности дает \((x+2)\ln(3) = 2x\ln(7)\). Хотя это уравнение кажется очень сложным, имейте в виду, что \(\ln(3)\) и \(\ln(7)\) — это просто константы. Уравнение \((x+2) \ln(3) = 2x \ln(7)\) на самом деле является линейным уравнением, и поэтому мы собираем все члены с \(x\) на одной стороне, а константы с другой. Затем мы делим обе части на коэффициент \(х\), который мы получаем путем факторизации.
9{2x}\справа)\). Правило мощности дает \((x+2)\ln(3) = 2x\ln(7)\). Хотя это уравнение кажется очень сложным, имейте в виду, что \(\ln(3)\) и \(\ln(7)\) — это просто константы. Уравнение \((x+2) \ln(3) = 2x \ln(7)\) на самом деле является линейным уравнением, и поэтому мы собираем все члены с \(x\) на одной стороне, а константы с другой. Затем мы делим обе части на коэффициент \(х\), который мы получаем путем факторизации. {\ln\left(\frac{1}{4}\right )}- 4\ln\left(\frac{1}{2}\right) & \\ & = & \frac{1}{4} \ln\left(\frac{1}{2}\right) — 4 \ln\left(\frac{1}{2}\right) = -\frac{15}{4} \ln\left(\frac{1}{2}\right) & \end{array} \номер\] 9{-0.1t} = \frac{1}{3}\), так что \(t = -10\ln\left(\frac{1}{3}\right)\), которое после быстрого применения Правило степени оставляет нам \(t = 10\ln(3)\). Если мы хотим избежать использования калькулятора для выбора тестовых значений, заметим, что, поскольку \(1 < 3\), \(0 = \ln(1) < \ln(3)\), так что \(10\ln( 3) > 0\). Поэтому мы выбираем \(t = 0\) в качестве тестового значения в \([0, 10 \ln(3))\). Поскольку \(3 < 4\), \(10 \ln(3) < 10 \ln(4)\), то последнее является нашим выбором тестового значения для интервала \((10 \ln(3), \infty)\). Наша диаграмма знаков находится ниже, а рядом с ней наш график \(y=T(t)\) из примера 6.1.2 с горизонтальной линией \(y = 100\). 9{x}\) растет относительно любого многочлена?
{\ln\left(\frac{1}{4}\right )}- 4\ln\left(\frac{1}{2}\right) & \\ & = & \frac{1}{4} \ln\left(\frac{1}{2}\right) — 4 \ln\left(\frac{1}{2}\right) = -\frac{15}{4} \ln\left(\frac{1}{2}\right) & \end{array} \номер\] 9{-0.1t} = \frac{1}{3}\), так что \(t = -10\ln\left(\frac{1}{3}\right)\), которое после быстрого применения Правило степени оставляет нам \(t = 10\ln(3)\). Если мы хотим избежать использования калькулятора для выбора тестовых значений, заметим, что, поскольку \(1 < 3\), \(0 = \ln(1) < \ln(3)\), так что \(10\ln( 3) > 0\). Поэтому мы выбираем \(t = 0\) в качестве тестового значения в \([0, 10 \ln(3))\). Поскольку \(3 < 4\), \(10 \ln(3) < 10 \ln(4)\), то последнее является нашим выбором тестового значения для интервала \((10 \ln(3), \infty)\). Наша диаграмма знаков находится ниже, а рядом с ней наш график \(y=T(t)\) из примера 6.1.2 с горизонтальной линией \(y = 100\). 9{x}\) растет относительно любого многочлена?
 005)}, \infty\right)\)
005)}, \infty\right)\) )
)
 Мне нужно собрать схему FSK-модема для моей научной работы в университете.
Требования:1. Модулятор в передатчике должен быть реализован на GMSK или 4-FSK (желательно не брать библиотечный…
Мне нужно собрать схему FSK-модема для моей научной работы в университете.
Требования:1. Модулятор в передатчике должен быть реализован на GMSK или 4-FSK (желательно не брать библиотечный… 04.2023
04.2023 Его возможности генерировать язык, похожий на человеческий, вдохновляют людей экспериментировать с его потенциалом в различных продуктах. Его крайне успешный запуск даже поставил давление на гигантов технологической отрасли, таких как Google, чтобы спешить выпустить свою собственную версию ChatGPT.
Его возможности генерировать язык, похожий на человеческий, вдохновляют людей экспериментировать с его потенциалом в различных продуктах. Его крайне успешный запуск даже поставил давление на гигантов технологической отрасли, таких как Google, чтобы спешить выпустить свою собственную версию ChatGPT. оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,…
оптический волновод , входные параметры, законы геометрической оптики , построение мод (волн) учитывая вышеперечисленные параметры,… Не получается реализовать low-pass фильтр в Simulink, но обо всём по порядку. Я пытаюсь сделать модель синхронного детектирования газов, в реальности установка такая: треугольный сигнал 2…
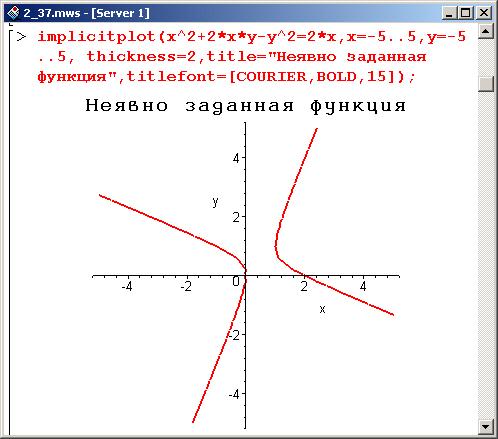
Не получается реализовать low-pass фильтр в Simulink, но обо всём по порядку. Я пытаюсь сделать модель синхронного детектирования газов, в реальности установка такая: треугольный сигнал 2… С помощью графического редактора уравнений вы также можете построить графики неявных функций , стандартных и общих форм из конических сечений и кривых уровня .
С помощью графического редактора уравнений вы также можете построить графики неявных функций , стандартных и общих форм из конических сечений и кривых уровня .


 Графический редактор уравнений отображает графики при вводе (по умолчанию).
Графический редактор уравнений отображает графики при вводе (по умолчанию). Изображение графиков появится под графиком уравнений . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
Изображение графиков появится под графиком уравнений . Затем вы можете использовать возможности вашего браузера, чтобы сохранить его или скопировать его в ваши документы.
 В противном случае некоторые компоненты графического редактора уравнений могут не отображаться или работать.
В противном случае некоторые компоненты графического редактора уравнений могут не отображаться или работать. Неявное дифференцирование — это процесс, в котором мы находим производную зависимой переменной. Это делается путем
Неявное дифференцирование — это процесс, в котором мы находим производную зависимой переменной. Это делается путем

 На этом веб-сайте есть и другие полезные онлайн-инструменты, которые вы можете использовать, такие как калькулятор третьей производной или калькулятор цепного правила с шагами. Такие инструменты могут сэкономить ваше время, которое вы тратите на ручные вычисления.
На этом веб-сайте есть и другие полезные онлайн-инструменты, которые вы можете использовать, такие как калькулятор третьей производной или калькулятор цепного правила с шагами. Такие инструменты могут сэкономить ваше время, которое вы тратите на ручные вычисления.
 Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:
Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные: Формула диагонали квадрата через диаметр описанной окружности:
Формула диагонали квадрата через диаметр описанной окружности:.jpg) Формула периметра квадрата через радиус описанной окружности:
Формула периметра квадрата через радиус описанной окружности: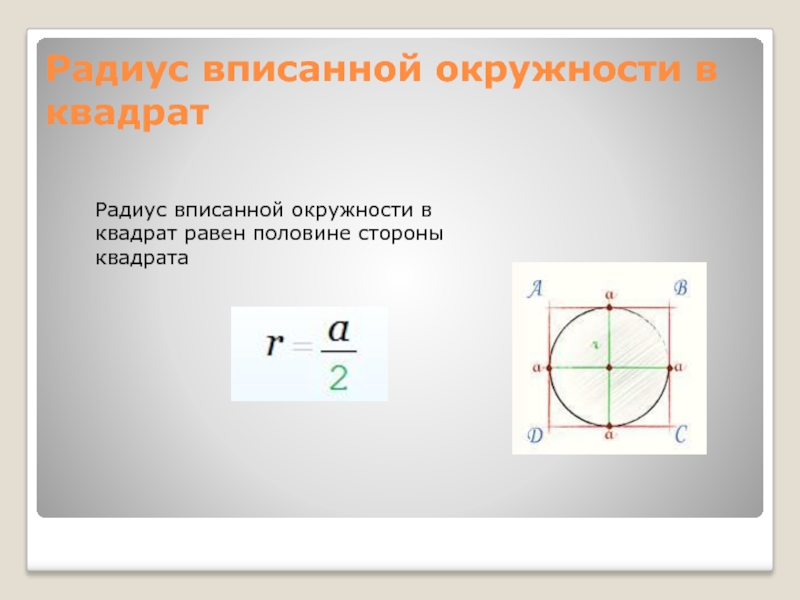 Формула площади квадрата через сторону квадрата:
Формула площади квадрата через сторону квадрата: Формула площади квадрата через длину отрезка l:
Формула площади квадрата через длину отрезка l:
 Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:
Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:

 Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
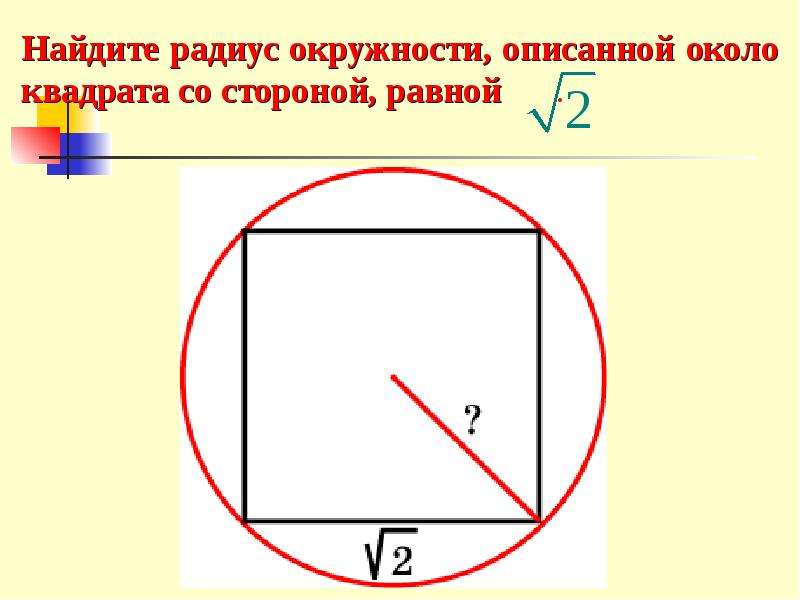
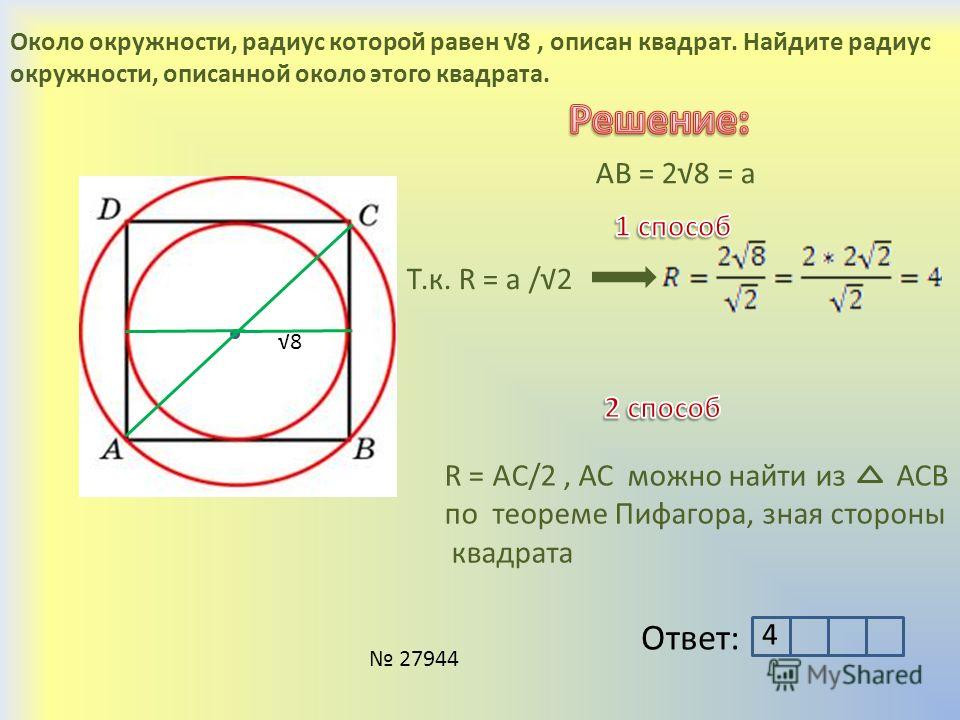
 ru Математика Геометрия Нахождение радиуса описанной вокруг квадрата окружности
ru Математика Геометрия Нахождение радиуса описанной вокруг квадрата окружности


 Поэтому вы оставляете ответ в виде 5000\pi 92
Поэтому вы оставляете ответ в виде 5000\pi 92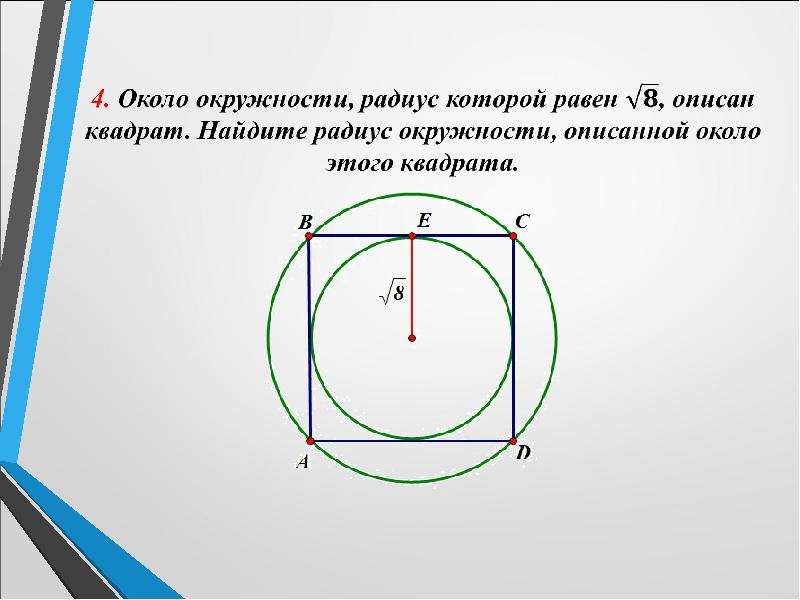
 Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.


 КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. (1/3)
(1/3) Сегодня ты умрёшь (2020)
Сегодня ты умрёшь (2020) К большому удивлению напарники продвигаются в деле и находят виновника произошедшего.
К большому удивлению напарники продвигаются в деле и находят виновника произошедшего. За помощью он снова обращается к Успенской.
За помощью он снова обращается к Успенской. Но может ли она себе это позволить? Это
где ей нужна небольшая помощь от вас.
Но может ли она себе это позволить? Это
где ей нужна небольшая помощь от вас. В данном случае неизвестно, сколько всего было
будет стоить.
В данном случае неизвестно, сколько всего было
будет стоить. Но у нее до сих пор нет
игры… или другой контроллер… или гарнитура.
Но у нее до сих пор нет
игры… или другой контроллер… или гарнитура. Они
математический способ сказать что-либо. Итак, когда мы говорили о Джо
баланс счета, мы фактически использовали уравнение:
Они
математический способ сказать что-либо. Итак, когда мы говорили о Джо
баланс счета, мы фактически использовали уравнение: мы не
действительно заботятся о семи играх в левой части уравнения. В
на самом деле, мы можем избавиться от этой семерки, если мы убедимся, что делаем
то же самое для обеих сторон уравнения.
мы не
действительно заботятся о семи играх в левой части уравнения. В
на самом деле, мы можем избавиться от этой семерки, если мы убедимся, что делаем
то же самое для обеих сторон уравнения. Это самая важная часть решения
уравнение. Изоляция переменной означает, что вы получили переменную
себя в левой части уравнения, а все остальное складывается
справа. Если вы можете изолировать переменную, значит, вы решили задачу.
уравнение — ответ просто выскакивает, например, х =
3 .
Это самая важная часть решения
уравнение. Изоляция переменной означает, что вы получили переменную
себя в левой части уравнения, а все остальное складывается
справа. Если вы можете изолировать переменную, значит, вы решили задачу.
уравнение — ответ просто выскакивает, например, х =
3 .
 Это сохраняет уравнение прежним.
Это сохраняет уравнение прежним. ..
..
 Двумя методами технического уровня для решения одновременных уравнений с несколькими неизвестными, используемыми при работе с двумя или тремя уравнениями, являются «подстановка» и «исключение». Чтобы решить для заданного числа неизвестных, мы требуем, чтобы такое же количество уравнений было предоставлено. Например, нам потребуется два уравнения для решения двух неизвестных величин. Нам потребовались бы три уравнения для решения трех неизвестных величин и так далее.
Двумя методами технического уровня для решения одновременных уравнений с несколькими неизвестными, используемыми при работе с двумя или тремя уравнениями, являются «подстановка» и «исключение». Чтобы решить для заданного числа неизвестных, мы требуем, чтобы такое же количество уравнений было предоставлено. Например, нам потребуется два уравнения для решения двух неизвестных величин. Нам потребовались бы три уравнения для решения трех неизвестных величин и так далее. Это оставит нам только одну неизвестную величину, x, для решения уравнения 2 вместо двух неизвестных, которые у нас были раньше.
Это оставит нам только одну неизвестную величину, x, для решения уравнения 2 вместо двух неизвестных, которые у нас были раньше.

 Если мы умножим Eq.1 на 8 и Eq.2 на -3, члены x станут 24x и -24x соответственно. Они компенсируют друг друга при суммировании двух уравнений.
Если мы умножим Eq.1 на 8 и Eq.2 на -3, члены x станут 24x и -24x соответственно. Они компенсируют друг друга при суммировании двух уравнений.


 Итак, вы добавляете компонент за компонентом.
Итак, вы добавляете компонент за компонентом.



 таблицу выше).
таблицу выше). также
также Максимальное количество строк – 8, максимальное количество столбцов – 8
Максимальное количество строк – 8, максимальное количество столбцов – 8 


 Сумма N матриц обычно получается путем суммирования элементов каждой матрицы.
Сумма N матриц обычно получается путем суммирования элементов каждой матрицы.
 д.). Тем не менее, существует прямая операция суммирования, которую можно использовать с матрицами разного размера.
д.). Тем не менее, существует прямая операция суммирования, которую можно использовать с матрицами разного размера.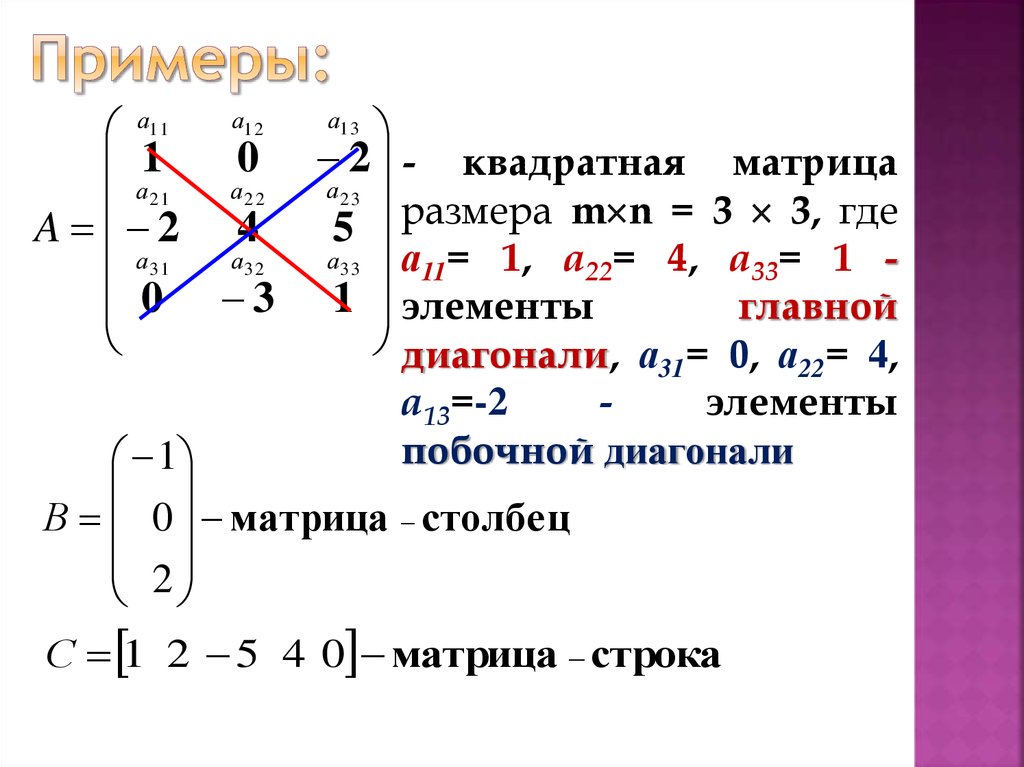
 Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты
Мы обязательно с ним ознакомимся и в 30-дневный срок ответим на указанный вами адрес электронной почты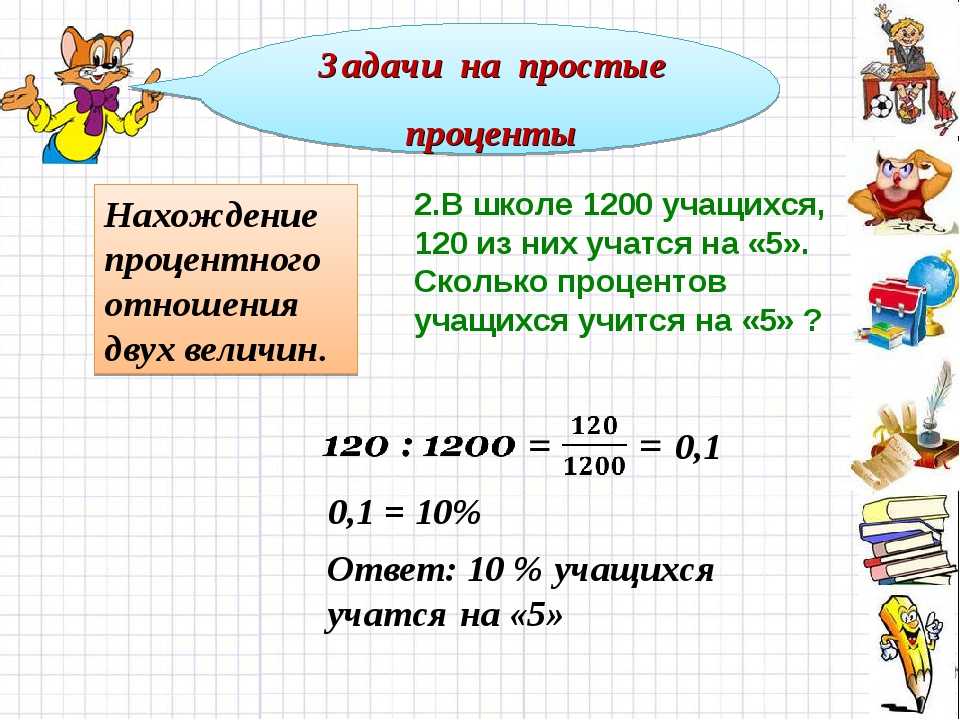 Хотя для обучения не может быть коротких путей, использование нескольких забавных методов, таких как игры и занятия, и плавное их сочетание с важными, но сложными концепциями может сделать обучение радостным.
Хотя для обучения не может быть коротких путей, использование нескольких забавных методов, таких как игры и занятия, и плавное их сочетание с важными, но сложными концепциями может сделать обучение радостным.
 Внутренние кредиты, когда вы начинаете делать платежи, более высокий процент ваших фиксированных ежемесячных платежей будет идти на проценты. Это связано с тем, что основной остаток больше в начале кредита; следовательно, таков интерес.
Внутренние кредиты, когда вы начинаете делать платежи, более высокий процент ваших фиксированных ежемесячных платежей будет идти на проценты. Это связано с тем, что основной остаток больше в начале кредита; следовательно, таков интерес. Более того, когда учащиеся учатся рассчитывать простые проценты, это делает их мудрыми в денежном отношении и помогает им принимать обоснованные финансовые решения. Поэтому давайте рассмотрим некоторые виды деятельности, которые помогут учащимся узнать о простых интересах.
Более того, когда учащиеся учатся рассчитывать простые проценты, это делает их мудрыми в денежном отношении и помогает им принимать обоснованные финансовые решения. Поэтому давайте рассмотрим некоторые виды деятельности, которые помогут учащимся узнать о простых интересах. Здесь следует отметить, что учащиеся должны указать проценты и суммы кредита каждого банка на листе бумаги, чтобы подсчитать и представить учителю.
Здесь следует отметить, что учащиеся должны указать проценты и суммы кредита каждого банка на листе бумаги, чтобы подсчитать и представить учителю.

 Попробуйте эти удивительные онлайн-игры, чтобы научиться простым интересам в визуально привлекательной форме.
Попробуйте эти удивительные онлайн-игры, чтобы научиться простым интересам в визуально привлекательной форме.

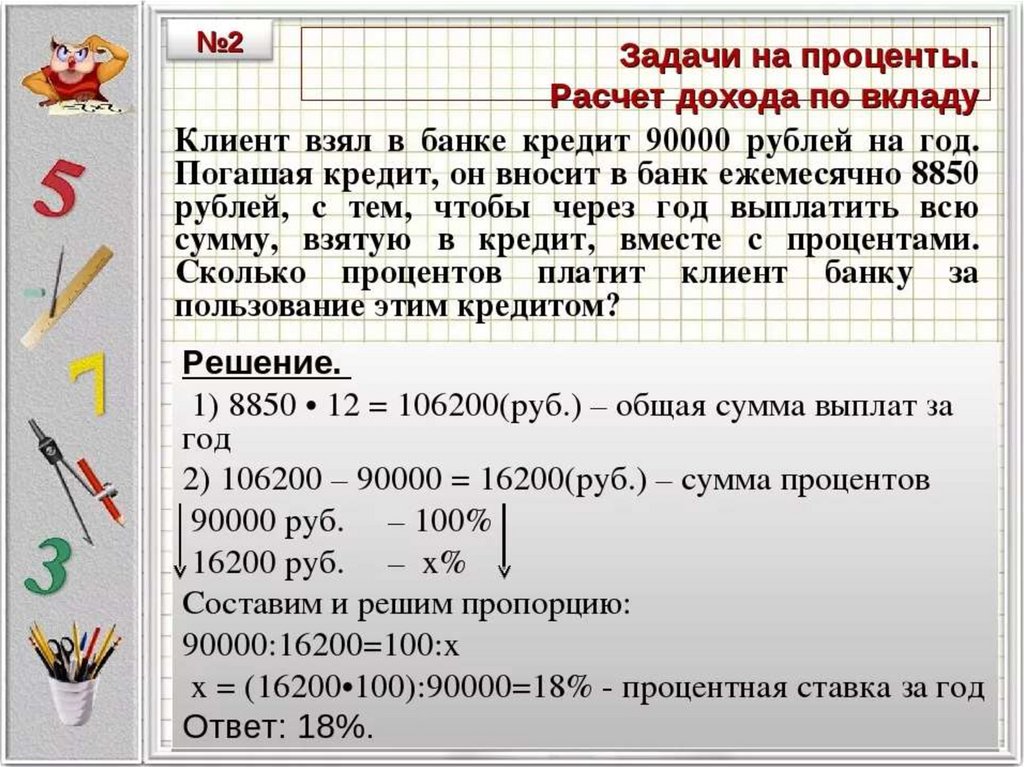 Это также развивает их способности критического мышления для решения вопроса.
Это также развивает их способности критического мышления для решения вопроса. За это время у меня была возможность испытать преподавание в классах на всех уровнях производительности, включая полное включение и продвинутые классы.
Я преподавал естествознание в средней школе (7-й и 8-й классы) и в старшей школе (9-й класс).наука с 1-го по 12-й класс), включая анатомию, астрономию, биологию, химию, науку об окружающей среде и физическую науку.
У меня есть PA Professional Certi
За это время у меня была возможность испытать преподавание в классах на всех уровнях производительности, включая полное включение и продвинутые классы.
Я преподавал естествознание в средней школе (7-й и 8-й классы) и в старшей школе (9-й класс).наука с 1-го по 12-й класс), включая анатомию, астрономию, биологию, химию, науку об окружающей среде и физическую науку.
У меня есть PA Professional Certi