Метод Гаусса онлайн
Назначение сервиса. Онлайн-калькулятор предназначен для решения системы линейных уравнений методом Гаусса, а также методом Гаусса-Жордано (чем они отличаются). Результат решения сохраняется в формате Word и Excel.- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
- Также решают
Инструкция. Для получения онлайн решения необходимо выбрать
количество переменных:
2345678
и количество строк
23456
Вместе с этим калькулятором также используют следующие:
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
По координатам вершин пирамиды найти
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Смысл метода: последовательно исключаем переменную за переменной, пока в одной из строк не будет однозначно определена переменная xi. Идею можно проиллюстрировать на простом примере:
Идею можно проиллюстрировать на простом примере:
x1 - x2 = 3
-x1 + 2x2 = 1
=========== (складываем строки)
-x2 + 2x2= 3 + 1 = 4 или x2 = 4
Откуда, x1 = 7
Суть метода можно понять, проанализировав пример решения.
Пример.
2x1-x2=0
-x1+x2+4x3=13
x1+2x2+3x3=14
Решение.
Запишем систему в виде расширенной матрицы:
|
Далее умножаем 2-ую строку на (2) и добавляем к первой:
|
|
Добавим 3-ую строку к 2-ой:
|
|
Умножим первую строчку на (3), 2-ую строку умножаем на (-1). Следующее действие: складываем первую и вторую строки:
Следующее действие: складываем первую и вторую строки:
|
|
Теперь исходную систему можно записать как:
x3 = 51/17
x2 = [27 - 7x3]/3
x1 = [14 - (2x2 + 3x3)]
Из 1-ой строки выражаем x3: 51/17 = 3
Из 2-ой строки выражаем x2: (27 - 7*3)/3 = 2
Из 3-ой строки выражаем x1: (14 - 2*2 - 3*3) = 1
Вывод: метод Гаусса является достаточно простым методом при небольшом количестве переменных и позволяет найти точное значение переменных. Процесс отыскания переменных можно упростить, если каждый раз сортировать столбцы по возрастанию.
Процесс отыскания переменных можно упростить, если каждый раз сортировать столбцы по возрастанию.
Метод Гаусса
Определение метода Гаусса
Пусть дана система , ∆≠0. (1)Метод Гаусса – это метод последовательного исключения неизвестных.
Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных.
Вычислительные схемы
- Схема единственного деления.
- Схема последовательного алгоритма. На первом шаге метода среди элементов aij определяют максимальный по модулю элемент. Первое уравнение системы и уравнение с номером i1 меняют местами. Далее стандартным образом производят исключение неизвестного xi1 из всех уравнений, кроме первого.
Схема единственного деления
Пусть a11≠0 (ведущий элемент) разделим на a11 первое уравнение. Получим
Получим
x1+a(1)12·x2+…+a(1)1n·xn=b(1)1 (2)
Пользуясь уравнением (2), легко исключить неизвестные x1 из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x1), то есть на первом шаге получим
.
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x2 (шаг 2).
После n шагов вместо (1) получим равносильную систему
(3)
Таким образом, на первом этапе мы получим треугольную систему (3).
 Этот этап называется прямым ходом.
Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения xn , xn-1, …, x1.
Обозначим полученное решение за x0. Тогда разность
ε=b-A·x0 называется невязкой.
Если ε=0, то найденное решение x0 является верным.
Вычисления по методу Гаусса выполняются в два этапа:
- Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
- Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.

Назначение метода Гаусса
Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.Виды метода Гаусса
- Классический метод Гаусса;
- Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k-ом шаге ведущим элементом оказывался наибольший по модулю элемент k-го столбца.
- Метод Жордано-Гаусса;
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.

Пример решения методом Гаусса
Решим систему:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x3:
Из 2-ой строки выражаем x2:
Из 3-ой строки выражаем x1:
Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 1 / 1 = 1 | 2 / 1 = 2 | -2 / 1 = -2 | 1 / 1 = 1 |
Разрешающий элемент равен (3).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.

Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 0 / 3 = 0 | 3 / 3 = 1 | 1 / 3 = 0.33 | 4 / 3 = 1.33 |
Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
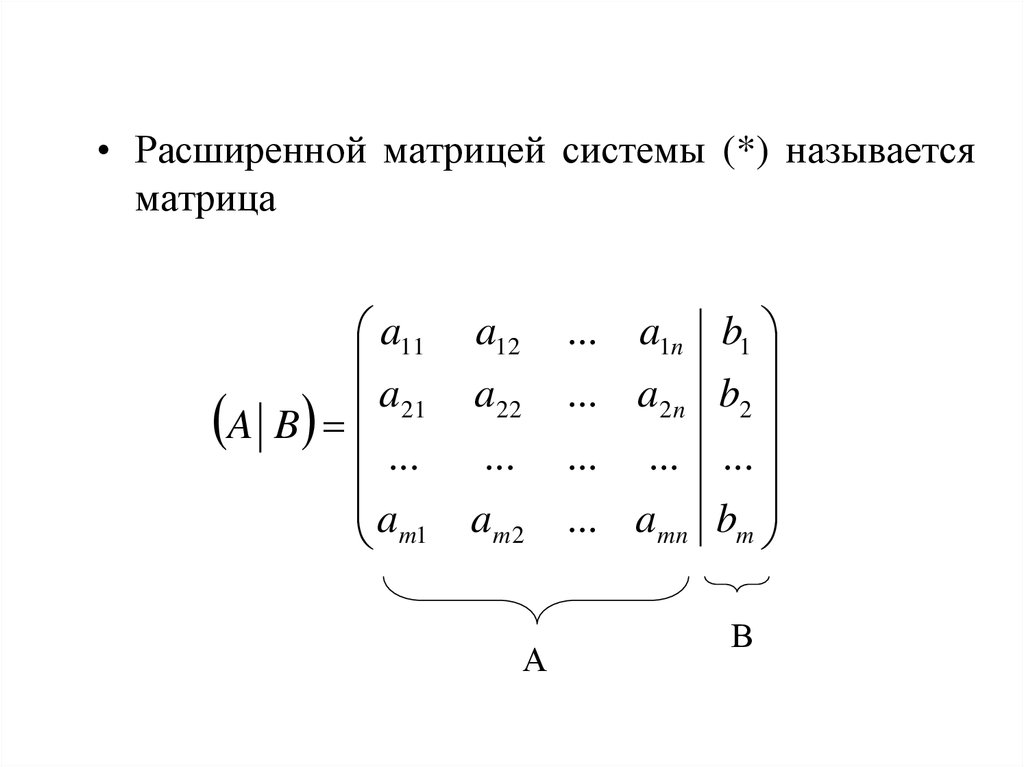
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | B |
| 0 / -4 = 0 | 0 / -4 = 0 | -4 / -4 = 1 | -4 / -4 = 1 |
Ответ: x1 = 1, x2 = 1, x3 = 1
| Показатель | Метод Гаусса | Метод Жордано-Гаусса |
| Вид матрицы | Треугольная матрица | Единичная матрица |
| Время решения | 0. 031 031 | 0.022 |
| Объем используемой памяти, байт | 5647 | 3277 |
Реализация метода Гаусса
Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi, а также имеется реализация метода Гаусса в онлайн режиме.Использование метода Гаусса
Применение метода Гаусса в теории игр
В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.Применение метода Гаусса при решении дифференциальных уравнений
Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.Применение метода Жордано-Гаусса в линейном программировании
В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.
Примеры
Пример №1. Решить систему методом Гаусса:x1 +2x2 — 3x3 + x4 = -2
x1 +2x2 — x3 + 2x4 = 1
3x1 -x2 + 2x3 + x4 = 3
3x1 +x2 + x3 + 3x4 = 2
- Решение
- Видео решение
Решение находим с помощью калькулятора.
Запишем систему в виде:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой
Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой
Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (0).
 Добавим 2-ую строку к 1-ой
Добавим 2-ую строку к 1-ой
Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x4
Из 2-ой строки выражаем x3
Из 3-ой строки выражаем x2
Из 4-ой строки выражаем x1
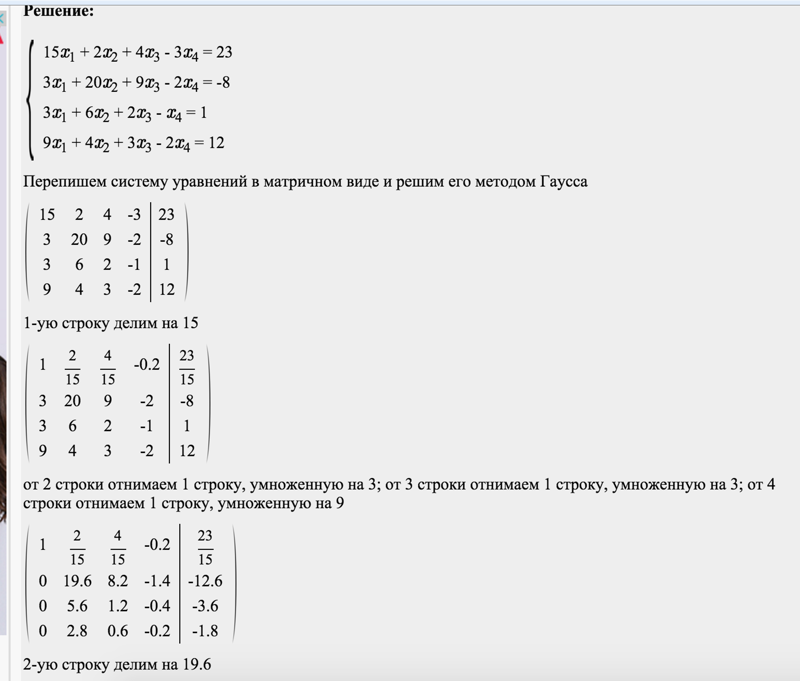
Пример №3.
- Решить СЛАУ методом Жордано-Гаусса. Запишем систему в виде:
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.5 -1 -1 3 1 2 3 6 4 3 2 9
Разрешающий элемент равен (5). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (5), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Разрешающий элемент равен (2.2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.1 -0.2 -0.2 0.6 0 2.2 3.2 5.4 0 3.8 2.8 6.6
Разрешающий элемент равен (-2.73). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.1 0 0.0909 1.09 0 1 1.45 2.45 0 0 -2.73 -2.73
x1 = 1.1 0 0 1 0 1 0 1 0 0 1 1  00, x2 = 1.00, x3 = 1.00
00, x2 = 1.00, x3 = 1.00
Перейти к решению своей задачи
Example1 - Систему линейных уравнений решить методом Гаусса
ПримерПосмотрите, как быстро можно определить, является ли система совместной
- Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения: Решение
- Example 4
- Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
Решение:xls - Решить систему линейных уравнений тремя способами: а) методом Гаусса последовательных исключений неизвестных; б) по формуле x = A-1b с вычислением обратной матрицы A-1; в) по формулам Крамера.
Решение:xls - Решить методом Гаусса следующую вырожденную систему уравнений.

Скачать решение doc - Решите методом Гаусса систему линейных уравнений записанную в матричной форме:
7 8 -3 x 92
2 2 2 y = 30
-9 -10 5 z -114
Перейти к онлайн решению своего примера
Решение системы уравнений методом сложения
Решите 6x+5y=3, 3x+3y=4 систему уравнений методом сложения.Решение.
6x+5y=3
3x+3y=4
Умножим второе уравнение на (-2).
6x+5y=3
-6x-6y=-8
============ (складываем)
-y=-5
Откуда y = 5
Находим x:
6x+5*5=3 или 6x=-22
Откуда x = -22/6 = -11/3
Пример №2. Решение СЛАУ в матричной форме означает, что исходную запись системы необходимо привести к матричной (так называемая расширенная матрица). Покажем это на примере.
Запишем систему в виде расширенной матрицы:
|
|
 Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой:
Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой:
|
|
|
x3 = -21/(-21) = 1
x2 = [29 — (14x3)]/15
x1 = [4 — (x3)]/3
Из 2-ой строки выражаем x2:
Из 3-ой строки выражаем x1:
Пример №3. Решить систему методом Гаусса:
x1 +2x2 — 3x3 + x4 = -2
Решить систему методом Гаусса:
x1 +2x2 — 3x3 + x4 = -2
x1 +2x2 — x3 + 2x4 = 1
3x1 -x2 + 2x3 + x4 = 3
3x1 +x2 + x3 + 3x4 = 2
Решение:
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:
Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой
Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой
Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой
Для удобства вычислений поменяем строки местами:
Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой
Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой
Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой
Добавим 2-ую строку к 1-ой
Из 1-ой строки выражаем x4
Из 2-ой строки выражаем x3
Из 3-ой строки выражаем x2
Из 4-ой строки выражаем x1
с шагами
Установите матрицу линейного уравнения и запишите ее элементы, чтобы найти решение, применяя метод исключения Гаусса с помощью этого калькулятора.
РЕКЛАМА
Размер матрицы:
2345678910
x
2345678910
МатрицаРЕКЛАМА
РЕКЛАМА
Содержание
| 1 | Что такое класс PriceEight? |
| 2 | Таблица классов priceeight: |
| 3 | Как рассчитать плотность priceeight (шаг за шагом): |
| 4 | Факторы, определяющие цену8 Классификация: |
| 5 | Для чего предназначен класс priceeight? |
| 6 | Упомянутая цена8 классов проверена официальными лицами? |
| 7 | Являются ли классы цен для UPS и FedEx одинаковыми? |
Получите виджет!
Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.
Получить код
Обратная связь
Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!
ОБРАТНАЯ СВЯЗЬ
Этот бесплатный калькулятор исключения Гаусса специально разработан, чтобы помочь вам решать системы уравнений. Да, теперь получить максимально точное решение уравнений можно всего за пару кликов.
Что такое алгоритм исключения Гаусса?В свете математического анализа:
«Особый метод, который используется для решения линейных уравнений путем составления расширенной матрицы чисел их коэффициентов, известен как алгоритм Гаусса»
Как подать заявку Алгоритм исключения Гаусса?Здесь мы собираемся применить эту теорему к примеру ниже. Поэтому для лучшего понимания просто оставайтесь сосредоточенными!
Пример № 01:
Найдите решение следующей системы уравнений, как показано ниже:
$$ 3x_{1} + 6x_{2} = 23 $$
$$ 6x_{1} + 2x_{2 } = 34 $$
Решение:
Без сомнения, наш широко используемый калькулятор исключения Гаусса с шагами покажет подробные вычисления для упрощения этих уравнений, но нам нужно проанализировать сценарий вручную.
Эквивалентная расширенная матричная форма приведенных выше уравнений выглядит следующим образом:
$$ \begin{bmatrix} 3&6&23 \\ 6&2&34 \\\end{bmatrix} $$
Шаги исключения по Гауссу:
Шаг № 01:
Разделить нулевую строку $2 \ на 3.
left[\begin{array}{cc|c}1&2& \frac{23}{3} \\6&2&34 \\\end{array}\right] $$
Шаг № 02:
Умножить первую строку на 6, а затем вычесть его из нулевой строки.
$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&-10&-12 \\\end{array}\right] $$
Шаг № 03:
Перейти к делению первой строки на -10.
$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&1&\frac{6}{5}\\\end{array}\right] $$
Шаг № 04:
Приступаем к нахождению произведения нулевой строки и 2. После этого вычитаем результат из первой строки.
$$ \left[\begin{array}{cc|c}1&0&\frac{26333333334}{5000000000}\\0&1& \frac{6}{5}\\\end{array}\right] $$
Как вы видите в левой части матрицы, мы получаем единичную матрицу. Таким образом, ответом в правой части уравнения будут значения переменных в уравнениях.
Таким образом, ответом в правой части уравнения будут значения переменных в уравнениях.
Таким образом, окончательные результаты следующие:
$$ b_{1} = 5,266 $$
$$ b_{2} = 1,2 $$
Те же результаты можно также проверить с помощью внешнего калькулятора исключения Гаусса. .
Как работает калькулятор метода исключения Гаусса?Получите представление о том, как этот бесплатный алгоритм уменьшения строки матрицы решения с методом исключения Гаусса упрощает системы уравнений.
Ввод:
- Сначала настройте порядок матрицы из выпадающих списков
- После этого нажмите кнопку «Установить матрицы», чтобы получить нужный формат матрицы
- Теперь извлеките числа из их полей
- После того, как вы закончите с материалом, нажмите кнопку расчета
Вывод:
Лучший калькулятор исключения Гаусса Джордана с шагами выполняет следующие вычисления:
- Показывает коэффициенты переменных
- Отображает шаги исключения Гаусса
Из источника Википедии: Исключение Гаусса, Операции со строками, Эшелонная форма, Вычисление определителей, обратная матрица, Ранги
Калькулятор Гаусса — это бесплатный онлайн-инструмент, используемый для преобразования матрицы в уменьшенную ступенчатую форму.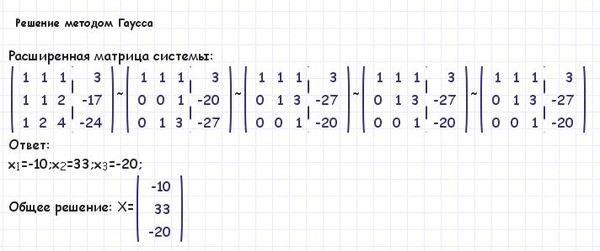 Он применяет операции со строками к матрице, чтобы найти обратную матрицу. Он может решить любую систему линейных уравнений методом исключения.
Он применяет операции со строками к матрице, чтобы найти обратную матрицу. Он может решить любую систему линейных уравнений методом исключения.
В математике всегда нужно решить систему линейных уравнений. Существует более двух методов решения системы линейных уравнений. Одним из таких методов является метод исключения Гаусса-Жордана.
Использование онлайн-инструмента — эффективный способ решить любую проблему. Итак, здесь мы представляем онлайн-инструмент, который является наиболее эффективным инструментом для поиска обратной матрицы.
Формула, используемая калькулятором метода исключения Гаусса
Исключение Гаусса Жордана — это алгоритм решения системы линейных уравнений путем представления ее в виде расширенной матрицы, сокращения ее с использованием операций со строками и представления системы в сокращенной строке- форма эшелона, чтобы найти решение.
Калькулятор Гаусса Жордана преобразует заданную матрицу в редуцированную ступенчатую форму для решения системы линейных уравнений и находит ее обратную. Сокращенную форму эшелона можно получить с помощью калькулятора исключения Гаусса, выполнив следующие шаги:
Сокращенную форму эшелона можно получить с помощью калькулятора исключения Гаусса, выполнив следующие шаги:
- Преобразуйте все диагональные записи в 1, применяя операции со строками и столбцами.
- Преобразование всех элементов, кроме диагоналей, в 0.
Сокращенная ступенчатая форма матрицы получается путем преобразования матрицы в единичную матрицу с помощью калькулятора исключения Жордана.
Как пользоваться калькулятором метода Гаусса-Жордана?
С помощью калькулятора Гаусса легко найти решение любой задачи, потому что он прост в использовании. Чтобы использовать этот инструмент, выполните следующие шаги:
- На первом этапе вам необходимо ввести количество строк и столбцов матрицы.
- Теперь введите значения всех элементов матрицы.
- Вы можете использовать случайную кнопку, чтобы выбрать случайный вариант.
- Нажмите кнопку расчета.
Вы получите пошаговое решение через несколько секунд после нажатия на кнопку расчета.
Зачем использовать калькулятор исключения Гаусса?
Концепция исключения в матрицах важна, потому что обычно она нам нужна для формирования эшелонированной и редуцированной эшелонированной формы. Эти две формы являются ключом к решению системы линейных уравнений.
Но ручные расчеты иногда становятся сложными. Эффективный и простой способ решить эту проблему — использовать онлайн-инструмент. Вы можете использовать калькулятор метода исключения Гаусса, потому что он прост в использовании.
Преимущества использования Калькулятора метода исключения Гаусса Джордана
В Интернете доступно множество математических инструментов, которые помогают решать многие задачи. Точно так же инструмент Gaussian преобразует матрицу в уменьшенную ступенчатую форму. Он имеет много полезных применений для улучшения ваших математических навыков. Вот некоторые из этих преимуществ:
- Калькулятор исключения Гаусса с шагами может исключить любую матрицу за короткий промежуток времени.

- Калькулятор исключения Гаусса может работать с матрицей до 4-го порядка.
- Он предоставляет вам пошаговое решение, чтобы вы могли легко его понять. Калькулятор исключения Джордана
- надежен, потому что он экономит ваше время и дает точный ответ.
- Gauss jordan калькулятор с шагами — это бесплатный онлайн-инструмент, поэтому вам не нужно подписываться на какой-либо платный план.
Другие связанные калькуляторы
Помимо этого калькулятора Гаусса, на этом веб-сайте есть много других связанных инструментов, которые вы можете использовать. Некоторые из бесплатных инструментов:
- Добавление калькулятора матриц
- Калькулятор вычитания матриц
- Калькулятор матриц умножения
- Определитель матричного калькулятора
- Калькулятор транспонирования матрицы
- Калькулятор обратной матрицы
- Ранг матричного калькулятора
- Матрица для калькулятора мощности
- Калькулятор собственных векторов
- Калькулятор собственных значений
- Недействительность матричного калькулятора
- Калькулятор матрицы трасс
- Калькулятор разложения Matrix Lu
- Калькулятор формы эшелона с уменьшенным рядом
- Калькулятор сопряженных матриц
Часто задаваемые вопросы
Что такое пошаговый калькулятор исключения Гаусса-Жордана и как он работает?
Калькулятор метода Гаусса-Жордана с шагами — это инструмент, используемый для решения систем линейных уравнений с использованием метода исключения Гаусса, также известного как исключение Гаусса-Жордана. Он использует серию операций со строками для преобразования матрицы в форму эшелона строк, а затем в сокращенную форму эшелона строк, чтобы найти решение системы уравнений.
Он использует серию операций со строками для преобразования матрицы в форму эшелона строк, а затем в сокращенную форму эшелона строк, чтобы найти решение системы уравнений.
Каковы преимущества использования калькулятора исключения Гаусса с шагами по сравнению с другими методами решения систем линейных уравнений?
Калькулятор метода Гаусса Джордана с шагами особенно полезен для решения систем уравнений с большим количеством переменных, поскольку он эффективен с точки зрения времени и пространства. Кроме того, его легко понять и реализовать, что делает его популярным среди студентов и профессионалов.
Могу ли я использовать калькулятор декомпозиции Гаусса Джордана для решения нелинейных уравнений?
Нет, матричный калькулятор исключения Гаусса предназначен только для решения систем линейных уравнений. Он не будет работать для нелинейных уравнений, потому что метод исключения Гаусса применяется только к матрицам, которые имеют форму эшелона строк или форму редуцированного эшелона строк, что невозможно для нелинейных уравнений.


 00, x2 = 1.00, x3 = 1.00
00, x2 = 1.00, x3 = 1.00


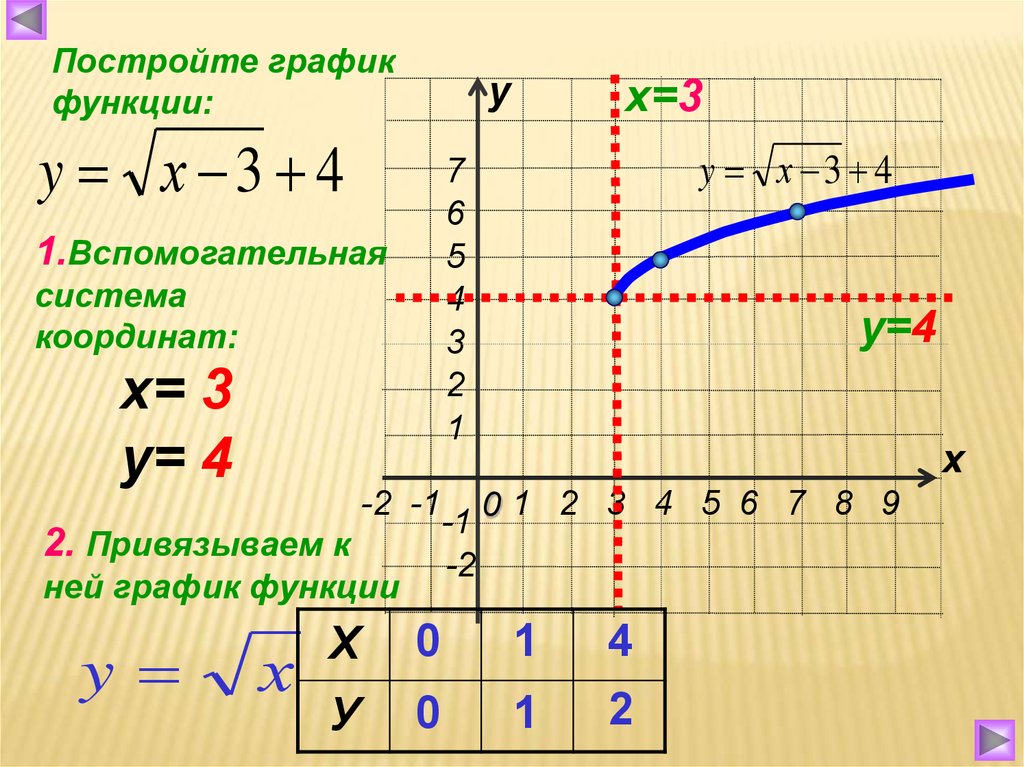 14159..
14159..

 2 равно минус 1 минус 1 равно тому, что 5 хорошо так что давайте посмотрим, какой вариант здесь правильный, мы видели, что номер варианта заставляет исправить хорошо извините отметьте наш первый, так что здесь необязательный самый быстрый правильный 5 хорошо спасибо
2 равно минус 1 минус 1 равно тому, что 5 хорошо так что давайте посмотрим, какой вариант здесь правильный, мы видели, что номер варианта заставляет исправить хорошо извините отметьте наш первый, так что здесь необязательный самый быстрый правильный 5 хорошо спасибо
 Речь о тенденциях. Вместо Ленина — Борис и Глеб. Вместо комсомольского задора — оголтелая клерикальная конъюнктура. Вместо защитников блокадного города — «блокадный ангел». Если завтрак на природе — то закусывают строители храма. Если семейный портрет — то постные лица на фоне церкви. Если пейзаж — то «Тропинка к храму» или «Золото божественной осени». На монументальных, то есть огромных, исторических полотнах — подозрительно напоминающие конников Буденного белогвардейцы в черкесках и Александр Невский под хоругвями. Апофеоз пошлости — портрет Александра Солженицына в лагерной робе, склоненного над утыканной свечами Землей: за его спиной проносятся «красные колеса».
Речь о тенденциях. Вместо Ленина — Борис и Глеб. Вместо комсомольского задора — оголтелая клерикальная конъюнктура. Вместо защитников блокадного города — «блокадный ангел». Если завтрак на природе — то закусывают строители храма. Если семейный портрет — то постные лица на фоне церкви. Если пейзаж — то «Тропинка к храму» или «Золото божественной осени». На монументальных, то есть огромных, исторических полотнах — подозрительно напоминающие конников Буденного белогвардейцы в черкесках и Александр Невский под хоругвями. Апофеоз пошлости — портрет Александра Солженицына в лагерной робе, склоненного над утыканной свечами Землей: за его спиной проносятся «красные колеса». 



 Никита, хоть и закоренелый пьяница,
не был пьян в тот день, потому что с последнего дня перед постом, когда он
пропил свое пальто и кожаные сапоги, зарекся пить и
свою клятву в течение двух месяцев и все еще соблюдал ее, несмотря на искушение
водка, которую повсюду пили в первые два дня
праздник.
Никита, хоть и закоренелый пьяница,
не был пьян в тот день, потому что с последнего дня перед постом, когда он
пропил свое пальто и кожаные сапоги, зарекся пить и
свою клятву в течение двух месяцев и все еще соблюдал ее, несмотря на искушение
водка, которую повсюду пили в первые два дня
праздник. Василий Андреевич не заплатил Никите восемьдесят
рублей в год стоил такой человек, но всего около сорока, которые он отдавал
ему наугад, небольшими суммами, да и то чаще всего не наличными, а
товары из собственного магазина и по высоким ценам.
Василий Андреевич не заплатил Никите восемьдесят
рублей в год стоил такой человек, но всего около сорока, которые он отдавал
ему наугад, небольшими суммами, да и то чаще всего не наличными, а
товары из собственного магазина и по высоким ценам. Итак, теперь, за два дня до праздника, Марта дважды была у
Василия Андреевича и получил от него муку пшеничную, чай, сахар и
кварту водки, партией по три рубля, а также пять рублей в
наличными, за что она поблагодарила его как за особую услугу, хотя он был должен
Никита хоть двадцать рублей.
Итак, теперь, за два дня до праздника, Марта дважды была у
Василия Андреевича и получил от него муку пшеничную, чай, сахар и
кварту водки, партией по три рубля, а также пять рублей в
наличными, за что она поблагодарила его как за особую услугу, хотя он был должен
Никита хоть двадцать рублей. Ты знаешь, что я служу тебе и беру
так много боли, как я бы для моего собственного отца. Я очень хорошо понимаю!
Никита ответил бы. Он прекрасно понимал, что Василий Андреевич обманывает
его, но в то же время он чувствовал, что бесполезно пытаться прояснить
свои счета с ним или объяснить свою сторону дела, и что до тех пор, пока
поскольку ему некуда было идти, он должен был принять то, что мог получить.
Ты знаешь, что я служу тебе и беру
так много боли, как я бы для моего собственного отца. Я очень хорошо понимаю!
Никита ответил бы. Он прекрасно понимал, что Василий Андреевич обманывает
его, но в то же время он чувствовал, что бесполезно пытаться прояснить
свои счета с ним или объяснить свою сторону дела, и что до тех пор, пока
поскольку ему некуда было идти, он должен был принять то, что мог получить. — Ну-ну, ну-ка, времени достаточно. Позвольте мне напоить вас
сначала, — продолжал он, обращаясь к лошади, как к тому, кто
понимал слова, которые употреблял, и взмахнув пыльным, бороздчатым
спине упитанного молодого жеребца с полой его пальто, он положил
уздечку на его красивую голову, поправил уши и чуб, и
сняв недоуздок, вывел его к воде.
— Ну-ну, ну-ка, времени достаточно. Позвольте мне напоить вас
сначала, — продолжал он, обращаясь к лошади, как к тому, кто
понимал слова, которые употреблял, и взмахнув пыльным, бороздчатым
спине упитанного молодого жеребца с полой его пальто, он положил
уздечку на его красивую голову, поправил уши и чуб, и
сняв недоуздок, вывел его к воде.
 Когда
все было почти готово, осталось только вожжи поправить, Никита
послал другого человека в сарай за соломой и в сарай за
наркотики
Когда
все было почти готово, осталось только вожжи поправить, Никита
послал другого человека в сарай за соломой и в сарай за
наркотики ‘Возьми меня с
ты! — закричал он, застегивая пальто на бегу.
‘Возьми меня с
ты! — закричал он, застегивая пальто на бегу.
 ‘Что
если погода ухудшится! Возьми его, ради всего святого!
‘Что
если погода ухудшится! Возьми его, ради всего святого!

 «Теперь все в порядке!»
«Теперь все в порядке!» В четверг днем в Москве валюта торговалась на уровне 54,2 за доллар, немного слабее, но все еще близко к семилетнему максимуму.
В четверг днем в Москве валюта торговалась на уровне 54,2 за доллар, немного слабее, но все еще близко к семилетнему максимуму.

 источники, доставляемые морем.
источники, доставляемые морем.
 Это означает, что, хотя Россия накопила огромный объем валютных резервов, поддерживающих ее валюту дома, она не может использовать эти резервы для удовлетворения своих импортных потребностей из-за санкций.
Это означает, что, хотя Россия накопила огромный объем валютных резервов, поддерживающих ее валюту дома, она не может использовать эти резервы для удовлетворения своих импортных потребностей из-за санкций. Россия приблизилась к дефолту в среду после того, как Минфин США допустил истечение срока ключевого исключения из санкций.
Россия приблизилась к дефолту в среду после того, как Минфин США допустил истечение срока ключевого исключения из санкций.
 14159..
14159.. {\circ} \leq \alpha
{\circ} \leq \alpha Покажем, что для тангенса и котангенса справедливы также следующие формулы:
Покажем, что для тангенса и котангенса справедливы также следующие формулы:
 {\circ}$) — период для функций $tg \alpha$ и $ctg \alpha$. Остается доказать, что $2 \pi$ — основной период для $\sin \alpha, \cos \alpha, sec \alpha$ и $cosec \alpha$, а $\pi$ — основной период для $tg \alpha$ и $ctg \alpha$. Докажем это только для $\sin \alpha$, а для остальных основных пяти функций советуем это сделать самостоятельно.
{\circ}$) — период для функций $tg \alpha$ и $ctg \alpha$. Остается доказать, что $2 \pi$ — основной период для $\sin \alpha, \cos \alpha, sec \alpha$ и $cosec \alpha$, а $\pi$ — основной период для $tg \alpha$ и $ctg \alpha$. Докажем это только для $\sin \alpha$, а для остальных основных пяти функций советуем это сделать самостоятельно.
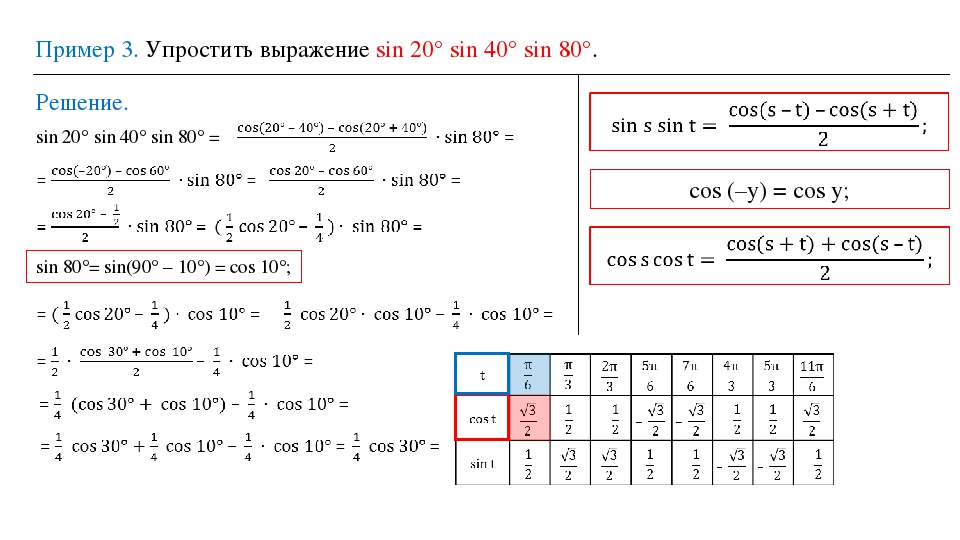 Следовательно, должно выполняться равенство $\frac{ \pi}{2} + A = \frac{ \pi}{2} + 2 \pi n$, откуда следует, что $A = 2\pi n$. Мы пришли к противоречию, предположив, что $0
Следовательно, должно выполняться равенство $\frac{ \pi}{2} + A = \frac{ \pi}{2} + 2 \pi n$, откуда следует, что $A = 2\pi n$. Мы пришли к противоречию, предположив, что $0
 После этого можно приступать к вычислениям.
После этого можно приступать к вычислениям.

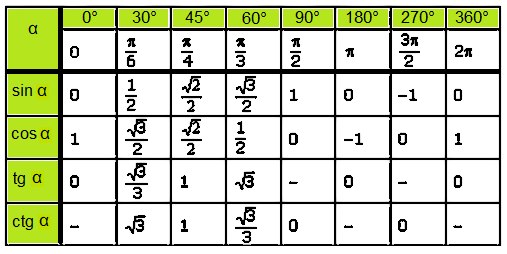 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор позволяет получить тригонометрическое разложение выражения. cos(−π) cos ( – π ). Шаг 1. Применить опорный угол, найдя угол с эквивалентными значениями триггера в первый …1 Ответ ; π=3,14159265… — трансцендентное число. Это предельная проблема ; х→π от cos x. cos x непрерывен в точке ; х=π . И cosπ+, и cosπ …Нажмите здесь, чтобы получить ответ на свой вопрос ✍️ Как найти точное значение cos – pi/3 ?… 90 и 270 градусов. Узнайте значение косинуса пи (π) с выводом на BYJU’S. … Мы знаем, что точное значение cos 0 градусов равно 1. Таким образом, cos 180 градусов равно … Ответ на: Если f(x) = cos pi x , найдите точное значение a такое, что frac{(f(1) – f(-1))}{1 – ( – 1)} = cos а. Зарегистрировавшись, вы получите… Привет! Я учусь в колледже по тригонометрии, и мы находимся в разделе, где мы должны найти точные значения и доказать, что выражение равно другому выражению, используя … Каково значение $\cos ( – \пи )$?. Ответ: Подсказка. Здесь вопрос имеет тригонометрическую функцию, нам нужно найти точное значение … Получите ответ на вопрос «Найдите точное значение cos pi/16» и найдите помощь в выполнении домашних заданий по другим вопросам по математике в eNotes.
cos(−π) cos ( – π ). Шаг 1. Применить опорный угол, найдя угол с эквивалентными значениями триггера в первый …1 Ответ ; π=3,14159265… — трансцендентное число. Это предельная проблема ; х→π от cos x. cos x непрерывен в точке ; х=π . И cosπ+, и cosπ …Нажмите здесь, чтобы получить ответ на свой вопрос ✍️ Как найти точное значение cos – pi/3 ?… 90 и 270 градусов. Узнайте значение косинуса пи (π) с выводом на BYJU’S. … Мы знаем, что точное значение cos 0 градусов равно 1. Таким образом, cos 180 градусов равно … Ответ на: Если f(x) = cos pi x , найдите точное значение a такое, что frac{(f(1) – f(-1))}{1 – ( – 1)} = cos а. Зарегистрировавшись, вы получите… Привет! Я учусь в колледже по тригонометрии, и мы находимся в разделе, где мы должны найти точные значения и доказать, что выражение равно другому выражению, используя … Каково значение $\cos ( – \пи )$?. Ответ: Подсказка. Здесь вопрос имеет тригонометрическую функцию, нам нужно найти точное значение … Получите ответ на вопрос «Найдите точное значение cos pi/16» и найдите помощь в выполнении домашних заданий по другим вопросам по математике в eNotes. Онлайн-расчет с помощью функция cos в соответствии с cos(pi)… допускает некоторые специальные значения, которые вычислитель может определить в точных формах.13 ian. 2018 — затем используйте тождество половинного угла, чтобы найти cos7,5°. cos15° = cos(45° – 30°). = cos45°cos30° + sin45° …Вопрос: используйте тождества, чтобы найти точное значение cos(Pi/12). Эта проблема решена! Вы получите подробное решение от эксперта в данной области, что … cos (pi/5) = 0,308. Мой калькулятор дает cos (pi/5) = 0,309.детали pi/5 = 72 … Как найти точное значение каждого тригонометрического отношения: 1) sin (300°) 2) …Сначала разделите угол на два угла, где известны значения шести тригонометрических функций. В этом случае π/12 можно разбить на π/3− … Аналогичные задачи из веб-поиска… пи-10-и-кос-пи-10. Смотрите объяснение. ВИДЕО ОТВЕТ: так что есть много способов решить, чтобы оценить кинематографические функции, не так ли? Eso с этим, вы можете оценить его на единицу … Вопрос 1036513: Найдите точное значение cos(pi) cos(3pi/4) + sin(pi) sin (3pi/4) Найдено 2 решения jim_thompson59{pi / 6} квадратный корень {1 + cos 2 x} dx По подписи …2 iun.
Онлайн-расчет с помощью функция cos в соответствии с cos(pi)… допускает некоторые специальные значения, которые вычислитель может определить в точных формах.13 ian. 2018 — затем используйте тождество половинного угла, чтобы найти cos7,5°. cos15° = cos(45° – 30°). = cos45°cos30° + sin45° …Вопрос: используйте тождества, чтобы найти точное значение cos(Pi/12). Эта проблема решена! Вы получите подробное решение от эксперта в данной области, что … cos (pi/5) = 0,308. Мой калькулятор дает cos (pi/5) = 0,309.детали pi/5 = 72 … Как найти точное значение каждого тригонометрического отношения: 1) sin (300°) 2) …Сначала разделите угол на два угла, где известны значения шести тригонометрических функций. В этом случае π/12 можно разбить на π/3− … Аналогичные задачи из веб-поиска… пи-10-и-кос-пи-10. Смотрите объяснение. ВИДЕО ОТВЕТ: так что есть много способов решить, чтобы оценить кинематографические функции, не так ли? Eso с этим, вы можете оценить его на единицу … Вопрос 1036513: Найдите точное значение cos(pi) cos(3pi/4) + sin(pi) sin (3pi/4) Найдено 2 решения jim_thompson59{pi / 6} квадратный корень {1 + cos 2 x} dx По подписи …2 iun. 3 (pi/7) является рациональным числом в форме p/q, где p и q — целые числа. Найти (p+q) См.: cos(pi/2) = 6,12323399573677e-17 sin(pi) = 1,22464679914735e-16 … когда вашему приложению необходимо использовать правильные значения для таких углов.3 dec. 2010 — На самом деле довольно легко найти точное значение cos (frac {pi} {5}), следуя по пути через комплексные числа. acum 3 zile — Как вычислить точные значения триггерных функций? · sin · cos · tan … Как только мы сможем найти синус, косинус и тангенс любого угла, мы можем использовать таблицу значений для построения графиков функций y = sin x, y = cos x и y …15 авг. 2022 — Ответ: либо 4 π 3, либо 5 π 3. 2. Найдите точное значение выражения без калькулятора, в …3 янв. 2014 — Не понимаю, почему вы находите cos(pi/4) неясным. Результат в Matlab является числовым приближением, конечно, в конце концов, вы используете программирование … Найдите точное значение cos(pi/12), используя формулу суммы или разности. … Тригонометрия Найдите точное значение cos ( (7pi)/12) cos ( 7π 12) cos ( 7 π 12) …4 апр.
3 (pi/7) является рациональным числом в форме p/q, где p и q — целые числа. Найти (p+q) См.: cos(pi/2) = 6,12323399573677e-17 sin(pi) = 1,22464679914735e-16 … когда вашему приложению необходимо использовать правильные значения для таких углов.3 dec. 2010 — На самом деле довольно легко найти точное значение cos (frac {pi} {5}), следуя по пути через комплексные числа. acum 3 zile — Как вычислить точные значения триггерных функций? · sin · cos · tan … Как только мы сможем найти синус, косинус и тангенс любого угла, мы можем использовать таблицу значений для построения графиков функций y = sin x, y = cos x и y …15 авг. 2022 — Ответ: либо 4 π 3, либо 5 π 3. 2. Найдите точное значение выражения без калькулятора, в …3 янв. 2014 — Не понимаю, почему вы находите cos(pi/4) неясным. Результат в Matlab является числовым приближением, конечно, в конце концов, вы используете программирование … Найдите точное значение cos(pi/12), используя формулу суммы или разности. … Тригонометрия Найдите точное значение cos ( (7pi)/12) cos ( 7π 12) cos ( 7 π 12) …4 апр. 2012 г. — cos(pi/12) ≈ 0,9659. Пожалуйста, дайте мне знать, если вам нужно сопоставить конкретный вариант ответа, например, некоторые из вчерашних задач. Спасибо.Тригонометрия Найдите точное значение cos ( (7pi)/12) cos ( 7π 12) cos ( 7 π 12) Перепишите 7π 12 7 π 12 как угол, где значения шести тригонометрических … Найдите точное значение cos( pi/12) с помощью формулы суммы или разности. Divida π12 π 12 em dois ângulos em que os valores das seis funções trigonométricas … sin( x )+sin( x 2 )=0, 0≤ x ≤ 2π · cos( x )−sin( x )=0 · sin(4) θ )−√32 = 0, ∀0≤ θ <2π · 2sin( x )+3=7sin( x ), x ∈ [0, 2π] · 3tan( A )−tan( A )=0, A ∈ [ 0, 3 …Sin cos tan диаграмма/таблица представляет собой диаграмму с тригонометрическими значениями синуса, косинуса… Найдите точные значения тригонометрических функций секанс, косеканс, … Пожалуйста, укажите 2 значения ниже, чтобы вычислить другие значения прямоугольного треугольника. Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/3, .
2012 г. — cos(pi/12) ≈ 0,9659. Пожалуйста, дайте мне знать, если вам нужно сопоставить конкретный вариант ответа, например, некоторые из вчерашних задач. Спасибо.Тригонометрия Найдите точное значение cos ( (7pi)/12) cos ( 7π 12) cos ( 7 π 12) Перепишите 7π 12 7 π 12 как угол, где значения шести тригонометрических … Найдите точное значение cos( pi/12) с помощью формулы суммы или разности. Divida π12 π 12 em dois ângulos em que os valores das seis funções trigonométricas … sin( x )+sin( x 2 )=0, 0≤ x ≤ 2π · cos( x )−sin( x )=0 · sin(4) θ )−√32 = 0, ∀0≤ θ <2π · 2sin( x )+3=7sin( x ), x ∈ [0, 2π] · 3tan( A )−tan( A )=0, A ∈ [ 0, 3 …Sin cos tan диаграмма/таблица представляет собой диаграмму с тригонометрическими значениями синуса, косинуса… Найдите точные значения тригонометрических функций секанс, косеканс, … Пожалуйста, укажите 2 значения ниже, чтобы вычислить другие значения прямоугольного треугольника. Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/3, . 3 от 0 до бесконечности · интегрируйте 1/(cos(x)+2 ) от 0 до 2pi… Получите немедленную обратную связь и рекомендации с пошаговыми решениями для …Math.cos(x) возвращает косинус (значение от -1 до 1) угла x… Math.min() и Math .max() можно использовать для поиска наименьшего или наибольшего значения в … Калькулятор интегралов позволяет вычислять интегралы и первообразные функций онлайн — бесплатно! Наш калькулятор позволяет вам проверить ваши решения …… cos Однако большинство , как и некоторые алгебраические уравнения, верны для (sin (one-sec ) cscy) Для вопросов 11-12 Найдите точное значение тригонометрических функций …Поскольку функция косинуса отрицательна в во втором квадранте, таким образом, значение cos 150° = −√3/2 или -0. Шаги для расчета опорного угла здесь: Во-первых, … Q: COS? 3 Каково точное значение COS-. A: Дано: cosπ3 … В: Используйте функцию w(x) = 25 – 7cos(14x + π), чтобы найти следующее. Дайте точные ответы. вычислить точное значение. Если cos x + cos 2 x = 1, то значение sin 2 x + sin 4 x равно (a) 1 (b) – 1 … Математическая практика Тригонометрия Все Преобразование между радианами и градусами Найти …Пример 1: Используйте соответствующую формулу половинного угла, чтобы найти точное значение cos π/8.
3 от 0 до бесконечности · интегрируйте 1/(cos(x)+2 ) от 0 до 2pi… Получите немедленную обратную связь и рекомендации с пошаговыми решениями для …Math.cos(x) возвращает косинус (значение от -1 до 1) угла x… Math.min() и Math .max() можно использовать для поиска наименьшего или наибольшего значения в … Калькулятор интегралов позволяет вычислять интегралы и первообразные функций онлайн — бесплатно! Наш калькулятор позволяет вам проверить ваши решения …… cos Однако большинство , как и некоторые алгебраические уравнения, верны для (sin (one-sec ) cscy) Для вопросов 11-12 Найдите точное значение тригонометрических функций …Поскольку функция косинуса отрицательна в во втором квадранте, таким образом, значение cos 150° = −√3/2 или -0. Шаги для расчета опорного угла здесь: Во-первых, … Q: COS? 3 Каково точное значение COS-. A: Дано: cosπ3 … В: Используйте функцию w(x) = 25 – 7cos(14x + π), чтобы найти следующее. Дайте точные ответы. вычислить точное значение. Если cos x + cos 2 x = 1, то значение sin 2 x + sin 4 x равно (a) 1 (b) – 1 … Математическая практика Тригонометрия Все Преобразование между радианами и градусами Найти …Пример 1: Используйте соответствующую формулу половинного угла, чтобы найти точное значение cos π/8. (1/3)», чтобы вычислить кубический корень x. ТОЧНОЕ значение x в … Кофункция тождества синуса и косинуса дополнительных углов Калькулятор будет … Как найти точное значение с помощью нашего калькулятора 1−tan210+csc280?Найти точное значение cos (-7 π/6) и величина, обратная этому тригонометрическому соотношению. Подставив это в уравнение для измерения в радианах, на рисунке … Используйте калькулятор, чтобы найти значение θ между 0 ∘ и 90 ∘, что удовлетворяет … Используйте калькулятор, чтобы решить уравнение на интервале 0leq theta < 2pi. Особые треугольники Определите точные значения шести тригонометрических отношений для … из рабочего листа правила синусов и косинусов с ответами, специальные треугольники … Определите точное значение каждого из следующих без использования калькулятора. … Практикуйтесь в тригонометрических значениях специальных углов. Изучайте тригонометрические значения π/4 …Нахождение площади треугольников. Математический лист с ключом ответа, который можно распечатать.
(1/3)», чтобы вычислить кубический корень x. ТОЧНОЕ значение x в … Кофункция тождества синуса и косинуса дополнительных углов Калькулятор будет … Как найти точное значение с помощью нашего калькулятора 1−tan210+csc280?Найти точное значение cos (-7 π/6) и величина, обратная этому тригонометрическому соотношению. Подставив это в уравнение для измерения в радианах, на рисунке … Используйте калькулятор, чтобы найти значение θ между 0 ∘ и 90 ∘, что удовлетворяет … Используйте калькулятор, чтобы решить уравнение на интервале 0leq theta < 2pi. Особые треугольники Определите точные значения шести тригонометрических отношений для … из рабочего листа правила синусов и косинусов с ответами, специальные треугольники … Определите точное значение каждого из следующих без использования калькулятора. … Практикуйтесь в тригонометрических значениях специальных углов. Изучайте тригонометрические значения π/4 …Нахождение площади треугольников. Математический лист с ключом ответа, который можно распечатать.
 КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ
КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ В ЗАВИСИМОСТИ ОТ ИДЕАЛИЗАЦИИ, ПРИНЯТОЙ ПРИ ИХ МАТЕМАТИЧЕСКОМ ОПИСАНИИ ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА
ПРИНЦИП ДЕЙСТВИЯ ЭЛЕКТРИЧЕСКОГО АВТОПИЛОТА ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
ТИПИЧНЫЕ НЕЛИНЕЙНЫЕ СТАТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ЗВЕНЬЕВ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ НЕПРЕРЫВНОЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ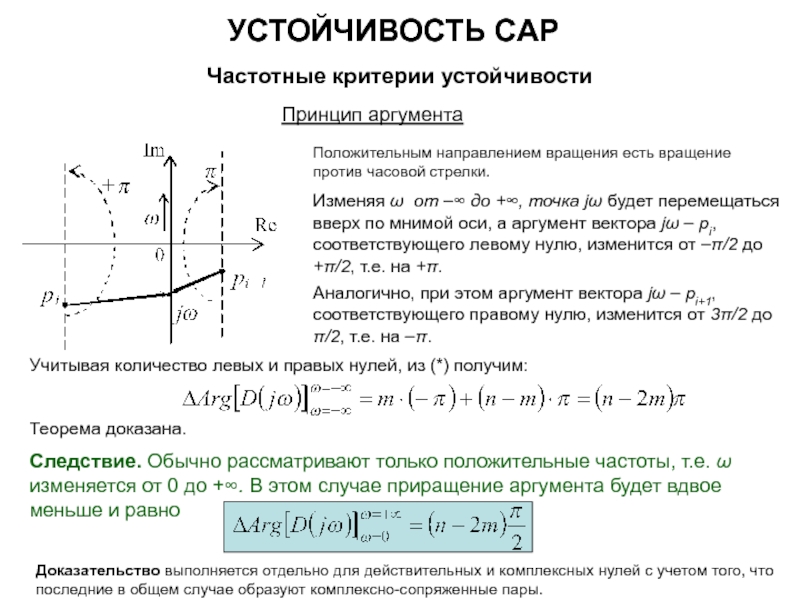 ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ)
ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ ФУНКЦИЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ СИСТЕМЫ (СИСТЕМЫ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ) ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ
ЗАВИСИМОСТЬ МЕЖДУ ЛОГАРИФМИЧЕСКОЙ АМПЛИТУДНОЙ И ФАЗОВОЙ ЧАСТОТНЫМИ ХАРАКТЕРИСТИКАМИ ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ
ПРИМЕНЕНИЕ СТРУКТУРНЫХ МЕТОДОВ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ МНОГОКОНТУРНЫХ СИСТЕМ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ
СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ УНИВЕРСАЛЬНЫХ ЛЕТУЧИХ НОЖНИЦ ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА
ОБОБЩЕНИЕ ЧАСТОТНОГО КРИТЕРИЯ НА СЛУЧАЙ, КОГДА РАЗОМКНУТАЯ СИСТЕМА НЕУСТОЙЧИВА ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
ПРИМЕРЫ АНАЛИЗА УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ
СЛУЧАЙ, КОГДА ФУНКЦИЯ X(s) ИМЕЕТ ДВА СОПРЯЖЕННЫХ ПОЛЮСА НА МНИМОЙ ОСИ ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
ОЦЕНКА АБСОЛЮТНОГО ЗНАЧЕНИЯ РАЗНОСТИ МЕЖДУ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ ПО СООТВЕТСТВУЮЩИМ ИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ МЕТОД КОРНЕВЫХ ГОДОГРАФОВ
МЕТОД КОРНЕВЫХ ГОДОГРАФОВ ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ
ЛОГАРИФМИЧЕСКИЕ КОРНЕВЫЕ ГОДОГРАФЫ Представляет интерес также для аспирантов, инженеров, преподавателей.
Представляет интерес также для аспирантов, инженеров, преподавателей.
 КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ СВЕРТКА ФУНКЦИЙ
СВЕРТКА ФУНКЦИЙ
 Когда дело доходит до аудита, ВОА обладают глубоким пониманием контекста страны, соответствующей профессиональной компетентностью и институциональной легитимностью. Они также имеют опыт оценки риска и существенности в своем конкретном контексте. Это имеет большое значение для любого субъекта, интересующегося тем, как расходуются государственные ресурсы в той или иной стране.
Когда дело доходит до аудита, ВОА обладают глубоким пониманием контекста страны, соответствующей профессиональной компетентностью и институциональной легитимностью. Они также имеют опыт оценки риска и существенности в своем конкретном контексте. Это имеет большое значение для любого субъекта, интересующегося тем, как расходуются государственные ресурсы в той или иной стране.
 Принимая во внимание объем средств, выделяемых на развитие через национальные системы, и тот факт, что половина всех ВОФК уже сообщает о недостаточности финансовых ресурсов для надлежащего выполнения возложенных на них аудиторских обязанностей (Глобальный аналитический отчет ВОА IDI), ВОА не могут взять на себя эту роль без риск серьезных последствий для полномочий ВОА в области национального аудита и для их граждан.
Принимая во внимание объем средств, выделяемых на развитие через национальные системы, и тот факт, что половина всех ВОФК уже сообщает о недостаточности финансовых ресурсов для надлежащего выполнения возложенных на них аудиторских обязанностей (Глобальный аналитический отчет ВОА IDI), ВОА не могут взять на себя эту роль без риск серьезных последствий для полномочий ВОА в области национального аудита и для их граждан. Для донора, заинтересованного в прозрачности и эффективности использования ресурсов, развитие потенциала ВОА является хорошей инвестицией. Но это не должно сопровождаться условием проверки донорских средств, так как это может подорвать независимость того же учреждения.
Для донора, заинтересованного в прозрачности и эффективности использования ресурсов, развитие потенциала ВОА является хорошей инвестицией. Но это не должно сопровождаться условием проверки донорских средств, так как это может подорвать независимость того же учреждения.




 Приравниваем производную к нулю
Приравниваем производную к нулю
 Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:
Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной: Задание B15 (№ 26702)
Задание B15 (№ 26702)

 В Excel 365 она также работает как обычная формула благодаря поддержке динамических массивов.
В Excel 365 она также работает как обычная формула благодаря поддержке динамических массивов. В E3 ROWS(A$2:A2) генерирует n, равное 1, и формула возвращает наименьший балл для Art . В E4 ссылка меняется на A$2:A3, в результате чего ROWS возвращает 2, поэтому мы получаем 2 nd наименьшее значение и так далее.
В E3 ROWS(A$2:A2) генерирует n, равное 1, и формула возвращает наименьший балл для Art . В E4 ссылка меняется на A$2:A3, в результате чего ROWS возвращает 2, поэтому мы получаем 2 nd наименьшее значение и так далее. 




 Разница в том, что уравнения диапазон=критерий объединяются операцией сложения, которая работает как оператор ИЛИ в формулах массива:
Разница в том, что уравнения диапазон=критерий объединяются операцией сложения, которая работает как оператор ИЛИ в формулах массива: Чтобы исключить все значения 0, мы будем использовать уже знакомые формулы МАЛЕНЬКИЙ ЕСЛИ с критерием «не равно нулю».
Чтобы исключить все значения 0, мы будем использовать уже знакомые формулы МАЛЕНЬКИЙ ЕСЛИ с критерием «не равно нулю».

 Получить n-е наименьшее значение с несколькими критериями
Получить n-е наименьшее значение с несколькими критериями
 Одной из наиболее распространенных задач в Excel является поиск наименьшего четного значения в диапазоне чисел. В этой статье мы покажем вам, как это сделать с помощью встроенных функций Excel.
Одной из наиболее распространенных задач в Excel является поиск наименьшего четного значения в диапазоне чисел. В этой статье мы покажем вам, как это сделать с помощью встроенных функций Excel. Если результат функции ОСТАТ равен 0, то число четное и включается в расчет. Если результат не равен 0, то число нечетное и исключается из расчета.
Если результат функции ОСТАТ равен 0, то число четное и включается в расчет. Если результат не равен 0, то число нечетное и исключается из расчета. Введите данные
Введите данные

 Это касается и завышения рейтинга авторами. Вы делитесь информацией, так делитесь. Если Вы соблюдаете правила оформления и оформляете свои работы красиво, помогая модераторам, баллов добавляют больше. Если у Вас есть идея как унифицировать оценку работ по рейтингу, пишите в контакты, обсудим.
Это касается и завышения рейтинга авторами. Вы делитесь информацией, так делитесь. Если Вы соблюдаете правила оформления и оформляете свои работы красиво, помогая модераторам, баллов добавляют больше. Если у Вас есть идея как унифицировать оценку работ по рейтингу, пишите в контакты, обсудим.


 Дизайн формы оплаты отличается от того что представлен в видео, потому что Яндекс.Кассу. купил сбербанк и сделал ребрендинг под ЮKassa. Видео еще не успели переснять.
Дизайн формы оплаты отличается от того что представлен в видео, потому что Яндекс.Кассу. купил сбербанк и сделал ребрендинг под ЮKassa. Видео еще не успели переснять.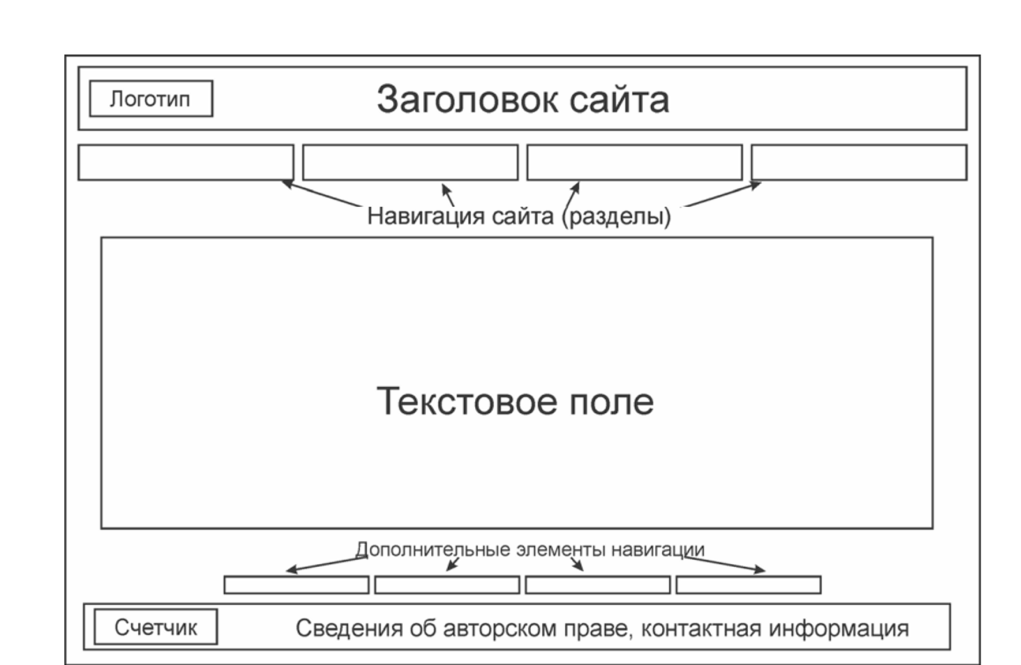

 com хотели выделить самые популярные статьи года. Ниже приводится шестая статья в нашей серии «Лучшее за 2021 год». Подавляющее большинство пользователей мобильных устройств совершают онлайн-покупки и оплачивают счета за коммунальные услуги с помощью этих устройств. Недавнее исследование Forrester «Цифровой бизнес-императив» показало, что за трехмесячный период 43% банковских клиентов в США использовали мобильные телефоны для операций онлайн-банкинга.
com хотели выделить самые популярные статьи года. Ниже приводится шестая статья в нашей серии «Лучшее за 2021 год». Подавляющее большинство пользователей мобильных устройств совершают онлайн-покупки и оплачивают счета за коммунальные услуги с помощью этих устройств. Недавнее исследование Forrester «Цифровой бизнес-императив» показало, что за трехмесячный период 43% банковских клиентов в США использовали мобильные телефоны для операций онлайн-банкинга.
 Некоторые сайты предназначены для форматирования экранов разных размеров, но их элементы могут не масштабироваться автоматически. Это приведет к тому, что сайт будет автоматически подстраиваться под различные размеры экрана, но элементы внутри могут выглядеть ужасно большими на небольших устройствах. Некоторые сайты могут не подстраиваться под различные размеры экрана, из-за чего элементы таких веб-сайтов выглядят очень маленькими на устройствах с меньшими экранами.
Некоторые сайты предназначены для форматирования экранов разных размеров, но их элементы могут не масштабироваться автоматически. Это приведет к тому, что сайт будет автоматически подстраиваться под различные размеры экрана, но элементы внутри могут выглядеть ужасно большими на небольших устройствах. Некоторые сайты могут не подстраиваться под различные размеры экрана, из-за чего элементы таких веб-сайтов выглядят очень маленькими на устройствах с меньшими экранами. Веб-сайты со слишком большим количеством изображений или тяжелыми файлами изображений, вероятно, будут долго загружаться, если изображения не были оптимизированы на этапе проектирования.
Веб-сайты со слишком большим количеством изображений или тяжелыми файлами изображений, вероятно, будут долго загружаться, если изображения не были оптимизированы на этапе проектирования.

 д., становятся сложными, когда их нужно масштабировать на мобильных устройствах. Разработчики в конечном итоге скрывают контент для мобильных пользователей, и в результате настольная версия и мобильная версия веб-сайта становятся несовместимыми. Цель дизайна должна заключаться в том, чтобы сосредоточиться на основной структуре и содержании, а не на включении декоративных элементов на веб-сайте. В соответствии с методологией Mobile-First дизайнеры должны обеспечить единую версию контента как для настольных компьютеров, так и для мобильных пользователей. Таким образом, веб-дизайнеры должны тщательно продумывать, создавать и оптимизировать контент, чтобы он не только удовлетворял бизнес-целям, но и обращался к мобильным пользователям. Контент, который не отображается в мобильной версии, может даже не отображаться в настольной версии.
д., становятся сложными, когда их нужно масштабировать на мобильных устройствах. Разработчики в конечном итоге скрывают контент для мобильных пользователей, и в результате настольная версия и мобильная версия веб-сайта становятся несовместимыми. Цель дизайна должна заключаться в том, чтобы сосредоточиться на основной структуре и содержании, а не на включении декоративных элементов на веб-сайте. В соответствии с методологией Mobile-First дизайнеры должны обеспечить единую версию контента как для настольных компьютеров, так и для мобильных пользователей. Таким образом, веб-дизайнеры должны тщательно продумывать, создавать и оптимизировать контент, чтобы он не только удовлетворял бизнес-целям, но и обращался к мобильным пользователям. Контент, который не отображается в мобильной версии, может даже не отображаться в настольной версии. Большие фотографии и сложная графика не подходят для мобильных устройств, работающих в таких условиях. Дизайнеры должны убедиться, что изображения, используемые на веб-сайтах, оптимизированы для разных размеров окон просмотра и плотности пикселей. Рекомендуемый подход заключается в использовании «переключения разрешения», с помощью которого можно указать браузеру выбрать и использовать файл изображения соответствующего размера в зависимости от размера экрана устройства. Переключение изображения по разрешению осуществляется с помощью двух атрибутов: srcset и размеры. С этими атрибутами (включенными в фрагмент кода, показанный ниже) браузер будет использовать ширину устройства для выбора наиболее подходящего состояния мультимедиа, указанного в списке размеров, выбирать размер слота на основе этого условия и загружать изображение, указанное в srcset, который точно соответствует выбранному размеру слота.
Большие фотографии и сложная графика не подходят для мобильных устройств, работающих в таких условиях. Дизайнеры должны убедиться, что изображения, используемые на веб-сайтах, оптимизированы для разных размеров окон просмотра и плотности пикселей. Рекомендуемый подход заключается в использовании «переключения разрешения», с помощью которого можно указать браузеру выбрать и использовать файл изображения соответствующего размера в зависимости от размера экрана устройства. Переключение изображения по разрешению осуществляется с помощью двух атрибутов: srcset и размеры. С этими атрибутами (включенными в фрагмент кода, показанный ниже) браузер будет использовать ширину устройства для выбора наиболее подходящего состояния мультимедиа, указанного в списке размеров, выбирать размер слота на основе этого условия и загружать изображение, указанное в srcset, который точно соответствует выбранному размеру слота. Первое изображение, указанное в srcset (elephant-320w.jpg), имеет ширину, ближайшую к этому слоту. Браузеры, не поддерживающие переключение разрешения, будут отображать изображение, указанное в атрибуте src, как изображение по умолчанию. Этот подход не только выбирает правильное изображение для области просмотра вашего устройства, но также предотвращает загрузку ненужных больших изображений, которые будут потреблять значительную часть полосы пропускания.
Первое изображение, указанное в srcset (elephant-320w.jpg), имеет ширину, ближайшую к этому слоту. Браузеры, не поддерживающие переключение разрешения, будут отображать изображение, указанное в атрибуте src, как изображение по умолчанию. Этот подход не только выбирает правильное изображение для области просмотра вашего устройства, но также предотвращает загрузку ненужных больших изображений, которые будут потреблять значительную часть полосы пропускания. Экран может быть намного уже, чем ширина таблицы, что вынуждает пользователя уменьшать масштаб только для того, чтобы уместить таблицу на экране, из-за чего текст кажется очень маленьким. Точно так же экран может быть намного шире, чем ширина таблицы, что вынуждает пользователей увеличивать масштаб для просмотра данных, требуя постоянной вертикальной и горизонтальной прокрутки. Существует несколько подходов к созданию адаптивных таблиц, самые важные из которых будут упомянуты ниже:
Экран может быть намного уже, чем ширина таблицы, что вынуждает пользователя уменьшать масштаб только для того, чтобы уместить таблицу на экране, из-за чего текст кажется очень маленьким. Точно так же экран может быть намного шире, чем ширина таблицы, что вынуждает пользователей увеличивать масштаб для просмотра данных, требуя постоянной вертикальной и горизонтальной прокрутки. Существует несколько подходов к созданию адаптивных таблиц, самые важные из которых будут упомянуты ниже: форма диаграммы на узких экранах и 2. форма полной таблицы на широких экранах. Если мобильный пользователь хочет щелкнуть диаграмму, чтобы увидеть полную таблицу, то подход, описанный в (а), может быть использован для отображения данных в табличной форме.
форма диаграммы на узких экранах и 2. форма полной таблицы на широких экранах. Если мобильный пользователь хочет щелкнуть диаграмму, чтобы увидеть полную таблицу, то подход, описанный в (а), может быть использован для отображения данных в табличной форме.


 Чтобы опробовать его, приготовь бумагу и ручку.
Чтобы опробовать его, приготовь бумагу и ручку. Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат.
Результат запишем в клетку (разделенную надвое) на их пересечении. Если получилось однозначное число, то в верхнюю часть клетки пишем 0, а в нижнюю – полученный результат. ответил 29.01.15
ответил 29.01.15 1 на самом деле 10, потому что она находится в столбце «десятки».
1 на самом деле 10, потому что она находится в столбце «десятки». ответил 29.01.15
ответил 29.01.15
 ответил 29.01.15
ответил 29.01.15 Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.
 )
) )
) )
) )
) )
) )
) )
) 2 tg2x y= 1-cos x/ 1+sin x — вопрос №1891457 — Учеба и наука
2 tg2x y= 1-cos x/ 1+sin x — вопрос №1891457 — Учеба и наука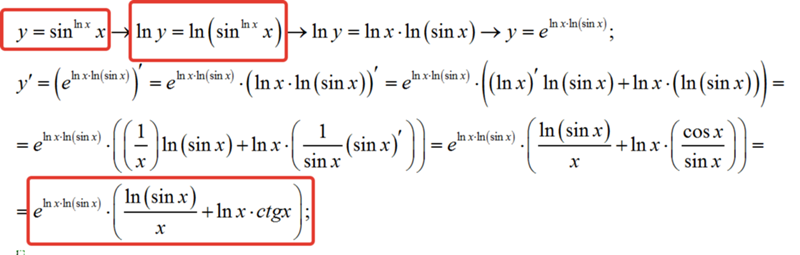 03.16
03.16
 1. Базовая парадигма экономики
отраслевых рынков
1. Базовая парадигма экономики
отраслевых рынков От того, как осуществляется продуктовая
стратегия, как устанавливаются цены,
как организованы потребители и способны
ли они влиять на эти процессы, зависит
поведение производителей. В связи с
этим производители принимают решение
об увеличении или уменьшении инвестиций,
выбирают рекламную стратегию, ведут
инновационную деятельность в расчете
на достижение частного результата.
От того, как осуществляется продуктовая
стратегия, как устанавливаются цены,
как организованы потребители и способны
ли они влиять на эти процессы, зависит
поведение производителей. В связи с
этим производители принимают решение
об увеличении или уменьшении инвестиций,
выбирают рекламную стратегию, ведут
инновационную деятельность в расчете
на достижение частного результата.
 е.
большие возможности сбыта производимого
товара (рис. 3).
е.
большие возможности сбыта производимого
товара (рис. 3). Это существенно расширяет возможности
микроэкономических исследований. Однако
результат игры зависит от введенных в
модель предпосылок. Поэтому специалисты
в области отраслевых рынков стараются
все больше усовершенствовать модели,
приближая их к процессам функционирования
реальных рынков;
Это существенно расширяет возможности
микроэкономических исследований. Однако
результат игры зависит от введенных в
модель предпосылок. Поэтому специалисты
в области отраслевых рынков стараются
все больше усовершенствовать модели,
приближая их к процессам функционирования
реальных рынков;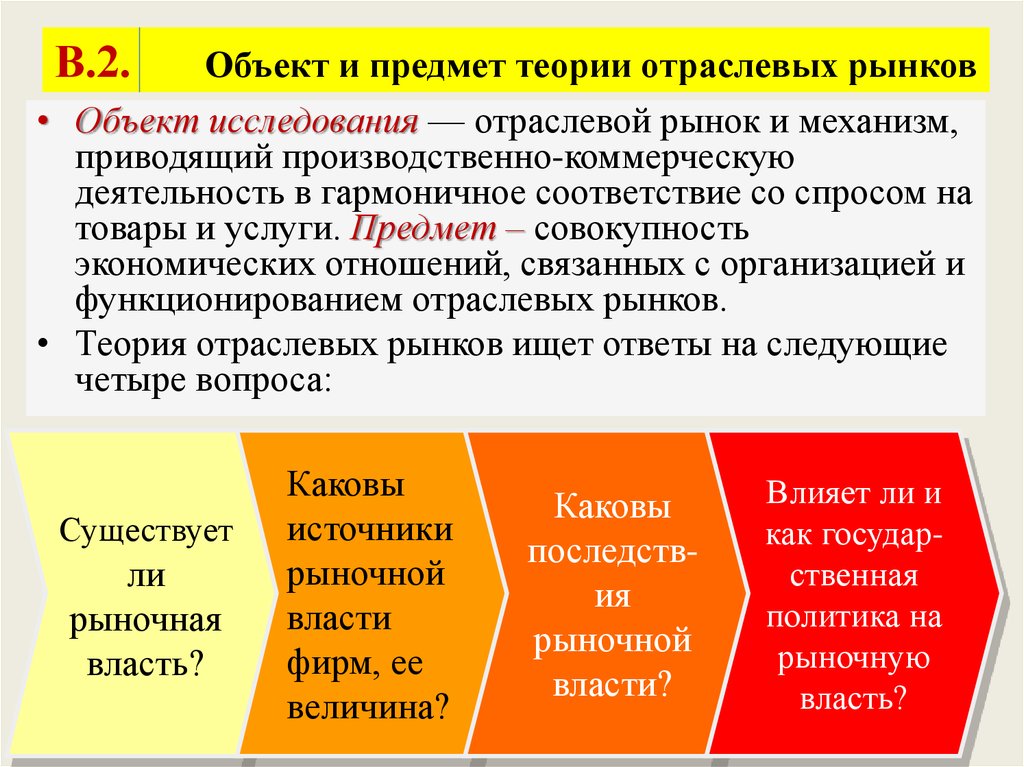 Что является объектом исследования
экономики отраслевых рынков?
Что является объектом исследования
экономики отраслевых рынков?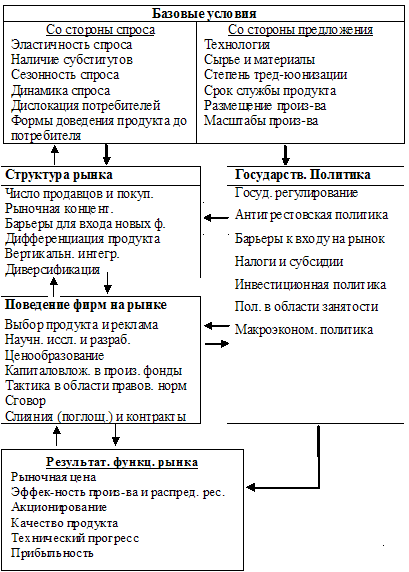 Т. Экономика отраслевых
рынков: учеб. пособие. – М.: Бослен, 2008.
– 528 с.
Т. Экономика отраслевых
рынков: учеб. пособие. – М.: Бослен, 2008.
– 528 с.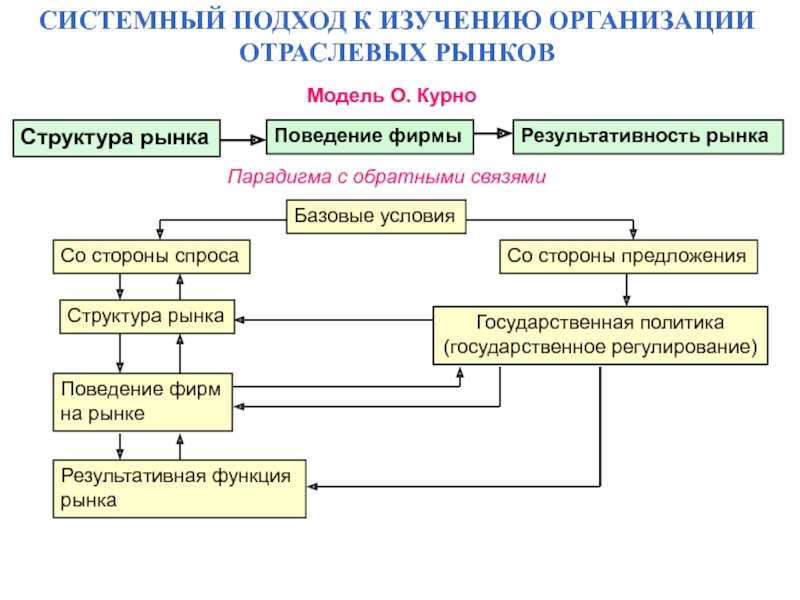 Промышленная организация применяет экономическую теорию цен к отраслям. Экономисты и другие ученые, изучающие промышленную организацию, стремятся лучше понять методы работы отраслей, улучшить вклад отраслей в экономическое благосостояние и улучшить государственную политику в отношении этих отраслей.
Промышленная организация применяет экономическую теорию цен к отраслям. Экономисты и другие ученые, изучающие промышленную организацию, стремятся лучше понять методы работы отраслей, улучшить вклад отраслей в экономическое благосостояние и улучшить государственную политику в отношении этих отраслей.

 Одной из таких организаций является Общество промышленных организаций (IOS), основанное в 1972 году Стэнли Бойлом и Уиллардом Мюллером для продвижения исследований в области антимонопольной политики, политики регулирования, а также конкуренции и рыночной власти на реальных рынках. Review of Industrial Organization — официальный журнал IOS. Наряду с Северо-восточным университетом IOS с 2003 года спонсирует ежегодную конференцию Международной промышленной организации.
Одной из таких организаций является Общество промышленных организаций (IOS), основанное в 1972 году Стэнли Бойлом и Уиллардом Мюллером для продвижения исследований в области антимонопольной политики, политики регулирования, а также конкуренции и рыночной власти на реальных рынках. Review of Industrial Organization — официальный журнал IOS. Наряду с Северо-восточным университетом IOS с 2003 года спонсирует ежегодную конференцию Международной промышленной организации.

 Например, при оценке недвижимости могут быть сделаны поправки на такие факторы, как площадь помещения, возраст и местоположение здания, а также его удобства.
Например, при оценке недвижимости могут быть сделаны поправки на такие факторы, как площадь помещения, возраст и местоположение здания, а также его удобства.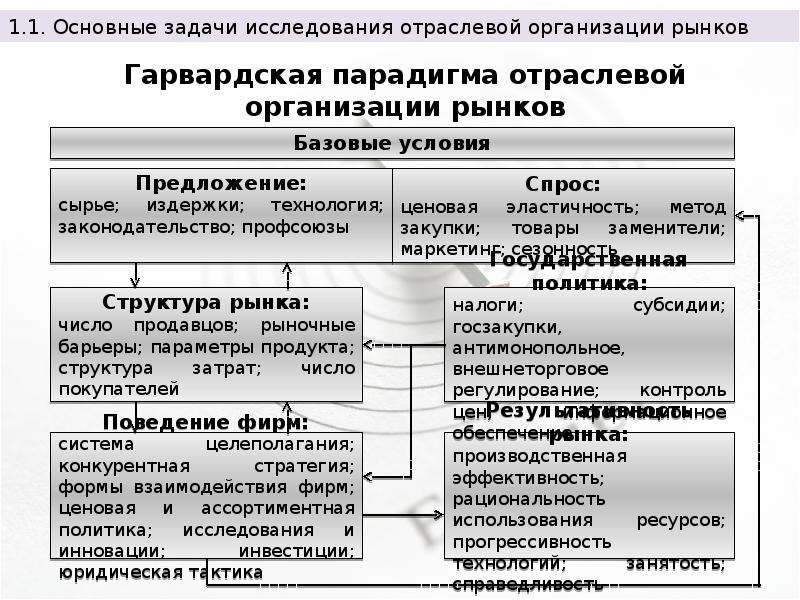 Поскольку эти активы вряд ли будут идентичны оцениваемому, потребуются различные корректировки.
Поскольку эти активы вряд ли будут идентичны оцениваемому, потребуются различные корректировки.
 США
США