Автор: 
Алгебраические выражения, коэффициент, виды выражений
- Коэффициент
- Виды выражений
Алгебраическое выражение — это запись, составленная со смыслом, в которой числа могут быть обозначены и буквами, и цифрами. Также она может содержать знаки арифметических действий и скобки.
Любую букву, обозначающую число, и любое число, изображённое с помощью цифр, принято считать в алгебре также алгебраическим выражением.
Алгебраические выражения, входящие в состав формул, могут применяться к решению частных арифметических задач, если в них заменить буквы данными числами и произвести указанные действия. Число, которое получится, если взять вместо букв какие-либо числа и произвести над ними указанные действия, называется численной величиной алгебраического выражения. Из этого легко сделать вывод, что одно и то же алгебраическое выражение при различных значениях входящих в него букв может иметь различные числовые величины.
Примеры:
1) Выражение
am + bn,
при a = 2, m = 5, b = 1, n = 4 вычисляется:
2 · 5 + 1 · 4 = 14,
а при a = 3, m = 4, b = 5, n = 1 вычисляется:
3 · 4 + 5 · 1 = 17 и т. д.
2) Выражение
abс,
при a = 1, b = 2, c = 3 равно:
1 · 2 · 3 = 6,
а при a = 2, b = 3, c = 4 равно:
2 · 3 · 4 = 24 и т. д.
Коэффициент
Коэффициент — это числовой множитель алгебраического выражения, представляющего собой произведение нескольких сомножителей. Коэффициент в выражении ставится перед всеми остальными буквенными множителями. Таким образом,
произведение чисел a, b, c, d, 4 записывается так: 4abcd;
произведение чисел m, n, , p записывается так: .
Числа 4 и — это коэффициенты.
Очевидно, что
4abcd = abcd + abcd + abcd + abcd
и точно также
.
Итак, коэффициент показывает, сколько раз целое алгебраическое выражение или известная его часть берется слагаемым.
Если в алгебраическом выражении нет числового множителя, то подразумевается, что коэффициент равен единице, так как
a = 1 · a; bc = 1 · bc
и так далее.
Виды выражений
Алгебраическое выражение, в которое не входят буквенные делители, называется целым, в противном случае дробным или алгебраической дробью.
Пример.
Целые алгебраические выражения:
| 7a2b, a2 + | 2 | bc . |
| 3 |
Дробные алгебраические выражения:
| a2 | , | m — n | |
| b3 | m + n | . |
Выражения, не содержащие корней, называются рациональными, а содержащие корни — иррациональными или радикальными. Например, все выражения, приведённые выше, являющиеся целыми или дробными, так же можно назвать и рациональными.
√a , 53√c + a√mn — иррациональные или радикальные выражения.
023. Алгебраические выражения
Алгебраическое выражение – это выражение, которое состоит из чисел, переменных и математических знаков. Выражение может содержать скобки, рациональную степень переменной (с целым или дробным показателем), знак модуля.
Например, алгебраические выражения – это: .
Область допустимых значений (ОДЗ) алгебраического выражения – это такие значения переменных, при которых это выражение имеет смысл.
Пример 3. Найдите ОДЗ алгебраического выражения: .
Решение. Если , то выражение не имеет смысла.
Ответ. ОДЗ: .
Пример 4. Найдите ОДЗ выражения: .
Решение. Из условия имеем:. Это значит, что если или , то выражение не имеет смысла.
Ответ. ОДЗ: .
Рассмотрим рисунок 3.1 подробнее, для этого дадим характеристику каждому компоненту рисунка.
Алгебраические выражения могут быть рациональными и иррациональными.
Рациональное выражение – это выражение, в котором содержатся действия сложения, вычитания, умножения, деления, возведения в степень (здесь показатель степени – это натуральное число).
Например, ; ; – это рациональные выражения.
Рациональные выражения могут быть Целыми и Дробными.
Целое рациональное выражение не содержит деления на буквенное выражение. Например, ; – это целые рациональные выражения.
Целые рациональные выражения подразделяются на одночлены и многочлены.
Одночлен – это произведение числового коэффициента на натуральную степень переменных.
Например, ; ; – это одночлены, где ; ; – это числовые коэффициенты; ; ; – это буквенные выражения.
Степень одночлена – это сумма показателей степеней всех переменных одночлена.
Например, одночлен – это одночлен шестой степени одночлен – это одночлен четвертой степени 7 – это одночлен нулевой степени.
Одночлен имеет Стандартный вид, если числовой коэффициент стоит на первом месте (перед буквенным выражением), а неизвестные множители записаны в алфавитном порядке.
Одночлены называются Подобными, если они имеют одинаковые буквенные выражения.
Привести подобные одночлены (члены) – это значит найти их сумму или разность.
Например, ; ; – это подобные одночлены.
Пример 5. Приведите подобные члены: .
Решение. ; ; .
Ответ. .
Многочлен – это алгебраическая сумма одночленов (их сумма или разность).
Например, – это многочлен.
Степень многочлена – это степень его старшего члена.
Например, многочлен – это многочлен четвертой степени; многочлен – это многочлен пятой степени.
Дробное рациональное выражение содержит деление на выражение с переменными. Дробное рациональное выражение называют алгебраической дробью.
Например, ; – это алгебраические дроби.
Используют и другое определение алгебраической дроби.
Выражение вида , где и – это многочлены или одночлены, называется Алгебраической дробью.
Область допустимых значений (ОДЗ) Алгебраической дроби это множество значений переменной, при которых ее знаменатель не равен нулю ().
Алгебраическая дробь равна нулю, если ее числитель равен нулю, т. е. .
Если в алгебраическом выражении используется возведение переменных в дробную степень (извлечение корня из переменных), то такое алгебраическое выражение называется Иррациональным.
Например, ; – это иррациональные выражения.
Алгебраические выражения могут быть рациональными и иррациональными.
Рациональные выражения разделяются на целые и дробные.
Целые рациональные выражения состоят из одночленов и многочленов.
Дробные рациональные выражения включают в себя алгебраические дроби.
| < Предыдущая | Следующая > |
|---|
буквенных уравнений | ChiliMath
Буквенные уравнения , проще говоря, представляют собой уравнения, содержащие две или более переменных. Ваша цель состоит в том, чтобы решить только одну переменную по отношению к другим. Если вы знаете, как решать регулярные уравнения, то я гарантирую вам, что решение буквальных уравнений будет легкой задачей.
Что такое буквальное уравнение?
Буквенное уравнение — это уравнение, включающее более одной переменной. Более того, переменная или «литерал» — это математический символ, представляющий произвольное значение или число.
Буквы в алфавите обычно используются для обозначения таких переменных, как a, b, c, x, y и z. Решить буквальное уравнение означает выразить одну переменную по отношению к другим переменным в уравнении.
Ключевая стратегия решения буквальных уравнений
«Суть» решения буквального уравнения в том, чтобы изолировать или оставить отдельно определенную переменную с одной стороны уравнения (слева или справа), а остальные – с противоположной стороны.
Если вы знаете, как решать обычные одношаговые уравнения, двухшаговые уравнения и многошаговые уравнения, процесс решения буквенных уравнений очень похож.
Поэтому вас не должны пугать буквальные уравнения, потому что у вас уже могут быть навыки для их решения. Это просто вопрос практики и знакомства.
Итак, ключевая идея выглядит так. Обратите внимание, что переменная, которую вы хотите решить, изолирована на одной стороне уравнения. В данном случае она находится на левой стороне. Обратите внимание, что переменная \color{red}\Large{x} сама по себе находится на одной стороне уравнения, а остальные — на противоположной.
Давайте рассмотрим несколько примеров!
Пример одношагового буквального уравнения
Пример 1 : Найдите s в буквальном уравнении P = 4s.
Помните эту формулу? Это периметр квадрата, где P означает периметр, а s – размер одной стороны квадрата. Таким образом, чтобы получить периметр квадрата, мы имеем P = s + s + s + s = 4s.
Чтобы найти s, нам нужно избавиться от коэффициента 4, который умножает s. Обратное умножение — это деление, поэтому мы должны делить обе части на 4!
- Мы можем изолировать переменную s с правой стороны.
- Разделите обе части на 4.
- Упрощение. Теперь, когда переменная \color{red}\Large{s} одна в правой части уравнения, мы закончили!
Примеры двухшаговых литеральных уравнений
Пример 2 : Найдите L в буквальном уравнении P = 2L + 2W.
Буквенное уравнение, упомянутое выше, также является формулой для определения периметра прямоугольника, где: P = периметр, L = длина и W = ширина.
Можно изолировать переменную L в правой части. Однако почему бы не перевернуть уравнение, чтобы мы могли оставить только переменную L слева? Что ж, звучит как план!
Пусть вас не пугает внешний вид. Просто сосредоточьтесь на вещах, которые вы хотите сделать, то есть на решении для L, а остальные шаги последуют за вами.
- Мы хотим решить L, верно?
- Переверните уравнение , чтобы изолировать переменную в левой части.
- Вычтите обе стороны на 2W.
- Упрощение.
- Разделите обе части на 2.
- Упрощение, теперь L стоит отдельно – решено!
Пример 3 : Найдите x в приведенном ниже буквальном уравнении.
Что делает это буквальное уравнение интересным, так это то, что мы собираемся изолировать переменную, которая является частью числителя дроби. Я не уверен, помните ли вы, что всякий раз, когда вы видите что-то подобное, постарайтесь сначала избавиться от знаменателя.
Это значительно упрощает весь процесс решения.
Поскольку знаменатель 3 делит выражение «x − y», противоположная операция, которая может его отменить, — умножение. Имеет смысл сначала умножить обе части на 3, а затем добавить на «y», чтобы оставить x отдельно. Не так уж плохо, верно?
- Хорошо, мы хотим найти x. Изолируем его с правой стороны.
- Начните с умножения обеих сторон на 3, что является знаменателем дроби.
- Упрощение. Это хорошо, знаменатель исчез.
- Добавить обе стороны по у. Это единственный способ убрать − y с правой стороны.
- Упрощение, x теперь счастлив сам по себе. Сделанный!
Примеры многошаговых буквенных уравнений
Пример 4 : Решите для C в буквальном уравнении ниже.
Это формула, используемая для преобразования меры температуры в единицах Цельсия в шкалу Фаренгейта. Обратите внимание: чтобы найти значение F (по Фаренгейту), нам нужно подставить некоторое значение C (по Цельсию).
Однако можем ли мы также использовать данную формулу для нахождения градусов Цельсия всякий раз, когда задано значение Фаренгейта?
Абсолютно да!
В конце концов, это буквальное уравнение, поэтому можно выразить C через F. Это то, что мы собираемся сделать сейчас…
- Все глаза прикованы к C. Цель состоит в том, чтобы изолировать его.
- Избавимся от 32 справа, вычтя обе части на 32.
- Это выглядит чище после упрощения.
- Затем умножьте обе части на 5, чтобы сократить знаменатель 5 под 9C.
- Мы на месте! Я предлагаю , а не , чтобы распределить 5 на (F — 32).
- Еще один шаг, разделите обе части на 9, чтобы окончательно изолировать переменную справа.
- Вот и все! Мы решили для C.
Пример 5 : Найдите h в буквальном уравнении 3h + g = 5h − hg.
Это действительно интересно! Некоторые из вас могут подумать, что невозможно изолировать переменную h, поскольку она находится почти в трех местах: одно h слева и два справа.
Ну не сдавайся еще! Открою вам небольшой «секрет».
Используйте метод факторинга, чтобы выбрать эту переменную h из группы. Но прежде чем вы сможете разложить h, убедитесь, что вы переместили все h на одну сторону уравнения.
Поскольку у нас есть два члена h в правой части, мы могли бы также переместить член 3h слева на другую сторону.
- Мы хотим h изолировать, верно?
- Сохраняем все наши h-члены справа. Мы можем сделать это, вычитая обе стороны на 3h.
- После упрощения замечательно видеть, что все наши h-термины находятся только справа.
- Очевидно, что шаг должен включать в себя факторизацию h.
Вау, это здорово! Всего одиночных ч с правой стороны.
- Само по себе выделение h означает, что мы должны избавиться от выражения (2−g).
Разделите обе части на (2 − g).
- Сделайте несколько отмен с правой стороны.
- Вот оно! Мы решили для h.
Пример 6 : Найдите x в приведенном ниже буквальном уравнении.
Самый простой способ решить это буквальное уравнение — выполнить перекрестное умножение . При этом знаменатели в обеих частях уравнения должны исчезнуть.
С этого момента мы можем применить ту же стратегию из примера 5, чтобы найти x , которая включает в себя сбор всех членов x на одной стороне уравнения, а затем, как мы надеемся, факторизацию x.
- В этом уравнении у нас есть два x с обеих сторон уравнения. Что еще более важно, они расположены в позиции числителя.
- Мы хотим, чтобы знаменатели исчезли, поэтому без колебаний мы должны применить метод перекрестного умножения. Затем просто примените распределительное свойство к обеим частям уравнения.
- На этом этапе мы решаем, где хранить или собирать все наши крестики. Для этого примера давайте оставим их слева.
Начните с , избавьтесь от -5x справа, добавив 5x с обеих сторон.
- Вот так это выглядит после упрощения. Следующим шагом будет работа с 3xy с правой стороны. Мы также хотим переместить его влево.
- Вычтите обе стороны на 3xy. Это должно оставить все наши крестики слева.
- Не забудьте написать 0 справа!
- Теперь -6 слева нужно переместить на правую сторону. Мы можем сделать это, добавив 6 к обеим сторонам.
- Становится лучше! У нас есть все наши x термины слева. Похоже, что мы можем исключить x.
- Ага! Мы только что сделали!
- Наконец, чтобы решить x, мы должны разделить обе части на выражение (8 − 3y). Выполните некоторые отмены.
- Готово!
Пройди тест !
Викторина по буквальным уравнениям
Вам может быть интересно:
Решение одношаговых уравнений
Решение двухэтапных уравнений
Решение многошаговых уравнений
Решение буквенных уравнений: обзор и примеры
Смотри, ты идешь! Теперь вы научились решать одношаговые уравнения, двухшаговые уравнения и многошаговые уравнения.
Теперь пришло время обсудить решение буквальных уравнений .
На этом уроке мы дадим определение буквенным уравнениям, рассмотрим примеры буквенных уравнений, а также научимся решать буквальные уравнения. Давайте буквально взволнован, чтобы начать!
Что мы рассматриваем
Что такое буквальное уравнение?
Напомним из нашего предыдущего исследования, что уравнение — это математическое предложение, в котором используется знак равенства = , чтобы показать, что два выражения равны. В отличие от других уравнений, с которыми вы уже работали, буквальные уравнения состоят в основном из букв и переменных.
Многие из буквальных уравнений, с которыми вы работали в своей жизни, были формулы. Хотя эти уравнения будут выглядеть иначе, чем наши обычные уравнения, они по-прежнему подчиняются тем же правилам решения.
Вернуться к оглавлению
Примеры буквенных уравнений
Хотя идея уравнений, состоящих в основном из букв, может показаться чуждой, вы много раз использовали буквальные уравнения в своей жизни.
Вот несколько примеров буквальных уравнений, с которыми вы уже работали в своей жизни:
Площадь прямоугольника
A = b \cdot h
Длина окружности
C = \pi \cdot D
Формула простых процентов
I = p \cdot r \cdot t
Каждая буква (или переменная) в буквальном уравнении имеет особое значение и изменяется от задачи к задаче.
Вернуться к оглавлению
Как решать буквенные уравнения
Решение буквенных уравнений следует тем же правилам, что и решение одношагового или двухэтапного уравнения. Идея «решения» буквального уравнения, по сути, означает, что мы переставляем буквы (или переменные), чтобы изолировать новую переменную. Буквальное уравнение «решено», когда интересующая переменная находится одна на одной стороне уравнения.
Ознакомьтесь с лицензиями школы Альберта !
Подобно решению уравнений, мы будем использовать обратные операции, чтобы изолировать переменную саму по себе.
Вот примеры обратных операций:
\text{Сложение} \leftrightarrow \text{Вычитание}
\text{Умножение} \leftrightarrow \text{Деление}
Вот несколько примеров решения буквенных уравнений:
Пример 1
Найдите h в следующем буквальном уравнении:
А = b \cdot h
Помните эту формулу? Как сказано выше, это площадь прямоугольника. Как отмечалось ранее, в буквенных уравнениях в основном используются буквы и переменные. Если бы это было простое уравнение, такое как 10 = 2x, мы бы просто разделили обе части на 2, чтобы получить мой окончательный ответ.
При «решении» буквенных уравнений мы следуем тем же правилам, что и простые уравнения. Следовательно, чтобы найти h в этом уравнении, нам нужно выделить его отдельно. Поэтому мы разделим обе части на b .
\dfrac{A}{b} = \dfrac{b \cdot h}{b}
Это изолирует h , что даст нам ответ:
h = \dfrac{A}{b}
Пример 2:
Хотя формулы являются распространенным примером буквенных уравнений, не все буквальные уравнения являются формулами.
Мы также можем изменить и «решить» буквальное уравнение для любой переменной. Например:
Найдите m в следующем уравнении:
| x = m + n | Исходное уравнение |
| x \textcolor{red}{- n} = m + n \textcolor{red}{- n} | Вычесть n с обеих сторон |
| x — n = m | m теперь изолировано |
| m = x — n |
Несмотря на то, что в уравнении не было чисел, мы «решили» буквальное уравнение для m .
Вернуться к оглавлению
Многошаговые буквенные уравнения
Пример 1
Не все буквальные уравнения решаются только за один шаг. Вот пример использования нескольких шагов для решения буквенных уравнений. 92}
Теперь у нас есть r, изолированный сам по себе, что дает нам новое буквальное уравнение:
r = \sqrt{\dfrac{V}{\pi h}}
Пример 2
Вот пример буквального уравнения, которое не является формулой, но которое мы можем решить для переменной.
Найдите x в следующем уравнении:
4(x + y) = P
Есть два способа решить эту проблему. Первый метод состоит в том, чтобы рассматривать его как уравнение и распределять 4 , а затем решать:
4x + 4y = Р
Затем мы можем вычесть 4y с каждой стороны:
4x + 4y \textcolor{red}{- 4y} = P \textcolor{red}{ — 4y}
Затем нам нужно разделить каждую сторону на 4 :
\dfrac{4x}{4} = \dfrac{P — 4y}{4}
Наконец, нам нужно упростить наше уравнение:
x = \dfrac{P}{4} — \dfrac{4y}{4}
х = \dfrac{P}{4} — у
Теперь мы, наконец, нашли x в буквальном уравнении. Давайте посмотрим, как можно решить уравнение, не упрощая в конце.
В другом методе мы можем просто разделить на 4 в начале, чтобы избежать использования свойства распределения. Например:
\dfrac{4(x + y)}{4} = \dfrac{P}{4}
Тогда нам просто нужно вычесть y с каждой стороны:
x + y \textcolor{red}{- y} = \dfrac{P}{4} \textcolor{red}{ — y}
Таким образом, мы получаем:
x = \dfrac{P}{4}- y
Обратите внимание, что уравнение уже упрощено, и никаких других шагов не требуется.
Вернуться к оглавлению
Вот короткое видео, демонстрирующее, как решать буквенные уравнения:
Буквенные уравнения с дробями
Давайте поработаем над некоторыми примерами буквенных уравнений с дробями!
Ознакомьтесь с лицензиями школы Альберта !
Пример 1
Многие буквенные уравнения и формулы в той или иной степени содержат дроби. Например, вот формула объема сферы:
93}Теперь, когда r изолировано, мы успешно нашли r .
Пример 2
Что произойдет, если мы просто захотим изменить уравнение для другой переменной?
Например, решите следующее уравнение для x :
y = \dfrac{x}{4} — \dfrac{1}{8}
Обратите внимание, что в уравнении две переменные, и наша конечная цель по-прежнему состоит в том, чтобы изолировать x .
Помните, мы можем убрать все дроби за один ход, умножив все члены на 9.0003 Наименьший общий знаменатель .
В этом буквальном уравнении наименьший общий знаменатель равен 8 . Следовательно, мы умножим каждое слагаемое на 8.
8 \cdot y = 8 \cdot \dfrac{x}{4} — 8 \cdot \dfrac{1}{8}
Это даст нам уравнение, в котором больше нет дробей:
8y = 2x — 1
Затем продолжайте решать, как обычное уравнение:
| 8y = 2x — 1 | Исходное уравнение |
| 8y \textcolor{red}{+ 1} = 2x — 1 \textcolor{red}{+ 1} | Добавить по 1 с каждой стороны |
| 8y + 1 = 2x | Упростить | 5 \fracd {8y + 1}{\textcolor{red}{2}} = \dfrac{2x}{\textcolor{red}{2}} | Разделите каждую сторону на 2 |
| \dfrac{8y}{2} + \dfrac{1}{2} = x | Упрощение |
| 4y + \dfrac{1}{2} = x | Упрощение |
Теперь, когда мы изолировали x отдельно, мы правильно «решил» буквальное уравнение.
Размеры рамы в сложенном виде без колес: 30 х 60 х 89 см. На раме под пластиковыми наличниками спрятаны надежные пружины, благодаря им коляска имеет очень мягкое укачивание, как при продольном качание, так и поперечном.
Прежде всего хочется сказать о ее главном плюсе, это вес (всего 12 кг) за счет этого коляска становится более транспортабельна и подходит для путешествий.
Внутренняя ткань выполнена из 100% хлопка, ее легко можно снять для стирки, внешняя ткань со специальной пропиткой против дождя.
В задние стойки встроены мягкие амортизаторы, благодаря которым перед препятствием коляска буквально пружинит.
02+17.19
27 — ClinVar — NCBI
4(BRCA1):c.594-2A>C
.. больше HGVS
… меньше HGVS
7 ЗК РФ установлено, что уполномоченный орган исполнительной власти или орган местного самоуправления, принявшие решение об изъятии, либо в случае, если решение об изъятии принято на основании ходатайства об изъятии, организация, подавшая такое ходатайство, обращаются от имени правообладателя изымаемой недвижимости без доверенности с заявлением о кадастровом учете земельных участков, подлежащих изъятию, земельных участков, предоставляемых взамен изымаемых земельных участков, или земельных участков, границы которых подлежат уточнению в связи с изъятием, если необходимо проведение государственного кадастрового учета таких земельных участков.
Являясь частью ведущей платформы мониторинга пациентов серии N, N1 оснащен интуитивно понятным дисплеем в стиле смартфона и основными параметрами, обеспечивающими высококачественную помощь, ориентированную на пациента. N1 служит комплексным многопараметрическим модулем, мощным транспортным монитором и универсальным прикроватным монитором — все в одном.
Дополнительный анализ ST и мониторинг интервала QT/QTc.
Кроме того, техническая удаленная поддержка доступна 24 часа в сутки, 7 дней в неделю бесплатно.
Мы известны своими потрясающими бутербродами. Который твой любимый?
Позвольте нам помочь вам сделать этот выпускной сезон особенным, если вы чествуете новых выпускников.
3N1 был очень приятным сюрпризом. У нас был сэндвич с пастрами и сэндвич с курицей Баха. Оба были вкусными. Отличный сервис и очень уютная атмосфера. Вы должны попробовать это место.
0LIT — Microsoft LiteratureLRF — Sony Portable ReaderMOBI — Mobipocket eBookPDB — Palm Media eBookRB — RocketEdition eBookTCR — Psion eBook7Z — 7-ZipZIP — ZipRAR — Roshal ArchiveJAR — Java ArchiveTAR — TarballTAR.GZ — TAR GZippedCAB — Cabinet
Мы обрабатываем все преобразования djvu в jpg в облаке, что означает, что никакие ресурсы вашего компьютера не будут использоваться в процессе.
и фотографии. Хотя этот формат становится все более распространенным, просмотр файлов DjVu может быть опасным, и для их открытия и расшифровки потребуются подключаемые модули или программы просмотра. Чтобы сделать файлы DjVu доступными, конвертируйте DjVu в JPEG, используя BitRecover Конвертер файлов DjVu в JPG. JPEG сделает документы DjVu подходящими для Интернета, электронной почты и многого другого.
Это одно автономное приложение, которое совместимо с большим преобразованием документов DjVu в широкий спектр форматов файлов, таких как JPG, PDF, DOC, DOCX, XLS, HTML, GIF, JPG, PNG, TIFF, PSD .
Как преобразовать файл DjVu в формат JPG?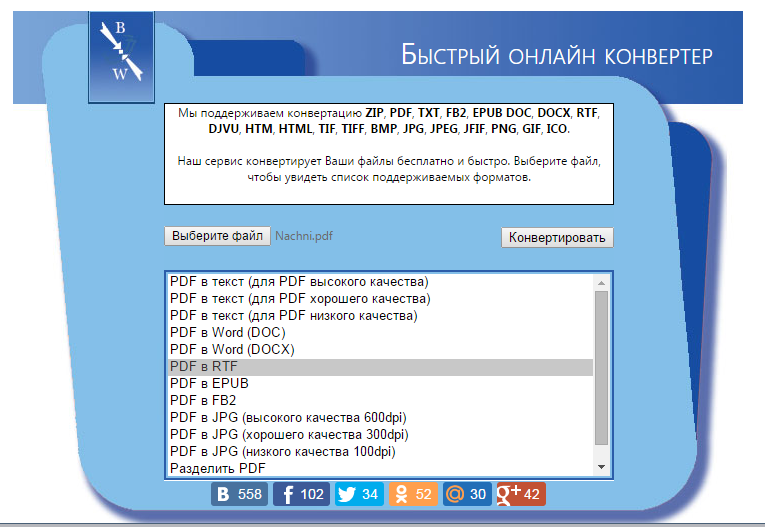
Отзывы показывают, что это программное обеспечение совместимо для преобразования больших файлов DjVu в формат JPEG. С ним вам никогда не придется ставить конфиденциальность и конфиденциальность данных .
Кроме того, вы можете установить «Параметры качества изображения», чтобы включить коэффициент сжатия изображения, значение по умолчанию — 25, а также вы можете ввести допустимые значения от 25 до 150.
Либо вы можете создать новую папку, либо оставить целевой путь сохранения без изменений.
Документы DJVU предназначены для того, чтобы дизайнеры контента могли просматривать цветные страницы книг, журналов и т. д. с высоким разрешением и распространять их в Интернете.
Размер по умолчанию, который предоставляет конвертер DjVu в JPG, составляет 25, но вы можете изменить его от 25 до 150 в соответствии с вашими потребностями.
03.2009, 19:04 
03.2009, 00:58 
03.2009, 01:11 
По-моему нужно так: 
..
02.2012, 00:31 
.. хочу найти о них какую-нибудь информацию. Спасибо за ответ.
Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует: 
е. предел зависит от пути, т.е. предела по двум переменным нет.
е. предел зависит от пути, т.е. предела по двум переменным нет.
07.2012, 00:22 
07.2012, 12:13 
07.2012, 19:02 
Следовательно если есть хотя бы в одном направлении значит просто — есть. Значит по аналогии и в пространстве — если есть хотя бы в одном направлении значит просто — есть.
А мне один раз уже закрыли мою тему, мотивировав, что таких тем уже полно и дескать не надо плодить — пишите в уже созданных.
Соответственно, у функции типа предела в бесконечности нет, поскольку упомянутая kw_artem
Тема
А у переменной точки таких направлений бесконечно много: слева направо, справа налево, по диагонали, по криволинейной траектории — как угодно.
Это выгодно. Ознакомиться с условиями занятий
На самом деле мы сконцентрируемся в основном на пределах функций двух переменных, но идеи можно распространить и на функции с более чем двумя переменными. 9- }} f\влево( х \вправо)\]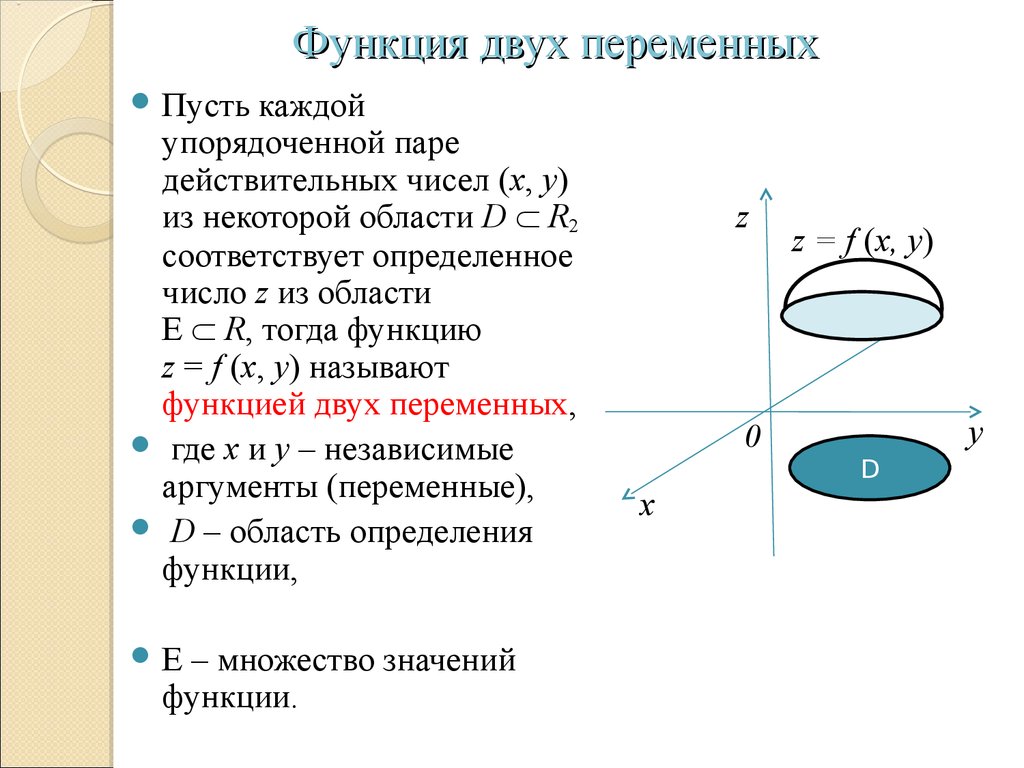
Давайте сначала обратимся к обозначениям и почувствуем, что мы собираемся просить в таких ограничениях.
Итак, если мы знаем, что функция непрерывна в точке, то все, что нам нужно сделать, чтобы получить предел функции в этой точке, — это подставить точку в функцию.
Однако для этой проблемы нам не о чем беспокоиться, поскольку точка, в которой мы берем предел, не находится на этой линии.
Однако в исчислении III это, как правило, исключение в примерах /problems, как будет показано в следующем наборе примеров. Другими словами, не ожидайте, что большинство этих типов ограничений будут просто факторизованы, а затем будут существовать, как в исчислении I. 94}}}\) Показать решение
Когда мы приближаемся к точке на пути, мы будем делать это, либо фиксируя \(x\) или \(y\), либо связывая \(x\) и \(y\) через некоторую функцию. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из исчисления I.
2}}}\) Показать решение
93}} \right) \to \left( {0,0} \right)} \frac{1}{2} = \frac{1}{2}\]
Тогда
92}<δ. \nonumber \]
Тогда верно каждое из следующих утверждений:
2}=0 \номер\] 92}=\tfrac{1}{2}. \nonumber \]
Уравнение этой линии \(y=kx\). Тогда предел становится
Например, если мы включаем половину границы круга \(δ\), но не другую половину, то множество не является ни открытым, ни закрытым. 92\) (Рисунок \(\PageIndex{4}\)).
2}<δ. \номер\] 92} \номер \]
\)
\) Это определение можно комбинировать с формальным определением (то есть эпсилон–дельта определение ) непрерывности функции одной переменной для доказательства следующих теорем:
3\)? Что значит быть непрерывным в точке в четырех измерениях? 92}<δ\большой\}. \nonumber \]
Используя закон произведения, степенной закон, разностный закон, постоянный множественный закон и закон тождества, 92}=2 \номер\]
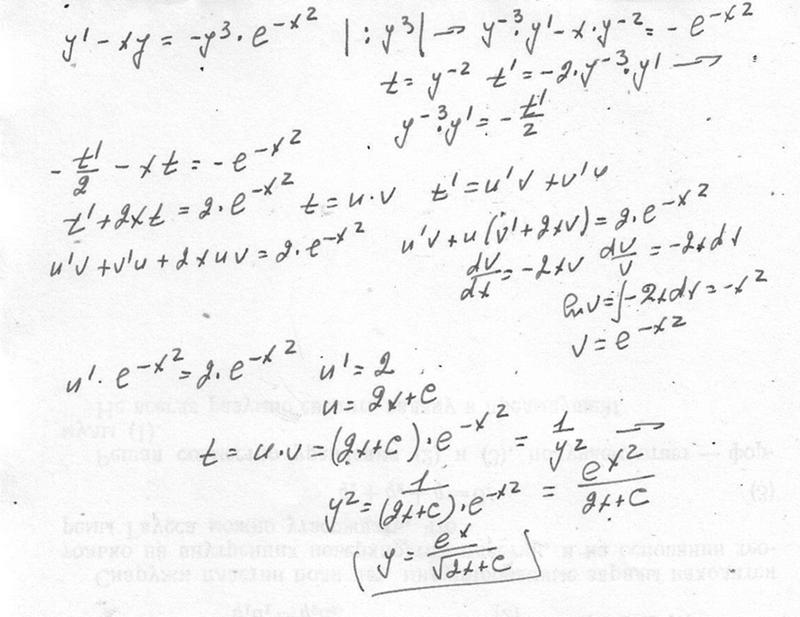
Получаем картину: диаграммы и графики 
Эксперименты: открытия в медицине или результаты, вводящие в заблуждение?
Материал предназначен для студентов-заочников и других читателей, которые хотят в самые короткие сроки освоить практику.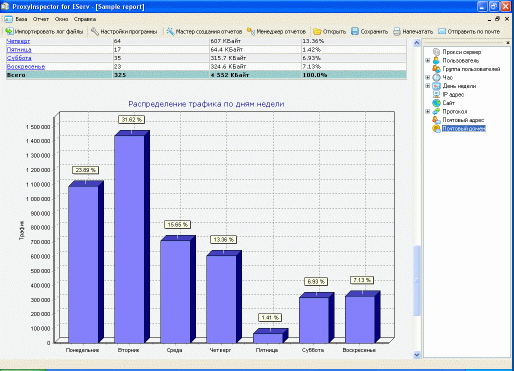
2.4. Исправленная выборочная дисперсия
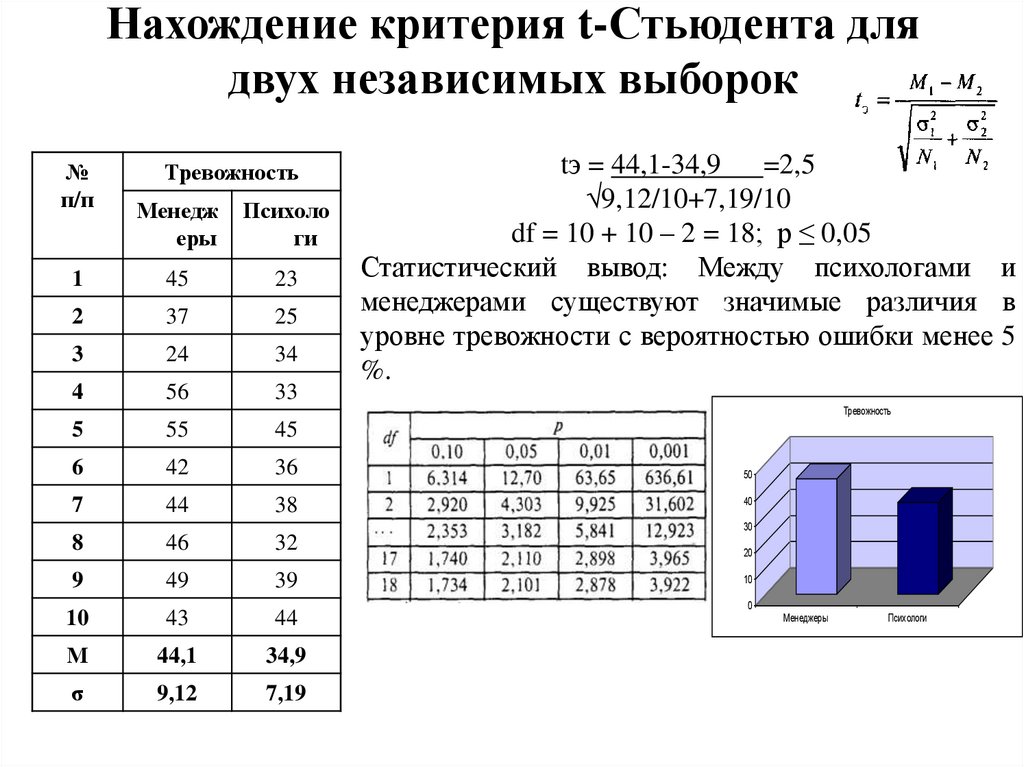5.1. Если генеральная дисперсия известна
4. Корреляционная зависимость и причинно-следственная связь и итоги по главе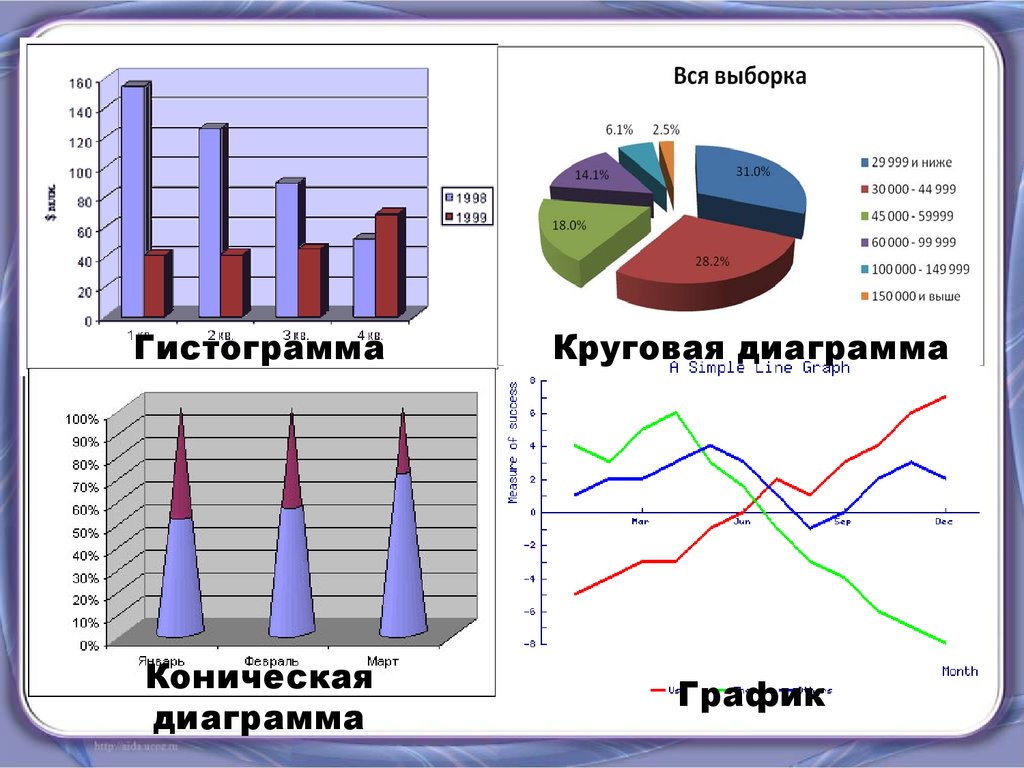
Но область статистики касается не только данных. Статистика — это весь процесс, связанный со сбором данных для ответов на вопросы о мире, в тех случаях, когда эти данные представляют собой числовые данные. Статистика для чайников предназначен для всех, кто хочет разобраться и оценить невероятное количество статистической информации, которая поступает к ним ежедневно. (Вы знаете, что это такое: диаграммы, графики, таблицы, а также заголовки, рассказывающие о результатах последнего опроса, опроса, эксперимента или другого научного исследования.) Эта книга вооружает вас способностью расшифровывать и принимать важные решения относительно статистические результаты, всегда осознавая, как люди могут ввести вас в заблуждение статистикой. Получите внутреннюю информацию о нюансах обработки чисел, а также о том, как вы можете
Статистика для чайников отличается от традиционных статистических текстов, справочников, дополнительных книг и учебных пособий следующим образом:
Wat cijfertjes над mijn leesgedrag:
Все действительно начинает обретать смысл, когда я читаю эту книгу.
Статистика требует времени!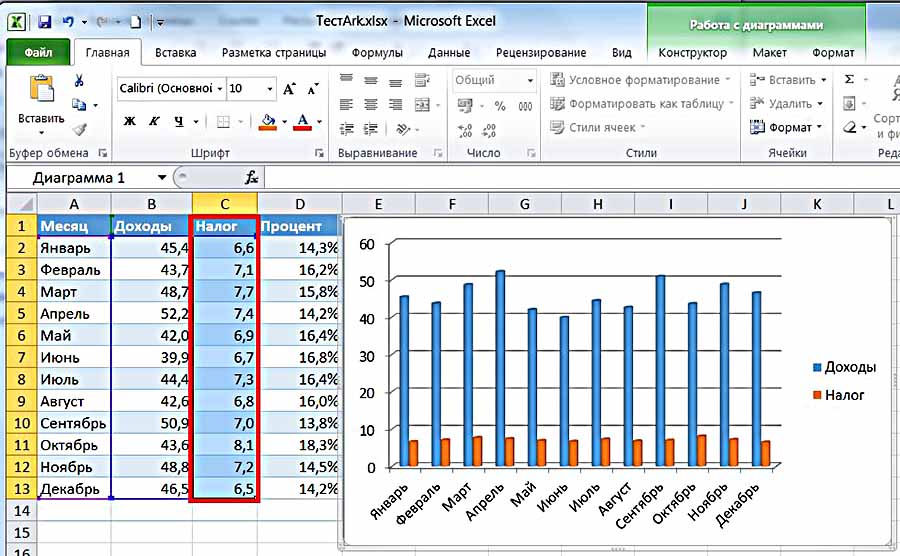 
Se trata де уна recopilacion де концепции, формулы у ejemplos sobre estadística descriptiva e inferencia estadística básicas. Adaptando аль currículo escolar español, cubre todas las materias de la educación secundaria (ESO y Bach) и incluso parte de algunas materias universitarias de introducción.
Включите повторение ejemplos. Eso Hace Que Si Lees Solo Capítulos sueltos, о salteados, не pierdas nada de información, pero Hace Que leerlo todo seguido acabe resultante cargante hasta el extremo.
Para ello, parte casi de cero, y puede ser leído por quien no tenga casi experiencia anterior con la estadística más allá de esa información diaria con la que se nos bombardea.
Stellenweise ein wenig zu viel Повторение, während an andren Orten ein wenig detaillierter auf die Konzepte eingegangen werden könnte. Alles in allem gut geeignet für alle die eine Auffrischung in Sachen Statistik oder eine erste Einführung benötigen.
Muy recomendable para aquellos Que necesitan «masticar» más las definiciones.
Вы получите выходные файлы Джипег одним кликом мыши.
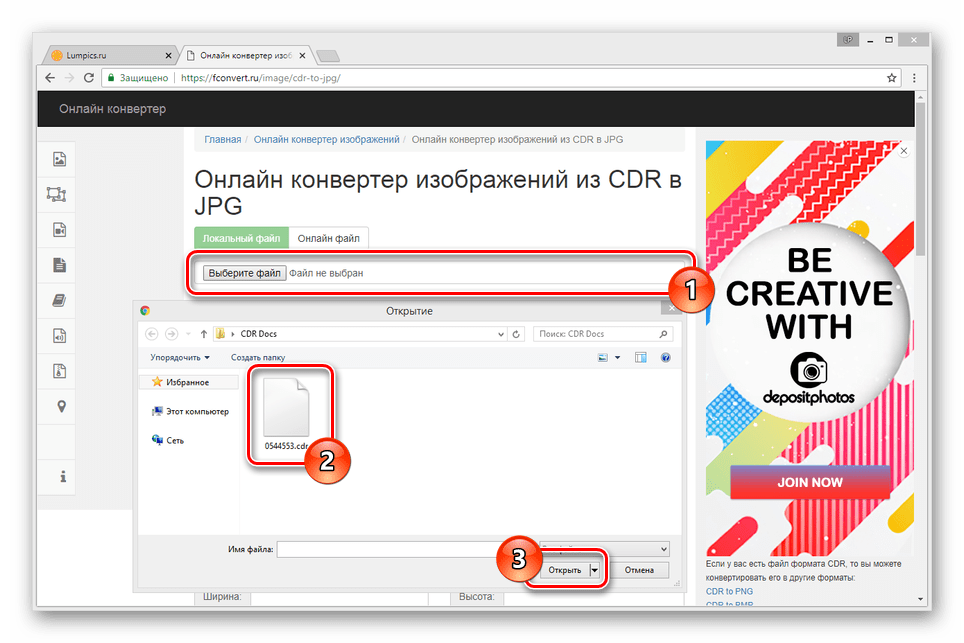
Именно это обозначение позволяет нам правильно обращаться с ними и использовать их. Можете ли вы представить, что произойдет, если вы получите PDF-файл от своего друга, но не сможете его открыть, потому что ваш читатель не распознал его? Вы бы сразу пришли к выводу, что на самом деле это не PDF-документ. Потому что программа для чтения PDF-файлов может открыть любой PDF-файл. В этом случае, даже если бы это был настоящий PDF-файл, вы все равно не смогли бы его открыть, если бы он не был помечен должным образом. И это то, что делает формат файла. Это обеспечивает плавный переход файлов и обработку между двумя сторонами.
Эти файлы хранятся в легком и удобном для перемещения формате, поскольку они обычно содержат важную информацию. Вы никогда не захотите, чтобы файл с ценной информацией застрял во время загрузки или скачивания.
Разные веб-сайты требуют разной информации и, следовательно, разных форматов изображений. Вы хотите иметь возможность конвертировать PNG в JPG бесплатно, чтобы ваши изображения могли соответствовать любым вещам, которые вам нужно делать в Интернете. 
Прежде всего, вам больше никогда не придется беспокоиться о том, что ваши изображения будут иметь какие-либо проблемы с совместимостью в Интернете. Вы можете просто перейти на веб-страницу инструмента и преобразовать свое изображение. См. пошаговое руководство ниже, чтобы узнать, как использовать инструмент
Здесь у вас есть три варианта. Либо загрузите из хранилища вашего устройства, либо загрузите с Google Диска, либо загрузите из Dropbox. Чтобы загрузить из своего хранилища, нажмите «Загрузить» и перейдите к файлу. Процедуры загрузки с Google Диска и Dropbox очень похожи.
Правильные ответы для сверки с учащимися отражаются на проекторе.
Итог урока
Для этого первую дробь переписываем без изменений и умножаем на перевернутую вторую. Сокращаем 18 и 36 на 18, 35 и 7 — на 7. В результате — неправильная дробь. Выделяем из нее целую часть.
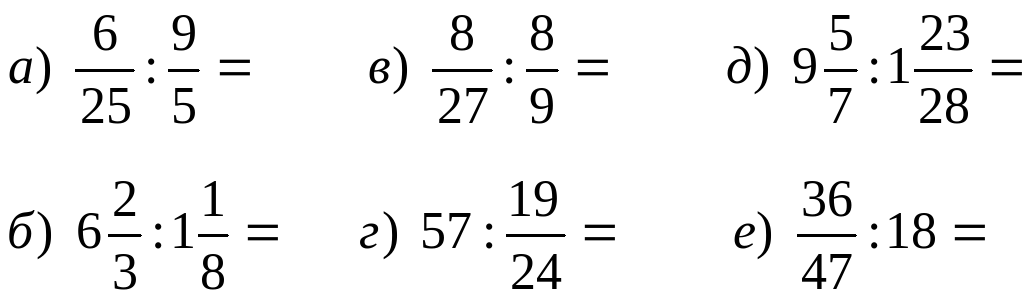
Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].
Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты: