Арксинус онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит арксинус, арккосинус, арктангенс, арккотангенс, арксеканс и арккосеканс и определит значение угла как в градусной, так и в радианной мере.
Введите число
арксинус (arcsin)арккосинус (arccos)арктангенс (arctg)арккотангенс (arcctg)арксеканс (arcsec)арккосеканс (arccosec)
Что такое арксинус угла
Арксинусом (arcsin x) числа x, является угол α заданный в радианной мере, такой, что sin α = x.
Вычислить арксинус, означает найти угол α, синус которого равен числу x.
Область значений (определяющее неравенства угла α в радианной и градусной мерах):
−π/2 ≤ α ≤ π/2
−90° ≤ α ≤ 90°
Область определения (определяющее неравенство числа x):
−1 ≤ x ≤ 1
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора.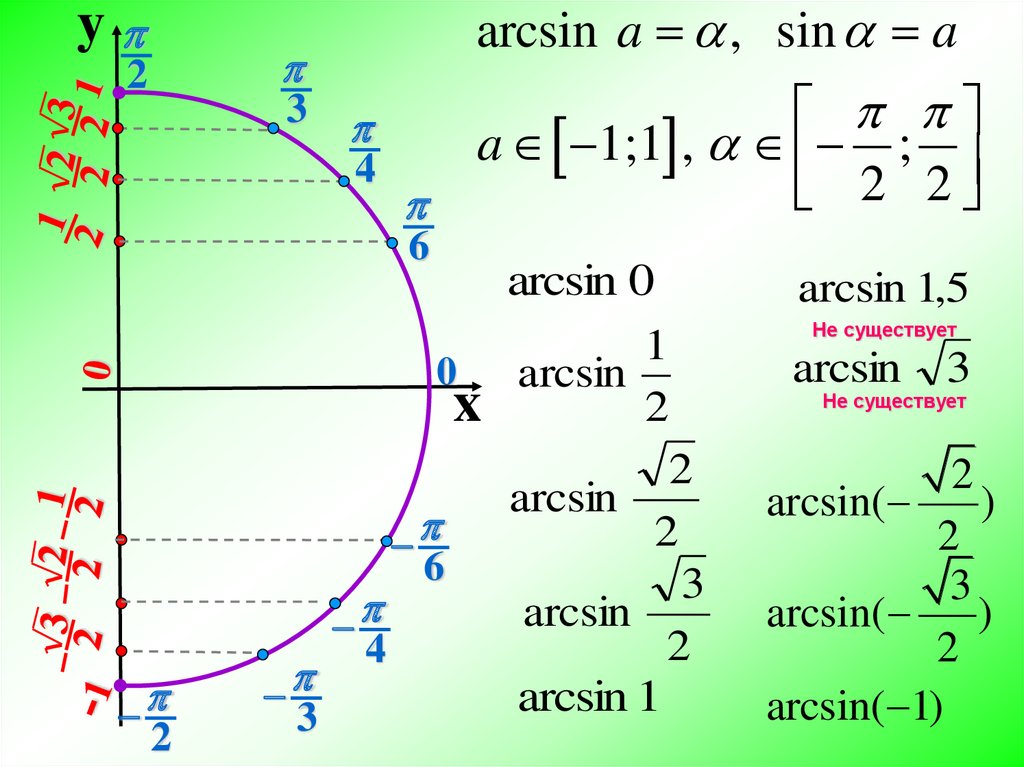 Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Арккосинус онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор вычислит арксинус, арккосинус, арктангенс, арккотангенс, арксеканс и арккосеканс и определит значение угла как в градусной, так и в радианной мере.
Введите число
арксинус (arcsin)арккосинус (arccos)арктангенс (arctg)арккотангенс (arcctg)арксеканс (arcsec)арккосеканс (arccosec)
Что такое арккосинус угла
Арккосинусом (arccos x) числа x, является угол α заданный в радианной мере, такой, что cos α = x.
Вычислить арккосинус, означает найти угол α, косинус которого равен числу x.
Область значений (определяющее неравенства угла α в радианной и градусной мерах):
0 ≤ α ≤ π
0° ≤ α ≤ 180°
Область определения (определяющее неравенство числа x):
−1 ≤ x ≤ 1
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Arcsin(x) Calculator — Калькулятор обратного синуса
Онлайн-калькулятор arcsin(x). Калькулятор обратного синуса.
Введите значение x (от -1 до 1) и нажмите кнопку «Рассчитать»
арксин
Угол в градусах
Угол в радианах
Расчет
Калькулятор синуса »
arcsin(x), sin -1 (x), функция обратного синуса.
- Определение арксинуса
- График арксинуса
- Правила арксинуса
- Таблица арксинуса
- Калькулятор арксинуса
Определение арксинуса
1≤x≤1 .
Когда синус y равен x:
sin y = x
Тогда арксинус x равен функции обратного синуса x, которая равна y:
arcsin x = sin -1 x = y
003
График арксинуса
Правила арксинуса
| Название правила | Правило |
|---|---|
| Синус арксинуса | sin( arcsin 2 39 x 0) 0) 0083 |
| Арксинус синуса | arcsin(sin) x ) = x +2 k π, когда k ∈ℤ ( k целое число) |
| Арксинус отрицательного аргумента | ) -03arcsin2(- грех x |
| Дополнительный угол sin α + arcsin( β ) = arcsin( α√ (1- β 2 ) + β√ (1- α 2 )) ) | |
| Разница арксинуса | арксинуса 3 α 042 β ) = arcsin( α√ (1- β 2 ) — β√ (1- α 2 )) ) |
| Косинус арксинуса | Тангенс арксинуса |
| Производная арксинуса | |
| Неопределенный интеграл арксинуса |
Таблица арксинуса
| x | arcsin(x) (рад) 075033 (°) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -1 | -π/2 | -90° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -√3/2 | -π/3 | -60° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -9/4082 -9/083/2 0083 | -45 ° | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| -1/2 | -π/6 | -30° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1/2 | π/6 | 30° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| π/4 | 45° | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
√ Калькулятор синуса 002 В настоящее время у нас есть около 5653 калькуляторов, таблиц преобразования и полезных онлайн-сервисов. инструменты и функции программного обеспечения для студентов, преподавателей и преподавателей, дизайнеров и просто для всех. инструменты и функции программного обеспечения для студентов, преподавателей и преподавателей, дизайнеров и просто для всех. Вы можете найти на этой странице финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы автокредита и калькуляторы лизинга, калькуляторы процентов, калькуляторы выплат, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, калькуляторы финансов, калькуляторы подоходного налога , калькуляторы сложных процентов, калькулятор зарплаты, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор ИМТ, калькуляторы калорий, калькулятор жировых отложений, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, калькулятор процентов, генератор случайных чисел, калькулятор треугольника, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор среднего балла, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, калькулятор преобразования генератора паролей и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebook (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook). Есть много очень полезных бесплатных онлайн-инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или пришлете нам какие-либо предложения по другим инструментам, которые придут вам на ум. Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или нуждается в лучшем переводе, сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее. Ниже перечислены наиболее часто используемые многими пользователями по всему миру.
И мы все еще разрабатываем больше. Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Поэтому все наши инструменты и сервисы абсолютно бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый из них строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите малейшую ошибку — ваш вклад чрезвычайно ценен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран. Нашли ошибку? Дайте нам знать!Мы получили ваше сообщение, мы свяжемся с вами в ближайшее время. Ой! Что-то пошло не так, обновите страницу и повторите попытку. Идентификатор страницы: 106 Калькулятор арксинуса для нахождения функции обратного синуса с шагами Онлайн-калькулятор арксинуса поможет вам вычислить \(арксинус(х)\) или обратный синус и отобразить результаты в радианах и градусах. В тригонометрии функция арксинуса представляет собой обратную функцию синуса. Его цель — вернуть угол, синус которого является заданным числом. Вы можете найти много устройств, которые состоят из кнопки арксинуса или иногда sin-1 для вычисления арксинуса. У каждой тригонометрической функции есть обратная функция. Такие функции всегда имеют одно и то же имя, но в качестве их первого имени будет добавлено слово «дуга». Вы можете найти много устройств, которые состоят из кнопки арксинуса или иногда sin-1 для вычисления арксинуса. Тем не менее, бесплатная версия онлайн-калькулятора обратного синуса — лучший способ приблизиться к тригонометрическим вычислениям обратного синуса. Поскольку функция арксинуса является обратной функцией \(y = sin(x)\). поэтому обратное уравнение греха будет:
В этой формуле \(k = {…, -2, -1,0,1, 2,}\). Каждый калькулятор арксинуса работает, чтобы следовать этому уравнению, как правило, для расчета точных результатов. Пример: Например, если \(sin30 = 0,5\), то синус 30 градусов равен 0,5. Следовательно, можно сказать, что в этом условии arcsin \( 0,5 = 30 \). Другими словами, угол, у которого sin равен 0,5, равен 30 градусам. Вы можете использовать арксинус всякий раз, когда вам известен синус любого конкретного угла и вам нужно знать фактический угол. Как рассчитать арксинус?Чтобы найти арксинус вручную, все, что вам нужно сделать, это взять уравнение и подставить в него значения, чтобы получить окончательный результат. Например, если, например, если значение синуса \(30°\) равно \(0,5\), то каким будет значение арксинуса?
Однако, чтобы избежать риска возможных ошибок в этом сложном расчете, использование калькулятора арксинуса будет отличной поддержкой. Точно так же онлайн-калькулятор arccos поможет вам вычислить обратную величину косинуса заданного числа. Использование арксинуса для нахождения угла?Предположим, у вас есть прямоугольный треугольник. Если известная длина стороны a равна \(52\), а гипотенуза c равна \(60\), то можно применить arcsin для определения угла \(α\) в точке A.
Однако, используя калькулятор арксинуса, вы можете избежать всех этих шагов и получить окончательные результаты за считанные секунды. Таблица для арксинуса: Помимо формулы арксинуса и калькулятора, вы также можете рассмотреть данную таблицу, которая поможет вам найти некоторые общие значения арксинуса. Ниже представлена таблица:
Домен, диапазон и другие свойства arcsin (x) могут быть представлены на графике следующим образом:
Однако калькулятор единичного круга позволяет определять различные тригонометрические значения угла, что помогает вычислять различные координаты единичного круга. Как работает калькулятор арксинуса?Калькулятор обратного синуса работает следующим образом, чтобы найти угол в градусах, радианах и других связанных единицах измерения. Ввод:
Калькулятор обратного синуса отобразит:
Косеканс является обратной величиной синуса. $$ sin-1x = arcsin x$$ Это означает, что дуга, синус которой равен x Сколько sin умножить на Arcsin?Чтобы понять это, взгляните на следующие четыре правила арксинуса:
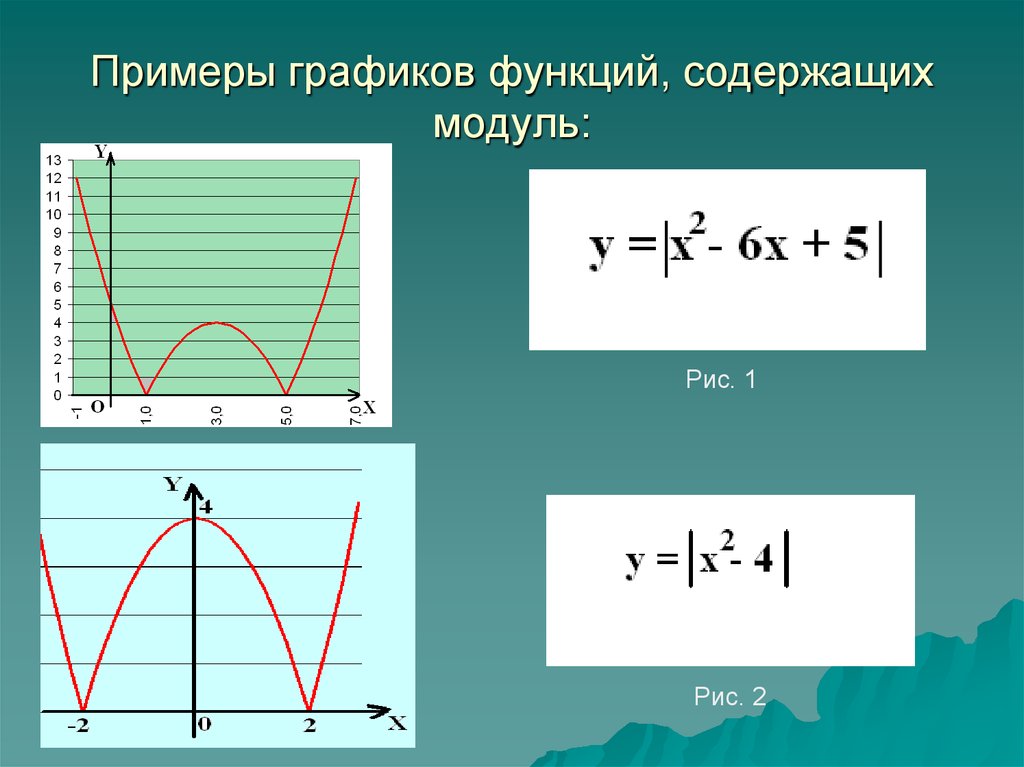
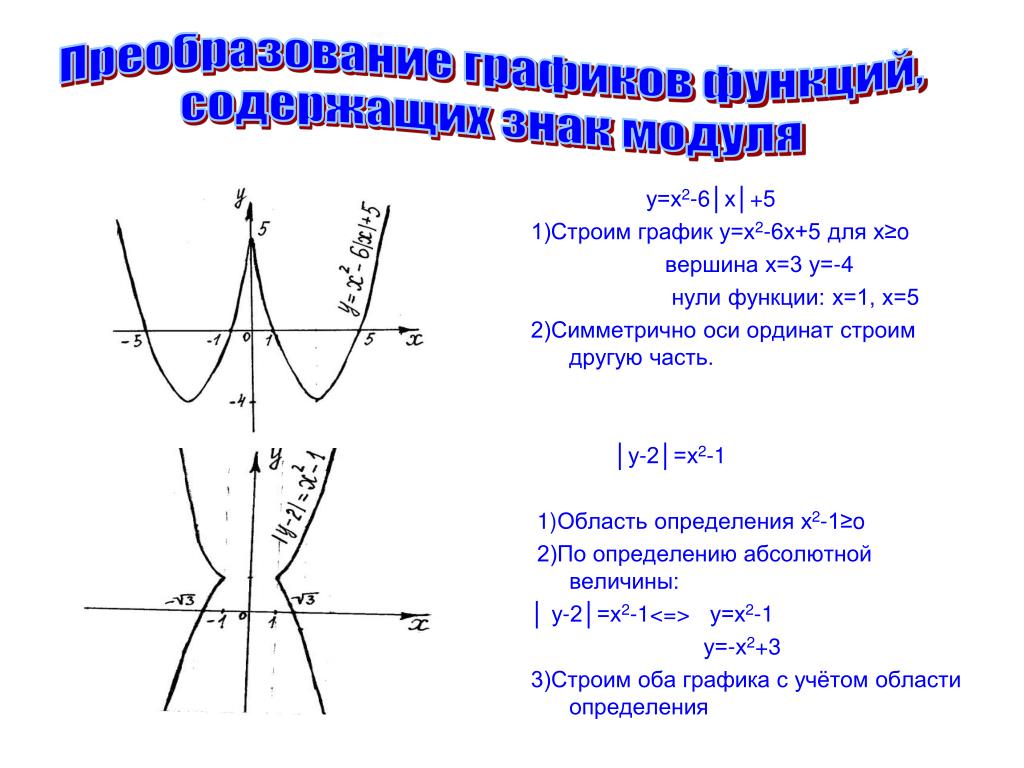
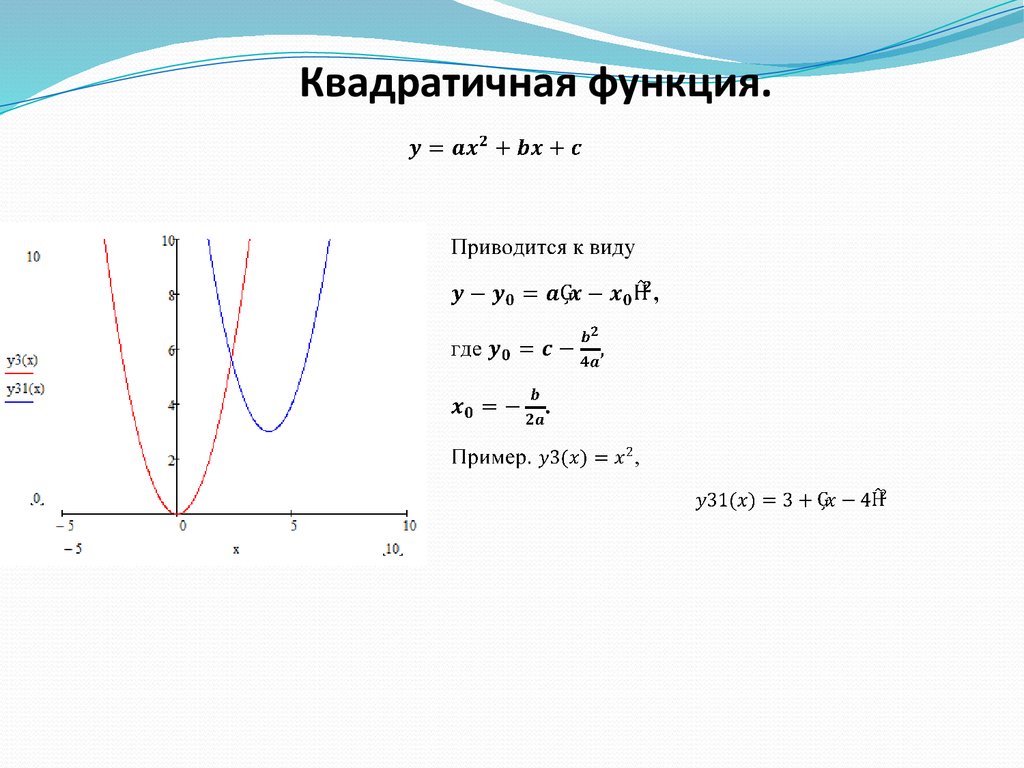
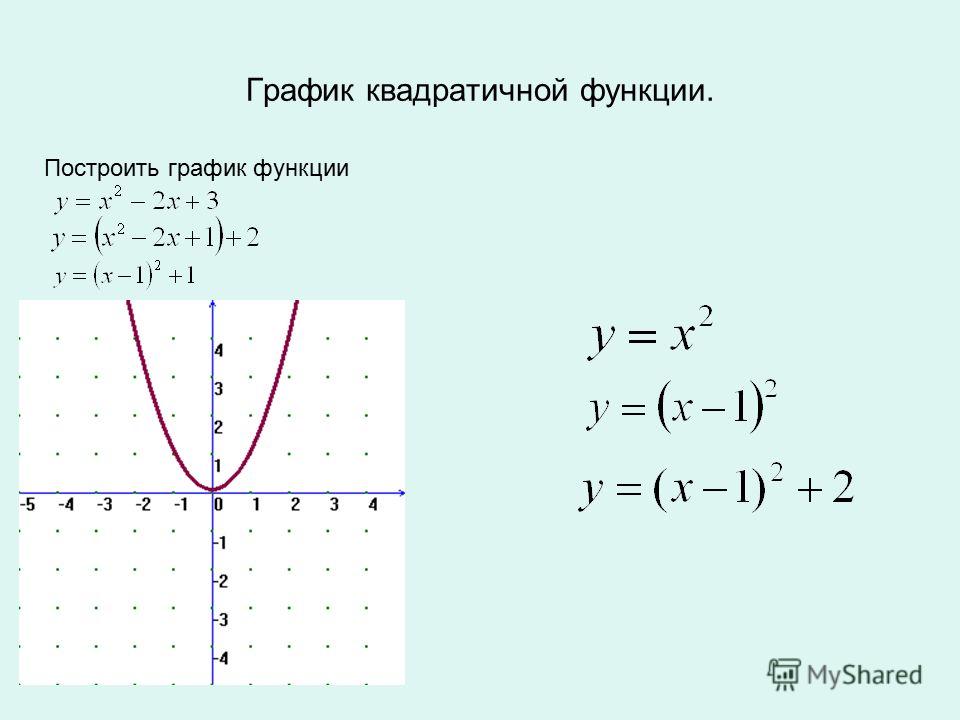
При обратном синусе необходимо выбрать угол в правой половине единичного круга, мера которого должна быть близка к нулю. Следовательно, \( sin-1(–½) = –30° или sin–1(–½) = –π/6\) . Когда дело доходит до вычисления обратного синуса, вам следует иметь калькулятор арксинуса для получения более точных и точных результатов. Таким образом, он служит эксклюзивной платформой для всех тех, кто стремится получить знания и хочет хорошо владеть функцией \( arcsin(x) \). Кроме того, этот калькулятор обратного синуса \( 100%\) бесплатен и одинаково полезен как для студентов, так и для преподавателей. Ссылка:Из источника Википедии: Обозначение, Принципиальные значения, Равенство тождественных тригонометрических функций. Источник открытого справочника по математике: большие и отрицательные углы, диапазон и область арксинуса. Из источника Mile Foot: обратные теоремы о взаимных тождествах, обратные симметричные тождества, теоремы об обратных кофункциональных тождествах. Из источника Shmoop: График функции обратного синуса, функция арксинуса. Построить график функции с модулем — один из видов задания 23 ОГЭ по математике. Рассмотрим примеры таких заданий. 1) Постройте график функции и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки. Решение: Область определения функции D(y): x∈R. 1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль: x-2=0, x=2. Найдём значение функции при x=2. y(2)=5·0-2²+5∙2-3∙0-6=0. Получили точку (2;0). 2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения. Если x-2>0, то есть при x>2, |х-2|=x-2, y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16. y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0). Координаты вершины параболы то есть вершина параболы — точка (5;9). 3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения. Если x-2<0, то есть при x<2, |х-2|=-(x-2), y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4. y=-x²+4 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x². Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2, строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16: График функции с модулем можно рассматривать и как график кусочной функции: Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4: Ответ: 0; 4. 2) Постройте график функции и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки. Решение: Область определения функции D(y): x∈R. 1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль: |6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1. y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0). Координаты вершины параболы Так как a=1, от вершины (3;-10) строим график y=x². |6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1. y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы от вершины (-3;-8) строим график y=x². Или: Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8: Ответ: -8; 1/36. 3) Постройте график функции и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки. Решение: Область определения функции D(y): x∈R. 1) Если x=0, y=|0|·0+3·|0|-5·0=0. 2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x. y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0). Координаты вершины параболы От вершины (1;-1) строим параболу y=x² (так как a=1). 3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x. y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0). Координаты вершины параболы От вершины (-4;16) строим параболу y=-x² (так как a=-1). Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x: Альтернативный вариант: Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16: Ответ: -1; 16. 4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс? Решение: Область определения функции D(y): x∈R. Построим график функции y=x²+2x-3. Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх. Координаты вершины параболы , то есть вершина параболы — точка (-1;-4). От вершины строим график функции y=x²: График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox. Или y=|x²+2x-3| Вершина параболы (-1;-4) при этом переходит в точку (-1;4): Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках). Ответ: 4. “Великое множество функций Изучение квадратичной функции с модулем
позволяет углубить знания учащихся в
преобразовании графиков квадратичной функции.
Учащиеся с большим интересом выполняют любые
задания с модулем. Рассмотренные приемы
построения графиков функции являются общими и
применяются не только к квадратичной, но и к
другим функциям. Функция – одно из основных математических и
общенаучных понятий, выражающее зависимость
между переменными величинами. Математика
рассматривает абстрактные переменные величины,
изучает законы их взаимосвязи, не углубляясь в
природу задачи. Математика же изучает эту зависимость в
отвлеченном виде, и она устанавливает, например,
что увеличение Х в 2 раза приведет к увеличению Y в
4 раза, и это заключение может применяться в любой
конкретной ситуации. Модуль и квадратичная функция Построение графиков функций:
1) Дать определение модуля числа Х 2) Дать определение квадратичной функции,
рассказать все, что известно об этой функции
(график, свойства). 3) Найти на рисунке график функции Y = –Х2 +
4Х – 3. 4) На каком рисунке изображен график функции Y =
–(Х + 1)(2 – Х)? 5) Вспомнить, как построить график функции Y = Х По определению модуля График функции Y = Х симметричен относительно
оси У. Y = АХ2 + ВX + C, Y = АХ2 + ВX + C, Y = АХ2 + ВХ + С Работа проводится в группах, т.к. графики в К–1
в) и К–3 в) одинаковы, их необходимо сравнить и
сделать вывод (всего 3 группы). Каждой группе
выдается карточка, в ней 3 задания. Учащиеся
должны построить графики квадратичной функции,
содержащей модуль, используя определение модуля
и сделать вывод: как построить график данной
функции, используя график квадратичной функции и
симметрию относительно осей координат. Работа в группах. Задание: построить график функции,
используя: а) определение модуля; а) Y = Х2 – 4 Х + 3 а) Y = Х2 + 2 Х – 3 а) Y = –Х2 + 4 Х – 3 Вопрос: а) Как построить график функции Y = f (X)? (1 способ. б) Как построить график функции Y = f (X) ? (Построить график функции Y = f (X) и точки с
отрицательными ординатами симметрично
отобразить относительно оси Х). в) Как построить график функции Y = f (X) ? (Построить график функции Y = f (X), если Х 0 и эту часть графика
симметрично отобразить относительно оси Y, а
потом точки с отрицательными ординатами
отобразить симметрично относительно оси Х.) г) Почему графики функций Y = –Х2 + 4X – 3 и Y
= Х2 – 4X + 3 одинаковы? (Так как А = А , –А = А) У рассмотренных функций под знаком модуля была
независимая переменная. Теперь рассмотрим
функции, где под знаком модуля стоит либо сама
функция, либо и функция, и независимая переменная
одновременно, т. Y =
АХ2 + ВX+ C и Y = АХ2
+ ВX + C Приведем конкретные примеры. а) Y = Х2 – 4X+ 3 По определению Построим график функции Y = f (X) и берем ту его
часть, которая расположена выше оси Х, т.к. Х2
– 4X+ 3 0 и добавим к ней ее
симметричное отображение относительно оси Х. б) Y = Х2 – 4X+ 3 Сначала строим график функции Y = Х2 – 4X+ 3 , а затем множество точек, координаты
которых удовлетворяют условию Y = Х2 – 4X+ 3 , т.е.
график функции Y = Х2
– 4X+ 3 отображаем
относительно оси Х. Дана функция Y = Х2 + 2X– 3 Выполнить всевозможные преобразования данной
квадратичной функции с модулем. Прямые линииРадикалы и т. Очевидно, рисовать прямые линии будет проще всего. Но большую часть времени вы будете строить графики для уравнений, которые, по крайней мере, немного сложнее. Первый шаг вверх — это графики абсолютных значений, которые состоят (по крайней мере, когда вы начинаете) из двух прямых линий, образующих своего рода букву «V», либо с правой, либо с обратной стороны. Содержание продолжается ниже. пример контекста, в котором мы должны быть осторожны, чтобы не забыть выбрать отрицательные значения x для нашей T-диаграммы. В противном случае очень легко забыть, что график абсолютного значения не будет просто одной непрерывной прямой линией. Например, предположим, что нам дано уравнение y = | x |. И предположим, что мы выбрали только положительные значения x , поэтому наша Т-диаграмма выглядит так: Тогда наши точки выглядят так: И мы соединим наши точки так: Мы только что завалили тест. Вместо этого давайте немного разнесем наши значения x и не забудем на этот раз построить отрицательное значение x или два. Наша новая Т-диаграмма выглядит так: Тогда наши точки выглядят следующим образом: Поскольку наши точки хорошо разбросаны, и поскольку мы не забыли включить пару «минусовых» x -значений, мы помним, что уравнения абсолютных значений отображаются в виде ломаных линий, поэтому прикладываем нашу линейку дважды, чтобы получилось: А это и есть правильный график! (Если вы хотите изучить эту тему более подробно, см. Графики функций абсолютного значения.) При графическом отображении квадратных уравнений/функций нам нужно нанести не только три точки; Я бы предложил минимум не менее пяти баллов, но от семи до девяти баллов будет лучше, если вы только начинаете. И мы должны ожидать, что нам также потребуется отображать отрицательные значения x . Например, предположим, что они дают нам y = x 2 − 6 x + 5. Есть множество вещей, которые мы можем сделать, чтобы помочь себе построить правильный график. Мы можем начать с поиска точек пересечения x и y . (Дополнительную информацию см. в разделе Перехваты.) В этом случае перехваты находятся в точках (1, 0), (5, 0) и (0, 5). Кроме того, мы можем найти вершину параболы, которая является самой высокой или самой низкой точкой на графике. (Дополнительную информацию см. в разделе Вершина.) В этом случае вершина — это самая нижняя точка на графике, и эта точка находится в точке (3, −4). Но в основном нам нужно потратить время, чтобы нанести довольно много точек, чтобы мы могли «увидеть» форму, прежде чем начать ее рисовать. Посмотрите, что часто происходит, когда новичок наносит только три точки: T-диаграмма Неправильный график Но приведенный выше график неверен; эта парабола должна выглядеть как «смайлик», а не как прямая линия. Итак, нам нужно нанести еще несколько точек. Мы уже нашли точки пересечения и вершину (выше). Добавим к этому еще один пункт, используя x = 6: Т-диаграмма Правильный график Гораздо лучше! Это график, который получит полные баллы! (Примечание: положительное квадратичное выражение можно рассматривать как графическое изображение «смайлика», а отрицательное квадратичное выражение можно рассматривать как графическое изображение «фрони». Да, это глупый способ выразить это, но вы победите) Забудьте об этом сейчас, хорошо? Если вы хотите изучить эту тему более подробно, пожалуйста, обратитесь к разделу Графики квадратичных функций.) URL: https://www.purplemath.com/modules/graphing2.htm Page 1Page 3 В главе 2 мы рассмотрели идею абсолютного значения и представили стратегии решения уравнений и неравенств с абсолютными значениями. В этом разделе наша цель — построить график функций абсолютного значения. Начнем с самой простой функции абсолютного значения, [latex]f(x)=|x|.[/latex] Напомним, что абсолютное значение числа — это его расстояние от нуля на числовой прямой. Как и в случае с любой функцией, мы можем использовать таблицу, чтобы помочь нам в построении графика. Поскольку мы не уверены в форме, мы хотим выбрать несколько точек, включая положительные и отрицательные стороны. Это приводит к таблице, приведенной ниже. Далее наносим точки. Если бы мы не выбрали достаточное количество точек, у нас может возникнуть соблазн нарисовать что-то более похожее на гладкую кривую через точки. Однако мы видим, что для этого потребуется более линейный график, за исключением того, что он, кажется, внезапно меняет направление в начале координат. Если бы мы выбрали только точки справа от 0, мы могли бы подумать, что график будет представлять собой простую прямую линию, а не форму буквы «V», которая в конечном итоге выглядит так. Окончательный график [latex]f(x)=|x|[/latex] показан ниже. Эта форма «V» будет появляться во всех простых функциях абсолютного значения, которые мы рассмотрим в этом разделе. Однако букву «V» можно сместить, сделать уже или шире или даже перевернуть. Знание основной формы графика абсолютного значения поможет нам в дальнейшем изучении абсолютных значений. Рассмотрим функцию [latex]f(x)=|x|-3[/latex]. Нанесение этих точек на график дает показанный ниже график. Мы видим ту же форму буквы «V», которую мы ожидаем от этого типа функции абсолютного значения. График [латекс]f(x)=|x|+2[/латекс]. Показать решение Стратегия построения графиков функций абсолютного значения вида [latex]f(x)=a|x|+b[/latex] В следующей задаче мы увидим, что происходит, когда перед абсолютным значением стоит коэффициент, отличный от 1. График [латекс]f(x)=2|x|[/латекс]. Показать решение В нашем последнем примере мы комбинируем некоторые идеи, которые видели. Кроме того, мы смотрим на влияние отрицательного коэффициента. График [латекс]f(x)=-2|x|+1[/латекс]. Показать решение Если вы хотите подробнее изучить графики абсолютных значений, ознакомьтесь с приведенным ниже разделом «Думай об этом». |
Теперь нанесем точки [латекс](-2,4), (-1,1), (0,0), (1,1), (2,4)[/латекс]
На первый взгляд может показаться, что эти точки образуют букву «V», как функции абсолютного значения, которые мы построили ранее. Но квадратичное семейство функций не рисуется прямыми линиями. Поскольку точек на линии , а не , вы не можете использовать линейку . Соедините точки как можно лучше, используя плавную кривую (не ряд прямых). Вы можете найти и нанести дополнительные точки (например, выделенные синим цветом ниже). Размещение стрелок на концах линий означает, что они продолжаются в этом направлении навсегда.
Обратите внимание, что форма похожа на букву U. Это называется параболой . Половина параболы является зеркальным отражением другой половины. Нижняя точка на этом графе называется вершиной . Вертикальная линия, проходящая через вершину, называется 9.{2}+c[/latex] выполните следующие действия:
- Распознайте форму квадратичной функции и то, что это будет парабола с центром вокруг точки x=0.


 Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других сайтов социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все видео, которые вы загружаете, загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, ALT-кодах для Mac, Windows и Linux и других полезных советах и инструментах (как написать смайлики онлайн и т. д.)
 Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий.
Наша цель — стать универсальным сайтом для людей, которым нужно быстро рассчитать или найти быстрый ответ для основных конверсий. Кроме того, этот бесплатный калькулятор обратного синуса отображает полный расчет, за которым следует формула арксинуса. Тем не менее, продолжайте читать, чтобы узнать, как вычислить арксинус. Но давайте начнем этот контекст с некоторых основ!
Кроме того, этот бесплатный калькулятор обратного синуса отображает полный расчет, за которым следует формула арксинуса. Тем не менее, продолжайте читать, чтобы узнать, как вычислить арксинус. Но давайте начнем этот контекст с некоторых основ!



 В прямоугольном треугольнике его можно выразить как отношение гипотенузы к катету, противолежащему данному углу.
В прямоугольном треугольнике его можно выразить как отношение гипотенузы к катету, противолежащему данному углу. Диапазон sin-1 ограничен \([–90°, 90°]\).
Диапазон sin-1 ограничен \([–90°, 90°]\).



 Например, в соотношении Y = Х2 математик
или геодезист увидит зависимость площади
квадрата от его стороны, а физик, авиаконструктор
или кораблестроитель может увидеть зависимость
силы Y сопротивления воздуха или воды от скорости
Х движения.
Например, в соотношении Y = Х2 математик
или геодезист увидит зависимость площади
квадрата от его стороны, а физик, авиаконструктор
или кораблестроитель может увидеть зависимость
силы Y сопротивления воздуха или воды от скорости
Х движения.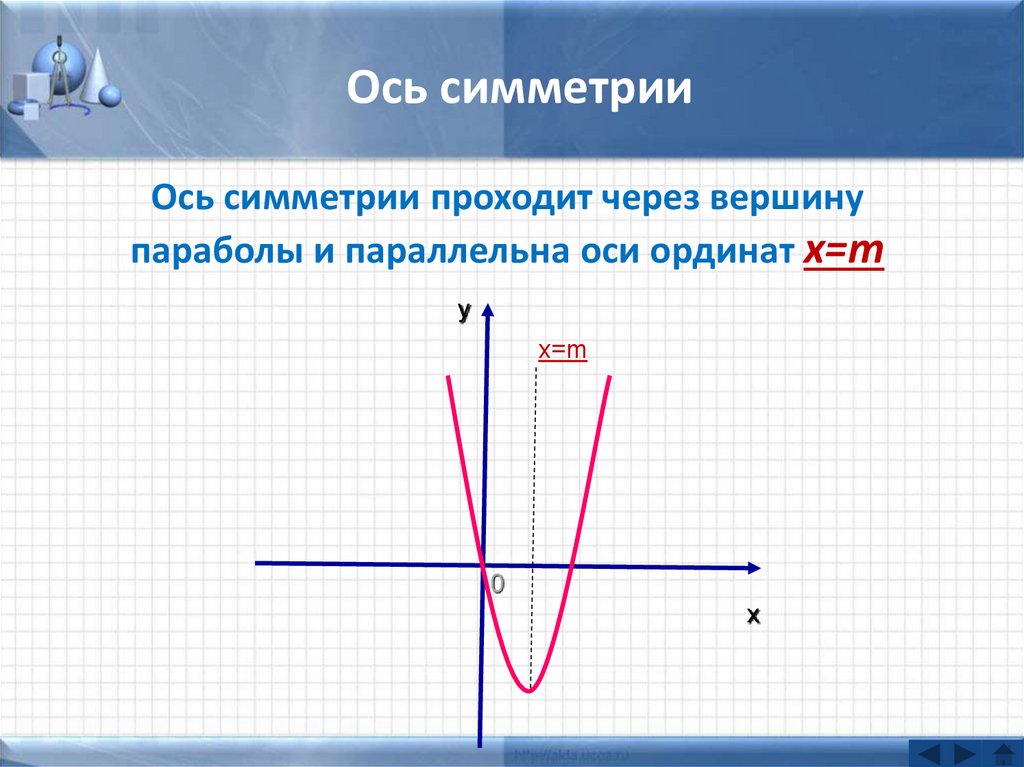

 Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х<
0.
Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х<
0. е. зависимости вида
е. зависимости вида д.
д.
 Три точки больше не будут сокращать его, потому что квадратичные графики представляют собой кривые линии, называемые «параболами».
Три точки больше не будут сокращать его, потому что квадратичные графики представляют собой кривые линии, называемые «параболами». (И, если вы внимательно посмотрите, нанесенные точки на самом деле даже не выстраиваются в прямую линию! Линейка провела линию как бы «между» точками, а не «сквозь» их.)
(И, если вы внимательно посмотрите, нанесенные точки на самом деле даже не выстраиваются в прямую линию! Линейка провела линию как бы «между» точками, а не «сквозь» их.) 3 Задачи обучения
3 Задачи обучения
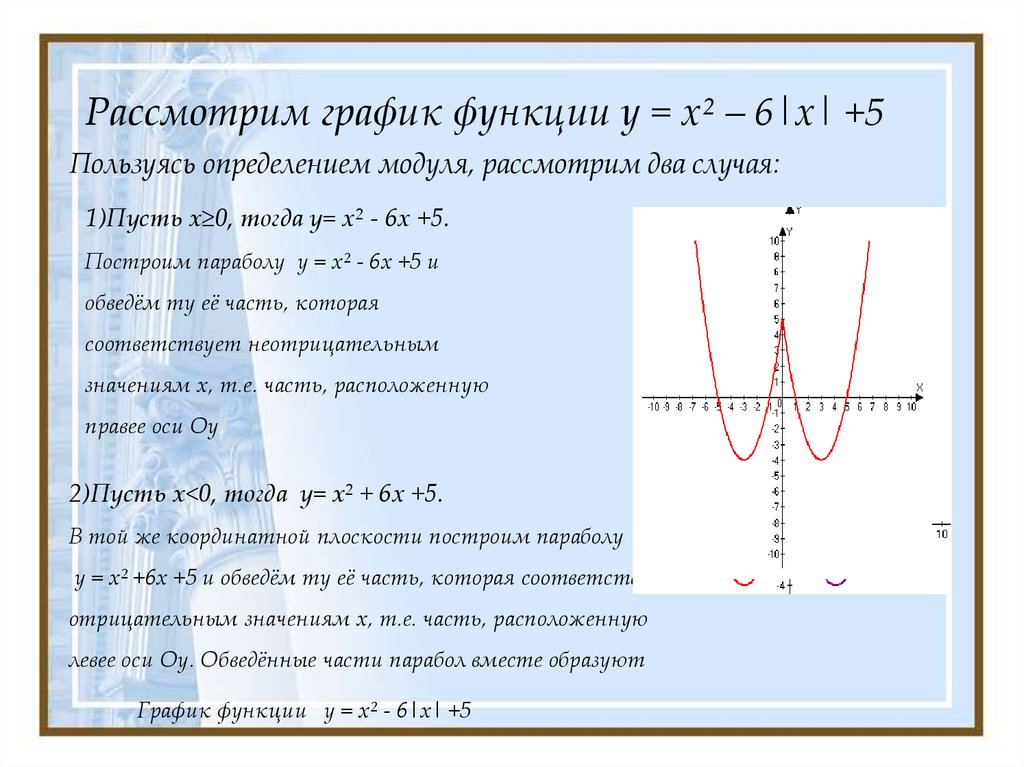 Давайте попробуем подставить те же значения для [latex]x[/latex], которые мы используем для базовой функции абсолютного значения.
Давайте попробуем подставить те же значения для [latex]x[/latex], которые мы используем для базовой функции абсолютного значения.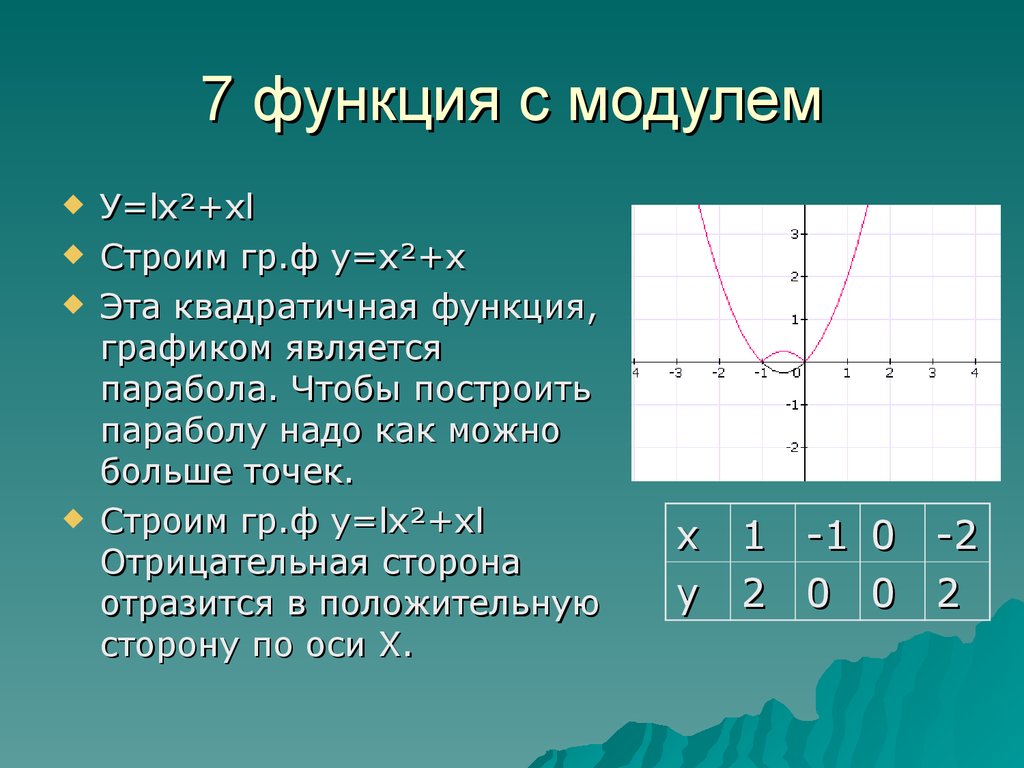 Однако не случайно обратите внимание, что кривая сместилась на 3 единицы вниз.
Однако не случайно обратите внимание, что кривая сместилась на 3 единицы вниз.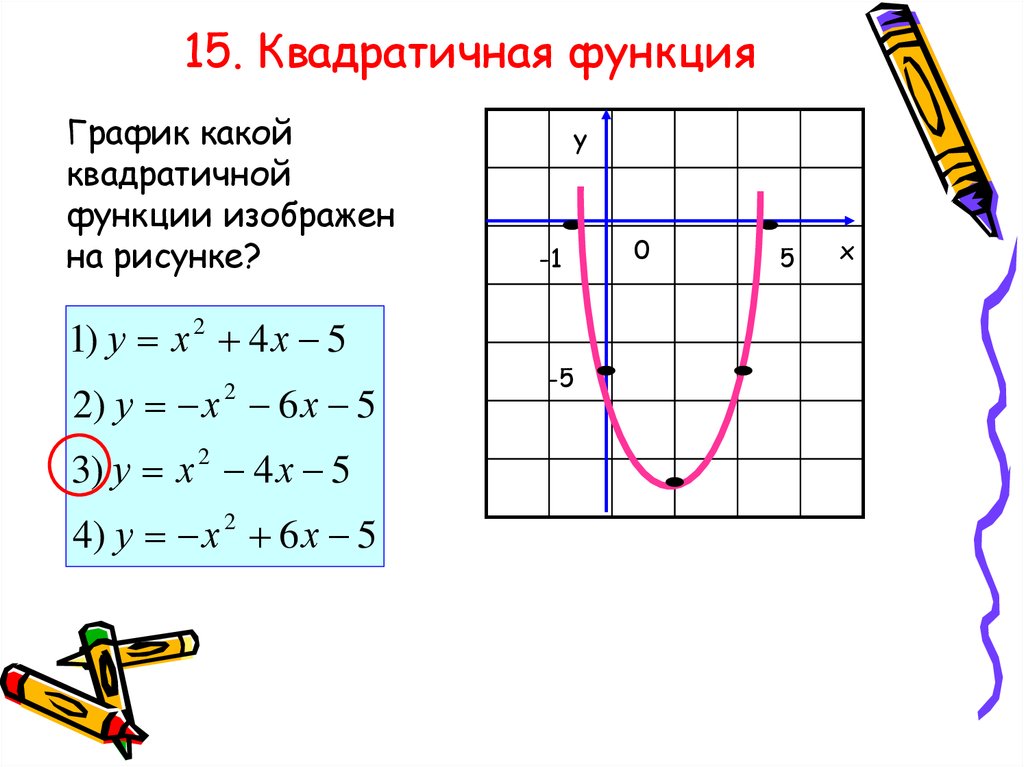 {2}[/latex]. 92=4[/латекс]
{2}[/latex]. 92=4[/латекс]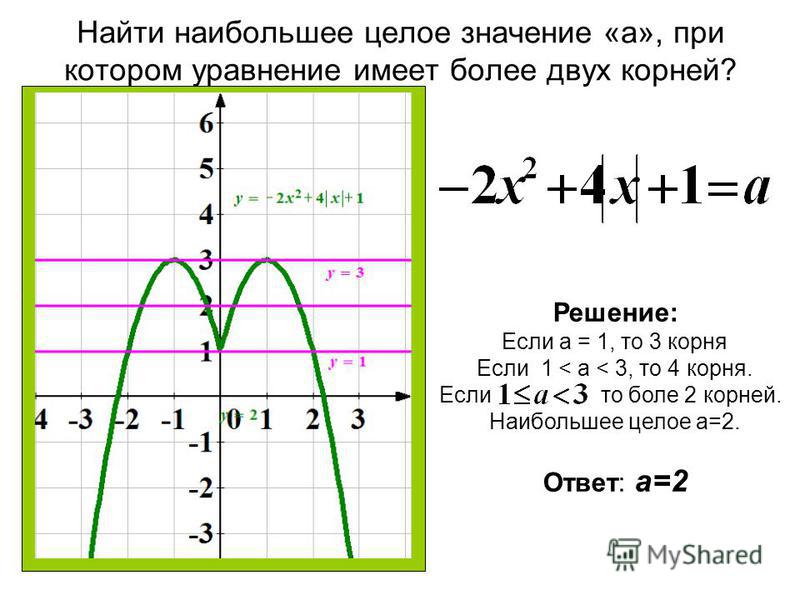
 В (Подробнее…)
В (Подробнее…) Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
 Оптимальным считается коричневый разных оттенков. Поправку делаем на цвет еды: много молочной продукции в рационе — стул будет светлее. Темнее, если поели блюдо с нори, чёрный бургер. Кроме того стоит задуматься о препаратах или БАДах, которые Вы можете принимать — препараты висмута, железа дают тёмный ближе к зелёному стул.
Оптимальным считается коричневый разных оттенков. Поправку делаем на цвет еды: много молочной продукции в рационе — стул будет светлее. Темнее, если поели блюдо с нори, чёрный бургер. Кроме того стоит задуматься о препаратах или БАДах, которые Вы можете принимать — препараты висмута, железа дают тёмный ближе к зелёному стул.

 В нем исследуются компоненты переработки всех пищевых продуктов (белков, жиров, углеводов), могут быть выявлены и описаны слизь, видимая кровь, клетки воспаления, иногда даже цисты простейших или яйца гельминтов.
В нем исследуются компоненты переработки всех пищевых продуктов (белков, жиров, углеводов), могут быть выявлены и описаны слизь, видимая кровь, клетки воспаления, иногда даже цисты простейших или яйца гельминтов. Их множество, начиная, с микроскопического иследования методом обогащения Parasep, вплоть до высокоточной ПЦР реакции отдельно к каждому типу возбудителя или панель из наиболее часто встречающихся.
Их множество, начиная, с микроскопического иследования методом обогащения Parasep, вплоть до высокоточной ПЦР реакции отдельно к каждому типу возбудителя или панель из наиболее часто встречающихся. Однако при анализе кала на скрытую кровь методом Colonview рекомендуется только ограничение вышеуказанных лекарственных средств.
Однако при анализе кала на скрытую кровь методом Colonview рекомендуется только ограничение вышеуказанных лекарственных средств.

 конусы сливок:
конусы сливок: 
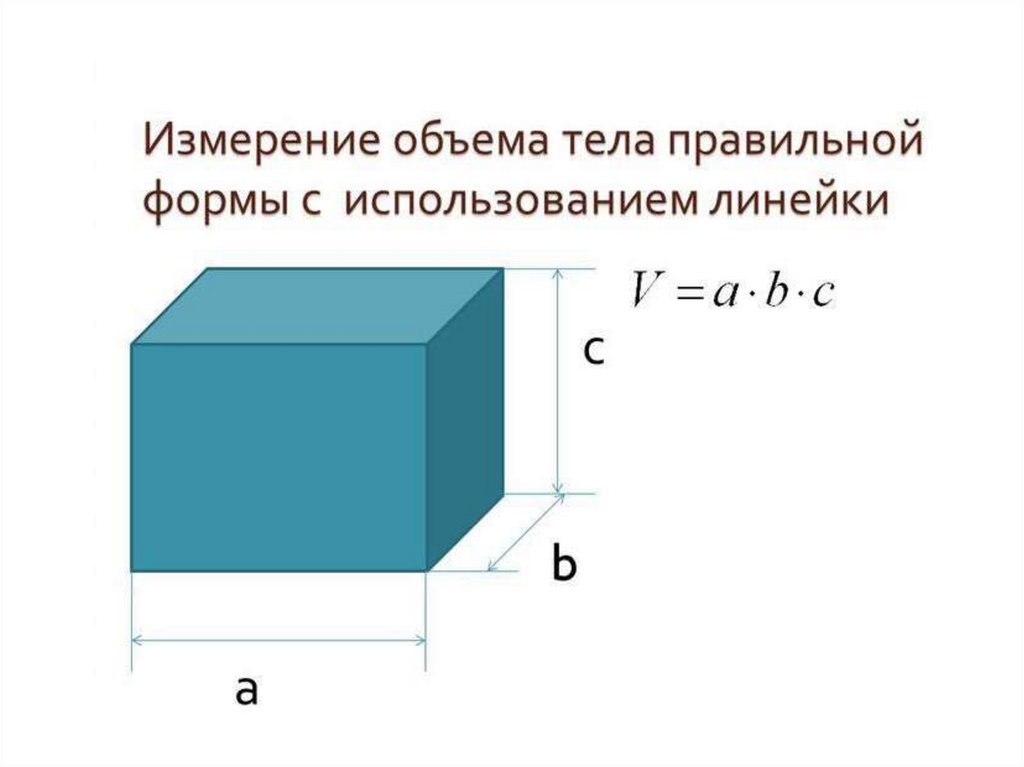
 Физические величины и измерения
>
Упражнение:
Вопросы с короткими/длинными ответами
>
Вопрос 6
Физические величины и измерения
>
Упражнение:
Вопросы с короткими/длинными ответами
>
Вопрос 6 Мы собираемся посмотреть, как вы можете определить объем обычного твердого тела, скажем, любой формы, например, латуни и различных типов камней. Вы можете его вынуть. Итак, описывая шаги с нужными диаграммами. Итак, первый шаг. Я собираюсь записать. Вы можете проверить это здесь, первый кусок, если у него есть измерительные устройства с вами. Слуховые аппараты, такие как измерительный цилиндр. Требуется измерительный прибор. .
Итак, следующее, что мы собираемся измерить, чтобы вы могли увидеть процедуру здесь. Итак, вы берете любой камень или что-то еще, вы берете один камень или что-то еще. Итак, давайте посмотрим здесь, в этом, как мы собираемся это выяснить.
Вы можете проверить здесь? Так что это первоначальный способ, это первое, что было дано по пятам в Shell. Хорошо, тогда я запишу это. Это исходная ситуация без какого-либо хранилища или какого-либо объекта, объем которого вы собираетесь измерять. Итак, после того, как мы вставляем предмет с ниткой, чтобы вы могли видеть процент установки камня, привязанного к нему с помощью нити, в измерительный инструмент, таким образом, измерительный цилиндр.
Мы собираемся посмотреть, как вы можете определить объем обычного твердого тела, скажем, любой формы, например, латуни и различных типов камней. Вы можете его вынуть. Итак, описывая шаги с нужными диаграммами. Итак, первый шаг. Я собираюсь записать. Вы можете проверить это здесь, первый кусок, если у него есть измерительные устройства с вами. Слуховые аппараты, такие как измерительный цилиндр. Требуется измерительный прибор. .
Итак, следующее, что мы собираемся измерить, чтобы вы могли увидеть процедуру здесь. Итак, вы берете любой камень или что-то еще, вы берете один камень или что-то еще. Итак, давайте посмотрим здесь, в этом, как мы собираемся это выяснить.
Вы можете проверить здесь? Так что это первоначальный способ, это первое, что было дано по пятам в Shell. Хорошо, тогда я запишу это. Это исходная ситуация без какого-либо хранилища или какого-либо объекта, объем которого вы собираетесь измерять. Итак, после того, как мы вставляем предмет с ниткой, чтобы вы могли видеть процент установки камня, привязанного к нему с помощью нити, в измерительный инструмент, таким образом, измерительный цилиндр. Итак, что здесь произошло, так что финал в
Объем 60 мл после введения. Это игровой банкомат, который вы можете увидеть здесь перед вставкой. Это просто HTML после его вставки. Получается 80мл. Итак, пекарня должна быть наполнена водой, какой угодно водой. Итак, если вы чувствуете внутри жидкость после введения камня, она увеличилась до 80 мл. Таким образом, способ измерения объема камня формула — это объем камня. Объем камня равен конечному объему или конечному объему данных, показывающих конечный объем за вычетом начального объема. Таким образом, окончательный объем вашего полета равен тому, насколько окончательный объем составляет 80 зубров HTML, а начальный объем составляет от 60. Таким образом, вы можете взять его в команду. SEC составляет 20. Таким образом, вы должны быть в состоянии измерить объем различных объектов. Надеюсь вы поняли это видео подпишитесь на канал для регулярных обновлений и спасибо за просмотр этого видео.»
Итак, что здесь произошло, так что финал в
Объем 60 мл после введения. Это игровой банкомат, который вы можете увидеть здесь перед вставкой. Это просто HTML после его вставки. Получается 80мл. Итак, пекарня должна быть наполнена водой, какой угодно водой. Итак, если вы чувствуете внутри жидкость после введения камня, она увеличилась до 80 мл. Таким образом, способ измерения объема камня формула — это объем камня. Объем камня равен конечному объему или конечному объему данных, показывающих конечный объем за вычетом начального объема. Таким образом, окончательный объем вашего полета равен тому, насколько окончательный объем составляет 80 зубров HTML, а начальный объем составляет от 60. Таким образом, вы можете взять его в команду. SEC составляет 20. Таким образом, вы должны быть в состоянии измерить объем различных объектов. Надеюсь вы поняли это видео подпишитесь на канал для регулярных обновлений и спасибо за просмотр этого видео.»



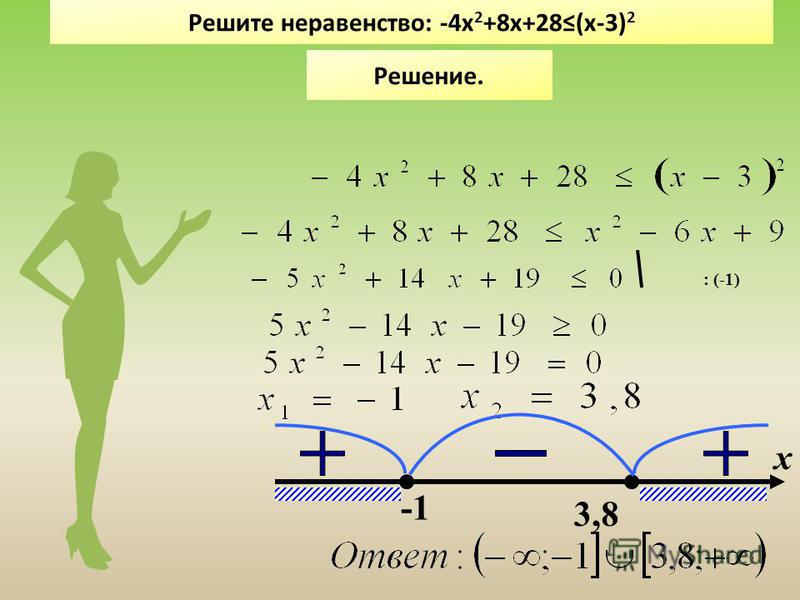 Левая часть имеет знак :
Левая часть имеет знак : Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
Здесь абитуриенты попадают в ловушку и теряют баллы. Будьте внимательны!
 Расставим знаки на каждом из них.
Расставим знаки на каждом из них.


 При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная.
При переходе через точку 4 знак меняется, степень соответствующего множителя нечетная. Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.
Правила просты: приводим неравенство к такому виду, что в его левой части – произведение множителей или дробь, а в правой – ноль. Находим точки, в которых левая часть обращается в ноль или не определена. Отмечаем на числовой оси эти точки. Они разбивают числовую ось (или координатную прямую) на интервалы, на каждом из которых функция в левой части неравенства сохраняет свой знак. Определяем знаки на интервалах, помня о правилах чередования знаков. И записываем ответ.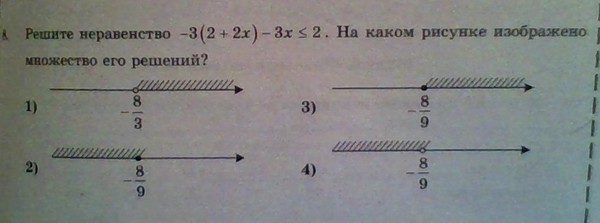

 Найди значения выражений и расположи их в порядке возрастания. Петерсон математика 6 класс ГДЗ. – Рамблер/класс467. Найди значения выражений и расположи их в порядке возрастания. Петерсон математика 6 класс ГДЗ. – Рамблер/класс
Найди значения выражений и расположи их в порядке возрастания. Петерсон математика 6 класс ГДЗ. – Рамблер/класс467. Найди значения выражений и расположи их в порядке возрастания. Петерсон математика 6 класс ГДЗ. – Рамблер/класс
 ..)
..) №18. Под руководством Ященко И.В.
№18. Под руководством Ященко И.В. Он использует какие-то очень странные выражения .
9Выражение 0111 «высмеивать» означает «высмеивать».
Судя по ее выражению , думаю, подарок был полной неожиданностью.
Мы видели, как выражение его лица изменилось с гневного на грустное.
Она носила самодовольный выражение .
Узнать больше
Он использует какие-то очень странные выражения .
9Выражение 0111 «высмеивать» означает «высмеивать».
Судя по ее выражению , думаю, подарок был полной неожиданностью.
Мы видели, как выражение его лица изменилось с гневного на грустное.
Она носила самодовольный выражение .
Узнать больше — Джейсон Петтигрю, SPIN , 19 апреля 2023 г.
Танцы и еда также являются важной частью культурного самовыражения чернокожих , так почему же это кажется таким… неправильным?
— Тайо Беро, , refinery29.com , 13 апреля 2023 г.
Дизайн, созданный HDR и Корганом, бескомпромиссен в своем смелом современном стиле 9.0111 выражение .
— Марк Ламстер, Dallas News , 12 апреля 2023 г.
Судья Венди Битлстоун, назначенный Обамой в Филадельфии, встал на сторону пользователей TikTok, которые были обеспокоены бесплатным выражением , в то время как судья Карл Николс, назначенный Трампом в Вашингтоне, округ Колумбия, основывал свое решение на федеральном регулирующем законе в иске, который подал сам TikTok. .
— Дэвид Ингрэм, NBC News , 8 апр.
— Джейсон Петтигрю, SPIN , 19 апреля 2023 г.
Танцы и еда также являются важной частью культурного самовыражения чернокожих , так почему же это кажется таким… неправильным?
— Тайо Беро, , refinery29.com , 13 апреля 2023 г.
Дизайн, созданный HDR и Корганом, бескомпромиссен в своем смелом современном стиле 9.0111 выражение .
— Марк Ламстер, Dallas News , 12 апреля 2023 г.
Судья Венди Битлстоун, назначенный Обамой в Филадельфии, встал на сторону пользователей TikTok, которые были обеспокоены бесплатным выражением , в то время как судья Карл Николс, назначенный Трампом в Вашингтоне, округ Колумбия, основывал свое решение на федеральном регулирующем законе в иске, который подал сам TikTok. .
— Дэвид Ингрэм, NBC News , 8 апр. 2023 г.
Как и Браун, ZelooperZ использует методы и текстуры левого поля в своем выражении .
— Андре Джи, Rolling Stone , 6 апреля 2023 г.
Выражение гена или то, как генетические изменения влияют на поведение и внешний вид, также может привести к эволюции вида.
— Сара Новак, Discover Magazine , 6 апреля 2023 г.
Вудс сказал, может быть, с малейшим озорством выражение .
— Фотографии Дуга Миллса, New York Times , 4 апреля 2023 г.
Трамп был виден публике во второй раз в здании суда около 14:30. и, с суровым выражением , снова прошел мимо охранников и милиции.
— Мэри Анджела Бок, Разговор , 3 апреля 2023 г.
Узнать больше
2023 г.
Как и Браун, ZelooperZ использует методы и текстуры левого поля в своем выражении .
— Андре Джи, Rolling Stone , 6 апреля 2023 г.
Выражение гена или то, как генетические изменения влияют на поведение и внешний вид, также может привести к эволюции вида.
— Сара Новак, Discover Magazine , 6 апреля 2023 г.
Вудс сказал, может быть, с малейшим озорством выражение .
— Фотографии Дуга Миллса, New York Times , 4 апреля 2023 г.
Трамп был виден публике во второй раз в здании суда около 14:30. и, с суровым выражением , снова прошел мимо охранников и милиции.
— Мэри Анджела Бок, Разговор , 3 апреля 2023 г.
Узнать больше Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах. » Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/expression. По состоянию на 29 апреля 2023 г.
существительное
» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/expression. По состоянию на 29 апреля 2023 г.
существительное


 Знаете ли вы, как отвечать на вопросы, которые вызывают самые ожесточенные споры по грамматике?
Знаете ли вы, как отвечать на вопросы, которые вызывают самые ожесточенные споры по грамматике?
 Привыкайте к этому.|Карла Миллер|4 февраля 2021 г.|Washington Post
Привыкайте к этому.|Карла Миллер|4 февраля 2021 г.|Washington Post Org|25 декабря 2014|DAILY BEAST
Org|25 декабря 2014|DAILY BEAST


 ru/.
ru/. dvpion.ru — общедоступный информационный портал с региональным и муниципальными сегментами, позволяющий семьям выбирать дополнительные общеобразовательные программы, соответствующие запросам, уровню подготовки и способностям детей с различными образовательными потребностями, возможностями.
dvpion.ru — общедоступный информационный портал с региональным и муниципальными сегментами, позволяющий семьям выбирать дополнительные общеобразовательные программы, соответствующие запросам, уровню подготовки и способностям детей с различными образовательными потребностями, возможностями.


 Это лишь предварительное оповещение организатора о желании обучаться
Это лишь предварительное оповещение организатора о желании обучаться ca с помощью IMAP Как получить доступ к своей учетной записи электронной почты Sfu.ca с помощью IMAP
ca с помощью IMAP Как получить доступ к своей учетной записи электронной почты Sfu.ca с помощью IMAP
 ca
ca  com >
Mahoroba.ne.jp (インターネットまほろば) >
126.ru >
Miomio.jp (IIJmio セーフティメール) >
Cheerful.com (mail.com) >
Anderledes.dk (Теленор Дания) >
Mindspring.com (EarthLink)>
com >
Mahoroba.ne.jp (インターネットまほろば) >
126.ru >
Miomio.jp (IIJmio セーフティメール) >
Cheerful.com (mail.com) >
Anderledes.dk (Теленор Дания) >
Mindspring.com (EarthLink)> Счета также были связаны с персоналом и пенсионерами.
Счета также были связаны с персоналом и пенсионерами.
 — Роджер Гейл, инструктор BCIT по кибербезопасности промышленных сетей
— Роджер Гейл, инструктор BCIT по кибербезопасности промышленных сетей 


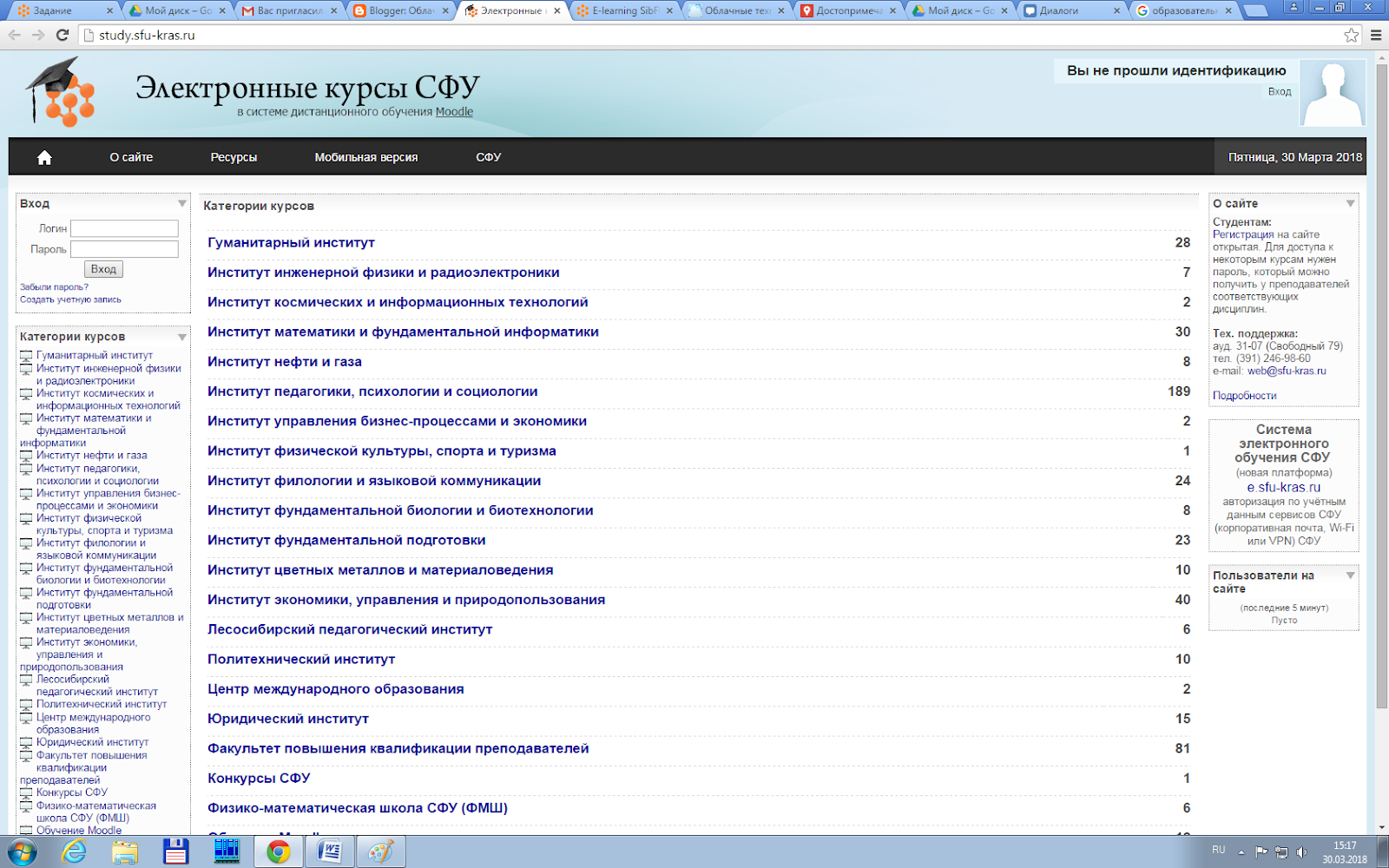


 к . D , то уравнение не имеет д ействительных корней.
к . D , то уравнение не имеет д ействительных корней.  3. Приведенным квадратным уравнением называется квадратное уравнение, первый коэффициент которого равен 1.
3. Приведенным квадратным уравнением называется квадратное уравнение, первый коэффициент которого равен 1.





 В случае, когда D = 0, обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0, квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
В случае, когда D = 0, обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0, квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
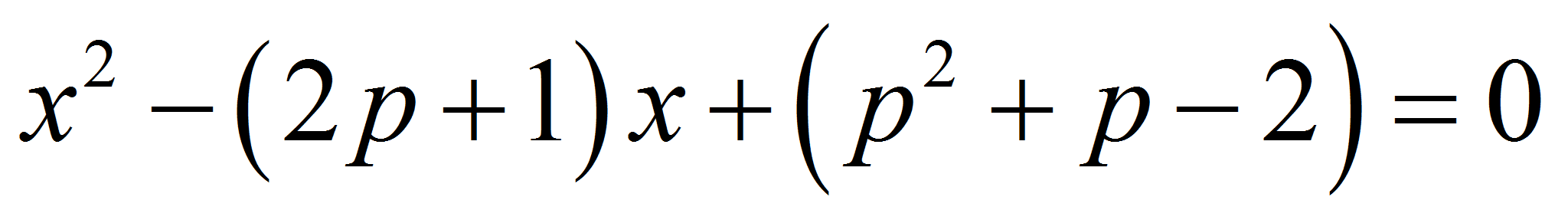
 Решение квадратных неравенств» нашего справочника.
Решение квадратных неравенств» нашего справочника. Эти два решения (значения x) также называются корнями квадратных уравнений и обозначаются как (α, β). Мы узнаем больше о корнях квадратного уравнения в нижеследующем содержании.
Эти два решения (значения x) также называются корнями квадратных уравнений и обозначаются как (α, β). Мы узнаем больше о корнях квадратного уравнения в нижеследующем содержании.

 Положительный знак и отрицательный знак могут быть альтернативно использованы для получения двух различных корней уравнения.
Положительный знак и отрицательный знак могут быть альтернативно использованы для получения двух различных корней уравнения.



 Существует четыре различных метода нахождения корней квадратного уравнения. Четыре метода решения квадратных уравнений заключаются в следующем.
Существует четыре различных метода нахождения корней квадратного уравнения. Четыре метода решения квадратных уравнений заключаются в следующем.
 Как правило, этого подробного метода избегают, и для получения требуемых корней используется только квадратичная формула.
Как правило, этого подробного метода избегают, и для получения требуемых корней используется только квадратичная формула. Решим эти два уравнения, чтобы найти условия, при которых эти уравнения имеют общий корень. Два уравнения решаются относительно x 2 и x соответственно.
Решим эти два уравнения, чтобы найти условия, при которых эти уравнения имеют общий корень. Два уравнения решаются относительно x 2 и x соответственно. При положительных значениях a (a > 0) квадратное выражение имеет минимальное значение при x = -b/2a, а при отрицательном значении a (a < 0) квадратное выражение имеет максимальное значение при x = -b /2а. x = -b/2a — координата x вершины параболы.
При положительных значениях a (a > 0) квадратное выражение имеет минимальное значение при x = -b/2a, а при отрицательном значении a (a < 0) квадратное выражение имеет максимальное значение при x = -b /2а. x = -b/2a — координата x вершины параболы.  Но в случаях, когда она не может быть решена факторизацией, используется квадратичная формула.
Но в случаях, когда она не может быть решена факторизацией, используется квадратичная формула.



 Здесь a и b — коэффициенты, c — постоянный член, а x — переменная. Поскольку переменная x имеет вторую степень, у этого квадратного уравнения есть два корня или ответа. Корни квадратного уравнения можно найти либо путем факторизации, либо с помощью квадратной формулы.
Здесь a и b — коэффициенты, c — постоянный член, а x — переменная. Поскольку переменная x имеет вторую степень, у этого квадратного уравнения есть два корня или ответа. Корни квадратного уравнения можно найти либо путем факторизации, либо с помощью квадратной формулы.


 Следовательно, дискриминант является важной и необходимой величиной, которая помогает легко найти природу корней квадратного уравнения.
Следовательно, дискриминант является важной и необходимой величиной, которая помогает легко найти природу корней квадратного уравнения. Один метод заключается в решении квадратного уравнения с помощью факторизации, а другой метод заключается в завершении квадратов. Всего существует три метода нахождения корней квадратного уравнения.
Один метод заключается в решении квадратного уравнения с помощью факторизации, а другой метод заключается в завершении квадратов. Всего существует три метода нахождения корней квадратного уравнения.
 Самый простой случай — система двух случайных величин, для которой принято находить математическое ожидание, дисперсию, среднеквадратичное отклонение, а также такие параметры, как ковариация (корреляционный момент) и корреляция.
Самый простой случай — система двух случайных величин, для которой принято находить математическое ожидание, дисперсию, среднеквадратичное отклонение, а также такие параметры, как ковариация (корреляционный момент) и корреляция.
 .. + a 1 (t )z «(t ) + a 0 (t )z (t ) = f (t )
.. + a 1 (t )z «(t ) + a 0 (t )z (t ) = f (t ) Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам .
Интегрирование неоднородного уравнения при наличии общего решения соответствующего однородного уравнения сводится, таким образом, к квадратурам . Аналогично случаю уравнений первого порядка, будем искать решение уравнения (2) в виде
Аналогично случаю уравнений первого порядка, будем искать решение уравнения (2) в виде  .,y n соответствующего однородного уравнения L(y)=0 и поэтому не равен нулю. Следовательно, существует единственное решение системы (8). Найдя его, получим функции C» j (x), j=1,2,…,n, а, следовательно, и C j (x), j=1,2,…,n Подставляя эти значения в (3), получаем решение линейного неоднородного уравнения.
.,y n соответствующего однородного уравнения L(y)=0 и поэтому не равен нулю. Следовательно, существует единственное решение системы (8). Найдя его, получим функции C» j (x), j=1,2,…,n, а, следовательно, и C j (x), j=1,2,…,n Подставляя эти значения в (3), получаем решение линейного неоднородного уравнения.  Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:
Решить линейные дифференциальные уравнения второго порядка с постоянными коэффициентами методом вариации произвольных постоянных:  В итоге получаем:
В итоге получаем: 


 В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.
В процессе интегрирования писали вместо С(x) просто С, чтобы не перегружать запись. А в конце вернулись к С(x), чтобы не путать С(x) с новой С.




 Узнайте, что такое производные и как Wolfram|Alpha их вычисляет. 92 x) wrt x
Узнайте, что такое производные и как Wolfram|Alpha их вычисляет. 92 x) wrt x Геометрически говоря, это наклон касательной в .
Геометрически говоря, это наклон касательной в .