Законы алгебры логики. Упрощение логических выражений.
Так же как и в привычной нам алгебре есть законы упрощения выражений, в алгебре логики действуют законы алгебры логики. Для удобства обработки информации алгебраические и логические выражения принято упрощать или приводить к нормальному виду. Большинство законов обеих алгебр схожи и уже знакомы вам. И лишь несколько вы узнаете впервые и, возможно, удивитесь. Упрощение сложных высказываний — это замена их на равносильные на основе законов алгебры высказываний с целью получения высказываний более простой формы. Нормальная форма выражений — это выражение где нет знаков операций импликации и эквивалентности, а инверсия применена только к отдельным высказываниям. Для обрабатывания выражений вы должны свободно ориентироваться между обозначениями операций. Основные три из них имеют следующие варианты обозначений: Инверсия (отрицание): Ø ,`A , не . Конъюнкция (умножение): & , L , × . Дизъюнкция (сложение): V, +. Для удобства записи и большей наглядности можно записывать знаки операций в логических выражениях в более привычной нам форме: умножение — знаком ×, а сложение — знаком +. Иначе говоря, упростить выражение — это найти в нём законы логики и их применить! Первое, что надо знать для упрощения — формулы замены операций (которых не должно быть в нормальной форме записи логических выражений): Итак, а теперь сами законы алгебры логики: Чтобы ими пользоваться их надо знать, т.е. выучить. Но на самом деле эти законы во многом повторяю законы обычной алгебры. Закон двойного отрицания напоминает нам ситуацию, когда «минус на минус даёт плюс», хотя так говорить и не грамотно, но зато именно так ученики его запоминают быстрее всего! Законы исключения третьего, операции с константами и законы повторения следуют из определения самих логических операций сложения (дизъюнкции) и умножения (конъюнкции). Переместительный, сочетательный и распределительный законы нам встречались и в обычной алгебре. Они и в алгебре логики работают точно так же! Правда распределительный закон относительно умножения на уроках математики применять никак нельзя, а в алгебре логики пожалуйста: a + b × c = (a + b)× (a + c) И последнее и самое интересное — это законы де Моргана (или двойного отрицания). Никак нельзя допускать при упрощении выражений оставлять знак отрицания более чем над одним высказыванием! С этой проблемой нам помогают бороться именно законы де Моргана. Запомнить их просто: отрицание раздается каждому высказыванию, находящемуся под общей чертой, а знаки + меняются на × , и наоборот × на +. Упрощение нескольких логических выражений представлено в следующем видео. Вы можете его ставить на паузу и сверяться с формулами законов в любом удобном для вас месте: com/embed/lpY0mporhBk?rel=0&wmode=opaque» frameborder=»0″ allowfullscreen=»true»> |
Упрощение логических выражений | Законы алгебры логики (курс pol 68 ч.) /informatika_10_68_pol/ (68 часов в уч. год)
Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, сокращенный курс, 2 часа в неделю)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 10 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, сокращенный курс, 2 часа в неделю) | Упрощение логических выражений
Содержание урока
Законы алгебры логики
Логические уравнения
Задачи
Для упрощения логических выражений используют законы алгебры логики. Они формулируются для базовых логических операций — «НЕ», «И» и «ИЛИ».
Закон двойного отрицания означает, что операция «НЕ» обратима: если применить ее два раза, логическое значение не изменится. Закон исключённого третьего основан на том, что в классической (двузначной) логике любое логическое выражение либо истинно, либо ложно («третьего не дано»). Поэтому если А = 1, то А = 0 (и наоборот), так что произведение этих величин всегда равно нулю, а сумма — единице.
Операции с константами и закон повторения легко проверяются по таблицам истинности операций «И» и «ИЛИ». Переместительный и сочетательный законы выглядят вполне привычно, так же, как и в арифметике. Почти везде «работает» аналогия с алгеброй чисел, нужно только помнить, что в логике 1 + 1 = 1, а не 2.
Распределительный закон для операции «ИЛИ» — это обычное раскрытие скобок. А вот для операции «И» мы видим незнакомое выражение, в алгебре чисел это равенство неверно. Доказательство можно начать с правой части, раскрыв скобки:
(А + В) • (А + С) = А • А + А • С + В • А + В • С.
Дальше используем закон повторения (А • А = А) и заметим, что
А + А • С = А • (1 + С) = А • 1 = А.
Аналогично доказываем, что А + В • А = А • (1 + В) = А, таким образом,
(А + В) • (А + С) = А + В • С.
Равенство доказано. Попутно мы доказали также и закон поглощения для операции «И» (для операции «ИЛИ» вы можете сделать это самостоятельно). Отметим, что из распределительного закона следует полезное тождество:
А + А • В = (А + А) • (А + В) = А + В.
Правила, позволяющие раскрывать отрицание сложных выражений, названы в честь шотландского математика и логика Огастеса (Августа) де Моргана. Обратите внимание, что при этом не просто «общее» отрицание переходит на отдельные выражения, но и операция «И» заменяется на «ИЛИ» (и наоборот). Доказать законы де Моргана можно с помощью таблиц истинности.
Теперь с помощью приведённых законов алгебры логики упростим полученное ранее логическое выражение для объединения областей 3 и 4 на диаграмме с тремя переменными (§ 20, рис. 3.15):
3.15):
(А • В • C) + А • В • C = (А + А) • В • C = В • C.
Здесь мы сначала вынесли общий множитель двух слагаемых за скобки, а затем применили закон исключённого третьего.
В общем случае можно рекомендовать такую последовательность действий.
1. Заменить все «небазовые» операции (исключающее ИЛИ, импликацию, эквивалентность и др.) на их выражения через базовые операции «НЕ», «И» и «ИЛИ».
2. Раскрыть отрицания сложных выражений по законам де Моргана так, чтобы операции отрицания остались только у отдельных переменных.
3. Используя вынесение общих множителей за скобки, раскрытие скобок и другие законы алгебры логики, упростить выражение.
Пример
(А + B) • (А + B) • (А + С)=(А + B) • А • B • (А + C = (А • А + B • А) • B • (А + С) = B • А • B • (А + С) = А • B • B • (А + С) = B • А • (А + С) = B • (А.
Здесь последовательно использованы закон де Моргана, распределительный закон, закон исключённого третьего, переместительный закон, закон повторения, снова переместительный закон и закон поглощения.
Следующая страница Логические уравнения
Cкачать материалы урока
Калькулятор булевой алгебры — онлайн-упрощение булевых логических выражений
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Калькулятор логических выражений
Инструмент/калькулятор для упрощения или минимизации логических выражений (булева алгебра), содержащих логические выражения с И, ИЛИ, НЕ, XOR.
Результаты
Калькулятор логических выражений — dCode
Метки: Символьные вычисления, Электроника
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Упрощение логических выражений
Калькулятор логических выражений/упрощение/минификаторФормат результата
Любой формат
Дизъюнктивная нормальная форма DNF (сумма произведений/SOP/Minterms)
Конъюнктивная нормальная форма CNF (произведение сумм/POS/Maxterms)
Только вентили НЕ-И (НЕ-И ⊼)
Только вентили ИЛИ-НЕ (НЕ-ИЛИ ⊽)
| Нотация | Алгебраические (*, +, !) Логические (∧, ∨, ¬) 9000 4 Программирование (&&, ||, ~) Буквенное (И, ИЛИ, НЕ) |
См. также: Таблица истинности — Решатель уравнений — Двоичный код
также: Таблица истинности — Решатель уравнений — Двоичный код
Ответы на вопросы (FAQ)
Что такое логическое выражение? (Определение)
A Логическое выражение (или Логическое выражение) — это математическое выражение, использующее Булева алгебра , которая использует логические значения (0 или 1, истина или ложь) в качестве переменных и имеет логические значения в качестве результата/упрощения. Выражение может содержать такие операторы, как конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ).
Как упростить/минимизировать логическое выражение?
Для упрощения булевых уравнений можно использовать различные методы: помимо классического развития через ассоциативность, коммутативность, дистрибутивность и т. д., таблицы истинности или диаграммы Венна обеспечивают хороший обзор выражений.
Пример: Исходное выражение (LaTeX) $$ \overline{a \land b \land (c \lor \bar{d})} \lor \bar{b} $$
dCode допускает несколько синтаксисов:
Алгебраическая запись
Пример: !(ab(c+!d))+!b с неявным умножением ab = a AND b и ! (восклицательный знак) для строки : логический НЕ .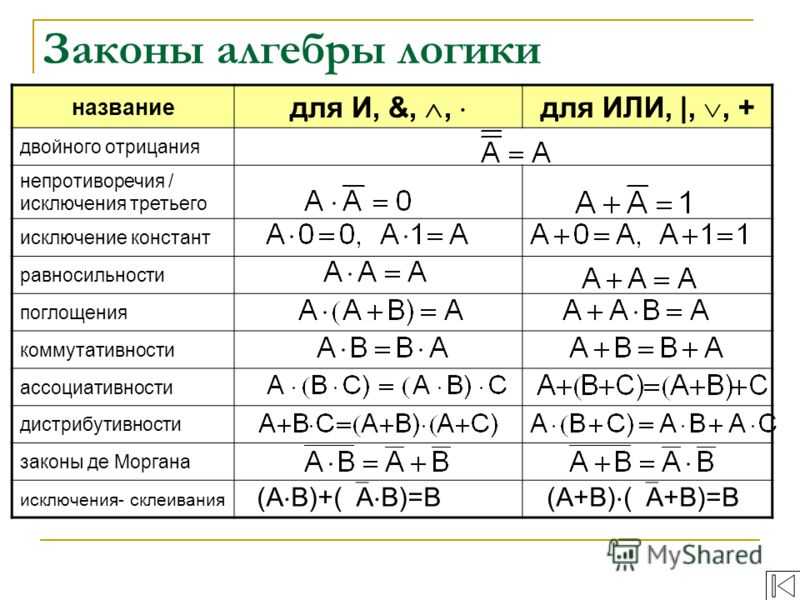
Логические/компьютерные обозначения
Пример: !(a&&b&&(c||!d))||!b с двойным символом и (амперсанд) для И и двойным символом | (прямая, вертикальная черта) для логического ИЛИ .
Буквенное обозначение
Пример: НЕ (a И b И (c ИЛИ НЕ d)) ИЛИ НЕ b
Для одного и того же выражения может быть несколько минимальных представлений, dCode предоставляет решение и выводит алгебраическое обозначение.
Некоторые обозначения неоднозначны, избегайте функционального обозначения ‘XOR(a,b)’ для записи a XOR b , также избегайте суффикса штрих/апостроф перед `a’ и предпочтите !a .
Что такое методы упрощения булевой алгебры?
Булева алгебра обладает многими свойствами (булевыми законами):
1 — Элемент тождества: $0$ нейтрален для логического ИЛИ, тогда как $1$ нейтрален для логического И
$$a + 0 = a \\a .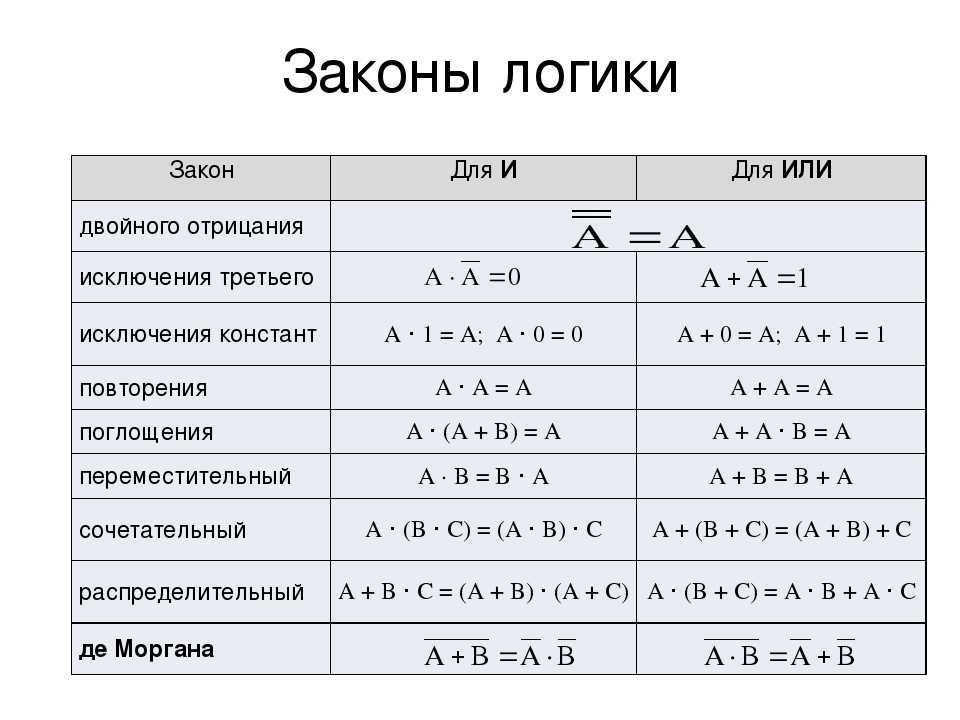 1 = a $$
1 = a $$
2 — Поглощение: $1$ поглощает для логического ИЛИ, а $0$ поглощает для логического И
$$ a + 1 = 1 \\ a.0 = 0 $$
3 — Идемпотентность: многократное применение одной и той же операции не меняет значение
$$ a + a = a + a + \cdots + а = а \ а . а = а . а . \cdots . a = a $$
4 — Инволюция или двойное дополнение: противоположность противоположности $ a $ est $ a $
$$ a = \overline{\overline{a}} = !(!a) $$
5 — Дополнительность по противоречию: $ a $ AND $ \text{not}(a) $ невозможно, поэтому ложно и равно $ 0 $
$$ а . \overline{a} = 0 $$
6 — Дополнительность по исключенному третьему: $ a $ OR $ \text{not}(a) $ всегда истинно, поэтому $ 1 $
$$ a + \overline{ a} = 1 $$
7 — Закон ассоциативности: скобки между одинаковыми операторами бесполезны
$$ a.(b.c) = (a.b).c = a.b.c \\ a+(b+c) = (a+b) +c = a+b+c $$
8 — Закон коммуникативности: порядок не имеет значения
$$ a.b = b. a \\ a+b = b+a $$
a \\ a+b = b+a $$
9 — Закон распределения: И распределено над ИЛИ, но также ИЛИ распределяется по И
$$ a.(b+c) = a.b + a.c \\ a+(b.c) = (a+b).(a+c) $$
10 — Законы Де Моргана (подробнее см. ниже)
$$ \overline{a+b} = \overline{a}.\overline{b} \\ \overline{a.b} = \overline{a}+\overline{b} $$
11 — Другие упрощения комбинации указанных выше
$$ a.(a+b) = a \\ a+(a.b) = a \\ (a.b) + (a.!b) = a \\ (a+b).(a+ !b) = a \\ a + (!a.b) = a + b \\ a.(!a + b) = a.b \\ a.b + \overline{a}.c = a.b + \overline{a}.c + b.c $$
Как показать/продемонстрировать, что 2 логических выражения равны?
Метод 1: упростите их , пока не получите то же самое написание в булевой алгебре .
Метод 2: путем вычисления их таблицы истинности , которая должна быть идентичной.
Что такое закон де Моргана?
Законы де Моргана часто используются для перезаписи логических выражений. Обычно они формулируются так: не (а и б) = (не а) или (не б) и не (а или б) = (не а) и (не б) . Вот эквивалентные логические записи:
Обычно они формулируются так: не (а и б) = (не а) или (не б) и не (а или б) = (не а) и (не б) . Вот эквивалентные логические записи:
$$ \overline{(a \land b)} \leftrightarrow (\overline{a}) \lor (\overline{b}) \iff \overline{AB} = \overline{a} + \overline{b } $$
$$ \overline{(a \lor b)} \leftrightarrow (\overline{a}) \land (\overline{b}) \iff \overline{a+b} = \overline{a} . \overline{b} $$
Что такое дизъюнктивная или конъюнктивная нормальная форма?
В логике можно использовать разные форматы для обеспечения лучшей читабельности или удобства использования.
Нормальная дизъюнктивная форма (DNF) использует сумму произведений (SOP):
Пример: (a&&c)||b
Нормальная конъюнктивная форма (CNF) или форма предложения использует произведение сумм (POS):
Пример: (a+b).( б +c)
Как показать пошаговые расчеты?
Шаги расчета, какими их может себе представить человек, для решателя не существуют. Выполняемые операции являются бинарными побитовыми и не соответствуют выполняемым при разрешении с помощью карандаша и бумаги.
Выполняемые операции являются бинарными побитовыми и не соответствуют выполняемым при разрешении с помощью карандаша и бумаги.
Исходный код
dCode сохраняет право собственности на исходный код «Калькулятора логических выражений». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Калькулятор логических выражений», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Булевых выражений». Функции калькулятора (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, script или доступ к API для «Калькулятора логических выражений» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Калькулятор логических выражений» или любых его результатов разрешено, если вы цитируете dCode!
Экспорт результатов в виде файла .csv или .txt можно выполнить бесплатно, щелкнув значок export .
Ссылка на источник (библиография):
30, https://www.dcode.fr/boolean-expressions-calculator
Сводка
- Упрощение логических выражений
- Что такое логическое выражение? (Определение)
- Как упростить/минимизировать логическое выражение?
- Что такое методы упрощения булевой алгебры?
- Как показать/продемонстрировать, что 2 логических выражения равны?
- Что такое закон де Моргана?
- Что такое дизъюнктивная или конъюнктивная нормальная форма?
- Как показать пошаговые расчеты?
Похожие страницы
- Таблица истинности
- Решатель уравнений
- Логические двойные
- Логические минитермы и макстермы
- Двоичный код
- Упрощение математических выражений
- Удалить Скобки
- СПИСОК ИНСТРУМЕНТОВ DCODE
Поддержка
- Paypal
- Patreon
- Подробнее
Форум/Справка
Ключевые слова
bool,boole,boolean,выражение,алгебра,логика,логический,упрощение,упрощение,и,или,не,xor,амперсанд,труба,восклицательный знак,морган
Ссылки
▲
Упрощение логических выражений
Упрощение логических выраженийУпрощение логических выражений
Примеры булевой алгебры Двоичный/булев основной индекс
[Примеры таблиц истинности] [Упрощение логических выражений] [Примеры логических вентилей]
Вот несколько примеров упрощений булевой алгебры. Каждая строка дает форму выражения, а
правило или правила
используется для получения его от предыдущего.
Как правило, есть несколько способов достичь результата.
Вот список правил упрощения.
Каждая строка дает форму выражения, а
правило или правила
используется для получения его от предыдущего.
Как правило, есть несколько способов достичь результата.
Вот список правил упрощения.- Упрощение: C + BC:
Выражение Используемые правила C + BC Исходное выражение С+(Б+С) Закон ДеМоргана. (С + С) + В Коммутативные, ассоциативные законы. Т + Б Закон о дополнении. Т Закон о личности. - Упрощение: AB(A + B)(B + B):
Выражение Используемые правила AB(A + B)(B + B) Исходное выражение АВ(А+В) Закон о дополнении, Закон о личности. (А+В)(А+В) Закон Де Моргана А + ВВ Распределительное право.  Этот шаг использует тот факт, что или распределяет по
и. Это может выглядеть немного странно
так как сложение не распределяется
над умножением.
Этот шаг использует тот факт, что или распределяет по
и. Это может выглядеть немного странно
так как сложение не распределяется
над умножением.А Дополнение, Идентификация. - Упрощение: (A + C)(AD + AD) + AC + C:
Выражение Используемые правила (A + C)(AD + AD) + AC + C Исходное выражение (А + С)А(Д + Д) + АС + С Распределительный. (А + С)А + АС + С Дополнение, Идентификация. А((А + С) + С) + С Коммутативный, Распределительный. А(А + С) + С Ассоциативный, идемпотентный. АА + АС + С Распределительный. А + (А + Т )С Идемпотент, Тождество, Распределение. А+С Личность дважды. 
Вы также можете использовать распределение или более и начиная с A(A+C)+C для достижения того же результата другим путем.
- Упрощение: A(A + B) + (B + AA)(A + B):
Выражение Используемые правила A(A + B) + (B + AA)(A + B) Исходное выражение АА + АВ + (В + А)А + (В + А)В Идемпотент (от АА до А), затем Дистрибутив, используется дважды. АВ + (В + А)А + (В + А)В Дополнение, затем Идентификация. (Строго говоря, мы также использовали коммутативный закон для каждого из этих Приложения.) АВ + БА + АА + ВВ + АВ Распределитель, два места. АБ + БА + А + АБ Идемпотент (для А), затем Дополнение и Идентичность для удаления ББ. АБ + АБ + А Т + АБ Коммутативный, Идентичность; подготовка к следующему шагу. 
Корень из 304: Mathway | Популярные задачи
2делители, простота, двоичный вид, куб, квадрат
Укажите число, чтобы получить всю информацию о нем:
Случайное число
Четность: Число 304 является четным.
Сумма цифр: 7 Произведение цифр: 0 Количество цифр: 3 Все делители числа 1 2 4 8 16 19 38 76 152 304 Количество делителей 10 Сумма делителей 620 Простое число Составное число
Квадратный корень 17,4355957741627 Кубический корень 6,72395081359793 Квадрат 92416 Куб 28094464 Обратное число 0,00328947368421053 Предыдущее число: 303 Следующее число: 305 Целое положительное число 304 является трехзначным.
 Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 304, равна 7, а их произведение равно 0.
Число 304 является четным.
Всего число 304 имеет 10 делителей:
1,
2,
4,
8,
16,
19,
38,
76,
152,
304,
. Сумма делителей равна 620. Куб числа 304 равен 92416, а квадрат составляет 28094464.
Квадратный корень рассматриваемого числа равен 17,4355957741627. Кубический корень равен 6,72395081359793.
Число, которое является обратным к числу 304, выглядит как 0,00328947368421053.
Оно записывается 3 цифрами.
Сумма цифр, из которых состоит число 304, равна 7, а их произведение равно 0.
Число 304 является четным.
Всего число 304 имеет 10 делителей:
1,
2,
4,
8,
16,
19,
38,
76,
152,
304,
. Сумма делителей равна 620. Куб числа 304 равен 92416, а квадрат составляет 28094464.
Квадратный корень рассматриваемого числа равен 17,4355957741627. Кубический корень равен 6,72395081359793.
Число, которое является обратным к числу 304, выглядит как 0,00328947368421053.
Квадратный корень из 304 — Как найти квадратный корень из 304? [Решено]
Квадратный корень из 304 выражается как √304 в радикальной форме и как (304) ½ или (304) 0,5 в экспоненциальной форме.
 Квадратный корень из 304, округленный до 8 знаков после запятой, равен 17,43559577. Это положительное решение уравнения x 2 = 304. Мы можем выразить квадратный корень из 304 в его низшей радикальной форме как 4 √19.
Квадратный корень из 304, округленный до 8 знаков после запятой, равен 17,43559577. Это положительное решение уравнения x 2 = 304. Мы можем выразить квадратный корень из 304 в его низшей радикальной форме как 4 √19.- Квадратный корень из 304: 17.435595774162696
- Квадратный корень из 304 в экспоненциальной форме: (304) ½ или (304) 0,5
- Квадратный корень из 304 в подкоренной форме: √304 или 4 √19
1. Что такое квадратный корень из 304? 2. Как найти квадратный корень из 304? 3. Является ли квадратный корень из 304 иррациональным? 4. Часто задаваемые вопросы Что такое квадратный корень из 304?
Квадратный корень из 304 (или корень из 304) — это число, которое при умножении само на себя дает произведение 304.
 Таким образом, квадратный корень из 304 = √304 = 4 √19 = 17,435595774162696.
Таким образом, квадратный корень из 304 = √304 = 4 √19 = 17,435595774162696.☛ Проверка: Калькулятор квадратного корня
Как найти квадратный корень из 304?
Значение √304 методом длинного деления
Объяснение:
- Формирование пар: 03 и 04
- Найдите число Y (1), квадрат которого <= 3. Теперь разделите 03 на 1 с частным 1.
- Снесите следующую пару 04 справа от остатка 2. Новое делимое теперь равно 204.
- Добавьте последнюю цифру частного (1) к делителю (1), т. е. 1 + 1 = 2. Справа от 2 найдите цифру Z (то есть 7), такую, что 2Z × Z <= 204. Найдя Z вместе 2 и Z (7) образуют новый делитель 27 для нового делимого 204.
- Разделите 204 на 27 с частным равным 7, получив остаток = 204 — 27 × 7 = 204 — 189 = 15.
- Теперь найдем десятичные разряды после частного 17.
- Уменьшите 00 справа от этого остатка 15. Новое делимое теперь равно 1500.

- Добавьте к делителю последнюю цифру частного, т. е. 7 + 27 = 34. Справа от 34 найдите цифру Z (то есть 4), такую, что 34Z × Z <= 1500. Вместе они образуют новый делитель (344) для новый дивиденд (1500).
- Разделите 1500 на 344 с частным равным 4, получив остаток = 1500 — 344 × 4 = 1500 — 1376 = 124.
- Снова наберите 00. Повторите описанные выше шаги, чтобы найти больше знаков после запятой для квадратного корня из 304.
Таким образом, квадратный корень из 304 по методу деления в большую сторону равен 17,4 прибл.
Является ли квадратный корень из 304 иррациональным?
Фактическое значение √304 не определено. Значение √304 до 25 знаков после запятой равно 17,43559.577416269420894793. Следовательно, квадратный корень из 304 — иррациональное число.
☛ Также проверьте:
- Квадратный корень из 729 — √729 = 27
- Квадратный корень из 25 — √25 = 5
- Квадратный корень из 106 — √106 = 10,29563
- Квадратный корень из 92 — √92 = 9,59166
- Квадратный корень из 52 — √52 = 7,21110
- Квадратный корень из 35 — √35 = 5,91608
- Квадратный корень из 113 — √113 = 10,63015
Квадратный корень из 304 решенных примеров
Пример 1: Решите уравнение x 2 − 304 = 0
Решение:
x 2 — 304 = 0, т.
 е. x 2 = 304
е. x 2 = 304
х = ±√304
Поскольку значение квадратного корня из 304 равно 17,436,
⇒ х = +√304 или -√304 = 17,436 или -17,436.Пример 2. Если площадь круга равна 304π в 2 . Найдите радиус окружности.
Решение:
Пусть ‘r’ будет радиусом окружности.
⇒ Площадь круга = πr 2 = 304π в 2
⇒ г = ±√304 в 90 157 Так как радиус не может быть отрицательным,
⇒ г = √304
Квадратный корень из 304 равен 17,436.
⇒ г = 17,436 вПример 3: Если площадь поверхности сферы составляет 1216π в 2 . Найдите радиус сферы.
Решение:
Пусть ‘r’ будет радиусом сферы.
⇒ Площадь сферы = 4πr 2 = 1216π в 2
⇒ г = ±√304 в 90 157 Так как радиус не может быть отрицательным,
⇒ г = √304
Квадратный корень из 304 равен 17,436.
⇒ г = 17,436 в
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о квадратном корне из 304
Каково значение квадратного корня из 304?
Квадратный корень из 304 равен 17,43559.
Почему квадратный корень из 304 является иррациональным числом?
При простой факторизации 304 т. е. 2 4 × 19 1 , 19 в нечетной степени. Следовательно, квадратный корень из 304 иррационален.
Является ли число 304 идеальным квадратом?
Разложение числа 304 на простые множители = 2 4 × 19 1 . Здесь простого множителя 19 нет в паре. Следовательно, 304 не является идеальным квадратом.




 Этот шаг использует тот факт, что или распределяет по
и. Это может выглядеть немного странно
так как сложение не распределяется
над умножением.
Этот шаг использует тот факт, что или распределяет по
и. Это может выглядеть немного странно
так как сложение не распределяется
над умножением.

 Квадратный корень из 304, округленный до 8 знаков после запятой, равен 17,43559577. Это положительное решение уравнения x 2 = 304. Мы можем выразить квадратный корень из 304 в его низшей радикальной форме как 4 √19.
Квадратный корень из 304, округленный до 8 знаков после запятой, равен 17,43559577. Это положительное решение уравнения x 2 = 304. Мы можем выразить квадратный корень из 304 в его низшей радикальной форме как 4 √19. Таким образом, квадратный корень из 304 = √304 = 4 √19 = 17,435595774162696.
Таким образом, квадратный корень из 304 = √304 = 4 √19 = 17,435595774162696.
 е. x 2 = 304
е. x 2 = 304 

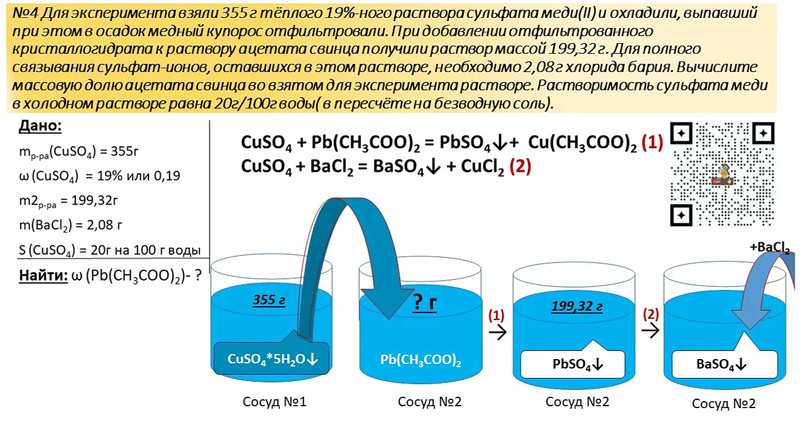
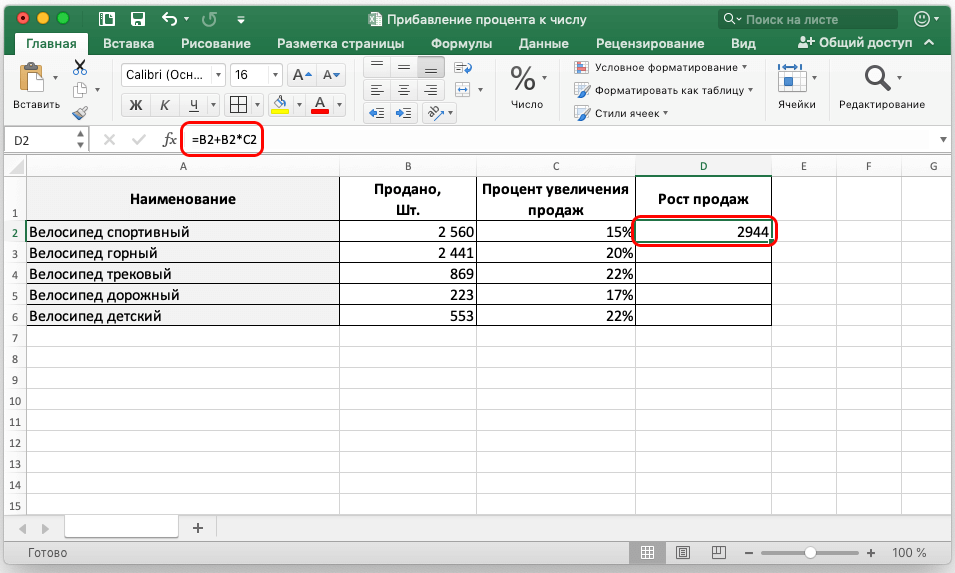
 Эта формула используется в Excel без последней части (*100). Это связано с тем, что при выборе процентного формата результирующее число автоматически изменяется на проценты.
Эта формула используется в Excel без последней части (*100). Это связано с тем, что при выборе процентного формата результирующее число автоматически изменяется на проценты.
 Если ответ отрицательный, это означает, что процентное изменение является уменьшением.
Если ответ отрицательный, это означает, что процентное изменение является уменьшением.


 2.
2.
 03. Затем в ячейку A4 введите (=A2*A3). Это даст вам сумму вашего повышения.
03. Затем в ячейку A4 введите (=A2*A3). Это даст вам сумму вашего повышения.

 Рассмотрим простой пример.
Рассмотрим простой пример.
 Допустим, вы хотите уменьшить определенную сумму на 25%, например, когда вы пытаетесь применить скидку. Здесь формула будет такой: = Цена * 1-Скидка%.
Допустим, вы хотите уменьшить определенную сумму на 25%, например, когда вы пытаетесь применить скидку. Здесь формула будет такой: = Цена * 1-Скидка%. Увеличение на 5 процентов будет означать, что если вы разделите исходное значение на 100 частей, это значение увеличится еще на 5 частей. Таким образом, если исходное значение увеличилось на 14 процентов, значение будет увеличиваться на 14 на каждые 100 единиц, на 28 на каждые 200 единиц и так далее. Чтобы сделать это еще более ясным, мы рассмотрим пример с использованием формулы процентного увеличения в следующем разделе.
Увеличение на 5 процентов будет означать, что если вы разделите исходное значение на 100 частей, это значение увеличится еще на 5 частей. Таким образом, если исходное значение увеличилось на 14 процентов, значение будет увеличиваться на 14 на каждые 100 единиц, на 28 на каждые 200 единиц и так далее. Чтобы сделать это еще более ясным, мы рассмотрим пример с использованием формулы процентного увеличения в следующем разделе.
 Через год стоимость снизилась до 1300 долларов. Процентное уменьшение будет рассчитываться следующим образом:
Через год стоимость снизилась до 1300 долларов. Процентное уменьшение будет рассчитываться следующим образом: Хотя процентное увеличение очень похоже на абсолютное увеличение, первое более полезно при сравнении нескольких наборов данных. Например, изменение с 1 на 51 и с 50 на 100 имеет абсолютное изменение 50, но процентное увеличение для первого составляет 5000%, а для второго — 100%, поэтому первое изменение выросло намного больше. . Вот почему увеличение в процентах является наиболее распространенным способом измерения роста .
Хотя процентное увеличение очень похоже на абсолютное увеличение, первое более полезно при сравнении нескольких наборов данных. Например, изменение с 1 на 51 и с 50 на 100 имеет абсолютное изменение 50, но процентное увеличение для первого составляет 5000%, а для второго — 100%, поэтому первое изменение выросло намного больше. . Вот почему увеличение в процентах является наиболее распространенным способом измерения роста . s для секунд, min для минут и т. д. Обратите внимание, что это не учитывает начисление сложных процентов.
s для секунд, min для минут и т. д. Обратите внимание, что это не учитывает начисление сложных процентов.


 Если вы запомните три шага и научитесь их применять, вы сможете быстро и точно вычислять проценты для правильного решения математических задач.
Если вы запомните три шага и научитесь их применять, вы сможете быстро и точно вычислять проценты для правильного решения математических задач.








 Например, Полярная — это α Малой Медведицы. Зная α Большой Медведицы, можно без особого труда отыскать Малую Медведицу. Если зрительно провести прямую линию от β к α Большой Медведицы, они укажут на полярную звезду. Самые яркие звезды северного полушария: α созвездия Лиры – звезда Вега, α Волопаса – Арктур, а в южном полушарии и на всем небе α Большого Пса – Сириус. К наиболее ярким звездам летнего периода относят: белые звезды: Вега в созвездии Лиры, Альтаир в созвездии Орла и Денеб в созвездии Лебедь, видны летом и осенью – так называемый летний треугольник.
Зодиакальные созвездия – созвездия, которые находятся на линии годичного движения Солнца – эта линия называется эклиптика. В каждом из них, Солнце находится около месяца. Сегодня принято считать, что зодиакальных созвездий 12, но на самом деле Солнце в своём движении пересекает 13 созвездий. 13 созвездие называется Змееносец и находится между созвездиями Скорпион и Стрелец, но для удобства оно было убрано из числа зодиакальных.
Например, Полярная — это α Малой Медведицы. Зная α Большой Медведицы, можно без особого труда отыскать Малую Медведицу. Если зрительно провести прямую линию от β к α Большой Медведицы, они укажут на полярную звезду. Самые яркие звезды северного полушария: α созвездия Лиры – звезда Вега, α Волопаса – Арктур, а в южном полушарии и на всем небе α Большого Пса – Сириус. К наиболее ярким звездам летнего периода относят: белые звезды: Вега в созвездии Лиры, Альтаир в созвездии Орла и Денеб в созвездии Лебедь, видны летом и осенью – так называемый летний треугольник.
Зодиакальные созвездия – созвездия, которые находятся на линии годичного движения Солнца – эта линия называется эклиптика. В каждом из них, Солнце находится около месяца. Сегодня принято считать, что зодиакальных созвездий 12, но на самом деле Солнце в своём движении пересекает 13 созвездий. 13 созвездие называется Змееносец и находится между созвездиями Скорпион и Стрелец, но для удобства оно было убрано из числа зодиакальных. Все звезды кажутся одинаково далёкими от нас, но истинное расстояние до них различно, и определить его можно только путем очень точных измерений и расчетов. Из-за осевого вращения Земли, звезды нам кажутся перемещающимися по небу, но при внимательном наблюдении можно заметить, что Полярная звезда почти не меняет своего положения относительно горизонта. Другие же звезды описывают в течении суток полный круг с центром вблизи Полярной. Это можно легко проверить, проведем небольшой опыт. Необходимо закрепить на штативе фотоаппарат, навести его на полярную звезду, и поставить длительную выдержку. В результате, мы получим фото, на котором увидим концентрические дуги – следы путей звезд. Общий центр этих дуг – точка, которая остается неподвижной при суточном движении звезд, условно называется северным полюсом мира. Диаметрально противоположная ему точка называется южным полюсом мира. Вращение звёзд происходит с Востока на Запад.
История астрономии
С тех самых пор, когда люди стали объединяться в группы, возникало множество проблем и вопросов, связанных с окружающим миром и природными явлениями, которые, так или иначе, влияли на жизнь человека.
Все звезды кажутся одинаково далёкими от нас, но истинное расстояние до них различно, и определить его можно только путем очень точных измерений и расчетов. Из-за осевого вращения Земли, звезды нам кажутся перемещающимися по небу, но при внимательном наблюдении можно заметить, что Полярная звезда почти не меняет своего положения относительно горизонта. Другие же звезды описывают в течении суток полный круг с центром вблизи Полярной. Это можно легко проверить, проведем небольшой опыт. Необходимо закрепить на штативе фотоаппарат, навести его на полярную звезду, и поставить длительную выдержку. В результате, мы получим фото, на котором увидим концентрические дуги – следы путей звезд. Общий центр этих дуг – точка, которая остается неподвижной при суточном движении звезд, условно называется северным полюсом мира. Диаметрально противоположная ему точка называется южным полюсом мира. Вращение звёзд происходит с Востока на Запад.
История астрономии
С тех самых пор, когда люди стали объединяться в группы, возникало множество проблем и вопросов, связанных с окружающим миром и природными явлениями, которые, так или иначе, влияли на жизнь человека. Вплоть до XIX века, астрономия была ограничена рамками познаний лишь в пределах Солнечной системы, объекты, находившиеся за её пределами и тем более за пределами нашей Галактики, были недосягаемы для изучения, и представления о них были лишь умозаключительными. Историческое развитие в астрономии заключается в том, что она формировалась, как наука вместе с изменяющейся в разные периоды общественной жизнью и культурой. В каждой народности были свои культура, мифы и обычаи, свои первооткрыватели, которые вносили вклад, делая открытия и давая объяснения тем или иным событиям, связанным с проявлениями природы и окружающего мира. Астрономия была необходима для охотников и мореплавателей, знание о расположении звёзд давало возможность для ориентации и навигации. Но для этого были необходимы длительные и регулярные наблюдения за светилами. Несмотря на то, что знание древних египтян о небесных светилах отставало от вавилонских, в задаче счёта времени жрецы Египта ушли вперёд. С развитие земледелия, возникает календарь (Рис.
Вплоть до XIX века, астрономия была ограничена рамками познаний лишь в пределах Солнечной системы, объекты, находившиеся за её пределами и тем более за пределами нашей Галактики, были недосягаемы для изучения, и представления о них были лишь умозаключительными. Историческое развитие в астрономии заключается в том, что она формировалась, как наука вместе с изменяющейся в разные периоды общественной жизнью и культурой. В каждой народности были свои культура, мифы и обычаи, свои первооткрыватели, которые вносили вклад, делая открытия и давая объяснения тем или иным событиям, связанным с проявлениями природы и окружающего мира. Астрономия была необходима для охотников и мореплавателей, знание о расположении звёзд давало возможность для ориентации и навигации. Но для этого были необходимы длительные и регулярные наблюдения за светилами. Несмотря на то, что знание древних египтян о небесных светилах отставало от вавилонских, в задаче счёта времени жрецы Египта ушли вперёд. С развитие земледелия, возникает календарь (Рис. 2), в котором год состоял из 12 месяцев, а месяц из 30 дней с добавочными 5 днями. Впоследствии этот календарь был положен в основу юлианского календаря, созданного в эпоху Древнего Рима.
Египтяне установили продолжительность года и создали систему летоисчисления.
…«Мир не только сфера, — говорит Платон. — Но сфера эта совершенна; Творец позаботился о том, чтобы поверхность ее была абсолютно гладкой, и это не без причин…»…
Длительные наблюдения светил помогли создать календарь, но привели к вопросу, который долгое время не находил ответа, что же находится в центре Земля или Солнце? Вопрос повис на многие столетия.
К VI в. до н.э. развитие культуры и науки в Европе способствовали созданию философских школ. Так известный древнегреческий философ и математик Пифагор (570-490 г. до н.э.) основал религиозно-философскую школу пифагорейцев. Он связывал сущность мира с соотношениями между числами. Пифагор считал, что Земля шарообразна и находится в центре, а Солнце, Луна и планеты вращаются вокруг неё.
2), в котором год состоял из 12 месяцев, а месяц из 30 дней с добавочными 5 днями. Впоследствии этот календарь был положен в основу юлианского календаря, созданного в эпоху Древнего Рима.
Египтяне установили продолжительность года и создали систему летоисчисления.
…«Мир не только сфера, — говорит Платон. — Но сфера эта совершенна; Творец позаботился о том, чтобы поверхность ее была абсолютно гладкой, и это не без причин…»…
Длительные наблюдения светил помогли создать календарь, но привели к вопросу, который долгое время не находил ответа, что же находится в центре Земля или Солнце? Вопрос повис на многие столетия.
К VI в. до н.э. развитие культуры и науки в Европе способствовали созданию философских школ. Так известный древнегреческий философ и математик Пифагор (570-490 г. до н.э.) основал религиозно-философскую школу пифагорейцев. Он связывал сущность мира с соотношениями между числами. Пифагор считал, что Земля шарообразна и находится в центре, а Солнце, Луна и планеты вращаются вокруг неё. Т.е. он был приверженцем геоцентрической системы мира.
Вопросов, которые бы решала сферическая астрономия очень много, помимо центра мира, неразрешимым вопросом было узнать расстояния до этих светил. Аристарх Самосский (310-230 гг. до н.э.) внёс огромный вклад в науку, он первый, кто задался вопросом о размерах и расстоянии до Луны и Солнца. Из всех сочинений Аристарха Самосского до нас дошло только одно, «О величинах и расстояниях Солнца и Луны». Поставив перед собой сложные задачи, он сам пытался их разрешить. К тому времени уже было представление о том, что Луна вращается вокруг Земли, во время затмений Луна заходит в тень Земли. Аристарх в доказательство своих теорий пользовался геометрическими теоремами, а условие теорем называл гипотезами.
В эпоху средневековья с рассветом культуры ислама, на востоке происходит большой научный подъём. Правители халифата были образованными людьми, и они способствовали развитию науки и образования для поддержания и развитости культуры в обществе.
Т.е. он был приверженцем геоцентрической системы мира.
Вопросов, которые бы решала сферическая астрономия очень много, помимо центра мира, неразрешимым вопросом было узнать расстояния до этих светил. Аристарх Самосский (310-230 гг. до н.э.) внёс огромный вклад в науку, он первый, кто задался вопросом о размерах и расстоянии до Луны и Солнца. Из всех сочинений Аристарха Самосского до нас дошло только одно, «О величинах и расстояниях Солнца и Луны». Поставив перед собой сложные задачи, он сам пытался их разрешить. К тому времени уже было представление о том, что Луна вращается вокруг Земли, во время затмений Луна заходит в тень Земли. Аристарх в доказательство своих теорий пользовался геометрическими теоремами, а условие теорем называл гипотезами.
В эпоху средневековья с рассветом культуры ислама, на востоке происходит большой научный подъём. Правители халифата были образованными людьми, и они способствовали развитию науки и образования для поддержания и развитости культуры в обществе. Астрономия и медицина были приоритетными науками. Вначале IX в. Аль-Мамун создал в Багдаде «Дом Мудрости» в котором находилась огромная библиотека и обсерватория. Он был похож на созданный в Александрии «Музей», который так же является прообразом «Академии Наук». Там учёные разных национальностей и конфессий занимались изучением древних сочинений – философии, астрономии, медицины, а так же занимались переводом литературы на арабский язык. Для решения сферических треугольников в IX-X веках исламскими математиками и астрономами был создан математический аппарат – сферическая тригонометрия — и инструмент, моделирующий преобразование координат – астролябия. Современной усовершенствованной астролябией является подвижная карта неба.
Классик персидской литературы Омар Хайям (1048 – 1122 гг. н.э.), автор знаменитых четверостиший – рубай, был астрономам. По его предложению был введён на Востоке один из самых точных календарей с високосными годами. Ошибка календаря была ничтожно малой – сутки за 4 500 лет.
Астрономия и медицина были приоритетными науками. Вначале IX в. Аль-Мамун создал в Багдаде «Дом Мудрости» в котором находилась огромная библиотека и обсерватория. Он был похож на созданный в Александрии «Музей», который так же является прообразом «Академии Наук». Там учёные разных национальностей и конфессий занимались изучением древних сочинений – философии, астрономии, медицины, а так же занимались переводом литературы на арабский язык. Для решения сферических треугольников в IX-X веках исламскими математиками и астрономами был создан математический аппарат – сферическая тригонометрия — и инструмент, моделирующий преобразование координат – астролябия. Современной усовершенствованной астролябией является подвижная карта неба.
Классик персидской литературы Омар Хайям (1048 – 1122 гг. н.э.), автор знаменитых четверостиший – рубай, был астрономам. По его предложению был введён на Востоке один из самых точных календарей с високосными годами. Ошибка календаря была ничтожно малой – сутки за 4 500 лет. Внук Тимура Улугбек (1394-1449 гг. н.э.) в 15 лет стал правителем Самарканда и прилегавших областей. При нём были сооружены грандиозные здания учебных заведений (Медресе). Он, с раннего детства пользуясь огромной библиотекой своего деда для самообразования, и оказался просвещённым правителем. В построенных в 1420 г. зданиях Медресе он основал университет, для преподавания в который были приглашены известные учёные, в том числе и астрономы. Через несколько лет, недалеко от Самарканда была создана большая обсерватория «Дворец наук», главным инструментом которой был огромный квадрант (по некоторым сведениям секстант). Часть его находилась в высеченной в скале траншее, а другая часть снаружи. Наземная часть дуги возвышалась над поверхностью земли приблизительно на двадцать метров, а глубина траншеи, в которой расположена сохранившаяся до нашего времени часть дуги (от 57 до 80 ), равна одиннадцати метрам. Квадрант размещался в плоскости меридиана и использовался для наблюдений кульминации и измерении угловых расстояний Солнца, Луны, планет и опорных звёзд.
Внук Тимура Улугбек (1394-1449 гг. н.э.) в 15 лет стал правителем Самарканда и прилегавших областей. При нём были сооружены грандиозные здания учебных заведений (Медресе). Он, с раннего детства пользуясь огромной библиотекой своего деда для самообразования, и оказался просвещённым правителем. В построенных в 1420 г. зданиях Медресе он основал университет, для преподавания в который были приглашены известные учёные, в том числе и астрономы. Через несколько лет, недалеко от Самарканда была создана большая обсерватория «Дворец наук», главным инструментом которой был огромный квадрант (по некоторым сведениям секстант). Часть его находилась в высеченной в скале траншее, а другая часть снаружи. Наземная часть дуги возвышалась над поверхностью земли приблизительно на двадцать метров, а глубина траншеи, в которой расположена сохранившаяся до нашего времени часть дуги (от 57 до 80 ), равна одиннадцати метрам. Квадрант размещался в плоскости меридиана и использовался для наблюдений кульминации и измерении угловых расстояний Солнца, Луны, планет и опорных звёзд. Точность наблюдений доходила до 1 После восьми лет наблюдений Улугбек составил каталог более 1000 звёзд, 700 попали в него впервые.
Знаменитый датский астроном Тихо Браге (1546-1601 гг. н.э.)– был искуснейшим наблюдателем дотелескопического периода. Каждую ясную ночь он проводил наблюдения, и это позволило ему составить очень точный звёздный каталог и собрать обширные данные наблюдений планеты Марс. Как лучший наблюдатель дотелескопической эры Тихо Браге достиг необходимой точности для обнаружения строгих закономерностей в движении планет.
Точность наблюдений доходила до 1 После восьми лет наблюдений Улугбек составил каталог более 1000 звёзд, 700 попали в него впервые.
Знаменитый датский астроном Тихо Браге (1546-1601 гг. н.э.)– был искуснейшим наблюдателем дотелескопического периода. Каждую ясную ночь он проводил наблюдения, и это позволило ему составить очень точный звёздный каталог и собрать обширные данные наблюдений планеты Марс. Как лучший наблюдатель дотелескопической эры Тихо Браге достиг необходимой точности для обнаружения строгих закономерностей в движении планет.
 Хорошо ли вы знаете электричество и магнетизм? Знакомы ли с законами Ома и Ньютона? Чем отличаются электроны от протонов? Ответы на эти и многие другие вопросы помогут найти тесты по физике!
Хорошо ли вы знаете электричество и магнетизм? Знакомы ли с законами Ома и Ньютона? Чем отличаются электроны от протонов? Ответы на эти и многие другие вопросы помогут найти тесты по физике! Давление
Давление  A
A джоуль на килограмм на кельвин
джоуль на килограмм на кельвин Думаете, черные дыры изучаются только в астрономии? Это не так — есть целая ветвь физики, изучающая материю, энергию и движение небесных тел. Среди наук математика, вероятно, соперничает с физикой в качестве предпосылки для понимания любой другой области. (И да, математика считается наукой!)
Думаете, черные дыры изучаются только в астрономии? Это не так — есть целая ветвь физики, изучающая материю, энергию и движение небесных тел. Среди наук математика, вероятно, соперничает с физикой в качестве предпосылки для понимания любой другой области. (И да, математика считается наукой!) Противоположным качеством является проводимость, то есть легкость прохождения тока.
Противоположным качеством является проводимость, то есть легкость прохождения тока.

 Технически, откровение Архимеда было больше связано с перемещением, но эта концепция тесно связана с плавучестью. И золото, и серебро слишком тяжелы, чтобы удержаться на плаву, но степень вытеснения ими воды различна, поэтому у Архимеда была точка отсчета для измерения того, сколько воды должна вытеснить корона.
Технически, откровение Архимеда было больше связано с перемещением, но эта концепция тесно связана с плавучестью. И золото, и серебро слишком тяжелы, чтобы удержаться на плаву, но степень вытеснения ими воды различна, поэтому у Архимеда была точка отсчета для измерения того, сколько воды должна вытеснить корона.
 Амперы — это единицы измерения электрического тока, а мы даже не говорили о джоулях или кулонах. Электричество — сложный предмет, несмотря на то, что мы пользуемся им ежедневно. Если вы действительно хотите понять это, вам лучше пройти курс электротехники, чем уроки физики.
Амперы — это единицы измерения электрического тока, а мы даже не говорили о джоулях или кулонах. Электричество — сложный предмет, несмотря на то, что мы пользуемся им ежедневно. Если вы действительно хотите понять это, вам лучше пройти курс электротехники, чем уроки физики.
 (Поворачивайте ложку вперед и назад, чтобы сразу увидеть это).
(Поворачивайте ложку вперед и назад, чтобы сразу увидеть это).






 Вот в чем фишка: физики знают, что это универсальный закон, но до сих пор не знают, почему масса создает гравитацию.
Вот в чем фишка: физики знают, что это универсальный закон, но до сих пор не знают, почему масса создает гравитацию.
 Но Джеймс Клерк Максвелл и Майкл Фарадей также были великими в этой области.
Но Джеймс Клерк Максвелл и Майкл Фарадей также были великими в этой области. Вот почему ее иногда называют «фундаментальной наукой». Но цикл Кребса, о том, как азот переходит из земной почвы в атмосферу и обратно, обычно изучается на уроках биологии.
Вот почему ее иногда называют «фундаментальной наукой». Но цикл Кребса, о том, как азот переходит из земной почвы в атмосферу и обратно, обычно изучается на уроках биологии. Они объясняют энергию, инерцию и энтропию.
Они объясняют энергию, инерцию и энтропию. Длины волн между ними по порядку: оранжевый, желтый, зеленый, синий и индиго.
Длины волн между ними по порядку: оранжевый, желтый, зеленый, синий и индиго. Почему эта сумма настолько особенная, что ее назвали в честь сэра Исаака Ньютона? Он представляет собой силу, которая заставила бы объект массой 1 кг ускориться на 1 метр в секунду в квадрате.
Почему эта сумма настолько особенная, что ее назвали в честь сэра Исаака Ньютона? Он представляет собой силу, которая заставила бы объект массой 1 кг ускориться на 1 метр в секунду в квадрате. Центростремительная сила противоположна и заставляет материю двигаться к центру вращения.
Центростремительная сила противоположна и заставляет материю двигаться к центру вращения.
 В химии важно точно измерять массу веществ, вступающих в реакцию и получающихся в результате нее. По определению моль является единицей количества вещества в СИ. Один моль содержит точно 6,02214076×10²³ элементарных частиц. Это значение численно равно константе Авогадро NA, если выражено в единицах моль⁻¹ и называется числом Авогадро. Количество вещества (символ n) системы является мерой количества структурных элементов. Структурным элементом может быть атом, молекула, ион, электрон или любая частица или группа частиц.
В химии важно точно измерять массу веществ, вступающих в реакцию и получающихся в результате нее. По определению моль является единицей количества вещества в СИ. Один моль содержит точно 6,02214076×10²³ элементарных частиц. Это значение численно равно константе Авогадро NA, если выражено в единицах моль⁻¹ и называется числом Авогадро. Количество вещества (символ n) системы является мерой количества структурных элементов. Структурным элементом может быть атом, молекула, ион, электрон или любая частица или группа частиц. Один моль чистого углерода-12 равен точно 12 г.
Один моль чистого углерода-12 равен точно 12 г. Молярная масса соединений равна сумме молярных масс элементов, из которых состоит соединение, с учетом количества атомов в соединении. Например, молярная масса воды (H₂O) приблизительно равна 1 × 2 + 16 = 18 г/моль.
Молярная масса соединений равна сумме молярных масс элементов, из которых состоит соединение, с учетом количества атомов в соединении. Например, молярная масса воды (H₂O) приблизительно равна 1 × 2 + 16 = 18 г/моль.
 Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
 », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
 По этой причине относительная атомная масса углерода и составляет 12 единиц.
По этой причине относительная атомная масса углерода и составляет 12 единиц. 
 Будут ли встречаться другие химические элементы с «не округленными» массами? Сомневаюсь.
Будут ли встречаться другие химические элементы с «не округленными» массами? Сомневаюсь. 
 68
68 белый порошок 55,12 фунта мешок Винтерсан Кемикал
белый порошок 55,12 фунта мешок Винтерсан Кемикал 
 Здесь это делается путем обработки оксида меди разбавленной серной кислотой. Кроме того, еще одним методом производства является медленное выщелачивание низкосортной медной руды на воздухе. Можно использовать бактерии для катализа этого процесса.
Здесь это делается путем обработки оксида меди разбавленной серной кислотой. Кроме того, еще одним методом производства является медленное выщелачивание низкосортной медной руды на воздухе. Можно использовать бактерии для катализа этого процесса. д.
д.


 Поэтому ставим 9 сверху и 81 снизу вот так:
Поэтому ставим 9 сверху и 81 снизу вот так:
 Мы также рассмотрим различные методы вычисления квадратного корня из 85 (как с компьютером/калькулятором, так и без него).
Мы также рассмотрим различные методы вычисления квадратного корня из 85 (как с компьютером/калькулятором, так и без него).
 На большинстве калькуляторов это можно сделать, набрав 85 и нажав клавишу √x. Вы должны получить следующий результат:
На большинстве калькуляторов это можно сделать, набрав 85 и нажав клавишу √x. Вы должны получить следующий результат: Однако мы можем превратить его в приблизительную дробь, используя квадратный корень из 85, округленный до сотых.
Однако мы можем превратить его в приблизительную дробь, используя квадратный корень из 85, округленный до сотых.
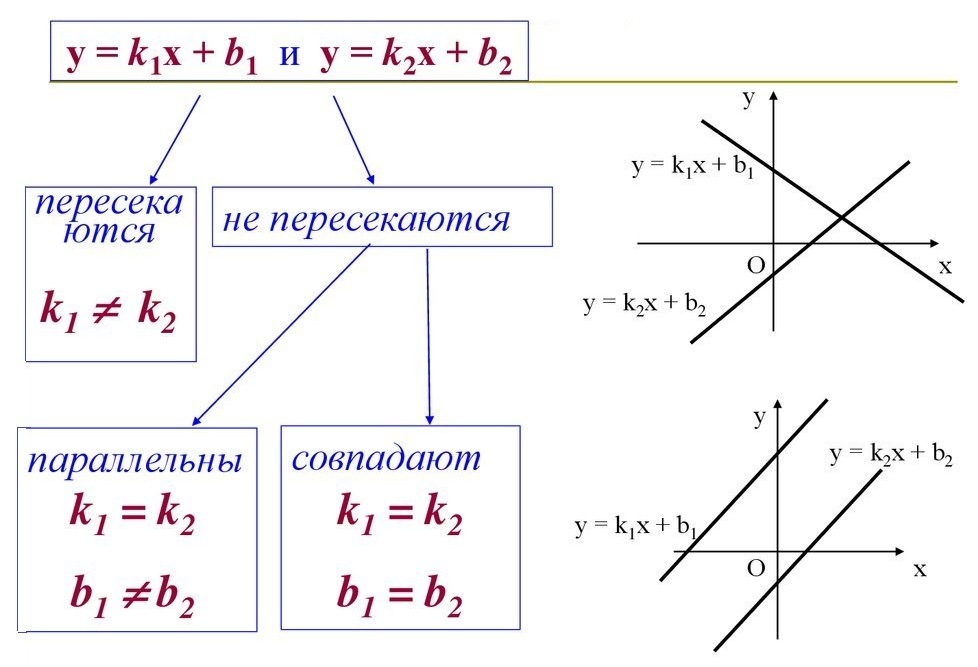
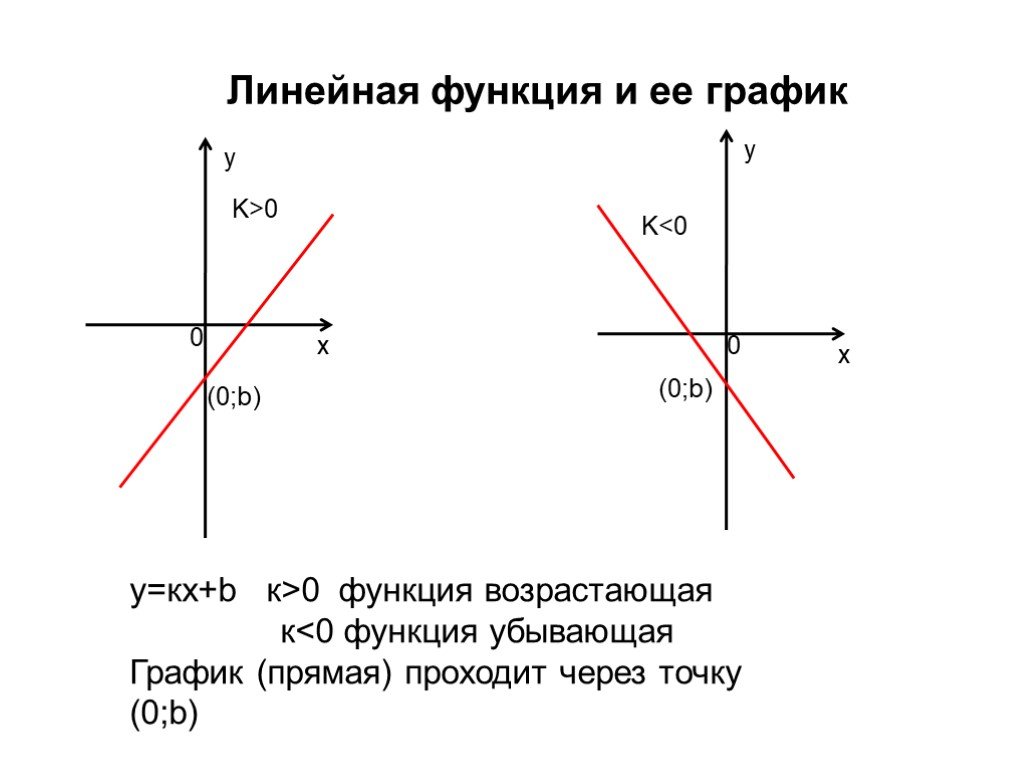
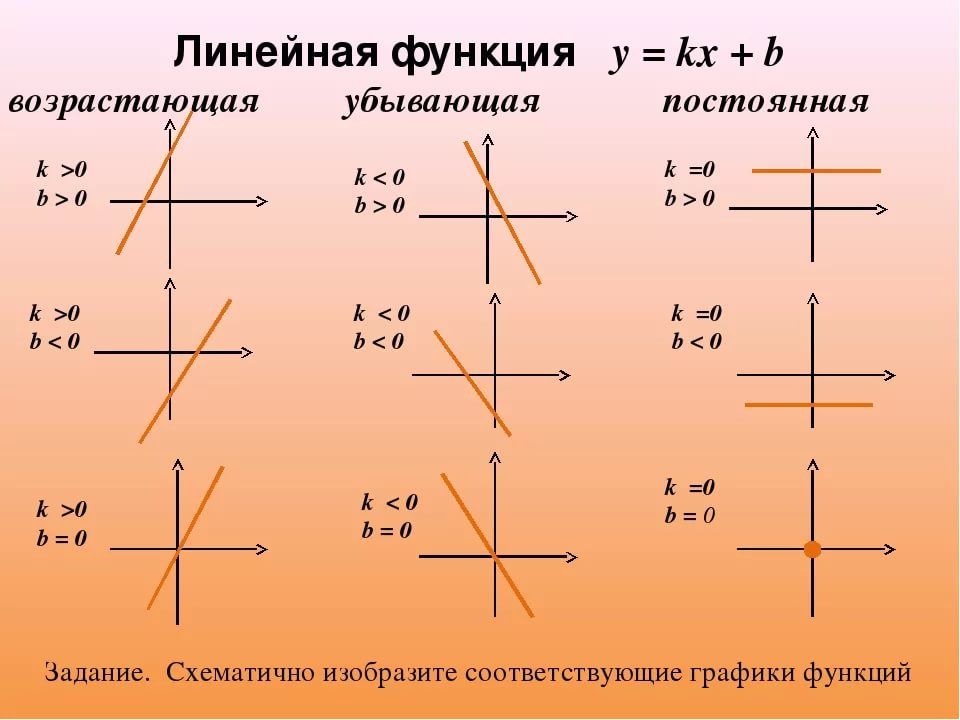
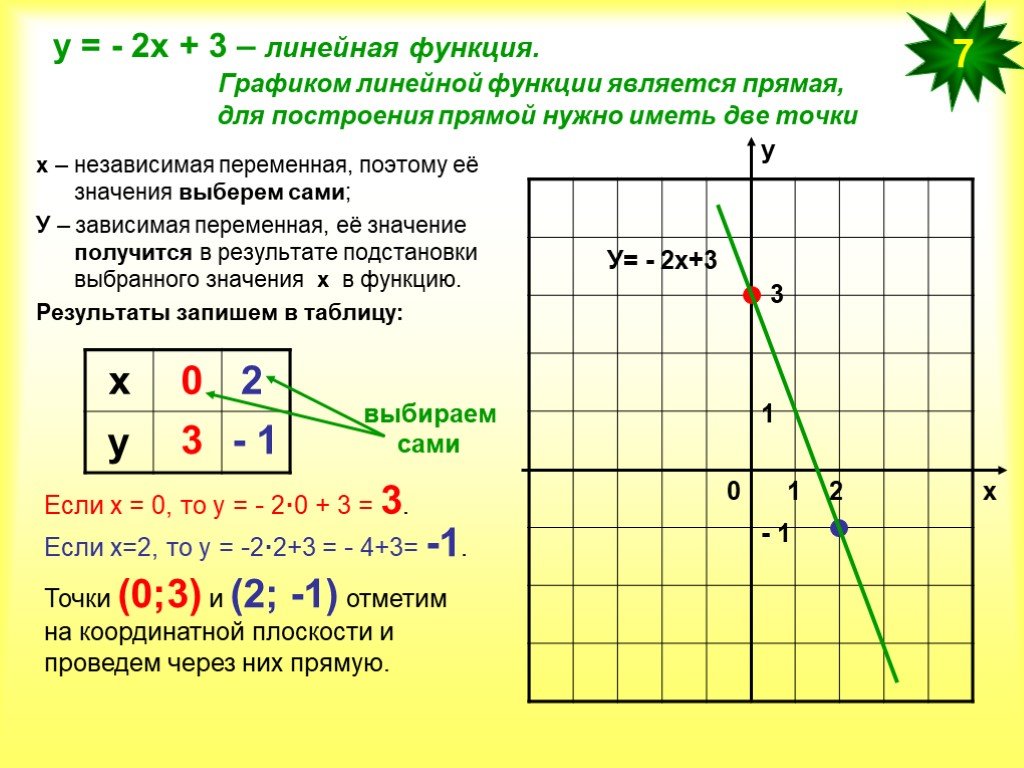
 Чему равен угловой коэффициент прямой y=-2x+3:
Чему равен угловой коэффициент прямой y=-2x+3:
 В Outlook результат формулы рассчитывается только при ее вставке, и получатель сообщения не сможет его изменить.
В Outlook результат формулы рассчитывается только при ее вставке, и получатель сообщения не сможет его изменить. Чтобы выделить несколько формул, удерживайте нажатой клавишу CTRL.
Чтобы выделить несколько формул, удерживайте нажатой клавишу CTRL.


 Всегда возвращает значение 0.
Всегда возвращает значение 0.

 Если хотя бы один из них является истинным, возвращает значение 1. Если оба аргумента являются ложными, возвращает значение 0. В основном используется в функции IF.
Если хотя бы один из них является истинным, возвращает значение 1. Если оба аргумента являются ложными, возвращает значение 0. В основном используется в функции IF. Округляет первый аргумент до заданного вторым аргументом количества десятичных разрядов. Если второй аргумент больше нуля (0), первый аргумент округляется до указанного количества десятичных разрядов (в меньшую сторону). Если второй аргумент равен нулю (0), первый аргумент округляется до ближайшего целого числа (в меньшую сторону). Если второй аргумент меньше нуля, первый аргумент округляется слева от десятичной запятой (в меньшую сторону).
Округляет первый аргумент до заданного вторым аргументом количества десятичных разрядов. Если второй аргумент больше нуля (0), первый аргумент округляется до указанного количества десятичных разрядов (в меньшую сторону). Если второй аргумент равен нулю (0), первый аргумент округляется до ближайшего целого числа (в меньшую сторону). Если второй аргумент меньше нуля, первый аргумент округляется слева от десятичной запятой (в меньшую сторону). Сравнивает указанный в скобках элемент с нулем (0). Если этот элемент больше нуля, возвращает значение 1; если равен нулю — 0; если меньше нуля — -1.
Сравнивает указанный в скобках элемент с нулем (0). Если этот элемент больше нуля, возвращает значение 1; если равен нулю — 0; если меньше нуля — -1. Если аргумент является истинным, возвращает значение 1, если ложным — 0. В основном используется в функции IF.
Если аргумент является истинным, возвращает значение 1, если ложным — 0. В основном используется в функции IF. Если ячейка является частью ссылки, она игнорируется.
Если ячейка является частью ссылки, она игнорируется. Здесь буква соответствует столбцу, а цифра — строке ячейки. Первый столбец таблицы обозначен буквой «A», а первая строка — цифрой «1». Приведенная ниже таблица содержит примеры записи ссылок в таком формате.
Здесь буква соответствует столбцу, а цифра — строке ячейки. Первый столбец таблицы обозначен буквой «A», а первая строка — цифрой «1». Приведенная ниже таблица содержит примеры записи ссылок в таком формате. 08.2015
08.2015
 Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
Опускать его, как принято во время письменных арифметических вычислений, недопустимо. То есть запись (2+3)5 Excel не поймет.
 Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь.
Те же манипуляции необходимо произвести для всех ячеек. Как в Excel задать формулу для столбца: копируем формулу из первой ячейки в другие строки. Относительные ссылки – в помощь. Это диапазон D2:D9
Это диапазон D2:D9 100%. Все правильно.
100%. Все правильно.





 Они позволяют вам ввести одну формулу в одну ячейку, а затем эта формула автоматически расширится до остальной части столбца сама по себе. Нет необходимости использовать команды «Заполнить» или «Копировать». Это может невероятно сэкономить время, особенно если у вас много строк. И то же самое происходит, когда вы меняете формулу; изменение также распространится на остальную часть вычисляемого столбца.
Они позволяют вам ввести одну формулу в одну ячейку, а затем эта формула автоматически расширится до остальной части столбца сама по себе. Нет необходимости использовать команды «Заполнить» или «Копировать». Это может невероятно сэкономить время, особенно если у вас много строк. И то же самое происходит, когда вы меняете формулу; изменение также распространится на остальную часть вычисляемого столбца. Это называется формулой структурированной ссылки , которая уникальна для таблиц Excel. Формат структурированной ссылки позволяет таблице использовать одну и ту же формулу для каждой строки. Обычная формула Excel для этого будет выглядеть так: =СУММ(B2:C2) , которую затем нужно будет скопировать или заполнить до остальных ячеек в столбце
Это называется формулой структурированной ссылки , которая уникальна для таблиц Excel. Формат структурированной ссылки позволяет таблице использовать одну и ту же формулу для каждой строки. Обычная формула Excel для этого будет выглядеть так: =СУММ(B2:C2) , которую затем нужно будет скопировать или заполнить до остальных ячеек в столбце Как правило, это не рекомендуется, поскольку это может помешать вашему столбцу автоматически обновляться в будущем, поскольку он не будет знать, какую формулу расширять при добавлении новых строк.
Как правило, это не рекомендуется, поскольку это может помешать вашему столбцу автоматически обновляться в будущем, поскольку он не будет знать, какую формулу расширять при добавлении новых строк.


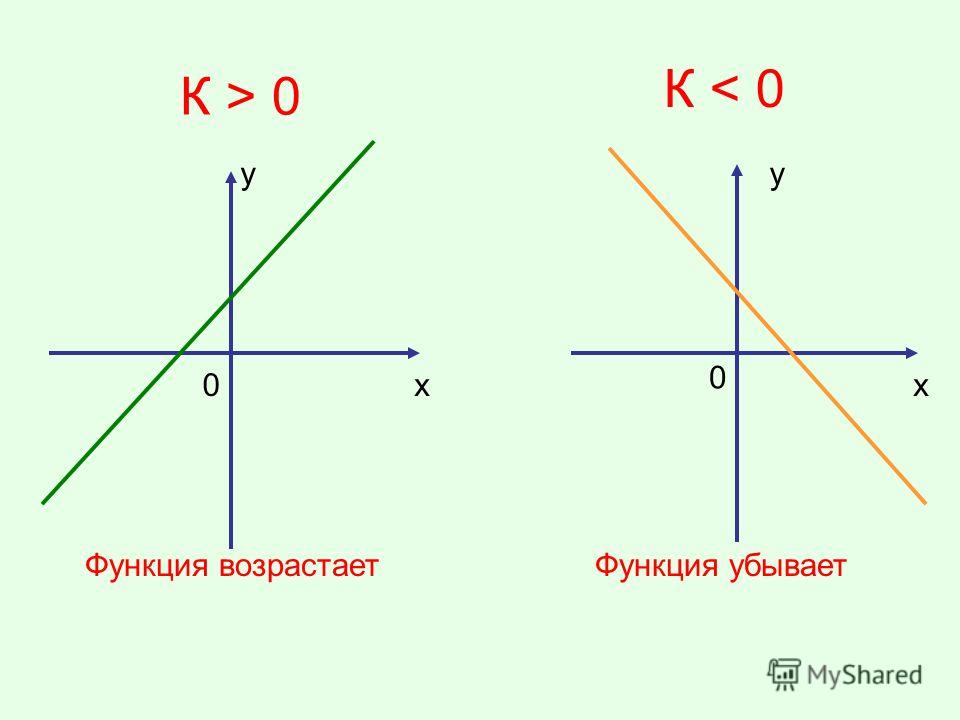
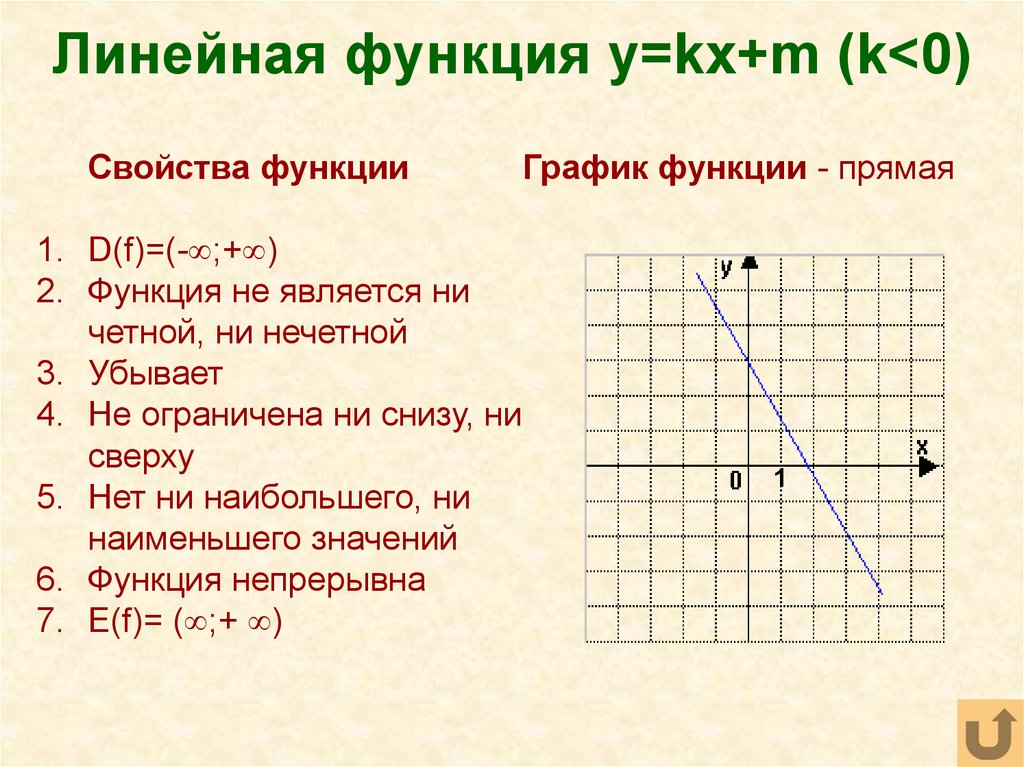
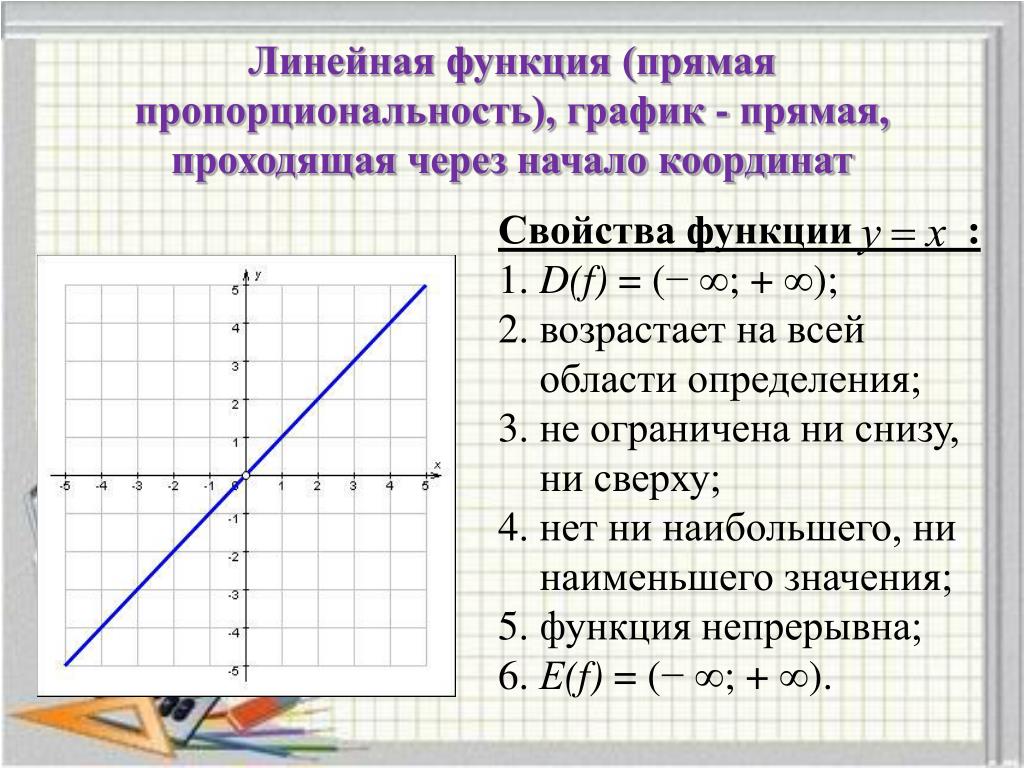
 Поэтому график зрительно «идет в гору».
Поэтому график зрительно «идет в гору».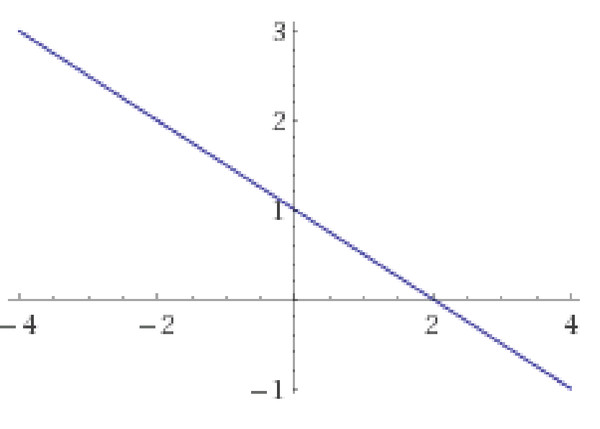


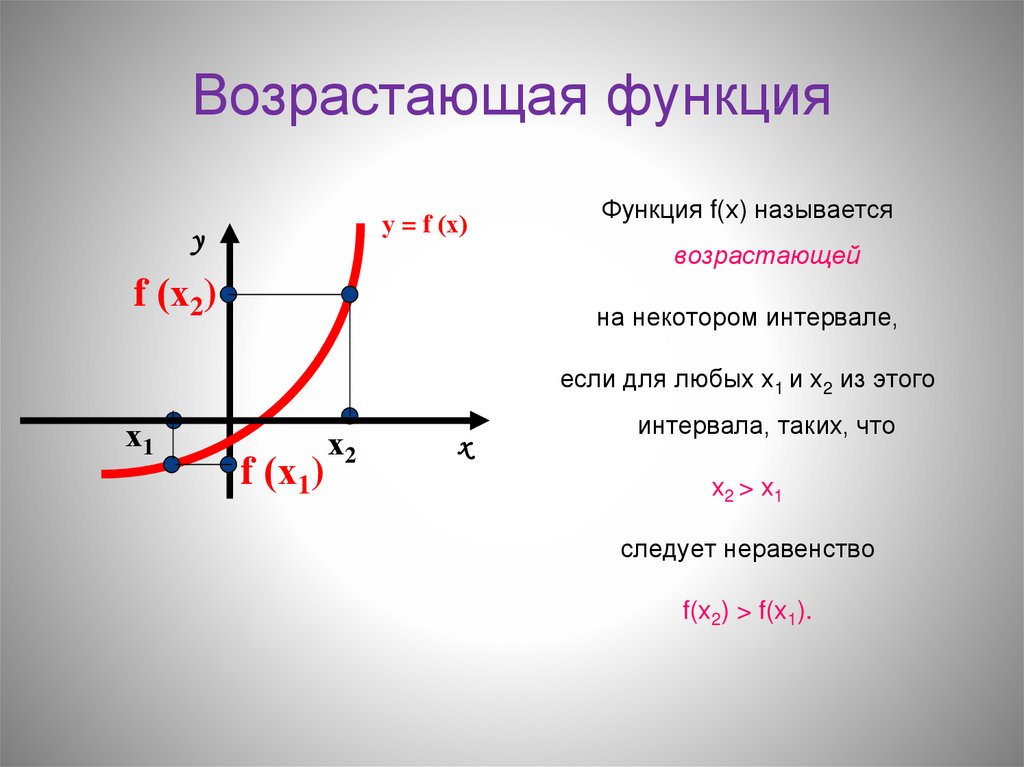
 Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения?
Но как доказать по формуле,
что функция « y = 1 − 3x » убывает на всей области определения? При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.
При
умножении неравенства на отрицательное число знак неравенства поменяется на
противоположный.
 Вместо
« x »
подставим « x1 » и « x2 ».
Вместо
« x »
подставим « x1 » и « x2 ».


 Значит, (x2-x1)(x2+x1+4)<0 и f(x2)<f(x1). Отсюда следует, что функция функция f(x)=x²+4x убывает на промежутке (-∞;-2).
Значит, (x2-x1)(x2+x1+4)<0 и f(x2)<f(x1). Отсюда следует, что функция функция f(x)=x²+4x убывает на промежутке (-∞;-2).


 В этой стратегии трейдеры используют модель нисходящего треугольника, чтобы предвидеть потенциальные прорывы, а индикаторы скользящих средних инициируют сигнал для открытия сделки.
В этой стратегии трейдеры используют модель нисходящего треугольника, чтобы предвидеть потенциальные прорывы, а индикаторы скользящих средних инициируют сигнал для открытия сделки.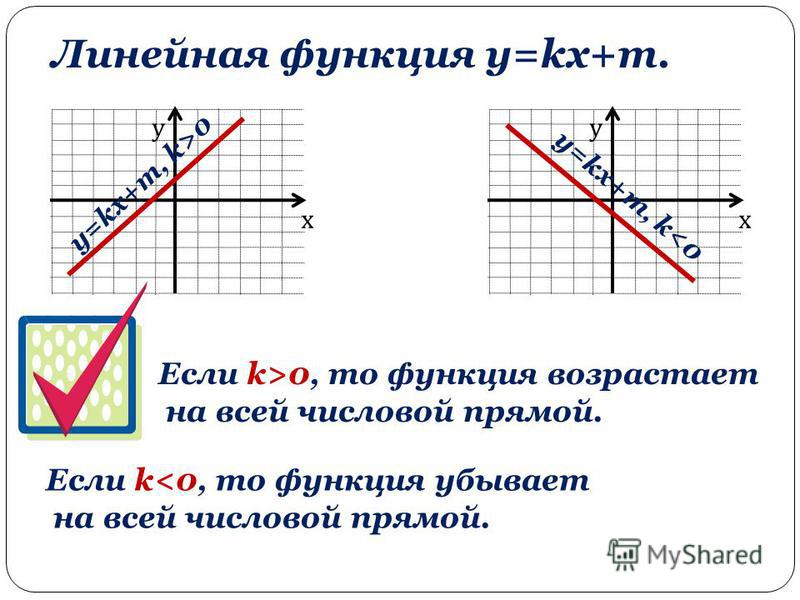 Нисходящий треугольник имеет горизонтальную нижнюю линию тренда и нисходящую верхнюю линию тренда. Восходящий треугольник имеет горизонтальную линию тренда на максимумах и восходящую линию тренда на минимумах.
Нисходящий треугольник имеет горизонтальную нижнюю линию тренда и нисходящую верхнюю линию тренда. Восходящий треугольник имеет горизонтальную линию тренда на максимумах и восходящую линию тренда на минимумах. Чем чаще цена касается уровней поддержки и сопротивления, тем надежнее модель графика.
Чем чаще цена касается уровней поддержки и сопротивления, тем надежнее модель графика. 

 19
19

 Председатель жюри конкурса, доктор филологических наук
Дмитрий Ермолович посвятил свою лекцию «Теория Комиссарова для
“чайников”» 95-летию со дня рождения одного из основателей
переводоведения. Директор Санкт-Петербургской Высшей школы
перевода Ирина Алексеева рассказала о том, как превратить знания
в личный стандарт качества переводчика. Переводчики-члены AIIC
Екатерина Шутова и Джулия Погер провели мастер-классы,
посвященные «боевому комплекту» умений и навыков устного
переводчика и использованию рисунков при ведении записей для
последовательного перевода. Секретами мастерства также поделились
доцент МГЛУ и член жюри конкурса Ирина Зубанова, мастер COSINES
Pi Борис Погодин, переводчик Е. М. Примакова и Б. Н. Ельцина
Виктор Немчинов, переводчик Президента РФ и генеральный консул РФ
в Касабланке Андрей Цыбенко, член команды переводчиков Президента
РФ Кирилл Казаков, переводчик посла Франции в РФ Ирэн Зайончек,
старший переводчик BCG Арсен Лазурский, эксперты COSINES Pi
Михаил Перегудов и Максим Гладков, ведущий переводчик института
лингвистики РГГУ Михаил Стровский и редактор МИА «Россия сегодня»
Ли Ялун.
Председатель жюри конкурса, доктор филологических наук
Дмитрий Ермолович посвятил свою лекцию «Теория Комиссарова для
“чайников”» 95-летию со дня рождения одного из основателей
переводоведения. Директор Санкт-Петербургской Высшей школы
перевода Ирина Алексеева рассказала о том, как превратить знания
в личный стандарт качества переводчика. Переводчики-члены AIIC
Екатерина Шутова и Джулия Погер провели мастер-классы,
посвященные «боевому комплекту» умений и навыков устного
переводчика и использованию рисунков при ведении записей для
последовательного перевода. Секретами мастерства также поделились
доцент МГЛУ и член жюри конкурса Ирина Зубанова, мастер COSINES
Pi Борис Погодин, переводчик Е. М. Примакова и Б. Н. Ельцина
Виктор Немчинов, переводчик Президента РФ и генеральный консул РФ
в Касабланке Андрей Цыбенко, член команды переводчиков Президента
РФ Кирилл Казаков, переводчик посла Франции в РФ Ирэн Зайончек,
старший переводчик BCG Арсен Лазурский, эксперты COSINES Pi
Михаил Перегудов и Максим Гладков, ведущий переводчик института
лингвистики РГГУ Михаил Стровский и редактор МИА «Россия сегодня»
Ли Ялун. Параллельно конкурсу устного перевода и мастер-классам
прошла конференция, где обсуждались вопросы профессионального
развития переводчиков, теория и практика перевода, специфика
перевода в различных сферах. Отдельная секция была посвящена
стандартам и нюансам юридического перевода.
Параллельно конкурсу устного перевода и мастер-классам
прошла конференция, где обсуждались вопросы профессионального
развития переводчиков, теория и практика перевода, специфика
перевода в различных сферах. Отдельная секция была посвящена
стандартам и нюансам юридического перевода. Садовничий: «Численность иранских студентов в российских вузах увеличилась»
Садовничий: «Численность иранских студентов в российских вузах увеличилась» Академик К.В. Анохин о программе «Очевидное — невероятное»
Академик К.В. Анохин о программе «Очевидное — невероятное»
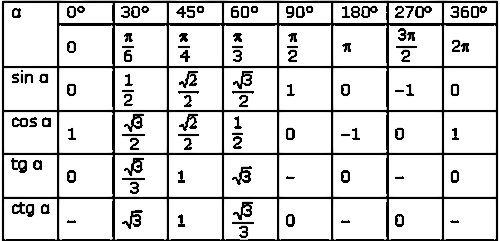 Вопрос в том, как мне узнать, как найти число, которое выходит, когда я знаю, что входит. Для косинуса числа (угла) мы можем «нарисовать» треугольник, как показано ниже, где угол при $A$ равен вход. Вызовите вход $A$. Тогда мы имеем, что $\cos(A) = \frac{h}{b}$. Так что в определенном смысле выход задается двумя числами (гипотенуза) и (прилегающее), но у нас просто один угол — один вход.
Вопрос в том, как мне узнать, как найти число, которое выходит, когда я знаю, что входит. Для косинуса числа (угла) мы можем «нарисовать» треугольник, как показано ниже, где угол при $A$ равен вход. Вызовите вход $A$. Тогда мы имеем, что $\cos(A) = \frac{h}{b}$. Так что в определенном смысле выход задается двумя числами (гипотенуза) и (прилегающее), но у нас просто один угол — один вход.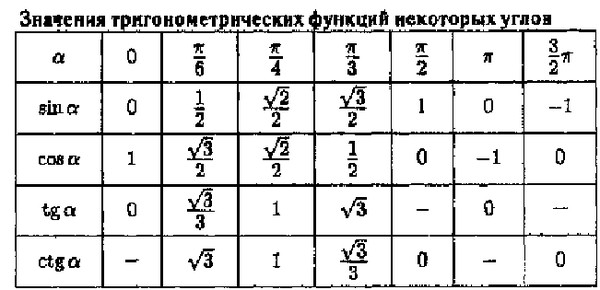 Это означает, что если бы я нарисовал изображение выше с помощью $\theta=\pi$, линия была бы горизонтальной, одна точка была бы связана с крайней левой точкой окружности, а другая — с радиусом. $\sin\theta$ равно нулю, так как высота (y) имеет нулевую длину. Однако $\cos \theta$ равно -1, потому что имеет отрицательную длину 1.
Это означает, что если бы я нарисовал изображение выше с помощью $\theta=\pi$, линия была бы горизонтальной, одна точка была бы связана с крайней левой точкой окружности, а другая — с радиусом. $\sin\theta$ равно нулю, так как высота (y) имеет нулевую длину. Однако $\cos \theta$ равно -1, потому что имеет отрицательную длину 1.