как найти общее решение системы линейных уравнений
Вы искали как найти общее решение системы линейных уравнений? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и найти общее решение неоднородной системы линейных уравнений, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как найти общее решение системы линейных уравнений».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как найти общее решение системы линейных уравнений,найти общее решение неоднородной системы линейных уравнений,найти общее решение системы линейных уравнений найти частное решение,общее и частное решение системы линейных уравнений,общие и частные решения отличаются по,системы линейных уравнений частное и общее решение,слау примеры решения,частное и общее решение системы линейных уравнений. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как найти общее решение системы линейных уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти общее решение системы линейных уравнений найти частное решение).
Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как найти общее решение системы линейных уравнений,найти общее решение неоднородной системы линейных уравнений,найти общее решение системы линейных уравнений найти частное решение,общее и частное решение системы линейных уравнений,общие и частные решения отличаются по,системы линейных уравнений частное и общее решение,слау примеры решения,частное и общее решение системы линейных уравнений. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как найти общее решение системы линейных уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, найти общее решение системы линейных уравнений найти частное решение).
Где можно решить любую задачу по математике, а так же как найти общее решение системы линейных уравнений Онлайн?
Решить задачу как найти общее решение системы линейных уравнений вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
2.3.6. Примеры решения задач по теме «Системы уравнений общего вида. Мет
Задача 1.
Указать базисный минор матрицы
Указание
Определите вначале ранг матрицы А, а затем найдите ненулевой минор, порядок которого равен R(A).
Решение
Определим R(A). Вторая и четвертая строки А равны, поэтому после вычитания из 4-й строки 2-й получаем:
Вычислим минор полученной матрицы, составленный из первых трех столбцов:
Таким образом, найден минор максимально возможного (3-го) порядка, не равный нулю. Следовательно, ранг матрицы А равен рангу преобразованной матрицы, то есть равен 3, а рассмотренный минор является базисным.
Ответ:
Задача 2.
Определить количество решений системы линейных уравнений
.
Указание
Сравните ранги матрицы системы и расширенной матрицы.
Решение
Сравним ранги матрицы системы
И расширенной матрицы
.
Для удобства вычислений будем искать ранг матрицы А1, отделив ее последний столбец вертикальной чертой. Тогда столбцы, стоящие слева от черты, образуют матрицу А, и мы одновременно найдем ранги обеих матриц.
А1 ~ .
Вычтем из второй строки удвоенную первую, а из третьей – первую, умноженную на 3:
А1 ~ ~ .
Таким образом, R(A) = 2, a R(A1) = 3, следовательно, система не имеет решений.
Ответ: система несовместна.
Задача 3.
Найти общее решение линейной системы
.
Указание
Убедившись в том, что система совместна, определите базисные и свободные неизвестные и выразите базисные неизвестные через свободные.
Решение
Найдем R(A) и R(A1):
Итак, R = R(A) = R(A1) = 2, а число неизвестных П = 5. Следовательно, R < N, и система имеет бесконечно много решений (совместна, но не определена).
Число базисных неизвестных равно R, то есть двум. Выберем в качестве базисных неизвестных Х1 и Х2, коэффициенты при которых входят в базисный минор преобразованной матрицы А: .
Соответственно Х3, Х4, Х5 – свободные неизвестные.
Запишем систему, равносильную исходной, коэффициентами в которой являются элементы полученной матрицы:
И выразим базисные неизвестные через свободные:
.
Получено общее решение системы. Одно из частных решений можно найти, положив все свободные неизвестные равными нулю: Х3 = Х4 = Х5 = 0. Тогда
Ответ:
Задача 4.
Найти общее решение системы, выразив в ответе первые неизвестные через последние:
Указание
Приведите расширенную матрицу к виду
Решение
Минор, состоящий из первых трех столбцов полученной матрицы,
Поэтому R(A) = R(A1) = 3, выбранный минор является базисным, а Х1, Х2, Х3, коэффициенты при которых составляют базисный минор, – базисными неизвестными. Тогда свободное неизвестное – Х4, и система, равносильная исходной, имеет вид:
Откуда
Ответ:
Задача 5.
Найти фундаментальную систему решений однородной линейной системы
Указание
Количество решений, образующих фундаментальную систему, равно числу
Свободных неизвестных. Задайте свободным неизвестным значения 1,0,0; 0,1,0; 0,0,1 и вычислите соответствующие значения базисных неизвестных.
Решение
Количество решений, образующих фундаментальную систему, равно числу Свободных неизвестных. |
Матрица А1 отличается от матрицы А только добавлением нулевого столбца свободных членов, поэтому все ее ненулевые миноры являются минорами матрицы А, то есть R(A) = R(A1). Найдем R(A):
Выберем в качестве базисного минора
Значит, R(A) = 2. Пусть Х4, Х5 – базисные неизвестные, Х1, Х2, Х3 – свободные неизвестные. Запишем для них новую систему:
Откуда
Фундаментальная система решений состоит из трех столбцов. Рассмотрим три набора значений свободных неизвестных:
1) Х1 = 1, Х2 = Х3 = 0.
Тогда Х4 = -0,2, Х5 = 1,2, и решение можно записать в виде столбца
2) Х1 = 0, Х2 = 1, Х3 = 0.
При этом Х4 = 1,2, Х5 = 3,8, и следующее решение системы имеет вид
3) Х1 = Х2 = 0, Х3 = 1. Отсюда Х4 = -0,8, Х5 = -0,2, и последний столбец
Фундаментальная система решений, построенная при таком выборе свободных неизвестных, называется Нормальной. Поскольку столбцы свободных неизвестных , , линейно независимы, это гарантирует линейную независимость решений Х1, Х2, Х3. |
Итак, в качестве фундаментальной системы решений можно выбрать
При этом любое решение данной системы имеет вид: Х = с1Х1 + С2Х2 + С3Х3, где С1, С2, С3 – произвольные постоянные. Эта формула задает общее решение системы.
Ответ:
Задача 6.
Составить однородную систему из двух уравнений, для которой столбцы
Образуют фундаментальную систему решений.
Указание
Пусть искомая система имеет вид:
Подставьте вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3 и решите полученную систему уравнений для коэффициентов Aij.
Решение
Существует бесконечно много систем однородных линейных уравнений, для каждой из которых фундаментальная система решений имеет указанный вид. Число уравнений в таких системах может быть различным. При этом можно указать их наименьшее требуемое количество, а увеличивать их число можно неограниченно. |
Определим вначале, из какого наименьшего числа уравнений может состоять такая система.
Число элементов каждого столбца равно пяти, следовательно, в системе пять неизвестных (П = 5). Количество столбцов, составляющих фундаментальную систему, равно трем, то есть N – R = 3, поэтому R = 5 – 3 = 2. Значит, матрица А должна иметь по крайней мере 2 строки. Следовательно, система уравнений с заданной фундаментальной системой решений может состоять из двух и более уравнений.
Пусть искомая система имеет вид:
Подставим вместо Х1, …, Х5 элементы столбцов Х1, Х2, Х3. Получим:
Разобьем полученные 6 уравнений на две системы, одна из которых содержит A1I, а вторая – A2I:
Найдем какое-либо частное решение этой системы. Приведем ее матрицу к треугольному виду:
Откуда
Следовательно,
Выберем А14 = А15 = 4, тогда А11 = 0, А12 = 8, А13 = -4.
2) Так же выглядит общее решение системы для A2I:
Выберем свободные неизвестные так, чтобы получить решение, линейно независимое с предыдущим.
Пусть А24 = 4, А25 = 0, тогда А21 = 5, А22 = 5, А23 = -3.
Итак, используя найденные значения коэффициентов, можно составить линейную однородную систему:
Фундаментальная система решений которой имеет вид, приведенный в условии задачи.
Ответ:
Задача 7.
Найти общее решение неоднородной линейной системы
С помощью фундаментальной системы решений соответствующей однородной системы.
Указание
Убедитесь в том, что система совместна. Затем составьте соответствующую однородную систему и найдите для нее фундаментальную систему решений. Далее используйте то, что общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы.
Решение
Убедимся в том, что система совместна:
Итак, R(A) = R(A1) = 2 – система совместна.
Составим по преобразованной матрице однородную систему:
И найдем для нее фундаментальную систему решений:
Фундаментальная система решений может быть выбрана так:
Общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы. |
Теперь найдем какое-нибудь частное решение неоднородной системы
Положим Х3 = Х4 = Х5 = 0, тогда . Следовательно,
и общее решение системы имеет вид:
Х = с1Х1 + С2Х2 + С3Х3 + Хчастн, где С1, С2, С3 – произвольные постоянные.
Ответ:
Задача 8.
Решить систему методом Гаусса:
.
Указание
Поменяйте местами 1-е и 2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице, а затем исключите Х из второго и третьего уравнений.
Решение
Метод Гаусса заключается в последовательном исключении неизвестных из уравнений системы. Для удобства его применения поменяем местами 1-е и
2-е уравнения, чтобы в первом уравнении коэффициент при Х равнялся единице:
Теперь исключим Х из второго и третьего уравнений. Для этого вычтем из второго уравнения первое, умноженное на 3, а из третьего – первое, умноженное на 2:
Далее можно легко исключить Z из третьего уравнения, если прибавить к нему второе:
Из последнего уравнения получаем, что У = 0. Подставляя это значение в первое и второе уравнения, находим остальные неизвестные: Z = 3, Х = 1.
Ответ: Х = 1, У = 0, Z = 3.
При применении метода Гаусса совсем не обязательно приводить систему к «классическому» треугольному виду: . Достаточно, чтобы матрица коэффициентов, например, системы трех уравнений с тремя неизвестными содержала два нуля в одном столбце и одновременно два нуля в одной строке, причем один из нулей стоял на пересечении этих строки и столбца. |
Задача 9.
Решить систему методом Гаусса:
Указание
Исключите Х2 из 2-го и 4-го уравнений, используя 1-е уравнение, а затем вычтите из 3-го уравнения 2-е, чтобы исключить Х3.
Решение
Исключим Х2 из 2-го и 4-го уравнений. Для этого из 2-го уравнения вычтем 1-е, а к 4-му прибавим 1-е, умноженное на 2:
Вычтем из 3-го уравнения 2-е, чтобы исключить Х3:
Теперь вычтем из 4-го уравнения удвоенное 3-е:
Из последнего уравнения находим . Тогда из 3-го уравнения Х1 = 0, из 2-го , из 1-го Х2 = 2.
Ответ:
| < Предыдущая | Следующая > |
|---|
Как решать однородные слау. Что такое однородная система линейных уравнений? Алгоритм решения систем линейных однородных уравнений
Системы линейных уравнений, у которой все свободные члены равны нулю, называются однородными :
Любая однородная система всегда совместна, поскольку всегда обладает нулевым (тривиальным ) решением. Возникает вопрос, при каких условиях однородная система будет иметь нетривиальное решение.
Теорема 5.2. Однородная система имеет нетривиальное решение тогда и только тогда, когда ранг основной матрицы меньше числа ее неизвестных.
Следствие . Квадратная однородная система имеет нетривиальное решение тогда и только тогда, когда определитель основной матрицы системы не равен нулю.
Пример 5.6. Определить значения параметра l, при которых система имеет нетривиальные решения, и найти эти решения:
Решение . Эта система будет иметь нетривиальное решение тогда, когда определитель основной матрицы равен нулю:
Таким образом, система нетривиальна, когда l=3 или l=2. При l=3 ранг основной матрицы системы равен 1. Тогда оставляя только одно уравнение и полагая, что y =a и z =b , получим x=b-a , т.е.
При l=2 ранг основной матрицы системы равен 2. Тогда, выбирая в качестве базисного минор:
получим упрощенную систему
Отсюда находим, что x=z /4, y=z /2. Полагая z =4a , получим
Множество всех решений однородной системы обладает весьма важным линейным свойством : если столбцы X 1 и X 2 — решения однородной системы AX = 0 , то всякая их линейная комбинация aX 1 + bX 2 также будет решением этой системы . Действительно, поскольку AX 1 = 0 и AX 2 = 0 , то A (aX 1 + bX 2) = aAX 1 + bAX 2 = a · 0 + b · 0 = 0. Именно вследствие этого свойства, если линейная система имеет более одного решения, то этих решений будет бесконечно много.
Линейно независимые столбцы E 1 , E 2 , E k , являющиеся решениями однородной системы, называется фундаментальной системой решений однородной системы линейных уравнений, если общее решение этой системы можно записать в виде линейной комбинации этих столбцов:
Если однородная система имеет n переменных, а ранг основной матрицы системы равен r , то k = n-r .
Пример 5.7. Найти фундаментальную систему решений следующей системы линейных уравнений:
Решение . Найдем ранг основной матрицы системы:
Таким образом, множество решений данной системы уравнений образует линейное подпространство размерности n — r = 5 — 2 = 3. Выберем в качестве базисного минор
Тогда оставляя только базисные уравнения (остальные будут линейной комбинацией этих уравнений) и базисные переменные (осталь-ные, так называемые свободные, переменные переносим вправо), по-лучим упрощенную систему уравнений:
Полагая, x 3 = a , x 4 = b , x 5 = c , находим
Полагая a = 1, b = c = 0, получим первое базисное решение; полагая b = 1, a = c = 0, получим второе базисное решение; полагая c = 1, a = b = 0, получим третье базисное решение. В результате, нормальная фундаментальная система решений примет вид
С использованием фундаментальной системы общее решение однородной системы можно записать в виде
X = aE 1 + bE 2 + cE 3 . à
Отметим некоторые свойства решений неоднородной системы линейных уравнений AX=B и их взаимосвязь соответствующей однородной системой уравнений AX = 0.
Общее решение неоднородной системы равно сумме общего решения соответствующей однородной системы AX = 0 и произвольного частного решения неоднородной системы . Действительно, пусть Y 0 произвольное частное решение неоднородной системы, т.е. AY 0 = B , и Y — общее решение неоднородной системы, т.е. AY = B . Вычитая одно равенство из другого, получим
A (Y-Y 0) = 0, т.е. Y — Y 0 есть общее решение соответствующей однородной системы AX =0. Следовательно, Y — Y 0 = X , или Y = Y 0 + X . Что и требовалось доказать.
Пусть неоднородная система имеет вид AX = B 1 + B 2 . Тогда общее решение такой системы можно записать в виде X = X 1 + X 2 , где AX 1 = B 1 и AX 2 = B 2 . Это свойство выражает универсальное свойство вообще любых линейных систем (алгебраических, дифференциальных, функциональных и т.д.). В физике это свойство называется принципом суперпозиции , в электро- и радиотехнике — принципом наложения . Например, в теории линейных электрических цепей ток в любом контуре может быть получен как алгебраическая сумма токов, вызываемых каждым источником энергии в отдельности.
Линейная система называется однородной , если все ее свободные члены равны 0.
В матричном виде однородная система
записывается:
.
Однородная система (2) всегда совместна .
Очевидно, что набор чисел
,
,
…,
удовлетворяет каждому уравнению
системы. Решение
называетсянулевым илитривиальным решением. Таким образом, однородная
система всегда имеет нулевое решение.
При каких условиях однородная система (2) будет иметь ненулевые (нетривиальные) решения?
Теорема 1.3 Однородная система (2)имеет ненулевые решения тогда и только тогда, когда рангr ее основной матрицыменьше числа неизвестныхn .
Система (2) – неопределенная
.
Следствие 1. Если число уравненийm однородной
системы меньше числа переменных
,
то система является неопределенной и
имеет множество ненулевых решений.
Следствие 2. Квадратная однородная
система
имеет ненулевые решения тогда и тогда,
когда основная матрица этой системывырождена, т.е. определитель
.
В противном случае, если определитель
,
квадратная однородная система имеетединственное нулевое решение
.
Пусть ранг системы (2)
т. е система (2) имеет нетривиальные
решения.
Пусть
и- частные решения этой системы, т.е.
и
.
Свойства решений однородной системы
Действительно, .
Действительно, .
Объединяя, свойства 1) и 2), можно
сказать, что если
…,
— решения однородной системы (2), то и
всякая их линейная комбинация-
также является ее решением. Здесь
—
произвольные действительные числа.
Можно найти
линейно независимых частных решений однородной системы (2), с помощью которых
можно получить любое другое частное
решение данной системы, т.е. получить
общее решение системы (2).
Определение 2.2 Совокупность
линейно независимых частных решений
…,
однородной системы (2) таких, что каждое
решение системы (2) можно представить
в виде их линейной комбинации, называетсяфундаментальной системой решений (ФСР) однородной системы (2).
Пусть
…,
— фундаментальная система решений, тогда
общее решение однородной системы (2)
можно представить в виде:
Где
.
Замечание. Чтобы получить
ФСР, нужно найти частные решения
…,
,
придавая поочередно какой-либо одной
свободной переменной значение «1», а
всем остальным свободным переменным –
значения «0».
Получим ,, …,- ФСР.
Пример. Найти общее решение и фундаментальную систему решений однородной системы уравнений:
Решение. Запишем расширенную матрицу системы, предварительно поставив на первое место последнее уравнение системы, и приведем ее к ступенчатому виду. Поскольку правые части уравнений в результате элементарных преобразований не меняются, оставаясь нулями, столбец
можно не выписывать.
̴
̴
̴
Ранг системы
где
— число переменных. Система неопределенная,
имеет множество решений.
Базисный минор при переменных
отличен
от нуля:
выбираем
в качестве базисных переменных, остальные
— свободные переменные (принимают любые
действительные значения).
Последней в цепочке матрице соответствует ступенчатая система уравнений:
(3)
Выразим базисные переменные
через свободные переменные
(обратный ход метода Гаусса).
Из последнего уравнения выразим
:
и подставим в первое уравнение. Получим.
Раскроем скобки, приведем подобные и
выразим:
.
Полагая
,
,
,
где
,
запишем
— общее решение системы.
Найдем фундаментальную систему решений
,,.
Тогда общее решение однородной системы можно записать в виде:
Замечание. ФСР можно было найти
другим путем, без предварительного
отыскания общего решения системы. Для
этого полученную ступенчатую систему
(3) нужно было решить трижды, полагая
для:
;
для:
;
для:
.
Однородная
система
всегда совместна и имеет тривиальное
решение
.
Для существования нетривиального
решения необходимо, чтобы ранг матрицыбыл меньше числа неизвестных:
.
Фундаментальной
системой решений однородной системы
называют систему решений в виде
векторов-столбцов
,
которые соответствуют каноническому
базису, т.е. базису, в котором произвольные
постоянные
поочередно полагаются равными единице,
тогда как остальные приравниваются
нулю.
Тогда общее решение однородной системы имеет вид:
где
— произвольные постоянные. Другими
словами, общее решение есть линейная
комбинация фундаментальной системы
решений.
Таким образом, базисные решения могут быть получены из общего решения, если свободным неизвестным поочередно придавать значение единицы, полагая все остальные равные нулю.
Пример . Найдем решение системы
Примем , тогда получим решение в виде:
Построим теперь фундаментальную систему решений:
.
Общее решение запишется в виде:
Решения системы однородных линейных уравнений имеют свойства:
Другими словами, любая линейная комбинация решений однородной системы есть опять решение.
Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений интересует математиков несколько столетий. Первые результаты были получены в XVIII веке. В 1750 г. Г.Крамер (1704 –1752) опубликовал свои труды по детерминантам квадратных матриц и предложил алгоритм нахождения обратной матрицы. В 1809 г. Гаусс изложил новый метод решения, известный как метод исключения.
Метод Гаусса, или метод последовательного исключения неизвестных, заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида. Такие системы позволяют последовательно находить все неизвестные в определенном порядке.
Предположим,
что в системе (1)
(что всегда возможно).
(1)
Умножая поочередно первое уравнение на так называемые подходящие числа
и складывая результат умножения с соответствующими уравнениями системы, мы получим эквивалентную систему, в которой во всех уравнениях, кроме первого, будет отсутствовать неизвестная х 1
(2)
Умножим
теперь второе уравнение системы (2) на
подходящие числа, полагая, что
,
и складывая его с нижестоящими, исключим переменную из всех уравнений, начиная с третьего.
Продолжая
этот процесс, после
шага мы получим:
(3)
Если
хотя бы одно из чисел
не равно нулю, то соответствующее
равенство противоречиво и система (1)
несовместна. Обратно, для любой совместной
системы числа
равны нулю. Число- это ни что иное, как ранг матрицы системы
(1).
Переход от системы (1) к (3) называется прямым ходом метода Гаусса, а нахождение неизвестных из (3) – обратным ходом .
Замечание : Преобразования удобнее производить не с самими уравнениями, а с расширенной матрицей системы (1).
Пример . Найдем решение системы
.
Запишем расширенную матрицу системы:
.
Прибавим к строкам 2,3,4 первую, умноженную на (-2), (-3), (-2) соответственно:
.
Поменяем строки 2 и 3 местами, затем в получившейся матрице добавим к строке 4 строку 2, умноженную на :
.
Прибавим
к строке 4 строку 3, умноженную на
:
.
Очевидно,
что
,
следовательно, система совместна. Из
полученной системы уравнений
находим решение обратной подстановкой:
,
,
,
.
Пример 2. Найти решение системы:
.
Очевидно,
что система несовместна, т.к.
,
а
.
Достоинства метода Гаусса :
Менее трудоемкий, чем метод Крамера.
Однозначно устанавливает совместность системы и позволяет найти решение.
Дает возможность определить ранг любых матриц.
Решение находим с помощью калькулятора . Алгоритм решения такой же, как и для систем линейных неоднородных уравнений.
Оперируя только со строками, находим ранг матрицы, базисный минор; объявляем зависимые и свободные неизвестные и находим общее решение.
Первая и вторая строки пропорциональны, одну из них вычеркнем:
.
Зависимые переменные – x 2 , x 3 , x 5 , свободные – x 1 , x 4 . Из первого уравнения 10x 5 = 0 находим x 5 = 0, тогда
; .
Общее решение имеет вид:
Находим фундаментальную систему решений, которая состоит из (n-r) решений. В нашем случае n=5, r=3, следовательно, фундаментальная система решений состоит из двух решений, причем эти решения должны быть линейно независимыми. Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 2. Достаточно придать свободным неизвестным x 1 и x 4 значения из строк определителя второго порядка, отличного от нуля, и подсчитать x 2 , x 3 , x 5 . Простейшим определителем, отличным от нуля, является .
Таким образом, первое решение: , второе – .
Эти два решения составляют фундаментальную систему решений. Заметим, что фундаментальная система не единственна (определителей, отличных от нуля, можно составить сколько угодно).
Пример 2
. Найти общее решение и фундаментальную систему решений системы
Решение.
,
отсюда следует, что ранг матрицы равен 3 и равен числу неизвестных. Значит, система не имеет свободных неизвестных, а поэтому имеет единственное решение – тривиальное.
Задание
. Исследовать и решить систему линейных уравнений.
Пример 4
Задание
. Найти общее и частное решения каждой системы.
Решение. Выпишем основную матрицу системы:
| 5 | -2 | 9 | -4 | -1 |
| 1 | 4 | 2 | 2 | -5 |
| 6 | 2 | 11 | -2 | -6 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 2-ую строку на (-5). Добавим 2-ую строку к 1-ой:
| 0 | -22 | -1 | -14 | 24 |
| 1 | 4 | 2 | 2 | -5 |
| 6 | 2 | 11 | -2 | -6 |
Умножим 2-ую строку на (6). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой:
Найдем ранг матрицы.
| 0 | 22 | 1 | 14 | -24 |
| 6 | 2 | 11 | -2 | -6 |
| x 1 | x 2 | x 3 | x 4 | x 5 |
Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x 1 ,x 2 , значит, неизвестные x 1 ,x 2 – зависимые (базисные), а x 3 ,x 4 ,x 5 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.
| 0 | 22 | 14 | -1 | -24 |
| 6 | 2 | -2 | -11 | -6 |
| x 1 | x 2 | x 4 | x 3 | x 5 |
Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
22x 2 = 14x 4 — x 3 — 24x 5
6x 1 + 2x 2 = — 2x 4 — 11x 3 — 6x 5
Методом исключения неизвестных находим нетривиальное решение :
Получили соотношения, выражающие зависимые переменные x 1 ,x 2 через свободные x 3 ,x 4 ,x 5 , то есть нашли общее решение :
x 2 = 0.64x 4 — 0.0455x 3 — 1.09x 5
x 1 = — 0.55x 4 — 1.82x 3 — 0.64x 5
Находим фундаментальную систему решений, которая состоит из (n-r) решений.
В нашем случае n=5, r=2, следовательно, фундаментальная система решений состоит из 3-х решений, причем эти решения должны быть линейно независимыми.
Чтобы строки были линейно независимыми, необходимо и достаточно, чтобы ранг матрицы, составленной из элементов строк, был равен количеству строк, то есть 3.
Достаточно придать свободным неизвестным x 3 ,x 4 ,x 5 значения из строк определителя 3-го порядка, отличного от нуля, и подсчитать x 1 ,x 2 .
Простейшим определителем, отличным от нуля, является единичная матрица.
Задача . Найти фундаментальный набор решений однородной системы линейных уравнений.
Линейное уравнение называется однородным , если его свободный член равен нулю, и неоднородным в противном случае. Система, состоящая из однородных уравнений, называется однородной и имеет общий вид:
Очевидно, что всякая однородная система совместна и имеет нулевое (тривиальное) решение. Поэтому применительно к однородным системам линейных уравнений часто приходится искать ответ на вопрос о существовании ненулевых решений. Ответ на этот вопрос можно сформулировать в виде следующей теоремы.
Теорема . Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных .
Доказательство : Допустим, система, ранг которой равен, имеет ненулевое решение. Очевидно, что не превосходит . В случае система имеет единственное решение. Поскольку система однородных линейных уравнений всегда имеет нулевое решение, то именно нулевое решение и будет этим единственным решением. Таким образом, ненулевые решения возможны только при .
Следствие 1 : Однородная система уравнений, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевое решение.
Доказательство : Если у системы уравнений , то ранг системы не превышает числа уравнений , т.е. . Таким образом, выполняется условие и, значит, система имеет ненулевое решение.
Следствие 2 : Однородная система уравнений с неизвестными имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю.
Доказательство : Допустим, система линейных однородных уравнений, матрица которой с определителем , имеет ненулевое решение. Тогда по доказанной теореме , а это значит, что матрица вырожденная, т.е. .
Теорема Кронекера-Капелли: СЛУ совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы. Система ур-ий называется совместной, если она имеет хотя бы одно решение.Однородная система линейных алгебраических уравнений .
Система m линейных ур-ий с n переменными называется системой линейных однородных уравнений, если все свободные члены равны 0. Система линейных однородных ур-ий всегда совместна, т.к. она всегда имеет, по крайней мере, нулевое решение. Система линейных однородных ур-ий имеет ненулевое решение тогда и только тогда, когда ранг её матрицы коэффициентов при переменных меньше числа переменных, т.е. при rang A (n. Всякая лин. комбинация
решений системы лин. однородн. ур-ий также является решением этой системы.
Система лин.независимых решений е1, е2,…,еk называется фундаментальной, если каждое решение системы является линейной комбинацией решений. Теорема: если ранг r матрицы коэффициентов при переменных системы линейных однородных уравнений меньше числа переменных n, то всякая фундаментальная система решений системы состоит из n-r решений. Поэтому общее решение системы лин. однордн. ур-ий имеет вид: с1е1+с2е2+…+сkеk, где е1, е2,…, еk – любая фундаментальная система решений, с1, с2,…,сk – произвольные числа и k=n-r. Общее решение системы m линейных ур-ий с n переменными равно сумме
общего решения соответствующей ей системы однородн. линейных ур-ий и произвольного частного решения этой системы.
7.Линейные пространства. Подпространства. Базис, размерность. Линейная оболочка. Линейное пространство называется n-мерным , если в нем существует система из линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число называется размерностью (числом измерений) линейного пространства и обозначается . Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве найдется система, состоящая из линейно независимых векторов, то такое пространство называют бесконечномерным (записывают: ). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.
Базисом n-мерного линейного пространства называется упорядоченная совокупность линейно независимых векторов (базисных векторов ).
Теорема 8.1 о разложении вектора по базису. Если — базис n-мерного линейного пространства , то любой вектор может быть представлен в виде линейной комбинации базисных векторов:
V=v1*e1+v2*e2+…+vn+en
и притом единственным образом, т.е. коэффициенты определяются однозначно. Другими словами, любой вектор пространства может быть разложен по базису и притом единственным образом.
Действительно, размерность пространства равна . Система векторов линейно независима (это базис). После присоединения к базису любого вектора , получаем линейно зависимую систему (так как это система состоит из векторов n-мерного пространства). По свойству 7 линейно зависимых и линейно независимых векторов получаем заключение теоремы.
Частное решение — это… Что такое Частное решение?
- Частное решение
- дифференциального уравнения F (x, y, y’,…, у (n)) = 0, решение у = φ(х), получающееся из общего решения (См. Общее решение) у = φ(х, C1,…, Cn) этого уравнения при некотором конкретном выборе произвольных постоянных C1,…, Cn. Например, общее решение уравнения у» + у = 0 есть у = C1cosx + C2sinx; полагая C1 = 2, C2 = —1, получим Ч. р. этого уравнения у = 2cosx — sinx.
Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.
- Частное право
- Частный поверенный
Смотреть что такое «Частное решение» в других словарях:
ЧАСТНОЕ РЕШЕНИЕ — дифференциального уравнения решение, получающееся из общего решения при некотором конкретном выборе произвольных постоянных … Большой Энциклопедический словарь
частное решение — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN partial solutionparticular solutionspecific solution … Справочник технического переводчика
частное решение — дифференциального уравнения, решение, получающееся из общего решения при некотором конкретном выборе произвольных постоянных. * * * ЧАСТНОЕ РЕШЕНИЕ ЧАСТНОЕ РЕШЕНИЕ дифференциального уравнения, решение, получающееся из общего решения при некотором … Энциклопедический словарь
частное решение — atskirasis sprendinys statusas T sritis fizika atitikmenys: angl. partial solution; particular solution vok. Einzellösung, f; Partiallösung, f; partikuläre Lösung, f rus. частное решение, n pranc. solution particulière, f … Fizikos terminų žodynas
ЧАСТНОЕ РЕШЕНИЕ — дифференциального уравнения, решение, получающееся из общего решения при нек ром конкретном выборе произвольных постоянных … Естествознание. Энциклопедический словарь
Частное решение — Частным решением дифференциального уравнения на интервале называется каждая функция y(x), которая при подстановке в уравнение вида обращает его в верное тождество на интервале . См. также Общее решение дифференциального уравнения … Википедия
Частное решение — особый вид решения на охрану ГГ, принимаемый начальником (командиром) пограничного соединения, воинской части в случае изменения обстановки на охраняемом участке ГГ. Оформляется приказом (распоряжением), в котором ставятся новые или уточняются… … Пограничный словарь
Частное решение дифференциального уравнения — Частным решением дифференциального уравнения на интервале называется каждая функция , которая при подстановке в уравнение вида обращает его в верное тождество на интервале . Зная общее решение однородного дифференциального уравнения и любое… … Википедия
Решение систем линейных алгебраических уравнений — Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений. Содержание 1 Однородные системы 1.1 Пример … Википедия
Решение СЛАУ: ФСР — Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений. Содержание 1 Однородные системы 1.1 Пример 2 Неоднородные системы … Википедия
Общее решение системы линейных уравнений — Студопедия.Нет
Решение систем линейных уравнений
Дана система линейных уравнений с неизвестными:
где — коэффициенты, стоящие перед неизвестными; — свободные члены системы ( ).
Прямоугольная таблица чисел:
,
составленная из коэффициентов, стоящих перед неизвестными, называется матрицей системы.
Матрица, получаемая приписыванием к матрице системы столбца свободных членов, называется расширенной матрицей:
Если ранг матрицы системы равен рангу расширенной матрицы, то такая система будет совместной. Совместной называется система, если она имеет хотя бы одно решение. Совместная система может иметь либо одно решение (называется определенной), либо бесконечно много решений (называется неопределенной). Система уравнений, не имеющая решений, называется несовместной. Если система уравнений содержит уравнение:
называемое противоречивым, то она несовместна.
Две системы, имеющие одни и те же решения, называются равносильными. Если в системе вычеркнуть одно или несколько уравнений:
называемых тривиальными, то получим систему уравнений, равносильную исходной.
Рассмотрим решение системы уравнений тремя способами: по формулам Крамера, матричным способом и методом исключения неизвестных – методом Гаусса.
Формулы Крамера
Система линейных уравнений, имеющая число уравнений, равное числу неизвестных , и определитель матрицы системы, отличный от нуля, имеет единственное решение.
Определитель, элементами которого являются коэффициенты, стоящие перед неизвестными, называется определителем системы:
Вспомогательные определители: …, составляются путем замены в определителе системы соответствующего столбца столбцом, состоящим из свободных членов:
Решение системы уравнений находится по формулам Крамера:
…,
Если определитель системы , то система имеет единственное решение (совместна и определенна). Если определитель системы и все вспомогательные определители …, также равны нулю, то такая система является совместной и имеет бесконечно много решений (неопределенна). Если определитель системы , но хотя бы один из вспомогательных определителей …, отличен от нуля, то такая система не имеет решений (несовместна или противоречива).
Пример 3.1. Решить систему уравнений:
Решение. Вычислим определитель системы уравнений:
Определитель системы отличен от нуля, следовательно, система имеет единственное решение, которое можно найти по формулам Крамера.
Вычислим вспомогательные определители:
По формулам Крамера находим решение системы:
Матричный способ
Запишем матрицу системы, т.е. матрицу, состоящую из коэффициентов при неизвестных
матрица, составленная из величин , называется матрицей-столбцом свободных членов. Составим еще матрицу-столбец неизвестных:
Тогда система уравнений в матричной форме примет вид:
Если то получим решение матричного уравнения:
На данной формуле и основан матричный способ решения систем линейных уравнений.
Пример 3.2. Решить матричным способом систему уравнений:
Решение. Для данной системы
Матрица, обратная к матрице , имеет вид:
Подставляя в формулу для решения матричного уравнения, имеем:
Таким образом,
Метод исключения неизвестных – метод Гаусса
Рассмотрим систему m – линейных уравнений с n – неизвестными:
Суть метода Гаусса заключается в том, что с помощью элементарных преобразований расширенная матрица системы приводится к равносильной матрице ступенчатого (треугольного или трапецеидального) вида. Это и есть прямой ход метода Гаусса.
На основании полученной ступенчатой матрицы составляется новая система уравнений, равносильная исходной, из которой последовательно, начиная с последнего уравнения, находятся все неизвестные; это суть обратного хода метода Гаусса.
Матрица А называется ступенчатой, если она имеет вид:
или
где – числа, отличные от нуля.
Элементарные преобразования матрицы:
1) отбрасывание строки, в которой все элементы равны нулю;
2) умножение всех элементов строки матрицы на число, не равное нулю;
3) изменение порядка строк матрицы;
4) прибавление к каждому элементу одной строки соответствующих элементов другой строки, умноженной на любое число.
Пример 3.3. Методом Гаусса решить систему уравнений:
Решение. Расширенная матрица системы имеет вид:
вычитая из элементов 3-й строки элементы 1-й, а из элементов 2-й строки элементы 1-й, умноженные на два, получим: Вычтем из элементов 2-й строки элементы 3-й, умноженные на семь, и поменяем местами 2-ю и 3-ю строки: Запишем систему уравнений с новыми коэффициентами:
Применим обратный ход метода Гаусса:
Решение системы:
Общее решение системы линейных уравнений
Неизвестное называется разрешенным, если какое-нибудь уравнение системы содержит с коэффициентом единица, а во всех остальных уравнениях системы неизвестное не содержится, т.е. содержится с коэффициентом нуль.
Система уравнений называется разрешенной, если каждое ее уравнение содержит разрешенное неизвестное. Например, система уравнений:
является разрешенной, так как неизвестные , и – разрешенные.
Если из каждого уравнения разрешенной системы уравнений выбрать по одному разрешенному неизвестному, то получим набор разрешенных неизвестных. Все остальные неизвестные будут называться свободными. В данной системе уравнений и – свободные неизвестные.
Общим решением совместной системы уравнений называется равносильная ей разрешенная система, в которой разрешенные неизвестные выражены через свободные. Если в общем решении свободным неизвестным придать какие-нибудь числовые значения, то получим решение данной системы, называемое частным.
Общее решение системы уравнений можно получить с помощью формул Крамера или методом Гаусса.
Пример 3.4. Исследоватьнасовместность,найти общее решение и одно частное решение системы уравнений с помощью формул Крамера:
Решение.
1.Запишем расширенную матрицу, найдем ее ранг и одновременно ранг матрицы системы уравнений:
~ ~
Таким образом, ранги матриц совпадают и равны 2. Следовательно, система уравнений является совместной.
2.Выберем минор , составленный из коэффициентов, стоящих перед неизвестными и первого и третьего уравнений. Этот минор отличен от нуля и его порядок равен рангу матрицы системы.
3.Выпишем первое и третье уравнения данной системы, содержащие строки минора M:
В этих уравнениях оставим в левой части неизвестные и , а остальные неизвестные перенесем в правую часть:
4.Решим полученную систему уравнений по формулам Крамера:
Запишем общее решение данной системы уравнений: Если свободные неизвестные положить , , то из общего решения находим , . Следовательно, , , , – частное решение исходной системы уравнений.
Пример 3.5. Найти с помощью метода Гаусса общее решение и одно частное решение системы уравнений:
Решение. Запишем систему уравнений в виде таблицы:
1.Данная система не содержит противоречивых и тривиальных уравнений. Первое уравнение не содержит разрешенного неизвестного. Неизвестное входит в это уравнение с коэффициентом единица. С помощью элементарных преобразований исключим из других уравнений и получим следующую систему уравнений:
2.Полученная система не содержит противоречивых и тривиальных уравнений. Третье уравнение содержит неизвестное с коэффициентом единица. Исключим неизвестное из остальных уравнений с помощью элементарных преобразований:
3.Данная система уравнений не содержит противоречивых и тривиальных уравнений. Она не является разрешенной, так как второе уравнение не содержит разрешенного неизвестного. Разделим это уравнение на -3:
С помощью элементарных преобразований исключим неизвестное из третьего и четвертого уравнений:
Запишем полученную разрешенную систему:
в которой , , –разрешенные неизвестные, а , – свободные неизвестные. Общее решение исходной системы уравнений имеет вид:
Если положить = =0, то частное решение исходной системы будет выглядеть следующим образом: = — 2; = 5; = 0; = -3; = 0.
Задания для самостоятельного решения:
Решить следующие системы уравнений:
3.1. 3.2. 3.3.
3.4. 3.5. 3.6.
3.7. 3.8. 3.9.
3.10. 3.11. 3.12.
3.13. 3.14. 3.15.
3.16. 3.17. 3.18.
3.19. 3.20. 3.21.
3.22. 3.23. 3.24.
3.25. 3.26. 3.27.
3.28. 3.29. 3.30.
3.31. 3.32. 3.33.
3.34. 3.35. 3.36.
3.37. 3.38. 3.39.
3.40. 3.41. 3.42.
3.43. 3.44. 3.45.
3.46. 3.47.
Общее решение системы уравнений
В ваших классах алгебры, если система уравнений имеет бесконечно много решений, вы просто напишете «бесконечно много решений» и перейдете к следующей задаче. Однако когда мы говорим «бесконечно много решений», происходит гораздо больше. В этой статье мы рассмотрим эту идею с общими решениями.
реклама
Содержание:
- Написание общего решения
- Нахождение конкретных решений на основе общего решения
- Краткое описание шагов
Выписка общего решения
Во-первых, давайте рассмотрим, как записать общее решение данной системы уравнений.Для этого рассмотрим пример.
Пример
Найдите общее решение системы уравнений:
\ (
\ begin {array} {c}
x_1 + 2x_2 + 8x_3 + 18x_4 = 11 \\
x_1 + x_2 + 5x_3 + 11x_4 = 10 \\
\ end {array} \)
Как и в любой системе уравнений, мы будем использовать расширенную матрицу и сокращение строки.
\ (
\ left [
\ begin {array} {cccc | c}
1 & 2 & 8 & 18 & 11 \\
1 & 1 & 5 & 11 & 10 \\
\ end {array}
\ right ]
\ sim
\ left [
\ begin {array} {cccc | c}
1 & 0 & 2 & 4 & 9 \\
0 & 1 & 3 & 7 & 1 \\
\ end {array}
\ right]
\)
Теперь запишите уравнения из этой сокращенной матрицы.
\ (
\ begin {array} {c}
x_1 + 2x_3 + 4x_4 = 9 \\
x_2 + 3x_3 + 7x_4 = 1 \\
\ end {array} \)
Обратите внимание на матрицу, что ведущие единицы (первая ненулевая запись в каждой строке) находятся в столбцах для \ (x_1 \) и \ (x_2 \).
Найдите эти переменные.
\ (
\ begin {array} {c}
x_1 = 9 — 2x_3 — 4x_4 \\
x_2 = 1 — 3x_3 — 7x_4 \\
\ end {array} \)
Остальные переменные — это свободных переменных , что означает, что они могут принимать любое значение.Значения \ (x_1 \) и \ (x_2 \) основаны на значениях этих двух переменных. В общем решении вы хотите это отметить.
Общее решение:
\ (
\ boxed {
\ begin {array} {l}
x_1 = 9 — 2x_3 — 4x_4 \\
x_2 = 1 — 3x_3 — 7x_4 \\
x_3 \ text {is free} \\
x_4 \ text { бесплатно} \\
\ end {array}
}
\)
Существует бесконечно много решений этой системы уравнений, все из которых используют разные значения двух свободных переменных.
Поиск конкретных решений
Предположим, вы хотите привести пример конкретного решения системы уравнений выше. Их бесконечно много, так что у вас есть большой выбор! Вам просто нужно рассмотреть возможные значения свободных переменных.
Пример решения
Лет:
\ (
\ begin {array} {l}
x_3 = 0 \\
x_4 = 1 \\
\ end {array}
\)
Не было особой причины выбирать 0 и 1. Опять же, это будет работать для ЛЮБОГО значения, которое вы выберете для этих двух переменных.
Используя эти значения, решение:
\ (
\ begin {array} {l}
x_1 = 9 — 2x_3 — 4x_4 = 9 — 2 (0) — 4 (1) \\
x_2 = 1 — 3x_3 — 7x_4 = 1 — 3 (0) — 7 (1) \\
x_3 = 0 \\
x_4 = 1 \\
\ end {array}
\ rightarrow
\ boxed {
\ begin {array} {l}
x_1 = 5 \\
x_2 = -6 \\
x_3 = 0 \\
x_4 = 1 \\
\ end {array}
}
\)
Чтобы убедиться, вы можете проверить эти значения в исходной системе уравнений:
\ (
\ begin {array} {l}
x_1 + 2x_2 + 8x_3 + 18x_4 = 11 \\
x_1 + x_2 + 5x_3 + 11x_4 = 10 \\
\ end {array}
\ rightarrow
\ begin {array} {l}
(5) + 2 (-6) + 8 (0) + 18 (1) = 11 \ text {(true)} \\
(5) + (-6) + 5 (0) +11 (1) = 10 \ text {(true)} \\
\ end {array}
\)
Поскольку оба уравнения верны для этих значений, мы знаем, что нашли одно из многих, многих решений.Если бы мы хотели найти больше решений, мы могли бы просто выбрать разные значения для двух свободных переменных \ (x_1 \) и \ (x_2 \).
объявление
Краткое описание шагов
Для данной системы уравнений шаги для написания общего решения следующие:
- Строка уменьшения расширенной матрицы для системы.
- Запишите уравнения матрицы с сокращенной строкой.
- Найдите переменные, у которых есть ведущая в столбце.
- Обозначьте остальные переменные как свободные.
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеОднородные и неоднородные системы
Однородные и неоднородные системы
Однородная система линейных уравнений — это одна в котором все постоянные члены равны нулю.Однородная система всегда хотя бы одно решение, а именно нулевой вектор. Когда строковая операция применительно к однородной системе новая система остается однородной. это Важно отметить, что когда мы представляем однородную систему в виде матрицы, мы часто опускаем последний столбец постоянных условий, так как применяя операции со строками не изменят этот столбец. Итак, мы используем обычную матрицу вместо расширенной матрицы. Конечно, ища решение, важно учитывать постоянные нулевые члены.
Неоднородная система имеет связанную однородную систему, который вы получаете, заменяя постоянный член в каждом уравнении нулем. Раздел 1.I.3 в учебнике посвящен пониманию структуры множества решений однородных и неоднородных систем. Основные теоремы которые подтверждены в этом разделе:
Теорема: множество решений однородная линейная система с $ n $ переменными имеет вид $ \ {a_1 \ vec v_1 + a_2 \ vec v_2 + \ cdots + a_k \ vec v_k \, | \, a_1, a_2, \ dots, a_k \ in \ R \} $, где $ k $ — количество свободных переменных в эшелонированной форме система и $ \ vec v_1, \ vec v_2, \ dots, \ vec v_k $ являются [постоянными] векторами в $ \ R ^ n.$
Теорема: Рассмотрим систему линейных уравнений в $ n $ переменных и предположим, что $ \ vec p $ — решение системы. Затем множество решений системы имеет вид $ \ {\ vec p + a_1 \ vec v_1 + a_2 \ vec v_2 + \ cdots + a_k \ vec v_k \, | \, a_1, a_2, \ dots, a_k \ in \ R \} $, где $ \ {a_1 \ vec v_1 + a_2 \ vec v_2 + \ cdots + a_k \ vec v_k \, | \, a_1, a_2, \ dots, a_k \ in \ R \} $ — множество решений ассоциированной однородной системы. (Итак, $ k $ по-прежнему количество свободных переменных в эшелонированной форме системы.)
Вектор $ \ vec p $ во второй теореме называется частное решение системы. (Помните, что для неоднородного системы, возможно, что не существует конкретного решения, а набор решений пуст.) Однородная система всегда имеет частным решением $ \ vec 0 $, а вторая Теорема применяется к однородным системам, взяв $ \ vec p = \ vec 0 $. Обратите внимание, что для данной системы векторы $ \ vec p $ и $ \ vec v_i $ не уникальны. Может быть много разных последовательностей операций со строками, которые можно использовать привести систему в эшелонированную форму.$ \ Vec p $ и $ \ vec v_i $, которые вы получите может зависеть от конкретной последовательности операций со строками, которые вы используете. Однако вы можно получить только разные способы написания одного и того же набора решений. (Возможно Удивительный факт, который еще не доказан, заключается в том, что независимо от того, в какой последовательности операций со строками, которые вы используете для приведения системы в эшелонированную форму, вы всегда получаете такое же количество свободных переменных. Это означает, что число $ k $ в система однозначно определяется системой.)
Эти теоремы на самом деле не меняют способ решения линейной системы, но это помогает нам понять структуру набора решений системы, и, в частности, геометрия множества решений.п $ это содержит происхождение. Добавление вектор $ \ vec p $ ко всем точкам в этом линейном пространстве дает «параллельную» линейную пространство, содержащее $ \ vec p $. Увидеть вторая картина в предыдущем разделе].
Другой важной темой в Разделе 1.I.3 учебника является особые и невырожденные матрицы. Это проблема только для квадратных матрицы. (Квадратная матрица — это матрица, в которой количество строк равно количеству столбцов.) Квадратная матрица — это ассоциированная матрица некоторой однородной системы.Поскольку матрица квадратная, однородная система имеет то же количество уравнений, что и переменные. Однородная система либо будет иметь единственное решение $ \ vec 0 $, либо у него будет бесконечное количество решений. Матрица называется невырожденный, если система имеет единственное решение. Она называется сингулярной, если система имеет бесконечную количество решений. (Только термины «единственное» и «неособое» применяются к квадратным матрицам.) Отметим, что по приведенным выше теоремам квадратная матрица является особенным тогда и только тогда, когда у него есть хотя бы одна свободная переменная, когда она помещается в форме эшелона, что, в свою очередь, верно тогда и только тогда, когда эшелон Форма матрицы имеет как минимум одну строку, содержащую только нули.n $ размерности $ n-1 $ (если уравнение не является тривиальное уравнение, $ 0 = 0 $.) И поскольку $ \ vec 0 $ является решением, это линейное пространство проходит через начало координат. Набор решений для всей системы: пересечение множеств решений для всех индивидуальных уравнений; то есть это пересечение $ n $ линейных пространств размерности $ n-1 $.
Например, если $ n = 2 $, мы смотрим на пересечение двух линий через начало координат; возможности заключаются в том, что линии пересекаются только в начале координат [невырожденная матрица] или что линии на самом деле идентичны [сингулярная матрица].Конечно, если вы выберете две строки наугад, маловероятно, что они идентичны. Это означает, что если вы выберете случайную матрицу $ 2 \ times2 $, это маловероятно. что это будет особенным.
Для $ n = 3 $ мы пересекаем три плоскости, содержащие начало координат. В пересечение двух плоскостей через начало координат является линией, если плоскости не происходят быть идентичным. Когда вы добавляете третью плоскость к перекрестку, вы скорее всего, пересекая эту плоскость линией, в результате получится один точка (а именно, начало координат), за исключением маловероятного случая, когда линия происходит полностью лежать в плоскости.n $ размерности $ n-1 $. Взяв пересечение этого пространства с множеством решений второе уравнение, вероятно, даст линейное пространство размерности $ n-2 $. Поскольку набор решений для каждого уравнения добавляется к пересечению, размер перекрестка, вероятно, уменьшится на единицу. Когда вы получаете до пересечения множеств решений для всех $ n $ уравнений, вы вероятно, будет пространство нулевого измерения — единственная точка, а именно источник. Опять же, если вы выберете случайную матрицу $ n \ times n $, это будет очень вряд ли будет единичным.(Слово «единственное число» означает «особенно необычный».)
Если посмотреть на неоднородную линейную систему $ n $ уравнений от $ n $ переменных, вы пересекаете множества решений, которые не обязательно содержат начало координат. Наиболее вероятная возможность пересечения — все еще одна точка, и бесконечное пересечение все еще возможно. Но у вас также есть возможность пустого перекрестка — нет решения — как, например, если бы вы пересекаете две параллельные линии.
Мы также можем подумать о том, что происходит, когда мы применяем сокращение строк к поместите матрицу $ n \ times n $ в эшелонированную форму.Рассмотрим матрицу как матрица однородной линейной системы, записанная без постоянного нуля члены из правых частей уравнений. $$ \ begin {pmatrix} c_ {11} & c_ {12} & \ cdots & c_ {1n} \\ c_ {21} & c_ {22} & \ cdots & c_ {2n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ c_ {n1} & c_ {n2} & \ cdots & c_ {nn} \ end {pmatrix} $$ Помните, что матрица квадратная, с тем же количеством строк, что и столбцов. Матрица формы эшелона, полученная в результате сокращения строк, будет иметь вид $$ \ begin {pmatrix} d_ {11} & d_ {12} & \ cdots & d_ {1n} \\ 0 & d_ {22} & \ cdots & d_ {2n} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & \ cdots & 0 & d_ {nn} \ end {pmatrix} $$ где все элементы ниже диагонали равны нулю (и некоторые из $ d_ {ij} $ также могут быть нулевыми).Но может быть нулевые строки внизу. То есть $ d_ {nn} $ может быть нулевым. Если $ d_ {nn} \ ne0 $, то свободных переменных нет, а однородные система имеет $ \ vec 0 $ в качестве единственного решения. Если $ d_ {nn} = 0 $, там — это хотя бы одна ненулевая строка, и не более $ n-1 $ из $ n $ строк ненулевые. Итак, существует не более $ n-1 $ ведущих переменных, что означает наличие хотя бы одной свободной Переменная; система имеет бесконечное количество решений.
Теперь предположим, что у нас есть неоднородная система с тем же матрица коэффициентов.Расширенная матрица для неоднородных система имеет вид $$ \ left (\ begin {array} {cccc | c} c_ {11} & c_ {12} & \ cdots & c_ {1n} & a_1 \\ c_ {21} & c_ {22} & \ cdots & c_ {2n} & a_2 \\ \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ c_ {n1} & c_ {n2} & \ cdots & c_ {nn} & a_n \ end {array} \ right) $$ Если мы применим метод Гаусса, используя те же строковые операции, что и для однородной системы получаем матрицу вида $$ \ left (\ begin {array} {cccc | c} d_ {11} & d_ {12} & \ cdots & d_ {1n} & b_1 \\ 0 & d_ {22} & \ cdots & d_ {2n} & b_2 \\ \ vdots & \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 0 & d_ {nn} & b_n \ end {array} \ right) $$ Теперь в случае $ d_ {nn} \ ne0 $ свободных переменных нет, и мы можем решить систему, чтобы получить уникальное решение.(Таким образом, линейная система, матрица коэффициентов которой квадратная, невырожденная матрица всегда будет иметь единственное решение.) В случае $ d_ {nn} = 0 $ мы должны учитывать постоянные сроки. Когда $ d_ {nn} = 0 $ и $ b_n \ ne 0 $, мы имеем уравнение вида $ 0 = k $, где $ k \ ne 0 $, и решения нет. Когда $ d_ {nn} = 0 $ и $ b_n = 0 $, у нас есть строка со всеми нулями. Однако, решения может все еще не быть, потому что одно из предыдущих уравнений может по-прежнему иметь вид $ 0 = k $, где $ k \ ne0 $. Однако мы можем говорят, что если таких строк нет, то мы имеем разрешимую систему с хотя бы одна свободная переменная, а количество решений бесконечно.
(к оглавлению)
Неоднородная система — обзор
Решение
В матричной форме система эквивалентна X ′ = 21−8−2X + sin3t0. Находим общее решение соответствующей однородной системы X ′ = 21−8−2X с DSolve.
Прозрачный [ x , y , xh, xp] homsol = DSolve [{ x ′ [ t ] == 2 x [ t ] + y [ t ] ], y ′ [ t ] == — 8 x [ t ] −2 y [ t ]}, { x [ t ], y [ t ]}, t ]
{{x [t] → 12C [2] Sin [2t] + C [1] (Cos [2t] + Sin [2t]), y [t] → C [2] (Cos [2t] −Sin [2t]) — 4C [1] Sin [2t]}}
Эти результаты показывают, что общее решение соответствующей однородной системы:
Xh = cos2t + sin2t12sin2t4sin2tcos2t − sin2tc1c2.
xh [t _] = {{ x [ t ]}, { y [ t ]}} /. Гомсол [[1]];Таким образом, ищем частное решение неоднородной системы вида Xp = asin3t + bcos3t, где a = a1a2 и b = b1b2. После определения A = 21−8−2 и Xp = asin3t + bcos3t, мы подставляем X p в неоднородную систему.
capa = {{2, 1}, {−8, −2}}; MatrixForm [capa]
21−8−2
XP [t _] = {{a1}, {a2}} Sin [3 t ] + {{b1}, {b2}} Cos [3 t ]; MatrixForm [xp [ t ]]
b1Cos [3t] + a1Sin [3t] b2Cos [3t] + a2Sin [3t]
step1 = xp ′ [ t ] == capa.xp [ t ] + {{Sin [3 t ]}, {0}}
{{3a1Cos [3 t ] −3b1Sin [3 t ]}, {3a2Cos [3 t ] −3b2Sin [3 t ]}} == {{b2Cos [3 t ] + Sin [3 t ] + a2Sin [3 t ] +2 (b1Cos [3 t ] + a1Sin [3 t ])}, {−8 (b1Cos [3 t ] + a1Sin [3 t ]) — 2 (b2Cos [3 t ] + a2Sin [3 t ])} }
Результат представляет собой систему уравнений, которая верна для всех значений t .В частности, замена t = 0 дает
eq1 = step1 /. t → 0
{{3a1}, {3a2}} == {{2b1 + b2}, {−8b1 — 2b2}}
, что эквивалентно системе уравнений
3a1 = 2b1 + b23a2 = −24b1 + b2.
Аналогично, замена t = π /2 даетeq2 = step1 /. t → Pi / 2
{{3b1}, {3b2}} == {{−1 — 2a1 −a2}, {8a1 + 2a2}}
, что эквивалентно системе уравнений
3b1 = −1−2a1 − a23b2−2−4a1 − a2.
Теперь мы используем Solve для решения этих четырех уравнений для a 1 , a 2 , b 1 и b 2coeffs = Solve [{eq1, eq2} ]
{{a1 → −25, a2 → 85, b1 → −35, b2 → 0}}
, а затем подставьте эти значения в X p , чтобы получить конкретное решение для неоднородной системы .
XP [t _] = XP [ t ] /. Coeffs [[1]]
{{−35Cos [3t] −25Sin [3t]}, {85Sin [3t]}}
A в целом решение неоднородной системы тогда дается формулой X = X h + X p .
xh [ t ]
{{12C [2] Sin [2t] + C [1] (Cos [2t] + Sin [2t])}, {C [2] (Cos [2t] −Sin [2t]) — 4C [1] Sin [2t]}}
x [t _] = xh [ t ] + xp [ t ]
{{−35Cos [3t] + 12C [2] Sin [2t] + C [1] (Cos [2t] + Sin [2t]) — 25Sin [3t]}, {C [2] (Cos [2t] −Sin [2t]) — 4C [1] Sin [2t] + 85Sin [3t]}}
Для решения задачи начального значения мы применяем начальное условие и решаем для неизвестных констант.
x [0]
{{−35 + C [1]}, {C [2]}}
cval = Решить [ x [0] == {{0}, {1}}]
{{C [1] → 35, C [2] → 1}}
Мы получаем решение задачи начального значения, подставляя эти значения обратно в общее решение.
x [t _] = x [ t ] /. Cvals [[1]] // Свести // Упростить
{110 (6Cos [2t] −6Cos [3t] + 11Sin [ 2t] −4Sin [3t]), Cos [2t] −175Sin [2t] + 85Sin [3t]}
Мы подтверждаем этот результат, построив графики x ( t ) и y ( t ) вместе на рисунке 6-19 (a), а также параметрически в B.
Рисунок 6-19. (а) x ( т, ) и x ( т, ). (b) Параметрический график x ( t ) по сравнению с y ( t )
p1 = График [Вычислить [ x [ t ]]], { t , 0, 4Pi }, PlotRange → {−2Pi, 2Pi}, AspectRatio → 1, PlotLabel → «(a)»]
p2 = ParametricPlot [ x [ t ], { t , 0, 4Pi}, PlotRange → {{- 6, 5}, {−5, 6}}, AspectRatio → 1, PlotLabel → «(b)»] Показать [GraphicsRow [{p1, p2}]]
Наконец, отметим, что DSolve может найти общее решение неоднородной системы
Очистить [ x , y , t ] Очистить [ x , y , xh, xp] homsol = DSolve [{ x ′ [ t ] == 2 x [ t ] + y [ t ], y ′ [ t ] == — 8 x [ t ] −2 y [ t ]}, { x [ t ], y [ t ]}, t ] 9 0003
{{x [t] → 12C [2] Sin [2t] + C [1] (Cos [2t] + Sin [2t]), y [t] → C [2] (Cos [2t] -Sin [2t]) — 4C [1] Sin [2t]}}
, а также решить задачу начального значения.
Прозрачный [ x , y , xh, xp] homsol = DSolve [{ x ′ [ t ] == 2 x [ t ] + y [ t ] ], y ′ [ t ] == — 8 x [ t ] −2 y [ t ], x [0] == 0, y [0] == 1}, { x [ t ], y [ t ]}, t ]
{{x [t] → 12Sin [2t], y [t] → Cos [2t] −Sin [2t]}}
Системы линейных уравнений: две переменные
Результаты обучения
- Решайте системы уравнений с помощью построения графиков, подстановок и сложений.
- Определить несовместимые системы уравнений, содержащие две переменные.
- Выразите решение системы зависимых уравнений, содержащей две переменные, в стандартных обозначениях.
Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, то есть сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он получает от продажи своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов необходимо произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.
(предоставлено Thomas Sørenes)
Введение в системные решения
Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам необходимо признать, что мы имеем дело с более чем одной переменной и, вероятно, более чем с одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Даже в этом случае это не гарантирует уникального решения.
В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
[латекс] \ begin {align} 2x + y & = 15 \\ [1 мм] 3x-y & = 5 \ end {align} [/ latex]
Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. В этом примере упорядоченная пара [латекс] (4,7) [/ латекс] является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем методы поиска такого решения, если оно существует.
[латекс] \ begin {align} 2 \ left (4 \ right) + \ left (7 \ right) & = 15 && \ text {True} \\ [1 мм] 3 \ left (4 \ right) — \ left (7 \ right) & = 5 && \ text {True} \ end {align} [/ latex]
Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Согласованная система уравнений имеет по меньшей мере одно решение. Согласованной системой считается независимая система , если она имеет единственное решение, такое как пример, который мы только что исследовали.Две линии имеют разные уклоны и пересекаются в одной точке на плоскости. Согласованной системой считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые точки пересечения y . Другими словами, линии совпадают, поэтому уравнения представляют одну и ту же линию. Каждая точка на линии представляет пару координат, удовлетворяющую системе. Таким образом, существует бесконечное количество решений.
Другой тип системы линейных уравнений — это несовместимая система , в которой уравнения представляют собой две параллельные линии.Линии имеют одинаковый наклон и разные точки пересечения y- . Для обеих линий нет общих точек; следовательно, у системы нет решения.
Общее примечание: Типы линейных систем
Существует три типа систем линейных уравнений с двумя переменными и три типа решений.
- Независимая система имеет ровно одну пару решений [латекс] \ left (x, y \ right) [/ latex]. Точка пересечения двух линий — единственное решение.
- Несогласованная система не имеет решения. Обратите внимание, что две линии параллельны и никогда не пересекутся.
- Зависимая система имеет бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
Ниже приводится сравнение графических представлений каждого типа системы.
Как сделать: для данной системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением.
- Подставьте упорядоченную пару в каждое уравнение системы.
- Определите, являются ли истинные утверждения результатом подстановки в обоих уравнениях; в таком случае заказанная пара является решением.
Пример: определение того, является ли упорядоченная пара решением системы уравнений
Определите, является ли упорядоченная пара [латекс] \ left (5,1 \ right) [/ latex] решением данной системы уравнений.
[латекс] \ begin {align} x + 3y & = 8 \\ 2x-9 & = y \ end {align} [/ latex]
Показать решениеПодставьте упорядоченную пару [латекс] \ left (5,1 \ right) [/ latex] в оба уравнения.
[латекс] \ begin {align} \ left (5 \ right) +3 \ left (1 \ right) & = 8 \\ [1mm] 8 & = 8 && \ text {True} \\ [3mm] 2 \ left (5 \ right) -9 & = \ left (1 \ right) \\ [1 мм] 1 & = 1 && \ text {True} \ end {align} [/ latex]
Упорядоченная пара [латекс] \ left (5,1 \ right) [/ latex] удовлетворяет обоим уравнениям, поэтому это решение системы.
Анализ решения
Мы можем ясно увидеть решение, построив график каждого уравнения. Поскольку решение представляет собой упорядоченную пару, удовлетворяющую обоим уравнениям, это точка на обеих прямых и, следовательно, точка пересечения двух прямых.
Попробуйте
Определите, является ли упорядоченная пара [латекс] \ left (8,5 \ right) [/ latex] решением следующей системы.
[латекс] \ begin {align} 5x-4y & = 20 \\ 2x + 1 & = 3y \ end {align} [/ latex]
Решение систем уравнений с помощью построения графиков
Существует несколько методов решения систем линейных уравнений. Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив систему уравнений на одном и том же наборе осей.
Пример: решение системы уравнений с двумя переменными с помощью построения графика
Решите следующую систему уравнений, построив график. Определите тип системы.
[латекс] \ begin {align} 2x + y & = — 8 \\ x-y & = — 1 \ end {align} [/ latex]
Показать решениеРешите первое уравнение для [латекс] y [/ латекс].
[латекс] \ begin {align} 2x + y & = — 8 \\ y & = — 2x-8 \ end {align} [/ latex]
Решите второе уравнение для [латекс] y [/ латекс].
[латекс] \ begin {align} x-y & = — 1 \\ y & = x + 1 \ end {align} [/ latex]
Изобразите оба уравнения на одном и том же наборе осей:
Кажется, что линии пересекаются в точке [латекс] \ влево (-3, -2 \ вправо) [/ латекс].Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.
[латекс] \ begin {align} 2 \ left (-3 \ right) + \ left (-2 \ right) & = — 8 \\ [1 мм] -8 = -8 && \ text {True} \\ [ 3 мм] \ left (-3 \ right) — \ left (-2 \ right) & = — 1 \\ [1 мм] -1 & = — 1 && \ text {True} \ end {align} [/ latex]
Решением системы является упорядоченная пара [латекс] \ left (-3, -2 \ right) [/ latex], поэтому система независима.
Попробуйте
Решите следующую систему уравнений, построив график.
[латекс] \ begin {собрано} 2x — 5y = -25 \\ -4x + 5y = 35 \ end {собрано} [/ latex]
Показать решениеРешением системы является упорядоченная пара [латекс] \ left (-5,3 \ right) [/ latex].
Вопросы и ответы
Можно ли использовать построение графиков, если система непоследовательна или зависима?
Да, в обоих случаях мы можем построить график системы для определения типа системы и решения. Если две линии параллельны, система не имеет решения и непоследовательна.Если две линии идентичны, система имеет бесконечное количество решений и является зависимой системой.
Попробуй
Постройте три различных системы с помощью онлайн-графического инструмента. Отнесите каждое решение к категории согласованных или несовместимых. Если система непротиворечива, определите, является ли она зависимой или независимой. Возможно, вам будет проще построить график каждой системы по отдельности, а затем очистить свои записи, прежде чем строить следующую.
1)
[латекс] 5x-3y = -19 [/ latex]
[латекс] x = 2y-1 [/ латекс]
2)
[латекс] 4x + y = 11 [/ latex]
[латекс] -2y = -25 + 8x [/ latex]
3)
[латекс] y = -3x + 6 [/ latex]
[латекс] — \ frac {1} {3} y + 2 = x [/ latex]
- Одно решение — последовательное, независимое
- Нет решений, непоследовательные, ни зависимые, ни независимые
- Множество решений — последовательные, зависимые
Решение систем уравнений подстановкой
Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод.Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную. Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.
Как: дана система двух уравнений с двумя переменными, решите, используя метод подстановки.
- Решите одно из двух уравнений относительно одной из переменных через другую.
- Подставьте выражение для этой переменной во второе уравнение, затем решите для оставшейся переменной.
- Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
- Проверьте решение в обоих уравнениях.
Пример: решение системы уравнений с двумя переменными подстановкой
Решите следующую систему уравнений путем подстановки.
[латекс] \ begin {align} -x + y & = — 5 \\ 2x-5y & = 1 \ end {align} [/ latex]
Показать решениеСначала мы решим первое уравнение для [латекс] y [/ латекс].
[латекс] \ begin {align} -x + y & = — 5 \\ y & = x — 5 \ end {align} [/ latex]
Теперь мы можем заменить выражение [latex] x — 5 [/ latex] на [latex] y [/ latex] во втором уравнении.
[латекс] \ begin {align} 2x — 5y & = 1 \\ 2x — 5 \ left (x — 5 \ right) & = 1 \\ 2x — 5x + 25 & = 1 \\ -3x & = — 24 \\ x & = 8 \ end {align} [/ latex]
Теперь мы подставляем [latex] x = 8 [/ latex] в первое уравнение и решаем относительно [latex] y [/ latex].
[латекс] \ begin {align} — \ left (8 \ right) + y & = — 5 \\ y & = 3 \ end {align} [/ latex]
Наше решение — [латекс] \ left (8,3 \ right) [/ latex].
Проверьте решение, подставив [latex] \ left (8,3 \ right) [/ latex] в оба уравнения.
[латекс] \ begin {align} -x + y & = — 5 \\ — \ left (8 \ right) + \ left (3 \ right) & = — 5 && \ text {True} \\ [3mm] 2x — 5y & = 1 \\ 2 \ left (8 \ right) -5 \ left (3 \ right) & = 1 && \ text {True} \ end {align} [/ latex]
Попробуйте
Решите следующую систему уравнений путем подстановки.
[латекс] \ begin {align} x & = y + 3 \\ 4 & = 3x — 2y \ end {align} [/ latex]
Показать решение[латекс] \ влево (-2, -5 \ вправо) [/ латекс]
Вопросы и ответы
Можно ли методом подстановки решить любую линейную систему с двумя переменными?
Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент 1 или –1, чтобы нам не приходилось иметь дело с дробями.
Следующее видео длится ~ 10 минут и представляет собой мини-урок по использованию метода подстановки для решения системы линейных уравнений.Мы представляем три разных примера, а также используем инструмент построения графиков, чтобы подытожить решение для каждого примера.
Решение систем уравнений с двумя переменными методом сложения
Третий метод решения систем линейных уравнений — это метод сложения , этот метод также называется методом исключения . В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю.Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения умножением, чтобы одна переменная была исключена сложением.
Как: решить систему уравнений методом сложения.
- Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
- Напишите одно уравнение над другим, выровняв соответствующие переменные.Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную. Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
- Решите полученное уравнение для оставшейся переменной.
- Подставьте это значение в одно из исходных уравнений и решите вторую переменную.
- Проверьте решение, подставив значения в другое уравнение.
Пример: решение системы методом сложения
Решите данную систему уравнений сложением.
[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \ end {align} [/ latex]
Показать решениеОба уравнения уже установлены равными константе. Обратите внимание, что коэффициент [латекс] x [/ латекс] во втором уравнении, –1, противоположен коэффициенту [латекс] x [/ латекс] в первом уравнении, 1.Мы можем сложить два уравнения, чтобы исключить [latex] x [/ latex] без умножения на константу.
[латекс] \ begin {align} x + 2y & = — 1 \\ -x + y & = 3 \\ \ hline 3y & = 2 \ end {align} [/ latex]
Теперь, когда мы удалили [latex] x [/ latex], мы можем решить полученное уравнение для [latex] y [/ latex].
[латекс] \ begin {align} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align} [/ latex]
Затем мы подставляем это значение для [latex] y [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].
[латекс] \ begin {align} -x + y & = 3 \\ -x + \ frac {2} {3} & = 3 \\ -x & = 3- \ frac {2} {3} \\ -x & = \ frac {7} {3} \\ x & = — \ frac {7} {3} \ end {align} [/ latex]
Решение этой системы — [латекс] \ left (- \ frac {7} {3}, \ frac {2} {3} \ right) [/ latex].
Проверьте решение в первом уравнении.
[латекс] \ begin {align} x + 2y & = — 1 \\ \ left (- \ frac {7} {3} \ right) +2 \ left (\ frac {2} {3} \ right) & = \\ — \ frac {7} {3} + \ frac {4} {3} & = \\ \ — \ frac {3} {3} & = \\ -1 & = — 1 && \ text {True} \ end {align} [/ латекс]
Анализ решения
Мы получаем важное представление о системах уравнений, глядя на графическое представление.Посмотрите на график ниже, чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.
Пример: использование метода сложения, когда требуется умножение одного уравнения
Решите данную систему уравнений методом сложения .
[латекс] \ begin {align} 3x + 5y & = — 11 \\ x — 2y & = 11 \ end {align} [/ latex]
Показать решениеДобавление этих уравнений в представленном виде не устраняет переменную.Однако мы видим, что первое уравнение содержит [latex] 3x [/ latex], а второе уравнение содержит [latex] x [/ latex]. Итак, если мы умножим второе уравнение на [latex] -3, \ text {} [/ latex], термины x прибавятся к нулю.
[латекс] \ begin {align} x — 2y & = 11 \\ -3 \ left (x — 2y \ right) & = — 3 \ left (11 \ right) && \ text {Умножаем обе стороны на} -3 \ \ -3x + 6y & = — 33 && \ text {Использовать свойство распределения}. \ end {align} [/ latex]
А теперь добавим их.
[латекс] \ begin {align} 3x + 5y & = — 11 \\ −3x + 6y & = — 33 \\ \ hline 11y & = — 44 \\ y & = — 4 \ end {align} [/ latex]
На последнем этапе мы подставляем [latex] y = -4 [/ latex] в одно из исходных уравнений и решаем для [latex] x [/ latex].
[латекс] \ begin {align} 3x + 5y & = — 11 \\ 3x + 5 \ left (-4 \ right) & = — 11 \\ 3x — 20 & = — 11 \\ 3x & = 9 \\ x & = 3 \ end {align} [/ latex]
Наше решение — упорядоченная пара [латекс] \ left (3, -4 \ right) [/ latex]. Проверьте решение в исходном втором уравнении.
[латекс] \ begin {align} x — 2y & = 11 \\ \ left (3 \ right) -2 \ left (-4 \ right) & = 3 + 8 \\ & = 11 && \ text {True} \ конец {align} [/ latex]
Попробуйте
Решите систему уравнений сложением.
[латекс] \ begin {align} 2x — 7y & = 2 \\ 3x + y & = — 20 \ end {align} [/ latex]
Показать решение[латекс] \ влево (-6, -2 \ вправо) [/ латекс]
Пример: использование метода сложения, когда требуется умножение обоих уравнений
Решите данную систему уравнений с двумя переменными сложением.
[латекс] \ begin {align} 2x + 3y & = — 16 \\ 5x — 10y & = 30 \ end {align} [/ latex]
Показать решениеОдно уравнение имеет [латекс] 2x [/ латекс], а другое — [латекс] 5x [/ латекс].Наименьшее общее кратное — [latex] 10x [/ latex], поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Давайте удалим [latex] x [/ latex], умножив первое уравнение на [latex] -5 [/ latex], а второе уравнение на [latex] 2 [/ latex].
[латекс] \ begin {align} -5 \ left (2x + 3y \ right) & = — 5 \ left (-16 \ right) \\ -10x — 15y & = 80 \\ [3 мм] 2 \ left (5x — 10y \ right) & = 2 \ left (30 \ right) \\ 10x — 20y & = 60 \ end {align} [/ latex]
Затем мы складываем два уравнения.
[латекс] \ begin {align} -10x-15y & = 80 \\ 10x-20y & = 60 \\ \ hline -35y & = 140 \\ y & = — 4 \ end {align} [/ latex]
Подставьте [латекс] y = -4 [/ latex] в исходное первое уравнение.
[латекс] \ begin {align} 2x + 3 \ left (-4 \ right) & = — 16 \\ 2x — 12 & = — 16 \\ 2x & = — 4 \\ x & = — 2 \ end {align} [ / латекс]
Решение: [латекс] \ left (-2, -4 \ right) [/ latex]. Проверьте это в другом уравнении.
[латекс] \ begin {align} 5x — 10y & = 30 \\ 5 \ left (-2 \ right) -10 \ left (-4 \ right) & = 30 \\ -10 + 40 & = 30 \\ 30 & = 30 \ end {align} [/ latex]
Пример: использование метода сложения в системах уравнений, содержащих дроби
Решите данную систему уравнений с двумя переменными сложением.
[латекс] \ begin {align} \ frac {x} {3} + \ frac {y} {6} & = 3 \\ [1 мм] \ frac {x} {2} — \ frac {y} {4 } & = 1 \ end {align} [/ latex]
Показать решениеСначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.
[латекс] \ begin {align} 6 \ left (\ frac {x} {3} + \ frac {y} {6} \ right) & = 6 \ left (3 \ right) \\ [1 мм] 2x + y & = 18 \\ [3 мм] 4 \ left (\ frac {x} {2} — \ frac {y} {4} \ right) & = 4 \ left (1 \ right) \\ [1 мм] 2x-y & = 4 \ end {align} [/ latex]
Теперь умножьте второе уравнение на [latex] -1 [/ latex], чтобы мы могли исключить x .
[латекс] \ begin {align} -1 \ left (2x-y \ right) & = — 1 \ left (4 \ right) \\ [1 мм] -2x + y & = — 4 \ end {align} [/ латекс]
Сложите два уравнения, чтобы исключить x , и решите полученное уравнение относительно y .
[латекс] \ begin {align} 2x + y & = 18 \\ −2x + y & = — 4 \\ \ hline 2y & = 14 \\ y & = 7 \ end {align} [/ latex]
Подставьте [латекс] y = 7 [/ латекс] в первое уравнение.
[латекс] \ begin {align} 2x + \ left (7 \ right) & = 18 \\ 2x & = 11 \\ x & = \ frac {11} {2} \\ & = 7.5 \ end {align} [/ latex]
Решение: [латекс] \ left (\ frac {11} {2}, 7 \ right) [/ latex]. Проверьте это в другом уравнении.
[латекс] \ begin {align} \ frac {x} {2} — \ frac {y} {4} & = 1 \\ [1 мм] \ frac {\ frac {11} {2}} {2} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {11} {4} — \ frac {7} {4} & = 1 \\ [1 мм] \ frac {4} {4} & = 1 \ end {align} [/ latex]
Попробуйте
Решите систему уравнений сложением.
[латекс] \ begin {align} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align} [/ latex]
Показать решение[латекс] \ влево (10, -4 \ вправо) [/ латекс]
В следующем видео мы представляем больше примеров того, как использовать метод сложения (исключения) для решения системы двух линейных уравнений.
Классифицируйте решения по системам
Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для выявления несовместимых систем. Напомним, что несовместимая система состоит из параллельных линий, которые имеют одинаковый наклон, но разные точки пересечения [латекс] y [/ латекс]. Они никогда не пересекутся. При поиске решения несовместимой системы мы получим ложное утверждение, например [latex] 12 = 0 [/ latex].
Пример: решение несовместимой системы уравнений
Решите следующую систему уравнений.
[латекс] \ begin {собрано} & x = 9 — 2y \\ & x + 2y = 13 \ end {собрано} [/ latex]
Показать решениеМы можем подойти к этой проблеме двумя способами. Поскольку одно уравнение для [латекс] x [/ латекс] уже решено, наиболее очевидным шагом является использование замены.
[латекс] \ begin {align} x + 2y & = 13 \\ \ left (9 — 2y \ right) + 2y & = 13 \\ 9 + 0y & = 13 \\ 9 & = 13 \ end {align} [/ latex]
Ясно, что это утверждение противоречит тому, что [латекс] 9 \ ne 13 [/ латекс].Следовательно, у системы нет решения.
Второй подход заключается в том, чтобы сначала манипулировать уравнениями так, чтобы они оба были в форме пересечения наклона. Мы манипулируем первым уравнением следующим образом.
[латекс] \ begin {собрано} x = 9 — 2y \\ 2y = -x + 9 \\ y = — \ frac {1} {2} x + \ frac {9} {2} \ end {собрано} [ / латекс]
Затем мы преобразуем второе уравнение в форму пересечения наклона.
[латекс] \ begin {собрано} x + 2y = 13 \\ 2y = -x + 13 \\ y = — \ frac {1} {2} x + \ frac {13} {2} \ end {собрано} [ / латекс]
Сравнивая уравнения, мы видим, что они имеют одинаковый наклон, но разные точки пересечения y .Следовательно, линии параллельны и не пересекаются.
[латекс] \ begin {gather} y = — \ frac {1} {2} x + \ frac {9} {2} \\ y = — \ frac {1} {2} x + \ frac {13} {2 } \ end {gather} [/ latex]
Анализ решения
Запись уравнений в форме пересечения наклона подтверждает, что система несовместима, потому что все линии в конечном итоге будут пересекаться, если они не параллельны. Параллельные линии никогда не пересекаются; таким образом, у этих двух линий нет общих точек. Графики уравнений в этом примере показаны ниже.
Попробуйте
Решите следующую систему уравнений с двумя переменными.
[латекс] \ begin {собрано} 2y — 2x = 2 \\ 2y — 2x = 6 \ end {собрано} [/ latex]
Показать решениеНет решения. Это противоречивая система.
Выражение решения системы зависимых уравнений, содержащих две переменные
Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют собой одну и ту же линию.Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии. После использования замены или добавления результирующее уравнение будет идентичным, например [латекс] 0 = 0 [/ латекс].
Пример: поиск решения зависимой системы линейных уравнений
Найдите решение системы уравнений с помощью метода сложения .
[латекс] \ begin {собрано} x + 3y = 2 \\ 3x + 9y = 6 \ end {собрано} [/ latex]
Показать решениеС помощью метода сложения мы хотим исключить одну из переменных, добавив уравнения.В этом случае давайте сосредоточимся на удалении [латекс] х [/ латекс]. Если мы умножим обе части первого уравнения на [latex] -3 [/ latex], то мы сможем исключить переменную [latex] x [/ latex].
[латекс] \ begin {align} x + 3y & = 2 \\ \ left (-3 \ right) \ left (x + 3y \ right) & = \ left (-3 \ right) \ left (2 \ right) \\ -3x — 9y & = — 6 \ end {align} [/ latex]
Теперь сложите уравнения.
[латекс] \ begin {align} −3x − 9y & = — 6 \\ + 3x + 9y & = 6 \\ \ hline 0 & = 0 \ end {align} [/ latex]
Мы видим, что будет бесконечное число решений, удовлетворяющих обоим уравнениям.
Анализ решения
Если бы мы переписали оба уравнения в форме пересечения наклона, мы могли бы знать, как будет выглядеть решение перед добавлением. Давайте посмотрим, что происходит, когда мы преобразуем систему в форму с пересечением наклона.
[латекс] \ begin {align} \ begin {gather} x + 3y = 2 \\ 3y = -x + 2 \\ y = — \ frac {1} {3} x + \ frac {2} {3} \ конец {собрано} \ hspace {2cm} \ begin {gather} 3x + 9y = 6 \\ 9y = -3x + 6 \\ y = — \ frac {3} {9} x + \ frac {6} {9} \ \ y = — \ frac {1} {3} x + \ frac {2} {3} \ end {gather} \ end {align} [/ latex]
Посмотрите на график ниже.Обратите внимание, что результаты такие же. Общее решение системы — [латекс] \ left (x, — \ frac {1} {3} x + \ frac {2} {3} \ right) [/ latex].
Написание общего решения
В предыдущем примере мы представили анализ решения следующей системы уравнений:
[латекс] \ begin {собрано} x + 3y = 2 \\ 3x + 9y = 6 \ end {собрано} [/ latex]
После небольшой алгебры мы обнаружили, что эти два уравнения в точности совпадают. Затем мы записали общее решение как [latex] \ left (x, — \ frac {1} {3} x + \ frac {2} {3} \ right) [/ latex].Зачем нам писать решение именно так? В некотором смысле это представление о многом говорит нам. Он говорит нам, что x может быть любым, x — x . Это также говорит нам, что y будет зависеть от x , точно так же, как когда мы пишем правило функции. В этом случае, в зависимости от того, что вы добавили для x , y будет определено в терминах x как [латекс] — \ frac {1} {3} x + \ frac {2} {3} [ /латекс].
Другими словами, существует бесконечно много пар ( x , y ), которые удовлетворяют этой системе уравнений, и все они попадают на линию [латекс] f (x) — \ frac {1} {3} x + \ frac {2} {3} [/ латекс].
Попробуйте
Решите следующую систему уравнений с двумя переменными.
[латекс] \ begin {собрано} y — 2x = 5 \\ -3y + 6x = -15 \ end {собрано} [/ latex]
Показать решениеСистема зависима, поэтому существует бесконечно много решений вида [латекс] \ left (x, 2x + 5 \ right) [/ latex].
Использование систем уравнений для исследования прибылиИспользуя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме производства скейтбордов в начале раздела.Функция дохода производителя скейтбордов — это функция, используемая для расчета суммы денег, которая поступает в бизнес. Это может быть представлено уравнением [латекс] R = xp [/ latex], где [latex] x = [/ latex] количество и [latex] p = [/ latex] цена. Функция дохода показана оранжевым цветом на графике ниже.
Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как аренда и заработная плата, и переменные затраты, такие как коммунальные услуги.Функция стоимости показана синим цветом на графике ниже. Ось x представляет количество в сотнях единиц. Ось y представляет собой стоимость или доход в сотнях долларов.
Точка пересечения двух линий называется точкой безубыточности . Из графика видно, что если произведено 700 единиц, стоимость составит 3300 долларов, а выручка также составит 3300 долларов. Другими словами, компания сломается, даже если произведет и продаст 700 единиц. Они не зарабатывают и не теряют деньги.
Заштрихованная область справа от точки безубыточности представляет объемы, от которых компания получает прибыль. Заштрихованная область слева представляет объемы, по которым компания терпит убытки. Функция прибыли — это функция дохода за вычетом функции затрат, записываемая как [латекс] P \ left (x \ right) = R \ left (x \ right) -C \ left (x \ right) [/ latex]. Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.
Пример: определение точки безубыточности и функции прибыли с помощью замещения
Дана функция стоимости [латекс] C \ left (x \ right) = 0.85x + 35 {,} 000 [/ latex] и функция дохода [latex] R \ left (x \ right) = 1,55x [/ latex], найдите точку безубыточности и функцию прибыли.
Показать решениеНапишите систему уравнений, используя [latex] y [/ latex], чтобы заменить обозначение функции.
[латекс] \ begin {align} y & = 0,85x + 35 {,} 000 \\ y & = 1,55x \ end {align} [/ latex]
Подставьте выражение [latex] 0.85x + 35 {,} 000 [/ latex] из первого уравнения во второе уравнение и решите относительно [latex] x [/ latex].
[латекс] \ begin {собрано} 0.85x + 35 {,} 000 = 1,55x \\ 35 {,} 000 = 0,7x \\ 50 {,} 000 = x \ end {в собранном виде} [/ latex]
Затем мы подставляем [латекс] x = 50 {,} 000 [/ latex] либо в функцию стоимости, либо в функцию дохода.
[латекс] 1,55 \ слева (50 {,} 000 \ справа) = 77 {,} 500 [/ латекс]
Точка безубыточности — [латекс] \ left (50 {,} 000,77 {,} 500 \ right) [/ latex].
Функция прибыли находится по формуле [латекс] P \ left (x \ right) = R \ left (x \ right) -C \ left (x \ right) [/ latex].
[латекс] \ begin {align} P \ left (x \ right) & = 1.55x- \ left (0,85x + 35 {,} 000 \ right) \\ & = 0,7x — 35 {,} 000 \ end {align} [/ latex]
Функция прибыли [латекс] P \ left (x \ right) = 0,7x — 35 {,} 000 [/ latex].
Анализ решения
Стоимость производства 50 000 единиц составляет 77 500 долларов США, а выручка от продажи 50 000 единиц также составляет 77 500 долларов США. Чтобы получить прибыль, бизнес должен произвести и продать более 50 000 единиц.
Как видно из графика ниже, функция прибыли имеет отрицательное значение до тех пор, пока [latex] x = 50 {,} 000 [/ latex] не пересечет ось x .Затем график переходит в положительные значения y и продолжает движение по этому пути, поскольку функция прибыли представляет собой прямую линию. Это показывает, что точка безубыточности для предприятий наступает, когда функция прибыли равна 0. Область слева от точки безубыточности представляет работу с убытками.
Написание системы линейных уравнений для ситуации
Редко можно получить уравнения, которые четко моделируют поведение, с которым вы сталкиваетесь в бизнесе, скорее, вы, скорее всего, столкнетесь с ситуацией, для которой вы знаете ключевую информацию, как в приведенном выше примере.Ниже мы суммируем три ключевых фактора, которые помогут вам преобразовать ситуацию в систему.
Как сделать: в ситуации, которая представляет собой систему линейных уравнений, напишите систему уравнений и найдите решение.
- Определите входные и выходные данные каждой линейной модели.
- Определите наклон и пересечение y каждой линейной модели.
- Найдите решение, установив две линейные функции равными другой и решив для x , или найдите точку пересечения на графике.
А теперь давайте попробуем применить эти ключевые факторы на практике. В следующем примере мы определяем, сколько разных типов билетов продано, учитывая информацию об общей выручке и количестве билетов, проданных на мероприятие.
Пример: запись и решение системы уравнений с двумя переменными
Стоимость билета в цирк составляет 25 долларов для детей и 50 долларов для взрослых. В определенный день посещаемость цирка составляет 2000 человек, а общий доход от ворот составляет 70 000 долларов.Сколько детей и сколько взрослых купили билеты?
Показать решениеПусть c = количество детей и a = количество взрослых, посещающих школу.
Общее количество человек — 2000 человек. Мы можем использовать это, чтобы написать уравнение для количества людей в цирке в тот день.
[латекс] c + a = 2 {,} 000 [/ латекс]
Доход от всех детей можно найти, умножив 25 долларов США на количество детей, [латекс] 25c [/ латекс]. Доход от всех взрослых можно найти, умножив 50 долларов.00 по количеству взрослых, [латекс] 50а [/ латекс]. Общий доход составляет 70 000 долларов. Мы можем использовать это, чтобы написать уравнение дохода.
[латекс] 25c + 50a = 70 {,} 000 [/ латекс]
Теперь у нас есть система линейных уравнений с двумя переменными.
[латекс] \ begin {собрано} c + a = 2,000 \\ 25c + 50a = 70 {,} 000 \ end {собрано} [/ latex]
В первом уравнении коэффициент обеих переменных равен 1. Мы можем быстро решить первое уравнение для [латекса] c [/ латекса] или [латекса] a [/ латекса].Решим за [латекс] [/ latex].
[латекс] \ begin {собрано} c + a = 2 {,} 000 \\ a = 2 {,} 000-c \ end {собрано} [/ latex]
Подставьте выражение [latex] 2 {,} 000-c [/ latex] во второе уравнение для [latex] a [/ latex] и решите относительно [latex] c [/ latex].
[латекс] \ begin {align} 25c + 50 \ left (2 {,} 000-c \ right) & = 70 {,} 000 \\ 25c + 100 {,} 000 — 50c & = 70 {,} 000 \ \ -25c & = — 30 {,} 000 \\ c & = 1 {,} 200 \ end {align} [/ latex]
Подставьте [latex] c = 1 {,} 200 [/ latex] в первое уравнение для решения относительно [latex] a [/ latex].
[латекс] \ begin {align} 1 {,} 200 + a & = 2 {,} 000 \\ a & = 800 \ end {align} [/ latex]
Мы обнаружили, что 1200 детей и 800 взрослых купили в тот день билеты в цирк.
Попробуйте
Билеты в цирк стоят 4 доллара для детей и 12 долларов для взрослых. Если было куплено 1650 билетов на питание на общую сумму 14 200 долларов, сколько детей и сколько взрослых купили билеты на питание?
Иногда система уравнений может помочь в принятии решения. В следующем примере мы помогаем ответить на вопрос: «Какая компания по аренде грузовиков предоставит наилучшую стоимость?»
Пример: построение системы линейных моделей для выбора компании по аренде грузовиков
Джамал выбирает между двумя компаниями по аренде грузовиков.Первый, Keep on Trucking, Inc., взимает предоплату в размере 20 долларов, затем 59 центов за милю. Второй, Move It Your Way, требует предоплаты в размере 16 долларов США, затем 63 цента за милю. Когда компания Keep on Trucking, Inc. станет лучшим выбором для компании Jamal?
Показать решениеДвумя важными величинами в этой задаче являются стоимость и количество пройденных миль. Поскольку нам нужно рассмотреть две компании, мы определим две функции.
| Ввод | d , пройденное расстояние в милях |
| Выходы | K ( d ): стоимость в долларах для аренды у Keep on Trucking M ( d ) стоимость в долларах для аренды у Move It Your Way |
| Начальное значение | Авансовый платеж: K (0) = 20 и M (0) = 16 |
| Скорость изменения | K ( d ) = 0 руб.59 за милю и P ( d ) = 0,63 доллара за милю |
Линейная функция имеет вид [латекс] f \ left (x \ right) = mx + b [/ latex]. Используя скорости изменения и начальные расходы, мы можем записать уравнения
[латекс] \ begin {align} K \ left (d \ right) = 0,59d + 20 \\ M \ left (d \ right) = 0,63d + 16 \ end {align} [/ latex]
Используя эти уравнения, мы можем определить, когда Keep on Trucking, Inc. будет лучшим выбором. Поскольку все, что нам нужно сделать, это затраты, мы ищем, когда Move It Your Way будет стоить меньше, или когда [латекс] K \ left (d \ right) Эти графики схематично изображены выше, причем K ( d ) выделены синим цветом. Чтобы найти пересечение, мы приравниваем уравнения и решаем: [латекс] \ begin {align} K \ left (d \ right) & = M \ left (d \ right) \\ 0,59d + 20 & = 0,63d + 16 \\ 4 & = 0,04d \\ 100 & = d \ \ d & = 100 \ end {align} [/ latex] Это говорит нам о том, что стоимость проезда для двух компаний будет одинаковой, если проехать 100 миль.Либо посмотрев на график, либо отметив, что [латекс] K \ left (d \ right) [/ latex] растет медленнее, мы можем сделать вывод, что Keep on Trucking, Inc. будет дешевле, когда больше, чем Проехано 100 миль, то есть [латекс] d> 100 [/ латекс]. Приложения для систем кажутся почти бесконечными, но мы просто покажем еще одно. В следующем примере мы определяем количество 80% раствора метана, которое нужно добавить к 50% раствору, чтобы получить окончательный раствор 60%. У химика есть 70 мл 50% раствора метана.Сколько 80% раствора она должна добавить, чтобы окончательный раствор состоял из 60% метана? Мы воспользуемся следующей таблицей, чтобы помочь нам решить эту проблему со смесью: Начнем с 70 мл раствора, и неизвестное количество может быть x .Часть представляет собой проценты или концентрацию раствора 0,5 для начала, 0,8 для доп. Добавьте столбец суммы, чтобы получить окончательную сумму.Часть этого количества равна 0,6, потому что мы хотим, чтобы окончательный раствор содержал 60% метана. Умножьте сумму на часть, чтобы получить сумму.обязательно распределить по последнему ряду: [латекс] (70 + х) 0,6 [/ латекс]. Если мы сложим начало и добавим записи в столбце «Итого», мы получим окончательное уравнение, которое представляет общую сумму и ее концентрацию. [латекс] \ begin {align} 35 + 0,8x & = 42 + 0,6x \\ 0,2x & = 7 \\ \ frac {0,2} {0,2} x & = \ frac {7} {0,2} \\ x & = 35 \ конец {align} [/ latex] 35 мл 80% раствора необходимо добавить к 70 мл 50% раствора, чтобы получить 60% раствор метана. Тот же процесс можно использовать, если к начальной и конечной сумме привязана цена, а не процент. метод сложения алгебраический метод, используемый для решения систем линейных уравнений, в которых уравнения складываются таким образом, чтобы исключить одну переменную, позволяя решить полученное уравнение для оставшейся переменной; затем используется подстановка для решения первой переменной точка безубыточности точка, в которой функция затрат пересекает функцию дохода; где прибыль равна нулю согласованная система система, для которой существует единственное решение для всех уравнений в системе, и это независимая система, или если существует бесконечное количество решений, и это зависимая система функция затрат функция, используемая для расчета затрат на ведение бизнеса; обычно состоит из двух частей: постоянных затрат и переменных затрат зависимая система система линейных уравнений, в которой два уравнения представляют одну и ту же линию; существует бесконечное количество решений для зависимой системы несовместимая система система линейных уравнений без общего решения, поскольку они представляют собой параллельные линии, не имеющие общей точки или прямой независимая система система линейных уравнений с ровно одной парой решений [латекс] \ left (x, y \ right) [/ latex] функция прибыли функция прибыли записывается как [латекс] P \ left (x \ right) = R \ left (x \ right) -C \ left (x \ right) [/ latex], выручка минус затраты функция дохода функция, которая используется для расчета дохода, просто записывается как [латекс] R = xp [/ latex], где [latex] x = [/ latex] количество и [latex] p = [/ latex] цена. метод подстановки алгебраический метод, используемый для решения систем линейных уравнений, в котором одно из двух уравнений решается для одной переменной, а затем подставляется во второе уравнение для решения для второй переменной система линейных уравнений набор из двух или более уравнений с двумя или более переменными, которые должны рассматриваться одновременно. Система дифференциальных уравнений, которую можно записать в виде: {y1 ′ = a1 & InvisibleTimes; 1 & ApplyFunction; (t) & InvisibleTimes; y1 + a1 & InvisibleTimes; 2 & ApplyFunction; (t) & InvisibleTimes; y2 +… + a1 & InvisibleTimes; n & ApplyFunction; (t) & InvisibleTimes; (t) & InvisibleTimes; y1 + a2 & InvisibleTimes; 2 & ApplyFunction; (t) & InvisibleTimes; y2 +… + a2 & InvisibleTimes; n & ApplyFunction; (t) & InvisibleTimes; yn = h3 & ApplyFunction; (t) ……………………………………………………………… ; 1 & ApplyFunction; (t) & InvisibleTimes; yn + an & InvisibleTimes; 2 & ApplyFunction; (t) & InvisibleTimes; y2 +… + an & InvisibleTimes; n & ApplyFunction; (t) & InvisibleTimes; yn = hn & InvisibleFunction; (t) (LS) & Z будем называть системой линейных
дифференциальные уравнения. Функции
ai & InvisibleTimes; j & ApplyFunction; (t) & ZeroWidthSpace;
называются коэффициентами, а функции
привет & ApplyFunction; (t) & ZeroWidthSpace;
называются бесплатными условиями системы. Систему (LS) часто записывают в матричной форме: y⃗ ′ = A & ApplyFunction; (t) & InvisibleTimes; y⃗ + h⃗ & ApplyFunction; (t) & ZeroWidthSpace; куда: y⃗ ′ = [y1′y2 ′… yn ′], A & ApplyFunction; (t) = [a1 & InvisibleTimes; 1 & ApplyFunction; (t) a1 & InvisibleTimes; 2 & ApplyFunction; (t)… a1 & InvisibleTimes; n & ApplyFunction; (t) a2 & InvisibleTimes; ; 2 & ApplyFunction; (t)… a2 & InvisibleTimes; n & ApplyFunction; (t) ………… an & InvisibleTimes; 1 & ApplyFunction; (t) an & InvisibleTimes; 2 & ApplyFunction; (t)… an & InvisibleTimes; n & ApplyFunction; (t)], h⃗ & ApplyFunction; (t)], h⃗ & ApplyFunction; (t)], h⃗ & ApplyFunction; (t)], h⃗ & ; (t) h3 & ApplyFunction; (t)… hn & ApplyFunction; (t)] & ZeroWidthSpace; Пример .Матричная форма системы: x ′ = t & InvisibleTimes; x − 2 & InvisibleTimes; y + ety ′ = x + t & InvisibleTimes; y − sin & ApplyFunction; t & ZeroWidthSpace; является: [x′y ′] = [t − 21t] & InvisibleTimes; [xy] + [et − sin & ApplyFunction; t] & ZeroWidthSpace; Упражнение . Запишите каждую из следующих систем в матрицу
форма: а) {x ′ = 3 & InvisibleTimes; x − 1t & InvisibleTimes; y + t2y ′ = — x + 4 & InvisibleTimes; y − tb) {x ′ = x − yy ′ = — x + 2 & InvisibleTimes; y + 1c) {x ′ = x− y + z + ty ′ = 2 & InvisibleTimes; x + 3 & InvisibleTimes; y − 5 & InvisibleTimes; z + 4z ′ = — 4 & InvisibleTimes; x + 2 & InvisibleTimes; y + 2 & InvisibleTimes; z + 3 & InvisibleTimes; t & ZeroWidthSpace; ОТВЕЧАТЬ Следующая теорема устанавливает достаточные условия для начального значения
проблема, связанная с (LS), чтобы иметь единственное решение. Теорема . Предположим, что функции
ai & InvisibleTimes; j & ApplyFunction; (t) & ZeroWidthSpace;
и
привет & ApplyFunction; (t) & ZeroWidthSpace;
(i, j = 1,…, n & ZeroWidthSpace;)
непрерывны на интервале
(а, б). & ZeroWidthSpace;
Тогда для каждого
t0 & Элемент; (a, b) & ZeroWidthSpace;
и каждый
y10, y20,…, yn0 & Element; R & ZeroWidthSpace;
существует единственное решение
y⃗ & ApplyFunction; (t) = (y1 & ApplyFunction; (t),…, yn & ApplyFunction; (t)) & ZeroWidthSpace;
системы (LS), удовлетворяющей начальным условиям
y⃗ & ApplyFunction; (t0) = (y10, y20,…, yn0).& ZeroWidthSpace; Метод исключения заключается в приведении системы
п & ZeroWidthSpace;
дифференциальные уравнения в одно дифференциальное уравнение порядка
n & ZeroWidthSpace ;.
Следующий пример объясняет это. Пример. Рассмотрим систему: (S) {x ′ = t & InvisibleTimes; x − y + 1y ′ = 2 & InvisibleTimes; x + t & InvisibleTimes; y − et & ZeroWidthSpace; Если мы решим первое уравнение (S) в
y & ZeroWidthSpace ;,
мы получили y = x ′ + t & InvisibleTimes; x + 1 & ZeroWidthSpace; и следовательно, у ‘= х’ ‘+ х + т & InvisibleTimes; х’ + 1.& ZeroWidthSpace; Подставляю сейчас
y & ZeroWidthSpace;
и
y ′ & ZeroWidthSpace;
таким образом выраженный
x & ZeroWidthSpace;
во второе уравнение получаем: x ′ ′ + x + t & InvisibleTimes; x ′ + 1 = 2 & InvisibleTimes; x + t & InvisibleTimes; (x ′ + t & InvisibleTimes; x + 1) −et & ZeroWidthSpace; После упрощения последнее уравнение принимает вид: x ′ ′ — (t2 + 1) и InvisibleTimes; x − t − 1 + et = 0 и ZeroWidthSpace; Таким образом, мы превратили систему (S) в единую систему второго порядка.
линейное уравнение. Следует отметить, что, наоборот, каждое линейное уравнение второго порядка может быть
превращается в систему двух линейных уравнений первого порядка. Чтобы увидеть это,
рассмотреть уравнение (*) y ′ ′ + p & ApplyFunction; (t) & InvisibleTimes; y ′ + q & ApplyFunction; (t) & InvisibleTimes; y = h & ApplyFunction; (t) & ZeroWidthSpace; Обозначение
y ′ & ApplyFunction; (t) & ZeroWidthSpace;
по
x & ApplyFunction; (t), & ZeroWidthSpace;
мы вводим новую функцию
х, & ZeroWidthSpace;
чья производная
x ′ = y ′ ′ & ZeroWidthSpace ;.Тогда уравнение (L) принимает вид x ′ + p & ApplyFunction; (t) & InvisibleTimes; x + q & ApplyFunction; (t) & InvisibleTimes; y = h & ApplyFunction; (t) & ZeroWidthSpace; который вместе с заменой
у ‘= х, & ZeroWidthSpace;
дает следующую систему: (**) {x ′ = — p & ApplyFunction; (t) & InvisibleTimes; x − q & ApplyFunction; (t) & InvisibleTimes; y + h & ApplyFunction; (t) y ′ = x & ZeroWidthSpace; Пример .Решим систему: (S) {x ′ = x − y + ety ′ = x + 3 & InvisibleTimes; y & ZeroWidthSpace; с начальными условиями
x & ApplyFunction; (0) = y & ApplyFunction; (0) = 0. & ZeroWidthSpace; РЕШЕНИЕ Решая первое уравнение для
y & ZeroWidthSpace ;,
мы получили
y = x − x ′ + et. & ZeroWidthSpace;
Следовательно
y ′ = x′ − x ′ ′ + et. & ZeroWidthSpace; Подстановка
y & ZeroWidthSpace;
и
y ′ & ZeroWidthSpace;
во втором уравнении получаем: x′ − x ′ ′ + et = x + 3 & InvisibleTimes; (x − x ′ + et) и ZeroWidthSpace; Итак, после упрощений получаем: (R1) x ′ ′ — 4 & InvisibleTimes; x ′ + 4 & InvisibleTimes; x = −2 & InvisibleTimes; et & ZeroWidthSpace; Мы получили линейное уравнение второго порядка в
Икс.& ZeroWidthSpace;
Соответствующее однородное уравнение: (R2)
x ′ ′ — 4 & InvisibleTimes; x ′ + 4 & InvisibleTimes; x = 0 & ZeroWidthSpace; Характеристическое уравнение (R2) имеет вид
λ2−4 & InvisibleTimes; λ + 4 = 0. & ZeroWidthSpace;
Имеет двойной корень
λ1,2 = 2 & ZeroWidthSpace ;. Таким образом, общее решение (R2) есть
x = (C1 + C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t. & ZeroWidthSpace; Теперь мы найдем частное решение (R1) методом неопределенных
коэффициенты.Ищем решение в виде
xp = A & InvisibleTimes; et. & ZeroWidthSpace; После дифференцирования получаем
xp ′ = xp ′ ′ = A & InvisibleTimes; et. & ZeroWidthSpace;
Подстановка
xp, xp ′ и ZeroWidthSpace;
и
xp ′ ′ & ZeroWidthSpace;
в уравнении (R1) получаем: A & InvisibleTimes; et − 4 & InvisibleTimes; A & InvisibleTimes; et + 4 & InvisibleTimes; A & InvisibleTimes; et = −2 & InvisibleTimes; et, & ZeroWidthSpace;
следовательно
А = -2.& ZeroWidthSpace; Таким образом, мы получили общее решение (R1): (X) x = (C1 + C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t − 2 & InvisibleTimes; et & ZeroWidthSpace; Из первого уравнения системы (S),
x ′ = x − y + et, & ZeroWidthSpace;
мы нашли
y = x − x ′ + et. & ZeroWidthSpace; Из (X) следует, что
x ′ = (C2 + 2 & InvisibleTimes; C1 + 2 & InvisibleTimes; C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t − 2 & InvisibleTimes; et.& ZeroWidthSpace;
Следовательно y = x − x ′ + et = (C1 + C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t − 2 & InvisibleTimes; et− (C2 + 2 & InvisibleTimes; C1 + 2 & InvisibleTimes; C2 & InvisibleTimes; times & evisibleTimes; ; и после упрощений (Y) y = (- C1 − C2 − C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t + et & ZeroWidthSpace; Таким образом, общее решение системы (1): x = (C1 + C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t − 2 & InvisibleTimes; et & ZeroWidthSpace; y = (- C1 − C2 − C2 & InvisibleTimes; t) & InvisibleTimes; e2 & InvisibleTimes; t + et & ZeroWidthSpace; Применяя начальные условия
x & ApplyFunction; (0) = y & ApplyFunction; (0) = 0 & ZeroWidthSpace;
к полученному выше
x & ZeroWidthSpace;
и
y, & ZeroWidthSpace;
мы получили {C1−2 = 0 − C1 − C2 + 1 = 0 & ZeroWidthSpace; Следовательно
C1 = 2 & ZeroWidthSpace;
и
С2 = -1.& ZeroWidthSpace; Решение системы (S) с заданными начальными условиями: x = (2-t) & InvisibleTimes; e2 & InvisibleTimes; t-2 & InvisibleTimes; et & ZeroWidthSpace; y = (t − 1) & InvisibleTimes; e2 & InvisibleTimes; t + et & ZeroWidthSpace; Упражнение . Найдите решение системы: (S) {x ′ = x + y − ety ′ = — x − y + et & ZeroWidthSpace; с начальными условиями
x & ApplyFunction; (0) = y & ApplyFunction; (0) = 1.& ZeroWidthSpace; ОТВЕЧАТЬ x = −et + 2 & InvisibleTimes; t − 2 & ZeroWidthSpace; y = et − 2 & InvisibleTimes; t & ZeroWidthSpace; РЕШЕНИЕ Решая первое уравнение в
y & ZeroWidthSpace ;,
у нас есть
y = x′ − x + et. & ZeroWidthSpace; Следовательно
y ′ = x ′ ′ — x ′ + и т.д. & ZeroWidthSpace;
Подстановка
y & ZeroWidthSpace;
и
y ′ & ZeroWidthSpace;
полученное таким образом ко второму уравнению, получаем x ′ ′ — x ′ + et = −x− (x′ − x + et) + et & ZeroWidthSpace; После упрощений получаем x ′ ′ = — et & ZeroWidthSpace; Последнее уравнение дает x ′ = — et + C1 & ZeroWidthSpace; и следовательно, (X) x = −et + C1 & InvisibleTimes; t + C2 & ZeroWidthSpace; Следовательно
y = x′ − x + et = & ZeroWidthSpace; −et + C1 — (- et + C1 & InvisibleTimes; t + C2) + et & ZeroWidthSpace; После упрощений получаем (Y) y = et-C1 & InvisibleTimes; t + C1-C2 & ZeroWidthSpace; Применяя начальные условия к (X) и (Y) соответственно, получаем -1 + C1 = 1 & ZeroWidthSpace; 1 + C1-C2 = 1 & ZeroWidthSpace; следовательно
С1 = С2 = 2.& ZeroWidthSpace; Требуемое решение: x = −et + 2 & InvisibleTimes; t − 2 & ZeroWidthSpace; y = et − 2 & InvisibleTimes; t & ZeroWidthSpace; Упражнение . Найдите решение системы: (S) {x ′ = x + yy ′ = 1t & InvisibleTimes; y + t & ZeroWidthSpace; с начальными условиями
x & ApplyFunction; (1) = y & ApplyFunction; (1) = 0. & ZeroWidthSpace; ОТВЕЧАТЬ x = & ZeroWidthSpace; x = -t2-t-1 + 3 & InvisibleTimes; et-1 & ZeroWidthSpace; y = t2 − t & ZeroWidthSpace; РЕШЕНИЕ Обратите внимание, что второе уравнение включает
y & ZeroWidthSpace;
только, поэтому мы можем решить его как одно уравнение. Перезапись
y ′ = 1t & InvisibleTimes; y + t & ZeroWidthSpace;
в виде (EY)
y′ − 1t & InvisibleTimes; y = t, & ZeroWidthSpace; мы идентифицируем его как линейное уравнение первого порядка. Умножая обе части (EY) на интегрирующий коэффициент
e∫ (−1t) & InvisibleTimes; dt = 1t, & ZeroWidthSpace;
у нас есть 1t & InvisibleTimes; y′ − 1t2 & InvisibleTimes; y = 1 & ZeroWidthSpace; (1t & InvisibleTimes; y) ′ = 1 & ZeroWidthSpace; 1t & InvisibleTimes; y = t + C & ZeroWidthSpace; y = t2 + C & InvisibleTimes; t & ZeroWidthSpace; Начальное состояние
y & ApplyFunction; (1) = 0 & ZeroWidthSpace;
подразумевает
0 = 1 + C, & ZeroWidthSpace;
следовательно
С = -1.& ZeroWidthSpace;
Следовательно
y = t2 − t. & ZeroWidthSpace; Теперь заменяем
y = t2 − t & ZeroWidthSpace;
в правой части первого уравнения (S), и получим: x ′ = x + t2 − t & ZeroWidthSpace; или (EX) x′ − x = t2 − t & ZeroWidthSpace; Это снова линейное уравнение первого порядка. Умножая обе стороны
(EX) интегрирующим множителем
e∫ (-1) & InvisibleTimes; dt = e-t, & ZeroWidthSpace;
у нас есть e − t & InvisibleTimes; x′ − e − t & InvisibleTimes; x = (t2 − t) & InvisibleTimes; e − t & ZeroWidthSpace; (e-t & InvisibleTimes; x) ′ = (t2-t) & InvisibleTimes; e-t & ZeroWidthSpace; e − t & InvisibleTimes; x = — (t2 + t + 1) & InvisibleTimes; e − t + C & ZeroWidthSpace; следовательно x = −t2 − t − 1 + C & InvisibleTimes; et & ZeroWidthSpace; Начальное состояние
x & ApplyFunction; (1) = 0 & ZeroWidthSpace;
подразумевает
0 = −3 + C & InvisibleTimes; e, & ZeroWidthSpace;
следовательно
C = 3e.& ZeroWidthSpace; Следовательно
x = −t2 − t − 1 + 3 & InvisibleTimes; et − 1. & ZeroWidthSpace; Решение системы (S) с заданными начальными условиями: x = & ZeroWidthSpace; x = -t2-t-1 + 3 & InvisibleTimes; et-1 & ZeroWidthSpace; y = t2 − t & ZeroWidthSpace; Упражнение . Решите систему: (S) {x ′ = y − ty ′ = x + t & ZeroWidthSpace; с начальными условиями
x & ApplyFunction; (1) = y & ApplyFunction; (1) = 0.& ZeroWidthSpace; ОТВЕЧАТЬ x = −t + 1 & ZeroWidthSpace; y = t − 1 & ZeroWidthSpace; РЕШЕНИЕ Решая первое уравнение для
y & ZeroWidthSpace;
дает
y = x ′ + t, & ZeroWidthSpace;
следовательно
y ′ = x ′ ′ + 1. & ZeroWidthSpace; Второе уравнение теперь принимает следующий вид: x ′ ′ + 1 = x + t & ZeroWidthSpace; или (EX) x ′ ′ — x = t − 1 & ZeroWidthSpace; Однородное уравнение, связанное с (EX): (EXH) x ′ ′ — x = 0 & ZeroWidthSpace; Корни его характеристического уравнения
λ2−1 = 0 & ZeroWidthSpace;
являются
λ1 = -1 & ZeroWidthSpace;
и
λ2 = 1.& ZeroWidthSpace; Поэтому общее решение (EXH): x = C1 & InvisibleTimes; e − t + C2 & InvisibleTimes; et & ZeroWidthSpace; Мы ищем частное решение (EX) в виде: xp = A & InvisibleTimes; t + B & ZeroWidthSpace; У нас есть
xp ′ = A & ZeroWidthSpace;
и
xp ′ ′ = 0. & ZeroWidthSpace;
Уравнение (EX) теперь дает: −A & InvisibleTimes; t − B = t − 1 и ZeroWidthSpace; Следовательно
A = -1 & ZeroWidthSpace;
и
B = 1, & ZeroWidthSpace;
так
xp = −t + 1 & ZeroWidthSpace; Таким образом, мы получили общее решение (EX):
x = C1 & InvisibleTimes; e − t + C2 & InvisibleTimes; et − t + 1.& ZeroWidthSpace;
Следовательно
x ′ = — C1 & InvisibleTimes; e − t + C2 & InvisibleTimes; et − 1. & ZeroWidthSpace; Из первого уравнения (S) имеем
y = x ′ + t = & ZeroWidthSpace; −C1 & InvisibleTimes; e − t + C2 & InvisibleTimes; et − 1 + t. & ZeroWidthSpace; Общее решение (S): x = C1 & InvisibleTimes; e-t + C2 & InvisibleTimes; et-t + 1 & ZeroWidthSpace; y = & ZeroWidthSpace; −C1 & InvisibleTimes; e − t + C2 & InvisibleTimes; et + t − 1 & ZeroWidthSpace; Применяя начальные условия
x & ApplyFunction; (1) = y & ApplyFunction; (1) = 0, & ZeroWidthSpace;
мы получили: 0 = C1 + C2 & ZeroWidthSpace; 0 = −C1 + C2 & ZeroWidthSpace; следовательно
С1 = С2 = 0.& ZeroWidthSpace; Требуемое решение (S) тогда: x = −t + 1 & ZeroWidthSpace; y = t − 1 & ZeroWidthSpace; Упражнение . Решите систему: {x ′ = y + 1y ′ = — x − 2 & InvisibleTimes; y & ZeroWidthSpace; с начальными условиями
x & ApplyFunction; (0) = y & ApplyFunction; (0) = 0. & ZeroWidthSpace; ОТВЕЧАТЬ х = -2 & InvisibleTimes; e-t-t & InvisibleTimes; e-t + 2 & ZeroWidthSpace; у = е-т + т & InvisibleTimes; е-т-1 & ZeroWidthSpace; Упражнение .Решите систему: {x ′ = x + 2 & InvisibleTimes; yy ′ = — x − y & ZeroWidthSpace; с начальными условиями
x & ApplyFunction; (0) = y & ApplyFunction; (0) = 1. & ZeroWidthSpace; ОТВЕЧАТЬ x = cos & ApplyFunction; t + 3 & InvisibleTimes; sin & ApplyFunction; t & ZeroWidthSpace; y = cos & ApplyFunction; t − 2 & InvisibleTimes; sin & ApplyFunction; t & ZeroWidthSpace; Международная конференция ОРГАНИЗАЦИЯ НА ОСНОВЕ ЗНАНИЙ Vol.XXIII № 3 2017 ОПРЕДЕЛЕНИЕ КОНКРЕТНОГО РЕШЕНИЯ ДЛЯ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ Василе Церняшу «Николае Бэлчешу « Николае Бэлчешу », , Румыния, u, .com, Land Forces Academy, Siba0003. Аннотация: Как и в случае линейных дифференциальных уравнений n-го порядка с постоянными коэффициентами, решаемая задача связана с определением частного решения, а затем с использованием общего решения присоединенной однородной системы линейных дифференциальных уравнений с постоянные коэффициенты, чтобы записать общее решение изначально заданной системы.Для однородных систем линейных дифференциальных уравнений с постоянными коэффициентами определение общего решения представляет собой метод исключения или сокращения , который превращает систему в линейное дифференциальное уравнение того же порядка, что и системы, и его К методам ее решения применяется или метод собственных значений и векторов. Если система неоднородна, то мы также должны определить конкретное решение, которое может быть выполнено в таким же образом, как и в случае дифференциальных уравнений n-го порядка с постоянными коэффициентами, если метод Независимо от метода , использованного для определения общего решения присоединенной однородной системы линейных дифференциальных уравнений с постоянными коэффициентами, использовался метод редукции или исключения или метод вариации констант.Какой бы метод не использовался, определить конкретное решение для системы линейных дифференциальных уравнений с постоянными коэффициентами сложно, в этом исследовании предлагается метод, аналогичный методу линейных дифференциальных уравнений n-го порядка с постоянными коэффициентами . Ключевые слова: системы линейных дифференциальных уравнений с постоянными коэффициентами, однородные системы линейных дифференциальных уравнений с постоянными коэффициентами, частное решение, общее решение 1.Введение В этом исследовании представлен простой и практичный метод для определения конкретного решения для системы линейных дифференциальных уравнений с постоянными коэффициентами , и начинается с наблюдения о том, как можно получить конкретное решение . к линейному дифференциальному уравнению n-го порядка с постоянными коэффициентами. Свободные члены системы могут быть частью того же класса функций, что свободный член может быть частью для линейных дифференциальных уравнений n-го порядка с постоянными коэффициентами , а именно комбинацией таких как: DOI: 10.1515 / kbo-2017-0152 © 2017. Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivatives 3.0. Без аутентификации Дата загрузки | 28.07.17, 7:01 Теперь, разобравшись с основными терминами, приступим к решению! Предположим, у нас есть две зависимые переменные, x и y , представляющие популяцию криля и яков.Представьте себе скорость изменения яков d x / d t , отрицательно зависящую от количества крилей. Точно так же в этом гипотетическом мире скорость изменения криля, d y / d t , отрицательно зависит от количества яков. Таким образом, наша гипотетическая связанная система линейных дифференциальных уравнений: Два неизвестных и два уравнения предлагают метод исключения из алгебры. Как мы увидим, запись d x / d t как D x выглядит так, как будто D умножает x .D, однако, является оператором на x , где операция дифференцирования. Фактически, даже умножение, как 4 умножение x на 4 x , является 4, действующим на x . В систему криль-як! Заменить d x / d t на D x и d y / d t на D y : Положив сначала x , мы получим следующее изменение: Умножая уравнение 2 на D, получаем: Умножая уравнение 1 на 4, получаем: Как видите, теперь мы исключаем 4D x из уравнения: Вычитая одно уравнение из другого, мы удалили 4D x . Как решить это уравнение? Подставляя в -36 y + D2 y = 0, получаем: -36e при + a 2 e при = 0. Разделив на «есть», мы получим: -36 + a 2 = 0. Решив для a , получим: a = ± 6. Таким образом: y = c 1 e6 t + c 2 e-6 t . Это повторение шага 3, но y исключены. Умножение уравнения 1 на D: Умножение уравнения 2 на 9: Удаление 9D y дает -36 x + D2 x = 0. Форма этого уравнения в x такая же, как и для y . Таким образом, решения для x и y одинаковы, за исключением индексов у констант: x = c 3 e6 t + c 4 e-6 t . Начальные условия — это переменная и значения ее первой производной в момент времени t = 0. Представьте себе в начале, y = 0 и d y / d t = 12. Подставляя t = 0 в это получаем: Поскольку, e0 = 1, y = ( c 1) 1 + ( c 2) 1. В момент времени t = 0, y = 0. Таким образом: c 1 + c 2 = 0. Теперь для начального состояния на d y / d t , которое вы можете увидеть здесь: При t = 0 получается следующее: В момент времени t = 0, d y / d t = 12: 6 c 1-6 c 2 = 12. Разделив на 6, получим: c 1 — c 2 = 2. Отлично! Два уравнения и два неизвестных: c 1 + c 2 = 0 c 1 — c 2 = 2 Решая для c 1 и c 2, получаем: c 1 = 1 и c 2 = -1. Таким образом: Решение для y используется для нахождения c 3 и c 4 в решении x . Продифференцируйте решение для x и подставьте в уравнение 1, D x = -9 y , которое вы можете увидеть здесь: Приравнивая члены e6 t , получаем: 6 c 3 = -9 или c 3 = -3/2. Приравнивая члены e-6 t , получаем: -6 c 4 = 9 или c 4 = -3/2. Таким образом: Если выражения для x и y верны, обратная подстановка в исходную систему уравнений делает эти уравнения истинными. Мы собираемся проверить, удовлетворяется ли исходная гипотетическая связанная система этими значениями x и y . и удовлетворяет У нас есть LHS (левая сторона): Упрощение до: -9e6 t + 9e-6 t . И у нас есть наша правая часть (правая часть), в которую мы подставляем -9 y , чтобы получить: -9e6 t + 9e-6 t . Проверить! Для второго уравнения: LHS: d y / d t = 6e6 t + 6e-6 t . RHS: замените на -4 x , чтобы получить , что упрощается до 6e6 t + 6e-6 t . Отлично, мы получили! График популяции криля x показывает начальное состояние x = 0 и положительный наклон. Это население растет в геометрической прогрессии. С другой стороны, популяция яков, и , начинается с -3 (мы не уверены, как будут функционировать яки с популяцией -3), с наклоном 0 и продолжает экспоненциально уменьшаться. Конечно, эта связь между яком и крилем чисто гипотетическая. Естественные хищники криля — тюлени, киты, пингвины, а не яки. Тем не менее, график показывает решение, согласующееся с уравнениями и начальными условиями, и это самое главное! Хорошо, давайте уделим пару минут, чтобы повторить, так как это было совсем немного! Как мы узнали, дифференциальное уравнение просто содержит производные. Мы также узнали, что если нет произведений зависимых переменных и если все производные и зависимые переменные возведены в первую степень, то дифференциальное уравнение будет линейным .С двумя или более уравнениями это система , а когда разные зависимые переменные появляются в одном и том же уравнении, система связана . Пример: решение проблемы химической смеси
Сумма Часть Всего Начало Добавить Финал Сумма Часть Всего Начало 70 мл 0,5 Добавить [латекс] x [/ латекс] 0,8 Финал [латекс] 70 + x [/ латекс] 0,6 Сумма Часть Всего Начало 70 мл 0,5 35 Добавить [латекс] x [/ латекс] 0,8 [латекс] 0,8x [/ латекс] Финал [латекс] 70 + x [/ латекс] 0,6 [латекс] 42 + 0,6x [/ латекс] Ключевые понятия
Глоссарий
Линейные системы дифференциальных уравнений. Метод исключения
Линейные системы дифференциальных уравнений. Метод устранения Решение линейных систем — метод исключения
(PDF) Определение частного решения для систем линейных дифференциальных уравнений с постоянными коэффициентами
Решение систем линейных дифференциальных уравнений методом исключения
Решение дифференциальных уравнений
Шаг 1. Используйте обозначение D для производной.
Шаг 2. Составьте уравнения.
Шаг 3: Решить методом исключения.
Шаг 4. Решите дифференциальное уравнение.
Шаг 5: Используя исключение, найдите другие переменные.
Шаг 6: Используя начальные условия, найдите константы.
Шаг 7. Проверьте решение.
Шаг 8: Составьте график и прокомментируйте решение:
Резюме урока



 Пусть этот коэффициент будет равен 2.
Для этого представим нынешний коэффициент при иксе как
и далее, производя действия с дробями, получаем:
Пусть этот коэффициент будет равен 2.
Для этого представим нынешний коэффициент при иксе как
и далее, производя действия с дробями, получаем: Найти предел .
Найти предел . Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела.
Представляем его как отношение синуса к косинусу.
Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела.
Представляем его как отношение синуса к косинусу. Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю. И дальнейшие преобразования. Всё
вышеописанное выглядит так:
Затем умножаем числитель и знаменатель на выражение, сопряжённое знаменателю. И дальнейшие преобразования. Всё
вышеописанное выглядит так: И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.
И большинство студентов, которые пропускают пары, заочно изучают этот курс или имеют преподавателей, которые сами не всегда понимают о чем объясняют, не могут вычислить самых элементарных примеров на замечательные пределы. Из формул первого замечательного предела видим, что с их помощью можно исследовать неопределенности типа ноль разделить на ноль для выражений с тригонометрическими функциями. Рассмотрим сначала ряд примеров на первый замечательный пределу, а потом изучим второй замечательный предел.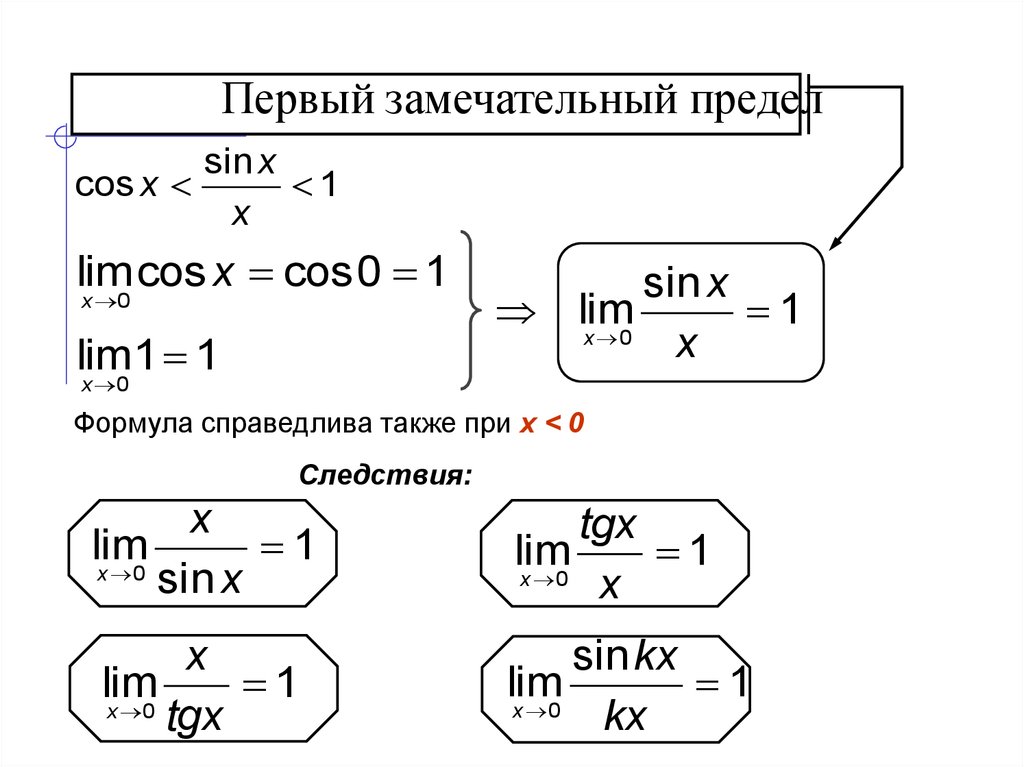 2
2  Далее выполняем замену переменных в пределе, и используем периодичность котангенса
Далее выполняем замену переменных в пределе, и используем периодичность котангенса (x-2)
(x-2) Для получения конечного значения используем формулу следствия 2 замечательного предела
Для получения конечного значения используем формулу следствия 2 замечательного предела Если заучить приведенные методики нахождения пределов Вам трудно, то всегда можете заказать контрольную работу на пределы у нас.
Если заучить приведенные методики нахождения пределов Вам трудно, то всегда можете заказать контрольную работу на пределы у нас. 2}<\left|AB\right|<\left|\overset\frown{ADB}\right|\)
2}<\left|AB\right|<\left|\overset\frown{ADB}\right|\) Подставим в двойное неравенство (в) и воспользуемся четностью косинуса и нечетностью синуса:
Подставим в двойное неравенство (в) и воспользуемся четностью косинуса и нечетностью синуса:
 0}2=1\)
0}2=1\)

 Таким образом, у нас есть так называемая неопределенность вида .
Таким образом, у нас есть так называемая неопределенность вида . Чистовой вариант решения может выглядеть так:
Чистовой вариант решения может выглядеть так:


 {0}\right]$
{0}\right]$ {2}-5 x+6}=-4$
{2}-5 x+6}=-4$ 307-68.
307-68.
 Какой должна быть стрелка, показано на
рисунке 6, б. Выносные линии выходят за концы стрелок размерной линии на 1…5
мм. Выносные и размерные линии проводят сплошной тонкой линией. Над размерной
линией, ближе к ее середине, наносят размерное число.
Какой должна быть стрелка, показано на
рисунке 6, б. Выносные линии выходят за концы стрелок размерной линии на 1…5
мм. Выносные и размерные линии проводят сплошной тонкой линией. Над размерной
линией, ближе к ее середине, наносят размерное число. 7. Нанесение размера окружностей
7. Нанесение размера окружностей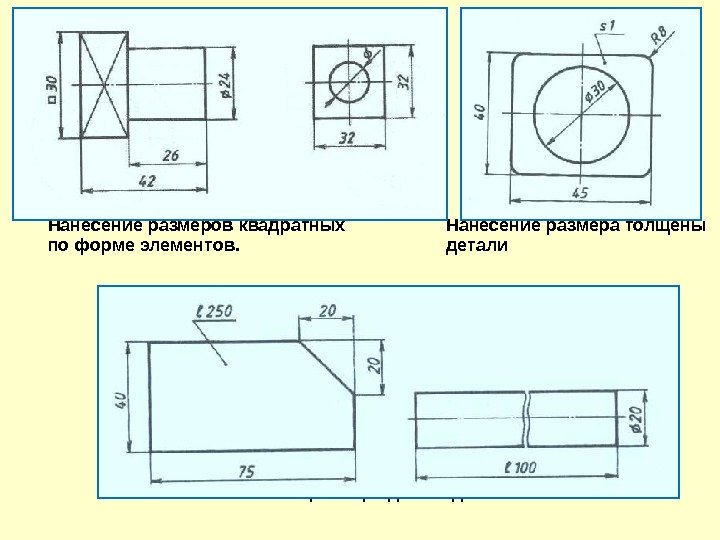 Например, запись на чертеже «3 отв. 0 10» означает, что в детали
имеются три одинаковых отверстия диаметром 10 мм.
Например, запись на чертеже «3 отв. 0 10» означает, что в детали
имеются три одинаковых отверстия диаметром 10 мм.
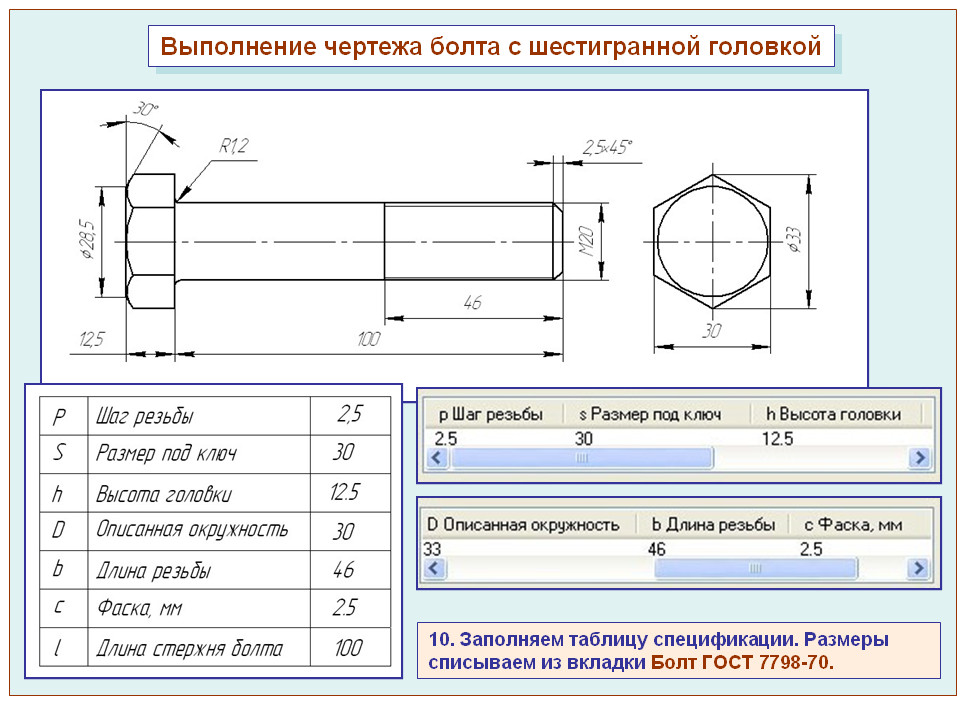 Сторона клетки равна 5 мм. Проставить размеры.
Работа выполняется на листе формата А4
Сторона клетки равна 5 мм. Проставить размеры.
Работа выполняется на листе формата А4 Приведите пример условных обозначений
применяемых на чертеже.
Приведите пример условных обозначений
применяемых на чертеже. Нанесите необходимые размеры, укажите толщину детали (она равна 4 мм).
Нанесите необходимые размеры, укажите толщину детали (она равна 4 мм). /
С.К. Боголюбов. — М.: Альянс, 2016. — 390 c.
/
С.К. Боголюбов. — М.: Альянс, 2016. — 390 c.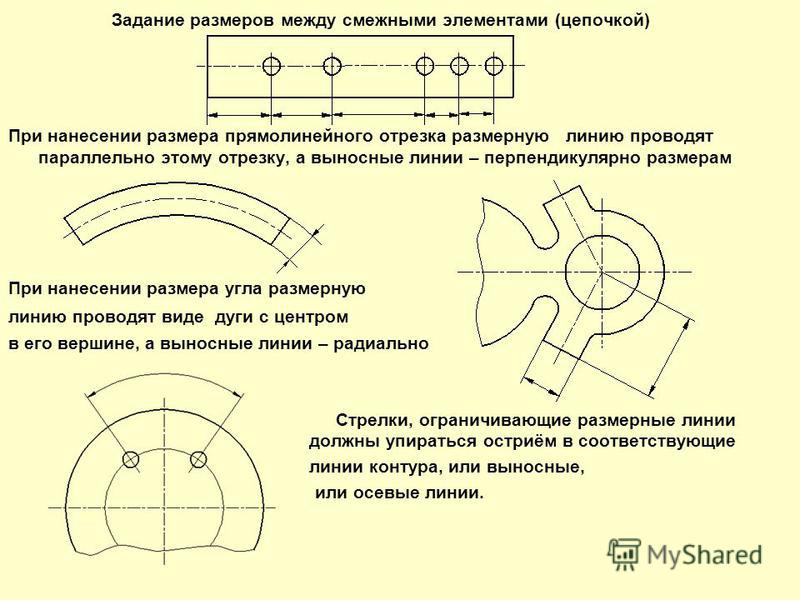 —
М.: ИЦ Академия, 2013. — 320 c.
—
М.: ИЦ Академия, 2013. — 320 c.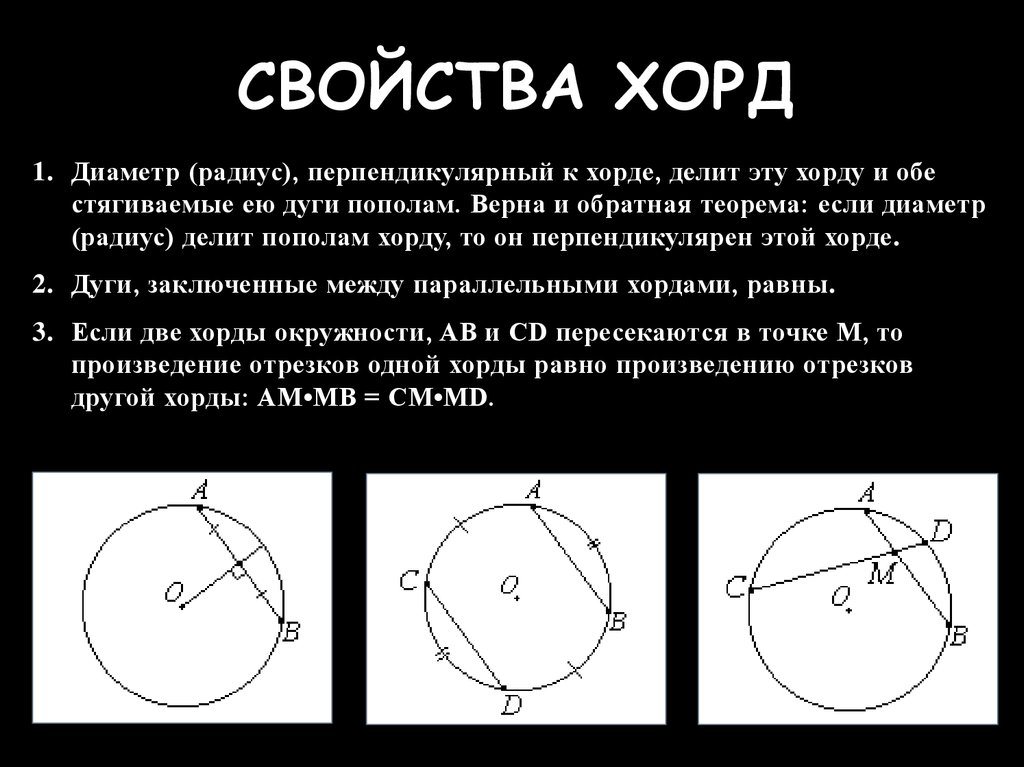 Возможна
простановка нескольких типов линейных, угловых, радиальных размеров,
диаметрального размера, размеров высоты и дуги. Кроме того, доступен
специальный способ простановки размеров, при котором тип размера автоматически
определяется системой.
Возможна
простановка нескольких типов линейных, угловых, радиальных размеров,
диаметрального размера, размеров высоты и дуги. Кроме того, доступен
специальный способ простановки размеров, при котором тип размера автоматически
определяется системой. Угловой размер
характеризует величину угла.
Угловой размер
характеризует величину угла. Расстояние между параллельными размерными линиями должно быть
не менее 7 мм.
(см. п. 1).
Расстояние между параллельными размерными линиями должно быть
не менее 7 мм.
(см. п. 1). (см. п: 1, 2, 3, 4, 5,
6).
(см. п: 1, 2, 3, 4, 5,
6).
 Текст размерной надписи может быть отредактирован
с помощью диалогового окна Задание размерной надписи.
Текст размерной надписи может быть отредактирован
с помощью диалогового окна Задание размерной надписи. 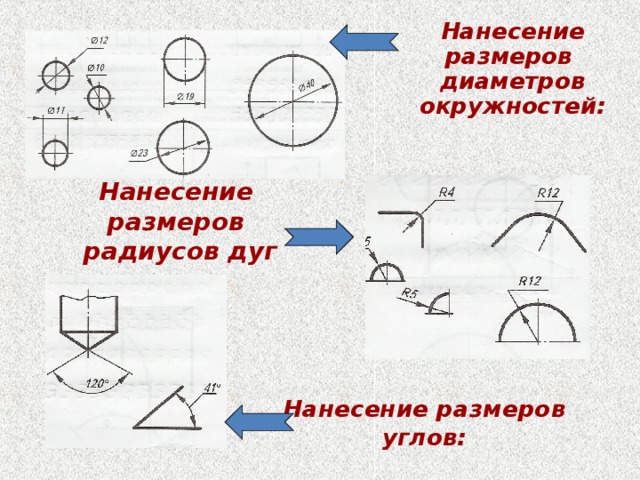
 Точки т1 и т2—точки привязки (точки выхода основных линий). Система
автоматически располагает выносные линии параллельно друг другу, а размерную
линию перпендикулярно им. Если длина размерной линии меньше суммарной длины
двух стрелок, стрелки автоматически будут сформированы снаружи выносных линий.
На расстоянии от 6 — 10 мм
от контура детали проводят параллельную ему размерную линию.
Точки т1 и т2—точки привязки (точки выхода основных линий). Система
автоматически располагает выносные линии параллельно друг другу, а размерную
линию перпендикулярно им. Если длина размерной линии меньше суммарной длины
двух стрелок, стрелки автоматически будут сформированы снаружи выносных линий.
На расстоянии от 6 — 10 мм
от контура детали проводят параллельную ему размерную линию.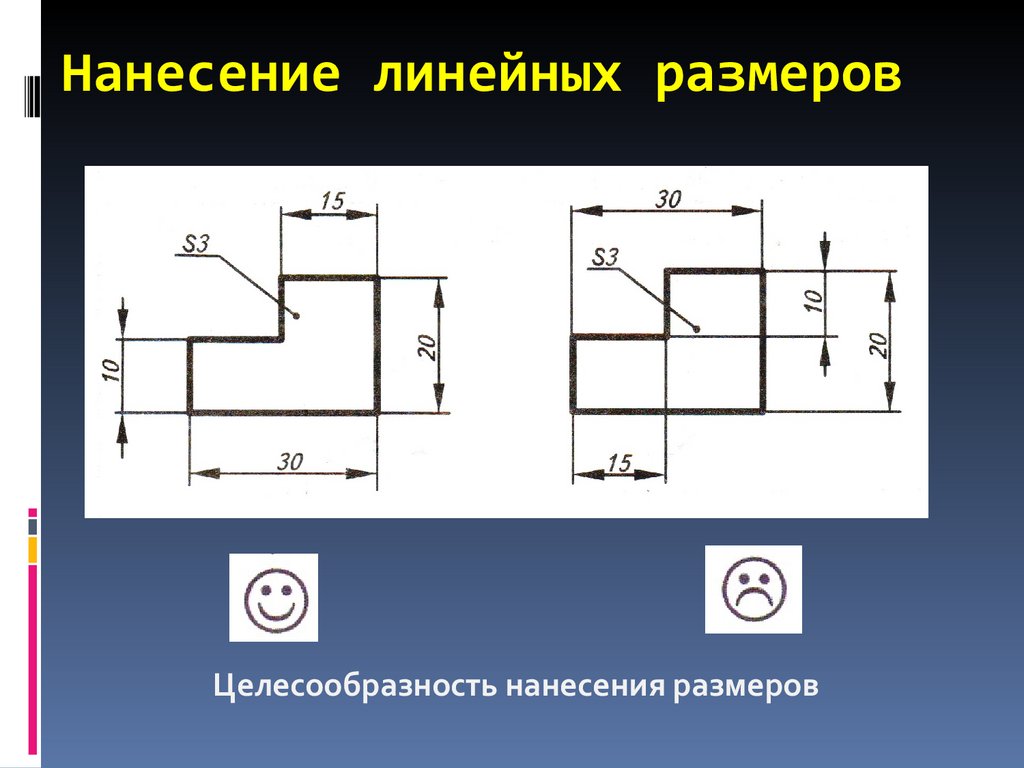 Равномерно распределяем размеры на все виды.
Осталось проставить размер окружности.
Равномерно распределяем размеры на все виды.
Осталось проставить размер окружности. Выберите кнопку Полная размерная линия.
Выберите кнопку Полная размерная линия.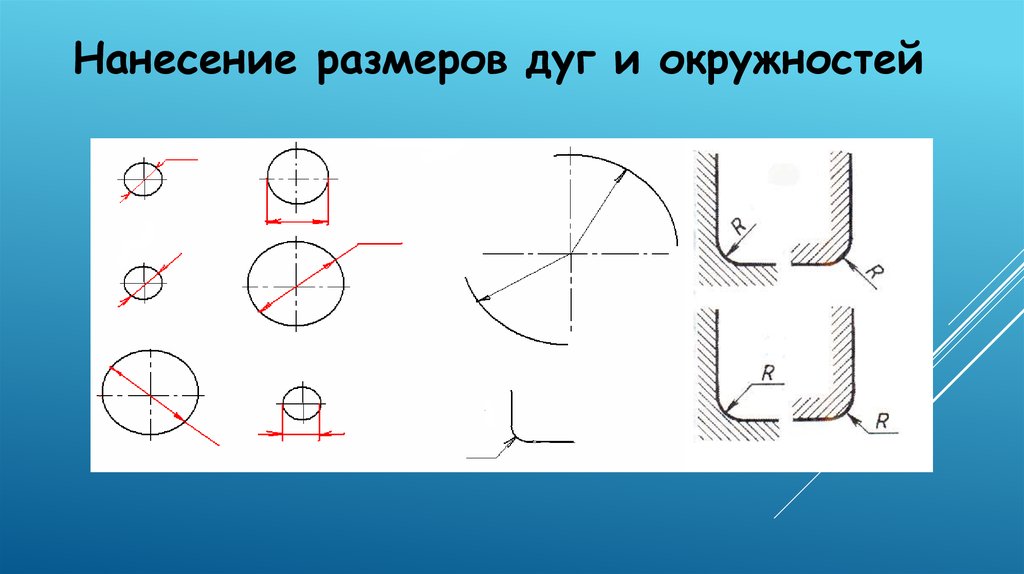 Местоположение
размера определяется наличием свободного места.
Местоположение
размера определяется наличием свободного места. Повторение изученного материала.
Повторение изученного материала.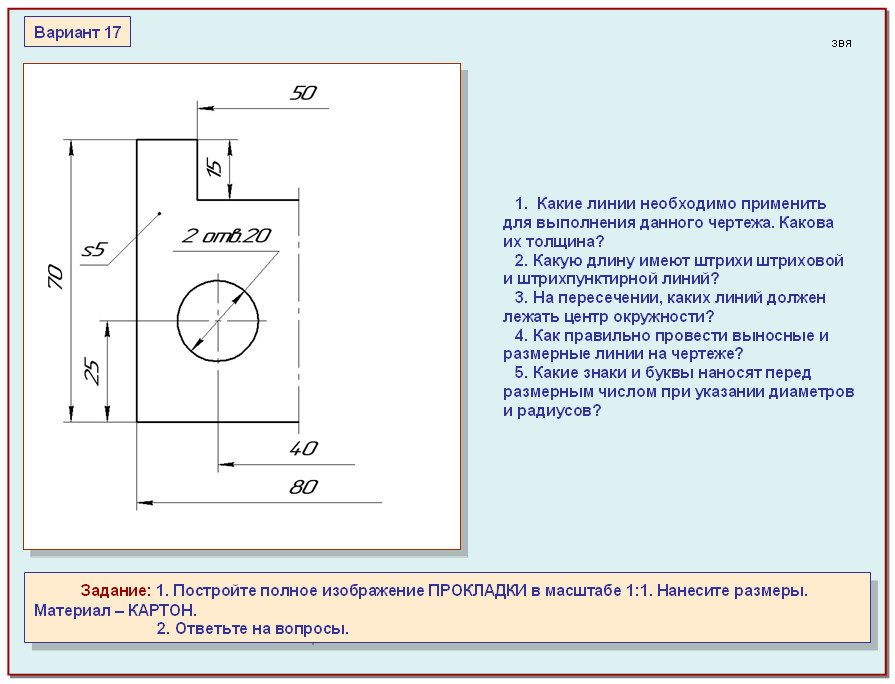 Линейные размеры на чертежах указывают в
миллиметрах, без обозначения единицы измерения.
Линейные размеры на чертежах указывают в
миллиметрах, без обозначения единицы измерения.
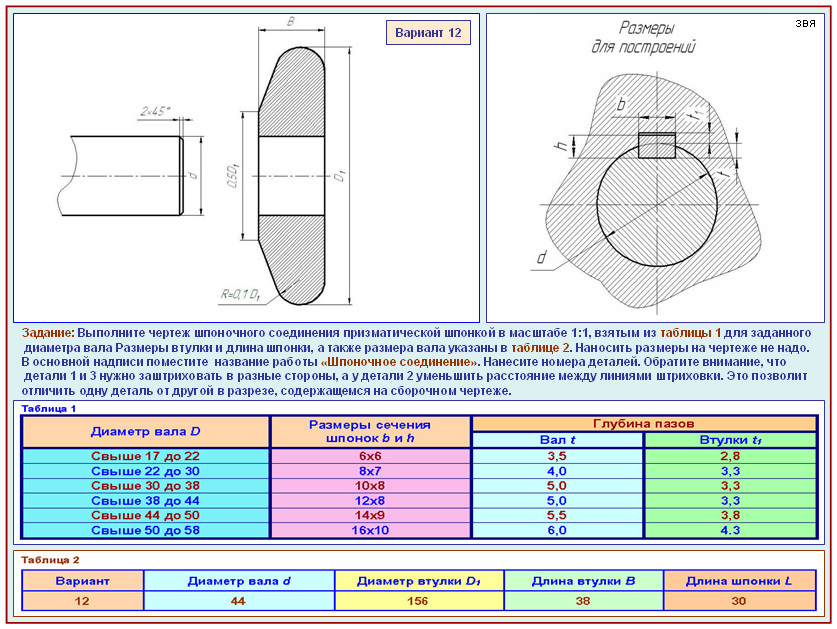
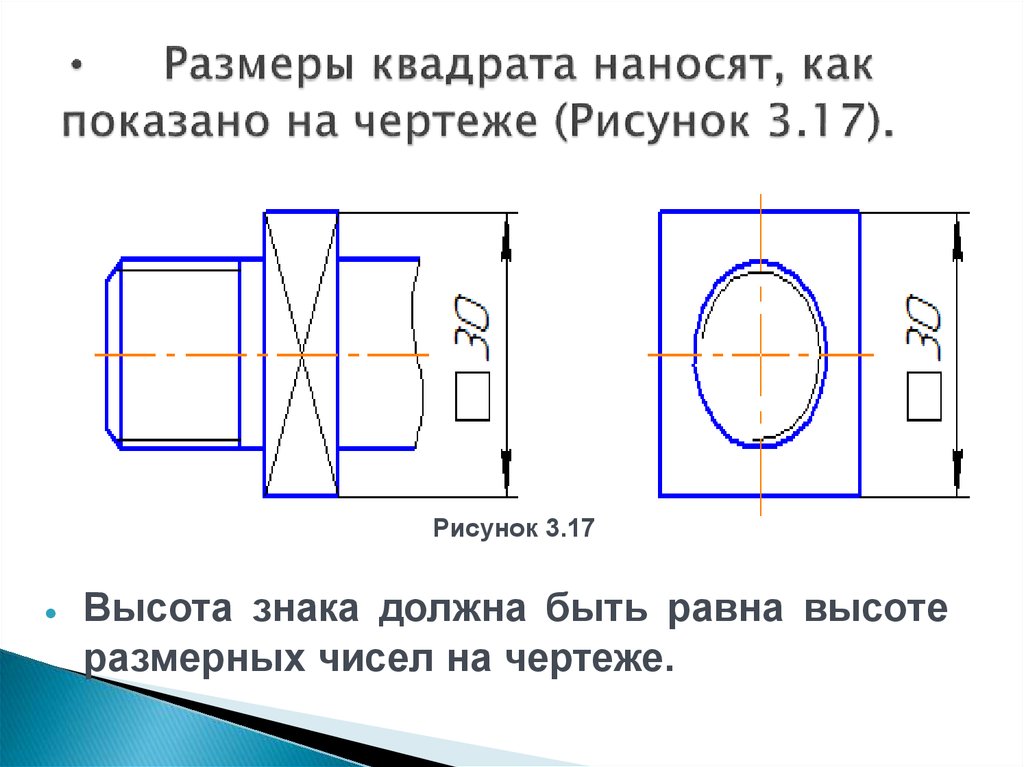 В заштрихованной
зоне наносить размерные числа не рекомендуется.
В этом случае размерные числа указывают на
горизонтально нанесенных полках.
В заштрихованной
зоне наносить размерные числа не рекомендуется.
В этом случае размерные числа указывают на
горизонтально нанесенных полках.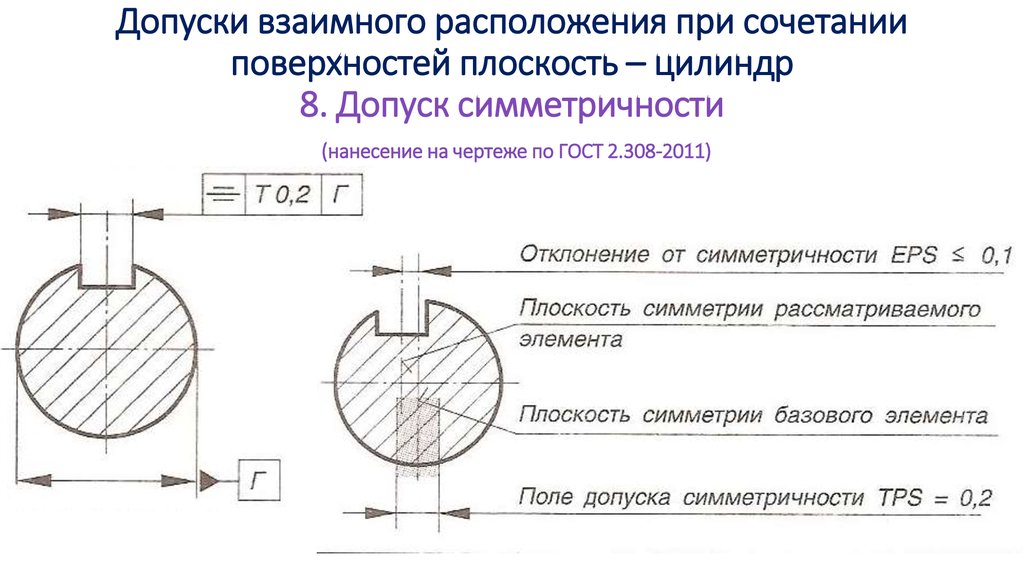
 38).
38). Если для нанесения размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на рис. 40, б; если недостаточно места для нанесения стрелок, то их наносят, как показано на рис. 40, в.
Если для нанесения размерного числа недостаточно места над размерной линией, то размеры наносят, как показано на рис. 40, б; если недостаточно места для нанесения стрелок, то их наносят, как показано на рис. 40, в.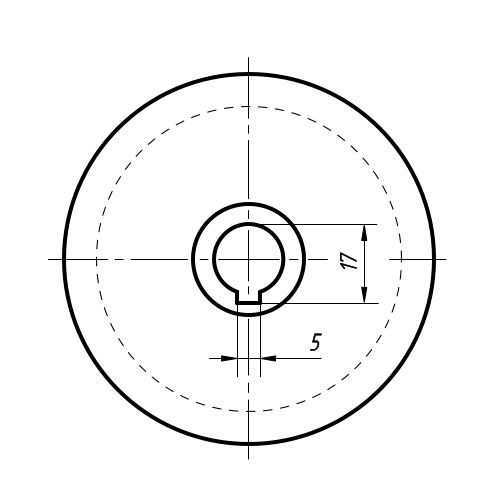 41, б).
41, б).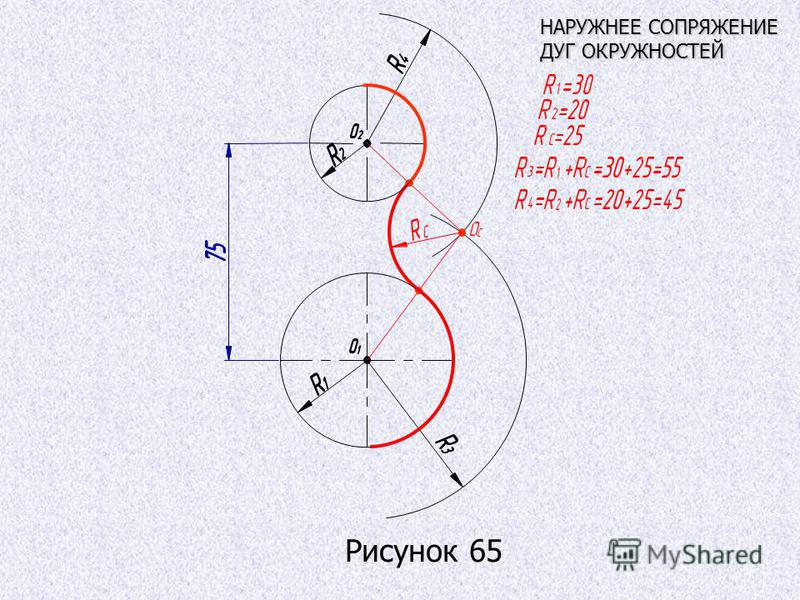

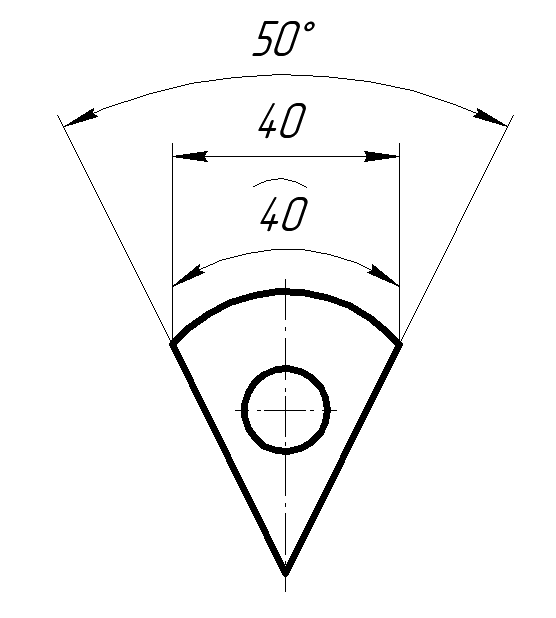
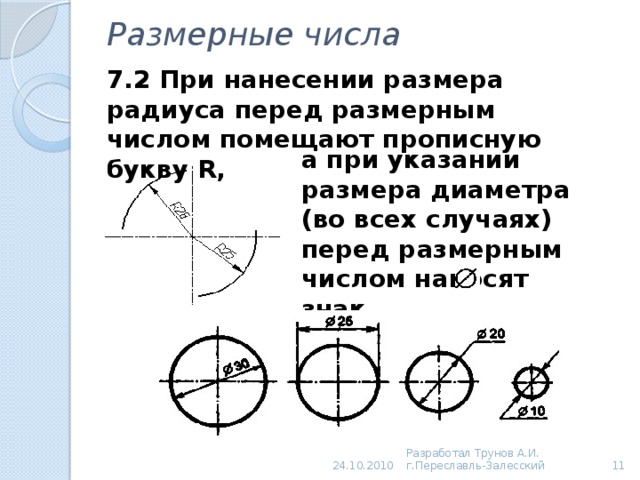
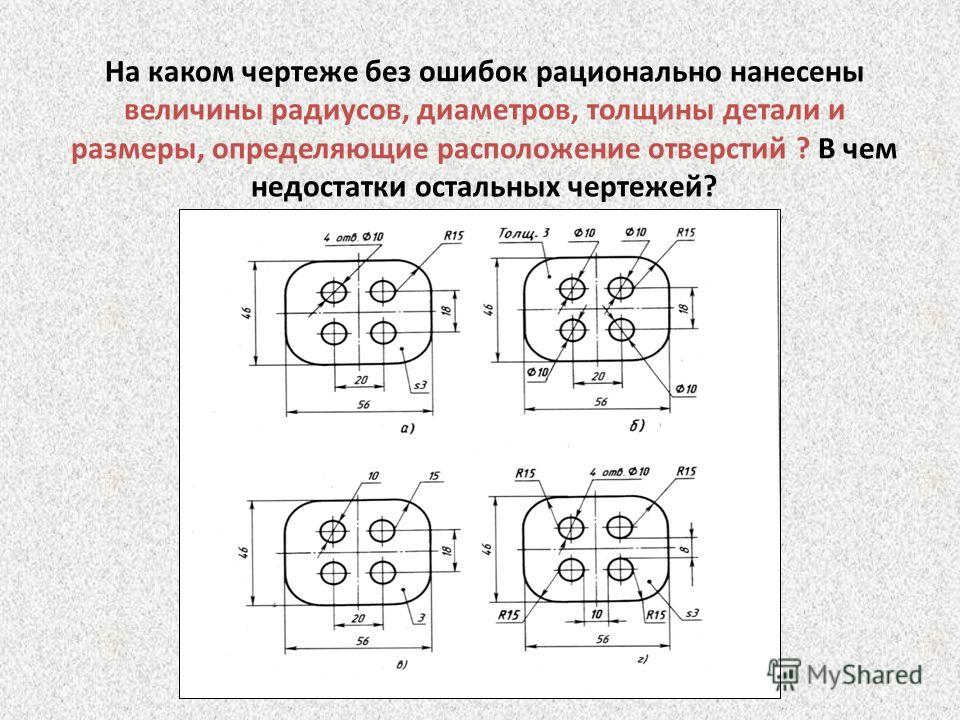 После чего на вкладках окна Modyfy Dimension Style задать характеристик размеров.
После чего на вкладках окна Modyfy Dimension Style задать характеристик размеров. Команда DIMLINEAR (DLI) ( Линейный ) Способы ввода команды:
Команда DIMLINEAR (DLI) ( Линейный ) Способы ввода команды: Откроется окно многострочного текстового редактора Multiline Text Editor, в котором можно внести изменения в размерный текст. Угловые скобки < > обозначают размерное число, определенное системой.
Откроется окно многострочного текстового редактора Multiline Text Editor, в котором можно внести изменения в размерный текст. Угловые скобки < > обозначают размерное число, определенное системой. Используется для нанесения вертикального размера. Система выдаст запрос на положение размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :
Используется для нанесения вертикального размера. Система выдаст запрос на положение размерной линии : Specify dimension line location or [ Mtext / Text / Angle ] :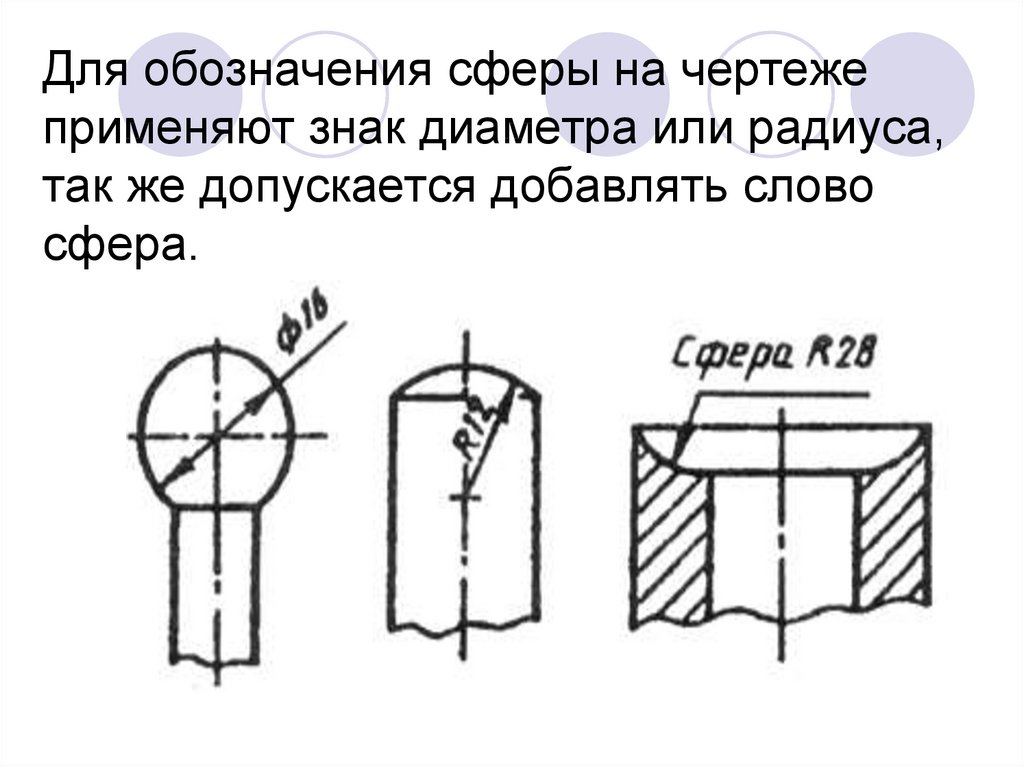 Выбрать опцию Rotated
Выбрать опцию Rotated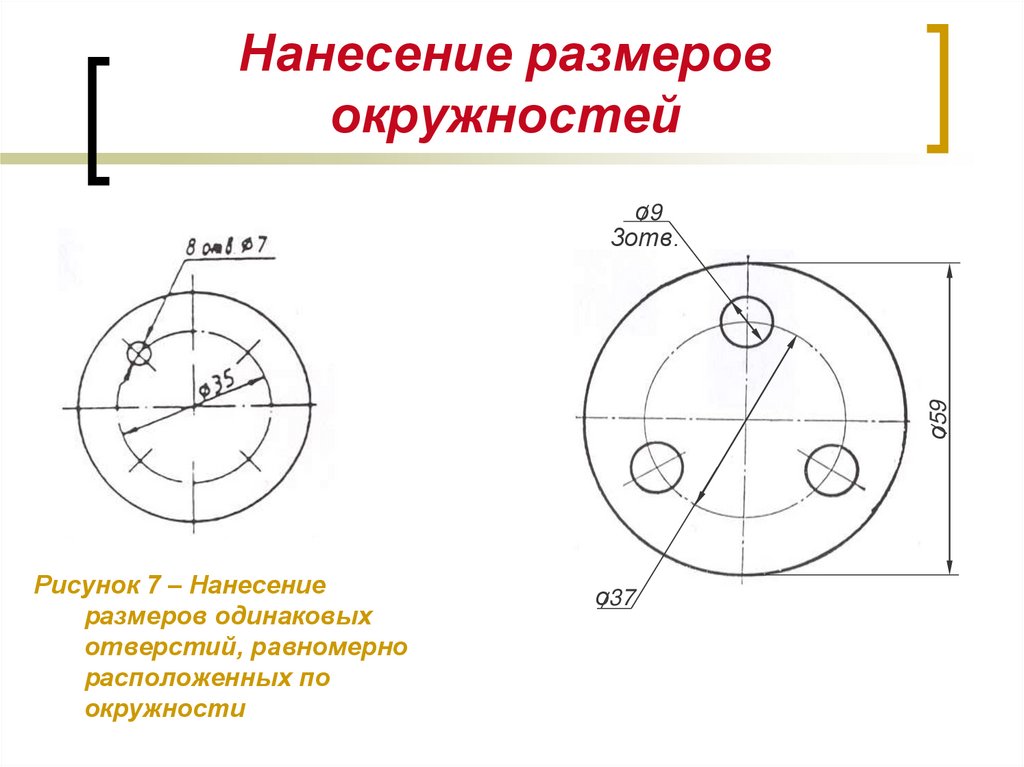 Размер наносится аналогично линейному.
Размер наносится аналогично линейному.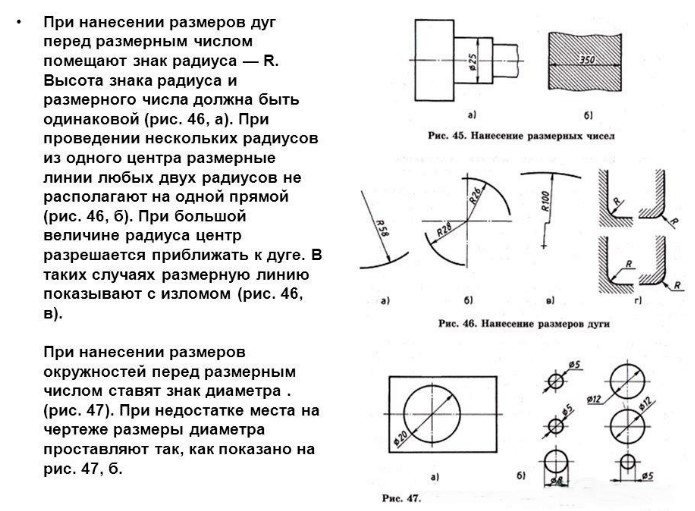
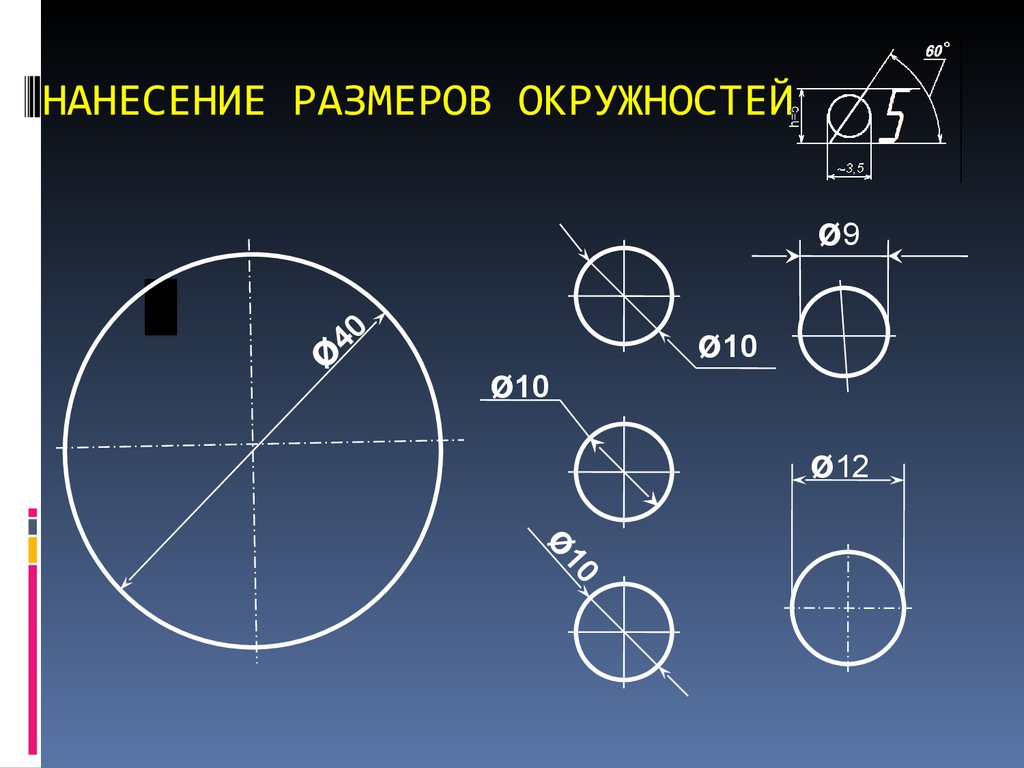
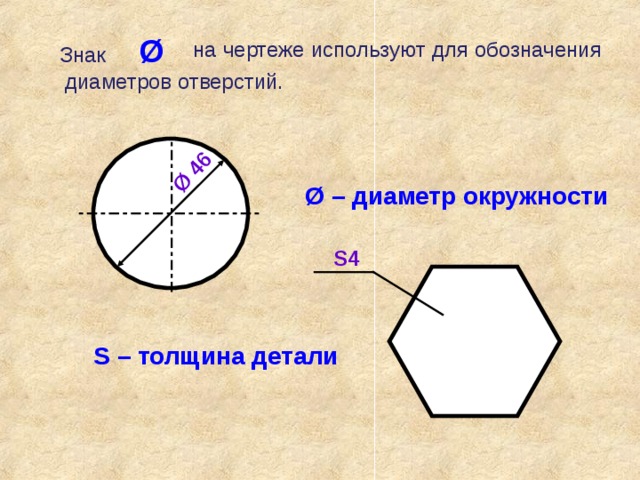
 Размерная линия для данного размере не должна быть вертикальной или горизонтальной.
Размерная линия для данного размере не должна быть вертикальной или горизонтальной.

 by/showthread.php?t=11&page=13web page example
<a title=»web page example» href=»https://superforum.diva.by/threads/%D0%9A%D0%B0%D0%BA-%D0%B2%D1%8B-%D1%83%D0%BA%D0%BB%D0%B0%D0%B4%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%D0%B5-%D0%B2%D0%BE%D0%BB%D0%BE%D1%81%D1%8B-%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D1%8B-%D0%BF%D1%80%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D1%82%D1%8B-%D0%B8%D0%BD%D1%81%D1%82%D1%80%D1%83%D0%BC%D0%B5%D0%BD%D1%82%D1%8B.159/page-10web page example
<a title=»web page example» href=»http://sfc.by/forum/viewtopic.php?p=440828#440828web page example
by/showthread.php?t=11&page=13web page example
<a title=»web page example» href=»https://superforum.diva.by/threads/%D0%9A%D0%B0%D0%BA-%D0%B2%D1%8B-%D1%83%D0%BA%D0%BB%D0%B0%D0%B4%D1%8B%D0%B2%D0%B0%D0%B5%D1%82%D0%B5-%D0%B2%D0%BE%D0%BB%D0%BE%D1%81%D1%8B-%D1%81%D0%BF%D0%BE%D1%81%D0%BE%D0%B1%D1%8B-%D0%BF%D1%80%D0%B5%D0%BF%D0%B0%D1%80%D0%B0%D1%82%D1%8B-%D0%B8%D0%BD%D1%81%D1%82%D1%80%D1%83%D0%BC%D0%B5%D0%BD%D1%82%D1%8B.159/page-10web page example
<a title=»web page example» href=»http://sfc.by/forum/viewtopic.php?p=440828#440828web page example Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).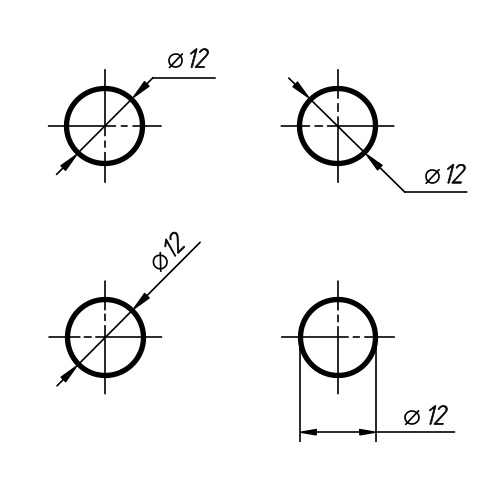 Так как угол 0-1-2 равен 30°, то для нахождения стороны
Так как угол 0-1-2 равен 30°, то для нахождения стороны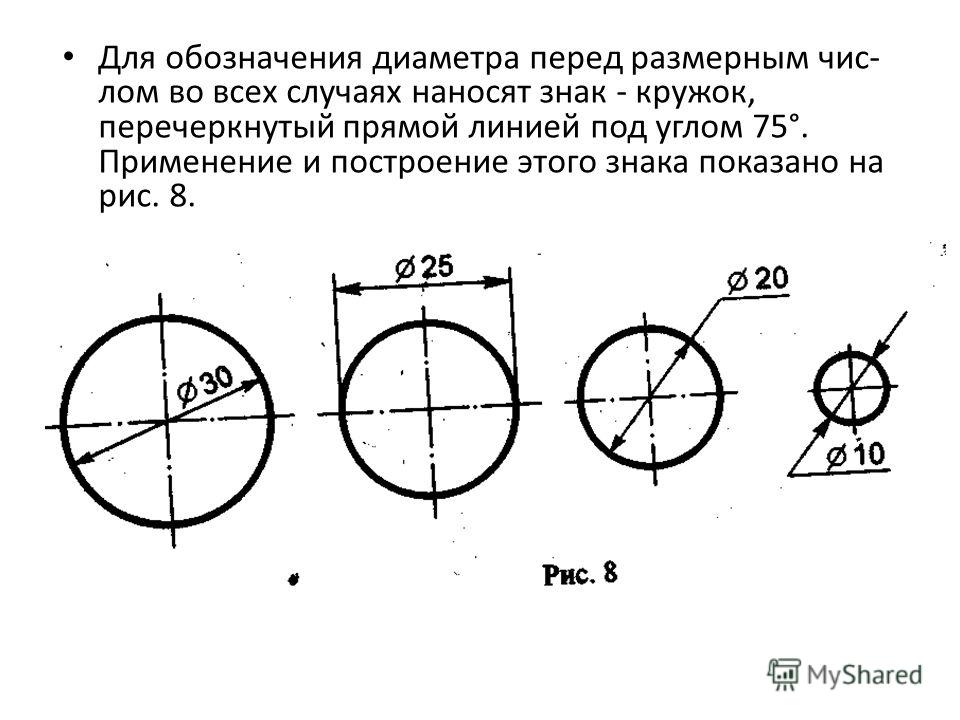 Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля. Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ?
Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ? При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
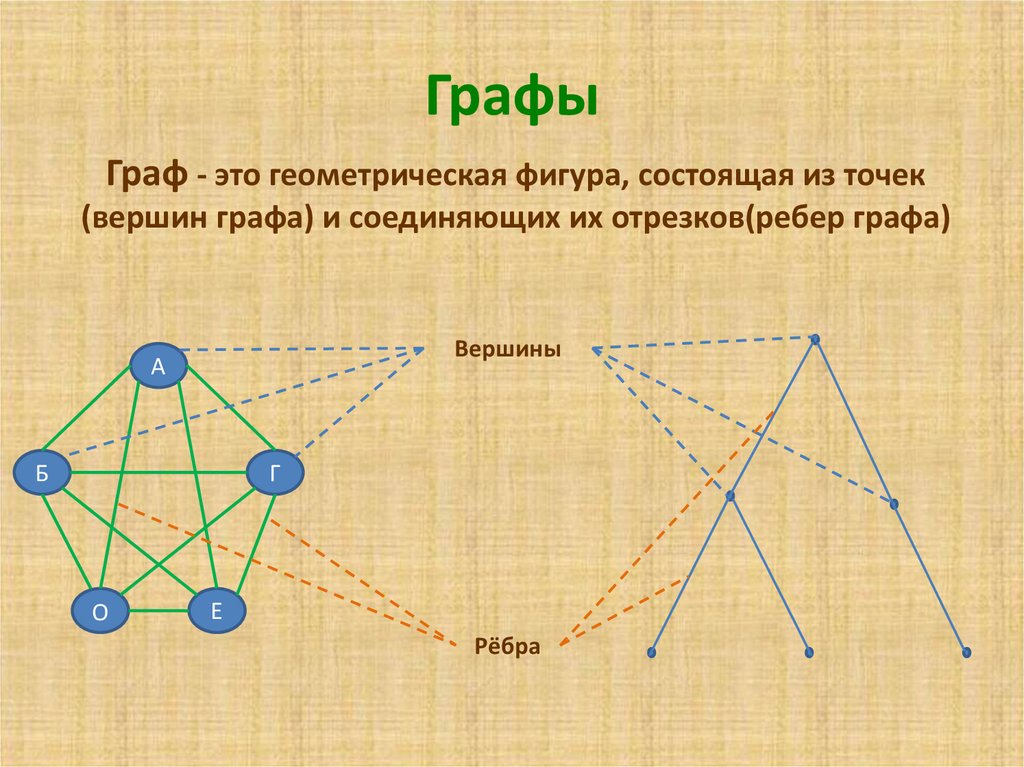 Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.
Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.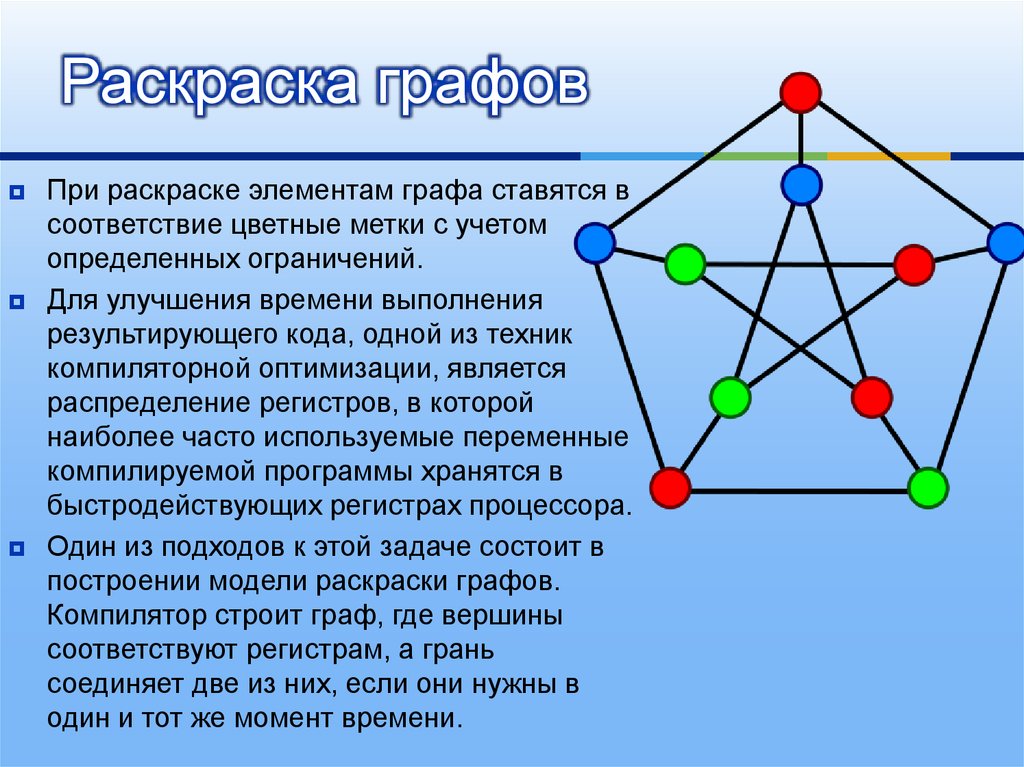 е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа.
е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа. ”
”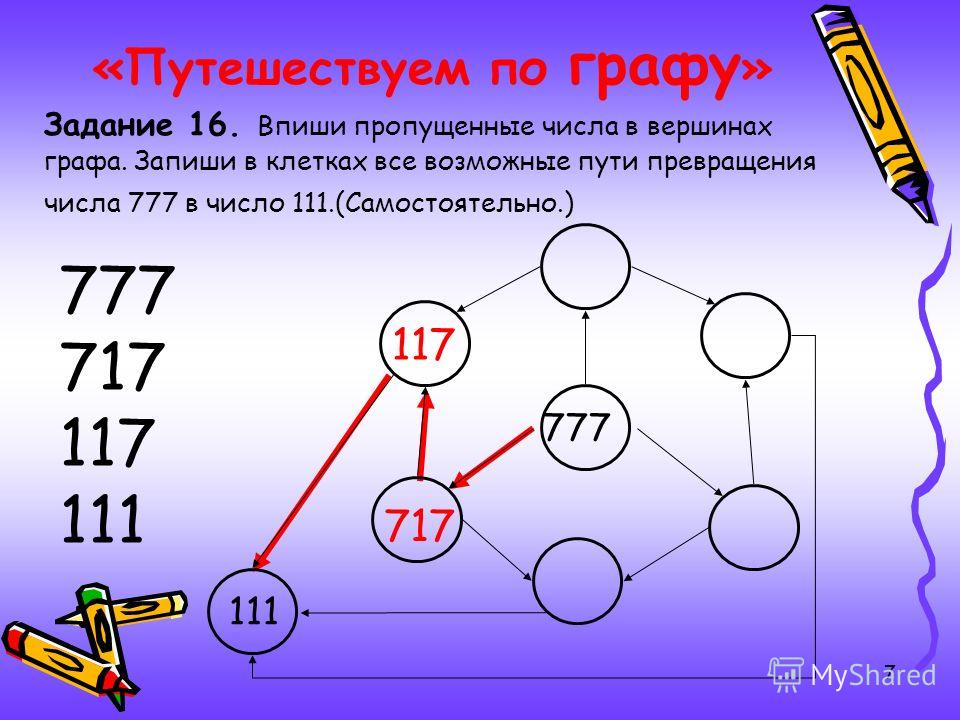 А так как
компонента связности – связный граф, то из
столицы существует путь по ковролиниям до города
Дальний, что и требовалось доказать.
А так как
компонента связности – связный граф, то из
столицы существует путь по ковролиниям до города
Дальний, что и требовалось доказать. То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.
То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.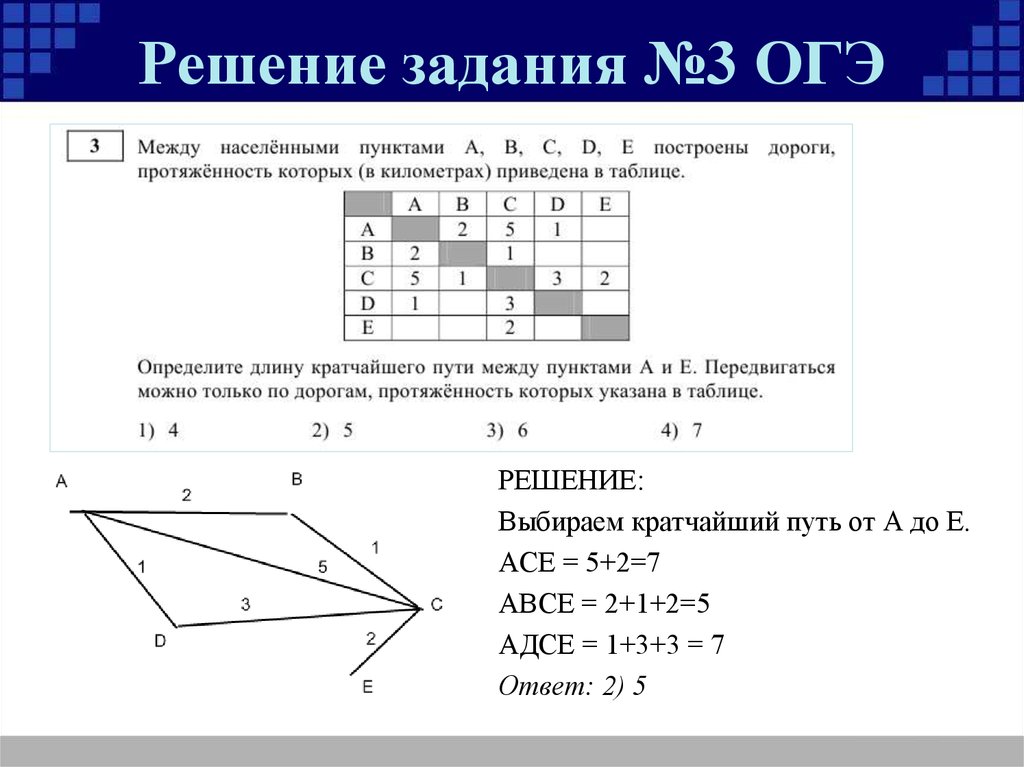 Занумеруем клетки доски, как
показано на рисунке:
Занумеруем клетки доски, как
показано на рисунке: Значит долететь из города 1 в город 9
нельзя.
Значит долететь из города 1 в город 9
нельзя.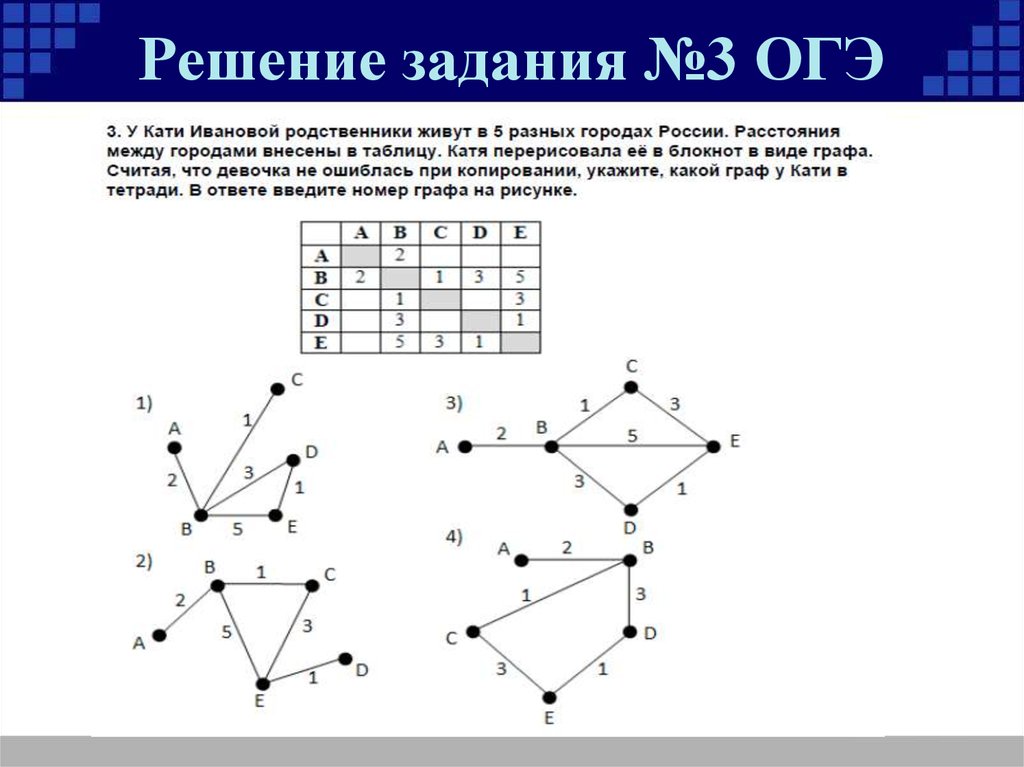 задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может.
задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может. Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист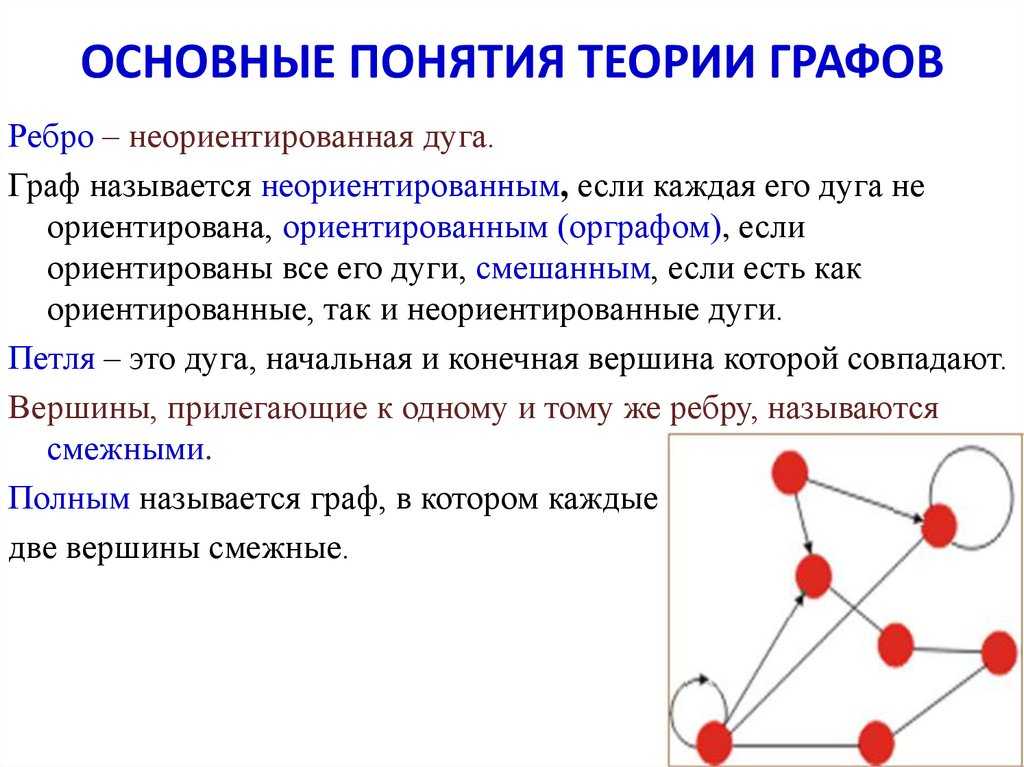
 Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса?
Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса? Среди девяти монет есть одна фальшивая, которая легче других. Определите ее с помощью двух взвешиваний на рычажных весах.
Среди девяти монет есть одна фальшивая, которая легче других. Определите ее с помощью двух взвешиваний на рычажных весах. Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу?
Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу? Сколько игр проведено к настоящему моменту и сколько еще осталось?
Сколько игр проведено к настоящему моменту и сколько еще осталось?
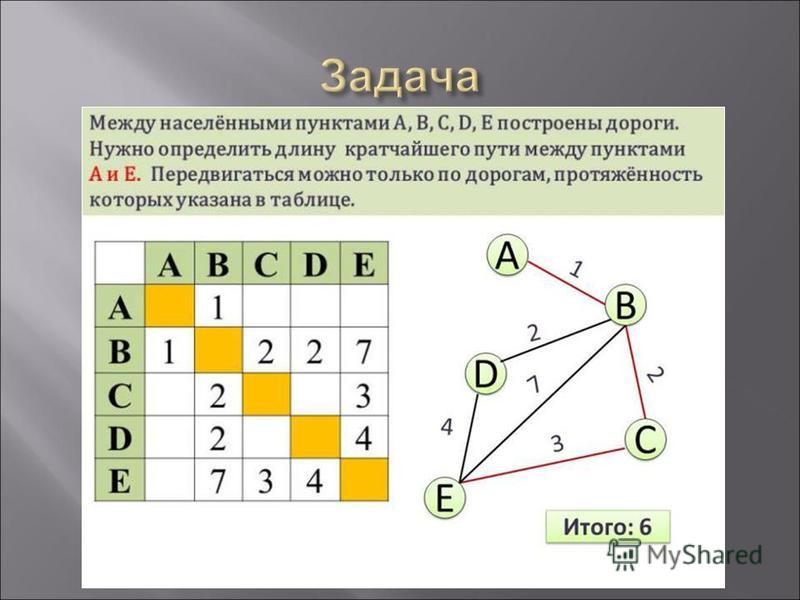 Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях.
Учебник — М.: Вентана-Граф (Российский учебник). Электронная ознакомительная версия для покупки пособия. Цитаты из книги использованы в учебных целях. Изучая математику, вы будете расширять список соответствующих моделей. Сейчас познакомимся с методом, применение которого основано на построении математической модели в виде геометрической фигуры. Заметим, что вы уже использовали элементы этого приёма, когда в задачах на движение строили различные схемы: движения в одном направлении, в противоположных направлениях, навстречу друг другу и т. п.
Изучая математику, вы будете расширять список соответствующих моделей. Сейчас познакомимся с методом, применение которого основано на построении математической модели в виде геометрической фигуры. Заметим, что вы уже использовали элементы этого приёма, когда в задачах на движение строили различные схемы: движения в одном направлении, в противоположных направлениях, навстречу друг другу и т. п.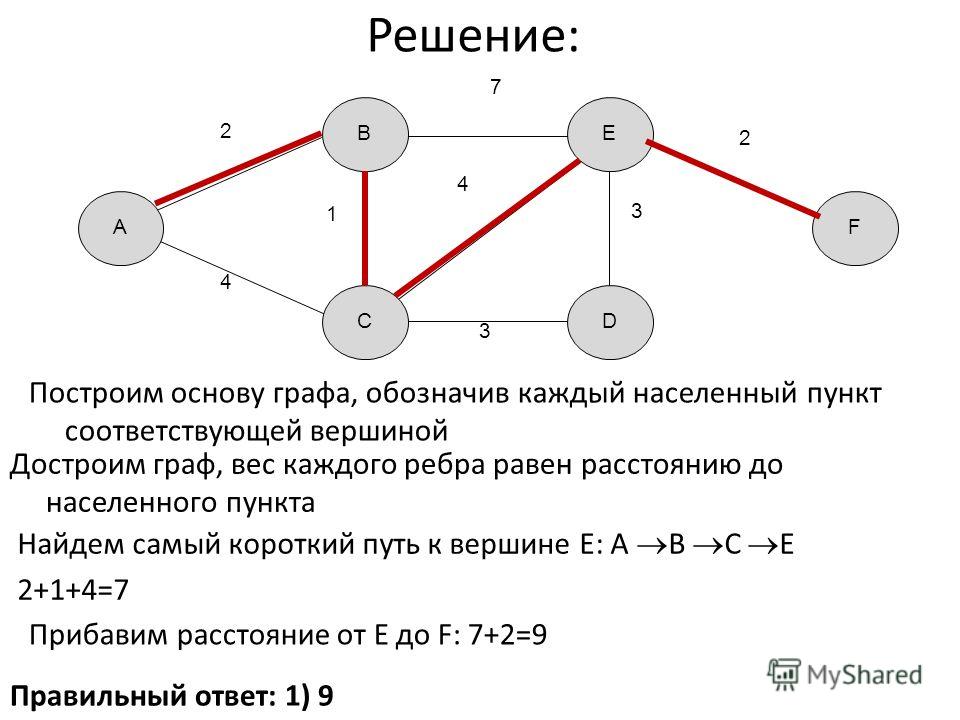 Подсчитаем, сколько отрезков будет на этой схеме. Имеем: 5*3 = 15 (отрезков). Однако при таком подсчёте каждый отрезок был учтён дважды. Получается, что количество отрезков равно 15/2. Это число не является целым. Получили противоречие.
Подсчитаем, сколько отрезков будет на этой схеме. Имеем: 5*3 = 15 (отрезков). Однако при таком подсчёте каждый отрезок был учтён дважды. Получается, что количество отрезков равно 15/2. Это число не является целым. Получили противоречие. Это слово произошло от латинского grafito — пишу.
Это слово произошло от латинского grafito — пишу. На самом деле имеет место более общий факт: в любом графе количество вершин, степень которых нечётная, является чётным числом. Он следует из того, что сумма степеней всех вершин графа равна удвоенному количеству его рёбер, а следовательно, является чётным числом.
На самом деле имеет место более общий факт: в любом графе количество вершин, степень которых нечётная, является чётным числом. Он следует из того, что сумма степеней всех вершин графа равна удвоенному количеству его рёбер, а следовательно, является чётным числом.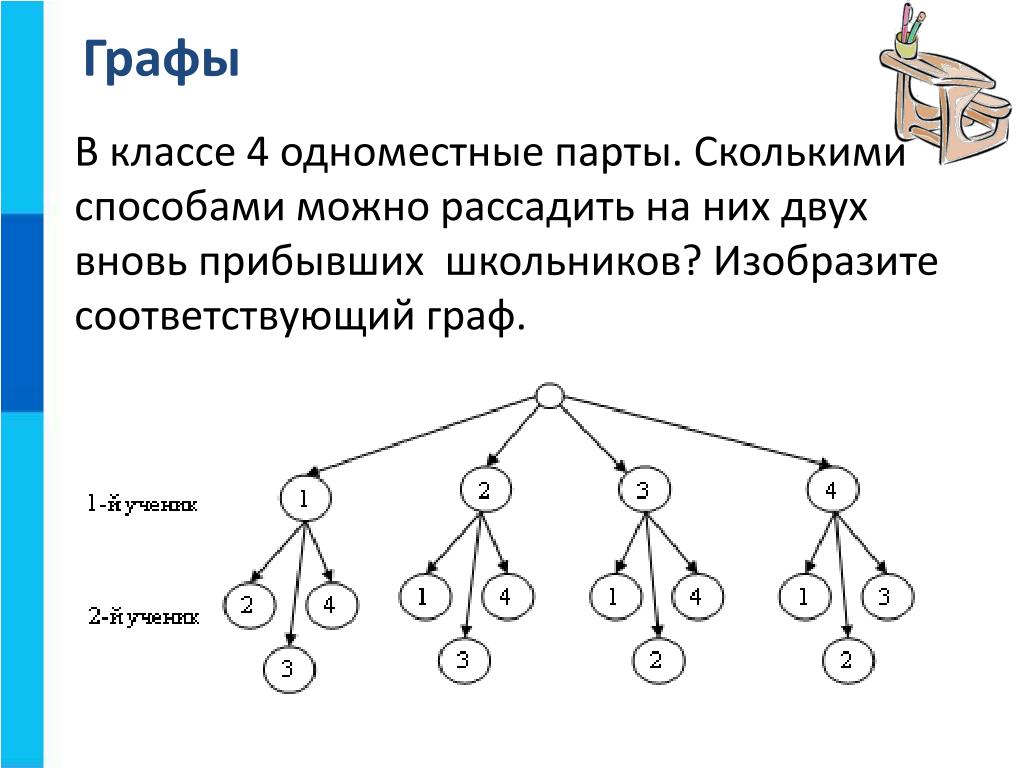
 Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 4. Решение задач с помощью графов.
Углубленный уровень: 7 класс. Учебник — М.: Вентана-Граф, 2019 (Российский учебник). 4. Решение задач с помощью графов. ) и повседневной жизни.
) и повседневной жизни. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.
Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.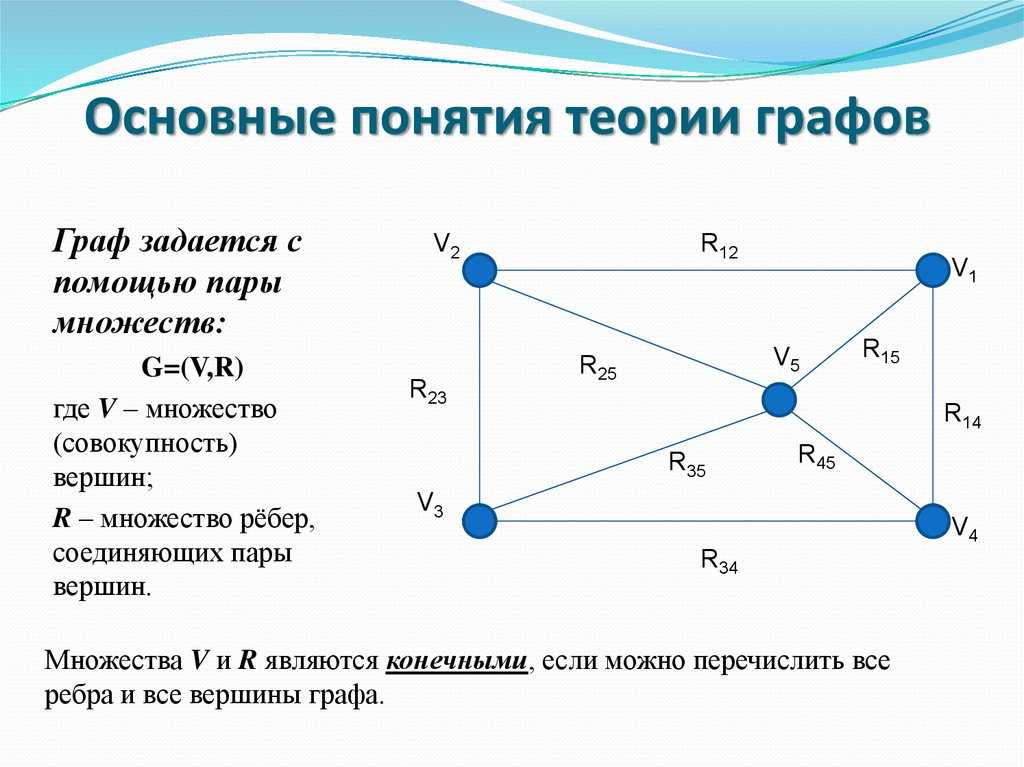 Линия указывает на связь между двумя точками.
Линия указывает на связь между двумя точками.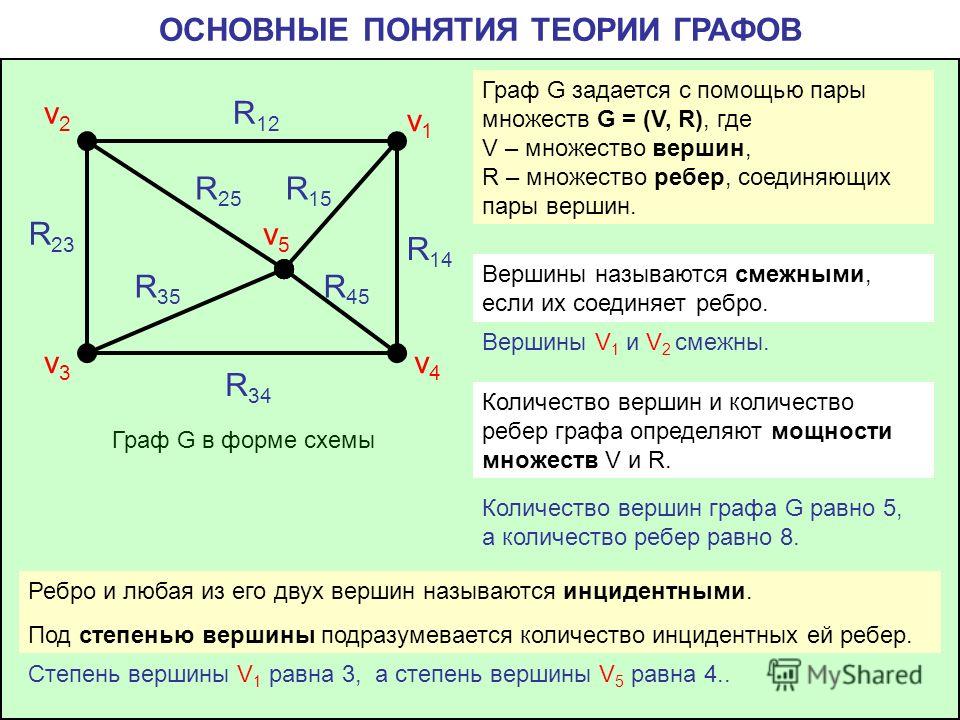
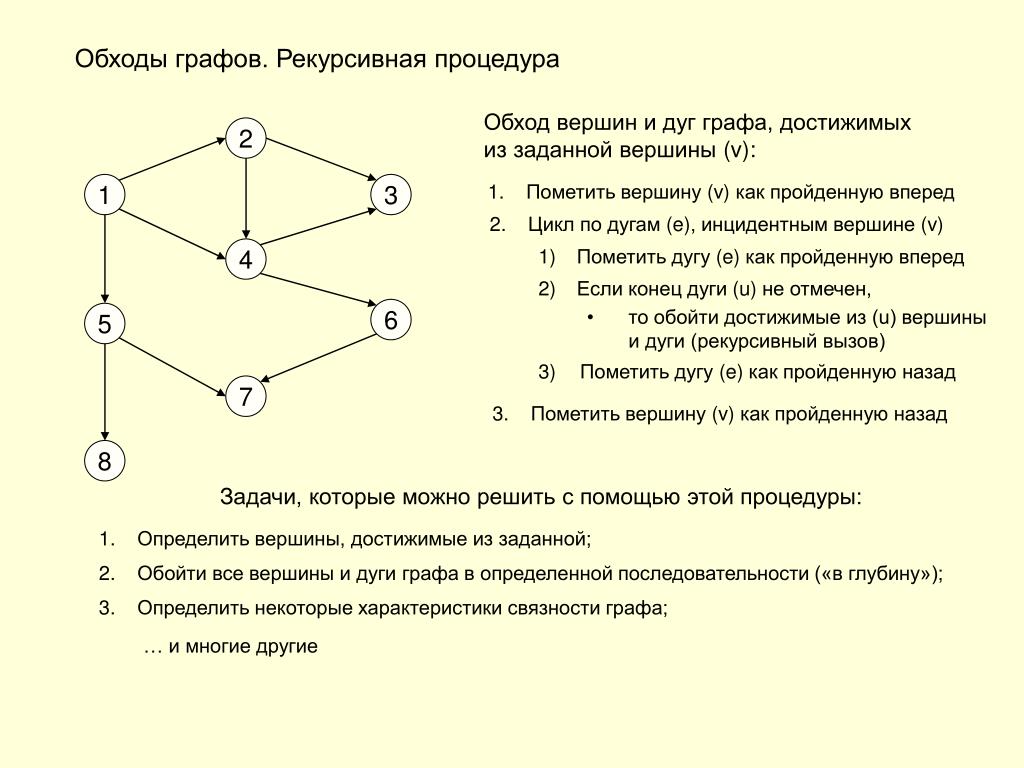 Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева.
Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева. Получается граф (2) дающий решение задачи.
Получается граф (2) дающий решение задачи.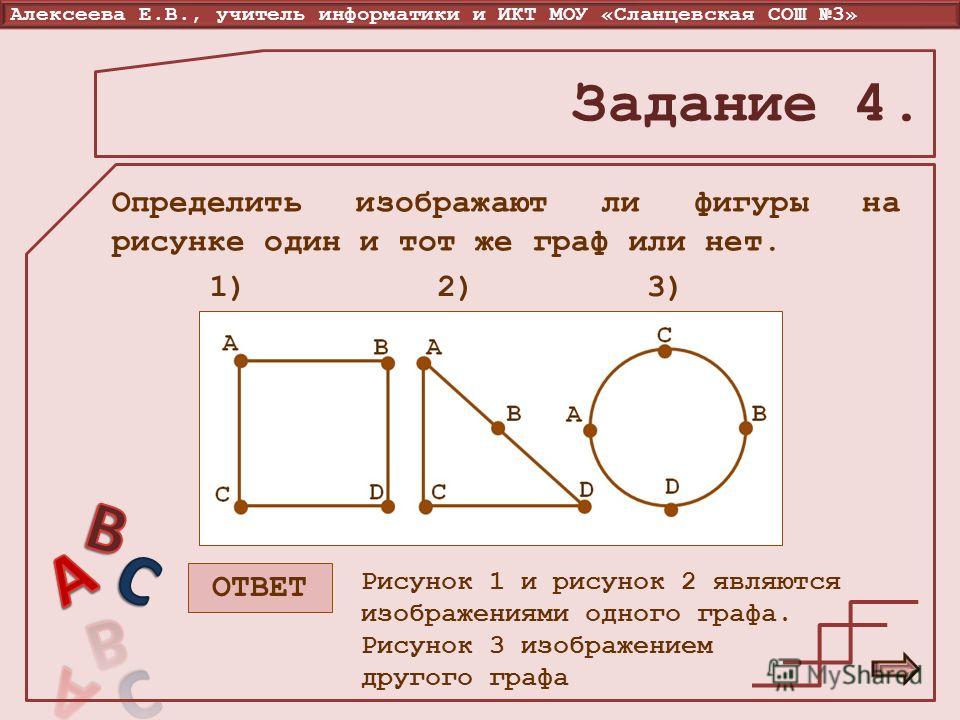
 Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места?
Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места? Нарисуй схему и сосчитай все возможные пути из города А в город В. Ответ: 6 партий .
Нарисуй схему и сосчитай все возможные пути из города А в город В. Ответ: 6 партий .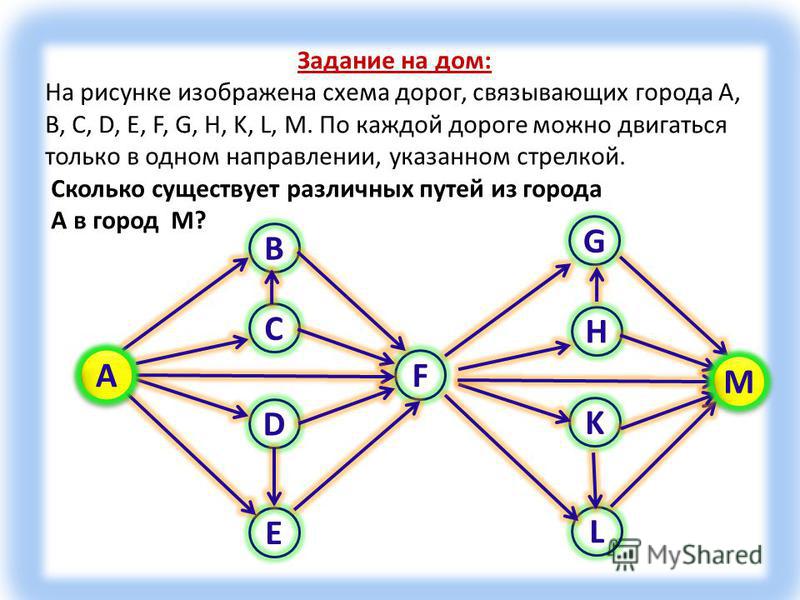 Информатика дает инструмент для познания любой научной дисциплины.
Информатика дает инструмент для познания любой научной дисциплины.
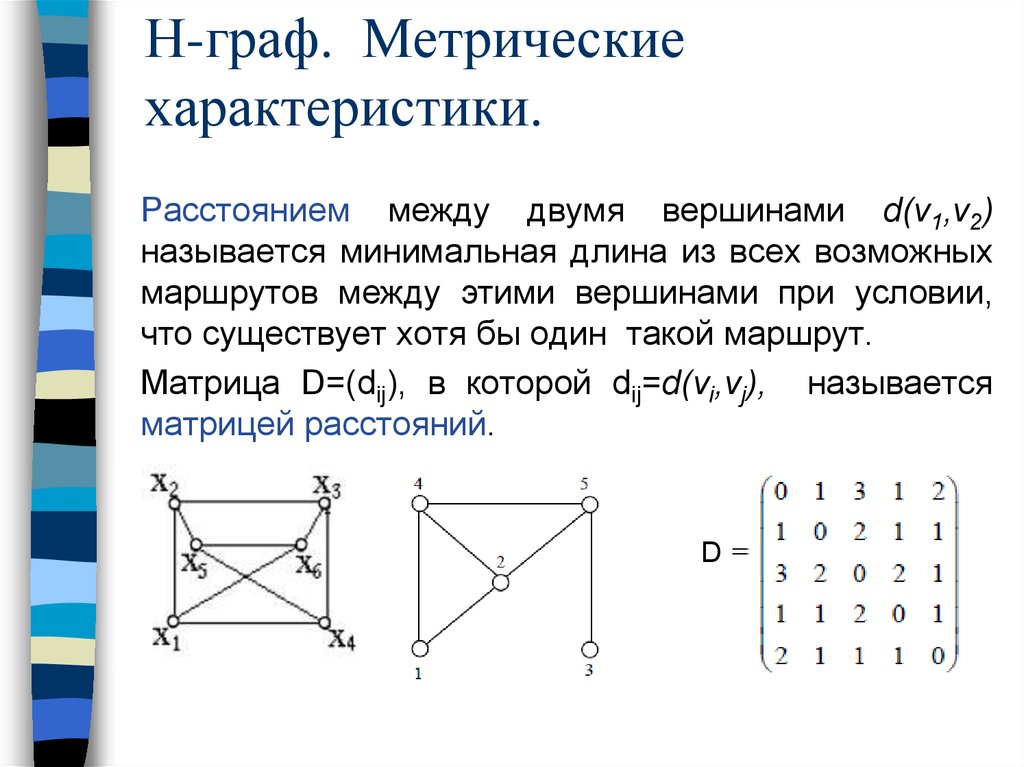
 Представление данных в виде графа придает им наглядность и простоту.
Представление данных в виде графа придает им наглядность и простоту.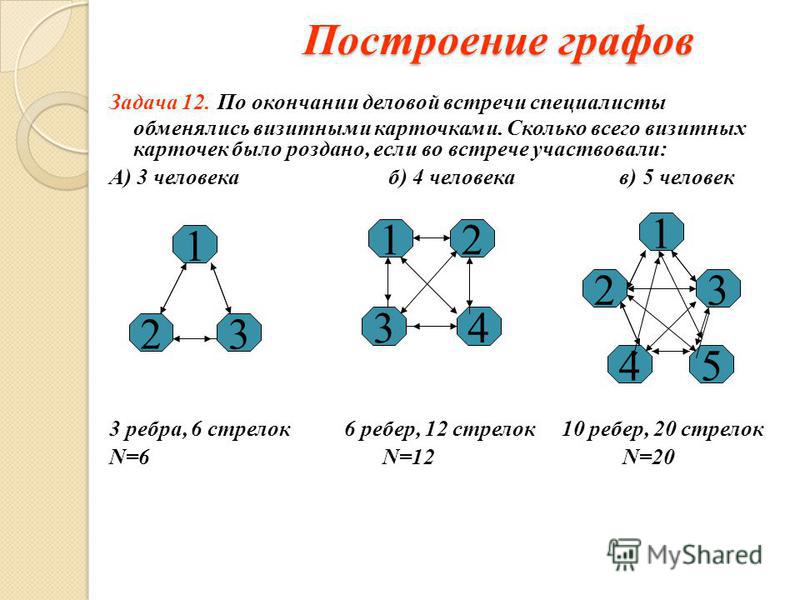

 Рис. 2
Рис. 2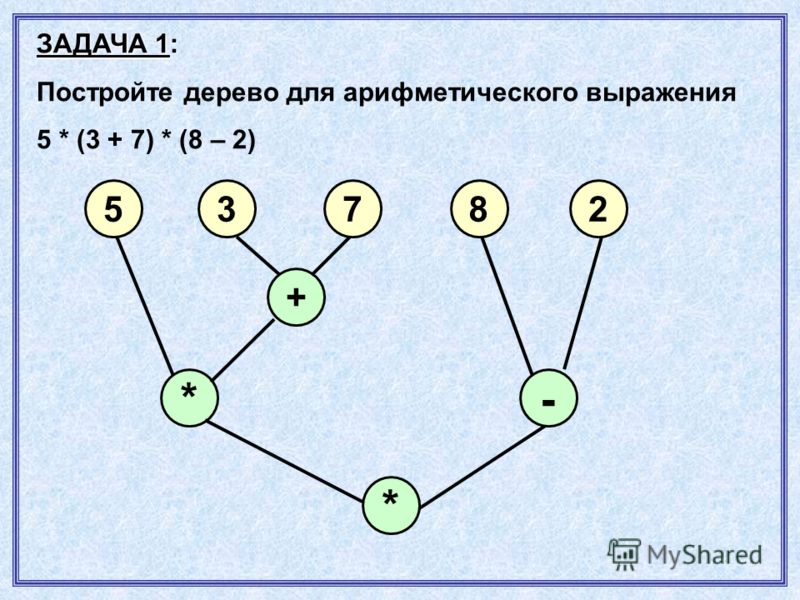 ..».
..».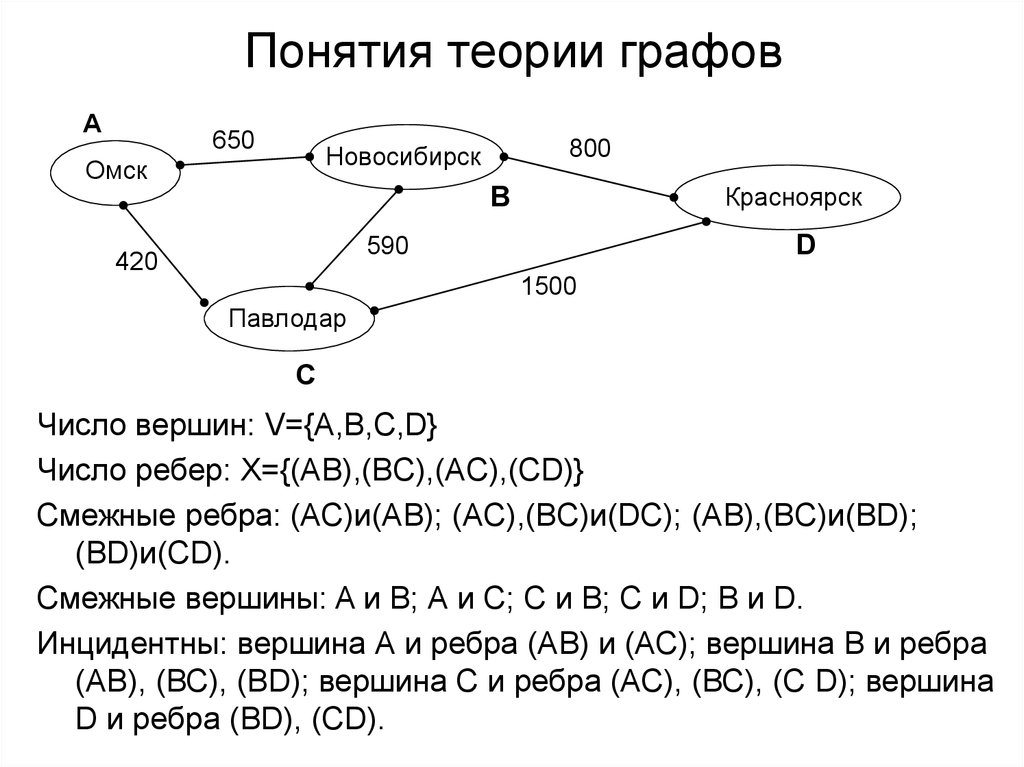 Точки называются вершинами графа, а соединяющие линии – рёбрами.
Точки называются вершинами графа, а соединяющие линии – рёбрами.  (рис.3)
(рис.3)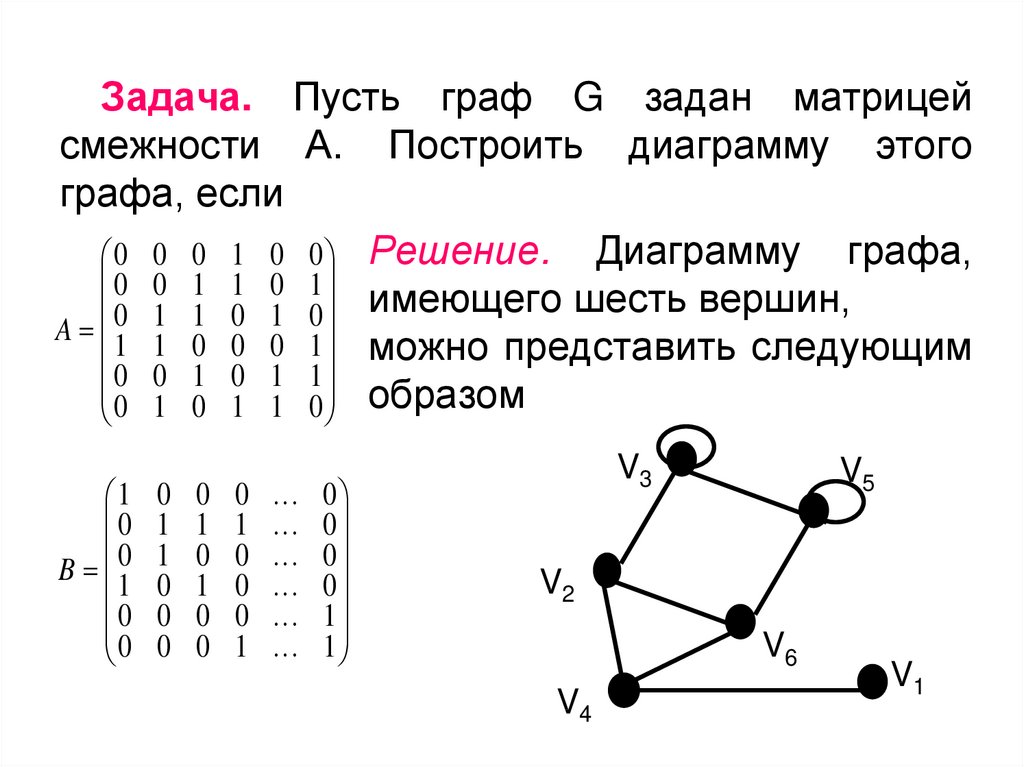
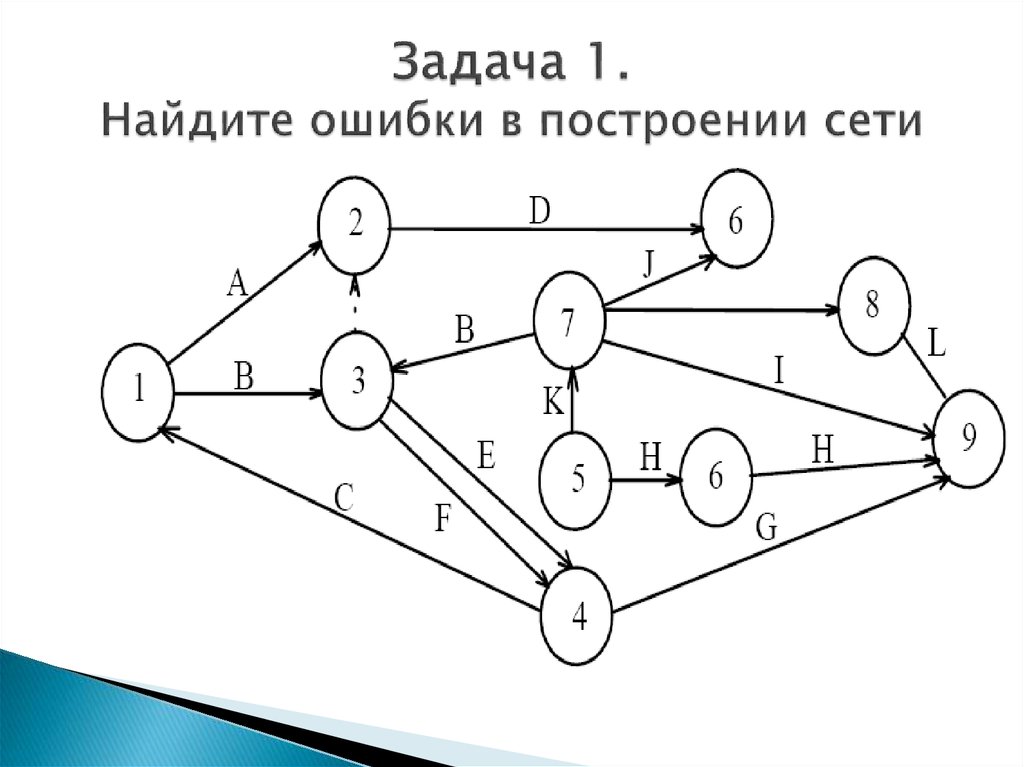
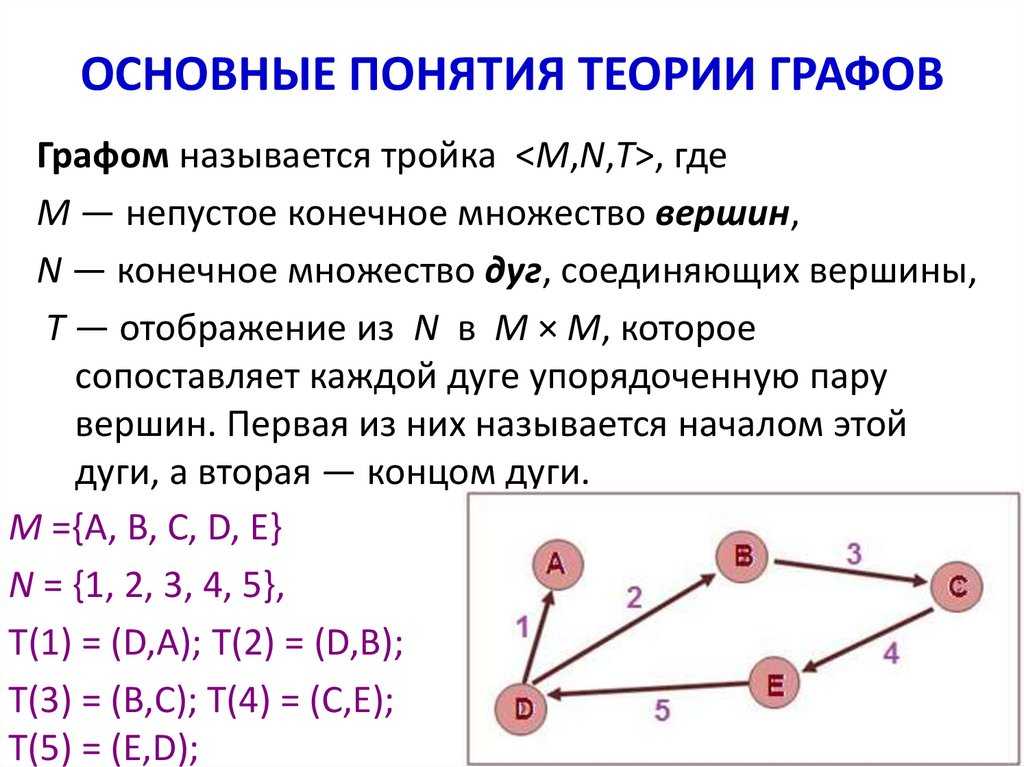 Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?
Стакан стоит около банки и сосуда с молоком. Куда налита каждая жидкость?
 Историк может говорить с математиком по-французски. Физик, биолог и математик не могут беседовать втроем на одном языке. Какими двумя языками владеет биолог (укажите названия языков в именительном падеже через пробел).
Историк может говорить с математиком по-французски. Физик, биолог и математик не могут беседовать втроем на одном языке. Какими двумя языками владеет биолог (укажите названия языков в именительном падеже через пробел). Получается граф G2 — решение задачи.
Получается граф G2 — решение задачи. Эту фигуру можно начертить одним росчерком. Основываемся при решении на
Эту фигуру можно начертить одним росчерком. Основываемся при решении на
 е. нельзя будет провести одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе ребер).
е. нельзя будет провести одно из ребер Б1, Б2 или Б3. которое не пересекло бы уже имеющихся в графе ребер). Что подтверждает нашу гипотезу.
Что подтверждает нашу гипотезу.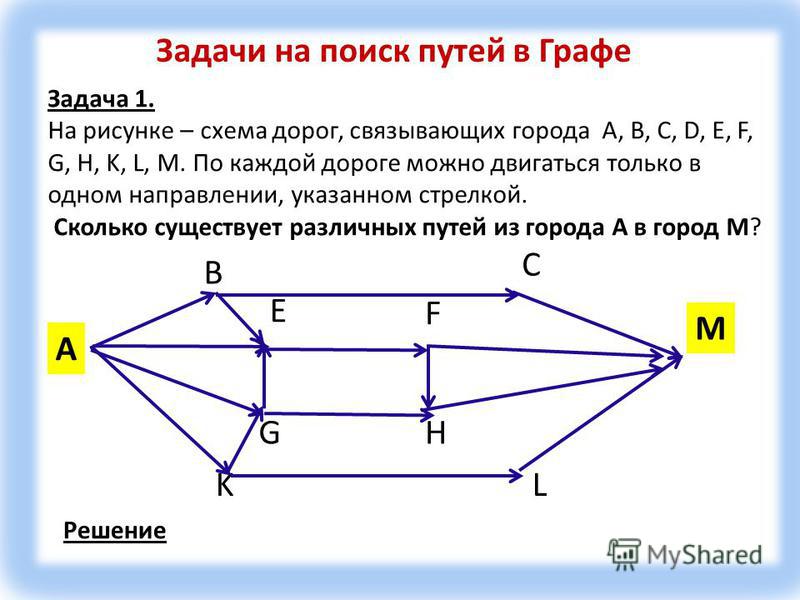 Весёлые задачи, Я. И. Перельман, Москва, 2003г
Весёлые задачи, Я. И. Перельман, Москва, 2003г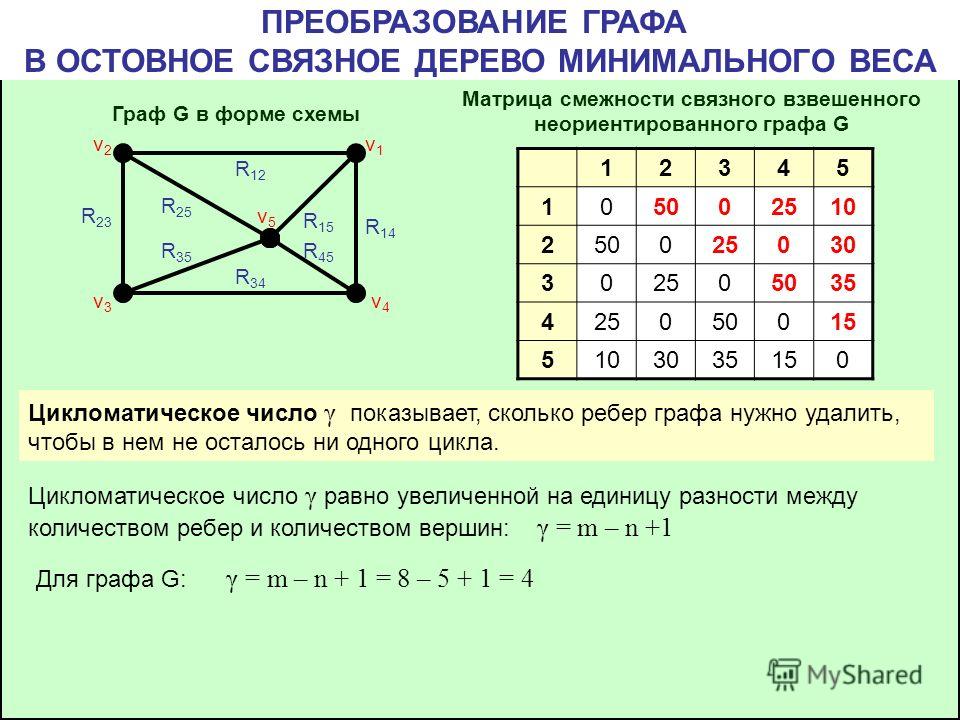
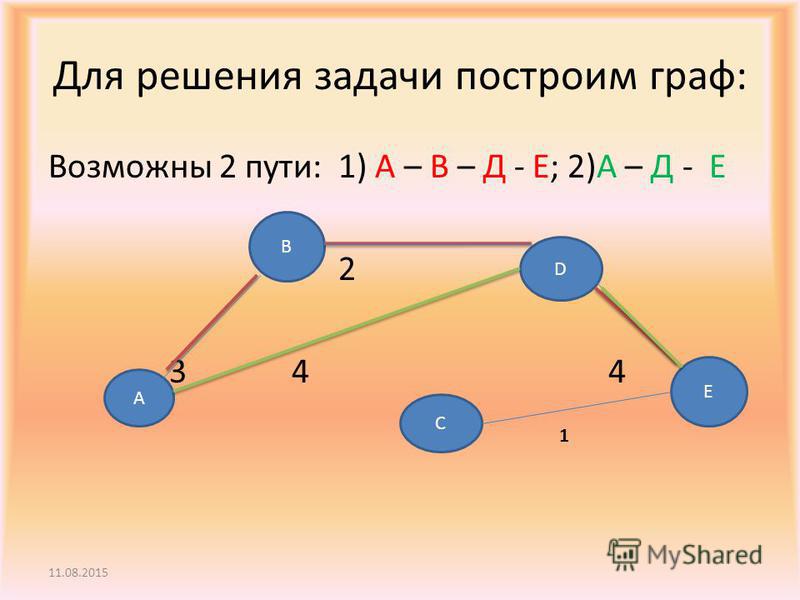
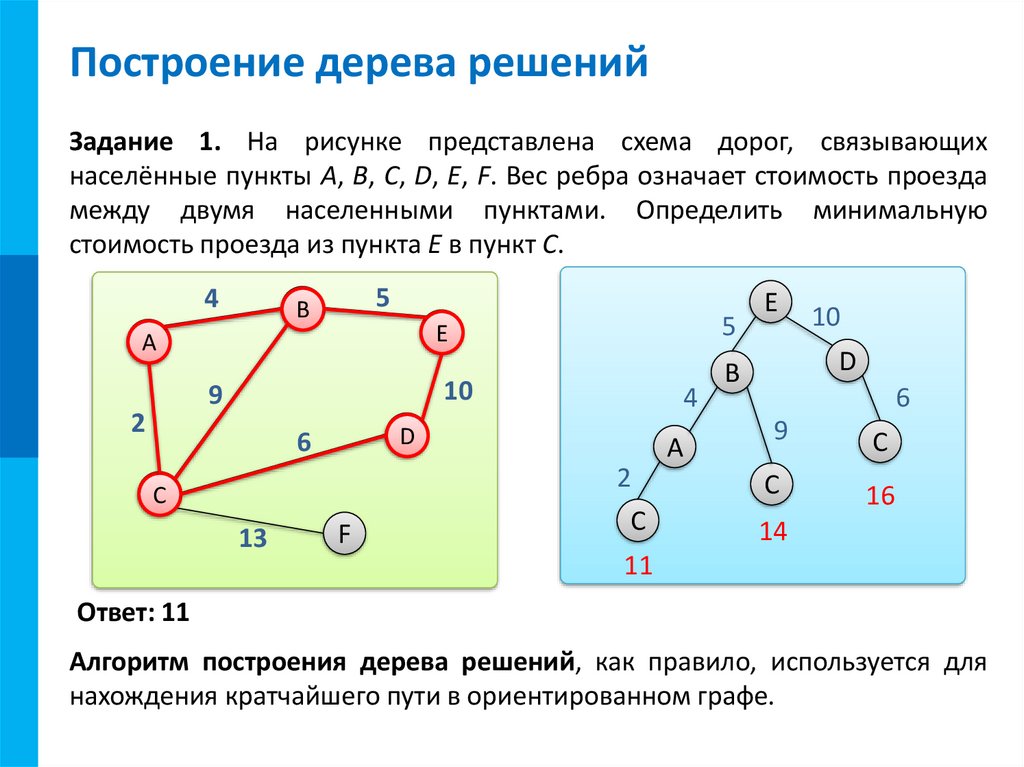 Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если ее степень равна единице и висячей, если ее степень равна нулю.
Степенью вершины графа называется число ребер, которым эта вершина принадлежит. Вершина называется изолированной, если ее степень равна единице и висячей, если ее степень равна нулю.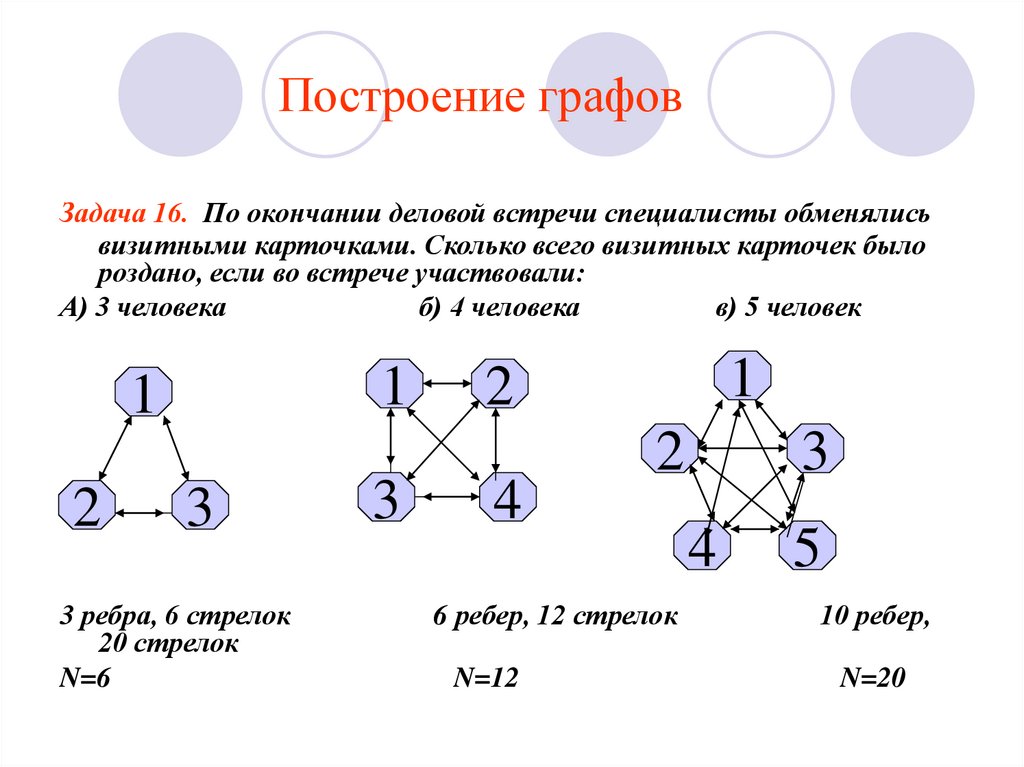 Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью.
Незамкнутый маршрут (путь) называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью. Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.
Записать матрицы смежности и инцидентности для графа, изображенного на рисунке.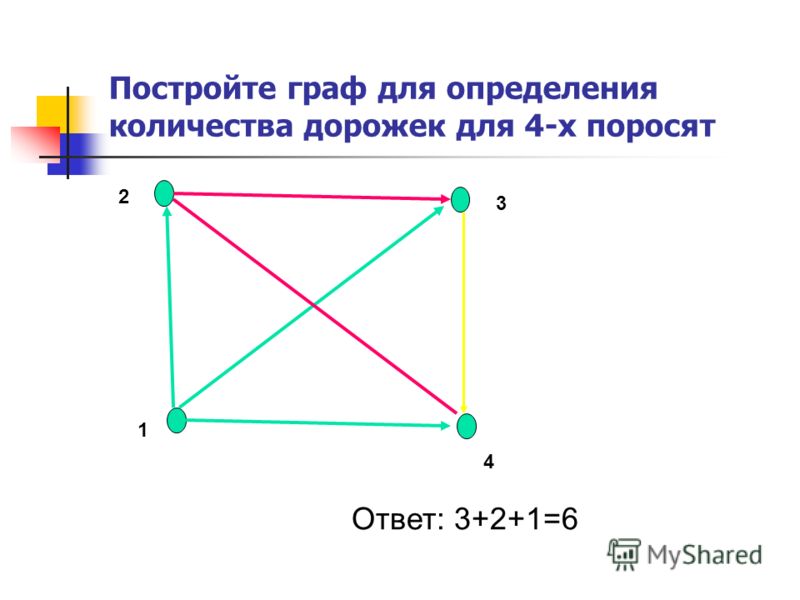 е. — матрица смежности.
е. — матрица смежности.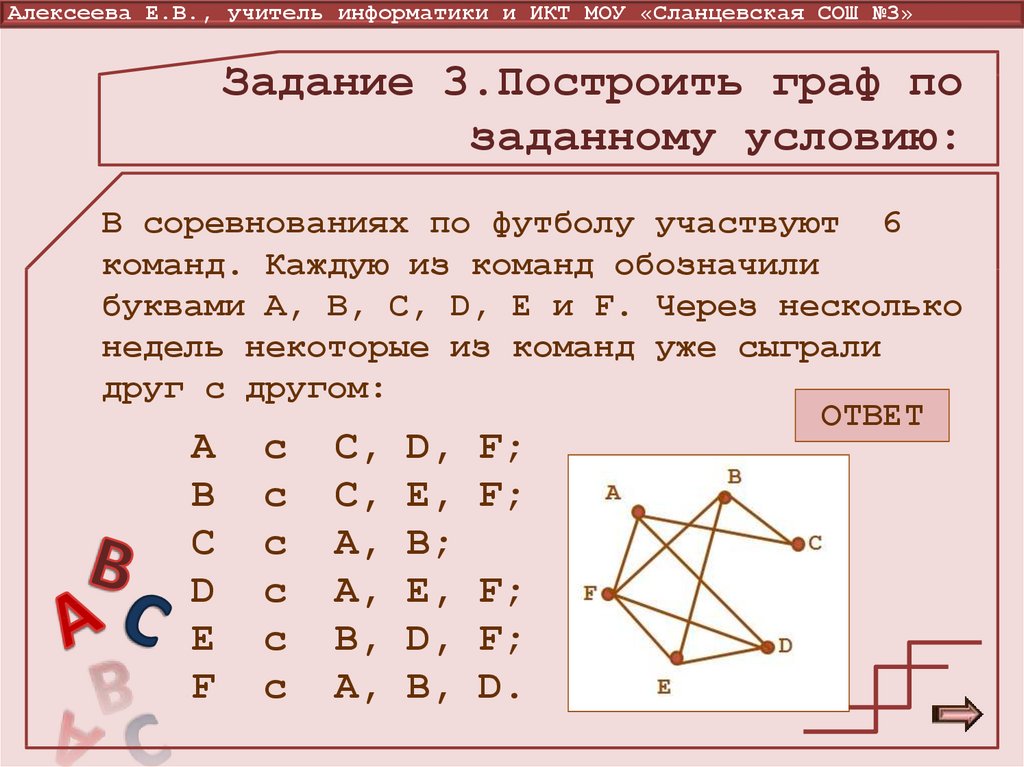
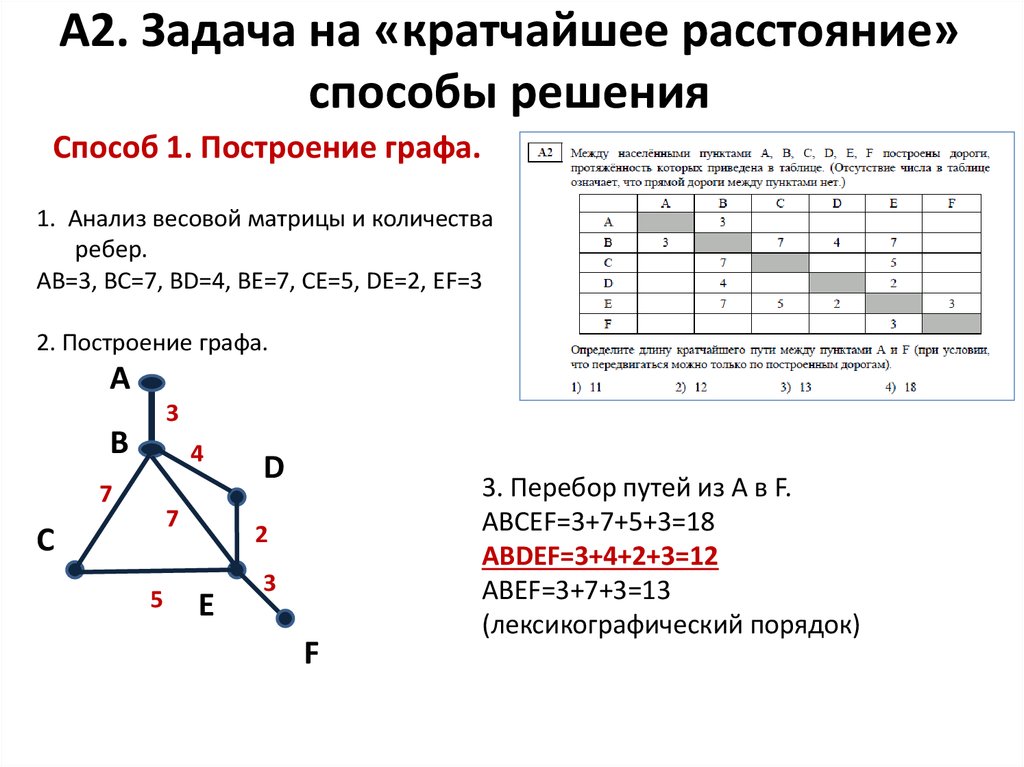
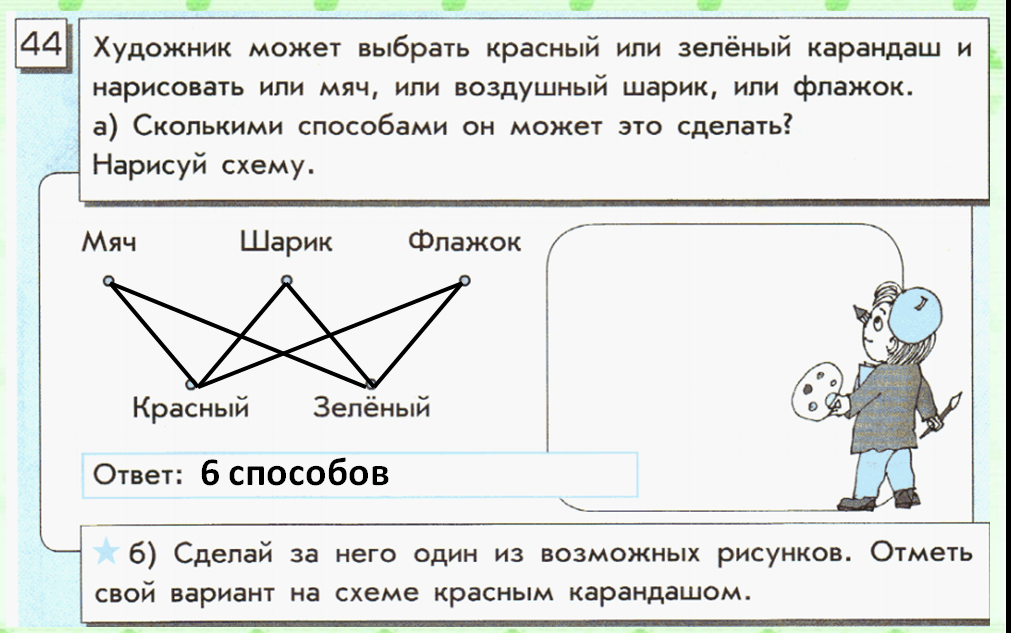



 ПОДРОБНО.
ПОДРОБНО.
 И нужно не только НОК, но и как его вычислили.
И нужно не только НОК, но и как его вычислили.
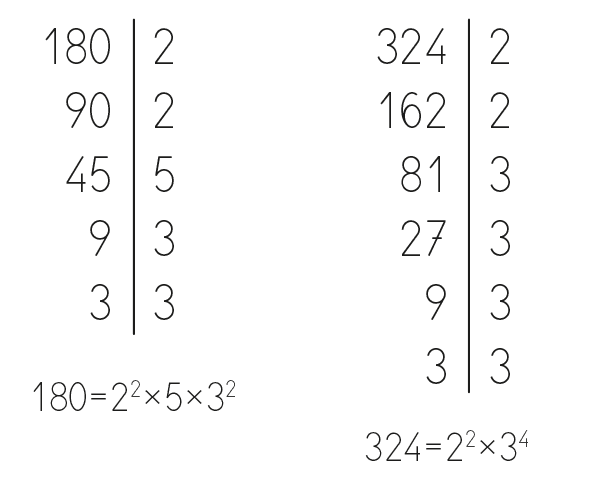
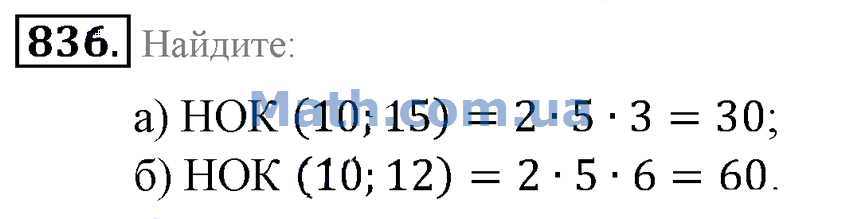 Например, НОД (24, 30,18) = 6.
Например, НОД (24, 30,18) = 6. 

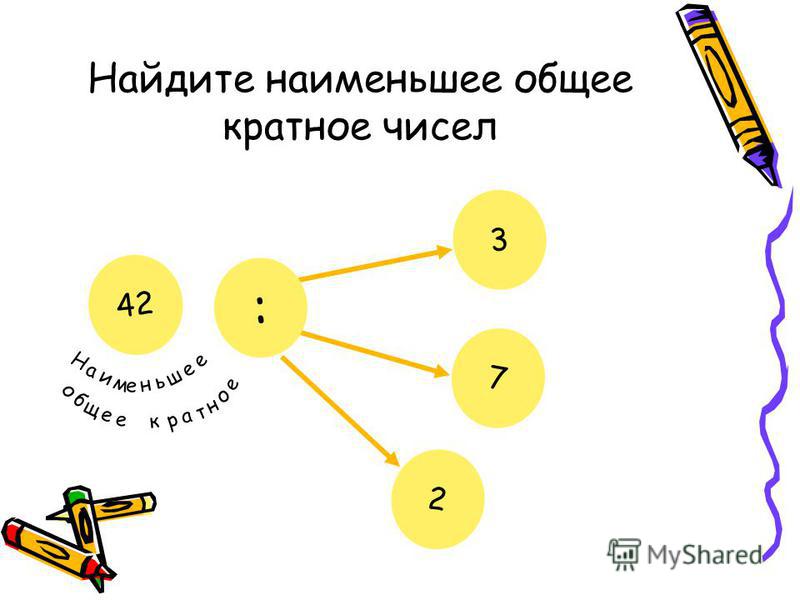
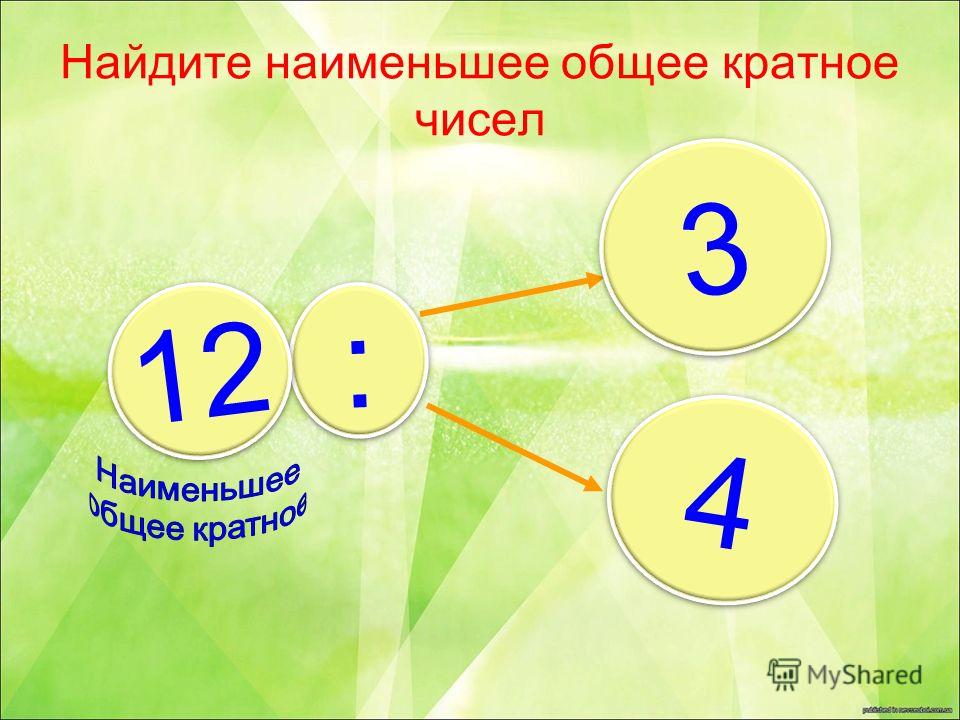



 Эти столбы решили заменить другими, поставив их на расстоянии 30 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, кроме столба в точке А.
Эти столбы решили заменить другими, поставив их на расстоянии 30 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого, кроме столба в точке А. 
 {3}}\) грамм.
{3}}\) грамм.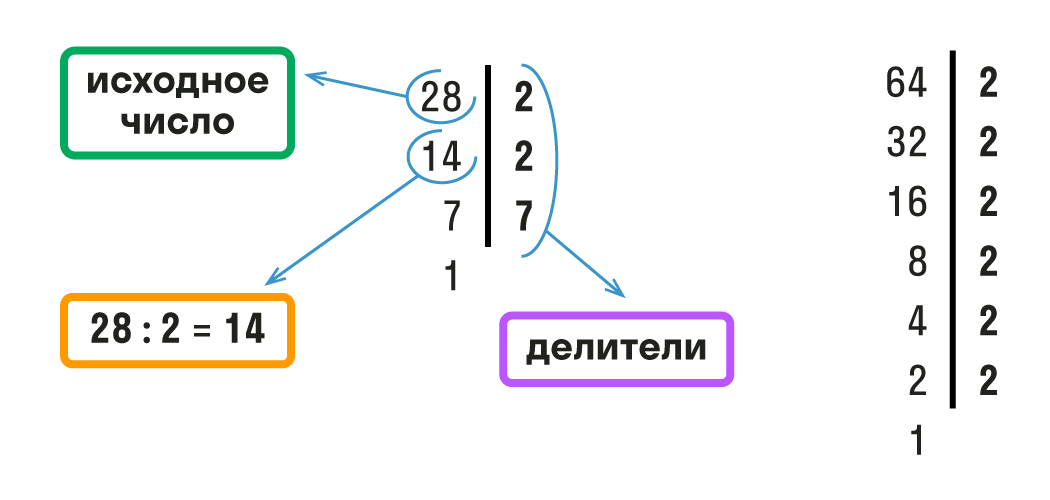 Теперь попробуем прочитать это определение:
Теперь попробуем прочитать это определение: Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение.
Для этого разделим 12 на все делители в диапазоне от 1 до 12. Если делитель позволит разделить 12 без остатка, то мы будем выделять его синим цветом и в скобках делать соответствующее пояснение. Для этого проверим все делители от 1 до 9
Для этого проверим все делители от 1 до 9 Числа выделенные синим цветом и являются делителями. Их и выпишем:
Числа выделенные синим цветом и являются делителями. Их и выпишем: Подчеркиваем обе двойки:
Подчеркиваем обе двойки: Оставшиеся числа в первом разложении перемножают и получают НОД.
Оставшиеся числа в первом разложении перемножают и получают НОД. Её и вычеркнем из первого разложения
Её и вычеркнем из первого разложения Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.

 Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ.
Первый способ заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этот способ. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК. Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12
Для этого мы выписали разложение первого числа и дописали туда множители из второго разложения, которых не было в первом разложении. В результате получили новое разложение 3 × 3 × 2 × 2. Нетрудно увидеть воочию, что в него одновременно входят разложение числа 9 и разложение числа 12 Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения:
Допишем множители 3 и 5 из второго разложения, и множитель 11 из третьего разложения: Значит наименьшее общее кратное чисел 24 и 12 равно 24
Значит наименьшее общее кратное чисел 24 и 12 равно 24 Найдите НОК чисел 40 и 32
Найдите НОК чисел 40 и 32 В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач.
В разделе мы дадим определение термина, рассмотрим теорему, которая устанавливает связь между наименьшим общим кратным и наибольшим общим делителем, приведем примеры решения задач. Так, для чисел 2 и 3 числа 16, −27, 5 009, 27 001 не будут общими кратными.
Так, для чисел 2 и 3 числа 16, −27, 5 009, 27 001 не будут общими кратными. Фактически, их число бесконечно.
Фактически, их число бесконечно.
 При этом оба равенства будут взаимно простыми числами.
При этом оба равенства будут взаимно простыми числами.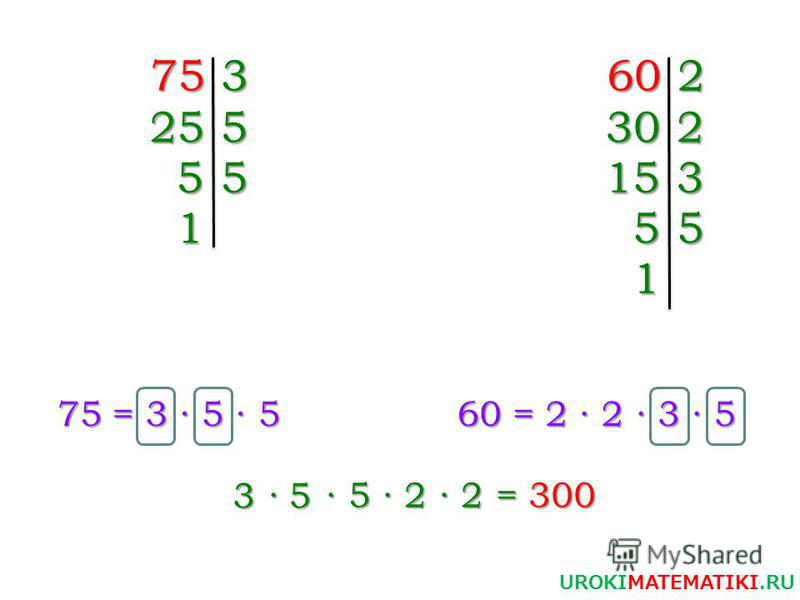

 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р. Для двух целых чисел a и b, обозначаемых НОК(a,b), НОК является наименьшим положительным целым числом, которое без остатка делится как на a, так и на b. Например, НОК(2,3) = 6 и НОК(6,10) = 30.
Для двух целых чисел a и b, обозначаемых НОК(a,b), НОК является наименьшим положительным целым числом, которое без остатка делится как на a, так и на b. Например, НОК(2,3) = 6 и НОК(6,10) = 30. У нас это выделено жирным шрифтом выше.
У нас это выделено жирным шрифтом выше.






 Т.е. возведем и числитель «3», и знаменатель «10» в третью степень.
Т.е. возведем и числитель «3», и знаменатель «10» в третью степень.



 Я знаком с методами как доказывают обратное. Все они не приемлемы. Вот внизу ролик поставили. Человек вычитывает степень числа которое приближается к нулю. Итог приближается к единице. Но во первых это не ноль, на самом деле это бесконечность. Ибо число приближается к нулю бесконечно. Значит тот число в его степени бесконечно приближается к единице. Но то число никогда не станет нулем, и степень ни когда не станет единицей. По этому такой подход не верный. Если использовать логарифму, получается то же самое. Ничего если возвести на степень ни чего, то ничего не будет происходить. Ибо нет какого либо числа, над чем можно работать. Ноль- на самом деле не число а дополнение, без которого математика просто не работает. А само по себе, это ни что. То есть нуля нет.
Я знаком с методами как доказывают обратное. Все они не приемлемы. Вот внизу ролик поставили. Человек вычитывает степень числа которое приближается к нулю. Итог приближается к единице. Но во первых это не ноль, на самом деле это бесконечность. Ибо число приближается к нулю бесконечно. Значит тот число в его степени бесконечно приближается к единице. Но то число никогда не станет нулем, и степень ни когда не станет единицей. По этому такой подход не верный. Если использовать логарифму, получается то же самое. Ничего если возвести на степень ни чего, то ничего не будет происходить. Ибо нет какого либо числа, над чем можно работать. Ноль- на самом деле не число а дополнение, без которого математика просто не работает. А само по себе, это ни что. То есть нуля нет. 0=0/0. А 0/0 не обязательно единица, это неопределенность, ведь на 0 делить нельзя))) это работает для выражения «а в степени b, где a и b стремятся к 0».
0=0/0. А 0/0 не обязательно единица, это неопределенность, ведь на 0 делить нельзя))) это работает для выражения «а в степени b, где a и b стремятся к 0». Просто математический закидон.
Просто математический закидон.
 Это и есть великая тайна сотворения мира. = 0!
Это и есть великая тайна сотворения мира. = 0! 2=9*4=36;$$
2=9*4=36;$$
 Примеры решения задания №9 из ЕГЭ по математике профильного уровня.
Примеры решения задания №9 из ЕГЭ по математике профильного уровня. Разбор основных методов и типов решения задач с параметром. Графический и аналитические методы.
Разбор основных методов и типов решения задач с параметром. Графический и аналитические методы. .. · a
.. · a Показатели кажутся довольно простыми… | Бретт Берри | Math Hacks
Показатели кажутся довольно простыми… | Бретт Берри | Math Hacks

 Возможного решения нет.
Возможного решения нет.
 Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
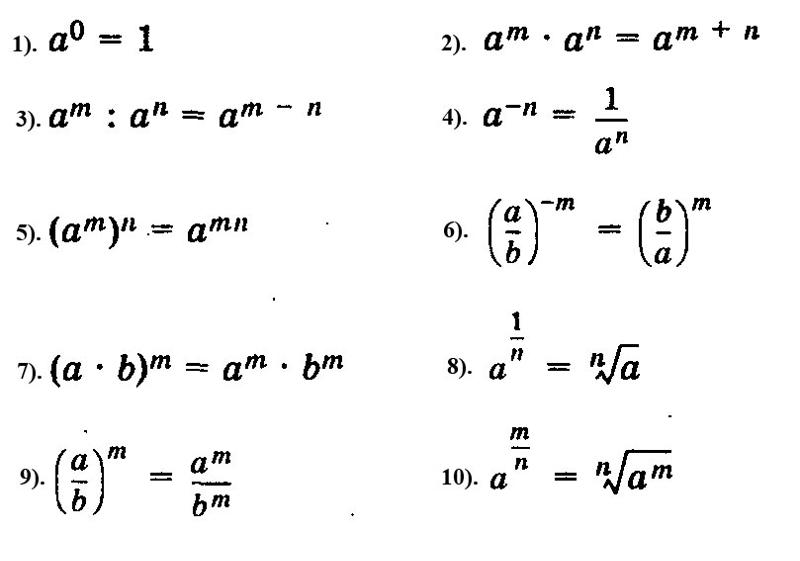 В этом калькуляторе вы можете узнать результат для отрицательного показателя степени. Просто поставьте знак минус перед числом в поле открытого поля, и результат будет рассчитан. (-n) =1/a n
В этом калькуляторе вы можете узнать результат для отрицательного показателя степени. Просто поставьте знак минус перед числом в поле открытого поля, и результат будет рассчитан. (-n) =1/a n  〖(a n ) 〗 m = a (n.m) Пример: Решите 〖(a 2 ) 〗 3
〖(a n ) 〗 m = a (n.m) Пример: Решите 〖(a 2 ) 〗 3  2)〗 2 =6 2
2)〗 2 =6 2  Если бы вы построили экспоненту известного основания, она показала бы линию, которая изгибается вверх и достигает почти идеального вертикального роста.
Эта концепция используется в калькуляторе сложного роста.
Если бы вы построили экспоненту известного основания, она показала бы линию, которая изгибается вверх и достигает почти идеального вертикального роста.
Эта концепция используется в калькуляторе сложного роста.
 Предположим, мы хотим изменить 1.0 на 9:
Предположим, мы хотим изменить 1.0 на 9: Давайте узнаем… 910 значит для тебя? Как это заставляет вас чувствовать? Вместо красивого аккуратного коэффициента масштабирования экспоненты хотят, чтобы мы чувствовали, заново переживали и даже ощущали запах процесса роста. Чем бы вы ни закончили, это ваш коэффициент масштабирования.
Давайте узнаем… 910 значит для тебя? Как это заставляет вас чувствовать? Вместо красивого аккуратного коэффициента масштабирования экспоненты хотят, чтобы мы чувствовали, заново переживали и даже ощущали запах процесса роста. Чем бы вы ни закончили, это ваш коэффициент масштабирования.
 А если разделить время на трети?
А если разделить время на трети? Каждая единица времени в «Фазе II» аналогична повторению всей фазы I:
Каждая единица времени в «Фазе II» аналогична повторению всей фазы I: 9x с точки зрения наблюдателя, а не производителя.
9x с точки зрения наблюдателя, а не производителя. 
 2=2=2 ОТДОВОГО РАБОТА.
2=2=2 ОТДОВОГО РАБОТА.  2 3 = 1/(2⋅2⋅2) = 1/8 = 0,125
2 3 = 1/(2⋅2⋅2) = 1/8 = 0,125
 Например, от 3 до 4-го (пишется 3) означает 3 х 3 х 3 х 3 = 81. Это не то же самое, что 3 х 4 (12).
Например, от 3 до 4-го (пишется 3) означает 3 х 3 х 3 х 3 = 81. Это не то же самое, что 3 х 4 (12).
 Предусмотрено восемь розеток на задней панели (четыре с расстоянием между стенами для размещения блока питания любого размера), а также три розетки на передней панели и USB-порт для зарядки для удобного питания персональных устройств. Надежный выключатель питания, прочные разъемы для розеток и стальная конструкция гарантируют бесперебойную работу Power-1 ночь за ночью.
Предусмотрено восемь розеток на задней панели (четыре с расстоянием между стенами для размещения блока питания любого размера), а также три розетки на передней панели и USB-порт для зарядки для удобного питания персональных устройств. Надежный выключатель питания, прочные разъемы для розеток и стальная конструкция гарантируют бесперебойную работу Power-1 ночь за ночью.
 треск, который я раньше слышал при включении некоторых устройств. Мне также нравится его цвет, определенно более привлекательный, чем у других на рынке».
треск, который я раньше слышал при включении некоторых устройств. Мне также нравится его цвет, определенно более привлекательный, чем у других на рынке».