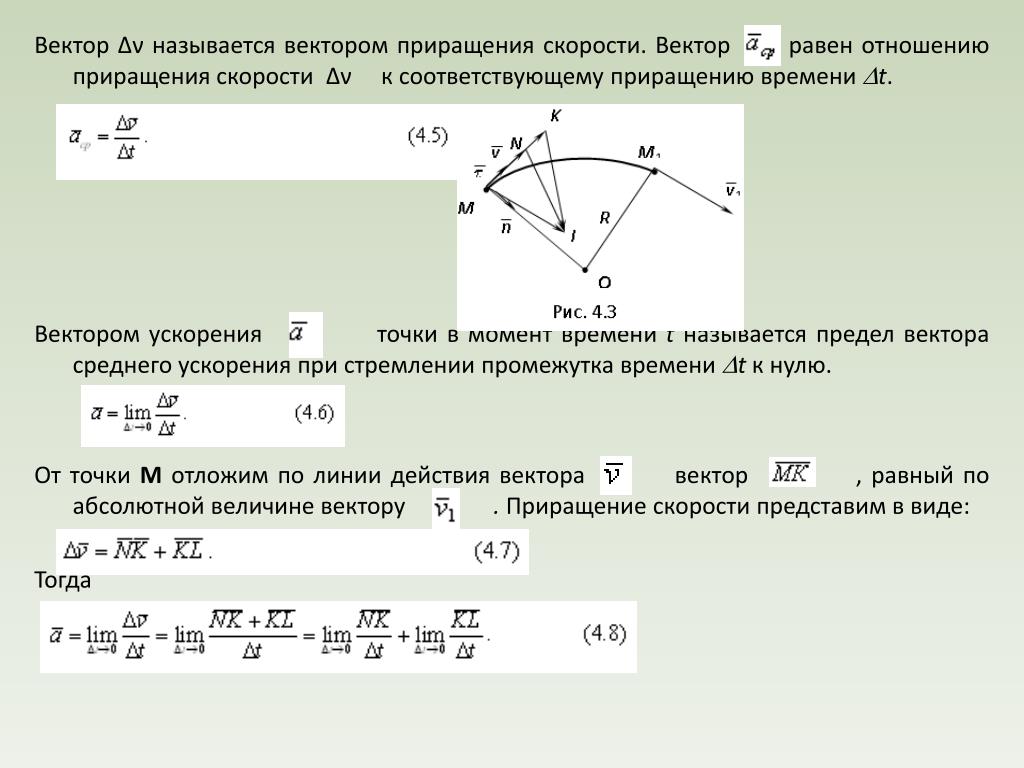
Построить график y 3x 1. Постройте график функции y=
Составим таблицу значений функции
Мы видим, что при (куб положительного числа положителен), а при (куб отрицательного числа отрицателен). Следовательно, график расположится на координатной плоскости в I и III четвертях. Заменим значение аргумента х противоположным значением тогда и функция примет противоположное значение; так как если , то
Значит, каждой точке графика соответствует точка того же графика, расположенная симметрично относительно начала координат.
Таким образом, начало координат является центром симметрии графика.
График функции изображён на чертеже 81. Эта линия называется кубической параболой.
В I четверти кубическая парабола (при ) «круто» поднимается
вверх (значения у «быстро» возрастают при возрастания х. см. таблицу), при малых значениях х линия «тесно» подходит к оси абсцисс (при «малых» значение у «весьма мало», см. таблицу). Левая часть кубической параболы (в III четверти) симметрична правой относительно начала координат.
Аккуратно вычерченный график может служить средством приближённого возведения чисел в куб. Так, например, положив найдём по графику
Для приближённого вычисления кубов составлены специальные таблицы.
Такая таблица имеется и в пособии В. М. Брадиса «Четырёхзначные математические таблицы».
Эта таблица содержит приближённые значения кубов чисел от 1 до 10, округлённые до 4-х значащих цифр.
Устройство таблицы кубов и правила пользования ею такие же, как и таблицы квадратов. Однако при увеличении (или уменьшении) числа в 10, 100 и т. д. раз его куб увеличивается (или уменьшается) в 1000, 1000 000 и т. д. раз. Значит, при пользовании таблицей кубов надо иметь в виду следующее правило переноса запятой:
Если в числе перенести запятую на несколько цифр, то в кубе этого числа надо перенести запятую в ту же сторону на утроенное количество цифр.
Поясним сказанное примерами:
1) Вычислить 2,2353. По таблице находим: ; прибавляем к последней цифре поправку 8 на последний знак:
2) Вычислить .2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке , потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U}
Напишите уравнение прямой, параллельной графику линейной функции y=3x-1 и проходящей через точку M(-1;1)
Понятие линейной функции
Линейными называются функции, выраженные общей формулой y = kx + b, где k и b — некоторые числа, именуемые коэффициентами. Графиком линейной функции выступает прямая, для построения которой достаточно взять две точки (переменная х — независимая, выбирается любая, переменная у — зависимая, высчитывается по формуле функции в соответствии с заданным х).
Свойства линейной функции
Областью определения линейной функции D(f) являются все действительные числа: x ∈ (-∞; ∞).
- Областью значений линейной функции Е(f) также являются все числа: у ∈ (-∞; ∞).
- Функция принимает значение 0 (у = 0) при x = -b / x.
Линейная функция возрастает при k > 0, убывает при k < 0.
Коэффициенты линейной функции
A функциях вида y = kx + b число k именуется угловым коэффициентом прямой. По его значению можно узнать угол α, который прямая образует с осью Ох (ее положительным направлением). Коэффициент k численно равен тангенсу угла α, поэтому при k > 0 угол α острый (меньше 90°), при k < 0 угол α — тупой (больше 90°).
Коэффициент b показывает смещение прямой y = kx + b вдоль оси Оу. Если b > 0, то график y = kx смещен вверх по оси Оу на b единичных отрезков, если b < 0, то график y = kx смещен вниз по оси Оу на |b| единичных отрезков.
Решение задачи
Нахождение уравнения прямой сводится к нахождению ее коэффициентов k и b.
Так как график искомой прямой параллелен графику линейной функции y = 3x — 1, то их угол наклона одинаков, значит k = 3. Имеем y = 3x + b.
Зная, что график прямой проходит через точку М(-1; 1), подставим ее координаты в формулу y = 3x + b и, решив полученное уравнение, найдем коэффициент b:
1 = 3 * (-1) + b
1 + 3 = b
b = 4.
Таким образом, формула искомой функции y = 3x + 4.
Ответ: y = 3x + 4.
x 1 3 функция
Вы искали x 1 3 функция? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и y 1 3 x, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x 1 3 функция».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как x 1 3 функция,y 1 3 x,y 1 3 x график,y 1 3 в степени x,y 1 3x,y 1 3x 1,y 1 3x график,y 1 x3,y 3 x 1 построить график функции,y 3 в степени x 1,y 3x 1 построить график функции,y x 1 3,y x 1 3 график,y x 1 3x 1,y x 3 1 график,y x 3 x 1,y x 3 x 1 построить график функции,y x в степени 1 3,график 1 3 в степени х,график y 1 3 x,график y 3 x 1,график y 3x 1,график y x 1 3,график y x 3 1,график функции y 1 3 x,график функции y 1 3x,график функции y 3 x 1,график функции y 3x 1,график функции y x 3 1,построить график y 1 3 x,построить график функции 1 y 3 x,построить график функции y 1 3 x,построить график функции y 3 x 1,построить график функции y 3x 1,построить график функции y x 1 3,постройте график функции y 3 x 1,постройте график функции y x 1 3,постройте график функции y x 1 3 x,у x 1 3,функция 1 3 x,функция x 3 1,функция y 1 3 x,функция y x 1 3,функция y x 3 1,функция y x 3 x 1. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и x 1 3 функция. Просто введите задачу в окошко и нажмите «решить» здесь (например, y 1 3 x график).
Где можно решить любую задачу по математике, а так же x 1 3 функция Онлайн?
Решить задачу x 1 3 функция вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
|
ЛИНЕЙНАЯ ФУНКЦИЯ
y = kx + b, где k,b — действительные числа Частные случаи линейной функции:
Взаимное расположение графиков линейных функций:
СВОЙСТВА ЛИНЕЙНОЙ ФУНКЦИИ y = kx + b
если k = 0, b > 0, то y > 0 при x R если k = 0, b y x R если k = 0, b = 0, то y = 0 при x R
Рассмотрим построение графика линейной функции по двум точкам:
Функция y = 3x + 2 строиться по двум точкам (x1;b) и (x2;b+k), при x1=0, а x2=1.
Теперь проведем через данные точки прямую:
Если k 0, b 0, можно выбрать точки (0;b) и (-b/k;0) на осях координат:
Например: y = 2x + 2
Если x1 = 0, то y1 = 2;
Через точки (0,2) и (-1;0) проведем прямую:
Если коэффициент перед х дробный, удобно выбирать х1 и х2 так, чтобы у1 и у2 были целыми.
y = — 1/3x + 2
Если x1 = 3, то y1 = 1;
Если x1 = -3, то y2 = 3;
Через точки (3;1) и (-3;3) провести прямую.
График функции y = kx + b можно получить из графика y = x в три этапа:
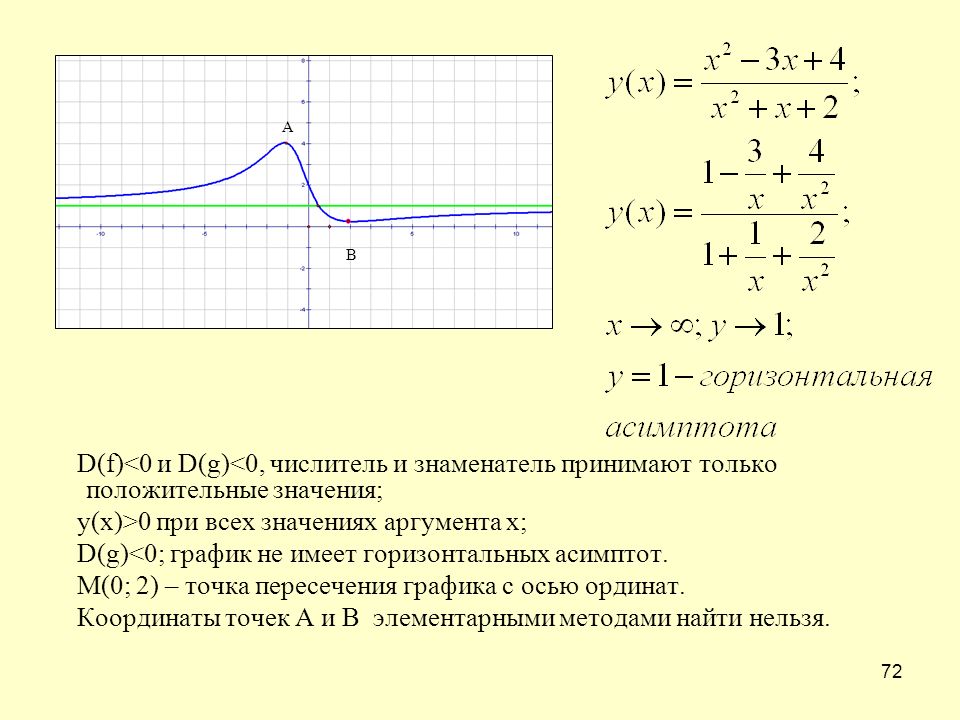
|
Как строить функцию в Excel — Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МS Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека. Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках. Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Известно, что одним из способов задания функции является графический. Графиком функции y=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания обладает очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
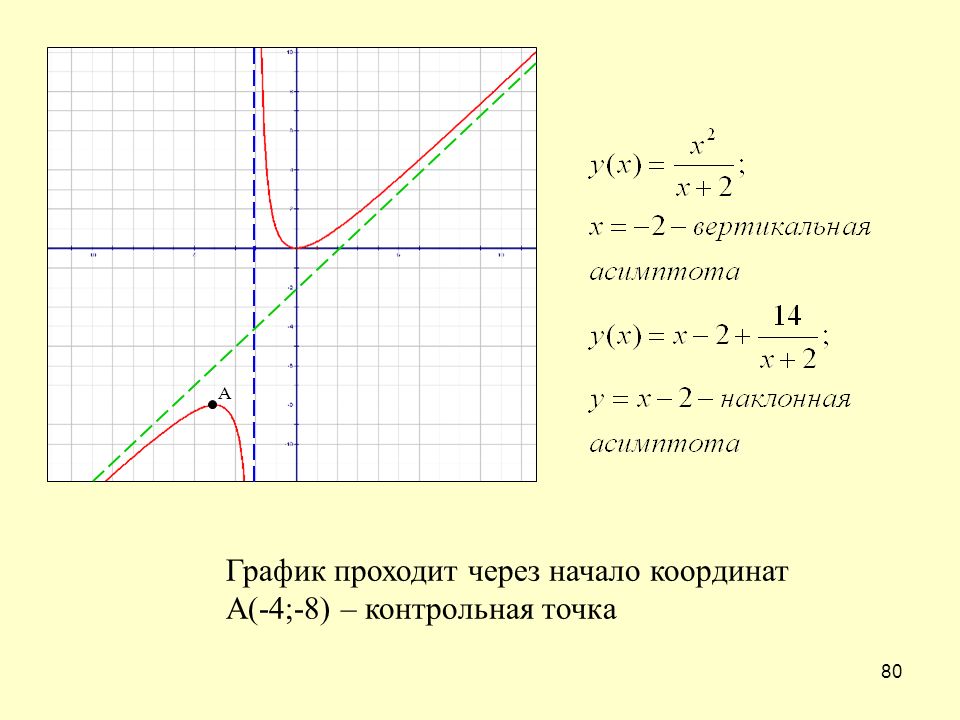
Учащимся 8-го класса известны следующие виды функций:
- y=kx+b;
- y=;
- y=|x|;
- y=kx2 (y=ax2+bx+c);
- y= ,
а также способы построения графиков функций y=f(x+l), y=f(x)+m, если известен график функции y=f(x) и элементарные методы исследования.
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и той системе координат для каждой группы, чтобы наглядно продемонстрировать их отличия. На уроке графики тех же функций дети построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1-я группа
- y=3x+5;
- y=x+5;
- y=3x+5;
- y=3x-1;
- y=-3x+5;
- y=-x+5;
2-я группа
3-я группа
- y=x2;
- y=x2-1;
- y=(x-1)2;
- y=x2-5x+4;
- y=-x2-1;
- y=-(x-1)2;
4-я группа
5-я группа
Работу учащихся опишем на примере построения графика функции y=:
- Определим промежуток построения графика функции. Пусть х1=-2, х2=2.
- В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежуток на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этого в ячейке А4 введем формулу =A3+0,1 и скопируем эту формулу в ячейки с А5 по А43.
Рис. 1. В ячейке А4 вводим формулу =A3+0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2). Для этого в ячейку В3 введем формулу: =(A3+1)/(F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1)в ячейки В4 — В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 — В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми». График функции y=построен. При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
Рис. 4. Построим график функции
Таким образом, учащиеся не только смогли получить навыки построения графиков функций в среде MS Excel, но и наглядно продемонстрировать отличительные характеристики каждой из функций в отдельно взятой группе.
Параграф 2.2. Свойства и графики основных функций.
Работу выполнила: Казанцева А.А. студентка группы 45.2
Пункт 2.2. Свойства и графики основных функций.
Объяснение и обоснование
1. Линейная функция y = kx + b.Линейной функцией называется функция вида
y = kx + b, где k и b — некоторые числа.
Обоснуем основные характеристики этой функции: область определения, область
значений, четность или нечетность, возрастание и убывание.
Область определения — множество всех действительных чисел: D (y) = R,
поскольку формула kx + b имеет смысл при всех действительных значениях
x, то есть для любого действительного x мы можем вычислить значение
kx + b (из свойств действительных чисел, которые строго доказываются в
курсах математического анализа, следует, что для любых действительных
чисел х, k и b однозначно определены произведение kх и сумма kх + b = у).
Область значений линейной функции будет разной в зависимости от зна-
чения коэффициента k.
Если k = 0, то функция имеет вид y = b, то есть ее
область значений состоит из одного числа b. В таком
случае графиком линейной функции y = b является
прямая, параллельная оси Ox, которая пересекает
ось Oy в точке b (рис. 19).
Если k ≠ 0, то E (y) = R (обоснование приведено в примере 3).
Четность и нечетность линейной функции существенно
зависит от значений коэффициентов b и k.
При b = 0 и k ≠ 0 функция y = kx + b превращается в функцию y = kx,
которая является нечетной, поскольку для всех x из ее области определения
Таким образом, график функции y = kx (рис. 22) симметричен относительно
точки O.
При k = 0 получаем функцию y = b, которая является
четной, поскольку для всех x из ее области определения
f (-x) = b = f (x). То есть график функции y = b
симметричен относительно оси Oy (рис. 21).
В общем случае при k ≠ 0 и b ≠ 0 функция
y = kx + b не является ни четной, ни нечетной, поскольку
f (-x) = k (-x) + b = -kx + b ≠ f (x) и также
f (-x) = -kx + b = -(kx — b) ≠ -f (x).
Возрастание и убывание линейной функции зависит от значения коэффициента k.
При k = 0 получаем функцию y = b — постоянную. При k > 0 функция y = kx + b
возрастает, а при k < 0 — убывает (обоснование приведено в примере 4).
В курсе геометрии было показано, что графиком линейной функции y = kx + b всегда является прямая линия.
Поскольку при x = 0 функция принимает значение y = b, то эта прямая всегда
пересекает ось Oy в точке b. Графики линейных функций приведены в таблице 3/
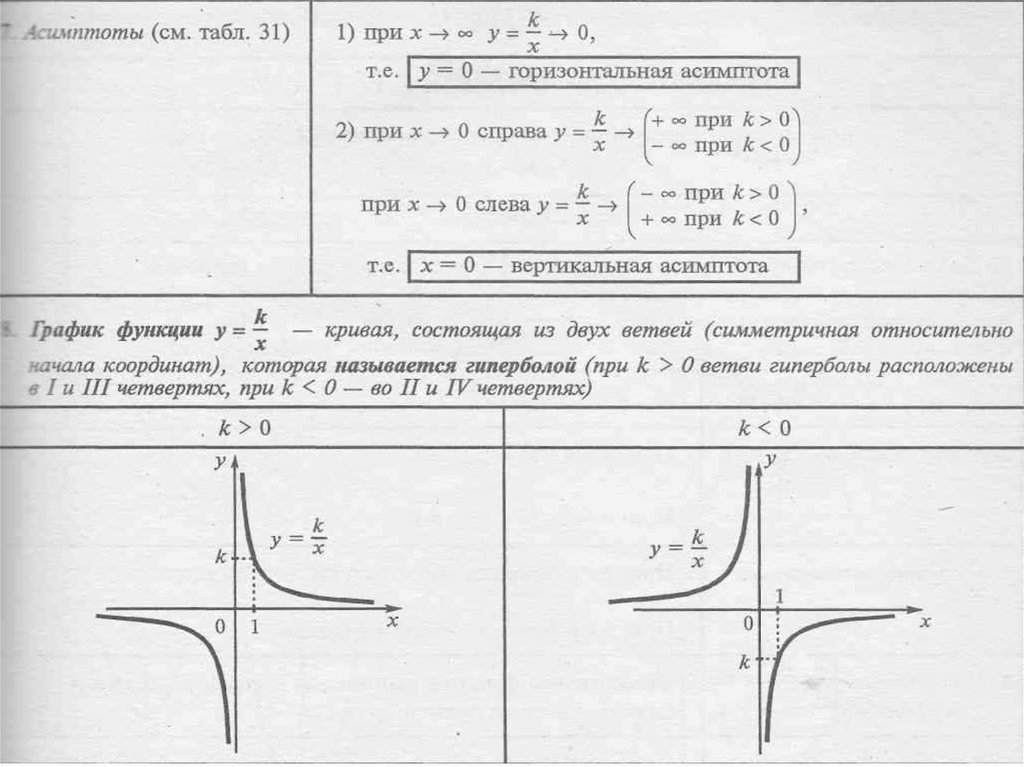
2. Функция y = k/x (k ≠ 0).
Эта функция выражает обратно пропорциональную зависимость.
Область определения: х ≠ 0. Это можно записать также так:
Область значений: у Ф 0. Это можно записать также так:
Для обоснования области значений функции y = k/x обозначим k/x = a.
Тогда из этого равенства получим x = k/a для всех a ≠ 0. То есть
для всех a ≠ 0 существует значение x = k/a, при котором
y =k/x = k/(k/a) = a. Таким образом, y принимает все
действительные значения, не равные нулю.
Функция нечетная, поскольку ее областью определения является множество,
симметричное относительно точки О, и f (-x) = -k/x = -f(x). Таким образом,
её график симметричен относительно начала координат (рис. 23).
Возрастание и убывание функции зависит от знака коэффициента k.
Если х2 > х1 (то есть х2 — х1 > 0), то для сравнения значений f(х2) и f(х1)
рассмотрим их разность: f(x2)-f(x1) = k/x2 — k/x1 = -k(x2-x1)/x2x1.
На промежутке (0; +∞) значение х1 > 0 и х2 > 0, следовательно, х1х2 > 0.
На промежутке (-∞;0) значение х1 < 0 и х2 < 0, значит, х1х2 > 0.
Учитывая, что х2 — х1 > 0 на каждом из промежутков (—∞; 0) или (0; +∞), при
k > 0 из равенства (1) получаем f(х2) — f(х1) < 0, а при k < 0 получаем f(х2) — f(х1) > 0.
При k > 0 на каждом из промежутков (—∞; 0) и (0; +∞), если х2 > х1, то f (х2) < f (х1),
таким образом, функция убывает на каждом из этих промежутков.
При k < 0 на каждом из промежутков (—∞; 0) и (0; +∞), если х2 > х1, то f (х2) > f (х1),
следовательно, функция возрастает на каждом из этих промежутков.
Из курса алгебры известно, что график функции у = k/x называется
гиперболой (она состоит из двух ветвей). При k > 0 ветви гиперболы
находятся в I и III координатных четвертях, а при k < 0 — во II и IV четвертях (рис. 23).
Замечание. Характеризируя возрастание или убывание функции у = k/x (k ≠ 0),
следует помнить, что, например, функция у = 1/x (рис. 24) убывает
каждом из промежутков (—∞; 0) и (0; +∞), но на всей области определения (х ≠ 0)
эта функция не является убывающей (и не является возрастающей).
Действительно, если взять х1 = —1 и х2 = 1, то x2 > x1, но f(x2) = f(1) = 1, а f(x1) = f(—1) = —1,
то есть большему значению аргумента не соответствует меньшее значение функции,
и на всей ее области определения функция f(x) = 1/x не является убывающей.
Поэтому же нельзя сказать, что функция f (x) = 1/x — убывает на
объединении интервалов (—∞; 0) U (0; +∞).
3. Функция y = ax² (a ≠ 0).Как известно из курса алгебры, графиком этой
функции является парабола, ветви которой направлены вверх при а > 0 (рис. 25, а)
и вниз при а < 0 (рис. 25, б). Поскольку при х = 0 значение у = 0, то график
всегда проходит через начало координат.
<Область определения: х ∈ R, поскольку значение у = ах² можно вычислить при
любых значениях х (из свойств действительных чисел, которые строго
доказываются в курсах математического анализа, следует, что для любых
действительных чисел х и а однозначно определены произведения х • х = х2 и ах²
и ax² = y).
Функция четная, поскольку f (—x) = а (—х)² = ах² = f (x). Таким образом, ее
график симметричен относительно оси Оу.
Область значений. Для нахождения области значений функции у = ax²
обозначим ax² = u. Поскольку а ≠ 0, то из этого равенства x² = u/a (*). При а > 0
уравнение (*) имеет решение для любого u ≥ 0, а при а < 0 уравнение (*) имеет
решение для любого u ≤ 0.
Следовательно, при а > 0 Е (у) = [0; +∞), а при а < 0 Е (у) = (—∞; 0].
Возрастание и убывание.
Если x2 > x1 ( то есть x2 — x1 >0), то для сравнения значений y(x2) и y(x1) рассмотрим их разность
y(x2)-y(x1) = ax2² — ax1² = a(x2² — x1²) = a(x2-x1)(x2+x1). (2)
На промежутке [0; +∞) значение х1 ≥ 0 и х2 > 0, следовательно, х2 + х1 > 0.
На промежутке (—∞; 0] значение х1 < 0 и х2 ≤ 0, значит, х2 + х1 < 0.
Учитывая, что х2 — х1 > 0 на каждом из указанных промежутков, из равенства (2)
получаем:
— при a > 0 на промежутке [0; +∞) у (х2) — у (х1) > 0, а на промежутке (—∞; 0]
y(x2) — y(x1) < 0.
— при a < 0 на промежутке [0; +∞) у (х2) — у (х1) < 0, а на промежутке (—∞; 0]
y(x2) — y(x1) > 0.
Следовательно, при х2 > х1, если a > 0, то на промежутке [0; +∞) у(х2) > y(x1)
функция возрастает, а на промежутке (—∞; 0] у (х2) < у (х1) функция убывает.
если же a < 0, то на промежутке [0; +∞) у (х2) < у (х1)
функция убывает, а на промежутке (—∞; 0] у (х2) > у (х1) функция возрастает.
Соответствующие графики приведены также в таблице 3.
4. Квадратичная функция y = ax² + bx + c (a ≠ 0).
Из курса агебры за 9 класс известно, что функция вида
y = ax² + bx +c, где a,b,c — действительные числа, причём
a≠0, называется квадратичной.Ее графиком является парабола,
ветви которой направлены вверх при а > 0 и вниз при а < 0.
Абсцисса вершины этой параболы x0 =-b/2a. Для обоснования этого
достаточно в заданном квадратном трехчлене выделить полный квадрат:
y = ax² + bx + c = a(x² + (b/a)x + c/a) = a(x + b/2a)² + (4ac — b²)/4a, то есть
y = ax² + bx + c = a(x + b/2a)² + y0, где y0 = (4ac — b²)/4a = -D/4a (3)
(D = b² — 4ac — дискриминант квадратного треёхчлена ax² + bx + c).
Напомним, что в зависимости от знака дискриминанта D парабола или
пересекает ось Ох (D > 0), или не пересекает (D < 0), или касается ее (D = 0).
Основные варианты расположения графика функции у = ax²2 + bx + с (a ≠ 0)
представлены в таблице 4.
Охарактеризуем свойства функции у = ax² + bx + с (a ≠ 0).
Область определения: D (у) = R, поскольку значение у = ax²2 + bx + с (a ≠ 0)
можно вычислить при любых значениях х (из свойств действительных чисел,
которые строго доказываются в курсах математического анализа, следует, что для
любых действительных чисел х, а, b и с однозначно определены произведения
х • х = х&, ах² и bx и суммы ах² + bx, (ax² + bx) + с = ax² + bx + с = у).
Область значений. Для нахождения области значений функции у = ax² + bx + с
используем формулу (3) и обозначим a(x + b/2a)² + y0 = u. Поскольку a ≠ 0, то
из этого равенства: (x + b/2a)² = (u — y0)/a.
ВОПРОСЫ ДЛЯ КОНТРОЛЯ:
1.Какая функция называется линейной? Назовите свойства линейной функции.
Какая линия является графиком линейной функции? Приведите примеры
линейных функций и их графиков.
2. Какая линия является графиком функции у = k/x (k≠ 0)? Приведите
графиков функций у = k/x при k > 0 и при k < 0. По графикам
укажите свойства этой функции при k > 0 и при k < 0. Докажите нечетность
функции у = k/x (k≠ 0).
3. Какая линия является графиком функции у = ax² (a ≠ 0)?
Как расположен этот график при а > 0 и при а < 0? Приведите примеры графиков функций
у = ax² при а > 0 и при а < 0. По графикам укажите свойства этой
функции при а > 0 и при а < 0. Докажите четность функции у = ax² (a ≠ 0).
4. Какая линия является графиком функции у = ax²2 + bx + с (a ≠ 0)?
Как расположен график при а > 0 и при а < 0? Как найти абсциссу
вершины графика функции у = ax²2 + bx + с (a ≠ 0)?
Приведите примеры графиков этой функции при а > 0 и при а < 0.
По графикам укажите свойства этой функции при а > 0 и при а < 0.
1. Постройте график функции:
1) y = 3x — 2; 2)y = -x + 4; 3) y = -2 4) y = -5x 5) y = 0 6)y = 4x
Есть ли среди этих функций чётные или нечётные? Ответ обоснуйте.
2. По приведёнными графикам функций y = kx + b (рис. 26) укажите знаки k и b в каждом случае.
Постройте график функции (3 — 5 ).
3. 1) y = -2/x; 2) y = 3/x 3) y = 1/x 4) y = 5/x
4. 1) y = -2x² 2) y = 3x² 3) y = -3x² 4) y = 5x²
5. 1) y = x² — 6x + 7 2) y = -x² + 4x + 2 3) y = 2x² — 2x + 1 4) y = -3x² + 6x
6. По приведённым графикам функции y = ax² + bx + c (a≠) (рис. 27)
укажите знаки a, b, c в каждом случае.
Y 3x 1 график. Постройте график функции y=
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке , потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U}
Решите Свойства прямой y = 3x + 1 Tiger Algebra Solver
Переставьте:
Переставьте уравнение, вычтя то, что находится справа от знака равенства из обеих частей уравнения:
y- (3 * x +1) = 0
Шаг 1:
Уравнение прямой линии
1.1 Решите y-3x-1 = 0
Тигр распознает, что здесь есть уравнение прямой. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).
«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат, в которой «y» — вертикальная ось, а «x» — горизонтальная ось.
В этой формуле:
y указывает нам, как далеко идет линия.
x сообщает нам, как далеко вдоль
м находится наклон или градиент, т.е. насколько крутой является линия.
b является точкой пересечения Y, т.е. Ось Y
Пересечения по осям X и Y и наклон называются свойствами линии. Теперь мы построим график линии y-3x-1 = 0 и вычислим ее свойства
График прямой линии:
Вычислите точку пересечения Y:
Обратите внимание, что когда x = 0, значение y равно 1 / 1, поэтому эта линия «разрезает» ось y при y = 1.00000
Y-Intercept = 1/1 = 1.00000
Вычислите X-Intercept:
Когда y = 0, значение x равно 1 / -3 Таким образом, наша линия «срезает» ось x в точке x = -0,33333
пересечение по оси x = 1 / -3 = -0,33333
Расчет наклона:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно 1.000, а для x = 2.000 значение y равно 7.000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 7.000 — 1.000 = 6.000 в год. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = ПОДЪЕМ / РАБОТА)
Наклон = 6.000 / 2.000 = 3.000
Геометрическая фигура: прямая линия
- Наклон = 6.000 / 2.000 = 3.000
- пересечение по оси x = 1 / -3 = -0,33333
- пересечение по оси y = 1/1 = 1,00000
Линейные графики — Xcelerate Math
Линейные графики названы так, потому что они представляют собой прямые линии .
Координаты считываются из начала координат (0,0) . Они находятся в порядке координаты x (по горизонтали) и координаты y (по вертикали) .
Поскольку это прямые линии, нужны только 3 точки . Две точки необходимы, чтобы провести линию, а третья точка используется для проверки правильности.
Графики не всегда проходят через начало координат (0,0).
Линейные уравнения записываются в виде:
y = м x + c
где
м — уклон (уклон)
c — точка пересечения оси y (точка, где график пересекает ось y)
m и c являются константами (фиксированными числами).
Примеры :
- В уравнении y = 3x + 2 градиент равен 3, а точка пересечения оси y равна 2.
- В уравнении y = 4x — 5 градиент равен 4, а точка пересечения оси y равна –5.
- В уравнении y = 1 ⁄ 2 x + 6, градиент равен 1 ⁄ 2 или 0,5, а точка пересечения оси y равна 6.
- В уравнении y = x градиент равен 1, а точка пересечения оси y равна 0.
Пример первый — покупка билетов на гонки на мотоциклах
Билеты на гонки на мотоциклах стоят 50 долларов каждый.Нарисуйте таблицу значений и линейный график, показывающий стоимость билетов.
Ответ:
Поскольку этот график представляет собой прямую линию, необходимо всего 3 точки: две точки для рисования линии и третья для проверки правильности.
Выберите x = 0, 1, 2, если в вопросе не указано иное.
| Кол-во билетов | 0 | 1 | 2 |
| Стоимость билетов | $ 0 | $ 50 | $ 100 |
Пример 2 — График y = x
(a) Что такое градиент в линейном уравнении y = x?
(b) Что такое точка пересечения по оси Y?
(c) Нарисуйте таблицу значений и график линейного уравнения y = x
Ответ:
(а) Градиент = 1
(b) пересечение оси y = 0
(c) Поскольку этот график представляет собой прямую линию, необходимо всего 3 точки: две точки для рисования линии, а третья — для проверки правильности.Выберите x = 0, 1, 2, если в вопросе не указано иное.
| x | 0 | 1 | 2 | |
| y = x | 0 | 1 | 2 | |
| Рабочий | y = x | y = 0 | y = x 9015 y = 0 | = 1 y = x y = 2 |
| Координаты | (0,0) | (1,1) | (2,2) |
Пример 3 — График y = 2x
(a) Что такое градиент в линейном уравнении y = 2x?
(b) Что такое точка пересечения по оси Y?
(c) Нарисуйте таблицу значений и график линейного уравнения y = 2x
Ответ:
(а) Градиент = 2
(b) пересечение оси y = 0
(c) Поскольку этот график представляет собой прямую линию, необходимо всего 3 точки: две точки для рисования линии, а третья — для проверки правильности.Выберите x = 0, 1, 2, если в вопросе не указано иное.
| x | 0 | 1 | 2 |
| y = 2x | 0 | 2 | 4 |
| Рабочий | y = 2x | 22 y = 2x y = 2x y = 2 × 1 y = 2 | y = 2x y = 2 × 2 y = 4 |
| Координаты | (0,0) | (1 , 2) | (2,4) |
Пример четвертый - график y = 2x + 3
(a) Что такое градиент в линейном уравнении y = 2x + 3?
(b) Что такое точка пересечения по оси Y?
(c) Нарисуйте таблицу значений и график линейного уравнения y = 2x + 3
Ответ:
(а) Градиент = 2
(б) точка пересечения по оси y = 3
(в)
| x | 0 | 1 | 2 |
| y = 2x + 3 | 3 | 5 | 7 |
| Рабочий | y = 2x + 3 y = 2x + 3 3 y = 3 | y = 2x + 3 y = 2 × 1 + 3 y = 5 | y = 2x + 3 y = 2 × 2 + 3 y = 7 |
| Координаты | (0,3) | (1,5) | (2,7) |
Вопросы
Что вы заметили в наклоне графиков y = 2 x и y = 2 x + 3?
Пример пятый - График y =
1 ⁄ 2 x + 1 (a) Каков градиент в линейном уравнении y = 1 ⁄ 2 x + 1?
(b) Что такое точка пересечения по оси Y?
(c) Нарисуйте таблицу значений и график линейного уравнения y = 1 ⁄ 2 x + 1
Ответ:
(a) Градиент = 1 ⁄ 2
( Обратите внимание, что график круче, чем y = 1 x, но не такой крутой, как y = 2 x и y = 2 x + 3 )
(b) точка пересечения по оси y = 1
(в)
| x | 0 | 1 | 2 | |||
| y = 1 ⁄ 2 x + 1 | 1 | 1 1 ⁄ | ||||
| y = 1 ⁄ 2 x + 1 y = 1 ⁄ 2 × 0 + 1 y = 1 |
y = 1 ⁄ 2 x + 1 y = 1 ⁄ 2 × 1 + 1 y = 1 1 ⁄ 2 |
y = 1 ⁄ 2 x + 1 y = 1 ⁄ 2 × 2 + 1 y = 2 | ||||
| Координаты | (0,1) | (1,1 1 ⁄ 2 ) | (2,2) |
Вопросы
Что вы заметили в коэффициенте при x (число, умноженном на x) и крутизне графика ?
Что вы заметили в константе (число в конце уравнения) и точке , где график пересекается с осью y ?
Пример шестой - График y = 3x - 1
(a) Что такое градиент в линейном уравнении y = 3x - 1?
(b) Что такое точка пересечения по оси Y?
(c) Изобразите уравнение y = 3x - 1, где –2
Ответ:
(a) Градиент = 3 ( Обратите внимание, что график круче, чем y = 1 x, y = 2 x и y = 2 x + 3 )
(b) пересечение оси y = –1
(c) В вопросе указано, что 3 значения x должны находиться в диапазоне от –2 до 2.Выберите x-значения –2, 0, 2.
| x | –2 | 1 | 2 |
| y = 3x - 1 | –7 | 1 | 3 |
| Рабочий | y = 3x - 1x - (–2) - 1 y = –6 - 1 y = –7 |
y = 3x - 1 y = 3 × 0 - 1 y = 0 - 1 y = –1 |
y = 3x - 1 y = 3 × 2 - 1 y = 4 - 1 y = 3 |
| Координаты | (–2, –7) | (0, –1 ) | (2,3) |
Вопрос
Нарисуйте таблицу значений, а затем изобразите уравнение y = 4x - 3 , где –3
(Помните, что ваш график будет правильным, если это прямая линия.)
Пример седьмой - График y = –2x + 5 (отрицательный градиент)
(a) Что такое градиент в линейном уравнении y = –2x + 5?
(b) Что такое точка пересечения по оси Y?
(c) Изобразите уравнение y = –2x + 5
Ответ:
(a) Градиент = –2 ( Обратите внимание, что график направлен в обратном направлении. )
(b) пересечение оси y = 5
(в)
| x | 0 | 1 | 2 |
| y = –2x + 5 | 5 | 3 | 1 |
| Рабочий | y = –2x (5 y = –2x 2) × 0 + 5 y = 0 + 5 y = 5 |
y = –2x + 5 y = (–2) × 1 + 5 y = (–2) + 5 y = 3 |
y = –2x + 5 y = (–2) × 2 + 5 y = (–4) + 5 y = 1 |
| Координаты | (0,5) | (1,3) | (2,1) |
1.2 + 4 на отдельном листе. Используя эти графики, сравните и сопоставьте форму и положение графиков.
(текстовое поле под вопросом)
Я знаю, что это обман, но мне нужны ответы, пожалуйста
Абсолютно нет!
Но если ВЫ публикуете то, о чем ВЫ ДУМАЕТЕ, кто-то может вам помочь.
Я не дам вам ответов, но скажу, что вам нужно сделать
1.2 - 81 = 0
разность квадратов ...
(x + 9) (x-9) = 0
и решения следующие .....
5. ......?
Вот правильные ответы;
1. С (-1/2, -5/2), (2,5)
2. A 0
3. В -1; 19
4. С -9,9
5. C экспоненциальный
ПОДХОДЯЩИЕ
6. A
7. D
8. C
9. B
10.ЭССЕ
Графические линейные уравнения с двумя переменными - Элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Распознавайте взаимосвязь между решениями уравнения и его графиком.
- Постройте линейное уравнение, нанеся точки.
- График вертикальных и горизонтальных линий.
Перед тем, как начать, пройдите тест на готовность.
- Оценить, когда.
Если вы пропустили эту проблему, просмотрите (рисунок). - Решите в общем.
Если вы пропустили эту проблему, просмотрите (рисунок).
Распознавать взаимосвязь между решениями уравнения и его графика
В предыдущем разделе мы нашли несколько решений уравнения. Они перечислены на (Рисунок). Итак, упорядоченные пары, и являются некоторыми решениями уравнения. Мы можем построить эти решения в прямоугольной системе координат, как показано на (Рисунок).
Обратите внимание, как точки идеально совпадают? Соединяем точки линией, чтобы получился график уравнения. См. (Рисунок). Обратите внимание на стрелки на концах каждой стороны линии. Эти стрелки указывают на продолжение линии.
Каждая точка на линии является решением уравнения. Кроме того, каждое решение этого уравнения представляет собой точку на этой прямой. Пункты , а не на линии, не являются решениями.
Обратите внимание, что точка с координатами находится на линии, показанной на (Рисунок).Если вы подставите и в уравнение, вы обнаружите, что это решение уравнения.
Итак, дело в решении уравнения. (Фраза «точка с координатами» часто сокращается до «точка».)
Значит, это не решение уравнения. Следовательно, дело не в контуре. См. (Рисунок). Это пример поговорки: «Картинка стоит тысячи слов». Линия показывает вам всех решений уравнения.Каждая точка на линии - это решение уравнения. И каждое решение этого уравнения находится на этой линии. Эта линия называется графиком уравнения.
График линейного уравнения
График линейного уравнения представляет собой линию.
- Каждая точка на линии является решением уравнения.
- Каждое решение этого уравнения представляет собой точку на этой прямой.
Используйте график, чтобы решить, будет ли каждая упорядоченная пара:
- решение уравнения.
- на линии.
ⓐ ⓑ
ⓐ да, да ⓑ да, да
Используйте график, чтобы определить, составляет ли каждая заказанная пара:
- решение уравнения
- по линии
ⓐ ⓑ
ⓐ нет, нет ⓑ да, да
Построение линейного уравнения по точкам
Есть несколько методов, которые можно использовать для построения графика линейного уравнения. Метод, который мы использовали для построения графиков, называется построением точек или методом построения точек.
Как построить уравнение по точкам
Постройте уравнение, нанеся точки.
Постройте уравнение, нанеся точки:.
Постройте уравнение, нанеся точки:.
Действия, которые необходимо предпринять при построении линейного уравнения путем нанесения точек, приведены ниже.
Постройте линейное уравнение путем нанесения точек.
- Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают. Если нет, внимательно проверьте свою работу.
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Это правда, что для определения линии нужны только две точки, но использование трех точек - хорошая привычка. Если вы нанесете только две точки, и одна из них неверна, вы все равно можете нарисовать линию, но она не будет представлять решения уравнения.Это будет неправильная линия.
Если вы используете три точки, а одна неверна, точки не выровняются. Это говорит о том, что что-то не так, и вам нужно проверить свою работу. Посмотрите на разницу между частью (a) и частью (b) на (Рисунок).
Приведем еще один пример. На этот раз мы покажем последние два шага в одной сетке.
Изобразите уравнение.
Решение
Найдите три точки, которые являются решениями уравнения. Здесь, опять же, легче выбрать значения для.Вы понимаете почему?
Перечислим точки на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Постройте уравнение, нанеся точки:.
Постройте уравнение, нанеся точки:.
Когда уравнение включает дробь в качестве коэффициента, мы все равно можем подставлять любые числа вместо. Но математика будет проще, если мы сделаем «правильный» выбор значений.Таким образом, мы избежим дробных ответов, которые сложно построить точным графиком.
Изобразите уравнение.
Решение
Найдите три точки, которые являются решениями уравнения. Поскольку в этом уравнении дробь является коэффициентом, мы будем тщательно выбирать значения. Мы будем использовать ноль в качестве одного варианта и кратное 2 для других вариантов. Почему значения, кратные 2, являются хорошим выбором?
Точки показаны на (Рисунок).
Постройте точки, убедитесь, что они совпадают, и проведите линию.
Изобразите уравнение.
Изобразите уравнение.
До сих пор все уравнения, которые мы построили на графике, были выражены в терминах. Теперь изобразим уравнение с одной и той же стороной и на одной стороне. Посмотрим, что получится в уравнении. Если в чем ценность?
Эта точка имеет дробную часть для координаты x , и, хотя мы можем построить график этой точки, трудно быть точным, указав дроби. Помните, что в этом примере мы тщательно выбирали значения для, чтобы вообще не отображать дроби.Если мы решим уравнение для, будет легче найти три решения уравнения.
Решения для, и показаны на (Рисунок). График представлен на (Рисунок).
Можете ли вы определить точку, которую мы нашли, пропустив на линии?
Изобразите уравнение.
Изобразите уравнение.
Изобразите уравнение.
Если вы можете выбрать любые три точки для построения линии, как вы узнаете, совпадает ли ваш график с тем, который показан в ответах в книге? Если точки пересечения графиков осей x и y совпадают, графики совпадают!
Уравнение на (Рисунок) было записано в стандартной форме, с обеими и на одной и той же стороне.Мы решили это уравнение всего за один шаг. Но для других уравнений в стандартной форме это не так просто решить, поэтому мы оставим их в стандартной форме. Мы все еще можем найти первую точку для построения, позволяя и решая для. Мы можем построить вторую точку, позволив, а затем решив для. Затем мы построим третью точку, используя другое значение для или.
Изобразите уравнение.
Решение
Мы перечисляем упорядоченные пары на (Рисунок). Нанесите точки, убедитесь, что они совпадают, и проведите линию.См. (Рисунок).
Изобразите уравнение.
Изобразите уравнение.
Вертикальные и горизонтальные линии графика
Можно ли построить уравнение только с одной переменной? Просто и нет, или просто без? Как мы составим таблицу значений, чтобы получить точки для построения?
Давайте рассмотрим уравнение. Это уравнение имеет только одну переменную,. Уравнение говорит, что всегда равно , поэтому его значение не зависит от. Независимо от того, что есть, ценность всегда есть.
Итак, чтобы составить таблицу значений, впишите все значения. Затем выберите любые значения для. Поскольку не зависит от, вы можете выбрать любые номера, которые вам нравятся. Но чтобы уместить точки на нашем координатном графике, мы будем использовать 1, 2 и 3 для координат y . См. (Рисунок).
Постройте точки из (Рисунок) и соедините их прямой линией. Обратите внимание на (рисунок), что мы построили вертикальную линию .
Вертикальная линия
Вертикальная линия - это график уравнения вида.
Линия проходит через ось x в точке.
Изобразите уравнение.
Изобразите уравнение.
Изобразите уравнение.
Что делать, если в уравнении есть, но нет? Давайте изобразим уравнение в виде графика. На этот раз значение y - является константой, поэтому в этом уравнении не зависит от. Заполните 4 для всех (рисунок), а затем выберите любые значения для. Мы будем использовать 0, 2 и 4 для координат x .
График представляет собой горизонтальную линию, проходящую через ось y в точке 4. См. (Рисунок).
Горизонтальная линия
Горизонтальная линия - это график уравнения вида.
Линия проходит по оси y в точке.
Постройте уравнение
Изобразите уравнение.
Изобразите уравнение.
Уравнения для вертикальных и горизонтальных линий очень похожи на уравнения типа В чем разница между уравнениями и?
Уравнение включает и.Значение зависит от значения. Координата y изменяется в зависимости от значения. Уравнение имеет только одну переменную. Значение постоянно. Координата y всегда равна 4. Она не зависит от значения. См. (Рисунок).
Обратите внимание, что на (Рисунок) уравнение дает наклонную линию, а дает горизонтальную линию.
График и в той же прямоугольной системе координат.
Решение
Обратите внимание, что в первом уравнении есть переменная, а во втором - нет.См. (Рисунок). Два графика показаны на (Рисунок).
График и в той же прямоугольной системе координат.
График и в той же прямоугольной системе координат.
Ключевые понятия
- Построение линейного уравнения по точкам
- Найдите три точки, координаты которых являются решениями уравнения. Разложите их в виде таблицы.
- Постройте точки в прямоугольной системе координат. Убедитесь, что точки совпадают.Если нет, внимательно проверьте свою работу!
- Проведите линию через три точки. Вытяните линию, чтобы заполнить сетку, и поместите стрелки на обоих концах линии.
Повседневная математика
Стоимость дома на колесах. Робинсоны арендовали дом на колесах на неделю, чтобы поехать в отпуск. Аренда дома на колесах обходится им в 594 фунта плюс 0,32 фунта за милю, поэтому линейное уравнение дает стоимость проезда на несколько миль. Рассчитайте стоимость аренды за 400, 800 и 1200 миль, а затем нарисуйте линию.
? 722,? 850,? 978
Еженедельный заработок. В художественной галерее, где он работает, Сальвадору платят 200 фунтов в неделю плюс 15% от продаж, которые он совершает, поэтому уравнение дает сумму, которую он зарабатывает на продаже произведений искусства в долларах. Подсчитайте сумму, которую Сальвадор зарабатывает от продажи 900, 1600 и 2000 фунтов стерлингов, а затем изобразите эту линию.
Письменные упражнения
Объясните, как выбрать три значения x , чтобы составить таблицу для построения графика линии.
В чем разница между уравнениями вертикальной и горизонтальной линии?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Уравнение точки и уклона прямой
Форма "точка-наклон" уравнения прямой:
Уравнение полезно, когда мы знаем:
- одна точка на линии: (x 1 , y 1 )
- и уклон линии: м ,
и хотите найти другие точки на линии.
Сначала поиграйте с ним (переместите точку, попробуйте разные уклоны):
Теперь давайте узнаем больше.
Что это означает?
(x 1 , y 1 ) - известная точка
м - уклон трассы
(x, y) - любая другая точка на линии
Разобраться в этом
Исходя из уклона:
Уклон м = изменение в y изменение x знак равно г - г 1 х - х 1
| Начиная с уклона: переставляем так:
чтобы получить это: |
Итак, это просто формула наклона по-другому!
Теперь давайте посмотрим, как его использовать.
Пример 1:
уклон "м" = 3 1 = 3
г - у 1 = м (х - х 1 )
Мы знаем m, а также знаем, что (x 1 , y 1 ) = (3,2), поэтому мы имеем:
Это отличный ответ, но мы можем его немного упростить:
г - 2 = 3х - 9
у = 3х - 9 + 2
у = 3х - 7
Пример 2:
м = −3 1 = −3
y - y 1 = m (x - x 1 )
Мы можем выбрать любую точку для (x 1 , y 1 ), поэтому давайте выберем (0,0), и у нас будет:
у - 0 = −3 (х - 0)
Что можно упростить до:
Пример 3: Вертикальная линия
Какое уравнение представляет собой вертикальная линия?
Наклон не определен!
На самом деле это особый случай , и мы используем другое уравнение, например:
Каждая точка на линии имеет координату x 1.5 ,
, поэтому его уравнение: x = 1,5
А как насчет y = mx + b?
Возможно, вы уже знакомы с формой «y = mx + b» (называемой формой уравнения линии с пересечением наклона).
Это то же уравнение, но в другой форме!
Значение «b» (называемое точкой пересечения оси y) - это точка пересечения линией оси y.
Таким образом, точка (x 1 , y 1 ) фактически находится в (0, b)
, и уравнение принимает следующий вид:
Начнем с y - y 1 = m (x - x 1 )
(x 1 , y 1 ) на самом деле (0, b): y - b = m (x - 0)
Это: y - b = mx
Положите b на другую сторону: y = mx + b
Форма линейного уравнения с пересечением наклона (Алгебра 1, Визуализация линейных функций) - Mathplanet
Ранее в этой главе мы выразили линейные уравнения, используя стандартную форму Ax + By = C.Теперь мы собираемся показать другой способ выражения линейных уравнений, используя форму углового пересечения y = mx + b.
В форме пересечения наклона вы используете наклон линии и точку пересечения по оси Y, чтобы выразить линейную функцию.
$$ y = mx + b $$
Где m - наклон, а b - точка пересечения с y.
Пример
Постройте уравнение
$$ y-2x = 1 $$
переписать в форме пересечения наклона
$$ y = 2x + 1 $$
Определите наклон и точку пересечения оси Y
m = 2 и b = 1
Постройте точку, соответствующую точке пересечения оси y, (0,1)
Значение m, наклон, говорит нам, что для каждого шага вправо по оси x мы перемещаемся на 2 шага вверх по оси y (поскольку m = 2)
И как только у вас будет вторая точка, вы можете просто провести линию через две точки и продлить ее в обоих направлениях.
Вы можете проверить правильность нарисованной линии, подставив координаты второй точки в исходное уравнение. Если уравнение верно, значит, верен второй пункт.
Наша вторая точка = (1, 3)
$$ y-2x = 1 $$
$$ 3-2 \ cdot 1 = 3-2 = 1 $$
Наш второй пункт - это решение уравнения, т. Е. Линия, которую мы нарисовали, верна.
Линия, проходящая через начало координат, имеет Y-пересечение нуля, b = 0, и представляет собой прямое изменение.
$$ y = mx $$
В прямой вариации ненулевое число m называется постоянной вариации.
Вы можете назвать функцию f, используя понятие функции
$$ f \ влево (x \ вправо) = mx + b $$
f (x) - другое имя для y и читается как «значение f в x» или «f of x». Для именования функций можно использовать буквы, отличные от f.
Группа функций со схожими характеристиками называется семейством функций. Все функции, которые можно записать в виде f (x) = mx + b, принадлежат семейству линейных функций.
Самая основная функция в семействе функций называется родительской функцией. Родительская функция всех линейных функций -
.$$ f \ влево (x \ вправо) = x $$
Видеоурок
График y = 3x - 2
Линейные уравнения в координатной плоскости (Алгебра 1, Визуализация линейных функций) - Mathplanet
Линейное уравнение - это уравнение с двумя переменными, график которого представляет собой линию. График линейного уравнения - это набор точек на координатной плоскости, которые все являются решениями уравнения.Если все переменные представляют собой действительные числа, можно изобразить уравнение, нанеся на график достаточно точек, чтобы распознать шаблон, а затем соединить точки, чтобы включить все точки.
Если вы хотите построить график линейного уравнения, у вас должно быть как минимум две точки, но обычно рекомендуется использовать более двух точек. При выборе очков старайтесь включать как положительные, так и отрицательные значения, а также ноль.
Пример
Постройте функцию y = x + 2
Начните с выбора пары значений для x e.г. -2, -1, 0, 1 и 2 и вычислите соответствующие значения y.
| х | Y = х + 2 | Заказанная пара |
| -2 | -2 + 2 = 0 | (-2, 0) |
| -1 | -1 + 2 = 1 | (-1, 1) |
| 0 | 0 + 2 = 2 | (0, 2) |
| 1 | 1 + 2 = 3 | (1, 3) |
| 2 | 2 + 2 = 4 | (2, 4) |
Теперь вы можете просто нанести пять упорядоченных пар на координатную плоскость
На данный момент это пример дискретной функции.Дискретная функция состоит из изолированных точек.
Проведя линию через все точки и продолжая линию в обоих направлениях, мы получаем противоположность дискретной функции, непрерывную функцию, которая имеет непрерывный график.
Если вы хотите использовать только две точки для определения вашей линии, вы можете использовать две точки, где график пересекает оси. Точка, в которой график пересекает ось x, называется отрезком x, а точка, в которой график пересекает ось y, называется отрезком y.Пересечение по оси x находится путем нахождения значения x, когда y = 0, (x, 0), а точка пересечения по оси y находится путем нахождения значения y, когда x = 0, (0, y).
Стандартная форма линейного уравнения -
$$ Ax + By = C, \: \: A, B \ neq 0 $$
Прежде чем вы сможете изобразить линейное уравнение в его стандартной форме, вы сначала должны решить уравнение относительно y.
$$ 2y-4x = 8 $$
$$ 2y-4x \, {\ color {green} {+ \, 4x}} = 8 \, {\ color {green} {+ \, 4x}} $$
$$ 2y = 4x + 8 $$
$$ \ frac {2y} {{\ color {green} 2}} = \ frac {4x} {{\ color {green} 2}} + \ frac {8} {{\ color {green} 2}}
$$$ y = 2x + 4 $$
Отсюда вы можете построить уравнение, как в примере выше.
График y = a представляет собой горизонтальную линию, где линия проходит через точку (0, a)
В то время как график x = a представляет собой вертикальную линию, проходящую через точку (a, 0)
Видеоурок
Постройте график линейного уравнения y = 3x - 2
Гигантский маятник в виде змеи, который будет выставлен перед Филлипс-холлом, посвященный искусству повсюду, в день 7 апреля, представляет собой идеальное сочетание искусства и науки.
Кинетическая скульптура размером 8 на 11 футов является детищем заведующего кафедрой математики Рича Маклафлина и заведующего кафедрой физики и астрономии Кристиана Илиадиса из Колледжа искусств и наук. Гиря на конце маятника — это 6-фунтовые дубинки Carolina blue.
К.э.н. по математике. Кандидат Франческа Бернарди исследует движение маятника змеи, который строится ко Дню искусств повсюду. (фото Кристен Чавес)Когда 17 маятников разной длины отпускаются одновременно, они создают волнообразный узор, похожий на скользящую змею.Затем маятник расцепляется и раскачивается отдельными моделями, прежде чем снова сойтись в большую волну. Цикл, на который смотреть гипнотизирует, занимает около минуты.
«Движение, которое они делают вместе, — это художественная часть, но в основе этого лежит наука», — сказал Илиадис. «Это гравитация, напряжение, энергия, количество движения, сопротивление воздуха, трение. Вы видите симметрию, но откуда эта симметрия? Это все уравнения «.
У преподавателей возникла идея увеличить в масштабе небольшой настольный маятник в виде змеи (с мячами для гольфа Carolina в качестве гирь), который стоит на рабочем столе Маклафлина.Он использовал эту уменьшенную версию в течение нескольких лет в своем летнем курсе математики для ученых-канцлеров.
Недавно в пятницу днем в магазине физики и астрономии на первом этаже Филлипс-холла Франческа Бернарди, доктор философии. кандидат математических наук, и Дэн Харрис, доктор математики, работали над настройкой маятника. Они использовали метроном, чтобы помочь координировать выпуск маятника, а также камеры iPhone и iPad для покадрового просмотра видеозаписи движения волн и внесения необходимых корректировок.Они составили план несколько недель назад, и управляющий магазином Фил Томпсон построил маятник. Проект поддержали средства Arts Everywhere.
Научный сотрудник математики Дэн Харрис корректирует маятник с помощью талрепа у основания скульптуры. (фото Кристен Чавес)По словам Харриса, сочетание искусства и науки было в центре его исследований на протяжении всей его выпускной карьеры.
«Любой, кто проходит мимо и видит маятник, будет заинтригован им, и это откроет дверь для разговора о том, что заставляет его работать — например, как изменение длины маятника меняет частоту», — сказал он.
Бернарди согласился и рассказал о недавнем опыте использования трехмерного принтера в производственном пространстве Hanes Art Center, который привел к разговору об искусстве и науке.
«Один из людей, которые там работали, спросил меня о подробностях нашего эксперимента. Искусство может сделать науку более доступной для всех », — сказала она.
Один из компонентов нового Плана повышения качества «Создание ученых» в Каролине направлен на интеграцию искусства и гуманитарных наук с научными курсами, чтобы обеспечить навыки критического мышления и понимание бесчисленных способов переплетения науки и культуры.
Дуэйн Дирдорф, директор студенческих лабораторий по физике и астрономии, сказал, что преподаватели кафедры используют все виды визуальных элементов в качестве учебных пособий.
«Эти вещи заставляют людей спрашивать: как это работает? Я подозреваю, что мы также будем показывать видео со змеиным маятником ».
Гири изготовлены из буровых долот Каролина синего цвета. (фото Кристен Чавес)Змеиный маятник также появится в Филлипс-холле на UNC Science Expo 22 апреля.
Рассказ Ким Спурр, фото Кристен Чавес, Колледж искусств и наук; видео любезно предоставлено кафедрой математики
.

 2+n-72)=1/(n+9)
2+n-72)=1/(n+9) Так
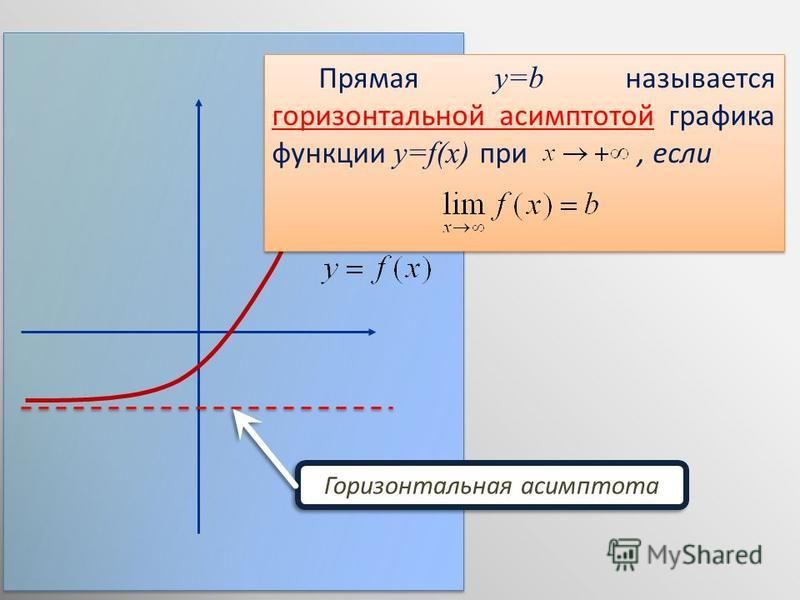
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
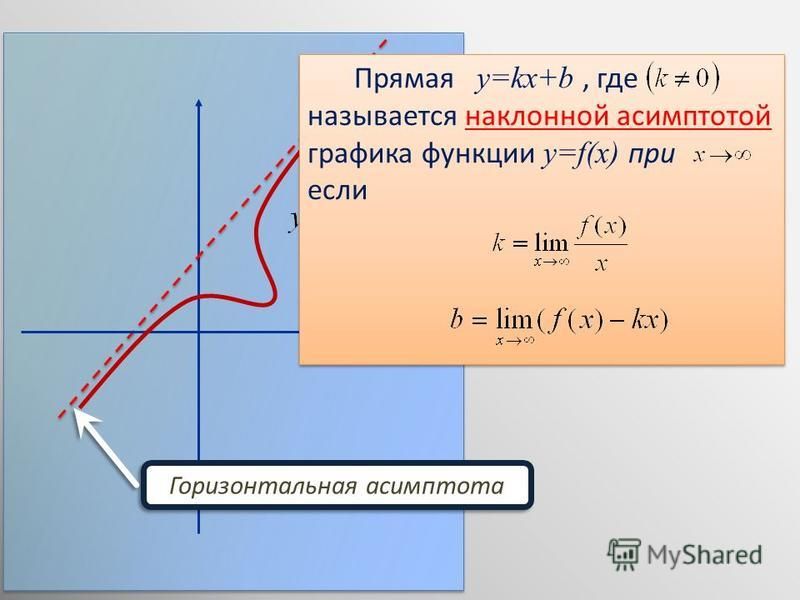
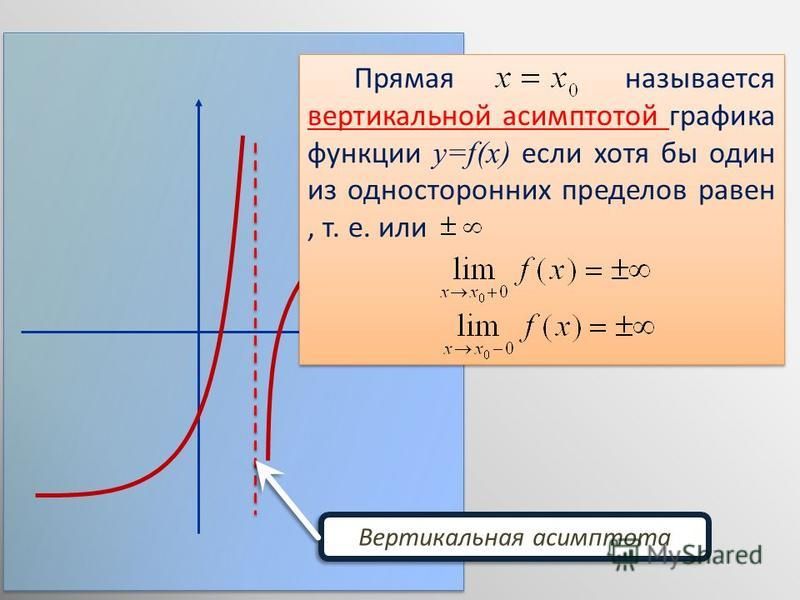
возможное расстояние, но так и не касается его.
Так
и с асимптотой: она постоянно стремится достигнуть кривой графика функции, приближается к нему на минимальное
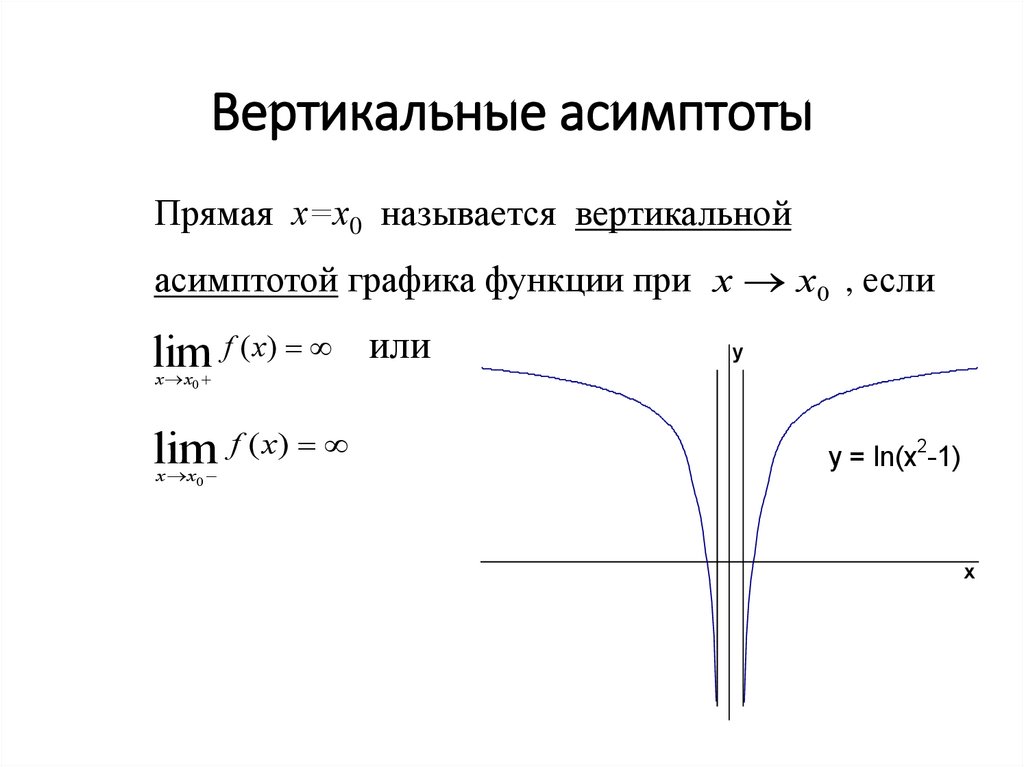
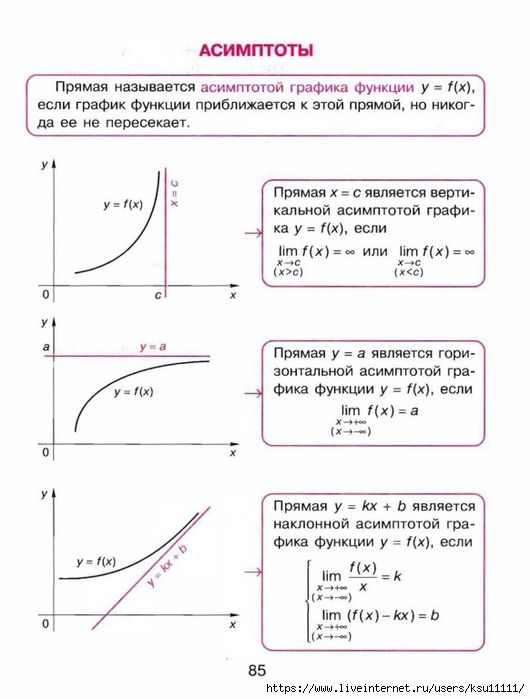
возможное расстояние, но так и не касается его.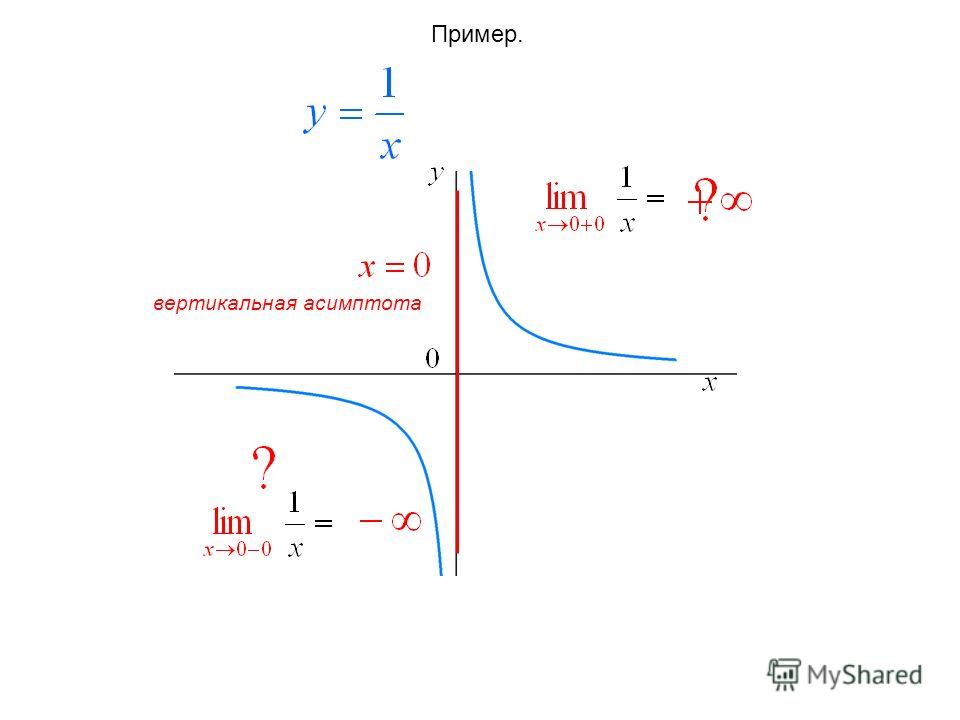 Прямая x = a
является вертикальной асимптотой графика функции, если точка x = a
является точкой разрыва второго рода для этой функции.
Прямая x = a
является вертикальной асимптотой графика функции, если точка x = a
является точкой разрыва второго рода для этой функции.
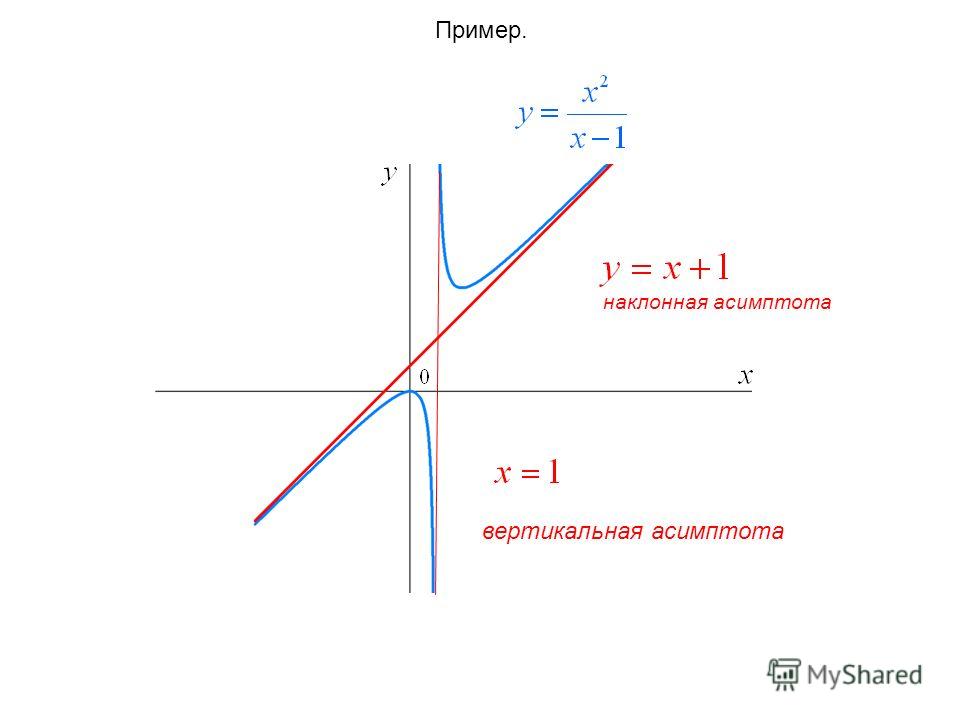
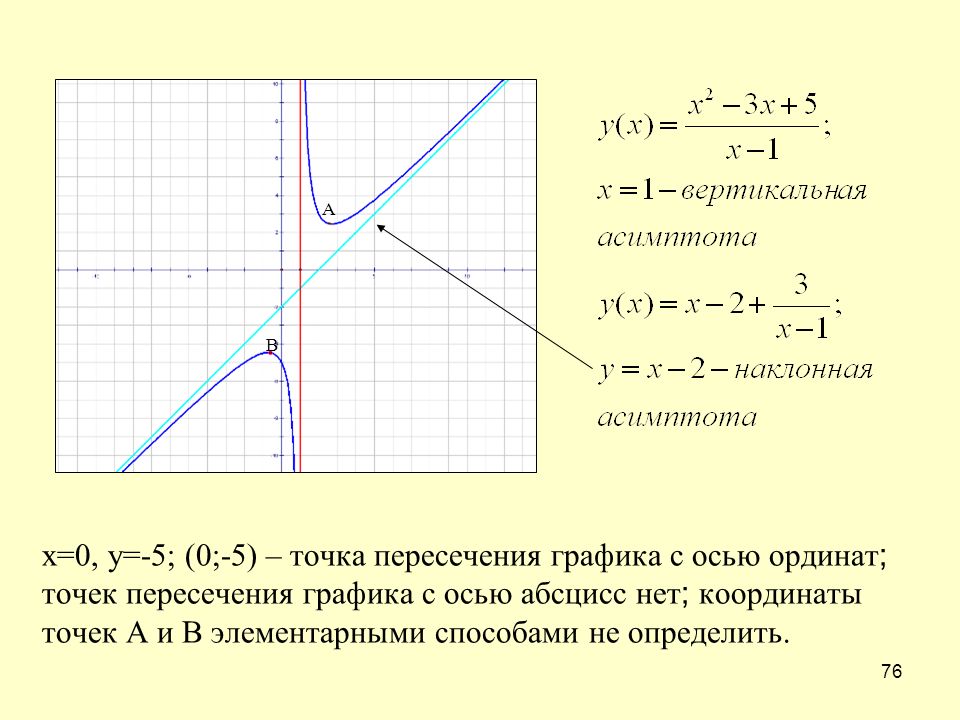
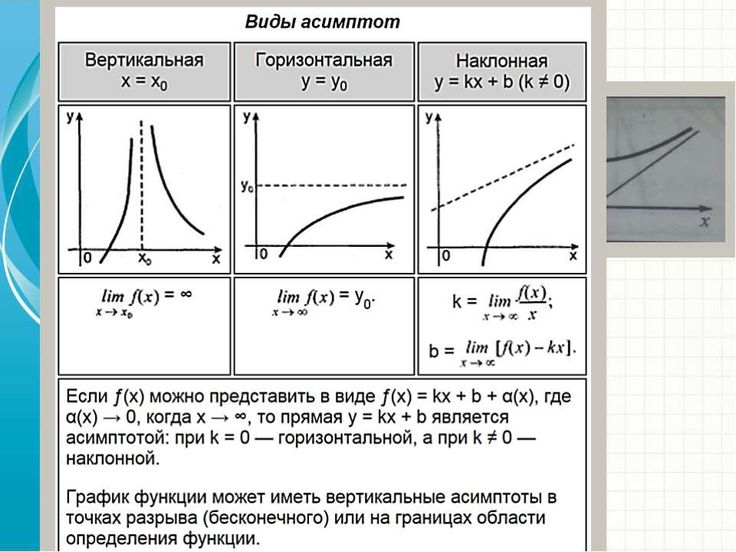
 Для наклонной асимптоты необходимо больше —
угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Для наклонной асимптоты необходимо больше —
угловой коэффициент k, который показывает угол наклона прямой, и свободный член b, который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом. Существование наклонной асимптоты определяется следующей теоремой,
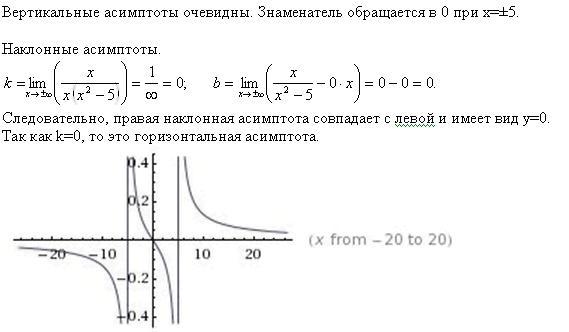
на основании которой и находят названные только что коэффициенты.
 Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
Прямая y = 2x является двусторонней
наклонной асимптотой графика данной функции (рис. внутри примера).
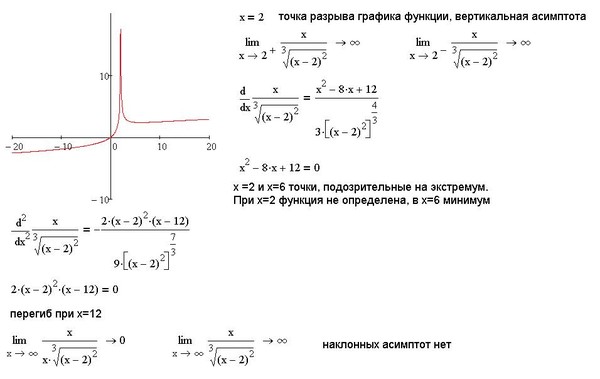
 Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
Заключение: x = 0 — точка
устранимого разрыва, поэтому у графика функции нет вертикальных асимптот.
 2*arctgh(x)*arcctgh(x)
2*arctgh(x)*arcctgh(x) 14159..
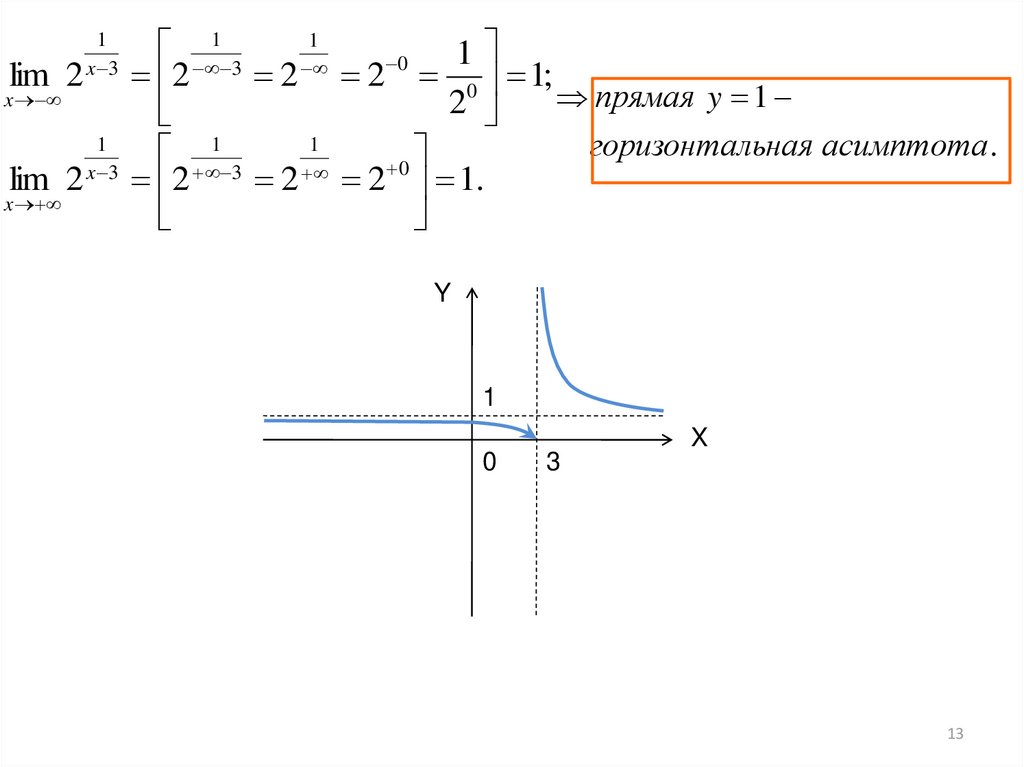
14159.. Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
Для многих функций существуют прямые, к которым графики функций неограниченно приближаются. Такие прямые называют асимптотами, и их точное определение мы дадим чуть позже. Как мы увидим далее, асимптоты бывают вертикальными, горизонтальными и наклонными. С вертикальными и горизонтальными асимптотами графика функции мы уже встречались, в частности, в разделе «Гипербола на координатной плоскости. График дробно-линейной функции». С наклонными асимптотами, за исключением горизонтальных, мы пока еще дела не имели.
 1)
1) 3)
3)
 Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет.
Следовательно, x = 0 – точка минимума функции (5). Других критических точек у функции (5) нет. Следует отдельно рассматривать случаи, когда аргумент стремится к бесконечности () и минус бесконечности ().
Следует отдельно рассматривать случаи, когда аргумент стремится к бесконечности () и минус бесконечности (). (5.873)
(5.873) е.
е. (4.71.5)
(4.71.5) Найдите все три горизонтальные, вертикальные и наклонные асимптоты с помощью этого калькулятора.
Найдите все три горизонтальные, вертикальные и наклонные асимптоты с помощью этого калькулятора.
 Теперь давайте научимся определять все эти типы.
Теперь давайте научимся определять все эти типы.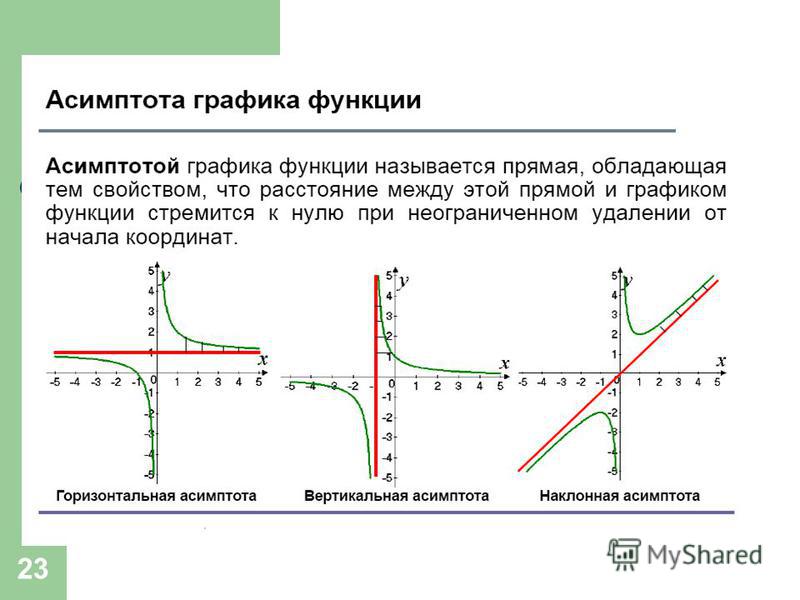 При сравнении числителя и знаменателя знаменатель оказывается большим выражением.
При сравнении числителя и знаменателя знаменатель оказывается большим выражением.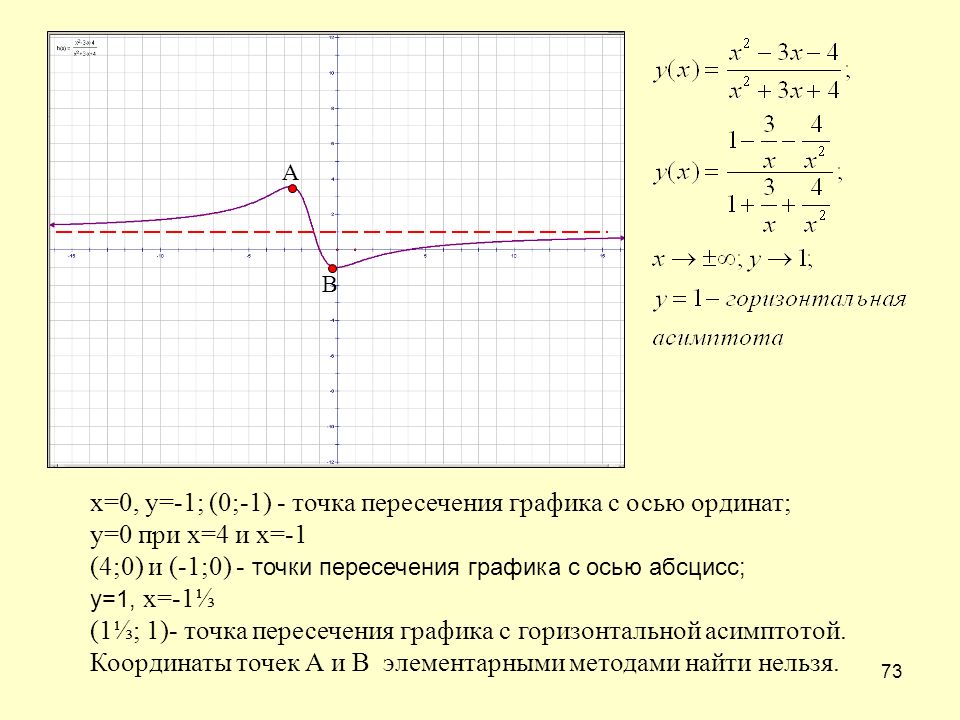

 Поскольку ничто не отменяется, асимптоты существуют при х = 6 и х = -6 .
Поскольку ничто не отменяется, асимптоты существуют при х = 6 и х = -6 .

 В нашем примере это значения 2x 2 и 7x 2 . Таким образом, разделив их, мы получим 2/7 . И это горизонтальное асимптотическое значение.
В нашем примере это значения 2x 2 и 7x 2 . Таким образом, разделив их, мы получим 2/7 . И это горизонтальное асимптотическое значение.
 рабочий лист решения задач 1 работа и сила
рабочий лист решения задач 1 работа и сила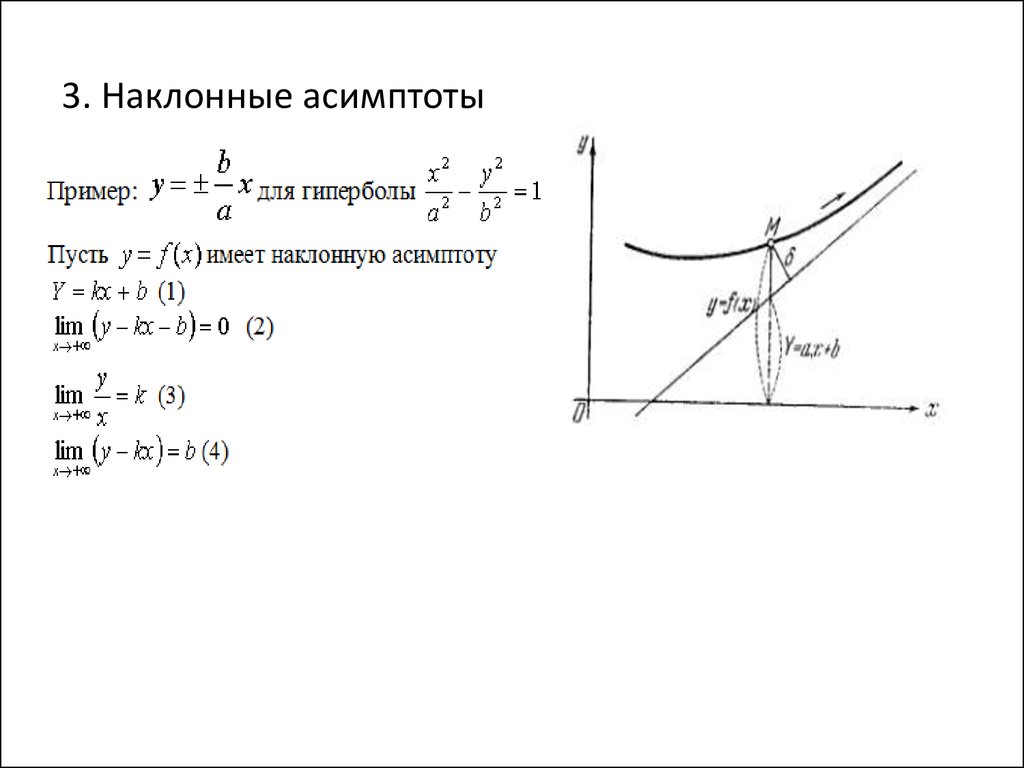 384 2 Макдугал Литтел
384 2 Макдугал Литтел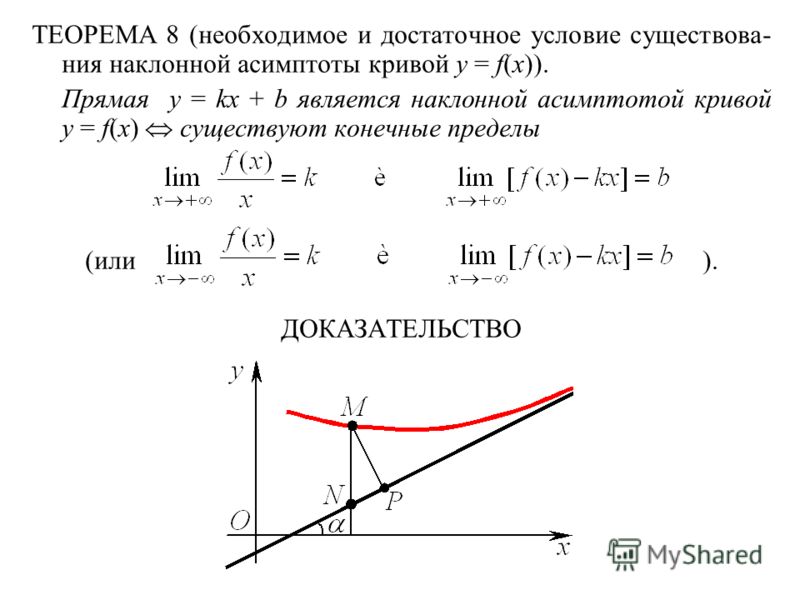 9
9 Почему важно знать, как упростить выражение в математике
Почему важно знать, как упростить выражение в математике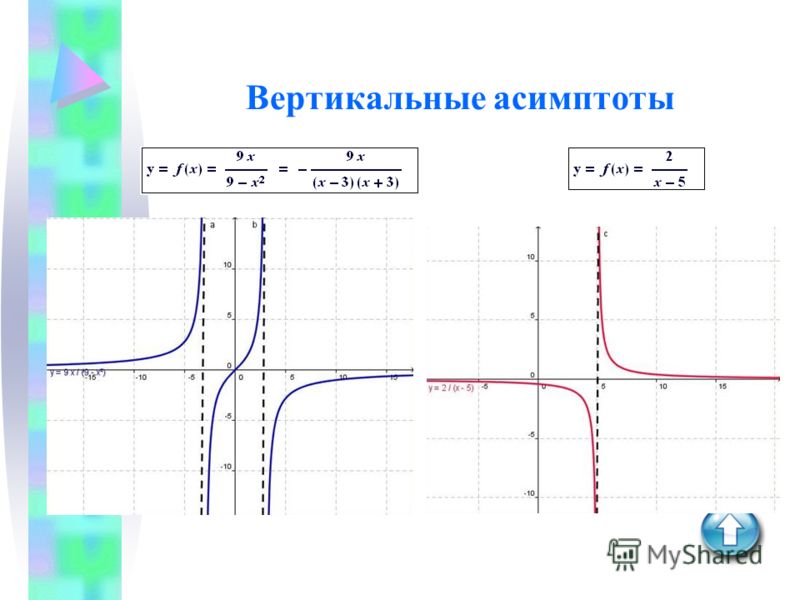
 ppt
ppt — экзамен по сурдсу
— экзамен по сурдсу pdf
pdf
 pdf
pdf com
com
 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Точно так же, когда мы приближаемся к \(x = 0\), функция снова сохраняет тот же знак, что и \(x\), но начинает становиться довольно большой. Вот набросок этого графика.
Точно так же, когда мы приближаемся к \(x = 0\), функция снова сохраняет тот же знак, что и \(x\), но начинает становиться довольно большой. Вот набросок этого графика. Рациональная функция будет равна нулю при определенном значении \(x\) только в том случае, если числитель равен нулю при этом \(x\), а знаменатель не равен нулю при этом \(x\). Другими словами, чтобы определить, равна ли когда-либо рациональная функция нулю, все, что нам нужно сделать, это установить числитель равным нулю и решить. Когда у нас есть эти решения, нам просто нужно
убедитесь, что ни одно из них не делает знаменатель равным нулю.
Рациональная функция будет равна нулю при определенном значении \(x\) только в том случае, если числитель равен нулю при этом \(x\), а знаменатель не равен нулю при этом \(x\). Другими словами, чтобы определить, равна ли когда-либо рациональная функция нулю, все, что нам нужно сделать, это установить числитель равным нулю и решить. Когда у нас есть эти решения, нам просто нужно
убедитесь, что ни одно из них не делает знаменатель равным нулю.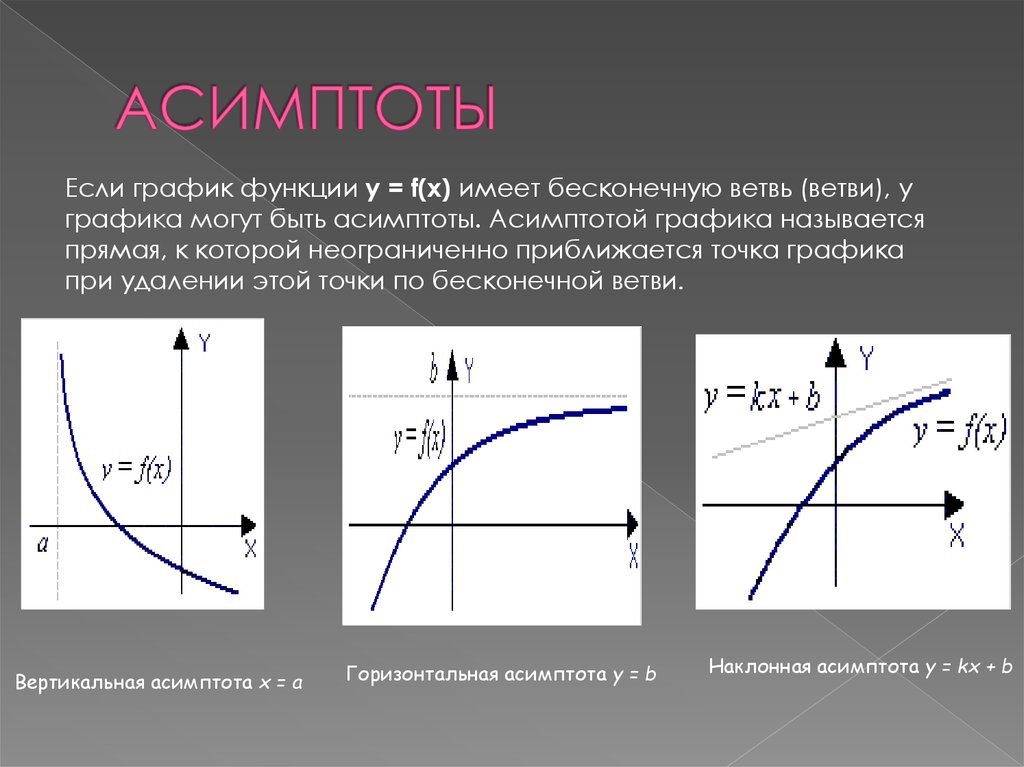
 Ему нужно только приблизиться к нему с одной стороны, чтобы он был горизонтальной асимптотой.
Ему нужно только приблизиться к нему с одной стороны, чтобы он был горизонтальной асимптотой.
 \(y\)-перехват равен
\(y\)-перехват равен Поскольку \(y\)-перехват и \(x\)-перехват уже находятся в левой области, нам не нужно будет получать там какие-либо точки. Это означает, что нам просто нужно получить точку в нужном регионе. На самом деле не имеет значения, какое значение \(x\) мы выбираем здесь, нам просто нужно, чтобы оно было достаточно маленьким, чтобы оно соответствовало нашему графику.
Поскольку \(y\)-перехват и \(x\)-перехват уже находятся в левой области, нам не нужно будет получать там какие-либо точки. Это означает, что нам просто нужно получить точку в нужном регионе. На самом деле не имеет значения, какое значение \(x\) мы выбираем здесь, нам просто нужно, чтобы оно было достаточно маленьким, чтобы оно соответствовало нашему графику.
 Это связано с тем, что в этой области есть несколько возможных вариантов поведения, и нам нужно определить фактическое поведение. Мы увидим другие основные варианты поведения в следующих примерах, так что на этом этапе это будет иметь больше смысла. 92} — 4x = x\left( {x — 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in}x = 0,\,\,x = 4\]
Это связано с тем, что в этой области есть несколько возможных вариантов поведения, и нам нужно определить фактическое поведение. Мы увидим другие основные варианты поведения в следующих примерах, так что на этом этапе это будет иметь больше смысла. 92} — 4x = x\left( {x — 4} \right) = 0\hspace{0.25in} \Стрелка вправо \hspace{0.25in}x = 0,\,\,x = 4\]

 Это может произойти, если ось x (горизонтальная ось) или ось y (вертикальная ось) движется к бесконечности. Асимптота — это линия, к которой приближается кривая, стремясь к бесконечности (не касаясь ее).
Это может произойти, если ось x (горизонтальная ось) или ось y (вертикальная ось) движется к бесконечности. Асимптота — это линия, к которой приближается кривая, стремясь к бесконечности (не касаясь ее).


 {2}-5x+10}{x-2 } \] 9{2}-6х$. После ввода первого полиномиального уравнения мы вводим вторую полиномиальную функцию в поле знаменателя; полиномиальная функция x-4.
{2}-5x+10}{x-2 } \] 9{2}-6х$. После ввода первого полиномиального уравнения мы вводим вторую полиномиальную функцию в поле знаменателя; полиномиальная функция x-4.
 е. наклонную асимптоту) в точке .
е. наклонную асимптоту) в точке .
 Асимптот нет.
Асимптот нет.



 , вектор скорости при поступательном движении тела).
, вектор скорости при поступательном движении тела). Два вектора, и , имеющие общую точку приложения, складываются по правилу параллелограмма. Разность векторов: .
Два вектора, и , имеющие общую точку приложения, складываются по правилу параллелограмма. Разность векторов: .  Вычисление длины (модуля) вектора в MS EXCEL
Вычисление длины (модуля) вектора в MS EXCEL е. в данном случае эквивалентна формуле =B8*B8+B9*B9
.
е. в данном случае эквивалентна формуле =B8*B8+B9*B9
.
 Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия Тогда для нашего вектора, если он задан на плоскости, а x = х к − х н,
Тогда для нашего вектора, если он задан на плоскости, а x = х к − х н, Для нахождения проекции вектора Пpab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
Для нахождения проекции вектора Пpab в онлайн режиме необходимо указать координаты векторов a и b. При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word. Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор.
 Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).

 »
и ввести в показатель степени число
-1
»
и ввести в показатель степени число
-1 2.10
приведен пример векторного произведения
векторов.
2.10
приведен пример векторного произведения
векторов. 2.10
приведен пример суммирования элементов
вектора.
2.10
приведен пример суммирования элементов
вектора. 3.2).
3.2). 3.1.
Диалоговое окно Text Styles (Стили текста)
3.1.
Диалоговое окно Text Styles (Стили текста) 3.4):
3.4): Ввести имя
переменной и знак просмотра, нажав
кнопку «=», detD=-3.
Ввести имя
переменной и знак просмотра, нажав
кнопку «=», detD=-3. Рис.
3.4).
Рис.
3.4).


 ,
причём при
.
,
причём при
.
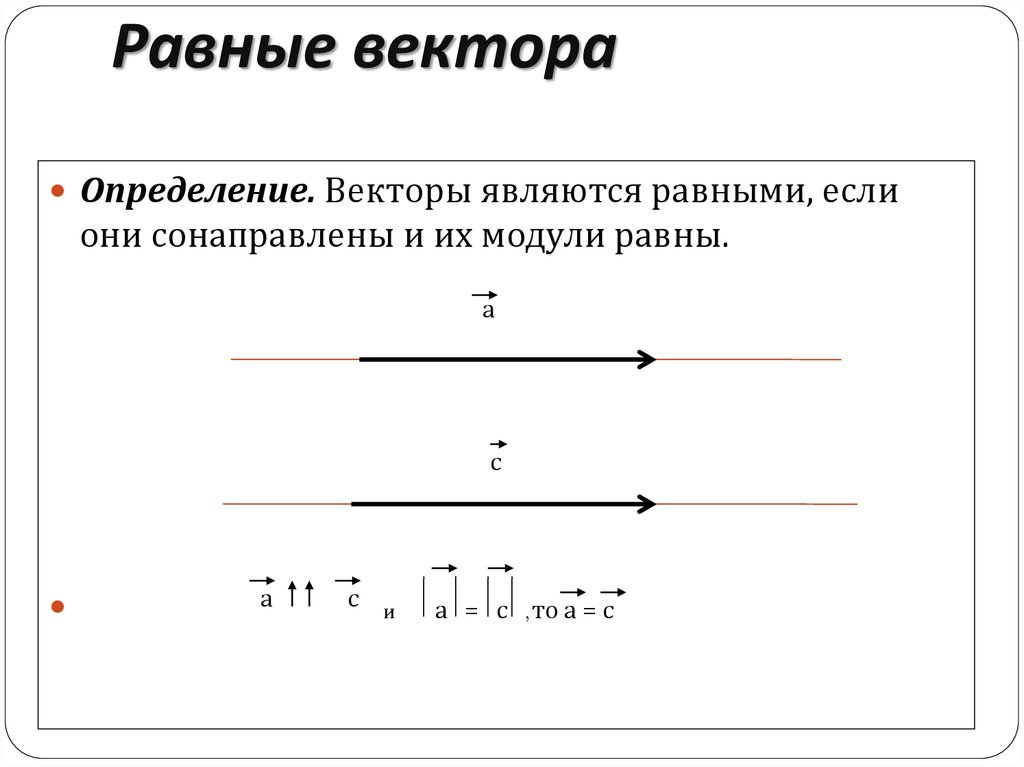
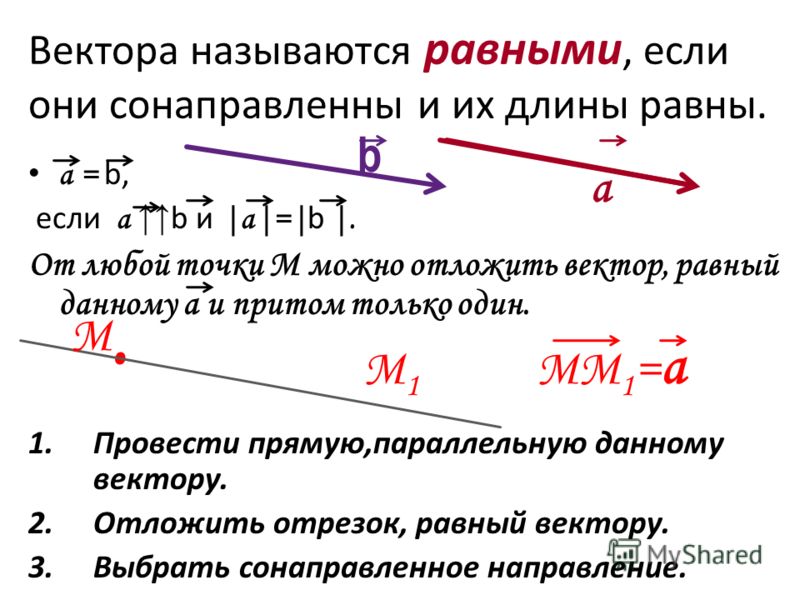
 (рис4) 1. 5. КАКАЯ СВЯЗЬ МЕЖДУ РАВЕНСТВОМ ВЕКТОРОВ И ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ? РАВНЫЕ ВЕКТОРЫ МОЖНО СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ, И, ОБРАТНО, ЕСЛИ ВЕКТОРЫ СОВМЕЩАЮТСЯ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ , ТО ЭТИ ВЕКТОРЫ ПАВНЫ.
(рис4) 1. 5. КАКАЯ СВЯЗЬ МЕЖДУ РАВЕНСТВОМ ВЕКТОРОВ И ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ? РАВНЫЕ ВЕКТОРЫ МОЖНО СОВМЕСТИТЬ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ, И, ОБРАТНО, ЕСЛИ ВЕКТОРЫ СОВМЕЩАЮТСЯ ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ , ТО ЭТИ ВЕКТОРЫ ПАВНЫ. Тогда суммой a будет +b вектор c начало которого совпадает с общим началом векторов, а конец — с , противоположной вершиной параллелограмма. (рис2)
Тогда суммой a будет +b вектор c начало которого совпадает с общим началом векторов, а конец — с , противоположной вершиной параллелограмма. (рис2) 5
5 8076615359
8076615359 11, GOST R 34.11-94, GOST(3425489)
11, GOST R 34.11-94, GOST(3425489) 52.68.209
52.68.209 02.2022
02.2022 02.2022 00:00
02.2022 00:00 04.2022 00:00
04.2022 00:00 80
80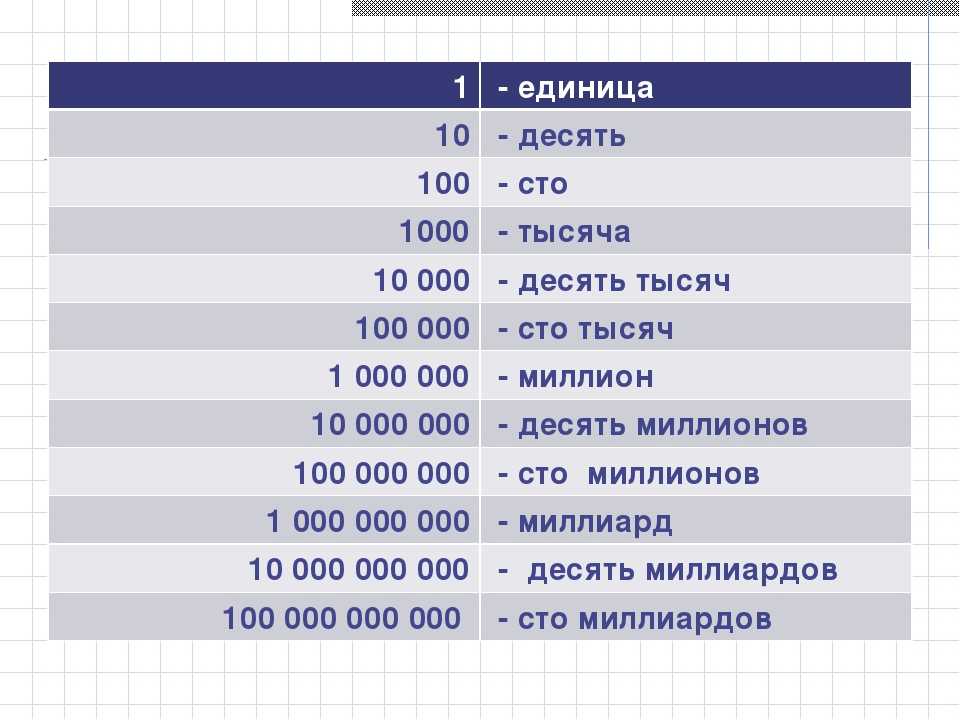 08.2022 00:00
08.2022 00:00 Иркутск, к/с 30101810900000000607 БИК 042520607. Суммы внесенных заявителями задатков возвращаются всем заявителям, за исключением победителя торгов, в течение пяти рабочих дней со дня подписания протокола о результатах проведения торгов.
Иркутск, к/с 30101810900000000607 БИК 042520607. Суммы внесенных заявителями задатков возвращаются всем заявителям, за исключением победителя торгов, в течение пяти рабочих дней со дня подписания протокола о результатах проведения торгов. 80 KZT
80 KZT
 При расчете используются официальные курсы национального банка Казахстана на сегодня. Для проведения вычисления выберите валюту, в которую хотите конвертировать и укажите сумму. В результате вы получите сумму, эквивалентную указанной сумме, только в целевой валюте.
При расчете используются официальные курсы национального банка Казахстана на сегодня. Для проведения вычисления выберите валюту, в которую хотите конвертировать и укажите сумму. В результате вы получите сумму, эквивалентную указанной сумме, только в целевой валюте.

 32
32 68
68 32
32 12
12

 ru/data/moduleImages/QRCodes/425/e6d0cb31f42d3fe95e9c387a8cd58cc5.png
ru/data/moduleImages/QRCodes/425/e6d0cb31f42d3fe95e9c387a8cd58cc5.png 615528128088
615528128088 Деньги так не читаются.
Деньги так не читаются. Новые века читаются как целые числа сотен. Мы не используем слово «тысяча», по крайней мере, не для чтения лет за последние 1000 лет.
Новые века читаются как целые числа сотен. Мы не используем слово «тысяча», по крайней мере, не для чтения лет за последние 1000 лет.
 Те, кто следует британским правилам письма, обычно используют «и». Например:
Те, кто следует британским правилам письма, обычно используют «и». Например: Постарайтесь помочь своим читателям.)
Постарайтесь помочь своим читателям.) Упражнение 1.5.
Упражнение 1.5. 1
1 ….
….



 д.
д. Один миллион…
Один миллион…  Файлы cookie
используется только для регистрации статистики анонимных посетителей и управления определенными
Основные функции страницы. Чтобы удалить это уведомление, нажмите;
в противном случае
нажмите для получения дополнительной информации о блокировке
печенье
Файлы cookie
используется только для регистрации статистики анонимных посетителей и управления определенными
Основные функции страницы. Чтобы удалить это уведомление, нажмите;
в противном случае
нажмите для получения дополнительной информации о блокировке
печенье 2, строка 3, вычеркнуть «семь
тысяча пятьсот шестьдесят» вставка «десять тысяч двадцать»
2, строка 3, вычеркнуть «семь
тысяча пятьсот шестьдесят» вставка «десять тысяч двадцать» 6, черты с 12 по 45
6, черты с 12 по 45 Государственный секретарь должен
внести сумму в фонд.
Государственный секретарь должен
внести сумму в фонд. В противном случае секретарь
Штат направляет факсимиле всех бланков регистраторам округов для
проверки, и регистраторы округа проверяют все бланки в соответствии с
процесс выше. Регистратор округа не должен проверять уже проверенные бланки. Регистратор округа должен
ежедневно сообщать о проверенных итогах государственному секретарю до тех пор, пока не будет принято решение
сделал, что было представлено достаточное количество проверенных квитанций. Если
достаточное количество подтвержденных квитанций было отправлено в один или несколько округов
регистраторы, регистраторы округа могут остановить процесс проверки.
В противном случае секретарь
Штат направляет факсимиле всех бланков регистраторам округов для
проверки, и регистраторы округа проверяют все бланки в соответствии с
процесс выше. Регистратор округа не должен проверять уже проверенные бланки. Регистратор округа должен
ежедневно сообщать о проверенных итогах государственному секретарю до тех пор, пока не будет принято решение
сделал, что было представлено достаточное количество проверенных квитанций. Если
достаточное количество подтвержденных квитанций было отправлено в один или несколько округов
регистраторы, регистраторы округа могут остановить процесс проверки.
 6. Тема
требованиям статьи IV, часть 1, раздел 1, Конституции штата Аризона,
раздел 16-953, Пересмотренный Устав штата Аризона, изменен следующим образом:
6. Тема
требованиям статьи IV, часть 1, раздел 1, Конституции штата Аризона,
раздел 16-953, Пересмотренный Устав штата Аризона, изменен следующим образом: А
кандидат-участник должен ежемесячно отчитываться перед комиссией о
статус спора по оспариваемым векселям. Любые деньги в
Предвыборный счет кандидатов после оплаты счетов должен быть возвращен незамедлительно
в фонд.
А
кандидат-участник должен ежемесячно отчитываться перед комиссией о
статус спора по оспариваемым векселям. Любые деньги в
Предвыборный счет кандидатов после оплаты счетов должен быть возвращен незамедлительно
в фонд. возвратить в фонд все денежные средства в
предвыборный счет кандидатов сверх суммы, достаточной для оплаты любых невыплаченных
счета за расходы, сделанные до даты, когда кандидат не прошел квалификацию
первичное голосование.
возвратить в фонд все денежные средства в
предвыборный счет кандидатов сверх суммы, достаточной для оплаты любых невыплаченных
счета за расходы, сделанные до даты, когда кандидат не прошел квалификацию
первичное голосование. END_STATUTE
END_STATUTE
 Неисключаемость
Неисключаемость




 Базовые
математические способности развивают в школе.
Базовые
математические способности развивают в школе.

 Родителям важно не упустить этот момент и
объяснить ребёнку, зачем вообще заниматься
математикой и учиться решать задачи.
Родителям важно не упустить этот момент и
объяснить ребёнку, зачем вообще заниматься
математикой и учиться решать задачи.
 Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических
способностей.
Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических
способностей.
 Мы знаем, как увлечь ребёнка математикой!
Мы знаем, как увлечь ребёнка математикой!
 Попробуйте
«Закономерности», «Логические задачи», «Умный счёт» и другие.
Попробуйте
«Закономерности», «Логические задачи», «Умный счёт» и другие.
 Чтобы помочь родителям и учителям, команда опытных методистов и педагогов
«ЛогикЛайк» регулярно создает новые уроки, упражнения и тесты.
Чтобы помочь родителям и учителям, команда опытных методистов и педагогов
«ЛогикЛайк» регулярно создает новые уроки, упражнения и тесты.
 Постепенно сложность нарастает, открываются новые
интересные задания.
Постепенно сложность нарастает, открываются новые
интересные задания.


 Составная на вычитание
или деление
Составная на вычитание
или деление









 Значит,
площадь четырёхугольника самая маленькая.
Значит,
площадь четырёхугольника самая маленькая.
 Проходит первая
четверть и способный ребёнок начинает скучать от однообразных или слишком простых для него
заданий.
Проходит первая
четверть и способный ребёнок начинает скучать от однообразных или слишком простых для него
заданий.
 В курсе мы чередуем
математические и логические задачи, закономерности, фигуры в пространстве и другие типы
заданий.
В курсе мы чередуем
математические и логические задачи, закономерности, фигуры в пространстве и другие типы
заданий.







 Кролик легче щенка, значит, правая более легкая
чаша с кроликом поднимется вверх.
Кролик легче щенка, значит, правая более легкая
чаша с кроликом поднимется вверх. Видеоуроки, советы и
подсказки помогут школьнику самостоятельно разобраться даже с очень сложными задачами.
Видеоуроки, советы и
подсказки помогут школьнику самостоятельно разобраться даже с очень сложными задачами.




 Миллиметр
Миллиметр Можно сказать, что её возраст не сильно отличается от возраста человечества. Математика помогает, с одной стороны, развивать абстрактное мышление, с другой — решать прикладные задачи в повседневной жизни.
Можно сказать, что её возраст не сильно отличается от возраста человечества. Математика помогает, с одной стороны, развивать абстрактное мышление, с другой — решать прикладные задачи в повседневной жизни. Детское любопытство и азарт позволяют вовлечься в мир абстрактных подсчётов и пройти путь от развлекательных задачек к настоящей сложной математике.
Детское любопытство и азарт позволяют вовлечься в мир абстрактных подсчётов и пройти путь от развлекательных задачек к настоящей сложной математике. Не обязательно использовать развёрнутое решение задачек по математике; можно проходит лабиринты, вырезать узоры, собирать по схемам различные поделки. Творческий подход приветствуется, ведь математика — это не всегда про сухие цифры.
Не обязательно использовать развёрнутое решение задачек по математике; можно проходит лабиринты, вырезать узоры, собирать по схемам различные поделки. Творческий подход приветствуется, ведь математика — это не всегда про сухие цифры. При правильном выполнении заданий дети получают кубки, медали и именные дипломы.
Наградами можно поделиться в социальных сетях, а диплом – распечатать.
При правильном выполнении заданий дети получают кубки, медали и именные дипломы.
Наградами можно поделиться в социальных сетях, а диплом – распечатать. Идёт запись
Идёт запись