дробный калькулятор с корнями
Вы искали дробный калькулятор с корнями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор дробей с корнями, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дробный калькулятор с корнями».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как дробный калькулятор с корнями,калькулятор дробей с корнями,калькулятор дробей со степенями и корнями,калькулятор дробей со степенями онлайн с решением,калькулятор квадратов чисел,калькулятор корень уравнения,калькулятор онлайн корней уравнений,калькулятор онлайн с дробями и корнями онлайн калькулятор,калькулятор онлайн с дробями и с корнями калькулятор,калькулятор онлайн с корнями и дробями онлайн калькулятор,калькулятор радикалов,калькулятор с дробями и корнями и степенями,калькулятор с корнями дробный,калькулятор с корнями и дробями,калькулятор с корнями и дробями и степенями,калькулятор с корнями и дробями онлайн,калькулятор с корнями и степенями и дробями,калькулятор с корнями с решением,калькулятор с кубами и квадратами,калькулятор сокращения дробей с буквами и степенями онлайн,калькулятор степеней с дробями онлайн,калькулятор уравнений с корнями,найти значение выражения с дробями и степенями онлайн,онлайн калькулятор квадратов,онлайн калькулятор корней с решением,онлайн калькулятор корней уравнений,онлайн решение выражений с корнями,онлайн решение примеров с корнями,онлайн решить пример с корнями,решение выражений с корнями онлайн,решение примеров онлайн с корнями,решение примеров с корнями онлайн,решение примеров с корнями онлайн калькулятор с решением,решить выражение онлайн с корнями,решить выражение с корнями онлайн,решить онлайн пример с корнями,решить пример онлайн с корнями,сложение корней калькулятор,сократить дробь с корнями онлайн калькулятор. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и дробный калькулятор с корнями. Просто введите задачу в окошко и нажмите «решить» здесь (например, калькулятор дробей со степенями и корнями).
Где можно решить любую задачу по математике, а так же дробный калькулятор с корнями Онлайн?
Решить задачу дробный калькулятор с корнями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор онлайн для расчетов процентов, дробей, степеней
Калькулятор давно и прочно вошел в нашу жизнь. Мы часто пользуемся им в повседневной жизни подбивая свои расходы за день, неделю, рассчитывая выплату коммунальных за месяц и т.д. С помощью онлайн калькулятора осуществляют простые арифметические расчеты студенты и школьники, продавцы в магазинах, торговцы на рынках, работники коммунальных служб, что позволяет сэкономить время, получить точные расчеты, избежать досадных ошибок.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| ( ) | ( ) | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin (α) | Синус угла |
| cos | cos (β) | Косинус |
| tan | tan (y) | Тангенс |
| sinh | sinh () | Гиперболический синус |
| cosh | cosh () | Гиперболический косинус |
| tanh | tanh () | Гиперболический тангенс |
| sin-1 | asin () | Обратный синус |
| cos-1 | acos () | Обратный косинус |
| tan-1 | atan () | Обратный тангенс |
| sinh-1 | asinh () | Обратный гиперболический синус |
| cosh-1 | acosh () | Обратный гиперболический косинус |
| tanh-1 | atanh () | Обратный гиперболический тангенс |
| x2 | ^2 | Возведение в квадрат |
| х3 | ^3 | Возведение в куб |
| xy | ^ | Возведение в степень |
| 10x | 10^() | Возведение в степень по основанию 10 |
| ex | exp () | Возведение в степень числа Эйлера |
| vx | sqrt (x) | Квадратный корень |
| 3vx | sqrt3 (x) | Корень 3-ей степени |
| yvx | sqrt (x,y) | Извлечение корня |
| log2x | log2 (x) | Двоичный логарифм |
| log | log (x) | Десятичный логарифм |
| ln | ln (x) | Натуральный логарифм |
| logyx | log (x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re () | Выделение целой действительной части |
| Im | Im () | Исключение действительной части |
| |x| | abs () | Модуль числа |
| Arg | arg () | Аргумент функции |
| nCr | ncr () | Биноминальный коэффициент |
| gcd | gcd () | НОД |
| lcm | lcm () | НОК |
| sum | sum () | Суммарное значение всех решений |
| fac | factorize () | Разложение на простые множители |
| diff | diff () | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
Виды калькуляторов
В зависимости от возможностей и сферы применения калькуляторы бывают простые, бухгалтерские, финансовые, инженерные.
- Бухгалтерскими калькуляторами пользуются бухгалтера и кассиры для арифметических расчетов с денежными суммами.
- Для финансовых расчетов пользуются финансовыми калькуляторами, у которых к стандартному набору математических функций добавлены операции со сложными процентами и функции, характерные для банковской сферы и финансовых приложений.
- Специализированные — это калькуляторы, применяемые для вычислений в конкретной сфере деятельности (строительные, ипотечные, статистические, медицинские).
- Печатающие — калькуляторы, которые с помощью печатающего устройства выводят полученные результаты, расчеты, графики и вычисления на бумажную ленту.
Отдельно выделяются:
- программируемые калькуляторы, используемые для выполнения сложных вычислений по заранее заложенной программе пользователя;
- графические, выполняющие построение и отображение графиков функций.
Простейший калькулятор предназначен выполнять ординарные арифметические расчеты (сложение, вычитание и т.п.), вычислять процент, извлекать квадратный корень, возводить число в степень. Помимо простых расчетов, строителям и архитекторам, инженерно-техническим и научным работникам, математикам и геодезистам, старшеклассникам и студентам технических специальностей очень часто приходится решать важнейшие инженерные задачи, осуществлять сложные математические расчеты.
Представленный на сайте тригонометрический калькулятор выполняет расчет:
- синусов;
- косинусов;
- тангенсов;
- котангенсов.
А также обратных тригонометрических функций:
- арксинусов;
- арккосинусов;
- арктангенсов;
- арккотангенсов.
Все тригонометрические расчеты с углами выполняются в радианах, градах и градусах.
На нашем сайте вы сможете пользоваться инженерным онлайн калькулятором, предназначенным для инженерных и научных расчетов разного уровня сложности.
Инженерный калькулятор позволяет:
- производить сложные расчеты с дробями;
- возводить любое число в степень, извлекать корень из числа;
- рассчитать онлайн проценты, логарифмы, интегралы любой сложности;
- выполнять необходимые математические операции с одной или несколькими матрицами;
- находить производную онлайн как от элементарной, так и от сложной функции;
- решать алгебраические, линейные, логарифмические, тригонометрические и другие уравнения.
Онлайн калькулятор прост и понятен в обращении, применять его не составит труда тем, кто пользуется настольным инженерным калькулятором, принципы работы функций и программ аналогичны. По своему виду инженерный калькулятор онлайн имитирует настоящий калькулятор, поэтому для ознакомления с ним вам не понадобится много времени.
решение уравнений онлайн со степенями
Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы? В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений.
Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы? В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений.
С его помощью вы сможете вводить данные, при этом используя интерфейсные визуальные кнопки либо непосредственно клавиатуру. Кроме этого предоставленный калькулятор онлайн позволить осуществить расчеты сложных выражений, к примеру:(21-45)/(1.52)(8+2*2)=-96.
Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы. В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений.
2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:
1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).
2. Если , то (правило извлечения корня из дроби).
3. Если , то (правило извлечения корня из корня).
4. Если , то (правило возведения корня в степень).
5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.
6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.
7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:
(правило умножения корней),
(правило деления корней),
8. Правило вынесения множителя из-под знака корня. При .
9. Обратная задача — внесение множителя под знак корня. Например,
10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.
При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним. Выполнить действия со степенями самостоятельно, а затем посмотреть решения.
Калькулятор предназначен для решения показательных уравнений онлайн.
Показательные уравнения – это уравнения, в которых переменная величина входит в аргумент показательной функции. Показательная функция это математическая функция вида f(x) = ax, где a является основанием степени, а x – показателем степени. Показательная функция всегда монотонна и она принимает только положительные значения.
Калькулятор предназначен для решения показательных уравнений онлайн.
Показательные уравнения – это уравнения, в которых переменная величина входит в аргумент показательной функции. Показательная функция это математическая функция вида f(x) = ax, где a является основанием степени, а x – показателем степени. Показательная функция всегда монотонна и она принимает только положительные значения.
Для того чтобы найти решение показательного уравнения, необходимо ввести это уравнение в ячейку. В ответе получаем корни уравнения, а также график показательной функции.
Калькулятор решает любые показательные уравнения онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step и Approximate form.
Решения показательных уравнений. Показательная функция всегда монотонна и она принимает только положительные значения.
https://okcalc.com/ru/equation/
https://www.function-x.ru/powers_and_radicals.html
https://allcalc.ru/node/667
Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.
Ответ: 23·(42−12)=32.
Пример 2Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Пример 3Представьте выражение со степенями 9-b3·π-12 в виде произведения.
Решение
Представим число 9 как степень 32 и применим формулу сокращенного умножения:
9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1
Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
Определение 2- ar·as=ar+s;
- ar:as=ar−s;
- (a·b)r=ar·br;
- (a:b)r=ar:br;
- (ar)s=ar·s.
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Пример 4Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.
Ответ: a2,5·(a2)−3:a−5,5=a2.
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5Найти значение степенного выражения 313·713·2123.
Решение
Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.
Есть еще один способ провести преобразования:
313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21
Ответ: 313·713·2123=31·71=21
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.
Решение
Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.
Ответ: t3−t−6.
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2
Ответ: 3·523·513-5-231+2·x2-3-3·x2=-122+x2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Пример 8
Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a0,3:
a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a
б) Обратим внимание на знаменатель:
x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162
Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т.е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12
Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.
Пример 9Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.
Получаем:
30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)
б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14
Ответ: а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10Выполните действия x12+1×12-1-x12-1×12+1·1×12.
Решение
Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:
x12-1·x12+1
Вычтем числители:
x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12
Теперь умножаем дроби:
4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12
Произведем сокращение на степень x12, получим 4×12-1·x12+1.
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.
Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1
Пример 11Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение
Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.
Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.
Переходим от последнего произведения к дроби x138x2,7+1.
Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить на x3·(x+1)0,2.
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12Представьте выражение x19·x·x36 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x≥0 и x·x3≥0 , которые задают множество [0, +∞).
На этом множестве мы имеем право перейти от корней к степеням:
x19·x·x36=x19·x·x1316
Используя свойства степеней, упростим полученное степенное выражение.
x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13
Ответ: x19·x·x36=x13.
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.
Теперь поделим обе части равенства на 72·x. Это выражение на ОДЗ переменной x принимает только положительные значения:
5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0
Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.
Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Комплексные корни и степени чисел онлайн
| Вы ввели следующее выражение |
| Результат вычисления степени |
| Результат выражения (альтернативный вывод) со всеми корнями |
Этот онлайн калькулятор рассчитывает любые степени действительных или комплексных чисел.
Поможет Вам рассчитать корень комплексного числа, возвести в степень действительное или комплексное выражение.
Рассчитывает степень любого числа
Хотелось бы заметить, что возведение любого действительного числа в дробную степень, не так сложно как может показаться на первый взгляд.
то есть, если мы хотим возвести число 3 в степень
то решение такое
Итого
Если речь идет о комплексных числах, то возведение степень и извлечени корня осуществляется по уравнению Муавра.
Формулы следующие:
Для возведения в степень
— модуль комплексного числа
— аргумент комплексного числа
Для извлечения корня
где p = 0, 1, …, k—1.
Есть еще третий возможный вариант, когда не только основание является комплексным числом, но и степень этого числа также число комплексное.
Конечно возникает желание использовать формулу Муавра и преобразовать её, для наших нужд, но мы воспользуемся первым вариантом вычисления степеней.
то есть вот этой формулой
Формула расчета логарифа комплексного числа известна
здесь k — может принимать любые целые значения, поэтому говорят, что логарифм комплексного числа многозначен.
Для практических целей используется главное значение(k=0)
Формула расчета экспоненты комплексного числа тоже
Таким образом у нас есть всё, что бы рассчитать на практике комплексную степень комплексного числа.
Синтаксис
Если используете XMPP клиент: step_i <запрос>
Если используете этот сайт: <запрос>
где запрос — состоит из двух чисел. Сначала идет основание потом в другом окне степень.
Основание может быть как действительным числом так и комплексным, положительным или отрицательным
Комплексное значение пишется как x:y где х- действительная часть числа, а y- мнимая часть, но можно написать и в нормальном виде через символ i
Степень может быть быть целым числом,как положительным так и отрицательным.
Степень может быть выражена также степенью двух целых чисел например 1/2 или -5/7. В таком случае альтернативный вывод покажет Вам, все 2 или все 7 корней соответственно.
Степень может быть комплексным числом записанным как в нормальной форме через символ i, так и через сокращенную запись x:y, где x- действительная часть числа, y — мнимая часть числа
Замечание: В поле можно вводить только числа и никак не выражение, если у Вас есть желание посчитать вот такое выражение
то эта страница вам не поможет, Вам надо использовать универсальный калькулятор комплексных чисел
где x- это основание, а y-степень
Примеры
Например: взять степень 2/5 от комплексного числа 1-2.5i
Пишем 1:-2.5 2/5 или если делаете запрос через Jabber step_i 1:-2.5 2/5
Ответ получим
Комплексное число 1:-2.5 в степени 2/5 равно
Действительная часть: 1.3209 Комплексная часть: -0.6812
Действительная часть: 1.0560 Комплексная часть: 1.0457
Действительная часть: -0.6682 Комплексная часть: 1.3275
Действительная часть: -1.4690 Комплексная часть: -0.2253
Действительная часть: -0.2396 Комплексная часть: -1.4667
Интересно, а чему будет равна мнимая единица в степени мнимой единицы?
пишем i i
и получаем что
возведем еще одно число в комплексную степень.
число 1+i в комплексную степень 1-i
результат вот такой
- Конвертер и калькулятор в разные системы счисления онлайн >>
Решить уравнение со степенями онлайн калькулятор. Решение показательных уравнений по математике
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.{nm}:\]
Прибавляем к исходному уравнению:
Вынесем за скобки \
Выразим \
Поскольку степени одинаковые, отбрасываем их:
Ответ: \
Где можно решить показательное уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат . Рекомендуется также ознакомиться с основными действиями над матрицами .Пример №1
. Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:
Пример №2
. Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3
. Задание. Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >
Удобный и простой онлайн калькулятор дробей с подробным решением может:
- Складывать, вычитать, умножать и делить дроби онлайн,
- Получать готовое решение дробей картинкой и удобно его переносить.
Результат решения дробей будет тут…
0
1
2
3
4
5
6
7
8
9
Знак дроби «/»
+
—
*
:
_cтереть
Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби «.
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .
Знаки используемые для записи в калькуляторе
Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.Возможности онлайн калькулятора дробей
Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.
Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.
Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.
Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобкуПроизведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Калькулятор Корней — Найдите квадратный корень
калькулятор корней онлайн корня поможет вам найти квадратный корень n-й степени любого положительного числа, которое вы хотите. Кроме того, этот калькулятор sqrt сообщает вам, что введенное вами число является точным квадратом или не является идеальным квадратом. Например; 4, 9 и 16 – это идеальные квадраты 2, 3 и 4 соответственно. Квадратный корень из числа – это число, которое при умножении на себя равно исходному числу. Например, квадрат 9 и 16 равен 3 и 4 соответственно. Если вы беспокоитесь о простом ручном вычислении, продолжайте читать, чтобы узнать формулу квадратного корня, вычисление дроби, отрицательные числа и многое другое!
Кроме того, вы можете попробовать наш онлайн калькулятор корней, который поможет вам вычислить значение любого числа, возведенного в любую степень.
Но давайте перейдем к основам!
Проведите по!
Как найти квадратный корень (шаг за шагом):Чтобы подготовиться к вычислению квадратного корня, вам следует запомнить основной идеальный квадратный корень. Поскольку квадрат 1, 4, 9, 16, 25, 100 равен 1, 2, 3, 4, 5 и 10.
Чтобы найти квадрат √25, давайте посмотрим!
√25 = √5 * 5
√25 = √52
√25 = 5
Это простейшие квадратные корни, потому что они всегда дают целое число, но что, если у числа нет точного квадратного корня? Например, вы должны оценить квадрат в 54?
- Как вы знаете, √49 = 7 & √64 = 8. Итак, √54 находится между 8 и 7.
- Число 54 ближе к 49, чем к 64. Итак, вы можете попробовать угадать √54 = 7,45.
- Затем возводя в квадрат 7,45, получаем 7,452 = 55,5, что больше 54. Поэтому вам следует попробовать меньшее число. Возьмем 7,3
- Если взять в квадрат 7,3, получим 53,29, что близко к 54.
- Это означает, что квадратный корень из 54 находится между 7,3 и 7,4. 1/2 = √a / √b = √a / b
Где a / b – любая дробь. Приведем еще один пример:
Пример:
Что такое квадратный корень из 9/25?
Решение:
√9 / 25 = √9 / √25
√9 / √25 = 3/5 = 0,6
Квадратный корень отрицательного числа:В школе нас учили, что квадратный корень из отрицательных чисел не может существовать. Но математики вводят общий набор чисел (Комплексные числа). В виде,
х = а + би
Где a – действительное число, а b – мнимая часть. Йота (i) – это комплексное число со значением:
я = √-1. Приведем несколько примеров:
Квадрат -4 = √-4 = √-1 * 9 = √ (-1) √9 = 3i
Чему равен квадратный корень из -17 = √-17 = √-1 * 17 = √ (-1) √17 = 17i
Как пользоваться калькулятором квадратного корня:С помощью этого калькулятор корней онлайн квадратный корень стало очень просто. Для точных расчетов вам просто нужно выполнить указанные шаги.
Читать дальше!
Входы:
- Прежде всего, нажмите вкладку, чтобы выбрать квадратный корень или корень n-й степени для любого числа.
- Затем введите число, для которого вы хотите произвести расчет в соответствии с выбранной опцией.
- Наконец, нажмите кнопку «Рассчитать».
Выходы:
Как только вы закончите, калькулятор покажет:
- Корень квадратный из числа.
- Корень N-й степени числа.
- Пошаговый расчет.
Заметка:
Независимо от того, какой параметр ввода, онлайн-калькулятор с корнями корня покажет вам точные результаты в соответствии с выбранным вводом.
Часто задаваемые вопросы (FAQ):Может ли число иметь более одного квадратного корня?Да, положительные числа имеют более одного sqrt, одно положительное, а другое отрицательное.
Является ли √2 рациональным числом?Нет, это иррациональное число.
Причина:
Квадратный корень из 2 не может быть выражен как частное двух чисел.
Рациональны ли квадратные корни?Некоторые корни рациональны, а другие иррациональны.
Конечное примечание:Квадратные корни часто встречаются в математических формулах, включая квадратную формулу, дискриминант, а также во многих законах физики. Кроме того, он используется во многих местах повседневной жизни, используется инженерами, плотниками, менеджерами по строительству, фельдшерами и многими другими. Когда дело доходит до вычислений для большого количества, это очень сложно и сложно. Просто попробуйте калькулятор корней онлайн, который поможет вам определить квадратный корень в соответствии с вашими потребностями.
Other languages: Square Root Calculator, Karekök Hesaplama, Kalkulator Akar Kuadrat, Kalkulator Pierwiastków, Wurzel Ziehen Rechner, 平方根 計算, 제곱근 계산, Kalkulačka Odmocniny, Calculadora De Raiz Quadrada, Calculatrice Racine Carré, Calculadora Raiz Cuadrada, Calcolo Radice Quadrata, حاسبة الجذر التربيعي, Neliöjuuri Laskin, Kvadratrot Kalkulator, Kvadratni Koren Kalkulator.
Онлайн-калькулятор предалгебры
Наших пользователей:
Я чувствую себя прекрасно, что больше не нужно выполнять домашние задания, задания и тесты. Я закончила школу. Наконец-то получил свой B.S. в телекоммуникациях. Ура! Спасибо за помощь и новую версию. Желаю тебе всего наилучшего.
S.D., ОрегонЯ хочу поблагодарить вас за вашу помощь. Ваша помощь в решении того, как решить проблему, помогла мне понять, как решать проблемы, и на самом деле получить правильный результат.Спасибо.
до н.э., ФлоридаЭто хорошая новость для любой школы, учителя или студента, когда такая фантастическая программа разработана специально для алгебры. Отличная работа!
Джеймс Мур, МичиганСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 25.02.2012:
- Уравнение радиуса для предварительной алгебры
- дроби стихотворения по математике
- LCD рабочие листы
- год Семь по математике {углы}
- умножение для начинающих
- ti 83 plus, найти ковариацию
- полууглов
- Определение «квадратного корня» четвертой степени
- сложнейшие задачи факторинга
- процентов формулы
- алгебра 2 glencoe Mathematics ответы
- преобразовать десятичное число в соотношение
- гипербола x3 + y3 целочисленных кубов
- Алгебра-умножение и деление выражений Руководство по решениям
- для математического опыта houghton mifflin
- Распечатки по математике для шестого класса бесплатно
- Упростить экспоненциальные выражения TI-84
- Алгебра 2-факторный калькулятор специальных продуктов
- калькулятор корней второго порядка
- преобразование смешанных дробей в десятичные
- статистика элементарных экзаменационных вопросов
- План урока с доказательством квадратичной формулы
- рабочие листы с пропорциями
- как решить линейные дифференциалы
- методы преобразования десятичной дроби в дробную
- буквальные уравнения для чайников
- метод замены на манекены
- формулы TI84
- Упростите калькулятор алгебраических дробей
- колледж + математика 100 бесплатных упражнений
- Корень квадратный из 7 в 9-й степени
- Решение задачи по дробям при делении
- программа для решения научных уравнений
- даже математика ответы эллипсы mathbook
- программа по алгебре для 9 класса
- ГЕОМЕТРИЧЕСКИЕ РЕШЕНИЯ ДЛЯ ПРЕСС-ЗАЛА
- процентных уравнений
- harcourt math georgia edition / практическое домашнее задание
- Дроби по математике ответы на вопросы
- Как решить пифагорейские тождества
- Калькулятор полиномиальных выражений делительной степени Код ответа на вопросы по книге прентис-холла
- Математические коды
- Калькулятор ТИ-83, корней
- Решатель полиномов факторинга
- решение алгебраических уравнений игры
- Справка по элементарной алгебре
- ключ ответа для алгебры гленко 1
- свертка для ti 89
- онлайн-решатель уравнений линейный
- Прентис Холл Алгебра 2 онлайн-учебник
- год 9 вопросов по математике продвинутого уровня
- вычислить 2 в 4-й степени
- расчет РАДИКАЛЬНЫЙ
- графические уравнения Прентиса Холла 89
- Рабочий лист «Test Of Genius»
- aptitude решен вопрос
- Программа факторинга ТИ-84
- объединяет две 3D-анимации в клене
- Системные уравнения 9-го класса
- степень решателя задач
- сложнейший математический вопрос
- многослойные листы третьего сорта
- онлайн-калькулятор экспонентов
- решение нескольких уравнений одновременно
- «Рабочий лист расширения»
- Самый простой способ найти LCM
- бесплатный калькулятор для решения уравнений с квадратными корнями
- Калькулятор квадратного уравнения и факторинга
- как делать множители по математике для детей
- художественная алгебра
- Макдугал Литтел Помощь в домашнем задании по структуре и методам алгебры Рабочий лист
- логарифмов
- бесплатных заданий по математике для девятого класса
- овладение физикой ключ ответа
- решить уравнение 3-го порядка
- Масштабные коэффициенты онлайн по математике
- Glencoe рабочая тетрадь по алгебре дополнение учителей
- Алгебра 2 ПО
- парабол; упрощенный коэффициент разницы
- предалгебра с pizzazz
- кубических сурда год 10
- Калькулятор экспонент и радикалов
- перевода рабочих листов по математике
- прентис холл алгебра 1 (издание 2004 г.) учитель том
Калькулятор дробных показателей | Как упростить рациональные экспоненты?
При работе с дробными показателями есть несколько условий.Вы можете увидеть их все и узнать, как решать дробные показатели с разными условиями. Они следующие
- Дробные экспоненты с числителем 1
- Дробные экспоненты с числителем, отличным от 1 (любые дроби)
Дробные экспоненты с числителем 1
Дробные экспоненты — это способ выражения степеней вместе с корнями в одной нотации. Давайте посмотрим на несколько примеров, числитель которых равен 1, и узнаем, как они называются.
36 1/2 = √36
27 3 = 27
Первый показатель степени 1/2 называется квадратным корнем, а следующий показатель степени 1/3 называется кубическим корнем. Если мы продолжим так же. Показатель 1 / k называется k-м корнем.
x 1 / k = k √x
Дробные экспоненты с числителем, отличным от 1 (любые дроби)
В случаях, когда числитель не равен 1 (n 1)
a = x н / д
Вам просто нужно возвести число в степень n и вынуть из него корень d.Вам не нужно беспокоиться о порядке, так как вы можете разделить его на две части.
- Целое число (n)
- Дробь Часть (1 / d)
x n / d = x ( n.1 / d ) = (x n ) 1 / d = (x 1 / d ) n
x n / d = d√x n = (d√x) n
Вы можете выбрать любой из удобных для вас методов и провести вычисления.
Пример: вычислить дробную экспоненту 16 3/2 ?
Раствор:
Дан дробный показатель степени 16 3/2
16 3/2 = 16 (3. 1/2)
= (16 3 ) 1/2
= √16 3
= √4096
= 64
Сделайте все свои математические задачи проще и быстрее с нашим онлайн-калькулятором.Сайт гуру предоставил бесплатные онлайн-калькуляторы для различных математических и статистических концепций.
Калькулятор дробной степени
Этот калькулятор дробной степени поможет вам — сюрприз, сюрприз — дробные показатели. Вы боретесь с концепцией дробных показателей? Отрицательные и дробные показатели — это для вас закрытая книга? Что ж, больше не о чем беспокоиться, прокрутите вниз, чтобы найти полезные объяснения.
Дробные показатели с числителем 1
Дробные показатели — это способ выражения степеней, а также корней в одном представлении .
Что именно это означает? Давайте сначала рассмотрим несколько простых примеров, где наш числитель равен 1 :
.- 64 (1/2) = √64
- 27 (1/3) = ³√27
Из приведенных выше уравнений мы можем вывести, что:
- Показатель степени 1/2 — это квадратный корень
- Показатель степени 1/3 — это кубический корень
- Показатель степени 1/4 — корень четвертой степени
- …
- Показатель степени 1 / k является корнем k-й степени
Но почему это так? Постараемся это доказать:Давайте воспользуемся законом экспонент, который гласит, что мы можем складывать показатели при умножении двух степеней с одинаковым основанием:
x a + b = x a * x b
так, например, если n = 2
x² = x¹⁺¹ = x¹ * x¹ = x * x
Попробуйте это с любым числом, которое вам нравится, это всегда правда!
Затем давайте посмотрим на дробные показатели x:
x = x¹ = x (1/2 + 1/2) = x (1/2) * x (1/2)
Как позвонить по номеру, умножение которого само на себя дает другой номер? Конечно, это квадратный корень из ! Итак, мы выяснили, что:
x (1/2) = √x
Если хотите, вы можете аналогичным образом проверить другие корни, например.г. кубический корень:
x = x (1/3 + 1/3 + 1/3) = x (1/3) * x (1/3) * x (1/3) = ³√x * ³√x * ³√x
т.
x (1/3) = ³√x
Теперь мы знаем, что x в степени одной трети равен кубическому корню из x.
Дробные показатели с числителем, отличным от 1 (любая дробь)
Итак, что произойдет, если наш числитель не равен 1 (n 1)?
Все, что вам нужно сделать, это возвести это число в степень n и взять корень d-th .Порядок не имеет значения, дробь n / d может быть разделена на две части:
- целое число (n)
- дробная часть (1 / d)
Давайте посмотрим на пример, где дробная экспонента = 3/2 и x = 16:
- 16 3/2 = 16 (3 * 1/2) = (16 3 ) 1/2 = √ (16³) = √4096 = 64
Или, как вариант, можно написать, что
- 16 3/2 = 16 (1/2) * 3 = (16 1/2 ) 3 = (√16) ³ = 4³ = 64
И результат действительно тот же.Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!
Отрицательный и дробный показатель степени
Положительные показатели говорят нам, сколько раз мы используем число при умножении:
Но что произойдет, если наша экспонента будет отрицательным числом, вы можете догадаться? Да, он говорит вам, сколько раз вам нужно разделить на это число:
Кроме того, вы можете просто вычислить положительную экспоненту (например, x 4 ), а затем взять обратную величину (в нашем случае 1 / x 4 ).Конечно, аналогично, если у нас есть отрицательная И дробная экспонента.
Калькулятор степени дроби — как использовать
Мы считаем, что этот инструмент настолько интуитивно понятен и прост, что никаких дополнительных пояснений не требуется, но для записи мы быстро объясним, как вычислить дробные показатели:
- Введите базовое значение . Например, введите 7.
- Введите числитель и знаменатель дроби .Если вы хотите использовать этот калькулятор как простой инструмент экспоненты — с целым числом в качестве показателя вместо дроби — введите 1 в качестве знаменателя. Предположим, наша дробь равна -2/5. Введите -2 в числитель и 5 в поле знаменателя (также отметьте обратную работу).
- Наслаждайтесь результатом, отображаемым нашим калькулятором дробной степени! Это 0,4592 для нашей примерной задачи.
Надо ли говорить о гибкости нашего инструмента? Вам не нужно переходить калькулятор сверху вниз — вычислите любое неизвестное, какое захотите! Введите любые три значения, и четвертое появится в мгновение ока.
Еще одна полезная функция калькулятора — дробью может быть не только показатель степени, но и основание ! Например, если вы хотите вычислить (1/16) 1/2 , просто введите 1/16 в базовое поле. Отлично!
Калькулятор дробей с показателями — Онлайн-калькулятор дробей с показателями
‘Cuemath’s Fractions with Exponents Calculator’ — это онлайн-инструмент, который помогает найти значение заданного показателя степени.
Что такое калькулятор дробей с показателями?
Онлайн-калькулятор дробей с показателямиCuemath поможет вам найти значение данного показателя дроби в течение нескольких секунд.
Как использовать дроби с калькулятором показателей?
Пожалуйста, выполните следующие шаги, чтобы найти значение заданной дробной экспоненты:
- Шаг 1: Введите базовое число, числитель экспоненты и знаменатель в данное поле ввода.
- Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти значение данной дробной экспоненты.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и найти значение другой дробной экспоненты.
Как найти дроби с показателями?
Показатель степени определяется как количество раз умножения основного числа на себя. Проще говоря, сколько раз конкретное число умножается само на себя, показано с помощью экспонент.
Показатель степени выражается в форме: x a / b , где x — это базовое число, a / b представляет дробь, a — числитель, а b — знаменатель
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример:Решить 4 -1/2 ?
Решение:= 4 -1/2
= 1/4 1/2
= 1 / √4
= 1/2
Аналогично, вы можете попробовать калькулятор, чтобы найти дроби с показателями для
1) 10 -3/2
2) 9 3/2
Калькулятор экспонент
Попробуйте бесплатную программу для решения математических задач или прокрутите вниз до учебных пособий!
Введите выражение, например.2-1 Пример задачи Ничья Количество решаемых уравнений: 23456789 Пример задачи Решить Введите неравенство в график, например.г. y Пример задачи Ничья Количество решаемых неравенств: 23456789 Пример задачи 908 Решить Наших пользователей:
Я никогда ничего подобного не видел! Постепенно я изучаю сложную алгебру вместе со своими детьми!
Лиза Шустер, Нью-ЙоркПока все отлично!
М.Б., ИллинойсПереезжать из города в город сложно, особенно когда нужно понимать, как преподает каждый учитель. С Алгебратором кажется, что есть только один учитель, и тоже хороший. Теперь мне не нужно беспокоиться о том, чтобы справиться с алгеброй. Я ищу помощи и в других областях.
Питер Гудман, TNСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2010-04-15:
- рабочий лист по математике для ks2
- лаплас для чайников
- прентис холл математика алгебра один
- Общая викторина для второклассников
- Советы по алгебре для детей
- www.math trivia.com
- как вычесть десятичные дроби powerpoint
- Семь — это нечетное число, как вы можете сделать это даже без добавления, вычитания, умножения или деления
- добавление 5 или 6 к числовому листу
- Упрощение калькулятора абсолютных значений
- примеры перестановок начальная школа Пример программы операций с квадратной формулой
- с использованием базового
- программное обеспечение
- учебники по компасу для курсов повышения квалификации по математике
- площадь без математических расчетов
- сравнение рабочих листов для упорядочивания целых чисел
- простой способ вычисления дробей
- делительный и умножающий корень
- решение дробных показателей
- добавить отрицательные положительные целые числа для печати бесплатно
- Клен решить сложное уравнение
- решить нелинейное уравнение символьный matlab
- CLEP Calculus бесплатное онлайн-руководство
- Калькулятор сложения и вычитания радикальных выражений
- комбинаций упражнений по математике
- Заданий по алгебре для 6 класса
- алгебраические уравнения для дробей
- алгебраические уравнения экспоненциальные
- Решение квадратных уравнений с отрицательными показателями
- математические ответы читы
- загрузить visual ti 84
- как взять 2 цифры после десятичной точки + java
- конвертировать y перехватить javascript
- Интересные мелочи по математике
- математическая культура один в майя
- Макдугал Литтел структура и метод алгебры и тригонометрии ответы
- Практика решения квадратных квадратичных листов Бухгалтерская книга
- саксонская алгебра 1 ответы
- парабола, изображения
- как решить дифференциальное уравнение с помощью Matlab
- поиск в Google / практический тест gre / перестановка
- бесплатные математические распечатки
- примеров математических мелочей с ответами за 4 класс
- как упростить показатели с помощью переменных
- Алгебра нахождение вершин по квадратичной формуле
- рабочие листы положительное отрицательное сложение вычитание
- слово проблема-образец и решения
- деление квадратного корня на дробь
- изучайте prealegbra онлайн бесплатно
- калькулятор трехчленов Алгебра
- , используемая в сети
- Калькулятор квадратного уравнения
- рудок «Глава 6», №7
- онлайн-эмулятор калькулятора ти-84
- бесплатных экзаменационных работ
- завершение вычисления квадрата
- Дискретная математика
- рабочий лист «уравнения баланса» математика
- вопросов для практики квадратичных функций 10 класс
- книга по математике формула 1 экзамен C3 график
- что такое разложение знаменателя на простые множители
- квадратных корня с использованием множителя
- Завершение квадратной конструкции
- Показатели по математике в шестом классе Калькулятор делителей
- общие ошибки при сложении и вычитании радикальных выражений помогают
- квадратные и квадратные корни, кубы и куберы
- графический калькулятор онлайн гипербола
- Калькулятор квадратного корня из дроби
- ks3 запись формулы рабочего листа
- texas ti-83 программное обеспечение для моделирования
- Упростить калькулятор квадратного корня
- решение уравнений 3-й степени
- преобразование десятичного числа в другое основание
- Учебник элементарной алгебры
- Рабочие листы по алгебре KS2
- Порядок операций решения логарифмов
- изменение предмета n алгебраических формул бесплатные рабочие листы
- Калькулятор алгебры продвинутого уровня
- решить систему на TI 83
- Как понимать алгебру
- Печатные листы с координатами для 5-го класса
- математика мелочи с ответами математика
- упростить вычисление корня
- как решить квадратные уравнения с использованием двух точек
- однородный дифференциал
- вопросов по начальной математике «Экзамены»
- Пирамиды сложения алгебры
- вычислить наибольший общий делитель
- TI-83 ROM скачать
- алгебра powerpoint по пропорциям
- контрольных по математике за год седьмой
- Упрощение алгебры калькулятор деление
- Образец онлайн-экзамена
- понятия дробей и квадратных корней
- решение однородных уравнений
- г. 8 учеников задачи по математике
Как оценить корни с помощью научного калькулятора — видео и стенограмма урока
Квадратный корень
Чтобы вычислить квадратный корень, воспользуйтесь кнопкой квадратного корня на вашем научном калькуляторе.Чтобы использовать эту кнопку, вам необходимо знать, как работает ваш калькулятор. В некоторых калькуляторах сначала нужно ввести число, а затем нажать кнопку извлечения квадратного корня. В других случаях вы сначала нажимаете кнопку извлечения квадратного корня, а затем свое число. Так, например, чтобы найти квадратный корень из 5, вы нажмете эти кнопки, если в вашем калькуляторе вы сначала вводите число.
Квадратный корень из 5 должен быть около 2,236.
Пользовательская кнопка корня
Чтобы найти другие корни, вы воспользуетесь специальной кнопкой, которая позволит вам выбрать корень.Если вы не видите такой кнопки, возможно, она находится в меню одной из функциональных клавиш.
Вы можете использовать настраиваемую корневую кнопку , чтобы найти кубический, четвертый и пятый корни или любой положительный целочисленный корень. Чтобы использовать эту кнопку, вам нужно посмотреть руководство к вашему калькулятору. В некоторых калькуляторах вы сначала вводите число, затем кнопку корня, а затем желаемый корень. В других случаях вы выполняете эти операции в обратном порядке, начиная с желаемого корня, затем кнопки корня и числа.
Чтобы найти кубический корень из 5 с помощью калькулятора, в который вы вводите желаемый корень последним, вы нажимаете следующие кнопки:
Кубический корень из 5 должен быть около 1,7.
Кнопка экспоненты
Если в вашем калькуляторе нет настраиваемой кнопки корня, вы можете использовать кнопку настраиваемой степени, чтобы найти корень.
Чтобы использовать кнопку настраиваемой экспоненты , преобразуйте желаемый корень в показатель степени, инвертируя его или используя 1 в качестве числителя и корня в качестве знаменателя дроби.Таким образом, кубический корень становится показателем 1/3, квадратный корень становится показателем или степенью 1/2, а корень пятой степени становится 1/5 и так далее.
После преобразования желаемого корня используйте кнопки в круглых скобках, чтобы сообщить калькулятору, что у вас есть дробная экспонента. Итак, чтобы ввести квадратный корень из 9, нажмите эти кнопки:
Помните, что в зависимости от вашего калькулятора вам может потребоваться сначала ввести дробную экспоненту, прежде чем нажимать кнопку настраиваемой экспоненты.символ). Если у вас есть, вы можете использовать его вместо кнопки настраиваемой экспоненты. Обе кнопки означают, что базовое число взято в степень.
Практическая задача
Давайте попробуем вычислить седьмой корень из 24. Если в вашем калькуляторе вы выбираете корень последним, вы нажимаете на кнопки, как это.
Вы должны получить ответ около 1,5746.
Резюме урока
На этом уроке вы узнали, как использовать научный калькулятор для вычисления корней.Корень в математике относится к этому символу:
Например, когда вы извлекаете квадратный корень из числа, вы ищете число, которое при умножении само на себя дает заданное число. Например, квадратный корень из 9 равен 3, потому что 3 умножения на себя равно 9.
Кубический корень числа — это число, которое при трехкратном умножении на себя дает данное число. Кроме того, любое положительное целое число может иметь корень.
При использовании научного калькулятора для нахождения корня вам необходимо следовать его руководству и посмотреть, вводите ли вы сначала число, а затем нажимаете кнопку корня, или наоборот. Пользовательская кнопка корня может использоваться для вычисления кубического, четвертого и пятого корней или любого положительного целочисленного корня.), которую можно использовать вместо кнопки настраиваемой экспоненты.
Интернет-научный калькулятор — инструмент
Скачать научный калькулятор eCalc
Версия для Windows Версия для Mac OSX Просмотреть больше загрузок
Онлайн-калькулятор и справка по математике
Поддержка кнопок и клавиш
Стек
Поддон Intro
Основные функции
Дополнение
Вычитание
Умножение
Дивизион
Знак
Площадь
Квадратный корень
Повышение мощности
Естественная экспонента
Логарифм
Натуральный логарифм
Обратный
Показатель
Факториал
PI
Тригонометрические функции онлайн
Синус
Обратный синус
Косинус
Обратный косинус
Касательная
Обратный тангенс
Косеканс
Обратный косеканс
Секант
Обратный секанс
Котангенс
Обратный котангенс
Онлайн-гиперболические тригонометрические функции
Гиперболический синус
Гиперболический косинус
Гиперболический тангенс
Гиперболический косеканс
Гиперболический секанс
Гиперболический котангенс
Обратный гиперболический синус
Обратный гиперболический косинус
Обратный гиперболический тангенс
Обратный гиперболический косеканс
Обратный гиперболический секанс
Обратный гиперболический котангенс
Меню
Формат
Уголок
Система координат
Режимы онлайн-калькулятора
Система координат
от десятичной дроби к дроби
Комплексные числа
Онлайн-конвертер единиц
Библиотека констант
Онлайн-решатель
Базовый преобразователь
Онлайн-калькулятор и справка по математике
eCalc — это бесплатный и простой в использовании научный калькулятор, который поддерживает множество расширенных функций, включая преобразование единиц измерения, решение уравнений и даже математику с комплексными числами.eCalc предлагается как бесплатный онлайн-калькулятор, так и в виде калькулятора для загрузки.
Режим ввода (алгебраический или RPN)
Онлайн-калькулятор работает либо с алгебраическим вводом (режим по умолчанию), либо с вводом RPN. Режим калькулятора устанавливается щелчком по символу «ALG / RPN» в строке состояния или путем изменения режима в диалоговом окне меню.
Алгебраический режим
Алгебраический режим ввода обычно называют «инфиксной записью» и широко используется в большинстве портативных калькуляторов.Выражения, вводимые в режиме алгебраического ввода, выполняются способом, который очень похож на естественную форму выражения, а порядок операций определяется приоритетом операторов и скобками.Режим RPN
RPN, что означает обратную польскую нотацию, представляет собой нотацию на основе стека, в которой операторы должны следовать за своими операндами. Например, чтобы оценить выражение «1 + 2» в RPN, пользователь должен ввести «1 2 +», и выражение вычисляется сразу после оператора.Выражения, содержащие круглые скобки, такие как «(1 + 2) * 3», оцениваются, отмечая порядок приоритета и вводя форму как «1 2 + 3 *».Поддержка графических кнопок и клавиатуры
Онлайн-калькулятор поддерживает ввод данных с помощью графической кнопки или традиционных клавиш компьютерной клавиатуры. Пользователю предоставляется возможность использовать любой метод ввода, и оба они одинаково действительны; тем не менее, существуют некоторые тригонометрические функции (как указано ниже), которые ограничены вводом с клавиатуры компьютера, поскольку для размещения графических кнопок доступно ограниченное пространство.
Стек
Стек — это функция калькулятора, которая позволяет просматривать историю результатов. В стеке одновременно отображаются только 4 элемента, но можно прокручивать вверх и вниз по стеку, щелкая стрелки вверх и вниз над стопкой. Значения в стеке также можно «вытолкнуть» вниз в поле ввода калькулятора, щелкнув стрелки вниз слева от строки в стеке.
Поддон Введение
Калькулятор разделен на две части: интерфейс научного калькулятора слева и панель калькулятора справа.Поддон обеспечивает область отображения для специальных функций. Некоторые из этих функций включают в себя: преобразователь единиц, библиотеку констант, решатель уравнений, полиномиальный решатель, базовое преобразование и преобразование десятичного числа в дробное.
Основные функции
Дополнение
Сложение (функция суммы) используется при нажатии кнопки «+» или с помощью клавиатуры. Функция дает a + b.
Вычитание
Вычитание (функция минуса) используется при нажатии кнопки «-» или с помощью клавиатуры.Функция приводит к a-b.
Умножение
Умножение (функция умножения) используется нажатием кнопки «x» или клавишей «*» на клавиатуре. Функция возвращает a * b. -1 или делению 1 на число.Икс. Числа автоматически отображаются в формате, когда число слишком велико или слишком мало для отображения. Чтобы ввести число в этом формате, используйте кнопку экспоненты «EEX». Для этого введите мантиссу (не экспоненциальную часть), затем нажмите «EEX» или введите «e», а затем введите показатель степени.
Факториал
Факториальная функция используется при нажатии «!» кнопку или введите «!».
PI
PI — математическая константа отношения длины окружности к ее диаметру.
Тригонометрические функции онлайн
синус
Функция Sine (SIN) используется при нажатии кнопки «SIN» или вводе «SIN ()». Результат — отношение длины противоположной стороны к длине гипотенузы прямоугольного треугольника.
Обратный синус
Для использования функции обратного синуса (ASIN или ARCSIN) нажмите кнопку «ASIN» или введите «ASIN ()». Результат действителен только от -pi / 2 до pi / 2.
Косинус
Функция косинуса (COS) используется при нажатии кнопки «COS» или вводе «COS ()».В результате получается отношение длины соседней стороны к длине гипотенузы прямоугольного треугольника.
Обратный косинус
Функция обратного косинуса (ACOS или ARCCOS) используется нажатием кнопки «ACOS» или вводом «ACOS ()». Результат действителен только от 0 до пи.
Касательная
Функция тангенса (TAN) используется при нажатии кнопки «TAN» или типа «TAN ()». Результат — отношение длины противоположной стороны к длине смежной стороны прямоугольного треугольника.
Обратная касательная
Функция обратной тангенсации (ATAN или ARCTAN) используется при нажатии кнопки «ATAN» или при вводе «ATAN ()». Результат действителен только от -pi / 2 до pi / 2.
Косеканс
Функция косеканса (CSC) используется при вводе «CSC ()». Косеканс — это мультипликативная обратная функция синусоиды.
Обратный косеканс
Функция обратного косеканса (ACSC) используется при вводе «ACSC ()». Результат действителен только от -pi / 2 до pi / 2, исключая 0.
Секант
Функция секанса (SEC) используется при вводе «SEC ()». Секанс — это мультипликативная величина, обратная функции косинуса.
Обратная секущая
Функция обратного секанса (ASEC) используется при вводе «ASEC ()». Результат действителен только от 0 до pi, исключая pi / 2.
Котангенс
Функция котангенса (COT) используется при вводе «COT ()». Котангенс — это мультипликативная обратная функция касательной.
Обратный котангенс
Функция обратного котангенса (ACOT) используется при вводе «ACOT ()». Результат действителен только от 0 до пи.
Онлайн-гиперболические тригонометрические функции
Гиперболический синус
Функция гиперболического синуса (SINH) используется при вводе «SINH ()».
Гиперболический косинус
Функция гиперболического косинуса (COSH) используется при вводе «COSH ()».
Гиперболический тангенс
Функция гиперболического тангенса (TANH) используется при вводе «TANH ()».
Гиперболический косеканс
Функция гиперболического косеканса (CSCH) используется при вводе «CSCH ()».
Гиперболический секанс
Функция гиперболического секанса (SECH) используется при вводе «SECH ()».
Гиперболический котангенс
Функция гиперболического котангенса (COTH) используется при вводе «COTH ()».
Обратный гиперболический синус
Функция обратного гиперболического синуса (ASINH) используется при вводе «ASINH ()».
Обратный гиперболический косинус
Функция обратного гиперболического косинуса (ACOSH) используется при вводе «ACOSH ()».
Обратный гиперболический тангенс
Функция обратного гиперболического тангенса (ATANH) Используется при вводе «ATANH ()».
Обратный гиперболический косеканс
Функция обратного гиперболического косеканса (ACSCH) используется путем ввода «ACSCH ()».
Обратный гиперболический секанс
Функция обратного гиперболического секанса (ASECH) используется путем ввода «ASECH ()».
Обратный гиперболический котангенс
Функция обратного гиперболического котангенса (ACOTH) используется при вводе «ACOTH ()».
Меню
Формат
Доступно 4 типа числовых форматов, и формат можно изменить, нажав кнопку «Меню». Доступные типы чисел: стандартные, фиксированные, научные и инженерные. В инженерии можно выбрать количество цифр для отображения в поле ввода в строке формата.Используемый числовой формат можно увидеть над стеком, это третий статус меню слева. Это место можно щелкнуть, чтобы изменить числовой формат.
Угол
Доступно 3 типа представления углов, и эти типы углов можно изменить, нажав кнопку «Меню». Форматы углов: радианы, градусы и градиенты. Формат угла отображается над стеком и является первым статусом меню. На это место можно щелкнуть, чтобы изменить формат угла.
Система координат
Для представления комплексных чисел доступны две системы координат. Системы координат бывают прямоугольными и полярными. Систему координат можно выбрать, нажав кнопку «Меню». Выбранная система координат отображается над стеком и является вторым статусом меню. Чтобы ввести число в прямоугольном формате, его необходимо ввести в формате «(3,4)». Чтобы ввести число в полярном формате, его необходимо ввести в формате «(3 @ 75)».Вместо символа «@» можно использовать символ угла клавиатуры калькулятора.
Режимы онлайн-калькулятора
Есть два режима онлайн-калькулятора: Алгебраический и RPN. Режим выбирается нажатием на кнопку «Меню». Режим калькулятора отображается в четвертом индикаторе состояния меню, при нажатии на это место режим изменяется. Нижняя зеленая кнопка «возврат» или «=» изменяется в зависимости от режима.
от десятичной дроби к дроби
Функция преобразования десятичной дроби в дробь этого калькулятора позволяет представить десятичное число в дробных оценках, а также в точном эквиваленте дроби.Функция преобразования десятичной дроби в дробь активируется нажатием кнопки «d> f» (десятичная дробь в дробную) на клавиатуре калькулятора. Откроется дисплей в боковом поддоне с полем ввода вверху. Десятичное значение можно ввести непосредственно в поле ввода, или, щелкнув стрелку ввода, будет введено значение из поля ввода калькулятора.
Комплексные числа
Онлайн-калькулятор полностью поддерживает комплексные числа. Комплексные числа являются расширением системы действительных чисел и включают второе число, которое является воображаемым, создавая плоскость комплексных чисел.Числовой формат для комплексных чисел — «a + bi», где a — действительное число, а b — мнимое число. Эти числа также могут быть представлены как величина и угол, когда система координат калькулятора находится в полярном режиме.
Онлайн-конвертер единиц
Онлайн-конвертер единиц отображается на поддоне, и его можно выбрать, нажав кнопку «Единицы». Конвертер единиц имеет 11 категорий: масса, скорость, время, мощность, объем, площадь, длина, энергия, температура, сила и давление.
Библиотека констант
Библиотека констант — это функция поддона, доступ к которой можно получить, щелкнув кнопку «CONST». Чтобы поместить константу в поле ввода калькулятора, просто нажмите на константу. Эта библиотека содержит множество популярных констант, которые используются регулярно. Библиотека констант включает в себя следующее: скорость света, кулоновская постоянная, ускорение гравитации, гравитационная постоянная, постоянная Планка, постоянная Больцмана, постоянная Фарадея, масса покоя электрона, масса покоя нейтрона, масса покоя протона, число Авогадро, заряд электронов, радиус Бора. , Молярная газовая постоянная, постоянная Ридберга, молярный объем, диэлектрическая проницаемость вакуума, постоянная Стефана-Больцмана, квант магнитного потока, проницаемость вакуума, магнетон Бора, постоянная Джозефсона, импеданс вакуума и квант проводимости.
Онлайн-решатель
В онлайн-калькуляторе есть два часто используемых решателя. Доступ к этим решателям можно получить, щелкнув кнопку палитры «РЕШИТЬ». Доступные решатели: Линейный решатель и Корневой решатель.
Линейный решатель
Линейный решатель выбирается одним из 4 вариантов. Этот решатель позволяет решать для переменных, когда существует равное количество уравнений, уникальных для каждой неизвестной переменной.Решатель требует, чтобы были введены коэффициенты уравнений. При вводе номеров переменных убедитесь, что каждая запись в столбце используется для одной и той же переменной. Коэффициенты комплексных чисел могут быть введены, как только все значения введены, щелкнув по кнопке «Решить». Результаты помечены как x1 … xn. X1 соответствует переменной, используемой в столбце 1 и x2, столбце 2 и так далее.Решатель полиномов
Решатель полиномов (решатель корня) выбирается щелчком по соответствующему порядку уравнения.Коэффициенты вводятся в поля ввода ниже. Затем нажмите «Решить», и результаты станут корнями уравнения.
Базовый преобразователь
Базовый преобразователь — это функция, которая включена в поддон, и к ней можно получить доступ, нажав кнопку «BASE».

 Для этого существует метод неопределённых коэффициентов, основанный
на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
Для этого существует метод неопределённых коэффициентов, основанный
на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
 Разложим знаменатель подынтегрального выражения на множители. Сначала
можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:
Разложим знаменатель подынтегрального выражения на множители. Сначала
можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь: В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим: Уравнения с многочленами в знаменателе имеют действительные корни,
а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее
разложение исходной дроби на простые дроби:
Уравнения с многочленами в знаменателе имеют действительные корни,
а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее
разложение исходной дроби на простые дроби: Шаг 1. Дан интеграл от рациональной функции
.
Шаг 1. Дан интеграл от рациональной функции
.







 Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:

 Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор
Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор  Если xj — комплексный корень кратности α полинома с действительными коэффициентами, то комплексно сопряженное число xj — тоже корень кратности α этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида , если xj, xj – корни кратности один. Если xj, xj – корни кратности α, то им соответствует α слагаемых и соответствующее разложение имеет вид
Если xj — комплексный корень кратности α полинома с действительными коэффициентами, то комплексно сопряженное число xj — тоже корень кратности α этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида , если xj, xj – корни кратности один. Если xj, xj – корни кратности α, то им соответствует α слагаемых и соответствующее разложение имеет вид


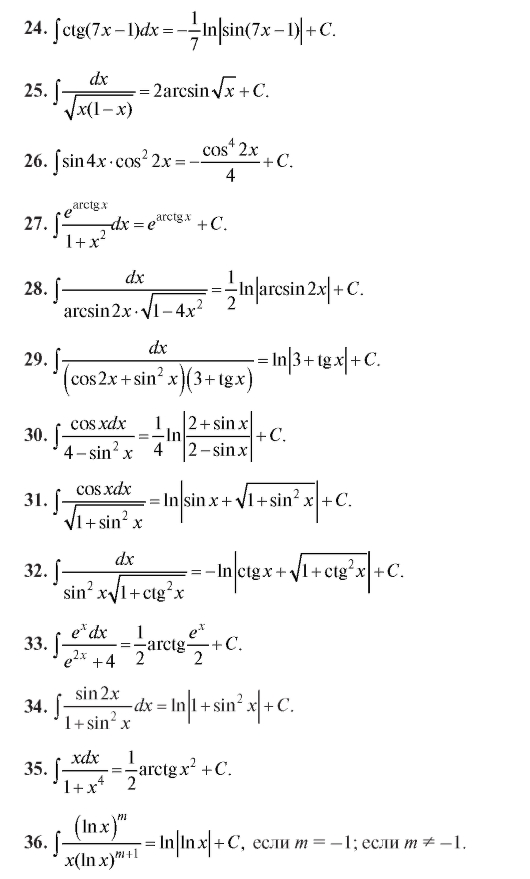


 Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены: 2), любую дробно-рациональную функцию — многочлены с действительными коэффициентами степени и соответственно, в общем случае можно представить суммой некоторого
2), любую дробно-рациональную функцию — многочлены с действительными коэффициентами степени и соответственно, в общем случае можно представить суммой некоторого
 е. При имеем откуда Наконец, приравнивая коэффициенты при получаем или Итак, вместо (2.31) запишем
е. При имеем откуда Наконец, приравнивая коэффициенты при получаем или Итак, вместо (2.31) запишем 32) получаем откуда
32) получаем откуда 33) подстановкой к табличному интегралу 13, а второй подстановкой — к интегралу
33) подстановкой к табличному интегралу 13, а второй подстановкой — к интегралу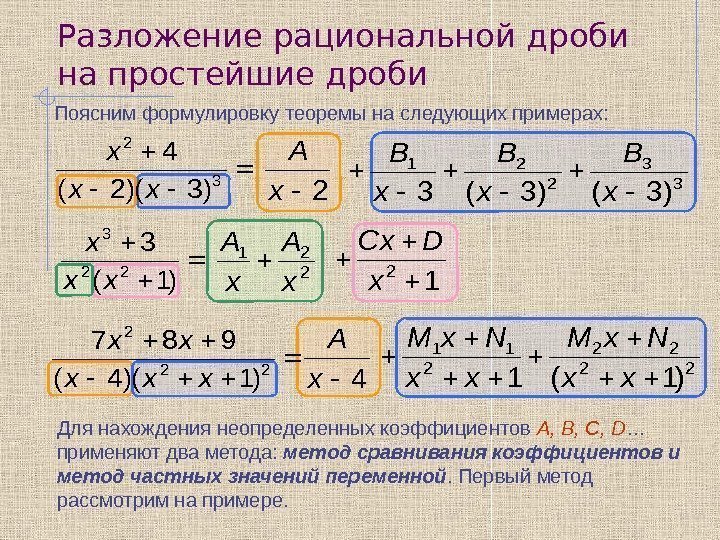


 Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители.
Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители. Найти интеграл
Найти интеграл

 Введем новую переменную tg . Тогда = =
Введем новую переменную tg . Тогда = =

 Интеграл от степенной функции легко вычислить по таблице интегралов.
Интеграл от степенной функции легко вычислить по таблице интегралов. Тогда Причем уже не являются корнями полинома . В этом случае из рациональной дроби тоже можно выделить некоторую элементарную рациональную дробь вида .
Тогда Причем уже не являются корнями полинома . В этом случае из рациональной дроби тоже можно выделить некоторую элементарную рациональную дробь вида .




 \]
\]
 Функция косеканса csc x
Функция косеканса csc x 0.3, Centos605 Обзор Redis — это высокоскоростная база данных памяти NoSQL, которая является системой хранения структуры данных в памяти, а …
0.3, Centos605 Обзор Redis — это высокоскоростная база данных памяти NoSQL, которая является системой хранения структуры данных в памяти, а … Такую низкоуровневую …
Такую низкоуровневую … обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс
обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс Он имеет область определения и множество значений .
Он имеет область определения и множество значений .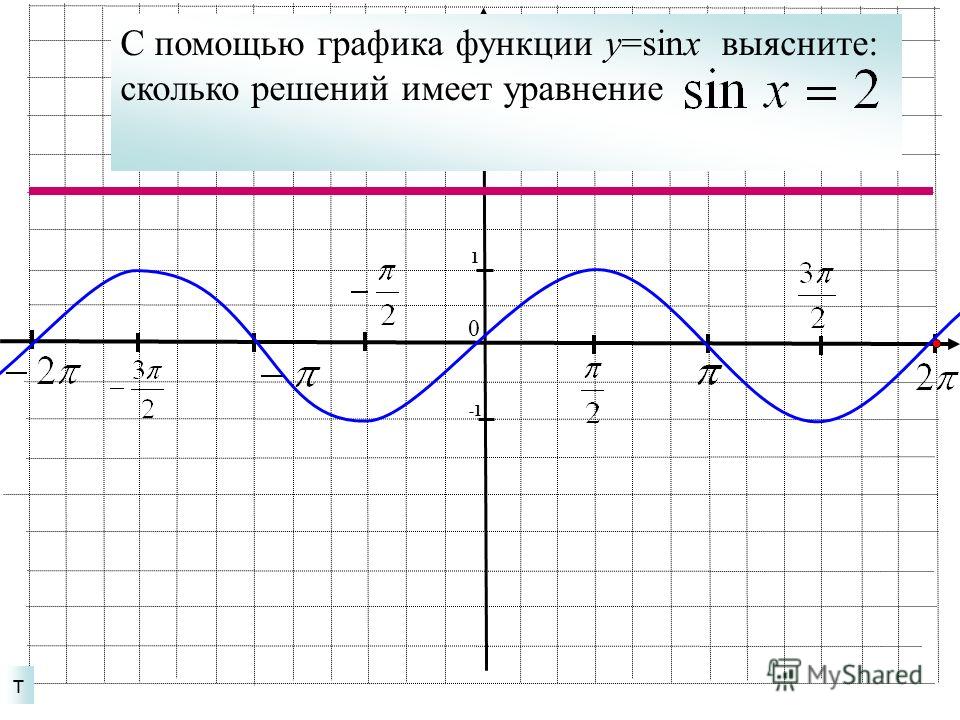 Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.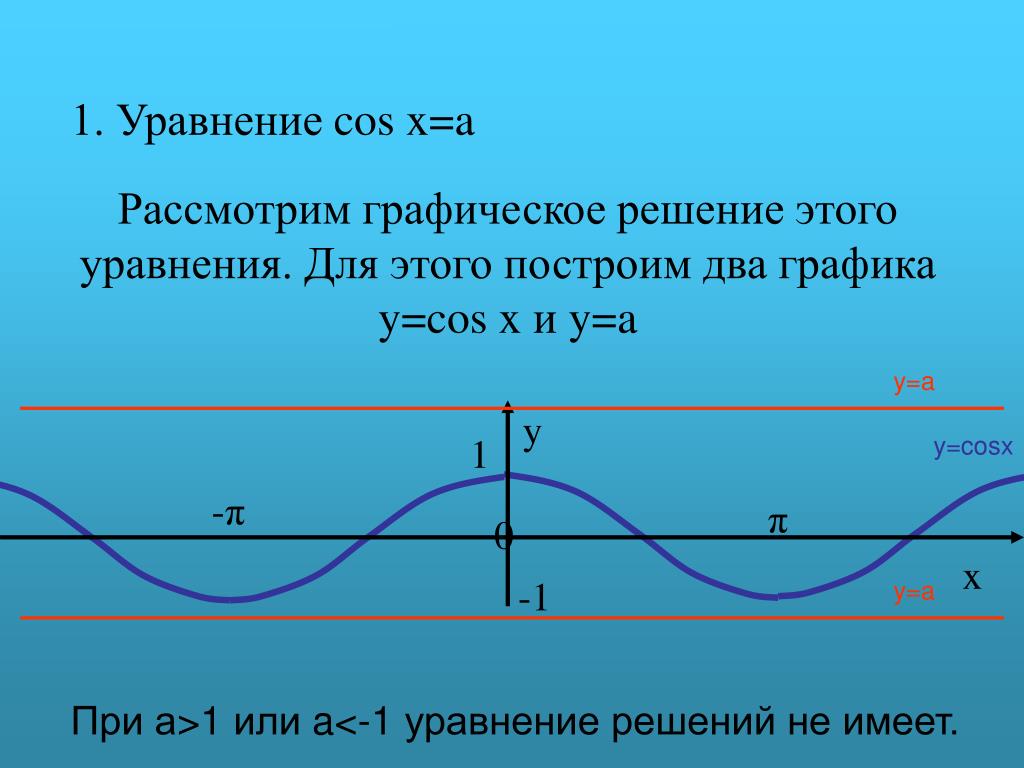 1 График функции y=arcsin х
1 График функции y=arcsin х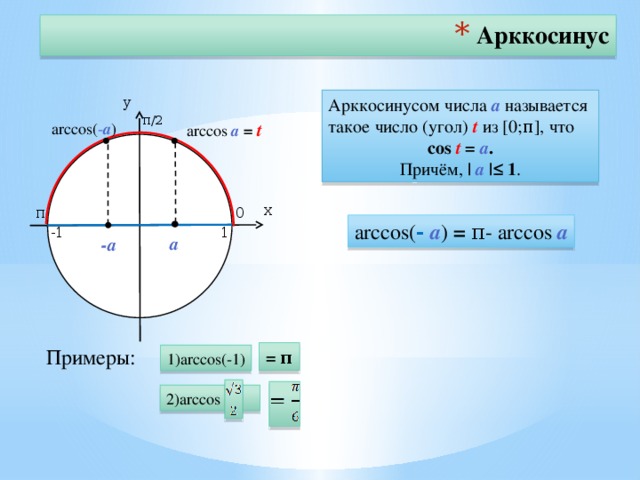 3 График функции y=arctgx
3 График функции y=arctgx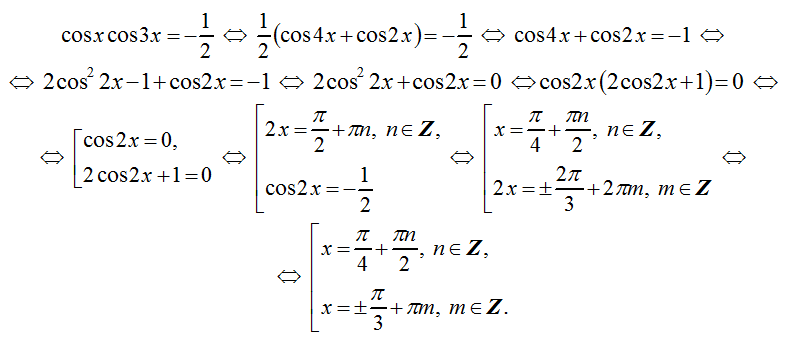 Другими словами, соответствие называется взаимнооднозначным, если каждому элементу x∈X соответствует единственный элемент y∈Y
и наоборот, каждому элементу y∈Y
соответствует единственный элемент x∈X. Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается f-1
и каждому элементу y∈Y
ставит в соответствие такой элемент x∈X,
что f (x) = y; этот факт записывают так: x=f-1 (y).
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных x↔y,
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что y=f-1 (x)
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции: D (f-1)=E (f)=Y.
Другими словами, соответствие называется взаимнооднозначным, если каждому элементу x∈X соответствует единственный элемент y∈Y
и наоборот, каждому элементу y∈Y
соответствует единственный элемент x∈X. Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается f-1
и каждому элементу y∈Y
ставит в соответствие такой элемент x∈X,
что f (x) = y; этот факт записывают так: x=f-1 (y).
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных x↔y,
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что y=f-1 (x)
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции: D (f-1)=E (f)=Y. Область значений обратной функции совпадает с множеством определения самой функции: E (f-1)=D (f)=X.
Область значений обратной функции совпадает с множеством определения самой функции: E (f-1)=D (f)=X.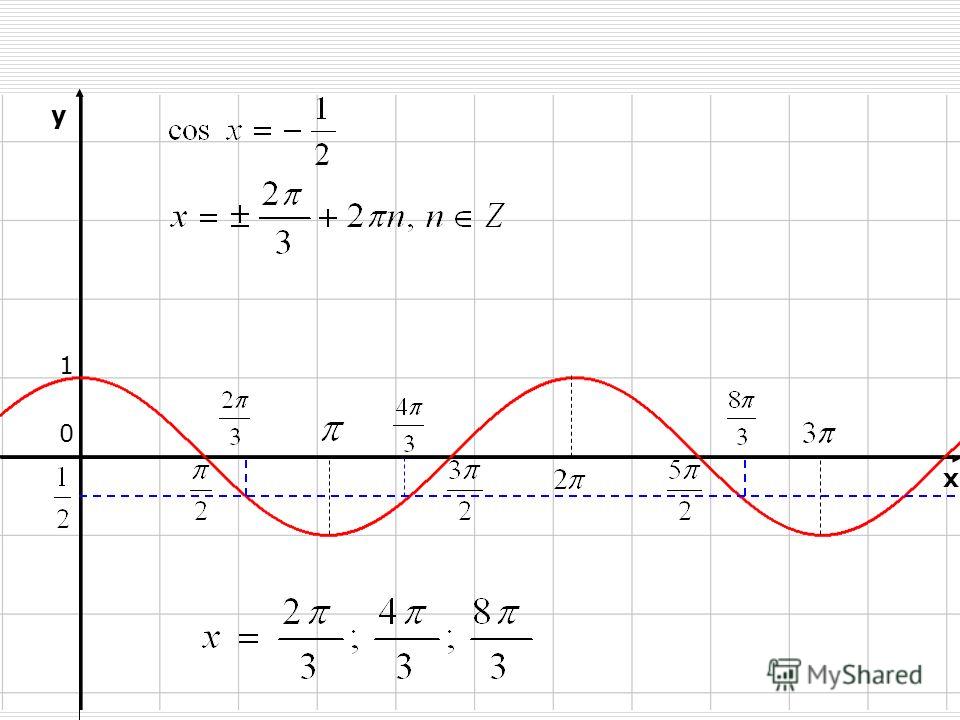

 Но у нас есть ограничения на y и z в виде неравенств -π2≤y≤π2, 0≤z≤π,
а для таких y и z равенство sin y = cos z возможно только при y=π2-z.
Следовательно, y+z=π2
и наконец arcsinx+arccosx=π2,
что и требовалось доказать.
Но у нас есть ограничения на y и z в виде неравенств -π2≤y≤π2, 0≤z≤π,
а для таких y и z равенство sin y = cos z возможно только при y=π2-z.
Следовательно, y+z=π2
и наконец arcsinx+arccosx=π2,
что и требовалось доказать.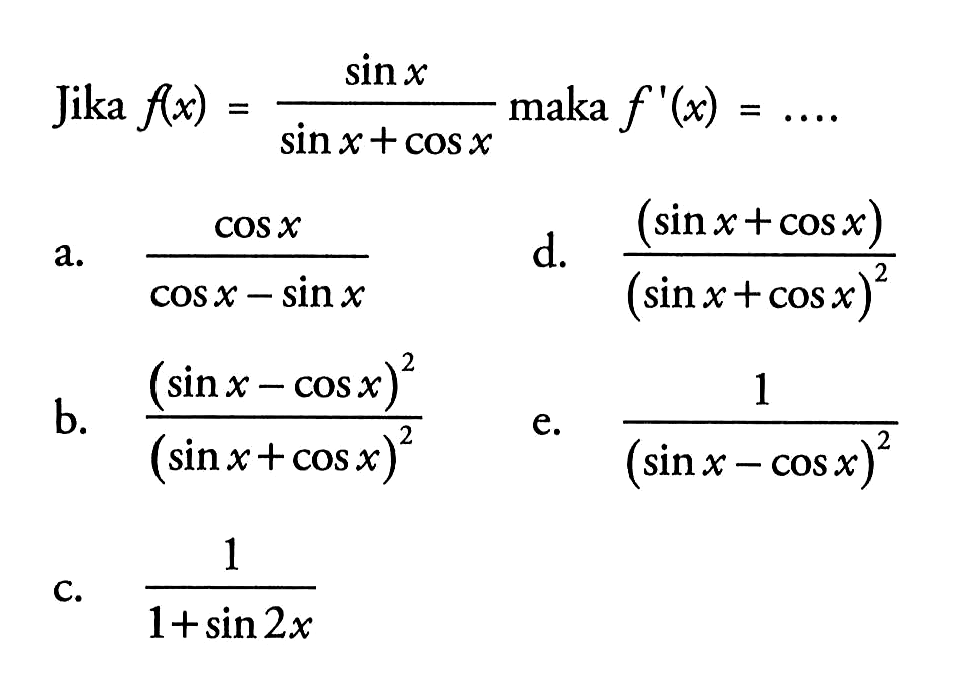 Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда sin(arccosx)=1-x2.
Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда sin(arccosx)=1-x2. 03.21
03.21 Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше
Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше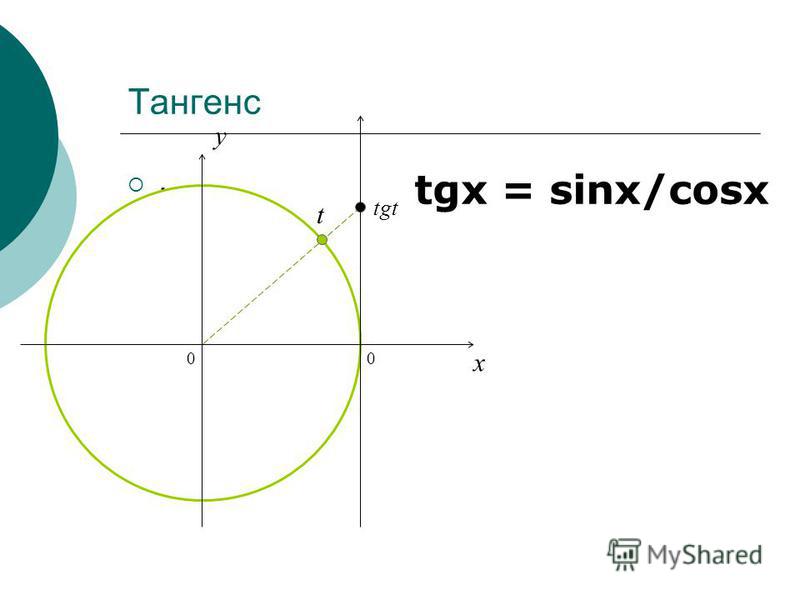 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
 Проверить навыки и умения студентов по вычислению производных простейших функций.
Проверить навыки и умения студентов по вычислению производных простейших функций. 18. y = ecos x * ctg8x3.
18. y = ecos x * ctg8x3. 7. у = arctg5x * log2(x — 3). 4.8. у = log3(x + 5) * arccos 3x.
7. у = arctg5x * log2(x — 3). 4.8. у = log3(x + 5) * arccos 3x. 25. у = lg(x — 3) * arcsin2 5x. 4.26. y = log2(x + 3) * arccos2x.
25. у = lg(x — 3) * arcsin2 5x. 4.26. y = log2(x + 3) * arccos2x. 5.12. у = 4(x — 7)6 * arcsin 3x5.
5.12. у = 4(x — 7)6 * arcsin 3x5.
 Для студентов и преподавателей вузов экономических и других специальностей, требующих изучения вероятностно-статистических методов, слушателей послевузовского образования.
Для студентов и преподавателей вузов экономических и других специальностей, требующих изучения вероятностно-статистических методов, слушателей послевузовского образования.


 Планируем за некоторое время собрать хорошую библиотеку классических и популярных книг и статей.
Планируем за некоторое время собрать хорошую библиотеку классических и популярных книг и статей.
 Весьма продуктивный и общий подход, который встречается не очень часто. Книга рассчитана на школьников старших классов.
Весьма продуктивный и общий подход, который встречается не очень часто. Книга рассчитана на школьников старших классов.  Ориентирована на студентов экономических вузов. Будет понятна и полезна заинтересованным школьникам, учителям, преподавателям вузов.
Ориентирована на студентов экономических вузов. Будет понятна и полезна заинтересованным школьникам, учителям, преподавателям вузов. Книга рассчитана на читателя, пожелавшего на элементарном уровне ознакомиться с теорией вероятностей и составить себе некоторое впечатление о ее применениях. Доступна школьникам старших классов. От себя добавим, что книга написана сжато, емко и не изобилует комбинаторными упражнениями, так характерными для современных российских курсов вероятности в вузах.
Книга рассчитана на читателя, пожелавшего на элементарном уровне ознакомиться с теорией вероятностей и составить себе некоторое впечатление о ее применениях. Доступна школьникам старших классов. От себя добавим, что книга написана сжато, емко и не изобилует комбинаторными упражнениями, так характерными для современных российских курсов вероятности в вузах. ..
.. Его лаконичная, написанная с юмором книга полна поучительных парадоксов и примеров, которые объединяет главная тема: рассказ о том, как теория игр влияет на наш…
Его лаконичная, написанная с юмором книга полна поучительных парадоксов и примеров, которые объединяет главная тема: рассказ о том, как теория игр влияет на наш… ..
.. ..
.. 448 с.
448 с. Для научных работников и инженеров. 640 с.
Для научных работников и инженеров. 640 с. Изложены элементы теории вероятностей в том виде, в каком они должны в первую очередь находить применение в астрономии и физике. 264 с.
Изложены элементы теории вероятностей в том виде, в каком они должны в первую очередь находить применение в астрономии и физике. 264 с. Книга будет полезной для студентов, для специалистов математиков, физиков и инженеров, занимающихся приложениями теории вероятностей. 156 с.
Книга будет полезной для студентов, для специалистов математиков, физиков и инженеров, занимающихся приложениями теории вероятностей. 156 с. 112 с.
112 с. 752 с.
752 с. Включено много полезных дополнений и упражнений. Книга может служить хорошим учебником для студентов и аспирантов, желающих серьезно изучить теорию случайных процессов, и отличным справочником для специалистов. 310 с.
Включено много полезных дополнений и упражнений. Книга может служить хорошим учебником для студентов и аспирантов, желающих серьезно изучить теорию случайных процессов, и отличным справочником для специалистов. 310 с. Для студентов математических специальностей, а также инженерных и научных работников, которые интересуются теорией вероятностей и ее применениями. 112 с.
Для студентов математических специальностей, а также инженерных и научных работников, которые интересуются теорией вероятностей и ее применениями. 112 с. Из путешествия читатель возвратится обогащенный понятиями и методами теории вероятностей, знанием областей ее применения. 90 с.
Из путешествия читатель возвратится обогащенный понятиями и методами теории вероятностей, знанием областей ее применения. 90 с. .. (1949, djvu, 6,26 Mb)
.. (1949, djvu, 6,26 Mb) Эта книга — одно из наиболее замечательных достижений математики ХХ века. 264 с.
Эта книга — одно из наиболее замечательных достижений математики ХХ века. 264 с. От других учебников, предназначенных для той же категории читателей, книга отличается большим вниманием к важным для приложений новым ветвям теории вероятностей (теории случайных процессов, теории информации, теории массового обслуживания и др.). 576 с.
От других учебников, предназначенных для той же категории читателей, книга отличается большим вниманием к важным для приложений новым ветвям теории вероятностей (теории случайных процессов, теории информации, теории массового обслуживания и др.). 576 с. В этих главах введены понятия вероятности, математического ожидания, независимости, случайной величины. Распространение этих понятий на общий случай дано в главах 6-12. Главы 13-16 посвящены некоторым задачам математической статистики. Каждая глава сопровождается небольшим количеством задач.
В этих главах введены понятия вероятности, математического ожидания, независимости, случайной величины. Распространение этих понятий на общий случай дано в главах 6-12. Главы 13-16 посвящены некоторым задачам математической статистики. Каждая глава сопровождается небольшим количеством задач. 
 На этой основе находятся различные характеристики случайных полей, возникающих в предлагаемой общей теоретико-вероятностной модели, изучается их вероятностное поведение (например, устанавливается марковское свойство), рассматриваются различные задачи прогнозирования, задачи идентификации и оценки параметров самой модели по статистическим данным и др. От читателя предполагается знание основ функционального анализа и теории вероятностей. 254 с.
На этой основе находятся различные характеристики случайных полей, возникающих в предлагаемой общей теоретико-вероятностной модели, изучается их вероятностное поведение (например, устанавливается марковское свойство), рассматриваются различные задачи прогнозирования, задачи идентификации и оценки параметров самой модели по статистическим данным и др. От читателя предполагается знание основ функционального анализа и теории вероятностей. 254 с. 224 с.
224 с. Книга ориентируется на умеренные аппетиты к строгости и детализации. Помимо классических разделов теории вероятностей в книге освещается ряд новых направлений: нелинейный закон больших чисел, асимптотическое агрегирование. Изложение сопровождается большим количеством примеров им парадоксов, способствующих рельефному восприятию материала. Затрагиваются многие прикладные области: управление запасами, биржевые игры, массовое обслуживание, страховое дело, стохастическая аппроксимация, обработка статистики. Несмотря на краткость, достаточно полно излагается теория информации с ответвлениями «энтропийно термодинамического» характера. Изложение построено так, что можно ограничиться любым желаемым срезом содержания. Для студентов, преподавателей, инженеров и научных работников. 216 с.
Книга ориентируется на умеренные аппетиты к строгости и детализации. Помимо классических разделов теории вероятностей в книге освещается ряд новых направлений: нелинейный закон больших чисел, асимптотическое агрегирование. Изложение сопровождается большим количеством примеров им парадоксов, способствующих рельефному восприятию материала. Затрагиваются многие прикладные области: управление запасами, биржевые игры, массовое обслуживание, страховое дело, стохастическая аппроксимация, обработка статистики. Несмотря на краткость, достаточно полно излагается теория информации с ответвлениями «энтропийно термодинамического» характера. Изложение построено так, что можно ограничиться любым желаемым срезом содержания. Для студентов, преподавателей, инженеров и научных работников. 216 с. Первый уровень рассчитан на студентов общетехнических специальностей, второй – на студентов специальностей, требующих повышенной математической подготовки. 592 с.
Первый уровень рассчитан на студентов общетехнических специальностей, второй – на студентов специальностей, требующих повышенной математической подготовки. 592 с. 160 с.
160 с. Теория вероятностей в примерах и задачах (2001, pdf,
Теория вероятностей в примерах и задачах (2001, pdf,  476 с.
476 с. Данное пособие предназначено для студентов и аспирантов естественно-научных и экономических факультетов. 119 с.
Данное пособие предназначено для студентов и аспирантов естественно-научных и экономических факультетов. 119 с. Может быть использован преподавателями, аспирантами и студентами высших учебных заведений. 295 c.
Может быть использован преподавателями, аспирантами и студентами высших учебных заведений. 295 c. Хобби. Досуг
Хобби. Досуг
 Виноделие
Виноделие
 Зарубежная
Зарубежная
 Ш.
Ш.
 С. Статистика. Вероятность. Комбинаторика
С. Статистика. Вероятность. Комбинаторика  (Школьное образование) ISBN 957-5-89415-561-0
(Школьное образование) ISBN 957-5-89415-561-0 
 В центре внимания автора — усвоение детьми 10—14 лет математических понятий в ходе занимательных игр.
В центре внимания автора — усвоение детьми 10—14 лет математических понятий в ходе занимательных игр.
 Р., Ященко И. В. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь
Р., Ященко И. В. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь
 Пособие для учащихся. М., «Просвещение», 1975. -223 с ил. (Мир знаний).
Пособие для учащихся. М., «Просвещение», 1975. -223 с ил. (Мир знаний).  17 Мб, 600dpi+OCR) ifolder или onlinedisk
17 Мб, 600dpi+OCR) ifolder или onlinedisk 23 Мб) ifolder.ru || onlinedisk
23 Мб) ifolder.ru || onlinedisk На большом количестве примеров изложены начальные понятия, идеи и методы комбинаторики, теории вероятностей и статистики. Даны задачи с решениями н ответами, а также упражнения с возрастающей степенью сложности для самостоятельной работы школьников (включая ответы). Содержатся рекомендации по примерному поурочному планированию учебного материала.
На большом количестве примеров изложены начальные понятия, идеи и методы комбинаторики, теории вероятностей и статистики. Даны задачи с решениями н ответами, а также упражнения с возрастающей степенью сложности для самостоятельной работы школьников (включая ответы). Содержатся рекомендации по примерному поурочному планированию учебного материала.
 В. Гнеденко.
В. Гнеденко.  В. Ященко. — М: МЦНМО: АО «Московские учебники», 2004.— 256 с: ил. ISBN 5-94057-161-1
В. Ященко. — М: МЦНМО: АО «Московские учебники», 2004.— 256 с: ил. ISBN 5-94057-161-1 ru || rghost.ru
ru || rghost.ru
 — 90 с.
— 90 с.
 38 Мб) ifolder.ru || onlinedisk
38 Мб) ifolder.ru || onlinedisk Для чтения файлов данного формата скачатьWinDjView-1.0 (885Кб) или страница с последней версией WinDjView
Для чтения файлов данного формата скачатьWinDjView-1.0 (885Кб) или страница с последней версией WinDjView д., а также, возможно, примеры «реальных» ситуаций, в которых они будут использоваться.0005
д., а также, возможно, примеры «реальных» ситуаций, в которых они будут использоваться.0005
 Красивое произведение на мой взгляд.
Красивое произведение на мой взгляд.
 1, 3-е издание
1, 3-е издание https://www.springer.com/gp/book/9783540438717
https://www.springer.com/gp/book/9783540438717 Расчетные геометрические характеристики рассматриваемых сечений.
Расчетные геометрические характеристики рассматриваемых сечений.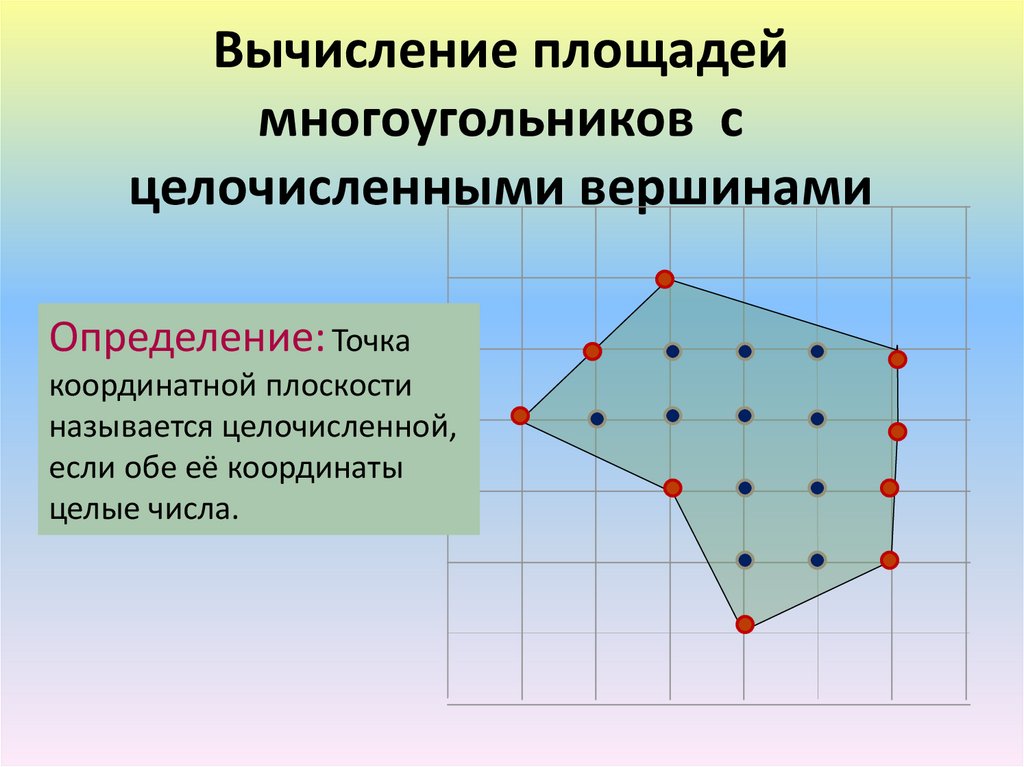
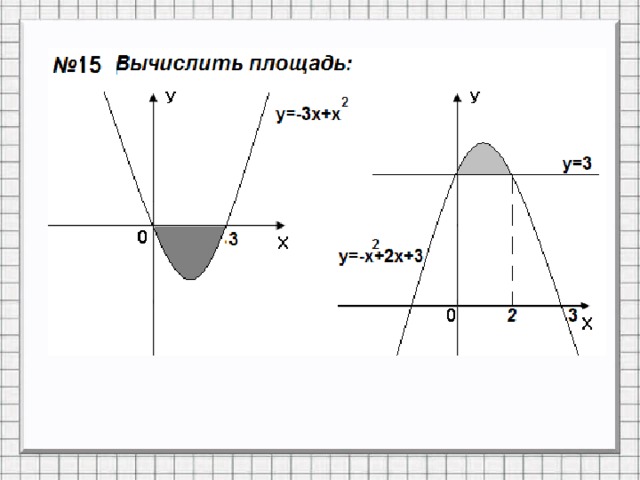 09.2022
09.2022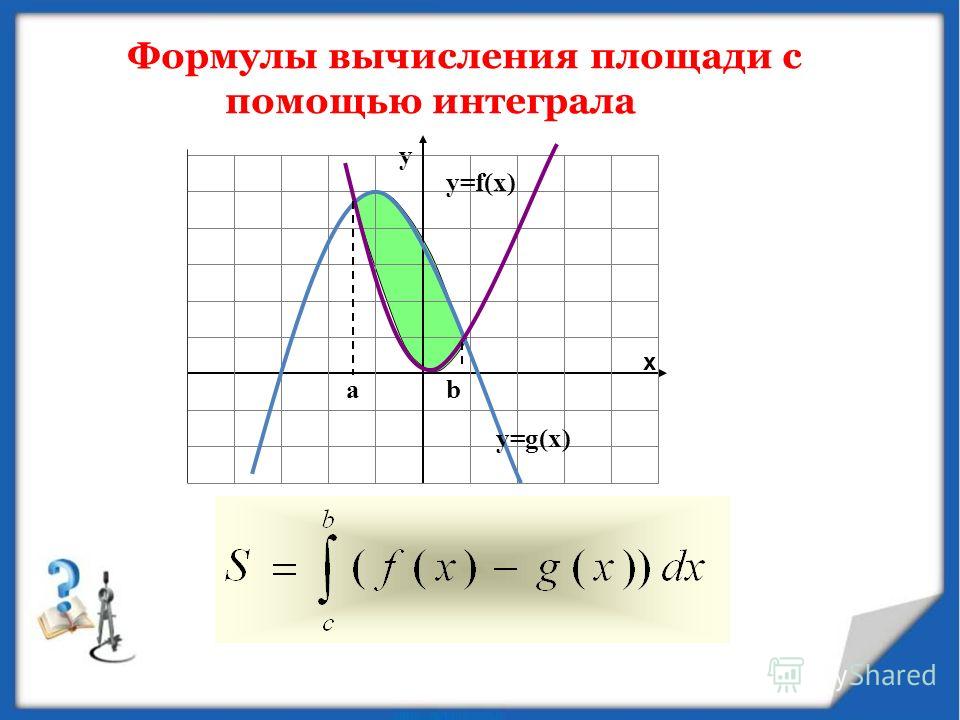 )
) Восстания)
Восстания) )
) Типанова, к Авиационной ул.)
Типанова, к Авиационной ул.) )
) )
) Добролюбова)
Добролюбова)
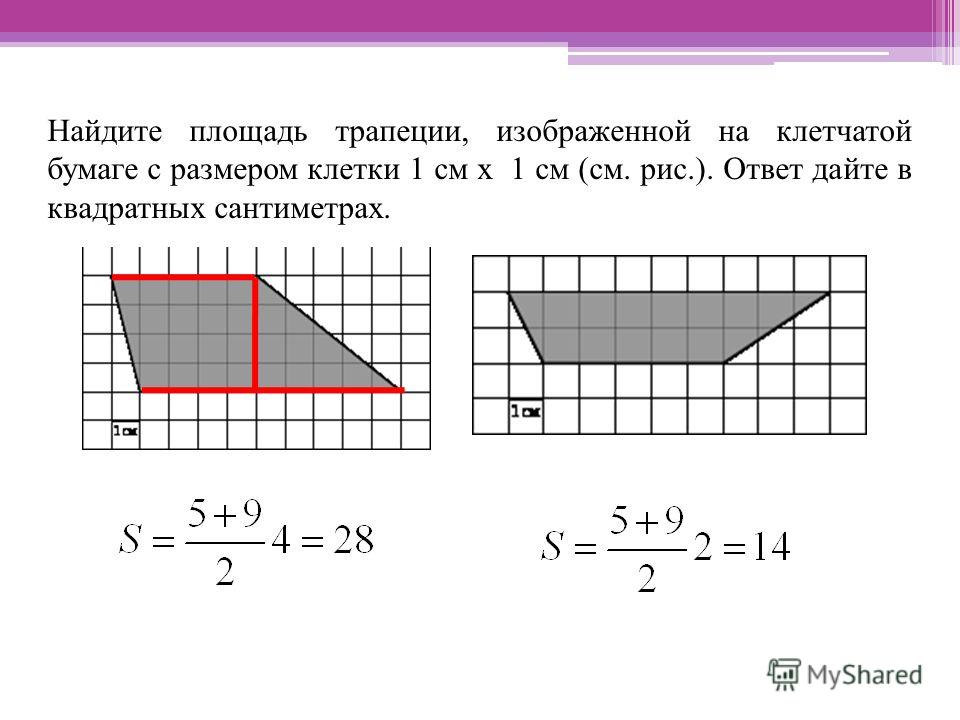 — пр. Металлистов — Кондратьевский пр. — Арсенальная ул. — ул. Комсомола — ул. Академика Лебедева — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала
— пр. Металлистов — Кондратьевский пр. — Арсенальная ул. — ул. Комсомола — ул. Академика Лебедева — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала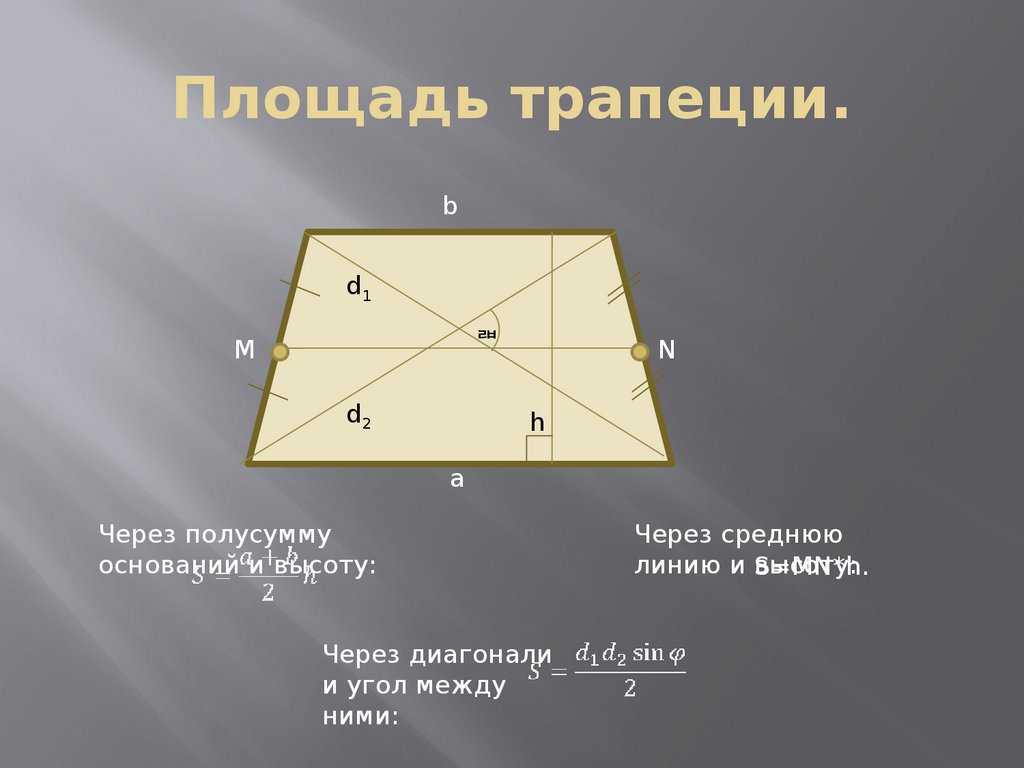 — станция метро «Чёрная речка»
— станция метро «Чёрная речка»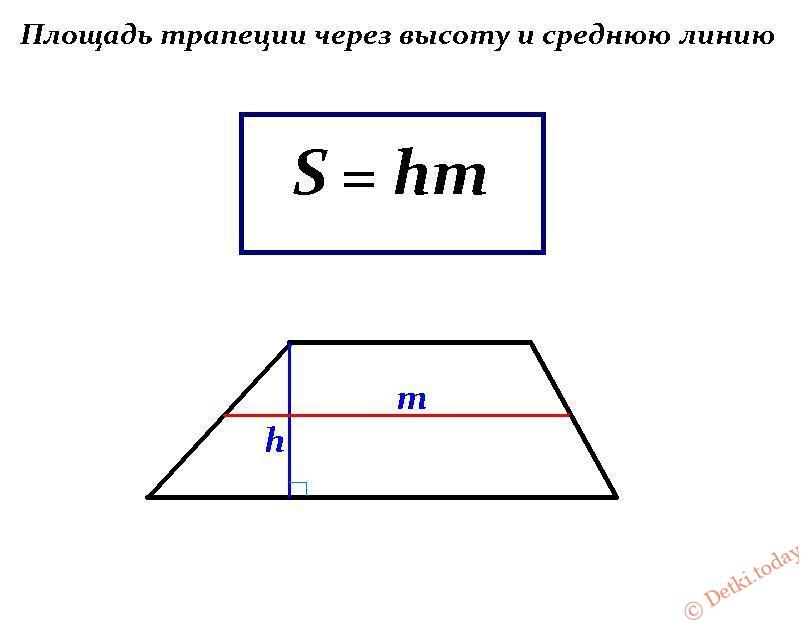 — ул. Комсомола — ул. Академика Лебедева — Литейный мост — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала
— ул. Комсомола — ул. Академика Лебедева — Литейный мост — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала Кораблестроителей — Тульская ул.
Кораблестроителей — Тульская ул. Обуховской Обороны)
Обуховской Обороны)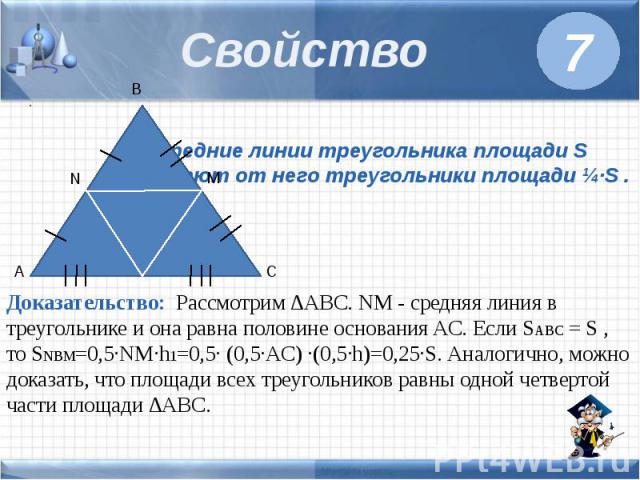 Костюшко
Костюшко Композиторов — пр. Просвещения — пр. Художников — пр. Луначарского — пр. Культуры — Тихорецкий пр. — Политехническая ул. — пл. Мужества
Композиторов — пр. Просвещения — пр. Художников — пр. Луначарского — пр. Культуры — Тихорецкий пр. — Политехническая ул. — пл. Мужества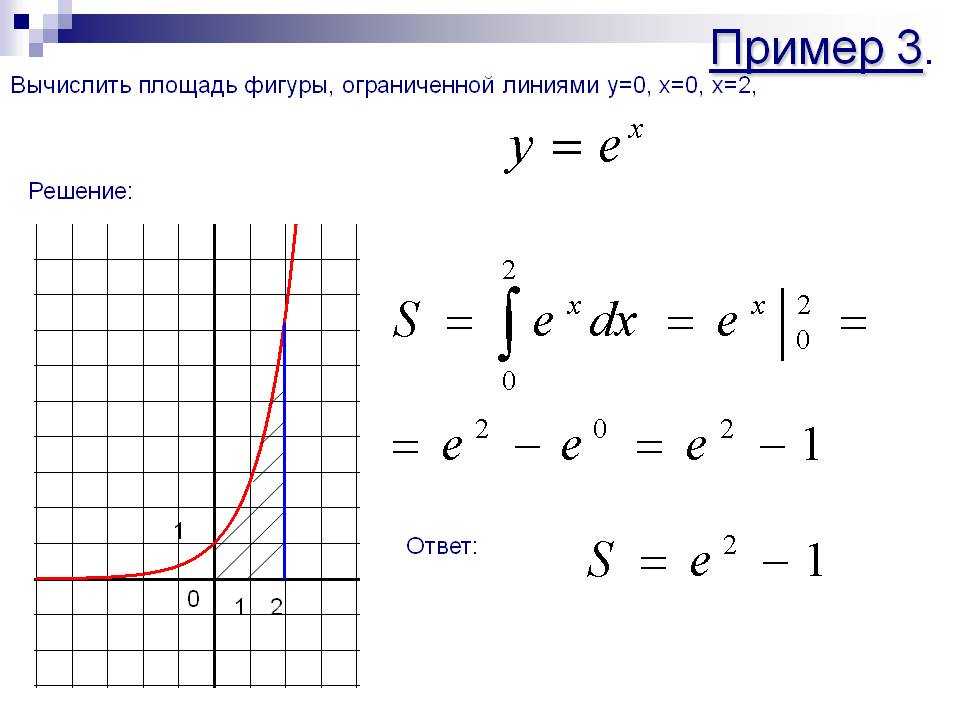 — Арцеуловская аллея.
— Арцеуловская аллея. Конституции
Конституции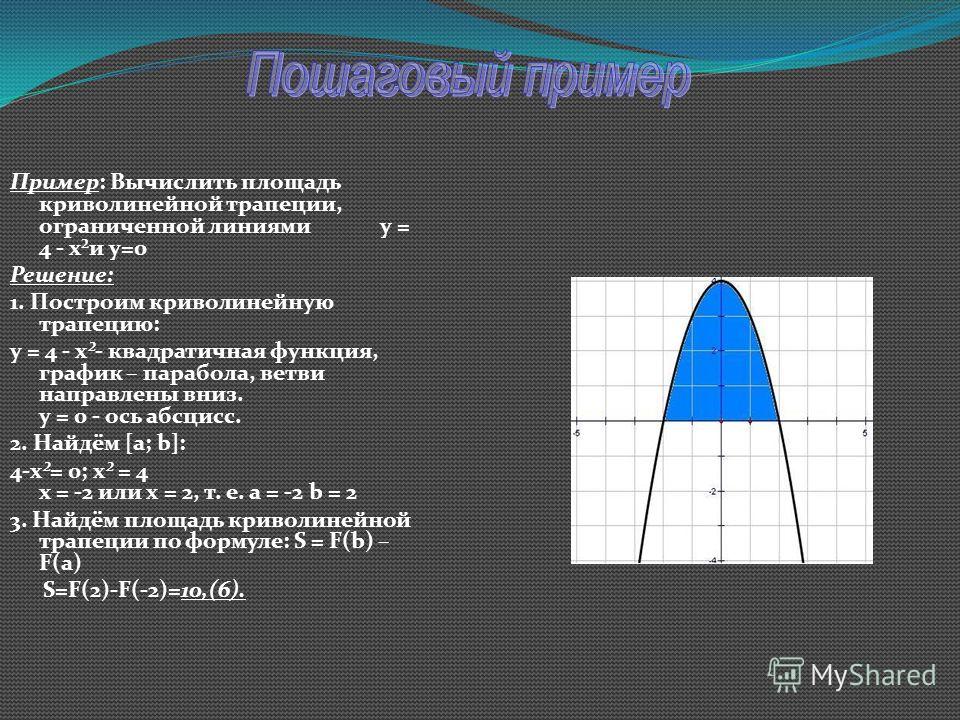 — пр. Добролюбова
— пр. Добролюбова — Суворовский пр.)
— Суворовский пр.) -д. станции Сортировочная — пр. Славы — Пражская ул. — ул. Белы Куна — Будапештская ул. — ул. Фучика — Белградская ул. — ул. Салова — Благодатная ул. — Московский пр. (обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.)
-д. станции Сортировочная — пр. Славы — Пражская ул. — ул. Белы Куна — Будапештская ул. — ул. Фучика — Белградская ул. — ул. Салова — Благодатная ул. — Московский пр. (обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.)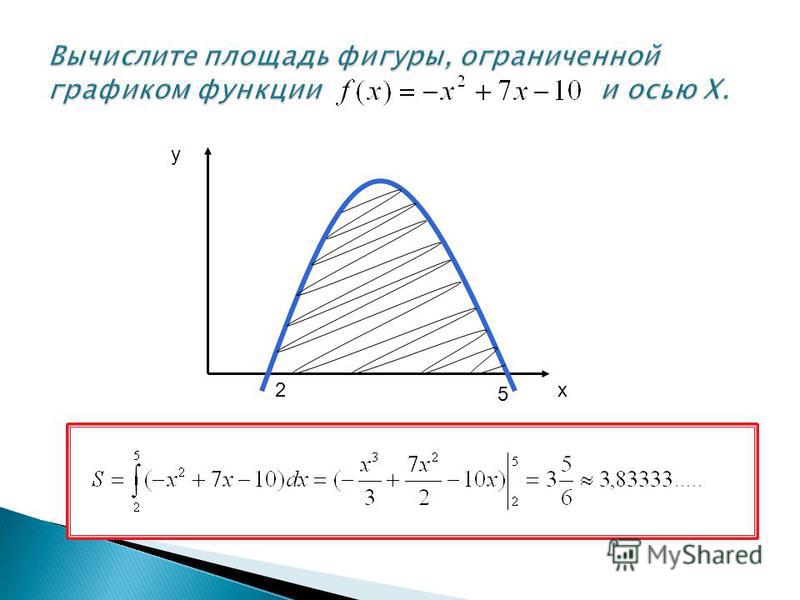 — ул. Салова — Благодатная ул. — Московский пр.(обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.)
— ул. Салова — Благодатная ул. — Московский пр.(обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.) (обратно: Камчатская ул. — Касимовская ул. — Бухарестская ул.)
(обратно: Камчатская ул. — Касимовская ул. — Бухарестская ул.) — пр. Героев
— пр. Героев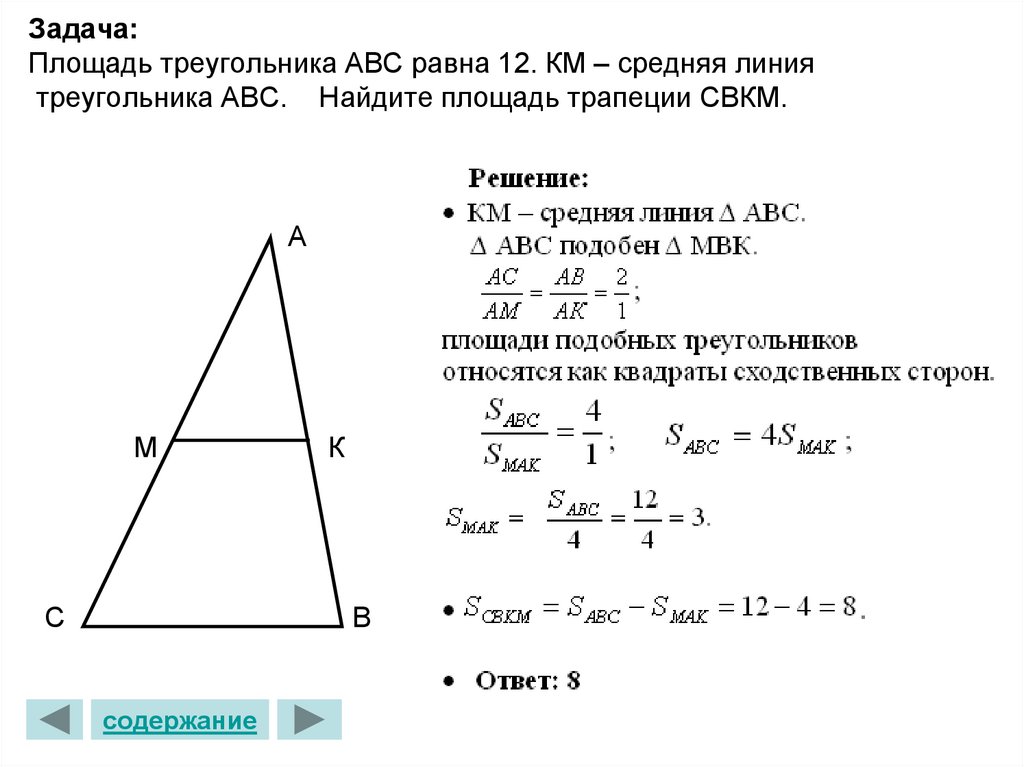 Партизана Германа — ул.Доблести — Ленинский пр.
Партизана Германа — ул.Доблести — Ленинский пр.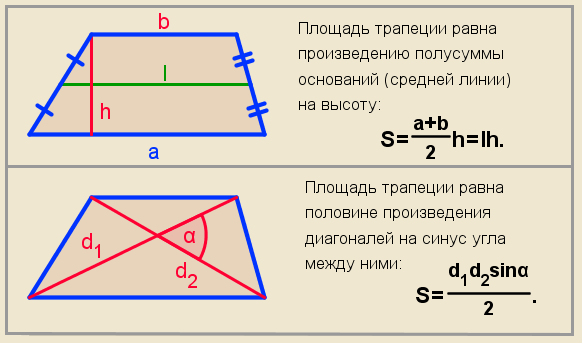
 Его можно обойти с любой стороны. Если Вы обойдете музей справа, то окажетесь ближе к кремлевской стене и мавзолею Ленина. Если обойдете музей с левой стороны, то путь Ваш будет идти через Воскресенские ворота, перед которыми установлен символический памятник Нулевой километр Автодорог России. Здесь можно бросить монетку и загадать желание.
Его можно обойти с любой стороны. Если Вы обойдете музей справа, то окажетесь ближе к кремлевской стене и мавзолею Ленина. Если обойдете музей с левой стороны, то путь Ваш будет идти через Воскресенские ворота, перед которыми установлен символический памятник Нулевой километр Автодорог России. Здесь можно бросить монетку и загадать желание.
 Поэтому те кто никогда не был в нашей столице часто спрашивают «Как добраться до Красной площади».
Поэтому те кто никогда не был в нашей столице часто спрашивают «Как добраться до Красной площади».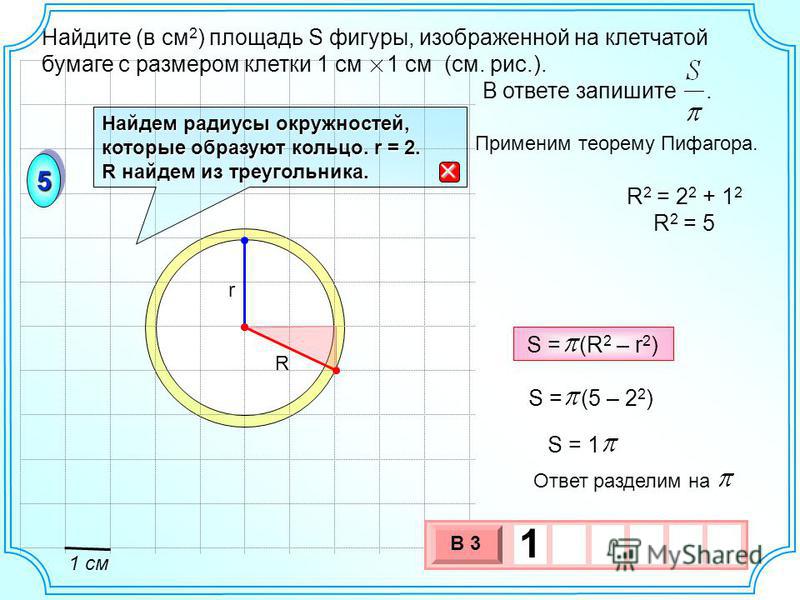
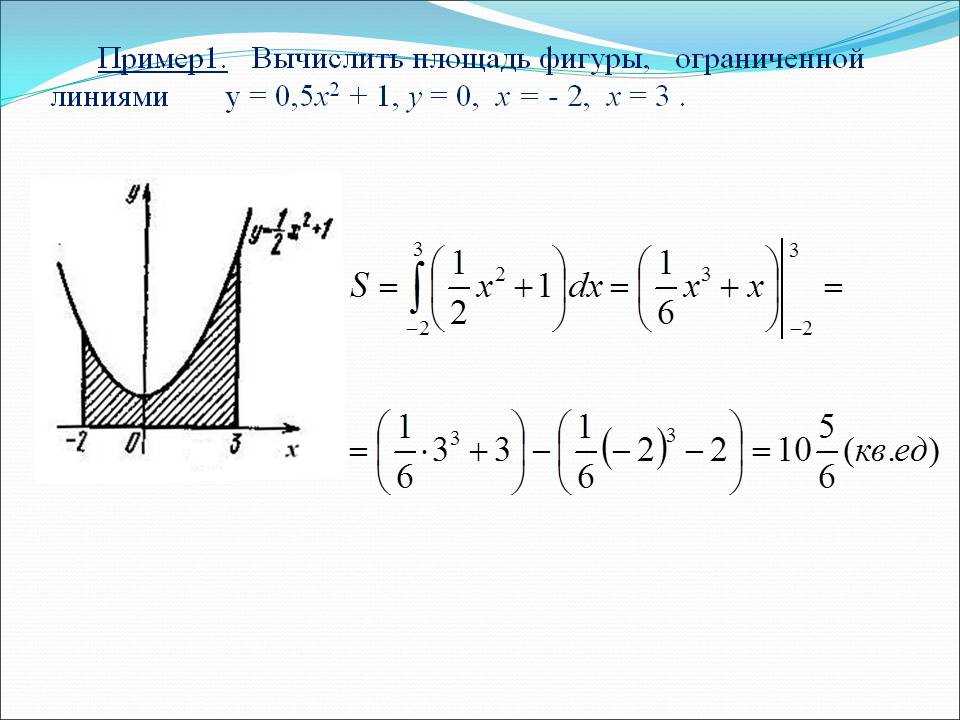 Реестры должны быть размещены в открытом доступе на официальных сайтах муниципалитетов, а если у органа местного самоуправления таковых нет, то – на порталах субъектов РФ.
Реестры должны быть размещены в открытом доступе на официальных сайтах муниципалитетов, а если у органа местного самоуправления таковых нет, то – на порталах субъектов РФ.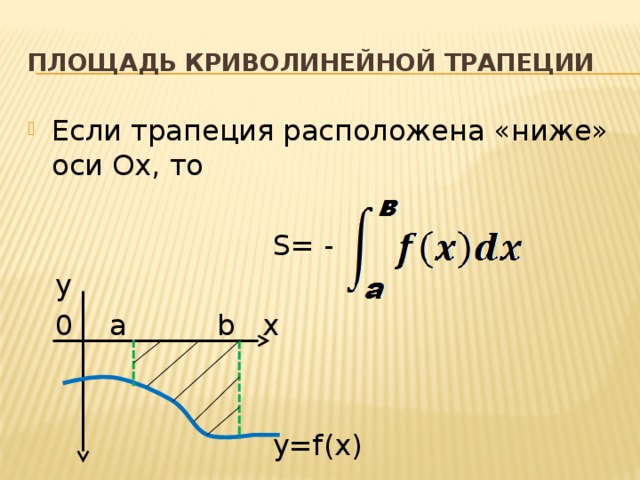 Для получения компенсации необходимо обратиться в отдел социальной защиты населения по месту жительства.
Для получения компенсации необходимо обратиться в отдел социальной защиты населения по месту жительства.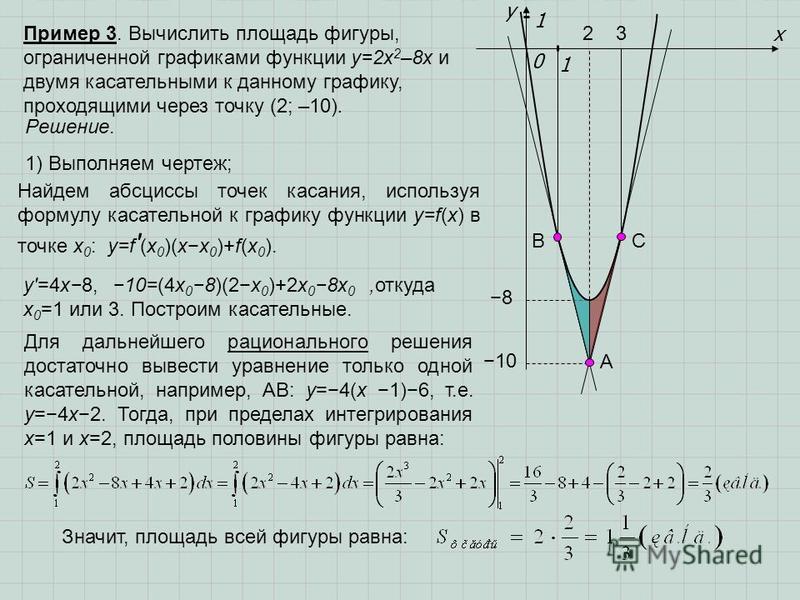

 При заключении договора с регоператором по обращению с ТКО нужно предоставить документ, подтверждающий, что зарегистрированный в доме или квартире человек проживает в другом месте. Это может быть документ о регистрации по факту временного пребывания, справка из учебного заведения. Полный перечень таких документов – в постановлении Правительства РФ № 354.
При заключении договора с регоператором по обращению с ТКО нужно предоставить документ, подтверждающий, что зарегистрированный в доме или квартире человек проживает в другом месте. Это может быть документ о регистрации по факту временного пребывания, справка из учебного заведения. Полный перечень таких документов – в постановлении Правительства РФ № 354.
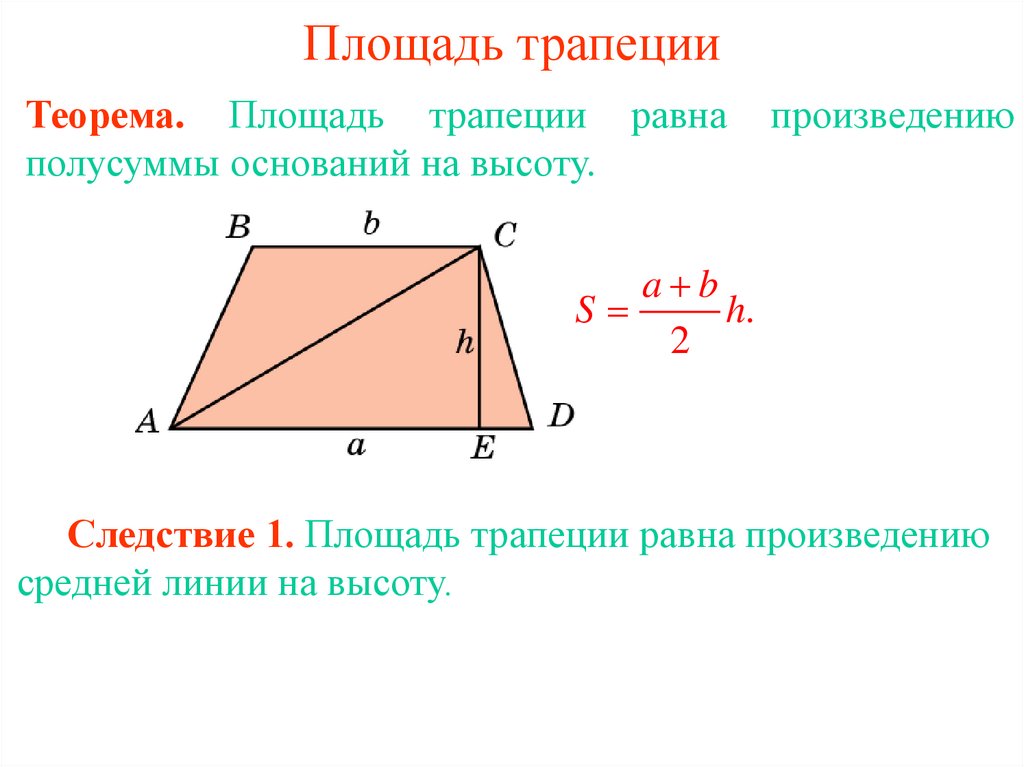
 6–24.13 Закона № 89-ФЗ.
6–24.13 Закона № 89-ФЗ.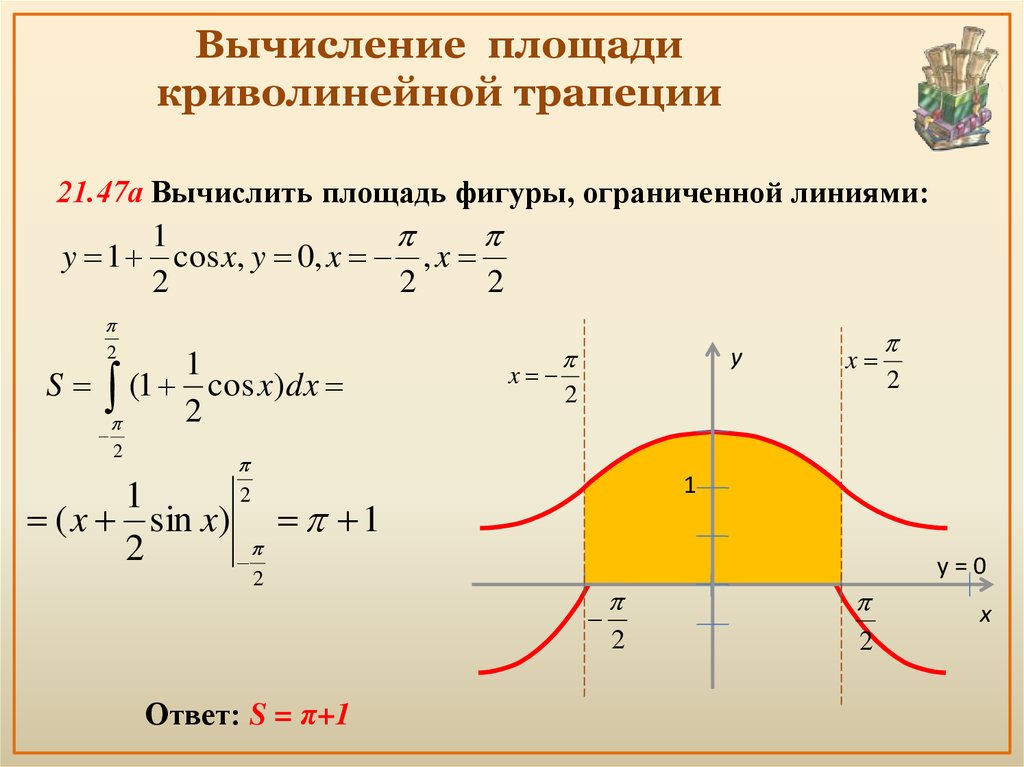 Условия образования ТКО обуславливают также особенность их удаления, которое осуществляется в настоящее время, в основном, путем захоронения, в ряде случаев с предварительной сортировкой. Виды отходов, отнесенные к ТКО, относятся к IV или V классу опасности в силу того, что в составе присутствуют в основном отходы материалов и изделий, отнесенных к IV и/или V классу опасности.
Условия образования ТКО обуславливают также особенность их удаления, которое осуществляется в настоящее время, в основном, путем захоронения, в ряде случаев с предварительной сортировкой. Виды отходов, отнесенные к ТКО, относятся к IV или V классу опасности в силу того, что в составе присутствуют в основном отходы материалов и изделий, отнесенных к IV и/или V классу опасности.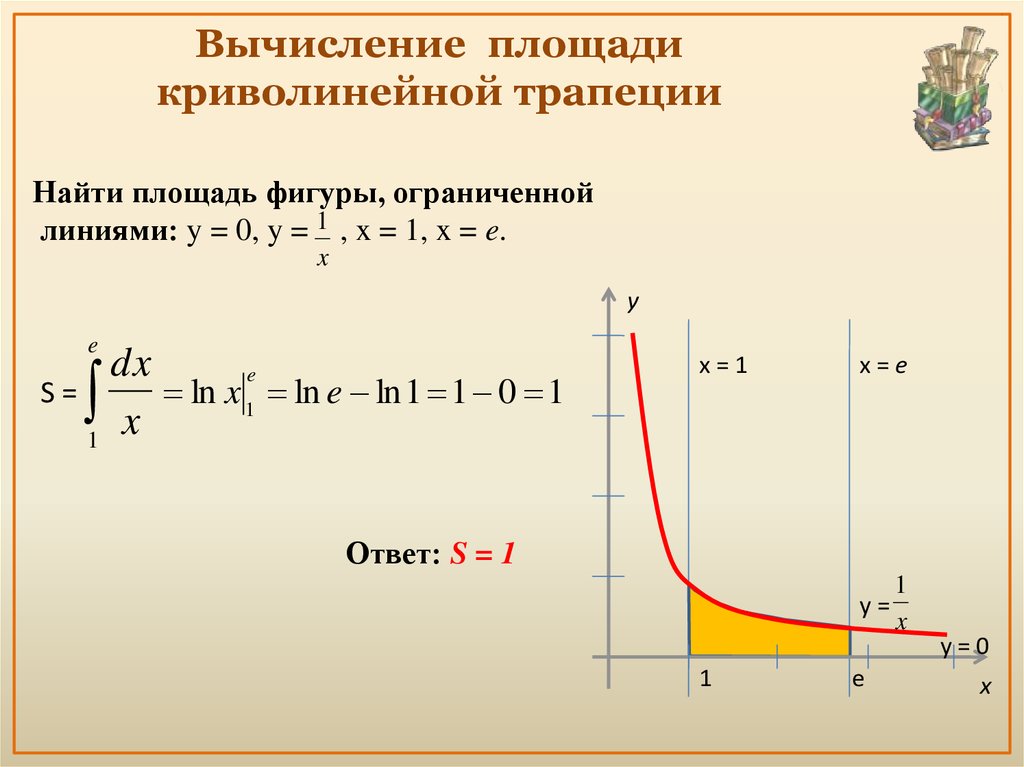
 Указанный договор заключается в порядке и в соответствии с требованиями, установленными гражданским законодательством Российской Федерации и законодательством Российской Федерации в области обращения с отходами производства и потребления.
Указанный договор заключается в порядке и в соответствии с требованиями, установленными гражданским законодательством Российской Федерации и законодательством Российской Федерации в области обращения с отходами производства и потребления.


 Кроме того, в некоторых субъектах РФ нормы накопления установлены для всей территории субъекта, а в некоторых – устанавливаются отдельно для каждого из городов, вплоть до самого небольшого муниципального района. Есть случаи, когда нормативы накопления в разных субъектах РФ указаны в различных единицах измерения. Аналогичная ситуация выявлена в случае анализа единых тарифов на услуги региональных операторов по обращению с ТКО. Нормативы накопления ТКО устанавливаются в м3 или кг на расчетную единицу. Расчетнойединицей является один проживающий или 1 кв. м общей площади.
Кроме того, в некоторых субъектах РФ нормы накопления установлены для всей территории субъекта, а в некоторых – устанавливаются отдельно для каждого из городов, вплоть до самого небольшого муниципального района. Есть случаи, когда нормативы накопления в разных субъектах РФ указаны в различных единицах измерения. Аналогичная ситуация выявлена в случае анализа единых тарифов на услуги региональных операторов по обращению с ТКО. Нормативы накопления ТКО устанавливаются в м3 или кг на расчетную единицу. Расчетнойединицей является один проживающий или 1 кв. м общей площади. 06.2016 № 505 (далее – Правила № 505), в целях сопоставления объема и массы ТКО определяется средняя плотность ТКО, рассчитываемая как отношение объема ТКО, принятых от собственников ТКО (без учета ТКО, коммерческий учет которых осуществляется исходя из их массы), к массе таких отходов, переданных на объекты обработки, утилизации, обезвреживания и захоронения отходов за последний истекший календарный год, а при отсутствии таких данных – как отношение установленного годового норматива накопления в объемных показателях к годовому нормативу накопления по массе (далее – средняя плотность ТКО).
06.2016 № 505 (далее – Правила № 505), в целях сопоставления объема и массы ТКО определяется средняя плотность ТКО, рассчитываемая как отношение объема ТКО, принятых от собственников ТКО (без учета ТКО, коммерческий учет которых осуществляется исходя из их массы), к массе таких отходов, переданных на объекты обработки, утилизации, обезвреживания и захоронения отходов за последний истекший календарный год, а при отсутствии таких данных – как отношение установленного годового норматива накопления в объемных показателях к годовому нормативу накопления по массе (далее – средняя плотность ТКО).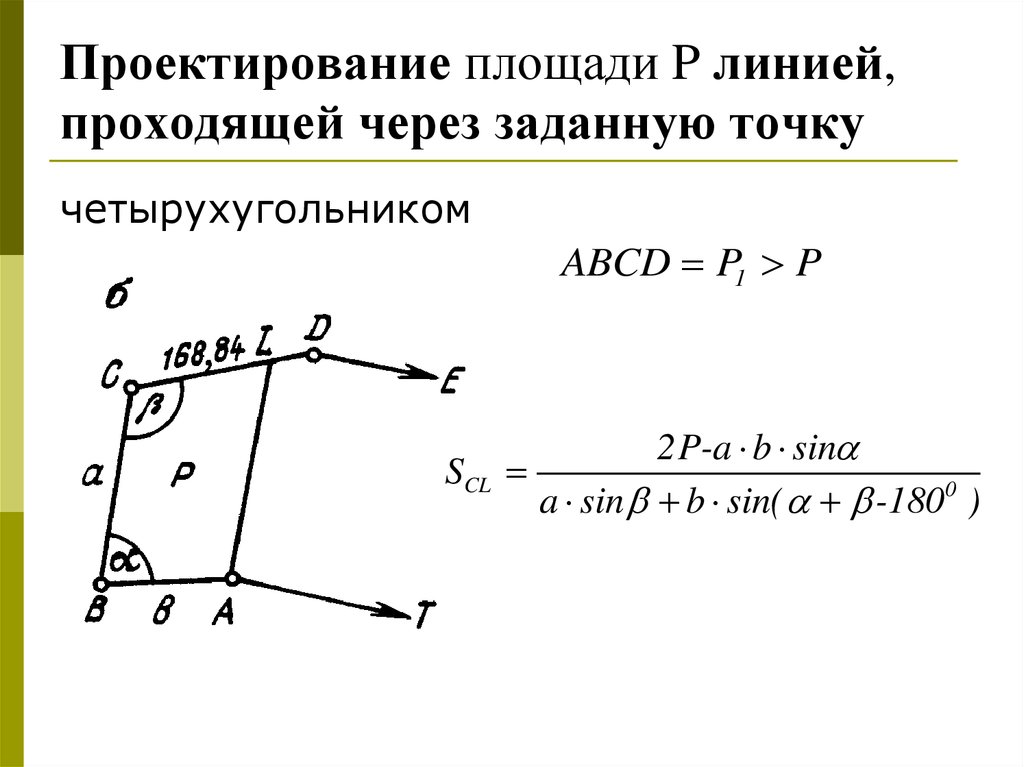

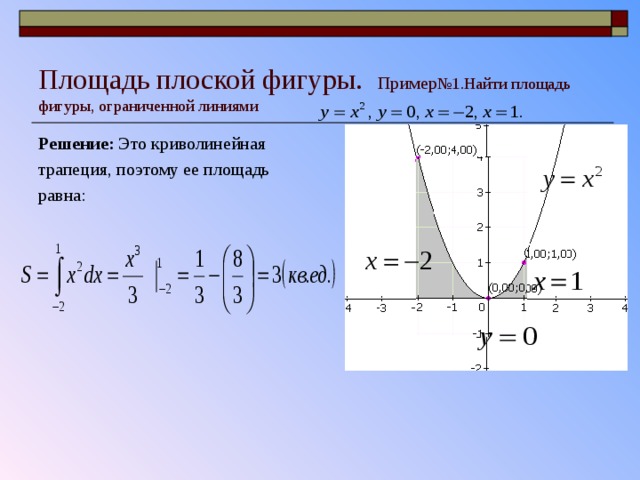
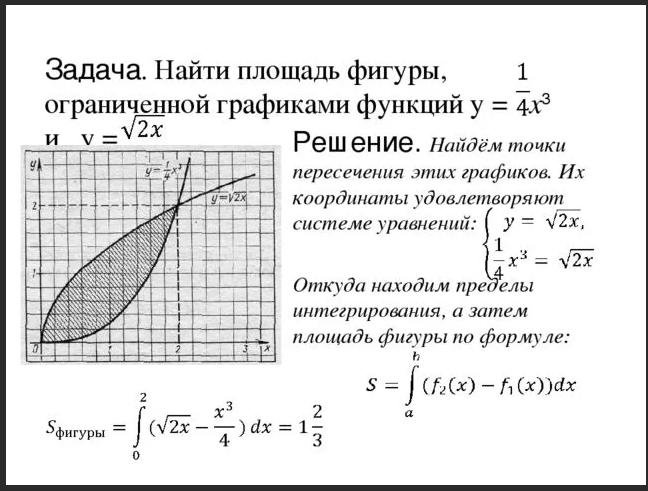

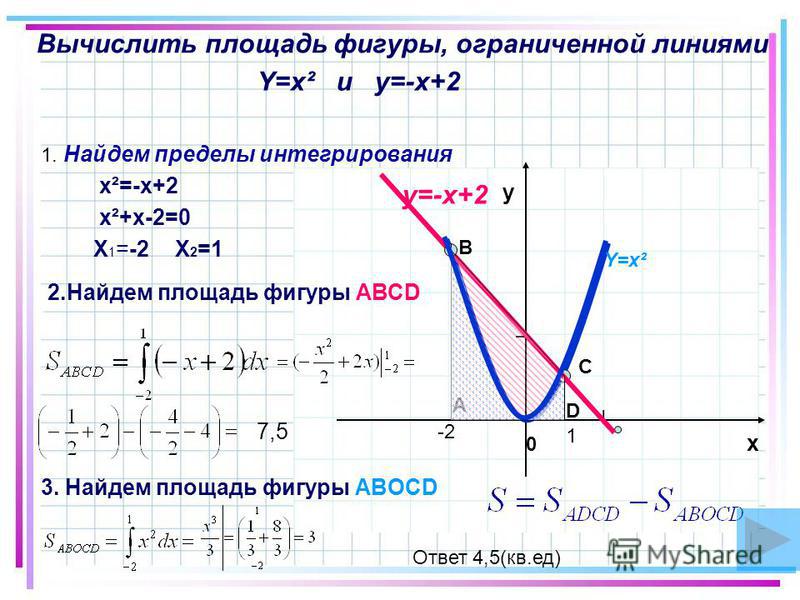
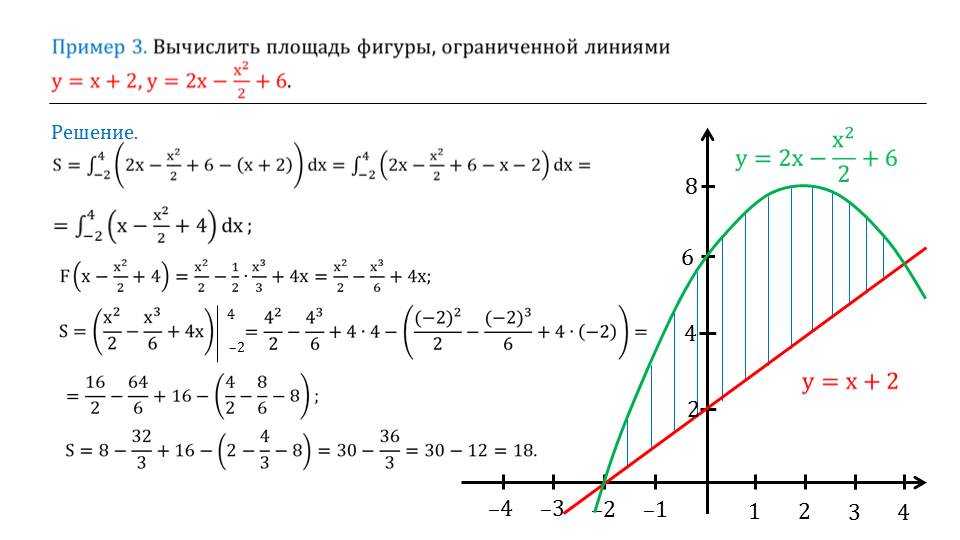 Одним из важнейших его событий традиционно остается программа «Музейная линия», где свои издательские проекты представляют различные музеи и галереи
Одним из важнейших его событий традиционно остается программа «Музейная линия», где свои издательские проекты представляют различные музеи и галереи Патронами события выступают Министерство цифрового развития, связи и массовых коммуникаций РФ и Российский книжный союз, поддерживают его федеральные министерства культуры и просвещения, а также правительство Москвы.
Патронами события выступают Министерство цифрового развития, связи и массовых коммуникаций РФ и Российский книжный союз, поддерживают его федеральные министерства культуры и просвещения, а также правительство Москвы.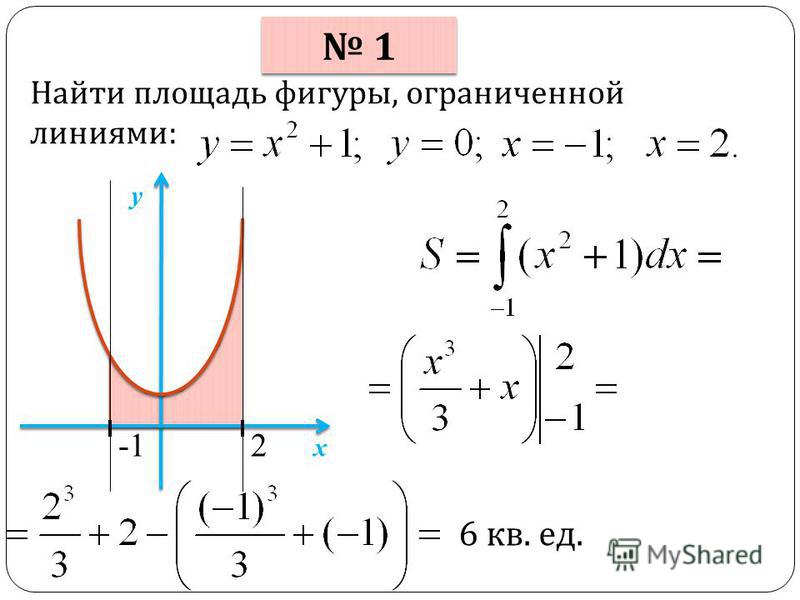 И.Харджиева. Русский авангард: материалы и документы из собрания РГАЛИ», каталог к проходившей в In artibus выставке «Французский рисунок из собрания Инны Баженовой» и другие.
И.Харджиева. Русский авангард: материалы и документы из собрания РГАЛИ», каталог к проходившей в In artibus выставке «Французский рисунок из собрания Инны Баженовой» и другие.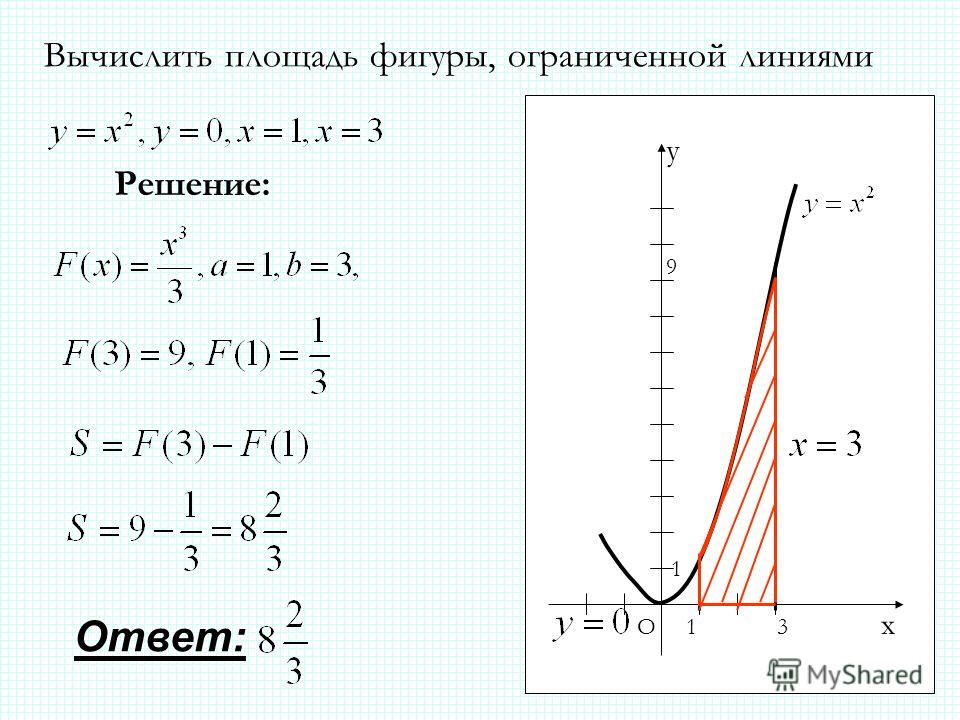
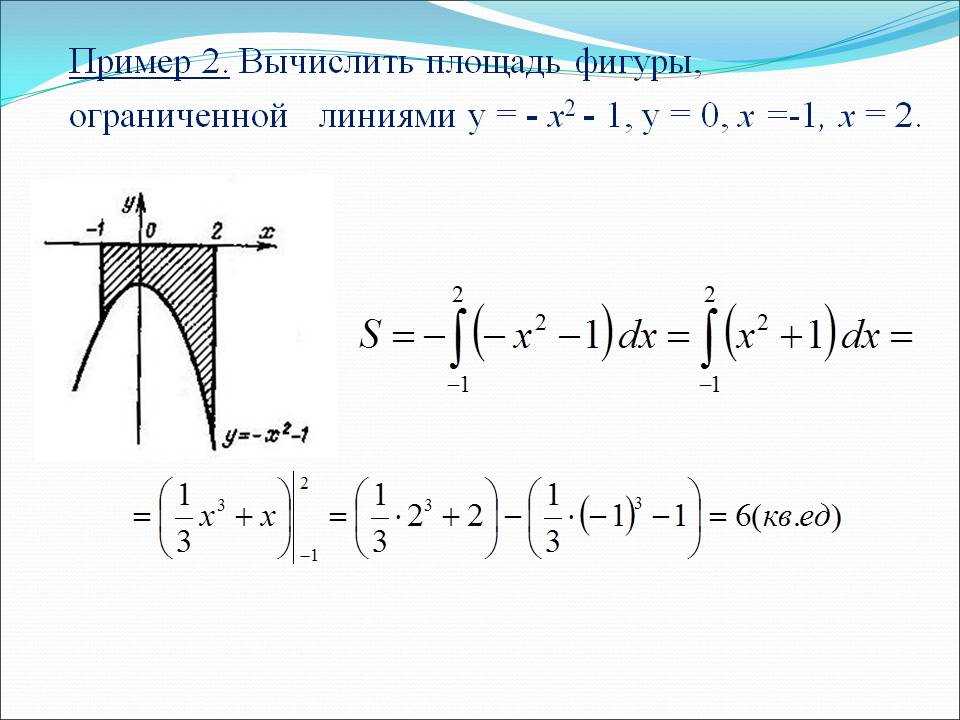 Numbered. Человек под номером» — это собрание портретов сотен людей, выживших в холокосте. Инициатива, возникшая в 2018 году, нашла отклик у 300 фотографов из 30 стран.
Numbered. Человек под номером» — это собрание портретов сотен людей, выживших в холокосте. Инициатива, возникшая в 2018 году, нашла отклик у 300 фотографов из 30 стран.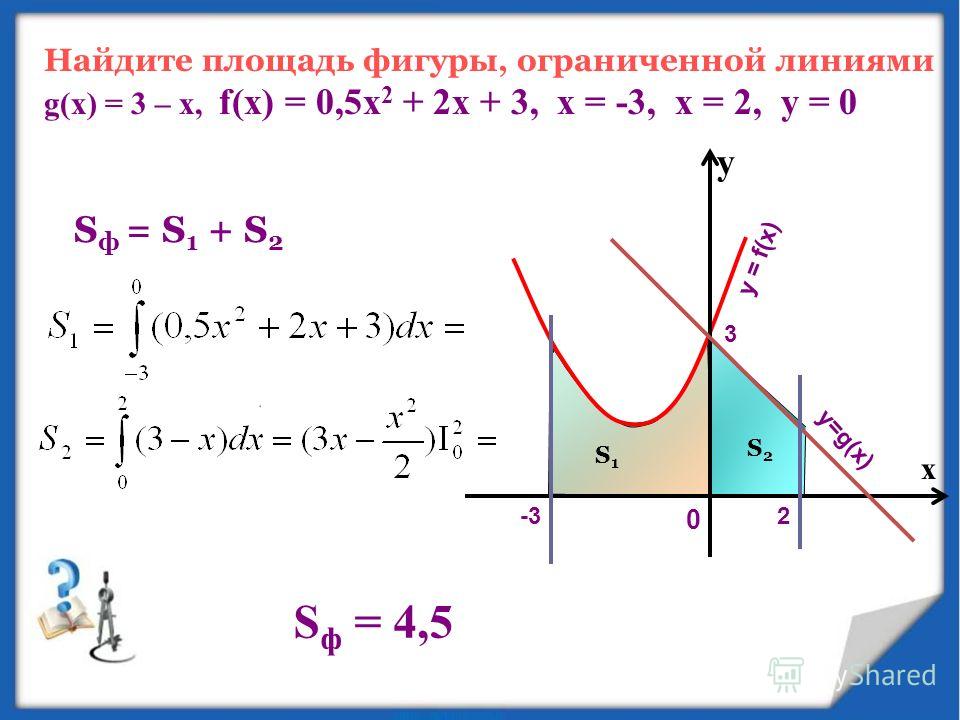 08.2022
08.2022 09.2022
09.2022 разделить на составные части. Это приводит к двум различным типам диаграмм с областями, по одному для каждого варианта использования.
разделить на составные части. Это приводит к двум различным типам диаграмм с областями, по одному для каждого варианта использования.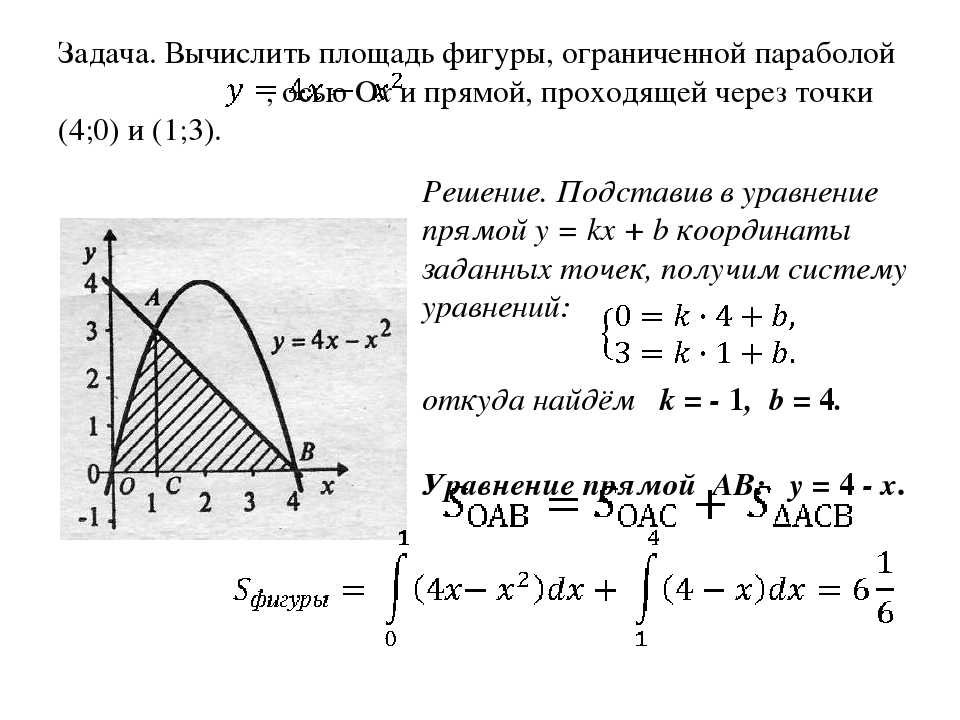 В этих случаях лучшим выбором будет просто придерживаться стандартной линейной диаграммы.
В этих случаях лучшим выбором будет просто придерживаться стандартной линейной диаграммы.
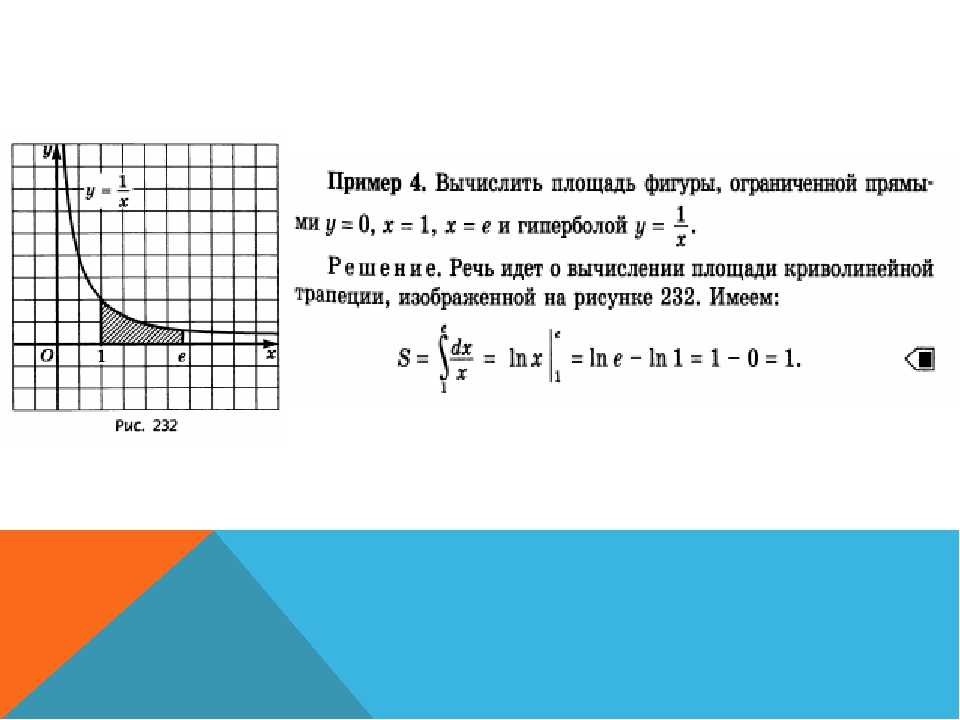 В каждом последующем столбце будет указан вертикальный вклад для каждой точки, по одному столбцу на серию, которую необходимо нанести на график. Этот формат применим как для перекрывающихся, так и для составных диаграмм с областями, при этом основное различие между диаграммами заключается в способе интерпретации значений для визуализации.
В каждом последующем столбце будет указан вертикальный вклад для каждой точки, по одному столбцу на серию, которую необходимо нанести на график. Этот формат применим как для перекрывающихся, так и для составных диаграмм с областями, при этом основное различие между диаграммами заключается в способе интерпретации значений для визуализации.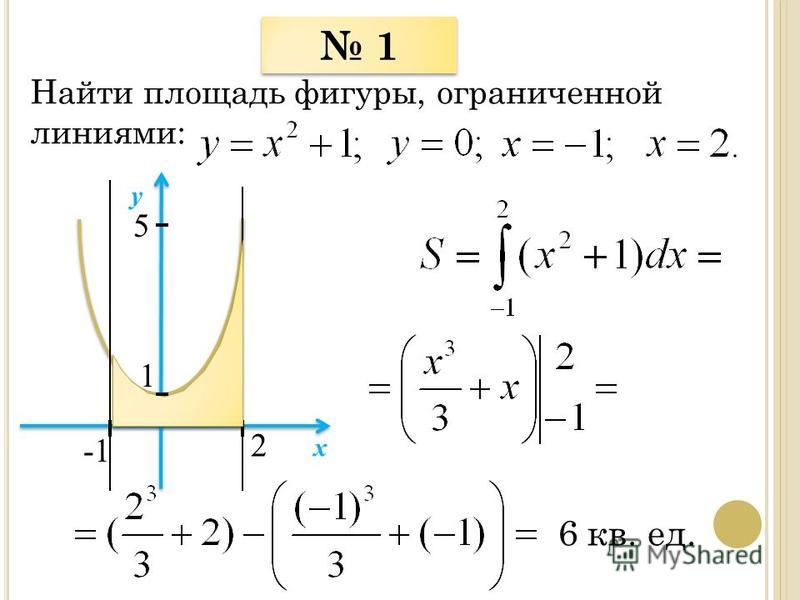 Таким образом, как и в гистограмме, обязательно наличие нулевой базовой линии, относительно которой должно выполняться затенение. Сокращение оси приведет к тому, что фактическое соотношение в значениях группы не будет соответствовать тому, что подразумевается на сгенерированном графике.
Таким образом, как и в гистограмме, обязательно наличие нулевой базовой линии, относительно которой должно выполняться затенение. Сокращение оси приведет к тому, что фактическое соотношение в значениях группы не будет соответствовать тому, что подразумевается на сгенерированном графике. Даже при наличии всего трех серий иногда бывает слишком много для отслеживания: три отдельных цвета, три попарных перекрытия и один цвет для всех трех перекрывающихся групп, всего семь цветов.
Даже при наличии всего трех серий иногда бывает слишком много для отслеживания: три отдельных цвета, три попарных перекрытия и один цвет для всех трех перекрывающихся групп, всего семь цветов.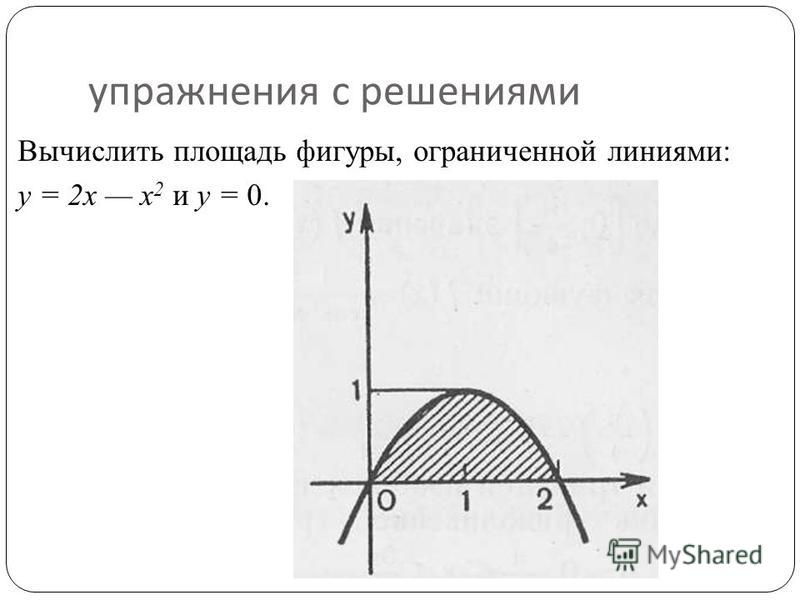 Как будет упомянуто в следующем разделе, чтение значений для любой отдельной группы, за исключением самой нижней, требует работы, поэтому рекомендуется сделать ее самой важной.
Как будет упомянуто в следующем разделе, чтение значений для любой отдельной группы, за исключением самой нижней, требует работы, поэтому рекомендуется сделать ее самой важной. Кроме того, когда у нас много значений, нас, вероятно, больше интересуют направление и наклон трендов, а не точные значения, когда линейные диаграммы работают лучше.
Кроме того, когда у нас много значений, нас, вероятно, больше интересуют направление и наклон трендов, а не точные значения, когда линейные диаграммы работают лучше.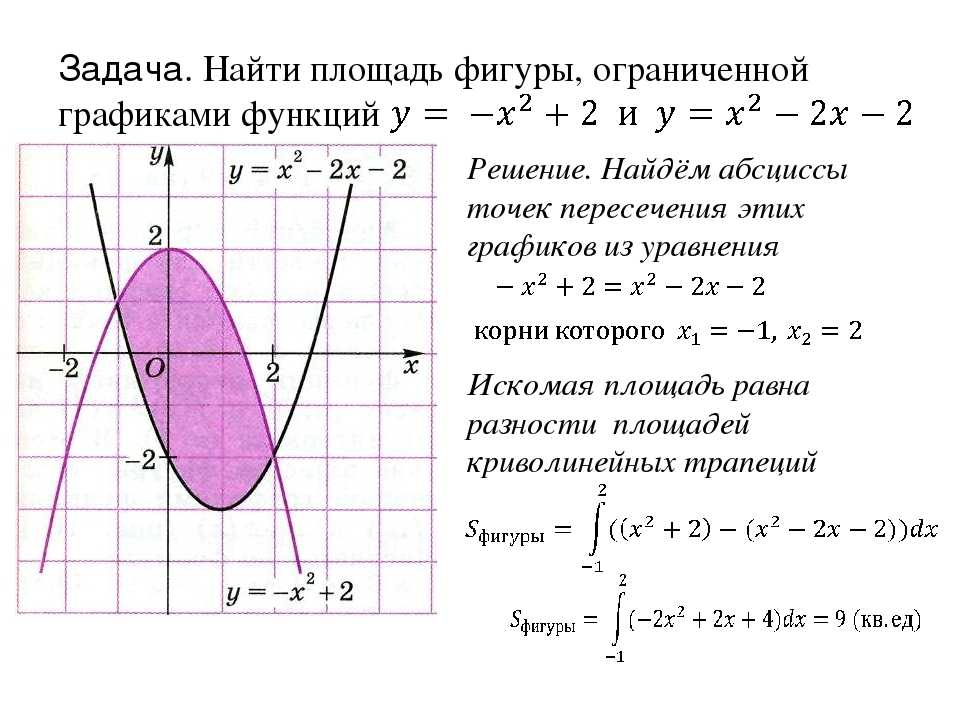
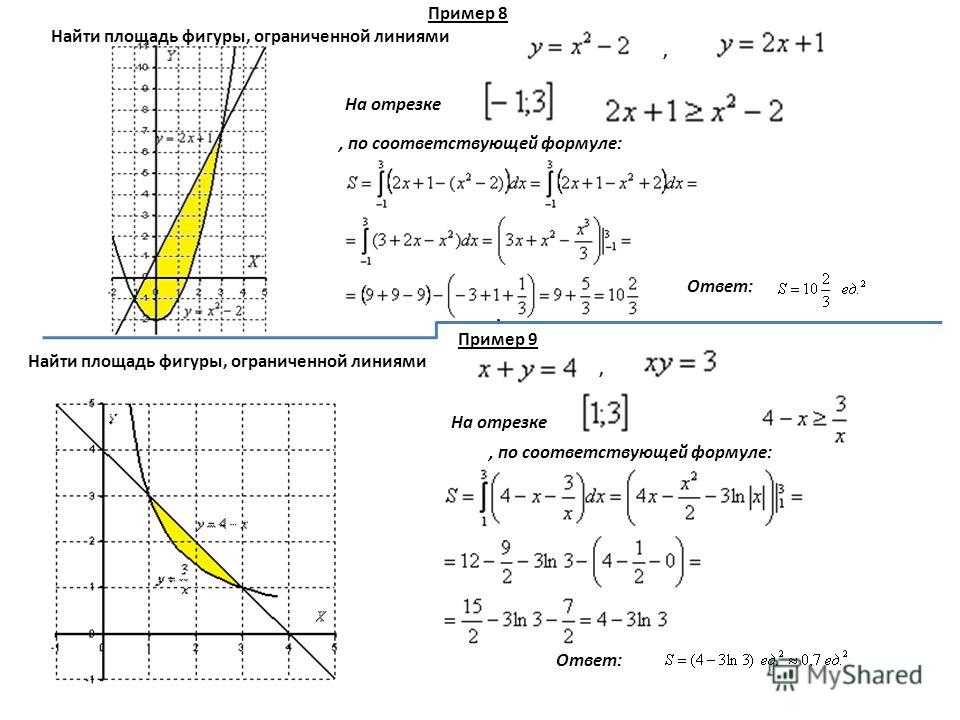 Если вы не уверены, что вас интересует диаграмма с областями, использование линейной диаграммы вряд ли приведет вас к неверному пути. Это особенно верно для диаграммы с перекрывающимися областями, где перекрывающиеся области могут быстро выйти из-под контроля. В качестве еще одного соображения, всегда можно просто создать больше графиков, если вы заинтересованы в проведении нескольких сравнений в своих данных, а не просто чувствуете необходимость выбрать только один тип диаграммы, чтобы нести как можно больше.
Если вы не уверены, что вас интересует диаграмма с областями, использование линейной диаграммы вряд ли приведет вас к неверному пути. Это особенно верно для диаграммы с перекрывающимися областями, где перекрывающиеся области могут быстро выйти из-под контроля. В качестве еще одного соображения, всегда можно просто создать больше графиков, если вы заинтересованы в проведении нескольких сравнений в своих данных, а не просто чувствуете необходимость выбрать только один тип диаграммы, чтобы нести как можно больше.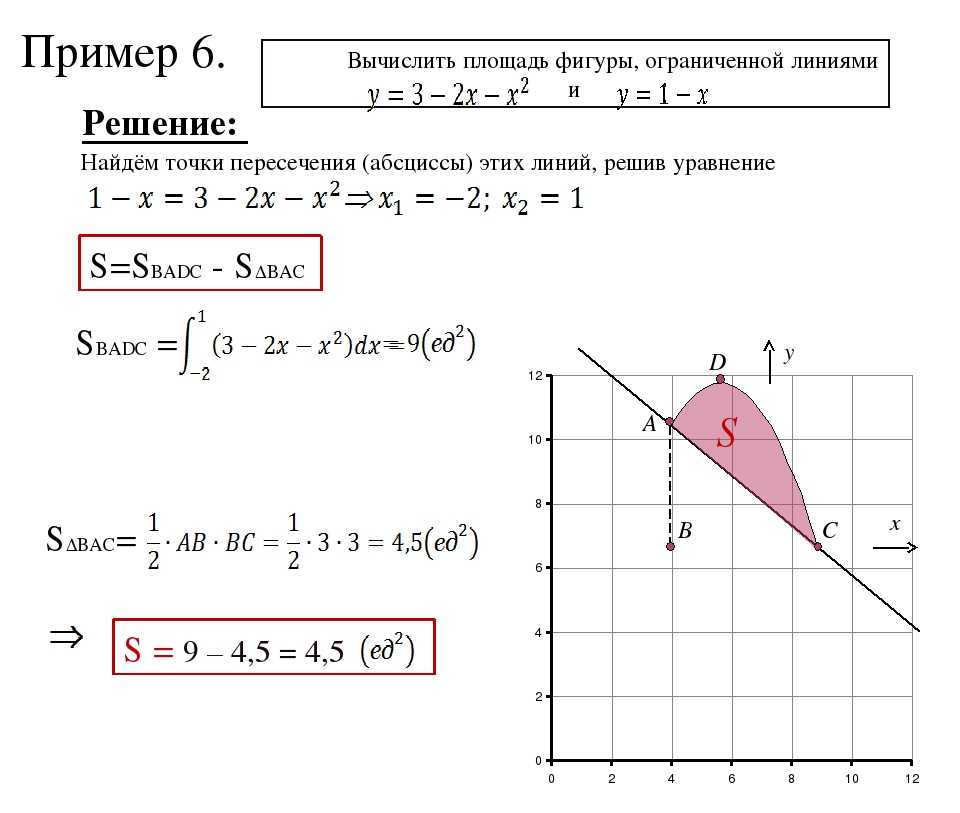 Таким образом, многие ограничения диаграммы с областями с накоплением также применимы к линейчатой диаграмме с накоплением. Однако одним из преимуществ столбцов, расположенных друг над другом, является то, что гораздо проще сделать последовательное суждение о стоимости в пределах каждого интервала горизонтальной оси. Заштрихованные области на диаграмме с областями могут искажаться, как показано выше, особенно когда линия меняет направление. Поскольку каждая область на линейчатой диаграмме с накоплением имеет прямоугольную форму, такого рода искажений можно избежать.
Таким образом, многие ограничения диаграммы с областями с накоплением также применимы к линейчатой диаграмме с накоплением. Однако одним из преимуществ столбцов, расположенных друг над другом, является то, что гораздо проще сделать последовательное суждение о стоимости в пределах каждого интервала горизонтальной оси. Заштрихованные области на диаграмме с областями могут искажаться, как показано выше, особенно когда линия меняет направление. Поскольку каждая область на линейчатой диаграмме с накоплением имеет прямоугольную форму, такого рода искажений можно избежать.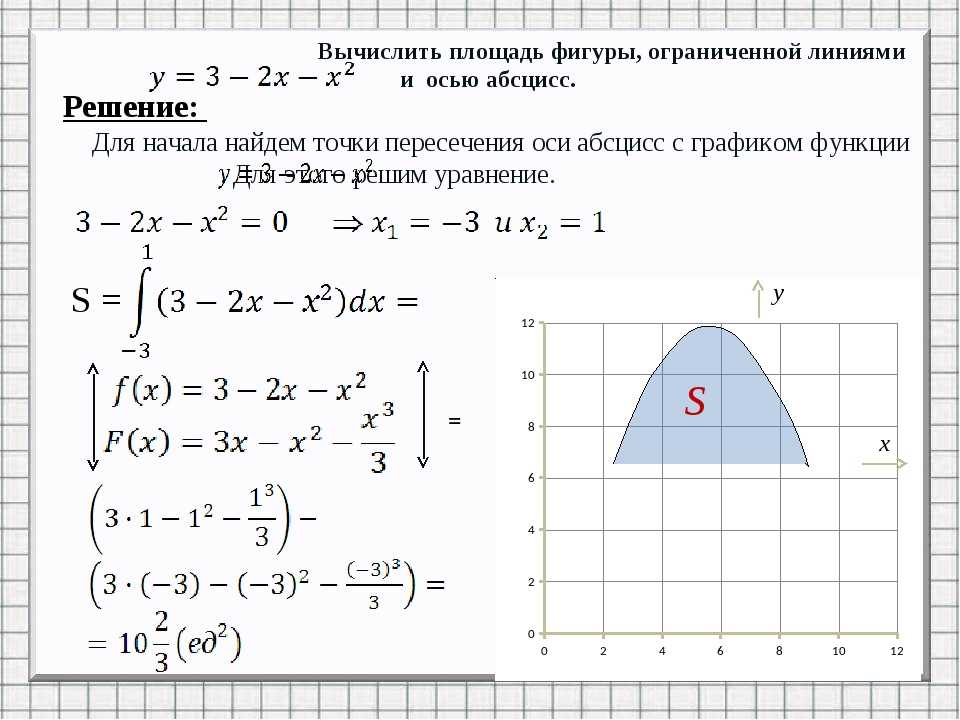
 Затем эти точки данных соединяются прямыми линиями, чтобы визуально показать тенденцию.
Затем эти точки данных соединяются прямыми линиями, чтобы визуально показать тенденцию. Когда этот год завершится, вы можете использовать существующую линейную диаграмму, чтобы показать, как на самом деле работала команда. Вы получите параллельное сравнение прогнозируемого роста и фактического роста.
Когда этот год завершится, вы можете использовать существующую линейную диаграмму, чтобы показать, как на самом деле работала команда. Вы получите параллельное сравнение прогнозируемого роста и фактического роста. Точки данных отмечаются на сетке XY, а затем соединяются в линию. Оттуда область между построенной линией и осью X заштрихована цветами или текстурами.
Точки данных отмечаются на сетке XY, а затем соединяются в линию. Оттуда область между построенной линией и осью X заштрихована цветами или текстурами. 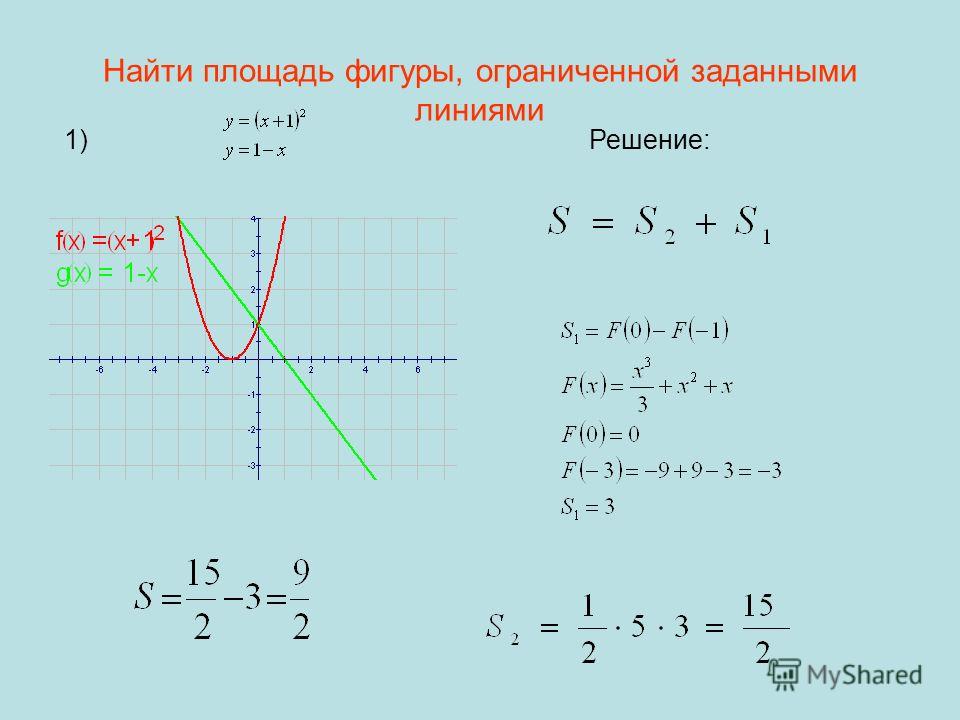 Диаграмма с областями, на которой сравниваются разные наборы данных, называется диаграммой с перекрывающимися областями. Например, если вы хотите узнать, сколько предметов женской и мужской одежды продала ваша компания по производству одежды в прошлом квартале, вы должны нанести точки данных для каждой категории и заполнить эти области другим цветом. Вы можете сразу увидеть, какая линия одежды показала лучшие результаты в квартальных продажах.
Диаграмма с областями, на которой сравниваются разные наборы данных, называется диаграммой с перекрывающимися областями. Например, если вы хотите узнать, сколько предметов женской и мужской одежды продала ваша компания по производству одежды в прошлом квартале, вы должны нанести точки данных для каждой категории и заполнить эти области другим цветом. Вы можете сразу увидеть, какая линия одежды показала лучшие результаты в квартальных продажах. 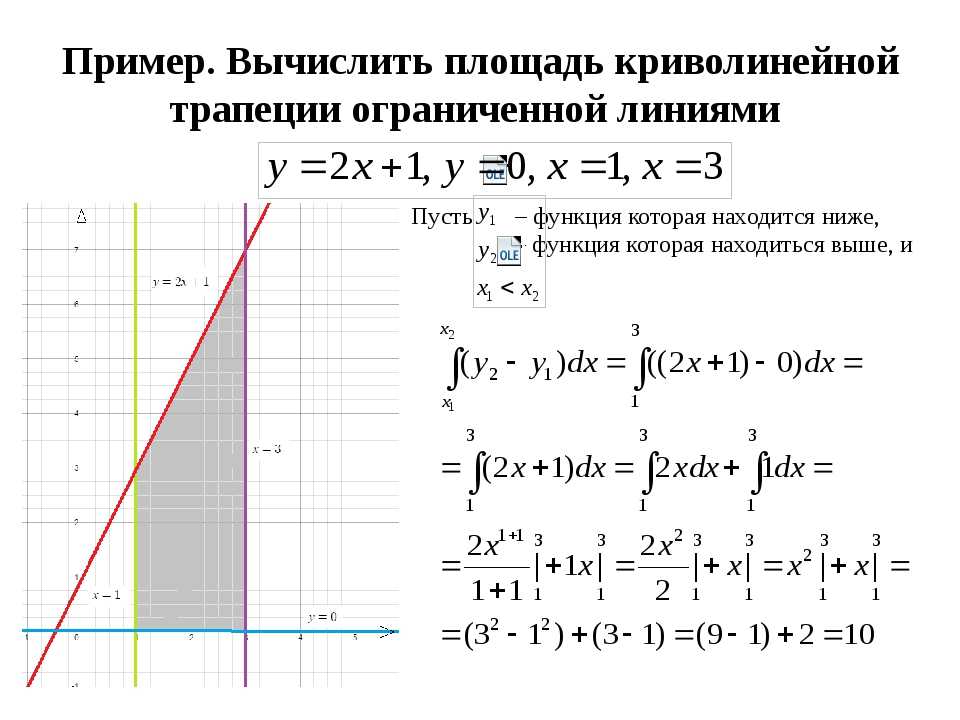 Они могут превратить скучные данные в профессиональные и легко читаемые диаграммы в вашей презентации. Линейные диаграммы хорошо отображают краткосрочные данные и точные точки данных, а диаграммы с областями отлично подходят для отображения долгосрочных данных и нескольких наборов данных.
Они могут превратить скучные данные в профессиональные и легко читаемые диаграммы в вашей презентации. Линейные диаграммы хорошо отображают краткосрочные данные и точные точки данных, а диаграммы с областями отлично подходят для отображения долгосрочных данных и нескольких наборов данных.  В диаграммах с областями
пространство под сегментами линий заполнено цветом, тогда как в
на линейных диаграммах визуализируются только линейные сегменты без дополнительных
окрашивание или затенение. Эти диаграммы облегчают визуализацию данных в течение
период времени (с использованием данных временных рядов) и выявление тенденций и
закономерности во всем диапазоне данных. Поддержка линейных и площадных диаграмм
визуализации как дискретных, так и непрерывных данных.
В диаграммах с областями
пространство под сегментами линий заполнено цветом, тогда как в
на линейных диаграммах визуализируются только линейные сегменты без дополнительных
окрашивание или затенение. Эти диаграммы облегчают визуализацию данных в течение
период времени (с использованием данных временных рядов) и выявление тенденций и
закономерности во всем диапазоне данных. Поддержка линейных и площадных диаграмм
визуализации как дискретных, так и непрерывных данных.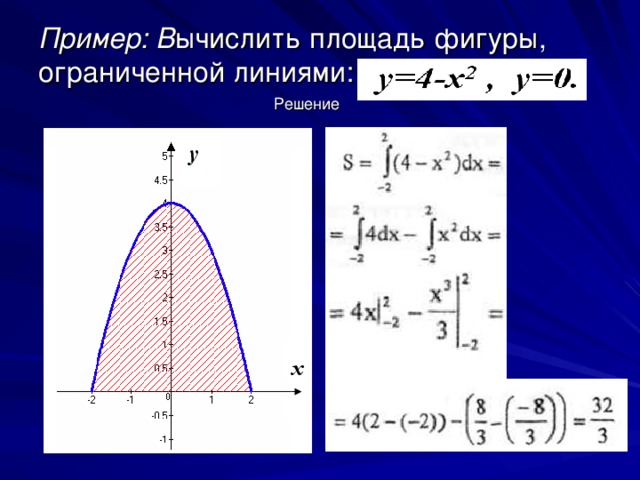
 сопоставляется с агрегацией оси Y
канал кодирования.
сопоставляется с агрегацией оси Y
канал кодирования.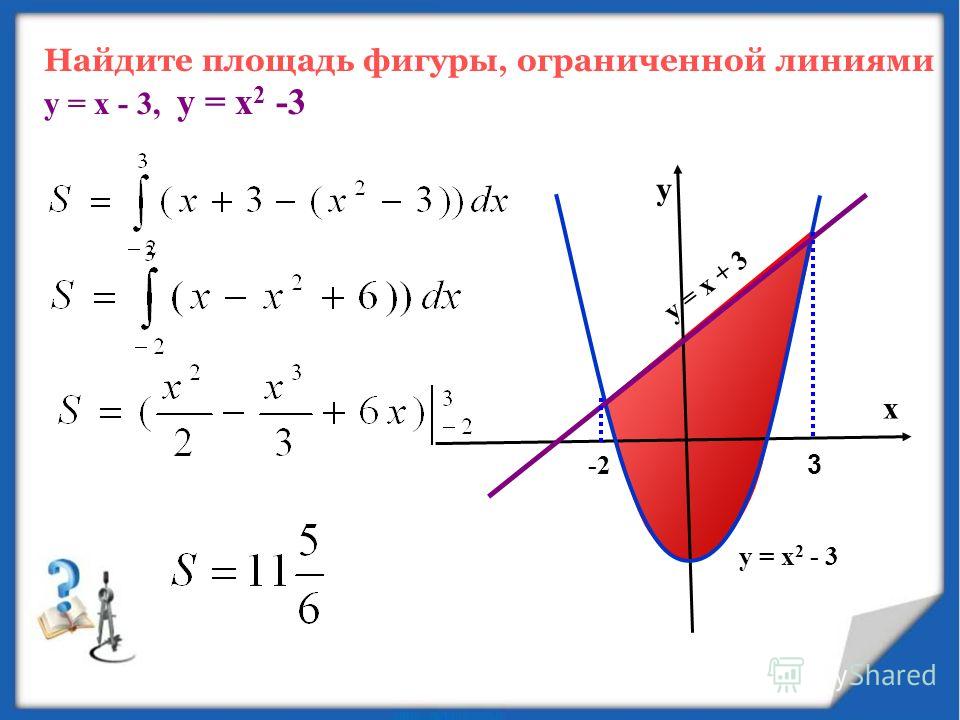 Непрерывные диаграммы не поддерживают агрегацию или группировку. непрерывный
график был бы полезен для визуализации цен закрытия акций с течением времени,
если предположить, что каждая цена закрытия исходит из отдельного документа в
набор данных.
Непрерывные диаграммы не поддерживают агрегацию или группировку. непрерывный
график был бы полезен для визуализации цен закрытия акций с течением времени,
если предположить, что каждая цена закрытия исходит из отдельного документа в
набор данных.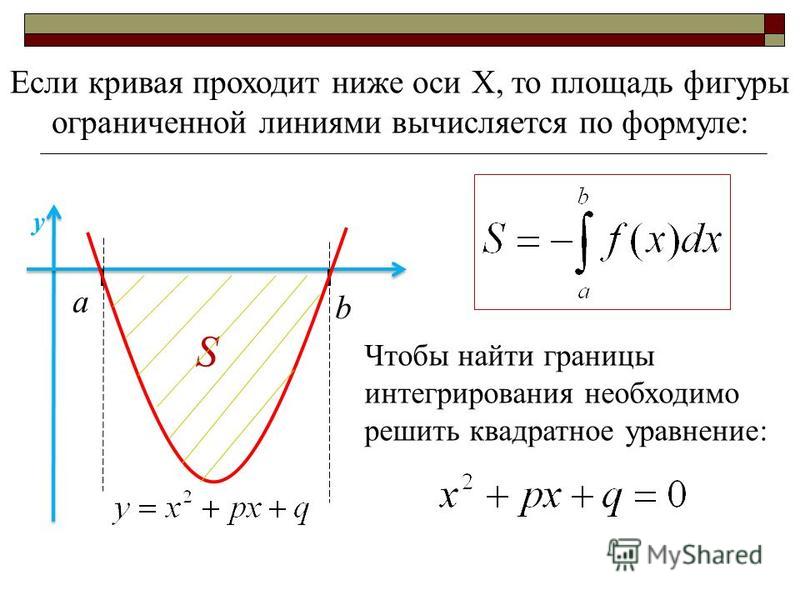

 Чтобы просмотреть все доступные параметры настройки, см.
Настроить диаграммы.
Чтобы просмотреть все доступные параметры настройки, см.
Настроить диаграммы.

 параметр.
параметр. Полученный файл ‘с потерями’ означает, что качество уже не может быть восстановлено. Этот формат часто используется в цифровых картах памяти камер. Файл JPG – отличный формат, так как нередко удается сжимать файлы до 1/10 размера исходного файла, что особенно хорошо для экономии трафика.
Полученный файл ‘с потерями’ означает, что качество уже не может быть восстановлено. Этот формат часто используется в цифровых картах памяти камер. Файл JPG – отличный формат, так как нередко удается сжимать файлы до 1/10 размера исходного файла, что особенно хорошо для экономии трафика. Может быть достигнута пропорция сжатия 100:1, хотя на этом уровне потери качества становятся заметны. Пропорции сжатия 10:1 или 20:01 дают незначительное ухудшение качества изображения.
Может быть достигнута пропорция сжатия 100:1, хотя на этом уровне потери качества становятся заметны. Пропорции сжатия 10:1 или 20:01 дают незначительное ухудшение качества изображения. doc
doc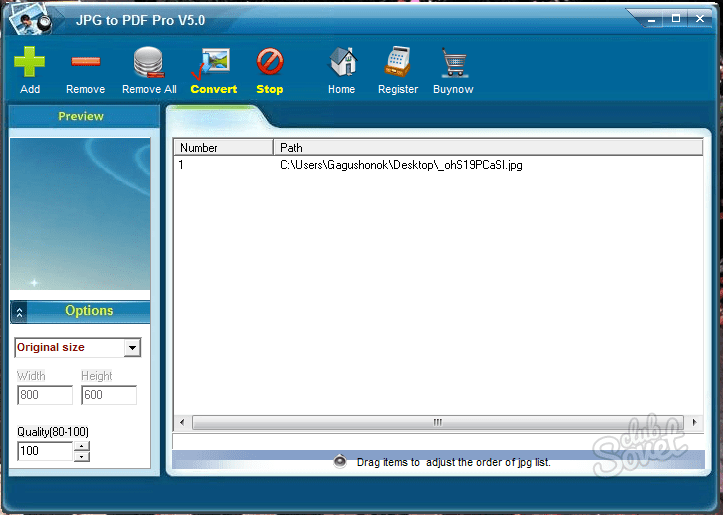 DOC файлы могут также содержать информацию о слиянии, что позволяет шаблону обработки слов быть использованным в сочетании с таблицей или базой данных.
DOC файлы могут также содержать информацию о слиянии, что позволяет шаблону обработки слов быть использованным в сочетании с таблицей или базой данных. Вы можете выполнить шаги, указанные ниже, чтобы Конвертировать JPG в Word.
Вы можете выполнить шаги, указанные ниже, чтобы Конвертировать JPG в Word.

 Наш конвертер JPG в Doc — это веб-сервис, совместимый со всеми операционными системами и устройствами. Вы не заметите никакой разницы в качестве или производительности этого инструмента, независимо от того, какое устройство вы используете.
Наш конвертер JPG в Doc — это веб-сервис, совместимый со всеми операционными системами и устройствами. Вы не заметите никакой разницы в качестве или производительности этого инструмента, независимо от того, какое устройство вы используете. DupliChecker предлагает самую безопасную платформу для всех, поскольку она не ставит под угрозу конфиденциальность пользователей. Базы данных конвертера JPG в Doc на нашем веб-сайте разработаны таким образом, что никакие данные пользователей не сохраняются после завершения конвертации. Вам больше не нужно беспокоиться о секретности важных файлов, поскольку наш онлайн-инструмент предлагает вам высший уровень безопасности для преобразования изображений JPG в Word.
DupliChecker предлагает самую безопасную платформу для всех, поскольку она не ставит под угрозу конфиденциальность пользователей. Базы данных конвертера JPG в Doc на нашем веб-сайте разработаны таким образом, что никакие данные пользователей не сохраняются после завершения конвертации. Вам больше не нужно беспокоиться о секретности важных файлов, поскольку наш онлайн-инструмент предлагает вам высший уровень безопасности для преобразования изображений JPG в Word. Мощный бесплатный онлайн JPG в Word конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мощный бесплатный онлайн JPG в Word конвертер документов легко. Установка программного обеспечения для настольных ПК, таких как Microsoft Word, OpenOffice или Adobe Acrobat, не требуется. Все конверсии вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. 
 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать. Никто не имеет доступа к вашим файлам. Преобразование файлов (включая JPG в WORD) абсолютно безопасно.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать. Никто не имеет доступа к вашим файлам. Преобразование файлов (включая JPG в WORD) абсолютно безопасно.
 Пожалуйста, смотрите полный список ниже.
Пожалуйста, смотрите полный список ниже. По функционалу они немного отличаются. Загрузите изображение в формате JPG или JPEG на сайт, используя окно загрузки.
По функционалу они немного отличаются. Загрузите изображение в формате JPG или JPEG на сайт, используя окно загрузки.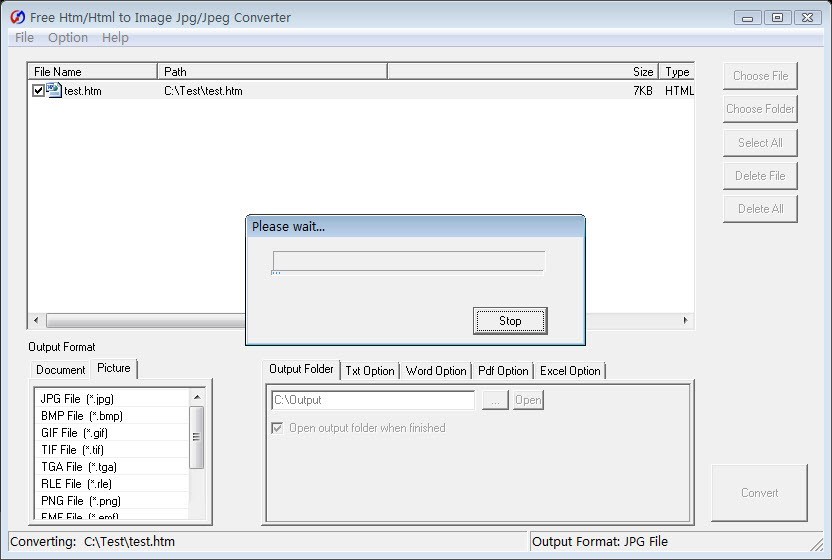 Сегодня нет необходимости перепечатывать существующий текст, тратя это драгоценное время. С этой работой помогают справиться многофункциональные устройства, которые выполняют ее в несколько этапов, избавляя человека от этой утомительной процедуры. Программное распознавание отсканированного текста и изображений позволяет быстро преобразовывать графические данные в цифровые. Полученные файлы можно редактировать.
Сегодня нет необходимости перепечатывать существующий текст, тратя это драгоценное время. С этой работой помогают справиться многофункциональные устройства, которые выполняют ее в несколько этапов, избавляя человека от этой утомительной процедуры. Программное распознавание отсканированного текста и изображений позволяет быстро преобразовывать графические данные в цифровые. Полученные файлы можно редактировать. 
 п. Работа с этими ресурсами действительно очень проста даже для тех, кто не совсем разбирается в вычислениях и новых технологиях, что позволяет конвертировать JPG в Word за очень короткое время.
п. Работа с этими ресурсами действительно очень проста даже для тех, кто не совсем разбирается в вычислениях и новых технологиях, что позволяет конвертировать JPG в Word за очень короткое время. Служба имеет ограничение нагрузки в 100 МБ и позволяет одновременно работать только с одним элементом, но, с другой стороны, предлагает расширенные возможности для изменения свойств преобразованных элементов. Таким образом, попробуйте прямо сейчас, и вы увидите, что вы не пожалеете об этом.
Служба имеет ограничение нагрузки в 100 МБ и позволяет одновременно работать только с одним элементом, но, с другой стороны, предлагает расширенные возможности для изменения свойств преобразованных элементов. Таким образом, попробуйте прямо сейчас, и вы увидите, что вы не пожалеете об этом. Если рассматриваемый файл находится в сети, вы можете указать URL копируя его из адресной строки веб-браузер и ударил его в поле Или введите URL-адрес файла, который вы хотите преобразовать в DOC:, При желании вы также можете конвертировать JPG в Word, выбрав исходный файл Dropbox, просто нажав кнопку Выберите из Dropbox и выбор элемента для действия.
Если рассматриваемый файл находится в сети, вы можете указать URL копируя его из адресной строки веб-браузер и ударил его в поле Или введите URL-адрес файла, который вы хотите преобразовать в DOC:, При желании вы также можете конвертировать JPG в Word, выбрав исходный файл Dropbox, просто нажав кнопку Выберите из Dropbox и выбор элемента для действия.
 Вы получите электронное письмо от ZamZar, содержащее ссылки для бесплатной загрузки ваших документов.
Вы получите электронное письмо от ZamZar, содержащее ссылки для бесплатной загрузки ваших документов. Затем укажите формат, в который вы хотите конвертировать файл JPG. Microsoft Word (DOCX).
Затем укажите формат, в который вы хотите конвертировать файл JPG. Microsoft Word (DOCX).
 По окончании регистрации (вы можете быстро пройти аутентификацию с Facebook, Google или Microsoft) снимите отметку с записи Да, мне нужны письма от новости. (чтобы не получать рассылку от ABBYY) и сначала нажмите кнопку Подтверждать а потом об этом reconocer начать конвертацию документа.
По окончании регистрации (вы можете быстро пройти аутентификацию с Facebook, Google или Microsoft) снимите отметку с записи Да, мне нужны письма от новости. (чтобы не получать рассылку от ABBYY) и сначала нажмите кнопку Подтверждать а потом об этом reconocer начать конвертацию документа. Есть программное обеспечение для Windows и MacOS, как бесплатное, так и платное. Все они очень просты в использовании, не волнуйтесь! Вам просто нужно выбрать то, что, по вашему мнению, может для вас больше всего, и загрузить его на свой компьютер, и все готово.
Есть программное обеспечение для Windows и MacOS, как бесплатное, так и платное. Все они очень просты в использовании, не волнуйтесь! Вам просто нужно выбрать то, что, по вашему мнению, может для вас больше всего, и загрузить его на свой компьютер, и все готово.
 Вам может показаться трудным и трудоемким редактировать файл JPG, но когда он преобразован в Word, редактирование становится простым.
Вам может показаться трудным и трудоемким редактировать файл JPG, но когда он преобразован в Word, редактирование становится простым.
 Многие бесплатные инструменты допускают только ограниченное количество конверсий за определенный период времени. С другой стороны, наш онлайн-конвертер JPG в Word предоставляет неограниченное количество конверсий для всех.
Многие бесплатные инструменты допускают только ограниченное количество конверсий за определенный период времени. С другой стороны, наш онлайн-конвертер JPG в Word предоставляет неограниченное количество конверсий для всех. Для преобразования файла JPG в формат Doc на нашем веб-сайте пользователям не нужно регистрироваться или создавать учетную запись.
Для преобразования файла JPG в формат Doc на нашем веб-сайте пользователям не нужно регистрироваться или создавать учетную запись. DupliChecker предлагает самую безопасную платформу для всех, поскольку она не ставит под угрозу конфиденциальность пользователей. Базы данных конвертера JPG в Doc на нашем сайте разработаны таким образом, что никакие данные пользователей не сохраняются после завершения конвертации. Вам больше не нужно беспокоиться о секретности важных файлов, так как наш онлайн-инструмент предлагает вам высочайший уровень безопасности для преобразования файлов JPG в Word.
DupliChecker предлагает самую безопасную платформу для всех, поскольку она не ставит под угрозу конфиденциальность пользователей. Базы данных конвертера JPG в Doc на нашем сайте разработаны таким образом, что никакие данные пользователей не сохраняются после завершения конвертации. Вам больше не нужно беспокоиться о секретности важных файлов, так как наш онлайн-инструмент предлагает вам высочайший уровень безопасности для преобразования файлов JPG в Word. Мощный бесплатный онлайн-конвертер документов JPG в Word очень прост. Не требуется установка программного обеспечения для настольных компьютеров, такого как Microsoft Word, OpenOffice или Adobe Acrobat. Все конвертации вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный.
Мощный бесплатный онлайн-конвертер документов JPG в Word очень прост. Не требуется установка программного обеспечения для настольных компьютеров, такого как Microsoft Word, OpenOffice или Adobe Acrobat. Все конвертации вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. 
 Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать по истечении этого периода времени. Никто не имеет доступа к вашим файлам. Преобразование файлов (в том числе JPG в WORD) абсолютно безопасно.
Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать по истечении этого периода времени. Никто не имеет доступа к вашим файлам. Преобразование файлов (в том числе JPG в WORD) абсолютно безопасно.
 Загрузите изображение в формате JPG или JPEG на сайт с помощью окна загрузки.
Загрузите изображение в формате JPG или JPEG на сайт с помощью окна загрузки. Сегодня нет необходимости перепечатывать существующий текст, тратя на это драгоценное время. Справиться с этой работой помогают многофункциональные устройства, которые выполняют ее в несколько этапов, освобождая человека от этой утомительной процедуры. Программное распознавание отсканированного текста и изображений позволяет быстро преобразовывать графические данные в цифровые. Полученные файлы можно редактировать.
Сегодня нет необходимости перепечатывать существующий текст, тратя на это драгоценное время. Справиться с этой работой помогают многофункциональные устройства, которые выполняют ее в несколько этапов, освобождая человека от этой утомительной процедуры. Программное распознавание отсканированного текста и изображений позволяет быстро преобразовывать графические данные в цифровые. Полученные файлы можно редактировать. 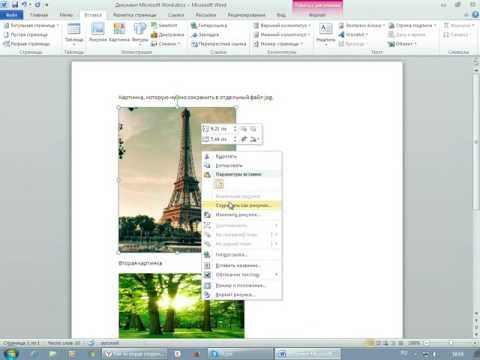

 0(
0( 0 (
0 (
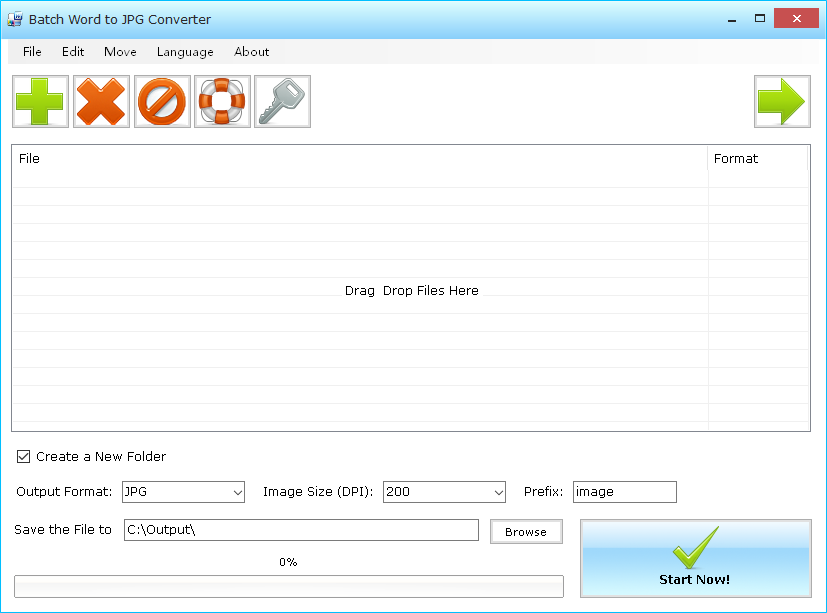 0(
0( 0(
0( ..Меньше
..Меньше

 В диалоговом окне Выберите изображение выберите поле Ссылка на файл .
В диалоговом окне Выберите изображение выберите поле Ссылка на файл .

 Если вы не вносили никаких изменений в настройки браузера по умолчанию, документ будет сохранен в папке Скачать Компьютер.
Если вы не вносили никаких изменений в настройки браузера по умолчанию, документ будет сохранен в папке Скачать Компьютер.
 Если, с другой стороны, в документе есть ошибки, используйте соответствующее поле на экране, чтобы внести все необходимые изменения, прежде чем продолжить загрузку.
Если, с другой стороны, в документе есть ошибки, используйте соответствующее поле на экране, чтобы внести все необходимые изменения, прежде чем продолжить загрузку. При желании вы также можете выбрать файлы, с которыми хотите работать, перетащив их прямо в окно браузера в соответствии с формулировкой или перетащив файлы . Если файл, который необходимо преобразовать, уже находится в сети, просто нажмите на вкладку URL Converter 9.0015 и введите его веб-адрес в отображаемое поле, чтобы загрузить его в службу.
При желании вы также можете выбрать файлы, с которыми хотите работать, перетащив их прямо в окно браузера в соответствии с формулировкой или перетащив файлы . Если файл, который необходимо преобразовать, уже находится в сети, просто нажмите на вкладку URL Converter 9.0015 и введите его веб-адрес в отображаемое поле, чтобы загрузить его в службу. Как? По почте! На самом деле вам просто нужно создать новое сообщение электронной почты с файлами, которые нужно преобразовать в качестве вложений, и отправить его на адрес [doc] @ zamzar.com или [docx] @ zamzar.com (на основе тип файла Word, в который вы хотите преобразовать документы). Через несколько минут вы получите электронное письмо со ссылкой для загрузки преобразованных документов. Удобнее, чем это?
Как? По почте! На самом деле вам просто нужно создать новое сообщение электронной почты с файлами, которые нужно преобразовать в качестве вложений, и отправить его на адрес [doc] @ zamzar.com или [docx] @ zamzar.com (на основе тип файла Word, в который вы хотите преобразовать документы). Через несколько минут вы получите электронное письмо со ссылкой для загрузки преобразованных документов. Удобнее, чем это?
 Затем нажмите кнопку Сканировать , расположенную в левом верхнем углу панели инструментов программы, чтобы начать сканирование документа.
Затем нажмите кнопку Сканировать , расположенную в левом верхнем углу панели инструментов программы, чтобы начать сканирование документа.