Как правильно объяснить ребёнку деление в столбик. Деление в столбик 648 разделить на 6 в столбик объяснение
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
- В 2-5 раз лучше запоминать тексты, лица, цифры, слова
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Для деления чисел из двух и более цифр (знаков) применяют деление в столбик .
По традиции, разбираться как делить столбиком будем на примере.
Вычислить:
Для начала запишем делимое и делитель в столбик. Выглядеть это будет так:
Их частное (результат) будем записывать под делителем. У нас это цифра «8
».
Начинаем делить «512
» на «8
» следующим образом:
- Определяем неполное частное . Для этого слева направо
сравниваем
цифры делимого и делитель.
Берём «5
».
Цифра «5
» меньше «8
», значит нужно взять еще одну цифру из делимого.
- «51
» больше «8
». Значит это неполное частное. Ставим точку в частном (под уголком делителя).
Запомните!
Для того, чтобы избежать ошибок, не забывайте определять количество цифр в частном.
Для этого посчитаем сколько цифр осталось в делимом, после неполного частного. У нас
после «51
» стоит только одно цифра
«2
». Значит и добавляем в результат ещё одну точку.
- Приступаем к делению. Вспоминая таблицу умножения на
«8
», находим ближайшее к
«51
» произведение.
«6 · 8 = 48
»
Записываем цифру «6
» в частное.Записываем «48
» под «51
».
Запомните!
При записи под неполном частным самая правая цифра неполного
частного должна стоять над самой правой цифрой произведения.
Между «51
» и «48
» слева поставим «−
» (минус). Вычтем по правилам
вычитания в столбик «48
» и под чертой запишем результат.
- В остатке получилось «3
».
Сравним остаток с делителем. «3
» меньше «8
».
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Математика. Деление уголком | Сайт Леонида Некина
Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
648 / 2.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
648 =
6 ∙ 100 + 4 ∙ 10 + 8 =
3 ∙ 2 ∙ 100 + 2 ∙ 2 ∙ 10 + 4 ∙ 2 =
( 3 ∙ 100 + 2 ∙ 10 + 4 ) ∙ 2 =
324 ∙ 2 .
После этого становится очевидно, что частное от деления равно
648 / 2 = 324.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:
156 / 2 = ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
156 =
15 ∙ 10 + 6 .
Поскольку число 15 не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
15 = 7 ∙ 2 + 1 = 14 + 1 .
Теперь мы можем продолжать расписывать наше делимое дальше:
156 =
15 ∙ 10 + 6 =
( 14 + 1 ) ∙ 10 + 6 =
14 ∙ 10 + 1 ∙ 10 + 6 =
14 ∙ 10 + 16 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 =
( 7 ∙ 10 + 8 ) ∙ 2 =
78 ∙ 2 .
Отсюда моментально получаем ответ:
156 / 2 = 78.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:
При делении первых двух разрядов ( 15 ) на двойку получается 7 плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
Умножаем на эту семерку наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ):
Теперь настало время вычислить остаток от деления 15-ти на 2 . Он равен, очевидно,
15 − 2 ∙ 7 = 15 − 14 .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:
У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:
В результате такого приписывания у нас получается число 16 . Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого:
Вычитаем последнюю строку из предпоследней и получаем 0:
1 | 5 | 6 | 2 | |
1 | 4 | | 7 | 8 |
| 1 | 6 | | |
| 1 | 6 | | |
| | 0 | | |
Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
156 : 2 = 78 (ост. 0).
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
157 : 2 = 78 (ост. 1).
Таблица для этого примера выглядит так:
1 | 5 | 7 | 2 | |
1 | 4 | | 7 | 8 |
| 1 | 7 | | |
| 1 | 6 | | |
| | 1 | | |
Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:
157 =
14 ∙ 10 + 17 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 + 1 =
( 7 ∙ 10 + 8 ) ∙ 2 + 1 =
7 8 ∙ 2 + 1
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
135674 : 259 = ?
Приступаем к заполнению таблицы:
В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
1356 : 259 = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
1356 / 259 ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 = 5 .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
1356 : 259 = 5 (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 | | | | | | |
259 ∙ 5 = | 1 | 2 | 9 | 5 | | | 5 | | |
Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 | | | | | | |
259 ∙ 5 = | 1 | 2 | 9 | 5 | | | 5 | | |
| | | 6 | 1 | | | | | |
Внимательно приглядимся к полученной разности ( 61 ). Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
1356 : 259 = 5 (ост. 61 ).
Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 | | | | | | |
259 ∙ 5 = | 1 | 2 | 9 | 5 | | | 5 | 2 | 3 |
| | | 6 | 1 | 7 | | | | |
| | | 1 | 1 | | | | | |
259 ∙ 2 = | | | 5 | 1 | 8 | | | | |
| | | | 9 | 9 | 4 | | | |
| | | | 1 | 2 | | | | |
259 ∙ 3 = | | | | 7 | 7 | 7 | | | |
| | | | 2 | 1 | 7 | | | |
Можно выписывать окончательный ответ:
135674 : 259 = 523 (ост. 217).
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:
2 | 6 | 2 | 7 | 4 | 0 | 8 | 7 | | |
2 | 2 | | | | | | | | |
2 | 6 | 1 | | | | 3 | 0 | 2 | 0 |
| | 1 | 7 | 4 | | | | | |
| | 1 | 1 | | | | | | |
| | 1 | 7 | 4 | | | | | |
| | | | 0 | | | | | |
Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf).
Теперь остается только тренироваться, тренироваться и тренироваться.
Из «бесконечного» сборника типовых упражнений
Деление нацело на однозначное число
Деление с остатком на однозначное число
Деление с остатком на однозначное число с возможным «приписыванием» нулей
Деление нацело на двузначное число
Деление с остатком на двузначное число
Деление нацело на трехзначное число
Деление с остатком на трехзначное число
Деление в столбик 648 разделить на 6. Как правильно объяснить ребёнку деление в столбик
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
- То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
- Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Научить ребенка делению столбиком просто. Необходимо объяснить алгоритм этого действия и закрепить пройденный материал.
- Согласно школьной программе, деление столбиком детям начинают объяснять уже в третьем классе. Ученики, которые схватывают все «на лету», быстро понимают эту тему
- Но, если ребенок заболел и пропустил уроки математики, или он не понял тему, тогда родители должны самостоятельно малышу объяснить материал. Нужно максимально доступно донести до него информацию
- Мамы и папы во время учебного процесса ребенка должны быть терпеливыми, проявляя такт по отношению к своему чаду. Ни в коем случае нельзя кричать на ребенка, если у него что-то не получается, ведь так можно отбить у него всю охоту к занятиям
Важно: Чтобы ребенок понял деление чисел, он должен досконально знать таблицу умножения. Если малыш плохо знает умножение, он не поймет деление.
Во время домашних дополнительных занятий можно пользоваться шпаргалками, но ребенок должен выучить таблицу умножения, прежде чем, приступать к теме «Деление».
Итак, как объяснить ребенку деление столбиком :
- Постарайтесь сначала объяснить на маленьких цифрах. Возьмите счетные палочки, например, 8 штук
- Спросите у ребенка, сколько пар в этом ряду палочек? Правильно — 4. Значит, если разделить 8 на 2, получится 4, а при делении 8 на 4 получится 2
- Пусть ребенок сам разделит другое число, например, более сложное: 24:4
- Когда малыш освоил деление простых чисел, тогда можно переходить к делению трехзначных чисел на однозначные
Деление всегда дается детям немного сложнее, чем умножение. Но усердные дополнительные занятия дома помогут малышу понять алгоритм этого действия и не отставать от сверстников в школе.
Начинайте с простого — деление на однозначное число:
Важно: Просчитайте в уме, чтобы деление получилось без остатка, иначе ребенок может запутаться.
Например, 256 разделить на 4:
- Начертите на листе бумаги вертикальную линию и разделите ее с правой части пополам. Слева напишите первую цифру, а справа над чертой вторую
- Спросите у малыша, сколько четверок помещается в двойке — нисколько
- Тогда берем 25. Для наглядности отделите это число сверху уголком. Опять спросите у ребенка, сколько помещается четверок в двадцати пяти? Правильно — шесть. Пишем цифру «6» в правом нижнем углу под линией. Ребенок должен использовать таблицу умножения для правильного ответа
- Запишите под 25 цифру 24, и подчеркните, чтобы записать ответ — 1
- Опять спрашивайте: в единице сколько помещается четверок — нисколько. Тогда сносим к единице цифру «6»
- Получилось 16 — сколько четверок помещается в этом числе? Правильно — 4. Записываем «4» рядом с «6» в ответе
- Под 16 записываем 16, подчеркиваем и получается «0», значит мы разделили правильно и ответ получился «64»
Письменное деление на двузначное число
Когда ребенок освоил деление на однозначное число, можно двигаться дальше. Письменное деление на двузначное число чуть сложнее, но если малыш поймет, как производится это действие, тогда ему не составит труда решать такие примеры.
Важно: Снова начинайте объяснять с простых действий. Ребенок научится правильно подбирать цифры и ему будет легко делить сложные числа.
Выполните вместе такое простое действие: 184:23 — как нужно объяснять:
- Разделим сначала 184 на 20, получается примерно 8. Но мы не пишем цифру 8 в ответ, так как это пробная цифра
- Проверяем, подходит 8 или нет. Умножаем 8 на 23, получается 184 — это именно то число, которое у нас стоит в делителе. Ответ будет 8
Важно: Чтобы ребенок понял, попробуйте вместо восьмерки взять 9, пусть он умножит 9 на 23, получается 207 — это больше, чем у нас в делителе. Цифра 9 нам не подходит.
Так постепенно малыш поймет деление, и ему будет легко делить более сложные числа:
- Разделим 768 на 24. Определите первую цифру частного — делим 76 не на 24, а на 20, получается 3. Записываем 3 в ответ под чертой справа
- Под 76 записываем 72 и проводим линию, записываем разность — получилось 4. Эта цифра делится на 24? Нет — сносим 8, получается 48
- Цифра 48 делится на 24? Правильно — да. Получается 2, записываем эту цифру в ответ
- Получилось 32. Теперь можно проверить — правильно ли мы выполнили действие деления. Сделайте умножение в столбик: 24х32, получается 768, значит все правильно
Если ребенок научился выполнять деление на двузначное число, тогда необходимо перейти к следующей теме. Алгоритм деления на трехзначное число такой же, как и алгоритм деления на двузначное число.
Например:
- Разделим 146064 на 716. Берем сначала 146 — спросите у ребенка делится это число на 716 или нет. Правильно — нет, тогда берем 1460
- Сколько раз число 716 поместится в числе 1460? Правильно — 2, значит пишем эту цифру в ответе
- Умножаем 2 на 716, получается 1432. Записываем эту цифру под 1460. Получается разность 28, записываем под чертой
- Сносим 6. Спросите у ребенка — 286 делится на 716? Правильно — нет, поэтому пишем 0 в ответе рядом с 2. Сносим еще цифру 4
- Делим 2864 на 716. Берем по 3 — мало, по 5 — много, значит получается 4. Умножаем 4 на 716, получается 2864
- Запишите 2864 под 2864, получается в разности 0. Ответ 204
Важно: Для проверки правильности выполнения деления, умножьте вместе с ребенком в столбик — 204х716=146064. Деление выполнено правильно.
Пришло время ребенку объяснить, что деление может быть не только нацело, но и с остатком. Остаток всегда меньше делителя или равен ему.
Деление с остатком следует объяснять на простом примере: 35:8=4 (остаток 3):
- Сколько восьмерок помещается в 35? Правильно — 4. Остается 3
- Делится эта цифра на 8? Правильно — нет. Получается, остаток 3
После этого ребенок должен узнать, что можно продолжать деление, дописывая 0 к цифре 3:
- В ответе стоит цифра 4. После нее пишем запятую, так как добавление нуля говорит о том, что число будет с дробью
- Получилось 30. Делим 30 на 8, получается 3. Записываем в ответ, а под 30 пишем 24, подчеркиваем и пишем 6
- Сносим к цифре 6 цифру 0. Делим 60 на 8. Берем по 7, получается 56. Пишем под 60 и записываем разность 4
- К цифре 4 дописываем 0 и делим на 8, получается 5 — записываем в ответ
- Вычитаем 40 из 40, получается 0. Итак, ответ: 35:8=4,375
Совет: Если ребенок что-то не понял — не злитесь. Пусть пройдет пару дней и снова постарайтесь объяснить материал.
Уроки математики в школе также будут закреплять знания. Пройдет время и малыш будет быстро и легко решать любые примеры на деление.
Алгоритм деления чисел заключается в следующем:
- Сделать прикидку числа, которое будет стоять в ответе
- Найти первое неполное делимое
- Определить число цифр в частном
- Найти цифры в каждом разряде частного
- Найти остаток (если он есть)
По такому алгоритму выполняется деление как на однозначные числа, так и на любое многозначное число (двузначное, трехзначное, четырехзначное и так далее).
Занимаясь с ребенком, чаще ему задавайте примеры на выполнение прикидки. Он должен быстро в уме подсчитать ответ. Например:
- 1428:42
- 2924:68
- 30296:56
- 136576:64
- 16514:718
Для закрепления результата можно использовать такие игры на деление:
- «Головоломка». Напишите на листе бумаги пять примеров. Только один из них должен быть с правильным ответом.
Условие для ребенка: Среди нескольких примеров, только один решен правильно. Найди его за минуту.
Видео: Игра арифметика для детей сложение вычитание деление умножение
Видео: Развивающий мультфильм Математика Изучение наизусть таблицы умножения и деления на 2
Калькулятор в столбик для Андроид устройств станет замечательным помощником для современных школьников. Программа не только дает правильный ответ на математическое действие, но и наглядно демонстрирует его пошаговое решение. Если же вам нужны более сложные калькуляторы – можете посмотреть или же продвинутый инженерный калькулятор.
Особенности
Главной особенностью программы является уникальность расчета математических операций. Отображение процесса вычислений столбиком дает возможность школьникам более подробно с ним ознакомиться, понять алгоритм решения, а не просто получить готовый результат и переписать его в тетрадь. Эта особенность имеет огромное преимущество перед другими калькуляторами, т.к. достаточно часто в школе учителя требуют расписать промежуточные вычисления, чтобы удостовериться, что школьник производит их в уме и действительно понимает алгоритм решения задач. Кстати, у нас есть еще одна программа похожего рода – .
Чтобы начать пользоваться программой, необходимо скачать калькулятор в столбик на Андроид. Сделать это можно на нашем сайте абсолютно бесплатно без дополнительных регистраций и смс. После установки откроется главная страница в виде тетрадного листа в клетку, на котором, собственно, и будут отображаться результаты вычислений и их подробное решение. Внизу располагается панель с кнопками:
- Цифры.
- Знаки арифметических действий.
- Удаление раннее введенных символов.
Ввод осуществляется по тому же принципу, что и на . Все отличие состоит только в интерфейсе приложения – все математические вычисления и их результат отображаются в виртуальной ученической тетради.
Приложение позволяет быстро и правильно выполнить стандартные для школьника математические вычисления столбиком:
- умножение;
- деление;
- сложение;
- вычитание.
Приятным дополнением в приложении является функция ежедневного напоминания о домашнем задании по математике. Хотите – делайте домашки. Для ее включения следует зайти в настройки (нажать кнопку в виде шестеренки) и установить галочку о напоминании.
Достоинства и недостатки
- Помогает школьнику не просто быстро получить правильный результат математических вычислений, но и понять сам принцип расчета.
- Очень простой, интуитивно понятный интерфейс для каждого пользователя.
- Установить приложение можно даже на самое бюджетное Андроид устройство с операционной системой 2.2 и более поздней версией.
- Калькулятор сохраняет историю проведенных математических вычислений, которую можно в любой момент очистить.
Калькулятор ограничен в математических операциях, поэтому применить его для сложных расчетов, с какими мог бы справиться инженерный калькулятор, не получится. Однако учитывая назначение самого приложения – наглядно продемонстрировать учащимся младшей школы принцип расчета в столбик, считать это недостатком не стоит.
Приложение также станет отличным помощником не только для школьников, но и для родителей, которые желают заинтересовать своего ребенка математикой и научить его правильно и последовательно производить вычисления. Если Вы уже пользовались приложением Калькулятор в столбик, оставьте свои впечатления ниже в комментариях.
4 класс. Моро. Учебник №1. Ответы к стр. 12
Числа от 1 до 1000
Четыре арифметических действия: сложение, вычитание, умножение, деление
Ответы к стр. 1254. Объясни, как разделили 864 на 4, и проверь деление умножением.
— 864|4 Х 216
8 |216 4
—6 864
4
— 24
24
0
55. Выполни деление и проверку.
— 748|2 Х 374 — 987|3 Х 329
6 |374 2 9 |329 3
—14 748 —8 987
14 6
— 8 —27
8 27
0 0
— 648|4 Х 162 — 756|6 Х 126
4 |162 4 6 |126 6
—24 648 —15 756
24 12
— 8 —36
8 36
0 0
56. Масса ящика с яблоками 12 кг, а масса пустого ящика в 6 раз меньше. Сколько килограммов яблок в этом ящике? Сколько таких ящиков нужно для 100 кг яблок?
1) 12 : 6 = 2 (кг) — масса пустого ящика
2) 12 — 2 = 10 (кг) — яблок в одном ящике ящика
3) 100 : 10 = 10 (ящ.) — для 100 кг яблок
О т в е т: 10 кг яблок в одном ящике; для 100 кг яблок нужно 10 ящиков.
57. Бабушка посадила 20 луковиц тюльпанов, а внучка — в 4 раза меньше. После этого у них осталось 10 луковиц. Сколько луковиц тюльпанов у них было сначала?
1) 20 : 4 = 5 (л.) — посадила внучка
2) 20 + 5 = 25 (л.) — посадили бабушка и внучка
3) 25 + 10 = 35 (л.)
О т в е т: сначала было 35 луковиц тюльпанов.
58. Найди периметр каждого многоугольника в миллиметрах.
№ 1: P = 28 + 23 + 15 + 15 + 40 = 121 (мм)
№ 2: P = 25 + 37 + 46 = 108 (мм)
№ 3: P = 25 • 4 = 100 (мм)
59.
300 — (90 + 70) + (86 — 46) = 180 0 • 8 + 7 = 7
90 : (10 • 9) : (9 : 9) = 1 0 • (8 + 7) = 0
91 : 13 • 7 = 49 84 : (14 • 3) = 2
Вычисли.
— 771|3 — 678|6
6 |257 6 |113
—17 —7
15 6
— 21 —18
21 18
0 0
ГДЗ по математике. Учебник. 4 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 4 класс
4 класс. Моро. Учебник №1. Ответы к стр. 12
3.9 (77.47%) от 79 голосующих
Контрольные работы по математике 4 класс
Просмотр содержимого документа
«КР№1 4кл 2014-2015»
Просмотр содержимого документа
«КР№10 4кл 2014-2015»
Просмотр содержимого документа
«КР№11 4л 2014-2015»
Просмотр содержимого документа
«КР№12 4кл 2014-2015»
Просмотр содержимого документа
«КР№2 4кл 2014-2015»
Просмотр содержимого документа
«КР№3 4кл 2014-2015»
Просмотр содержимого документа
«КР№4 4кл 2014-2015»
Просмотр содержимого документа
«КР№5 4кл 2014-2015»
Просмотр содержимого документа
«КР№6 4кл 2014-2015»
Просмотр содержимого документа
«КР№7 4кл 2014-2015»
Деление в столбик 648 разделить на 6. Как делить десятичные дроби
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|
| 5 | цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- |
| . | точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 |
| + | знак плюс | Сложение чисел (целые, десятичные дроби) |
| — | знак минус | Вычитание чисел (целые, десятичные дроби) |
| ÷ | знак деления | Деление чисел (целые, десятичные дроби) |
| х | знак умножения | Умножение чисел (целые, десятичные дроби) |
| √ | корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 |
| x 2 | возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 |
| 1 / x | дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число |
| % | процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» |
| ( | открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 |
| ) | закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки |
| ± | плюс минус | Меняет знак на противоположный |
| = | равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. |
| ← | удаление символа | Удаляет последний символ |
| С | сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.
Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Вычисление процентов от числа
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта. Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
- Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление натуральных чисел, особенно многозначных, удобно проводить особым методом, который получил название деление столбиком (в столбик) . Также можно встретить название деление уголком . Сразу отметим, что столбиком можно проводить как деление натуральных чисел без остатка , так и деление натуральных чисел с остатком .
В этой статье мы разберемся, как выполняется деление столбиком. Здесь мы поговорим и о правилах записи, и о всех промежуточных вычислениях. Сначала остановимся на делении столбиком многозначного натурального числа на однозначное число. После этого остановимся на случаях, когда и делимое и делитель являются многозначным натуральными числами. Вся теория этой статьи снабжена характерными примерами деления столбиком натуральных чисел с подробными пояснениями хода решения и иллюстрациями.
Навигация по странице.
Правила записи при делении столбиком
Начнем с изучения правил записи делимого, делителя, всех промежуточных выкладок и результатов при делении натуральных чисел столбиком. Сразу скажем, что письменно выполнять деление столбиком удобнее всего на бумаге с клетчатой разлиновкой – так меньше шансов сбиться с нужной строки и столбца.
Сначала в одной строке слева направо записываются делимое и делитель, после чего между записанными числами изображается символ вида . Например, если делимым является число 6 105
, а делителем – 5
5, то их правильная запись при делении в столбик будет такой:
Посмотрите на следующую схему, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком.
Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого, и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места. Например, при делении столбиком натурального числа 614 808
на 51 234
(614 808
– шестизначное число, 51 234
– пятизначное число, разница в количестве знаков в записях равна 6−5=1
) для промежуточных вычислений потребуется меньше места, чем при делении чисел 8 058
и 4
(здесь разница в количестве знаков равна 4−1=3
). Для подтверждения своих слов приводим законченные записи деления столбиком этих натуральных чисел:
Теперь можно переходить непосредственно к процессу деления натуральных чисел столбиком.
Деление столбиком натурального числа на однозначное натуральное число, алгоритм деления столбиком
Понятно, что разделить одно однозначное натуральное число на другое достаточно просто, и делить эти числа в столбик нет причин. Однако будет полезно отработать начальные навыки деления столбиком на этих простых примерах.
Пример.
Пусть нам нужно разделить столбиком 8
на 2
.
Решение.
Конечно, мы можем выполнить деление при помощи таблицы умножения , и сразу записать ответ 8:2=4
.
Но нас интересует, как выполнить деление этих чисел столбиком.
Сначала записываем делимое 8
и делитель 2
так, как того требует метод:
Теперь мы начинаем выяснять, сколько раз делитель содержится в делимом. Для этого мы последовательно умножаем делитель на числа 0
, 1
, 2
, 3
, … до того момента, пока в результате не получим число, равное делимому, (либо число большее, чем делимое, если имеет место деление с остатком). Если мы получаем число равное делимому, то сразу записываем его под делимым, а на место частного записываем число, на которое мы умножали делитель. Если же мы получаем число большее, чем делимое, то под делителем записываем число, вычисленное на предпоследнем шаге, а на место неполного частного записываем число, на которое умножался делитель на предпоследнем шаге.
Поехали: 2·0=0
; 2·1=2
; 2·2=4
; 2·3=6
; 2·4=8
. Мы получили число, равное делимому, поэтому записываем его под делимым, а на место частного записываем число 4
. При этом запись примет следующий вид:
Остался завершающий этап деления однозначных натуральных чисел столбиком. Под числом, записанным под делимым, нужно провести горизонтальную черту, и провести вычитание чисел над этой чертой так, как это делается при вычитании натуральных чисел столбиком . Число, получающееся после вычитания, будет остатком от деления. Если оно равно нулю, то исходные числа разделились без остатка.
В нашем примере получаем
Теперь перед нами законченная запись деления столбиком числа 8
на 2
. Мы видим, что частное 8:2
равно 4
(и остаток равен 0
).
Ответ:
8:2=4
.
Теперь рассмотрим, как осуществляется деление столбиком однозначных натуральных чисел с остатком.
Пример.
Разделим столбиком 7
на 3
.
Решение.
На начальном этапе запись выглядит так:
Начинаем выяснять, сколько раз в делимом содержится делитель. Будем умножать 3
на 0
, 1
, 2
, 3
и т.д. до того момента, пока не получим число равное или большее, чем делимое 7
. Получаем 3·0=07
(при необходимости обращайтесь к статье сравнение натуральных чисел). Под делимым записываем число 6
(оно получено на предпоследнем шаге), а на место неполного частного записываем число 2
(на него проводилось умножение на предпоследнем шаге).
Осталось провести вычитание, и деление столбиком однозначных натуральных чисел 7
и 3
будет завершено.
Таким образом, неполное частное равно 2
, и остаток равен 1
.
Ответ:
7:3=2 (ост. 1)
.
Теперь можно переходить к делению столбиком многозначных натуральных чисел на однозначные натуральные числа.
Сейчас мы разберем алгоритм деления столбиком . На каждом его этапе мы будем приводить результаты, получающиеся при делении многозначного натурального числа 140 288
на однозначное натуральное число 4
. Этот пример выбран не случайно, так как при его решении мы столкнемся со всеми возможными нюансами, сможем подробно разобрать их.
Сначала мы смотрим на первую слева цифру в записи делимого. Если число, определяемое этой цифрой, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого, и работать дальше с числом, определяемым двумя рассматриваемыми цифрами. Для удобства выделим в нашей записи число, с которым мы будем работать.
Первой слева цифрой в записи делимого 140 288
является цифра 1
. Число 1
меньше, чем делитель 4
, поэтому смотрим еще и на следующую слева цифру в записи делимого. При этом видим число 14
, с которым нам и предстоит работать дальше. Выделяем это число в записи делимого.
Следующие пункты со второго по четвертый повторяются циклически, пока деление натуральных чисел столбиком не будет завершено.
Сейчас нам нужно определить, сколько раз делитель содержится в числе, с которым мы работаем (для удобства обозначим это число как x
). Для этого последовательно умножаем делитель на 0
, 1
, 2
, 3
, … до того момента, пока не получим число x
или число больше, чем x
. Когда получается число x
, то мы записываем его под выделенным числом по правилам записи, используемым при вычитании столбиком натуральных чисел. Число, на которое проводилось умножение, записывается на место частного при первом проходе алгоритма (при последующих проходах 2-4
пунктов алгоритма это число записывается правее уже находящихся там чисел). Когда получается число, которое больше числа x
, то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место частного (или правее уже находящихся там чисел) записываем число, на которое проводилось умножение на предпоследнем шаге. (Аналогичные действия мы проводили в двух примерах, разобранных выше).
Умножаем делитель 4
на числа 0
, 1
, 2
, …, пока не получим число, которое равно 14
или больше 14
. Имеем 4·0=014
. Так как на последнем шаге мы получили число 16
, которое больше, чем 14
, то под выделенным числом записываем число 12
, которое получилось на предпоследнем шаге, а на место частного записываем число 3
, так как в предпоследнем пункте умножение проводилось именно на него.
На этом этапе из выделенного числа вычитаем столбиком число, расположенное под ним. Под горизонтальной линией записывается результат вычитания. Однако, если результатом вычитания является нуль, то его не нужно записывать (если только вычитание в этом пункте не является самым последним действием, полностью завершающим процесс деления столбиком). Здесь же для своего контроля не лишним будет сравнить результат вычитания с делителем и убедиться, что он меньше делителя. В противном случае где-то была допущена ошибка.
Нам нужно вычесть столбиком из числа 14
число 12
(для корректности записи нужно не забыть поставить знак «минус» слева от вычитаемых чисел). После завершения этого действия под горизонтальной чертой оказалось число 2
. Теперь проверяем свои вычисления, сравнивая полученное число с делителем. Так как число 2
меньше делителя 4
, то можно спокойно переходить к следующему пункту.
Теперь под горизонтальной чертой справа от находящихся там цифр (или справа от места, где мы не стали записывать нуль) записываем цифру, расположенную в том же столбце в записи делимого. Если же в записи делимого в этом столбце нет цифр, то деление столбиком на этом заканчивается. После этого выделяем число, образовавшееся под горизонтальной чертой, принимаем его в качестве рабочего числа, и повторяем с ним со 2
по 4
пункты алгоритма.
Под горизонтальной чертой справа от уже имеющейся там цифры 2
записываем цифру 0
, так как именно цифра 0
находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой образуется число 20
.
Это число 20
мы выделяем, принимаем в качестве рабочего числа, и повторяем с ним действия второго, третьего и четвертого пунктов алгоритма.
Умножаем делитель 4
на 0
, 1
, 2
, …, пока не получим число 20
или число, которое больше, чем 20
. Имеем 4·0=0
Проводим вычитание столбиком. Так как мы вычитаем равные натуральные числа, то в силу свойства вычитания равных натуральных чисел в результате получаем нуль. Нуль мы не записываем (так как это еще не завершающий этап деления столбиком), но запоминаем место, на котором мы его могли записать (для удобства это место мы отметим черным прямоугольником).
Под горизонтальной линией справа от запомненного места записываем цифру 2
, так как именно она находится в записи делимого 140 288
в этом столбце. Таким образом, под горизонтальной чертой мы имеем число 2
.
Число 2
принимаем за рабочее число, отмечаем его, и нам еще раз придется выполнить действия из 2-4
пунктов алгоритма.
Умножаем делитель на 0
, 1
, 2
и так далее, и сравниваем получающиеся числа с отмеченным числом 2
. Имеем 4·0=02
. Следовательно, под отмеченным числом записываем число 0
(оно было получено на предпоследнем шаге), а на месте частного справа от уже имеющегося там числа записываем число 0
(на 0
мы проводили умножение на предпоследнем шаге).
Выполняем вычитание столбиком, получаем число 2
под горизонтальной чертой. Проверяем себя, сравнивая полученное число с делителем 4
. Так как 2
Под горизонтально чертой справа от числа 2 дописываем цифру 8
(так как она находится в этом столбце в записи делимого 140 288
). Таким образом, под горизонтальной линией оказывается число 28
.
Принимаем это число в качестве рабочего, отмечаем его, и повторяем действия 2-4
пунктов.
Здесь никаких проблем возникнуть не должно, если Вы были внимательны до настоящего момента. Проделав все необходимые действия, получается следующий результат.
Осталось последний раз провести действия из пунктов 2
, 3
, 4
(предоставляем это Вам), после чего получится законченная картина деления натуральных чисел 140 288
и 4
в столбик:
Обратите внимание, что в самой нижней строчке записано число 0
. Если бы это был не последний шаг деления столбиком (то есть, если бы в записи делимого в столбцах справа оставались цифры), то этот нуль мы бы не записывали.
Таким образом, посмотрев на законченную запись деления многозначного натурального числа 140 288
на однозначное натуральное число 4
, мы видим, что частным является число 35 072
, (а остаток от деления равен нулю, он находится в самой нижней строке).
Конечно же, при делении натуральных чисел столбиком Вы не будете настолько подробно описывать все свои действия. Ваши решения будут выглядеть примерно так, как в следующих примерах.
Пример.
Выполните деление в столбик, если делимое равно 7 136
, а делителем является однозначное натуральное число 9
.
Решение.
На первом шаге алгоритма деления натуральных чисел столбиком мы получим запись вида
После выполнения действий из второго, третьего и четвертого пунктов алгоритма запись деления столбиком примет вид
Повторив цикл, будем иметь
Еще один проход дет нам законченную картину деления столбиком натуральных чисел 7 136
и 9
Таким образом, неполное частное равно 792
, а остаток от деления равен 8
.
Ответ:
7 136:9=792 (ост. 8)
.
А этот пример демонстрирует, как должно выглядеть деление в столбик.
Пример.
Разделите натуральное число 7 042 035
на однозначное натуральное число 7
.
Решение.
Удобнее всего выполнить деление столбиком.
Ответ:
7 042 035:7=1 006 005
.
Деление столбиком многозначных натуральных чисел
Поспешим Вас обрадовать: если Вы хорошо усвоили алгоритм деления столбиком из предыдущего пункта этой статьи, то Вы уже почти умеете выполнять деление столбиком многозначных натуральных чисел . Это действительно так, так как со 2
по 4
этапы алгоритма остаются неизменными, а в первом пункте появляются лишь незначительные изменения.
На первом этапе деления в столбик многозначных натуральных чисел нужно смотреть не на первую слева цифру в записи делимого, а на такое их количество, сколько знаков содержится в записи делителя. Если число, определяемое этими цифрами, больше делителя, то в следующем пункте нам предстоит работать с этим числом. Если же это число меньше, чем делитель, то нам нужно добавить к рассмотрению следующую слева цифру в записи делимого. После этого выполняются действия, указанные во 2
, 3
и 4
пункте алгоритма до получения конечного результата.
Осталось лишь посмотреть применение алгоритма деления столбиком многозначных натуральных чисел на практике при решении примеров.
Пример.
Выполним деление столбиком многозначных натуральных чисел 5 562
и 206
.
Решение.
Так как в записи делителя 206
участвуют 3
знака, то смотрим на первые 3
цифры слева в записи делимого 5 562
. Эти цифры соответствуют числу 556
. Так как 556
больше, чем делитель 206
, то число 556
принимаем в качестве рабочего, выделяем его, и переходим к следующему этапу алгоритма.
Теперь умножаем делитель 206
на числа 0
, 1
, 2
, 3
, … до того момента, пока не получим число, которое либо равно 556
, либо больше, чем 556
. Имеем (если умножение выполняется сложно, то лучше выполнять умножение натуральных чисел столбиком): 206·0=0556
. Так как мы получили число, которое больше числа 556
, то под выделенным числом записываем число 412
(оно было получено на предпоследнем шаге), а на место частного записываем число 2
(так как на него проводилось умножение на предпоследнем шаге). Запись деления столбиком принимает следующий вид:
Выполняем вычитание столбиком. Получаем разность 144
, это число меньше делителя, поэтому можно спокойно продолжать выполнение требуемых действий.
Под горизонтальной линией справа от имеющегося там числа записываем цифру 2
, так как она находится в записи делимого 5 562
в этом столбце:
Теперь мы работаем с числом 1 442
, выделяем его, и проходим пункты со второго по четвертый еще раз.
Умножаем делитель 206
на 0
, 1
, 2
, 3
, … до получения числа 1 442
или числа, которое больше, чем 1 442
. Поехали: 206·0=0
Проводим вычитание столбиком, получаем нуль, но сразу его не записываем, а лишь запоминаем его позицию, потому что не знаем, завершается ли на этом деление, или придется еще раз повторять шаги алгоритма:
Теперь мы видим, что под горизонтальную черту правее запомненной позиции мы не можем записать никакого числа, так как в записи делимого в этом столбце нет цифр. Следовательно, на этом деление столбиком закончено, и мы завершаем запись:
- Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
- Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Поручни для инвалидов | Готовые комплекты поручней для инвалидов в ванную и туалет
Обеспечить комфортное передвижение человеку с ограниченными возможностями помогут поручни для инвалидов и пожилых людей, изготовленные с учетом всех основных запросов клиентов. Воспользоваться удобными приспособлениями могут люди любого возраста, пола, которые испытывают проблемы, вызванные нарушениями опорно-двигательного аппарата. Компания «Натеко» предлагает для инвалидов готовые комплекты настенных поручней из нержавеющей стали и ударопрочного пластика.
Виды поручней
Наша компания производит следующие виды поручней:
- для санузла – помогают пользоваться ванной, туалетом, раковиной или душевой кабиной;
- для коридоров – монтируются на стену, помогают передвигаться между помещениями;
- для жилых комнат – прикроватные модели, с помощью которых удобно подниматься с кровати.
У нас можно купить для инвалидов поручни из нержавеющей стали откидные или стационарные.
Продукция выпускается из прочных, надежных материалов. Изделия отличаются конструктивными особенностями, функциональностью, сроком службы. Их можно разделить на три основные категории:
- пластиковые – прочные, легкие, отличаются удобным монтажом, имеют низкую цену. Не всегда способны выдержать высокую нагрузку;
- металлические – прочные, имеют длительный срок службы, выдерживают высокую статическую и динамическую нагрузку, устойчивы к коррозии. Могут устанавливаться на стену или борт ванны;
- вакуумные – срабатывают при нажатии на кнопку, могут устанавливаться в жилых комнатах, коридорах, санузлах. Отличаются высокой стоимостью.
Все виды конструкций обеспечивают возможность самостоятельно подняться, присесть на кровати. Комплект поручней для инвалидов из нержавейки обеспечит уверенность, безопасность, позволит самостоятельно обслуживать себя при решении бытовых нужд.
Особенности поручней
Компания «Натеко» — производитель поручней. Наша продукция соответствует следующим требованиям:
- прочность – конструкции выдерживают высокие нагрузки;
- надежность – перила рассчитаны на динамическое воздействие;
- влагостойкость – продукция предназначена для помещений с высокой влажностью;
- гигиеничность – на поверхности не скапливается грязь, за ней легко ухаживать без применения специальных средств;
- долговечность – срок эксплуатации более 10 лет;
- простой монтаж – удобные, практичные крепления позволяют надежно зафиксировать перила на стене или ванной.
При изготовлении мы учитываем, что конструкция не должна мешать передвижению или создавать опасность получения травмы.
Как выбрать поручни
Предлагаем купить в Москве продукцию для любой комнаты и коридора дома, квартиры. При выборе рекомендуется учитывать размер, форму, используемые материалы. Для крепежных кронштейнов должно быть достаточно свободного места на стене. Опорные приспособления должны фиксировать поручень на удобной высоте. Учитывается исполнение конструкции – выпускаются левосторонние и правосторонние модели.
Вы не знаете, где купить поручни для инвалидов для санузла или ванной? Испытываете затруднения при выборе удобной конструкции? Заполните форму обратной связи и консультанты компании «Натеко» помогут решить все ваши вопросы.
648 разделить на 4 | 648 разделить на 4 с остатком
Ответ на математические задачи Этапы решения
Математические ответы на деление дроби 648/4
6484 = 162
162 = 1620 с точностью до десятых
162 = 162 с точностью до сотых
162 = 162 с точностью до тысячных
= 0 с точностью до десятых
= 0 с точностью до сотых
= 0 с точностью до тысячных
Другие разделы Домашнее задание по математике —
648 делим пополам плюс 20
Домашнее задание ответов: (648/2) + 20 = 344
648 делим пополам плюс 40
Домашнее задание ответов: (648/2) + 40 = 364
648/4 разделить на 2
Ответ: (648/4) ÷ 2 = 81
Домашнее задание
Division Math можно легко решить с помощью этого бесплатного инструмента.Чтобы решить домашнее задание или задание, все, что вам нужно сделать, это ввести значение в соответствующее поле и нажать «вычислить», чтобы получить математические ответы.
Что такое числитель / знаменатель
Числитель: мы называем верхнее число числителем, это число в верхней части имеющейся у вас дроби.
Знаменатель: мы называем нижнее число знаменателем, это целое число внизу, это число, на которое делится.
Шаги преобразования дробей в десятичные
Шаг 1: Найдите число, которое можно умножить на нижнюю часть дроби, чтобы получилось 10, 100, 1000 или любая единица с последующими нулями.
Шаг 2: Умножьте верхнюю и нижнюю части на выбранное вами число.
Шаг 3. Затем запишите только верхнее число, поместив десятичную запятую в правильное место, то есть на один пробел с правой стороны для каждого нуля в нижнем числе.
a / b = c В приведенных выше выражениях a называется делимым, b называется делителем, а c называется частным; в выражении a / b, a также называется числителем, а b также называется знаменателем.
Этот калькулятор дробей также можно использовать для вычисления доли в процентах, скидок на покупки, купонов, жировых отложений, валовой прибыли, потери веса, любви, налогов, увеличения и уменьшения населения, прибыли от продаж.Как только вы знаете значения, определить% легко.
Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты. отправьте электронное письмо в контакт на нашем сайте.
Вперед Назад
% PDF-1.6
%
14765 0 объектов>
эндобдж
xref
14765 379
0000000016 00000 н.
0000010363 00000 п.
0000010500 00000 п.
0000010705 00000 п.
0000010745 00000 п.
0000010801 00000 п.
0000010847 00000 п.
0000010980 00000 п.
0000011042 00000 п.
0000011183 00000 п.
0000011315 00000 п.
0000011452 00000 п.
0000012206 00000 п.
0000012719 00000 п.
0000013347 00000 п.
0000013679 00000 п.
0000013861 00000 п.
0000014045 00000 п.
0000014149 00000 п.
0000014338 00000 п.
0000017060 00000 п.
0000021702 00000 п.
0000021935 00000 п.
0000022159 00000 п.
0000022222 00000 п.
0000022329 00000 п.
0000022419 00000 п.
0000022465 00000 п.
0000022590 00000 н.
0000022701 00000 п.
0000022813 00000 п.
0000022946 00000 п.
0000023065 00000 п.
0000023208 00000 п.
0000023335 00000 п.
0000023462 00000 п.
0000023638 00000 п.
0000023729 00000 п.
0000023830 00000 п.
0000023992 00000 п.
0000024090 00000 п.
0000024276 00000 п.
0000024416 00000 п.
0000024555 00000 п.
0000024722 00000 п.
0000024885 00000 п.
0000025046 00000 п.
0000025209 00000 п.
0000025344 00000 п.
0000025479 00000 п.
0000025643 00000 п.
0000025798 00000 п.
0000025908 00000 н.
0000026077 00000 п.
0000026223 00000 п.
0000026369 00000 п.
0000026529 00000 п.
0000026673 00000 п.
0000026841 00000 п.
0000027055 00000 п.
0000027210 00000 п.
0000027364 00000 н.
0000027529 00000 п.
0000027686 00000 н.
0000027837 00000 н.
0000027996 00000 н.
0000028149 00000 п.
0000028315 00000 п.
0000028486 00000 п.
0000028603 00000 п.
0000028735 00000 п.
0000028887 00000 п.
0000029004 00000 п.
0000029139 00000 п.
0000029291 00000 п.
0000029434 00000 п.
0000029574 00000 п.
0000029727 00000 н.
0000029828 00000 п.
0000029968 00000 н.
0000030116 00000 п.
0000030265 00000 п.
0000030420 00000 п.
0000030579 00000 п.
0000030731 00000 п.
0000030899 00000 п.
0000031060 00000 п.
0000031169 00000 п.
0000031320 00000 н.
0000031498 00000 п.
0000031596 00000 п.
0000031738 00000 п.
0000031897 00000 п.
0000032025 00000 п.
0000032148 00000 п.
0000032249 00000 п.
0000032367 00000 п.
0000032474 00000 п.
0000032590 00000 н.
0000032705 00000 п.
0000032834 00000 п.
0000032950 00000 п.
0000033091 00000 п.
0000033191 00000 п.
0000033325 00000 п.
0000033472 00000 п.
0000033592 00000 п.
0000033717 00000 п.
0000033871 00000 п.
0000034001 00000 п.
0000034092 00000 п.
0000034256 00000 п.
0000034384 00000 п.
0000034538 00000 п.
0000034660 00000 п.
0000034798 00000 п.
0000034968 00000 н.
0000035108 00000 п.
0000035235 00000 п.
0000035370 00000 п.
0000035533 00000 п.
0000035703 00000 п.
0000035880 00000 п.
0000036039 00000 п.
0000036206 00000 п.
0000036352 00000 п.
0000036499 00000 н.
0000036646 00000 п.
0000036760 00000 п.
0000036866 00000 н.
0000036977 00000 п.
0000037137 00000 п.
0000037302 00000 п.
0000037424 00000 п.
0000037558 00000 п.
0000037679 00000 п.
0000037825 00000 п.
0000037974 00000 п.
0000038106 00000 п.
0000038244 00000 п.
0000038383 00000 п.
0000038521 00000 п.
0000038659 00000 п.
0000038764 00000 п.
0000038895 00000 п.
0000039030 00000 н.
0000039152 00000 п.
0000039297 00000 п.
0000039440 00000 п.
0000039586 00000 п.
0000039729 00000 п.
0000039874 00000 п.
0000040016 00000 н.
0000040143 00000 п.
0000040299 00000 п.
0000040470 00000 п.
0000040573 00000 п.
0000040683 00000 п.
0000040810 00000 п.
0000040955 00000 п.
0000041097 00000 п.
0000041253 00000 п.
0000041374 00000 п.
0000041559 00000 п.
0000041701 00000 п.
0000041843 00000 п.
0000042027 00000 н.
0000042195 00000 п.
0000042325 00000 п.
0000042422 00000 п.
0000042536 00000 п.
0000042680 00000 п.
0000042835 00000 п.
0000042955 00000 п.
0000043105 00000 п.
0000043256 00000 п.
0000043385 00000 п.
0000043533 00000 п.
0000043684 00000 п.
0000043831 00000 п.
0000043931 00000 н.
0000044088 00000 п.
0000044208 00000 п.
0000044333 00000 п.
0000044447 00000 п.
0000044580 00000 п.
0000044705 00000 п.
0000044828 00000 п.
0000044950 00000 п.
0000045091 00000 п.
0000045225 00000 п.
0000045341 00000 п.
0000045453 00000 п.
0000045570 00000 п.
0000045681 00000 п.
0000045817 00000 п.
0000045937 00000 п.
0000046071 00000 п.
0000046194 00000 п.
0000046355 00000 п.
0000046476 00000 п.
0000046602 00000 п.
0000046763 00000 н.
0000046875 00000 п.
0000046990 00000 н.
0000047112 00000 п.
0000047278 00000 п.
0000047388 00000 п.
0000047516 00000 п.
0000047651 00000 п.
0000047788 00000 п.
0000047908 00000 н.
0000048032 00000 п.
0000048167 00000 п.
0000048320 00000 н.
0000048445 00000 п.
0000048565 00000 п.
0000048727 00000 н.
0000048897 00000 н.
0000049064 00000 н.
0000049226 00000 п.
0000049396 00000 п.
0000049550 00000 п.
0000049716 00000 п.
0000049874 00000 п.
0000050030 00000 н.
0000050202 00000 п.
0000050312 00000 п.
0000050448 00000 п.
0000050617 00000 п.
0000050768 00000 п.
0000050907 00000 п.
0000051061 00000 п.
0000051183 00000 п.
0000051326 00000 п.
0000051510 00000 п.
0000051666 00000 п.
0000051818 00000 п.
0000051940 00000 п.
0000052085 00000 п.
0000052234 00000 п.
0000052369 00000 п.
0000052496 00000 п.
0000052648 00000 п.
0000052786 00000 п.
0000052937 00000 п.
0000053070 00000 п.
0000053204 00000 п.
0000053357 00000 п.
0000053504 00000 п.
0000053624 00000 п.
0000053748 00000 п.
0000053883 00000 п.
0000053996 00000 п.
0000054130 00000 п.
0000054263 00000 п.
0000054432 00000 п.
0000054563 00000 п.
0000054670 00000 п.
0000054827 00000 н.
0000054925 00000 п.
0000055050 00000 п.
0000055230 00000 п.
0000055361 00000 п.
0000055481 00000 п.
0000055598 00000 п.
0000055762 00000 п.
0000055893 00000 п.
0000056055 00000 п.
0000056154 00000 п.
0000056312 00000 п.
0000056447 00000 п.
0000056599 00000 п.
0000056709 00000 п.
0000056858 00000 н.
0000057098 00000 п.
0000057207 00000 п.
0000057376 00000 п.
0000057522 00000 п.
0000057652 00000 п.
0000057818 00000 п.
0000057922 00000 п.
0000058056 00000 п.
0000058166 00000 п.
0000058323 00000 п.
0000058420 00000 п.
0000058580 00000 п.
0000058726 00000 п.
0000058865 00000 п.
0000059045 00000 п.
0000059193 00000 п.
0000059341 00000 п.
0000059523 00000 п.
0000059693 00000 п.
0000059828 00000 п.
0000059981 00000 п.
0000060105 00000 п.
0000060239 00000 п.
0000060360 00000 п.
0000060525 00000 п.
0000060643 00000 п.
0000060778 00000 п.
0000060903 00000 п.
0000061052 00000 п.
0000061219 00000 п.
0000061379 00000 п.
0000061548 00000 п.
0000061718 00000 п.
0000061864 00000 п.
0000062019 00000 п.
0000062181 00000 п.
0000062329 00000 п.
0000062449 00000 п.
0000062572 00000 п.
0000062690 00000 н.
0000062807 00000 п.
0000062927 00000 н.
0000063050 00000 п.
0000063179 00000 п.
0000063296 00000 н.
0000063414 00000 п.
0000063534 00000 п.
0000063664 00000 п.
0000063804 00000 п.
0000063938 00000 п.
0000064077 00000 п.
0000064207 00000 п.
0000064339 00000 н.
0000064481 00000 п.
0000064633 00000 н.
0000064762 00000 п.
0000064907 00000 н.
0000065054 00000 п.
0000065192 00000 п.
0000065310 00000 п.
0000065428 00000 п.
0000065553 00000 п.
0000065723 00000 п.
0000065817 00000 п.
0000066055 00000 п.
0000066237 00000 п.
0000066362 00000 п.
0000066514 00000 п.
0000066706 00000 п.
0000066907 00000 п.
0000067081 00000 п.
0000067215 00000 п.
0000067351 00000 п.
0000067505 00000 п.
0000067656 00000 п.
0000067844 00000 п.
0000067976 00000 п.
0000068160 00000 п.
0000068302 00000 п. 5Qf; oqXRks? S
Повышенное соотношение возбуждения и ингибирования стабилизирует синапс и возбудимость цепи в четырех моделях мышей для аутизма
Основные особенности
- •
Четыре модели мыши аутизма имеют общее увеличение соотношения ЭИ в сенсорной коре
- •
Изменения соотношения ЭИ действовали для стабилизации синаптической деполяризации и всплеска
- •
Сенсорно-вызванная частота возбуждения in vivo была удивительно нормальной, а иногда и
- •
Эти данные свидетельствуют о том, что изменения соотношения EI являются компенсаторными при аутизме
Резюме
Предполагается, что различные генетические формы аутизма имеют общее увеличение соотношения возбуждения и торможения (EI) в коре головного мозга, вызывая повышенная возбудимость и чрезмерные спайки.Мы проводим систематическую проверку этой гипотезы на 4 моделях мышей ( Fmr1 — / y , Cntnap2 — / — , 16p11.2 del / + , Tsc2 +/− ), уделяя особое внимание соматосенсорной коре. Все мутанты с аутизмом показали пониженное ингибирование с прямой связью в слое 2/3 в сочетании с более умеренным, переменным снижением прямого возбуждения, что привело к общему увеличению отношения проводимости E-I.Несмотря на это, спайк с прямой связью, синаптическая деполяризация и спонтанный спайк были в основном нормальными. Моделирование показало, что изменения проводимости E и I у каждого мутанта были количественно согласованы, чтобы дать стабильную, а не повышенную синаптическую деполяризацию для клеток, близких к порогу спайков. Соответственно, пик, вызванный усами, не увеличивался in vivo , несмотря на обнаруживаемое снижение ингибирования. Таким образом, повышенное отношение E-I является фенотипом общей цепи, но, по-видимому, отражает гомеостатическую стабилизацию синаптического возбуждения, а не стимулирует гипервозбудимость сети при аутизме.
Ключевые слова
EI ratio
кора головного мозга
соматосенсорная кора
возбудимость контура
Fragile X
гомеостаз
аутизм
возбуждение
статьи
торможение
Рекомендуемые статьи
Цитирующие статьи
powerbi — Как разделить каждую строку вычисляемого столбца на сумму другого вычисляемого столбца?
Я не могу правильно определить деление по этим образцам данных:
Расчетный столбец Другой расчет.столбец
48 207
257 370
518 138
489 354
837 478
1 005 648
1 021 2 060
1,463 2,164
2 630 1818
2 993 2358
3 354 3 633
4,332 5,234
4,885 6,108
4,514 6,008
4 356 6 888
4 824 7 382
7 082 5 988
7 498 6 059
4865
4192
3 816
2 851
2 768
2,093
2 207
770
397
149
178
336
167
124
18
Я пытаюсь создать новый вычисляемый столбец.
Для каждой строки я хочу получить значение Расчетный столбец и разделить его на Итого Другой расчет. столбец .
Всего Еще вычисл. столбец = 82826
Это желаемый результат в новом вычисляемом столбце, назовем его % Столбец :
% Столбец
0,000579528167484
0,0031028735
0,006254074807428
.
.
.
ПРИМЕЧАНИЕ — эти 3 столбца: Расчетный столбец , Другой расчетный столбец.столбцы и % Столбцы находятся в одной таблице и представляют собой вычисляемых столбцов .
Я перепробовал множество формул, но ни одна из них не дала желаемого результата. : | Я предполагаю, что это из-за природы вычисляемых столбцов или я не понимаю сути.
Возможно ли это вообще, или я должен пойти другим путем, используя Меру?
Можете пролить свет?
####### РЕДАКТИРОВАТЬ #######
Я собрал образец файла, чтобы помочь отладить это.Вот:
https://drive.google.com/open?id=1r7kiIkwgHnI5GUssJ6KlXBAoeDRISEuC
Как видите:
-
Earned Daily% HARDCODED работает нормально, потому что 82826 жестко запрограммирован в качестве знаменателя. -
Earned Daily% by StelioK и Earned Daily% by Alexis Olson выводят одно и то же неверное значение для деления при использовании формулы СУММ .
Я использую последнюю версию Power BI Desktop, если это важно: Версия: 2.70.5494.701, 64-разрядная версия (июнь 2019 г.)
% PDF-1.5
%
185 0 объект
>
эндобдж
xref
185 30
0000000015 00000 н.
0000001777 00000 н.
0000001869 00000 н.
0000001891 00000 н.
0000002158 00000 п.
0000002448 00000 н.
0000002747 00000 н.
0000003043 00000 н.
0000003334 00000 н.
0000003620 00000 н.
0000003894 00000 н.
0000004170 00000 н.
0000004827 00000 н.
0000005488 00000 н.
0000005621 00000 п.
0000005945 00000 н.
0000006078 00000 н.
0000006555 00000 н.
0000006737 00000 н.
0000006915 00000 н.
0000007088 00000 н.
0000007261 00000 н.
0000008857 00000 н.
0000060773 00000 п.
0000065137 00000 п.
0000071315 00000 п.
0000075586 00000 п.
0000086280 00000 п.
0000086736 00000 п.
0000087355 00000 п.
трейлер
]
>>
startxref
0
%% EOF
186 0 объект
>
эндобдж
187 0 объект
>
эндобдж
188 0 объект
> / XObject> / ProcSet [/ PDF
/ Text / ImageC] >> / Аннотации [195 0 R 194 0 R 193 0 R 192 0 R 191 0 R 190 0 R 189 0 R] >>
эндобдж
189 0 объект
>>>
эндобдж
190 0 объект
>>>
эндобдж
191 0 объект
>>>
эндобдж
192 0 объект
>>>
эндобдж
193 0 объект
>>>
эндобдж
194 0 объект
>>>
эндобдж
195 0 объект
>>>
эндобдж
196 0 объект
>
эндобдж
197 0 объект
>
эндобдж
198 0 объект
>
эндобдж
199 0 объект
> / Вт [1 [160 250
142 219 333 513 680 498 277 275 813 697 716 566 443 852 368 447 371 455 378 395 453 202 407 195 704 458 455 447 283 310 255 446 377
585 384 949]] / FontDescriptor 204 0 R >>
эндобдж
200 0 объект
>
эндобдж
201 0 объект
> / W [1 [190 711
169 405 405 204 286 204 455 476 476 476 476 476 476 476 476 476 269 269 840 613 573 673 709 558532 704 748 322 320 643 550 853 734
546 612 483 705 623 876 406 489 405 497 420 262 438 495 238 239 448 231 753 500 492490 490 324 345 294 487 421 639 399 431 500 208
356 356 546 509 741 1015 485 561]] / FontDescriptor 205 0 R >>
эндобдж
202 0 объект
>
эндобдж
203 0 объект
>
эндобдж
204 0 объект
>
эндобдж
205 0 объект
>
эндобдж
206 0 объект
>
ручей
xXn7} ߯ G (: Hԩ ߗ (yF٦
~ z ~ 4J; a_hLy2JGe? v „> OvViX.* m * & U͏ovM #
Колонна | Игровой клуб, очные виды спорта, чтобы оставаться активными
От восхода до заката перед студентами-спортсменами Дивизиона I стоит задача сбалансировать полную академическую нагрузку с утренними тренировками, тренировками и другими программными мероприятиями. Хотя некоторым студентам, возможно, нравилось быть спортсменом в старшей школе, у них может не быть времени или возможностей, чтобы перенести это на уровень колледжа.
К счастью, у Питта есть множество вариантов, которые позволяют учащимся оставаться активными, не принимая на себя такую же степень приверженности занятиям спортом первого дивизиона.Если вы хотите поиграть на соревнованиях или просто провести время с друзьями, в Pitt нет недостатка в возможностях.
Клубный спорт — это способ, которым учащиеся могут играть организованно и соревновательно, без обязательств на уровне университетской команды. Клубные команды, как правило, имеют атрибуты, похожие на школьные, такие как пробы, тренировки и поездки на игры, но не имеют жестких соревнований и временных затрат, как в университетских видах спорта. Хотя время, затрачиваемое на каждый клубный вид спорта, варьируется, обычно оно включает несколько тренировок в неделю в дополнение к играм, разбросанным в течение семестра.
Клубные команды соревнуются с другими клубными командами из других университетов региона. Питт часто играет в других известных школах региона, например, в университетах штата Пенсильвания, штата Огайо и Роберта Морриса.
Для тех, кто ищет более непринужденную обстановку, очные виды спорта являются еще одним популярным вариантом на территории кампуса. Pitt Campus Recreation предлагает очные виды спорта, такие как корнхол, вышибалы, кикбол, пиклбол и волейбол. Внутренние виды спорта обычно проводятся в одном из многочисленных мест на территории кампуса Питта, а именно в залах Trees и Bellefield.
Лично я, играя в бейсбол более десяти лет, прежде чем поступить в Питт, я знал, что мне будет не хватать участия в легкой атлетике и общего чувства соревнования. К счастью, я быстро обнаружил, что у меня все еще будет возможность участвовать в занятиях, которые мне нравились в старшей школе.
Начало моего опыта с Питтом во время объявленного «Года COVID» было, мягко говоря, интересным. Мои друзья и я изо всех сил пытались найти, чем заняться после уроков или в выходные дни, поэтому мы решили присоединиться к очной лиге вышибалы.
Мы ходили в Trees Hall каждый понедельник и час или около того играли в вышибалу. Это был долгожданный перерыв от обычных занятий и работы, особенно в год, полный ограничений на то, что вы можете делать, и неуверенности в пандемии. Это, безусловно, было одним из ярких моментов моего первого года обучения.
Но клубные и очные виды спорта подходят не всем — у учащихся все еще есть возможности оставаться активными и конкурентоспособными, продолжая посещать уроки и выполнять работу вне учебы.Многочисленные зеленые насаждения и фитнес-центры Питта позволяют студентам работать в своем собственном темпе. Когда погода начинает нагреваться, студенты часто будут сталкиваться со своими сверстниками, которые занимаются спортом, например, игрой в Spikeball, бросая фрисби или бросая футбольный мяч на лужайке у Собора, за пределами Мемориального зала солдат и моряков или в верхней части кампуса.
Доступность Питта к зеленым насаждениям — это то, что мне очень понравилось в первый год. Учитывая ограниченность того, что мы могли делать с социальной точки зрения, выходить на улицу в хороший день никто не считал само собой разумеющимся.Некоторые из моих лучших воспоминаний из прошлого года остались на лужайке у Собора, когда мои друзья играли во что угодно, от Spikeball до Cornhole.
Независимо от того, хотят ли поступающие первокурсники продолжать заниматься любимым спортом или просто оставаться в хорошей физической форме, безусловно, существует широкий спектр вариантов, из которых можно выбирать и строить с учетом желаний и потребностей каждого.
Государственный университет Дакоты по легкой атлетике — Троянский женский баскетбол, похоже, вернется в норму в победной колонке, на этой неделе сыграны две игры
Женский баскетбол — вторник, дек.10, 2019
11 декабря 2019
ПРИМЕЧАНИЯ К ИГРЕ (PDF)
Трансляция в среду: ВИДЕО — ЖИВОЕ АУДИО — СТАТИСТИКА В РЕЖИМЕ
Покрытие в прямом эфире по воскресеньям: ВИДЕО В РЕЖИМЕ — 9 СОСТОЯНИЕ В РЕЖИМЕ 9 Превью на этой неделе
MADISON, SD (10 декабря 2019 г.) — Женская баскетбольная команда Trojan из Университета Дакоты (общий рекорд 2–6) отходит в сторону от своего расписания конференции North Star, продолжая свой непростой график вне конференции.Вечером среды троянцы остаются дома, пока они принимают давнюю соперницу Дакоту Уэслиан (Южная Дакота) (общий рекорд 8: 3). Подсказка назначена на 17:30. в DSU Fieldhouse. Тигры выиграли первую встречу в этом сезоне в Sanford Pentagon в Су-Фолс, Южная Дакота. 2 ноября со счетом 94-74.
DSU отправились в путь в воскресенье вечером, столкнувшись с другим соперником из Атлетической конференции Great Plains. Троянцы отправляются в Центр Ньюмана Фланагана (3303 Rebecca Street) в Су-Сити, штат Айова, чтобы сразиться с Брайар-Клифф (штат Айова) (общий рекорд 2-8) на 6 очках.м. Зарядные устройства выиграли первую встречу ранее в этом сезоне 85-73 на DSU Fieldhouse 28 октября.
Троянцы проиграли пару игр на прошлой неделе, опустившись на 5-ю позицию Дордта (Айова) 90-76 в рейтинге. Road 2 декабря. DSU открыла конференцию North Star с 80-70 неудач на своем поле в Белвью (Небраска) 7 декабря. Дакота Уэслиан сходит с дистанции 100-72 на конференции, заняв первое место в Дивизионе II NAIA. Конкордия (Небраска) 7 декабря. Тигры победили Маунт Марти (SD) 73-42 дома 7 декабря.4. Брайар Клифф проиграл четвертый и пятый игры подряд после проигрыша № 11 Северо-Западного (Айова) 75-56 4 декабря и № 8 Морнингсайд (Айова) 95-56 7 декабря.
Далее: Штат Дакота возвращается в Су-Сити, штат Айова, 18 декабря, когда они сталкиваются с Морнингсайдом № 8 (Айова) в спортзале RVSC-Allee. 20 декабря DSU принимает Стерлинг (Канада) в последней домашней игре 2019 календарного года.
Быстрые хиты этой недели
+ Дакота Стэйт (Южная Дакота) стремится к своей первой победе над соперником Great Plains Athletic Conference в этом сезоне.
+ Дакота Уэслиан (SD) выиграла первую встречу в этом сезоне в 4-м ежегодном NAIA-South Dakota Pentagon Classic 94-74 2 ноября. Тигры выиграли 16 встреч с троянцами, последняя победа DSU ожидается в ноябре. 2, 2010 (78-73 победы на DSU Fieldhouse).
+ DSU — это 2-3 рекорда дома в этом сезоне, а DWU — 2-3 рекорда на выезде. Браяр Клифф (Айова) дома — 1-4 рекорда.
+ Троянцы продолжают занимать 5-е место в NAIA Division II по проценту попаданий с игры до 3-х очков.Дакота Стэйт реализовала 72 из 188 трехочковых бросков с игры, что составляет 38,3 процента.
+ Линдси Фогл лидирует по проценту попаданий с игры 3-х очков перед играми на этой неделе. Она истощила 19 трехочковых в 33 попытках (57,6%). Джесси Джайлз также занимает седьмое место в дивизионе NAIA II с 51,6% попаданий с трехочковой дуги (16 из 31).
+ Штат Дакота стремится к своей первой победе над Брайар Клифф (Айова) с 29 ноября 2008 года.
+ У троянцев осталось семь неконференционных игр в расписании на 2019 год, включая пару игр во Флориде во время зимних каникул.
+ DSU совершат прямые рейсы в Су-Сити, штат Айова, 15 декабря в Брайар-Клифф (штат Айова) и 18 декабря в Морнингсайд (штат Айова).
Примечательно …
ТРОЯНЫ ИЩУТ ПЕРВЫХ ПОБЕД над GPAC: Штат Дакота (Южная Дакота) стремится одержать первые победы над противником Great Plains Athletic Conference в этом сезоне. В последний раз троянцы победили оппонента с конференции GPAC 27 октября 2017 года в матче с колледжем Святой Марии (Небраска) в DSU Fieldhouse.
DSU С ПОЛЯ: Согласно статистическому сайту DakStats-NAIA на вторник, троянские программы занимают 10-е место в стране по проценту попаданий с игры (46,5%). Морган Кёпселл лидирует в команде с 60,3 процентами попаданий с игры (41 из 68), что является седьмым лучшим результатом во втором дивизионе NAIA.
ОСТАВШИЕСЯ ДОМАШНИЕ ИГРЫ В ДЕКАБРЕ: У DSU есть две оставшиеся домашние игры в течение декабря, включая соревнование с соперницей Дакотой Уэслиан (С.D.) в среду. 20 декабря троянцы проводят свою последнюю домашнюю игру в 2019 календарном году Стерлинг (Канада), а 4 января они вернутся домой против Оглала Лакота (Южная Дакота) после поездки во Флориду 30-31 декабря.
ГОРЯЧИЙ СЧЕТ: Дакота Стэйт набрала не менее 70 очков во всех восьми играх этого сезона. Троянцы набирают в среднем 81,0 очка за игру (648 очков), что является 20-м показателем в рейтинге NAIA Division II. Четыре игрока (Джесси Джайлс, Морган Кёпселл, Саванна Уолсдорф, Линдси Фогл) имеют в среднем двузначные числа для DSU.
DSU JUNIOR VARSITY ВЫИГРЫВАЕТ ДОМА: Женская юношеская баскетбольная команда штата Дакота завершает свою часть расписания 2019 года домашней победой 76-71 над Riverland CC (Миннесота) 10 декабря. Троянцы берут зимние каникулы. и продолжат свое домашнее противостояние с пятью играми 13 января против Northwestern (Айова).
Троянцы упорно сражаются, падают в (5) Дордт (Айова)
Сиу-Центр, Айова (2 декабря 2019 г.) — Штат Дакота (SD) вернулся в строй впервые в 20-2020 гг. продолжительность дня в гимназии ДеВитта.«Троянцы» сыграли свой первый выездной поединок в сезоне, столкнувшись с 5-м номером в национальном рейтинге Дордтом (штат Айова). Защитники оторвались от троянцев 90-76.
Дордт удерживал небольшое преимущество 22-20 после первой четверти и увеличил свое преимущество до 42-32 к перерыву. В третьей четверти троянцы разогнали счет 13: 2, что было подчеркнуто трехочковым Сидни Фиком, который вывел DSU вперед 45-44 с 7:05 на часах в третьей. Лидерство DSU было недолгим, поскольку DC ответил счетом 9: 0 и никогда не оглядывался назад, чтобы обеспечить победу.
Четыре троянца записали двузначные числа в игре, Фик и Джесси Джайлз набрали по 14 очков каждый. Линдси Фогл и Морган Кёпселл добавили по 13 очков каждая. Кёпселл сделал шесть подборов и зафиксировал четыре блок-шота на игровом уровне. Эшлин Макдональд и Саванна Уолсдорф сделали по пять подборов.
Дордт бросил 42,5 процента с игры (31 из 73) по сравнению со штатом Дакота — 39,1 процента (25 из 64). Защитники превзошли троянцев 49-38.
Брюинз использует всплеск третьей четверти для победы над троянами
Мэдисон, С.Д. (7 декабря 2019 г.) — Стейт Дакота (Южная Дакота) возглавляла Белвью (Небраска) 33–30 в перерыве в первой встрече женской баскетбольной конференции North Star Athletic Association в DSU Fieldhouse. В третьей четверти «Брюинз» использовали ход 26–14 и отбили троянов со счетом 80–70.
Обе команды изо всех сил пытались стрелять в первые двадцать минут игры: DSU стрелял 30,6% (11 из 36), а BU — 27% с игры (10 из 37). Белвью набрала 61,1% в третьем квартале, обогнав Дакота Стэйт.В заключительной четверти троянцы не смогли набрать больше четырех очков в двух разных случаях.
Морган Кёпселл спровоцировала наступательную атаку «Троянцев», забив рекорд сезона 26 очков с игры 10 из 14 и выполнив все шесть штрафных бросков. Она сделала пять подборов и зафиксировала два блока. Джесси Джайлз прибавила 14 очков и отдал 5 передач. Эшлин Макдональд набрала 12 очков и сделала девять подборов.
Белвью бросил 40 процентов с игры (26 из 65 попаданий с игры) по сравнению с Дакота Стэйт 39.4 процента (26 из 66 попаданий с игры). BU получил 21 из 27 штрафных бросков (77,8 процента), а DSU — 13 из 21 штрафных бросков (61,9 процента). Трояны превзошли Bruins 46-38.
Взгляд вперед на троянский женский баскетбол
Madison, S.D. (10 декабря 2019 г.) — В штате Дакота (Южная Дакота) осталось шесть игр в декабре. В среду троянцы будут дома против Дакоты Уэслиан, занимающей 13-е место в рейтинге.
Планируется, что троянцы совершат поездку в Су-Сити, штат Айова, на две игры подряд, посетив Брайар-Клифф (штат Айова) в воскресенье и No.8-е место в Морнингсайде (Айова) 18 декабря перед возвращением домой 20 декабря против Стерлинга (Канзас).
После игры Стерлинга у штата Дакота будет рождественский перерыв, прежде чем он вернется в бой. Троянцы отправятся во Флориду для пары игр, посетив Webber International (Флорида) 30 декабря и Warner (Флорида) 31 декабря, чтобы завершить свою часть своего расписания на 2019 год.
Штат Дакота будет дома шесть раз в течение Нового года, начиная с 4 января против Оглала Лакота (С.Д.). Планируется, что троянцы проведут свой сезонный домашний бой из пяти игр в DSU Fieldhouse, начав с пары соревнований на конференциях North Star Athletic Association 17-18 января, за которыми последует финал вне конференции против Mount Marty (SD). ) 22 января.
Лидеры женских баскетбольных команд DSU 2019-20
- Очки / Очки за игру: Джесси Джайлз — 15,1 очка за игру (121 общий балл)
- Процент бросков с игры: Морган Кёпселл — 60.3 процента попаданий с игры (41 из 68 попаданий с игры)
- Процент попаданий с игры с 3-мя попаданиями: Линдси Фогл — 57,6% 3-х очковых попаданий с игры (19 из 33 3-х очковых попаданий с игры)
- Бесплатно -Процент бросков: Эшлин Макдональд — 90,0% штрафных бросков (9 из 10 штрафных бросков)
- Подборов / подборов за игру: Морган Кёпселл — 6,5 подбора за игру (52 подбора)
- передач / передач за игру: Джесси Джайлс — 2,4 передачи за игру (19 передач)
- Перехватов / перехватов за игру: Саванна Уолсдорф — 1.

 ..
.. Икс вершины:
Икс вершины: ..
.. ..
..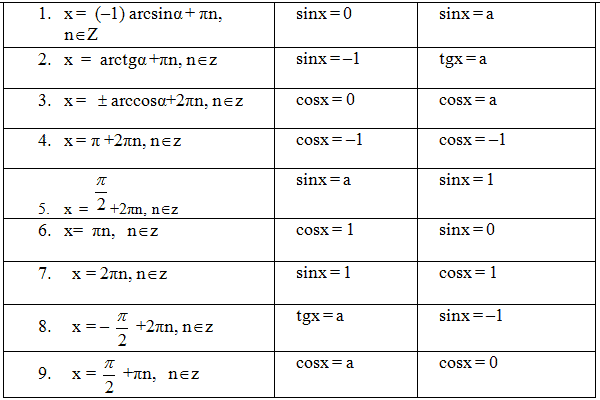 е. в том числе для любых треугольников):
е. в том числе для любых треугольников): ..
.. ..
.. ..Меньше
..Меньше

 Формула также отображается в строке формул вверху окна Excel.
Формула также отображается в строке формул вверху окна Excel. Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.
Например, можно выделить ячейки B7 и C7, нажать кнопку Автосумма и суммировать два столбца одновременно.

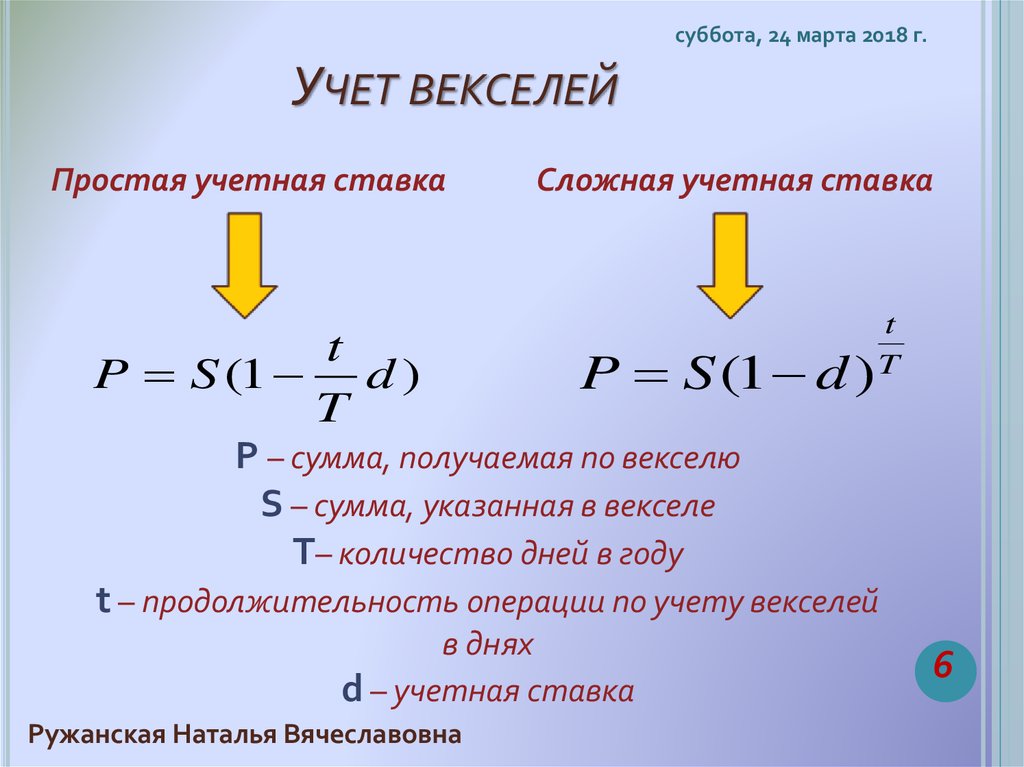 Например, если вам нужно спасти человечество в разгар энергетического кризиса, предотвратить разлив нефти, сохранить шедевр в Лувре или поставить сложный трюк для голливудского блокбастера. В книге «Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций» (издательство «Альпина Паблишер»), переведенной на русский язык Анной Туровской, британский математик Крис Уоринг рассказывает о пользе уравнений на примере не только бытовых, но и экстраординарных событий. Предлагаем вам ознакомиться с фрагментом, посвященным поиску простого числа, состоящего из ста миллионов знаков.
Например, если вам нужно спасти человечество в разгар энергетического кризиса, предотвратить разлив нефти, сохранить шедевр в Лувре или поставить сложный трюк для голливудского блокбастера. В книге «Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций» (издательство «Альпина Паблишер»), переведенной на русский язык Анной Туровской, британский математик Крис Уоринг рассказывает о пользе уравнений на примере не только бытовых, но и экстраординарных событий. Предлагаем вам ознакомиться с фрагментом, посвященным поиску простого числа, состоящего из ста миллионов знаков. Решим поставленную перед нами задачу — докажем состоятельность человечества. От нас требуется найти простое число, состоящее из ста миллионов знаков. За это инопланетяне в подробностях поведают о своих наиболее важных достижениях. Благодаря им мы сумеем свести к нулю выбросы углекислого газа и, остановив таким образом глобальное потепление, спасем собственную планету. Сумеете ли вы обнаружить настолько монструозное число?
Решим поставленную перед нами задачу — докажем состоятельность человечества. От нас требуется найти простое число, состоящее из ста миллионов знаков. За это инопланетяне в подробностях поведают о своих наиболее важных достижениях. Благодаря им мы сумеем свести к нулю выбросы углекислого газа и, остановив таким образом глобальное потепление, спасем собственную планету. Сумеете ли вы обнаружить настолько монструозное число? Первая категория мала: один-единственный делитель есть только у единицы. Вторая категория включает простые числа, которые делятся на нее и на себя. Вот несколько первых простых чисел: 2, 3, 5, 7, 11, 13, 17. Доказано, что существует бесконечное множество простых чисел. Они стоят особняком и могут здорово помочь вам при совершении покупок в интернете (этот момент мы разберем в подробностях чуть позже).
Первая категория мала: один-единственный делитель есть только у единицы. Вторая категория включает простые числа, которые делятся на нее и на себя. Вот несколько первых простых чисел: 2, 3, 5, 7, 11, 13, 17. Доказано, что существует бесконечное множество простых чисел. Они стоят особняком и могут здорово помочь вам при совершении покупок в интернете (этот момент мы разберем в подробностях чуть позже). Каждый из приведенных примеров — уникальный, единственно возможный вариант представления составных чисел при разложении на простые множители. Поэтому мы вправе утверждать, что простые числа — своего рода ДНК всех прочих чисел.
Каждый из приведенных примеров — уникальный, единственно возможный вариант представления составных чисел при разложении на простые множители. Поэтому мы вправе утверждать, что простые числа — своего рода ДНК всех прочих чисел. Переходите к следующему невычеркнутому числу — это будет 3. А затем избавляетесь от невычеркнутых чисел, кратных тройке. Возобновляете процесс: следующее число, которым вы еще не занимались, должно быть простым, в чем вы убедитесь, попытавшись разложить его на меньшие множители.
Переходите к следующему невычеркнутому числу — это будет 3. А затем избавляетесь от невычеркнутых чисел, кратных тройке. Возобновляете процесс: следующее число, которым вы еще не занимались, должно быть простым, в чем вы убедитесь, попытавшись разложить его на меньшие множители. Ну а кому-нибудь еще нужны эти простые числа? Да, нужны. Простые числа используются для шифрования сетевого трафика, а в наши дни без интернета не проживешь.
Ну а кому-нибудь еще нужны эти простые числа? Да, нужны. Простые числа используются для шифрования сетевого трафика, а в наши дни без интернета не проживешь. Именно по этому вы можете быть спокойны, делая покупки в интернете: на страже ваших банковских данных стоят простые числа.
Именно по этому вы можете быть спокойны, делая покупки в интернете: на страже ваших банковских данных стоят простые числа. Есть и другие ухищрения, но даже если вычеркнуть 90 процентов чисел со 100 миллионами знаков, вас тем не менее ждет уйма работы с очень большими числами. Допустим, у вас есть самый мощный в мире компьютер, который проанализирует оставшиеся числа, — но все равно на поиск и проверку нужного числа уйдут долгие годы.
Есть и другие ухищрения, но даже если вычеркнуть 90 процентов чисел со 100 миллионами знаков, вас тем не менее ждет уйма работы с очень большими числами. Допустим, у вас есть самый мощный в мире компьютер, который проанализирует оставшиеся числа, — но все равно на поиск и проверку нужного числа уйдут долгие годы. Достичь хотя бы первого уровня человечеству может помочь антиматерия (подробнее см. главу 18).
Достичь хотя бы первого уровня человечеству может помочь антиматерия (подробнее см. главу 18).
 Это было выявлено в 1903 году, спустя 250 лет после смерти Мерсенна.
Это было выявлено в 1903 году, спустя 250 лет после смерти Мерсенна.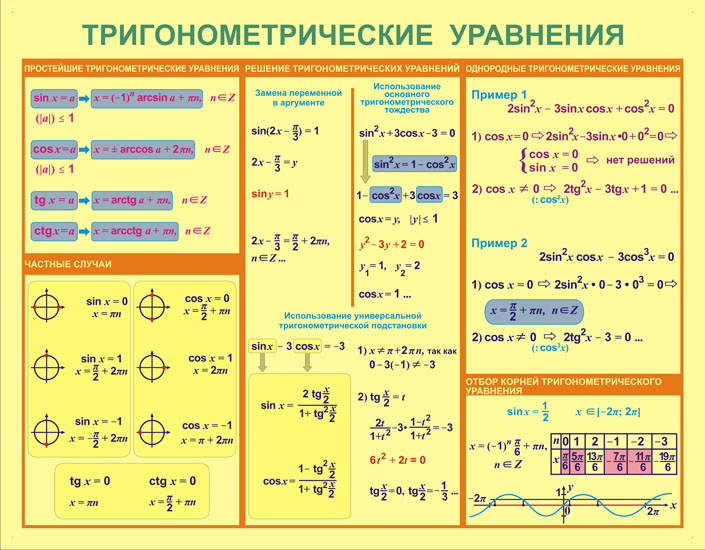
 Но есть одно ухищрение. Возведение в степень — это результат многократного умножения числа на себя. К этой хитрости и прибегнем. 1099999999 — это 10, умноженное само на себя 99 999 999 раз. Будь у вас достаточно времени (и бумаги), вы могли бы записать нужное выражение таким образом:
Но есть одно ухищрение. Возведение в степень — это результат многократного умножения числа на себя. К этой хитрости и прибегнем. 1099999999 — это 10, умноженное само на себя 99 999 999 раз. Будь у вас достаточно времени (и бумаги), вы могли бы записать нужное выражение таким образом: Экспресс-анализ сообщает, что в M31, обнаруженном Леонардом Эйлером в 1772 году (2 147 483 647), уже 10 цифр. Как знать, может, победителем станет M2147483647?
Экспресс-анализ сообщает, что в M31, обнаруженном Леонардом Эйлером в 1772 году (2 147 483 647), уже 10 цифр. Как знать, может, победителем станет M2147483647? Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций / Крис Уоринг : Пер. с англ. [Анны Туровской] — М.: Альпина Паблишер, 2022. — 194 с., ил.
Формулы на все случаи жизни: Как математика помогает выходить из сложных ситуаций / Крис Уоринг : Пер. с англ. [Анны Туровской] — М.: Альпина Паблишер, 2022. — 194 с., ил. Экономистам, чтобы делать перерасчет цен, анализировать показатели компании. Менеджерам — вести базу клиентов. Аналитикам — строить и проверять гипотезы.
Экономистам, чтобы делать перерасчет цен, анализировать показатели компании. Менеджерам — вести базу клиентов. Аналитикам — строить и проверять гипотезы.
 Округляет дробное число до целого в большую или меньшую сторону. Укажите ячейку с нужным числом, в качестве второго значения — 0.
Округляет дробное число до целого в большую или меньшую сторону. Укажите ячейку с нужным числом, в качестве второго значения — 0. Вычисляет квадратный корень числа в ячейке.
Вычисляет квадратный корень числа в ячейке.
 Обычно критерий — числовой промежуток или предел.
Обычно критерий — числовой промежуток или предел.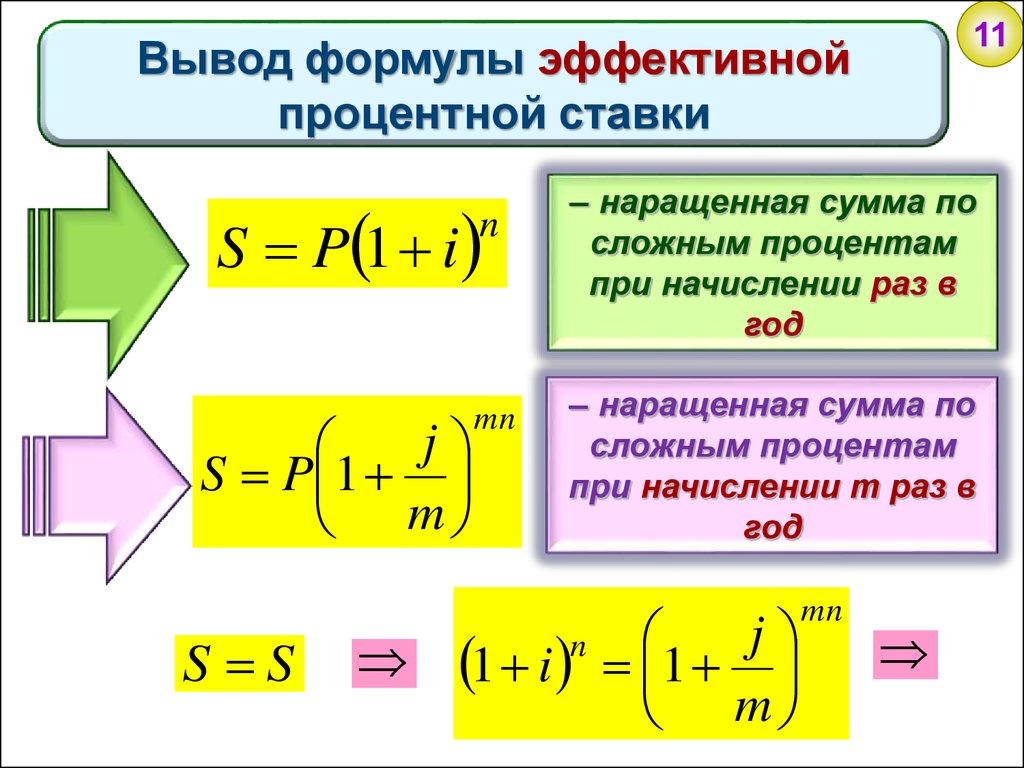 Например, вам нужно найти сумму двух чисел. Если значение больше 65, сумму нужно умножить на 1,5. Если меньше — на 2.
Например, вам нужно найти сумму двух чисел. Если значение больше 65, сумму нужно умножить на 1,5. Если меньше — на 2.
 Чтобы ее вписать, используют символы = ( ) ; : .
Чтобы ее вписать, используют символы = ( ) ; : .
 .. Меньше
.. Меньше

 ..Меньше
..Меньше
 Excel умножает два последних числа и прибавляет к результату первое число.
Excel умножает два последних числа и прибавляет к результату первое число.

 Это связано с тем, что ячейка содержит или равна формуле и вычисляемому ею значению.
Это связано с тем, что ячейка содержит или равна формуле и вычисляемому ею значению.
 Вокруг указанной ячейки появится красная рамка .
Вокруг указанной ячейки появится красная рамка . Формула в ячейке B3 автоматически пересчитает и отобразит новое значение в ячейке B3.
Формула в ячейке B3 автоматически пересчитает и отобразит новое значение в ячейке B3.
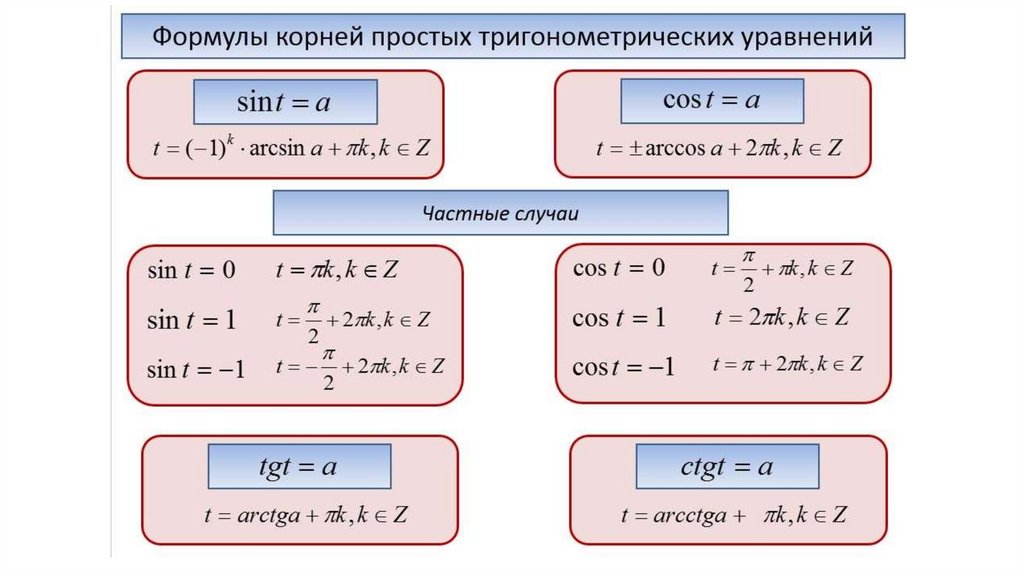 Просмотрите наш урок об относительных и абсолютных ссылках на ячейки, чтобы узнать больше.
Просмотрите наш урок об относительных и абсолютных ссылках на ячейки, чтобы узнать больше.
 Если вы хотите, вы можете использовать нашу рабочую тетрадь.
Если вы хотите, вы можете использовать нашу рабочую тетрадь.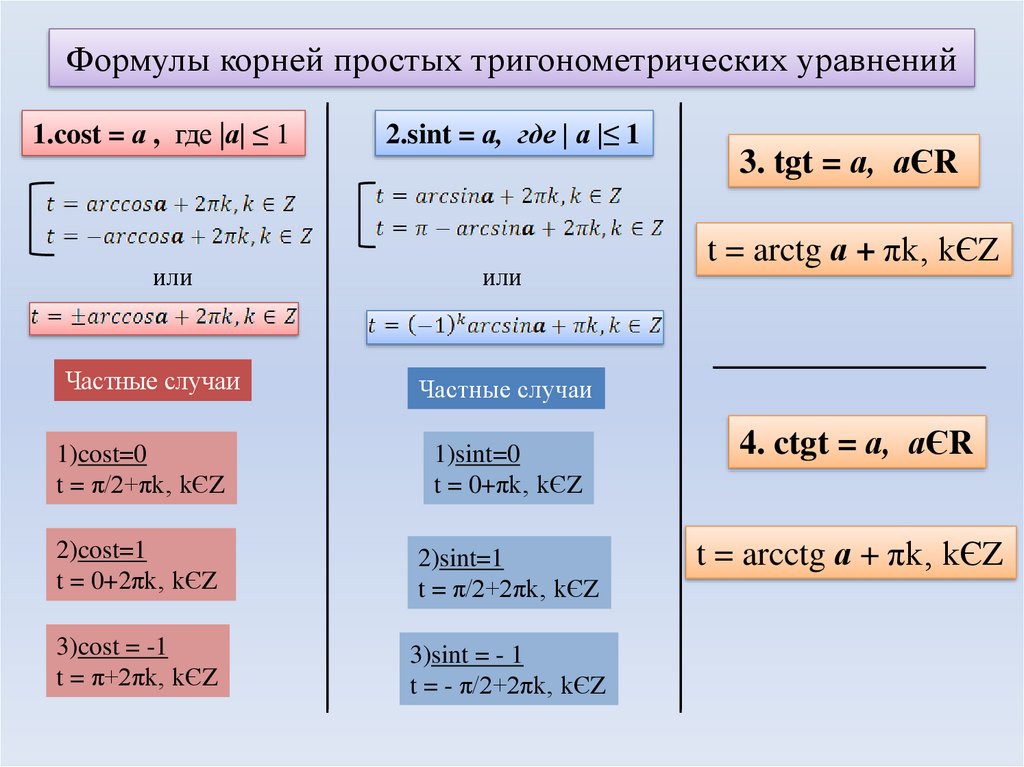

 .
.

 В противном случае он покажет ошибку.
В противном случае он покажет ошибку. Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев.
читать далее
Это условная функция Excel, которая возвращает результат на основе выполнения или невыполнения заданных критериев.
читать далее Найдём точки
пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1).
Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу
после этого теретического экскурса.
Найдём точки
пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1).
Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу
после этого теретического экскурса. Зная точки A и B пересечения граничной прямой с осями
координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две
части, лежащие справа и слева (выше и ниже) от этой прямой.
Зная точки A и B пересечения граничной прямой с осями
координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две
части, лежащие справа и слева (выше и ниже) от этой прямой. Начертим прямую
Начертим прямую Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
 Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).
Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).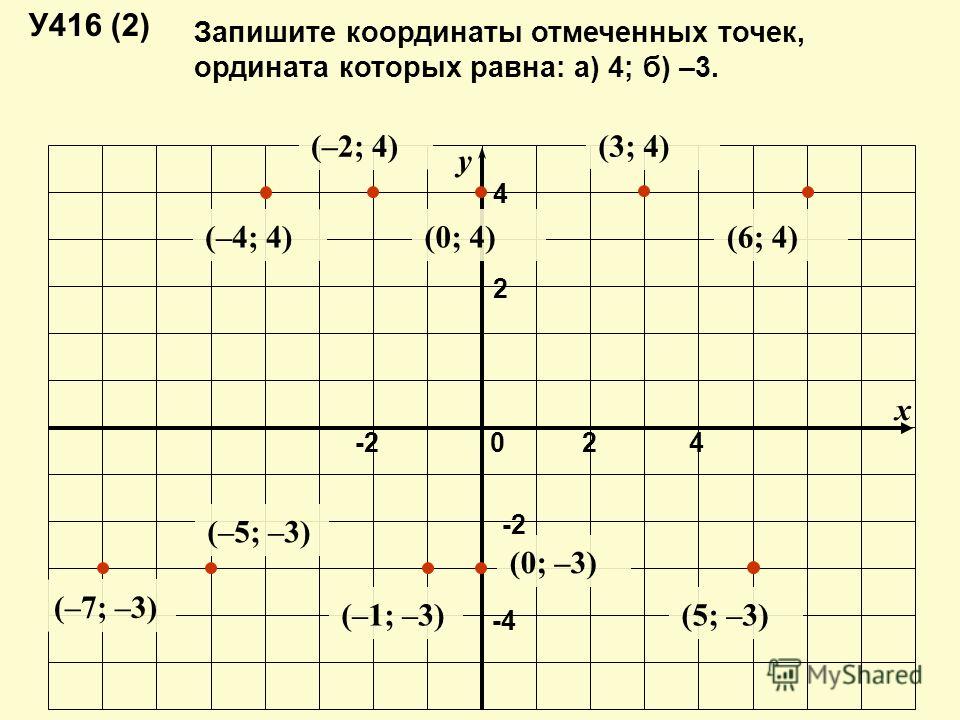 Пересечение всех этих
полупространств образует многогранник решений. Но изобразить этот многогранник (называемый
симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть
в действительном пространстве, многогранник решений можно изобразить геометрически.
Пересечение всех этих
полупространств образует многогранник решений. Но изобразить этот многогранник (называемый
симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть
в действительном пространстве, многогранник решений можно изобразить геометрически. На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.
На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.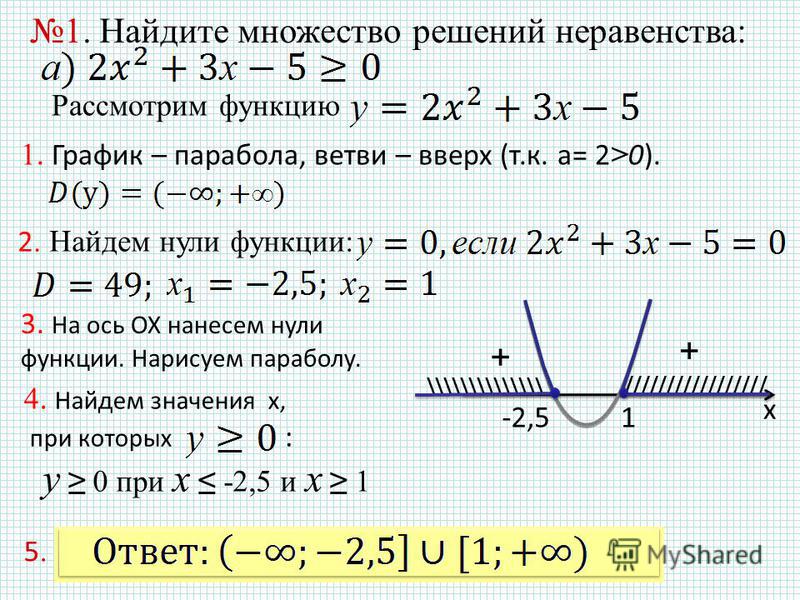 Теорема Кронекера-Капелли
Теорема Кронекера-Капелли В качестве «пробной»
точки выбирают любую точку, не принадлежащую
граничной прямой. Полуплоскость,
в которой неравенство выполняется,
отмечают стрелками, направленными
внутрь данной полуплоскости.
В качестве «пробной»
точки выбирают любую точку, не принадлежащую
граничной прямой. Полуплоскость,
в которой неравенство выполняется,
отмечают стрелками, направленными
внутрь данной полуплоскости.

 192 Из
Казани в Наб.Челны необходимо перевезти
оборудование трех типов: I
типа- 95 ед., II
типа – 100 ед., III
типа – 185 ед. Для перевозки оборудования
завод может заказать три вида транспорта.
Количество оборудования каждого типа,
вмещаемого на определенный вид транспорта,
приведено в таблице 2. Записать условия
перевозки оборудования из Казани в
Наб.Челны и установить, сколько единиц
транспорта каждого вида для этого
потребуется.
192 Из
Казани в Наб.Челны необходимо перевезти
оборудование трех типов: I
типа- 95 ед., II
типа – 100 ед., III
типа – 185 ед. Для перевозки оборудования
завод может заказать три вида транспорта.
Количество оборудования каждого типа,
вмещаемого на определенный вид транспорта,
приведено в таблице 2. Записать условия
перевозки оборудования из Казани в
Наб.Челны и установить, сколько единиц
транспорта каждого вида для этого
потребуется. 193 На
товарные станции А1 и А2 прибыло по 45
комплектов мебели. Перевозка одного
комплекта со станции А1 в магазины М1,
М2 и М3 обходится соответственно в 1, 3 и
5 ден. ед., а перевозка комплекта со
станции А2 в те же магазины – в 3, 5 и 4
ден. ед.. В каждый магазин надо доставить
одинаковое количество мебели. Записать
в математической форме условия доставки
мебели в магазины, если транспортные
расходы определены в 270 ден. ед. и найти
план перевозки мебели со станций в
магазины.
193 На
товарные станции А1 и А2 прибыло по 45
комплектов мебели. Перевозка одного
комплекта со станции А1 в магазины М1,
М2 и М3 обходится соответственно в 1, 3 и
5 ден. ед., а перевозка комплекта со
станции А2 в те же магазины – в 3, 5 и 4
ден. ед.. В каждый магазин надо доставить
одинаковое количество мебели. Записать
в математической форме условия доставки
мебели в магазины, если транспортные
расходы определены в 270 ден. ед. и найти
план перевозки мебели со станций в
магазины. Определить какое количество сырья
следует перерабатывать по каждой
технологии, чтобы выполнить плановое
задание по выпуску изделий.
Определить какое количество сырья
следует перерабатывать по каждой
технологии, чтобы выполнить плановое
задание по выпуску изделий.
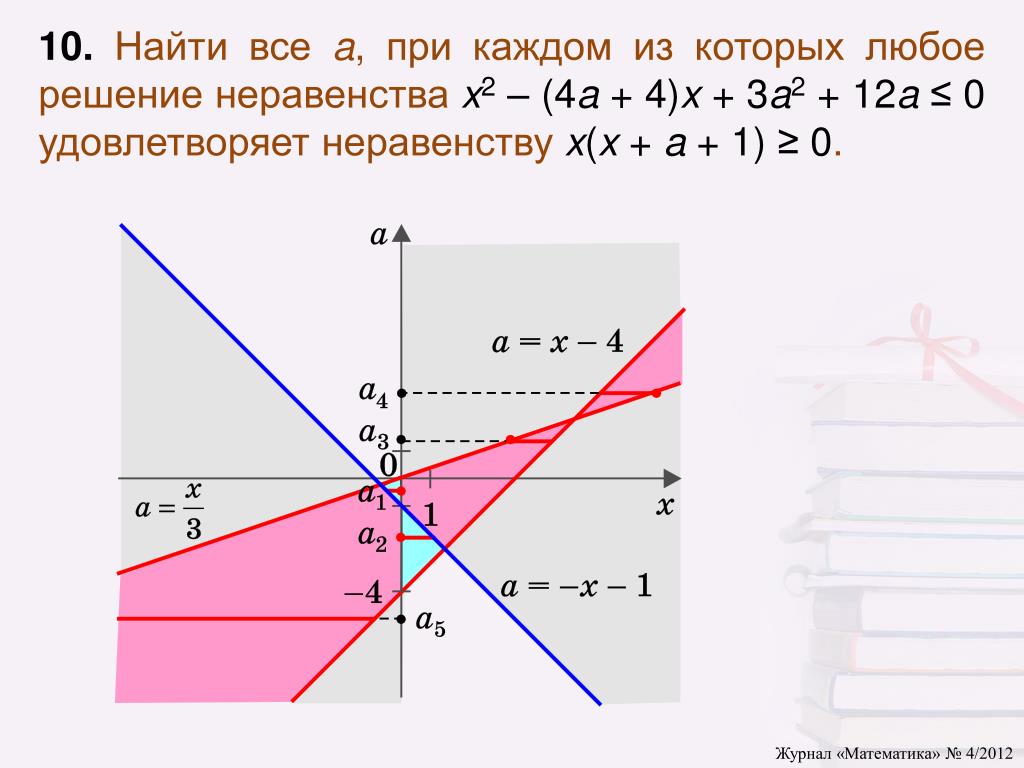 ед.
ед.
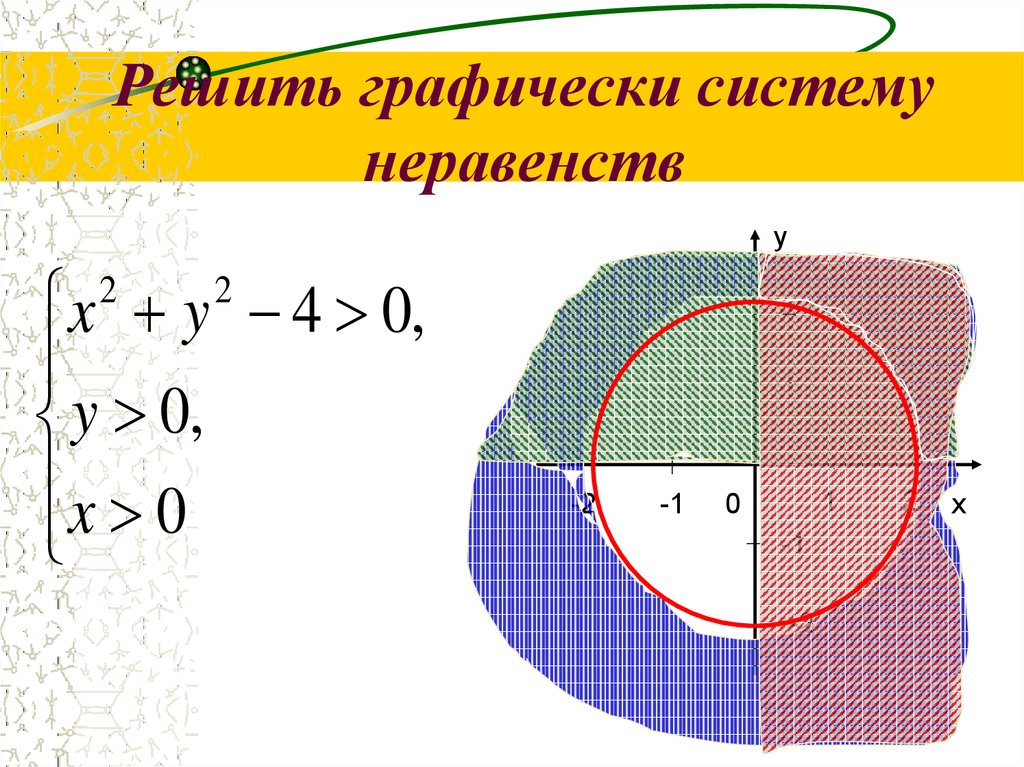 Построить графически область
допустимых вариантов формирования
поездов.
Построить графически область
допустимых вариантов формирования
поездов.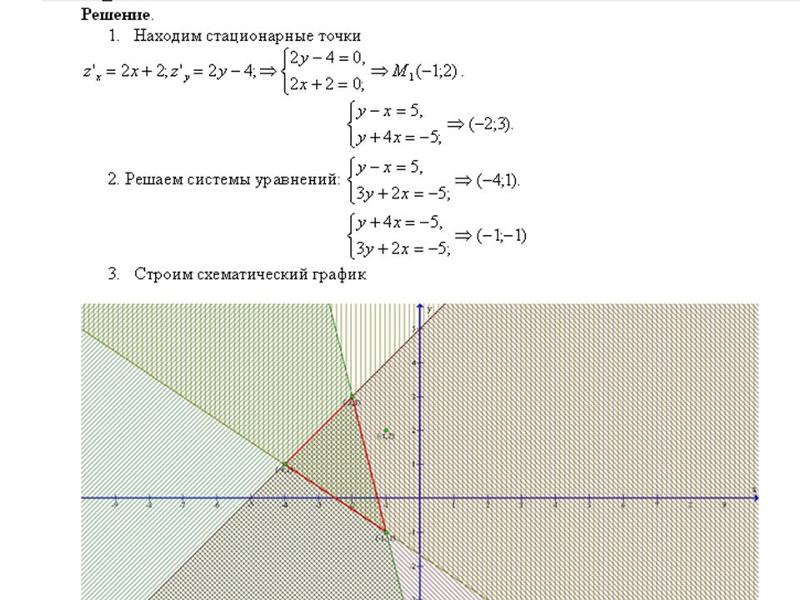 12.2011
12.2011
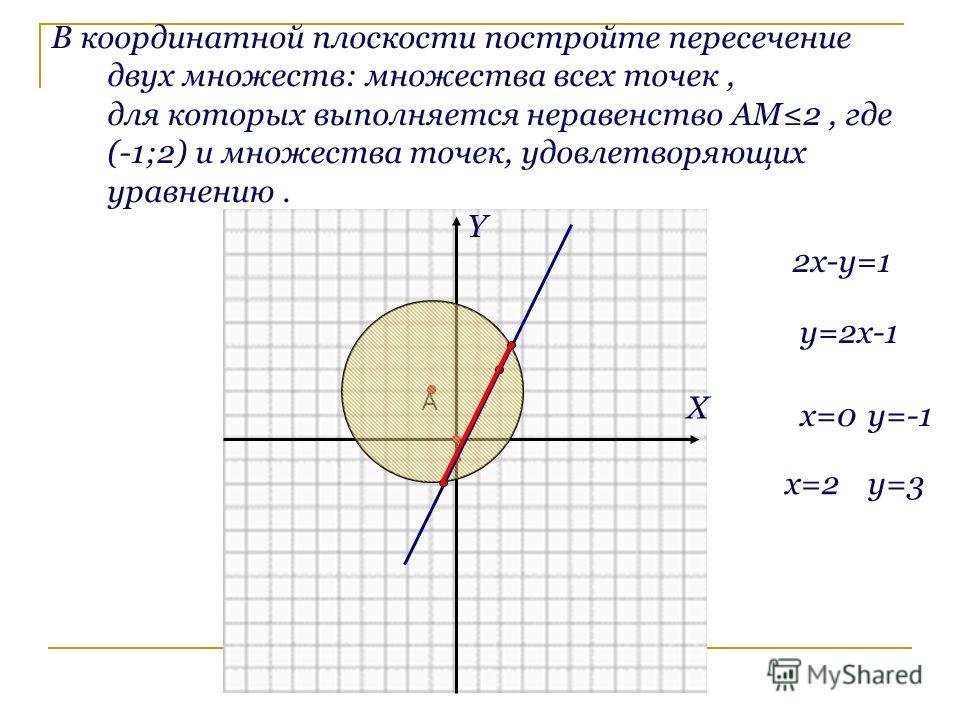



 Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.
Если знак функции совпадает со знаком неравенства, то эта полуплоскость и будет решением неравенства.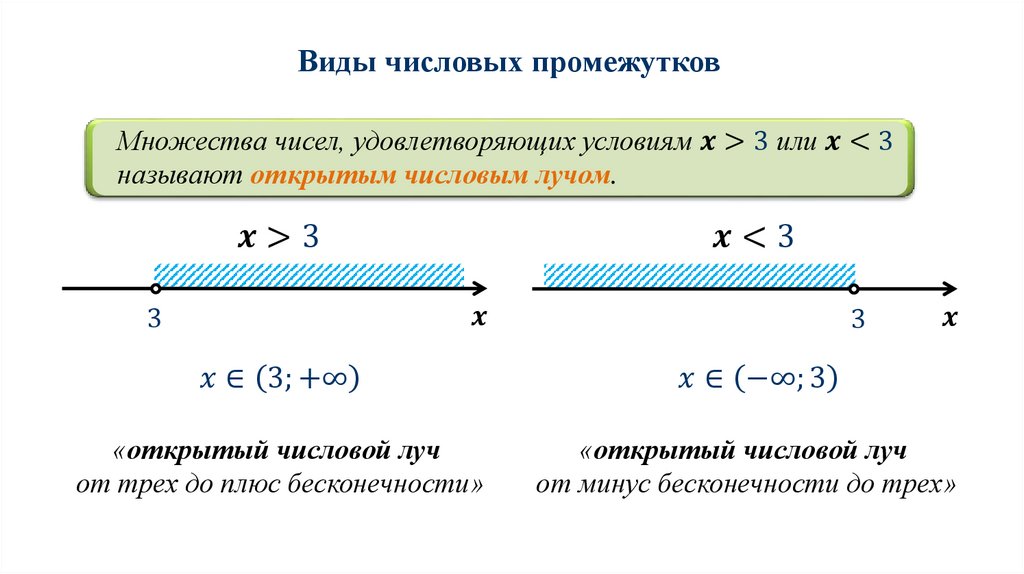
 Закрепление ранее изученного материала.
Закрепление ранее изученного материала.


 Выразить переменную у через переменную х:
Выразить переменную у через переменную х: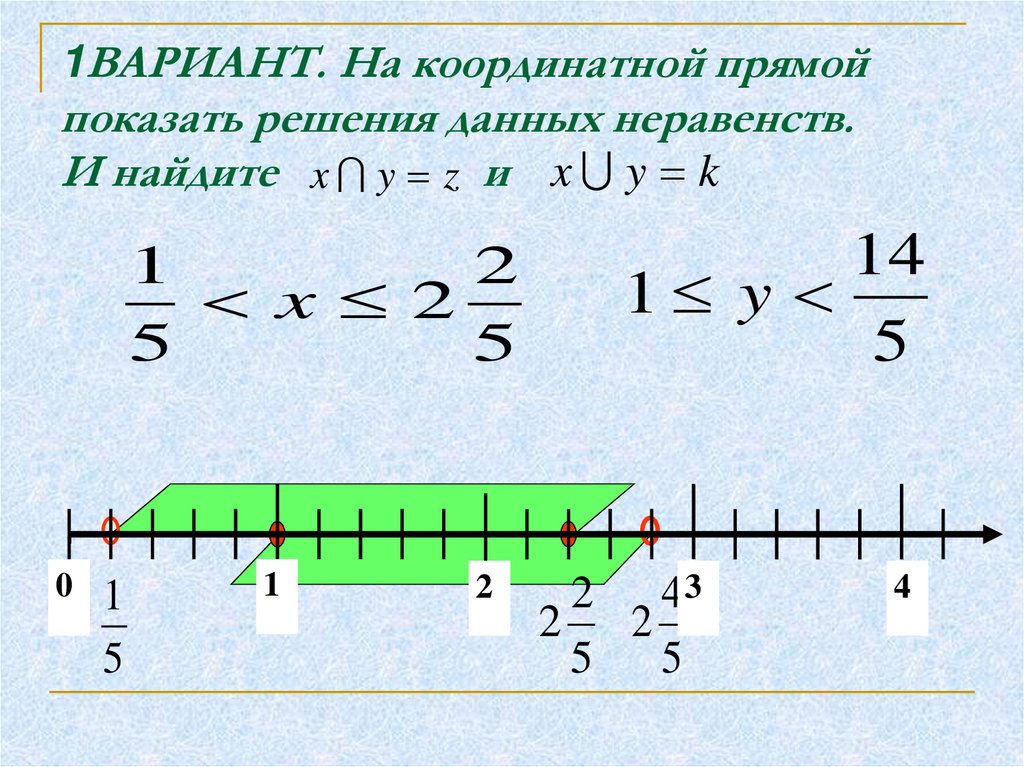

 — на с. 92 (в последнем случае
— на с. 92 (в последнем случае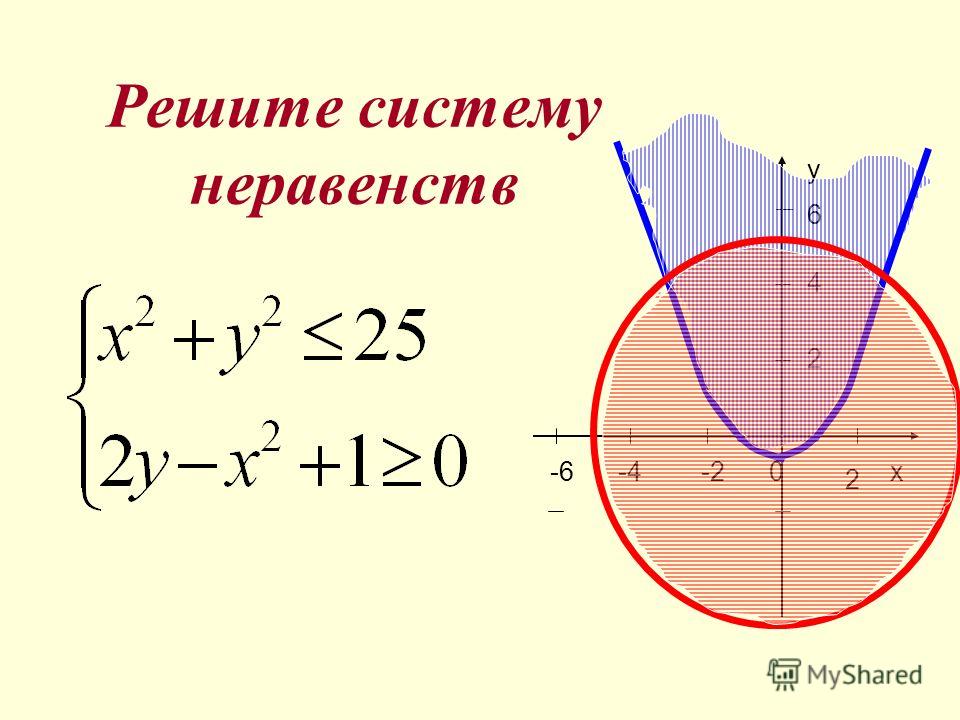

 !Я 1 t * / ✓ и
!Я 1 t * / ✓ и Поскольку каждая точка М1 графика
Поскольку каждая точка М1 графика Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем:
Учитывая, что точки М и М1 симметричны относительно оси Оу (рис. 51) , получаем: = ~2——. Поэтому
= ~2——. Поэтому Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой).
Множество точек, ко-ординаты которых удовлетворяют неравенству у < -х2, является объ-единением точек параболы у = -х2 и точек координатной плоскости, находящихся ниже параболы (на ри-сунке это множество обозначено вер-тикальной штриховкой). Множество точек, координаты которых удовлет-воряют неравенству у > х — 2, состоит из точек координатной плоскости, находящихся выше прямой у = х — 2 (на рисунке это множество обозначено горизонтальной штриховкой). Ориентир
Ориентир
 Постройте эскиз графика функции:
Постройте эскиз графика функции: В одном случае это множество может сузиться, то есть корни будут потеряны, в другом — расшириться, то есть появятся посторонние корни.
В одном случае это множество может сузиться, то есть корни будут потеряны, в другом — расшириться, то есть появятся посторонние корни.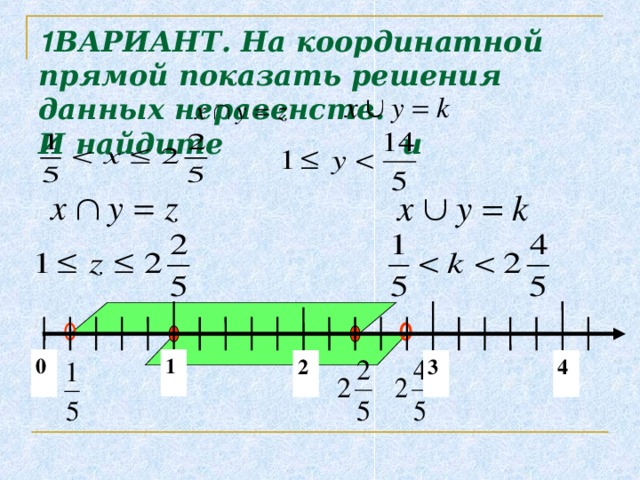 Рассмотрим некоторые из этих причин.
Рассмотрим некоторые из этих причин.

 Появление же посторонних корней возможно за счет корней уравнения Следовательно, полученное уравнение — следствие уравнения, данного в условии.
Появление же посторонних корней возможно за счет корней уравнения Следовательно, полученное уравнение — следствие уравнения, данного в условии. Поскольку функция не является обратимой, то уравнения не являются равносильными.
Поскольку функция не является обратимой, то уравнения не являются равносильными. Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
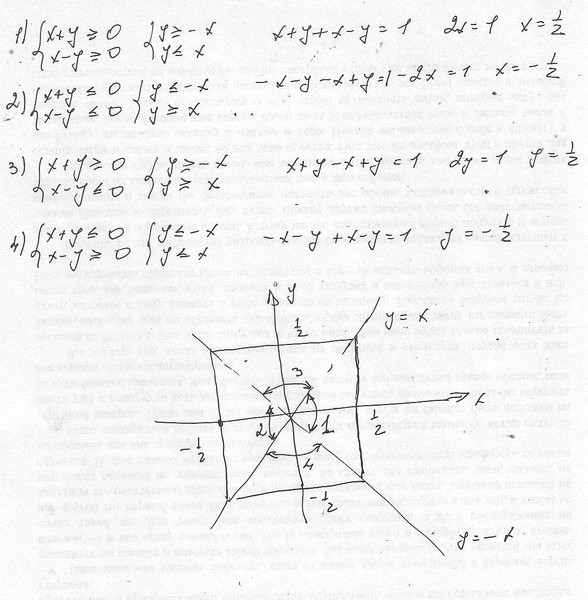 Вместе с тем нахождение области определения уравнения — путь вполне естественный.
Вместе с тем нахождение области определения уравнения — путь вполне естественный. Очевидно, что число 0 является корнем данного уравнения.
Очевидно, что число 0 является корнем данного уравнения. 34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек».
34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек». Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
 Геометрические преобразования графика уравнения
Геометрические преобразования графика уравнения 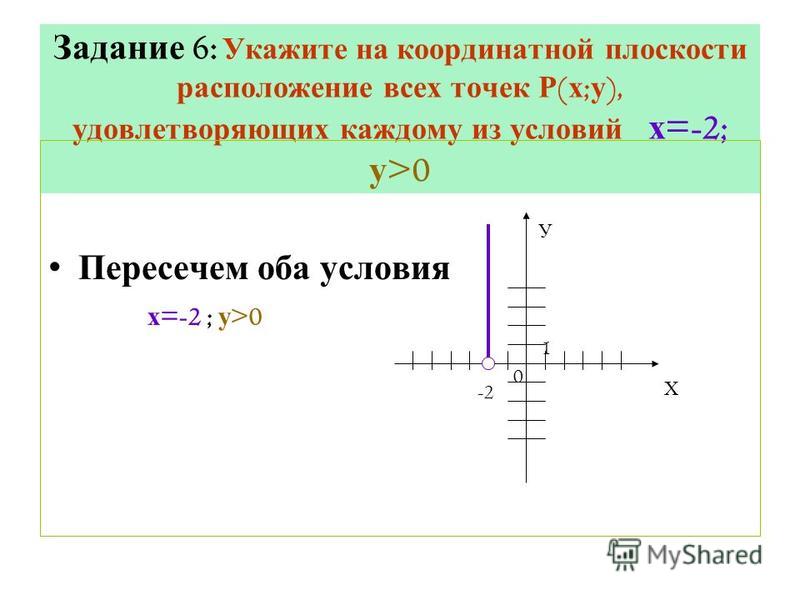


 60, в). Аналогично, если на плоскости есть изображение окружности , то графиком неравенства будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства , а на рисунке 62 — график неравенства .
60, в). Аналогично, если на плоскости есть изображение окружности , то графиком неравенства будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства , а на рисунке 62 — график неравенства .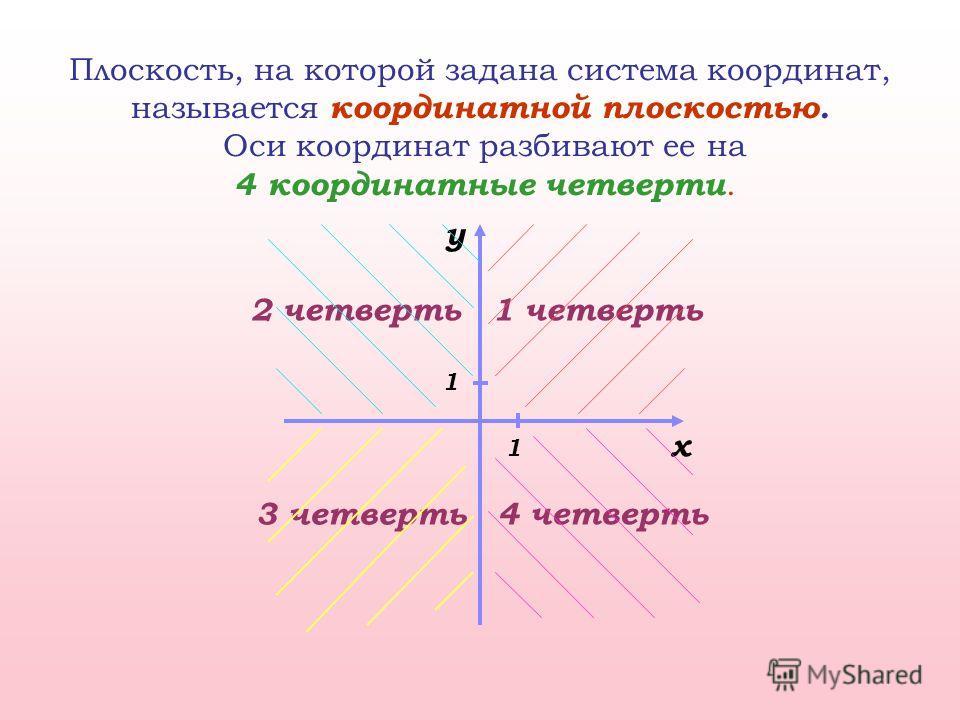

 Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции
Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции 65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству , состоит из точек координатной плоскости, находящихся выше прямой (на рисунке это множество обозначено горизонтальной штриховкой).
65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству , состоит из точек координатной плоскости, находящихся выше прямой (на рисунке это множество обозначено горизонтальной штриховкой).
 67, б).
67, б). Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте подставить в неравенство координаты x и y точек A и B; вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства.
Каждая упорядоченная пара в заштрихованной области под линией является решением [латекс]y<2x+5[/латекс], так как все точки под линией сделают неравенство верным. Если вы сомневаетесь в этом, попробуйте подставить в неравенство координаты x и y точек A и B; вы увидите, что они работают. Итак, заштрихованная область показывает все решения этого неравенства. Давайте использовать [latex]y<2x+5[/latex] и [latex]y>−x[/latex], так как мы уже построили график каждого из них.
Давайте использовать [latex]y<2x+5[/latex] и [latex]y>−x[/latex], так как мы уже построили график каждого из них. Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.
Алгебраически проверим, является ли точка решением линейного уравнения или неравенства.
 Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что система не имеет решения. Аналогичный результат мы получим для следующей системы линейных неравенств.
Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что система не имеет решения. Аналогичный результат мы получим для следующей системы линейных неравенств.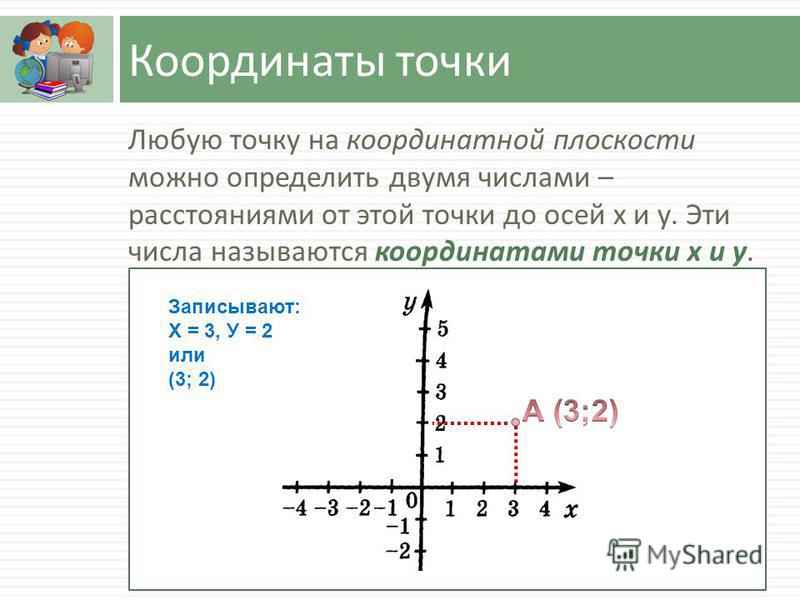
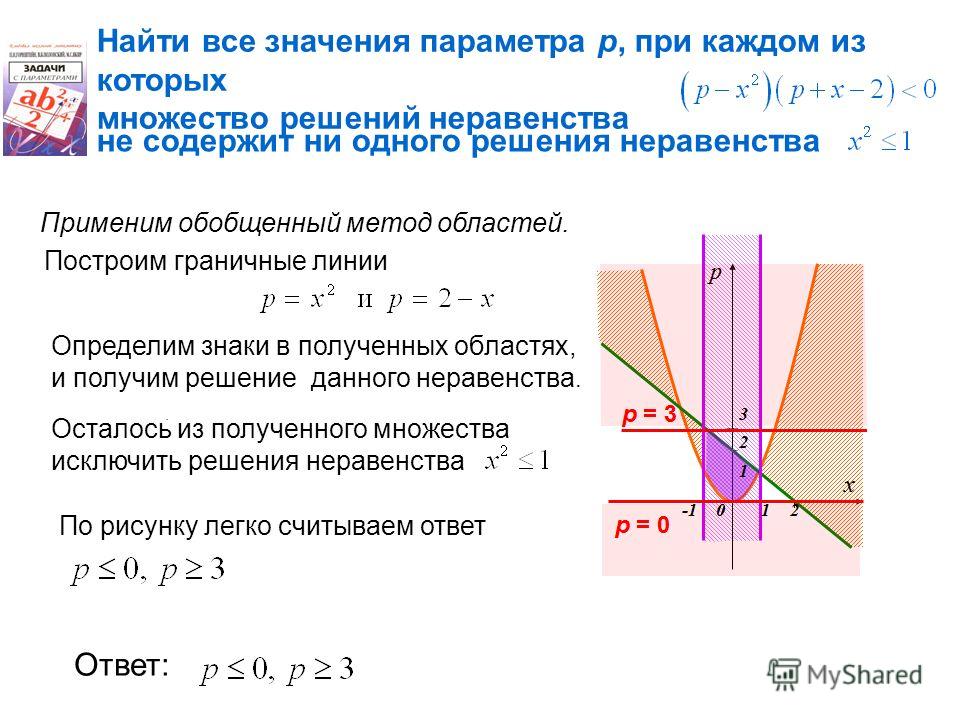
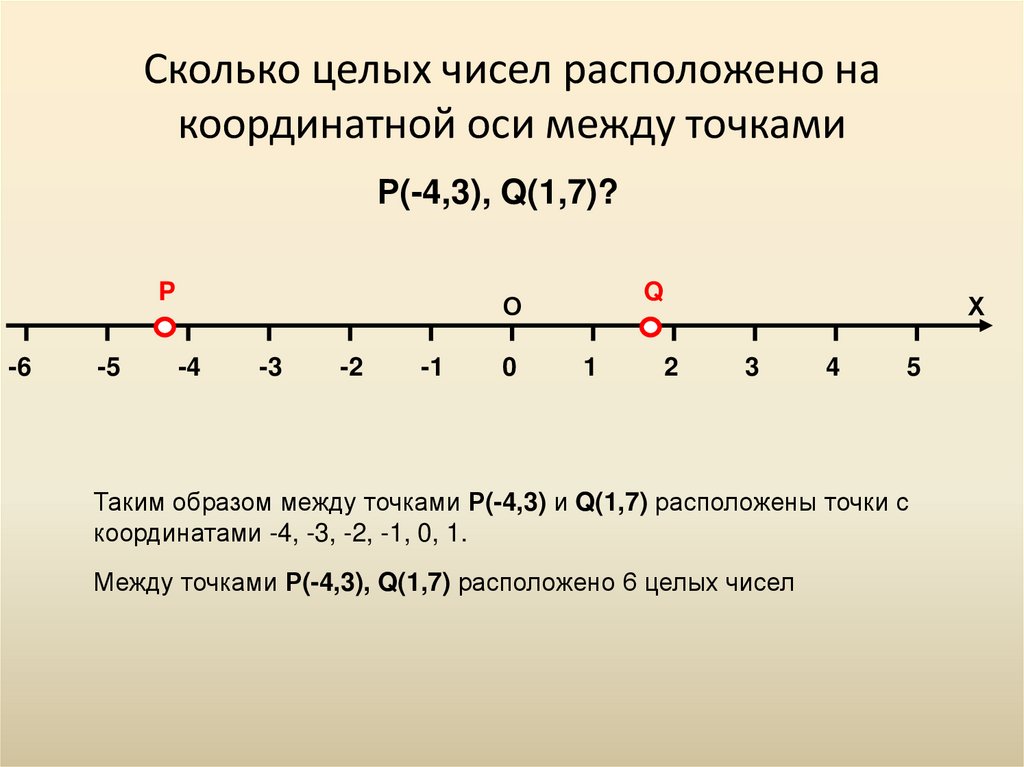 Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.
Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным. Посмотрите на каждую заказанную пару. 9Координата 0015 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?
Посмотрите на каждую заказанную пару. 9Координата 0015 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?

 Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.
Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.

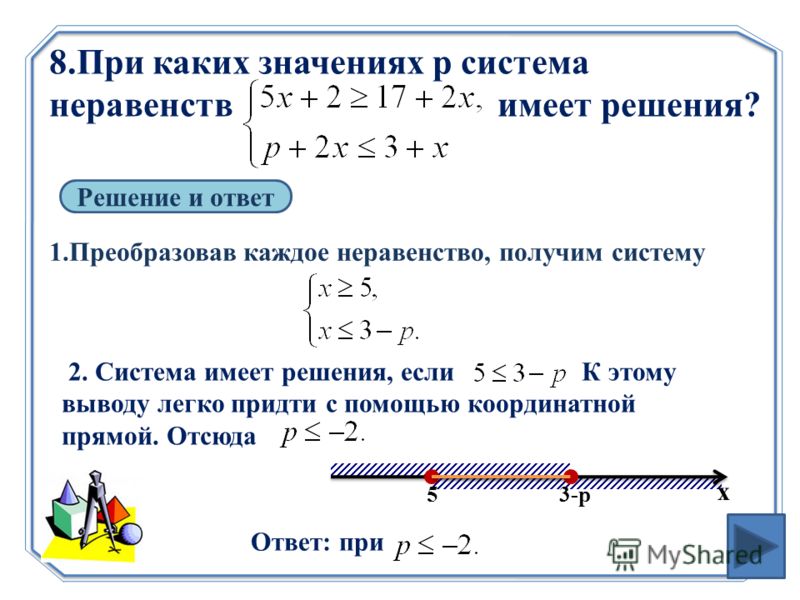
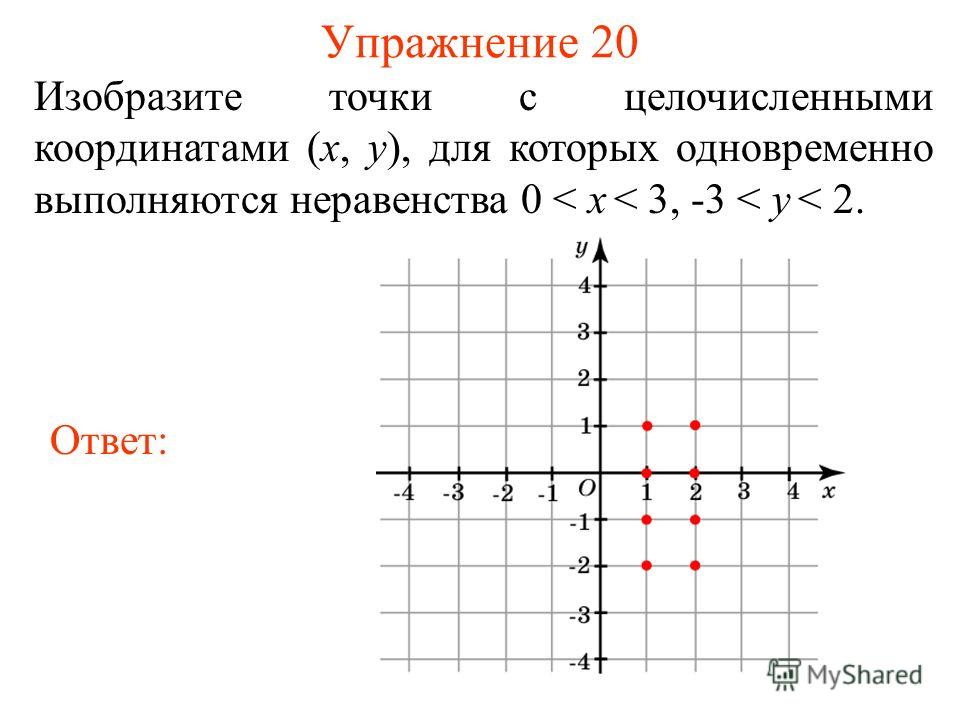 Граница неравенства рисуется сплошной линией, если точки на самой линии удовлетворяют неравенству, как в случаях ≤ и ≥. Она рисуется штриховой линией, если точки на прямой не удовлетворяют неравенству, как в случаях < и >. Вы можете сказать, какую область закрасить, проверив некоторые точки в неравенстве. Использование координатной плоскости особенно полезно для визуализации области решений неравенств с двумя переменными.
Граница неравенства рисуется сплошной линией, если точки на самой линии удовлетворяют неравенству, как в случаях ≤ и ≥. Она рисуется штриховой линией, если точки на прямой не удовлетворяют неравенству, как в случаях < и >. Вы можете сказать, какую область закрасить, проверив некоторые точки в неравенстве. Использование координатной плоскости особенно полезно для визуализации области решений неравенств с двумя переменными.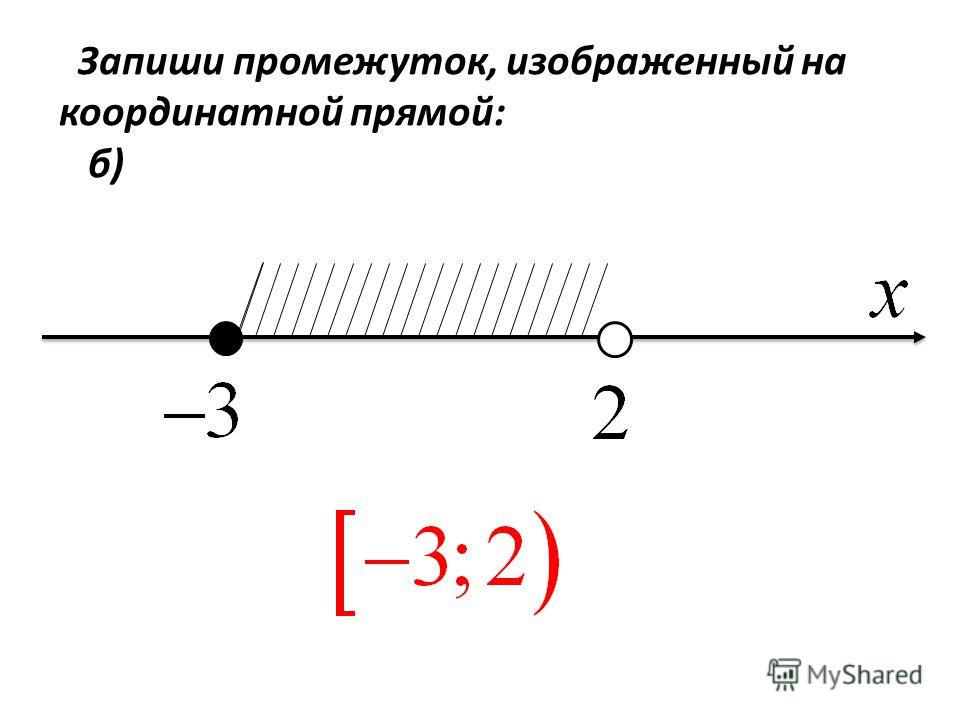


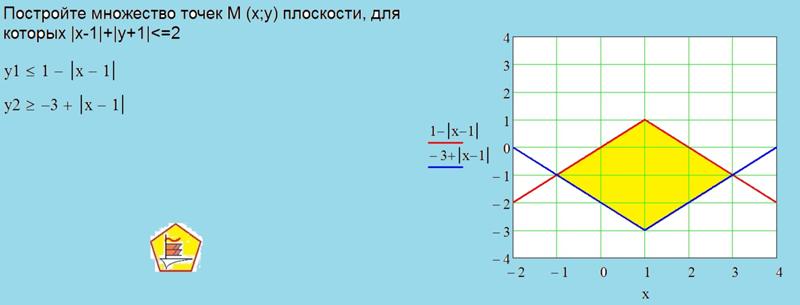
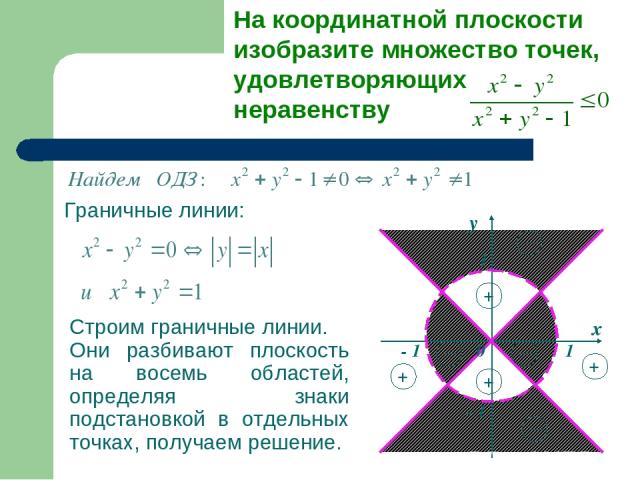 В плоской прямоугольной системе координат точка пересечения осей; график (0,0).
В плоской прямоугольной системе координат точка пересечения осей; график (0,0).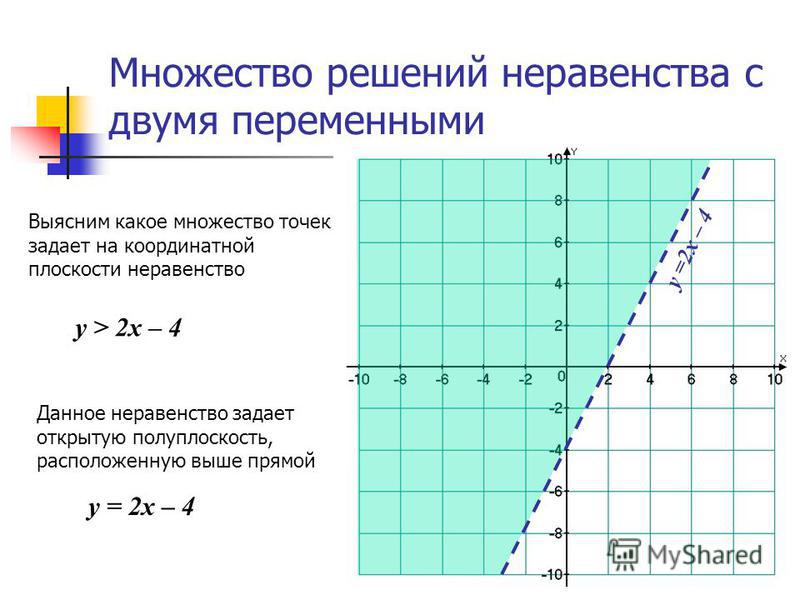
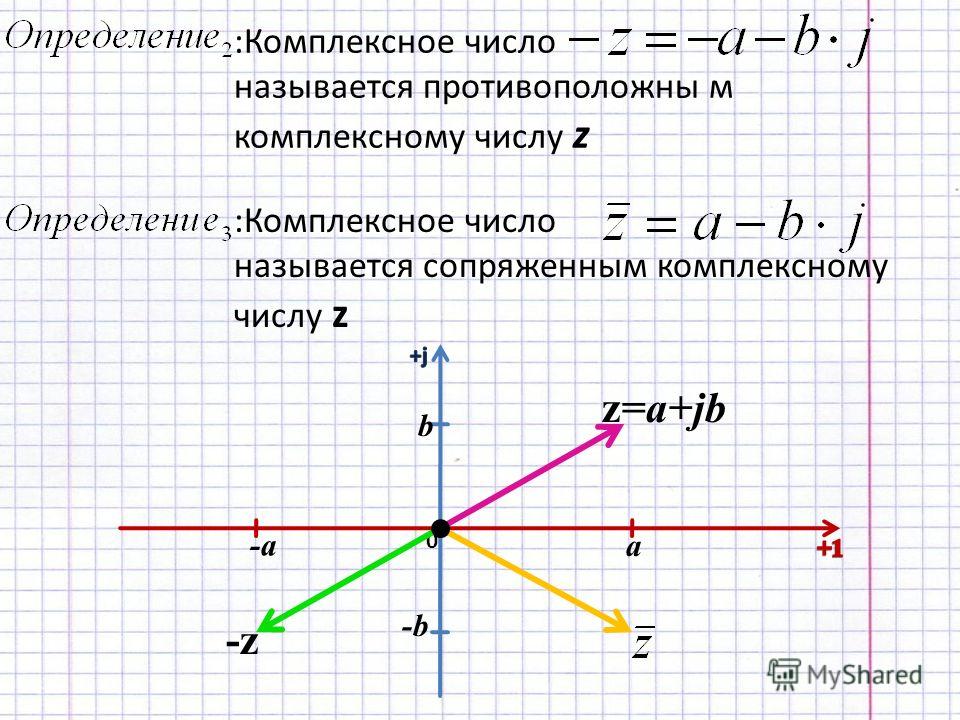


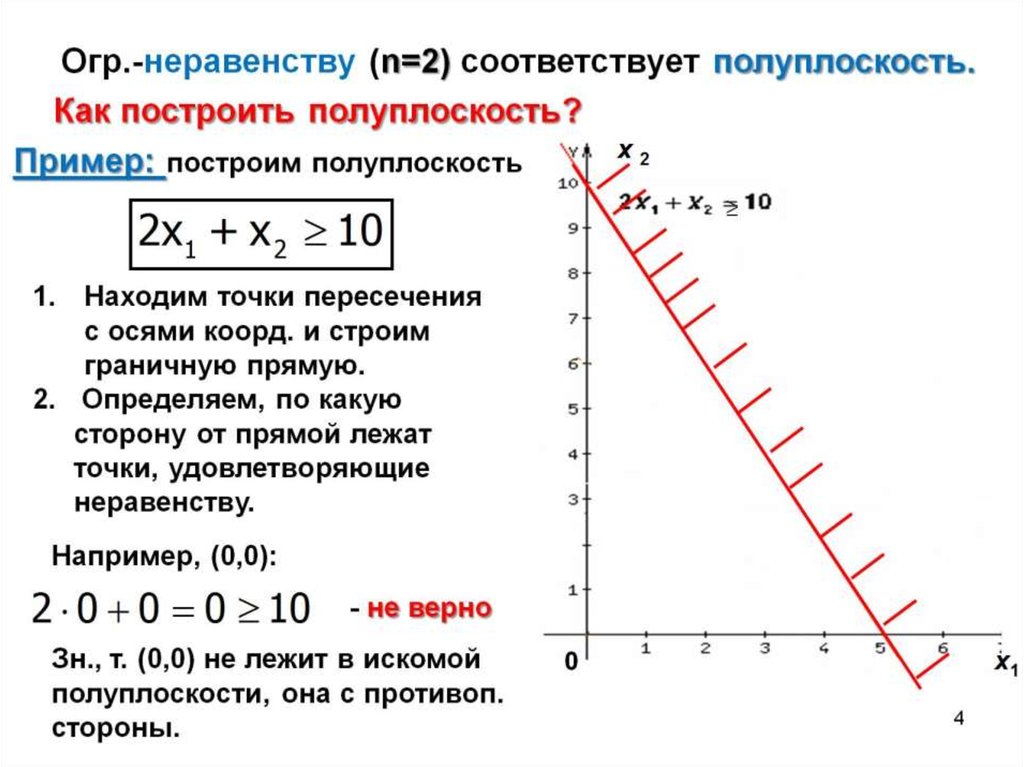
 Линейное неравенство с двумя переменными. Неравенство, связывающее линейные выражения с двумя переменными. Множество решений представляет собой область, определяющую половину плоскости. С другой стороны, имеет множество решений, состоящее из области, определяющей половину плоскости.
Линейное неравенство с двумя переменными. Неравенство, связывающее линейные выражения с двумя переменными. Множество решений представляет собой область, определяющую половину плоскости. С другой стороны, имеет множество решений, состоящее из области, определяющей половину плоскости. Если у нас есть строгое неравенство <, мы будем использовать пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Если у нас есть строгое неравенство <, мы будем использовать пунктирную линию, чтобы указать, что эти точки не включены в набор решений. Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано включающее неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги построения графика набора решений для неравенства с двумя переменными показаны в следующем примере.
Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано включающее неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги построения графика набора решений для неравенства с двумя переменными показаны в следующем примере. Поскольку контрольная точка (0, 0) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, не содержащую эту контрольную точку. В этом случае заштрихуйте выше линии границы.
Поскольку контрольная точка (0, 0) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, не содержащую эту контрольную точку. В этом случае заштрихуйте выше линии границы. 4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1.
4. Непрерывность функции в точкеВидеолекция (часть 1)Lecture 1. Differential calculus of functions of a single variableВидеолекция (часть 2)Lecture 2. Differentiation of a function given parametricallyПрактическое занятие 1. Правила дифференцированияПрактическое занятие 2. Логарифмическое дифференцирование. Дифференцирование функции, заданной параметрическиPractical lesson 1. Logarithmic differentiation. Differentiating a function defined parametricallyPractical lesson 2. Rules of differentiationЗадачи для самостоятельной работыРешения задачТаблица производныхТест 1.1.5 Производная функцииВидеолекция 1. Геометрический и физический смысл производнойLecture 1. Geometric and physical meaning of the derivativeВидеолекция 2. Дифференциал функцииLecture 2. Differential of a functionПрактическое занятие 1. Геометрический смысл производнойPractical lesson 1. The geometric meaning of the derivativeПрактическое занятие 2. Производные и дифференциалы высших порядковPractical lesson 2. Higher-order derivatives and differentialsЗадачи для самостоятельной работыРешения задачТест 1. 1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.
1.6. Геометрический и физический смысл производнойQuiz 1.1.6. Geometric and physical sense of the derivativeВидеолекция 1. Основные теоремы дифференциального исчисления.Lecture 1. Basic theorems of differential calculusВидеолекция 2. Исследование функций на монотонность и выпуклостьLecture 2. The study of the monotonicity of the functionПрактическое занятие 1. Исследование свойств функций с помощью производнойPractical lesson 1. Studying the properties of functions using a derivativeПрактическое занятие 2. Правило ЛопиталяPractical lesson 2. L’Hospital’s ruleЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.1.7 (часть 1). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 1)Тест 1.1.7 (Часть 2). Исследование свойств функции с помощью производнойQuiz 1.1.7 (part 2)Теоретический материал (Часть 1)Задачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Теоретический материал (Часть 2)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1. 1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2.
1.8. Асимптоты графика функцииВидеолекция. Дифференциальное и интегральное исчислениеLecture. Differential and Integral CalculationЗадачи для самостоятельной работыРешения задачТаблица интеграловТест 1.2.1. Неопределенный интегралВидеолекция. Неопределенный интеграл: методы интегрирования.Lecture. Indefinite integral: methods of integration.Практическое занятие. Внесение функции под знак дифференциалаPractical lesson. Adding a function under the sign of the differentialЗадачи для самостоятельной работыРешения задачТест 1.2.2. Методы интегрированияВидеолекция 1. Интегрирование дробно-рациональных функций (часть1)Lecture 1. Integration of fractional-rational functions (part 1)Видеолекция 2. Интегрирование дробно-рациональных функций (часть 2)Lecture 2. Integration of fractionally rational functions (part 2)Практическое занятие 1. Интегрирование иррациональных выражений (часть 1)Practical lesson 1. Integration of irrational expressions (part 1)Практическое занятие 2. Интегрирование тригонометрических функцийPractical lesson 2. Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1.
Integration of trigonometric functionsЗадачи для самостоятельного решенияРешения задачТест 1.2.3. Интегрирование рациональных дробей, тригонометрических и иррациональных функцийВидеолекция. Определенный интеграл: интеграл РиманаLecture. Definite integral: Riemann integral. Практическое занятие 1. Вычисление определенного интегралаPractical lesson 1. Calculating a certain integralЗадачи для самостоятельной работыРешения задачТест 1.2.4. Определенный интегралВидеолекция LectureЗадачи для самостоятельного решенияРешения задачТест 1.2.5 Приложения определенного интегралаВидеолекция. Несобственный интегралыLecture. Improper integralЗадачи для самостоятельного решенияРешения задачТест 1.2.6. Несобственные интегралыВидеолекция 1. Функции нескольких переменныхLecture 1. Functions of Multiple VariablesВидеолекция 2. Частные производныеLecture 2. Partial derivativesПрактическое занятие. Функция двух переменныхPractical lesson. Function of several variablesЗадачи для самостоятельной работыРешения задачТест 1. 3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3.
3.1. Функции нескольких переменных (основные понятия)Quiz 1.3.1Видеолекция Дифференцируемость функции двух переменныхLecture. Differentiable functions of two variablesПрактическое занятие 1. Производные и дифференциалы высших порядковПрактическое занятие 2. Понятие дифференциала первого и второго порядкаPractical lesson 2. The concept of the first- and second-order differentialЗадачи для самостоятельной работыРешения задач Тест 1.3.2. Дифференцирование функции нескольких переменныхQuiz 1.3.2Видеолекция 1. Дифференцирование сложной функции, заданной неявноLecture 1. Differentiation of a complex function and a function given implicitlyВидеолекция 2. Производная по направлению. ГрадиентLecture 2. The directional derivative and the gradientПрактическое занятие 1. Производная по направлению, градиентPractical lesson 1. The directional derivative, the gradientПрактическое занятие 2. Исследование свойств функций по определениюPractical lesson 2. Investigating function properties by defenition Практическое занятие 3. Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1.
Дифференцирование сложной функции и дифференцирование функции, заданной неявноPractical lesson 3. Differentiation of a composite function and differentiation of implicitly defined functionЗадачи для самостоятельного решенияРешения задачТест 1.3.3. Частные производныеQuiz 1.3.3Видеолекция 1. Экстремум функции двух переменныхВидеолекция 2. Экстремумы функции в замкнутой областиЗадачи для самостоятельной работы (Часть 1)Решения задач (Часть 1)Задачи для самостоятельной работы (Часть 2)Решения задач (Часть 2)Тест 1.3.4. Экстремум функции двух переменныхQuiz 1.3.4Видеолекция 1. Двойной интеграл Lecture 1. Double integral Видеолекция 2. Вычисление двойного интегралаLecture 2. Calculation of the double integralПрактическое занятие 1. Вычисление двойного интегралаPractical lesson 1. Calculating a certain integralПрактическое занятие 2. Вычисление двойного интегралаPractical lesson 2. Calculating a certain integralЗадачи для самостоятельного решения (Часть 1)Решения задач (Часть 1)Задачи для самостоятельного решения (Часть 2)Решения задач (Часть 2)Тест 1. 3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3).
3.5. Двойной интегралQuiz 1.3.5Видеолекция. Криволинейные интегралыLecture. Curvilinear integralsПрактическое занятие. Вычисление криволинейные интегралов I и II родаPractical lesson. Calculating curvilinear integrals 1 and 2 kind Задачи для самостоятельного решенияРешения задачТест 1.3.6. Криволинейные интегралыАттестация по модулю 1Итоговое тестирование по курсу (2-1)Видеолекция 1. Система линейных уравнений: основные понятияПрактическое занятие 1. Системы линейных уравненийPractical lesson (part 1). Systems of linear equationsТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Видеолекция 2. Решение систем линейных уравнений методом ГауссаПрактическое занятие 2. Решение систем линейных уравнений методом гауссаPractical lesson (part 2). The system of linear equationsТеоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Видеолекция 3. Исследование систем линейных уравненийLecture 3. A system of linear equationsPractical lesson (part 3). The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1.
The system of linear equationsПрактическое занятие 3. Исследование систем линейных уравненийТеоретический материал (лекция 3)Задачи для самостоятельной работы 3Решения задач 3Тест 2.1.1. Системы линейных уравненийСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Векторное пространствоLecture 1. Vector spaceВидеолекция 2. линейная зависимость векторов. Базис векторного пространстваLecture 2. Linear dependence of vectors and the concept of the basis of the vector systemПрактическое занятие 1. Арифметическое векторное пространствоPractical lesson 1. Arithmetic vector spaceПрактическое занятие 2. Линейная зависимость векторов. Базис векторного пространстваPractical lesson 2. Linear dependence of vectors and the concept of the basis of the vector systemТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Тест 2.1.2. Арифметическое n-мерное векторное пространствоСправочник (часть 1)Справочник (часть 2)Видеолекция 1. Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.
Исследование систем линейных уравненийLecture 1. Study systems of linear equationsВидеолекция 2. Однородная система линейных уравненийLecture 2. Homogeneous system of equationsПрактическое занятие 1. Фундаментальная система решений однородной системы линейных уравненийPractical lesson 1. Fundamental system of solutionsПрактическое занятие 2Practical lesson 2Теоретический материал (лекция 1)Теоретический материал (лекция 2)Задачи для самостоятельной работыРешения задачТест 2.1.3. Исследование систем линейных уравненийСправочникВидеолекция 1. Матрицы и определителиLecture 1. Matrix determinantВидеолекция 2. Операции над матрицамиLecture 2. Operations on matricesВидеолекция 3. Обратная матрицаLecture 3. Inverse matrixПрактическое занятие 1. Операции над матрицамиPractical lesson 1. The operations on matrices Практическое занятие 2. Вычисление определителейТеоретический материал (лекция 1)Задачи для самостоятельной работы 1Решения задач 1Теоретический материал (лекция 2)Задачи для самостоятельной работы 2Решения задач 2Теоретический материал (лекция 3)Тест 2.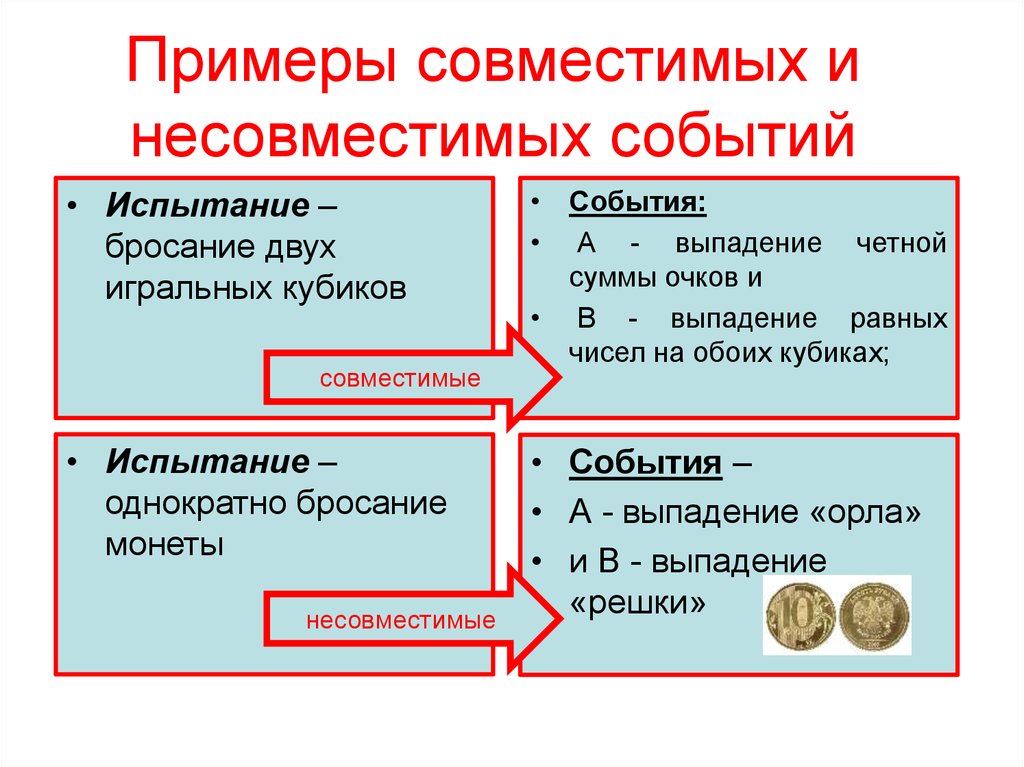 1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов.
1.4. МатрицыQuiz 2.1.4. MatricesСправочник (часть 1)Справочник (часть 2)Справочник (часть 3)Видеолекция 1. Прямоугольная декартова система координатLecture 1. Rectangular Cartesian coordinate systemТеоретический материалПрактическое занятие. Решение задач в координатахPractical lesson. Solution of problems in coordinatesЗадачи для самостоятельной работыРешения задачТест 2.2.1. Декартова система координатСправочникВидеолекция 1. Скалярное произведение векторовLecture 1. Scalar product of vectorsТеоретический материал (Часть 1)Видеолекция 2. Векторное и смешанное произведения векторовLecture 2. Vector and mixed products of vectorsПрактическое занятие 1. Скалярное произведение векторовPractical lesson 1. Scalar product of vectorsПрактическое занятие 2. Применение произведений векторов при решении задачPractical lesson 2. vector and mixed product of vectors to solve themТеоретический материал (Часть 2)Задачи для самостоятельной работы 1Решения задач 1Тест 2.2.2.(часть 1). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson.
Длина вектора. Векторное произведение векторов. Смешанное произведение векторовЗадачи для самостоятельной работы 2Решения задач 2Тест 2.2.2. (часть2). Скалярное произведение векторов. Длина вектора. Векторное произведение векторов. Смешанное произведение векторовСправочник (Часть 1)Справочник (Часть 2)Видеолекция. Уравнения прямой на плоскости и в пространствеLecture. Equation of a straight line on a plane and in spaceТеоретический материалПрактическое занятие 1. Уравнения прямой на плоскостиPractical lesson 1. Related to the equation of a straight line on a planeЗадачи для самостоятельной работы 1Решение задач 1Практическое занятие 2. Взаимное расположение прямыхPractical lesson 2. The relative position of straight lines.Задачи для самостоятельной работы 2Решение задач 2Тест 2.2.3. Уравнения прямойСправочникВидеолекция. Уравнение плоскости. Взаимное расположение прямой и плоскостиТеоретический материалПрактическое занятие. Уравнение плоскости. Взаимное расположение прямой и плоскости Practical lesson. Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1.
Equation of a plane Задачи для самостоятельной работы 1Решение задач 1Задачи для самостоятельной работы 2Практическое занятие 2. Взаимное расположение плоскостейPractical lesson 2. Relative position of planesРешение задач 2Тест 2.2.4. Уравнения плоскостиСправочникВидеолекция 1. ЭллипсLecture 1. EllipseТеоретический материал Часть 1Практическое занятие 1. ЭллипсPractical lesson 1. EllipseЗадачи для самостоятельной работы 1Решение задач 1Видеолекция 2. Гипербола и параболаLecture 2. Hyperbola and parabolaТеоретический материал (Часть 2)Практическое занятие 2. Гипербола и параболаЗадачи для самостоятельной работы 2Решение задач 2Тест 2.2.5. Кривые второго порядкаСправочник (Часть 1)Справочник (Часть 2)Аттестация по модулю 2Анкета обратной связиИтоговое тестирование по курсу (1-2)Итоговое тестирование по курсу (2)Видеолекция 1. Основные понятия теории вероятностей Lecture 1. Basic concepts of probability theoryВидеолекция 2. Вероятность случайного событияLecture 2. Probability of a random eventПрактическое занятие 1. Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТест 3.
Классическая вероятностьPractical lesson 1. Classical probabilityЗадачи для самостоятельной работы (часть 1)Решения задач (часть 1)Практическое занятие 2. Операции над событиями. Practical lesson (part 2). Algebra of events. Properties of probabilitiesЗадачи для самостоятельно работы (часть 2)Решения задач (часть 2)Теоретический материалТест 3.1.1. Классическая вероятностьВидеолекция 1. Условная вероятностьLecture 1. Conditional probabilityПрактическое занятие 1. Условная вероятность. Формула полной вероятности. Формула БайесаPractical lesson 1. Conditional probability. The formula of total probability, Bayes ‘ formulaЗадачи для самостоятельной работы. Условная вероятностьРешения задач. Условная вероятностьВидеолекция 2. Повторные независимые опыты и формула БернуллиLecture 2. Repeated Independent Experiments and the Bernoulli FormulПрактическое занятие 2. Схема БернуллиPractical lesson 2. Bernoulli’s formulaЗадачи для самостоятельной работы. Схема БернуллиРешения задач. Схема БернуллиТест 3. 1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.
1.2. Условная вероятностьВидеолекция 1. Дискретные лучайные величиныLecture 1. Discrete random variablesВидеолекция 2. Числовые характеристики дискретных случайных величинПрактическое занятие. Дискретные случайные величиныPractical lesson. Discrete random variablesЗадачи для самостоятельного решенияРешения задачЛабораторная работа. Законы распределения дискретных случайных величинLaboratory work 1. Distribution Laws of Discrete Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3.2.1. Дискретные случайные величиныВидеолекция 1. Непрерывные случайные величиныВидеолекция 2. Частные случаи распределений случайных величинLecture 2. Special cases of distributions of random variablesПрактическое занятие. Непрерывные случайные величиныPractical lesson. Continuous random variableЗадачи для самостоятельного решенияРешения задачЛабораторная работа (видео). Законы распределения непрерывных случайных величинLaboratory work (video). Distribution Laws of Continuous Random VariablesЛабораторная работаРешения задач (лабораторная работа)Теоретический материалТест 3. 2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3.
2.2. Непрерывные случайные величиныТеоретический материалТест 3.3.1. Законы больших чиселВидеолекция 1. Система случайных величин (часть 1)Видеолекция 2. Система случайных величин (часть 2)Lecture 2. Systems of random variables (part 2)Практическое занятие. Система случайных величинЗадачи для самостоятельной работыРешения задачЛабораторная работаРешение задачи (лабораторная работа)Теоретический материалТест 3.4.1. Совместный закон распределенияВидеолекция 1. Характеристическая функция случайной величиныLecture 1. Characteristic function of a random variableВидеолекция 2. Свойства характеристической функции случайной величиныLecture 2. Properties of characteristic functions random variable Практическое занятие 1. Вычисление характеристической функции случайной величиныPractical lesson 1. Calculation of Characteristic Functions Практическое занятие 2. Проверка устойчивости для стандартных распределенийPractical lesson 2. Testing the robustness for standard distributions.Задачи для самостоятельного решения (часть 1)Задачи для самостоятельного решения (часть 2)Решения задач (часть 1)Решения задач (часть 2)Тест 3. 4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2.
4.2. (данное тестирование по теме 1)Видеолекция. Основные понятия математической статистикиLecture. The basic concepts of mathematical statisticsЛабораторная работа (видео). Основные понятия математической статистикиLaboratory work (video). Basic concepts of mathematical statisticsТеоретический материалЛабораторная работа. Основные понятия математической статистикиРешения задач (лабораторная работа)Тест 3.5.1. Основные понятия математической статистикиQuiz 3.5.1.Видеолекция. Статистические оценки параметров генеральной совокупности. Lecture. Statistical estimates of general population parametersЛабораторная работа 1 (видео). Статистические оценки параметров генеральной совокупностиLaboratory work 1 (video). Statistical estimators of the parameters of the populationЛабораторная работа 1. Статистические оценки параметров генеральной совокупностиРешения задач 1Лабораторная работа 2 (видео). Минимальный или оптимальный объем выборочной совокупностиLaboratory work 2(video). Minimum or optimal sample sizeЛабораторная работа 2. Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2.
Минимальный или оптимальный объем выборочной совокупностиРешения задач 2Теоретический материалТест 3.5.2. Статистические оценкиQuiz 3.5.2Видеолекция. Зависимость между величинами. Виды зависимостейLecture. Dependence between quantities. Types of dependenciesТеоретический материал 1Лабораторная работа 1 (видео, часть 1). Парный корреляционный анализLaboratory work 1 (video, part 1). Pair correlation analysisЛабораторная работа 1. Парный корреляционный анализЛабораторная работа 1 (видео, часть 2). Множественный корреляционный анализРешение задач 1Лабораторная работа 2 (видео, часть 2). Парный регрессионный анализLaboratory work 2 (video, part 2). Paired Regression AnalysisЛабораторная работа 2. Парный регрессионный анализРешения задач 2Теоретический материал 2Тест 3.5.3. Зависимость между величинамиQuiz 3.5.3Лекция. Статистические гипотезы Теоретический материалЛабораторная работа (видео). Статистический критерий хи-квадратLaboratory work. The Chi-Square StatisticЛабораторная работа 1. Критерий хи-квадратРешения задач (Критерий хи-квадрат)Лабораторная работа 2. Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2).
Критерий ПирсонаЛабораторная работа (расчетная таблица)Решения задач (Критерий Пирсона)Тест 3.6.1. Проверка статистических гипотез: основные понятияQuiz 3.6.1Видеолекция. Проверка статистических гипотезLecture. Testing statistical hypothesesЛабораторная работа 1 (видео). Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейLaboratory work 1. Comparison of Sampled Population Means with Known Population VariancesЛабораторная работа 1. Сравнение средних выборочных совокупностей при известных дисперсиях генеральных совокупностейРешения задач (лабораторная работа 1)Лабораторная работа 2 (часть 1). Сравнение средних независимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 1). Comparison of means of independent sample populations with unknown variances of general populationsЛабораторная работа 2 (часть 2). Сравнение средних зависимых выборочных совокупностей при неизвестных дисперсиях генеральных совокупностейLaboratory work 2 (part 2). Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3)
Comparison of mean dependent sample populations with unknown variances of general populationsЛабораторная работа 2. Проверка статистических гипотез о сравнении средних выборочных совокупностей, если не известны дисперсии генеральных совокупностейРешения задач (лабораторная работа 2)Теоретический материалТест 3.6.2. Проверка гипотезQuiz 3.6.2Аттестация по модулю 3Итоговое тестирование по курсу 1-2-3Итоговое тестирование по курсу для математических специальностейИтоговое тестирование по курсу (3) Испытания сопровождаются их исходами (событиями).
Испытания сопровождаются их исходами (событиями).
 Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.
Например, если событие А – появление числа 2 при одном бросании кости, а событие В – появление чётного числа в этом же бросании, то события А и В совместные, а событие С – появление числа 2 при одном бросании кости и событие D – появление числа 3 в этом бросании – события несовместные.

 Доказать по определению условной
вероятности.
Доказать по определению условной
вероятности.
 Событие ( , ) означает, что выпала
грань, содержащая
красный (соответственно синий, зеленый) цвета.
Событие ( , ) означает, что выпала
грань, содержащая
красный (соответственно синий, зеленый) цвета. Как известно, со случайными событиями можно проводить арифметические действия, главными из которых являются сложение и умножение событий. Теория вероятностей позволяет с помощью своих основных теорем найти вероятность суммы и произведения событий, т.е. определить либо вероятность появления хотя бы одного из рассматриваемых событий, либо вероятность одновременного появления этих событий.
Как известно, со случайными событиями можно проводить арифметические действия, главными из которых являются сложение и умножение событий. Теория вероятностей позволяет с помощью своих основных теорем найти вероятность суммы и произведения событий, т.е. определить либо вероятность появления хотя бы одного из рассматриваемых событий, либо вероятность одновременного появления этих событий. Обозначим через т А и т В число элементарных событий благоприятствующих событиям А и В соответственно. Так как события А и В несовместны, то сумме этих событий А + В благоприятствуют т А + т В элементарных событий. Поэтому .
Обозначим через т А и т В число элементарных событий благоприятствующих событиям А и В соответственно. Так как события А и В несовместны, то сумме этих событий А + В благоприятствуют т А + т В элементарных событий. Поэтому . 1 окончательно получаем .■
1 окончательно получаем .■ Обозначим его буквой D и найдем его вероятность. Применяя классическую формулу, получим
Обозначим его буквой D и найдем его вероятность. Применяя классическую формулу, получим


 Однако это так называемые крайние случаи. Наибольший интерес возникает тогда, когда наступление события В как-то изменяет (увеличивает или уменьшает) вероятность появления события А , не превращая его в достоверное или невозможное при новых условиях событие. Характеристикой такого влияния одного события на другое служит условная вероятность.
Однако это так называемые крайние случаи. Наибольший интерес возникает тогда, когда наступление события В как-то изменяет (увеличивает или уменьшает) вероятность появления события А , не превращая его в достоверное или невозможное при новых условиях событие. Характеристикой такого влияния одного события на другое служит условная вероятность. В задаче требуется найти вероятность события А , при условии, что событие В произошло, т.е. найти . Если событие В произошло, то в урне осталось 13 шаров, из которых 5 белых. Следовательно, вероятность вынуть белый шар из 13, среди которых 5 белых равна .■
В задаче требуется найти вероятность события А , при условии, что событие В произошло, т.е. найти . Если событие В произошло, то в урне осталось 13 шаров, из которых 5 белых. Следовательно, вероятность вынуть белый шар из 13, среди которых 5 белых равна .■ е. вероятность события А совпадает с условной вероятностью этого события. Сами же события А и В являются независимыми в данном испытании.
е. вероятность события А совпадает с условной вероятностью этого события. Сами же события А и В являются независимыми в данном испытании. Объем правильного тетраэдра
Объем правильного тетраэдра
 Расчёт объёма усечённой пирамиды
Расчёт объёма усечённой пирамиды 14
14 до н. э. царем города, в котором они жили.
до н. э. царем города, в котором они жили. Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
Гиерон разгневался на то, что его провели, и, не находя способа уличить это воровство, попросил Архимеда хорошенько подумать об этом. Тот, погруженный в думы по этому вопросу, как-то случайно пришел в баню и там, опустившись в ванну, заметил, что из нее вытекает такое количество воды, каков объем его тела, погруженного в ванну. Выяснив себе ценность этого факта, он, не долго думая, выскочил с радостью из ванны, пошел домой голым и громким голосом сообщал всем, что он нашел то, что искал. Он бежал и кричал одно и то же по-гречески: «Эврика, эврика! (Нашел, нашел!)».
 Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см 3) или кубических метрах (м 3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см 3) или граммы на миллилитр (г/мл).
Прежде чем вычислить плотность тела, необходимо найти его объем. Если тело имеет правильную геометрическую форму, его объем можно рассчитать при помощи простой формулы. Объем измеряется обычно в кубических сантиметрах (см 3) или кубических метрах (м 3). Используя найденный объем тела, легко рассчитать его плотность. Для измерения плотности служат граммы на кубический сантиметр (г/см 3) или граммы на миллилитр (г/мл).
 Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье.
Ниже приведены формулы для нахождения объема перечисленных выше фигур. Более подробные сведения и иллюстрации можно найти в статье. Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.
Для большинства тел простой формы понадобится измерить высоту; если у фигуры круглое основание, необходимо также определить его радиус, если же в основании лежит прямоугольник – его длину и ширину.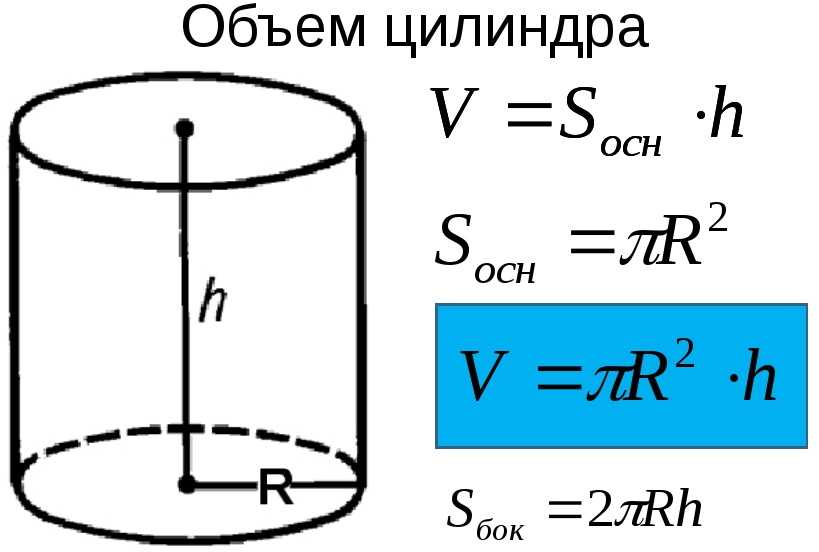 После полученной величины обязательно напишите единицы, в которых она измеряется.
После полученной величины обязательно напишите единицы, в которых она измеряется.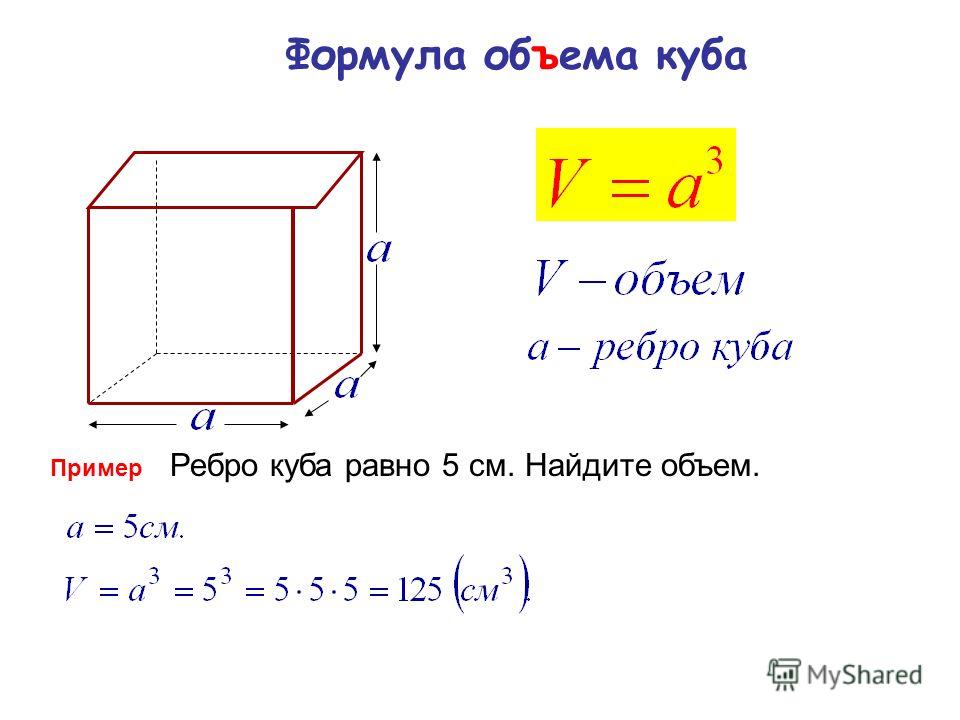
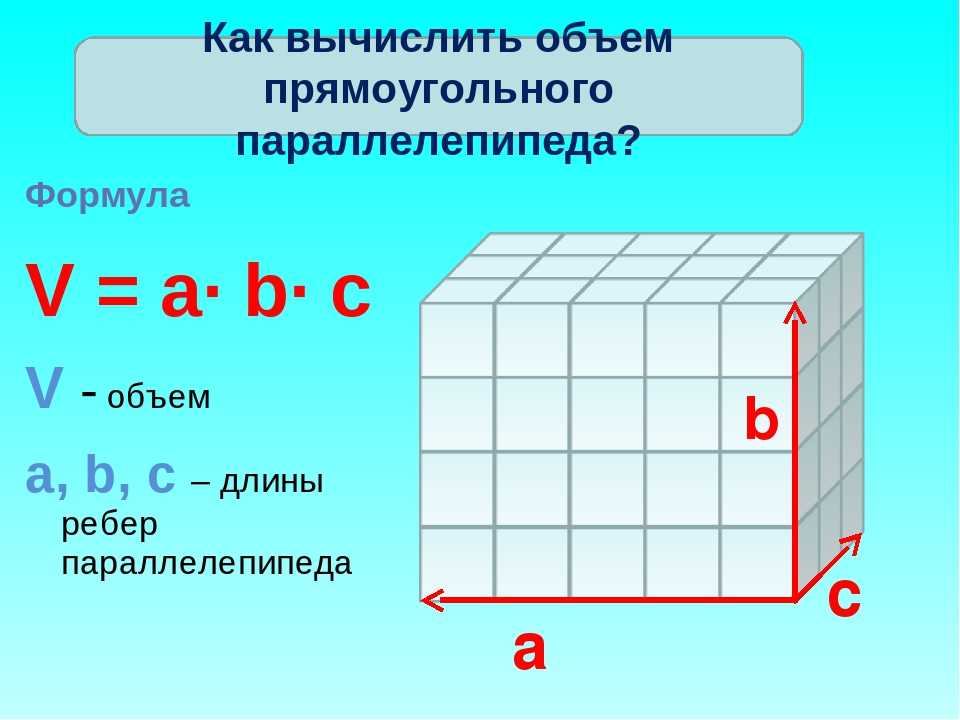 Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.
Обычно объем жидкостей измеряют в миллилитрах, но один миллилитр как раз и равен одному кубическому сантиметру.
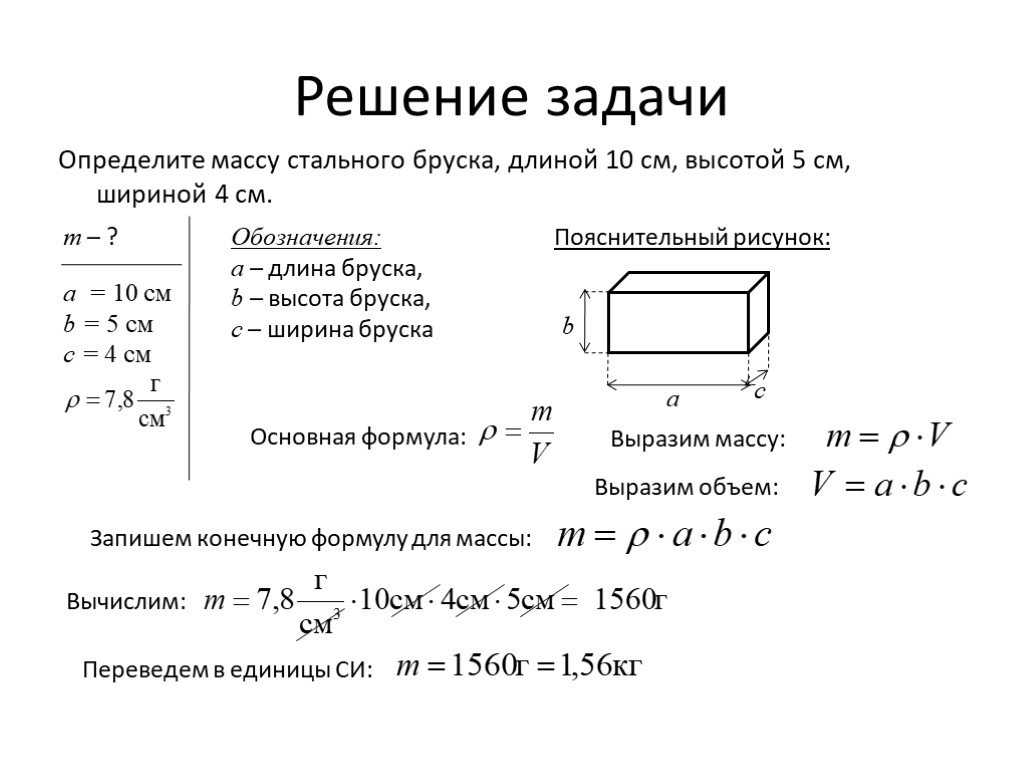
 Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.
Объем рассчитать при помощи современных технологий сегодня несложно, достаточно вашего нахождения тут.


 Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза.
Калькулятор объёмов простой и удобный в применении, он выдаст результаты как объёма коробки так и груза. Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас.
Как рассчитать кубатуру вы знаете, поэтому всё остальное в ваших руках, теперь выбор транспорта зависит от вас. Так можно узнать объём (V). Когда газ находится в нормальных условиях — н. у., то его Vm — объём в молях составляет 22,4 л./моль. Если в условии сказано, сколько вещества в молях имеется (n), то нужно подставить данные в формулу и выяснить конечный результат.
Так можно узнать объём (V). Когда газ находится в нормальных условиях — н. у., то его Vm — объём в молях составляет 22,4 л./моль. Если в условии сказано, сколько вещества в молях имеется (n), то нужно подставить данные в формулу и выяснить конечный результат.
 Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще.
Объект может иметь сравнительно небольшой V и большую S, например, так устроен мозг человека. Вычислить данные показатели для простых геометрических фигур гораздо проще. Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
Куб – это частный случай параллелепипеда, в котором все 6 граней представляют собой равные квадраты. В этом случае, чтобы найти V, нужно узнать длину только одной стороны и возвести ее в третью степень.
 Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей.
Типовые задачи, как правило, не содержать большого количества вычислений и сложных дробей. Часто школьнику предлагают как найти объем неправильной геометрической фигуры. В таких случаях следует помнить простое правило, что общий объем равен сумме V-ов составных частей. Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн.
Например, какого объема необходим бак для воды на дачном участке, или каким размером делать бассейн. Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно.
Главное — это знать требуемые значения, без которых выполнить расчет будет невозможно. В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров.
В этом случае объем этого объекта определяется следующим образом: 10x3x1,5=45 кубометров, или 45 кубических метров. При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
При этом выделяют несколько видов фигур. Принцип расчета не имеет конкретных отличий, но сами фигуры внешне отличаются. Итак, можно выделить такие виды:
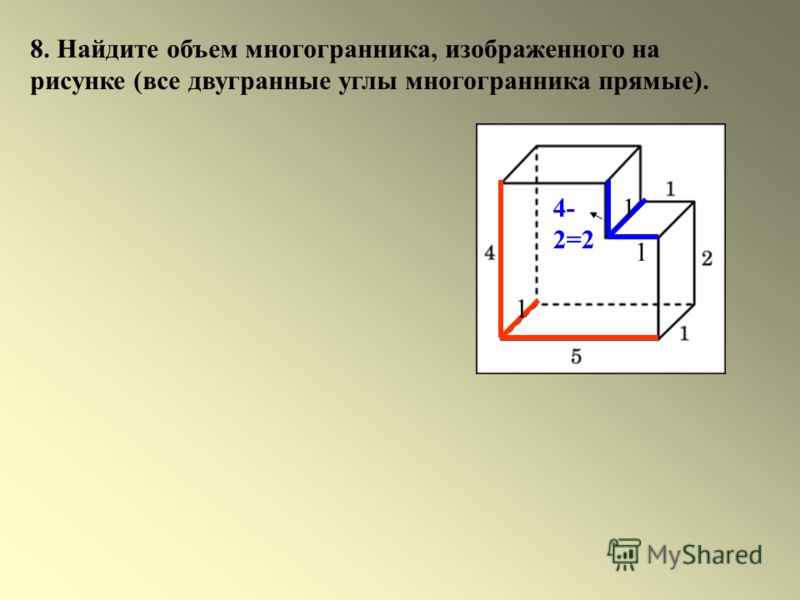 3$ — эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.
3$ — эта запись означает, что объём некоторого сосуда равен 3-м, если в качестве единицы измерения взят кубический миллиметр.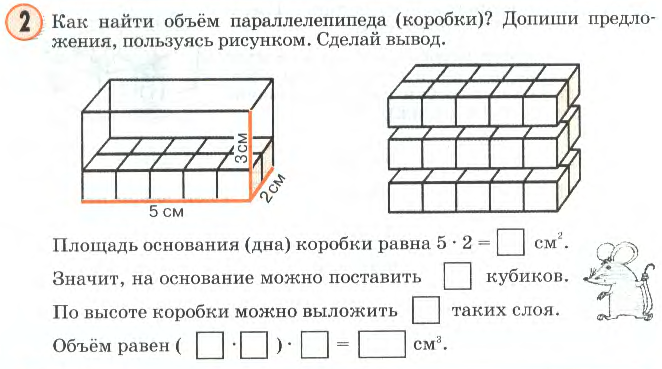

 3$, где $R$ — радиус шара.
3$, где $R$ — радиус шара.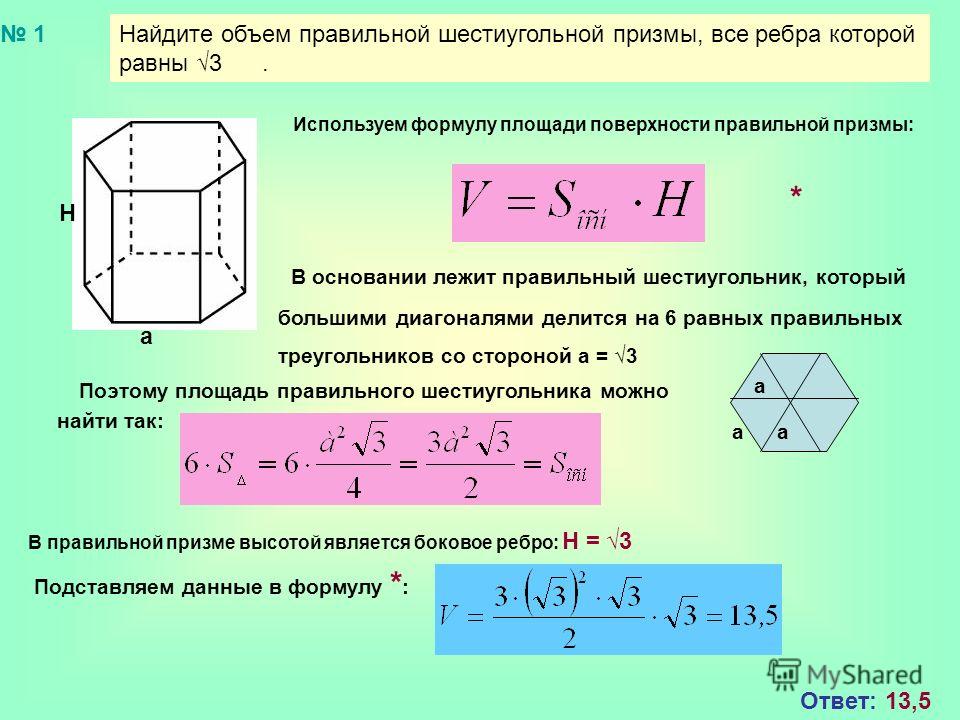 3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту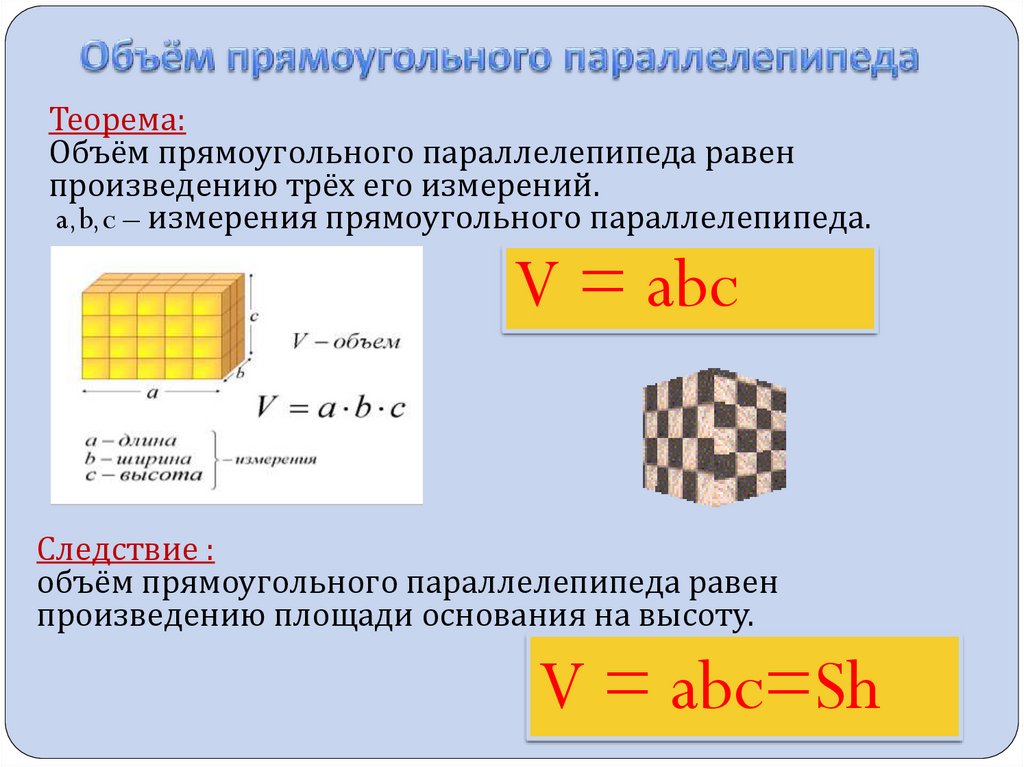 Площадь умножить на высоту. 2,5 х 20 =50 куб.
Площадь умножить на высоту. 2,5 х 20 =50 куб.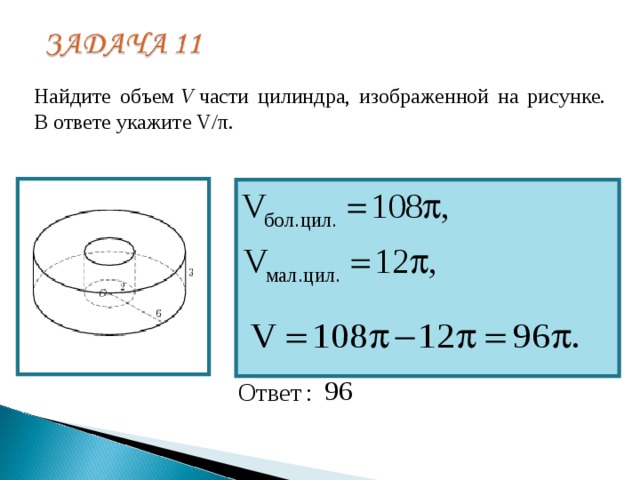
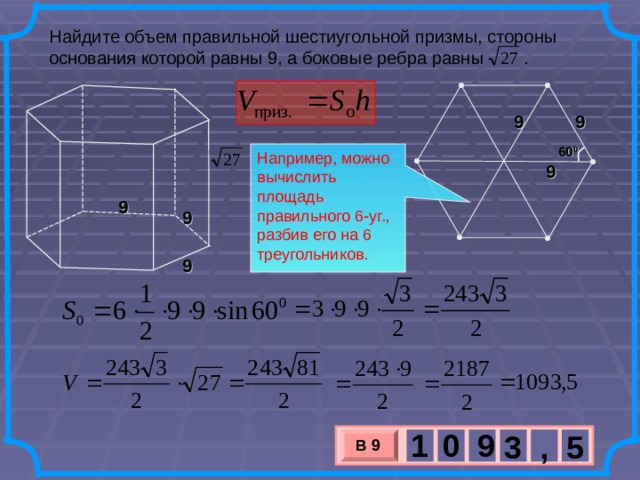 Меченосцев можно подсаживать до 10 животных.
Меченосцев можно подсаживать до 10 животных.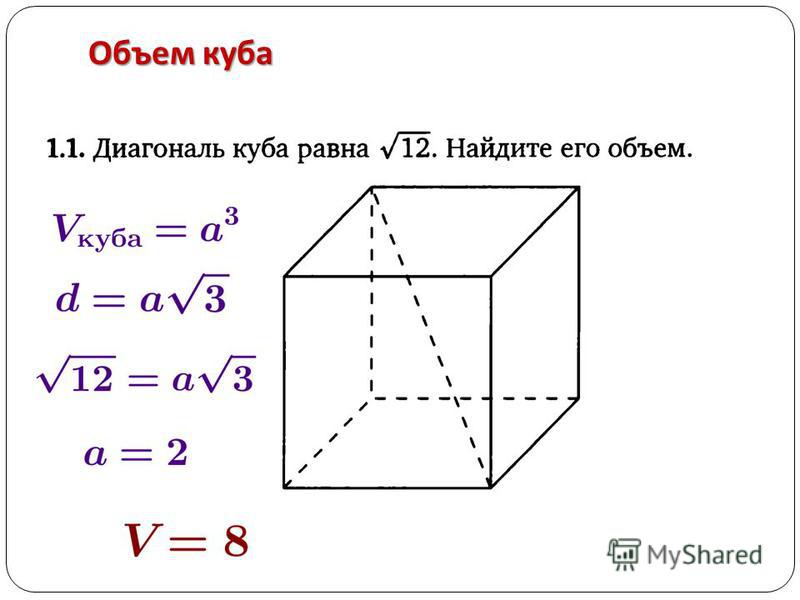 Меченосцы – 6 шт. Моллинезии – 6 шт.
Меченосцы – 6 шт. Моллинезии – 6 шт. 2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту:
2} — это формула площади круга, а в нашем случае — площадь основания. Поэтому формулу объема цилиндра можно записать через площадь основания и высоту: 14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3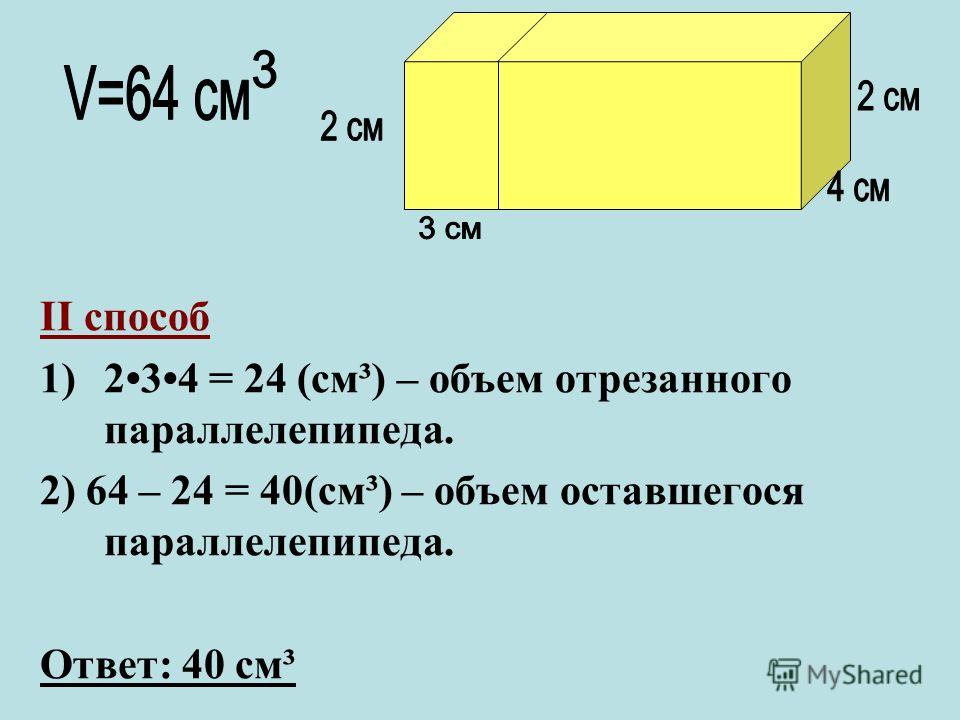
 Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом: То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра. )
)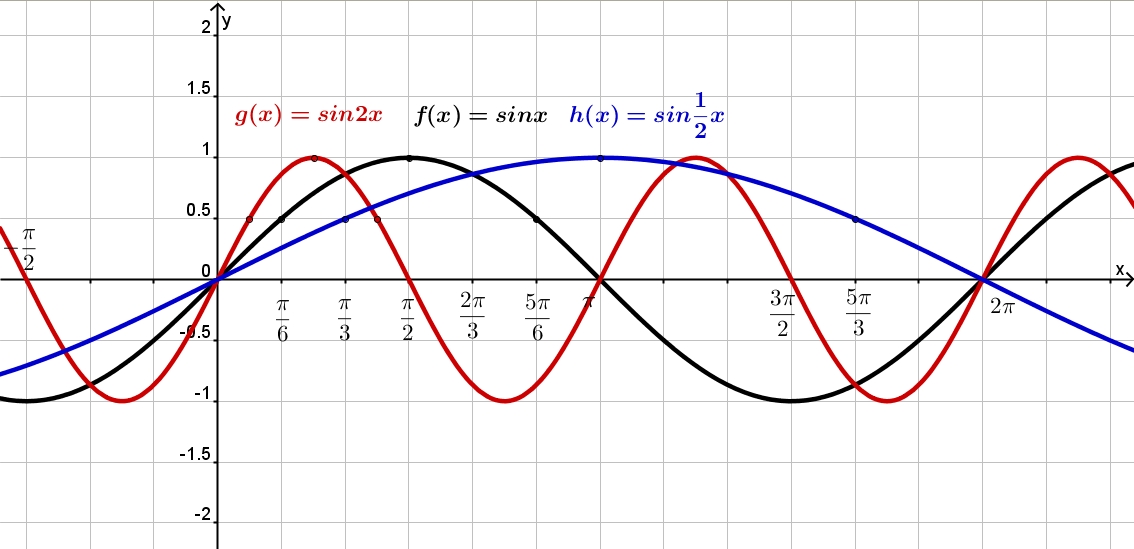 )
)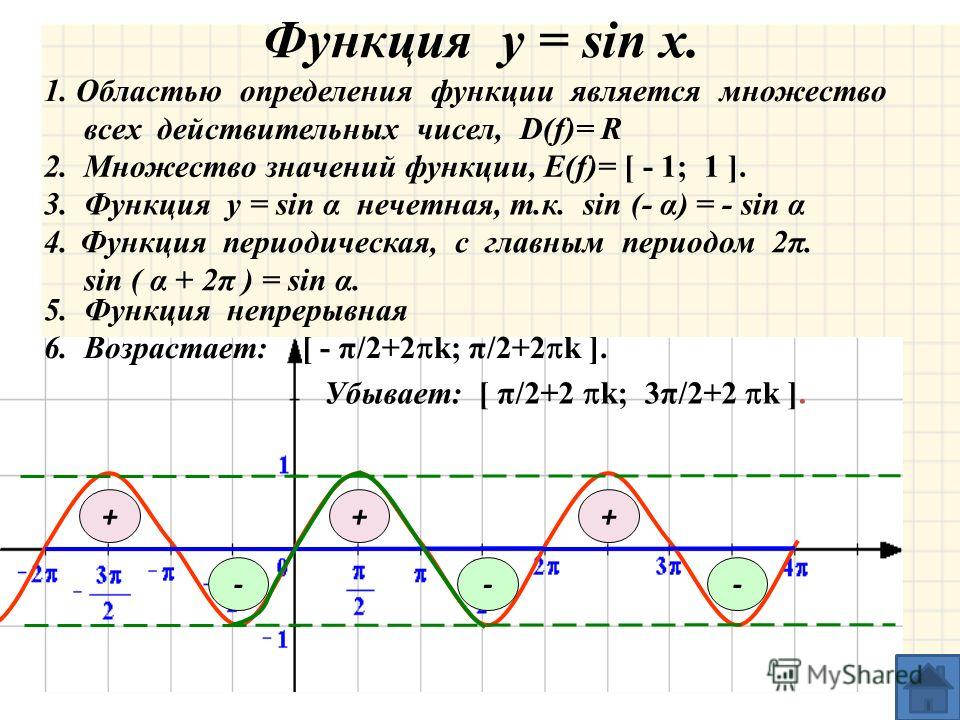 )
) )
) )
) )
) )
) )
) Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию
Каждому действительному числу соответствует единственное значение синуса. Такое соответствие определяет тригонометрическую функцию  75), значит, значения синусов этих углов также совпадают, т. е.
75), значит, значения синусов этих углов также совпадают, т. е.  76). Это означает, что ее график состоит из повторяющихся частей, поэтому достаточно его построить на отрезке длиной (например, а затем повторить построение на каждом следующем отрезке длиной
76). Это означает, что ее график состоит из повторяющихся частей, поэтому достаточно его построить на отрезке длиной (например, а затем повторить построение на каждом следующем отрезке длиной  79, а).
79, а). 82). График функции называется синусоидой.
82). График функции называется синусоидой. е.
е. 
 84).
84). Область значений функции.
Область значений функции.
 = 1
= 1 = 1 при х = π/2 + 2πn , n Z
= 1 при х = π/2 + 2πn , n Z
 Когда, в свою очередь, арабские математические трактаты попали к европейским математикам, те перевели джайб на латинский, благо под рукой как раз было изящное слово, обозначающее складку или пазуху на римской тоге — слово sinus. Родственную функцию назвали complementi sinus, дополнительный синус. Позже утвердилось современное сокращение: sin и cos.
Когда, в свою очередь, арабские математические трактаты попали к европейским математикам, те перевели джайб на латинский, благо под рукой как раз было изящное слово, обозначающее складку или пазуху на римской тоге — слово sinus. Родственную функцию назвали complementi sinus, дополнительный синус. Позже утвердилось современное сокращение: sin и cos. Восприятие, осмысление, первичное закрепление
Восприятие, осмысление, первичное закрепление

 Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017.
Дидактические материалы к учебнику Алгебра и начала математического анализа (углублённый уровень) – М.: «Вентана-Граф», 2017. С учётом этого факта продолжим построение графика влево, то точки -π:
С учётом этого факта продолжим построение графика влево, то точки -π: