5 способов создать векторную картинку в Adobe Illustrator
Микростокер и иллюстратор Ольга Захарова рассказала несколько способов, которыми она пользуется при создании очередной иллюстрации на продажу или для коммерческого заказа. Способы просты и, наверняка, большинство практикующих иллюстраторов о них знает, однако, все они сопряжены с нюансами, на которые стоит обратить внимание.
Когда я только начинала вести этот блог, я совсем ничего не понимала в стоках и очень мало знала о создании векторной иллюстрации. Поэтому мне хотелось делиться с миром каждым важным открытием — я понимала, что также, как недавно страдала я, не зная, как сделать бесшовную текстуру, сейчас страдает еще кто-то 🙂
Сейчас стало труднее. Потому что этап «новичковости» уже прошел, и очень многие вещи мне кажутся настолько очевидными, что пока кто-то из новичков не начинает задавать про них вопросы, мне не приходит в голову о них написать. Поэтому, ребята, не стесняйтесь писать комментарии, задавать все вопросы, даже те, которые кажутся глупыми (глупых вопросов не бывает).
Три картинки — три разных способа создания. Угадаете, где какой? 🙂
Это я все к тому, что меня тут как-то недавно спросили — а как удобнее обрисовывать картинку в Иллюстраторе?
Ведь существует великое множество способов превратить идею или скетч в векторную картинку с помощью нашей любимой программы 🙂 И я решила описать самые известные способы — с их плюсами и минусами. Сама я пользуюсь разными способами — в зависимости от результата, который хочу получить.
Трейс / Image Trace
Самый автоматизированный способ сделать из скетча векторную картинку и, как мне казалось раньше, самый быстрый (дисклеймер — сейчас я уже так не думаю).
Трейс картинки осуществляется с помощью панели image trace (верхняя панель Window — Image Tace) — просто помещаете свой скетч на рабочую область, открываете панельку, в выпадающем меню выбираете один из пресетов (у всех разные настройки, выбрать лучший можно методом тыка) — например, sketch — и через минуту-другую ваш файл превращен в вектор. Потом нужно только не забыть удалить “мусор” — разные пустые пути, которые образуются в процессе. Для этого не снимая выделение с оттрейсенного объекта надо пойти в верхнее меню Object — Path — Clean Up.
Трейс готов! Как говорили на одной моей прошлой работе “нажал кнопку — и в кассу”. Но, увы, все не так просто.
Результат трейса выглядит круто только тогда, когда исходная картинка-скетч была высокого качества (четкие линии с минимумом рукодрожания, не ворсистыми линиями и тп), потом она была сканирована с приличным DPI и хотя бы немного обработана в фотошопе (выбеливание фона, добавление контраста). Во всех остальных случаях трейс требует доработки.
Я делаю так: включаю видимость путей (cmd+H), выбираю контрастный цвет для них по отношению к обводке (двойной клик по названию слоя) — и, увеличив картинку до 200-300% проверяю аккуратность линий. В этом мне сильно помогают обычный карандаш — он мне нравится больше, чем сглаживающий — и плагин от Astute Graphics Smart Remove Brush Tool, которым можно удалять лишние точки, минимально изменяя линию.
Тут важно не переусердствовать в “вылизывании” картинки — если вам нужно идеальные ровные линии — быстрее использовать один из инструментов, о которых речь пойдет ниже. Трейс разумно использовать тогда, когда хочется сохранить эффект “нарисованности вручную”.
Я на данный момент использую трейс только для цитат вроде такой:
Плюсы и минусы трейса:
+ Можно относительно быстро превратить хороший скетч в векторную картинку с сохранением hand drawn эффекта
– Нужно потратить время, чтобы обработать
– Весь объект уже векторный, то есть труднее поменять толщину линий
– Линии не будут идеально ровными (это же и плюс)
Мой вердикт таков — использовать трейс надо с умом, применяя его ни ко всему подряд, чтобы сэкономить время на обработку, а к избранным картинкам, чтобы сохранить “ручной” эффект и некую небрежность линий.
Блоб браш / Blob Brush
Из всех инструментов иллюстратора больше всего на настоящую, живую, кисточку похож блоб браш. За это его очень любят художники, которые переходят с живого рисования или рисования в фотошопе на вектор. Всю прелесть этого инструмента могут оценить только те, у кого есть графический планшет – с его помощью можно контролировать толщину линий нажимом.
У этого инструмента так много поклонников, что мне даже как-то неловко признаваться, что я его не люблю и практически совсем не использую. Это вызывает у людей примерно такие же эмоции, как когда я говорю, что мне не нравится “Мастер и Маргарита”. Но что есть — то есть 🙂 Примеры употребления блоб браша в моем портфолио можно найти только на очень-очень старых картинках, которые, скорее всего, будут удалены во время следующей чистки.
Одна из моих первых картинок, нарисованная блоб брашем
Блоб брашем можно рисовать линии также, как вы это делаете фломастером на бумаге (сравнивать с кистью, мне кажется, не совсем верно, тк прозрачность блоб браша не регулируется нажимом), при условии, повторюсь, наличия планшета.
Плюсы и минусы блоб браша:
+ Облегчает художникам переход с растра на вектор
+ Имитирует “живое” рисование
– Нужен планшет, чтобы оценить всю прелесть (и умение рисовать тоже не помешает)
– Толщину линий можно задавать только перед рисованием, как только линия проведена — она по сути является векторным объектом с заливкой, — как и в случае с трейсом регулировать толщину постфактум сложно
Пентул / Pentool
Самый, наверное, непонятный инструмент для новичков, который оказывается крайне удобной и функциональной штукой, когда узнаешь его поближе. Совсем скоро я добавлю урок в магазин про то, как сделать кривые Безье своими лучшими друзьями, потому что сама в свое время потратила на них немало нервов.
Перо — инструмент наиболее далекий от художников и близкий графическим дизайнерам, потому что чтобы нарисовать линию — нужно не провести ее кисточкой/карандашом и тп, а поставить точку, потом еще одну — и так далее, регулируя изгиб и длину ручками кривой.
Почему-то мне видится, что блоб брашем больше рисуют девочки, а пентулом — мальчики, потому что он такой строгий и серьезный. И да, это мой любимый инструмент. Правда, не стандартный пентул, а апгрейд от Астуте Графикс под названием Вектор Скрайб.
Плюсы и минусы пентула:
+ Чистые и аккуратные линии
+ Можно регулировать толщину нарисованных линий/картинки в любой момент за пару секунд, пока не сделан экспанд (который нужно делать перед отправкой на стоки, но лучше сохранять в рабочем файле неэкспанднутую копию)
+ Пентул — отличный способ создавать картинки на стоки для тех, кто не умеет рисовать в классическом понимании этого слова
– Все рисование сводится к расстановке точек и повороту ручек — многих креативных людей это напрягает
– Полезно также освоить инструмент Shape Builder Tool и панель Pathfinder, потому что обычный ластик удалить лишнее не поможет
– Чтобы научиться уверенно обращаться с пентулом, нужно освоить какое-то количество теории и много, много практиковаться, при этом первое время линии будут получаться кривоватыми и на отрисовку будет уходить много времени
Кисточка (обычная) / Brush
Компромисс между пентулом и блоб брашем для тех, кто хочет проводить линии, а не ставить точки, и при этом иметь больший контроль над тем, как линия выглядит.
Что на линию, проведенную кистью, что на “пентульную” можно “насадить” огромное количество самых разных кистей — из стандартной библиотеки (правда, официально на стоки их использовать нельзя), либо !! своих собственных, каждый раз получая новый результат. Потом нужно не забыть все это дело отэкспандить (то есть превратить в вектор с помощью команды Object — Expand).
Плюсы и минусы кисточки:
+ Сохраняется возможность редактирования линий и можно рисовать руками (не точками)
– Нужен планшет
– Линии почти всегда получаются не такими, как хочется, — может у меня руки кривые, но по моим ощущениям тот же блоб браш позволяет точнее контролировать линию
У блоб браша и кисточки есть свои индивидуальные настройки, добраться до которых можно, дважды кликнув по конкретному инструменту в левой панельке.
У кисточки можно настроить чувствительность и сглаживаемость линии, у блоб браша также можно включить или отключить автоматическое слипание объектов одного цвета друг с другом. Подробно про настройки мне рассказать нечего, тк у меня стоят стандартные.
Простые геометрические формы
Речь о квадрате, круге, линиях, многоугольниках — чаще всего, конечно, они используются не сами по себе, а в сочетании с пентулом. Рисование с помощью геометрических фигур подходит тем, кто любит геометричность в картинках, кайфует от четких форм и минимума точек на путях 🙂 Раньше я использовала формы только для каких-то очевидных действий — например, делала глаза персонажу с помощью круга, или каркас дома с помощью квадрата.
Посмотрев курс Illustration for Designers: Create Your Own Geometric Animal (Иллюстрация для дизайнеров: Создайте свое собственное геометричное животное) на Skillshare я переосмыслила роль форм в картинках и мне стало интересно научиться видеть формы в объектах. Так родилась серия животных, которую я скоро планирую продолжить:
Плюсы и минусы рисования формами:
+ Линии получаются идеальными, не нужно думать о том, куда поставить точку и как потянуть за ручку
– Перестроиться на «мышление формами» большинству людей очень сложно
– Все равно придется использовать дополнительные инструменты — пентул, панель пасфайндер или шейп билдер тул
Примерно 80% моих текущих картинок нарисованы плагином InkScribe — тот самый аналог пентула от Astute Graphics, о котором я уже говорила (я, кстати, планирую написать отдельный пост про астутовские плагины, как только меня перестанет пугать потенциальный размер этого поста).
Остальные 20% — это трейс, простые формы и иногда — Dynamic Sketch Tool. Это что-то вроде карандаша, только более аккуратный и с большим количеством настроек (опять же, астутовский).
Каким инструментом будет удобнее/быстрее рисовать лично вам кроме вас никто решить не сможет. Поэтому мой главный совет — пробуйте их все, применяйте для разных картинок, разных стилей, в разных ситуациях и не позволяйте чужому мнению на вас влиять. Потому что для кого-то блоб браш всех прекраснее и милее, а кому-то, чтобы рисовать крутые картинки, и планшет не нужен — справляются мышкой и пентулом.
Фото на обложке: ShutterStock
Векторные инструменты рисования в Фотошопе
Базовые векторные инструменты в Adobe Photoshop идентичны Illustrator-у. Но, отмечу, для рисования в чистом виде они не созданы. Почему? Во первых, для рисования в векторе есть отличные программы Illustrator или Corel Draw. Вот там присутствует весь необходимый для рисования функционал. Во вторых, скупость настроек в фотошопе для вектора. В Фотошопе имеются только инструменты рисования и некоторые примитивы. Что с одной стороны правильно. Вот отличная программа для растровой графики, а вот отличная программа для векторной. Да, в векторной бывает необходимо поработать с растром, а в растровой бывает нужен вектор. Так лучше связать их и продавать пакетом.
Из картинки видно — все контуры, из которых состоит фигура, остаются внутри слоя. Таким образом фигуру можно быстро и легко изменить. Хотя векторный Adobe Photoshop способен на куда большее. Например, данные эскизы для одного старого сайта я исполнял в векторе. Изображение я кистью с твердыми краями. Затем выделял слой и переводил выделение в контуры. Из контуров делал залитые слои с векторной маской. Таким образом я достигал отсутствующего в фотошопе сглаживания контура.
Инструмент Pen Tool
Первым у нас идет инструмент Pen Tool и его разновидности. Тот же самый набор можно найти в Illustrator-е. Это удобно при переходе из одной программы в другую, не надо переучиваться. Тем более что все векторные инструменты перекочевали в Photoshop прямо из Illustrator-а.
Pen Tool — перо Безье, модулировать им векторный контур проще простого, но для новичков может оказаться весьма сложным занятием. Подробные описания всех приемов управления с направляющими заняли бы отдельную статью или главу. Фактически это самый основной и головной инструмент модулирования фигур и контуров в векторе. И, что удобно, одинаковый во всех векторных программах.
Попробуем изобразить пару контуров. Выберите инструмент Pen Tool, и следите чтобы в настройках инструмента у вас стояла опция Path. Не то чтобы это было особенно важно, но если вместо Path там будет Shape Layer, то вы будете рисовать заливками с векторной маской, а не просто контурами. Подробнее об этих режимах я написал в статье Shape Layers, Path и Fill Pixel в Фотошопе.
Теперь кликните в любом месте. Когда вы кликнули, у вас появилась ключевая точка (якорь, ключик, штучка, название не имеет значения). Протяните мышь в любую сторону, продолжая зажимать кнопку. Если все правильно, вы увидите направляющие.
Кликните в любом другом месте. Вы увидите как от первой точки к второй протянулась линия. Начинайте отводить мышку, не отпуская клавишу. Ваш контур формируется в зависимости от того, как вы выставите направляющие ко второй ключевой точке.
Понять в какой зависимости от чего строятся линии в зависимости от направляющих пожалуй самое базовое понимание векторной графики. На панельке настроек векторных инструментов у Pen Tool есть одна интересная настройка — Auto Add/Delete. Это фактически автоматизированные Add и Delete Anchor Point Tools о которых речь пойдет дальше. Кликните по этой галочке и ваша кисть сможет прямо во время рисования добавлять точки на уже отрисованные контуры и удалять ненужные точки. Вы сможете делать это прямо во время рисования контура, а не после. И для этого не придется переключаться на бесполезные Add и Delete Anchor Point Tools
Freeform Pen Tool
Если для работы с Pen Tool необходимо понять принципы построения векторных кривых, то Freeform Pen Tool — инструмент, свободный от всяких правил и принципов. Просто кликайте по нему и рисуйте контур, так как вы рисовали бы обычной кистью. Идеальный круг или праздник геометрических форм им конечно не изобразить, а вот кляксу вполне. Этот инструмент подойдет для создания коллекций фигур в индустриальном стиле. Рисовать кляксы им самое то. Ну а если мастерство рисования доведено до совершенства, то… думаю лучше использовать программу Illustrator, если конечно вы не из тех, кто для развлечения ваяет шедевры в MS Paint (:
У инструмента Freeform Pen Tool пожалуй есть ещё одна интересная настройка. В панели настроек Freeform Pen Tool есть галочка Magnetic. Это спрятанный аналог инструмента Magnetic Lasso Tool. Работает точно так же. Просто включите эту галочку. Подведите курсор к какому-то четко выраженному объекту, с высококонтрастной кромкой и начинайте обводить. Конечно, идеальной геометрии ждать от этого инструмента не нужно.
Add Anchor Point Tool и Delete Anchor Point Tool
Add Anchor Point Tool — тот инструмент добавляет на уже отрисованный контур дополнительные точки, для изменения или коррекции формы контура. Просто нарисуйте контур, затем переключитесь на этот инструмент и поставьте не хватающие узелки в нужных вам местах. Для чего это нужно? Ну может вам необходимо поставить побольше точек, что бы контур был больше похож на то что вам нужно.
Delete Anchor Point Tool — соответственно данный инструмент удаляет лишние точки векторной кривой. Область применения этого инструмента та же что и у Add Anchor Point Tool, только в случае уменьшения точек линия контура становится по понятным причинам более ровной и мягкой.
Convert Point Tool
Этот инструмент помогает в редактировании направляющих точки кривой. При нажатии на точку инструмент сбрасывает направляющие. Удерживая кнопку мыши, отводим мышку в сторону. Так мы изменяем формы и направление направляющих, против их первоначального значения. А если зацепить инструментом Convert Point Tool одну из направляющих, можно придать ей независимое направление.
И ещё раз. Вы захватываетесь инструментом Convert Point Tool, за точку. От такой близости у точки сбрасываются направляющие. Не отпуская кнопку мыши, отводите мышь в сторону, выстраивая новые направляющие. А при желании, можете захватить за одну из направляющих и настроить её в индивидуальном порядке. А теперь обсудим детали.
Выпадающее меню векторных инструментов
Выпадающее меню векторных инструментов раскрывает нам разные интересные фичи, многие из которых завязаны на других темах, так что я не буду расписывать их слишком глубоко. Логично, не разбираться же нам в том что такое маска, в статье про инструменты рисования. Выбираем любой из инструментов, рисуем подобие круга, как у меня, и щелкаем правой кнопкой мыши. Нарисовать цельный круг важно, иначе не все опции меню будут доступны. Обратите внимание, сейчас кликать надо по контуру.
Delete Anchor Point
Все очень просто. Кликаете по непонравившейся точке и удаляете её. Мне так даже проще чем инструментом Delete Anchor Point Tool. Тем более если такая точка всего одна. Эта опция меню сменная. Сейчас там Delete Anchor Point, потому что я подвел мышку ровно к точке. Если кликнуть мышкой по любому месту контура Delete сменится на Add Anchor Point, то есть речь идет о добавлении новой точки на контур.
Create Vector Mask
Является шорткатом на опцию Layer > Vector Mask > Current Path Что делает эта опция? Создает векторную маску конечно. Сейчас я покажу как это делается. Поместите на палитру какое-нибудь фото. Я например выбрал фотографию своего попугая Чучи. Контур должен быть виден. Сбрасывать его нельзя. Поместите фото прямо под контур или контур под фото. Или нарисуйте новый контур именно так, как вам хочется. Теперь нажимаем на Create Vector Mask и получаем результат! Векторный контур превратился в векторную маску. А попугай Чуча в кружок!
Delete Vector Mask
Название говорит само за себя. Попугай Чуча превращается в прямоугольную фотографию. Маска уходит в небытие. Контур становится обычным контуром.
Define Custom Shape
Контур превращается в векторную фигуру-заготовку. То есть, данная опция сохраняет контур, помещает его в специальную библиотеку, откуда его далее можно всегда достать и не хитро воспользоваться. Просто впишите название вашего контура.
И найдите его по адресу инструмента Custom Shape Tool в меню настроек инструмента среди других зверюшек и стрелочек.
Make Selection — Эта опция из вектора создает выделение. Разберем поподробнее что предлагает нам меню.
Feather Radius — радиус размытия. Если вы свое выделение далее зальете, края будут рызмытыми. Чем больше значение тем больше размытие. Внимание на экран:
Anti-aliased — смягчает края. Без функции Anti-aliased заливка будет залита попиксельно. Функция Anti-aliased создает на краях заливки полутона.
Fill Path
Дальний родственник опции Edit > Fill. Но в отличии от последней имеет пару апгрейдов. У него есть идентичная графа Content, что в целом значит, чем заливать то будем? Есть графа Blending, отвечающая за режимы наложения. А так же важная галочка Preserve transparency. При выставлении этой галочки заливка учитывает прозрачные места и не заливает их.
Stroke Path
Подчеркивает выделение. Причем подчеркивает чем угодно. В меню Stroke Path можно выбрать любой инструмент, хоть резинку, хоть блендер, хоть кисть. Чаще всего конечно нужна кисть. Stroke Path пользуется настройками инструмента, которые выставленны в данный момент. Например если последний раз вы рисовали твердой кистью 10 px, то подчеркиваться контур будет именно ею. Опция Simulate Pressure симулирует давление.
Clipping Path
Разновидность маскирования в фотошопе и не только. Наиболее часто Clipping Path применяют при отделении заднего фона от объекта. Не поверите, но на западе существуют целые студии занимающиеся этой работой, а работники маскировщики называются — специалисты по маскированию. Вот уж специалисты так специалисты! По сути, Clippping Path крепит контур к растровому изображению. Нарисуйте, например, контур на семейной фотографии, или выделите контуром объект. Сохраните в формате PDF и откройте в Illustratore. Ваше изображение помещено внутрь контура, точно так же как при векторной маске. По правде говоря этот Clipping Path является для меня черным пятном. Загадочность Clipping Path заставила меня подробным образом изучить эту опцию, о чем я и написал в своей статье Что такое Clipping Path
Free Transform Path
Изменяет форму контура или отдельной группы точек. Изменение формы объекта в представлении не нуждается. И без того интуитивно ясно как это делается. Квадратик крутится во все стороны, зажимая уголки меняется размер. А при зажатии клавиши Ctrl меняется перспектива фигуры.
Автор:
Как нарисовать изогнутую стрелку в PowerPoint
Стрелки – довольно частый элемент презентации – связи, указатели, ссылки, – всего этого на слайдах хватает. Однако если нарисовать прямую стрелку обычно очень легко, то попытка немного усложнить задачу и добавить к слайду изогнутую стрелку, почти наверняка с первого раза не удастся. Впрочем, учитывая тот факт, что простые, прямые стрелки скучны до безобразия, нам придется что-то придумать.
К счастью, есть очень просто рецепт, которым я с вами сейчас поделюсь.
Основа для стрелкиПервым делом добавим контур нашей супер-стрелки, для этого в группе «рисование» на панели «Главная» выберем инструмент «Кривая». По сравнению с другими инструментами этой группы, «кривая» строится по принципу кривых Безье – с каждым щелчком мыши по слайду, на экране будет возникать не кратчайший путь от точки к точке, а плавный, точно выверенный маршрут. Как только кривая будет доведена до конца – нажмите «Esc», чтоб зафиксировать её положение. Если вышло совсем не так ровно, как хотелось – не страшно, сейчас мы это исправим.
Нарисую в PowerPoint два блока и соединю их кривой
Придаем стрелке форму.Выделяем нашу кривую, нажимаем на ней правой кнопкой мыши и выбираем в контекстном меню пункт «Начать изменение узлов». Линия изменит цвет, а узловые точки (места, где мы щелкали мышью) станут вновь активными. Перемещая узловые точки, придадим кривой аккуратный, ровный вид.
Обратите внимание: при выборе узловой точки, повторный вызов контекстного меню правой кнопки мыши, выведет ряд дополнительных настроек (добавление, удаление узловых точек, изменение их свойств).
А теперь, займемся кривыми Безье
Заканчиваем создание стрелкиУ наших кривых кое-чего не хватает, верно? Придадим им более соответствующий вид: выделяем кривую, нажимаем на ней правой кнопкой мыши и выбираем в контекстном меню пункт «Формат фигуры». В появившемся окне настроек, нас интересуют в первую очередь пункты «Тип конечной стрелки» и «Размер конечной стрелки» – они определяющие «навершие» нашей кривой.
Я немного дорисовал исходный рисунок. теперь превратим кривые в полноценные стрелки.
После того, как все встанет на свои места, можно дополнительно визуализировать наши стрелки. Для примера, я раскрасил их разными цветами («Цвет») и задал разную толщину – по степени важности («Ширина»).
Итоговая схема с закругленными стрелками
ᐈ Нарисовать Логотип в Векторе Киев — Цены 2021, Стоимость
Нарисовать логотип в векторе в Киеве
Логотип – знак отличия бренда, который значительно влияет на его узнаваемость и помогает его продвижению. Чтобы это было действительно так, важно, чтобы разработка логотипов велась дизайнером, который профессионально ориентируется в рекламной сфере. Без этого логотип будет просто красивым значком – и не сможет нести в себе информацию, ценную для целевой аудитории.
Логотипы обычно разрабатывают в 4 этапа:
- сбор необходимой информации;
- разработка концепции;
- подготовка черновиков и вариантов;
- утверждение и внедрение итогового варианта.
На первом этапе разработка логотипов заключается в обсуждении элементов, которые должен включать знак. Ориентирами могут служить направление работы компании, вид ее продукции, особенности целевой аудитории. После этого принимается решение, каким будет логотип: в виде рисунка, надписи, сочетания символа и текста. Каким бы ни было решение, всегда нужно исходить из максимальной простоты – перегруженные логотипы никто не запомнит.
Работая над созданием логотипа, дизайнер (художник) не только придумывает несколько вариантов, а и продумывает, как будет выглядеть логотип на упаковках с продукцией, на фирменных бланках, визитках и т.п. В целом создание знака может занять много времени – ведь еще важно протестировать результат на аудитории и, если нужно, внести изменения.
Прайс: Нарисовать логотип в векторе в городе Киев
| Цены на дизайн сайта | Цена, грн |
|---|---|
| Дизайн сайта-представительства | от 1500 грн |
| Дизайн промо-сайта | от 2500 грн |
| Дизайн сайта-каталога | от 3500 грн |
| Дизайн интернет-магазина | от 4000 грн |
| Дизайн нестандартного проекта | от 8000 грн |
| Стоимость дизайна интерьера | Цена, грн |
| Обмерный чертеж | от 100 грн |
| Варианты перепланировки (2-3 варианта) | от 300 грн |
| План демонтажных работ | от 120 грн |
| План монтажных работ | от 150 грн |
| План расстановки мебели | от 170 грн |
| Схема разводки сантехнической системы, узлы, сечение | от 300 грн |
| Схемы размещения приборов отопительной системы | от 200 грн |
| Схемы дверных проемов | от 150 грн |
| Схемы вентиляции и кондиционирования | от 130 грн |
| Сечение полов, потолков | от 150 грн |
| План напольных покрытий с ведомостью материалов | от 150 грн |
| План теплого пола | от 155 грн |
| План потолков с привязками | от 160 грн |
| План осветительного оборудования с привязкой выключателей | от 170 грн |
| План размещения розеток и выключателей | от 180 грн |
| Раскладка плитки | от 190 грн |
| Детальные схемы мебели под заказ (кухня, гардеробная, шкаф и т.п.) | от 300 грн |
| Развертка стен всех помещений | от 300 грн |
| Ведомость отделки помещения | от 700 грн |
| Фотореалистичная 3D – визуализация интерьера каждого помещения | от 500 грн |
| Цена разработки логотипа | Цена, грн. |
| Разработка 3 вариантов логотипа | от 1000 грн |
| Разработка 5 вариантов логотипа | от 1500 грн |
| Разработка 10 вариантов логотипа | от 2000 грн |
| Разработка больше 20 вариантов логотипа | от 5000 грн |
| Редизайн логотипа | от 3000 грн |
| Разработка фирменного стиля | от 10000 грн |
| Цены на дизайн баннера | Цена, грн |
| Дизайна макета биг-борда (3х6м) | от 1000 грн |
| Дизайна макета сити-лайта | от 800 грн |
| Дизайна макета вывески | от 500 грн |
| Дизайн баннерной сетка | от 500 грн |
*Цена актуальная на Июль 2021
Профессиональная разработка логотипов в Киеве может стоить недорого. Это реально, если заказать ее у специалиста напрямую, минуя рекламные агентства и других посредников. Найти хорошего дизайнера или художника можно через сервис Kabanchik.ua, при этом стоимость разработки логотипа будет на 30-50% ниже, чем у рекламных агентств. Самые важные преимущества – заказчик сам выбирает специалиста, сам определяет дату сдачи работы и сумму гонорара.
Metod Draw — векторный редактор онлайн ⋆ Lifeservice
Наверно каждый сталкивался или слышал о мифическом и каком то совсем сложном формате изображений вектор — который идеально подходит для логотипов, макетирования страниц, иллюстраций, которые можно масштабировать до любого размера. Признанными программами для профессионалов, конечно является CorelDRAW, Adobe Illustrator но они достаточно сложны, дороги, неповоротливы, требуют установки и часто не подходят, для создания простого логотипа, несложной иллюстрации или рекламной надписи. Есть и бесплатное ПО скажете вы и будете правы, Inkscape пожалуй лучший представить свободного программного обеспечения. Как быть тому, кому не подходят все эти программы? Обычный браузер вполне справится с такой задачей. О онлайн редакторе графики я уже рассказывал, в продолжении темы поговорим о векторных иллюстрациях, которые можно создать или редактировать онлайн, не устанавливая никаких программ. Для этого понадобятся минимальные навыки , идея и желание для осуществления. Для этого нужен только браузер и доступ в сет
На Metod Draw внушительный набор функций, даже поначалу не верится, что это возможно в простом браузере. Тот, кто хотя бы раз открывал Adobe Illustrator меня поймет: множество параметров, координат и инструментов. В Metod Draw все просто и наглядно, напоминает привычный Paint в windows. Возможным недостатком может быть отсутствие поддержки русского языка, благо терминов немного и разобраться легко.
Возможности:
- Поддерживает горячие клавиши. Стандартный набор (Ctrl + C, Ctrl + V, Ctrl + Z…).
- Есть неплохая библиотека готовых символов и форм. Палитра цветов.
- Открывает файлы формата .SVG конвертировать из другого векторного формата можно тут.
- Загрузка и растрирование изображений.
- Сохраняем в .PNG что упрощает использование в web разработке.
- Свобода творчества. Бесплатно. Креативно.
comments powered by HyperComments
Лучшие уроки по векторной графике
Поиск лучших руководств по векторной графике позволит вам добавить личный штамп к своим проектам, создав собственную векторную графику. Хотя в сети есть куча стоковых векторных изображений, бывают моменты, когда вам нужно что-то более особенное.
Мы провели поиск по всему миру и собрали лучшие учебники по векторной графике, чтобы дать вам возможность создавать бесконечно гибкие цифровые творения. Они подойдут новичкам, желающим начать, и опытным профессионалам, желающим отточить свою технику.Каким бы ни был ваш уровень, мы вам поможем.
Во всех этих руководствах используется программное обеспечение, такое как Illustrator CC, Affinity Designer или Sketch, чтобы продемонстрировать, как создать собственный векторный дизайн (наш список руководств по рисованию может помочь вам с дизайном). Требуется программное обеспечение? Вот лучшие скидки на Creative Cloud. Если вы предпочитаете использовать стоковый вектор или вам нужно вдохновение, ознакомьтесь с нашим списком веб-сайтов с лучшими бесплатными векторными изображениями.
Лучшие на сегодня предложения Adobe Creative Cloud
После того, как вы ознакомились с ними, почему бы не добавить еще несколько инструментов в свой набор инструментов и не попробовать наши учебники по Photoshop и Illustrator?
Что такое векторная графика?
В отличие от изображений на основе пикселей, созданных в таких инструментах, как Photoshop CC, векторы основаны на математически определенных линиях и точках, которые объединяются в формы.Поэтому, как бы вы ни масштабировали векторную графику вверх или вниз, она никогда не станет размытой или потеряет четкость.
Чтобы узнать больше о разнице между векторными и растровыми изображениями, а также узнать о других удобных работах и фразах, которые могут вас запутать, прочтите нашу публикацию о ключевых терминах, которые должен знать каждый графический дизайнер.
Во все более цифровом мире растет спрос на векторную графику. Итак, давайте начнем с лучших руководств по векторной графике.
Получите Adobe Illustrator прямо сейчас
Один из лучших и простых способов создания потрясающих векторных изображений — это Adobe Illustrator.Вы можете купить программное обеспечение через опцию Adobe CC All Apps, которая дает вам доступ ко всему набору CC настольных и мобильных творческих приложений. План также включает 100 ГБ облачного хранилища, Adobe Portfolio, Adobe Fonts и Adobe Spark с дополнительными функциями. (В качестве альтернативы, если вы студент или преподаватель, вы можете сэкономить до 60% на CC.) View Deal
01. Начните создавать иллюстрации
Если вы новичок в создании векторной графики в Adobe Illustrator, вот отличное место для начала.Создатели программного обеспечения объясняют, как легко создавать свои произведения из простых векторных фигур, которые можно настраивать, комбинировать и раскрашивать, чтобы создавать привлекательные иллюстрации.
02. Создание и редактирование фигур
Продолжая предыдущее введение, в этом руководстве Adobe изложены основы создания и редактирования фигур в Adobe Illustrator CC, в том числе способы рисования комбинирования и обводки фигур.
03. Объяснение векторов! Учебное пособие по Affinity Designer
Adobe Illustrator — не единственный инструмент, доступный для создания векторной графики: все более популярной альтернативой является Affinity Designer.В этом руководстве по Affinity Designer объясняется, как векторы сравниваются с растровыми / растровыми изображениями, как создаются векторы, какие приложения используют векторы, почему вам нужно экспортировать свою работу, а также лучшие советы по сохранению четкости и четкости вашего окончательного дизайна.
04. Руководство для начинающих по векторам в Affinity Designer
Здесь Майк Мангиаларди предоставляет подробное руководство по созданию базового векторного графического изображения с помощью этого программного обеспечения, которому может следовать любой человек на любом уровне. Даже если вы не используете Affinity Designer, здесь вы узнаете много нового о векторах, которые можно применить к своей работе с помощью других инструментов.
05. Создание векторной иллюстрации от начала до конца
Pro иллюстратор и блогер Крис Спунер считает, что набор инструментов Illustrator для создания фигур можно использовать для создания классных векторных иллюстраций абсолютно чего угодно. Он демонстрирует это здесь, проходя через процесс создания простой иллюстрации водяного пистолета. Все это делается с помощью основных инструментов Illustrator, а затем используется инструмент Live Paint для добавления цвета.
06. Переход с Adobe Illustrator на Affinity Designer
Может быть, вы уже практиковались в создании векторной графики в Illustrator, но когда дело касается Affinity Designer, вы новичок? Чтобы помочь вам, Андрей Стефан проведет вас через процесс перехода с Adobe Illustrator на Affinity Designer, перечисляя ключевые препятствия, которые вам, возможно, придется преодолевать на этом пути.
07. Как писать от руки в векторном формате
Хотите преобразовать рукописный текст в формат векторной графики? В этом видео Скотт Бирсак показывает, как именно это сделать в Adobe Illustrator.
08. Создание красочных векторных изображений персонажей
В этом уроке Illustrator от Digital Arts вы узнаете, как превратить нарисованный от руки эскиз в цветной цифровой векторный файл, с учетом корректировки цвета, глубины и композиции.Базовые навыки, которые вы здесь изучите, помогут вам снова и снова создавать масштабируемые векторы символов.
09. Как создать значок галочки
В этом уроке Андрей Стефан проведет вас через процесс создания простого векторного значка, галочки или галочки с помощью Adobe Illustrator от начала до конца.
Следующая страница: Промежуточные уроки по векторному искусству
Как рисовать векторных людей в Adobe Illustrator | автор: Toffu Co
Привет, друзья! Мы так рады загрузить наш первый учебник Как рисовать векторных людей в Adobe Illustrator .
В этом наполовину учебном видео, посвященном рисованию на половинной скорости, вы можете выполнить шаги по рисованию нашего простого набора, который вы можете скачать здесь .
Напоминаем, что во время рисования я использовал перьевой планшет, но мышь тоже работает.
Ладно, приступим!
# step1 настройка документа
Мы начинаем с создания нового rgb-документа размером 30×30 см с настройками по умолчанию.
Когда появится пустая страница, перетащите эталонное изображение (вы можете скачать его здесь) в проект, затем щелкните преобразование и измените его размер.Высота «H» должна составлять 30 см. Обратите внимание на маленькую иконку, на которой она должна быть рядом с размерами W и H.
После изменения размера изображения перетащите его в центр страницы и заблокируйте слой 1, щелкнув место рядом со значком глаза под панелью «Слои».
(ps Если вы не видите панель слоев, перейдите в раздел «Окно» в верхней части экрана и нажмите «Слои».)
# step2 новые слои + контур и формы
Когда все выглядит Хорошо нажмите кнопку Create New Layer под панелью слоев и переименуйте его в jacket .
Когда выбран слой куртки , щелкните инструмент «Карандаш» (N) слева и нарисуйте контур куртки.
После рисования контура куртки щелкните инструмент «Пипетка» (I) слева, затем щелкните желтую часть куртки.
Когда форма будет выглядеть нормально, щелкните инструмент «Прямое выделение» (A) слева и щелкните опорные точки, которые необходимо отредактировать.
Вам следует удалить все точки привязки, которые выглядят ненужными, или преобразовать их в угловые или сглаженные с верхней панели.Чтобы улучшить форму, перетащите ручки узловых точек и измените форму прикрепленных линий.
После завершения всей куртки создайте новый слой как брюки и повторите процесс прямого выбора карандашом и пипеткой, затем перетащите куртку слой (включая верх) над другими слоями.
Создайте новый слой с именем skin и закройте другие слои, щелкнув значки глаз рядом с ними. Повторите процесс прямого выделения карандашом и пипеткой, нарисуйте лицо и руки, затем перетащите слой кожа наверх.
Создайте новый слой с именем , волосы и повторите тот же процесс. Для лучшего обзора не забудьте закрыть другие слои, прежде чем рисовать волосы. Повторите процесс прямого выбора, волосы и форма лица должны хорошо подходить.
Создайте новый слой с именем зонт и щелкните на инструменте Pen Tool (P) слева. Щелкните по углам и завершите ребро.
Когда все будет готово, создайте слой зонт2 и нарисуйте тканевую часть зонтика с помощью Pen Tool (P).
После перекраски зонта и расположения слоев (слой зонтика2 должен находиться между слоями куртки и штанов) создайте новый слой для сигареты, я использовал имя oth (сокращенная форма других) . Когда выбран слой oth , нажмите Pencil Tool (N) и нарисуйте контур сигареты. Перетащите слой oth под слой skin .
Создайте еще один слой oth для рисования части сигареты, которая появляется на коже, затем нарисуйте ее с помощью Pencil Tool (N) и уточните с помощью Direct Selection Tool (A).
# step3 редактирование шаблонов
Пока все хорошо, мы почти закончили рисование. Убедитесь, что все слои видны, и под панелью «Слои» щелкните кружок рядом со слоем jacket . Это позволяет выбрать сразу все содержимое слоя. Выбрав Копировать (cmd + c) (ctrl + c) и Вставить на место (cmd + shift + v) (ctrl + shift + v) и , нажмите Swatches> Swatches Libraries menu> Patterns> Deco > Vonster Patterns> Splatterz справа.
Я выбрал этот узор из-за схожести с исходным фото, при желании можно попробовать что-нибудь другое. После выбора выкройки закройте слой jacket со значком глаза под панелью слоев. Теперь используйте инструмент «пипетка» и нажмите на синюю часть куртки. Дважды щелкните раздел «Заливка» слева и скопируйте цветовой код на экране «Палитра цветов».
Снова откройте раздел «Образцы» и дважды щелкните использованный узор. Когда появится экран редактирования рисунка, щелкните синюю часть рисунка> Заливка> Палитра цветов и вставьте сюда код цвета.
Наконец, повторите это для остальных цветов. Для облегчения я изменил;
синий> синий # 0f9abe
розовый> красный # cd360f
зеленый> черный # 141319
И результат;
Надеюсь будет полезно. Продолжайте следить!
Создание векторной графики и работа с ней в Adobe Photoshop
Adobe Illustrator — это стандартное приложение для графического дизайна. Это лучший инструмент для работы с векторными файлами.
К сожалению, не у всех есть Illustrator, но у многих есть Photoshop. В Photoshop есть базовая поддержка векторных изображений. В этом руководстве мы рассмотрим, как создавать векторные изображения в Photoshop в качестве замены Illustrator.
Что такое векторное изображение?
Photoshop в первую очередь предназначен для растровых изображений. Это многоугольные изображения, нарисованные попиксельно. Они поддерживают большое количество деталей и используются для фотографий.Однако размеры файлов могут быть большими, и вы не можете увеличить их без потери качества.
Векторные изображения — это линии и кривые, построенные по математическим формулам. Это означает, что вы можете изменять их размер бесконечно, а размеры файлов часто очень малы. Векторы отлично подходят для работы с графическим дизайном, включая создание логотипов и значков. Вы даже можете конвертировать изображения в векторную графику в Adobe Illustrator.
Часть векторной графики состоит из нескольких объектов.Каждый объект представляет собой линию или фигуру, край которой определяется путем. В Photoshop путь показан тонкой синей линией (хотя технически она невидима).
К каждому объекту можно применить два типа цвета:
- Обводка — это линия, которая следует за траекторией.
- Заливка добавляет сплошной цвет или узор в пространство, окруженное траекторией.
Вы устанавливаете оба параметра на панели параметров в верхней части экрана. Вы также можете установить Без цвета , если хотите, чтобы они оставались пустыми. Для обводки также можно установить толщину в пикселях и стиль. По умолчанию используется сплошная линия.
В Photoshop вы рисуете векторные изображения с помощью фигур, линий и текста.
Рисование векторных фигур и линий
Photoshop поставляется с инструментами для рисования нескольких распространенных форм.По умолчанию выделен инструмент «Прямоугольник » . Нажмите и удерживайте этот значок, чтобы открыть полный набор инструментов:
- Инструмент Прямоугольник
- Инструмент «Прямоугольник со скругленными углами»
- Инструмент «Эллипс»
- Инструмент «Многоугольник»
- Инструмент линии
- Инструмент Custom Shape
Вы всегда можете выбрать выделенный инструмент, нажав U на клавиатуре.Или нажмите Shift + U , чтобы переключаться между инструментами, пока не найдете тот, который вам нужен.
Чтобы работать быстрее, рекомендуется изучить дополнительные сочетания клавиш Photoshop.
Рисование основных векторных фигур
Выберите инструмент для фигуры, которую хотите нарисовать, затем добавьте цвета Fill и Stroke .
Теперь щелкните и перетащите на холст. Фигура рисуется из угла в любом направлении, в котором вы перетаскиваете.Чтобы создать симметричную форму, такую как круг или квадрат, нажмите и удерживайте клавишу Shift .
Чтобы нарисовать треугольник, выберите инструмент Polygon Tool . Щелкните один раз на холсте, чтобы открыть окно настроек Create Polygon . Установите Количество сторон с на 3 .
Изменение и редактирование векторных фигур
При создании векторной графики в Photoshop вы не ограничены базовыми формами.Их можно очень быстро изменить.
Сначала выберите форму. Это выделит фигуру и покажет точки привязки на ее пути. Это точки, в которых форма имеет углы или кривые.
Выберите Direct Selection Tool на панели инструментов (щелкните и удерживайте значок Path Selection Tool , чтобы найти его, или нажмите Shift + A ). Теперь щелкните одну из опорных точек и перетащите ее в любом направлении, чтобы деформировать форму.
Для более сложного редактирования перемещайте две или более точек привязки одновременно.
Щелкните один, чтобы выделить его, затем Shift + щелкните другой. Теперь используйте клавиши курсора на клавиатуре для одновременного перемещения обеих точек.
Слияние и объединение векторных фигур
Для еще более сложных форм вы можете использовать Path Operations .Это позволяет объединить несколько фигур в одну новую.
Начните с рисования фигуры на холсте. Затем нажмите кнопку Path Operations на панели параметров в верхней части экрана. Обычно каждый новый путь или фигура располагается на отдельном слое. Измените это, нажав Объединить фигуры .
Теперь нарисуйте еще одну фигуру. Это будет на том же слое, что и ваша первая фигура.
Если вам нужно переместить объекты по отдельности, используйте инструмент Path Selection Tool .
Перетащите вторую фигуру так, чтобы она перекрывала первую. Два сливаются в единую фигуру, хотя остаются отдельными объектами. Щелкните Объединить компоненты формы в Операции с контурами , чтобы объединить их в один объект.
Используйте инструмент Path Selection Tool , чтобы выбрать вторую фигуру, которую вы нарисовали. Теперь в Path Operations выберите Subtract Front Shape .Фигура будет удалена вместе с областью, где она перекрывается с первой фигурой.
Выделите обе формы. В Path Operations выберите Intersect Shape Areas . Это удаляет обе формы, за исключением областей, где они перекрываются. Мы используем эту опцию для создания полукруга.
Наконец, выделите обе формы и выберите Исключить перекрывающиеся формы .Это удаляет область, где две формы перекрываются, и оставляет все остальное нетронутым.
Эти инструменты — эффективный способ создания новых фигур, а также разделения или вырезания частей из существующих. Они также работают с инструментами Pen Tool и Text .
Нарисовать векторные линии
Есть два других инструмента, связанных с фигурой, о которых следует знать. Во-первых, это инструмент Line Tool .
Выберите инструмент и установите Высота на панели параметров. Это устанавливает толщину линии. Затем щелкните и перетащите документ, чтобы нарисовать его. Удерживайте нажатой клавишу Shift , чтобы привязать линию к нулю или 90 градусам.
У этого инструмента есть несколько скрытых функций, но по большей части вы будете использовать его для рисования прямой линии.
Рисование пользовательских векторных фигур
Наконец, инструмент Custom Shape Tool .Задайте цвета заливки и обводки, затем щелкните параметр Форма на панели параметров. Здесь вы можете выбрать одну из бесчисленных предустановленных пользовательских форм, которые предоставляет Photoshop.
Чтобы добавить больше фигур, помимо начального выбора, щелкните шестеренку Settings и выберите категорию для добавления. Существуют формы для любого использования — значки, пузыри речи, стрелки, текстуры и т. Д. Вы также можете загружать сторонние фигуры.
Щелкните и перетащите, чтобы добавить фигуру к изображению. Вы также можете щелкнуть холст, чтобы указать точную ширину и высоту.
Если у вас есть опыт работы с Illustrator, вы знаете, что используете Paintbrush Tool для рисования от руки. В Photoshop есть инструмент «Кисть», который выполняет аналогичную работу. Но в Photoshop этот инструмент не является векторным, поэтому не стоит использовать его для рисования. Вместо этого вам следует использовать Pen Tool .
Инструмент «Перо» — одна из самых мощных функций Photoshop. Вы будете часто использовать его при редактировании фотографий в Photoshop, поскольку он позволяет создавать очень точные выделения. Он также отлично подходит для рисования и векторной графики.
Начало работы с инструментом «Перо»
Инструмент «Перо» работает, рисуя путь между опорными точками, которые вы создаете, когда нажимаете на холст. Добавьте обводку к контуру, и вы сможете нарисовать контур; добавьте заливку, и вы сможете нарисовать сплошной объект.
Вот краткое руководство для начала:
- Выберите инструмент Pen Tool (P) . Щелкните холст изображения, чтобы поставить точку привязки.
- Переместите курсор на несколько дюймов и щелкните еще раз, чтобы опустить еще одну точку привязки. Будет создан путь для их соединения. Установите обводку на 5 пикселей, черный цвет, чтобы вам было лучше видно.
- Щелкните еще несколько раз, чтобы развернуть путь. Щелкните и перетащите, чтобы создать изогнутый путь. Это также добавит руль к точке привязки. Перетащите их, чтобы контролировать угол и глубину кривой.
- Щелкните Введите , чтобы создать открытый путь (линию), или щелкните первую точку привязки, чтобы создать замкнутый путь (форму).
Инструмент «Перо» так полезен тем, что вы можете вернуться и отредактировать форму в любое время:
- Возьмите Direct Selection Tool (A) .Выберите опорную точку на пути и перетащите ее в новое положение. Используйте этот инструмент с ручками опорной точки, чтобы редактировать кривую.
- Выберите инструмент Добавить опорную точку , нажав и удерживая инструмент «Перо». Щелкните где-нибудь на пути, чтобы вручную добавить новую точку привязки, затем перетащите ее на место. Это позволяет вам точно настроить свою форму.
Инструменты с тремя ручками
Photoshop предлагает три разных ручки для рисования:
- Pen Tool — это наиболее гибкий вариант по умолчанию.Новичкам мы рекомендуем использовать это в первую очередь для рисования прямых линий. По мере того, как вы станете более продвинутыми, вы можете использовать его для всего.
- Инструмент Freeform Pen Tool позволяет рисовать от руки, аналогично Brush Tool. Он по-прежнему создает путь, который вы можете настроить и отредактировать позже. Точки привязки генерируются автоматически по мере рисования. Это отличный инструмент, если вы используете графический планшет.
- Инструмент Curvature Pen Tool позволяет легко рисовать кривые без необходимости играть с рулем, как вы это делаете с основным инструментом Pen Tool.
Трассировка изображения как вектора в Photoshop
Как только вы научитесь использовать различные инструменты пера, вы сможете использовать их для трассировки изображений. Таким образом вы превращаете отсканированный эскиз или объект на фотографии в векторное изображение.
Откройте изображение в Photoshop и увеличьте масштаб. Теперь выберите инструмент «Перо» и поместите первую точку привязки на границу объекта, который вы хотите обвести.Ваш новый рисунок автоматически перейдет на отдельный слой. Продолжайте щелкать по краям, чтобы создать свой путь.
Если объект, который вы отслеживаете, находится на простом фоне, попробуйте инструмент Freeform Pen Tool с опцией Magnetic , активированной на панели параметров. Это привяжет ваш путь к краю объекта.
Работа с векторным текстом в Photoshop
Использование текста в Photoshop не требует пояснений.Выберите инструмент Horizontal Text Tool (T) , щелкните холст изображения, чтобы создать текстовое поле, затем введите. Вы можете настроить шрифт, размер, вес и все остальное, как и в любом другом приложении.
Для обычного текста установите цвет заливки, но не обводку. Применяйте обводку только для сильно стилизованного текста.
Когда вы закончите, вы можете преобразовать текст в векторный объект. Выделите текст и перейдите к Type> Convert to Shape .Это позволяет вам получить доступ к точкам привязки на каждом персонаже, поэтому вы можете настраивать их индивидуально. Это хорошо для изменения цвета отдельной буквы или настройки внешнего вида шрифта.
После преобразования текст больше не доступен для редактирования. Рекомендуется продублировать, а затем скрыть исходный текстовый слой, на всякий случай, если вам понадобится резервная копия.
Управление векторными объектами
Чтобы создать произведение искусства, вам нужно, чтобы все эти объекты были в правильном положении и в нужном размере.Вот как это сделать:
- Переместите объекты , выделив их инструментом Path Selection Tool (A) и перетащив на место.
- Измените размер объектов , выбрав их с помощью инструмента выбора пути , затем нажав Ctrl + T в Windows или Cmd + T на Mac. Это показывает рамку вокруг объекта. Возьмите руль за край и потяните внутрь или наружу, чтобы изменить размер.Удерживайте клавишу Shift , чтобы сохранить исходное соотношение сторон.
- Поверните объект , удерживая мышь за пределами одного из рулей, пока курсор не превратится в значок поворота. Теперь щелкните и перетащите.
- Измените порядок объектов , щелкнув слой и перетащив его выше или ниже другого слоя.
- Выровняйте объекты , выбрав их все с помощью инструмента перемещения (V) (или удерживая Shift и щелкнув несколько слоев), а затем используя элементы управления выравниванием на панели параметров.
Векторная графика в Photoshop: соединяем все вместе
Теперь, когда вы знаете, как использовать все инструменты, вы можете собрать их вместе, чтобы создать свои собственные векторные изображения:
Хотя Photoshop не является настоящей альтернативой Illustrator для профессионального графического дизайна, он на удивление эффективен. Для простых вещей, таких как логотипы, значки и небольшие изображения, которые вы хотите использовать в других документах, этого более чем достаточно.
Adobe Illustrator vs.Photoshop: в чем разница?Мы устраняем любую путаницу в различиях между этими двумя наборами для редактирования изображений.
Читать далее
Об авторе Энди Беттс (Опубликовано 222 статей)Энди — бывший печатный журналист и редактор журнала, который пишет о технологиях уже 15 лет.За это время он внес вклад в бесчисленное количество публикаций и написал работы по копирайтингу для крупных технологических компаний. Он также предоставил экспертные комментарии для средств массовой информации и организовал панели на отраслевых мероприятиях.
Более От Энди БеттсаПодпишитесь на нашу рассылку новостей
Подпишитесь на нашу рассылку, чтобы получать технические советы, обзоры, бесплатные электронные книги и эксклюзивные предложения!
Нажмите здесь, чтобы подписаться
учебных пособий по Illustrator: 34 новых урока по векторной графике для изучения рисования и иллюстрации | Учебники
Лучшие бесплатные уроки Illustrator, видеоуроки помогут вам рисовать векторную графику, иллюстрации и дизайн персонажей.В этой коллекции руководств мы собрали свежие идеи, которые лучше всего подходят для начинающих и опытных дизайнеров-иллюстраторов. Эти учебные пособия помогут научиться пользоваться Adobe Illustrator и инструментами Illustrator, а также очень помогут, пошаговая презентация того, что упростило изучение и понимание. Я надеюсь! Эти уроки Adobe Illustrator могут улучшить ваши навыки иллюстрации и улучшить качество ваших работ.
Вы также можете быть заинтересованы в следующих новых статьях.
Неограниченные загрузки
Более 1500000+ шрифтов, мокапов, бесплатных материалов и материалов для дизайна
Узнайте, как создавать векторную графику в Adobe Illustrator
Без сомнения! Adobe Illustrator — это мощный инструмент для создания векторных иллюстраций, цифровых иллюстраций и полезных иллюстраций, который можно использовать в проектах веб-дизайна и графического дизайна . Эти уроки научат вас создавать векторный портрет, 3D-моделирование, векторную графику , векторные логотипы, векторные символы, узоры и многие другие полезные объекты и эффекты.
Так чего же вы ждете? Посмотрите лучшие уроки по Illustrator и выведите свои знания о векторной графике на новый уровень. Наслаждаться!
Как создать акварельную кисть в Adobe Illustrator
Из этого урока вы узнаете, как создать кисть в Illustrator. Следуйте за мной, я покажу вам, насколько это просто. Но сначала позвольте нам порекомендовать вам несколько потрясающих кистей, прежде чем мы перейдем к уроку по кистям.
Ссылка на учебное пособие
Как нарисовать ретро-дизайн персонажа-талисмана в Illustrator
В сегодняшнем уроке Adobe Illustrator мы собираемся повеселиться, создав ретро-дизайн персонажа-талисмана хот-дога, вдохновленный классическим мультяшным стилем 1930-х годов, известным как «резиновый шланг».Представьте себе первых персонажей Disney или Fleischer Studios с их изогнутыми конечностями, глазами в форме пирожка и трехпалыми руками в белых перчатках.
Ссылка на учебное пособие
Узнайте, как создать самолет в Adobe Illustrato
Из этого урока вы узнаете, как нарисовать припаркованный самолет на взлетно-посадочной полосе в Adobe Illustrator. Мы будем использовать базовые формы, такие как эллипсы, прямоугольники и прямоугольники с закругленными углами, чтобы постепенно создавать нашу иллюстрацию. Далее вы будете использовать набор градиентов вместе с различными техниками и эффектами, чтобы максимально приблизиться к реалистичности.
Ссылка на учебное пособие
Как нарисовать кита в векторе в Adobe Illustrator
В этом уроке иллюстратора вы узнаете, как нарисовать вектор кита, используя базовые геометрические фигуры в Adobe Illustrator. Мы научимся работать с «Живыми углами», инструментом «Ножницы», панелью «Обработка контуров» и будем использовать другие полезные векторные инструменты и функции.
Ссылка на учебное пособие
Как создать шаблон векторной инфографики в Illustrator
Следующие шаги помогут вам создать шаблон инфографики в Adobe Illustrator.Для начала вы узнаете, как настроить простую сетку. Используя основные инструменты и все преимущества сетки и привязки к сетке, вы узнаете, как создать шаблон макета инфографики. Вы узнаете, как работать с основными инструментами и эффектами, как легко настраивать и умножать фигуры или контуры и как добавлять тонкие блики. Если вы новичок в дизайне инфографики, это небольшое руководство может стать вашим первым шагом к тому, чтобы стать иллюстратором инфографических шаблонов.
Ссылка на учебное пособие
Как нарисовать иллюстрацию единорога в Illustrator
В этом уроке Illustrator мы научимся иллюстрировать единорога, используя очень простые техники.
Ссылка на учебное пособие
Как создать шаблон векторного макета футболки в Adobe Illustrator
В этом уроке вы узнаете, как использовать инструмент Mesh Tool в Adobe Illustrator для создания векторного шаблона макета футболки!
Ссылка на учебное пособие
Как сделать иконку милого медведя в Adobe Illustrator
В этом уроке мы создадим симпатичного плоского плюшевого мишку, используя простые геометрические формы и различные инструменты и функции, которые помогут нам изменить эти формы, создав черты лица.
Ссылка на учебное пособие
Как создать текстурную кисть в Illustrator
Это руководство предназначено для тех, кто хочет использовать технику рисования в реальном мире в цифровом рисовании. Если вам нравятся текстуры, гранж или кисти, или если вам нравится рисовать в Illustrator и вы хотите иметь более разнообразный арсенал кистей, оставайтесь здесь. В этом кратком руководстве вы узнаете, как создать и установить кисть в Illustrator. Я обещаю, что это легко, и после этого урока вы захотите создать еще несколько десятков из них!
Ссылка на учебное пособие
Как создать эффект золотого текста в Adobe Illustrator
Этот урок по иллюстратору будет интересен всем, кто работает с текстовыми стилями и эффектами в Adobe Illustrator.Мы будем создавать эффект золотого текста, живой и редактируемый, который вы можете скачать с Envato Elements.
Ссылка на учебное пособие
Как сделать изометрические художественные иконки еды в Adobe Illustrator
В следующем уроке вы узнаете, как создать минимальный набор изометрических иконок еды в Adobe Illustrator. Если вы новичок в изометрическом рисовании, то этот урок для вас, потому что вы научитесь создавать свою собственную изометрическую сетку, а значки создаются с использованием только основных форм.
Ссылка на учебное пособие
Как нарисовать печать в векторном руководстве Illustrator
В этом новом руководстве вы узнаете, как создать забавную летнюю иллюстрацию мультяшного тюленя, сидящего в плавучем бассейне в Adobe Illustrator.
Ссылка на учебное пособие
Как создавать узоры и кисти с эффектом полутонов в Photoshop и Illustrator
В этом уроке я покажу вам, как добиться эффекта полутонов в Photoshop. Вы можете применить эти шаги к любому изображению по своему вкусу, чтобы получить черно-белый полутон и цветной полутон.Мы также рассмотрим, как создавать собственные полутоновые кисти в Photoshop, которые помогут вам добавить отличные детали к вашим работам. Наконец, мы рассмотрим, как создавать полутоновые кисти в Illustrator. Это идеально, если вы только начинаете заниматься иллюстрацией и хотите развить свои навыки и стиль.
Ссылка на учебное пособие
Как нарисовать милого кролика в Adobe Illustrator Vector Tutorial
В этом уроке векторной графики вы научитесь рисовать милого кролика в Adobe Illustrator.Мы будем использовать простые формы, и с базовыми навыками Pen Tool (P) вы сможете создать этого милого кролика и других персонажей животных в этом стиле в будущих проектах.
Ссылка на учебное пособие
Как сделать узор шеврона в иллюстраторе
В этом уроке я покажу вам, как создать узор в Illustrator, в частности, бесшовный узор шеврона. Процесс довольно прост, и после того, как вы попробуете его один раз, вы полностью поймете, как создать повторяющийся узор в Illustrator.
Ссылка на учебное пособие
Как создать значок SmartWatch в Adobe Illustrator Tutorial
В этом уроке для иллюстратора мы подробно рассмотрим процесс создания значка умных часов с использованием основных геометрических фигур и простых инструментов, имеющихся в Adobe Illustrator.
Ссылка на учебное пособие
Как создать узор из углеродного волокна в Illustrator
Следующие шаги помогут вам создать узор из углеродного волокна в Illustrator.Для начала вы узнаете, как создать простую сетку, которая поможет вам создать идеальный узор в Illustrator. Затем, используя базовые инструменты и техники смешивания, а также набор переходов, вы узнаете, как создать узор в Illustrator. Далее вы узнаете, как применить заливку узором в Illustrator и как создать узор из углеродного волокна второго типа в Illustrator. Наконец, вы узнаете, как добавить узорную заливку Illustrator для полностью редактируемого фрагмента текста.
Ссылка на учебное пособие
Как создать классную доску в Adobe Illustrator Урок
В этом уроке я покажу вам, как создать классную доску в Adobe Illustrator.Мы будем использовать основные инструменты, некоторые техники построения векторных форм, а также некоторые градиенты и эффекты для достижения финального результата. Учебник относительно прост и может быть применен ко многим другим проектам Illustrator.
Ссылка на учебное пособие
Как создать арабский узор в Illustrator
В этом уроке вы узнаете, как сделать узор в Illustrator пошагово. Мы будем делать образец иллюстратора арабского узора, используя Adobe Illustrator.
Ссылка на учебное пособие
Как нарисовать мультипликационный персонаж в Adobe Illustraot Учебное пособие
Если вам нравится дизайн персонажей, следуйте этому руководству и узнайте, как нарисовать симпатичного мальчика в Adobe Illustrator.
Ссылка на учебное пособие
Как создать кисть в Illustrator
В этом уроке я поделюсь с вами некоторыми из моих секретных рецептов и поделюсь с вами, когда начну создавать три разные кисти с нуля. Затем я покажу вам, как вы можете использовать их, чтобы оживить вашу иллюстрацию.
Ссылка на учебное пособие
Создайте симпатичный значок блокнота в Adobe Illustrator
Ссылка на учебное пособие
Как нарисовать робота в Adobe Illustrator Tutorial
В этом новом руководстве вы узнаете, как создать дружелюбного персонажа-робота в Adobe Illustrator.Мы будем использовать в основном базовые формы, градиенты, переходы и эффекты, чтобы сделать его как можно более симпатичным.
Ссылка на учебное пособие
Как создать вкусный ломтик арбуза в учебнике Illustrator
В этом туториале иллюстратора вы научитесь создавать основные формы ломтика арбуза, используя основные формы. Двигаясь дальше, вы узнаете, как добавить цвет, детали, используя набор градиентов, а также некоторые базовые эффекты. Наконец, вы узнаете, как добавить легкую тень и простой фон.
Ссылка на учебное пособие
Как сделать красочный фон в Adobe Illustrator Урок
В этом подробном видеоуроке по иллюстратору вы узнаете, как создать красочный векторный фон в Illustrator.
Ссылка на учебное пособие
Как создать векторный логотип лисы в Adobe Illustrator Tutorial
В этом кратком видеоуроке по иллюстратору вы узнаете, как создать векторный логотип Fox в Illustrator.
Ссылка на учебное пособие
Узнайте, как создать логотип с бейсбольным значком в учебном пособии Illustrator
В этом новом уроке я покажу вам, как создать логотип бейсбольного значка.Используя инструменты Rectangle Tool, Ellipse Tool или Pen Tool, вы создадите основные формы. Позже, используя технику построения базовой векторной формы и некоторые эффекты деформации, вы получите окончательный логотип.
Ссылка на учебное пособие
Узнайте, как создать точечный рисунок геометрической формы в Adobe Illustrator
Используйте этот удивительный сценарий и набор эффектов, чтобы быстро и легко создавать потрясающие произведения искусства в Adobe Illustrator. Вам понравятся советы и рекомендации, описанные в этом видео!
Ссылка на учебное пособие
Как создать плоскую иконку в Adobe Illustrator CC Учебное пособие
В этом уроке Adobe Illustrator CC мы научимся создавать дизайн плоских иконок для начинающих.Если вы не понимаете какую-либо часть видеоурока, дайте мне знать в разделе комментариев, с указанием сроков этой конкретной части видеоурока Illustrator CC, я буду более чем обязан ответить, если смогу.
Ссылка на учебное пособие
Создание фона абстрактного красочного геометрического в Adobe Illustrator
Ссылка на учебное пособие
Как создать дизайн логотипа в виде шестиугольника в Уроке Illustrator
Из этого видеоурока вы узнаете, как создать потрясающий шестиугольный логотип для вашего бизнеса с нуля, теперь это очень просто.Просто следуйте инструкциям и получите потрясающий дизайн логотипа.
Ссылка на учебное пособие
Как нарисовать векторный портретный набросок в Adobe Illustrator Tutorial
В этом удивительном уроке вы узнаете, как создать набросок, набросал векторную иллюстрацию художественного портрета из линий из вашей фотографии в Adobe Illustrator. И вам не нужно использовать Pen Tool, Pencil Tool или даже планшет для рисования. Всего можно добиться с помощью фотографии с хорошо сбалансированным освещением.
Ссылка на учебное пособие
Как создать красочный дизайн инфографических шагов в учебнике Illustrator
Ссылка на учебное пособие
Как создать векторный портрет
Превратить красивый портрет в векторную иллюстрацию — это увлекательная задача, которая не требует выдающихся навыков рисования и может дать вам отличный финальный образец дизайна.Однако это требует много времени и терпения. В этом уроке мы прольем свет на то, как создать векторный портрет на основе изображения.
Начните с выбора хорошего изображения
Окончательный результат будет во многом зависеть от того, какой тип изображения вы выберете. Ищите что-то не только красивое, но также с хорошим освещением, контрастом (что значительно облегчит вашу работу, как вы увидите позже) и хорошими деталями. По крайней мере, но не в последнюю очередь, предпочтительно использовать высококачественное изображение, потому что вы можете сильно увеличивать и уменьшать масштаб.Если вам нужно удалить отвлекающий фон, см. Наше руководство по удалению фона с изображения.
Это изображение, которое мы будем использовать в этом уроке. Это красивый портрет с хорошим освещением и контрастом, а также с некоторыми интересными деталями.
Создайте новый документ
Для начала откройте Gravit Designer и создайте новый документ с Infinite Canvas , чтобы было достаточно места для работы. Для этого оставьте поля Ширина и Высота пустыми и нажмите «Создать!» .
Импортировать изображение
Когда документ готов, пора импортировать изображение, которое вы выбрали ранее, на холст Gravit. Для этого вы можете использовать опцию Разместить изображение на кнопке панели инструментов или перейти в меню Файл> Импорт> Поместить изображение .
Однако самый простой способ — перетащить изображение прямо из папки вашего компьютера на холст Gravit.
Доминирование над основными инструментами рисования
Для остальной части этого урока необходимо иметь хорошее представление о том, как использовать основные инструменты рисования, Перо и Безигон.Если вы уже освоили их, вперед!
Если нет, ознакомьтесь с нашими руководствами и руководством пользователя, чтобы узнать о приемах использования инструментов рисования Gravit Designer. И помните: практика делает это совершенным.
Базовые формы
Пора начинать. Существует множество различных подходов, техник и стилей для создания векторного портрета или любой другой иллюстрации, но в этом уроке мы будем использовать один конкретный стиль и следовать определенному пути. Начнем с основных форм портрета.
Теперь вы в основном обрисовываете основные «фрагменты» изображения с помощью пера или безигона. В случае с фото, которое мы выбрали, основными частями являются лицо, волосы, блузка, руки, шея, стол и фон.
Выбор использования ручки или Bezigon полностью зависит от вас. Используйте тот инструмент, который позволяет вам рисовать более комфортно, или даже оба! Перо — это скорее инструмент «бесплатного рисования», а Bezigon поможет вам добиться идеальных кривых.
Это окончательный результат обрисовки.Вы можете увидеть, как это выглядит только с контуром, без заливки слева и с заливкой справа.
Пока не стоит особо беспокоиться о финальных цветах, поскольку это можно будет определить позже. А пока используйте любые цвета, которые считаете нужными, чтобы продолжить работу.
Совет: заблокируйте слой изображения, чтобы избежать его ошибочного перемещения при создании контуров.
Основные функции
Теперь, когда у вас есть основные формы, вы можете начать с основных функций, таких как брови, глаза, рот и аксессуары.Процесс тот же: набросайте с помощью инструментов Pen или Bezigon.
Оставьте основные формы скрытыми или оставьте видимым только контур, чтобы вы могли видеть остальную часть изображения, чтобы продолжить его очерчивание. Также заблокируйте базовые формы, чтобы избежать их ошибочного перемещения, как и в случае со слоем изображения.
Свет, тени, полутона и контуры
Остальную часть процесса можно разделить на четыре этапа: свет, полутона, тени и контуры. Как вы можете видеть на картинке, помимо более светлых рефлексов, у нас есть более темные области, которые мы назовем полутона , и даже более темные части, которые мы назовем тенями .Кроме того, в некоторых точках пересечения нам нужно будет добавить более твердый контур , чтобы лучше их очертить. Одним из примеров этого является место, где пальцы касаются других участков кожи, и часть рук, которая сгибается.
Следующий шаг — начать создавать твердые формы с помощью инструментов рисования для теней, света, полутонов и контуров. Вы можете начать с того места, где вам удобнее, но в этом уроке давайте начнем с более легких частей.
Поэтому проще выбрать изображение с хорошим контрастом света / тени и цветов.Если ваше изображение более размытое или вы думаете, что можете использовать больше контраста, вы добавите немного контраста с помощью эффекта Gravit’s Color Adjust.
Светлые пятна
Источник света на изображении определяет, где есть более светлые тона, а где более темные. Вы можете видеть на этом снимке, что свет исходит откуда-то сверху / спереди женщины из-за световых рефлексов, например, на макушке волос, на лице и на ее плече.
Свет воздействует не только на кожу и волосы, но и на все твердые тела, которых он касается.Черная блузка, губы и даже глаза и веки имеют более темные и светлые детали, даже если они очень тонкие.
Совет: вам не нужно слишком беспокоиться о создании «идеальной» формы, в конце концов, тени и световые рефлексы размыты и размыты, и мы собираемся представить их как твердые формы для этого стиля портрет. Вам просто нужно придерживаться того, что вы видите на исходном изображении, и заново представить его как твердую форму.
Мы оставим аксессуары напоследок, поэтому вам пока не нужно о них беспокоиться.
Средние тона
Перейдите к следующему шагу с более темными оттенками, которые мы называем средними тонами, и очертите их. Пока что мы предлагаем вам три различных тона: основной цвет кожи, светлые и темные формы.
Можно использовать разные оттенки для представления более темных тонов и не очень темных тонов, например, для век. Даже зубы и ногти имеют более темный оттенок, поэтому обращайте внимание на детали.
Тени
Пришло время создать формы, представляющие самые темные тона изображения, такие как левая сторона лица, шея, внутренняя часть рук и части прямо под руками.Черная блузка также имеет более темные оттенки, поскольку сама блузка не на 100% черная, и на нее отражается свет.
Обратите внимание, что необходимо добавить темную форму даже прямо под аксессуарами, поскольку они отбрасывают темную тень на кожу.
Окончательные контуры
Наконец, пришло время добавить несколько более темных контуров, где вы обнаружите необходимость лучше очертить формы. Это будет происходить в основном с линиями пальцев, рук и разделением между лицом и шеей.
Принадлежности
Мы приберегли аксессуары напоследок, потому что, поскольку они сделаны из металла, световые рефлексы работают немного иначе. Начиная с браслетов, помимо основного цвета вы добавите более светлый цвет, а затем еще более светлые небольшие рефлексы, представляющие то, как свет падает на металлическую деталь.
По такому же принципу можно применить и серьги, и кулон. Обратите внимание, что у колец на правой руке не так много световых рефлексов, как у других частей.
В колье есть не только два тона бликов, но и несколько теней.
И вы пришли к финишу! Это пока окончательный результат. Не стесняйтесь настраивать цветовую палитру и изменять некоторые оттенки и насыщенность.
Вы даже можете использовать эффект «Регулировка цвета», чтобы внести некоторые изменения.
Последний штрих
Закончив настройку цветовой палитры, вы все равно можете добавить последнюю дополнительную деталь. Создайте прямоугольник того же размера, что и фон, и поместите его поверх иллюстрации.Установите режим наложения слоя на Screen на панели Appearance.
А теперь вы можете поиграть с цветом и прозрачностью, чтобы создать крутой цветовой эффект. Вы также можете попробовать разные режимы наложения.
Для окончательного результата этого урока используйте цвет # 9900FF с режимом наложения Screen с 14% непрозрачностью .
Различные стили
Это лишь один из множества различных стилей, которые вы можете использовать для преобразования изображения в векторный портрет.Возможностей много: вы можете использовать размытые формы вместо сплошных, стиль минимализма или более реалистичный, или даже использовать рисунок в оттенках серого.
Это лишь некоторые примеры, опубликованные на странице Gravit Designer в Instagram:
Надеюсь, это руководство было для вас полезным. Дайте нам знать в комментариях и не забудьте поделиться с нами работой, которую вы создаете с помощью Gravit Designer!
Как нарисовать вектор милой лягушки в Adobe Illustrator
На этот раз мы воспользуемся основными геометрическими фигурами и различными инструментами Adobe Illustrator, чтобы создать простого и привлекательного мультяшного персонажа — зеленой лягушки! Следуйте этому руководству, и давайте вместе научимся рисовать милых животных!
Подробности руководства
- Программа: Adobe Illustrator CS6 — CC
- Сложность: Средний
- Охваченные темы: Построение фигуры, Панель обводки, Смещение контура
- Приблизительное время выполнения: 20 минут
Окончательное изображение: вектор милой лягушки
Шаг 1
Начнем с головы нашего милого вектора лягушки.Возьмите инструмент Ellipse Tool (L) и нарисуйте светло-зеленую фигуру 260 x 170 пикселей .
Шаг 2
Возьмите инструмент Direct Selection Tool (A) и выберите точку привязки справа. Щелкните нижний маркер и немного потяните его вниз, чтобы форма стала более квадратной и плоской внизу. Повторите то же самое для противоположной стороны эллипса.
Используйте направляющие ( Control-R и перетащите горизонтальную линию на холсте), чтобы упростить выравнивание ручек.
Шаг 3
Давайте добавим глаза с помощью инструмента Ellipse Tool (L) . Создайте круг 75 x 75 пикселей и поместите его поверх головы.
Дублируйте круг ( Shift-Alt и перетащите), чтобы создать второй глаз.
Шаг 4
Выделите оба круга и перейдите к Object> Path> Offset Path. Установите значение Offset на -15 пикселей , чтобы создать новые круги внутри глаз.
Шаг 5
Залейте созданные круги белым цветом, изображая глазные яблоки.
Выделите белые кружки и снова перейдите к Offset Path . На этот раз установите значение смещения на -7 пикселей . Залейте созданные формы темным цветом для радужки.
Шаг 6
Давайте добавим треугольный блик в глаза. Прежде всего, переключитесь на инструмент Polygon Tool (вы можете найти его в том же раскрывающемся меню, что и инструмент Rectangle Tool ). Дважды щелкните Инструмент многоугольника на панели инструментов Инструменты и установите для параметра Стороны значение 3 . Создайте маленький белый треугольник и поместите его поверх глаза, как показано на изображении.
Сгруппируйте (Control-G) все элементы глаза и поместите копию ( Shift-Alt и перетащите) на противоположную сторону головы.
Шаг 7
Теперь создадим рот. Создайте эллипс 95 x 85 пикселей и установите цвет обводки на темно-серый на панели Color .Установите цвет Fill на None.
Выберите верхнюю опорную точку с помощью Direct Selection Tool (A) и удалите ее. Теперь у нас есть только нижняя половина эллипса, образующая улыбку.
Шаг 8
Не снимая выделения с формы рта, откройте панель Stroke ( Window> Stroke ) и установите Weight на 8 pt , Cap to Round Cap. Таким образом мы делаем обводку толще.
Используйте инструмент «Перо» (P) или инструмент «Отрезок линии» (\) , чтобы сделать короткий штрих с закругленными колпачками для ноздри.
Также добавьте вторую ноздрю.
Шаг 9
Инструментом Ellipse Tool (L) нарисуйте пару розовых форм для румян на щеках. Этот элемент всегда помогает сделать героев мультфильмов симпатичнее.
Шаг 10
Давайте добавим последний штрих нашему персонажу, сделав его более детальным.Используйте инструмент «Перо» (P) или инструмент «Отрезок линии» (\) , чтобы нарисовать прямую линию. Установите Weight на 8 pt и Cap на Round Cap на панели Stroke . Скопируйте линию дважды и поверните копии в противоположных направлениях, чтобы создать стилизованные ресницы.
Установите цвет Stroke на такой же светло-зеленый, что и для головы, и прикрепите ресницы к верхней части глаз.
Ура! Наш милый вектор лягушки готов!
Отличная работа, ребята, мы закончили наш персонаж! Надеюсь, вам понравилось следовать этому руководству, и вы открыли для себя несколько новых советов и приемов для ваших будущих работ.
Удачи!
Автор: Юлия Соколова
2D / 3D-художник и инструктор по созданию персонажей, иконок, надписей и иллюстраций.
Как рисовать векторную графику с помощью Scratch 3
Scratch — популярный язык визуального программирования для создания видеоигр и анимации. В нем также есть инструмент векторного рисования, который любой может использовать для создания уникальных игровых ресурсов и искусства.
Scratch 1.0 был написан на Smalltalk, чрезвычайно хакерском языке программирования, который позволял пользователям заглядывать за кулисы программного обеспечения. Он был популярен на разных платформах и был даже разветвлен Raspberry Pi Foundation для расширенной поддержки.
Scratch 3.0 был переписан с нуля. Он основан на HTML5 и JavaScript, что означает, что он работает на планшете или мобильном телефоне так же хорошо, как на ноутбуке или настольном компьютере.
Что такое векторы?
Векторный рисунок отличается от рисования в обычном приложении для рисования.Векторные изображения выглядят гладкими независимо от того, насколько сильно вы увеличиваете или уменьшаете масштаб. Нет пикселизации. Векторы создают гладкий и законченный продукт любого размера.
В Scratch игровые персонажи называются спрайтами . В Scratch есть библиотека готовых спрайтов, которые можно использовать в проектах, но вы также можете нарисовать свои собственные, используя встроенную программу рисования или встроенное векторное приложение.
Как съесть слона
Для рисования векторами навыки рисования не требуются.Вместо того, чтобы рисовать объект за один раз, разбейте его на отдельные формы. Ищите круги, овалы, треугольники и прямоугольники. Может быть полезно использовать фотографии или живую модель объекта, который вы рисуете.
Я продемонстрирую все основные моменты рисования векторного спрайта в Scratch, объясняя, как рисовать яблоко, но вы можете применить этот метод к любому объекту, который хотите создать.
Инструменты для рисования
Набор инструментов для векторного рисованияScratch — это то место, где вы найдете инструменты, необходимые для рисования объектов:
И вот некоторые термины, связанные с рисованием векторной графики:
- Холст : Где вы рисуете; шахматная доска бело-серая прозрачная
- Узел : точка на пути объекта, определяющая форму объекта
- Объект : круг, квадрат или линия на холсте
- Инструмент «Стрелка» : захват, изменение размера и поворот объектов с помощью этого инструмента
- Инструмент «Узел» : добавляйте, перемещайте и выбирайте узлы с помощью этого инструмента
Начало работы
Чтобы начать рисование, откройте веб-браузер и перейдите в Scratch.mit.edu. Если вы используете Scratch Desktop, откройте приложение.
Чтобы открыть новый проект, выберите Создать в верхнем меню. Чтобы открыть приложение для векторного рисования Scratch, щелкните синий значок Scratch Cat, затем выберите значок Paintbrush. Это создаст новый холст спрайта.
Есть два способа создать собственный спрайт:
- Чтобы создать совершенно новый спрайт, используйте и комбинируйте любые инструменты рисования в наборе инструментов.
- Чтобы изменить внешний вид существующего спрайта, щелкните значок спрайта в правом нижнем углу, чтобы сделать его активным, затем щелкните инструмент «Стрелка» на панели инструментов, щелкните спрайт на холсте и внесите нужные изменения.
Предупреждение: если вы нажмете кнопку « Convert to Bitmap » в нижней части экрана рисования, ваша иллюстрация превратится в пиксельное растровое изображение, и вы не сможете восстановить его в вектор.
Нарисуйте форму яблока
- Выберите пустой холст спрайта, затем выберите инструмент Circle . Создайте круг, щелкнув пустой холст и перетащив мышь. Нажатие клавиши Shift при этом создает идеальный круг.
- Чтобы изменить цвет круга, выберите инструмент Стрелка , щелкните круг, чтобы выбрать его, и щелкните раскрывающееся меню под Заливка . Это открывает возможности для изменения цвета, насыщенности и яркости формы.
— Если вы хотите, чтобы форма была прозрачной, выберите белое поле с диагональной красной линией, чтобы установить цвет «нет».
— Если вы хотите добавить или удалить цветную рамку вокруг объекта, выберите раскрывающееся меню в разделе Контур . - Выберите инструмент Узел . Щелкните центр объекта, чтобы выделить его. Вы увидите четыре узла, равномерно расположенных по краю круга.
Перемещение любого из узлов изменит форму круга. Вы можете добавить дополнительные узлы, щелкнув край круга. Если вы переместите узел слишком сильно или случайно добавите узел, вы можете отменить последний шаг, щелкнув значок со стрелкой назад в верхней части экрана. Вы также можете отменить, нажав Ctrl + Z. - Яблоки обычно меньше снизу, чем сверху.Щелкните и перетащите через два боковых узла, чтобы выбрать их. Узлы становятся синими, когда они выбраны.
Выбрав узлы, нажмите стрелку вверх на клавиатуре, чтобы переместить узлы к вершине круга. - Добавьте два узла в нижнюю часть круга — один слева от исходного нижнего узла, другой — справа. Слегка приподнимите исходный нижний центральный узел, чтобы создать отступ.
- Теперь аналогичным образом добавьте два узла к вершине круга.Слегка опустите исходный центральный верхний узел, чтобы создать отступ.
- Продолжайте настраивать и добавлять узлы, пока не будете довольны формой яблока.
Нарисуйте шток
- Выберите инструмент Прямоугольник . Нарисуйте длинный тонкий прямоугольник на холсте в том месте, где вы хотите разместить стебель.
- Используйте инструмент Узел , чтобы придать прямоугольнику форму, напоминающую стержень. Измените заливку на желаемый цвет.
- Выберите стержень, используя инструмент «Стрелка».Чтобы переместить стебель за яблоком, нажмите кнопку Назад над холстом.
Добавьте форму выделения
- Выберите инструмент Линия . Нарисуйте треугольник на форме яблока, соединяя каждую новую линию с концом предыдущей. Это превратит линии в законченную форму.
- Выберите треугольник с помощью инструмента Стрелка и измените его цвет на более светлый, например белый, с помощью инструмента Заливка .
- Добавьте и настройте узлы с помощью инструмента Узел , чтобы создать форму выделения. Если узлы слишком острые и заостренные, их можно изменить на изогнутые. Выберите узел (ы), которые вы хотите изогнуть, затем нажмите кнопку Curved .
— Совет для профессионалов: чтобы выбрать более одного узла за раз, нажмите и удерживайте Shift при выборе каждого узла.
И вот так вы нарисовали бесконечно масштабируемое яблоко.
Если вы хотите использовать свое изображение вне Scratch, щелкните правой кнопкой мыши эскиз костюма и выберите «Экспорт».Ваш рисунок будет загружен в виде файла .svg.
Чтобы использовать изображение в проекте Scratch, вернитесь на вкладку кода. Ваш новый спрайт появится в правом углу вместе с остальными спрайтами проекта. Используйте его в своем проекте Scratch, поделитесь им с другими пользователями Scratch на веб-сайте Scratch и, прежде всего, рисуйте больше интересных вещей с помощью векторов.
.
 g. http://48ers.com/magnacarta.pdf
g. http://48ers.com/magnacarta.pdf PDF файл может быть любой длины, содержать любое количество шрифтов и изображений и предназначен для того, чтобы обеспечить создание и передачу продукции, готовой к печати.
PDF файл может быть любой длины, содержать любое количество шрифтов и изображений и предназначен для того, чтобы обеспечить создание и передачу продукции, готовой к печати. txt
txt Unicode является соперничающим форматом для текстовых файлов. Простой текстовый файл должен содержать только несколько непечатных символов, таких как новые строки, табуляция и перевод страницы
Unicode является соперничающим форматом для текстовых файлов. Простой текстовый файл должен содержать только несколько непечатных символов, таких как новые строки, табуляция и перевод страницы 0 File)
0 File) com
а также
aspose.cloud
com
а также
aspose.cloud

 Этот онлайн сервис может конвертировать файлы PDF даже со сложной структурой. Наш конвертер проанализирует содержимое PDF до мельчайших деталей и воссоздаст соответствующие элементы в целевом текст формате. В результате получается компактный текст документ, готовый к редактированию или отправке по электронной почте.
Этот онлайн сервис может конвертировать файлы PDF даже со сложной структурой. Наш конвертер проанализирует содержимое PDF до мельчайших деталей и воссоздаст соответствующие элементы в целевом текст формате. В результате получается компактный текст документ, готовый к редактированию или отправке по электронной почте. Это также отличное решение, если мы хотим автоматически извлечь текст из PDF.
Это также отличное решение, если мы хотим автоматически извлечь текст из PDF.
 Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа.
Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа. Для решения этой задачи пользователю нужно выполнить преобразование между этими форматами файлов.
Для решения этой задачи пользователю нужно выполнить преобразование между этими форматами файлов.
 При преобразовании в обычный текст сохраняются только текстовые данные из исходного файла.
При преобразовании в обычный текст сохраняются только текстовые данные из исходного файла.
 Помимо прямого конвертирования в другие форматы, в приложении имеются опции, оптимизированные под определенные устройства для чтения разных производителей.
Помимо прямого конвертирования в другие форматы, в приложении имеются опции, оптимизированные под определенные устройства для чтения разных производителей. В этой программе вы можете перевести PDF в TXT. Здесь также имеется поддержка извлечения изображений из исходного файла.
В этой программе вы можете перевести PDF в TXT. Здесь также имеется поддержка извлечения изображений из исходного файла.

 На сервисе имеется возможность преобразовать PDF в TXT онлайн бесплатно.
На сервисе имеется возможность преобразовать PDF в TXT онлайн бесплатно.

 Просто нажмите и удерживайте Ctrl и щелкните файлы в той же папке один за другим.
Просто нажмите и удерживайте Ctrl и щелкните файлы в той же папке один за другим. Вот несколько ключевых особенностей программы:
Вот несколько ключевых особенностей программы:
 Как конвертировать TXT в PDF?
Как конвертировать TXT в PDF?
 Контроллер MY HEAT PRO имеет массу уникальных возможностей:
управление каскадом до 6-ти котлов;
управление бойлером косвенного нагрева;
упр….
Контроллер MY HEAT PRO имеет массу уникальных возможностей:
управление каскадом до 6-ти котлов;
управление бойлером косвенного нагрева;
упр…. Вопрос {{ 8 }} ТЗ 8 Тема 1-0-0 Сводную бухгалтерскую информацию получают с помощью измерителей натуральных трудовых денежных 9. Вопрос {{ 9 }} ТЗ 9 Тема 1-0-0 Хозяйственный учет включает в себя следующие составляющие основные средства, оборотные средства и отвлеченные средства оперативный, бухгалтерский и статистический виды учета основные и оборотные средства основные средства и средства в сфере производства Предмет и метод бухгалтерского учета. Бухгалтерский баланс 10. Вопрос {{ 10 }} ТЗ 10 Тема 2-0-0 Автором первой книги, изданной в 1494 г по бухгалтерскому учету, в которой раскрыты специфические методы учета, признан Гюгли Рудановский Шерр Пачоли 11. Вопрос {{ 11 }} ТЗ 11 Тема 2-0-0 стр. 5 из 27 созданный в процессе хозяйственной деятельности 24. Вопрос {{ 24 }} ТЗ 24 Тема 2-0-0 Инвестированный собственниками капитал выступает в форме уставного капитала добавочного капитала резервного капитала нераспределенной прибыли 25. Вопрос {{ 25 }} ТЗ 25 Тема 2-0-0 Созданный в процессе функционирования организации собственный капитал существует в форме уставного капитала добавочного капитала нераспределенной прибыли резервного капитала 26.
Вопрос {{ 8 }} ТЗ 8 Тема 1-0-0 Сводную бухгалтерскую информацию получают с помощью измерителей натуральных трудовых денежных 9. Вопрос {{ 9 }} ТЗ 9 Тема 1-0-0 Хозяйственный учет включает в себя следующие составляющие основные средства, оборотные средства и отвлеченные средства оперативный, бухгалтерский и статистический виды учета основные и оборотные средства основные средства и средства в сфере производства Предмет и метод бухгалтерского учета. Бухгалтерский баланс 10. Вопрос {{ 10 }} ТЗ 10 Тема 2-0-0 Автором первой книги, изданной в 1494 г по бухгалтерскому учету, в которой раскрыты специфические методы учета, признан Гюгли Рудановский Шерр Пачоли 11. Вопрос {{ 11 }} ТЗ 11 Тема 2-0-0 стр. 5 из 27 созданный в процессе хозяйственной деятельности 24. Вопрос {{ 24 }} ТЗ 24 Тема 2-0-0 Инвестированный собственниками капитал выступает в форме уставного капитала добавочного капитала резервного капитала нераспределенной прибыли 25. Вопрос {{ 25 }} ТЗ 25 Тема 2-0-0 Созданный в процессе функционирования организации собственный капитал существует в форме уставного капитала добавочного капитала нераспределенной прибыли резервного капитала 26. Вопрос {{ 26 }} ТЗ 26 Тема 2-0-0 Краткосрочный привлеченный капитал организации составляют краткосрочные кредиты и займы добавочный капитал резервный капитал уставный капитал 27. Вопрос {{ 27 }} ТЗ 27 Тема 2-0-0 Долги, относящиеся к обязательствам по распределению – это долги поставщикам дебиторов работникам по начисленной оплате труда 28. Вопрос {{ 28 }} ТЗ 28 Тема 2-0-0 Собственные источники образования средств предприятия дебиторская задолженность прибыль долгосрочные займы 29. Вопрос {{ 29 }} ТЗ 29 Тема 2-0-0 Долгами, относящимися к обязательствам по расчетам, являются долги учредителей поставщикам акционеров 30. Вопрос {{ 30 }} ТЗ 30 Тема 2-0-0 Предметом бухгалтерского учета является стр. 6 из 27 кругооборот хозяйственных средств отражение состояния и использования средств хозяйства в процессе их кругооборота контроль за использованием средств финансово-хозяйственная деятельность организации 31. Вопрос {{ 31 }} ТЗ 31 Тема 2-0-0 Под методом бухгалтерского учета понимают совокупность приемов отражения предмета бухгалтерского учета способы отражения предмета бухгалтерского учета совокупность способов и приемов отражения объектов бухгалтерского учета 32.
Вопрос {{ 26 }} ТЗ 26 Тема 2-0-0 Краткосрочный привлеченный капитал организации составляют краткосрочные кредиты и займы добавочный капитал резервный капитал уставный капитал 27. Вопрос {{ 27 }} ТЗ 27 Тема 2-0-0 Долги, относящиеся к обязательствам по распределению – это долги поставщикам дебиторов работникам по начисленной оплате труда 28. Вопрос {{ 28 }} ТЗ 28 Тема 2-0-0 Собственные источники образования средств предприятия дебиторская задолженность прибыль долгосрочные займы 29. Вопрос {{ 29 }} ТЗ 29 Тема 2-0-0 Долгами, относящимися к обязательствам по расчетам, являются долги учредителей поставщикам акционеров 30. Вопрос {{ 30 }} ТЗ 30 Тема 2-0-0 Предметом бухгалтерского учета является стр. 6 из 27 кругооборот хозяйственных средств отражение состояния и использования средств хозяйства в процессе их кругооборота контроль за использованием средств финансово-хозяйственная деятельность организации 31. Вопрос {{ 31 }} ТЗ 31 Тема 2-0-0 Под методом бухгалтерского учета понимают совокупность приемов отражения предмета бухгалтерского учета способы отражения предмета бухгалтерского учета совокупность способов и приемов отражения объектов бухгалтерского учета 32. Вопрос {{ 32 }} ТЗ 32 Тема 2-0-0 Элементами метода бухгалтерского учета являются документация и инвентаризация система счетов и двойная запись сверка документов оценка и калькуляция выборка бухгалтерский баланс и отчетность 33. Вопрос {{ 33 }} ТЗ 33 Тема 2-0-0 Операция «Выплачена из кассы заработная плата работникам организации» относится к … типу. первому второму третьему четвертому Счета и двойная запись 34. Вопрос {{ 34 }} ТЗ 34 Тема 3-0-0 Одним из элементов метода бухгалтерского учета является бухгалтерский баланс ведение записей на карточках или в таблицах открытие на каждую группу (вид средств или источников отдельного счета отражение по каждому счету остатков и оборотов 35. Вопрос {{ 35 }} ТЗ 35 Тема 3-0-0 Счет — это способ отражения и текущей группировки имущества, источников и хозяйственных операций по однородным признакам с учетом их изменений текущего учета, контроля источников и хозяйственных процессов группировки и текущего учета имущества и хозяйственных операций стр.
Вопрос {{ 32 }} ТЗ 32 Тема 2-0-0 Элементами метода бухгалтерского учета являются документация и инвентаризация система счетов и двойная запись сверка документов оценка и калькуляция выборка бухгалтерский баланс и отчетность 33. Вопрос {{ 33 }} ТЗ 33 Тема 2-0-0 Операция «Выплачена из кассы заработная плата работникам организации» относится к … типу. первому второму третьему четвертому Счета и двойная запись 34. Вопрос {{ 34 }} ТЗ 34 Тема 3-0-0 Одним из элементов метода бухгалтерского учета является бухгалтерский баланс ведение записей на карточках или в таблицах открытие на каждую группу (вид средств или источников отдельного счета отражение по каждому счету остатков и оборотов 35. Вопрос {{ 35 }} ТЗ 35 Тема 3-0-0 Счет — это способ отражения и текущей группировки имущества, источников и хозяйственных операций по однородным признакам с учетом их изменений текущего учета, контроля источников и хозяйственных процессов группировки и текущего учета имущества и хозяйственных операций стр. 7 из 27 36. Вопрос {{ 36 }} ТЗ 36 Тема 3-0-0 По отношению к балансу все счета подразделяются на активные пассивные синтетические аналитические 37. Вопрос {{ 37 }} ТЗ 37 Тема 3-0-0 Активные счета – это счета для учёта имущества источников образования средств результатов хозяйственной деятельности 38. Вопрос {{ 38 }} ТЗ 38 Тема 3-0-0 Пассивные счета – это счета для учёта хозяйственных средств источников образования имущества результатов хозяйственной деятельности 39. Вопрос {{ 39 }} ТЗ 39 Тема 3-0-0 Сальдо конечное по активному счету равно нулю, если в течение месяца по счету не было движения средств оборот по дебету равен обороту по кредиту сальдо начальное плюс оборот по дебету равны обороту по кредиту сальдо начальное плюс оборот по дебету меньше оборота по кредиту 40. Вопрос {{ 40 }} ТЗ 40 Тема 3-0-0 Сальдо конечное по пассивному счету равно нулю, если в течение месяца по счету не было движения сальдо начальное плюс кредитовый оборот равны обороту по дебету оборот по кредиту равен обороту по дебету сальдо начальное плюс кредитовый оборот меньше дебетового 41.
7 из 27 36. Вопрос {{ 36 }} ТЗ 36 Тема 3-0-0 По отношению к балансу все счета подразделяются на активные пассивные синтетические аналитические 37. Вопрос {{ 37 }} ТЗ 37 Тема 3-0-0 Активные счета – это счета для учёта имущества источников образования средств результатов хозяйственной деятельности 38. Вопрос {{ 38 }} ТЗ 38 Тема 3-0-0 Пассивные счета – это счета для учёта хозяйственных средств источников образования имущества результатов хозяйственной деятельности 39. Вопрос {{ 39 }} ТЗ 39 Тема 3-0-0 Сальдо конечное по активному счету равно нулю, если в течение месяца по счету не было движения средств оборот по дебету равен обороту по кредиту сальдо начальное плюс оборот по дебету равны обороту по кредиту сальдо начальное плюс оборот по дебету меньше оборота по кредиту 40. Вопрос {{ 40 }} ТЗ 40 Тема 3-0-0 Сальдо конечное по пассивному счету равно нулю, если в течение месяца по счету не было движения сальдо начальное плюс кредитовый оборот равны обороту по дебету оборот по кредиту равен обороту по дебету сальдо начальное плюс кредитовый оборот меньше дебетового 41. Вопрос {{ 41 }} ТЗ 41 Тема 3-0-0 Двойная запись — это способ группировки объектов учета (имущества, источников и др.) отражения на двух взаимосвязанных счетах хозяйственных операций по дебету одного и кредиту другого счета в одной и той же сумме обобщения данных бухгалтерского учета 42. Вопрос {{ 42 }} ТЗ 42 Тема 3-0-0 Корреспонденция счетов – взаимосвязь между счетами стр. 10 из 27 Классификация счетов по структуре предназначена для изучения принципов построения бухгалтерских счетов построения системы контроля удобства работы соизмерения дебетовых и кредитовых оборотов по счету 57. Вопрос {{ 57 }} ТЗ 57 Тема 3-0-0 Основные счета служат источником информации для определения финансовых результатов составления бухгалтерского баланса определения стоимости имущества 58. Вопрос {{ 58 }} ТЗ 58 Тема 3-0-0 Основные счета подразделяются на инвентарные (имущественные) дополнительные фондовые (капитала) счета для учета расчетов собирательно-распределительные 59. Вопрос {{ 59 }} ТЗ 59 Тема 3-0-0 Инвентарные (имущественные) счета – это счета пассивные активные активно – пассивные 60.
Вопрос {{ 41 }} ТЗ 41 Тема 3-0-0 Двойная запись — это способ группировки объектов учета (имущества, источников и др.) отражения на двух взаимосвязанных счетах хозяйственных операций по дебету одного и кредиту другого счета в одной и той же сумме обобщения данных бухгалтерского учета 42. Вопрос {{ 42 }} ТЗ 42 Тема 3-0-0 Корреспонденция счетов – взаимосвязь между счетами стр. 10 из 27 Классификация счетов по структуре предназначена для изучения принципов построения бухгалтерских счетов построения системы контроля удобства работы соизмерения дебетовых и кредитовых оборотов по счету 57. Вопрос {{ 57 }} ТЗ 57 Тема 3-0-0 Основные счета служат источником информации для определения финансовых результатов составления бухгалтерского баланса определения стоимости имущества 58. Вопрос {{ 58 }} ТЗ 58 Тема 3-0-0 Основные счета подразделяются на инвентарные (имущественные) дополнительные фондовые (капитала) счета для учета расчетов собирательно-распределительные 59. Вопрос {{ 59 }} ТЗ 59 Тема 3-0-0 Инвентарные (имущественные) счета – это счета пассивные активные активно – пассивные 60. Вопрос {{ 60 }} ТЗ 60 Тема 3-0-0 Инвентарные счета предназначены для учета источников образования имущества имущества заемных средств 61. Вопрос {{ 61 }} ТЗ 61 Тема 3-0-0 Фондовые счета или счета капитала – это счета пассивные активные забалансовые 62. Вопрос {{ 62 }} ТЗ 62 Тема 3-0-0 Фондовые (капитала) счета предназначены для учета хозяйственных процессов источников образования имущества имущества стр. 11 из 27 63. Вопрос {{ 63 }} ТЗ 63 Тема 3-0-0 Счета для учета расчетов подразделяются на активные пассивные собирательно-распределительные сопоставляющие активно-пассивные 64. Вопрос {{ 64 }} ТЗ 64 Тема 3-0-0 Активные счета для учета расчетов отражают задолженность кредиторскую дебиторскую бюджету по налогам организациям по займам 65. Вопрос {{ 65 }} ТЗ 65 Тема 3-0-0 Пассивные счета для учета расчетов отражают кредиторскую задолженность дебиторскую задолженность задолженность подотчетных лиц расходы будущих периодов 66. Вопрос {{ 66 }} ТЗ 66 Тема 3-0-0 Регулирующие счета используются для учета источников образования активов имущества уточнения оценки объектов учета процесса заготовления 67.
Вопрос {{ 60 }} ТЗ 60 Тема 3-0-0 Инвентарные счета предназначены для учета источников образования имущества имущества заемных средств 61. Вопрос {{ 61 }} ТЗ 61 Тема 3-0-0 Фондовые счета или счета капитала – это счета пассивные активные забалансовые 62. Вопрос {{ 62 }} ТЗ 62 Тема 3-0-0 Фондовые (капитала) счета предназначены для учета хозяйственных процессов источников образования имущества имущества стр. 11 из 27 63. Вопрос {{ 63 }} ТЗ 63 Тема 3-0-0 Счета для учета расчетов подразделяются на активные пассивные собирательно-распределительные сопоставляющие активно-пассивные 64. Вопрос {{ 64 }} ТЗ 64 Тема 3-0-0 Активные счета для учета расчетов отражают задолженность кредиторскую дебиторскую бюджету по налогам организациям по займам 65. Вопрос {{ 65 }} ТЗ 65 Тема 3-0-0 Пассивные счета для учета расчетов отражают кредиторскую задолженность дебиторскую задолженность задолженность подотчетных лиц расходы будущих периодов 66. Вопрос {{ 66 }} ТЗ 66 Тема 3-0-0 Регулирующие счета используются для учета источников образования активов имущества уточнения оценки объектов учета процесса заготовления 67. Вопрос {{ 67 }} ТЗ 67 Тема 3-0-0 Регулирующие счета подразделяются на сопоставляющие дополнительные контрарные собирательно-распределительные контрарно-дополнительные бюджетно-распределительные 68. Вопрос {{ 68 }} ТЗ 68 Тема 3-0-0 Регулирующие дополнительные счета … оценку объекта учета уменьшают увеличивают не изменяют стр. 12 из 27 69. Вопрос {{ 69 }} ТЗ 69 Тема 3-0-0 Регулирующие контрарные счета … оценку объекта учета уменьшают увеличивают не изменяют 70. Вопрос {{ 70 }} ТЗ 70 Тема 3-0-0 Операционные счета подразделяются на собирательно-распределительные финансово-результативные калькуляционные сопоставляющие контрарные 71. Вопрос {{ 71 }} ТЗ 71 Тема 3-0-0 Калькуляционные счета используются для уточнения оценки объектов, отраженных на основных счетах учета источников образования активов учета затрат и исчисления себестоимости продукции, работ, услуг учета косвенных расходов, подлежащих распределению по объектам бухгалтерского учета 72. Вопрос {{ 72 }} ТЗ 72 Тема 3-0-0 Сопоставляющие счета используются для определения финансовых результатов исчисления себестоимости определение результатов по заготовлению предметов труда 73.
Вопрос {{ 67 }} ТЗ 67 Тема 3-0-0 Регулирующие счета подразделяются на сопоставляющие дополнительные контрарные собирательно-распределительные контрарно-дополнительные бюджетно-распределительные 68. Вопрос {{ 68 }} ТЗ 68 Тема 3-0-0 Регулирующие дополнительные счета … оценку объекта учета уменьшают увеличивают не изменяют стр. 12 из 27 69. Вопрос {{ 69 }} ТЗ 69 Тема 3-0-0 Регулирующие контрарные счета … оценку объекта учета уменьшают увеличивают не изменяют 70. Вопрос {{ 70 }} ТЗ 70 Тема 3-0-0 Операционные счета подразделяются на собирательно-распределительные финансово-результативные калькуляционные сопоставляющие контрарные 71. Вопрос {{ 71 }} ТЗ 71 Тема 3-0-0 Калькуляционные счета используются для уточнения оценки объектов, отраженных на основных счетах учета источников образования активов учета затрат и исчисления себестоимости продукции, работ, услуг учета косвенных расходов, подлежащих распределению по объектам бухгалтерского учета 72. Вопрос {{ 72 }} ТЗ 72 Тема 3-0-0 Сопоставляющие счета используются для определения финансовых результатов исчисления себестоимости определение результатов по заготовлению предметов труда 73. Вопрос {{ 73 }} ТЗ 73 Тема 3-0-0 Особенность строения сопоставляющих счетов заключается в наличии двух остатков сразу отсутствии остатков отражении одновременно двух и более объектов учета отражении одного объекта учета в двух разных оценках 74. Вопрос {{ 74 }} ТЗ 74 Тема 3-0-0 Собирательно-распределительные счета используются для уточнения оценки объектов, отраженных на основных счетах учета источников образования имущества распределения затрат по отчетным периодам учета косвенных расходов, подлежащих распределению по объектам бухгалтерского учета стр. 15 из 27 средствами труда трудовыми ресурсами предметами труда Принципы учета основных хозяйственных процессов 88. Вопрос {{ 88 }} ТЗ 88 Тема 5-0-0 Под фактической заготовительной себестоимостью предметов труда понимается плановая себестоимость первоначальная стоимость стоимость предметов труда по договорным ценам покупная стоимость приобретенных предметов труда плюс транспортно- заготовительные расходы 89. Вопрос {{ 89 }} ТЗ 89 Тема 5-0-0 Затраты по снабжению организации предметами труда могут отражаться на счетах «Основные средства» «Вложения во внеоборотные активы» «Материалы» «Основное производство» «Заготовление и приобретение материальных ценностей» 90.
Вопрос {{ 73 }} ТЗ 73 Тема 3-0-0 Особенность строения сопоставляющих счетов заключается в наличии двух остатков сразу отсутствии остатков отражении одновременно двух и более объектов учета отражении одного объекта учета в двух разных оценках 74. Вопрос {{ 74 }} ТЗ 74 Тема 3-0-0 Собирательно-распределительные счета используются для уточнения оценки объектов, отраженных на основных счетах учета источников образования имущества распределения затрат по отчетным периодам учета косвенных расходов, подлежащих распределению по объектам бухгалтерского учета стр. 15 из 27 средствами труда трудовыми ресурсами предметами труда Принципы учета основных хозяйственных процессов 88. Вопрос {{ 88 }} ТЗ 88 Тема 5-0-0 Под фактической заготовительной себестоимостью предметов труда понимается плановая себестоимость первоначальная стоимость стоимость предметов труда по договорным ценам покупная стоимость приобретенных предметов труда плюс транспортно- заготовительные расходы 89. Вопрос {{ 89 }} ТЗ 89 Тема 5-0-0 Затраты по снабжению организации предметами труда могут отражаться на счетах «Основные средства» «Вложения во внеоборотные активы» «Материалы» «Основное производство» «Заготовление и приобретение материальных ценностей» 90. Вопрос {{ 90 }} ТЗ 90 Тема 5-0-0 Затраты по снабжению организации средствами труда отражаются на счете «Основные средства» «Вложения во внеоборотные активы» «Основное производство» «Заготовление и приобретение материальных ценностей» «Отклонение в стоимости материальных ценностей» 91. Вопрос {{ 91 }} ТЗ 91 Тема 5-0-0 Процесс производства – это совокупность операций, связанных с заготовлением предметов труда производством продукции, работ и услуг заготовлением средств труда продажей продукции, работ и услуг 92. Вопрос {{ 92 }} ТЗ 92 Тема 5-0-0 Расходы, связанные с затратами во вспомогательном производстве, отражаются на счете 23 20 25 26 стр. 16 из 27 93. Вопрос {{ 93 }} ТЗ 93 Тема 5-0-0 Общепроизводственные расходы отражаются на счете 80 45 28 25 94. Вопрос {{ 94 }} ТЗ 94 Тема 5-0-0 Общехозяйственные расходы организации отражаются на счете 25 70 26 76 95. Вопрос {{ 95 }} ТЗ 95 Тема 5-0-0 Затраты в зависимости от объема производства делятся на постоянные и прямые постоянные и переменные условно-постоянные и условные одноэлементные и компенсационного характера 96.
Вопрос {{ 90 }} ТЗ 90 Тема 5-0-0 Затраты по снабжению организации средствами труда отражаются на счете «Основные средства» «Вложения во внеоборотные активы» «Основное производство» «Заготовление и приобретение материальных ценностей» «Отклонение в стоимости материальных ценностей» 91. Вопрос {{ 91 }} ТЗ 91 Тема 5-0-0 Процесс производства – это совокупность операций, связанных с заготовлением предметов труда производством продукции, работ и услуг заготовлением средств труда продажей продукции, работ и услуг 92. Вопрос {{ 92 }} ТЗ 92 Тема 5-0-0 Расходы, связанные с затратами во вспомогательном производстве, отражаются на счете 23 20 25 26 стр. 16 из 27 93. Вопрос {{ 93 }} ТЗ 93 Тема 5-0-0 Общепроизводственные расходы отражаются на счете 80 45 28 25 94. Вопрос {{ 94 }} ТЗ 94 Тема 5-0-0 Общехозяйственные расходы организации отражаются на счете 25 70 26 76 95. Вопрос {{ 95 }} ТЗ 95 Тема 5-0-0 Затраты в зависимости от объема производства делятся на постоянные и прямые постоянные и переменные условно-постоянные и условные одноэлементные и компенсационного характера 96. Вопрос {{ 96 }} ТЗ 96 Тема 5-0-0 Под прямыми расходами на производство продукции понимаются расходы, которые могут быть отнесены непосредственно на себестоимость продукции расходы, возникшие независимо от объема производства все производственные расходы 97. Вопрос {{ 97 }} ТЗ 97 Тема 5-0-0 Под косвенными расходами понимаются расходы связанные с изготовлением конкретного изделия которые не могут быть списаны на прямую себестоимость продукции возникшие в структурном подразделении (цехе, участке) по основному виду деятельности 98. Вопрос {{ 98 }} ТЗ 98 Тема 5-0-0 Остаток по счету «Основное производство» характеризует величину затрат за квартал затрат в незавершенном производстве затрат за декаду полной фактической себестоимости готовой продукции 99. Вопрос {{ 99 }} ТЗ 99 Тема 5-0-0 Дебетовый оборот по счету «Основное производство» характеризует величину стр. 17 из 27 затрат отчетного периода затрат за квартал затрат за декаду полной фактической себестоимости готовой продукции 100.
Вопрос {{ 96 }} ТЗ 96 Тема 5-0-0 Под прямыми расходами на производство продукции понимаются расходы, которые могут быть отнесены непосредственно на себестоимость продукции расходы, возникшие независимо от объема производства все производственные расходы 97. Вопрос {{ 97 }} ТЗ 97 Тема 5-0-0 Под косвенными расходами понимаются расходы связанные с изготовлением конкретного изделия которые не могут быть списаны на прямую себестоимость продукции возникшие в структурном подразделении (цехе, участке) по основному виду деятельности 98. Вопрос {{ 98 }} ТЗ 98 Тема 5-0-0 Остаток по счету «Основное производство» характеризует величину затрат за квартал затрат в незавершенном производстве затрат за декаду полной фактической себестоимости готовой продукции 99. Вопрос {{ 99 }} ТЗ 99 Тема 5-0-0 Дебетовый оборот по счету «Основное производство» характеризует величину стр. 17 из 27 затрат отчетного периода затрат за квартал затрат за декаду полной фактической себестоимости готовой продукции 100. Вопрос {{ 100 }} ТЗ 100 Тема 5-0-0 Кредитовый оборот по счету «Основное производство» характеризует величину затрат за квартал затрат в незавершенном производстве фактической производственной себестоимости выпущенной готовой продукции затрат за декаду 101. Вопрос {{ 101 }} ТЗ 101 Тема 5-0-0 Готовая продукция – продукция выпущенная из производства и сданная на склад отгруженная покупателям оплаченная покупателями 102. Вопрос {{ 102 }} ТЗ 102 Тема 5-0-0 Выпущенная из производства готовая продукция оценивается по окончании отчетного периода по фактической производственной себестоимости договорной стоимости хозрасчетной себестоимости рыночной стоимости 103. Вопрос {{ 103 }} ТЗ 103 Тема 5-0-0 На стадии процесса реализации проданная продукция учитывается на счете 40 90 20 104. Вопрос {{ 104 }} ТЗ 104 Тема 5-0-0 Под полной фактической себестоимостью проданной продукции понимается сметная себестоимость производства в целом фактическая себестоимость производства и ее продажи фактическая себестоимость единицы продукции 105.
Вопрос {{ 100 }} ТЗ 100 Тема 5-0-0 Кредитовый оборот по счету «Основное производство» характеризует величину затрат за квартал затрат в незавершенном производстве фактической производственной себестоимости выпущенной готовой продукции затрат за декаду 101. Вопрос {{ 101 }} ТЗ 101 Тема 5-0-0 Готовая продукция – продукция выпущенная из производства и сданная на склад отгруженная покупателям оплаченная покупателями 102. Вопрос {{ 102 }} ТЗ 102 Тема 5-0-0 Выпущенная из производства готовая продукция оценивается по окончании отчетного периода по фактической производственной себестоимости договорной стоимости хозрасчетной себестоимости рыночной стоимости 103. Вопрос {{ 103 }} ТЗ 103 Тема 5-0-0 На стадии процесса реализации проданная продукция учитывается на счете 40 90 20 104. Вопрос {{ 104 }} ТЗ 104 Тема 5-0-0 Под полной фактической себестоимостью проданной продукции понимается сметная себестоимость производства в целом фактическая себестоимость производства и ее продажи фактическая себестоимость единицы продукции 105. Вопрос {{ 105 }} ТЗ 105 Тема 5-0-0 Расходы, связанные с продажей продукции, называются комплексными общепроизводственными коммерческими расходами (внепроизводственными) стр. 20 из 27 сокращения объема первичной документации 118. Вопрос {{ 118 }} ТЗ 118 Тема 6-0-0 Документы по способу их составления подразделяются на разовые и накопительные машинные и ручные комбинированные и бухгалтерского оформления первичные и сводные 119. Вопрос {{ 119 }} ТЗ 119 Тема 6-0-0 Документы по объему отраженной в них информации подразделяются на разовые и накопительные распорядительные и оправдательные типовые и стандартизированные 120. Вопрос {{ 120 }} ТЗ 120 Тема 6-0-0 Документы по месту составления подразделяются на внутренние накопительные внешние сводные 121. Вопрос {{ 121 }} ТЗ 121 Тема 6-0-0 Документы при поступлении в бухгалтерию подвергаются проверке арифметической плановой формальной внезапной по существу отражаемых операций 122. Вопрос {{ 122 }} ТЗ 122 Тема 6-0-0 Формальная проверка документов – это проверка полноты и правильности заполнения реквизитов правильности подсчета стоимостных показателей законности совершения операций 123.
Вопрос {{ 105 }} ТЗ 105 Тема 5-0-0 Расходы, связанные с продажей продукции, называются комплексными общепроизводственными коммерческими расходами (внепроизводственными) стр. 20 из 27 сокращения объема первичной документации 118. Вопрос {{ 118 }} ТЗ 118 Тема 6-0-0 Документы по способу их составления подразделяются на разовые и накопительные машинные и ручные комбинированные и бухгалтерского оформления первичные и сводные 119. Вопрос {{ 119 }} ТЗ 119 Тема 6-0-0 Документы по объему отраженной в них информации подразделяются на разовые и накопительные распорядительные и оправдательные типовые и стандартизированные 120. Вопрос {{ 120 }} ТЗ 120 Тема 6-0-0 Документы по месту составления подразделяются на внутренние накопительные внешние сводные 121. Вопрос {{ 121 }} ТЗ 121 Тема 6-0-0 Документы при поступлении в бухгалтерию подвергаются проверке арифметической плановой формальной внезапной по существу отражаемых операций 122. Вопрос {{ 122 }} ТЗ 122 Тема 6-0-0 Формальная проверка документов – это проверка полноты и правильности заполнения реквизитов правильности подсчета стоимостных показателей законности совершения операций 123. Вопрос {{ 123 }} ТЗ 123 Тема 6-0-0 Арифметическая проверка документов – это проверка полноты заполнения реквизитов правильности их оформления правильности подсчета стоимостных показателей законности совершения операций 124. Вопрос {{ 124 }} ТЗ 124 Тема 6-0-0 стр. 21 из 27 Проверка по существу отражаемых в документах операций – проверка полноты заполнения реквизитов законности и целесообразности совершения операций правильности его оформления правильности подсчета стоимостных покупателей 125. Вопрос {{ 125 }} ТЗ 125 Тема 6-0-0 Под документооборотом понимается общее количество поступивших в организацию документов движение документов от составления до регистрации его в учетных регистрах движение документов от момента составления (получения) до передачи в архив 126. Вопрос {{ 126 }} ТЗ 126 Тема 6-0-0 Причинами проведения инвентаризаций являются составление сметы затрат на производство хищение, злоупотребление отсутствие первичных документов при отпуске ценностей подготовка годовой отчетности получение выписок банка с расчетного счета 127.
Вопрос {{ 123 }} ТЗ 123 Тема 6-0-0 Арифметическая проверка документов – это проверка полноты заполнения реквизитов правильности их оформления правильности подсчета стоимостных показателей законности совершения операций 124. Вопрос {{ 124 }} ТЗ 124 Тема 6-0-0 стр. 21 из 27 Проверка по существу отражаемых в документах операций – проверка полноты заполнения реквизитов законности и целесообразности совершения операций правильности его оформления правильности подсчета стоимостных покупателей 125. Вопрос {{ 125 }} ТЗ 125 Тема 6-0-0 Под документооборотом понимается общее количество поступивших в организацию документов движение документов от составления до регистрации его в учетных регистрах движение документов от момента составления (получения) до передачи в архив 126. Вопрос {{ 126 }} ТЗ 126 Тема 6-0-0 Причинами проведения инвентаризаций являются составление сметы затрат на производство хищение, злоупотребление отсутствие первичных документов при отпуске ценностей подготовка годовой отчетности получение выписок банка с расчетного счета 127. Вопрос {{ 127 }} ТЗ 127 Тема 6-0-0 Инвентаризации по охвату объектов имущества подразделяются на перманентные плановые полные частичные внезапные 128. Вопрос {{ 128 }} ТЗ 128 Тема 6-0-0 Недостачи товарно-материальных ценностей, выявленные в ходе инвентаризации, отражаются на счете 80 82 94 129. Вопрос {{ 129 }} ТЗ 129 Тема 6-0-0 Недостачи материалов на складе, выявленные в ходе инвентаризации, отражаются записью Д 94 К 10 Д 10 К 94 Д 94 К 26 Д 91 К 94 стр. 22 из 27 130. Вопрос {{ 130 }} ТЗ 130 Тема 6-0-0 Бухгалтерская запись Д 50 К 91 означает поступление наличных денег от дочерних организаций оприходование излишка денежных средств, выявленного при инвентаризации в кассе поступление денег в кассу от подотчетных лиц списание недостачи денег в кассе 131. Вопрос {{ 131 }} ТЗ 131 Тема 6-0-0 Недостача ценностей в пределах норм естественной убыли в цехе основного производства списывается с кредита счета 94 в дебет счета 20 23 26 132. Вопрос {{ 132 }} ТЗ 132 Тема 6-0-0 Недостача материалов, выявленная в ходе инвентаризации, если виновное лицо не установлено, списывается в конечном итоге с кредита счета 94 в дебет счета 83 91 99 84 133.
Вопрос {{ 127 }} ТЗ 127 Тема 6-0-0 Инвентаризации по охвату объектов имущества подразделяются на перманентные плановые полные частичные внезапные 128. Вопрос {{ 128 }} ТЗ 128 Тема 6-0-0 Недостачи товарно-материальных ценностей, выявленные в ходе инвентаризации, отражаются на счете 80 82 94 129. Вопрос {{ 129 }} ТЗ 129 Тема 6-0-0 Недостачи материалов на складе, выявленные в ходе инвентаризации, отражаются записью Д 94 К 10 Д 10 К 94 Д 94 К 26 Д 91 К 94 стр. 22 из 27 130. Вопрос {{ 130 }} ТЗ 130 Тема 6-0-0 Бухгалтерская запись Д 50 К 91 означает поступление наличных денег от дочерних организаций оприходование излишка денежных средств, выявленного при инвентаризации в кассе поступление денег в кассу от подотчетных лиц списание недостачи денег в кассе 131. Вопрос {{ 131 }} ТЗ 131 Тема 6-0-0 Недостача ценностей в пределах норм естественной убыли в цехе основного производства списывается с кредита счета 94 в дебет счета 20 23 26 132. Вопрос {{ 132 }} ТЗ 132 Тема 6-0-0 Недостача материалов, выявленная в ходе инвентаризации, если виновное лицо не установлено, списывается в конечном итоге с кредита счета 94 в дебет счета 83 91 99 84 133. Вопрос {{ 133 }} ТЗ 133 Тема 6-0-0 Недостача ценностей, возникшая по вине материально-ответственного лица, списывается с кредита счета 94 в дебет счета 71 73 76 91 134. Вопрос {{ 134 }} ТЗ 134 Тема 6-0-0 Способы проверок документов по форме по существу по характеру заполнения документа арифметическая 135. Вопрос {{ 135 }} ТЗ 135 Тема 6-0-0 Корректировка меньшей суммы на большую при правильной корреспонденции счетов осуществляется способом дополнительной бухгалтерской записи пунктировки корректурным стр. 25 из 27 148. Вопрос {{ 148 }} ТЗ 148 Тема 7-0-0 Основным регистром по отдельным счетам при журнально-ордерной форме учета является… Главная книга оборотная ведомость журнал-ордер 149. Вопрос {{ 149 }} ТЗ 149 Тема 7-0-0 Признак, положенный в основу строения журналов-ордеров произвольный кредитовый дебетовый 150. Вопрос {{ 150 }} ТЗ 150 Тема 7-0-0 Основным регистром по отдельным счетам при мемориально-ордерной форме учета является мемориальный ордер Главная книга оборотная ведомость 151.
Вопрос {{ 133 }} ТЗ 133 Тема 6-0-0 Недостача ценностей, возникшая по вине материально-ответственного лица, списывается с кредита счета 94 в дебет счета 71 73 76 91 134. Вопрос {{ 134 }} ТЗ 134 Тема 6-0-0 Способы проверок документов по форме по существу по характеру заполнения документа арифметическая 135. Вопрос {{ 135 }} ТЗ 135 Тема 6-0-0 Корректировка меньшей суммы на большую при правильной корреспонденции счетов осуществляется способом дополнительной бухгалтерской записи пунктировки корректурным стр. 25 из 27 148. Вопрос {{ 148 }} ТЗ 148 Тема 7-0-0 Основным регистром по отдельным счетам при журнально-ордерной форме учета является… Главная книга оборотная ведомость журнал-ордер 149. Вопрос {{ 149 }} ТЗ 149 Тема 7-0-0 Признак, положенный в основу строения журналов-ордеров произвольный кредитовый дебетовый 150. Вопрос {{ 150 }} ТЗ 150 Тема 7-0-0 Основным регистром по отдельным счетам при мемориально-ордерной форме учета является мемориальный ордер Главная книга оборотная ведомость 151. Вопрос {{ 151 }} ТЗ 151 Тема 7-0-0 В журналах-ордерах синтетические и аналитические записи совмещаются способами шахматным, смешанным смешанным, линейным линейно-позиционным, шахматным, смешанным 152. Вопрос {{ 152 }} ТЗ 152 Тема 7-0-0 Оборотная ведомость по синтетическим счетам при журнально-ордерной форме бухгалтерского учета составляется не составляется 153. Вопрос {{ 153 }} ТЗ 153 Тема 7-0-0 Главная книга при журнально-ордерной форме учета раскрывает подробно дебет счетов, а кредит счетов дается в ней общей суммой не содержит остатки по счетам 154. Вопрос {{ 154 }} ТЗ 154 Тема 7-0-0 Бухгалтерский баланс при журнально-ордерной форме учета составляется по данным остатков в журналах-ордерах Главной книге оборотной ведомости по синтетическим счетам 155. Вопрос {{ 155 }} ТЗ 155 Тема 7-0-0 стр. 26 из 27 При журнально-ордерной форме бухгалтерского учета баланс по данным Главной книги составляется не составляется 156. Вопрос {{ 156 }} ТЗ 156 Тема 7-0-0 Приход денежных средств по счету «Касса» при журнально-ордерной форме учета отражается журнале-ордере № 1 оборотной ведомости по синтетическим счетам ведомости № 1 157.
Вопрос {{ 151 }} ТЗ 151 Тема 7-0-0 В журналах-ордерах синтетические и аналитические записи совмещаются способами шахматным, смешанным смешанным, линейным линейно-позиционным, шахматным, смешанным 152. Вопрос {{ 152 }} ТЗ 152 Тема 7-0-0 Оборотная ведомость по синтетическим счетам при журнально-ордерной форме бухгалтерского учета составляется не составляется 153. Вопрос {{ 153 }} ТЗ 153 Тема 7-0-0 Главная книга при журнально-ордерной форме учета раскрывает подробно дебет счетов, а кредит счетов дается в ней общей суммой не содержит остатки по счетам 154. Вопрос {{ 154 }} ТЗ 154 Тема 7-0-0 Бухгалтерский баланс при журнально-ордерной форме учета составляется по данным остатков в журналах-ордерах Главной книге оборотной ведомости по синтетическим счетам 155. Вопрос {{ 155 }} ТЗ 155 Тема 7-0-0 стр. 26 из 27 При журнально-ордерной форме бухгалтерского учета баланс по данным Главной книги составляется не составляется 156. Вопрос {{ 156 }} ТЗ 156 Тема 7-0-0 Приход денежных средств по счету «Касса» при журнально-ордерной форме учета отражается журнале-ордере № 1 оборотной ведомости по синтетическим счетам ведомости № 1 157. Вопрос {{ 157 }} ТЗ 157 Тема 7-0-0 Движение денежных средств на расчетном счете организации при мемориально-ордерной форме раскрывается в мемориальном ордере № 2 мемориальном ордере № 1 накопительной ведомости 158. Вопрос {{ 158 }} ТЗ 158 Тема 7-0-0 Упрощенная форма бухгалтерского учета предназначена для использования если у организации имеются собственные основные средства если у организации отсутствуют собственные основные средства только субъектами малого предпринимательства 159. Вопрос {{ 159 }} ТЗ 159 Тема 7-0-0 «Книга учета хозяйственных операций» является регистром… синтетического учета аналитического учета комбинированным 160. Вопрос {{ 160 }} ТЗ 160 Тема 7-0-0 В «Книге учета хозяйственных операций» синтетические и аналитические записи совмещаются способом линейно-позиционным шахматным комбинированным 161. Вопрос {{ 161 }} ТЗ 161 Тема 7-0-0 В «Книге учета хозяйственных операций» хозяйственные операции регистрируются в хронологическом порядке в течение месяца квартала года 162.
Вопрос {{ 157 }} ТЗ 157 Тема 7-0-0 Движение денежных средств на расчетном счете организации при мемориально-ордерной форме раскрывается в мемориальном ордере № 2 мемориальном ордере № 1 накопительной ведомости 158. Вопрос {{ 158 }} ТЗ 158 Тема 7-0-0 Упрощенная форма бухгалтерского учета предназначена для использования если у организации имеются собственные основные средства если у организации отсутствуют собственные основные средства только субъектами малого предпринимательства 159. Вопрос {{ 159 }} ТЗ 159 Тема 7-0-0 «Книга учета хозяйственных операций» является регистром… синтетического учета аналитического учета комбинированным 160. Вопрос {{ 160 }} ТЗ 160 Тема 7-0-0 В «Книге учета хозяйственных операций» синтетические и аналитические записи совмещаются способом линейно-позиционным шахматным комбинированным 161. Вопрос {{ 161 }} ТЗ 161 Тема 7-0-0 В «Книге учета хозяйственных операций» хозяйственные операции регистрируются в хронологическом порядке в течение месяца квартала года 162. Вопрос {{ 162 }} ТЗ 162 Тема 7-0-0 стр. 27 из 27 Форма учета с использованием регистров учета имущества применяется на малых предприятиях, если имеются собственные основные средства отсутствуют собственные основные средства средняя численность работников за отчетный период не превышает в промышленности 100 человек используются все поступившие в отчетном месяце предметы труда 163. Вопрос {{ 163 }} ТЗ 163 Тема 7-0-0 Основными регистрами, применяемыми в форме учета с использованием регистров учета имущества, являются ведомости формы В-1 – В-8 систематические (шахматная) формы В-9 хронологические 164. Вопрос {{ 164 }} ТЗ 164 Тема 7-0-0 Форма учета с использованием регистров учета имущества, применяемых на малых предприятиях предполагает составление для контрольных функций ведомостей накопительной шахматной оборотной
Вопрос {{ 162 }} ТЗ 162 Тема 7-0-0 стр. 27 из 27 Форма учета с использованием регистров учета имущества применяется на малых предприятиях, если имеются собственные основные средства отсутствуют собственные основные средства средняя численность работников за отчетный период не превышает в промышленности 100 человек используются все поступившие в отчетном месяце предметы труда 163. Вопрос {{ 163 }} ТЗ 163 Тема 7-0-0 Основными регистрами, применяемыми в форме учета с использованием регистров учета имущества, являются ведомости формы В-1 – В-8 систематические (шахматная) формы В-9 хронологические 164. Вопрос {{ 164 }} ТЗ 164 Тема 7-0-0 Форма учета с использованием регистров учета имущества, применяемых на малых предприятиях предполагает составление для контрольных функций ведомостей накопительной шахматной оборотной Правильные варианты ответа отмечены символом «+».
Правильные варианты ответа отмечены символом «+». Назовите принцип бухгалтерского учета:
Назовите принцип бухгалтерского учета:
 Актив баланса − это группировка средств по
Актив баланса − это группировка средств по В пассиве баланса отражаются
В пассиве баланса отражаются Сальдо конечное по пассивному счету равно нулю, если
Сальдо конечное по пассивному счету равно нулю, если План счетов бухгалтерского учета – это
План счетов бухгалтерского учета – это 51 «Расчетные счета»
51 «Расчетные счета» При отражении суммы НДС по приобретенным материалам составляется запись
При отражении суммы НДС по приобретенным материалам составляется запись 08 «Вложения во внеоборотные активы»
08 «Вложения во внеоборотные активы» Тот факт, что его члены становятся бесконечно малыми, не является достаточным для обеспечения сходимости. Например, следующий ряд
Тот факт, что его члены становятся бесконечно малыми, не является достаточным для обеспечения сходимости. Например, следующий ряд
 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.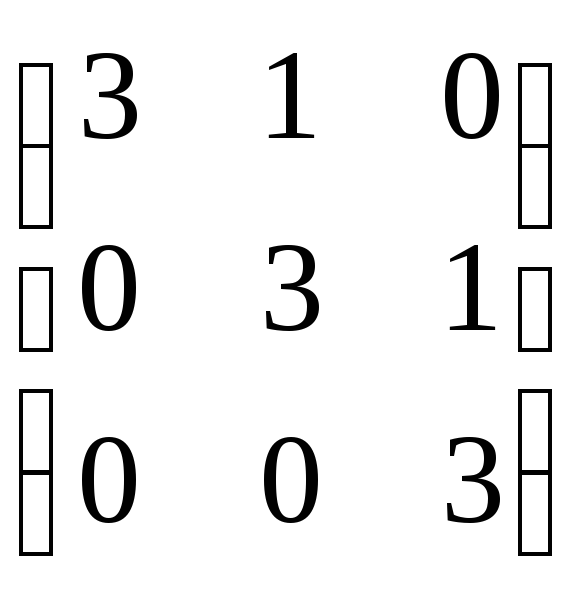 Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта

 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
 Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта Начнем с функций. Итак,
чтобы перемножить две матрицы a иbпо всем правилам
математики, запишем следующую команду:
Начнем с функций. Итак,
чтобы перемножить две матрицы a иbпо всем правилам
математики, запишем следующую команду:
 ones(9)
np.dot(a, b) # значение 45
ones(9)
np.dot(a, b) # значение 45 resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b)
resize(3, 3)
b.resize(3, 3)
a @ b # аналог np.matmul(a, b) array([1, 2])
np.dot(b, a) # array([14, 20, 26])
array([1, 2])
np.dot(b, a) # array([14, 20, 26]) Изначально, уравнение можно записать в векторно-матричном виде:
Изначально, уравнение можно записать в векторно-матричном виде:
 qr()
qr()
 eig()
eig()
 pinv()
pinv()
 Объединение и разделение массивов | NumPy уроки
Объединение и разделение массивов | NumPy уроки {*} v_n.
$$
{*} v_n.
$$ Как и для векторов, при умножении матрицы на число $c$ мы получим новую матрицу, в которой все элементы умножены на $c$, а при сложении двух матриц одинаковых размеров мы получим новую матрицу, все элементы которой являются суммой соответствующих элементов двух исходных матриц.
Как и для векторов, при умножении матрицы на число $c$ мы получим новую матрицу, в которой все элементы умножены на $c$, а при сложении двух матриц одинаковых размеров мы получим новую матрицу, все элементы которой являются суммой соответствующих элементов двух исходных матриц.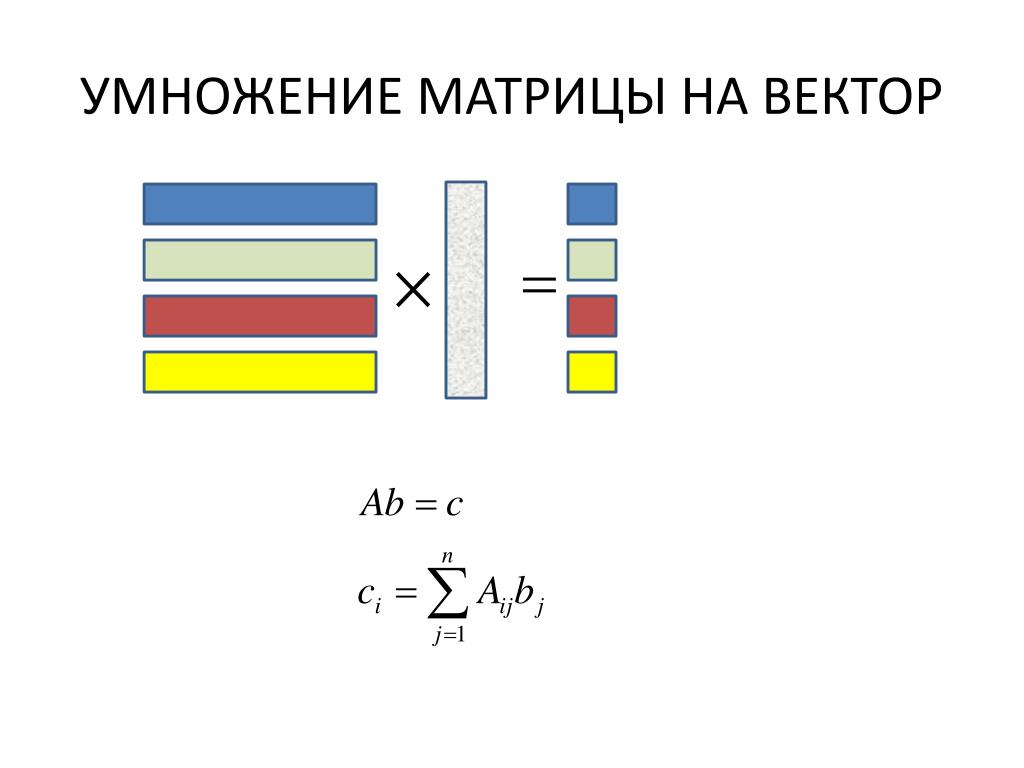 \dagger$.
\dagger$.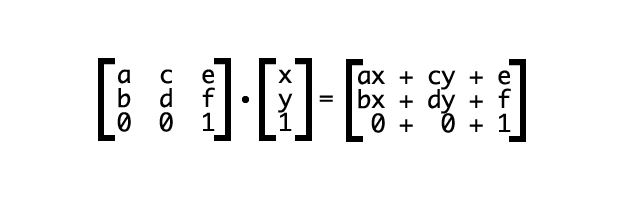 Тензорным произведением двух матриц $M$ размером $m\times n$ и $N$ размером $p \times q$ является более крупная матрица $P=M\otimes N$ размером $mp \times nq$, которая вычисляется на основе $M$ и $N$ по такой формуле:
Тензорным произведением двух матриц $M$ размером $m\times n$ и $N$ размером $p \times q$ является более крупная матрица $P=M\otimes N$ размером $mp \times nq$, которая вычисляется на основе $M$ и $N$ по такой формуле: {\otimes 2}=\begin{bmatrix} 0 &0&0&1 \\ 0 &0&1&0 \\ 0 &1&0&0\\ 1 &0&0&0\end{bmatrix}.
\end{align}
{\otimes 2}=\begin{bmatrix} 0 &0&0&1 \\ 0 &0&1&0 \\ 0 &1&0&0\\ 1 &0&0&0\end{bmatrix}.
\end{align} Первые полторы тысяч разложений.
Первые полторы тысяч разложений.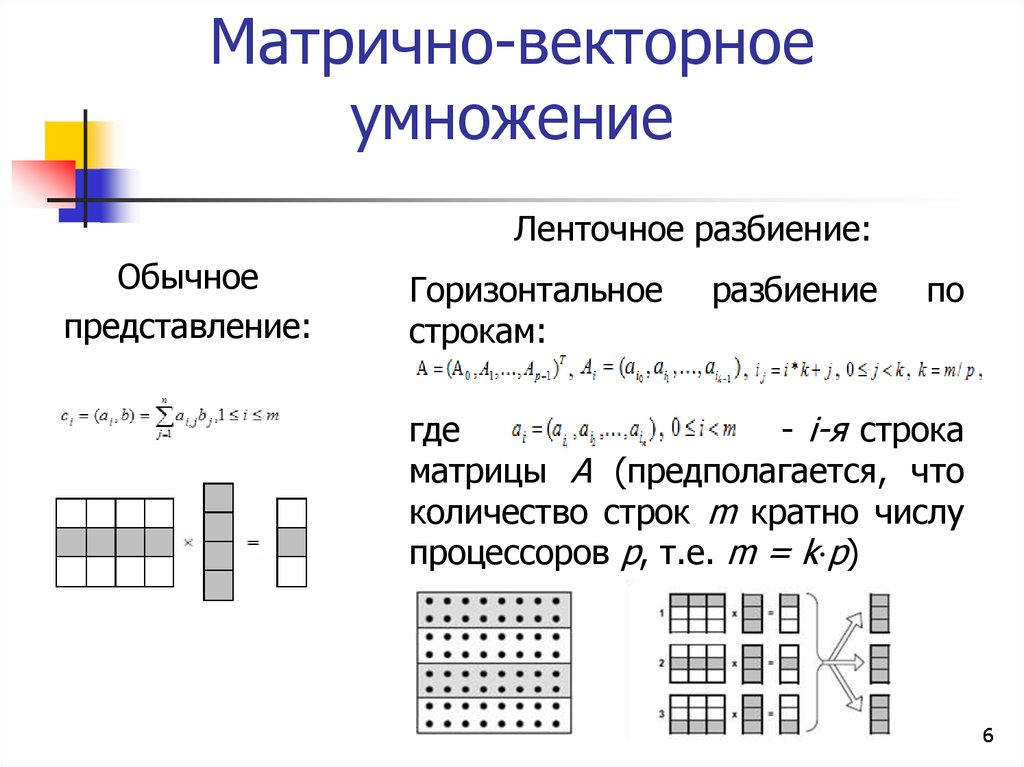 Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.
Одностолбцовую матрицу будем называть вектор-столбцом, а однострочную матрицу — вектор-строкой.
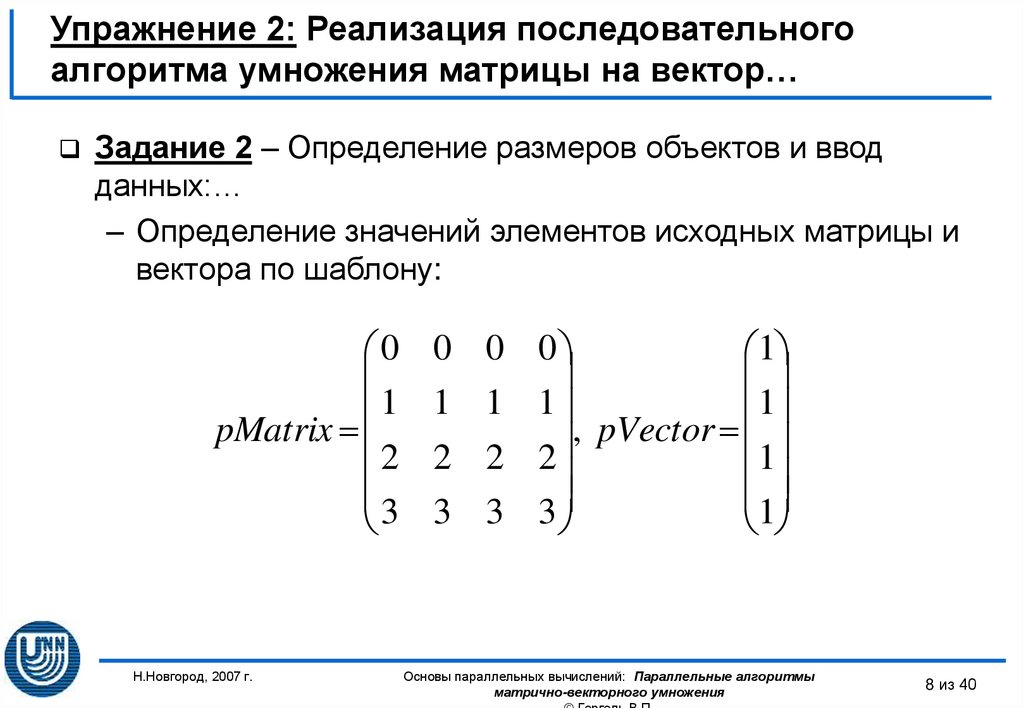 Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн )
) )
) )
) )
) )
) )
) )
)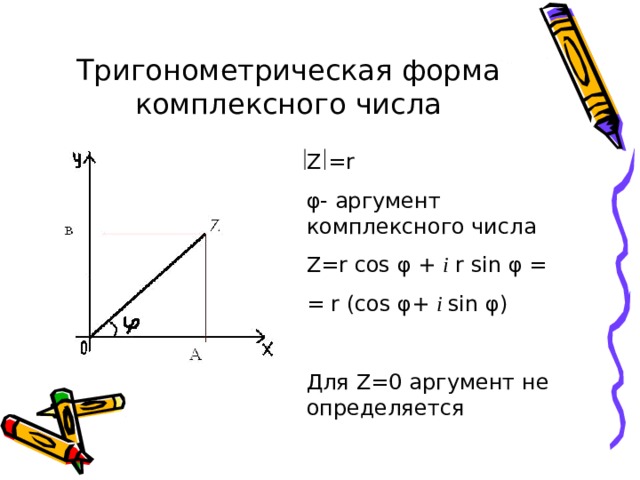 )
)
 Е. и др., Учебник комплект под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Е. и др., Учебник комплект под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
 Данная формула справедлива для любых значений a и b.
Данная формула справедлива для любых значений a и b. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде: 4.3. Тригонометрическая форма записи комплексных чисел
4.3. Тригонометрическая форма записи комплексных чисел
 Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

 Найдём z из уравнения
Найдём z из уравнения .., n мы будем получать разные комплексные числа, а при k = n имеем:
.., n мы будем получать разные комплексные числа, а при k = n имеем:
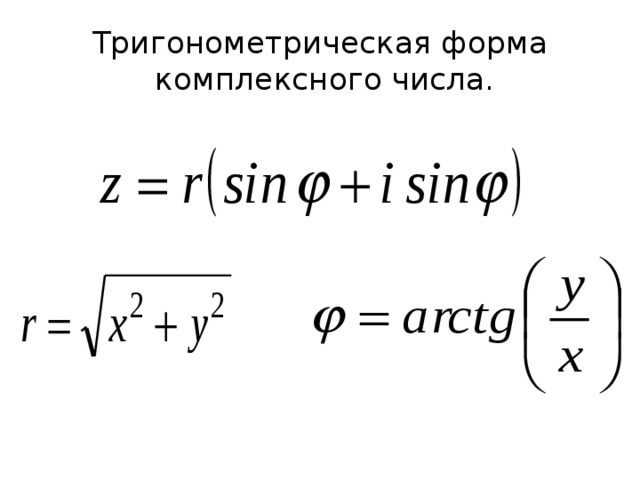
 2}}\) и j=\(arctg {b \over a}\)
2}}\) и j=\(arctg {b \over a}\) Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки.
Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки. А.П. Чехова
А.П. Чехова . Имею большой опыт обучения иностранным языкам (немецкий
и английский), последние 18 лет работала учителем в лингвистической гимназии. Есть богатый опыт работы с учебными пособиями иностранных издательств Hueber, Oxford, Cambridge, подготовки учеников к международным экзаменам. Владею коммуникативной методикой обучения и ориентируюсь на личность ученика, его пожелания, цели, уровень владения иностранным языком. Готовлю к ЕГЭ, ОГЭ, ВПР, результаты от 65 до 100 баллов. Выпускники успешно обучаются в ведущих вузах страны, а также за рубежом.
Буду рада сотрудничеству! До встречи!
. Имею большой опыт обучения иностранным языкам (немецкий
и английский), последние 18 лет работала учителем в лингвистической гимназии. Есть богатый опыт работы с учебными пособиями иностранных издательств Hueber, Oxford, Cambridge, подготовки учеников к международным экзаменам. Владею коммуникативной методикой обучения и ориентируюсь на личность ученика, его пожелания, цели, уровень владения иностранным языком. Готовлю к ЕГЭ, ОГЭ, ВПР, результаты от 65 до 100 баллов. Выпускники успешно обучаются в ведущих вузах страны, а также за рубежом.
Буду рада сотрудничеству! До встречи! Равнобедренный треугольник (вариант 2)
Равнобедренный треугольник (вариант 2) По определению синуса и косинуса:
По определению синуса и косинуса:
 Рассмотрим несколько примеров на представление комплексных чисел в тригонометрической форме.
Рассмотрим несколько примеров на представление комплексных чисел в тригонометрической форме.
 335). Длина такого вектора равна 5, а угол, который он образует с осью абсцисс, равен π . Поэтому
335). Длина такого вектора равна 5, а угол, который он образует с осью абсцисс, равен π . Поэтому Могут ли аргументом комплексного числа одновременно быть углы φ и — φ ?
Могут ли аргументом комплексного числа одновременно быть углы φ и — φ ? У полюса r = 0, а φ не определено. Для всех остальных точек r > 0, а φ определено с точностью до слагаемого кратного 2π. При этом парам чисел (r; φ) и (r 1 ; φ 1) сопоставляется одна и та же точка, если .
У полюса r = 0, а φ не определено. Для всех остальных точек r > 0, а φ определено с точностью до слагаемого кратного 2π. При этом парам чисел (r; φ) и (r 1 ; φ 1) сопоставляется одна и та же точка, если . 3. Тригонометрическая форма комплексного числа
3. Тригонометрическая форма комплексного числа  Найти алгебраическую форму комплексного числа .
Найти алгебраическую форму комплексного числа .
 Аргумент не определён для единственного
числа:.
Аргумент не определён для единственного
числа:. Найдем его модуль и аргумент. Очевидно,
что.
Формальный расчет по формуле:.
Очевидно,
что(число
лежит непосредственно на действительной
положительной полуоси). Таким образом,
число в тригонометрической форме:.
Найдем его модуль и аргумент. Очевидно,
что.
Формальный расчет по формуле:.
Очевидно,
что(число
лежит непосредственно на действительной
положительной полуоси). Таким образом,
число в тригонометрической форме:. Проверка:
Проверка: C
модулем проблем не возникает, всегда
следует использовать
формулу
.
А вот формулы для нахождения аргумента
будут разными, это зависит от того, в
какой координатной четверти лежит число.
При этом возможны три варианта (их
полезно переписать):
C
модулем проблем не возникает, всегда
следует использовать
формулу
.
А вот формулы для нахождения аргумента
будут разными, это зависит от того, в
какой координатной четверти лежит число.
При этом возможны три варианта (их
полезно переписать):

 называется алгебраическое выражение вида
называется алгебраическое выражение вида е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.
е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.


 Тригонометрическая запись комплексных чисел.
Тригонометрическая запись комплексных чисел. Длина вектора
, изображающего комплексное число z , называется модулем этого числа и обозначается
или r .
Длина вектора
, изображающего комплексное число z , называется модулем этого числа и обозначается
или r .
 ru Математика Алгебра Формы записи комплексного числа: тригонометрическая, показательная
ru Математика Алгебра Формы записи комплексного числа: тригонометрическая, показательная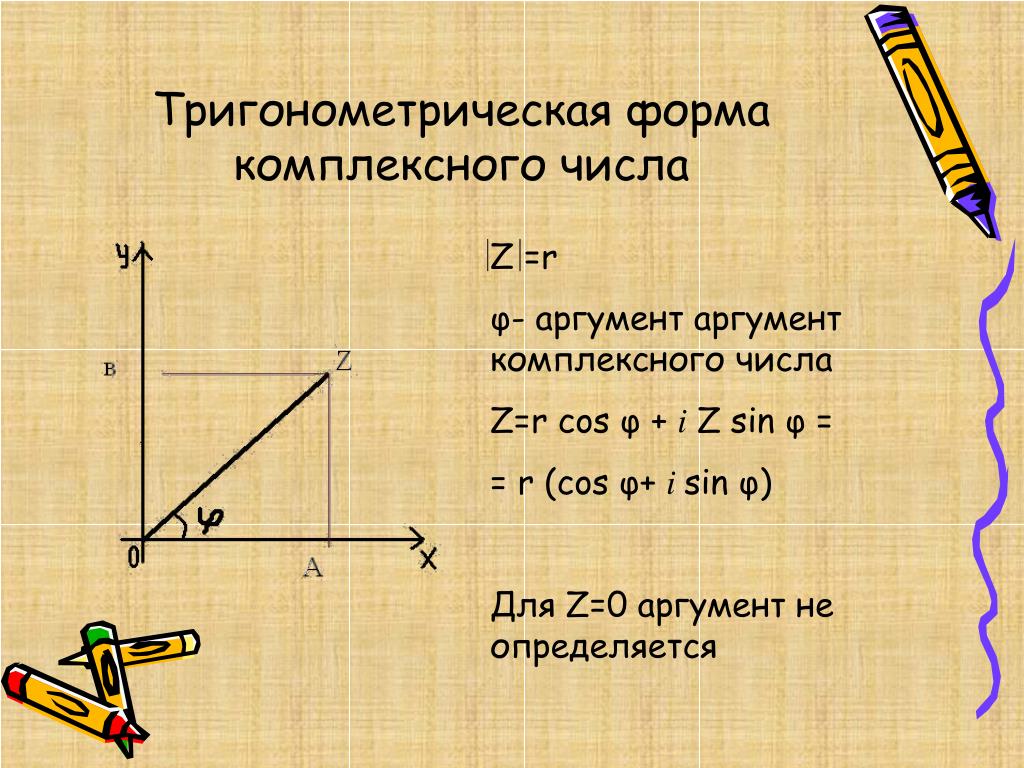
 нуля) вида z = a + bi можно записать в показательной форме:
нуля) вида z = a + bi можно записать в показательной форме: )/3
)/3 Эта форма называется тригонометрической формой и является важной формой комплексных чисел, потому что намного легче найти корни и степени комплексных чисел, когда они находятся в их тригонометрических формах.
Эта форма называется тригонометрической формой и является важной формой комплексных чисел, потому что намного легче найти корни и степени комплексных чисел, когда они находятся в их тригонометрических формах.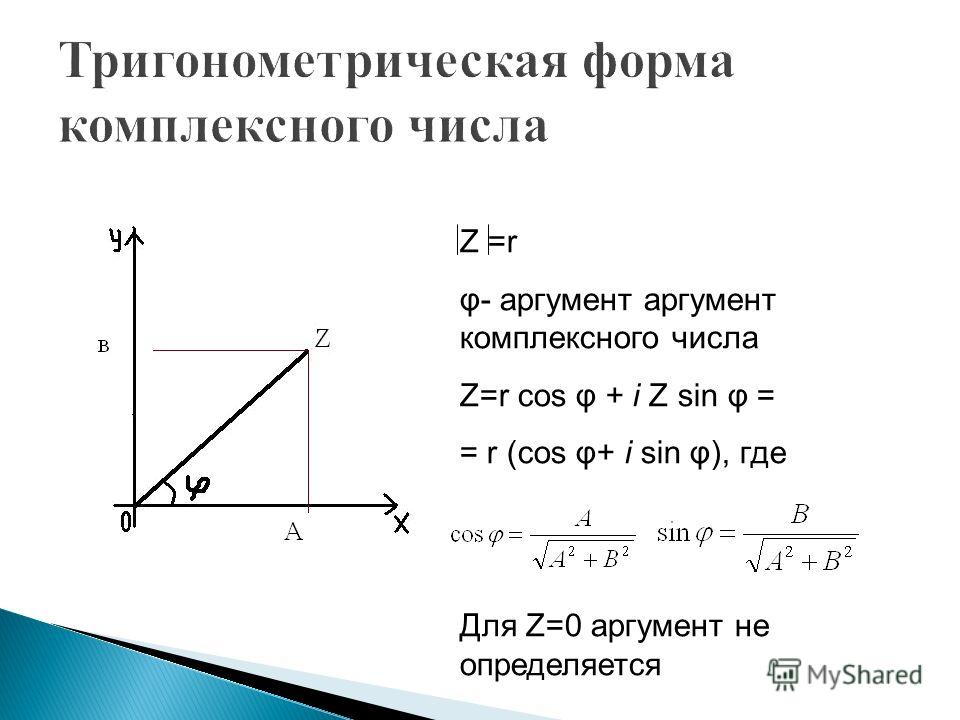

 Но мы оставим это для вас, чтобы вы могли попробовать сами. ( Подсказка : используйте метод ФОЛЬГИ и разностные свойства синуса и косинуса).
Но мы оставим это для вас, чтобы вы могли попробовать сами. ( Подсказка : используйте метод ФОЛЬГИ и разностные свойства синуса и косинуса). 2}$. Между тем аргумент или $\theta$ можно определить, взяв тангенс, обратный $\dfrac{b}{a}$. 9{\circ})\end{align}$
2}$. Между тем аргумент или $\theta$ можно определить, взяв тангенс, обратный $\dfrac{b}{a}$. 9{\circ})\end{align}$ Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.  \]
\]
 Проиллюстрируем на примере.
Проиллюстрируем на примере. Это оказывается правдой в целом.
Это оказывается правдой в целом.




 Если \(r\) является величиной \(z\) (то есть расстоянием от \(z\) до начала координат) и \(\theta\) угол \(z\) образует с положительным действительным ось, затем 9{2}}, \cos(\theta) = \dfrac{a}{r}\]
Если \(r\) является величиной \(z\) (то есть расстоянием от \(z\) до начала координат) и \(\theta\) угол \(z\) образует с положительным действительным ось, затем 9{2}}, \cos(\theta) = \dfrac{a}{r}\]
 gvsu.edu/books/12
gvsu.edu/books/12



 е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Пример этого показан на рисунке ниже. 92}} \) — это не что иное, как длина вектора, который мы используем для представления комплексного числа \(z = a + bi\). Эта интерпретация также говорит нам, что неравенство \(\left| {{z_1}} \right| < \left| {{z_2}} \right|\) означает, что \({z_1}\) ближе к началу координат ( в комплексной плоскости), чем \({z_2}\).
Пример этого показан на рисунке ниже. 92}} \) — это не что иное, как длина вектора, который мы используем для представления комплексного числа \(z = a + bi\). Эта интерпретация также говорит нам, что неравенство \(\left| {{z_1}} \right| < \left| {{z_2}} \right|\) означает, что \({z_1}\) ближе к началу координат ( в комплексной плоскости), чем \({z_2}\). Обратите внимание, что это означает, что существует буквально бесконечное количество вариантов для \(\theta \).
Обратите внимание, что это означает, что существует буквально бесконечное количество вариантов для \(\theta \). 92}} \]
92}} \] Это имеет смысл, если учесть следующее.
Это имеет смысл, если учесть следующее. Продолжая в том же духе, мы снова можем видеть, что каждое новое значение аргумента будет найдено путем вычитания кратного \(2\pi \) из исходного значения аргумента.
Продолжая в том же духе, мы снова можем видеть, что каждое новое значение аргумента будет найдено путем вычитания кратного \(2\pi \) из исходного значения аргумента. Обратите внимание, что неравенства на обоих концах диапазона говорят о том, что отрицательное действительное число будет иметь главное значение аргумента \({\mathop{\rm Arg}\nolimits} z = \pi \).
Обратите внимание, что неравенства на обоих концах диапазона говорят о том, что отрицательное действительное число будет иметь главное значение аргумента \({\mathop{\rm Arg}\nolimits} z = \pi \). \[г = \влево| г \ справа | = \sqrt {1 + 3} = 2\]
\[г = \влево| г \ справа | = \sqrt {1 + 3} = 2\] Так что, если вы используете калькулятор, будьте осторожны. Вам нужно будет вычислить оба и определить, какой из них попадает в правильный квадрант, чтобы соответствовать комплексному числу, которое у нас есть.
потому что только один из них будет в правильном квадранте.
Так что, если вы используете калькулятор, будьте осторожны. Вам нужно будет вычислить оба и определить, какой из них попадает в правильный квадрант, чтобы соответствовать комплексному числу, которое у нас есть.
потому что только один из них будет в правильном квадранте. Вот полярная форма \(z = — 1 + i\,\sqrt 3 \).
Вот полярная форма \(z = — 1 + i\,\sqrt 3 \). Для полноты здесь приведены все возможные значения аргумента любого отрицательного числа.
Для полноты здесь приведены все возможные значения аргумента любого отрицательного числа. Однако все, что нам нужно сделать, чтобы получить аргумент, — это подумать о том, где находится это комплексное число в комплексной плоскости. В комплексной плоскости чисто мнимые числа лежат либо на положительной оси \(у\), либо на отрицательной оси \(у\) в зависимости от знака мнимой части.
Однако все, что нам нужно сделать, чтобы получить аргумент, — это подумать о том, где находится это комплексное число в комплексной плоскости. В комплексной плоскости чисто мнимые числа лежат либо на положительной оси \(у\), либо на отрицательной оси \(у\) в зависимости от знака мнимой части. 2} \ theta} = r \] 9{i\,\left( {{\theta _{\,1}}\, — \,\,{\theta _{\,2}}} \right)}}\label{eq:eq11}\end {выровнять}
2} \ theta} = r \] 9{i\,\left( {{\theta _{\,1}}\, — \,\,{\theta _{\,2}}} \right)}}\label{eq:eq11}\end {выровнять} Например, рассмотрим \({z_1} = i\) и \({z_2} = — 1\). В этом случае мы имеем \({z_1}{z_2} = — i\) и главное значение аргумента для каждого равно
Например, рассмотрим \({z_1} = i\) и \({z_2} = — 1\). В этом случае мы имеем \({z_1}{z_2} = — i\) и главное значение аргумента для каждого равно {i\,{\theta _{\,2}}}}\). Также предположим, что мы знаем, что \({z_1} = {z_2}\). В данном случае имеем 9{я\,{\тета _{\,2}}}}\]
{i\,{\theta _{\,2}}}}\). Также предположим, что мы знаем, что \({z_1} = {z_2}\). В данном случае имеем 9{я\,{\тета _{\,2}}}}\] Борна
Борна ………(1)
………(1)  Мы можем получить α и R г. с использованием
калькулятор, похожий на то, как мы это делали с комплексными числами
раздел.
Мы можем получить α и R г. с использованием
калькулятор, похожий на то, как мы это делали с комплексными числами
раздел.



 …. (1)
…. (1) Выразить 7 sin θ + 12 cos θ в виде R cos ( θ − α), где 0 ≤ α < π/2.
Выразить 7 sin θ + 12 cos θ в виде R cos ( θ − α), где 0 ≤ α < π/2. Выразить 2,348 sin θ − 1,251 cos θ в виде −R cos ( θ ), где 2,348 sin θ + α
Выразить 2,348 sin θ − 1,251 cos θ в виде −R cos ( θ ), где 2,348 sin θ + α


















 е. число делят на сумму чисел, то необходимо выполнить действия в скобках (если это возможно), и только потом делимое число разделить на результат, полученный в скобках.
е. число делят на сумму чисел, то необходимо выполнить действия в скобках (если это возможно), и только потом делимое число разделить на результат, полученный в скобках.
 е. исходное выражение можно записать следующим образом:
е. исходное выражение можно записать следующим образом:






 Переменной a присвоили значение 2 , переменной b присвоили значение 3 . В результате буквенное выражение a+b+4 обращается в обычное числовое выражение 2+3+4 значение которого можно найти:
Переменной a присвоили значение 2 , переменной b присвоили значение 3 . В результате буквенное выражение a+b+4 обращается в обычное числовое выражение 2+3+4 значение которого можно найти: Число 3 в этом произведении называют коэффициентом . Этот коэффициент показывает во сколько раз будет увеличена переменная a . Данное выражение можно прочитать как «a три раза» или «трижды а «, или «увеличить значение переменной a в три раза», но наиболее часто читается как «три a «
Число 3 в этом произведении называют коэффициентом . Этот коэффициент показывает во сколько раз будет увеличена переменная a . Данное выражение можно прочитать как «a три раза» или «трижды а «, или «увеличить значение переменной a в три раза», но наиболее часто читается как «три a «
 В этом случае коэффициентом является единица:
В этом случае коэффициентом является единица:
 В принципе, данная задача очень проста. Достаточно уметь правильно умножать числа.
В принципе, данная задача очень проста. Достаточно уметь правильно умножать числа.
 Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
Но нам ничего не мешает, заменить вычитание сложением. Тогда мы снова получим выражение, состоящее из слагаемых:
 Эту операцию называют приведением подобных слагаемых .
Эту операцию называют приведением подобных слагаемых .