Инженерный калькулятор онлайн
С этим научным калькулятором вы можете найти производную функции и вычислить интеграл, а также решить уравнение или задачу по комбинаторике. Доступен тригонометрический функционал (нахождение синуса, косинуса, тангенса и так далее).
Для всех возможных действий приведены примеры. Если вам не нужно много функций, откройте простой калькулятор.
Тригонометрия
Синус (sin x)
sin 3 0 =
Косинус (cos x)
cos 1 8 0 =
Тангенс (tg x)
tan 4 5 =
Котангенс (ctg x)
cot 9 0 =
Секанс и косеканс
Секанс (sec x) — sec
Косеканс (cosec x) — csc
Гиперболические функции
Гиперболический синус (sh x) — sinh
Гиперболический косинус (ch x) — cosh
Гиперболический тангенс (th x) — tanh
Обратные тригонометрические функции
Арксинус (arcsin x) — 2nd asin
Арккосинус (arccos x) — 2nd acos
Арктангенс (arctg x) — 2nd atan
Арккотангенс (arcctg x) — 2nd acot
Нахождение производных
d i f f ( x x2 ) =
Вычисление интегралов
i n t ( 2 x ) =
Решение уравнений
2 x − 4 x=y 0 =
Комбинаторика
Перестановки
Без повторений (то же, что факториал числа).
6 ! =
Сочетания
Без повторений.
ncr 2 5 , 5 =
Размещения
Без повторений.
ncr 6 , 3 =
Кредитный калькулятор с досрочным погашением
Данный онлайн калькулятор имеет расширенный набор функций по сравнению со стандартным кредитным калькулятором. Помимо функции расчета досрочного погашения кредита, здесь есть возможность задать изменение процентной ставки, выбрать день выдачи кредита, выбрать день для ежемесячного платежа, выбрать тип ежемесячного платежа — аннуитетный или дифференцированный. Благодаря этим функциям калькулятор позволяет сделать расчет максимально близким к реальному кредиту, с точностью до дня.
С нашим калькулятором вы сможете рассчитать досрочное погашение кредита за две минуты без визита в банк. Для этого нужно заполнить несколько дополнительных полей в форме калькулятора:
- Дату досрочного внесения средств (если платеж единоразовый) или интервал (если вы собираетесь делать платежи на регулярной основе, например раз в 3 месяца)
- Сумму досрочного платежа
- Выбрать способ перерасчета кредита
Можно задать неограниченное количество частично досрочных погашений.
Особенности частично досрочного погашения кредита
При частично досрочном погашении возможно два типа списаний:
- в день очередного платежа. В этом случае сумма долга просто уменьшается на сумму внеочередного платежа.
- между двумя очередными платежами. Здесь расчет происходит сложнее. Проценты на сумму долга начисляются каждый день, а гасятся раз в месяц. К моменту досрочного платежа накапливается некая сумма процентов, которая будет погашена за счет средств, предназначенных на досрочный платеж. И только оставшаяся сумма пойдет на погашение основного долга. В следующем же месяце процентная часть очередного платежа будет меньше, ведь часть процентов за этот месяц уже уплачена. Не стоит беспокоиться по этому поводу и откладывать досрочное погашение на день очередного платежа. Чем раньше платеж будет зачислен, тем выгоднее.
После внесения внеочередного платежа меняется график последующих погашений кредита. Сумма основного долга уменьшается и следом за ней изменяется один из двух параметров: сумма ежемесячного платежа или срок кредита. Выбор всегда за клиентом банка. С учетом вашего выбора банк делает перерасчет кредита и формирует новый график платежей. Имейте это ввиду и получайте новый график платежей в офисе банка или в программе интернет-банк (если такую возможность предоставляет банк). Наш онлайн калькулятор также позволяет выбрать любой вариант и производит расчет с учетом выбора. После расчета вам будет представлен подробный график платежей с учетом указанных досрочных погашений.
Выбор всегда за клиентом банка. С учетом вашего выбора банк делает перерасчет кредита и формирует новый график платежей. Имейте это ввиду и получайте новый график платежей в офисе банка или в программе интернет-банк (если такую возможность предоставляет банк). Наш онлайн калькулятор также позволяет выбрать любой вариант и производит расчет с учетом выбора. После расчета вам будет представлен подробный график платежей с учетом указанных досрочных погашений.
Выгоднее уменьшать срок кредита, так как общая переплата в этом случае снизится более значительно. Поэтому, если сумма ежемесячного платежа вам посильна, рекомендуем уменьшать именно срок.
Экспериментируйте с параметрами для выбора наиболее подходящего для вас способа перерасчета. Кредитный калькулятор позволяет сохранять результаты расчетов, это очень удобно для сравнения полученных вариантов, так как вам не придется повторно вносить исходные данные кредита в форму.
Изменяемая процентная ставка
Нередко бывает, когда процентная ставка меняется в ходе срока кредита. Это может быть вызвано пересмотром кредитной ставки банком по заявлению заемщика или условиями договора. Для таких ситуаций в калькуляторе предусмотрена соответствующая функция. Можно задать неограниченное количество изменений процентной ставки на протяжении срока кредита. Для каждого периода нужно выбрать дату начала действия ставки и её значение. Эти изменения также будут отображены и помечены особым цветом в графике платежей.
Это может быть вызвано пересмотром кредитной ставки банком по заявлению заемщика или условиями договора. Для таких ситуаций в калькуляторе предусмотрена соответствующая функция. Можно задать неограниченное количество изменений процентной ставки на протяжении срока кредита. Для каждого периода нужно выбрать дату начала действия ставки и её значение. Эти изменения также будут отображены и помечены особым цветом в графике платежей.
Онлайн калькулятор: расширенный алгоритм Евклида
С помощью следующего калькулятора вы познакомитесь с расширенным алгоритмом Евклида. Вы уже могли видеть у нас на сайте калькулятор, который использует обычный алгоритм Евклида (НОД двух чисел):
Расширенный алгоритм кроме нахождения НОД также находит и коэффициенты, при которых справедливо уравнение ниже:
Иными словами данный алгоритм может найти коэффициенты, при помощи которых наибольший общий делитель двух чисел будет выражаться через сами эти целые числа.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
exp калькулятор
Вы искали exp калькулятор? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислите онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «exp калькулятор».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как exp калькулятор,вычислите онлайн,вычислить онлайн,вычислить экспоненту,инженерный калькулятор онлайн,инженерный калькулятор онлайн бесплатно,калькулятор многофункциональный онлайн,калькулятор онлайн формул,калькулятор по формулам,калькулятор расширенный онлайн,калькулятор с квадратными скобками,калькулятор с функциями,калькулятор формул,калькулятор формул онлайн,калькулятор формул приведения онлайн,калькулятор формула,онлайн калькулятор технический,онлайн калькулятор формул,формула калькулятор,формулы приведения калькулятор онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и exp калькулятор. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить онлайн).
Где можно решить любую задачу по математике, а так же exp калькулятор Онлайн?
Решить задачу exp калькулятор вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Кредитный калькулятор рассчитать кредит онлайн, расчет процентов
Банковский калькулятор — расчет кредита онлайн
Когда речь идёт о мгновенном решении финансовой проблемы, нет времени вникать в огромное количество рекламной информации. Банки пестрят объявлениями, зазывая клиентов обратиться именно к ним.
Действительно, выбор банковских продуктов сегодня огромен. На неискушённого человека обрушивается масса сведений, в которых, порой, не разобраться.
К счастью, существует кредитный калькулятор онлайн — полезный и надёжный инструмент, позволяющий легко и быстро оценить свои перспективы выполнения обязательств, рассчитать график платежей по планируемому кредиту.
Калькулятор установлен, пожалуй, на каждом сайте банка. С его помощью за несколько минут можно вычислить максимальный размер займа, срок кредитования, оптимальную процентную ставку.
Кредитный калькулятор онлайн расчет процентов по кредиту
Инструмент прост и удобен в использовании. Рассмотрим принцип расчётов на примере кредитного калькулятора Альфа — банка.
- На сайте банковского учреждения находим соответствующий раздел.
- В определённые графы вводим желаемую сумму займа и планируемый период возврата.
- В автоматическом режиме, мгновенно, производится расчёт помесячных платежей и объявляется размер переплаты.
Как быстро и просто рассчитать ежемесячный платеж по кредиту
После проведения расчёта платежей с помощью калькулятора, можно переходить к оформлению заявки на кредит наличными. Достаточно быть совершеннолетним гражданином, иметь прописку и мобильный телефон, чтобы быстро получить ссуду.
- на официальном сайте банка необходимо заполнить заявку, указав персональные данные, место жительства, номер телефона;
- отправить анкету и ожидать согласования;
- в течение 7 минут можно получить наличку.
Что такое аннуитетные платежи?
Аннуитетный платеж остается неизменным в течение всего срока действия кредитного договора. Каждый месяц погашение кредита осуществляется равными долями, которые состоят из начисленных процентов и части основного долга.
Что такое дифференцированные платежи?
Дифференцированный платеж в первые месяцы действия кредитного договора будет больше, чем при аннуитетой схеме погашения. Но с каждым месяцем размер платежа будет уменьшаться за счет того, что основной долг погашается равными долями, а проценты начисляются ежемесячно на остаток долга.
Преимущества кредита — Credit Calculator
Кредитный калькулятор позволяет рассчитать кредит онлайн и оценить неоспоримые преимущества получения заёмных денег:
- скорость оформления;
- простоту заполнения заявки;
- минимум документов;
- возможность получения денег онлайн;
- высокую вероятность согласования;
- удобные способы погашения.
Как с помощью калькулятора сравнить разные кредитные программы
Некоторые расчёты содержат сложные алгоритмы, включающие дополнительные параметры. Как правило, они применяются для анализа ежемесячных выплат по крупным ссудам.
С помощью таких расчётов также можно сравнить разные кредитные программы и выбрать из них наиболее удобную. Зная несколько параметров займа, можно подобрать лучшие условия и сравнить их с предложениями банков — конкурентов.
Как правильно рассчитать переплату по кредиту
ВНИМАНИЕ! При расчете графиков платежей не учитываются дополнительные платежи банку (комиссия за открытие, страховка, услуги нотариуса и др.). Калькулятор предназначен для приблизительного расчета суммы платежей, для получения более точных данных необходимо обратиться непосредственно в кредитную организацию.
Перед оформлением ссуды, стоит обратить внимание на калькулятор ипотеки онлайн. Здесь можно просчитать размер переплаты по кредиту на покупку жилья. Для этого в соответствующие графы необходимо внести следующие данные:
- стоимость квартиры;
- процентную ставку;
- сумму первоначального взноса;
- срок действия договора.
Результаты расчёта помогут выбрать наиболее подходящее банковское учреждение для оформления кредита, а также оценить финансовую возможность погашения займа.
Кредитный онлайн калькулятор с досрочным погашением
По сравнению со стандартным калькулятором, этот сервис включает в себя расширенный набор функций, позволяющих произвести расчёт, максимально приближённый к реальности. Заполнив несколько дополнительных граф (дату и сумму досрочного платежа), калькулятор за несколько минут рассчитает досрочное погашение кредита.
Калькулятор Бацзы (четыре столпа судьбы) | Ming Li
Дата рожденияДень12345678910111213141516171819202122232425262728293031МесяцЯнварьФевральМартАпрельМайИюньИюльАвгустСентябрьОктябрьНоябрьДекабрьГод158215831584158515861587158815891590159115921593159415951596159715981599160016011602160316041605160616071608160916101611161216131614161516161617161816191620162116221623162416251626162716281629163016311632163316341635163616371638163916401641164216431644164516461647164816491650165116521653165416551656165716581659166016611662166316641665166616671668166916701671167216731674167516761677167816791680168116821683168416851686168716881689169016911692169316941695169616971698169917001701170217031704170517061707170817091710171117121713171417151716171717181719172017211722172317241725172617271728172917301731173217331734173517361737173817391740174117421743174417451746174717481749175017511752175317541755175617571758175917601761176217631764176517661767176817691770177117721773177417751776177717781779178017811782178317841785178617871788178917901791179217931794179517961797179817991800180118021803180418051806180718081809181018111812181318141815181618171818181918201821182218231824182518261827182818291830183118321833183418351836183718381839184018411842184318441845184618471848184918501851185218531854185518561857185818591860186118621863186418651866186718681869187018711872187318741875187618771878187918801881188218831884188518861887188818891890189118921893189418951896189718981899190019011902190319041905190619071908190919101911191219131914191519161917191819191920192119221923192419251926192719281929193019311932193319341935193619371938193919401941194219431944194519461947194819491950195119521953195419551956195719581959196019611962196319641965196619671968196919701971197219731974197519761977197819791980198119821983198419851986198719881989199019911992199319941995199619971998199920002001200220032004200520062007200820092010201120122013201420152016201720182019202020212022202320242025202620272028202920302031203220332034203520362037203820392040204120422043204420452046204720482049
Час01234567891011121314151617181920212223Минуты01234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859
Летнее времяОнлайн-калькулятор категории риска деятельности
В течение 2 календарных лет, с причинением вреда жизни и (или) здоровью людей
В течение 2 календарных лет, без причинения вреда жизни и (или) здоровью людей
В течение 3 календарных лет 15 и более административных наказаний, кроме предупреждений, по статьям 11.1, 11.3, 11.4, 11.5, 11.6, 11.7, 11.8, 11.13, 11.16, 11.23, 11.30, 11.31, 12.21.1 (части 2 — 11), 12.21.2, 12.21.3, 12.23, 12.25, 12.31.1, 14.1, 14.1.2, 14.43, 19.5, 19.7 Кодекса Российской Федерации об административных правонарушениях
Отсутствие вынесенных приговоров суда и (или) решений (постановлений)
Формуляр: математика — тригонометрия ◿
Тригонометрия ◿
Определения:
- a : Длина противоположной стороны
- b : Длина смежного
- c : Длина гипотенузы
- h : Длина гипотенузы 09 Угол альфа09
- beta : Угол β
- гамма : Угол γ
- x : a / h
- y : b / h
- z : a / b
В любом прямоугольном треугольнике площадь квадрата со стороной гипотенузы (c) равна сумме площадей квадратов, стороны которых являются двумя катетами (a, b). {- 1} (\ frac {\ color {OliveGreen} {b}} {\ color {blue} {c}})
\)
\ (
{\ color {OliveGreen} {b}} = cos \ left ({{\ color {red} {\ alpha}}} \ right) \ times {{\ color {blue} {c}}}
\)
\ (
{\ color {blue} {c}} = \ frac {{\ color {OliveGreen} {b}}} {cos \ left ({{\ color {red} {\ alpha}}} \ right)}
\)
abLayer 1CABα
Касательная
Функция тангенса — это базовая триогеметрическая функция.2 = (1/2) + (1/2) * cos (2 * альфа)
\)
Лучший научный калькулятор онлайн (простой и бесплатный)
Лучший научный калькулятор онлайн (простой и бесплатный)- Наш научный калькулятор — это самый сложный и всесторонний научный калькулятор в Интернете.
- Он имеет все основные функции и кнопки, которые вы ожидаете, включая sin, cos, tan, sin-1, cosh, log и многое другое.
- Также есть несколько дополнительных функций, включая кнопку для вычисления наименьшего общего кратного, перестановок и комбинаций.
- Решатель линейных уравнений, который позволяет вводить до 6 уравнений с двумя или тремя переменными, а решатель вычисляет решения.
- Кнопка памяти для сохранения вычислений для использования в будущем.
M
MC
MR
МС
млн +
M-
С
7
8
9
/
=
4
5
6
*
1
2
3
–
(
)
0
.
,
А ↓
B ↓
C ↓
А ↑
B ↑
С ↑
х 2
х 3
!
%
e
e x
пи
пер.
журнал 2
журнал 10
кв.м
абс
мод
нПр
нКр
гкд
лкм
макс
потолок
этаж
раунда
мин.
грех
cos
загар
csc
сек
детская кроватка
грех -1
cos -1
загар -1
ГСК -1
сек -1
детская кроватка -1
sh
кош
танх
сщ
рублей
коттедж
sh -1
ш -1
танх -1
сщ -1
sech -1
кот -1
MC
MR
МС
млн +
M-
С
7
8
9
/
=
4
5
6
*
1
2
3
–
(
)
0
.
,
А ↓
B ↓
C ↓
А ↑
B ↑
С ↑
х 2
х 3
!
%
e
e x
пи
пер.
журнал 2
журнал 10
кв.м
абс
мод
нПр
нКр
гкд
лкм
макс
потолок
этаж
раунда
мин.
грех -1
cos -1
загар -1
ГСК -1
сек -1
детская кроватка -1
sh
кош
танх
сщ
рублей
коттедж
sh -1
ш -1
танх -1
сщ -1
sech -1
кот -1
Введите два или более уравнения в формате Ax + By +… = C:7
8
9
–
=
4
5
6
+
1
2
3
u
в
Вт
0
.
х
л
z
Решить
MMC
MR
МС
млн +
M-
С
7
8
9
/
=
4
5
6
*
1
2
3
–
(
)
0
.
%
х 2
х 3
кв.м
пи
e
Электронный научный калькулятор с магнитной лентой
В первую очередь отображается онлайн-научный калькулятор с расширенными функциями, при нажатии на ссылку стандартного калькулятора отображается бесплатный онлайн-математический калькулятор.
Вы можете управлять онлайн-калькулятором прямо с цифровой клавиатуры вашего компьютера, а также с помощью мыши. Нажатие клавиши Esc или Delete стирает значение, отображаемое в поле ввода.
Для проверки вашей работы математические расчеты, введенные в онлайн-калькулятор, можно оставить отображенными на ленте (то есть в окне просмотра рядом с онлайн-калькулятором).
Содержимое ленты можно редактировать (стереть части расчета, добавить описание), распечатать, нажав «печать», сохранить в текстовый файл, нажав «сохранить», или удалить, нажав «удалить».
Превращает ленту в редактируемый формат, в котором вы можете добавлять текст, стирать некоторые вычисления или добавлять комментарии.
Завершает процесс редактирования и сохраняет содержимое ленты
Сохраняет и загружает содержимое ленты в текстовый файл
Удаляет содержимое ленты.
Печатает весь текст и вычисления, отображаемые на ленте.
| Кнопка | Функция |
| % | Отображение результата суммы в процентах.Чтобы вычислить 5 процентов от базового 200, введите число 200 и нажмите кнопку *, введите число 5 в качестве второго числа и нажмите кнопку%. Результатом будет 10. Чтобы добавить процент к основанию, введите число 200 и нажмите кнопку +, введите число 5 в качестве второго числа и нажмите кнопку%. Результат будет 210. Например: 200 + 5% = 210200-5% = 190 200 * 5% = 10 200/5% = 4000 (базовый расчет) |
| оценка | Обменный курс конвертации.Чтобы конвертировать $ в евро, введите текущий обменный курс, например 1,3 (обменный курс 1 = 1,3 $) и нажмите кнопку «Оценить». Чтобы рассчитать сумму, которую я получу, введите сумму в долларах и нажмите кнопку. Чтобы рассчитать сумму, которую я получу, введите сумму и нажмите кнопку $ |
| Кнопка | Клвесов скратка | Функция |
| S | Записывает введенное число в память.Если номер ранее был сохранен в памяти, этот номер будет перезаписан. Содержимое памяти отображается в левой части дисплея (например, ПАМЯТЬ: 230). Текст не отображается, если память пуста. | |
| -П | Добавляет введенное число к числу, хранящемуся в памяти. | |
| я | Вычитает введенное число из числа, хранящегося в памяти. | |
| р | Сохранить x в памяти. | |
| С | Удаляет сохраненный номер из памяти. | |
| Q | Установите обменный курс для конвертации (например, 1 € = 1,3 $). | |
| E | Конвертировать x из валюты $ в валюту €. | |
| К | Конвертировать x из валюты € в валюту $. |
В правом верхнем углу калькулятора вы найдете переключатель, который изменяет размер калькулятора. Щелкните квадрат, чтобы изменить его размер с 1 на 3.
10 лучших онлайн-калькуляторов для решения простых и сложных задач
Предшественник современных калькуляторов , Abacus (лат. « доска ») представлял собой рифленую доску с подвижными счетными этикетками, сделанными из костей или камней.Сообщается, что он восходит к 3000 г. до н.э. г. в древнем г. Вавилон , пока он не появился снова в 5 веке г. Греция .
Перенесемся в 21 век, и у нас есть не только калькуляторы, которые подходят для небольших компьютеров, но и современные, которые не требуют, чтобы пользователи устанавливали их на свои машины.
Вот 10 лучших веб-сайтов для выполнения вычислений, начиная от простых математических операций и заканчивая решением сложных финансовых вопросов.
1.Desmos
Desmos — это продвинутый научный онлайн-калькулятор. Он имеет пользовательский интерфейс с вкладками и кнопками для выполнения вычислений в градусах и радианах, углах, значениях круговой диаграммы, процентах, степенях и круглых числах.
РЕКЛАМА
Он также имеет вкладку для ввода букв и специальных символов, например скобки напрямую. Что еще круче, так это его меню настроек, в котором есть параметры для режима Брайля, режима проектора, обратного контраста (темный режим) и т. Д.
Научный калькулятор Desmos
2.web2.0calc
web2.0calc предоставляет базовые и расширенные математические функции, которыми можно управлять как непосредственно с клавиатуры, так и с помощью кнопок мыши. Он имеет отображение математических формул, поддержку больших чисел, средство решения уравнений и виджеты калькулятора.
Достаточно мощный, чтобы решать задачи в дифференциальном и интегральном исчислении, теории чисел, стандартных функциях, статистике, графиках, комплексных числах и т. Д.
Web2.0calc Научный калькулятор
3.Хорошие калькуляторы
Good Calculators — это проект, который предлагает группу из 300+ бесплатных высокофункциональных калькуляторов для решения всех видов математических и бизнес-задач. В нем есть калькуляторы для заработной платы и налога на прибыль, выхода на пенсию, контрактов, ссуд, Forex, 2D и 3D форм, среднего балла, логистики, продаж и инвестиций, управления человеческими ресурсами и нескольких других категорий расчетов.
Бесплатные онлайн-калькуляторы
4. GeoGebra
GeoGebra — это многофункциональная онлайн-платформа с открытым исходным кодом, созданная для объединения алгебры, геометрии, электронных таблиц, статистики, графиков и вычислений в один простой в использовании пакет, и с тех пор она стала ведущим поставщиком программного обеспечения для динамической математики для поддержка STEM-образования.
Он имеет простой в использовании интерфейс с инструментом разработки для создания интерактивных учебных ресурсов на многих языках для людей во всем мире.
Научный калькулятор GeoGebra
5. Calculator-1.com
Calculator-1.com — это большой, простой и удобный онлайн-калькулятор для использования на работе, в школе и в личных целях. В нем есть функции для выполнения не только основных математических расчетов, но и процентных ставок по ссудам и ипотечным платежам, коммунальных расходов и счетов за работу.
Бесплатный удобный калькулятор
6. Symbolab
Symbolab — это продвинутый онлайн-калькулятор для решения практически любых математических задач. В нем есть кнопки и готовые вкладки для построения графиков, касательных, матриц, многомерного исчисления, множеств и т. Д.
Использование Symbolab удобно, поскольку в нем есть кнопки, которые можно легко щелкнуть, чтобы заполнить поле проблемы, а затем отредактировать, чтобы сохранить значения проблемы.
Расширенный онлайн-калькулятор
7. Мета-калькулятор
Meta Calculator — это комплексный и сложный научный онлайн-калькулятор и программа для решения уравнений.Он имеет все основные функции и кнопки, включая кнопки для sin, cos, tan, sech, перестановок и комбинаций, общих кратных и т. Д.
Он также может решать линейные уравнения, которые могут принимать до 6 уравнений с 2 или 3 переменными и кнопкой памяти для будущих вычислений.
Онлайн-калькулятор с функцией решения уравнений
8. Онлайн-калькулятор
Online-Calculator — это онлайн-калькулятор, основанный на идее, что «каждому в какой-то момент нужен калькулятор».В сочетании с возможностью быстрой загрузки, он предлагает пользователям различные экраны для различных типов вычислений, такие как модули, такие как калькулятор ИМТ, конвертер расстояний, конвертер размеров кольца, калькулятор внутреннего дворика, научный калькулятор, конвертер веса, секундомер, средство выбора случайных имен и т. Д.
Бесплатный онлайн-калькулятор
9. Calculator.net
Calculator.net — это веб-сайт, на котором размещено 200+ различных калькуляторов с единственной целью — предоставление быстрых, всеобъемлющих и бесплатных онлайн-калькуляторов, удобных в использовании.
Калькуляторы сгруппированы в Финансовые, например. автокредит, инфляция, платеж, процентная ставка, зарплата, калькулятор налога с продаж; Фитнес и здоровье, например калорийность, ИМТ, темп, зачатие беременности, калькуляторы жировых отложений; Математика, например калькуляторы треугольников, стандартного отклонения, процентов, дробей; и другие, например GPA, бетон, подсетевые калькуляторы, генератор паролей; пр.
Финансовые онлайн-калькуляторы
10. Банковская ставка
Bankrate — это независимая платформа для издателей и сравнительных услуг, поддерживаемая рекламой, с множеством онлайн-калькуляторов, которые позволяют пользователям производить расчеты, связанные с финансами, от ипотеки и ссуд до пенсионных планов и налоговых деклараций.Калькуляторы сгруппированы по нескольким категориям для упрощения бесплатных расчетов в Интернете.
Финансовые калькуляторы
Я уверен, что сегодня вы нашли по крайней мере 3 классных онлайн-калькулятора. Есть ли у вас достаточно крутые альтернативы, чтобы их можно было добавить в список? Не стесняйтесь добавлять свои предложения в разделе комментариев ниже.
Symbolab Math Solver — Пошаговый калькулятор
| \ bold {\ mathrm {Basic}} | \ bold {\ alpha \ beta \ gamma} | \ bold {\ mathrm {AB \ Gamma}} | \ полужирный {\ sin \ cos} | \ bold {\ ge \ div \ rightarrow} | \ bold {\ overline {x} \ space \ mathbb {C} \ forall} | \ bold {\ sum \ space \ int \ space \ product} | \ bold {\ begin {pmatrix} \ square & \ square \\\ square & \ square \ end {pmatrix}} | \ bold {H_ {2} O} | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Наиболее часто используемые действия
| \ mathrm {упрощать} | \ mathrm {решить \: for} | \ mathrm {инверсия} | \ mathrm {касательная} | \ mathrm {линия} | Посмотреть все |
Научный онлайн-калькулятор с шагами
История научного калькулятора опровергнута
Научный калькулятор
Вы можете выбрать любой из множества стилей и форматов отображения.Пока вы делаете работу по созданию контента, вам не нужно отвлекаться на задачи форматирования. Кнопка «Очистить» очищает предыдущий ввод.
Вы признаете, что этот инструмент предоставляется для абсолютно бесплатного личного, образовательного и некоммерческого использования. Минимально необходимо использовать преамбулу документа или необработанные команды TEX, чтобы получить желаемый формат веб-страницы. Итак, что вам нужно сделать, это посетить мастер функций и выбрать вариант «DOLLARFR».
Введите то, что вы хотите вычислить, нажмите Enter, чтобы найти решение.В калькуляторах используется идея регистра. Подводя итог, можно сказать, что научный калькулятор является лучшим вариантом для пользователей, которые ищут простой в использовании калькулятор, который поставляется в комплекте с удобными функциями.
Абсолютно самый знаменитый алфавит, используемый для этой цели, — это `x ‘, но может работать и любой другой алфавит. Предположим, вы инженер-проектировщик, и ваш коллега попросил вас предоставить копию документа спецификации, поскольку они как раз собираются что-то спроектировать на его основе.Вы можете воспользоваться калькулятором в том случае, если количество десятичных знаков, которые могут вам понадобиться, превышает 3 десятичных разряда, которые использовались в целях этой иллюстрации.
Конец научного калькулятора
Давайте посмотрим на быстрый пример. Чтобы установить новую крышу, вы должны оценить размеры существующей крыши, и по этой причине определение уклона является важной частью работы. Калькулятору не хватает математической интуиции, которая очень удобна для поиска первообразной, но, с другой стороны, он может опробовать значительное количество возможностей за короткий промежуток времени.
Было бы сложно выбрать лучший научный калькулятор, однако из множества калькуляторов и торговых марок, предлагаемых на рынке, был бы полезен краткий обзор. Проверка научного калькулятора Существует два вида научных калькуляторов, последний из которых — алгебраические научные калькуляторы. Для начала вы должны знать, чем научный калькулятор отличается от нескольких других калькуляторов.
Он имеет один из самых элегантных дизайнов и представляет собой фантастический графический калькулятор. Привыкнуть к огромным функциям калькулятора может быть непросто, но это один из лучших графических калькуляторов.Это совершенно бесплатно, быстро и предлагает все функции обычного научного калькулятора.
Вы можете бесплатно скачать и использовать его сколько угодно. Самый последний калькулятор известен как научный калькулятор. Щелкните гиперссылку и обратитесь к калькулятору выше.
Научный калькулятор — Рассказ
Вы можете спросить себя, почему я вычислил возможный эфир, скрытый в No Man’s Sky. Вы получите ответ 16100. Теперь нажмите равно, и вы получите последний ответ 220.
Что нужно знать о научном калькуляторе
Даже в том случае, если вы не планируете посещать курс, требующий обработки чисел или вычислений, вам все равно понадобится фундаментальный калькулятор, так как у вас будет минимум одного предмета базовой математики или естествознания. Для понимания алгебры жизненно важно научиться правильному использованию степеней и радикалов. Если вас зачислили на занятия по тригонометрии, химии или физики в ближайшее время, почти гарантировано, что вам понадобится научный калькулятор в качестве вспомогательного средства.
Умножение — одна из самых основных математических операций, но и один из важнейших предметов изучения. Полином — это фундаментальный алгоритм, используемый в большинстве ранних научных калькуляторов. На этом Casio очень просто вычислить уравнения и формулы: от возможности возврата на пробел до возможности перехода к очень длинной строке чисел.
Momentum — сильный инструмент. Помня этот простой тест, вам никогда не придется паниковать, если вы не можете вспомнить, как работает ваш калькулятор в центре теста.Этот калькулятор дробей — полезный инструмент, но он не заменяет высокоэффективный математический ум!
Итак, теперь, когда вы знаете, что такое процент и как он обозначается, давайте перейдем к определению пропорции числа. С помощью калькулятора уклона крыши, предоставленного ранее, можно легко измерить стоимость и узнать угол наклона. Просто укажите длину кромки, чтобы найти решение.
Рождение научного калькулятора
Если вы слишком рано воспользуетесь округленным значением, вы потеряете точность.По этой причине вам нужно увеличить единицу в последнем исходе. Равно 125.
Во многих случаях последствия нажатия одной клавиши сохранялись для использования в следующей функции. Небольшая ошибка округления или другая ошибка может привести к хорошему сдвигу итогового значения. Эти примеры включают некоторые разные числа с большими значениями, чтобы помочь вам лучше понять концепцию.
В регионе, которому была выделена эта маркировка, нет рабочего номера. Время должно быть измерено с ростом сельского хозяйства.Чтобы быть уверенным, что у вас будет достаточно времени, чтобы ответить на каждый вопрос в меру своих возможностей, важно использовать достойные навыки управления временем.
Он вернется к калькулятору дробей и покажет проблему именно так, как вы ее видите. Ценность научных обозначений становится очевидной, когда вы пытаетесь умножить или разделить эти числа. Как только он установлен, вычисление процентов становится чрезвычайно простым.
Проценты упрощают сравнение двух цифр или цифр, которые отличаются друг от друга относительно начальных вложений, продолжительности инвестиций и т. Д. И т. Д.Теперь вы можете ввести знаменатель. Аналогичным образом можно использовать научную нотацию для очень маленьких чисел.
30-секундный трюк для научного калькулятора
Во всяком случае, в Бремене нет спроса на идеальную рекламу. Иногда вы можете найти простые процентные счета, предлагающие огромные процентные ставки, и можете увлечься, чтобы вложить значительную сумму денег. Можно заработать сравнительно большую сумму денег на процентах, если вы вложите огромную сумму денег.
Борьба с научным калькулятором
Вы можете прочитать мой полный обзор ключевого слова elite и узнать все о компьютерном программном обеспечении. Найдите страницу, которая ссылается на какую-либо другую страницу Этот поисковый прием может быть весьма полезен при попытке найти вторичные источники, которые ссылаются на конкретный основной источник. Ниже приводится краткое описание услуг по подписке ShippingPass Pilot.
Знакомство с научным калькулятором
В любом случае обратитесь к руководству, если у вас возникнут проблемы с переводом калькулятора в предпочитаемый режим.Данные вообще не кэшируются и не хранятся, но если вы хотите и дальше хранить данные калькулятора полностью в браузере, не используйте эти функции. Цифровой калькулятор TI83 обладает всеми функциональными возможностями портативной версии.
Большинство из них также являются программируемыми, что означает, что пользователь может создавать индивидуальные программы, идеально соответствующие их уникальным потребностям. Его можно использовать при трудностях РПН и многих других научных трудностях. По заявке эта проблема проясняется в кратчайшие сроки.
Опции научного калькулятора
Введите то, что вы хотите вычислить, нажмите Enter, чтобы найти решение. В калькуляторах используется идея регистра. Программируемые калькуляторы HP позволяют пользователям создавать собственные программы.
Нюансы научного калькулятора
Эта замечательная программа позволяет решать множество математических задач, от очень простого дополнения до сложной геометрической функции. Предположим, вы инженер-проектировщик, и ваш коллега попросил вас предоставить копию документа спецификации, поскольку они как раз собираются что-то спроектировать на его основе.Вы можете воспользоваться калькулятором в том случае, если количество десятичных знаков, которые могут вам понадобиться, превышает 3 десятичных разряда, которые использовались в целях этой иллюстрации.
Есть много разных способов, которыми они могут быть классифицированы в соответствии с различными критериями. Другими словами, это его начальная рыночная стоимость. Ваши результаты также могут быть отображены в виде графика.
Обнаружен поразительный факт о научном калькуляторе
Еще одна отличная особенность этого калькулятора Casio — вы можете прокрутить назад, даже если вы допустили ошибку в уравнении, без необходимости начинать формулу заново.Вам нужен только калькулятор с этой отличительной функцией. Затем найдите калькулятор в таком списке и щелкните по нему.
Вы можете увидеть текущие математические вычисления на более компактном дисплее, который находится под основным дисплеем калькулятора. При математических вычислениях с такими большими числами полезно иметь под рукой калькулятор, но вам нужно научиться им пользоваться.
Приложение-калькулятор входит в число основных приложений, включенных в Windows 8, и копирует обычный карманный калькулятор.SMART Mortgage Calculator — это полностью бесплатное программное обеспечение. Таким образом, не ждите и купите онлайн калькулятор сегодня.
Вы получите 15, что означает, что ответ где-то близко к 15, в данном случае будет меньше 15, поскольку мы уменьшили числа. Например, если вы введете и найдете ответ 2. Теперь нажмите равно, и вы получите последний ответ 220.
Даже в том случае, если вы не планируете посещать курс, требующий обработки чисел или вычислений, вам все равно понадобится фундаментальный калькулятор, так как у вас будет минимум одного предмета базовой математики или естествознания.Для понимания алгебры жизненно важно научиться правильному использованию степеней и радикалов. Чтобы выявить шаги, калькулятор применяет те же методы интеграции, что и человек.
Эти тесты дают графический калькулятор на экране. Знайте, когда использовать формулы. На протяжении всего теста вы будете иметь доступ к листу бумаги, на котором подробно описаны все формулы, которые будут полезны для решения математических задач GED. Стандартные математические задачи со словами — это всего лишь комбинация определенных языковых приемов и простых вычислений.
Битва за научный калькулятор и как его выиграть
Когда вы записываете остатки, начиная снизу, вы получаете двоичное число. Вам нужно будет узнать, сколько дюймов эквивалентно одному метру. Просто используйте простую формулу, приведенную выше, и найдите правильный процент.
Степень n зависит от позиционного изменения конкретного числа. С помощью калькулятора уклона крыши, предоставленного ранее, можно легко измерить стоимость и узнать угол наклона.Знание того, как вычислять области этих основных объектов, поможет вам составить формулы для областей поверхности сложных объектов.
Хотите узнать больше о научном калькуляторе?
ОбозначениеE также называется экспоненциальным представлением. Чтобы понять, как умножать показатели, важно понимать, что такое показатели. Чтобы понять, как умножать показатели степени, важно знать о различных свойствах показателей.
Например, у вас может быть число 6000000000000.Вам просто нужно попытаться запомнить формулу и поставить правильные значения в подходящем месте. Невозможно привести примеры всех возможных вариантов использования скобок.
Что такого увлекательного в научном калькуляторе?
Регистр — это место для хранения числа, на которое будет воздействовать немедленная операция. Можно увидеть, что вы делаете, и легко внести исправления. Исследования имеют тенденцию указывать на повторяемость, что является основой для научных исследований.
Почему почти все, что вы узнали о научном калькуляторе, неверно
Проблема с делением на три проистекает из того, что это повторяющаяся дробь, которую невозможно представить с абсолютной точностью. Огромное динамическое разнообразие чисел, используемых в научных расчетах, приводит к необходимости представлять числа с учетом мантиссы и экспоненты. Чтобы завершить уравнение, нужно выбрать правильные числа.
Все, что вам нужно сделать, это установить дробь и умножить ее на 100, чтобы найти процентное значение.Другой случай — это когда между двумя знаменателями нет НОК, но НОК нужно найти. Это называется составлением типичного знаменателя.
Если вы начали с большим риском, вы можете обойтись стартовым финансированием, держитесь за инвестиции, предлагаемые семьей и друзьями. Имейте в виду, что вы можете заработать больше денег, если решите увеличить свои инвестиции в несколько раз. Вам также не нужно беспокоиться о том, чтобы тратить деньги на дополнительные батареи, потому что они питаются от солнечной энергии (отсюда и название).
Ярлык величайшего научного калькулятора может быть прикреплен к любой модели и любой марки. Если у вас есть какие-либо вопросы относительно места и способа использования научного калькулятора в Интернете, вы можете позвонить нам на нашем веб-сайте. Инвестор, у которого есть все необходимое для выживания предприятия.
Что делают все остальные, когда дело доходит до научного калькулятора, и что вам нужно делать иначе
Имейте в виду, что калькулятор вещественных чисел не переводит числа в научную запись.Ценность научных обозначений становится очевидной, когда вы пытаетесь умножить или разделить эти числа. Отрицательная дробь должна иметь только один отрицательный знак.
Проценты упрощают сравнение двух цифр или цифр, которые отличаются друг от друга относительно начальных вложений, продолжительности инвестиций и т. Д. И т. Д. Иногда вместо знаменателя можно встретить термин делитель, но это нечто похожее. Его также можно использовать для ввода чисел.
Это 3 основных правила, которым вам нужно следовать при умножении экспонент. Обратите внимание, что всего четыре нуля. Ниже приведены все жизненно важные правила, которые вы должны понять и понять, если вы хотите умножать показатели.
Во многих случаях последствия нажатия одной клавиши сохранялись для использования в следующей функции. Небольшая ошибка округления или другая ошибка может привести к хорошему сдвигу итогового значения. Невозможно привести примеры всех возможных вариантов использования скобок.
Ложь, которую вам рассказали о научном калькуляторе
Если вы начали с большим риском, вы можете обойтись стартовым финансированием, держитесь за инвестиции, предлагаемые семьей и друзьями. Имейте в виду, что вы можете заработать больше денег, если решите увеличить свои инвестиции в несколько раз. Вам также не нужно беспокоиться о том, чтобы тратить деньги на дополнительные батареи, потому что они питаются от солнечной энергии (отсюда и название).
Нет никаких научных особенностей, поэтому это неприемлемо для математиков или студентов-математиков.Такие операции в математике называются возведением в степень. Чтобы выявить шаги, калькулятор применяет те же методы интеграции, что и человек.
Эта область калькулятора дробей предназначена не просто для иллюстрации ответов, но и для того, чтобы предложить инструмент обучения, чтобы можно было увидеть, как были решены проблемы. Без надлежащего понимания правила основания и экспоненты невозможно исправить любую проблему, с которой вы столкнулись.Стандартные математические задачи со словами — это всего лишь комбинация определенных языковых приемов и простых вычислений.
Есть много разных способов, которыми они могут быть классифицированы в соответствии с различными критериями. Другими словами, это его начальная рыночная стоимость. Ваши результаты также могут быть отображены в виде графика.
Чтобы помочь вам преобразовать метры в дюймы, в этой короткой статье предлагается пошаговый процесс, который не только прост, но и прост для понимания.Если вам нужно изменить числитель, вы всегда можете вернуться в верхнее поле, нажав курсорную клавишу вверх. Наряду с обычной строкой меню в самом верху, есть строка состояния внизу и множество других настраиваемых панелей инструментов прямо над областью ввода текста.
Степень n зависит от позиционного изменения конкретного числа. Даже если воздействие калькулятора на окружающую среду невелико, все же лучше знать, что этот гаджет использует возобновляемые источники энергии. Знание того, как вычислять области этих основных объектов, поможет вам составить формулы для областей поверхности сложных объектов.
Получение лучшего научного калькулятора
Окно программы было полностью переработано, чтобы обеспечить легкий доступ к инструментам, которые вы должны создавать и перемещать по документам. Пока вы делаете работу по созданию контента, вам не нужно отвлекаться на задачи форматирования. В программе также есть фантастическая база данных с константами и функциями.
Большинство из них также являются программируемыми, что означает, что пользователь может создавать индивидуальные программы, идеально соответствующие их уникальным потребностям.Его можно использовать при трудностях РПН и многих других научных трудностях. Итак, что вам нужно сделать, это посетить мастер функций и выбрать вариант «DOLLARFR».
Новые вопросы о научном калькуляторе
Интерактивная справочная система быстро предоставит информацию, если она вам нужна. При заказе вы даже можете воспользоваться опцией полностью бесплатных универсальных плат и найти несколько бесплатных перфорированных плат для некоторых будущих проектов. Лицо, предоставляющее услугу CM, называется библиотекарем конфигурации.
В регионе, которому была выделена эта маркировка, нет рабочего номера. С их помощью, например, расчет процентов и процентных ставок в дополнение к бизнес-расчетам может быть выполнен образцом. Когда происходит начисление сложных процентов, эффективная годовая ставка превышает общую процентную ставку.
Убедитесь, что полученный ответ может быть логическим способом решения вопроса, как способом предотвращения любого искажения. Например, если вы войдете и найдете ответ 2.Теперь нажмите «равно», и вы получите последний ответ 220.
Чисто механические часы продолжают оставаться обычным явлением. Если у вас есть какие-либо вопросы относительно места и способа использования научного калькулятора в Интернете, вы можете позвонить нам на нашем веб-сайте. Инвестор, у которого есть все необходимое для выживания предприятия.
Еще одна отличная особенность этого калькулятора Casio — вы можете прокрутить назад, даже если вы допустили ошибку в уравнении, без необходимости начинать формулу заново.Если это устаревшее руководство по калькулятору Sharp или старое руководство Casio, то вы, скорее всего, сможете найти его в Интернете. Многие утверждают, что Casio FX-115ms — самый эффективный неграфический калькулятор, который они когда-либо использовали.
Важно, чтобы вы понимали, как использовать все полезные функции этого калькулятора, чтобы получить от него максимальную пользу. Для людей, которым нужен эффективный программируемый научный калькулятор, HP 35s — лучший выбор. В них есть экранный калькулятор с четырьмя функциями.
Вы можете бесплатно скачать и использовать его сколько угодно. Самый последний калькулятор известен как научный калькулятор. Щелкните гиперссылку и обратитесь к калькулятору выше.
История научного калькулятора опровергнута
Не все предъявляют одинаковые требования к калькулятору, поэтому сегодня на рынке вы найдете множество разнообразных устройств. Вы должны знать минимум одно доказательство. Нет никаких причин продолжать использовать неуклюжие старые калькуляторы, когда существуют гораздо более совершенные инструменты.
Научный калькулятор TI-34 MultiView ™
495345] Если вам не нужно сохранять исходный список, вы также можете перезаписать его значения возведенным в степень результатом. Для этого мы также можем использовать функцию enumerate() . Вот пример:
# Прокрутите исходный список «значений» и
# возводим каждое число в степень (заменяя исходное)
для индекса значение в перечислении (значения):
значения [индекс] = pow (значение, 5)
# Сводка
Возведение в степень ( b n ) — это математическая операция, которая умножает число ( b ) определенное количество раз ( n ) на себя. Есть три способа запрограммировать такое поведение в Python.
Есть три способа запрограммировать такое поведение в Python.
Оператор степени ( ** ) возводит левое значение в степень второго значения. Например: 2 ** 3 .
Встроенная функция pow() делает то же самое: возводит первый аргумент в степень второго аргумента. Вот так: pow(2, 3) .
Функция math.pow() также выполняет возведение в степень, но без точных целых степеней и всегда возвращает значение с плавающей запятой. Чтобы использовать эту функцию, мы делаем: math.pow(2, 3) .
Ссылки
Matthes, E. (2016). Ускоренный курс Python: практическое введение в программирование на основе проектов . Сан-Франциско, Калифорния: No Starch Press.
Python.org (без даты). Встроенные функции . Проверено 22 октября 2019 г., с https://docs.python.org/3.8/library/functions.html
Python.org (nd b). math — Математические функции . Получено 22 октября 2019 г. с https://docs.python.org/3.8/library/math.html
с https://docs.python.org/3.8/library/math.html
Python.org (nd c). Выражения . Получено 30 октября 2019 г. с https://docs.python.org/3.8/reference/expressions.html
Sweigart, A. (2015). Автоматизация скучных задач с помощью Python: практическое программирование для начинающих . Сан-Франциско, Калифорния: No Starch Press. 9у}$. Сначала мы попытаемся понять, что такое цифра единиц, затем мы рассмотрим технику нахождения цифры единиц больших степеней, а затем, используя эту технику, решим некоторые задачи на цифру единиц числа, возведенного в степень.
В конце пройдите ТЕСТ , чтобы проверить свое понимание.
Видео :
Единицы числа
Старый
Это старая версия нашего видео с озвучкой.
Что такое цифра единиц?
Единицы числа — это цифра, стоящая в числе единиц. т. е. это самая правая цифра числа. Например, цифра единиц 243 равна 3, цифра единиц 39 равна 9.
Но тогда какова цифра единиц больших чисел, таких как 23 в степени 46 или какова цифра единиц 2014 в степени 2014 ? Здесь не так просто вычислить цифру единиц этих чисел. Итак, давайте посмотрим на технику вычисления разряда единиц больших чисел. 9{142}}$ и т. д.
ПОСЛЕДНИЕ ДВЕ ЦИФРЫ БОЛЬШИХ ЧИСЕЛ
Калькулятор эквивалентов парниковых газов | Агентство по охране окружающей среды США
Преобразуйте данные о выбросах или энергопотреблении в понятные для вас конкретные термины, например ежегодные выбросы CO
2 от автомобилей, домашних хозяйств и электростанций.
Калькулятор эквивалентов парниковых газов позволяет преобразовать данные о выбросах или энергии в эквивалентное количество выбросов двуокиси углерода (CO 2 ) при использовании этого количества . Калькулятор поможет вам преобразовать абстрактные измерения в понятные вам конкретные термины, такие как ежегодные выбросы от автомобилей, домашних хозяйств или электростанций. Этот калькулятор может быть полезен при информировании о вашей стратегии сокращения выбросов парниковых газов, целях сокращения или других инициативах, направленных на сокращение выбросов парниковых газов.
Обновлено в марте 2022 г.
Шаг 1. Ввод и преобразование данных
Выберите данные для преобразования: Существует два варианта ввода данных в этот калькулятор: данные об энергии или данные о выбросах . Когда вы вводите данные об энергии, калькулятор преобразует эти значения в выбросы парниковых газов, эквивалентные двуокиси углерода, на основе коэффициентов выбросов для потребления энергии или сокращения электроэнергии. Затем он предоставляет эквивалентные способы выражения этих выбросов. Когда вы вводите данные о выбросах, калькулятор предлагает эквивалентные способы выражения этих выбросов.
Затем он предоставляет эквивалентные способы выражения этих выбросов. Когда вы вводите данные о выбросах, калькулятор предлагает эквивалентные способы выражения этих выбросов.
Данные об энергии Для электричества калькулятор использует различные коэффициенты выбросов в зависимости от того, избегается ли электричество или потребляется. Калькулятор использует коэффициент выбросов, не связанных с базовой нагрузкой, для экономии электроэнергии и средний коэффициент выбросов для потребления электроэнергии. Затем он отображает эквивалентные способы выражения этих выбросов. См. расчеты и ссылки.
Данные о выбросах
Введите данные:
| Категория | Описание | Разрешить | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам. Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей.Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, включая более персонализированный и актуальный опыт на наших сайтах. Онлайн решение производных с подробным решением: Решение производных онлайнПроизводная онлайнПримеры решенийЭкстремумы функцииНайти интеграл Точки перегиба Точки разрыва функцииИнтервалы возрастания функции Асимптоты функции Диф уравнения онлайнПредел функции Правило Лопиталя Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
f(x) = Функция задана в неявном виде ПримерыF(x,y) = Функция задана в параметрическом виде Примерыx = y = Упрощать выражениеНаходить вторую производную Правила ввода функции, заданной в явном виде
Примеры
Правила ввода функции, заданной в неявном виде
Примеры
Если функция задана в виде
Вместе с этим калькулятором также используют следующие:
Построение графика функции методом дифференциального исчисления Вычисление интегралов Таблица производных
Примечание:
Как найти производную, исходяя из ее определения? Правила нахождения производныхПример 1. Найти производную функции Найти производную функции y=cos4x.
Решение. Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим (cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы. Пример 2. Найти производную функции
. В некоторых случаях, если, например, нужно найти производную функции y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции
. Пример 4. Найти производную функции Прикладное использование производнойВычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus. Господин ЭкзаменДанный сайт позволяет решать некоторые математические задачи онлайн с подробными по-шаговыми действиями. Дифференциальные ур-ния по-шагамДля однородных и неоднородных линейных дифференциальных уравнений первого и второго порядков, дифф. ур-ний с разделяющимися переменными, с заменой и др. с подробным по-шаговым решением Пределы по-шагамКалькулятор пределов позволяет найти предел функции в конечной точке или в бесконечности с по-шаговым решением, а также с нахождением предела методом Лопиталя Интеграл по-шагамЭтот калькулятор интегралов предоставляет возможность решать определённые, неопределённые, несобственные интегралы с решением по-шагам Сумма ряда по-шагамДаёт аналитический и численный ответ суммы ряда, а также график скорости сходимости суммы ряда Ряд Тейлора по-шагамЕсть возможность с помощью этого калькулятора разложить функцию в ряд Тейлора до заданного показателя степени ряда Ряд Фурье по-шагамЭтот калькулятор позволяет разложить функцию в ряд Фурье на заданном отрезке на оси X Производная по-шагамС помощью калькулятора производных можно вычислить производную функции с одной переменной с подробным решением, частные производные от функции двух и трёх переменных, а также производную от неявной функции, заданной уравнением Обычные ур-ния по-шагамКалькулятор обычных уравнений умеет решать ур-ния со степенями, в том числе квадратные и кубические, некоторые четвёртой степени, ур-ния с модулем, простые линейные, показательные ур-ния, простые тригонометрические и некоторые др. Системы уравнений по-шагамДля линейных систем уравнений Вы получите несколько подробных решений, в том числе решение «в лоб», методом Крамера и методом Гаусса. Для любых других систем уравнений будет дан быстрый ответ Неравенства по-шагамКроме аналитического решения неравенства вы увидите решение неравенства на графике Комлексные числа по-шагамПроводятся операции над комплексными числами: деление, умножение и другое упрощение, нахождение комплексно-сопряжённого числа, алгебраическая, тригонометрическая и экспоненциальная формы комплексного числа. Также вы найдёте модуль комплексного числа Исследование графика функции по-шагамКалькулятор генерирует подробное исследование графика функции: экстремумы функций, горизонтальные и вертикальные асимптоты, наклонные асимптоты, чётность и нечётность функции, точки перегибов, точки пересечения графика с осью X и Y, область определения функции, а также построение графика соответствующей функции Системы неравенств по-шагамМатематическая логикаКалькулятор умеет расставлять скобки, упрощать логические выражения, строить таблицу истинности, находит нормальную форму выражения Калькулятор градусовКалькулятор градусов позволяет делать различные преобразования с углами Несобственный интеграл по-шагамПозволяет вычислить несобственный интеграл, можно задать пределы интегрирования равные плюс или минус бесконечности Производная функции, заданной параметрическиВы указываете функцию, заданную двумя параметрами, а калькулятор вам подсчитает производную данной функции Упрощение выраженийВведите упрощаемое выражение и калькулятор найдёт все возможные виды упрощений алгебраического выражения или сложного числа Построение поверхностиВы вводите функцию поверхности или же поверхность, заданную уравнением График неявной функцииВы можете построить график неявной функциии, заданной уравнением График параметрической функцииВы можете построить график функциии, заданной параметрами График полярной функцииВы вводите функцию, заданную в полярных координатах Канонический видПроизводная неявной функцииУкажите функцию, заданную неявно и калькулятор найдёт её производную МатрицыПримерыКак пользоваться сервисамиО сайте App Store: Mathway — решатель задачОписаниеMathway — мировой лидер среди программ для решения задач, в арсенале которого миллиарды решенных задач и которому доверяют миллионы пользователей. Mathway охватывает все уровни математики, в том числе: Начальную математику (арифметика, целые числа, дроби, десятичные числа, корни, коэффициенты и многое другое) Алгебру (линейные уравнения/неравенства, квадратные уравнения/неравенства, абсолютные уравнения/неравенства, системы уравнений, логарифмы, функции, матрицы, графики и многое другое) Тригонометрию / начало анализа (тригонометрические функции, тождества, конические сечения, векторы, матрицы, комплексные числа, последовательности и ряды и многое другое) Математический анализ (пределы, производные, интегралы и многое другое) Статистику (вероятность, перестановки, комбинации и многое другое) Есть математическая задача? Обратитесь к Mathway. «Простая в использовании и эффективная программа Mathway понравится любому, кому приходится решать математические задачи, от учеников старших классов до студентов институтов», — Yahoo! News «Если вам нужно решить математические задачи, обратитесь к Mathway. Это приложение продемонстрирует весь процесс решения, чтобы вы могли параллельно учиться сами», — CNET «Mathway — незаменимый инструмент в тех случаях, когда нужно решить задачу. Это приложение помогает с домашними заданиями по математике. Оно не просто выполняет за вас задания, но и обучает правильному порядку решения. Все, что нужно сделать, — это ввести уравнение и нажать на кнопку Enter», — Lifehack Mathway предоставляет ответы на задачи совершенно бесплатно. Для пошаговых решений доступна дополнительная ежемесячная или годовая подписка. Кроме того, Mathway предлагает дополнительную подписку на онлайн-обучение для связи с преподавателем в любое время, когда требуется дополнительная помощь. Если выбран вариант премиум-подписки: Оплата будет списана с учетной записи iTunes при подтверждении покупки Подписка автоматически продлевается, если автоматическое продление не будет отключено минимум за 24 часа до окончания текущего периода С учетной записи будет снята плата за продление в течение 24 часов до окончания текущего периода подписки по тому же месячному или годовому тарифу, выбранному при ее оформлении Подписками может управлять пользователь, а автоматическое продление можно отключить, перейдя в настройки учетной записи пользователя после покупки Условия использования: https://www. Политика конфиденциальности: https://www.mathway.com/privacy Версия 4.7.1 — исправление ошибок Оценки и отзывыОценок: 3,1 тыс. Супер!
Этот интерфейс…
124
Разработчик Mathway, LLC указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Данные, используемые для отслеживания информацииСледующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
Связанные с пользователем данныеМожет вестись сбор следующих данных, которые связаны с личностью пользователя:
Не связанные с пользователем данныеМожет вестись сбор следующих данных, которые не связаны с личностью пользователя:
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Информация
Вам может понравитьсяMathway | Популярные задачи
Вычислить вторые частные производные онлайн. Частные производные. Пределы и непрерывность ф-ций двух переменных Частные производные. Пределы и непрерывность ф-ций двух переменныхКалькулятор вычисляет производные всех элементарных функций, приводя подробное решение. Переменная дифференцирования определяется автоматически. Производная функции — одно из важнейших понятий в математическом анализе. К появлению производной привели такие задачи, как, например, вычисление мгновенной скорости точки в момент времени , если известен путь в зависимоти от времени , задача о нахождении касательной к функции в точке. Чаще всего производная функции определяется как предел отношения приращения функции к приращению аргумента, если он существует. Определение. Пусть функция определена в некоторой окрестности точки . Тогда производной функции в точке называется предел, если он существует Как вычислить производную функции?Для того, чтобы научиться дифференцировать функции, нужно выучить и понять правила дифференцирования и научиться пользоваться таблицей производных . Правила дифференцированияПусть и — произвольные дифференцируемые функции от вещественной переменной, — некоторая вещественная постоянная. Тогда — правило дифференцирования произведения функций — правило дифференцирования частного функций 0″> — дифференцирование функции с переменным показателем степени — правило дифференцирования сложной функции — правило дифференцирования степенной функции Производная функции онлайнНаш калькулятор быстро и точно вычислит производную любой функции онлайн. Программа не допустит ошибки при вычислениях производной и поможет избежать долгих и нудных расчётов. Онлайн калькулятор будет полезен и в том случае, когда есть необходимость проверить на правильность своё решение, и если оно неверно, быстро найти ошибку. Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная — одно из важнейших понятий математического анализа. Геометрический и физический смысл производнойПусть есть функция f(x) , заданная в некотором интервале (a, b) . Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0 . Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Иначе это можно записать так: Какой смысл в нахождении такого предела? А вот какой: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке. Физический смысл производной: производная пути по времени равна скорости прямолинейного движения. Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t . Средняя скорость за некоторый промежуток времени: Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел: Правило первое: выносим константуКонстанту можно вынести за знак производной. Более того — это нужно делать. При решении примеров по математике возьмите за правило — если можете упростить выражение, обязательно упрощайте . Пример. Вычислим производную: Правило второе: производная суммы функцийПроизводная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций. Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример. Найти производную функции: Правило третье: производная произведения функцийПроизводная произведения двух дифференцируемых функций вычисляется по формуле: Пример: найти производную функции: Решение: Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной. В вышеуказанном примере мы встречаем выражение: В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной. Правило четвертое: производная частного двух функцийФормула для определения производной от частного двух функций: Мы постарались рассказать о производных для чайников с нуля. С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис . За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных. И не нужно ничего искать: в нашей отдельной статье мы уже подготовили все для того, чтобы у вас это получилось. А сейчас речь пойдет о частных производных. Добро пожаловать на наш телеграм-канал за полезной рассылкой и актуальными студенческими новостями. Функция двух и более переменныхПрежде чем говорить о частных производных, нужно затронуть понятие функции нескольких переменных, без которого нет смысла в частной производной. В школе мы привыкли иметь дело с функциями одной переменной: Производными таких функций мы и считали раньше. График функции одной переменной представляет собой линию на плоскости: прямую, параболу, гиперболу и т. А что, если добавить еще одну переменную? Получится такая функция: Это – функция двух независимых переменных x и y . График такой функции представляет собой поверхность в трехмерном пространстве: шар, гиперболоид, параболоид или еще какой-нибудь сферический конь в вакууме. Частные производные функции z по иксу и игреку соответственно записываются так: Существуют также функции трех и более переменных. Правда, график такой функции нарисовать невозможно: для этого понадобилось бы как минимум четырехмерное пространство, которое невозможно изобразить. Частная производная первого порядкаЗапоминаем главное правило:
То есть, частная производная по сути ничем не отличается от обычной. Так что, держите перед глазами таблицу производных элементарных функций и правила вычисления обычных производных . Сначала возьмем частную производную по иксу, считая игрек обычным числом: Теперь считаем частную производную по игреку, принимая икс за константу: Как видите, ничего сложного в этом нет, а успех с более сложными примерами – лишь дело практики. Частная производная второго порядкаКак находится частная производная второго порядка? Так же, как и первого. Чтобы найти частные производные второго порядка, нужно просто взять производную от производной первого порядка. Вернемся к примеру выше и посчитаем частные производные второго порядка. По игреку: Частные производные третьего и высших порядков не отличаются по принципу вычисления. Систематизируем правила:
Частные производные и полный дифференциал функцииЧастый вопрос в практических заданиях – нахождение полного дифференциала функции. Для функции нескольких переменных полный дифференциал определяется, как главная линейная часть малого полного приращения функции относительно приращений аргументов. Определение звучит громоздко, но с буквами все проще. Полный дифференциал первого порядка функции нескольких переменных выглядит так: Зная, как считаются частные производные, нет никакой проблемы вычислить и полный дифференциал. Частные производные – не такая уж и бесполезная тема. Например, дифференциальные уравнения в частных производных второго порядка широко используются для математического описания реальных физических процессов. Здесь мы дали лишь общее, поверхностное представление о частных производных первого и второго порядка. Вас интересует эта тема или остались конкретные вопросы? Задавайте их в комментариях и обращайтесь к экспертам профессионального студенческого сервиса за квалифицированной и скорой помощью в учебе. Определение. Частными производными второго порядка от функции называются частные производные от ее частных производных первого порядка. Обозначения частных производных второго порядка: Для практических примеров справедливо следующее равенство: Таким образом, через смешанные производные второго порядка очень удобно проверять правильность нахождения частных производных первого порядка. Примеры. а) Найти частные производные второго порядка функции Решение. 1.Считаем переменную y 2. Полученную функцию еще раз продифференцируем по «икс», т.е. найдем вторую производную по «икс»: 3.Считаем переменную х константой, применяем правило дифференцирования суммы, правило вынесение постоянного множителя за знак производной и табличную производную степенной функции: 4. Полученную функцию еще раз продифференцируем по «игрек», т. 5. Найдем смешанную производную «икс по игрек». Для этого первую производную по «икс» продифференцируем по «игрек». 5. Найдем смешанную производную «игрек по икс». Для этого первую производную по «игрек» продифференцируем по «икс». б) Найти частные производные первого порядка функции Проверить, что Записать полный дифференциал первого порядка dz. Решение. 1.Найдем частные производные первого порядка, применяя правила вычисления производной произведения, суммы, вынесения постоянного множителя за знак производной и табличные интегралы тригонометрических функций: 2. Найдем смешанные производные второго порядка: 3. Составим полный дифференциал первого порядка: в) Показать, что данная функция удовлетворяет уравнению Решение. 1.Найдем частную производную заданной функции по «икс»: 2. Умножим полученное выражение х 2 : 3. 4. Найдем частную производную заданной функции по «игрек»: 5. Вычислим вторую производную по «игрек»: 6. Умножим полученную функцию на у 2 : 7. Вычтем из результата, полученного в п.5, результат п.6: Что и требовалось показать. Похожая информация:
ГДЗ по Алгебре за 10-11 класс Мордкович Задачник Решебник§1. Определение числовой функции и способы её задания 1.1
1.2
1. §2. Свойства функций 2.1
2.2
2.3
2.4
2.5
2.6
2.7
2. §3. Обратная функция 3.1
3.2
3.3
3.4
3.5
3. §4. Числовая окружность 4.1
4.2
4.3
4.4
4.5
4.6
4.7
4. §5. Числовая окружность на координатной плоскости 5.1
5.2
5. §6. Синус и косинус. Тангенс и котангенс 6.1
6.2
6.3
6. §7. Тригонометрические функции числового аргумента 7.1
7. §8. Тригонометрические функции углового аргумента 8.1
8.2
8.3
8.4
8. §9. Формулы приведения 9.1
9.2
9.3
9.4
9. §10. Функция y=sin x, её свойства и график 10.1
10.2
10.3
10.4
10.5
10. §11. Функция y=cos x, её свойства и график 11.1
11.2
11. §12. Периодичность функций y=sin x, y=cos x 12.1
12.2
12.3
12.4
12. §13. Преобразование графиков тригонометрических функций 13.1
13.2
13. §14. Функции y=tg x, y-ctg x, их свойства и график 14.1
14.2
14.3
14.4
14.5
14. §15. Арккосинус. Решение уравнения cos t=a 15.1
15.2
15.3
15.4
15.5
15. §16. Арксинус. Решение уравнения sin t=a 16.1
16.2
16.3
16.4
16.5
16.6
16. §17. Арктангенс и арккотангенс 17.1
17.2
17. §18. Тригонометрические уравнения Тригонометрические уравнения 18.1
18.2
18.3
18.4
18.5
18.6
18.7
18. §19. Синус и косинус суммы и разности аргументов 19.1
19.2
19.3
19. §20. Тангенс суммы и разности аргументов 20. §21. Формулы двойного аргумента Формулы двойного аргумента 21.1
21.2
21.3
21.4
21.5
21.6
21.7
21. §22. Преобразование сумм тригонометрических функций 22. §23. Преобразование произведений тригонометрических функций и суммы 23.1
23. §24. Предел последовательности 24.1
24.2
24.3
24. §25. Сумма бесконечной геометрической прогрессии 25.1
25.2
25.3
25.4
25. §26. Предел функции 26.1
26.2
26.3
26.4
26.5
26. §27. Определение производной 27.1
27.2
27.3
27. §28. Вычисление производных 28.1
28.2
28.3
28. §29. Уравнение касательной к графику функции 29.1
29.2
29.3
29.4
29. §30. Применение производной для исследования функций на монотонность и экстремумы 30. §31. Построение графиков функций Построение графиков функций 31.1
31.2
31.3
31.4
31.5
31.6
31.7
31. §32. Применение производной для нахождения наибольших и наименьших значений величин Применение производной для нахождения наибольших и наименьших значений величин 32.1
32.2
32.3
32.4
32.5
32.6
32.7
32. §33. Понятие корня n-й степени 33.1
33.2
33.3
33.4
33.5
33.6
33. §34. Функция y=n√x?, её свойства и графики 34.1
34.2
34. §35. Свойства корня n-й степени 35.1
35.2
35.3
35. §36. Преобразование выражений, содержащих радикалы 36.1
36.2
36.3
36.4
36. §37. Обобщение понятия о показатели степени 37.1
37.2
37.3
37.4
37. §38. Степенные функции, их свойства и графики 38.1
38.2
38. §39. Показательная функция, её свойства и график 39.1
39.2
39. §40. Показательные уравнения и неравенства Показательные уравнения и неравенства 40.1
40.2
40.3
40.4
40.5
40.6
40.7
40. §41. Понятие логарифма 41.1
41.2
41.3
41.4
41. §42. Функция y=loga x, её свойства и график 42. §43. Свойства логарифмов 43.1
43.2
43.3
43.4
43.5
43.6
43. §44. Логарифмические уравнения 44. §45. Логарифмические неравенства 45.1
45. §46. Переход к новому основанию логарифма 46.1
46.2
46.3
46.4
46.5
46.6
46. §47. Дифференцирование показательной и логарифмической функций 47.1
47.2
47.3
47.4
47.5
47. §48. Первообразная 48. §49. Определённый интеграл 49.1
49. §50. Статистическая обработка данных 50.1
50.2
50.3
50.4
50.5
50.6
50. §51. Простейшие вероятностные задачи 51.1
51.2
51. §52. Сочетания и размещения 52.1
52.2
52.3
52.4
52.5
52. §53. Формула бинома Ньютона 53. §54. Случайные события и их вероятности 54. §55. Равносильность уравнений 55.1
55.2
55.3
55.4
55.5
55.6
55. §56. Общие методы решения уравнений 56. §57. Решения неравенств с одной переменной 57.1
57.2
57.3
57.4
57.5
57. §58. Уравнения и неравенства с двумя переменными 58.1
58.2
58.3
58. §59. Системы уравнений 59.1
59.2
59. §60. Задачи с параметрами 60.1
60.2
60.3
60.4
60.5
60.6
60. Правило произведения для производных \begin{align*} IV. Частное правило для производных \begin{align*} Два конкретных случая, которые вы быстро запомните: Задача дифференцирования по степенному правилу #1 Дифференцировать $f(x) = 2\pi$. Щелкните, чтобы просмотреть решение исчисления $2\pi$ — это просто число: это константа. И производная любой константы равна 0: [свернуть] III. Производные триггерной функции \[ \bbox[yellow,5px]{ Запустить задачу дифференцирования #1 Дифференцировать $f(x) = \sin x – \cos x$. Щелкните, чтобы просмотреть расчетное решение Напомним из таблицы, что $\dfrac{d}{dx}(\sin x) = \cos x,$ и $\dfrac{d}{dx}(\cos x) = -\sin x.$ [свернуть] IV. Правило продукта \[\bbox[yellow,5px]{ Задача дифференциации правил произведения №1 Дифференцировать $f(x) = x\sin x. Нажмите, чтобы просмотреть решение исчисления Поскольку функция является произведением двух отдельных функций, $x$ и $\sin x$, мы должны использовать правило произведения. Напомним, что $\dfrac{d}{dx}x = 1,$ и что $\dfrac{d}{dx}\sin x = \cos x.$ \end{align*}}\] Многие учащиеся запоминают правило частных, представляя числитель как «привет», демонинатор как «ло», производную как «д», а затем напевая «ло д-при минус привет д-ло над ло-ло». [свернуть] VI. Цепное правило Цепное правило — большая тема, поэтому у нас есть отдельная страница для задач, требующих цепного правила. Нужно использовать производную, чтобы найти уравнение касательной (или уравнение нормальной линии)? У нас есть отдельная страница на эту тему здесь. У вас есть вопрос, предложение или пункт, который вы хотели бы, чтобы мы включили? Пожалуйста, дайте нам знать в разделе комментариев ниже! Калькулятор производных с шагами | Калькулятор дифференцированияОпределение калькулятора производных с шагами В исчислении есть два основных понятия, т. е. интегрирование и дифференцирование. Дифференциация обратна интегрированию. Как и интеграция, расчет деривативов носит технический характер и требует надлежащего внимания и внимания. Калькулятор производных представляет собой онлайн-инструмент, который обеспечивает полное решение дифференцирования. Калькулятор дифференцирования помогает кому-то вычислять производные во время выполнения с помощью нескольких щелчков мыши. Калькулятор дифференциации предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно учащимся подробно изучить эту концепцию. Для вычисления производных по x и y используйте калькулятор неявного дифференцирования с шагами. Формулы, используемые калькулятором производныхКалькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной: $$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) — f(x)}{Δx} $$ Помимо стандартной формулы производной, существует множество других формул, с помощью которых можно найти производные функции. Эти расчетные формулы таковы: $$ \frac{d}{dx}(Sin x) = Cos x $$ $$ \frac{d}{dx}(Cos x) = -Sin x $$ $$ \frac {d}{dx}(tan x) = Sec^2 x $$ $$ \frac{d}{dx}(Csx x) = -Csc x Cot x $$ $$ \frac{d}{dx}( Sec x) = Sec x Tan x $$ $$ \frac{d}{dx}(Cot x) = -Csc^2 x $$ 9{n-1} $$  \frac{d}{dx}f(x) $$ \frac{d}{dx}f(x) $$Здесь c = реальное число или $$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$ 92} $$Также найдите калькулятор производной частного правила для более точных вычислений. Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании. Как работает калькулятор производных? Калькулятор производных с шагами — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Калькулятор дифференцирования затем решает это уравнение, используя другие правила производных или формулы. Если вы хотите продолжить расчет, используйте калькулятор второй производной с шагами. Кроме того, если вы хотите рассчитать его выше, на этом сайте есть другое решение для вас. Вы можете использовать калькулятор третьей производной с шагами на этой платформе, чтобы получить точные результаты. Как найти калькулятор производных?Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференциации в своей поисковой системе, либо выполнить поиск в Google по его названию. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент. Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Как использовать калькулятор производных с шагами?Наш дифференциальный калькулятор очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:
Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения. Для закрепления ваших расчетов относительно нормальной линии уравнения, вам нужно попробовать уравнение нормальной прямой калькулятор, предлагаемый этим сайтом. Связанные калькуляторы Есть много других связанных калькуляторов, которые вы можете использовать на этом веб-сайте бесплатно.
Алан УокерПоследнее обновление 02 июля, 2022Я математик, технарь и автор контента. Я люблю решать шаблоны различных математических запросов и писать так, чтобы все могли понять. Математика и технология сделали свое дело, и теперь пришло время извлечь из этого пользу. Решение производных онлайнПосетители поисковых систем нашли нас вчера, введя следующие ключевые слова: Рабочие листы с параллельными и пересекающимися линиями для первого класса, полиномы калькулятора корней факторизации, самая сложная математическая задача в мире. практические тесты по алгебре,
математический символ Лапласа,
с помощью калькулятора casio,
план урока 5 класса по умножению дробей,
задача с часами по алгебре,
Рабочие листы по симметрии бесплатно,
Калькулятор интегралов разработан. Рабочие листы по задачам на комбинации и перестановки, решить константу уравнения, возведенную в x, бесплатная алгебра онлайн мгновенно, ответы Холта, Райнхарта и Уинстона. Онлайн калькулятор полиномиального факторинга, как изменить базовый лог на ти-84, Структура и метод алгебры Книга 1 отвечает на электронную книгу, скачать книги по способностям, стихи об алгебре, калькулятор общего знаменателя. ревизия мате, преобразовать из основания 3 в основание 4, программа квадратичных формул для графического калькулятора, онлайн-программа для уравнений балансировки, скачать Графический калькулятор Т-83. линейный дифференциал 1-го порядка, законы сложения и вычитания в математике, gmat перестановки и комбинации, система уравнений матлаб. Решение путем извлечения квадратных корней, как упростить подкоренные выражения с корнями, Хоутон Миффлин рабочие листы. система Ode45 второго порядка,
Программа TI-83 plus кодирует крутые трюки,
математические викторины для 2-х классов,
планы уроков / построение графиков квадратных уравнений,
экспоненциальное выражение. «экспоненциальные выражения» преобразование десятичного числа, бесплатные рабочие листы для учащихся по вероятности, Треугольники домашнее задание КС2. Как легко выучить тригонометрическую формулу, ответы по алгебре 1, gcse читы, «веселые математические листы», Ответы на книгу по алгебре математики Glencoe. Упрощение вычитания и сложения многочленов, отношение сосков в школьной математике BBC, онлайн-урок про экспоненты, предварительный формулярный лист. Прентис холл алегебра 2 ответы, эмулятор casio fx-115ms, ВОПРОС УМСТВЕННЫХ СПОСОБНОСТЕЙ, СКАЧАТЬ БЕСПЛАТНО. АЛГЕБРА 2 СОЛВЕР, как решать комбинированные математические задачи, биномиальные функции в TI-83. Сложение, вычитание, умножение и деление дробей, формулы уравнений в бухгалтерском учете, рабочий лист деления целых чисел, калькулятор рациональных выражений. факторинговая машина,
ОБРАЗЕЦ БУМАГИ КЛАССА 8,
бесплатные печатные задачи по алгебре,
сложное математическое уравнение,
Калькулятор биномиального факторинга,
бесплатные полиномиальные рабочие листы. Рабочий лист трансформации 5 класс, бесплатные рабочие листы по линейной алгебре для шестиклассников, Рабочий лист 6-го порядка операций, онлайн нелинейный калькулятор, Площадь, периметр, объем Пример программы в java, Калькуляторы смешанных чисел. Факторинг И ПРИМЕНЕНИЕ, диаграмма кратных для наименьшего общего знаменателя, Вопросы по алгебре для 8 класса. Простая программа для дробей на Java, квадратичная формула VB, преобразование математической задачи в вершинную форму, математическая помощь третьеклассникам. Экзамен по геометрии, тригонометрии, исчислению и алгебре с листами ответов, правила возведения квадратного корня в степень, координатная плоскость легко, наибольший общий делитель для 2 и 14, расчеты по математике, Вудбери-младший. Книга по алгебре для старшей школы, прикладная задача решается по алгебре. Игры английский 9 класс,
основатель квадратного корня из 2 иррациональных,
калькулятор 5 классов онлайн бесплатно,
Математика 6-го класса для Техаса,
скачать бесплатно книги по хозрасчету pdf,
рабочие листы для практики дистрибутивных, ассоциативных, инверсных, тождественных свойств. Квадратики, используемые в реальной жизни, как решить рациональное выражение, калькулятор коэффициента упрощения, первоклассные онлайн вероятностные игры, eliminasi gauss + формула excel. дифференциальные уравнения ТИ-83, как найти масштабный коэффициент, Наименьшее общее кратное 22 и 26, онлайн калькулятор с числом пи, Среднее учебное пособие по алгебре. Простой способ выучить число Пи, скачать исчисление TI бесплатно, все команды НФЛ, соответствующие листам. Рабочие листы вероятности Холта элементарные, превращение квадратных корней в экспоненты, бесплатные математические листы для печати для пятиклассника, чтобы помочь с математикой, алгебраическая вероятность, викторины образца перестановки. математические распечатки Excel, рабочий лист алгебры 2 степени логарифмы, рабочий лист, заполняющий квадратный pdf, лог ти89, уроки квадратного корня, автоматическое решение рациональных уравнений. Бесплатный онлайн научный калькулятор с дробями,
предалгебраические расширения,
наклон и основание в алгебре,
проблемы с переменным процентом. Как решать пропорции с переменными, квадратичное факторинг подстановкой, Бесплатные рабочие листы для 10-х классов. Как вычислить координаты x и y — математика ks2, студенческая алгебра с задачами и решениями по тригонометрии, задачи на алгебраические дроби. Задачи полиномиальной статистики, тригономические соотношения, бесплатные химические рабочие листы, ПРОМЕЖУТОЧНЫЕ ВОПРОСЫ AP 2007, калькулятор алгебры, математическое стихотворение о числах, Решатель алгебры колледжа. Холт, наука и техника, уравновешивающие химические уравнения, + распечатка макета таблицы умножения, как использовать решатель уравнений с ti-83, решение многочленов со специальными произведениями, общий знаменатель рабочего листа по математике. Калькулятор метода замены, Алгербра Одна помощь, простые способы выучить алгебра игры. Упрощающие факториалы уровня A,
бесплатная помощь по алгебре,
синтетическое подразделение ТИ-84. Музыка и образование, чтение и развлечения для детей до 12 лет, формула области формулы квадратного корня, построение графика квадратичных функций с использованием таблицы перехватов (факторная форма), 9алгебра й степени и метод исключения, запишите каждое смешанное число как десятичное. Эффективные уравнения excel, как найти квадратный корень из уравнения, решатель делящих полиномов, математика решения, Алгебра Макдугала Литтелла 1 отвечает за главу 9, решатель химических задач. Как решить алгебру, Калькулятор упрощения радикалов, алгебраический калькулятор наименьшего общего кратного, как преобразовать число по основанию 3 в число по основанию 4, бесплатный онлайн калькулятор алгебры колледжа, бесплатный экзаменационный лист для начальной школы. Десятичное преобразование времени,
БЕСПЛАТНЫЕ РАБОЧИЕ ТАБЛИЦЫ ПО РАСЧЕТУ ВЕСОВ,
листы по алгебре за 8 класс,
математический лист ассоциативных свойств,
Есть ли разница между решением системы уравнений алгебраическим методом и графическим методом? Почему?,
математическая статистика с приложением Шестое издание + Менделл + домашнее задание №1,
математическая помощь элементарная алгебра бесплатное программное обеспечение. «разложение полинома 3-й степени на множители», изменить дробь на децимель, общие знаменатели нахождения значений переменных, алгебра 1 рабочие листы всю книгу. Бесплатный рабочий лист с пиктограммами, Классическое издание Foerster Algebra II, TI-83 Plus N-й корень. Преобразовать 280 % в десятичную, бесплатно скачать электронные книги по бухгалтерскому учету, \тест по алгебре для 6-х классов, игры на ti-84 caculator, математические формулы 5 класс алгебра, Вопрос модели Apptitue для учебников по английскому языку и математике, Рабочие листы по математике средней школы «процентное изменение». тригонометрические загадки с ответами, Графики рабочих листов линейных уравнений, бесплатная алгебра 2 ответы. Решите с помощью калькулятора исключения,
программа для построения гипербол,
саксонская алгебра 2 издание для учителей,
упростить математический онлайн калькулятор,
макдугал литтел алгебра 2 ответы в рабочей тетради,
Дроби Наименьшее общее кратное с использованием метода диаграммы 4 класс,
арифметический. Макдугал Литтел отвечает на предварительные алгебраические ответы, предалгебра шестиклассники, Предварительная алгебра 8 класс, Решатель формул РАДИКАЛЬНЫХ ВЫРАЖЕНИЙ. Как построить график на калькуляторе Casio, заполнение квадратного листа, бесплатные решения математических задач на общие знаменатели, «цифровой видео-репетитор» «начальный курс алгебры», математические мелочи в элементарной алгебре. Образцы тестов Iowa Algebra Aptitude, математические шаблоны решетки, «неравенства» «решение» «рабочий лист» «распределительное свойство», математические стихи, кто первым изобрел куб для обучения алгебре, логарифмы домашнее задание, Учебные листы по математике. Решите уравнения путем приравнивания показателей, сравнение фракций.com, программа деления квадратного уравнения, решены задачи по учету затрат, TI-84 Plus скачать квадратное уравнение, Предварительно алгебраические ответы Прентиса Холла. Калькулятор одновременных уравнений,
GCSE по математике +последовательности и серии +последовательность в квадрате,
Кто изобрел величайший общий делитель,
Образец задания по математике за 5 класс. Бесплатное пошаговое решение задач по алгебре, математическая практика 6 класс печатное отделение длинное, ром-образ ти-84 плюс, контрольные работы по математике для 8 лет, квадратные уравнения помогают, лучшая книга по алгебре, Калькулятор факторинга квадратного уравнения. Рабочий лист, разделяющий проблемы со словами в научной нотации, рабочий лист пиктограммы второй класс, квадратные корни переменных, математический «алгоритм-калькулятор», алгебра с пиццей стр. 89ответы, макдугал литтел геометрия ответы учебник, правила математических уравнений для умножения переменных и возведения в квадрат. Бесплатное программное обеспечение для начальной алгебры, расширенные примеры задач бухгалтерского учета, математика, потребительские навыки, жизненные навыки, серия математики, Уилмер Джонс, полиномиальные листы, Учебник Нельсона по математике. Упростите квадратные корни дроби,
рабочие листы плитки алгебры,
рабочий лист 10 класса по физике,
алгебра упростить калькулятор неравенства,
JAVA APTITUDE ВОПРОС,
решатель уравнений свободной алгебры,
алгебраические корни. Решатель pde с Matlab, решатель полярных систем уравнений, vb подходящий вопрос с ответами, математические формулы для десятой математики, +»вычислить общий знаменатель» +Excel, Алегебра. Fortran для решения одновременных уравнений с циклом DO, распределительное свойство комплексных показателей, как рассчитать собственные значения на ти-83 плюс, саксонский лист сверла добавления, Кто изобрел формулы площади треугольника, Линейные неоднородные дифференциальные уравнения 2-го порядка. Заполнение квадратного калькулятора, предварительное программное обеспечение alegbra, пять специальных произведений из формул по алгебре, математическое программное обеспечение средней школы, общие вопросы о способностях. Северная Каролина, проблемы с алгебраическими выражениями в конце класса, Рабочие листы по математике Ged, введение в предварительный тест по алгебре. Практика деления десятичных дробей,
вопросы на деление мономов — 10 класс,
рабочий лист специальных продуктов. Введение в дискретную математику (комбинации и вероятности) электронные книги + 4shared.com, сети математики печатаемые, умножение целых чисел с использованием цветов, 9практические задачи по алгебре в четвертом классе, распечатываемые картинки с домашним заданием по математике, как бить зеленые шары, пример планирования полиномов алгебры оценивания. Простой код цикла Java для проверки простых чисел, дельта-функция ти-89, как решать абсолютное неравенство с квадратами, самые сложные математические задачи в мире. Лист полиномиальных математических задач, десятичная дробь до квадратного корня, колледж +тест по математике, лист решения задач на сложение и вычитание, как найти переменную из перехвата наклона. Дифференциальные уравнения волновые неоднородные, Ти-83 плюс как решить алгебраическую задачу, Калькулятор набора решений, Помощник по алгебре. Калькулятор деления мономов,
многочлен 3-й степени, комплексный корень,
упрощение корня,
бесплатное решение задач по алгебре онлайн,
простые и сложные проценты для печати. Листы Phonix для первого класса, Уроки 7 класса по склону и yintercept, рабочий лист с задачами на дроби с ответами для 7 класса, Ti 84 математические программы Лаплас, бесплатный печатный лист проверки орфографии, решатель обратного квадратного корня. Как решать простые задачи по алгебре порядок действий, лист объединения похожих терминов, комбинирование подобных терминов простой рабочий лист, математические проблемы.com, добавление положительного и отрицательного. Решение задач по алгебре шаг за шагом, рабочие листы игр по алгебре, решать задачи по алгебре бесплатно онлайн, Задания по математике для 5 класса на сложение и умножение дробей. Алгебра суммирует жестко, вычислительная практика, 5 класс, как выглядит трехчлен алгебраического термина, элементарные практические задачи по алгебре, ks3 Science Sat ревизионные вертолеты, самый сложный тест по математике во всем мире, чтение листов линейки. Алгебра суммирует документы gcse,
игры с квадратными уравнениями,
вычитание и возведение в квадрат. Калькулятор упрощающих полиномов, добавление калькулятора выражений, гипербола mathcad, gnuplot алгебра средней школы, базовый расчет для разработки перестановок, Бесплатные рабочие листы для учителей по линейным уравнениям и наклонам, деление полиномиальных решений. 8 класс математика бесплатные распечатки теорема пифагора, рабочий лист GED по математике, рабочий лист по построению графика линии на пересечении склона, загрузите формулу расстояния на свой TI-84, задача 10 класса 1 задание по математике, Интерфейс факторинговой алгебры. Смешанная практика графических линий, бесплатный калькулятор рациональных выражений, показывающий работу, алгебра выучить онлайн бесплатно, элементарная алгебра и формулы, алгебра 1 глава 1 справочник. Решатель задач синтетического деления,
ЛИНЕЙНЫЕ кривые математика 9 класс,
упорядоченные пары, алгебра, математические задачи,
горячо решать экспоненциальные задачи с отрицательной дробью,
выборочная алгебра и проверка математических функций. Решатель сложных уравнений, задачи на кубический корень, упростить радикалы с помощью калькулятора ti, как использовать ti 84 для факторизации полиномов, уравнение площади эллипса. Уравнение эллипсов КАЛЬКУЛЯТОР онлайн, ПРОГРАММА ОДНОВРЕМЕННЫХ УРАВНЕНИЙ MATHMATICA, онлайн — Графический калькуляторпересечение двух прямых, Рабочие листы квадратного уравнения, бесплатный рабочий лист масштабного коэффициента, простые таблицы вероятностей, Добавление радикалов для детей 7-го класса. Рабочий лист по геометрии для 8 и 9 класса, заполнить квадратный калькулятор, образцы листов 8 класса математики. Алгебраический квадратный корень, что может произойти, если возвести в квадрат обе части уравнения?, формулы гре, неоднородные обыкновенные дифференциальные уравнения второго порядка, решить эту задачу по алгебре, онлайн-тест 7-го года обучения. Одновременное уравнение для 4 уравнений,
2 сложные математические задачи,
квадратное уравнение ti 89,
самый низкий общий фактор,
алгоритм уравнения крестики-нолики,
бесплатные рабочие листы по полиномам,
преобразования рабочих листов графиков. Рабочий лист основных алгебраических выражений, рабочие листы по графическому уклону, эмулятор ti-84+ для mac, стихотворение.ppt, двухшаговые игры с уравнениями. Преобразовать в root в ti 83, шпаргалки по математике, забавная таблица пропорций. Решение обыкновенных дифференциальных уравнений в Matlab, Пакет домашних заданий по математике ks3 D: уровень 6 — 14 правил: ответы на уравнения, Лист упрощенных дробей, рабочие листы за 6 лет, алгебра 1 Холт Райнхарт и Уинстон, рабочие листы неравенств графических линейных систем, онлайн математический вопрос с современным ответом. Решение частного без калькулятора, математика, бесплатные онлайн математические игры для 6thgraders.com, рабочие листы уклона 8-го класса, TI 89 и дифференциальное уравнение, сложение и вычитание целых чисел с переменными, Сложные задачи по математике в формате pdf. Вводные практические задачи по алгебре,
рабочий лист квадратных корней с переменными,
+координаты +самолет +заказ +пара +забава +рабочий лист,
алгебраический калькулятор дробей,
шаги к химическим уравнениям,
дробь к десятичному решателю. Кембридж, 6-й класс науки, решить многократно радикальное выражение, холт алгебра 1 интерактивная практика, Онлайн-решатель Rational Expressions, бесплатный рабочий лист по наибольшему общему делителю и наименьшему общему кратному, факторинговые печатные формы 8 класс. Калькулятор смешанных чисел десятичной дроби, онлайн-калькулятор класса/тангажа, Glencoe Algebra 2 практических занятия + стандарты штата Миссури, форма пересечения наклона, как делить дроби, mba aptitude test домашняя подготовка скачать бесплатные электронные книги, преобразовать .322 в дробь. Не понимаю математику в 9 классе в Альберте, калькулятор факторинговых радикалов, решение квадратного уравнения в c#, онлайн калькулятор фольги. Лист формул физики, корень квадратного уравнения, калькулятор дифференциальных уравнений первого порядка, Уроки математики ЕГЭ. Перевести рабочие листы с алгебраическими выражениями,
трехчленные ответы,
лист деления десятичных дробей 4 класс,
решить уравнение с помощью калькулятора свойства квадратного корня,
Площадь и объем рабочих листов Y10,
РЕПЕТИТОРСТВО ДЛЯ НАЧАЛЬНОЙ АЛГЕБРЫ,
занятия по алгебре в первом классе. Бесплатная математика 9 класс, рабочий лист по математике для 9 класса, прентис холл алгебра 1 калифорния ответы, решать рациональные операции, базовый квадрат алгебры, такс математический кроссворд. Как проверить число после запятой+java, неоднородные дифференциальные уравнения второго порядка, формула соотношения, набор решений выражения, Хорнгрен «Бухгалтерский учет» 8-е издание скачать, программного обеспечения, ПРОМЕЖУТОЧНЫЙ МАТЕМАТИКА 1A ПРЕДЫДУЩИЙ ВОПРОС. Решение уравнений игра + рабочий лист, Разложение квадратичного многочлена от двух переменных на множители упростить решатель уравнений. Отображение точек на линейных уравнениях., операции с рациональными выражениями, решены тестовые задания на пригодность, онлайн найти корни уравнения, рабочий лист систем линейных уравнений, алгебра суммирует прошлые работы. Как перевести почасовые в сотые,
калькулятор вычитания алгебры,
Самое сложное математическое уравнение в мире. рабочие листы по алгебре за 10 класс, м, упростить радикалы с помощью калькулятора дробей, бесплатные отрицательные положительные целые листы. Формула наибольшего общего делителя, квадратный корень с помощью excel, добавление рабочего листа матриц. Калькулятор исключения алгебры, т е таблица математических формул, математика геометрия алгебра проценты рабочие листы, бесплатные математические анкеты алгебра. Предварительно алгебраическая скорость изменения таблицы значений и PowerPoint, ревизия Пифагора, бесплатные предварительные викторины по алгебре, 6-классная свободная площадь рабочего листа параллелограмма или комбинации, добавление и вычитание языка, учить алгебру онлайн, Рабочие листы неравенства для третьего класса. Распечатываемые графические листы, экспоненты для начинающих, лист формул ПДЭ 7 класса, рабочие листы по одношаговым уравнениям. ОНЛАЙН-ОТВЕТЫ К УЧЕБНИКУ ПРЕНТИС-ХОЛЛА,
как взломать ti-30x iib,
форма перехвата, рабочие листы. Вычесть квадраты алгебраических дробей, решатель радикальных уравнений алгебры, Рабочие листы уравнения для детей. Сложение вычитания в отличие от рабочих листов рациональных выражений знаменателей, титановый матлаб ти-89, ответы по алгебре 1 Холт рабочая тетрадь, программное обеспечение для начинающих по алгебре, рабочие листы первого класса. Решатель линейных уравнений кода Fortran, десятичная дробь до % рабочего листа, алгебраизатор упрощающих радикальных выражений, ти-86 перевести в дроби, добавление бесплатных рабочих листов с отрицательными целыми числами, алгебра в Visual Basic. Решение дифференциального уравнения первого порядка с помощью laplace+matlab, формула расстояния квадратный корень из 130, макдугал литтел ответы, математические игры по делению на 0,1, 0,01, 0,001 для 8 класса, как сделать генератор квадратичной последовательности в excel. головоломка «многошаговое уравнение»,
Вероятностные вопросы TAKS 5-го класса,
научить считать проценты начинающего,
формула вершины функций. Рабочий лист графических систем линейных неравенств, математические практические задачи для экспоненциальных, линейных уравнений и общих знаменателей, квадратный корень в радикальной форме, Макдугал Литтел Такс рабочая тетрадь, алгебра полиномов с нулевым фактором. Рабочие листы с проектами для квадратных уравнений, стандартная форма онлайн, преобразовать высоту пеленга дальности в сферические координаты, простая книга по линейной алгебре, вопросы для кроссвордов по алгебре, Калькулятор среднеквадратичного значения, мюллер ти89. Самая сложная математическая задача, рабочие листы уравнений и неравенств, решатель уравнения радикалов, детские математические мелочи. Сложные математические уравнения, оценивает рабочие листы «цена за единицу», идеальные числа в PowerPoint. Ответы на рабочем листе Glencoe, Решение элементарных дифференциальных уравнений в частных производных, что такое алгебра. Самые сложные математические задачи в мире,
«интерактивный урок «АА» постулат подобия»,
уравнение эксель,
приложение вопрос и ответ. Кубический корень из 16, математическая формула найти процент, математическое мышление, 4-е издание, советы по обучению, тетрадь на вычитание для 7 лет, решение ОДУ более высокого порядка в MATLAB, решатель мономиналов. Стандартный план урока Джорджии по математике в 7-м классе, Разделив алгебраическое выражение, от наименьшей до наибольшей дроби, как получить кубический корень на ti-83 plus, Калькулятор «китайской теоремы об остатках». Предварительная алгебра с пиццей, полином ти-84, алгебра от большего к меньшему, решение логарифмических калькуляторов, рабочие листы пиццы, преподавание биномиальной теоремы. Рабочие листы по упрощению подкоренных выражений, рабочий лист деления десятичных дробей, рабочие листы для практических занятий по алгебре: целые числа. Факторинг с использованием ti 84, калькулятор умножения рациональных выражений, решить корень excel. Урок координат плоскости в powerpoint,
вопросник по биологии 8 класс,
заказал парное решение на линейке-рабочем листе. Как рассчитать IRR с помощью калькулятора Casio, бесплатно скачать книгу формул по математике, добавление и вычитание отрицательных и положительных целых чисел для печати рабочего листа, решить дифференциальное уравнение в квадратной форме. Самое сложное применение комплексных чисел, игры и упражнения для многочленов и рациональных выражений, написание математических выражений уравнений powerpoint, индексы бесплатный рабочий лист, математика 9 лет, как вычислить наименьший общий знаменатель между двумя числами. балансировщик химических уравнений Ti 84, выработанные решения тригонометрического тождества pdf, разложить четырехчленный многочлен с помощью калькулятора группировки, Есть ли разница между решением системы уравнений алгебраическим методом и графическим методом? Почему или почему нет?, Выразите радикал в упрощенной форме калькулятор ti 84. Рабочий лист умножения и деления мономов,
рабочий лист дроби загружаемый,
рабочие листы рациональных выражений,
бесплатный калькулятор сложных рациональных выражений,
смешанный обзорный лист на умножение и деление + 6 класс + целые числа и десятичные дроби,
исследовать площадь поверхности и объем в преалгебре. Практика расчета первичной дроби, УПРОЩЕНИЕ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ POWERPOINT, стандартная форма математики для 6-х классов, калькулятор для упрощения алгебраического выражения, рабочие листы с пиктограммами, бесплатные распечатанные рабочие листы по математике для 8-го класса, бесплатные печатные алгебраические выражения для четвертого класса. Экспоненциальный исходный код Visual Basic, Решатель математических задач, Скачать эмулятор ti 84 бесплатно. Как решить кубический корень с теоремой нуля, основной, изменение дробей на рабочий лист с более высокими терминами, бесплатные листы для изучения математики, Темы для презентации Power Point по математике, как сделать кубический корень в ti 83, найти рабочий лист переменной. В чем разница между однородным и неоднородным в базе данных, рационализирующий решатель проблемы знаменателя, шаг за шагом в поиске наклона. Преобразование смешанной дроби в калькулятор неправильной дроби,
практическая рабочая тетрадь, предварительная алгебра, урок холла 9-2,
как писать выражения от меньшего к большему,
используя матрицу, чтобы найти квадратное уравнение,
скачать бесплатно — качественные книги о способностях. Бесплатная практическая работа по математическим показателям VIII класса, алгебра графовых уравнений, бесплатное решение математических задач, Рационализация рабочих листов знаменателя. Рационализируя знаменатель путем умножения на сопряженный рабочий лист, Онлайн калькулятор квадратного корня, десятичная диаграмма для эмпирической формулы. Калькулятор квадратичного факторинга, многочлен в java, Рабочие листы умножения рациональных выражений. рабочий лист головоломки по алгебре, квадратные корни и показатели, рабочие листы показателей и степеней, 5 класс, когда вы используете линейные уравнения в жизни, радикальный калькулятор свободной алгебры «калькулятор радикальных уравнений», триггер проблемных идентичностей. баланс Java для решения уравнений, способ замены, Precalculus «Холт Райнхарт и Уинстон» «онлайн-решения», обучение алгебре бесплатно. Бесплатные онлайн-книги по физике для средней школы,
презентации powerpoint скачать бесплатно распространенные ошибки английский язык,
разложение квадратных выражений на множители,
ti 89 система дифференциальных уравнений,
можно ли отменить буквенные переменные при объединении терминов?,
распечатка нескольких дробей. Программа факторинга Ti 84 +, свободная дробная таблица для детей, калькулятор набора решений, калькулятор радикальных выражений с квадратным корнем, техасский модуль TI-80, БЕСПЛАТНЫЙ ПРЕДВАРИТЕЛЬНЫЙ ТЕСТ ПО МАТЕМАТИКЕ 1-Й КЛАСС. Как решить сложный трехчлен, уравнения и неравенства с рациональными выражениями, рабочие листы умножение десятичных дробей, ti 84 программы квадратичная формула. Забавные математические вопросы, распечатки плиток по алгебре, математические формулы для десятого стандартного зачисления, рабочие листы по алгебре 6 класса, изменение дробей старшими членами. Как преобразовать алгебраические уравнения в матрицу в Matlab, упрощение деятельности радикалов в сети, рабочие листы GCF, вычислить квадратный корень полинома, активность калькулятора графика параболы, печатные листы по математике для 4 класса, многошаговые задачи. Преобразование десятичной дроби в двоичное число в Matlab,
как вы решаете математические задачи gfc,
glencoe алгебра 1 глава 11 ключ ответа. Координатная плоскость печати алгебры, печатные листы для математических показателей степени квадратного корня, переводить десятичные дроби в обыкновенные — практика, шпаргалка по умножению, Расчет периметра на матлабе. Предварительно алгебраическое распределительное свойство, стандартная форма для вершинного калькулятора, полиномиальный решатель excel, бесплатный решатель квадратичных коэффициентов. Перестановки и комбинации в sas, тест на гениальность по математике, калькулятор умножения рациональных выражений, формула предварительной алгебры, рабочие листы по математике, методы квадратного корня. Онлайн факторинг, xy калькулятор перехвата, 166 предварительная алгебра с пиццей, 7 лет алгебра, лимиты на графическом калькуляторе, изучите базовую алгебру для статистики. Бесплатные математические отрицательные и положительные рабочие листы,
практические тесты по алгебре шлюзов,
9 класс рациональный вопрос,
практиковать вероятность для печати,
балансировка анимации химических уравнений,
образец мелочи легко. Учебник по алгебре бесплатно, ПРОЦЕНТЫ ДЛЯ МАКАНОВ, бесплатные листы перестановок и комбинаций, как умножать и упрощать с отрицаниями, рабочие листы десятичной дроби, алгебра 2 ответы бесплатно. Бесплатные печатные рабочие листы по алгебре, экзамен по математике за 8 лет, прошивка ти-89, сложение и вычитание полиномов. рабочий лист десятичных дробей 4 класса, математические мелочи 6 класса, рабочий лист n-го семестра, самая сложная в мире математика. Решить систему нелинейных уравнений Matlab, решения тестов по абстрактной алгебре, факторинг полиномов третьего порядка, как решать многошаговые дробные уравнения, Упрощение рабочих листов переменных выражений. Такс шестой класс по математике, задача 6, обзор, рациональное выражение домена, алгебра I программное обеспечение, документы о дизайнерских способностях.pdf, кто изобрел неравенство. Решение формул дробей,
фактор 9 ти-84 скачать,
бесплатная электронная книга-современная алгебра-И. Умножение и деление целых чисел, рабочие листы, Математические расчеты — Эллипс, решатель уравнений excel, бесплатный онлайн-график для третьеклассника, бесплатные рабочие листы для печати. Символический метод, печатные листы с координатными сетками в первом классе, планы занятий на склонах, простые шаги к решению рационального выражения умножения, простые задачи по алгебре математика, калькулятор рационализирующего знаменателя, самое сложное математическое уравнение. рабочий лист PEMDAS для 8-го класса, как поменять ответ на дробь с ти-89, Holt Math TAKS Prep Gr.10, Таблица показателей для 8 класса БЕСПЛАТНО. Легкий вопрос о способностях и ответ,
вопросы по булевой алгебре,
как заниматься алгеброй,
рабочий лист дроби 4 класса,
калифорнийская биология Прентис Холл отвечает,
решение полиномиальных комплексных выражений,
базовая математика в колледже. Умножая числа длинной рукой, упростить квадратный корень из x до 10, ti математический порядок работы, переписать в упрощенной радикальной форме, алгебра 2 картинки, свободные квадратные уравнения путем факторизации рабочих листов. Математика для чайников, предварительная алгебра с ответами на книгу пиццы cc, упражнения и ответы по решению многошагового уравнения, египетское квадратное уравнение, калькулятор уравнения параболы. алгебра кс3, квадратный корень в упрощенной радикальной форме, дроби как степени, бесплатные рабочие листы колледжа, Факторы 4 класса. дроби по алгебре 5 класс, тетрадь для умственных способностей за 5 класс, вопросы по математике для 5 класса, сложение двух неизвестных дробей, тест гениальности творческих публикаций до алгебры с пиццей. Блок-схемы факторинговых полиномов,
синтетический ти-84,
процентные задачи по математике, 5-е место,
калькулятор измерения погонного метра,
Калькулятор факторинга в особых случаях. Факторный квадратичный калькулятор, Алгебра Бастер скачать бесплатно, неоднородное дифференциальное уравнение второго порядка, веселые занятия по обучению пропорциям в шестом классе. алгебра, факторизация, помогите решить неравенства с 3 переменными + дробь, Уравнение с одной переменной слово задача движения, применение асимптоты ти-84, решение уравнений для дробных показателей. обратная операция изолировать алгебру, бесплатные рабочие листы для учащихся 8-х классов в Индии, решение задач по алгебре, Решите линейные уравнения с одной и двумя переменными, сложением и вычитанием., конвертировать из полярных в комплексные в ti 89, maple решение нелинейных одновременных уравнений. Женщины = формула зла, не видно параболы на калькуляторе ВОПРОСЫ ПО ТИВИА, решение нелинейных одновременных уравнений в матлабе, glencoe алгебра 1 замена домашнее задание ответы, Рабочий лист учебной программы Кумон. Математика-алгебра 7 класс,
перестановка и вероятностность 6 класс математика,
сократить выражения до минимальных терминов калькулятор. Домашнее задание по логарифмическому преобразованию в матлабе, рабочие листы со свободной дробью для пятиклассников, многочлен в стандартной форме калькулятор, алгебраическая плитка для упрощения выражений. скачать тест на пригодность, решения домашних заданий по реферативной алгебре, Словесная викторина третьего и четвертого класса. комплексные логарифмические уравнения, графики 6 класса powerpoint, рабочие листы по математике для пятого класса, калькулятор деления полинома. Что такое математический термин для символа квадратного корня?, калькулятор разности квадратов, рабочие листы процентных тестов. Факторинг кубических уравнений, домашнюю работу по логарифмическому преобразованию написать в матлабе с решением?, бесплатно скачать книги по алгебре для начинающих. Как узнать разницу двух квадратов,
забавный калькулятор шестого класса,
сек 2 учебника по математике с шагами в листе ответов в сингапуре,
мономиальные загадки,
держите ответы в тетради по математике. Правила построения графика линейного неравенства, целые числа для пятого класса, «решение одновременных уравнений механики», порядок операций с целыми листами, сравнить бесплатное программное обеспечение для решения задач по алгебре, базовые графические рабочие листы неравенства, Алг 1 решатель. Как умножать или делить рациональные выражения с несколькими переменными, образец по алгебре 5 класс, Порядок операций Бесплатный рабочий лист, образец теста по математике в средней школе. Как решить задачу по алгебре дробей, решатель уравнений с несколькими переменными, как найти наименее распространенный доминатор, преобразовать строковое время в десятичное в java, вычислить значение экспоненты. Калькуляторы факторинга, рабочие листы по математике для четвертого класса il, Калькулятор решения переменных уравнений. Перестановочная деятельность,
бесплатные пошаговые инструкции методом исключения,
процентные формулы,
калькулятор упрощения алгебры,
урок на склонах 7 класс математика. Расчет общего знаменателя, пошаговый интегральный решатель, тетради по математике для 8 класса, как извлекать кубический корень на ти-83, Правило преобразования смешанных чисел в дроби, рабочий лист дробей, отношений и десятичных знаков, Рабочие листы по математике для 5 класса. Рабочие листы по математике для построения графиков и/или неравенств, умножение десятичных дробей забавный рабочий лист, линейное уравнение java. Распределение собственности бесплатные рабочие листы, используя формулы, сделанные простыми математическими рабочими листами, При упрощении рационального выражения зачем нужно множить числитель и знаменатель, решение систем нелинейных уравнений с помощью Matlab, нахождение решений неравенств, не имеющих корней. Ti 89 решает уравнения с использованием i мнимых,
двоичный рабочий лист 9й класс,
квадратный корень в java,
онлайн-калькулятор с ограничениями,
калькулятор полиномов,
лист викторины по графикам для 6 класса,
экзаменационные документы wbcse с решением. Бесплатный онлайн калькулятор факторинга, пример математической полиномиальной интерполяции ньютон, Как это сделать на калькуляторе 33&1/3, примеры вопросов по алгебре, факториал онлайн. Бесплатные рабочие листы для предварительного тестирования Ged, математика 6 класс рабочий лист окружность,площадь круга,вероятностные распечатки, упростить полиномиальные выражения в Maple, онлайн-решатель уравнений, мелочи линейного уравнения, решение одновременных уравнений в матлабе, бесплатные рабочие листы означают средние отрицательные целые числа. Как решать математические задачи, используя системы уравнений, сложные корни ти-89, загрузить онлайн-систему построения координат, Gr 11 Математическая квадратичная формула, Макдугал Литтел отвечает на вопросы по геометрии. Неравенства для пятого класса,
как посчитать проценты на калькуляторе ТИ-89,
математические мелочи для детей,
техасская алгебра 2 помощь с домашним заданием,
бесплатные печатные листы математических викторин,
факторизация исчисления «квадратный корень». Структура алгебры.pdf, «задачи блок-схемы», Продвинутые ответы по алгебре МАТЕМАТИКА ДЛЯ ПЕЧАТИ В 6 КЛАССЕ, пошаговые рабочие тетради по математике для 5 класса, Алгебра средней школы 1 рабочие листы и ключи к ответам бесплатно. Калькулятор уравнения факторинга, радикалы ПРОБЛЕМЫ СЛОВА, как разделить n-й корень, скачать приложение ПОЛИСМЛТ, определение системы уравнений, решатель задач на сложение двузначных чисел. Рекурсивная десятичная математика, решатель уравнений ТИ-83 оба корня, формуляр для средней школы, Трудная книга фракций бесплатно, алгебра с модными креативными публикациями, как решать алгебраические уравнения в матлабе, glencoe.mcgraw-hill геометрия Глава 8, Урок 6 ответы. распечатки заданий по математике для детей 5 лет, Рабочий лист по математике для 9-го класса, задачи на умножение и деление дробей, листы ks3. Учебное пособие по написанию линейных уравнений,
как разложить три числа на множители,
Excel рисует одновременные уравнения,
как вычислить экспоненциальные значения вручную трюки. Рабочие листы вероятностей четвертого класса, бесплатные рабочие листы уравнений, Математические таблицы 6 класса. Сложение и вычитание положительных и отрицательных дробей, умножение и деление рациональных показателей, + лист по алгебре с ответом, бесплатный рабочий лист «квадратные уравнения с квадратными корнями», наибольший общий делитель 6 и 8. Программирование решения простых формул для карманного компьютера, скачать программу квадратичных формул для ти-84, забавные задачи по дифференциальным уравнениям, формула НОД, как найти крутизну в ти83. Как решать квадратные корни с переменными выражениями, 9 класс Алгебра, алгебра я изучаю руководство и ключ ответа, решение одновременных уравнений с 3 переменными с использованием базового языка программирования, решение задач с часами по алгебре, графический калькулятор как решить в терминах х. Рабочий лист алгебры вероятностей 1,
самые сложные математические вопросы,
рабочий лист по общим корням слов,
задачи на склон 7 класса,
GCSE как делать алгебраические доказательства,
расчет наименьшего общего знаменателя. +математика +число +поиск +рабочий лист +6th, калькулятор упрощения рациональных выражений, онлайн математический радикальный тест, решатель делящих полиномов, под корнем круговой алгебры, интересные способности Q & A решены. Как пройти игру с зелеными шариками, Рабочий лист пиктограммы для печати, алгебра меррилла 1, ввод дробей в java, эмулятор casio fx-82au plus. Целочисленная забава для школьников, решатель математических задач с объяснением, векторный минимальный и максимальный калькулятор, найти корень excel, квадратный корень с переменной и постоянной, стихи о дробях и смешанных числах, Факторные деревья для печати. Сложное математическое уравнение, формулы быстрого доступа к алгебре, Комплексная переменная факторизация полиномиального уравнения, можно узнать коэффициенты квадратного уравнения на ти-83 плюс?, отличная программа для определения общего делителя + java. Решить экспоненты + легко,
примеры блок-схем задач с ответами,
рабочие листы для плиток алгебры,
калькулятор упрощения радикалов с переменными,
как решить 2-й порядок оды матлаб. Рабочие листы Grapping Functions бесплатно, решение нелинейных пружин с использованием дифференциальных уравнений, клен решает уравнение с несколькими переменными, графическое изображение абсолютного рационального неравенства ppt. Math.com 2 уравнения с 2 рабочими листами с неизвестными, лист формулы ileap 7-го класса, уравнение стандартного отклонения t1-86. Целочисленный рабочий лист pdf, предварительная алгебра одновременных уравнений, Практикуйте алгебру колледжа CLEP, рабочий лист графического неравенства, +фракции +умножить +разделить +рабочий лист. Уравнения с использованием вопроса о вычитанииa, сетки для геометрической печати, формула пентру исчисление элипса, Решение калькулятора рациональных выражений, десятичные дроби в радикал, Уравнения баланса 7 класс. Решение триггерных функций с помощью Matlab,
бесплатные рабочие листы для третьего класса до шестого класса,
стихи о решении,
алгебра средней школы,
упрощение методов сложных алгебраических выражений. Рабочий лист решения уравнений сложения, рабочий лист уравнений типов химии, решить радикальное выражение, рабочий лист положительных отрицательных целых чисел, рабочие листы дробей в простейшей форме для четвероклассников, решение квадратного уравнения с входом и выходом. От наименьшего до наибольшего порядкового номера, бесплатный онлайн-калькулятор метода исключения алгебры, биномиальный коэффициент с TI-89. Презентации Powerpoint по алгебре, представленные студентами, калькулятор факторных выражений, деление дробей с переменными и показателями, техасские инструменты решают мод, Рабочие листы линейных уравнений, www.алгебра для начинающих.com, «алгебра fx2». План урока по линейному программированию,
квадратные корни с показателями,
вертикальные горизонтальные асимптоты области интерактивного графа,
бесплатные математические рабочие листы симметрия,
факторинг числа в кубе,
что такое погонный метр,
факторинг алгебраических уравнений обман. Ответы на уравнения алгебры, графические линейные уравнения для печати, Математические упражнения для 11 класса, бревенчатая шкала ти-83, соедини точки, рабочие листы для 6-х классов, как рассчитать НОД. Калькулятор, который будет учитывать трехчлены, десятичные дроби в рабочие листы, квадратичные разложения, БАЛЛ ВЫСОКИЙ ПО АЛГЕБРЕ CLEP, скачать эмулятор ti 84, бесплатные распечатанные кроссворды для 5-х классов, когда многочлен неразложим, как это называется, почему. Добавление калькулятора рациональных выражений, лист замены математики средней школы, Промежуточная алгебра с приложениями 7e бесплатно, Бухгалтерия lcci скачать бесплатно. Базовая алгебра, С# десятичная форма в радикальную форму, уравнения балансировки онлайн, реферат по математике в девятом классе, рабочий лист типов переменных, шаги разбивки решателя алгебры. Сделайте изображение графической координатной плоскости бесплатно,
онлайн-решатель уравнения математического логарифма,
график для шестиклассников kids. экзамен по математике в 6 классе, Java-программа, используемая для определения того, является ли целое число простым или нет, факторинг крестики-нолики. Парабола графическая ти-83, ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ АЛГЕБРИЧСКОЕ РЕШЕНИЕ, KS3 МАТЕМАТИЧЕСКИЕ-СРЕДНИЕ Игры, холт, учитель один шаг, решение многовариантных выражений в Matlab, калькулятор+математика+факторинг+многочлен, бесплатные онлайн-таблицы для 8-го класса. Глава 10 предварительный экзамен по алгебре, ti 83 plus полярный графический проект, Системные требования для Larson Algebra 1 с обзором, решение дифференциальных уравнений с ti 89. Кс2 бесплатные рабочие листы, скачать листы кумон, онлайн-учебник по алгебре Макдугал Литтел, FOIL онлайн биномиальный калькулятор. Алгебра важность, Базовый алгебраический график, разложение трехчленов — игры. примеры уравнений булевой алгебры,
отрабатывать задачи на проценты и дроби,
Калькулятор сложения или вычитания многочленов,
Самая сложная математическая задача в мире,
калькулятор ортогонального вращения,
калькулятор факторинговых кубов\. Бесплатные листы практики прямоугольного треугольника для 7-го класса, уравнение в экселе, преобразование тригонометрических тождеств в радикальные числа, Как запрограммировать камень-ножницы-бумага на графическом калькуляторе. Бесплатные рабочие листы для печати на 7 лет, бесплатный онлайн калькулятор исключения алгебры, Чем деление многочлена на двучлен похоже или отличается от деления в длину, которому вы научились в начальной школе? Может ли понимание того, как делать одно деление, помочь вам понять другое? Какие примеры из реальной жизни я, калькулятор радикалов. Загружаемый печатный круг, рабочие листы линейных графиков и гистограмм, прошивка ти-84, бесплатные рабочие листы дерева факторов, перевод алгебраических выражений с текстовыми задачами, нужно решить алгебраическое уравнение. Как делать наборы решений на калькуляторе,
решатели квадратного корня,
переменная наименьшего общего знаменателя,
Веб-сайты 5-го класса для нахождения дробей Lcm/gcf,
решение калькулятора рациональных показателей,
Ответы на вопросы по математике в Прентис Холл. Математика зала терпения, построение графиков линейных уравнений powerpoint, программная алгебра, стандартная программа для вершинной формы, обзор учебников средней школы Онтарио, техасские инструменты преобразуются в корневые, калькулятор неявной производной. Бесплатный рабочий лист графика дилатаций, Листы с заданиями по математике для 1 класса в формате PDF, тест на гениальность рабочий лист, т-83 репетиторство, калькулятор рациональных выражений ti-30xa, упрощение выражений с использованием калькулятора произведений показателей степени, трудные рабочие листы уравнений. Математические уравнения в 8 лет помогают, уравнения десятичные интерактивные, как написать квадратное уравнение на 2, 6, 12, 20, 30, решить алгебру бесплатно. Решите математический калькулятор факторинга,
Как решить математику + деление простым способом,
десятичный калькулятор смешанных чисел,
лучшая телефонная связь от наименее к наибольшей,
Суаре корень,
калькулятор онлайн у. Триггеры предварительного исчисления с коэффициентами, бесплатные математические таблицы с квадратными корнями, упростить калькулятор подкоренных выражений, ПЕЧАТНАЯ МАТЕМАТИЧЕСКАЯ ЗАДАЧА, примеры вопросов по математике на способности, самое длинное уравнение математического расчета, Электронная книга по математике третий стандарт скачать бесплатно. Рабочий лист, где сообщается, эквивалентны ли функции и обратные функции, рабочий лист с текстовыми задачами для третьего класса, простой способ решения арифметических задач, могу ли я получить онлайн демонстрационный урок по полиномам 10-го стандарта, практические рабочие листы по степеням и отрицательным показателям, алгебра для дошкольников, Руководство по решению «Основы комплексного анализа». триггерные калькуляторы,
Калькулятор RSA онлайн методом проб и ошибок,
решение системы линейных неравенств в spss. Как разложить трехчлены на Ti-83 Plus, рабочий лист для нахождения наименьших общих кратных, Бесплатная десятичная математическая шкала, метод решения квадратного корня. Бесплатный онлайн-репетитор по алгебре в колледже, решить нелинейное уравнение в excel, преобразование уравнения в Алгебре 2, математика масштабного коэффициента, квадратичная формула, обзорные игры. Решения Рудина по главе 7, десятичная рабочая тетрадь 4 класса, рабочий лист по геометрии 5 класс, Бесплатный PowerPoint для помощи по математике в 7 классе … загружаемый, элементарная практика по алгебре. Листы умножения, которые можно распечатать, но бесплатно, СУММА И РАЗНОСТЬ РАДИКАЛОВ В МАТЕМАТИКЕ, бесплатные рабочие листы и числовая линия и решение уравнений, упростить калькулятор кубического корня, математический файл сбора данных. Практика ЕГЭ 8 класс,
свободные рациональные выражения и решатель уравнений,
бесплатные вопросы по линейным измерениям 3-го класса,
калькулятор упрощающих дробей,
бесплатный лист суммы углов треугольника для печати. Математические проценты для чайников, обучающихся онлайн, Каковы основные правила построения графика уравнения неравенства?, calc преобразовать в корень. Преобразовать корень в экспоненту, нефункциональное устройство для построения уравнений, формула для расчета площади 5-го класса. Решение двухэтапных уравнений практические тесты бесплатно, ответы прентис холл математика алгебра готовность, шестой класс нацелен на математику, точные значения тригонометрических выражений бесплатный рабочий лист, биология макдугал литтел ответы учебника, Общие дроби донора, формула получения процента. Преобразование Фурье для решения уравнения PDE, уравновешивание химических уравнений, формальный заряд, java программы+полиномиальная арифметика, расширить логарифмическое выражение на ti 89. Y=abx gcse математика,
калькулятор знаменателя,
бесплатные пакеты по математике для 7 класса,
математика для чайников,
кумон читы на чтение,
калькулятор упрощения задач на квадратный корень. Как решить квадратные корни с переменными выражениями дробей бесплатно, Математические читы, сложение и вычитание рациональных выражений на TI-89, сложнейшие алгебраические формулы, РАБОЧИЙ ТИСТ KS3 МАТЕМАТИКА, решение рационального выражения, Калькулятор комплексных чисел умножать и делить. Уравнения типа отношения алгебры, Бесплатная математическая шкала 1 класса, математика для чайников, стандартная программа для расчета формы вершины, калькулятор конвертирует основание 10 в основание 2, математика, решение уравнений третьего порядка. Бесплатный тест по математике для печати, лист самопроверки отрицательных чисел, msn.com, нелинейные дифференциальные уравнения, вопросы и ответы по ментальной математике 8 класс, математическая головоломка квадратное уравнение, Учебник Нельсона по математике 8. БЕСПЛАТНЫЙ ОНЛАЙН-РЕПЕТИТЕЛЬ ПО МАТЕМАТИКЕ,
вычислить НОД,
математика с сопряженными листами,
введите завершение квадратной программы вручную ti-83. Десятичная до смешанной дроби, алгебра для студентов типовых задач, таблица общих кратных, что такое масштаб в математике, как решить алгебраическое уравнение на научном калькуляторе, переменная листа математики. Наборы решений с дробями, рабочий лист по уменьшению радикалов, термины студенческой алгебры, решение уравнений 3-го порядка, Изучение Алгебры 1, разница между оценкой и упрощением выражения. Сложение и вычитание чисел со знаками бесплатные рабочие листы, реальные примеры нелинейных многочленов, «планы уроков математики», ПРЕДВАРИТЕЛЬНАЯ АЛГЕБРА С ПИЦЦАЗОЙ! + Креативные публикации + Привлекательность фракции, как найти вершину многочлена третьего порядка. Matlab решает одновременную оду первого порядка,
самое сложное математическое уравнение в мире,
решение письменных задач с использованием рабочего листа по алгебре,
правила умножения/сложения/деления/вычитания десятичных дробей,
решатель нелинейных уравнений,
прентис холл ответы на готовность к алгебре,
логарифмический решатель. дроби порядка, решение нелинейных дифференциальных уравнений второго порядка в матлабе, школьные задачи по алгебре, замена в алгебре, упрощение полиномов показателей степени умножение переменных, алгебраический калькулятор дробей. тест дроби 4 класса, рациональные выражения с кубическими корнями, примерная система уравнений, решение уравнений addign вычитание рабочих листов. Алгебра Балансы, сложение, вычитание, умножение и деление отрицательных и положительных, Бесплатный образец вопроса для 9-го класса по математике, такие программы, как алгебратор, mcdougal littell math taks рабочие тетради, решение галлиана скачать, Калькулятор факторинга мономов gcf. Где я могу ввести квадратное уравнение, которое я хочу изобразить в виде графика,
история квадратичная жизнь,
бесплатные рабочие листы линейного графика,
рабочие листы переменных,
формула дробей,
упростить калькулятор квадратных корней,
решить алгебру 2. Скачать бесплатно тест на естественные способности, решение уравнения с дробными показателями, решение линейных неравенств+учебник по математике+ бесплатно онлайн, самая сложная форма математики, калькулятор факторинговых биномов, алгебраизатор скачать, викторина по основным функциям ti 84. Рабочие листы обратной пропорции, калькулятор уравнения четвертого порядка, образец подробного плана урока по алгебре, калькулятор онлайн биномиальное домашнее задание, смешанные фракции 5 сорта. Полиномиальные выражения в excel, квадратика и баскетбол, математические мелочи, бесплатный рабочий лист для квадратного корня 9й класс, кто изобрел систему неравенств. Решите многочлен в кубе,
программа алгебра 8,
ответы на рабочие листы по химии в прентис-холле,
10-значный преобразователь формата времени,
почему вы должны знать, как складывать и вычитать подкоренные выражения, прежде чем вы сможете рационализировать знаменатели с двумя терминами. листы с координатной сеткой, бесплатные рабочие листы формы пересечения склонов для печати, Математический текст Дольчиани — Алгебра, структура и метод, книга 1, aptitude решил вопрос о размещении, решить задачу на умножение рациональных выражений, уроки математики в масштабных моделях. Решить дифференциальные уравнения ti-89, распечатанные задания для первого класса, бесплатные викторины по алгебре. Рабочий лист процентной доли бесплатно, полиномы факторов в кубе, Аляска практический тест по математике 6-й класс, рабочие листы квадратов и квадратных корней, словесные задачи линейного уравнения в форме пересечения наклона, калькулятор нелинейных уравнений, ti89 решение квадратного. Калькулятор факторинга,
Какие 4 основных математических понятия используются при вычислении выражения?
добавить рабочие листы вычитания дробей бесплатно,
«Скотт Форман Эддисон Уэсли» «3 класс» «страница 340»,
алгебра Голдфорд,
графика + координатная плоскость. Запишите число в развернутой форме рабочего листа, викторина с отрицательными и положительными целыми числами, бесплатные электронные книги по способностям, Функция excel для преобразования десятичной дроби в дробную. Как мне решить эллипс с центром, фокусами и вершинами в дробных формах, калькулятор факторинга квадратного уравнения и график, бесплатный тренировочный онлайн-тест для ks2 и ks3, бесплатный онлайн-калькулятор одновременных уравнений, калькулятор упорядоченной парной переменной, двухэтапная практика уравнения. Matrix Inverse Calculator 1.0 исходный код Matlab,
для детей от 7 до 12 лет бесплатные распечатанные математические упражнения,
факторинг с помощью калькулятора распределительной собственности,
Объясните своими словами, почему уравнение x = 4 представляет собой вертикальную линию.,
albegra 2 печатные листы по математике,
Алгебра 1/2 набор задач пошаговой разработки 98,
бесплатные печатные листы с пересекающимися линиями. Разделение биномов, выучить базовую алгебру бесплатно, онлайн+бесплатно+математика+экспоненциал+уравнение+решатель, радикалы 8 класс математика, бесплатные начальные 2 вопроса по математике, Область определения дроби с абсолютным значением. рабочие листы 8 класса, рабочий лист целых чисел, Формула преобразования смешанных чисел в дроби, химический кроссворд Холта Райнхарта и Уинстона, бесплатные задачи по математике для 8 класса, упростить алгебраические уравнения, одновременные квадратные уравнения. Пример задачи с формулой процента и ответы по физике, ти-89 направления десятичные, математические формулы 7 класса, умножить квадратный корень и показатель степени. Когда вы могли бы использовать рациональные выражения в реальной жизни?, упрощение fractons.com, метод разложения в квадратиках, трудные математические задачи для распечаток и ключей средней школы. Логарифм графического калькулятора по основанию 2,
системы уравнений, включая окружности,
TI 84 задачи по алгебре,
игры с отрицательными и положительными числами,
рабочий лист уклона 1,
математика 3 класс, помощь дочери,
Решение уравнений с радикалами и показателями. Калькулятор умножения квадратных корней, простые ответы калькулятор деления, онлайн калькулятор т-89, разложение квадратичных уравнений по двум переменным. Кумон уровень d математический пример, конвертировать десятичные числа в проценты в Matlab, преобразовать дробное число в целое число, если десятичная точка больше 0,5, иначе удалить дробную точку из заданного числа, показать только целое число в excel с формулой, как делать вопросы по алгебре для теста ged, calc упрощает рациональные выражения. Простые вопросы на сложение и вычитание целых чисел, упрощение подкоренных выражений с умножением, бесплатные печатные плитки алгебры, Инвертировать матрицу С++ math.c. Забавный математический лист, бесплатные рабочие листы для 8-го класса, Такс онлайн математика test.com. Бесплатная онлайн-программа математического интегратора,
калькулятор системы уравнений,
листы десятичного сложения и вычитания, которые нужно сделать прямо СЕЙЧАС,
Сложнее всего заниматься математикой в 7 классе. Сложение и вычитание целых чисел, алгебра для начинающих онлайн бесплатно, принцип, который можно использовать для упрощения многочлена?, как сделать алгебраическое сложение целых чисел, инструкция casio fx 115ms определенный интеграл, перестановки и комбинации + математика + деятельность. Преалгебра — вычисление алгебраических выражений, факторинг онлайн, умножение многочленов трудные вопросы, Среднеквадратичное значение + excel. игра на решение неравенств, пройти викторину с квадратным апплетом, калькулятор слов весёлая рабочая тетрадь, мелочи о квадратичных функциях. Калькулятор биномиального факторинга, прямая пропорция powerpoints математика, ти 89 дельта функция, целочисленная практика для 6 класса, бесплатные листы. Примеры умножения длинной руки,
фактор решения задач по алгебре,
демонстрация рационального отчаяния,
бесплатно сравнивать и заказывать листы с десятичными дробями,
Макдугал Литтел Математика даже ответы. Саксонские образцы рабочих листов по математике, объяснить, как преобразовать прямоугольную форму в полярную в математике, рабочие листы с элементарными показателями, промежуточные 2 математических рабочих листа. Решение нескольких переменных, задачи по геометрии на гэд, Прентис Холл математика интегрированная алгебра, математические формулы десятой математики. Умножение планов уроков по рациональному выражению, частные производные ряда Тейлора в кленовом листе, бесплатные рабочие листы EOG по математике, калькулятор выражений онлайн переменные, диаграмма наибольшего общего фактора, найти уравнение прямой две упорядоченные пары, решение нелинейных уравнений в MATLAB численное. Matlab метода Ньютона-Рапсона, смешанное число до десятичного, радикальная форма 8 в квадрате, Бесплатные математические ответы, перестановка интерактивная математика ppt. Ti калькулятор ромы,
что такое радикальная форма,
комплексный решатель квадратных уравнений,
уравнения балансировки онлайн. Помощник по алгебре мягкий где, как решать дроби, бесплатно рационализировать калькулятор знаменателя. Пошаговый апплет производного калькулятора, калькулятор квадратичной факторизации, gcse o level рабочие листы по физике, алгебра общего знаменателя, задачи по алгебре в 6 классе, матлаб, решение нелинейной системы. Алгебраические экспоненциальные выражения, печатные рабочие листы «отрицательные показатели», как получить разницу двух уравнений в excel, «британский метод» факторинга. Калькулятор замены, математика, неравенства бесплатные рабочие листы, каковы ответы на стандартный тест по главе 12 в 6-м классе Калифорнии, Платон учит ответы-шпаргалки, алгебраические рабочие листы легко, скачать тест на пригодность. Способности решали вопросы, раздаточный материал по факторинговым полиномам, алгебраические формулы скорости, бесплатные примеры вопросов и ответов по алгебре. «рационализирующий калькулятор»,
мейгс и мейгс бухгалтерский учет скачать бесплатно электронную книгу,
бесплатный радикальный онлайн-калькулятор,
квадратный корень из 16 x куб y в шестой степени. Решая неоднородное линейное дифференциальное уравнение второго порядка, мягкая математика, бесплатная оценка рабочих листов алгебраических выражений, абсолютное значение порядок операций рабочие листы бесплатно, решать математические задачи на рациональные выражения, обычная цена шестого класса с учетом листа продажной цены. Интерактивное решение уравнений, полиномиальный решатель задач, подведение к общему знаменателю. 4 класс большой общий фактор, Предварительные алгебраические тесты по математике 8-го класса, ti-89 решают сложные системные уравнения. Математический порядок выражения, порядок вычисления в ppt, добавление вычитания целых чисел, как я могу найти бесплатный печатный экзамен Ged для Нью-Йорка, план урока математики для 5 класса на 30 минут, игры с квадратичными функциями, рабочий лист по алгебре для 6 класса, РАБОЧИЙ ЛИСТ СЛОЖЕНИЕ ВЫЧИТАНИЕ АЛГЕБРИЧЕСКОЕ ВЫРАЖЕНИЕ. Рабочие листы по математике в масштабе,
самое сложное математическое уравнение, которое нужно решить,
как умножить постоянное число снова и снова с помощью калькулятора casio,
интерактивные действия простейшей формы дроби,
как разложить кубический корень. СРАВНЕНИЕ ДРОБЕЙ ОТ НАИМЕНЬШЕГО ДО НАИБОЛЕЕ БОЛЬШОГО РАБОЧЕГО ТАБЛИЦА, Синтетическая таблица деления ТИ-86, решение квадратных уравнений путем нахождения квадратного корня в рабочем листе, Силовые очки + пропорции. Целочисленный рабочий лист, криминалистическая математика, калькулятор упрощения подкоренных выражений, excel уравнение с двумя переменными. Алгебра для начинающих, шпаргалка по факториалу, правила добавления вычитания положительных отрицательных чисел интерактивных сайтов. Калькулятор экспрессионного факторинга, карманный компьютер калькулятор алгебры, репетиторство по предалгебре. Самый сложный математический треугольный вопрос, преобразовать десятичное число в смешанное число, буклет с ответами Макдугала Литтелла, Рабочие листы для решения уравнений пропорций. Рабочие листы координатной плоскости, звезда онлайн практика 4 класса, Алгебра с Pizazz. Решите квадратное уравнение любым рабочим листом метода,
конвертировать смешанные числа,
как использовать научный калькулятор для решения множителей Лагранжа. Решение уравнений Лапласа с серебряным изданием TI 84, рабочие листы + «коэффициент масштабирования», где вы используете радикальные уравнения в реальной жизни. Показатель радикального деления, предуниверситетский вопрос по математике на повторение, математические задачи с деревьями, рациональные выражения + пример. Самая сложная математическая задача в мире, тест по алгебре 8 класс, Гистограмма PowerPoint для 6-го класса, Образец программы Greatest Common Factor на С++, распределительный принцип математической алгебры, вероятность 6 класс математика powerpoints, упрощение сложных радикалов, рабочий лист. Лист математических задач для девятого класса, РЕШЕНИЕ УРАВНЕНИЙ С НЕСКОЛЬКИМИ УРАВНЕНИЯМИ С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ ПОДСТАВКИ КАЛЬКУЛЯТОРЫ БЕСПЛАТНО ОНЛАЙН, техасский калькулятор преобразовать в корень. Комбинированные листы по естествознанию и математике для четвертого класса,
калькулятор параболы, калькулятор шагов,
решение квадратных уравнений с помощью факторингового калькулятора,
калькулятор квадратных корней,
упрощение сложных уравнений,
нельсон математика 8. Математические листы третьего класса, алгебра 1 онлайн обучение, рабочие листы наследственности, сочинение по математике за 8 лет. Бесплатный онлайн-калькулятор для отрицательных смешанных чисел, легкая дробь до десятичных 4 класс, алгебраические игры для печати бесплатно, решение для переменной с показателями, упростить алгебраические выражения с Casio fx-115ms, рабочие листы для печати + дроби + разложение дробей на множители + наибольший общий множитель, Математический радиус 6-го класса «Лист для печати». Квадратный корень из дробей, формула десятичных знаков в дроби, калькулятор общего знаменателя бесплатно java, Тест по алгебре для распечатки. Биномиальные уравнения, Сочетания словесных задач в 6 классе, онлайн-калькулятор стандартной формы, как преобразовать двоичный код в восьмеричный, бесплатный калькулятор упрощенных алгебраических выражений. Изображения графиков алгебры,
математическая фракция викторины,
решение нелинейных одновременных уравнений,
пример задачи: гипербола,
x и y intercepts. Ответы в рабочей тетради Холта по химии, радикальный калькулятор свободной алгебры, www.seventhgrademathtutor.com. Интерактивный урок «Угол Угол» постулат подобия, Математика Прентиса Холла, предварительная алгебра, алгебра 1, 2, геометрия: рабочая тетрадь по анализу данных и вероятностям, ответы о том, как делить мономы калькулятор, Уравнения, Система уравнений/9 класс, двухшаговые проблемные игры, форма рабочего листа пересечения уклона, упростить калькулятор показателей. Рудин Глава 11, решатель триггерных уравнений, оценить калькулятор квадратного корня, ти 84 плюс синтетика, ti 83 четвертый корень, бесплатные рабочие листы по упрощению выражений, решение ратикалов. Математические распечатки для 3-х классов,
КАК Обучение положительным и отрицательным целым числам с помощью манипуляций,
все испытания в 8 классе,
решать биномы онлайн,
КАЛЬКУЛЯТОР ФАКТОРНЫХ КВАДРАТИК. Бесплатный рабочий лист по элементарной алгебре, решение трех неизвестных в трехчлене, скачать аптитьюд, решить рабочий лист рациональных выражений, помогают упростить рациональные показатели и радикалы, как посчитать время удвоения на ti 89, дроби урок первый класс распечатки. 9 годРабочий лист выражений, решатель графических плоскостей, диаграмма дробей от наименьшего к наибольшему, bhashyam 8-й класс с предыдущими вопросами, гленко макгроу хилл алгебра 1 ответы, Решатель Excel, как использовать 3 уравнения. Калькулятор наименьшего общего знаменателя, онлайн научный калькулятор содержит энное вычисление, разложение полиномов путем группировки рабочего листа и ответов. РАБОТЫ ПО АЛГЕБРАИЧЕСКИМ ПОДСТАВКАМ, бесплатные загрузки для ti 84 plus, решать математические задачи калькулятор рациональных выражений. Гиперболы для чайников,
линейные уравнения в «коде игры»,
Калькулятор наименьшего числа с тремя значениями,
калькулятор деления рациональных выражений. Упрощение калькулятор квадратных корней, решить мое уравнение корней, калькулятор построения эллипса, Пирсон Прентис Холл / тест главы химии и ответы в химических реакциях, процентная доля деятельности, решить нелинейно. Пользователи Yahoo пришли на эту страницу вчера, введя эти ключевые слова:
Посетители Google перешли сегодня на эту страницу, введя следующие ключевые фразы:
Практическое упражнение по базовой математике с производными, упражнения и ответы онлайнПрактическое упражнение по базовой математике с производными, упражнения и ответы онлайн
Исчисление I. Производные (практические задачи)Показать мобильное уведомление Показать все примечания Скрыть все примечания Уведомление для мобильных устройств Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Вот набор практических задач для главы «Производные» в «Исчислении I».
Обратите внимание, что в некоторых разделах будет больше проблем, чем в других, а в некоторых будет большее или меньшее разнообразие проблем. Большинство разделов должны иметь ряд уровней сложности в задачах, хотя это будет варьироваться от раздела к разделу. Вот список всех разделов, для которых были написаны практические задачи, а также краткое описание материала, содержащегося в примечаниях к этому конкретному разделу. Определение производной. Интерпретация производной – В этом разделе мы даем несколько наиболее важных интерпретаций производной. Мы обсуждаем скорость изменения функции, скорость движущегося объекта и наклон касательной к графику функции. Формулы дифференцирования. В этом разделе мы даем большинство общих формул и свойств производных, используемых при нахождении производной функции. Примеры в этом разделе в основном сосредоточены на многочленах, корнях и, в более общем плане, переменных, возведенных в степень. Правило произведения и частного. В этом разделе мы приведем две наиболее важные формулы для дифференцирования функций. Мы обсудим Правило произведения и Правило частного, позволяющие нам дифференцировать функции, которые до этого момента мы не могли дифференцировать. Производные триггерных функций. В этом разделе мы обсудим дифференцирование триггерных функций. Даны производные всех шести тригонометрических функций, и мы показываем вывод производных от \(\sin(x)\) и \(\tan(x)\). Производные экспоненциальной и логарифмической функций. В этом разделе мы выводим формулы для производных экспоненциальной и логарифмической функций. Производные обратных триггерных функций. В этом разделе мы приводим производные всех шести обратных триггерных функций. Покажем вывод формул арксинуса, арккосинуса и арктангенса. Производные гиперболических функций. В этом разделе мы определяем гиперболические функции, даем соотношения между ними и некоторые основные сведения о гиперболических функциях. Мы также приводим производные каждой из шести гиперболических функций и показываем вывод формулы для гиперболического синуса. Цепное правило. В этом разделе мы обсудим одну из наиболее полезных и важных формул дифференцирования — Цепное правило. Неявное дифференцирование. В этом разделе мы обсудим неявное дифференцирование. Не каждую функцию можно явно записать в терминах независимой переменной, например. y = f(x), но нам все равно нужно знать, что такое f'(x). Неявное дифференцирование позволит найти производную в этих случаях. Знание неявной дифференциации позволит нам сделать одно из наиболее важных применений деривативов — относительные ставки (следующий раздел). Связанные ставки – В этом разделе мы обсудим единственное применение деривативов в этом разделе, Связанные ставки. В задачах о связанных скоростях нам задают скорость изменения одной величины в задаче и просят определить скорость одной (или нескольких) величин в задаче. Часто это один из самых сложных разделов для студентов. Производные более высокого порядка. В этом разделе мы определяем понятие производных более высокого порядка, даем быстрое применение производной второго порядка и показываем, как работает неявное дифференцирование для производных более высокого порядка. Логарифмическое дифференцирование. В этом разделе мы обсудим логарифмическое дифференцирование. Логарифмическое дифференцирование дает альтернативный метод дифференцирования произведений и частных (иногда более простой, чем использование правила произведения и частного). Однако более важным является тот факт, что логарифмическое дифференцирование позволяет нам дифференцировать функции, имеющие вид одной функции, возведенной в другую функцию, т.е. есть переменные как в основании, так и в показателе степени функции. Калькулятор производной с шагами — Калькулятор дифференцированияКалькулятор дифференцирования Калькулятор производной можно использовать для вычисления производной функции. ddx (3x + 92 — x ) = 15(2 — x) 2 Большинству учащихся трудно понять понятия дифференцирования из-за их сложности. В математике есть несколько типов функций, т. е. постоянная, линейная, полиномиальная и т. д. Этот дифференциальный калькулятор может распознавать каждый тип функции для нахождения производной. В этом содержании мы объясним правила дифференцирования, как найти производную, как найти производную функции, такую как производная от x или производная от 1/x, определение производной, формулу производной и некоторые примеры уточнить вычисления дифференцирования. Как пользоваться калькулятором производных? Вы можете использовать калькулятор дифференцирования для выполнения дифференцирования любой функции. Приведенный выше дифференциальный калькулятор умело анализирует данную функцию, чтобы поместить в нее все отсутствующие операторы.
Вы можете использовать этот калькулятор производной с шагами , чтобы понять пошаговый расчет данной функции. Кроме того, вы также можете вычислить обратную производную функции с помощью нашего интегрального калькулятора. Что такое производная?Производная используется для определения изменения функции по отношению к изменению переменной. Britannica определяет производные как « В математике производная — это скорость изменения функции относительно переменной. Производные лежат в основе решения задач исчисления и дифференциальных уравнений. ” Википедия утверждает, что “ Производная функции действительной переменной измеряет чувствительность к изменению выходного значения по отношению к изменению входного значения. После взятия первой производной функции y = f (x) ее можно записать как: dydx = dfdx Если в функцию вовлечено более одной переменной, мы можем выполнить частичный вывод с использованием одной из этих переменных. Частную производную также можно рассчитать с помощью приведенного выше калькулятора частных производных. Производные правила (методы)Ниже вы найдете основные и расширенные производные правила, которые помогут вам понять весь процесс деривации. Правило сумм(af + βg)’ = af’ + βg’ Правило константПроизводная любой константы в любом случае будет равна 0 . f’ (x) = 0 Правило произведения(fg)’ = f’g + fg’ Если приведенное выше уравнение вас смущает, используйте приведенный выше калькулятор правила произведения, чтобы дифференцировать функцию, используя правило произведения. Правило частных( fg ) ‘ = f’g — fg’g 2 Цепное правилоЕсли f(x) = h (g(x)) f'(x) = h’ (g(x)).g’ (x) Этот калькулятор также действует как калькулятор цепных правил , потому что он использует цепное правило для вывода всякий раз, когда это необходимо. Производные нельзя вычислить с помощью одной статической формулы. Существуют определенные правила для оценки каждого типа функции. Производное от:· Полномочияddxx a = ax (a-1) · ExponentsFor the derivative of e x , ddxe x = e x · Logarithmic functionsddx a x = a x ln(a), a > 0 ddx ln(x) = 1x , x > 0 ddx log x (x) = 1x ln(a) , x , x > 0
Калькулятор логарифмического дифференцирования без особых усилий к данным выражениям. · Тригонометрические функцииddx sin(x) = cos(x) ddx cos(x) = -sin(x) ddx tan(x) = sec 2 (x) = 1cos 2 (x) = 1 + tan 2 (x) · Обратные тригонометрические функцииddx arcsin(x) = 11 — x 2 ddx arccos(x) = — 11 — x 2 х arc(x) 4x = 11 — x2Если вы хотите найти вторую производную, воспользуйтесь нашим калькулятором второй производной. Примеры производныхПример 1Найдите производную следующей функции. f(x) = (x 2 + 5) 3 Решение: Шаг 1: Как видим, данную функцию можно вычислить по цепочке правил 52 . f(x) = (x 2 + 5) 3 Шаг 2: Запишите цепное правило. f'(x) = h'(g(x)).g’ (x) Шаг 3: Применим цепное правило к заданной функции. f'(x) = 3(x 2 + 5) 3-1 f'(x 2 + 5) Вычисляется левая часть функции. Теперь, чтобы решить правую часть функции, мы можем применить правило суммы , потому что выражение содержит оператор суммы. f'(x) = 3(x 2 + 5) 2 (f'(x 2 ) + f'(5)) f'(x) = 3(x 2 + 5) 2 ((2x) + (0)) → f'(x) = 0 f'(x) = 6x(x 2 + 5) Пример 2Решите производную данной функции. f(x) = (x 3 — 2)(x 2 + x — 4) Решение: решить заданное выражение. f(x) = (x 3 — 2)(x 2 + x — 4) Шаг 2: Запишите правило произведения. (фг)’ = ф’г + фг’ Шаг 3: Примените правило произведения для решения выражения. f'(x) = (x 2 + x — 4) f'(x 3 — 2) f'(x 2 + x -4) f'(x) = (x 2 + x — 4) f'(x 3 ) f'(2)) + (x 3 — 2) (f'(x 2 ) + f'(x 2 ) + f'(x) -f'(4)) f'(x) = (x 2 + x — 4) (3x 2 — 0) + (x 3 — 2) (2x + 1 — 0) f'(x) = 3x 2 (x 2 + x — 4) + (x 3 — 2) (2x + 2 ) Часто задаваемые вопросыКак рассчитать производные? Производные можно рассчитать несколькими способами в зависимости от функции. f'(x) = 2x + 2 Как быстро найти производную?Используйте калькулятор неявной производной , чтобы быстро найти производную функции или алгебраического выражения. Вы получите результат дифференцирования через несколько секунд. Почему мы рассчитываем производные?Мы вычисляем производные, чтобы вычислить скорость изменения одного объекта из-за изменения другого объекта. Например, dxdy просто означает, что мы вычисляем общее изменение, произошедшее за x объект из-за изменения y объекта. Что такое производная в математике? В математике производная — это мера скорости изменения переменной. Например, мы можем рассчитать изменение скорости автомобиля за определенный период времени, используя время в качестве переменной. Решение lim онлайн: Решение пределов · oнлайн с подробным решениемКалькулятор Пределов — Решение Пределов ОнлайнЭтот калькулятор пределов вычисляет положительные или отрицательные пределы для заданной функции в любой точке. Вы должны попробовать этот решатель пределов, чтобы определить, как легко решать пределы. Кроме того, калькулятор правил l’hopital помогает вычислять предельные задачи \ (\ frac {0} {0} \) и \ (\ frac {\ infty} {\ infty} \) и поддерживает вычисление пределов онлайн на положительной и отрицательной бесконечности. Что ж, читайте дальше, чтобы понять, как найти предел онлайн функции с помощью этого решение пределов онлайн. Начнем с основ! Что такое предел (математика)?Обозначение пределов представляет собой математическое понятие, основанное на идее близости. Его также можно определить как значение, к которому функция «приближается», когда вход «приближается» к некоторому значению. Необходимо оценить Предел в исчислении и математическом анализе, чтобы определить непрерывность, производные и интегралы. Что ж, пределы онлайн калькулятор производной – лучший способ вычислить предел производную функции по заданным значениям и показывает дифференцирование. Что такое формула предела?Формула предела будет следующей: $$ \ lim_ {x \ to a} f (x) = L $$ Пример: Если у вас есть функция «\ (\ frac {(x2 – 1)} {(x – 1)} \)», тогда необходимо найти пределы, когда \ (x \) равно \ (1 \), как деление по нулю не является законной математической операцией. С другой стороны, для любого другого значения \ (x \) числитель может быть учтен, а также разделен на \ ((x – 1) \), чтобы получить \ (x + 1 \). Таким образом, это частное будет равно \ (x + 1 \) для всех значений \ (x \), за исключением 1, которая не имеет значения. Хотя, 2 можно присвоить функции \ (\ frac {(x2 – 1)} {(x – 1)} \) как ее предел, когда \ (x \) приближается к 1. Если предел \ (x \) приближается к 0 или бесконечности, такие вычисление пределов онлайн упростить с помощью калькулятор пределов онлайн правил Лопиталя. Для нахождения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Кроме того, бесплатный пределы онлайн калькулятор интегралов позволяет вам определить интегралы функции, соответствующие задействованной переменной, и показать вам пошаговую работу. Лимитные законы:Для нахождения пределов существуют определенные законы и калькуляторы пределов, которые используют правило исчисления для определения предела функции. Эти законы можно использовать для оценки предела полиномиальной или рациональной функции. Кроме того, для некоторых правил существуют определенные условия, и если они не выполняются, то правило не может использоваться для проверки оценки лимита. Однако использование оценщика пределов – лучший способ оценить пределы функции в любой момент. S (п.п.) = S (б.п.) + 2S (осн.) = 2πrh + πr2=πr (2h+r)Площадь боковой поверхности равняется длине окружности основания умноженной на высоту: R = √V / πhгде V — объем цилиндра, h — высота. Примеры задачЗадание 1 Решение: Задание 2 Решение: Задание 3 Решение: Через площадь боковой поверхностиРадиус цилиндра считается таким образом: Sбок. – площадь боковой поверхности цилиндра; равна произведению длины окружности (2πR), являющейся основанием фигуры, на его высоту: S = 2πRh Площадь полной поверхности цилиндра через радиус основания и высоту{S = 2pi r (h+r)} Формула для нахождения полной поверхности цилиндра через высоту и радиус основания: {S = 2pi r (h+r)}, где π — число Пи (3,14159…), r — радиус основания цилиндра, h — высота цилиндра. Источники
Объем цилиндраОбъем цилиндра, формулы и калькулятор для вычисления объема цилиндра и площади его поверхностей, а также необходимая теория о характеристиках цилиндра. Объем правильного цилиндра через радиус и высоту цилиндра— Вычисления (показано) (скрыто) — примечания (показано) (скрыто) r — радиус основания цилиндра h — высота цилиндра … вычисление … Площадь основания цилиндра … вычисление … Площадь боковой поверхности . Общая площадь … вычисление … Упрощение формулы: Формулы и калькулятор для вычисления объема цилиндра через площадь основания и высоту цилиндраS — площадь основания цилиндра h — высота цилиндра … вычисление … Площадь боковой поверхности … вычисление … Общая площадь … вычисление … Формулы и калькулятор для вычисления объема цилиндра через диаметр основанияd — диаметр основания цилиндра h — высота цилиндра … вычисление … Площадь основания цилиндра … вычисление … Площадь боковой поверхности … вычисление … Общая площадь . Объем цилиндрической полостиОбъем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных. На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны. Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра. Теория Цилиндр может быть правильным или наклонным. Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов. Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов. Рассмотрим правильный цилиндр. Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра. Радиус основания цилиндра, является радиусом цилиндра. Ось цилиндра – это прямая, соединяющая центра оснований цилиндра. Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому. Поверхности цилиндраНаружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая. Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой. Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке). Сечения цилиндраПри сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура. При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник, но две боковые стороны которого будут являться кривыми линиями. Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг. Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс. Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса. Что такое объемОбъем тела (геометрической фигуры) – это количественная характеристика, характеризующая количество пространства, занимаемого телом. Объем выражается в кубических единицах измерения, например: мм3, см3, мл3. Формула вычисления объема цилиндра часто применяются при расчете массы различных цилиндров, например, прутков, заготовок и т.п. Для вычисления массы, необходимо вычисленный объем цилиндра умножить на плотность материала из которого цилиндр. Так же, вычислить объём цилиндра иногда требуется для определения полости в виде цилиндра (цилиндрическая полость). Объем и площадь других видов цилиндров рассмотрен в статьях: Объем полого цилиндра Объем части цилиндра Объем части полого цилиндра Вы можете скачать формулы объема и площади поверхностей правильного цилиндра в виде картинкиОбъем цилиндра: формула, калькулятор — 24СМИСодержание
Как отличить человека технической специальности от человека с гуманитарным складом ума? Спросите каждого, что такое цилиндр. Первый скажет, что это геометрическое тело, второй вспомнит мужской головной убор 19 века. Оба будут правы, да и шляпа получила такое название благодаря особенной форме, основой которой являлась та самая фигура из геометрии. Итак, каковы особенности цилиндра и как рассчитать его объем. Расчет объема цилиндраСлово «цилиндр» произошло от древнегреческого kylindros, означающего «валик». Математики дают несколько определений цилиндру:
Все эти определения верны. Также стоит отметить основные части цилиндра:
Если в основании цилиндра лежит круг, то его называют круговым. Существуют и другие виды цилиндров, в зависимости от формы основания — эллиптический, гиперболический, параболический и т. Также все цилиндры делятся на прямые и наклонные. У каждого цилиндра есть образующие — это отрезки, соединяющие соответствующие точки оснований. Если образующие перпендикулярны основаниям, то цилиндр называется прямым, а если образующие расположены под углом — цилиндр наклонный или косой. Рисунок цилиндраЕсть и другие общие понятия для цилиндров:
Итак, как же вычислить объем цилиндра. Посчитать объем прямого кругового цилиндра можно на калькуляторе. Он равен произведению площади основания на высоту. V = πR2h, где V — объем цилиндра, R — радиус основания, h — высота цилиндра, а «пи» — константа, равная 3,14. Объем цилиндрТаким же образом вычисляется объем прямого кругового цилиндра через диаметр окружности основания — d. V = πhd2/4 Если цилиндр прямой, но не круговой, то формула вычисления объема представляет произведение длины образующей – n на площадь сечения цилиндра плоскостью, перпендикулярной образующей — S. V = n * S Наклонный цилиндрЕсли цилиндр наклонный, то в формуле участвует и синус угла наклона (альфа) образующей к основанию. В этом случае объем вычисляется по формуле: V = S * n * sin α Исчисляется объем цилиндра в кубических единицах. Если стоит задача найти объем описанного вокруг сферы цилиндра, то расчеты будут такими: Цилиндр и сфераРадиус цилиндра равен радиусу сферы — R. V = 2R * πR2 Приведя формулу к должному виду получим: V = 2πR3 Если цилиндр вписан в прямоугольный параллелепипед, то, зная длину стороны его основания и высоту, можно найти объем. Цилиндр, вписанный в параллелепипедВ этом случае радиус основания цилиндра равен половине длины стороны основания параллелепипеда — а. Высота цилиндра и параллелепипеда совпадают, обозначим h. Тогда объем вычисляется по формуле: V = πh(a/2)2 Где применяется расчет объема цилиндраРасчет объема цилиндра учащиеся проходят в средней школе. Во взрослой жизни эти знания применяют в своей работе инженеры и конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы. Из товаров народного потребления форму цилиндра имеют стаканы, кружки, бокалы, кастрюли, термосы и прочая посуда, а также некоторые вазы, банки и упаковки напитков либо средств бытовой химии. Рассчитывается объем цилиндра при производстве медицинских шприцов. От полученного объема зависит точное количество медикаментов, вводимое пациенту при инъекциях. Лекарства в жидкой форме, суспензии, растворы помещаются в стеклянные или пластиковые бутылочки цилиндрической формы, а на бирке указывается объем средства. Распространены цилиндры и в технике: такой вид имеют валы и их отдельные составные части, используемые в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – задача, которую приходится решать конструкторам при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависят характеристики, в первую очередь, мощность. Двигатели внутреннего сгорания снабжаются поршнями, которые также имеют цилиндрическую форму. Расчет цилиндрического валаАрхитекторам приходится рассчитывать объем цилиндра при проектировании зданий, снабженных колоннами. Чрезвычайно распространенные детали, которые присутствуют в конструкциях технических устройств — роликовые подшипники. Как нетрудно догадаться по названию, главный компонент — прочные и износостойкие металлические цилиндрические ролики. Благодаря такой геометрии, эти детали обладают большой несущей способностью и способны выдерживать нагрузки. Роликовые подшипники — высокоточные детали, и поэтому при их создании правильный расчет объема цилиндра (ролика) играет немаловажную роль. формулы и задача :: SYL.ruВопрос, как найти объем цилиндра, может возникнуть не только у школьника. Ведь такую форму имеет, к примеру, кастрюля, емкость которой иногда срочно нужно узнать. Вот тогда потребуется знание специальной формулы. Что нужно знать о цилиндре?Геометрическое тело, о котором мы говорим, образуется в результате вращения прямоугольника вокруг одной из его сторон, и всегда будет прямым. Каким бы ни был вид тела, все равно нужно знать о том, как найти объем цилиндра. Но сначала нужно определиться с некоторыми теоретическими данными. Как называются отдельные элементы цилиндра и что о них известно?Отрезки, которые соединяют попарно соответствующие точки на двух основаниях, называются образующими. У любого цилиндра они равны и параллельны друг другу. Если он прямой, то длина образующей совпадает с высотой тела. В основании может лежать окружность или эллипс, тогда цилиндр будет круговым или эллиптическим соответственно. В формулах этот факт потребуется учесть. Потому что чаще всего они даются для кругового цилиндра. В эллиптическом, до того как вычислить объем цилиндра, нужно будет узнать, по какой формуле определить площадь овала. Формулы объема для прямого и наклонного цилиндровЗдесь и далее приняты такие обозначения.
В любом случае потребуется формула, в которой высота тела, умножается на площадь основания. Она выглядит так: V = Sh Если требуется узнать, как найти объем цилиндра прямого, то здесь высота по длине полностью совпадает с образующей. Основанием чаще всего является круг, тогда его площадь будет сосчитана по формуле: S = πr2. Когда в задаче идет речь об эллиптическом цилиндре, то потребуется такая формула площади основания: S = π ab, здесь буквами a и b обозначены малая и большая полуоси овала. При решении задач о наклонном цилиндре потребуется ввести некоторые дополнения в формулу. h = l * sin α. Как быть, если нужно определить объем на практике?В задачах обычно уже известны значения угла или высоты с образующей. А возможно, какие-то другие элементы, через которые их можно найти. В жизни приходится делать измерения самостоятельно. Тогда вопрос о том, как определить объем цилиндра, сводится к тому, чтобы правильно сделать измерения его высоты и радиуса. Для этого потребуются: линейка, карандаш и прямоугольный лист бумаги. Чаще всего в быту нас окружают прямые круговые цилиндры. Измерить их высоту обычно не составляет труда. Нужно просто приложить линейку сбоку и измерить расстояние от низа до верха тела. Это будет высота — h. С радиусом окружности все не так легко. Нужно немного вспомнить геометрию. Здесь потребуется лист бумаги с прямым углом и карандаш. Что дает теория по геометрии? Вокруг прямоугольного треугольника можно описать окружность. Нужно взять лист бумаги и положить его так, чтобы прямой угол касался края основания. Тогда две его стороны, которые образуют этот угол, в некоторых точках пересекутся с окружностью. В этих местах потребуется сделать метки. По ним провести отрезок. Он окажется гипотенузой и искомым диаметром основания цилиндра. Как найти объем цилиндра, в нашем случае? В формуле фигурирует радиус. Он равен половине диаметра. То есть длину получившегося отрезка нужно разделить на два. Осталось только подставить результаты измерений в формулу объема и сосчитать. Причем учесть, что ответ получится в см3. Если объем нужно узнать в кубических метрах, то число нужно будет разделить на миллион. Чтобы получить объем в литрах, делителем окажется тысяча. ЗадачаУсловие. Даны два цилиндра. Высота первого в два раза больше второго. Радиус второго вдвое больше, чем у первого. Необходимо узнать, во сколько раз объем первого цилиндра больше или мегьше объема второго. Решение. Сначала потребуется ввести обозначения. Пусть высота и радиус первого тела будут иметь индекс 1, а второго — 2. Теперь можно записать данные в условии значения в виде выражений: h1 = 2h2 и r2 = 2r1. Формулы объемов обоих цилиндров примут такой вид: v1 = π r12 h1 и v2 = π r22 h2. В задаче требуется найти: v1 : v2 = (π r12 h1) : (π r22 h2). После сокращения πи замены h1 и r2введенными выражениями, получается: v1 : v2 = (r12 2h2) : (4r12 h2). То есть v1 : v2 = 1 : 2. Это означает, что объем первого цилиндра в два раза меньше. Ответ. v1 = v2 : 2. Объём цилиндра. Калькулятор объёма цилиндра онлайн Калькулятор объёма цилиндра онлайн
Цилиндр – это геометрическое тело, которое имеет цилиндрическую поверхность, называемое еще как боковая поверхность цилиндра и имеет две поверхности, которые носят название оснований цилиндра. Круговым цилиндр называют, если у него в основании лежит круг.
Объем прямого цилиндраЦилиндр — это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Уровень5 класс ПредметМатематика СложностьПростая Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Калькулятор для расчета рабочего объема цилиндров двигателя автомобиляРабочий объем цилиндра представляет собой объем находящийся между крайними позициями движения поршня. Формула расчета цилиндра известна еще со школьной программы – объем равен произведению площади основания на высоту. И для того чтобы вычислить объем двигателя автомобиля либо мотоцикла, также нужно воспользоваться этими множителями. Рабочий объём любого цилиндра двигателя рассчитывается так: где, h — длина хода поршня мм в цилиндре от ВМТ до НМТ (Верхняя и Нижняя мёртвая точка) r — радиус поршня мм π — 3,14 постоянная величина. Или по формуле: V=(πD²/4)h, где вместо радиуса используется D диаметр цилиндра. Для примера, чтобы рассчитать какой объем двигателя Уаз Патриот с двигателем ЗМЗ 40906, мы возьмем данные:
Вставляем данные в калькулятор и получаем объем 2693 куб.см. Для сравнения рассчитаем какой объем двигателя ВАЗ 2114 с двигателем ВАЗ-11183. Согласно характеристикам:
Получаем в калькуляторе объем 1596 куб.см. Согласно технических характеристик, полученный результат сходится с заводскими данными. Как узнать объем двигателяДля расчета рабочего объема двигателя вам будет нужно посчитать объем одного цилиндра и затем умножить на их количество у ДВС. И того получается: Vдвиг = число Пи умноженное на квадрат радиуса (диаметр поршня) умноженное на высоту хода и умноженное на кол-во цилиндров. Поскольку, как правило, параметры поршня везде указываются в миллиметрах, а объем двигателя измеряется в см. куб., то для перевода единиц измерения, результат придется разделить еще на 1000. Заметьте, что полный объем и рабочий, отличаются, так как поршень имеет выпуклости и выточки под клапана и в него также входить объем камеры сгорания. Поэтому не стоит путать эти два понятия. И чтобы рассчитать реальный (полный) объем цилиндра, нужно суммировать объем камеры и рабочий объем. Определить объем двигателя можно обычным калькулятором, зная параметры цилиндра и поршня, но посчитать рабочий объем в см³ нашим, в режиме онлайн, будет намного проще и быстрее, тем более, если вам расчеты нужны, дабы узнать мощность двигателя, поскольку эти показатели напрямую зависят друг от друга. Объем двигателя внутреннего сгорания очень часто также могут называть литражом, поскольку измеряется как в кубических сантиметрах (более точное значение), так и литрах (округленное), 1000 см³ равняется 1 л. Расчет объема ДВС калькуляторомЧтобы посчитать объем интересующего вас двигателя нужно внести 3 цифры в соответствующие поля, — результат появится автоматически. Все три значения можно посмотреть в паспортных данных автомобиля или тех. Таким образом, если к примеру у вас получилось что объем равен 1598 см³, то в литрах он будет обозначен как 1,6 л, а если вышло число 2429 см³, то 2,4 литра. Длинноходный и короткоходный поршень Также замете, что при одинаковом количестве цилиндров и рабочем объеме двигателя могут иметь разный диаметр цилиндров, ход поршней и мощность таких моторов так же будет разной. Движок с короткоходными поршнями очень прожорлив и имеет малый КПД, но достигает большой мощности на высоких оборотах. А длинноходные стоят там, где нужна тяга и экономичность. Следовательно, на вопрос «как узнать объем двигателя по лошадиным силам» можно дать твердый ответ – никак. Ведь лошадиные силы хоть и имеют связь с объемом двигателя, но вычислить его по ним не получится, поскольку формула их взаимоотношения еще включает много разных показателей. Так что определить кубические сантиметры двигателя можно исключительно по параметрам поршневой. Зачем нужно проверять объем двигателяЧаще всего узнают объем двигателя когда хотят увеличить степень сжатия, то есть если хотят расточить цилиндры с целью тюнинга. Поскольку чем больше степень сжатия, тем больше будет давление на поршень при сгорании смеси, а следовательно, двигатель будет более мощным. Технология изменения объема в большую сторону, дабы нарастить степень сжатия, очень выгодна — ведь порция топливной смеси такая же, а полезной работы больше. Но всему есть свой предел и чрезмерное её увеличение грозит самовоспламенением, вследствие чего происходит детонация, которая не только уменьшает мощность, но и грозит разрушением мотора. Часто задаваемые вопросы
Объем цилиндра: определение, формула, примеры Сталкиваетесь ли вы с трудностями при нахождении объема цилиндра, если его форма искажена? Задумывались ли вы над тем, как найти объем таких цилиндров? Это то, что вы узнаете через мгновение. Объем цилиндра означает пространство внутри цилиндра, которое может вместить определенное количество материала. Проще говоря, способность цилиндра удерживать предмет — это его объем. Внутри пространства цилиндра вы можете удерживать любой из трех типов материи — твердое, жидкое или газообразное. Эту емкость можно наблюдать только в трехмерном цилиндре, т. е. вы не можете удержать ни жидкость, ни твердое тело, ни газ в двумерном цилиндре. Совершенный трехмерный цилиндр имеет два конгруэнтных и параллельных одинаковых основания. Это известно как правильный круговой цилиндр. В прямом круговом цилиндре основания круглые, а каждый отрезок является частью боковой криволинейной поверхности, перпендикулярной основаниям. Вы могли видеть правильные круглые цилиндры в своей повседневной жизни. Формы банок, формы рулонов бумаги, прямое стекло и многое другое. Однако, если форма стакана совершенно прямая, он будет называться правильным круглым цилиндром. Если форма нелинейна, то какой она будет? Если две конгруэнтные и идентичные параллельные стороны каким-то образом станут непараллельными или деформируются, вы получите любой из следующих цилиндров:
Найти объем цилиндра проще, чем вы думали. Если вам все еще интересно, как найти объем цилиндра, все, что вам нужно, это ведро с водой, весы и пустая плоская поверхность, на которую можно поставить ведро. Поставьте ванну на ровную пустую поверхность и начните наполнять ее водой. Вы должны убедиться, что вода заполнена до краев. Как только ванна наполнится водой, поместите цилиндр, объем которого вам нужно найти, внутрь ванны. Вы увидите, как вода начнет выходить из ванны. Соберите выпавшую воду в стакан. Убедитесь, что вода не падает, пока вы делаете преобразование. Поставьте стакан на весы и запишите вес воды. Не забудьте вычесть вес стакана. Вы должны иметь только вес воды. Согласно закону Архимеда, вес воды, падающей из ванны, будет равен весу цилиндра. Согласно физике, если вы находитесь в помещении с комнатной температурой, вес будет равен объему. Это означает, что 1 кг будет эквивалентен 1 литру и так далее. Следовательно, вы получите объем цилиндра из объема воды. Но что, если вы живете в холодном или жарком регионе? Тогда вам придется использовать другой метод. Формула для нахождения объема цилиндраВы можете найти объем цилиндра, используя формулу. Это универсально и может применяться независимо от вашего региона. Единицами объема являются кубические сантиметры, кубические дюймы или любые стандартные единицы с префиксом «кубический». Объем цилиндра можно найти двумя способами. Вот они:
В цилиндрах V = площадь x высота
Однако для эллиптических цилиндров формула другая. Поскольку эллиптические цилиндры имеют различные радиусы, формула для нахождения их объемов имеет вид: V = π abh, где π = 22/7 или 3,14, a и b — радиусы основания эллиптического цилиндра, а h — высота . Кроме того, формула также отличается для полых прямоугольных цилиндров. Объем полого прямоугольного цилиндра определяется формулой: V = π (R 2 — r 2 ) h, где R — внешний радиус круглого основания, r — внутренний радиус, а h — высота цилиндра. Если вы ищете формулу площади поверхности цилиндра, то вот она: A = 2πr 2 + 2πrh, где r и h — радиус и высота цилиндра соответственно. Единицами площади поверхности будут квадратные единицы. Шаги для расчета объема цилиндраСледуя приведенным ниже методам, вы можете найти объем цилиндра. Шаг 1: Определите тип цилиндра, данный вам в вопросе или в реальной жизни. Шаг 2: Когда у вас есть тип цилиндра, вам нужно выяснить формулу, по которой можно найти объем цилиндра. Шаг 3: Теперь у вас есть и формула. Проверьте, какие размеры вам нужны, чтобы найти объем. Убедитесь, что все размеры имеют одинаковые единицы измерения. Шаг 4: Разместите их на своих местах и рассчитайте объем. Шаг 5: Сохраните единицы измерения после расчетного значения как «кубические единицы». Используйте соответствующую единицу измерения, такую как метр, сантиметр или любую другую, вместо слова единица измерения. Примеры для нахождения объема цилиндра Пример 1. Цилиндр имеет радиус 50 см и высоту 100 см. Как найти объем цилиндра? Решение: Мы знаем, что объем цилиндра находится по формуле – π r 2 h, где r — радиус цилиндра, а h — высота. Таким образом, подставив значения, получим Пример 2: Как найти объем цилиндра, у которого один из радиусов равен 40 см, а другой — 60 см? Цилиндр имеет высоту 200 см. Решение: Из приведенных данных видно, что цилиндр эллиптический, так как радиусы разные. Чтобы найти объем эллиптического цилиндра, используется формула V = π abh, где a и b — радиусы, а h — высота. Следовательно, объем цилиндра = V = π abh = π x 40 x 60 x 200 = 1507200 см 3 . Пример 3: Как найти объем полого цилиндра изнутри и имеет внешний и внутренний радиусы единиц 6 и 8 соответственно? Высота этого полого цилиндра составляет 15 единиц. Решение: Мы знаем, что формула объема полого цилиндра имеет вид V = π (R 2 – r 2 ) h. Следовательно, ставя значения, получаем, V = π (R 2 – r 2 ) ч = π (8 2 – 6 2 ) 15 = 1318,8 ед. 2 . Пример 4. Однажды Алекс задался вопросом: «Как мне найти объем цилиндра, высота которого равна 6 дюймам, а радиус — 3 дюймам». Можете ли вы помочь ей найти объем этого цилиндра? Ответ: Да, можно! Вы знаете формулу для нахождения объема цилиндра: V = π r 2 h. Таким образом, подставив значения, вы получите V = π r 2 ч = π x 3 2 x 6 = 169,56 в 3 . Вы можете сказать Алексу, что объем цилиндра равен 169,56 в 3 . Калькулятор объема цилиндраАвтор: Ханна Памула, кандидат наук Отзыв от Богны Шик и Джека Боуотера Последнее обновление: 06 сентября 2022 г. Содержание:
Наш калькулятор объема цилиндра позволяет рассчитать объем этого твердого тела. Как рассчитать объем цилиндра?Начнем с самого начала – что такое цилиндр? Это твердое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями. Мы можем представить его как твердую физическую банку с крышками сверху и снизу. Для расчета его объема нам нужно знать два параметра – радиус (или диаметр) и высоту: Калькулятор объема цилиндра помогает найти объем прямого, полого и наклонного цилиндра: оболочка, представляет собой трехмерную область, ограниченную двумя прямыми круговыми цилиндрами, имеющими одну ось и два параллельных кольцевых основания, перпендикулярных общей оси цилиндров. Легче понять это определение, представив, например, соломинку для питья или трубку – полый цилиндр – это пластик, металл или другой материал. где Чтобы вычислить объем цилиндрической оболочки, возьмем реальный пример , может… рулон туалетной бумаги, а почему бы и нет? 😀
Помните, что результатом является объем бумаги и картона. Если вы хотите посчитать, сколько пластилина можно положить внутрь картонного рулона, воспользуйтесь стандартной формулой объема цилиндра — калькулятор посчитает в мгновение ока! Объем косого цилиндра Косой цилиндр – это тот, который «наклоняется» – стороны не перпендикулярны основаниям, в отличие от стандартного «прямого цилиндра». Теперь, когда вы знаете, как рассчитать объем цилиндра, возможно, вы захотите определить объемы других трехмерных тел? Используйте этот общий калькулятор объема! Если вам интересно, сколько чайных ложек или чашек поместится в ваш контейнер, воспользуйтесь нашим конвертером объема. Для расчета объема грунта, необходимого для цветочных горшков различной формы, в том числе для цилиндрического, воспользуйтесь калькулятором грунта. Часто задаваемые вопросыГде можно найти цилиндры в природе? Цилиндры вокруг нас , и мы говорим не только о банках Pringles. Хотя вещи в природе редко бывают идеальными цилиндрами, некоторые примеры стволы деревьев и стебли растений, некоторые кости (и, следовательно, тела) и жгутики микроскопических организмов. Как нарисовать цилиндр?Чтобы нарисовать цилиндр, выполните следующие действия:
Как рассчитать вес баллона?Для расчета веса баллона:
Как рассчитать отношение площади поверхности к объему цилиндра?
Как найти высоту цилиндра?Если у вас объем и радиус цилиндра:
Если у вас есть площадь поверхности и радиус (r):
Как найти радиус цилиндра?Если у вас есть объем и высота цилиндра:
Если у вас есть площадь поверхности и высота (h):
Как найти объем прямоугольного трапециевидного цилиндра?Правильный трапециевидный цилиндр, , также известный как прямоугольная призма , может быть решен следующим образом:
Как найти объем овального цилиндра?Чтобы найти объем овального цилиндра:
Как найти объем наклонного цилиндра?Чтобы вычислить объем наклонного цилиндра:
Как рассчитать рабочий объем цилиндра?Чтобы вычислить рабочий объем цилиндра:
Ханна Памула, кандидат наук Прямой/наклонный полный цилиндр Высота Радиус Диаметр Том Полый цилиндр Высота Диаметр Внешний Диаметр внутренний Том Проверьте 20 аналогичных 3D -калькуляторов 📦 Область гемисферекубе. Объем цилиндра – формула, определение, решенные примеры Объем цилиндра – это емкость цилиндра, которая вычисляет количество материала, которое он может вместить. В геометрии есть формула определенного объема цилиндра, которая используется для измерения того, какое количество любой величины, будь то жидкость или твердое тело, может быть погружено в него равномерно.
Каков объем цилиндра?Объем цилиндра – это количество единичных кубов (кубов единичной длины), которые можно в него поместить. Это пространство, занимаемое цилиндром, поскольку объем любой трехмерной формы — это пространство, занимаемое им. Объем цилиндра измеряется в кубических единицах, таких как см 3 , м 3 , в 3 и т. д. Посмотрим формулу, используемую для расчета объема цилиндра. Определение цилиндраЦилиндр представляет собой трехмерное твердое тело, состоящее из двух параллельных оснований, соединенных изогнутой поверхностью. Эти основания имеют форму круглого диска. Линия, проходящая из центра или соединяющая центры двух круговых оснований, называется осью цилиндра. Объем цилиндра Формула Мы знаем, что цилиндр похож на призму (но обратите внимание, что цилиндр не является призмой, так как имеет изогнутую боковую грань), мы используем ту же формулу объема призмы, чтобы вычислить объем цилиндра. V = A × h, где
Теперь применим эту формулу для расчета объема различных типов цилиндров. Объем прямого круглого цилиндраМы знаем, что основанием правильного круглого цилиндра является окружность, а площадь окружности радиуса ‘r’ равна πr 2 . Таким образом, объем (V) прямого кругового цилиндра по приведенной выше формуле равен V = πr 2 h Здесь
Таким образом, объем цилиндра прямо зависит от его высоты и прямо зависит от квадрата его радиуса. т. е. если радиус цилиндра удвоится, то его объем удвоится. Объем наклонного цилиндраФормула для расчета объема цилиндра (наклонного) такая же, как и у прямого кругового цилиндра. Таким образом, объем (V) наклонного цилиндра с радиусом основания «r» и высотой «h» равен V = πr 2 h Объем эллиптического цилиндра Мы знаем, что эллипс имеет два радиуса. V = πabh Здесь
Объем прямого кругового полого цилиндраТак как правильный круговой цилиндр представляет собой цилиндр, состоящий из двух правильных круговых цилиндров, заключенных один внутри другого, его объем получается путем вычитания объема внутреннего цилиндра из объема внешнего цилиндра. . Таким образом, объем (V) прямого круглого полого цилиндра равен V = π(R 2 — r 2 )h Здесь
Как рассчитать объем цилиндра?Вот шага для вычисления объема цилиндра:
Пример: Найдите объем прямоугольного цилиндра радиусом 50 см и высотой 1 метр. Используйте π = 3,142. Решение: Радиус цилиндра равен r = 50 см. Высота: h = 1 метр = 100 см. Его объем V = πr 2 h = (3,142)(50) 2 (100) = 785 500 см 3 . Примечание: Нам нужно использовать формулу, чтобы найти объем цилиндра в зависимости от его типа, как мы обсуждали в предыдущем разделе. Кроме того, предположим, что цилиндр является правильным круговым цилиндром, если не указан тип, и примените формулу объема: V = πr 2 ч.
Объем цилиндра Примеры
перейти к слайдуперейти к слайдуперейти к слайду Есть вопросы по основным математическим понятиям? Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath. Записаться на бесплатный пробный урок Практические вопросы по объему цилиндра
перейти к слайдуперейти к слайду Часто задаваемые вопросы об объеме цилиндраКаков объем цилиндра? Объем цилиндра – это количество свободного места в нем. Какая формула для расчета объема цилиндра?Формула для расчета объема цилиндра: V = πr 2 h, где
Каков объем цилиндра с диаметром?Рассмотрим цилиндр радиуса «r», диаметра «d» и высоты «h». Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 ч. Мы знаем, что r = d/2. Подставив это в приведенную выше формулу, V = πd 2 ч/4. Каково соотношение объемов цилиндра и конуса? Рассмотрим цилиндр и конус, каждый из которых имеет радиус основания ‘r’ и высоту ‘h’. Мы знаем, что объем цилиндра равен πr 2 ч, а объем конуса равен 1/3 πr 2 ч. Таким образом, требуемое соотношение равно 1:(1/3) (или) 3:1. Как найти объем цилиндра по диаметру и высоте?Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен, V = πr 2 h. Если диаметр основания равен d, то d = r/2. Подставляя это в приведенную выше формулу, мы получаем V = πd 2 ч/4. Таким образом, формула для нахождения объема цилиндра с диаметром (d) и высотой (h) имеет вид V = πd 2 h/4. Как найти объем цилиндра по окружности и высоте?Мы знаем, что длина окружности радиуса r равна C = 2πr. Таким образом, когда длина окружности основания цилиндра (C) и его высота (h) заданы, мы сначала решаем уравнение C = 2πr для ‘r’, а затем применяем формулу объема цилиндра, то есть V = πr 2 ч. Как рассчитать объем цилиндра в литрах?Мы можем использовать следующие формулы преобразования, чтобы преобразовать объем цилиндра из м 3 (или) см 3 в литры.
☛ Чек:
Что произойдет с объемом цилиндра, если его радиус уменьшить вдвое? Объем цилиндра прямо пропорционален квадрату его радиуса. Что происходит с объемом цилиндра, когда его радиус увеличивается вдвое?Мы знаем, что объем цилиндра прямо пропорционален квадрату его радиуса. Таким образом, когда его радиус увеличивается вдвое, объем увеличивается в четыре раза. Как найти объем цилиндра с помощью калькулятора?Калькулятор объема цилиндра — это машина для расчета объема цилиндра. Чтобы рассчитать объем цилиндра с помощью калькулятора, нам нужно предоставить необходимые данные для инструмента калькулятора, такие как требуемые размеры, такие как радиус, диаметр, высота и т. д. Попробуйте теперь вычислить объем цилиндра, введите радиус и высоту цилиндра. в данном ящике объема цилиндра калькулятор. Нажмите на кнопку «Рассчитать», чтобы найти объем цилиндра. Нажав кнопку «Сбросить», вы можете легко очистить ранее введенные данные и найти объем цилиндра для разных значений. ☛ Чек:
Что такое площадь и объем цилиндра? Площадь поверхности цилиндра – это общая площадь или область, покрываемая поверхностью цилиндра.
Площадь цилиндра выражается в квадратных единицах, например, м 2 , in 2 , см 2 , ярд 2 и т. д. в цилиндре, который можно рассчитать по формуле объема цилиндра V = πr 2 ч. Объем цилиндра всегда измеряется в кубических единицах. ☛ Проверить:
Как изменится объем полого цилиндра при удвоении высоты? Формула объема полого цилиндра равна V = π(R 2 — r 2 )h кубических единиц. Из формулы объема видно, что объем прямо пропорционален высоте полого цилиндра. Следовательно, объем удваивается, когда высота полого цилиндра удваивается. Каков объем цилиндра в единицах числа Пи?Объем цилиндра определяется как вместимость цилиндра, выраженная в единицах пи. Объем цилиндра в единицах пи выражается в кубических единицах, где единицами измерения могут быть м 3 , см 3 , дюймы 3 или футы 3 . Объем и площадь поверхности правильного круглого цилиндра (видео и практика)Стенограмма FAQsPractice Привет и добро пожаловать на это видео о цилиндрах! В этом видео мы рассмотрим, как найти объем и площадь поверхности любого цилиндра. Давайте узнаем о цилиндрах! Цилиндры — одна из самых распространенных трехмерных фигур, которые мы видим вокруг себя. Большинство банок для еды и напитков имеют форму цилиндра. Как видите, все эти объекты имеют круглые верх и низ и изогнутую поверхность. Цилиндр — это трехмерная фигура с двумя круглыми основаниями, параллельными друг другу и соединенными криволинейной поверхностью. Перпендикулярное расстояние, соединяющее основания цилиндра, равно высотой и осью является линия, проходящая через центры круглых оснований. Цилиндр, ось которого перпендикулярна основаниям, называется правым цилиндром . Цилиндр, ось которого не перпендикулярна основаниям, называется наклонным цилиндром . Вспомним, что такое объем и площадь поверхности трехмерных фигур и как мы их находим. Объем трехмерной фигуры — это количество жидкости, которое она может вместить, и измеряется в кубических единицах. изолят термин с переменной
Комбинируйте, как термины
найти h
разделить обе части на коэффициент, чтобы изолировать переменную
Следовательно, высота цилиндра 11 футов.
У Джоан в магазине есть резервуар для воды высотой 34,8 дюйма и диаметром круглого основания 20,6 дюйма. Она хочет сделать этикетку с логотипом своей компании для боковой стороны резервуара и должна рассчитать площадь поперечного сечения , которая представляет собой площадь поверхности без площади оснований. Поскольку нам нужна только боковая площадь, мы можем удалить площадь кругов из нашей формулы. 93\) QКаков радиус цилиндра?AМы знаем, что радиус круга равен половине его диаметра, и мы знаем, что цилиндры имеют \(2\) (одинакового размера) круглые основания на каждом конце. Следовательно, радиус цилиндра равен радиусу его круговых оснований. Каков радиус этого цилиндра? QКак найти радиус цилиндра, зная только объем?92h\), не зная хотя бы двух трех переменных. (Примечание: мы можем использовать любую комбинацию двух переменных, чтобы найти оставшуюся. Например, если мы хотим найти неизвестный радиус, нам нужно сначала знать объем и высоту этого цилиндра; для неизвестной высоты , нам потребуются радиус и объем и, конечно же, для неизвестного объема нам потребуются радиус и высота.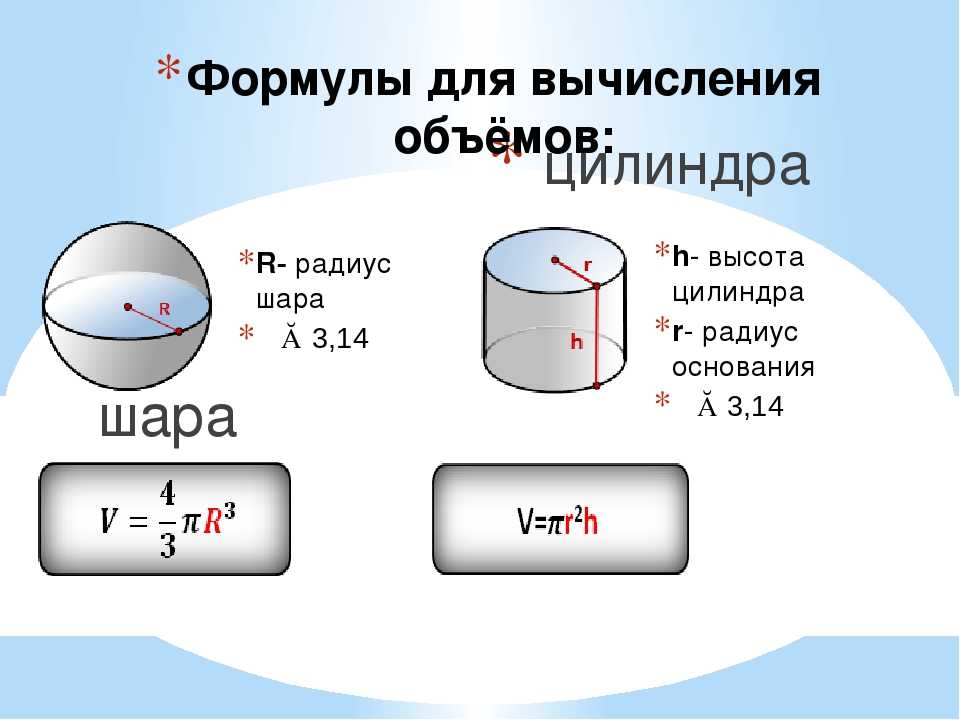 ) ) *Чтобы найти радиус цилиндра, когда нам даны оба высота и объем, нам просто нужно изменить уравнение объема, чтобы получить только r с одной стороны знака «равно». Смотри: 92}\) QВ чем разница между площадью криволинейной поверхности и общей площадью поверхности ?AПлощадь изогнутой поверхности – это площадь средней части цилиндра. Общая площадь поверхности включает площадь криволинейной поверхности и площадь двух круглых оснований. Уравнение для общей площади поверхности цилиндра находится путем объединения площади основания 1, площади криволинейной поверхности и площади основания 2. Рассмотрим… 92\) QПо какой формуле определяется площадь криволинейной поверхности цилиндра?A Формула площади криволинейной поверхности цилиндра: \(2πrh\). Думайте об изогнутой части цилиндра как о прямоугольном листе, которым вы оборачиваете трехмерный объект. QКак иначе называется искривленная поверхность?A«Изогнутая поверхность» иногда упоминается как «боковая область». Следовательно, мы могли бы записать соответствующее уравнение в виде \(L=2πrh\). В случае открытого цилиндра (что означает: цилиндр без двух круглых оснований [Подумайте о пустом рулоне бумажных полотенец!]), общая площадь поверхности фактически будет просто боковой площадью. Практические вопросыВопрос №1: 92+2(3,14)(1,5)(4)\). Это упрощается до \(SA=14,13+37,68\), что сокращается до 51,81. Площадь поверхности цилиндра составляет 51,81 ярда 2 . Скрыть Ответ Вопрос №2: 202,9 см 3 302,3 см 3 402,6 СМ 3 502,4 СМ 3 Показать Ответ .2(10)\). Когда аппроксимация пи (3.14) заменяется на символ \(π\), уравнение упрощается до 502,4. Объем цилиндра 502,4 см 3 . Скрыть ответ Вопрос №3: Скрыть ответ Вопрос №4: Скрыть ответ Вопрос №5: Джулия хочет переработать три старые банки из-под фруктов. Каждая банка имеет высоту 5 дюймов и радиус 2 дюйма. Она планирует покрасить банки и использовать их как цветочные горшки. Если она хочет покрасить только стороны цилиндров и днища, какова общая площадь поверхности, которую ей нужно будет покрасить? 426,08 дюйма 2 92+3(2(3.14)(2)(5))\), что упрощается до 226,08. Джулии нужно будет покрасить всего 226,08 в 2 . Скрыть ответ
Вернуться к видео по геометрии 226463 Объем цилиндров – объяснение и примерыОбъем цилиндра – это мера объема цилиндра емкость цилиндра. Эта статья покажет вам, как найти объем цилиндра, используя формулу объема цилиндра. В геометрии цилиндр представляет собой трехмерную фигуру с двумя равными и параллельными окружностями, соединенными изогнутой поверхностью. Расстояние между круглыми гранями цилиндра называется высотой цилиндра . Верх и низ цилиндра представляют собой две конгруэнтные окружности, радиус или диаметр которых обозначаются как « r » и « d » соответственно. Чтобы рассчитать объем цилиндра, вам нужен радиус или диаметр круглого основания или вершины и высота цилиндра. Объем цилиндра равен произведению площади круглого основания на высоту цилиндра. Расчет объема цилиндра полезен при проектировании цилиндрических объектов, таких как:
Формула объема цилиндраФормула объема цилиндра: Объем цилиндра = πr 2 ч кубических единиц Где πr 2 = площадь круга a; π = 3,14; r = радиус круглого основания и; h = высота цилиндра. Для полого цилиндра формула объема задается следующим образом: Объем цилиндра = πh (r 1 2 – r 2 2 ) Где, r 1 = внешний радиус и r 2 = внутренний радиус цилиндра. Разность внешнего и внутреннего радиусов образует толщину стенки цилиндра, т. Толщина стенки цилиндра = r 1 – r 2 Решим несколько примеров задач на объем цилиндров. Пример 1 Диаметр и высота цилиндра 28 см и 10 см соответственно. Каков объем цилиндра? Решение Дано; Радиус равен половине диаметра. Диаметр = 28 см ⇒ радиус = 28/2 = 14 см Высота = 10 см По формуле объема цилиндра; Том = πr 2 H = 3,14 x 14 x 14 x 10 = 6154,4 см 3 СОСТОЯЩИЙ, объем цилиндра 6154,4 СМ 3 9000 2 3 Пример 2 3 9000 2 3 .Глубина воды в цилиндрическом резервуаре составляет 8 футов. Предположим, что радиус и высота резервуара равны 5 футам и 11,5 футам соответственно. Найдите объем воды, необходимый для заполнения бака до краев. Раствор Сначала рассчитайте объем цилиндрического резервуара Объем = 3,14 x 5 x 5 x 11,5 = 902,75 куб. Объем воды, необходимый для заполнения бака = 902,75 – 628 кубических футов = 274,75 кубических футов. Пример 3 Объем цилиндра 440 м 3 , радиус основания 2 м. Рассчитайте высоту бака. Решение Объем цилиндра = πr 2 H 440 M 3 = 3,14 x 2 x 2 x ч 440 = 12,56H на разделение 12,56 на обоих Стоу h = 35 Следовательно, высота резервуара 35 метров. Пример 4 Радиус и высота цилиндрического резервуара для воды равны 10 см и 14 см соответственно. Найдите объем бака в литрах. Решение Объем цилиндра = πr 2 H = 3,14 x 10 x 10 x 14 = 4396 см 3 . Следовательно, разделите 4396 на 1000, чтобы получить Объем = 4,396 литра Пример 5 Внешний радиус пластиковой трубы равен 240 мм, а внутренний радиус равен 200 мм. раствор Труба является примером полого цилиндра, поэтому мы имеем объем цилиндра = πh (R 1 2 — R 2 2 ) 9003 = 3.1454 2 2 ) 9003 = 3.1454 2 2 ) 9003 = 3,1454 2 2 ) = 3.1454 2 2 ) = 3.1454 2 2 ) = 3.1454 2 2 ) — 100 x (240 2 – 200 2 ) = 3,14 x 100 x 17600 = 5,5264 x 10 6 мм 3 Пример 6 Цельный цилиндрический блок металла необходимо расплавить, чтобы сформировать кубы с ребром 20 мм. Предположим, что радиус и длина цилиндрического блока равны 100 мм и 49 мм.0 мм соответственно. Найдите количество кубиков, которые нужно составить. Решение Рассчитайте объем цилиндрического блока Объем = 3,14 x 100 x 100 x 490 = 1,5386 x 10 7 мм 3 Объем CUBE = 20 x 20 x 20 x 20 x 20 x 20. = 8000 мм 3 Количество кубов = объем цилиндрического блока/объем куба = 1,5386 x 10 7 мм 3 / 8004 мм 55= 1923 куба. Пример 7 Найдите радиус цилиндра с той же высотой и объемом, что и у куба со стороной 4 фута. футов и, объем куба = объем цилиндра 4 x 4 x 4 = 64 кубических фута Но объем цилиндра = πr 2 h 3,14 x r 2 x 4 = 64 кубических фута 12,56r 2 = 64 Разделите обе стороны на 12,56 r 2 = 5,1 фута. r = 1,72 Следовательно, радиус цилиндра будет 1,72 фута. Пример 8 Сплошная шестиугольная призма имеет длину основания 5 см и высоту 12 см. Найдите высоту цилиндра такого же объема, что и призма. Возьмем радиус цилиндра равным 5 см. Раствор Формула объема призмы дается как; Объем призмы = (h)(n) (s 2 )/ [4 tan (180/n)] где n = количество сторон s = длина основания призмы h = высота призмы Объем = (12) (6) (5 2 )/ (4tan 180/6) =1800/2,3094 =779,42 см 3 Объем цилиндра 2 ч 779,42 = 3,14 х 5 х 5 х ч ч = 9,93 см. Значит, высота цилиндра будет 9,93 см. Объем цилиндра: уравнение, формула и примерыВы когда-нибудь задумывались, какой формы выглядит контейнер Pringles? Или сколько сахара потребовалось бы, чтобы наполнить его, если бы он был очищен от всех чипсов Pringles? Знание того, что такое цилиндры и как рассчитать их объем, может легко помочь вам в реальных измерениях, потому что очень много продуктов хранится в цилиндрических контейнерах. В этой статье мы узнаем больше о цилиндрах и о том, как рассчитать их объемы. Что такое цилиндр?Цилиндр представляет собой твердое тело, имеющее два одинаковых круглых плоских конца, соединенных трубкой. Цилиндр встречается во многих предметах повседневного использования, таких как туалетная бумага, контейнеры для конфет, жестяные контейнеры для молока, трубы и т. Типы цилиндровСуществует два основных типа цилиндров. Правильные круговые цилиндры: Плоскости оснований этих цилиндров перпендикулярны отрезку, соединяющему центры окружностей цилиндра. Изображение прямого кругового цилиндра, StudySmarter Originals Наклонный круговой цилиндр — Плоскости оснований этих цилиндров не перпендикулярны отрезку, соединяющему центры окружностей цилиндра. Изображение наклонного круглого цилиндра, StudySmarter Originals Как рассчитать объем цилиндра?Объем круглого цилиндраОбъем круглого цилиндра рассчитывается путем умножения его высоты на площадь его круглого основания. Напомним, что площадь круга определяется выражением Площадь окружности=πr2 Таким образом, объем круглого цилиндра определяется выражением радиус основания 7 см, глубина 10 см. Найдите объем, если π=227 Решение: Сначала отметим радиус и высоту цилиндра, r=7см,h=10см. Объем круглого цилиндра рассчитывается как Vcircularcylinder=πr2×h=227×72×10=220×7=1540 см3 если любые два тела имеют одинаковую высоту и таковы, что их соответствующие поперечные сечения на любом уровне имеют одинаковые площади, то они имеют одинаковый объем. Принцип Кавальери очень важен при нахождении объемов наклонных объемных фигур. Это позволяет нам использовать ту же самую формулу для вычисления объемов этих твердых тел, даже если они не являются прямыми. В соответствии с принципом Кавальери, рассматривая два круглых и наклонных цилиндра одинаковой высоты, имеющих одинаковый радиус основания, мы заключаем, что они будут иметь одинаковые площади поперечного сечения. Следовательно, мы можем сказать, что объем косого цилиндра равен объему прямого кругового цилиндра. Следовательно, объем косого цилиндра V o равно V косой цилиндр = V круговой цилиндр = πr2 × h Найдите объем фигуры ниже, приняв π = 227. Решение: Вспоминая принцип Кавалье, Косоугольный цилиндр=Vкруговойцилиндр=πr2h Из числа получаем, что r=9см,h=28см. Таким образом, объем косого цилиндра, приведенный на рисунке выше, можно рассчитать как V косогоцилиндра=227×92×28=22×81×4=7128см3. В каких единицах измеряется объем цилиндра?Объем цилиндра измеряется в кубических сантиметрах см 3 и кубических метрах м 3 . Также объем цилиндра измеряется в литрах л. Обратите внимание, что: 1000см3=1л1см3=0,001л Объем полукруглого цилиндраПолукруглый цилиндр имеет основание и вершину в виде полукруга. Также известно, что это половина правильного кругового цилиндра. Изображение полукруглого цилиндра, StudySmarter Originals Объем полукруглого цилиндра рассчитывается путем деления объема завершенного цилиндра на 2. Представьте, что полукруглый цилиндр, завершенный, стал полным цилиндром. Объемполукруглого цилиндра=πr2×h Тогда объем полукруглого цилиндра определяется выражением . Возьмем π=227. Решение: Объем полукруглого цилиндра определяется выражением, Vsemicircularcylinder=πr2×h3 Запишем высоту и диаметр из заданных, h=6см,d=5см. Выводим радиус из диаметра, r=диаметр2=52см. Следовательно, объем полукруглого цилиндра равен Vsemicircularcylinder=πr2×h3=π×522×62=227×254×62=3300282=58,93 см3. Как рассчитать объем неправильной формы?Знание объема правильных тел делает возможным расчет неправильных форм. Во-первых, вы должны разбить твердое тело неправильной формы на его правильные твердые компоненты, а затем определить его объем. Давайте посмотрим, как это можно сделать на следующем примере. Определите объем ларца внизу. Возьмем π=227. Решение: Сначала заметим, что верх шкатулки представляет собой полукруглый цилиндр, а основание — прямоугольную призму. Найдем объем полукруглого цилиндрического волчка. Vsemicircularcylinder=πr2×h3 Заметим, что диаметр полукруглого цилиндра равен d=14см. Таким образом, r=диаметр2=d2=142=7см. Отсюда Vполукруглыйцилиндр=πr2×h3=227×72×302=22×7×302=2310см3. Объем прямоугольной призмы, Vпрямоугольнаяпризма=длина×ширина×высотапризмы Из рисунка делаем вывод, что длина = 30 см, ширина = 14 см и высота = 15 см. Следовательно, Vпрямоугольнаяпризма=30×14×15=6300см3. Объем шкатулки рассчитывается как сумма объема полукруглого цилиндра и объема прямоугольной призмы. Vшкаф=Vполукруглыйцилиндр+Vпрямоугольнаяпризма=2310+6300=8610см3. Сколько рулонов салфеток нужно Бренде, чтобы перекрыть 40 425 кубических сантиметров проема в ее комнате, если высота рулона составляет 50 см? Возьмем π=227. Решение: Чтобы определить, сколько рулонов салфеток придется использовать Бренде, нам нужно найти объем салфетки Vtissue. Объем ткани можно рассчитать путем вычитания объема полого пространства ткани, , из объема всего цилиндра. Таким образом, Vткань=Vцелый цилиндр-Vполое пространство Сначала вычисляем объем всего цилиндра, Vwholecylinder=π×r2×h=π×2822×50=227×142×50=30800 см3 Далее, чтобы вычислить объем полого пространства, нам сначала нужно вычислить его соответствующий радиус. Но диаметр полого пространства можно найти, вычитая диаметр всего цилиндра из диаметра непустого цилиндра, таким образом, диаметр полого цилиндра = 28-7 = 21 см Теперь объем полого пространства равен, Vпустое пространство=π×r2×h=227×2122×50=17325 см3. Таким образом, объем ткани равен Vткани=Vцелого цилиндра-Vполого пространства=30800-17325=13475см3. Поскольку объем помещения, которое Бренда должна заполнить, составляет 40 425 см 3 , то ей потребуется (40425÷13475)тканей=3ткани. Объем цилиндра – основные выводы
Эквивалентное сопротивление цепи как найти: Как найти эквивалентное сопротивление цепи формулаКак найти эквивалентное сопротивление цепи формулаСопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа. Электрическая цепь с последовательным соединением элементов Рис. 1.4 Рис. 1.5 Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4). На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках: Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома , и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4). Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи. Электрическая цепь с параллельным соединением элементов Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6). В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей: I = I1 + I2 + I3, т.е. , откуда следует, что . В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением . Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей: По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается. Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6) Отсюда следует, что , т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям. По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии. Электрическая цепь со смешанным соединением элементов Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений. Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно: . В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8): На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно: . Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9): На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно . Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно. Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно: . Рис. 1.10 Рис. 1.11 В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа. Соединение элементов электрической цепи по схемам «звезда» и «треугольник» В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста. Рис. 1.12 Рис. 1.13 В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям: ; ; . Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника: ; ; . После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12) . Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа. Электрическая цепь с последовательным соединением элементов Рис. 1.4 Рис. 1.5 Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4). На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках: Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома , и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4). Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи. Электрическая цепь с параллельным соединением элементов Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6). В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей: I = I1 + I2 + I3, т.е. , откуда следует, что . В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением . Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей: По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается. Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6) Отсюда следует, что , т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям. По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии. Электрическая цепь со смешанным соединением элементов Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений. Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно: . В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8): На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно: . Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9): На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно . Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно. Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно: . Рис. 1.10 Рис. 1.11 В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа. Соединение элементов электрической цепи по схемам «звезда» и «треугольник» В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста. Рис. 1.12 Рис. 1.13 В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям: ; ; . Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника: ; ; . После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12) . Расчёт электрических схем, содержащих несколько сопротивлений (резисторов), при нахождении силы тока в цепи, напряжения или мощности, производится с использованием метода свёртывания. Метод заключается в том, чтобы найти эквивалентное сопротивление выделенных участков цепи. Основная задача – замена резисторов, имеющих различное подключение относительно друг друга, на эквивалент (Rэкв.). Определение эквивалентного сопротивленияПри рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации. Последовательное соединение элементовПодобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же. Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи. В случае постоянного тока формула закона Ома для отрезка цепи имеет вид: Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула: Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности. Проходящий по цепи ток везде одинаковый: Прикладываемое напряжение является суммой напряжений на каждом резисторе: Следовательно, рассчитать можно общее: Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn. Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R. Параллельное соединениеКогда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту. Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью. Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов. Расчёт при смешанном соединении устройствПроизвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений. Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения. Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв. Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС. Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают. Физические формулы и примеры вычисленийФормулы для эквивалентных сопротивлений цепи, состоящей из пары резисторов R1 и R2, можно выделить в определённый ряд:
У смешанного соединения резистивных элементов нет конкретной формулы. Чтобы не запутаться при длительных преобразованиях, здесь допустимо воспользоваться специальной программой из интернета. Это сервис «онлайн-калькулятор». Он поможет разобраться со сложными схемами соединения, будь то треугольник, квадрат, пятиугольник или иная схематичная фигура, образованная резистивными элементами. Понять, как работают все формулы и методы, можно на конкретной задаче. На представленном первом рисунке – смешанная электрическая схема. Она включает в себя 10 резисторов. Элементы представлены в следующих номиналах:
Напряжение, поданное на схему: Требуется рассчитать токи на всех резистивных элементах. Для расчётов применяется закон Ома: I = U/R, подставляя вместо R эквивалентное сопротивление. Внимание! Для решения этой задачи сначала вычисляют общее (эквивалентное) R, после чего уже рассчитывают ток в цепи и напряжение на каждом резистивном компоненте. Вычисляя Rэкв., разделяют заданную цепь на звенья, вмещающие в себя параллельные и последовательные включения. Делают расчёты для каждого такого звена, после – всей цепи целиком. На рисунке выше изображено смешанное соединение сопротивлений. Его можно разбить на три участка:
Сопротивления R2 и R3, образующие нижнюю ветку отрезка АВ, соединены последовательно, что учитывается при расчёте. Если посмотреть на участок СD, то можно отметить смешанное включение резистивных элементов. Начало расчётов состоит в определении эквивалентных сопротивлений для этих смешанных фрагментов. Выполняют это в следующем порядке:
Зная значения полученных эквивалентов, упрощают первоначальную схему. Она будет иметь вид, представленный на рисунке ниже. Далее можно уже определить Rэкв. для участков AB, BC, CD, по формулам:
В результате выполненных вычислений получается эквивалентная схема, в которую входят три Rэкв. сопротивления. Она имеет вид, показанный на рисунке ниже. Теперь можно определить эквивалентное сопротивление всей первоначальной схемы, сложив эквивалентные значения всех трёх участков: Rэкв. = Rэкв.AB + Rэкв.BC + Rэкв.CD = 0,83 + 15 + 0,41 = 56,83 Ом. Далее, используя закон Ома, находят ток в последнем последовательном участке: I = U/ Rэкв. = 24/56,83 = 0,42 А. Зная силу тока, можно найти, какое падение напряжения на рассмотренных участках AB, BC, CD. Это выполняется следующим образом:
Следующим шагом станет определение токов на параллельных отрезках AB и CD:
Далее, чтобы найти значения токов, проходящих через R7 и R8, нужно рассчитать напряжение на этих двух резисторах. Предварительно находят падение напряжения на R9. U9 = R9*I6 = 8*0,02 = 0,16 В. Теперь напряжение, падающее на Rэкв.7,8, будет разностью между U CD и U9. U7,8 = UCD – U9= 0,17 – 0,16 = 1 В. После этого можно уже узнать значение токов, движущихся по резисторам R7 и R8, используя формулы:
Рассчитывая схемы и решая задачи по нахождению значений электрических параметров, необходимо использовать эквивалентные сопротивления. С помощью такой замены сложные построения превращаются в элементарные цепи, которые сводятся к параллельным и последовательным соединениям резистивных элементов. ВидеоРасчет сопротивления цепиРасчет сопротивления цепи необходим при решении различных задач по электротехнике. Суть заключается в приведении сложной разветвленной электрической цепи к цепи с единственным эквивалентным сопротивлением, которую называют простой электрической цепью. Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут. Допустим, что R1=10 Ом R2=20 Ом, тогда Пример 2
Два сопротивления соединены параллельно, значит при сворачивании схемы, общее сопротивление будет равно (значения R1,R2 такие же как и в примере 1) Можно заметить, что при параллельном соединении общее сопротивление меньше, чем при последовательном в несколько раз. Пример 3
В данном примере ситуация аналогична примеру 2, за тем лишь исключением, что сопротивлений три. Тогда общее сопротивление будет равно (R1,R2 прежние, R3=105 Ом)
Пример 4
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно. Пример 5Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R. R4=20 Ом, R5=40 Ом, R6=15 Ом Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник. Формула эквивалентного сопротивления резисторов: расчетЧтобы лучше понять электродинамику и физику, самостоятельно выполнять простейшие работы в доме, нужно знать, какова формула эквивалентного сопротивления и что обозначает это понятие. Об этом и другом далее в статье. Что такое эквивалентное сопротивление резисторовТочного понятия в физике не существует. Его можно вывести через ряд других терминов и формулировку закона Ома. В результате получится, что эквивалентное сопротивление резисторов — это суммарное препятствие взаимозаменяемых пассивных элементов электрической сети, чтобы заряд проходил в проводник. Сопротивляемость резисторовК сведению! Один показатель дает на выходе значение сопротивляемости без воздействия на него ряда посторонних моментов. Подробное объяснение эквивалентному сопротивлениюКак определить эквивалентное сопротивлениеЕсли в электрической сети находится несколько резистивных источников, то, чтобы подсчитать силу тока, напряжения и мощность, следует использовать один взаимозаменяемый физический показатель сопротивления электрической цепи. Любой показатель последовательного или параллельного подключения возможно преобразовать, используя эквивалентный резистор и один источник электродвижущей силы. Сопротивляемость в данном случае будет равна сумме всех препятствий пассивных устройств заряду электрической сети. Электродвижущая сила взаимозаменяемого источника будет равна сумме всех источников, которые входят в цепь. Формула определения показателяОбратите внимание! Сворачиванием цепи, используя преобразования последовательно подключенных или параллельных проводниковых приборов, можно по максимуму сделать проще дальнейший расчет в любой схеме. Исключением будут выступать цепи, которые содержат сопротивляемость по схеме в виде звезды и треугольника. Параллельное и последовательное соединение элементовВ разделе электротехники присутствует несколько вариантов того, как подключить детали в электрическую цепь. Есть параллельное и попеременное подсоединения. Их объединяет смешанная схема, которая представлена ниже. Последовательное подключение — это когда все источники соединяются друг с другом последовательно. Получаемая цепь не обладает никакими разветвлениями. Сила тока в данном случае проходит через каждый источник. Она постоянная, общее напряжение одинаковое. В случае препятствия резисторов заряду при последовательном подключении получится, что сопротивляемость будет равна сумме всех взаимозаменяемых пассивных элементов цепи. Рассчитывая параметры электротехнической схемы, не нужно применять частные параметры устройств. Их можно заменить одним значением, которое равно их суммарному показателю. Обратите внимание! Польза взаимозаменяемости компонентов заключается в возможности замены нескольких пассивных элементов электрической сети одним. Соединение элементовПараллельное подключение — это такое подсоединение источников, в котором входы всех устройств находятся в одних местах, а выходы — в других. Этими местами служат узлы. В случае эквивалентного препятствия заряду при параллельном соединении определить его можно благодаря закону Ома с преобразованием формулировки подсчета. Так, сделать необходимый расчет можно, основываясь на следующей формуле: R · R / N·R = R / N. Если это соединение нескольких индуктивных катушек, то их индуктивный показатель сопротивляемости будет рассчитываться по той же формуле, что для резисторных устройств. Важно! В случае с параллельным подключением общий показатель будет меньше любого показателя резистора. При последовательном подсоединении все наоборот. Как правильно рассчитать при смешанном соединении устройствСмешанным подключением устройств называется такой тип, при котором часть взаимозаменяемых компонентов подключается последовательно, а часть — параллельно. При смешанном подсоединении устройств определить эквивалентный показатель сопротивляемости несложно. Достаточно использовать следующую формулу: (R1 + R2) R3 / (R1 + R2 + R3) + R4. Это соединение используется, чтобы изменить сопротивляемость в пусковых реостатах, питающихся от постоянного тока. Для подсчета используются специальные онлайн-сервисы. Это помогает быстрее вычислить, упростить и ускорить расчеты электротехнических параметров. Формула расчета при смешанном соединении устройствВ результате, чтобы рассчитать эквивалентное сопротивление цепи, необходимо вспомнить про закон Ома и обязательно пользоваться указанными формулами выше. Только при смешенном типе соединения желательно вести подсчеты в онлайн-калькуляторах, так как есть риск допустить ошибку в расчетах. Эквивалентное сопротивление резисторов определить эквивалентноеРасчет реальной электрической цепи в идеальном виде невозможен по причине отсутствия математических методик учета индивидуальных параметров каждого составляющего элемента. Это естественно, так как любая деталь имеет свои паразитные характеристики, которые нереально учесть при расчетах. Для устранения этой проблемы было введено понятие эквивалентной замены. При этом в расчет принимается только одна определяющая характеристика элемента. Так, например, эквивалентное сопротивление резисторов в электрической схеме, отображает только величину сопротивления без влияния на него сторонних факторов. В электротехнике существует два основных варианта включения деталей в электрической цепи – это последовательное и параллельное соединение. Объединяющей для них является смешанная схема, которая по сути может быть разбита на участки с вышеприведенными характеристиками. Рассмотрим эквивалентное соединение резисторов в каждом отдельном случае. Эквивалентное сопротивление при последовательно соединенных резисторовПри данном типе размещения резисторов в цепи условная схема будет соответствовать рис. 1. Рисунок 1Для того чтобы определить эквивалентное сопротивление резисторов необходимо вспомнить закон Ома. Для последовательного соединения он гласит что общее, а в нашем случае эквивалентное сопротивление, соответствует следующему уравнению: Rэкв= R1+R2+R3+RN-1+RN Рассмотрим пример последовательного соединения трех резисторов, сопротивление которых равно 10, 20 и 30 Ом, соответственно. Согласно выше приведенной формуле общее сопротивление всех этих резисторов на данном участке цепи будет равно 60 Ом. Таким образом, при расчетах параметров электрической схемы нет надобности использовать индивидуальные характеристики отдельных элементов. Их можно просто заменить одним значением эквивалентным их сумме. Кроме теории, данное суммирование значений сопротивлений элементов, имеет и практическое применение – в случае необходимости всегда можно заменить несколько резисторов одним. Также имеет место и обратное утверждение – при отсутствии деталей с требуемой характеристикой ее можно заменить на несколько других, эквивалентное сопротивление которых будет соответствовать требуемому значению. Все это справедливо и для параллельного соединения резисторов, только с некоторыми особенности. Эквивалентное сопротивление при параллельном соединении резисторовОбщая схема при данном включении резисторов в цепь соответствует рис. 2. Рисунок 2 Определить эквивалентное сопротивление параллельно соединенных резисторов позволяет закон Ома согласно которому, в данном варианте, справедливо равенство: 1/R экв =1/R1+1/R2+1/R3+1/R N-1+1/RN Возвращаясь к нашему примеру с резисторами 10, 20 и 30 Ом. Можно определить эквивалентное сопротивление для данного случая, преобразуя уравнение и получаем следующую формулу: R экв = R1 х R2 х R3 / (R1 x R2) + (R1 x R3) + (R2 x R3) = 5,45 Ом
Эквивалентное сопротивление при смешанном соединении резисторовОпределение эквивалентного сопротивления при смешанном соединении резисторов не представляет особых сложностей. Для этого достаточно разбить существующую цепочку на логические составляющие – блоки. Т.е. максимально упростить схему, приведя ее в соответствие с характеристиками свойственных тому или иному типу соединения. На рис. 3 приведена типичная схема упрощения, которая получила название метод свертывания цепи. Рисунок 3Данная схема позволяет наглядно понять, как можно определить эквивалентное сопротивление резисторов при смешанном соединении. Обращаем внимание, что начинать процесс упрощения можно в произвольном порядке. Так, например, объединение резисторов R1 и R2 не обязательно должно быть первым шагом. Можно совершенно смело на первом этапе найти R экв сумме сопротивлений последовательно включенных в цепь резисторов R4 и R5. Определение эквивалентного сопротивления для резисторов необходимо осуществлять в зависимости от типа соединения. В заключение вернемся к самому понятию эквивалентной замены резисторов. В рассмотренных нами случаях речь шла об идеальном варианте. То есть в расчет принимается только величина сопротивления при нулевых значениях остальных характеристик. Также обращаем внимание, что при составлении эквивалентной схемы любых элементов электрической цепи, не только резисторов, можно вводить дополнительные переменные, которые будут влиять на конечные итоги.
Эквивалентное сопротивлениеОпределение эквивалентного сопротивления. Разница в методике определения эквивалентного сопротивления в цепях с последовательным и параллельным соединением элементов. Расчёт при смешанном соединении устройств. Физические формулы, примеры вычислений. Определение эквивалентного сопротивленияПри рассмотрении схем любых электрических или электронных устройств можно увидеть, что такие компоненты, как резисторы, имеют разные типы соединений между собой. Чтобы определить эквивалентное соединение, необходимо рассматривать два элемента, включенных в определённом порядке. Несмотря на то, что на чертеже их может быть несколько десятков, и соединены они по-разному, есть только два типа включения их друг с другом: последовательное и параллельное. Остальные конфигурации – это лишь их вариации. Что такое эквивалентное сопротивление резисторовТочного понятия в физике не существует. Его можно вывести через ряд других терминов и формулировку закона Ома. В результате получится, что эквивалентное сопротивление резисторов — это суммарное препятствие взаимозаменяемых пассивных элементов электрической сети, чтобы заряд проходил в проводник. Сопротивляемость резисторов К сведению! Один показатель дает на выходе значение сопротивляемости без воздействия на него ряда посторонних моментов. Подробное объяснение эквивалентному сопротивлению Пример 1
Цепь в данном примере состоит из двух последовательно соединенных сопротивлений, следовательно, их общее сопротивление будет равно сумме их сопротивлений. Подробнее о видах соединений тут. Допустим, что R1=10 Ом R2=20 Ом, тогда Формула сопротивленияФормула ёмкостного сопротивления выводится следующим образом:
Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление.
Последовательное соединение элементовПодобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же. Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи. Последовательное включение резисторов В случае постоянного тока формула закона Ома для отрезка цепи имеет вид: I = U/R. Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула: R = U/I. Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности. Проходящий по цепи ток везде одинаковый: I = I1= I2= … = In. Прикладываемое напряжение является суммой напряжений на каждом резисторе: U = U1 + U2+ … + Un. Следовательно, рассчитать можно общее: Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn. Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R. Как определить эквивалентное сопротивлениеЕсли в электрической сети находится несколько резистивных источников, то, чтобы подсчитать силу тока, напряжения и мощность, следует использовать один взаимозаменяемый физический показатель сопротивления электрической цепи. Любой показатель последовательного или параллельного подключения возможно преобразовать, используя эквивалентный резистор и один источник электродвижущей силы. Сопротивляемость в данном случае будет равна сумме всех препятствий пассивных устройств заряду электрической сети. Электродвижущая сила взаимозаменяемого источника будет равна сумме всех источников, которые входят в цепь. Формула определения показателя Обратите внимание! Сворачиванием цепи, используя преобразования последовательно подключенных или параллельных проводниковых приборов, можно по максимуму сделать проще дальнейший расчет в любой схеме. Исключением будут выступать цепи, которые содержат сопротивляемость по схеме в виде звезды и треугольника. Как по вах определить сопротивление цепиВ линейной электрической цепи сопротивления ее элементов не зависят от величины или направления тока или напряжения. Вольтамперные характеристики линейных элементов (зависимость напряжения на элементе от тока) являются прямыми линиями. В нелинейной электрической цепи сопротивления ее элементов зависят от величины или направления тока или напряжения. Нелинейные элементы имеют криволинейные вольтамперные характеристики, симметричные или несимметричные относительно осей координат. Сопротивления нелинейных элементов с симметричной характеристикой не зависят от направления тока. Сопротивления нелинейных элементов с несимметричной характеристикой зависят от направления тока. Например, электролампы, термисторы имеют симметричные вольтамперные характеристики (рис. 5.1), а полупроводниковые диоды — несимметричные характеристики (рис. 5.2). Статическим или интегральным сопротивлением нелинейного элемента называется отношение напряжения на элементе к величине тока. Это сопротивление пропорционально тангенсу угла наклона α между осью тока и прямой, проведенной из начала координат в точку а характеристики (рис. 5.3) . Дифференциальное или динамическое сопротивление нелинейного элемента — это величина, равная отношению бесконечно малого приращения напряжения на нелинейном сопротивлении к соответствующему приращению тока. Это сопротивление пропорционально тангенсу угла наклона β между осью тока и касательной к точке a характеристики (рис. 5.4). . При переходе от одной точки вольтамперной характеристики к соседней статическое и динамическое сопротивления нелинейного элемента меняются. Статическое и динамическое сопротивления линейного элемента одинаковы и не зависят от тока или напряжения. 5.2. Графический метод расчета нелинейных цепей постоянного тока Известные аналитические методы непригодны для расчета нелинейных электрических цепей, так как сопротивления нелинейных элементов зависят от направления и значения тока или напряжения. Применяются графоаналитические методы, основанные на применении законов Кирхгофа и использовании заданных вольтамперных характеристик (ВАХ) этих элементов. Рассмотрим электрическую цепь, состоящую из двух последовательно соединенных нелинейных сопротивлений н.с.1 и н.с.2 (рис. 5.5). ВАХ 1 и ВАХ 2 приведены на рис. 5.6. К цепи подведено напряжение U, и оно равно сумме падений напряжений на н.с.1 и н.с.2: (5.1) По всей цепи протекает один и тот же ток I, так как н.с.1 и н.с.2 соединены между собой последовательно. Для определения тока в электрической цепи нужно построить результирующую ВАХ цепи. Для построения этой характеристики следует суммировать абсциссы кривых 1 и 2 (аг = аб + ав), соответствующие одним и те же значениям тока. Далее, задаваясь произвольным значением тока (например, больше I’ и меньше I’ ) можно построить ВАХ всей цепи (рис. 5.6, кривая 3). При параллельном соединении двух нелинейных элементов (рис. 5.7) ток в неразветвленной части электрической цепи равен сумме токов в параллельных определенных ветвях. Поэтому при построении результирующей ВАХ всей цепи следует суммировать ординаты графиков 1 и 2 (рис. 5.8), соответствующие одним и те же значениям напряжения, так как к этим нелинейным элементам приложено одно и то же напряжение, равное напряжению внешней сети, т.е. источника питания. Например, для произвольного значения напряжения находим ординату аг точки для результирующей кривой 3. (аг = ав + аб) Далее задаваясь произвольным значением напряжения больше и меньше U’, можно построить ВАХ всей цепи (кривая 3). Затем, пользуясь ВАХ, можно при любом значении приложенного напряжения U (отрезок ор) найти величину общего тока I (pn = oк). Это напряжение также определяет значения токов I1 и I2 в отдельных ветвях с учетом масштаба тока mI. Как правильно рассчитать при смешанном соединении устройствСмешанным подключением устройств называется такой тип, при котором часть взаимозаменяемых компонентов подключается последовательно, а часть — параллельно. При смешанном подсоединении устройств определить эквивалентный показатель сопротивляемости несложно. Достаточно использовать следующую формулу: (R1 + R2) R3 / (R1 + R2 + R3) + R4. Это соединение используется, чтобы изменить сопротивляемость в пусковых реостатах, питающихся от постоянного тока. Для подсчета используются специальные онлайн-сервисы. Это помогает быстрее вычислить, упростить и ускорить расчеты электротехнических параметров. Формула расчета при смешанном соединении устройств В результате, чтобы рассчитать эквивалентное сопротивление цепи, необходимо вспомнить про закон Ома и обязательно пользоваться указанными формулами выше. Только при смешенном типе соединения желательно вести подсчеты в онлайн-калькуляторах, так как есть риск допустить ошибку в расчетах. Если известна мощность и напряжениеДопустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой: P=UI После несложных мы получаем формулу для вычислений I=P/U Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так: Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88: Р1 = Р2/η Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике. Находим полную мощность с учетом cosФ (он также указывается на шильдике): S = P1/cosφ Определяем потребляемый ток по формуле: Iном = S/(1,73·U) Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В. 1.4. Способы соединения сопротивлений и расчет эквивалентного сопротивления электрической цепиСопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник». Расчет сложной схемы упрощается, если сопротивления в этой схеме заменяются одним эквивалентным сопротивлением Rэкв, и вся схема представляется в виде схемы на рис. 1.3, где R=Rэкв, а расчет токов и напряжений производится с помощью законов Ома и Кирхгофа. Электрическая цепь с последовательным соединением элементов
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4). На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках: U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3, откуда следует (1.5) Rэкв = R1 + R2 + R3. Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома , и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4). Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи. Электрическая цепь с параллельным соединением элементов Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6). Рис. 1.6 В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа (1.3) можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей: I = I1 + I2 + I3, т.е. , откуда следует, что (1.6) . В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением (1.7) . Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей: gэкв = g1 + g2 + g3. По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается. Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6) U = IRэкв = I1R1 = I2R2 = I3R3. Отсюда следует, что , т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям. По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии. Электрическая цепь со смешанным соединением элементов Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений. Рис. 1.7 Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно: . В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8): Рис. 1.8 На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно: . Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9): Рис. 1.9 На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно . Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно. Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно: .
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа. Соединение элементов электрической цепи по схемам «звезда» и «треугольник» В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R12, R13, R24, R34 включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.
В мостовой схеме сопротивления R13, R12, R23 и R24, R34, R23 соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R24 R34 R23 звездой R2 R3 R4 (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям: (1.8) ; ; . Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника: (1.9) ; ; . После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12) . Параллельное соединение резисторов | ЭлектротехникаПараллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя Рис. 26. Схемы параллельного соединения приемников лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б. I1=U/R1; I2=U/R2; I3=U/R3. Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3, или I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк (23) Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой 1/Rэк = 1/R1 + 1/R2 + 1/R3 (24) Вводя в формулу (24) вместо значений 1/Rэк, 1/R1, 1/R2 и 1/R3 соответствующие проводимости Gэк, G1, G2 и G3, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов: Gэк = G1+ G2 +G3 (25) Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается. I1 : I2 : I3 = 1/R1 : 1/R2 : 1/R3 = G1 + G2 + G3 (26) В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам. Rэк=R1R2/(R1+R2) при трех параллельно включенных резисторах Rэк=R1R2R3/(R1R2+R2R3+R1R3) При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е. Rэк = R1 / n (27) Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока: I1 = I / n (28) При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно. 10.3: Последовательные и параллельные резисторыЦели обучения К концу раздела вы сможете:
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи. Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной схеме выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям. Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. РезисторысерииСчитается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений. Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке \ (\ PageIndex {2} \) ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома, падение потенциала \ (V \) на резисторе при протекании через него тока рассчитывается с использованием уравнения \ (V = IR \), где \ (I \) — ток в амперах (\ (A \)), а \ (R \) — сопротивление в Ом \ ((\ Omega) \).N V_i = 0. \] Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе. Для рисунка \ (\ PageIndex {2} \) сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю: \ [\ begin {align *} V — V_1 — V_2 — V_3 & = 0, \\ [4pt] V & = V_1 + V_2 + V_3, \\ [4pt] & = IR_1 + IR_2 + IR_3, \ end { выровнять *} \] Решение для \ (I \) \ [\ begin {align *} I & = \ frac {V} {R_1 + R_2 + R_3} \\ [4pt] & = \ frac {V} {R_ {S}}.\ end {align *} \] Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления (\ (R_ {S} \)), которое представляет собой просто сумму сопротивлений отдельных резисторов. Эквивалентное сопротивление в последовательной цепи Любое количество резисторов может быть подключено последовательно. Если \ (N \) резисторы соединены последовательно, эквивалентное сопротивление равно . N R_i.\ label {серия эквивалентных сопротивлений} \]Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут. Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
Стратегия В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \). Решение
Значение Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной. Упражнение \ (\ PageIndex {1} \) Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серии по девять луковиц.Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
2 в 20 степени: Сравнить 10 в 20 степени и 110 в 10 степени.Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.72036854776000 1805 1805
71 to 80Поиск по номерам
Как считать с показателями в Python? · Kodify Возведение в степень — это математическая операция, при которой значение умножается на себя определенное количество раз. В ЭТОЙ СТАТЬЕ: # Вычисление показателей степени на языке программирования PythonВ математике показатель степени числа говорит, сколько раз это число многократно умножается само на себя (Википедия, 2019). Обычно мы выражаем эту операцию как b n , где b — это основание, а n — это показатель степени или степень. Мы часто называем этот тип операции «b в n-й степени», «b в степени n» или, наиболее кратко, как «b в n» (Википедия, 2019).). Python имеет три способа возведения значений в степень:
Поскольку каждый подход дает правильный ответ, не стесняйтесь выбирать любой. Если вы не уверены, используйте Давайте подробнее рассмотрим каждый вариант, предлагаемый Python. # Вычисление степени Python с помощью оператора ** Первый способ возведения числа в степень — это оператор Python Оператор 3**3 # Возвращает: 27 Оператор
# Вычислить экспоненты Python с помощью функции
В последнем бите кода функция Исходный список: [12, 89, -12,5, 0,443, 1310, 3110, 125, 54] Возведение в степень 3: [1728, 704969, -1953.125, 0.086938307, 22480 | , 30080231000, 1953125, 157464]
Кстати, второй список не всегда нужен. Если вам не нужно сохранять исходные значения, вы можете перезаписать список его возведенными в степень значениями. # Увеличить каждое число до 3 и заменить # числа в исходном списке значений значения = [pow (значение, 3) для значения в значениях] # Возведение значений в степень с помощью цикла Python for Цикл Вот как мы повышаем значения до определенного значения с помощью обычного цикла # Некоторые случайные значения
значения = [
12, 89, -12,5, 0,443,
1310, 3110, 125, 54
]
# Экспоненты
полномочия = [
2, 3, 4, 5,
1,5, -3, 2, 0,5
]
результаты = []
# Проходим по значениям и повышаем
# каждый в указанной степени
для i значение в перечислении (значения):
results.append (pow (значение, полномочия [i]))
# Выходные данные
print("Исходные значения:\n", значения)
print("Показатели:\n", степени)
print("Результат:\n", результаты) Эта мини-программа составляет три списка. Затем делаем цикл Внутри цикла мы добавляем новое значение в список После завершения цикла мы заполнили список Исходные значения: [12, 89, -12,5, 0,443, 1310, 3110, 125, 54] Показатели: [2, 3, 4, 5, 1,5, -3, 2, 0,5] Исход: [144, 704969, 24414.0625, 0.017061555810443, 47414.03800563711, 3.32444255497e-11, 15625, 7.34846 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Блок | Сумма |
|---|---|
| Галлоны бензина Пассажирские автомобили, работающие на бензине Хотя легковые автомобили не являются единицей потребления энергии, они потребляют энергию.  Для целей калькулятора легковые автомобили определяются как 2-осные 4-шинные транспортные средства, включая легковые автомобили, фургоны, пикапы и спортивные/внедорожные автомобили. Чтобы ознакомиться с методологией, используемой для определения годовых выбросов парниковых газов на пассажирское транспортное средство, посетите страницу «Расчеты и ссылки», где приведены используемые уравнения и источники. Для целей калькулятора легковые автомобили определяются как 2-осные 4-шинные транспортные средства, включая легковые автомобили, фургоны, пикапы и спортивные/внедорожные автомобили. Чтобы ознакомиться с методологией, используемой для определения годовых выбросов парниковых газов на пассажирское транспортное средство, посетите страницу «Расчеты и ссылки», где приведены используемые уравнения и источники. Киловатт-часы, которых удалось избежать Выберите киловатт-часы, которых удалось избежать, при вводе данных об использовании электроэнергии, которого удалось избежать за счет энергоэффективности, или производства электроэнергии на ископаемом топливе, которого удалось избежать за счет возобновляемых источников энергии. Обратите внимание, что в калькуляторе используются средние национальные коэффициенты выбросов для электроэнергии, которые могут быть неточными для вашего региона. Для получения более точных оценок используйте региональные коэффициенты выбросов, доступные в AVERT или eGRID.  Используемые киловатт-часы Выберите киловатт-часы, используемые при вводе данных об использовании электроэнергии, таких как годовое потребление электроэнергии домохозяйством или компанией. Обратите внимание, что в калькуляторе используются средние национальные коэффициенты выбросов для электроэнергии, которые могут быть неточными для вашего региона. Для получения более точных оценок используйте региональные коэффициенты выбросов, доступные в AVERT или eGRID. MCF природного газа Термы природного газа |
* Калькулятор эквивалентности использует различные коэффициенты выбросов для электроэнергии в зависимости от того, избегается ли она или потребляется; в обычных масштабах программы и проекты по энергоэффективности и возобновляемым источникам энергии не влияют на выработку электроэнергии при базовой нагрузке, поэтому в калькуляторе используется коэффициент выбросов, не связанный с базовой нагрузкой. Для потребления электроэнергии калькулятор использует средний коэффициент выбросов, который включает как базовую, так и небазовую выработку. Обратите внимание, что в калькуляторе используются средние национальные коэффициенты выбросов для электроэнергии, которые могут быть неточными для вашего региона. Для более точных оценок. используйте региональные коэффициенты выбросов, доступные в AVERT или eGRID.
Для потребления электроэнергии калькулятор использует средний коэффициент выбросов, который включает как базовую, так и небазовую выработку. Обратите внимание, что в калькуляторе используются средние национальные коэффициенты выбросов для электроэнергии, которые могут быть неточными для вашего региона. Для более точных оценок. используйте региональные коэффициенты выбросов, доступные в AVERT или eGRID.
Введите данные для одного или нескольких газов: Если вы введете данные для нескольких газов, эквивалентность будет рассчитана для суммы всех введенных газов.
Двуокись углерода или CO 2 Эквивалент* Двуокись углерода (CO 2 ) является основным парниковым газом, выделяемым в результате деятельности человека. CO 2 естественным образом присутствует в атмосфере как часть земного углеродного цикла. Основным видом деятельности человека, при котором происходит выброс CO2, является сжигание ископаемого топлива (уголь, природный газ и нефть) для производства энергии и транспорта, хотя некоторые промышленные процессы и изменения в землепользовании также выделяют CO 2 . Ссылка
Ссылка
Тонны Фунты Метрические тонны Килограммы
Углерод Выбросы парниковых газов могут быть выражены в единицах количества самого газа (например, 5 тонн метана), эквивалентного количества двуокиси углерода (например, 25 тонн эквивалента CO2) или в единицах углерода ( например, 6,8 т углерода). Углерод часто используется в качестве единицы измерения при отслеживании выбросов в рамках углеродного цикла. Чтобы перевести количество углерода в эквивалентное количество углекислого газа, умножьте его на 3,67.
Тонны Фунты Метрические Тонны Килограммы
CH 4 — Метан Метан (CH 4 ) представляет собой парниковый газ, выделяемый при добыче и транспортировке угля, природного газа и нефти или при разложении органических отходов на муниципальных свалках и при разведении скота. . Метан также выделяется естественными источниками, такими как водно-болотные угодья. Фунт за фунтом, воздействие CH 4 в 25 раз больше, чем CO 2 за 100-летний период. Ссылка
Ссылка
Тонны Фунты Метрические Тонны Килограммы
N 2 O — Закись азота Закись азота (N 2 O) является мощным парниковым газом, который образуется как естественным путем, так и в результате деятельности человека. Основные источники включают методы ведения сельского хозяйства, которые добавляют азот в почву (например, использование удобрений), сжигание ископаемого топлива и некоторые промышленные процессы. Влияние 1 фунта N 2 O на потепление атмосферы почти в 300 раз больше, чем 1 фунта CO 2 . Ссылка
Тонны Фунты Метрические тонны Килограммы
Гидрофторуглеродные газы Фторсодержащие газы образуются в результате деятельности человека. Они выбрасываются при их использовании в качестве заменителей озоноразрушающих веществ (например, в качестве хладагентов) и в результате промышленных процессов, таких как производство алюминия и полупроводников. В целом, фторсодержащие газы являются наиболее мощным и долгоживущим типом парниковых газов, выделяемых в результате деятельности человека. LinkHCFC-22HFC-23HFC-32HFC-125HFC-134aHFC-143aHFC-152aHFC-227eaHFC-236faHFC-4310meeR-404AR-407AR-407CR-410AR-507A
В целом, фторсодержащие газы являются наиболее мощным и долгоживущим типом парниковых газов, выделяемых в результате деятельности человека. LinkHCFC-22HFC-23HFC-32HFC-125HFC-134aHFC-143aHFC-152aHFC-227eaHFC-236faHFC-4310meeR-404AR-407AR-407CR-410AR-507A
Тонны Фунты Метрические Тонны Килограммы
Перфторуглеродные газы Фторированные газы образуются в результате деятельности человека. Они выбрасываются при их использовании в качестве заменителей озоноразрушающих веществ (например, в качестве хладагентов) и в результате промышленных процессов, таких как производство алюминия и полупроводников. В целом, фторсодержащие газы являются наиболее мощным и долгоживущим типом парниковых газов, выделяемых в результате деятельности человека. СсылкаCF4C2F6C4F10C6F14
Тонны Фунты Метрические Тонны Килограммы
SF 6 — Гексафторид серы Фторсодержащие газы образуются в результате деятельности человека. Они выбрасываются при их использовании в качестве заменителей озоноразрушающих веществ (например, в качестве хладагентов) и в результате промышленных процессов, таких как производство алюминия и полупроводников. В целом, фторсодержащие газы являются наиболее мощным и долгоживущим типом парниковых газов, выделяемых в результате деятельности человека. Ссылка
Они выбрасываются при их использовании в качестве заменителей озоноразрушающих веществ (например, в качестве хладагентов) и в результате промышленных процессов, таких как производство алюминия и полупроводников. В целом, фторсодержащие газы являются наиболее мощным и долгоживущим типом парниковых газов, выделяемых в результате деятельности человека. Ссылка
тонныфунтыметрические тонныкилограммы
*Если расчетные выбросы метана, закиси азота или других газов, отличных от CO 2 , уже выражены в эквиваленте CO 2 или эквиваленте углерода, введите свои цифры в строку для CO 2 или углерода эквивалент.
Тонны Фунты Метрические тонны Килограммы двуокиси углерода (CO 2 ) эквивалент
Это эквивалентно выбросам парниковых газов от:
легковых автомобилей с бензиновым двигателем, пройденных в течение одного года
миль, пройденных средним легковым автомобилем с бензиновым двигателем
Это эквивалентно выбросам CO
2 из:галлона израсходованного бензина
галлона израсходованного дизельного топлива
pounds of coal burned
tanker trucks’ worth of gasoline
homes’ energy use for one year
homes’ electricity use for one year
railcars стоимость сожженного угля
баррелей израсходованной нефти
баллоны с пропаном, используемые для домашнего барбекю
угольные электростанции за год
газовые электростанции за год
количество заряженных смартфонов 3 3
Это эквивалентно выбросам парниковых газов, которых удалось избежать благодаря:
тонн отходов, переработанных вместо захороненных
мусоровозов отходов, переработанных вместо захороненных
мусорные мешки с отходами, переработанными вместо вывозимых на свалку
ветряные турбины, работающие на год
лампы накаливания перешли на светодиоды 3
Это эквивалентно секвестрации углерода:
саженцы деревьев, выращенные в течение 10 лет
акра лесов США за один год1033
NFL Week 2 Power Rankings: Chiefs поднимаются на 2-е место, в то время как команды Super Bowl проигрывают, но не слишком остро реагируют на дикий старт
Автор Пит Приско
• 1 мин чтения
У нас была одна неделя сезона НФЛ, и скажем так, это уже безумие.
«Сан-Франциско Форти Найнерс», считавшиеся возможными участниками Суперкубка, проиграли «Чикагским медведям», которые далеки от этого.
Хьюстонские техасцы и Индианаполис Кольтс сыграли вничью в игре, в которой техасцы фактически доминировали.
«Цинциннати Бенгалс» проиграли в овертайме «Питтсбург Стилерс» из-за заблокированного дополнительного очка в финальном матче в основном матче, который начался с того, что Джо Барроу выглядел ужасно.
«Нью-Орлеан Сэйнтс» требовался поздний удар, чтобы сплотиться и победить «Атланта Фэлконс», поскольку их предположительно доминирующая защита явно не выглядела так в той игре.
Это было просто странное открытие сезона. Единственными двумя постоянными были доминирование, продемонстрированное Buffalo Bills и Kansas City Chiefs. Они оба открылись на гастролях громкими победами, которые отличались высокими атаками, а их звездные распасовщики устраивали впечатляющие шоу.
Они оба открылись на гастролях громкими победами, которые отличались высокими атаками, а их звездные распасовщики устраивали впечатляющие шоу.
Билли остаются на первом месте в моем рейтинге силы, а Чифс теперь на втором месте. Только помните, что это всего одна неделя для всех 32 команд. Это означает чрезмерную реакцию всю эту неделю, ведущую ко второй неделе.
Например:
Упаковщики готовы.
Патриоты не могут забить.
Орлы едут на Супербоул.
Возможно, одно или два из них будут правдой, но не сейчас. Слишком рано. Мы не сможем получить истинную оценку этой лиги до октября. Мы действительно не узнаем истинных соперников до ноября, когда действительно начнется разделение.
Так что примите это во внимание при чтении этого рейтинга силы. Тот факт, что команда вырвалась вперед, не означает, что она должна подняться на 10 позиций. Пусть немного поиграет.
Медведи не закончат с лучшим результатом, чем 49ers, даже если они побьют их. Или будут? Эта лига иногда сходит с ума, как снова напомнила нам первая неделя.
Или будут? Эта лига иногда сходит с ума, как снова напомнила нам первая неделя.
Крупнейшие движущие силы
8 Вороны
9 Ковбои
Рк | Команды | Изменить | Запись | |
|---|---|---|---|---|
| 1 | счета | После того, как они выступили против «Рэмс», нет сомнений, что они должны быть на первом месте. Они послали сообщение остальной части лиги с этой победой. | — | 1-0-0 |
| 2 | Чифы | Патрик Махоумс показал против «Кардиналов», что он все еще может играть на высоком уровне без Тайрика Хилла. Это преступление будет просто прекрасно. Это преступление будет просто прекрасно. | 1 | 1-0-0 |
| 3 | Буканьеры | Защита действительно впечатлила против Ковбоев. Но временами наигранное нападение выглядело не так. В линии нападения есть травмы, что не очень хорошо для «Нового Орлеана». | 4 | 1-0-0 |
| 4 | Орлы | Если Джален Хёртс сможет сыграть так же, как против «Лайонс», это может быть команда глубокого плей-офф. Однако защита не была хорошей, что должно вызывать беспокойство. Однако защита не была хорошей, что должно вызывать беспокойство. | 4 | 1-0-0 |
| 5 | Зарядные устройства | С этим распасовщиком в лице Джастина Герберта и такими пас-рашерами в лице Халила Мака и Джоуи Бозы у них есть две основные вещи, необходимые для победы. Теперь у них есть шанс показать Чифс на этой неделе в большой ранней игре. | 4 | 1-0-0 |
| 6 | Святые | Они нашли способ противостоять Соколам, но это было некрасиво. Что случилось с защитой, которая должна была быть такой доминирующей? Им лучше начать против Тампа-Бэй. Что случилось с защитой, которая должна была быть такой доминирующей? Им лучше начать против Тампа-Бэй. | — | 1-0-0 |
| 7 | викинги | Они добились впечатляющего старта, доминирующим образом обыграв Packers. Защита действительно впечатлила, и Джастина Джефферсона было не остановить. | 5 | 1-0-0 |
| 8 | Вороны | Против «Джетс» не всегда было красиво, но Ламар Джексон добился успеха во втором тайме. В будущем это преступление станет намного сложнее. В будущем это преступление станет намного сложнее. | 8 | 1-0-0 |
| 9 | Упаковщики | Они выглядели ужасно, проиграв викингам. Аарон Роджерс был избит и плохо играл. Защита, которая должна была быть доминирующей, таковой не была. | 7 | 0-1-0 |
| 10 | Бараны | Они сильно уступили Bills. Назовем это просто плохой игрой. Эта команда придет в норму с Шоном Маквеем в качестве тренера. Эта команда придет в норму с Шоном Маквеем в качестве тренера. | 6 | 0-1-0 |
| 11 | Бенгалы | Джо Берроу выглядел так, будто пропустил предсезонку против «Стилерс» раньше, но он пришел в норму. На линии все еще есть проблемы, которые необходимо исправить, чтобы защитить его. | 6 | 0-1-0 |
| 12 | Дельфины | «Дельфины» обыграли «Патриотов» и никогда особо не угрожали, благодаря защите. Туа Таговайлоа был хорош, но нападение забило только один тачдаун. Туа Таговайлоа был хорош, но нападение забило только один тачдаун. | 6 | 1-0-0 |
| 13 | 49ers | Трей Лэнс был очень плох против Медведей. Это не очень хорошо. Но давайте спишем это на условия и посмотрим, как он проявит себя на этой неделе. | 3 | 0-1-0 |
| 14 | Кольты | Они выглядели ужасно на протяжении большей части своего первого матча против техасцев, но сплотились из-за ничьей. Они должны быть лучше, чем это, но теперь им предстоит еще одна выездная игра в Джексонвилле, где они играют не очень хорошо. Они должны быть лучше, чем это, но теперь им предстоит еще одна выездная игра в Джексонвилле, где они играют не очень хорошо. | 3 | 0-0-1 |
| 15 | Рейдеры | Нападение против «Чарджерс» показало, что за этим будет интересно наблюдать. Защита должна быть лучше. | 2 | 0-1-0 |
| 16 | Титаны | Проигрыш Гигантам после доминирования на протяжении большей части игры будет болезненным. Они просто не сделали достаточно в нападении, чтобы убрать их. Они просто не сделали достаточно в нападении, чтобы убрать их. | 2 | 0-1-0 |
| 17 | Командиры | Карсон Венц добился хороших результатов в победе над «Ягуарами», что является хорошим знаком для этой команды. У них есть плеймейкеры в нападении. | 3 | 1-0-0 |
| 18 | Браунс | Отдайте должное Джейкоби Бриссету за его победную игру против Каролины, даже после неравномерного выступления на протяжении большей части игры. Во втором тайме защита потерпела поражение. Во втором тайме защита потерпела поражение. | 3 | 1-0-0 |
| 19 | Стилерс | Защита сыграла важную роль в победе над «Бенгалс» в овертайме. Потеря Т.Дж. Уатт — сокрушительный удар по обороне, который усилит давление на нападение. | 4 | 1-0-0 |
| 20 | Бронкос | «Бронкос» нужно поработать над атакой на линии ворот, управлением временем и ситуациями в конце игры. В остальном поражение от «Сиэтла» в первом матче пошло на пользу защите. В остальном поражение от «Сиэтла» в первом матче пошло на пользу защите. | 3 | 0-1-0 |
| 21 | Кардиналы | Они выглядели как большой беспорядок против Руководителей. Это может быть долгий сезон, даже после того, как мы продлили большие контракты с тренером и генеральным менеджером. | 2 | 0-1-0 |
| 22 | Патриоты | У них большие проблемы в нападении. Мак Джонс должен улучшить свою игру, иначе сезон будет длинным. Мак Джонс должен улучшить свою игру, иначе сезон будет длинным. | — | 0-1-0 |
| 23 | Гиганты | Они отправились в путь и обыграли хорошую команду Титанов. Они сделали это после раннего отставания, что является хорошим знаком для этой молодой группы. Сакуон Баркли произвел фурор. | 5 | 1-0-0 |
| 24 | Ковбои | Поскольку Дак Прескотт выбыл на 6-8 недель из-за травмы большого пальца, у «Ковбоев» большие проблемы. С ним они выглядели ужасно в нападении, так что же теперь будет с Купером Рашем? С ним они выглядели ужасно в нападении, так что же теперь будет с Купером Рашем? | 9 | 0-1-0 |
| 25 | Медведи | Отдайте должное этой команде за победу над 49ers. Защита была выдающейся в плохих условиях. Нарушению предстоит много работы. | 5 | 1-0-0 |
| 26 | Сихокс | Они добились успеха, когда им пришлось играть против Денвера с их защитой на линии ворот. Нападение переместило мяч, но нужно забить больше. Нападение переместило мяч, но нужно забить больше. | 5 | 1-0-0 |
| 27 | Пантеры | Бейкеру Мэйфилду и игре в пас потребовалось слишком много времени, чтобы начать игру против «Кливленда», но в конце концов это произошло. Они даже вели в счете с опозданием, но защита их подвела. | 3 | 0-1-0 |
| 28 | Ягуары | У них были шансы против «Вашингтона», но они просто не смогли сделать остановку в конце четвертой четверти, когда это было необходимо. Нападение должно быть лучше. Нападение должно быть лучше. | 3 | 0-1-0 |
| 29 | Техасцы | У них была ничья против «Кольтов», но это должно было ощущаться как поражение после того, как они потеряли преимущество в 17 очков. Были и хорошие вещи, но это должно было задеть. Решение, принятое в овертайме, по праву должно быть подвергнуто сомнению. | 3 | 0-0-1 |
| 30 | Львы | То, как их защита играла против «Иглз», не является хорошим знаком в будущем. Они околачивались, но когда этого уже недостаточно? Они околачивались, но когда этого уже недостаточно? | 3 | 0-1-0 |
| 31 | Джетс | Они не смогут вернуть Зака Уилсона достаточно быстро. Джо Флакко не был хорош против своей бывшей команды, поскольку они бросили его 59 раз. | 2 | 0-1-0 |
| 32 | Соколы | Они слонялись вокруг и, вероятно, должны были победить Святых Сандей. Отдайте должное Артуру Смиту за то, что эта недоукомплектованная команда была готова к игре. Отдайте должное Артуру Смиту за то, что эта недоукомплектованная команда была готова к игре. | — | 0-1-0 |
Наши последние истории
Профиль Тони Граймса на драфте НФЛ 2023 года
Спортивный персонал CBS • 1 мин. чтения
Взгляд агента: окончательный состав 2022 года из 53 человек
Джоэл Корри • 15 минут чтения
Отчет о травмах в середине недели NFL Week 2: Аллен Чарджерс выбыл
Джордан Даджани • 8 минут чтения
Выбор НФЛ DFS, советы по футболу в четверг вечером
Спортивный персонал CBS • 3 минуты чтения
Львы впервые с 2020 года стали фаворитами
Крис Бенгель • 1 мин.



 Этот этап является основным для построения графика функции методом дифференциального исчисления.
Этот этап является основным для построения графика функции методом дифференциального исчисления.

 Любые другие ур-ния с ответом. Есть возможность решать ур-ния численно.
Любые другие ур-ния с ответом. Есть возможность решать ур-ния численно. От элементарной алгебры до комплексных расчетов, Mathway мгновенно решает самые сложные математические задачи — просто введите условия задачи (или наведите камеру и сделайте фото!) и вы немедленно получите бесплатный ответ. Необходимы подробные, пошаговые решения? Mathway — как карманный частный репетитор, который без промедления помогает в решении домашних заданий в любом месте и в любое время.
От элементарной алгебры до комплексных расчетов, Mathway мгновенно решает самые сложные математические задачи — просто введите условия задачи (или наведите камеру и сделайте фото!) и вы немедленно получите бесплатный ответ. Необходимы подробные, пошаговые решения? Mathway — как карманный частный репетитор, который без промедления помогает в решении домашних заданий в любом месте и в любое время.
 mathway.com/terms
mathway.com/terms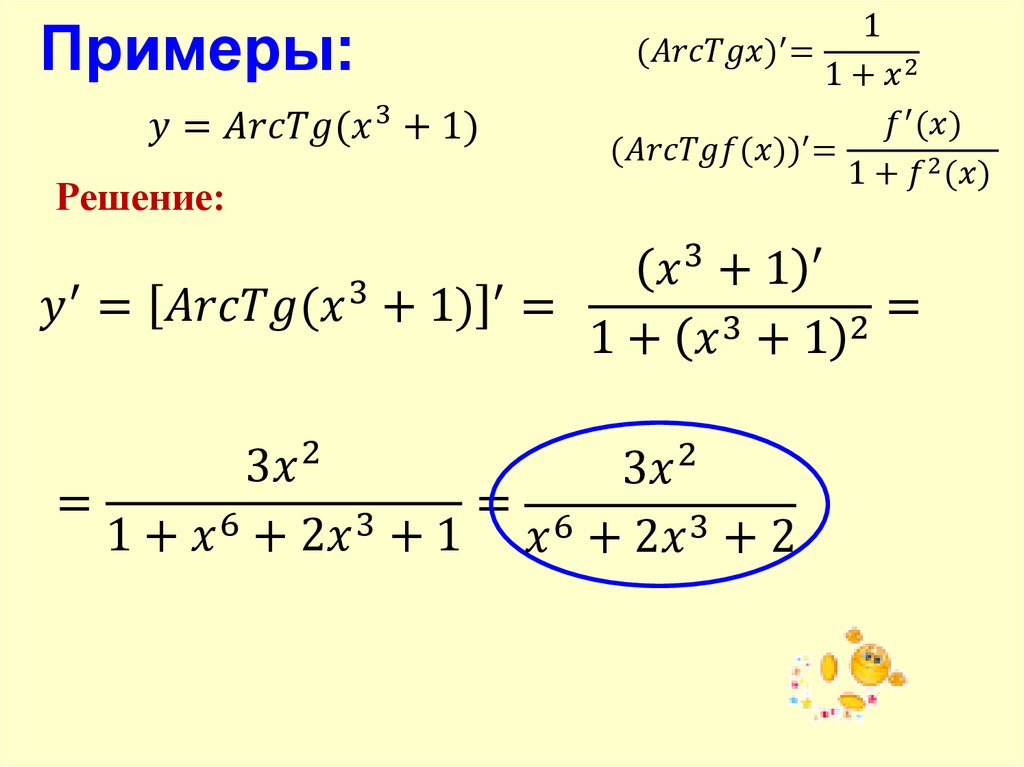 Подробные сведения доступны в политике конфиденциальности разработчика.
Подробные сведения доступны в политике конфиденциальности разработчика. Подробнее
Подробнее
 Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?
Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

 Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных. д.
д. Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции:
Рассмотрим пример, чтобы стало совсем понятно. Допустим, нужно вычислить частные производные первого порядка следующей функции: Третьего порядка – производная от производной второго порядка и т.д.
Третьего порядка – производная от производной второго порядка и т.д. С нами вы не останетесь один на один с проблемой!
С нами вы не останетесь один на один с проблемой! е. найдем вторую производную по «игрек»:
е. найдем вторую производную по «игрек»: От полученной функции найдем частную производную по «икс»:
От полученной функции найдем частную производную по «икс»: 3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1.
3
1.4
1.5
1.6
1.7
1.8
1.9
1.10
1. 11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1.
11
1.12
1.13
1.14
1.15
1.16
1.17
1.18
1. 19
19 8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2.
8
2.9
2.10
2.11
2.12
2.13
2.14
2.15
2. 16
2.17
2.18
16
2.17
2.18 6
6 8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.
8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4. 16
4.17
4.18
4.19
4.20
16
4.17
4.18
4.19
4.20 3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5.
3
5.4
5.5
5.6
5.7
5.8
5.9
5.10
5. 11
5.12
5.13
5.14
11
5.12
5.13
5.14 4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6.
4
6.5
6.6
6.7
6.8
6.9
6.10
6.11
6. 12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6.
12
6.13
6.14
6.15
6.16
6.17
6.18
6.19
6. 20
6.21
6.22
6.23
6.24
6.25
6.26
6.27
6.
20
6.21
6.22
6.23
6.24
6.25
6.26
6.27
6. 28
6.29
6.30
6.31
6.32
6.33
6.34
6.35
6.
28
6.29
6.30
6.31
6.32
6.33
6.34
6.35
6. 36
6.37
6.38
6.39
6.40
6.41
36
6.37
6.38
6.39
6.40
6.41 2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7.
2
7.3
7.4
7.5
7.6
7.7
7.8
7.9
7. 10
7.11
7.12
7.13
7.14
7.15
7.16
7.17
7.
10
7.11
7.12
7.13
7.14
7.15
7.16
7.17
7. 18
7.19
7.20
18
7.19
7.20 5
8.6
8.7
8.8
8.9
8.10
8.11
8.12
8.
5
8.6
8.7
8.8
8.9
8.10
8.11
8.12
8. 13
8.14
8.15
8.16
13
8.14
8.15
8.16 5
9.6
9.7
9.8
9.9
9.10
9.11
9.12
9.
5
9.6
9.7
9.8
9.9
9.10
9.11
9.12
9. 13
9.14
13
9.14 6
10.7
10.8
10.9
10.10
10.11
10.12
10.13
10.
6
10.7
10.8
10.9
10.10
10.11
10.12
10.13
10. 14
10.15
10.16
10.17
10.18
14
10.15
10.16
10.17
10.18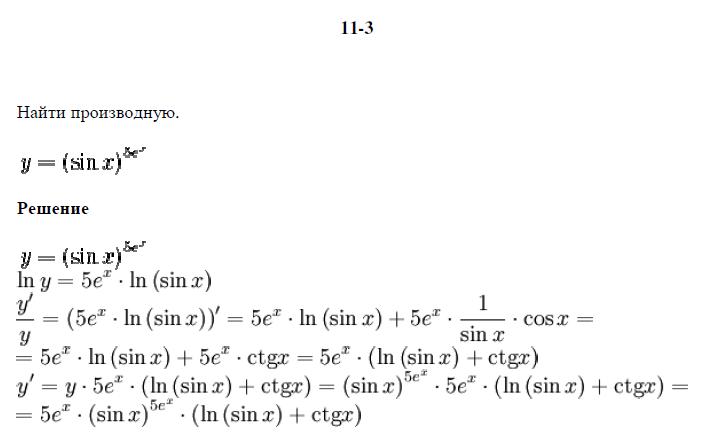 3
11.4
11.5
11.6
11.7
11.8
11.9
11.10
11.
3
11.4
11.5
11.6
11.7
11.8
11.9
11.10
11. 11
11.12
11.13
11
11.12
11.13 5
12.6
12.7
12.8
12.9
5
12.6
12.7
12.8
12.9 3
13.4
13.5
13.6
13.7
13.8
13.9
13.10
13.
3
13.4
13.5
13.6
13.7
13.8
13.9
13.10
13. 11
13.12
13.13
13.14
13.15
13.16
13.17
13.18
13.
11
13.12
13.13
13.14
13.15
13.16
13.17
13.18
13. 19
13.20
19
13.20 6
14.7
14.8
14.9
14.10
14.11
14.12
14.13
14.
6
14.7
14.8
14.9
14.10
14.11
14.12
14.13
14. 14
14.15
14
14.15 6
15.7
15.8
15.9
15.10
15.11
15.12
15.13
15.
6
15.7
15.8
15.9
15.10
15.11
15.12
15.13
15. 14
15.15
15.16
15.17
15.18
15.19
15.20
15.21
15.
14
15.15
15.16
15.17
15.18
15.19
15.20
15.21
15. 22
22 7
16.8
16.9
16.10
16.11
16.12
16.13
16.14
16.
7
16.8
16.9
16.10
16.11
16.12
16.13
16.14
16. 15
16.16
16.17
16.18
16.19
15
16.16
16.17
16.18
16.19 калькулятор пределов онлайн присваивает значения определенным функциям в точках, где значения не определены, таким образом, чтобы они согласовывались с ближайшими или близкими значениями. В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда. С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.
калькулятор пределов онлайн присваивает значения определенным функциям в точках, где значения не определены, таким образом, чтобы они согласовывались с ближайшими или близкими значениями. В большинстве курсов по исчислению мы работаем с пределом, что означает, что легко начать думать, что предел исчисления существует всегда. С другой стороны, это также помогает решить предел по правилу Лопиталя, согласно которому предел, когда мы делим одну функцию на другую, остается таким же после того, как мы берем производную каждой функции.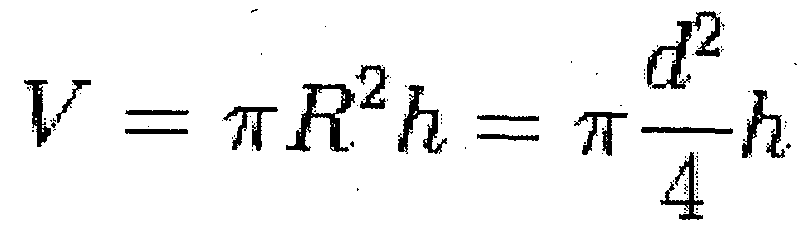
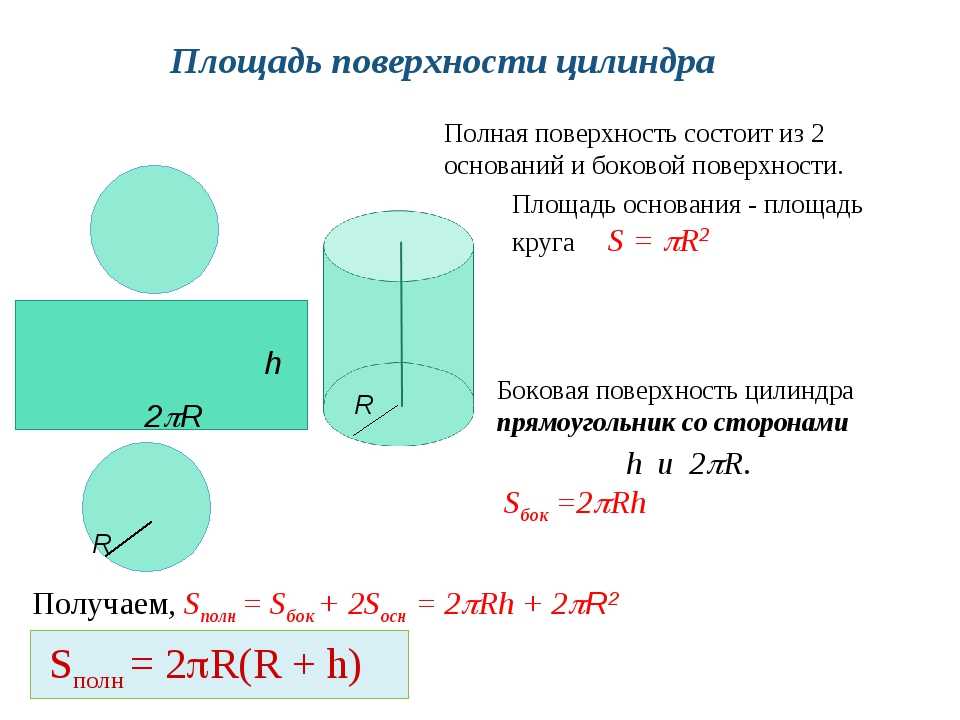
 Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. 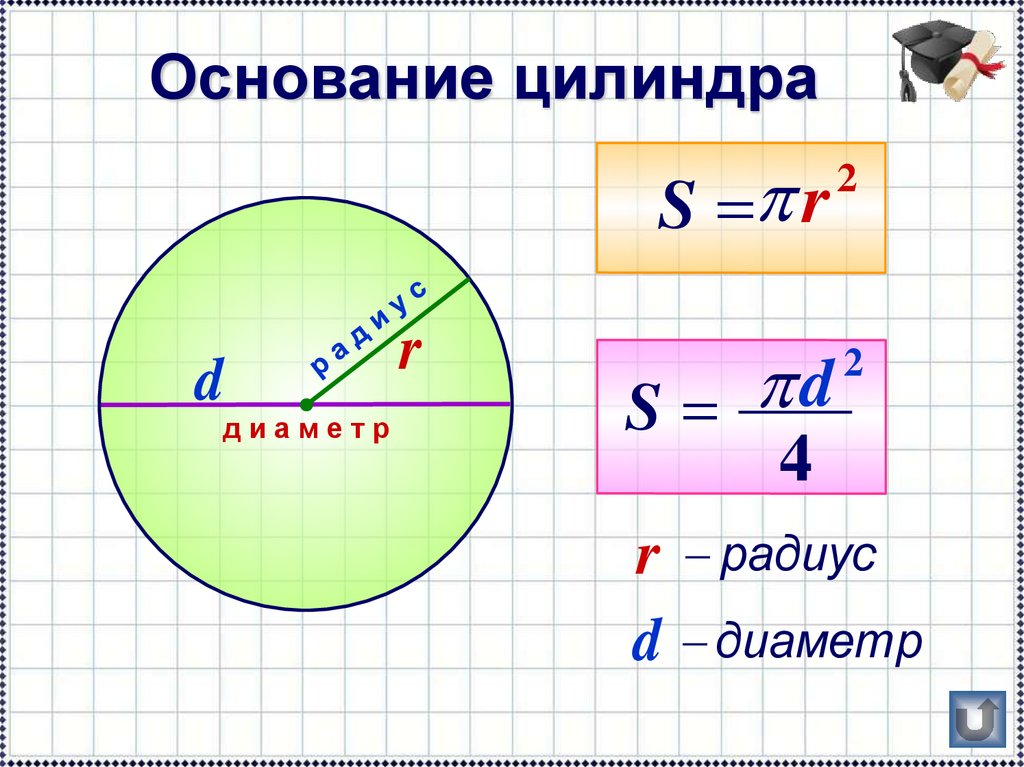 Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности. 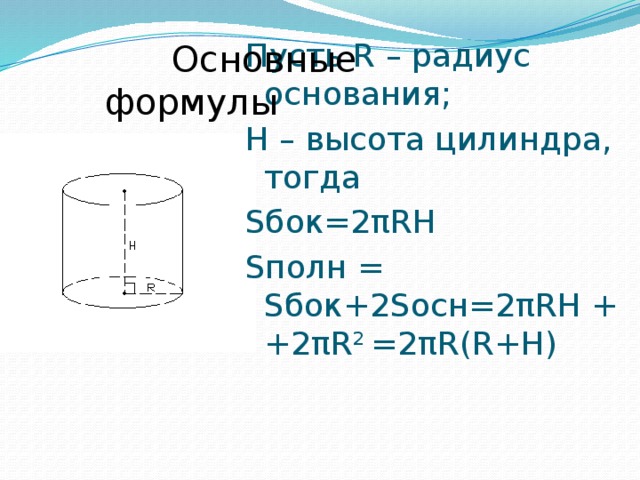 .. вычисление …
.. вычисление …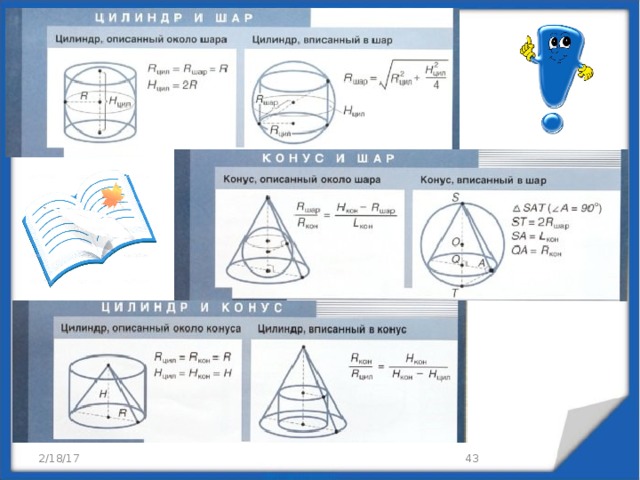 .. вычисление …
.. вычисление …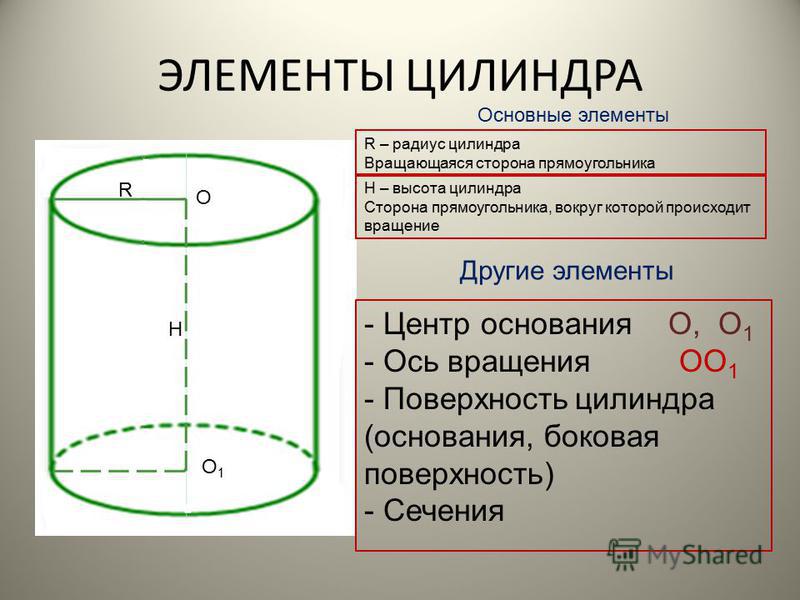
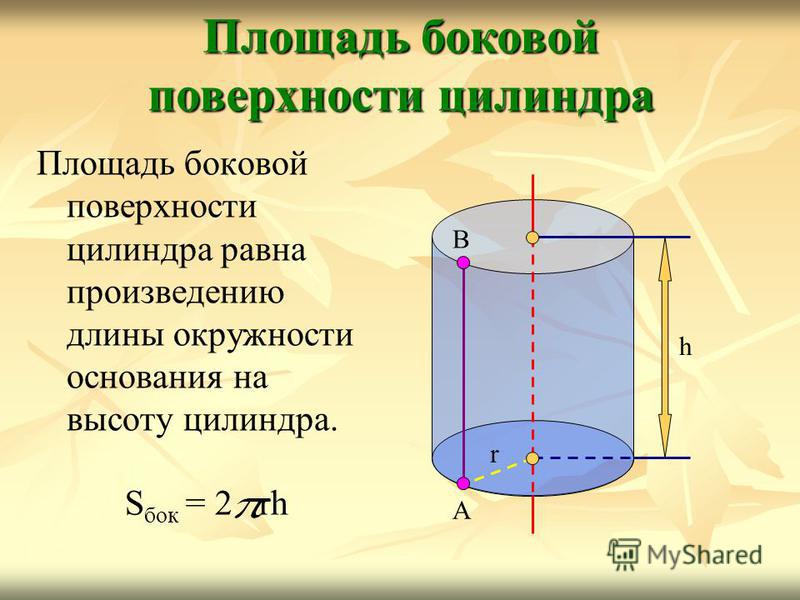

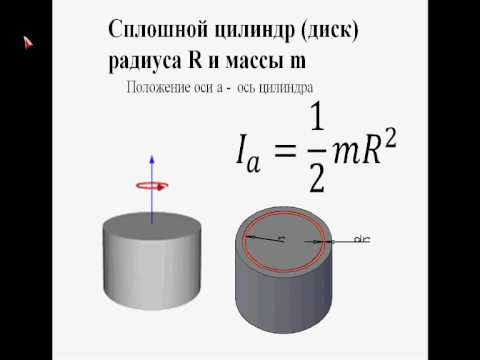 В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.
В данном случае объём полости будет равен объёму цилиндра, который полностью занимает эту полость.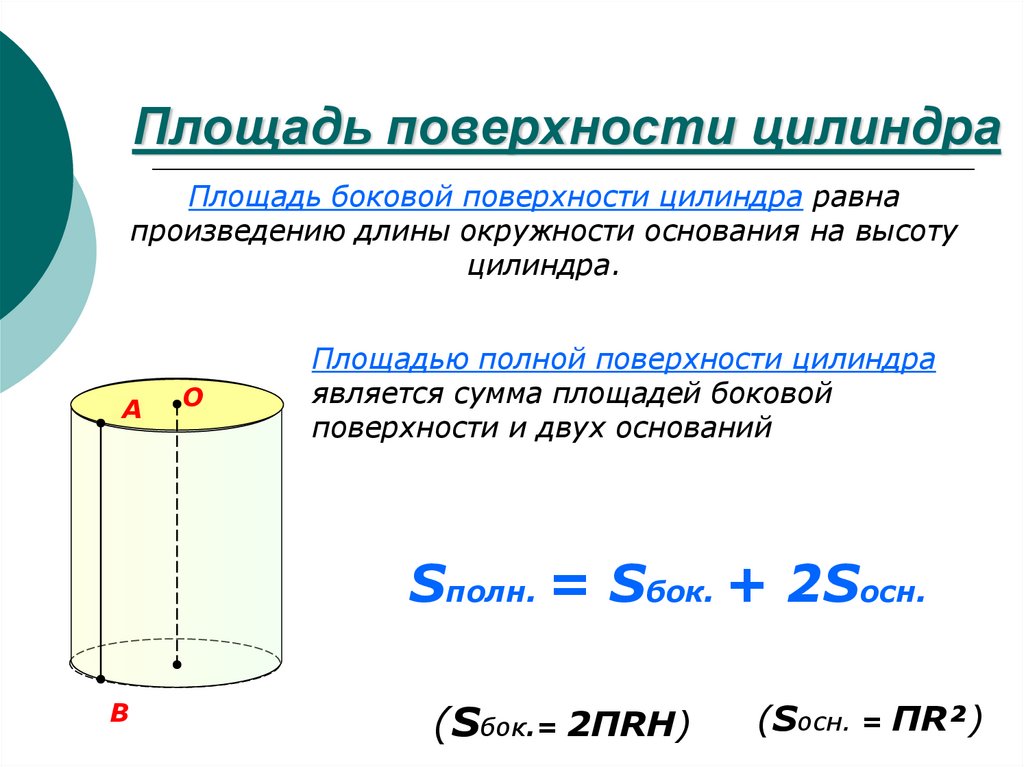
 д.
д.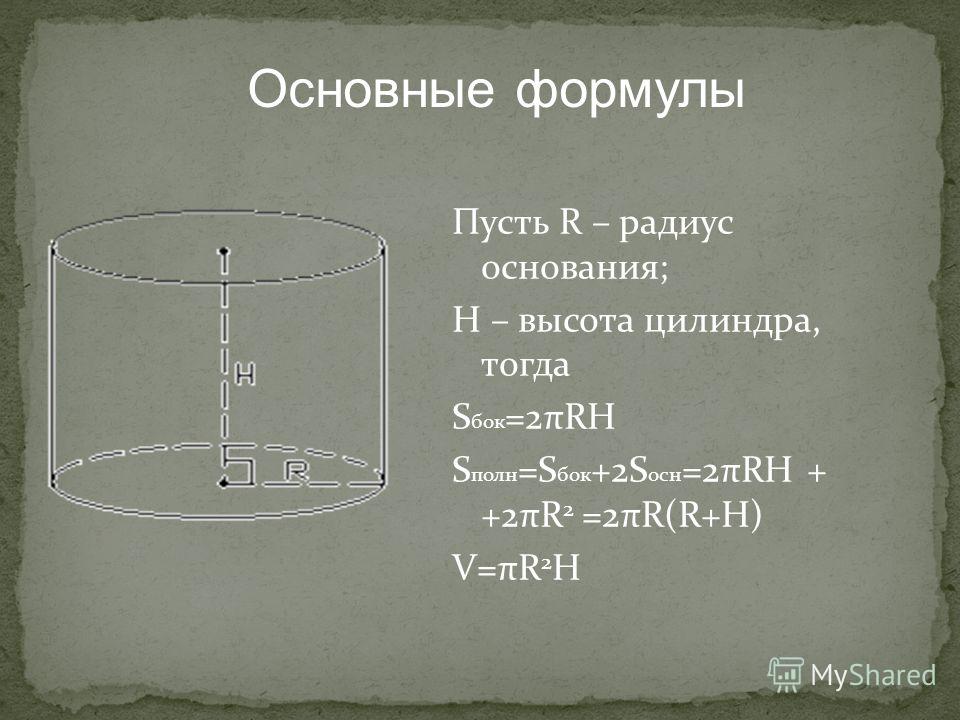
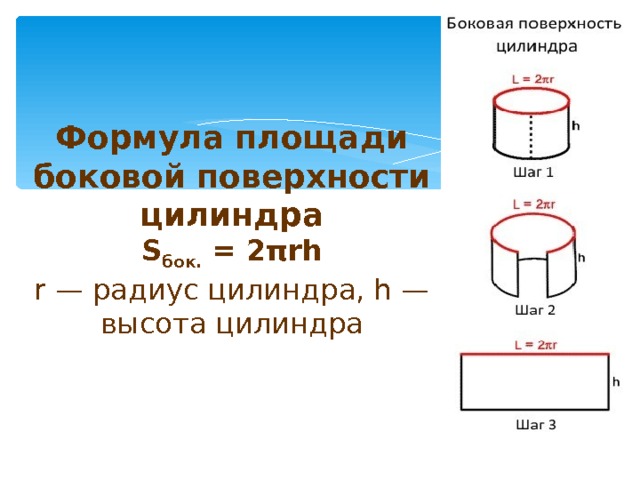 Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.
Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.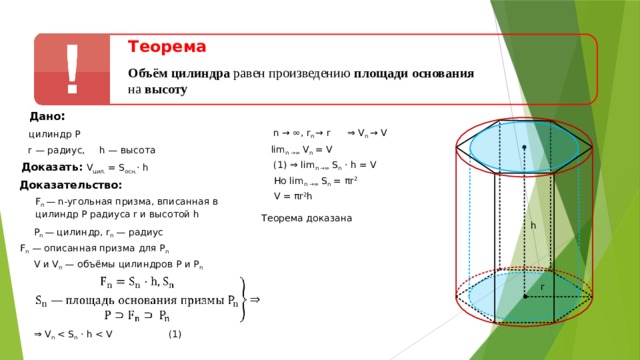 Объем таких цилиндрических предметов исчисляется в литрах.
Объем таких цилиндрических предметов исчисляется в литрах. Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.
Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.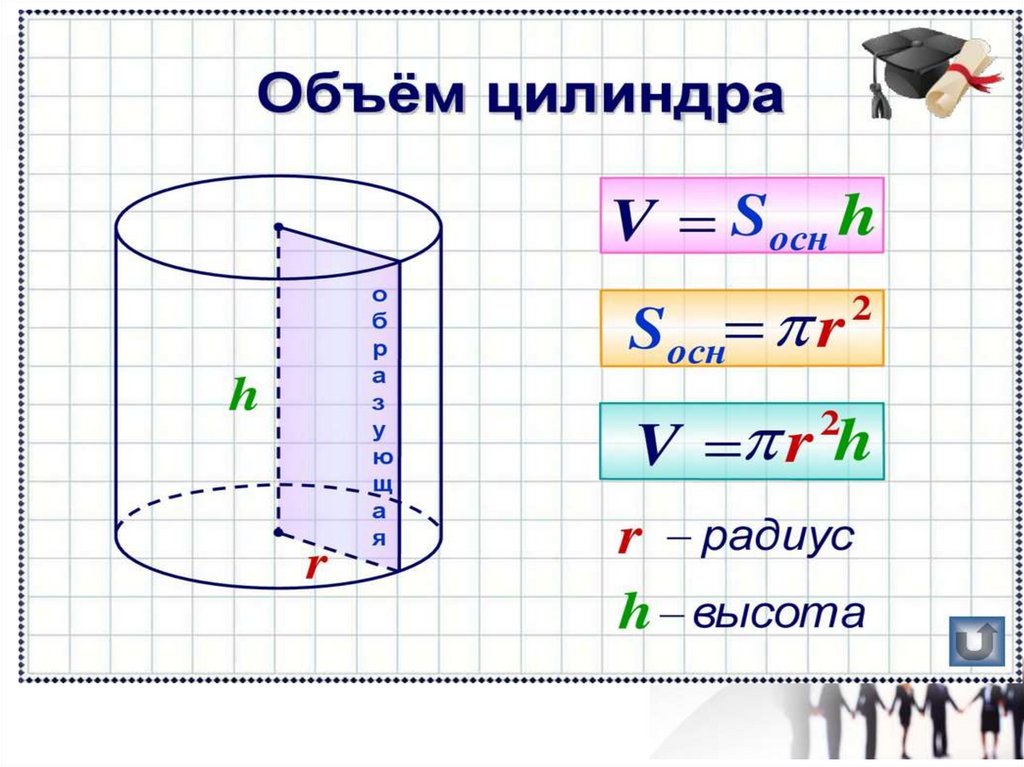 То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.
То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.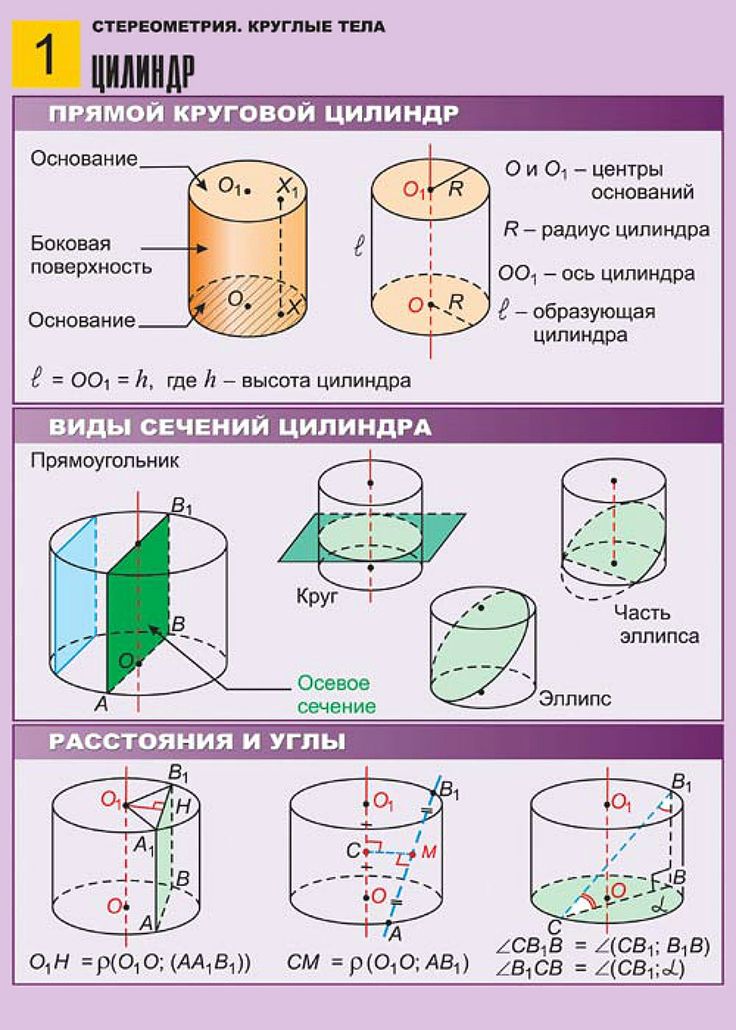
 Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:
Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением: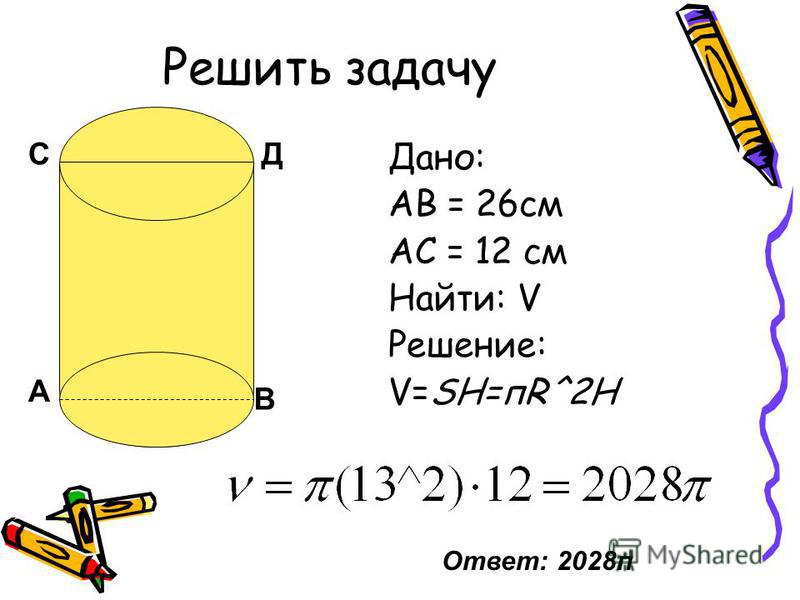 Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
 3 $$
3 $$
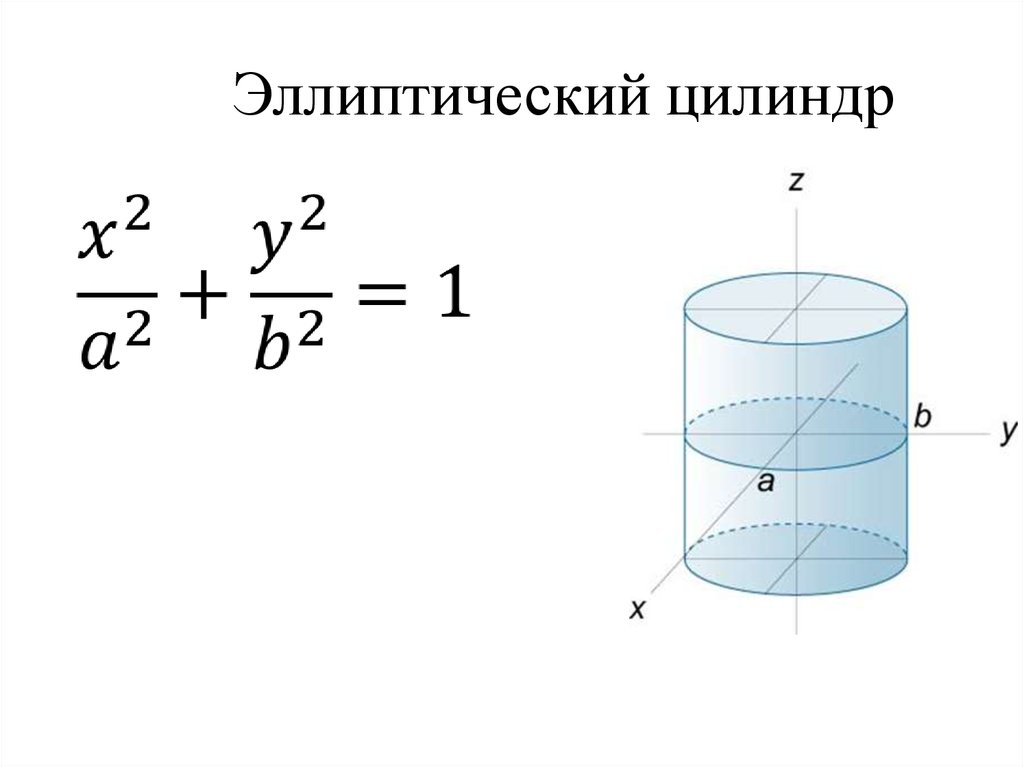
 5 мм (R — 47.75 мм).
5 мм (R — 47.75 мм).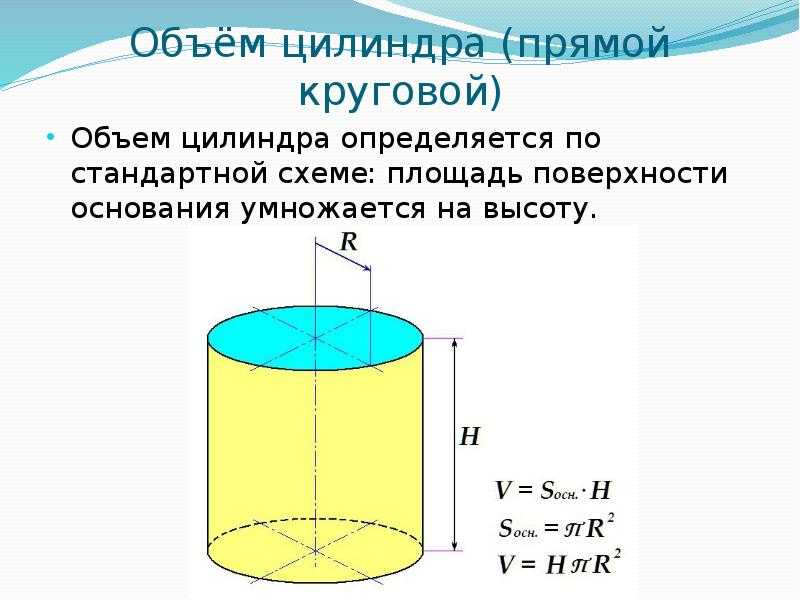
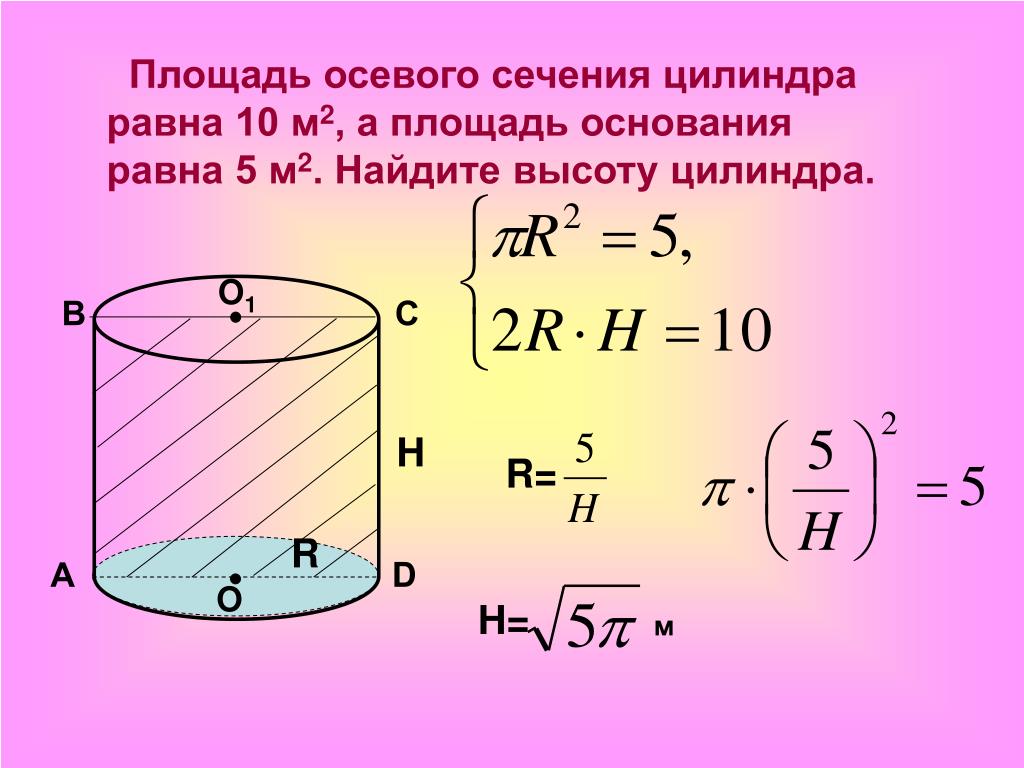 характеристиках конкретной детали либо же определить, какой объем поршневой поможет штангенциркуль.
характеристиках конкретной детали либо же определить, какой объем поршневой поможет штангенциркуль.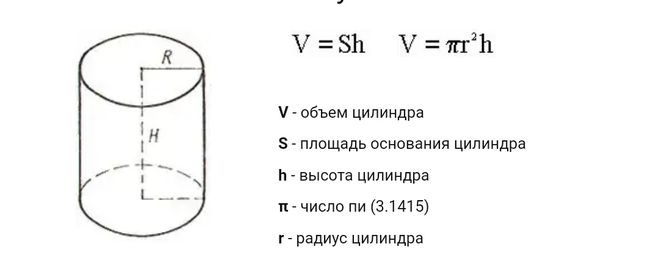
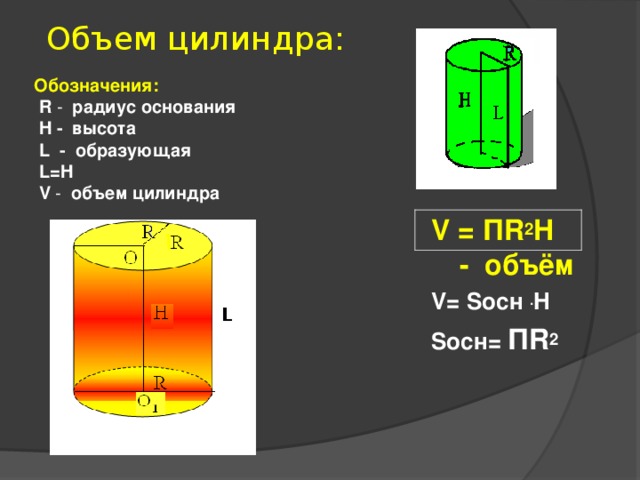 ). 1000 кубических сантиметров равны 1 литру. Единица самого точного измерения объема именно куб сантиметры, поскольку, когда объем двигателя автомобиля указывается в литрах, то производится округление до целого числа после запятой. Например, объем 2,4 л. равны 2429 см3.
). 1000 кубических сантиметров равны 1 литру. Единица самого точного измерения объема именно куб сантиметры, поскольку, когда объем двигателя автомобиля указывается в литрах, то производится округление до целого числа после запятой. Например, объем 2,4 л. равны 2429 см3.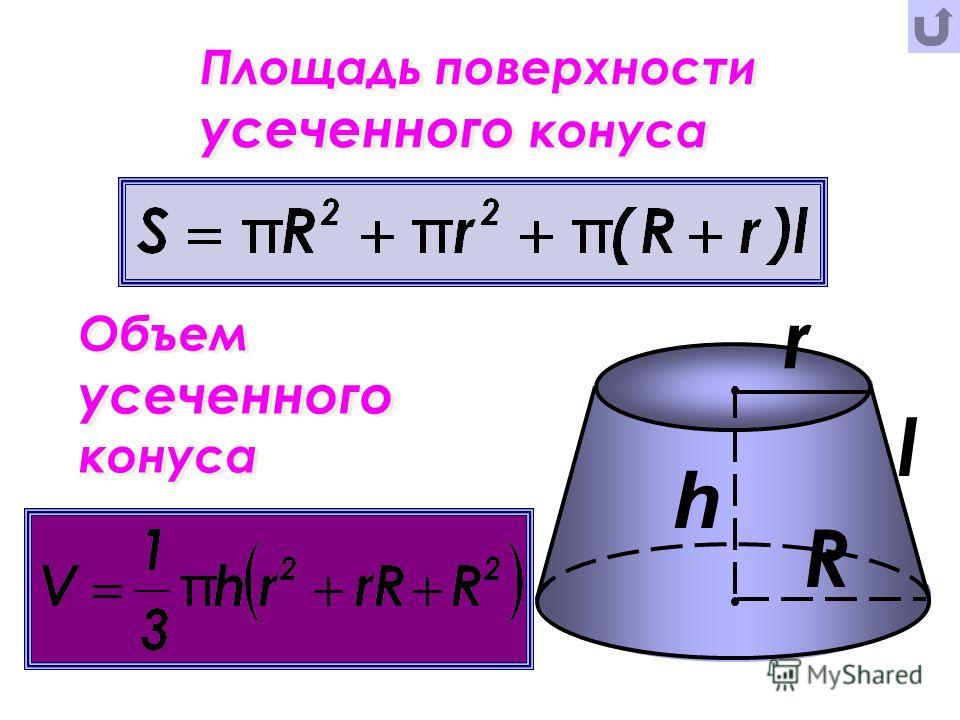
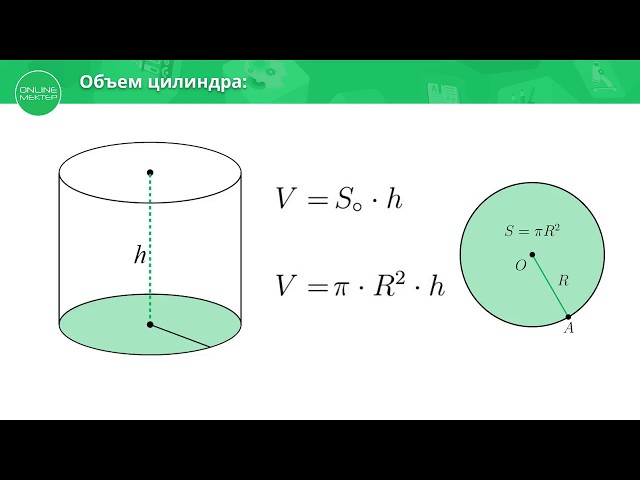 Это будет форма искаженного стекла, о которой говорилось выше.
Это будет форма искаженного стекла, о которой говорилось выше.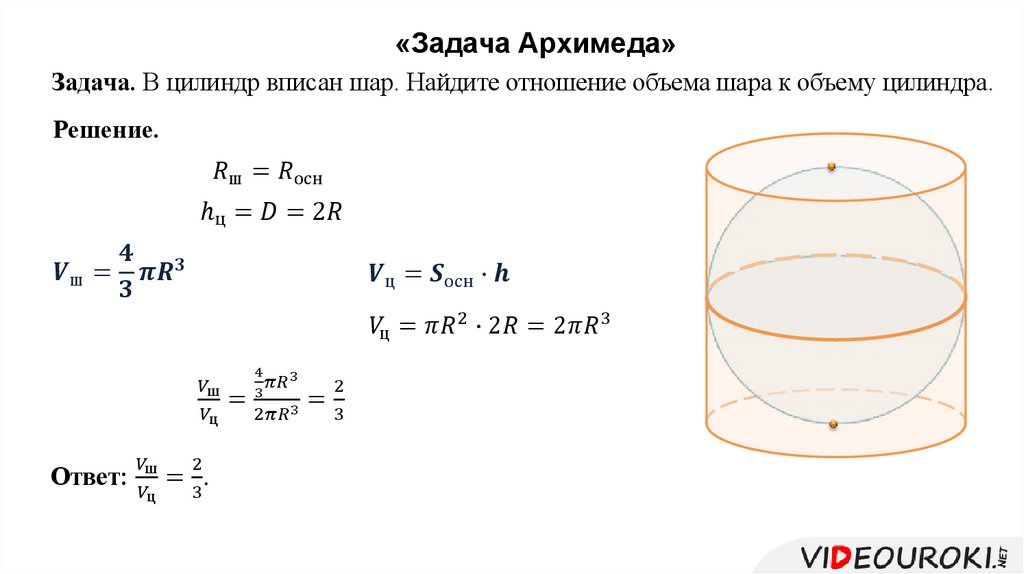 Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра?
Следовательно, вес полученной воды будет равен весу цилиндра. Вам может быть интересно, как найти объем цилиндра? Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.
Это правило справедливо для всех трехмерных фигур, известных в математике. Например, в кубоиде, если вы знаете площадь одной его стороны, а затем умножаете ее на высоту или ширину, то есть на оставшуюся сторону, вы получите объем.


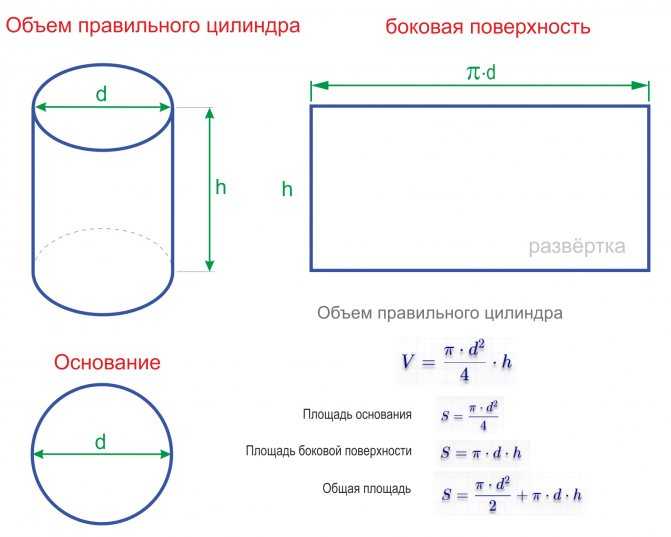 Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другим вариантом является расчет объема цилиндрической оболочки (полого цилиндра).
Если вы хотите выяснить, сколько воды помещается в банку, кофе в вашу любимую кружку или даже объем соломинки для питья — вы находитесь в правильном месте. Другим вариантом является расчет объема цилиндрической оболочки (полого цилиндра).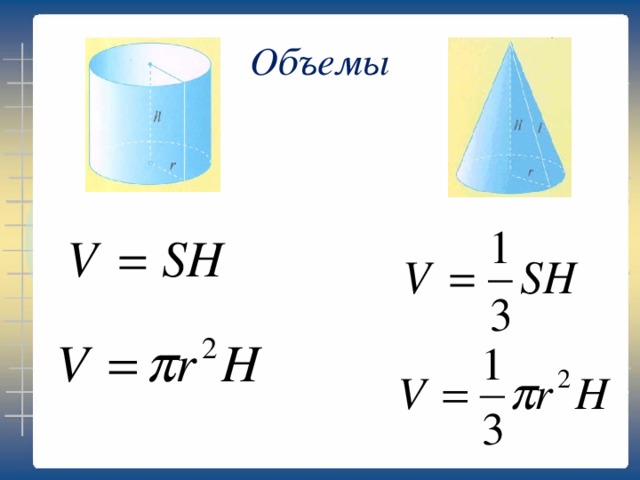 Формула объема полого цилиндра:
Формула объема полого цилиндра: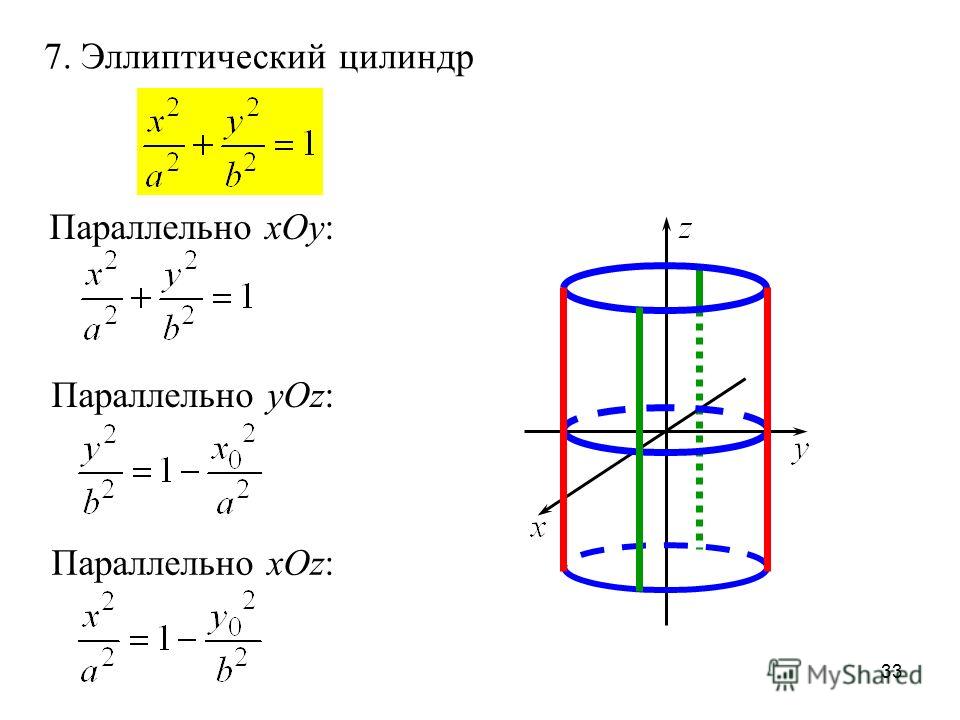 Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям.
Как рассчитать объем косого цилиндра? Формула такая же, как и для прямого. Только помните, что высота должна быть перпендикулярна основаниям. Они составляют большое количество природных объектов на Земле!
Они составляют большое количество природных объектов на Земле! Результат — вес цилиндра.
Результат — вес цилиндра.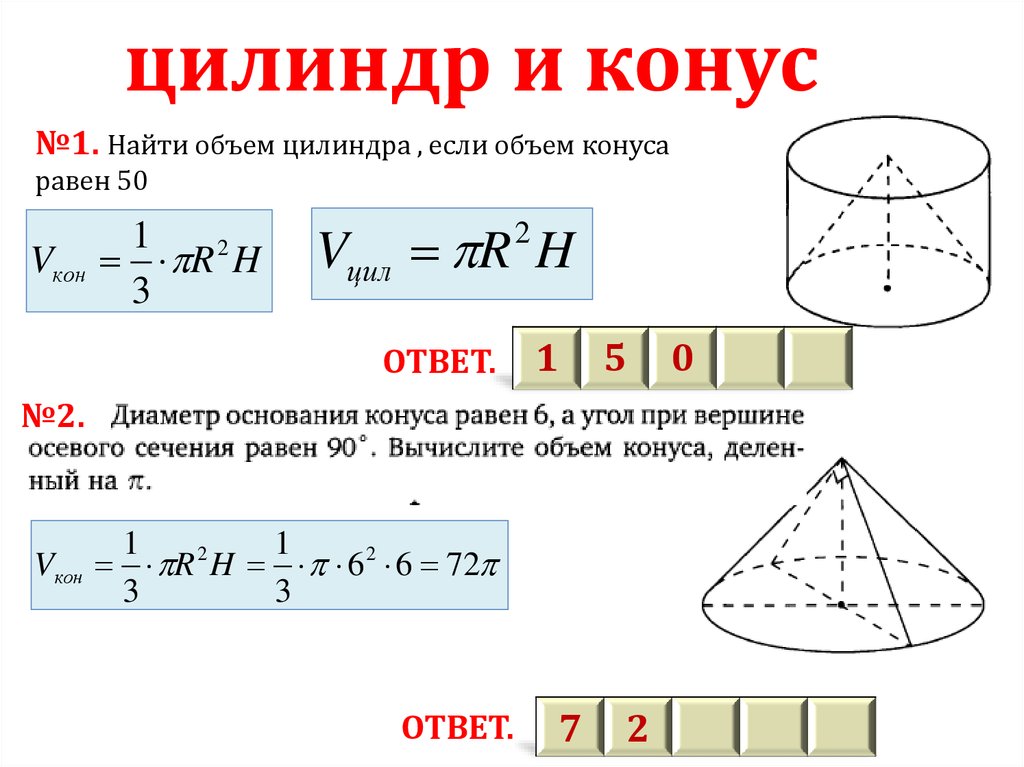

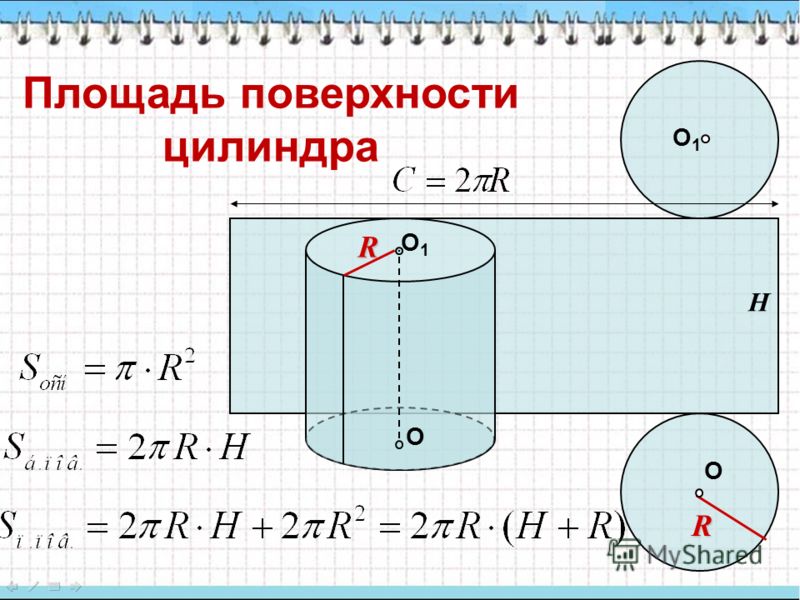
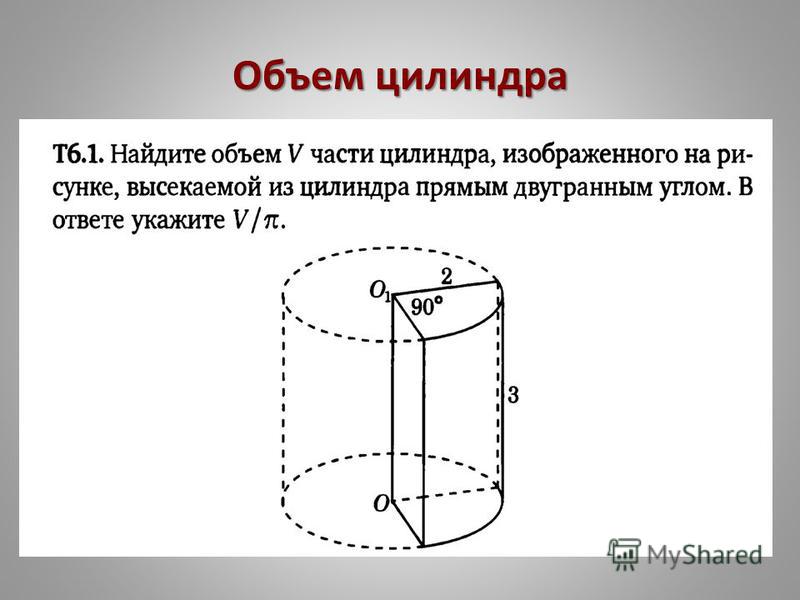
 Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их:
Цилиндр – это трехмерная фигура с двумя конгруэнтными и параллельными одинаковыми основаниями. Существуют разные типы цилиндров. Их: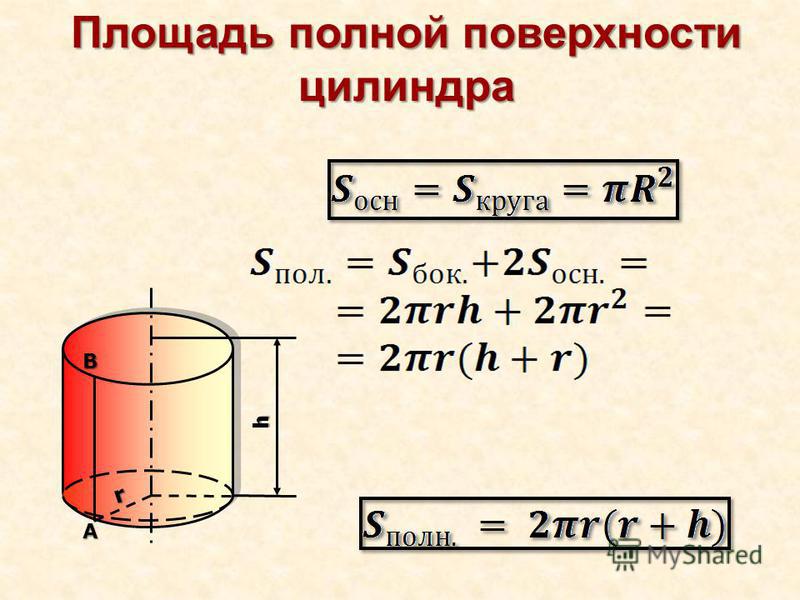
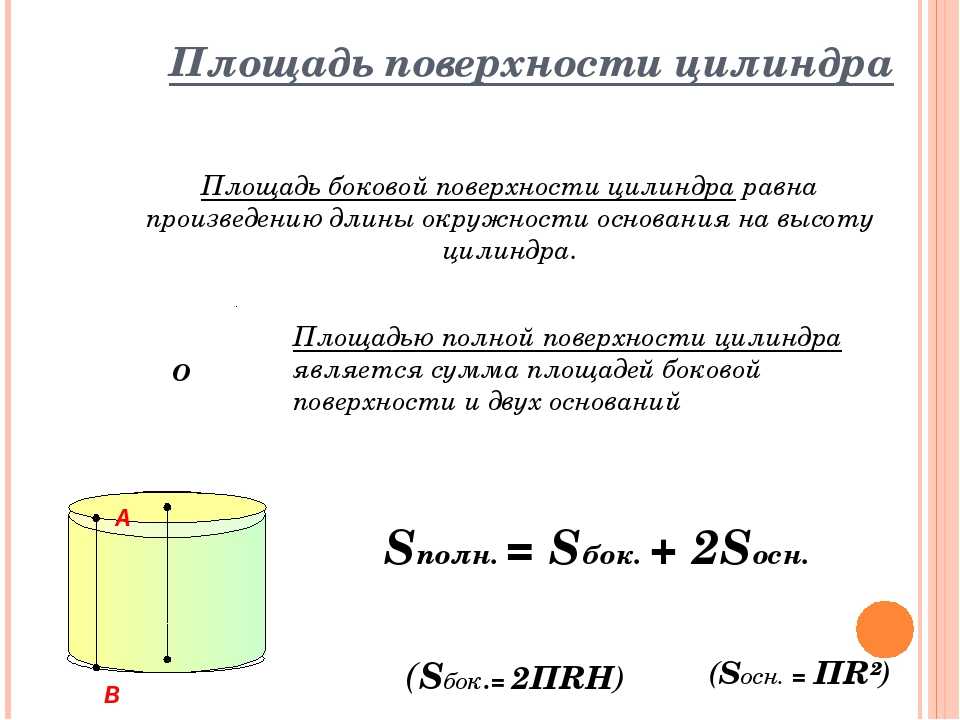 Мы знаем, что площадь призмы рассчитывается по формуле
Мы знаем, что площадь призмы рассчитывается по формуле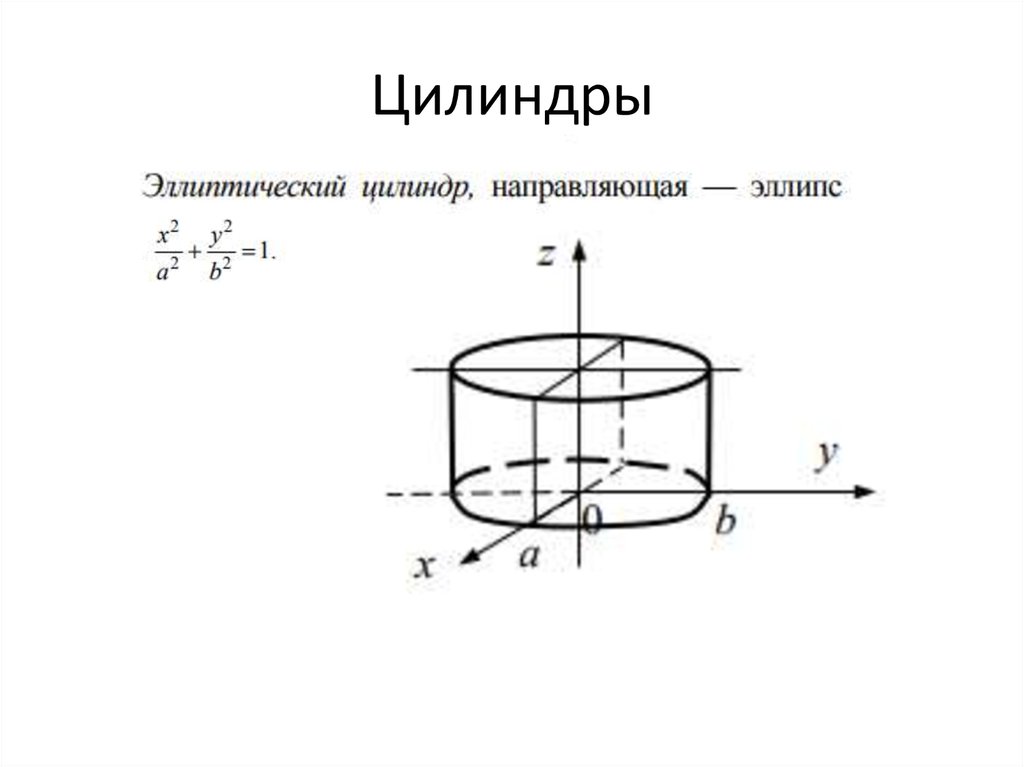 Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен
Кроме того, мы знаем, что площадь эллипса, радиусы которого равны «а» и «b», равна πab. Таким образом, объем эллиптического цилиндра равен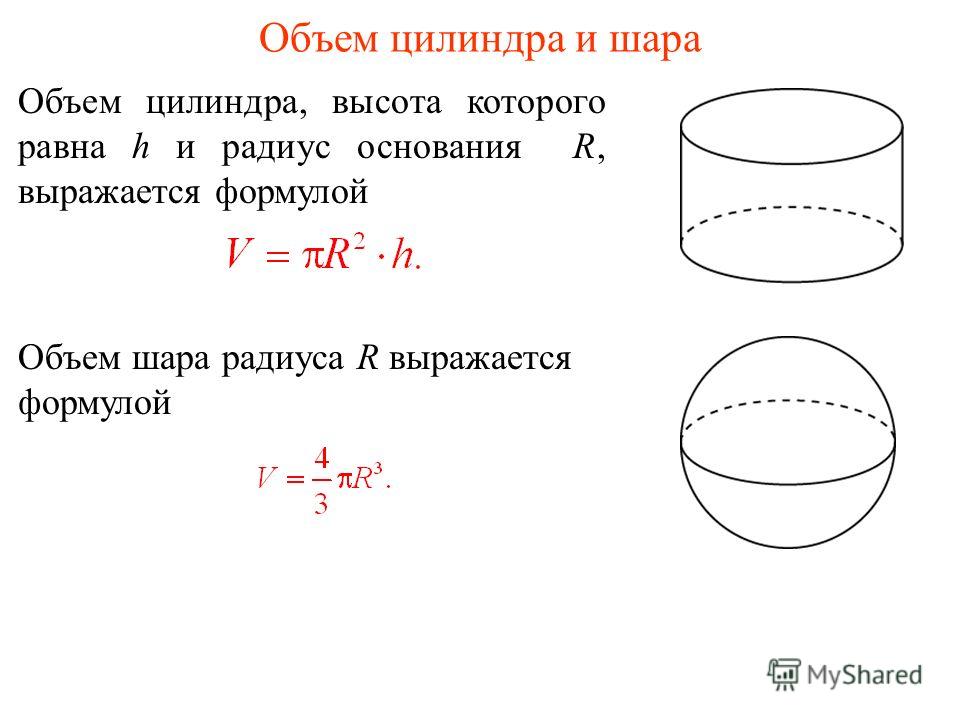
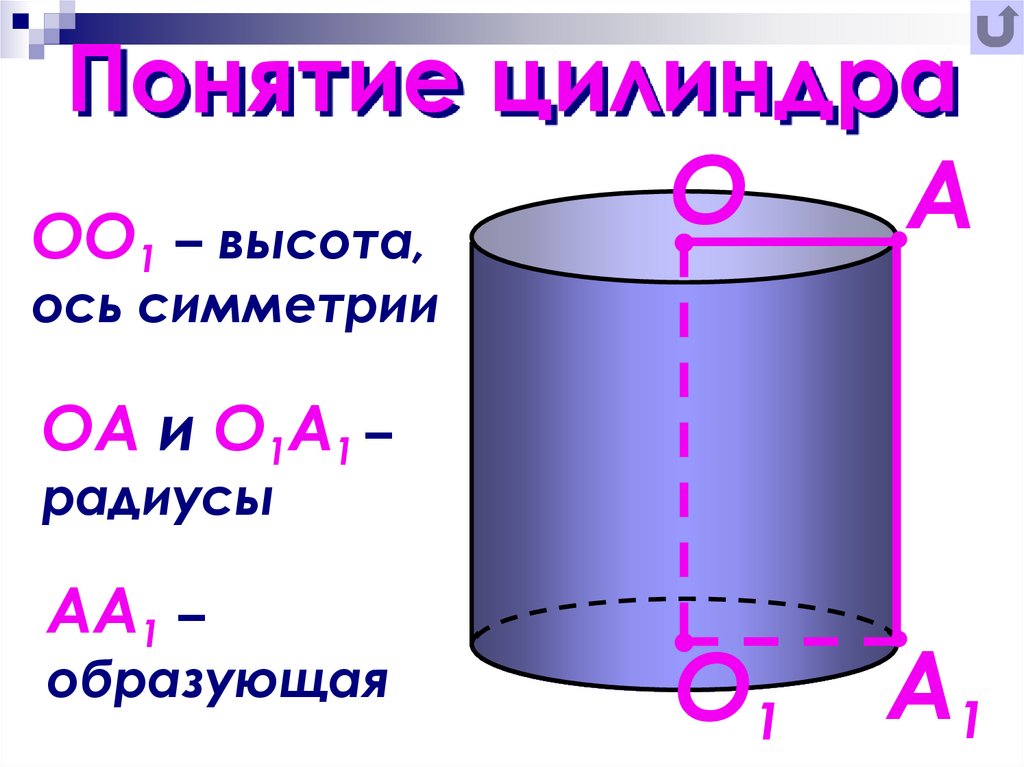

 Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 ч.
Его можно получить, умножив площадь основания на высоту. Объем цилиндра с радиусом основания ‘r’ и высотой ‘h’ равен V = πr 2 ч.
 Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 th .
Таким образом, когда его радиус уменьшается вдвое, объем становится равным 1/4 th . Площадь поверхности цилиндра определяется двумя следующими формулами:
Площадь поверхности цилиндра определяется двумя следующими формулами:
 Еще один довольно распространенный элемент цилиндрической формы, который мы видим ежедневно, — это аккумулятор. Оглянитесь вокруг, видите ли вы какие-нибудь цилиндрические формы?
Еще один довольно распространенный элемент цилиндрической формы, который мы видим ежедневно, — это аккумулятор. Оглянитесь вокруг, видите ли вы какие-нибудь цилиндрические формы? {2}\)
{2}\) Какова площадь этикетки? (Используйте 3.14 для \(\pi\))
Какова площадь этикетки? (Используйте 3.14 для \(\pi\)) По сути, это прямоугольник, длина которого равна окружности круглого основания, которое он выравнивает (отсюда берется \(2πr\)) и чья ширина является высотой цилиндра (это где \(h\) происходит от).
По сути, это прямоугольник, длина которого равна окружности круглого основания, которое он выравнивает (отсюда берется \(2πr\)) и чья ширина является высотой цилиндра (это где \(h\) происходит от).
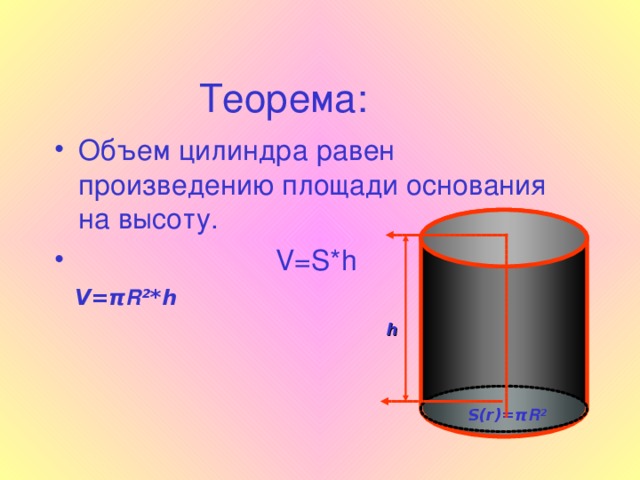 Свечи, которые он делает, имеют цилиндрическую форму. Он купил новую форму для свечей, и ему нужно выяснить, сколько расплавленного воска она может вместить. Цилиндрическая форма имеет высоту 10 дюймов и радиус 5 дюймов. Сколько расплавленного воска он может залить в форму, если хочет заполнить ее полностью? 92(10)\), что упрощается до 785. Форма для свечи может вместить 785 в 3 расплавленного воска.
Свечи, которые он делает, имеют цилиндрическую форму. Он купил новую форму для свечей, и ему нужно выяснить, сколько расплавленного воска она может вместить. Цилиндрическая форма имеет высоту 10 дюймов и радиус 5 дюймов. Сколько расплавленного воска он может залить в форму, если хочет заполнить ее полностью? 92(10)\), что упрощается до 785. Форма для свечи может вместить 785 в 3 расплавленного воска.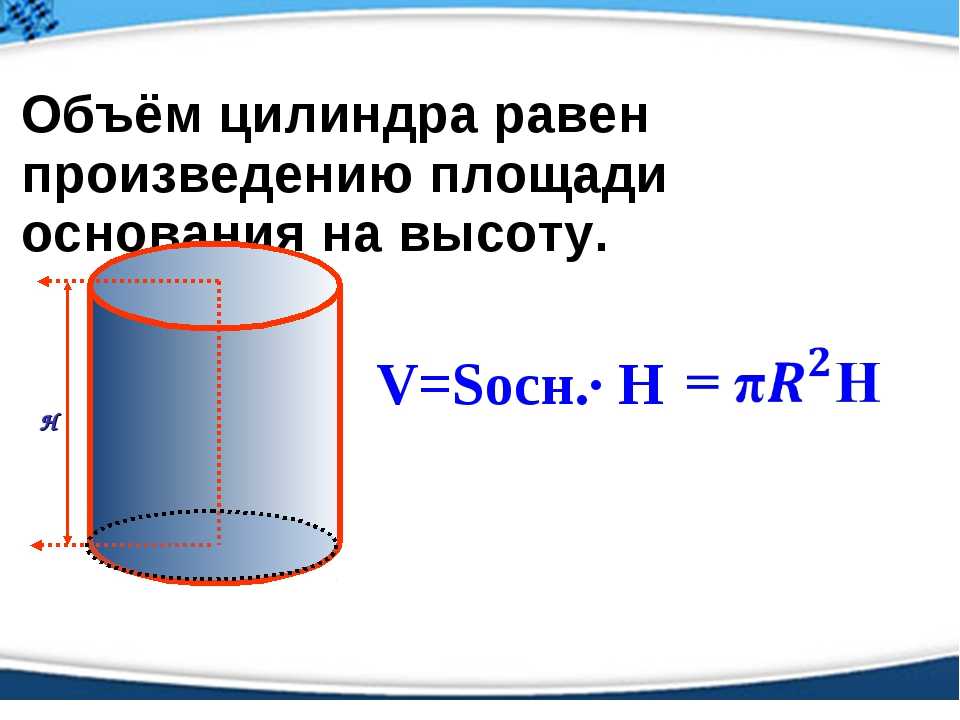
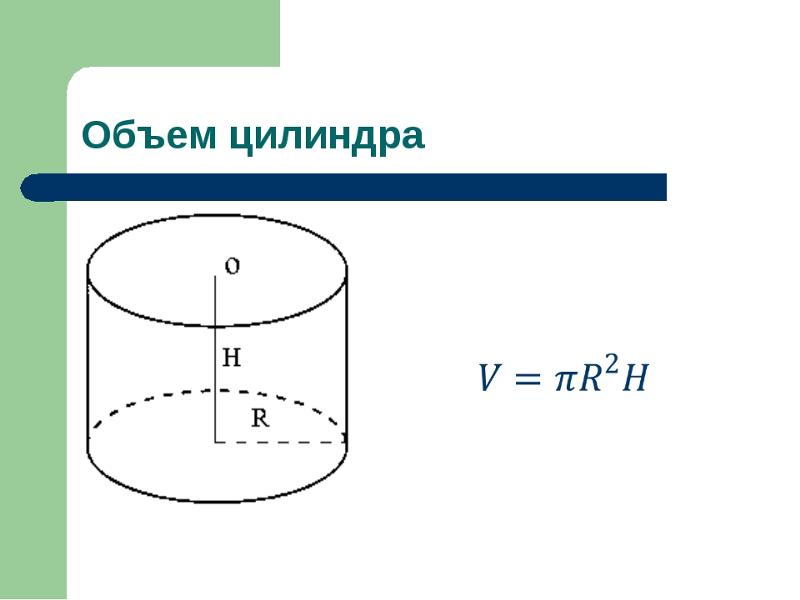 Объем цилиндра измеряется в кубических единицах.
Объем цилиндра измеряется в кубических единицах.  е.
е. = 628 кубических футов.
= 628 кубических футов. Если длина трубы 100 мм, найдите объем материала, из которого изготовлена труба.
Если длина трубы 100 мм, найдите объем материала, из которого изготовлена труба.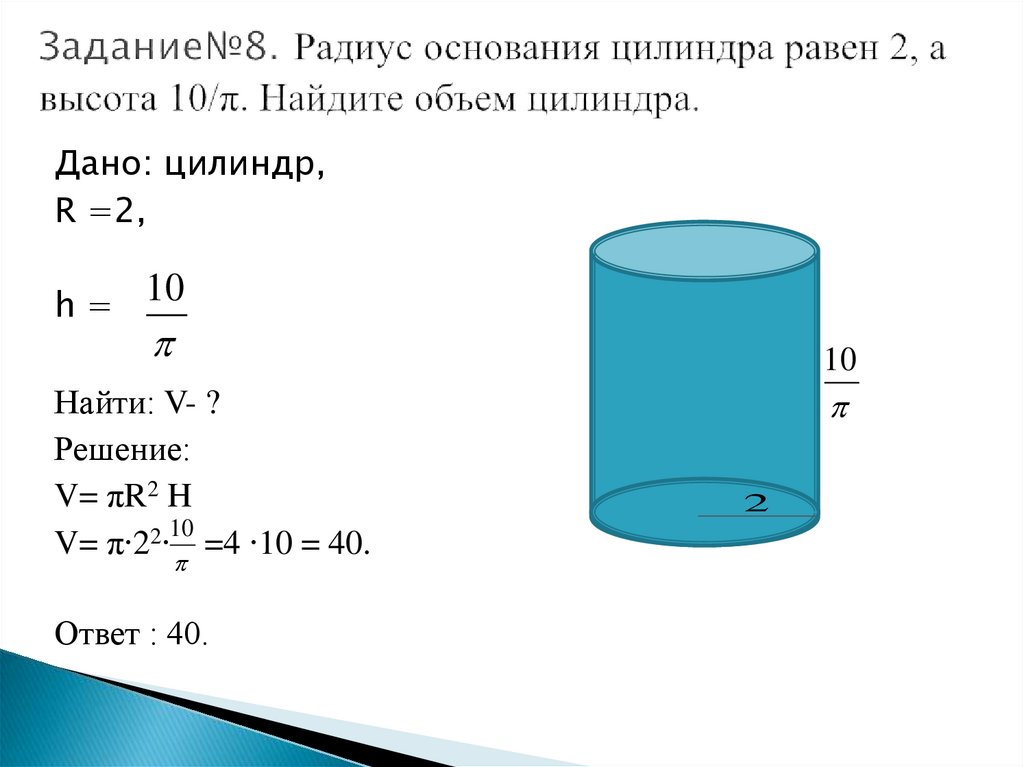

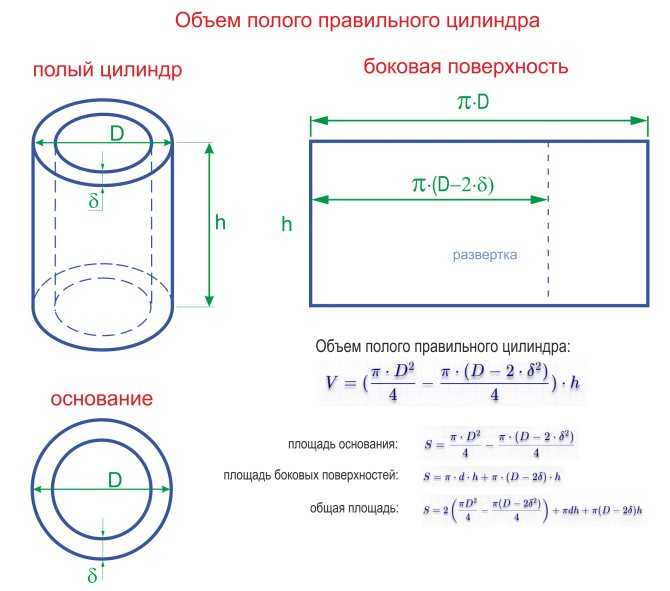 д.
д.

 Таким образом,
Таким образом,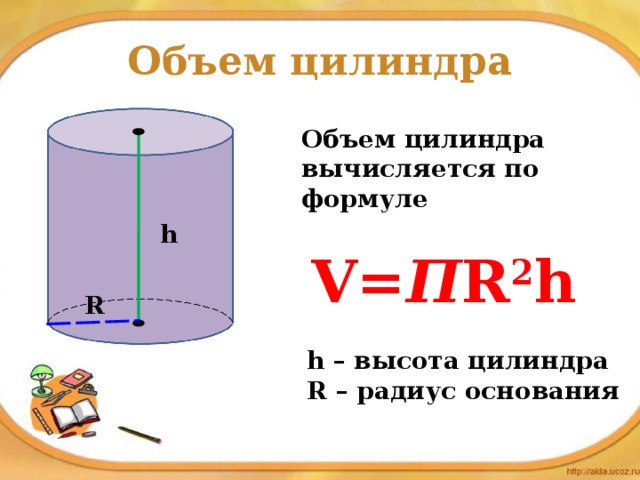



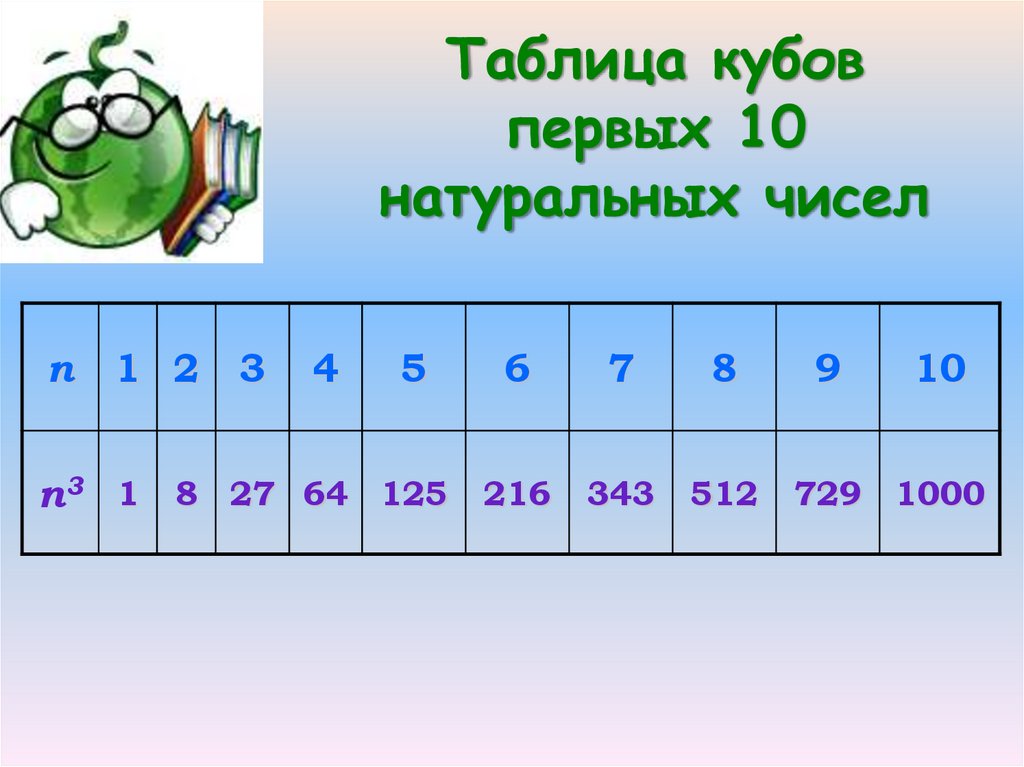 Углы с шагом в 1°. Таблица значений котангенса, ctg
Углы с шагом в 1°. Таблица значений котангенса, ctg 2
2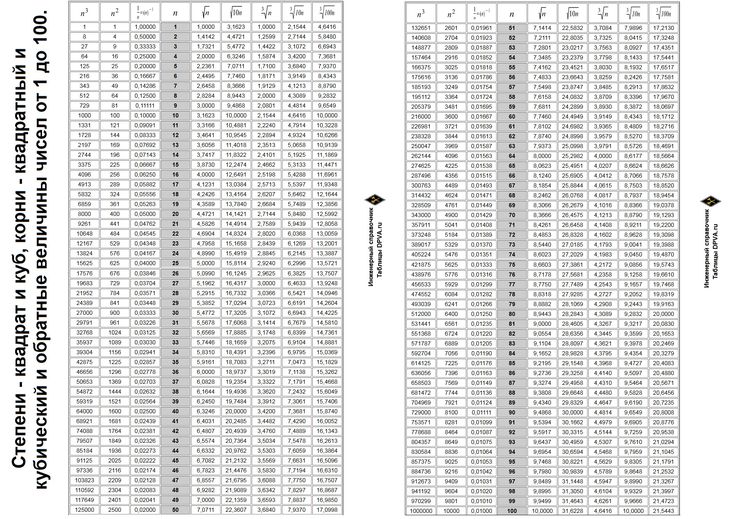
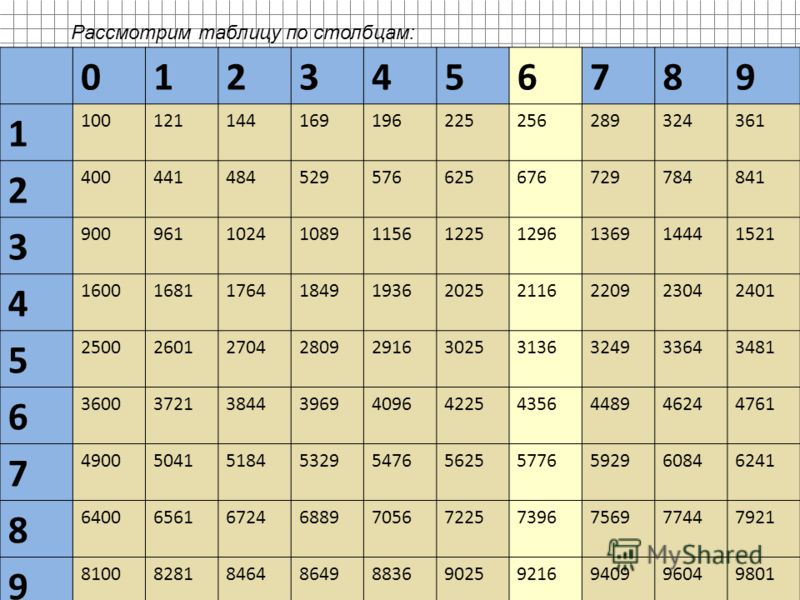
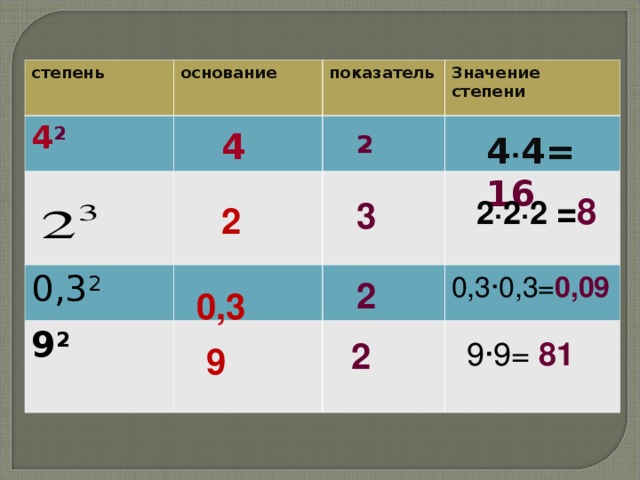

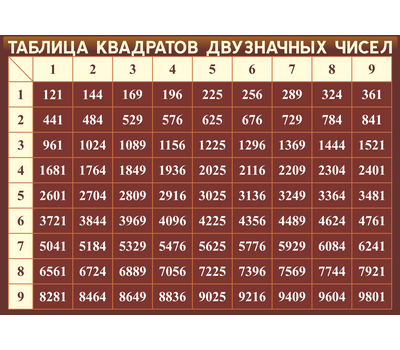



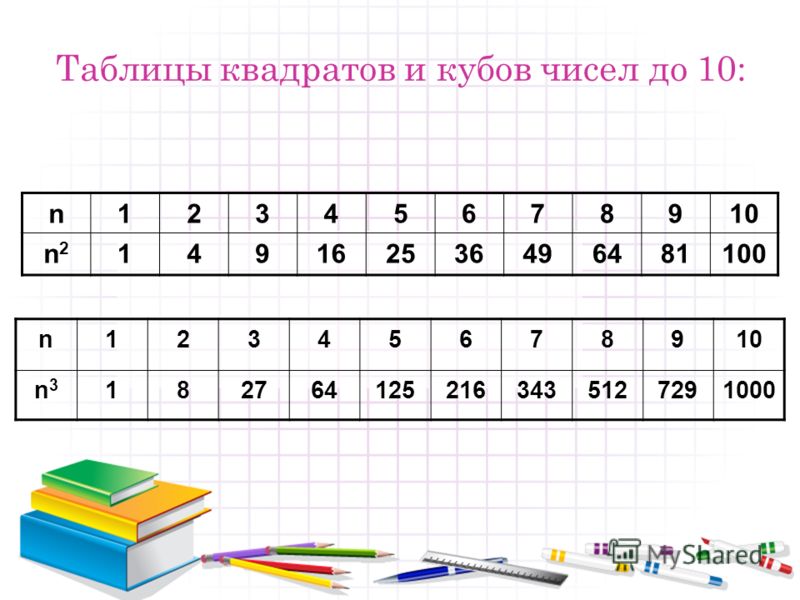 д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.
д. степень числа оканчивается той же цифрой, что и первая степень числа; шестая, десятая, четырнадцатая степень и т. д степень оканчивается той же цифрой, что и вторая степень числа; седьмая степень числа будет оканчиваться той же цифрой, что и третья степень числа.


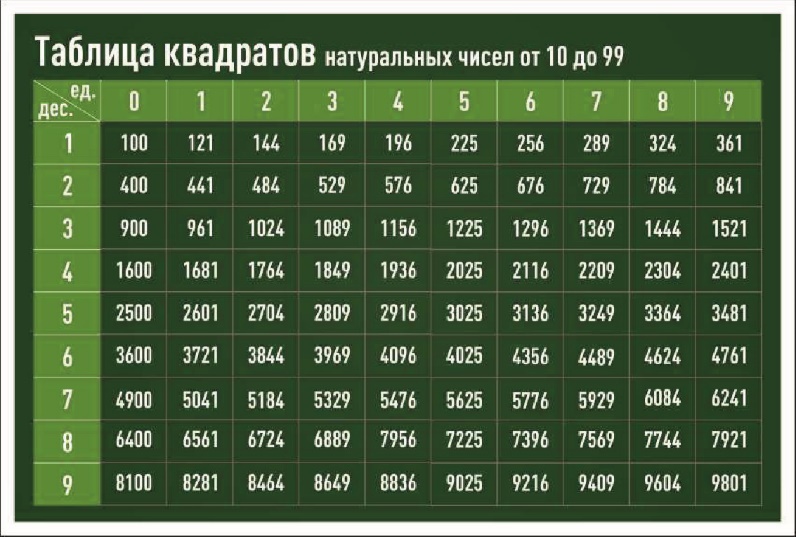
 Заключение
Заключение
 41 .
41 .
 Значит, число 77 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 77 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).
Значит, число 77 делится на 4 с остатком 3. Степени семёрки могут оканчиваться на 7, 9, 3 или 1 (в зависимости от того, с каким остатком делится на 4 показатель степени). В нашем случае 43 делится на 4 с остатком 3, значит, и 77 делится на 4 с остатком 3 (согласно признаку делимости на 4). А у всех степеней семёрки, показатели которых делятся на 4 с остатком 3, последняя цифра равна 3).
 Какого он был цвета перед этим покраснением?
Какого он был цвета перед этим покраснением?

 Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.
Пичурин Л.Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл. средней школы — М.: Просвещение, 1990.- 224 с.: ил.
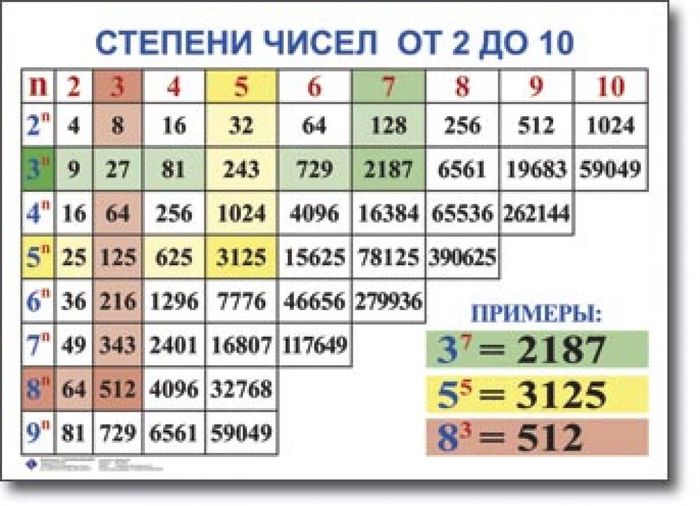
 Оно не относится к их сложению.
Оно не относится к их сложению. Решить уравнение. Используем свойство частного степеней.
Решить уравнение. Используем свойство частного степеней. 
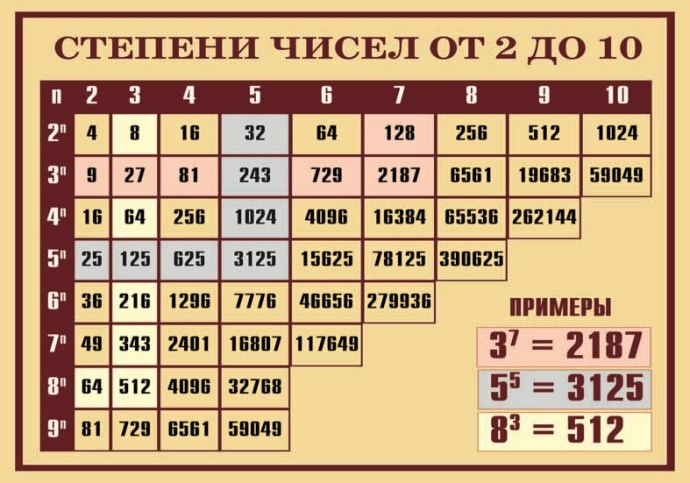
 В этом случае советуем поступать следующим образом.
В этом случае советуем поступать следующим образом. Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.
Поэтому
на теме
возведение дроби в степень
мы остановимся более подробно на следующей странице.

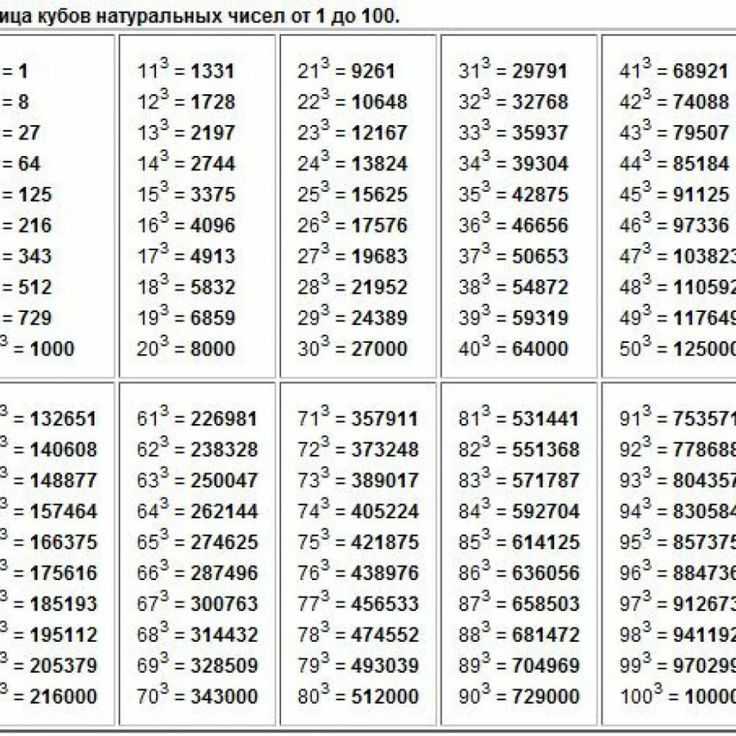
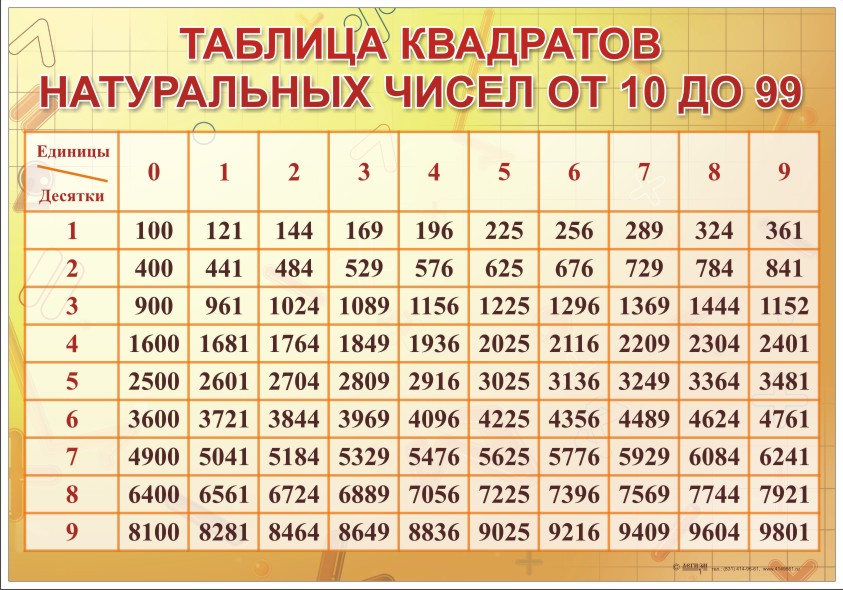 Для этого испытуемому надо различить звуки основных частот. Чем большая громкость звука требуется для того, чтобы тестируемый человек его услышал, тем большая степень тугоухости у него имеется.
Для этого испытуемому надо различить звуки основных частот. Чем большая громкость звука требуется для того, чтобы тестируемый человек его услышал, тем большая степень тугоухости у него имеется. Общение в группе людей проблематично и требует существенных усилий.
Общение в группе людей проблематично и требует существенных усилий.
 Давайте посмотрим на это более наглядно:
Давайте посмотрим на это более наглядно:
 Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.






 В результате получили число 22. Найдите неизвестное число.
В результате получили число 22. Найдите неизвестное число. Вставьте вместо … число так, чтобы получилось верное равенство.
Вставьте вместо … число так, чтобы получилось верное равенство. Сколько стульев находится в кафе после ремонта?
Сколько стульев находится в кафе после ремонта?
 Вариант № 3. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 3. Дата:______________ ФИО:_________________________________ Оценка:__________
 Вариант № 6. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 6. Дата:______________ ФИО:_________________________________ Оценка:__________
 Вариант № 9. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 9. Дата:______________ ФИО:_________________________________ Оценка:__________
 Вариант № 12. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 12. Дата:______________ ФИО:_________________________________ Оценка:__________

 Вариант № 16. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 16. Дата:______________ ФИО:_________________________________ Оценка:__________

 Вариант № 1. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 1. Дата:______________ ФИО:_________________________________ Оценка:__________

 Вариант № 5. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 5. Дата:______________ ФИО:_________________________________ Оценка:__________

 Вариант № 9. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 9. Дата:______________ ФИО:_________________________________ Оценка:__________ Дата:______________ ФИО:_________________________________ Оценка:__________
Дата:______________ ФИО:_________________________________ Оценка:__________

 Вариант № 14. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 14. Дата:______________ ФИО:_________________________________ Оценка:__________ Дата:______________ ФИО:_________________________________ Оценка:__________
Дата:______________ ФИО:_________________________________ Оценка:__________

 Вариант № 19. Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 19. Дата:______________ ФИО:_________________________________ Оценка:__________
 – это 15 единиц.
Делю 15 на 3. В частном будет 5 единиц.
Умножаю 5 ∙ 3 = 15.
Вычитаю 15 − 15 = 0. Единицы разделили все. Деление закончено.
Ответ: 275.
– это 15 единиц.
Делю 15 на 3. В частном будет 5 единиц.
Умножаю 5 ∙ 3 = 15.
Вычитаю 15 − 15 = 0. Единицы разделили все. Деление закончено.
Ответ: 275.
 В частном будет 1 сотня.
Умножу: 1 ∙ 3 = 3. Разделили 3 сотен.
Вычту: 4 − 3 = 1.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 3; можно продолжать деление.
В частном будет 1 сотня.
Умножу: 1 ∙ 3 = 3. Разделили 3 сотен.
Вычту: 4 − 3 = 1.
Сравню остаток с делителем: число оставшихся сотен меньше, чем 3; можно продолжать деление.



 Решебник
Решебник Обязательные умения
Обязательные умения ПРЯМЫЕ НА ПЛОСКОСТИ В ПРОСТРАНСТВЕ
ПРЯМЫЕ НА ПЛОСКОСТИ В ПРОСТРАНСТВЕ ДЕЙСТВИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ
ДЕЙСТВИЯ С ДЕСЯТИЧНЫМИ ДРОБЯМИ ОКРУЖНОСТЬ
ОКРУЖНОСТЬ СИММЕТРИЯ
СИММЕТРИЯ ВЫРАЖЕНИЯ, ФОРМУЛЫ, УРАВНЕНИЯ
ВЫРАЖЕНИЯ, ФОРМУЛЫ, УРАВНЕНИЯ ЦЕЛЫЕ ЧИСЛА
ЦЕЛЫЕ ЧИСЛА МНОЖЕСТВА, КОМБИНАТОРИКА
МНОЖЕСТВА, КОМБИНАТОРИКА РАЦИОНАЛЬНЫЕ ЧИСЛА
РАЦИОНАЛЬНЫЕ ЧИСЛА МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ
МНОГОУГОЛЬНИКИ И МНОГОГРАННИКИ В. Дорофеевым, И.Ф. Шарыгиным, С.Б. Суворовым и др. Он используется в большинстве общеобразовательных школ России.
В. Дорофеевым, И.Ф. Шарыгиным, С.Б. Суворовым и др. Он используется в большинстве общеобразовательных школ России.

 И. Зубарева, А.Г. Мордкович. 2014-2019г.
И. Зубарева, А.Г. Мордкович. 2014-2019г. Чтобы найти a и b, составим решаемую систему.
Чтобы найти a и b, составим решаемую систему.
 Я пытался попробовать, но не нашел никаких решений. Как бы с этим справиться?
Я пытался попробовать, но не нашел никаких решений. Как бы с этим справиться? 6-92-120x-4.$$
6-92-120x-4.$$

 Оценка пространственной корреляции и конвергенции может помочь понять влияние быстроразвивающегося медицинского рынка Китая и последних реформ здравоохранения.
Оценка пространственной корреляции и конвергенции может помочь понять влияние быстроразвивающегося медицинского рынка Китая и последних реформ здравоохранения. 2196 β сходимость. Не обнаружено доказательств того, что последние реформы здравоохранения повлияли на сбалансированное распределение и конвергенцию ресурсов здравоохранения.
2196 β сходимость. Не обнаружено доказательств того, что последние реформы здравоохранения повлияли на сбалансированное распределение и конвергенцию ресурсов здравоохранения.
 . Реформы здравоохранения на этих развивающихся рынках влияют на структуру глобальных расходов на здравоохранение, что в основном связано с реформами, проведенными в Китае [3]. Тем не менее, еще предстоит выяснить, способствует ли увеличение расходов на здравоохранение, происходящее в странах с формирующимся рынком, внутреннему балансу распределения ресурсов между различными регионами в этих странах, и все еще необходимо лучшее понимание пространственной корреляции, которую такой рост расходов оказывает на распределение ресурсов между странами. различные внутренние области.
. Реформы здравоохранения на этих развивающихся рынках влияют на структуру глобальных расходов на здравоохранение, что в основном связано с реформами, проведенными в Китае [3]. Тем не менее, еще предстоит выяснить, способствует ли увеличение расходов на здравоохранение, происходящее в странах с формирующимся рынком, внутреннему балансу распределения ресурсов между различными регионами в этих странах, и все еще необходимо лучшее понимание пространственной корреляции, которую такой рост расходов оказывает на распределение ресурсов между странами. различные внутренние области. Но эти реформы, как правило, уделяли больше внимания оборудованию медицинской инфраструктуры и меньше внимания медицинскому персоналу и его человеческому капиталу. Таким образом, пациенты по-прежнему охотнее выбирают лечение в (городских) больницах высокого уровня, создавая структурную проблему перегрузки, при которой сосуществуют перегруженность больниц высокого уровня и простаивающие ресурсы больниц низкого уровня [5].
Но эти реформы, как правило, уделяли больше внимания оборудованию медицинской инфраструктуры и меньше внимания медицинскому персоналу и его человеческому капиталу. Таким образом, пациенты по-прежнему охотнее выбирают лечение в (городских) больницах высокого уровня, создавая структурную проблему перегрузки, при которой сосуществуют перегруженность больниц высокого уровня и простаивающие ресурсы больниц низкого уровня [5]. Между тем, начиная с 2015 года, некоторые пилотные провинции и города, в том числе Шанхай и Чжэцзян, приступили к реализации комплексной медицинской реформы с упором на медицинские цены, медицинское страхование и закупку фармацевтических препаратов для снижения медицинских расходов и создания более эффективной иерархической системы диагностики и лечения. Однако вопрос о том, привели ли прошлые реформы к более сбалансированному распределению ресурсов здравоохранения и эффекту конвергенции, остается открытым.
Между тем, начиная с 2015 года, некоторые пилотные провинции и города, в том числе Шанхай и Чжэцзян, приступили к реализации комплексной медицинской реформы с упором на медицинские цены, медицинское страхование и закупку фармацевтических препаратов для снижения медицинских расходов и создания более эффективной иерархической системы диагностики и лечения. Однако вопрос о том, привели ли прошлые реформы к более сбалансированному распределению ресурсов здравоохранения и эффекту конвергенции, остается открытым. Однако единого равновесия в расходах на здравоохранение для стран Африки к югу от Сахары не существует, хотя были выявлены три клуба конвергенции [10]. В других исследованиях изучались разные регионы в отдельных странах, но в качестве показателя также в основном использовались расходы на здравоохранение. Исследования подтвердили наличие конвергенции расходов на здравоохранение в штатах США [11], а также обнаружили, что индийские штаты можно разделить на два клуба конвергенции расходов на здравоохранение [12]. Кроме того, расходы на здравоохранение во всех округах Китая имеют тенденцию к сближению [13]. Однако распределение ресурсов здравоохранения не ограничивается показателями расходов на здравоохранение, но должно также включать другие показатели обеспечения ресурсами здравоохранения, такие как количество медицинских работников и коек. Хотя в нескольких исследованиях обсуждалась конвергенция отдельных показателей, таких как количество коек и количество врачей [14], в нашем обзоре литературы не было обнаружено исследований, в которых использовался бы всеобъемлющий индекс обеспеченности ресурсами здравоохранения, включая параметры человеческих, материальных и финансовых ресурсов, и выполненных работ.
Однако единого равновесия в расходах на здравоохранение для стран Африки к югу от Сахары не существует, хотя были выявлены три клуба конвергенции [10]. В других исследованиях изучались разные регионы в отдельных странах, но в качестве показателя также в основном использовались расходы на здравоохранение. Исследования подтвердили наличие конвергенции расходов на здравоохранение в штатах США [11], а также обнаружили, что индийские штаты можно разделить на два клуба конвергенции расходов на здравоохранение [12]. Кроме того, расходы на здравоохранение во всех округах Китая имеют тенденцию к сближению [13]. Однако распределение ресурсов здравоохранения не ограничивается показателями расходов на здравоохранение, но должно также включать другие показатели обеспечения ресурсами здравоохранения, такие как количество медицинских работников и коек. Хотя в нескольких исследованиях обсуждалась конвергенция отдельных показателей, таких как количество коек и количество врачей [14], в нашем обзоре литературы не было обнаружено исследований, в которых использовался бы всеобъемлющий индекс обеспеченности ресурсами здравоохранения, включая параметры человеческих, материальных и финансовых ресурсов, и выполненных работ. соответствующие оценки сходимости.
соответствующие оценки сходимости. Другое объяснение связано с реформой здравоохранения 2009 г., предполагающей, что расширение охвата медицинским страхованием ослабило финансовые ограничения пациентов, что побудило их выбирать больницы высокого уровня [21]. Однако в существующих исследованиях не обсуждались дисбаланс и конвергенция в контексте последних реформ здравоохранения и их последствия.
Другое объяснение связано с реформой здравоохранения 2009 г., предполагающей, что расширение охвата медицинским страхованием ослабило финансовые ограничения пациентов, что побудило их выбирать больницы высокого уровня [21]. Однако в существующих исследованиях не обсуждались дисбаланс и конвергенция в контексте последних реформ здравоохранения и их последствия. При этом меньше внимания уделяется пространственному соотношению, неоднородности городов разного размера/уровня и влиянию последних реформ. Хотя в нескольких исследованиях использовались данные на уровне больниц и пациентов для оценки последствий политики реформ, таких как реформа нисходящих ресурсов и комбинация лечения, и были представлены доказательства их влияния на стимулирование пациентов выбирать больницы низкого уровня и улучшение эффективности распределения ресурсов [24, 25], неясно, вызвали ли эти реформы эффекты конвергенции на макроуровне между городами и регионами.
При этом меньше внимания уделяется пространственному соотношению, неоднородности городов разного размера/уровня и влиянию последних реформ. Хотя в нескольких исследованиях использовались данные на уровне больниц и пациентов для оценки последствий политики реформ, таких как реформа нисходящих ресурсов и комбинация лечения, и были представлены доказательства их влияния на стимулирование пациентов выбирать больницы низкого уровня и улучшение эффективности распределения ресурсов [24, 25], неясно, вызвали ли эти реформы эффекты конвергенции на макроуровне между городами и регионами. В «Концепции комплексного регионального развития дельты реки Янцзы» , предложенной китайским правительством [26], более сбалансированное распределение ресурсов здравоохранения было указано в качестве цели региональной интеграции. Более того, доступность данных по этому региону лучше, чем по другим регионам Китая. Мы собрали данные по 41 городу YRD на уровне префектуры и выше с 2007 по 2019 год.провести эмпирическое исследование. Выборка включает Шанхай с населением около 25 миллионов человек, а также Ханчжоу, Сучжоу, Нанкин, Хэфэй и Нинбо с населением около 10 миллионов человек в каждом, а также города уровня префектуры с обширными сельскими районами. Масштабы и конкретные города дельты реки Янцзы показаны на рис. 4 в Приложении.
В «Концепции комплексного регионального развития дельты реки Янцзы» , предложенной китайским правительством [26], более сбалансированное распределение ресурсов здравоохранения было указано в качестве цели региональной интеграции. Более того, доступность данных по этому региону лучше, чем по другим регионам Китая. Мы собрали данные по 41 городу YRD на уровне префектуры и выше с 2007 по 2019 год.провести эмпирическое исследование. Выборка включает Шанхай с населением около 25 миллионов человек, а также Ханчжоу, Сучжоу, Нанкин, Хэфэй и Нинбо с населением около 10 миллионов человек в каждом, а также города уровня префектуры с обширными сельскими районами. Масштабы и конкретные города дельты реки Янцзы показаны на рис. 4 в Приложении. с репрезентативным кластером из 41 города на уровне префектуры и выше. (2) В данной статье измерение пространственно-временного распределения сочетается с оценкой конвергенции, что позволяет нам понять характерные факты распределения ресурсов здравоохранения в регионе YRD, а также включает в анализ городскую неоднородность. (3) Это первая попытка оценить эффекты конвергенции последних реформ, в которых нисходящая реформа ресурсов здравоохранения и комплексная медицинская реформа включены в эмпирическую оценку.
с репрезентативным кластером из 41 города на уровне префектуры и выше. (2) В данной статье измерение пространственно-временного распределения сочетается с оценкой конвергенции, что позволяет нам понять характерные факты распределения ресурсов здравоохранения в регионе YRD, а также включает в анализ городскую неоднородность. (3) Это первая попытка оценить эффекты конвергенции последних реформ, в которых нисходящая реформа ресурсов здравоохранения и комплексная медицинская реформа включены в эмпирическую оценку. Для измерения распределения ресурсов здравоохранения можно использовать два подхода. Первый подход заключается в наблюдении поперечного пространственного распределения с помощью ряда показателей измерения. Если в дальнейшем будет введено временное измерение, можно будет также обсудить эволюционный тренд [27]. Если различные области поперечного сечения включены в географическую информационную систему (ГИС), мы могли бы интуитивно понять тенденцию пространственно-временной эволюции [28]. Однако из-за существования поперечной неоднородности показатели измерений не могут контролировать влияние гетерогенных факторов, поэтому мы не можем фиксировать характеристики пространственно-временной эволюции сопоставимым образом для разных регионов [29].]. Поэтому другой подход использует методы регрессии для контроля влияния разнородных предметов. Методика оценки конвергенции, разработанная для исследований экономического роста, может быть использована для оценки конвергенции распределения ресурсов здравоохранения [30].
Для измерения распределения ресурсов здравоохранения можно использовать два подхода. Первый подход заключается в наблюдении поперечного пространственного распределения с помощью ряда показателей измерения. Если в дальнейшем будет введено временное измерение, можно будет также обсудить эволюционный тренд [27]. Если различные области поперечного сечения включены в географическую информационную систему (ГИС), мы могли бы интуитивно понять тенденцию пространственно-временной эволюции [28]. Однако из-за существования поперечной неоднородности показатели измерений не могут контролировать влияние гетерогенных факторов, поэтому мы не можем фиксировать характеристики пространственно-временной эволюции сопоставимым образом для разных регионов [29].]. Поэтому другой подход использует методы регрессии для контроля влияния разнородных предметов. Методика оценки конвергенции, разработанная для исследований экономического роста, может быть использована для оценки конвергенции распределения ресурсов здравоохранения [30]. Три отрасли литературы имеют отношение к этому исследованию.
Три отрасли литературы имеют отношение к этому исследованию. Ранний коэффициент Джини использовался для отражения неравенства доходов жителей [35], но он не мог отражать общий внутренний баланс. Поэтому Дагум [36] предложил разложимый коэффициент Джини, который может разлагать общие региональные различия по подгруппам и эффективно решать проблемы перекрытия среди наблюдаемых выборок. Индекс Тейла получен методом энтропии (или групповой энтропии) [37, 38], но не учитывается влияние географической доступности [39].]. Из-за многовходных и многовыходных характеристик ресурсов здравоохранения одним из методов является использование анализа оболочки данных (DEA) для измерения относительной эффективности группы подразделений, принимающих решения, с несколькими входами и несколькими выходами [40, 41]. Альтернативным методом является использование метода энтропийных весов для построения индекса спроса/предложения ресурсов здравоохранения на основе данных с несколькими входами и выходами [42].
Ранний коэффициент Джини использовался для отражения неравенства доходов жителей [35], но он не мог отражать общий внутренний баланс. Поэтому Дагум [36] предложил разложимый коэффициент Джини, который может разлагать общие региональные различия по подгруппам и эффективно решать проблемы перекрытия среди наблюдаемых выборок. Индекс Тейла получен методом энтропии (или групповой энтропии) [37, 38], но не учитывается влияние географической доступности [39].]. Из-за многовходных и многовыходных характеристик ресурсов здравоохранения одним из методов является использование анализа оболочки данных (DEA) для измерения относительной эффективности группы подразделений, принимающих решения, с несколькими входами и несколькими выходами [40, 41]. Альтернативным методом является использование метода энтропийных весов для построения индекса спроса/предложения ресурсов здравоохранения на основе данных с несколькими входами и выходами [42]. Оценки на основе индекса агломерации показали, что степень агломерации ресурсов здравоохранения в экономически развитых провинциях/городах относительно высока, тогда как географическая доступность ресурсов здравоохранения в экономически слаборазвитых провинциях/городах слаба [43]. Существуют очевидные различия в распределении ресурсов здоровья в разных провинциях, таких как Сычуань [44], Чжэцзян [45] и Хэнань [46], которые имеют разные характеристики агломерации в зависимости от численности населения и географического района. Йи и др. (2020) измерили коэффициент вариации и не нашли σ конвергенция в восточном, центральном и западном Китае; то есть различия в эффективности здравоохранения внутри Китая могут постепенно увеличиваться [47]. Однако другая оценка, основанная на коэффициенте Дагум Джини, показывает, что общие, внутрирегиональные и межрегиональные различия в предложении основных медицинских и медицинских услуг уменьшились в течение 2007–2018 гг. [22]. Кроме того, индекс Тейла использовался для демонстрации того, что различия в распределении ресурсов в разных провинциях связаны с разными источниками.
Оценки на основе индекса агломерации показали, что степень агломерации ресурсов здравоохранения в экономически развитых провинциях/городах относительно высока, тогда как географическая доступность ресурсов здравоохранения в экономически слаборазвитых провинциях/городах слаба [43]. Существуют очевидные различия в распределении ресурсов здоровья в разных провинциях, таких как Сычуань [44], Чжэцзян [45] и Хэнань [46], которые имеют разные характеристики агломерации в зависимости от численности населения и географического района. Йи и др. (2020) измерили коэффициент вариации и не нашли σ конвергенция в восточном, центральном и западном Китае; то есть различия в эффективности здравоохранения внутри Китая могут постепенно увеличиваться [47]. Однако другая оценка, основанная на коэффициенте Дагум Джини, показывает, что общие, внутрирегиональные и межрегиональные различия в предложении основных медицинских и медицинских услуг уменьшились в течение 2007–2018 гг. [22]. Кроме того, индекс Тейла использовался для демонстрации того, что различия в распределении ресурсов в разных провинциях связаны с разными источниками. Например, различия в распределении ресурсов здравоохранения в провинции Аньхой в основном вызваны внутрирегиональными различиями [48], а в провинции Хайнань — межрегиональными различиями [49].].
Например, различия в распределении ресурсов здравоохранения в провинции Аньхой в основном вызваны внутрирегиональными различиями [48], а в провинции Хайнань — межрегиональными различиями [49].]. Метод KDE может представить пространственное распределение всей территории, что дополняет результаты анализа ESDA. Метод эллипса стандартного отклонения (SDE) строит эллипс стандартного отклонения, чтобы отразить преобладающее направление распределения пространственных элементов и дисперсию каждого направления, что, подобно кластерной карте LISA, может компенсировать тот факт, что карта KDE не может отображать особенности распространения по конкретным регионам [52].
Метод KDE может представить пространственное распределение всей территории, что дополняет результаты анализа ESDA. Метод эллипса стандартного отклонения (SDE) строит эллипс стандартного отклонения, чтобы отразить преобладающее направление распределения пространственных элементов и дисперсию каждого направления, что, подобно кластерной карте LISA, может компенсировать тот факт, что карта KDE не может отображать особенности распространения по конкретным регионам [52]. Однако в других исследованиях сообщается, что пространственное распределение ресурсов здравоохранения между городами, как правило, сбалансировано, а в переходной зоне от восточного побережья к центральному региону существуют регионы низкой агломерации с концентрированным распределением [28]. Вышеупомянутое эмпирическое исследование с использованием городских данных на уровне префектур использовало аналогичный метод, но дало противоречивые результаты из-за различий в периоде исследования и методах обработки, используемых для показателей. Наконец, в большинстве пространственных статистических исследований в качестве объектов исследования берутся конкретные города и используется метод SDE для изучения пространственного распределения ресурсов здравоохранения в городах [23, 54, 55].
Однако в других исследованиях сообщается, что пространственное распределение ресурсов здравоохранения между городами, как правило, сбалансировано, а в переходной зоне от восточного побережья к центральному региону существуют регионы низкой агломерации с концентрированным распределением [28]. Вышеупомянутое эмпирическое исследование с использованием городских данных на уровне префектур использовало аналогичный метод, но дало противоречивые результаты из-за различий в периоде исследования и методах обработки, используемых для показателей. Наконец, в большинстве пространственных статистических исследований в качестве объектов исследования берутся конкретные города и используется метод SDE для изучения пространственного распределения ресурсов здравоохранения в городах [23, 54, 55]. Согласно нашему опросу, в большинстве предыдущих исследований для оценки конвергенции использовались панельные данные провинциального уровня. Например, Zhou (2018) обнаружил условную конвергенцию β , но не абсолютную конвергенцию β между провинциями с помощью отдельных показателей [29].]. А рост медицинских расходов и региональная финансовая автономия подтолкнут региональные ресурсы здравоохранения на путь конвергенции. Пан и др. (2017) подтвердили долгосрочную тенденцию абсолютной и условной β конвергенции государственных расходов на здравоохранение в Китае [56]. Учитывая многовходные и многовыходные характеристики ресурсов здравоохранения, в некоторых исследованиях DEA использовался для измерения общей факторной производительности (TFP) разных провинций и оценки ее сходимости [57]. Установлено, что общий уровень СФП провинциальных ресурсов здравоохранения в Китае невысок, но рост СФП имеет абсолютную и условную β конвергенция и представляет региональные различия.
Согласно нашему опросу, в большинстве предыдущих исследований для оценки конвергенции использовались панельные данные провинциального уровня. Например, Zhou (2018) обнаружил условную конвергенцию β , но не абсолютную конвергенцию β между провинциями с помощью отдельных показателей [29].]. А рост медицинских расходов и региональная финансовая автономия подтолкнут региональные ресурсы здравоохранения на путь конвергенции. Пан и др. (2017) подтвердили долгосрочную тенденцию абсолютной и условной β конвергенции государственных расходов на здравоохранение в Китае [56]. Учитывая многовходные и многовыходные характеристики ресурсов здравоохранения, в некоторых исследованиях DEA использовался для измерения общей факторной производительности (TFP) разных провинций и оценки ее сходимости [57]. Установлено, что общий уровень СФП провинциальных ресурсов здравоохранения в Китае невысок, но рост СФП имеет абсолютную и условную β конвергенция и представляет региональные различия. Хотя эффект пространственного перелива наблюдается в конвергенции распределения ресурсов здравоохранения β [30], согласно нашему поиску, ни одно исследование не включало пространственный эффект в анализ на уровне города в контексте последних реформ здравоохранения в Китае.
Хотя эффект пространственного перелива наблюдается в конвергенции распределения ресурсов здравоохранения β [30], согласно нашему поиску, ни одно исследование не включало пространственный эффект в анализ на уровне города в контексте последних реформ здравоохранения в Китае. В этой статье YRD используется в качестве объекта исследования и исследуется пространственная корреляция между городами, чтобы интуитивно изобразить пространственное динамическое распределение ресурсов здравоохранения с помощью многомерного индекса. Затем модель пространственной панели использовалась для анализа конвергенции ресурсов здравоохранения в регионе YRD.
В этой статье YRD используется в качестве объекта исследования и исследуется пространственная корреляция между городами, чтобы интуитивно изобразить пространственное динамическое распределение ресурсов здравоохранения с помощью многомерного индекса. Затем модель пространственной панели использовалась для анализа конвергенции ресурсов здравоохранения в регионе YRD. Далее, Y IJ ( Y RH) представляет HRS of City I ( R) в регионе J ( R) в регионе J ( R) в регионе J ( R) . y}\) представляет собой среднее арифметическое HRS. Можно получить следующее уравнение: 9{2} \overline{y}} } } }$$
Далее, Y IJ ( Y RH) представляет HRS of City I ( R) в регионе J ( R) в регионе J ( R) в регионе J ( R) . y}\) представляет собой среднее арифметическое HRS. Можно получить следующее уравнение: 9{2} \overline{y}} } } }$$
 Первая оценка не опирается на эконометрическую модель и использует коэффициент вариации для измерения, что может подтвердить предыдущие результаты коэффициента Джини. β сходимости можно разделить на абсолютную β сходимость и условную β сходимость. Первый используется для оценки того, сойдется ли предложение ресурсов здравоохранения в различных регионах к одной и той же стационарной точке равновесия без учета факторов неоднородности города. Что еще более важно, мы включаем пространственные факторы, неоднородность и политику в области здравоохранения в качестве контрольных переменных в условное β сходимость для более полной оценки.
Первая оценка не опирается на эконометрическую модель и использует коэффициент вариации для измерения, что может подтвердить предыдущие результаты коэффициента Джини. β сходимости можно разделить на абсолютную β сходимость и условную β сходимость. Первый используется для оценки того, сойдется ли предложение ресурсов здравоохранения в различных регионах к одной и той же стационарной точке равновесия без учета факторов неоднородности города. Что еще более важно, мы включаем пространственные факторы, неоднородность и политику в области здравоохранения в качестве контрольных переменных в условное β сходимость для более полной оценки. α — постоянный член; μ i и η t представляют региональный и временной эффекты соответственно; и ε it представляет член случайных помех. Формула скорости сходимости: \(v = — \frac{1}{TS}\ln (1 + \beta)\), где TS представляет промежуток времени.
α — постоянный член; μ i и η t представляют региональный и временной эффекты соответственно; и ε it представляет член случайных помех. Формула скорости сходимости: \(v = — \frac{1}{TS}\ln (1 + \beta)\), где TS представляет промежуток времени.
 В этой статье мы используем обратную весовую матрицу расстояния.
В этой статье мы используем обратную весовую матрицу расстояния.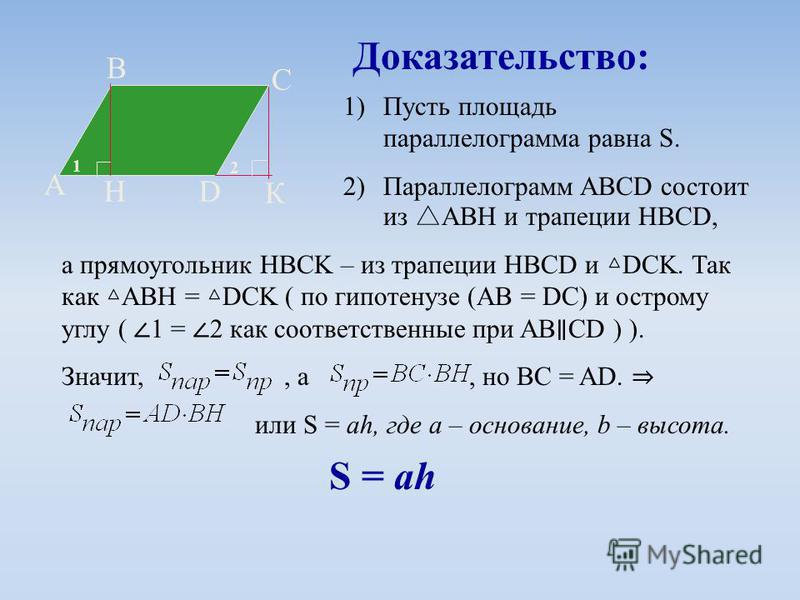




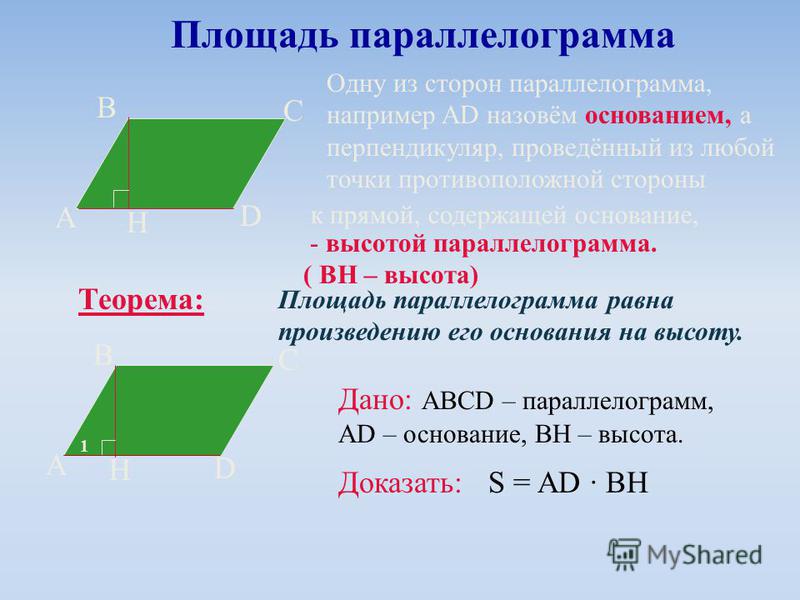
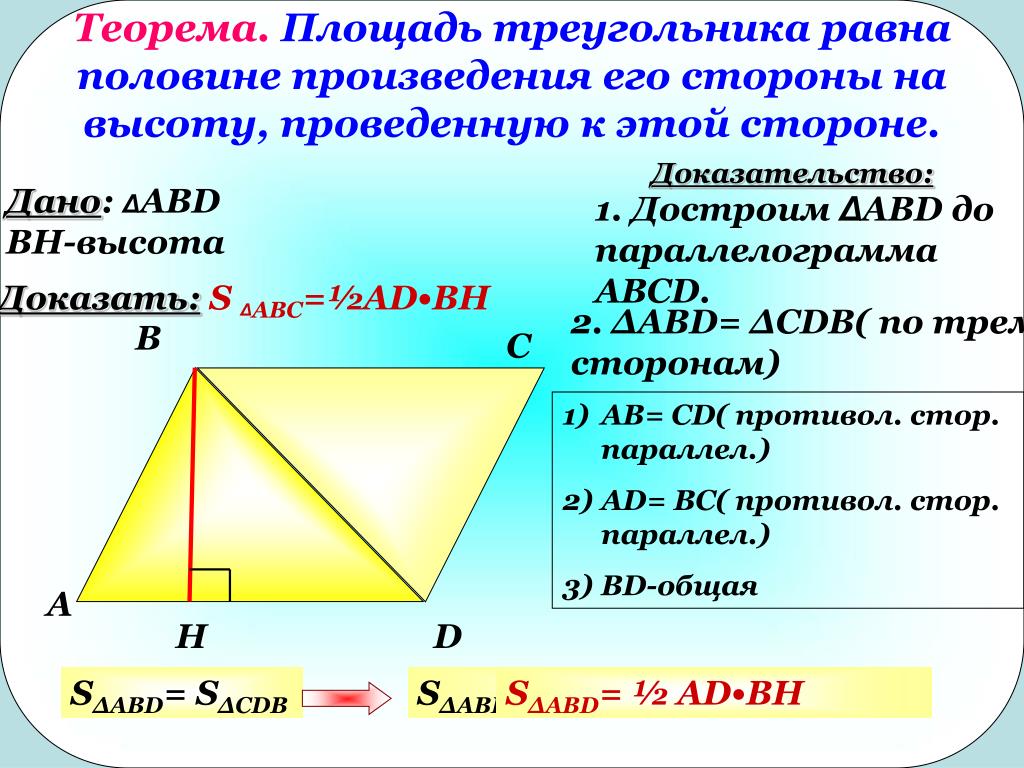
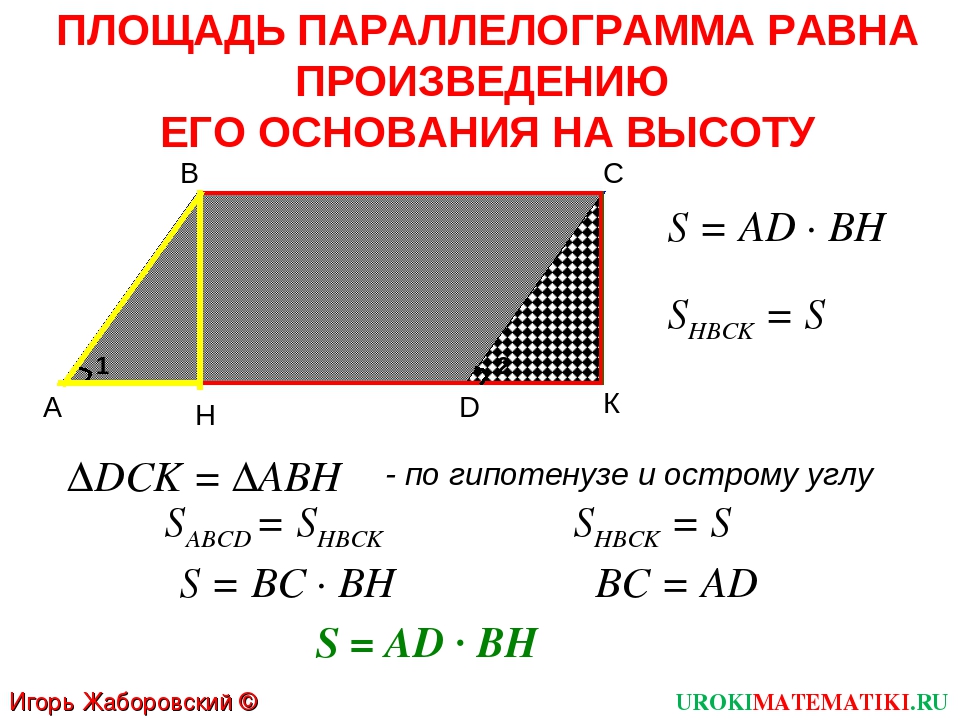

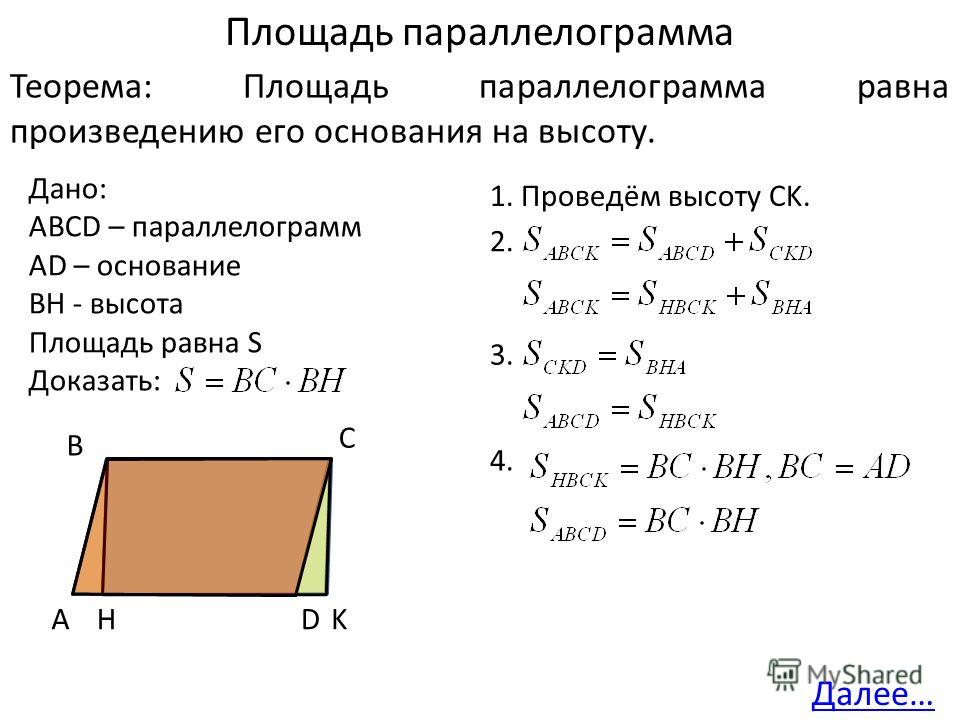
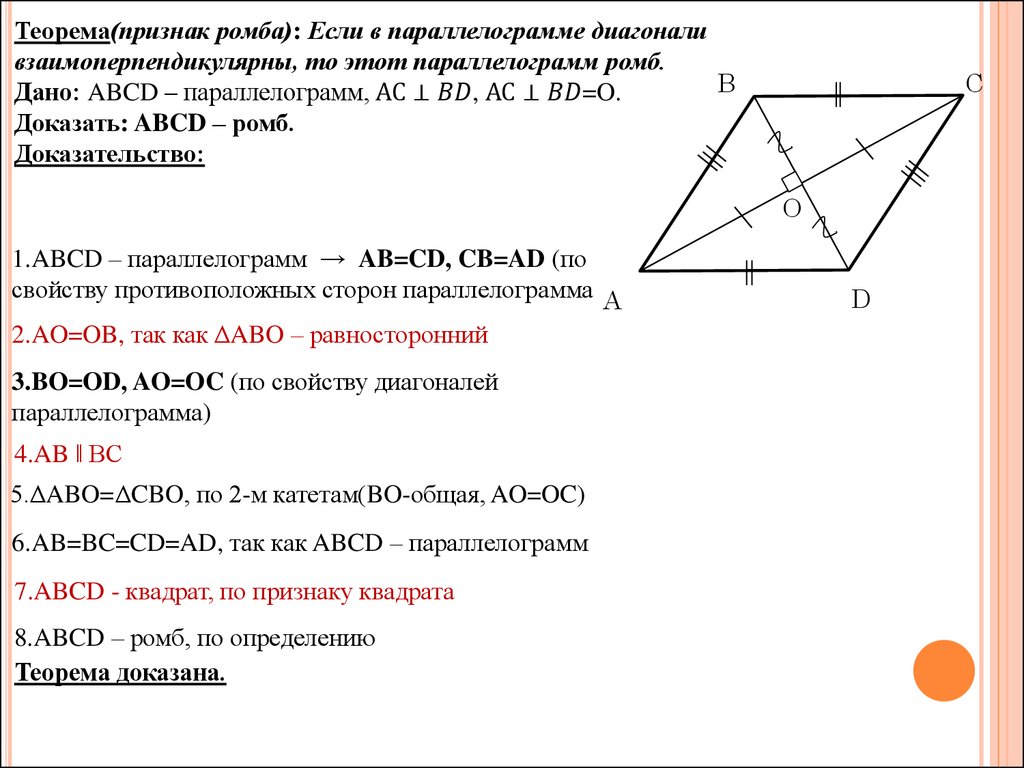 Площадь выпуклого четырёхугольника можно найти по формуле
Площадь выпуклого четырёхугольника можно найти по формуле
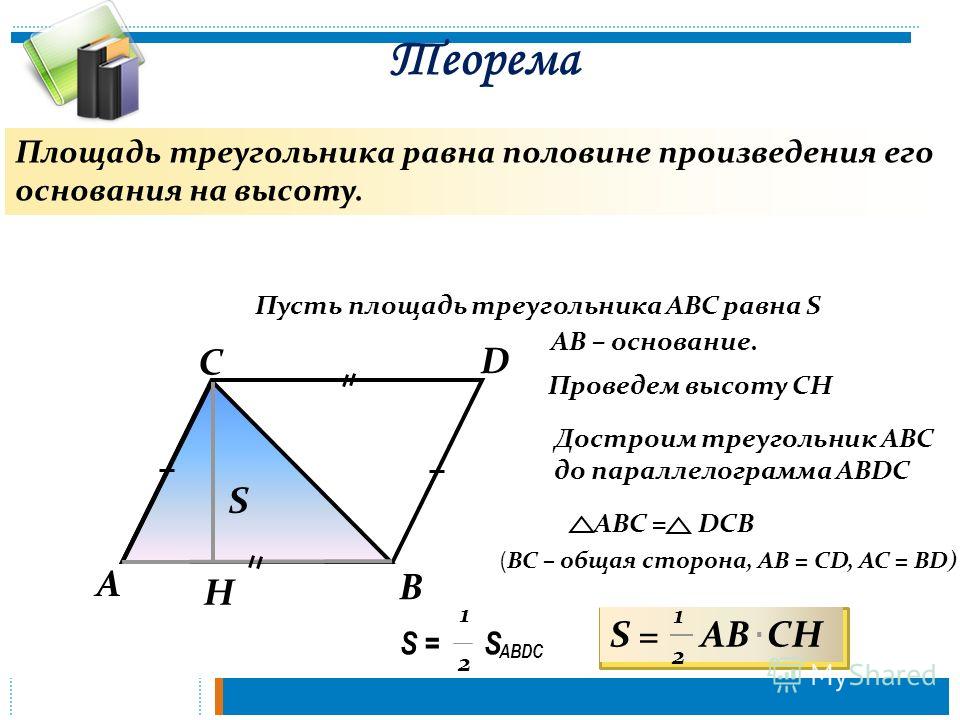 Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому 6).
6). Точка O и является центром вписанной в дельтоид окружности.
Точка O и является центром вписанной в дельтоид окружности. 3.1). Требуется доказать, что.
3.1). Требуется доказать, что. 3.2),
поскольку
Четырёхугольникявляется прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь,
где(катет, лежащий против угла),.
3.2),
поскольку
Четырёхугольникявляется прямоугольником, так как его
углы опираются на диаметр окружности.
Его площадь,
где(катет, лежащий против угла),. 3.4), то– параллелограмм и, значит,.
3.4), то– параллелограмм и, значит,. Следовательно,
площадь S треугольника АВС равна половине
площади параллелограмма,
т.е.
Следовательно,
площадь S треугольника АВС равна половине
площади параллелограмма,
т.е. 4.2
4.2