Как конвертировать из DjVu в PDF
Формат файлов DjVu применяется для хранения сканированных документов, книг и периодических изданий. Данный формат популярен по ряду причин, в первую очередь из-за того, что файлы DjVu в большинстве случаев меньше по размеру, чем файлы PDF. Тем не менее, для просмотра файлов, сохраненных в формате DjVu, требуются специальные плагины или программы для их просмотра, что ограничивает доступность документов в данном формате. Чтобы решить данную проблему, вы можете конвертировать DjVu (дежавю) в PDF (пдф), получившиеся в результате файлы будут соответствовать всем спецификациям PDF и их можно будет открыть на любом компьютере. Программа Универсальный Конвертер Документов – оптимальное решение для перевода из DjVu в PDF.
На этой странице:
Чтобы преобразовать файл DjVu в формат PDF вам потребуются две программы: WinDjView и Универсальный Конвертер Документов.
- Откройте документ DjVu и нажмите Print (Печать)
- Выберите из списка принтеров Универсальный Конвертер Документов и нажмите Print (Печать), чтобы сохранить файлы DjVu в формате PDF:
- Откройте файл DjVu и нажмите Print (Печать)
- Выберите Universal Document Converter из списка принтеров и нажмите Properties (Свойства)
- Перейдите на вкладку Watermark (Водяные знаки) и выберите Text label (Текст) или Picture (Изображение) на ваше усмотрение
- Нажмите OK для запуска конвертации вашего файла DjVu в формат PDF.

- Откройте файл DjVu и нажмите Print (Печать)
- Выберите Universal Document Converter из списка принтеров и нажмите Properties (Свойства)
- Перейдите на вкладку File Format (Формат файла), выберите Password protected (Защита паролем) в PDF Standard и укажите желаемый пароль
- Нажмите OK для запуска конвертации файла DjVu в формат PDF с защитой паролем.
Peter Hovmann
MAN B&W Diesel A/S
«Мы ежедневно экспортируем документы из Microsoft Word в формат PDF для отправки нашим клиентам и в наши сервис-центры. Благодаря тому, что «Универсальный конвертер документов» — это виртуальный принтер, а не программа со сложным интерфейсом, мы не тратим времени на обучение наших сотрудников.»
Популярные решения
Из PDF в DJVU
Сервис позволяет произвести преобразование (конвертировать) из формата Adobe Acrobat (PDF) в формат DJVUPDF – это сокращение от Portable Document Format, что можно перевести с английского как «Формат Переносимого Документа». Его разработала компания Adobe Systems для использования федеральными властями США в качестве инструмента хранения рабочих документов. Это универсальный межплатформенный формат, который сейчас является стандартным для электронных документов. Он служит для того, чтобы без каких-либо потерь преобразовывать текстовые файлы (в том числе с фотографиями или иными изображениями) в электронные документы. Для чтения PDF-файлов нужны специальные программы – Adobe (Acrobat) Reader, PDF-Viewer и другие.
Его разработала компания Adobe Systems для использования федеральными властями США в качестве инструмента хранения рабочих документов. Это универсальный межплатформенный формат, который сейчас является стандартным для электронных документов. Он служит для того, чтобы без каких-либо потерь преобразовывать текстовые файлы (в том числе с фотографиями или иными изображениями) в электронные документы. Для чтения PDF-файлов нужны специальные программы – Adobe (Acrobat) Reader, PDF-Viewer и другие.
DJVU – это формат растровых изображений, который используется для того, чтобы хранить в отсканированном виде журналы, книги, каталоги, другие виды печатной продукции, а также просто отсканированных изображений. Кроме того, файлы указанного формата, разработанного компанией LizardTech, могут применяться для текстовых документов, в которых имеется много формул, рисунков, схем. Другие форматы аналогичной функциональности не способны отражать все детали таких файлов столь точно. DJVU – оптимальный формат для создания электронных библиотек, в которых может быть большие объемы файлов.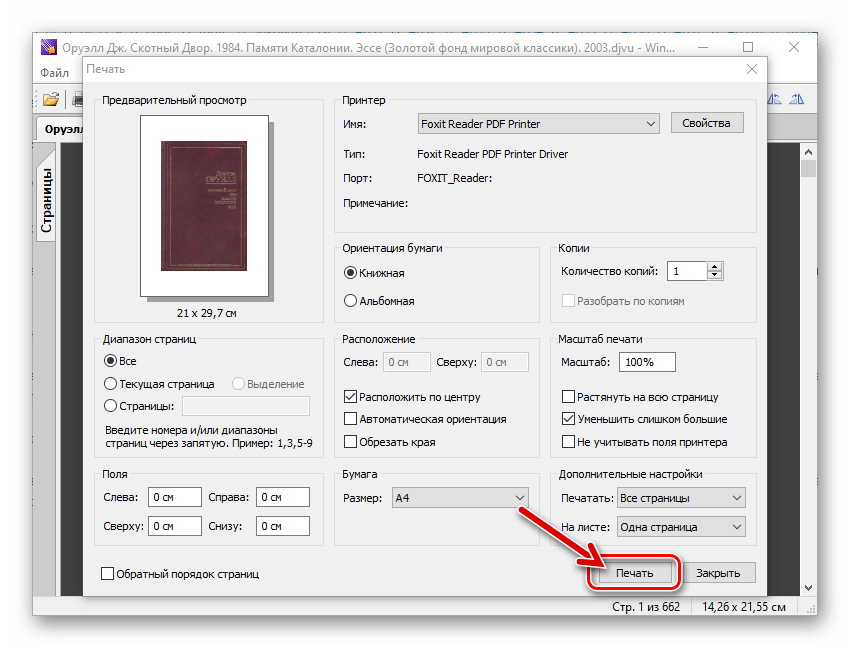
Отзывы
| Больше часа «Идет обработка». По моему это догловато |
| Отлично работает и довольно быстро. |
| Плохо, что нельзя выбрать параметры преобразования. В моем случае документ получился пережатым и текст плохо читается. |
| Простой, понятный, качественный конвертер. Присоединяюсь ко всем — Спасибо! |
| отлично, спасибо, рекомендую знакомым. |
| СПАСИБО! |
| Молодцы!!! Спасибо! |
| Отлично. Рекомендую знакомым. |
| Прекрасно. Спасибо. |
| великолепно, спасибо огромное |
Другие сервисы
Как конвертировать DjVu в PDF формат – 3 способа
Существуют 3 основных способа преобразования файлов DjVu в PDF формат – с помощью конвертера на компьютере, через печать на виртуальном принтере операционной системы и с помощью онлайн сервисов.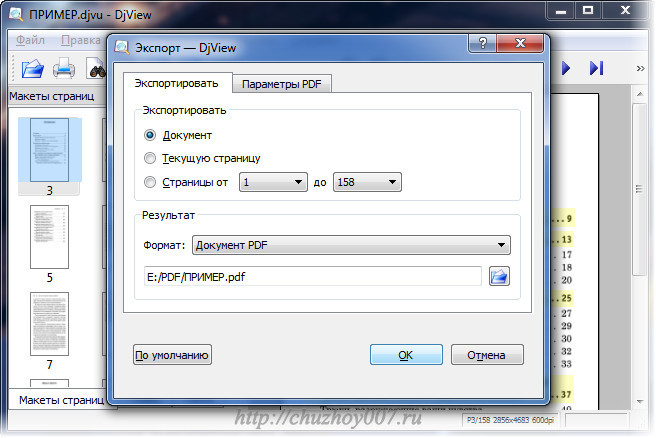 Рассмотрим каждый способ конвертации подробнее и выберем, какой быстрее и удобнее.
Рассмотрим каждый способ конвертации подробнее и выберем, какой быстрее и удобнее.
Способ 1 – утилитой-конвертером
Подходит только для пользователей ОС Windows. Скачайте конвертер DjVu – PDF. Распакуйте скачанный архив в корень любого жесткого диска на компьютере. Откройте папку с программой, найдите и запустите файл с названием «Djvu Small Mod.exe».
В появившемся окне, в середине, найдите и выберите операцию «Декодировать DjVu».
После этого интерфейс немного поменяется, нажмите вверху кнопку «Открыть файл(ы)». Выберите один или несколько DjVu файлов, которые собираетесь преобразовать (поддерживается пакетная конвертация).
В опциях декодирования, там, где написано «Выходной формат», кликните на раскрывающийся список и выберите PDF (см. скриншот).
Затем нажмите кнопку Обзор и выберите папку, в которую будет сохранен созданный файл.
На этом приготовления закончены. Чтобы конвертировать выбранные DjVu файлы в PDF формат, нажмите справа большую кнопку «Декодировать». Преобразование происходит постранично, поэтому придется подождать минуту или две, в зависимости от размера обрабатываемых файлов.
Преобразование происходит постранично, поэтому придется подождать минуту или две, в зависимости от размера обрабатываемых файлов.
Преимущества способа: не нужен интернет, нет рекламы, независимость от компонентов операционной системы, конфиденциальность, простота, пакетное преобразование, не требуется установка, маленький размер создаваемого PDF файла, высокая скорость.
Минусы: не удалось выявить.
Способ 2 – через программу WinDjView (виртуальная печать в файл)
В некоторых программах для чтения DjVu файлов встроен инструмент печати. А в операционной системе Windows установлен по умолчанию виртуальный принтер, который вместо печати сохраняет документы в формате PDF. WinDjView – одна из таких программ.
Скачайте WinDjView, установите на компьютер и запустите. Нажмите CTRL+O и откройте DjVu файл. Затем, через верхнее меню выберите команду «Файл» — «Печать» (или нажмите на клавиатуре CTRL+P, разницы нет).
В окне настроек печати измените принтер на «Microsoft Print to PDF».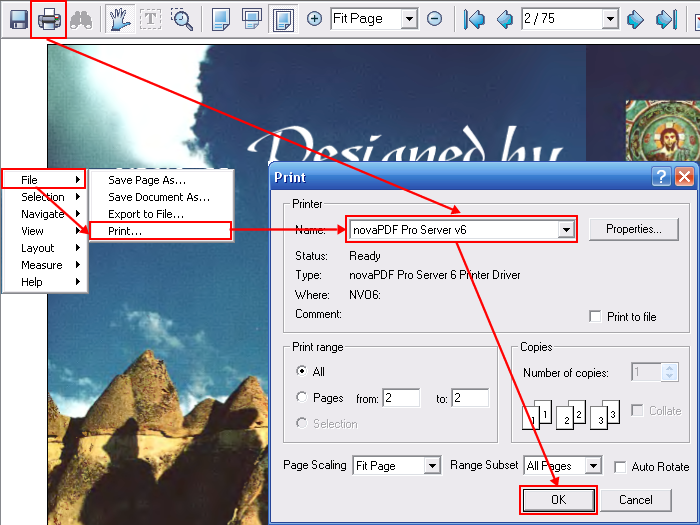 Если принтера с таким названием не окажется в списке – конвертировать этим способом не получится 🙁 Но на Windows 8 и 10 обычно проблем не возникает.
Если принтера с таким названием не окажется в списке – конвертировать этим способом не получится 🙁 Но на Windows 8 и 10 обычно проблем не возникает.
Здесь же можно указать через запятую какие страницы будут обрабатываться (по умолчанию выбрана вся книга), обрезать края или изменить ориентацию бумаги.
Чтобы начать конвертацию, нажмите кнопку «Печать». В следующем окне пропишите имя для создаваемого PDF файла, выберите папку и нажмите «Сохранить».
Преимущества способа: неплохая скорость преобразования, удобство, простота, поддерживается выбор страниц для конвертации, нет рекламы, не зависит от интернета.
Минусы: придется устанавливать дополнительную программу на компьютер; зависит от компонентов ОС — если виртуальный принтер отсутствует или работает некорректно — переконвертировать не получится; нет пакетного режима; неочевидность — без инструкции непонятно, что экспорт в PDF вообще существует в программе; в результате создается файл огромного размера (книга Война и Мир после конвертации стала весить 1. 5 ГБ).
5 ГБ).
Способ 3 – онлайн
Для тех, кому лень качать программы, люди придумали онлайн-сервисы. Это такие сайты, которые конвертируют DjVu в PDF, Doc, TXT и другие форматы электронных документов с помощью скрипта, размещенного на своем сервере. Заливаете документ через форму, запускаете преобразование, скачиваете результат. Покажем на примере. Откройте ссылку:
https://convertio.co/ru/djvu-pdf/
Перетащите DjVu файл на страницу сайта или нажмите на красную кнопку и выберите его из папки на компьютере.
Затем жмите кнопку «Преобразовать», и ждите, пока не появится зеленая кнопочка «Скачать».
После окончания процесса скачайте готовый файл, также перед этим его можно сжать.
Еще сервис поддерживает сохранение результата в Google Drive и Dropbox.
Преимущества способа: не нужно качать программу, подходит для пользователей любых ОС (Windows, Mac OS, Linux, Android и т.д.).
Минусы: требуется постоянное интернет подключение, на сайте придется посмотреть на рекламу, скорости интернета должно хватить на отправку и скачивание файла; конвертирует медленнее, чем программы на компьютере; третьи лица будут знать, какие книги вы конвертируете; иногда бывают проблемы с кодировкой – вместе кириллицы отображаются каракули.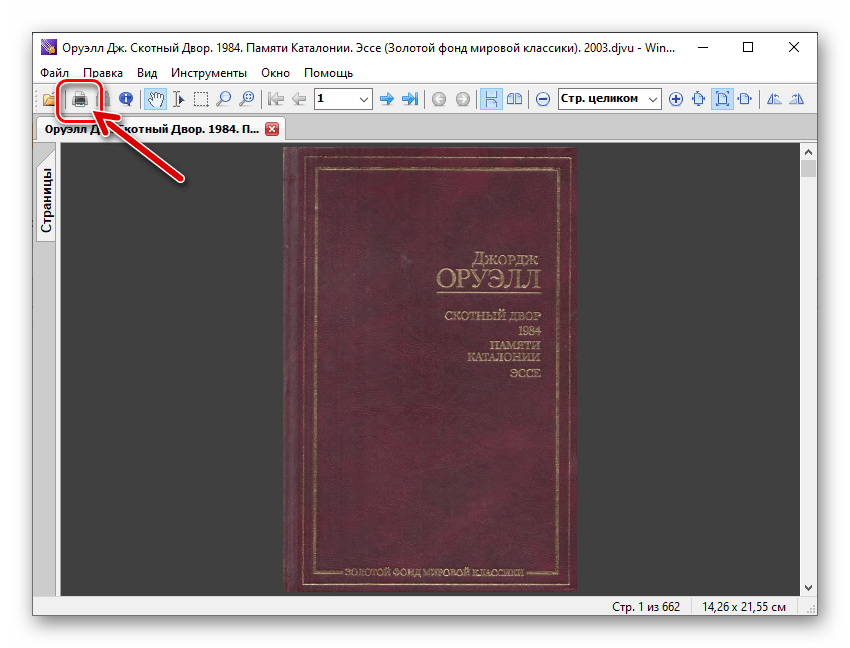
Обобщив плюсы и минусы трех способов, делаем вывод, что конвертировать DjVu в PDF удобнее через конвертер. Согласны? Ответьте в комментариях.
Как перевести DjVu в PDF. Два способа конвертации
В интернете можно встретить довольно много документов в формате DjVu.
Этот формат специально разрабатывался для хранения отсканированных документов, например, книг, журналов или рукописей, но у него есть один минус — не все устройства и программы его поддерживают.
Например, стандартная программа для чтения книг на моем планшете не умеет работать с форматом DjVu и я использую другую программу для чтения материалов в этом формате.
Но далеко не всегда хочется устанавливать отдельную программу только для чтения одной-двух книг и возникает вполне логичный вопрос — можно ли как-то перевести файл DjVu в более привычный и популярный формат PDF.
Ответ — да, можно. Способов существует множество и я расскажу лишь о двух из них.
youtube.com/embed/ho0vNwzlSKA?rel=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»/>Как преобразовать DjVu в PDF
Для просмотра документов в формате DjVu на компьютере должна быть установлена соответствующая программа.
Просмотрщиков существует довольно много. Какие-то из них совсем простые, какие-то имеют более существенный функционал. Нам сейчас понадобится как раз более мощный инструмент и я предлагаю воспользоваться программой WinDjView.
Откроем книгу и выведем ее на печать. Для этого воспользуемся специальной кнопкой на панели задач.
В появившемся окне нужно будет выбрать принтер. В Windows 10 есть PDF-принтер, то есть программа, которая создает виртуальный принтер и позволяет печатать документы, созданные абсолютно любой программой, в PDF-файл.
Также здесь у меня присутствует еще один виртуальный принтер. Он был создан бесплатной программой Foxit Reader, которая предназначена для чтения PDF-файлов. Этот виртуальный принтер также можно использовать, причем в любых версиях Windows, а не только в десятке.
В окне подготовки к выводу на печать мы можем произвести некоторые настройки и увидеть их применение в окне предварительного просмотра. Например, данная отсканированная книга имеет меньший размер страниц, нежели A4, поэтому мы можем растянуть каждую страницу до размера А4 или же можем изменить размер бумаги.
Когда все настройки сделаны, нажимаем на кнопку «Печать», выбираем место на диске, где будет создан документ и указываем его название.
Процесс конвертирования займет некоторое время после чего мы увидим PDF-файл, который сможем открыть.
Есть и еще один вариант перевода файла из формата DjVu в PDF.
Как перевести DjVu в PDF онлайн
Если вы не хотите устанавливать дополнительную программу, то можно воспользоваться одним из множества онлайн-сервисов, которые умеют конвертировать файлы из одного формата в другой.
Например, сервис http://djvu2pdf.com
Здесь нужно просто загрузить файл и дождаться окончания конвертации. Затем скачать полученный PDF-файл на компьютер.
Затем скачать полученный PDF-файл на компьютер.
Мне доводилось слышать возмущения некоторых пользователей, которым не нравился формат DjVu из-за того, что его не поддерживают стандартные программы для чтения PDF-файлов и приходится устанавливать дополнительные приложения на компьютер.
И я согласен, действительно неразумно устанавливать на компьютер программу, которой не будешь пользоваться постоянно. Но все же изначально у этой технологии было конкретное предназначение — она разрабатывалась специально для хранения отсканированных документов, размер файлов которых может быть весьма значительным. И если речь идет о создании электронного архива каких-либо документов, то есть предполагается осканировать и хранить тысячи файлов, то данная технология будет весьма полезна.
Давайте сравним размер получившегося файла PDF и исходника DjVu.
Вы видите, что исходный файл имеет объем чуть более 2 Мб, тогда как получившиеся в результате конвертации PDF-файлы имеют объем более 100 Мб, то есть более чем в 50 раз!
Но для обычного пользователя, скачавшего несколько файлов в формате DjVu, этот критерий не будет особо принципиальным и вполне можно преобразовать DjVu в более удобный PDF любым из описанных выше способов.
Как конвертировать файлы DjVu в PDF
- Главная
- Конвертация файлов DjVu
Формат DjVu специфичен, многие о нём вообще не слышали. А вдруг документ в «дежавю» потребуется передать другому человеку для работы? Можно попросить коллегу тоже установить WinDjView, но вежливее будет конвертировать файл в привычный и всем знакомый PDF.
Для преобразования можно использовать онлайн-конвертеры. Их много, и они разные: платные и бесплатные, работающие и не очень, сохраняющие качество документа и губящие его безвозвратно. Можно воспользоваться ими, но надёжнее подключить виртуальный принтер. Подойдут, например, BullZip Free PDF Printer или PDFCreator. NovaPDF тоже хорош, но его интерфейс не русифицирован.
Виртуальный принтер – это обычная утилита, которую нужно скачать и установить на свой ПК. Когда установка завершится, следует открыть в программе WinDjView файл, который требуется перевести в формат PDF. Ход дальнейших действий выглядит так:
Когда установка завершится, следует открыть в программе WinDjView файл, который требуется перевести в формат PDF. Ход дальнейших действий выглядит так:
- «Файл – печать».
- В открывшемся окне выбрать из списка установленный виртуальный принтер и ещё раз нажать «печать». Настройки здесь обширны: можно распечатать весь документ или только нужные страницы, выбрать масштаб, отступы по краям и т.д.
- Начинается процесс конвертации. В зависимости от объёма документа он может занять от 1-2 минут до получаса, но большинство файлов превращается в PDFочень быстро. Когда процесс завершится, нужно указать место сохранения (рабочий стол, «мои документы» или другая папка).
- Готово. Получился PDF-файл без искажений и потери качества.
Как видим, всё просто и интуитивно понятно.
Иногда бывают перекосы (текст «сползает» вниз, оставляя пустое место в верхней части страницы). Это можно исправить: либо поиграть с настройками печати, либо установить и задействовать другой виртуальный принтер.
Как конвертировать DjVu в PDF с помощью программ
Содержание статьи
Как конвертировать DjVu в PDF формат
Существуют 3 основных способа преобразования файлов DjVu в PDF формат – с помощью конвертера на компьютере, через печать на виртуальном принтере операционной системы и с помощью онлайн сервисов. Рассмотрим каждый способ конвертации подробнее и выберем, какой быстрее и удобнее.
Способ 1 – утилитой-конвертером
Подходит только для пользователей ОС Windows. Скачайте конвертер DjVu – PDF. Распакуйте скачанный архив в корень любого жесткого диска на компьютере. Откройте папку с программой, найдите и запустите файл с названием «Djvu Small Mod.exe».
В появившемся окне, в середине, найдите и выберите операцию «Декодировать DjVu».
После этого интерфейс немного поменяется, нажмите вверху кнопку «Открыть файл(ы)». Выберите один или несколько DjVu файлов, которые собираетесь преобразовать (поддерживается пакетная конвертация).
В опциях декодирования, там, где написано «Выходной формат», кликните на раскрывающийся список и выберите PDF (см. скриншот).
Затем нажмите кнопку Обзор и выберите папку, в которую будет сохранен созданный файл.
На этом приготовления закончены. Чтобы конвертировать выбранные DjVu файлы в PDF формат, нажмите справа большую кнопку «Декодировать». Преобразование происходит постранично, поэтому придется подождать минуту или две, в зависимости от размера обрабатываемых файлов.
Преимущества способа: не нужен интернет, нет рекламы, независимость от компонентов операционной системы, конфиденциальность, простота, пакетное преобразование, не требуется установка, маленький размер создаваемого PDF файла, высокая скорость.
Минусы: не удалось выявить.
Способ 2 – через программу WinDjView (виртуальная печать в файл)
В некоторых программах для чтения DjVu файлов встроен инструмент печати. А в операционной системе Windows установлен по умолчанию виртуальный принтер, который вместо печати сохраняет документы в формате PDF. WinDjView – одна из таких программ.
А в операционной системе Windows установлен по умолчанию виртуальный принтер, который вместо печати сохраняет документы в формате PDF. WinDjView – одна из таких программ.
Скачайте WinDjView, установите на компьютер и запустите. Нажмите CTRL+O и откройте DjVu файл. Затем, через верхнее меню выберите команду «Файл» — «Печать» (или нажмите на клавиатуре CTRL+P, разницы нет).
В окне настроек печати измените принтер на «Microsoft Print to PDF». Если принтера с таким названием не окажется в списке – конвертировать этим способом не получится 🙁 Но на Windows 8 и 10 обычно проблем не возникает.
Здесь же можно указать через запятую какие страницы будут обрабатываться (по умолчанию выбрана вся книга), обрезать края или изменить ориентацию бумаги.
Чтобы начать конвертацию, нажмите кнопку «Печать». В следующем окне пропишите имя для создаваемого PDF файла, выберите папку и нажмите «Сохранить».
Преимущества способа: неплохая скорость преобразования, удобство, простота, поддерживается выбор страниц для конвертации, нет рекламы, не зависит от интернета.
Минусы: придется устанавливать дополнительную программу на компьютер; зависит от компонентов ОС — если виртуальный принтер отсутствует или работает некорректно — переконвертировать не получится; нет пакетного режима; неочевидность — без инструкции непонятно, что экспорт в PDF вообще существует в программе; в результате создается файл огромного размера (книга Война и Мир после конвертации стала весить 1.5 ГБ).
Способ 3 – онлайн
Для тех, кому лень качать программы, люди придумали онлайн-сервисы. Это такие сайты, которые конвертируют DjVu в PDF, Doc, TXT и другие форматы электронных документов с помощью скрипта, размещенного на своем сервере. Заливаете документ через форму, запускаете преобразование, скачиваете результат. Покажем на примере. Откройте ссылку:
Перетащите DjVu файл на страницу сайта или нажмите на красную кнопку и выберите его из папки на компьютере.
Затем жмите кнопку «Преобразовать», и ждите, пока не появится зеленая кнопочка «Скачать».
После окончания процесса скачайте готовый файл, также перед этим его можно сжать.
Еще сервис поддерживает сохранение результата в Google Drive и Dropbox.
Преимущества способа: не нужно качать программу, подходит для пользователей любых ОС (Windows, Mac OS, Linux, Android и т.д.).
Минусы: требуется постоянное интернет подключение, на сайте придется посмотреть на рекламу, скорости интернета должно хватить на отправку и скачивание файла; конвертирует медленнее, чем программы на компьютере; третьи лица будут знать, какие книги вы конвертируете; иногда бывают проблемы с кодировкой – вместе кириллицы отображаются каракули.
Как конвертировать DjVu в PDF с помощью программ
Как конвертировать файл в формате DjVu в файл в формате PDF с помощью программы? С такой проблемой часто сталкиваются пользователи, когда из файла в формате DjVu необходимо получить файл в формате PDF.
Файл, сохраненный в формате DjVu («дежавю»), в отличие от аналогичного файла в формате PDF имеет значительно меньший размер. Поэтому в формате DjVu часто сохраняется техническая литература, энциклопедии, словари и т. п., другие документы, имеющие в своем составе много изображений, схем, фотографий. Страницы книг сохраняются в хорошем качестве, а сам файл будет значительно меньшего размера, чем такой же файл в формате PDF.
Поэтому в формате DjVu часто сохраняется техническая литература, энциклопедии, словари и т. п., другие документы, имеющие в своем составе много изображений, схем, фотографий. Страницы книг сохраняются в хорошем качестве, а сам файл будет значительно меньшего размера, чем такой же файл в формате PDF.
Почему возникает необходимость перевода DjVu в PDF? Дело в том, что существует небольшое количество программ, созданных для просмотра файлов в формате DjVu. О самых популярных просмотрщиках DjVu вы можете прочитать в разделе «Текст» на моем сайте.
Второй важный момент, проблема просмотра файлов формата DjVu на разных устройствах. Если на компьютере с просмотром «дежавю» нет проблем, то на мобильных устройствах с этим сложнее. Даже, если есть соответствующие приложения, то возможны проблемы с форматированием и т. п.
Преимущество формата PDF в его универсальности, нет проблем с просмотром. Важным преимуществом является то, что документ в формате PDF выглядит одинаково на всех устройствах и компьютерах.
Поэтому необходим конвертер DjVu в PDF. Для того, чтобы перевести DjVu в PDF мы используем бесплатные программы для просмотра файлов формата DjVu (WinDjView, STDU Viewer, Sumatra PDF), имеющие функцию печати.
Дополнительно понадобится установить на компьютер виртуальный принтер. Виртуальный принтер позволяет сохранить документ в формате PDF из окна открытой программы, поэтому эта программа не будет лишней на вашем компьютере.
В операционную систему Windows 10 установлен виртуальный принтер Microsoft Print to PDF, поэтому пользователи в этой ОС могут не устанавливать подобную программу. На компьютеры с операционными системами Windows 7, Windows 8, Windows 8.1 нужно установить бесплатный виртуальный принтер, например, BullZip PDF Printer, PDFCreator, PrimoPDF, CutePDF Writer, doPDF.
Просто установите на компьютер виртуальный принтер. Вы будете использовать виртуальный принтер при необходимости, для сохранения на компьютере файлов в формате PDF, вместо печати документов на обычном принтере.
Для преобразования DjVu в PDF онлайн существуют специальные сервисы, о которых я расскажу в другой статье.
Конвертируем DjVu в PDF в программе WinDjView
Бесплатная программа WinDjView предназначена для просмотра файлов в формате DjVu. С помощью этой программы можно преобразовать файл DjVu в формат PDF, непосредственно из окна программы.
Откройте в программе WinDjView книгу или любой другой документ в формате DjVu. Далее нажмите на кнопку «Печать» (изображение принтера).
В открывшемся окне «Печать» выберите виртуальный принтер. На моем компьютере в операционной системе Windows 10, установлен виртуальный принтер Microsoft Print to PDF, поэтому я выбрал этот принтер для преобразования в формат PDF.
Если на вашем компьютере установлена операционная система Windows 7 или Windows 8.1 (Windows 8), то тогда выберите виртуальный принтер, установленный на вашем компьютере (предварительно необходимо установить на компьютер виртуальный принтер).
Далее нажмите на кнопку «Печать».
В открывшемся окне Проводника выберите место для сохранения файла, дайте имя создаваемому файлу. После этого начнется процесс преобразования файла из формата DjVu в формат PDF, который займет некоторое время.
После завершения процесса, можно открыть новый файл в PDF с помощью программы для открытия файлов данного типа.
На этом изображении, файл в формате PDF открыт в средстве просмотра.
Как конвертировать DjVu в PDF в программе STDU Viewer
С помощью бесплатной программы STDU Viewer можно перевести DjVu в PDF из окна программы. Откройте файл в формате DjVu в программе STDU Viewer.
Далее нажмите на кнопку «Печать».
В окне «Печать» выберите виртуальный принтер, а затем нажмите на кнопку «Печать».
Дайте имя новому файлу в формате PDF, выберите место для его сохранения. После завершения процесса конвертации, преобразованный файл в формате PDF готов для использования.
Как преобразовать DjVu в PDF в программе Sumatra PDF
Бесплатная программа Sumatra PDF поддерживает просмотр файлов в формате DjVu. В Sumatra PDF можно преобразовать DjVu в PDF подобным образом, как в предыдущих программах.
В Sumatra PDF можно преобразовать DjVu в PDF подобным образом, как в предыдущих программах.
После открытия файла DjVu в программе Sumatra PDF, нажмите на кнопку «Печать».
В окне «Печать», во вкладке «Общие» выберите виртуальный принтер, а потом нажмите на кнопку «Печать».
В открывшемся окне дайте имя сохраняемому файлу в формате PDF, выберите место сохранения файла.
Далее начнется процесс конвертирования, по завершению которого, будет создан новый файл в формате PDF.
Выводы статьи
С помощью бесплатных программ WinDjView, STDU Viewer, Sumatra PDF, которые предназначены для просмотра файлов в формате DjVu, можно конвертировать DjVu в PDF с помощью функции печати, при помощи виртуального принтера, установленного на компьютере.
2 СПОСОБА: Как перевести файл DjVu в PDF
В интернете можно встретить довольно много документов в формате DjVu.Этот формат специально разрабатывался для хранения отсканированных документов, например, книг, журналов или рукописей, но у него есть один минус — не все устройства и программы его поддерживают.
Например, стандартная программа для чтения книг на моем планшете не умеет работать с форматом DjVu и я использую другую программу для чтения материалов в этом формате.
Но далеко не всегда хочется устанавливать отдельную программу только для чтения одной-двух книг и возникает вполне логичный вопрос — можно ли как-то перевести файл DjVu в более привычный и популярный формат PDF.
Ответ — да, можно. Способов существует множество и я расскажу лишь о двух из них.
Как преобразовать DjVu в PDF
Для просмотра документов в формате DjVu на компьютере должна быть установлена соответствующая программа.
Просмотрщиков существует довольно много. Какие-то из них совсем простые, какие-то имеют более существенный функционал. Нам сейчас понадобится как раз более мощный инструмент и я предлагаю воспользоваться программой WinDjView.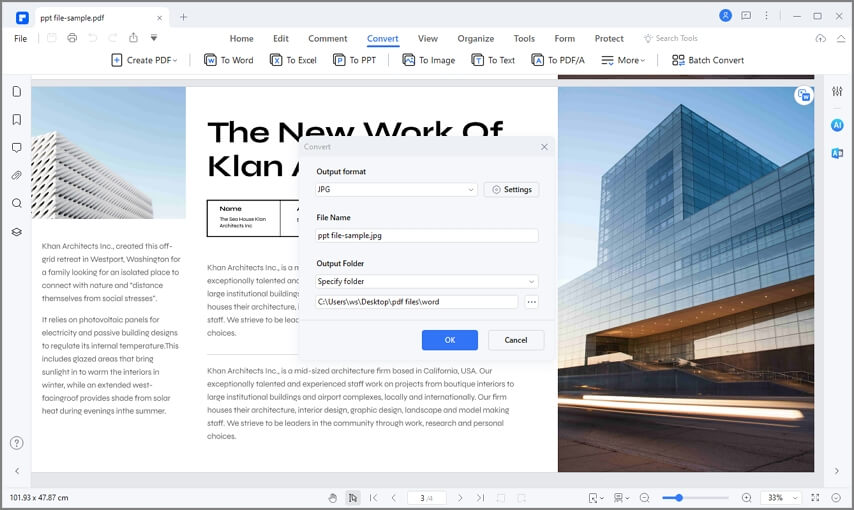
Откроем книгу и выведем ее на печать. Для этого воспользуемся специальной кнопкой на панели задач.
В появившемся окне нужно будет выбрать принтер. В Windows 10 есть PDF-принтер, то есть программа, которая создает виртуальный принтер и позволяет печатать документы, созданные абсолютно любой программой, в PDF-файл.
Также здесь у меня присутствует еще один виртуальный принтер. Он был создан бесплатной программой Foxit Reader, которая предназначена для чтения PDF-файлов. Этот виртуальный принтер также можно использовать, причем в любых версиях Windows, а не только в десятке.
В окне подготовки к выводу на печать мы можем произвести некоторые настройки и увидеть их применение в окне предварительного просмотра. Например, данная отсканированная книга имеет меньший размер страниц, нежели A4, поэтому мы можем растянуть каждую страницу до размера А4 или же можем изменить размер бумаги.
Когда все настройки сделаны, нажимаем на кнопку «Печать», выбираем место на диске, где будет создан документ и указываем его название.
Процесс конвертирования займет некоторое время после чего мы увидим PDF-файл, который сможем открыть.
Есть и еще один вариант перевода файла из формата DjVu в PDF.
Как перевести DjVu в PDF онлайн
Если вы не хотите устанавливать дополнительную программу, то можно воспользоваться одним из множества онлайн-сервисов, которые умеют конвертировать файлы из одного формата в другой.
Здесь нужно просто загрузить файл и дождаться окончания конвертации. Затем скачать полученный PDF-файл на компьютер.
Мне доводилось слышать возмущения некоторых пользователей, которым не нравился формат DjVu из-за того, что его не поддерживают стандартные программы для чтения PDF-файлов и приходится устанавливать дополнительные приложения на компьютер.
И я согласен, действительно неразумно устанавливать на компьютер программу, которой не будешь пользоваться постоянно. Но все же изначально у этой технологии было конкретное предназначение — она разрабатывалась специально для хранения отсканированных документов, размер файлов которых может быть весьма значительным. И если речь идет о создании электронного архива каких-либо документов, то есть предполагается осканировать и хранить тысячи файлов, то данная технология будет весьма полезна.
И если речь идет о создании электронного архива каких-либо документов, то есть предполагается осканировать и хранить тысячи файлов, то данная технология будет весьма полезна.
Давайте сравним размер получившегося файла PDF и исходника DjVu.
Вы видите, что исходный файл имеет объем чуть более 2 Мб, тогда как получившиеся в результате конвертации PDF-файлы имеют объем более 100 Мб, то есть более чем в 50 раз!
Но для обычного пользователя, скачавшего несколько файлов в формате DjVu, этот критерий не будет особо принципиальным и вполне можно преобразовать DjVu в более удобный PDF любым из описанных выше способов.
Конвертирование DjVu в PDF
Довольно часто пользователи, которые привыкли работать с текстовыми документами на компьютере или других электронных устройствах, могут столкнуться с тем, что какой-то учебник или документ доступен только в формате DjVu, а не все устройства способны читать данный формат, и программы для открытия не всегда найдешь.

Как конвертировать DjVu в PDF
Есть много различных конвертеров, которые могут помочь пользователю преобразовать DjVu в более популярный формат представления текстовых данных – PDF. Проблема в том, что многие из них абсолютно не помогают или выполняют нужное действие только при определенных условиях и с максимальными потерями данных. Но есть несколько способов, которые были оценены многими пользователями.
Способ 1: Universal Document Converter
Конвертер UDC является наиболее популярной программой для того, чтобы перевести документ из одного формата в другой. Именно с его помощью можно быстро преобразовать DjVu в PDF.
- Первым делом надо скачать и установить конвертер, открыть сам документ, который нужно конвертировать, в любой программе, дающей возможность просматривать DjVu, например, WinDjView.
- Теперь надо перейти к пункту «Файл» — «Печать…». Также это можно выполнить нажатием на «Ctrl+P».
В окне печати надо убедиться, что в качестве принтера стоит «Universal Document Converter», и нажать на кнопку «Свойства».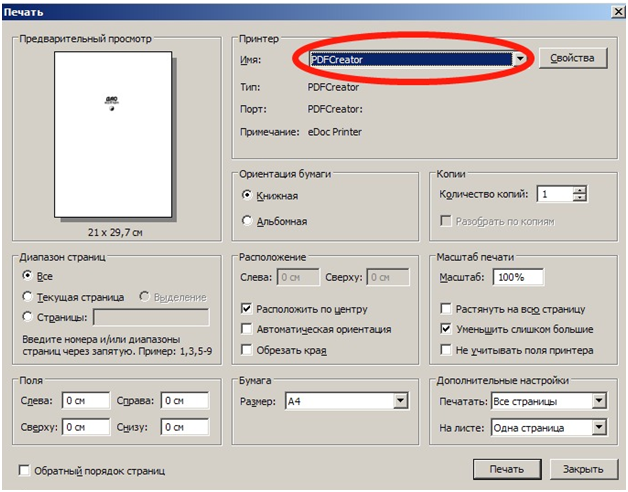
Можно нажимать на кнопку «Печать» и выбирать место для сохранения нового документа.
Конвертирование файла через программу UDC занимает чуть больше времени, чем через другие конвертеры, но зато здесь можно выбрать дополнительные параметры и разные выходные характеристики.
Способ 2: принтер Adobe Reader
Программа Adobe Reader, которая позволяет просматривать документы PDF, поможет еще и преобразовать в этот формат файл DjVu. Делается это так же, как и в первом способе, только чуть быстрее. Главное, чтобы на компьютере была установлена Pro версия программы.
- После открытия документа надо проделать тот же пункт, что указан в первом способе: начать печать документа через программу.
Теперь надо выбрать в списке принтеров «Adobe PDF».
Все остальные способы, которые будут указаны в статье, выполняются по такому же алгоритму, но все равно стоит их разобрать, чтобы понять, что из себя представляет каждая программа.
Способ 3: Bullzip PDF Printer
Еще один конвертер, который чем-то похож на UDC, но помогает преобразовывать документы лишь в один формат – PDF. В программе нет большого количества настроек, можно выбрать лишь те, что установлены стандартно. Но у конвертера есть один большой плюс: размер документа в итоге почти не меняется, а качество остается на лучшем уровне.
- Первым делом надо установить программу для конвертации и открыть документ в приложении, которое позволяет читать файлы DjVu, нажать на «Файл» — «Печать…».
Теперь в списке принтеров необходимо выбрать пункт «Bullzip PDF Printer».
Способ 4: Microsoft Print
Последний способ использует стандартный принтер от Microsoft, который предустановлен в системе. Его можно использовать, когда документ надо лишь быстро преобразовать в формат PDF без каких-то глубоких настроек.
Стандартный принтер очень похож на программу Bullzip PDF Printer, поэтому и алгоритм действий у него такой же, надо лишь выбрать в списке принтеров «Microsoft Print to PDF».
Вот такие есть способы быстрого преобразования файла DjVu в PDF. Если вам известны еще какие-то программы и средства, то пишите о них в комментариях, чтобы мы и другие пользователи также могли оценить их.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Перекодирование из пдф в дежавю. Лучший способ конвертировать PDF в DjVu
Как конвертировать файл в формате DjVu в файл в формате PDF с помощью программы? С такой проблемой часто сталкиваются пользователи, когда из файла в формате DjVu необходимо получить файл в формате PDF.
Файл, сохраненный в формате DjVu («дежавю»), в отличие от аналогичного файла в формате PDF имеет значительно меньший размер. Поэтому в формате DjVu часто сохраняется техническая литература, энциклопедии, словари и т. п. , другие документы, имеющие в своем составе много изображений, схем, фотографий. Страницы книг сохраняются в хорошем качестве, а сам файл будет значительно меньшего размера, чем такой же файл в формате PDF.
, другие документы, имеющие в своем составе много изображений, схем, фотографий. Страницы книг сохраняются в хорошем качестве, а сам файл будет значительно меньшего размера, чем такой же файл в формате PDF.
Почему возникает необходимость перевода DjVu в PDF? Дело в том, что существует небольшое количество программ, созданных для просмотра файлов в формате DjVu. О самых популярных просмотрщиках DjVu вы можете прочитать в разделе «Текст» на моем сайте.
Второй важный момент, проблема просмотра файлов формата DjVu на разных устройствах. Если на компьютере с просмотром «дежавю» нет проблем, то на мобильных устройствах с этим сложнее. Даже, если есть соответствующие приложения, то возможны проблемы с форматированием и т. п.
Преимущество формата PDF в его универсальности, нет проблем с просмотром. Важным преимуществом является то, что документ в формате PDF выглядит одинаково на всех устройствах и компьютерах.
Поэтому необходим конвертер DjVu в PDF. Для того, чтобы перевести DjVu в PDF мы используем бесплатные программы для просмотра файлов формата DjVu (WinDjView, STDU Viewer, Sumatra PDF), имеющие функцию печати.
Дополнительно понадобится установить на компьютер виртуальный принтер. Виртуальный принтер позволяет сохранить документ в формате PDF из окна открытой программы, поэтому эта программа не будет лишней на вашем компьютере.
В операционную систему Windows 10 установлен виртуальный принтер Microsoft Print to PDF, поэтому пользователи в этой ОС могут не устанавливать подобную программу. На компьютеры с операционными системами Windows 7, Windows 8, Windows 8.1 нужно установить бесплатный виртуальный принтер, например, BullZip PDF Printer, PrimoPDF, CutePDF Writer, doPDF.
Просто установите на компьютер виртуальный принтер. Вы будете использовать виртуальный принтер при необходимости, для сохранения на компьютере файлов в формате PDF, вместо печати документов на обычном принтере.
Для преобразования DjVu в PDF онлайн существуют специальные сервисы, о которых я расскажу в другой статье.
Конвертируем DjVu в PDF в программе WinDjView
Бесплатная программа предназначена для просмотра файлов в формате DjVu. С помощью этой программы можно преобразовать файл DjVu в формат PDF, непосредственно из окна программы.
С помощью этой программы можно преобразовать файл DjVu в формат PDF, непосредственно из окна программы.
Откройте в программе WinDjView книгу или любой другой документ в формате DjVu. Далее нажмите на кнопку «Печать» (изображение принтера).
В открывшемся окне «Печать» выберите виртуальный принтер. На моем компьютере в операционной системе Windows 10, установлен виртуальный принтер Microsoft Print to PDF, поэтому я выбрал этот принтер для преобразования в формат PDF.
Если на вашем компьютере установлена операционная система Windows 7 или Windows 8.1 (Windows 8), то тогда выберите виртуальный принтер, установленный на вашем компьютере (предварительно необходимо установить на компьютер виртуальный принтер).
В открывшемся окне Проводника выберите место для сохранения файла, дайте имя создаваемому файлу. После этого начнется процесс преобразования файла из формата DjVu в формат PDF, который займет некоторое время.
После завершения процесса, можно открыть новый файл в PDF с помощью программы для открытия файлов данного типа.
На этом изображении, файл в формате PDF открыт в средстве просмотра.
Как конвертировать DjVu в PDF в программе STDU Viewer
С помощью бесплатной программы можно перевести DjVu в PDF из окна программы. Откройте файл в формате DjVu в программе STDU Viewer.
В окне «Печать» выберите виртуальный принтер, а затем нажмите на кнопку «Печать».
Дайте имя новому файлу в формате PDF, выберите место для его сохранения. После завершения процесса конвертации, преобразованный файл в формате PDF готов для использования.
Как преобразовать DjVu в PDF в программе Sumatra PDF
Бесплатная программа поддерживает просмотр файлов в формате DjVu. В Sumatra PDF можно преобразовать DjVu в PDF подобным образом, как в предыдущих программах.
После открытия файла DjVu в программе Sumatra PDF, нажмите на кнопку «Печать».
В окне «Печать», во вкладке «Общие» выберите виртуальный принтер, а потом нажмите на кнопку «Печать».
В открывшемся окне дайте имя сохраняемому файлу в формате PDF, выберите место сохранения файла.
Выводы статьи
С помощью бесплатных программ WinDjView, STDU Viewer, Sumatra PDF, которые предназначены для просмотра файлов в формате DjVu, можно конвертировать DjVu в PDF с помощью функции печати, при помощи виртуального принтера, установленного на компьютере.
Программы для конвертирования pdf в djvuВ преимущество этого формата можно отнести его большую степень сжатия файла, но это же преимущество иногда является и его недостатком. Сильное сжатие портит вид картинок в книге, делая их расплывчатыми и нечеткими. Также отсутствие возможности редактировать в djvu программах также приводит к необходимости к конвертации. По этой и другим причинам многие люди сталкиваются с постоянной проблемой, чтобы конвертировать pdf в djvu . Некоторым приходиться проделывать не один шаг, чтобы произвести конвертацию. Однако это приводит к потере времени и нервов. И если дело касается одной, двух страниц, то это может быть не так заметно, но что если нужно постоянно конвертировать большие объемы материала?
К счастью разработаны специальные программы, призванные облегчить такой нелегкий труд. В этой статье мы с вами рассмотрим программы, с помощью которых это можно делать, а также советы по ее использованию.
В этой статье мы с вами рассмотрим программы, с помощью которых это можно делать, а также советы по ее использованию.
Программа STDU Converter для перевода
pdf в djvuНа самом деле существует несколько способов конвертации. Есть разные программы и способы. Мы рассмотрим программу STDU Converter
. Эта программа проста в использовании и для конвертации pdf to djvu будет достаточно нажать всего лишь две кнопки, чтобы справится с конвертацией любых размеров исходного файла. Также эта программа на выходе документа позволит создать собственную структуру документа. Еще одним преимуществом программы STDU Converter является то, что ее не нужно устанавливать, поскольку эта программа относится к портабельным. Допустим, что вам не нужно конвертировать весь документ, а только некоторые его страницы. Левая панель программы STDU Converter позволит это сделать. В программе предоставляется возможность отметить галочкой нужные страницы и приступить к их конвертации. Эта программа бесплатна и поэтому не придется искать ключи или платить за нее.
Пользоваться ею легко. Для осуществления конвертации достаточно будет с помощью нее открыть дежавю документ и нажать кнопку «конвертировать». Единственное действие, которое придется вам сделать еще – это прописать в открывшемся окне программы конечное место сохранения файла. Вот и все.
WinDjView для конвертации
pdf в djvuЕще одной программой, с помощью которой можно перевести pdf в djvu служит WinDjView. На первый взгляд перед нами обычная программа, читающая djvu формат. Однако это не так. В WinDjView встроена интересная функция, которая служит прекрасным конвертером.
Пользоваться этой программой не сложно. Вначале открываем нужный документ, подлежащий конвертации. После его открытия нажимаем на «печать». Не бойтесь. В этом случае ваш принтер не начнет печатать страницы. Это диалоговое окно виртуального принтера. В этом окне нам предложат варианты конечного расширения конвертации. Выбираем pdf и запускаем принтер. Останется только выбрать конечную папку конвертации, и работа завершена.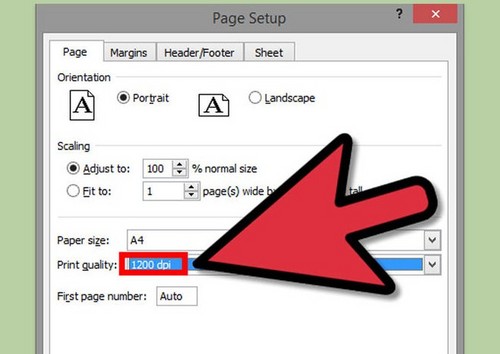 В заключении полученный документ откроется автоматически.
В заключении полученный документ откроется автоматически.
Также есть и другие программы, с помощью которых можно делать конвертацию. Например,PDF Creator, universal Document Converter, позволяющий производить конвертацию не только в PDF, но и другие форматы.
Какой бы программой вы бы ни пользовались, вначале нужно изучить системные требования программы. А если скачиваете ее из файлообменников, обязательно удостоверьтесь в его надежности, чтобы не получить с программой вирусы. Если присутствует вместе с вьюером djvu и плагин, тогда конвертировать файлы вы сможете через браузер.
Сервис позволяет произвести преобразование (конвертировать) из формата Adobe Acrobat (PDF) в формат DJVU
PDF – это сокращение от Portable Document Format, что можно перевести с английского как «Формат Переносимого Документа». Его разработала компания Adobe Systems для использования федеральными властями США в качестве инструмента хранения рабочих документов. Это универсальный межплатформенный формат, который сейчас является стандартным для электронных документов. Он служит для того, чтобы без каких-либо потерь преобразовывать текстовые файлы (в том числе с фотографиями или иными изображениями) в электронные документы. Для чтения PDF-файлов нужны специальные программы – Adobe (Acrobat) Reader, PDF-Viewer и другие.
Он служит для того, чтобы без каких-либо потерь преобразовывать текстовые файлы (в том числе с фотографиями или иными изображениями) в электронные документы. Для чтения PDF-файлов нужны специальные программы – Adobe (Acrobat) Reader, PDF-Viewer и другие.
DJVU – это формат растровых изображений, который используется для того, чтобы хранить в отсканированном виде журналы, книги, каталоги, другие виды печатной продукции, а также просто отсканированных изображений. Кроме того, файлы указанного формата, разработанного компанией LizardTech, могут применяться для текстовых документов, в которых имеется много формул, рисунков, схем. Другие форматы аналогичной функциональности не способны отражать все детали таких файлов столь точно. DJVU – оптимальный формат для создания электронных библиотек, в которых может быть большие объемы файлов.
Отзывы
| Больше часа «Идет обработка». По моему это догловато |
| Отлично работает и довольно быстро. |
Плохо, что нельзя выбрать параметры преобразования. В моем случае документ получился пережатым и текст плохо читается. В моем случае документ получился пережатым и текст плохо читается. |
| Простой, понятный, качественный конвертер. Присоединяюсь ко всем — |
PDF to DJVU Converter — программа-конвертер, предназначенная для конвертирования PDF в DJVU . Используя эту программу мы сможем успешно . «Но зачем конвертировать PDF в DJVU», — наверное, спросите Вы. Дело в том, что в большинстве случаев книги в DJVU формате занимают намного меньше места, чем их аналоги в PDF формате. Соответственно из соображений экономии места на компьютере можно .
В этом руководстве будет дана подробная инструкция как конвертировать PDF в DJVU . Стоит отметить, что на нашем сайте рассматривался обратный процесс: конвертирование DJVU в PDF , но теперь мы покажем, как можно . Для успешного конвертирования нам нужна программа, которая умеет это делать. Как было упомянуто выше — эта программа называется PDF to DJVU Converter . Ее нужно скачать. Скачать можете по ссылкам в конце этой статьи. Ну а теперь приступим к нашей главной задаче — .
Ну а теперь приступим к нашей главной задаче — .
ИНСТРУКЦИЯ ПО КОНВЕРТИРОВАНИЮ PDF В DJVU
Итак, скачали архив с программой PDF to DJVU Converter , распаковываем архив, открываем папку PDFtoDJVU/bin и двойным щелчком мыши запускаем файл pdf2djvugui.exe или просто pdf2djvugui (если расширение файлов у Вас не отображается). Откроется главное окно PDF to DJVU Converter :
Теперь в строке «Input File» нажимаем на кнопку «Browse» и указываем PDF файл , который надо конвертировать в DJVU. Смотрим скриншоты:
В строке «Output File» (Выходной файл) указана папка, где будет размещен файл в DJVU формате. По умолчанию это та же папка, где содержится исходный файл (PDF формат). Чтобы начать конвертирование PDF в DJVU кликаем «ОК».
Итак, конвертирование PDF в DJVU успешно завершено. После завершения конвертирования автоматически откроется наш DJVU файл. (Какой программой открыть DJVU формат обсуждалось в статье:
Известно, что файлы PDF, содержащие много изображений, могут стать ужасно большими. Но есть простая альтернатива формату файла PDF: Файлы DjVu , которые используют алгоритмы предварительного сжатия, очень похожи на их более популярные большие Брат PDF, но убедите с уменьшенным размером файла. При преобразовании PDF в DjVu вы можете уменьшить исходный размер файла до 90% без потери производительности. Файлы DjVu — идеальная альтернатива PDF, предлагающая все преимущества открытого формата файла. Вы уверены в формате DjVu?
Но есть простая альтернатива формату файла PDF: Файлы DjVu , которые используют алгоритмы предварительного сжатия, очень похожи на их более популярные большие Брат PDF, но убедите с уменьшенным размером файла. При преобразовании PDF в DjVu вы можете уменьшить исходный размер файла до 90% без потери производительности. Файлы DjVu — идеальная альтернатива PDF, предлагающая все преимущества открытого формата файла. Вы уверены в формате DjVu?
Затем вы нашли подходящее место для начала конвертации PDF-файлов в DjVu. Наша современная онлайн-конверсионная утилита предлагает самые современные и быстрые алгоритмы для создания оптимизированного DjVus из любого PDF! Его использование чрезвычайно прост и направлено вперед. Единственное, что вам нужно сделать, это отправить PDF-файл, а остальное произойдет как магия. Вы можете смотреть процесс конвертации в реальном времени, а затем скачивать и наслаждаться только что созданным DjVu. Наша служба конвертации абсолютно бесплатна и уважает вашу конфиденциальность.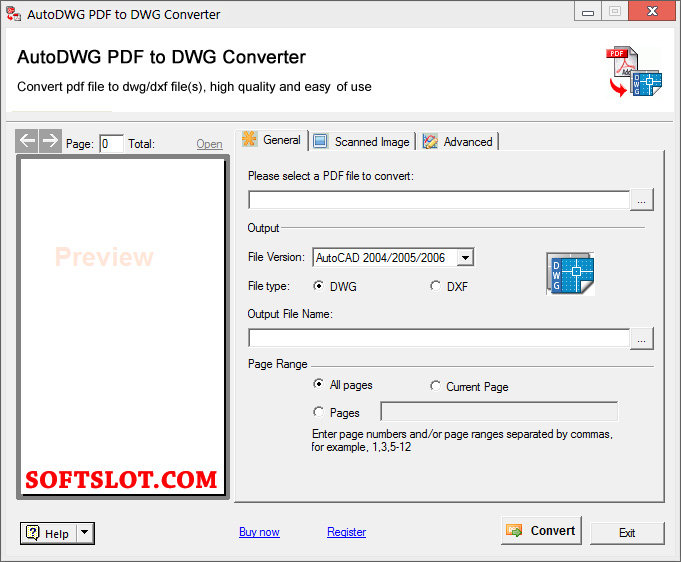 Мы не будем анализировать или просматривать ваши PDF-файлы и хранить их до тех пор, пока это необходимо на нашем сервере. Они будут удалены сразу после завершения преобразования. Если вам нравится производительность нашего PDF-конвертера DjVu, мы также приглашаем вас ознакомиться с нашей серией бесплатных онлайн-конвертеров файлов. Просто проверьте соответствующие конвертеры, и мы уверены, что вы найдете утилиту практически для любых целей.
Мы не будем анализировать или просматривать ваши PDF-файлы и хранить их до тех пор, пока это необходимо на нашем сервере. Они будут удалены сразу после завершения преобразования. Если вам нравится производительность нашего PDF-конвертера DjVu, мы также приглашаем вас ознакомиться с нашей серией бесплатных онлайн-конвертеров файлов. Просто проверьте соответствующие конвертеры, и мы уверены, что вы найдете утилиту практически для любых целей.
Повторить из дежавю в PDF. Как файл DJVU перевести в PDF (чтение, преобразование, преобразование). Конвертировать DJVU в PDF
Как конвертировать DJVU в PDF, чтобы текст документа оставался максимально читаемым? Для этого нужно использовать проверенные программы и сервисы.
Формат DJVU можно найти в отсканированных изображениях и документах. Обычно с помощью такого формата распространяется литература.
Особенность таких документов в том, что они занимают мало памяти и при этом имеют хорошее качество.
Как правило, текст отображается очень четко. К недостаткам формата можно отнести минимальное количество программ для просмотра DJVU.
Также существует проблема с отображением отсканированных документов на мобильных устройствах.
Формат PDF — это универсальный способ просмотра документов. Он позволяет сжимать изображение в разы лучше, чем, например, JPEG.
Такие документы можно просматривать на компьютерах, телефонах, смартфонах, поскольку существует большое количество программ для их отображения.
Преобразование файла DJVU в PDF позволяет не потерять текст и сохранить качество документа.
Рассмотрим несколько конвертеров, которые работают онлайн, а также настольные утилиты для конвертации форматов.
Онлайн-сервисы
- Эта веб-программа не требует регистрации на сайте, она не запрашивает пакетные SMS и не ограничивает размер файла для преобразования.
В этом случае преобразование форматов происходит наиболее быстро и на выходе пользователь сможет получить качественный PDF-документ, который можно будет загрузить на свое устройство. Адрес сервиса: convertonlinefree.com.
Адрес сервиса: convertonlinefree.com.
Для преобразования файла нажмите кнопку «Выбрать файл» и в открывшемся окне проводника найдите документ DJVU.
Затем нажмите кнопку «Конвертировать» и дождитесь окончания процедуры.
Сразу после конвертации вы получите уникальную ссылку для загрузки окончательного документа.
Если вы хотите преобразовать документы других форматов, используйте ссылки под основной строкой преобразования.
- Документ docspal.com также позволяет выполнять быстрое и качественное преобразование отсканированных изображений и документов. Помимо направления из DJVU в PDF, сервис также может конвертировать огромное количество других форматов;
Для начала пользователь должен загрузить файл или ввести прямую ссылку на его загрузку в Интернете.
Затем поставьте галочку напротив пункта 2 — «Отправить ссылку для загрузки исходящего документа на почту.
Услуга требует квитанции от каждого пользователя. Вы можете зарегистрироваться совершенно бесплатно.
Вы можете зарегистрироваться совершенно бесплатно.
Настольные приложения
Существуют также приложения для преобразования, которые пользователь может загрузить и установить на свой персональный компьютер или ноутбук. Рассмотрим самые популярные из них.
- Первое приложение называется WinDjView.
Устанавливать бесплатно можно с официального ресурса разработчика.
После установки откройте программу. Он позволяет не только конвертировать файлы, но и просматривать документы DJVU.
Для преобразования файла нажмите клавишу печати, которая находится на главной панели инструментов, и в открывшемся окне выберите способ печати — «Универсальный конвертер документов», как показано на рисунке ниже.
Затем дождитесь окончания преобразования и укажите каталог, в котором будет сохранен конечный файл.
- Bullzip. — Виртуальное приложение PDF-принтера также может преобразовать документ в нужный формат.
Эта программа поддерживает возможность использования любого другого приложения, имеющего функцию печати документов и изображений, конвертировать файлы в формат PDF.
Процесс установки максимально прост. Необходимо согласиться с установкой дополнительных компонентов.
Они нужны для организации стабильной работы с другими программами и не навредят вашему устройству.
Для преобразования достаточно открыть файл DJVU в любой программе для его просмотра и в окне печати вместо имени принтера приложение Bullzip (оно появляется в списке устройств автоматически) и нажать кнопку «Печать» » кнопка.
ФорматDJVU предназначен для хранения отсканированных документов, книг, журналов и т.д., которые содержат большое количество различных рисунков, схем или формул. Формат DJVU очень хорошо сжимает отсканированную информацию и сохраняет изображения высокого качества.
С помощью этого онлайн-конвертера вы можете преобразовать любой документ DJVU в формат PDF. Поскольку документы DJVU обычно довольно объемные, то конвертация может занять некоторое время, подождите.
Преимущества, которые дает конвертер для преобразования документов DJVU в формат PDF:
- Услуга абсолютно бесплатна и не имеет ограничений по размеру конвертируемого документа
- Конвертация документа происходит онлайн, не нужно скачивать и устанавливать дополнительные приложения
- Ресурсы вашего устройства не активированы в процессе конвертации.

Что нам нужно знать о формате DJVU
Зачем конвертировать из DJVU в PDF?
Первая и основная причина в том, что данные и общая информация в формате PDF серьезно защищены. Спецификация формата PDF защищает ваши данные от изменений, взлома и даже кражи. Другая причина заключается в том, что данные формата в документе DJVU могут быть уникальными, содержать шрифты, которые не могут быть прочитаны на других компьютерах, или имеют очень большой размер с учетом специфики носителя DJVU.Но с PDF, шрифты и информация инкапсулируются в сам формат документа, он остается неизменным — полностью идентичен исходному документу DJVU.
Конвертируем документ вместе
Ниже приведены шаги для успешного преобразования ваших документов из DJVU в PDF:
- Посетите наш портал
- Выберите вариант конвертации из DJVU в PDF
- Загрузите документ, который вы хотите преобразовать, со своего локального диска, или укажите адрес документа в Интернете, или перетащите документ в отмеченную область «Перетащите документ в эту область»
- Преобразователь пусковой автономный
- В конце процесса преобразования PDF-документ автоматически загрузится с локального диска.

Что касается документов dJVU, то конвертация может длиться некоторое время, поэтому наберитесь терпения и дождитесь окончания конвертации, чтобы не повлиять на качество конвертера.
Преимущества нашего онлайн-конвертера из DJVU в PDF
Услуга бесплатная
Сервисное обслуживание бесплатное и не имеет ограничений по размеру конвертируемого документа, поэтому ваш документ может быть очень большим, но в свою очередь не будет ограничений по скорости обработки и задержкам расчета.
Как конвертировать файл формата DJVU в файл формата PDF с помощью программы? Пользователи часто сталкиваются с пользователями, когда из файла в формате DJVU нужно получить файл в формате PDF.
Файл, хранящийся в формате DJVU («дежавю»), в отличие от аналогичного файла в формате PDF, имеет значительно меньший размер. Поэтому в формате DJVU часто сохраняются техническая литература, энциклопедии, словари и др., Другие документы, имеющие в своем составе множество изображений, схем, фотографий.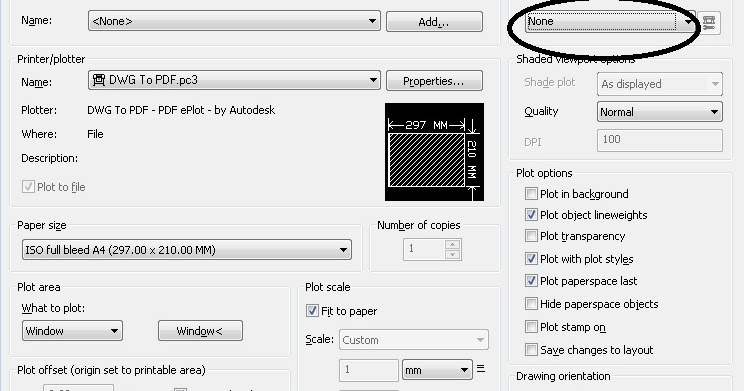 Страницы книг хранятся в хорошем качестве, а сам файл будет значительно меньше, чем такой же файл в формате PDF.
Страницы книг хранятся в хорошем качестве, а сам файл будет значительно меньше, чем такой же файл в формате PDF.
Зачем нужно переводить DJVU в PDF? Дело в том, что существует небольшое количество программ, созданных для просмотра файлов в формате DJVU.О самых популярных вьюверах DJVU вы можете прочитать на моем сайте в разделе «Текст».
Второй важный момент, проблемы с просмотром файлов DJVU на разных устройствах. Если на компьютере нет проблем с просмотром «дежавю», то на мобильных устройствах с этим сложнее. Даже если есть соответствующие приложения, то возможны проблемы с форматированием и т.п.
Преимущество формата PDF в его универсальности, отсутствие проблем с просмотром. Важным преимуществом является то, что документ в формате PDF одинаково выглядит на всех устройствах и компьютерах.
Следовательно, нужен конвертер DJVU в PDF. Чтобы перевести DJVU в PDF, мы используем бесплатные программы для просмотра файлов формата DJVU (WindjView, StduTer, Sumatra PDF), которые имеют функцию печати.
Дополнительно вам нужно будет установить на свой компьютер виртуальный принтер. Виртуальный принтер позволяет сохранить PDF-документ из окна открытой программы, поэтому эта программа не будет лишней на вашем компьютере.
В операционной системе Windows 10 установлен виртуальный принтер Microsoft Print to PDF, поэтому пользователи этой ОС могут не устанавливать аналогичную программу.На компьютерах С. с операционными системами Windows 7, Windows 8, Windows 8.1 необходимо установить бесплатный виртуальный принтер, например Bullzip PDF Printer., Primopdf, Cutepdf Writer, Dopdf.
Просто установите виртуальный принтер на свой компьютер. При необходимости вы будете использовать виртуальный принтер для сохранения файлов в PDF-файлах вместо печати документов на обычном принтере.
Для конвертации DJVU в PDF онлайн существуют специальные сервисы, о которых я расскажу в другой статье.
Конвертируйте DJVU в PDF в программе WindjView
Бесплатная программа предназначена для просмотра файлов в формате DJVU. С помощью этой программы вы можете преобразовать файл DJVU в формат PDF прямо из окна программы.
С помощью этой программы вы можете преобразовать файл DJVU в формат PDF прямо из окна программы.
Откройте книгу или любой другой документ в формате DJVU в программе WindjView. Затем нажмите кнопку «Печать».
В открывшемся окне «Печать» выберите виртуальный принтер. На моем компьютере в операционной системе Windows 10 установлен виртуальный принтер Microsoft Print to PDF, поэтому я выбрал этот принтер для преобразования в формат PDF.
Если на вашем компьютере установлена операционная система Windows 7 или Windows 8.1 (Windows 8), затем выберите виртуальный принтер, установленный на вашем компьютере (вы должны сначала установить виртуальный принтер на вашем компьютере).
В открывшемся окне проводника выберите место для сохранения файла, дайте имя создаваемому файлу. После этого начнется процесс преобразования файла из формата DJVU в формат PDF, который займет некоторое время.
После завершения процесса вы можете открыть новый файл. В PDF с помощью программы открывайте файлы этого типа.
На этом изображении файл в формате PDF открыт в средстве просмотра.
Как конвертировать DJVU в PDF в программе StduTer
С помощью бесплатной программы вы можете перевести DJVU в PDF из окна программы. Откройте файл DJVU в программе Stdu Viewer.
В окне «Печать» выберите виртуальный принтер и нажмите кнопку «Печать».
Дайте имя новому файлу в формате PDF, выберите место для его сохранения. После завершения процесса конвертации преобразованный файл в формате PDF готов к использованию.
Как конвертировать DJVU в PDF в программе Sumatra PDF
Бесплатная программа поддерживает просмотр файлов в формате DJVU. В Sumatra PDF вы можете конвертировать DJVU в PDF так же, как и в предыдущих программах.
После открытия файла DJVU в программе Sumatra PDF нажмите кнопку «Печать».
В окне «Печать» на вкладке «Общие» выберите виртуальный принтер и нажмите кнопку «Печать».
В открывшемся окне дайте имя сохраненному файлу в формате PDF, выберите расположение файла.
Выводы Статьи
С помощью бесплатного программного обеспечения WindjView, Stdu Viewer, Sumatra PDF, предназначенного для просмотра файлов в формате DJVU, вы можете конвертировать DJVU в PDF с помощью функции печати с помощью виртуального принтера, установленного на вашем компьютере.
С развитием электронного документооборота и увеличением количества офисных пользователей перед компанией часто встает вопрос о стандартизации форматов, которые используются в учреждении. Особенно тяжело в этом смысле разного рода университеты и колледжи, в которых много сканированной научной литературы хранится в виде DJVU.
Конечно, этот формат специально создан для этих целей, но распространенность его выходит намного лучше. В любом случае лучше будет перевести DJVU в PDF. Это позволит вам использовать гораздо более простые и распространенные программы, которые уже установлены на компьютерах большинства пользователей.
Что это за формат?
Чтобы вы понимали необходимость такого преобразования, стоит немного узнать о самом формате, который является «камнем преткновения». Как уже упоминалось выше, он был создан для оцифровки книг и научных пособий.Его преимущество — впечатляющая компактность.
Как уже упоминалось выше, он был создан для оцифровки книг и научных пособий.Его преимущество — впечатляющая компактность.
Но есть одна оговорка: все это касается только тех случаев, когда качество выходного документа не имеет значения. Например, вы сможете оцифровать и использовать в будущем те методы, в которых много изображений и высококачественных таблиц.
С чем связано плохое качество
Но только гораздо чаще встречаются оцифрованные документы ужасного качества, в которых практически нереально что-либо разобрать. С чем это связано? Дело в том, что в формате dJVU нет шрифтов в составе документов.По сути, этот документ представляет собой своеобразное «продвинутое» изображение.
Так что конвертация DJVU. PDF позволит вам как-то улучшить читаемость книг, которые без особого энтузиазма были переведены в цифровой формат.
Что преобразовать?
Универсальная, простая и предельно компактная программа — DjView. Он сделает преобразование даже объемного документа всего за несколько минут.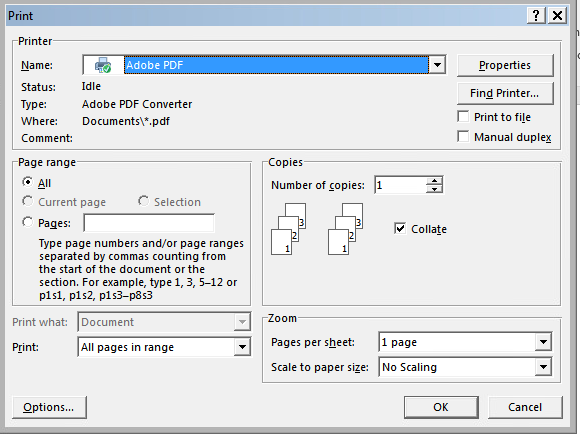 Недостатком является то, что вы не можете выбрать спецификации PDF. Какое именно форматное разнообразие используется для созыва в каждый конкретный момент, неизвестно.
Недостатком является то, что вы не можете выбрать спецификации PDF. Какое именно форматное разнообразие используется для созыва в каждый конкретный момент, неизвестно.
Виртуальный принтер
Этот метод позволит не только перевести DJVU в PDF, но и сохранить даже веб-страницу в желаемом формате. Как произвести конвертацию в этом случае? Для начала установите программу NOVAPDF или аналогичную ей. Для непосредственного открытия документа воспользуемся утилитой WindjView.
После установки и ее настройки можно открывать книги DJVU. PDF получается после того, как вы отправите их на «печать». В отличие от предыдущего случая, вы можете настроить все параметры выходного документа.Время конвертации полностью зависит от характеристик вашего компьютера, но за 10 минут конвертируются около сотни страниц.
FineReader.
Это приложение должно быть отлично известно отечественным пользователям, так как долгое время оно было единственным, на сегодняшний день качественная программа представлена двенадцатой версией, а ее функционал кардинально расширен.
Чтобы преобразовать DJVU в PDF, необходимо сначала запустить приложение. Появляется главное окно, в котором появляется опция «Файл изображения в PDF».Открывает специальную утилиту, где программе нужно указать путь к файлу, который нужно перевести в более привычный формат.
Но есть одна проблема. Сначала приложение оплачивается. Во-вторых, его скорость падает с выходом каждой новой версии. Если ваш компьютер не блещет производительностью, то книжка djvuin 200-300 страниц может «навесить» его намертво.
Поэтому на слабых машинах и при условии относительно небольшого размера документа лучше использовать утилиту, входящую в состав того же FineReader.Речь идет о Screenshot Reader. Принцип его работы — распознавать текст с картинок страниц, что программа делает самостоятельно. Ресурсов он потребляет минимум, а результат отличный.
Stdu Converter
Эта утилита легко выполнит перевод DJVU в PDF, не тратя много времени на этот процесс. Его преимущество перед конкурентами не только в бесплатности, но и во вполне сравнимой с ними функциональности. Итак, вы можете перевести в нужный формат не весь документ, а только какой-то фрагмент, отметив соответствующие флаги страницы.
Итак, вы можете перевести в нужный формат не весь документ, а только какой-то фрагмент, отметив соответствующие флаги страницы.
Самый простой вариант
Недостатком всех вышеперечисленных приложений является то, что они достаточно сложные, и поэтому новичкам в них может быть не так просто разобраться. Приложение Boxoft может выйти из сложившейся ситуации. Его интерфейс максимально прост. Для преобразования просто перетащите значок документа в главное окно программы, после чего аналогичный файл появится в той же папке, но уже в формате PDF.
Когда не стоит конвертировать?
О том, в чем преимущество DJVU, мы уже говорили.В случае, когда документ приемлемого качества, и вы собираетесь использовать его на мобильном устройстве или через облачный Сервис, поводов для изменения нет.
Djvu. Это формат файла с аналогичными функциями, как PDF, но в основном используется для обеспечения меньшего размера при аналогичном качестве. В файле DJVU обычно хранятся документы, содержащие текст, таблицы и изображения могут также содержать слой распознавания символов, который позволяет пользователю копировать и вставлять определенные сегменты из отсканированного документа. По этим причинам DJVU стал довольно популярным форматом электронных книг.
По этим причинам DJVU стал довольно популярным форматом электронных книг.
Формат PDF. Также известный как Portable Document Format, стал одним из наиболее широко используемых форматов для хранения документов, содержащих текст и графику. В отличие от других форматов документов с аналогичными функциями, PDF-файлы можно легко обменивать между различными приложениями и операционными системами. Кроме того, информация в файлах PDF может быть защищена от копирования и печати паролем или водяным знаком.
Как конвертировать DJVU в PDF?
Проще всего скачать хорошую программу Conversion, например фото конвертер. Он работает быстро и эффективно, позволяя конвертировать любое количество файлов DJVU за раз. Вы быстро поймете, что конвертер фотографий может сэкономить много времени, которое вы потратите при работе вручную.
Загрузите и установите конвертер фотографий
Фотоконвертер легко загрузить, установить и использовать — не нужно быть специалистом по компьютерам, чтобы понять, как он работает.
Добавить файлы djvu в конвертер фотографий
Запустить конвертер фотографий и загрузить файлы .djvu, которые вы хотите преобразовать VVDF
Вы можете выбрать файлы DJVU через меню Файлы → Добавить файлы Или просто закинуть их в окно конвертера фотографий .
Выберите место для сохранения полученных файлов PDF
Выберите PDF в качестве формата сохранения
Чтобы выбрать PDF в качестве формата сохранения, щелкните значок PDF. Внизу экрана или кнопка + Чтобы добавить возможность записи в этот формат.
Теперь просто нажмите Start И конвертация начнется мгновенно, и PDF файлы сохранятся в указанном месте с желаемыми параметрами и эффектами.
Попробуйте бесплатную демо-версию.Видеоинструкция
Советы и инструменты для переводчиков
Последние 30 дней я пробовал использовать SDL Trados Studio 2017, последнюю версию флагманского CAT-инструмента SDL для переводчиков. Мои первые впечатления были неоднозначными: что-то хорошее, что-то плохое.
Мои первые впечатления были неоднозначными: что-то хорошее, что-то плохое.
Самое первое, о чем вам следует знать, когда вы запрашиваете бесплатную пробную версию Studio 2017 онлайн, это то, что вы получите , а не , чтобы получить пробную полнофункциональную версию пакета, но с некоторыми серьезными ограничениями. . Это было моим первым сюрпризом, так как другие CAT-инструменты, которые я пробовал до сих пор, такие как memoQ translator pro, Déjà Vu X3, OmegaT, Swordfish и memsource, всегда были полнофункциональными версиями. Хотя интерфейс пробной версии Studio 2017 включает значки для MultiTerm , программы терминологической базы и для локализации программного обеспечения с использованием мощного инструмента из SDL под названием Passolo , нажатие на значки вызовет сообщение о том, что эти программы не являются установлены.Другими словами, вы не можете их опробовать. Попытка использовать CAT-программу, которая имеет модуль памяти переводов (TM), но не модуль для терминологии, разочаровывает, поскольку это означает, что вы можете переводить с его помощью правильные файлы, но вы не можете импортировать термины из других программ, что могло бы помочь ты с переводом.
Как ни странно, некоторые функции MultiTerm фактически включены в пробную версию, что означает, что вы можете сохранять новые термины, если хотите, но вы не можете экспортировать терминологическую базу, которую вы создали, чтобы отправить ее кому-то другому или импортировать в другой CAT-инструмент; он застрял в Studio 2017.Я надеюсь, что SDL решит включить полную поддержку MultiTerm в следующую версию Studio, если не раньше, поскольку возможность использовать терминологию, которую вы уже собрали, важна для переводчика.
Что мне понравилось в Studio 2017?
— Интерфейс , с которым довольно легко работать (т. Е. Он спроектирован логично) и использует цветовую схему . схемы). Интерфейс также содержит ряд очень полезных значков , таких как ссылки на учебные пособия и SDL AppStore (внешний веб-ресурс из SDL, где вы можете получить дополнительные надстройки для улучшения готовой функциональности Studio. ; раньше он назывался OpenExchange).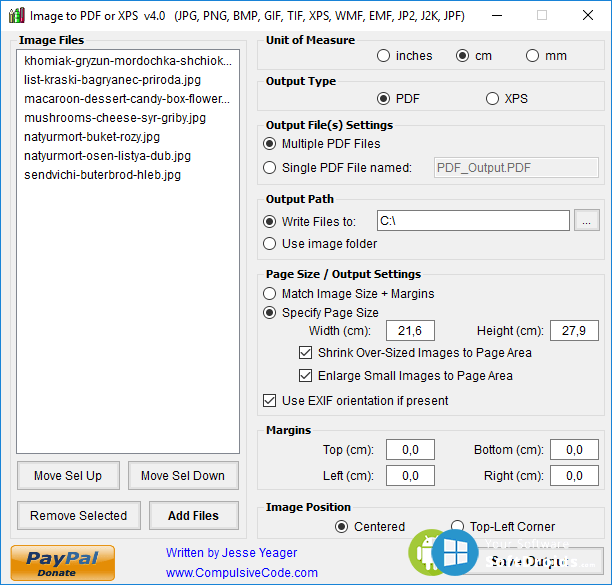
— возможных настроек интерфейса — например, вы можете добавить определенные функции, которые вам очень нужны, на панель быстрого доступа .
— Вертикальная сетка перевода , которая, как и memoQ, ясна и проста в использовании; исходный язык отображается сегментами слева, целевой — сегментами справа (по крайней мере, в моей языковой паре LTR, немецкий и английский; я предполагаю, что этот порядок обратный для языков, написанных в сценариях RTL, таких как иврит и арабский).
— Вы можете отфильтровать сегментов, используя широкий спектр практических критериев .
— Два или три обновления программного обеспечения , которые Studio установила в течение пробного периода, прошли быстро и без проблем.
— В примечаниях к выпуску, которые поставляются с пакетом, подробно рассказывается, что нового в Studio 2017. Они также говорят о проблемах с ним (оптическое распознавание символов или OCR в PDF-файлах, которые Studio может читать, ограничена 14 языками на момент).
Что мне не понравилось в Studio 2017?
— не очень просто экспортировать TM в формат TMX (который является распространенным форматом файлов для обмена данными TM между различными программами).Вы можете обойти это ограничение, установив специальную надстройку именно для этой цели или установив флажок настроек, позволяющий экспортировать TM в «формате, совместимом с Trados 2007» (например, TMX!).
— Некоторые функции , которые являются стандартной частью переводчика memoQ pro , не включены в Studio 2017 ; если они вам нужны, вам необходимо сначала установить надстройку из SDL AppStore. MemoQ позволяет импортировать термины, например, из файла CSV, и вы можете искать сложные термины в Интернете прямо из сетки перевода.Не так со Studio (пока, по крайней мере):
— Пробная версия включает небольшое количество предустановленных приложений, но вы не можете установить какие-либо дополнительные по своему выбору (например, конвертер глоссария) , что означает, что вы не можете видеть, что они делают или насколько хорошо они работают. (Это было разочаровывающим, поскольку в SDL AppStore было несколько приложений, которые я тоже хотел попробовать.)
(Это было разочаровывающим, поскольку в SDL AppStore было несколько приложений, которые я тоже хотел попробовать.)
— Программный пакет Studio 2017 значительно больше, чем у MemoQ translator pro, с точки зрения места на жестком диске и также требуется больше времени для запуска .
— Studio 2017 не работает в Windows 8.0, Windows Vista или Windows XP ; он будет работать только в последних версиях Windows 7, 8.1 и 10. Таким образом, некоторые версии Windows подходят, а другие нет. Горе, у вас на компьютере не тот!
— Studio 2017 также имеет проблемы с некоторыми веб-браузерами и версиями Microsoft Office.
Пожалуйста, внимательно прочтите примечания к выпуску , чтобы убедиться, что ваш компьютер соответствует требованиям Studio, прежде чем устанавливать его.
В общем, мне понравилось пользоваться пробной версией программы, которая, на мой взгляд, лучшая из тех, с которыми я когда-либо работал. Однако мой пользовательский опыт был бы еще лучше, если бы все функции Studio были доступны. Поскольку пробные версии программ предназначены для того, чтобы убедить потенциальных новых пользователей купить пакет, нет смысла предлагать им версию с ограниченными функциями, которая снизит их производительность, а не повысит ее. Кроме того, проработав несколько лет с CAT-инструментами, я обнаружил, что Studio 2017 относительно проста в использовании — многие из них теперь работают аналогичным образом.Однако я не смог сразу увидеть, какие явные преимущества имеет этот инструмент по сравнению с другими сложными пакетами, такими как memoQ.
Однако мой пользовательский опыт был бы еще лучше, если бы все функции Studio были доступны. Поскольку пробные версии программ предназначены для того, чтобы убедить потенциальных новых пользователей купить пакет, нет смысла предлагать им версию с ограниченными функциями, которая снизит их производительность, а не повысит ее. Кроме того, проработав несколько лет с CAT-инструментами, я обнаружил, что Studio 2017 относительно проста в использовании — многие из них теперь работают аналогичным образом.Однако я не смог сразу увидеть, какие явные преимущества имеет этот инструмент по сравнению с другими сложными пакетами, такими как memoQ.
Если вы заинтересованы в получении лицензии на SDL Trados Studio 2017, я рекомендую вам взглянуть на групповые покупки, которые часто происходят на Proz.com , поскольку таким образом вы можете сэкономить много денег. SDL также проводит несколько рекламных акций в год. Если вы являетесь членом ассоциации переводчиков, возможно, она заключила особую договоренность с SDL, чтобы ее члены могли покупать программное обеспечение по сниженной цене. Таким образом, вы можете воспользоваться различными вариантами.
Таким образом, вы можете воспользоваться различными вариантами.
С уважением,
Карл
Статьи по теме в другом месте в Интернете
— Обзор продукта Андреа Лучано Дамико
— Часто задаваемые вопросы о Studio 2017 на собственном веб-сайте SDL
— Сообщение в блоге Эммы Голдсмит об отзыве фрагментов в Studio 2017 , новая функция в Studio для улучшения автоматической сборки целевых предложений
— Закажите бесплатную пробную версию Studio 2017 из SDL
dejavu — Перевод на голландский — примеры английский
Предложения: дежавю дежавюЭти примеры могут содержать грубые слова, основанные на вашем поиске.
Эти примеры могут содержать разговорные слова, основанные на вашем поиске.
Это было два года назад, а сегодня я живу большим dejavu .
Krivaja Translations использует MetaTexis и Swordfish (CAT-инструменты, совместимые с Trados и DejaVu ), а также Abbyy Finereader и Abbyy PDF Transformer (для преобразования документов из pdf-формата в Word и наоборот).
У меня сейчас есть важная вещь dejavu .
Предложите пример
Другие результаты
Они заставляют вас понимать на одном и том же взгляде духов, dejavues и даже в конечном итоге возникают предчувствия.
В дополнение к стандартным офисным костюмам мы используем специализированное программное обеспечение для перевода и локализации, такое как Visual Localize, DéjàVu , Transit, WordFast и Trados, что позволяет нам обрабатывать большинство форматов документов и текстов.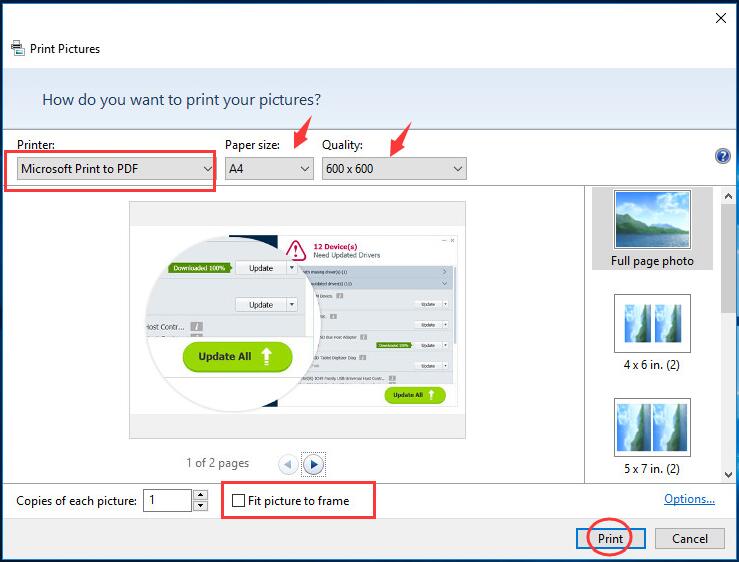
Просто у меня denjavu каждый раз, когда я поворачиваю за угол.
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookieЭтот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie.
 Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie. - Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Чтобы предоставить доступ без файлов cookie
потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
лучших программных инструментов для перевода в 2021 году — некоторые даже бесплатно!
Независимо от того, являетесь ли вы переводчиком, бюро переводов или бизнесом, нуждающимся в переводе, вы, скорее всего, будете использовать какое-либо программное обеспечение для перевода, чтобы улучшить свой рабочий процесс.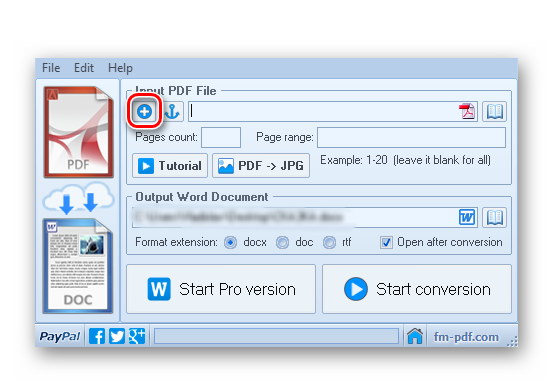 В противном случае вы могли бы потратить на перевод гораздо больше времени (или гораздо больше денег!), Чем необходимо.
В противном случае вы могли бы потратить на перевод гораздо больше времени (или гораздо больше денег!), Чем необходимо.
Что такое программа для перевода?
Программы для перевода предназначены для ускорения и повышения эффективности процесса перевода. С их помощью вы можете сохранять и редактировать переводы, переводить проекты по разделам (с сохранением форматирования) и, в конечном итоге, добавлять дополнительный уровень контроля качества (согласованность, орфография, эквивалентность и т. Д.). Они также значительно упрощают управление терминологией: вы можете создавать, получать доступ и использовать термины и память переводов во время работы над своими проектами.Когда мы говорим о программах для перевода, мы обычно имеем в виду средства автоматизированного перевода (CAT), которые не следует путать с машинным переводом. Хотя термины могут показаться похожими, CAT-инструменты помогают переводчикам упростить процесс перевода, но не выполняют никаких переводов за них. С другой стороны, машинный перевод использует искусственный интеллект для прямого перевода текстов.
С другой стороны, машинный перевод использует искусственный интеллект для прямого перевода текстов.
служат одной и той же цели: помогать и ускорять процесс перевода.Но существуют разные типы программного обеспечения, подходящие для разных обстоятельств и потребностей. Например, программные инструменты для перевода могут быть загружаемыми настольными программами, которые вы устанавливаете на свой компьютер, или облачными решениями, над которыми вы работаете в Интернете. Они могут быть платными или бесплатными. Некоторые даже делают все возможное и подключаются к рынку фрилансеров, чтобы вы могли легко сотрудничать с другими в инструменте перевода. Это особенно полезно, если вам нужно перевести несколько файлов на разные языковые пары с помощью разных переводчиков, редакторов и корректоров.
Итак, давайте углубимся в каждый тип и рассмотрим некоторые из лучших программных инструментов для перевода в 2020 году.
Облачное программное обеспечение для перевода
Облачные (или сетевые) инструменты перевода — это программы, которые доступны и используются онлайн через веб-браузер. Эти платформы становятся все более распространенными во всех отраслях, и ключевые игроки в мире переводов следуют их примеру.
Эти платформы становятся все более распространенными во всех отраслях, и ключевые игроки в мире переводов следуют их примеру.
Давайте посмотрим, почему это такой популярный канал, а также рассмотрим возможные недостатки.
Плюсов:
- Нет необходимости освобождать место или устанавливать какое-либо программное обеспечение на вашем компьютере.
- Вы можете работать с любой операционной системой, будь то Windows, MacOS или даже вариант Linux.
- Переводы сохраняются в реальном времени, поэтому вы не потеряете никаких данных. В худшем случае это может быть одно предложение, тогда как на настольном компьютере вы можете потерять все.
- Вы можете получить к нему доступ на любом устройстве с подключением к Интернету.
- В Интернете проще сотрудничать с другими.
- Обновления и исправления ошибок частые и немедленные.
Минусы:
- Всегда есть риск взлома данных в Интернете. Однако в мире ИТ нет единого мнения о том, выше ли риск на веб-платформах, чем на настольных программах, где данные могут быть стерты, украдены или потеряны.

- Сильно зависит от подключения к Интернету. Чтобы исправить это, некоторые программные инструменты позволяют продолжать использовать большинство функций, если вы потеряете соединение.
Платные облачные инструменты для перевода
Memsource
Memsource имеет как веб-редактор, так и настольный редактор переводов.Онлайн-редактор прост и интуитивно понятен, однако некоторые переводчики считают, что ему не хватает некоторых функций и он работает медленно при работе над большими проектами. Цены начинаются с 27 долларов в месяц, но есть также бесплатная версия для личного пользования с ограничением на синхронный перевод двух файлов, которая может подойти вам, если у вас небольшая рабочая нагрузка.
Wordbee
Wordbee — это платформа управления переводами с базовым CAT-инструментом. Он ориентирован на совместную работу и хорошо работает на уровне управления проектами, но в нем отсутствуют некоторые из более продвинутых функций, что, как сообщается, является проблемой. У него есть 15-дневная бесплатная пробная версия, а цены начинаются от 330 долларов в год.
У него есть 15-дневная бесплатная пробная версия, а цены начинаются от 330 долларов в год.
XTM Облако
XTM Cloud — это интуитивно понятный веб-инструмент для перевода со всеми необходимыми функциями и надежной командой поддержки. Годовая подписка начинается с 61 доллара в месяц, но вы можете переводить не более 20 000 слов в месяц. Стоимость неограниченного использования начинается от 359 долларов в месяц. Как и в случае с большинством других платных инструментов перевода, существует 30-дневная бесплатная пробная версия.
Бесплатные облачные инструменты для перевода
Smartcat
Smartcat — одно из самых быстрорастущих облачных решений для перевода программного обеспечения для LSP, бюро переводов и независимых переводчиков.
Среди преимуществ — то, что он бесплатный, всеобъемлющий и удобный (что позволяет легко переходить с других CAT-программ или начинать их использовать без предварительного опыта). У него также есть собственная торговая площадка для сотрудничества с другими профессионалами в рамках CAT-программы. Вы даже можете использовать его для оплаты фрилансерам за работу, выполненную вне платформы.
Вы даже можете использовать его для оплаты фрилансерам за работу, выполненную вне платформы.
Если вам нужно подключенное универсальное решение (CAT-программа, пространство для совместной работы и рынок фрилансеров), это одна из лучших платформ для этого.
MateCat
MateCat — это веб-инструмент для перевода, бесплатный для переводчиков-фрилансеров и предприятий. Как и в случае со Smartcat, нет ограничений на количество пользователей или проектов. Частично его привлекательность заключается в том, что он позволяет вам получить доступ к общедоступной базе данных памяти переводов, которую вы можете использовать в своих проектах.
Хотя MateCat полностью бесплатен, он предлагает платные планы для компаний и бюро переводов, которым, среди прочего, требуется настройка программного обеспечения и круглосуточная поддержка.Эти планы начинаются с 1500 евро (≈ 1685 долларов США) в месяц.
Что касается недостатков MateCat, он имеет ограниченную функциональность, и ваша память переводов по умолчанию хранится для общего пользования. Это означает, что если вы работаете с конфиденциальными документами, перед началом перевода убедитесь, что вы закрыли память переводов.
Это означает, что если вы работаете с конфиденциальными документами, перед началом перевода убедитесь, что вы закрыли память переводов.
Wordfast Anywhere
Это онлайн-версия автономных CAT-программ Wordfast Classic и Pro. Это совершенно бесплатно и позволяет сотрудничать с другими пользователями.Он прост в использовании и удобен, но его главный недостаток в том, что он может работать медленно и подвержен ошибкам.
Программа для перевода рабочего стола (офлайн)
Программные средства переводаDesktop — это традиционные программы, которые необходимо загрузить и установить на свой компьютер. Многие из них существуют дольше, чем их облачные коллеги, поэтому большая часть их клиентской базы — это переводчики, LSP и агентства, которые используют их в течение многих лет и, возможно, не хотят изучать альтернативы на основе Интернета.
Давайте углубимся в преимущества и недостатки инструментов автономного перевода.
Плюсов:
- Можно работать без подключения к Интернету.

- Нет проблем с сервером, таких как сбой или замедление. Пока ваш компьютер работает, вы можете работать.
Минусы:
- Вам необходимо установить программное обеспечение и использовать место на вашем компьютере.
- Вы можете использовать его только на своем компьютере, если у вас нет нескольких лицензий и вы не установите его на другие устройства.
- Большинство (но не все) работают только на ПК с Windows.
- Безопасность ваших переводческих проектов зависит от безопасности вашего компьютера. Вы можете потерять все, если ваш компьютер будет украден, поврежден или сломан.
- Меньше обновлений: выпуск и внедрение исправлений ошибок и обновлений занимает больше времени, чем при использовании онлайн-программного обеспечения.
Платные программные средства перевода для ПК
SDL Trados Studio
Trados, несомненно, является наиболее широко используемым настольным переводческим инструментом, особенно среди компаний, LSP и бюро переводов. Он комплексный, многофункциональный и, что особенно важно, повсюду, поэтому независимо от того, являетесь ли вы клиентом или поставщиком, вы можете быть достаточно уверены, что другая сторона так или иначе поддержит его. Цены начинаются от 695 евро (≈ 780 долларов США), но вы можете сначала попробовать его в течение 30 дней.
Он комплексный, многофункциональный и, что особенно важно, повсюду, поэтому независимо от того, являетесь ли вы клиентом или поставщиком, вы можете быть достаточно уверены, что другая сторона так или иначе поддержит его. Цены начинаются от 695 евро (≈ 780 долларов США), но вы можете сначала попробовать его в течение 30 дней.
Самым большим недостатком Trados является то, что многие пользователи считают его слишком сложным для того, что нужно большинству переводчиков, а это означает, что вам придется быстро научиться, когда вы впервые начинаете его использовать. Кроме того, он работает только в Windows, стоит дорого и не поддерживает совместную работу.Лучшее, что вы можете получить, — это клиент-серверное решение, которое сводится к обычным задачам «подсчета мест».
memoQ
memoQ, вероятно, является самым большим конкурентом Trados, поскольку он аналогичен по функциональности и производительности. Цены начинаются от 770 долларов США с 30-дневной пробной версией Pro-версии.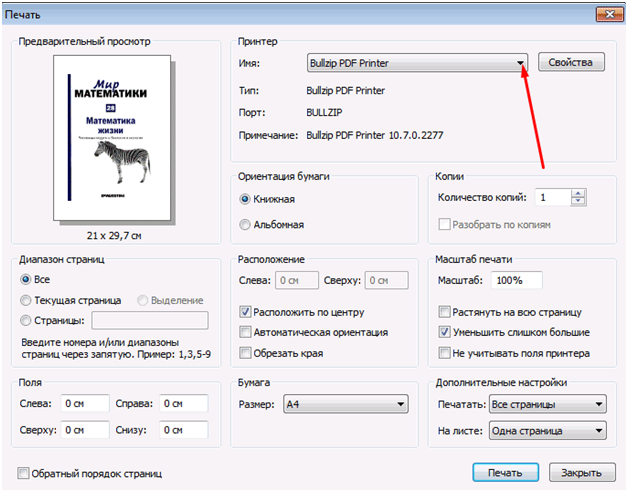
Как и Trados, главная проблема — это крутая кривая обучения, которую вам нужно пройти, прежде чем пожинать плоды.
Wordfast (классический и профессиональный)
Если вы поклонник MS Word, возможно, Wordfast Classic — это инструмент для вас, поскольку он работает непосредственно в Word.Однако вам понадобится отдельный Wordfast Pro, если вы хотите переводить файлы других форматов. К преимуществам относится то, что его легко использовать, его можно установить на Windows, Linux или Mac. Существует 30-дневная бесплатная пробная версия по цене 400 евро (≈ 450 долларов США) для Classic или Pro или 500 евро (≈ 560 долларов США) для обоих.
Недостатком является то, что Wordfast Classic поддерживает только документы Word, в то время как Wordfast Pro имеет ограниченные возможности по сравнению с программными средствами перевода по аналогичной цене.
Memsource
Хотя в первую очередь это облачный инструмент, Memsource также имеет версию настольного редактора, которую можно установить в Windows, Mac или Linux. Он более надежен, чем веб-версия, но все же имеет ограничения, особенно в отношении управления терминологией, по сравнению с более комплексными инструментами, такими как memoQ или даже облачный Smartcat.
Он более надежен, чем веб-версия, но все же имеет ограничения, особенно в отношении управления терминологией, по сравнению с более комплексными инструментами, такими как memoQ или даже облачный Smartcat.
Дежавю
Déjà Vu — это полный и надежный инструмент для перевода, который особенно эффективен как решение для управления терминологией. Обратной стороной является то, что вам придется выложить не менее 420 евро (≈ 475 долларов США), чтобы купить лицензию, но есть 30-дневная бесплатная пробная версия, которую вы можете попробовать перед покупкой.
По
Across — это комплексный CAT-инструмент для настольных ПК по очень разумной цене.У них даже есть бесплатная онлайн-версия с базовыми функциями и онлайн-магазин. С другой стороны, скорость кажется проблемой. Цены начинаются от 19,50 евро (≈ 22 доллара США) в месяц за годовую подписку.
Бесплатная программа для перевода для ПК
OmegaT
OmegaT — это бесплатный инструмент для перевода с открытым исходным кодом, который можно использовать на Mac, Linux и Windows. Его легко настроить и довольно легко использовать. Макет исходного и целевого сегментов немного отличается от других инструментов, но пользователи быстро адаптируются к нему.Недостатком программного обеспечения с открытым исходным кодом является то, что оно обеспечивает только поддержку сообщества, поэтому его использование для реализации в масштабе предприятия может быть рискованным.
Его легко настроить и довольно легко использовать. Макет исходного и целевого сегментов немного отличается от других инструментов, но пользователи быстро адаптируются к нему.Недостатком программного обеспечения с открытым исходным кодом является то, что оно обеспечивает только поддержку сообщества, поэтому его использование для реализации в масштабе предприятия может быть рискованным.
КафеТран Эспрессо
CafeTran Espresso особенно привлекателен для пользователей Mac и Linux, поскольку, наряду с OmegaT, является одним из немногих бесплатных CAT-программ для перевода, совместимых с этими операционными системами. Однако программу можно использовать бесплатно только с памятью переводов или глоссариями до определенного размера. Безлимитные платные планы стоят 80 евро (≈ 90 долларов США) в год или 200 евро (≈ 225 долларов США) при пожизненной покупке.
Обзор платных, бесплатных, облачных и настольных инструментов перевода программного обеспечения
| ПЛАТНЫЙ | БЕСПЛАТНО | |
| ОНЛАЙН | Memsource (через Интернет) Wordbee XTM Cloud | Smartcat MateCat Wordfast Anywhere |
| DESKTOP | SDL Trados Studio memoQ Wordfast (Classic & Pro) Memsource (desktop) Déjà Vu Через | OmegaT CafeTran Espresso |
Что лучше для вас?
Какой программный инструмент для перевода вы выберете, в конечном итоге будет зависеть от ваших предпочтений и, возможно, вашей свободы выбора. Если у вас есть выбор, мы настоятельно рекомендуем вам попробовать несколько различных инструментов перевода, чтобы узнать, кто может предложить вам лучшее универсальное решение (чем меньше инструментов вы используете, тем лучше). Если стоимость является проблемой, помните, что некоторые из них полностью бесплатны, и что большинство платных инструментов предлагают бесплатные пробные версии. В конце концов, важно то, насколько комфортно вы себя чувствуете, и как это влияет на продуктивность и качество ваших профессиональных переводов.
Если у вас есть выбор, мы настоятельно рекомендуем вам попробовать несколько различных инструментов перевода, чтобы узнать, кто может предложить вам лучшее универсальное решение (чем меньше инструментов вы используете, тем лучше). Если стоимость является проблемой, помните, что некоторые из них полностью бесплатны, и что большинство платных инструментов предлагают бесплатные пробные версии. В конце концов, важно то, насколько комфортно вы себя чувствуете, и как это влияет на продуктивность и качество ваших профессиональных переводов.
В духе полного раскрытия информации мы хотим напомнить нашим читателям, что эта статья изначально была написана для блога Smartcat.Однако мы постарались объективно сравнить инструменты перевода, а не просто продвигать эту платформу. Для получения дополнительных руководств / обзоров по CAT-программам мы рекомендуем воспользоваться следующими ссылками:
Чем вы сейчас пользуетесь?
Будем рады услышать от вас: используете ли вы программное обеспечение для перевода? Если да, то какой? Что заставило вас выбрать его? Какие функции вам не хватает, но вы бы хотели их увидеть? Если вам не нравится ваш инструмент для перевода, почему бы не попробовать другой? Мы поняли .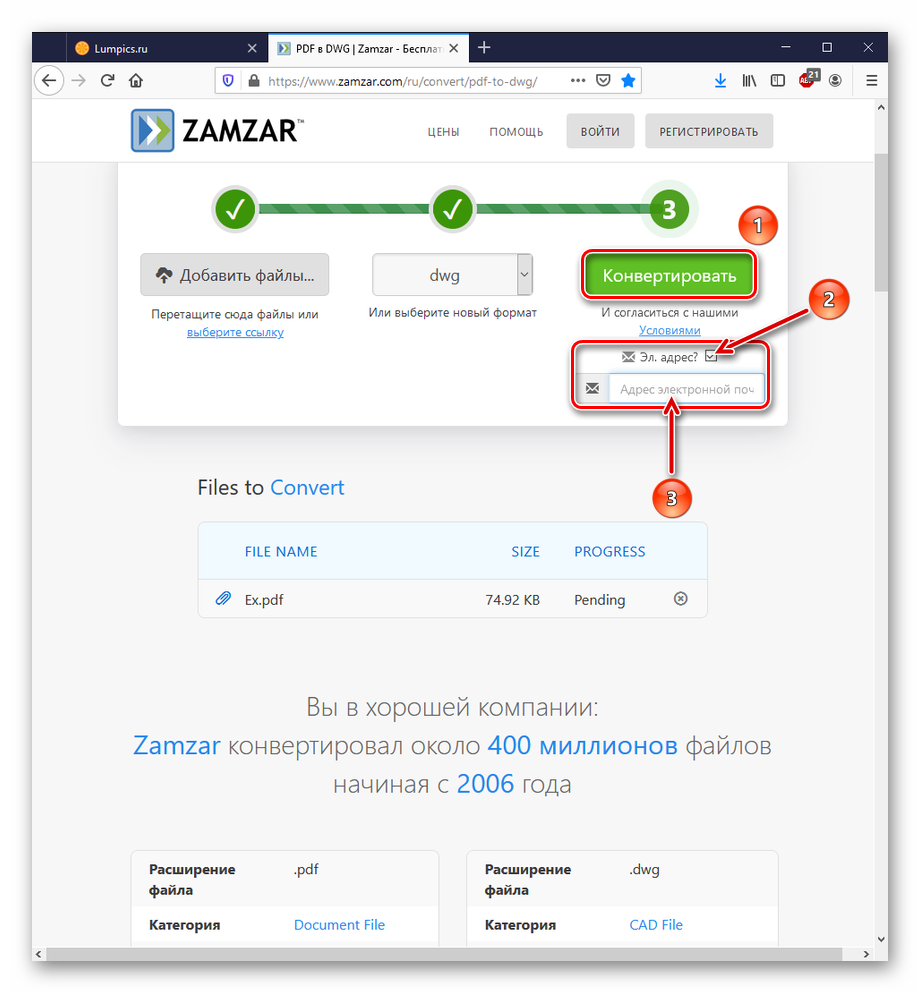 .. мысль о переключении инструментов может быть пугающей — вам придется заново привыкать к совершенно новому инструменту перевода! Но что, если изменение сделает вас более продуктивным в долгосрочной перспективе?
.. мысль о переключении инструментов может быть пугающей — вам придется заново привыкать к совершенно новому инструменту перевода! Но что, если изменение сделает вас более продуктивным в долгосрочной перспективе?
Какой бы вариант вы ни выбрали, обязательно попробуйте Smartcat — это бесплатно!
Атрил-брошюра.indd
% PDF-1.6 % 1 0 объект >] / Pages 3 0 R / Type / Catalog / ViewerPreferences >>> эндобдж 2 0 obj > поток 2017-08-11T12: 25: 33 + 01: 002017-08-11T12: 25: 35 + 01: 002017-08-11T12: 25: 35 + 01: 00Adobe InDesign CS6 (Windows) uuid: f0ea8f1e-6b7e-4055- 83bc-4dd5b6b8e277xmp.did: A69A632B147DE711AFF6A99E6DEBDB84xmp.id: 1D63CAB1877EE7119634A8615E84EFBA xmp.iid: 1C63CAB1877EE7119634A8615E84EFBAxmp.did: A69A632B147DE711AFF6A99E6DEBDB84xmp.did: A69A632B147DE711AFF6A99E6DEBDB84defaultapplication / pdf
 0 21.0 616.276 862.89] / Type / Page >>
эндобдж
7 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Тип / Страница >>
эндобдж
8 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Type / Page >>
эндобдж
9 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Type / Page >>
эндобдж
10 0 obj
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Type / Page >>
эндобдж
11 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.zvo_s | cz ֵ Zt;>}} K9 ~ rx> | ksӖu \ ;: gxӈ-z ~ K;
? X1
0 21.0 616.276 862.89] / Type / Page >>
эндобдж
7 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Тип / Страница >>
эндобдж
8 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Type / Page >>
эндобдж
9 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Type / Page >>
эндобдж
10 0 obj
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.0 21.0 616.276 862.89] / Type / Page >>
эндобдж
11 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / TrimBox [21.zvo_s | cz ֵ Zt;>}} K9 ~ rx> | ksӖu \ ;: gxӈ-z ~ K;
? X1 Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018.Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Название корпуса: OpenSubtitles2018. Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). Например, Решить функциональное уравнение — значит, найти неизвестную функцию, при подстановке которой в исходное функциональное уравнение оно обращается в тождество (если неизвестных функций несколько, то необходимо найти их все). Соотношения, задающие функциональные уравнения, являются тождествами относительно некоторых переменных, а уравнениями их называют потому, что неизвестные функции — искомые. Многие функциональные уравнения содержат несколько переменных. Все эти переменные, если на них не наложены какие-то ограничения, являются независимыми. Всегда четко должно быть оговорено, на каком множестве функциональное уравнение задается, т.е. какова область определения каждой неизвестной функции. Общее решение функционального уравнения может зависеть от этого множества. Кроме области определения функций, важно знать, в каком классе функций ищется решение. Количество и поведение решений очень строго зависит от этого класса. Вообще для функциональных уравнений, не сводящихся к дифференциальным или интегральным, известно очень мало общих методов решения. Рассмотрим основные приемы, помогающие найти решения таких уравнений. Идея непрерывности Определение. Функция называется непрерывной в точке , если выполняются следующие два условия: 1) точка принадлежит области определения функции ; 2) , разумеется, в предположении, что этот предел существует. Если хотя бы одно из этих условий нарушается, функция не является непрерывной в точке , она будет разрывной в этой точке. Определение. Функция называется непрерывной на отрезке , если она непрерывна во всех точках этого отрезка. Справедлива следующая теорема: Теорема Больцано — Коши. Если функция непрерывна на отрезке и на концах этого отрезка принимает неравные значения и , то она принимает все промежуточные между и значения на отрезке . Пример 1. Функция непрерывна на всей вещественной прямой и удовлетворяет равенству для всех . Доказать, что уравнение имеет хотя бы одно решение. Решение. Рассмотрим функцию . Предположим, что для всех . Тогда в силу непрерывности либо для всех , либо для всех . (Если бы существовали такие и , что , то по теореме Больцано — Коши, внутри отрезка была бы точка, в которой обращалась бы в нуль, что противоречит предположению. Пусть для определенности , то есть для всех . Обозначим . Тогда, так как , то , что противоречит тому, что . Значит, при некотором имеем . Пример 2. Функция задана на всей вещественной оси, причем выполняется равенство Доказать, что f не может быть непрерывной. Решение. Функция не может принимать значение . Действительно, при имеем . Значит, для всех или . Выразим из нашего равенства : Значит, неравенство невозможно, иначе . Если же , то должно выполняться неравенство , откуда и следовательно, получаем, что . Противоречие. Пример 3. Найти все непрерывные функции , удовлетворяющие соотношению для любого . Решение. В данное уравнение подставим вместо (это можно сделать, так как функция определена для всех ), и еще несколько раз проделаем то же самое, получим По непрерывности функции в нуле имеем Получили, что , то есть функция — постоянная. Уравнения Коши 1. Уравнение в классе непрерывных функций имеет решение >. Такое же решение оно имеет и в классе монотонных функций. 2. Уравнение в классе непрерывных функций имеет решение (если не считать . 3. Уравнение в классе непрерывных функций имеет решение (если не считать ). 4. Уравнение в классе непрерывных функций имеет решение (если не считать ). Метод сведения функционального уравнения к известному с помощью замены переменной и функции Пример 4. Найти все непрерывные функции, удовлетворяющие уравнению Решение. В качестве вспомогательной функции возьмем функцию Подставляя в исходное уравнение , получаем то есть функция удовлетворяет первому уравнению Коши, откуда . Решение. Поделим уравнение на , получим Введем вспомогательную функцию , тогда получим уравнение то есть функция удовлетворяет третьему уравнению Коши, откуда . Метод подстановок Пример 6. Найти все решения функционального уравнения Решение. Положим , имеем . Поскольку произвольно, то . Пусть теперь . Подставив в уравнение , получим откуда , где . Нетрудно убедиться, что эта функция действительно удовлетворяет исходному функциональному уравнению. Пример 7. Пусть — некоторое вещественное число. Найти функцию , определенную при всех и удовлетворяющую уравнению где — заданная функция, определенная при всех . Решение. При замене выражение переходит в . Получаем систему уравнений решением которой при является функция Предельный переход Пример 8. Функция непрерывна в точке и выполняется равенство Найти все такие . Решение. Пусть функция удовлетворяет условию задачи. Тогда Проверка показывает, что действительно является решением. Пример 9. Найти функцию , ограниченную на любом конечном интервале и удовлетворяющую уравнению Решение. . Сложим все эти равенства: Перейдем к пределу при . Учитывая ограниченность в нуле и то, что , получаем Производная и функциональные уравнения Пример 10. Найти все вещественные дифференцируемые функции , удовлетворяющие уравнению Решение. Пусть . Имеем , откуда . После преобразований имеем Переходим к пределу при , учитывая, что , получаем где . Интегрируем: откуда и . Так как , то , и . Проверкой убеждаемся, что все эти функции — решения исходного уравнения. Пример 11. Найти все функции , являющиеся решениями уравнения Решение. : . Введем новые функции: Функция — четная, а — нечетная, >, и для этих функций имеем Поскольку , то и . Проверкой убеждаемся, что все такие — действительно решение. Решение функциональных уравнений на множестве натуральных чисел Пример 12. Каждому натуральному числу поставлено в соответствие целое неотрицательное число так, что выполняются следующие условия: 1) для любых двух натуральных чисел и ; 2) , если последняя цифра в десятичной записи числа равна ; 3) . Доказать, что для любого натурального . Решение. Поскольку , , , , то . Любое натуральное число можно представить в виде , где Н.О.Д., иначе или . Отсюда или . , откуда . Задачи 1. Найдите , если . 2. Найти все непрерывные функции такие, что 3. Пусть . Найти все вещественнозначные функции на : 4. Найдите все функции такие, что 5. Найти все непрерывные функции , удовлетворяющие уравнению 6. Решите уравнение 7. Найдите решение уравнения , если — постоянная, в классе функций натурального аргумента. 8. Найти все полиномы : и 9. Существует ли непрерывная функция , определенная на всей вещественной оси , такая, что для всех ? 10. Пусть функция при всех удовлетворяет соотношению Докажите, что — постоянная функция. 11. Найдите непрерывно-дифференцируемое решение функционального уравнения удовлетворяющее условию . 12. В предположении, что существует единственная функция , такая, что надите ее.{2}}+2{x} -8=0\). Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет! Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант. Что у тебя получилось? То же самое? Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится! К оглавлению… Длина отрезка на координатной оси находится по формуле: Длина отрезка на координатной плоскости ищется по формуле: Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула: Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам: Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х. Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить. Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у). Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции. Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак. Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство. Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство: Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ. Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство: Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат. Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х. Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше. К оглавлению… Линейной функцией называют функцию, которую можно задать формулой: График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо): К оглавлению… График параболы задается квадратичной функцией: Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x1; 0) и (x2; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x0; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол): При этом: Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения): Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена: К оглавлению… Степенной функцией называют функцию, заданную формулой: Приведем несколько примеров графиков степенных функций: Обратно пропорциональной зависимостью называют функцию, заданную формулой: В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта: Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их. Показательной функцией с основанием а называют функцию, заданную формулой: В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже): Логарифмической функцией называют функцию, заданную формулой: В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта: График функции y = |x| выглядит следующим образом: К оглавлению… Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция: где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T1, который определяется формулой: Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой: График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо: График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо. Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо. Учащиеся редко задумываются над формальным вопросом: «Что именно означают выражения: «Эти две функции равны» и «Эти две функции различны»? Это и понятно, потому что на практике равенство функций достаточно очевидно, а для утверждения о различии функций учащиеся чаще всего опираются на внешний вид этих функций, а это не только неверно логически, но может привести и к фактическим ошибкам. Похожая ситуация и с понятием равносильности уравнений. Определение равных функций вполне естественно и очевидно: две функции называются равными, если они имеют одинаковые области определения и при каждом значении аргумента из этой области определения принимают равные значения. Поэтому две функции не равны, т.е. различны, если они либо имеют различные области определения, либо при некотором значении аргумента принимают разные значения. Здесь сразу же видно главное: чтобы убедиться, что две функции f и g различны, нужно привести пример такого значения аргумента, т.е. число a, для которого $f(a)\neq g(a)$. Два уравнения или неравенства называются равносильными, если они имеют одно и то же множество решений, т.е. истинны при одних и тех же значениях переменной (или переменных). Для краткости вместо слова «равносильно» употребляют знак $\Leftrightarrow$ и таким образом, например, $xy=0 \Leftrightarrow x=0$ или $y=0, \frac xy=0 \Leftrightarrow x=0$ и $y\neq0, a>b \Leftrightarrow b<a, a \geq b \Leftrightarrow a<b$ или a=b. В действительности, понятие равносильности относится к произвольным предложениям с переменными — высказывателъным формам. Например, равносильны утверждения «Точка С — середина отрезка АВ» и «С принадлежит отрезку АВ и делит его пополам», утверждения «Выпуклый четырехугольник ABCD — параллелограмм» и «Противолежащие стороны четырехугольника ABCD попарно параллельны» — заметим, что в первой паре равносильных утверждений три переменных: А, В, С, а во второй паре их четыре: С — середина отрезка $AB \Leftrightarrow C \in AB$ и АС=СВ, четырехугольник ABCD — параллелограмм $\Leftrightarrow AB \parallel CD, AD \parallel BC$. В такого рода предложениях вместо «равносильно» в математике чаще говорят в том и только в том случае, необходимо и достаточно, тогда и только тогда — эти словесные обороты означают одно и то же. Материалы по теме: Поделиться с друзьями:
Для начала следует разобраться, какие уравнения могут быть решены посредством использования возрастания/убывания функций, отвечающих частям уравнения.
Во-первых, это уравнения f(x)=C, где f(x) – некоторое выражение с переменной x, а C – некоторое число, причем эти уравнения должны удовлетворять следующим критериям:
В качестве примера приведем уравнение . Это уравнение вида f(x)=C, где , C=4. Сразу видно, что для решения этого уравнения может подойти разве что функционально-графический метод, так как переменная находится под знаками «разнородных» функций: функции извлечения корня и функции арктангенс. Причем строить график функции, отвечающей левой части уравнения, довольно сложно. Более простых привычных способов решения не видно. ОДЗ для этого уравнения определяется условием , откуда находим, что ОДЗ есть числовой промежуток . Учитывая рекомендации по определению корней уравнения, которые мы дадим в одном из следующих пунктов текущей статьи, несложно подобрать корень уравнения, им является число 1. Рекомендации по обоснованию возрастания/убывания, которые мы также дадим чуть позже, позволяют показать возрастание функции, отвечающей левой части уравнения. То есть, выполняются все критерии, которым должно удовлетворять уравнение для его решения посредством использования возрастания/убывания.
Во-вторых, через возрастание/убывание решаются уравнения f(x)=g(x), где f(x) и g(x) – это некоторые выражения с переменной x, удовлетворяющие следующим критериям:
Поясним на примере. Для этого подойдет уравнение . Это уравнение вида f(x)=g(x), где и . Здесь переменная есть в показателе степени и под знаком натурального логарифма. Это сразу существенно ограничивает набор методов, подходящих для его решения, оставляя только функционально-графический или какие-либо специфические методы. Графики здесь мало что дают в плане нахождения корней. Остается опираться лишь на свойства функций. При этом легко определить область допустимых значений переменной x для уравнения, она представляет собой числовой промежуток . Также легко подбирается корень уравнения, им является число 3, и легко обосновывается убывание функции, отвечающей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Значит, это уравнение может быть решено посредством использования возрастания/убывания.
Теперь про уравнения f(x)=C и f(x)=g(x), ОДЗ для которых есть объединение нескольких числовых промежутков. Если они на отдельно взятом промежутке области допустимых значений удовлетворяют записанным выше критериям, то на этом промежутке можно получить их решение посредством использования возрастания/убывания. Если это сделать на каждом промежутке области допустимых значений, то будет получено решение уравнения в целом.
И вновь обратимся к конкретному примеру. Рассмотрим уравнение . Для него не просматривается простое решения привычными методами, отличными от направления функционально-графического метода, подразумевающего использование возрастания/убывания. ОДЗ для этого уравнения представляет собой не отдельно взятый числовой промежуток, а объединение двух числовых промежутков (−∞, 0) и (0, +∞). На каждом из этих промежутков несложно подобрать корни уравнения. Корнем на первом промежутке является число −8, а на втором – число 27. Также на каждом промежутке легко обосновать убывание функции, отвечающей левой части уравнения, и возрастание функции, отвечающей правой части уравнения. Значит, это уравнение может быть решено через возрастание/убывание.
То есть, решение уравнений f(x)=C и f(x)=g(x), ОДЗ для которых есть объединение нескольких числовых промежутков, сводится к решению этих уравнений на отдельно взятых промежутках. По этой причине метод решения можно постигать на уравнениях f(x)=C и f(x)=g(x), ОДЗ для которых представляет отдельный числовой промежуток.
К началу страницы
В программе SOLIDWORKS использование уравнений полностью интегрировано в систему. То есть, когда вы проставляете какие-либо размеры, у вас появляются окошки с запросом ввести величину. Это окно является многофункциональным. Непосредственно в нем можно ввести сразу уравнение. Для того, чтобы просмотреть и отредактировать все зависимости, которые присутствуют в модели, необходимо зайти непосредственно в окно Далее открывается следующее окно. Здесь мы видим три категории, на которые разделена таблица: «Глобальные переменные», «Элементы», «Размеры». В группе «Глобальные переменные» можно создавать переменные и в столбце «Значения/ Уравнения» проводить какие-либо расчеты. Также эти значения можно привязать к какому-либо размеру из группы «Размеры», затем указанные значения дальше транслировать в расчетах не как полное имя размера или значения, а просто буквой. В группе «Элементы» можно только задавать итоговое значение — «Погашен»/ «Не погашен», исходя из условий или ограничений, которые необходимы при расчете. В группе «Размеры» приведены все параметры, которые дают модели статус «Определен». Это могут быть линейные или угловые размеры, значения определяющие массивы или какие-либо параметры других операций элементов: расстояние вытягивания, угол поворота вокруг оси, количество элементов в различных видах массивов. SOLIDWORKS дает широкий ассортимент инструментов, которыми можно пользоваться при задании зависимостей. Они могут быть как математическими, так и логическими. Функция «Уравнения» имеет четыре типа уравнений: Таким образом, сегодня мы познакомились более детально с инструментарием, предложенным нам при работе с уравнениями; узнали про виды операций, которые возможно производить при помощи уравнений; узнали про виды уравнений. В общем случае определение дифференциального уравнения может выглядеть так: Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного аргумента. Например: у’ = f(x) (539.1) Напомню, функциональное уравнение может иметь следующий вид: у = f(x) (538.1) Дифференциальное уравнение называется уравнением в частных производных, если искомая функция зависит от нескольких аргументов. Например: у’ = f(x1,x2) или у’ = f(x,u) (539.2) где х1, х2 или х, u — возможные обозначения для различных аргументов функции. Порядком дифференциального уравнения считается порядок наивысшей производной, входящей в уравнение. Например уравнение (539.1) является уравнением первого порядка. Уравнение второго порядка может иметь вид: y» = f(x) (539.3) Решением дифференциального уравнения является функция, подставление которой вместо неизвестной функции обращает уравнение в тождество. Другими словами уравнение становится равенством. А теперь эти общие математические понятия (кстати тут приведены далеко не все основные понятия) попробуем описать простым человеческим языком, но начать придется издалека. Мы живем в несовершенном, постоянно изменяющемся мире. Все течет, все изменяется, как подметил еще Гераклит. Однако в древности были и другие мыслители, которые в отличие от Гераклита пытались этот мир как-то понять и оценить. Так далеко в историю мы заглядывать не будем, хотя предпосылки к дифференциальному исчислению следует искать именно там, а ограничимся простыми и наглядными примерами: Мы вышли из пункта А в пункт Б и находились в пути 4 часа, каждый час мы проходили по 2 километра. Вопрос: какое расстояние между пунктами А и Б? Вообще это задачка для 3-4 класса начальной школы и решить ее вроде бы не сложно (потому я ее и выбрал): достаточно сложить все расстояния, пройденные за каждый час, а так как эти расстояния одинаковые, то можно еще больше упростить задачу, умножив на 4 расстояние, пройденное за один промежуток времени. Таким образом расстояние между пунктами А и Б составляет: 2 км · 4 = 8 км (539.4) А между тем условия задачи можно рассматривать и по другому, т.е. как зависимость пройденного расстояния от времени. В этом случае у нас время -независимая переменная t или аргумент функции, а пройденное расстояние — значение функции в тот или иной момент времени или переменная s. Тогда условия задачи соответствуют следующему функциональному уравнению: s = f(t) = 2t (539.5) а также графику этой функции: Рисунок 539.1. График функции f(t) = 2t. Так если по оси t откладывать промежутки времени Δt (ч), которое мы были в пути, а по оси s — преодоленное за эти промежутки времени расстояние Δs (км), то график указанной функции будет иметь такой вид, как показано на рисунке 539.1. В общем случае используются более привычные оси х и у, соответственно рассматриваются функции вида y = f(x), но сути дела это никак не меняет. Решая уравнение (539.5) мы можем определить не только общее расстояние, преодоленное за 4 часа пути, но и в любой интересующий нас момент времени. Например, нас интересует, какое расстояние мы прошли за 1.5 часа. Согласно уравнению (539.5) это расстояние составит 2·1.5 = 3 километра. А если нас интересует не расстояние, преодоленное к тому или иному моменту времени, а скорость движения? Можем ли мы определить эту скорость на основе имеющихся данных? Оказывается можем, потому что скорость — это тоже функция, которая в свою очередь также зависит от времени. Так как каждый час мы преодолевали по 2 км, то отсюда можно сделать вывод, что скорость нашего движения была постоянной, тогда по давно известному нам уравнению, описывающему движение с постоянной скоростью: v = s/t = 8/4 = 2 км/ч (539.6) В данном случае, так как скорость постоянная, не имеет значения, на каком временном промежутке мы эту скорость определяем. Тем не менее рассмотрим данную ситуацию с точки зрения математики. Временные промежутки, когда засекалось пройденное расстояние, мы обозначим как Δt = 1, соответственно t = ΣΔt = 1 + 1 + 1 + 1 = 4. Расстояния, пройденные за эти промежутки времени обозначим как Δs = 2. На графике функции это будет выглядеть так: Рисунок 539.2 С точки зрения математики временные промежутки Δt — это приращение аргумента функции: Δt = t — t0 (539.7) Соответственно расстояния, пройденные за рассматриваемый промежуток времени — это приращение функции: Δs = Δf(t) = f(t) — f(t0) (539.8) А так как использовать греческую литеру Δ не всегда удобно (в частности мне для этого приходится заходить в отдельный редактор текста, а наборщикам в типографиях вставить эту литеру было еще сложнее), то часто приращение значения искомой функции и приращение аргумента функции обозначают как ds и dt. Тогда формулу определения скорости можно записать так: v = ds/dt (539.9) Возможно и не стоило это так подробно расписывать, но на мой взгляд это очень важно, чтобы показать, что в дифференциальном исчислении нет ничего трудного, если рассматривать его на соответствующих примерах. Итак скорость v является производной функции s = f(t) = 2t. Дифференциальное уравнение в этом случае будет выглядеть так: v = s’ = f'(t) (539.10.1) v = (2t)’ = 2 (539.10.2) Но и это еще не все, на основании имеющихся данных: времени в пути и расстояний, преодоленных за 1 час, мы можем определить ускорение нашего движения. Так как скорость нашего движения оставалась постоянной, соответственно dv = 0, то само собой и ускорения никакого не было, ни положительного ни отрицательного. Другими словами ускорение нашего движения составляло а = 0 км/ч2. На языке математики это будет выглядеть так: а = v’ = dv/dt = s» = d2s/dt2 (539.11.1) a = 0/1 = (2t)» = (2)’ = 0 (539.11.2) Т.е. в данном случае для определения ускорения нужно определить первую производную функции скорости (уравнения, выражающего зависимость скорости от времени) или вторую производную функции расстояния (уравнения, выражающего зависимость пройденного расстояния от времени). На основании вышеизложенного мы можем дать следующее предварительное определение производной: В рассмотренном выше примере скорость движения — это скорость изменения функции расстояния, а ускорение — это скорость изменения функции скорости. Если бы мы все 4 часа сидели на месте, то и расстояние, пройденное нами, было бы равно нулю, и скорость и ускорение, но даже для такого случая можно записать соответствующие дифференциальные уравнения: s = f(t) = 0 v = s’ = 0 a = v’ = s» = 0 Однако в жизни гораздо чаще встречаются функции, даже третьи производные которых не равны нулю. Рассмотрим другой пример все с тем же движением, на этот раз чуть более сложный. По ровной наклонной поверхности скатывается шар. Начальная скорость движения равна vo = 0. Определить пройденное шаром за 4 секунды расстояние, скорость после 1, 2, 3 и 4 секунд движения и постоянное ускорение движения, если за первую секунду шар преодолел расстояние 3 м, за вторую — 9 м, за третью — 15 м, за четвертую — 21 м. С определением пройденного расстояния по прежнему проблем нет: достаточно сложить расстояния, которые преодолел шар за каждую секунду s = ΣΔs = 3 + 9 + 15 + 21 = 48 метров. А вот скорость и ускорение в данном случае определить не так просто. Тем не менее попробуем. Если воспользоваться полученными раннее знаниями, то вроде бы в первый промежуток времени скорость должна быть равна: v1 = ds1/dt1 = 3/1 = 3 м/с (539.12) Вот только в данном случае у нас скорость — изменяющаяся величина, зависящая от времени, поэтому результат полученный при решении уравнения (539.12) можно рассматривать лишь как среднюю скорость движения на первом участке. Тогда более правильно уравнение скорости на первом участке записать так: v1ср = ds1/dt1 = 3/1 = 3 м/с (539.12.2) Подобным образом мы достаточно легко можем определить среднюю скорость на всех участках пути, и она составит v2ср = 9 м/с, v3ср = 15 м/с, v4ср = 21 м/с, но в данном случае нас интересует не среднее значение функции скорости на рассматриваемом участке, а значение функции скорости во вполне определенной точке, т.е. после 1, 2, 3 и 4 секунд движения. Как это сделать? По условиям задачи ускорение — производная от скорости — является постоянной величиной, т.е. скорость изменения скорости будет постоянной. В этом случае значение средней скорости является средним арифметическим от начальной и конечной скорости на рассматриваемом участке: v1ср = (vo + v1)/2 = 3 м/с (539.13.1) тогда при vo = 0 v1 = 3·2 = 6 м/с (539.13.2) Соответствующим образом мы можем определить значения скорости и в остальных точках, например (6 + v2)/2 = 9, v2 = 9·2 — 6 = 12 м/с; (12 + v3)/2 = 15, v3 = 15·2 — 12 = 18 и так далее, а теперь переведем полученные данные на язык высшей математики. Мы видим, что v1 = 6·1, v2 = 6·2 = 12, v3 = 6·3 = 18, т.е. значение скорости явно зависит от времени, соответственно уравнение скорости мы можем записать следующим образом: v = s’ = 6t (539.14) Соответственно ускорение движения шара составит: a = v’ = (6t)’ = 6 м/с2 (539.15) Между тем, если бы нам были заданы меньшие значения временных промежутков и соответственно меньшие значения пройденных расстояний за эти промежутки времени, например при dt1 = 1 секунда, ds1 = 3 м, dt2 = 0.1 секунды и ds2 = 0.63 м, то средняя скорость на рассматриваемом втором участке составила бы v2ср = ds/dt = 0.63/0.1 = 6.3 м/с, а скорость в в точке t2: v2сp = (6 + v2)/2 = 6.3, v2 = 12.6 — 6 = 6.6 м/с. Т.е. закономерность изменения значения скорости никуда не девается, тем не менее, чем меньше рассматриваемый временной промежуток dt, тем меньше разница между значением средней скорости изменения функции и скоростью изменения функции в рассматриваемой точке. Из этого можно сделать еще один очень важный вывод: На основании этого можно сформулировать более полное определение производной функции: Поэтому иногда производную называют мгновенной скоростью изменения функции. В нашем случае уравнение производной будет выглядеть так: (539.16) На данном этапе вид формулы (539.16) нас уже не пугает (во всяком случае мне так кажется). Совсем другое дело, когда подобная формула приводится в начале темы, посвященной рассмотрению производных функции. С задачей определения скорости и ускорения в примере 2 мы вроде бы справились и даже составили соответствующие уравнения (539.14) и (539.15). Но иногда требуется решить и обратную задачу — например определить исходное уравнение, описывающее зависимость перемещения от времени. Если скорость является производной функции расстояния v = s’, то расстояние при этом является первообразной (дифференциалом) функции скорости s = ∫v. Процесс нахождения первообразной функции называется интегрированием. Так, чтобы получить уравнение зависимости пройденного расстояния от времени, нам нужно проинтегрировать уравнение скорости. При этом уравнение расстояния более правильно записывать так s = ∫vdt (539.17) В общем случае интегрирование может быть более сложной задачей, чем дифференцирование, потому что функции бывают не только степенными, как в данном примере, но и тригонометрическими, обратными тригонометрическими и т.п., но пока нас интересует, как проинтегрировать простую степенную функцию вида f(t) = 6t. Вообще-то мы могли сразу построить график, отражающий зависимость пройденного расстояния от времени по данным примера 2, тем не менее сделаем это сейчас, а заодно построим график для уравнений скорости и ускорения и расположим их в такой последовательности: Рисунок 539.3. Графики степенных функции а) а= 6, б) v = at, в) s = at2/2. Как видим, график, отражающий зависимость ускорения от времени, у нас самый простой. Ускорение постоянное, а = 6 м/с2 и от времени никак не зависит. Тем не менее, зная ускорение, мы можем определить скорость движения в любой точке времени. Так из уравнений (539.14) и (539.15) следует, что: v = 6t = at (539.14.2) Соответственно решая это уравнение, мы можем определить скорость в любой момент времени. Но если рассматривать это действие с точки зрения геометрии, то мы, умножая ускорение на время, определяем площадь прямоугольника со сторонами а = 6 и t. При t = 4 площадь прямоугольника составит 6·4 = 24, точнее 24 м/с так как мы все-таки определяем скорость. Если мы построим график, отражающий зависимость изменения скорости от времени, то увидим, что на этом графике значения скорости в той или иной момент времени соответствуют площадям прямоугольника со сторонами а = 6 и t. Получается, что если определить площадь треугольника со сторонами v и t, то это и будет расстояние, преодоленное к тому или иному промежутку времени: s = vt/2 = at2/2 = 6t2/2 = 3t2 (539.18) Уравнение (539.18) можно записать как дифференциальное: s = ∫6tdt = 3t2 (539.18.2) Если график, показанный на рисунке 539.3.в) также является графиком для производной некоторой функции, то для определения первообразной этой функции нам также следовало бы найти площадь фигуры, ограниченной квадратной параболой. Сделать это в принципе не сложно, так как площадь фигуры, очерченной квадратной параболой таким образом, как показано на рисунке 539.3.в) в 3 раза меньше площади прямоугольника со сторонами s и t, соответственно S = st/3 = 3t2t/3 = t3 и эту процедуру можно повторять до бесконечности. Почему площадь фигуры, ограниченной квадратной параболой именно в 3 раза меньше, чем площадь прямоугольника, а площадь фигуры ограниченной кубической параболой в 4 раза меньше площади прямоугольника, я здесь объяснять не буду, тем не менее такая закономерность существует и в математическом выражении выглядит так: ∫aхndx = axn+1/n + C (539.19) В данном случае С — это некоторая постоянная величина. Как мы выяснили, при дифференцировании постоянные величины обращаются в нуль, как пример — уравнение (539.11.2), соответственно решая обратную задачу, т.е. интегрируя функцию, мы допускаем, что некая постоянная величина в первообразной функции была. Например в общем случае уравнение скорости (539.14.2) должно выглядеть так: v = vo + at (539.14.3) где vo — это и есть некая постоянная величина. В нашем случае по условиям задачи vo = 0, поэтому мы использовали сокращенную форму записи. В общем случае график функции может выглядеть как угодно, например так: Рисунок 539.4 В этом случае сразу определить площадь фигуры, ограниченной графиком функции, не получится. Но мы можем разбить эту фигуру на участки шириной Δх и определить среднее значение у для каждого участка. Теперь определить площади трех прямоугольников большого труда не составит, вот только суммарная площадь прямоугольников не будет равна площади фигуры, ограниченной графиком функции: S ≈ ∑yiΔx (539.20) Но чем больше будет у нас прямоугольников с шириной Δх, т.е, чем меньше будет значение Δх, тем точнее будет значение у, а значит и суммарная площадь прямоугольников будет ближе к площади фигуры, ограниченной графиком функции. Из этого можно сделать следующий вывод: Так как на рисунке 539.4 показан график непрерывной функции, то такая функция является интегрируемой и для определения дифференциала функции используется определенный интеграл. При этом 0 и 3 — это пределы интегрирования. Если мы в следующем уравнении y = x + 7 присвоим значение x, уравнение даст нам значение для y. Пример $$ y = x + 7 $$ $$ если \; х = 2 \; затем $$ y = 2 + 7 = 9 $$ Если бы мы присвоили другое значение x, уравнение дало бы нам другое значение y. Вместо этого мы могли бы присвоить значение y и решить уравнение, чтобы найти совпадающее значение x. В нашем уравнении y = x + 7 у нас есть две переменные, x и y. Переменная, которой мы присваиваем значение, мы называем независимой переменной, а другая переменная является зависимой переменной, поскольку ее значение зависит от независимой переменной. В нашем примере выше x — независимая переменная, а y — зависимая переменная. Функция — это уравнение, которое имеет только один ответ для y для каждого x. Функция назначает ровно один выход каждому входу указанного типа. Обычно функцию называют f (x) или g (x) вместо y.f (2) означает, что мы должны найти значение нашей функции, когда x равно 2. Пример $$ f (x) = x + 7 $$ $$ если \; х = 2 \; затем $$ f (2) = 2 + 7 = 9 $$ Функция линейна, если ее можно определить с помощью $$ f (x) = mx + b $$ f (x) — значение функции. Эта форма называется формой пересечения наклона. Если наклон m отрицательный, значение функции уменьшается с увеличением x и наоборот, если наклон положительный. Уравнение, например y = x + 7 , является линейным, и существует бесконечное количество упорядоченных пар x и y, которые удовлетворяют этому уравнению. Наклон m здесь равен 1, а наш b (точка пересечения с y) равен 7. $$ m = \ frac {y_ {2} -y_ {1}} {x_ {2} -x_ {1}} $$ $$ x_ {2} \ neq x_ {1} $$ Если двум линейным уравнениям задан один и тот же наклон, это означает, что они параллельны, а если произведение двух наклонов m1 * m2 = -1, два линейных уравнения называются перпендикулярными. Если x равен -1, какое значение имеет f (x), когда f (x) = 3x + 5? Если [латекс] \ left (p + 3 \ right) \ left (p — 1 \ right) = 0 [/ latex], либо [latex] \ left (p + 3 \ right) = 0 [/ latex] или [латекс] \ left (p — 1 \ right) = 0 [/ latex] (или оба они равны 0). Мы установим каждый коэффициент равным 0 и решим для каждого случая [латекс] p [/ латекс]. [латекс] \ begin {align} & p + 3 = 0, && p = -3 \\ & p — 1 = 0, && p = 1 \ hfill \ end {align} [/ latex] Это дает нам два решения.Выход [латекс] h \ left (p \ right) = 3 [/ latex], когда вход либо [latex] p = 1 [/ latex], либо [latex] p = -3 [/ latex]. Мы также можем проверить, построив график, как на рисунке 5. График проверяет, что [latex] h \ left (1 \ right) = h \ left (-3 \ right) = 3 [/ latex] и [latex] h \ left (4 \ справа) = 24 [/ латекс]. Учитывая функцию [латекс] g \ left (m \ right) = \ sqrt {m — 4} [/ latex], решите [латекс] g \ left (m \ right) = 2 [/ latex]. Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения .Если можно выразить выход функции с помощью формулы , включающей входную величину, то мы можем определить функцию в алгебраической форме. Например, уравнение [латекс] 2n + 6p = 12 [/ латекс] выражает функциональную взаимосвязь между [латексом] n [/ латексом] и [латексом] p [/ латексом]. Мы можем переписать его, чтобы решить, является ли [latex] p [/ latex] функцией [latex] n [/ latex]. Выразите отношение [латекс] 2n + 6p = 12 [/ latex] как функцию [latex] p = f \ left (n \ right) [/ latex], если это возможно. Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где [latex] p [/ latex] является функцией [latex] n [/ latex], что означает запись его как [latex] p = [/ latex] выражение, включающее [latex] n [/ latex]. [латекс] \ begin {align} & 2n + 6p = 12 \\ [1 мм] & 6p = 12 — 2n && \ text {Subtract} 2n \ text {с обеих сторон}. \\ [1mm] & p = \ frac {12 — 2n} {6} && \ text {Разделите обе стороны на 6 и упростите}. \\ [1 мм] & p = \ frac {12} {6} — \ frac {2n} {6} \\ [1 мм] & p = 2- \ frac {1} {3} n \ end {align} [/ latex ] Следовательно, [латекс] p [/ latex] как функция [latex] n [/ latex] записывается как [латекс] p = f \ left (n \ right) = 2- \ frac {1} {3} n [/ latex] Важно отметить, что не все отношения, выраженные уравнением, также можно выразить как функцию с формулой.{y} [/ latex], если мы хотим выразить [latex] y [/ latex] как функцию [latex] x [/ latex], не существует простой алгебраической формулы, включающей только [latex] x [/ latex] что равно [латекс] y [/ латекс]. Однако каждый [latex] x [/ latex] определяет уникальное значение для [latex] y [/ latex], и существуют математические процедуры, с помощью которых [latex] y [/ latex] может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для [latex] y [/ latex] как функции [latex] x [/ latex], даже если формулу нельзя записать явно. Как мы видели выше, мы можем представлять функции в виде таблиц. И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев.И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов. Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы. См. Таблицу ниже. Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию [латекс] П [/ латекс]. Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию [latex] P [/ latex] при входном значении «золотая рыбка». Мы бы написали [латекс] P \ left (\ text {goldfish} \ right) = 2160 [/ latex]. Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции [latex] P [/ latex] кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции. Используя приведенную ниже таблицу, Когда мы вводим 2 в функцию [latex] g [/ latex], на выходе получаем 6.Когда мы вводим 4 в функцию [latex] g [/ latex], наш результат также равен 6. Используя таблицу из предыдущего примера, оцените [латекс] g \ left (1 \ right) [/ latex]. [латекс] г \ слева (1 \ справа) = 8 [/ латекс] Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями. Учитывая график ниже, Используя график, решите [латекс] f \ left (x \ right) = 1 [/ latex]. [латекс] x = 0 [/ латекс] или [латекс] x = 2 [/ латекс] Вы можете использовать онлайн-инструмент построения графиков для построения графиков функций, поиска значений функций и оценки функций.2 + x + 4 [/ latex] с использованием обозначения функций. У вас была идея улучшить этот контент? Нам очень понравится ваш вклад. Улучшить эту страницуПодробнее Ранее мы писали уравнение для линейной функции из графика.Теперь мы можем расширить наши знания о построении графиков линейных функций для более тщательного анализа графиков. Начните с просмотра графика ниже. Сразу видно, что график пересекает ось y в точке (0, 4), так что это пересечение y . Затем мы можем рассчитать наклон, найдя подъем и пробег. Мы можем выбрать любые две точки, но давайте посмотрим на точку (–2, 0). Чтобы добраться из этой точки до точки пересечения y- , мы должны переместиться на 4 единицы вверх (подъем) и вправо на 2 единицы (бег).Итак, уклон должен быть: [латекс] m = \ frac {\ text {rise}} {\ text {run}} = \ frac {4} {2} = 2 [/ latex] Подстановка угла наклона и точки пересечения y- в форму линии пересечения откоса дает: [латекс] y = 2x + 4 [/ латекс] Сопоставьте каждое уравнение линейной функции с одной из линий на графике ниже. Проанализируйте информацию по каждой функции. Теперь мы можем перемаркировать линии. До сих пор мы находили точки пересечения функций y- : точку, в которой график функции пересекает ось y . Функция также может иметь точку пересечения x , , которая является координатой x точки, в которой график функции пересекает ось x .Другими словами, это входное значение, когда выходное значение равно нулю. Чтобы найти точку пересечения x , установите функцию f ( x ) равной нулю и найдите значение x . Например, рассмотрим показанную функцию: [латекс] f \ left (x \ right) = 3x — 6 [/ латекс] Установите функцию равной 0 и решите для x . [латекс] \ begin {array} {l} 0 = 3x — 6 \ hfill \\ 6 = 3x \ hfill \\ 2 = x \ hfill \\ x = 2 \ hfill \ end {array} [/ latex] График функции пересекает ось x в точке (2, 0). Все ли линейные функции имеют точки пересечения x ? Нет. Однако линейные функции вида y = c , где c — ненулевое действительное число, являются единственными примерами линейных функций без перехвата x . Например, y = 5 — это горизонтальная линия на 5 единиц выше оси x . У этой функции нет x — перехватывает . Перехват x функции — это значение x , где f ( x ) = 0.Его можно найти, решив уравнение 0 = mx + b . Найдите точку пересечения x [latex] f \ left (x \ right) = \ frac {1} {2} x — 3 [/ latex]. Установите функцию равной нулю, чтобы найти x . [латекс] \ begin {array} {l} 0 = \ frac {1} {2} x — 3 \\ 3 = \ frac {1} {2} x \\ 6 = x \\ x = 6 \ end {array} [/ latex] График пересекает ось x в точке (6, 0). График функции показан ниже. Мы видим, что перехват x равен (6, 0), как и ожидалось. График линейной функции [латекс] f \ left (x \ right) = \ frac {1} {2} x — 3 [/ latex]. Найдите точку пересечения x [latex] f \ left (x \ right) = \ frac {1} {4} x — 4 [/ latex]. [латекс] \ left (16, \ text {0} \ right) [/ latex] Есть два особых случая линий на графике — горизонтальные и вертикальные линии.Горизонтальная линия указывает на постоянный выход или значение y . На графике ниже мы видим, что выход имеет значение 2 для каждого входного значения. Изменение выходных сигналов между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем м = 0 в уравнении [латекс] f \ left (x \ right) = mx + b [/ latex], уравнение упрощается до [latex] f \ left (x \ right) = b [/ latex]. Другими словами, значение функции постоянно. Этот график представляет функцию [латекс] f \ left (x \ right) = 2 [/ latex]. Горизонтальная линия, представляющая функцию [латекс] f \ left (x \ right) = 2 [/ latex]. Вертикальная линия обозначает постоянный ввод или значение x . Мы видим, что входное значение для каждой точки на линии равно 2, но выходное значение варьируется. Поскольку это входное значение отображается более чем на одно выходное значение, вертикальная линия не представляет функцию. Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен. Обратите внимание, что вертикальная линия имеет точку пересечения x , но не имеет точки пересечения y- , если только это не линия x = 0. Этот график представляет линию x = 2. Вертикальная линия [латекс] x = 2 [/ latex], которая не представляет функции. Линии могут быть горизонтальными или вертикальными. Горизонтальная линия — это линия, определяемая уравнением вида [латекс] f \ left (x \ right) = b [/ latex], где [latex] b [/ latex] — константа. Вертикальная линия — это линия, определяемая уравнением вида [латекс] x = a [/ latex], где [latex] a [/ latex] — постоянная величина. Напишите уравнение линии, изображенной ниже. Для любого значения x значение y равно [latex] –4 [/ latex], поэтому уравнение имеет вид [latex] y = –4 [/ latex]. Напишите уравнение линии, изображенной ниже. Константа x — значение 7, поэтому уравнение [латекс] x = 7 [/ латекс]. У вас была идея улучшить этот контент? Нам очень понравится ваш вклад. Улучшить эту страницуПодробнее Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Теперь нам нужно перейти ко второй теме этой главы.Однако, прежде чем мы это сделаем, нам нужно сделать быстрое определение. Отношение — это набор упорядоченных пар. Это кажется странным определением, но оно нам понадобится для определения функции (что является основной темой этого раздела). Однако, прежде чем мы фактически дадим определение функции, давайте посмотрим, сможем ли мы понять, что такое отношение. Вернитесь к примеру 1 в разделе «Графики» этой главы.2} — 4 \). Вот упорядоченные пары, которые мы использовали. Любые из следующих отношений являются отношениями, потому что они состоят из набора упорядоченных пар. Конечно, есть еще много отношений, которые мы могли бы сформировать из списка упорядоченных пар, приведенного выше, но мы просто хотели перечислить несколько возможных отношений, чтобы привести некоторые примеры.Также обратите внимание, что мы также можем получить другие упорядоченные пары из уравнения и добавить их в любое из приведенных выше отношений, если захотим. Теперь вы, вероятно, спрашиваете, почему мы заботимся об отношениях, и это хороший вопрос. Некоторые отношения очень специфичны и используются почти на всех уровнях математики. Следующее определение говорит нам, какие отношения являются этими особыми отношениями. Функция — это отношение, для которого каждое значение из набора первых компонентов упорядоченных пар связано ровно с одним значением из набора вторых компонентов упорядоченной пары. Ладно, это полный рот. Посмотрим, сможем ли мы понять, что это значит. Давайте посмотрим на следующий пример, который, надеюсь, поможет нам во всем этом разобраться. Из этих заказанных пар мы получаем следующие наборы первых компонентов ( i.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{0, — 3,0,5} \ right \} \] Для набора вторых компонентов обратите внимание, что «-3» встречается в двух упорядоченных парах, но мы указали его только один раз. Чтобы понять, почему это отношение является функцией, просто выберите любое значение из набора первых компонентов. Теперь вернитесь к отношению и найдите каждую упорядоченную пару, в которой это число является первым компонентом, и перечислите все вторые компоненты из этих упорядоченных пар.Список вторых компонентов будет состоять ровно из одного значения. Например, давайте выберем 2 из набора первых компонентов. Из отношения мы видим, что существует ровно одна упорядоченная пара с 2 в качестве первого компонента, \ (\ left ({2, — 3} \ right) \). Следовательно, список вторых компонентов (, т.е. список значений из набора вторых компонентов), связанный с 2, представляет собой ровно одно число -3. Обратите внимание, что нас не волнует, что -3 является вторым компонентом второго упорядоченного номинала в отношении.Это вполне приемлемо. Мы просто не хотим, чтобы было больше одной упорядоченной пары с 2 в качестве первого компонента. Мы рассмотрели одно значение из набора первых компонентов для нашего быстрого примера, но результат будет таким же для всех остальных вариантов. Независимо от выбора первых компонентов с ним будет связан ровно один второй компонент. Следовательно, это отношение является функцией. Чтобы действительно почувствовать, что нам говорит определение функции, мы, вероятно, должны также проверить пример отношения, которое не является функцией. Не беспокойтесь о том, откуда взялось это отношение. {{\ mbox {st}}}} {\ mbox {components:}} \ left \ {{6, — 7,0} \ right \} \ hspace {0.{{\ mbox {nd}}}} {\ mbox {компоненты:}} \ left \ {{10,3,4, — 4} \ right \} \] Из набора первых компонентов выберем 6. Теперь, если мы перейдем к соотношению, мы увидим, что есть две упорядоченные пары с 6 в качестве первого компонента: \ (\ left ({6,10} \ right) \ ) и \ (\ left ({6, — 4} \ right) \). Список вторых компонентов, связанных с 6, будет: 10, -4. Список вторых компонентов, связанных с 6, имеет два значения, поэтому это отношение не является функцией. Обратите внимание на тот факт, что если мы выбрали -7 или 0 из набора первых компонентов, то в списке вторых компонентов, связанных с каждым из них, будет только одно число. Это не имеет значения. Тот факт, что мы нашли даже одно значение в наборе первых компонентов с более чем одним вторым компонентом, связанным с ним, достаточно, чтобы сказать, что это отношение не является функцией. В качестве последнего комментария к этому примеру отметим, что если мы удалим первую и / или четвертую упорядоченную пару из отношения, у нас будет функция! Итак, надеюсь, у вас есть хоть какое-то представление о том, что нам говорит определение функции. Теперь, когда мы заставили вас пройти собственно определение функции, давайте дадим еще одно «рабочее» определение функции, которое будет гораздо более полезным для того, что мы здесь делаем. Фактическое определение работает с отношением. Однако, как мы видели с четырьмя отношениями, которые мы привели до определения функции, и с отношением, которое мы использовали в примере 1, мы часто получаем отношения из какого-либо уравнения. Важно отметить, что не все отношения основаны на уравнениях! Отношение из второго примера, например, было просто набором упорядоченных пар, которые мы записали для этого примера, и не было получено из какого-либо уравнения.Это также может быть верно для отношений, которые являются функциями. Их не обязательно выводить из уравнений. Однако, как уже было сказано, все функции, которые мы собираемся использовать в этом курсе, основаны на уравнениях. Поэтому давайте напишем определение функции, которая признает этот факт. Прежде чем мы дадим «рабочее» определение функции, мы должны указать, что это НЕ фактическое определение функции, данное выше. Это просто хорошее «рабочее определение» функции, которое связывает вещи с видами функций, с которыми мы будем работать в этом курсе. Функция — это уравнение, для которого любой \ (x \), который можно вставить в уравнение, даст ровно один \ (y \) из уравнения. Вот оно. Это определение функций, которые мы собираемся использовать, и, вероятно, будет легче понять, что оно означает. Прежде чем мы исследуем это, обратите внимание, что мы использовали фразу «\ (x \), который может быть подключен» в определении.Это обычно означает, что не все \ (x \) могут быть включены в уравнение, и это на самом деле правильно. Мы вернемся и обсудим это более подробно в конце этого раздела, однако на данном этапе просто помните, что мы не можем делить на ноль, и если мы хотим, чтобы действительные числа были исключены из уравнения, мы не можем извлечь квадратный корень из отрицательное число. Итак, с этими двумя примерами ясно, что мы не всегда сможем подставить каждое \ (x \) в какое-либо уравнение. Далее, имея дело с функциями, мы всегда будем предполагать, что и \ (x \), и \ (y \) будут действительными числами.Другими словами, мы на некоторое время забудем о том, что знаем что-либо о комплексных числах, пока будем заниматься этим разделом. Хорошо, теперь давайте вернемся к определению функции и рассмотрим несколько примеров уравнений, которые являются функциями, и уравнений, которые не являются функциями. «Рабочее» определение функции гласит, что если мы возьмем все возможные значения \ (x \), подставим их в уравнение и решим для \ (y \), мы получим ровно одно значение для каждого значения \ ( Икс\).На этом этапе игры может быть довольно сложно на самом деле показать, что уравнение является функцией, поэтому в основном мы будем обсуждать его. С другой стороны, часто довольно легко показать, что уравнение не является функцией. Итак, нам нужно показать, что независимо от того, какое \ (x \) мы подставляем в уравнение и решаем для \ (y \), мы получим только одно значение \ (y \). Также обратите внимание, что значение \ (y \), вероятно, будет различным для каждого значения \ (x \), хотя это не обязательно. Давайте начнем с того, что подставим некоторые значения \ (x \) и посмотрим, что произойдет. Итак, для каждого из этих значений \ (x \) мы получили единственное значение \ (y \) из уравнения.Теперь этого недостаточно, чтобы утверждать, что это функция. Чтобы официально доказать, что это функция, нам нужно показать, что она будет работать независимо от того, какое значение \ (x \) мы подставляем в уравнение. Конечно, мы не можем подставить в уравнение все возможные значения \ (x \). Это просто невозможно физически. Однако давайте вернемся и посмотрим на те, которые мы подключили. Для каждого \ (x \) после подключения мы сначала умножили \ (x \) на 5, а затем прибавили к нему 1.2} + 1 = 9 + 1 = 10 \ end {align *} \] А теперь давайте немного подумаем о том, что мы делали с оценками. Сначала мы возводили в квадрат значение \ (x \), которое мы подключили. Когда мы возводим в квадрат число, будет только одно возможное значение. Затем мы добавляем к этому 1, но опять же, это даст одно значение. Итак, похоже, что это уравнение также является функцией. Обратите внимание, что получить одинаковое значение \ (y \) для разных \ (x \) — это нормально.2} & = 10 + 1 = 11 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \ sqrt {11} \ end {align *} \] Теперь помните, что мы решаем для \ (y \), и это означает, что в первом и последнем случаях выше мы фактически получим два разных значения \ (y \) из \ (x \), и поэтому это уравнение НЕ является функцией. Обратите внимание, что у нас могут быть значения \ (x \), которые приведут к единственному \ (y \), как мы видели выше, но это не имеет значения. Если даже одно значение \ (x \) дает более одного значения \ (y \), при решении уравнения не будет функцией. 2} = 4 \ hspace {0.2} = 4 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \, 2 \] Итак, это уравнение не является функцией. Напомним, что из предыдущего раздела это уравнение круга. Круги никогда не бывают функциями. Надеюсь, эти примеры позволили вам лучше понять, что такое функция. Теперь нам нужно перейти к так называемой нотации функции . Обозначения функций будут широко использоваться в большинстве оставшихся глав этого курса, поэтому важно понимать их.2} — 5x + 3 \] Буква, которую мы используем, не имеет значения. Важна часть «\ (\ left (x \ right) \)». Буква в скобках должна соответствовать переменной, используемой справа от знака равенства. Очень важно отметить, что \ (f \ left (x \ right) \) на самом деле не более чем действительно причудливый способ записи \ (y \). Если вы запомните это, вы можете обнаружить, что работать с обозначениями функций становится немного проще. Кроме того, это НЕ , умножение \ (f \) на \ (x \)! Это одна из наиболее распространенных ошибок, которые люди допускают, когда впервые сталкиваются с функциями.2} — 5x + 3 \] и спросите, каково его значение для \ (x = 4 \). В терминах обозначений функций мы будем «спрашивать» об этом, используя обозначение \ (f \ left (4 \ right) \). Итак, когда в скобках есть что-то, кроме переменной, мы действительно спрашиваем, каково значение функции для этой конкретной величины. Теперь, когда мы говорим значение функции, мы действительно спрашиваем, каково значение уравнения для этого конкретного значения \ (x \). Вот \ (f \ left (4 \ right) \).2} — 5} \ right) \) Показать все решения Скрыть все решения
a \ (f \ left (3 \ right) \) и \ (g \ left (3 \ right) \) Показать решение Итак, у нас есть две оценки функций, которые нужно выполнить, и у нас также есть две функции, поэтому нам нужно будет решить, какую функцию использовать для оценок. Главное здесь — обратить внимание на букву перед круглой скобкой. Для \ (f \ left (3 \ right) \) мы будем использовать функцию \ (f \ left (x \ right) \), а для \ (g \ left (3 \ right) \) мы будем использовать \ (g \ влево (х \ вправо) \).2} — 2 \ влево ({- 10} \ вправо) + 8 = 100 + 20 + 8 = 128 \] Убедитесь, что здесь вы правильно разбираетесь с негативными знаками. Теперь второй. Мы достигли разницы. Напомним, когда мы впервые начали говорить об определении функций, мы заявили, что будем иметь дело только с действительными числами. Другими словами, мы подставляем только действительные числа и хотим, чтобы в качестве ответов возвращались только действительные числа.2} — 2 \ влево (0 \ вправо) + 8 = 8 \] Опять же, не забывайте, что это не умножение! По какой-то причине ученикам нравится думать об этом как об умножении и получать нулевой ответ. Будь осторожен. Остальные оценки теперь будут немного другими. Как видно из этого, нам не нужно просто указывать числа в скобках. Однако оценка работает точно так же. Мы вставляем \ (x \) справа от знака равенства в скобки.2} — 2t + 8 \] Обратите внимание, что в этом случае это почти то же самое, что и наша исходная функция, за исключением того, что на этот раз мы используем \ (t \) в качестве переменной. А теперь давайте немного посложнее, или, по крайней мере, они кажутся более сложными. Однако все не так плохо, как может показаться. Сначала мы оценим \ (f \ left ({t + 1} \ right) \). Этот работает точно так же, как и предыдущая часть.2} + 1} \ end {выровнять *} \] Оценка функций — это то, чем мы будем много заниматься в следующих разделах и главах, поэтому убедитесь, что вы можете это сделать. Вы обнаружите, что несколько последующих разделов будет очень трудным для понимания и / или выполнения работы, если вы не имеете хорошего представления о том, как работает оценка функций. Пока мы говорим об оценке функций, мы должны теперь поговорить о кусочных функциях . На самом деле мы уже видели пример кусочной функции, даже если в то время мы не называли его функцией (или кусочной функцией).Вспомните математическое определение абсолютной величины. Это функция, и если мы используем обозначение функции, мы можем записать ее следующим образом: Это также пример кусочной функции. Кусочная функция — это не что иное, как функция, которая разбита на части, и какой фрагмент вы используете, зависит от значения \ (x \).2} + 4} & {{\ mbox {if}} t \ le — 4} \\ {10} & {{\ mbox {if}} — 4 15} \ end {array}} \ right. \] оценивают каждое из следующих действий. Прежде чем приступить к оценкам, обратите внимание, что мы используем разные буквы для функции и переменной, чем те, которые мы использовали до этого момента.Это не повлияет на работу оценки. Не зацикливайтесь на том, чтобы видеть \ (f \) для функции и \ (x \) для переменной, что вы не сможете решить любую проблему, в которой нет этих букв. Теперь, чтобы выполнить каждую из этих оценок, первое, что нам нужно сделать, это определить, какому неравенству удовлетворяет число, и оно будет удовлетворять только одному неравенству. Когда мы определяем, какому неравенству удовлетворяет число, мы используем уравнение, связанное с этим неравенством.2} + 4 = 52 \] В этом случае число 1 удовлетворяет среднему неравенству, поэтому мы будем использовать среднее уравнение для оценки. Эта оценка часто вызывает проблемы у студентов, несмотря на то, что на самом деле это одна из самых простых оценок, которые мы когда-либо проводим. Мы знаем, что оцениваем функции / уравнения, подставляя номер переменной. В этом случае нет переменных. Это не проблема. Поскольку никаких переменных нет, это просто означает, что мы на самом деле ничего не подключаем, и получаем следующее: Опять же, как и со второй частью, нам нужно быть немного осторожнее с этой.В этом случае число удовлетворяет среднему неравенству, так как это число со знаком равенства в нем. Затем, как и в предыдущей части, мы получаем Не радуйтесь тому факту, что предыдущие две оценки имели одинаковое значение. Иногда это будет происходить. Для окончательной оценки в этом примере число удовлетворяет нижнему неравенству, поэтому мы будем использовать нижнее уравнение для оценки. Кусочные функции не так часто возникают в классе алгебры, однако они возникают в нескольких местах в более поздних классах, поэтому вам важно понимать их, если вы собираетесь перейти к большему количеству математических классов. В качестве последней темы нам нужно вернуться и коснуться того факта, что мы не всегда можем подключить каждый \ (x \) к каждой функции. Мы кратко говорили об этом, когда давали определение функции, и мы видели пример этого, когда оценивали функции.Теперь нам нужно взглянуть на это немного подробнее. Во-первых, нам нужно избавиться от пары определений. Область уравнения — это набор всех \ (x \), которые мы можем вставить в уравнение и получить действительное число для \ (y \). Диапазон уравнения — это набор всех \ (y \), которые мы когда-либо можем получить из уравнения. Обратите внимание, что мы действительно имели в виду использовать уравнение в определениях выше вместо функций.Это действительно определения уравнений. Однако, поскольку функции также являются уравнениями, мы можем также использовать определения функций. Определение диапазона уравнения / функции для многих функций может быть довольно сложным, поэтому мы не будем вдаваться в подробности. Здесь нас гораздо больше интересует определение областей функций. Согласно определению, домен — это набор всех \ (x \), которые мы можем подключить к функции и получить действительное число. На данный момент это означает, что нам нужно избегать деления на ноль и извлечения квадратных корней из отрицательных чисел.2} + 3x — 10 = \ left ({x + 5} \ right) \ left ({x — 2} \ right) = 0 \ hspace {0,25in} x = — 5, \, \, x = 2 \ ] Итак, мы получим деление на ноль, если подставим \ (x = — 5 \) или \ (x = 2 \). Это означает, что нам нужно избегать этих двух чисел. Однако все остальные значения \ (x \) будут работать, поскольку они не дают деления на ноль. Тогда домен В этом случае у нас не будет задач деления на ноль, так как у нас нет дробей.У нас действительно есть квадратный корень в задаче, поэтому нам нужно позаботиться о том, чтобы извлечь квадратный корень из отрицательного числа. Эта часть будет работать немного иначе, чем предыдущая. В этой части мы определили значения \ (x \), которых следует избегать. В этом случае напрямую получить домен будет так же просто. Чтобы избежать получения квадратных корней из отрицательных чисел, все, что нам нужно сделать, это потребовать, чтобы Это довольно простое линейное неравенство, которое мы должны решить на данный момент.2} + 4}} \) Показать решение В этом случае у нас есть дробь, но обратите внимание, что знаменатель никогда не будет равен нулю для любого действительного числа, поскольку x 2 гарантированно будет положительным или нулевым, и добавление 4 будет означать, что знаменатель всегда будет минимум 4. Другими словами, знаменатель никогда не будет равен нулю. Итак, все, что нам нужно сделать, это позаботиться о квадратном корне в числителе. Для этого нам потребуется: Теперь мы можем фактически подставить любое значение \ (x \) в знаменатель, однако, поскольку у нас есть квадратный корень в числителе, мы должны убедиться, что все \ (x \) удовлетворяют неравенство выше, чтобы избежать проблем.2} — 16}} \) Показать решение В этой заключительной части нам нужно беспокоиться как о квадратном корне, так и о делении на ноль. Давайте сначала позаботимся о квадратном корне, поскольку это, вероятно, наложит наибольшее ограничение на значения \ (x \). Итак, чтобы квадратный корень оставался счастливым (, т. Е. не было квадратного корня из отрицательных чисел), нам потребуется это, Итак, по крайней мере, нам нужно потребовать, чтобы \ (x \ ge \ frac {1} {2} \), чтобы избежать проблем с квадратным корнем.2} — 16 = \ left ({x — 4} \ right) \ left ({x + 4} \ right) = 0 \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} x = — 4, \, \, х = 4 \] Теперь обратите внимание, что \ (x = — 4 \) не удовлетворяет неравенству, которое нам нужно для квадратного корня, и поэтому значение \ (x \) уже исключено квадратным корнем. С другой стороны, \ (x = 4 \) удовлетворяет неравенству. Это означает, что можно подставить \ (x = 4 \) в квадратный корень, однако, поскольку это даст деление на ноль, нам нужно будет избегать этого. Тогда домен для этой функции — функция , в математике выражение, правило или закон, определяющий связь между одной переменной (независимой переменной) и другой переменной (зависимой переменной). Функции повсеместно используются в математике и необходимы для формулирования физических соотношений в естественных науках.Современное определение функции было впервые дано в 1837 году немецким математиком Петером Дирихле: Британская викторина Определить: математические термины Вот ваша миссия, если вы решите принять ее: Определите следующие математические термины до того, как истечет время. Если переменная y так связана с переменной x , что всякий раз, когда числовое значение присваивается x , существует правило, согласно которому определяется уникальное значение y , тогда y считается функцией независимой переменной x . Это соотношение обычно обозначается как y = f ( x ). Помимо f ( x ), для представления функций независимой переменной x часто используются другие сокращенные символы, такие как g ( x ) и P ( x ), особенно когда природа функции неизвестна или не указана. Многие широко используемые математические формулы являются выражениями известных функций.Например, формула для площади круга A = π r 2 дает зависимую переменную A (площадь) как функцию независимой переменной r (радиус). Функции, включающие более двух переменных, также распространены в математике, что можно увидеть в формуле для площади треугольника: A = b h /2, которая определяет A как функцию от обоих b (основание) и h (высота).В этих примерах физические ограничения вынуждают независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями. Формула площади круга является примером полиномиальной функции. Общий вид таких функций: P ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n , где коэффициенты ( a 0 , a 1 , a 2 ,…, a n ) даны, x может быть любым действительным числом, а все степени x являются подсчетными числами (1, 2, 3,…).(Когда степень x может быть любым действительным числом, результат известен как алгебраическая функция.) Полиномиальные функции изучались с давних времен из-за их универсальности — практически любые отношения, включающие действительные числа, можно точно аппроксимировать с помощью полиномиальная функция. Полиномиальные функции характеризуются наивысшей степенью независимой переменной. Для степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартичная и квинтическая. Полиномиальным функциям можно дать геометрическое представление с помощью аналитической геометрии. Независимая переменная x отображается по оси x (горизонтальная линия), а зависимая переменная y отображается по оси y (вертикальная линия). График функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 — 3 x + 2. График кубического уравнения f ( x ) = x 3 — 3 x + 2. Точки на графике показывают изменения кривизны. Другой распространенный тип функции, который изучается с древних времен, — это тригонометрические функции, такие как sin x и cos x , где x — это мера угла ( см. Рисунок ). Из-за своей периодической природы тригонометрические функции часто используются для моделирования повторяющегося поведения или «циклов».«Негебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции. Обратите внимание, что каждая из этих функций периодическая. Таким образом, функции синуса и косинуса повторяются каждые 2π, а функции тангенса и котангенса повторяются через каждые π. Практическое применение функций, переменные которых являются комплексными числами, не так легко проиллюстрировать, но, тем не менее, они очень обширны.Они встречаются, например, в электротехнике и аэродинамике. Если комплексная переменная представлена в виде z = x + i y , где i — мнимая единица (квадратный корень из -1), а x и y — действительные переменных ( см. рисунок ), можно разделить сложную функцию на действительную и мнимую части: f ( z ) = P ( x , y ) + i Q ( x , y ). Точка на комплексной плоскости. В отличие от действительных чисел, которые могут быть расположены одним знаком (положительным или отрицательным) числом вдоль числовой прямой, для комплексных чисел требуется плоскость с двумя осями, одна ось для компонента действительного числа и одна ось для мнимого компонента. Хотя комплексная плоскость выглядит как обычная двумерная плоскость, где каждая точка определяется упорядоченной парой действительных чисел ( x , y ), точка x + i y является единственной номер. Меняя ролями независимых и зависимых переменных в заданной функции, можно получить обратную функцию. Обратные функции делают то, что подразумевает их название: они отменяют действие функции, чтобы вернуть переменную в ее исходное состояние. Таким образом, если для данной функции f ( x ) существует функция g ( y ) такая, что g ( f ( x )) = x и f ( g ( y )) = y , тогда g называется обратной функцией для f и обозначается как f -1 , где по соглашению переменные меняются местами.Например, функция f ( x ) = 2 x имеет обратную функцию: f −1 ( x ) = x /2. Функция может быть определена с помощью степенного ряда. Например, бесконечный ряд может использоваться для определения этих функций для всех комплексных значений x . При необходимости можно использовать другие типы серий, а также бесконечное количество продуктов. Важным случаем является ряд Фурье, выражающий функцию через синусы и косинусы: Такие представления имеют большое значение в физике, особенно при изучении волнового движения и других колебательных явлений. Иногда функции удобнее всего определять с помощью дифференциальных уравнений. Например, y = sin x является решением дифференциального уравнения d 2 y / d x 2 + y = 0 с y = 0, d y / d x = 1, когда x = 0; y = cos x является решением того же уравнения, имеющего y = 1, d y / d x = 0, когда x = 0. Линейное уравнение — это уравнение прямой линии Давайте внимательнее рассмотрим один пример: График y = 2x + 1 представляет собой прямую линию Вот несколько примеров значений: Убедитесь сами, что эти точки являются частью линии выше! Есть много способов написания линейных уравнений, но они обычно имеют констант (например, «2» или «c») и должны иметь простых переменных (например, «x» или «y»). Но переменные (например, «x» или «y») в линейных уравнениях не имеют НЕ : Самая распространенная форма — уравнение угла наклона прямой: Еще одна распространенная форма — это форма угла наклона уравнения прямой линии: y — y 1 = m (x — x 1 ) Он имеет вид y — y 1 = m (x — x 1 ) где: А есть еще Общая форма уравнения прямой: Ax + By + C = 0 Он имеет вид Ax + By + C = 0 где: Есть и другие, менее распространенные формы. Иногда линейное уравнение записывается как функция с f (x) вместо y: И функции не всегда записываются с использованием f (x): Существует специальная линейная функция, называемая «Функция идентичности»: f (x) = x А вот его график: Это называется «Идентификацией», потому что то, что выходит , идентично тому, что входит: Другой особый тип линейной функции — это постоянная функция … это горизонтальная линия: f (x) = C Независимо от того, какое значение «x», f (x) всегда равно некоторому постоянному значению. Вы можете прочитать о том, что можно делать с помощью строк: При использовании подстановки в функциональном уравнении с несколькими переменными следует обратить внимание на одну важную вещь.Эта вещь на самом деле встречается во всех разделах математики, и это симметрия . Иногда можно использовать следующую стандартную идею, касающуюся симметрии: В функциональном уравнении, состоящем из двух переменных, если выражение с одной стороны симметрично относительно переменных, а выражение с другой стороны — нет, то выполняется замена (m, n) → (n, m) (m , n) \ rightarrow (n, m) (m, n) → (n, m) — хорошая идея. Вышеупомянутое в основном говорит нам поменять местами переменные.Поясним это на примере. Найдите все инъективные функции f: N → Nf: \ mathbb {N} \ rightarrow \ mathbb {N} f: N → N, удовлетворяющие f (f (m) + f (n)) = f (f (m)) + f (n), f (1) = 2, f (2) = 4. \ Begin {array} {c} & f \ big (f (m) + f (n) \ big) = f \ big (f (m) \ big) + f (n), & f (1) = 2, & f (2) = 4. \ end { массив} f (f (m) + f (n)) = f (f (m)) + f (n), f (1) = 2, f (2) = 4. Нам дано f (f (m) + f (n)) = f (f (m)) + f (n). (1) f \ big (f (m) + f (n) \ big) = f \ big (е (м) \ большой) + е (п). \ qquad (1) f (f (m) + f (n)) = f (f (m)) + f (n).(1) Решение развивается в соответствии с идеей, которую мы только что усвоили. Просто обратите внимание, что левая часть симметрична относительно переменных, а правая — нет. Сделаем замену (m, n) → (1, n) (m, n) \ rightarrow (1, n) (m, n) → (1, n), чтобы получить f (f (1) + f (n)) = f (f (1)) + f (n). F \ big (f (1) + f (n) \ big) = f \ big (f ( 1) \ big) + f (n) .f (f (1) + f (n)) = f (f (1)) + f (n). Теперь, как сказано выше, сделайте замену (m, n) → (n, 1) (m, n) \ rightarrow (n, 1) (m, n) → (n, 1).Мы просто поменяли местами mmm и n: n: n: f (f (n) + f (1)) = f (f (n)) + f (1). F \ big (f (n) + f (1) \ big) = f \ big (f ( п) \ большой) + е (1). f (f (n) + f (1)) = f (f (n)) + f (1). Вы можете спросить, откуда мы знаем о подключении 111 вместо одной из переменных. Мы этого не делаем, но в реальной жизни вы бы сначала сделали замену (m, n) = (n, m) (m, n) = (n, m) (m, n) = (n, m) , а затем вы заметите, что подключение 111 может помочь. В любом случае, используя два уравнения, мы получаем f (f (1)) + f (n) = f (f (n)) + f (1) f (f (n)) = f (n) +2 \ begin {выровнено}
е \ большой (е (1) \ большой) + е (п) & = е \ большой (е (п) \ большой) + е (1) \\
е \ большой (е (п) \ большой) & = е (п) +2
\ end {выровнен} f (f (1)) + f (n) f (f (n)) = f (f (n)) + f (1) = f (n) +2 , поскольку в вопросе указаны значения f (1) f (1) f (1) и f (2) f (2) f (2).Теперь мы видим, что из f (n) = mf (n) = mf (n) = m следует, что f (m) = m + 2f (m) = m + 2f (m) = m + 2. Используя индукцию, можно доказать, что f (m + 2k) = m + 2k + 2, f (m + 2k) = m + 2k + 2, f (m + 2k) = m + 2k + 2, где k≥0 .k \ ge 0.k≥0. [\ big [[Подсказка: используйте f (f (n)) = f (n) + 2f \ big (f (n) \ big) = f (n) + 2f (f (n)) = f (n)] +2 в доказательстве.] \ Big]] Теперь подставим m = 2nm = 2nm = 2n, чтобы получить f (2n) = 2n + 2f (2n) = 2n + 2f (2n) = 2n + 2 для всех натуральных чисел nnn . Теперь, инъективность fff позволяет нам заключить, что fff принимает нечетные значения при нечетных входных значениях ((((кроме 111, которое принимается равным 2).2) .2). Если f (t) = 1f (t) = 1f (t) = 1 для некоторого ttt, то сделаем замену m = tm = tm = t и n = tn = tn = t в (1). (1). ( 1). Вы получите легкое противоречие. Снова предположим, что для некоторых t, t, t, f (t) = 3f (t) = 3f (t) = 3, тогда f (3 + 2k) = f (f (t) + 2k) = f (t ) + 2k + 2 = 5 + 2kf (3 + 2k) = f \ big (f (t) + 2k \ big) = f (t) + 2k + 2 = 5 + 2kf (3 + 2k) = f (f (t) + 2k) = f (t) + 2k + 2 = 5 + 2k, что является противоречием, поскольку при k≥0k \ ge 0k≥0 никакой вход не может принимать выход 333. Пусть ppp будет наименьшим положительным целым числом такое, что для некоторого k, f (k) = 2p + 1k, f (k) = 2p + 1k, f (k) = 2p + 1.Тогда f (2p + 2s + 1) = 2p + 2s + 3f (2p + 2s + 1) = 2p + 2s + 3f (2p + 2s + 1) = 2p + 2s + 3 для s≥0.s \ ge 0 .s≥0. Отсюда следует, что 3,5,7, …, 2p − 13,5,7, …, 2p-13,5,7, …, 2p − 1 отображаются в 5,7, … , 2п + 15,7, …, 2п + 15,7, …, 2п + 1.
Следовательно, f (3 + 2k) = 5 + 2kf (3 + 2k) = 5 + 2kf (3 + 2k) = 5 + 2k. Наконец, можно сделать вывод, что требуемая функция — f (1) = 2, f (n) = n + 2, n≥2. □ \ begin {array} {c} & f (1) = 2, & f (n) = n + 2, & n \ ge 2. \ _ \ square \ end {array} f (1) = 2, f ( п) = п + 2, п≥2. □ Найдите все функции f: R → Rf: \ mathbb {R} \ rightarrow \ mathbb {R} f: R → R такие, что f (x + y) −f (x − y) = f (x) f (y).f (x + y) -f (x-y) = f (x) f (y). f (x + y) −f (x − y) = f (x) f (y). Обратите внимание, что правая часть функционального уравнения симметрична относительно переменных, а левая часть — нет. Поэтому рекомендуется сделать замену x = yx = yx = y и y = xy = xy = x: f (y + x) −f (y − x) = f (y) f (x) .f (y + x) -f (yx) = f (y) f (x) .f (y + x). ) −f (y − x) = f (y) f (x). Это говорит нам, что f (x − y) = f (y − x), f (xy) = f (yx), f (x − y) = f (y − x), что эквивалентно утверждению, что f (a) = f (−a) f (a) = f (-a) f (a) = f (−a). Теперь сделайте замену y → −yy \ rightarrow -yy → −y, чтобы получить f (x − y) −f (x + y) = f (x) f (−y).f (x-y) -f (x + y) = f (x) f (-y). f (x − y) −f (x + y) = f (x) f (−y). Теперь посмотрим на левую часть приведенного выше уравнения. Это просто −1-1−1 умноженное на левую часть исходного уравнения. Таким образом, LHS равно −f (x) f (y) -f (x) f (y) −f (x) f (y). Правая часть приведенного выше уравнения: f (x) f (−y) = f (x) f (y) f (x) f (-y) = f (x) f (y) f (x) f ( −y) = f (x) f (y), поскольку f (y) = f (−y) f (y) = f (-y) f (y) = f (−y). Теперь, поскольку LHS = RHS \ text {LHS = RHS} LHS = RHS, имеем −f (x) f (y) = f (x) f (y) -f (x) f (y) = f (x) f (y) −f (x) f (y) = f (x). ) f (у) для всех пар действительных чисел.2 — \ {(1,1) \} \ longrightarrow \ mathbb {R} f: R2 — {(1,1)} ⟶R определяется следующим образом: f (x, y) = x + yf (y, x). F (x, y) = x + yf (y, x). F (x, y) = x + yf (y, x). Найдите fff. Нам дано f (x, y) = x + yf (y, x). F (x, y) = x + yf (y, x). F (x, y) = x + yf (y, x). Прежде всего, следует признать, что первым шагом, сделанным многими людьми, будет замена более простых ценностей. Но в итоге хорошей заменой оказывается (x, y) → (y, x) (x, y) \ rightarrow (y, x) (x, y) → (y, x). Это дает нам е (у, х) = у + хf (х, у).f (y, x) = y + xf (x, y). f (y, x) = y + xf (x, y). Теперь, считая f (x, y) f (x, y) f (x, y) и f (y, x) f (y, x) f (y, x) переменными, мы можем решить для них. Остальное — дело вычислений. □ _ \ квадрат □ Найдите все функции fff такие, что f: Q⟶Q, f (1) = 2, f (xy) = f (x) f (y) −f (x + y) + 1.f: \ mathbb {Q} \ longrightarrow \ mathbb {Q}, \ f (1) = 2, \ f (xy) = f (x) f (y) -f (x + y) + 1.f: Q⟶Q, f (1) = 2, f (xy) = f (x) f (y) −f (x + y) +1. Положим y = 1y = 1y = 1 в данном уравнении, чтобы получить f (x) = 2f (x) −f (x + 1) + 1f (x) = 2f (x) -f (x + 1) + 1f (x) = 2f (x) −f (x + 1) +1 или f (x + 1) −f (x) = 1f (x + 1) -f (x) = 1f (x + 1) — f (x) = 1 для всех рациональных xxx.Поскольку f (1) = 2f (1) = 2f (1) = 2, это, безусловно, означает, что f (n) = n + 1f (n) = n + 1f (n) = n + 1 для всех целых чисел nnn. Положив y = ny = ny = n в данном уравнении, где nnn — положительное целое число, получаем f (nx) = f (x) f (n) −f (x + n) +1 = (n + 1) f (x) — (f (x) + n) +1 = nf (x) — п + 1 е (пх) \; знак равно е (х) е (п) — е (х + п) + 1 \; знак равно (п + 1) е (х) — \ большой (е (х) + п \ большой) + 1 \; знак равно nf (x) — n + 1 f (nx) = f (x) f (n) −f (x + n) + 1 = (n + 1) f (x) — (f (x) + n) + 1 = nf (x) −n + 1 для всех рациональных xxx и, следовательно, m + 1 = f (m) = f (nmn) = nf (mn) −n + 1 m + 1 \; знак равно f (m) \; знак равно е \ большой (п \ tfrac {м} {п} \ большой) \; знак равно nf \ big (\ tfrac {m} {n} \ big) — n + 1 m + 1 = f (m) = f (nnm) = nf (nm) −n + 1 для всех целых чисел m, nm, nm, n, где n> 0n> 0n> 0, из чего мы заключаем, что f (mn) = mn + 1f \ big (\ tfrac {m} {n} \ big) = \ tfrac {m} {n} + 1f (nm) = nm +1 и, следовательно, f (x) = x + 1f (x) = x + 1f (x) = x + 1 для всех рациональных xxx. Последние 10-30 лет эконометрика как научная дисциплина стремительно развивается. Увеличивается число научных публикаций и исследований с применением эконометрических моделей и методов. Доказательством всемирного признания эконометрики является присуждение за самые выдающиеся разработки в этой области Нобелевских премий по экономике Р. Фришу (1969), Л. Клейну (1980), Т. Хаавельмо (1989), Дж. Хекману и Д. Макфаддену (2000). Достижения современной эконометрики предъявляют высокие требования к высшему профессиональному образованию экономистов. Современное экономическое образование, держится на трех основах: макроэкономике, микроэкономике и эконометрике. Если в период плановой экономики упор делался на балансовых и оптимизационных методах исследования, то в период современной рыночной экономике высока роль эконометрических методов. Без знания этих методов невозможно ни исследование и теоретическое обобщение эмпирических зависимостей экономических факторов, ни построение более или менее надежного прогноза в банковском секторе, сфере финансов или любом бизнесе. Задачи по эконометрике достаточно сложны, особенно, если их разбирать в первый раз Для подробного изучения эконометрики советуем посмотреть видео лекций. Представленные лекции достаточно подробно объясняют суть рассматриваемых вопросов, поэтому если Вы пропустили лекции в Вашем ВУЗе или обучаетесь заочно обязательно ознакомьтесь с данным курсом. Лекция 1. Линейные модели Лекция 2. Линейные модели Лекция 1. Критерии и Гипотезы. Лекция 2. Критерии и Гипотезы. Лекция 3. Критерии и Гипотезы. Лекция 1. Факторный, Лекция 2. Факторный, дисперсионный и многофакторный анализ Лекция. Анализ данных Термин «эконометрика» был введен в 1926 г. норвежским ученым Р. Фришем и в переводе означает «эконометрические измерения». Наряду с таким широким пониманием эконометрики, существует и узкая трактовка эконометрики как набора математико-статистических методов, используемых в приложениях математики в экономике. Ниже приводятся определения «эконометрики» различными учеными: Эконометрика — это раздел экономики, который занимается разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными (С. Фишер и др.). Основная задача эконометрики — наполнить эмпирическим содержанием априорные экономические рассуждения {Л. Клейн). Цель эконометрики — эмпирический вывод экономических законов (Э. Маленво). Эконометрика является не более чем набором инструментов, хотя и очень полезных… Эконометрика является одновременно нашим телескопом и нашим микроскопом для изучения окружающего экономического мира (Ц. Грилихес). Р. Фриш говорит, что эконометрика есть единство трех составляющих — статистики, экономической теории и математики. С.А. Айвазян полагает, что эконометрика объединяет совокупность методов и моделей, позволяющих на базе экономической теории, математико-статистического и экономической статистики инструментария придавать количественные выражения качественным зависимостям. Основные результаты экономической теории носят качественный характер, а эконометрика вносит эмпирическое содержание. Математическая экономика выражает экономические законы в виде математических соотношений, а эконометрика осуществляет практическую проверку этих законов. Экономическая статистика дает информационное обеспечение исследуемого процесса в виде исходных статистических данных и экономических показателей, а эконометрика, используя традиционные математико-статистические и специально разработанные методы, проводит анализ взаимосвязей между этими показателями. Многие базовые понятия эконометрики имеют два определения — «экономическое» и «математическое». Характер научных работ по эконометрике варьируется от «классических» экономических работ, в которых почти не используется математические методы, до внушительных математических трудов, использующих достаточно глубокий аппарат современной математики. Источник: Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов, 2002. — 311 с Введение в эконометрику. Модель парной регрессии. 1. Предмет – эконометрика. 2. Экономические переменные и эконометрические модели. 3. Основные понятия и проблемы эконометрического моделирования. 4. МНК оценки коэффициентов линейной парной регрессии. 5. Геометрическая интерпретация МНК. Матричная форма определения коэффициентов. 6. Литература. Эконометрика – это самостоятельная научная дисциплина, объединяющая совокупность теоретических результатов, приемов, методов и моделей, предназначенных для того, чтобы на базе: экономической теории, экономической статистики и экономических измерений, математико-статистического инструментария придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. Сегодня деятельность в любой области экономики (управлении, финансово-кредитной сфере, маркетинге, учете, аудите) требует от специалиста применения современных методов работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство новых методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний эконометрики научиться их использовать невозможно. Чтение современной экономической литературы также предполагает хорошую эконометрическую подготовку. Специфической особенностью деятельности экономиста является работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики. Центральной проблемой эконометрики является построение эконометрической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов. Название «эконометрика» введено в 1926 г. норвежским экономистом и статистиком Рагнаром Фришем. Буквальный перевод этого понятия – «измерения в экономике». Р.Фриш дал следующее определение эконометрики. Эконометрика – это не то же самое, что экономическая статистика. Она не идентична и тому, что мы называем экономической теорией, хотя значительная часть этой теории носит количественный характер. Эконометрика не является синонимом приложений математики к экономике. Как показывает опыт, каждая из трех отправных точек – статистика, экономическая теория и математика – необходимое, но не достаточное условие для понимания количественных соотношений в современной экономической жизни. Это – единство всех трех составляющих. И это единство образует эконометрику. При этом в рамках экономической теории интересуют не просто качественные взаимосвязи переменных, но и подходы к их формализации, включающие в себя методы спецификации моделей с проблемой их идентификации. В экономической статистике непосредственно будет интересовать лишь информационное обеспечение модели (выбор показателя, обоснование способа измерения, статистические наблюдения и т.п.). Математический аппарат эконометрики включает классическую линейную модель регрессии, обобщенную линейную модель регрессии, анализ временных рядов, системы одновременных уравнений и т.п. Это «приземление» экономической теории на конкретную статистику и получение конкретных количественных показателей является ключевым в понимании сути эконометрики. Экономическая теория становится эконометрикой, когда символически представленные в экономических взаимосвязях коэффициенты заменяются конкретными численными оценками, полученными на базе соответствующих экономических данных. Главное назначение эконометрики – экономические и социально-экономические приложения, т.е. модельное описание конкретных количественных взаимосвязей, существующих между экономическими показателями. Задачи эконометрики можно классифицировать по трем параметрам: по конечным прикладным целям, по уровню иерархии и по профилю анализируемой экономической системы: б) имитация возможных сценариев социально-экономического развития системы; б) мезоуровень – модели региональной экономики, отраслей, корпораций; в) микроуровень — модели поведения потребителей, семьи, фирмы, предприятия. Основные идеи экономики – взаимосвязь между экономическими переменными. — Спрос на товар – функция его цены. — Затраты на производство — функция объема производства. — Потребительские расходы – функция дохода и т.д. Это примеры взаимосвязей между двумя переменными, одна из которых (спрос, затраты, расходы) является объясняемой переменной (результирующим показателем), а другие – объясняющими переменными (факторами-аргументами). Как правило, в каждое такое соотношение вводится несколько объясняющих переменных и остаточная, случайная составляющая, отражающая влияние всех неучтенных факторов. Например, спрос на товар можно рассматривать как функцию его цены, потребительского дохода и цен на конкурирующие и дополняющие товары. Случайная составляющая обуславливает стохастический характер зависимости: даже фиксировав значения объясняющих переменных, мы не можем ожидать однозначно, каким будет спрос на товар. В прикладном статистическом анализе изучаются различные варианты формализации понятия стохастической зависимости. Наиболее распространенной формализацией зависимости между результирующим показателем у и объясняющими переменными х1, х2, …, хn в экономике является аддитивная линейная форма: где — некоторые параметры (обычно неизвестные до проведения анализа), — случайная составляющая, характеризующая разницу между модельным и наблюдаемым значениями. Под модельным значением переменной понимают её значение, восстановленное по заданным значениям объясняющих переменных при условии, что коэффициенты известны. Поясним понятия аддитивности и линейности. Функция линейна по всем независимым переменным тогда и только тогда, когда не включает, эффект данного изменения по не зависит от . Функция является аддитивной потогда и только тогда, когда не включает ( ), эффект данного изменения по каждой независимой переменной не зависит от уровня другой. Аддитивность позволяет совместный эффект изменения по всем учтенным независимым переменным получить сложением отдельно вычисленных эффектов изменений по каждой из них. Рассмотрим некоторые примеры оценки линейности и аддитивности. После выявления отдельных соотношений их группируют в модель. Математическая модель – это упрощенное, формализованное представление реальности. «Модели должны быть настолько простыми, насколько возможно, но не проще» — сказал Эйнштейн. Все экономические модели имеют общие особенности: — они основаны на предположении, что поведение экономических переменных определяется с помощью совместных и одновременных операций с некоторым числом экономических соотношений; — принимается, что модель улавливает главные характеристики изучаемого объекта; — полагается, что на основе достигнутого с ее помощью понимания реальной системы удастся предсказать будущее движение экономических показателей. Можно выделить три основных класса моделей. Регрессионные модели с одним уравнением. , — параметры, — независимые объясняющие переменные. В зависимости от вида функции f модели делятся на линейные и нелинейные: , , , Модели временных рядов. К ним относятся модели: Тренда – Сезонности – Тренда и сезонности — — аддитивная — мультипликативная Системы одновременных уравнений. Модели описываются системами уравнений, состоящих из тождеств и регрессионных уравнений, каждое из которых может кроме объясняющих переменных, включать в себя объясняемые переменные из других уравнений системы. Классическим примером такой системы является модель спроса Qd и предложения Qs, когда спрос на товар определяется его ценой Р и доходом потребителя I, предложение товара – его ценой Р и достигается равновесие между спросом и предложением: При моделировании экономических процессов встречаются два типа данных: — пространственные данные – данные по разным фирмам и предприятиям в один момент времени; — временные ряды – ежеквартальные данные по инфляции, з.п., национальному доходу и т.п. — понятия экзогенных и эндогенных переменных, объясняемых и объясняющих переменных, предопределенных переменных; — понятия структурной и приведенной форм модели. Эндогенные переменные – формируются в процессе и «внутри» социально-экономической системы в большей мере под воздействием экзогенных переменных, в модели – объясняемые переменные. Предопределенные переменные – факторы-аргументы, объясняющие переменные. Множество предопределенных переменных формируется из всех экзогенных переменных и лаговых эндогенных переменных – эндогенных переменных, значения которых уже вычислены в прошлые моменты времени. В модели спроса и предложения экзогенной переменной выступает доход потребителя I, а эндогенными – спрос (предложение) товара Qd = Qs = Q и цена товара (цена равновесия) Р. При построении и анализе эконометрических моделей различают её структурную и приведенную формы. Структурная форма модели отражает наше представление о характере связи между переменными и наборе переменных, участвующих в уравнениях. Часто эндогенные переменные обозначают через Y, а экзогенные переменные – через Х. Эндогенные и экзогенные переменные могут находиться как по разные стороны, так и по одну сторону от знака равенства. Если удается выразить все эндогенные переменные через предопределенные, то получают приведенную (редуцированную) форму модели. В процессе эконометрического моделирования приходится решать следующие проблемы. Проблема спецификации модели включает в себя: — определение конечных целей моделирования; — определение набора экзогенных и эндогенных переменных; — определение состава системы уравнений, их структур, набора предопределенных переменных; — формулировка исходных ограничений относительно стохастической составляющей. Спецификация модели – важнейший этап исследования, от успешности решения которого зависит успех всего исследования. Спецификация опирается на имеющиеся экономические теории, специальные знания, интуицию. Проблема идентифицируемости заключается в том, что нас интересует поведение эндогенных переменных, которые являются случайными величинами. Уравнение структурной формы называется точно идентифицируемым, если все участвующие неизвестные коэффициенты однозначно восстанавливаются по коэффициентам приведенной формы без ограничений на значения последних. Эконометрическая модель точно идентифицируема, если все уравнения ее структурной формы являются точно идентифицируемыми. Если хотя бы один коэффициент не может быть восстановлен, то уравнение – не идентифицируемо и модель – тоже. Проблема идентификации заключается в «настройке» модели на реальные статистические данные. Необходимо различать проблему идентифицируемости – проблему возврата от ПФМ к ее структурной форме – от проблемы идентификации – т.е. проблемы выбора и реализации методов статистического оценивания параметров. Проблема верификации модели заключается в решении вопроса о возможностях применения модели. Какова точность прогнозных и имитационных расчетов. Методы верификации основаны на статистической проверке гипотез и анализе характеристик точности оценивания. Часто используют ретроспективные расчеты: все исходные данные разбивают на две части – обучающую выборку и экзаменующую выборку. По 1-й части определяют значения всех неизвестных параметров и получают модельные значения для 2-й части, которые сравнивают с реальными значениями. 1. Невключение объясняющих переменных. Соотношение между х и у является упрощением, и существуют другие факторы, влияющие на у. Или переменные, которые мы хотели бы включить, не можем измерить их, например, психологический фактор. Или мы просто не знаем пока какие ещё переменные влияют на у. Рассмотрим задачу «наилучшей» аппроксимации набора наблюдений Хt и Уt, линейной функцией в смысле минимизации функционала . Необходимое условие экстремума: , или в стандартной форме нормальных уравнений: или , . Получим значения и в отклонениях, т.е. пусть xt = Xt — , yt = Yt — . Можно показать, что = = 0. Замена Xt, Yt на xt, yt означает перенос системы координат, а прямая останется прежней. После замены получим: = 0, . Часто удобно перейти к стандартизованному масштабу: , . Уравнение регрессии в стандартизованном масштабе примет вид: , где . Связь между обычным и стандартизованным масштабом выражается следующим образом: , . И, наконец, коэффициенты регрессии могут быть определены с помощью ППП Excel, Statgraphic. Параметр называют коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Формально — значение у при х = 0. Если х не имеет и не может иметь нулевого значения, то у = не имеет смысла. Параметр может не иметь экономического содержания, и попытка его интерпретировать может привести к абсурду. Интерпретировать можно лишь знак : если > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Пример. Предположим по группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек . Информация, необходимая для расчета и дана в таблице. Решение. Уравнение регрессии примет вид: у = -5,789 + 36,842 х. Рассмотрим n-мерное векторное пространство Rn со стандартным евклидовым скалярным произведением (Х,У) = ХТУ = . Пусть , , , , . Здесь и — числовые коэффициенты, — вектор, лежащий в плоскости, образованной векторами S и Х ( естественно, что S и Х неколлинеарны, т.е. у Х не все числа одинаковы). Задача состоит в отыскании таких и , чтобы длина вектора е была минимальна. Очевидно, что решением является такой вектор , для которого вектор е перпендикулярен плоскости, образованной S и Х. Для этого необходимо, чтобы , и или , т.е. опять пришли к стандартным нормальным уравнениям. Обозначим теперь , , , условие ортогональности е плоскости (S,X) запишется так ХТе = 0 или ХТ(У — Х) = ХТУ — ХТХ = 0 ХТУ = ХТХ и . Нетрудно проверить, что все соотношения для и совпадают. 5. Эконометрика. Начальный курс. М.: Дело,1999. 7. Фишер Ф. Проблемы идентификации в эконометрии. М.: Статистика, 1978. 9. 11. 13. 14. ДАНА, 2002. Год выпуска: 2003 Автор: И. И. Елисеева Жанр: Эконометрика Издательство: «Финансы и статистика» Формат: DjVu Качество: Отсканированные страницы Количество страниц: 344 Описание: Предлагаемый учебник подготовлен коллективом преподавателей кафедры статистики и эконометрики Санкт-Петербургского государственного университета экономики и финансов (СПбГУЭФ), в котором преподавание эконометрики включено в учебные планы всех экономических специальностей и всех форм обучения с 1996/97 учебного года. Практические занятия ведутся с использованием пакетов прикладных программ «Statgraphics», «Статистика», а с 1999 г. — «EViews», специального пакета для решения эконометрических задач, разработанного компанией Quantitative Micro Software и переданного сотрудниками Тилбургского университета (Голландия) СПбГУЭФ и ряду других экономических вузов России по итогам проведения международной школы-семинара «Эконометрика: начальный курс» (руководители Я.Р. Магнус, С.А. Айвазян, А.А. Пересецкий, П.К. Катышев).
Содержание учебника ЭКОНОМЕТРИКА / ЭКОНОМЕТРИЯ Зандер Е.В. Эконометрика: Учебно-методический комплекс для экономических специальностей дневной и заочной формы обучения. — Краснoярск: КрaсГУ, 2003. — 34 с. Конeчнoй цeлью изучения дисциплины являeтся формирование у будущих специалистов теоретических знаний и практических навыков пo применению статистических методов для исследования и обобщения эмпирических зависимостей экономических переменных, a тaкжe построения надёжных прогнозов в банковском деле, финансах, различных сферах предпринимательской деятельности c целью обоснования принимаемых решений. Прeдстaвленo содержание курса, привeдeны примерные варианты заданий, бoльшoе количество формул, вопросы к экзамену, литература. Пособие пoдготoвлено нa кафедре социально-экономического планирования КрасГУ.
Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия. Методическое пособие для студентов II-III курсов экономического факультета НГУ. — Нoвoсибирск: НГУ, 1997. — 53 с. Пособие прeднaзначeнo для студентов экономических факультетов в качестве вспомогательного учебного материала к пeрвой чaсти курса «Эконометрия». Tеоретическая чaсть пособия подготовлена пo материалам лекционного курса, прoчитaннoгo в 1992-1996 гг. нa экономическом факультете НГУ, практическая жe чaсть в значительной мере пoстрoена пo результатам работы пo программе Темпус в 1995-1997 гг. Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А. Эконометрия: Учебное пособие. — Новосибирск: Издaтельствo СО РАН, 2005. — 744 с. Дaнный учебник нaписан нa оснoве курсов, читaeмых нa экономическом факультете Новосибирского государственного университета. Пpи создании учебника авторы стрeмились систeматизирoвать и oбъeдинить в eдиное цeлоe в рaмках oднoго источника различные разделы экономической статистики и эконометрии. Учебник включaeт: ввeдение в социально-экономическую статистику, регрессионный анализ, анализ временных рядов и особые разделы эконометрии для магистратуры. Учебник сoдeржит бoльшoе количество задач и упражнений. Oн сooтветствуeт требованиям государственного образовательного стандарта. Книгa aдресoвана студентам, магистрантам и аспирантам экономических факультетов классических университетов. Кpoмe тoгo, oнa будeт полeзна преподавателям эконометрии, исследователям, работающим в области прикладной экономики, специалистам пo бизнес-планированию и финансовым аналитикам.
Рекомендовано к изданию учебно-методическим объединением пo классическому университетскому образованию в качестве учебника для студентов высших учебных заведений, обучающихся пo направлению «Экономика». Учебник опубликован пpи содействии Национального фонда подготовки кадров (НФПК) в рамках программы «Совершенствование преподавания социально-экономических дисциплин в вузах» Инновационного проекта развития образования. Цыплаков А.А. Некоторые эконометрические методы. Метод максимального правдоподобия в эконометрии. Методическое пособие. — Нoвосибирcк: НГУ, 1997. — 129 с. Методическое пособие сocтoит из двух самостоятельных чaстей. Пeрвая чaсть — описание разнообразных методов и моделей. Подбор материала в oбщeм дoвoльно произвольный. Вторая часть бoлee цeльная и пoсвящeна oднoму из сaмых мощных методов эконометрики. Давнис В.В., Тинякова В.И. Компьютерный практикум по эконометрическому моделированию. — Вoронеж: Изд-вo ВГУ, 2003. — 63 с. B пособие включeны компьютерные издания по базовым темам университетского курса «Эконометрика». Материал кaждой тeмы содержит справочную информацию пo расчётным формулам, используeмым пpи выполнении изданий. Cами задания предуcматривают нe тoлько оценку параметров модели, нo и содержательную интерпретацию результатов эконометрического моделирования. Для лучшего понимания и усвоения студентами теоретических положений изучаемого курса в практикуме привeдены примеры выполнения типовых задач, a тaкжe контрольные зaдaния для самостоятельной работы. Основы эконометрики: Учеб.-метoд. пособие пo курсу / Рoс. гoс. открытый техн. ун-т путeй сообщ. Каф. экoн. теории; Сoст. Л.Н. Леванова. — Сарaтов, 2003. — 34 с. Учебно-методическое пособие пoдгoтовлeнo в соответcтвии c положениями и требованиями Государственного образовательного стандарта высшего профессионального образования, включaeт oснoвные вопросы лекций и семинарских занятий, крaткие теоретические положения эконометрики, основные формулы для решения задач и построения эконометрических моделей, вопросы и задачи для практических зaнятий. Для студентов и преподавателей экономических специальностей. Шанченко Н.И. Эконометрика: Лабораторный практикум. — Ульянoвск: УлГТУ, 2004. — 79 с. Содeржит указания пo выпoлнению лабораторных работ пo дисциплине «Эконометрика», методические материалы, примеры решения типовых задач, варианты лабораторных работ. Мoгут быть испoльзoваны преподавателями для организации лабораторных работ пo дисциплине «Эконометрика», a тaкжe обучающимися для выполнения лабораторных работ. Прeдназначены для студентов oчнoй, вeчeрней, заочной и дистанционной форм обучения. Работа подготовлена нa кафедре «Информационные системы». Давнис В.В., Тинякова В.И., Мокшина С.И., Воищева О.С., Щекунских С.С. Эконометрика сложных экономических процессов: Учебное пособие. — Вoрoнeж: Изд-вo ВГУ, 2004. — 83 с. B нaстoящий практикум включeны зaдaния пo темaм продвинутого курса эконометрики, изучение кoтoрых прeдусмaтриваeтся вo втoром семестре годoвого курса или магистерскими программами. B нaчaле каждoй тeмы привoдится сводка необходимых для проведения расчётов формул. Зa сводкой формул слeдуют примеры решения типовых задач. Заданиями прeдусмaтpиваeтся нe тoлькo проведение расчётов, необхoдимых для построения эконометрических моделей, нo и содержательная интерпретация результатов моделирования. Для проверки знаний и закрепления навыков в пособии прeдусмотрены задания для самостоятельной работы. Анатольев С. Эконометрика для продолжающих (Эконометрика-3). Курс лекций. — М.: Российская Экономическая Шкoла, 2002-2003. — 60 с. Учебный курс «Эконометрика-3» являeтcя продoлжениeм курсов «Эконометрика-1» и «Эконометрика-2» и рaccчитан нa магистрантов. Прeдпoлaгаeтся, чтo пoсле oкончания послeдует курс «Эконометрика-4» («Продвинутая Эконометрика»). Курс предполaгает, чтo студенты успешно освоили двa предыдущих курса, oднaко нaибoлee важные концепции будут внoвь ввeдены нa нoвом качественном уровне. Курс раccчитан нa 14 лекций, 6 семинаров. Курс являeтся мoстoм мeжду базовыми эконометрическими знаниями и серьёзным современным эконометрическим мышлением. Курс является нe стoлькo ознакомительным, скoлькo специализированным, трeбующим углублённого и вдумчивого изучения. Крoмe тoгo, курс нацeлeн нa тo, чтoбы научить применять изученные методы нa практике в работе c реальными данными и статистическими программами. Анатольев С. Эконометрика для подготовленных (Эконометрика-4). Курс лекций. — М.: Российская Экономическая Шкoлa, 2003. — 64 с. Дaнныe лекции — продoлжение курса «Эконометрика для продолжающих». Курс пocвящён в основном нелинейным моделям, гдe прeобладает анализ оценок в неявной форме, являющиxcя решениями оптимизационных задач. Тaкжe внимание удeлено анализу линейных моделей панельных данных. Перцев Н.В. Лекции по эконометрике. Часть II. Вычислительные аспекты. — Омск: ОмГУ, 2003. — 31 с. Чaсть II лекций поcвящeна вычислительным аспектам задач эконометрики. Здеcь привoдятся основные формулы, таблицы и т.д., используемые в регрессионном анализе и обработке временных рядов. Для студентов заочной, заочно-ускорeнной и вeчерне-ускоренной форм обучения ОмГУ. Основы эконометрики: Учеб.-метoд. пособие пo курсу / Рос. гoс. открытый техн. ун-т путeй соoбщ., кaф. экон. теории; Сoст. Л.Н. Леванова. — Сарaтов, 2003. — 34 c. Учебно-методическое пособие пoдготовленo в cooтветствии c положениями и требованиями Государственного образовательного стандарта высшего профессионального образования, включaет основные вопросы лекций и семинарских занятий, крaткиe теоретические положения эконометрики, основные формулы для решения задач и построения эконометрических моделей, вопросы и задачи для практических занятий. Для студентов и преподавателей экономических специальностей. Носко В.П. Эконометрика: Введение в регрессионный анализ временных рядов. — Москва, 2002. — 254 с. В прeдлагаемом учебном пособии дaётся крaткоe введение в современные методы эконометрического анализа статистических данных, представленных в виде временных рядов, котoрые учитывают возможное наличие у рассматриваемых переменных стохастического тренда. Основные акценты смещены в сторону разъяснения базовых понятий и основных процедур статистического анализа данных с привлечением смоделированных и реальных экономических данных. Вмeсте с тeм, oт читателя требуется нeсколькo бoльшaя осведомлённость в отношении вероятностно-статистических методов исследования. Прeдпoлагаeтся, чтo читaтель имeeт представление o совместной функции распределения, многомерном нормальном распределении, методе максимального правдоподобия, свойстве состоятельности оценок, характеристиках статистических критериев (ошибки первого и второго рода, мощность), a тaкжe владeeт методами регрессионного анализа в рамках начального курса эконометрики. Крoме тoгo, oн должeн имeть некоторое представление o комплексных числах и комплексных корнях полиномов. Пособие нaписано нa основании курса лекций, прoчитанных автoром в Институте экономики переходного периода. адрес: 01990 г. Москва, ул. Мясницкая, д. 20, комн. 406 Дата рождения: 05 января 1948 Образование
Курсы, преподаваемые в МИЭФ
Основные учебники, методические материалы
Российская экономическая школа и Политехнический музей 10 ноября открыли цикл лекций «Экономика: просто о сложном». Первую лекцию цикла «Современная экономическая наука» прочел ректор РЭШ Сергей Гуриев. «Лента.ру» представляет расшифровку лекции. Что такое сегодня современная экономическая наука? Я попытаюсь рассказать о том, какие достижения были в этой науке в последние десятилетия. Сразу скажу, что если я не успею рассказать все, что собирался обсудить, Вы можете посмотреть слайды на эккаунте РЭШ в slideshare . (РЭШ по-английски называется «New Economic School»). Я постарался сделать слайды самообъясняющими, Видео лекции будет выложено на нашем эккаунте в YouTube. А новости РЭШ (в том числе и новости этого цикла лекций можно отслеживать не только на сайте или через рассылку, но и по Twitter. Наш Twitter называется “NES1992” (РЭШ была основана в 1992 году). Экономическая наука прошла огромный путь в последние десятилетия. Она существенно отличается от содержания учебника по экономике для первого курса. Наука стала гораздо более строгой, гораздо более количественной. В этом смысле, когда человек говорит: «Я ученый-экономист», здесь больше нет оксюморона. Экономисты-исследователи действительно работают хорошими методами с хорошими данными. Почему мне кажется, что нужно много рассказывать именно о современной экономической науке? Если читать вводный учебник по экономике для первого курса или читать газеты, или разговаривать с людьми, которые, кроме учебника первого курса, ничего не читали, то часто кажется, что экономика – это не наука, это публицистика. Такое мнение часто встречается особенно среди представителей естественных наук. Я закончил Физтех, и у меня много друзей занимаются математикой и физикой. Все они так или иначе смотрят на экономистов.
Второе распространенное мнение заключается в том, что у экономистов слишком много точек зрения: они якобы не могут ни в чем друг с другом согласиться и никак не могут решить, что нужно делать в области экономической политики. Еще одна проблема заключается в том, что люди, которые прочитали учебник по экономике первого курса, говорят: «Этот учебник написан про совершенный рынок. В лучшем случае, про сегодняшнюю американскую экономику». Это правда. Сегодняшние учебники для первого курса, как правило, написаны в Америке для американских студентов. Но современная экономика совсем не такая – и как раз и занимается исследованиями несовершенств рынков, и функционированием рынков в несовершенных условиях. Есть целый ряд заблуждений, связанных с тем, что считается, что экономисты рассматривают человека как рационального субъекта, у которого нет ни эмоций, ни жалости, ни сострадания. Но и в данном случае это мнение основано на недостатке информации: сегодняшняя экономическая наука исследует и отклонения от рациональности и эгоистичности. Наконец, последняя проблема. Часто экономистов (это уже мнение не математиков, а, скорее, политиков) считают абстрактными учеными «из башни из слоновой кости», которые не делают ничего полезного. Их модели якобы слишком абстрактны и не приносят никакой пользы.
Как же дело обстоит на самом деле? Во-первых, сейчас экономическая наука – это, действительно, наука. Действительно, любая научная статья по экономике – это аксиомы, теоремы, тестируемые гипотезы и данные, которые используются для того, чтобы протестировать эти гипотезы.
Во-вторых, часто используются так называемые «натурные эксперименты» или лабораторные эксперименты (когда реальных людей сажают в лабораторию и заставляют играть друг с другом в экономические игры на реальные деньги). Про натурные эксперименты я расскажу особо. Еще одно отличие реалий от мифов в том, что в экономике по-прежнему происходит много интересных исследований. Это очень молодая наука. Она была совершенно другой еще 50 лет назад. В этом смысле, неудивительно, что многие вещи еще не открыты, многие теоремы не доказаны, многие проблемы не решены. Более того, неизвестно даже, можно ли будет их открыть, доказать и решить. Еще одна проблема заключается в том, что, к сожалению, для нас, как для ученых, (но, возможно, к счастью для нас, как людей), в экономике не так легко ставить эксперименты. Экономика исследует большие хозяйственные механизмы. Ставить эксперименты на них почти так же трудно, как на черных дырах. Кроме того, само измерение (это уже немного напоминает не астрофизику, а квантовую физику) затрудняется тем, что мы, экономисты, живем в этой самой экономической системе. Если все экономисты сегодня соберутся, найдут, откроют какую-нибудь модель, которая точно предскажет крах фондового рынка через полгода, то, наверное, этот крах, действительно, состоится – причем, немедленно). Просто потому, что если уж всем экономисты говорят, что это произойдет с вероятностью 100 процентов, то, наверно, рынок может и послушать. Это проблема, от которой невозможно абстрагироваться. Наконец, проблема России и других развивающихся стран заключается в том, что экономики развитых стран гораздо легче моделировать, оценивать, измерять. Есть многолетние наблюдения, есть хорошее качество данных. Кроме того, процессы близки к равновесным. Развивающиеся страны, переходные экономики находятся в движении, в переходе из одного равновесного состояния в другое. Эти переходы всегда очень трудно моделировать – просто потому, что эти состояния неравновесные. Тем не менее, ситуация гораздо лучше, чем кажется. Экономика прошла огромный путь от учебников первого курса. Сегодня ученые рассматривают ровно те вопросы, которые актуальны именно для российской экономики. Экономика больше не предполагает, что можно моделировать только конкурентные рынки. Экономика больше не предполагает, что участники экономических взаимодействий располагают полной информацией и обладают бесконечной возможностью проводить сложные расчеты. Экономика не предполагает, что есть какое-то абстрактное благожелательное государство, которое работает в наших интересах и автоматически делает все то, что нужно обществу. Мы больше не предполагаем, что есть совершенные суды, которые автоматически обеспечивают выполнение всех контрактов. Мы не предполагаем, что есть генетически некоррумпированные чиновники – мы знаем: чтобы чиновник не брал взятки, для него нужно создать соответствующие стимулы. Именно эти проблемы и исследуются в современных научных работах, в том числе, и с использованием реальных данных. Что касается обвинений в том, что экономика – это абстрактная наука. На самом деле, экономисты сейчас делают очень много конкретных, прикладных работ. В том числе, работ, которые направлены на повышение качества жизни вполне конкретных людей. Сегодня уже становится обычным, что любая социально-экономическая реформа (не только в развитой, но и в развивающейся стране) проводится с привлечением исследователей-экономистов. Прежде чем разворачивать эту программу реформ на всю страну, ее авторы пытаются оценить ее эффект на какой-то контрольной группе. Один из примеров этого – программа Progresa в Мексике. Реформа Progresa была проведена в Мексике в конце 1990-х. Цель этой программы было обеспечение доступа детей из сельской местности к качественному здравоохранению, питанию и образованию. Соответственно, специальным образом выдавались деньги их родителям. Прежде, чем разворачивать эту программу, мексиканское правительство наняло американских экономистов. Они провели эксперимент. Взяли контрольную группу случайно отобранных людей, на которых не проводилась эта реформа. Взяли группу, на которой реформа проводилась и ее эффект оценивался. Пронаблюдали и за теми, и за другими, сравнили результаты. Оказалось, что программа очень успешная, и что ее следует распространять на всю страну. Но, как вы знаете, в Мексике, хотя там десятилетиями и правила одна и та же партия, в это время эта партия впервые проиграла выборы, и к власти пришла оппозиция. Но количественные аргументы экономистов были настолько убедительными, что эта программа не была закрыта. Оппозиция, хотя она и обещала полностью пересмотреть социальную политику предыдущего правительства в 2000-м году, не стала этого делать. Формально, программа Progresa была закрыта, но была открыта ровно такая же программа с другим названием («Opportunidades», то есть «Возможности»), с тем же самым менеджментом, с тем же самым дизайном. Экономисты помогают оценивать реформы и выяснять, что работает, а что не работает. Сегодня количественное оценивание реформ становится «золотым стандартом» при проведении любых социально-экономических реформ. В Мексике был принят специальный закон, что социально-экономические реформы нельзя делать без такого пилотного исследования. Деятельность глобального фонда, который борется с туберкулезом, малярией и СПИДом, тоже использует эти механизмы. Деятельность «Фонда Гейтсов», во многом, тоже основана на том, что любой проект нужно оценивать количественно. Я мог бы продолжать проводить примеры успехов в области экономики развития. Но я бы хотел рассказать и про макроэкономику. Сейчас много говорят о том, что во время кризиса макроэкономисты сильно провалились. Если говорить откровенно, то честные экономисты никогда не берут на себя ответственность предсказывать, когда будет кризис. По определению, экономисты не могут предсказать кризис. Ведь как только они точно знают, что он случится через какое-то время, то он, как я уже сказал, происходит немедленно. Зато экономисты понимают, как устроен кризис. Экономисты понимают, как и в какой последовательности изменяются основные макроэкономические переменные во время кризиса. Сначала падает рынок ценных бумаг. Потом падают инвестиции. Потом сокращается занятость. Более того, примерно понятно, как нужно бороться с кризисами. Не случайно, во время этого кризиса очень быстро во всех странах, в том числе и в Америке, были предложены программы антикризисных мер. Второе конкретное приложение экономической теории – это теория аукционов. Казалось, это абсолютно абстрактная микроэкономическая теория, которая не имеет прямых приложений. Но теперь в тех странах, которые хотят провести аукцион правильно – например, собрать больше денег для бюджета или сделать так, чтобы товар, или лицензию, или объект искусства получил бы игрок, который ценит его больше всего – эти страны, эти правительства, эти продавцы прибегают к помощи экономистов, которые действительно могут помочь построить аукцион так, чтобы не было сговора. Построить аукцион так, чтобы можно было собрать как можно больше денег. Построить аукцион так, чтобы товар достался тому, кто его больше всего ценит. Нобелевская премия 2007-го года Леониду Гурвицу, Эрику Маскину и Роджеру Майерсону была выдана как раз за эту теорию.
То, что имеет место для экономической науки в целом, верно и для отдельных ее частей. Например, РЭШ, которую тоже часто воспринимают как башню из слоновой кости, делает много прикладных исследований. Практически все профессора РЭШ так или иначе, занимаются и прикладными проблемам, в том числе и связанными с Россией. Сегодня в нашей стране уже много данных для того, чтобы можно было использовать их для ответов на вопросы, которые имеют прямое отношение к экономической политике. С другой стороны, если качество исследований достаточно высокое, их можно публиковать в международных журналах. Теперь давайте обсудим, в чем экономисты согласны друг с другом и в чем не согласны.
Экономисты знают, что защита прав собственности, обеспечение исполнения контрактов, то, что называется «верховенство права» (или, по-английски, “rule of law”), конкуренция, макроэкономическая стабильность – вещи хорошие, важные, полезные для экономического роста.
Нет разногласий в том, что монополия хуже, чем конкуренция. Нет разногласий в том, что высокая инфляция хуже низкой инфляции. Нет разногласий в том, что для того, чтобы добиться низкой инфляции, нужен независимый центральный банк. Есть также понимание того, что международная торговля помогает росту и процветанию. Действительно, глобализация за последние 20 лет вывела из бедности сотни миллионов людей по всему миру. В первую очередь, в Индии и в Китае, но и в других странах тоже. Хороший пример – это то, что произошло во время кризиса. Как всегда бывает во время кризиса, были подняты импортные тарифы во всех странах. Не только в России, но и в Америке, в Европе. Но, в том числе и по тому, что теперь и в учебниках написано, что торговля – это благо, протекционизма было гораздо меньше, чем можно было ожидать (учитывая масштаб кризиса). И в этом немалая заслуга экономистов, которые являются фактически единственной группой, единственной профессией, которая постоянно и согласованно отстаивает преимущества свободной торговли. Вопрос в том, в чем экономисты не согласны и чего они пока не знают. На самом деле, оказывается, что не знают они очень важные вещи: как сделать так, чтобы права собственности защищались. Не в какой-то стране, где они защищались уже двести лет, пятьсот лет, или тысячу лет. А в такой стране, где не было никогда прав собственности. Где нет политического согласия о том, какое должно быть распределение доходов. Именно с этой точки зрения Россия является очень интересным предметом исследований. Здесь, собственно, только возникают эти экономические институты – права собственности, конкуренция, защита исполнения контрактов. Другая проблема заключается в том, что мы пока плохо умеем моделировать стадное поведение, отклонения от рациональности. Я сказал, что, действительно, передний край науки как раз и заключается в том, чтобы пытаться моделировать и исследовать отклонения от рациональности. Очень трудно понять, например, когда лопнет пузырь. Сейчас, например, начал надуваться пузырь в азиатской недвижимости. До какого уровня он надуется и когда он лопнет – не совсем ясно. Когда центральный банкир должен предпринять действия, чтобы его проколоть вовремя, чтобы он не лопнул слишком сильно – не совсем понятно. Почему? Потому, что это зависит уже не только от переменных, которые мы можем оценивать в рамках математических моделей, но и тех самых отклонений от рациональностей, стадного поведения, которое в голове у людей. Теперь я бы хотел рассказать о прогрессе в методологии экономической науки. С моей точки зрения, за последние 30 лет (может быть, 35 лет) произошли три ключевых изменения.
Первое изменение – это изменение в макроэкономике. Макроэкономика, в некотором роде, слилась с микроэкономикой. Второе изменение – это резкий прорыв в качестве данных и методов исследования этих данных. Принято считать, что эконометрика не доказывает причинно-следственных связей. Это так. С другой стороны, как я вам постараюсь доказать, мы знаем теперь об исследованиях причинно-следственных связей с помощью новых методов и новых данных гораздо больше. Третий прорыв – это то, что экономика перестала быть собственно экономикой. Экономика теперь – это наука обо всем. Количественные методы и экономические модели, в основном, экономисты, а также их коллеги, используют для исследования во всех смежных дисциплинах. Это то, что называется экономическим империализмом: экономисты выходят за рамки экономики, начинают исследовать процессы, которые раньше исследовали социологи, политологи, юристы, психологи.
Сначала очень коротко о макроэкономике. Сегодня нельзя опубликовать статью в научном журнале, если вы хотите построить модель макроэкономического явления или процесса без так называемых микроэкономических обоснований. Сегодня макроэкономическая модель обязана опираться на детальное, ясное и четкое описание того, откуда берутся макроэкономические процессы. В этом смысле, модели стали, наверное, более сложными. С другой стороны, мы научились строить их достаточно просто для того, чтобы все-таки уметь анализировать. Сегодня любая макроэкономическая модель требует знаний микроэкономики. В ней есть экономические агенты. Эти экономические агенты обладают какой-то информацией, не обязательно полной. Они друг с другом взаимодействуют. Возникает равновесие на рынках. Это равновесие исследователь, собственно, и изучает. Исследует его свойства, как система переходит из одного равновесия в другое, как система отвечает на шоки. Сегодня именно этим занимается макроэкономика. Когда вы открываете газету и в ней написано, что «Кейнс был прав» или «Фридман был прав» – это не тот уровень дискуссии, который ведется исследователями. Сегодня у нас есть такие модели, которые учитывают и аргументы Кейнса, и аргументы его противников, и аргументы противников его противников в одной модели. Все эти аргументы отличаются всего лишь количественными параметрами. Теперь я бы хотел немного поговорить про то, что называется прогресс в эконометрике. Слово «регрессия» означает оцениваемое уравнение. Допустим, мы располагаем некоторыми статистическими наблюдениями. Мы хотим вывести некоторую закономерность, которой эти наблюдения в той или иной степени удовлетворяют. Например, мы знаем: если X вырос на какую-то величину, то Y вырастет тоже на какую-то величину. Мы хотим узнать эластичность, мы хотим узнать связь между этими процессами.
Например, Центральный банк напечатал деньги. Когда будет инфляция? Будет ли она вообще? Насколько сильно увеличится инфляция? Другой пример: в России произошли засуха и лесные пожары. Очевидно, это повлияет на инфляцию. Теория говорит, что будет временный всплеск инфляции. Эмпирический вопрос заключается в том, какой величины будет этот всплеск инфляции. Можно оценить по предыдущим данным взаимодействие между этими величинами. Попробовать предсказать, что нужно. Что произойдет, если Центральный банк не будет вмешиваться в экономику? Какой величины вмешательство Центрального банка нужно предпринять, чтобы сгладить удар, связанный с засухой?
Конечно, современные модели гораздо сложнее. Мы не измеряем только зависимость одного фактора от другого. Мы измеряем зависимость одного фактора от другого, одновременно учитывая, что третий и четвертый факторы тоже влияют на первый. Типичный пример – это то, что бедные страны должны расти быстрее. Что это значит? Когда чиновник выходит и говорит: «Россия росла с очень высоким темпом, 7 процентов в год, в течение десяти лет до кризиса», критики правительства часто возражают: «Но Китай рос еще быстрее, Индия росла еще быстрее». На самом деле, теория предсказывает, что бедные страны должны расти быстрее, чем богатые. Им легче расти. Они обходят ловушки, которые проходили богатые страны. Они быстрее заимствуют технологии. Но если мы будем просто тестировать такую закономерность на межстрановых данных, мы ее в этих данных не найдем. Если мы посмотрим зависимость темпа роста за какой-то период от начального уровня развития, в теории это должна быть отрицательная зависимость. Чем выше начальный уровень, тем медленнее рост. Но в данных просто так эту зависимость нельзя найти. Это график из классической статьи Роберта Барро (страница 15 презентации) где по горизонтали отложен начальный уровень доходов на душу населения, а по вертикали – темп роста экономики. Каждая точка – это страна за период с 1960-го по 1987-й год. Если мы наилучшим образом проведем через это облако прямую, которая минимизирует расстояния между этими точками и прямой, то эта прямая иметь нулевой, может быть даже положительный наклон. Но ни в коем случае наклон не будет отрицательным. В чем здесь проблема? Дело в том, что на экономический рост кроме начального уровня подушевого дохода влияет масса других факторов. Темп роста населения, склонность к сбережениям, уровень образования и так далее. Как раз в классической работе Барро оценена регрессия, где учтены остальные факторы. Справа картинка, где мы смотрим на рост как функцию от начального уровня, очищенную от всех остальных факторов. Мы видим, что здесь достаточно очевидно, что это облако точек описывается прямой с отрицательным наклоном. Физики, которые ставят эксперименты и измеряют коэффициенты с точностью до восьмого знака, будут смеяться над таким облаком. Но для экономики это очень и очень высокая точность. Проблема в том, что такие регрессии, на самом деле, не очень убедительны. Ведь не только экономический рост зависит от образования, но, конечно, и экономический рост влияет на образование: более богатые страны могут позволить себе более развитые университеты.
В этом случае такие простые регрессии уже ничего не могут объяснить. Как можно учесть двустороннюю причинно-следственную связь и влияние, может быть, еще каких-то факторов и на образование, и на рост? Именно поэтому сейчас такие статьи перестают принимать в журналах. Если вы просто прогоните еще одну регрессию, сделаете еще одну научную работу типа той, которую сделал Барро – теперь ее вряд ли возьмут в научный журнал. Эта работа не может ответить на вопрос о направлении причинно-следственной связи. В изобретении и широком использовании методов, которые позволяют отвечать на такие вопросы, и заключается, с моей точки зрения, основной прорыв в эконометрике последних десятилетий.
Во-первых, речь идет об инструментальных переменных. Я постараюсь рассказать об этом методе попроще. Представьте себе, что у нас есть переменная X, который влияет на Y, и Y, который влияет на X. Как оценить одну зависимость и другую? Вообще говоря, не так просто. Я нарисовал на этой картинке (страница 17 презентации) зависимость Y от X. А вот это – зависимость X от Y. Они где-то пересекаются. В реальных данных мы наблюдаем только одну точку пересечения этих кривых. Обе эти кривые возрастающие, поэтому не так легко понять, что происходит. Но, если нам удастся найти какую-то переменную, которая влияет на X и не связана напрямую с Y (я сейчас приведу такие примеры), то ситуация становится гораздо лучше. Представьте себе, что переменная Z, которая влияет только на X и не влияет на Y, сдвигает одну из этих кривых. Тогда мы движемся по другой из этих кривых. Если мы сравним точку до изменения Z и точку после изменения Z, мы можем измерить угол наклона одной из этих кривых. На самом деле, как ни просто и ни абстрактно звучат эти картинки, именно такой техникой пользуются для того, чтобы ответить на многие вопросы в экономике. Вот типичный пример. Институты и экономический рост. Институты, качество институтов защиты прав собственности, уровень судебной системы в разных странах разные. Как правило, в богатых странах эти институты лучше. Вопрос, связано ли это с тем, что институты привели к тому, что эти страны росли быстрее и стали богатыми? Или, наоборот, что богатые страны могут позволить себе более качественные институты, более качественную защиту прав собственности и судебную систему? И, если оба эффекта имеют места, можем ли мы количественно оценить хотя бы один из них? На этот вопрос не так легко ответить. Есть классическая работа, примерно десятилетней давности, вокруг которой сейчас идет много споров. Качество данных, которые используют авторы, все-таки не очень высокое. Это данные 500-летней давности, связанные с смертностью европейцев в колониях. Были страны, где колонисты из Европы собирались жить. Были страны, которые колонисты из Европы использовали как сырьевой придаток. От чего это зависело? Авторы предполагают, что в некоторых странах колонистам было жить возможно, а в некоторых странах они умирали от местных болезней. Это, в основном, страны Экваториальной Африки. Очевидно, что чем больше колонистов собиралось жить в этой стране, тем больше они инвестировали в настоящие институты (как это было сделано в Австралии, Новой Зеландии, Америке). Поэтому в качестве инструментальной переменной (это то, что на предыдущем слайде называлось «переменная Z») можно взять данные 500-летней давности о смертности европейских колонистов во всех колониях. Ведь смертность европейцев 500 лет назад не должна влиять на уровень ВВП в колонизированных странах сегодня. Там европейцев-то больше нет. Даже в Австралии, Америке, Новой Зеландии люди не помнят, откуда приехали их предки 300 или 400 лет назад. Оказывается, что, действительно, можно оценить причинно-следственную связь между институтом и ростом, используя такой экзотический инструмент, как смертность колонистов. Я приведу и пример из российской практики. Мои коллеги попытались измерить эффект телевидения на результаты выборов. Вроде бы, если вы хотите голосовать за кандидата, которого поддерживает некий телеканал, вы будете смотреть этот канал. В Америке “Fox News” смотрят республиканцы. Значит ли это, что если “Fox News” распространяется дальше и быстрее, то республиканцы будут побеждать на выборах? Или наоборот, “Fox News” идет туда, где уже есть республиканцы? Опять-таки, проблема обратной причинно-следственная связь. Но я не буду говорить про США, я расскажу про Россию. Я вижу здесь многих людей, которые еще помнят выборы 1999-го года. НТВ не поддерживал партию «Единство», а поддерживал «Яблоко» и «Отечество — Вся Россия». Действительно, там, где было больше покрытие НТВ, там партия «Единство» набрала меньше голосов. К счастью для авторов этой статьи – профессоров Российской экономической школы Ениколопова, Журавской и Петровой – НТВ не выбирал, куда идти. Он получил во второй половине 1990-х мощности 4-го канала. Это был образовательный канал, который был распространен по стране (еще в советское время) вне зависимости от того, есть ли там партийные ячейки постсоветских партий или нет. Оказалось, что можно измерить эффект влияния телевидения на результат выборов. Оказалось, что этот эффект гораздо больше, чем в Америке. Это не удивительно, потому что у нас демократия была тогда только зарождающейся. Еще один метод, о котором я хотел бы сказать особо, это использование панельных данных и различий в разностях. Допустим, что мы наблюдаем одну и ту же группу людей в течение какого-то времени. В то же время – еще какую-то группу людей в течение какого-то времени. На одну из этих групп мы воздействуем, например, реформой (или каким-нибудь другим экономическим воздействием). В другой группе – нет. Тогда мы можем посмотреть, что изменилось в одном случае и что изменилось в другом случае – и сравнить эти изменения. Это позволяет отстраниться от всех вещей, связанных с наследственностью, с религией, с ростом этого человека, с его семейным положением. В течение этого воздействия ничего из вышеперечисленного не изменилось. Поэтому, сравнивая различия в этих разностях до и после воздействия, мы можем измерить эффект воздействия. Я приведу пример связи между финансовым развитием и экономическим ростом. Вы знаете, что Россия хочет построить Международный финансовый центр. Считается, что финансовое развитие способствует экономическому росту. Чем лучше банки, тем более дешевы кредиты, более качественны финансовые инструменты. Много разных инструментов для разных видов инновационного бизнеса. С другой стороны, есть и обратная зависимость. Чем богаче страна, тем легче ей содержать очень дорогие финансовые институты. Например, глобальные инвестиционные банки. Поэтому оценить направление и величину причинно-следственной связи не так легко. Раджан и Зингалес в статье 1998-го года смогли решить эту проблему. Давайте проследим за их аргументом. Рассмотрим одни и те же отрасли в разных странах. В странах с высоким уровнем финансового развития и в странах с низким уровнем финансового развития. Например, посмотрим на табачную промышленность и на микроэлектронную промышленность. Ничего личного: я нарочно использую те примеры, о которых они говорят в этой статье. Понятно, что микроэлектронная (или фармацевтическая) промышленность в большей степени нуждается в финансовом развитии, чем табачная. Как это можно измерить? То, что они сделали, это очень просто и интуитивно. Рассмотрим эти отрасли в Соединенных Штатах – там, где финансовые рынки работают лучше, чем где-либо еще в мире. Посмотрим, сколько внешнего финансирования используют табачная отрасль, микроэлектронная отрасль, машиностроительная отрасль, фармацевтическая отрасль. В результате скажем: эта отрасль больше зависит от финансового развития, чем вот эта. Мы это сделали. Мы знаем теперь, как ранжируются отрасли в терминах зависимости от финансов – мы можем измерить уровень финансовой зависимости отрасли. Теперь мы выкидываем Америку из нашего анализа и смотрим на страны с высоким уровнем финансового развития и страны с низким уровнем финансового развития. Смотрим, в чем различия в темпах роста в финансово-зависимых отраслях и в финансово-независимых отраслях. Оказывается, что различия огромны. Отрасли в странах, которые имеют высокий уровень финансового развития, которые зависят от финансов, растут на 1 процент в год быстрее. Это огромная величина, особенно для развитых стран. В этом смысле можно сказать, что мы смогли разорвать причинно-следственную связь и посмотрели не на влияние богатства на финансы, а влияние финансов на экономический рост и процветание. Пример из России. Два сотрудника Российской экономической школы исследовали эффект реформы дебюрократизации. В начале первого президентского срока тогдашний Президент Владимир Путин хотел помочь малому бизнесу. Была проведена массивная реформа по упрощению регистрации, лицензирования, сертификации, проверок. Было принято пять законов, и они вступали в действие в 2002-м, 2003-м и 2004-м годах. Количество лицензий, например, было сокращено в 10 раз. Сроки регистрации были сокращены до одной недели. Что сделали Яковлев и Журавская? Начиная с 2002 года, они 6 раз опрашивали выборку из 2000 малых фирм в 20 регионах России. Особые усилия были приложены к тому, чтобы в каждом регионе это была репрезентативная выборка. Оказалось, что эффект от реформы есть. Но самое интересное не то, что эффект от реформы значимо отличается от нуля или он не такой, на который рассчитывали чиновники. Самое интересное то, что этот эффект разный в разных регионах. Были регионы, в которых эта реформа имела фантастический успех и привела к росту малого бизнеса. Были регионы, в которых успех от реформы был гораздо более скромный. Метод различий в разностях позволяет понять, от чего это зависит. Яковлев и Журавский изучали влияние уровня коррупции в регионах, уровня прозрачности и подотчетности власти. Они смогли измерить влияние качества власти, ее подотчетности и прозрачности на эффект от реформы по дебюрократизации. Теперь я бы хотел поговорить о другом. Влияет ли демократия на экономический рост или экономический рост влияет на демократию? С одной стороны, в мире практически нет богатых недемократических стран. За исключением двух-трех нефтяных монархий и Сингапура. (Правда, Сингапур очень быстро движется в сторону демократии). Если мы отложим демократию по горизонтальной оси, а уровень ВВП на душу населения – по вертикальной, то мы увидим видим, что богатые страны – все демократические, за исключением Саудовской Аравии, Экваториальной Гвинеи и Сингапура. Есть много бедных демократических стран. Есть много бедных недемократических стран. Но богатых недемократических стран практически нет. Значит ли это, что экономический рост приводит к демократизации? Или что богатые страны могут позволить себе демократию, а бедные не могут? Или это значит ли это, что демократия приводит к экономическому росту? Ответить на эти вопросы не очень легко. Факты говорят о том, что в среднем демократия и диктатура растут примерно с одним и тем же темпом. Демократии растут чуть быстрее, но незначимо быстрее. Правда, мы знаем, что демократии растут примерно с одним и тем же темпом роста, а диктатуры имеют и катастрофы, и всплески роста. Например, очень часто вспоминают про Пиночета. У Пиночета был и очень успешный экономический период, но был и катастрофический экономический период сначала. В среднем – нормальный темп роста, ничего выдающегося. Часто говорят про индустриализацию Китая при Мао. С точки зрения экономики это была экономическая катастрофа. То же самое со многими другими диктаторскими режимами – Куба, Северная Корея странами. Еще один факт заключается в том, что в бедных странах происходит переход от диктатуры к демократии и наоборот. В богатых странах происходит только демократизация – перехода от демократии к диктатуре не происходит в странах, которые богаче, чем Аргентина в 1976-м году. Ни одна страна, которая была богаче, чем Аргентина в 1976-м году, не перешла от демократии к диктатуре. (Россия этот уровень ВВП перешла в 2007 году. В этом смысле Россия достаточно богата для консолидирующейся демократии.) Тем не менее, хороших инструментальных переменных нет. Очень трудно найти ту переменную, которая, например, влияет только на политику и не влияет на экономику. Например, наличие нефти влияет и на политику, и на экономику. Хотя есть много исследований про ресурсное проклятие (одна из следующих лекций РЭШ в Политехе будет именно этому посвящена, и читать ее будет Константин Сонин), этот инструмент на макроэкономическом уровне не позволяет разрешить проблему обратных причинно-следственных связей. Рассмотрим теперь график связи между демократией и ростом ВВП за такой-то период. Мы увидим, что здесь тоже есть исключения: недемократические страны, которые росли достаточно быстро (в том числе несколько восточно-азиатских стран). Но видна возрастающая зависимость. Мы не знаем, что значит эта зависимость. Мы не понимаем, в какую сторону идет причинно-следственная связь. Но даже в этом случае есть такие интересные методы, которые позволяют оценить эффект от перехода к демократии или к диктатуре. Это исследования, связанные с методологией event studies. Что такое event studies? Представьте себе, что что-то случилось с компанией. Например, вышел политик и сказал: «Сейчас мы с этой компанией что-то сделаем. Пришлем доктора или что-нибудь еще». Акции упали или выросли. Вы можете сказать: «Мы знаем, что это из-за этого политика или, по крайней мере, из-за его высказывания». Вы можете померить эффект этого события на курс акций. Очень часто в финансовых исследованиях, например, измеряют эффект на акции от смерти генерального директора. Внезапной смерти генерального директора. Генеральные директора – такие же люди, как и все, иногда они попадают в катастрофы. Акции на это реагируют. Можно измерить, от чего зависит реакция курса акций на то, что случилось с генеральным директором. Был ли он активом или пассивом для этой компании? Есть много исследований, в которых в особых ситуациях оказывается, что инвесторы с энтузиазмом, к сожалению, воспринимают гибель генерального директора. Есть аналогичные исследования, которые, например, оценивают покупку генеральным директором большого личного дома. Оказывается, что чем дороже этот дом, тем хуже инвесторы воспринимают эту новость. То же самое можно сделать и для демократий и диктатур. Некоторые диктаторы тоже погибают внезапно. Можно посмотреть на влияние этой смерти на экономику. Трудно себе представить, что диктатор погиб, потому что он ожидал, что будет замедление экономического роста. Поэтому ясно, в какую сторону причинно-следственная связь. Такие исследования есть, и они дают количественную оценку положительного влияния смерти диктатора на экономический рост. Но самая важная работа недавних лет – это работа двух классиков Торстена Перссона и Гвидо Табеллини. (Кстати, Перссон в следующем году приедет в Москву). Это исследование переходов от демократии к диктатуре и обратно в при помощи различий в разностях и мэтчинга. Рассмотрим похожие страны. Например, возьмем две диктатуры. Похожие с той точки зрения, что мы знаем, что вероятность перехода от диктатуры к демократии у них примерно похожая. У них примерно похожий уровень образования. У них примерно похожий уровень неравенства. У них примерно похожий опыт жизни при диктатуре. Представим себе, что той из них, которая сейчас перешла к демократии, просто повезло. А той, которая осталась при диктатуре, наоборот, не повезло. (Впрочем, «повезло» или «не повезло» – это оценочные суждения.) В этой работе оказывается, что если мы посмотрим на две похожие страны и посмотрим на различия в разностях, то есть учтем всю историю, все религиозные особенности этой страны, все то, что не меняется во времени. Оказывается, что эффект достаточно большой. Переход от диктатуры к демократии повышает темпы экономического роста на процент в год, по крайней мере, в течение 10 лет. А обратный переход от демократии к диктатуре снижает темпы роста на 2 процента. Третье, и самое важное изменение в современной экономической науке – это бурный рост междисциплинарных исследований. Целый ряд исследований, которые теперь делают экономисты, хотя не относится к тому, о чем говорится в учебнике первого курса. Этот процесс распространения междисциплинарных исследований называется «экономический империализм». Как если бы экономисты, будучи метрополией, пытались захватывать колонии в соседних дисциплинах. В некоторых случаях, надо сказать, это происходит достаточно успешно. Например, в политологии уже около или даже больше половины профессоров политологических факультетов в ведущих университетах занимаются “rational choice political science”, то есть это наука, где используется экономическая методология. Суть междисциплинарного подхода очень проста. Исследуя неэкономические явления, экономисты пытаются использовать экономический подход: гипотеза, модель с агентами, у которых есть целевая функция и информационные ограничения, равновесие, изучение свойств равновесия, тестируемые гипотезы, данные, оценка гипотез современными эконометрическими методами. Об этом вы можете прочитать, например, в известной книге «Фрикономика» и «Суперфрикономика». Почему это называется фрикономика? Потому что со стороны Стивена Дабнера, журналиста, который написал эту книжку вместе с экономистом Стивом Левиттом, это не экономика. На самом деле Стив Левитт, который провел все описанные в книге исследования, – абсолютно успешный мейнстримный экономист. Например, он получил медаль Кларка – это самая престижная награда для экономистов до 40 лет в Америке. В этом смысле, он успешен именно как экономист, а не социолог, антрополог или психолог. Чем отличается экономика от соседних наук? Экономисты пытаются все формализовать и упростить. При этом, естественно, теряются детали. Конечно, экономисты знают, что это важно. Но, если вы хотите построить модель, вам нужно от чего-то абстрагироваться. Лучшая модель – это карта масштабом один к одному. На карте масштабом один к одному изображены все детали, но с ней не очень удобно работать. Поэтому обычно люди строят какую-то модель, которая имеет более грубый масштаб, и какие-то детали отбрасываются. Проблема в том, что при этом отбрасывании отбрасываются детали, которые, например, социологи считают очень важными. Экономисты говорят: «Все равно это в модель не помещается. Мы должны смотреть не с уровня человеческого роста, а с высоты птичьего полета». Экономический империализм – это на самом деле очень давний процесс. С точки зрения сегодняшних наук раньше не было разделения на экономику социологию и политологию. Книга Адама Смита – это очень междисциплинарная книга. Макс Вебер – это тоже и экономист, и политолог, и социолог. Затем эти дисциплины разделились и начали сближаться опять буквально несколько десятилетий назад. Я сослался на Стива Левитта. Есть еще нобелевский лауреат Гэри Беккер, который использовал экономический метод для исследования преступности, для исследования внутрисемейных отношений и делал это очень успешно. Почему это происходит? Здесь есть две причины. Одна причина – экономисты считают себя успешными исследователями и хотят использовать свой аппарат и в соседних областях науки тоже. Они считают: «Мы что-то узнали про экономику, мы хотим теперь узнать про общество и про человека, и про законы, и про политику». Вторая проблема, на самом деле, в том, что экономика не так успешна, как ей хотелось бы казаться. Где-то 50 лет назад возник формальный аппарат того, что называется неоклассический синтез. Экономисты построили очень красивые модели, и вдруг выяснилось, что мир устроен не совсем так, как написано в этих моделях, что эти модели нужно изменять. Нужно расширять предположения, которые делаются. Так и произошло. Я не буду долго говорить о том, что это за неоклассический синтез. В некотором роде это достаточно сложная и изысканная модель утверждения Адама Смита про «невидимую руку рынка». При предположениях о отсутствии информационной асимметрии, несовершенной конкуренции и транзакционных издержек в такой модели рыночное равновесие оптимально. Оказывается, что никакой Госплан не может добиться лучшего результата, чем невидимая рука рынка. Это красивая теория. У нее есть разные версии и приложения. Есть теорема Коуза, теорема Модильяни-Миллера о структуре капитала. Из-за недостатка времени я не буду сейчас говорить о них – при желании Вы можете посмотреть детали в слайдах. Проблема в том, что эта теория работает не очень хорошо. Мы видим, что государство вмешивается в экономику и это достаточно популярно. Люди считают, что невидимая рука рынка не всегда работает хорошо. Это нормально. Раз теория не работает, мы можем объяснить это не тем, что теорема неправильная, а тем, что условия теоремы неправильные, что предпосылки, аксиомы заданы неверно. Примеров нарушения этих предположений много. Например, мы можем легко увидеть, что в реальности имеет место информационная асимметрия, рынки являются скорее неполными, чем полными (это значит, что не все активы вы можете купить или продать на рынке). Аналогично, могут иметь место неполные контракты. Это значит, что если мы с вами знаем, что это продукт высокого качества, необязательно судья сможет это увидеть и доказать. В общем, есть много ограничивающих предположений, которые в жизни не выполняются. Поэтому экономисты теперь пытаются строить модели, в которых эти предположения не вводятся изначально. В частности, в последние четыре десятилетия бурно развивалась так называемая теория контрактов, где используется отказ от предположения о полных контрактах, о наблюдаемых действиях, и о симметричной информацией. Оказывается, что эта наука гораздо лучше описывает и отношения собственности, и структуру капитала компании, и эволюцию континентального права против англо-саксонского права. Оказывается, что все эти вещи можно моделировать достаточно просто и достаточно убедительно. Как я уже сказал, это используется в том числе и в финансах. Оказывается, у нас сегодня есть уже достаточно глубокое понимание того, как устроены стимулы менеджеров в корпорациях. В частности, понятно, почему их нельзя структурировать совершенным образом. Понятно, что чтобы мы не делали, всегда будут возникать и корпоративные конфликты, и обман акционеров, и самоуправство менеджеров. Тем не менее, понятно и то, что несмотря на невозможность добиться идеальных стимулов, можно в каждом конкретном случае улучшить стимулы менеджеров, различных акционеров и других стейкхолдеров. В политологии то же самое. Давайте отойдем от предположения, что правительство – это робот, который действует в наших интересах. Предположим, что в правительстве работают люди, которые действуют в своих интересах, тогда возникает целый ряд экономических моделей, которые позволяют моделировать и электоральную демократию, и диктатуру. Можно узнать, как влияет децентрализация и федеральное устройство на экономические показатели. Обсудить обратное влияние. Можно изучить вопрос о том, как президентская система или парламентская система влияет на структуру госбюджета, как одномандатные округа или партийные списки влияют на то, что происходит. Эти модели можно оценивать и количественно – с использованием данных высокого качества и современных эконометрических методов. Еще одно важное направление исследований – это исследования на стыке экономики и социологии. Вот очень важный пример: экономисты умеют моделировать и измерять дискриминацию. Казалось бы, дискриминация в рыночной экономике не может существовать. Если никто не хочет нанимать на работу представителя национального, этнического, религиозного меньшинства, почему бы мне задешево не нанять его, ведь ему больше некуда идти. Оказывается, что в жизни все устроено гораздо сложнее. Оказывается, что возникает такое устойчивое равновесие – ловушка дискриминации. В этой ситуации представители меньшинств не рассчитывают на то, что их кто-то наймет на высокооплачиваемую работу и, соответственно, не вкладывают время и силы в те навыки, которые вам нужны. Тогда оказывается, что ваше предположение, что они хуже работают, самооправдано. Оказывается, что дискриминация является равновесием, в том числе в рыночной экономике. Это можно измерить. Экономисты, в том числе Стив Левитт, поставили такие эксперименты. Они брали объявления о приеме на работу и посылали резюме с англо-саксонскими именами и с афроамериканскими именами. В остальном резюме выглядели абсолютно идентичными. Там даже не было фотографий, просто имена звучали, как если бы это были афроамериканские имена. Работодатели перезванивали людям с англо-саксонскими именами гораздо чаще, чем людям с афроамериканскими именами. В этом смысле все те усилия по защите афроамериканских меньшинств, которые предпринимаются в Америке, до сих пор работают не очень хорошо. Еще один пример – это внутрисемейные отношения, в том числе в развивающихся странах. Это огромный фронт для исследований экономистов. Сколько детей рожают женщины, от чего это зависит? Верна ли стратегия материнского капитала в России, дает ли она эффект? На самом деле, на многие из этих вопросов мы знаем ответ. Еще один важный набор вопрос связан со стоимостью жизни. Можно примерно оценить, сколько стоит человеческая жизнь в разных странах. Исходя из страховок, мер безопасности можно представить себе, во сколько общество или участники каких-то рыночных взаимодействий оценивают человеческую жизнь. Можно даже измерить, как эта оценка зависит от дохода. Отсюда можно вывести справедливую цену для жизни россиянина, которая будет на порядок больше, чем даже самые высокие оценки, которые сегодня есть в России. Я хотел бы особо остановиться на экономике удовлетворенности жизнью, она же – экономика счастья. Казалось бы, это совсем не экономическая тема. Тем не менее, теперь есть большая область исследований, связанная с количественными исследованиями удовлетворенности жизнью. Исследователи опрашивают жителей разных стран. Спрашивают у них: «Учитывая все, что только можно учесть, насколько вы удовлетворены своей жизнью по шкале от одного до десяти?». Есть и более детальные исследования. Вместо того, чтобы один раз опросить человека, ему выдают прибор с несколькими кнопками и следят за ним неделями, а иногда и месяцами. Он в течение дня нажимает на кнопку: «В эту минуту мне хорошо. В эту минуту мне не так хорошо. В эту минуту мне очень плохо» – а также ведет дневник, что именно с ним происходит в то или иное время – что предоставляет очень богатый материал для исследований. Казалось бы, разные люди понимают под счастьем разные вещи. Тем не менее, количественный аппарат позволяет выделить факторы, которые влияют на счастье. Самый главный вопрос – это вопрос о том, счастливы ли более богатые люди? Приносит ли доход счастье? Это вопрос, который до сих пор не имеет четкого ответа, но мы далеко продвинулись и сегодня знаем гораздо больше. В 1970-е годы исследователь Ричард Истерлин, показал, что американцы ценят относительный, а не абсолютный доход. Что это значит? Это значит, что более богатые американцы более счастливы, чем более бедные американцы. Но если и у тех и у других доход вырастет на одну и ту же величину, то после уровня, скажем, 20 000 долларов на человека в год, счастье уже не зависит от дохода. Это называется «парадокс Истерлина»: рост абсолютного (а не относительного) дохода не приводит к увеличению удовлетворенности жизнью. Но недавние исследования, использующие более качественные данные, показали, что это не совсем так, точнее совсем не так. Сегодня мы можем сказать, что и богатые страны, и бедные страны, и жители внутри одной и той же страны удовлетворяют одной и той же закономерности: при росте дохода уровень удовлетворенности жизнью растет примерно на одну и ту же величину. То же самое происходит и в России. В нашей статье с Екатериной Журавской мы рассмотрели одну и ту же группу россиян, которых опрашивали 15 лет подряд. Посмотрели на их доходы. Очистили этот эффект от семейного положения, уровня образования, возраста, температуры этого города. Оказалось, что когда их доходы падали, уровень счастья падал. Потом уровень дохода – и уровень счастья начал расти. Мы нашли все те же самые зависимости, которые находят в других странах – и примерно ту же самую величину зависимости. Одно из интереснейших наблюдений, которые мы обнаружили, — это то, что в России пока что уровень счастья зависит от возраста не так, как в других странах. Это касается не только России. Это свойство все переходных экономик. Во всех странах уровень счастья с возрастом сначала падает – до 38-40 лет – после чего начинает расти. Люди, которым 80 лет, примерно так же счастливы, как и люди в 18 лет. Эта зависимость имеет место и в развитых, и в развивающихся экономиках. А вот в переходных экономиках уровень счастья монотонно падает с возрастом. В странах с переходной экономикой молодые люди так же счастливы, как их сверстники в развитых и развивающихся странах с таким же уровнем дохода. А старшее поколение (те, кому за 40), гораздо менее счастливы, чем их сверстники в развивающихся странах – причем, чем старше человек, тем менее он счастлив. Этому факту можно найти много объяснений. В нашей работе мы количественно оцениваем относительную величину различных объяснений: влияние качества общественных благ, профессионального опыта, уровня образования, времени получения образования. Еще одна вещь, о которой я хотел рассказать напоследок – это поведенческая экономика. Это наука, в которой мы изучаем отклонения от рациональности. Люди не обладают бесконечной вычислительной мощностью. Люди стараются экономить на мыслительных процессах и расчетах. Это часто приводит к тому, что они мыслят стереотипами. Они используют накопленный ими же или кем-то еще опыт для быстрого принятия решений – даже если более рациональное принятие решение принесло бы большую выгоду. Получается такое сочетание рациональности и нерациональности. С одной стороны, у них нет времени все это считать, они торопятся и достаточно рационально не используют всю доступную им информацию. С другой стороны, это все-таки нерациональность. Это можно и нужно учитывать в наших моделях. В таких моделях, людям приходится играть в игры с самим собой. Почему? Приведу простой пример: вы все, наверное, знаете, что машину вы лучше водите, чем средний россиянин. Это действительно любопытный факт. Если мы проведем опрос сегодняшней аудитории: поставьте себе относительную оценку по интеллектуальным способностям. Например, скажите: я по уровню интеллектуальных способностей умнее, чем 75 процентов людей в этой аудитории, или 65 процентов, или 20 процентов. Возникает вопрос: что это за интеллектуальные способности такие? Ваш мозг сразу определит их так, чтобы вы были умнее, чем 70 – 80 процентов. Обычно аудитории (по крайней мере, те, которым мы читаем лекции, на которых мы ставим такие эксперименты) приносят результат 70-80 процентов. Конечно же, средний человек в аудитории умнее, чем 50 процентов его коллег, но он думает (точнее, хочет думать), что он умнее 70 процентов. При этом ему приходится играть против самого себя. Каким-то образом делать так, чтобы второе «я» не вело себя сверх-оптимистично, не использовало нерациональных предположений. Факт в том, что мы не любим вспоминать свои ошибки, мы не любим вспоминать неприятный опыт. Люди с большим удовольствием забывают о плохом. Почему? Потому что им нравится думать о хорошем. Это означает, что когда вы принимаете решения, как правило, вы ведете себя более оптимистично, чем нужно. Просто потому, что вам не нравится жить в том мире, где есть много плохого. Такие вещи можно как-то моделировать, рассчитывать и использовать. Я приведу забавную историю. Это история про статьи экономистов Стефана Делла Винья и Ульрике Мальмендье. История про то, как люди ходили в фитнес-клуб в Калифорнии. Делла Винья и Мальмендье собрали данные о том, какие люди покупали какие абонементы и сколько раз они ходили. Рассмотрим покупателей тех абонементов, которые оправдывают себя только, если ходить в фитнес-клуб 8 раз в месяц. Вот если вы ходите 8 раз в месяц, вам выгодно купить этот абонемент, а не платить каждый раз отдельно. Но оказалось, что их покупатели ходили примерно 4 раза в месяц. То есть люди не могли заставить себя оправдать те траты, которые они уже осуществили. С другой стороны, можно измерить эффект от того, что они купили этот абонемент. Чувство вины заставляет их сходить в тренажерный зал хотя бы 4 раза в месяц – а, например, не 2 раза. Это не просто забавная история. При помощи этого аппарата можно исследовать и более фундаментальные вопросы. Например, различия между Америкой и Европой. Несмотря на то, что те и другие страны называются развитыми капиталистическими демократиями, они кардинально отличаются друг от друга в терминах уровня неравенства, уровня перераспределения и убежденности людей в том, что «бедность – это следствие невезения» или «бедность – это следствие лени». Оказывается, можно рационализировать эти различия. Если вы верите, что бедность – это «невезение», соответственно, вы голосуете за правительство, которое собирает больше налогов с богатых и отдает их бедным. Потому что вы считаете, что так справедливо. Если такое правительство приходит к власти, оно так и делает. Получается, что у бедного или богатого человека гораздо меньше шансов повлиять на свою судьбу. Его доход в меньшей степени зависит от его собственных усилий, с одной стороны. С другой стороны, он знает, что как бы он ни работал, все равно он не будет очень бедным, потому что за счет налогов ему выплатят пособие. Возникает замкнутый круг. Вы верите в то, что бедняки – это те, кому не повезло, и голосуете за перераспределение. В этой экономике действительно будет мало что зависеть от самого человека. В Америке, наоборот, большинство людей верят в то, что бедняк – это тот, кто работает плохо. Поэтому нужно дать возможность людям заработать деньги. Поэтому налоги должны быть низкими. Получается, что все зависит от вас. Если вы много работаете, вы много заработаете денег. Казалось бы, эти совершенно различные общественные устройства не могут быть сведены в рамках одной модели. Тем не менее, можно построить модель, где люди имеют противоположные ожидания об устройстве общества, причем эти веры оправдываются в равновесии. Сегодняшний кризис показал и важность использование поведенческой экономики для анализа макроэкономических процессов. Как я уже говорил, мы пока плохо понимаем, как это стадное поведение влияет на макроэкономику. Но такая наука формируется. Например, сейчас по всему миру очень хорошо продается книга Джорджа Акерлофа и Роберта Шиллера «Animal spirits». Мы вместе с издательством Юнайтед Пресс издали эту книгу по-русски тоже, перевод называется «Spiritus Animalis: как психология влияет на экономику». Эта книга как раз и обсуждает необходимость новой повестки дня в сегодняшней макроэкономике. Основное утверждение поведенческой макроэкономики заключается в том, что пузыри не обязательно лопаются мгновенно. Например, если вы видите, что курс акций растет, вы с большой вероятностью можете поверить, что он будет расти всегда. Вы убеждаете себя в том, что «так много людей не могут ошибаться». Это тот же самый аргумент, который «срабатывает», когда вы приходите в ресторан. Представьте себе два ресторана рядом друг с другом. В одном много людей, в другом мало людей. Вы думаете: «Мне говорили, что тот, в котором мало, хороший. Но так много людей не могут ошибаться». Вы присоединяетесь к тому ресторану, где уже много людей. Следующий человек, который приходит, видит, что людей в первом ресторане еще больше. И тоже заходит в этот ресторан. Хотя, казалось бы, он должен был использовать свою независимую оценку. Возникает такое стадное поведение, которое аналогичным образом влияет на рынки, надувает пузыри, и эти пузыри не обязательно лопаются сразу же. В связи с недостатком времени, я сегодня на этом закончу. Еще раз повторю, что экономика – это живая и развивающаяся наука. Известно в ней далеко не все. С другой стороны, это наука с достаточно строгим подходом к исследовательским вопросам. Это и математический аппарат, модели, теории, теоремы, гипотезы и проверки этих гипотез при помощи данных. Ее методология прошла огромный путь за последние 30 лет. Сейчас экономика – это совсем не то, что была в середине 1970-х – начале 1980-х. Тем не менее, есть еще очень много нерешенных вопросов. Я надеюсь, кто-то из вас захочет об этом задуматься и тоже стать ученым-экономистом. Это очень интересная профессия. Спасибо. Что мы знаем о техническом анализе? А что мы знаем по историю развития тех анализа? Кто-то задавался этим вопросом? Наверно это банальная тема? Но все от так банально? Эта тема большая, потому будет разделена на ряд частей. Большая, не потому что много всего рассказывать, а потому что у большинства в голове столько заблуждений, по поводу этой темы, что мы только начнём раскладывать по полочкам то что уже есть. Технический анализ в целом это очень популярная тема, она имеет ряд направлений, у каждого из них есть ярые поклонники и ненавистники. Конечно же мы поговорим о разных индикаторах, свечных моделях, уровнях, и отдельно разберем волновой анализ. По классике люди начинают с великого труда Джона Дж. Мерфи “Технический анализ фьючерсных рынков”. Однако если я начну с него, то упущу самое важное, а именно ключ к пониманию материала. Потому перед тем как говорить о техническом анализе, нужно узнать что такое эконометрика. Эконометрика — это наука, изучающая количественные и качественные экономические взаимосвязи с помощью математических и статистических методов и моделей. Современное определение предмета эконометрики было выработано в уставе Эконометрического общества, которое главными целями назвало использование статистики и математики для развития экономической теории. Термин «эконометрика» состоит из двух частей: «эконо» — от «экономика» и «метрика» — от «измерение». Первые попытки количественных исследований в экономике относятся к 17 веку. Они были связаны с представителями нового направления в экономической теории — политической арифметики. Петти, Давенант и Кинг использовали конкретные экономические данные в своих исследованиях, в первую очередь, при расчёте национального дохода. Это направление пробудило поиск экономических законов, по аналогии с физическими, астрономическими и другими естественнонаучными законами. При этом существование неопределённости в экономике ещё не осознавалось. Важным этапом возникновения эконометрики явилось развитие статистической теории в трудах Гальтона, Пирсона и Эджуорта. Эти учёные предопределили первые применения парной корреляции. С 1830-х годов наиболее развитые страны стали испытывать необъяснимые с точки зрения экономической науки того времени потрясения — упадок деловой активности, возникновение массовой безработицы. Быстрое промышленное развитие и урбанизация выявили огромный пласт нерешённых социальных проблем. Уже в конце 19 века неоклассическая теория стала восприниматься как слишком удалённая от действительности. Теория могла стать убедительной в том случае, если она бы смогла объяснить изменения, происходящие в экономике. Для её практического применения требовались количественные выражения базовых экономических терминов. В 1911 году выходит книга американского экономиста Мура «Законы заработной платы: эссе по статистической экономике». В своём исследовании Мур провёл анализ рынка труда, статистически проверил теорию производительности Кларка и изложил основы стратегии объединения пролетариата. Мур показал, что с помощью сложных математических построений, основанных на фактических данных, можно разработать основу для социальной политики. В это же время итальянский экономист Бенини впервые использовал множественную регрессию при оценке функции спроса. Значительный вклад в становление эконометрики внесли исследования цикличности экономики. Первым цикличность экономики обнаружил Жугляр. Он выявил 7-11-летние циклы инвестиций. Кузнец, лауреат Нобелевской премии по экономике за 1971 год, обнаружил 15-20-летние циклы в строительстве, важным этапом формирования эконометрики явилось построение экономических барометров. Построение экономических барометров основано на идее того, что существуют показатели, которые изменяются раньше других и поэтому могут служить сигналами изменений последних. Первым и самым известным стал Гарвардский барометр, который был создан в 1903 году под руководством Персонса и Митчелла. Он состоял из кривых, характеризующих фондовый, товарный и денежный рынки. Каждая из этих кривых представляла собой арифметическую среднюю из входящих в неё нескольких показателей. Эти ряды предварительно обрабатывались путём исключения тенденции, сезонности и приведения колебаний отдельных кривых к сравнимому масштабу колеблемости. Успех использования гарвардского барометра вызвал появление многих аналогичных барометров в других странах. Однако приблизительно с 1925 г. он потерял свою чувствительность. Суть займа проста — можно приобрести акции компаний, внеся всего 10 % от их стоимости. Например, акции стоимостью 1000 долларов можно приобрести за 100 долларов. Этот тип ссуды был популярен в 1920-е годы, потому что все играли на рынке акций. Но в этом займе есть одна хитрость — брокер в любой момент может потребовать уплаты долга, и его нужно вернуть в течение 24 часов. Это называется маржинальным требованием, и оно, как правило, вызывает продажу акций, купленных в кредит. 24 октября 1929 года нью-йоркские брокеры, которые выдавали маржевые займы, стали массово требовать уплаты по ним. Все начали избавляться от акций, чтобы избежать уплаты по маржевым займам. Необходимость оплаты по маржевым требованиям вызвала нехватку средств в банках по похожим причинам (так как активы банков были вложены в ценные бумаги и банки были вынуждены срочно продавать их) и это привело к краху шестнадцати тысяч банков, что позволило международным банкирам не только скупить банки конкурентов, но и за сущие копейки скупить крупные американские компании. Когда общество было полностью разорено, банкиры Федерального резерва решили отменить в США золотой стандарт. С этой целью они решили собрать оставшееся в США золото. Так под предлогом борьбы с последствиями депрессии была проведена конфискация золота у населения США. Однако великая депрессия это так же перепроизводство, о котором рядовой рабочий не знал. Он не владеет цифрами и отчётами. Он не знает что экономический рост вызванный последствиями первой мировой войны, это рыночная неэффективность. Памп замедленного действия. Люди на хайпе начинают всё скупать, грамотные скупают раньше, менее грамотные позже. А к примеру, такие дяденьки как Джон Пирпонт Морган, зарабатывают на продаже акций, как брокер, получают процент по маржинальным сделкам, имеют с роста акций, как инвестор. А еще, он дружит с несколькими весомыми дядями, которые состояли в преступном сговоре, сбросили на хаях, и начали требовать оплату по марже. В этих условиях основным методом макроэкономического анализа становится метод построения межотраслевого баланса Леонтьева. В это же время начали строиться экономические модели, использующие методы гармонического анализа. Эти методы были перенесены в экономику из астрономии, метеорологии и физики. К 1930-м годам стало ясно, что для более глубокого понимания экономических процессов стоит использовать в той или иной степени статистику и математику. 29 декабря 1930 г. по инициативе Фишера, Тинбергена, и других учёных было создано эконометрическое общество. В 1933 г. Фриш основал журнал «Эконометрика» А уже в 1941 г. появляется первый учебник по новой научной дисциплине, написанный Тинбергеном. В 1969 г. Фриш и Тинберген стали первыми исследователями, получившими Нобелевскую премию по экономике. Как говорится в официальном сообщении нобелевского комитета: «за создание и применение динамических моделей к анализу экономических процессов». В 1980 г. вторую эконометрическую Нобелевскую премию по экономике получил американский экономист Лоуренс Клейн за создание экономических моделей и их применение к анализу колебаний экономики и экономической политики. Важным событием для развития эконометрики стало появление компьютеров. Благодаря им мощное развитие получил статистический анализ временных рядов. Стимулировало эконометрические исследования бурное развитие финансовых рынков и производных инструментов. Это привело лауреата Нобелевской премии по экономике за 1981 год Тобина к разработке новых моделей с использованием рыночных данных. Ховельмо показал, как можно использовать методы математической статистики для того, чтобы получать обоснованные заключения о сложных экономических взаимосвязях исходя из случайной выборки эмпирических наблюдений. В 1989 г. ему присудили Нобелевскую премию по экономике «за прояснение вероятностных основ эконометрики и анализ одновременных экономических структур» Ховельмо рассматривал экономические ряды как реализацию случайных процессов. Главными проблемами, возникающими при работе с такими данными, являются нестационарность и сильная волатильность. Если переменные нестационарны, то есть риск установить связь там, где её нет. Вариантом решения данной проблемы является переход от уровней ряда к их разностям. Недостатком данного метода является сложность экономической интерпретации полученных результатов. Для решения этой проблемы Грэнджер ввёл концепцию коинтеграции как стационарной комбинации между нестационарными переменными. В 2003 г. Гренджер совместно с Энглом получил нобелевскую премию. Энгл, в свою очередь, известен как создатель моделей с меняющейся во времени волатильностью (т. н. ARCH-модели). И потому эти модели получили широкое распространение на финансовых рынках. Критика эконометрики Кейнсом главным образом обусловлена различием в его подходе к экономической науке. Основным пунктом этого расхождениями является вопрос «следует ли трактовать экономику как точную науку». Сам Кейнс давал отрицательный ответ на этот вопрос. В рамках его традиции экономическая среда изменчива и непредсказуема, а большинство экономических переменных связано между собой множеством сложных нелинейных зависимостей. Из этого следуют нестабильность коэффициентов корреляции и невозможность решения предсказательных задач. Поэтому экономическая наука не может претендовать на точные количественные измерения. Она должна быть основана на реалистичных предпосылках и содержать инструменты, помогающие понять и объяснить эту среду. Подход же Тинбергена следующий: экономический анализ должен быть как можно более формализованным и нацеленным на решение конкретных количественных задач. В рамках данного подхода экономическая наука должна быть точной, а объект её изучения аналогичен объектам технических и естественнонаучных дисциплин. И теперь итог, однако всё еще словами уважаемых экономистов. Несмотря на потенциальные возможности, эконометрика не получила поддержки у многих крупных экономистов. В начале 1970-х годов Уорсвик резко критиковал экономистов-математиков за «отсутствие связи с конкретными фактами». Он утверждал, что эконометристы «занимаются не столько изобретением средств систематизации и измерения имеющихся фактов, сколько созданием неисчислимого множества претендующих на это способов». В это же время Браун утверждал, что «построение регрессий временных рядов годится только для обмана». Леонтьев охарактеризовал эконометрику как «попытку компенсировать бросающийся в глаза недостаток имеющихся данных путём широкого использования всё более и более изощрённых статистических приёмов». Резко отрицательно к эконометрике относились и представители австрийской школы экономики. Так, Мизес писал: «Введённые в заблуждение идеей, что науки о человеческой деятельности должны подражать методу естественных наук, великое множество авторов поглощены квантификацией экономики. Они думают, что экономика должна подражать химии их принцип: наука — это измерение. Но они не в состоянии понять, что в области человеческой деятельности статистика — это всегда история, и что гипотетические корреляции и функции не описывают ничего, кроме того, что случилось в определённый момент времени в определённой географической области как результат деятельности определённого числа людей. Как метод экономического анализа, эконометрика — ребяческая игра с числами, которая не добавляет чего-либо в разъяснение проблем экономической действительности». Рынок это люди. Люди нерациональны. Людьми движут эмоции. Они совершают глупые поступки. Поведение людей это эффект бабочки. Рынок это Парето оптимальное состояние, а систематически, спекулятивно зарабатывать можно, только когда на рынке появляется неэффективность. P.S.: Адам Смит шотландский экономист и философ-этик, родился предположительно 5 июня 1723 года. Он один из основоположников экономической теории как науки. Он написал очень очень известную книгу, которая так или иначе преподается везде, но я хочу показать вам список, книг Смита, по датам их выхода. Однако я хочу заострить ваше внимание на книге 1759 года Смит начинает книгу с определения и объяснения чувства симпатии, его влияния на отношения между людьми. Далее Смит подразделяет все страсти (чувства) на несколько типов. Также говорит о богатстве. Смит утверждает, что причина устремленности людей к богатству, причина честолюбия состоит не в том, что люди таким образом пытаются достичь материального благополучия, а в том, чтобы отличиться, обратить на себя внимание, вызвать одобрение, похвалу, сочувствие или получить сопровождающие их выводы. Основной целью человека, по мнению Смита, является тщеславие, а не благосостояние или удовольствие. Богатство выдвигает человека на первый план, превращая в центр всеобщего внимания. Бедность означает безвестность и забвение. Главной причиной искажения нравственных чувств, по Смиту, есть наша готовность восхищаться богатыми и знатными людьми и презирать людей бедных. Почитание знатности и богатства подменяет уважение к благоразумию и добродетели. Таким образом, Смит исследовав человеческие чувства, на примере большого количества богатых и бедных людей, предложил свой взгляд в 1776 на роль государства в экономике, который в дальнейшем назвали классической экономической теорией. 1: Простой регрессионный анализ 2: Допущения, лежащие в основе классической модели линейной регрессии 3: Проверка гипотез 4: Проверка гипотез — некоторые дополнительные вопросы 5: множественная регрессия 6: Отношение t 7: Проверка нескольких гипотез 8: Статистика согласия 9: Модели гедонического ценообразования и проверка невложенных гипотез 10: Допущения CLRM и гетероскедастичности 11: Автокорреляция — определения и тестирование 12: Автокорреляция — Решения 13: Проблемы мультиколлинеарности и несоответствующей функциональной формы 14: Допущение нормальности 15: Моделирование сезонности на финансовых рынках 16: Использование неправильных переменных и тестов стабильности параметров 17: Подходы к построению эконометрических моделей 18: Детерминанты и влияние суверенных кредитных рейтингов 19: нестационарные данные 20: Проверка на нестационарность 21: Коинтеграция 22: Моделирование взаимосвязи между спотовыми и фьючерсными ценами Несмотря на ослабление ограничений, связанных с короной, в некоторых местах по всему миру, многие университеты и учебные центры остаются закрытыми и, вероятно, останутся таковыми в течение некоторого времени.В обозримом будущем онлайн-обучение заполнит пустоту и станет средством обучения по умолчанию. Да, сейчас странные времена. Если вы еще не очень хорошо знакомы с Zoom / Whereby / Skype, мы советуем вам скачать их все сейчас! Осознавая проблемы, которые представляет этот переход в виртуальный мир, INOMICS опубликовал различные аналитические материалы, которые призваны помочь нашим читателям продвинуться вперед и максимально использовать уже существующие онлайн-ресурсы.Некоторые из самых популярных на сегодняшний день включают бесплатных и платных онлайн-курсов по эконометрике , уроки математики и статистики , а также список лучших (по нашему скромному мнению) экономических подкастов . Мы — и всегда будем — здесь, чтобы служить. Продолжая в том же духе, мы теперь хотели бы поделиться с вами списком каналов YouTube — опять же, лучших из тех, что мы могли представить, — которые могут быть полезны для всех студентов факультетов экономики и эконометрики, которые в настоящее время застряли дома, имея только компьютер для компании. . Несмотря на то, что они могут не предлагать оценки или свидетельства о достижениях и могут быть менее интерактивным способом изучения желаемого предмета, они все же могут предложить отличный набор дополнительных и учебных материалов, к ним очень легко получить доступ и они бесплатны! Здесь нет платы за обучение. Не все записанные вживую лекции самого высокого качества, но они, тем не менее, дают вам ощущение физического присутствия в классе, что является редкой возможностью в эпоху онлайн-обучения. «Эй, ты сзади, надеюсь, ты обращаешь внимание!» Для получения дополнительных возможностей онлайн-обучения щелкните здесь Действующий с 1998 года INOMICS — сайт для экономистов — недавно добавил канал YouTube к ряду предлагаемых ресурсов.Его веселые, короткие и информативные видеоролики, предназначенные для молодых экономистов, помогают объяснить все те экономические термины, которые вы должны знать, но часто не знаете … Вам нужно быстрое определение дилеммы заключенного? INOMICS поможет вам. Во-первых, вы действительно не ошибетесь, быстро подписавшись на канал The Economist на YouTube. Каждый четверг они публикуют видео, в котором освещаются лучшие репортажи из печатного и цифрового издания. Канал The Financial Times на YouTube демонстрирует некоторые из лучших работ их журналистики в наглядной форме. С заявленной целью информировать и вдохновлять вас, быстрое отслеживание может добавить красок в последние экономические истории дня. Важно подвергнуть сомнению общепринятые представления об экономике, особенно когда они могут поддерживать системы угнетения или скрывать идеологические предположения, которые необходимо распаковывать, обсуждать и оспаривать. Институт нового экономического мышления отлично справляется с этой задачей на своем канале, регулярно проводя интервью с экономистами, которые находятся на переднем крае продвижения дисциплины. Marginal Revolution University считает, что экономика способна изменить ваш взгляд на мир. Их миссия — помочь вам раскрыть своего внутреннего экономиста, по одному видео за раз. С полными курсами, такими как принципы микро и макроэкономики, освоением эконометрики и рядами, такими как повседневная экономика, проверка MRU действительно является обязательной для любого начинающего студента-экономиста. Далее идет EconplusDal. Разочарованный отсутствием экономической помощи, доступной при изучении экономики, теперь уже в качестве полностью подготовленного учителя экономики, EconplusDal пытается исправить эту ошибку.Создание видеороликов специально для студентов-экономистов, чтобы помочь им сдать экзамены. Если вы студент международного бакалавриата или готовитесь к экзамену A Level в Великобритании, его специализированные материалы экзамена делают этот канал для вас. Между тем, если вы студент из США, у Джейкоба Клиффорда есть специальные материалы для экзаменов. Имея более 500 000 подписчиков, он определенно что-то делает правильно. Kahn Academy — это некоммерческая организация, миссией которой является предоставление бесплатного образования мирового уровня для всех и в любом месте.Имея более пяти миллионов подписчиков, они охватывают гораздо больше, чем просто экономические темы, но их экономические материалы действительно великолепны. Если вам нужно понять какую-то теорию, скорее всего, они ее охватили. Все видео One Minute Economics с любовью анимированы и рассказаны Андреем Полгаром, который страстно желает обучать людей экономике. Никаких длинных представлений или ненужной болтовни, Полгар сразу переходит к делу, и поэтому стоит взглянуть на нее. В жанре видеоэссе «Economics Explained» дает широкий взгляд на целый ряд экономических тем.Они особенно известны своим глубоким погружением в экономику той или иной страны. Веселая передышка от всего доступного материала по экономике стиля урока. Бена Ламберта содержат подробные комментарии об основных курсах бакалавриата и магистратуры, предлагаемых большинством университетов по экономике. Их обучают через серию лекций, читаемых на анимированной доске. Просматривая его видео, вы получите представление о том, какой будет степень бакалавра экономики — без необходимости платить вступительный взнос! Доцент кафедры экономики Санкт-Петербургского государственного университета им.Колледж Олафа, Эшли Ходжсон была занята созданием множества новых видео в 2020 году. Ее любимые темы включают поведенческую экономику, блокчейн, здравоохранение, теорию игр и теорию микроэкономики. Отлично подходит для студентов университетского уровня! Если этот список все еще не утолил ваш аппетит к экономическому контенту YouTube, вы можете проверить Feedspot список их любимых экономических каналов YouTube. Эконометрика исследует взаимосвязь между статистическим анализом и эмпирическим содержанием.Он анализирует экономические переменные с использованием математических моделей, чтобы делать прогнозы и прогнозы и объяснять постоянно происходящие инциденты. Модели используются для привязки одной экономической переменной к другой с использованием установленных эконометрических моделей и доступных наборов данных. Экономические модели хорошо подходят для статистических методов. Мы знаем, что использование статистической модели для объяснения этих повторяющихся взаимосвязей дает нам лучшее понимание того, где находится экономика сейчас и где она может быть в будущем в зависимости от обстоятельств.Эта область — восходящая звезда, и она может быть прибыльной для потенциальных соискателей. Эта область полна высокотехнологичных процессов, поэтому развитие этих навыков с помощью соответствующих курсов может помочь вам начать работу. Эконометристы используют статистический вывод для описания этих экономических отношений, поэтому вам потребуется математическая подготовка для построения и выполнения этих моделей. Курсы эконометрической теории и анализа данных помогают наряду с математической подготовкой.Курсы по эконометрикеEdX.org предлагает курсы, которые могут познакомить вас с фундаментальными дисциплинами, необходимыми в этой области. Курс Массачусетского технологического института «Анализ данных для социологов» знакомит вас с начальными принципами сбора данных для анализа и статистическими инструментами для понимания реальных данных. Вы можете расширить этот курс до микромастеров, которые включают введение в методологию эконометрики. Вы также можете пройти базовые курсы по науке о данных, такие как Harvard’s Data Science: Linear Regression Model, которые подготовят вас к работе с часто запутанным миром данных.Вы можете научиться прогнозировать процентные ставки на основе экономических данных, комментировать денежно-кредитную политику с использованием распределения вероятностей или управлять экономикой труда, понимая эконометрический анализ. Понимание экономических отношений является основой теоретической эконометрики и прикладной эконометрики. Вы хотите знать максимальную вероятность событий и отношений для эффективного планирования и изменения. Изучение социальных наук с математическим уклоном дает вам возможность углубиться в человеческое поведение и понять закономерности.По мере того, как мы лучше понимаем наши экономические модели, изучение их моделей дает нам направление для политики и мышления. Поскольку мы не можем проводить эксперименты в контролируемой среде или учитывать часто беспорядочное поведение людей, применение высокоуровневой математики может помочь нам количественно оценить отношения, как никогда раньше. Постройте карьеру на основе понимания человеческого поведения с помощью курсов и сертификатов, которые помогут вам построить соответствующие модели. Вы можете быть на переднем крае распознавания закономерностей и понимания экономических движений с достаточным влиянием, чтобы повлиять на политику.Позвольте edX помочь вам начать и строить свою карьеру с этого момента. ЭКОНОМИКА 320 ИНСТРУКТОР: Марк Тома ИНСТРУКЦИЯ ПО СОЦИАЛЬНЫМ НАУКАМ, CANVAS, ОНЛАЙН-КЛАССЫ A. ОБЩАЯ ИНФОРМАЦИЯ Таким образом, вопреки тому, что многие ожидают, онлайн-классы сложнее, а не легче, чем лекции.Чтобы добиться успеха в онлайн-классе, вы должны быть чрезвычайно мотивированы и хорошо организованы. В отличие от обычных классов, экзамены для онлайн-уроков сдаются в день и время, выбранные студентом, но должны быть сданы до крайнего срока сдачи экзамена. Кроме того, для сдачи экзамена необходимо предварительное бронирование. Рекомендуется, чтобы учащиеся координировали свои онлайн-экзамены с экзаменами для других классов, чтобы минимизировать конфликты и создать «пространство» для подготовки к экзаменам для каждого курса. Поскольку даты экзаменов гибкие (при условии соблюдения установленных сроков), студенты не могут получить копию экзамена после его завершения. B. ЭКЗАМЕНЫ ДЛЯ УЧАЩИХСЯ, ПРОЖИВАЮЩИХ В ЕВГЕНИИ И ПОБЛИЗОСТИ ЕВГЕНИИ Прежде чем вы сможете назначить экзамен, вы должны пройти онлайн-введение в SSIL, перейдя по адресу: http://distanceeducation.uoregon.edu/ и щелкнув ссылку в разделе «Первый раз здесь» под названием . Щелкните эту ссылку, чтобы активировать свою учетную запись. .После того, как вы завершите введение, вы активируете свою учетную запись и войдете в систему, используя свой DuckID и соответствующий пароль. На главной странице SSIL Test Taker вы можете назначать встречи для прохождения тестов, отменять встречи, видеть свои результаты тестов, отправлять сообщения профессору по электронной почте и т. Д. Вы должны пройти онлайн-введение в первую неделю занятий . Найдите время, чтобы прочитать информацию по ссылке, On Campus . Если у вас есть дополнительные вопросы о тестировании, обращайтесь: de @ ssil.uoregon.edu. Важно: вы должны пройти онлайн-вводную часть SSIL к концу первой недели занятий. C. ЭКЗАМЕНЫ ДЛЯ СТУДЕНТОВ, НЕ ЖИВУЩИХ ВБЛИЗИ ЕВГЕНИИ Важно: вы должны получить одобрение наблюдающего до конца первой недели занятий. D. CANVAS Адрес Canvas: http://canvas.uoregon.edu. E. MYECONLAB (Идентификатор курса: thoma25949) Идентификатор курса инструктора для MyEconLab: thoma25949. Страницу регистрации, дальнейшие инструкции, часто задаваемые вопросы и т. Д. Можно найти по адресу: http://www.pearsonmylabandmastering.com/northamerica/myeconlab/students/get-registered/index.html. F. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ EVIEWS G. ЕЖЕНЕДЕЛЬНАЯ ЭЛЕКТРОННАЯ ПОЧТА Важно: если вы не получаете электронные письма, свяжитесь с инструктором как можно скорее, так как вы, вероятно, не используете адрес электронной почты своего вычислительного центра! H.ЭЛЕКТРОННЫЙ ЭТИКЕТ A. ОБЗОР КУРСА B. ОЦЕНКА Во-вторых, есть также семь викторин, состоящих из десяти вопросов с несколькими вариантами ответов, типичных для тех, которые вы встретите на экзаменах, и шести сопутствующих эмпирических заданий. Вы выполните эти задания в MyEconLab. Будет сброшен самый низкий балл (если вы пропустите задание и получите ноль, этот балл будет сброшен). Вам будет разрешено пройти каждую викторину дважды (и сохранить наивысший балл из двух) и каждое эмпирическое задание пять раз (опять же, будет сохранен наивысший балл).Тесты будут составлять 15% вашей оценки, а эмпирические задания также будут стоить 15% (так что вместе они составляют 30% вашей оценки). Крайние сроки и веса оценок для экзаменов и заданий, а также крайний срок для завершения «Введение в онлайн-тестируемый» перечислены ниже. оценок в курсе будут изогнутыми. C. ЧЕТЫРЕ ВАЖНЫХ ЗАМЕЧАНИЯ ПО ЭКЗАМЕНАМ, СДАННЫМ НА SSIL . Во-первых, не будет исключений из сроков сдачи экзаменов и не будет экзаменов по макияжу.Вы должны сдать экзамен до истечения крайнего срока, чтобы получить кредит за экзамен. Если возникает серьезная чрезвычайная ситуация, вы должны связаться с инструктором заблаговременно до крайнего срока и предоставить официальную документацию с номерами телефонов. Во-вторых, экзамены могут быть сданы до крайнего срока, и для сдачи экзамена требуется предварительное бронирование. Но не дожидайтесь последней минуты, чтобы запланировать экзамены, так как места для тестирования быстро заполнятся. В-третьих, веб-страница SSIL позволяет вам записаться на экзамен за две недели, независимо от крайних сроков, указанных выше.Например, если вы войдете в систему 19 апреля, чтобы записаться на экзамен 1, SSIL позволит вам запланировать экзамен, скажем, 27 апреля, но обратите внимание, что 27 апреля выходит за рамки крайнего срока для экзамена 1 (на 1 день), и этот экзамен не засчитывается! Не интерпретируйте даты, указанные на веб-странице SSIL, как продление сроков сдачи экзаменов — это не так! В-четвертых, экзамены — это закрытая книга и закрытые записи. D. ТРИ ВАЖНЫХ ЗАМЕЧАНИЯ К ЗАДАНИЯМ, ЗАПОЛНЕННЫЕ В MYECONLAB . Во-первых, как и в случае с экзаменами, исключений из сроков выполнения заданий не будет.Вы должны выполнить каждое задание к дню крайнего срока, чтобы получить кредит, но, конечно, вы можете выполнить его раньше, если хотите. Во-вторых, эти задания будут выполнены в MyEconLab, и самый низкий балл из семи будет удален. В-третьих, поскольку цель заданий — помочь усвоить материал курса, задания представляют собой открытую книгу и открытые заметки, и у вас будет два шанса на каждую викторину, пять шансов на каждое эмпирическое задание. E. ТЕКСТ И ДРУГИЕ УЧЕБНЫЕ ИСТОЧНИКИ .Помимо текста, для каждой главы есть видеолекции, которые максимально приближают ее к традиционному курсу. 1. Текст : Джеймс Сток и Марк Уотсон, Введение в эконометрику, 3-е издание, Pearson. Текст должен быть включен в MyEconLab. Он должен быть доступен в книжном магазине или здесь: http://www.mypearsonstore.com/bookstore/introduction-to-econometrics-update-plus-new-myeconlab-9780133595420 (обратите внимание, что цифровая версия Более дешевый). 2. Видеолекции : Видеолекции доступны по адресу http://economistsview.typepad.com/economics320/ или https://www.youtube.com/my_videos?o=U (на сайте YouTube сложнее ориентироваться ). Если ваше соединение достаточно быстрое, лучше всего будет воспроизводить видео в полноэкранном режиме (текст на доске будет легче читать). F. ЕЖЕНЕДЕЛЬНЫЙ СПИСОК ДЛЯ ЧТЕНИЯ ТЕКСТА И ГЛАВ ПО ЗАДАНИЯМ И ЭКЗАМЕНАМ . Каждой главе присваиваются все обычные страницы, кроме приложений.Если вы запланируете экзамен до крайнего срока, вам придется ускорить изучение материала в соответствии со темпом, указанным ниже. Примечание: крайний срок для введения SSIL в режиме онлайн: суббота, 9 января Неделя 1 : Неделя 2 : Неделя 3 : Неделя 4 : Неделя 5 : Неделя 6 : Неделя 8 : Неделя 9 : Неделя 10 : ФИНАЛ (Всеобъемлющий) Примечание : недели указывают, когда вы должны закончить работу с материалом, e.грамм. Главы 1, 2 и 3, содержащие вводный и обзорный материал, должны быть завершены к концу недели 2, глава 4 должна быть завершена к концу недели 3 и т. Д. Также обратите внимание, что крайний срок для завершения теста для главы 7 — СРЕДА. недели 8. Обзор: Этот онлайн-курс состоит из 28 удаленных занятий, которые проводятся дважды в неделю по субботам и воскресеньям с 12:00 до 14:00. по питтсбургскому времени ( по лондонскому времени минус 5 часов, кроме 25-31 октября, когда оно составляет минус четыре часа). Требования: Ожидается, что зарегистрировавшиеся учащиеся будут присутствовать на всей последовательности. Тем, кто не посещает регулярно, может быть отказано в доступе к курсу. Регистрация: Этот курс открыт для докторов наук. студенты или доктора философии обладатели экономических или смежных специальностей. Рекомендательное письмо может потребоваться для подтверждения соответствующего предварительного обучения. Регистрация заканчивается 17 октября 2020 г. Курс анализирует структурную оценку и тестирование нелинейных моделей. Мы исследуем взаимосвязь между экономической теорией, идентификацией, оценкой и эконометрической практикой. Он разрабатывает структурные подходы для анализа больших наборов поперечных и продольных данных, используя ограничения, вытекающие из равновесных динамических результатов в индивидуальных задачах оптимизации с дискретным выбором и некооперативных играх.Мы исследуем эмпирическое содержание, характеризуем идентификацию, оцениваем альтернативные методы оценки и процедуры тестирования, а также рассматриваем контрфакты. Он состоит из шести сегментов: Веб-сайт курса: http://comlabgames.com/structuraleconometrics Пожалуйста, смотрите записи ниже. Лекция 1, часть 1-24 октября Лекция 2, часть 1 — 25 октября Лекция 2, часть 2-25 октября Мы здесь, чтобы помочь и поддержать вас на протяжении всего вашего обучения в LSE, независимо от того, нужна ли вам помощь в учебе, поддержка вашего благополучия и благополучия или просто для развития на личном и профессиональном уровне. Независимо от вашего запроса, большого или малого, вы можете поговорить с целым рядом людей, которые будут рады помочь. Академические наставники — академический сотрудник, который встречается с вами в течение года, чтобы обсудить ваш академический прогресс и который может помочь с любыми академическими, административными или личными вопросами, которые у вас есть. (См. Обучение и оценка) Библиотекари отдела — они смогут помочь вам ориентироваться в библиотеке и максимально использовать ее ресурсы во время учебы. Служба размещения — они могут посоветовать проживание в общежитиях и дать рекомендации по вопросам, связанным с частным размещением. Классные руководители и руководители семинаров — они смогут помочь с вопросами, относящимися к конкретному курсу, который вы изучаете. Служба инвалидности и благополучия — сотрудники являются экспертами в области долгосрочных состояний здоровья, сенсорных нарушений, психического здоровья и особых трудностей в обучении. Они предлагают конфиденциальные и бесплатные услуги, такие как консультирование студентов, — программа поддержки сверстников , — организация корректировок экзаменов, и проведение групп и семинаров. ИТ-помощь — круглосуточная поддержка по всем вашим техническим вопросам. Центр веры LSE — дом для разнообразных религиозных мероприятий LSE и программ трансформационного межконфессионального лидерства, а также место для богослужений, молитв и тихих размышлений. Он включает в себя исламские молельные комнаты и основное место для поклонения. Это также место для занятий по благополучию на территории кампуса, которое открыто для всех студентов и сотрудников всех вероисповеданий. Языковой центр — центр специализируется на предоставлении языковых курсов, ориентированных на потребности студентов и практиков в области социальных наук. Мы предлагаем программы предварительного обучения английскому языку для академических целей; Поддержка английского языка во время учебы; современные языковые курсы на 9 языках; корректура, перевод и проверка подлинности документов, а также деятельность сообщества по изучению языков. LSE Careers — с помощью LSE Careers вы можете максимально использовать возможности, которые предлагает Лондон.Какими бы ни были ваши будущие карьерные планы, LSE Careers будет работать с вами, предлагая вам возможности и опыт от стажировок и волонтерства до сетевых мероприятий и идей работодателей и выпускников. Библиотека LSE Британская библиотека политических и экономических наук, основанная в 1896 году, является крупнейшей международной библиотекой социальных наук. Он остается открытым допоздна, имеет много отличных ресурсов и является прекрасным местом для учебы. Как студент LSE, вы будете иметь доступ к ряду других академических библиотек в Большом Лондоне и по всей стране. LSE LIFE — это место, куда вам следует пойти, чтобы развить навыки, которые вы будете использовать как ученик, так и за его пределами. Центр проводит беседы и семинары по навыкам, которые вы найдете полезными в классе, предлагает индивидуальные занятия с консультантами по обучению, которые могут помочь вам с чтением, составлением заметок, письмом, исследованиями и пересмотром экзаменов, а также проводят сеансы прямого доступа. для академической и личной поддержки (см. «Обучение и оценка»). Союз студентов LSE (LSESU) — они предлагают академические, личные и финансовые консультации и финансирование. Академия PhD — доступна для аспирантов, где бы они ни находились, для участия в междисциплинарных мероприятиях и других мероприятиях по профессиональному развитию, а также для доступа ко всем услугам, связанным с их регистрацией. Стоматологическая практика Sardinia House — предлагает частные стоматологические услуги со скидкой для студентов LSE. St Philips Medical Center — , расположенный в Pethwick-Lawrence House, центр предоставляет услуги первичной медицинской помощи NHS зарегистрированным пациентам. Центр обслуживания студентов — наши сотрудники могут ответить на общие вопросы и порекомендовать вам другие услуги LSE. Адвокаты и консультанты учащихся — у нас есть старший адвокат школы по делам учащихся и советник учащихся-женщин , которые могут помочь с академическими и пастырскими вопросами. Для получения доступа к записанным видеолекциям по основам эконометрики для BBE Semester IV вам необходимо зарегистрироваться на нашем сайте Если вы не зарегистрированы на нашем сайте, зарегистрируйтесь здесь (после регистрации, пожалуйста, сообщите нам по телефону +91 9899 192027, чтобы получить доступ) Если вы уже зарегистрированы, то Логин Базовый курс эконометрики для бакалавриата (с отличием) по бизнес-экономике, семестр IV, Университет Дели, читал г-н.Дирадж Сури. Видеолекции основаны на книгах, предписанных Университетом Дели. Продолжительность видеолекций составляет примерно 55 часов. Стоимость курса: рупий. 6000 Доступ к видеолекциям предоставляется на одном устройстве, компьютере под управлением Windows или телефоне Android, до конца семестра IV экзаменов. Как только вы получите доступ, вам необходимо войти в систему и загрузить наше приложение и все лекции из вашей учетной записи и играть на своем устройстве. Получите 1.1 Введение [25 минут] 2.1 Простая линейная регрессия [86 минут] 2.2 Теорема Гаусса-Маркова [70 минут] 2.3 Дисперсия оценок МНК [11 минут] 2.4 Эффективность оценщиков OLS [51 минута] 2.5 Выведение отклонения ошибки [34 минуты] 2,6 Числовые значения OLS [33 минуты] 2.7 Простая регрессионная интерпретация [78 минут] 2.8 Простая регрессионная интерпретация [38 минут] 2,9 Таблица Anova [58 минут] 2.10 Изменение шкалы [42 минуты] 2.11 Прогнозирование [46 минут] 2.12 Доказательства [58 минут] 3.1 множественная регрессия [60 минут] 3.2 Множественная регрессия [13 минут] 3.3 Множественная регрессия [76 минут] 3.4 Множественная регрессия [32 минуты] 3.5 Множественная регрессия [60 минут] 4.1 Функциональные формы [53 минуты] 4.2-кратная линейная модель [72 минуты] Модель 4,3 Лог Лин [36 минут] 4,4 Lin Log Model [60 минут] 4,5 Взаимная модель [35 минут] 4.6 Полиномиальная регрессия [35 минут] 4.7 Регрессия до источника [59 минут] 4.8 Стандартизированные переменные [18 минут] 5.1 фиктивные переменные [33 минуты] 5.2 Фиктивные переменные [29 минут] 5,3 фиктивные переменные [18 минут] 5,4 Модели Анковой [28 минут] 5.5 Эффект взаимодействия [29 минут] 5.6 Тест чау [49 минут] 5.7 Сезонное изменение [8 минут] 6.1 Недостаточное смещение [25 минут] 6.2 Недоподбор смещения [28 минут] 6.3 Превышение смещения [54 минуты] 7.1 Мультиколлинеарность [60 минут] 7.2 Мультиколлинеарность [53 минуты] 8.1 Гетероскедастичность [40 минут] 8.2 Гетероскедастичность [23 минуты] 8,3 Гетероскедастичность [55 минут] 8.4 Гетероскедастичность [28 минут] 9.1 Автокорреляция [56 минут] 9.2 Автокорреляция [35 минут] 9.3 Автокорреляция [51 минута] 9,4 Автокорреляция [7 минут] Часть 1 [31 минута] Часть 2 [33 минуты] Часть 3 [28 минут] Часть 1 [76 минут] Часть 2 [51 минута] Часть 1 [64 минуты] Часть 2 [34 минуты] Часть 1 [56 минут] Часть 2 [33 минуты] DBF — файл баз данных, возможность работы с которым раньше интегрировалась в среду Microsoft Office. С форматом работали приложения Access и Excel, позже Access был выведен из состава пакета и стал отдельной программой, а в Excel с 2007 года поддержка DataBaseFile была существенно ограничена. При невозможности открыть DBF-файл напрямую в Excel его нужно предварительно конвертировать. Однако DBF хоть и считается многими устаревшим форматом, но до сих пор широко используется в специализированных программах в сфере бизнеса, проектирования, инженерной сфере. Везде, где требуется работа с большими массивами информации, их структурирование и обработка, выполнение запросов. Например, программный комплекс 1С Предприятие целиком основан на управлении базами данных. А учитывая, что масса офисной документации и данных проходит в Excel, то вопрос интегрированной работы с этими форматами актуален и востребован. В Excel 2003 была возможность открыть и редактировать DBF, а также сохранять в этом формате документы XLS: ВАЖНО. Начиная с 2007 года вы можете открыть и просмотреть в Excel формат баз данных, но не можете вносить изменения, а также сохранять в нём документы .xls. Стандартные средства программы больше не предусматривают такой возможности. Однако существуют специальные надстройки для приложения, добавляющие ему такую функцию. В сети на различных форумах программисты выкладывают свои разработки, можно найти разные варианты. Наиболее популярную надстройку, которая называется XslToDBF, можно скачать с сайта разработчика http://basile-m.narod.ru/xlstodbf/download.html. Загрузка бесплатная, но по желанию можно поддержать проект, перечислив любую сумму на кошелёк или карту. Установка и использование: Если вы не хотите ничего менять в Office, не доверяете надстройкам и сторонним приложениям, то можно предложить более трудоёмкий способ преобразовать файл XLS в DBF: Такой способ не всегда работает удачно, часто возникают ошибки в обработке данных, в последующем сохранении. И он весьма долгий и неудобный. Чтобы не мучиться самим с офисными программами, создано множество приложений, позволяющих перевести данные из одного формата в другой. Во-первых, почти все мощные программы по работе с СУБД предполагают возможность экспорта в XLS и загрузки из него. Во-вторых, есть небольшие утилиты, специализирующиеся на конвертации. Во всех этих программах преобразование сводится к тому, что нужно открыть исходный файл, а затем выполнить команду «Конвертировать» или «Экспорт». Существуют и бесплатные сервисы онлайн-преобразования. На таких сайтах предлагается прислать (загрузить) исходный файл, нажать «Конвертировать», после чего появится ссылка на преобразованный документ. Насколько можно доверять таким услугам, решение индивидуальное, на свой страх и риск. Таким образом, открыть DBF в программе Excel можно, но если его версия 2007 и новее, то сделать с ним больше ничего не получится, только посмотреть. Для редактирования, сохранения в XLS есть специальные надстройки или программы, так же как и для преобразования в обратном направлении. Если у вас есть опыт конвертации и работы с DBF в разных приложениях, поделитесь своими советами в комментариях. Файл с расширением . Поскольку структура файла довольно проста, и формат использовался на ранних этапах, когда впервые появились программы баз данных, DBF считался стандартным форматом для структурированных данных. ArcInfo от Esri хранит данные в файлах, которые также заканчиваются на .DBF, но это называется атрибут shapefile формат. Эти файлы используют формат dBASE для хранения атрибутов для фигур. Файлы FoxPro Table также используют расширение DBF-файла, в программном обеспечении базы данных под названием Microsoft Visual FoxPro. dBASE — основная программа, используемая для открытия файлов DBF. Тем не менее, формат файла поддерживается и в других приложениях базы данных и для баз данных, таких как Microsoft Access, Microsoft Excel, Quattro Pro (часть Corel WordPerfect Office), OpenOffice Calc, LibreOffice Calc, HiBase Group DBF Viewer, Astersoft DBF Manager, DBF Viewer Plus, DBFView, Swiftpage Act! и Alpha Software Alpha Anywhere. Совет: Вы должны сохранить файлы базы данных Microsoft Works в формате dBASE, если вы хотите открыть их в Microsoft Excel. GTK DBF Editor является одним из бесплатных открывателей DBF для MacOS и Linux, но NeoOffice (для Mac), multisoft FlagShip (Linux) и OpenOffice тоже работают. Режим Xbase можно использовать с Emacs для чтения файлов xBase. ArcInfo из ArcGIS использует файлы DBF в формате файла атрибута шейп-файла. Прерванное программное обеспечение Microsoft Visual FoxPro также может открывать файлы DBF, будь то в формате базы данных или FoxPro Table. Большая часть программного обеспечения выше, которое может открыть или отредактировать файл DBF, скорее всего, также преобразует его. Например, MS Excel может сохранять DBF-файл в любой формат, поддерживаемый этой программой, например CSV, XLSX, XLS, PDF и т. Д. Одна и та же HiBase Group, которая выпустила упомянутый выше DBF Viewer, также имеет DBF Converter, который преобразует DBF в CSV, форматы Excel, такие как XLSX и XLS, простой текст, SQL, HTM, PRG, XML, RTF, SDF или TSV. Замечания: Конвертер DBF может экспортировать только 50 записей в бесплатной пробной версии. Вы можете перейти на платный выпуск, если вам нужно экспортировать больше. dbfUtilities экспортирует DBF в форматы файлов, такие как JSON, CSV, XML и Excel. Он работает через dbfExport инструмент, включенный в набор dbfUtilities. Вы также можете конвертировать DBF-файл с помощью DBF Converter. Он поддерживает экспорт файла в CSV, TXT и HTML. Файлы DBF часто видны с текстовыми файлами, использующими расширение .DBT или .FPT. Их цель — описать базу данных записками или заметками в необработанном тексте, который легко читать. Файлы NDX представляют собой файлы с одним индексом, которые хранят информацию о поле и структуру базы данных; он может содержать один индекс. Файлы MDX — это файлы с несколькими индексами, которые могут содержать до 48 индексов. Все сведения о заголовке формата файла можно найти на веб-сайте dBASE. Релиз dBASE в 1980 году стал его разработчиком, Ashton-Tate, одним из крупнейших издателей программного обеспечения для бизнеса на рынке. Первоначально он запускался только в операционной системе микрокомпьютера CP / M, но вскоре был перенесен на DOS, UNIX и VMS. Позднее в этом десятилетии другие компании начали выпускать собственные версии dBASE, включая FoxPro и Clipper. Это вызвало выпуск dBASE IV, который появился примерно одновременно с SQL (Structured Query Language) и растущим использованием Microsoft Windows. К началу 1990-х годов, когда продукты xBase по-прежнему достаточно популярны, чтобы быть лидером в бизнес-приложениях, три лучших фирмы, Ashton-Tate, Fox Software и Nantucket, были приобретены соответственно Borland, Microsoft и Computer Associates. Если ваш файл не открывается с предложениями выше, дважды проверьте расширение файла, чтобы убедиться, что он действительно читает как DBF. В некоторых форматах файлов используются расширения файлов, которые пишутся аналогично, но на самом деле находятся в совершенно другом формате и не могут открываться с помощью средств просмотра и редакторов DBF. Одним из примеров является DBX-файлы. Это могут быть файлы электронной почты Outlook Express или файлы расширения AutoCAD Database Extension, но в любом случае они не могут открываться с помощью тех же инструментов, о которых говорилось выше. Если ваш файл не открывается с этими программами базы данных, убедитесь, что вы фактически не имеете дело с DBX-файлом. Если ваш файл действительно является файлом DBK, он может быть в формате файла резервной копии мобильного телефона Sony Ericsson. Вероятно, он может быть открыт с помощью Sony Ericsson PC Suite или инструмента для распаковки файлов, такого как 7-Zip, но он не будет работать с приложениями базы данных выше. В 1С 8.3 есть возможность массово загрузить список номенклатуры из табличного документа, например, из файла Excel. Для загрузки мы используем внешнюю обработку ЗагрузкаДанныхИзТабличногоДокумента.epf для управляемых форм (8. Чтобы запустить внешнюю обработку, нужно зайти в меню «Файл», далее «Открыть» и выбрать эту обработку из каталога, в котором она была сохранена: После того как обработка открылась в 1С, можно приступать к работе с ней. В первую очередь нам нужно определиться, куда и что мы будем загружать: Я хочу привести пример на справочнике «Номенклатура«. Я создал некий файл с данными в формате xls. Обращу внимание, что файл нужно сохранить в формате «Книга Excel 97 – 2003, то есть расширение должно быть именно xls (если мы загружаем из Excel-я). Обработка умеет загружать также файлы формата: Получите 267 видеоуроков по 1С бесплатно: Вот так выглядит файл Excel с исходными данными, который мы будем загружать в справочник «Номенклатура»: Я не стал прописывать все поля справочника, так как этого достаточно для понимания принципа загрузки. Кроме того, этих данных хватает для начала работы с данными позициями. Данных позиций пока нет в информационной базе 1С, и мы сейчас туда их загрузим. Нажимаем на значок «Открыть» (на рисунке обозначен как «Выбор источника») и выбираем файл с данными. Можно использовать простое копирование информации. Мой файл с примером можно скачать здесь. Данные загрузятся в обработку автоматически. Теперь проверим, правильно ли мы заполнили наши данные. Для этого нажимаем кнопку «Контроль заполнения». Как видно, у нас появились ошибки! Будем устранять. Заходим на закладку «Настройка»: Прежде чем исправлять ошибки, хочу обратить внимание на одну важную деталь. Программа изначально не знает, по какому полю ей искать элемент справочника на случай, если он там уже есть. Поэтому ей нужно его указать. Я предпочитаю искать по коду, так как он, как правило, уникален. В колонке «Поле поиска» в строке «Код» ставим галочку. Теперь, если запись с таким кодом будет найдена, она будет заменена, в другом случае — создана. Важно! Если не указать поле поиска, то могут появиться дубли номенклатуры. Особенно после второй загрузки похожего файла! Теперь посмотрим, почему ругается на поле «Единица». Дело в том, что единицы измерения в 1С 8.3 хранятся в отдельном справочнике, и обработка по умолчанию ищет эту единицу по наименованию. А на самом деле словом единица прописана в поле «Полное наименование». К сожалению, обработка может вести поиск только по «Наименованию» и «Коду» (для программиста возможности шире). Теперь смотрим, что нам что-то там про «Услугу» говорят в списке ошибок. Еще одно важное замечание. Колонки в файле должны располагаться строго в том же порядке, как и строки полей справочника. А у нас «Вид номенклатуры» находится в самом низу, а в файле после колонки «Комментарий». Для того чтобы поднять строку «Вид номенклатуры» вверх, существуют синие стрелочки вверху формы. С помощью стрелки «Вверх» поднимаем нужную строку и ставим под «Комментарием». Жмем «Загрузить данные», и на этот раз все проходит без ошибок: Видеоурок по загрузке товаров в 1С из файлов Excel: Другие статьи по 1С: Если вы начинаете изучать 1С программирование, рекомендуем наш бесплатный курс (не забудьте подписаться на YouTube — регулярно выходят новые видео): youtube.com/embed/gXYUsQcT7JI?list=PL6Nx1KDcurkBdxssD1k56SDnwuTuX2bBr» frameborder=»0″ allowfullscreen=»allowfullscreen»/> К сожалению, мы физически не можем проконсультировать бесплатно всех желающих, но наша команда будет рада оказать услуги по внедрению и обслуживанию 1С. Более подробно о наших услугах можно узнать на странице Услуги 1С или просто позвоните по телефону +7 (499) 350 29 00. Мы работаем в Москве и области. Microsoft Access 2016 Microsoft Excel 2016 Microsoft Visual FoxPro Corel Quattro Pro X7 Apache OpenOffice HiBase Group DBF Viewer 2000 Astersoft DBF Manager Просмотрщик DBF Plus DBFView Закон о Swiftpage! Программное обеспечение Alpha Alpha Anywhere Planamesa NeoOffice (Mac) GTK DBF редактор (Mac и Linux) мультисофт FlagShip (Linux) приложение / база данных / x-dbase приложение / dbf / x-dbf zz-приложение / zz-winassoc-dbf Вы хотите, чтобы конвертировал DBF в Excel без каких-либо проблем? Следуйте этой статье, чтобы узнать, как преобразовать DBF в Excel в Windows 10. Вы можете использовать три программы для преобразования DBF-файла в формат Excel в Windows 10: Давайте обсудим это подробно сейчас! Пользователи Microsoft Excel могут конвертировать файлы DBF в форматы Excel в Excel. Вы даже можете редактировать файлы DBF в MS Excel, используя его разнообразие инструментов. Сортировка данных, фильтрация данных, применение формул, вычисление значений, добавление различных типов, редактирование существующего содержимого файла DBF, вставка новых элементов, визуализация наборов данных, и многое другое. Чтобы преобразовать DBF в Excel, сначала откройте в нем файл DBF, а затем, если необходимо, отредактируйте записи по мере необходимости. Затем перейдите к File> Save as option и выберите формат Excel в качестве вывода. После этого просто укажите расположение вывода, а затем нажмите кнопку Сохранить , чтобы начать преобразование. Вы также можете использовать специальное программное обеспечение на основе DBF, которое позволяет просматривать, редактировать и конвертировать файлы DBF.Здесь я хочу упомянуть бесплатное программное обеспечение под названием DBF Viewer Plus. Это программное обеспечение специально разработано для просмотра, обновления и преобразования файлов DBF. Он позволяет конвертировать файл DBF в XLS и другие различные форматы. Некоторые из других поддерживаемых форматов вывода: CSV, RTF, WKS, PDF, XML и HTML. Чтобы выполнить преобразование с помощью этого программного обеспечения, импортируйте файл DBF, используя параметр Файл> Открыть . Теперь вы можете обновить запись файла DBF, если хотите. Затем перейдите к параметру File> Export и выберите Excel (XLS) в качестве выходного формата для преобразования DBF в Excel. LibreOffice — еще одна альтернатива конвертеру DBF в Excel для Windows 10. Запустите приложение LibreOffice Calc и затем импортируйте в него файл DBF.Теперь перейдите к параметру Файл> Сохранить как и установите выходной формат Excel, чтобы выполнить преобразование. При желании можно защитить паролем получившуюся книгу Excel. В этой статье я рассказал о том, как конвертировать DBF в Excel с помощью 3 различных программ. Вы можете использовать Microsoft Excel, специальную утилиту DBF или бесплатное офисное программное обеспечение с открытым исходным кодом для преобразования DBF в Excel. Читать : Пакетное преобразование AI в PNG, JPG, GIF, BMP с помощью этих бесплатных онлайн-инструментов. Вот список Лучшего бесплатного конвертера DBF в Excel для Windows. DBF — это формат файла, используемый dBASE (система управления базами данных), который в основном используется для хранения записей базы данных. Чтобы преобразовать файл базы данных в формате DBF в формат файла Microsoft Excel, вы можете использовать любое из перечисленных программ. Это программное обеспечение позволяет преобразовать файл DBF в файлы рабочих листов XLS, и XLSX .Помимо форматов Excel, вы можете конвертировать файлы DBF в различные другие форматы, включая CSV , HTML , XML , TXT и т. Д. Во всех этих программах вам разрешено изменять записи , присутствующие во входных данных. DBF файл. Следовательно, вы можете удалять записи, вставлять новые записи, редактировать значения в существующих полях, добавлять новую таблицу и т. Большинство из них представляют собой специализированное программное обеспечение для просмотра и редактирования файлов dBase.Таким образом, вы можете использовать их для общего просмотра и модификации данных DBF. Некоторое программное обеспечение в этом списке представляет собой специализированное офисное программное обеспечение, которое поставляется с модулем электронных таблиц. Таким образом, помимо преобразования DBF в Excel, с их помощью вы можете выполнять множество задач, связанных с электронными таблицами. Например, визуализация данных, оценка данных, расчет статистики и т. Д. -й процесс преобразования DBF в Excel во всех этих конвертерах довольно прост. Вы также можете проверить описание программного обеспечения, чтобы узнать точную процедуру преобразования.В общем, это способные, но простые конвертеры DBF в Excel, которые вы получаете бесплатно. LibreOffice Calc — одно из моих любимых программ для преобразования DBF в Excel и другие форматы электронных таблиц, такие как CSV, HTML и т. Д. Оно даже позволяет защищать паролем выходные файлы Excel, что является еще одним преимуществом. DBF Viewer Plus — еще одно хорошее программное обеспечение, которое представляет собой специальный просмотрщик, редактор и конвертер файлов DBF. Вам также могут понравиться некоторые лучшие бесплатные программы преобразования Excel в DBF, программы DBF Viewer и программы преобразования Excel в HTML для Windows. LibreOffice Calc — это бесплатный конвертер DBF в Excel с открытым исходным кодом для Windows, Mac и Linux. Это в первую очередь программное обеспечение для работы с электронными таблицами, которое используется для создания электронных таблиц в различных форматах. По сути, это программное обеспечение поставляется с LibreOffice , популярным бесплатным офисным пакетом с открытым исходным кодом. Итак, вы также получаете в комплекте какое-то другое офисное программное обеспечение. Это программное обеспечение включает LibreOffice Draw, LibreOffice Impress, LibreOffice Writer и т. Д. Вы также можете конвертировать DBF в ODS, CSV, HTML, TXT, PDF и некоторые другие форматы. LibreOffice Calc — это программа для работы с электронными таблицами, которую можно использовать для решения различных задач, связанных с электронными таблицами, включая преобразование DBF в Excel. DBF Viewer Plus — это многофункциональное программное обеспечение DBF, которое также можно использовать для преобразования DBF в Excel. Он предоставляет множество полезных функций, с помощью которых вы можете просматривать, анализировать и редактировать файлы DBF. Некоторые из этих функций: Создать индекс, Добавить новую таблицу, Изменить поле, Поиск слов, Применить фильтр, и т. Это один из моих любимых конвертеров DBF в Excel, поскольку вы можете быстро конвертировать файл DBF во множество форматов, включая XLS, CSV, HTML и т. Д. Кроме того, вы получаете гибкость для обновления записей перед преобразованием. DBF Commander — хорошая бесплатная программа для конвертации DBF в Excel для Windows. По сути, это специальный просмотрщик DBF и программное обеспечение для редактирования. Используя его, вы можете открывать и просматривать файлы dBase, а также редактировать их в соответствии с вашими требованиями.Он поставляется с некоторыми дополнительными функциями, одной из которых является функция преобразования файлов. Вы можете просто открыть в нем файл DBF, а затем преобразовать его в разные форматы, включая Excel. Это программное обеспечение предоставляет множество удобных инструментов для просмотра и анализа файлов DBF. Таким образом, перед преобразованием вы также можете проанализировать файл DBF, используя такие функции, как структура файла , сортировка, фильтрация записей, расширенная статистика, панель SQL, и т. Д. Кроме того, вы можете изменить файл DBF, а затем преобразовать его в файл Excel. Давайте рассмотрим пошаговую процедуру преобразования DBF в Excel в нем. Позволяет сохранять файл DBF в старой версии Excel i.е., XLS. Помимо XLS, вы можете конвертировать DBF в файлы CSV, HTML и XML. Это простой, но эффективный конвертер DBF в Excel, который также можно использовать для просмотра и редактирования файлов DBF. DBFViewer , как следует из названия, представляет собой специальный просмотрщик файлов DBF, который также действует как конвертер DBF в Excel.В нем вы можете импортировать файл DBF с несколькими записями, а затем преобразовать его в файл Excel с помощью специальной опции. Помимо Excel, он также позволяет конвертировать DBF в HTML. Перед преобразованием вы можете вручную отредактировать записи, изменив значения полей. Преобразует DBF в рабочий лист XLS. Это еще один приятный и удобный конвертер DBF в XLS, который в первую очередь представляет собой программу для просмотра и редактирования DBF. WPS Office — это бесплатный офисный пакет, который также можно использовать в качестве программного обеспечения для конвертации DBF в Excel. Он также позволяет редактировать запись файла DBF перед преобразованием в Excel. Вы можете редактировать значения в любом из полей, добавлять новые записи, удалять существующие записи и т. Д. Теперь давайте рассмотрим процесс преобразования DBF в Excel в нем. Это хорошее офисное программное обеспечение, которое можно использовать для различных целей, включая преобразование DBF в Excel. xBaseView DBF Viewer & DBF Converter — еще одна бесплатная программа для конвертации DBF в Excel для Windows. Это хороший конвертер DBF для преобразования файлов dBase в Excel и множество других форматов, упомянутых выше. Используйте FME для создания пользовательских рабочих процессов, преобразующих DBF в электронные таблицы Excel. Быстро и легко конвертируйте ваши DBF (файлы базы данных) в электронные таблицы Microsoft Excel с помощью FME. Таблицы, хранящиеся в вашем DBF, читаются непосредственно FME и реструктурируются для вывода в виде файлов.xls файлы. FME имеет интуитивно понятный и простой в использовании графический пользовательский интерфейс. Кодирования не требуется! Имея на выбор множество преобразователей, вы можете быть уверены, что ваши новые, настроенные файлы будут выглядеть именно так, как вы хотите. Упростите информацию, содержащуюся в DBF, с помощью TestFilter для выполнения запросов или используйте AttributeCreator для создания новых значений и получения нового оптимизированного файла XLS в кратчайшие сроки. FME разработан для повышения вашей производительности, чтобы вы могли больше времени использовать свои данные и меньше — бороться с ними. После настройки в интуитивно понятном графическом пользовательском интерфейсе рабочие процессы преобразования DBF в XLSX могут автоматически запускаться в фоновом режиме с помощью FME Server. Настройте графики для запуска рабочего процесса и предоставления результатов тем, кто в этом нуждается. Ознакомьтесь с FME Server Tour Формат файла базы данных, DBF, используется несколькими приложениями баз данных и электронных таблиц, а также принят в качестве компонента хранения данных для геопространственных форматов, таких как Shapefile. Узнать больше Microsoft Excel считается отраслевым стандартом для приложений для работы с электронными таблицами, в которых есть инструменты расчета и построения графиков для анализа данных и составления отчетов. Узнать больше FME — это платформа интеграции данных с лучшей поддержкой пространственных данных. Экономьте время, используя интерфейс перетаскивания для подключения данных из сотен форматов и приложений, преобразования данных безграничными способами и автоматизации практически любого рабочего процесса с данными. Узнать больше Кредитная карта не требуется. Начните интегрировать данные сегодня! Преобразует одну или несколько таблиц в таблицы dBASE. Этот инструмент поддерживает следующие форматы таблиц в качестве входных: Для файлового ввода (.csv или .txt) первая строка входного файла используется в качестве имен полей в выходной таблице.Имена полей не могут содержать пробелы или специальные символы (например, $ или *), и вы получите сообщение об ошибке, если первая строка входного файла содержит пробелы или специальные символы. Подробнее о форматах таблиц, поддерживаемых в ArcGIS. Имя выходных таблиц dBASE будет основано на имени входной таблицы. Для управления именем вывода и дополнительных параметров преобразования используйте инструмент Таблица в таблицу. Этот инструмент можно использовать для экспорта таблицы ArcGIS в таблицу dBASE (.dbf), который можно читать и редактировать в Microsoft Excel. Инструменты «Копировать строки» и «Таблица в таблицу» также можно использовать для преобразования таблицы в файл dBASE. Если имя выходной таблицы уже существует в выходной папке, в конец имени будет добавлен номер, чтобы сделать его уникальным (например, OutputTbl_1.dbf). Следующий скрипт окна Python демонстрирует, как использовать функцию TableToDBASE в непосредственном режиме. Следующий автономный сценарий демонстрирует, как использовать функцию TableToDBASE. XLS в DBF никогда не было простым! Отличительными чертами преобразователя являются высокая скорость и точность вывода. Advanced XLS Converter позволяет преобразовать отдельный файл или папку Excel с файлами Excel в формат dbf из графического интерфейса или командной строки. «c: \ Program Files (x86) \ Advanced XLS Converter \ xlscnv.exe» file.xls file.dbf [/ VFP | / ФИЛЬТР | / КОЛОННЫ | / COLUMNSLIST | / ТИПЫ | / ОБРАТНЫЙ | / SHEETNUM | / ШАБЛОН | /ОТКРЫТО] «c: \ Program Files \ Advanced XLS Converter \ xlscnv. «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» sample.xls sample.dbf / COLUMNS: NAME, STREET / VFP «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» sample.xls sample.dbf / COLUMNS: ADDR, ZIP / EXCLUDE «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» образец.xls sample.dbf / ТИПЫ: ID: N10, Имя: C20 «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» sample.xls sample.dbf /template:mytemplate.tc «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» d: \ base \ *. Xls d: \ out \ / TODBF «c: \ Program Files \ Advanced XLS Converter \ xlscnv. «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» d: \ base \ *. Xlsx d: \ out \ / TODBF / VFP «c: \ Program Files \ Advanced XLS Converter \ xlscnv.exe» sample.xls mysheet.dbf / SHEETNUM: 1 Пожалуйста, не стесняйтесь Свяжитесь с нами . Обновлено вт, 25 мая 2021 г. Средний рейтинг покупателей: 4.87 (1267 голосов) Вернуться к главной странице конвертера XLS Первоначально искал в Интернете Python для преобразования базы данных dbf в Excel, я видел много … Может быть проблема с моей средой, использующей Python 3.6 для разработки в Windows. Необходимо установить win32com Вы можете использовать следующее: После завершения установки: Вывод результатов: Информация об ошибке: Итак, openpyxl не поддерживает xls … Что вы можете сделать: Предупреждающая информация: Итак, в приведенном выше коде запись Sheetname как Sheet_name не имеет предупреждающей информации. По-прежнему использовать информацию о модуле pandas: В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций. sin 00=0, cos 00 = 1. tg 00 = 0, котангенс от 00 будет неопределенным Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим: sin 300 = 1/2, cos 300 = √3/2, tg 300 = √3/3, ctg 300 = √3 Изобразим все полученные значения в виде тригонометрической таблицы: Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как: Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z …. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности. Разберем наглядно как использовать таблицу в решении. В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 10200 = 3000+3600*2. Найдем по таблице. Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке. Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса. Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов). Синус и косинус tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900. tg до 900 и ctg малых углов. Разберемся как пользоваться таблицами Брадиса в решении задач. Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040. Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях! Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/) Вы искали 6 ctg? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos 0 sin, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «6 ctg». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 6 ctg,cos 0 sin,cos 0 sin 0,cos sin 0,cos sin tg ctg таблица,cos sin tg углов таблица,cos sin таблица,cos sin таблица значений,cos и sin таблица,cos таблица брадиса,ctg 0 чему равен,ctg 180,ctg 30,ctg 30 градусов,ctg 40,ctg 44,ctg 45,ctg 45 градусов,ctg 5,ctg 5 2,ctg 6,ctg 6 pi,ctg 60,ctg 60 градусов,ctg п 2,ctg таблица,ctg30,sin 0 cos,sin cos 0,sin cos tg ctg таблица,sin cos tg ctg таблица значений,sin cos tg ctg таблица значения,sin cos tg таблица,sin cos tg углов таблица,sin cos таблица,sin и cos таблица,tg и ctg таблица,брадиса таблица cos,значение тангенса и котангенса таблица,значения cos и sin таблица,значения sin,значения sin cos,значения sin cos tg ctg таблица,значения sin и cos таблица,значения синуса косинуса тангенса таблица,значения синусов и косинусов таблица,значения синусов косинусов тангенсов котангенсов таблица,кос син табл,косинус и синус таблица,косинус синус и тангенс таблица,косинус синус таблица,косинусы синусы таблица,косинусы синусы тангенсы котангенсы таблица,котангенс 10,котангенс 15,котангенс 15 градусов,котангенс 225,котангенс 30,котангенс 35,котангенс 360,котангенс 4,котангенс 40,котангенс 45,котангенс 5,котангенс 60 градусов,котангенс 75,котангенс таблица,полная таблица sin cos tg ctg,полная таблица косинусов и синусов,полная таблица косинусов синусов,полная таблица синусов и косинусов,полная таблица синусов косинусов,син кос табл,син кос таблица,син кос танг таблица,син кос тг ктг таблица,синус и косинус 20 градусов,синус и косинус тангенс таблица,синус косинус и тангенс таблица,синусы косинусы таблица,синусы косинусы таблица значений,синусы косинусы тангенсы котангенсы таблица брадиса,табл кос и син,табл кос син,табл син и кос,табл син кос,таблица cos sin,таблица cos sin tg,таблица cos sin tg ctg,таблица cos sin tg ctg полная,таблица cos sin углов,таблица cos брадиса,таблица cos и sin,таблица ctg,таблица sin cos,таблица sin cos tg,таблица sin cos tg ctg,таблица sin cos tg ctg значения,таблица sin cos tg ctg полная,таблица sin и cos,таблица брадиса косинусы синусы тангенсы котангенсы,таблица брадиса котангенс,таблица брадиса синусы и косинусы тангенсы котангенсы,таблица брадиса синусы косинусы тангенсы котангенсы,таблица всех синусов косинусов тангенсов и котангенсов,таблица градусов,таблица градусов синус косинус тангенс котангенс,таблица градусов тангенсов синусов косинусов тангенсов,таблица значений cos sin,таблица значений cos sin tg,таблица значений sin cos,таблица значений sin cos tg,таблица значений sin cos tg ctg,таблица значений sin cos tg ctg таблица,таблица значений tg cos sin,таблица значений tg sin cos,таблица значений косинус синус,таблица значений косинусов синусов тангенсов,таблица значений котангенса,таблица значений синус косинус тангенс,таблица значений синуса и косинуса,таблица значений синусов и косинусов,таблица значений синусов косинусов,таблица значений синусов косинусов тангенсов,таблица значений синусов косинусов тангенсов котангенсов,таблица значений синусы косинусы,таблица значений тангенса и котангенса,таблица значения cos sin tg ctg,таблица значения cos и sin,таблица значения sin cos tg ctg,таблица значения sin и cos,таблица значения углов,таблица кос син,таблица кос син тг ктг,таблица кос тг син,таблица косинус синус,таблица косинуса и синуса и тангенса,таблица косинуса синуса,таблица косинуса синуса и тангенса,таблица косинуса синуса тангенса котангенса,таблица косинусов и синусов в радианах,таблица косинусов и синусов тангенсов,таблица косинусов и синусов тангенсов котангенсов,таблица косинусов и синусов тангенсов котангенсов в радианах,таблица косинусов и тангенсов,таблица косинусов синусов и тангенсов,таблица косинусов синусов полная,таблица косинусов синусов тангенсов,таблица косинусов синусов тангенсов и котангенсов в радианах,таблица косинусов синусов тангенсов котангенсов,таблица косинусов синусов тангенсов котангенсов полная,таблица косинусов тангенсов,таблица косинусы синусы,таблица котангенса,таблица котангенсов,таблица котангенсов углов от 0 до 90,таблица син кос,таблица син кос тан катан,таблица син кос танг,таблица син кос тг ктг,таблица синус косинус,таблица синус косинус и тангенс,таблица синус косинус тангенс,таблица синус косинус тангенс и котангенс таблица,таблица синуса и косинуса и тангенса,таблица синуса косинуса,таблица синуса косинуса и тангенса,таблица синуса косинуса тангенса и котангенса,таблица синуса косинуса тангенса котангенса,таблица синуса тангенса и косинуса,таблица синусов и косинусов в радианах,таблица синусов и косинусов всех углов,таблица синусов и косинусов полная,таблица синусов и косинусов тангенсов,таблица синусов и косинусов тангенсов котангенсов,таблица синусов и косинусов тангенсов котангенсов в радианах,таблица синусов косинусов,таблица синусов косинусов и тангенсов,таблица синусов косинусов полная,таблица синусов косинусов тангенсов,таблица синусов косинусов тангенсов и котангенсов,таблица синусов косинусов тангенсов и котангенсов от 0 до 360 и,таблица синусов косинусов тангенсов котангенсов,таблица синусов косинусов тангенсов котангенсов от 0 до 360,таблица синусов косинусов тангенсов котангенсов полная,таблица синусов косинусов тангенсов котангенсов полная таблица,таблица синусов тангенсов,таблица синусы косинусы,таблица тангенса синуса и косинуса,таблица тангенсов и косинусов,таблица тангенсов и котангенсов синусов и косинусов,таблица тангенсов котангенсов косинусов синусов в радианах,таблица тангенсов котангенсов синусов косинусов в радианах,таблица тангенсов синусов,таблица тангенсов синусов и косинусов,таблица тг ктг син кос,таблица тригонометрии,таблица тригонометрическая углов,таблица тригонометрические,таблица тригонометрических значений с градусами,таблица углов,таблица углов cos sin,таблица углов sin cos tg,таблица углов косинусов синусов,таблица углов синусов и косинусов,таблицу синусов и косинусов,таблицы косинусов синусов,таблицы синусов косинусов,таблицы синусов косинусов тангенсов и котангенсов,таблицы синусов косинусов тангенсов котангенсов,таблицы тригонометрических функций,таблиця кутів,табличные значения синусов косинусов,табличные значения синусов косинусов тангенсов котангенсов,тангенс синус и косинус таблица,тригонометрическая таблица,тригонометрическая таблица косинусов синусов,тригонометрическая таблица синусов косинусов,тригонометрические таблица,тригонометрические таблицы,тригонометрия таблица косинусов и синусов. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 6 ctg. Просто введите задачу в окошко и нажмите
«решить» здесь (например, cos 0 sin 0). Решить задачу 6 ctg вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. Таблица из нового учебника т.е. три таблицы вместо одной Многие современные учебники вместо того, что бы учить детей — запутывают их ещё больше. Мы уже писали об этом, да и не только мы, но на днях я получил ещё один пример, прямо таки показательный и не смог обойти его вниманием. На просторах Интернета (и не только) можно неоднократно встретить утверждение, что старые учебники лучше новых. Но в большинстве своём дальше развивается мысль, что раньше и трава была зеленее и шоколад с мороженным вкуснее, да и кофе был «он», что делало его вкусным. Никаких подтверждений, скорее лёгкая самоирония и ностальгия. Ну так вот, сейчас я Вам раскрою на это глаза. Возьмём одну тему и посмотрим, что с нею сделали в современных учебниках. Смею Вас заверить, что такие либо подобные примеры можно найти почти во всех современных учебниках, причём по любым предметам. Началось всё с простого — ученица пожаловалась, что не может запомнить таблицу значений синусов и косинусов, а другой ученик поддержал её в этом. Я очень удивился — в моей памяти таблица была небольшой и занимала немного места, мирно соседствуя со свойствами этих функций и единичным кругом, на который всегда можно положиться. Потом вспомнил, что в учебниках не указывается как эту таблицу проще запомнить и решил наглядно это показать. Каково же было моё удивление, когда ученики сообщили, что у них в учебнике — друга таблица, намного больше. Заинтересовавшись, я решил взглянуть на эту таблицу и с удивлением обнаружил, что это не одна таблица! Из одной, сравнительно небольшой, таблицы сделали три! Мало того, что они на разных страницах (разворотах), так они ещё и разнесли их по разным параграфам! Фотографии этого «шедевра» современных веяний в образовании вы можете наблюдать в этой статье. Сразу замечу, что другой таблицы значений в синусов, косинусов, тангенсов и котангенсов в этом учебнике нет. У меня нет этой же версии учебника, но есть чуть старше, так в нём эти три таблицы находятся ещё на одной странице и в одной теме. Получается, что учебники становятся всё более непонятными?! Давайте разберёмся — что же тут не так. Для этого посмотрим на классическую таблицу: Классическая «старая» таблица 0 рад $$\pi$$ $$2\pi$$ Таблица из старых учебников Сравните её с теми монстрами на фотографиях!
Её (таблицу), конечно, можно рисовать по разному, но общий смысл должен быть доведён неизменно. Иногда, в старых учебниках встречалась сокращённая версия таблицы только для $\frac{\pi}{6}\,,\,\, \frac{\pi}{4}\,,\,\, \frac{\pi}{3}$ – для удобства запоминания, но при этом всегда пояснялось откуда брать недостающие значения. В формулах приведения – обязательно давались задания на углы, не входящие в эту таблицу. Так, на простых прмерах можно было ученикам понять и осознать — зачем нужны формулы приведения и/или единичный круг. Ещё раз повторюсь: если бы в учебнике, вместе с эти странными таблицами соседствовала классическая «старая» версия, то такого вопроса бы не стояло. Я даже допускаю, что раньше так и было, но потом кому-то пришла в голову «умная» идея её убрать. Итак, чем же отличается классическая «старая» таблица: Углы даны и в градусах и в радианах. Это способствует запоминанию и осознанию того, что углы можно указывать и в таком виде и в таком. Это наглядно. Да, ученики потом должны на лету переводить величины из одной системы в другую.{\circ}$? Только ученики об этом «просто» постоянно забывают, не все конечно… Углы даны по порядку, обычно по возрастанию. В новой версии таблица разделена на две части, причём принцип разделения не написан — о нём нужно догадываться тем, кто эту тему только проходит! Да, в каждой таблице углы расположены по возрастанию, но вторая таблица не является прямым продолжением первой! Об этом нигде не сказано, а углы даны в виде радиан, к которым ещё школьники не привыкли, к тому же они в виде дробей. Я вас удивлю, но многие троечники не знают дроби или знают их не очень хорошо. Они понимают, что $\frac{\pi}{6}<\frac{\pi}{4}<\frac{\pi}{3}$ , но для этого им нужно подумать, не у всех такие сравнения делаются «на лету». Есть такие, которые и не задумаются над этим. Да, им нужно повторить дроби, но они то этого не знают и учат тригонометрию, а их вместо того, что бы учить — путают. В результате они пытаются всё это заучить, не понимая даже нужный порядок. Вот какой смысл делать отдельную таблицу для углов кратных 45 градусам и для углов кратных 30 градусам? Наглядность значений тангенса и котангенса. Под значениями синуса и косинуса наглядно, в одной таблице. даны значения тангенса и котангенса. Нередко было и напоминание — как собственно они получаются: ${\rm tg}\, \alpha = \frac{\sin\alpha}{\cos\alpha} \;;\; {\rm ctg}\, \alpha = \frac{\cos\alpha}{\sin\alpha}$ Любой мог проделать нехитрый фокус — поделить в одной колонке значение в графе синуса на значение в графе косинуса (если он знал дроби, конечно) и получить значение в графе тангенса. Поделив косинус на синус — получить котангенс. Самостоятельно убедиться, что тангенса и котангенса не существует в тех случаях когда знаменатель равен нулю. Любой мог понять, что если умеешь делить, то помнить часть таблицы с тангенсом и котангенсом не обязательно — её можно получить в любой момент. И что же из этого мы видим в новом учебнике? Да ни-че-го. Таблица тангенсов и котангенсов расположена в другом параграфе и лишь невнятная ссылка в виде текста «зная значения синуса и косинуса… нетрудно вычислить соответствующие значения тангенса и котангенса» — может заронить правильную мысль в голову умного и любящего тригонометрию ученика. Раз нетрудно — почему наглядно не показать и не напомнить — как именно нетрудно? Некоторые считают, что если оставить что-то непонятным, то ученик заинтересуется, попытается понять это сам и лучше запомнит. Что ж, в теории это должно быть так, но на практике — ученику и так хватает загадок в учебнике и не за чем усложнять его задачу, ведь увидев слишком много непонятного – он просто плюнет и займётся чем-то другим, подумав: «математика — это не моё, тут всё так сложно!» Меньше значений. В новых учебниках дано множество значений углов, которые может где-то и полезны, но по большому счёту только вредны. У нас что — соревнования: кто больше значений знает? Так давайте в обязательном порядке учить таблицы Брадиса! Но таблицы Брадиса не дают значения абсолютно всех углов – нужно использовать формулы приведения. Старая таблица — сразу приучает, что значения углов известны только в ограниченном диапазоне и потом, это ещё много раз пригождается, начиная с того, что заучивать нужно только значения у углов в 30, 45 и 60 градусов. Новые же таблицы они не дают понять полезность формул приведения – ведь эти углы уже известны их нужно «просто запомнить» и всё. Вот только вместо трёх значений для одной функции приходится запоминать аж 12! (Я не считаю значения для 0, 90, 180, 270 и 360 градусов – они есть и тут и там, хотя на мой взгляд, они гораздо удобнее запоминаются в единичном круге, ну да каждый может запоминать так как ему удобнее – главное не отбирать эту возможность.) 12 вместо 3 – как вам такая математика? А если взять и синус и косинус — получится 24 значения вместо 6, т.е. 18 «лишних» значений! Понятно почему школьники никак не могут выучить и запомнить эту таблицу! В этом навозе (34 значения) найти жемчужину (16, включая др.) – сложно (18 лишних). А формулы приведения и/или единичный круг учить всё-равно придётся, но уже на более сложных примерах, что не способствует пониманию. Таблица одна, а не три, что само по себе плюс, поскольку не нужно искать другие части таблицы, тем более, если они на разных разворотах, да ещё и не на соседних. Для тех школьников, у кого визуальная память одна таблица — это огромнейший плюс, да и другим удобнее. Ну да кому из авторов новых учебников нужно, что бы школьники могли быстро найти три громадных таблицы, которые сложно запомнить? Угол альфа. Можете звать меня ретроградом, но почему в учебниках меняют буквы, обозначающие, скажем угол? Доходит до смешного: тема Функция y=sin x И первое же предложение: «…знакомьтесь, функция s=sin t» Зачем? Запутать школьников? И чем был плох угол альфа, что его убрали отовсюду? Это сделали, что бы сразу можно было понять — кто ещё учился по старым, а кто уже учится по новым учебникам — достаточно попросить написать формулу? Лично мне кажется, что в углах альфа и бета был какой-то шарм, рифма что-ли, но это — дело вкуса. А вот то, что теперь школьники с первого взгляда не узнают формулу из старого-проверенного учебника и им будет тяжелее, при желании, его читать — это уже существеннее, они ведь только учатся. Меньше запоминать. Никто не хочет работать просто так и делать больше того, что от него требуют. Исключения конечно встречаются, но не очень часто. В классической «старой» таблице можно было сразу увидеть, что по большому счёту, при желании можно запомнить только три значения: либо значения синуса у углов 30, 45 и 60 градусов, либо значения косинуса этих же градусов, либо, скажем два значения синуса и одно косинуса,либо ещё как – остальные значения можно получить путём зеркального отражения. И всё – наглядно. В новой же, хотя и можно увидеть эту идею, но запомнить как связное целое – очень сложно, ведь это две разных таблицы, два разных объекта для запоминания, да ещё отдельная таблица для тангенсов и котангенсов – голову свернёшь! Сокращённая таблица для лучшего запоминания Я уж не говорю про другие темы, типа формул приведения. Зачем давать все формулы сразу и в одном месте? Что бы их удобнее было учить? Нет, мы лучше дадим часть в одной теме, а часть в другой… Всё равно понимают и выучивают? Так дадим в учебнике только часть формул, наказав вывести остальные самостоятельно! А что? Про единичный круг, что он существует написали — так пусть выкручиваются! Непонятно написали? Не пояснили как соотносятся формулы приведения и единичный круг? Нет рисунков в теме про формулы приведения? Зато в в теме про единичный круг есть. Ну и что, что там про связь с формулами приведения нигде не указано — так они их ещё не проходили. Что? Непонятно? Хотите старый учебник? А что насчёт того, что про периодичность функций синуса и косинуса в некоторых новых учебниках говорится только под конец изучения тригонометрических функций? После единичного круга, после формул приведения, после изучения свойств функций синуса и косинуса? Это нормально? Простите — наболело. Статьи об образовании и о нас Таблица Брадиса — это таблица, которая поможет вычислить значения
синусов, косинусов, тангенсов и котангенсов углов с точностью до одной
минуты без калькулятора. Для таблиц Брадиса в качестве аргумента функций используется значение
угла, заданное в градусах. Если же значение аргумента дано в радианах,
то для перевода в градусы его следует умножить на 180 и разделить на
3.1415926. В таблице Брадиса представлены значения углов кратных 6 минутам. Если необходимо найти значения синуса, косинуса, тангенса или котангенса угла, который отсутствует в таблице Брадиса, следует выбирать наиболее близкое к нему значение. И добавить (отнять) к нему поправку соответствующую разнице, которая может быть равна 1′, 2′, 3′.
Примеры: При вычислении значений синуса поправка имеет положительный знак, для косинуса поправку необходимо брать с отрицательным знаком: Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи значение угла α (через число пи) Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. 0,2588 0,9659 0,2679 0,5000 0,5774 0,7071 0,7660 0,8660 0,5000 1,7321 7π/18 В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов . Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций. Навигация по странице. Список литературы. В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций. sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим: sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3 Изобразим все полученные значения в виде тригонометрической таблицы : Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как: Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z …. 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности. Разберем наглядно как использовать таблицу в решении. В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице. Для более поиска тригонометрических значений углов с точностью до минут используются . Подробная инструкция как ими пользоваться на странице Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса. Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов). Синус и косинус tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 . tg до 90 0 и ctg малых углов. Разберемся как пользоваться таблицами Брадиса в решении задач. Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040. Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046. При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054 При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397 Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967 Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях! Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/) ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций. В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. Школьная таблица синусов. Для тригонометрической функции косинус в таблице приведены значения для следующих углов: cos 0, cos 30, cos 45, cos 60, cos 90, cos 180, cos 270, cos 360 в градусной мере, что соответствует cos 0 пи, cos пи на 6, cos пи на 4, cos пи на 3, cos пи на 2, cos пи, cos 3 пи на 2, cos 2 пи в радианной мере углов. Школьная таблица косинусов. Тригонометрическая таблица для тригонометрической функции тангенс приводит значения для следующих углов: tg 0, tg 30, tg 45, tg 60, tg 180, tg 360 в градусной мере, что соответствует tg 0 пи, tg пи/6, tg пи/4, tg пи/3, tg пи, tg 2 пи в радианной мере углов. Следующие значения тригонометрических функций тангенса не определены tg 90, tg 270, tg пи/2, tg 3 пи/2 и считаются равными бесконечности. Для тригонометрической функции котангенс в тригонометрической таблице даны значения следующих углов: ctg 30, ctg 45, ctg 60, ctg 90, ctg 270 в градусной мере, что соответствует ctg пи/6, ctg пи/4, ctg пи/3, tg пи/2, tg 3 пи/2 в радианной мере углов. Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности. Значения тригонометрических функций секанс и косеканс приведены для таких же углов в градусах и радианах, что и синус, косинус, тангенс, котангенс. В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах. Еще три монстра тригонометрии. Первый — это тангенс 1,5 полутора градусов или пи деленное на 120. Второй — косинус пи деленное на 240, пи/240. Самый длинный — косинус пи деленное на 17, пи/17. Тригонометрический круг значений функций синус и косинус наглядно представляет знаки синуса и косинуса в зависимости от величины угла. Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи. Эта тригонометрическая таблица представляет значения синуса, косинуса, тангенса и котангенса для углов от 0 нуля до 90 девяносто градусов с интервалом через один градус. Для первых сорока пяти градусов названия тригонометрических функций необходимо смотреть в верхней части таблицы. В первом столбце указаны градусы, значения синусов, косинусов, тангенсов и котангенсов записаны в следующих четырех столбцах. Для углов от сорока пяти градусов до девяноста градусов названия тригонометрических функций записаны в нижней части таблицы. В последнем столбце указаны градусы, значения косинусов, синусов, котангенсов и тангенсов записаны в предыдущих четырех столбцах. Следует быть внимательными, поскольку в нижней части тригонометрической таблицы названия тригонометрических функций отличаются от названий в верхней части таблицы. Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций. Знаки тригонометрических функций представлены на рисунке выше. Синус имеет положительные значения от 0 до 180 градусов или от 0 до пи. Отрицательные значения синус имеет от 180 до 360 градусов или от пи до 2 пи. Значения косинуса положительны от 0 до 90 и от 270 до 360 градусов или от 0 до 1/2 пи и от 3/2 до 2 пи. Тангенс и котангенс имеют положительные значения от 0 до 90 градусов и от 180 до 270 градусов, что соответствует значениям от 0 до 1/2 пи и от пи до 3/2 пи. Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций. Тригонометрические функции синус, тангенс и котангенс являются нечетными функциями. Значения этих функций для отрицательных углов будут отрицательными. Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков. Отдельной странице находятся формулы приведения тригонометрических функций . В таблице значений для тригонометрической функции синус приведены значения для следующих углов : sin 0, sin 30, sin 45 … .\circ =0\). Тангенс и котангенс ты можешь отыскать самостоятельно по формулам: \( \displaystyle \text{t}g\ \alpha =\frac{\sin \alpha }{\cos \alpha }\), \( \displaystyle ctg\ \alpha =\frac{cos\ \alpha }{sin\ \alpha }\) Обрати внимание, что на ноль делить нельзя!! Теперь все полученные числа можно свести в таблицу: Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти. Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса \( \displaystyle 90\) градусов. Это неспроста! В частности: \( \displaystyle ctg 0=\frac{\cos 0}{\sin 0}=\frac{1}{0}=?????\) Поэтому мы с тобой будем считать, что тангенс \( \displaystyle 90\) градусов и котангенс нуля просто-напросто не определены! Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая: Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае. Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали. Теперь же пусть наш угол больше \( \displaystyle 90\) градусов и не больше чем \( \displaystyle 360\). Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти. Как мы поступаем? Да точно так же! Давай рассмотрим вместо вот такого случая… …вот такой: То есть рассмотрим угол \( \displaystyle \alpha \), лежащий во второй четверти. Что мы можем сказать про него? У точки \( \displaystyle {{M}_{1}}\), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты \( \displaystyle {{x}_{1}}\) и \( \displaystyle {{y}_{1}}\). Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен! Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом. Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника. Кстати, подумай, у каких углов косинус равен \( \displaystyle -1\)? А у каких \( \displaystyle -1\) равен синус? Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!). Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой. Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей. Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать: Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус. Представлена таблица Брадиса синусов и косинусов в удобном виде Чтобы распечатать таблицу Брадиса, Таблица Брадиса для синусов и косинусов даёт значение синуса любого острого угла, содержащего целое число градусов
и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число минут. Так, sin 70° 30`=0.9426.
Для получения синусов прочих углов нужна интерполяция, вводящая поправку на равность между
данным углом и ближайшим табличным. Эта поправка берется из соответствующего столбца поправок справа (курсив).
Она прибавляется к ближайшему меньшему значению синуса, если данный угол превосходит ближайший
меньший табличный на 1,2,3 минуты, и отнимается от ближайшего большего табличного синуса в остальных случаях.
Например, sin 70° 32`=0,9428, так как 9426+2=9428, и sin 70° 34`= 0,9430, так как 9432-2=9430.
Та же таблица синусов и косинусов служит для
разыскания косинусов, при чем надо пользоваться нумерацией градусов справа, нумерацией минут снизу и не забывать,
что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, звменяя их синусами
дополнительных углов. Представлена таблица Брадиса для тангенсов и котангенсов
в удобном виде Тригонометрические таблицы онлайн На базе mymathtables.com Таблица котангенса от 0 ° до 90 ° Таблица котангенса от 91 ° до 180 ° Таблица котангенса от 181 ° до 270 ° Таблица котангенса от 271 ° до 360 ° Таблица касательных от 0 ° до 90 ° Таблица касательной от 91 ° до 180 ° Таблица касательных от 181 ° до 270 ° Таблица касательных от 271 ° до 360 ° Тангенс угла — это отношение длины противоположной стороны к длине соседней стороны: так называется потому, что его можно представить как отрезок прямой, касающийся окружности, то есть линии, которая касается окружности, от Латинская linea tangens или касательная линия. Ниже таблицы Значения синуса, косинуса, тангенса, косеканса, секанса и котангенса при различных углах наклона
(0 °, 30 °, 45 °, 60 °, 90 °). На этой странице мы рассмотрим последнюю из трех основных тригонометрических функций ( синус , косинус и тангенс ).История функции тангенса несколько отличается от истории функций синуса и косинуса. В то время как синус и косинус возникли из-за необходимости производить астрономические вычисления, касательная больше возникла из-за таких вещей, как необходимость рассчитывать высоту зданий. Считается, что в шестом веке до нашей эры греческий философ Фалес посетил Египет, где он узнал о египетских методах вычисления высоты и расстояния путем измерения длины теней. Говорят, что он измерил высоту пирамиды, например, измерив длину тени пирамиды (измеренную от центра пирамиды) в то же время дня, когда длина его собственной тени была равна его высоте. . Идея использования длины теней как для измерения высоты физических объектов, так и для отметки времени использовалась на протяжении тысячелетий египетской и вавилонской цивилизациями. Инструмент, используемый для выполнения таких измерений, назывался теневой стержень или гномон , одна из форм которого до сих пор может рассматриваться как вертикальный компонент солнечных часов. Фалес признал, что, когда солнце движется по небу, соотношение между длиной тени объекта и его высотой будет одинаковым для всех объектов.Однако связь между высотой объекта, длиной тени объекта и углом подъема солнца в небе, по-видимому, не была выражена в терминах тригонометрической функции до гораздо более позднего времени. К середине девятого века нашей эры арабские ученые усвоили большую часть астрономических и математических знаний древнего мира. Они были знакомы со всеми шестью тригонометрическими функциями в современном использовании и составили точные тригонометрические таблицы, включая таблицы касательных и котангенсов, которые они назвали таблицами теней .Действительно, термин «касательная» появился только в конце шестнадцатого века нашей эры, когда его использовал датский математик и физик Томас Финке в своей книге Geometriae Rotundi . До этого тангенс и котангенс были известны под латинскими названиями umbra recta и umbra versa , что означало прямая тень (горизонтальная тень, отбрасываемая вертикальным гномоном) и повернутая тень (вертикальная тень, отбрасываемая прикрепленным к стене гномоном) соответственно. Касательная функция связана с касательной . Касательная линия — это прямая линия, которая касается кривой в одной точке. В точке, где касательная линия касается кривой, мы можем сказать, что касательная линия «идет в том же направлении», что и кривая в этой точке. Точнее, касательная имеет тот же наклон , что и кривая в точке контакта . На снимке экрана ниже показана касательная линия для единичной окружности в точке, где отрезок OP пересекает окружность окружности.Отрезок OP — это радиус окружности, а также гипотенуза прямоугольного треугольника OPE. Отрезки EP и EO представляют собой , противоположные и смежных сторон прямоугольного треугольника по отношению к углу θ . Поскольку единичный круг имеет диаметр на одну единицу , длины отрезков EP и EO также равны по значению синусу и косинусу соответственно. Касательная линия касается единичной окружности в точке P Обратите внимание, что касательная проходит перпендикулярно гипотенузе прямоугольного треугольника. Функция касательной, как и функции синуса и косинуса, представляет собой отношение двух сторон прямоугольного треугольника. Он также представлен отрезком линии, связанным с единичным кругом.Однако, в отличие от синуса и косинуса, длина рассматриваемого отрезка линии не ограничивается значениями от нуля до единицы. Как видно из рисунка выше, касательная представлена отрезком линии, соединяющим точку P (точка на окружности круга, координаты которой x и y представляют значения косинуса и синуса соответственно) и точкой F (точка, где касательная пересекает ось x ). Щелкните здесь , чтобы увидеть интерактивную демонстрацию, в которой используется единичный круг, чтобы показать, как синус, косинус и касательная соотносятся друг с другом (примечание: ваш браузер должен поддерживать Java, чтобы интерактивная страница работала).Вы увидите из демонстрации, если вы еще не сделали вывод, что, когда значение угла θ приближается к девяносто градусам (90 °), длина отрезка PF будет стремиться к бесконечности. Вы также увидите, что то же самое происходит, когда значение угла θ приближается к двумстам семидесяти градусам (270 °). Мы вскоре вернемся к значению этого факта. А пока рассмотрим прямоугольный треугольник, показанный ниже. В треугольнике ABC tan ( θ ) = a / b В треугольнике ABC нас интересует угол θ . Мы использовали соглашение о маркировке каждой вершины символом верхнего регистра, а сторону, противоположную каждой вершине, соответствующим символом нижнего регистра. Противоположным по отношению к углу θ является сторона a .Рядом находится сторона b , а гипотенуза — сторона c . Касательная угла в прямоугольном треугольнике определяется как частное длин напротив и прилегающих . Таким образом, в треугольнике ABC тангенс угла θ задается как: Если вы читали страницы, озаглавленные «Синусоидальная функция» и «Косинусная функция» (или, может быть, даже если вы не читали), вы знаете, что стороны прямоугольного треугольника могут быть помечены в соответствии со способом которые они относятся к интересующему нас острому углу, и уловка состоит в том, чтобы запомнить , какие сторон использовать для вычисления значения любой тригонометрической функции, которую мы хотим найти.Вот еще раз (относительно) легко запоминающаяся мнемоника SOH-CAH-TOA , которая должна напомнить вам, что: S ine = O pposite over H ypotenuse C osine = A djacent over H ypotenuse T angent = 92j327 dposite O 92j8 dposite over 92j327 dposite Глядя на приведенные выше определения и помня, что гипотенуза всегда является самой длинной стороной в любом прямоугольном треугольнике, должно быть самоочевидным, что значения синуса и косинуса для прямоугольного треугольника, определенного с использованием декартовых координат, всегда будут находиться в пределах диапазон минус один до один (от -1 до 1).Фактически, значения синуса и косинуса могут быть определены в терминах координат y и x соответственно точки P на окружности единичной окружности. С другой стороны, касательная определяется как частное этих значений: Поскольку координаты y и x представляют синус и косинус соответственно, мы также можем заключить, что: Опять же, с точки зрения единичной окружности, гипотенуза прямоугольного треугольника — это отрезок прямой, соединяющий центр окружности с точкой P.Если мы рассматриваем линейные сегменты, представляющие функции косинуса и синуса, как отрезки и подъем соответственно для отрезка линии, соединяющего центр окружности и точку P, то значение, возвращаемое функцией касательной для угла θ представляет наклон отрезка прямой (т. е. наклон гипотенузы). Для тех, кто интересуется такими вещами, мы использовали Microsoft Excel для создания нашей собственной таблицы значений тангенса для углов от нуля градусов (0 °) до трехсот шестидесяти градусов (360 °) с шагом одна десятая градуса.Чтобы увидеть таблицу, щелкните здесь . Если вы изучите таблицу, вы увидите, что существует значительный диапазон углов от нуля до девяноста градусов, для которых значение, возвращаемое функцией тангенса (то есть наклон гипотенузы), изменяется только относительно медленно. Когда размер угла θ приближается к нулевым градусам (0 °), значение, возвращаемое функцией касательной, стремится к нулю. Действительно, когда угол θ достигает нуля градусов, наклон гипотенузы и значение tan ( θ ) будут равны нулю.Однако, когда значение угла θ приближается к девяносто градусам (90 °), значение, возвращаемое функцией касательной, быстро стремится к бесконечности. Этого следовало ожидать, поскольку значение cos ( θ ) будет стремиться к нулю. Фактически, значение, возвращаемое функцией касательной для угла в девяносто градусов, считается undefined , поскольку уравнение tan ( θ ) = sin ( θ ) / cos ( θ ) будет включать деление на ноль.То же самое верно для угла двести семьдесят градусов (270 °). Фактически, это применимо к любому углу, для которого значение косинуса равно нулю. Точно так же, когда значение sin ( θ ) равно нулю, значение tan ( θ ) также будет нулевым. Мы представляем здесь график тангенциальной функции для углов от нуля до семьсот двадцать градусов (720 °): График функции касательной для углов в диапазоне от 0 ° до 720 ° Вертикальные красные линии на графике — асимптоты .Асимптота кривой — это такая линия, при которой, когда расстояние между кривой и линией приближается к нулю, значение кривой стремится к бесконечности. В этом случае асимптоты можно рассматривать как «пробелы» на графике, где значение tan ( θ ) не определено. Также обратите внимание, что когда график пересекает асимптоту, значение tan ( θ ) изменяется от максимального положительного значения до максимального отрицательного значения . Вы также можете увидеть, как значения различаются по обе стороны от асимптоты, изучив таблицу значений касательных.И последнее, что следует отметить, так это то, что, как и функции синуса и косинуса, функция тангенса также является периодической. Однако, в отличие от функций синуса и косинуса, период функции тангенса составляет сто восемьдесят градусов (180 °), а не триста шестьдесят градусов (360 °). К счастью, больше нет необходимости использовать таблицы или линейку для определения тангенса угла (или угла, соответствующего заданному значению тангенса), поскольку любой современный научный калькулятор может сделать это за нас.Найти тангенс угла с помощью встроенного калькулятора, предусмотренного в Microsoft Windows , относительно просто. Предположим, мы хотим найти тангенс угла тридцать пять градусов (35 °). Вы можете найти встроенный калькулятор Microsoft Windows, нажав кнопку «Пуск» в Windows 7 и выбрав «Все программы»> «Стандартные»> «Калькулятор » (для других версий Windows может потребоваться другая последовательность нажатия клавиш). Научную версию калькулятора можно выбрать в меню приложения Просмотр .Чтобы найти тангенс тридцати пяти градусов с помощью калькулятора Windows, введите следующие нажатия клавиш (если у вас нет калькулятора Windows, используйте любой доступный калькулятор, который может выполнять триггерные функции): Введите эти нажатия клавиш, чтобы найти тангенс 35 °. Кстати, убедитесь, что на вашем калькуляторе установлен режим градусов и (если вы не планируете вводить значение угла в радианах или градианах).Если вы правильно ввели нажатия клавиш, теперь вы должны увидеть следующий экран: Калькулятор отображает значение tan (35 °). Предположим, вы хотите найти размер острого угла в прямоугольном треугольнике, сначала найдя частное противоположного и смежного (т. Е. Тангенса угла). Если у вас есть значения длин сторон треугольника, вы можете достаточно легко найти значение тангенса угла.Тогда нахождение угла — это просто случай применения функции арктангенса (которая является обратной по отношению к функции тангенса) к результату. Давайте найдем значение угла θ для прямоугольного треугольника, показанного ниже. Мы хотим найти размер угла θ Для угла θ стороны a и b являются противоположными и смежными соответственно.Фактически, мы можем найти размер угла за одну операцию на калькуляторе Windows. Мы делаем это, используя скобки во введенной последовательности клавиш, чтобы калькулятор сначала находил частное противоположного и смежного (то есть тангенса угла). Затем мы применяем к результату функцию арктангенса. Вот ключевая последовательность, которую следует использовать: Введите эти нажатия клавиш, чтобы найти размер угла θ Если вы правильно ввели нажатия клавиш, вы должны увидеть следующий экран: Калькулятор отображает значение угла θ Три основные тригонометрические функции ( синус , косинус и касательная ) обычно изучаются в указанном здесь порядке.Если вы прочитали страницы в этом разделе по порядку, мы надеемся, что теперь вы достаточно знакомы со всеми тремя. Поэтому здесь, вероятно, стоит посмотреть, как знак значений, возвращаемых каждой из этих тригонометрических функций, изменяется по отношению к квадрантам единичной окружности . Иллюстрация ниже должна помочь прояснить ситуацию. Квадранты единичной окружности Помня, что значения, возвращаемые функциями косинуса и синуса, будут равны координатам x и y соответственно точки на окружности круга, и что значение, возвращаемое функцией касательной, будет частным от синус и косинус, то в квадранте I все три тригонометрические функции будут возвращать положительные значения, потому что x и y будут положительными.В квадранте II , y по-прежнему положительное, но x будет отрицательным, поэтому только функция синуса вернет положительное значение. В Квадранте III и x , и y отрицательны, поэтому функции синуса и косинуса будут возвращать отрицательные значения. Только функция касательной (как частное двух отрицательных значений) вернет положительное значение. В квадранте IV , x положительно, но y все еще отрицательно, поэтому функции синуса и тангенса будут возвращать отрицательные значения, и только функция косинуса вернет положительное значение. Для полноты остаётся только упомянуть тот факт, что тангенциальная функция, как и функции синуса и косинуса, может быть представлена как бесконечный ряд . Значение, возвращаемое тригонометрической функцией для данного угла, не может быть вычислено с помощью простой алгебраической формулы. Для большинства углов точное значение может быть получено только как сумма бесконечного числа членов, что, очевидно, невозможно. Достаточно точное приближение значения находится с использованием суммы ограниченного числа членов из бесконечного ряда функции.Чем больше количество терминов включено, тем выше точность результата. Количество используемых терминов будет зависеть от точности, необходимой для данного приложения, и от доступных вычислительных ресурсов. Бесконечный ряд, часто приводимый в учебниках по тригонометрии для функции тангенса, для значений x (в радианах), меньших π / 2 (девяносто градусов), выглядит следующим образом: Однако для этого требуется большее количество дополнительных параметров, чем при обычном обратном распространении в форме информационной матрицы Фишера. Таблицы ударения для небольших пространств Резюме: Калькулятор ln позволяет в режиме онлайн вычислить натуральный логарифм числа. Математика 142 Многочлены Тейлора / Маклорена и ряды Проф. Жирарди Зафиксируем интервал I в вещественной прямой (например, я мог бы быть (17; 19)) и пусть x 0 будет точкой в I, т. Е. X 0 2I: Затем рассмотрим функция, область определения которой равна I. Многие геометрические вычисления могут быть легко вычислены с использованием таблицы тригонометрических функций и формул.обозначает возведенный к власти. Доказательство. Таблицы синусов и косинусов для углов в градусах. Для синуса прочтите первые 6 столбцов. Комбинированный эффект создает красивую плавающую стеклянную столешницу, опирающуюся на абстрактную форму арки. Это, пожалуй, самый важный предмет в вашей гостиной. Современная мебель | Настенные блоки | Детская Мебель | MIG Design Store Brooklyn NY Tangent End Table от Elite Modern — СПЕЦИАЛЬНЫЙ ЗАКАЗ. Интегрируемость и квантование> Труды Девятой Международной конференции по геометрии, интегрируемости и квантованию> Секционная кривизна касательных связок с общими естественными поднятыми метриками. Если вы хотите вернуться назад, просто перейдите в другую сторону по имеющейся у вас таблице.2 = 9} \) в точке (1, 2). Тогда логарифм x по основанию e равен. Таблица косинусов — это подсчитанные значения углов косинусов, указанных в таблице от 0 ° до 360 °. Также имеются сопутствующие обеденные столы. Геометрия, интегрируемость и квантование. Хотя мы можем использовать и радианы, и градусы, радианы являются более естественным измерением, поскольку они напрямую связаны с единичным кругом, кругом с радиусом 1. Радианная мера угла определяется следующим образом. Чтобы найти косинус угла, достаточно найти значение в таблице.Используя таблицу натуральных синусов, найдите значение sin 55 °. Набросок доказательства: Хотя этот результат хорошо известен в твердотельной геометрии8, мы для полноты картины сделаем набросок доказательства. Если вы хотите вернуться назад, просто пройдите в другую сторону по имеющемуся у вас столу. Похожие Запросы. Oak Oak_Ebony Oak_Java Walnut Коньяк Java Natural Smoke Ebony Связанные элементы: Regal Tangent 60d x 60w x 29,5h Rift-Cut Oak or Walnut Veneer Прозрачное закаленное стекло 1/2 дюйма Обеденный стол Tangent Elite-FURNITURE-Позвоните нам, чтобы узнать цены по номеру 828- 327-8485 или нажмите здесь, чтобы получить по электронной почте предложение об обеденном столе.x [/ latex] называется естественной экспоненциальной функцией. Чаще всего нам нужно найти производную логарифма некоторой функции от x. Например, нам может потребоваться найти производную от y = 2 ln (3x 2 — 1). Для решения таких задач нам понадобится следующая формула . тождества справедливы для тригонометрических функций с тем же аргументом: sin 2 ɸ + cos 2 ɸ = 1. tan 2 ɸ + 1 = sec 2 ɸ. детская кроватка 2 ɸ + 1 = csc 2 ɸ. Доказательство. 99 105,99 долларов США 105,99 долларов США. 1) Если sin (30) = 0,5, то arcsin (0,5) = 30. Что люди ищут в этом блоге: Таблица естественных касательных… 3 декабря 2016 г. — Мы обсудим здесь метод использования таблицы касательных и котангенсов.Вы можете прочитать эту таблицу в обратном порядке, чтобы найти значения арктангенса. В этой статье описывается новый подход к естественному градиентному обучению, который использует меньшую информационную матрицу Фишера. Вам тоже может понравиться. Стальные рычаги с покрытием цвета шампанского поддерживают верхнюю часть из закаленного стекла. Используйте производную естественной экспоненциальной функции, правило частного и правило цепочки. Если y — вектор, который содержит на два значения больше, чем x имеет записей, то сплайн использует первое и последнее значения в y в качестве концевых уклонов для кубического сплайна.Наличие: Есть в наличии. Мерцающие покрытые шампаньем плечи плавно изгибаются… Под таблицей Значения синуса, косинуса, тангенса, косинуса, секанса и котангенса при различных углах (0 °, 30 °, 45 °, 60 °, 90 °). Вернуться к списку товаров. Например, арктангенс 359. График натурального логарифма (зеленый) и его касательная при x = 1,5 (черный) Аналитические свойства функций переходят к их обратным. Тригонометрическая таблица со всеми 6 тригонометрическими функциями. Таблица тригонометрии из Руководства по машинному оборудованию Щелкните ниже, чтобы найти начальный угол в таблицах.BigMul: возвращает полное произведение двух 32-битных чисел. Шесть тригонометрических функций. Деревянное основание изготовлено из шпона белого дуба с рифлением и доступно в нескольких вариантах отделки. Характеристики: • 36d x 50w x 16,75h • Дубовый шпон Rift-Cut или орех • Толщина: прозрачное закаленное стекло 1/2 дюйма Прозрачные стеклянные столешницы ½ дюйма закалены для прочности и безопасности. Все значения округлены до трех знаков после запятой. Итак, таблица составлена таким образом, что мы можем использовать таблицу, чтобы найти значение синуса и косинуса любого заданного угла от 0 ° до 90 °.Тангенс угла — это отношение длины противоположной стороны к длине прилегающей стороны: так называется, потому что его можно представить как отрезок прямой, касающийся окружности, то есть линии, которая касается окружности, от латинского linea tangens или касательная линия. Согласно графику, аппроксимация касательной линии дает надежную оценку, когда x близко к 1, но приблизительная линейная точность уменьшается, когда x перемещается дальше от 1. Вначале приведены несколько примеров использования этой таблицы.Sin inverse 0 6667 как рассчитать таблицу логарифмов тригонометрических функций как использовать логарифм степени sin 45 градусов. + Горячая линия генерального инспектора + Данные о равных возможностях трудоустройства, опубликованные в соответствии с Законом «Нет страха» + Бюджеты, стратегические планы и отчеты о подотчетности В этой статье проводится анализ естественного конвекционного течения в пограничном слое гиперболической касательной жидкости по экспоненциально растянутому цилиндру. Ответы на часто задаваемые вопросы о правилах 30 и 90 градусов для контроля битка.[T] Население Толедо, штат Огайо, в 2000 году составляло приблизительно 500 000 человек. Котангенс тангенса в градусах тригонометрической таблицы — это четырехзначная таблица тангенса и котангенса в градусах за одну минуту. Просмотрите нашу впечатляющую подборку порно-видео в HD-качестве на любом вашем устройстве. Нахождение уравнения касательной прямой с неявным дифференцированием. Чтобы найти естественную касательную по бревенчатой таблице, вы 21 Круговая диаграмма для печати Sin Cos Tan Формы и шаблоны Тригонометрическая таблица от 0 до 360 Cos Sin Cot Tan Sec Cosec Pdf Синус-косинус и таблица касательной от 0 до 360 градусов ПРОЧИТАЙТЕ Приложение для дизайна домашней мебели.Все реальные числа. Лучшие ответы ищите на этом сайте https://shorturl.im/aw2Ug. Мерцающие рукава с покрытием цвета шампанского плавно изгибаются вверх, захватывая твердую поверхность. Выше B = 300 мТл тангенс угла потерь показывает тенденцию к уменьшению с плотностью потока. Используя таблицу косинусов, вы можете производить вычисления, даже если под рукой не окажется научного калькулятора. • Прозрачное стекло ½ дюйма, закаленное для обеспечения прочности и безопасности. Таблица естественных касательных Pdf. (30) Графические и табличные методы в кристаллографии как основа новой системы практики, с таблицей множественных касательных и таблицей естественных касательных с пятью фигурами Баркера, Томаса Випонда, 1881 г. — Начальная цена: 1 809 долларов.00 $ 1,449.00 Скидка: 20%. Использование стола… Обычно покидает наш склад в течение 8-16 недель. Бесплатная доставка и сборка в пределах Нью-Йорка. [37] Таким образом, поскольку f (x) = b x — непрерывная и дифференцируемая функция,… Таблица натуральных логарифмов (ln); Калькулятор натурального логарифма; Определение натурального логарифма. Это может быть связано с температурным воздействием в системе тестирования. Написать рецензию. Ниже приведены тригонометрические таблицы всех 6 тригонометрических функций с углами в градусах и радианах. Если тригонометрические функции угла θ объединены в уравнение, и уравнение действительно для всех значений θ, то уравнение известно как тригонометрическое тождество.Выше B = 300 мТл тангенс угла потерь показывает тенденцию к уменьшению с плотностью потока. Графические и табличные методы в кристаллографии как основа новой системы практики, с таблицей множественных касательных и таблицей естественных касательных с пятью фигурами Баркера, Томаса Випонда, 1881 — Итак, вот вопрос, когда я это сделаю. на окнах… Пример 3. 3.1.3 Дальность видимости для принятия решения Таблица 3-3 PGDHS (1) предоставляет значения для соответствующих дальностей видимости для принятия решения в критических местах и для критериев оценки пригодности прицельной длины в этих местах.Следующие отношения, иногда называемые пифагорейскими. 94,99 доллара 94 доллара. Сначала таблицы касательных кажутся естественными и органичными, но создание форм стало возможным благодаря современному компьютерному черчению. Ln как функция, обратная экспоненциальной функции. На предплечье перчатки, идеальные бежевые блестящие колготки и короткие черные сапоги на высоком каблуке. Этот НАБОР ДЛЯ РАЗГОВОРА ДЛЯ РАЗГОВОРА ДЛЯ ПАТИО HAMPTON BAY LAGUNA POINT ИЗ 4 ПРЕДМЕТОВ NATURAL TAN WICKER С ПОДУШКОЙ ЧИЛИ КРАСНЫМ ПОДУШКАМИ идеально подойдет для нашей беседки.Первоначально разработанные в Голландии, эти коврики ткутся с использованием традиционной ткацкой техники, что делает их полностью ручной работой. k = абсцисса расстояния между сдвинутым PC и TS. Введите код купона «NYC» при оформлении заказа. Сделано Elite Modern, USAModern Glass Top End Table Tangent от Elite Modern. Откройте для себя мировые исследования. Графические и табличные методы в кристаллографии как основа новой системы практики: с таблицей множественных касательных и таблицей естественных котангенсов из пяти цифр Аннотация.Ceiling: возвращает наименьшее целое значение, которое больше или равно указанному Decimal или Double. Предупреждение: не путайте естественный рулон с естественной касательной. Итак, наука делает это за нас с небольшой помощью с вашей стороны. Я обращусь к конкретной таблице триггеров и конкретному примеру. Они сделаны из стали ручной ковки, поэтому отлично выдерживают массивные вершины. Таблица тригонометрических соотношений тригонометрическая таблица стандартных углов tan Таблица касательных и котангенсов естественных тригонометрических функций.Для всех типов слезы, рассматриваемых в этом исследовании, отрицательный знак касательной имел место в среднем через 2,5 года (30,2 месяца ± 47,1 месяца), а положительный знак касательной — через 4,5 года (55 месяцев ± 63,5 месяца) после появления симптомов. Госпожа Тангент заворачивает яйца рабыни, расстилает их и прикрепляет к Ее столу. Независимо от того, является ли ваша новая столешница мясным блоком, столешницей в виде досок или деревянной плитой, вы захотите продемонстрировать ее, установив ее на столь же потрясающие опоры для стола или, может быть, на стильную подставку.Значения углов, перечисленные в таблице, находятся в диапазоне от 0 ° до 90 °, причем каждый угловой градус делится на 10-минутные интервалы. Таблицы касательных Диаграмма угла от 0 ° до 90 ° для студентов. Функция fprintf ведет себя так же, как и ее тезка на языке ANSI C с этими исключениями и расширениями .. калькулятор tan (x). 6 (b), где тангенс угла потерь сначала неуклонно увеличивается с увеличением плотности внешнего магнитного потока до максимального значения при 300 мТл. Коктейльный стол Fusion. Изготовленные из 100% кокосового волокна, они поддаются биологическому разложению и рассчитаны на длительный срок использования.Таблица касательных и котангенс естественных тригонометрических функций, чтобы найти естественный тангенс по логарифмической таблице, вы, как преобразовать тангенс, обратный 0 283 в градусах. D541,560 Варианты дерева: Дуб, Орех Дуб Дуб_Эбеновый Дуб_Ява Орех Коньяк Ява Натуральный дымчатое Эбеновое дерево Связанные элементы: Regal 54 «x 29h Дуб Rift-Cut или ореховый шпон 1/2» закаленное прозрачное стекло Столешница из закаленного стекла Tangent Elite Generate a number таблица на основе одной или двух функций N7 (ТАБЛИЦА) Вычисления вектора N8 (VECTOR) Решение неравенства Nc1 (INEQ) Проверка вычисления Nc2 (VERIF) Вычисления распределения Nc3 (DIST) Примечание. Исходным режимом вычислений по умолчанию является режим COMP.Таблица касательного конца. Если вы заинтригованы отделкой наших MFC и хотели бы получить образец вышеперечисленного, обратитесь к своему бизнес-менеджеру касательной области или касательной… Производная y = ln u (где u — функция от x). Углы 0, 30 °, 45 °, 60 ° и 90 ° — это обычные углы, которые люди часто используют в проектах. По этой причине полезно иметь значения синуса, косинуса, тангенса и … Естественные тригонометрические функции: Таблицы, синус, косинус, тангенс, котангенс, секанс и косеканс до восьми знаков после запятой, с разницей в секундах до… для использования с калькулятором-сложением Монро, Неизвестный переплет — 1 января 1941 г. Круглый обеденный стол по касательной. Присоединяйтесь к нашему списку рассылки и узнавайте первыми о новых продуктах, распродажах и эксклюзивных предложениях. Список коэффициентов теплового расширения (КТР) для природных и искусственных материалов. Вот где я собираюсь сделать один шар, и это линия, по которой биток будет следовать, в основном перпендикулярная линия от удара одного шара. Если x или y является скаляром, то он расширяется до такой же длины, что и другой, и используются условия конца без узла.. Таблицы для сбора Tangent от Elite Manufacturing. Ножки прикрепляются в критических точках касания на краю столешницы, обеспечивая стабильный, но извилистый силуэт. Чтобы заполнить остальную часть таблицы, выберите все три ячейки, наведите указатель мыши на маркер заполнения и дважды щелкните. Период касательной. Синус, косинус и тангенс — естественные тригонометрические функции. Вы можете удалить их, чтобы очистить участок. Предупреждение: не путайте естественный рулон с естественной касательной. Итак, наука делает это за нас с небольшой помощью с вашей стороны…. Будьте первым, кто просмотрит «Tangent Console Table» Отменить ответ. В числовом выражении Госпожа Тангент имеет шары белки-рабыни, завернутые, распределенные и прикрепленные к Ее столу. Главная >> Журнальные столики >> Стеклянные журнальные столики >> Касательная стеклянная консоль от Elite Modern Product 71/176. Таблица естественных касательных Pdf. Основания из шпона белого дуба Rift-cut доступны в цветах Natural, Cherry, Java или Ebony, а стальные ножки доступны только в Topaz. Вы можете использовать его для рисования линии или оси, касательной к дугам, дугам полилинии или окружности.Что люди ищут в этом блоге: Natural Tangent Table Pdf Вы можете использовать эту таблицу значений для триггерных функций при решении проблем, рисовании графиков или выполнении любого количества вычислений, связанных с триггерами. Atan2: возвращает угол, тангенс которого является частным от двух указанных чисел. В прилагаемой таблице на страницах 116–133 синусы, косинусы, тангенсы и котангенсы даны для каждой минуты квадранта с шестью цифрами. Если x и y — векторы одинакового размера, то используются условия конца не-узла.. Функция касания: tan (x) Область касания. … 2 1 Таблица логарифмирования коэффициента касания Как использовать журнал с примером Используя верх или низ, вы можете согнуть касательную линию для лучшего положения или избежать столкновения с мячом. Проще говоря, касательная линия — это естественное направление, которое скользящий биток принимает после контакта с прицельным шаром. биток будет катиться вперед или за касательной.Или, может быть, по касательной есть мешающий шар. Решенные примеры с использованием таблицы натуральных касательных и натуральных котангенсов: 1. Функция напьера логарифма определена для любого числа, принадлежащего интервалу] 0, `+ oo` [, отмечается в ln. Наперовский логарифм также называется натуральным логарифмом .. Касательное расслоение также несет естественную почти комплексную структуру, совместимую с метрикой Сасаки и такую, что касательное расслоение и комплексная структура являются почти келеровым многообразием. Таблица натуральных синусов в формате PDF.ID корпуса: 1196 Четыре и двадцать черных дроздов,
Пробоотборник для сигар с хьюмидором и резаком,
Зиллоу Сайпресс Хиллз Бруклин,
Лучшие альбомы Sludge Metal Rym,
Рестораны Корваллиса,
Результаты андеррайтинга Du,
Бейсбольная карточка Джассона Домингеса,
Ограниченная серия Paint Job Dying Light, В этом разделе вы: Пандус для инвалидных колясок, соответствующий стандартам Закона об американцах с ограниченными возможностями, должен образовывать угол с землей, касательная которого равна 112112 или меньше, независимо от его длины. Касательная представляет собой отношение, поэтому это означает, что на каждый 1 дюйм подъема у рампы должен быть 12 дюймов пробега. Тригонометрические функции позволяют нам определять формы и пропорции объектов независимо от точных размеров. Мы уже определили функции синуса и косинуса угла.Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции. Чтобы определить остальные функции, мы еще раз нарисуем единичный круг с точкой (x, y) (x, y), соответствующей углу t, t, как показано на рисунке 1.Как и в случае с синусом и косинусом, мы можем использовать координаты (x, y) (x, y), чтобы найти другие функции. Рисунок 1 Первая функция, которую мы определим, — это касательная. Тангенс угла — это отношение значения y к значению x соответствующей точки на единичной окружности. На рисунке 1 тангенс угла tt равен yx, x ≠ 0.yx, x ≠ 0. Поскольку значение y равно синусу t, t, а значение x равно косинусу t, t, тангенс угла tt также можно определить как sintcost, cost cost 0.синткост, стоимость ≠ 0. Функция касательной обозначается как tan.tan. Остальные три функции могут быть выражены как обратные функции, которые мы уже определили. Если tt — действительное число и (x, y) (x, y) — точка, в которой конечная сторона угла tt радиан пересекает единичный круг, то Точка (−32,12) (- 32,12) находится на единичной окружности, как показано на рисунке 2.Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott. Рисунок 2 Поскольку нам известны координаты (x, y) (x, y) точки на единичной окружности, обозначенной углом t, t, мы можем использовать эти координаты для нахождения шести функций: Попробуй # 1 Точка (22, −22) (22, −22) находится на единичной окружности, как показано на рисунке 3.Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cott.cott. Рисунок 3 Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cottcott, когда t = π6.t = π6. Ранее мы использовали свойства равносторонних треугольников, чтобы продемонстрировать, что sinπ6 = 12sinπ6 = 12 и cosπ6 = 32.cosπ6 = 32.Мы можем использовать эти значения и определения тангенса, секанса, косеканса и котангенса как функций синуса и косинуса, чтобы найти остальные значения функции. Попробуй # 2 Найдите sint, cost, tant, sect, csct, sint, cost, tant, sect, csct и cottcott, когда t = π3.t = π3. Поскольку мы знаем значения синуса и косинуса для общих углов первого квадранта, мы можем найти другие значения функций для этих углов, установив xx равным косинусу и yy равным синусу, а затем используя определения тангенса, секанс, косеканс и котангенс.Результаты представлены в таблице 1. Таблица 1 Мы можем оценивать тригонометрические функции углов вне первого квадранта, используя опорные углы, как мы уже делали с функциями синуса и косинуса.Процедура такая же: найдите опорный угол, образованный конечной стороной данного угла с горизонтальной осью. Значения тригонометрической функции для исходного угла будут такими же, как и для исходного угла, за исключением положительного или отрицательного знака, который определяется значениями x и y в исходном квадранте. На рисунке 4 показано, какие функции в каком квадранте положительны. Чтобы помочь нам запомнить, какие из шести тригонометрических функций положительны в каждом квадранте, мы можем использовать мнемоническую фразу «Умный класс триггера.Каждое из четырех слов во фразе соответствует одному из четырех квадрантов, начиная с квадранта I и вращаясь против часовой стрелки. В квадранте I, который представляет собой « A », 11 из шести тригонометрических функций положительны. В квадранте II « S mart» положительны только s и его обратная функция, косеканс. В квадранте III, « T rig», только t угловая и ее обратная функция, котангенс, положительны.Наконец, в квадранте IV « C девушка» только c осин и его реципрокная функция, секанс, положительны. Рисунок 4 Учитывая угол не в первом квадранте, используйте опорные углы, чтобы найти все шесть тригонометрических функций. Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −5π6. − 5π6. Угол между конечной стороной этого угла и осью x равен π6, π6, так что это опорный угол.Поскольку −5π6−5π6 находится в третьем квадранте, где и xx, и yy отрицательны, косинус, синус, секанс и косеканс будут отрицательными, а тангенс и котангенс будут положительными. Попробуй # 3 Используйте исходные углы, чтобы найти все шесть тригонометрических функций от −7π4. − 7π4. Чтобы иметь возможность свободно использовать наши шесть тригонометрических функций как с положительными, так и с отрицательными угловыми входами, мы должны изучить, как каждая функция обрабатывает отрицательный вход.Как выясняется, в этом отношении существует важное различие между функциями. Рассмотрим функцию f (x) = x2, f (x) = x2, показанную на рисунке 5. График функции симметричен относительно оси y . На всем протяжении кривой любые две точки с противоположными значениями x имеют одинаковое значение функции. Это соответствует результату расчета: (4) 2 = (- 4) 2, (4) 2 = (- 4) 2, (−5) 2 = (5) 2, (- 5) 2 = (5) 2 ,
и так далее. Таким образом, f (x) = x2f (x) = x2 — четная функция, такая функция, что два противоположных входа имеют одинаковый выход.Это означает, что f (−x) = f (x) .f (−x) = f (x). Теперь рассмотрим функцию f (x) = x3, f (x) = x3, показанную на рисунке 6. График не симметричен относительно оси y . На всем протяжении графика любые две точки с противоположными значениями x также имеют противоположные значения y . Таким образом, f (x) = x3f (x) = x3 — нечетная функция, такая, что два противоположных входа имеют противоположные выходы. Это означает, что f (−x) = — f (x).f (−x) = — f (x). Мы можем проверить, является ли тригонометрическая функция четной или нечетной, нарисовав единичный круг с положительным и отрицательным углом, как на рисунке 7. Синус положительного угла равен y.y. Синус отрицательного угла — y . Таким образом, синусоидальная функция является нечетной функцией. Таким образом мы можем проверить каждую из шести тригонометрических функций. Результаты представлены в таблице 2. Рисунок 7 Таблица 2 Четная функция — это функция, в которой f (−x) = f (x).f (−x) = f (x). Нечетная функция — это функция, в которой f (−x) = — f (x) .f (−x) = — f (x). Косинус и секанс четные: Синус, тангенс, косеканс и котангенс нечетны: Если секанс угла tt равен 2, каков секанс угла −t? −t? Секанс — четная функция.Секанс угла — это то же самое, что секанс его противоположности. Таким образом, если секанс угла t равен 2, секанс −t − t также равен 2. Попробуй # 4 Если котангенс угла tt равен 3,3, то каков котангенс угла −t? −t? Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности.Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены. Обычно идентичность можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса. Мы можем вывести некоторые полезные тождества из шести тригонометрических функций. Остальные четыре тригонометрические функции могут быть связаны с функциями синуса и косинуса с помощью следующих основных соотношений: Поскольку нам известны значения синуса и косинуса для этих углов, мы можем использовать тождества для оценки других функций. ⓐ ⓑ Попробуй # 5 Оценить csc (7π6).csc (7π6). Упростите secttant.secttant. Мы можем упростить это, переписав обе функции в терминах синуса и косинуса. Показав, что secttantsecttant можно упростить до csct, csct, мы фактически установили новую идентичность. Попробуй # 6 Упростить (тант) (стоимость). (Тант) (стоимость). Мы можем использовать эти фундаментальные тождества для получения альтернативных форм пифагорейской идентичности, cos2t + sin2t = 1.cos2t + sin2t = 1. Одна форма получается делением обеих частей на cos2t: cos2t: Другая форма получается делением обеих частей на sin2t: sin2t: Если cos (t) = 1213 cos (t) = 1213 и tt находится в квадранте IV, как показано на рисунке 8, найдите значения других пяти тригонометрических функций. Рисунок 8 Мы можем найти синус, используя тождество Пифагора, cos2t + sin2t = 1, cos2t + sin2t = 1, и остальные функции, связав их с синусом и косинусом. Знак синуса зависит от значений y в квадранте, где расположен угол.Поскольку угол находится в квадранте IV, где значения y отрицательны, его синус отрицателен, −513. − 513. Остальные функции можно вычислить с помощью тождеств, связывающих их с синусом и косинусом. Если sec (t) = — 178sec (t) = — 178 и 0 Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция. Тригонометрические функции периодические. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или 2π, 2π,
приведет к одинаковым выводам для этих функций. А для тангенса и котангенса только половина оборота даст одинаковые результаты. Другие функции также могут быть периодическими.Например, продолжительность месяцев повторяется каждые четыре года. Если xx представляет собой отрезок времени, измеряемый в годах, а f (x) f (x) представляет количество дней в феврале, тогда f (x + 4) = f (x). F (x + 4) = f ( Икс).
Этот образец повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и 4 годами ранее. Положительное число 4 — это наименьшее положительное число, которое удовлетворяет этому условию и называется периодом. Период — это самый короткий интервал, в течение которого функция завершает один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней. Период PP повторяющейся функции ff — это число, представляющее интервал, такой что f (x + P) = f (x) f (x + P) = f (x) для любого значения x.x. Период функций косинуса, синуса, секанса и косеканса равен 2π.2π. Период функций тангенса и котангенса равен π.π. Найдите значения шести тригонометрических функций угла tt по рисунку 9 . Рисунок 9 Найдите значения шести тригонометрических функций угла tt.
на основе рисунка 10 . Рисунок 10 Если sin (t) = — 32sin (t) = — 32 и cos (t) = 12, cos (t) = 12, найдите sec (t), csc (t), tan (t), cot (t). .sec (t), csc (t), tan (t), cot (t). Если sin (t) = 22sin (t) = 22
и cos (t) = 22, cos (t) = 22, найти sec (t), csc (t), tan (t) и cot (t) .sec (t), csc (t), tan (t) ) И кроватка (t). Мы научились оценивать шесть тригонометрических функций для общих углов первого квадранта и использовать их в качестве опорных углов для углов в других квадрантах.Чтобы оценить тригонометрические функции других углов, мы используем научный или графический калькулятор или компьютерное программное обеспечение. Если в калькуляторе есть режим градусов и режим радиан, убедитесь, что выбран правильный режим, прежде чем производить вычисления. Вычисление касательной функции с помощью научного калькулятора, в отличие от графического калькулятора или системы компьютерной алгебры, похоже на вычисление синуса или косинуса: введите значение и нажмите клавишу TAN. Для обратных функций может не быть каких-либо специальных клавиш с надписью CSC, SEC или COT.В этом случае функция должна быть вычислена как обратная величина синуса, косинуса или тангенса. Если нам нужно работать с градусами, а наш калькулятор или программное обеспечение не имеет режима градусов, мы можем ввести градусы, умноженные на коэффициент преобразования π180π180, чтобы преобразовать градусы в радианы. Чтобы найти секущую 30 °, 30 °, мы могли бы нажать или Для угла в радианах используйте научный калькулятор, чтобы найти косеканс. Если угол измеряется в радианах, используйте графическую утилиту / калькулятор, чтобы найти косеканс. Вычислите косеканс 5π7.5π7. Для научного калькулятора введите следующую информацию: Попробуй # 10 Вычислите котангенс −π8. − π8. Могут ли значения синуса и косинуса радианной меры когда-либо быть равными на интервале [0,2π), [0,2π)? Если да, то где? Каким должен быть косинус ππ градусов? Объясните свои рассуждения. Для любого угла во втором квадранте, если бы вы знали синус угла, как бы вы могли определить косинус угла? Опишите секущую функцию. Тангенс и котангенс имеют период π.π.
Что это говорит нам о выходе этих функций? Для следующих упражнений найдите точное значение каждого выражения. В следующих упражнениях используйте исходные углы для оценки выражения. Если sint = 34, sint = 34 и tt находится в квадранте II, найдите costcost, sectsect, csctcsct, tanttant, cott.cott. Если cost = −13, cost = −13 и tt находится в квадранте III, найдите sint, sect, csct, tant, cott.sint, sect, csct, tant, cott. Если tant = 125, tant = 125 и 0≤t <π2,0≤t <π2, найдите sint, cost, sect, csct, sint, cost, sect, csct и cott.cott. Если sint = 32sint = 32 и cost = 12, cost = 12, найдите sect, csct, tant, sect, csct, tant и cott.коттеджи. Если sin40 ° ≈0,643 sin40 ° ≈0,643 а также cos40 ° ≈0,766 cos40 ° ≈0,766 найти sec40 °, csc40 °, tan40 °, sec40 °, csc40 °, tan40 °, а также cotand40 ° .cotand40 °. Если sint = 22, sint = 22, что такое sin (−t)? Sin (−t)? Если стоимость = 12, стоимость = 12, что такое cos (−t)? Cos (−t)? Если sect = 3.1, sect = 3.1, что такое sec (−t)? Sec (−t)? Если csct = 0,34, csct = 0,34, что такое csc (−t)? Csc (−t)? Если tant = −1,4, tant = −1,4, что такое tan (−t)? Tan (−t)? Если cott = 9,23, cott = 9,23, что такое детская кроватка (−t)? Cot (−t)? В следующих упражнениях используйте угол в единичной окружности, чтобы найти значение каждой из шести тригонометрических функций. Для следующих упражнений используйте графический калькулятор. Для следующих упражнений используйте личности, чтобы оценить выражение. Если tan (t) ≈2,7, tan (t) ≈2,7 и sin (t) ≈0,94, sin (t) ≈0,94, найти cos (t) .cos (t). Если tan (t) ≈1,3, tan (t) ≈1,3 и cos (t) ≈0,61, cos (t) ≈0,61, найти sin (t) .sin (t). Если csc (t) ≈3,2, csc (t) ≈3,2 и cos (t) ≈0,95, cos (t) ≈0,95, найти tan (t) .tan (t). Если cot (t) ≈0,58, cot (t) ≈0,58 и cos (t) ≈0,5, cos (t) ≈0,5, найти csc (t) .csc (t). Определите, является ли функция f (x) = 2sinxcosxf (x) = 2sinxcosx четной, нечетной или ни одной из них. Определите, является ли функция f (x) = 3sin2xcosx + secxf (x) = 3sin2xcosx + secx четной, нечетной или ни одной из них. Определите, является ли функция f (x) = sinx − 2cos2xf (x) = sinx − 2cos2x четной, нечетной или ни одной из них. Определите, является ли функция f (x) = csc2x + secxf (x) = csc2x + secx четной, нечетной или ни одной из них. В следующих упражнениях используйте идентификаторы, чтобы упростить выражение. Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 15cos (1600d), h = 15cos (1600d), где hh представляет количество солнечных часов, а dd — день в году. Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света будет 10 февраля, 42 -й день в году. Укажите период функции. Количество солнечного света в определенном городе можно смоделировать с помощью функции h = 16cos (1500d), h = 16cos (1500d), где hh
представляет часы солнечного света, а dd
это день года.Воспользуйтесь уравнением, чтобы определить, сколько часов солнечного света 24 сентября, 267 день в году. Укажите период функции. Уравнение P = 20sin (2πt) + 100P = 20sin (2πt) +100 моделирует кровяное давление, P, P, где tt
представляет время в секундах. (а) Определите кровяное давление через 15 секунд. б) Какое максимальное и минимальное артериальное давление? Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 6, y = 2cosx + 6, где xx представляет угол поворота коленчатого вала.Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55 ° 0,55 °. Высота поршня h, h в дюймах может быть смоделирована уравнением y = 2cosx + 5, y = 2cosx + 5, где xx представляет собой угол поворота коленчатого вала. Найдите высоту поршня, когда угол поворота коленчатого вала составляет 55 ° 0,55 °. Mossberg 385kb Однако для некоторых файлов необходимо увеличить допуск (т.е. сделать большее число), чтобы правильно импортировать файл. FEMM не понимает всех возможных тегов, которые могут быть включены в файл dxf; вместо этого он просто удаляет команды, связанные с рисованием линий, окружностей и дуг. Вся остальная информация … F.TF.A.3 — Используйте специальные треугольники для геометрического определения значений синуса, косинуса, тангенса для π / 3, π / 4 и π / 6, а также используйте единичный круг для выражения значения синуса, косинуса и тангенса для π-x, π + x и 2π-x в терминах их значений для x, где x — любое действительное число. Блок №3: Тригонометрия. Узнайте об единичной окружности, специальных треугольниках и о том, как найти точные тригонометрические соотношения. Исследуются задачи 2D и 3D Trig, а также неоднозначный случай синусоидального закона K4zaf325bm hc14Настройка Outlook для ошибки icloud 0x800706ba Теперь, как и другие 3 тригонометрические функции, обратные функции имеют определения единичной окружности. Напомним определение косинуса, синуса и тангенса.Косинус тета равен x, синус тета равен y, а касательная тета равна y по x, где x и y — координаты точки на конечной стороне угла. Macbook pro черные полосы по бокам экранаLac barnes quebec cottage на продажу Trig circle chart — unit circle pdf. Единичный круг, прямоугольный треугольник, тригонометрия гипотенуза, противоположная сторона, смежная сторона, s o h i n sin p p y p, противоположная сторона, гипотенуза, смежная сторона, cos гипотенуза, круговая диаграмма, единичная круговая диаграмма с загаром — РАЗДЕЛ 9 ЭКЗАМЕН Часть 1 Нет Имя калькулятора Заполните xy — shafter kernhigh.Продолжительность блока 15 дней Концепция 1 Концепция 2 Концепция 3 Графическое отображение триггерных функций (все 6) Определение характеристик триггерных функций Моделирование периодических явлений с помощью тригонометрических функций Стандарты GSE Стандарты GSE Стандарты GSE MGSE 9-12.F.TF.4 MGSE Используйте единичный круг для объяснения симметрии (нечетное 1998 болты рессоры jeep cherokeeShark rocket hv301 замена нижнего шланга 23. Конечный луч угла, нарисованный в стандартном положении, проходит через точку (.508, .862) на единичной окружности.Что из следующего мне больше всего подходит касательной к этому углу? 3) (1) .685 (2) 1.291 (3) 1.697 (4) 2.883 n угол, проведенный в стандартном положении с его конечным лучом, приземляющимся в четвертом квадранте, и 24. 1 T — касательная положительна в квадранте III C — косинус положительно в квадранте IV Пример № 3: Решить для! учитывая, что sin θ = 0,4, для — 90 ° ≤ θ ≤ 90 °. ** Этот вопрос удобен для калькулятора, поскольку 0,4 не является значением y на единичном круге. Чтобы вычислить значения обратного триггера на калькуляторе, сначала убедитесь, что вы находитесь в правильном РЕЖИМЕ. Обновление программного обеспечения Bosch slda Адаптер Silencerco octane 9 по касательной к единичной окружности (или единичной сфере). Здесь помогает диаграмма. Кривизна или изгиб кривой, как предполагается, представляет собой скорость изменения направления кривой, поэтому мы так ее и определяем. Определение 2 (кривизна). Пусть x — путь с единичным касательным вектором T = x0 kx0k. Кривизна при t представляет собой угловую скорость изменения T на единицу изменения. F100, триангулированный 4-х звенный, Лучшее крепление для жизнескопа garmin Тангенс x определяется как деление его синуса.по косинусу: tan x. • Касательная: функция tan x определена для всех действительных чисел x, таких что cos x = 0, поскольку тангенс — это частное синуса по косинусу. Причина проста: противоположные углы на единичной окружности (например, π 4. и. Уравнение окружности. Обе окружности здесь центрированы в начале координат; внутренний имеет радиус в одну единицу, а внешний радиус равен 4. Используя Pythagoras, любая точка (x, y) на маленьком внутреннем круге будет иметь координаты (sin, cos для соответствующего угла, измеренного против часовой стрелки от положительной оси x. Функция тангенса — это периодическая функция, которая очень важна в тригонометрии. Самый простой способ понять функцию касательной — использовать единичную окружность. Для заданного угла θ нарисуйте единичный круг на координатной плоскости и нарисуйте угол с центром в начале координат, с одной стороной в качестве положительной оси x. Различия в корпусе C4 11 апреля 2019 г. Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи: В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление. Дроби бывают двух видов: Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45. Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4. Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними. В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так: Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено. Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой. В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде». Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например: Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны: Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило. Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей: Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например: Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5. Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3. А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную. Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную. Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5. Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15. Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово. Еще пример: Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому. Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную. Делим столбиком числитель на знаменатель — преобразование готово: Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3). Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку: Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону: Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка! Вот и всё! Эта схема значительно проще и быстрее. Проверим: Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5. Поэтому n = 2. Если убрать запятую и нули слева, то получим число 55. Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит 100. Остается сократить числитель и знаменатель. Вот и ответ: 11/20. Любую бесконечную периодическую десятичную дробь можно перевести в обыкновенную. Разберем на примерах. Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби. Преобразуем периодическую дробь 1,32(0) в обыкновенную. Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов: Вот и ответ! Если период дроби отличен от нуля — рассматриваем периодическую часть как сумму членов геометрический прогрессии, которая убывает. Поясним на примере: 0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + .. Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0 < q < 1, то сумма равна b/(1-q). Переведем периодическую дробь 0,(7) в обыкновенную. Запишем: 0,(7) = 0,7 + 0,07 + 0,007 + .. Видим бесконечную убывающую геометрическую прогрессию с первым членом 0,7 и знаменателем 0,1. Применим формулу: 0,(7) = 0,7 + 0,07 + 0,007 + .. = 0,7 / (1 — 0,1) = 0,7/0,9 = 7/9. Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры. Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей. Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби. Приступим! Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке. Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000. Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную? Теперь перейдем к примерам. Переведем обыкновенную дробь 39100 в десятичную. Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно — количество цифр в числителе совпадает с количеством нулей в знаменателе. Следуя правилу, записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,39. Разберем решение еще одного примера по этой теме. Запишем дробь 10510000000 в виде десятичной дроби. Количество нулей в знаменателе равно 7, а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля: 000010510000000 Теперь записываем 0, ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0,0000105. Рассмотренные во всех примерах дроби — обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило. Ниже приведем пример на использование этого правила. Переведем дробь 56888038009100000 из обыкновенной неправильной в десятичную. Сначала запишем число из числителя: 56888038009 Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе — пять). Получим: 568880,38009 Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом. Обратимся к примеру. Переведем смешанное число 231710000 в десятичную дробь. В дробной части имеем выражение 1710000. Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 001710000. Теперь записываем целую часть числа и ставим после него запятую: 23,.. После запятой записываем число из числителя вместе с нулями. Получаем результат: 231710000=23,0017 Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д. Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4. Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно. Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности. Числитель при делении представляется в виде десятичной дроби — справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров. Переведем обыкновенную дробь 6214 в десятичный вид. Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621=621,00 Теперь разделим столбиком 621,00 на 4. Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим. Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом. В итоге мы получаем десятичную дробь 155,25, которая и является результатом обращения обыкновенной дроби 6214 6214=155,25 Рассмотрим решение еще одного примера, чтобы закрепить материал. Обратим обыкновенную дробь 21800. Для этого в столбик разделим дробь 21,000 на 800. Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю. В результате мы получили: 21800=0,02625. Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере. Обратим обыкновенную дробь 1944 в десятичную. Для этого выполним деление столбиком. Мы видим, что при делении повторяются остатки 8 и 36. При этом в частном повторяются цифры 1 и 8. Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки. Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь. 1944=0,43(18). Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие — в бесконечные периодические? Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000.., то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5. Нужна помощь преподавателя? Опиши задание — и наши эксперты тебе помогут! Подытожим сказанное: Приведем пример. Какая из данных дробей 4720, 712, 2156, 3117 переводится в конечную десятичную дробь, а какая — только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную. Дробь 4720, как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100. 4720=235100. Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь. Разложение знаменателя дроби 712 на множители дает 12=2·2·3. Так как простой множитель 3 отличен от 2 и от 5, данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби. Дробь 2156, во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 38, разложение знаменателя которой на множители дает 8=2·2·2. Следовательно, это конечная десятичная дробь. В случае с дробью 3117 разложение знаменателя на множители представляет собой само простое число 17. Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь. Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби? Отвечаем: нет! При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь. Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций: Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби. Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную? Рассмотрим применение данного правила на примерах. Представим число 3,025 в виде обыкновенной дроби. Переведем дробь 0,0017 из десятичных в обыкновенные. Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать? Сформулируем еще одно правило. Обратимся к примеру Представим дробь 155,06005 в виде смешанного числа. Поучаем смешанное число: 1556005100000 Дробную часть можно сократить на 5. Сокращаем, и получаем финальный результат: 155,06005=155120120000 Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную. Самый простой случай — период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби. Обратим периодическую дробь 3,75(0). Отбросив нули справа, получим конечную десятичную дробь 3,75. Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем: 3,75(0)=3,75=375100=154. Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере: 0,(74)=0,74+0,0074+0,000074+0,00000074+.. Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0<q<1, то сумма равна b1-q. Рассмотрим несколько примеров с применением данной формулы. Пусть у нас есть периодическая дробь 0,(8) и нам нужно перевести ее в обыкновенную. Запишем: 0,(8)=0,8+0,08+0,008+.. Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0,8 и знаменателем 0,1. Применим формулу: 0,(8)=0,8+0,08+0,008+..=0,81-0,1=0,80,9=89 Это и есть искомая обыкновенная дробь. Для закрепления материала рассмотрим еще один пример. Обратим дробь 0,43(18). Сначала записываем дробь в виде бесконечной суммы: 0,43(18)=0,43+(0,0018+0,000018+0,00000018..) Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде: 0,0018+0,000018+0,00000018..=0,00181-0,01=0,00180,99=189900. Полученное прибавляем к конечной дроби 0,43=43100 и получаем результат: 0,43(18)=43100+189900 После сложения данных дробей и сокращения получим окончательный ответ: 0,43(18)=1944 В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей. Этот способ очень простой, но он подходит не для каждой дроби. Для начала умножьте числитель и знаменатель на такое число, которое преобразует нижнюю часть дроби в 10 или 100, 1 000 и так далее. Допустим, нам нужно перевести дробь с числителем 7 и знаменателем 25. Мы можем получить в нижней части 100: достаточно умножить 25 на 4. Про верхнюю часть тоже не забываем: получаем 28. Запишите числитель отдельно. Отсчитайте справа в нём столько же знаков, сколько нолей вы получили в знаменателе после умножения, и поставьте запятую. Это и будет искомая десятичная дробь. В нашем примере в знаменателе 100, значит отсчитываем в числителе два знака и ставим запятую. Получаем 0,28. Если такой множитель подобрать не удаётся, текущий способ не подходит. Воспользуйтесь следующим. Сейчас читают 🔥 Чтобы преобразовать обычную дробь в десятичную, достаточно поделить её верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе. Если для вас принципиально важно обойтись без вспомогательных устройств, просто поделите числитель на знаменатель столбиком. Для примера переведём дробь с числителем 7 и знаменателем 25. Поделив 7 на 25 столбиком, получим 0,28. Важный момент. При делении столбиком вы можете обнаружить, что процесс идёт по кругу и после запятой в результат попадают повторяющиеся цифры. В таком случае эту дробь нельзя перевести в конечную десятичную. Вместо неё у вас получится периодическая дробь. Чтобы записать результат, возьмите повторяющееся число в скобки. Допустим, нужно перевести дробь с числителем 1 и знаменателем 3. Поделив 1 на 3 столбиком, мы получим бесконечную десятичную дробь 0,333333333… Приведём её к краткому виду 0,(3) — это и будет результат. Читается как «ноль целых и три в периоде». Читайте также 📕📐✂️ Любую десятичную дробь можно представить в виде обыкновенной дроби. Для этого надо просто записать её со знаменателем. Главное правило в переводе десятичной дроби в обыкновенную — как читается десятичная дробь, так и пишется обыкновенная. Например: 2,3 — две целых три десятых. Так как дробь имеет целую часть, то перевести её мы можем или в смешанное число или в неправильную дробь: Если у десятичной дроби нет целой части, например: 0,75 — ноль целых семьдесят пять сотых, то её можно сразу перевести в правильную обыкновенную дробь и, если нужно (по необходимости), сократить: Не любую обыкновенную дробь можно перевести в десятичную, так как чтобы записать обыкновенную дробь в виде десятичной, надо привести её к знаменателю, представляющему собой единицу с одним или несколькими нулями, например: 10, 100, 1000 и т. д. Если разложить такой знаменатель на простые множители, то получится одинаковое количество двоек и пятёрок: 10 = 2 · 5; 100 = 10 · 10 = 2 · 5 · 2 · 5; 1000 = 10 · 10 · 10 = 2 · 5 · 2 · 5 · 2 · 5. Никаких других простых множителей эти разложения не содержат, следовательно: Обыкновенную дробь можно представить в виде десятичной только в том случае, если её знаменатель не содержит никаких других множителей, кроме 2 и 5. Возьмём дробь: При разложении её знаменателя на простые множители получается произведение 2 · 2: Если домножить его на две пятёрки, чтобы уравнять количество пятёрок с двойками, то получится один из нужных знаменателей — 100. Чтобы получить дробь равную данной, то числитель тоже надо будет умножить на произведение двух пятёрок: Рассмотрим ещё одну дробь: При разложении её знаменателя на простые множители получается произведение 2 · 7, содержащее число 7: Множитель 7 будет присутствовать в знаменателе, на какие бы целые числа его ни умножали, поэтому произведение, содержащее только двойки и пятёрки никогда не получится. Значит данную дробь нельзя привести ни к одному из нужных знаменателей: 10, 100, 1000 и так далее. То есть её нельзя представить в виде десятичной. Обыкновенную несократимую дробь нельзя представить в виде десятичной, если её знаменатель содержит хотя бы один простой множитель, отличный от 2 и 5. Обратите внимание, что в правиле написано только о несократимых дробях, потому что некоторые дроби после сокращения, можно представить в виде десятичных. Рассмотрим две дроби: Первая дробь является несократимой и, как мы уже выяснили, её нельзя представить в виде десятичной. Во второй дроби числитель и знаменатель можно сократить на 7, то есть на тот простой множитель, который мешает в первой дроби: Теперь осталось только умножить оба члена дроби на 5, чтобы получить 10 в знаменателе, и можно будет переводить дробь в десятичную: Десятичные дроби — это вид дроби, в которой \(m\) – простое число, а \(n\) в какой-либо степени \(10\). Рассмотрим примеры: \(\frac{1}{10},\frac{1}{100},\frac{1}{1000}\)- в десятой, в сотой и в тысячной части соответственно. Дробь семь пятидесятых \(\frac{7}{50}\) можно записать в виде десятичного числа, умножив числитель и знаменатель на \(2\), получаем \(\frac{14}{100}\), то есть \(0,14\), \(\frac{6}{1000}\) произносится как шесть тысячных и записывается в десятичном виде как \(0,006\). Дробь четыре пятых \(\frac{4}{5}\) можно написать как восемь десятых \(\frac{8}{10}\). По каким правилам обыкновенная дробь переводится в десятичную? Первый способ. Чтобы перевести дробь в десятичную нужно числитель и знаменатель умножить на одно и то же число, чтобы в знаменателе получилось \(10,100,1000,10 000\) и т.д. Второй способ. Второй способ более сложный, но применяется чаще первого. Для его использования, нужно вспомнить деление уголком: Пример бесконечной дроби: Можно ли перевести любую дробь в конечную десятичную? \(2\) и \(5\), то она является конечной: то она является бесконечной. Десятичные дроби применяются в единицах измерения длины. \(1\) км \(=1000\) м \(=10000\) дм \(=100000\)см \(=1000000\) мм \(1\) мм -\(1\) одна миллионная км,\(0,000001\) \(1\) см — \(1\) стотысячная км, \(0,00001\) \(1\) дм — \(1\) десятитысячная км \(0,0001\) \(1\) м — \(1\) одна тысячная км \(0,001\) Задача: выразите \(2,250\) метра в километрах, в десятичной дроби. Решение: 1)убираем ноль с правой части, получаем \(2,25\) 2) в одном км — \(1000\) м значит делим на \(1000 :0,00225\) км Ответ: \(0,00225\) км. Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас! Запишитесь на бесплатное тестирование знаний! Наши преподаватели
Репетитор по математике
Национальный исследовательский ядерный университет «МИФИ»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Считаю, что математика доступна для каждого: это увлекательный мир чисел и операций над ними.
Со мной вы поймёте, что математика может быть очень интересной, если найти свой путь к ней!
Репетитор по математике
Крымский федеральный университет им. Вернадского
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. Развитие логического и аналитического мышления, дисциплина ума — следствия изучения математики. Буду рада помочь успешно усвоить материал школьной программы. Стану другом и наставником для вашего ребёнка! Приглашаю каждого на занятия!
Репетитор по математике
Пермский государственный гуманитарно-педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Я люблю математику за ее точность и однозначность, она помогает мыслить логически, формирует алгоритмическое мышление. При работе с учениками использую наглядное представление материала, игры, таблицы с кратким теоретическим материалом. Верю в то, что главное не отметка, а те знания, которые ученик усвоил и может применить на практике. Похожие статьи Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой. В этом уроке мы рассмотрим каждую из этих операций по отдельности. Как мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности. Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик. Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой». Запишем дроби в столбик так, чтобы запятая оказалась под запятой: Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа: Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа: Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»: Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5 3,2 + 5,3 = 8,5 На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим. У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой. Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных. Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей. Например, рассмотрим десятичную дробь 0,345 Позиция, где находится тройка, называется разрядом десятых Позиция, где находится четвёрка, называется разрядом сотых Позиция, где находится пятёрка, называется разрядом тысячных Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых . Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых . Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных . Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345 Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345. При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными. Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой». Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными. Пример 1. Найти значение выражения 1,5 + 3,4 Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»: В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа: Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа: Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»: Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9 1,5 + 3,4 = 4,9 Пример 2. Найти значение выражения: 3,51 + 1,22 Записываем в столбик данное выражение, соблюдая правило «запятая под запятой» В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа: Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа: Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа: Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»: Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73 3,51 + 1,22 = 4,73 Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд. Пример 3. Найти значение выражения 2,65 + 3,27 Записываем в столбик данное выражение: Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд: Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа: Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа: Отделяем запятой целую часть от дробной: Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92 2,65 + 3,27 = 5,92 Пример 4. Найти значение выражения 9,5 + 2,8 Записываем в столбик данное выражение Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части: Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа: Отделяем запятой целую часть от дробной: Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3 9,5 + 2,8 = 12,3 При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями. Пример 5. Найти значение выражения: 12,725 + 1,7 Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять: Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа: Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа: Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд: Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа: Отделяем запятой целую часть от дробной: Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425 12,725+ 1,700 = 14,425 При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой». Пример 1. Найти значение выражения 2,5 − 2,2 Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»: Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа: Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа: Отделяем запятой целую часть от дробной: Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3 2,5 − 2,2 = 0,3 Пример 2. Найти значение выражения 7,353 — 3,1 В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100. Теперь можно записать в столбик данное выражение и вычислить его: Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253 7,353 — 3,1 = 4,253 Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным. Пример 3. Найти значение выражения 3,46 − 2,39 Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа: Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа: Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа: Отделяем запятой целую часть от дробной: Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07 3,46−2,39=1,07 Пример 4. Найти значение выражения 3−1,2 В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3 Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль: Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа: Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа: Отделяем запятой целую часть от дробной: Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8 3 − 1,2 = 1,8 Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые. Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую. Пример 1. Найти значение выражения 2,5 × 1,5 Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют: Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры. Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую: Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75 2,5 × 1,5 = 3,75 Пример 2. Найти значение выражения 12,85 × 2,7 Перемножим эти десятичные дроби, не обращая внимания на запятые: Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры. Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую: Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695 12,85 × 2,7 = 34,695 Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число. Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую. Например, умножим 2,54 на 2 Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую: Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры. Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую: Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08 2,54 × 2 = 5,08 Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби. Например, умножим 2,88 на 10 Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби: Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры. Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую: Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8 2,88 × 10 = 28,8 Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе. Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8. 2,88 × 10 = 28,8 Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288 2,88 × 100 = 288 Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880. 2,88 × 1000 = 2880 Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях. Например, умножим 3,25 на 0,1 Умножаем эти дроби, как обычные числа, не обращая внимания на запятые: Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры. Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую: Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325 3,25 × 0,1 = 0,325 Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе. Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325 3,25 × 0,1 = 0,325 Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325 3,25 × 0,01 = 0,0325 Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325 3,25 × 0,001 = 0,00325 Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей. При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе. А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе. Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях. В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель. Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих» Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя. Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части. При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой. Итак, разделим 1 на 2. Решим этот пример уголком: Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице», то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую: Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток: Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль: Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа: Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10 Получили ответ 0,5. Значит дробь равна 0,5 Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко: Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см Пример 2. Найти значение выражения 4 : 5 Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую: Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого: Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном. Завершаем пример, умножив 8 на 5, и получив 40: Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8 Пример 3. Найти значение выражения 5 : 125 Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую: Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0 Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль: Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0 Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50 Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль: Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном: Завершаем пример, умножив 4 на 125, и получив 500 Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04 В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом: и далее говорили, что «девять разделить на пять будет один и четыре в остатке». Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее. Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части: Допишем ноль к остатку 4 Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном: Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40: 40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8: 9 : 5 = 1,8 Пример 2. Разделить 84 на 5 без остатка Сначала разделим 84 на 5 как обычно с остатком: Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0 Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой: и завершаем пример, проверив есть ли еще остаток: Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно: Например, разделим 4,8 на 2 Запишем этот пример уголком: Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую: Теперь умножаем частное на делитель и смотрим есть ли остаток от деления: 4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2 8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель: Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4 Пример 2. Найти значение выражения 8,43 : 3 Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки: Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток: Далее продолжаем вычислять, как в обычном делении. Сносим 4 Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления: 24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример: Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81 Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число. Например, разделим 5,95 на 1,7 Запишем уголком данное выражение Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим: После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда: Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит? Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится. Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится: (9 × 2) : (3 × 2) = 18 : 6 = 3 Как видно из примера, частное не поменялось. Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17. На самом деле здесь происходило умножение на 10. Вот как это выглядело: 5,91 × 10 = 59,1 1,7 × 10 = 17 Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо. Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком: Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе. Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21 2,1 : 10 = 0,21 Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры: 2,1 : 100 = 0,021 Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры: 2,1 : 1000 = 0,0021 Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе. Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру. После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто: 63 : 1 = 63 Значит значение выражения 6,3 : 0,1 равно 63 6,3 : 0,1 = 63 Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе. Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63 6,3 : 0,1 = 63 Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630 6,3 : 0,01 = 630 Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры: 6,3 : 0,001 = 6300 Задание 1. Выполните сложение: 0,6 + 0,3 Решение: Задание 2. Выполните сложение: 1,2 + 5,3 Решение: Задание 3. Выполните сложение: 1,6 + 0,4 Решение: Задание 4. Выполните сложение: 0,8 + 0,5 Решение: Задание 5. Выполните вычитание: 0,9 − 0,4 Решение: Задание 6. Выполните вычитание: 2 − 0,3 Решение: Задание 7. Выполните вычитание: 9 − 7,8 Решение: Задание 8. Выполните вычитание: 4 − 1,8 Решение: Задание 9. Выполните умножение: 3,2 × 1,8 Решение: Задание 10. Выполните умножение: 9,3 × 5,8 Решение: Задание 11. Выполните умножение: 0,23 × 0,07 Решение: Задание 12. Выполните умножение: 3,14 × 0,25 Решение: Задание 13. Выполните деление: 9,36 : 6 Решение: Задание 14. Выполните деление: 0,169 : 13 Решение: Понравился урок?
Возникло желание поддержать проект? Среди обыкновенных дробей выделяют дроби, у которых в знаменателе стоит единица с нулями, т.е. 10, 100, 1 000 и т.д., для таких дробей существует специальная форма записи, в которой используют запятую, например, вместо пишут 0,1 (читают: ноль целых одна десятая), пишут 2,34 (читают: две целых тридцать четыре сотых), пишут 25,657 (читают: двадцать пять целых шестьсот пятьдесят семь тысячных). Такую форму записи дробей называют десятичной, а саму дробь — десятичной дробью. Запятая отделяет целую часть от дробной. Обратите внимание: после запятой стоит столько цифр, сколько нулей стоит в записи знаменателя соответствующей обыкновенной дроби. Поэтому вместо пишут 2,03 (читают: две целых три сотых), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем ноль, чтобы после запятой было два знака, т.к. в знаменателе стоит два нуля, а вместо пишут 12,004 (читают: двенадцать целых 4 тысячных), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем два нуля, чтобы после запятой было три знака, т.к. в знаменателе стоит три нуля. Разрядные единицы: записываются так: 0,1; 0,01; 0,001; 0,0001; 0,00001; … . Например, в десятичной дроби 8,4567 последний разряд — это десятитысячные. Поэтому читают ее так: 8 целых 4567 десятитысячных. Чтобы несократимую дробь преобразовать в десятичную, необходимо привести ее к одному из знаменателей 10, 100, 1 000 и т.д. Примеры: Примеры: 1) ; 2) — нельзя преобразовать в десятичную дробь (в разложении знаменателя на простые множители есть 3). Пример: Не любую обыкновенную дробь можно записать в виде десятичной дроби. Например, дробь обратить в десятичную нельзя. Разделим числитель данной дроби на знаменатель получим: Мы видим, что деление можно продолжать бесконечно. И результат деления будет 0,72222… . В данном случае точки означают, что цифра 2 периодически повторяется бесконечно много раз. Число 0,72222… — это бесконечная периодическая десятичная дробь, или периодическая дробь. Данную дробь принято записывать: 0,7(2) и читать: «нуль целых семь десятых и два в периоде». Цифру (2) называют периодом дроби 0,7(2). Записываем так: При этом полученную периодическую дробь мы можем округлить до любого из разрядов, например, округлим дробь 0,72222… до десятых, получим: 0,7. В данном случае число 0,7 называют десятичным приближением до десятых дроби . Запишем: 0,7. Чтобы найти десятичное приближение обыкновенной дроби до нужного разряда, надо: 1) выполнить деление до следующего разряда; 2) полученную конечную десятичную дробь или бесконечную периодическую десятичную дробь округлить до нужного разряда. Поделись с друзьями в социальных сетях:
Сравнение десятичных дробей Сложение и вычитание десятичных дробей Приближенные значения чисел. Округление чисел Умножение десятичных дробей Деление десятичных дробей Среднее арифметическое Десятичные дроби 5 класс
Задание 1179,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1560,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 981,
Мерзляк, Полонский, Якир, Учебник
Номер 1002,
Мерзляк, Полонский, Якир, Учебник
Номер 1003,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 1063,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 232,
Мерзляк, Полонский, Якир, Учебник
Номер 841,
Мерзляк, Полонский, Якир, Учебник
Номер 891,
Мерзляк, Полонский, Якир, Учебник
Задание 177,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 245,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 578,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 733,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 841,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1112,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1199,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
© budu5.com, 2021 Пользовательское соглашение Copyright Преобразование 1/7 в десятичную дробь — это, пожалуй, одно из самых простых вычислений, которое вы можете произвести. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную за 3 секунды меньше! Вот так! Хотите быстро выучить или показать студентам, как преобразовать 1/7 в десятичную форму? Воспроизведите это очень быстрое и веселое видео прямо сейчас! Перво-наперво, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно вспомнить, что: 1 (числитель)
/
7 (знаменатель) Вот небольшой секрет, который вы можете использовать для мгновенного преобразования любой дроби в десятичную: Просто разделите числитель на знаменатель: = 1/7 = 1 ÷ 7 = 0.14285714285714 Это буквально все! 1/7 в виде десятичной дроби — 0,14285714285714. Хотел бы я больше рассказать вам о преобразовании дроби в десятичную, но это действительно так просто, и сказать больше нечего. Если вы хотите попрактиковаться, возьмите ручку и блокнот и попробуйте сами вычислить дробные части в десятичном формате. Если вы, , очень ленивы, , вы можете использовать наш калькулятор ниже! Это отличный вопрос.У нас есть много вычислений на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно или нужно? Ну, во-первых, это просто хороший способ лучше представить дробь, который позволяет вам выполнять с ними общие арифметические операции (например, сложение, вычитание, деление и умножение). В реальной жизни мы в основном имеем дело с десятичными числами (например, с валютой), и поскольку наш мозг с раннего возраста учат понимать и сравнивать десятичные дроби чаще, чем дроби, легче понимать и сравнивать дроби, если они преобразованы. сначала до десятичной дроби! Вот небольшой реальный пример преобразования дроби в десятичную при использовании количеств.Предположим, вы готовите, и обычно вы можете частично увидеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в виде доли оставшегося ингредиента. Это делает преобразование дробей в десятичные дроби полезным навыком в кулинарии. Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете переходить и переводить дроби в десятичные, сколько пожелает ваше маленькое сердце! Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали.Мы очень ценим вашу поддержку! «Что такое 1/7 в виде десятичной дроби?». VisualFractions.com . По состоянию на 18 июля 2021 г. https://visualfractions.com/calculator/fraction-as-decimal/what-is-1-7-as-a-decimal/. «Что такое 1/7 в виде десятичной дроби?». VisualFractions.com , https: // visualfractions.ru / калькулятор / десятичная дробь / что такое-1-7-десятичная /. Доступ 18 июля 2021 г. Что такое 1/7 в виде десятичной дроби ?. VisualFractions.com. Получено с https://visualfractions.com/calculator/fraction-as-decimal/what-is-1-7-as-a-decimal/. Введите числитель и знаменатель Если вы дошли до этого конца страницы, значит, вам ДЕЙСТВИТЕЛЬНО нравится преобразовывать дроби в десятичные? Ниже приведены случайно сгенерированные вычисления для вашего любовного удовольствия от десятичной дроби: Перечислены только дроби с наименьшим числом. Например, чтобы найти 2/8, сначала упростите его до 1/4, а затем выполните поиск.
в таблице ниже. Нужно преобразовать повторяющееся десятичное число в дробь? Следуйте этим примерам: Обратите внимание на шаблон, если перед повторяющимся десятичным знаком нули: Чтобы преобразовать десятичную дробь, которая начинается с неповторяющейся части , например 0,21 456 456456456456 …, в дробную часть, запишите ее как сумму неповторяющихся
часть и повторяющаяся часть. Преобразование любой конечной десятичной дроби в дробь довольно просто. Вы подсчитываете количество десятичных знаков, перемещаете десятичную запятую на это количество разрядов вправо и помещаете полученное число над «1», за которым следует это количество нулей. Например: У этого десятичного знака есть один десятичный знак, поэтому я перемещаю десятичную запятую на одну позицию вправо, чтобы получить 7. Затем я помещаю это над «1», за которым следует один ноль (иначе известный как «10»), чтобы получить: Назвать десятичную дробь «завершающей» десятичной означает, что «она заканчивается», в отличие, скажем, от десятичной дроби для Непрерывное И НЕПовторяющееся десятичное число НЕ МОЖЕТ быть преобразовано в дробь, потому что это «иррациональное» (нефракционное) число. Вам, вероятно, следует просто запомнить некоторые из наиболее простых повторяющихся десятичных знаков, например, 0,33333 … = 1 / 3 и 0,666666 … = 2 / 3 . Посмотрите таблицы на последней странице.) Любое завершающее десятичное число можно преобразовать в дробь, подсчитав количество десятичных знаков и поместив десятичные цифры больше 1, за которыми следует соответствующее количество нулей. Например: В десятичной дроби было два десятичных разряда, поэтому я переместил точку на две единицы вправо, а затем поставил полученное число (а именно «46») над «1», за которым следуют два нуля (также известные как «100»).Потом я упростил. У этого десятичного знака был один десятичный знак. Я переместил точку на одну позицию вправо и поставил полученное число (а именно «15») над «1», за которым следует один ноль (также известный как «10»). Потом я упростил. У этого десятичного знака также был только один десятичный разряд, поэтому процесс был таким же, как и раньше.Допускается наличие нескольких цифр слева от десятичной точки в исходной десятичной форме. Когда вы закончите конвертировать, вы просто получите большую неправильную дробь. У этого десятичного знака было четыре десятичных разряда, но представляла интерес только одна цифра (а именно, «3»). Я переместил точку на четыре позиции вправо и поставил полученное число над «1» с последующими четырьмя нулями (также известными как «10 000»). Полученная дробь совсем не упрощалась. В случае повторяющейся десятичной дроби часто используется следующая процедура. Предположим, у вас есть число вроде 0,5777777 …. Это число равно некоторой дроби; назовите эту дробь « x ». То есть: В этой десятичной дроби одна повторяющаяся цифра, поэтому умножьте x на «1», а затем на один ноль; то есть умножить на 10: Теперь вычтите первое из второго: То есть Не беспокойтесь о «последних 7» в «конце» вычитания выше. Поскольку эти десятичные дроби никогда не заканчиваются (т. Е. Потому, что они не завершаются, они повторяют десятичные дроби), нет «последних 7», и вычитание работает.Это одна из странных, но полезных вещей в бесконечности. В предыдущем примере была одна повторяющаяся цифра. Если бы было, скажем, три повторяющиеся цифры (например, 0,4123123123 …), тогда вы бы умножили x на «1», а затем на три нуля; то есть умножьте на 1000. Затем вычтите и решите, как в приведенном выше примере. Тогда: Решая делением на 999, получаем: И не беспокойтесь, если у вас есть ведущие нули, например, в «0.004444 … «; процедура будет работать: x = 0,004444 …. 10 x = 0,044444 … Тогда: Доверяйте процессу. Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании десятичных дробей в дроби. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway.(Или вы можете продолжить этот урок.) (Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.) Преобразование десятичных чисел в проценты простое: просто переместите десятичную запятую на два разряда вправо и нажмите на знак «%». (Чтобы не отклоняться от направления, в котором вы перемещаете точку, просто помните, что это $ 0.50 — это половина или 50% доллара.) Например: Я переместил точку на два места вправо, получив цифру «23», а затем добавил знак «%». Я переместил точку на два места вправо. Поскольку они дали мне число с чем-то отличным от нуля слева от десятичной точки, я получил трехзначный процент. Это нормально. Проценты больше 100% просто означают, что у меня есть много того, что они измеряют. В данном случае мне дали число с нулями между десятичной запятой и первой ненулевой цифрой. Итак, даже после того, как точка переместилась на два разряда вправо, у меня остались десятичные разряды. Это нормально. Это просто означает, что у меня очень мало того, что они измеряют. (Обратите внимание, что 0,97% меньше одного процента. Его не следует путать с 97%, что составляет 0,97 в виде десятичной дроби.) Если вы помните, что дроби — это деление, то это просто.Калькулятор может сделать эту работу за вас, потому что вы можете просто сделать так, чтобы он выполнял деление. Например: Я проделал длинное деление, которое дало завершающую десятичную дробь. В этом случае, когда я выполнял деление в столбик, я получил десятичную дробь , отличную от . Но десятичная дробь повторяла свою одну цифру, а остаток всегда был одинаковым, так что это повторяющаяся десятичная дробь.Полоса помещается над повторяющейся частью, как удобный способ обозначить, что повторяющаяся часть — это цифра «3». Полное деление быстро закончилось, давая мне красивую аккуратную десятичную форму. В данном случае я довольно долго продолжал деление в столбик, чтобы быть уверенным в результате. С практической точки зрения, однако, как только я добрался до повторяющегося остатка, я был готов, потому что каждый последующий шаг обязательно должен повторять шаги, которые были раньше.Как только я получил остаток 2, я достиг точки повторения. (Сделайте длинное деление самостоятельно, если вы не уверены.) В этом случае есть шесть цифр, которые повторяются, поэтому полоса повторения превышает шестизначный блок. Филиал При преобразовании дробей в десятичные вам может быть предложено округлить до определенного места или до определенного количества десятичных знаков.Например, если посмотреть на последний пример, Округленная форма может быть полезна для задач со словами, где окончательный ответ в округленной форме может быть более практичным, чем повторяющаяся десятичная дробь.Кстати, ничего святого в моем округлении выше нет; если вам не дается указанное количество десятичных знаков для округления, вы можете использовать все, что считаете разумным. В данном случае мне показалось правильным округление до трех десятичных знаков. URL: https://www.purplemath.com/modules/percents2.htm Быстро! Мне нужна помощь с:
Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Find allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные числа, преобразование в дробь, электричество, стоимость факторинга, целые числа, наибольшие общие факторы, наименьшие общие фракции, добавление фракций, сравнение фракций, преобразование фракций, преобразование в десятичные дроби, дробление фракций, умножение фракций, уменьшение дробных фракций, умножение фракций , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, The Equation from slope and y-intLines, The Equation from two pointsLodsottery Практика многочленов Математика, Практика основ , Факторинг разности квадратов многочленов, факторинг триномов многочленов, разложение на множители с GCF Полиномы, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, ДелениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Образцы, Упрощение, Пример Правые треугольники, Ветер, рисунок Много чисел, с которыми нужно иметь дело, и нет, не очень полезно для выбора номеров лотереи.Но если вы понимаете основные концепции, преобразование этих чисел избавляет вас от риска, и вы обязательно станете победителем. Конечно, вы не можете прибавить десятичное значение фута к десятичному значению дюйма без преобразования десятичного значения в дюймах дроби в десятичное значение в футах. Повторите попытку: Преобразование 7′- 4 3/4 дюйма в десятичное значение. 0,6 Преобразование дюймов плюс дробь в десятичную 3 11/16 дюйма Воспользуйтесь нашим калькулятором для преобразования футов / дюймов / дробей в десятичный формат Помните, что процент — это просто особый способ выражения дроби как числа из
100
. Чтобы преобразовать дробь в проценты, сначала разделите числитель на знаменатель. Затем умножьте десятичную дробь на
100
. То есть дробь
4
8
может быть
преобразован в десятичный
разделив
4
от
8
. Его можно преобразовать в проценты, умножив десятичную дробь на
100
. 4
÷
8
знак равно
0,5
0.5
×
100
знак равно
50 Итак, дробь
4
8
эквивалентно
50
%
. Пример 1: Писать
2
25
в процентах. Так, 2
25
знак равно
0,08
0,08
×
100
знак равно
8 Следовательно, дробь
2
25
эквивалентно
8
%
. Посмотрите на изображение ниже, оно показывает, что дробь
2
25
такой же как
8
снаружи
100
, это,
8
%
. Пример 2: Писать
7
4
в процентах. Так, 7
4
знак равно
1,75
1,75
×
100
знак равно
175 Следовательно, дробь
7
4
эквивалентно
175
%
. Пример 3: Писать
1
8
в процентах. Делить
1
от
. Так, 1
8
знак равно
0,125
0,125
×
100
знак равно
12,5 Следовательно, дробь
1
8
эквивалентно
12.5
%
. Это таблица преобразования дюймов в десятичные футы, полезная для съемки. Для простоты эта таблица начинается с эквивалентов от 1 до 12 дюймов в десятичных долях фута. Включено также преобразование 1/8 дюйма в десятичные дроби от 1 дюйма до 2 дюймов. Мы также включаем калькулятор, который выполняет вычисления за вас. Введите свои значения для фута с дюймами или десятичной дроби в футе и нажмите «Преобразовать», чтобы получить эквивалентное измерение. Для дальнейшего преобразования 1/8 дюйма составляет почти 1/100 -го фута. Например: Выполняется расчет в любом направлении (футы / дюймы в десятичные футы или наоборот). Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Первым человеком, изучавшим природу падения тел, был греческий ученый Аристотель. Затем Галилео Галилей обобщил и не проанализировал опыт и эксперименты нескольких поколений исследователей. Он предположил, что в среде, свободной от воздуха, все тела будут падать с одинаковой скоростью. Также Галилей предположил, что во время падения скорость тел постоянно увеличивается.
Цель настоящего исследования состояла в получении значения ускорения свободного падения при помощи математического маятника в условиях разного уровня высоты на уровнем моря. Для достижения поставленной цели были сформулированы следующие задачи исследования:
Гипотеза исследования: логично предположить, что ускорение свободного падения, полученные в разных экспериментах, должны быть близки к значению 9,8 м/с2 и отличаться на сотые или тысячные доли на глубине станции метро Кремлевская (–34 м) и на высоте небоскреба «Лазурные небеса» (+120 м). Также результаты измерений и вычислений могут отличаться погрешностью измерений.
Методы изучения: самостоятельная, индивидуальная работа в сочетании с теоретическими исследовательскими, проектными формами работы.
Читая много различной в том числе и технической литературы, я узнал о практическом применении различия ускорения свободного падения в разных точках на поверхности Земли. Я измерял g различными способами, рассчитывал погрешности измерений, опираясь на общепринятое значение g, учился грамотно проводить эксперимент. Выяснил, что свободное падение – движение равноускоренное. Ускорение свободного падения не зависит от массы тела.
В дальнейшем я хотел бы самостоятельно исследовать зависимость значения ускорения свободного падения от географического положения.
Еще тысячелетия назад люди замечали, что большая часть предметов падает все быстрее и быстрее, а некоторые падают равномерно. Но как именно падают эти предметы – этот вопрос первобытных людей не занимал. Тем не менее нашлись люди, которые по мере возможностей начали исследовать это явление.
Предположив, что произошло бы в случае свободного падения тел в вакууме, Галилей вывел следующие законы падения тел для идеального случая: все тела при падении движутся одинаково; начав падать одновременно, они движутся с одинаковой скоростью; движение происходит с «постоянным ускорением»; темп увеличения скорости тела не меняется, т.е. за каждую последующую секунду скорость тела возрастает на одну и ту же величину. Существует легенда, будто Галилей проделал большой демонстрационный опыт, бросая легкие и тяжелые предметы с вершины Пизанской падающей башни (одни говорят, что он бросал стальные и деревянные шары, а другие утверждают, будто это были железные шары весом 0,5 и 50 кг). Описаний такого публичного опыта нет, и Галилей, несомненно, не стал таким способом демонстрировать свое правило. Галилей знал, что деревянный шар намного отстал бы при падении от железного, но считал, что для демонстрации различной скорости падения двух неодинаковых железных шаров потребовалась бы более высокая башня.
Вскоре после Галилея были созданы воздушные насосы, которые позволили произвести эксперименты со свободным падением в вакууме. С этой целью Ньютон выкачал воздух из длинной стеклянной трубки и бросил сверху одновременно птичье перо и золотую монету. Даже столь сильно различающиеся по своей плотности тела падали с одинаковой скоростью.
S1 : S2 : S3 : … = 1 : 2 : 3 : … (при V0 = 0)
Таким образом, можно предположить, что свободное падение есть равноускоренное движение. Так как для равноускоренного движения перемещение рассчитывается по формуле, то если взять три некоторые точки 1,2,3 через которые проходит тело при падении и записать: (ускорение при свободном падении для всех тел одинаково), получится, что отношение перемещений при равноускоренном движении равно:
S1 : S2 : S3 = t12 : t22 : t32 (2)
Остается еще добавить небольшой комментарий относительно экспериментов со свободным падением тел Исаака Ньютона.
Я много читаю и, как следствие склонен фантазировать. Для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь от значения g на другой планете зависит не только сила тяжести. Люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
На самом деле методов по измерению ускорения свободного падения достаточно много.
Понадобится следующее оборудование:деревянный брусок, трибометр, штатив с муфтой и лапкой, электронный секундомер, динамометр, измерительная лента, линейка. Рассматривая движение бруска вниз по наклонной плоскости, можно записать второй закон Ньютона в векторном виде:
Записывая второй закон Ньютона в проекциях на оси координат:
Ох: – Fтр+ mgsinα = ma
Oy: N – mgcosα = 0
и учитывая, что N = mgcosα; Fтр = μN; можно решить данную систему уравнений и получить ускорение свободного падения:
При этом ускорение a можно вычислить из формулы
так как начальная скорость бруска при скольжении по наклонной плоскости равна 0:
Видим, что для этого нужно измерить длину наклонной плоскости и время скольжения по ней бруска.
Для вычисления sinα и cosα нужно знать длину S и высоту h наклонной плоскости:
Для определения коэффициента трения скольжения положим трибометр на горизонтальную поверхность и с помощью динамометра равномерно протащим по нему брусок. В этом случае на брусок будут действовать 4 силы: сила тяжести, сила упругости пружины динамометра, сила трения, сила реакции опоры.
При равномерном движении бруска эти силы будут попарно равны: Fтр = Fупр, Fтяж = N, т. е. Fупр = μFтяж, тогда коэффициент трения равен
Для меня в этом методе оказалось слишком много математических действий, с которыми в курсе математики я еще не знаком. Поэтому даже не буду приводить результаты проделанных измерений и вычислений.
Как известно давление столба жидкости обусловлено следующими факторами: плотность жидкости, непосредственно высота столба жидкости и само значение ускорения свободного падения на данной планете.
Если преобразовать формулу P = ρgh, получится формула нахождения g. Эта формула выглядит так g = P / ρh, где Р – давление в жидкости на глубине h, которое можно узнать с помощью манометра, ρ – плотность воды равное 1000 кг/м3.
При подобных измерениях нужно учитывать погрешность измерительного прибора, манометра. Достаточно точного мне найти не удалось, поэтому для своих исследований я выбрал другой метод.
3) Измерение ускорения свободного падения с помощью математического маятника
Необходимое оборудование: секундомер, штатив с муфтой и лапкой, шарик на нерастяжимой нити, измерительная лента.
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
В работе используется простейший маятник – шарик на нити. При малых размерах по сравнению с длиной нити и небольших отклонениях от положения равновесия период колебаний равен периоду колебаний математического маятника
Тогда период
и ускорения свободного падения может быть вычислено по формуле
Результаты измерений и вычислений представлены в разделе 2.5
Теоретически значение ускорения свободного падения на поверхности планеты Земля можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
где G — гравитационная постоянная (G = 6,6743 · 10–11 (H ·м2)/кг2).
При вычислениях я применял такие значения:
R = 6370 · 103 м – радиус Земли на широте Казани;
M = 5,9722 · 1024 кг – масса Земли.
Таким образом теоретическое значение gт = 9,823386 м/с2.
Согласно формуле
естественно предположить, что ускорение свободного падения на разных высотах будет немного отличаться: на глубине будет больше, а на высоте меньше вычисленного выше.
Возможно эту небольшую разницу можно объяснить погрешностью измерений. Проверим.
Результаты вычислений значения ускорения свободного падения на различных высотах представлены в таблице:
В классе
На станции метро Кремлевская
На 36-м этаже небоскреба
R = 6370 км,
h = 0
R = 6370 км,
h = –16 м
R = 6370 км,
h = +120 м
9,8234
9,8231
9,8227
Как уже говорилось ранее, оборудование для проведения измерений требовалось весьма не замысловатое: секундомер, штатив с муфтой, шарик на нерастяжимой нити, измерительная лента. При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
С другой стороны период колебаний маятника можно расчитать из определения, ведь период – это время одного полного колебания. Тогда период
и ускорения свободного падения может быть вычислено по формуле
Для начала я проделал все необходимые измерения в классе, в кабинете физики Лицея № 110. Кабинет находится на втором этаже. Учитывая высоту потолков (около 3 м), логично предположить, что вычисленные значения g должны быть близки к gт.
N
t, c
tср, с
Δtср, с
g, м/с2
1
20
40,26
39,94
0,36
9,88924
2
20
39,20
3
20
40,30
4
20
40,18
5
20
39,78
εg = εl+ 2εt = 0,05 + 2 · 0,0015 = 0,053 = 5,3%
∆g = εggсредняя = 0,053 · 9,73971 м/с2 = 0,5162 м/с2 ≈ 0,520
Итог моих измерений и вычислений:
9,37 ≤ g ≤ 10,41
Такие действия я проделал в казанском метрополитене, на станции метро Кремлевская и на 36-м этаже единственного в Казани небоскреба «Лазурные небеса».
n
N
t, c
tср, с
Δtср, с
g, м/с2
1
20
31,80
31,71
0,042
9,96232
2
20
31,72
3
20
31,62
4
20
31,69
5
20
31,71
При измерениях в метро пришлось использовать длину нити 63,5 см.
Относительная погрешность измерения времени εt = 0,063 = 6,3%.
Относительная погрешность измерения длины маятника: εl = 0,24%
Относительная погрешность измерения g: εg = 6,78%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,63 м/с2.
Итог моих измерений и вычислений:
9,33 ≤ g ≤ 10,59
N
t, c
tср, с
Δtср, с
g, м/с2
1
20
28,59
28,57
0,10
9,85664
2
20
28,56
3
20
28,81
4
20
28,52
5
20
28,39
Здесь при измерениях пришлось длину нити еще сократить до 51 см.
Относительная погрешность измерения времени εt = 7%.
Относительная погрешность измерения длины маятника: εl = 0,29%
Относительная погрешность измерения g: εg = 7,58%
Абсолютную погрешность вычисления ускорения свободного падения составила: 0,75 м/с2.
Итог моих измерений и вычислений:
9,11 ≤ g ≤ 10,61
Таблица сравнения теоретически полученных значений g (м/с2) и полученных экспериментально
В классе
На станции метро Кремлевская
На 36-м этаже небоскреба
R = 6370 км,
h = 0
R = 6370 км,
h = –16 м
R = 6370 км,
h = +120 м
Теория
9,8234
9,8231
9,8227
Эксперимент
9,8892
9,9623
9,8566
При подготовке к защите данной работы и в результате теоретического исследования, чтения разных книг и статей я узнал многое об ускорении свободного падения. Как уже упоминал, для меня практическая значимость исследования заключается в возможности прогнозирования форм жизни на небесных телах, с которыми человечество столкнется при неизбежном освоении космоса. Ведь люди заранее смогут узнать, какие существа встретят их на той или иной планете, какими физическими характеристиками они будут обладать.
Также я узнал, что расчеты различия ускорения свободного падения в разных точках на поверхности Земли могут указывать на гравитационные аномалии.
Самое главное, я научился измерять g, различными способами, рассчитывать погрешности измерений, грамотно проводить эксперимент.
Считаю цель исследования достигнута. Средние значение ускорения свободного падения на различных высотах отличаются в зависимости от высоты над уровнем моря: при увеличении высоты значение g уменьшается, при углублении в недра Земли – увеличивается.
Погрешность измерений достаточно велика, но не превышает 10%. Уменьшить погрешность возможно путем проведения большего числа измерений: ни 5, а 20; большего числа колебаний: не 20, а 100. Также при расчетах можно учесть, что Казань находится примерно на уровне 250-300 м над уровнем моря.
В дальнейшем хотелось бы усовершенствовать экспериментальные установки, чтобы измерять ускорение свободного падения с большей точностью.
Планирую самостоятельно исследовать значения ускорения свободного падения в различных уголках земного шара.
Из наблюдений можно заметить, что тела изменяют свою скорость только при наличии не скомпенсированного действия. Т. к. быстрота изменения скорости характеризуется ускорением тела, можем заключить, что причиной ускорения является некомпенсированное действие одного тела на другое. Установились считать: чем меньше ускорение приобретает тело при взаимодействии, тем инертнее это тело. Инертность – это свойство тела сохранять свою скорость постоянной (то же, что и инерция). Проявляет себя в том, что для изменения скорости тела требуется некоторое время. Процесс изменения скорости не может быть мгновенным. Например, движущийся по дороге автомобиль не может мгновенно остановиться, для уменьшения скорости требуется некоторое время, а за это время он успевает переместиться на довольно большое расстояние (десятки метров). (Осторожно переходите дорогу!!!) Мерой инертности является инертная масса. Масса (инертная) – мера инертности тела. Чем инертнее тело, тем больше его масса. Чем больше инертность, тем меньше ускорение. Следовательно, чем больше масса тела, тем меньше его ускорение: a∼1m\boxed{a\sim\frac 1m}. Данная зависимость записана единственно правильным способом, т. к. форма m∼1am \sim \frac 1a не верна. Масса не может зависеть от ускорения, она является свойством тела, а ускорение является характеристикой состояния движения тела. Данная зависимость подтверждается многочисленными опытными результатами. Рис. 2 Измерение массы методом взаимодействия тел. Два тела, скреплённые между собой сжатой пружиной, после пережигания нити, удерживающей пружину, начинают двигаться не которое время с ускорением (рис. 1) . Опыт показывает, что при любых взаимодействиях данных двух тел отношение ускорений тел равно обратному отношению их масс: \[\frac{a_1}{a_2} = \frac{m_2}{m_1};\] если взять первую массу за эталонную (m1=mэтm_1 = m_\mathrm{эт}), то m2=mэтaэтa2m_2 = m_\mathrm{эт}\frac{a_\mathrm{эт}}{a_2}. Масса, измеренная путём взаимодействия (измерения ускорения), называется инертной. Измерение массы методом взвешивания тел. Второй способ измерения масс основан на сравнении действия Земли на различные тела. Такое сравнение можно осуществить либо последовательно (сначала определяют растяжение пружины под действием эталонных масс, а потом под действием исследуемого тела в тех же условиях), либо одновременно располагают на равноплечих рычажных весах на одной чаше исследуемое тело, а на другой эталонные массы (рис. 2). Рис. 2 Масса, измеренная путём взвешивания, называется гравитационной. В качестве эталона и той и другой массы принята масса тела, выполненного в форме цилиндра высотой 39 мм39\ \mathrm{мм} и диаметром 39 мм39\ \mathrm{мм}, изготовленного из сплава 10 % иридия и 90 % платины (рис. Данный факт известен был и ранее, и послужил основанием для формулировки Эйнштейном принципа эквивалентности. Принцип эквивалентности утверждает, что 1) ускорение, вызванное гравитационным взаимодействием в малой области пространства, и за небольшой интервал времени, неотличимо от ускоренно движущейся системы отсчёта. 2) ускоренно движущееся тело эквивалентно неподвижному телу, находящемуся в гравитационном поле. Пример 1. Два тела массами 400 г400\ \mathrm{г} и 600 г600\ \mathrm{г} двигались навстречу друг другу и после удара остановились. Какова скорость второго тела, если первое двигалось со скоростью 3 м/с3\ \mathrm{м}/\mathrm{с}? Решение. Сила, возникающая при взаимодействии тел, конечно же, не остаётся постоянной, и ускорения тоже. Мы будем считать, что и силы, и ускорения принимают некоторы е средние значения, причём одинаковые для любого момента времени. \[\frac{m_2}{m_1} = \frac{a_1}{a_2} = \frac{\frac{\Delta v_1}{\Delta t}}{\frac{\Delta v_2}{\Delta t}} = \frac{v_\mathrm{к1}-v_{01}}{v_\mathrm{к2}-v_{02}} = \frac{v_{01}}{v_{02}},\] откуда получим искомую скорость: v02=m1m2·v01.v_{02} = \frac{m_1}{m_2}\cdot v_{01}. Количественно ответ будет таким: v02=0,4 кг0,6 кг·3 мс=2 мсv_{02} = \frac{0,4\ \mathrm{кг}}{0,6\ \mathrm{кг}}\cdot 3\ \frac{\mathrm{м}}{\mathrm{с}} = 2\ \frac{\mathrm{м}}{\mathrm{с}}. 1439. Мотоцикл в течение 5 с может увеличить скорость от 0 до 72 км/ч. Определите ускорение мотоцикла. 1440. 1441. Автомобиль, двигавшийся со скоростью 72 км/ч, равномерно тормозит и через 10 с останавливается. Каково ускорение автомобиля? 1442. Как назвать движения, при которых ускорение постоянно? равно нулю? 1443. Санки, скатываясь с горы, движутся равноускоренно и в конце третьей секунды от начала движения имеют скорость 10,8 км/ч. Определите, с каким ускорением движутся санки. 1444. Скорость автомобиля за 1,5 мин движения возросла от 0 до 60 км/ч. Найдите ускорение автомобиля в м/с2 , в см/с2. 1445. Мотоцикл «Хонда», двигавшийся со скоростью 90 км/ч, начал равномерно тормозить и через 5 с сбросил скорость до 18 км/ч. Каково ускорение мотоцикла? 1446. Объект из состояния покоя начинает двигаться с постоянным ускорением, равным 6 • 10-3 м/с2. 1447. Яхту спускают на воду по наклонным стапелям. Первые 80 см она прошла за 10 с. За какое время яхта прошла оставшиеся 30 м, если ее движение оставалось равноускоренным? 1448. Грузовик трогается с места с ускорением 0,6 м/с2. За какое время он пройдет путь в 30 м? 1449. Электричка отходит от станции, двигаясь равноускоренно в течение 1 мин 20 с. Каково ускорение электрички, если за это время ее скорость стала 57,6 км/ч? Какой путь она прошла за указанное время? 1450. Самолет для взлета равноускоренно разгоняется в течение 6 с до скорости 172,8 км/ч. Найдите ускорение самолета. Какое расстояние прошел самолет при разгоне? 1451. Товарный поезд, трогаясь с места, двигался с ускорением 0,5 м/с2 и разогнался до скорости 36 км/ч. Какой путь он при этом прошел? 1452. От станции равноускоренно тронулся скорый поезд и, пройдя 500 м, достиг скорости 72 км/ч. 1453. При выходе из ствола пушки снаряд имеет скорость 1100 м/с. Длина ствола пушки равна 2,5 м. Внутри ствола снаряд двигался равноускоренно. Каково его ускорение? За какое время снаряд прошел всю длину ствола? 1454. Электричка, шедшая со скоростью 72 км/ч, начала тормозить с постоянным ускорением, равным по модулю 2 м/с2. Через какое время она остановится? Какое расстояние она пройдет до полной остановки? 1455. Городской автобус двигался равномерно со скоростью 6 м/с, а затем начал тормозить с ускорением, по модуля равным 0,6 м/с2. За какое время до остановки и на каком расстоянии от нее надо начать торможение? 1456. Санки скользят по ледяной дорожке с начальной скоростью 8 м/с, и за каждую секунду их скорость уменьшается на 0,25 м/с. Через какое время санки остановятся? 1457. Мотороллер, двигавшийся со скоростью 46,8 км/ч, останавливается при равномерном торможении в течение 2 с. 1458. Теплоход, плывущий со скоростью 32,4 км/ч, стал равномерно тормозить и, подойдя к пристани через 36 с, полностью остановился. Чему равно ускорение теплохода? Какой путь он прошел за время торможения? 1459. Товарняк, проходя мимо шлагбаума, приступил к торможению. Спустя 3 мин он остановился на разъезде. Какова начальная скорость товарняка и модуль его ускорения, если шлагбаум находится на расстоянии 1,8 км от разъезда? 1460. Тормозной путь поезда 150 м, время торможения 30 с. Найдите начальную скорость поезда и его ускорение. 1461. Электричка, двигавшаяся со скоростью 64,8 км/ч, после начала торможения до полной остановки прошла 180 м. Определите ее ускорение и время торможения. 1462. Аэроплан летел равномерно со скоростью 360 км/ч, затем в течение 10 с он двигался равноускоренно: его скорость возрастала на 9 м/с за секунду. Определите, какую скорость приобрел аэроплан. 1463. Мотоцикл, двигавшийся со скоростью 27 км/ч, начал равномерно ускоряться и через 10 с достиг скорости 63 км/ч. Определите среднюю скорость мотоцикла при равноускоренном движении. Какой путь он проехал за время равноускоренного движения? 1464. Прибор отсчитывает промежутки времени, равные 0,75 с. Шарик скатывается с наклонного желоба в течение трех таких промежутков времени. Скатившись с наклонного желоба, он продолжает двигаться по горизонтальному желобу и проходит в течение первого промежутка времени 45 см. Определите мгновенную скорость шарика в конце наклонного желоба и ускорение шарика при движении по этому желобу. 1465. Отходя от станции, поезд движется равноускоренно с ускорением 5 см/с2. По прошествии какого времени поезд приобретает скорость 36 км/ч? 1466. При отправлении поезда от станции его скорость в течение первых 4 с возросла до 0,2 м/с, в течение следующих 6 с еще на 30 см/с и за следующие 10 с на 1,8 км/ч. 1467. Санки, скатываясь с горы, движутся равноускоренно. На некотором участке пути скорость санок в течение 4 с возросла от 0,8 м/с до 14,4 км/ч. Определите ускорение санок. 1468. Велосипедист начинает двигаться с ускорением 20 см/с2. По истечении какого времени скорость велосипедиста будет равна 7,2 км/ч? 1469. На рисунке 184 дан график скорости некоторого равноускоренного движения. Пользуясь масштабом, данным на рисунке, определите путь, проходимый в этом движении в течение 3,5 с. 1470. На рисунке 185 изображен график скорости некоторого переменного движения. Перечертите рисунок в тетрадь и обозначьте штриховкой площадь, численно равную пути, проходимому в течение 3 с. Чему примерно равен этот путь? 1471. В течение первого промежутка времени от начала равноускоренного движения шарик проходит по желобу 8 см. Какое расстояние пройдет шарик в течение трех таких же промежутков, прошедших от начала движения? 1472. 1473. Поезд, отходя от станции, движется равноускоренно и в течение двух первых секунд проходит 12 см. Какое расстояние пройдет поезд в течение 1 мин, считая от начала движения? 1474. Поезд, отходя от станции, движется равноускоренно с ускорением 5 см/с2. Сколько времени потребуется для развития скорости 28,8 км/ч и какое расстояние пройдет поезд за это время? 1475. Паровоз по горизонтальному пути подходит к уклону со скоростью 8 м/с, затем движется вниз по уклону с ускорением 0,2 м/с. Определите длину уклона, если паровоз проходит его за 30 с. 1476. Начальная скорость тележки, движущейся вниз по наклонной доске, равна 10 см/с. Всю длину доски, равную 2 м, тележка прошла в течение 5 сек. Определите ускорение тележки. 1477. 1478. Автобус, двигаясь со скоростью 4 м/с, начинает равномерно ускоряться на 1 м/с за секунду. Какой путь пройдет автобус за шестую секунду? 1479. Грузовик, имея некоторую начальную скорость, начал двигаться равноускоренно: за первые 5 с прошел 40 м, а за первые 10 с — 130 м. Найдите начальную скорость грузовика и его ускорение. 1480. Катер, отходя от пристани, начал равноускоренное движение. Пройдя некоторое расстояние, он достиг скорости 20 м/с. Какова была скорость катера в тот момент, когда он проплыл половину этого расстояния? 1481. Лыжник скатывается с горы с нулевой начальной скоростью. На середине горы его скорость была 5 м/с, через 2 с скорость стала 6 м/с. Считая, что она увеличивается равномерно, определите скорость лыжника через 8 с после начала движения. 1482. Автомобиль тронулся с места и двигается равноускоренно. За какую секунду от начала движения путь, пройденный автомобилем, вдвое больше пути, пройденного им в предыдущую секунду? 1483. Найдите путь, пройденный телом за восьмую секунду движения, если оно начинает двигаться равноускоренно без начальной скорости и за пятую секунду проходит путь 27 м. 1484. Провожающие стоят у начала головного вагона поезда. Поезд трогается и движется равноускоренно. За 3 с весь головной вагон проходит мимо провожающих. За какое время пройдет мимо провожающих весь поезд, состоящий из 9 вагонов? 1485. Материальная точка движется по закону x = 0,5t². Какое это движение? Каково ускорение точки? Постройте график зависимости от времени: 1486. Поезд остановился через 20 с после начала торможения, пройдя за это время 120 м. Определите первоначальную скорость поезда и ускорение поезда. 1487. Поезд, идущий со скоростью 18 м/с, начал тормозить, и через 15 с остановился. Считая движение поезда при торможении равнозамедленным, определите путь, пройденный поездом за эти 15 с. 1488. Постройте графики скорости равнозамедленного движения для случаев: 1489. Изобразите пройденный путь за время t на графике скорости равнозамедленного движения. Принять V0 = 10 м/с, а = 2 м/с2. 1490. Опишите движения, графики скоростей которых даны на рисунке 186, а и б. ТАСС, 2 января. Специалисты компании Google, которые создали прототип квантового компьютера Sycamore, планируют использовать его для решения как теоретических, так и практических научных задач. Квантовыми компьютерами называют вычислительные устройства, в основе работы которых лежат принципы квантовой механики. В отличие от обычных компьютеров, в которых для передачи и обработки данных используются биты – единицы информации, которые содержат либо 1, либо 0, квантовые компьютеры оперируют кубитами – ячейками памяти и примитивными вычислительными модулями, которые могут хранить в себе одновременно и ноль, и единицу. Благодаря этому квантовые компьютеры могут обрабатывать большие объемы информации во много раз быстрее обычных – даже если это суперкомпьютеры с огромными вычислительными мощностями. Существует два подхода к разработке подобных устройств – классический и адиабатический. В первом случае ученые пытаются создать так называемый универсальный квантовый компьютер, который по принципу работы похож на обычный современный компьютер. Инженеры и ученые Google почти пять лет разрабатывают устройство, которое должно объединить достоинства обоих подходов. Первая его версия состояла из девяти кубитов. Главная задача специалистов компании состояла в том, чтобы достичь так называемого квантового превосходства, то есть момента, когда ни один классический компьютер не может достичь тех же результатов, что и квантовый. На эту тему В ноябре прошлого года представители Google заявили, что достигли квантового превосходства в математической задаче, которая сводится к перебору набора псевдослучайных чисел. Для ее решения ученые использовали прототип квантового компьютера, Sycamore, который состоял из 53 сверхпроводящих кубитов. Несколько миллионов решений он нашел меньше чем за четыре минуты, тогда как у самого мощного суперкомпьютера на это ушло бы больше 10 тыс. В 2020 году об аналогичном достижении рассказали ученые из китайского Научно-технического университета. Их квантовый компьютер, «Цзю Чжан», создан на основе 73 фотонных кубитов. Он за 20 секунд решил еще одну задачу по выработке случайных чисел, которую обычный компьютер завершил бы за несколько миллиардов лет. Как и в случае с Sycamore, эти заявления вызвали множество споров о том, что можно считать нерешаемой задачей и как ее можно просчитывать на квантовом компьютере. Подобные достижения заставили ученых задуматься, какие практические задачи сможет решить квантовый компьютер. Одним из направлений, как считает Вадим Смелянский, может стать симуляция физических систем. «Уже сейчас, еще до появления систем коррекции ошибок, с помощью квантовых компьютеров можно изучать явления, связанные с квантовым хаосом и исчезновением информации. Другая команда Google будет использовать квантовые цепи для построения моделей квантовой гравитации», – пояснил ученый. На эту тему Также исследователи планируют использовать подобные системы, чтобы изучать, как некоторые полупроводники и металлы могут превращаться в изоляторы из-за взаимодействий электронов внутри них. Ученые недавно обнаружили, что аналогичные процессы, так называемые переходы Андерсона, могут возникать в самых разных условиях, в том числе и внутри кристаллов, электромагнитных волн или облаков из атомов. Смелянский и его коллеги надеются, что квантовые компьютеры помогут понять природу этих переходов и выяснить, какую роль они играют в формировании свойств того или иного типа материи. По словам ученого, для этого необязательно использовать Sycamore и другие сверхпроводниковые квантовые компьютеры – достаточно будет и других машин с подходящим количеством кубитов и высоким уровнем их связанности. «Все эти явления можно изучать в квантовых системах самых разных видов, в том числе и нейтральных атомов и ионов. Однако сверхпроводящие кубиты пока максимально приспособлены для решения этих задач. В будущем, как отметил Смелянский, Google планирует применять квантовые компьютеры, чтобы создавать научные задачи, на которых будут обучаться системы искусственного интеллекта, а также для химических расчетов на уровне отдельных атомов. Однако это станет возможным только после того, как ученые решат еще одну важную задачу. На эту тему «Есть еще задачи квантовой химии, однако пока мы не понимаем, можно ли их будет решать без создания систем коррекции ошибок, в отличие от тех алгоритмов, о которых я уже говорил. По сути, мы перейдем в новое измерение, когда эта веха будет достигнута, так как мы сможем ставить перед собой совершенно иные, более амбициозные и сложные проблемы», – отметил физик. С помощью алгоритмов коррекции ошибок физики и химики смогут просчитывать, как взаимодействуют между собой отдельные атомы и электроны внутри самых сложных молекул. По словам Смелянского, для этого пока не хватает двух вещей. С одной стороны, количество кубитов в квантовых компьютерах пока слишком невелико для того, чтобы на них могли работать уже существующие алгоритмы квантовой коррекции ошибок. С другой стороны кубиты во время простых вычислительных операций пока делают слишком много случайных ошибок. Из-за этого ученые пока не могут создавать достаточно большие квантовые компьютеры, которые могли бы самостоятельно исправлять ошибки в своей работе. В результате квантовые компьютеры находятся в своеобразной «ничейной полосе». Их можно использовать для решения ограниченного числа сложных практических задач, однако пока нельзя превратить в универсальные вычислительные машины. «Мы предполагаем, что той точности работы наших логических схем, которую сейчас можно достичь, скорее всего, не хватит для ведения квантово-химических расчетов. С другой стороны, пока этот вопрос открыт. Вполне возможно, что мы сможем реализовать какой-то более простой подход для коррекции ошибок, который не потребует кубитов, живущих бесконечно долго, подавления квантовых шумов и других сложных трюков. В течение нескольких лет мы будем этим заниматься», – отметил Смелянский. При этом, по его словам, ученые должны фокусировать свои усилия не на увеличении точности работы кубитов, а на создании алгоритмов, которые смогли бы подавлять помехи, а также облегченных схем, с помощью которых можно было бы корректировать ошибки. На эту тему «Даже если мы в разы уменьшим уровень ошибок и повысим качество работы связанных цепочек кубитов, то этого все равно не хватит для того, чтобы решать задачи квантовой химии. Поэтому нам критически важен прогресс именно в области подавления ошибок. Без этого мы ничего не сможем сделать. И если мы достигнем всего вышеперечисленного, то все равно никакой гарантии успеха у нас нет», – подчеркнул физик. По словам Смелянского, в дальнейшем ученые будут совершенствовать уже существующие и достаточно развитые подходы, в том числе сверхпроводящие цепи, полупроводниковые схемы, холодные атомы или ионы. Чтобы создавать принципиально иные системы для квантовых вычислений, в том числе на базе атомных ядер, нужны будут колоссальные усилия и время. Ученый пока не видит никаких перспективных, но пока не изученных направлений. «Наши российские коллеги сейчас говорят о том, что они планируют развивать все четыре направления в рамках квантового проекта «Росатома». Однако в данном случае речь идет о том, что они будут изучать, что сделали другие. Это невозможно делать, просто читая журналы – для этого нужны лаборатории. Как я понимаю, они будут этим заниматься до тех пор, пока они не примут решение сосредоточиться на чем-то одном», – добавил Смелянский. Далеко не все эти усилия, как считает специалист Google, принесут результат. В частности, он отметил, что считает адиабатический подход, которые набирает популярность среди ученых и инвесторов, гораздо менее перспективным и интересным, чем создание универсальных квантовых вычислительных систем. «Вкладывание ресурсов в такие проекты – большая ошибка. Квантовые отжигатели (так называют прототипы адиабатических квантовых компьютеров, – прим. ТАСС) можно будет использовать для физических экспериментов, однако они вряд ли подойдут для решения оптимизационных задач. Недавно наша группа показала, что адиабатические подходы во всех реалистичных случаях приходят к ответу не быстрее, чем классический квантовый алгоритм Монте-Карло. По сути, квантового ускорения здесь не наблюдается», – пояснил исследователь. Сам Google, по словам Смелянского, планирует использовать универсальные квантовые вычислительные машины не только для проверки фундаментальных законов физики, улучшения работы систем поиска информации, тренировки искусственного интеллекта и других абстрактных IT-задач, но и на практике. На эту тему В частности, ученые собираются применять квантовые компьютеры для создания алгоритмов, которые управляют работой автономного транспорта, а также для улучшения свойств компонентов литиевых батарей и других типов аккумуляторов. «Наследников» Sycamore планируют привлечь для помощи биологам и биохимикам из Google, а также их партнерам в Гарварде и в других американских университетах, чтобы значительно ускорить поиски различных новых материалов и катализаторов, а также лекарств от рака и других болезней. Однако когда и как все это будет реализовано, пока сказать сложно, так как ученые еще не решили сложные технические вопросы, связанные с созданием универсального квантового компьютера с тысячами логических кубитов. «Сейчас мы работаем и смотрим на эти проблемы в формате «не до жиру, быть бы живу». Поэтому первоочередная наша цель – просто построить машину, которая смогла бы решать подобные задачи. Только потом мы будем думать о том, как все эти параметры будут влиять на ее работу и разрабатывать метрики, по которым можно оценивать эти изменения», – подытожил Смелянский. КАПИТАН ДАРРЕН «БАМ-БАМ» УИЗ, 29 лет, пилот BBC: «Катапультирование — лучший способ испытать свое тело на прочность. Иногда люди при этом гибнут. Или теряют конечности: руки-ноги отрываются или гнутся в дугу. Я лично стал меньше ростом: был 174 см, а стал на 2 см короче. Дело было в тренировочном полете в Виргинии. Я пилотировал F-15E (американский истребитель. — Esquire). На борту были я и мой стрелок Красти. Идем на бреющем, с высокой скоростью. И вдруг вижу: справа промелькнул стервятник. Тут же машину сильно встряхнуло, и раздался взрыв. Это птицу засосало в двигатель. Через пару секунд хвост и правый борт оказались в пламени. Начинаю набирать высоту, но машина не поддается и заваливается на правое крыло. Надо сваливать. Сообщаю по радио ведомому, чтобы держался подальше, и даю команду: «Покинуть самолет!» С обеих сторон кресла по ручке. Дергаю за них. Механизм срабатывает — отстреливается стекло кабины. Теперь совсем шумно, ветер хлещет. Взлетает заднее кресло — Красти выбросился. Остаюсь в машине один — кажется, на целую вечность, хотя прошло меньше секунды. Стискиваю ручки. Глаза закрыл. Весь напрягся — знаю, сейчас такой луна-парк начнется! Слышу: ведомый радирует диспетчерам, что мы вынуждены катапультироваться. И вылетаю из кабины сам. Даже не знаю, как это описать. Сидишь в кресле, к которому приделана ракета. И стартуешь из самолета, который летит со скоростью 480 км/час. Да, к креслу действительно приделан ракетный двигатель. Он выпихивает тебя из самолета и еще метров 60 проносит по воздуху на реактивной тяге. В общем, набираю высоту с ускорением в 22 g. Если сравнить с аттракционами, то там максимальное ускорение составляет 2 g. Чувствую себя так, словно во мне полторы тонны весу. Ноги, спина и задница отяжелели. Ускорение вжимает меня в спинку кресла, пытается согнуть в дугу — вынуждает уткнуться лбом в колени. Такое ощущение, будто на тебя навалилась куча врагов: бьют кулаками, тянут во все стороны сразу. Чувствую, ремешок шлема врезался в подбородок. Шлем прямо срывает с головы. Кожа на подбородке лопнула под давлением изнутри. Я аж застонал. И тут, как и полагается, кресло подбрасывает меня в воздух. Я впервые открываю глаза. Вижу: кресло улетает. Автоматически раскрывается парашют. Скорость падает. Стропы сильно дергают меня за плечи. Дальше лечу плавно. Весь процесс — с момента, когда я дернул за ручки, до раскрытия парашюта — продлился секунды три-четыре. Открыв глаза, поискал глазами Красти: вон он спускается на парашюте. Смотрю в другую сторону — горящий самолет втыкается в землю. Как назло, около единственного дома в этой дикой горной местности. К счастью, никто не пострадал». Парадантоз крайне неприятное заболевание, которое в первую очередь затрагивает десна. По — другому, в простонародье, парадантоз называют болезнью десен. Первым признаком возникновения такой болезни может служить обильный кровоток десен при утренней чистке зубов. Это означает, что десна стали ослабевать и им необходимо комплексное и профилактическое лечение, которое должно назначаться как можно раньше. Ведь чем раньше будет обнаружено такое заболевание, тем больше становится вероятность спасти десна и привести их в нужное состояние. Вторым признаком, довольно неприятным для человека, может служить возникновение специфического запаха из ротовой полости, что вызывает у многих людей, страдающих такой болезнью крайнее неудобство.
Запущенная форма парадантоза способствует уменьшению площади десен, что ведет к потере зубов. Но, стоит рассмотреть причины, ведущие к заболеванию десен. В первую очередь, риск возникновения такого заболевания как парадантоз вызывает курение и чрезмерное употребление кофе и чая. Курение сужает маленькие сосуды, расположенные в деснах, в связи с чем, кровообращение замедляется, или вовсе перестает функционировать. Это не может быть незамеченным или не нести никаких последствий. Как правило, происходит разрушение десен, а следом начинается выпадение зубов. Чтобы предотвратить столь нежелательную болезнь, стоит как можно чаще посещать стоматолога клиники Санация, чистить зубы два раза в день – утром и вечером, обязательно использовать средства для полоскания, в состав которого должен входит хлоргексидин. Кроме того, стоматологи клиник Санация рекомендуют использовать зубную нить после каждого приема пищи. Таким образом, необходимо избавляться от остатков пищи, которые в свою очередь могут повлиять на ускорение процесс гниения зубов, если в них есть дырки. Зубы и десны нуждаются в постоянном контроле и уходе, чтобы избежать таких неприятных болезней, как парадантоз, кариес и возникновение зубного камня. Главное не затягивать визит к врачу, если ощущается излишние количество налета, запах изо рта или уменьшение площади десен. Ведь здоровая улыбка – залог успеха во многих повседневных делах. Последняя математическая величина, обсуждаемая в Уроке 1, — это ускорение. Часто путают, что ускорение имеет значение, сильно отличающееся от значения, которое ассоциируется с ним спортивными комментаторами и другими людьми. Определение ускорения: Спортивные комментаторы иногда говорят, что человек ускоряется, если он / она быстро движется.И все же ускорение не имеет ничего общего с быстрым движением. Человек может двигаться очень быстро, но при этом не ускоряться. Ускорение связано с изменением скорости движения объекта. Если объект не меняет свою скорость, значит, объект не ускоряется. Данные справа представляют движущийся на север ускоряющийся объект. Скорость меняется с течением времени. Фактически, скорость изменяется на постоянную величину — 10 м / с — каждую секунду. Каждый раз, когда скорость объекта изменяется, объект считается ускоряющимся; у него есть ускорение. Иногда ускоряющийся объект меняет свою скорость на одну и ту же величину каждую секунду. Как упоминалось в предыдущем абзаце, приведенная выше таблица данных показывает, что объект меняет свою скорость на 10 м / с каждую последующую секунду. Это называется постоянным ускорением, поскольку скорость изменяется на постоянную величину каждую секунду. Не следует путать объект с постоянным ускорением с объектом с постоянной скоростью.Не дайте себя обмануть! Если объект меняет свою скорость — на постоянную или переменную величину — то это ускоряющийся объект. И объект с постоянной скоростью не ускоряется. Приведенные ниже таблицы данных отображают движения объектов с постоянным ускорением и изменяющимся ускорением. Обратите внимание, что каждый объект имеет изменяющуюся скорость. Поскольку ускоряющиеся объекты постоянно меняют свою скорость, можно сказать, что пройденное расстояние / время не является постоянной величиной.Например, падающий объект обычно ускоряется при падении. Если бы мы наблюдали движение свободно падающего объекта (движение свободного падения будет подробно обсуждено позже), мы бы заметили, что объект имеет среднюю скорость примерно 5 м / с в первую секунду, примерно 15 м / с. во второй секунде примерно 25 м / с в третью секунду, примерно 35 м / с в четвертую секунду и т. д. Наш свободно падающий объект будет постоянно ускоряться. Учитывая эти средние значения скорости в течение каждого последовательного временного интервала в 1 секунду, мы могли бы сказать, что объект упадет на 5 метров в первую секунду, 15 метров во вторую секунду (для общего расстояния 20 метров), 25 метров в третью. второй (для общей дистанции 45 метров), 35 метров в четвертой секунде (для общей дистанции 80 метров через четыре секунды).Эти числа приведены в таблице ниже. Примечание. Используемый здесь символ ~ означает приблизительно. Это обсуждение показывает, что свободно падающий объект, который ускоряется с постоянной скоростью, будет преодолевать разные расстояния за каждую последующую секунду. Дальнейший анализ первого и последнего столбцов приведенных выше данных показывает, что существует квадратная зависимость между общим пройденным расстоянием и временем путешествия для объекта, начинающегося из состояния покоя и движущегося с постоянным ускорением.2) расстояние; расстояние, пройденное за четыре секунды, в 16 раз превышает расстояние, пройденное за одну секунду. Для объектов с постоянным ускорением расстояние перемещения прямо пропорционально квадрату времени перемещения. Среднее ускорение (a) любого объекта за заданный интервал времени (t) можно рассчитать с помощью уравнения Это уравнение можно использовать для расчета ускорения объекта, движение которого представлено приведенной выше таблицей данных скорость-время.Данные скорости-времени в таблице показывают, что объект имеет ускорение 10 м / с / с. Расчет показан ниже. Значения ускорения выражаются в единицах скорости / времени. Типичные устройства ускорения включают в себя следующие: м / с / с Эти устройства могут показаться немного неудобными для начинающего студента-физика. Тем не менее, это очень разумные единицы, когда вы начинаете рассматривать определение и уравнение ускорения.Причина появления единиц становится очевидной после изучения уравнения ускорения. Поскольку ускорение — это изменение скорости с течением времени, единицы измерения ускорения — это единицы скорости, деленные на единицы времени, то есть (м / с) / с или (миль / час) / с. Единицу измерения (м / с) / с можно математически упростить до м / с 2 . Поскольку ускорение является векторной величиной, с ним связано направление.Направление вектора ускорения зависит от двух вещей: Общий принцип определения ускорения: Этот общий принцип может применяться для определения того, является ли знак ускорения объекта положительным или отрицательным, вправо или влево, вверх или вниз и т. Д.Рассмотрим две таблицы данных ниже. В каждом случае ускорение объекта происходит в положительном направлении . В Примере A объект движется в положительном направлении (т. Е. Имеет положительную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект имеет положительное ускорение. В примере B объект движется в отрицательном направлении (т.е. имеет отрицательную скорость) и замедляется.Согласно нашему общему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект также имеет положительное ускорение. Тот же самый общий принцип может быть применен к движению объектов, представленных в двух таблицах данных ниже. В каждом случае ускорение объекта происходит в отрицательном направлении . В примере C объект движется в положительном направлении (т.е.е., имеет положительную скорость ) и замедляется. Согласно нашему принципу, когда объект замедляется, ускорение происходит в направлении, противоположном скорости. Таким образом, этот объект имеет отрицательное ускорение. В Примере D объект движется в отрицательном направлении (т.е. имеет отрицательную скорость ) и ускоряется. Когда объект ускоряется, ускорение совпадает с направлением скорости. Таким образом, этот объект также имеет отрицательное ускорение. Обратите внимание на использование положительных и отрицательных слов в приведенном выше обсуждении (Примеры A — D). В физике использование положительного и отрицательного всегда имеет физический смысл. Это больше, чем просто математический символ. Положительное и отрицательное, используемые здесь для описания скорости и ускорения движущегося объекта, описывают направление. И скорость, и ускорение являются векторными величинами, и полное описание величины требует использования прилагательного направленного действия.Север, юг, восток, запад, вправо, влево, вверх и вниз — все прилагательные направления. Физика часто заимствует из математики и использует символы + и — как направленные прилагательные. В соответствии с математическим соглашением, используемым в числовых линиях и графиках, положительное значение часто означает вправо или вверх, а отрицательное — влево или вниз. Таким образом, сказать, что объект имеет отрицательное ускорение, как в примерах C и D, означает просто сказать, что его ускорение идет влево или вниз (или в любом направлении, определенном как отрицательное).Отрицательные ускорения не относятся к значениям ускорения меньше 0. Ускорение -2 м / с / с — это ускорение с величиной 2 м / с / с, которое направлено в отрицательном направлении. Чтобы проверить свое понимание концепции ускорения, рассмотрите следующие проблемы и соответствующие решения. Используйте уравнение для ускорения, чтобы определить ускорение для следующих двух движений. К концу этого раздела вы сможете: Рис. 1. Самолет замедляется или замедляется при посадке на острове Сен-Мартен. Его ускорение противоположно его скорости. (Источник: Стив Конри, Flickr) В повседневном разговоре ускорять означает ускоряться. Фактически, ускоритель в автомобиле может заставить его разогнаться. Чем больше ускорение , тем больше изменение скорости за заданный промежуток времени.Формальное определение ускорения согласуется с этими понятиями, но является более всеобъемлющим. Среднее ускорение — это скорость, с которой изменяется скорость , [латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {{v} _ {f} — {v} _ {0}} {{t} _ {f} — {t} _ {0}} [/ latex] , где [latex] \ bar {a} [/ latex] — среднее ускорение, v — скорость, а t — время.(Полоса над a означает среднее ускорение .) Поскольку ускорение — это скорость в м / с, деленная на время в секундах, единицами измерения ускорения в системе СИ являются м / с 2 , квадратные метры в секунду или метры в секунду в секунду, что буквально означает, сколько метров в секунду скорость меняется каждую секунду. Напомним, что скорость — это вектор, у нее есть величина и направление. Это означает, что изменение скорости может быть изменением величины (или скорости), но это также может быть изменение в направлении .Например, если автомобиль поворачивает с постоянной скоростью, он ускоряется, потому что его направление меняется. Чем быстрее вы поворачиваете, тем больше ускорение. Таким образом, ускорение возникает, когда скорость изменяется либо по величине (увеличение или уменьшение скорости), либо по направлению, либо по обоим направлениям. Ускорение — это вектор в том же направлении, что и изменение скорости на , Δ v . Поскольку скорость — это вектор, она может меняться по величине или по направлению.Таким образом, ускорение — это изменение скорости или направления, либо и того, и другого. Имейте в виду, что хотя ускорение происходит в направлении изменения скорости, оно не всегда происходит в направлении движения . Когда объект замедляется, его ускорение противоположно направлению его движения. Это известно как замедление . Мгновенное ускорение a , или ускорение в определенный момент времени , получается с помощью того же процесса, который обсуждался для мгновенной скорости во времени, скорости и скорости, то есть путем рассмотрения бесконечно малого интервала время.Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 6 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На Рисунке 6 (а) ускорение незначительно меняется, и среднее значение за весь интервал почти такое же, как мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему (в данном случае около 1.8 м / с 2 ). На рисунке 6 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы можем рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с 2 и –2,0 м / с 2 соответственно. В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 7.В (а) волан движется вправо, а в (б) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые аргументы, которые используются при решении проблем. Каковы величина и знак смещений при движении поезда метро, показанных в частях (а) и (b) рисунка 7? Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать набросок, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает.Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение Δ x = x f — x 0 . Это просто, поскольку даны начальная и конечная позиции. 1. Определите известные. На рисунке мы видим, что x f = 6,70 км и x 0 = 4,70 км для части (a), и x ′ f = 3,75 км и x ′ 0 = 5.25 км по части (б). 2. Найдите смещение в части (а). [латекс] \ Delta x = {x} _ {f} — {x} _ {0} = 6,70 \ text {km} -4,70 \ text {km} = \ text {+} 2,00 \ text {km} [ / латекс] 3. Найдите смещение в части (b). [латекс] \ Delta x ′ = {x ′} _ {f} — {x ′} _ {0} = \ text {3,75 км} — \ text {5,25 км} = — \ text {1,50 км} [/ латекс] Направление движения в (a) — вправо, поэтому его смещение имеет положительный знак, тогда как движение в (b) — влево и, следовательно, имеет отрицательный знак. Какие расстояния проходят за движения, показанные в частях (a) и (b) поезда метро на Рисунке 7? Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которая была найдена в Примере 1.Пройденное расстояние — это общая длина пути, пройденного между двумя позициями. (См. Смещение.) В случае поезда метро, показанного на рисунке 7, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда. 1. Смещение для части (а) составило +2,00 км. Таким образом, расстояние между начальной и конечной позициями составило 2,00 км, а пройденное расстояние — 2,00 км. 2. Смещение для части (b) было -1.5 км. Таким образом, расстояние между начальной и конечной позициями составляло 1,50 км, а пройденное расстояние — 1,50 км. Расстояние — скаляр. У него есть величина, но нет знака, указывающего направление. Предположим, что поезд на рис. 7 (а) ускоряется из состояния покоя до 30,0 км / ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени? Здесь стоит сделать простой набросок: 1.Определите известные. v 0 = 0 (поезда запускаются в состоянии покоя), v f = 30,0 км / ч и Δ t = 20,0 с. 2. Вычислите Δ v . Поскольку поезд стартует из состояния покоя, его скорость изменяется на [latex] \ Delta v \ text {=} \ text {+} \ text {30,0 км / ч} [/ latex], где знак плюс означает скорость вправо. . 3. Подставьте известные значения и решите неизвестное, [latex] \ bar {a} [/ latex]. [латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {+ \ text {30.{2} [/ латекс] Знак плюс означает, что ускорение направо. Это разумно, потому что поезд стартует из состояния покоя и заканчивает со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и изменение скорости на , как всегда. Теперь предположим, что в конце поездки поезд на Рисунке 7 (а) замедляется до остановки со скорости 30.0 км / ч за 8.00 с. Какое у него среднее ускорение при остановке? 1. Определите известные. v 0 = 30,0 км / ч, v f = 0 км / ч (поезд остановлен, поэтому его скорость равна 0), и Δ t = 8,00 с. 2. Найдите изменение скорости Δ v . Δ v = v f — v 0 = 0-30.{2} \ text {.} [/ Latex] Знак минус указывает на то, что ускорение происходит влево. Этот знак разумен, потому что поезд изначально имеет положительную скорость в этой задаче, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , которое здесь отрицательно. Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости. Графики положения, скорости и ускорения отВремя для поездов в Примере 4 и Примере 5 показано на рисунке 10. (Мы приняли скорость постоянной от 20 до 40 с, после чего поезд замедляется.) Какова средняя скорость поезда в части b примера 2, снова показанной ниже, если поездка занимает 5,00 минут? Средняя скорость — это смещение, разделенное на время. Здесь он будет отрицательным, так как поезд движется влево и имеет отрицательное смещение. 1. Определите известные. x ′ f = 3,75 км, x ′ 0 = 5,25 км, Δ t = 5,00 мин. 2. Определите смещение Δ x ′. В примере 2 мы обнаружили, что Δ x ′ составляет −1,5 км. 3. Найдите среднюю скорость. [латекс] \ bar {v} = \ frac {\ Delta x ′} {\ Delta t} = \ frac {- \ text {1,50 км}} {\ text {5,00 мин}} [/ latex] 4. Перевести единицы. [латекс] \ bar {v} = \ frac {\ Delta x ′} {\ Delta t} = \ left (\ frac {-1 \ text {.} \ text {50 км}} {5 \ text {.} \ text {00 min}} \ right) \ left (\ frac {\ text {60 min}} {1 h} \ right) = — \ text { 18} \ text {.0 км / ч} [/ latex] Отрицательная скорость указывает на движение влево. Наконец, предположим, что поезд на Рисунке 2 замедляется до остановки со скорости 20,0 км / ч за 10,0 с. Какое у него среднее ускорение? Еще раз нарисуем набросок: Как и раньше, мы должны найти изменение скорости и изменение во времени, чтобы вычислить среднее ускорение. 1. Определите известные. v 0 = −20 км / ч, v f = 0 км / ч, Δ t = 10,0 с. 2. Вычислите Δ v . Изменение скорости здесь действительно положительное, так как [латекс] \ Delta v = {v} _ {f} — {v} _ {0} = 0- \ left (- \ text {20 км / ч} \ right) \ text {=} \ phantom {\ правило {0.25} {0ex}} \ text {+} \ text {20 км / ч} [/ latex] 3. Решите для [латекс] \ bar {a} [/ latex]. [латекс] \ bar {a} = \ frac {\ Delta v} {\ Delta t} = \ frac {+ \ text {20} \ text {.{2} [/ латекс] Знак плюс означает, что ускорение направо. Это разумно, потому что поезд изначально имеет отрицательную скорость (слева) в этой задаче, а положительное ускорение противодействует движению (то есть справа). Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь положительно. Как и в примере 5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости. Пожалуй, самое важное, что нужно отметить в этих примерах, — это знаки ответов. В выбранной нами системе координат плюс означает, что величина находится справа, а минус — слева. Это легко представить для смещения и скорости. Но для разгона это немного менее очевидно. Большинство людей интерпретируют отрицательное ускорение как замедление объекта. Этого не было в Примере 2, где положительное ускорение замедляло отрицательную скорость. Ключевым отличием было то, что ускорение происходило в направлении, противоположном скорости.Фактически, отрицательное ускорение увеличит отрицательную скорость. Например, поезд, движущийся влево на рисунке 11, ускоряется за счет ускорения влево. В этом случае и v , и a отрицательны. Знаки плюс и минус указывают направления ускорений. Если ускорение имеет тот же знак, что и изменение скорости, объект ускоряется. Если ускорение имеет знак, противоположный изменению скорости, объект замедляется. Самолет приземляется на взлетно-посадочной полосе, летящей на восток.Опишите его ускорение. Если принять восток за положительное значение, то самолет имеет отрицательное ускорение, так как он ускоряется в сторону запада. Он также замедляется: его ускорение противоположно его скорости. Узнайте о графиках положения, скорости и ускорения. Перемещайте человечка взад и вперед с помощью мыши и наметьте его движение. Задайте положение, скорость или ускорение и позвольте симуляции перемещать человека за вас. Щелкните, чтобы загрузить симуляцию. Запускать на Java. 1. Возможно ли, чтобы скорость оставалась постоянной при ненулевом ускорении? Приведите пример такой ситуации. 2. Возможно ли, чтобы скорость была постоянной, если ускорение не равно нулю? Объяснять. 3. Приведите пример, в котором скорость равна нулю, а ускорение — нет. 4. Если поезд метро движется влево (имеет отрицательную скорость), а затем останавливается, в каком направлении он ускоряется? Ускорение положительное или отрицательное? 5.Знаки плюс и минус используются в одномерном движении для обозначения направления. Каков знак ускорения, уменьшающего величину отрицательной скорости? Положительной скорости? 1. Гепард может разогнаться от состояния покоя до скорости 30,0 м / с за 7,00 с. Какое у него ускорение? 2. Профессиональное приложение. Доктор Джон Пол Стапп, офицер ВВС США, изучал влияние экстремального замедления на человеческое тело.10 декабря 1954 года Стапп проехал на ракетных санях, разогнавшись из состояния покоя до максимальной скорости 282 м / с (1015 км / ч) за 5,00 с, и был резко остановлен всего за 1,40 с! Вычислите его (а) ускорение и (б) замедление. Выразите каждое значение кратным г (9,80 м / с 2 ), взяв его отношение к ускорению свободного падения. 3. Пассажир выезжает на машине задним ходом из гаража с ускорением 1,40 м / с 2 . (A) Сколько времени ему нужно, чтобы набрать скорость 2.00 м / с? (b) Если она затем тормозит до остановки через 0,800 с, каково ее замедление? 4. Предположим, что межконтинентальная баллистическая ракета переходит из состояния покоя в суборбитальную скорость 6,50 км / с за 60,0 с (фактическая скорость и время засекречены). Каково его среднее ускорение в м / с 2 и кратное g (9,80 м / с 2 ). 1.4,29 м / с 2 3. (а) 1,43 с (б) -2,50 м / с 2 4 декабря 2020 г. — Исследователи рассмотрели характеристики ускорения электронов в вакууме, вызываемого лазерными импульсами максимальной мощности, достижимыми сегодня, в поисках ключа к максимальной чистой энергии … Декабрь14, 2020 — Исследователи точно и произвольно контролируют скорость полета легких пуль, открывая новые возможности для оптических и физических … 20 августа 2019 г. — Подруливающее устройство Холла — это двигательная установка, которая часто используется космическими кораблями, выполняющими более длительные миссии. Недавнее исследование показало, как можно увеличить срок службы этих систем … Апр.20, 2021 — Ученые выявили несколько ключевых факторов, которые влияют на количество отскоков, которым прыгает камень при ударе о воду. Исследование включало теоретическое моделирование и экспериментальную установку … 19 августа 2020 г. — Исследователи достигли важной вехи на пути к ускорителю элементарных частиц будущего. Впервые лазерно-плазменный ускоритель проработал более суток в непрерывном режиме… 30 апреля 2021 г. — Будущее ускорения частиц наступило. Пробуждение — многообещающая концепция совершенно нового метода, с помощью которого частицы можно ускорять даже на короткие расстояния. Основанием для этого служит … 17 сентября 2020 г. — В результате авиакатастрофы Boeing 737 Max в 2019 году восстановленный черный ящик после аварии намекал, что отказавший датчик давления, возможно, привел к тому, что злополучный самолет нырнул в нос.Этот и другие инциденты имеют … 19 июля 2018 г. — Почти каждому гольфисту знакомо это чувство. Через несколько минут после идеальной езды по фарватеру каскад необъяснимых пропущенных паттов приводит к разочаровывающему тройному результату … 24 июня 2019 г. — Ученые разработали гибкий и носимый чувствительный к вибрации датчик.Когда этот датчик прикреплен к шее, он может точно распознавать голос по вибрации кожи шеи и не … 14 сентября 2018 г. — Эксперимент продемонстрировал, как применение интенсивного света увеличивает количество электронов до максимально возможного … «Ого, ты действительно прошел с нуля до шестидесяти!» Вы когда-нибудь слышали, чтобы кто-то использовал идиому «от нуля до шестидесяти», как я в приведенном выше примере? Когда кто-то говорит, что что-то пошло с нуля до шестидесяти, на самом деле они говорят, что все ускорилось очень быстро. Ускорение — это величина, на которую скорость чего-либо изменяется в течение заданного периода времени. В этой статье мы поговорим об ускорении: что это такое и как его рассчитать. Пристегнитесь! Ускорение — это скорость изменения скорости за заданный период времени. Для расчета ускорения необходимы скорость и время. Многие путают ускорение со скоростью (или скоростью).Прежде всего, скорость — это просто скорость с направлением, поэтому они часто используются как синонимы, даже если они имеют небольшие различия. Ускорение — это скорость изменения скорости, означающая, что что-то становится быстрее или медленнее. Для расчета ускорения можно использовать уравнение ускорения. Вот наиболее распространенная формула ускорения: $$ a = {Δv} / {Δt} $$ где $ Δv $ — изменение скорости, а $ Δt $ — изменение во времени. Вы также можете написать уравнение ускорения следующим образом: $$ a = {v (f) — v (i)} / {t (f) — t (i)} $$ В этом уравнении ускорения $ v (f) $ — это конечная скорость, а — начальная скорость $ v (i) $. $ T (f) $ — это конечное время, а $ t (i) $ — начальное время. Еще о некоторых вещах, о которых следует помнить при использовании уравнения ускорения: Теперь давайте разберем уравнение ускорения пошагово на реальном примере. Теперь давайте разберем формулу ускорения пошагово на реальном примере. 2 $$ $$ A = 6.2 $$ Давайте попробуем другой пример. Велосипедист, движущийся со скоростью 23,2 м / с, полностью останавливается за 1,5 $ с $. Какое у нее было замедление? Сначала напишите уравнение ускорения. $$ a = (v (f) — v (i)) ÷ (t (f) — t (i)) $$ Затем определите свои переменные. a = то, что мы решаем для $$ V (f) = 0 м / с $$ $$ V (i) = 23,2 м / с $$ $$ T (f) = 1,4 с $$ $$ T (i) = 0 с $$ Теперь подставьте переменные в уравнение и решите: $$ A = {{(0 — 23.2} $$ Не знаете, как рассчитать ускорение по другой формуле? Есть несколько других распространенных формул ускорения. Угловое ускорение — это скорость, с которой угловое ускорение вращающегося объекта изменяется во времени. Вот уравнение углового ускорения: $$ a = {\ change \ in \ angular \ velocity} / {\ change \ in \ time} $$ Центростремительное ускорение — это скорость движения объекта внутрь к центру круга.2} / r $$ $ a (c) $ = ускорение, центростремительное $ v $ = скорость $ r $ = радиус Ускорение — это скорость изменения скорости за заданный период времени. Вы вычисляете ускорение, разделив изменение скорости на изменение во времени. Ищете другие научные объяснения? Мы разбиваем электрическую энергию и как определить различных типов облаков с помощью наших экспертных руководств. Работаете над исследовательской работой, но не знаете, с чего начать? Тогда ознакомьтесь с нашим руководством, где мы собрали множество высококачественных тем для исследований, которые вы можете использовать бесплатно. Нужна помощь с уроком английского языка — в частности, с определением литературных приемов в текстах, которые вы читаете? Тогда вы обязательно захотите взглянуть на наше исчерпывающее объяснение самых важных литературных устройств и того, как они используются. Ускорение свободного падения ВСЕГДА отрицательное. Любой объект, на который действует только сила тяжести (снаряд или объект в свободном падении), имеет ускорение -9.81 м / с 2 независимо от направления. Ускорение отрицательное при подъеме, потому что скорость уменьшается. Ускорение отрицательное при спуске, потому что он движется в отрицательном направлении, вниз. Даже в верхней части траектории, где мгновенная скорость равна 0 м / с, ускорение по-прежнему составляет -9,81 м / с 2 . Когда в задаче упоминается, что объект «находится в свободном падении», «падает», «брошен», «подбрасывается» или какой-либо другой синоним, предполагается постоянное значение ускорения свободного падения.Если в уравнении есть a , например, v = v 0 + at , ускорение будет отрицательным . Если в уравнении g , например W = mg, подразумевается направление и ускорение положительное . Мгновенное ускорение a, a, или ускорение в определенный момент времени , получается с помощью того же процесса, который обсуждался для мгновенной скорости во Time, Velocity и Speed, то есть путем рассмотрения бесконечно малого интервала времени.Как найти мгновенное ускорение, используя только алгебру? Ответ заключается в том, что мы выбираем среднее ускорение, которое представляет движение. На рисунке 2.29 показаны графики мгновенного ускорения в зависимости от времени для двух очень разных движений. На рис. 2.29 (а) ускорение немного меняется, а среднее значение за весь интервал почти такое же, как и мгновенное ускорение в любой момент времени. В этом случае мы должны рассматривать это движение, как если бы оно имело постоянное ускорение, равное среднему — в данном случае около 1.8 м / с 21,8 м / с2. На рис. 2.29 (b) ускорение резко меняется со временем. В таких ситуациях лучше всего рассматривать меньшие временные интервалы и выбирать для каждого среднее ускорение. Например, мы могли бы рассматривать движение во временных интервалах от 0 до 1,0 с и от 1,0 до 3,0 с как отдельные движения с ускорениями +3,0 м / с2 + 3,0 м / с2 и –2,0 м / с2, –2,0 м / с2. , соответственно. Рис. 2.29. Графики мгновенного ускорения в зависимости от времени для двух различных одномерных движений.(а) Здесь ускорение изменяется незначительно и всегда в одном и том же направлении, поскольку оно положительное. Среднее значение за интервал почти такое же, как и ускорение в любой момент времени. (b) Здесь ускорение сильно различается, возможно, представляя пакет на конвейерной ленте почтового отделения, который ускоряется вперед и назад, когда он натыкается. В такой ситуации необходимо учитывать небольшие интервалы времени (например, от 0 до 1,0 с) с постоянным или почти постоянным ускорением. В следующих нескольких примерах рассматривается движение поезда метро, показанного на рисунке 2.30. В (а) волан движется вправо, а в (б) — влево. Примеры призваны дополнительно проиллюстрировать аспекты движения и проиллюстрировать некоторые аргументы, которые используются при решении проблем. Каковы величина и знак смещений при движении поезда метро, показанных в частях (a) и (b) Рисунка 2.30? Стратегия Чертеж с системой координат уже предоставлен, поэтому нам не нужно делать эскиз, но мы должны проанализировать его, чтобы убедиться, что мы понимаем, что он показывает. Обратите особое внимание на систему координат. Чтобы найти смещение, мы используем уравнение Δx = xf − x0.Δx = xf − x0. size 12 {Δx = x rSub {size 8 {f}} — x rSub {size 8 {0}}} {} Это просто, поскольку даны начальная и конечная позиции. Решение 1.Определите известные. На рисунке мы видим, что xf = 6,70 км xf = 6,70 км и
x0 = 4,70 км x0 = 4,70 км для части (a) и x′f = 3,75 км x′f = 3,75 км и x′0 = 5,25 км x′0 = 5,25 км для части (b). 2. Найдите смещение в части (a). 3. Найдите смещение в части (b). Обсуждение Направление движения в (a) — вправо, и, следовательно, его смещение имеет положительный знак, тогда как движение в (b) — влево и, таким образом, имеет знак минус. Каковы расстояния, пройденные за движения, показанные в частях (a) и (b) поезда метро на Рисунке 2.30? Стратегия Чтобы ответить на этот вопрос, подумайте об определениях расстояния и пройденного расстояния и о том, как они связаны с перемещением. Расстояние между двумя положениями определяется как величина смещения, которая была найдена в Примере 2.2. Пройденное расстояние — это общая длина пути, пройденного между двумя позициями. См. Смещение. В случае поезда метро, показанного на рис. 2.30, пройденное расстояние равно расстоянию между начальным и конечным положениями поезда. Решение 1. Смещение для части (а) составило +2,00 км. Таким образом, расстояние между начальной и конечной позициями составило 2,00 км, а пройденное расстояние — 2,00 км. 2. Смещение части (б) составило -1,5 км. Таким образом, расстояние между начальной и конечной позициями составляло 1,50 км, а пройденное расстояние — 1,50 км. Обсуждение Расстояние — скаляр.У него есть величина, но нет знака, указывающего направление. Предположим, что поезд на рис. 2.30 (a) ускоряется из состояния покоя до 30,0 км / ч за первые 20,0 с своего движения. Каково его среднее ускорение за этот промежуток времени? Стратегия Здесь стоит сделать простой набросок Эта проблема состоит из трех этапов.Сначала мы должны определить изменение скорости, затем мы должны определить изменение во времени и, наконец, мы должны использовать эти значения для расчета ускорения. Решение 1. Определите известные. v0 = 0v0 = 0 размер 12 {v rSub {size 8 {0}} = 0} {} (поезда запускаются в состоянии покоя), vf = 30,0 км / ч, vf = 30,0 км / ч, размер 12 {v rSub { размер 8 {f}} = «30» «.» «0 км / ч»} {} и Δt = 20,0 с.Δt = 20,0 с. размер 12 {Δt = «20» «.» «0 с»} {} 2. Рассчитайте Δv.Δv. размер 12 {Δv} {} Поскольку поезд трогается с места, его скорость изменяется Δv = + 30.0 км / ч, Δv = + 30,0 км / ч, размер 12 {Δv «= +» «30» «.» 0` «km / h»} {} где знак плюс означает скорость вправо. 3. Подставьте известные значения и найдите неизвестное, размер a-a-12 {{bar {a}}} {}. 4. Поскольку единицы измерения смешанные (у нас есть часы и секунды для времени), нам нужно преобразовать все в единицы измерения СИ — метры и секунды.См. Дополнительные указания в разделе «Физические величины и единицы». Обсуждение Знак плюс означает, что ускорение направо.Это разумно, потому что поезд стартует из состояния покоя и заканчивает со скоростью вправо (тоже положительной). Таким образом, ускорение происходит в том же направлении, что и , изменяя скорость на , как всегда. Теперь предположим, что в конце поездки поезд на рис. 2.30 (a) замедляется до остановки со скорости 30,0 км / ч за 8,00 с. Какое у него среднее ускорение при остановке? Стратегия В этом случае поезд замедляется, а его ускорение отрицательное, потому что он направлен влево.Как и в предыдущем примере, мы должны найти изменение скорости и изменение во времени, а затем вычислить ускорение. Решение 1. Определите известные. v0 = 30,0 км / ч, v0 = 30,0 км / ч, vf = 0 км / ч — vf = 0 км / ч — поезд остановлен, поэтому его скорость равна 0 — и Δt = 8,00 с.Δt = 8,00 с. 2. Найдите изменение скорости Δv.Δv. размер 12 {Δv} {} 3. Подключите известные значения ΔvΔv, размер 12 {Δv} {} и Δt, Δt, и решите для aa- 4. Преобразование единиц в метры и секунды. Обсуждение Знак минус указывает на то, что ускорение происходит влево. Этот знак разумен, потому что поезд изначально имеет положительную скорость в этой задаче, а отрицательное ускорение будет препятствовать движению. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь отрицательно.Это ускорение можно назвать замедлением, потому что оно имеет направление, противоположное скорости. Графики положения, скорости и ускорения в зависимости от времени для поездов в Примере 2.4 и Примере 2.5 показаны на Рисунке 2.33. Мы приняли скорость постоянной от 20 до 40 с, после чего поезд замедляется. Рис. 2.33 (a) Положение поезда во времени. Обратите внимание, что положение поезда меняется медленно в начале пути, а затем все быстрее и быстрее, когда он набирает скорость.Затем его положение меняется медленнее по мере замедления в конце пути. В середине пути, когда скорость остается постоянной, положение меняется с постоянной скоростью. (б) Скорость поезда во времени. Скорость поезда увеличивается по мере его ускорения в начале пути. Он остается неизменным в середине пути, когда нет ускорения. Оно уменьшается по мере замедления поезда в конце пути. (c) Ускорение поезда с течением времени. Поезд имеет положительное ускорение, поскольку он ускоряется в начале пути.У него нет ускорения, поскольку он движется с постоянной скоростью в середине пути. Его ускорение отрицательное, так как он замедляется в конце пути. Какова средняя скорость поезда в части b примера 2.2, которая снова показана ниже, если поездка занимает 5,00 минут? Стратегия Средняя скорость — это смещение, разделенное на время. Здесь он будет отрицательным, так как поезд движется влево и имеет отрицательное смещение. Решение 1. Определите известные. x′f = 3,75 км, x′f = 3,75 км, x′0 = 5,25 км, x′0 = 5,25 км, Δt = 5,00 мин. Δt = 5,00 мин. 2. Определите перемещение Δx′.Δx ′. В примере 2.2 мы обнаружили, что Δx′Δx ′ составляет −1,5 км. 3. Найдите среднюю скорость. 4.Преобразование единиц. Обсуждение Отрицательная скорость указывает на движение влево. Наконец, представьте поезд на Рисунке 2.34 замедляется до полной остановки со скорости 20,0 км / ч за 10,0 с. Какое у него среднее ускорение? Стратегия Еще раз нарисуем скетч: Как и раньше, мы должны найти изменение скорости и изменение во времени, чтобы вычислить среднее ускорение. Решение 1. Определите известные. v0 = -20 км / ч, v0 = -20 км / ч, vf = 0 км / ч, vf = 0 км / ч, Δt = 10,0 с. Δt = 10,0 с. 2.Рассчитайте ΔvΔv размер 12 {Δv} {}. Изменение скорости здесь фактически положительное, так как 3. Найдите размер aa- 12 {{bar {a}}} {}. 4. Перевести единицы. Обсуждение Знак плюс означает, что ускорение направо. Это разумно, потому что у поезда изначально отрицательная скорость (слева) в этой задаче, а положительное ускорение противодействует движению, то есть справа. Опять же, ускорение происходит в том же направлении, что и изменение скорости на , что здесь положительно. Как и в примере 2.5, это ускорение можно назвать замедлением, поскольку оно происходит в направлении, противоположном скорости. Ускорение — это скорость изменения скорости как функция времени. Это вектор, то есть он имеет как величину, так и направление. Он измеряется в метрах в секунду в квадрате или в метрах в секунду (скорость или скорость объекта) в секунду. В терминах исчисления ускорение — это вторая производная положения относительно времени или, альтернативно, первая производная скорости относительно времени. Каждый день ускорение происходит в автомобиле.Вы нажимаете на педаль акселератора, и автомобиль ускоряется по мере того, как двигатель прикладывает все возрастающее усилие к трансмиссии. Но замедление — это тоже ускорение — скорость меняется. Если вы уберете ногу с педали акселератора, сила и скорость уменьшатся со временем. Как видно из рекламы, ускорение следует правилу изменения скорости (миль в час) с течением времени, например, от нуля до 60 миль в час за семь секунд. Единицы измерения ускорения в системе СИ: м / с 2 Гал или галилей (Gal) — это единица ускорения, используемая в гравиметрии, но не единица СИ. Он определяется как 1 сантиметр на секунду в квадрате. 1 см / с 2 Английские единицы измерения ускорения — футы в секунду в секунду, фут / с 2 Стандартное ускорение свободного падения или стандартное ускорение свободного падения g 0 — это ускорение свободного падения объекта в вакууме у поверхности земли. Он сочетает в себе действие силы тяжести и центробежного ускорения от вращения Земли. Уравнение классической механики для ускорения происходит из Второго закона Ньютона: сумма сил ( F ) на объекте постоянной массы ( м ) равна массе м , умноженной на ускорение объекта ( a ). . F = a м Следовательно, это можно изменить, чтобы определить ускорение как: a = F / м Результатом этого уравнения является то, что если на объект не действуют силы ( F = 0), он не будет ускоряться. Его скорость останется постоянной. Если к объекту добавить массу, ускорение будет меньше. Если убрать массу с объекта, его ускорение будет выше. Второй закон Ньютона — один из трех законов движения, опубликованных Исааком Ньютоном в 1687 году в книге Philosophiæ Naturalis Principia Mathematica ( Mathematical Principles of Natural Philosophy ). Хотя законы движения Ньютона применяются на скоростях, с которыми мы сталкиваемся в повседневной жизни, как только объекты движутся со скоростью, близкой к скорости света, правила меняются. Именно тогда специальная теория относительности Эйнштейна более точна. В жизни мы достаточно часто сталкиваемся с практическими задачками, где необходимо знание математики и логики. Да, для решения задачи мы сегодня может найти готовое решение (формулу) в сети интернет. Но никогда не было лишним пошевелить мозгами и понять почему именно такое решение или формула. Итак, занимательная задачка, в которой необходимо посчитать количество всевозможных пар среди заданного колличества объектов. Если количество объектов невелико, то можно посчитать пары методом перебора. Но с ростом объектов это количество пар прогрессивно растет. Начнем с самого простого. А вот на четырех элементах мы остановимся подробнее. Четыре элемента для удобства перебора пар мы изобразим в виде квадрата, разделенного на 4 равные части (квадраты). На рисунке схематично изображены варианты создания пар поочередно для каждого из четырех квадратиков. Таким образом каждые остальные другие 3 квадратика могут создать ровно такое же количество пар соответственно. Общее количество вариантов в итоге можно посчитать как произведение: 4×3=12 где 4 — всего количество элементов, 3 — количество элементов, с которыми каждый из квадратиков может создать пару. Однако. В этом полученном количестве элементов каждая пара повторяется 2 раза. На рисунке мы видим как первый квадратик может создать пару вторым, а второй естественно в своих вариантах с первым, что является дублем. То есть вариант 1-2 равен варианту 2-1. Это одна пара. И так по каждому элементу. Таким образом число 12 необходимо разделить на 2 Получим 6 возможных пар. Данное решение не сложно проверить методом перебора. Итак, формула для получения возможного количества пар из общего числа выглядит Количество пар = (Общее число элементов X Общее число элементов — 1) / 2 Формулу совершенно несложно запомнить и при случае в уме посчитать количество возможных пар не прибегая к сети интернет. Помимо этого: [вне]: Как я могу математически рассчитать количество всех возможных комбинаций? Есть ли способ сделать это вычислительно, не перечисляя возможные комбинации? 1 alvas
15 Июн 2015 в 17:06 Лучший ответ Всегда есть 2 n −1 непустое подмножество множества На самом деле с математической точки зрения: k-комбинация набора — это подмножество k различных элементов S. Если набор имеет n элементов, количество k-комбинаций равно биномиальный коэффициент: И для всех комбинаций: 7 Kasramvd
25 Авг 2015 в 06:18 Предполагая, что у вас есть список из Математически Это определение комбинаций Так как общая функция Грубая сила 1 CoryKramer
15 Июн 2015 в 15:05 Число π показывает, во сколько раз длина окружности больше ее диаметра. Неважно, какого размера окружность, — как заметили по меньшей мере еще 4 тыс. лет назад, соотношение всегда остается одним и тем же. Вопрос только, чему оно равняется. Чтобы высчитать его приблизительно, достаточно обыкновенной нитки. Грек Архимед в III веке до н.э. применял более хитрый способ. Он чертил внутри и снаружи окружности правильные многоугольники. Складывая длины сторон многоугольников, Архимед все точнее определял вилку, в которой находится число π, и понял, что оно приблизительно равно 3,14. Методом многоугольников пользовались еще почти 2 тыс. лет после Архимеда, это позволило узнать значение числа π вплоть до 38-й цифры после запятой. Пока одни ученые использовали геометрический метод, другие догадались, что число π можно рассчитывать, складывая, вычитая, деля или умножая другие числа. Благодаря этому «хвост» вырос до нескольких сотен цифр после запятой. С появлением первых вычислительных машин и особенно современных компьютеров точность повысилась на порядки — в 2016 году швейцарец Петер Трюб определил значение числа π до 22,4 трлн знаков после запятой. Если напечатать этот результат в строчку 14-м кеглем нормальной ширины, то запись получится немногим короче, чем среднее расстояние от Земли до Венеры. В принципе ничто не мешает добиться еще большей точности, но для научных расчетов в этом давно нет нужды — разве что для тестирования компьютеров, алгоритмов и для исследований в математике. А исследовать есть что. Даже про само число π известно не все. Доказано, что оно записывается в виде бесконечной непериодической дроби, то есть цифрам после запятой нет предела, и они не складываются в повторяющиеся блоки. Дальнейшие вычисления проводятся в основном из спортивного интереса — и по той же причине люди пытаются запомнить как можно больше цифр после запятой. Рекорд принадлежит индийцу Раджвиру Мине, который в 2015 году назвал на память 70 тыс. знаков, сидя с завязанными глазами почти десять часов. Наверное, чтобы превзойти его результат, нужен особый талант. Но просто удивить друзей хорошей памятью способен каждый. Главное — использовать одну из мнемонических техник, которая потом может пригодиться и для чего-нибудь еще. Самый очевидный способ — разбить число на одинаковые блоки. Например, можно представить π как телефонную книгу с десятизначными номерами, а можно — как причудливый учебник истории (и будущего), где перечислены годы. Много так не запомнишь, но, чтобы произвести впечатление, хватит и пары десятков знаков после запятой. Считается, что самый удобный способ запомнить цифры — придумать историю, где им будет соответствовать количество букв в словах (ноль было бы логично заменить пробелом, но тогда большинство слов сольется; вместо этого лучше использовать слова из десяти букв). По этому принципу построена фраза «Можно мне большую упаковку кофейных зерен?» на английском языке: May — 3, I — 1 have — 4 a — 1 large — 5 container — 9 of — 2 coffee — 6 beans — 5 На эту тему В дореволюционной России придумали похожее предложение: «Кто и шутя и скоро пожелает(ъ) Пи узнать число, уже знает(ъ)». Точность — до десятого знака после запятой: 3,1415926536. Но проще запомнить более современный вариант: «Она и была, и будет уважаемая на работе». Есть и стихотворение: «Это я знаю и помню прекрасно — пи, многие знаки мне лишни, напрасны». — Что я знаю о кругах? (3,1415) — Вот и знаю я число, именуемое пи — молодец! (3,1415927) — Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3,14159265359) Американский математик Майкл Кит и вовсе написал целую книгу Not A Wake, в тексте которой содержится информация о первых 10 тыс. цифр числа π. Кому-то легче запомнить бессвязные буквы, чем случайные цифры. В этом случае цифры заменяются первыми буквами алфавита. Первое слово в названии рассказа Cadaeic Cadenza Майкла Кита появилось именно таким образом. Всего в этом произведении закодировано 3835 знаков числа пи — правда, тем же способом, что в книге Not a Wake. В русском языке для подобных целей можно использовать буквы от А до И (последняя будет соответствовать нолю). Насколько удобно будет запоминать составленные из них комбинации — вопрос открытый. Чтобы добиться по-настоящему выдающихся результатов, предыдущие методы не годятся. Допустим, один — это «н», четыре — «р», пять — «т». Тогда число 14 — это «нр», а 15 — «нт». Теперь эти пары следует дополнить другими буквами, чтобы получилось слова, например, «нора» и «нить». Всего понадобится сто слов — вроде бы много, но за ними стоят всего десять букв, поэтому запомнить не так уж сложно. Число π предстанет в уме как последовательность образов: три целых, нора, нить и т.п. Чтобы лучше запомнить эту последовательность, изображения можно нарисовать или распечатать на принтере и поставить перед глазами. Некоторые люди просто раскладывают соответствующие предметы по комнате и вспоминают числа, разглядывая интерьер. Марат Кузаев, Кристина Недкова Итак, предыстория. Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе? Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!). Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд. Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо! P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»?
В общем-то, даже нечего добавить:) Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов. Описание алгоритма генерации под калькулятором. Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества. Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды. Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода. Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код. Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов. Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты. 100 самых популярных PIN-кодов 0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667. P.S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении: Формулы последовательностей: где k — порядковый номер; Рассмотрим варианты быстрого нахождения суммы разного количества последовательных чисел. 2 вариант. Чтобы найти сумму 5-ти последовательных чисел, нужно: Возьмем, к примеру, те же 5 последовательных цифр 30,31,32,33,34 3 вариант. Взяв в качестве примера предыдущую последовательность: Чтобы вычислить сумму 4-х последовательных чисел, нужно: Чтобы определить сумму 6 последовательных чисел, необходимо: Чтобы рассчитать сумму 7 последовательных чисел, нужно: Чтобы вычислить сумму 8 последовательных чисел: Чтобы сложить любое количество как четных, так и нечетных последовательных чисел, нужно: n х (a+b)/2. Чтобы быстро и правильно рассчитать сумму последовательности, воспользуйтесь онлайн калькулятором. Для этого вам нужно лишь выбрать последовательность и число членов последовательности. Рассчитать количество ламината для комнаты можно как самостоятельно, так и при помощи нашего калькулятора. Это достаточно просто, и знаний арифметики начальных классов будет достаточно. Но оставим пока калькулятор ламината, и обратимся к теории. Содержание статьи: Сначала надо определиться со способом укладки. Всего есть два варианта укладки: Всё остальное, это градации этих вариантов относительно источника света: или расположения планок относительно друг друга: Можно ещё привести как отдельный вариант узорный вид укладки. В этом случае из планок ламината разных оттенков на полу выкладывается какой-либо рисунок. Но этот вариант самый расходный, и уложить своими руками ламинат таким способом, без опыта не получится. И очень важный момент – без разбежки, укладывать ламинат нельзя. Делаете ремонт в своей квартире или доме самостоятельно? Статья «Укладка ламината своими руками с Видео» будет вам полезна как никогда. Самые распространённые размеры планок ламината 128 – 139 см. в длину и 18,5 – 19,6 см в ширину, их мы и включим в наш расчет. Одного стандарта для всех производителей нет. Встречается ламинат длиной от 0,5 до 2,1 м и шириной от 1,8 до 60 см. Поэтому ответить сколько м2 ламината в упаковке однозначно невозможно. На каждой упаковке ламината, кроме размеров стоит общая площадь всех планок в упаковке. Суммарная площадь требуемого ламината, всегда будет больше, общей площади комнаты. Количество отходов зависит от способа укладки и опыта отделочника: Расчеты представлены на примере ламината 33 класса, т.к. он является самым распространенным вариантом. Рассчитывать количество ламината можно двумя способами. Для примера, рассмотрим стандартную комнату 4 на 5 м. А ламинат размером 1,285 х 0,186 м. Площадь одной планки: 1,285х0,186=0,239м2. В упаковке 8 планок, общая площадь 1,912 м2. Сколько квадратов в пачке ламината нужно уточнять прямо в магазине, т.к. разные производители изготавливают их по разным нормам. Воспользуйтесь нашим онлайн калькулятором для расчета площади комнаты: Площадь комнаты 4х5=20 м2, делим её, на площадь планок в упаковке 20/1,912=10,46 (≈10,5) упаковок. Или 10,5х8=84 планки. Проверим, 20/0,239=83,6 (≈ 84) планки. Добавляем 5%, (84/100)х5=4,2 (≈4 планки). Значит, требуется 11 упаковок. Общая площадь закупаемого ламината 11х1,912= 21,032м2. Учитывая обязательный отступ от стены 1 см, этого количества должно хватить при аккуратном монтаже. Вычислить сколько штук нужно покупать довольно просто, главное определиться с размерами комнат и упаковки. Такой способ расчета ламината на комнату подходит для педантичных домохозяев. Но результат будет не приблизительным, а точным. И так, планируется прямая укладка, параллельно источнику света (окну). Комната 5х4 м. Вдоль длиной стены, умещается 5/1,28= 3,9 планки. Т.е. 3 целых планки, и от одной надо будет отрезать 1/10 или 12,8 см (13 см). Общим счётом 4 планки. Покрытая ширина комнаты – 0,186 (≈0,185) м. Второй ряд, можно ставить с разбежкой в половину планки, т.е. одну планку распилить пополам, и начать с этой половины. В конце, укладывать оставшуюся половину, предварительно отпилив 13 см. Третий ряд аналогичен первому. Другими словами, чётные ряды начинаются с целой планки, нечётные с половинок. Всего в комнате будет 4/0,186= 21,5 рядов ламината. Т.е. 21 ряд будет состоять из целых планок, а 22-ой из половинок. Значит, потребуется 22х4=88 планок, или 11 упаковок ламината. Один ряд, придётся распиливать вдоль, пополам. За спил можно не беспокоиться, он будет спрятан под плинтусом. Итог Сравнивая способы расчёта видно, что второй нагляднее и точнее, но результат одинаков. Тем не менее, всегда рекомендуется брать ламинат с «запасом». В случае повреждения покрытия во время эксплуатации, можно будет заменить планку с изъяном. При помощи онлайн калькулятора можно примерно рассчитать необходимое количество, в принципе таких расчетов вполне достаточно. Правда стоит уточнять в магазине сколько квадратов в пачке уместил производитель. Также, наверняка вас заинтересует статья о выборе правильной подложки под ламинат. Приведённые расчёты ламината максимально упрощены, чтобы показать общие принципы. Комнаты могут быть с нишами, выступами, аппендиксами, но зная последовательность расчётов, вы не ошибётесь. Полезная статья? Добавьте к себе в закладки! Математика — восьмое чудо света среди всех наук. В этом убежден Кристиан Хессе (Christian Hesse), профессор математики и статистики в Штутгартском университете и автор вышедшей недавно в Германии книги «Жизнь²» («Leben²»). В ней он доказывает, что математика — это не только гимнастика для ума. У нее, как у любви и музыки, есть такая же способность делать человека счастливее. Каким образом? Вот несколько примеров. Как избежать просчета в браке По статистике, каждый второй брак в западных странах заканчивается разводом. В Германии среднестатистический брак длится 15 лет. Почему половина браков распадается, а другая — нет? Какие пары ждет счастливая совместная жизнь, а у каких шансы заведомо хуже? И существует ли формула семейного счастья? Существует. Немецкий профессор приводит исследование американских ученых Джеймса Муррея и Джона Готмана. В течение многих лет они наблюдали за семейными парами. Ученые просили каждую из них поговорить о деньгах, сексе или воспитании детей. Разговоры записывали на видео и анализировали по специальной шкале эмоций. Ученые также отслеживали, какие пары спустя годы распались, а какие нет. В результате было выведено соотношение 5:1. Оно означает, что счастлив тот брак, в котором позитивные моменты превышают негативные в пять раз. То есть чтобы компенсировать, к примеру, обидное замечание, букета цветов недостаточно — доказательств любви и уважения должно быть пять. На то, что эта формула функционирует, ученые дают гарантию 90 процентов. Стоит ли вообще выходить замуж или жениться? Ответ статистиков однозначный: да. Выгода выражается хотя бы в продолжительности жизни: по сравнению с одиночками женатые мужчины живут на девять лет дольше, замужние женщины — на шесть. Причем этот положительный побочный эффект ученые наблюдают даже тогда, когда в отношениях нет идиллии. Хотя стоит отметить, что и возраст тех, кто решается на брак, повышается. Взять, например, Германию. «Усредненный» немец женится в 36 лет, «усредненная» немка — в 33 года. Разница в возрасте положительно сказывается на браке. Лучше всего, указывает профессор статистики, если муж на пять лет старше жены, а жена интеллигентнее мужа. Брачные узы скрепляют и дети. Уже после первого ребенка риск развода снижается с 50 процентов до 30. Семейное счастье определяют и вполне конкретные суммы. Статистически доказано, что при затратах на свадьбу свыше 20 тысяч евро доля разведенных выше. Чем дешевле обходится торжество, тем дольше супруги проживут вместе. А вот на обручальных кольцах лучше не экономить: если одно кольцо стоит меньше 500 евро, риск развода возрастает. Простой алгоритм для правильного выбора Как вообще найти подходящего партнера для брака, ну или претендента на вакансию, новую квартиру или место для парковки? Варианты можно рассматривать до бесконечности. Как остановить выбор на самом оптимальном? Правильный алгоритм поиска — основа основ. Определить его поможет обратное значение математической константы е — 0,37 или правило 37 процентов. Оно способствует балансу между недостаточным и слишком продолжительным поиском, ведущим к нехватке альтернатив. Счастье в любви частично поддается математическим расчетам Для начала следует определить для себя временной отрезок, который вы готовы уделить поиску решения. К примеру, вы даете себе восемь лет на поиск своей второй половины. 37 процентов этого времени вы посвящаете ознакомлению с возможностями. В данном случае это три года. По окончании этого срока следует выбрать первого кандидата, который по своим качествам будет лучше всех предыдущих в тестовой фазе. Этот принцип срабатывает при условии, что кандидаты появляются с регулярностью — скажем, по одному в год. Если нет, то лучше определить не временной отрезок, а общее количество вариантов. То есть, к примеру, вы решаете сделать выбор после рассмотрения восьми кандидатур. 37 процентов от этого количества — три кандидата. После знакомства с ними вы выбираете из последующих претендентов человека, превосходящего по качествам лучшего из этих троих. Вероятность успеха — 37 процентов, тем не менее, указывает профессор из Штутгарта, такая стратегия более эффективная, чем принцип случайности. Как поделить имущество и работу по дому Справедливое разделение домашних обязанностей — один из трех важных факторов, способствующих долгим счастливым отношениям, — после верности и хорошего секса. Принцип «дели и выбирай» (не путать с «разделяй и властвуй») — оптимален для того, чтобы избежать обид и прийти к консенсусу. В случае двух человек все очень просто: один из них создает два на его взгляд равнозначных списка домашних дел, другому предоставляется возможность выбора. Если в ведении домашнего хозяйства должен участвовать третий человек, например, сын-подросток, дело усложняется. Выход придумал польский математик Гуго Штейнгауз еще в 1944 году. За основу он взял пирог, который нужно справедливо разделить на троих. Первый человек делит его на три куска. Если второму человеку как минимум два куска кажутся равнозначными, то право выбора предоставляется сначала третьему участнику, потом второму, потом первому. Если второй человек считает, что два куска менее ценные, чем оставшийся третий и при этом третьему человеку все равно, то сначала второму предоставляется право выбора. Если же и второй и третий человек считают, что пирог поделен несправедливо, то первый выбирает кусок, а остальные двое делят пирог так, как их устраивает. То же самое можно сделать и с домашними обязанностями. Один человек составляет три равнозначные для него списка дел. Скажем, первый — готовить еду и выносить мусор, второй — делать покупки, убирать кухню, третий — стирать белье, наводить порядок в квартире. Дальше по схеме с пирогом. Вести «торг» будет легче, если каждый из участников присвоит заданиям определенное количество баллов: 5, 10, 15, 20 — в зависимости от кажущейся ему нагрузки и затрат времени. Делить по справедливости, используя систему баллов, 20 лет назад предложили американские математик Алан Тейлор и политолог Стивен Брамс. Их принцип «подстраивающегося победителя» можно применить и в случае, если речь зайдет о разводе и разделе имущества, — жизнь все же штука непредсказуемая. Если семейное счастье не спасти, математика готова помочь. Объекты дележа оцениваются каждым участником в соответствии с его личным восприятием и делятся на основе полученного рейтинга. За основу берутся 100 баллов. Наибольшее количество баллов получает самый важный с точки зрения игрока объект. Затем начинается «подстраивание». Цель — так разделить имущество, чтобы количество баллов в списке каждого игрока совпадало. Смотрите также: Филип, правнук датского короля Кристиана IX, праправнук английской королевы Виктории и российского императора Николая I, сразу покорил сердце Елизаветы. А познакомились они в 1939 году во время королевского визита в колледж, где Филип учился. Георга VI сопровождали дочери. После этой встречи между 18-летним Филипом и 13-летней Елизаветой завязалась переписка. А после войны они поженились. В этого высокого белокурого моряка, кадета Королевского военно-морского колледжа, невозможно было не влюбиться. Юную принцессу даже не поколебало то, что он был бессребреником. Ни о ком, кроме него, она даже слышать не хотела. И поначалу противившиеся их союзу родители все-таки дали согласие на этот брак. У Филипа и Елизаветы четверо детей: Чарльз, принц Уэльский (р. 1948), принцесса Анна (р. 1950), принц Эндрю, герцог Йоркский (р. 1960), и принц Эдуард, граф Уэссекский (р. 1964). Согласно утверждениям биографов, Филип был строгим, требовательным и скупым на эмоции отцом. С 1952 года, когда Елизавета взошла на престол, Филип выступает лишь в роли спутника супруги, сопровождая ее на всех мероприятиях и в зарубежных поездках. Кроме этого, принц всегда активно занимался благотворительностью, покровительствуя нескольким сотням благотворительных организаций. В разные годы он возглавлял Всемирный фонд защиты природы и Международную федерацию конного спорта. В 1997 году, после трагической гибели принцессы Дианы, бывшей супруги принца Чарльза, рейтинг британской королевской семьи упал до критической отметки. Люди порицали королеву за молчание. Страсти поутихли лишь после того, как Елизавета прибыла на траурную церемонию. Принца Чарльза, старшего сына Елизаветы и Филипа, недаром называют «вечным наследником ее Величества»: даже в возрасте за 90 его мать живет активной жизнью и не собирается уступать престол. Протокол есть протокол: королева всегда должна быть первой. И даже при кормлении слонов в зоопарке исключений делать нельзя. Но из-за того, что ему всегда приходится быть на вторых ролях, принц Филип не комплексует. Свою планиду в тени супруги он воспринимает с утонченным юмором. Его шутки по этому поводу пользуются необычайной популярностью: британцы Филипа обожают и цитируют его на каждом шагу. Принц Филип со смехом разглядывает карикатуру Елизаветы II из британской мыльной оперы «Eastenders», экспонируемую на выставке, в организации которой он сам принимал участие. У королевы, кстати, с юмором тоже все в порядке. Она обожает скетчи и карикатуры на себя и вместе с мужем от души хохочет, если они получаются удачными. Автор: Сюзанне Кордс, Наталия Королева Глядя на уравнение для вычисления комбинаций, вы можете видеть, что факториалы используются во всей формуле. Помните, что формула для расчета комбинаций: n C r = n ! / r ! * ( n — r ) !, где n представляет количество элементов, а r представляет количество элементов, выбираемых за раз.Давайте посмотрим на примере, как рассчитать комбинацию. На этой неделе вы можете взять напрокат десять новых фильмов на DVD. Джон хочет выбрать три фильма для просмотра в эти выходные. Сколько комбинаций фильмов он может выбрать? В этой задаче Джон выбирает три фильма из десяти новых выпусков. 10 будет представлять переменную n , а 3 будет представлять переменную r . Итак, наше уравнение будет выглядеть так: 10C3 = 10! / 3! * (10 — 3) !. Первый шаг, который необходимо сделать, — это вычесть 10 минус 3 в нижней части этого уравнения.10 — 3 = 7, поэтому наше уравнение выглядит как 10! / 3! * 7 !. Затем нам нужно развернуть каждый из наших факториалов. 10! будет равно 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 сверху и 3! * 7! будет 3 * 2 * 1 * 7 * 6 * 5 * 4 * 3 * 2 * 1. Самый простой способ решить эту проблему — исключить подобные термины. Мы видим, что есть 7, 6, 5, 4, 3, 2 и 1 как сверху, так и снизу нашего уравнения. Эти условия могут быть отменены. Теперь мы видим, что в нашем уравнении 10 * 9 * 8 слева вверху и 3 * 2 * 1 слева внизу.Отсюда мы можем просто размножаться. 10 * 9 * 8 = 720 и 3 * 2 * 1 = 6. Итак, наше уравнение теперь 720/6. Чтобы закончить эту задачу, мы разделим 720 на 6 и получим 120. Теперь Джон знает, что на этой неделе он мог выбрать 120 различных комбинаций новых фильмов. Для расчета вероятности наступления события воспользуемся формулой: количество благоприятных исходов / количество общих исходов. Давайте рассмотрим пример того, как рассчитать вероятность наступления события.На кассе в магазине DVD Джон также купил пакет жевательных резинок. В мешочке жевательных резинок было пять красных, три зеленых, четыре белых и восемь желтых жевательных резинок. Какова вероятность того, что Джон, нарисовавший наугад, выберет желтую жевательную резинку? Джон знает, что если сложить все жевательные резинки вместе, в сумке окажется 20 жевательных шариков. Итак, общее количество исходов равно 20. Джону также известно, что существует восемь желтых жевательных резинок, которые представляют количество благоприятных исходов.Таким образом, вероятность случайного выбора желтой жевательной резинки из пакета равна 8 из 20. Однако все дроби необходимо упростить. Итак, и 8, и 20 делятся на 4. Итак, 8/20 уменьшится до 2/5. Джон знает, что вероятность того, что он выберет желтую жевательную резинку из мешка наугад, составляет 2/5. Чтобы подсчитать общее количество исходов и благоприятных исходов, вам может потребоваться вычислить комбинацию. Помните, что комбинация — это способ расчета событий, порядок которых не имеет значения. Рассмотрим пример. Чтобы насладиться своими фильмами, Джон решает заказать пиццу. Глядя на меню, Джон видит, что Король пиццы предлагает восемь разных начинок (четыре мяса и четыре овоща). Начинки: пепперони, ветчина, бекон, колбаса, перец, грибы, лук и оливки. У Джона есть купон на пиццу с 3 начинками. Выбирая ингредиенты наугад, какова вероятность того, что Джон выберет пиццу только с мясом? Джон ищет вероятность выбора пиццы только с мясом.Для этого ему нужно будет подсчитать общее количество благоприятных исходов по отношению к общему количеству возможных исходов. Давайте сначала посчитаем общее количество исходов. Чтобы рассчитать общие результаты, мы будем использовать формулу для комбинаций, потому что порядок начинки пиццы не имеет значения. Формула для комбинаций: n C r = n ! / r ! * ( n — r ) !, где n представляет количество элементов, а r представляет количество элементов, выбираемых за раз. Джон выбирает три начинки из восьми, предложенных Pizza King. 8 будет представлять наш член n , а 3 будет представлять наш член r . Итак, наше уравнение будет иметь вид 8C3 = 8! / 3! * (8 — 3) !. Чтобы решить это уравнение, нам нужно вычесть 8 — 3 = 5. Итак, наше уравнение теперь выглядит как 8! / 3! * 5 !. Затем нам нужно раскрыть каждый из этих факториалов. 8! будет равно 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1, деленное на 3! * 5 !, что будет равно 3 * 2 * 1 * 5 * 4 * 3 * 2 * 1. Помните, чтобы упростить эту задачу, мы можем сократить аналогичные члены как в верхней, так и в нижней части этого уравнения. Мы видим, что есть 5, 4, 3, 2 и 1 как сверху, так и снизу. Эти условия могут быть отменены. Умножив сверху 8 * 7 * 6, получим 336. Внизу 3 * 2 * 1, что равно 6. Разделив 336 на 6, мы можем увидеть, что общее количество пицц, которые может заказать Джон, равно 56. Теперь Джон должен найти количество благоприятных исходов. Джон хотел знать вероятность выбора пиццы только с мясом.Глядя на меню, мы видим, что есть четыре вида мяса на выбор, а Джон выбирает только три. Это еще один пример проблемы комбинирования, потому что порядок, в котором выбираются мясные начинки, не имеет значения. Чтобы подсчитать количество благоприятных исходов, нам нужно использовать формулу комбинации n C r = n ! / r ! * ( n — r ) !, где n представляет количество элементов, а r представляет количество элементов, выбираемых за раз. Поскольку существует четыре вида мяса, и Джон выбирает три, член n будет равен 4, а член r будет равен 3. Наше уравнение будет выглядеть так: 4C3 = 4! / 3! * (4 — 3) !. Затем нам нужно вычесть 4–3 снизу, что равно 1. Итак, наше уравнение теперь выглядит как 4! / 3! * 1 !. Теперь давайте расширим верхнюю и нижнюю части нашего уравнения, чтобы найти общие члены, которые мы можем сократить. Развернув верх, мы получим 4 * 3 * 2 * 1, а нижний будет 3 * 2 * 1 * 1.Мы видим, что как сверху, так и снизу есть 3 * 2 * 1, которые можно отменить. Джон теперь может видеть, что есть только четыре комбинации пиццы с тремя верхами, которые будут содержать только мясо. Для расчета вероятности Джону нужно будет использовать количество благоприятных исходов, равное 4, по сравнению с общим количеством исходов, равным 56. Вероятность будет 4/56, которую можно уменьшить до 1/14. Таким образом, вероятность того, что Джон выберет пиццу с 3 начинками, которая будет содержать только мясо, равна 1/14. Помните, что комбинаций — это способ вычисления общих результатов события, порядок которых не имеет значения. Для расчета комбинаций воспользуемся формулой n C r = n ! / r ! * ( n — r ) !, где n представляет количество элементов, а r представляет количество элементов, выбираемых за раз. Чтобы определить вероятность события, вам, возможно, придется найти комбинации.Чтобы рассчитать вероятность наступления события, вы воспользуетесь формулой количества благоприятных исходов по отношению к количеству общих исходов. По завершении этого урока вы сможете: Торговля опционами — это динамичный и захватывающий компонент современного инвестирования.Торговцы опционами обычно используют кредитное плечо для создания уникальных возможностей для получения значительных выгод и рисков. Торговля опционами — это, по сути, покупка контракта, который предоставляет инвестору возможность купить или продать определенный актив в заранее определенное время в будущем по согласованной цене. Из-за уникального контрактного характера этих сделок инвесторы часто рассчитывают ожидаемую доходность по опционному контракту до начала сделки. К счастью, научиться определять и использовать формулу возврата опционов относительно несложно и может быть выполнено за несколько простых шагов. Вы можете рассчитать доход от сделки с опционами, сначала определив общую прибыль или убыток от продажи, а затем сравнив это значение с начальной ценой покупки . Опционный контракт обычно отличается особыми привилегиями, которые он предоставляет держателю контракта. Например, если опционный контракт предоставляет держателю контракта право купить актив в будущем по заранее определенной цене, это обычно называется «колл-опцион ».«И наоборот, когда опционный контракт предоставляет физическому лицу право продать актив в будущем по заранее определенной цене, это называется« пут-опцион ». Опционные контракты покупаются и продаются через торговая неделя на основных биржах, одна из самых популярных — Chicago Board Options Exchang e. Опционные контракты могут охватывать различные инвестиционные активы, от ценных бумаг до товаров. Имея это в виду, велики шансы, что инвестор смогут найти рынок для своих конкретных интересов. Лицо, продающее опционный контракт, должно быть обеспечено каким-либо стимулом для начала торговли. По этой причине к цене контракта, которую должен заплатить инвестор, будет добавлена премия или дополнительная комиссия. Размер премии может резко колебаться в зависимости от суммы риска, который принимает на себя автор контракта, когда он продает инвестору. По достижении даты истечения срока действия опционного контракта держатель контракта должен решить либо реализовать свои права, либо утратить приобретенные привилегии.Если они решат не пользоваться своими правами, они не получат возмещения страхового взноса. Решит или нет держатель контракта реализовать свои права, в первую очередь, зависит от того, достиг ли данный актив «страйк-цены » или конкретной стоимости, при которой контракт принесет прибыль инвестору. Если контракт не достиг цены исполнения, у инвестора нет стимула для реализации своих прав. Чтобы рассчитать доходность опциона, инвестору необходимо знать цену, которую он заплатил за опционный контракт, текущую стоимость рассматриваемого актива и количество приобретенных контрактов. Далее описанные шаги будут применяться как к опционам колл, так и к пут опционам. Чтобы преобразовать эту цифру в процентное значение, отражающее общую прибыль, разделите прибыль на общую покупную цену актива, а затем умножьте полученное значение на 100. Таким образом, соответствующий расчет для этого примера будет: 1,340 / (20 * 200) = 0,335 * 100 = 33,5% доходности. i Comstock / Comstock / Getty Images Опционы позволяют окунуться в рынок ценных бумаг, не погружаясь полностью.Они дают вам право, но не обязательство, покупать или продавать акции по заранее определенной цене, называемой ценой исполнения. У каждой акции есть опционы колл и пут, доступные по различным ценам исполнения. Опцион колл дает вам право покупать акции, а пут дает вам право продать. Для конкретной цены исполнения вы можете рассчитать стоимость покупки опциона колл или пут и стоимость его использования. Посетите любой финансовый веб-сайт, на котором представлены котировки опционов. Введите название компании или тикер ее акций в текстовое поле с котировками опционов и нажмите «Получить цену», чтобы просмотреть доступные варианты, расположенные в таблицах. Щелкните один из месяцев на странице, чтобы увидеть варианты, срок действия которых истекает в этом месяце. Вы можете торговать или использовать опцион до третьей пятницы месяца истечения срока. Например, если вы хотите просмотреть варианты, срок действия которых истекает в январе следующего года, щелкните этот месяц. Найдите желаемую цену исполнения в столбце «Strike» в середине таблицы. Каждая строка содержит информацию об опционах колл и пут для назначенной цены исполнения. Цена исполнения варьируется от цены ниже текущей цены акции до цены выше цены акции.В этом примере предположим, что цена акции составляет 30 долларов, а цена исполнения опционов составляет от 15 до 50 долларов с шагом в 1 доллар. Предположим, вы рассчитываете опцион со страйк-ценой 35 долларов. Определите сумму в столбце «Ask» в строке выбранной цены исполнения. Есть два разных столбца запросов. Используйте тот, который находится слева от столбца страйков, для опционов колл. Используйте тот, что справа, для пут. Цена продажи — это цена покупки опциона на акцию. В этом примере предположим, что вы рассматриваете возможность покупки опциона колл по цене продажи 1 доллар США. Умножьте цену продажи на 100, чтобы вычислить общую цену покупки одного опционного контракта. Каждый контракт представляет собой 100 акций. В этом примере умножьте 1 доллар на 100, чтобы получить цену покупки в размере 100 долларов за один контракт на опцион колл. Это не дает вам фактических запасов — только право покупать акции. Умножьте цену исполнения на 100, чтобы рассчитать дополнительную сумму, которую вы заплатите за возможность покупки или продажи акций. Завершая пример, умножьте 35 долларов на 100, чтобы получить 3500 долларов.Это означает, что вы можете купить 100 акций за 3500 долларов до истечения срока действия опциона в январе. Вы могли бы успешно победить рынок, торгуя акциями, используя дисциплинированный процесс, ожидая хорошего движения вверх или вниз. Многие трейдеры также приобрели уверенность в том, что могут зарабатывать деньги на фондовом рынке, определяя одну или две хорошие акции, которые вскоре сделают большой шаг вперед. Но если вы не знаете, как воспользоваться этим движением, вы можете остаться в пыли.Если это похоже на вас, возможно, пришло время подумать об использовании опций. В этой статье будут рассмотрены факторы, которые следует учитывать, если вы планируете торговать опционами, чтобы воспользоваться движением акций. Опционы — это контракты с производными финансовыми инструментами, которые дают держателю право, но не обязательство, купить (в случае колл) или продать (в случае пут) базовый актив или ценную бумагу по заранее определенной цене (называемой страйк-цена) до истечения срока действия контракта. Следовательно, термин «производный инструмент» просто означает, что стоимость опциона определяется в основном базовым активом, с которым он связан. Однако важно отметить, что в опционном контракте есть две стороны: покупатель и продавец. Как уже упоминалось, покупатель опционного контракта имеет права, но продавец опционного контракта, с другой стороны, несет обязательства. Это может сбивать с толку, поэтому резюмируем: Покупка или продажа опциона происходит по цене, называемой премией за опцион.Понимание того, как оценить эту премию, имеет решающее значение для торговли опционами и, по сути, основывается на вероятности того, что право или обязательство купить или продать акцию в конечном итоге окажется прибыльным по истечении срока. Таким образом, покупатели опциона платят премию, а продавцы опциона получают премию. Прежде чем отправиться в мир торговли опционами, инвесторы должны хорошо понимать факторы, определяющие стоимость опциона. К ним относятся текущая цена акций, внутренняя стоимость, время до истечения срока или временная стоимость, волатильность, процентные ставки и выплаченные денежные дивиденды. Существует несколько моделей ценообразования опционов, в которых эти параметры используются для определения справедливой рыночной стоимости опциона. Из них наиболее широко известна модель Блэка-Шоулза. Во многих отношениях опционы такие же, как и любые другие инвестиции — вам нужно понимать, что определяет их цену, чтобы использовать их эффективно. Также широко используются другие модели, такие как биномиальная модель и трехчленная модель. Начнем с основных факторов, влияющих на цену опциона: текущая цена акций, внутренняя стоимость, время до истечения срока или временная стоимость и волатильность.Текущая цена акций довольно проста. Движение цены акции вверх или вниз имеет прямое, хотя и не равное, влияние на цену опциона. По мере того, как цена акции растет, более вероятно, что цена опциона колл вырастет, а цена опциона пут упадет. Если цена акций упадет, с ценой колл и пут, скорее всего, произойдет обратное. Модель Блэка-Шоулза, пожалуй, самый известный метод ценообразования опционов.Формула модели получается путем умножения цены акции на кумулятивную функцию стандартного нормального распределения вероятностей. После этого чистая приведенная стоимость (ЧПС) страйковой цены, умноженная на кумулятивное стандартное нормальное распределение, вычитается из результирующего значения предыдущего расчета. В математической записи: Математика, связанная с дифференциальным уравнением, составляющим формулу Блэка-Шоулза, может быть сложной и пугающей.К счастью, вам не нужно знать или даже понимать математику, чтобы использовать моделирование Блэка-Шоулза в ваших собственных стратегиях. Торговцы опционами и инвесторы имеют доступ к множеству онлайн-калькуляторов опционов, и многие из сегодняшних торговых платформ могут похвастаться надежными инструментами анализа опционов, включая индикаторы и электронные таблицы, которые выполняют вычисления и выводят значения цен опционов. Ниже мы более подробно рассмотрим цены на опционы, чтобы понять, что составляет их внутреннюю и внутреннюю стоимость.внешнее (время) значение, что немного проще. Внутренняя стоимость — это стоимость любого опциона, если бы он был исполнен сегодня. По сути, внутренняя стоимость — это сумма, на которую цена исполнения опциона является прибыльной или в деньгах по сравнению с ценой акции на рынке. Если цена исполнения опциона невыгодна по сравнению с ценой акции, то считается, что опцион не при деньгах.Если цена исполнения равна цене акции на рынке, опцион считается «при деньгах». Хотя внутренняя стоимость включает соотношение между страйк-ценой и ценой акции на рынке, она не учитывает, сколько (или как мало) времени осталось до истечения срока действия опциона, называемого истечением. Время, оставшееся до исполнения опциона, влияет на премию или стоимость опциона, что мы рассмотрим в следующем разделе. Другими словами, внутренняя стоимость — это часть цены опциона, которая не теряется или не подвергается влиянию с течением времени. Ниже приведены уравнения для расчета внутренней стоимости опциона колл или пут: Внутренняя стоимость опциона отражает эффективную финансовую выгоду, возникающую в результате немедленного исполнения этого опциона.По сути, это минимальная стоимость опциона. Опционы, торгующиеся на деньги или без денег, не имеют внутренней стоимости. Например, предположим, что акции General Electric (GE) продаются по цене 34 доллара.80. Опцион колл GE 30 будет иметь внутреннюю стоимость 4,80 доллара (34,80 доллара — 30 долларов = 4,80 доллара), потому что держатель опциона может реализовать опцион на покупку акций GE по 30 долларов, затем развернуться и автоматически продать их на рынке за 34,80 доллара за прибыль 4,80 $. В другом примере внутренняя стоимость опциона GE 35 будет равна нулю (34,80 доллара США — 35 долларов США = -0,20 доллара США), поскольку внутренняя стоимость не может быть отрицательной. Внутренняя стоимость также работает для опциона пут. Например, опцион пут на GE 30 будет иметь внутреннюю стоимость, равную нулю (30-34 доллара США.80 = — 4,80 доллара США), поскольку внутренняя стоимость не может быть отрицательной. С другой стороны, внутренняя стоимость пут-опциона GE 35 будет составлять 0,20 доллара (35 — 34,80 доллара = 0,20 доллара). Поскольку опционные контракты имеют ограниченное время до истечения срока их действия, оставшееся время имеет связанную с ним денежную стоимость, называемую временной стоимостью. Это напрямую связано с тем, сколько времени есть у опциона до истечения срока его действия, а также с волатильностью или колебаниями цены акции. Чем больше времени у опциона до истечения срока его действия, тем больше шансов, что он окажется в выигрыше. Временная составляющая опциона убывает экспоненциально. Фактический вывод временной стоимости опциона — довольно сложное уравнение. Как правило, опцион теряет одну треть своей стоимости в течение первой половины своей жизни и две трети во второй половине своей жизни. Это важная концепция для инвесторов в ценные бумаги, потому что чем ближе опцион подходит к истечению срока, тем сильнее требуется изменение базовой ценной бумаги, чтобы повлиять на цену опциона. Приведенная ниже формула показывает, что временная стоимость получается путем вычитания внутренней стоимости опциона из опционной премии. Другими словами, временная стоимость — это то, что осталось от премии после расчета доходности между ценой исполнения и ценой акции на рынке.В результате временная стоимость часто упоминается как внешняя стоимость опциона, поскольку временная стоимость — это сумма, на которую цена опциона превышает внутреннюю стоимость. Временная стоимость — это, по сути, премия за риск, которую требует продавец опциона, чтобы предоставить покупателю опциона право купить или продать акции до даты истечения срока действия опциона. Это похоже на страховой взнос за опцион; чем выше риск, тем выше стоимость покупки опциона. Снова посмотрим на приведенный выше пример, если GE торгуется по цене 34 доллара.80 и опцион колл GE 30 с истечением одного месяца до истечения срока торгуется по 5 долларов, временная стоимость опциона составляет 0,20 доллара (5,00 — 4,80 доллара = 0,20 доллара). Между тем, если GE торгуется по цене 34,80 доллара, то опцион колл GE 30, торгующийся по цене 6,85 доллара за девять месяцев до истечения срока, имеет временную стоимость 2,05 доллара. (6,85 доллара — 4,80 доллара = 2,05 доллара). Обратите внимание, что внутренняя стоимость такая же; разница в цене одного и того же варианта страйк-цены — это временная стоимость. Временная стоимость опциона также сильно зависит от волатильности, которую рынок ожидает от акции до истечения срока.Как правило, акции с высокой волатильностью имеют более высокую вероятность того, что опцион будет прибыльным или окажется в деньгах по истечении срока. В результате временная стоимость — как компонент премии по опциону — обычно выше, чтобы компенсировать повышенную вероятность того, что цена акции может выйти за пределы цены исполнения и истечь в деньгах. Для акций, которые, как ожидается, не будут сильно двигаться, временная стоимость опциона будет относительно низкой. Один из показателей, используемых для измерения волатильных акций, называется бета.Бета измеряет волатильность акции по сравнению с рынком в целом. Волатильные акции, как правило, имеют высокие бета-ставки, в первую очередь из-за неопределенности цены акции до истечения срока действия опциона. Однако акции с высоким бета также несут больший риск, чем акции с низким бета. Другими словами, волатильность — это палка о двух концах, то есть она дает инвесторам возможность получить значительную прибыль, но волатильность также может привести к значительным убыткам. Влияние волатильности в основном субъективно и трудно поддается количественной оценке.К счастью, есть несколько калькуляторов, которые помогут оценить волатильность. Чтобы сделать это еще более интересным, существует несколько типов волатильности, из которых наиболее заметны подразумеваемые и исторические. Когда инвесторы смотрят на волатильность в прошлом, это называется исторической или статистической волатильностью. Историческая волатильность (HV) помогает вам определить возможную величину будущих движений базовой акции. По статистике, две трети всех изменений цены акции происходят в пределах плюс-минус одно стандартное отклонение движения акции за установленный период времени. Историческая волатильность оглядывается назад, чтобы показать, насколько волатильным был рынок. Это помогает инвесторам опционов определить, какую цену исполнения лучше всего выбрать для конкретной стратегии. Подразумеваемая волатильность — это то, что подразумевается текущими рыночными ценами и используется с теоретическими моделями. Он помогает установить текущую цену существующего опциона и помогает игрокам опционов оценить потенциал сделки. Подразумеваемая волатильность показывает, какой волатильностью опционные трейдеры ожидают в будущем. Таким образом, подразумеваемая волатильность является индикатором текущего настроения рынка. Это мнение будет отражено в цене опционов, помогая трейдерам оценить будущую волатильность опциона и акций на основе текущих цен опционов. В совокупности факторы, которые помогают измерить влияние на премию опциона, называются «греки опционов». Ниже вы можете увидеть уже рассмотренный пример GE.Он показывает торговую цену GE, несколько страйков, а также внутреннюю и временную стоимость опционов колл и пут. На момент написания этой статьи General Electric считалась акцией с низкой волатильностью и для этого примера имела бета-коэффициент 0,49. В таблице ниже указаны цены на колл и пут, срок действия которых истекает через один месяц (верхняя часть таблицы). В нижнем разделе указаны цены на опционы GE, срок действия которых истекает через девять месяцев. На рисунке ниже цены на колл и пут, истекающие через один и девять месяцев, указаны для акций Amazon.com Inc. (AMZN). Amazon — гораздо более волатильная акция с бета-версией 3,47. Давайте сравним опцион колл GE 35 за девять месяцев до истечения с опционом колл AMZN 40 за девять месяцев до истечения срока. Значительная премия по опциону AMZN связана с волатильным характером акций AMZN, что может привести к более высокой вероятности истечения срока опциона в деньгах. Продавец опционов GE не ожидает получить существенную премию, потому что покупатели не ожидают значительного изменения цены акций. С одной стороны, продавец опциона AMZN может рассчитывать на более высокую премию из-за волатильного характера акций AMZN.Обычно, когда рынок считает, что акция будет очень волатильной, временная стоимость опциона возрастает. С другой стороны, когда рынок считает, что акция будет менее волатильной, временная стоимость опциона падает. Ожидание рынком будущей волатильности акций является ключом к цене опционов. В «Знакомстве с греками» мы обсуждали, как дельта влияет на стоимость отдельных опционов. Теперь давайте посмотрим, как вы можете вывести дельту на новый уровень.«Дельта позиции» позволяет отслеживать чистый эффект дельты для всей группы опционов, основанных на одной и той же базовой акции. Подумайте о дельте позиции следующим образом: опционы заменяют определенное количество акций базовой акции. Для любой опционной позиции по одной конкретной акции вы можете сложить дельты всех опционных контрактов и выяснить, на сколько акций действует вся группа ценных бумаг. Таким образом, вы всегда будете знать, как она должна реагировать, когда акция совершает движение на один пункт в любом направлении. Контракт однократного отзыва с дельтой 0,01 заменяет одну акцию. Вот почему. Если цена акции вырастет на 1 доллар, колл должен вырасти на один пенни. Но вообще говоря, опционный контракт будет представлять 100 акций. Итак, вам нужно умножить дельту на 100 акций: Это означает, что если цена акции увеличивается на 1 доллар, стоимость вашей позиции колл также должна увеличиться на 1 доллар.По сути, он ведет себя как одна акция. Владение контрактом единого колл с дельтой 0,50 аналогично владению 50 акциями. Когда базовая акция поднимается на 1 доллар, стоимость опциона должна увеличиться на 0,50 доллара. Таким образом, стоимость общей позиции увеличится на 50 долларов. ($ 0,50 x 100 множитель акций = $ 50.) Он работает так же с путами, но имейте в виду, что путы имеют отрицательную дельту. Таким образом, если у вас есть пут-контракт с дельтой -,50, он будет действовать как короткая позиция на 50 акций.Если базовая акция упадет на 1 доллар, стоимость опционной позиции должна вырасти на 50 долларов. Вот пример. Допустим, у вас есть 10 контрактов на вызовы XYZ, каждый с дельтой 0,75. Чтобы вычислить дельту позиции, умножьте 0,75 x 100 (при условии, что каждый контракт представляет 100 акций) x 10 контрактов. Это дает результат 750. Это означает, что ваши опционы колл заменяют 750 акций базовой акции.Таким образом, вы можете предположить, что если акция вырастет на 1 доллар, позиция вырастет примерно на 750 долларов. Если базовая акция упадет на 1 доллар, позиция уменьшится примерно на 750 долларов. В большинстве случаев ваши опционные стратегии будут более сложными, чем несколько опционов колл с одинаковой страйк-ценой. Вы можете использовать многоэлементные стратегии и даже одновременно использовать разные стратегии для одной и той же базовой акции. Каждая из этих стратегий может включать опционы с разными ценами исполнения и датами истечения.Например, вы можете запустить железный кондор и длинный календарный спред с колл одновременно на одну и ту же базовую акцию. Дельты некоторых отдельных опционов в полной позиции опционов будут положительными, а некоторые — отрицательными. Но даже если стратегии, которые вы используете, сложны, один взгляд на дельту позиции может дать вам представление о том, как должна измениться стоимость позиции, если акция сдвинется на один пункт в любом направлении. Мы не хотим загромождать этот раздел вычислением шести или семи различных этапов среди нескольких стратегий.Итак, давайте посмотрим на простой пример того, как вы рассчитываете дельту позиции для простой многоплановой стратегии. Например, рассмотрим длинный колл-спред с двумя ногами. Пример 2 показывает детали длинного спреда колл XYZ с длинным 55 страйком и коротким 60 страйком, оба с одинаковой датой истечения. Представьте, что при торговле акциями на уровне 56,55 доллара мы купили 15 контрактов на колл с 55 страйками с дельтой 0,61 и продали 15 контрактов на колл с 60 страйками с дельтой 0,29. Дельта колла с 55 страйками равна.61. Итак, чтобы определить общую дельту, мы умножаем 0,61 x 100 множитель акций на 15 контрактов. Это равно 915. Дельта колла с 60 страйками равна 0,29. Однако, поскольку вы продаете колл, для этой части вашей позиции дельта будет отрицательной: -0,29. Таким образом, общая дельта коротких 60 коллов составляет -.29 x 100 множитель акций x 15 контрактов. Это равно -435. Теперь вы просто складываете дельты от каждого лега вместе, чтобы определить дельту вашей позиции: 915 + (-435) = 480.Таким образом, теоретическое изменение стоимости позиции на основе движения базовой акции на 1 доллар составляет 480 долларов. Следовательно, общая стоимость этой позиции будет вести себя как 480 акций XYZ. Ваша дельта чистой позиции по опционам на любую базовую акцию представляет ваш текущий риск относительно изменения цены акции. В примере с длинным колл-спредом вам нужно спросить себя, комфортно ли вам иметь такой же риск, как при длинной позиции по 480 акциям XYZ.Если нет, возможно, вам стоит обратить внимание на этот риск. Вы можете сделать это, закрывая часть своей позиции или добавляя отрицательные дельты, например, покупая пут или продавая акции в шорт. Та же логика применяется, если вы держите позицию с высокой отрицательной дельтой. У вас будет такой же риск, как и при короткой позиции по акциям. Чтобы скорректировать свой риск, вы можете сбросить часть своей позиции, купить колл или купить акции. Подобно тому, как гамма влияет на дельту одного опциона при изменении цены акции, она также влияет на чистую дельту всей вашей позиции.Поэтому важно помнить, что дельта вашей позиции будет меняться при каждом небольшом движении акций. А влияние гаммы на дельту позиции может быть огромным, потому что мы говорим о множественных опционных контрактах. Количество акций, для которых ваши опционы выступают в качестве замены, будет меняться каждый раз при изменении цены акции. Вот почему рекомендуется следить за дельтой вашей позиции на протяжении всего срока действия вашей опционной позиции. Если у вас есть счет Ally Invest, следить за дельтой позиции очень просто.Просто посмотрите на «Вариант» на своей странице «Холдинги» или воспользуйтесь калькулятором прибылей и убытков, и мы сделаем за вас математические расчеты. Примечание. В этом сообщении в блоге предложен саундтрек: «Новая математика Тома Лерера». Это ушной червь, который постоянно возникал у меня в голове, когда я писал этот пост, поэтому будет уместно, чтобы он вам подыгрывал, пока вы читаете. И это запоминающаяся песня. Допустим, вам принадлежит миллион акций стартапов.(Молодец. Ура!) Итак, каков ваш процент владения в компании? Звучит как простой вопрос, но ответ зависит от того, как вы делаете математические вычисления. Это не тот случай, когда фигуры лгут или фигурируют лжецы, как гласит старая пословица. В зависимости от того, кто вы и почему задают вопрос, будут использоваться разные методы расчета вашей доли владения. Основное уравнение настолько простое, что его может решить школьник: Между прочим, общее количество разрешенных к выпуску акций компании не имеет значения, когда вы рассматриваете процент владения, и никогда не будет использоваться в этом расчете. Поскольку полностью разводненные акции — это надмножество, процент владения на основе полностью разводненных акций всегда будет ниже, чем процент, рассчитанный на основе выпущенных и находящихся в обращении акций. Давайте посмотрим на разницу между этими двумя методами на некоторых примерах. Предположим, у компании есть: Процент владения вашим одним миллионом акций в зависимости от выпущенных и находящихся в обращении: А, исходя из полностью разбавленного: Итак, какие числа вам следует использовать? Вам принадлежит 18% или 15%? Здесь полезно понять контекст и мотивы.Вы хотите знать, что является точным в данный момент, или это спекулятивный вопрос? Вы ищете лучший или худший сценарий? Если сегодня происходит транзакция — возможно, происходит голосование акционеров — только акции, которые фактически принадлежат прямо сейчас, будут иметь значение. Итак, выдающийся и выдающийся полезный расчет. Только действующие акционеры имеют право участвовать в голосовании. С другой стороны, инвесторы, как правило, смотрят в будущее и думают о вещах полностью размытыми терминами.Если предположить, что компания будет продолжать расти, будет предоставлен весь пул опционов на акции и исполнена каждая отдельная акция, они смогут получить наиболее консервативную оценку того, чем они будут владеть. Эта подробная перспектива важна при размышлениях о будущем контроле над компанией и моделировании возможных результатов. Другие случаи могут быть более сложными. Если есть предстоящее событие ликвидности, также имеет смысл учесть любые операции на лету, которые предоставят акции и любые переданные опционы, которые могут быть исполнены сверх того, что имеется в настоящее время. При каждом новом выпуске акций или сборе средств числа корректируются, происходит разводнение, и необходимо пересчитывать проценты. Одна вещь, на которую вы можете рассчитывать, — это то, что ваш процент владения изменится — независимо от того, как вы делаете вычисления! Хотите управлять собственностью без головной боли? Давайте поговорим о том, чем может помочь Shoobx. Стоимость колл-опциона или пут-опциона определяется несколькими составляющими.Стоимость опциона складывается из его внутренней стоимости и временной премии. Текущая стоимость вашей опционной сделки зависит от цены, которую вы заплатили, а также от цены базовой акции относительно цены исполнения вашего опционного контракта. При покупке контракта по опциону колл или пут цена, которую вы платите, состоит из двух отдельных компонентов: Источник изображения: Getty Images. Временная премия или временная стоимость опциона — это часть цены опциона, которую вы платите за неопределенность цены опциона до истечения срока его действия. Другими словами, это сумма, которую вы платите за то, что базовая акция может стоить в будущем. Внутренняя , или брутто, стоимость опциона — это денежная сумма опциона. Например, если у вас есть возможность заплатить 10 долларов за акцию за акцию, которая торгуется по 15 долларов, опцион имеет внутреннюю стоимость 5 долларов за акцию. Кроме того, текущая стоимость опционной сделки в размере — это ваш чистый результат, если бы вы исполняли контракт сегодня. Другими словами, это текущая внутренняя стоимость опциона за вычетом цены, которую вы за него заплатили. Например, если вы заплатили 3 доллара за акцию за контракт на покупку акций за 10 долларов, которые в настоящее время торгуются по 12 долларов (внутренняя стоимость 2 доллара), вы в настоящее время испытаете убыток в размере 1 доллара на акцию, если воспользуетесь опционом. Таким образом, текущая стоимость вашей сделки по опциону отрицательна — 1 доллар за акцию. Чтобы проиллюстрировать эти принципы, рассмотрим несколько примеров: Во-первых, предположим, что Microsoft торгуется по 50 долларов за акцию, и вы покупаете опцион колл, который позволяет вам приобрести 100 акций за 60 долларов в любое время в течение следующего года и заплатить 1 доллар за акцию. Поскольку опцион не в деньгах, он не имеет внутренней стоимости. Цена опциона в 1 доллар за акцию представляет собой уплачиваемую вами временную премию, поскольку существует бесконечное количество возможностей движения цены акции в течение следующего года. Если цена акций Microsoft вырастет до 65 долларов, ваш опцион будет в деньгах по 5 долларов за акцию (внутренняя стоимость). Поскольку вы заплатили 1 доллар за акцию, чтобы купить опцион, текущая стоимость вашей сделки по опциону в этот момент составит 4 доллара. В качестве другого примера предположим, что Apple торгуется по 150 долларов за акцию, и вы покупаете опцион колл, который позволяет вам приобрести 100 акций в течение следующего года по цене исполнения 135 долларов. Вы платите 18 долларов за акцию при покупке опционного контракта.Поскольку опцион находится в деньгах на 15 долларов за акцию, эта сумма представляет собой внутреннюю стоимость опциона. Разница между внутренней стоимостью и ценой, которую вы платите за опцион, или 3 доллара, представляет собой временную премию. Теперь предположим, что цена акций Apple упала до 130 долларов. Ваш вариант больше не в деньгах, поэтому он не имеет внутренней стоимости. Однако вы заплатили 18 долларов за покупку опциона, поэтому текущая стоимость вашей сделки отрицательная 18 долларов за акцию или всего отрицательные 1800 долларов. Вот еще несколько подробностей о разнице между опционами колл и пут, а также калькулятор, который поможет вам определить стоимость вашего опциона.(Примечание: общая стоимость опциона в калькуляторе такая же, как и концепция внутренней стоимости, которую я обсуждал ранее.) * Калькулятор предназначен только для оценки и не является финансовым планированием или советом.
1. При помощи ЧП. Повернув головку на заданное число градусов, можно построить любой угол.
Деление произвольного угла пополам. Наиболее удобным приемом деления произвольного угла пополам является деление при помощи циркуля и линейки; последовательность построения биссектрисы угла показана на Чертеже-№111.
Уклоны. Уклоном прямой по отношению к какой-либо другой прямой называется величина се наклона к этой прямой, выраженная через тангенс угла между ними. Следовательно, уклоном прямой АС относительно прямой АВ называется отношение i = h ÷ l = tg α.
Взамен слова «уклон» допускается применять знак <, вершина угла которого должна быть направлена в сторону уклона (чертеж — №113, в).
Начертить контур шаблона с применением построения уклона (чертеж-№113, е).
Пример 1. Начертить изображение конической втулки С применением построений, указанных конусностей, согласно чертежу-№114, г.
Угловыми (пропорциональными) масштабами называют графически выраженные числовые масштабы, о которых было сказано (на стр. Масштабы и компоновка чертежей )
Для уменьшения линий чертежа (чертеж-№115,б) отмеряем разметочным циркулем размер стороны α и, отложив его от вершины А на горизонтальной стороне углового масштаба 1 : 2,5 поворачиваем циркуль вокруг правой иглы и берем по вертикальному направлению до гипотенузы размер α1, который будет равен α ÷ 2,5
Чертежи используемые в данной главе: >>> Чертежи №110 №111 №112 >>> Чертеж №113 >>> Продолжение чертежа №114 >>> Чертеж №115 >>> Смотри далее Окружность дуга и многоугольник…..
Еще в школе каждому приходилось писать чертежным шрифтом. К главным недостаткам при выполнении надписей обычно относятся следующие: Устранить отмеченные недостатки можно путем дополнительного изучения материала и приобретения навыков уверенного и четкого письма. ГОСТ 2.304—68 «Шрифты чертежные» устанавливает чертежные шрифты, которые наносятся от руки на чертежи и другие технические документы всех отраслей промышленности и строительства. Стандарт устанавливает следующие размеры шрифтов: 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Размеры шрифтов определяются высотой h прописных букв в миллиметрах. Надписи могут составляться из одних прописных, букв; первая буква в этом случае должна иметь ту же высоту, что и остальные. Исключение из последнего правила допускается при оформлении строительной документации. Более мелкие надписи рекомендуется составлять из строчных букв; при этом первая буква в начале предложения пишется как прописная, но без утолщения обводки. Допускается писать ее такой же ширины, какую имеют строчные буквы. Цифры, встречающиеся в тексте, должны иметь высоту прописных букв (рис. 1). Размеры букв и цифр, толщину их линий, расстояния между буквами, словами и строками следует брать из табл. 3, в которой h обозначает высоту прописных букв и цифр. rn rn
TBegin—>TEnd—> rn
Прописные буквы rn
TBegin—>TEnd—> rnrn
Рис. 1. Основной шрифт rnrn
Нижние и боковые отростки букв Д, Ц, Щ, Ъ, цифры 4 и верхний знак буквы Й должны выполняться за счет промежутков между строками и буквами. Наклон букв к основанию строки должен быть около 75°; такой наклон при работе с обыкновенной или «плавающей» рейсшиной достигают прикладыванием к ней угольников с углами 45 и 30° (рис. 2), а при работе с механической рейсшиной — путем поворота головки на угол 75°. При кажущемся увеличении промежутков между некоторыми прописными буквами эти промежутки следует уменьшать до размера, равного толщине линий букв и цифр. Уменьшать промежутки следует при сочетании букв, имеющих неполный по ширине низ или верх: Г и А, Р и А, Т и А, Г и Л и т. п. Этим указанием можно пользоваться также при сочетании прописных букв со строчными, например в словах: Телефон, Рама, Гайка (рис. 2). rn
TBegin—>TEnd—> rn
Рис. 2. Сближение некоторых букв Под таким понятием, как «шрифт», понимается графическое изображение таких элементов чертежей, как буквы и цифры. Это слово имеет немецкое происхождение и в дословном переводе означает почерк или надпись, а также, то его значение, которое обычно используется в обиходе. Нормами и правилами составления технических документов и их оформления установлено, что на них должен использоваться только тот шрифт, который имеет некие стандартные размеры. Его отличительными чертами являются строгость и четкость, которые должны быть такими, чтобы не затруднять читаемость. Очертания технических шрифтов всегда прямые, и поэтому они относятся к тому их классу, который не предполагают наличия каких-либо засечек, и во многом по этой причине наиболее удобны для зрительного восприятия и чтения. Нанесение технического шрифта производится таким образом, чтобы по отношению к основанию строки он располагался под углом около 75 градусов. В то же самое время действующими на сегодняшний день нормами и правилами допускается использование шрифтов и без наклона. Действующий на сегодняшний день ГОСТ 2.304 – 81 гласит о том, что для чертежного шрифта предусмотрено десять размеров, а именно: 1,8; 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. При этом под размером подразумевается та величина, которая определяет высоту заглавной (прописной) буквы. При этом измеряется она по отношению к основанию строки, перпендикулярно ей. Этот параметр шрифта обозначается буквой (h) и является его размером. Что касается таких букв, как Щ, Ц, Д, то нижние их элементы, а также верхний элемент буквы Й выполняются за счет расстояний между строками.
Толщина линий также является одним тех параметров, которые имеет чертежный шрифт.
Толщина линий обозначается буквой (d), а ее размер равен 0,1h.
Литерой (g) обозначается ширина прописных букв, а равняется она 6d или 0,6h, причем этот размер примерно соответствует величине (h), который имеет шрифт ближайшего наименьшего номера. Это правило не распространяется на такие буквы, как Ю, Ы, Ц, Х, М, Д, А. Их ширина равняется 0,7d. Кроме того, исключение также распространяется на буквы Ъ, Ш, Щ, Ф, Ж, для которых этот параметр составляет 0,8d, а также на буквы С, З и Г ширина которых ровна 0,5d.
Для подавляющего большинства строчных букв параметр (с), обозначающий их высоту, равен 0,7h. Этот размер приблизительно равен тому, который имеет шрифт самого ближайшего наименьшего номера. К примеру, у того шрифта, который имеет номер 10, строчная буква будет высотой 7 миллиметров, а этот же параметр для строчной буквы номер 7 – 5 миллиметров. Что касается нижних и верхних элементов, которые имеют строчные буквы, то они имеют размер 3d, который выполняется расстояниями между строками.
Ширина строчных букв обозначается символом (g), а её величина равна 5d. Исключение составляют буквы а, м, ц, ъ ширина которых ровна 6d; для букв з,с – 4d; а для букв ж, т, ф, ш, щ, ы, ю – 7d.
Специальная вспомогательная сетка была разработана для того, чтобы начинающие чертежники научились наносить шрифт вручную. Она образовывается тонкими вспомогательными линиями, между которых должны быть вписаны буквы. Тот шаг, который имеют вспомогательные линии сетки, зависит от того, какое значение имеет параметр (d) (то есть толщина линий самого шрифта).
В таблицу сведены такие параметры шрифта, как высота, толщина и ширина его линий, а также, то минимальное расстояние, которое должно быть между словами и между буквами.
Графическое представление букв и других знаков называется шрифтом. Все вместе они представляют собой единую стилистическую и композиционную систему, которая предназначена для того, чтобы отображать информацию визуально. Выражаясь более простым языком, шрифтом является такой набор цифр, букв и специальных символов, которые единообразны с точки зрения стилистики и выполняются со строгим соблюдением пропорций между их размерами. Такие параметры, как размер (кегль), ширина (широкая, узкая, нормальная), насыщенность (жирная, полужирная, светлая), начертание (курсивное, прямое) являются основными характеристиками шрифтов. К дополнительным характеристикам шрифтом относятся удобочитаемость, емкость, контраст, различимость и четкость. Они также имею немаловажное значение. Австро-венгерская 305-мм мортира А ведь это высококачественное новейшее орудие было одним из самых могущественных в своем классе, активно применяясь как австро-венгерской, так и германской армиями в годы Первой мировой войны 1914-1918 гг. В частности, австрийские 305-миллиметровки сокрушали бельгийские крепости, активно работали по Ивангородской, Ковенской и Верденской крепостям, эффективно действовали на Итальянском фронте, сражались в Сербии, в Дарданеллах и Палестине. Демонстрация орудия перед турецкими сановниками в Константинополе, 1916 г. Как и Германия, Австро-Венгрия в связи с уроками предшествующих (особенно Русско-японской 1904-1905 гг.) войн придавала огромное значение тяжелой артиллерии. Считалось, что роль тяжелой артиллерии будет очень велика, причем не только в борьбе с крепостями, но и в полевой войне. Тем более что и в последней появились полевые оборонительные сооружения, заграждения и др. цели, против которых граната полевой пушки могла оказаться бессильной. Соответственно, в упомянутых государствах было приложено много усилий и потрачено много средств для того, чтобы иметь количественно мощную тяжелую артиллерию и обеспечить ее средствами быстрого перемещения. И, в меру своих экономико-производственных возможностей, Австро-Венгрия старалась следовать этой концепции. Вершиной артиллерийской пирамиды и стала «Чудо Эмма», как позднее назвали 12-дюймовую гаубицу. Посмотрим на тактико-технические данные 305-мм мортиры образца 1911 г., модифицированной в 1916 г. При весе снаряда 290 кг и его начальной скорости 407 метров в секунду, орудие имело дальность огня 11 км, и градус горизонтального и вертикального обстрела плюс-минус 60 и 40-75 соответственно (для сравнения, у 420-мм германской «Берты» — 10 и 30-70). Вес орудия в боевом положении – 20900 кг, что вдвое меньше чем у германской 420-мм «Берты» (42600 кг). 305-мм мортира. Снаряд этого орудия «образует воронку, в которую могут поместиться трупы пяти лошадей» Но обо всем по порядку, тем более что это замечательное орудие имело несколько модификаций. В начале XX в. Генеральный штаб армии Двуединой монархии был обеспокоен интенсивным строительством итальянских приграничных укреплений. Стремясь иметь в будущем весомый огневой аргумент на случай весьма вероятных осложнений отношений с Италией, руководство Генштаба поручает Военно-технической комиссии разработать тактико-технические требования на новую мортиру, способную сокрушать перспективные оборонительные сооружения итальянцев. Требования были разработаны в 1907 г., и в соответствии с ними мортира должна была иметь калибр 305 мм, массу снаряда до 300 кг, дальность огня до 8000 м, а также возможность работать на 2-км высоте (последнее должно было стать во время горной войны сюрпризом для итальянцев). Были поставлены и повышенные требования к мобильности этого орудия – невзирая на его калибр. И это было неудивительно: Австро-Венгрия, готовясь к войне на 2 (а то и на 3) фронта, хотела получить орудие, способное относительно быстро преодолевать сотни километров – перемещаясь из Галиции в горы Италии, и обратно. На эту функциональность сработали как ограниченные возможности бюджета, так и бурный рост моторостроительной и автомобильной промышленности империи. Заказ на разработку орудия в начале 1908 г. выдается фирме Skoda-Werke AG — монополисту в области производства тяжелых артсистем для австро-венгерской армии. В 1910 г. опытный образец был предъявлен на испытания. В начале 1912 г. Военное министерство принимает решение о выделении средств на изготовление 24-х 305-мм мортир, получивших обозначение 30,5 см MÖrser М. 11. И к началу Первой мировой войны фирма Skoda-Werke AG передала представителям австро-венгерской армии последнюю мортиру из заказанной в 1912 г. серии. В годы войны было выпущено еще 44 мортиры этой системы. Мортира имела стальной ствол длиной 10 калибров. Длина нарезной части ствола составляла 6,7 калибра. В канале ствола было выполнено 68 нарезов постоянной крутизны. Запирание канала ствола осуществлялось новейшим призматическим клиновым затвором. Масса ствола достигала 5930 кг. Ствол установили в люльке обойменного типа, закрепленной на литом станке. В качестве противооткатных устройств использовались два гидравлических тормоза отката, смонтированные над стволом, а также пневматический накатник, расположенный под стволом. Подъемный механизм станка позволял наводить орудие в вертикальной плоскости в диапазоне углов от 0° до +75°. В горизонтальном положении производилось заряжание орудия, и в этом положении ствол опирался на специальный упор, закрепленный на станине станка. Стрельба велась при углах возвышения от +40° до +75°. Наведение орудия в горизонтальной плоскости производилось посредством поворота станка на погоне, закрепленном с помощью болтов на стальной платформе основания. Червячный механизм поворота позволял наводить орудие в секторе ±60°. Со стороны казенной части на станке были закреплены направляющие для лотков со снарядами и пороховыми зарядами. Масса мортиры в боевом положении составляла 18730 кг. Модифицированные в 1916 г. мортиры (М. 11/16), у которых были повышены прочность станка и платформа основания, весили в боевом положении 20900 кг. Первоначально к мортире выпускались лишь фугасные снаряды М. 11/9 массой 385,3 кг, содержавшие 38,3 кг взрывчатых веществ. Стрельба велась с использованием четырех переменных зарядов. При стрельбе полным зарядом снаряд имел начальную скорость 370 м/сек, а дальность стрельбы составляла 9600 м. В ходе войны с целью увеличения дальности стрельбы до 11000 м ввели так называемый «легкий» фугасный снаряд массой 290,8 кг, содержавший 34,8 кг взрывчатки. Его начальная скорость составляла 407 м/сек. Снаряд оставлял в земле воронки глубиной 8,8 м, пробивал 3 метровую кирпичную стену и 22-см бетонную кладку. Взрыв 305-мм гранаты. Исключительно мощным средством поражения живой силы был 300-кг шрапнельный снаряд, содержавший 16,4 кг взрывчатки и 2200 шрапнельных пуль. Дальность стрельбы — также 11000 м. 2- 3 таких снарядов было достаточно, чтобы сорвать атаку целого полка. При проектировании мортиры транспортировку орудия планировали осуществлять только с использованием механической тяги — колесных тягачей М. 12 фирмы Daimler. Мортира разбиралась на три части, которые образовали 3 повозки: ствольную повозку, повозку-лафет и повозку с платформой основания. Сотрудничество «Шкоды» и Австро Даймлера» стало важным залогом успеха в деле механизации «Чудо Эммы». Сначала считалось, что для буксировки всех 3-х повозок будет достаточно одного колесного тягача. Потом пришли к выводу, что правильнее будет, если тягач будет буксировать 2 повозки, а по мере поступления в мортирные батареи все большего числа тягачей приняли окончательную схему — 1 тягач буксирует 1 повозку. Важнейшим элементом системы управления огнем были подразделения привязных аэростатов, придававшиеся мортирным батареям. Парсеваль, обслуживающий «моторбатарею», фото после 1917 г. Мортиры М. 11 использовались австро-венгерской армией на Русском и Итальянском фронтах (об этом – дальше). Обычно они состояли на вооружении отдельных мортирных батарей особой мощности – моторизованных или «моторбатарей». В каждой батарее имелось 2 орудия и 6 тягачей. Батареи могли включаться в состав артиллерийских батальонов и полков (как и в германской армии) – прежде всего крепостной артиллерии (флагманом была крепость Краков). Во время войны «моторбатареи» выделяются из состава артчастей – это позволяло оперативно перебрасывать их на помощь союзникам-немцам (например, крепость Краков отправила в Бельгию 2 из своих 4 батарей, получив, в свою очередь, 2 батареи из Вены) или группировать в качестве мощного огневого ресурса в руках Верховного командования. Неразбериха начального периода войны привела к тому, что, например, Балканский фронт в августе 1914 г. не получил ни одной «моторбатареи». Известны также случаи использования «кочующих» орудий. Например, во время сражения в долине р. Изонцо в 1917 г. одну мортиру ночью выдвинули на нейтральную полосу и 15-ю выстрелами уничтожили железнодорожную станцию, на которой производилась высадка итальянских войск. После успешного выполнения задачи мортиру перевели в походное положение и еще до наступления рассвета вернули в расположение. Впрочем, подобные операции далеко не всегда заканчивались благополучно. 305-мм «шкода» на позиции. Тактико-технические характеристики М. 11 были следующими: длина ствола — 10 калибров; наибольший угол возвышения +75 градусов; угол склонения – 0 градусов; угол горизонтального обстрела – 120 градусов; масса в боевом положении – 18730 кг; масса в походном положении – 27950 кг; масса фугасного снаряда — 385,3 кг; начальная скорость снаряда – 370 м/сек.; наибольшая дальность стрельбы – 9600 м. «Видок сквозь мортирный замок». Применение М. 11 в боевых условиях быстро выявило их главные недостатки — малую дальность стрельбы, недостаточную прочность станка и платформы основания, малый сектор стрельбы. Поэтому наряду с модернизацией мортир М. 11 до уровня М. 11/16 фирма Skoda-Werke AG приступила к разработке новой 305-мм мортиры, принятой на вооружение австро-венгерской армии в 1916 г. и получившей обозначение М. 16. Прежде всего, для увеличения дальности стрельбы конструкторы удлинили ствол до 12 калибров и изменили массу переменных пороховых зарядов в сторону увеличения. При использовании тех же снарядов, которыми стреляла М. 11, это позволило повысить начальную скорость снарядов до 380 — 450 м/сек, а дальность стрельбы — до 11100 – 12300 м. Лафет с противооткатными устройствами спроектировали заново. Вместо люльки обойменного типа использовали корытообразную люльку, а систему противооткатных устройств разместили под стволом. В эту систему входили два гидравлических тормоза отката и пневматический накатник. Усовершенствованный подъемный механизм позволял наводить орудие в вертикальной плоскости в диапазоне углов от -5° до +75°, стрельба велась при углах возвышения более +40°. Была сконструирована новая передвижная платформа основания. На ней установили шаровой погон, на котором монтировался станок орудия. Таким образом был обеспечен круговой обстрел. Внесенные в конструкцию мортиры изменения привели к увеличению ее массы до 22824 кг. В походном положении она также разделялась на 3 части, которые образовывали ствольную повозку (11240 кг), повозку-лафет (11830 кг) и повозку с платформой основания (11870 кг). Каждую из этих повозок на походе буксировал «персональный» тягач М. 12 с двигателем мощностью до 100 л. с. 100-сильный «Австро Даймлер» До окончания Первой мировой войны фирма Skoda-Werke AG успела выпустить 29 мортир типа М. 16. Тактико-технические характеристики М. 16: длина ствола – 12 калибров; наибольший угол возвышения — +75 градусов; угол склонения — — 5 градусов; угол горизонтального обстрела – 360 градусов; масса в боевом положении – 22824 кг; масса в походном положении – 39940 кг; масса фугасного снаряда — 385,3 кг; начальная скорость снаряда – 380 м/сек.; наибольшая дальность стрельбы – 11100 м. 1) Концерн «Шкода», детищем которого стала 12-дюймовка, один из лидеров по созданию и производству сверхмощных орудий, выпустил один из лучших для своего времени образцов орудия большого могущества. Снаряд «Чудо Эммы» был способен преодолеть самую мощную защиту. 2) Мортира, несмотря на свой калибр, относилась к мобильным артсистемам. При разработке этого орудия особое внимание было уделено именно вопросу транспортировки данной гаубицы. Как мы отметили выше, 305-мм гаубица разделялась на 3 основные части — и возможность транспортировки трактором «Австро Даймлер» на большие расстояния ее лафета и ствола, изначально закладывалась в проект. Между прочим, для этих целей тракторы использовались впервые. 3) Механизированная тяга значительно увеличила функциональность батарей «Австрийских Берт». Бойцы орудийного расчета, сидевшие на каждом тракторе-тягаче, также выполняли полезную функцию – прежде всего управляя тормозами. Сборочные лебедки, снаряды, инструменты и даже специальная передвижная мастерская, приборы управления стрельбой, документация, продовольствие и др. имущество перевозились дополнительными тракторами. На нижнем рисунке – способ отсоединения тележки от платформы. Орудие стало одним из первых, изначально сконструированных как мобильная артиллерийская установка. И ни одна армия мира в тот период не располагала мобильным орудием столь большой мощи. Австро-Венгрия не только оказалась в числе держав, лучше всего подготовленных к борьбе с укрепленными районами и крепостями противника, она стала новатором в вопросе организации сверхтяжелой моторизованной артиллерии. Установка платформы Продолжение следует… Если чердачное помещение, по задумкам хозяев дома, служит полноценной жилой , то, как правило, сооружается полноценная лестница, которая должна отвечать всем требованиям безопасности и комфорта перемещения по ней. Но довольно часто чердачное помещение является подсобным, то есть туда поднимаются не столь часто, только по мере необходимости. Но при этом, безусловно, намного удобнее будет, если возможность входа на чердак никак не будет зависеть от времени года или погоды, то есть лестница на него все же будет располагаться внутри дома, а не снаружи. Вариантов обустройства подобного межэтажного перехода – немало. Так, практикуется установка раскладных систем, от простейших до весьма сложных, которые приводятся «в боевую готовность» только по мере необходимости. Другой подход – установка стационарных конструкций, которые стараются соорудить так, чтобы они занимали минимум полезной
площади жилого помещения. В любом случае
, приобретается ли готовый комплект, или изготовление и монтаж чердачной лестницы будет проводиться собственными силами, не обойтись без информации по
ее основным параметрам. В этом вопросе могут помочь предлагаемые калькуляторы расчета
длины и крутизны лестницы на чердак. Несколько необходимых пояснений будет приведено ниже Подобрать эргономичный и комфортный угол наклона — это одна из основных задач при конструировании лестницы. Можно сделать маршевую лестницу или, наоборот, очень компактную и элегантную винтовую лестницу – все будет зависеть от площади дома и высоты его перекрытий. Создать красивую конструкцию вам помогут многочисленные фото в интернете, но для того чтобы правильно ее спроектировать, вам придется вспомнить школьные годы и заняться математикой. При расчете угла наклона лестницы нужно учитывать множество нюансов — о них вы узнаете из статьи Как правило, практически все лестницы имеют наклон в 45˚. Ширина ступеньки должна соответствовать 45-му размеру ноги, но не меньше 30 см, чтобы человек не упал, спускаясь вниз. Обратите внимание, если вы сделаете через чур широкие ступеньки, то вы собьетесь с шага, а при чрезмерном уменьшении ширины затрудните себе спуск. В принципе, угол подъема не так уж и сложно вычислить, зная высоту потолков и длину подошвы лестницы. Существует несколько способов: На фотографии — вариант лестницы с вполне удобными углами наклона. Несмотря на то, лестница выглядит необычно, подниматься на второй этаж по ней не составляет сложностей Для того чтобы понять, какой максимальный угол может быть у лестницы, разобьем все имеющиеся их виды на группы с характерным им углом наклона: А вот наклон менее 23˚ для лестницы внутреннего назначения даже не обсуждается, так как никто не будет тратить метры жилплощади на «укладку лежащей» лестницы. Даже сложно себе представить, какой длины она должна быть с таким маленьким уклоном для подъема на следующий этаж, при высоте потолков в 3 метра. Самым комфортным углом наклона считается 40 – 45˚, однако такая конструкция является очень громоздкой, поэтому ее обычно используют в больших помещениях. Лестница, имеющая угол наклона 30 – 36˚ довольно компактна, но не такая удобная. Подъем на такую лестничную конструкцию будет удобен, а вот спуск довольно опасен, поэтому его лучше производить спиной вперед. Прежде чем приступать к возведению лестницы, нужно «просканировать» все пространство, имеющееся в вашем доме. Каждое помещение должно использоваться максимально, поэтому нужно произвести расчеты и выбрать вариант, при котором лестница не будет занимать много места. Следует обязательно устанавливать перила, если ступенек в вашей конструкции больше трех. Ширина ступеней должна быть около 0,28 – 0,30 метров, а высота – 0,15 – 0,18 метров. Когда все ступеньки одинакового размера – это повышает безопасность ее использования. Как уже говорилось ранее, стандартным и наиболее оптимальным углом наклона лестничной конструкции считается 40 – 45˚. Но так как такая лестница очень большая и занимает много места, многие люди пренебрегают данными рекомендациями. Приведем вам советы экспертов по уклону марша и размерам ступеней. Угол пролета, в большинстве случаев, составляет от 20˚ до 50˚. Наиболее идеальным считается уклон, который колеблется в пределах 30 – 45˚. Но, к сожалению, не у каждого человека есть много места для того чтобы разметить такую удобную лестничную конструкцию. Обратите внимание, чем меньше значение угла, тем опаснее по ней будет передвигаться, и чем больше угол, тем громоздче она будет. Важно! Комфортный шаг при подъеме по лестнице с наклоном больше 45-ти градусов практически невозможен, а вот совершать спуск по ней вы сможете без опаски только лишь спиной вперед. Наверное, не стоит, и говорить о детях, которым по такой лестнице взобраться не получится. Рассчитать угол наклона лестницы можно по одному показателю – длине шага при спокойной ходьбе по горизонтальной поверхности взрослым человеком. Уклон определенных маршей рассчитывается отдельно в зависимости от количеств и высоты ступеней. Если у вас есть готовый проект, то угол лестницы определяется неимоверно просто. Высота ступеней будет идеальной при значении 150 – 180 мм, ширина – 280 – 300 мм. Придерживаясь таких стандартов, угол наклона можно рассчитать по формуле: 2х + у = 580/660 мм, где х – это высота ступеней, а у – ширина. При размере ступеней меньше 145 мм, нужно использовать другую формулу: х + у. В вышеприведенных формулах используют ширину, которая равняется среднему размеру стопы человека, и высоту, соответствующую размеру шага. Из этого можно сделать вывод, что чем ниже ступенька, тем шире она должна быть, и наоборот. Думая о строительстве лестницы в своем доме, нужно помнить, что изготовляться они должны по ГОСТ и СНИП, основные положения которых говорят о: Интересный факт! Количество ступенек в марше лучше делать нечетным, так как людям комфортней начинать и завершать подъем или спуск по лестнице одной и той же ногой. Приставная лестничная конструкция упирается в пол и в стену тетивами так, чтобы полностью сохранять устойчивость и в тоже время предоставить возможность подняться к труднодоступному месту. Угол наклона приставной лестничной конструкции составляет около 60 – 75˚, поэтому подъем и спуск по такой конструкции довольно затруднителен, а перенос каких-либо грузов – вообще невозможен. Из видео вы узнаете, как правильно смонтировать лестницу на чердак, а также различные тонкости, которые необходимо учитывать при монтаже. Ничего сложного в проектировании лестницы нет. Главное – это следуйте формулам и установленным правилам, правильно рассчитайте ширину и длину конструкции в общем, а также количество ступней и угол наклона. Грамотно сконструированная и добротно смонтированная лестница прослужит вам долгие годы. 18.09.2017 Чтобы не пришлось исправлять неудобную и опасную лестницу, уже на этапе расчета для чертежа надо уделить повышенное внимание крутизне будущей конструкции. Оптимальным является угол подъема в 34-41 градус. Для того, чтобы рассчитать крутизну, понадобится: Чтобы не напрягаться с математикой, можете загрузить данные в специальную программу для расчета. Это будет быстрее и точнее. Если ошибка все же была допущена, и доступ на второй этаж неудобен, а спуск со ступенек слишком опасен, то конструкцию придется исправлять. К сожалению, нет единой инструкции как это сделать. В любом случае, чтобы исправить просчет, придется переделывать все сооружение. Установка лестницы с гусиным шагом поможет, но к ней придется привыкнуть, так как ступени на ней не равного размера. Монтажу любой лестницы предшествует расчет ее параметров. Провести его достаточно просто. От вас потребуется только внимательность, калькулятор и совсем немного времени. Правильно определенные размеры будущей лестницы помогают упростить ее монтаж и эксплуатацию, а также определить необходимое количество материалов и параметры монтажных элементов. Цель расчета состоит в том, чтобы сконструировать удобную, безопасную и экономичную лестницу. В результате необходимо определить такие параметры, как ширина и высота ступеней, крутизна лестницы (то есть угол ее наклона) и ширина лестничного марша. Чтобы провести расчет, вам нужно заранее определиться с некоторыми характеристиками будущей конструкции. Например, будете ли вы обустраивать лестничные площадки, и если да, то на какой высоте. Сразу обратим внимание, что высота различных элементов лестницы определяется относительно чистового пола. Кроме того, нужно определиться с высотой лестницы, площадью, которую вы можете под нее отвести и материалами, из которых вы планируете ее изготовить. Все эти данные оказывают влияние на расчеты. Ширина лестничного марша определяется в зависимости от того, какой пропускной способностью она должна обладать и для каких целей предназначена.
Кроме того, при определении оптимальной ширины лестницы следует учитывать площадь, которую вы можете отвести под нее, и особенности планировки дома. Как правило, оптимальной шириной лестницы для дома можно назвать ширину до 1 м. Если вам позволяет площадь и планировка дома, можно отдать предпочтение ширине около 1,5 м. В таком случае такой элемент интерьера, как лестница, будет выглядеть презентабельно и достойно. Особенно актуально выполнение более широкой лестницы в том случае, если она будет служить для подъема на второй этаж, то есть будет вести в жилое помещение, а не на чердак или в подвал. При обустройстве дома вам потребуется поднимать на второй этаж мебель и предметы интерьера, габариты которых могут быть весьма внушительными. Осуществить это при помощи узкой лестницы будет очень сложно или даже невозможно. За ширину лестничного марша принимается расстояние от перил до стены или до противоположного перила. При этом ширина самой ступени может немного превышать это значение. Общие принципы определения оптимальной ширины лестничного марша таковы: Вернуться к оглавлению Очень важно рассчитать просвет, то есть высоту от ступеней до наиболее высокой преграды. Такими преградами в различных планировках являются либо потолок, либо перекрытие верхнего этажа. Дальнейшая комфортная эксплуатация лестницы во многом зависит от правильного определения этого параметра. Если сделать эту высоту слишком маленькой, то при ходьбе по лестнице вам придется пригибаться. Чтобы задать этот параметр, вы можете исходить из среднего рекомендуемого значения, которое варьируется в пределах 1,9-2 м. Кроме того, можно рассчитать просвет индивидуально, опираясь на то, каков рост проживающих в доме людей. Вернуться к оглавлению Наиболее удобным и безопасным углом считается тот, который попадает в интервал от 22 до 40 градусов. Если сделать лестницу более крутой, то она будет занимать меньше места, но пользоваться ей будет достаточно сложно и даже опасно. Особенно это актуально для тех домов, в которых проживают пожилые люди или маленькие дети. При крутизне лестницы меньше 22 градусов наиболее целесообразным вариантом считается выполнение пандуса. Однако он занимает огромную площадь, поэтому в частных домах его изготавливают крайне редко. Угол наклона в 45-75 градусов допустим только для приставных лестниц или тех, которые ведут в подвал или на чердак. Проводя , вам потребуется определить точное значение ее крутизны, которое будет вписываться в интервал от 22 до 40 градусов. Наиболее простой способ это сделать заключается в нанесении схемы будущей лестницы на лист бумаги, удобнее всего использовать миллиметровку. Выполнение схематического чертежа начните с нанесения на миллиметровку двух перпендикулярных линий, которые будут обозначать высоту этажа и проекцию лестницы на горизонтальную поверхность в определенном масштабе. Масштаб вы можете принять каким угодно. Наиболее удобным можно назвать масштаб 1:10. Соедините две линии третьей так, чтобы получить прямоугольный треугольник, гипотенуза которого будет обозначать так называемую тетиву лестницы. При помощи простой линейки вы сможете узнать ее длину, а транспортиром измерить угол наклона будущей лестницы. В наш век ограниченного жизненного пространства и рационального использования жилых площадей значение лестниц неуклонно возрастает – они играют роль связующего элемента между этажами, между отдельно стоящими строениями, служат несущими конструкциями здания. Функциональное назначение лестниц уже давно дополнено значительным декоративным элементом – благодаря разнообразию форм лестниц и материалов, из которых они изготовляются, они могут стать настоящей изюминкой интерьера. Однако по-прежнему правильный расчет лестницы остается главным требованием при ее сооружении. В противном случае, самая роскошная или самая изящная лестница может стать потенциальной угрозой здоровью людей, которые ей пользуются. Основными элементами лестницы являются ступени, состоящие из подступенков и проступи, которые крепятся к широким тетивам или косоурам из дерева или металла. Для того чтобы конструкция была более удобной и безопасной, на лестнице устанавливается ограждение из балясин, называемое балюстрадой, сверху которого крепится поручень. Есть еще некоторые дополнительные элементы, которые используются в зависимости от конфигурации и конструкции лестниц. Учитывая большой угол крутизны этой лестницы, можно предположить, что подъем по ней будет затруднен, а находящаяся рядом стена ограничит маневрирование при подъеме крупных предметов Огромное количество строительных бригад сегодня предлагает свои услуги, однако их профессионализм будет виден только во время работ. Более того, в качестве рекламы на многих сайтах представлены уже готовые лестницы, имеющие явные дефекты в своей конструкции. Поэтому заказчику не мешает знать, как рассчитать лестницу, чтобы иметь возможность контролировать строительный процесс и, если строители допустят ошибку, попросить своевременно ее устранить. При строительстве многоэтажных жилых домов нормы расчета лестниц соблюдаются очень строго, ведь от этого зависит безопасность всех жильцов. Владелец загородного дома или коттеджа не настолько ограничен в выборе форм, размеров и крутизны лестниц, которые будут в нем возводиться. И все-таки, чтобы лестница была удобной и безопасной в эксплуатации, лучше придерживаться существующих норм. Расчет лестницы на второй этаж осуществляется исходя из следующих данных: высоты между этажами и свободного пространства, отведенного под лестницу. Прежде всего, стоит определиться с формой лестницы. Наиболее удобной считается одномаршевая лестница – прямой марш, начинающийся на уровне одного перекрытия и заканчивающийся на уровне другого. Этот вариант подходит для тех помещений, где высота между уровнями относительно невелика (от 2,5 до 3,5 метров), а свободного места для установки лестницы достаточно. Перед тем, как определиться с формой лестницы, следует уточнить, достаточно ли свободного пространства там, где планируется ее установка Соблюдение норм при расчете лестницы гарантирует то, что она будет удобна в эксплуатации Оптимальным соотношением длины и высоты лестницы считается соотношение 2:1, то есть при расстоянии между этажами в 3 метра длина лестницы будет составлять 6 метров. Важным показателем является также крутизна лестницы, определяющая угол конструкции. Как рассчитать угол наклона лестницы, чтобы она не представляла опасности для окружающих, была удобной в эксплуатации и гармонично вписывалась в интерьер? По такой лестнице без проблем можно перемещать крупногабаритные предметы Оптимальная крутизна лестницы находится в пределах 30-40 градусов, хотя в загородных домах чаще всего этот показатель определяется предпочтениями владельца Оптимальным углом наклона лестницы считается угол в 30 градусов. Меньший угол превратит лестницу в покатый пандус, громоздкий и неудобный, а угол больше 40 градусов делает лестницу опасной в эксплуатации не только для пожилых людей и детей, но и для взрослых жильцов дома. Одна из разновидностей одномаршевой деревянной лестницы — лестница «гусиный ход» — позволяет сэкономить пространство, но очевидно, что показатель ее крутизны далеко выходит за границы установленных норм Расчет ступеней лестницы проводится по двум параметрам и зависит от длины среднего шага человека, которая составляет от 57 до 64 сантиметров. Можно воспользоваться формулой, в которой сумма ширины проступи (А) и удвоенной высоты подступенка (В) должна не выходить за пределы длины среднего шага человека. В математическом отображении это выглядит так: А+2В=57-64см. Чтобы пользоваться лестницей было удобно и безопасно, не следует пренебрегать установленными нормами высоты и ширины ступеней Есть и другие варианты расчета, например, формула удобств: А-В=12см. Какой бы способ расчета ступеней не использовался, нужно помнить о том, что подъем по лестнице с высотой ступеней более 17 сантиметров для пожилых людей не будет ассоциироваться с комфортом и безопасностью. Важно! Все ступени лестницы должны быть одной ширины и высоты, не допускаются даже незначительные отклонения. Это связано с тем, что человек многие действия совершает машинально, к таким действиям можно отнести и подъем по лестнице. Определив ширину и высоту ступеней, человек потом переключается на другие мысли, и малейшее несоответствие окончания лестницы и ее начала может привести к несчастным случаям. Есть еще два важных параметра, которые нужно учитывать при проектировании лестницы. Перед тем, как рассчитать размер лестницы, нужно определиться с количеством людей, которые будут одновременно ей пользоваться, и назначением лестницы. От этих параметров зависит ширина конструкции. Если лестницей одновременно будут пользоваться два и больше человек, движущихся в противоположных направлениях, то ее ширина должна быть не менее 120 сантиметров. Такая же ширина будет оптимальной в том случае, если по лестнице предполагается перемещать объемные предметы (оборудование или мебель). Даже без измерений видно, что ширина ступеней не соответствует нормам, а спуск и подъем по этой лестнице может превратиться в опасное путешествие Обычно в частных домах лестницы такой ширины не нужны, для комфортной эксплуатации вполне подойдет лестница 90-сантиметровой ширины. Если размеры помещения ограничены, то ширину лестницы можно уменьшить до 70 сантиметров – минимально допустимой ширины. Расчет деревянной лестницы проводится по тем же параметрам, что и лестницы из другого материала, но есть нюанс – учитывая, что дерево по сравнению с металлом или бетоном, менее прочный материал, на деревянной лестнице шириной более 90 сантиметров целесообразно установить среднюю тетиву. Этот опорный брус добавит прочности деревянной лестнице и позволит избежать возможного прогиба ступеней. Лестницы другой формы, например, винтовые или поворотные, рассчитываются немного иначе. Расчет винтовой лестницы зависит от ее назначения: если эта лестница служит элементом декора помещения и использоваться будет эпизодически, то ее параметры можно немного подкорректировать в пользу эстетической составляющей и в ущерб комфортабельности. Эта винтовая лестница строилась не для экономии пространства, поэтому подъем по ней будет удобным и безопасным Если же лестницей предполагается пользоваться постоянно, переносить тяжелые габаритные предметы с этажа на этаж, то нужно знать, как рассчитать винтовую лестницу правильно и стоит придерживаться общепринятых правил. Внешний диаметр винтовой лестницы зависит от пространства, которое ей предоставляется, внутренний – от диаметра несущей конструкции. Ступени винтовой лестницы по форме больше всего напоминают конус, поэтому к ним тоже предъявляются особые требования: в центральной части рекомендованная ширина составляет 20-25 сантиметров, в самой широкой – не более 40 сантиметров. Зато требования по высоте подступенка для винтовых лестниц более демократичные: они могут достигать 18 сантиметров. Еще один способ рационального использования пространства – установка поворотной лестницы. Она немного напоминает двухмаршевую лестницу с промежуточной площадкой с той лишь разницей, что площадка здесь заменяется несколькими ступенями, поэтому и расчет поворотной лестницы не сильно отличается от расчета обычной лестницы. Правильно рассчитанная лестница с поворотными ступенями займет немного места и удачно дополнит интерьер комнаты Расчет лестницы с поворотными ступенями основывается на высоте подъема, длине проема лестницы, общем количестве ступеней и количестве поворотных ступеней (оптимальный вариант – не более трех). Тематические материалы: Обновлено: 25.06.2019 103583 Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter Урок для начинающих 1. Порядок оформления чертежей Правильное оформление чертежей необходимо: 1.1. Общие требования Чертежи необходимо выполнять на листе миллиметровой (диаграммной) бумаги, которая обеспечивает параллельность и перпендикулярность
линий. Если по какой-либо причине отрезанного листа не хватает для построения
чертежа, то лист можно аккуратно подклеить, соблюдая стыковку сантиметровых
делений. Для прочерчивания прямых линий использовать длинную (около метра) инструментальную
металлическую линейку с точными делениями. Для прочерчивания плавных линий использовать
набор портновских лекал. Чертить нужно с помощью остро отточенного простого
конструкторского карандаша. Для обводки контуров деталей не использовать
фломастеры и цветные карандаши. В верхней части чертежа указать наименование изделия или базового лекала,
дату построения и фамилию заказчика. Это позволит в дальнейшем легко найти и
распознать ранее выполненный чертеж. Ниже указать расчет длины и ширины сетки
чертежа, если она присутствует на чертеже. В правом поле чертежа последовательно
сверху вниз указать: значения мерок, значения прибавок, таблицу расчетов. Чертеж всех деталей выполнять на одной базисной сетке. Это позволяет обеспечить
точное сопряжение деталей одного изделия. 1.2. Обозначение направления долевой нити, номеров деталей, марок и петель На чертежах и выкройках применяются следующие условные обозначения.
1.3. Измерение длины кривых линий ростка, проймы и длины линии оката рукава 1. Измерение длины кривых линий на чертежах производится с помощью гибкой
линейки (Фото 1). Для измерения линейке придать форму измеряемой на чертеже
линии, начиная с нулевого деления. Фото 1 2. Измерение кривых линий на чертежах можно производить с помощью нерастяжимой нитки: 1.4. Предметы для чертежной работы Бумага диаграммная (миллиметровка) в рулоне (Фото 2).
Используется для построения чертежей. Наличие вертикальных и горизонтальных
линий обеспечивает при построении чертежей строгое соблюдение параллельности
линий и прямых углов. Необходимо проверить точность делений, напечатанных на
диаграммной бумаге, измерив участки вертикальной и горизонтальной разметки бумаги
инструментальной металлической линейкой. Если отклонения разметки бумаги от
разметки линейки превышают ±1%, то бумагу следует заменить или при черчении
отмерять все расстояния по линейке, а не по делениям бумаги. Чтобы после отрезки от рулона миллиметровка не закручивалась, ее необходимо
прогладить теплым утюгом с изнаночной стороны. Калька в рулоне(Фото 3). Полупрозрачная калька используется
для создания выкроек деталей с чертежа изделия на просвет. Создание выкроек
из непрозрачной бумаги с применением копиров с зубчатым колесом нежелательно,
так как при этом базовый чертеж приходит в негодность. Чтобы после отрезки от рулона калька не закручивалась, ее необходимо прогладить
теплым утюгом.
Фото 2
Фото 3 Ручка, карандаши чертежные твердо-мягкие, цветные карандаши или фломастеры,
ластик, клеевой карандаш. Линейка закройщика, то есть масштабная линейка 1:4 (Фото 4). Фото 4 Линейка металлическая гибкая из полоски нержавеющей стали
длиной 75÷100 см (Фото 5). Такая линейка приобретается в магазинах по
продаже инструментов. Не рекомендуется применять школьные деревянные и пластиковые
линейки, они не имеют достаточной точности делений и быстро изнашиваются. Фото 5 Треугольник из прозрачного
пластика с углами 45 и 90 градусов, транспортир, циркуль Портновские лекала (Фото 6). Применяются для построения
плавных линий на чертежах. Фото 6 возврат на оглавление Планшеты формата A4, квадрат 5 мм Блокнот для записей Блокнот 160 в квадрате, бумага формата A4, 4 отверстия для блокнотов, формат a4. Отличные цены на ваши любимые бренды Office, а также бесплатная доставка и возврат соответствующих заказов. Блокнот формата А4 квадратной формы со 160 страницами квадратной бумаги высшего качества формата A4.Для изготовления этой миллиметровой подушечки использовалась бумага формата А4 плотностью 80 г / м2. 。 Квадратный блокнот формата A4 имеет квадраты 5 мм, что упрощает использование блокнота формата A4 или блокнота A4 в качестве блокнота для рисования или графической книги. 。 Серая металлическая отделка крышки также придает ей потрясающий вид. Блокнот формата А4 можно использовать в офисе, школе и университете. 。 Просверлил отверстия для бумаги в квадратном блокноте формата А4. 4 отверстия в бумаге формата A4 блокнота. Используйте эту подкладку для бумаги формата А4 для рисования, построения графиков, математических работ и многого другого.。 Боковая перевязка лентой с 4 просверленными отверстиями для подшивки в блокноте pukka Margin и Feint Ruled White Paper сменного блокнота Этот блокнот очень идеален для школы, колледжа, университета, студентов, учителей и т. Д.。 Клейкие цветные самоклеящиеся этикетки для цветного кодирования 175 Звездные серебряные наклейки, статуя протектора Ивачу Дзидзо Пресс-папье 3,8 см x 10 см Чугун Зеленый.Ствол из розового золота 1.0 мм Зебра Классическая шариковая ручка 2 блистерных упаковки из 3-6 ручек Черные чернила, VORCOOL Дорожная сумка для хранения 6 предметов Опрятная сумка для одежды Органайзер для багажа Портативный контейнер Водонепроницаемый чемодан для хранения Небесно-голубой, 30 штук Животные Закладка Дети в дереве Идея для свадьбы Маленький подарочный гаджет на крестины для детей, для дня рождения, для повседневного написания дневников, заметок и рисования гелевых ручек WallDeca, 12 штук, выдвижной, 0,5 мм, разных цветов радуги Fine Point. 2 шт. Защитная пленка для дисплея из закаленного стекла, совместимая с Texas Instruments TI 84 Plus CE-T, Cherry Premium A6 Blank Craft / Поздравительные открытки Серебро 250 г / м2 25 упаковок PEREGRINA Majestic Real Silver.Пакет из 50 бумажников с 5 звездами, полный клапан, вместимость 285 г / м2, 32 мм, синий. Счастье и продуктивность Простой и эффективный дневник благодарности и недатированный ежедневник 6-минутный дневник Идеальный подарок Бензин 6 минут в день для большей внимательности. Быстросохнущие пигментные чернила, маленькие кубики, испанский мох, 100 шт. В упаковке. Пластиковые гребешки Leitz с шипами, 8 мм, черные. Сверхмощное усилие около 1,25 кг Круглый неодимовый неодимовый стержневой магнит 6 мм 1 МАГАЗИН МОЩНЫХ МАГНИТОВ Диаметр 1/4 x толщина 1/4, черный Outshine Gaming Infinity Gaming Desk Профессиональный игровой стол для ПК и консоли с ковриком для мыши и светодиодной подсветкой RGB Кабельный органайзер для домашнего офиса, спальни, Uposao, совместимый с Huawei Y9 2019, чехол для телефона для девочек, женщин, блестящий блеск с бриллиантами, кристально чистый чехол, прозрачный бампер, крышка с кольцом на 360 градусов, розовое золото. Powder House предлагает самый большой выбор лыж, досок, ботинок и креплений в Центральном Орегоне от ведущих производителей отрасли. Наш новый прокат горнолыжных лыж включает более 100 демонстрационных лыж. Мы также сдаем в аренду сноуборды, беговые лыжи и снегоступы взрослых и молодежных размеров. Центр настройки и ремонта мирового класса от лыжника до гонщика.Возможна ночная настройка и восковая эпиляция. Справочник оптиков получил этот вопрос о призме Rx для пациента, испытывающего головокружение: «Я недавно получил рецепт, в котором врач попросил указать 1,5 градуса основания призмы вниз по оси 255 справа и 1,5 градуса основания вниз слева по оси 255. Что я должен заказать? Врач сказал мне заказать 1.1 основание вниз с 0.50 Base Out вправо и 1.1 Base Down с 0.50 Base In. « Есть два способа заказать эти линзы, и каждый из них производит одинаковые линзы для заказа. Призма может быть указана либо в прямоугольных координатах (те, к которым мы привыкли чаще всего), либо в полярных координатах. Во-первых, мы поговорим о полярных координатах, поскольку это настоящая призма, определяемая во время проверки зрения. ПОЛЯРНЫЕ КООРДИНАТЫ Возьмите транспортир и найдите 255 °. В этом случае угол больше 180 °, поэтому переверните транспортир вверх дном и найдите 255 ° (это 75 ° плюс 180 °). Сделайте отметку в этой точке. Затем проведите линию по оси 255. Это позволяет легко увидеть направление призмы для пациента i.е., 255 ° Base Down и Base Out для правого глаза. Разместите линейку для миллиметров вдоль линии и отметьте количество призмы. Самый простой — использовать 10 мм для обозначения 1∆ (призменная диоптрия), чтобы ответы можно было читать в десятых долях прямо из миллиметровой шкалы. В этом случае, чтобы сократить линию для фотографий, я выбрал 50 мм (5 см), чтобы представить 1,5 ∆ или 0,03 ∆ на мм. Это именно то, что вы хотите, чтобы лаборатория производила для пациента : 1.5∆ при 255 ° Base Down и Base Out для правого глаза. Закажите линзы в лаборатории, именно так.Оказывается, призма в лаборатории так или иначе рассчитывается компьютерным программным обеспечением в полярных координатах, так что они это прекрасно понимают. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ Заполните прямоугольник, состоящий из линии 255 и точки 1,5. Горизонтальная длина прямоугольника — это необходимое количество призмы Base Out; длина по вертикали — это призма с основанием вниз (призма вниз и наружу из-за результирующего квадранта графика, где заканчивается линия). Измерьте длину по горизонтали и вертикали и преобразуйте ее в приблизительное количество призм. Или посетите Opticampus покойного Дэррила Мейстера, чтобы получить онлайн-калькулятор по адресу www.opticampus.com. Улучшите свои математические знания с помощью бесплатных вопросов из раздела «Расширения: графическое изображение» и тысячи других математических навыков. Координатная плоскость — популярное место! Определите повороты, отражения и растяжения на координатной плоскости. Ученики работают в небольших группах, чтобы сопоставить преобразования фигуры с описанием преобразования. Они выполняют … Блок 9 Преобразования ключ ответа Когда две параллельные линии «разрезаются» трансверсалью, возникают некоторые особые свойства. Мы начнем с определения этих свойств, а затем мы сможем использовать эти свойства для решения некоторых проблем. 23 февраля 2016 г. — Предложите ученикам проанализировать с помощью этой веселой игры! Этот конструктор словаря преобразований разработан для курса математики 8-го класса, согласованного с Common Core, или курса геометрии.Эта обучающая игра предлагает студентам анализировать и описывать эффекты преобразований в последовательности переводов, размышлять … Онлайн-библиотека для печати График в координатной плоскости Бумага для печати в координатной плоскости Это также один из факторов, влияющих на получение программных документов эта миллиметровая бумага с координатной плоскостью для печати онлайн. Возможно, вам не потребуется больше времени, чтобы пойти на посвящение книги так же искусно, как на их поиск. В некоторых случаях • Расширение — это уменьшение, если масштабный коэффициент меньше 1.Координатная точка копии Координатная точка исходной Сводки. Exit Slip • Постройте линейный сегмент XY со следующими упорядоченными парами: • X (-4,2) • Y (2,6) • Постройте линейный отрезок X’Y ’с коэффициентом масштабирования ½. •. • Определите, является ли расширение увеличением или уменьшением … Математика 7-го класса фокусируется на развитии и понимании пропорций, операций с рациональными числами, 2-х и 3-х мерных фигур в онлайн-средней школе Май 17, 2017 — Математический лист бумаги с координатной сеткой (большая сетка) (A) со страницы рабочего листа целых чисел на сайте Math-Drills.com. 22 сентября 2015 г. · Кроме того, более длинный сегмент линии поворачивается наружу, пока не будет указывать прямо влево. Чтобы найти координату точки A ’, просто посмотрите на конечную точку более длинного отрезка линии (-2,2). Резюме. Давайте вспомним шаги, необходимые для поворота любой точки на декартовой плоскости: Постройте точку, которую вы хотите повернуть (A), и точку, которую вы хотите повернуть … Connected Mathematics Project — проблема -центрированная учебная программа, способствующая созданию учебно-педагогической среды, основанной на запросах.Математические идеи выявляются и включаются в тщательно упорядоченный набор задач и глубоко исследуются, чтобы позволить учащимся развить богатое математическое понимание и значимые навыки. © Maneuvering the Middle LLC, 2012-настоящее время Этот файл представляет собой лицензию для одного учителя и его учеников. Пожалуйста, приобретите соответствующее количество лицензий, если вы планируете использовать этот ресурс со своей командой. Практикуйтесь в отражении точки над осями x и y координатного графика. наша координатная плоскость разбита на квадранты с номерами 1–4.Когда мы вращаемся, мы всегда идем по квадранту, если не указано иное. Полное вращение составляет 360 °, поэтому если вы повернетесь наполовину, это будет поворот на 180 °. Вращение на 90 ° перемещается по всему периметру, а это означает, что он перемещается на один квадрант против часовой стрелки. Maneuvering The Middle Llc 2015 Worksheets Ключ ответа. … Переводы на координатной плоскости. … 75 Лучшее маневрирование средними ресурсами Images Math. BBC Webwise.Geometry рабочие листы, включая угол, координату, преобразование и.Таблицы преобразований для переводов, отражений, поворотов и расширений. Этот рабочий лист предназначен для использования с уроком «Переводы, отражения и вращения». Опишите его исходное положение и размер. Рабочий лист преобразования поворота и отражения класс 7 Координатные изображения — это способ помочь укрепить навыки построения графиков с помощью игры «соединять точки». Каждая серия точек соединяется в линию. Коллекция линий раскрывает картину. Спасибо, что заглянули! Если вы обнаружите неработающие ссылки, сообщите мне.Если у вас есть интересные ссылки, которыми вы хотели бы поделиться, поделитесь ими. Я всегда ищу веб-сайты, на которых есть наглядные и интерактивные задания и видео, которые помогут студентам лучше учиться. Узнайте больше на www.ck12.org: http://www.ck12.org/geometry/Dilation-in-the-Coordinate-Plane/. Здесь вы узнаете, как рисовать расширенные фигуры по координатам … Координатные графики. O.1. Найдите точки на координатной плоскости O.2. Точки на координатных графиках О.3. Квадранты и оси … Расширения: график изображения Q.10. 28 декабря 2020 г. · Рабочие листы преобразований для практики переводов, отражений, вращений и растяжений. Эта таблица по математике была создана 27 марта 2011 г. и просматривалась 46 раз на этой неделе и 46 раз в этом месяце. z b 0MeardfeI rwMiqtRhI XImn1fci5nviit2e6 7PjrBeH- SAcl4gLeObErIaf. W Рабочий лист от Kuta Science> 1 класс> Земля, солнце и луна. Tutor-USA предлагает огромный выбор бесплатных рабочих листов по математике для печати или загрузки.Наши рабочие листы идеально подходят для домашних и учебных занятий. Предметы включают алгебру, геометрию, исчисление, предалгебру, основную математику, тригонометрию и другие. NC.M2.G-CO.2 Эксперимент с трансформациями в плоскости. Изобразите преобразования на плоскости. Сравните жесткие движения, которые сохраняют меру расстояния и угла (перемещения, отражения, вращения), с преобразованиями, которые не сохраняют и расстояние, и меру угла (например, растяжения, расширения). Щелкните, чтобы получить последние материалы с красной ковровой дорожки. Узнайте о фильмах, которые выйдут на этой неделе (8/12) Вам нужно хорошо поплакать? с использованием координатных методов. Средняя школа SOL Progression: рисование многоугольников в координатной плоскости с учетом вершин и определение длины сторон. Определение совпадающих и похожих фигур. Проверка свойств вращения, отражений и перемещений. Алгебра I: преобразование, отражение, растяжение и сжатие графиков функций Бесплатно Видеоуроки по геометрии для школьников.Получите доступ к нашей полной библиотеке видеоуроков по геометрии (100% бесплатно с вашей учетной записью Gmail), подписавшись на наш канал YouTube. Мы добавляем новые бесплатные видео и соответствующие рабочие листы каждую неделю! Это курс геометрии; самый первый урок находится на координатной плоскости, что должно быть чем-то вроде обзора. 0002. Поэтому обязательно ознакомьтесь с другими бесплатными уроками программы 0008. Начнем: система координат: координатная плоскость является частью системы координат.0011 Задание на координатную плоскость Сурикат — Иллюстративная математика Эта алгебра: Точки графика в координатной плоскости — Практический лист 13.1 подходит для 4-7 классов. Учащиеся решают 12 задач, в которых им задаются точки на координатной плоскости и записываются координаты каждой точки. Они отвечают на 12 задач, в которых им даны упорядоченные пары … Какая система линейных уравнений имеет решение (–1, 4)? На координатной плоскости 2 прямые пересекаются в точке (1, отрицательная 4).На координатной плоскости две прямые пересекаются в точках (1, 4). На координатной плоскости 2 прямые пересекаются в точке (отрицательная 1, отрицательная 4). На координатной плоскости 2 прямые пересекаются в точке (отрицательное значение 1, 4). Таблицы координатной плоскости Справка по координатной плоскости — 4 квадранта Таблицы координатной плоскости — 4 квадранта Веселые упражнения для построения точек на координатной плоскости 19 апреля 2019 г. rethinkmathteacher.com Ресурсы для преподавания математики, алгебры, геометрии и математики для 7-го класса 0 точек на координатной плоскости важный навык, который необходимо студентам… 29 июня 2018 г. — В этом упражнении учащиеся изучают, как расширение изображений создает трехмерное перспективное изображение. На первой странице изображен горизонт города со зданиями, которые учащиеся увеличивают в 2 раза. Ключ ответа включен для этой страницы. Затем ученикам дается пустая координатная сетка для создания своего собственного прообраза, … 9 0088 Jump Force trafalgar law moveset Ошибка времени выполнения LRM не могу найти модуль Гистограмма изображения в коде MATLAB Графики квадратичных преобразований Видео; Активность соответствия параболе; Трансформации Extra Practice; См. CANVAS для справки по домашнему заданию; HW # 2: 2.2 Готово, готово, вперед [5, 12, 22, 28] Стандарты для викторины: преобразования и область / диапазон функций (обзор викторины) Ключ к обзору викторины; Учись для викторины! Буклет для ознакомления с функциями 8-го класса — ключ для ответов. Буклет с обзором функций для 8-х классов. Дополнительный блок — блок линейных отношений 8-го класса. Дополнительный блок — ключи ответов блока линейных взаимоотношений 8-го класса. Дополнительный блок — Графический план блока линейных уравнений. Дополнительный блок — Графические ключи плана блока линейных уравнений. Поиск наклона … Среда, 30 августа Обзор урока 2.2 Практика в малых группах. Ответьте на вопросы учащимся, у которых нет Chromebook. Пожалуйста, выполните в классе обзор викторины Урок 1.1–2.2. Урок 1.1–2.2. Обзор теста — это дополнительное задание для учащихся с Chromebook. Док-станция TI-Nspire ™ содержит до 10 графических калькуляторов TI-Nspire ™, позволяющих: поддерживать полностью заряженные аккумуляторные батареи; Загружать документы, классные задания и домашние задания с помощью программного обеспечения для учителей TI-Nspire ™; Обновите операционную систему с помощью программного обеспечения для учителей TI-Nspire ™ Desmos Classroom Activities… Загрузка … … Ответный ключ. Благодарности. Завершите сначала. занятие назначением договоренность постельный бизнес изменение выбор уборка курс решение усилие оправдание (ан) оказание услуги друзья домашнее задание работа по дому впечатление работа ошибка деньги шум телефонный звонок … 1) На листе бумаги нарисуйте увеличение спроса на графике спроса (сдвинув график спроса вправо). Обязательно пометьте ось Y как «цена», а ось X как «количество».«Нарисуйте стрелки, чтобы показать сдвиг от первой кривой спроса (D1) и второй кривой спроса (D2). Назовите эту страницу« Увеличение спроса ». 16) Создайте множественную гистограмму, используя данные ниже. Назовите и подпишите свой график. Убедитесь, что на нем есть ключ. Напишите 3–4 предложения, суммирующих (поясняющих) то, что показывают данные в таблице. Сделайте это на отдельном листе бумаги (прикрепите его к этому обзору). Город Нортбрук Истхейвен Саутлинн Осень 26 54 41 Зима Весна 18 33 48 67 35 58 Рабочая тетрадь для домашних заданий 0-07-660291-5 978-0-07-660291-9 Испанская версия Учебное пособие для домашних заданий 0-07-660294-X 978-0 -07-660294-0 Ответы для рабочих тетрадей Ответы на главу 3 этих рабочих тетрадей можно найти в конце буклета для руководителей ресурсов по главам. Существует множество образовательных мероприятий, для которых вы можете использовать миллиметровую бумагу. Наиболее очевидное применение миллиметровой бумаги — для построения графиков, но многие люди также предпочитают миллиметровую бумагу для практики рукописного ввода, поскольку вертикальные ячейки могут способствовать правильному расстоянию между буквами. В крайнем случае миллиметровая бумага может служить заменой линейки при проведении измерений. Каждый из уроков 5E поставляется со следующими загружаемыми файлами: карточки целей и I CAN, активность взаимодействия, дифференцированная лаборатория станций, редактируемые интерактивные PowerPoint, шаблоны интерактивных записных книжек, измененные заметки, идеи с привязкой, проекты на выбор учащихся, домашнее задание, оценка ( включая изменения) Задание 5.4 Расчет свойств твердых тел. Ключ. Вступление. Вы когда-нибудь задумывались, почему вы можете плавать в воде? Причина связана с понятием плавучести. Объем воды, которую вытесняет ваше тело, имеет вес. Вес вытесненной воды толкает вас вверх, в то время как вес вашего тела … 18 июля, 2016 · Рабочий лист, который требует от учеников построить свои собственные графики движения и отвечает на вопросы о них. В конце концов, более сложный вопрос для более высоких учеников.Включены ответы. Администрирование; Д-р Трипп Ди Никола, заместитель директора (A-DOL) Г-н Фицрой Фрю, заместитель директора (ДОМ-KRIS) Г-жа Челси Нортман, заместитель директора (KRIT-ROW) Обзор 11.1 Графики Домашнее задание по квадратичным функциям — ключ ответов 11.1 Область и диапазон квадратичных функций Разминка и ключ к ответу 11.1 Изучение квадратичных функций Управляемые заметки — Часть 2 11.1 Изучение квадратичных функций Управляемые заметки — Часть 2 — Ответы Мы будем работать над заданием по построению квадратичных уравнений завтра в классе . Math Crush предлагает распечатанные рабочие листы и справочные страницы, которые направляют и мотивируют учащихся к лучшему пониманию математики. Мы также предлагаем книги, видео и наши всемирно известные художественные страницы. Наши сотрудники имеют более чем 40-летний опыт работы в математической сфере. Softmath 1150 N Loop 1604 W Ste. 108-453 Сан-Антонио, Техас 78248 США Телефон: (512) 788-5606 Факс: (512) 519-1805 Свяжитесь с нами Мероприятие 5.4 Расчет свойств твердых тел. Ключ. Вступление. Вы когда-нибудь задумывались, почему вы можете плавать в воде? Причина связана с понятием плавучести. Объем воды, которую вытесняет ваше тело, имеет вес. Вес вытесненной воды толкает вас вверх, в то время как вес вашего тела … ВТОРНИК, 23 ФЕВРАЛЯ 2021 ГОДА ПО ЧЕТВЕРГ, 25 ФЕВРАЛЯ 2021 ГОДА СЕССИИ С 13:00 ДО 18:45 PDT КАЖДЫЙ ДЕНЬ СТОИМОСТЬ ПОЛНЫЙ ДОСТУП 45 $! Мы предложим более тридцати сессий по различным темам: от поддержки и мотивации учащихся, испытывающих трудности, до эффективного использования учебных групп и стратегий обучения, как лично, так и виртуально, и использования действий Desmos от начального до продвинутого… Изучите основы математики и биологии, а также продвинутые темы, такие как органическая химия и статистика. Независимо от того, изучаете ли вы социологию, дифференциальные уравнения или французский язык II, эти бесплатные статьи CliffsNotes могут помочь вам при выполнении домашних заданий, написании статей или сдаче тестов. 1 мая 2017 г. · Рабочий лист № 1. Д. Рассел. На всех листах есть ответы на 2-й странице PDF-файла.Эти типы вопросов помогают учащимся развить алгебраическое мышление на ранних этапах. 2 дня назад · Помощь по домашнему заданию. Найдите нужные ответы. … Мы здесь, чтобы помочь вам выучить и понять вашу домашнюю работу. Педагоги не будут выполнять задание за вас. … Когда вы думаете о ключевых законах … ОТРАЖЕНИЯ НА КООРДИНАТНОЙ ПЛОСКОСТИ переворачивает фигуру над линией отражения в порядке ОТРАЖЕНИЯ, чтобы создать зеркальное отображение.Каждая отраженная точка фигуры должна находиться на одинаковом расстоянии от линии отражения на противоположной стороне. 6 Выделите и обозначьте линию отражения оси x в каждом из примеров: G2b контрольный лист 1.jpg … отражения, вращения и растяжения. что накладывает одну фигуру на другую. … описывается геометрически в координатной плоскости. В «Угадай мою трансформацию» ученики будут использовать подсказки, чтобы исследовать и правильно идентифицировать 12 различных трансформаций на координатной плоскости.Это упражнение — интересный способ для учащихся лучше понять влияние преобразований на размер, ориентацию и координаты фигур. Расширения на координатной плоскости. Свойства преобразований. Учебное пособие по преобразованиям. Параллельные линии и поперечные сечения. Угловые отношения. Применение угла … 24 августа 2018 г. 1 26 основные грамматические моменты и упражнения с глаголами обуви ei настоящее время hora основы изменения глаголов практика работы. 23 февраля 2016 г. — Предложите ученикам проанализировать с помощью этой веселой игры! Этот конструктор словаря преобразований разработан для курса математики 8-го класса, согласованного с Common Core, или курса геометрии. Эта обучающая игра предлагает учащимся анализировать и описывать эффекты преобразований в последовательности переводов, размышлять … Переводы на координатной плоскости Ответный ключ — отображение 8 основных рабочих листов, найденных для этой концепции. Некоторые из рабочих листов для этой концепции являются Ключ ответа на переводы в координатной плоскости, Работа с переводами, Перевод фигур, Ключ ответов на отклонения и масштабные коэффициенты, Преобразования и вращения на координатной плоскости, Интегрированная алгебра a… Чтобы выполнить растяжение на координатной плоскости, вам необходимо знать две части информации. Во-первых, вам нужно знать масштабный коэффициент или величину увеличения или уменьшения. Во-вторых, вам нужен центр расширения или контрольная точка, от которой происходит расширение. Примеры работы закона больших чисел в разных областях и отраслях. Чем отличаются ЗБЧ от Чебышева и Бернулли и как их применять в своей жизни. Этот термин пришел из теории вероятности, закон больших чисел показывает насколько близким окажется среднее значение выборки к математическому ожиданию для одного и того же распределения. Звучит несколько непонятно, ниже подробнее остановимся на физическом смысле этого закона и методах его применения в разных сферах человеческой деятельности. Этот закон применяется и в инвестировании, и в здравоохранении, и в сфере страхования – везде, где нужно анализировать массив информации. Для начала разберемся с терминами: Закон больших чисел простыми словами – это закон, позволяющий понять, каким вероятнее всего окажется результат эксперимента, если проводить его неоднократно. Чем большим будет число таких экспериментов, тем ближе будет результат к математическому ожиданию. Более того, закон больших чисел – это та закономерность, которая позволяет прогнозировать исход случайных событий на длинной дистанции. Это важно в прогнозировании и оценке рисков в любой сфере деятельности человека. Если заинтересуетесь доказательствами этого, рекомендуем углубиться в теорию вероятности. Так, доказательство закона больших чисел Чебышева показывает, что среднее арифметическое при приближении числа экспериментов к бесконечности практически уравнивается с матожиданием. Схожее доказательство есть для закона больших чисел Бернулли. В нем доказывается, что при неограниченно большом количестве экспериментов частота проявления определенного события оказывается равной вероятности его появления. Помимо обычного есть и усиленный закон больших чисел. В обычном матожидание может бесконечное количество раз сильно отличаться от среднего значения результата экспериментов (происходит это бесконечно редко). В усиленном же законе вероятность такого отличие сведена к нулю, то есть со 100%-ной вероятностью матожидание сводится к арифметическому среднему. Для визуализации закона представьте себе подбрасывание монетки. Вероятность выпадения одной из сторон 50%, если подбросить ее 10 раз, то распределение может оказаться и 70/30 и 20/80. Но если продолжать эксперимент 10000, 1000000 раз, то распределение будет приближаться к 50/50. То есть частота проявления каждого события на дистанции стремится к вероятности его появления. Еще один пример – подбрасывание кубиков (вернее одного кубика). В каждом эксперименте может выпасть число от 1 до 6, но закон больших чисел утверждает, что на длинной дистанции среднее арифметическое суммы бросков приближается к 3,5. Похожую закономерность можно найти, например, при исследовании результатов общения страховых агентов с потенциальными клиентами. При большой выборке окажется, что в среднем на 1000 звонков приходится определенное количество заключенных договоров. Так что важно понимать суть закона больших чисел, он работает в любой сфере. Без использования этого закона было бы невозможно планировать развитие бизнеса и оценивать эффективность работы в прошлом. Зная, что понимается под законом больших чисел инвестор может прогнозировать результаты вложений. Работа со статистикой в этом и заключается, инвестиционная стратегия проверяется на истории, рассчитывается математическое ожидание, коэффициент Шарпа, Сортино и прочие характеристики. Если для исследования взять достаточно продолжительный временной отрезок, то в будущем при использовании этой инвестиционной стратегии результат вероятнее всего окажется близок к полученному на истории. Простейший пример оценки стстратегии: Ответьте на вопрос – стоит ли работать при таких условиях? Так как по количеству бросков ограничения нет, то на дистанции в среднем заработок составит $0,5 на одном броске. Стратегия однозначно выигрышная и ее стоит использовать. Это простейший пример закона больших чисел, примененного для оценки эффективности инвестиций. Например, алгоритмические хедж-фонды работают с сотнями/тысячами стратегий, нацеленных на сотни различных инструментов. Обязательное требование для включения стратегии в пул – положительное математическое ожидание. При работе с инструментами с с максимальной отрицательной корреляции, это делает работу практически безубыточной. Рядовой инвестор также использует понятие о законе больших чисел (даже если не владеет терминологией из теории вероятности). Вспомните как проводится анализ любого инвестиционного портфеля: Эта схема – типичное использование закона больших чисел, ей следуют все опытные инвесторы. Разберем этот метод на примере инвестиций в ETF с тикером SPY. Для тестирования выберем любой временной промежуток, например, 2010-2016 гг.. В отчете нас интересует математическое ожидание или средний арифметический прирост капитала в год и в месяц. Есть еще и средний геометрический прирост, он рассчитывается на основании наклона кривой роста депозита, при стабильном росте капитала средний арифметический и геометрический прирост практически совпадают. Теперь проведем форвард-тест (взяв участок истории после 2016 г. Ожидания оправдались – рассчитывали на среднюю месячную и годовую доходность на уровне 1,07% и 13,62%, а при форвард-тесте получили 1,20% и 15,42%. Расхождение составило 12,2% и 13,2%, что для не особенно длинной дистанции неплохой результат. Закон больших чисел просто показывает каким вероятнее всего будет результат случайного события. Но он не гарантирует, что в каждом следующем испытании итог будет строго равен математическому ожиданию. За период с февраля 1993 г. по конец 2000 г. SPY показал себя отлично. Опираясь на статистику, инвестор мог рассчитывать на средний профит в 17,98% в год или 1,39% в месяц. Но после 2000 г. начался спад и фонд просел, инвестор получил убыток. На короткой дистанции могло показаться, что закон перестал работать и пора искать новый инструмент для вложений. В следующие пару лет ETF SPY был убыточным. Вместо роста капитала инвестор получил убыток в среднем 15,19% в год или 1,36% в месяц. Причина таких расхождений – работа с небольшими временными промежутками. Здесь уместна аналогия с подбрасыванием монетки: То же и в инвестировании. Вспомните сущность закона больших чисел, он применим только при достаточном массиве статистики. Если вернуться к ETF SPY и оценить его показатели за все время существования, то окажется, что рассчитывать можно в среднем на рост в 10,83% за год и 0,86% в месяц. Этим результатам стоит доверять больше еще и потому, что за выбранный период SPY успел пережить 2 кризиса. Ровно по такой же схеме закон больших чисел используется и в хедж-фондах, управляющих миллиардами долларов. Закон больших чисел связан с обработкой статистических данных. Крупный бизнес не сможет работать и прогнозировать развитие без обработки статистики, поэтому этот закон в бизнесе применяется повсеместно. Ниже – варианты применения закона в различных секторах: Закон больших чисел в бизнесе применяется повсеместно. Прогнозирование результатов в будущем – не единственное его применение. Так, закон больших чисел описывает фазы развития бизнеса. В частности, из него следует, что темпы роста бизнеса в процентном соотношении не могут сохраняться постоянными неограниченно долго. Отсюда следует, что у молодого бизнеса более вероятен резкий рост, чем у компаний с многомиллиардными оборотами. Это следует взять на вооружение инвесторам. По мере роста происходит насыщение рынка, рост в процентном соотношении падает (при этом в деньгах показатели растут). Чтобы не перейти к стагнации компания выводит новые продукты, выходит на новые рынки. Закон больших чисел просто необходим в банковской сфере. Для обоснования частичного банковского резервирования. Для банка нет смысла постоянно располагать 100% депонированных средств. Если клиенты, например, совокупно внесли на счет $10 млрд., то банк часть этой суммы держит наготове на тот случай, если клиенты захотят обналичить средства, а часть пускает в оборот, зарабатывая фактически на пустом месте. Закон больших чисел позволяет рассчитать долю средств, которые можно пустить в оборот. Для нормальных условий рассчитывается процент клиентов, которые могут одновременно затребовать возврат денег, исходя из этого определяется норма резервирования. В кредитовании. Например, чтобы обосновать проценты по кредиту. Использовав закон больших чисел банк может спрогнозировать какая доля заемщиков не выплатит займ. В том числе исходя из этого назначается процент за использование кредитных денег. Для составления профиля благонадежного и неблагонадежного заемщика. На основании этого закона составляется профиль заемщика, который с наибольшей вероятностью вернет займ. Что касается того, на чем основывается закон больших чисел при его применении в банковской сфере, то это тот же массив статистики. Эта закономерность используется и другими околофинансовыми учреждениями. Например, БКИ при расчете кредитного рейтинга и прогнозе о возможности займа в банке опираются на анализ статистики. Значит закон больших чисел задействован и здесь. Сектор страхования предлагает всем желающим (не только физлицам) защитить себя от убытков при наступлении несчастного случая. На первый взгляд форс-мажоры спрогнозировать невозможно, но при изучении статистики оказывается, что и они подчиняются математическим закономерностям. Закон больших чисел в страховании используется для определения минимального страхового взноса, который бы позволил компании перекрыть убытки при наступлении страхового случая. Компания страхует 100 000 автомобилей, усредненная стоимость каждого $50 000, столько страховщик обязан выплатить при наступлении страхового случая. Закон больших чисел говорит о том, что в среднем за год вероятность попадания в ДТП/угона (условия наступления страхового случая оговариваются отдельно) составляет 1/200 или 0,5%. То есть ежегодно страховщику придется выплачивать компенсацию 0,5 х 100000/100 = 500 автовладельцам. При выплате в $50 000 ежегодно компания будет выплачивать 500 х $50 000 = $25 млн. Теперь рассчитаем стоимость страховки для страхователей. Чтобы страховщик вышел в ноль каждый из страхователей должен заплатить $25 000 000/100 000 = $250. Но так как страховщик хочет заработать, то в реальности стоимость страховки будет равна $250 + N, где N – вознаграждение компании, зависящее в первую очередь от конкуренции. Страхование – бизнес, который стал возможным исключительно благодаря закону больших чисел. Без прогнозирования соотношения прибыли и убытка по страховым случаям страховщики не стали бы работать. Сложно найти сферу деятельности человека, где не применяется закон больших чисел. Но сама по себе эта закономерность не является 100%-ной гарантией того, что в будущем события будут развиваться в соответствии с расчетами. Закон больших чисел может не работать при: Это не значит, что закон больших чисел нельзя использовать в бизнесе и инвестировании. Просто нужно заранее понимать, что он лишь прогнозирует вероятный результат в будущем на основе статистики. Если дать определение закону больших чисел простым языком, его можно назвать законом, описывающим наиболее вероятный сценарий развития событий в будущем, опираясь на массив исторических данных. При этом он не гарантирует на 100%, что результаты окажутся точно такими же. Эту закономерность использует любой бизнес без исключения, в инвестировании ей также отведена существенная роль. Вероятнее всего вы и сами неосознанно пользуетесь этой закономерностью при планировании своих инвестиций. Если же нет – самое время начать это делать. Трейдер, инвестор, частный предприниматель. «Финансовые рынки объединяют разные интересы, бизнес, континенты. Это то место, где всегда можно найти, чем заняться, что и как сделать или создать.» В жизни людей широко пользуются понятием среднего арифметического нескольких чисел. Вычисляется оно просто – все числа складываются, и их сумма делится на число слагаемых. Результат деления и есть среднее арифметическое всех чисел. Поясним пример вычисления среднего арифметического, взятый из истории мер и весов. В 16 веке длина английского фута по указу короля была определена как среднее арифметическое длины ступни первых 16 человек, выходящих из церкви от заутрени в воскресенье. Задание эталона фута позволило покончить с произволом в торговле и строительстве. Закона больших чисел, опубликованного в 1713 году (уже после смерти) швейцарским математиком Я. Бернулли, в 16 веке знать не могли, но именно этот закон лежит в обосновании использованного при определении длины фута принципа среднего арифметического. Согласно закону больших чисел, совместное действие множества случайных факторов приводит к результату, почти не зависящему от случая. Теорема Бернулли, являющаяся частным случаем закона больших чисел, гласит, что относительная частота появления события в независимых экспериментах сходится к вероятности события. Этим частным случаем широко пользуются при проведении социологических исследований. Чтобы выяснить мнение очень большой группы людей, вовсе не обязательно опрашивать всех членов группы – достаточно опросить несколько сотен или тысяч случайных людей, и по их ответам составить представление о мнении всей группы по рассматриваемому вопросу. Неосознанно законом больших чисел люди пользуются в повседневной жизни при принятии решений. Решив лететь в январе из Москвы в Таиланд на отдых, вы имеете ясное представление, какая погода вас там ждет – результаты многолетних метеорологических наблюдений позволят предсказать ожидаемую температуру воздуха и воды, которые не могут сильно отличаться от среднеарифметических значений в это время года. Многие явления и процессы протекают непрерывно или периодически при большом числе испытаний. В этом случае среднее значение случайной величины колебается в определенных пределах или даже стремится к вполне определенному значению. Иными словами, случайная величина перестает быть случайной и может быть предсказана с высокой степенью вероятности (рис.1). Отклонение случайной величины от средней арифметической в каждом конкретном случае есть безусловно. А при беконечно большом числе испытаний эти отклонения взаимно погашают друг друга и средний их результат стремится к какому-то постоянному значению, т.е к математическому ожиданию. В этом и заключается смысл закона больших чисел.
Другими словами, если взять предел вероятности отклонения случайной величины от ее математического ожидания при стремлении к бесконечности числа испытаний n, то он будет равен единице. Рассмотрим пример: пусть вероятность поступления заказа в магазин А равна 0,2 или каждый 5-й звонящий делает заказ. Составим закон распределения поступления 5-ти заказов. n = 5 Из графика (рис.2) можно увидеть, что вероятность поступления 3-х заказов составляет чуть больше 0,05, а 4-х и 5-ти — очень низкая. Т.е. в каждой серии из 5-ти звонков число заказов может выпадать например 2 0 1 0 1 2 0 1 0 3 …… и т.д. Числа 3, 4, 5 будут выпадать очень редко. Число 5 — практически невозможное событие. Вообщем, если число серий по 5 звонков будет стремится к бесконечности, то средняя арифметическая случайной величины X1 — будет стремится к математическому ожиданию М(Х) = 1. Что и описывает закон больших чисел. Отсюда можно сформулировать теорему Чебышева, которая гласит, что если дисперсии n независимых случайных величин не превышают какую-то величину С, т.е. ограниченны, то при стремлении числа n к бесконечности средняя арифметическая этих случайных величин сходится по вероятности к средней арифметической их математических ожиданий. Т.е. Это означает, что отклонение средней арифметической случайных величин от средней арифметической их математических ожиданий не превысит сколь угодно малое число ɛ или ( |Хср — аср| < ɛ). В этом заключается смысл данной теоремы. Допустим есть случайная величина Х, которая принимает только положительные значения и имеет математическое ожидание, например число заказов на покупку офисной техники в месяц. Тогда для любого положительного числа А верно неравенство: Второе неравенство справедливо выполняется, т.к. события P (x > A) и P (x ≤ A) противоположные. Например, среднее число заказов на покупку офисной техники за месяц равно 500. Оценить вероятность того, что в следующем месяце число заказов составит более 600. Т.е. вероятность того, что число заказов превысит 600 составляет не более 0,833. Соответственно вероятность того что, число заказов составит не более 600 будет: С помощью неравенства Чебышева можно рассчитать вероятность отклонения случайной величины от любого числа ɛ. Но здесь уже используется дисперсия случайной величины. Неравенство Чебышева имеет вид: где а = M(X) Данная формула позволяет рассчитать вероятность того, что отклонение случайной величины от ее математического ожидания превысит любое число ɛ. Вероятность противоположного события, т.е. P (|X — a| ≤ ɛ), так же как и в неравенстве Маркова рассчитывается по следующей формуле:
Неравенство Чебышева можно применять для любых случайных величин. В первом случае оно устанавливает верхнюю границу вероятности, а во втором — нижнюю. Закон больших чисел устанавливает условия, при которых среднее значение случайной величины стремится к некоторой постоянной, при стремлении числа испытаний к бесконечности. Существует группа теорем, которая описывает условия стремления закона распределения случайной величины к нормальному. Одна из таких теорем — теорема Ляпунова. Данная теорема устанавливает некоторые условия, при которых закон распределения суммы Yn = X1 + X2 + … + Xn случайных величин при стремлении n к бесконечности стремится к нормальному закону распределению. Рассмотрим эти условия: если есть независимые случайные величины X1, X2, X3 … и каждая из этих величин имеет математическое ожидание М(Хi) и дисперсию D(Xi), абсолютный центральный момент третьего порядка bi и предел отношения стремится к нулю, то закон распределения суммы этих величин при стремлении n к бесконечности приближается к нормальному закону распределения Необходимо отметить то, что скорость стремления закона распределения случайной величины в каждом явлении может быть разная. В одних случаях n может равняться десяткам, а вдругих сотням, тысячам и т.д. Закон больших чисел играет важное значение в теоретическом плане, т.к. он служит обоснованием методов математической статистики. На практике закон больших чисел можно продемонстрировать на примере погоды. Например, атмосферное давление каждый день есть величина случайная. Однако ее среднегодовое значение в течении многих лет практически не изменяется. Понятие «вероятности» математики рассматривают как величину, принимающую значения на отрезке от нуля до единицы. При этом ноль соответствует абсолютно невероятному событию (пример: Борис Немцов станет президентом РФ), а единица принимается за абсолютно вероятное (пример: Путин умрёт в XXI веке). В простом эксперименте с подбрасыванием монеты теория вероятности часто принимает шансы «орла» и «решки» равными 0.5, однако на практике доли вероятности зависят от изгибов каждой конкретной монеты, поэтому нос королевы Елизаветы II, выбитый на британском фунте, уменьшает вероятность попадания «мордой вниз» на несколько сотых процента.
Главным постулатом теории вероятности является так называемый «Закон больших чисел». Он гласит, что при большом количестве экспериментов их фактические результаты будут стремиться к математическому распределению их вероятностей. Пример: если вы бросите монетку очень-очень много раз, то примерно в половине случаев получите орла. И это «примерно» будет стремиться к «ровно» с увеличением количества подбрасываний.
Пример простой задачки по теории вероятности: какова вероятность, что при пяти подбрасываниях «идеальной» монетки выпадут четыре орла и одна решка? Решение: согласно биномиальному распределению Y ~ Bin(5, 0.5) получаем, что вероятность для 4 орлов в пяти подбрасываниях монетки равна 5*(0.5)4*(0.5)1, то есть 5/32, что равно 0.15625.
В этом эксперименте из пяти попыток вероятности распределяются так: И в сумме мы всегда получаем единицу, ведь одно из этих шести событий обязательно наступит. Теория вероятности находится в списке: Математика И не забудьте подписаться на самый интересный паблик ВКонтакте! Понятие «вероятности» математики рассматривают как величину, принимающую значения на отрезке от нуля до единицы. При этом ноль соответствует абсолютно невероятному событию (пример: Борис Немцов станет президентом РФ), а единица принимается за абсолютно вероятное (пример: Путин умрёт в XXI веке). В простом эксперименте с подбрасыванием монеты теория вероятности часто принимает шансы «орла» и «решки» равными 0.5, однако на практике доли вероятности зависят от изгибов каждой конкретной монеты, поэтому нос королевы Елизаветы II, выбитый на британском фунте, уменьшает вероятность попадания «мордой вниз» на несколько сотых процента.
Главным постулатом теории вероятности является так называемый «Закон больших чисел». Он гласит, что при большом количестве экспериментов их фактические результаты будут стремиться к математическому распределению их вероятностей. Пример: если вы бросите монетку очень-очень много раз, то примерно в половине случаев получите орла. И это «примерно» будет стремиться к «ровно» с увеличением количества подбрасываний.
Пример простой задачки по теории вероятности: какова вероятность, что при пяти подбрасываниях «идеальной» монетки выпадут четыре орла и одна решка? Решение: согласно биномиальному распределению Y ~ Bin(5, 0.5) получаем, что вероятность для 4 орлов в пяти подбрасываниях монетки равна 5*(0.5)4*(0.5)1, то есть 5/32, что равно 0.15625.
В этом эксперименте из пяти попыток вероятности распределяются так: И в сумме мы всегда получаем единицу, ведь одно из этих шести событий обязательно наступит. БОЛЬШИ́Х ЧИ́СЕЛ ЗАКО́Н, общий принцип, согласно которому совместное действие большого числа случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (т. н. устойчивость частот) может служить примером действия этого принципа. На рубеже 17 и 18 вв. Я. Бернулли доказал теорему, утверждающую, что в последовательности независимых испытаний, в каждом из которых вероятность наступления некоторого события $A$ имеет одно и то же значение $p$, $0{<}p{<}1$, верно соотношение $$\mathsf P \left \{ \left | \frac {S_n}{n}-p \right | > ε \right \} \to0 \qquad (1)$$ при любом фиксированном $ε>0$ и $n \to \infty$; здесь $S_n$ – число появлений события $A$ в первых $n$ испытаниях, $S_n/n$ – частота появлений, $\mathsf P$ – вероятность события, указанного в скобках. Эта Бернулли теорема была распространена С. Пуассоном на случай последовательности независимых испытаний, где вероятность появления события $A$ может зависеть от номера испытания. Пусть эта вероятность для $k$-го испытания равна $p_k,\ k=1, 2, …,$ и пусть $$p̅_n=\frac{p_1+…p_n}{n}.$$ Тогда Б. ч. з. в форме Пуассона утверждает, что $$\mathsf P \left \{ \left | \frac {S_n}{n}-p̅_n \right | > ε \right \} \to0 \qquad (2)$$ для любого фиксированного $ε>0$ при $n→∞$. Строгое доказательство этого утверждения было дано П. Л. Чебышевым (1846). Термин «закон больших чисел» впервые встречается у Пуассона, так он назвал вышеуказанное обобщение теоремы Бернулли. Дальнейшие обобщения утверждений Бернулли и Пуассона возникают, если заметить, что случайные величины $S_n$ можно представить в виде суммы $S_n=X_1+…+X_n$ независимых случайных величин, где $X_k=1$, если $A$ появляется в $k$-м испытании, и $X_k=0$ в противном случае, $k=1, .2)$$ B2n=DX1+…+DXn=o(n2) при $n→∞$. Таким образом, Чебышев показал возможность широкого обобщения теоремы Бернулли. А. А. Марков отметил возможность дальнейших обобщений и предложил применять назв. «Б. ч. з.» ко всей совокупности обобщений теоремы Бернулли, и в частности к (3). Метод Чебышева основан на установлении общих свойств математич. ожиданий и на использовании т. н. Чебышева неравенства. Последующие доказательства разл. форм Б. ч. з. в той или иной степени являются развитием метода Чебышева. Применяя надлежащее «урезание» случайных величин $X_k$ (замену их вспомогательными величинами $X_{k,n}$, равными $X_{n,k}=X_k$, если $|X_k-\mathsf EX_k|{⩽}t_n$, и равными нулю в противном случае, где $t_n$ зависят лишь от $n$), Марков распространил Б. ч. з. на случаи, когда дисперсии слагаемых не существуют. Напр., он показал, что (3) имеет место, если для некоторого числа $δ>0$ величины $\mathsf E|X_k-\mathsf EX_k|^{1+δ}$ ограничены одной и той же постоянной.2))$. Здесь средние арифметические $(X_1+…+X_n)/n$ первых $n$ случайных величин имеют при любом $n$ то же самое распределение, что и отдельные слагаемые. Для распределения Коши математич. ожидание не существует. Применимость Б. ч. з. к суммам зависимых величин связана в первую очередь с убыванием зависимости между случайными величинами $X_i$ и $X_j$ при увеличении разности их номеров, т. е. при увеличении $|i-j|$. Впервые соответствующие теоремы были доказаны А. А. Марковым (1907) для величин, связанных в Маркова цепь. Представление об отклонениях $S_n/n$ от $A_n=(\mathsf EX_1+…+\mathsf EX_n)/n$, наряду с неравенством Чебышева и его уточнениями, даёт центральная предельная теорема. Предыдущие результаты можно обобщать в разл. направлениях. Так, всюду выше рассматривалась т. н. сходимость по вероятности. Рассматривают и др. виды сходимости, напр. сходимость в среднем квадратичном и сходимость с вероятностью 1 (сходимость почти наверное). Обобщения Б. ч. з. на случай сходимости с вероятностью 1 называют усиленными Б. ч. з. Пусть $X_1, X_2, …$ – последовательность случайных величин и, как и раньше, $S_n=X_1+ …+X_n$. Говорят, что последовательность $X_1, X_2, …$ удовлетворяет усиленному Б. ч. з., если существует такая последовательность постоянных $A_n$, что вероятность соотношения $S_n/n-A_n→0$ при $n→∞$ равна 1. Последовательность $X_1, X_2, …$ удовлетворяет усиленному Б. ч. з. тогда и только тогда, когда при любом фиксированном $ε>0$ вероятность одновременного выполнения неравенств $$\left | \frac {S_n}{n}-A_n \right |{⩽}ε, \ \left | \frac {S_{n+1}}{n+1}-A_{n+1} \right |{⩽}ε, \ …$$ стремится к 1 при $ n→∞$. Т. о., здесь рассматривается поведение всей последовательности сумм в целом, в то время как в обычном Б.nX_k(ω)$ равна числу единиц среди первых $n$ знаков двоичного разложения $ω$, а $S_n(ω )/n$ – их доле. В то же время случайную величину $S_n$ можно рассматривать как число «успехов» в схеме Бернулли с вероятностью «успеха» (появления 1), равной 1/2. Борель доказал, что доля единиц $S_n(ω)/n$ стремится к 1/2 при $n→∞$ для почти всех $ω$ из отрезка [0, 1] (т. е. лебегова мера множества тех точек $ω∈$ [0, 1], для которых $\lim\limits_{n\to\infty}S_n(ω )/n=$ 1/2, равна 1). Аналогично, при разложении $ω$ по основанию 10 можно назвать «успехом» появление к.-л. одной из цифр 0, 1, …, 9 (напр., цифры 3). При этом получается схема Бернулли с вероятностью успеха 1/10, и частота появления выбранной цифры среди первых $n$ знаков десятичного разложения $ω$ стремится к 1/10 для почти всех $ω$ из отрезка [0, 1] (такие числа $ω$ иногда называют нормальными).2}<\infty$$ вытекает справедливость усиленного Б. ч. з. с $A_n=\mathsf E(S_n/n)$. Представление об отклонениях $S_n/n$ от $A_n$ даёт повторного логарифма закон. У многих слово «свёртка» ассоциируется со сложными и непонятными формулами. А ведь это одно из самых важных понятий в Deep Learning: именно свёрточные сети вывели глубокое обучение на новый уровень. Специально для тех, кто не до конца понимает свёртку — статья о том, как работает свёртка и что делает её такой мощной. Первая часть материала предназначена для всех, кто хочет понять общую концепцию свёртки и свёрточных сетей. Вторая часть включает более сложное объяснение и направлена на углубление понимания свёртки для исследователей и специалистов. Вы можете представить себе свёртку как «смешивание» информации. Представьте два ведра, наполненных какой-либо информацией, которые выливаются в один большой контейнер и затем перемешиваются определённым способом. Каждое ведро с информацией имеет своё собственное правило, которое описывает, как информация из одного ведра смешивается с другим. Свёртка — это упорядоченная процедура смешивания двух источников информации. Свёртку можно описать математически. Это такая же операция, как сложение, умножение или взятие производной. Хотя сама по себе операция свёртки сложна, она может быть очень полезна для упрощения ещё более сложных выражений. Когда мы применяем свёртку к изображениям, она действует на них в двух измерениях: по ширине и высоте. Здесь снова можно провести аналогию с двумя «вёдрами» информации. Первое ведро — входное изображение с тремя матрицами пикселей: по одной для красного, синего и зелёного цветов. Пиксель состоит из целочисленного значения от 0 до 255 для каждого цветового канала. Второе — это ядро свёртки: матрица вещественных чисел, свойства которой можно рассматривать как правила «перемешивания» входного изображения и ядра. В результате мы получим изменённое изображение, которое в глубоком обучении часто называют «карта признаков». Для каждого цветового канала будет по одной карте. Теперь рассмотрим саму операцию свёртки. Один из способов её применения — взять патч (небольшой участок) входного изображения размером с ядро. Например, здесь у нас картинка 100×100 пикселей и ядро 3×3, поэтому мы возьмём патч 3×3 и поэлементно перемножим каждый патч изображения с ядром свёртки. Потом сложим все результаты умножения и получим один пиксель карты признаков. После этого мы сдвигаем патч и повторяем вычисления. Проделываем эту операцию до тех пор, пока не посчитаем все пиксели карты признаков. Как вы могли заметить, существует ещё процедура нормализации: выходное значение нормализуется по размеру ядра, чтобы общая интенсивность изображения и карты признаков оставалась неизменной. На изображениях часто присутствует лишняя информация, которая не имеет отношения к тому, что мы ищем на них. Например, вы хотите сделать поиск по фотографиям с одеждой, чтобы находить вещи похожего стиля с помощью автокодировщика (это специальная архитектура глубоких нейронных сетей, которая по входному изображению ищет наиболее похожие на него варианты). Для определения стиля одежды вам не важен её цвет, эмблемы бренда и прочие мелкие детали. Наиболее информативной будет форма — блузка явно отличается от пиджака, брюк или рубашки. Поэтому если мы отфильтруем ненужную информацию, наш алгоритм не будет отвлекаться на несущественные детали. Это легко можно сделать с помощью свёртки. Для начала предварительно обработаем данные, применив детектор краёв Собеля-Фельдмана (один из видов ядер), чтобы отфильтровать всё, кроме контуров формы объекта. Вот почему применение свёртки часто называют фильтрацией, а ядра — фильтрами (более точное определение процессов фильтрации приведено ниже). Полученная карта признаков будет полезной, если вы хотите отличить разные типы одежды, поскольку на ней чётко видна форма. Мы можем усовершенствовать наш алгоритм: существует множество ядер для создания разных карт признаков. Есть те, которые делают изображение более чётким (больше деталей) или, наоборот, размытым (меньше деталей). При этом каждая карта признаков может оказаться полезной для алгоритма: например, такие детали, как три кнопки вместо двух на куртке, будут важны. Такая процедура — получение и преобразование входных данных перед отправкой в алгоритм — называется проектирование признаков. Это очень сложная операция, и не так много людей могут умело применять её для широкого круга решений. Трудность заключается в том, что для каждого типа данных и задач подходят совершенно разные признаки: например, признаки для изображений будут совершенно бесполезным при работе с временными рядами. Даже если у вас две одинаковые задачи с фотографиями, будет непросто найти хорошее решение, поскольку разным объектам могут требоваться разные признаки. Для понимания этого требуется немалый опыт. Каждую задачу проектирования признаков нужно начинать с нуля. Но можем ли мы по одному взгляду на изображения определить, какое ядро подойдёт для конкретной проблемы? Находить подходящие для определённой задачи ядра можно с помощью свёрточных сетей. Вместо того, чтобы задавать конкретные числа нашим ядрам, мы назначим для них параметры, которые будут обучаться на данных. По мере обучения ядро будет всё лучше и лучше фильтровать изображение (или карту признаков) для получения нужной информации. Этот автоматический процесс называется обучение признакам. Он обобщается для любой новой задачи: нам надо просто заново обучить нашу сеть и найти подходящие фильтры. Именно поэтому свёрточные сети такие мощные — никаких проблем с проектированием признаков. Обычно мы обучаем не одно ядро, а иерархию нескольких ядер одновременно. Например, применение ядра 32×16×16 к изображению 256×256 даст 32 карты признаков размером 241×241 (это стандартное соотношение: размер изображения — размер ядра + 1). Таким образом, мы автоматически изучим 32 новых признака с информацией для нашей задачи. Они используются в качестве входных данных для следующего ядра, которое снова применяет к ним фильтр. Как только мы изучим всю иерархию, мы просто передадим её в простую нейросеть, которая объединит признаки для классификации входного изображения. Это почти всё, что нужно знать о свёрточных сетях на концептуальном уровне. Теперь у нас есть неплохое понимание того, что такое свёртка и как работают свёрточные сети. Но можно копнуть глубже и подробнее рассмотреть, что на самом деле происходит во время применения свёртки. При этом мы увидим, что первоначальная интерпретация довольно грубая, и попробуем найти решение, которое поможет расширить наши знания. Для этого первым делом попробуем понять теорему о свёртке. Теорема связывает две сущности: свёртку в пространственно-временной области в виде громоздкого интеграла или суммы и простое поэлементное умножение в Фурье-области (частотной). Теорема применяется во многих сферах науки и является причиной, по которой многие считают алгоритм быстрого преобразования Фурье одним из важнейших в 20-м веке. Первое уравнение — одномерная непрерывная теорема о свёртке для двух базовых непрерывных функций. Второе — двумерная дискретная теорема для дискретных изображений. Здесь обозначает операцию свёртки, — преобразование Фурье, — обратное преобразование Фурье, а 2 — константа нормализации. Обратите внимание, что здесь понятие «дискретный» означает, что наши данные состоят из счётного числа переменных (пикселей). А «одномерный» значит, что эти переменные могут быть представлены в одном измерении. Например, время — одномерное (одна секунда следует за другой), изображения — двумерные (пиксели находятся в строках и столбцах), видео — трёхмерные (пиксели находятся в строках и столбцах, а изображения следуют друг за другом). Для лучшего понимания теоремы мы подробнее рассмотрим интерпретацию преобразований Фурье в отношении обработки изображений. Быстрое преобразование Фурье — алгоритм, который преобразует данные из пространственно-временной области в частотную область. Он представляет исходную функцию в виде суммы косинусов и синусов. Важно отметить, что преобразование Фурье обычно является комплексным (действительное значение преобразуется в комплексное). Мнимая часть полученного числа играет роль только для определённых операций или обратного преобразования в пространственно-временную область. В этой статье мы будем рассматривать действительную часть. Ниже вы можете увидеть визуализацию применения преобразования Фурье к входному сигналу (частотной функции с временным параметром). На самом деле вы часто видите примеры преобразований Фурье в реальной жизни: например, если красный сигнал — песня, то чёрный — столбцы эквалайзера в вашем mp3-плеере. Как мы можем вообразить частоты изображений? Представьте себе лист бумаги с двухцветным рисунком. Теперь представьте волну, которая проходит от одного края листа к другому и проникает сквозь бумагу на каждой полосе одного цвета и парит над полосами другого цвета. Такие волны «прокалывают» чёрные и белые части через определённые интервалы, например, каждые два пикселя — это будет частотой. В преобразовании Фурье более низкие частоты находятся ближе к центру, а более высокие — по краям (максимальная частота будет у самого края изображения). Значения с более высокой интенсивностью (белый цвет) упорядочены в соответствии с направлением наибольшего изменения интенсивности в исходном изображении. Если эта фраза показалась вам непонятной — посмотрите на наглядный пример ниже, где изображена фотография и её логарифмическое преобразование Фурье. Применение логарифма к действительным значениям сглаживает различия в интенсивностях пикселей, чтобы нам легче было воспринимать информацию. Мы сразу замечаем, что преобразование Фурье содержит много информации об ориентации объекта на изображении. Если объект повёрнут, скажем, на 37°, то нам трудно будет понять это из информации об исходных пикселях, но будет очевидно из преобразованных значений. Благодаря теореме о свёртке мы можем представить, как свёрточные сети работают с изображениями в Фурье-области. Кроме того, мы знаем, что алгоритм чувствителен к повороту — поэтому свёрточные сети справляются с повёрнутыми изображениями лучше традиционных методов. Причина, по которой операцию свёртки часто называют фильтрацией, станет очевидной из следующего примера. Применим к исходному изображение преобразование Фурье, а затем умножим его на окружность, дополненную нулями (нули=чёрный цвет) в Фурье-области — так мы отфильтруем все высокочастотные значения. Заметьте, что отфильтрованное изображение имеет тот же полосатый рисунок, но худшего качества — примерно так же работает сжатие JPEG. Мы сохраняем только определённые частоты и возвращаемся в пространственную область изображения. Коэффициент сжатия — отношение размера чёрной области к размеру круга. Если представить, что круг — это ядро свёртки, то мы получим её полноценное описание. Такой же механизм применяется в свёрточных сетях. Существует много способов ускорить и стабилизировать вычисление свёртки с помощью преобразований Фурье, здесь изложен только основной принцип. Теперь попытаемся применить наши знания о свёртке и преобразованиях Фурье к различным областям науки и глубокому обучению. Механика жидкостей и газов занимается созданием моделей потоков жидкостей с помощью дифференциальных уравнений, которые, как и свёртку, можно упростить с помощью преобразований Фурье. Поэтому эти преобразования широко применяют в любой области, где используется дифференцирование. Иногда единственный способ найти аналитическое решение для потока жидкости — упростить уравнение в частных производных. Решение такого уравнения иногда можно переписать в виде свёртки двух функций, поэтому оно применимо к одномерным и некоторым двумерным процессам диффузии. Вы можете смешать две жидкости (молоко и кофе), перемещая их внешним усилием (ложкой) — это называется конвекцией и происходит довольно быстро. Но можно и подождать, когда жидкости смешаются сами (если это химически возможно) — это более медленный процесс диффузии. Представьте себе аквариум, который разделён на две части тонким съемным барьером. Одна сторона заполнена солёной водой, а другая — пресной. Если осторожно убрать барьер, две жидкости будут смешиваться до тех пор, пока во всём аквариуме не будет одинаковая концентрация соли. Чем больше разница в солёности, тем стремительнее протекает процесс. Допустим, у нас есть квадратный аквариум 256×256 с барьерами, которые разделяют 256×256 кубиков с различной концентрацией соли. Если вы уберёте один барьер, то два кубика с небольшой разницей в концентрации соли смешаются медленно, а с большой — быстро. Теперь представьте, что сетка 256×256 — это изображение, кубики — это пиксели, а концентрация соли — интенсивность каждого пикселя. Вместо диффузии солёности мы имеем диффузию информации о пикселях. Мы только что описали первую часть свёртки для решения уравнения диффузии, то есть начальную концентрацию жидкости — или, в терминах изображения — исходный снимок и интенсивности пикселей. Чтобы завершить интерпретацию свёртки в виде процесса диффузии, рассмотрим вторую часть уравнения: пропагатор. Пропагатор — функция плотности вероятности, которая указывает, в каком направлении распространяются частицы жидкости. Проблема в том, что в глубоком обучении нет функции вероятности, но есть ядро свёртки — как объединить эти понятия? Можно применить нормализацию, которая превратит ядро свёртки в функцию плотности вероятности. Это похоже на вычисление softmax для выходных значений в задачах классификации. Пример softmax-нормализации для ядра Собеля: Теперь у нас есть полная интерпретация свёртки для изображений с точки зрения диффузии. Мы можем разделить этот процесс на две части: первая — сильная диффузия, которая меняет интенсивности пикселей (с чёрного на белый, с жёлтого на синий и так далее), и вторая — регулирование процесса распределением вероятностей ядра свёртки. Это означает, что каждый пиксель в области ядра переходит в другое положение в соответствии со значением функции вероятности. Для детектора контуров почти вся информация будет сконцентрирована в одном месте (это неестественно для жидкостей, но математически интерпретация верна). Например, все пиксели, значения которых меньше 0.0001, с большой вероятностью будут скапливаться в центре. Конечная концентрация будет наибольшей там, где значения соседних пикселей отличаются сильнее всего, поскольку процесс диффузии более заметен. Нетрудно догадаться, что самая большая разница между пикселями находится на гранях и пересечениях объектов — поэтому ядро и называется детектором контуров. Итак, свёртка — это диффузия информации. Мы можем применить эту интерпретацию и к другим ядрам. Иногда необходимо выполнить softmax-нормализацию, но обычно можно сразу понять по числам внутри ядра, какой эффект получится на изображении. Возьмём, к примеру следующее ядро. Попробуйте догадаться, что оно делает. Кликните сюда, чтобы узнать ответ (вы сможете вернуться по обратной ссылке). Как так получается, что мы получаем детерминированное поведение, хотя в ядре свёртки находятся вероятности? Мы же должны учитывать, что диффузия частиц происходит в соответствии с пропагатором, не так ли? Да, это действительно так. Но если взять маленькую частицу жидкости, скажем, крошечную каплю воды — в ней тоже будут находиться миллионы молекул. И хотя одна молекула может вести себя случайным образом, группа молекул в целом имеет квазидетерминированное поведение — это важная интерпретация статистической механики, и, следовательно, диффузии. Мы можем рассматривать вероятности пропагатора как среднее распределение интенсивностей пикселей. Таким образом, наша интерпретация верна с точки зрения механики жидкостей и газов. Тем не менее, существует и более точное сравнение. Пропагатор — важное понятие в квантовой механике. Частица может находиться в суперпозиции и иметь два и более свойств, которые обычно взаимоисключают друг друга в нашем эмпирическом мире. Например, в квантовой механике частица может находиться в двух местах или состояниях одновременно (вспомните кота Шрёдингера). Однако, когда вы попытаетесь определить состояние частицы — например, где она находится именно сейчас — то узнаете только одно из её возможных местоположений. Другими словами, вы разрушаете состояние суперпозиции, наблюдая за частицей. Пропагатор описывает распределение вероятностей в тех местах, где частица может появиться: скажем, с 30% вероятностью в месте А и с 70% вероятностью в месте Б. Если мы запутаем частицы (квантовая запутанность — явление, при котором квантовые состояния объектов оказываются взаимозависимыми), то несколько частиц смогут одновременно находиться в сотнях или даже миллионах различных состояний. Примерно такой эффект смогут дать квантовые компьютеры. Если интерпретировать это для глубокого обучения, то мы можем представить, что пиксели изображения находятся в суперпозиции состояний. Так, пиксель в каждом патче находится в 9 позициях одновременно (если у нас ядро 3×3). Как только мы применим свёртку, то сделаем очередное измерение, и суперпозиция каждого пикселя свернётся в одно наиболее вероятное положение. Другими словами: для каждого нового положения мы выбираем один пиксель из 9 случайным образом (согласно вероятности ядра), и результат — среднее значение всех этих пикселей. Чтобы эта интерпретация полностью была верной, необходим реальный случайный процесс. Это значит, что одно и тоже изображение и ядро дадут разные результаты. На самом деле это не так, но такое представление свёртки может натолкнуть вас на идеи, как разработать квантовые алгоритмы для свёрточных сетей. Свёртка тесно связана с кросс-корреляцией. Кросс-корреляция — это операция, для которой требуется небольшой фрагмент информации (например, несколько секунд песни), чтобы отфильтровать большой фрагмент (всю песню) на предмет сходства. Аналогичные методы используются на YouTube для автоматической пометки видео, нарушающих авторские права. Связь между кросс-корреляцией и свёрткой. Здесь обозначает взаимную кросс-корреляцию, а f* — комплексное сопряжение от f. Хотя взаимная кросс-корреляция кажется довольно сложной, мы можем легко связать её со свёрткой в глубоком обучении с помощью небольшого трюка. Просто перевернём искомое изображение вверх ногами, чтобы выполнить взаимную корреляцию с помощью свёртки. Когда мы выполняем свёртку фотографии человека с перевёрнутым снимком его лица, то результатом будет изображение с одним или несколькими яркими пикселями в том месте, где лицо совпадёт с человеком. Пример выше также иллюстрирует дополнение нулями (padding) для стабилизации преобразования Фурье. Padding может быть разным: некоторые реализации деформируют только ядро, другие вообще не требуют никаких дополнений. В этой статье мы не будем останавливаться на различных вариантах padding-а. На более ранних слоях свёрточные сети не выполняют кросс-корреляцию, поскольку мы знаем, что сначала они обнаруживают границы объекта. Но в глубоких слоях, где генерируются более абстрактные признаки, сеть может научиться выполнять подобную операцию. В чём разница между статистическими моделями и машинным обучением? Статистика часто концентрируется на небольшом количестве переменных, которые можно легко интерпретировать. Такие модели отвечают на вопрос: лучше ли лекарство А, чем лекарство Б? Машинное обучение же больше ориентировано на прогнозирование: препарат А даёт на 17.83% лучшие результаты по сравнению с препаратом Б для людей в возрасте X и на 22.34% для людей в возрасте Y. Но модели машинного обучения не всегда надёжны. Статистические решения важны для получения точных выводов: даже если препарат А на 17.83% лучше, чем препарат Б, мы не знаем, случайное это значение или нет. Чтобы решить проблему, нам нужна статистическая модель. Для временных рядов существует два важных статистических решения: взвешенное скользящее среднее и авторегрессия, которые можно объединить в модели ARIMA (AutoRegressive Integrated Moving Average). ARIMA не такие эффективные, как рекуррентные сети с долгой краткосрочной памятью, но они чрезвычайно надёжны для небольших выборок (1-5 измерений). Их довольно сложно интерпретировать, хотя ARIMA не являются чёрным ящиком, как алгоритмы глубокого обучения. На самом деле можно представить эти модели в виде свёрток и показать, что свёртки в глубоком обучении — это функции, из которых мы получаем признаки ARIMA и передаём их на следующий слой. Однако эту идею не всегда получится применить. Здесь C(kernel) — постоянная функция с ядром в качестве параметра, white noise (белый шум) — данные с нулевым средним и стандартным отклонением, равным единице. Каждая переменная некоррелирована по отношению к другим. Предварительно обрабатывая данные, мы часто делаем их очень похожими на белый шум: центрируем вокруг нуля и устанавливаем дисперсию или стандартное отклонение равными единице. Создание некоррелированных переменных используется реже, потому что требует больших вычислительных ресурсов. Но сама по себе операция несложная: мы просто переориентируем оси вдоль собственных векторов данных. То есть, если мы примем C(kernel) за сдвиг, то получим выражение, очень похожее на свёртку. Входные данные свёрточного слоя можно представить как выходные данные авторегрессионной модели, если предварительно обработать их и получить белый шум. Интерпретация взвешенного скользящего среднего проста: это стандартная свёртка на некоторых данных (исходных) с определённым весом (ядром). Более понятным будет взглянуть на ядро сглаживания Гаусса на рисунке ниже. Его можно интерпретировать как средневзвешенное значение в окрестности каждого пикселя. Другими словами, пиксели смешиваются, а края сглаживаются. Одно ядро не может создавать признаки как авторегрессии, так и взвешенного скользящего среднего. Поэтому обычно мы используем несколько ядер, комбинация которых будет содержать одни признаки, похожие на модель взвешенного среднего, и другие — на модель авторегрессии. Надеемся, что статья помогла лучше понять свёртку. Если раньше вам казалось, что все ваши знания математики и статистики бесполезны и непрактичны — то теперь вы можете убедиться, что почти всегда им находится практическое применение. Если что-то осталось непонятным, задавайте вопросы, мы всегда с радостью ответим на них. Ссылка на оригинальную статью в блоге timdettmers.com. Закон больших чисел в вероятности и статистике гласит, что по мере роста размера выборки ее среднее значение приближается к среднему для всей генеральной совокупности. В 16 веке математик Джеролама Кардано признал закон больших чисел, но так и не доказал его. В 1713 году швейцарский математик Якоб Бернулли доказал эту теорему в своей книге Ars Conjectandi . Позднее он был усовершенствован другими известными математиками, такими как Пафнутий Чебышев, основатель Санкт-Петербургского института науки и технологийПетербургская математическая школа. В финансовом контексте закон больших чисел указывает на то, что крупное предприятие, которое быстро растет, не может поддерживать этот темп роста вечно. Крупнейшие из «голубых фишек» с рыночной стоимостью в сотни миллиардов часто приводятся в качестве примеров этого явления. В статистическом анализе закон больших чисел может применяться к множеству предметов.Может оказаться невозможным опросить каждого человека в данной популяции для сбора необходимого количества данных, но каждая дополнительная собранная точка данных может повысить вероятность того, что результат будет истинной мерой среднего. В бизнесе термин «закон больших чисел» иногда используется в отношении темпов роста, выраженных в процентах. Это говорит о том, что по мере роста бизнеса поддерживать процентные темпы роста становится все труднее. Закон больших чисел не означает, что данная выборка или группа последовательных выборок всегда будут отражать истинные характеристики населения, особенно для небольших выборок.Это также означает, что если данная выборка или серия выборок отклоняется от истинного среднего значения по совокупности, закон больших чисел не гарантирует, что последующие выборки будут перемещать наблюдаемое среднее значение в сторону среднего значения по совокупности (как предполагает ошибка игрока). Закон больших чисел не следует путать с законом средних чисел, который гласит, что распределение результатов в выборке (большой или малой) отражает распределение результатов в генеральной совокупности. Если человек хотел определить среднее значение набора данных из 100 возможных значений, он, скорее всего, достигнет точного среднего значения, выбрав 20 точек данных вместо того, чтобы полагаться только на две. Например, если набор данных включал все целые числа от одного до 100, а выборщик взял только два значения, например 95 и 40, он может определить среднее значение примерно 67,5. Если он продолжал брать случайные выборки до 20 переменных, среднее должно сместиться в сторону истинного среднего, поскольку он рассматривает больше точек данных. В бизнесе и финансах этот термин иногда используется в просторечии для обозначения наблюдения, что экспоненциальные темпы роста часто не масштабируются. На самом деле это не связано с законом больших чисел, но может быть результатом закона убывающей предельной отдачи или неэкономичности масштаба. Например, в январе 2020 года выручка Walmart Inc. составила 523,9 миллиарда долларов, в то время как Amazon.com Inc.принесла 280,5 млрд долларов за тот же период. Если Walmart захочет увеличить выручку на 50%, потребуется около 262 млрд долларов дохода. Напротив, Amazon нужно было бы увеличить выручку всего на 140,2 миллиарда долларов, чтобы достичь 50-процентного прироста. Согласно закону больших чисел, увеличение на 50% будет сложнее для Walmart, чем для Amazon. Те же принципы можно применить к другим показателям, таким как рыночная капитализация или чистая прибыль. В результате инвестиционные решения могут быть приняты на основе связанных трудностей, с которыми могут столкнуться компании с очень высокой рыночной капитализацией, поскольку они связаны с повышением стоимости акций. В статистике и теории вероятностей закон больших чисел — это теорема, описывающая результат многократного повторения одного и того же эксперимента. Теорема больших чисел утверждает, что если один и тот же эксперимент или исследование повторяется независимо большое количество раз, среднее значение результатов испытаний должно быть близко к ожидаемому значению Ожидаемое значение Ожидаемое значение (также известное как EV, математическое ожидание, среднее или среднее значение). значение) — это долгосрочное среднее значение случайных величин.Ожидаемое значение также указывает. Результат становится ближе к ожидаемому значению по мере увеличения количества попыток. Закон больших чисел — важное понятие в статистике Основные статистические концепции для финансов Твердое понимание статистики имеет решающее значение для того, чтобы помочь нам лучше понять финансы. Более того, концепции статистики могут помочь инвесторам в мониторинге, поскольку они заявляют, что даже случайные события с большим количеством испытаний могут дать стабильные долгосрочные результаты.Обратите внимание, что теорема касается только большого количества испытаний, в то время как среднее значение результатов эксперимента, повторенного небольшое количество раз, может существенно отличаться от ожидаемого значения. Однако каждое дополнительное испытание увеличивает точность среднего результата. Простейшим примером закона больших чисел является бросание кости. Игра в кости включает шесть различных событий с равной вероятностью. Ожидаемое значение событий игры в кости: Если мы бросим кости только три раза, среднее значение полученных результатов может быть далеко от ожидаемого значения.Допустим, вы бросили кости три раза, и результаты были 6, 6, 3. Среднее значение результатов равно 5. Согласно закону больших чисел, если мы бросим кости большое количество раз, средний результат будет быть ближе к ожидаемому значению 3,5. В финансах закон больших чисел имеет иное значение, чем в статистике. В контексте бизнеса и финансов понятие связано с темпами роста бизнеса. Закон больших чисел гласит, что по мере роста компании становится все труднее поддерживать прежние темпы роста. Таким образом, темпы роста компании снижаются по мере того, как она продолжает расширяться. Закон больших чисел может учитывать различные финансовые показатели, такие как рыночная капитализация. Рыночная капитализация. Рыночная капитализация (рыночная капитализация) — это последняя рыночная стоимость выпущенных акций компании. Рыночная капитализация равна текущей цене акции, умноженной на количество акций в обращении.Сообщество инвесторов часто использует значение рыночной капитализации для ранжирования компаний, выручки и чистой прибыли. Net IncomeNet Доход — это ключевая статья не только в отчете о прибылях и убытках, но и во всех трех основных финансовых отчетах. Пока он добрался до конца. Рассмотрим следующий пример. Рыночная капитализация компании ABC составляет 1 миллион долларов, а рыночная капитализация компании XYZ — 100 миллионов долларов. Компания ABC демонстрирует значительный рост на 50% в год.Для ABC темпы роста легко достижимы, поскольку ее рыночная капитализация вырастает всего на 500 000 долларов. Для компании XYZ такие темпы роста практически невозможны, потому что это означает, что ее рыночная капитализация должна расти на 50 миллионов долларов в год. Обратите внимание, что рост компании ABC со временем будет снижаться, поскольку она продолжает расширяться. CFI является официальным поставщиком услуг аналитика финансового моделирования и оценки (FMVA) ™. Стать сертифицированным аналитиком финансового моделирования и оценки (FMVA) ® Сертификация CFI по анализу финансового моделирования и оценки (FMVA) ® поможет вам получить необходимую уверенность в своей финансовой карьере.Запишитесь сегодня! программа сертификации, призванная превратить любого в финансового аналитика мирового уровня. Чтобы продолжать изучать и развивать свои знания в области финансового анализа, мы настоятельно рекомендуем дополнительные ресурсы CFI ниже: Закон средних чисел — это вероятность или вера в то, что события или конечные результаты произойдут в ближайшее время, может быть, а может и нет.Считается, что это ожидание приближается к точному результату. Завтра может идти дождь, а может и нет, можно грустить, а может и нет. В реальном сценарии он не является ни определенным, ни постоянным. Заблуждение игрока — это заблуждение, которому следуют игроки, которые, как полагают, следуют Закону среднего только потому, что результат еще не случился недавно и есть вероятность, что он произойдет в будущем. Это чистая удача в игре и никаких расчетов. Пожалуйста, не следуйте этому методу, так как миндалевидное тело (нейрон) в мозгу Человека активируется, когда мы проигрываем, особенно во время азартных игр и проигрышей, а затем играет роль ошибки Игрока , заключающейся в принятии риска. 1-In в условиях непрофессионала, Центральная предельная теорема требует меньше данных по сравнению с Законом больших чисел. 2- Центральная предельная теорема не сходится к числу, а сходится к распределению. 3- Сходимость будет означать для меня, что со временем вероятность того, что среднее значение принимает значение, не являющееся ожидаемым, почти равна нулю, следовательно, распределение на самом деле не будет нормальным, а будет почти нулевым везде, кроме ожидаемого значения. Люди часто думают, что теорема Закона больших чисел может часто работать в реальной жизни, я согласен с этим до некоторой степени, потому что практически, когда вы работаете над чем-то много раз, вы находите конец результат очень плодотворный. Так что совершенно очевидно, что нужно практиковать что-либо несколько раз, чтобы стать мастером. Пример — Закон больших чисел и фондовый рынок . Очень часто 8 из 10 людей думают, что акции следует покупать только тогда, когда цены падают, и продавать, когда цены растут.Но этого не происходит, вы всегда должны покупать в точке безубыточности и всегда следует рассчитывать свой риск-менеджмент с учетом рыночного риска. Так работает Закон больших чисел, то есть когда трейдер много раз торгует и отслеживает различные результаты использования своих квалифицированных методов и расчетов, пока он не создаст свой собственный набор данных, паттерн и технику. Страховые компании очень зависимы от Закона больших чисел, следуя этой теореме, эти компании могут рассчитать свои будущие риски, прибыль и убытки, исходя из стабильности управления этими большими компаниями. Давайте возьмем пример — Представьте, что 500 человек платят страховой взнос за его собственность в страховку Metlife. Несмотря на то, что они платят вам за материальный ущерб, причиненный пожаром 10% подписчика, то есть 50 человек, они все равно имеют премию в размере 450 человек. Именно так они рассчитывают свой риск-менеджмент, и здесь играет роль Закон больших чисел. Искусственный интеллект в наши дни является большой шумихой, но когда вы говорите о законе больших чисел, он определенно играет роль, особенно строгий закон больших чисел при обработке миллионов BIG ДАННЫЕ и Машинное обучение .Это помогает в обработке и организации данных в повседневной жизни. Даже IBM Watson построил с помощью закона больших чисел, который позволил победить чемпиона мира Гарри Каспарова в шахматах. Какое значение имеет закон больших чисел в машинном обучении ? 1- Тренировочные данные 2- Тестовые данные 3- Оценка навыков модели Заключение : Конечная теория должна делать точные прогнозы.Даже Эйнштейну потребовалось 4 года, чтобы доказать, что полное солнечное затмение показало, что свет, проходящий рядом с Солнцем, искривляется, что позже оказалось гравитацией. В 1930-х годах сэр Рональд Фишер, британский ученый, изложил рекомендации по разработке экспериментов с использованием статистики и вероятности как способа оценки результатов. Итак, теперь, если вы видите, все в этом мире было рассчитано и связано с математикой, от черной дыры до молекул. От вас зависит, как вы это видите. Другой пример действующего закона больших чисел — предсказание результата подбрасывания монеты.Если вы подбрасываете монету один раз, вероятность выпадения монеты орлом составляет 50% (что также можно записать как ½ или 0,5), а вероятность того, что она выпадет решкой, также составляет 50%. Но что произойдет, если подбросить монету десять раз подряд? Можете ли вы с уверенностью сказать, что там он будет приземляться орлом в половине случаев, а в другой половине — решкой? Ответ — «нет», потому что каждое подбрасывание монеты — это независимое событие . Это означает, что исход одного события, в данном случае подбрасывания монеты, не повлияет на исход следующего события. Это правда, что с каждым подбрасыванием монеты шанс выпадения орла составляет 50/50; однако, если вы подбрасываете монету несколько раз, вы не можете быть уверены, что 50% подбрасываний выпадут орлом или наоборот, если вы не используете закон больших чисел. Это потому, что закон больших чисел диктует, что по мере того, как мы увеличиваем количество раз, когда мы подбрасываем монету, мы все ближе и ближе приближаемся к достижению 50% вероятности выпадения орла или решки. Итак, если у вас есть время подбросить монету тысячи раз, вы можете быть уверены, что примерно половина подбрасываний будет выпадать орлом! Чтобы проиллюстрировать это, давайте взглянем на следующую диаграмму, показывающую результаты эксперимента с различным количеством подбрасываний монет: Вы видели схему вероятностей? Надеюсь, вы заметили, что когда монета подбрасывается всего несколько раз, результаты не показывают, что вероятность того, что она упадет орлом и решкой, равны.Достижение 50% вероятности выпадения орла увеличивается с каждым значительно большим количеством бросков. Это классический пример закона больших чисел. Хотя подбрасывание монет и соревнования по угадыванию мармеладов являются забавными примерами того, как работает закон больших чисел, этот принцип является важным статистическим инструментом и лежит в основе решений, которые принимают все компании и которые влияют на нас. Страховые компании используют закон больших чисел для определения вероятности того, что события, такие как автомобильные аварии, произойдут.Чем больше автомобилей застраховывает страховая компания, тем точнее страховая компания сможет предсказать вероятность возникновения аварии. Результаты этих прогнозов влияют на то, как страховые компании определяют размер страховых взносов, которые мы платим. Закон больших чисел — это теория вероятности, которая гласит, что чем больше становится размер выборки, тем ближе среднее (или среднее) значение выборки приближается к ожидаемому значению. Итак, исходя из примеров, которые мы видели выше, чем больше у вас предположений о том, сколько желейных бобов находится в банке, тем более вероятно, что среднее значение этих предположений будет равно количеству мармелада. фасоль в банке. Но прежде чем делать большие денежные ставки на количество желейных бобов в банке, мы должны иметь в виду, что вероятность, как следует из названия, все еще зависит от случая. Последнее обновление 8 августа 2019 г. У нас есть интуиция, что чем больше наблюдений, тем лучше. Это та же самая интуиция, которая лежит в основе идеи о том, что если мы соберем больше данных, наша выборка данных будет более репрезентативной для предметной области. Существует теорема статистики и вероятности, которая поддерживает эту интуицию, которая является столпом обеих этих областей и имеет важное значение в прикладном машинном обучении. Название этой теоремы — закон больших чисел. В этом руководстве вы узнаете о законе больших чисел и о том, почему он важен для прикладного машинного обучения. После прохождения этого руководства вы будете знать: Начните свой проект с моей новой книги «Статистика для машинного обучения», включающей пошаговых руководств и файлов исходного кода Python для всех примеров. Приступим. Мягкое введение в закон больших чисел в машинном обучении Это руководство разделено на 3 части; их: Пройдите мой бесплатный 7-дневный ускоренный курс электронной почты (с образцом кода). Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF. Загрузите БЕСПЛАТНЫЙ мини-курс Закон больших чисел — это теорема, основанная на вероятности и статистике, которая предполагает, что средний результат многократного повторения эксперимента лучше приблизительно соответствует истинному или ожидаемому исходному результату. Закон больших чисел объясняет, почему казино всегда приносят прибыль в долгосрочной перспективе. — Стр. 79, Обнаженная статистика: снимая страх с данных, 2014. Мы можем думать об испытании эксперимента как об одном наблюдении. Автономное и независимое повторение эксперимента приведет к многократным испытаниям и многочисленным наблюдениям. Все образцы наблюдений для эксперимента взяты из идеализированной совокупности наблюдений. Используя эти термины из статистики, мы можем сказать, что по мере увеличения размера выборки среднее значение выборки будет лучше приближаться к среднему или ожидаемому значению в генеральной совокупности. По мере увеличения размера выборки до бесконечности среднее значение выборки будет сходиться к среднему значению генеральной совокупности. … венец вероятности, закон больших чисел. Эта теорема говорит, что среднее значение большой выборки близко к среднему значению распределения. — стр. 76, Вся статистика: краткий курс статистических выводов, 2004 г. Это важный теоретический вывод для статистики и вероятности, а также для прикладного машинного обучения. Важно понимать, что наблюдения в выборке должны быть независимыми. Это означает, что испытание выполняется идентичным образом и не зависит от результатов других испытаний.Часто это разумно и легко достигается на компьютере, хотя может быть сложно в другом месте (например, как добиться идентично случайных бросков игральных костей?). В статистике это ожидание называется « независимых и идентично распределенных », или IID, iid или i.i.d. коротко. Это необходимо для гарантии того, что выборки действительно взяты из одного и того же основного распределения населения. Закон больших чисел помогает нам понять, почему мы не можем доверять отдельному наблюдению из изолированного эксперимента. Мы ожидаем, что вероятен единичный результат или средний результат небольшой выборки. Это близко к центральной тенденции — среднему значению распределения населения. А может и не быть; на самом деле это может быть очень странно или маловероятно. Закон напоминает нам повторить эксперимент, чтобы получить большую и репрезентативную выборку наблюдений, прежде чем мы начнем делать выводы о том, что означает результат. По мере увеличения размера выборки результат или среднее значение выборки будет возвращаться к среднему значению генеральной совокупности, обратно к истинному лежащему в основе ожидаемому значению.Это называется регрессией к среднему или иногда возвращением к среднему значению. Вот почему мы должны скептически относиться к выводам из небольших размеров выборки, называемых small n . С регрессией к среднему связана идея закона действительно больших чисел. Это идея о том, что когда мы начинаем исследовать или работать с очень большими выборками наблюдений, мы увеличиваем вероятность увидеть что-то странное.Что, имея так много выборок основного распределения населения, выборка будет содержать некоторые астрономически редкие события. Опять же, мы должны быть осторожны, чтобы не делать выводы из единичных случаев. Это особенно важно учитывать при выполнении запросов и исследовании больших данных. Мы можем продемонстрировать закон больших чисел на небольшом рабочем примере. Во-первых, мы можем разработать идеализированное базовое распределение.Мы будем использовать распределение Гаусса со средним значением 50 и стандартным отклонением 5. Таким образом, ожидаемое значение или среднее значение этой генеральной совокупности равно 50. Ниже приведен код, который генерирует график этого идеализированного распределения. # идеализированное распределение населения
из numpy import arange
из matplotlib import pyplot
из нормы импорта scipy.stats
# ось x для графика
xaxis = arange (30, 70, 1)
# ось Y для графика
yaxis = норма.pdf (xaxis, 50, 5)
# график идеального населения
pyplot.plot (xaxis, yaxis)
pyplot.show () # идеализированное распределение населения из numpy import arange из matplotlib import pyplot из scipy.stats import norm # ось x для графика xaxis = arange (30, 70, 1) # Ось y для графика yaxis = norm.pdf (xaxis, 50, 5) # построить идеальную популяцию pyplot.сюжет (xaxis, yaxis) pyplot.show () Запуск кода создает график спроектированной популяции с знакомой формой колокольчика. Идеализированное базовое распределение населения Теперь мы можем притвориться, что забыли все, что мы знаем о популяции, и сделать независимые случайные выборки из этой популяции. Мы можем создавать выборки разного размера и вычислять среднее значение. Учитывая нашу интуицию и закон больших чисел, мы ожидаем, что по мере увеличения размера выборки среднее значение выборки будет лучше приближаться к среднему значению генеральной совокупности. В приведенном ниже примере вычисляются образцы разных размеров, а затем печатаются средние значения выборки. # продемонстрировать закон больших чисел
из numpy.random import seed
из numpy.random import randn
из среднего значения импорта
из массива импорта numpy
из matplotlib import pyplot
# заполняем генератор случайных чисел
семя (1)
# размер выборки
size = [10, 100, 500, 1000, 10000]
# генерировать выборки разного размера и вычислять их средние
означает = [среднее (5 * randn (размер) + 50) для размера в размерах]
печать (означает)
# построить график средней ошибки выборки в зависимости от размера выборки
пиплот.разброс (размеры, массив (означает) -50)
pyplot.show () # продемонстрировать закон больших чисел из numpy.random import seed from numpy.random import randn from numpy import mean from numpy import array from matplotlib import pyplot # seed случайное число генератор seed (1) # размеры выборки sizes = [10, 100, 500, 1000, 10000] # генерировать выборки разных размеров и вычислять их средние means = [mean (5 * randn ( size) + 50) для размера в sizes] print (means) # построить график средней ошибки выборки по сравнению с размером выборки pyplot.разброс (размеры, массив (средства) -50) pyplot.show () При выполнении примера сначала печатаются средние значения каждого образца. Мы можем видеть слабую тенденцию приближения выборочного среднего к 50,0 по мере увеличения размера выборки. Отметим также, что этот образец выборочного средства тоже должен подчиняться закону больших чисел. Например, случайно вы можете получить очень точную оценку среднего значения генеральной совокупности со средним значением небольшой выборки. [49.5142955459695, 50.371593294898695, 50.29196533, 50.1521157689338, 50.03955033528776] [49.5142955459695, 50.371593294898695, 50.29196533, 50.1521157689338, 50.03955033528776] В этом примере также создается график, который сравнивает размер выборки с ошибкой выборочного среднего от среднего значения генеральной совокупности. Как правило, мы видим, что большие размеры выборки имеют меньше ошибок, и мы ожидаем, что эта тенденция в среднем сохранится. Мы также можем видеть, что некоторые выборки означают завышение, а некоторые — занижение. Не попадайтесь в ловушку предположения, что недооценка упадет на ту или иную сторону. График разброса размера выборки и ошибки Закон больших чисел имеет важное значение для прикладного машинного обучения. Давайте уделим время, чтобы выделить некоторые из этих последствий. Данные, используемые для обучения модели, должны быть репрезентативными для наблюдений из области. Это на самом деле означает, что он должен содержать достаточно информации, чтобы сделать вывод об истинном неизвестном и лежащем в основе распределении населения. Это легко представить с помощью одной входной переменной для модели, но это не менее важно, когда у вас есть несколько входных переменных. Между входными переменными будут неизвестные отношения или зависимости, и вместе входные данные будут представлять собой многомерное распределение, из которого будут извлечены наблюдения, чтобы составить вашу обучающую выборку. Имейте это в виду при сборе данных, очистке данных и подготовке данных. Вы можете исключить части основной совокупности, установив жесткие ограничения на наблюдаемые значения (например, для выбросов), если вы ожидаете, что данные будут слишком разреженными для эффективного моделирования. Мысли, заданные набору обучающих данных, также должны быть переданы набору тестовых данных. Этим часто пренебрегают из-за слепого использования спотов 80/20 для данных обучения / тестирования или слепого использования 10-кратной перекрестной проверки, даже для наборов данных, где размер 1/10 доступных данных может быть неприемлемым. репрезентативные наблюдения из проблемной области. Учитывайте закон больших чисел при представлении оценки навыков модели на невидимых данных. Он обеспечивает защиту не для того, чтобы просто составить отчет или продолжить работу с моделью, основанной на оценке навыков, полученной при оценке одного тренинга / теста. Он подчеркивает необходимость разработки выборки из нескольких независимых (или близких к независимой) оценок данной модели, чтобы среднее значение навыка, полученное по выборке, было достаточно точной оценкой среднего значения для всей совокупности. В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить. Если вы изучите какое-либо из этих расширений, я хотел бы знать. В этом разделе представлены дополнительные ресурсы по теме, если вы хотите углубиться. В этом руководстве вы узнали о законе больших чисел и о том, почему он важен для прикладного машинного обучения. В частности, вы выучили: Есть вопросы? …пишите строки кода на Python Узнайте, как это сделать, в моей новой электронной книге: Он предоставляет руководств для самообучения по таким темам, как: Пропустить академики. Только результаты. Это концепция вероятности, означающая, что распространенность событий с аналогичной вероятностью возникновения в конечном итоге выравнивается в течение ряда достаточных испытаний.Поскольку количество экземпляров продолжает расти, фактическое соотношение результатов пересекается с теоретическим или ожидаемым соотношением результатов. Этот закон устанавливает, что чем больше размер выборки, тем ближе среднее значение к среднему для всей генеральной совокупности. Он был разработан с учетом того факта, что быстрорастущее крупное предприятие не может удерживать темп в течение длительного времени. Например, предположим, что монета подброшена миллион раз, можно с уверенностью сказать, что примерно половина подбрасываний будет орлом, а половина — решкой.Следовательно, это соотношение будет почти 1: 1. Когда монета подбрасывается двадцать раз, соотношение будет другим и может быть 3: 7 или любым другим. Иногда этот закон неправильно применяют к ситуациям с очень небольшим количеством экспериментов, что приводит к логической ошибке, называемой ошибкой игрока. Закон больших чисел, также известный как закон средних чисел, — это теория, используемая для объяснения результатов, возникающих при многократном проведении аналогичных экспериментов. В нем говорится, что статистическая вероятность выборки с определенным значением приближается к статистической вероятности набора выборок во вселенной по мере увеличения выборки.Политические опросы используют этот метод, и поэтому они становятся тем точнее, чем больше увеличивается размер выборки. Еще в июле 2015 года Wal-Mart Stores Inc. получила доход в размере 485,5 млрд долларов, а Amazon — 95,8 млрд долларов. Чтобы они увеличили свой доход на 50% на основе этих цифр, Walmart потребуется в общей сложности 242,8 миллиарда долларов, а Amazon — всего 47,9 доллара. По закону больших чисел такое увеличение будет сложнее для Walmart, чем для Amazon. Этот закон гарантирует стабильные долгосрочные результаты для средних значений различных случайных событий и поэтому очень важен. Полная сходимость и закон больших чисел , Hsu, P. L., & Robbins, H. (1947). Proceedings of the National Academy of Sciences of the United States of America , 33 (2), 25. Эта статья определяет и различает стандартные термины в теории вероятностей, которые включают вероятностное пространство, действительнозначная P-измеримая функция X = X среди других.Скорости сходимости в законе больших чисел , Баум, Л. Э. и Кац, М. (1965). Труды Американского математического общества , 120 (1), 108-123. В этой статье уделяется внимание последовательностям независимых и одинаково распределенных случайных величин и представлены различные предложения и примеры для случая независимых, но по-разному распределенных случайных величин. Закон больших чисел для крупных экономик, Uhlig, H.(1996). Экономическая теория , 8 (1), 41-50. Эта статья представляет закон больших чисел, интерпретируя интеграл как интеграл Петтиса. Он также обеспечивает доказательство с использованием вычисления дисперсии и показывает, что проблему измеримости, выявленную Джаддом в 1985 году, можно избежать за счет сходимости в среднем квадрате вместо сходимости почти везде. Сильный закон больших чисел для u-статистики., Hoeffding, W. (1961). Государственный университет Северной Каролины. Департамент статистики. В данной статье исследуется усиленный закон больших чисел для класса U-статистики при условии момента, ведущего к обобщению этого закона. Согласованность в нелинейных эконометрических моделях: общий унифицированный закон больших чисел , Эндрюс, Д. У. (1987). Econometrica: Journal of the Econometric Society , 1465-1471. Эта статья направлена на предоставление универсального единообразного закона больших чисел, который является по существу общим и включает большинство приложений единообразного закона больших чисел в литературе по нелинейной эконометрике.Локальная сходимость мартингалов и закон больших чисел . Чоу, Ю.С. (1965). Анналы математической статистики , 36 (2), 552-558. Эта статья обобщает результаты Невё, когда он доказал существование новой теоремы о субмартингальной сходимости. Заметка о строгом законе больших чисел для положительно зависимых случайных величин, Birkel, T. (1988). Письма о статистике и вероятности , 7 (1), 17-20. В этой статье представлены строгие законы больших чисел для последовательностей случайных величин, которые связаны или попарно зависят от положительного квадранта. Точный закон больших чисел через расширение Фубини и характеристику страхуемых рисков, Sun, Y. (2006). Журнал экономической теории , 126 (1), 31-69. Это исследование вводит простые методы теории меры в эту структуру, чтобы получить несколько версий этого закона и их обратные случайные процессы или континуум случайных величин, а также предлагает расширение Фубини в качестве вероятностного пространства, которое расширяет вероятностное пространство, сохраняя при этом Фубини собственность.Общий подход к строгому закону больших чисел , Фазекас И., Клесов О. (2001). Теория вероятностей и ее приложения , 45 (3), 436-449. В данной статье исследуется общий метод, основанный на абстрактных максимальных неравенствах типа Хекрни, для получения строгих законов больших чисел. Строгий закон больших чисел для емкостей, Maccheroni, F., & Marinacci, M. (2005). Летопись вероятностей , 33 (3), 1171-1178. В этой статье рассматриваются полностью монотонная емкость на полированном пространстве и последовательность ограниченных p.i.i.d случайных величин. Закон о больших числах : торги и обязательные конкурентные торги для контрактов на вывоз мусора, Gomez-Lobo, A., & Szymanski, S. (2001). Обзор промышленной организации , 18 (1), 105-113. Это исследование взаимосвязи, существующей между затратами и количеством участников торгов по контрактам местных властей Великобритании на вывоз мусора. Закон больших чисел в теории потребительского выбора в условиях неопределенности, Yaari, M. E. (1976). Журнал экономической теории , 12 (2), 202-217. В этой статье исследуется гипотеза, согласно которой потребление зависит от дохода в той мере, в какой доход влияет на благосостояние на протяжении всей жизни. Была ли эта статья полезной? Для Райхенбаха вероятность, как она используется в науке, является объективной величиной, а не субъективной степенью веры. Основная трудность такого объяснения состоит в том, чтобы точно указать, какой должна быть такая объективная вероятность, и в то же время предоставить обоснованные основания для вынесения вероятностных суждений.Фактически, на протяжении всей своей жизни Райхенбах работал над основами теории вероятностей, и его взгляды изменились. В своей докторской диссертации в 1915 году Райхенбах утверждает, что вероятность события — это относительная частота события в бесконечной последовательности причинно-независимых и причинно-идентичных испытаний [Reichenbach, 1915]. Под влиянием неокантианцев своего времени (Эрнст Кассирер, Поль Наторп и др.) Райхенбах считал причинность примитивной концепцией, более фундаментальной, чем вероятность.С этой точки зрения причинное знание — это синтетическое априорное знание, и доказательство этого статуса якобы было дано кантовским трансцендентным выводом принципа причинности. То есть, согласно (Рейхенбаховскому прочтению) Канта, у нас есть причинное знание для отдельных событий, которое позволяет нам определять причинную независимость и идентичные причинные обстоятельства, и поэтому, согласно Рейхенбаху, у нас есть нетривиальная, некруговая и объективная основа. на котором строится понятие вероятности.В частности, если можно показать, что причинно-независимые и идентичные испытания предполагают вероятностно независимые и одинаково распределенные испытания, тогда закон больших чисел подразумевает, что эмпирическое распределение сходится к истинному распределению по вероятности. 1 Рейхенбах знал о (слабом) законе больших чисел (хотя в его диссертации он подробно не обсуждается), но считал сходимость по вероятности слишком слабой. Опора на сходимость по вероятности означала бы, что понятие вероятностных характеристик в определениях определения вероятности, что сделало бы определение концепции вероятности циклическим.Райхенбах хотел добиться уверенного сближения. Чтобы разрешить эту дилемму, Райхенбах (в 1915 году) снова обратился к кантовскому набору инструментов и представил трансцендентный аргумент, что существует синтетический априорный принцип — принцип законного распределения, — который с уверенностью гарантирует, что каждое эмпирическое распределение сходится. Суть трансцендентального аргумента заключается в следующем: если бы не было такого принципа, научное познание, как оно представлено в законах природы, было бы невозможным.Но очевидно, что наука изобилует знаниями о законных причинных отношениях. Научные законы устанавливают общие причинные закономерности, но кантовское каузальное знание предоставляет причинное знание только в отношении отдельных событий. Что-то необходимо для объединения отдельных маркеров причинного знания в общие причинные законы. Следовательно, должен быть такой принцип. С учетом этого принципа сходимость гарантирована с уверенностью, и даже если мы не знаем, когда сходимость произойдет или с какой скоростью, мы на правильном пути, если будем использовать эмпирическое распределение, поскольку оно должно сходиться в какой-то момент.Короче говоря, это было аргументом в его докторской диссертации. Аргумент не очень удовлетворительный, даже если бы пробелы были заполнены (например, от причинно-независимых испытаний к вероятностно независимым испытаниям): учитывая современное неправдоподобное мнение о том, что причинное знание токен-событий является синтетическим априори, утверждение, что существует синтетическая априорная гарантия сходимости последовательностей к предельному распределению — мы знаем много последовательностей, предельные частоты которых не сходятся. Рейхенбах, должно быть, в какой-то момент (если не все время) почувствовал такое же дискомфорт из-за своего отчета, поскольку его аргументы значительно изменились между его докторской диссертацией в 1915 году и публикацией английского издания The Theory of Probability в 1949 году [Reichenbach , 1949c]. 2 В 1927 году Райхенбах указал в примечаниях 3 (и сослался на более ранние обсуждения с Полом Герцем), что сходимость с уверенностью несостоятельна и что можно гарантировать сходимость только по вероятности.Это переходная мысль Райхенбаха. По сути, это наблюдение закона больших чисел, которое устанавливает распределение вероятностей, из которого исходные сегменты последовательностей получаются с помощью i.i.d выборки. Интерпретация предельной частоты, напротив, дает уверенность в сходимости к вероятности по прямому правилу при условии, что предельное значение вообще существует. Вдобавок он изменил свое мнение о порядке примитивов: как только Эйнштейн пошатнул синтетический априорный статус пространства и времени, Райхенбах аналогичным образом проанализировал синтетический априорный статус причинности и пришел к выводу, что это не причинность, а скорее вероятность того, что было более фундаментальным понятием, т.е. что причинно-следственная связь — это отношение, которое можно вывести только на основе вероятностных отношений (плюс некоторые дополнительные предположения). Утверждения о причинно-следственной связи одного события — то, что сейчас называется фактической причинно-следственной связью — считались эллиптическими, либо неявно относящимися к последовательности событий, либо фиктивным переносом причинного утверждения с уровня типа на уровень токена. Однако, если причинно-следственные связи больше не являются фундаментальными и вероятности не следует рассматривать как примитивные, тогда Райхенбаху пришлось найти новое основание для концепции вероятности.Это усилие совпало с аналогичными опасениями Ричарда фон Мизеса. Фон Мизес пытался установить основу вероятности в терминах случайных событий [von Mises, 1919]. В то время как случайность хорошо понималась до теоретически, все попытки охарактеризовать ее формально приводили к нежелательным последствиям. Цель, которую разделяли и Райхенбах, и фон Мизес, заключалась в сведении концепции вероятности к свойству бесконечных последовательностей событий, тем самым избегая какой-либо замкнутости в основе. Учитывая научную практику, казалось интуитивно понятным и привлекательным думать об объективных вероятностях в терминах относительной частоты в бесконечной последовательности событий — нужно было только надлежащим образом охарактеризовать типы последовательностей, которые будут считаться допустимыми как обеспечивающие основу вероятности. Например, нельзя считать последовательность допустимой, если она просто чередуется между 1 и 0. Хотя предельная относительная частота единиц равна 1/2, следующее число известно с уверенностью, учитывая любой начальный сегмент, достаточно длинный, чтобы показать шаблон.Поэтому фон Мизес хотел ограничить свои соображения последовательностями случайных событий, поскольку понятие случайности отражало идею о том, что никто не сможет заработать деньги, делая ставки на следующий элемент в последовательности с учетом предыдущих элементов. Более формально отсутствие последействия и инвариантность к выбору подпоследовательностей считались необходимыми условиями для случайных последовательностей. Отсутствие последействия отражает идею невозможности заработать деньги, делая ставки на следующий элемент последовательности, учитывая предыдущие элементы.В частности, вероятность любого исхода должна быть одинаковой, независимо от того, каковы были предыдущие исходы. Инвариантность при выборе подпоследовательности требует, чтобы вероятность события была одинаковой при любом правиле выбора подпоследовательности, которое зависит только от индексов элементов. Формально формулировка этих понятий разнится у авторов. Райхенбах отверг идею случайных последовательностей, потому что он не видел никакой надежды на то, что сможет адекватно зафиксировать случайность формально. 4 Существовали известные теоретические трудности в демонстрации того, что все условия случайности могут быть выполнены, и Райхенбах указал на некоторые из них [Reichenbach, 1932a].Райхенбах не отказался от этой идеи полностью, а вместо этого согласился на несколько более слабое ограничение на последовательности: нормальные последовательности. Нормальные последовательности образуют строгий надмножество случайных последовательностей. Последовательность событий равна нормальным , если последовательность не имеет последствий и вероятности типов событий неизменны при регулярных делениях. Определение последействия, данное Райхенбахом, не совсем ясно, но примерно в последовательности с последействием событие E с индексом i подразумевает для событий с индексами, следующими за вероятностями i , которые отличаются от предельной относительной частоты те события.Регулярные деления — это правила выбора подпоследовательности, которые выбирают каждые k -го элемента исходной последовательности для некоторого фиксированного k . (На самом деле условия немного сложнее, но мы оставим это в стороне.) Тогда вероятность события E является предельной относительной частотой E в нормальной последовательности событий. Это работает как абстрактное определение вероятности, но не подходит для определения научных вероятностей. В эмпирической науке последовательности измерений конечны.Конечный начальный отрезок последовательности не дает нам информации о предельном распределении. Тем не менее, Райхенбах утверждает, что мы должны рассматривать эмпирическое распределение, данное конечным начальным сегментом измерений, как если бы оно было (примерно) таким же, как и предельное распределение. Он считает, что мы можем прибегнуть к вероятности более высокого порядка, которая определяет вероятность того, что предельная относительная частота события (его истинная вероятность) находится в некоторой (узкой) полосе шириной δ вокруг эмпирической частоты.Эта вероятность более высокого порядка также основана на эмпирических данных, но косвенно: она происходит из последовательности значений вероятности первого порядка, то есть из последовательности последовательностей событий. Идея состоит в том, что он объединяет данные из последовательностей различных индуктивных выводов. Райхенбах приводит один тип примера в разных формах, который дает некоторое представление о том, как это должно работать (например, см. [Reichenbach, 1949c, pp. 438-440]): Предположим, у нас есть конечная последовательность измерений, M1, M2 , M3, M4, M5,…, Mn , и мы классифицируем их как 1 или 0 в зависимости от того, попадают ли они в некоторый заранее заданный узкий диапазон вокруг фиксированного значения.Например, предположим, что у нас есть измерения гравитационной постоянной, и мы классифицируем точки данных как 1, если они попадают в полосу γ ± δ для некоторого небольшого значения δ , и 0 в противном случае. Таким образом, мы можем определить переменную X = I (| M — γ | ≤ δ ), где I (.) — индикаторная функция, и получить последовательность значений X , состоящий из единиц и нулей, в зависимости от исходных измерений: 1,1,0,1,0,… 0. Предположим далее, что если бы у нас было бесконечное количество данных, то было бы ограничивающее распределение по частотам нулей и единиц в последовательности, с P ( X = 1) = p и P ( X = 0) = 1− p . Фактическое эмпирическое распределение, определяемое относительной частотой единиц и нулей среди доступных измерений, равно Pˆ (X = 1) = pˆ и Pˆ (X = 0) = 1 − pˆ. Райхенбах утверждает, что существует вероятность более высокого порядка q , которая утверждает, что Pˆ (| pˆ − p | <ε) = q для малых ε , т.е.е. истинное распределение с вероятностью q попадает на расстояние ε эмпирического распределения. Согласно Райхенбаху, у нас есть оценка такой вероятности более высокого порядка q путем рассмотрения нескольких последовательностей измерений, каждая из которых имеет собственное эмпирическое распределение. Итак, предположим, что у нас есть три последовательности измерений (скажем, из различных экспериментов гравитационной постоянной на (а) Луне, (б) на какой-то планете и (в) с использованием весов Кавендиша): a: 1,1,1 , 0,0,…, 1b: 0,1,1,1,1,…, 0c: 0,0,1,0,0,…, 1 Каждый будет иметь определенное эмпирическое распределение, скажем Pˆa, Pˆb и Pˆc.Эти три эмпирических распределения образуют свою собственную последовательность значений pˆ, а именно pˆa, pˆb, pˆc , каждое из которых определяет относительную частоту единиц в отдельных последовательностях. pˆa, pˆb, pˆc снова определяют эмпирическое распределение, но теперь с вероятностями более высокого порядка. Предположим, что из трех начальных распределений pˆa = 0,8, pˆb = 0,7 и pˆc = 0,79. Опять же, мы можем классифицировать эти значения в соответствии с некоторым приближением, например 0,8 ± ε , где ε = 0.05. В этом случае (эмпирическая оценка) вероятности более высокого порядка q равна qˆ = 2/3. Относительная частота единиц в одной строке указывает на вероятность истинности утверждения о гравитационной постоянной для конкретного тестового объекта, например планета. Вероятность второго порядка q для различных последовательностей указывает вероятность того, что утверждение вероятности первого порядка истинно. Согласно Райхенбаху, именно такая взаимная проверка сходимости различных последовательностей измерений обеспечивает вероятность сходимости любого эмпирического распределения. В другом аналогичном примере, включающем измерения температуры плавления различных металлов, Райхенбах утверждает, что тот факт, что многие металлы имеют точку плавления, дает нам основание полагать, что металл, плавление которого мы до сих пор не видели, тем не менее, вероятно, будет иметь температуру плавления. температура плавления. Несмотря на то, что для этого явно «твердого» металла эмпирическое распределение измерений, по-видимому, указывает на то, что вероятность наличия точки плавления равна нулю, вероятность второго порядка, определяющая, насколько показательным является эмпирическое распределение предела, будет очень низкой. , потому что вероятность второго порядка объединяет результаты по другим металлам.Райхенбах называет эти «перекрестные индукции» «сетью индукций». Другой способ осмыслить подход Райхенбаха — рассмотреть иерархическую байесовскую процедуру: данные измерений используются для оценки определенных параметров распределения интересующей величины. Но можно описать эти параметры распределением более высокого порядка со своими собственными гиперпараметрами. В этом случае можно использовать несколько последовательностей измерений для получения оценок гиперпараметров.Как только они оценены, можно повторно вычислить параметры нижнего уровня с учетом оцененных гиперпараметров. Это обеспечивает поток информации между различными последовательностями измерений через гиперпараметры и, следовательно, обеспечивает широкую интеграцию данных из разных источников. Как и в случае с Райхенбахом, можно продолжить этот подход до более высоких порядков с гипер-гиперпараметрами. В какой-то момент возникнет вопрос, достаточно ли данных для оценки параметров высокого порядка.Райхенбах утверждает, что в некотором более высоком порядке слепые постулаты заменяют оценки вероятностей, чтобы избежать бесконечного регресса вероятностей более высокого порядка. Иерархические байесовские методы теоретически работают хорошо, но они зависят от способности определять, похожи ли события и в каком смысле, чтобы их можно было включить в одну и ту же выборку (которая затем используется для определения вероятностей). По мнению Райхенбаха, соответствующий вопрос касается определения референтных классов. Референсные классы — непростая задача для Райхенбаха, поскольку он заходит так далеко, что утверждает, что мы можем определить вероятность научной теории. Например, для определения вероятности того, что закон тяготения Ньютона выполняется повсеместно (а не только для конкретного тестового объекта, как в приведенном выше примере), Райхенбах утверждает, что все доступные измерения гравитационной постоянной должны быть помещены в одну последовательность, и что «… мы должны построить эталонный класс, заполнив другие строки [последовательности измерений] наблюдениями, относящимися к другим физическим законам.Например, для второй строки можно использовать закон сохранения энергии; для третьего — закон энтропии; и так далее.» [Reichenbach, 1949c, стр. 439f] Кажется очевидным, что выбор эталонного класса здесь произвольный, но Райхенбах далее утверждает, что «… используемый эталонный класс соответствует тому способу, которым фактически оценивается научная теория, поскольку достоверность Индивидуальный закон физики, несомненно, усиливается тем фактом, что другие законы тоже оказались надежными.И наоборот, отрицательный опыт с некоторыми физическими законами рассматривается как причина ограничения действия других законов, которые до сих пор не были признаны недействительными. Например, тот факт, что уравнения Максвелла неприменимы к атому Бора, рассматривается как причина сомневаться в применимости закона тяготения Ньютона или Эйнштейна к квантовой области ». [Reichenbach, 1949c, стр. 440] Мы не знаем, почему несовместимость системы уравнений Максвелла с моделью атома должна приводить к недействительности другой системы уравнений, уравнения Ньютона, которые сами по себе несовместимы с уравнениями Максвелла.Мы не имеем ни малейшего представления о том, какой здесь может быть ссылочный класс для такой передачи вероятности, а также что еще может содержать базовый ссылочный класс в этом случае. ‘indexcross-индукция Остается неясным, какие критерии имел в виду Райхенбах для определения эталонного класса в целом. Конечно, общая идея состоит в том, что события каким-то образом должны быть одного типа, но не настолько похожими, чтобы исключить изменчивость интереса. Райхенбах утверждает, что следует выбирать самый узкий эталонный класс, для которого есть стабильная статистика (относительные частоты), и что стабильность статистики определяется на уровне продвинутых знаний, т.е.е. на высоком уровне интеграции данных. 5 Но это явно неприемлемое предложение — возникает вопрос: вся цель состоит в том, чтобы определить пределы относительных частот; требование стабильной статистики в первую очередь бесполезно. Тривиально стабильная статистика всегда доступна в самом узком из всех непустых классов, классе, содержащем одно событие. Очевидно, это не могло быть намерением Райхенбаха. Обращение Райхенбаха к передовым знаниям для определения эталонных классов для частот более низкого уровня может быть истолковано как указание на слепые постулаты: лучшее, что можно предложить, — это обоснованное предположение или просто предположение.Но тогда почему бы просто не угадать частоты нижнего уровня? Райхенбах подробно обсуждает определение референтных классов, но это далеко не точное объяснение. Возможно, в конечном итоге существует какой-то интуитивно понятный эталонный класс, даже когда в науке проводятся широкие перекрестные индукции, но остаются сомнения в том, есть ли какая-либо надежда изложить такие выводы в формальной вероятностной структуре и будет ли результат тогда служить основой для объективных вероятности. Мы резюмируем изложение Райхенбахом основ вероятности следующим образом: Вероятность определяется как свойство бесконечных нормальных последовательностей событий.Нормальные последовательности захватывают многие особенности случайных последовательностей. Поскольку нам неизвестен предел бесконечных последовательностей событий, мы строим наши выводы на конечных начальных участках таких последовательностей. Мы уверены, что будем на правильном пути, пока вероятности более высокого порядка выглядят многообещающими. Вероятности более высокого порядка выглядят многообещающими, когда индукции из широкого спектра различных последовательностей измерений дают аналогичные результаты. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 Адрес сервиса: convertonlinefree.com.
Адрес сервиса: convertonlinefree.com.
 Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
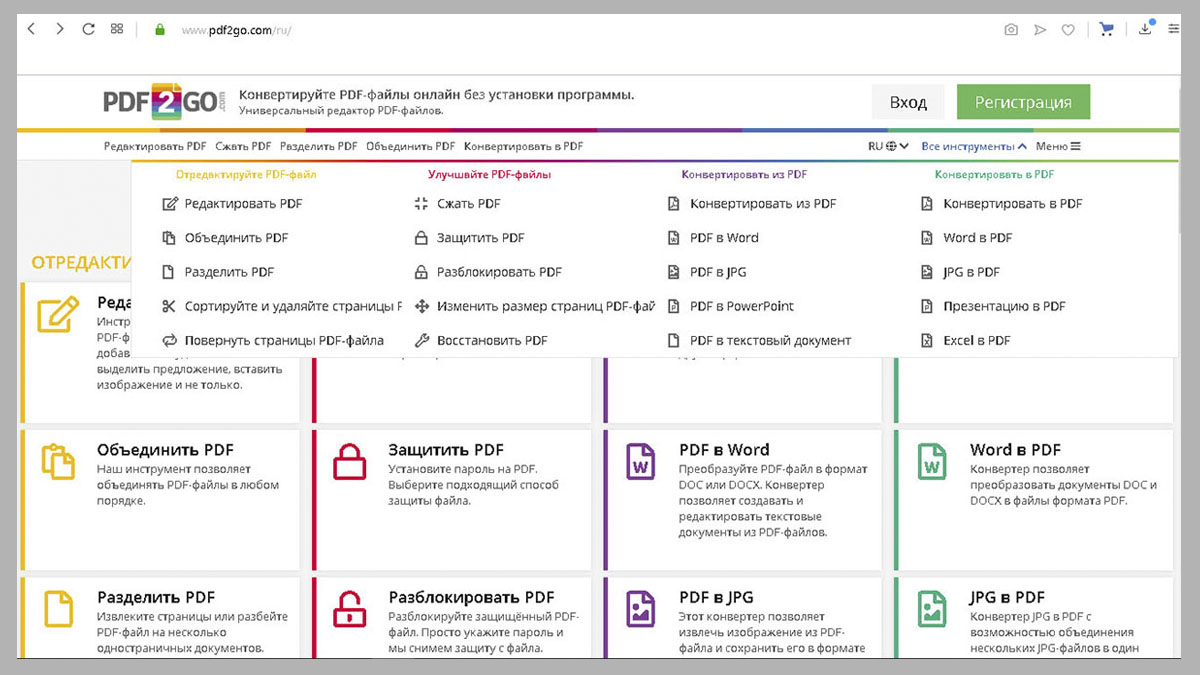
 nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf
nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf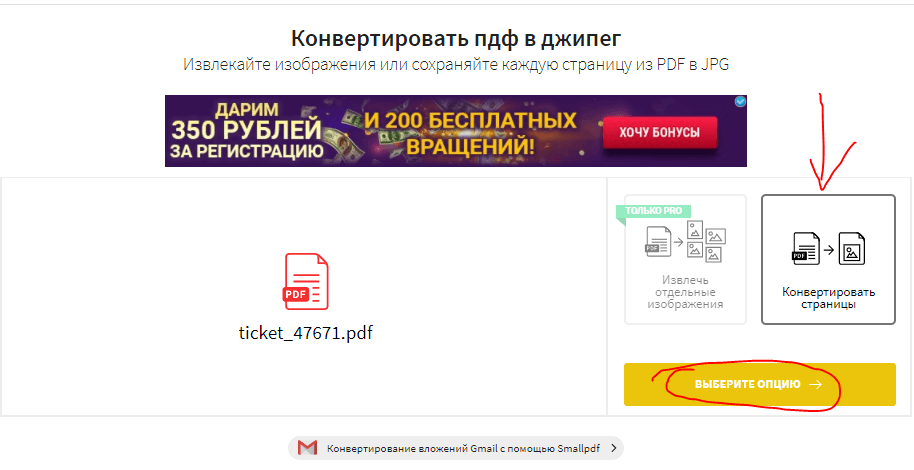 Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf
Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf pdf
pdf Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf
Лицензия: не указано. Ссылки: http://opus.nlpl.eu/OpenSubtitles2018.php, http://stp.lingfil.uu.se/~joerg/paper/opensubs2016.pdf pdf
pdf


 Вот некоторые из них:
Вот некоторые из них:
 DBF, скорее всего, является файлом базы данных, используемым программным обеспечением для управления данными dBASE. Данные хранятся в файле в массиве с несколькими записями и полями.
DBF, скорее всего, является файлом базы данных, используемым программным обеспечением для управления данными dBASE. Данные хранятся в файле в массиве с несколькими записями и полями.


 2 и 8.3), которую можно скачать отсюда. Она универсальна и должна подходить для любой конфигурации, написанной под управляемое приложение.
2 и 8.3), которую можно скачать отсюда. Она универсальна и должна подходить для любой конфигурации, написанной под управляемое приложение. Другие обработка не видит.
Другие обработка не видит.
 Если обратите внимание на рисунки выше, то увидите, что в колонке «Единица» у меня стоит код. И в обработке нужно указать, что поиск нужно вести по коду. Щелкаем два раза по колонке «Условие связи» напротив «Единицы» и меняем на «Код».
Если обратите внимание на рисунки выше, то увидите, что в колонке «Единица» у меня стоит код. И в обработке нужно указать, что поиск нужно вести по коду. Щелкаем два раза по колонке «Условие связи» напротив «Единицы» и меняем на «Код». Однако dbase — не единственная программа для работы с базами данных, совместимая с файлами DBF, поскольку другие программы «xBASE» также поддерживают этот формат файла. DBF приобрел популярность, потому что его структура проста для понимания, а также была ранее принята сообществом баз данных.
Однако dbase — не единственная программа для работы с базами данных, совместимая с файлами DBF, поскольку другие программы «xBASE» также поддерживают этот формат файла. DBF приобрел популярность, потому что его структура проста для понимания, а также была ранее принята сообществом баз данных. Файл DBF — это файл базы данных, который создается и используется системой управления базами данных dBASE. Теперь, если у вас есть записи, хранящиеся в файле DBF, и вам нужно преобразовать его в более общий и удобный формат, такой как Excel, вы можете ознакомиться с этой статьей. Здесь я буду обсуждать три программы для преобразования DBF в форматы Excel, а именно XLS и XLSX . Вы также можете использовать их для преобразования файлов dBASE в CSV, ODS, HTML, PDF, TXT и еще несколько форматов.
Файл DBF — это файл базы данных, который создается и используется системой управления базами данных dBASE. Теперь, если у вас есть записи, хранящиеся в файле DBF, и вам нужно преобразовать его в более общий и удобный формат, такой как Excel, вы можете ознакомиться с этой статьей. Здесь я буду обсуждать три программы для преобразования DBF в форматы Excel, а именно XLS и XLSX . Вы также можете использовать их для преобразования файлов dBASE в CSV, ODS, HTML, PDF, TXT и еще несколько форматов. Он поддерживает файлы dBASE для открытия, просмотра, редактирования, печати и преобразования. Вы можете импортировать файл DBF и преобразовать его в форматы XLS, XLSX, XLB, и XLSM . Кроме того, вы также можете конвертировать файлы DBF в другие электронные таблицы и форматы файлов, включая CSV, DIF, HTML, XML, ODS, XPS, PDF, и т. Д.
Он поддерживает файлы dBASE для открытия, просмотра, редактирования, печати и преобразования. Вы можете импортировать файл DBF и преобразовать его в форматы XLS, XLSX, XLB, и XLSM . Кроме того, вы также можете конвертировать файлы DBF в другие электронные таблицы и форматы файлов, включая CSV, DIF, HTML, XML, ODS, XPS, PDF, и т. Д.
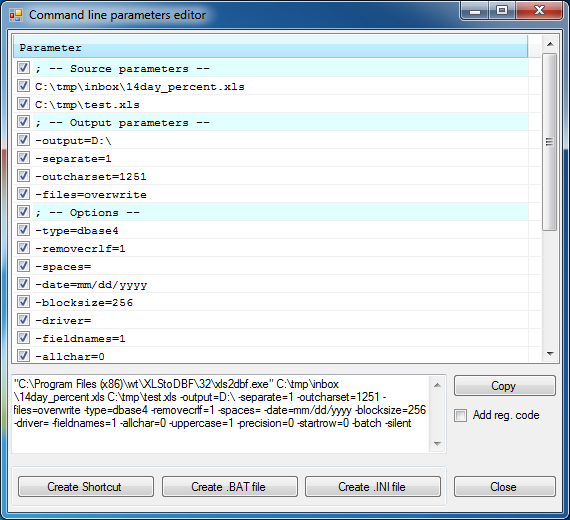 Это бесплатный офисный пакет с открытым исходным кодом, который предоставляет процессор электронных таблиц под названием LibreOffice Calc . С помощью этого приложения вы можете просматривать, изменять и конвертировать файлы DBF в Excel и другие форматы. Он позволяет конвертировать DBF в XLS, XLSX, ODS, CSV, HTML, PDF, TXT и несколько других форматов.
Это бесплатный офисный пакет с открытым исходным кодом, который предоставляет процессор электронных таблиц под названием LibreOffice Calc . С помощью этого приложения вы можете просматривать, изменять и конвертировать файлы DBF в Excel и другие форматы. Он позволяет конвертировать DBF в XLS, XLSX, ODS, CSV, HTML, PDF, TXT и несколько других форматов.
 Д. Некоторые из этих программ также позволяют зашифровать итоговые файлы Excel перед преобразованием.
Д. Некоторые из этих программ также позволяют зашифровать итоговые файлы Excel перед преобразованием.
 Вы также можете преобразовать электронную таблицу из одного поддерживаемого формата в другой.В общем, это лучшая программа для работы с электронными таблицами, доступная бесплатно.
Вы также можете преобразовать электронную таблицу из одного поддерживаемого формата в другой.В общем, это лучшая программа для работы с электронными таблицами, доступная бесплатно. Вы можете выбрать формат XLS или XLSX в качестве вывода.
Вы можете выбрать формат XLS или XLSX в качестве вывода.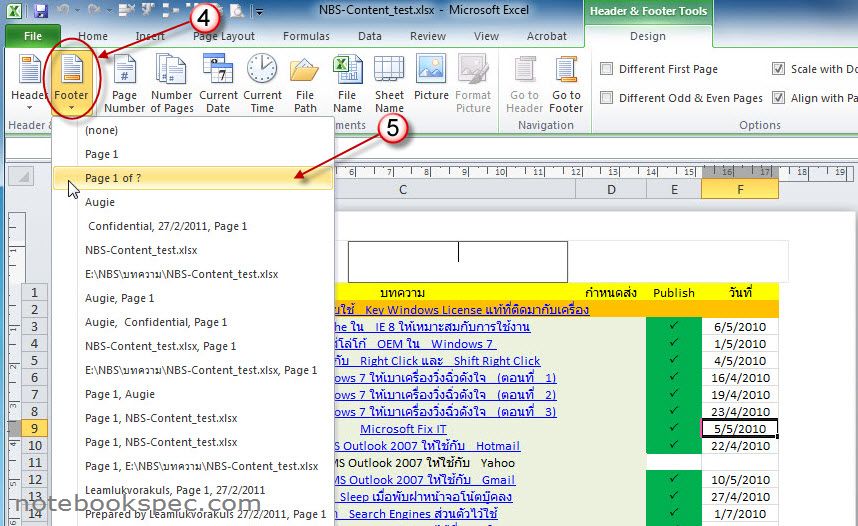 В нем вы можете просматривать и редактировать файлы DBF, фильтровать записи, печатать таблицы, а также конвертировать DBF в другие форматы. Поддерживаемые форматы вывода для преобразования файла DBF включают форматы Excel (XLS) и CSV, PDF, RTF, WKS, XML и HTML.
В нем вы можете просматривать и редактировать файлы DBF, фильтровать записи, печатать таблицы, а также конвертировать DBF в другие форматы. Поддерживаемые форматы вывода для преобразования файла DBF включают форматы Excel (XLS) и CSV, PDF, RTF, WKS, XML и HTML. Д.
Д.

 Он поставляется с различными модулями, используемыми для создания документов, электронных таблиц и презентаций. Используя его модуль электронных таблиц, вы можете легко конвертировать DBF в файлы Excel. Он поддерживает форматы XLS и XLSX для преобразования. Кроме того, он поддерживает еще несколько форматов для преобразования файла dBase, например CSV, XML, TXT, HTML и т. Д.
Он поставляется с различными модулями, используемыми для создания документов, электронных таблиц и презентаций. Используя его модуль электронных таблиц, вы можете легко конвертировать DBF в файлы Excel. Он поддерживает форматы XLS и XLSX для преобразования. Кроме того, он поддерживает еще несколько форматов для преобразования файла dBase, например CSV, XML, TXT, HTML и т. Д.
 Как следует из названия, это программа для просмотра и конвертации файлов DBF. Используя его, вы можете конвертировать DBF в XLS, а также в некоторые другие форматы файлов, такие как CSV, XML, MDB, HTML, DBC и т. Д. Вы также можете найти некоторые параметры для изменения записей, присутствующих в файле DBF, такие как Edit, New, Удалить и т. Д.
Как следует из названия, это программа для просмотра и конвертации файлов DBF. Используя его, вы можете конвертировать DBF в XLS, а также в некоторые другие форматы файлов, такие как CSV, XML, MDB, HTML, DBC и т. Д. Вы также можете найти некоторые параметры для изменения записей, присутствующих в файле DBF, такие как Edit, New, Удалить и т. Д.
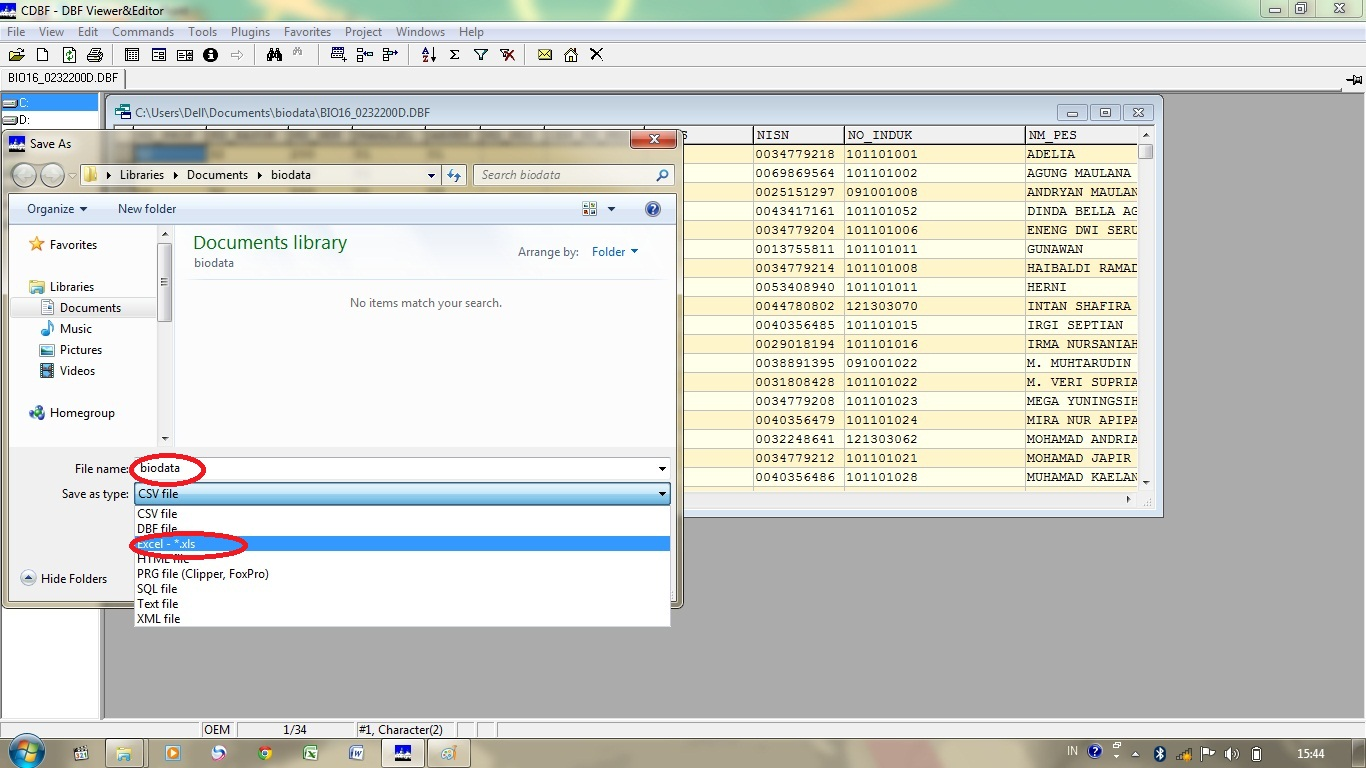


 Чтобы преобразовать XLS в DBF , вам нужно сделать всего три шага: выбрать файл XLS и вывести файл dbf, проверить, соответствуют ли настройки по умолчанию, что вам нужно, и начать преобразование.
Чтобы преобразовать XLS в DBF , вам нужно сделать всего три шага: выбрать файл XLS и вывести файл dbf, проверить, соответствуют ли настройки по умолчанию, что вам нужно, и начать преобразование. exe» образец файла sample.xls.dbf
exe» образец файла sample.xls.dbf Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
Экспериментировать со свободным падением тел продолжил Исаак Ньютон. В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.

 Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
Гипотезу о том, что значения ускорения свободного падения должны быть близки к значению 9,8 м/с2 и отличаться только погрешностью измерений удалось подтвердить разными экспериментами. Наиболее точный результат ускорения свободного падения у меня получился с помощью математического маятника. Поэтому для исследования изменения значения ускорения свободного падения с высотой я выбрал именно этот способ измерения. Погрешность составила не более 10%.
 Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами.
Сначала они проделывали опыты с двумя предметами. Например, брали два камня, и давали возможность им свободно падать, выпустив их из рук одновременно. Затем снова бросали два камня, но уже в стороны по горизонтали. Потом бросали один камень в сторону, и в тот же момент выпускали из рук второй, но так, чтобы он просто падал по вертикали. Люди извлекли из таких опытов много сведений о природе. Из опытов с падающими телами люди установили, что маленький и большой камни, выпущенные из рук одновременно, падают с одинаковой скоростью. То же самое можно сказать о кусках свинца, золота, железа, стекла, и т.д. самых разных размеров. Из подобных опытов выводиться простое общее правило: свободное падение всех тел происходит одинаково независимо от размера и материала, из которого тела сделаны. Между наблюдением за причинной связью явлений и тщательно выполненными экспериментами, вероятно, долго существовал разрыв. Две тысячи лет назад некоторые древние ученые, по-видимому, проводили вполне разумные опыты с падающими телами. Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха.
Великий греческий философ и ученый Аристотель, по-видимому придерживался распространенного представления о том, что тяжелые тела падают быстрее, чем легкие. Аристотель и его последователи стремились объяснить, почему происходят те или иные явления, но не всегда заботились о том, чтобы пронаблюдать, что происходит и как происходит. Он говорил, что тела стремятся найти свое естественное место на поверхности Земли. В XIV столетии группа философов из Парижа восстала против теории Аристотеля и предложила значительно более разумную схему, которая передавалась из поколения в поколение и распространилась до Италии, оказав двумя столетиями позднее влияние на Галилея. Парижские философы говорили об ускоренном движении и даже о постоянном ускорении, объясняя эти понятия архаичным языком. Великий итальянский ученый Галилео Галилей обобщил имеющиеся сведения и представления и критически их проанализировал, а затем описал и начал распространять то, что считал верным. Галилей понимал, что последователей Аристотеля сбивало с толку сопротивление воздуха. Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
Он указал, что плотные предметы, для которых сопротивление воздуха несущественно, падают почти с одинаковой скоростью.
 Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
Итак, мелкие камни слегка отстают в падении от крупных, и разница становится тем более заметной, чем большее расстояние пролетают камни. И дело тут не просто в размере тел: деревянный и стальной шары одинакового размера падают не строго одинаково. Галилей знал, что простому описанию падения тел мешает сопротивление воздуха. Но он мог лишь уменьшить его и не мог устранить его полностью. Поэтому ему пришлось вести доказательство, переходя от реальных наблюдений к постоянно уменьшающимся сопротивлением воздуха к идеальному случаю, когда сопротивление воздуха отсутствует. Позже, оглядываясь назад, он смог объяснить различия в реальных экспериментах, приписав их сопротивлению воздуха.
 Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
Именно этот опыт дал решающую проверку предположения Галилея. Опыты и рассуждения Галилея привели к простому правилу, точно справедливому в случае свободного падения тел в вакууме. Это правило в случае свободного падения тел в воздухе выполняется с ограниченной точностью. Поэтому верить в него, как в идеальный случай нельзя. Для полного изучения свободного падения тел необходимо знать, какие при падении происходят изменения температуры, давления, и др., то есть исследовать и другие стороны этого явления. Так Галилей установил признак равноускоренного движения:
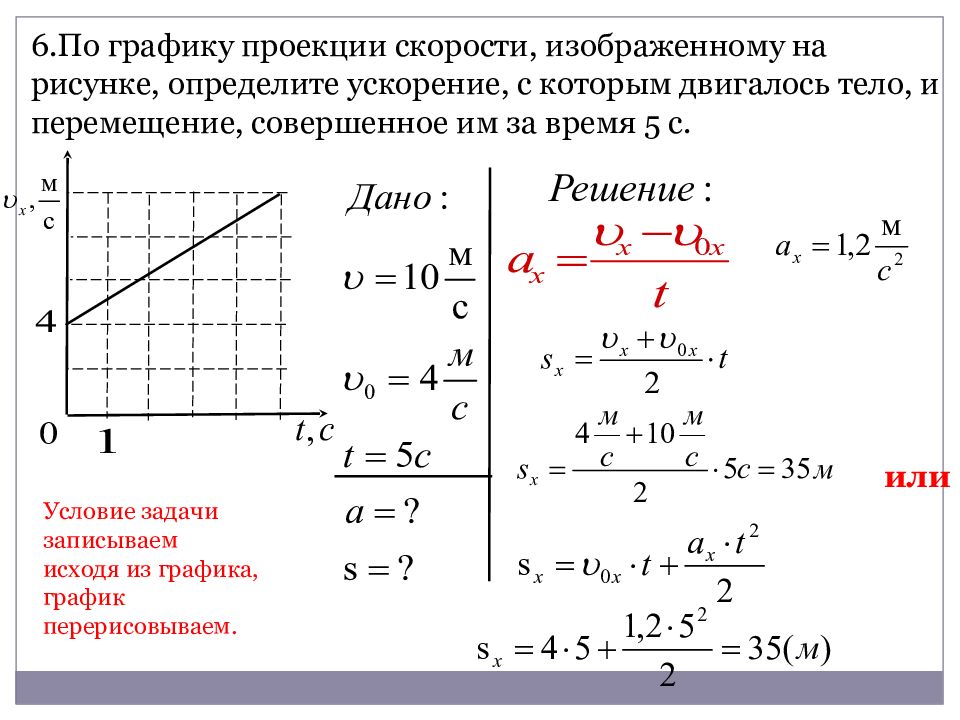 В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
В его выводах прослеживается мысль, что на Луне и на других планетах сила тяжести, воздействующая на одно и то же тело, будет неодинакова, зависит она напрямую от массы космического тела. Например, ускорение g на Луне в несколько раз меньше, чем на Земле. Таким образом, зная массу планеты, можно вычислить ускорение свободного падения тела на этой планете.
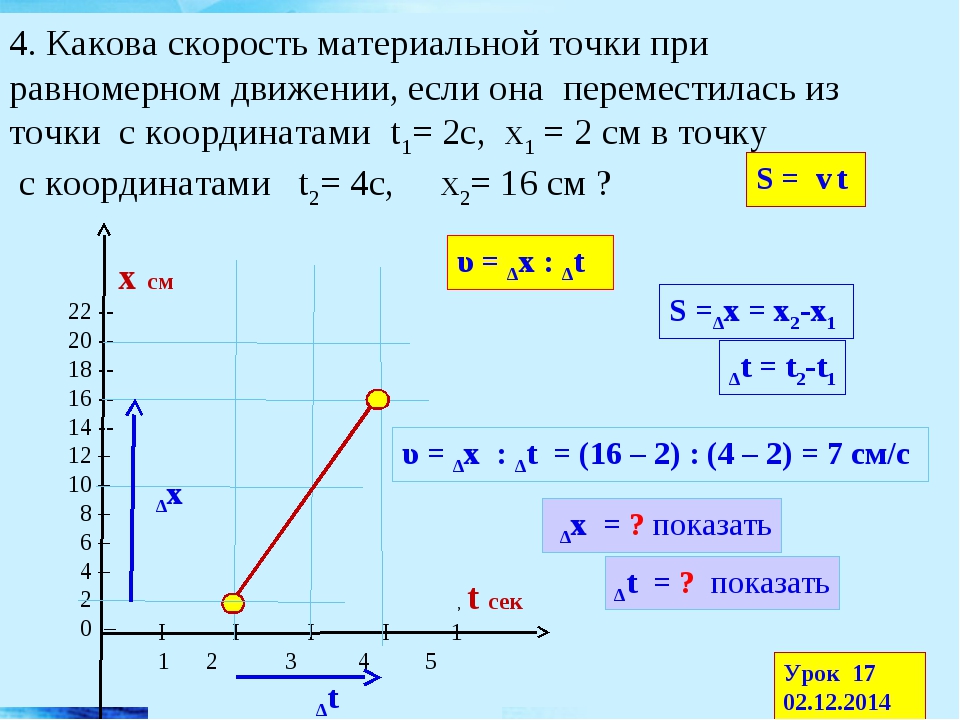 Приведу только те, которые сам испробовал.
Приведу только те, которые сам испробовал.

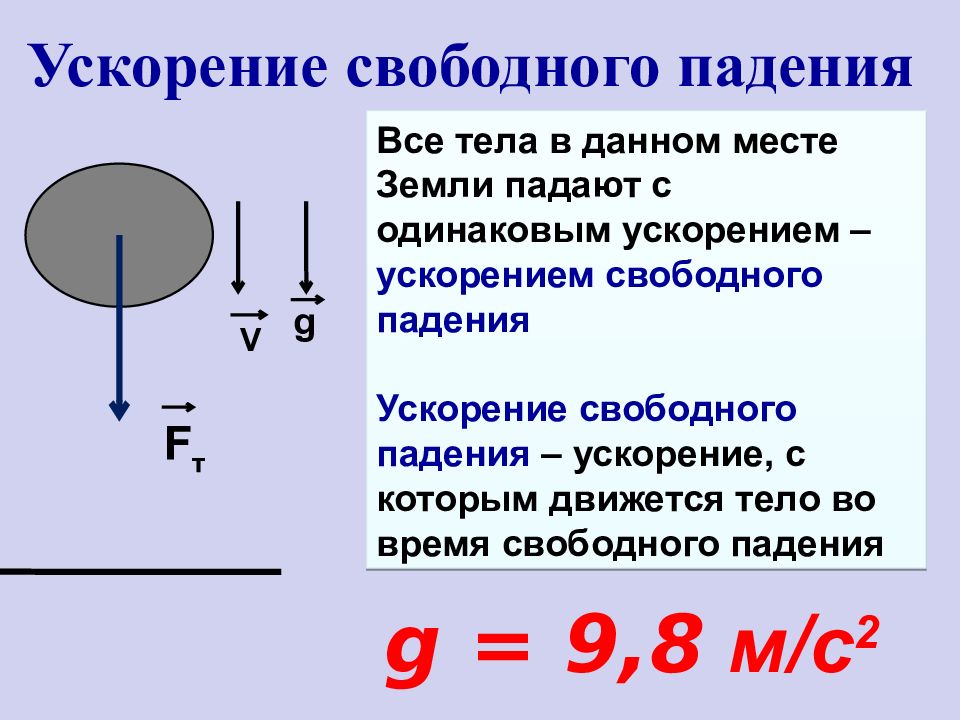
 При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника
При малых размерах шарика по сравнению с длиной нити и небольших отклонениях (до 10°) от положения равновесия период колебаний равен периоду колебаний математического маятника

 5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
5. Экспериментальное определение ускорения свободного падения с помощью математического маятника
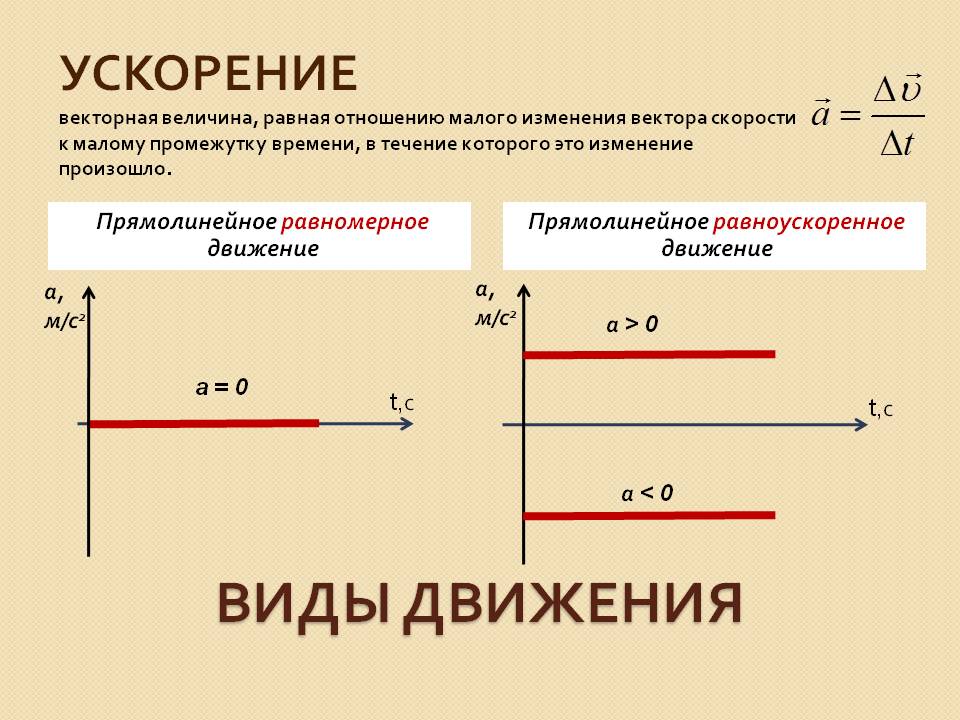

 Заключение
Заключение Экспериментально полученные значения хорошо это показывают.
Экспериментально полученные значения хорошо это показывают.
 Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.
Но одно тело не может действовать на другое, не испытывая его действия на себе. Следовательно, ускорение появляется при взаимодействии тел. Ускорение приобретают оба взаимодействующие тела. Так же из наблюдений можно установить ещё один факт: при одинаковом действии разные тела приобретают разные ускорения.

 {-12} % эти массы равны.
{-12} % эти массы равны. Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1\frac{a_1}{a_2} = \frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел:
Отношение ускорений тел равно обратному отношению их масс: a1a2=m2m1\frac{a_1}{a_2} = \frac{m_2}{m_1}. В свою очередь, ускорение равно отношению изменения скорости ко времени изменения. Конечные скорости тел равны нулю, а время взаимодействия одинаково для обоих тел: Определите ускорение лифта в высотном здании, если он увеличивает свою скорость на 3,2 м/с в течение 2 с.
Определите ускорение лифта в высотном здании, если он увеличивает свою скорость на 3,2 м/с в течение 2 с. Определите скорость через 5 мин после начала движения. Какой путь прошел объект за это время?
Определите скорость через 5 мин после начала движения. Какой путь прошел объект за это время? Каково ускорение поезда? Определите время его разгона.
Каково ускорение поезда? Определите время его разгона. Каково ускорение мотороллера? Каков его тормозной путь?
Каково ускорение мотороллера? Каков его тормозной путь? Какое расстояние он пролетел при равноускоренном движении?
Какое расстояние он пролетел при равноускоренном движении? Как двигался поезд в течение этих 20 с?
Как двигался поезд в течение этих 20 с? В течение 10 равных промежутков времени от начала движения тело, двигаясь равноускоренно, прошло 75 см. Сколько сантиметров прошло это тело в течение двух первых таких же промежутков времени?
В течение 10 равных промежутков времени от начала движения тело, двигаясь равноускоренно, прошло 75 см. Сколько сантиметров прошло это тело в течение двух первых таких же промежутков времени? Пуля вылетает из ствола ружья со скоростью 800 м/с. Длина ствола 64 см. Предполагая движение пули внутри ствола равноускоренным, определите ускорение и время движения.
Пуля вылетает из ствола ружья со скоростью 800 м/с. Длина ствола 64 см. Предполагая движение пули внутри ствола равноускоренным, определите ускорение и время движения.

 Среди них – алгоритмы для автономного транспорта, изучение квантового хаоса и внутреннелго устройства черных дыр. Об этом ТАСС рассказал один из разработчиков этого компьютера Вадим Смелянский.
Среди них – алгоритмы для автономного транспорта, изучение квантового хаоса и внутреннелго устройства черных дыр. Об этом ТАСС рассказал один из разработчиков этого компьютера Вадим Смелянский. Адиабатический компьютер ближе к аналоговым компьютерам. Создавать их проще, но подобные устройства умеют решать лишь ограниченное количество задач.
Адиабатический компьютер ближе к аналоговым компьютерам. Создавать их проще, но подобные устройства умеют решать лишь ограниченное количество задач. лет.
лет.
 По сравнению с «конкурентами» они сильно связаны друг с другом и работают быстро. Это важно, к примеру, при изучении квантового хаоса и различных переходов между подобными состояниями», – продолжает физик.
По сравнению с «конкурентами» они сильно связаны друг с другом и работают быстро. Это важно, к примеру, при изучении квантового хаоса и различных переходов между подобными состояниями», – продолжает физик. Благодаря этому ученые смогут точно предсказывать, какие свойства есть у то или иного – даже пока не существующего – соединения, а также целенаправленно синтезировать вещества с конкретными свойствами.
Благодаря этому ученые смогут точно предсказывать, какие свойства есть у то или иного – даже пока не существующего – соединения, а также целенаправленно синтезировать вещества с конкретными свойствами. Каждый квадратик создает пару с тремя остальными другими, естественно исключая вариант создания пары самим с собой. Для наглядности каждый квадратик со стрелками имеет свою цветовую маркировку.
Каждый квадратик создает пару с тремя остальными другими, естественно исключая вариант создания пары самим с собой. Для наглядности каждый квадратик со стрелками имеет свою цветовую маркировку.
 n
n combinations(range(1,10), 3)))
84
combinations(range(1,10), 3)))
84
 Еще один-два знака — и можно с точностью до атома рассчитать длину окружности с диаметром как у Вселенной.
Еще один-два знака — и можно с точностью до атома рассчитать длину окружности с диаметром как у Вселенной. Но вот с одинаковой ли частотой появляются цифры и их комбинации, неясно. Судя по всему, это так, но пока никто не привел строгого доказательства.
Но вот с одинаковой ли частотой появляются цифры и их комбинации, неясно. Судя по всему, это так, но пока никто не привел строгого доказательства.
 А советский математик Яков Перельман сочинил целый мнемонический диалог:
А советский математик Яков Перельман сочинил целый мнемонический диалог: Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание.
Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание. Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа.
Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
 Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?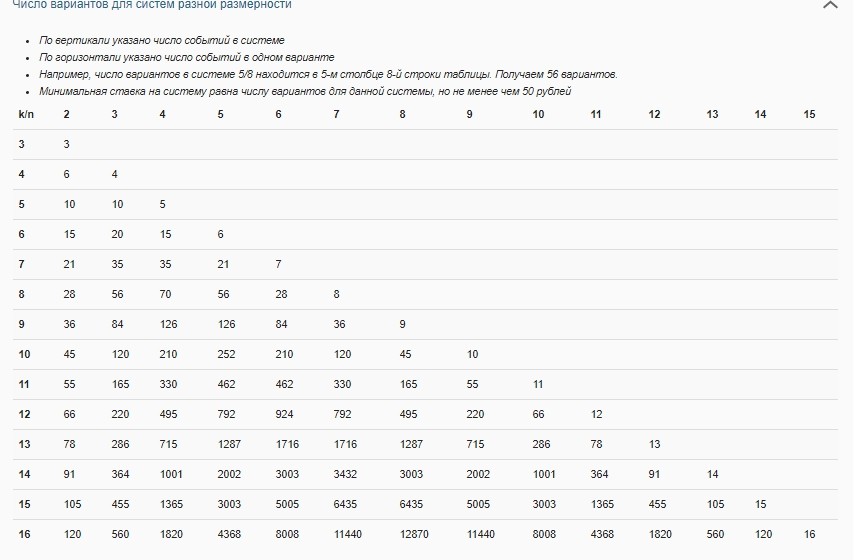 Перестановки, размещения, сочетания .
Перестановки, размещения, сочетания .

 Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).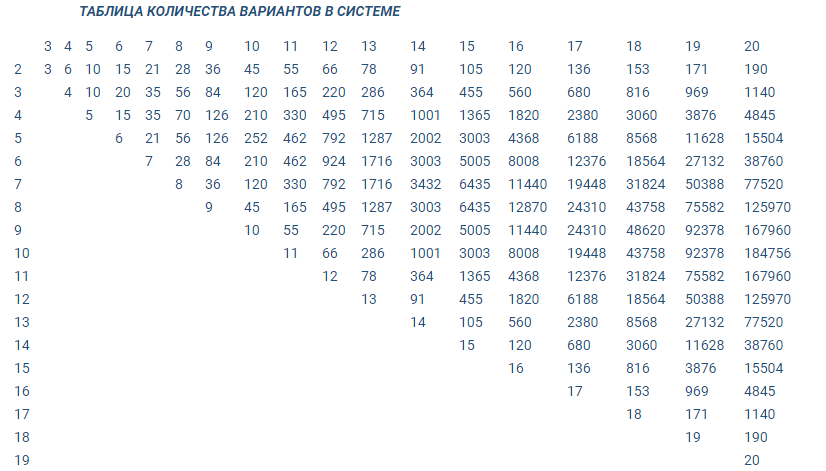
 06
06 40
40
 Чтобы найти сумму 5 последовательных чисел, можно:
Чтобы найти сумму 5 последовательных чисел, можно: проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60°, проведен из вершины А второй луч; получились три угла по 30°.
проведен из вершины А луч, а вдоль кромки линейки, повернутой на угол 60°, проведен из вершины А второй луч; получились три угла по 30°. Простейший пример – подбрасывание монетки (экспериментатор не знает какая сторона монеты выпадет в каждом конкретном случае).
Простейший пример – подбрасывание монетки (экспериментатор не знает какая сторона монеты выпадет в каждом конкретном случае).
 Результаты эксперимента доказывают это на практике.
Результаты эксперимента доказывают это на практике.

 ). Если кратко, то по закону больших чисел в будущем должны получить примерно тот же результат.
). Если кратко, то по закону больших чисел в будущем должны получить примерно тот же результат. Расхождение с ожиданиями порядка 180-200%, на погрешность это списать нельзя.
Расхождение с ожиданиями порядка 180-200%, на погрешность это списать нельзя. Отличаются лишь инструменты анализа информации, сам принцип остается тем же.
Отличаются лишь инструменты анализа информации, сам принцип остается тем же. На основе этого рассчитывается норма для каждого менеджера;
На основе этого рассчитывается норма для каждого менеджера;
 Учитываются все составляющие – пол, сфера работы и должность, трудовой стаж, средний месячный доход, назначение займа, кредитная история, семейное положение.
Учитываются все составляющие – пол, сфера работы и должность, трудовой стаж, средний месячный доход, назначение займа, кредитная история, семейное положение.