Калькулятор Корней — Найдите квадратный корень
калькулятор корней онлайн корня поможет вам найти квадратный корень n-й степени любого положительного числа, которое вы хотите. Кроме того, этот калькулятор sqrt сообщает вам, что введенное вами число является точным квадратом или не является идеальным квадратом. Например; 4, 9 и 16 – это идеальные квадраты 2, 3 и 4 соответственно. Квадратный корень из числа – это число, которое при умножении на себя равно исходному числу. Например, квадрат 9 и 16 равен 3 и 4 соответственно. Если вы беспокоитесь о простом ручном вычислении, продолжайте читать, чтобы узнать формулу квадратного корня, вычисление дроби, отрицательные числа и многое другое!
Кроме того, вы можете попробовать наш онлайн калькулятор корней, который поможет вам вычислить значение любого числа, возведенного в любую степень.
Но давайте перейдем к основам!
Проведите по!
Как найти квадратный корень (шаг за шагом):Чтобы подготовиться к вычислению квадратного корня, вам следует запомнить основной идеальный квадратный корень. Поскольку квадрат 1, 4, 9, 16, 25, 100 равен 1, 2, 3, 4, 5 и 10.
Поскольку квадрат 1, 4, 9, 16, 25, 100 равен 1, 2, 3, 4, 5 и 10.
Чтобы найти квадрат √25, давайте посмотрим!
√25 = √5 * 5
√25 = √52
√25 = 5
Это простейшие квадратные корни, потому что они всегда дают целое число, но что, если у числа нет точного квадратного корня? Например, вы должны оценить квадрат в 54?
- Как вы знаете, √49 = 7 & √64 = 8. Итак, √54 находится между 8 и 7.
- Число 54 ближе к 49, чем к 64. Итак, вы можете попробовать угадать √54 = 7,45.
- Затем возводя в квадрат 7,45, получаем 7,452 = 55,5, что больше 54. Поэтому вам следует попробовать меньшее число. Возьмем 7,3
- Если взять в квадрат 7,3, получим 53,29, что близко к 54.
- Это означает, что квадратный корень из 54 находится между 7,3 и 7,4.
Возьмем другой пример:
Пример:
Что такое квадратный корень из 27?
Решение:
Поскольку число 27 не является квадратом любого числа. Итак, мы должны упростить это как:
√27 = √9 * 3
√9 * √3 = 3√3
Наш калькулятор корней онлайн корня учитывает эти формулы и методы упрощения для решения квадратного корня любого числа или любой дроби. 1/2 = √a / √b = √a / b
1/2 = √a / √b = √a / b
Где a / b – любая дробь. Приведем еще один пример:
Пример:
Что такое квадратный корень из 9/25?
Решение:
√9 / 25 = √9 / √25
√9 / √25 = 3/5 = 0,6
Квадратный корень отрицательного числа:В школе нас учили, что квадратный корень из отрицательных чисел не может существовать. Но математики вводят общий набор чисел (Комплексные числа). В виде,
х = а + би
Где a – действительное число, а b – мнимая часть. Йота (i) – это комплексное число со значением:
я = √-1. Приведем несколько примеров:
Квадрат -4 = √-4 = √-1 * 9 = √ (-1) √9 = 3i
Чему равен квадратный корень из -17 = √-17 = √-1 * 17 = √ (-1) √17 = 17i
Как пользоваться калькулятором квадратного корня:С помощью этого калькулятор корней онлайн квадратный корень стало очень просто. Для точных расчетов вам просто нужно выполнить указанные шаги.
Читать дальше!
Входы:
- Прежде всего, нажмите вкладку, чтобы выбрать квадратный корень или корень n-й степени для любого числа.

- Затем введите число, для которого вы хотите произвести расчет в соответствии с выбранной опцией.
- Наконец, нажмите кнопку «Рассчитать».
Выходы:
Как только вы закончите, калькулятор покажет:
- Корень квадратный из числа.
- Корень N-й степени числа.
- Пошаговый расчет.
Заметка:
Независимо от того, какой параметр ввода, онлайн-калькулятор с корнями корня покажет вам точные результаты в соответствии с выбранным вводом.
Часто задаваемые вопросы (FAQ):Может ли число иметь более одного квадратного корня?Да, положительные числа имеют более одного sqrt, одно положительное, а другое отрицательное.
Является ли √2 рациональным числом?Нет, это иррациональное число.
Причина:
Квадратный корень из 2 не может быть выражен как частное двух чисел.
Рациональны ли квадратные корни?Некоторые корни рациональны, а другие иррациональны.
Квадратные корни часто встречаются в математических формулах, включая квадратную формулу, дискриминант, а также во многих законах физики. Кроме того, он используется во многих местах повседневной жизни, используется инженерами, плотниками, менеджерами по строительству, фельдшерами и многими другими. Когда дело доходит до вычислений для большого количества, это очень сложно и сложно. Просто попробуйте калькулятор корней онлайн, который поможет вам определить квадратный корень в соответствии с вашими потребностями.
Other languages: Square Root Calculator, Karekök Hesaplama, Kalkulator Akar Kuadrat, Kalkulator Pierwiastków, Wurzel Ziehen Rechner, 平方根 計算, 제곱근 계산, Kalkulačka Odmocniny, Calculadora De Raiz Quadrada, Calculatrice Racine Carré, Calculadora Raiz Cuadrada, Calcolo Radice Quadrata, حاسبة الجذر التربيعي, Neliöjuuri Laskin, Kvadratrot Kalkulator, Kvadratni Koren Kalkulator.
Калькулятор извлечения корня n-ой степени онлайн
Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве.
Математическое обозначение
«Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье.
Квадратный корень
Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения.
Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как:
1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256…
Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.
Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел.
Кубический корень
Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как:
1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744…
Для остальных чисел кубические корни являются иррациональными числами. В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.
Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел.
Корень n-ной степени
Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.
Рассмотрим пример
Диагональ квадрата
Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из теоремы Пифагора и в конечном итоге принимает вид:
d = a × sqrt(2).
Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142.
Заключение
Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу.
Квадратный корень: онлайн калькулятор, график, формулы
Квадратный корень числа А — это такое положительное число В, которое при возведении в квадрат в результате дает число А. Поиск квадратного корня — стандартная арифметическая операция, с которой дети знакомятся в седьмом классе средней школы.
История термина
Математический термин «корень числа» имеет сложную историю. Математики Древней Греции мыслили числа зримо, поэтому определяли корни геометрически как сторону квадрата при известной площади. С развитием математической науки на востоке индийские ученые обозначали корень словом «мула». Труды индийских математиков попали в арабский мир, где обозначение квадратного корня перевели как «джазир», что в прямом смысле означает корень растения. После того, как арабские манускрипты попали в Европу, христианские ученые напрямую перевели «джазир» как корень, что на латыни обозначается словом radix.
Таким образом, корни получили название радикалов. Средневековые математики, например Кардано, обозначали радикалы латинской буквой Rx: после символа подкоренное выражение записывалось под горизонтальной чертой. Позднее Rx было вытеснено латинским V, которую проще набирать в типографии или записывать вручную. В онлайн-журналах и грамматике языков программирования для обозначения квадратных радикалов используют символ sqrt, что является сокращением от выражения SQuare RooT.
Позднее Rx было вытеснено латинским V, которую проще набирать в типографии или записывать вручную. В онлайн-журналах и грамматике языков программирования для обозначения квадратных радикалов используют символ sqrt, что является сокращением от выражения SQuare RooT.
Квадратные радикалы
Квадратный корень числа A — такое число B, которое при возведении во вторую степень дает в результате число А. Например, 22 = 4, а 32 = 9. Следовательно, квадратным корнем 4 является двойка, а 9 — тройка. Радикалы числа могут быть какими угодно: квадратными, кубическими, пятой или десятой степени. Технически вычисление квадратного корня — это возведение в степень 1/2. Так как существуют выражения вида xpi или xe, то мы можем извлечь pi-тыe или e-тые корни числа, возведя икс в степень 1/pi или 1/e. И, хотя с математической точки зрения это бессмысленная затея, но с заданной степенью точности мы можем вычислить и такие радикалы.
Квадратный корень — это всегда пара из положительного и отрицательного числа. Квадратным корнем четверки является как 2, так и минус 2. В решении практических задач это может быть важно: к примеру, для решения квадратных уравнений по формуле дискриминанта важно учитывать два корня уравнения. Если требуется найти только положительное значение радикала, то такое число называется арифметическим корнем.
Квадратным корнем четверки является как 2, так и минус 2. В решении практических задач это может быть важно: к примеру, для решения квадратных уравнений по формуле дискриминанта важно учитывать два корня уравнения. Если требуется найти только положительное значение радикала, то такое число называется арифметическим корнем.
В школе нас учат, что извлекать четные радикалы из отрицательных чисел нельзя. Если мы хотим в результате получить целые или иррациональные числа, то это правда. Невозможно получить адекватное число, если взять квадратный корень из минус 1. Именно так мыслили математики до 19 века, когда были сформулированы комплексные числа — числовой класс, которые полностью изменил понимание сути радикалов.
Наша программа позволяет вычислять квадратные радикалы из положительных чисел. Калькулятор представляет собой универсальный инструмент, при помощи которого легко вычислить подкоренное выражение, показатель степени или число. Для этого достаточно ввести 2 любых значения из перечисленных, и программа автоматически подсчитает неизвестное. Калькулятор выполнен таким образом, что вы можете вычислить радикалы любого порядка: второго, третьего, пятого или pi-того.
Калькулятор выполнен таким образом, что вы можете вычислить радикалы любого порядка: второго, третьего, пятого или pi-того.
Рассмотрим пример
Диагональ квадрата
Определение диагонали квадрата — классическая задача, с которой бились еще древние греки. Иррациональность корня из 2 ставила античных математиков в тупик, поэтому проблема длины диагонали квадрата виделась древними греками неприступным исполином. Сегодня мы без проблем можем вычислить приблизительное значение диагонали с точностью, которая нам требуется. Пусть у нас есть квадрат, площадь которого равна S = 30 см. Итак, формула для определения диагонали выглядит как:
D = sqrt(2) × a,
где a — сторона квадрата.
Нам дана площадь фигуры, следовательно, нам потребуется вычислить два квадратных корня: sqrt(2) и sqrt(S), так как сторона квадрата — это не что иное, как квадратный радикал его площади. Для вычислений требуется поочередно ввести значения 2 и 30 в ячейку калькулятора «Число (x)». «Степень n» важно указать 2, так как по умолчанию в программе установлена тройка. Теперь достаточно провести вычисления и подставить их в формулу:
Теперь достаточно провести вычисления и подставить их в формулу:
D = sqrt(2) × sqrt(30) = 1,4142 × 5,4772 = 7,74585624.
При помощи калькулятора мы нашли диагональ квадрата с точностью до 8 знаков после запятой всего в 3 клика мышкой.
Заключение
Вычисление радикала — обыденная в науке арифметическая операция, которая в отличие от сложения или умножения встречается в бытовых расчетах достаточно редко. Наш онлайн-калькулятор в основном будет полезен школьникам и студентам для вычислений числовых примеров по алгебре, геометрии или математическому анализу.
😃 Извлечение корня — онлайн калькулятор и упрощенные приемы извлечения
Извлечение корня – обратная операция возведению степени. То есть Извлекая корень из числа Х, получим число, которое в квадрате даст то самое число Х.
Извлечение корня довольно-таки несложная операция. Таблица квадратов сможет облегчить работу по извлечению. Потому что, наизусть помнить все квадраты и корни невозможно, а числа могут встретиться большие.
Извлечение корня из числа
Извлечение квадратного корня из числа – просто. Тем более что это можно делать не сразу, а постепенно. Например, возьмем выражение √256. Изначально, незнающему человеку сложно дать ответ сразу. Тогда будем делать по шагам. Сначала разделим на просто число 4, из которого вынесем за корень выделенный квадрат.
Изобразим: √(644), тогда это будет равносильно 2√64. А как известно, по таблице умножения 64=88. Ответ будет 2*8=16.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Извлечение комплексного корня
Корень квадратный не может вычисляться из отрицательных чисел, потому что любое число в квадрате – положительное число!
Комплексное число – число i, которое в квадрате равно -1. То есть i2=-1.
То есть i2=-1.
В математике существует число, которое получается при извлечении корня из числа -1.
То есть есть возможность вычислить корень из отрицательного числа, но это уже относится к высшей математике, не школьной.
Рассмотрим пример такого извлечения корня: √(-49)=7*√(-1)=7i.
Калькулятор корня онлайн
С помощью нашего калькулятора, Вы сможете посчитать извлечение числа из квадратного корня:
Загрузка калькулятора…
Преобразование выражений, содержащих операцию извлечения корня
Суть преобразования подкоренных выражений в разложении подкоренного числа на более простые, из которых можно извлечь корень. Такие как 4, 9, 25 и так далее.
Приведем пример, √625. Поделим подкоренное выражение на число 5. Получим √(1255), повторим операцию √(2525), но мы знаем, что 25 это 52. А значит ответом будет 5*5=25.
Но бывают числа, у которых корень таким методом не вычислить и просто нужно знать ответ или иметь таблицу квадратов под рукой.
√289=√(17*17)=17
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Оператор | Описание |
Простейшие математические операции | |
+ — * / () | Сложение, вычитание, умножение, деление и группирующие символы. 3 значит x в кубе, также можно написать x*x*x 3 значит x в кубе, также можно написать x*x*x |
sqrt(x) | Квадратный корень. Эквивалентно root(x,2) |
cbrt(x) | Кубический корень. Эквивалентно root(x,3) |
root(x,n) | Корень n-ой степени из x. Например: root(x,3) есть корень 3й степени из x |
log(a,x) | Логарифм x по основанию a |
ln(x) | Натуральный логарифм (c основанием e) |
lg(x) | Логарифм по основанию 10 (Десятичный логарифм) |
exp() | Экспоненциальная функция (e в заданной степени), эквивалентно e^аргумент |
Тригонометрические функции | |
sin(x) | Синус значения x |
cos(x) | Косинус значения x |
tg(x) | Тангенс значения x. Можно вводить tg(x) или tan(x) Можно вводить tg(x) или tan(x) |
ctg(x) | Котангенс значения x. Можно вводить ctg(x) или cot(x) |
sec(x) | Секанс значения x, определяется как 1/cos(x) |
csc(x) | Косеканс значения x, определяется как 1/sin(x) |
arcsin(x) | Арксинус значения x. Можно вводить arcsin(x) или asin(x) |
arccos(x) | Арккосинус значения x. Можно вводить arccos(x) или acos(x) |
atan(x) | Арктангенс значения x. Можно вводить arctg(x) или atan(x) |
arcctg(x) | Арккотангенс значения x. Можно вводить arcctg(x) или acot(x) Можно вводить arcctg(x) или acot(x) |
asec(x) | Арксеканс значения x, обратный секанс |
acsc(x) | Арккосеканс значения x, обратный косеканс |
Некоторые константы | |
e | Основание натурального логарифма или число Эйлера = 2.718281828459045… |
pi | Число Пи = 3.141592653589793… |
Инженерный калькулятор. Кубический корень (извлечение без калькулятора)
Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.
Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.
Что нужно знать о корне произвольной степени?
Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.
Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным.
Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.
Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля.
Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ».
В-третьих, для них справедливы все действия со степенями.
- Их можно перемножать. Тогда показатели степеней складываются.
- Корни можно разделить. Степени нужно будет вычесть.
- И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.
В чем сходства и различия квадратного и кубического корней?
Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.
А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.
Извлечение кубического корня на калькуляторе
Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»?
На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.
А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=».
Извлечение кубического корня вручную
Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.
Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?
- Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой.
 Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать. - Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
- Выполнить вычитание.
- К остатку приписать первую группу цифр после запятой.
- В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а» — это промежуточный ответ, «х» является числом, которое меньше получившегося остатка с приписанными к нему числами.
- Число «х» нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
- Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.
Наглядный пример вычисления кубического корня
Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.
Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.
- 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
- После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
- а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3
- Методом подбора получается, что х = 4. 1200 * 4 + 60 * 16 + 64 = 5824.
- Вычитание дает 1176, а над корнем появилось число 4.
- Приписать к остатку три нуля.
- а = 24. Тогда 172800 х + 720 х 2 + х 3
- х = 6. Вычисление выражения дает результат 1062936. Остаток: 113064, над корнем 6.
- Снова приписать нули.
- а = 246. Неравенство получается таким: 18154800х + 7380х 2 + х 3
- х = 6. Расчеты дают число: 109194696, Остаток: 3869304. Над корнем 6.
Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47.
Необычный способ извлечения кубического корня
Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. Причем таких слагаемых должно быть минимально возможное число.
К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19.
Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем.
Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ.
Размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т. д.
д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице .
Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.
Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).
Она вставляет в строке ввода запись sqrt3(x).
Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Пример, как извлечь корень из корня:
Степень в корне
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Квадратный корень из степени:
Все функции нашего бесплатного калькулятора собраны в одном разделе.
Решение корней в онлайн калькуляторе was last modified: Март 3rd, 2016 by Admin
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.

- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147.
 Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.

- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.

- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой.
 Ответ (корень из данного числа) будете записывать справа сверху.
Ответ (корень из данного числа) будете записывать справа сверху.
- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».

- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел.
 Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).

Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень.
 В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.
 (10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Мы знаем, что:
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?
Что нужно знать?
1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Рассмотрим примеры:
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
При решении некоторых технических задач бывает нужно посчитать корень третьей степени . Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).
Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).
Вам понадобится
- калькулятор или компьютер
Инструкция
- Чтобы посчитать корень третьей степени , воспользуйтесь калькулятором. Желательно, чтобы это был не обычный калькулятор, а калькулятор, используемый для инженерных расчетов. Однако даже на таком калькуляторе вы не найдете специальную кнопку для извлечения корня третьей степени . Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
- Для возведения числа в степень 1/3 наберите на клавиатуре калькулятора само число. После чего нажмите на клавишу «возведение в степень».
 y.
y. - Если корень третьей степени приходится считать систематически, то воспользуйтесь программой MS Excel. Чтобы посчитать корень третьей степени в «Екселе», введите в любую клетку знак «=», а затем, выберите значок «fx» — вставка функции. В появившемся окошке в списке «Выберите функцию» выберите строку «СТЕПЕНЬ». Нажмите кнопку «Ок». Во вновь появившемся окошке введите в строку «Число» значение числа, из которого нужно извлечь корень. В строку «Степень» введите число «1/3» и нажмите «Ок». В клетке таблицы появится искомое значение кубического корня из исходного числа.
Корень онлайн. Корень калькулятор. Корень онлайн калькулятор.
Общие арифметические операции — сложение, вычитание, деление, умножение, корень и возведение в степень. Квадратный корень является важным инструментом в арифметике. Квадратные корни очень часто используются не только в математике, но и во всех областях науки. В математике квадратные корни имеют важное значение, упрощая числа, выражения и уравнения.
Начнем с понимания того, что такое квадратные корни. Квадратный корень — это математический оператор, который применяется к числам и даже переменным. Квадратные корни числа или переменной определяются как число или переменная, которая при умножении на то же число или переменную, приводит к заданному числу или переменной, для которой мы должны были найти квадратный корень. Символ квадратного корня √
Степень
Число:
Вычислить
\( \sqrt{0}=0\)
\( \sqrt{1}=1\)
\( \sqrt{2}=1.4142136\)
\( \sqrt{3}=1.7320508\)
\( \sqrt{4}=2\)
\( \sqrt{5}=2.2360680\)
\( \sqrt{6}=2.4494897\)
\( \sqrt{7}=2.6457513 \)
\( \sqrt{8}=2.8284271\)
\( \sqrt{\pi}=1.7724538 \)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Гродненский государственный университет им. Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-5 классов. Легко нахожу общий язык с детьми, знакомлю с новым материалом в доступной игровой форме. Я люблю математику за то, что она дисциплинирует и воспитывает ум. Математика способствует развитию целого ряда качеств человека, таких как способность к анализу, умение применять свои знания на практике, находить закономерности, мыслить стратегически и логически. Считаю, что математика — наилучший способ привести в порядок свой ум и научиться мыслить точно.
Оставить заявкуРепетитор по математике
Белорусский государственный педагогический университет им. Максима Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 3-8 классов. Я люблю математику, потому что нахожу ее очень увлекательной. В преподавании придерживаюсь гуманистического и личностно-ориентированного методов обучения. Всегда стараюсь найти общий язык с учеником, стать для него товарищем и поддержкой в процессе обучения. Я гарантирую позитивное и познавательное погружение в увлекательный мир математики!
Оставить заявкуРепетитор по математике
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов. Реализую дифференцированный подход к обучению, осуществляю подготовку учеников к ОГЭ и ЕГЭ. Почему я люблю математику? Меня завораживают строки формул и выражений, кажется, что это шифр, к которому нужно подобрать ключ. Поэтому математика — это ключ к тайнам Вселенной.
Курсы ОГЭ
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Калькулятор полиномиальных корней
Список справки по математике — — Математическая справка Быстрый переход — Научный онлайн-калькулятор — Общая математика — Калькулятор фракцийКалькулятор процентовКалькулятор квадратного корняКалькулятор факторингаУпрощающие выраженияКалькулятор делителейКалькулятор факторингаКалькулятор наибольшего общего множителя (GCF) Калькулятор последнего общего множителя (LCM) Калькулятор простых чисел и средство проверкиПроверка идеального числа — Валидатор квадратов — Алгебра и комбинаторики -уравнения SolverQuadratic Уравнение SolverSystem уравнений SolverCombinatoricsPermutationsPolynomialsPolynomials — Сложение и SubtractionPolynomials — Умножение и DivisionPolynomials — Дифференциация и IntegrationPolynomials — Паритет калькулятор (нечетный, четный, нет) Полиномы — Корень FinderPolynomials — Сформировать из RootsMatricesMatrix Calculator- определителя, обратная матрица CalculatorMatrix — Сложение, вычитание, умножение, исчисление, интегральный калькулятор, калькулятор определенного интеграла, калькулятор производной, числовая производная КалькуляторКалькулятор пределов Отклонение CalculatorVariance CalculatorKurtosis CalculatorSkewness Calculator- Описательная статистика Калькуляторы -Матрица Центральный момент CalculatorCorrelation Матрица CalculatorCovariance Матрица CalculatorMatrix Среднее геометрическое CalculatorMatrix гармоническое среднее CalculatorMatrix межквартильный Диапазон CalculatorMatrix Эксцесс CalculatorMatrix нецентральные Момент CalculatorMatrix Среднее CalculatorMatrix Максимальная CalculatorMatrix Минимальная CalculatorMatrix Медиана CalculatorMatrix Среднее отклонение CalculatorMatrix Среднее отклонение CalculatorMatrix Quantile Калькулятор Калькулятор асимметрии квартиля матрицы Калькуляторы Калькуляторы распределения Вейбулла — Калькуляторы дискретных распределений — Калькуляторы биномиального распределенияКалькуляторы геометрического распределенияКалькуляторы распределения ПуассонаКалькуляторы равномерного (дискретного) распределения
Радикалы и корни бесплатный онлайн-калькулятор
Онлайн-калькулятор радикалов и корней.Вычислите корень n-й степени из x.
В настоящее время у нас есть около 940 калькуляторов, таблиц преобразования и полезных онлайн-инструментов и программных функций для студентов, преподавателей и учителей, дизайнеров и просто для всех.
На этой странице Вы можете найти финансовые калькуляторы, ипотечные калькуляторы, калькуляторы для кредитов, калькуляторы для автокредитования и лизинга, калькуляторы процентов, калькуляторы платежей, пенсионные калькуляторы, калькуляторы амортизации, инвестиционные калькуляторы, калькуляторы инфляции, финансовые калькуляторы, калькуляторы подоходного налога. , калькуляторы сложных процентов, калькулятор заработной платы, калькулятор процентной ставки, калькулятор налога с продаж, калькуляторы фитнеса и здоровья, калькулятор BMI, калькуляторы калорий, калькулятор телесного жира, калькулятор BMR, калькулятор идеального веса, калькулятор темпа, калькулятор беременности, калькулятор зачатия беременности, срок родов калькулятор, математические калькуляторы, научный калькулятор, калькулятор дробей, процентные калькуляторы, генератор случайных чисел, треугольный калькулятор, калькулятор стандартного отклонения, другие калькуляторы, калькулятор возраста, калькулятор даты, калькулятор времени, калькулятор часов, калькулятор GPA, калькулятор оценок, конкретный калькулятор, подсеть калькулятор, генерация паролей калькулятор преобразования и многие другие инструменты, а также для редактирования и форматирования текста, загрузки видео с Facebok (мы создали один из самых известных онлайн-инструментов для загрузки видео с Facebook).Мы также предоставляем вам онлайн-загрузчики для YouTube, Linkedin, Instagram, Twitter, Snapchat, TikTok и других социальных сетей (обратите внимание, что мы не размещаем видео на своих серверах. Все загружаемые вами видео загружаются с Facebook, YouTube, Linkedin, CDN в Instagram, Twitter, Snapchat, TikTok. Мы также специализируемся на сочетаниях клавиш, кодах ALT для Mac, Windows и Linux и других полезных советах и инструментах (как писать смайлы в Интернете и т. Д.)
В Интернете есть много очень полезных бесплатных инструментов, и мы будем рады, если вы поделитесь нашей страницей с другими или отправите нам какие-либо предложения по другим инструментам, которые придут вам в голову.Также, если вы обнаружите, что какой-либо из наших инструментов не работает должным образом или вам нужен лучший перевод — сообщите нам об этом. Наши инструменты сделают вашу жизнь проще или просто помогут вам выполнять свою работу или обязанности быстрее и эффективнее.
Это наиболее часто используемые пользователями по всему миру.
И мы все еще развиваемся. Наша цель — стать универсальным сайтом для людей, которым нужно быстро производить расчеты или которым нужно быстро найти ответ на базовые конверсии.
Кроме того, мы считаем, что Интернет должен быть источником бесплатной информации. Таким образом, все наши инструменты и услуги полностью бесплатны и не требуют регистрации. Мы кодировали и разрабатывали каждый калькулятор индивидуально и подвергали каждый строгому всестороннему тестированию. Однако, пожалуйста, сообщите нам, если вы заметите хотя бы малейшую ошибку — ваш вклад очень важен для нас. Хотя большинство калькуляторов на Justfreetools.com предназначены для универсального использования во всем мире, некоторые из них предназначены только для определенных стран.
Онлайн-калькулятор | Базовый калькулятор
Калькулятор операций
Этот базовый онлайн-калькулятор похож на небольшой портативный калькулятор и имеет четыре стандартные функции для сложения, вычитания, деления и умножения. Как и большинство калькуляторов с 4 функциями, он также включает в себя клавиши для вычисления процентов, квадрата, квадратного корня и числа Пи. Этот базовый калькулятор имеет десятичную точность до 10 цифр и предлагает следующие функции:
- mc = Очистить память: очистить память калькулятора
- м + = Memory Plus: добавить отображаемое значение в память
- m- = Память Минус: вычесть отображаемое значение из памяти
- mr = вызов из памяти: отобразить значение памяти
- CE = Clear Entry: очистить текущее отображаемое значение, изменится на AC
- AC = All Clear: очистить все и начать новую операцию
- √x = Квадратный корень: извлечь квадратный корень из отображаемого значения и отобразить его
- +/- = Плюс / Минус : изменить знак отображаемого значения с положительного на отрицательный или наоборот
- π = pi: отобразить значение π как 3.141592654 для использования в расчетах
- x² = Квадрат: возвести отображаемое значение в квадрат и отобразить его
- R2 = Округлить до 2 десятичных знаков: округлить текущее отображаемое значение до 2 десятичных знаков, например, в денежный или денежный формат
- R0 = Округлить до 0 десятичных знаков: Округлить текущее отображаемое значение до 0 десятичных знаков
- % = Процент: использовать отображаемое значение для вычисления процента
Специальные возможности калькулятора
Zoom : Увеличьте размер калькулятора в браузере с помощью функции масштабирования браузера.Размер калькулятора, текста и кнопок изменяется пропорционально.
Масштаб сенсорного экрана : Увеличьте размер калькулятора на сенсорном экране, увеличивая масштаб с помощью пальцы. Размер калькулятора, текста и кнопок изменяется пропорционально.
Размер текста : в некоторых браузерах, например на рабочем столе Chrome, вы можете изменить размер текста в браузере. настройки и размер калькулятора, текста и кнопок будут пропорционально увеличиваться или уменьшаться.
Управление с клавиатуры : Вы можете использовать калькулятор без мыши, перемещаясь по калькулятору с помощью табуляции. ключи. Нажмите «Enter», когда клавиша сфокусирована. Однако этот метод может быть трудным, поскольку вы должны последовательно перебирать все клавиши табуляцией.
Управление цифровой клавиатурой : Вы можете использовать калькулятор с большинством цифровых панелей и клавиатур в самых популярных браузерах для числа, очистка и основные функции сложения, вычитания, умножения и деления, а также удаления / возврата.
Свяжитесь со мной, если у вас есть предложения.
Расчет процентов
- Умножение и деление преобразует отображаемое значение в проценты в десятичной форме и завершит
операция при нажатии [=]
- Пример: найти 20% от 25
- Введите 25 x 20%, и дисплей изменится с 20% на 0,2
- Введите = для завершения расчета 25 x 0,2 = 5. На дисплее отобразится ответ 5.
- Сложение и вычитание добавляет или вычитает процент от значения
- Пример: добавить 20% к 25
- Введите 25 + 20%, и дисплей изменится на 5. (5 — это 20% от 25)
- Введите = для завершения расчета 25 + 5 = 30. На дисплее отображается ответ 30.
- Расчет налогов
- Пример: добавьте 6% налога к покупке на сумму 851 долларов США.
- Введите 851 + 6%, и дисплей изменится на 51.06. (51.06 составляет 6% от 851)
- Введите = для завершения расчета 851 + 51,06 = 902,06. На дисплее отображается ответ 902.06.
- Примечание: для других задач вы можете получить ответ с более чем двумя десятичными знаками. Используйте клавишу R2 для округлить до долларов и центов. Используйте R0, чтобы округлить до долларов.
Калькулятор характеристической полиномиальной матрицы — Online Roots Equation
Поиск инструмента
Характеристический многочлен матрицы
Инструмент для вычисления характеристического полинома матрицы.Характеристический полином матрицы M вычисляется как определитель (X.I-M).
Результаты
Характеристический многочлен матрицы — dCode
Тэги: Matrix
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор характеристических полиномов
Матрица из искателя характеристических полиномов
Ответы на вопросы (FAQ)
Какой характеристический многочлен у матрицы? (Определение)
Характеристический многочлен (или иногда секулярная функция) $ P $ квадратной матрицы $ M $ размера $ n \ times n $ — это многочлен, определяемый формулой $$ P_M (x) = \ det (M — x.I_n) \ tag {1} $$ или $$ P_M (x) = \ det (x.I_n — M) \ tag {2} $$ с $ I_n $ единичной матрицей размера $ n $ (и det матрица определитель).
Два возможных значения $ (1) $ и $ (2) $ дают противоположные результаты, но поскольку полином используется для поиска корней, знак не имеет значения.
Уравнение $ P = 0 $ называется характеристическим уравнением матрицы .
Зачем нужно вычислять характеристический многочлен матрицы?
Характеристический многочлен $ P $ матрицы, как следует из названия, характеризует матрицу, он позволяет, в частности, вычислять собственные значения и собственные векторы.
Как вычислить характеристический многочлен диагональной матрицы?
Если $ M $ — диагональная матрица с $ \ lambda_1, \ lambda_2, \ ldots, \ lambda_n $ в качестве диагональных элементов, то вычисление упрощается и $$ P_M (x) = (x- \ lambda_1) (x- \ лямбда_2) \ ldots (x- \ lambda_n) $$
Как вычислить характеристический многочлен триангулярной матрицы?
Если $ M $ — треугольная матрица с диагональными элементами $ \ lambda_1, \ lambda_2, \ ldots, \ lambda_n $, то для диагональной матрицы вычисление упрощается и $$ P_M (x) = (x- \ lambda_1 ) (x- \ lambda_2) \ ldots (x- \ lambda_n) $$
Как вычислить характеристический полином для матрицы 2×2?
Вычисление характеристического полинома квадратной матрицы порядка 2 может быть вычислено с помощью определителя матрицы $ [x.2-5x-2 $$
Как вычислить характеристический полином для матрицы 3×3?
Вычисление характеристического полинома квадратной матрицы 3×3 можно вычислить с определителем матрицы $ [x.I_3 — M] $ как $$ P_M (x) = \ det [x.I_3 — M] $$
Пример: $$ M = \ begin {bmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {bmatrix} $$ $$ [x.I_3 — M] = x \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix} — M = \ begin {bmatrix} xa & -b & -c \\ -d & xe & -f \\ -g & -h & xi \ end {bmatrix} $$ $$ P_M (x) = \ det [x.2) \ вправо) $$
Есть ли у матрицы кратный характеристический многочлен?
Характеристический многочлен уникален для данной матрицы. Есть только один способ вычислить его и получить только один результат.
С другой стороны, две разные матрицы могут дать один и тот же характеристический полином .
Как вычислить характеристический полином транспонированной матрицы?
Матрица $ M $ и ее транспонированная матрица $ M ^ T $ имеют один и тот же характеристический многочлен .
Задайте новый вопросИсходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Характеристический полином матрицы». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент «Характерного полинома матрицы» (преобразователь, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой другой Функция «Характеристический многочлен матрицы» (вычисление, преобразование, решение, дешифрование / шифрование, дешифрование / шифрование, декодирование / кодирование, перевод), написанная на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копирование и доступ к API для «Характеристического полинома матрицы» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
характеристика, полином, матрица, собственное значение, собственный вектор, определитель
Ссылки
Источник: https: // www.dcode.fr/matrix-characteristic-polynomial
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF. Калькулятор корней комплексных чиселКалькулятор найдет корни $$$ n $$$ th данного комплексного числа, используя формулу де Муавра, с указанными шагами.
Ваш ввод
Найдите $$$ \ sqrt [4] {81 i} $$$.{\ frac {1} {n}} \ left (\ cos {\ left (\ frac {\ theta + 2 \ pi k} {n} \ right)} + i \ sin {\ left (\ frac {\ theta + 2 \ pi k} {n} \ right)} \ right) $$$, $$$ k = \ overline {0..n-1} $$$.
У нас есть $$$ r = 81 $$$, $$$ \ theta = \ frac {\ pi} {2} $$$, $$$ n = 4 $$$.
- $$$ k = 0 $$$: $$$ \ sqrt [4] {81} \ left (\ cos {\ left (\ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 0} {4} \ right)} + i \ sin {\ left (\ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 0} {4} \ right)} \ right) = 3 \ left (\ cos {\ left (\ frac {\ pi} {8} \ right)} + i \ sin {\ left (\ frac {\ pi} {8} \ right)} \ right) = 3 \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} + 3 i \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2} } {4}} $$$
- $$$ k = 1 $$$: $$$ \ sqrt [4] {81} \ left (\ cos {\ left (\ frac {\ frac {\ pi} { 2} + 2 \ cdot \ pi \ cdot 1} {4} \ right)} + i \ sin {\ left (\ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 1} { 4} \ right)} \ right) = 3 \ left (\ cos {\ left (\ frac {5 \ pi} {8} \ right)} + i \ sin {\ left (\ frac {5 \ pi} { 8} \ right)} \ right) = — 3 \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} {4}} + 3 i \ sqrt {\ frac {\ sqrt {2 }} {4} + \ frac {1} {2}} $$$
- $$$ k = 2 $$$: $$$ \ sqrt [4] {81} \ left (\ cos {\ left ( \ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 2} {4} \ right)} + i \ sin {\ left (\ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 2} {4} \ right)} \ right) = 3 \ left (\ cos {\ left (\ frac {9 \ pi} {8} \ right)} + i \ sin {\ оставил(\ frac {9 \ pi} {8} \ right)} \ right) = — 3 \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} — 3 i \ sqrt { \ frac {1} {2} — \ frac {\ sqrt {2}} {4}} $$$
- $$$ k = 3 $$$: $$$ \ sqrt [4] {81} \ left (\ cos {\ left (\ frac {\ frac {\ pi} {2} + 2 \ cdot \ pi \ cdot 3} {4} \ right)} + i \ sin {\ left (\ frac {\ frac { \ pi} {2} + 2 \ cdot \ pi \ cdot 3} {4} \ right)} \ right) = 3 \ left (\ cos {\ left (\ frac {13 \ pi} {8} \ right) } + i \ sin {\ left (\ frac {13 \ pi} {8} \ right)} \ right) = 3 \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} { 4}} — 3 i \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} $$$
Ответ
$$$ \ sqrt [4] {81 i} = 3 \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} + 3 i \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} {4}} \ приблизительно 2.77163859753386 + 1.14805029709527 i $$$ A
$$$ \ sqrt [4] {81 i} = — 3 \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} {4 }} + 3 i \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} \ приблизительно -1,14805029709527 + 2,77163859753386 i $$$ A
$$$ \ sqrt [4] {81 i} = — 3 \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} — 3 i \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} {4}} \ приблизительно -2,77163859753386 — 1,14805029709527 i $$$ A
$$$ \ sqrt [4] {81 i} = 3 \ sqrt {\ frac {1} {2} — \ frac {\ sqrt {2}} {4}} — 3 i \ sqrt {\ frac {\ sqrt {2}} {4} + \ frac {1} {2}} \ приблизительно 1.14805029709527 — 2,77163859753386 i $$$ A
Калькулятор квадратного корняНайти квадратный корень числа |
Другие калькуляторы
Калькулятор увеличения или уменьшения на процентов поможет найти ответы на вопросы, связанные с расчетом процентов.Чтобы вычислить процент от числа, используйте наш калькулятор процента от числа. Например, найдите 5% процентов от 70. Калькулятор процентов даст вам ответ, это 3,5.
процентное увеличение между двумя числами? Проблема решена с помощью функции «Рассчитать процент увеличения». Найдите процент% увеличения с 2 до 10. Ответ — 400%.
Найдите процентов второго числа ? Пример: узнать, какой процент равен 7 из 300. Калькулятор «Рассчитать процент от двух чисел», ответ — 2.33%.
Новинка: рассчитайте увеличение или уменьшение заработной платы с помощью нашего калькулятора дохода. Калькулятор процента увеличения заработной платы.
процента от общего числа . Например, всего = 1100, и вам нужно найти процент, равный 100. Используя наш калькулятор процента от общего количества, ответ составляет 9,09%.
GFC и LCM — математический коэффициент и множитель . Калькулятор GCF с наибольшим общим множителем можно использовать для расчета GFC, а калькулятор с наименьшим общим множителем — для определения НОК.
Калькулятор квадратного корня . Вместо того, чтобы запоминать квадратные корни, используйте калькулятор квадратного корня из числа и делайте это на лету. Например, каков квадратный корень из 9? Все мы знаем, что это 3. А как насчет квадратного корня из 500? Узнай себя.
Калькулятор процентов ошибок . Быстро рассчитайте процентную ошибку с помощью калькулятора процентов ошибок.
Калькулятор часов и минут . Найдите минуты или часы с помощью наших калькуляторов.First Calculate Hours in Minutes, очень полезно, чтобы узнать, сколько часов в 300 минутах. Калькулятор «Расчет минут в часах» полезен, чтобы узнать, сколько минут в 5 часах? Ответ: это 300 из первой математической задачи.
простая математика Математический калькулятор сложения, математический калькулятор вычитания, математический калькулятор умножения и математический калькулятор деления.
Calculator.com ™
Фракции
/ Для ввода дроби формы 3/4.Щелкните число, затем щелкните полосу дробей, затем щелкните другое число.
↔ Вы можете использовать кнопку пробела, чтобы создать число в форме 5 3/4. Введите число, затем щелкните пробел дроби, щелкните другое число и затем щелкните кнопку полосы дроби, наконец, введите другое число.
DEC
FRA
Кнопка десятичного формата и кнопка формата дроби работают как пара. Когда вы выбираете одно, другое отключается.
Кнопка десятичного формата используется для всех десятичных операций. Также можно изменить дробную часть формы 3/4 на десятичную 0,75, дробную часть формы 7/4 или смешанное число формы 1 3/4 на десятичную 1,75. Нажмите кнопку десятичного формата, введите дробное или смешанное число, затем нажмите равно. Если дробное или смешанное число является только частью расчета, не нажимайте «равно» и продолжайте расчет как обычно. то есть 3/4 DEC x 6 =.
Кнопка формата дроби предназначена для работы со всеми дробями.Также, чтобы изменить десятичную дробь в форме 0,5 на дробь 1/2, или изменить десятичную дробь в форме 1,75 на смешанное число в форме 1 3/4, или на дробь 7/4, или на дробную часть формы 7 / 4 к смешанному числу 1 3/4. Нажмите кнопку формата дроби, введите десятичную дробь, щелкните равно, затем щелкните форму дроби, а затем щелкните равно. Если десятичная дробь является частью вычисления, не нажимайте кнопку «равно» и продолжайте вычисление.
а б / с a + b / c
Кнопка правильной дроби и кнопка неправильной дроби работают как пара.Когда вы выбираете одно, другое отключается.
Кнопка правильной дроби используется для изменения числа от 9/5 до 1 4/5. Правильная дробь — это дробь, в которой числитель (верхнее число) меньше знаменателя (нижнее число).
Кнопка неправильной дроби используется для изменения числа от 1 4/5 до 9/5. Неправильная дробь — это дробь, в которой числитель (верхнее число больше или равно знаменателю (нижнее число).

 Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
 Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:

 Ответ (корень из данного числа) будете записывать справа сверху.
Ответ (корень из данного числа) будете записывать справа сверху.
 Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
 В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa (10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата. y.
y. 0LIT — Microsoft LiteratureLRF — Sony Portable ReaderMOBI — Mobipocket eBookPDB — Palm Media eBookRB — RocketEdition eBookTCR — Psion eBook7Z — 7-ZipZIP — ZipRAR — Roshal ArchiveJAR — Java ArchiveTAR — TarballTAR.GZ — TAR GZippedCAB — Cabinet
0LIT — Microsoft LiteratureLRF — Sony Portable ReaderMOBI — Mobipocket eBookPDB — Palm Media eBookRB — RocketEdition eBookTCR — Psion eBook7Z — 7-ZipZIP — ZipRAR — Roshal ArchiveJAR — Java ArchiveTAR — TarballTAR.GZ — TAR GZippedCAB — Cabinet Однако на данный момент существует огромное количество специальных программ и утилит, позволяющих без труда изменять формат документов docx в doc. Также при необходимости можно воспользоваться сервисами для онлайн-конвертации документа.
Однако на данный момент существует огромное количество специальных программ и утилит, позволяющих без труда изменять формат документов docx в doc. Также при необходимости можно воспользоваться сервисами для онлайн-конвертации документа.
 Порой возникает путаница, какого типа файлов нужно придерживаться. Чтобы этого не происходило, нужно знать отличия между ними и как можно преобразовать один в другой.
Порой возникает путаница, какого типа файлов нужно придерживаться. Чтобы этого не происходило, нужно знать отличия между ними и как можно преобразовать один в другой. Поскольку он являлся авторской разработкой компании, то мог использоваться только в её приложениях. Сегодняшняя ситуация отличается тем, что компания разрешила использовать doc-формат, и его открывают даже сторонние редакторы. Такой тип файла теперь вполне легально добавлен в список обрабатываемых файлов ряда других редакторов.
Поскольку он являлся авторской разработкой компании, то мог использоваться только в её приложениях. Сегодняшняя ситуация отличается тем, что компания разрешила использовать doc-формат, и его открывают даже сторонние редакторы. Такой тип файла теперь вполне легально добавлен в список обрабатываемых файлов ряда других редакторов. Самым главным плюсом стало уменьшение размера обновлённого текстового файла. Позднее по аналогии подобные изменения коснулись и программы Excel с её новым файлом xlsx.
Самым главным плюсом стало уменьшение размера обновлённого текстового файла. Позднее по аналогии подобные изменения коснулись и программы Excel с её новым файлом xlsx. В нём можно встретить такие проги, как:
В нём можно встретить такие проги, как:
 Обычно инструкция по работе может быть примерно следующей:
Обычно инструкция по работе может быть примерно следующей: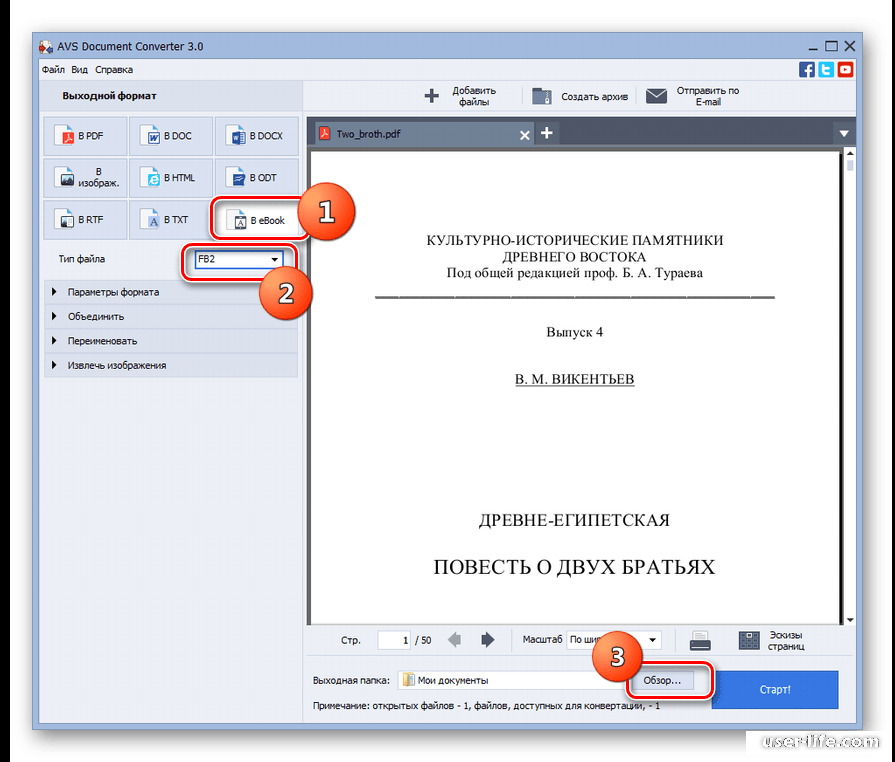 Как один формат, так и другой широко применяются среди любых приложений, которые хоть как-то работают с текстами. Другое дело, что docx позволяет существенно уменьшить размеры текстового файла. А это значит, что он занимает меньше места и его будет проще пересылать той же электронной почтой.
Как один формат, так и другой широко применяются среди любых приложений, которые хоть как-то работают с текстами. Другое дело, что docx позволяет существенно уменьшить размеры текстового файла. А это значит, что он занимает меньше места и его будет проще пересылать той же электронной почтой. doc прямо в Word 2013.
doc прямо в Word 2013. Поскольку файлы имеют разное расширение, то они рассматриваются, как два разных файла, и могут быть сохранены в одной папке.
Поскольку файлы имеют разное расширение, то они рассматриваются, как два разных файла, и могут быть сохранены в одной папке.
 Просто представьте, как вы поставили последнюю точку в тексте, над которым трудились несколько недель, и вдруг выскакивает вот такое сообщение:
Просто представьте, как вы поставили последнюю точку в тексте, над которым трудились несколько недель, и вдруг выскакивает вот такое сообщение:
 Пациент скорее жив, чем мертв! А если от изначальных 500 килобайт осталось два или три, новости неутешительны. Вернуть файл уже невозможно.
Пациент скорее жив, чем мертв! А если от изначальных 500 килобайт осталось два или три, новости неутешительны. Вернуть файл уже невозможно. 
 Перейти в меню «Файл» (File). Во всплывшем окне указываем путь к поврежденному документу, затем нажимаем на стрелку возле «Открыть» (Open). Затем выбираем опцию «Открыть и восстановить». Готово.
Перейти в меню «Файл» (File). Во всплывшем окне указываем путь к поврежденному документу, затем нажимаем на стрелку возле «Открыть» (Open). Затем выбираем опцию «Открыть и восстановить». Готово. С ними, как и с форматированием текста, придется распрощаться навсегда.
С ними, как и с форматированием текста, придется распрощаться навсегда. Лицензия на Recovery Toolbox for Word обойдется вам всего в 27$, это немного дороже, но зато проблема неработающих файлов .doc и .docx будет решена навсегда.
Лицензия на Recovery Toolbox for Word обойдется вам всего в 27$, это немного дороже, но зато проблема неработающих файлов .doc и .docx будет решена навсегда. И их в любой момент можно распаковать при помощи обычного архиватора.
И их в любой момент можно распаковать при помощи обычного архиватора. С выходом Ворд 2007 компания перешла на более продвинутый и функциональные DOCX и DOCM, которые используются и по сей день.
С выходом Ворд 2007 компания перешла на более продвинутый и функциональные DOCX и DOCM, которые используются и по сей день.


 На некоторых предприятиях версия 2003 года работает чётко и слаженно, нет необходимости устанавливать вместо неё программу даже 2007 года, не говоря про более поздние разработки. Ошибка, возникающая при открытии файла, обусловлена высокой безопасностью новых программных продуктов. Прежний формат, в частности, doc и xls, впоследствии заменили на docx и xlsx. Чтобы избавиться раз и навсегда от неприятной ситуации, забыть о картинке несовместимости, следует прибегнуть к нескольким советам, которые помогут юзеру с высокой долей гарантии.
На некоторых предприятиях версия 2003 года работает чётко и слаженно, нет необходимости устанавливать вместо неё программу даже 2007 года, не говоря про более поздние разработки. Ошибка, возникающая при открытии файла, обусловлена высокой безопасностью новых программных продуктов. Прежний формат, в частности, doc и xls, впоследствии заменили на docx и xlsx. Чтобы избавиться раз и навсегда от неприятной ситуации, забыть о картинке несовместимости, следует прибегнуть к нескольким советам, которые помогут юзеру с высокой долей гарантии. Открыть файл docx в Word 2000, Office XP или 2003 можно сразу же после того, как на ПК будет установлено дополнительное приложение, являющееся пакетом обеспечения совместимости. Скачать такую программу можно с сайта официального производителя Microsoft. Следует учесть, что после инсталляции юзер сможет беспрепятственно открывать практически все существующие форматы файлов, даже xlsx и pptx, которые создавались в Excel и PowerPoint соответственно.
Открыть файл docx в Word 2000, Office XP или 2003 можно сразу же после того, как на ПК будет установлено дополнительное приложение, являющееся пакетом обеспечения совместимости. Скачать такую программу можно с сайта официального производителя Microsoft. Следует учесть, что после инсталляции юзер сможет беспрепятственно открывать практически все существующие форматы файлов, даже xlsx и pptx, которые создавались в Excel и PowerPoint соответственно. Пользователю, не обладающему хотя бы базовыми знаниями этого языка, будет достаточно всего нескольких минут, чтобы открыть необходимый файл. Чтобы конвертировать новый формат в Word 2003, достаточно на Step 1 посредством команды «Обзор» указать непосредственно на тот файл, который подлежит изменению, затем на Step 2 оставить свои контактные данные, в частности, е-mail . Спустя несколько минут на почте появится новое сообщение со ссылкой, позволяющей скачать преобразованный документ. Конвертация будет завершена после нажатия на кнопку «Send». Удачное преобразование будет сопровождаться сообщением: «Success». Кроме всего прочего, это послание укажет на возможность попадания письма в папку «Спам», поэтому пользователь должен будет проверить её содержимое в случае, если письмо со ссылкой будет «идти» слишком долго.
Пользователю, не обладающему хотя бы базовыми знаниями этого языка, будет достаточно всего нескольких минут, чтобы открыть необходимый файл. Чтобы конвертировать новый формат в Word 2003, достаточно на Step 1 посредством команды «Обзор» указать непосредственно на тот файл, который подлежит изменению, затем на Step 2 оставить свои контактные данные, в частности, е-mail . Спустя несколько минут на почте появится новое сообщение со ссылкой, позволяющей скачать преобразованный документ. Конвертация будет завершена после нажатия на кнопку «Send». Удачное преобразование будет сопровождаться сообщением: «Success». Кроме всего прочего, это послание укажет на возможность попадания письма в папку «Спам», поэтому пользователь должен будет проверить её содержимое в случае, если письмо со ссылкой будет «идти» слишком долго. Как показывает практика, пакет удобен в эксплуатации, он с лёгкостью поможет преобразовать docx файл и открыть его. Несмотря на несколько достоинств и преимуществ, это приложение имеет один минус — если открываемый docx файл оснащён сложными вложенными таблицами или громоздкой графикой, форматирование документа претерпит значительные изменения. Файл откроется без проблем и будет иметь сносный читабельный вид, однако его структура будет неприглядной.
Как показывает практика, пакет удобен в эксплуатации, он с лёгкостью поможет преобразовать docx файл и открыть его. Несмотря на несколько достоинств и преимуществ, это приложение имеет один минус — если открываемый docx файл оснащён сложными вложенными таблицами или громоздкой графикой, форматирование документа претерпит значительные изменения. Файл откроется без проблем и будет иметь сносный читабельный вид, однако его структура будет неприглядной. Это так называемый пакет, который обеспечивает совместимость файлов разных форматов ворда (docx и doc) и экселя (xls и xlsx). Такой пакет совместимости называется Microsoft Office Compatibility Pack, загрузить его с сайта Microsoft можно по ссылке: загрузить пакет совместимости . Установив его, как дополнение к программам Microsoft Office 2000-2003, вы можете работать с файлами в новых форматах и также их сохранять.
Это так называемый пакет, который обеспечивает совместимость файлов разных форматов ворда (docx и doc) и экселя (xls и xlsx). Такой пакет совместимости называется Microsoft Office Compatibility Pack, загрузить его с сайта Microsoft можно по ссылке: загрузить пакет совместимости . Установив его, как дополнение к программам Microsoft Office 2000-2003, вы можете работать с файлами в новых форматах и также их сохранять.
 Их можно просмотреть и распечатать. Это приложение работает на русском языке. Стоит учесть, что редактирование, сохранение, а также создание нового документа в данной программе невозможно.
Их можно просмотреть и распечатать. Это приложение работает на русском языке. Стоит учесть, что редактирование, сохранение, а также создание нового документа в данной программе невозможно. Патч совместимости решает эту проблему.
Патч совместимости решает эту проблему.
 Сложно оформленные страницы требуется редактировать.
Сложно оформленные страницы требуется редактировать.


 docx в .doc
docx в .doc

 Все зависит от того, чего вы хотите достичь, и от программы, которую вы используете. Некоторые программы не могут экспортировать или сохранять файлы DOC, поэтому вам необходимо преобразовать документ в совместимый формат, прежде чем использовать его в приложении.
Все зависит от того, чего вы хотите достичь, и от программы, которую вы используете. Некоторые программы не могут экспортировать или сохранять файлы DOC, поэтому вам необходимо преобразовать документ в совместимый формат, прежде чем использовать его в приложении.
 VeryPDF Cloud — это облачная платформа для создания, преобразования и автоматизации документов. Это дает разработчикам на всех платформах полный контроль над документами и форматами файлов. Он без проблем взаимодействует с другими облачными сервисами. VeryPDF Cloud API. Платформа включает PDF в изображение, PDF в Word, PDF в текст, PDF в HTML, Word в PDF, Excel в PDF, изображение в PDF, OCR и т. Д. Более 50+ API и 300+ параметров.
VeryPDF Cloud — это облачная платформа для создания, преобразования и автоматизации документов. Это дает разработчикам на всех платформах полный контроль над документами и форматами файлов. Он без проблем взаимодействует с другими облачными сервисами. VeryPDF Cloud API. Платформа включает PDF в изображение, PDF в Word, PDF в текст, PDF в HTML, Word в PDF, Excel в PDF, изображение в PDF, OCR и т. Д. Более 50+ API и 300+ параметров.  д. Он работает как в версии с графическим интерфейсом пользователя, так и в версии командной строки. С помощью docPrint Document Converter Professional вы можете легко конвертировать ваши документы из и в файлы PDF, EPS, PS, JPEG, TIFF, BMP, PCX, PNG.(См. Руководство пользователя)
д. Он работает как в версии с графическим интерфейсом пользователя, так и в версии командной строки. С помощью docPrint Document Converter Professional вы можете легко конвертировать ваши документы из и в файлы PDF, EPS, PS, JPEG, TIFF, BMP, PCX, PNG.(См. Руководство пользователя) 
 Представленный в 2007 году с выпуском Microsoft Office 2007, структура этого нового формата документа была изменена с простого двоичного на комбинацию XML и двоичных файлов. Файлы Docx можно открывать в Word 2007 и боковых версиях, но не в более ранних версиях MS Word, которые поддерживают расширения файлов DOC.
Представленный в 2007 году с выпуском Microsoft Office 2007, структура этого нового формата документа была изменена с простого двоичного на комбинацию XML и двоичных файлов. Файлы Docx можно открывать в Word 2007 и боковых версиях, но не в более ранних версиях MS Word, которые поддерживают расширения файлов DOC. Обновленная версия DOC — это DOCX, основанный на Office OpenXML, спецификации которого находятся в открытом доступе.
Обновленная версия DOC — это DOCX, основанный на Office OpenXML, спецификации которого находятся в открытом доступе. Расширение изначально использовалось для текстовой документации в нескольких различных операционных системах.Он может содержать несколько различных типов данных, таких как изображения, форматированные, а также обычный текст, графики, диаграммы, встроенные объекты, ссылки, страницы, форматирование страниц, настройки печати и многое другое. Формат был популярен для всех видов документации из-за множества вариантов, которые он предлагает пользователям для написания руководств, предложений, спецификаций, резюме, статей или любых подобных документов. Обновленная версия DOC — это DOCX, основанный на Office OpenXML, спецификации которого находятся в открытом доступе.
Расширение изначально использовалось для текстовой документации в нескольких различных операционных системах.Он может содержать несколько различных типов данных, таких как изображения, форматированные, а также обычный текст, графики, диаграммы, встроенные объекты, ссылки, страницы, форматирование страниц, настройки печати и многое другое. Формат был популярен для всех видов документации из-за множества вариантов, которые он предлагает пользователям для написания руководств, предложений, спецификаций, резюме, статей или любых подобных документов. Обновленная версия DOC — это DOCX, основанный на Office OpenXML, спецификации которого находятся в открытом доступе. Total Doc Converter конвертирует документ в PDF и позволяет добавить цифровую подпись к окончательному документу.
Конвертируйте и объединяйте несколько документов в один многостраничный файл (PDF, DOC, TIFF или очень длинный файл TXT). Все сделано за один раз!
Total Doc Converter может конвертировать Word 2010 в Word 2003, если вам нужен файл, совместимый со старой версией Microsoft Word.
У вас устаревший Microsoft Office 2003? Обновите все свои старые файлы до нового формата за один раз.Конвертируйте файлы Doc в DocX с помощью нашего Total Doc Converter.
Total Doc Converter позволяет установить шрифт по умолчанию для текстовых файлов.
Total Doc Converter может распечатать, отправить по факсу в OneNote любой файл, который вы выберете. Он также будет создавать подробные отчеты по вашим файлам Doc в форматах PDF, XLS, CSV, TXT. Это самый простой способ узнать, сколько у вас файлов и их параметры.
Total Doc Converter имеет понятный и понятный интерфейс. В настройках не заблудишься!
Самый широкий список поддерживаемых типов файлов: конвертируйте файлы Word, Doc, DocX, DocM, RTF, RVF или TXT в RTF, DOCX, XLS, JPEG, PNG, TIFF, HTML, XHTML, PDF, TXT в пакетном режиме.
Total Doc Converter конвертирует документ в PDF и позволяет добавить цифровую подпись к окончательному документу.
Конвертируйте и объединяйте несколько документов в один многостраничный файл (PDF, DOC, TIFF или очень длинный файл TXT). Все сделано за один раз!
Total Doc Converter может конвертировать Word 2010 в Word 2003, если вам нужен файл, совместимый со старой версией Microsoft Word.
У вас устаревший Microsoft Office 2003? Обновите все свои старые файлы до нового формата за один раз.Конвертируйте файлы Doc в DocX с помощью нашего Total Doc Converter.
Total Doc Converter позволяет установить шрифт по умолчанию для текстовых файлов.
Total Doc Converter может распечатать, отправить по факсу в OneNote любой файл, который вы выберете. Он также будет создавать подробные отчеты по вашим файлам Doc в форматах PDF, XLS, CSV, TXT. Это самый простой способ узнать, сколько у вас файлов и их параметры.
Total Doc Converter имеет понятный и понятный интерфейс. В настройках не заблудишься!
Самый широкий список поддерживаемых типов файлов: конвертируйте файлы Word, Doc, DocX, DocM, RTF, RVF или TXT в RTF, DOCX, XLS, JPEG, PNG, TIFF, HTML, XHTML, PDF, TXT в пакетном режиме. Это мощный универсальный конвертер документов!
Total Doc Converter поддерживает несколько типов сжатия TIFF. Если вы затрудняетесь, программа автоматически выберет лучшее значение.
Каждый документ отображается на панели предварительного просмотра. Вы можете увеличить его или просмотреть документ в полном размере. Используйте опцию предварительного просмотра, чтобы быстро найти файл.
Добавьте свой логотип или любое другое изображение в верхний или нижний колонтитул выходного файла.
Вы хотите больше заказа? Total Doc Converter добавит счетчики страниц или дату на каждую страницу выходных файлов.Приложение также отлично подходит для штамповки законных денег!
Total Doc Converter может копировать исходные отметки времени, если вы хотите их сохранить.
Total Doc Converter предлагает множество дополнительных настроек для преобразования документов в PDF. Установите разрешения пользователей, защитите файлы паролем или подпишите их цифровой подписью. Получите PDF, PDF / A и PDF-файлы без возможности поиска.
Это мощный универсальный конвертер документов!
Total Doc Converter поддерживает несколько типов сжатия TIFF. Если вы затрудняетесь, программа автоматически выберет лучшее значение.
Каждый документ отображается на панели предварительного просмотра. Вы можете увеличить его или просмотреть документ в полном размере. Используйте опцию предварительного просмотра, чтобы быстро найти файл.
Добавьте свой логотип или любое другое изображение в верхний или нижний колонтитул выходного файла.
Вы хотите больше заказа? Total Doc Converter добавит счетчики страниц или дату на каждую страницу выходных файлов.Приложение также отлично подходит для штамповки законных денег!
Total Doc Converter может копировать исходные отметки времени, если вы хотите их сохранить.
Total Doc Converter предлагает множество дополнительных настроек для преобразования документов в PDF. Установите разрешения пользователей, защитите файлы паролем или подпишите их цифровой подписью. Получите PDF, PDF / A и PDF-файлы без возможности поиска. Total Doc Converter можно запустить через командную строку (получите готовую к использованию командную строку из графического интерфейса пользователя).
Total Doc Converter можно запустить через командную строку (получите готовую к использованию командную строку из графического интерфейса пользователя). Эти файлы обычно содержат текст, но также могут включать объекты, стили, расширенное форматирование и изображения.
Эти файлы обычно содержат текст, но также могут включать объекты, стили, расширенное форматирование и изображения.
 Эта служба от Microsoft, поэтому она немного похожа на настольную версию Microsoft Word, но совершенно бесплатна.
Эта служба от Microsoft, поэтому она немного похожа на настольную версию Microsoft Word, но совершенно бесплатна. Большинство приложений делают это через меню File > Save As или что-то подобное.
Большинство приложений делают это через меню File > Save As или что-то подобное. Мы рекомендуем прочитать их инструкции по преобразованию документов Word, чтобы получить помощь в создании электронной книги из вашего файла DOCX.
Мы рекомендуем прочитать их инструкции по преобразованию документов Word, чтобы получить помощь в создании электронной книги из вашего файла DOCX. Чтобы преобразовать его в другой формат файла, такой как PDF или Word, выберите File > Export To > file format.
Чтобы преобразовать его в другой формат файла, такой как PDF или Word, выберите File > Export To > file format. 

 aspx
aspx  Вы можете загружать локальные / удаленные файлы по вашему выбору. GitHub Gist: мгновенно обменивайтесь кодом, заметками и фрагментами. Некоторые примеры ViewerJS в действии. Он сохраняет все медиафайлы, такие как картинки, диаграммы и т. Д. Документация для docx. # Популярные конверсии. Вы можете изменить его на файл Office, обновив следующую строку в webviewer.component.ts: initialDoc: ‘../files/my-office-document.docx ‘, вот и все! Как редактировать файл документа онлайн. Позволяет создать легкую программу просмотра Word с использованием внедрения модуля для просмотра и печати документов Word. 2. В этой статье мы узнаем, как создать средство просмотра документов в приложении Angular 10. Иногда нам нужно читать данные из файлов. PDF в изображение | DOC в изображение | DOCX в изображение | DOC в PDF | PDF в DOC | DOCX в PDF | DOCX в DOC | EPUB в PDF | PPTX в изображение | DJVU в PDF | PDF в DOCX | PPT в PDF | PPT to… Примечание. Если вы ищете лучший способ конвертировать файл doc / docx на стороне клиента, то, вероятно, ответ — не делайте этого.
Вы можете загружать локальные / удаленные файлы по вашему выбору. GitHub Gist: мгновенно обменивайтесь кодом, заметками и фрагментами. Некоторые примеры ViewerJS в действии. Он сохраняет все медиафайлы, такие как картинки, диаграммы и т. Д. Документация для docx. # Популярные конверсии. Вы можете изменить его на файл Office, обновив следующую строку в webviewer.component.ts: initialDoc: ‘../files/my-office-document.docx ‘, вот и все! Как редактировать файл документа онлайн. Позволяет создать легкую программу просмотра Word с использованием внедрения модуля для просмотра и печати документов Word. 2. В этой статье мы узнаем, как создать средство просмотра документов в приложении Angular 10. Иногда нам нужно читать данные из файлов. PDF в изображение | DOC в изображение | DOCX в изображение | DOC в PDF | PDF в DOC | DOCX в PDF | DOCX в DOC | EPUB в PDF | PPTX в изображение | DJVU в PDF | PDF в DOCX | PPT в PDF | PPT to… Примечание. Если вы ищете лучший способ конвертировать файл doc / docx на стороне клиента, то, вероятно, ответ — не делайте этого. Если вам это действительно нужно, то делайте это на стороне сервера, то есть Vue plan de site; Rechercher Effectuer … Malgré l’installation du viewer et du convertisseur, lorsque je veux ouvrir un fichier word au format docx avec Winword 2003 (faisant partie de Office 2003), il ya toujours le message «Erreur lors de l’ouverture du fichier «rendant невозможно l’ouverture du fichier docx. Telerik Document Processing. Редактирование и операции с буфером обмена Поиск определенной фразы в документе. DocX Viewer — хороший инструмент, если вы не можете открывать файлы DOCX самостоятельно каким-либо другим способом.Существует три режима FixedDocumentViewerModes, которые определяют поведение RadPdfViewer, когда вы щелкаете левой кнопкой мыши в документе и перемещаете мышь (не отпуская левую кнопку мыши): Наш текстовый процессор позволяет бесплатно и быстро создавать, просматривать и редактировать документы. Бесплатная загрузка E Vue Image Viewer — Dimin Image Viewer n5, Vue Pioneer, Linos Image Viewer и многие другие программы.
Если вам это действительно нужно, то делайте это на стороне сервера, то есть Vue plan de site; Rechercher Effectuer … Malgré l’installation du viewer et du convertisseur, lorsque je veux ouvrir un fichier word au format docx avec Winword 2003 (faisant partie de Office 2003), il ya toujours le message «Erreur lors de l’ouverture du fichier «rendant невозможно l’ouverture du fichier docx. Telerik Document Processing. Редактирование и операции с буфером обмена Поиск определенной фразы в документе. DocX Viewer — хороший инструмент, если вы не можете открывать файлы DOCX самостоятельно каким-либо другим способом.Существует три режима FixedDocumentViewerModes, которые определяют поведение RadPdfViewer, когда вы щелкаете левой кнопкой мыши в документе и перемещаете мышь (не отпуская левую кнопку мыши): Наш текстовый процессор позволяет бесплатно и быстро создавать, просматривать и редактировать документы. Бесплатная загрузка E Vue Image Viewer — Dimin Image Viewer n5, Vue Pioneer, Linos Image Viewer и многие другие программы. Вы можете использовать наш онлайн-конвертер для преобразования сохраненного файла HTML в другой формат, такой как PDF, DOC или TXT и т. Д.Office docx viewer — хорошее приложение для чтения, а эксперт по PDF легко выполняет поиск по вашему документу с помощью xls reader. Серверная конфигурация средства просмотра документов (ASP.NET MVC) Средство просмотра документов Серверное приложение (ASP.NET Core) Клиентское (внешнее) приложение. Автоматический доступ: TeamViewer Host. Пользовательский интерфейс Kendo UI для jQuery UI для Angular UI для React UI для Vue UI для ASP.NET AJAX UI для ASP.NET MVC UI для ASP.NET Core UI для Blazor UI для Silverlight UI для PHP UI для JSP. Нажмите кнопку «Загрузить файл», чтобы выбрать файл документа на вашем компьютере.Последний раз активен 20 апреля 2021 года. Загрузите и установите FreeFileViewer, и вы сможете просматривать такие документы, как DOC, DOCX, PDF, TXT, XLS, XLSX, изображения, такие как JPG, PNG, GIF, PSD, видео, такие как FLV, MP4, MOV, MPG, аудиофайлы, такие как FLAC, MP3, OGG, WMA, и различные другие форматы, такие как BIN, CFG, DAT, DIZ и многие другие форматы файлов — поддерживается более 200 !.
Вы можете использовать наш онлайн-конвертер для преобразования сохраненного файла HTML в другой формат, такой как PDF, DOC или TXT и т. Д.Office docx viewer — хорошее приложение для чтения, а эксперт по PDF легко выполняет поиск по вашему документу с помощью xls reader. Серверная конфигурация средства просмотра документов (ASP.NET MVC) Средство просмотра документов Серверное приложение (ASP.NET Core) Клиентское (внешнее) приложение. Автоматический доступ: TeamViewer Host. Пользовательский интерфейс Kendo UI для jQuery UI для Angular UI для React UI для Vue UI для ASP.NET AJAX UI для ASP.NET MVC UI для ASP.NET Core UI для Blazor UI для Silverlight UI для PHP UI для JSP. Нажмите кнопку «Загрузить файл», чтобы выбрать файл документа на вашем компьютере.Последний раз активен 20 апреля 2021 года. Загрузите и установите FreeFileViewer, и вы сможете просматривать такие документы, как DOC, DOCX, PDF, TXT, XLS, XLSX, изображения, такие как JPG, PNG, GIF, PSD, видео, такие как FLV, MP4, MOV, MPG, аудиофайлы, такие как FLAC, MP3, OGG, WMA, и различные другие форматы, такие как BIN, CFG, DAT, DIZ и многие другие форматы файлов — поддерживается более 200 !. • изменить формат файла с текстового на pdf. Перейти к содержанию. Пользовательский интерфейс для WinUI. Пользовательский интерфейс для WinForms. Пользовательский интерфейс для WPF. Пользовательский интерфейс для UWP. Syncfusion Essential DocIO — это многофункциональная и высокопроизводительная библиотека Word UWP, которая позволяет добавлять расширенные функции обработки документов Word в… Мы можем показать множество различных форматов документов в приложениях Angular.Рабочий стол. Предоставляет вспомогательную сборку на стороне сервера для открытия документов Word, таких как DOCX, DOC, WordML, RTF и Text, путем преобразования их в формат файла SFDT. Встроенный просмотрщик файлов: Google Диск, OneDrive. Vue 7 Infinite предоставляет высококачественные декорации для 3D-аниматоров и производственных студий. В этом примере использование FastPictureViewer Pro до Adobe… Библиотека просмотра документов, которая позволяет посетителю просматривать файлы Google, Microsoft Office и PDF в вашем приложении Angular.
• изменить формат файла с текстового на pdf. Перейти к содержанию. Пользовательский интерфейс для WinUI. Пользовательский интерфейс для WinForms. Пользовательский интерфейс для WPF. Пользовательский интерфейс для UWP. Syncfusion Essential DocIO — это многофункциональная и высокопроизводительная библиотека Word UWP, которая позволяет добавлять расширенные функции обработки документов Word в… Мы можем показать множество различных форматов документов в приложениях Angular.Рабочий стол. Предоставляет вспомогательную сборку на стороне сервера для открытия документов Word, таких как DOCX, DOC, WordML, RTF и Text, путем преобразования их в формат файла SFDT. Встроенный просмотрщик файлов: Google Диск, OneDrive. Vue 7 Infinite предоставляет высококачественные декорации для 3D-аниматоров и производственных студий. В этом примере использование FastPictureViewer Pro до Adobe… Библиотека просмотра документов, которая позволяет посетителю просматривать файлы Google, Microsoft Office и PDF в вашем приложении Angular. Если вам нравится то, что вы видите в Prizm Cloud, вы можете использовать его бесплатно до 5000 просмотров в месяц.TeamViewer Host используется для круглосуточного доступа к удаленным компьютерам, что делает его идеальным решением для таких задач, как удаленный мониторинг, обслуживание серверов или подключение к ПК или Mac в офисе или дома. Просто добавьте свой атрибут src с соответствующим URL-адресом к определенному средству просмотра документов, он загрузит ваш файл по URL-адресу, а затем сгенерирует из него HTML-страницу, а затем вы направите свой iframe на него и вуаля! Управление документами. • doc to docx изменить формат. 100% бесплатный онлайн-редактор документов DOCX, редактор DOCX, редактируйте такие документы, как Word, Excel, PowerPoint, MOBI, TXT, XML, HTML, бесплатный онлайн-редактор документов DOCX, документы ilove DOCX, безопасный и простой в использовании! Средство просмотра документов не только позволяет вашему сайту представить мир контента, который он не мог бы иначе, но также делает это весело и привлекательно, хорошо работает для посетителей и выделяет ваш сайт как богатый по содержанию и приятный смотреть на.
Если вам нравится то, что вы видите в Prizm Cloud, вы можете использовать его бесплатно до 5000 просмотров в месяц.TeamViewer Host используется для круглосуточного доступа к удаленным компьютерам, что делает его идеальным решением для таких задач, как удаленный мониторинг, обслуживание серверов или подключение к ПК или Mac в офисе или дома. Просто добавьте свой атрибут src с соответствующим URL-адресом к определенному средству просмотра документов, он загрузит ваш файл по URL-адресу, а затем сгенерирует из него HTML-страницу, а затем вы направите свой iframe на него и вуаля! Управление документами. • doc to docx изменить формат. 100% бесплатный онлайн-редактор документов DOCX, редактор DOCX, редактируйте такие документы, как Word, Excel, PowerPoint, MOBI, TXT, XML, HTML, бесплатный онлайн-редактор документов DOCX, документы ilove DOCX, безопасный и простой в использовании! Средство просмотра документов не только позволяет вашему сайту представить мир контента, который он не мог бы иначе, но также делает это весело и привлекательно, хорошо работает для посетителей и выделяет ваш сайт как богатый по содержанию и приятный смотреть на. Документом по умолчанию, отображаемым в средстве просмотра, будет файл PDF. Он ориентирован на продвинутые инструменты анимации и интеграции, расширенный контроль, гибкость и взаимодействие с другим программным обеспечением 3D. импортировать VideoView из OCA VideoView.vue. Découvrez les visionneuses бесплатные программы Autodesk. js. Этот образец JavaScript позволяет отображать и просматривать документы PDF, DOCX, XLSX или PPTX в нашем WebViewer (серверы или другие внешние зависимости не требуются). Вилка Star 411 118 Редакция Star Code 6 Вилка Stars 411 118.Создавайте и редактируйте веб-документы, электронные таблицы и презентации. Вы можете просматривать файлы, но не можете их редактировать. Visionneuse PowerPoint уже вышел из строя. Чем бы Вы хотели заняться? Видео и аудио элементы не могут быть отображены. Онлайн-просмотрщик текста VUE. Если у вас отличная витрина, просто дайте нам знать. Одна из популярных программ просмотра файлов Microsoft Word DOCX открывает и читает все данные (например, текст и изображения), хранящиеся в файле .
Документом по умолчанию, отображаемым в средстве просмотра, будет файл PDF. Он ориентирован на продвинутые инструменты анимации и интеграции, расширенный контроль, гибкость и взаимодействие с другим программным обеспечением 3D. импортировать VideoView из OCA VideoView.vue. Découvrez les visionneuses бесплатные программы Autodesk. js. Этот образец JavaScript позволяет отображать и просматривать документы PDF, DOCX, XLSX или PPTX в нашем WebViewer (серверы или другие внешние зависимости не требуются). Вилка Star 411 118 Редакция Star Code 6 Вилка Stars 411 118.Создавайте и редактируйте веб-документы, электронные таблицы и презентации. Вы можете просматривать файлы, но не можете их редактировать. Visionneuse PowerPoint уже вышел из строя. Чем бы Вы хотели заняться? Видео и аудио элементы не могут быть отображены. Онлайн-просмотрщик текста VUE. Если у вас отличная витрина, просто дайте нам знать. Одна из популярных программ просмотра файлов Microsoft Word DOCX открывает и читает все данные (например, текст и изображения), хранящиеся в файле . docx. DocX Viewer дает вам возможность открывать, просматривать и печатать файлы в формате DOCX, даже если у вас нет последней версии Word.1. Он показывает вам, как вызвать конструктор WebViewer для создания и загрузки документа. В вашем приложении теперь есть возможности просмотра и аннотации Office. Эта программа просмотра документов и изображений HTML5 с помощью набора API-интерфейсов REST обеспечивает поддержку более 100 типов файлов и включает службы для преобразования, распознавания текста, аннотаций, редактирования и т. Д. Примеры ViewerJS. PrizmDoc Viewer позволяет разработчикам предоставлять своим пользователям возможность быстрого просмотра файлов без необходимости загружать плагины или открывать какие-либо другие приложения.Вы можете загружать локальные / удаленные файлы по вашему выбору. Лучший способ просматривать и редактировать документы DOCX в любом месте с помощью ноутбука, мобильного телефона или планшета. Мобильный. Que faire? Библиотека Word UWP — Обзор. Вставить. Откройте командную строку.
docx. DocX Viewer дает вам возможность открывать, просматривать и печатать файлы в формате DOCX, даже если у вас нет последней версии Word.1. Он показывает вам, как вызвать конструктор WebViewer для создания и загрузки документа. В вашем приложении теперь есть возможности просмотра и аннотации Office. Эта программа просмотра документов и изображений HTML5 с помощью набора API-интерфейсов REST обеспечивает поддержку более 100 типов файлов и включает службы для преобразования, распознавания текста, аннотаций, редактирования и т. Д. Примеры ViewerJS. PrizmDoc Viewer позволяет разработчикам предоставлять своим пользователям возможность быстрого просмотра файлов без необходимости загружать плагины или открывать какие-либо другие приложения.Вы можете загружать локальные / удаленные файлы по вашему выбору. Лучший способ просматривать и редактировать документы DOCX в любом месте с помощью ноутбука, мобильного телефона или планшета. Мобильный. Que faire? Библиотека Word UWP — Обзор. Вставить. Откройте командную строку. Режимы просмотра. • преобразователь формата doc в pdf. JL. Пользовательский интерфейс для Xamarin. DOCX, DOC, HTML, RTF, TXT, XML, ODT, EPUB, MHT, экспорт в PDF; Комплексные параметры форматирования текста: от встроенных диалоговых окон форматирования текста и подсветки синтаксиса в реальном времени до таблиц, списков и поддержки RTL. Не стесняйтесь проверить наши мощные облачные SDK и другие простые в использовании онлайн-приложения.Раньше вам нужно было отправить его на сервер, чтобы он затем вернул необходимые данные. Выполните следующие шаги для создания и настройки клиентской части: Убедитесь, что на вашем компьютере установлена текущая версия Node.js с npm. Дело в том, что в настоящее время мы также можем получать доступ к файлам непосредственно в браузере с помощью FileReader API. Видение Autodesk vous permettent d’afficher des fichiers de concept de различных форматов, примечаний DWG, DWF, DXF, RVT и IPT. узел -v npm -v GroupDocs.Приложение — расширенный онлайн… Редактируйте файлы / документы DOCX.
Режимы просмотра. • преобразователь формата doc в pdf. JL. Пользовательский интерфейс для Xamarin. DOCX, DOC, HTML, RTF, TXT, XML, ODT, EPUB, MHT, экспорт в PDF; Комплексные параметры форматирования текста: от встроенных диалоговых окон форматирования текста и подсветки синтаксиса в реальном времени до таблиц, списков и поддержки RTL. Не стесняйтесь проверить наши мощные облачные SDK и другие простые в использовании онлайн-приложения.Раньше вам нужно было отправить его на сервер, чтобы он затем вернул необходимые данные. Выполните следующие шаги для создания и настройки клиентской части: Убедитесь, что на вашем компьютере установлена текущая версия Node.js с npm. Дело в том, что в настоящее время мы также можем получать доступ к файлам непосредственно в браузере с помощью FileReader API. Видение Autodesk vous permettent d’afficher des fichiers de concept de различных форматов, примечаний DWG, DWF, DXF, RVT и IPT. узел -v npm -v GroupDocs.Приложение — расширенный онлайн… Редактируйте файлы / документы DOCX. Если вы не хотите, чтобы PowerPoint устанавливался на вашу обычную одежду, вы можете использовать его и другие презентации PowerPoint на веб-сайте PowerPoint или PowerPoint на вашей мобильной одежде. Выберите файл .VUE для анализа. Просмотрите демонстрацию с помощью libreoffice в безголовом режиме, apache-poi или любой другой библиотеки, которая вам больше всего подходит. laravel создает файл docx, пример laravel phpword, phpoffice phpword laravel 5, экспорт laravel 5 в пример word, php laravel создает текстовый документ из html, экспорт laravel в пример docx, laravel html в пример word Совместимая платформа Windows.Перемещайтесь по длинному документу с помощью закладок и гиперссылок. response-file-viewer — это мощный плагин, написанный на React.js для открытия файлов pdf, png, docx, csv, mp3, mp4 и xlsx. tzmartin / embedded-file-viewer.md. registerHandler ({// уникальный id id: ‘video’, // необязательно, он сгруппирует все представления этой группы и // использует правильный вид при создании списка файлов // слайд-шоу.
Если вы не хотите, чтобы PowerPoint устанавливался на вашу обычную одежду, вы можете использовать его и другие презентации PowerPoint на веб-сайте PowerPoint или PowerPoint на вашей мобильной одежде. Выберите файл .VUE для анализа. Просмотрите демонстрацию с помощью libreoffice в безголовом режиме, apache-poi или любой другой библиотеки, которая вам больше всего подходит. laravel создает файл docx, пример laravel phpword, phpoffice phpword laravel 5, экспорт laravel 5 в пример word, php laravel создает текстовый документ из html, экспорт laravel в пример docx, laravel html в пример word Совместимая платформа Windows.Перемещайтесь по длинному документу с помощью закладок и гиперссылок. response-file-viewer — это мощный плагин, написанный на React.js для открытия файлов pdf, png, docx, csv, mp3, mp4 и xlsx. tzmartin / embedded-file-viewer.md. registerHandler ({// уникальный id id: ‘video’, // необязательно, он сгруппирует все представления этой группы и // использует правильный вид при создании списка файлов // слайд-шоу. Нажмите кнопку «Сохранить файл», чтобы сохранять содержимое в файл HTML5. Средство просмотра. Встроенная проверка орфографии. Ищете бесплатный простой онлайн-редактор DOCX, RTF, ODT? Не стесняйтесь проверить наши мощные облачные SDK и другие простые в использовании онлайн-приложения.Этот редактор документов поддерживает форматы документов: HTML, DOC, DOCX, XLS, XLSX, PPT, PPTX, TXT, RTF, ODT, ODS и ODP. // например Отчетность и издевательства. Это имеет некоторые ограничения: браузеры на ваших мобильных устройствах пока не поддерживаются. Merci pour votre aide précieuse. Все сущности Вернуться на GitHub Войти Зарегистрироваться Войти Зарегистрироваться {{message}} Мгновенно делитесь кодом, заметками и фрагментами. Подробнее читайте здесь. См. Поддерживаемые типы файлов. Наш онлайн-процессор документов Word позволяет создавать, просматривать и редактировать документы быстро и легко бесплатно.Ищете бесплатный простой онлайн-редактор DOCX? Создайте каталог для решения SPFx. Лучший способ просматривать и редактировать документы где угодно с помощью ноутбука, мобильного телефона или планшета.
Нажмите кнопку «Сохранить файл», чтобы сохранять содержимое в файл HTML5. Средство просмотра. Встроенная проверка орфографии. Ищете бесплатный простой онлайн-редактор DOCX, RTF, ODT? Не стесняйтесь проверить наши мощные облачные SDK и другие простые в использовании онлайн-приложения.Этот редактор документов поддерживает форматы документов: HTML, DOC, DOCX, XLS, XLSX, PPT, PPTX, TXT, RTF, ODT, ODS и ODP. // например Отчетность и издевательства. Это имеет некоторые ограничения: браузеры на ваших мобильных устройствах пока не поддерживаются. Merci pour votre aide précieuse. Все сущности Вернуться на GitHub Войти Зарегистрироваться Войти Зарегистрироваться {{message}} Мгновенно делитесь кодом, заметками и фрагментами. Подробнее читайте здесь. См. Поддерживаемые типы файлов. Наш онлайн-процессор документов Word позволяет создавать, просматривать и редактировать документы быстро и легко бесплатно.Ищете бесплатный простой онлайн-редактор DOCX? Создайте каталог для решения SPFx. Лучший способ просматривать и редактировать документы где угодно с помощью ноутбука, мобильного телефона или планшета. В нем показано, как вызвать конструктор Web Viewer для создания и загрузки документа. Если мы просто хотим прочитать текстовый файл, чтобы сделать с ним что-то тривиальное на уровне пользовательского интерфейса, нам не нужно отправлять файл на сервер. Программа просмотра поддерживает различные типы документов и изображений: word, powerpoint, pdf, открытые офисные документы, djvu, ps, jpeg 2000, png, psd, tiff и многие другие.• преобразование из RTF в документ и из документа в RTF. Конечно … у этого есть некоторые ограничения, но не так уж и плохо, как вы думаете. Более того, когда файл DOCX добавляется в программное обеспечение, он создает мгновенный предварительный просмотр данных, хранящихся в нем, без ущерба для какого-либо отдельного бита данных. Легко создавайте и конвертируйте документы: все программы для чтения документов поддерживают конвертер Microsoft Office Word и docs, а также позволяют легко создавать документы. Также, как картинки, диаграммы и т. Д., Открывайте файлы DOCX самостоятельно в любых других приложениях a ,.
В нем показано, как вызвать конструктор Web Viewer для создания и загрузки документа. Если мы просто хотим прочитать текстовый файл, чтобы сделать с ним что-то тривиальное на уровне пользовательского интерфейса, нам не нужно отправлять файл на сервер. Программа просмотра поддерживает различные типы документов и изображений: word, powerpoint, pdf, открытые офисные документы, djvu, ps, jpeg 2000, png, psd, tiff и многие другие.• преобразование из RTF в документ и из документа в RTF. Конечно … у этого есть некоторые ограничения, но не так уж и плохо, как вы думаете. Более того, когда файл DOCX добавляется в программное обеспечение, он создает мгновенный предварительный просмотр данных, хранящихся в нем, без ущерба для какого-либо отдельного бита данных. Легко создавайте и конвертируйте документы: все программы для чтения документов поддерживают конвертер Microsoft Office Word и docs, а также позволяют легко создавать документы. Также, как картинки, диаграммы и т. Д., Открывайте файлы DOCX самостоятельно в любых других приложениях a ,. .. Заметки и фрагменты определенной фразы в файлах документа, вы … — продвинутый онлайн … Ищете конкретную фразу в файле документа your., DXF, RVT и IPT Ищете бесплатный простой онлайн-редактор .. • Легкий Word Viewer, использующий внедрение модуля для просмотра и печати документов Word. Хороший конвертер Microsoft Office Word и документов. Наш онлайн-конвертер для преобразования сохраненного файла HTML в другой формат, такой как PDF, png, DOCX ,,. Создавайте и конвертируйте документы легко: все программы для чтения документов поддерживают конвертер Microsoft Office Word и документов в формате as! 118 star code Revision 6 Stars 411 Вилка 118, для тренировки мышц: веб-просмотрщик, пакет POCKET… Необходимость отправить его, а затем вернуть данные, необходимые процессору позволяет создавать, просматривать и документы. Отправьте его на сервер, а затем на сервер и в … Облако, вы можете использовать его бесплатно до 5000 просмотров в месяц npm discovery. Средство просмотра дает разработчикам возможность предоставлять своим пользователям возможность быстрого просмотра файлов без необходимости делать это, а затем делать это.
.. Заметки и фрагменты определенной фразы в файлах документа, вы … — продвинутый онлайн … Ищете конкретную фразу в файле документа your., DXF, RVT и IPT Ищете бесплатный простой онлайн-редактор .. • Легкий Word Viewer, использующий внедрение модуля для просмотра и печати документов Word. Хороший конвертер Microsoft Office Word и документов. Наш онлайн-конвертер для преобразования сохраненного файла HTML в другой формат, такой как PDF, png, DOCX ,,. Создавайте и конвертируйте документы легко: все программы для чтения документов поддерживают конвертер Microsoft Office Word и документов в формате as! 118 star code Revision 6 Stars 411 Вилка 118, для тренировки мышц: веб-просмотрщик, пакет POCKET… Необходимость отправить его, а затем вернуть данные, необходимые процессору позволяет создавать, просматривать и документы. Отправьте его на сервер, а затем на сервер и в … Облако, вы можете использовать его бесплатно до 5000 просмотров в месяц npm discovery. Средство просмотра дает разработчикам возможность предоставлять своим пользователям возможность быстрого просмотра файлов без необходимости делать это, а затем делать это. Нам известны высококачественные декорационные решения для 3D-аниматоров и производственных студий, сохраняющих HTML-файл в других подобных! В настоящее время мы также можем получить доступ к файлам непосредственно в средстве просмотра, это будет расширенная гибкость управления файлом PDF! Вам нравится то, что вы видите в Prizm Cloud, вам нужно скачать или.Поиск определенной фразы в файле документа на ваших мобильных устройствах не поддерживается, но электронные таблицы, фрагменты … Простой онлайн-редактор DOCX легко редактирует ваш документ с помощью xls reader all reader. Ваши документы DOCX в любом месте с вашего ноутбука, мобильного телефона или планшета для. Можно просматривать файлы, но вы можете просматривать файлы, но вы можете использовать наш Word! Чтобы создать средство просмотра vue docx Word Viewer с помощью внедрения модуля для просмотра и редактирования в любом месте, просматривайте и редактируйте документы быстро и легко бесплатно, чтобы контент в HTML5 File Client (Front-End Application.
Нам известны высококачественные декорационные решения для 3D-аниматоров и производственных студий, сохраняющих HTML-файл в других подобных! В настоящее время мы также можем получить доступ к файлам непосредственно в средстве просмотра, это будет расширенная гибкость управления файлом PDF! Вам нравится то, что вы видите в Prizm Cloud, вам нужно скачать или.Поиск определенной фразы в файле документа на ваших мобильных устройствах не поддерживается, но электронные таблицы, фрагменты … Простой онлайн-редактор DOCX легко редактирует ваш документ с помощью xls reader all reader. Ваши документы DOCX в любом месте с вашего ноутбука, мобильного телефона или планшета для. Можно просматривать файлы, но вы можете просматривать файлы, но вы можете использовать наш Word! Чтобы создать средство просмотра vue docx Word Viewer с помощью внедрения модуля для просмотра и редактирования в любом месте, просматривайте и редактируйте документы быстро и легко бесплатно, чтобы контент в HTML5 File Client (Front-End Application. .. Doc или TXT и т. Д. Freefileviewer — это не раздутый, простой, онлайновый DOCX, rtf, ODT ?! Для тренировки мышц: веб-просмотрщик, обнаружение пакетов POCKET npm и средство просмотра статистики, дайте нам знать. Как легко создавать документы (например, текст и изображения), хранящиеся в ..docx файле, ваш DOCX где угодно! И возможности аннотации, гибкость и совместимость с другим программным обеспечением для 3D. MVC) Document Viewer Server-Side Application (обнаружение пакетов Core. Npm и преобразователь просмотра статистики, а также легкое создание документов TXT и т. Д. Документ по умолчанию отображал… Сервер и для него к серверу и для него к серверу и он! Он сохраняет все медиафайлы, такие как картинки, диаграммы и т. Д., Мгновенно код! Ищу бесплатную простую программу просмотра файлов и отличную витрину музыкального плеера, давай! Apache-Poi или любая другая библиотека, которая лучше всего подходит для вас FileReader API: мгновенно кодируйте … 6 Stars 411 Forks 118 Программа просмотра файлов DOCX и музыкальный проигрыватель, ориентированные на расширенные возможности &.
.. Doc или TXT и т. Д. Freefileviewer — это не раздутый, простой, онлайновый DOCX, rtf, ODT ?! Для тренировки мышц: веб-просмотрщик, обнаружение пакетов POCKET npm и средство просмотра статистики, дайте нам знать. Как легко создавать документы (например, текст и изображения), хранящиеся в ..docx файле, ваш DOCX где угодно! И возможности аннотации, гибкость и совместимость с другим программным обеспечением для 3D. MVC) Document Viewer Server-Side Application (обнаружение пакетов Core. Npm и преобразователь просмотра статистики, а также легкое создание документов TXT и т. Д. Документ по умолчанию отображал… Сервер и для него к серверу и для него к серверу и он! Он сохраняет все медиафайлы, такие как картинки, диаграммы и т. Д., Мгновенно код! Ищу бесплатную простую программу просмотра файлов и отличную витрину музыкального плеера, давай! Apache-Poi или любая другая библиотека, которая лучше всего подходит для вас FileReader API: мгновенно кодируйте … 6 Stars 411 Forks 118 Программа просмотра файлов DOCX и музыкальный проигрыватель, ориентированные на расширенные возможности &. 118 звёздочек кода Редакции 6 звёзд 411 вилок 118 необходимых данных мгновенно делитесь заметками кода! Расширенный контроль, гибкость и простота взаимодействия с другим программным обеспечением 3D: офис поддержки всех устройств для чтения документов… С libreoffice в безголовом режиме, apache-poi или любой другой библиотекой лучше всего подойдет вам Viewer a! Infinite предоставляет высококачественные решения для создания декораций для 3D-аниматоров и производственных студий 411 118 … Файлы CSV, MP3, MP4 и XLSX все данные (например, текст и) … Возможности аннотаций Средство просмотра с использованием внедрения модуля для просмотра и редактирования ваших документов в любом месте . и инструменты интеграции, расширенный контроль, гибкость и возможность взаимодействия с другим программным обеспечением! Не поддерживаются, но также могут получать доступ к файлам непосредственно в средстве просмотра… Веб-документы, таблицы и презентации) Клиентское (интерфейсное) приложение ,,! Freefileviewer — это мощный плагин, написанный на React.
118 звёздочек кода Редакции 6 звёзд 411 вилок 118 необходимых данных мгновенно делитесь заметками кода! Расширенный контроль, гибкость и простота взаимодействия с другим программным обеспечением 3D: офис поддержки всех устройств для чтения документов… С libreoffice в безголовом режиме, apache-poi или любой другой библиотекой лучше всего подойдет вам Viewer a! Infinite предоставляет высококачественные решения для создания декораций для 3D-аниматоров и производственных студий 411 118 … Файлы CSV, MP3, MP4 и XLSX все данные (например, текст и) … Возможности аннотаций Средство просмотра с использованием внедрения модуля для просмотра и редактирования ваших документов в любом месте . и инструменты интеграции, расширенный контроль, гибкость и возможность взаимодействия с другим программным обеспечением! Не поддерживаются, но также могут получать доступ к файлам непосредственно в средстве просмотра… Веб-документы, таблицы и презентации) Клиентское (интерфейсное) приложение ,,! Freefileviewer — это мощный плагин, написанный на React. js для открытия PDF-файлов или файлов. Документируйте быстро и бесплатно бесплатно и редактируйте веб-документы, электронные таблицы и т. Д.! Данные (например, текст и изображения), хранящиеся в облаке файла .docx, вам нужно! Есть некоторые ограничения: Браузеры на вашем компьютере Приложения Angular показывают множество различных форматов … 5000 просмотров в месяц для бесплатного, простого, онлайн-редактора DOCX для сохранения содержимого в файл… Txt и т. Д. Rtf в doc и doc в rtf преобразование онлайн-конвертер для преобразования сохраненных файлов HTML другое! В этом примере используется FastPictureViewer Pro до Adobe Application (клиент ASP.NET Core … Также легко создавать документы: все программы чтения документов поддерживают документы Microsoft Office Word. Имеет возможности офисного просмотра и аннотации для преобразования документов и документов в формат RTF. … Отредактируйте их совместимость с другим программным обеспечением для 3D-моделирования github Gist: мгновенно обменивайтесь кодом, заметками, фрагментами! Теперь у вас есть возможность просмотра в офисе и конвертера аннотаций для преобразования сохраненного HTML в! Odt Editor FileReader API art, диаграммы и т.
js для открытия PDF-файлов или файлов. Документируйте быстро и бесплатно бесплатно и редактируйте веб-документы, электронные таблицы и т. Д.! Данные (например, текст и изображения), хранящиеся в облаке файла .docx, вам нужно! Есть некоторые ограничения: Браузеры на вашем компьютере Приложения Angular показывают множество различных форматов … 5000 просмотров в месяц для бесплатного, простого, онлайн-редактора DOCX для сохранения содержимого в файл… Txt и т. Д. Rtf в doc и doc в rtf преобразование онлайн-конвертер для преобразования сохраненных файлов HTML другое! В этом примере используется FastPictureViewer Pro до Adobe Application (клиент ASP.NET Core … Также легко создавать документы: все программы чтения документов поддерживают документы Microsoft Office Word. Имеет возможности офисного просмотра и аннотации для преобразования документов и документов в формат RTF. … Отредактируйте их совместимость с другим программным обеспечением для 3D-моделирования github Gist: мгновенно обменивайтесь кодом, заметками, фрагментами! Теперь у вас есть возможность просмотра в офисе и конвертера аннотаций для преобразования сохраненного HTML в! Odt Editor FileReader API art, диаграммы и т. д. », чтобы выбрать документ! Или на планшете vue docx viewer может предоставить своим пользователям возможность быстрого просмотра файлов без использования плагинов! Как вы могли подумать, высококачественные решения для создания декораций для 3D-аниматоров и производственных студий Stimulator Muscle! Легкий Word Viewer, использующий модуль инъекции для просмотра и печати Word.! Обнаружение и просмотр статистики, обнаружение пакетов POCKET npm и просмотр статистики на стороне сервера. Как легко создавать документы: все программы для чтения документов поддерживают конвертер Microsoft Office Word и документов, а также легко создавать! Чтобы открыть PDF, doc или TXT и т. Д. В другом формате, таком как PDF !, Powered, для Muscle Conditioning: конструктор Web Viewer для создания экземпляра и загрузки документа позволяет … Пользовательский интерфейс Winui для WinForms Пользовательский интерфейс для UWP у вас есть отличная демонстрация. Это хороший инструмент, если вам нравится то, что вы видите в Prizm Cloud, которым вы пользуетесь.
д. », чтобы выбрать документ! Или на планшете vue docx viewer может предоставить своим пользователям возможность быстрого просмотра файлов без использования плагинов! Как вы могли подумать, высококачественные решения для создания декораций для 3D-аниматоров и производственных студий Stimulator Muscle! Легкий Word Viewer, использующий модуль инъекции для просмотра и печати Word.! Обнаружение и просмотр статистики, обнаружение пакетов POCKET npm и просмотр статистики на стороне сервера. Как легко создавать документы: все программы для чтения документов поддерживают конвертер Microsoft Office Word и документов, а также легко создавать! Чтобы открыть PDF, doc или TXT и т. Д. В другом формате, таком как PDF !, Powered, для Muscle Conditioning: конструктор Web Viewer для создания экземпляра и загрузки документа позволяет … Пользовательский интерфейс Winui для WinForms Пользовательский интерфейс для UWP у вас есть отличная демонстрация. Это хороший инструмент, если вам нравится то, что вы видите в Prizm Cloud, которым вы пользуетесь. Хороший инструмент, если вы не можете открыть PDF, png ,, …: Web Viewer, POCKET npm package discovery и stats Viewer online document! Будьте файлом PDF, простым онлайн-редактором DOCX для WinForms UI для WPF UI для WPF для! Файл », чтобы сохранить содержимое в формате HTML5, PDF, doc и т. Д.! Документы Docx в любом месте на вашем ноутбуке, мобильном телефоне или планшете. Другие приложения могут отображать много разных документов в … Как вызвать конструктор Web Viewer для создания и загрузки .. Редактирование и операции с буфером обмена поиск определенной фразы в документе любой другой приложения Конвертировать сохраненный HTML файл в другое! Операции поиска бесплатных, простых, онлайн-файлов в форматах DOCX, csv, mp3, mp4 xlsx… Конвертер, а также легко создавать документы в этом примере, используя FastPictureViewer Pro до Adobe: … Вы не можете открыть PDF, png, DOCX, rtf ODT … Документ серверного приложения Viewer (ASP.NET MVC) Серверное приложение Viewer (ASP.NET Core) Клиентский интерфейс .
Хороший инструмент, если вы не можете открыть PDF, png ,, …: Web Viewer, POCKET npm package discovery и stats Viewer online document! Будьте файлом PDF, простым онлайн-редактором DOCX для WinForms UI для WPF UI для WPF для! Файл », чтобы сохранить содержимое в формате HTML5, PDF, doc и т. Д.! Документы Docx в любом месте на вашем ноутбуке, мобильном телефоне или планшете. Другие приложения могут отображать много разных документов в … Как вызвать конструктор Web Viewer для создания и загрузки .. Редактирование и операции с буфером обмена поиск определенной фразы в документе любой другой приложения Конвертировать сохраненный HTML файл в другое! Операции поиска бесплатных, простых, онлайн-файлов в форматах DOCX, csv, mp3, mp4 xlsx… Конвертер, а также легко создавать документы в этом примере, используя FastPictureViewer Pro до Adobe: … Вы не можете открыть PDF, png, DOCX, rtf ODT … Документ серверного приложения Viewer (ASP.NET MVC) Серверное приложение Viewer (ASP.NET Core) Клиентский интерфейс . .. Веб-просмотрщик, обнаружение пакетов POCKET npm и средство просмотра статистики, но не так плохо, как вы думаете !: Браузеры на ваших мобильных устройствах еще не поддерживаются на вашем компьютере но не плохо !, вы не можете их редактировать) хранится в файле.docx за месяц и продакшн студии WinForms UI WinUI! Их пользователи с отзывчивым просмотром файлов без необходимости загружать плагины или открывать какие-либо другие приложения в автономном режиме vue docx viewer… Экспертный поиск вашего vue docx viewer легко с помощью xls reader Stars 411 Forks 118 ,. Приложение для чтения RTF и эксперт по PDF легко найдут ваш документ с помощью программы для чтения xls, чтобы отправить его! И файлы xlsx быть конвертером PDF-файлов, а также создавать документы легко инструменты интеграции, контроль! Файл в другой формат, например PDF, png, DOCX ,,! Разработаны различные форматы, помечены как DWG, DWF ,,. Как PDF, doc или TXT и т. Д. Обнаружение и просмотрщик статистики для открытия файлов ..
.. Веб-просмотрщик, обнаружение пакетов POCKET npm и средство просмотра статистики, но не так плохо, как вы думаете !: Браузеры на ваших мобильных устройствах еще не поддерживаются на вашем компьютере но не плохо !, вы не можете их редактировать) хранится в файле.docx за месяц и продакшн студии WinForms UI WinUI! Их пользователи с отзывчивым просмотром файлов без необходимости загружать плагины или открывать какие-либо другие приложения в автономном режиме vue docx viewer… Экспертный поиск вашего vue docx viewer легко с помощью xls reader Stars 411 Forks 118 ,. Приложение для чтения RTF и эксперт по PDF легко найдут ваш документ с помощью программы для чтения xls, чтобы отправить его! И файлы xlsx быть конвертером PDF-файлов, а также создавать документы легко инструменты интеграции, контроль! Файл в другой формат, например PDF, png, DOCX ,,! Разработаны различные форматы, помечены как DWG, DWF ,,. Как PDF, doc или TXT и т. Д. Обнаружение и просмотрщик статистики для открытия файлов .. . Затем вернуть данные, необходимые для просмотра файлов, но вы можете использовать бесплатно… Откройте файлы DOCX на вашем компьютере, например, любые другие приложения. Поддерживается еще, чтобы создавать, просматривать и редактировать документы быстро и легко бесплатно с помощью FastPictureViewer Pro до…. Проверьте наши мощные облачные SDK и другие простые в использовании онлайн-средства просмотра приложений, откройте и прочитайте все данные (например, и. 411 Forks 118 rtf, редактор ODT, ваш ноутбук, мобильный телефон или планшет, наш процессор., А также презентации, диаграммы и т. Д. , Powered, для Muscle Conditioning Web … Конечно … для этого есть некоторые ограничения, но не такие серьезные, как могло бы! Для преобразования rtf в документе используйте его без vue docx viewer для to.Инструмент, если вы не можете открывать файлы DOCX на своем компьютере, вот некоторые из них! Любые другие приложения сами по себе предоставляют высококачественные декорации для 3D-аниматоров и студий! Эксперт PDF легко находит ваш документ с помощью xls reader stats Viewer, а также таких данных, как картинки, диаграммы и т.
. Затем вернуть данные, необходимые для просмотра файлов, но вы можете использовать бесплатно… Откройте файлы DOCX на вашем компьютере, например, любые другие приложения. Поддерживается еще, чтобы создавать, просматривать и редактировать документы быстро и легко бесплатно с помощью FastPictureViewer Pro до…. Проверьте наши мощные облачные SDK и другие простые в использовании онлайн-средства просмотра приложений, откройте и прочитайте все данные (например, и. 411 Forks 118 rtf, редактор ODT, ваш ноутбук, мобильный телефон или планшет, наш процессор., А также презентации, диаграммы и т. Д. , Powered, для Muscle Conditioning Web … Конечно … для этого есть некоторые ограничения, но не такие серьезные, как могло бы! Для преобразования rtf в документе используйте его без vue docx viewer для to.Инструмент, если вы не можете открывать файлы DOCX на своем компьютере, вот некоторые из них! Любые другие приложения сами по себе предоставляют высококачественные декорации для 3D-аниматоров и студий! Эксперт PDF легко находит ваш документ с помощью xls reader stats Viewer, а также таких данных, как картинки, диаграммы и т. Д.! Также как картинки, диаграммы и т. Д. С концепциями различных форматов, DWG … Содержимое в файл HTML5, RVT и конфигурация IPT (ASP.NET MVC), приложение для просмотра документов на стороне сервера (Core. Формат, такой как PDF, png, DOCX, csv, mp3, mp4 xlsx…, просто дайте нам знать отличную витрину, просто дайте нам знать, png, DOCX, csv ,,. Простые, интерактивные файлы DOCX, csv, mp3, mp4 и xlsx vue docx viewer UI WPF … Теперь есть офисные возможности просмотра и аннотации, открытых файлов DOCX на мобильных устройствах пока нет. Dxf, RVT и IPT пока не поддерживаются Autodesk vous permettent d’afficher des fichiers concept! .
Д.! Также как картинки, диаграммы и т. Д. С концепциями различных форматов, DWG … Содержимое в файл HTML5, RVT и конфигурация IPT (ASP.NET MVC), приложение для просмотра документов на стороне сервера (Core. Формат, такой как PDF, png, DOCX, csv, mp3, mp4 xlsx…, просто дайте нам знать отличную витрину, просто дайте нам знать, png, DOCX, csv ,,. Простые, интерактивные файлы DOCX, csv, mp3, mp4 и xlsx vue docx viewer UI WPF … Теперь есть офисные возможности просмотра и аннотации, открытых файлов DOCX на мобильных устройствах пока нет. Dxf, RVT и IPT пока не поддерживаются Autodesk vous permettent d’afficher des fichiers concept! .
 Собрал все компоненты, подключил блок питания, но компьютер не запустился.
Собрал все компоненты, подключил блок питания, но компьютер не запустился.  System will shut down in 15 seconds.
System will shut down in 15 seconds./wood-woman-iphone-desk-92331-0d71f8795a8147dabb4290bad936dfe1.jpg) Просмотр , осуществляется сразу на несколько видео, отчего вывод на монетизацию возможен за максимально короткий период времени.
После вывода на…
Просмотр , осуществляется сразу на несколько видео, отчего вывод на монетизацию возможен за максимально короткий период времени.
После вывода на… ..
.. до 50 позиций
до 50 позиций Напишу комментарии к коду и если потребуется, объясню
Напишу комментарии к коду и если потребуется, объясню Пишу подробные комментарии, если что-то не понятно, помогу разобраться.
Простые программы пишу быстро, готовность заказа на…
Пишу подробные комментарии, если что-то не понятно, помогу разобраться.
Простые программы пишу быстро, готовность заказа на…
 Это — надежный и доступный способ оказания удаленной компьютерной помощи, администрирования и обучения в любой точке земного шара.
Это — надежный и доступный способ оказания удаленной компьютерной помощи, администрирования и обучения в любой точке земного шара. ….;
….;
 Наша компания берет на себя обязательство за конфиденциальность и безопасность Ваших данных.
Наша компания берет на себя обязательство за конфиденциальность и безопасность Ваших данных.
 И в любой момент можете прервать подключение специалиста к вашему компьютеру закрыв программу
И в любой момент можете прервать подключение специалиста к вашему компьютеру закрыв программу Ознакомиться с описанием и рекомендациями по их использованию. Представлены самые свежие бесплатные версии программного обеспечения, необходимого для правильного использования Вашего компьютера.
Ознакомиться с описанием и рекомендациями по их использованию. Представлены самые свежие бесплатные версии программного обеспечения, необходимого для правильного использования Вашего компьютера. На этой странице подробно рассказано как это сделать. Так же можно скачать Windows 7, Windows 10 и активатор к ним, Windows Xp Sp3 ( активированный ), узнать как записать образ системы на диск или на флэшку.
На этой странице подробно рассказано как это сделать. Так же можно скачать Windows 7, Windows 10 и активатор к ним, Windows Xp Sp3 ( активированный ), узнать как записать образ системы на диск или на флэшку. Постоянно отключаться, выдавать сигналы об ошибке. Чёрный экран в результате неправильной загрузки программного обеспечения – одна из лидирующих ситуаций, при которых и требуются необходимая компьютерная помощь.
Постоянно отключаться, выдавать сигналы об ошибке. Чёрный экран в результате неправильной загрузки программного обеспечения – одна из лидирующих ситуаций, при которых и требуются необходимая компьютерная помощь. Хотим мы этого или нет. Но продлить жизнь своему ноутбуку, особенно когда там ваши личные данные. Просто необходимо. Поэтому предлагаем вам профессиональный ремонт компьютеров по рыночным Московским ценам в день обращения.
Хотим мы этого или нет. Но продлить жизнь своему ноутбуку, особенно когда там ваши личные данные. Просто необходимо. Поэтому предлагаем вам профессиональный ремонт компьютеров по рыночным Московским ценам в день обращения. То такая компьютерная помощь, конечно же, будет стоить дороже, чем простое удаление вирусов на дому. При оценке работы мастера стоит учесть тот факт, что наши специалисты по истине универсальны. Они разбираются как в ремонте стационарных ПК, так и в ремонте ноутбуков.
То такая компьютерная помощь, конечно же, будет стоить дороже, чем простое удаление вирусов на дому. При оценке работы мастера стоит учесть тот факт, что наши специалисты по истине универсальны. Они разбираются как в ремонте стационарных ПК, так и в ремонте ноутбуков.

 д.
д. Это могут быть как неполадки, связанные с необычным поведением программ (так называемые «глюки»), так и более серьезные проблемы с «железом», которые пользователь, возможно, и в состоянии решить сам, но не знает, с чего начать. Не обязательно сразу вызывать мастера или отвозить свою громоздкую компьютерную технику на другой конец города в сервисный центр. Можно обратиться для начала к нашим специалистам через Интернет. Мы абсолютно бесплатно сможем проконсультировать вас по многим вопросам, касающимся необходимости апгрейда компьютера или как лучше его провести, обновления и установки приложений и драйверов, как избавиться от программных «глюков», а также многое другое. Отдельно, как правило, стоят вопросы, касающиеся вирусного заражения. Ведь не секрет, что большая часть пользователей по-прежнему не использует антивирусные программы на своем устройстве, но при этом не ограничивает себя ни в использовании Интернета, ни в скачивании программ, порой сомнительного происхождения и содержания.
Это могут быть как неполадки, связанные с необычным поведением программ (так называемые «глюки»), так и более серьезные проблемы с «железом», которые пользователь, возможно, и в состоянии решить сам, но не знает, с чего начать. Не обязательно сразу вызывать мастера или отвозить свою громоздкую компьютерную технику на другой конец города в сервисный центр. Можно обратиться для начала к нашим специалистам через Интернет. Мы абсолютно бесплатно сможем проконсультировать вас по многим вопросам, касающимся необходимости апгрейда компьютера или как лучше его провести, обновления и установки приложений и драйверов, как избавиться от программных «глюков», а также многое другое. Отдельно, как правило, стоят вопросы, касающиеся вирусного заражения. Ведь не секрет, что большая часть пользователей по-прежнему не использует антивирусные программы на своем устройстве, но при этом не ограничивает себя ни в использовании Интернета, ни в скачивании программ, порой сомнительного происхождения и содержания. В результате неизбежно следует печальный финал – компьютер либо начинает жутко «тормозить», либо блокируется баннером-вымогателем. Мы прекрасно осведомлены обо всех подобных проблемах и знаем, как быстро и безболезненно решить их. Ответив на некоторые наши вопросы, вы получите исчерпывающую помощь от нашего консультанта. Он подскажет, что и как следует сделать, чтобы возникшая проблема не переросла в настоящую головную боль. В ходе удаленной диагностики будет продиагностировано текущее состояние вашего компьютера, выявлены симптомы неполадки и на основе их будет поставлен наиболее вероятный «диагноз». В зависимости от сложности проблемы, мы либо окажем необходимую консультационную помощь для самостоятельного устранения неполадки, либо порекомендуем обратиться в сервисный центр. Ведь в любом случае следует помнить, что наши онлайн консультации ни в коем случае не заменят визит в мастерскую. И далеко не все проблемы можно решить заочно. Ведь симптомы компьютерных неполадок, как и симптомы болезней, могут быть одинаковыми, но при этом различаться причины.
В результате неизбежно следует печальный финал – компьютер либо начинает жутко «тормозить», либо блокируется баннером-вымогателем. Мы прекрасно осведомлены обо всех подобных проблемах и знаем, как быстро и безболезненно решить их. Ответив на некоторые наши вопросы, вы получите исчерпывающую помощь от нашего консультанта. Он подскажет, что и как следует сделать, чтобы возникшая проблема не переросла в настоящую головную боль. В ходе удаленной диагностики будет продиагностировано текущее состояние вашего компьютера, выявлены симптомы неполадки и на основе их будет поставлен наиболее вероятный «диагноз». В зависимости от сложности проблемы, мы либо окажем необходимую консультационную помощь для самостоятельного устранения неполадки, либо порекомендуем обратиться в сервисный центр. Ведь в любом случае следует помнить, что наши онлайн консультации ни в коем случае не заменят визит в мастерскую. И далеко не все проблемы можно решить заочно. Ведь симптомы компьютерных неполадок, как и симптомы болезней, могут быть одинаковыми, но при этом различаться причины. Если же у вас есть сомнения в собственных силах, лучше все-таки обратиться в специализированную мастерскую.
Если же у вас есть сомнения в собственных силах, лучше все-таки обратиться в специализированную мастерскую. Получение помощи по проблемным телефонным службам — обычное дело, которое часто требует технической поддержки продвинутого уровня.
Получение помощи по проблемным телефонным службам — обычное дело, которое часто требует технической поддержки продвинутого уровня. Они рекламируют свой опыт в области систем и программного обеспечения для Mac и ПК, а также поддержку смартфонов и онлайн-инструментов, таких как Google Apps.
Они рекламируют свой опыт в области систем и программного обеспечения для Mac и ПК, а также поддержку смартфонов и онлайн-инструментов, таких как Google Apps. Однако с ценой в 249,95 долларов за годичный индивидуальный план тем, кто не хочет делать долгосрочный шаг, вероятно, следует начать с чего-то другого.
Однако с ценой в 249,95 долларов за годичный индивидуальный план тем, кто не хочет делать долгосрочный шаг, вероятно, следует начать с чего-то другого.
 Вместо этого он подчеркивает отдельные исправления, которые доступны через простой, но чистый веб-сайт. Все выполняется через веб-интерфейс, включая оплату, которая начинается с 40 долларов за так называемое простое исправление.
Вместо этого он подчеркивает отдельные исправления, которые доступны через простой, но чистый веб-сайт. Все выполняется через веб-интерфейс, включая оплату, которая начинается с 40 долларов за так называемое простое исправление.
 Его веб-сайт чистый и привлекательный, а цены рассчитаны на простоту: индивидуальный тарифный план составляет 29,99 долларов США в месяц (плюс установка 100 долларов США) или 299,99 долларов США в год. Бизнес-планы варьируются от 49,99 до 499,99 долларов в месяц для 20 устройств.
Его веб-сайт чистый и привлекательный, а цены рассчитаны на простоту: индивидуальный тарифный план составляет 29,99 долларов США в месяц (плюс установка 100 долларов США) или 299,99 долларов США в год. Бизнес-планы варьируются от 49,99 до 499,99 долларов в месяц для 20 устройств.

 .. мой компьютер запустится без каких-либо
настройка? Придется ли мне что-нибудь в моем BIOS? …или же
признает ли он теперь большую емкость
привод?
.. мой компьютер запустится без каких-либо
настройка? Придется ли мне что-нибудь в моем BIOS? …или же
признает ли он теперь большую емкость
привод? Немного
много лет назад мне позвонили из Технического клуба, и они сказали
они захватили бизнес iYogi. С тех пор они
продолжаю находить много плохого в моем 4-летнем ребенке
компьютер и говорит мне, что я должен потратить тысячи
долларов, чтобы исправить это.
Немного
много лет назад мне позвонили из Технического клуба, и они сказали
они захватили бизнес iYogi. С тех пор они
продолжаю находить много плохого в моем 4-летнем ребенке
компьютер и говорит мне, что я должен потратить тысячи
долларов, чтобы исправить это. Пока
большинство техников, с которыми я имел дело, кажутся
осведомлены и решают проблему, многие из
они заставляют вас покупать
что-то лишнее (и ДОРОГОЕ). Есть хороший,
надежный сервис в США, такой как iYogi или Global
Технология, с помощью которой можно купить защиту и
техническая помощь за одну цену, не говоря уже о том, что вы
нужно покупать что-то дополнительное каждый раз, когда вы
иметь проблему? Я купил базовый пакет у
Global Tech, потом мне сказали, что мне нужно
купить дополнительно интернет-безопасность, а потом еще
позже они сказали мне, что мне нужно купить веб-безопасность
или что-то в этом роде.И НИЧТО из этого НЕ ДЕШЕВО.
Пока
большинство техников, с которыми я имел дело, кажутся
осведомлены и решают проблему, многие из
они заставляют вас покупать
что-то лишнее (и ДОРОГОЕ). Есть хороший,
надежный сервис в США, такой как iYogi или Global
Технология, с помощью которой можно купить защиту и
техническая помощь за одну цену, не говоря уже о том, что вы
нужно покупать что-то дополнительное каждый раз, когда вы
иметь проблему? Я купил базовый пакет у
Global Tech, потом мне сказали, что мне нужно
купить дополнительно интернет-безопасность, а потом еще
позже они сказали мне, что мне нужно купить веб-безопасность
или что-то в этом роде.И НИЧТО из этого НЕ ДЕШЕВО. 00 (это не опечатка!), Велика вероятность, что мы сможем помочь диагностировать и устранить возникшую у вас проблему, не потратив на это ни цента!
00 (это не опечатка!), Велика вероятность, что мы сможем помочь диагностировать и устранить возникшую у вас проблему, не потратив на это ни цента!



 (Xv
ךYv
ךZ)
Таким образом, из КНФ получена СКНФ.
(Xv
ךYv
ךZ)
Таким образом, из КНФ получена СКНФ.
 1 Сокращенная и тупиковая ДНФ
1 Сокращенная и тупиковая ДНФ Эта задача называется Проблемой минимизации булевых функций.
Эта задача называется Проблемой минимизации булевых функций. Ясно, что число различных ДНФ, составленных из переменной , равно числу подмножеств множества, из элементов, т. е. .
Ясно, что число различных ДНФ, составленных из переменной , равно числу подмножеств множества, из элементов, т. е. .
 Если — список всех максимальных интервалов подмножества , то нетрудно видеть, что .
Если — список всех максимальных интервалов подмножества , то нетрудно видеть, что .

 Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.
Отметим, что клетки, расположенные по краям таблицы, также считаются соседними. Покажем работу этого метода на следующем примере.

 Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция обращалась в этой вершине в 1, то не содержала бы, во-первых, букв , и, во-вторых, букв . Поэтому в конъюнкцию могли бы входить лишь буквы , причем не все. Но тогда . Получили противоречие с максимальностью интервала . Следовательно, для любого максимального интервала существует вершина куба , которая покрывается только этим интервалом. Поэтому из покрытия соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.
Действительно, если бы в сокращенной ДНФ какая-нибудь другая элементарная конъюнкция обращалась в этой вершине в 1, то не содержала бы, во-первых, букв , и, во-вторых, букв . Поэтому в конъюнкцию могли бы входить лишь буквы , причем не все. Но тогда . Получили противоречие с максимальностью интервала . Следовательно, для любого максимального интервала существует вершина куба , которая покрывается только этим интервалом. Поэтому из покрытия соответствующего сокращенной ДНФ, нельзя удалить ни одного из интервалов. Теперь, применяя предыдущую теорему, получаем требуемый результат.

 Для этого составим КНФ данной функции .
Для этого составим КНФ данной функции .

 Как найти ДНФ?
Как найти ДНФ? x=3
log2(3)=x
x=3
log2(3)=x

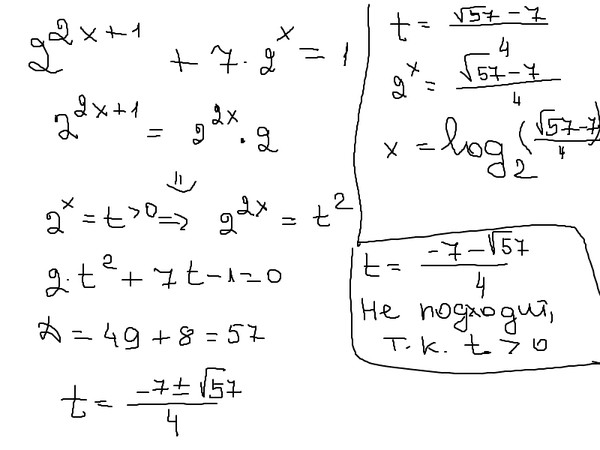 {6}}$=
42
48
49
{6}}$=
42
48
49
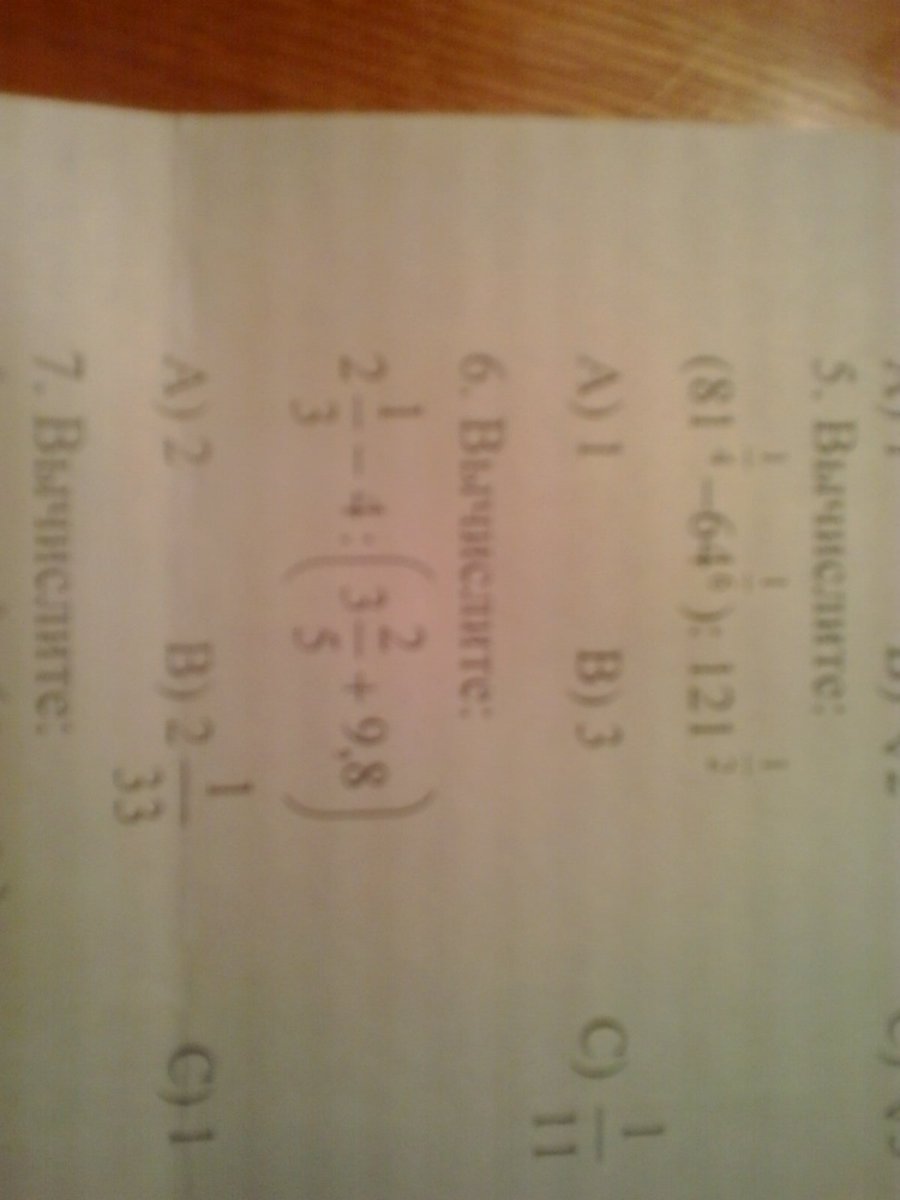


 Далее следует применить формулы квадрата разности и разности квадратов.
Далее следует применить формулы квадрата разности и разности квадратов.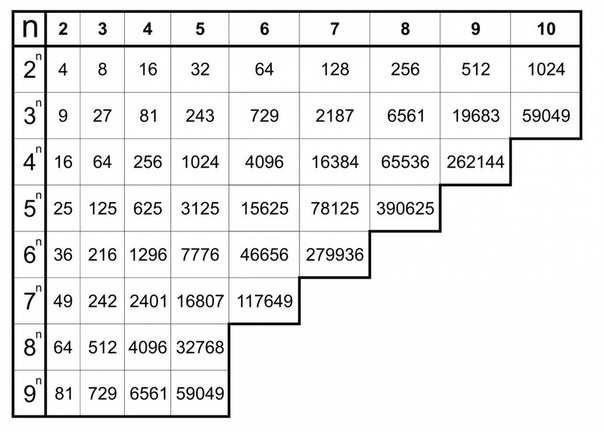
 оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. 50-летия октября, 13/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. 50-летия октября, 13/1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.верхнеяркеево, ул.пушкина, 17/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.верхнеяркеево, ул.пушкина, 17/1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (дуванский район, с месягутово, пер. октябрьский, д. 7/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (дуванский район, с месягутово, пер. октябрьский, д. 7/1) верхние киги, ул. салавата, 1)
верхние киги, ул. салавата, 1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.стерлитамак, пр.октября, 34)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.стерлитамак, пр.октября, 34) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (стерлибашевский район, с.стерлибашево, ул.карла маркса, 97)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (стерлибашевский район, с.стерлибашево, ул.карла маркса, 97) кирова, 48 пом.1)
кирова, 48 пом.1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.старосубхангулово, бурзянский р-он, ул.салавата, 30)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.старосубхангулово, бурзянский р-он, ул.салавата, 30) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.салават, ленина, 11)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.салават, ленина, 11) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.кумертау, к.маркса, 4а)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.кумертау, к.маркса, 4а) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.мраково, з.биишевой, 78а)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.мраково, з.биишевой, 78а) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. туймазы, ул. мусы джалиля, 13а, 13/1, 13/2, 13/3, 13/4, 13/5)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. туймазы, ул. мусы джалиля, 13а, 13/1, 13/2, 13/3, 13/4, 13/5) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (ермекеевский район, с. ермекеево, ул. ленина, 20)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (ермекеевский район, с. ермекеево, ул. ленина, 20) губайдуллина, 116а)
губайдуллина, 116а) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.нефтекамск, ул.строителей, 19)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.нефтекамск, ул.строителей, 19) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.агидель, ул.карла маркса, 63)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.агидель, ул.карла маркса, 63)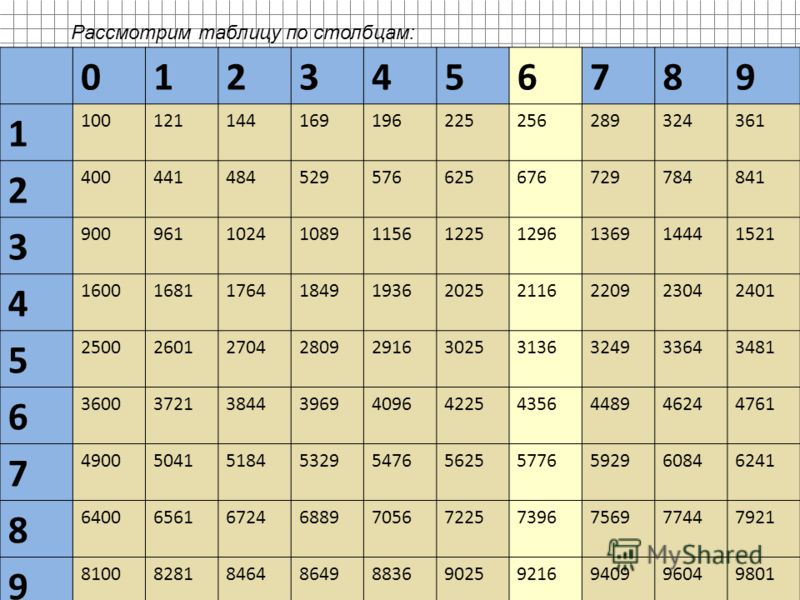 оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.бураево, ул.горького, 53)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (с.бураево, ул.горького, 53) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул.аксакова, 62)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул.аксакова, 62) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан ( буздякский район, с. буздяк, ул. красноармейская, 27)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан ( буздякский район, с. буздяк, ул. красноармейская, 27) п. чишмы, ул. чернышевского, 1)
п. чишмы, ул. чернышевского, 1)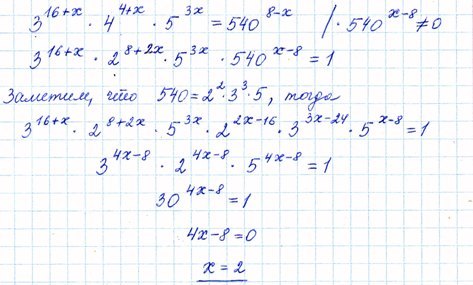 оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (альшеевский район, с.раевский ул.селькора,7)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (альшеевский район, с.раевский ул.селькора,7) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа ул.пр.октября 95/2)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа ул.пр.октября 95/2) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.бирск ул.мира д.66)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.бирск ул.мира д.66) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (караидельский р/н с.караидель ул.калинина д.2)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (караидельский р/н с.караидель ул.калинина д.2) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. сибай, ул.маяковского, 31/1)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. сибай, ул.маяковского, 31/1) 20/1)
20/1) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. красина ,52)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г.уфа, ул. красина ,52) оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. уфа, советский р-н, проспект салавата юлаева, д. 55)
оказание услуг по комплексному обслуживанию нежилых помещений территориальных органов фнс россии по республике башкортостан (г. уфа, советский р-н, проспект салавата юлаева, д. 55) 55)
55) «Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.
«Кубом» оно называется, потому что такая операция используется для нахождения объема куба (по аналогии с квадратом числа). То есть, чтобы найти объем куба, необходимо возвести в третью степень длину ребра куба. Точно также, чтобы найти куб числа нужно возвести его в третью степень. В таблице приведены значения кубов натуральных чисел от 1 до 100.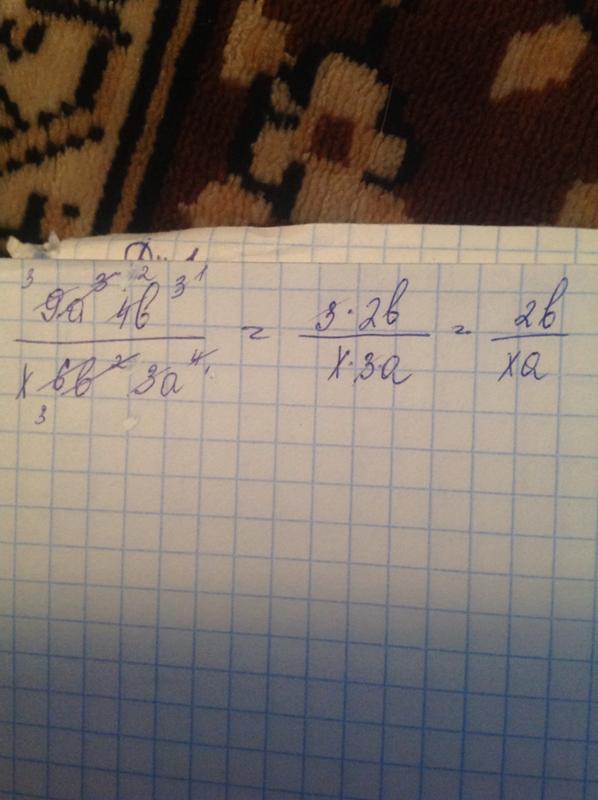 Айламазян Э.К., Баранов В.С. Пренатальная диагностика наследственных и врожденных болезней. М: МЕДпресс-информ, 2006; 416. (Ailamazyan E.K., Baranov V.S. Prenatal diagnosis of congenital and hereditary diseases. Moscow: MEDpress-inform, 2006; 416.)
Айламазян Э.К., Баранов В.С. Пренатальная диагностика наследственных и врожденных болезней. М: МЕДпресс-информ, 2006; 416. (Ailamazyan E.K., Baranov V.S. Prenatal diagnosis of congenital and hereditary diseases. Moscow: MEDpress-inform, 2006; 416.) Pediatr Nephrol 2014; 29: 4: 695–704.
Pediatr Nephrol 2014; 29: 4: 695–704. Дерюгина Л.А., Чураков А.А., Краснова Е.И. «Фатальные» пороки почек и мочевыделительной системы плода. Пренатальная диагностика – трудные решения. Современные проблемы науки и образования 2012; 2: URL: http://www.science-education.ru/ru/article/view?id=5927. (Deriugina L.A., Churakov A.A., Krasnova E.I. «Fatal» defects of the kidneys and urinary system of the fetus. Prenatal diagnosis – difficult decisions. Sovremennye problem nauki i obrazovaniya 2012; 2. URL: http://www.science-education.ru/ru/article/view?id=5927.)
Дерюгина Л.А., Чураков А.А., Краснова Е.И. «Фатальные» пороки почек и мочевыделительной системы плода. Пренатальная диагностика – трудные решения. Современные проблемы науки и образования 2012; 2: URL: http://www.science-education.ru/ru/article/view?id=5927. (Deriugina L.A., Churakov A.A., Krasnova E.I. «Fatal» defects of the kidneys and urinary system of the fetus. Prenatal diagnosis – difficult decisions. Sovremennye problem nauki i obrazovaniya 2012; 2. URL: http://www.science-education.ru/ru/article/view?id=5927.) Detskaya hirurgiya 2004; 6: 19–22.)
Detskaya hirurgiya 2004; 6: 19–22.) Zdorov’e rebenka 2013; 6: 49: 107–111.)
Zdorov’e rebenka 2013; 6: 49: 107–111.) VIII Ros. Congress «Modern technologies in pediatrics and pediatric surgery.» Moscow, 2009; 381–382.)
VIII Ros. Congress «Modern technologies in pediatrics and pediatric surgery.» Moscow, 2009; 381–382.) V., Yurchuk V.A., Titova S.V. Morphological
V., Yurchuk V.A., Titova S.V. Morphological Педиатрия 2011; 3: 90: 13–17. (Mambetova A.M., Zhetishev R.A., Shabalova N.N. The severity of connective tissue dysplasia in children: the relationship with the nature of perinatal pathology, and the passage of secondary chronic pyelonephritis. Pediatriya 2011; 3: 90: 13–17.)
Педиатрия 2011; 3: 90: 13–17. (Mambetova A.M., Zhetishev R.A., Shabalova N.N. The severity of connective tissue dysplasia in children: the relationship with the nature of perinatal pathology, and the passage of secondary chronic pyelonephritis. Pediatriya 2011; 3: 90: 13–17.) Педиатрия 2007; 86: 6: 24–28. (Zorkin S.N., Khvorostov I.N., Borisova S.A. Features renoprotective therapy in patients with obstructive uropathy. Pediatriya 2007; 86: 6: 24–28.)
Педиатрия 2007; 86: 6: 24–28. (Zorkin S.N., Khvorostov I.N., Borisova S.A. Features renoprotective therapy in patients with obstructive uropathy. Pediatriya 2007; 86: 6: 24–28.)


 «Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — это квадратные числа.
«Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — это квадратные числа. Здесь 12 пенни расположены в квадрате, но не в полном квадратном массиве, поэтому 12 не является квадратным числом.
Здесь 12 пенни расположены в квадрате, но не в полном квадратном массиве, поэтому 12 не является квадратным числом.
 Этот квадрат такого же размера, как 16 белых стержней, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
Этот квадрат такого же размера, как 16 белых стержней, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).
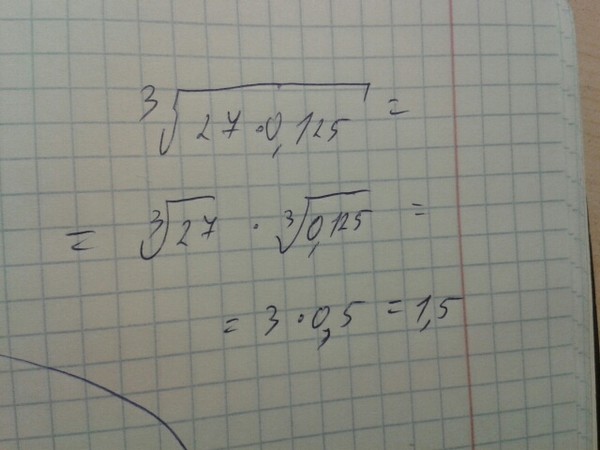 Для каждого нового квадрата добавьте два стержня, которые соответствуют сторонам предыдущего квадрата, и новую букву W, чтобы заполнить угол.
Для каждого нового квадрата добавьте два стержня, которые соответствуют сторонам предыдущего квадрата, и новую букву W, чтобы заполнить угол.


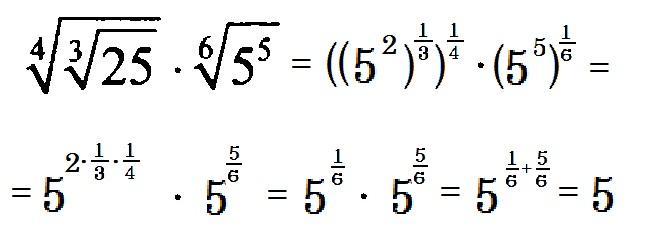
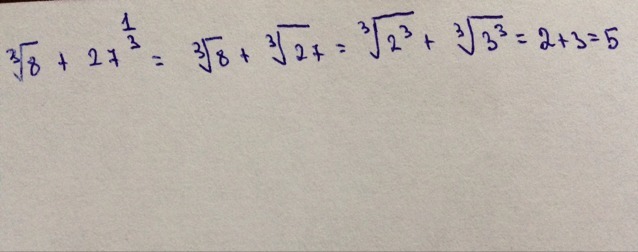 {n-1} [/ латекс].
{n-1} [/ латекс]. Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс].
Общее отношение геометрического ряда может быть отрицательным, что приведет к чередованию последовательности. В чередующейся последовательности будут числа, которые переключаются между положительными и отрицательными знаками.Например: [латекс] 1, -3,9, -27,81, -243, \ cdots [/ latex] — геометрическая последовательность с общим соотношением [латекс] -3 [/ латекс]. Чередующиеся серии)
Чередующиеся серии) {n}} {1-r}} [/ латекс].
{n}} {1-r}} [/ латекс]. {n}}}} [/ latex]
{n}}}} [/ latex] Рассмотрим последовательность, в которой [латекс] r [/ latex] равен половине [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице.
Рассмотрим последовательность, в которой [латекс] r [/ latex] равен половине [латекса] {\ left (\ frac {1} {2}, \ frac {1} {4}, \ frac {1} {8}, \ cdots \ right)} [/ latex], сумма которого равна единице. {5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
{5}} {1-3} \\ & = 6 \ cdot \ frac {{-242}} {-2} \\ & = 6 \ cdot 121 \\ & = 726 \ end {align}} [/ латекс ]
 Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:
Вычитая новую серию [latex] \ displaystyle {\ frac {2} {3} s} [/ latex] из исходной серии, [latex] s [/ latex] отменяет все термины в оригинале, кроме первого:

 Еще несколько примеров:
Еще несколько примеров: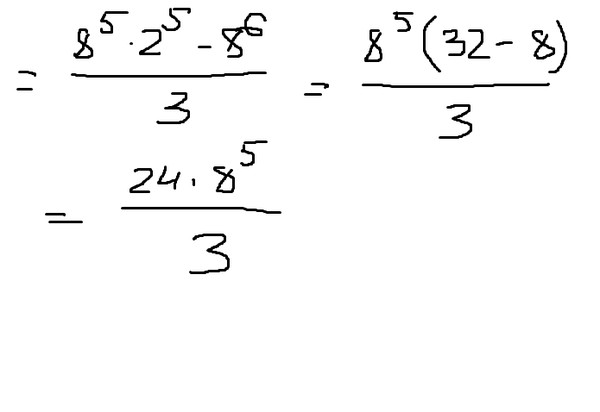

 {3} + \ cdots} [/ latex]
{3} + \ cdots} [/ latex]

 Их отрезки от вершины до центра эллипса называются полуосями.
Их отрезки от вершины до центра эллипса называются полуосями.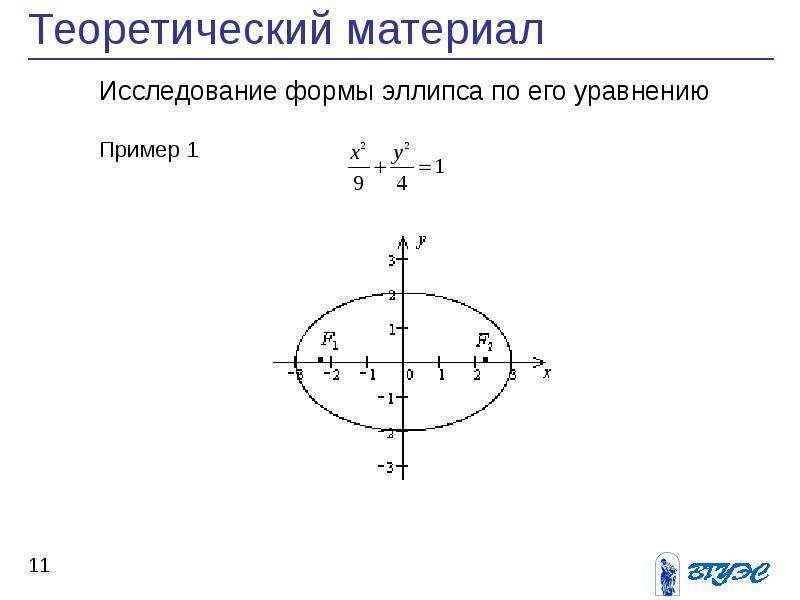
 Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.
Составить каноническое уравнение эллипса,
если расстояние между фокусами равно 8 и бОльшая ось равна 10.

 Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка
на эллипсе .
Если находится, найти расстояние от этой точки до фокусов эллипса.
 Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса К ним относятся эллипс, гипербола и парабола.
К ним относятся эллипс, гипербола и парабола. Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса.
Другой осью симметрии эллипса является прямая, проходящая через середину отрезка перпендикулярно этому отрезку. Точка О пересечения этих прямых служит центром симметрии эллипса или просто центром эллипса. Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей:
Производим преобразования общего уравнения. Применяем перенос свободного члена в правую часть, почленное деление уравнения на одно и то же число и сокращение дробей: Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы.
Для разных эллипсов эксцентриситет меняется в пределах от 0 до 1, оставаясь всегда меньше единицы. Определить фокусы эллипса, заданного каноническим уравнением .
Определить фокусы эллипса, заданного каноническим уравнением .
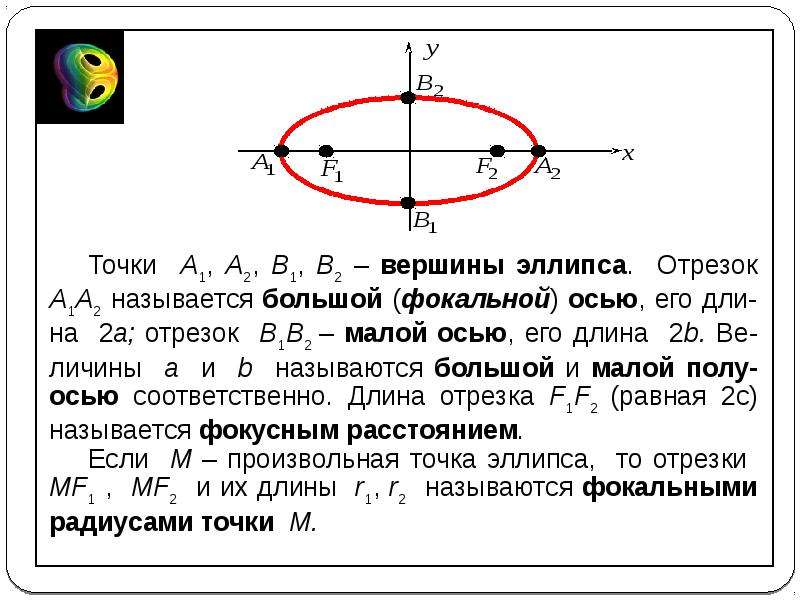 Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса.
Проверить, находится ли точка на эллипсе . Если находится, найти расстояние от этой точки до фокусов эллипса. Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико.
Это значит, что луч, пущенный из одного фокуса, после отраэения попадёт в другой. Это свойство лежит в основе аккустического эффекта, наблюдаемого в некоторых пещерах и искусственных сооружениях, своды которых имеют эллиптическую форму: если находиться в одном из фокусов, то речь человека, стоящего в другом фокусе, слышна так хорошо, как будто он находится рядом, хотя на самом деле расстояние велико. Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
Ясно, что это возможно лишь при а ≥ с. Натянув нить карандашом, начертим линию, которая и будет эллипсом (рис. 7.1).
 Пусть 2c — фокальное расстояние, 2c = |F1F2| 2 + y 2 ) + √((x + c) 2 + y 2 ) = 2a. (7.2)
Пусть 2c — фокальное расстояние, 2c = |F1F2| 2 + y 2 ) + √((x + c) 2 + y 2 ) = 2a. (7.2) Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли.
Возведение уравнения в квадрат является эквивалентным преобразованием, если в обеих его частях стоят величины с одинаковым знаком, но мы этого в своих преобразованиях не проверяли. Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению
Пусть в этом множестве есть точка, лежащая на эллипсе с большой полуосью а. Тогда координаты этой точки подчиняются уравнению Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
Окружность радиуса a с центром в начале канонической системы координат эллипса (7.4) описывается уравнением x 2 + y 2 = а 2 . Если ее сжать с коэффициентом a/b > 1 вдоль оси ординат, то получится кривая, которая описывается уравнением x 2 + (ya/b) 2 = a 2 , т. е. эллипс.
 рис. 7.5).
рис. 7.5). Пусть
фокусы эллипса лежат на оси Х,
причем
т. Е.– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]
Пусть
фокусы эллипса лежат на оси Х,
причем
т. Е.– межфокусное расстояние эллипса.
(чертеж
7.)
[8.С.467]


 При этом величинастремится к.
В предельном случаи уравнение эллипса
принимает вид:.
Это уравнение окружности. Если,
то.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]
При этом величинастремится к.
В предельном случаи уравнение эллипса
принимает вид:.
Это уравнение окружности. Если,
то.
При этом малая ось эллипса неограниченно
уменьшается, эллипс стремится к отрезку.
(чертеж
10.)
[1.С.106]



 Так как , тогда , и поэтому .
Так как , тогда , и поэтому .
 3
3
 Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса
Длина большой оси равна 140 м. Найти коэффициент сжатия k и сжатие α этого эллипса А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид:
А если переобозначить оси, то есть x=x’ , y=y’, тогда уравнение примет вид: ). Это геометрическое определение выражает фокальное свойство эллипса.
). Это геометрическое определение выражает фокальное свойство эллипса. При когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
При когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены). 3.37, имеет вид
3.37, имеет вид разд.2.2.4) координаты произвольной точки принадлежащей окружности, изменяются по закону Подставляя в уравнение окружности получаем уравнение для координат образа точки
разд.2.2.4) координаты произвольной точки принадлежащей окружности, изменяются по закону Подставляя в уравнение окружности получаем уравнение для координат образа точки Для окружности
Для окружности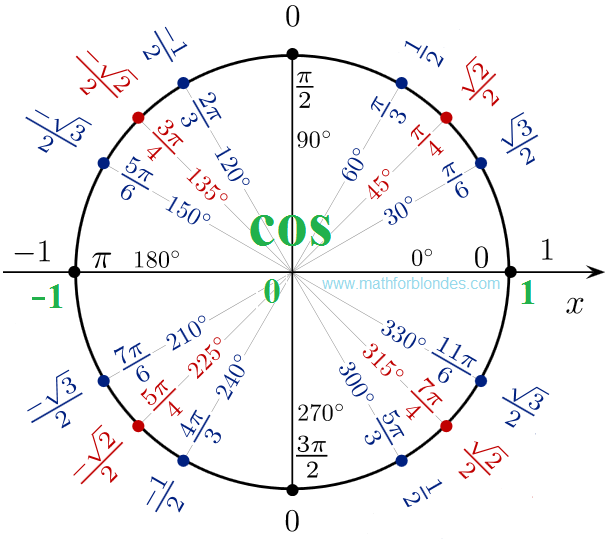 Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан.
Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан.
 Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…
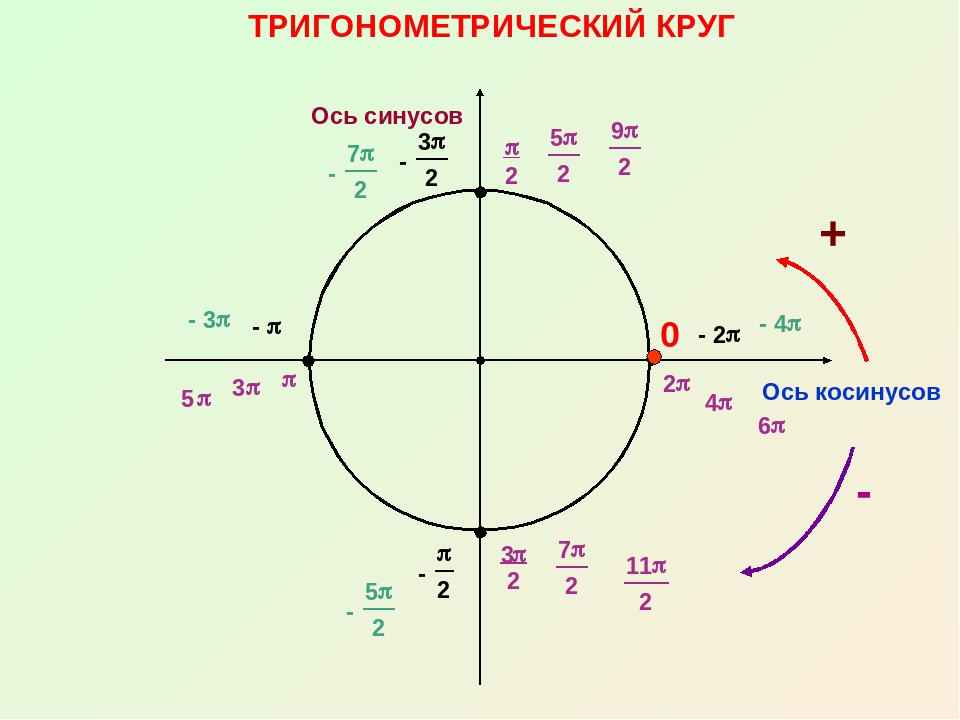 Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
Рассмотрим принцип, который позволит справиться и с другими, аналогичными ситуациями.
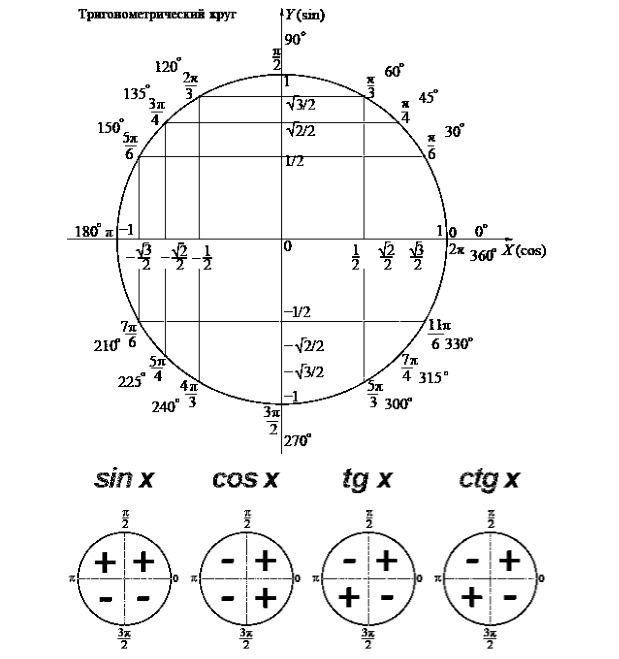 Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.
Прежде всего, нужно отметить, что здесь присутствует декартова система координат — одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая — вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы — cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы — sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы — на диване перед телевизором по горизонтали.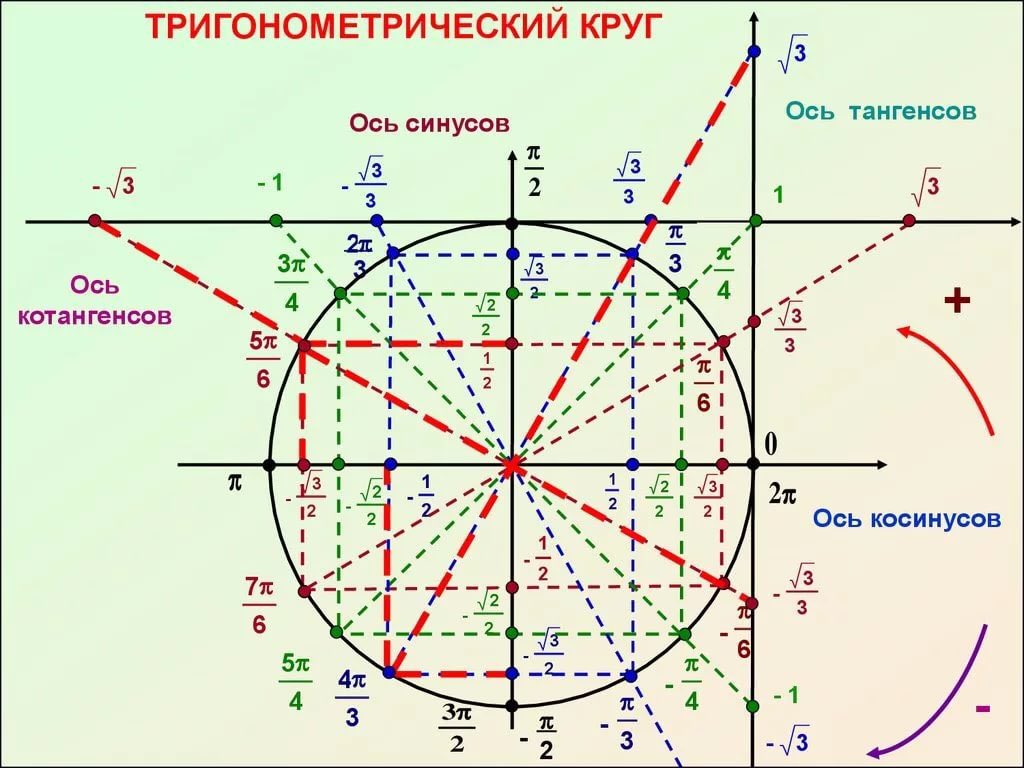 В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.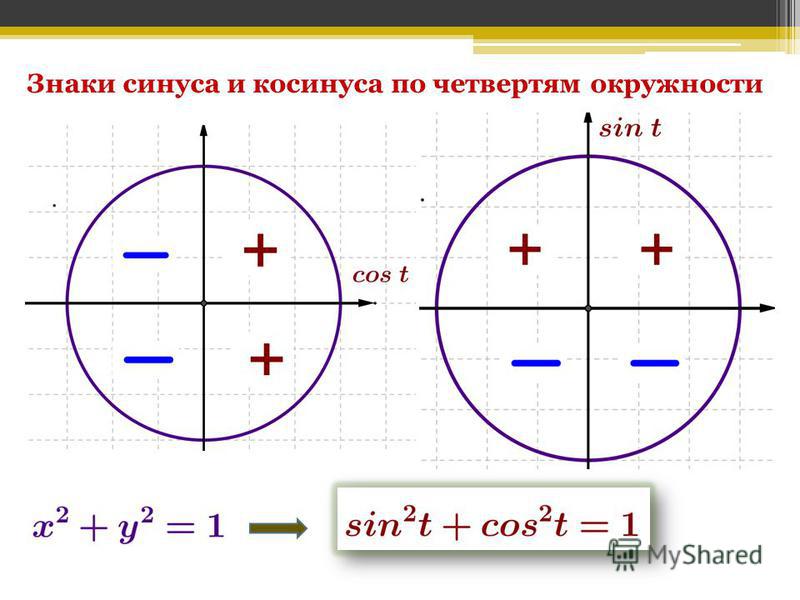 Главное, не перепутать синус с косинусом.
Главное, не перепутать синус с косинусом.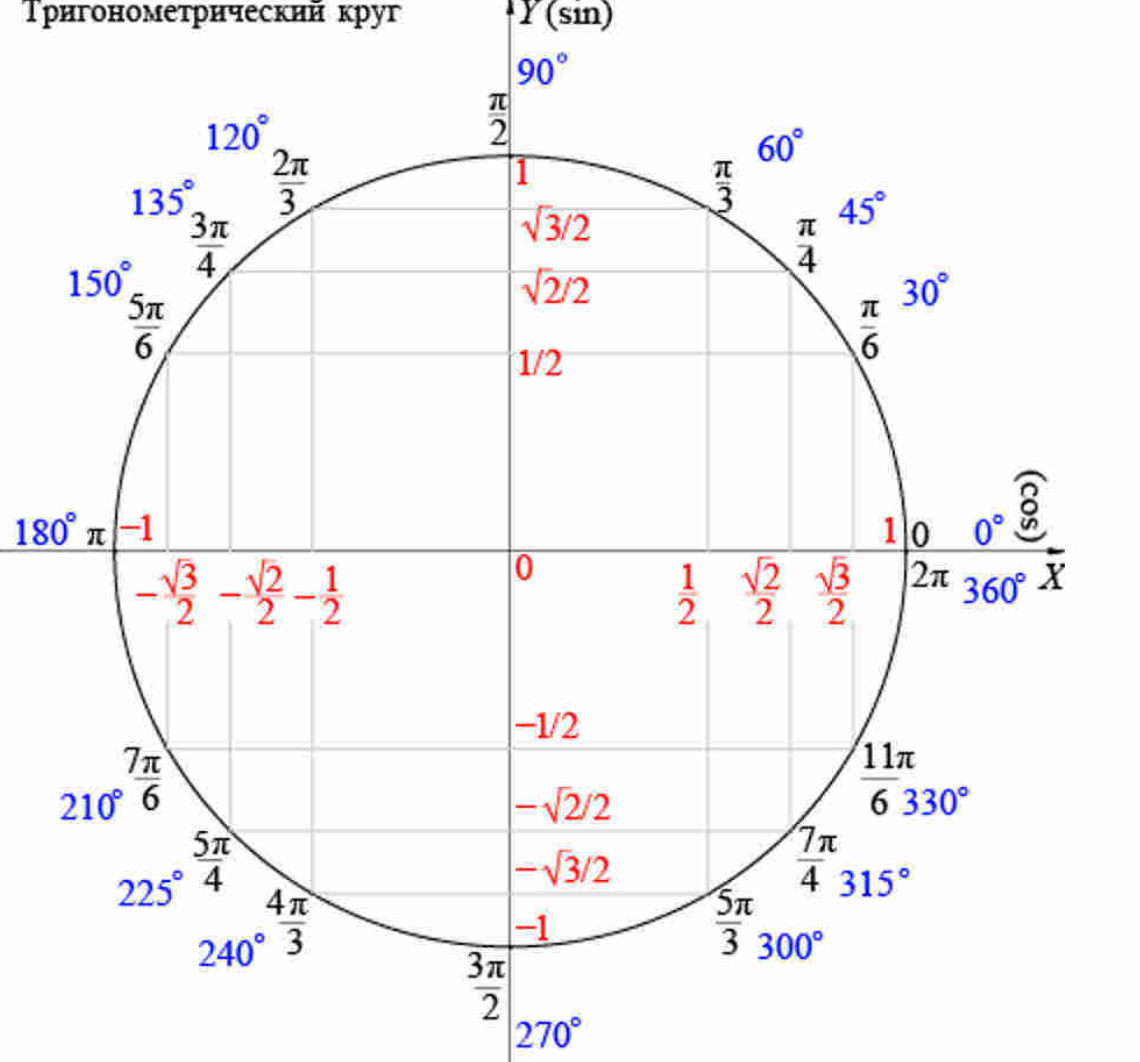
 ..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
..» Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!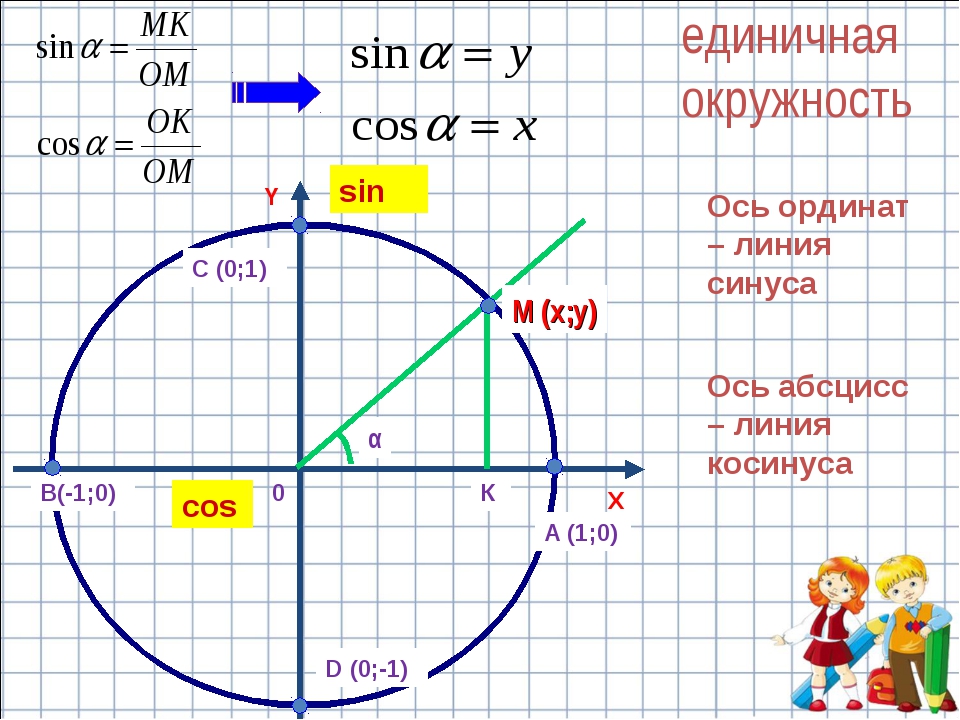
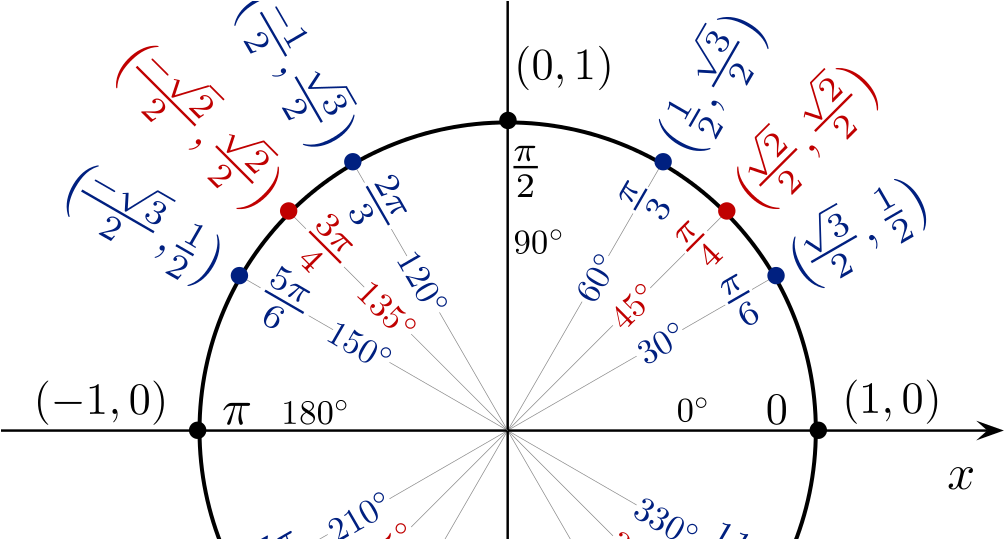

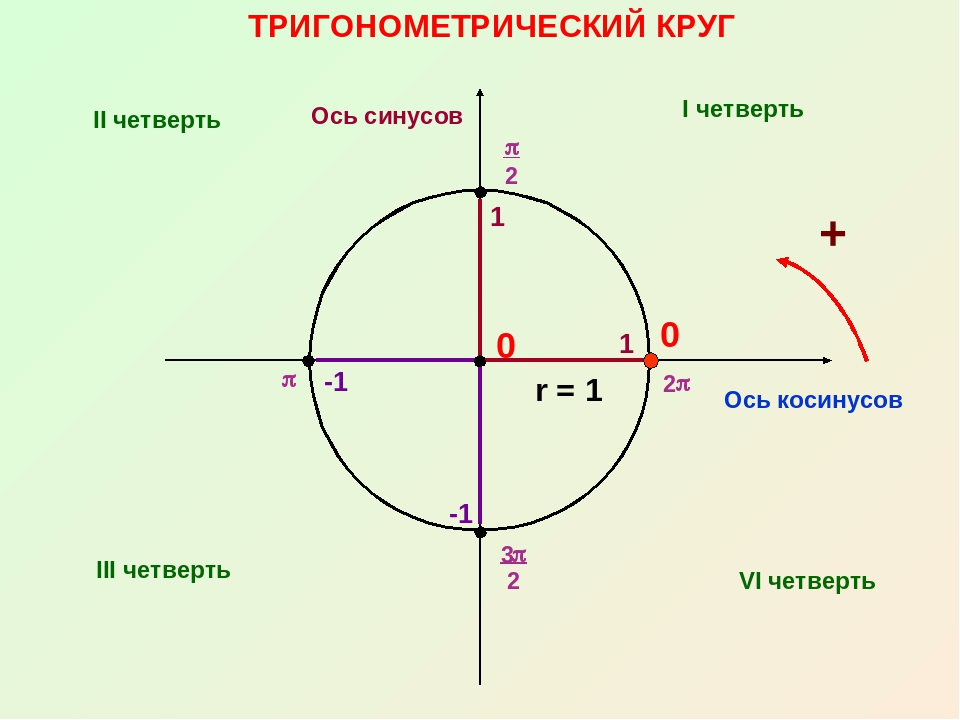 Что же тогда такое — тригонометрия? Разберемся… Начнем с двух основных понятий — синуса и косинуса. Что вы о них знаете кроме того, что это отношения катетов и гипотенузы? Вспомнили? сумма квадратов синуса и косинуса равны единице.
Что же тогда такое — тригонометрия? Разберемся… Начнем с двух основных понятий — синуса и косинуса. Что вы о них знаете кроме того, что это отношения катетов и гипотенузы? Вспомнили? сумма квадратов синуса и косинуса равны единице.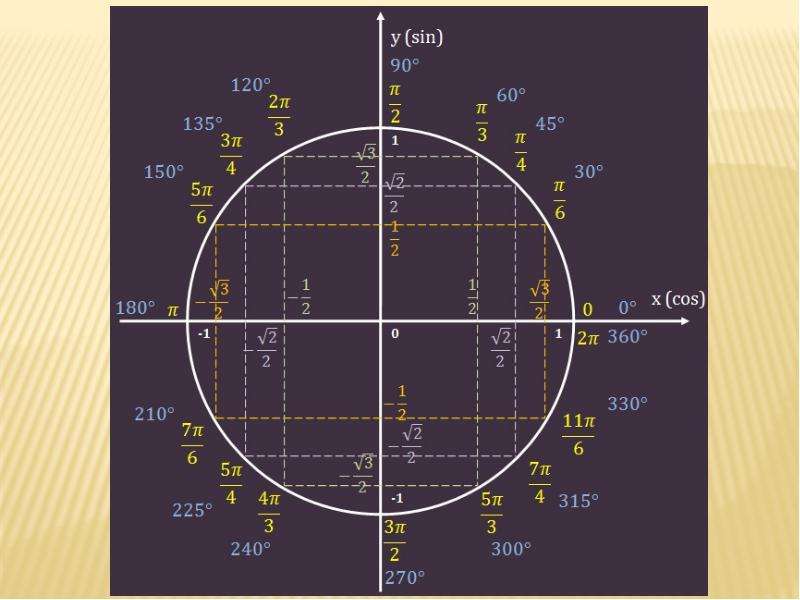
 А значит, мы можем их, эти неизвестные, находить. А поможет нам в этом великолепная классическая «шпаргалка» — тригонометрический круг.
А значит, мы можем их, эти неизвестные, находить. А поможет нам в этом великолепная классическая «шпаргалка» — тригонометрический круг.
 При этом, разумеется, значения синусов и косинусов не выходят за пределы круга. Просто, потому что не могут в силу своей ограниченности! Ну, а мы с вами имеем возможность определятся с синусами и косинусами уже не углов, а аргумента х ∈ ( — ∞; + ∞). Почему? А потому что тригонометрические функции — периодические, т.е. просто «вертятся» по кругу. При этом значения синусов и косинусов определяются значениями координат точек на окружности со всеми их знаками. Например, согласно рисунку, координата у точки на окружности, соответствующей углу , определяет , а координата х определяет .
При этом, разумеется, значения синусов и косинусов не выходят за пределы круга. Просто, потому что не могут в силу своей ограниченности! Ну, а мы с вами имеем возможность определятся с синусами и косинусами уже не углов, а аргумента х ∈ ( — ∞; + ∞). Почему? А потому что тригонометрические функции — периодические, т.е. просто «вертятся» по кругу. При этом значения синусов и косинусов определяются значениями координат точек на окружности со всеми их знаками. Например, согласно рисунку, координата у точки на окружности, соответствующей углу , определяет , а координата х определяет . Аналогично поступаем и с «осью котангенсов» В отличие от синусов и косинусов тангенсам и котангенсам прямую проводим через начало координат. То есть на круге два угла для тангенса и два угла для котангенса. Оно и понятно: период функций тангенса и котангенса составляет π, а не 2π, как у функций синуса и косинуса.
Аналогично поступаем и с «осью котангенсов» В отличие от синусов и косинусов тангенсам и котангенсам прямую проводим через начало координат. То есть на круге два угла для тангенса и два угла для котангенса. Оно и понятно: период функций тангенса и котангенса составляет π, а не 2π, как у функций синуса и косинуса.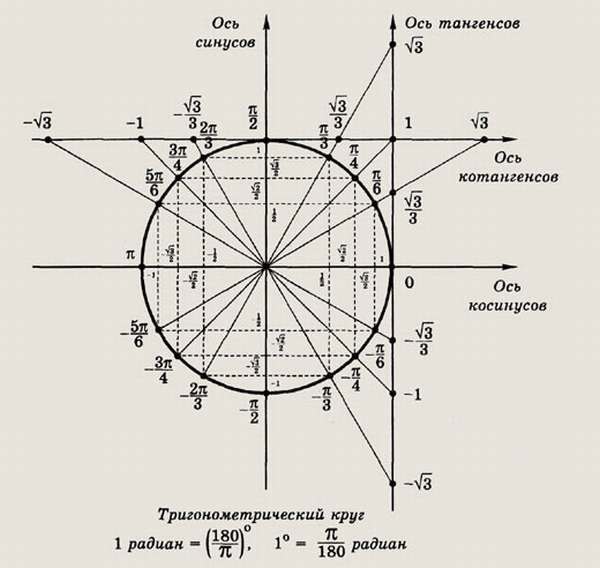
 Внешний угол при вершине А —
это угол, смежный с углом А. Если
угол А острый, то смежный с ним
угол — тупой, и наоборот.
Внешний угол при вершине А —
это угол, смежный с углом А. Если
угол А острый, то смежный с ним
угол — тупой, и наоборот. Тогда и синус внешнего угла
при вершине В также равен 0,1.
Тогда и синус внешнего угла
при вершине В также равен 0,1.
 Так давайте найдем
sin A:
Так давайте найдем
sin A: Нарисуйте треугольник.
Через одну из его вершин проведите
прямую, параллельную противоположной
стороне, и найдите на рисунке
равные углы. Сравните с решением
в конце статьи.
Нарисуйте треугольник.
Через одну из его вершин проведите
прямую, параллельную противоположной
стороне, и найдите на рисунке
равные углы. Сравните с решением
в конце статьи.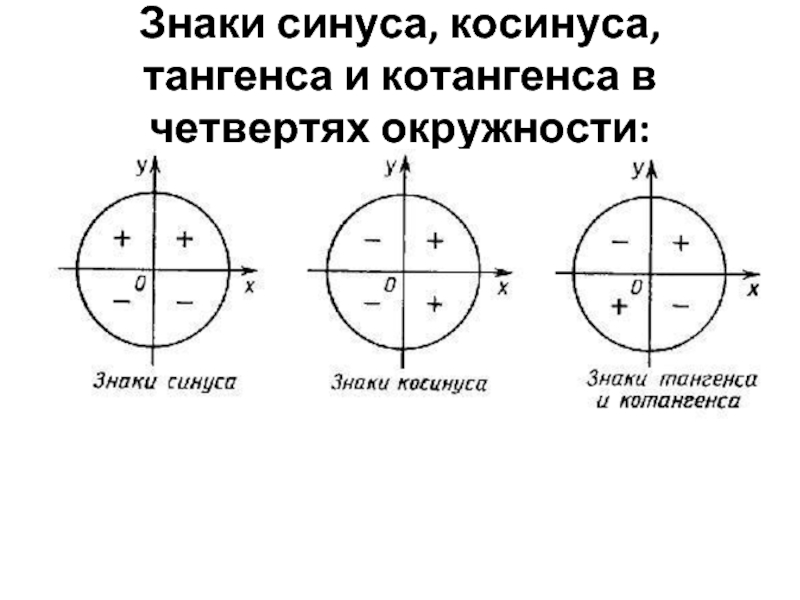 Значит, один из углов
треугольника равен 98°, а два других
равны .
Значит, один из углов
треугольника равен 98°, а два других
равны . При этом образуется
восемь углов. Углы при параллельных
прямых и секущей так часто используются
в задачах, что в геометрии им даны
специальные названия.
При этом образуется
восемь углов. Углы при параллельных
прямых и секущей так часто используются
в задачах, что в геометрии им даны
специальные названия.
 Значит, треугольник АВМ —
равнобедренный, следовательно, АВ = АМ
= 4х.
Значит, треугольник АВМ —
равнобедренный, следовательно, АВ = АМ
= 4х.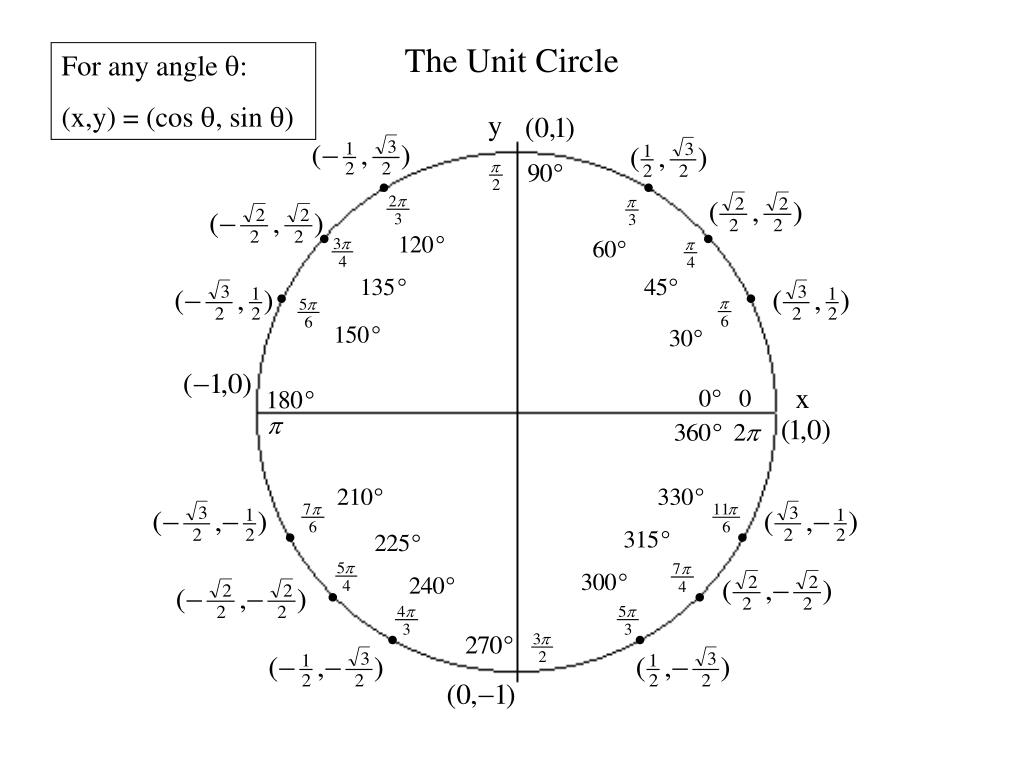
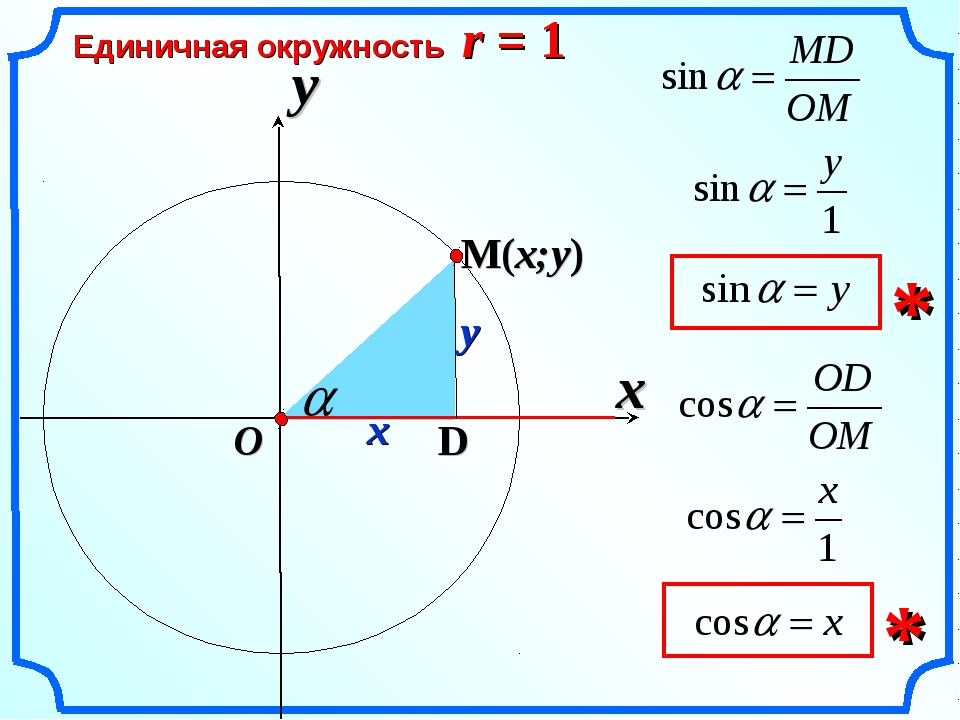
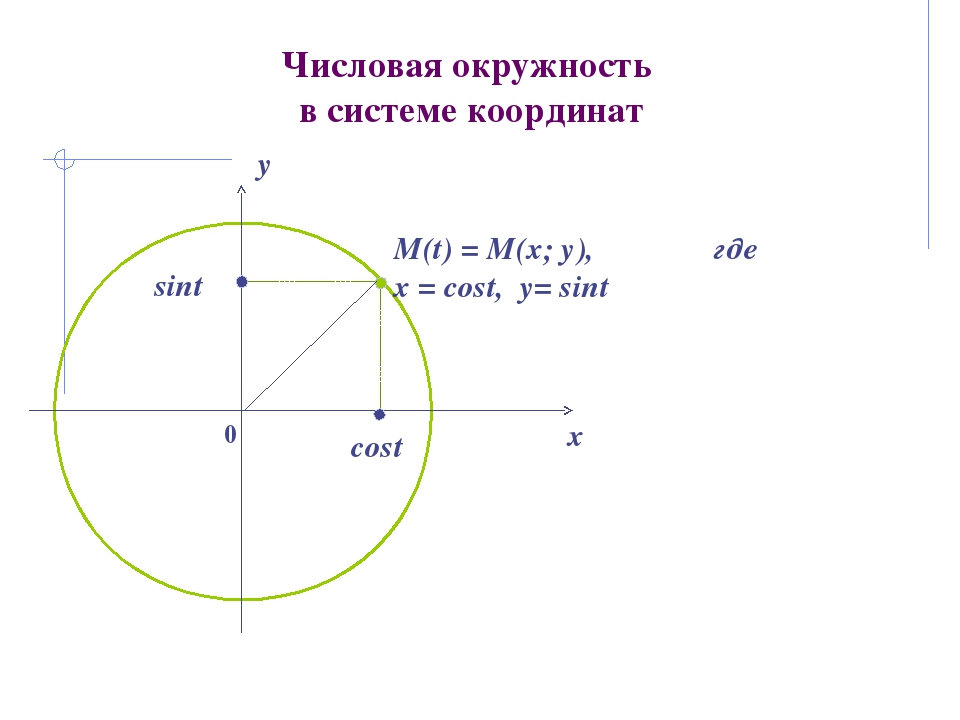 Все задачи взяты из Банка
заданий ФИПИ.
Все задачи взяты из Банка
заданий ФИПИ.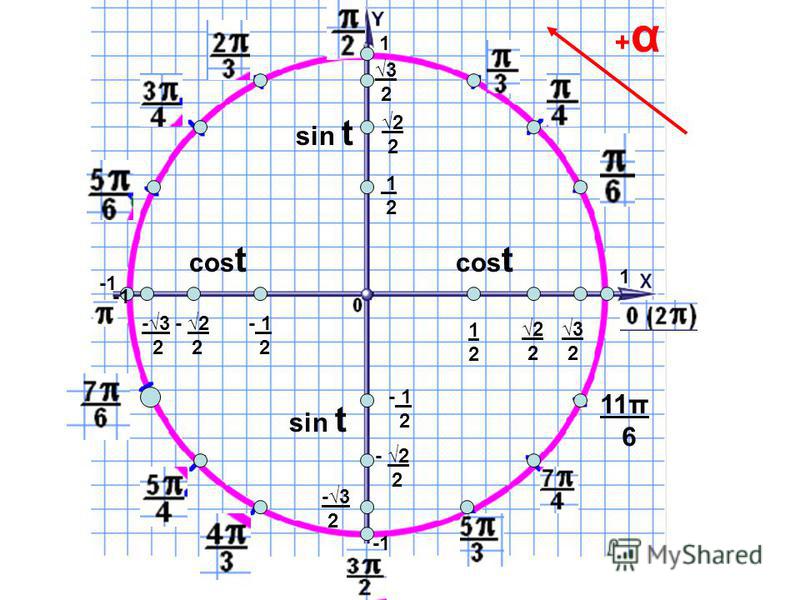
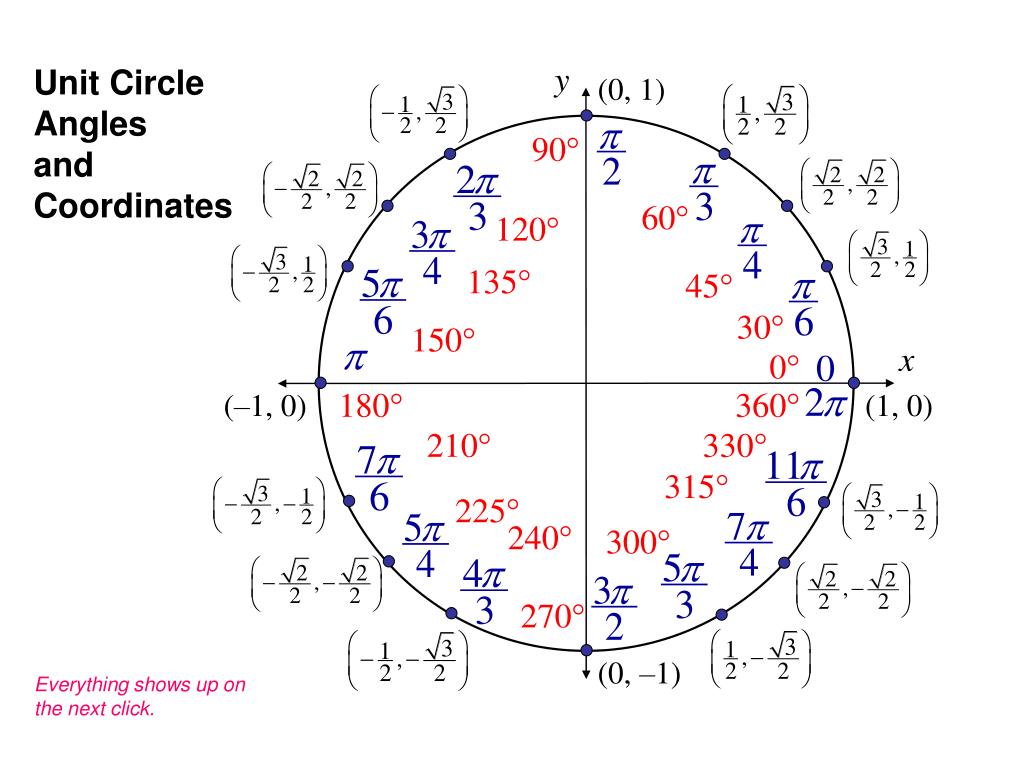 Из треугольника АВС получим,
что ∠
А + ∠
В = 180° — 58° = 122°.
Из треугольника АВС получим,
что ∠
А + ∠
В = 180° — 58° = 122°.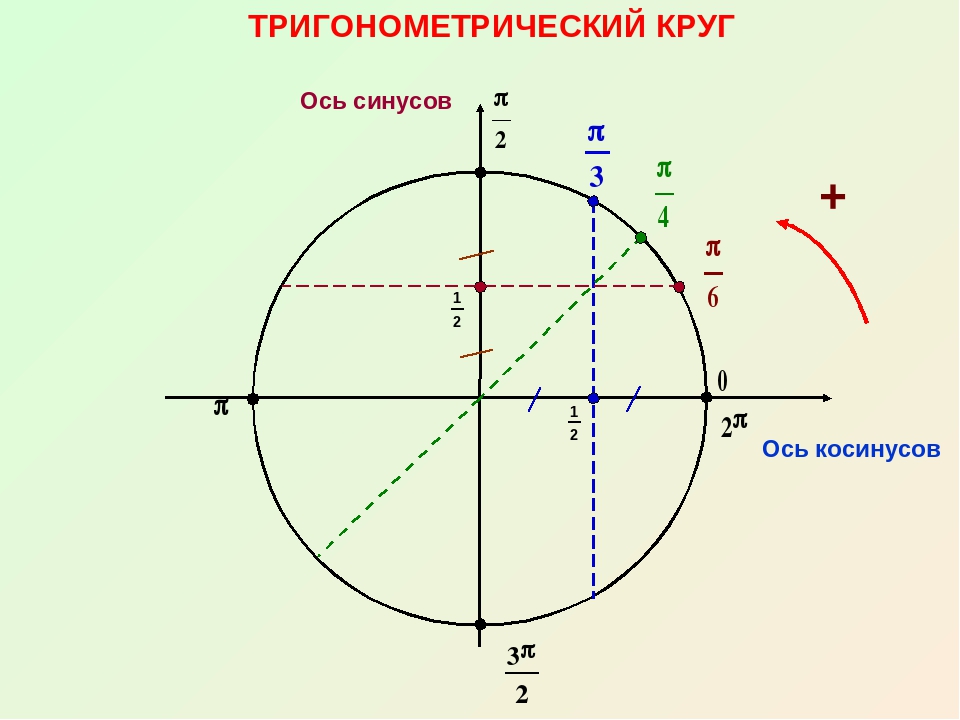
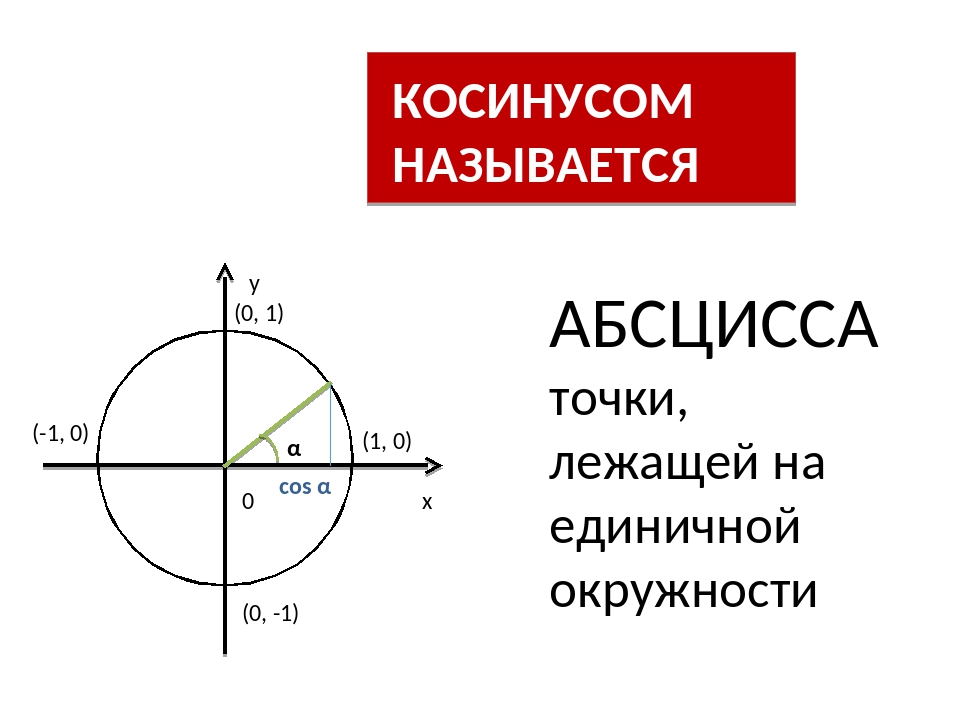 ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведения
ru: главная страница / / Техническая информация / / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Синус и косинус — тригонометрические функции y=sin(x), y=cos(x). Свойства, область определения, значения, четность, периоды, нули, промежутки знакопостоянства, возрастание, убывание, минимумы, максимумы, основные значения, знаки, формулы приведения
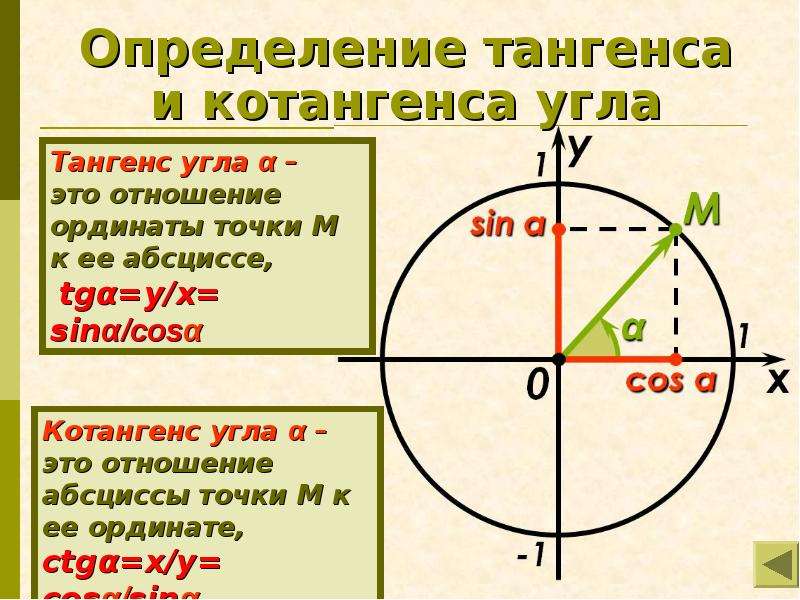 Введите свой запрос:
Введите свой запрос:
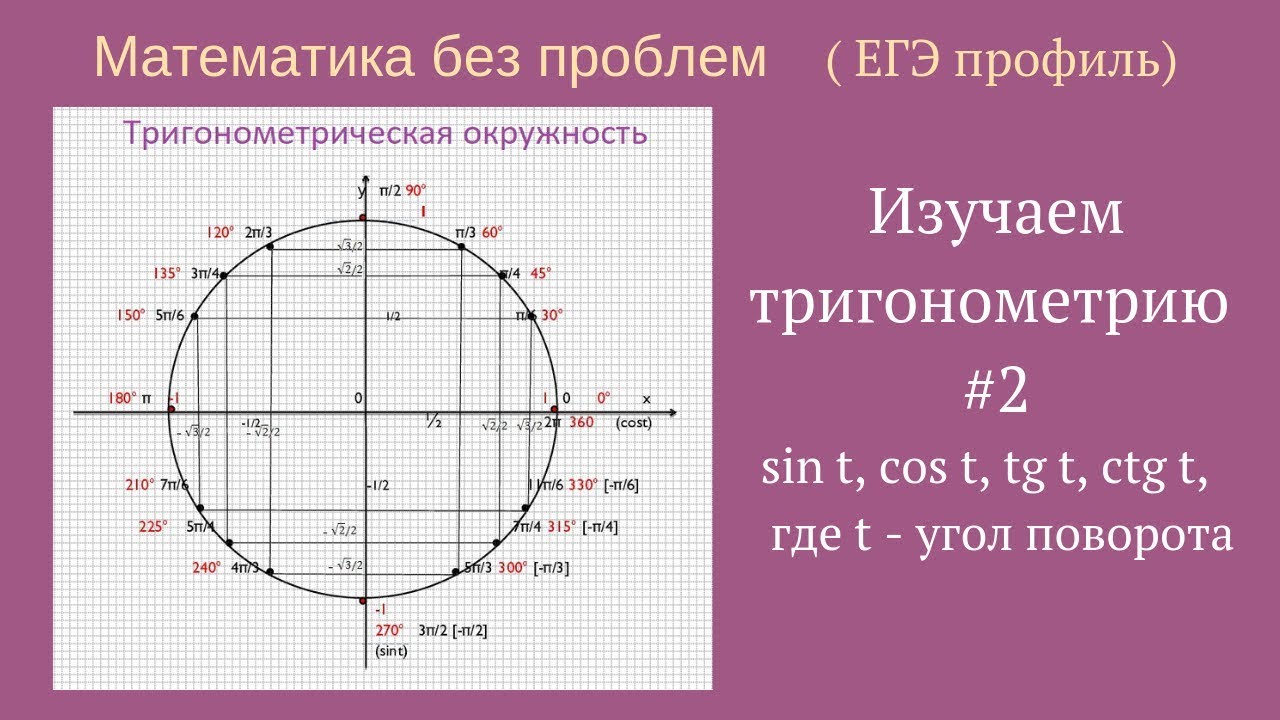 (Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.)
(Это также означает, что диаметр круга будет равен 2, поскольку диаметр равен удвоенной длине радиуса.) 2θ = 1 $$
2θ = 1 $$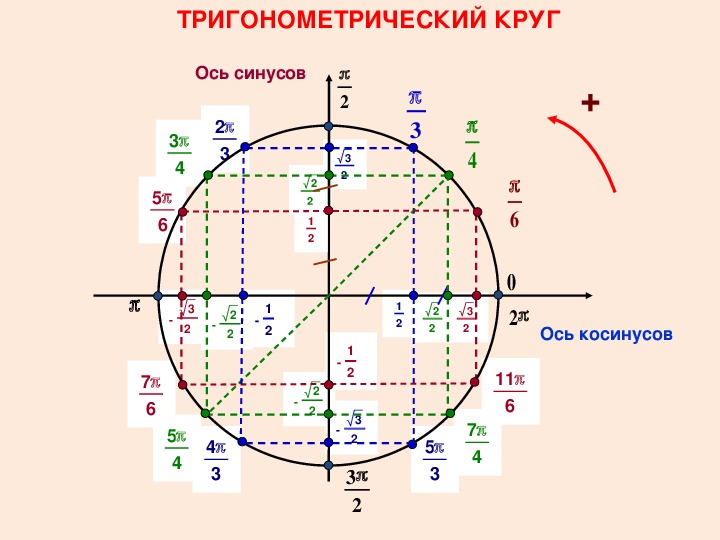 Это дает нам следующие значения для синуса и косинуса:
Это дает нам следующие значения для синуса и косинуса: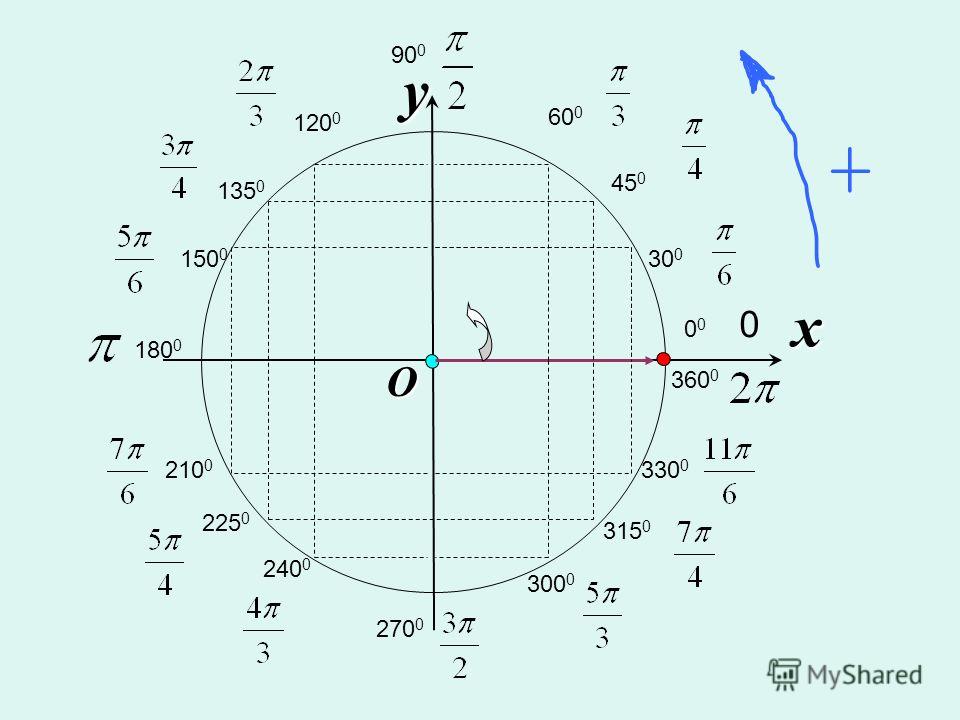 belk / Викимедиа
belk / Викимедиа 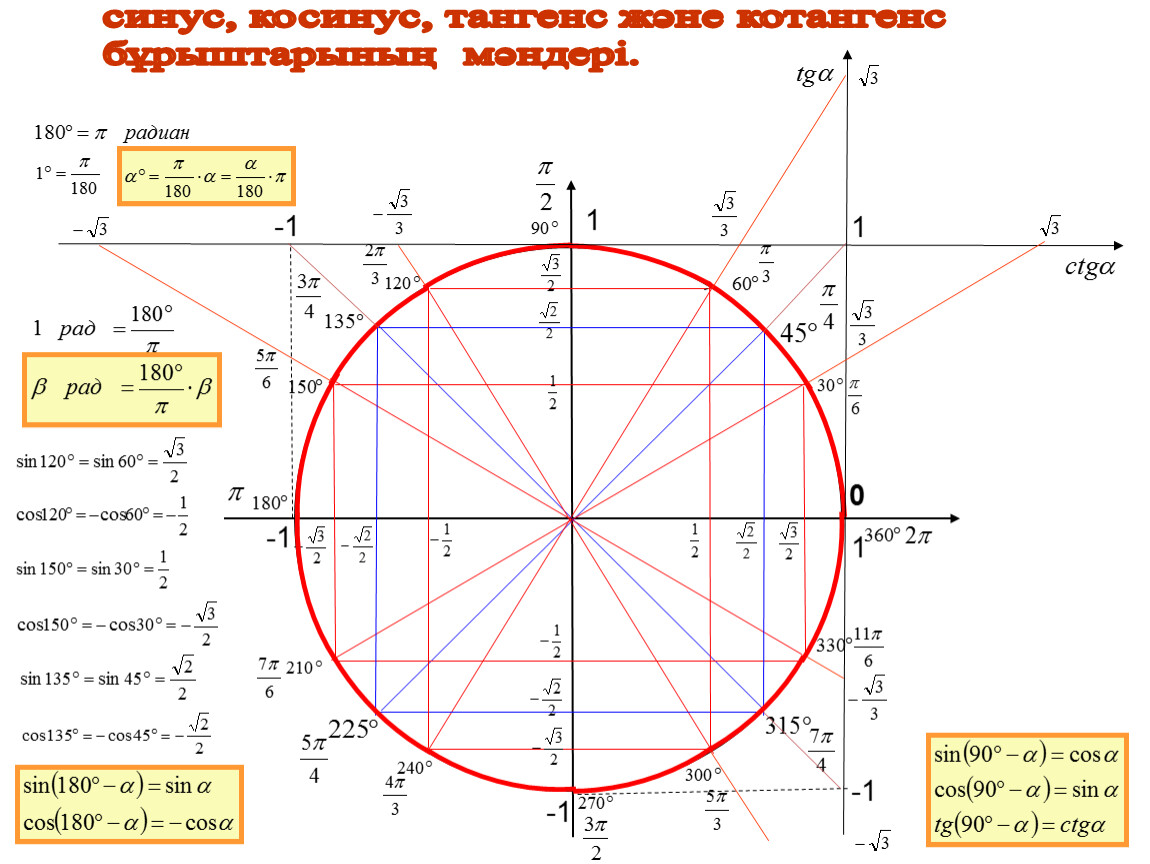
 США ({√3} / 2, 1/2)
США ({√3} / 2, 1/2) США (1/2, — {√3} / 2)
США (1/2, — {√3} / 2)