Таблица степеней, таблица степеней для чисел от 1 до 10, полная таблица степеней
Таблица степеней — перечень чисел от 1 до 10 возведенных в степень от 1 до 10. Таблица степеней редко применяется в учебе, но когда она нужна, без нее просто не обойтись. Ведь не сразу вспомнишь сколько будет 6 в 4-ой степени! Всятаблица степеней представлена ниже. На нашем сайте помимо таблицы степеней советуем посмотреть программы для решения задач по теории вероятности, геометрии и математике! Также на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1n | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2n | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
| 3n | 3 | 9 | 27 | 81 | 243 | 729 | 2187 | 6561 | 19683 | 59049 |
| 4n | 4 | 16 | 64 | 256 | 1024 | 4096 | 16384 | 65536 | 262144 | 1048576 |
| 5n | 5 | 25 | 125 | 625 | 3125 | 15625 | 78125 | 390625 | 1953125 | 9765625 |
| 6n | 6 | 36 | 216 | 1296 | 7776 | 46656 | 279936 | 1679616 | 10077696 | 60466176 |
| 7n | 7 | 49 | 343 | 2401 | 16807 | 117649 | 823543 | 5764801 | 40353607 | 282475249 |
| 8n | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 |
| 9n | 9 | 81 | 729 | 6561 | 59049 | 531441 | 4782969 | 43046721 | 387420489 | 3486784401 |
| 10n | 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 | 10000000000 |
Таблица степеней от 1 до 10
11=1 12=1 13=1 14=1 15=1 16=1 17=1 18=1 19=1 110=1 | 21=2 22=4 23=8 24=16 25=32 26=64 27=128 28=256 29=512 210=1024 | 31=3 32=9 33=27 34=81 35=243 36=729 37=2187 38=6561 39=19683 310=59049 | 41=4 42=16 43=64 44=256 45=1024 46=4096 47=16384 48=65536 49=262144 410=1048576 | 51=5 52=25 53=125 54=625 55=3125 56=15625 57=78125 58=390625 59=1953125 510=9765625 |
61=6 62=36 63=216 64=1296 65=7776 66=46656 67=279936 68=1679616 69=10077696 610=60466176 | 71=7 72=49 73=343 74=2401 75=16807 76=117649 77=823543 78=5764801 79=40353607 710=282475249 | 81=8 82=64 83=512 84=4096 85=32768 86=262144 87=2097152 88=16777216 89=134217728 810=1073741824 | 91=9 92=81 93=729 94=6561 95=59049 96=531441 97=4782969 98=43046721 99=387420489 910=3486784401 | 101=10 102=100 103=1000 104=10000 105=100000 106=1000000 107=10000000 108=100000000 109=1000000000 1010=10000000000 |
Остались вопросы?
Здесь вы найдете ответы.x=3 log2(3)=x
90 в 10 степени
90 в 10 =34867844009999998976.00000
12 в степени 1/3
Сложная формула но в кратце ответ — 6
Слишком сложно?
Таблица степеней не по зубам? Тебе ответит эксперт через 10 минут!
Степени поражения легких: КТ1, КТ2, КТ3, КТ4
Главная статьи Степени поражения легких: КТ1, КТ2, КТ3, КТ4Компьютерная томография (КТ) легких считается «золотым стандартом» диагностики воспаления легких, в частности пневмонии, ассоциированной с COVID-19. На томограммах — множественных сканах дыхательного органа в трех плоскостях — визуализируются нефункциональные участки уплотнения или инфильтрации легочной ткани.
Когда говорят о поражении легких при пневмонии, то имеют в виду, что альвеолы — маленькие пузырькообразные полости легких, которые отвечают за хранение воздуха и газообмен, заполняются жидкостью, слизью, фиброзной тканью и «выходят из строя».
На ранних стадиях пневмония может протекать практически бессимптомно или вызывать незначительный дискомфорт: кашель, затрудненное дыхание, повышение температуры. Однако она быстро переходит в более тяжелую форму и человек начинает ощущать нехватку воздуха, спазм в груди, вызванный отеком легких, или острый респираторный дистресс-синдром — обширный воспалительный процесс, который дает осложнение на сердце и в некоторых случаях приводит к летальному исходу.
В этой связи очень важно вовремя распознать пневмонию и начать лечение. КТ легких — единственный метод диагностики, который позволяет выявить очаги инфильтрации и оценить степень их выраженности, даже если поражено менее 5% легких.
После компьютерной томографии легких, особенно при наличии подозрений на вирусную пневмонию, пациентов в первую очередь интересуют результаты и расшифровка обследований. В этой статье мы расскажем о том, что означает КТ1, КТ2, КТ3, КТ4 в заключении, и на что следует обратить внимание, если пневмония все-таки была обнаружена.
Что означает КТ1, КТ2, КТ3, КТ4 при вирусной пневмонии COVID-19?
Чтобы врачи могли объективно оценивать объем поражения легких, взвешивать риски и реагировать на вызовы, был принят единый стандарт классификации вирусных пневмоний по степени тяжести, где:
КТ-0 — отсутствие признаков вирусной пневмонии;
КТ-1 — легкая форма пневмонии с участками «матового стекла», выраженность патологических изменений менее 25%;
КТ-2 — умеренная пневмония, поражено 25-50% легких;
КТ-3 — среднетяжелая пневмония, поражено 50-75% легких;
КТ-4 — тяжелая форма пневмонии, поражено >75% легких.
Процент деструкции легочной ткани определяется по томограммам. Врач-рентгенолог оценивает по пятибалльной шкале каждую из пяти долей легких.* Если признаки пневмонии не выявлены, то значение соответствует 0; 1 балл свидетельствует о поражении легких 5%, и так далее.
* Согласно «Временным методическим рекомендациям» Министерства Здравоохранения РФ от октября 2020 г., принятая и описанная выше балльная система оценки легочных сегментов и долей упразднена. Объективность оценки поддерживается программным обеспечением и медицинской экспертизой.
Иными словами, сокращение КТ1, КТ2, КТ3 или КТ4, которое врач-рентгенолог пишет в заключении, указывает на объемы нефункциональной легочной ткани в совокупности с другими признаками, характерными для той или иной стадии. Это эмпирическая визуальная шкала, принятая рентгенологами.
Данную шкалу визуальной оценки легких по результатам компьютерной томографии (или МСКТ) разработали только во время пандемии новой коронавирусной инфекции. Ее ввели специалисты из Центра диагностики и телемедицины США, изучив КТ-исследования 13 003 человек, которые составили основную выборку.
Примечательно, что скорость перехода пневмонии к следующей, более осложненной степени зависит не только от возраста пациента (чем старше, тем быстрее), но и от текущей стадии заболевания. А именно, если вирусная пневмония SARS-CoV-2 у пациента была выявлена еще на первой стадии (КТ1), то предотвратить переход к следующей (КТ2) будет легче как минимум потому, что сравнительно малому числу вирионов требуется больше времени, чтобы распространиться по легким и спровоцировать более обширный воспалительный процесс. В то время как переход от КТ3 к КТ4 происходит очень быстро, и тогда жизнь пациента находится под угрозой. Анализируя уже упомянутую группу пациентов, ученые из США пришли к выводу, что при переходе в следующую группу, риск летального исхода при коронавирусе увеличивался примерно на 38%.
Процент вовлечения паренхимы (собственно поражения) легких в заключениях обычно указан приблизительно, поэтому диапазон значений может быть довольно широким, однако это не главный показатель. При определении степени тяжести воспаления легких учитываются и другие признаки воспаления легких:
1) Наличие «матовых стекол» на сканах КТ, их локализация, консолидация. «Матовые стекла» — это светлые участки легких на томограммах, которые свидетельствуют об очагах инфильтрации. Плотная ткань не пропускает рентгеновские лучи. «Матовые стекла» — основной признак поражения легких на КТ. Их распространенность и консолидация соответствует тяжелым стадиям пневмонии КТ3 и КТ4.
2) Утолщение междолькового пространства легких или «симптом булыжной мостовой» — ткань легких на сканах КТ имеет внешнее визуальное сходство с брусчаткой. Соответствует тяжелой стадии пневмонии КТ4.
3) Симптом «обратного гало» или «ободка́» — на томограммах выглядит как светлые кольца. Это участки уплотнения вокруг очага инфекции. Считается признаком организующейся пневмонии.
4) Ретикулярные изменения — тонкие линии патологически измененного легочного интерстиция, формирующие сеть.
Если в заключении указана «полисегментарная пневмония», это значит, что признаки воспалительного процесса обнаружены в обоих легких, в нескольких сегментах.
Поражение легких КТ1
На сканах КТ легких обнаружены «матовые стекла» — менее трех. Диаметр очага инфильтрации не превышает 3 см, иные патологические изменения легких не обнаружены. У пациента может быть высокая температура, затрудненное дыхание, кашель, иногда явные симптомы отсутствуют. Лечиться от внебольничной пневмонии КТ1 можно в амбулаторных условиях и дома после консультации врача.
Поражение легких КТ2
КТ2 означает, что обнаружено более трех участков воспаления легких по типу «матового стекла» диаметром не более 5 см. Также как и в случае с КТ1, это внебольничная пневмония, при которой не нужна госпитализация. Пациент лечится дома, соблюдая рекомендации врача. КТ легких поможет ответить на вопрос — имеется ли активный воспалительный процесс и тенденция к консолидации «матовых стекол». Если лечение не помогает, и становится хуже, рекомендовано сделать повторное КТ легких, чтобы оценить динамику и скорректировать лечение. Поскольку у пациента с умеренной пневмонией КТ2 может быть поражено до 50% легких, после основного лечения необходима реабилитация.
Поражение легких КТ3
Обнаружены множественные участки «матового стекла» с тенденцией к консолидации. Это основной признак, но возможны и другие: ретикулярные изменения, «дерево в почках» или центрилобулярные очаги. При пневмонии КТ3 поражено более 50% легких, нужна срочная госпитализация и интенсивная терапия. Множественные инфекционные очаги и подавленные защитные силы организма способствуют тому, что переход от КТ3 к КТ4 происходит быстрее и легче, чем от КТ1 к КТ2.
Поражение легких КТ4
Критическая стадия поражения легких, когда более 75% легких не участвует в газообмене. На томограммах визуализируется как диффузное поражение лёгочной ткани с ретикулярными изменениями и симптомом «булыжной мостовой», гидроторакс. Пациент может нуждаться в реанимации с искусственной вентиляцией легких (ИВЛ).
Квалификации на уровне высшего образования
Ниже перечислены квалификации, которые вы можете получить в университете или высшем учебном заведении.
Степень специалиста
- Продолжительность — 2 года
- Предыдущее обучение — 12 класс или его эквивалент, сертификат III или сертификат IV
- Подробности — Степень специалиста (Associate Degree) — это короткий вариант программы уровня высшего образования, который может помочь вам в карьере, если вы уже работаете, и у вас нет времени на получение полноценной степени бакалавра. Эта степень может вести к получению степени бакалавра или диплома продвинутого уровня по специализированным отраслевым направлениям. Associate Degree охватывает общие понятия или основы знаний в выбранной вами области. Вы изучите общую теорию и освоите базовые навыки, необходимые при трудоустройстве.
Степень бакалавра
- Продолжительность — 3 года
- Предыдущее обучение — 12 класс или его эквивалент, сертификат III или сертификат IV
- Подробности — Степень бакалавра — это базовая квалификация для работы в определенной области. В рамках этих программ вы получите систематизированные знания, освоите основные принципы и подходы решения задач, которые вам понадобятся для профессиональной деятельности. Содержание учебных программ этого уровня более глубокое, чем на уровне специалиста. Вы сможете расширить знания и развить навыки до уровня, который поможет вам при желании продолжить своё обучение в аспирантуре.
Степень бакалавра (с отличием)
- Продолжительность — 4 года
- Предыдущее обучение — Степень бакалавра
- Подробности — Если вы добьетесь значительных успехов по программе бакалавриата, ваше учебное заведение может позволить вам учиться еще один год и получить степень с отличием.
Сертификат об окончании курса высшего учебного заведения
- Продолжительность — 6 месяцев
- Предыдущее обучение — Степень бакалавра
- Подробности — Сертификат об окончании курса высшего учебного заведения свидетельствует о дальнейшем развитии индивидуальных навыков, полученных по программе высшего образования, или о получении углубленных профессиональных знаний и навыков в новой предметной области.
Диплом об окончании курса высшего учебного заведения
- Продолжительность — 1 год
- Предыдущее обучение — Степень бакалавра
- Подробности — Диплом об окончании курса высшего учебного заведения свидетельствует о получении профессиональных знаний в различных областях с целью применения в профессиональной или высококвалифицированной деятельности, а также предоставляет возможности для дальнейшего роста и обучения.
Степень магистра
- Продолжительность — 1 — 2 года
- Предыдущее обучение — Степень бакалавра (с отличием) или степень бакалавра
- Подробности — Степень магистра присваивается по окончании курса, который может строиться как индивидуальная исследовательская (research) или традиционная курсовая (coursework) работа или их сочетание. Эта программа сделает вас лидером в своей области. Для получения степени магистра требуется один год обучения после получения степени бакалавра с отличием или два года после получения степени бакалавра.
Докторская степень
- Продолжительность — Как правило, 3 года
- Предыдущее обучение — Степень магистра
- Подробности — Докторская степень — это высшая ученая степень, присваиваемая австралийскими университетами. Несмотря на то, что она присваивается за проведение исследовательской работы, некоторые программы могут содержать элементы курсовой работы.
Докторская степень включает три компонента:
- аналитический обзор литературы, экспериментальный или системный подход к знаниям.
- оригинальный исследовательский проект, внесший значительный вклад в развитие знаний или понимание вашей предметной области.
- солидная и грамотно организованная диссертация, демонстрирующая взаимосвязь исследовательской работы с предметной областью.
Аденоиды у ребенка — откуда берутся, признаки и симптомы
“Кажется, у нашего ребёнка аденоиды!”– с такими сомнениями чаще всего приходят родители с малышом на прием к оториноларингологу, начитавшись статей в интернете, или после разговора с «всезнающими» мамами в песочнице/садике/школе. В этой статье мы постараемся разобрать наиболее частые вопросы об аденоидных вегетациях и попробуем понять, настолько ли все страшно.
Что такое аденоиды и откуда они берутся
Аденоидные вегетации (носоглоточная миндалина) – это лимфоидная ткань в своде носоглотки. Она имеется у всех без исключения детей и является периферическим органом иммунной системы, частью лимфоидного глоточного кольца. Главной функцией данного анатомического образования является борьба с проникающими в организм ребёнка бактериями или вирусами. Главное ее отличие от остальных миндалин — поверхность покрыта особым эпителием, который продуцирует слизь. Увеличение (гипертрофию) аденоидной ткани провоцируют частые аллергические и респираторные заболевания вирусной или бактериальной этиологии. Поэтому пик гипертрофии аденоидной ткани приходится как раз на возраст 3-7 лет. Затем лимфоидная ткань постепенно редуцируется в возрасте 10–12 лет. К 17 годам нередко остаются только фрагменты ткани, у здоровых же взрослых людей аденоидная ткань отсутствует. Гипертрофию аденоидной ткани принято делить на несколько степеней по ее объёму в носоглотке от первой, где аденоиды закрывают носовые ходы (хоаны) на 1/3 , до третьей-четвертой степени, когда происходит полная обтурация носоглотки с невозможностью носового дыхания.
Клинические проявления
Воспаление аденоидной ткани называется аденоидит. Течение его бывает острым, подострым и хроническим. Коснемся кратко основных симптомов, на которые стоит обращать внимание родителям:
1. Насморк, чаще всего он имеет затяжное течение.
2. Преимущественное дыхание через рот. Обусловлено затрудненным носовым дыханием. Степень затруднения напрямую зависит от степени гипертрофии аденоидной ткани. Часто появляется гнусавость. При длительном течении хронического аденоидита и дыхании через рот, возможно изменение лицевого скелета, что в дальнейшем проявляется стойким нарушением произношения речи.
3. Ночной храп, беспокойный сон.
4. Утренний кашель, обусловленный поперхиванием слизью, стекающей из носоглотки за ночь.
5. Снижение слуха, рецидивирующие отиты из-за механической обтурации слуховых труб аденоидными вегетациями. При этом гипертрофия может быть и 1-2 степени, при расположении аденоидов возле устьев слуховых труб, которые отвечают за вентиляцию среднего уха через слуховую трубу. Ребенок начинает постоянно переспрашивать или смотреть мультики слишком громко.
6. Быстрая утомляемость, апатия. Обусловлены постоянным кислородным голоданием головного мозга, особенно при хроническом аденоидите. Возможно отставание от сверстников в умственном и физическом развитии.
Методы исследования аденоидных вегетаций
В обычном состоянии без дополнительных оптических приспособлений эту миндалину увидеть невозможно. Существует ряд исследований, которые помогают установить степень аденоидных вегетаций: пальцевое исследование, задняя риноскопия зеркалом, рентгенография носоглотки, эндоскопия носоглотки, трёхмерное рентгенологическое исследование или КТ носоглотки. Наиболее современными методами на сегодняшний день являются:
- эндоскопия носоглотки и полости носа. Процедура выполняется в нашей клинике под местной анестезией на приеме ЛОР врача. Полностью безболезненна, позволяет оценить не только степень аденоидных вегетаций, но и характер воспаления, состояние устьев слуховых труб, а также осмотреть задние отделы полости носа.
- трёхмерное рентгенологическое исследование / КТ носоглотки. Методы по информативности значительно превосходят обычный рентген носоглотки, так как позволяют определить не только размер, но и соотношение аденоидных вегетаций к остальным структурам носоглотки (устья слуховых труб, хоаны и др). Лучевая нагрузка практически в 3 раза меньше (0,009м3в), а длительность исследования не более 2 мин. Пройти данное исследование можно в клинике на Усачева.
Лечение аденоидита
Лечение аденоидита принято разделять на консервативное и оперативное. Консервативное лечение требует от родителей, в первую очередь, большого терпения (надо научить малыша правильно высмаркиваться, проводить с ним туалет полости носа иногда несколько раз в день!), посещения процедур (промывание носа ЛОР врачом, физиолечение и др.), четкого выполнения всех назначений врача. Это далеко не быстрый процесс, но если родители и врач заодно, и действуют сплоченной командой, то результат не заставляет себя ждать! Но бывают случаи, когда консервативное лечение неэффективно, тогда врач принимает решение об оперативном вмешательстве, и не всегда это зависит только от степени аденоидов. Чаще всего показаниями к оперативному лечению являются: полное отсутствие носового дыхания, рецидивирующие отиты (тубоотиты), ночное апное, стойкое снижение слуха.
«Если они участвуют в иммунном ответе, зачем их удалять? Ничего лишнего в организме нет!»
Действительно, аденоидная ткань является частью лимфоидного кольца глотки, как было сказано выше, но только частью! Здесь важно оценивать соотношение вреда и пользы для организма. В случае хронического аденоидита сама миндалина становится местом обитания и размножения патогенных микроорганизмов, что явно не приносит пользы ребёнку, а частые обострения приводят к увеличению аденоидной ткани в размере, вызывая параллельно заболевание ушей, с последующим стойким снижением слуха.
«Если их удалить — они вырастут заново!»
На данном этапе развития медицины это мнение является ошибочным. Операция аденотомия выполняется под общим наркозом, с использованием эндоскопической техники. Современное оснащение позволяет удалять аденоидную ткань полностью под визуальным контролем, тем самым гарантируя отсутствие рецидивов. При аденотомии под местной анестезией, как выполнялось ранее повсеместно, действительно высок риск повторных аденотомий, так как чаще всего часть миндалины не удаляется с первого раза, что и вызывает рецидив.
Совет от доктора
Как обобщение, хочу сказать, что всем известная шутка про лечение насморка за 7 дней и за неделю с детьми не работает! Те, кто относятся к насморку ребенка как к «обычным соплям, которые и сами пройдут», сталкиваются чаще всего в дальнейшем с целой кипой осложнений. Поэтому, чем раньше вы обратитесь к ЛОР врачу и начнете грамотное лечение, тем выше вероятность, что проблема аденоидов обойдет вас стороной!
Запишитесь к детскому врачу-оториноларингологу по телефону единого контакт-центра в Москве +7 (495) 775 75 66, заполните форму on-line записи или обратитесь в регистратуру клиники «Семейный доктор».
Здоровья вам и вашим малышам!
Цельная передняя ручка, ширина 12,2 мм, прозрачная анодированная, высота 3 U
Поставщики в вашем регионе
Ниже приведен список местных поставщиков, которые в настоящее время имеют этот товар на складе:
| Дистрибьютор | Количество | Дата наличия на складе | Цена | |
|---|---|---|---|---|
| Информация отсутствует. |
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ИЗДЕЛИИ
Ручка может крепиться к блочному каркасу или 19-дюймовой передней панели. Поставляется с прозрачным или черным анодным покрытием. Ручки крепятся болтами с задней стороны.
Заказывайте комплект для сборки отдельно.
Обратите внимание, что поставки доступны в указанных стандартных товарных партиях (товарная партия, например, 5 шт., 10 шт., 50 шт. и т. д.). Другие объемы заказов (например, 2 шт.) могут округляться вверх до следующего возможного размера стандартной товарной партии.
Комплектность поставки
В комплект поставки этого изделия входят следующие позиции:
| Изделие | Описание | Количество | |
|---|---|---|---|
| 1 | Передняя ручка, анодированный алюминиевый профиль | 1 |
СКОЛИОЗ | Научно-практический центр детской психоневрологии
Руководитель центра профессор, доктор медицинских наук Сампиев Мухаммад Таблиханович
Профессор кафедры травматологии и ортопедии РУДН.
Хирургией позвоночника занимается с 1997 года.
Специализация деформации позвоночника и дегенеративные заболевания позвоночника.
Проходил стажировку в Германии, Франции, Чехии, Голландии, Швецарии, США, Англии.
Является автором 90 печатных работ, 10 авторских свидетельств и 1 иностранных патента, 1 монографии.
Награды: автор научного открытия, диплом №114
Заместитель руководителя центра профессор, доктор медицинских наук Лака Александр Андреевич
Профессор кафедры травматологии и ортопедии РУДН.
Почетный профессор Университета Тимишоара, Румыния
Хирургией позвоночника занимается с 1969 года.
Специализация деформации позвоночника.
Проходил стажировку в Германии, Франции, Чехии, Голландии, Швецарии, Англии.
Является автором более 200 печатных работ, 10 авторских свидетельств и 1 иностранного патента, 3 монографий, 1 учебника
Награды: лауреат премии Призвание “За создание нового метода лечения” 2004 г.
Золотая медаль Brussels Eureka 2003 за конструкцию LSZ (скользящая система)
кандидат медицинских наук Балашов Степан Петрович
Хирургией позвоночника занимается с 2004 года.
Специализация хирургия деформации позвоночника и дегенеративных заболеваний, детская ортопедия
Проходил стажировку в Германии, Франции, Чехии, Голландии, Швецарии, Англии.
Является автором более 50 печатных работ, 1 патента, 4 учебно-методических работы.
СКОЛИОЗ
Сколиоз! Это слово сегодня очень часто можно услышать с экрана телевизора, прочитать в газетах и журналах. Оно вызывает чувство страха и паники, если вдруг прозвучит рядом с фамилией вашего ребенка. Часто мы даже не знаем достоверно, что это такое. Что-то, где-то слышали… Но в наших глазах видится «изогнутое тело», «страшный горб» и как итог испорченная жизнь. Что делать? К кому бежать за помощью? Неизвестность во многих вопросах. Желание помочь и бессилие. Так что же такое сколиоз? Что делать, если в амбулаторной карте вашего ребенка появляется такой диагноз?
Что такое сколиоз?
Сколиоз — это одна из наиболее актуальных проблем современной ортопедии (особенно детской). Сколиоз как болезнь – сложная деформация позвоночника, характеризующаяся искривлением его в трех плоскостях.
Сложная трехмерная деформация позвоночника приводит к деформации ребер и грудной клетки в целом, изменению ее формы (формирование реберного горба), нарушению нормального взаиморасположения органов грудной клетки и систем человеческого организма. У больных сколиозом развивается физическая неполноценность, возникают глубокие психические страдания вследствие больших косметических дефектов.
Таким образом, сколиоз это не просто деформация отдельно взятого сегмента человеческого организма, это болезнь которая затрагивает и приводит к нарушениям в нескольких системах (опорно-двигательная, дыхательная, сердечно-сосудистая, нервная). Искривление позвоночника в этом случае является ведущим и первоочередным проявлением болезни, но не единственным! Исходя из этого важно понимать, что вовремя начатое лечение заболевание поможет предупредить развитие не только тяжелой деформации позвоночника и грудной клетки, но и изменения со стороны дыхательной, сердечно-сосудистой и нервной системы.
Причины развития сколиоза?
Причины возникновения заболевания неизвестны. В течение столетий врачи и ученые пытаются разобраться и понять причины, вызывающие идиопатический (беспричинный ) сколиоз. Было высказано много предположений, разработано множество теорий, но пока ни одна из них не нашла 100% подтверждения. Сегодня мы можем предполагать, что в основе заболевания лежат несколько процессов:
Наследственная предрасположенность
Изменения нервной системы
Нарушение эндокринной сферы
Изменения со стороны соединительнотканных и костных структур позвоночника.
К сожалению, у 80% обращающихся к нам пациентов причину сколиоза выяснить не удается. Такой сколиоз носит название идиопатический сколиоз (idiopathic scoliosis). Очевидно одно: бытовавшие долгое время теории «рахитического» и «школьного» сколиозов полностью остались достоянием истории. Нет связи с рахитом, нет связи с посадкой за школьной партой. Последнее особенно важно подчеркнуть, так как учителя и родители больных до сих пор часто склонны объяснять развитие болезни именно «неправильным» сидением за партой.
Влияет ли возраст и пол на развитие сколиоза?
Сколиоз может появиться практически в любом возрасте, но наиболее часто это происходит в период полового созревания – в возрасте 12-14 лет, причем у девочек немного раньше. Вообще в 80% случаев сколиозом страдают девушки.
Принято разделять сколиозы в зависимости от возраста в котором он проявился на (Э.В. Ульрих, А.Ю. Мушкин, 2004) :
Сколиоз детей младшего возраста: развиваются в первые 2 года жизни, чаще наблюдаются у мальчиков, в большинстве случаев регрессируют.
Ювенильный сколиоз: развивается между 3-м годом жизни и началом пубертатного периода, чаще наблюдается у девочек, чаще прогрессирует.
Сколиоз подростков: начало развития совпадает с периодом полового созревания и продолжается до завершения роста костей (18-20 лет). В подавляющем большинстве случаев (до 85%) отмечаются у девочек, прогрессирует.
Сколиозы взрослых: развивается после завершения костного роста (после 18 лет).
Симптомы сколиоза.
Сколиоз достаточно прост в диагностики. Уже по внешнему виду пациента и расспросу родителей опытный врач сможет поставить диагноз и определить степень деформации. Точный диагноз устанавливается только после выполнения рентгенографического исследования позвоночника.
Основные признаки, по которым вы можете заподозрить сколиоз:
Вид со спины
Асимметрия надплечий – когда одно плечо расположено выше другого
Асимметрия стояния лопаток – при развитии сколиоза лопатка на выпуклой стороне деформации становится выше чем лопатка на вогнутой стороне, а формирующийся реберный горб “выталкивает ” ее кнаружи.
Основным симптомом является изменение линии остистых отростков, которая из прямой переходит либо в С либо в образную сколиотическую дугу.
Перекос туловища – сколиоз приводит к изменению баланса туловища, когда как показано на рисунки происходит наклон оси туловища в сторону вершины деформации.
Вид в наклоне
При наклоне вперед (тест Адамса) удается четче проследить деформацию позвоночника, а также измерить величину реберного горба.
Мы перечислили только самые основные признаки сколиоза, которые можно выявить без специальной аппаратуры. В клинике, исследование больного включает всестороннее клиническое обследование пациента , обязательно рентгенографическое исследование позвоночника, КТ или МРТ по показаниям и консультации специалистов для решения вопроса о степени изменений в других органах и системах.
Прогрессирование сколиоза
Практически всегда сколиоз прогрессирует. Врачу всегда хочется точно знать какова будет скорость этого прогресса. Но, дело в том, что не существует абсолютно надежных признаков прогрессирования сколиотической деформации. Есть лишь косвенные указания на относительно большую или меньшую вероятность увеличения искривления, причем оценивать их нужно только в комплексе.
На данный момент врач прежде всего оценивает следующие параметры:
возраст
степень имеющийся патологии
степень окончания роста скелета (тест Риссера)
наследственность
наличие других заболеваний особенно нервной или гормональной систем
Исходя из знания о скорости прогрессирования сколиоза, ортопед выбирает метод лечения сколиоза. Хочется отметить важность проблемы прогрессирования сколиоза и ее опасность так как очень часто мы встречаемся с запущенными, тяжелыми сколиотическими деформациями превышающими 100 градусов, прогрессировавшие у ребенка только из за того что по тем или иным причинам была выбрана неправильная тактика лечения ребенка без учета прогрессирования заболевания.
Забегая вперед, нужно предупредить, наличие малой степени деформации при ее неуклонном прогрессировании на сегодняшний день является ПРЯМЫМ ПОКАЗАНИЕМ К ХИРУРГИЧЕКОЙ КОРРЕКЦИИ СКОЛИОЗА.
По данным мировых исследований, на сегодняшний день ни один из методов консервативной терапии (массаж, ЛФК, мануальная терапия, ношение корсета, электростимуляция мышц и т.д) не может является средством ЛЕЧЕНИЯ и КОРРЕКЦИИ СКОЛИОЗА.
ЛЕЧЕНИЕ СКОЛИОЗА ДЕТЕЙ
Хирургическое лечение детей с прогрессирующим сколиозом в возрасте до 10 лет, чрезвычайно сложная мировая проблема хирургии позвоночника т.к. в этом возрасте структуры позвоночника до конца не сформированы и рост позвоночника не завершен. В связи с чем, применение техники операций как у взрослых или подростков приводит к ограничению роста позвоночника.
В лечении сколиоза детей принято несколько схем лечения.
(часто используется в Америке и Европе). Этапное хирургическое лечение – выполняют оперативную коррекцию конструкцией, затем данную конструкцию удлиняют каждые 1-2 года, до 14-15 лет и затем выполняют установку стабильной конструкции.
Плюсы:
своевременное хирургическое лечение
возможность сохранить рост позвоночника ребенка
Минусы:
- Регулярные операции с интервалом в полгода или год, в среднем 5-6 операций до 15 лет.
- Каждая последующая операция увеличивает риск осложнений
- Статистически высокий процент осложнений как связанных с конструкцией так и хирургических (до 50% осложнений)
- Несовершенство “растущих” конструкций/li>
Одномоментная коррекция с применением стабильной конструкции (в настоящее время, не рекомендуется применять). Выполнять сразу операцию с установкой стабильной конструкции, чревато тяжелым осложнением – синдромом “коленчатого вала” когда сколиоз продолжает прогрессировать с уже установленной конструкций на позвоночнике.
Пример.
Выжидательная тактика (часто встречается в России)- ребенка наблюдают, выполняют консервативное лечение до возраста 16-17 лет (завершения роста позвоночника) и затем выполняют операцию с использованием статической конструкции
Применение выжидательной тактики приводит к формированию тяжелейшего сколиоза к 16-17 годам, который очень трудно поддается коррекции. Также, формируются изменения со стороны сердца и легких. Часто пациенты обращаются с настолько тяжелой формой сколиоза при котором выполнить операцию невозможно.
Пример.
У нас в Центре был прооперирован больной 15 лет с такой историей болезни:
|
5 лет |
8 лет |
11 лет |
14 лет |
|
Деформация 25 град |
Деформация 63 град |
Деформация 94 град |
Деформация 116 град (!) |
Как видите, сколиоз выявлен в 5 лет, на тот момент это II степень деформации. Через 3 год сколиоз прогрессировал уже до IV степени. Хирургическая коррекция была показана уже на тот момент времени. К сожалению, в наш Центр пациент обратился только в возрасте 15 лет с тяжелейшей деформацией более 116 град. Мы выполнили операцию по коррекции сколиоза с установкой конструкции LSZ3. Результата коррекции составил порядка 50% от исходной деформации.
Если бы, выполнить операцию в возрасте 7-8 лет, результат был бы намного лучше.
Мы считаем, что перечисленные выше схемы лечения не применимы в условиях детского прогрессирующего сколиоза.
Схема лечения сколиоза детей, используемая в Центре коррекции сколиозов.
При обращении к нам пациента со сколиозом в возрасте до 12 лет мы используем двухэтапный хирургический метод лечения.
Первый этап выполняется операция по коррекции сколиоза, устанавливается конструкция LSZ5.
Подробнее о данной конструкции.
Пациент выписывается на 10-12 сутки и наблюдается в Центре ежегодно, до 14-15 лет.
За это время позвоночник растет в условиях коррекции конструкцией LSZ, сколиоз не прогрессирует.
Второй этап лечения. После достижения пациентом 14-15 лет, выполняется плановая операция по замене скользящей системы LSZ5 на стабильную транспедикулярную конструкцию.
Данная конструкция устанавливается пожизненно.
Такая тактика позволяет
- Выполнить коррекцию сколиоза у детей в возрасте от 5 лет
- Сохранить рост позвоночника
- Выполнить коррекцию деформацию дважды
- Не допустить развития крайне тяжелых форм сколиоза
Примеры лечения сколиоза детей.
Ребенок 6 лет.
Диагноз:Врожденный прогрессирующий сколиоз IV степени. Деформация 82 градуса. На фоне сколиоза прогрессирует нарушение баланса туловища, перекос таза,укорочение левой нижней конечности.
Ребенку была выполнена хирургическая коррекция сколиоза с применением конструкции LSZ .
Результат. Коррекция сколиоза составила 58%. Баланс туловища восстановлен, компенсирован перекос таза и укорочение левой нижней конечности.
Пример №2
Ребенок 7 лет
Идиопатический прогрессирующий сколиоз IV степени.
Деформация – 100 градусов
Течение сколиоза прогрессирующие, Ребенку была выполнена хирургическая коррекция сколиоза с применением скользящей конструкции LSZ
ЛЕЧЕНИЕ ПОДРОСТКОВОГО СКОЛИОЗА
В связи с тем, что рост позвоночника у подростков практически закончен, лечение подросткового сколиоза проводится с применением стабильных спинальных конструкций. В отличие от “растущих” конструкций или LSZ конструкции, данные системы исправляют позвоночник и жестко фиксируют его и не предусматривают замену инструментария в дальнейшем.
В Центра коррекции сколиозов мы используем только проверенный, современный инструментарий на ряду с мировыми клиниками, это конструкции фирм Medtronic, Depuy, Alphatec.
Современная конструкция Котреля – Дюбуссе – CD HORIZON® LEGACY™
Данный инструментарий состоит из набора винтов и крючков которые будучи установлены на поясничном и грудном отделах позвоночника фиксируются к стержням коррекции. Во время операции выполняется коррекция деформации – т.н. деротационный маневр, благодаря чему позвонки выравниваются, а деформация значительно исправляется.
История конструкции Котреля – Дюбуссе
CD® инструментарий был запатентован в 1987 году. С тех пор система постоянно совершенствовалась и на сегодняшний день является наиболее широко применяемым инструментарием в мире для коррекции деформаций позвоночника. С момента внедрения в 87 году во всем мире было выполнено более 450 тыс. операций по установке данной системы.
О истории создания и технических особенностях инструментария вы можете прочитать нашу статью Стабильные спинальные системы
Деротационный маневр, позволяет развернуть позвонки в нужную плоскость
Преимущества использования винтовых конструкций в лечение подросткового сколиоза.
- <Возможность выполнить деротационный маневр – “развренуть” повернутые позвонки и зафиксировать их в нужной плоскости.
- Все элементы конструкции находятся внутрикостно
- Конструкция после операции не прощупывается под кожей.
- Высокая эффективность коррекции
- Высокое качество конструкции и исключительная надежность в послеоперационном периоде.
Примеры операций по лечению подросткового сколиоза в Центре коррекции сколиозов.
Пациентка А., 16 лет.<
Диагноз: Идиопатический, прогрессирующий сколиоз 3 степени.
Грудной сколиоз 58 градусов
Сколиоз после операции. Остаточная дуга 17 градусов.
Коррекция сколиоза составила 71%
Кровопотеря за операцию 300 мл, препараты крови (донорские) ни во время ни после операции не использовались.
Вертикализация начало самостоятельной ходьбы – 4 сутки после операции
Снятие швов, выписка – 10 сутки после операции.
Разрешено посещать школу ч/з 1,5 мес после операции.
Пациентка, Г., 15 лет. Диагноз: Идиопатический сколиоз 3 степени тип I A –
Выполнена операция – коррекция сколиоза системой Котреля – Дюбуссе CD HORIZON® LEGACY™. Применение только винтовой фиксации обеспечила практически 100% ррентгенографический и клиничекский результата в лечении сколиоза.
Фотографии и рентегнограммы пациентки Г., 15 лет со сколиозом до и после операции
Пайиентка Г., 15 лет. Идиопатический сколиоз 3 степени
Пайиентка Г., 15 лет. Фото после операции по коррекуции сколиоза
Коррекция сколиоза составила 99%
Кровопотеря за операцию 350 мл, препараты крови (донорские) ни во время ни после операции не использовались.
Вертикализация начало самостоятельной ходьбы – 4 сутки после операции
Снятие швов, выписка – 12 сутки после операции.
Разрешено посещать школу ч/з 1,5 мес после операции.
Пациентка Т., 17 лет. Диагноз: Идиопатический, прогрессирующий сколиоз 4 степени.
Операция – коррекция сколиоза системой Depuy Expedium
Фотографии и рентегнограммы пациентки со сколиозом до и после операции
Пациентка Т., 17 лет. Грудная сколиотическая дуга 62 градуса
Коррекция сколиоза составила 80 %
ЛЕЧЕНИЕ ТЯЖЕЛЫХ ФОРМ СКОЛИОЗА
Вопрос лечения тяжелых форм сколиоза, запущенных деформаций является весьма актуальным в мире. К крайне тяжелым сколизам относят деформации 90-100 градусов. В практике Центра коррекции сколиозов деформации свыше 100 градусов встретились у порядка 25% пациентов.
Хирургия крайне тяжелых деформаций позвоночника не допускает “шаблонного” подхода, результативна при возможности выбора инструментария и владения разными методами коррекции .
В Центре коррекции сколиозов мы используем несколько типов операций в случае запущенных форм сколиоза
Вариант лечения запущенного сколиоза №1
Одноэтапная операция – исправление сколиоза с применение только дорсальной транспедикулярной конструкции
Пример
Пациентка, 12 л. Идиопатический сколиоз 4 ст. До операции.
Этот идеальный вариант в лечении запущенных сколиозов, но он очень редко применим. Обычно сколиозы свыше 90 градусов очень жесткие деформация сопровождается выраженными изменениями анатомии позвоночника. Для достижения хорошего результата в коррекции сколиоза приходится использовать двухэтапный подход.
Вариант лечения запущенного сколиоза №2
Двухэтапное хирургическое лечение очень тяжелого сколиоза
Выполняются две операции, первая релиз позвоночника – выполняется спереди – цель её сделать позвоночник мобильным, подготовить его к основному этапу. Операция выполняется спереди, положение пациента на боку, разрез кожи производится в зависимости от локализации вершины деформации, обычно по 10 межреберью (рисунок 1). Выполняется торокотомия (открывается грудная клетка), выполняется доступ к передним отделам позвоночника – телам позвонков и межпозвонковым дискам (рисунок 2). Межпозвонковые диски на вершине деформации удаляются, за счет чего увеличивается мобильность позвоночника (рис 3 и 4).
|
Рис.1 |
Рис.2 |
Рис.3 |
Рис.4 |
Вторая операция выполняется через 5-7 дней после первой. Цель второй операции выполнить коррекция сколиоза с использованием дорсальной (задней) коррегирующей системы. Коррекция по классической схеме: доступ к позвоночнику осуществляется сзади, производится установка транспедикулярных винтов, монтаж конструкции, выполнение корригирующего маневра. Подробно данная операция описана здесь.
Пример двухэтапного лечения тяжелого сколиоза в Центре коррекции сколиозов
Пацинтка, возраст 13 лет, диагноз идиопатический подростковый сколиоз IV степени.
Величина основной дуги 116 градусов, поясничной дуги 85. В связи с тяжестью деформации было решено выполнить двух этапное хирургическое лечение.
Первым этапом выполнена дискэктомия (удаление дисков) на уровнях Th8-Th9, Th9-Th20, Th21-Th22 c установкой двух Mesh на уровне Th21-Th20 и Th20-Th9.
Вторым этапом чрез 1 неделю после релиза выполнена задняя коррекция деформация с уровня Th3-L4 . При оценки рентгенограмм остаточная деформация основной дуги составила 33 град, поясничной дуги 25 град. Коррекция сколиоза составила 70%
Пацинтка, возраст 13 лет, диагноз идиопатический сколиоз, 6 мес. после операции.
Преимущество данного метода:
Золотой стандарт в лечение крайне тяжелых сколиозов
Хороший результат коррекции
Коррекция сколиоза достигается за одну госпитализацию
Недостатки
Длительная госпитализация – 20-30 дней.
Две операции
Первый этап сопряжен с торокотомией – открытием грудной клетки
Два послеоперационных рубца.
Вариант лечения запущенного сколиоза №3
На ряду с представленным методом лечения запущенных деформаций позвоночника который является классическим в мировой практике в Центре коррекции сколиозов применяется авторский метод лечения.
Его суть в том что все хирургические вмешательства выполняются только сзади.
Первым этапом выполняется коррекция сколиоза конструкцией LSZ.
Вторым этапом через несколько лет после первой операции конструкция меняется на винтовую систему с выполнением дополнительной коррекции.
Примеры этапного метода лечения сколиоза с применением растущей системы LSZ и последующей ей заменой на винтовую конструкцию.
Пациентка, возраст 14 лет, диагноз идиопатический подростковый сколиоз IV степени.
Величина основной дуги 114 градусов. Первичное обращение в 2012 году выполнена операция – коррекция сколиоза системой LSZ –растущая. Коррекция сколиоза составила 60%, остаточная дуга 55 град. За время наблюдения в течении 3х лет прибавка в росте составила 6 см, позвоночник “перерос” конструкцию о чем свидетельствуют выскользнувшие из блоков крепления прижимы.
В 2013 году выполнена операции по замене коррегирующей конструкции, система LSZ удалена, выполнена коррекция сколиоза системой Zodiac.
При оценки рентгенограмм остаточная деформация основной дуги составила 23 град.
Итоговая коррекция сколиоза составила 80%
2012 г. Пациентки16 лет. Контрольный осмотр. Остаточная деформация 55 градусов. Позвоноик “перерос” конструкцию. Рост 182 см
Преимущество данного метода:
Лучший результат коррекции
Один послеоперационный рубец (со стороны спины)
Возможность нарастить коррекцию
Более легкая реабилитация
Отсутствие рисков сопряженных с торокотомией
Недостатки
Две операции
КИФОЗ, КИФОТИЧЕСКАЯ ДЕФОРМАЦИЯ ПОЗВОНОЧНИКА
Кифоз (др.-греч. κύφος согнутый, горбатый) — искривление позвоночника в сагиттальной плоскости с образование выпуклости обращенной кзади.
Кифоз может быть патологическим и физиологическим.
Физиологический кифоз
Кифоз в грудном отделе позвоночника – часть НОРМАЛЬНОЙ анатомии позвоночника у ЛЮБОГО человека. Надо знать:
Физиологические значения грудного кифоза вариабельны: от 15 – 50°, в среднем 35°
У девочек кзначения кифоза выше чем у мальчиков
Кифоз грудного отдела у ребенка формируется у ребенка в возрасте 6-8 мес с возрастам его значение увеличивается
Патологический кифоз
Патологическим кифоз становится в случае когда искривления превышает значение в 40 градусов и в этом случае говорят о гиперкифозе или кифотической деформации, что является болезнью требующей лечения.
Часто встречающиеся кифотические деформации:
1) Кифотическая деформация на фоне болезни Щойермана-Мау
2) Идиопатический гиперкифоз
3) Врожденная кифотическая деформация
Формируется на фоне аномалий развития позвонков (может быть в любом отделе позвоночника)
Лечение патологического кифоза
Лечение деформаций позвоночника только одно – хирургическое. Остальные виды лечения – массаж, физиолечение, корсет, лфк – поддерживающие виды терапии которые могут использоваться для улучшения самочувствия пациента.
Подробнее о операция при кифотической деформации позвоночика смотрите здесь
Профессор Сампиев М.Т. о болезни Шойрмана-Мау и лечении гиперкифоза
Ожоги. Особенности и степени тяжести. Первая помощь
Уважаемые родители чудесных мальчиков и девочек, а также их бабушки и дедушки! Окружающий мир не только прекрасен и интересен для вашего ребенка, но и таит опасные для него ситуации. Вы всегда рядом и первыми сможете помочь вашему малышу.
Скоро лето – пора отпусков и детских каникул, а это значит, что дети большее время будут проводить дома и на улице, в сельской местности и в походе у костра. Как дерматолог хочу обратить ваше внимание на часто встречающийся вид травмы – ожоги.
Ожоги – один из распространенных видов травм у детей и взрослых.
Ожоги бывают термические, химические, электрические, лучевые. Термические ожоги составляют более 90% от всех видов – это ожоги пламенем, горячим паром, горячей или горящей жидкостью, кипятком, ожоги от соприкосновения с раскаленными предметами, солнечные ожоги. Особенно опасны ожоги для детей и пожилых людей.
Малыши чаще получают ожоги, опрокидывая на себя кипяток, горячее молоко или суп, прикасаясь к раскаленным предметам (батарея, утюг, электрическая плита, лампочка). Дети постарше, как правило, страдают при неосторожном обращении с огнем дома или на природе.
В зависимости от глубины поражения кожи различают степени тяжести ожогов.
Ожог 1 степени — это поражением самого поверхностного слоя кожи. Развивается выраженное покраснение кожи, ее отек, в пораженном месте отмечаются боли, чувство жжения. Эти явления стихают в течении 2-х дней, а через неделю наступает полное выздоровление.
При ожоге 2 степени верхний слой кожи полностью погибает и отслаивается, при этом образуются пузыри, заполненные прозрачной жидкостью. Первые пузыри появляются уже через несколько минут после ожога, однако еще в течение 1 суток могут образовываться новые пузыри, а уже существующие — увеличиваться в размерах. Если течение болезни не осложнится инфицированием раны, то заживление наступает через 10-12 дней.
При ожогах 3 степени кожа поражается практически на всю глубину. При этом образуются массивные пузыри с толстой оболочкой, заполненные кровянистым содержимым, напряженные и очень болезненные.
Ожог 4 степени — это полная гибель всех слоев кожи, включая подкожно-жировую клетчатку, а также и нижележащих тканей — мышц, сухожилий, костей.
Каждый повреждающий фактор имеет свои особенности:
- Пламя. Площадь ожога относительно большая, по глубине преимущественно 2-я степень. При первичной обработке раны представляет сложность удаление остатков обгоревшей одежды, незамеченные нити ткани могут в последующем служить очагами развития инфекции. Могут поражаться органы зрения, верхние дыхательные пути. Очень опасны ожоги пламенем в закрытых помещениях, так как к повреждению поверхности тела добавляются ожоги дыхательных путей горячим дымом, отравление угарным газом.
- Горячая жидкость. Площадь ожога небольшая, но относительно глубокая, преимущественно 2—3-й степеней.
- Пар. Площадь ожога большая, но неглубокая. Очень часто поражаются дыхательные пути.
- Раскалённые предметы. Площадь ожога всегда ограничена размерами предмета и имеет относительно чёткие границы и значительную глубину.
Как практикующий врач, хочу обратить ваше внимание на то, что, к сожалению, в большинстве случаев ожоги наносят не только физическую травму и косметические дефекты, но и длительную психологическую травму. Поэтому своевременная первая помощь и специализированная врачебная имеют огромное значение.
ЧТО ДЕЛАТЬ?
Первое, что надо сделать при оказании помощи пострадавшему — это прекратить воздействие поражающего фактора. Если речь идет про ожог кипятком, то необходимо как можно быстрее снять (срезать) пропитанную горячей жидкостью одежду.
При воздействие пламенем наиболее правильным будет потушить горящую одежду водой, а потом снять. Если достаточного количества воды нет, тушить следует подручными средствами — плотной тканью, песком, землей. При этом не следует закрывать пострадавшего с головой — это может привести к вдыханию продуктов горения с последующим ожогом дыхательных путей и отравлению.
Не следует также сбивать пламя голыми руками, так как при этом спасатель сам может перейти в разряд пострадавших. Если пострадавший находился в закрытом помещении, как можно скорее вынесите его на свежий воздух.
Одежду и обувь с ребенка нужно обязательно снять полностью, так как в большинстве случаев мы не можем достоверно оценить, какие участки тела подверглись воздействию высокой температуры. Нужно помнить, что волосы также могут пострадать и вести себя как тлеющая одежда, концентрируя тепло и обжигать кожу головы, уши и лицо ребенка.
Удалять приставшую к телу одежду не следует, поскольку при этом есть риск дополнительно повредить обожженную поверхность.
ОСОБЫЕ ПРЕДОСТОРОЖНОСТИ НАДО СОБЛЮДАТЬ, ЕСЛИ ОДЕЖДА СИНТЕТИЧЕСКАЯ, ТАК КАК ПРИ ГОРЕНИИ ОНА ПЛАВИТСЯ И ПРИЛИПАЕТ К КОЖЕ.
Ни в коем случае не пытайтесь счищать прикипевший полимер!
При ожогах следует незамедлительно снять кольца, часы, браслеты, цепочки, бусы, поскольку в дальнейшем будет развиваться отек пораженного участка, и эти предметы могут сдавливать ткани с нарушением кровообращения вплоть до развития омертвления тканей.
Обязательно следует охладить пораженный участок — погружением в холодную воду, снег. Длительность воздействия холода колеблется от 3-5 до 15-20 минут. Слишком долго охлаждать обожженное место не следует, чтобы не вызвать спазм сосудов с последующим нарушением кровообращения в пораженном участке. Эта мера эффективна в течение 2 часов после получения ожога и не только уменьшает боль, но и — глубину поражения. Даже когда действие поражающего фактора прекращено, ожог продолжает развиваться и углубляться за счет того, что поверхностные слои кожи играют роль горячего компресса для нижележащих. Охлаждая поверхность тела, можно прервать этот процесс.
Параллельно охлаждению необходимо адекватное обезболивание. Для этого используют обезболивающие препараты — Парацетамол или Анальгин. На пораженную кожу наложить чистую сухую марлевую повязку и в короткие сроки показать врачу.
В случае глубоких ожогов следует воздерживаться от каких-либо манипуляций. Не надо пытаться самостоятельно очистить рану от приставших обрывков одежды и других загрязнений (данная манипуляция может привести к отслоению больших участков кожи, кровотечению, а впоследствии и к инфицированию ран), не следует самостоятельно вскрывать пузыри. На ожоговую рану следует наложить сухую стерильную повязку (при обширных ожогах завернуть пострадавшего в чистую простыню), после чего обратиться к врачу.
Масляные мази и другие жиросодержащие продукты при ожогах применять категорически нельзя. Такое действие только усугубит тяжесть поражения, а персоналу в больнице придётся удалять масляную плёнку, причиняя дополнительные страдания пострадавшему.
В случае любых ожогов обязательна незамедлительная консультация врача!
экспонентов: основные правила | Purplemath
Purplemath
Экспоненты — это сокращение для многократного умножения одного и того же самого на себя. Например, сокращение для умножения трех копий числа 5 показано справа от знака «равно» в (5) (5) (5) = 5 3 . «Показатель», равный 3 в этом примере, означает, сколько раз умножается значение.То, что умножается, в этом примере равно 5, называется «базой».
Этот процесс использования экспонент называется «возведением в степень», где показатель — это «степень». Выражение «5 3 » произносится как «пять в третьей степени» или «пять в третьей степени».
MathHelp.com
Есть две специально названные степени: «до второй степени» обычно произносится как «в квадрате», а «до третьей степени» обычно произносится как «в кубе». Итак, «5 3 » обычно произносится как «пять кубов».
Когда мы имеем дело с числами, мы обычно просто упрощаем; мы предпочли бы иметь дело с «27», чем с «3 3 ».Но для переменных нам нужны показатели степени, потому что мы предпочли бы иметь дело с « x 6 », чем с « xxxxxx ».
У экспонентовесть несколько правил, которые мы можем использовать для упрощения выражений.
Чтобы упростить это, я могу думать в терминах того, что означают эти показатели. «До третьей» означает «умножение трех копий», а «до четвертой» означает «умножение четырех копий». Используя этот факт, я могу «расширить» два фактора, а затем вернуться к упрощенной форме.Сначала расширяю:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
Теперь я могу убрать скобки и сложить все множители:
( xxx ) ( xxxx ) = xxxxxxx
Это семь копий переменной.«Умножение семи копий» означает «в седьмой степени», поэтому это можно переформулировать как:
xxxxxxx = x 7
Собираем все вместе, шаги следующие:
( x 3 ) ( x 4 ) = ( xxx ) ( xxxx )
= xxxxxxx
= x 7
Тогда упрощенная форма ( x 3 ) ( x 4 ) будет:
Обратите внимание, что x 7 также равно x (3 + 4) .Это демонстрирует первое основное правило экспоненты:
Всякий раз, когда вы умножаете два члена с одинаковым основанием, вы можете складывать экспоненты:
( x м ) ( x n ) = x (m + n)
Однако мы НЕ можем упростить ( x 4 ) ( y 3 ), потому что основания разные: ( x 4 ) ( y 3 ) = xxxxyyy = ( x 4 ) ( y 3 ).Ничего не сочетается.
Теперь, когда я знаю правило (а именно, что я могу добавлять силы к одной и той же базе), я могу начать с перемещения баз, чтобы расположить все одинаковые базы рядом друг с другом:
( a 5 b 3 ) ( a b 7 ) = ( a 5 ) ( a ) ( b 3 ) ( б 7 )
Теперь я хочу добавить мощности на a и b .Однако у второго и , похоже, нет мощности. Что мне добавить для этого срока?
Все, что не имеет силы, в техническом смысле «возведено в степень 1». Все, что находится в степени 1, является самим собой, поскольку оно «умножает одну копию» самого себя. Таким образом, приведенное выше выражение можно переписать как:
( a 5 ) ( a ) ( b 3 ) ( b 7 ) = ( a 5 ) ( a 1 ) ( b 3 ) ( б 7 )
Теперь могу комбинировать:
( a 5 ) ( a 1 ) ( b 3 ) ( b 7 ) = a 5 + 1 b 3 + 7 = a 6 b 10
Если сложить все вместе, моя ручная работа будет выглядеть так:
( a 5 b 3 ) ( a b 7 ) = ( a 5 a 1 ) ( b 3 b 7 ) =
В следующем примере есть две силы, одна из которых в некотором смысле «внутри» другой.
Чтобы сделать упрощение, я могу начать с размышлений о том, что означают показатели степени. «До четвертого» снаружи означает, что я умножаю четыре копии любого основания, заключенного в круглые скобки. В этом случае база четвертой степени равна x 2 . Умножение четырех копий этой базы дает мне:
Каждый фактор в приведенном выше расширении — это «умножение двух копий» переменной.Это расширяется как:
( x 2 ) ( x 2 ) ( x 2 ) ( x 2 ) = ( xx ) ( xx ) ( xx ) ( xx )
Убрав круглые скобки, получим:
( xx ) ( xx ) ( xx ) ( xx ) = xxxxxxxx
Это строка из восьми копий переменной.«Умножение восьми копий» означает «в восьмой степени», поэтому это означает:
xxxxxxxx = x 8
Собираем все вместе:
( x 2 ) 4 = ( x 2 ) ( x 2 ) ( x 2 ) ( x 2 )
= ( xx ) ( xx ) ( xx ) ( xx )
= xxxxxxxx
= x 8
Обратите внимание, что ( x 2 ) 4 = x 8 , и что 2 × 4 = 8.Это демонстрирует правило второй степени:
Всякий раз, когда у вас есть выражение в степени, которое возведено в степень, вы можете упростить, умножив внешнюю степень на внутреннюю степень:
Если у вас есть продукт в круглых скобках и сила в скобках, то сила идет на каждый элемент внутри. Например:
( xy 2 ) 3 = ( xy 2 ) ( xy 2 ) ( xy 2 )
= ( xxx ) ( y 2 y 2 y 2 )
= ( xxx ) ( yyyyyy )
= x 3 y 6
= ( x ) 3 ( y 2 ) 3
Другой пример:
Предупреждение. Это правило НЕ работает, если в скобках указана сумма или разница.Экспоненты, в отличие от умножения, НЕ «распределяются» по сложению.
Например, учитывая (3 + 4) 2 , НЕ поддавайтесь искушению сказать: « Эй, это равно 3 2 + 4 2 = 9 + 16 = 25 », потому что это неправильный. На самом деле (3 + 4) 2 = (7) 2 = 49, а не 25.
Если сомневаетесь, запишите выражение в соответствии с определением мощности. Например, учитывая ( x — 2) 2 , не пытайтесь делать это в уме.Вместо этого запишите это; «в квадрате» означает «умножение двух копий», поэтому:
( x — 2) 2 = ( x — 2) ( x — 2)
= x ( x — 2) — 2 ( x — 2)
= xx — 2 x — 2 x + 4
= x 2 — 4 x + 4.
Ошибка в виде ошибочной попытки «распределить» экспоненту чаще всего совершается, когда ученик пытается делать все в своей голове, вместо того, чтобы показать свою работу.Делайте все аккуратно, и вы вряд ли совершите эту ошибку.
Теперь, когда я знаю правило о полномочиях на полномочия, я могу провести 4 по каждому из факторов внутри. (Мне нужно помнить, что у c внутри скобок это «в степени 1».)
( a 2 ) 4 ( b 3 ) 4 ( c 1 ) 4
= ( a 2 × 4 ) ( b 3 × 4 ) ( c 1 × 4 )
= a 8 b 12 c 4
Партнер
Есть еще одно правило, которое может или не может быть рассмотрено в вашем классе на данном этапе:
Все, что находится в нулевой степени, равно «1» (пока «что-нибудь» не является нулем само по себе).
Это правило объясняется на следующей странице. Однако на практике это правило означает, что некоторые упражнения могут быть намного проще, чем может показаться на первый взгляд:
Упростить [(3
x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0
Кого волнует эта фигня в квадратных скобках? Я точно не знаю, потому что нулевая мощность снаружи означает, что значение всего этого равно 1.Ха!
[(3 x 4 y 7 z 12 ) 5 (–5 x 9 y 3 z 4 ) 2 ] 0 = 1
Между прочим, как только ваш класс охватит «до нуля», вам следует ожидать упражнения, подобного приведенному выше, на следующем тесте.Это распространенный вопрос с подвохом, призванный заставить вас тратить кучу вашего ограниченного времени, но он работает только в том случае, если вы не обращаете внимания.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в упрощении выражений с помощью экспонент. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок, или просмотрите здесь множество рабочих примеров.)
Щелкните здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите ознакомиться с их программным обеспечением или получить дополнительную информацию.
URL: https://www.purplemath.com/modules/exponent.htm
Таблицы экспонент и образцы
В таблицах степеней целых чисел можно найти много интересных закономерностей.
Полномочия 2 | Полномочия 3 | Полномочия 4 |
| 2 1 знак равно 2 | 3 1 знак равно 3 | 4 1 знак равно 4 |
| 2 2 знак равно 4 | 3 2 знак равно 9 | 4 2 знак равно 16 |
| 2 3 знак равно 8 | 3 3 знак равно 27 | 4 3 знак равно 64 |
| 2 4 знак равно 16 | 3 4 знак равно 81 год | 4 4 знак равно 256 |
| 2 5 знак равно 32 | 3 5 знак равно 243 | 4 5 знак равно 1024 |
| 2 6 знак равно 64 | 3 6 знак равно 729 | 4 6 знак равно 4096 |
| 2 7 знак равно 128 | 3 7 знак равно 2187 | 4 7 знак равно 16384 |
| 2 8 знак равно 256 | 3 8 знак равно 6561 | 4 8 знак равно 65536 |
| 2 9 знак равно 512 | 3 9 знак равно 19683 | 4 9 знак равно 262144 |
| 2 10 знак равно 1024 | 3 10 знак равно 59049 | 4 10 знак равно 1048576 |
Одна вещь, которую вы можете заметить, — это закономерности в цифрах.В полномочиях 2 таблица, единичные цифры образуют повторяющийся узор 2 , 4 , 8 , 6 , 2 , 4 , 8 , 6 , … . В полномочиях 3 таблица, единичные цифры образуют повторяющийся узор 3 , 9 , 7 , 1 , 3 , 9 , 7 , 1 , … . Мы предоставляем вам разобраться, почему это происходит!
В полномочиях 4 таблица, чередуются единицы цифр: 4 , 6 , 4 , 6 . Фактически, вы можете видеть, что полномочия 4 такие же, как четные степени 2 :
4 1 знак равно 2 2 4 2 знак равно 2 4 4 3 знак равно 2 6 и т.п.
Такая же связь существует между полномочия 3 и полномочия 9 :
Полномочия 3 | Полномочия 9 |
| 3 1 знак равно 3 | 9 1 знак равно 9 |
| 3 2 знак равно 9 | 9 2 знак равно 81 год |
| 3 3 знак равно 27 | 9 3 знак равно 729 |
| 3 4 знак равно 81 год | 9 4 знак равно 6561 |
| 3 5 знак равно 243 | 9 5 знак равно 59 049 |
| 3 6 знак равно 729 | 9 6 знак равно 531 441 |
| 3 7 знак равно 2187 | 9 7 знак равно 4,782,969 |
| 3 8 знак равно 6561 | 9 8 знак равно 43 046 721 |
| 3 9 знак равно 19 683 | 9 9 знак равно 387 420 489 |
| 3 10 знак равно 59 049 | 9 10 знак равно 3 486 784 401 |
В полномочия 10 легко, потому что мы используем база 10 : для 10 п просто напишите » 1 » с участием п нули после него.Для отрицательные силы 10 — п , написать » 0. » с последующим п — 1 нули, а затем 1 . Полномочия 10 широко используются в научная нотация , так что будет неплохо с ними освоиться.
Полномочия 10 | |
| 10 1 знак равно 10 | 10 0 знак равно 1 |
| 10 2 знак равно 100 | 10 — 1 знак равно 0.1 |
| 10 3 знак равно 1000 | 10 — 2 знак равно 0,01 |
| 10 4 знак равно 10 000 | 10 — 3 знак равно 0,001 |
10 5 знак равно 100 000 (сто тысяч) | 10 — 4 знак равно 0.0001 (одна десятитысячная) |
10 6 знак равно 1 000 000 (один миллион) | 10 — 5 знак равно 0,00001 (стотысячная) |
10 7 знак равно 10 000 000 (десять миллионов) | 10 — 6 знак равно 0.000001 (одна миллионная) |
10 8 знак равно 100 000 000 (сто миллионов) | 10 — 7 знак равно 0,0000001 (одна десятимиллионная) |
10 9 знак равно 1 000 000 000 (один миллиард) | 10 — 8 знак равно 0.00000001 (стомиллионная) |
10 10 знак равно 10 000 000 000 (десять миллиардов) | 10 — 9 знак равно 0,000000001 (одна миллиардная) |
Нажмите здесь для получения дополнительных имен для действительно большие и очень маленькие числа .
Еще одно последствие использования нами база 10 хороший образец между отрицательными степенями 2 и полномочия 5 .
Степень 2 | Степени 5 |
| 2 — 5 знак равно 1 32 знак равно 0.03125 | 5 — 5 знак равно 1 3125 знак равно 0,00032 |
| 2 — 4 знак равно 1 16 знак равно 0,0625 | 5 — 4 знак равно 1 625 знак равно 0.0016 |
| 2 — 3 знак равно 1 8 знак равно 0,125 | 5 — 3 знак равно 1 125 знак равно 0,008 |
| 2 — 2 знак равно 1 4 знак равно 0.25 | 5 — 2 знак равно 1 25 знак равно 0,04 |
| 2 — 1 знак равно 1 2 знак равно 0,5 | 5 — 1 знак равно 1 5 знак равно 0.2 |
| 2 0 знак равно 1 | 5 0 знак равно 1 |
Уроки по упрощению экспонент — Уроки Wyzant
Прежде чем мы углубимся в упрощение экспоненты, давайте потратим некоторое время, чтобы узнать, что именно такое экспонента. Показатель степени — это надстрочный индекс
или небольшое число, написанное в верхнем правом углу числа, переменной или набора круглых скобок.Пример одного показан
ниже.
2 3
Это говорит вам умножить 1 на число столько раз, сколько указано в экспоненте.
В приведенном выше примере 2 в третьей степени (в третьей степени.
означает, что показатель степени равен 3). Это эквивалентно задаче умножения ниже, потому что 1 умножается на 2 три
раза.
1 * 2 * 2 * 2
8
Как видите, 1 * 2 * 2 * 2 можно упростить до 8, что является ответом на проблему.
Экспоненты
Изучите следующую проблему:
-3 6
Эта задача заменена на задачу умножения, описанную ниже. Из-за порядка операций (объясненного в следующем уроке)
сначала упрощается показатель степени, а затем к ответу добавляется отрицательный знак.
1 * 3 * 3 * 3 * 3 * 3 * 3
-729
Как видите, умножение упрощается до числа -729. Вы можете проделать эту работу в уме, на полях
бумаги или с помощью калькулятора, если это возможно.
Экспоненты
Следующая проблема показана ниже:
(-3) 6
На этот раз -3 заключен в круглые скобки. Вместо того, чтобы переносить отрицательный знак, каждые 3 становятся отрицательными.
1 * -3 * -3 * -3 * -3 * -3 * -3
729
Как видите, умножение упрощается до 729. Обратите внимание, что помимо
результат предыдущего примера отрицательный, результат
здесь тот же.Уделяйте особое внимание нахождению показателей степени при отрицательных
знаках, так как это частый источник ошибок.
Особые случаи
Нулевой показатель
Каждая из этих проблем решается путем умножения 1 на число,
— количества раз, которое указывает показатель степени. Если показатель степени равен 0, то
вообще не умножается на число. Следовательно, ответ — 1.
Это важное правило, о котором следует помнить.
Ноль с показателем степени:
В большинстве случаев ноль с показателем степени можно вычислить так же, как и любое другое число
и показатель степени.
Обратите внимание, что до тех пор, пока 1 умножается хотя бы на один 0, конечный результат
равен 0. Следовательно, мы можем заключить, что 0 для любого положительного показателя степени всегда равно нулю.
Другой особый случай — 0 0 . Ноль с показателем степени
ноль не определен и не может быть вычислен.
Будьте осторожны, не соблюдайте правила для нулевых показателей! От нуля до любой положительной степени
всегда равно нулю, потому что независимо от того, сколько раз вы умножаете 1 на
ноль, ответ всегда будет нулем.Но 0 0 не определено.
Показатель 1:
Рассмотрим этот пример, в котором rasies число возведено в первую степень.
Если вы попробуете любой аналогичный пример, такой как 10 1 или 100 1 , вы
обнаружите, что результатом всегда будет исходное число или основание. Это
, потому что 1, умноженное на любое другое число, всегда равно второму числу.
Итак, чтобы упростить случай, когда число возводится в первую степень, мы можем
просто удалить показатель степени.
Экспоненты
От десяти до любой степени
Этот совет может сэкономить вам много времени: Десять в любой степени — это просто число 1
, за которым следует количество нулей, обозначенных показателем степени.
Пример показан ниже.
Обратите внимание, что результатом является единица с пятью нулями, потому что показатель степени на
10 равен 5.
Показатели чтения
В общем проблема типа
5 10
читается как «пять в десятой степени.”
Специальные случаи для чтения экспонент
У некоторых экспонентов есть особые способы произнесения. Это немного упрощает определение
, но совсем не обязательно, чтобы вы их использовали.
- Вторая степень: 3 2 — может читаться как «тройка во второй степени» или «тройка в квадрате».
- The Third Power: 10 3 — можно читать как «Десять в третьей степени» или «10 в кубе».
Показатели числа ресурсов
electric — Могу ли я использовать провод 12-2 на 20-амперном выключателе для питания всей ванной комнаты?
Вы,
, должны использовать 12AWG с выключателем на 20 А для этого прогонаВаша «полуванна» по определению NEC по-прежнему является ванной, поскольку в ней есть туалет и раковина, известная как раковина:
Санузел. Область, включающая бассейн с одним или несколькими следующее: унитаз, писсуар, ванна, душ, биде и т. д. сантехника.
В результате тот факт, что у вас есть розетка в этой цепи, делает ее ответвленной цепью для ванной комнаты, которая подпадает под NEC 210.11 (C) (3) и исключение из нее:
(3) Ответвительные цепи для ванных комнат. В дополнение к количеству ответвления, требуемые другими частями этого раздела, по крайней мере одна параллельная цепь на 120 вольт и 20 ампер должна быть обеспечена для поставьте в ванную (ые) розетку (и).Такие цепи должны других розеток нет.
Исключение: там, где 20-амперный контур питает одну ванную комнату, розетки для другого оборудования в той же ванной комнате должны быть разрешены поставляться в соответствии с 210.23 (A) (1) и (A) (2).
Для этого требуется, чтобы цепь была цепью на 20 А, с использованием провода 12AWG на всем протяжении. Между прочим, совсем не редкость или необычность, когда одна ванная комната полностью питается от выделенной ответвленной цепи на 20 А, как вы описываете, поэтому не беспокойтесь о каких-либо глупых представлениях о предоставлении «слишком большой мощности» свету.
Единственное, что вам нужно знать, это то, что вентилятор для ванны должен потреблять не более 10 А, чтобы соответствовать правилу 50% в NEC 210.23 (A) (2):
.(2) Утилизационное оборудование закреплено на месте. Общий рейтинг Утилизационное оборудование, закрепленное на месте, кроме светильников, не должно превышать 50 процентов от силы тока параллельной цепи. рейтинг, при котором осветительные приборы, подключение по шнуру и розетке оборудование, не закрепленное на месте, или и то, и другое, также поставляются.
Если у вас нет такого причудливого вентилятора для ванны с подогревом, у вас не должно возникнуть проблем с соблюдением этого правила, поскольку обычный вентилятор для ванны потребляет всего несколько ампер.
Обратите внимание, что вам понадобится AFCI для вашего выключателя на 20A, и, вероятно, вы захотите подать питание на двухблочную коробку на туалетном столике для розетки GFCI и выключателя света, с отдельными 12/2 ветками, идущими оттуда к лампам / вентилятору. . Если у вас установлена только одна групповая коробка и вы не можете ее изменить, вы все равно можете это сделать, но вы застрянете с комбинацией GFCI / переключатель, что означает, что ваш вентилятор и свет будут на одном переключателе, останавливаясь у вас есть таймер для вентилятора.
Калькулятор экспоненты (степени)— Калькулятор капитана
Калькулятор экспонент
Обратите внимание: для работы этого калькулятора требуется JavaScript.Определение — Что такое показатель степени?
Показатель степени — это количество раз, когда число умножается само на себя.
Запишите показатель степени в виде увеличенного числа. В числе 2 4 (2 в степени 4 или 2 в степени 4) «4» является показателем. «2» — это число, которое нужно умножить на себя в 4 раза.В этом случае 2 x 2 x 2 x 2 = 16.
Формула— как найти экспоненту
Найдите показатель степени числа, умножив это число на само число раз.
число 2 = число x число
число 3 = число x число x число
число 4 = число x число x число x число
Пример
3 2 = 3 x 3 = 9
9 5 = 9 x 9 x 9 x 9 x 9 = 59 049
5 10 = 5 x 5 x 5 x 5 x 5 x 5 x 5 x 5 x 5 x 5 = 9,765,625
Правила экспонент (законы экспонент)
Продукт с той же базой
Чтобы умножить одинаковые основания, оставьте основание одинаковым и сложите экспоненты.
x a • x b = x (a + b)
Пример: 7 3 • 7 5 = 7 (3 + 5) = 7 8 = 5,764,801
Показатель экспоненты (или степени в степени)
Чтобы вычислить показатель степени, умножьте показатели вместе.
(x a ) b = x (a • b) = x ab
Пример: (4 3 ) 2 = 4 (3 • 2) = 4 6 = 4 096
Деление чисел на экспоненты (частные с одинаковым основанием)
Чтобы разделить два основания с одинаковым показателем, вычтите показатель знаменателя из показателя числителя.
x a ÷ x b = x (a — b)
Пример: 5 7 ÷ 5 3 = 5 (7-3) = 5 4 = 625
Умножение чисел на экспоненту
Оба числа, умноженные в степень, могут быть возведены в эту степень.
(xy) z = x z • y z
Пример: (9x) 5 = 9 5 x 5 = 59,049x 5
Деление на показатель
Чтобы разделить дробь, возведенную в степень, укажите показатель степени как в числителе, так и в знаменателе.
(x ÷ y) z = x z ÷ y z
Пример: (7 ÷ 5) 4 = 7 4 ÷ 5 4 = 2,401 ÷ 625 = 3,8416
Показатель 0
Любое число в степени 0 равно 1.
х 0 = 1
Пример: 450 0 = 1
Отрицательные экспоненты
Отрицательные экспоненты могут быть преобразованы в 1, деленную на основание экспоненты
x -a = 1 ÷ 1 a
Пример: 6 -4 = 1 ÷ 6 4 = 1 ÷ 1,296 = 0.0007716
Деление на отрицательную экспоненту
Числа с отрицательной степенью в качестве знаменателя можно заменить на числитель, а показатель степени сделать положительным.
1 ÷ x -a = x a
Пример: 1 ÷ 3 -4 = 3 4 = 81
Как набирать экспоненты
- В Microsoft Word и других продуктах Office щелкните правой кнопкой мыши и выберите «Шрифт», чтобы открыть меню шрифтов. Выберите «Надстрочный индекс».
- В Документах Google и других продуктах выделите текст, который вы хотите использовать в качестве показателя степени.символ перед экспонентой. Если в экспоненте более одного символа, заключите их в (скобки).
Таблица экспонент
Обратите внимание: для работы этой таблицы требуется JavaScript.Часто задаваемые вопросы
Что такое показатель степени (в математике)?
Показатель — это количество раз, когда число умножается само на себя. Например, от 3 до 4 (написано 3) означает 3 x 3 x 3 x 3 = 81. Это не то же самое, что 3 x 4 (12).
В чем разница между «Power Of» и «Exponent»?
Это одно и то же.Большинство людей используют термины «в степени» и «в степени» как синонимы.
Мы находим, что при описании вещи «показатель степени» является более естественным термином. («Какой показатель у числа в этом уравнении?» Звучит лучше, чем «Какова степень у числа в этом уравнении?»).
При описании действия более естественным термином является «степень из» («вычислить пять в степени трех» звучит лучше, чем «вычислить пять в степени три»).
Что такое отрицательная экспонента?
Отрицательная экспонента означает, сколько раз нужно разделить число.3 4 (положительный показатель степени) означает 3-кратное умножение самого себя 4 раза (3 x 3 x 3 x 3 = 81). 3 -4 (отрицательный показатель степени) означает разделить 3 на себя 4 раза (3 ÷ 3 ÷ 3 ÷ 3 = 0,012346).
Источники и другие ресурсы
Другие калькуляторы экспонент
Как использовать функцию Excel POWER
В геометрии формула для расчета объема конуса: Формула для расчета объема конуса основана на формуле для расчета объема пирамиды.Поскольку основанием конуса является …
В геометрии сфера определяется как набор точек, находящихся на одинаковом расстоянии (r) от данной точки в трехмерном пространстве. Формула для расчета площади поверхности шара: Греческий …
В геометрии сфера определяется как набор точек, находящихся на одинаковом расстоянии (r) от данной точки в трехмерном пространстве.Кубический корень числа можно вычислить вручную, возведя число до (1 / …
В геометрии формула для расчета площади поверхности правого конуса: Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле …
В этом примере показан один из способов расчета ИМТ (индекса массы тела) в Excel. Стандартная формула ИМТ: ИМТ = вес (кг) / рост (м) 2 Используемый здесь подход состоит в том, чтобы сначала преобразовать высоту из дюймов и футов в метры, а.), с номером слева и мощностью справа. Итак, в …
В геометрии площадь, ограниченная кругом радиуса (r), определяется по следующей формуле: πr2 Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π равно …
Функция КОРЕНЬ полностью автоматическая и возвращает квадратный корень из любого положительного числа. Например, чтобы получить квадратный корень из 25: = SQRT (25) // возвращает 5 Если вы дадите SQRT отрицательное число, он вернет # ЧИСЛО…
В геометрии формула для расчета объема цилиндра: Греческая буква π («пи») представляет собой отношение длины окружности к ее диаметру. В Excel π представлено в формуле с …
Что такое экспонента
Показатель — это количество раз, когда определенное число умножается само на себя.2` читается как «5 в степени 2» или «5 в степени 2».
Товарная форма номеров
Большие числа, разбитые на более мелкие формы, известны как числовые продукты.
Чтобы найти числовую форму продукта, скажем, 4 7
4 7 записывается в форме продукта как 4 7 = 4 × 4 × 4 × 4 × 4 × 4 × 4Выражение формы произведения чисел показателем
Чтобы выразить произведение чисел на экспоненты, мы считаем, сколько раз число умноженное само на себя.Это показатель этого числа.
Чтобы найти числа в экспоненциальной форме, скажем, 32.
Запишите форму произведения 32. 32 = 2 x 2 x 2 x 2 x 2 = 2 5 .
Здесь 2 умножается на себя в 5 раз. Так что показатель степени равен 5, а основание равно дано 2.
Мы получаем показатель степени 2 5 .Простой пример
2 7Пояснение:
Давайте найдем простые множители 128.
2 4
128 = 2 х 2 х 2 х 2 х 2 х 2 х 2 = 2 7
Здесь 2 умножается на себя в 7 раз. Так что показатель степени равен 7, а основание дано 2.
Получаем показатель степени 2 7 .Пояснение:
Давайте найдем простые делители 32.
32 = 2 х 2 х 2 х 2 = 2 4
Здесь 2 умножается на себя в 5 раз. Таким образом, показатель степени равен 4, а основание — 2.
Получаем показатель степени 2 4 .Квадрат числа
Квадрат числа является произведением некоторого целого числа на себя.2.
Квадрат отрицательного числа является положительным числом. Простой пример
1225Пояснение:
пл.35.
= (-35) 2
= (-35) × (-35)
= 1225Примеры квадрата переменных:
- 1. ab 2 = a × b × b
- 2. (ab) 2 = ab × ab
- 3.(ab) -2 = — (ab) × (-ab) = (ab) 2
Куб числа
Куб числа — это просто число, умноженное на себя в 3 раза.
Например, чтобы найти куб из 3.
Примечание:
Куб из 3 равен 3 умноженным на 3.
Куб из 3 = 3 × 3 × 3 = 27.
Мы можем выразить это в экспоненциальной форме как 3 3
- Куб отрицательного числа является отрицательным числом.
Простой пример
15625Пояснение:
Найдите куб 25.
= (-25) 3
= (-25) × (-25) × (-25)
= -15625Примеры куб переменных:
- 1.ab 3 = a × b × b x b
- 2. (ab) 3 = ab × ab × ab
Какое значение имеют числа в экспоненциальной форме?
Найти значение 3 5 .Мы можем найти значение чисел, представленных в экспоненциальной форме, умножив основание с самим собой, сколько раз дан показатель степени.
3 5 означает умножение 3 на себя 5 раз.
3 5 = 3 × 3 × 3 × 3 × 3
3 × 3 × 3 × 3 × 3 = 243.Показатель: проблемы со словами
См. Картинку ниже. Ящики находятся в группе по 4. Подсчитайте количество ящиков в группе. и запишите их в форме экспоненты и продукта.Как ты мог прочитать этот номер? Найдите значение этого числа в экспоненциальной форме.
64Пояснение:
Групповые номера ящиков — 3.В каждой группе по 4 бокса. Так что база равно 4, а показатель степени равен 3. Мы можем записать это в форме экспоненты как 4 3 .
Форма произведения 4 3 = 4 × 4 × 4
Мы можем читать 4 3 как 4, увеличенное до 3.
Значение 4 3 = 4 × 4 × 4 = 64Пожалуйста, смотрите картинку ниже.Звезды в группе из 12. Подсчитайте количество звезд в группе. и запишите их в форме экспоненты и продукта. Как ты мог прочитать этот номер? Найдите значение этого числа в экспоненциальной форме.
20736Пояснение:
Групповые номера звезд — 4.В каждой группе по 12 звезд. Так что база равно 12, а показатель степени равен 4. Мы можем записать это в форме экспоненты как 12 4 .
Форма продукта 12 4 = 12 × 12 × 12 × 12
Мы можем читать 12 4 как 12, увеличенное до 4.
Значение 12 4 = 12 × 12 × 12 × 12 = 20736Правила экспоненты
Любое число с показателем степени 0 (кроме 0) равно 1.Таким образом, x 0 = 1.
Примеры: 5 0 = 1, 15 0 = 1, 123 0 = 1, 154 0 = 1, 120 0 = 1Когда база увеличена до положительного значения мощности; х 1 = х
Примеры: (10) 1 = 10, (15) 1 = 15, (124) 1 = 124 и (-10) 1 = -10, (-15) 1 = -15, (-124) 1 = -124Простой пример
64/729Пояснение:
(2/3) 6
Здесь 2/3 — основание, а 6 — показатель степени.
Для (2/3) 6 среднее значение 2/3 равно 6 раз. Так что,
(2/3) 6 = 2/3 × 2/3 × 2/3 × 2/3 × 2/3 × 2/3 = 2 × 2 × 2 × 2 × 2 × 2/3 × 3 × 3 × 3 × 3 × 3 = 64/729Когда база увеличена до отрицательного значения мощности; х -1 = 1 / х.
1/20736
Примеры: 5 -6 = 1/5 6 , 4 -3 = 1/4 3 , 7 -5 = 1/7 5Пояснение:
(12) -4
Здесь 12 — основание, а -4 — показатель степени.
Для (12) -4 среднее 1 / (12) 4
(12) -4 = 1 / (12) 4
= 1/12 × 1/12 × 1/12 × 1/12 = 1 × 1 × 1 × 1/12 × 12 × 12 × 12 = 1/20736Объем воды
Задача Word:
Емкость кубической формы на треть заполнена керосиновым маслом.Каждая сторона контейнера 9 дюймов в длину. Какой объем керосина в кубических дюймах?
243 кубических дюймаПояснение:
Объем куба = (сторона) 3
Объем кубической емкости = 9 3 = 9 × 9 × 9 = 729.
Объем кубической тары 729 кубических дюймов.
Объем керосина в кубических дюймах
= 729/3 = 243 кубических дюймаПравило умножения при одинаковом основании
Когда мы умножаем числа с одинаковым основанием, основание продукта остается то же и показатели добавляются, чтобы получить индекс продукта.
Например: 8 4 × 8 5 = 8 4 + 5 = 8 9
Примечание:
- Если a — любое рациональное число, а m и n — любые положительные целые числа, то m × a n = a m + n
Простой пример
7 9Пояснение:
7 5 × 7 4
= (7 × 7 × 7 × 7 × 7) × (7 × 7 × 7 × 7)
= (7 × 7 × 7 × 7 × 7 × 7 × 7 × 7 × 7)
= число 7, (5 + 4) умноженное на = 7 9
Таким образом, 7 5 × 7 4 = 7 9Средний Пример:
(7/5) 3 × (7/5) 8
= (7/5) 3 + 8
= (7/5) 11Предварительный пример:
(y) 4 × (y) 6
= (y) 4 + 6
= (y) 10Пример из реальной жизни: проблема со словами
Группе работодателей был дан проект, состоящий из трех частей.Есть 3 2 способов заполнить 2 документа в Части A. Есть 3 2 способов заполнить 2 документа в Части B. Сколько существует способов завершить проект? Все 4? документы?
Есть 81 способ завершить проект.
Пояснение:
Есть 3 2 способов заполнить 2 документа в Части A. Всего 3 2 способов заполнить 2 документа в Части Б. Количество способов завершить проект все 4 документа являются продуктом 3 2 и 3 2
Произведение 3 2 и 3 2
= 3 2 × 3 2
= 3 2 + 2
= 3 4
= 81Правило деления при одинаковом основании
Если a — любое рациональное число, отличное от 0, а m и n — любые положительные целые числа, такие что m> n, тогда a m ÷ a n = a m-n
Примечание:
- Когда мы делим числа с одинаковым основанием, основание остается прежним и показатели вычитаются.
- Если индекс дивиденда больше, чем у делителя, вычесть показатель степени. делителя от дивиденда.
Простой пример
1/8 5Пояснение:
= 8 9-4
= 8 5
8 4 ÷ 8 9
= 1/8 9-4
= 1/8 5Средний Пример:
1296Пояснение:
6 8 ÷ 6 4
= (6 × 6 × 6 × 6 × 6 × 6 × 6) ÷ (6 × 6 × 6 × 6)
= (6 × 6 × 6 × 6)
= 1296Предварительный пример:
32/243Пояснение:
= (2/3) 8 -3
= (2/3) 5
= (2/3) × (2/3) × (2/3) × (2/3) × (2/3)
= 2 × 2 × 2 × 2 × 2/3 × 3 × 3 × 3 × 3
= 32/243Предварительный пример;
(а) 4 × (а) 6
= 1 / (а) 6-4
= 1 / (а) 2Пример из реальной жизни
В обществе проводится опрос о работе на дому для женщин и мужчин.Установлено, что 7 6 женщин выполняли работу из дома, но только 7 2 мужчины выполняли работу из дома. Во сколько раз больше женщин выполняли работу из дома?
Еще 2401 женщина выполняла работу из дома.Пояснение:
Чтобы больше женщин работали из дома, мы должны разделить эти два выражения показаны для женщин и мужчин. То есть 7 6 и 7 2
7 6 /7 2
= 7 6-2
= 7 4
70005 = 7 7 × 7
= 2401Правило индексации числа в индексной форме
Если мы скажем, (2 3 ) 5Если x — любое рациональное число, а m и n — натуральные числа, то
(x м ) n = (x) m × n
(2 3 ) 5
Умножьте индекс.
(2 3 ) 5 = (2) 3 × 5 = 2 15Простой пример
(а 4 ) 5
(а 4 ) 5
= а 4 × 5
= а 20Средний Пример
81/256Пояснение:
[(-3/4) 2 ] 2
Умножим числовые индексы.
= (-3/4) 2 × 2
= (-3/4) 4
= -3 × -3 × -3 × -3 / 4 × 4 × 4 × 4
= 81/256Правило индексации продукта
Если мы скажем, (4 × 3) 7 .Если x и y — любые рациональные числа, а m — любые положительные целые числа, то
(x × y) м = x м × y м .
(4 × 3) 7 = (4) 7 × (3) 7Простой пример
(а × б) 5
(а × б) 5 = (а) 5 × (б) 5Средний Пример:
1000Пояснение:
(5 × 2) 3
= (5) 3 × (2) 3
= (5 × 5 × 5) × (2 × 2 × 2)
= 1000Предварительный пример:
4/225Пояснение:
(1/3 × 2/5) 2
= (1/3) 2 × (2/5) 2
= 1 × 1 × 2 × 2/3 × 3 × 5 × 5
= 4/225Правило индексации числа в форме числитель-знаменатель
Если x / y — любое рациональное число, а m — любое натуральное число, то
(x / y) м = x м / y мСкажем,
(3/5) 2 = 3 2 /5 2 и (x / y) 2 = х 2 / у 2Простой пример
625/16Пояснение:
(5/2) 4
= (5) 4 / (2) 4
= (5 × 5 × 5 × 5) / (2 × 2 × 2 × 2)
= 625/16Средний Пример:
36/25Пояснение:
(-6/5) 2
= (-6) 2 / (5) 2
= (-6 × -6) / (5 × 5) 9 · 1072 = 36/25Дополнительные примеры с большим количеством правил вместе
Предварительный пример:
100Пояснение:
(5 × 2) 3 ÷ (5 × 2) 1
Сначала мы вычтем здесь индекс.
= (5 × 2) 3 -1
= (5 × 2) 2
= (5) 2 × (2) 2
= 5 × 5 × 2 × 2
= 100
3125Пояснение:
Сначала мы добавим сюда индекс.
= (5 1 ) 2 + 3
= (5 1 ) 5
= 5 1 × 5
= 5 5
= 3125
1/36Пояснение:
(а × б) 3 ÷ (а × б) 5
= 1 / (а × б) 5 -3
= 1 / (а × б) 2
= 1 / (2 × 3) 2 поместите значение для a = 2 и b = 3
= 1 / (2) 2 × (3) 2
1/2 × 2 × 3 × 3
= 1/36
1Пояснение:
(а) 0 ÷ (б) 0
= (15) 0 ÷ (17) 0 поместите значение для a = 15 и b = 17
= 1 ÷ 1
= 1Дробный индекс
Квадрат числа отображается записью числа с показателем 2.
Индекс ½ представляет собой квадратный корень из числа.
Они известны как дробные индексы.Скажем, квадрат 4, мы запишем как 4 2 .
Теперь, если мы хотим записать квадратный корень из 4, мы запишем как 4 1/2 .
Также как кубический корень из 8 записывается как 8 1/3Примечание:
- Корень n-й степени числа отображается индексом 1 / n.
Как читать числа как дробные индексы?
См. Следующие примеры:
9 1/2 означает квадратный корень из 9.
1000 1/3 означает кубический корень из 1000.
625 1/4 означает четвертый корень из 625.
1000 1 / 10 означает квадратный корень из 1000.Простой пример
4Пояснение:
4 × 4 × 4 × 4 = 256.
Следовательно, 4 4 = 256.
И наоборот, 4 — это корень четвертой степени из 256.
16Пояснение:
16 × 16 = 256.
Следовательно, 16 2 = 256.
И наоборот, 16 — это квадратный корень из 256.Средний Пример:
Найдите значения следующих индексных чисел.
- 125 1/3 = кубический корень из 125 = 5
- 144 1/2 = квадратный корень из 144 = 12
- 216 1/3 = кубический корень из 216 = 6
- 169 1/2 = квадратный корень из 169 = 13
Дробные индексы умножения
Как вы знаете, если a — любое рациональное число, а m и n — любые положительные целые числа, то
a m × a n = a m + n
То же правило применяется для дробных индексов, когда мы умножаем числа как индексная форма с той же базой.Если мы скажем, 7 1/2 × 7 1/3
Сложите порядковые номера. 7 1/2 × 7 1/3 = 7 1/2 + 1/3
Упростите добавленную форму индекса. 7 1/2 + 1/3 = 7 3 + 2/6
7 3 + 2/6 = 7 5/6 означает 5 th мощность 6 -я корень из 7.Простой пример
9 2/3 означает степень 2 и степень из 3 -го корня из 9.Пояснение:
9 1/3 × 9 1/3
= 9 1/3 + 1/3
= 9 1 + 1/3
= 9 2/3
14 9/20 означает 9 -ю степень из 20 -го корень из 14.Пояснение:
14 1/4 × 14 1/5
= 14 1/4 + 1/5
= 14 5 + 4/20
= 14 9/20
x 8/15 означает 8 -ю степень из 15 -го корня x.Пояснение:
x1 / 3 x 1/5
= х 1/3 + 1/5
= х 5 + 3/15
= х 8/15Деление дробных индексов
Если a — любое рациональное число, отличное от 0, а m и n — любые положительные целые числа, такие что m> n, тогда a m ÷ a n = a m-n
То же правило применяется для дробных индексов, когда мы умножаем числа как индексная форма с той же базой.
Если мы скажем,
7 1/3 ÷ 7 1/3
Вычтите порядковые номера. 7 1/3 ÷ 7 1/3 = 7 1/3 — 1/3
Упростите форму индекса. = 7 1/3 — 1/3 = 7 0
Запишите значение. 7 0 = 1Простой пример
9 2/3 означает степень 2 и степень из 3 -го корня из 9.Пояснение:
13 1/4 ÷ 13 1/5
m 2/15 означает степень 2 и из 15 -го корня из m.
= 13 1 / 4- 1/5
= 13 5-4 / 20
= 13 1/20
13 1/20 означает корень 20 -го из 13.Пояснение:
м 1/3 ÷ м 1/5
8 1/12 означает 12 -й корень из 8.
= м 1/3 — 1/5
= м 5-3 / 15
= м 2/15Пояснение:
8 1/4 ÷ 8 1/6
= 8 1/4 — 1/6
= 8 3-2 / 12
= 8 1/12Правило индекса числа для дробных индексов
Если мы говорим , (2 1/3 ) 1/5Если x — любое рациональное число, а m и n — натуральные числа, то
(x м ) n = x m × n
Умножьте числовые индексы.(2 1/3 ) 1/5 = 2 1/3 × 1/5
Упростите форму индекса. 2 1/3 × 1/5 = 2 1/15
Запишите значение. 2 1/15Простой пример
25 1/4Пояснение:
(25) 1/2 × 1/2
Умножьте числовые индексы.
= 25 1/4
8 1/18Пояснение:
8 1/2 × 1/9
Умножьте числовые индексы.
= 8 1/18
л 1/6Пояснение:
y 1/2 × 1/3
Умножьте числовые индексы.
= у 1/6Правило индекса продукта для дробных индексов
Можно сказать,Если x и y — любые рациональные числа, а m — любые положительные целые числа, то
(x × y) м = x м × y м .
(5 × 3) 1/7 = (5) 1/ 7 × (3) 1/ 7
Или (a × b) 1/5 = (a) 1/ 5 × (b) 1/ 5Простой пример
Упростить (5 × 9) 1/3
(5 × 9) 1/3
= (5) 1/ 3 × (9) 1/ 3Средний Пример:
10Пояснение:
(125 × 8) 1/ 3
= (125) 1/ 3 × (8) 1/ 3
= 5 × 2
= 10
80Пояснение:
(100 × 64) 1/ 2
= (100) 1/ 2 × (64) 1/ 2
= 10 × 8
= 80Дополнительные примеры с большим количеством правил вместе
Простой пример:
20Пояснение:
(625 × 256) 1/ 2 ÷ (625 × 256) 1/ 4
= (625 × 256) 1/ 2 — 1/ 4
= (625 × 256) 1/ 4
= (625) 1/ 4 × (256) 1/ 4
= 5 × 4
= 20
27Пояснение:
[(81) 1 ] 1/2 × [(81) 1 ] 1/4
= [(81) 1 ] 1/2 + 1/4
= (81 ) 3/4
Означает степень 3 и корня 4 из 81.
= 27Предварительный пример:
2 2/15 × 3 2/15Пояснение:
(a × b) 1/ 3 ÷ (a × b) 1/ 5 поместите значение для a = 2 и b = 3
= (2 × 3) 1/ 3 ÷ (2 × 3) 1/ 5
= (2 × 3) 1 / 3- 1/5
= (2 × 3) 5-3 / 15
= (2 × 3) 2/15
= 2 2/15 × 3 2/15
Что следует помнитьДля любого заданного числа составлять пары…
Советы
- Когда мы умножаем / делим индексы с одинаковым основанием, основание остается неизменным.
- Чтобы записать числа как степень 10, первое число должно быть от 1 до 10 и другой — степень 10.
Думаю:
.
- Какой из них больше 73 или 37?
- Каким может быть значение (1) 1000
- Если дано 8 3 ÷ 3 2 . Вы можете добавить экспоненты? Если нет! ‘Почему’?



 Согласно определению, когда n четное, то при любом положительном значении а верно
равенство
Согласно определению, когда n четное, то при любом положительном значении а верно
равенство
 В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так,
выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.
В частности, знаком корня служил символ Rx (от латинского слова radix — корень). Так,
выражение 24+374 в символике Шюке имело вид R¯x424p¯R¯x237.
 е. x=±54.
е. x=±54. Решить
уравнение
Решить
уравнение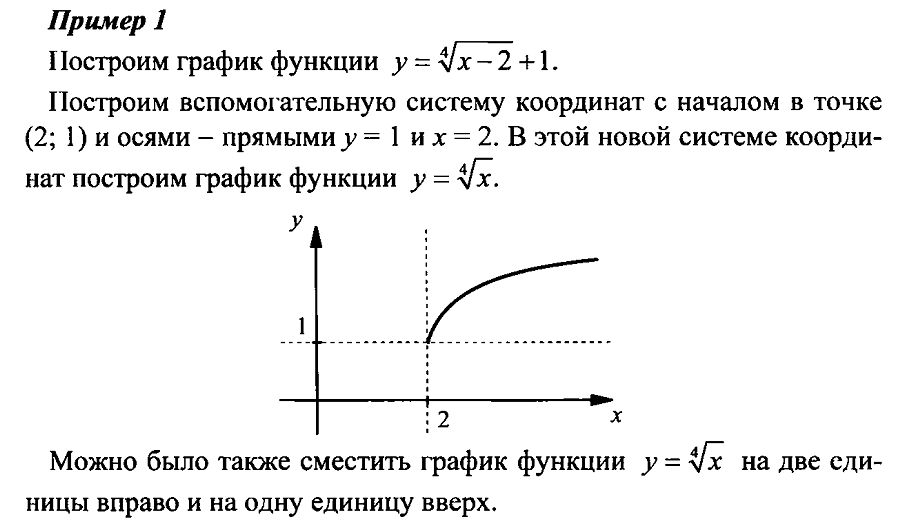 24°
24°


 37°
37°


 53
53 И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 корень 3 степени из х производная».
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «3 корень 3 степени из х производная». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 корень 3 степени из х производная. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как найти производную корня).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и 3 корень 3 степени из х производная. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как найти производную корня). Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.
Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.





 Можно вводить arcctg(
Можно вводить arcctg( Едем дальше. А если перед нами такое выражение:
Едем дальше. А если перед нами такое выражение: {2}}\cdot 2}=7\sqrt{2}\)
{2}}\cdot 2}=7\sqrt{2}\) Но нам он, конечно, по зубам. Ну что, начнем раскладывать \( 4225\) на множители?
Но нам он, конечно, по зубам. Ну что, начнем раскладывать \( 4225\) на множители? 
 Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так:
Известно, что для того, чтобы взять корень n из числа, необходимо возвести его в степень 1/n. Соответственно, извлечение квадратного корня из числа 4 будет выглядеть так: 3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")
sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds
3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = 4 ** 0.5
print("** time: {:>.3f}".format(monotonic() - start) + " seconds")
start = monotonic()
for a in range(iterations):
x = pow(4, 0.5)
print("pow time: {:>.3f}".format(monotonic() - start) + " seconds")
sqrt time: 0.266 seconds
** time: 0.109 seconds
pow time: 0.453 seconds
 py", line 2, in
x = sqrt(-4)
ValueError: math domain error
py", line 2, in
x = sqrt(-4)
ValueError: math domain error Кроме того оператор ** оказался наиболее быстрым при тестировании.
Кроме того оператор ** оказался наиболее быстрым при тестировании.
 {2}} {5} && \ text {Упростить}. \\ \ end {align} [/ latex]
{2}} {5} && \ text {Упростить}. \\ \ end {align} [/ latex] {\ frac {2} {3}} [/ латекс] как радикал.{\ frac {23} {15}} [/ латекс]
{\ frac {2} {3}} [/ латекс] как радикал.{\ frac {23} {15}} [/ латекс] ..или:
..или: Например:
Например: Подумайте об этом: предположим, вы начали с числа –2. Тогда:
Подумайте об этом: предположим, вы начали с числа –2. Тогда: С другой стороны, если они дадут вам что-то вроде x 4/5 , вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что пятый корень не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».)
С другой стороны, если они дадут вам что-то вроде x 4/5 , вам не нужно заботиться о том, является ли x положительным или отрицательным, потому что пятый корень не имеет проблем с отрицательными. (Между прочим, эти соображения не имеют значения, если в вашей книге указано, что вы должны «предполагать, что все переменные неотрицательны».) (2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.
(2/3) «в ячейку, электронная таблица Microsoft» Excel «возвращает ошибку» # ЧИСЛО! «, Еще один бесполезный ответ.
 a n = a m + n
a n = a m + n 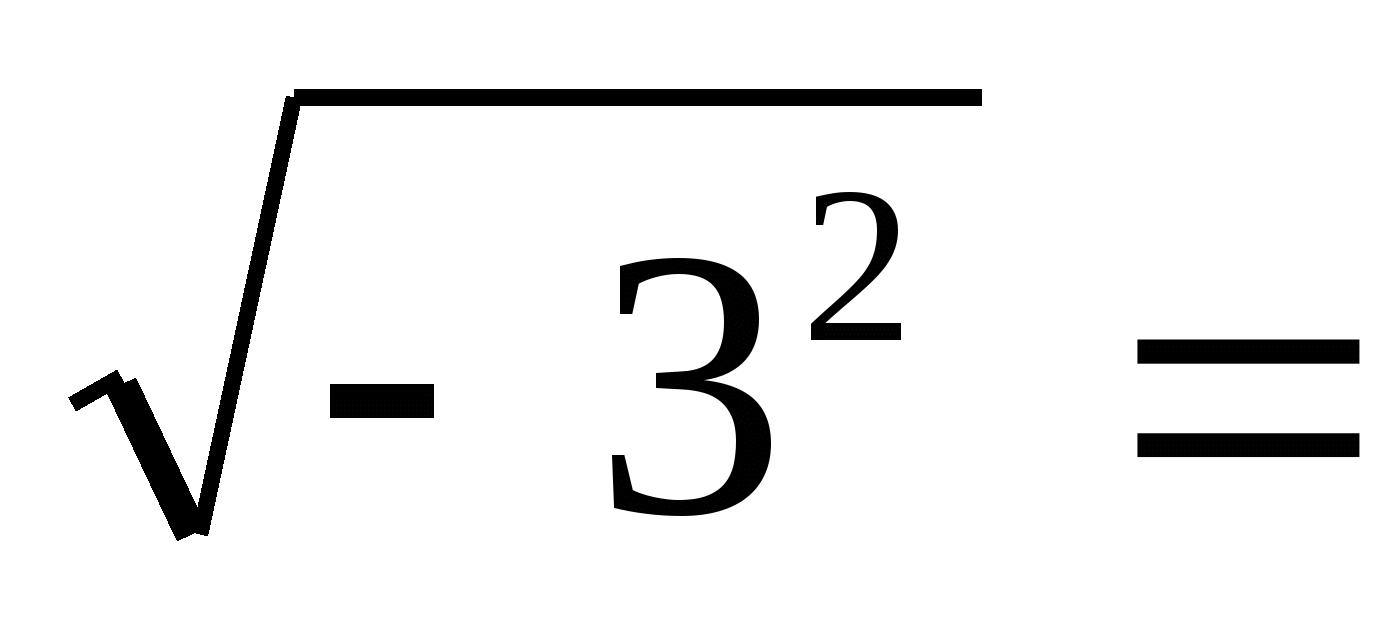 Упростить (7.5 * 10 5 ) / (25 * 10 -4 )
Упростить (7.5 * 10 5 ) / (25 * 10 -4 )
 08 * (2 2 ) 0,22 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ]
08 * (2 2 ) 0,22 ] 10 / [16 0,16 * (2 4 ) 0,74 * (4 2 ) 0,1 ] При помощи нити ролик привязан к динамометру (5). При вращении ролик натянет нить, и динамометр покажет некую силу F, тем бо’льшую, чем быстрее вращается диск.
При помощи нити ролик привязан к динамометру (5). При вращении ролик натянет нить, и динамометр покажет некую силу F, тем бо’льшую, чем быстрее вращается диск. То есть за секунду совершается один оборот. Следовательно, период T = 1 с. Вычисляя центростремительное ускорение ролика по формуле a = 4p2R/T2, получим: 4 · 3.142 · 0.2 / 12 » 8 м/с2. Именно это число и записано в клетке «ускорение».
То есть за секунду совершается один оборот. Следовательно, период T = 1 с. Вычисляя центростремительное ускорение ролика по формуле a = 4p2R/T2, получим: 4 · 3.142 · 0.2 / 12 » 8 м/с2. Именно это число и записано в клетке «ускорение».
 (1)
(1) Инертная масса
Инертная масса Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
«до теории относительности» корректна.
Его называют массой покоя тела.
Поэтому формулы (1), (2), (3) следовало бы записать
так: P = m0v, F = m0a,
.
Однако для малых скоростей, как видно из формулы
(5), инертная масса равна массе покоя, m = m0, и поэтому запись (1), (2), (3) в разделе
«до теории относительности» корректна.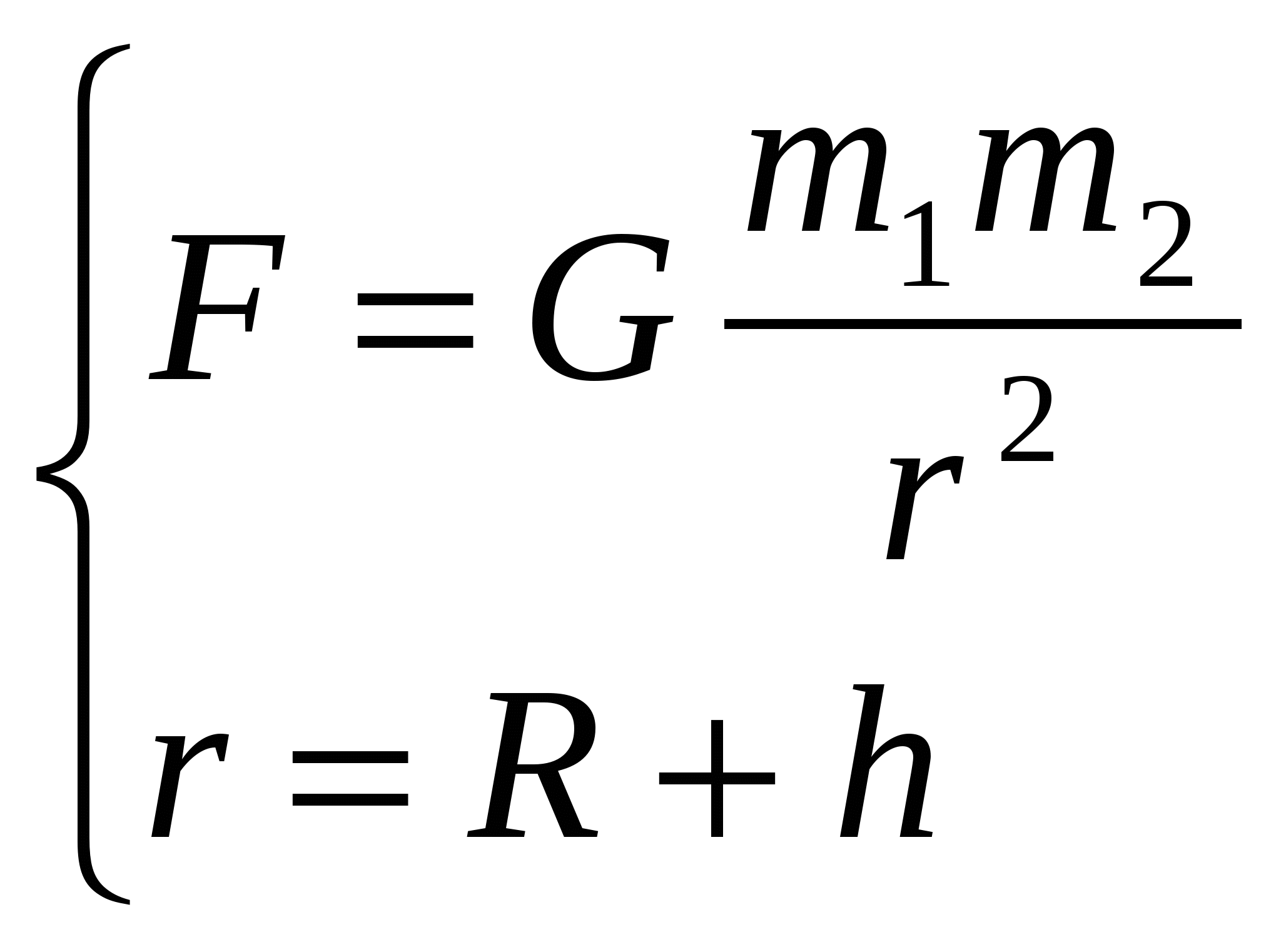 Однако существует собственная
скорость хода часов.
Однако существует собственная
скорость хода часов. Однако в этом
случае не существует какого либо выделенного
значения инертной массы. Либо, можно сказать,
выделенное значение равно нулю.
Однако в этом
случае не существует какого либо выделенного
значения инертной массы. Либо, можно сказать,
выделенное значение равно нулю. Фейнману предложить простой способ
операционного определения инертной массы,
основанный на формуле (9) и справедливый для любой
скорости. «Массу можно измерить так: просто
привязать предмет на веревочке, крутить его с
определенной скоростью и измерять ту силу,
которая необходима, чтобы удержать его.» [4]
Фейнману предложить простой способ
операционного определения инертной массы,
основанный на формуле (9) и справедливый для любой
скорости. «Массу можно измерить так: просто
привязать предмет на веревочке, крутить его с
определенной скоростью и измерять ту силу,
которая необходима, чтобы удержать его.» [4] Гравитационная масса
Гравитационная масса Два, доселе различных понятия,
соединяются в одно.
Два, доселе различных понятия,
соединяются в одно.
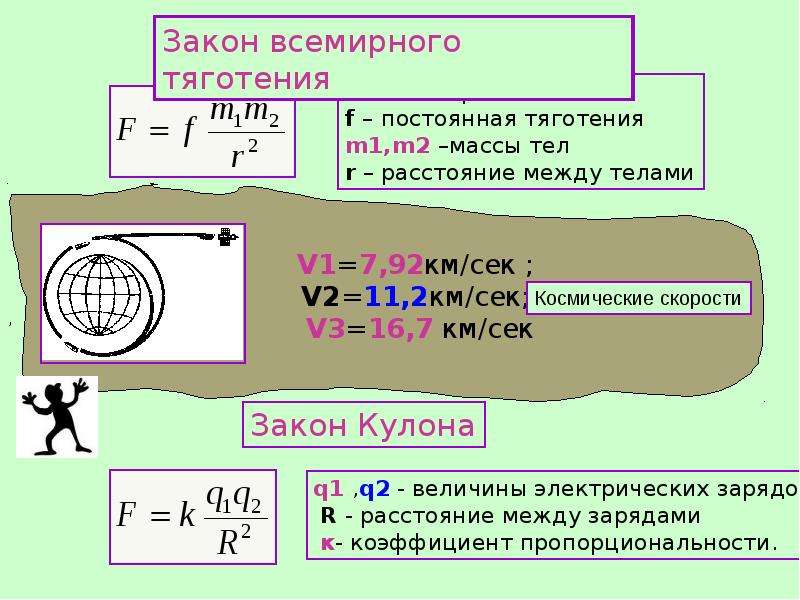 (15)
(15) Точно так же, когда говорят о
дефекте массы покоя при ядерных реакциях, имеют в
виду не массу покоя, определяемую формулой (15), а
сумму масс покоя частей системы.
Точно так же, когда говорят о
дефекте массы покоя при ядерных реакциях, имеют в
виду не массу покоя, определяемую формулой (15), а
сумму масс покоя частей системы.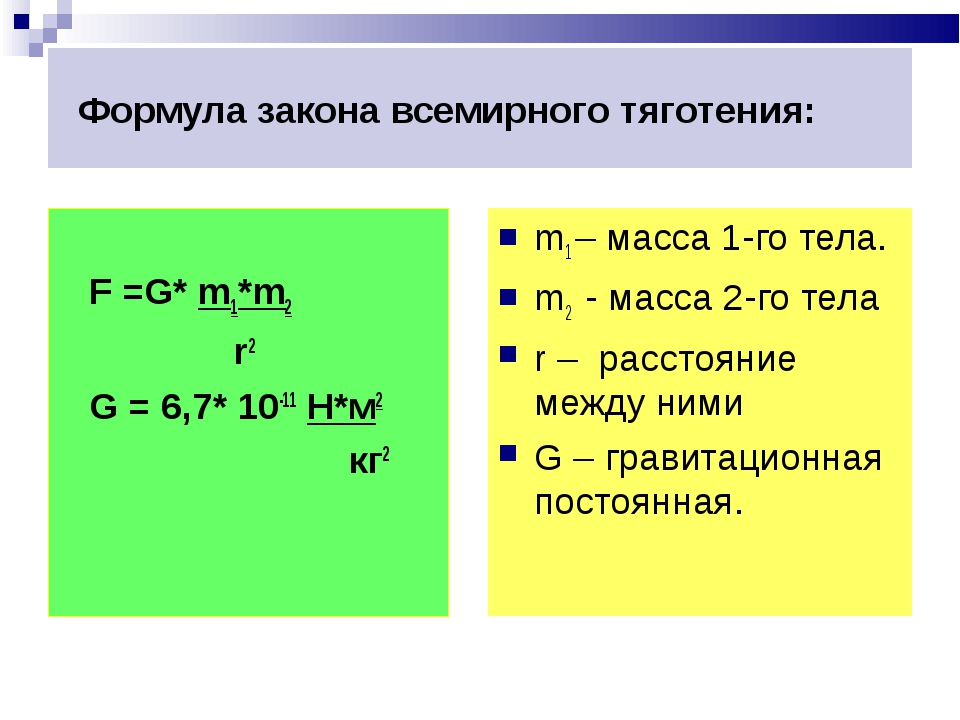 [1] , стр. 1365) и мешает
проявлению закона сохранения массы покоя. Фотоны
и частицы, движущиеся со скоростью света, не
обладают массой покоя. Операционное определение
массы покоя частицы предполагает торможение ее
до малой скорости без использования информации о
текущем состоянии частицы.
[1] , стр. 1365) и мешает
проявлению закона сохранения массы покоя. Фотоны
и частицы, движущиеся со скоростью света, не
обладают массой покоя. Операционное определение
массы покоя частицы предполагает торможение ее
до малой скорости без использования информации о
текущем состоянии частицы.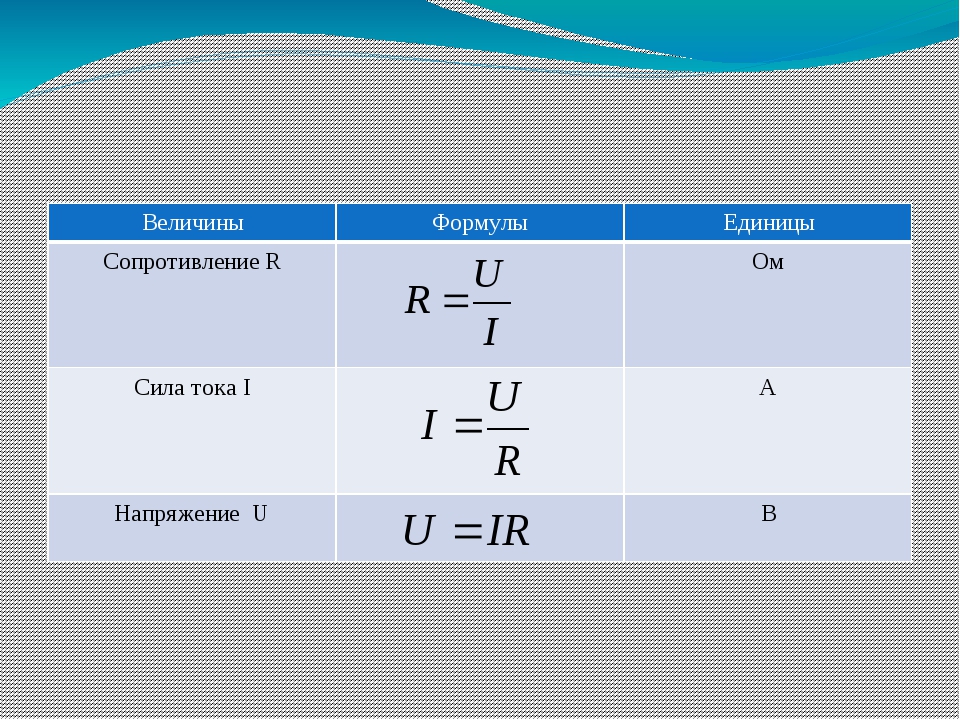

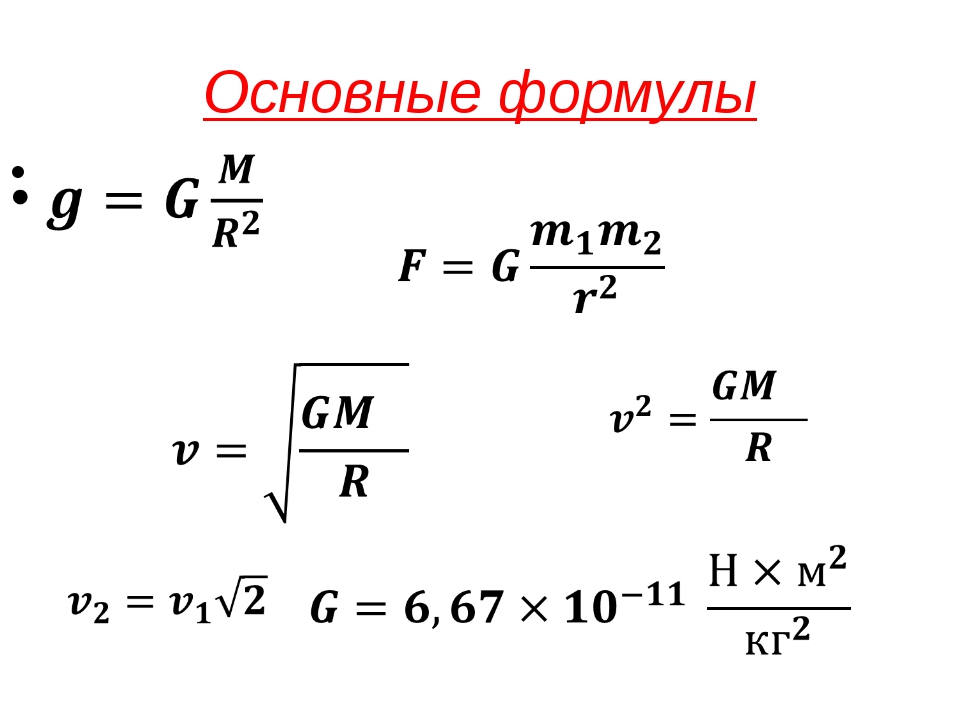 » [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
«Известия вузов. Физика», «Квант», «American Journal of Physics»,
«Physics Education» (Bristol), «Physics Today».
» [11] К сожалению, великая идея
релятивистской массы тщательно изолируется от молодежи. На данный момент статья
[1, 2] отклонена редакциями следующих журналов:
«Известия вузов. Физика», «Квант», «American Journal of Physics»,
«Physics Education» (Bristol), «Physics Today».
 -496p.
-496p.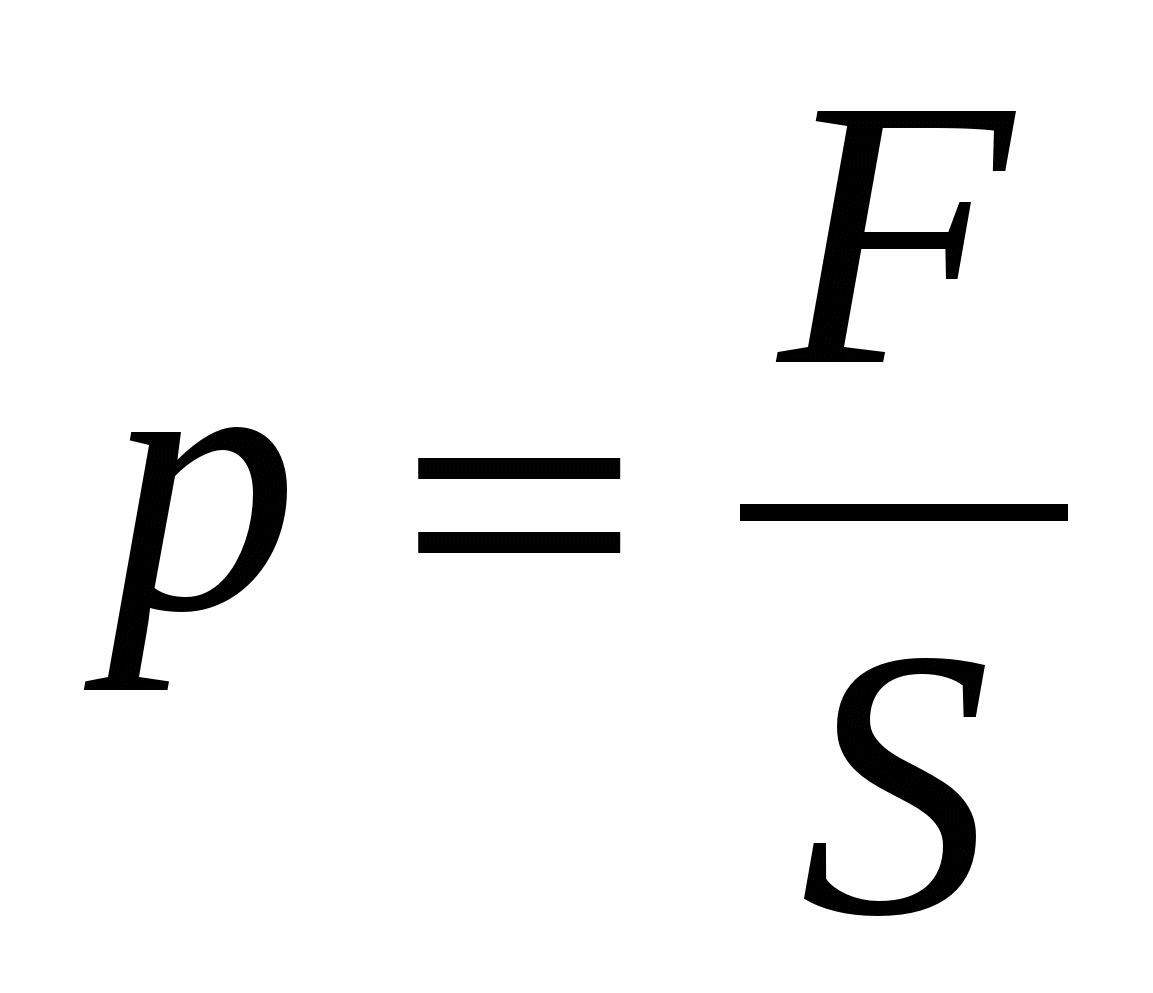

 Вставьте в текст пропущенные слова из следующего ряда: действие, скорость, направление, деформация, нагревание.
Вставьте в текст пропущенные слова из следующего ряда: действие, скорость, направление, деформация, нагревание. : Сила. Второй закон Ньютона :.
: Сила. Второй закон Ньютона :. Если, к примеру, ми изучаем движение автомобиля, то знаем, что он взаимодействует с поверхностью Земли. Нас интересует движение автомобиля, а не Земли.
Как известно, числовые значения ускорений двух взаимодействующих тел обратно пропорциональны их массам:
Если, к примеру, ми изучаем движение автомобиля, то знаем, что он взаимодействует с поверхностью Земли. Нас интересует движение автомобиля, а не Земли.
Как известно, числовые значения ускорений двух взаимодействующих тел обратно пропорциональны их массам:
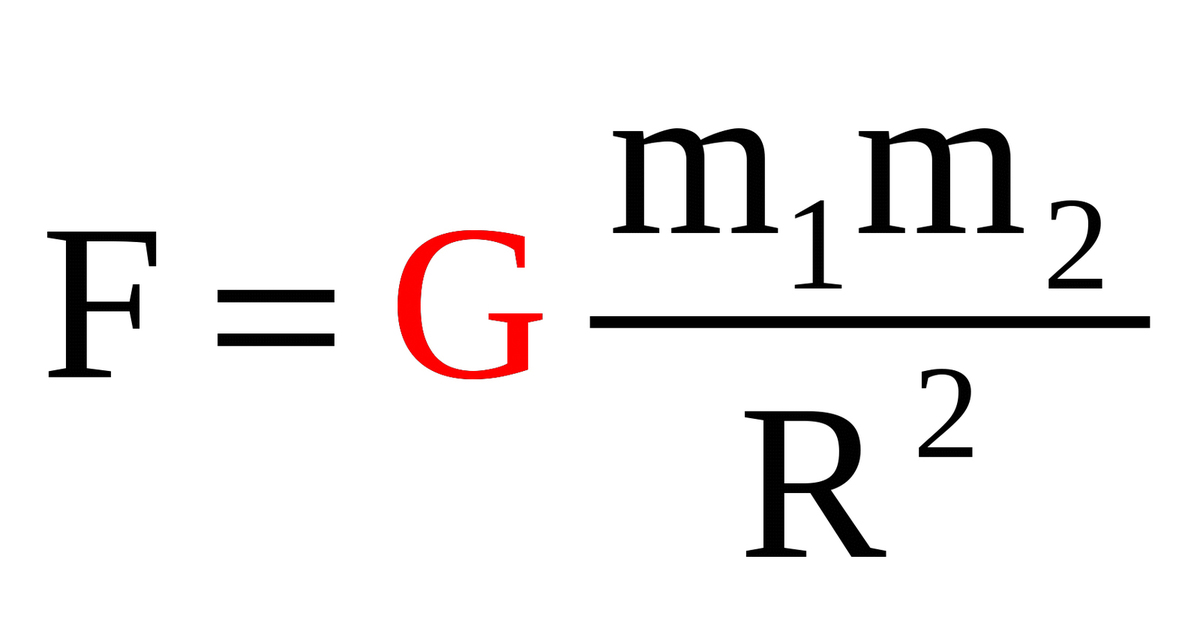 А при умножении вектора на скаляр получаем вектор того же направления, изменяется только его значение.
А при умножении вектора на скаляр получаем вектор того же направления, изменяется только его значение. Эти силы можно сложить по правилу параллелограмма и найти равнодействующею всех приложенных сил. Ускорение, которое телу сообщают все силы вместе равно ускорению, которое получило бы тело под действием равнодействующей силы.
Эти силы можно сложить по правилу параллелограмма и найти равнодействующею всех приложенных сил. Ускорение, которое телу сообщают все силы вместе равно ускорению, которое получило бы тело под действием равнодействующей силы. В соответствии со вторым законом Ньютона это значит, что к телу приложена постоянная сила Fx, направленная вдоль оси и равная по модулю max.
В соответствии со вторым законом Ньютона это значит, что к телу приложена постоянная сила Fx, направленная вдоль оси и равная по модулю max.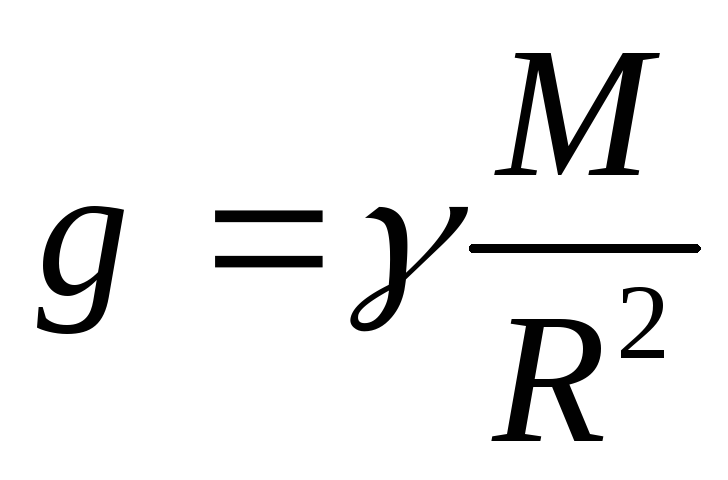 Груз m1 взаимодействует с наклонной плоскостью, нитью и Землёй. Данные тела являются источниками четырёх си: силы реакции опоры N, силы трения скольжения µ N, сила натяжения нити Т, и сила тяжести m1g. Груз m2 взаимодействует лишь с Землёй и нитью, поэтому к нему приложены только две силы – сила тяжести m2g,и сила натяжения нити Т.(Пример №1).
Если приложенных к грузам сил отлична от нуля, то грузы начнут двигаться с ускорением, которое можно найти с помощью второго закона Ньютона. Направления движения тел в общем случае зависят от масс тел, угла наклона плоскости и коэффициента трения.
Если перетягивая груз m2,то сила трения, приложенная к телу m1, оказывается направленной вниз. Применительно к телу m1 второй закон Ньютона, записывается в проекциях на оси X и Y, даёт:
m1a= T-m1gsina- µ N,
0=N-m1gcosa,
Применяя тот же закон к телу m2, получаем:
m2а= m2п-Т,
Из этих уравнений находим ускорение:
а=((m2-m1sina- µm1cosa)/m2+m1)g,
Если предположить, что перетягивает тело m1(сила трения изменяется на противоположную), получаем другой ответ:
а=((msina-m2-µm1cosa)/m2+m1)g,
Так как модули ускорения а>0, то заданных значениях а(угол) и µ, первое из получившихся уравнений справедливо при условии:
m2>=m1(sina+µcosa),
а второе:
m2,
Следовательно второй закон Ньютона позволяет добить массу информации о рассматриемай системе.
Груз m1 взаимодействует с наклонной плоскостью, нитью и Землёй. Данные тела являются источниками четырёх си: силы реакции опоры N, силы трения скольжения µ N, сила натяжения нити Т, и сила тяжести m1g. Груз m2 взаимодействует лишь с Землёй и нитью, поэтому к нему приложены только две силы – сила тяжести m2g,и сила натяжения нити Т.(Пример №1).
Если приложенных к грузам сил отлична от нуля, то грузы начнут двигаться с ускорением, которое можно найти с помощью второго закона Ньютона. Направления движения тел в общем случае зависят от масс тел, угла наклона плоскости и коэффициента трения.
Если перетягивая груз m2,то сила трения, приложенная к телу m1, оказывается направленной вниз. Применительно к телу m1 второй закон Ньютона, записывается в проекциях на оси X и Y, даёт:
m1a= T-m1gsina- µ N,
0=N-m1gcosa,
Применяя тот же закон к телу m2, получаем:
m2а= m2п-Т,
Из этих уравнений находим ускорение:
а=((m2-m1sina- µm1cosa)/m2+m1)g,
Если предположить, что перетягивает тело m1(сила трения изменяется на противоположную), получаем другой ответ:
а=((msina-m2-µm1cosa)/m2+m1)g,
Так как модули ускорения а>0, то заданных значениях а(угол) и µ, первое из получившихся уравнений справедливо при условии:
m2>=m1(sina+µcosa),
а второе:
m2,
Следовательно второй закон Ньютона позволяет добить массу информации о рассматриемай системе.
 время подъема
время подъема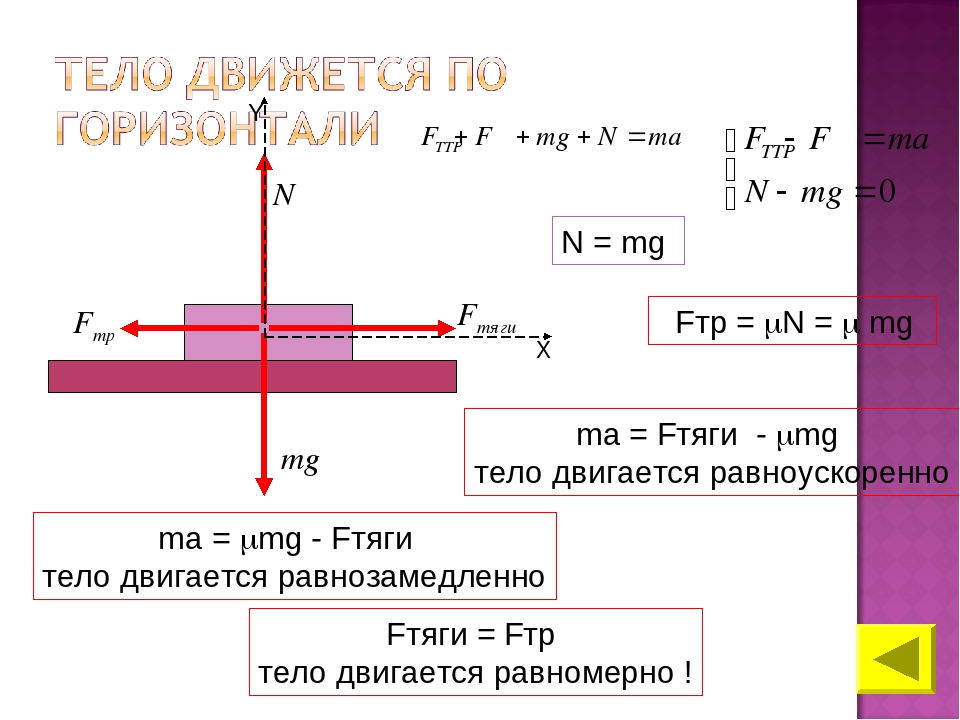 смещение x = Asin(t
+ 0),
2. скорость v = Acos(t
+ 0),
vmax = A
смещение x = Asin(t
+ 0),
2. скорость v = Acos(t
+ 0),
vmax = A  Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.)
Казалось, что сейчас вас так и выбросит на обочину. И если вспомнить законы механики Ньютона, то получается, что раз вас буквально вдавливало в дверцу, значит на вас действовала некая сила. Ее обычно называют «центробежная сила». Именно из-за центробежной силы так захватывает дух на крутых поворотах, когда эта сила прижимает вас к бортику автомобиля. (Между прочим, этот термин, происходящий от латинских слов centrum («центр») и fugus («бег»), ввел в научный обиход в 1689 году Исаак Ньютон.) В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета.
В обеих системах отсчета события описываются одинаково и для этого описания используются одни и те же уравнения. Единственным отличием будет интерпретация происходящего внешним и внутренним наблюдателем. В этом смысле центробежная сила напоминает силу Кориолиса (см. Эффект Кориолиса), которая также действует во вращающихся системах отсчета. Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v2/r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv2/r.
Тело, движущееся с постоянной скоростью по окружности, движется с ускорением, поскольку оно всё время меняет направление. Это ускорение равно v2/r, где v — скорость, а r — радиус окружности. Соответственно, наблюдатель, находящийся в движущейся по окружности системе отсчета, будет испытывать центробежную силу, равную mv2/r. Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим:
Согласно второму закону механики Ньютона, отношение между силой и ускорением в этом случае F = ma. Подставив в это уравнение формулу ускорения для тела, движущегося по окружности, получим: На ЕГЭ встречается в номерах 1-7, 27-29. Примерно половина экзамена! Неудивительно, ведь механика в физике включает понятия скорости, ускорения, силы, массы, энергии, колебаний, волн. Хотите полностью освоить тему? Подумайте о курсах подготовки к ЕГЭ. Там дают много полезного материала, он пригодится на итоговой аттестации, для учебы в университете. В статье изучим основы механики в физике, рассмотрим главные формулы для ЕГЭ.
На ЕГЭ встречается в номерах 1-7, 27-29. Примерно половина экзамена! Неудивительно, ведь механика в физике включает понятия скорости, ускорения, силы, массы, энергии, колебаний, волн. Хотите полностью освоить тему? Подумайте о курсах подготовки к ЕГЭ. Там дают много полезного материала, он пригодится на итоговой аттестации, для учебы в университете. В статье изучим основы механики в физике, рассмотрим главные формулы для ЕГЭ. Путь — участок траектории, пройденный материальной точкой за определенный промежуток времени. Отношение перемещения ко времени называется скоростью: v = s / t. Задачи по механике в физике иногда рассматривают две скорости, связанные с разными системами координат. Применяется закон сложения скоростей v2 = v1 + v. Здесь v2, v1 — скорости точки в двух системах отсчета, v — скорость системы 1, движущейся относительно системы 2.
Путь — участок траектории, пройденный материальной точкой за определенный промежуток времени. Отношение перемещения ко времени называется скоростью: v = s / t. Задачи по механике в физике иногда рассматривают две скорости, связанные с разными системами координат. Применяется закон сложения скоростей v2 = v1 + v. Здесь v2, v1 — скорости точки в двух системах отсчета, v — скорость системы 1, движущейся относительно системы 2.  Ускорение — быстрота изменения направления
Ускорение — быстрота изменения направления Второй закон Ньютона выражает соотношение F = ma. В формуле появляется понятие силы — меры взаимодействия (влияния друг на друга) тел. В механике различают силы трения, упругости, гравитационные силы. В задачах иногда встречается принцип суперпозиции: если на тело действует сразу несколько сил, их складывают, представив в виде одной, называемой равнодействующей. С силой связан третий закон Ньютона: для каждого действия есть противодействие, равное по модулю, противоположное по направлению. Запишем в виде F1 = -F2 или m1a1 = -m2a2. Еще несколько важных сил:
Второй закон Ньютона выражает соотношение F = ma. В формуле появляется понятие силы — меры взаимодействия (влияния друг на друга) тел. В механике различают силы трения, упругости, гравитационные силы. В задачах иногда встречается принцип суперпозиции: если на тело действует сразу несколько сил, их складывают, представив в виде одной, называемой равнодействующей. С силой связан третий закон Ньютона: для каждого действия есть противодействие, равное по модулю, противоположное по направлению. Запишем в виде F1 = -F2 или m1a1 = -m2a2. Еще несколько важных сил:  Fтр = μN;
Fтр = μN; В номерах 3, 4 изучаемые расстояния намного больше радиуса Земли, ее можно считать материальной точкой.
В номерах 3, 4 изучаемые расстояния намного больше радиуса Земли, ее можно считать материальной точкой. 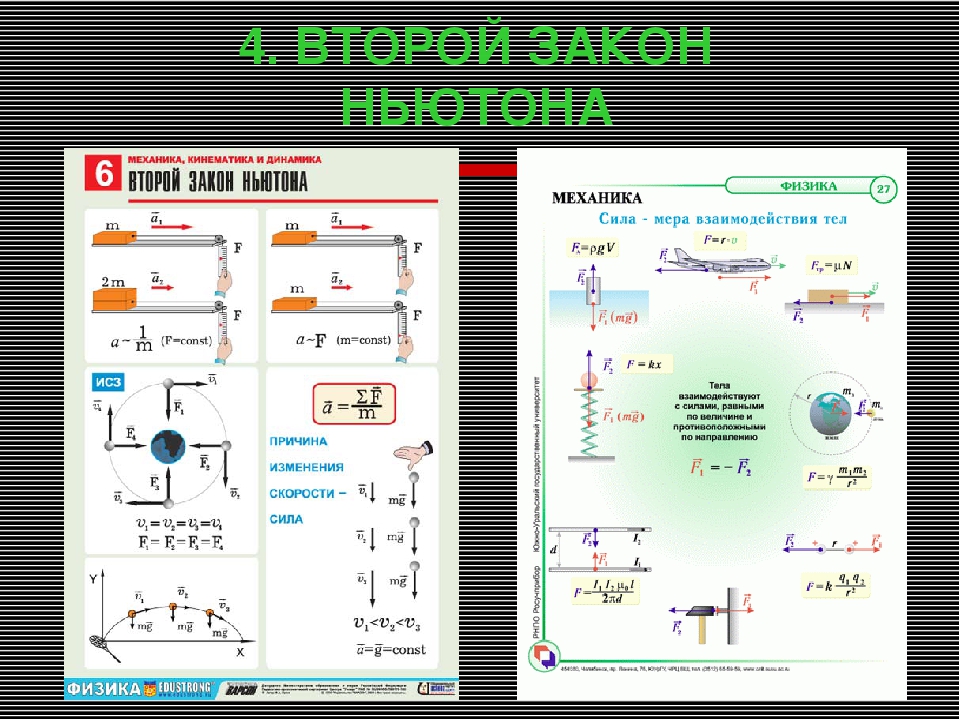 Кроме того, уменьшится потенциальная энергия, общая механическая также станет меньше.
Кроме того, уменьшится потенциальная энергия, общая механическая также станет меньше. 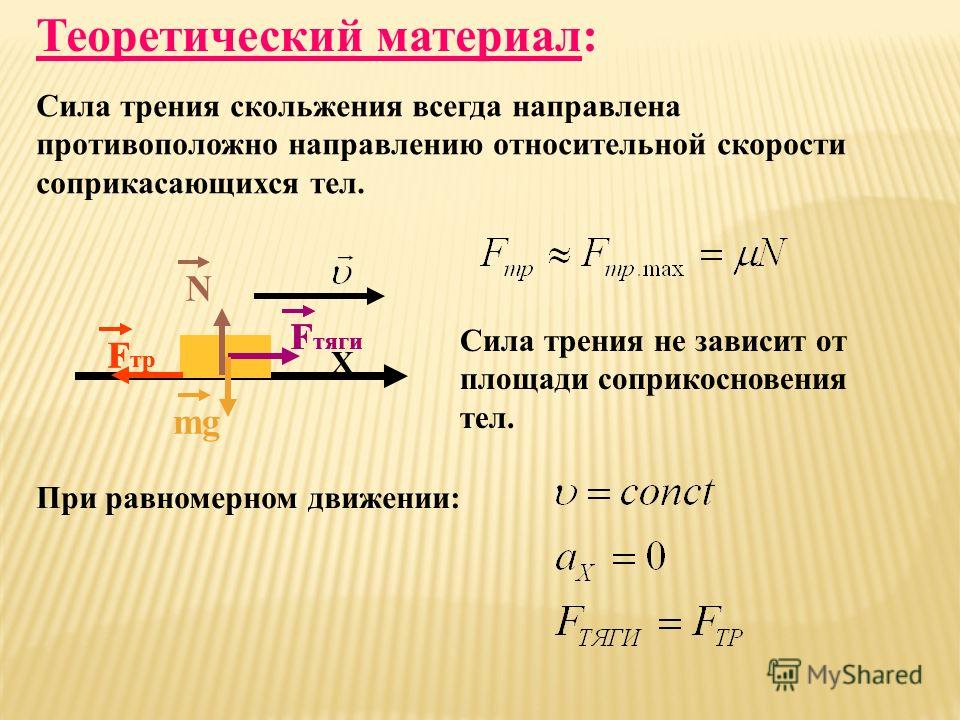
 Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона.На самом деле существуют точные вращательные аналоги как силы, так и массы.
Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона.На самом деле существуют точные вращательные аналоги как силы, так и массы.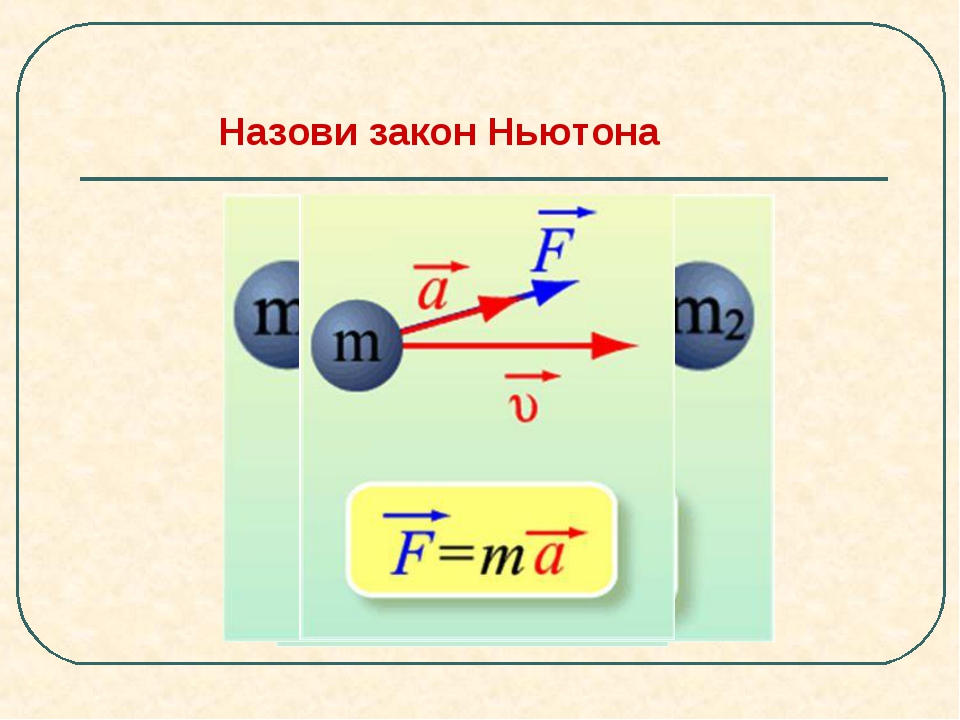 Поскольку сила перпендикулярна r, ускорение [latex] \ text {a} = \ text {F} / \ text {m} [/ latex] получается в направлении F. Мы можем изменить это уравнение так, чтобы F = ma, а затем поищите способы связать это выражение с выражениями для вращательных величин.Заметим, что a = rα, и подставляем это выражение в F = ma, получая:
Поскольку сила перпендикулярна r, ускорение [latex] \ text {a} = \ text {F} / \ text {m} [/ latex] получается в направлении F. Мы можем изменить это уравнение так, чтобы F = ma, а затем поищите способы связать это выражение с выражениями для вращательных величин.Заметим, что a = rα, и подставляем это выражение в F = ma, получая:
 Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес — это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением:
Масса материи, которой обладает объект, не зависит от его местоположения во Вселенной. С другой стороны, вес — это сила тяжести, с которой Земля притягивает к себе объект. Поскольку гравитационные силы меняются в зависимости от местоположения, вес объекта на поверхности Земли отличается от его веса на Луне. Вес, как сила, чаще всего выражается в метрических единицах измерения в ньютонах. Каждое место во Вселенной характеризуется постоянной гравитационного поля, представленной символом g (иногда называемое ускорением свободного падения).Вес (или F grav ) и масса ( м ) связаны уравнением: В форме уравнения можно сказать, что a = F net / m . Чистая сила — это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.
В форме уравнения можно сказать, что a = F net / m . Чистая сила — это векторная сумма всех индивидуальных значений силы. Если величина и направление отдельных сил известны, то эти силы могут быть добавлены как векторы для определения результирующей силы. Следует обратить внимание на векторную природу силы. Направление важно. Поднимающую силу и прижимающую силу можно добавить, присвоив прижимной силе отрицательное значение, а восходящей силе положительное значение. Аналогичным образом, сила, направленная вправо, и сила, направленная влево, могут быть добавлены путем присвоения левой силе отрицательного значения и правой силы положительного значения.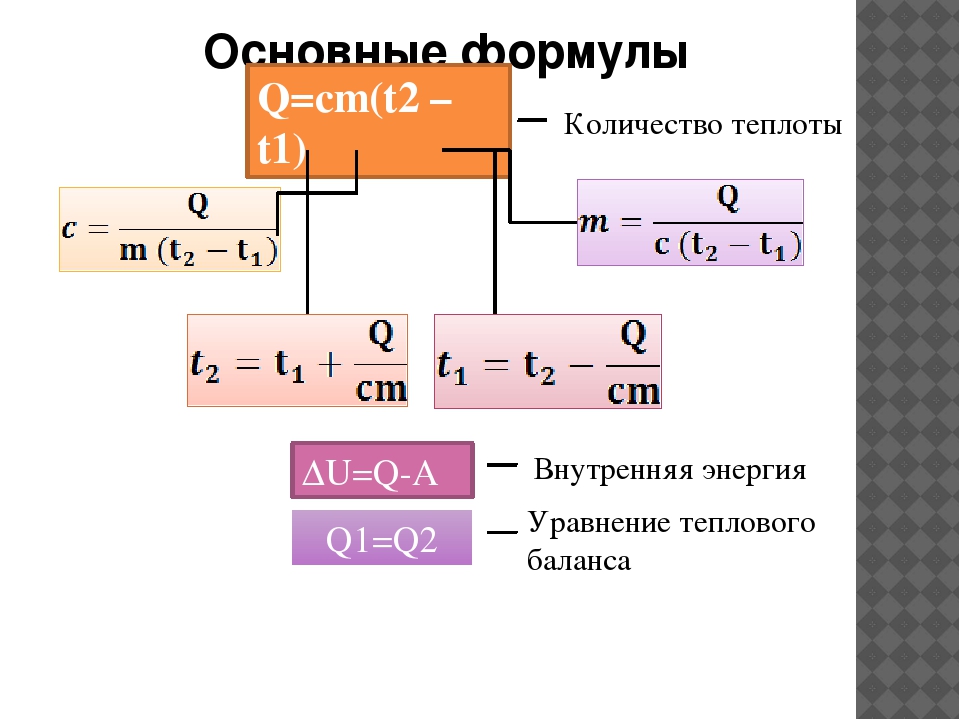 При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.
При использовании уравнения в качестве руководства к размышлениям необходимо учитывать прямые и обратные отношения между ускорением и чистой силой и массой. Двукратное или трёхкратное увеличение чистой силы вызовет такое же изменение ускорения, удвоение или утроение его значения.Увеличение массы в два или три раза вызовет обратное изменение ускорения, уменьшив его значение в два или три раза.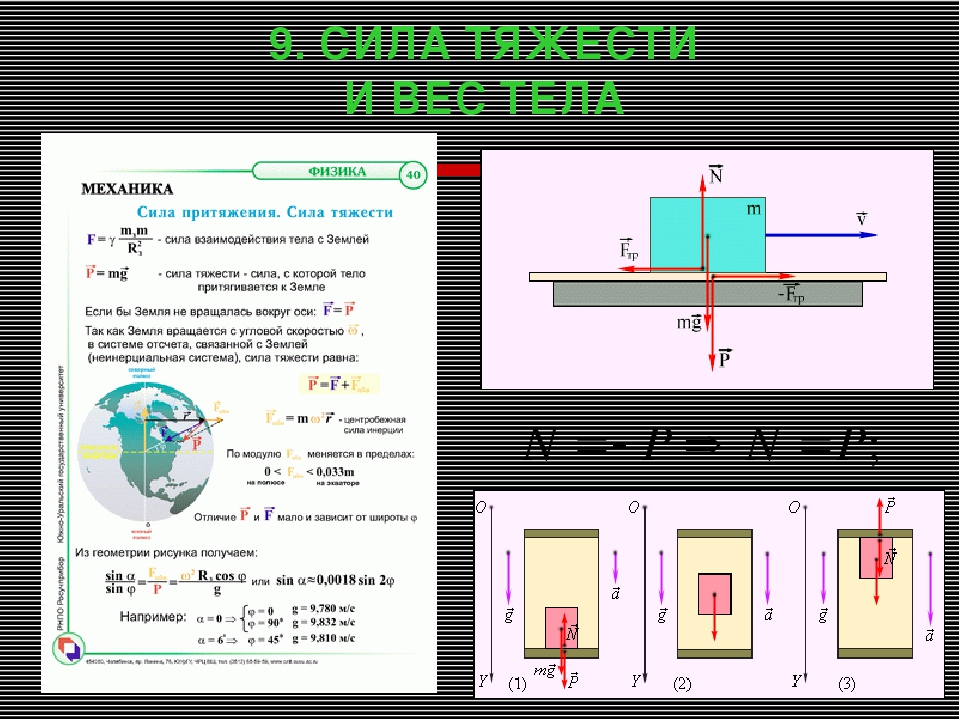 Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.
Если величины всех отдельных сил известны, диаграмму можно использовать для определения чистой силы. И если ускорение и масса известны, то можно рассчитать чистую силу, и диаграмму можно использовать для определения значения единственной неизвестной силы.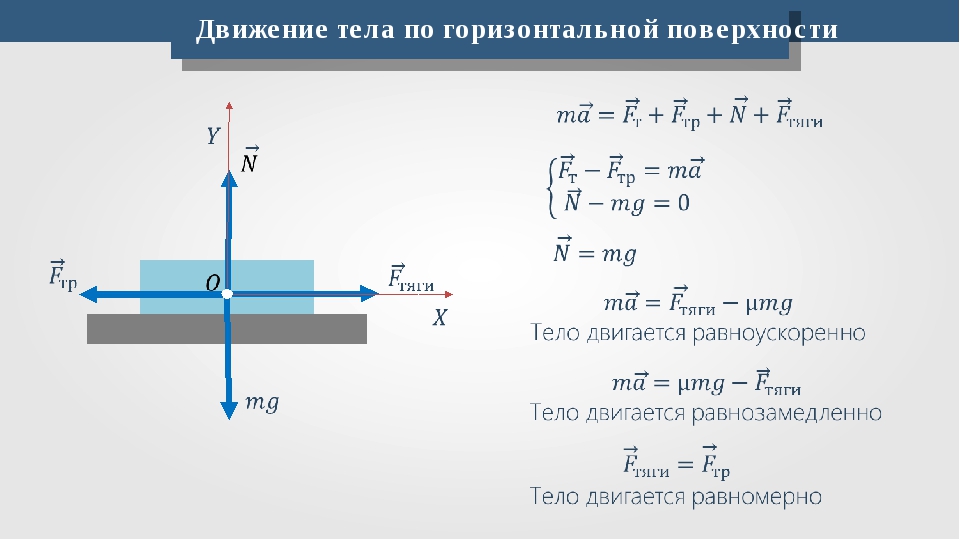 Четыре уравнения перечислены ниже.
Четыре уравнения перечислены ниже.

 Второй закон гласит, что сумма сил (F) на объекте равна его массе (m), умноженной на ускорение объекта (a).
Второй закон гласит, что сумма сил (F) на объекте равна его массе (m), умноженной на ускорение объекта (a).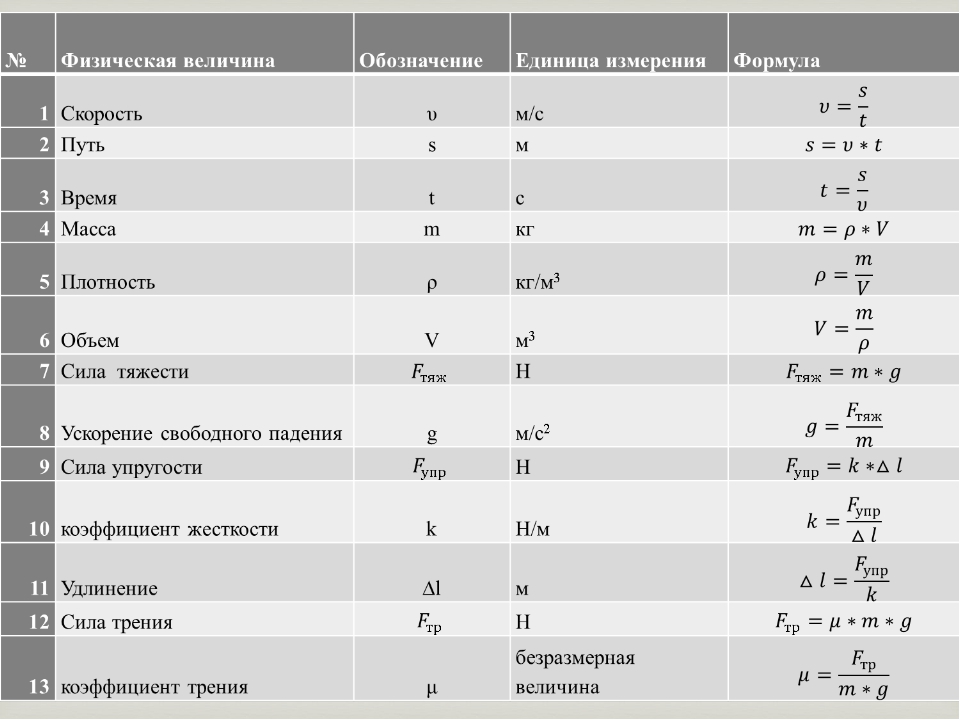 Первые шаги уже были проверены на странице энергии-импульса и здесь не повторяются.Посетите страницу E = pc, чтобы узнать о первых шагах вывода. Более подробную информацию можно найти в статье Key Physics Equations and Experiments . .
Первые шаги уже были проверены на странице энергии-импульса и здесь не повторяются.Посетите страницу E = pc, чтобы узнать о первых шагах вывода. Более подробную информацию можно найти в статье Key Physics Equations and Experiments . . Объекты в состоянии равновесия (состояние, при котором все силы уравновешены) не будут ускоряться.Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.
Объекты в состоянии равновесия (состояние, при котором все силы уравновешены) не будут ускоряться.Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Присутствие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или одновременно скорость и направление.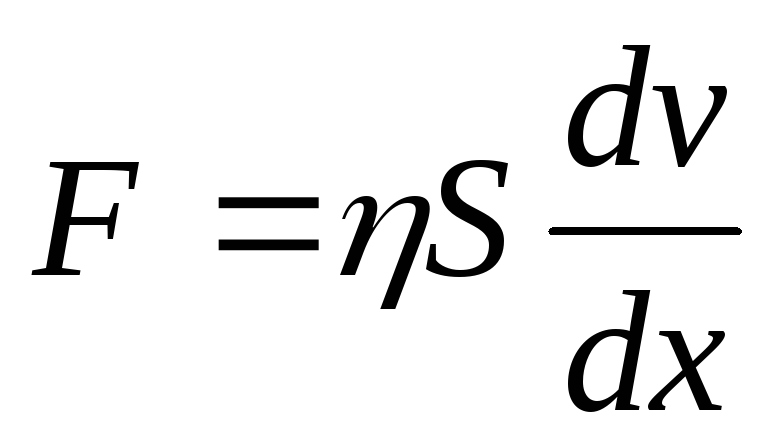
 При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.
При необходимости просмотрите этот принцип, вернувшись к практическим вопросам в Уроке 2.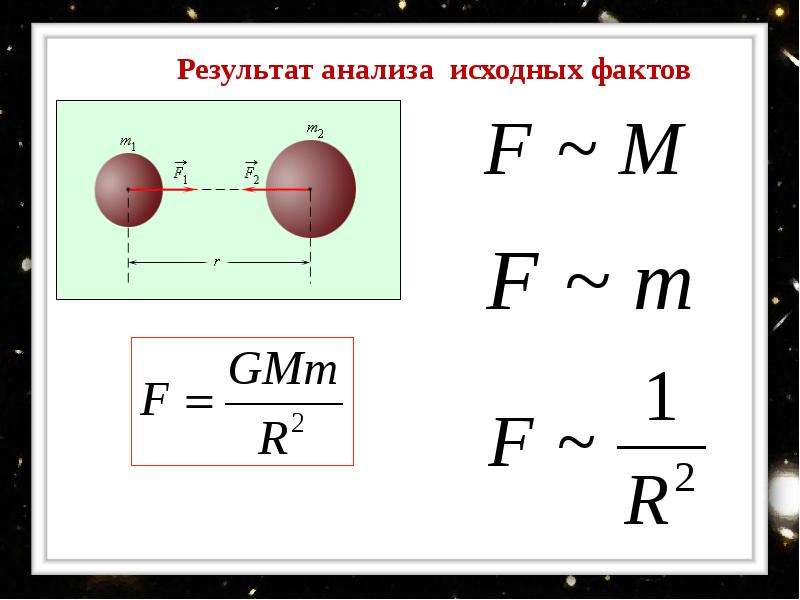 )
)  Ускорение прямо пропорционально чистой силе.
Ускорение прямо пропорционально чистой силе. Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
Удвойте, утроите или учетверите массу, и ускорение составит половину, одну треть или одну четвертую от первоначального значения.
 Проверьте свое понимание
Проверьте свое понимание 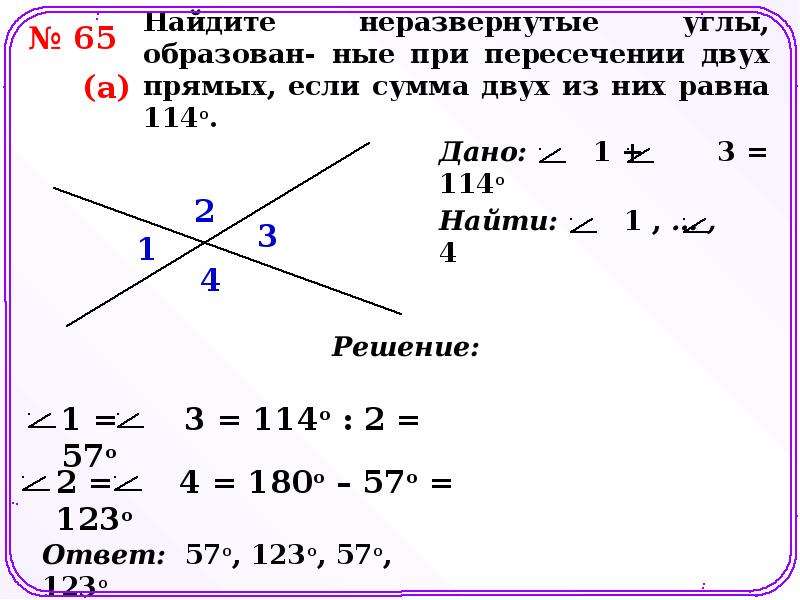 Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.
Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение. Рассмотрим формулировку.
Рассмотрим формулировку.
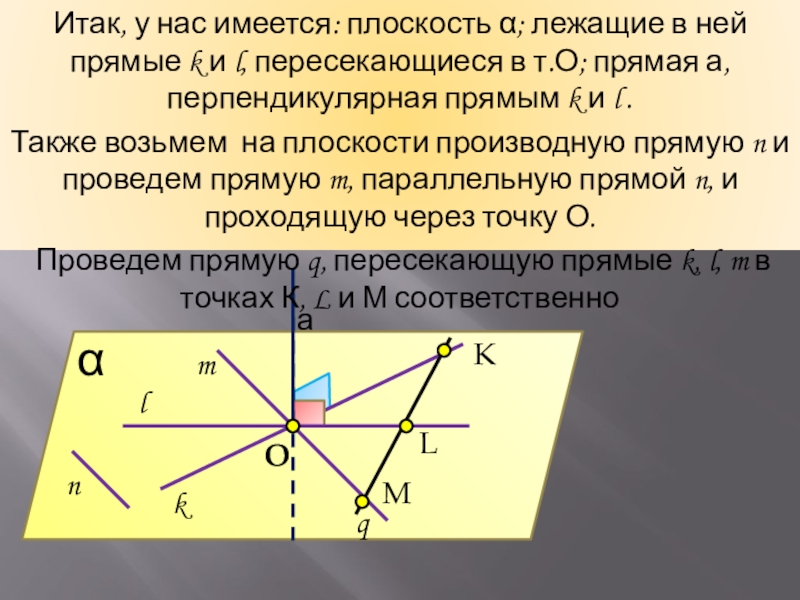
 Для выявления их перпендикулярности найдем скалярное произведение векторов.
Для выявления их перпендикулярности найдем скалярное произведение векторов.


 Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.
Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.


 Выражение будет записано:
Выражение будет записано: Для выявления их перпендикулярности найдем скалярное произведение векторов.
Для выявления их перпендикулярности найдем скалярное произведение векторов.
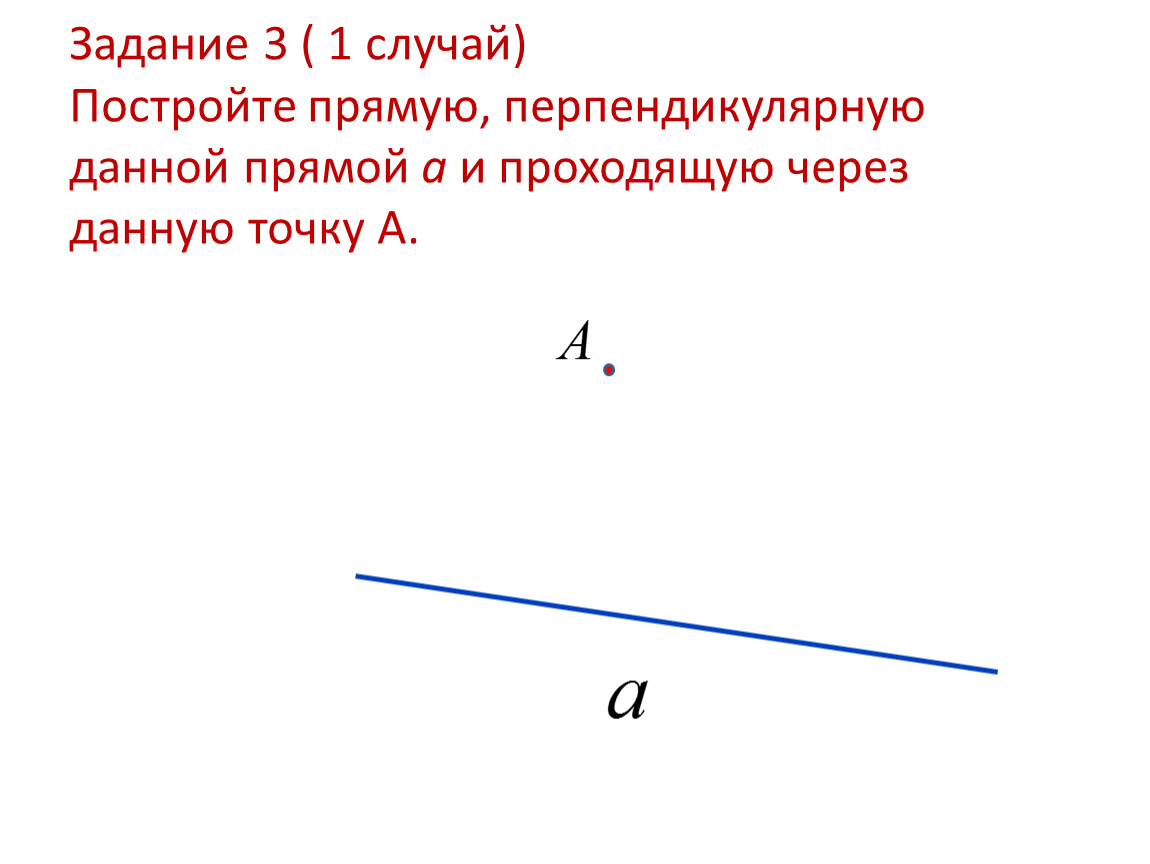
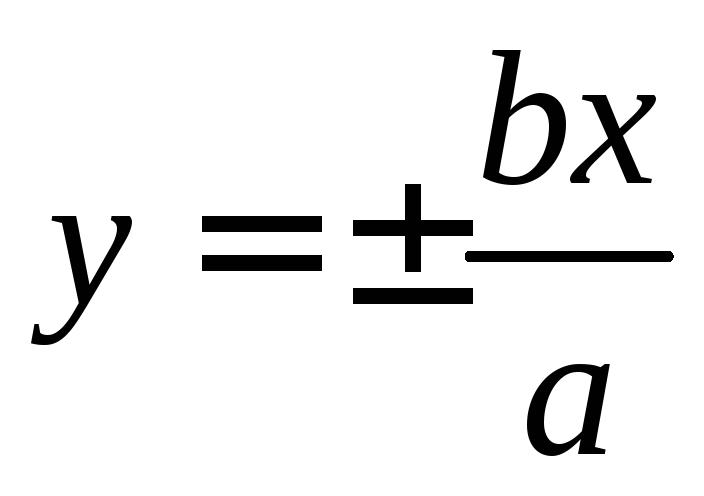

 192.
192. — КиберПедия
— КиберПедия


 Значит, выполняется условие перпендикулярности заданных прямых.
Значит, выполняется условие перпендикулярности заданных прямых. Перепишем уравнение в виде , откуда видны координаты нормального вектора этой прямой: .
Перепишем уравнение в виде , откуда видны координаты нормального вектора этой прямой: .
 Следовательно, заданные прямые не перпендикулярны.
Следовательно, заданные прямые не перпендикулярны.
 Плоскость в пространстве R3. Уравнение плоскости.
Плоскость в пространстве R3. Уравнение плоскости.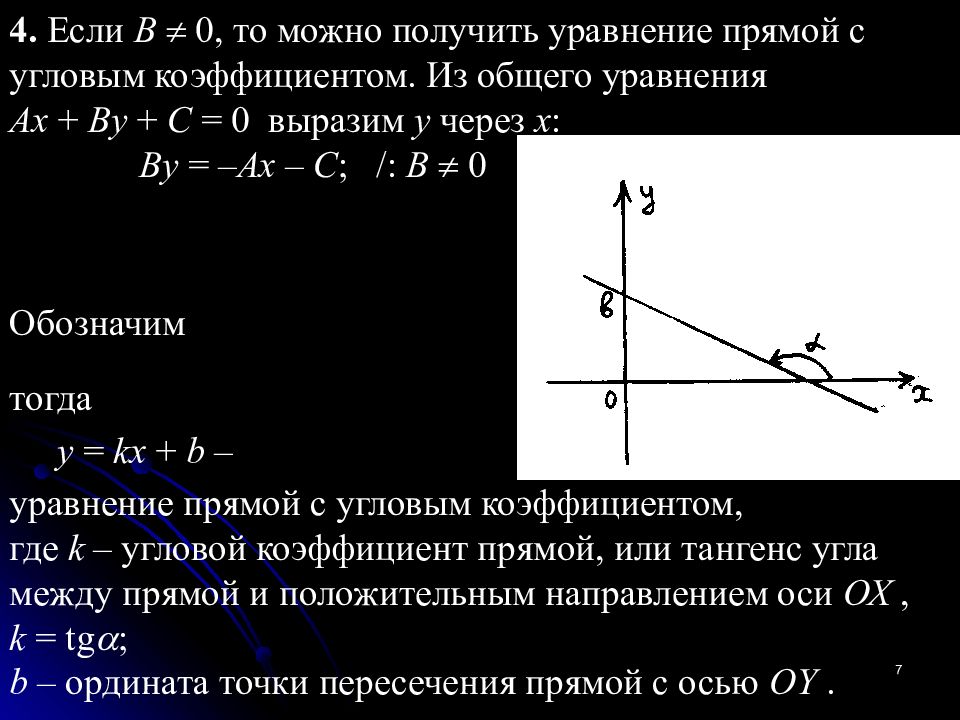 е. уравнение вида
Ax + By + Cz + D = 0. (3.21)
Коэффициенты при х, у и z являются координатами вектора, который перпендикулярен плоскости (рис. 57).
е. уравнение вида
Ax + By + Cz + D = 0. (3.21)
Коэффициенты при х, у и z являются координатами вектора, который перпендикулярен плоскости (рис. 57).
 Ax + By+ Cz + (-Ax0 — By -Cz0)= 0
Ax + By+ Cz + (-Ax0 — By -Cz0)= 0
 Действительно, пусть точка H2 лежит в плоскости и отлична от точки H1. Очевидно, треугольник М2H1H2 является прямоугольным, в нем М1H1 – катет, а M1H2 – гипотенуза, следовательно, . Кстати, отрезок M1H2 называется наклонной, проведенной из точки М1 к плоскости . Итак, перпендикуляр, опущенный из заданной точки на заданную плоскость, всегда меньше наклонной, проведенной из этой же точки к заданной плоскости.
Действительно, пусть точка H2 лежит в плоскости и отлична от точки H1. Очевидно, треугольник М2H1H2 является прямоугольным, в нем М1H1 – катет, а M1H2 – гипотенуза, следовательно, . Кстати, отрезок M1H2 называется наклонной, проведенной из точки М1 к плоскости . Итак, перпендикуляр, опущенный из заданной точки на заданную плоскость, всегда меньше наклонной, проведенной из этой же точки к заданной плоскости.

 Взаимное расположение прямой и плоскости в пространстве R3.
Взаимное расположение прямой и плоскости в пространстве R3. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальныеуравнения системы, находим координаты искомой точки.
Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальныеуравнения системы, находим координаты искомой точки. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.
Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.


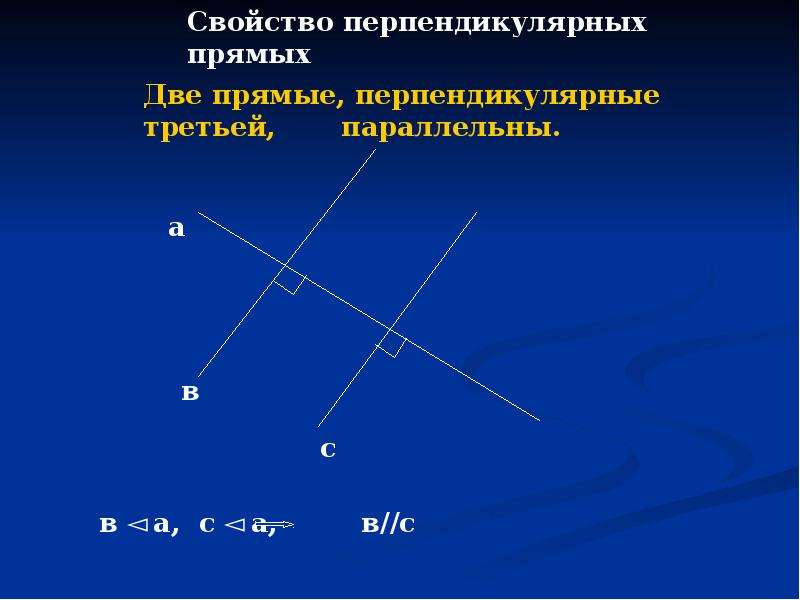 Выражение будет записано:
Выражение будет записано: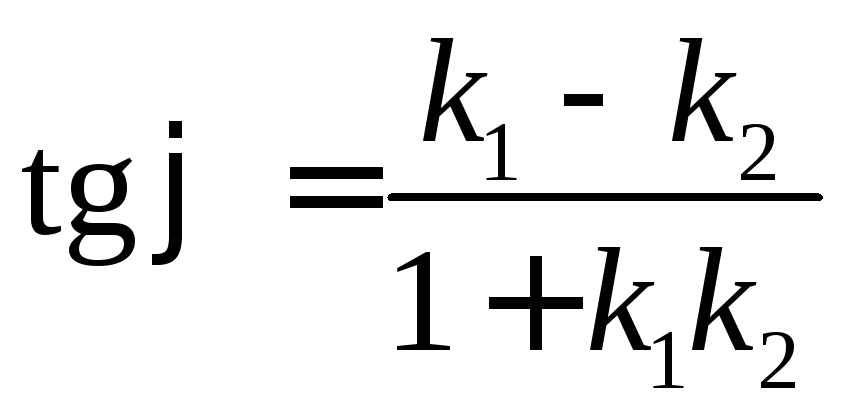 Для выявления их перпендикулярности найдем скалярное произведение векторов.
Для выявления их перпендикулярности найдем скалярное произведение векторов.


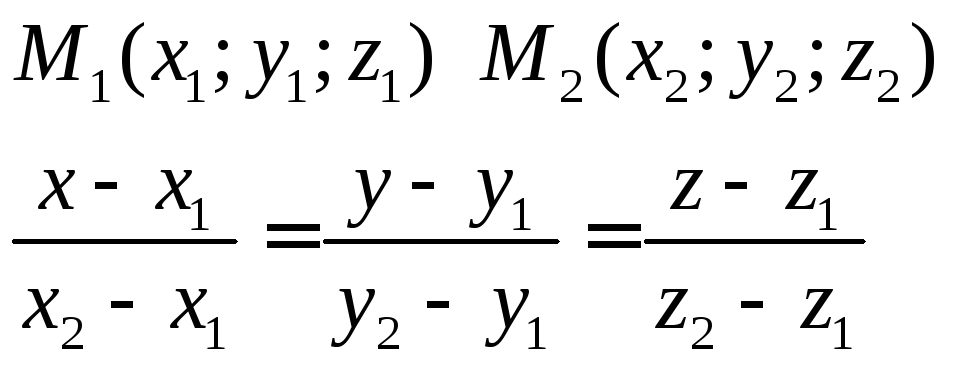

 Именно его авторству принадлежит Теорема Пифагора, которая крайне востребована в решениях задач.
Именно его авторству принадлежит Теорема Пифагора, которая крайне востребована в решениях задач.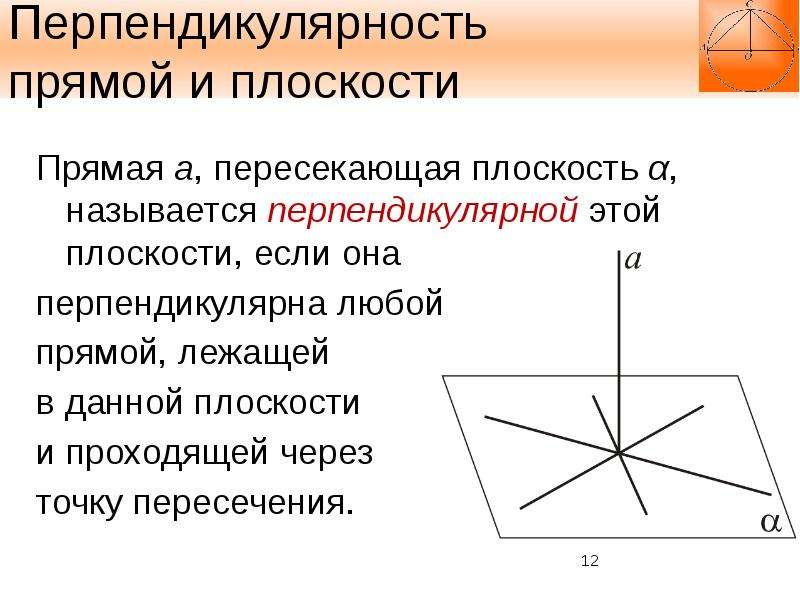


 Чтобы создать две перпендикулярные прямые, нам необходимо совместить одну из двух сторон прямого угла нашего
Чтобы создать две перпендикулярные прямые, нам необходимо совместить одну из двух сторон прямого угла нашего Пересекающиеся прямые имеют только одну общую точку, непересекающиеся прямые — ни одной общей точки, у совпадающих прямых все точки общие.
Пересекающиеся прямые имеют только одну общую точку, непересекающиеся прямые — ни одной общей точки, у совпадающих прямых все точки общие. 3).
3). 1
1 7
7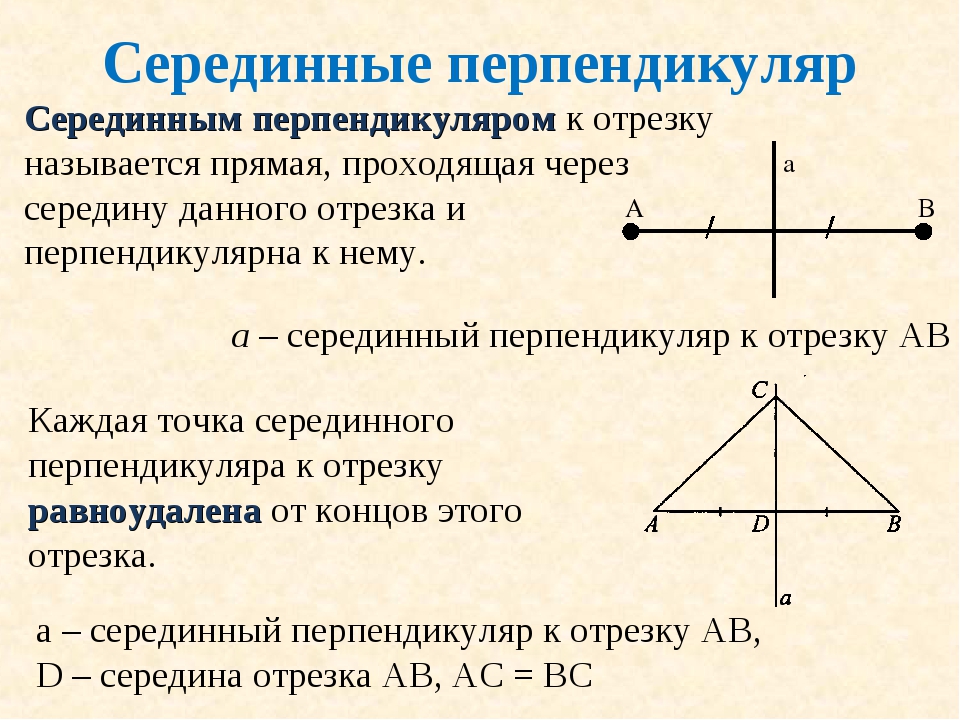
 13, 14, 15.
13, 14, 15.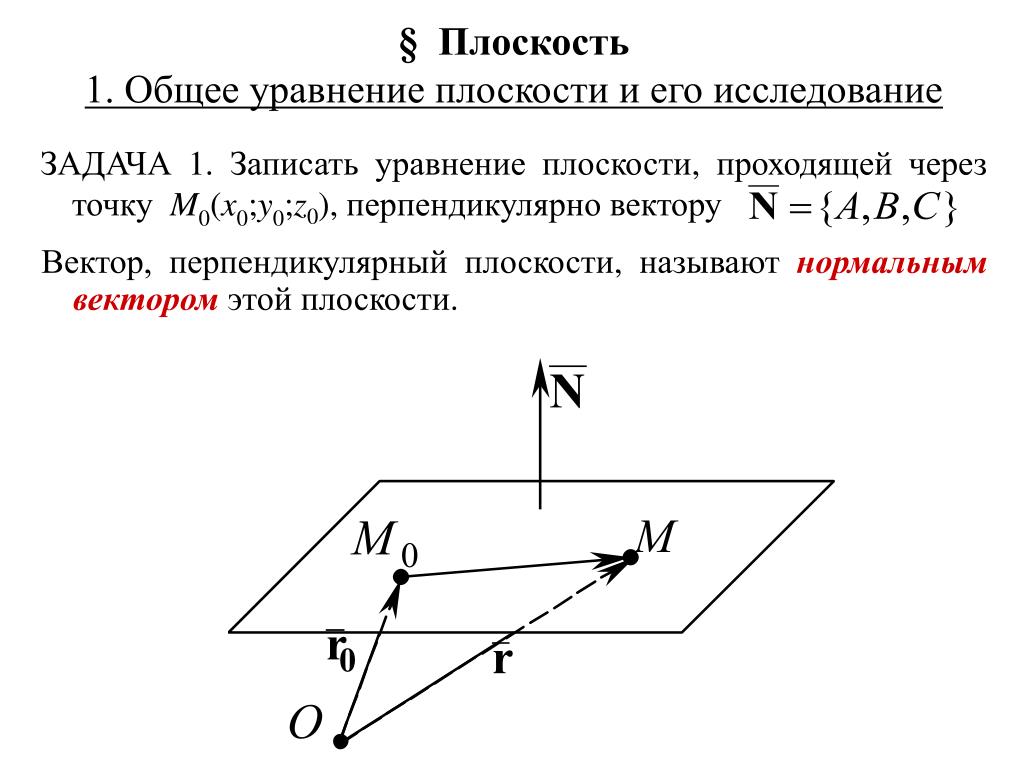

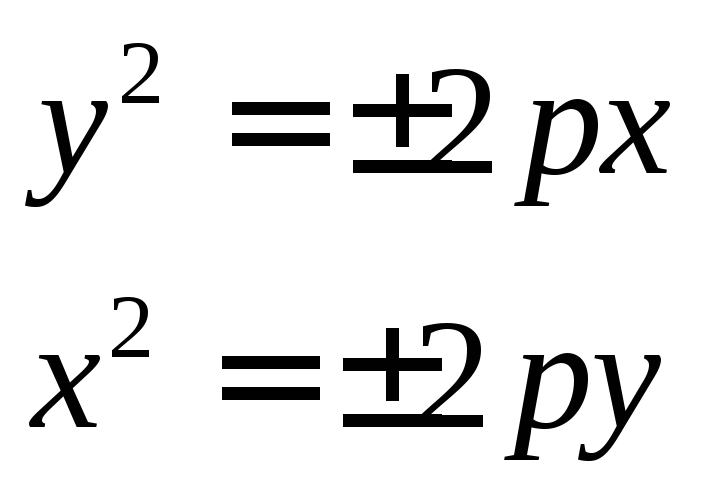
 9)
9) В прямоугольной системе координат Оху возьмем какую либо точку , координаты которой удовлетворяют уравнению (4.11)
В прямоугольной системе координат Оху возьмем какую либо точку , координаты которой удовлетворяют уравнению (4.11)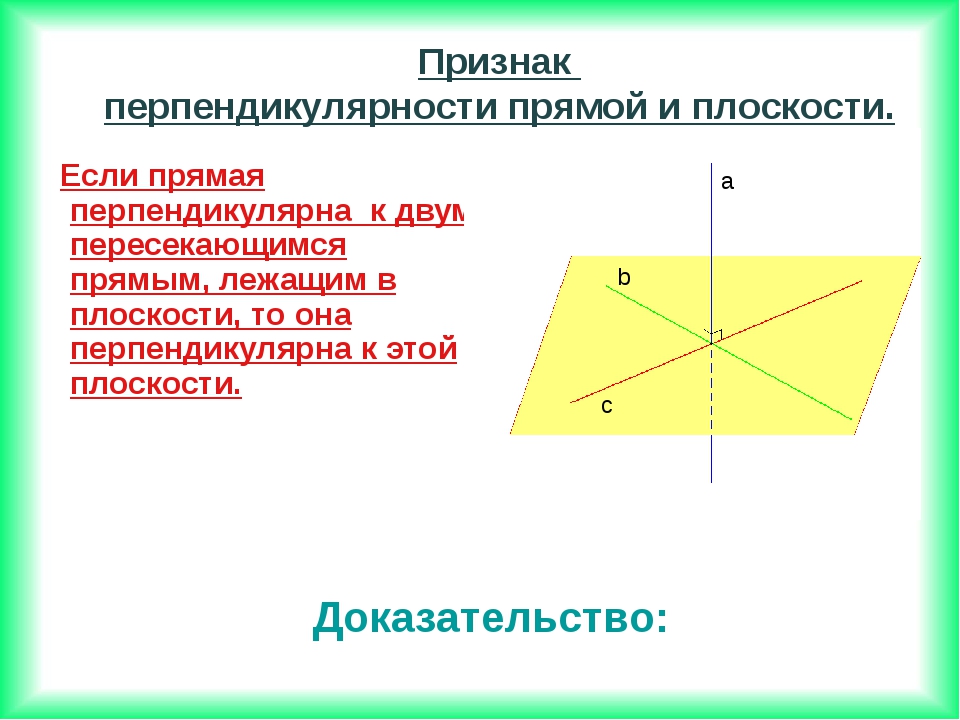 1).
1). 19)
19) Если угол равен 90°, то прямые а и b перпендикулярны.
Если угол равен 90°, то прямые а и b перпендикулярны. Прямая а перпендикулярна плоскости. Докажем, что и прямая а1 перепендикулярна плоскости.
Прямая а перпендикулярна плоскости. Докажем, что и прямая а1 перепендикулярна плоскости. Здесь a = 2, b = -5, c = 2 . Имеем D = b 2 — 4 ac = (-5) 2- 4*2*2 = 9 . Так как D > 0 , то уравнение имеет два корня. Найдем их по формуле (2)
Здесь a = 2, b = -5, c = 2 . Имеем D = b 2 — 4 ac = (-5) 2- 4*2*2 = 9 . Так как D > 0 , то уравнение имеет два корня. Найдем их по формуле (2) Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.

 Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .
Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения . Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число.
Такая ситуация возникает, когда в формуле под корнем
оказывается отрицательное число. Приступим!
Содержание статьи:
Приступим!
Содержание статьи: Всё правильно, так и есть, но…
Всё правильно, так и есть, но… Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.
Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть
статью у Инны Фельдман.


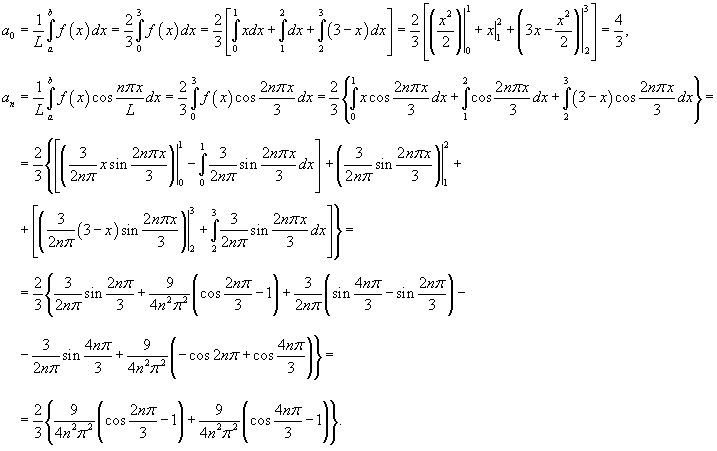

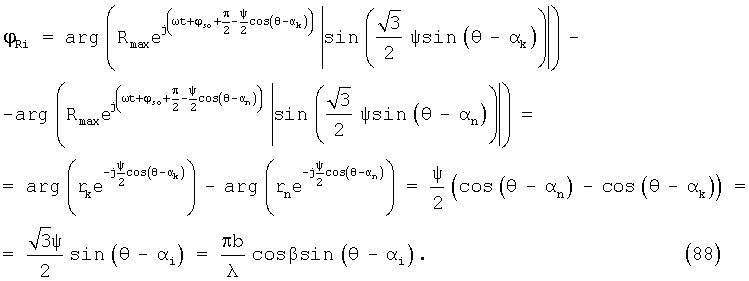
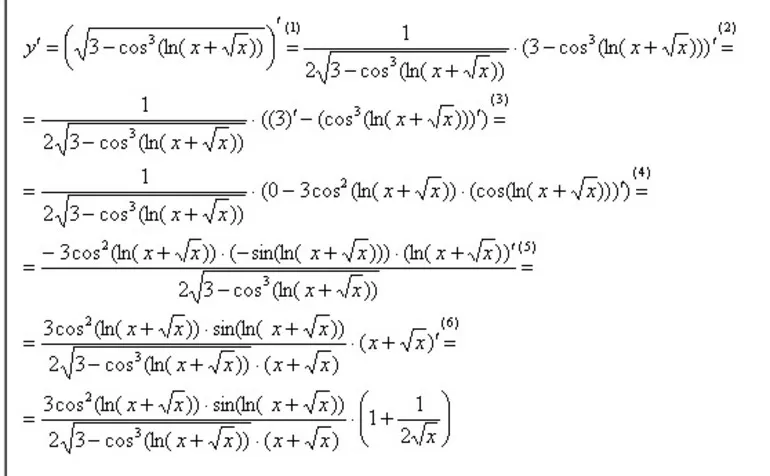 ..»)
..»)
 По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:
По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду: Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !
Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !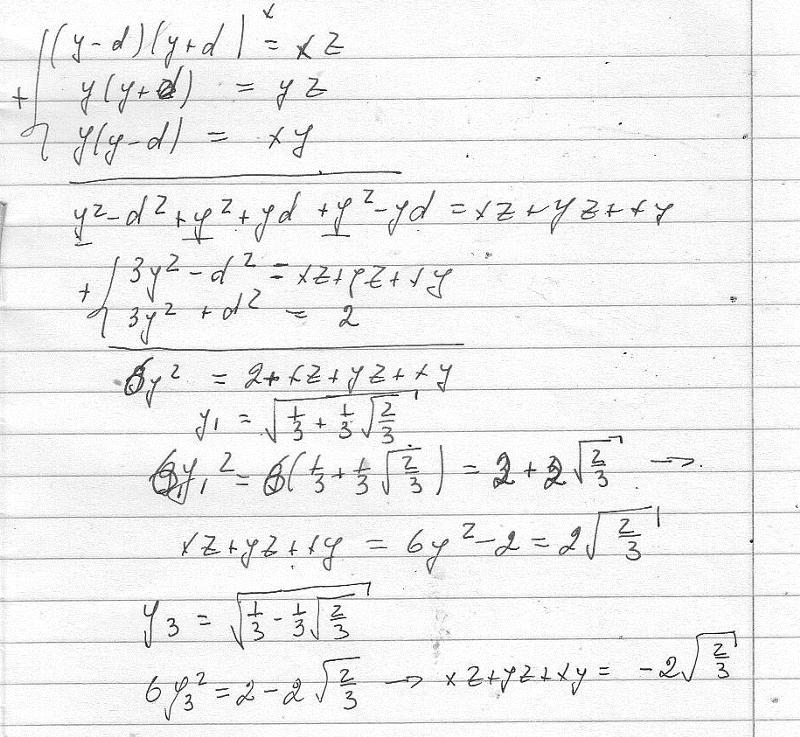 Этот злой пример с кучей минусов решится запросто и без ошибок!
Этот злой пример с кучей минусов решится запросто и без ошибок!
 Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:
Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений: Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.
Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.  Вы поняли, что ключевое слово здесь – внимательно?
Вы поняли, что ключевое слово здесь – внимательно? 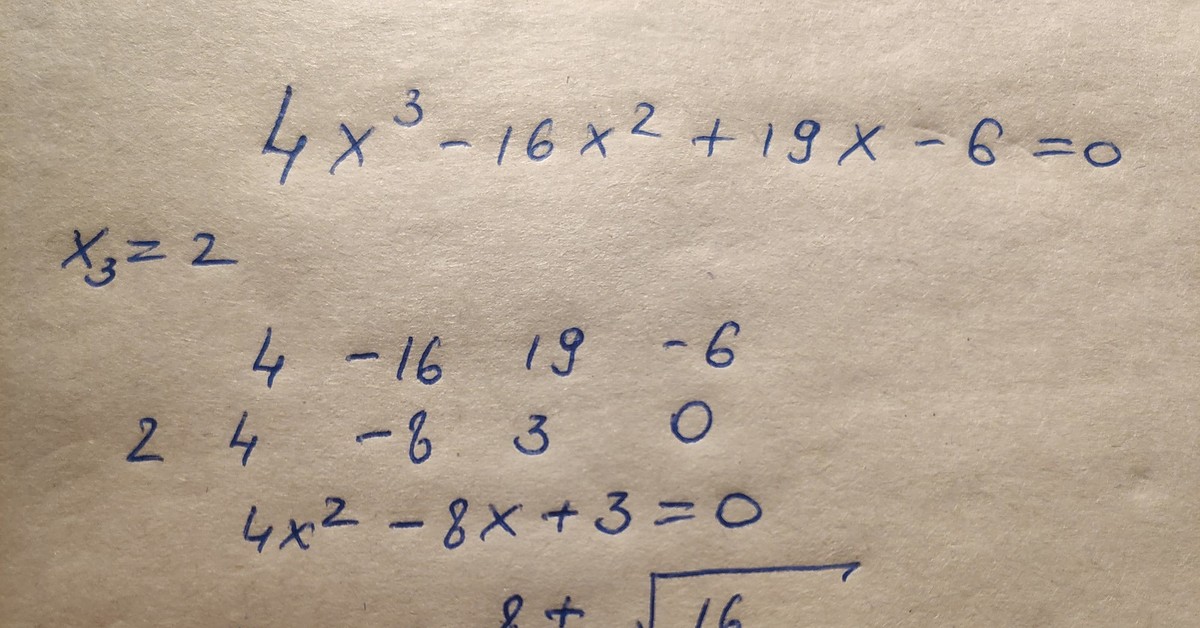 Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1.
Дорешайте самостоятельно.
У вас должны получиться корни 2 и -1. Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…
Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…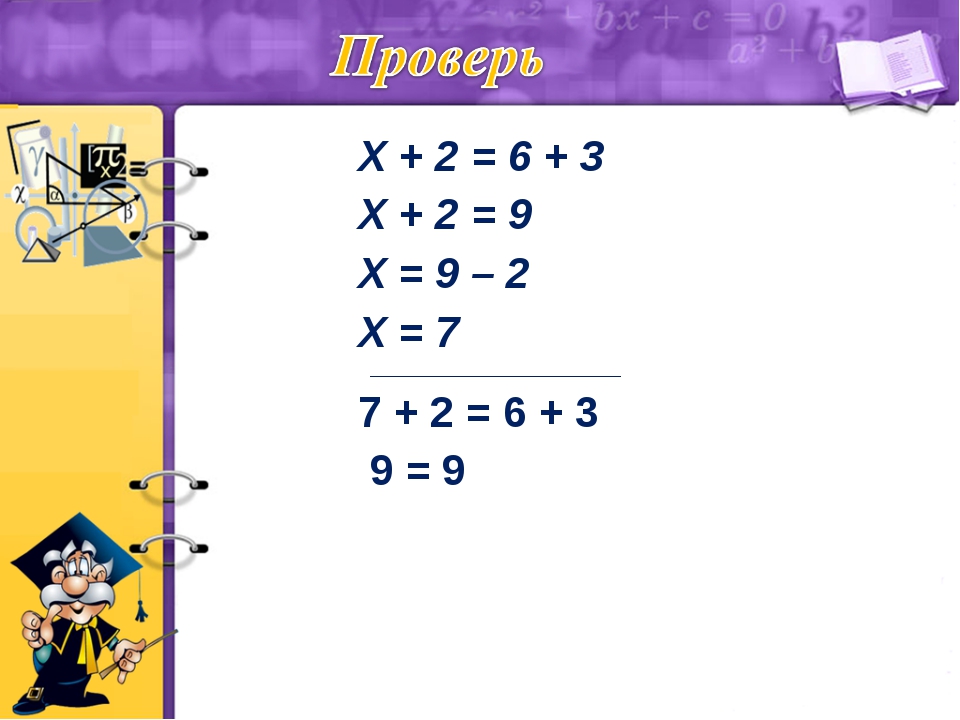 Делайте это!
Делайте это!  Они представлены в таблице ниже.
Они представлены в таблице ниже. Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими:
Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими: Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.
Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу. В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.
В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.

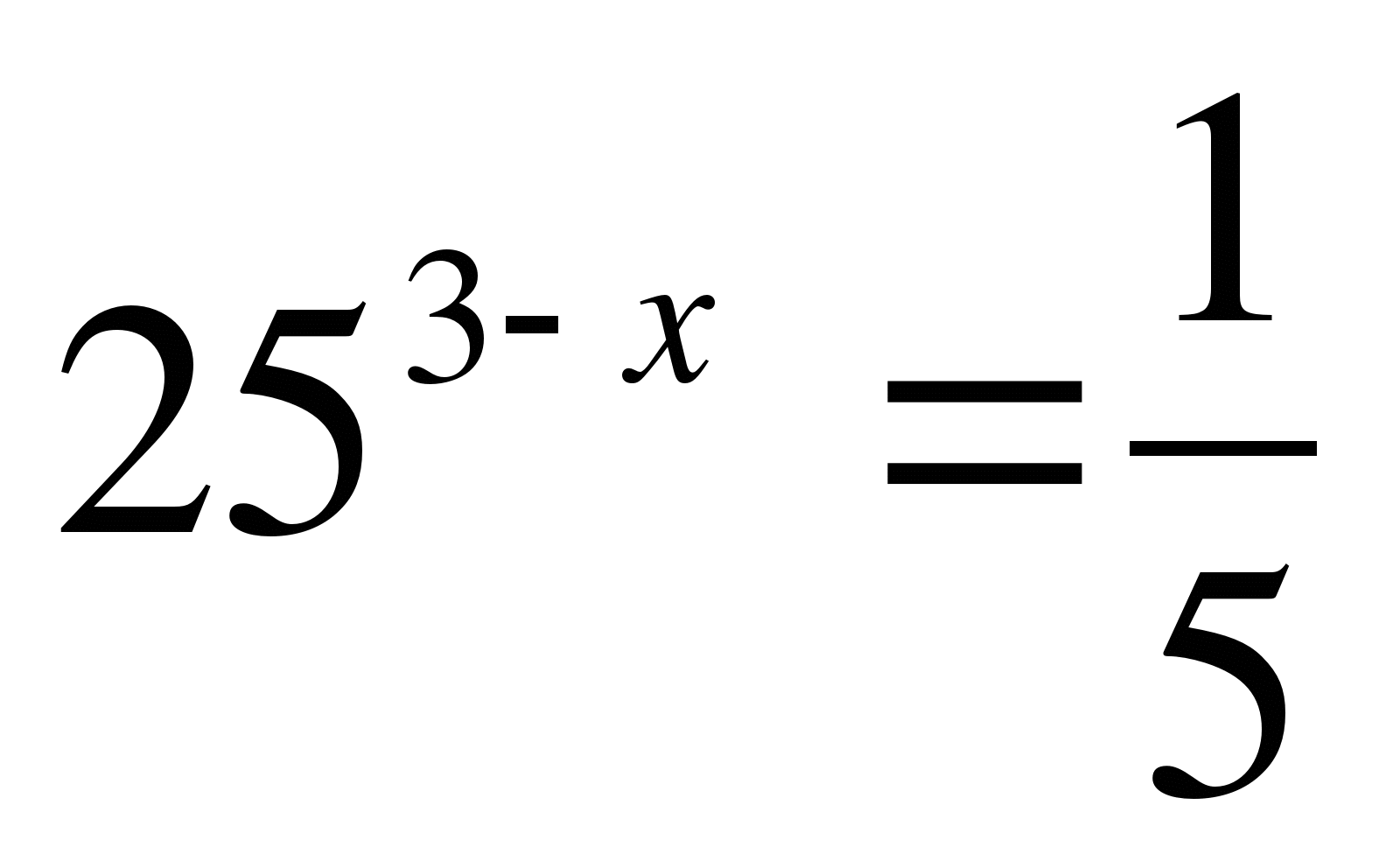
 К числу таких заданий можно отнести задание С3 – «Цепочка органических веществ», С2 – «Реакции между неорганическими веществами и их растворами».
К числу таких заданий можно отнести задание С3 – «Цепочка органических веществ», С2 – «Реакции между неорганическими веществами и их растворами». Атом углерода карбонильной группы (СО) отдаст 2 электрона атому кислорода, но частично компенсирует недостачу, приняв 1 электрон от атома водорода. Следовательно, его степень окисления будет равна +1:
Атом углерода карбонильной группы (СО) отдаст 2 электрона атому кислорода, но частично компенсирует недостачу, приняв 1 электрон от атома водорода. Следовательно, его степень окисления будет равна +1: Свойства перманганата натрия должны быть аналогичны свойствам перманганта калия, который в зависимости от кислотности среды способен давать различные продукты:
Свойства перманганата натрия должны быть аналогичны свойствам перманганта калия, который в зависимости от кислотности среды способен давать различные продукты: Такими свойствами могут быть некоторые индивидуальный свойства простых веществ и их соединений, например, реакция лития или магния с азотом:
Такими свойствами могут быть некоторые индивидуальный свойства простых веществ и их соединений, например, реакция лития или магния с азотом: Так растворы амфотерных гидроксидов в избытке щелочи обладают всеми свойствами щелочей. Они способны вступать в реакции с кислотами и кислотными оксидами:
Так растворы амфотерных гидроксидов в избытке щелочи обладают всеми свойствами щелочей. Они способны вступать в реакции с кислотами и кислотными оксидами: В результате чего могут протекать обменные реакции в водных растворах:
В результате чего могут протекать обменные реакции в водных растворах: Можно использовать концентрированную фосфорную кислоту:
Можно использовать концентрированную фосфорную кислоту:
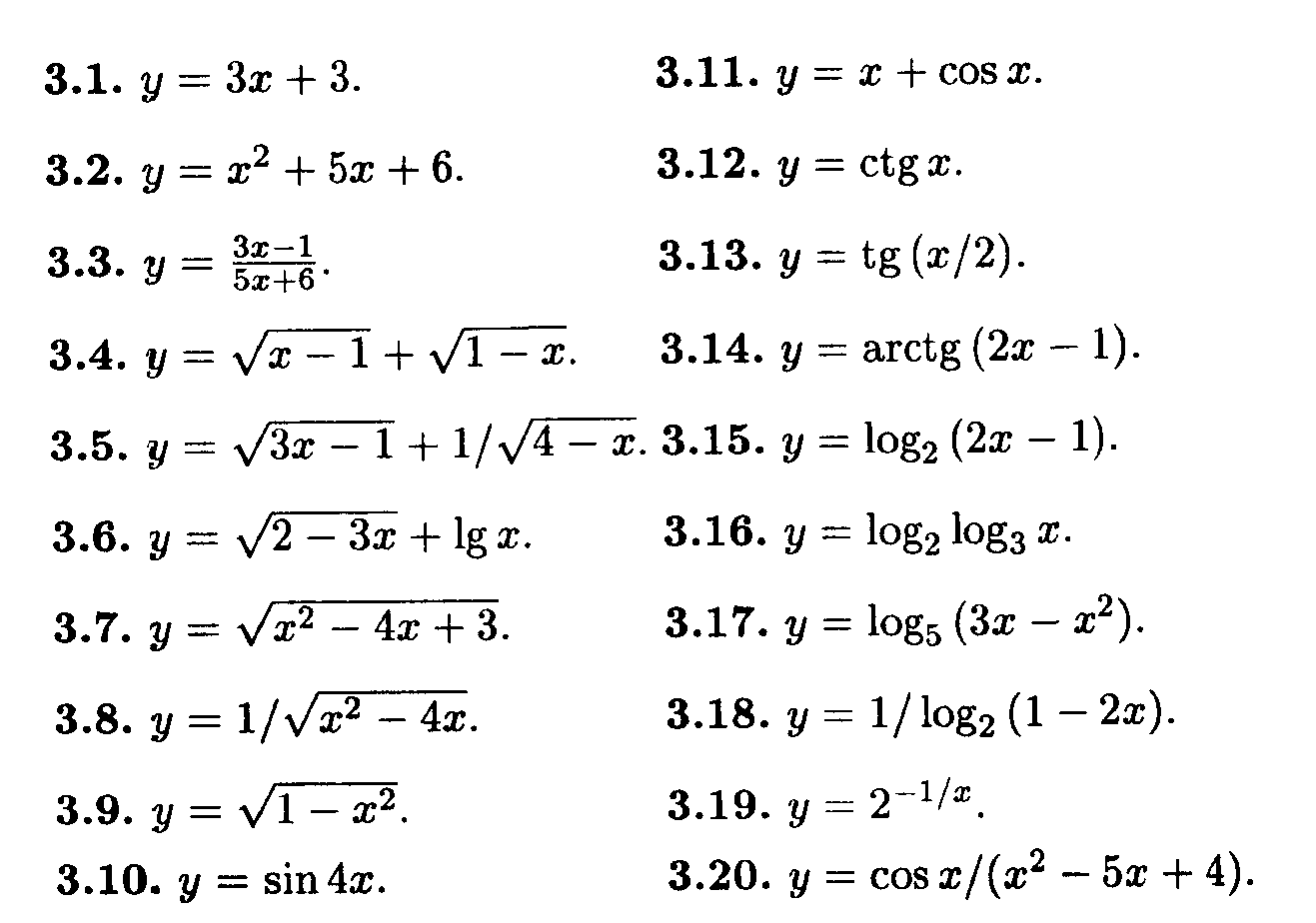 ) ® С6Н5-СНОН-СН3 + KBr
) ® С6Н5-СНОН-СН3 + KBr Но и у них даже, казалось бы, самые легкие задания могут вызвать затруднения. На каких моментах часто спотыкаются участники экзамена и как можно избежать ошибок, рассказывает Наталия Покровская, эксперт Московского центра качества образования, ответственный секретарь предметной комиссии ЕГЭ по химии.
Но и у них даже, казалось бы, самые легкие задания могут вызвать затруднения. На каких моментах часто спотыкаются участники экзамена и как можно избежать ошибок, рассказывает Наталия Покровская, эксперт Московского центра качества образования, ответственный секретарь предметной комиссии ЕГЭ по химии.
