Вычисление разницы во времени — Служба поддержки Майкрософт
Excel
Формулы и функции
Другие функции
Другие функции
Вычисление разницы во времени
Excel для Microsoft 365 Excel 2021 Excel 2019 Excel 2016 Excel 2013 Excel 2010 Excel 2007 Еще…Меньше
Предположим, что вы хотите узнать, сколько времени сотруднику требуется на завершение работы в строке сборки или заказ на питание для обработки в пиковые часы. Существует несколько способов вычисления разницы между двумя значениями времени.
Существует два подхода, которые можно использовать для того, чтобы представить результаты в стандартном формате времени (часы: минуты : секунды). Для поиска разницы между значениями времени используется оператор вычитания(-),а затем сделайте следующее:
Применив к ячейке пользовательский код формата, с помощью следующих элементов:
Выделите ячейку.
На вкладке Главная в группе Число щелкните стрелку рядом с полем Общие и выберите другие числовые форматы.
В диалоговом окне Формат ячеек в списке Категория выберите настраиваемый формат, а затем в поле Тип выберите пользовательский формат.
Для форматирование времени используйте функцию ТЕКСТ. При использовании кодов формата времени количество часов не превышает 24, минуты никогда не превышают 60, а секунды никогда не превышают 60.
Пример таблицы 1.
 Представляем результат в стандартном формате времени
Представляем результат в стандартном формате времени
Скопируйте таблицу ниже на пустой лист и при необходимости измените ее.
|
A |
B |
|
|---|---|---|
|
1 |
Время начала |
Время окончания |
|
2 |
09. |
09.06.2007, 15:30 |
|
3 |
Формула |
Описание (результат) |
|
4 |
=B2-A2 |
Часы между двумя разами (4). |
|
5 |
=B2-A2 |
Часы и минуты между двумя разами (4:55). К ячейке необходимо вручную применить пользовательский формат «ч:мм». |
|
6 |
=B2-A2 |
Часы, минуты и секунды между двумя временами (4:55:00). К ячейке необходимо вручную применить пользовательский формат «ч:мм:сс». |
|
7 |
=ТЕКСТ(B2-A2;»h») |
Часы между двумя ячейками с форматом «ч» с помощью функции ТЕКСТ (4). |
|
8 |
=ТЕКСТ(B2-A2;»ч:мм») |
Часы и минуты между двумя ячейками с форматом «ч:мм» с помощью функции ТЕКСТ (4:55). |
|
9 |
=ТЕКСТ(B2-A2;»ч:мм:сс») |
Часы, минуты и секунды между двумя ячейками с форматом «ч:мм:сс» с помощью функции ТЕКСТ (4:55:00). |
Примечание: Если использовать оба формата с функцией ТЕКСТ и применить к ячейке числовом формате, функция ТЕКСТ имеет приоритет над форматированием ячейки.
Дополнительные сведения об использовании этих функций см. в функциях ТЕКСТ и Отображение чисел в виде дат и времени.
Пример таблицы 2. Представляем результат на основе одной единицы времени
Для этого нужно использовать функцию INT или функции ЧАС,МИНУТЫ и СЕКУНДЫ,как показано в примере ниже.
Скопируйте таблицу ниже на пустой лист и при необходимости измените ее.
|
A |
B |
|
|---|---|---|
|
1 |
Время начала |
Время окончания |
|
2 |
09. |
09.06.2007, 15:30 |
|
3 |
Формула |
Описание (результат) |
|
4 |
=INT((B2-A2)*24) |
Общее количество часов между двумя временами (4) |
|
5 |
=(B2-A2)*1440 |
Общее количество минут между двумя числами времени (295) |
|
6 |
=(B2-A2)*86400 |
Общее количество секунд между двумя числами времени (17700) |
|
7 |
=ЧАС(B2-A2) |
Разница в единицах времени между двумя значениями времени. |
|
8 |
=МИНУТЫ(B2-A2) |
Разница в единицах времени между двумя значениями времени. Это значение не может превышать 60 (55). |
|
9 |
=СЕКУНДЫ(B2-A2) |
Разница в единицах секунды между двумя значениями времени. Это значение не может превышать 60 (0). |
Дополнительные сведения об использовании этих функций см. в функциях INT,HOUR,MINUTEи SECOND.
в функциях INT,HOUR,MINUTEи SECOND.
Как правильно посчитать часы на работе
Здоровье › Больничный › Как посчитать норму часов с учетом больничного листа
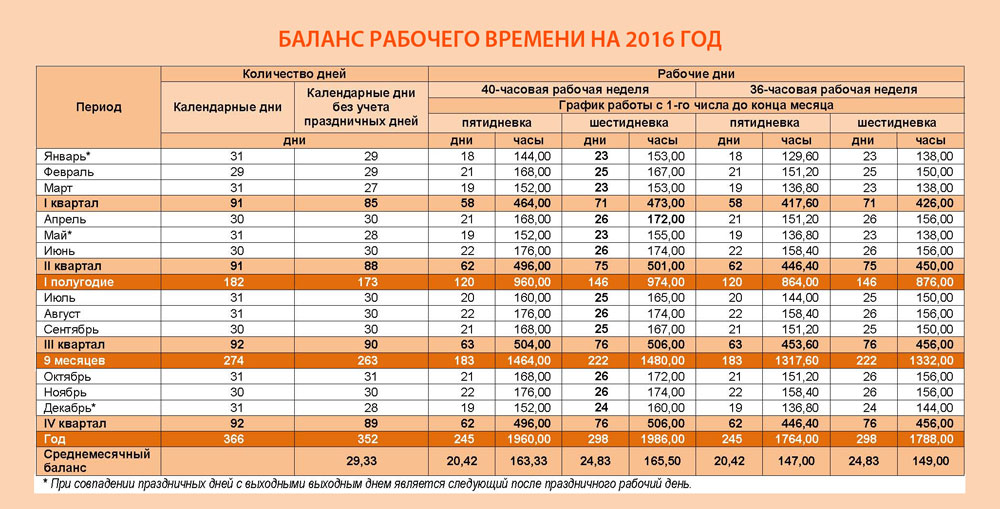
Если требуется рассчитать рабочее время на год, умножать нужно на количество рабочих дней не в месяце, а в году. Не забудьте учесть сокращение на час в предпраздничные дни. Для 2020 года при пятидневной рабочей неделе формула будет выглядеть так: (40 часов / 5 дней × 248 дней) — 5 часов = 1 979 часов.
Таким образом, норма рабочего времени конкретного месяца рассчитывается следующим образом: продолжительность рабочей недели (40, 39, 36, 30, 24 и т.д. часов) делится на 5, умножается на количество рабочих дней по календарю пятидневной рабочей недели конкретного месяца и из полученного количества часов вычитается количество часов в данном месяце, на которое производится сокращение рабочего времени накануне нерабочих праздничных дней.
- Необходимо учитывать количество рабочих дней в году при расчете рабочего времени на год
- Сокращение на час в предпраздничные дни должно быть учтено
- Для рассчета нормы рабочего времени нужно делить продолжительность рабочей недели на 5 и умножать на количество рабочих дней в месяце
- Норма рабочего времени одинакова для пятидневной рабочей недели и режима «сутки через трое»
- Счетчик часов в табеле рабочего времени включает число отработанных дней и часов за полмесяца и итоговое число дней и часов за месяц
- Расчет сумм за сверхурочную работу производится путем распределения количества переработанных часов на количество смен
- Исторически 8-часовой рабочий день был введен Робертом Оуэном
- Нормальная продолжительность рабочего времени — 40 часов в неделю, но может быть сокращена для отдельных категорий работников
- Норма рабочего времени — это количество времени, которое работник должен отработать за определенный период времени, исчисляемый исходя из продолжительности рабочего времени в неделю.

- Как посчитать свое рабочее время
- Как правильно рассчитать норму часов
- Как посчитать часы по табелю
- Как считать переработки
- Почему 8 часовой рабочий день
- Как считается рабочий день
- Какие часы считаются рабочими
- Что входит в норму рабочего времени
- Сколько часов нужно отработать на ставку
- Чему равен 1 человеко час
- Как рассчитать человеко часов пример
- Как посчитать трудозатраты в человеко часах
- Как считается переработка по часам
- Что считается переработкой часов
- Как правильно оплачивать переработку
- Как учитывается обед в рабочее время
- Сколько времени длится рабочий день
- Сколько должны платить за 12 часовой рабочий день
- Как рассчитать норму рабочего времени при суммированном учете
- Как рассчитать количество часов на ставку
- Как считать часы в графике
- Что такое учет рабочего времени
- Как считать минуты в табеле
- Сколько часов переработки в месяц
- Сколько часов переработки допустимо в неделю
- Сколько часов работник должен отработать в месяц
- Как посчитать норму часов на 0 75 ставки
- Что такое 40 часовая рабочая неделя
- Что такое норма часов
- Чем отличается график от табеля учета рабочего времени
- Можно ли в табеле ставить минуты
- Можно ли в табеле ставить 12 часов
- Сколько норма часов в день
- Как считать отпуск в норму часов при сменном графике
- Как рассчитать норму часов с отпуском
Как посчитать свое рабочее время
Иными словами, норма рабочего времени одинаково подсчитывается как для пятидневной рабочей недели с двумя выходными днями, так и для режима «сутки через трое». Так, например, норма рабочего времени при 40-часовой рабочей неделе в марте 2018 года составляла 159 часов (40 / 5 × 20 р. д.
Так, например, норма рабочего времени при 40-часовой рабочей неделе в марте 2018 года составляла 159 часов (40 / 5 × 20 р. д.
Как правильно рассчитать норму часов
Рабочее времяЧтобы рассчитать месячную норму рабочего времени как нормальную, нужно продолжительность рабочей недели (не более 40 часов) разделить на пять и умножить на количество рабочих дней по календарю пятидневной рабочей недели заданного месяца.
Как посчитать часы по табелю
Вот как правильно считать часы в табеле рабочего времени организации:
- в 5-й графе указывают число отработанных дней и часов за каждые полмесяца;
- в 6-й графе — итоговое число дней и часов за месяц.
Как считать переработки
Расчет причитающихся работнику сумм за сверхурочную работу в учетном периоде производится путем распределения количества переработанных часов на количество смен в учетном периоде. После чего первые два часа каждой смены оплачиваются в полуторном размере, а оставшиеся часы каждой смены в двойном размере.
Почему 8 часовой рабочий день
В конце XVIII века, чтобы приносить максимум пользы, заводы должны были работать практически без остановок. Поэтому люди трудились по 10–16 часов в сутки. Но человек по имени Роберт Оуэн начал движение за 8-часовой рабочий день.
Как считается рабочий день
Нормальная продолжительность рабочего времени — это 40 часов в неделю (ст. 91 ТК РФ). В то же время продолжительность рабочего времени по ТК сокращается для отдельных категорий работников (например, для инвалидов I или II группы — до 35 часов в неделю, для «вредников» — до 36 часов в неделю).
Какие часы считаются рабочими
109 ТК РФ). Нормальная продолжительность рабочего времени — это 40 часов в неделю (ст. 91 ТК РФ).
Что входит в норму рабочего времени
Норма рабочего времени — это то количество времени, которое работник должен отработать в течение календарного периода времени (за месяц, квартал, год). Норма рабочего времени за конкретный период исчисляется исходя из продолжительности рабочего времени в неделю.
Сколько часов нужно отработать на ставку
Нормальная продолжительность рабочего времени, согласно трудовому законодательству, составляет 40 часов в неделю и является нормой рабочего времени для всех сотрудников в России, независимо от организационно-правовой формы предприятия, режима рабочего времени, вида трудового договора и иных условий.
Чему равен 1 человеко час
Человеко-час (некоторые пишут «человекочас», но это неправильно) — это единица учета рабочего времени, которая соответствует 1 часу работы 1 человека. Эта единица наиболее удобна для планирования рабочего времени, определения количества необходимых работников, а также установления сроков выполнения работы.
Как рассчитать человеко часов пример
Можно вычислить этот показатель на каждого постоянного работника, при условии, что он работает целый месяц по 8 часов в день. При пятидневной работе получится: 21 рабочий день умножить на восемь часов = 168 человеко-часов в день. Обычно эту формулу применяют при нормированном рабочем дне.
Как посчитать трудозатраты в человеко часах
Можно рассчитать трудозатраты на выполнение определенной задачи, если известно, сколько времени она занимает у одного специалиста. Для этого нужно использовать следующую формулу: Ч = К * Т. Ч — это искомые трудозатраты в человеко-часах. Т — выбранная единица времени, как правило, час.
Как считается переработка по часам
Сверхурочная работа оплачивается за первые два часа работы не менее чем в полуторном размере, за последующие часы — не менее чем в двойном размере.
Что считается переработкой часов
Что такое переработка
Если в компании используется суммированный учёт рабочего времени, то переработкой считаются часы, отработанные помимо установленной в трудовом договоре нормы за учётный период.
Как правильно оплачивать переработку
В соответствии со ст. 152 ТК РФ сверхурочная работа оплачивается за первые два часа работы не менее чем в полуторном размере, за последующие часы — не менее чем в двойном размере.
Как учитывается обед в рабочее время
Перерыв для отдыха и питания не включается в рабочее время и не оплачивается. Продолжительность перерыва должна быть не менее 30 минут и не более 2 часов. У некоторых категорий работников (железнодорожников, водителей и др.) при 8 часовом рабочем дне перерыв может быть разбит на две части.
Сколько времени длится рабочий день
Обычная рабочая неделя состоит из пяти 8-часовых рабочих дней, всего 40 часов (или 38, 36 и т. д). Бывают четырёхдневные рабочие недели с 10-часовым рабочим днём, трёхдневные с 12-часовой сменой (предполагающие компенсацию за длительность).
Сколько должны платить за 12 часовой рабочий день
1 ст. 99 ТК РФ). Работа сверх нормального числа рабочих часов за учетный период оплачивается за первые два часа работы не менее чем в полуторном размере, а за все остальные часы — не менее чем в двойном (ст. 152 ТК РФ).
Как рассчитать норму рабочего времени при суммированном учете
Как правильно определить норму рабочего времени при его суммированном учете?:
- при 40-часовой рабочей неделе — восьми часов;
- при продолжительности рабочей недели, равной менее 40 часов, — количества часов, получаемого в результате деления установленной продолжительности рабочей недели на пять дней.

Как рассчитать количество часов на ставку
Чтобы определить размер указанной ставки, оклад необходимо разделить на среднемесячное количество рабочих часов в зависимости от установленной работнику продолжительности рабочей недели в часах. Среднемесячное количество рабочих часов рассчитывается путем деления годовой нормы рабочего времени в часах на 12.
Как считать часы в графике
Подсчет нормы часов производится следующим образом: количество рабочих часов ежедневно умножается на число дней за соответствующий период (за основу берется количество рабочих часов при 5-дневной неделе).
Что такое учет рабочего времени
Учет рабочего времени — это фиксирование и наблюдение за действиями подчиненных для контроля рабочего процесса и поддержания рабочей дисциплины в компании.
Как считать минуты в табеле
Для расчета в «табеле универсальном» МИНУТЫ всегда переводятся в ДЕСЯТЫЕ ДОЛИ часа. Т. е. 36часов 40 минут = 36,67 ч.
Сколько часов переработки в месяц
Сколько часов в месяц можно работать по Трудовому кодексу
Продолжительность сверхурочной работы не должна превышать для каждого работника 4 часов в течение 2 дней подряд. Есть и другое ограничение: сверхурочные работы не должны превышать для каждого работника 120 часов в год (ст. 99 ТК РФ).
Есть и другое ограничение: сверхурочные работы не должны превышать для каждого работника 120 часов в год (ст. 99 ТК РФ).
Сколько часов переработки допустимо в неделю
Продолжительность сверхурочной работы не должна превышать для каждого работника 4 часов в течение двух дней подряд и 120 часов в год, за исключением случаев, предусмотренных ТК РФ.
Сколько часов работник должен отработать в месяц
За установленный в трудовом договоре оклад работник в месяц должен отработать месячную норму рабочих часов. Месячная норма часов определяется, исходя из установленной Трудовым кодексом РФ для конкретной категории работников продолжительности рабочей недели. Для большинства работников она составляет 40 часов.
Как посчитать норму часов на 0 75 ставки
Нормальное рабочее время — 40 часов в неделю, а 0,75 ставки соответствует 30 рабочим часам в неделю. Если у вас каждый день обед длится 1 час, то по указанному вами графику выходит большее количество часов, чем 30, то есть ставка не 0,75.
Что такое 40 часовая рабочая неделя
Так, при 40-часовой рабочей неделе норма рабочего времени — 8 часов, при продолжительности рабочей недели 36 часов она составит 7,2 часа, при 24-часовой рабочей неделе — 4,8 часа.
Что такое норма часов
Норма рабочего времени — это предельное количество часов в день или дней в неделю, на которые работника можно привлекать к труду.
Чем отличается график от табеля учета рабочего времени
Табелем отражается фактическое отработанное время, а индивидуальным графиком отражается Норма времени (планируемое).
Можно ли в табеле ставить минуты
Так, в табеле можно указать, например, 3 часа 45 минут или 2 часа 25 минут. Обосновывается это следующим. Работодатель обязан вести учет времени, фактически отработанного каждым работником (ч. 4 ст.
Можно ли в табеле ставить 12 часов
Ставить в табеле необходимо столько рабочих часов, сколько работник отработал по факту. Если работнику установлен 12 часовой рабочий день из них час перерыв, то и отразить в табеле необходимо именно 11 часов, следовательно и оплате подлежат 11, а не 12 часов работы. Цитата (91. Понятие рабочего времени.
Цитата (91. Понятие рабочего времени.
Сколько норма часов в день
Нормальная продолжительность рабочего времени по ТК РФ — это не более 40 часов в неделю (ст. 91 ТК РФ). Соответственно, при пятидневной рабочей неделе с двумя выходными днями полный рабочий день должен длиться 8 часов (Порядок, утв. Приказом Минздравсоцразвития РФ от 13.08.2009 № 588н).
Как считать отпуск в норму часов при сменном графике
Он позволяет корректировать время недоработки и переработки по графику. Подсчет нормы часов производится следующим образом: количество рабочих часов ежедневно умножается на число дней за соответствующий период (за основу берется количество рабочих часов при 5-дневной неделе).
Как рассчитать норму часов с отпуском
Норма рабочего времени, приходящаяся на время отпуска или болезни рассчитывается следующим образом: продолжительность рабочей недели (например, 40 часов) делится на 5, умножается на количество рабочих дней отпуска или болезни при пятидневной рабочей неделе.
- Как правильно рассчитать зарплату по часам
- Как правильно считать количество часов
- Как правильно считать часы переработки
- Как правильно считать часы работы
- Как рассчитать зарплату по норме часов
- Как рассчитать человеко часы формула
- Как рассчитать человеко-часов пример
- Как рассчитываются часы
- Как считают часы работы
- Как считаются норма часы
- Какая норма часов работы
Как рассчитать количество отработанных часов
Обновлено: 2 сентября 2022 г. — Марк Мэтьюз и Алисса Гуле
Время — деньги. И если вы должным образом не отслеживаете часы работы сотрудников, время наносит ущерб вашей прибыли. Как убедиться, что вы все делаете правильно, платите своим сотрудникам достойную заработную плату и защищаете свой чистый доход от ошибок? Считайте это вашим кратким руководством по подсчету отработанных часов.
2 Методы подсчета отработанных часов
Существует несколько различных методов подсчета отработанных часов. Первый — ручной подсчет часов. Во-вторых, программное обеспечение часов.
Как рассчитать количество рабочих часов вручную
Существуют различные методы подсчета рабочих часов. Наиболее распространенные из них включают запись времени начала и окончания рабочего времени. Некоторые работодатели требуют, чтобы их сотрудники записывали свое рабочее время на бумаге, в то время как другие используют систему хронометража для регистрации часов. После регистрации рабочего времени работодатель должен будет подсчитать итоги для начисления заработной платы.
Пример расчета общего количества отработанных часов Чтобы выяснить, сколько часов работают сотрудники, вам нужен процесс сбора этой информации от рабочих перед каждым платежным периодом. Оттуда вы можете найти общую сумму для начисления заработной платы.
Пример расчета общего количества отработанных часов
Во-первых, вам потребуется время начала и окончания. В качестве примера возьмем время начала 8:45 и время окончания 15:45.
- Преобразовать все время в 24-часовой формат (военное время):
- Преобразование 8:45 утра в 08:45 часов
- Преобразование 15:45 в 15:45 часов
- Затем вычтите время начала из времени окончания.
- У вас есть фактические часы и минуты, отработанные за день.
Крайне важно обеспечить точность расчетов, поскольку любая человеческая ошибка может привести к огромным затратам. Согласно отчету Gartner, недобросовестные данные обходятся компаниям в 12,9 млн долларов в год.
Как подсчитать количество отработанных часов с помощью программного обеспечения Вы можете использовать программное обеспечение для упрощения процесса подсчета отработанных часов. Убедитесь, что вы ввели все правильные значения для почасовой ставки и ставки сверхурочной работы, если она у вас есть. После этого можно переходить к расчету заработной платы.
После этого можно переходить к расчету заработной платы.
Использование отработанных часов для расчета валовой заработной платы
Чтобы определить заработную плату работника, необходимо преобразовать часы и минуты в десятичный формат. После этого умножьте отработанное время на заработную плату, чтобы найти валовую заработную плату.
Например, если сотрудник работает 8:30 минут, это 8,5 часа после десятичного преобразования. Когда вы умножаете это число на почасовую заработную плату работника, в результате получается сумма, которую вы будете платить.
Ниже вы найдете таблицу, которая поможет вам преобразовать минуты в десятичные числа.
Таблица преобразования минут в десятичные числа
Инструменты для учета рабочего времени сотрудников
Министерство труда США предоставляет рекомендации, которые помогут вам точно отслеживать рабочее время сотрудников. Вот несколько приемлемых способов отслеживания времени:
- Ручка и бумажные табели учета рабочего времени
- Механические часы
- Бесплатные калькуляторы времени
- Программное обеспечение часов
Давайте рассмотрим каждый из этих вариантов более подробно.
Табели рабочего времени с ручкой и бумагой
Карандаш и бумага могут показаться простым способом начать работу, но они подходят не для всех предприятий и работников. Воровство времени может быть серьезной проблемой при использовании метода карандаша и бумаги, поскольку трудно гарантировать, что все отчеты сотрудников о часах точны.
Это также может снизить производительность, так как вам или кому-то из вашей команды всегда нужно будет просматривать эти табели учета рабочего времени и подсчитывать количество отработанных часов для каждого сотрудника.
Механические часы
Это устройство проставляет дату и время на бумажной карте учета рабочего времени. Для этого работодатель выдает каждому сотруднику табель учета рабочего времени на период оплаты. Затем сотрудники на месте используют часы для отслеживания своего рабочего времени.
Сотрудник обязан приходить и уходить в нужное время. Они прошивают табель учета рабочего времени всякий раз, когда приходят или уходят с работы. Затем работник подсчитывает отработанное время, и сотрудник получает оплату.
Затем работник подсчитывает отработанное время, и сотрудник получает оплату.
Бесплатные калькуляторы учета рабочего времени
В Интернете можно найти множество бесплатных онлайн-калькуляторов карт учета рабочего времени, которые подсчитывают отработанные часы. OnTheClock предлагает несколько бесплатных различных калькуляторов времени:
- Калькулятор учета рабочего времени с обедом и сверхурочными
- Калькулятор тайм-карт Excel
- Преобразование часов и минут в десятичные часы
- Преобразовать десятичные часы в часы и минуты
Программное обеспечение Time Clock для учета рабочего времени сотрудников
Более удобным вариантом для учета отработанного времени является программа учета рабочего времени. OnTheClock предоставляет несколько функций, которые могут быть полезны вашему бизнесу.
- Быстрая и простая установка
- Автоматический расчет часов
- Отслеживание посещаемости и отгулов сотрудников
- Расширенные функции геолокации
- Простое отслеживание проекта и расчет стоимости работ
- Отправка часов работы сотрудников непосредственно в программу расчета заработной платы
- Мобильные и браузерные приложения для простоты
Демистификация процесса подсчета отработанных часов
Не оставляйте записи об отработанных часах и выплаченной заработной плате на волю случая. Узнайте больше о том, что OnTheClock может сделать для вашего бизнеса, и попробуйте его бесплатно в течение 30 дней. Если у вас есть только один или два сотрудника для вашего бизнеса, вы можете использовать OnTheClock бесплатно.
Узнайте больше о том, что OnTheClock может сделать для вашего бизнеса, и попробуйте его бесплатно в течение 30 дней. Если у вас есть только один или два сотрудника для вашего бизнеса, вы можете использовать OnTheClock бесплатно.
a мысль От SHERI 15.06.2021 …
Я ИСПОЛЬЗУЮ ТАБЛИЦУ ПРЕОБРАЗОВАТЕЛЯ, ЧТОБЫ ПОДЧИСЛИТЬ ОТРАБОТАННОЕ ВРЕМЯ СОТРУДНИКОВ. ПЛАТИТЬ ИМ ЗА 75 МИНУТ ИЛИ КОНВЕРТИРОВАТЬ В 45 МИНУТ?
ответ от OTC — Привет, Шери, при подсчете отработанных часов обычно используются десятичные дроби. Вы можете использовать конвертер десятичных чисел или наши часы для сотрудников, чтобы конвертировать десятичные дроби в минуты. Например, 8,75 часа преобразуются в 8 часов 45 минут. 0,75 — это представление 75% часа (что составляет 45 минут). Мы надеемся, что это поможет.
мысль От janet m comfort 16.05.2021 …
получил мой первый платежный чек в качестве замены, в котором говорилось, что я проработал 8 часов. я захожу в 9утра и не могу пробиться до 13:15. Почему я заплатил только за 8 часов?
я захожу в 9утра и не могу пробиться до 13:15. Почему я заплатил только за 8 часов?
ответ от OTC — Привет, Джанет, спасибо за обращение. Основываясь на времени, которое вы указали в своем комментарии, с 9:00 до 13:15 будет 4,25 часа. Это при условии, что перерывы не были вычтены. Мы надеемся, что эта информация будет полезной.
мысль От Майра от 16.04.2021 …
В разделе этой статьи о переводе часов в часы и неполные часы вы приводите пример, что 8:45 должно быть 8,45 часа. Это неправильно, не так ли? Я всегда считал, что это 8,75 часа. Я ошибаюсь? Если нет, исправление этих примеров может быть хорошей идеей. 🙂 Спасибо Майра
ответ от OTC — Здравствуйте Майра, спасибо за отличный комментарий. Хитрость здесь заключается в том, чтобы набрать максимальное число, отбросить час и сохранить 13 минут. Этот пример просто показывает, как производить расчеты, используя часы/минуты, а не десятичные преобразования. Мы надеемся, что это поможет с вашим вопросом. Хорошего дня и не стесняйтесь поделиться этой статьей в социальных сетях, чтобы помочь другим.
Мы надеемся, что это поможет с вашим вопросом. Хорошего дня и не стесняйтесь поделиться этой статьей в социальных сетях, чтобы помочь другим.
мысль От Cindy Henrie от 08.01.2021 …
Привет, у меня проблема с нашими старыми школьными часами отсчета времени. введите мое время, оно рассчитывается так, как если бы я работал только в 12-часовую смену, как мне ввести это
ответ от OTC — Здравствуйте, Синди, спасибо за вопрос. Мы действительно не можем объяснить, как это сделать на старых часах, так как мы не знаем систему. Благодаря технологиям, улучшающим бизнес-операции, наши современные часы автоматически подсчитывают отработанные часы с момента прихода и ухода сотрудника. Мы рекомендуем использовать наше приложение часов или порекомендовать его вашему работодателю. Мы будем рады ответить на любые вопросы, которые могут возникнуть у вас или у вашего работодателя о нашей системе учета рабочего времени. Пожалуйста, свяжитесь с нами по телефону 888-753-5999. Хорошего дня.
Хорошего дня.
мысль От Кевин Газлей от 06.10.2020 …
человек работает в первый день (воскресенье) расчетного периода 11 часов 15 минут @$36.час, во второй день (пн) 12 часов 00 минут @$18.hr,/день третий (вторник) на 10 часов 40 минут @$18.hr,/день 4 (wens) на 10 часов,35 минут, (6hrs05mins@$18,hr/4hrs30mins@$27.hr) день 5 (чт) на 10 часов. 30 минут @ 27 долларов в час, / день 6 (пт) в течение 9 часов 42 минуты, @ 27 долларов в час // общая валовая заработная плата составляет 1562,04 доллара / это правильно ??? или я ошибаюсь??? Пожалуйста, ответьте тем же, спасибо
ответ от OTC — Привет, Кевин! Мы не являемся профессионалами в области расчета заработной платы, но мы предлагаем несколько бесплатных ценных инструментов для отслеживания рабочего времени, которые помогут вам в вашей ситуации. Пожалуйста, обратитесь к нашим бесплатным инструментам здесь. Мы надеемся, что это поможет.
мысль От Оксана Берина от 20. 06.2020 …
06.2020 …
За две недели отработала 80 часов. Заплатили только за 56. Правильно?
ответ от OTC — Здравствуйте и спасибо за вопрос. Это будет зависеть от того, когда ваша рабочая неделя начинается и заканчивается. Это также зависит от того, когда цикл расчета заработной платы вашей компании начинается и заканчивается. См. наш блог Как настроить периоды оплаты для работы с датами оплаты, чтобы лучше понять, как ваш работодатель может организовать свою рабочую неделю. Мы надеемся, что это поможет.
мысль От Эфраим от 08.07.2019 …
Как рассчитать мое время Время начала с 14:50 до 00:00
Ответ от OTC — Здравствуйте, Эфраим, вот ссылка калькулятор часов. https://www.ontheclock.com/Free-Online-Time-Card-Calculator.aspx Не стесняйтесь указывать отработанное время, включая перерывы. Спасибо, что обратились к нам 🙂
мысль От Барбара от 03.04.2019 …
Пожалуйста, помогите мне рассчитать мои часы до военного времени. Я работал с 16:03 до 23:00 и не понимаю, как мой работодатель придумал 6,9.5 часов?
Я работал с 16:03 до 23:00 и не понимаю, как мой работодатель придумал 6,9.5 часов?
ответ от OTC — Привет Барбара! Вот ссылка, которая позволяет вам конвертировать часы и минуты в десятичные часы. Мы надеемся, что это поможет. https://www.ontheclock.com/convert-hours-minutes-to-decimal-hours.aspx
мысль От Wasif 25.03.2019 …
Мои расчеты: 5×12 = 60 долларов 20 минут х 12 = 4 доллара = 64 доллара. Я работаю с 16:00 до 21:20. Расчет машины учета рабочего времени: 16:00 — 21:20 = 5.20 5,20 х 12 = 62,40 доллара. Не могли бы вы помочь мне понять, почему существует разница между моими расчетами и расчетами машины с карточками учета рабочего времени?
ответ от OTC — Привет Васиф, Возможно, вам поможет наш калькулятор десятичных часов: https://www.ontheclock.com/convert-hours-minutes-to-decimal-hours.aspx
мысль От Дебра Энн Лапаран от 04. 03.2019 ..
03.2019 ..
Это помогает мне понимать простые вещи, очень хорошо помогает также студентам понимать математику
ответ от OTC — Привет, Дебра, Мы очень рады услышать, что мы можем помочь студентам понять математику.
мысль От Джеймс 10.02.2019 …
Привет на работе, я прибываю в 4.15, но когда они считают мои часы, они начинают считать в 5.00, пожалуйста, мне нужна помощь.
ответ от OTC — Привет, Джеймс! Если ваш работодатель использует нашу систему для отслеживания рабочего времени сотрудников, возможно, администратор учетной записи включил «пробивное округление». Попросите человека, который контролирует учетную запись, связаться с нами, и мы сможем помочь ему. Спасибо, Безрецептурная команда
мысль От Кей от 15.12.2018 …
Я хочу рассчитать свои часы
Ответ от OTC — Привет Кей,
Зарегистрируйтесь и начните подсчитывать свои часы, нажав на предоставленную ссылку. Надеюсь это поможет. https://www.ontheclock.com/frmRegStepOne.aspx
Надеюсь это поможет. https://www.ontheclock.com/frmRegStepOne.aspx
мысль От Эрик от 02.11.2018 …
Привет, что мне делать, когда мой работодатель ежемесячно платит мне меньше базовой зарплаты ?
ответ от OTC — Привет, Эрик! Спасибо, что связались с нами. Вам платят меньше, чем вы должны получать за отработанное время? Вы также упоминаете о зарплате, если у вас зарплата, то вы должны платить столько же каждый месяц. Ваша валовая заработная плата за год должна соответствовать контракту о заработной плате.
мысль От Трейси 01.10.2018 …
Я обнаружил, что мой работодатель сокращает мне часы.
мысль Из Тим. от 20.07.2018 …
Законно ли, что компания платит вам за 37 часов, а они заставляют вас работать 40 часов.
ответ от OTC — Привет, Тим, это определенно незаконно. Я бы предложил начать с вас начать с разговора с вашим работодателем. Если вы не добились там никакого прогресса, зайдите на сайт жалоб сотрудников DOL — DOL 9.0003
Если вы не добились там никакого прогресса, зайдите на сайт жалоб сотрудников DOL — DOL 9.0003
мысль От Лесли от 07.01.2018 …
Как программа часов рассчитывает сверхурочные для сотрудников? А как насчет недели, на которой есть официальный выходной?
ответ от OTC —
Привет, Лесли! Программное обеспечение OnTheClock предоставляет список предустановленных правил сверхурочной работы. Работодатель выберет правило сверхурочной работы, которое лучше всего соответствует его требованиям к сверхурочной работе. Рабочие часы и сверхурочные автоматически программным обеспечением. Я могу связаться с вами напрямую, чтобы узнать, каковы ваши требования и как мы можем помочь.
Что касается государственных праздников, наше программное обеспечение позволяет отслеживать PTO (оплачиваемый отпуск). Используя функции PTO, запись выходных, личных и больничных дней очень проста. Рабочие часы также могут быть отмечены как оплачиваемые или неоплачиваемые. ~Марк
~Марк
Оставь свои мысли…
Ваше имя
(обязательно, будет показано)
Ваш адрес электронной почты
(обязательно, не отображается)
Комментарий
разница во времени, сложение, вычитание и суммирование времени
В этом учебном пособии рассматриваются различные способы расчета времени в Excel. Вы найдете несколько полезных формул для сложения и вычитания времени, расчета разницы во времени или прошедшего времени и многого другого.
В статье на прошлой неделе мы подробно рассмотрели особенности формата времени Excel и возможности основных функций времени. Сегодня мы углубимся в вычисления времени в Excel, и вы узнаете еще несколько формул для эффективного управления временем на ваших листах.
Сегодня мы углубимся в вычисления времени в Excel, и вы узнаете еще несколько формул для эффективного управления временем на ваших листах.
Как рассчитать разницу во времени в Excel (истекшее время)
Для начала давайте посмотрим, как можно быстро посчитать прошедшее время в Excel, т.е. найти разницу между временем начала и временем окончания. И, как это часто бывает, существует более одной формулы для расчета времени. Какой из них выбрать, зависит от вашего набора данных и того, какого именно результата вы пытаетесь достичь. Итак, давайте пробежимся по всем методам, по одному.
Формула 1. Вычесть один раз из другого
Как вы, наверное, знаете, время в Excel — это обычные десятичные числа, отформатированные так, чтобы они выглядели как время. И поскольку это числа, вы можете складывать и вычитать время так же, как и любые другие числовые значения.
Самая простая и очевидная формула Excel для расчета разницы во времени:
= Время окончания — Время начала
В зависимости от вашей структуры данных, фактическая формула разницы во времени может принимать различные формы, например:
| Формула | Пояснение |
=А2-В2 | Вычисляет разницу между значениями времени в ячейках A2 и B2. |
=ЗНАЧ ВРЕМЕНИ("20:30") - ЗНАЧ ВРЕМЕНИ("6:40") | Вычисляет разницу между указанными значениями времени. |
=ВРЕМЯ(ЧАС(A2),МИНУТА(A2),СЕКУНД(A2)) - ВРЕМЯ(ЧАС(B2),МИНУТА(B2),СЕКУНД(B2)) | Вычисляет разницу во времени между значениями в ячейках A2 и B2, игнорируя разницу в датах, когда ячейки содержат значения даты и времени. |
Помня, что во внутренней системе Excel время представлено дробными частями десятичных чисел, вы, скорее всего, получите результаты, подобные этому:
Десятичные дроби в столбце D абсолютно верны, но не очень значимы. Чтобы сделать их более информативными, вы можете применить собственное форматирование времени с помощью одного из следующих кодов:
| Временной код | Пояснение |
| ч | Прошедшее время, отображается как 4. |
| ч:мм | Истекшие часы и минуты, отображаемые в формате 4:10. |
| ч:мм:сс | Истекшие часы, минуты и секунды, отображаемые как 4:10:20. |
Чтобы применить пользовательский формат времени, нажмите Ctrl + 1, чтобы открыть диалоговое окно Формат ячеек , выберите Пользовательский из списка категорий и введите временные коды в поле Введите . Подробные инструкции см. в разделе Создание пользовательского формата времени в Excel.
А теперь давайте посмотрим, как наша формула разницы во времени и временные коды работают на реальных рабочих листах. Если Время начала находится в столбце A, а Время окончания — в столбце B, вы можете скопировать следующую формулу из столбцов C через E:
=$B2-$A2
Прошедшее время отображается по-разному в зависимости от формата времени, примененного к столбцу:
Примечание. Если прошедшее время отображается в виде решеток (#####), то либо ячейка с формулой недостаточно широка, чтобы вместить время, либо результатом ваших расчетов времени является отрицательное значение.
Формула 2. Вычисление разницы во времени с помощью функции ТЕКСТ
Еще один простой способ расчета продолжительности между двумя периодами времени в Excel — использование функции ТЕКСТ:
- Рассчитать часов между двумя временами:
=ТЕКСТ(B2-A2, "h") - Возврат часов и минут между 2 раза:
=ТЕКСТ(B2-A2, "ч:мм") - Возврат часов , минут и секунд между 2 раза:
=ТЕКСТ(B2-A2, "ч:мм:сс")
Примечания:
- Значение, возвращаемое функцией ТЕКСТ, всегда является текстом. Обратите внимание на выравнивание по левому краю текстовых значений в столбцах C:E на снимке экрана выше. В некоторых сценариях это может быть существенным ограничением, поскольку вы не сможете использовать возвращенное «текстовое время» в других вычислениях.
- Если результатом является отрицательное число, формула ТЕКСТ возвращает #ЗНАЧ! ошибка.

Формула 3. Подсчет часов, минут или секунд между двумя значениями времени
Чтобы получить разницу во времени в одной единице времени (часах, минутах или секундах), вы можете выполнить следующие вычисления.
Расчет часов между двумя временами :
Чтобы представить разницу между двумя временами в виде десятичного числа , используйте следующую формулу:
=( Время окончания — Время начала ) * 24
Предположим, что ваше время начала указано в A2, а время окончания в B2, вы можете использовать простое уравнение B2-A2, чтобы вычислить разницу между двумя временами, а затем умножить ее на 24, что является количеством часов в одном дне:
=(B2-A2) * 24
Чтобы получить число полных часов , используйте функцию INT для округления результата до ближайшего целого числа:
=ЦЕЛОЕ((B2-A2) * 24)
Всего минут между двумя повторами :
Чтобы рассчитать количество минут между двумя периодами времени, умножьте разницу во времени на 1440, что равно количеству минут в одном дне (24 часа * 60 минут = 1440).
=( Время окончания — Время начала ) * 1440
Как показано на следующем снимке экрана, формула может возвращать как положительные, так и отрицательные значения, последние возникают, когда время окончания меньше времени начала, как в строке 5:
=(B2-A2)*1440
Всего секунд между моментами :
Чтобы получить общее количество секунд между двумя событиями, вы умножаете разницу во времени на 86400, что является количеством секунд в одном дне (24 часа * 60 минут * 60 секунд = 86400).
=( Время окончания — Время начала ) * 86400
В нашем примере формула выглядит следующим образом:
=(B2-A2)* 86400
Примечание. Чтобы результаты отображались корректно, Общий формат следует применять к ячейкам с вашей формулой разницы во времени.
Формула 4. Расчет разницы в одной единице времени без учета других
Чтобы найти разницу между 2 значениями времени в определенную единицу времени, игнорируя остальные, используйте одну из следующих функций.
- Разница в часов , без учета минут и секунд:
=ЧАС(B2-A2) - Разница в минут , без учета часов и секунд:
=МИНУТЫ(B2-A2) - Разница в секунд , без учета часов и минут:
= ВТОРОЙ (B2-A2)
При использовании функций Excel ЧАС, МИНУТА и СЕКУНД помните, что результат не может превышать 24 для часов и 60 для минут и секунд.
Примечание. Если время окончания меньше времени начала (т. е. результатом формулы является отрицательное число), функция #ЧИСЛО! возвращается ошибка.
Формула 5. Расчет времени, прошедшего с момента начала до настоящего времени
Чтобы рассчитать, сколько времени прошло с момента начала до настоящего момента, вы просто используете функцию СЕЙЧАС, чтобы получить текущую дату и текущее время, а затем вычесть из них дату и время начала.
Предположим, что начальная дата и время находятся в вызове A2, приведенная ниже формула возвращает следующие результаты, при условии, что вы применили соответствующий формат времени к столбцу B, ч:мм в этом примере:
=СЕЙЧАС()-A2
В случае, если прошедшее время превышает 24 часа , используйте один из этих форматов времени, например d «days» h:mm:ss , как показано на следующем снимке экрана:
Если ваши начальные точки содержат только значения времени без дат, вам необходимо использовать функцию ВРЕМЯ для правильного расчета прошедшего времени. Например, следующая формула возвращает время, прошедшее с момента значения времени в ячейке A2 до настоящего времени:
Например, следующая формула возвращает время, прошедшее с момента значения времени в ячейке A2 до настоящего времени:
=ВРЕМЯ(ЧАС(СЕЙЧАС()), МИНУТЫ(СЕЙЧАС()), СЕКУНДЫ(СЕЙЧАС())) - A2
Примечание. Прошедшее время не обновляется в режиме реального времени, оно обновляется только при повторном открытии или пересчете рабочей книги. Чтобы принудительно обновить формулу, нажмите либо Shift + F9, чтобы пересчитать активную электронную таблицу, либо нажмите F9, чтобы пересчитать все открытые книги.
Формула 5. Отображение разницы во времени как «XX дней, XX часов, XX минут и XX секунд»
Вероятно, это самая удобная формула для расчета разницы во времени в Excel. Вы используете функции HOUR, MINUTE и SECOND для возврата соответствующих единиц времени и функцию INT для вычисления разницы в днях. Затем вы объединяете все эти функции в одну формулу вместе с текстовыми метками:
=ЦЕЛОЕ(B2-A2) & "дни", & ЧАС(B2-A2) & "часы", & МИНУТЫ(B2-A2) & "минуты и" & СЕКУНДЫ(B2-A2) & "секунды"
Чтобы скрыть нулевые значения в формуле разницы во времени в Excel, вставьте в нее четыре функции ЕСЛИ:
=ЕСЛИ(ЦЕЛОЕ(B2-A2)>0, ЦЕЛОЕ(B2-A2) & " дней, ","") & ЕСЛИ(ЧАС(B2-A2)>0, ЧАС(B2-A2) & " часов , ","") & ЕСЛИ(МИНУТЫ(B2-A2)>0, МИНУТЫ(B2-A2) & " минут и ","") & ЕСЛИ(СЕКУНДЫ(B2-A2)>0, СЕКУНДЫ(B2-A2) ) & "секунды","")
Синтаксис может показаться чрезмерно сложным, но он работает 🙂
Кроме того, вы можете рассчитать разницу во времени, просто вычитая время начала из времени окончания (например, = B2-A2 ), а затем применив к ячейке следующий формат времени:
d «дни», h «часы», m «минуты» и «s» секунды
Преимущество этого подхода заключается в том, что результатом будет обычное значение времени, которое можно использовать в других расчетах времени, в то время как результатом сложной формулы, описанной выше, является текстовое значение. Недостатком является то, что пользовательский формат времени не может различать нулевые и ненулевые значения и игнорировать последние. Чтобы отобразить результат в других форматах, см. Как показать время за 24 часа, 60 минут, 60 секунд.
Недостатком является то, что пользовательский формат времени не может различать нулевые и ненулевые значения и игнорировать последние. Чтобы отобразить результат в других форматах, см. Как показать время за 24 часа, 60 минут, 60 секунд.
Как рассчитать и отобразить отрицательное время в Excel
При расчете разницы во времени в Excel вы иногда можете получить результат в виде ошибки ######, поскольку разница представляет собой отрицательное время. Но есть ли способ правильно отображать отрицательное время в Excel? Способ конечно есть, и даже не один 🙂
Способ 1. Измените систему дат Excel на систему дат 1904
Самый быстрый и простой способ нормально отображать отрицательное время (со знаком минус) — переключиться на 1904 система даты. Для этого щелкните Файл > Параметры > Дополнительно , прокрутите вниз до раздела При расчете этой рабочей книги и поставьте галочку в поле Использовать систему дат 1904 .
Нажмите OK , чтобы сохранить новые настройки, и теперь отрицательные времена будут отображаться правильно, как отрицательные числа:
Способ 2.
 Расчет отрицательного времени в Excel по формулам
Расчет отрицательного времени в Excel по формуламЕсли изменить систему дат по умолчанию в Excel невозможно, то вы можете заставить отрицательное время отображаться правильно, используя одну из следующих формул:
=ЕСЛИ(A2-B2>0, A2-B2, "-" и ТЕКСТ(ABS(A2-B2),"ч:мм"))
=ЕСЛИ(A2-B2>0, A2-B2, ТЕКСТ(ABS(A2-B2),"-ч:мм"))
Обе формулы проверяют, больше ли разница во времени (A2-B2) 0, и если да, то возвращают эту разницу. Если разница во времени меньше нуля, первая формула вычисляет абсолютную разницу и объединяет знак минус. Вторая формула дает точно такой же результат при использовании отрицательного формата времени «-h::mm «.
Примечание. Имейте в виду, что в отличие от первого метода, который обрабатывает отрицательное время как отрицательное числовое значение, результатом функции ТЕКСТ всегда является текстовая строка, которую нельзя использовать в вычислениях или других формулах.
Добавление и вычитание времени в Excel
По сути, есть 2 способа складывать и вычитать время в Excel:
- Использование функции ВРЕМЯ
- Использование арифметических вычислений на основе количества часов (24), минут (1440) и секунд (86400) в одних сутках
Функция ВРЕМЯ(час, минута, секунда) делает вычисление времени в Excel действительно простым, однако она не позволяет добавлять или вычитать более 23 часов, 59 минут или 59 секунд. Если вы работаете с большими временными интервалами, то используйте один из арифметических расчетов, показанных ниже.
Если вы работаете с большими временными интервалами, то используйте один из арифметических расчетов, показанных ниже.
Как прибавить или вычесть часы ко времени в Excel
Чтобы добавить часы к заданному времени в Excel, вы можете использовать одну из следующих формул.
Функция ВРЕМЯ для добавления до 24 часов
= Время начала + ВРЕМЯ( N часов , 0, 0)
Например, если ваше время начала находится в ячейке A2, и вы хотите добавить к нему 2 часа, формула будет выглядеть следующим образом:
=A2 + ВРЕМЯ(2, 0, 0)
Примечание. Если вы попытаетесь добавить более 23 часов с помощью функции ВРЕМЯ, указанные часы будут разделены на 24, а остаток будет добавлен к значению времени начала. Например, если вы попытаетесь добавить 25 часов к «02.06.2015, 10:00» (ячейка A4), используя формулу =A4 + TIME(25, 0, 0) , результатом будет «02.06.2015 11:00», т.е. A4 + 1 час.
Формула для прибавления любого количества часов (меньше или больше 24 часов)
Следующая формула не имеет ограничений на количество часов, которые вы хотите добавить:
= Время запуска + ( N часов / 24)
Например, чтобы добавить 28 часов к времени начала в ячейке A2, введите следующую формулу:
=А2 + (28/24)
До вычтите часов из данного времени, вы используете аналогичные формулы, и просто замените «+» знаком минус:
Например, чтобы вычесть 3 часа из времени в ячейке A2, подойдет любая из следующих формул:
=А2-(3/24)
=A2-ВРЕМЯ(3,0,0)
Чтобы вычесть более 23 часов, используйте первый.
Как прибавить/вычесть минуты ко времени в Excel
Чтобы добавить минуты к заданному времени, используйте те же методы, которые мы только что использовали для добавления часов.
Для прибавления или вычитания до 60 минут
Используйте функцию ВРЕМЯ и укажите минуты, которые вы хотите добавить или вычесть, во втором аргументе:
= Время начала + ВРЕМЯ(0, N минут , 0)
А вот пара реальных формул для расчета минут в Excel:
Чтобы добавить 20 минут ко времени в A2: =A2 + TIME(0,20,0)
Чтобы вычесть 30 минут из времени в A2: =A2 — TIME(0,30,0)
Чтобы добавить или вычесть более 60 минут
При расчете разделите количество минут на 1440 (количество минут в сутках) и прибавьте частное к времени начала:
= Время запуска + ( N минут / 1440)
Чтобы вычесть минуты из времени, просто замените плюс знаком минус. Например:
Чтобы добавить 200 минут: =A2 + (200/1440)
Чтобы вычесть 300 минут: =A2 -(300/1440)
Как прибавить/вычесть секунды к заданному времени
Вторые вычисления в Excel выполняются аналогичным образом.
Чтобы добавить менее 60 секунд к заданному времени, вы можете использовать функцию ВРЕМЯ:
= Время начала + ВРЕМЯ(0, 0, N секунд )
Чтобы добавить более 59 секунд, используйте следующую формулу:
= Время начала + ( N секунд / 86400)
Чтобы вычесть секунды, используйте те же формулы со знаком минус (-) вместо плюса (+).
На листах Excel формулы могут выглядеть примерно так:
Чтобы добавить 30 секунд к A2: =A2 + TIME(0,0,31)
Чтобы добавить 1200 секунд к A2: =A2 + (1200/86400)
Чтобы вычесть 40 секунд из A2: =A2 - TIME(0,0,40)
Чтобы вычесть 900 секунд из A2: =A2 - (900/86400)
Как суммировать время в Excel
Формула суммирования времени в Excel — это обычная функция СУММ, и применение правильного формата времени к результату — вот что помогает.
Предположим, у вас есть несколько проектных времен в столбце B, и вы хотите их суммировать. Вы пишете простую формулу СУММ, как показано ниже, и получаете результат в формате по умолчанию, таком как чч:мм:сс .
Вы пишете простую формулу СУММ, как показано ниже, и получаете результат в формате по умолчанию, таком как чч:мм:сс .
=СУММ(B2:B4)
В некоторых случаях формат времени по умолчанию работает просто отлично, но иногда вам может понадобиться больше, например, для отображения общего времени в виде минут и секунд или только секунд. Хорошей новостью является то, что никаких других вычислений не требуется, все, что вам нужно сделать, это применить пользовательский формат времени к ячейке с помощью формулы СУММ.
Щелкните ячейку правой кнопкой мыши и выберите Формат ячеек в контекстном меню или нажмите Ctrl + 1, чтобы открыть диалоговое окно Формат ячеек . Выберите Custom из списка категорий и введите один из следующих форматов времени в поле Введите :
- Для отображения общего времени в минутах и секундах: [м]:сс
- Для отображения общего времени в секундах: [сс]
Результат будет выглядеть следующим образом:
Как суммировать данные за 24 часа в Excel
Чтобы суммировать более 24 часов, вы используете ту же формулу СУММА, что обсуждалась выше, и примените к ячейке один из следующих форматов времени:
| Формат | Отображается как | Пояснение |
| [ч]:мм | 30:10 | Часы и минуты |
| [ч]:мм:сс | 30:10:20 | Часы, минуты и секунды |
| [ч] «часы», мм «минуты», сс «секунды» | 30 часов 10 минут 20 секунд | |
| д ч:мм:сс | 1 06:10:20 | Дни, часы, минуты и секунды |
| д «день» ч:мм:сс | 1 день 06:10:20 | |
| д «день», ч «часы», м «минуты» и «с» секунды | 1 день, 6 часов, 10 минут и 20 секунд |
Чтобы увидеть, как эти настраиваемые форматы времени могут выглядеть на вашем листе Excel, взгляните на снимок экрана ниже, где в ячейки A9 введена та же формула СУММ. до А13:
до А13:
=СУММ($B$2:$B$4)
Примечание. Приведенные выше пользовательские форматы времени работают только для положительных значений. Если результат ваших расчетов времени является отрицательным числом, например. когда вы вычитаете большее время из меньшего, результат будет отображаться как #####. Чтобы по-другому отображать отрицательные значения времени, см. пользовательский формат для отрицательных значений времени.
Кроме того, имейте в виду, что формат времени, примененный к ячейке, изменяет только представление на дисплее, не изменяя значение ячейки. Например, на скриншоте выше ячейка A13 выглядит как текст, но на самом деле это обычное значение времени, которое хранится в виде десятичной дроби во внутренней системе Excel. Это означает, что вы можете свободно ссылаться на эту ячейку в других формулах и вычислениях.
Для получения дополнительной информации см. Как рассчитать и показать за 24 часа, 60 минут, 60 секунд.
Мастер формул даты и времени — быстрый способ расчета времени в Excel
Теперь, когда вы знаете множество различных формул для сложения и вычитания времени в Excel, позвольте мне показать вам инструмент, который может все это сделать. Ладно, почти все 🙂
Ладно, почти все 🙂
А вот и мастер формул даты и времени Ablebit для Excel:
В мастере даты и времени , вы переключаетесь на вкладку Добавить или Вычесть , в зависимости от того, какую операцию вы хотите выполнить, и делаете следующее:
- Нажмите на ссылку Показать поля времени в левой части окна.
- Введите значения или ссылки на ячейки для аргументов формулы. По мере заполнения полей аргументов мастер строит формулу в выбранной ячейке.
- По завершении нажмите кнопку Вставить формулу
Вот оно! Например, вот как вы можете добавить указанное количество часов, минут и секунд ко времени в формате A4:
Если вам нужно скопировать формулу в другие ячейки, зафиксируйте все ссылки, кроме ячейки, содержащей исходное время (A4), со знаком $, как показано на снимке экрана ниже (по умолчанию мастер всегда использует относительные ссылки). Затем дважды щелкните маркер заполнения, чтобы скопировать формулу вниз по столбцу, и все готово!
Помимо расчета времени, мастер также может добавлять и вычитать даты, получать разницу между двумя датами и вычислять возраст по дате рождения.

 06.2007, 10:35
06.2007, 10:35 К ячейке необходимо вручную применить пользовательский формат «а».
К ячейке необходимо вручную применить пользовательский формат «а».
 06.2007, 10:35
06.2007, 10:35 Это значение не может превышать 24 (4).
Это значение не может превышать 24 (4).



 Деление многочлена на многочлен
Деление многочлена на многочлен Измерение углов
Измерение углов Получить подробную информацию можно здесь.
Получить подробную информацию можно здесь. Прямоугольный треугольник – это трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов называется прямым углом , отсюда и название прямоугольного треугольника. Мы выбираем один из двух оставшихся углов и обозначаем его 9.0006 c и третий угол мы обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , то мы знаем, что значение d :
Прямоугольный треугольник – это трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов называется прямым углом , отсюда и название прямоугольного треугольника. Мы выбираем один из двух оставшихся углов и обозначаем его 9.0006 c и третий угол мы обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , то мы знаем, что значение d :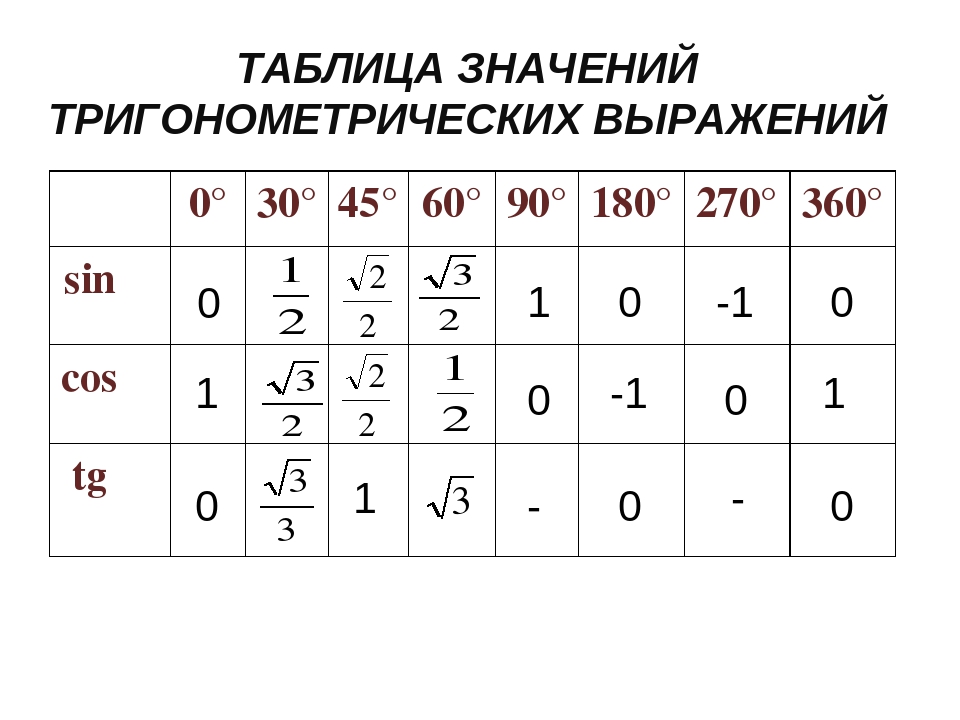 Угол c образован пересечением гипотенузы h и прилежащей стороны a .
Угол c образован пересечением гипотенузы h и прилежащей стороны a . Чтобы продемонстрировать этот факт, давайте изучим три фигуры в середине страницы. В этом примере у нас есть 8-футовая лестница, которую мы собираемся прислонить к стене. Стена имеет высоту 8 футов, и мы нарисовали белые линии на стене и синие линии вдоль земли с интервалом в один фут. Длина лестницы фиксированная. Если мы наклоним лестницу так, чтобы ее основание находилось в 2 футах от стены, лестница образует с землей угол около 75,5 градусов. Лестница, земля и стена образуют прямоугольный треугольник. Отношение расстояния от стены (а – примыкающей) к длине лестницы (h – гипотенуза) равно 2/8 = 0,25. Это определяется как косинус с = 75,5 градусов. (На другой странице мы покажем, что если бы лестница была в два раза длиннее (16 футов) и наклонена под тем же углом (75,5 градусов), то она располагалась бы в два раза дальше (4 фута) от стены. Соотношение остается одинаковым для любого прямоугольного треугольника с углом 75,5 градусов.) Если мы измерим точку на стене, где лестница соприкасается (o — напротив), расстояние составит 7,745 фута.
Чтобы продемонстрировать этот факт, давайте изучим три фигуры в середине страницы. В этом примере у нас есть 8-футовая лестница, которую мы собираемся прислонить к стене. Стена имеет высоту 8 футов, и мы нарисовали белые линии на стене и синие линии вдоль земли с интервалом в один фут. Длина лестницы фиксированная. Если мы наклоним лестницу так, чтобы ее основание находилось в 2 футах от стены, лестница образует с землей угол около 75,5 градусов. Лестница, земля и стена образуют прямоугольный треугольник. Отношение расстояния от стены (а – примыкающей) к длине лестницы (h – гипотенуза) равно 2/8 = 0,25. Это определяется как косинус с = 75,5 градусов. (На другой странице мы покажем, что если бы лестница была в два раза длиннее (16 футов) и наклонена под тем же углом (75,5 градусов), то она располагалась бы в два раза дальше (4 фута) от стены. Соотношение остается одинаковым для любого прямоугольного треугольника с углом 75,5 градусов.) Если мы измерим точку на стене, где лестница соприкасается (o — напротив), расстояние составит 7,745 фута. Вы можете проверить это расстояние, используя Теорему Пифагора , которая связывает стороны прямоугольного треугольника: 92 = 64 – 4 = 60
Вы можете проверить это расстояние, используя Теорему Пифагора , которая связывает стороны прямоугольного треугольника: 92 = 64 – 4 = 60 Математики называют эту ситуацию функцией. Отношение прилежащего катета к гипотенузе зависит от угла c , поэтому мы можем записать символ как cos(c) = value .
Математики называют эту ситуацию функцией. Отношение прилежащего катета к гипотенузе зависит от угла c , поэтому мы можем записать символ как cos(c) = value .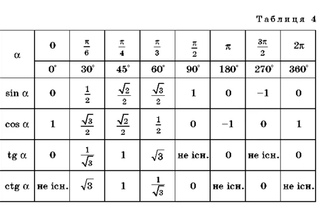 Позже, если мы знаем значение угла в прямоугольном треугольнике, таблицы сообщают нам отношение сторон треугольника. Если мы знаем длину любой стороны, мы можем найти длину других сторон. Или, если мы знаем отношение любых двух сторон прямоугольного треугольника, мы можем найти значение угла между сторонами. Мы можем использовать таблицы для решения задач. Некоторые примеры задач, связанных с треугольниками и углами, включают спуск планера, крутящий момент на шарнире, работу балансиров подъемной силы и лобового сопротивления братьев Райт, а также определение отношения подъемной силы к лобовому сопротивлению для самолета.
Позже, если мы знаем значение угла в прямоугольном треугольнике, таблицы сообщают нам отношение сторон треугольника. Если мы знаем длину любой стороны, мы можем найти длину других сторон. Или, если мы знаем отношение любых двух сторон прямоугольного треугольника, мы можем найти значение угла между сторонами. Мы можем использовать таблицы для решения задач. Некоторые примеры задач, связанных с треугольниками и углами, включают спуск планера, крутящий момент на шарнире, работу балансиров подъемной силы и лобового сопротивления братьев Райт, а также определение отношения подъемной силы к лобовому сопротивлению для самолета.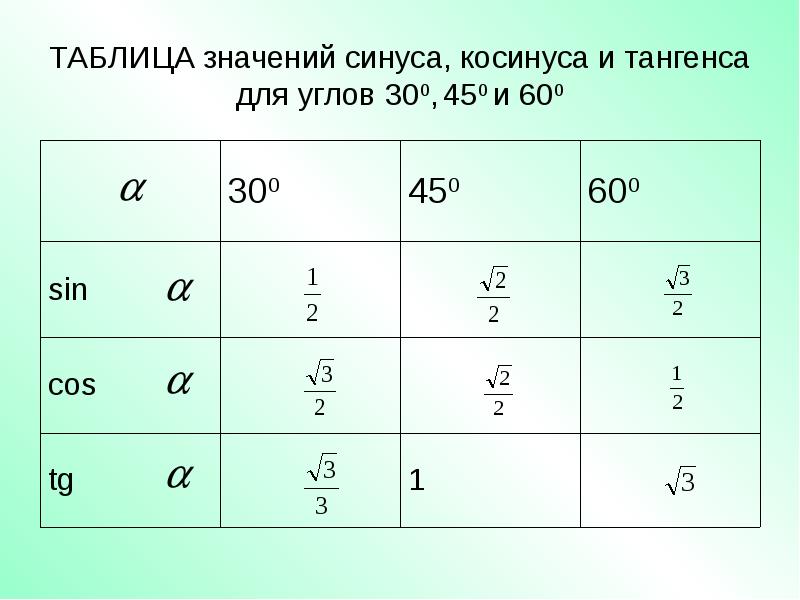 в ваш мозг, пока он не готов взорваться. А потом вы столкнулись с проблемой физики. Тот, который требует от вас знания синуса или косинуса? – 60 градусов.
в ваш мозг, пока он не готов взорваться. А потом вы столкнулись с проблемой физики. Тот, который требует от вас знания синуса или косинуса? – 60 градусов.  Если учащиеся что-нибудь помнят о тригонометрии, то это, вероятно, SOH CAH TOA (см. ниже), что напоминает нам о том, что синус (S) угла равен длине противоположной стороны треугольника (O), деленной на гипотенузу (H ), косинус (C) угла равен прилежащей стороне (A), деленной на гипотенузу (H), а тангенс (T) равен противолежащей стороне (O), деленной на прилежащую сторону (A).
Если учащиеся что-нибудь помнят о тригонометрии, то это, вероятно, SOH CAH TOA (см. ниже), что напоминает нам о том, что синус (S) угла равен длине противоположной стороны треугольника (O), деленной на гипотенузу (H ), косинус (C) угла равен прилежащей стороне (A), деленной на гипотенузу (H), а тангенс (T) равен противолежащей стороне (O), деленной на прилежащую сторону (A).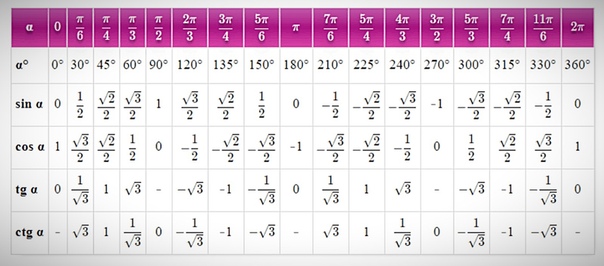
 ≈ 0,7 и ≈ 0,9.
≈ 0,7 и ≈ 0,9. 




 . (Зима) Слайд №1
. (Зима) Слайд №1 найди сумму чисел 6и 8 (14)
найди сумму чисел 6и 8 (14) Введение в тему урока. Работа в группах (по рядам)
Введение в тему урока. Работа в группах (по рядам) (Решение уравнений и задач) Открываю тему.
(Решение уравнений и задач) Открываю тему. (Можно найти значение Х, при котором равенство будет верным)
(Можно найти значение Х, при котором равенство будет верным) (решил самостоятельно, без помощи учителя и класса, поэтому ставлю себе 5)
(решил самостоятельно, без помощи учителя и класса, поэтому ставлю себе 5) (Некоторые ученики работают по карточкам) Слайд №10
(Некоторые ученики работают по карточкам) Слайд №10 82 №3 (1)
82 №3 (1) Самооценка
Самооценка Рефлексия деятельности на уроке. Слайд №15 (белый)
Рефлексия деятельности на уроке. Слайд №15 (белый) .(себя оценить, составлять самому уравнения)
.(себя оценить, составлять самому уравнения) .(получил хорошую отметку,)
.(получил хорошую отметку,) В. Дорофеева
В. Дорофеева
 Решите уравнение (на доске)!!!!! Найди ошибку???? (7 слайд)
Решите уравнение (на доске)!!!!! Найди ошибку???? (7 слайд)



 Часто требуется немного практики, чтобы преобразовать английское предложение в математическое предложение, что является одним из первых шагов к решению текстовых задач. В приведенной ниже таблице слова или фразы, обычно связанные с математическими операторами, распределены по категориям. Текстовые задачи часто содержат эти или похожие слова, поэтому полезно посмотреть, какие математические операторы с ними связаны.
Часто требуется немного практики, чтобы преобразовать английское предложение в математическое предложение, что является одним из первых шагов к решению текстовых задач. В приведенной ниже таблице слова или фразы, обычно связанные с математическими операторами, распределены по категориям. Текстовые задачи часто содержат эти или похожие слова, поэтому полезно посмотреть, какие математические операторы с ними связаны. Обратите внимание, что 9 стоит первым в предложении, а выражение
Обратите внимание, что 9 стоит первым в предложении, а выражение



 Рекорд среди мужчин на той же трассе был установлен в 1994 Тома Джонсона, завершившего дистанцию со временем 5:33:21. [2]
Рекорд среди мужчин на той же трассе был установлен в 1994 Тома Джонсона, завершившего дистанцию со временем 5:33:21. [2]  Теперь, когда мы знаем скорость каждого бегуна, мы можем ответить на вопросы об отдельных дистанциях или времени.
Теперь, когда мы знаем скорость каждого бегуна, мы можем ответить на вопросы об отдельных дистанциях или времени. T , обычно измеряется в месяцах), что деньги остаются на счете. Сумма, заработанная с течением времени, называется процентами ( I ), которые затем передаются покупателю.
T , обычно измеряется в месяцах), что деньги остаются на счете. Сумма, заработанная с течением времени, называется процентами ( I ), которые затем передаются покупателю.

 Например, рассмотрим прямоугольник с длиной 8 и шириной 3. В прямоугольнике две длины и две ширины (противоположные стороны), поэтому мы добавляем [латекс]8+8+3+3=22[/латекс ]. Поскольку в прямоугольнике две длины и две ширины, периметр прямоугольника можно найти по формуле [латекс]{P}=2\left({L}\right)+2\left({W}\right )[/латекс], где
Например, рассмотрим прямоугольник с длиной 8 и шириной 3. В прямоугольнике две длины и две ширины (противоположные стороны), поэтому мы добавляем [латекс]8+8+3+3=22[/латекс ]. Поскольку в прямоугольнике две длины и две ширины, периметр прямоугольника можно найти по формуле [латекс]{P}=2\left({L}\right)+2\left({W}\right )[/латекс], где В следующем примере показано, как изолировать переменную в формуле перед заменой известных размеров или значений в формулу.
В следующем примере показано, как изолировать переменную в формуле перед заменой известных размеров или значений в формулу. {2}[/латекс], через высоту, ч .
{2}[/латекс], через высоту, ч . Для этого разделите обе части на , чтобы получить . Важно понимать, что вопрос касается не значения , а скорее значения выражения . Чтобы найти этот ответ, подключите и выражение будет выглядеть так . Затем это равно , что дает правильный ответ .
Для этого разделите обе части на , чтобы получить . Важно понимать, что вопрос касается не значения , а скорее значения выражения . Чтобы найти этот ответ, подключите и выражение будет выглядеть так . Затем это равно , что дает правильный ответ . Для этого возьмите и разделите обе части на . Это оставляет вас с . Конечно, вопрос касается не значения , а значения . Итак, подключитесь , и выражение будет выглядеть так: что есть . Это упрощает , давая вам окончательный ответ.
Для этого возьмите и разделите обе части на . Это оставляет вас с . Конечно, вопрос касается не значения , а значения . Итак, подключитесь , и выражение будет выглядеть так: что есть . Это упрощает , давая вам окончательный ответ. В этом случае оба варианта одинаково хороши, и вы должны использовать тот метод, который наиболее удобен. Однако, как правило, решение напрямую является лучшим вариантом в разделе SAT без калькулятора.
В этом случае оба варианта одинаково хороши, и вы должны использовать тот метод, который наиболее удобен. Однако, как правило, решение напрямую является лучшим вариантом в разделе SAT без калькулятора. Ваше упрощенное уравнение должно выглядеть так:
Ваше упрощенное уравнение должно выглядеть так: Это дает вам:
Это дает вам:

 Убедившись, что траектория точки
М пересекает плоскость найти:
Убедившись, что траектория точки
М пересекает плоскость найти: 1
1



 2
2 в д&
в д&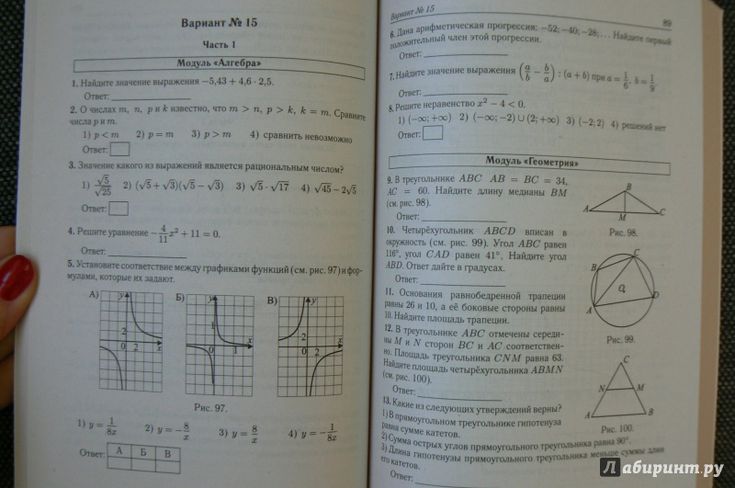 в.биркун
в.биркун ru. Хотите тоже свой сайт?
ru. Хотите тоже свой сайт? В книге рассматриваются прямоугольные декартовы координаты в трехмерном пространстве и деление интервала в заданном отношении. Примеры вопросов касаются задач, связанных с равнобедренными треугольниками, вершинами и центром тяжести равных масс. Книга определяет понятие вектора, а затем перечисляет проблемы, касающиеся закона треугольника и скалярного произведения двух векторов. Другие задачи сосредоточены на уравнениях поверхности и кривой и на вопросах, связанных с пересечением трех поверхностей. В тексте перечислены другие задачи, такие как уравнение плоскости, вектор направления прямой линии и различные задачи, относящиеся к уравнениям плоскости, прямой линии и сферы в векторе направления. Подборка полезна для преподавателей аналитической геометрии и других курсов физико-математических и общетехнических дисциплин.
В книге рассматриваются прямоугольные декартовы координаты в трехмерном пространстве и деление интервала в заданном отношении. Примеры вопросов касаются задач, связанных с равнобедренными треугольниками, вершинами и центром тяжести равных масс. Книга определяет понятие вектора, а затем перечисляет проблемы, касающиеся закона треугольника и скалярного произведения двух векторов. Другие задачи сосредоточены на уравнениях поверхности и кривой и на вопросах, связанных с пересечением трех поверхностей. В тексте перечислены другие задачи, такие как уравнение плоскости, вектор направления прямой линии и различные задачи, относящиеся к уравнениям плоскости, прямой линии и сферы в векторе направления. Подборка полезна для преподавателей аналитической геометрии и других курсов физико-математических и общетехнических дисциплин. Элементарные задачи трехмерной аналитической геометрии
Элементарные задачи трехмерной аналитической геометрии  Уравнение плоскости через ее пересечения с осями координат
Уравнение плоскости через ее пересечения с осями координат  В.
В. В книге обсуждаются элементарные задачи плоской аналитической геометрии. Текст представляет темы на оси и интервалы на оси и координаты на прямой линии. Книга также определяет, что такое прямоугольные декартовы координаты на плоскости, деление интервала в заданном отношении и показывает, как вычислить площадь треугольника. Уравнение кривой, функции двух переменных и понятие уравнения кривой объясняются на примерах и задачах. Автор также обращается к геометрическим свойствам кривых второго порядка, уравнениям прямой, окружности, эллипса, гиперболы и параболы. Затем в тексте обсуждается общая теория кривых второго порядка с упором на уравнения центральных кривых второго порядка. Автор цитирует упрощение этих уравнений как применимое к теоретической механике. Этот сборник задач может быть использован учителями аналитической геометрии и их учениками.
В книге обсуждаются элементарные задачи плоской аналитической геометрии. Текст представляет темы на оси и интервалы на оси и координаты на прямой линии. Книга также определяет, что такое прямоугольные декартовы координаты на плоскости, деление интервала в заданном отношении и показывает, как вычислить площадь треугольника. Уравнение кривой, функции двух переменных и понятие уравнения кривой объясняются на примерах и задачах. Автор также обращается к геометрическим свойствам кривых второго порядка, уравнениям прямой, окружности, эллипса, гиперболы и параболы. Затем в тексте обсуждается общая теория кривых второго порядка с упором на уравнения центральных кривых второго порядка. Автор цитирует упрощение этих уравнений как применимое к теоретической механике. Этот сборник задач может быть использован учителями аналитической геометрии и их учениками. Аналитическая геометрия на плоскости
Аналитическая геометрия на плоскости  Уравнение прямой через ее пересечения на осях. Совместность уравнений двух и трех прямых
Уравнение прямой через ее пересечения на осях. Совместность уравнений двух и трех прямых 
 Иногда совершить такие действия в уме очень непросто, что приводит к получению неправильного и недостоверного ответа. Вычисление процента от числа при помощи онлайн калькулятора — это быстрый и точный результат моментально.
Иногда совершить такие действия в уме очень непросто, что приводит к получению неправильного и недостоверного ответа. Вычисление процента от числа при помощи онлайн калькулятора — это быстрый и точный результат моментально.

 д.
д. Это, без сомнения, один из самых полных инструментов, а также хороший инструмент для инженеров.
Это, без сомнения, один из самых полных инструментов, а также хороший инструмент для инженеров.
 Программа превращает ваш мобильный телефон Android в инструмент, способный выполнять практически любые вычисления, что делает ее одним из лучших решений для студентов начального и продвинутого уровней.
Программа превращает ваш мобильный телефон Android в инструмент, способный выполнять практически любые вычисления, что делает ее одним из лучших решений для студентов начального и продвинутого уровней.

 В свою очередь, для химиков он способен решать химические уравнения с одной или несколькими переменными.
В свою очередь, для химиков он способен решать химические уравнения с одной или несколькими переменными.
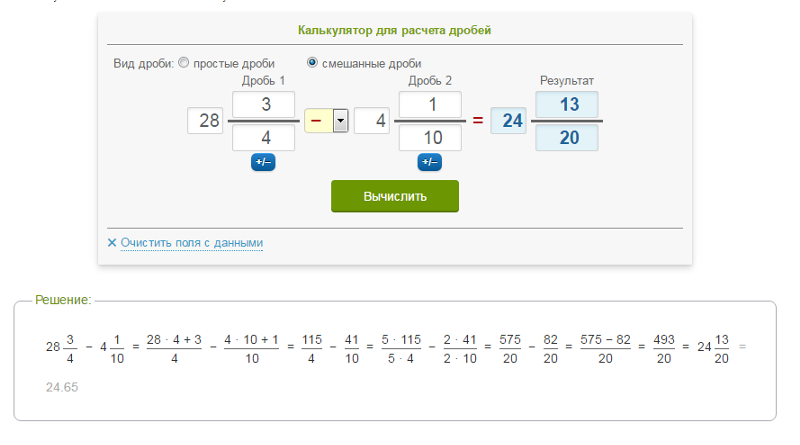
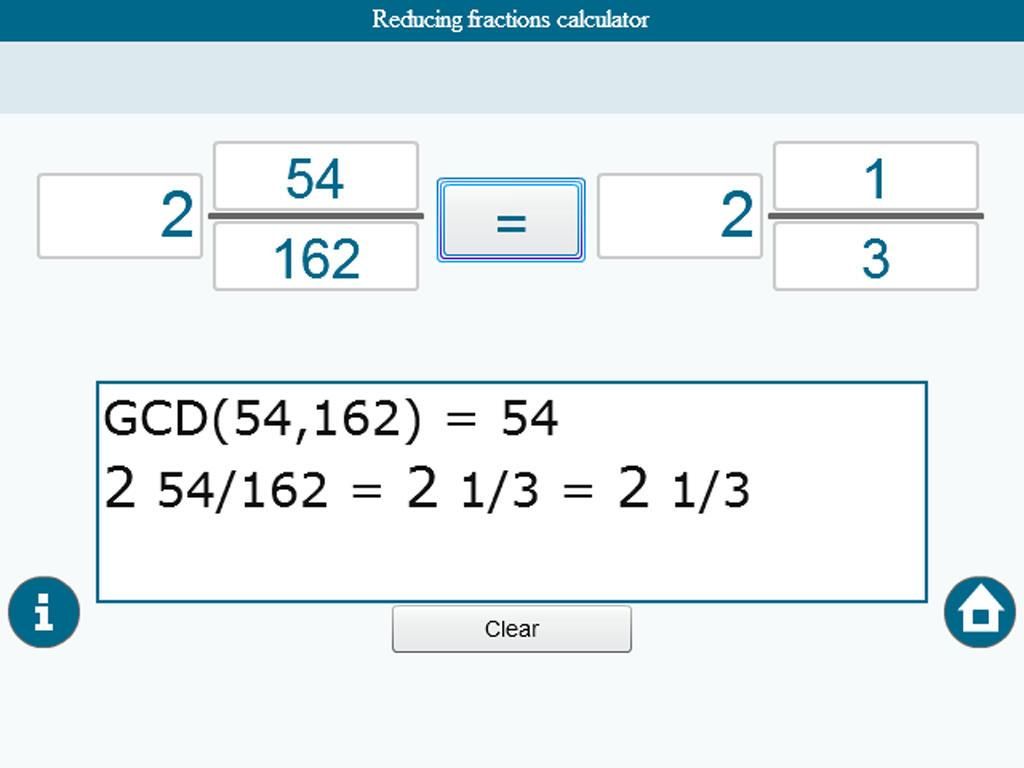
 Этот уникальный калькулятор решает задачи на дроби на лету и имеет множество применений.
Этот уникальный калькулятор решает задачи на дроби на лету и имеет множество применений.




 К дополнительным преимуществам платной версии относятся одновременное конвертирование нескольких файлов PPT или PPTX и неограниченный размер файлов.
К дополнительным преимуществам платной версии относятся одновременное конвертирование нескольких файлов PPT или PPTX и неограниченный размер файлов.
 Люди могут просматривать слайды, даже если у них нет PowerPoint, но они не могут вносить в них изменения.
Люди могут просматривать слайды, даже если у них нет PowerPoint, но они не могут вносить в них изменения.
 Сохраните презентацию в формате PDF
Сохраните презентацию в формате PDF Однако вы можете установить более высокое или более низкое качество печати PDF-файла.
Однако вы можете установить более высокое или более низкое качество печати PDF-файла.
 Благодаря нескольким полезным онлайн-инструментам, готовым к использованию, редактирование файлов никогда не было таким простым.
Благодаря нескольким полезным онлайн-инструментам, готовым к использованию, редактирование файлов никогда не было таким простым. Это сделано для борьбы с любым, кто может захотеть просмотреть ваши данные. Кроме того, мы не будем передавать или продавать ваши данные кому-либо еще.
Это сделано для борьбы с любым, кто может захотеть просмотреть ваши данные. Кроме того, мы не будем передавать или продавать ваши данные кому-либо еще.

 Если неверно, значит, набор S не соответствует первичному определению, следовательно, S Î S.
Если неверно, значит, набор S не соответствует первичному определению, следовательно, S Î S.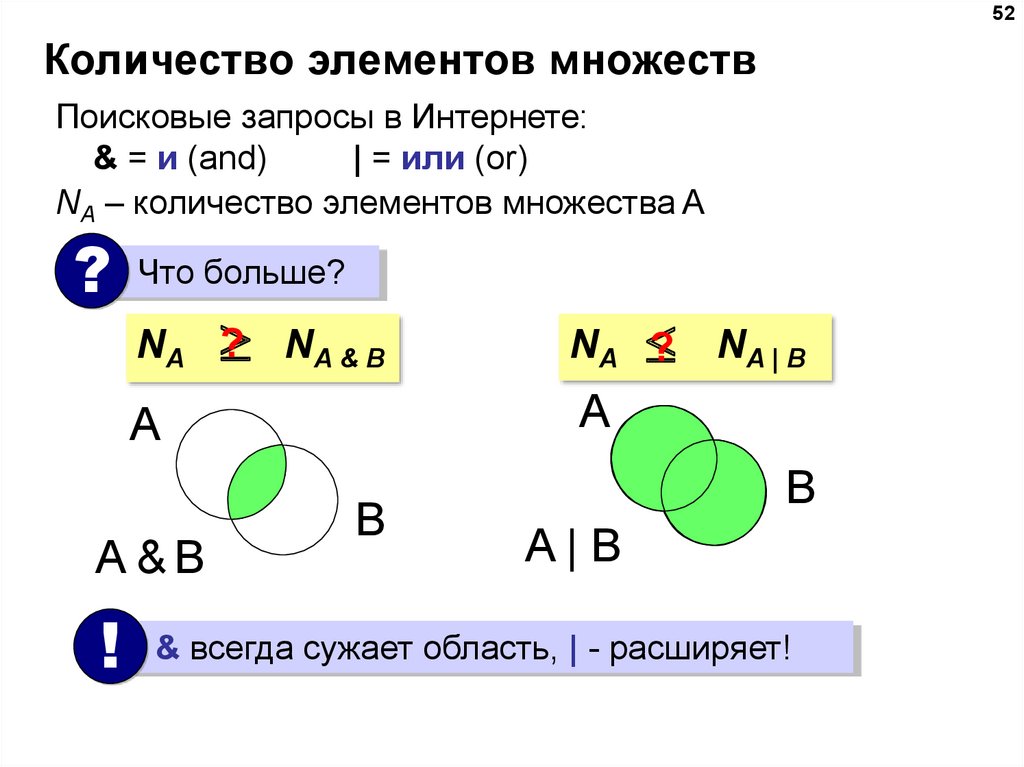 Это означает, что наш объект выглядит как А = {1, 2, 3, 4,}. Согласно формуле, для A существует 24 = 16 подмножества: 14 собственных и 2 несобственных. При помощи калькулятора рассчитаем эти составляющие. Мы получим:
Это означает, что наш объект выглядит как А = {1, 2, 3, 4,}. Согласно формуле, для A существует 24 = 16 подмножества: 14 собственных и 2 несобственных. При помощи калькулятора рассчитаем эти составляющие. Мы получим: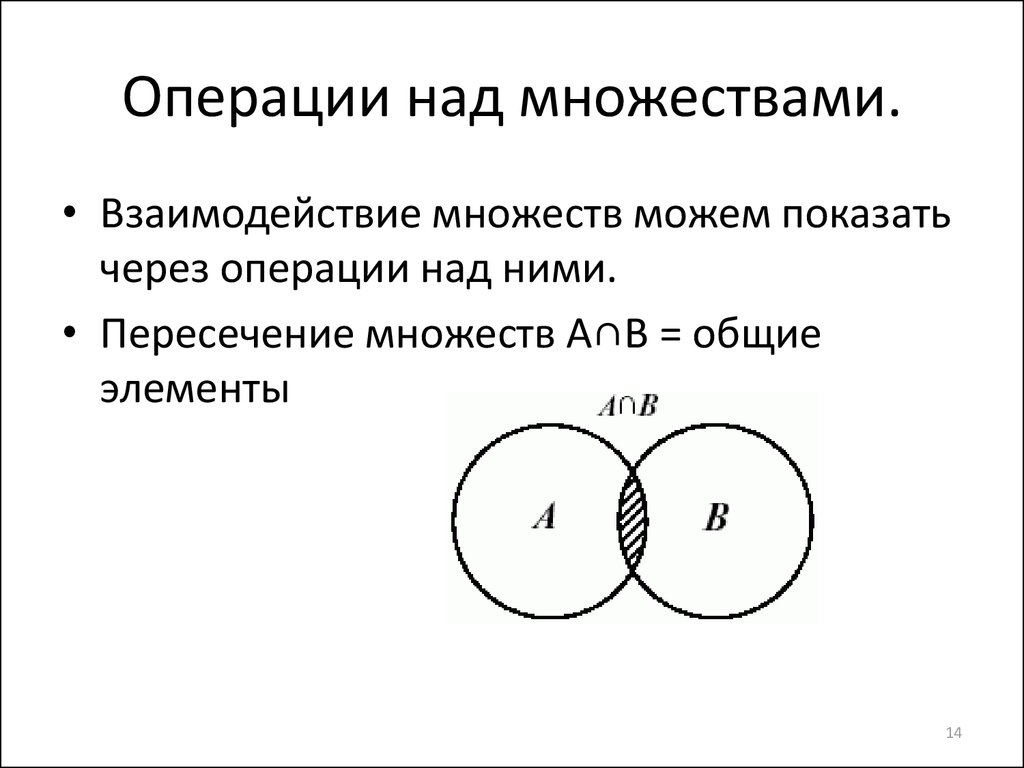
 Наивной его теория стала в результате образования нескольких логических парадоксов, которые были успешно решены при трансформации канторовской теории в аксиоматическую теорию множеств.
Наивной его теория стала в результате образования нескольких логических парадоксов, которые были успешно решены при трансформации канторовской теории в аксиоматическую теорию множеств.
 Однако это верно только для множеств с неразличимыми элементами, то есть для обычного набора чисел. Если же важен порядковый номер элементов множества, то результат противоположный и {3, 11} не является подмножеством {1, 3, 5, 7, 11, 13}.
Однако это верно только для множеств с неразличимыми элементами, то есть для обычного набора чисел. Если же важен порядковый номер элементов множества, то результат противоположный и {3, 11} не является подмножеством {1, 3, 5, 7, 11, 13}.

 В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов.
В химии любое вещество, которое нельзя разложить на более простые вещества с помощью обычных химических процессов. com
com Также этот калькулятор сообщает о подмножествах с определенным количеством элементов. Здесь мы объясним разницу между подмножеством и правильным подмножеством и как найти подмножества данного набора.
Также этот калькулятор сообщает о подмножествах с определенным количеством элементов. Здесь мы объясним разницу между подмножеством и правильным подмножеством и как найти подмножества данного набора.

 n\) 93 – 1$$
n\) 93 – 1$$


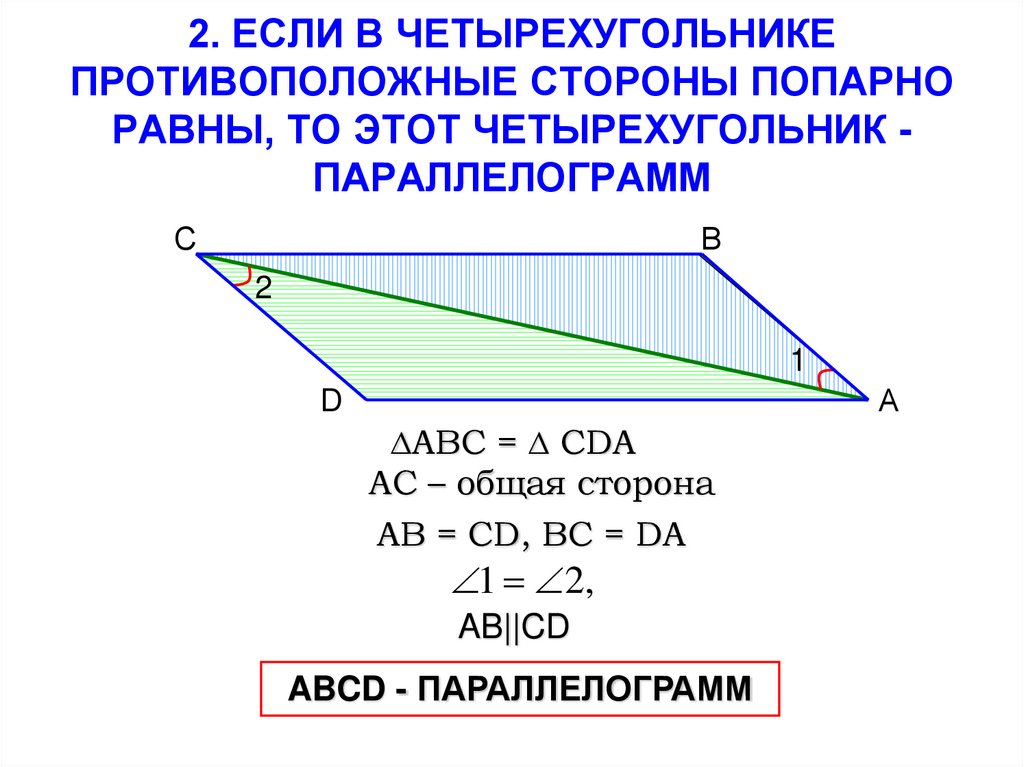
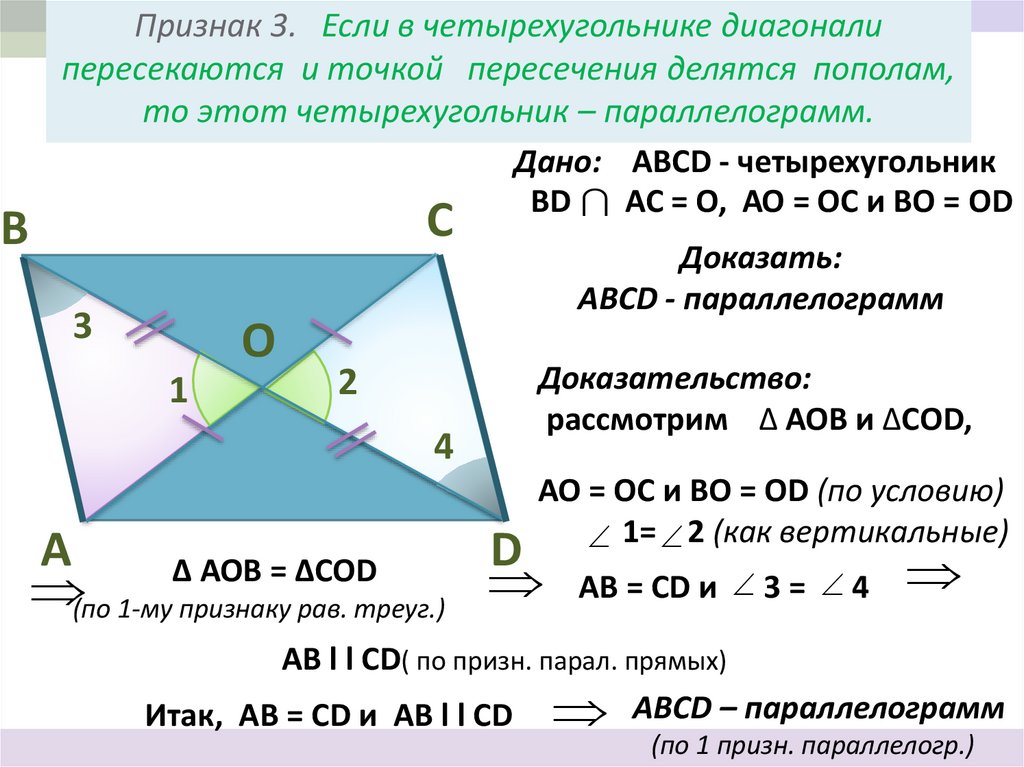 (2 признак равенства треугольников)
(2 признак равенства треугольников)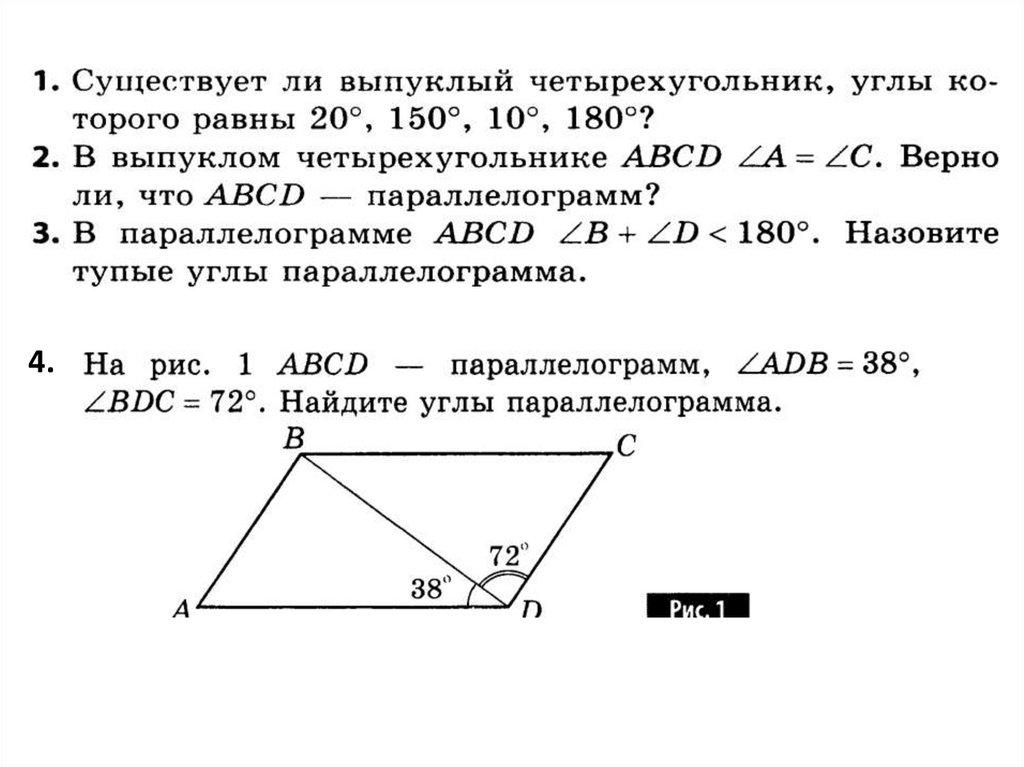
 (теорема косинусов).
(теорема косинусов).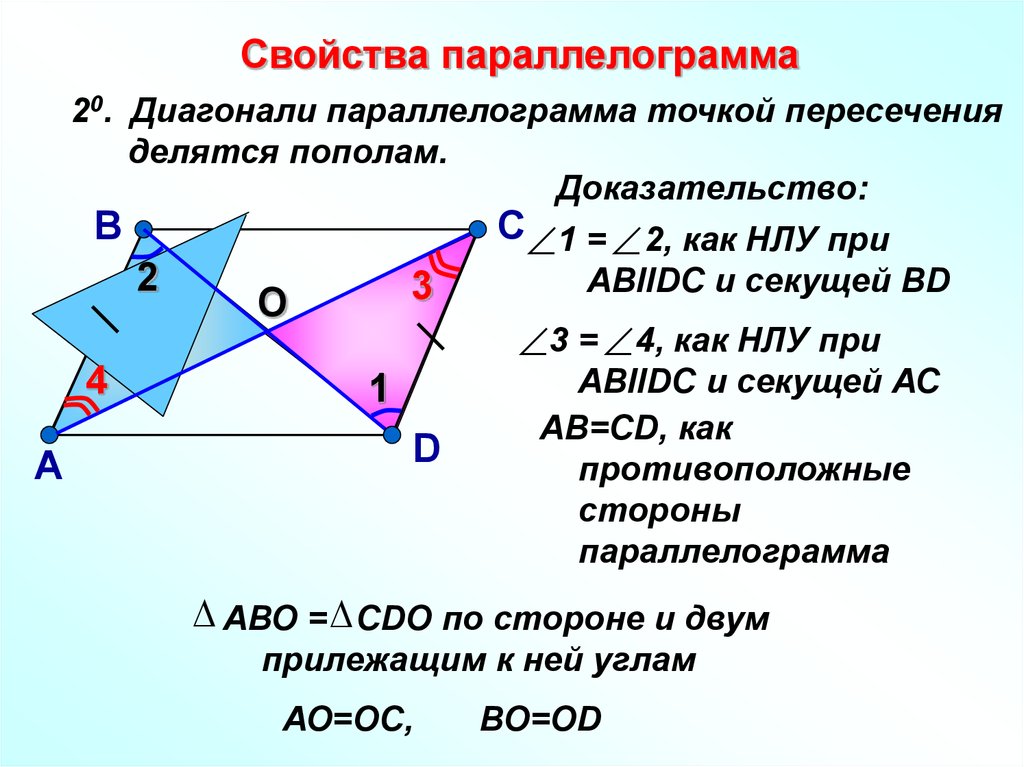




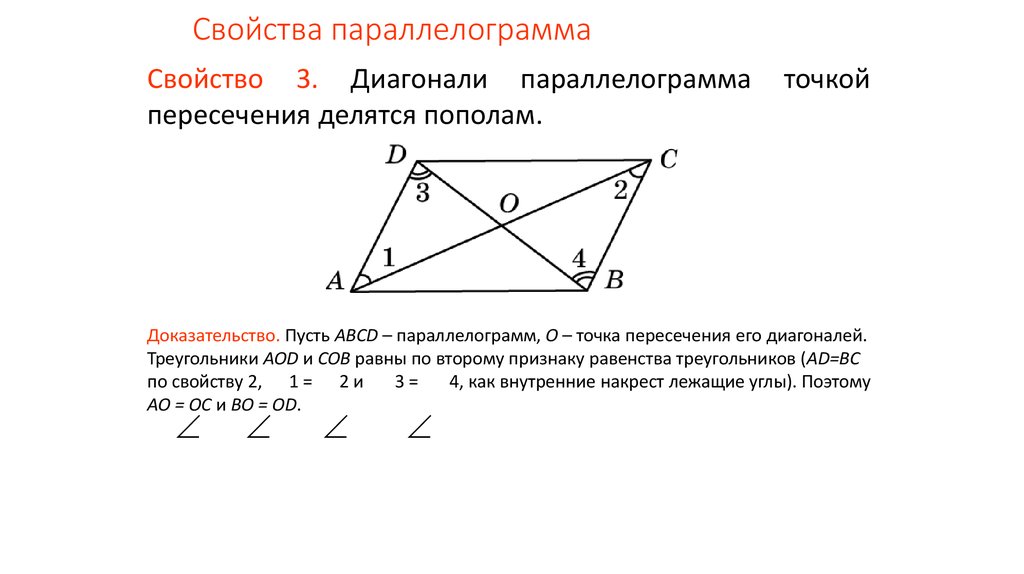 Если они при этом еще и перпендикулярны, то этот прямоугольник – квадрат).
Если они при этом еще и перпендикулярны, то этот прямоугольник – квадрат).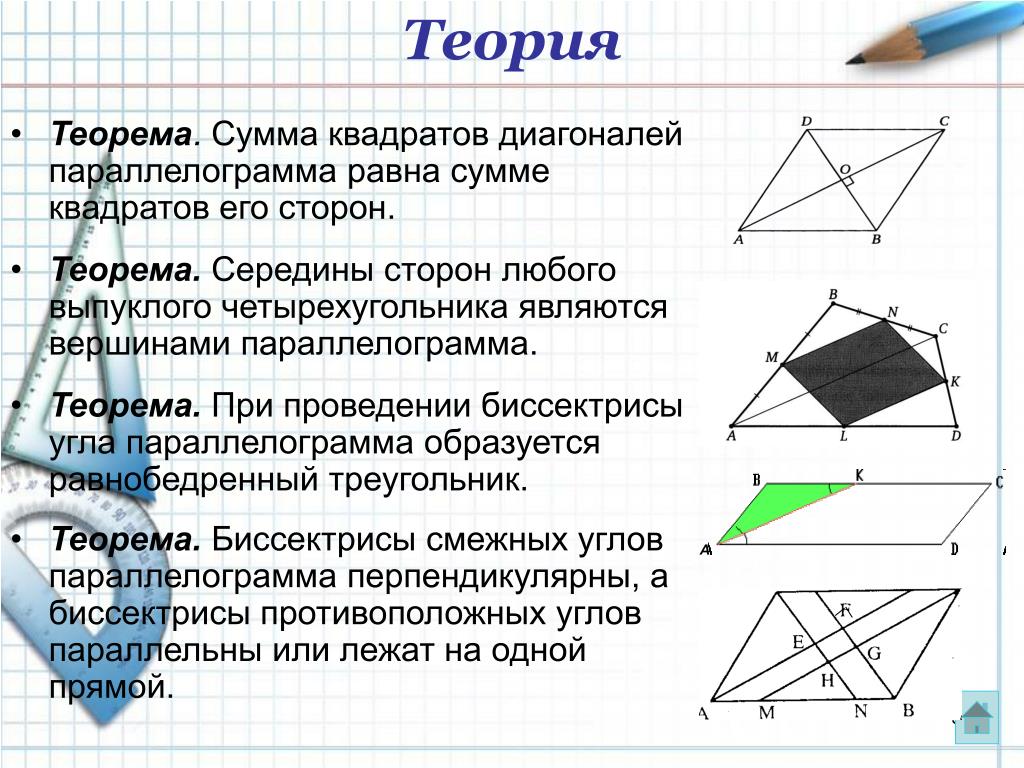


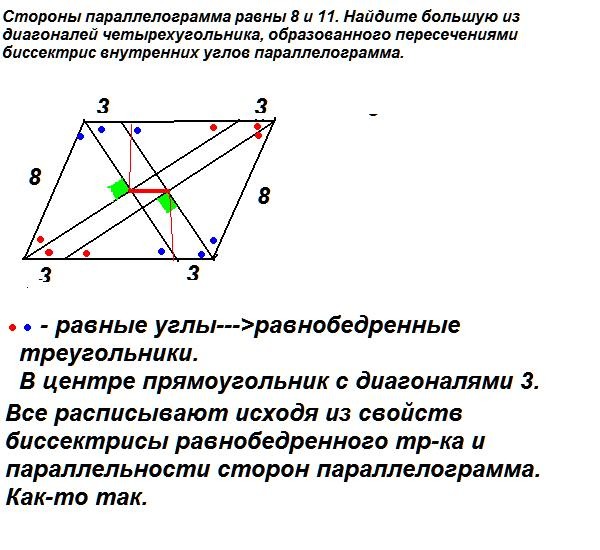 Если взять два произвольных равнобедренных треугольника, то три угла одного из них не обязательно будут соответственно равны трем углам другого).
Если взять два произвольных равнобедренных треугольника, то три угла одного из них не обязательно будут соответственно равны трем углам другого).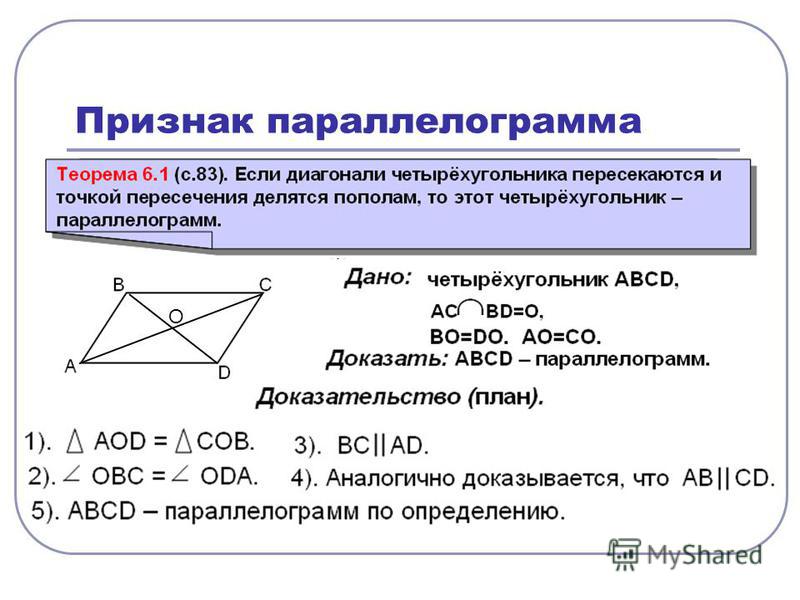

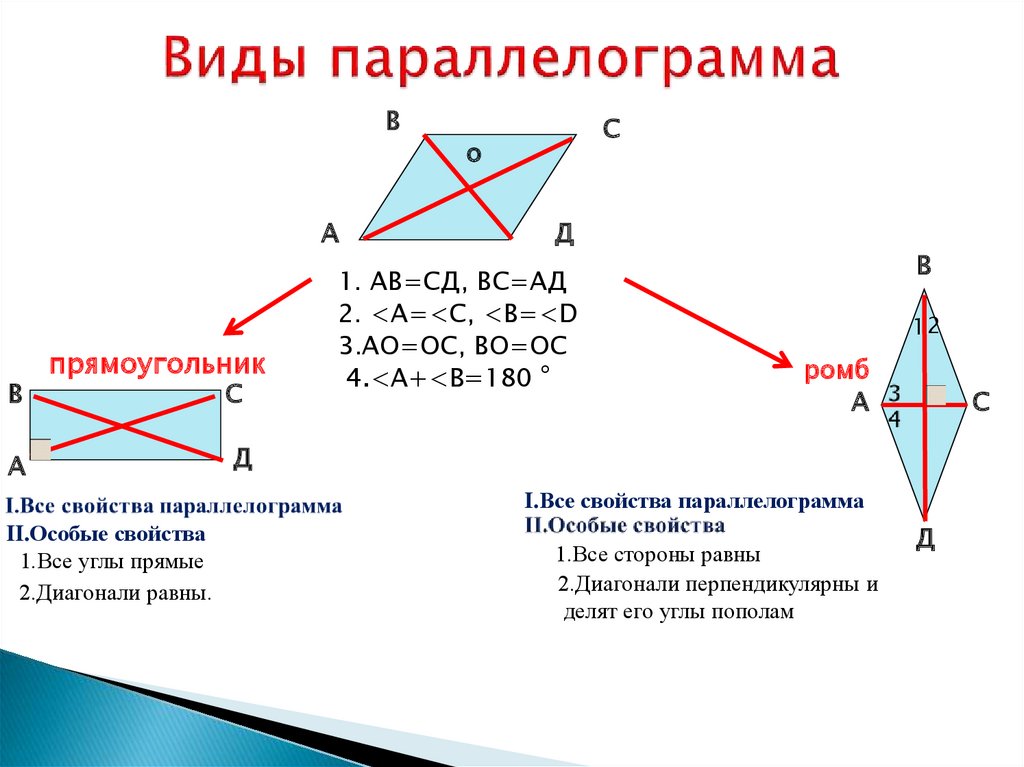



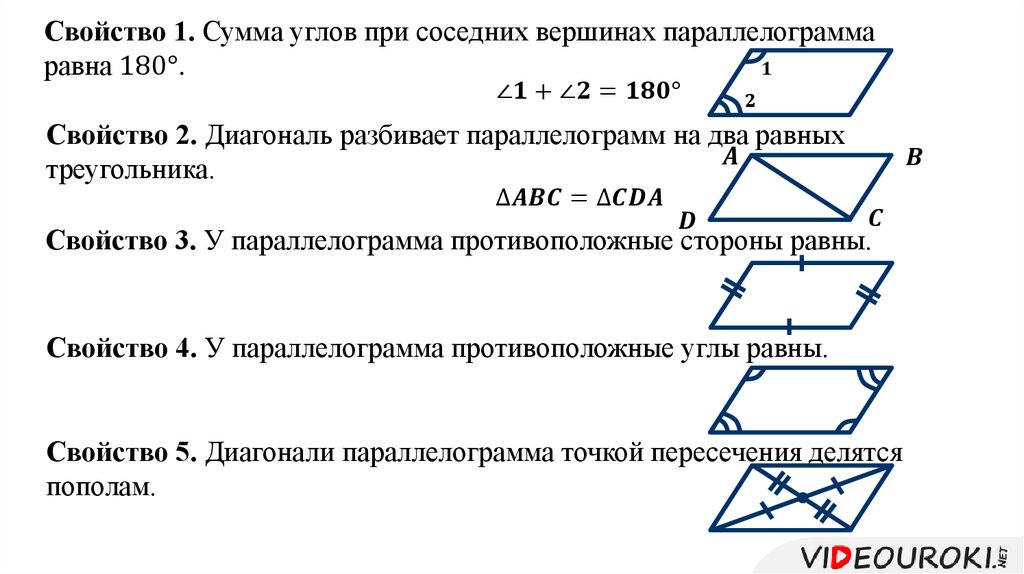
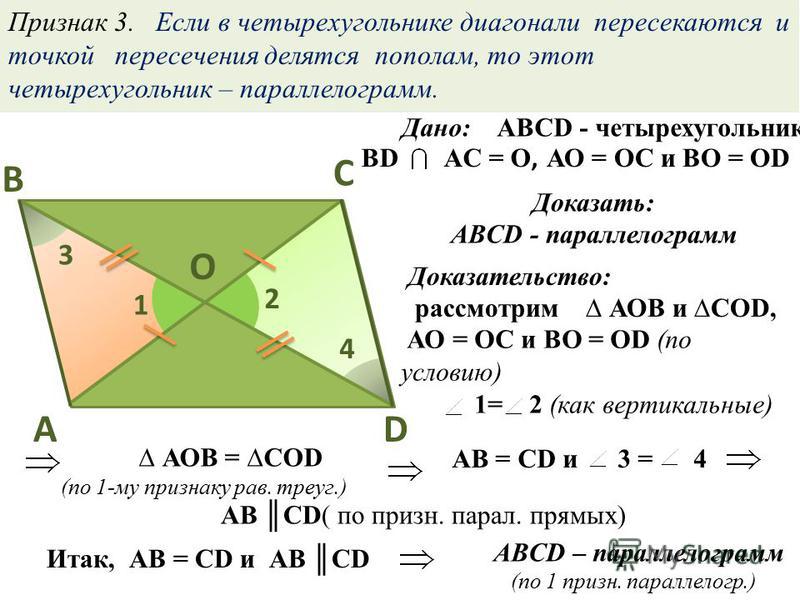
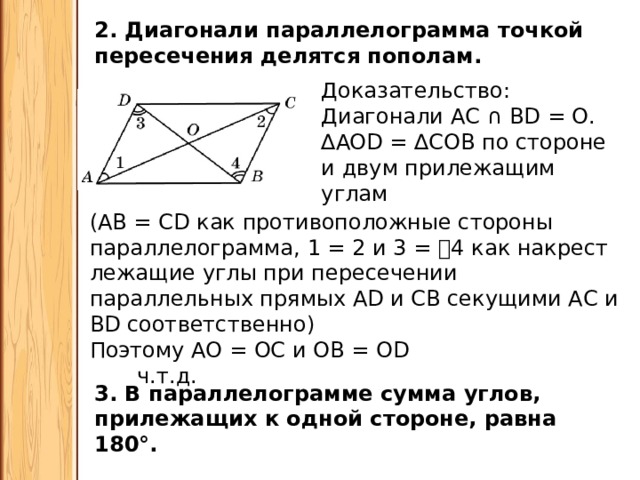 Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной.
Через точку, лежащую на этой прямой, можно провести только одну прямую перпендикулярную данной. 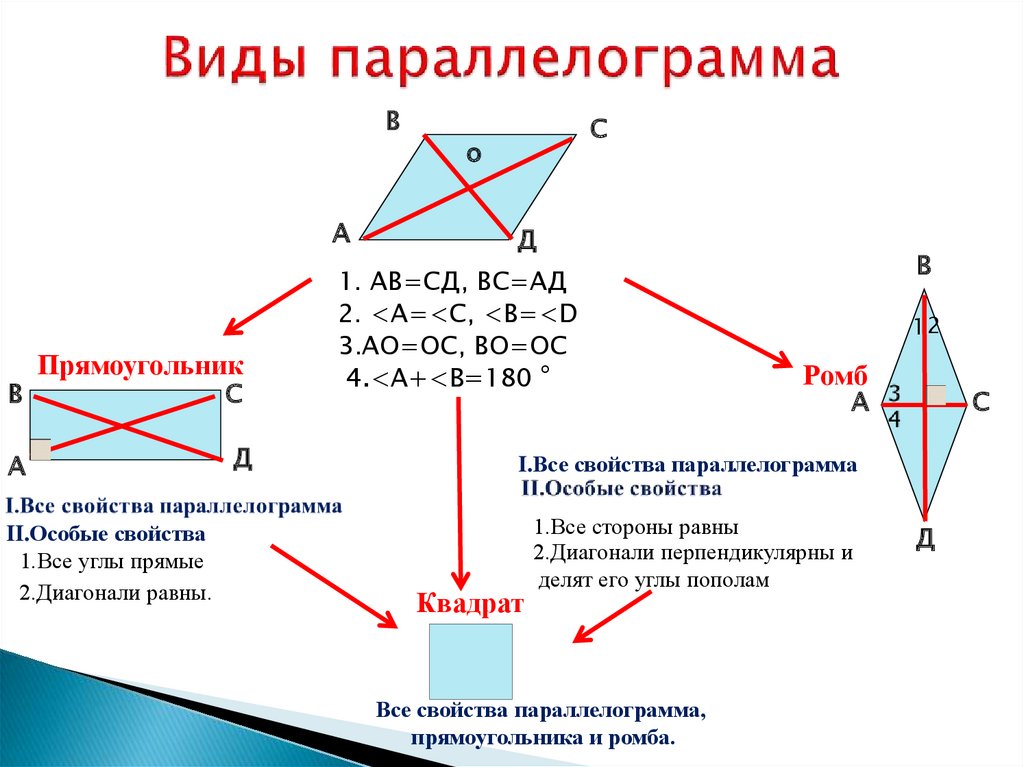

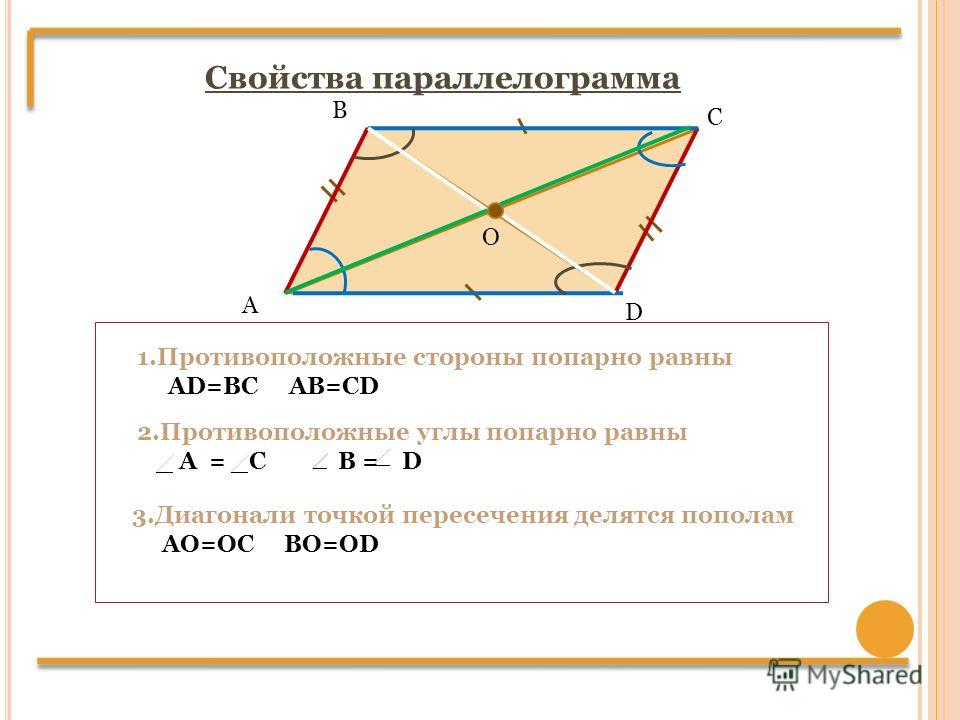

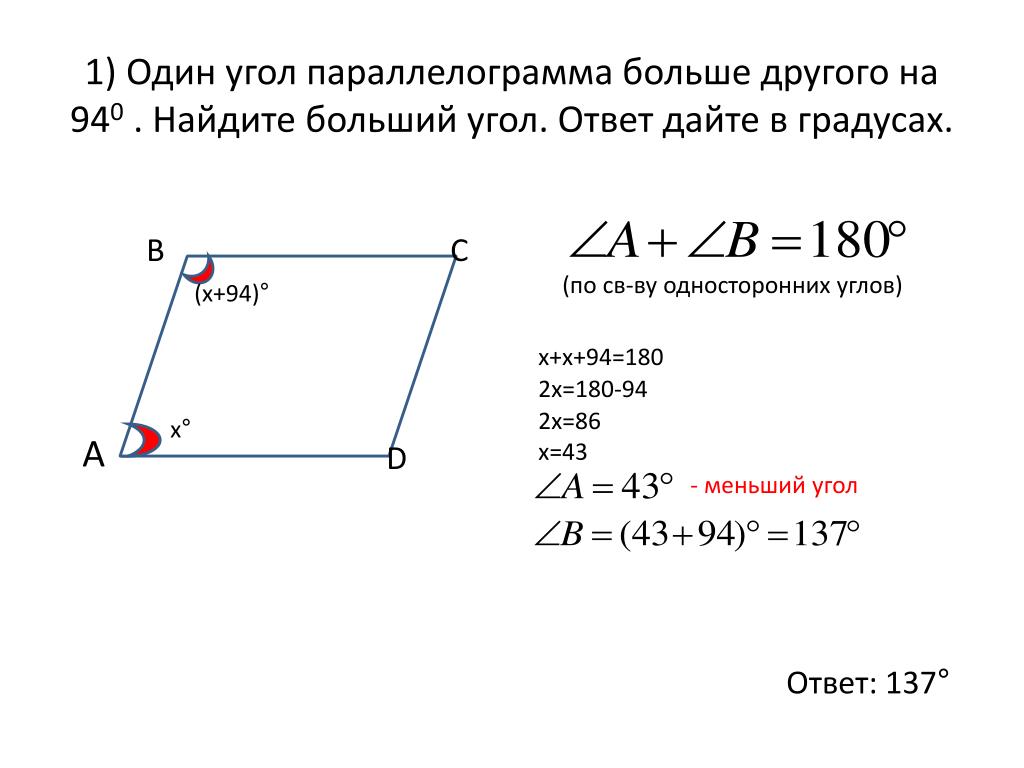

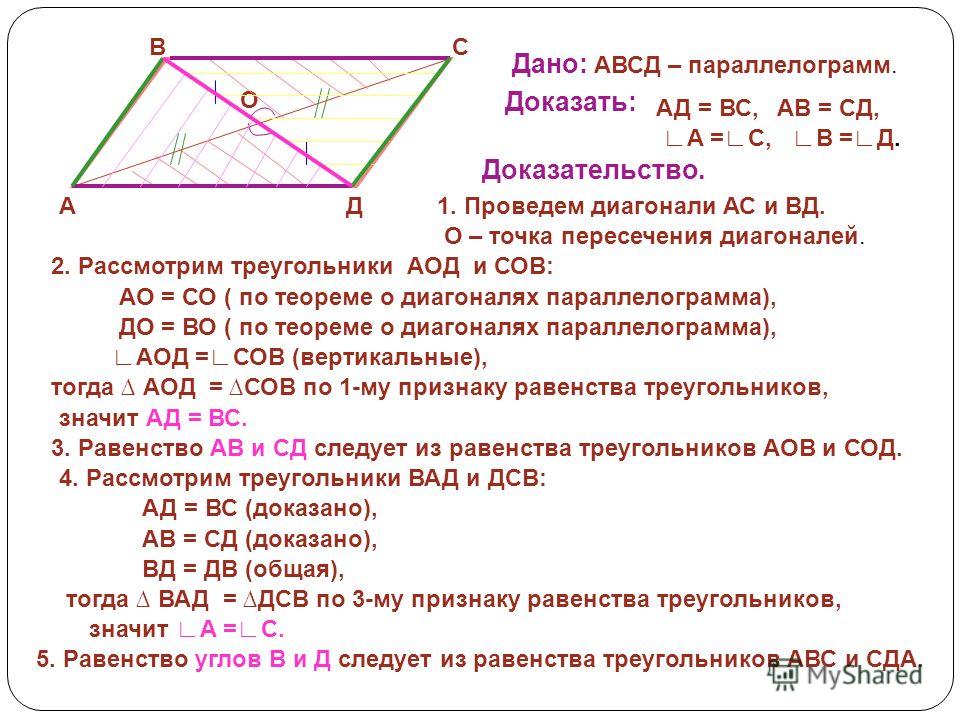
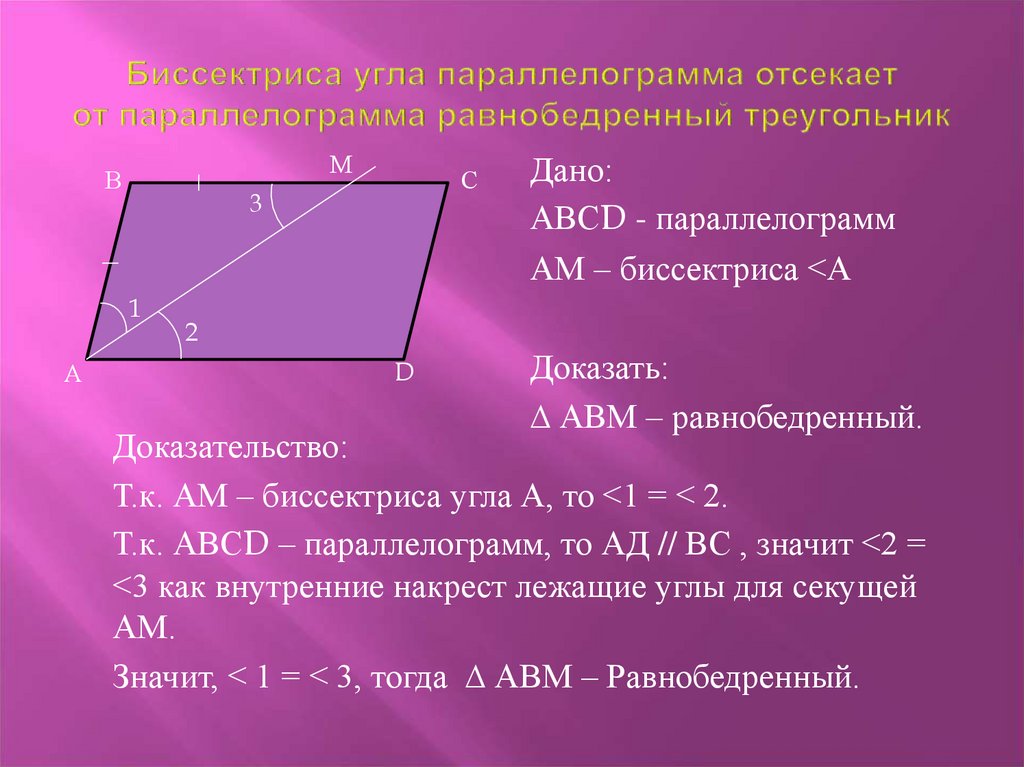


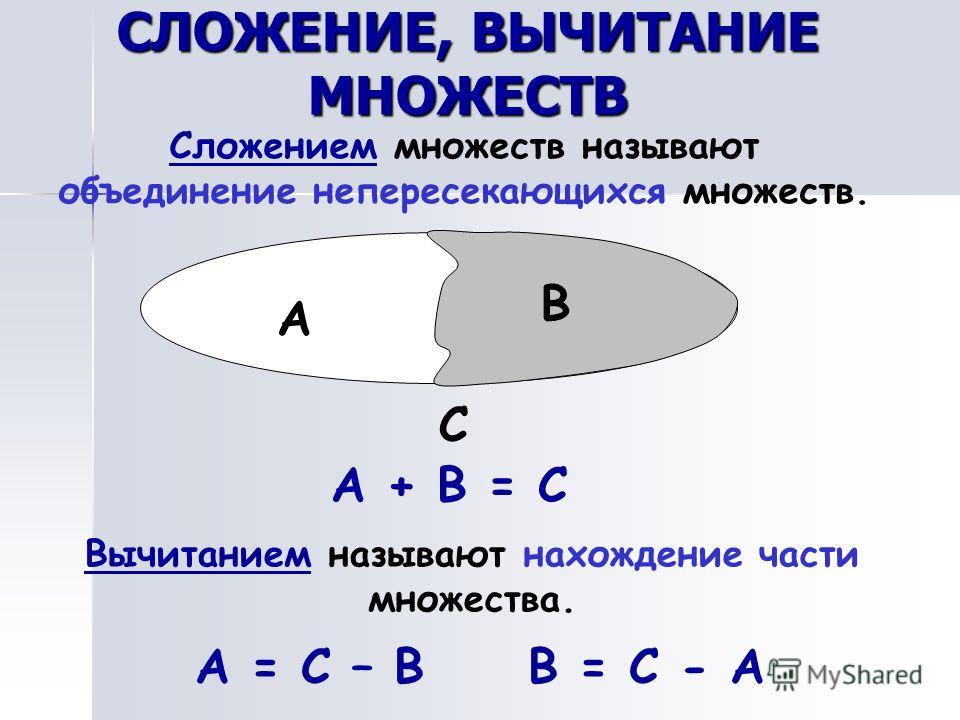
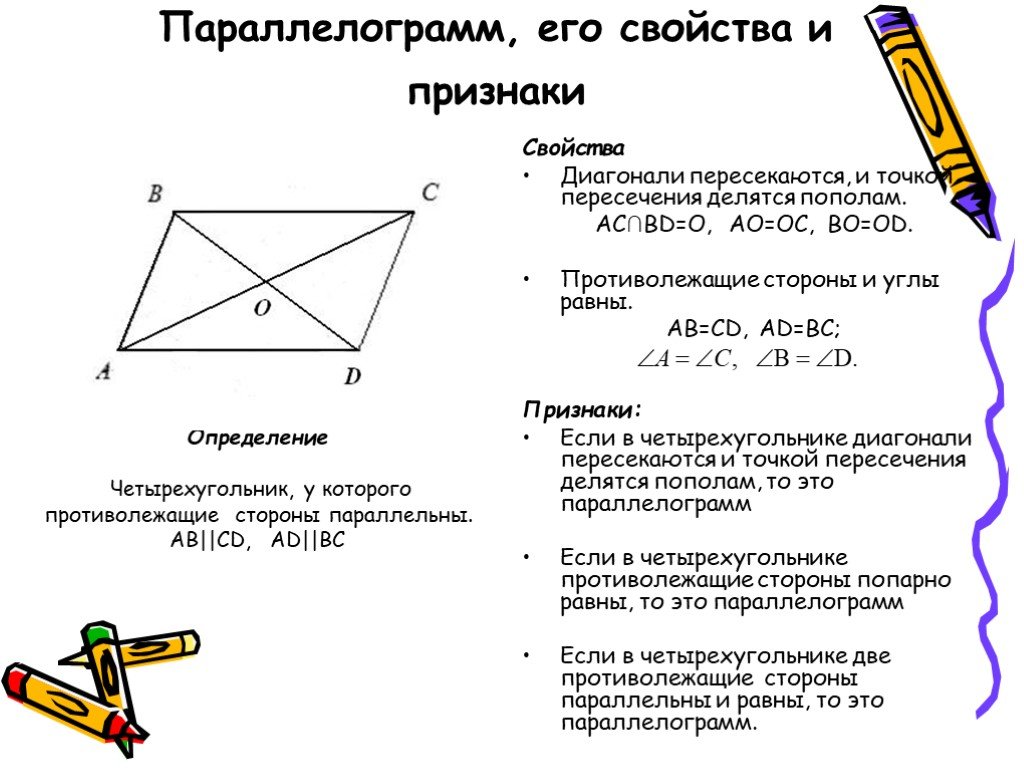
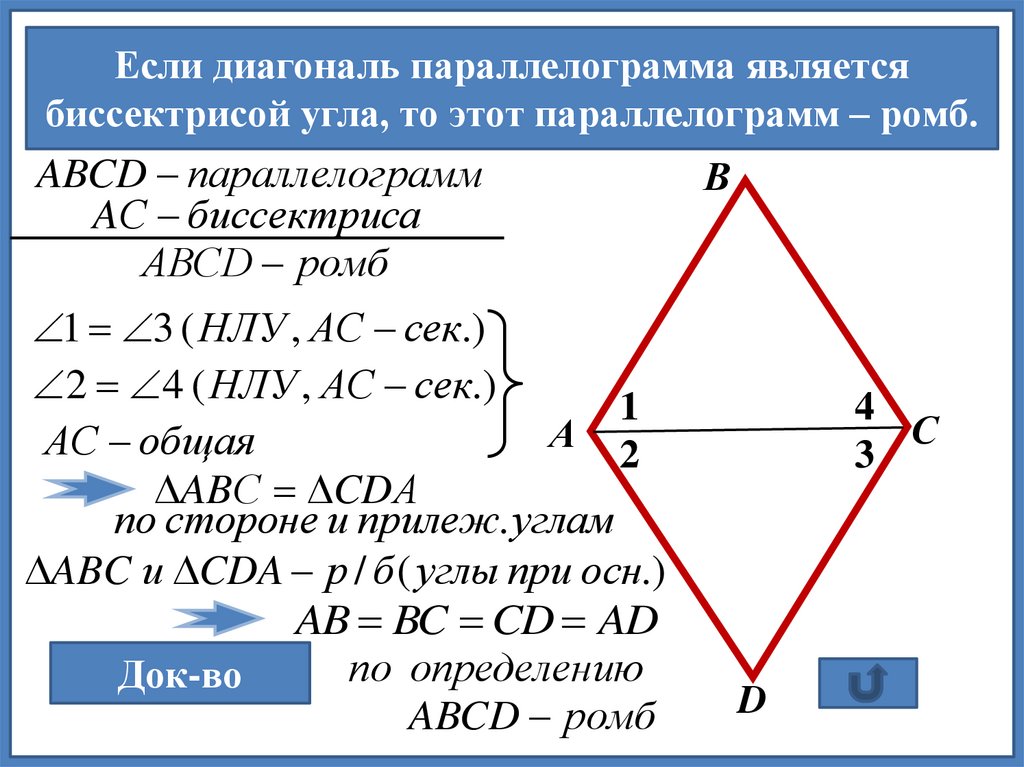 Какие из следующих утверждений верно?
Какие из следующих утверждений верно?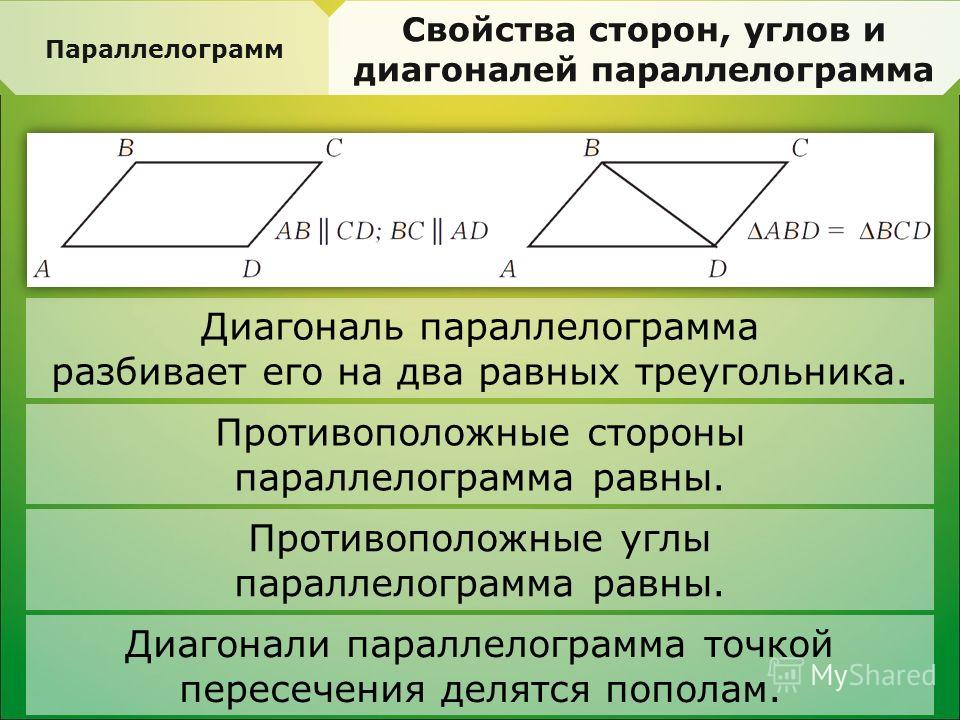 В параллелограмме диагонали пересекаются под прямым углом.
В любом четырехугольнике, если пара противоположных сторон равны, он является параллелограммом.
Если все углы четырехугольника равны, то это параллелограмм.
Если три стороны четырехугольника равны, то это параллелограмм.
Если три угла четырехугольника равны, то это параллелограмм.
Если все стороны четырехугольника равны, то это параллелограмм
В параллелограмме диагонали пересекаются под прямым углом.
В любом четырехугольнике, если пара противоположных сторон равны, он является параллелограммом.
Если все углы четырехугольника равны, то это параллелограмм.
Если три стороны четырехугольника равны, то это параллелограмм.
Если три угла четырехугольника равны, то это параллелограмм.
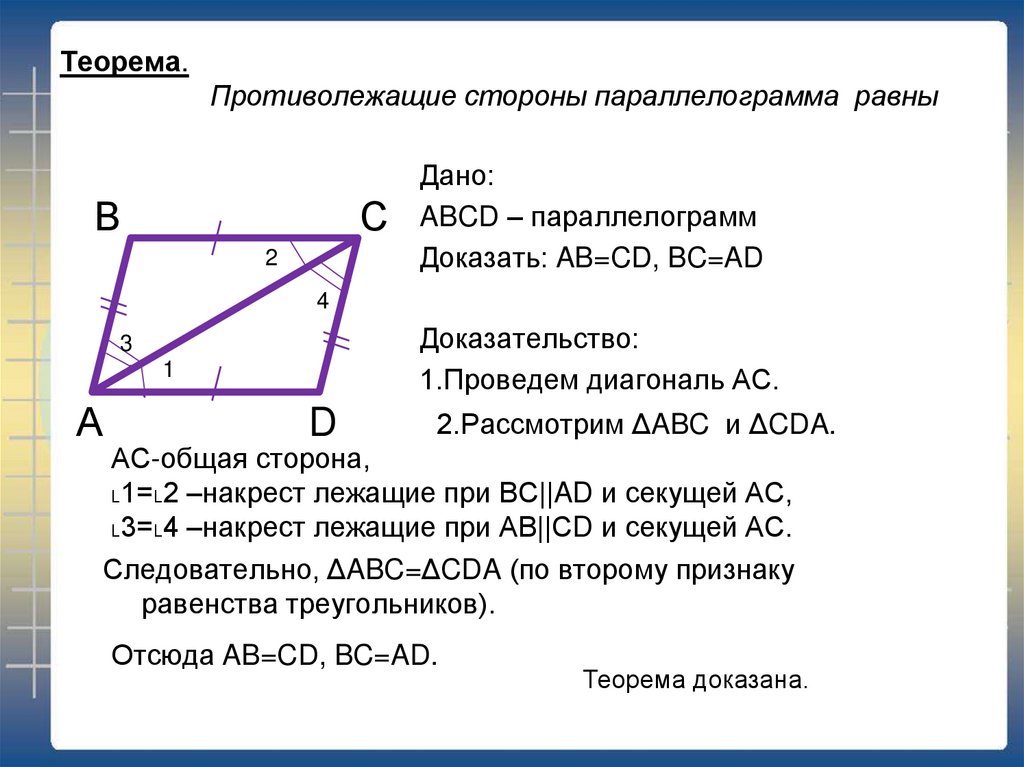
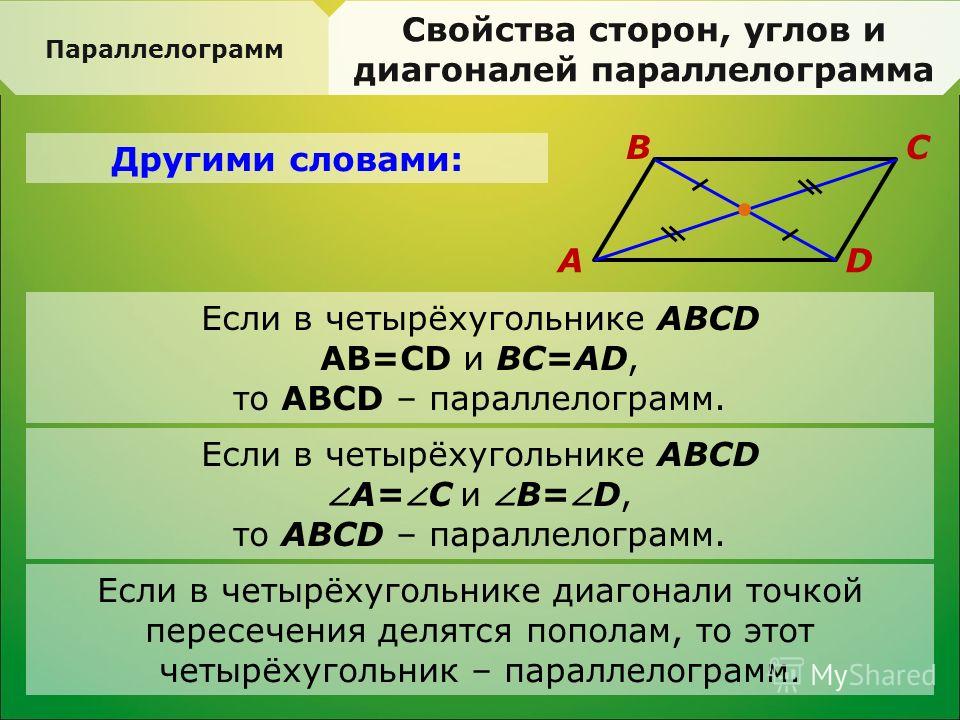
Если все стороны четырехугольника равны, то это параллелограмм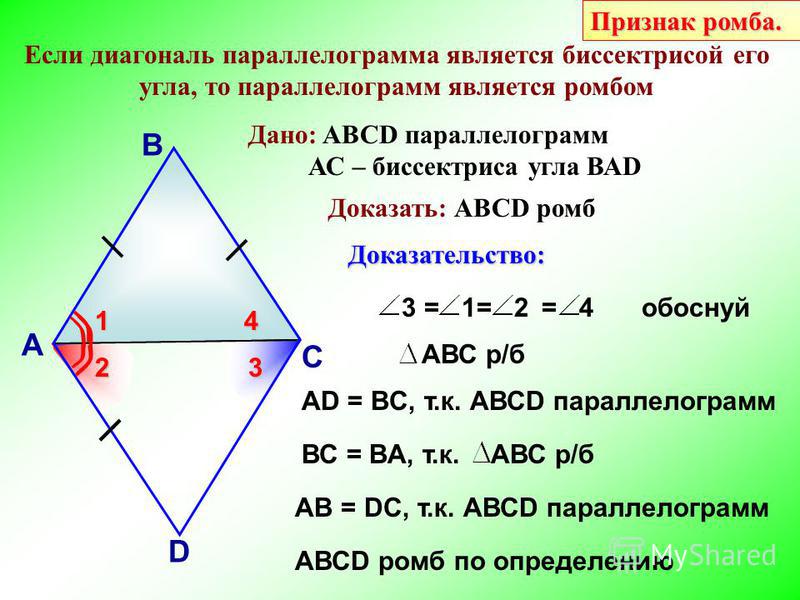 (vi) Ложь. Основным условием параллелограмма является параллельность сторон.
(vii) Ложь. Обе пары противоположных углов должны быть равны, чтобы четырехугольник можно было назвать параллелограммом.
(viii) Верно. Если все стороны равны, то равны и противоположные стороны.
(vi) Ложь. Основным условием параллелограмма является параллельность сторон.
(vii) Ложь. Обе пары противоположных углов должны быть равны, чтобы четырехугольник можно было назвать параллелограммом.
(viii) Верно. Если все стороны равны, то равны и противоположные стороны.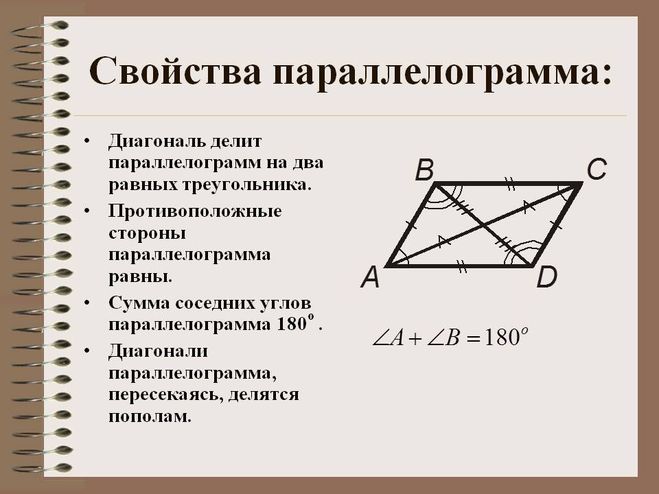
 नहीं करते हैं, तो चतुर्भुज एक समान्तर चतुर्भुह तो
नहीं करते हैं, तो चतुर्भुज एक समान्तर चतुर्भुह तो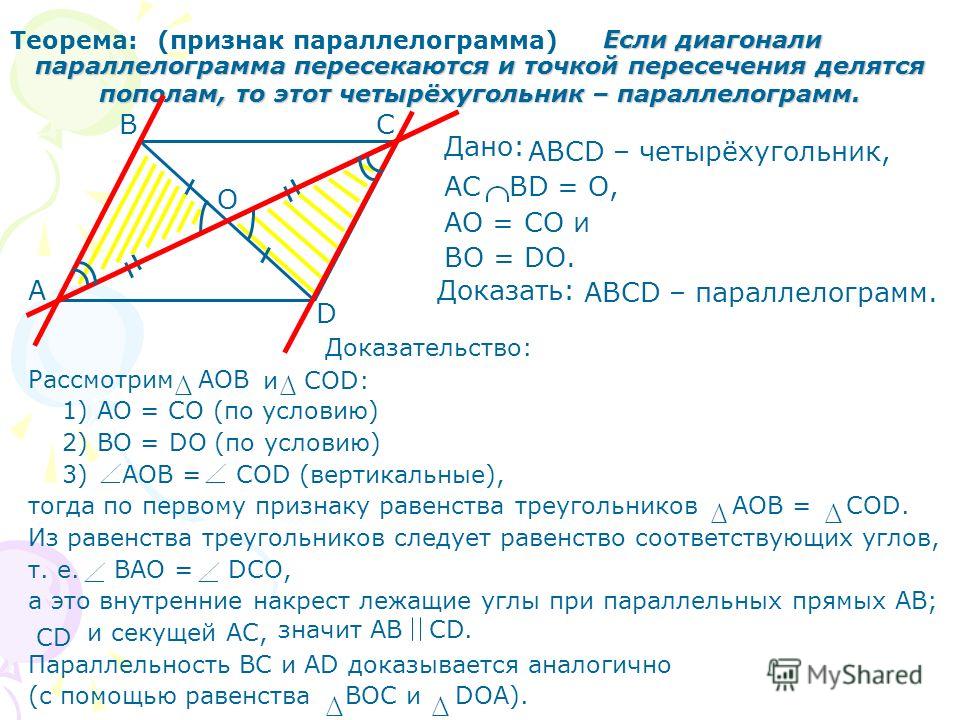



 Тогда
Тогда Примеры и описание
Примеры и описание Элементы отделяются точкой с запятой.
Элементы отделяются точкой с запятой.
 Перед
k-ым
слагаемым появляется коэффициент
(-1)
, если элементы матрицы
А
в произведении упорядочены по номеру строки, а количество инверсий в
k-ой
перестановке множества номеров столбцов нечетно.
Перед
k-ым
слагаемым появляется коэффициент
(-1)
, если элементы матрицы
А
в произведении упорядочены по номеру строки, а количество инверсий в
k-ой
перестановке множества номеров столбцов нечетно.  д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.
д. — это элементы матрицы. Теперь поясним, как были сформированы индексы у элементов, т.е. почему, например, есть слагаемое а11*а22*а33, а нет а11*а22*а13.

 д.
д. В дальнейшем для решения линейных уравнений методом обращения матриц нам необходимо применить эту концепцию. Перекрестное произведение двух векторов легко запоминается путем вычисления определителей.
В дальнейшем для решения линейных уравнений методом обращения матриц нам необходимо применить эту концепцию. Перекрестное произведение двух векторов легко запоминается путем вычисления определителей. Детерминанты принимают квадратную матрицу на входе и возвращают одно число на выходе.
Детерминанты принимают квадратную матрицу на входе и возвращают одно число на выходе.

 Но любую строку/любой столбец можно использовать для вычисления определителей.
Но любую строку/любой столбец можно использовать для вычисления определителей. Вот простой способ найти его.
Вот простой способ найти его.



 (-1 -(-9) — 3. (-3 -(-6) + 2.(-9 -(-2))
(-1 -(-9) — 3. (-3 -(-6) + 2.(-9 -(-2))
 Он получается путем умножения элементов любой строки или столбца на соответствующие им коэффициенты и сложения произведений.
Он получается путем умножения элементов любой строки или столбца на соответствующие им коэффициенты и сложения произведений. Его определитель можно вычислить как: |D| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\) |D| = (8×4) – (6×3) = 32 – 18 = 14.
Его определитель можно вычислить как: |D| = \(\left|\begin{array}{ll}8 & 6 \\3 & 4\end{array}\right|\) |D| = (8×4) – (6×3) = 32 – 18 = 14.


 Таким образом, определители могут быть отрицательными. Если определители отрицательны, это означает, что матрица изменила ориентацию своего базового вектора. |-А| = (-1) n |А|. Возьмите любой положительный определитель, поменяйте местами любые две строки или столбца матрицы и найдите его определитель, в результате чего будет отрицательный определитель.
Таким образом, определители могут быть отрицательными. Если определители отрицательны, это означает, что матрица изменила ориентацию своего базового вектора. |-А| = (-1) n |А|. Возьмите любой положительный определитель, поменяйте местами любые две строки или столбца матрицы и найдите его определитель, в результате чего будет отрицательный определитель. Определитель определен только для квадратных матриц.
Определитель определен только для квадратных матриц.
 Определитель представляет собой сумму этих значений, чередующихся сложением и вычитанием.
Определитель представляет собой сумму этих значений, чередующихся сложением и вычитанием.
 {\circ}=6 \cdot \frac{1}{2}=3
\)
{\circ}=6 \cdot \frac{1}{2}=3
\)
 На
практике, они позволяют не делать лишних
операций и сократить время выполнения
задач. Поэтому, будущим специалистам
очень важно понять теорию векторов и
научиться решать задачи с ними.
На
практике, они позволяют не делать лишних
операций и сократить время выполнения
задач. Поэтому, будущим специалистам
очень важно понять теорию векторов и
научиться решать задачи с ними.
 Найти угол между векторами
и
Найти угол между векторами
и
 Вычислить объем пирамиды, построенной
на векторах
,
,
Вычислить объем пирамиды, построенной
на векторах
,
, 15
Дж
15
Дж 15
Дж
15
Дж

 Давайте посмотрим на пример ниже, чтобы лучше понять концепцию.
Давайте посмотрим на пример ниже, чтобы лучше понять концепцию. Для приведенного выше вектора v угол градиента равен a. Затем мы можем определить соотношение между углом и величиной компонентов с помощью тригонометрии.
Для приведенного выше вектора v угол градиента равен a. Затем мы можем определить соотношение между углом и величиной компонентов с помощью тригонометрии.
 Источник: Огулкан Тезкан, StudySmarter.
Источник: Огулкан Тезкан, StudySmarter.