Ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Найти координаты точек пересечения графика с функции с осями координат:1)y=-1,5x+3;2)y=-2x+4;3)y=-1,5x-6;4)y=0,8x-0,6;5)y=1/4x+2;6)y=2/3x-5.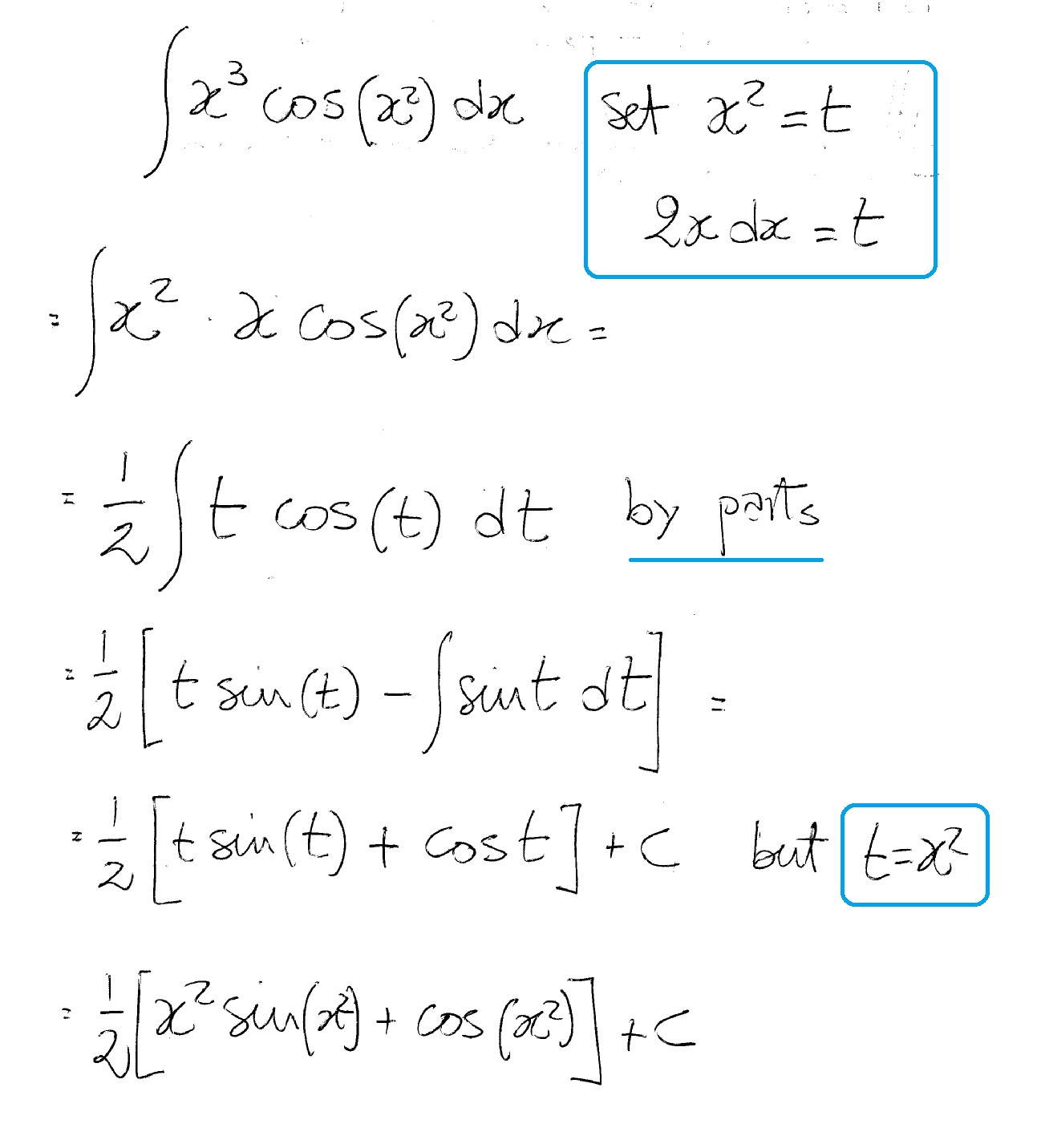
задача для 5 класса. После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?ответы майл ру помогите решить задачу какое наименьшее количество карандашей надо прибавить к 146 уже имеющимя карандашам, чтобы получившееся
периметр прямоугольника 150 дм,длина его больше ширины на 150 см. Вычислите длину и ширину прямоугольника.
Пользуйтесь нашим приложением| 1 | Найти производную — d/dx | бревно натуральное х | ||||||||||||
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | ||||||||||||
| 3 | Найти производную — d/dx | 92)|||||||||||||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | ||||||||||||
| 22 | Найти производную — d/dx | грех(2x) | ||||||||||||
| 23 | Найти производную — d/dx | 9(3x) по отношению к x|||||||||||||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | ||||||||||||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | ||||||||||||
| 43 | Оценка интеграла 9бесконечность | |||||||||||||
| 45 | Найти производную — d/dx | х/2 | ||||||||||||
| 46 | Найти производную — d/dx | -cos(x) | ||||||||||||
| 47 | Найти производную — d/dx | грех(3x) | 92+1||||||||||||
| 68 | Оценить интеграл | интеграл от sin(x) по x | ||||||||||||
| 69 | Найти производную — d/dx | угловой синус(х) | ||||||||||||
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | ||||||||||||
| 85 | Найти производную — d/dx | лог х | ||||||||||||
| 86 | Найти производную — d/dx | арктан(х) | ||||||||||||
| 87 | Найти производную — d/dx | бревно натуральное 5х92(3x))dx
Вопрос Обновлено: 26/04/2023Рекомендуемые вопросы 9 видеоРЕКЛАМА Ab Padhai каро бина объявления ке Khareedo DN Про и дехо сари видео бина киси ад ки рукаават ке! Похожие видео 026 257120645 00:44 সমাকলন করো : ∫sin3xcos3xdx 333025075 02: 23 ∫cos3xdx = 474018671 02:03 ∫√2+sin3x. Вы умеете решать неравенства? Уверены? Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя. При решении неравенств мы можем: 1. Умножать обе части неравенства на число или выражение, не равное нулю. При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный. 2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны 3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный. Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. 4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя). 5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени. Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты. 1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем. Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов. > 0 > 0 Получаем, что < 0 или > . 2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет. Как, например, решить неравенство > Перенесем все в левую часть неравенства, чтобы в правой остался ноль. > 0 Разложим левую часть на множители. > 0 Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: < или > . Запомним: ответы типа « > » абсурдны. Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: . 4. Возводить обе части неравенства в квадрат можно только если они неотрицательны. 5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. 6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений. 7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать. При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе. Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений. А теперь – полезный лайфхак для решения дробно-рациональных неравенств. Решите неравенство Запишем ОДЗ: Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени. Может быть, сделаем проще? Представим дробь в виде суммы дробей и . Продолжаем упрощать левую часть: Теперь можно и привести дроби к одному знаменателю. Все, больше ничего не пишем. Решаем неравенство методом интервалов. Ответ: . Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Решение неравенств: основные ошибки и полезные лайфхаки» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта. Публикация обновлена:
07.04.2023 Докажите, что при любых любых значениях p истинно неравенство
Когда на тестах по математике стоит такая задача, то необходимо вначале решить неравенство.
137 Практические тесты
Вопрос дня
Карточки
Learn by Concept SAT Mathematics Help »
Неравенства и абсолютное значение »
Понимание неравенств Какое из следующих выражений выражает полный набор значений для , которые удовлетворяют приведенному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: Неравенства можно решать так же, как уравнения, с одной важной оговоркой: если вы умножаете или делите на отрицательное число, вы должны перевернуть знак неравенства. Затем добавьте 2 к обеим сторонам, чтобы выделить член: Затем разделите обе части на 3, чтобы получить одно: Сообщить об ошибке Какое из следующих значений представляет собой полный набор значений , которые удовлетворяют приведенному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: Эта задача демонстрирует важную концепцию работы с неравенствами. Если вы умножаете или делите неравенство на отрицательное число, вы должны перевернуть знак неравенства. Здесь вы можете разделить обе части исходного неравенства на , чтобы остаться в одиночестве. Однако, если вы это сделаете, вы должны перевернуть знак, чтобы получить: Вы можете выбрать число, соответствующее вашему ответу, чтобы убедиться, что оно удовлетворяет исходному неравенству. Обратите внимание, что во многих задачах можно избежать умножения/деления на отрицательное число путем прибавления или вычитания (для которых нет таких ограничений) членов к сторонам неравенства, где они будут положительными. Например, учитывая , если вы прибавите к обеим сторонам и вычтете 10 из обеих сторон, вы получите , и теперь вы будете делить на положительное 2, и вам не придется беспокоиться о смене знака, чтобы получить . Сообщить об ошибке Если , что из следующего должно быть правдой? I. II. III. Возможные ответы: Только I и III Только I Только II и III Ни один из этих ответов не должен быть верным Объяснение: На первый взгляд, вы можете просто умножить обе части исходного неравенства на и поверить, что . В результате ни одно из этих утверждений «не должно быть истинным», поэтому правильный ответ «ни одно из этих утверждений не должно быть истинным». Сообщить об ошибке Если , что из следующего должно быть правдой? Возможные ответы: Правильный ответ: Объяснение: Неравенства можно решать точно так же, как уравнения (с оговоркой, что если вы умножаете/делите на минус, вы должны поменять знак неравенства, но это не играет роли в этой задаче). 1) Прибавьте 2 к обеим сторонам, чтобы получить: 2) Разделите обе части на 2, чтобы получить: Сообщить об ошибке представляет собой полный набор значений , которые удовлетворяют приведенному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: Неравенства можно решать так же, как и уравнения, с одной важной оговоркой, как вы увидите в этой задаче: если вы умножаете или делите на отрицательное число, вы должны изменить направление знака неравенства. Здесь вы можете начать с умножения обеих сторон на 2, чтобы исключить знаменатель. Это приводит вас к: Теперь у вас есть выбор, как вы перемещаете оставшиеся члены, чтобы изолировать и найти переменную. Здесь обратите внимание, что для решения набора решений вам придется разделить на -1, чтобы удалить минус. Если вы это сделаете, вам нужно будет изменить направление знака, чтобы получить правильный ответ: Теперь также признайте, что вы могли бы вообще избежать шага деления на минус. На этом этапе: Вы могли бы прибавить к обеим сторонам, чтобы получить: И затем, когда вы вычтете 8 из обеих сторон, вы также получите правильный ответ: Сообщить об ошибке Что из следующего представляет собой полный набор значений , которые удовлетворяют указанному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: Неравенства можно решать так же, как уравнения, с той лишь оговоркой, что если вы умножаете или делите на отрицательное число, вы должны поменять знак неравенства. Во-первых, ваша цель состоит в том, чтобы получить все термины с одной стороны и числовые термины с другой. Для этого вы можете прибавить к обеим сторонам и вычесть из обеих сторон, чтобы получить: Теперь вы хотите остаться наедине, так что вы можете разделить обе стороны на . Это оставляет: или сокращенную дробь . Обратите внимание, что вы можете читать неравенства слева направо или справа налево, поэтому здесь «две трети больше, чем» — это то же самое, что «меньше двух третей». Таким образом, вы найдете ответ, записанный как . Обратите внимание, что вы можете проверить значение, близкое к вашему неравенству, чтобы убедиться, что оно работает. Поскольку у вас есть , вы можете попробовать . Если вы подключите это к заданному неравенству, вы увидите, что оно работает, возвращая истинное утверждение . Это поможет подтвердить ваш ответ. Сообщить об ошибке Что из следующего представляет собой полный набор решений для значений , которые удовлетворяют приведенному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: При работе с неравенствами очень важно учитывать, что всякий раз, когда вы умножаете или делите на отрицательное число, вы должны перевернуть знак неравенства. Обратите внимание, что вы также можете справиться с этим, используя только сложение/вычитание, где правила точно такие же, как и в уравнениях. Для этого сложите и вычтите из обеих частей данного неравенства. затем становится: Затем вы делите на положительное число, , чтобы изолировать . Это дает вам соответствие правильному ответу, указанному выше. Сообщить об ошибке Какое из следующих неравенств представляет собой полный набор решений для значений , удовлетворяющих приведенному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: Неравенства можно решать так же, как и уравнения — проделайте то же самое с обеими сторонами, пока не изолируете переменную — за одним важным исключением. Здесь, если вычесть из обеих частей, вы можете получить все члены в одной части уравнения, причем с положительным коэффициентом, поэтому вам не нужно беспокоиться о делении на отрицательное. Это дает вам: Затем прибавьте к обеим сторонам, чтобы изолировать переменную справа: Разделите на и вы получите ответ: , который совпадает с Сообщить об ошибке 900 выражает полный набор значений для , которые удовлетворяют приведенному выше неравенству? Возможные ответы: Правильный ответ: Объяснение: Чтобы ответить на этот вопрос, мы должны иметь в виду, что неравенства подчиняются тем же правилам и операциям, что и уравнения, за одним важным исключением. В этом случае мы начинаем с того, что избавляемся от знаменателя, умножая обе части нашего неравенства на 4 мы можем затем вычесть два из обеих сторон, чтобы получить и разделить обе части на -3, (имейте в виду, что при этом нам нужно перевернуть знак!) Сообщить об ошибке Уведомление об авторских правах 137 Практические тесты
Вопрос дня
Карточки
Учитесь по концепции Обновлено 14 мая 2018 г. Неравенство с большим количеством отрицаний и абсолютных значений. Помощь! Когда переворачивать знак неравенства? Не бойся! Есть пара случаев, когда вы переворачиваете неравенство, и мы рассмотрим их ниже. TL;DR (слишком длинный; не читал) Перевернуть знак неравенства, когда вы умножаете или делите обе части неравенства на отрицательное число. Также часто приходится менять знак неравенства при решении неравенств с абсолютными значениями. Основная ситуация, когда вам нужно перевернуть знак неравенства, — это когда вы умножаете или делите обе части неравенства на отрицательное число. Например, рассмотрим следующую задачу: 3_x_ + 6 > 6_x_ + 12 Чтобы решить, нужно получить все x -es на одной стороне неравенства. Вычтите 6_x_ с обеих сторон, чтобы слева было только x . 3_x_ −6_x_ + 6 > 6_x_ −6_x_ + 12 −3_x_ + 6 > 12 Теперь изолируем x в левой части, переместив константу 6 в другую часть неравенства. − 3_x_ + 6 − 6 > 12 − 6 −3_x_ > 6 Теперь разделите обе части неравенства на −3. Поскольку вы делите на отрицательное число, вам нужно перевернуть знак неравенства . −3_x_ (÷ −3) < 6 (÷ − 3) x < − 2. То же правило применимо, если вы умножаете обе части на дробь. Умножение и деление являются противоположностями одного и того же процесса, вроде сложения и вычитания, поэтому к ним применяются одни и те же правила. Вам также нужно подумать об изменении знака неравенства, когда вы имеете дело с задачами с абсолютными значениями . Возьмем следующий пример. Если у вас есть: | 3_x_ | + 6 < 12, Тогда, прежде всего, вы хотите выделить выражение абсолютного значения в левой части неравенства (это облегчает жизнь). Вычтите 6 с обеих сторон, чтобы получить: | 3_x_ | < 6. Теперь вам нужно переписать это выражение в виде составного неравенства . | 3_x_ | < 6 можно записать двумя способами: 3_x_ < 6 («положительная» версия) или 3_x_ > −6 («отрицательная» версия). Эти два утверждения также можно записать в одну строку: −6 < 3_x_ < 6. Вывод выражения абсолютного значения всегда положителен, но « x » внутри знаков абсолютного значения может быть отрицательное, поэтому нужно рассмотреть случай, когда x отрицательное. По сути, мы умножаем на −1: мы умножаем 9.0347 x на отрицательную единицу слева (но поскольку она находится внутри знаков абсолютного значения, результат все еще положительный), а затем мы умножаем правую часть на отрицательную и меняем знак неравенства, потому что мы только что умножили на отрицательное. Это дает нам два наших неравенства (или наше «составное неравенство»). Мы можем легко решить обе из них. 3_x_ < 6 становится x < 2, когда мы делим обе части на 3. Электронный учебник Периодический закон, открытый Д. И. Менделеевым был выражен в таблице. Периодическая таблица химических элементов,
или таблица менделеева. 1 H 1.008 2 He 4.003 3 Li 6.938 4 Be 9.012 5 B 10.806 6 C 12.01 7 N 14.006 8 O 15.999 9 F 18.998 10 Ne 20.18 11 Na 22.99 12 Mg 24.304 13 Al 26.982 14 Si 28.084 15 P 30.974 16 S 32.059 17 Cl 35.446 18 Ar 39.948 19 K 39.098 20 Ca 40.078 21 Sc 44.956 22 Ti 47.867 23 V 50.942 24 Cr 51. 25 Mn 54.938 26 Fe 55.845 27 Co 58.933 28 Ni 58.693 29 Cu 63.546 30 Zn 65.38 31 Ga 69.723 32 Ge 72.63 33 As 74.922 34 Se 78.971 35 Br 79.901 36 Kr 83.798 37 Rb 85.468 38 Sr 87.62 39 Y 88.906 40 Zr 91.224 41 Nb 92.906 42 Mo 95.95 44 Ru 101.07 45 Rh 102.906 46 Pd 106.42 47 Ag 107.868 48 Cd 112.414 49 In 114.818 50 Sn 118.71 51 Sb 121.76 52 Te 127.6 53 I 126.904 54 Xe 131.293 55 Cs 132.905 56 Ba 137.327 57 La 138.905 72 Hf 178. 73 Ta 180.948 74 W 183.84 75 Re 186.207 76 Os 190.23 77 Ir 192.217 78 Pt 195.084 79 Au 196.967 80 Hg 200.592 81 Tl 204.382 82 Pb 207.2 83 Bi 208.98 58 Ce 140.116 59 Pr 140.908 60 Nd 144.242 62 Sm 150.36 63 Eu 151.964 64 Gd 157.25 65 Tb 158.925 66 Dy 162.5 67 Ho 164.93 68 Er 167.259 69 Tm 168.934 70 Yb 173.045 71 Lu 174.967 90 Th 232.038 91 Pa 231.036 92 U 238.029 В таблице менделеева колонки называются группами, строки называются периодами. Элементы в группах как правило имеют
одинаковые электронные конфигурации внешних оболочек, например, благородные газы — последняя группа, имеют законченную
электронную конфигурацию. Как заполняется электронная конфигурация элементов подробно описано в статье Скачать таблицу менделеева в хорошем качестве © 2015-2022 — K-Tree.ru • Электронный учебник Копия материалов, размещённых на данном сайте, допускается только по письменному разрешению владельцев
сайта. Степень окисления (СО) – это условное обозначение в химии, служащее для того, чтобы определять заряд атома у какого-либо химического элемента (или группы элементов). Без степеней окисления не решается ни одна задача, не составляется ни одно уравнение, но самое главное – без них мы не можем чётко определить свойства элемента и то, какую роль он будет играть в различных соединениях. Знаменательно, что периодическая система (ПС) Д.И. Менделеева сгруппирована гениальнейшим образом: все элементы разделены по периодам, группам, подгруппам, их порядковые номера также соответствуют определённым показателям. Благодаря этому нам не приходится заучивать качества каждого химического элемента (ХЭ) наизусть, потому что легко можно найти его в таблице и определить всё, что требуется. Однако даже в таком случае некоторые люди, забывая школьные знания по курсу химии (или пренебрегая ими когда-то), вынуждены вернуться к изучению данной темы подробнее. Итак, для начала необходимо сформировать верные объективные представления о хроме (Cr), разобраться с его положением в ПС, а затем можно будет приступить к наиболее важной части – практике. ХЭ располагается в VI группе, 4 периоде, носит порядковый номер 24 и обладает атомной массой равной 52 г/моль. Благодаря пассивированию хром не взаимодействует с серной (H2SO4) и азотной (HNO3) кислотами, проявляет устойчивость в воздухе. Это амфотерный металл – значит, он может растворяться как в кислотах, так и в щелочах. Элемент растворяется в сильных разбавленных кислотах (например, соляная кислота HCl), в нормальных условиях (н.у.) взаимодействует только с фтором (F). При нагревании хром может осуществлять взаимодействие с элементами VII группы (галогены), кислородом O2, бором B, азотом N2, серой S2, кремнием Si. Теперь поговорим непосредственно о том, какие степени окисления бывают у данного ХЭ: он может приобретать СО +4, +6, а также +2 в безвоздушном пространстве, +3 – в пространстве с воздухом. Хром, как любой другой металл, является сильным восстановителем. С правилом «крест-накрест» вы наверняка уже знакомы. А что, если соединение имеет, например, целых три элемента? В этом случае мы смотрим на последний элемент вещества, определяем его степень окисления и умножаем на коэффициент, находящийся справа (конечно, если он есть). Рассмотрим пример: Степени окисления в следующих формулах попробуйте расставить сами: Хром – один из самых интересных химических элементов, соединения с которым – штука сложная, но необходимая для понимания. Будет замечательно, если данные примеры помогут разобраться со столь кропотливой темой. Редакция «Учисьучись.рф» По завершении этого раздела вы сможет Хром представляет собой твердый стальной серый металл, обладающий высокой устойчивостью к окислению даже при высоких температурах. Это шестой по распространенности элемент в земной коре, где он сочетается с железом и кислородом в виде хромитовой руды. Начало страницы Хром используется в трех основных отраслях промышленности Эти отрасли промышленности являются наиболее важными промышленными источниками хрома в атмосфере [EPA 1998; АТСДР 2000]. Использование хрома в огнеупорах включает магнезит-хромовый огнеупорный кирпич для футеровки металлургических печей и гранулированный хромит для различных других жаропрочных применений. Начало страницы Хром существует в ряде степеней окисления от -2 до +6 валентность. Наиболее важными стабильными состояниями являются 0 (элементарный металл), +3 (трехвалентный) и +6 (шестивалентный). Хром в хромитовой руде находится в трехвалентном состоянии; промышленные процессы также производят элементарный металл и шестивалентный хром. Воздействие хрома на здоровье в первую очередь связано с валентным состоянием металла во время воздействия. Трехвалентные (Cr[III]) и шестивалентные (Cr[VI]) соединения считаются наиболее биологически значимыми. Cr(III) является важным диетическим минералом в низких дозах. Соединения Cr(VI) канцерогенны. Cr(VI) обычно считается в 1000 раз более токсичным, чем Cr(III) [EPA 1998; АТСДР 2000; Даян и Пейн, 2001]. Cr(III) является важным диетическим питательным веществом. Требуется для потенцирования инсулина и для нормального метаболизма глюкозы. Дефицит Cr (III) был связан с Cr(III) содержится в большинстве свежих продуктов и питьевой воде. Диетические источники, богатые Cr(III), включают Другими важными источниками Cr(III) являются минеральные добавки, пивные дрожжи и пиво. Национальная академия наук установила безопасное и адекватное суточное потребление Cr(III) для взрослых в размере 50-200 мкг в день. В среднем взрослые в США получают с пищей около 60-80 мкг Cr(III) в день. Поэтому диета многих людей может не содержать достаточного количества Cr(III) [ATSDR 2000]. Считается, что биологически активная форма органического комплекса Cr(III), часто называемая фактором толерантности к глюкозе (GTF), способствует взаимодействию инсулина с его клеточными рецепторами. Исследования показали, что добавление Cr(III) у субъектов с дефицитом и предельным дефицитом может привести к быстрому устранению многих симптомов дефицита хрома [Cohen, Kargacin et al. Начало страницы Начало страницы Являясь библиотекой, NLM предоставляет доступ к научной литературе. Перспектива охраны окружающей среды. 1991 май; 92: 7–11. doi: 10.1289/ehp.91927 PMCID: PMC1519378 PMID: 1935853 Информация об авторе Информация об авторских правах и лицензии Отказ от ответственности Хром, названный в честь его разноцветных соединений, существует в степенях окисления — от 2 до +6 включительно. Соединения демонстрируют широкий спектр геометрических форм, включая квадратно-плоские, тетраэдрические, октаэдрические и различные искаженные геометрические формы. Хром встречается в природе главным образом в виде хромитовой руды FeCr2O4, в которой хром находится в состоянии +3. Существование определенной степени окисления зависит от многих факторов, включая pH, окислительно-восстановительный потенциал и кинетику. Полный текст доступен в виде отсканированной копии оригинальной печатной версии. Получите копию для печати (файл PDF) полной статьи (972K) или щелкните изображение страницы ниже, чтобы просмотреть страницу за страницей. тож самое.ищем корни D=1-4*4*(-3)=49 Х1 и х2=1+ или — корень из 49 все делим на 2 х1=(1-7)\2=-3 х2=(1+7)\2=4 раскладываем на множители:4(х+3)(х-4)<0 отмечаем на числовой прямой числа -3 и 4 Ответ:(-3;4) 1 2 >
>> Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье. Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства! Темы для повторения: New Решаем задачи из сборника И. В. Ященко, 2021 Квадратичные неравенства Метод интервалов Уравнения и неравенства с модулем Иррациональные неравенства Показательные неравенства Логарифмические неравенства Метод замены множителя (рационализации) Решение неравенств: основные ошибки и полезные лайфхаки Решаем задачи из сборника И. Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15 Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15 Логарифмические неравенства повышенной сложности Разберем неравенства разных типов из вариантов ЕГЭ по математике. Дробно-рациональные неравенства 1. Решите неравенство: Сделаем замену Тогда , а Получим: Решим неравенство относительно t методом интервалов: Получим: Вернемся к переменной x: Ответ: Показательные неравенства 2. Решите неравенство Сделаем замену Получим: Умножим неравенство на Дискриминант квадратного уравнения Значит, корни этого уравнения: Разложим квадратный трехчлен на множители. . Вернемся к переменной x. Внимание. Ответ: Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ. 3. Решите неравенство Сделаем замену Получим: Вернемся к переменной Первое неравенство решим легко: С неравенством тоже все просто. Но что делать с неравенством ? Ведь Представляете, как трудно будет выразить х? Оценим Для этого рассмотрим функцию Сначала оценим показатель степени. Пусть Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом Мы получили, что Тогда , и это значит, что Значение не достигается ни при каких х. Но если и , то Мы получили: Ответ: Логарифмические неравенства 4. Решите неравенство Запишем решение как цепочку равносильных переходов. Ответ: Следующее неравенство — комбинированное. И логарифмы, и тригонометрия! 5. Решите неравенство ОДЗ: Замена Ответ: А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический. 6. Решите неравенство: Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что . Используем также условия Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, Поскольку Согласно методу замены множителя, выражение заменим на Получим систему: Решить ее легко. Ответ: . Разберем какое-нибудь нестандартное неравенство. 7. Решите неравенство: ОДЗ: Привести обе части к одному основанию не получается. Ищем другой способ. Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4. Функции и — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз. Поскольку при x=9 значение монотонно возрастающей функции равно 4, при значения этой функции меньше 4. Конечно, при этом , то есть x принадлежит ОДЗ. Ответ: Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. В тексте пересечение прямых обозначают символом ∩. — Вторая группа — обозначения логических операций, составляющая синтаксическую основу геометрического языка. А(А`, А») – точка А задана на комплексном чертеже горизонтальной и фронтальной проекциями; α(А, b) – плоскость α задана прямой b и точкой А. А`≡ В` – горизонтальные проекции точек А и В совпадают. Дуга окружности. Слово «дуга» иногда заменяется знаком . Дуга обозначается двумя или тремя буквами, из которых две ставятся на концах дуги, а третья — у какой-нибудь точки дуги. На чертеже 88 обозначены две дуги: АСВ и ADB. В том случае, когда дуга меньше полуокружности, она обычно обозначается двумя буквами. этот знак значит принадлежит. Линии уровня обозначают: h — горизонталь, f — фронталь, p — профильная прямая. Для прямых используют также следующие обозначения: (АВ) — прямая, проходящая через точки А и В; IABI — длина отрезка АВ (расстояние между точками А и В). К самым распространённым относятся: Дуга вниз в геометрии— знак пересечения. С помощью этих фигур мы определим все остальные геометрические фигуры, а точку и прямую можем попытаться только представить: точку — как что-то бесконечно малое, а прямую — как что-то бесконечно простирающееся в обе стороны. Точка начала луча разделяет прямую на две части. Обычно луч обозначают малой латинской буквой (например, луч h), либо двумя большими латинскими буквами, первая из которых обозначает начало луча, а вторая — какую-нибудь точку на луче (например, луч АО). Чтобы обозначить плоскость на письме, традиционно используются маленькие греческие буквы, например, α, γ или π . Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм. Вертикальная плоскость, расположенная перед нами, называется фронтальной плоскостью проекций и обозначается латинской буквой V (вэ). Под прямым углом к фронтальной плоскости располагается горизонтальная плоскость проекций, которая обозначается латинской буквой Н (аш). Плоскость – основные понятия, обозначения и изображение. Мы уже имеем представление о точке и прямой на плоскости. Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Планиме́трия (от лат. planum — «плоскость», др. -греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости: треугольники, окружности, параллелограммы и т. Определение. Доказательство – рассуждение, устанавливающее какое-либо свойство. Теорема – утверждение, устанавливающее некоторое свойство и требующее доказательства. … Аксиома – утверждение, устанавливающее некоторое свойство и принимаемое без доказательства. Функции модуля pygame.draw рисуют геометрические примитивы на поверхности – экземпляре класса Surface. В качестве первого аргумента они принимают поверхность. Поэтому при создании той или иной поверхности ее надо связать с переменной, чтобы потом было что передать в функции модуля draw. Поскольку мы пока используем только одну поверхность – главную оконную, то ее будем указывать в качестве первого параметра, а при создании свяжем с переменной: В большинстве случаев фигуры прорисовывают внутри главного цикла, так как от кадра к кадру картинка на экране должна меняться. Поэтому на каждой итерации цикла в функции модуля draw передаются измененные аргументы (например, каждый раз меняется координата x). Однако у нас пока не будет никакой анимации, и нет смысла перерисовывать фигуры на одном и том же месте на каждой итерации цикла. Поэтому создавать примитивы будем в основной ветке программы. На данном этапе цикл while нужен лишь для того, чтобы программа самопроизвольно не завершалась. После прорисовки, чтобы увидеть изменения в окне игры, необходимо выполнить функцию update() или flip() модуля display. Иначе окно не обновится. Рисование на поверхности – одно, а обновление состояния главного окна – другое. Представьте, что в разных местах тела главного цикла на поверхности прорисовываются разные объекты. Если бы каждое такое действие приводило к автоматическому обновлению окна, то за одну итерацию оно обновлялось бы несколько раз. Это приводило бы как минимум к бессмысленной трате ресурсов, так как скорость цикла связана с FPS. Итак, первый аргумент функций рисования – поверхность, на которой размещается фигура. В нашем случае это будет Далее идут специфичные для каждой фигуры аргументы. Последним у большинства является толщина контура. Все функции модуля draw возвращают экземпляры класса Rect – прямоугольные области, имеющие координаты, длину и ширину. Не путайте функцию rect() модуля draw и класс Rect, это разные вещи. Начнем с функции rect() модуля draw: Если указывается толщина контура (последний аргумент во второй строке), то прямоугольник будет незаполненным, а цвет определит цвет рамки. Третьим аргументом является кортеж из четырех чисел. Первые два определяют координаты верхнего левого угла прямоугольника, вторые – его ширину и высоту. Следует отметить, что в функцию draw. Обычно цвета выносят в отдельные переменные-константы. Это облегчает чтение кода: Чтобы нарисовать линию, а точнее – отрезок, надо указать координаты его концов. При этом функция line() рисует обычную линию, aaline() – сглаженную (толщину для последней указать нельзя): Координаты можно передавать как в виде списка, так и кортежа. Функции lines() и aalines() рисуют ломанные линии: Координаты определяют места излома. Количество точек может быть произвольным. Третий параметр (True или False) указывает замыкать ли крайние точки. Функция polygon() рисует произвольный многоугольник. Задаются координаты вершин. Сглаженная ломаная здесь повторяет контур многоугольника, чем сглаживает его ребра. Так же как в случае rect() для polygon() можно указать толщину контура. Функция circle() рисует круги. Указывается центр окружности и радиус: В случае эллипса передается описывающая его прямоугольная область: Наконец, дуга: Указывается прямоугольник, описывающий эллипс, из которого вырезается дуга. Четвертый и пятый аргументы – начало и конец дуги, выраженные в радианах. Нулевая точка справа. На данном этапе мы уже готовы создать анимацию. Никакого движения объектов на экране монитора нет. Просто от кадра к кадру изменяются цвета пикселей экрана. Суть алгоритма в следующем. Берем фигуру. Рисуем ее на поверхности. Обновляем главное окно, человек видит картинку. Стираем фигуру. Рисуем ее с небольшим смещением от первоначальной позиции. Снова обновляем окно и так далее. Как «стереть» старую фигуру? Для этого используется метод fill() объекта Surface. В качестве аргумента передается цвет, т. е. фон можно сделать любым, а не только черным, который задан по-умолчанию. Ниже в качестве примера приводится код анимации круга. Объект появляется с левой стороны, доходит до правой, исчезает за ней. После этого снова появляется слева. Ваша задача написать код анимации квадрата, который перемещается от левой границе к правой, касается ее, но не исчезает за ней. Курс с примерами решений практических работ: В математике дуга определяется как часть границы окружности или кривой. Его также можно назвать открытой кривой. Граница круга — это периметр или расстояние вокруг круга, также известное как длина окружности. Итак, дуга — это расстояние между любыми двумя точками, проведенными по его окружности. Поясним это на примере: На этом рисунке расстояние между точками A и B представляет собой дугу, проведенную по окружности окружности. Вы можете назвать это дугой AB. Дуга обозначается символом «⌢». Итак, дугу AB можно записать в виде $\widehat{AB}$. Вы также можете записать его как $\widehat{BA}$. Порядок точек не имеет значения. Чтобы построить дугу, вам понадобится либо хорда, либо центральный угол. Хорда — это отрезок, соединяющий любые две точки окружности. Центральный угол — это угол между любыми двумя радиусами окружности. Например, центральный угол на диаграмме между радиусами QA и QB, как показано ниже, равен 60°. Вы, должно быть, заметили, что дуга делит окружность на две части. У одного расстояние между двумя конечными точками меньше (малая дуга), а у другого расстояние больше (большая дуга). Если не указано иное, дуга всегда будет считаться второстепенной дугой. Чтобы указать большую дугу, вы можете взять третью точку на дуге окружности и использовать три буквы в имени. На приведенной выше диаграмме $\widehat{AB}$ — это малая дуга, а $\widehat{ADB}$ — большая дуга. Полуокружность — это дуга, концы которой совпадают с диаметром окружности. Вы можете рассчитать длину дуги, используя приведенную ниже формулу. Длина дуги окружности = $\frac{y}{360}$ ✕ $2 π r$ Где r = радиус окружности y = угол (в градусах), образуемый дугой в центре круга 360 = угол одного полного оборота. Значение $π$ (пи) = 3,14 Пример 1: Вычислить длину дуги, образующей угол 60 градусов в центре круга радиусом 5 см. Решение : Мы знаем, что формула длины дуги $\frac{y}{360} ✕ $2 π r$ В этом примере y = 60 и r = 5 например, мы получаем Длина дуги = $\frac{60}{360}$ ✕ 2 ✕ 3,14 ✕ 5 = 5,23 см Пример 2. Вычислите длину дуги, образующей угол 40 градусов в центре окружности с радиус 6 см. Решение: Мы знаем, что формула длины дуги $\frac{y}{360}$ ✕ $2 π r$ В этом примере y = 40 и r = 6 Подставляя эти значения в Например, мы получаем Длина дуги = $\frac{40}{360}$ ✕ 2 ✕ 3,14 ✕ 6 = 4,186 см Пример 3: Определите большую дугу в этом круге. Мы знаем, что большая дуга — это большое расстояние между двумя конечными точками. Итак, здесь $\widehat{ADC}$ — это большая дуга, а $\widehat{ABC}$ — меньшая дуга. 1 20,93 см 10,93 см 14,56 см 30,46 см Правильный ответ: 20,93 см 2 $\widehat{AB}$ $\widehat{BD}$ $\widehat{DA}$ $\widehat{ADB}$ Правильный ответ: $\widehat{AB}$ 3 90° 60° 45° 30° Правильный ответ: 90° 4 81° 76° 45° 99° Правильный ответ: 99° Что такое дуга полукруга? Полуокружность — это дуга, концы которой лежат на диаметре окружности. Здесь и $\widehat{AB}$, и $\widehat{ACB}$ являются полуокружностями. Что такое центральный угол дуги? Центральный угол — это угол, на который опирается дуга в центре. Может ли дуга быть прямой линией? Нет. Дуга всегда является открытой кривой. Круги просты, но у них есть части. Одна часть — это дуга, отрезок круга, кусок его окружности. Сами дуги бывают разных типов, например, большие дуги, полуокружности и малые дуги. Окружность — это множество всех точек, равноудаленных от данной точки. Окружность – это расстояние по окружности. Круги могут иметь углы, образованные двумя радиусами. Это 90 199 центральных углов 90 200 и почти всегда обозначаются либо их точным измерением угла (или радиана), либо греческой буквой тета, θ\thetaθ. Окружности также могут иметь углы, образованные двумя хордами (отрезками линий с концами на окружности) с общей конечной точкой на окружности. Эти углы называются вписанными углами. Как центральные, так и вписанные углы образуют большую и малую дуги. Дуга – это часть окружности, которая меньше всей окружности. Поскольку это допускает почти все возможные части, математики разбивают дуги следующим образом:0007 В типичном рисунке окружности читатель понимает, что речь идет о малой дуге. На этом рисунке нас интересует малая дуга, определяемая центральным углом θ\thetaθ. Для маркировки малой дуги требуются только ее конечные точки на окружности. Вот второстепенная дуга GO : Если вам нужна большая дуга, выберите и пометьте обе конечные точки дуги и случайную точку между ними. Дуги обычно обозначаются в письменной форме с помощью их точек (две для малой дуги, три для большой дуги), а затем рисуется крошечная короткая дуга, проведенная над буквами. Дуги имеют два измерения: Одним из способов измерения дуги является центральный угол окружности. Это угол дуги 90 199 90 200 . Вы помещаете строчную букву m перед письменной формой дуги, например: Таким образом, вы можете написать mFUN⌢=45°m\overset\frown{FUN}=45°mFUN⌢=45° и сказать: «Большая дуга FUN измеряет 45 градусов . » Другой способ измерения дуг — их расстояние по окружности окружности. Это длина дуги . Чтобы записать длину дуги словами, вы ставите маленькую букву l перед письменной формой, например: Таким образом, вы можете написать lGO⌢=13. Пусть дано квадратное уравнение Применим к квадратному трехчлену те же преобразования, которые мы выполняли ранее, когда доказывали теорему о том, что графиком функции с является парабола. Имеем Обычно выражение обозначают буквой D и называют дискриминантом квадратного уравнения (или дискриминантом квадратного трехчлена ). Таким образом, Значит, квадратное уравнение можно переписать в виде и далее Любое квадратное уравнение можно преобразовать к виду (1), удобному, как мы сейчас убедимся, для того, чтобы определять число корней квадратного уравнения и находить эти корни. Теорема 1 Если D <0, то квадратное уравнение не имеет корней. Доказательство. Если D < 0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней. Пример 1. Решить уравнение Решение. Здесь а = 2, b = 4, с = 7, Так как D < 0, то по теореме 1 данное квадратное уравнение не имеет корней. Теорема 2 Если D = О, то квадратное уравнение имеет один корень, который находится по формуле Доказательство. Если D = 0, то уравнение (1) принимает вид Значит, единственный корень уравнения. Замечание 1. Помните ли вы, что абсцисса вершины параболы, которая служит графиком функции ? Почему именно это значение оказалось единственным корнем квадратного уравнения ? «Ларчик» открывается просто: если D = 0, то, как мы установили ранее, Графиком же функции является парабола с вершиной в точке (см., например, рис. 98). Значит, абсцисса вершины параболы и единственный корень квадратного уравнения при D = 0 — одно и то же число. Пример 2. Решить уравнение 4х2 — 20х + 25 = 0. Решение. Здесь а = 4, b = -20, с = 25, D = b2 — 4ас = (-20)2 — 4 • 4 • 25 = 400 — 400 = 0. Так как D = 0, то по теореме 2 данное квадратное уравнение имеет один корень. Этот корень находится по формуле Значит, . Ответ: 2,5. Замечание 2. Обратите внимание, что 4х2 — 20х +25 — полный квадрат: 4Х2 — 20х + 25 = (2х — 5)2. Если бы мы это заметили сразу, то решили бы уравнение так: (2х — 5)2 = 0, значит, 2х — 5 = 0, откуда получаем х = 2,5. Вообще, если D = 0, то ах2 + bх + с = Теорема 3. Если D > О, то квадратное уравнение ах2 + bх + с = О имеет два корня, которые находятся по формулам Доказательство. Перепишем квадратное уравнение в виде (1) Положим тогда уравнение (1) примет вид По условию, D > О, значит, правая часть уравнения положительное число. Тогда из уравнения (2) получаем, что Ho , таким образом, задача свелась к решению двух уравнений: Из первого уравнения находим Из второго уравнения находим Итак, заданное квадратное уравнение имеет два корня: Замечание 3. Пример 3. Решить уравнение Зх2 + 8x — 11 = 0. Решение. Здесь а = 3, b = 8, с = —11, D = b2 — 4ас = 82 — 4 • 3 • (—11) = 64 4- 132 = 196. Так как D > 0, то по теореме 3 данное квадратное уравнение имеет два корня. Эти корни находятся по формулам (3) Ответ: 1, Фактически мы с вами выработали следующее правило: Похожие презентации: Элементы комбинаторики ( 9-11 классы) Применение производной в науке и в жизни Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде» Знакомство детей с математическими знаками и монетами Тренажёр по математике «Собираем урожай». Счет в пределах 10 Методы обработки экспериментальных данных Лекция 6. Корреляционный и регрессионный анализ Решение задач обязательной части ОГЭ по геометрии Дифференциальные уравнения Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи English
Русский
Правила регистр
Логин Найдите свой запрос Уравнение типа ax2+ bx + c = 0, где a≠ 0, которое содержит только одну переменную и ‘2’ в его высшей степени, называется квадратным уравнением. i. Чистое квадратное уравнение: Квадратное уравнение формы ax 2 + c = 0, где отсутствует средний член, содержащий степень 1, известно как чистое квадратное уравнение. напр. х 2 = 9 или, х 2 — 9 = 0 ii. Измененное квадратное уравнение: Стандартная форма квадратного уравнения известна как искаженное квадратное уравнение. ax 2 + bx + c = 0 — это квадратное уравнение. напр. x 2 — 9x — 15 = 0 Квадратное уравнение представляет собой уравнение второй степени с одной переменной . Таким образом, мы получаем два решения переменной, содержащейся в этом уравнении. Решение квадратного уравнения известно как корни. Следовательно, квадратное уравнение имеет два корня. Решение корней, полученных из квадратного уравнения, должно удовлетворять уравнению. Существует три основных метода решения квадратного уравнения: а) Решение квадратного уравнения методом факторизации: В этом методе квадратное уравнение ax 2 + bx+ c = 0 факторизуется и выражается как произведение двух линейных множителей. Здесь x 2 — 7x + 6 = 0 или, x 2 — 7x = -6 или, x 2 — 2.x.(7/2) + (7/ 2) 2 = (7/2) 2 — 6 или (х — 7/2) 2 = 14/2 — 6 или (х — 7/2) 2 = 7 — 6 или, (х — 7/2) 2 = (±1) 2 Избегая квадрата с обеих сторон, мы получаем x — 7/2 = ±1 или, x = 7/2±1 Теперь, взяв знак +ve , получаем х = 7/2 + 1 = 7+2/2 = 9/2 = 4,5 Теперь, взяв знак -ve, получаем х = 7/2 — 1 = 7-2/2 = 5/2 = 2,5 ∴ x = 4,5 или 2,5 Следовательно, два корня квадратного уравнения x 2 — 4x + 6 = 0 равны 2,5 и 4,5. Здесь x 2 — 7x + 6 = 0 или, x 2 — 7x = -6 или, x 2 — 2.x.(7/2) + ( 7/ 2) 2 = (7/2) 2 — 6 или (х — 7/2) 2 = 14/2 — 6 или (х — 7/2) 2 = 7 — 6 или, (x — 7/2) 2 = (±1) 2 Исключая квадрат с обеих сторон, получаем x — 7/2 = ±1 или, x = 7/2±1 Теперь, взяв знак +ve, получаем х = 7/2 + 1 = 7+2/2 = 9/2 = 4,5 Теперь, взяв знак -ve, получаем х = 7/2 — 1 = 7-2/2 = 5/ 2 = 2,5 ∴ x = 4,5 или 2,5 Следовательно, два корня квадратного уравнения x 2 — 4x + 6 = 0 равны 2,5 и 4,5. Здесь, х 2 — 8х + 12 = 0 или, х 2 — (6 + 2)х + 12 = 0 или, х 2 — 6х — 2х + 12 = 0 или, х (х — 6) -2 (х — 6) = 0 или, (х — 6) (х — 2) = 0 ∴ х — 6 = 0 или, х = 6 Опять же, x — 2 = 0 или, x = 2 ∴ x = 2 и 6 Теперь проверка, Когда x = 2 L. = 2 2 — 8*2 + 12 = 4 — 16 +12 = 0 = R.H.S доказано, что верно Снова, когда х = 6 , Л.Х.С. = х 2 — 8x + 12 = 6 2 — 8*6 + 12 = 36 — 48 + 12 = 0 = R.H.S. доказано, что верно ∴ x = 2 и 6 удовлетворяют уравнению. Следовательно, два корня квадратного уравнения x 2 — 8x +12 = 0 равны 2 и 6. Здесь, сравнивая уравнение x 2 — 8x + 12 = 0 с ax 2 — bx + c = 0, Получаем, a = 1, b = -8 и c = 12,92 — 4*1*12)}{2*1}\) = \(\frac{(8) ±\sqrt(64 — 48)}{2}\) =\(\frac{( 8) ±\sqrt(16)}{2}\) =\(\frac{8± 4 }{2}\) Теперь, взяв знак +ve, получаем x =\(\frac {8 + 4}{2}\) = 6 Снова со знаком -ve получаем x =\(\frac{8 — 4}{2}\) = 2 ∴ 2 или 6 Теперь проверка, Когда x = 2, L. = 2 2 — 8*2 + 12 = 4 — 16 +12 = 0 = П.С. доказано, что верно Когда x = 6, Л.Х.С. = x 2 — 8x + 12 = 6 2 — 8*6 + 12 = 36 — 48 + 12 = 0 = R.H.S. доказано, что верно ∴ x = 2 и 6 оба удовлетворяют уравнению. Здесь, х 2 — 5х + 20 = 0 или, х 2 — 5х = -6 или, (х) 2 — 5х = -6 или, (х) 2 — 2.х.(5/2) + (5/2) 2 = (5/2) 2 -6 или, (х — 5/2) 2 = 25/4 — 6 или, (х — 5/2) 2 = 25 — 24/4 или, (х — 5/2) 2 = 1/4 или, (x — 5/2) 2 = (± 1/2) 2 Избегая квадратов с обеих сторон, x — 5/ 2 =±1/2 x = 5/2± 1/2 Теперь, взяв знак +ve, получаем x = 5+1/2 = 3 Принимая знак -ve, получаем x = 5-1/2 = 2 ∴ x = 3 или 2 Теперь проверка, При x = 2, Л. = 2 2 — 5*2 + 6 = 4 — 10 + 6 = 0 = R.H.S. доказано, что верно. Когда x = 3, L.H.S. = x 2 — 5x + 6 = 3 2 — 5*3 + 6 = 9 — 15 + 6 = 0 = RHS доказано, что верно ∴ x = 2 и 3 оба удовлетворяют уравнению. Здесь (x — 1) (x + 4) = 0 Либо x — 1 = 0…………(i) , либо x + 4 = 0. ………..(ii) Теперь, из уравнения (i), x — 1 = 0 или, x = 1 Опять же, из уравнения (ii), х + 4 = 0 или, х = -4 ∴ х = 1 и -4. Здесь (x — 3 ) (x + 2) = 0 Либо x — 3 = 0…………(i) Или x + 2 = 0…………(ii) Теперь из уравнения (i) x — 3 = 0 или x = 3 Теперь из уравнения ( ii), х + 2 = 0 или, х = -2 ∴ х = 3 или -2 Здесь, х 2 — 49 = 0 или, х 2 — (7) 2 = 0 или, (x + 7) (x — 7) = 0 Либо, x + 7 = 0 . Или, x — 7 = 0 ………………….(ii) Теперь из уравнения (i) или, x + 7 = 0 или, x = -7 Теперь из уравнения (ii) или x — 7 = 0 или x = 7 ∴ x =±7 оба удовлетворяют уравнению. Здесь, сравнивая уравнение 3x 2 — 5x — 2 = 0 с осью 92 — 4*3*-2)}{2*3}\) = \(\frac{(5) ±\sqrt(25 + 24)}{6}\) = \(\frac{ 5 ±\sqrt(49)}{6}\) = \(\frac{5 ± 7}{6}\) Теперь, взяв знак +ve, получаем x = \(\frac{ 5 + 7}{6}\) = 2 Снова со знаком -ve получаем x = \(\frac{5 — 7}{6}\) = \(\frac { -1} {3}\) ∴ x = 2 или \(\frac {-1} {3}\) Теперь проверка, Когда x = 2 L.H.S. = 3x 2 — 5x — 2 = 3*2 2 — 5 * 2 — 2 = 12 — 10 — 2 = 0 = R.H.S, что верно Когда x =\(\frac {-1} {3}\ ) L. = 3*(\(\frac {-1} {3}\)) 2 — 5\(\frac {-1} {3}\) — 2 = 1 +\(\frac {5} {3}\) — 2 = 0 = R.H.S, что верно ∴ x = 2 и \(\frac {-1} {3}\) оба удовлетворять уравнению. Здесь х = х 2 — 7х + 12 = 0 или, х 2 — (4 + 3)х + 12 = 0 или, х 2 -4х -3х + 12 = 0 или, x(x — 4) -3(x — 4) = 0 или, (x — 4) (x — 3) = 0 Либо, x — 4 = 0 ∴x = 4 Или, x — 3 = 0 ∴x = 3 Теперь проверка, Когда, x = 4 L.H.S. = х 2 — 7х + 12 = 0 = 4 2 — 7*4 + 12 = 16 — 28 + 12 = 0 = R.H.S, что верно Когда x = 3 L.H.S = x 2 — 7x + 12 = 3 2 — 7*3 + 12 9 0003 = 9 — 21 + 12 = 0 = RHS, что верно ∴ x = 4 и 3 оба удовлетворяют уравнению. Здесь х 2 — 25 = 0 или, х 2 — (5) 2 = 0 или, (х + 5) (х — 5) = 0 Либо, х + 5 = 0……………..(i) Или, х — 5 = 0………… ……..(ii) Теперь из уравнения (i), или, x + 5 = 0 или, x = -5 Теперь из уравнения (ii), или, x — 5 = 0 или, x = 5 ∴ x =±5 оба удовлетворяют уравнению. Здесь, х 2 — 15х + 36 = 0 или, х 2 — (12 + 3)х + 36 = 0 или, х 2 — 12х — 3х + 36 = 0 или, х (х — 12) -3 (х — 12) = 0 или, (х — 12) (х — 3) = 0 ∴ x — 12 = 0 или, x = 12 Опять же, x — 3 = 0 или, x = 3 ∴ x = 12 и 3 Теперь проверка , Когда х = 12 Л.Х.С. = x 2 — 15x + 36 = 12 2 — 8*12 + 36 = 144 — 180 + 36 = 0 = R. Снова, когда x = 3, L.H.S. = x 2 — 8x + 12 = 3 2 — 8*3 + 36 = 9 — 45 + 36 = 0 = R.H.S. доказано, что верно ∴ x = 3 и 12 удовлетворяют уравнению. Следовательно, два корня квадратного уравнения x 2 — 8x +12 = 0 равны 3 и 12. Здесь, сравнивая уравнение x 2 — 15x + 36 = 0 с осью 92 — 4*1*36)}{2*1}\) = \(\frac{(15) ±\sqrt(225 — 144)}{2}\) =\(\frac{( 15) ±\sqrt(81)}{2}\) =\(\frac{15 ± 9 }{2}\) Теперь, взяв знак +ve, получаем x =\(\frac {15 + 9}{2}\) = 12 Снова со знаком -ve получаем x =\(\frac{15 — 9}{2}\) = 3 ∴ 3 или 12 Теперь проверка, Когда x = 3, L.H.S. = х 2 — 15х + 36 = 3 2 — 15*3 + 36 = 9 — 45 +36 = 0 = П. Когда x = 12, Л.Х.С. = x 2 — 15x + 36 = 12 2 — 15*12 + 36 = 144 — 180 + 36 = 0 = R.H.S. доказано, что верно ∴ x = 3 и 12 оба удовлетворяют уравнению. Здесь (2x — 5 ) (x + 3) = 0 Либо, 2x — 5 = 0……………(i) Или, x + 3 = 0………….(ii) Теперь из уравнения (i) 2x — 5 = 0 или, x = 5/2 Теперь из уравнения (ii) x + 3 = 0 или, x = -3 ∴ x = 5/2 или -3 Теперь проверка при x = 5 /2 L.H.S = (2x — 5) (x +3) = (2*5/2 — 5) (5/2 + 3) = 0 = R.H.S доказано, что верно при x = -3 L.H.S = (2x — 5) (x + 3) = (2*-3 — 5) (-3 + 3) = 0 = RHS доказано, что верно ∴ 5/2 и -3 оба удовлетворяют уравнению. Здесь x 2 — 100 = 0 или, x 2 — 10 2 = 0 или, (x — 10) (x + 10) = 0 Либо, х — 10 = 0. Или, x + 10 = 0…………(ii) Теперь , х — 10 = 0 или, х = 10 Опять же, x + 10 = 0 или, x = -10 ∴x = ±10 Теперь проверка , когда x = 10 L.H.S = x 90 027 2 — 100 = 10 2 — 100 = 0 = R.H.S доказано, что верно 27 2 — 100 = 0 = правая сторона доказано, что верно ∴ Следовательно, x = 10 и -10 оба удовлетворяют уравнению. © 2019-20 Куллабс. Все права защищены. Решение квадратных уравнений методом факторизации. Сравните решения в различных представлениях (график, уравнение и таблица). Основные стандарты, рассмотренные в этом уроке Основные понятия, которые учащиеся должны продемонстрировать или понять для достижения цели урока Fishtank Plus Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся. Задания, предназначенные для изучения ключевых моментов урока, и наводящие вопросы, помогающие ученикам понять Каждый из наборов A и B включает квадратичную функцию, представленную в виде уравнения, графика и таблицы. Определите, совпадают ли все три представления в каждом наборе. Если нет, объясните, как бы вы изменили одно или несколько представлений, чтобы они совпадали. Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной задачи. Решение какой из приведенных ниже квадратичных функций имеет наибольшее положительное значение $$x$$? Создайте бесплатную учетную запись или войдите, чтобы получить доступ к наводящим вопросам для этой основной проблемы. |
Умножение столбца чисел на одно и то же число
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel для Windows Phone 10 Еще…Меньше
Предположим, нужно умножить столбец чисел на одно и то же число в другой ячейке. Для этого перед копированием формулы ее нужно изменить, добавив в адрес ячейки множителя символы $.
В нашем примере ниже требуется умножить все числа в столбце A на число 3 в ячейке C2. Формула =A2*C2 даст правильный результат (4500) в ячейке B2. Однако копирование формулы в последующие ячейки столбца B не будет работать, поскольку ссылка на ячейку C2 изменяется на C3, C4 и т. д. Так как в этих ячейках нет данных, результат в ячейках от B3 до B6 будет равен нулю.
Чтобы умножить все числа в столбце A на ячейку C2, добавьте символы $ в ссылку на ячейку следующим образом: $C$2, как показано в следующем примере.
Символ$ $ Excel, что ссылка на ячейку C2 является «абсолютной», поэтому при копировании формулы в другую ячейку она всегда будет ссылаться на ячейку C2. Чтобы создать формулу:
-
В ячейке B2 введите знак равенства (=).
-
Щелкните ячейку A2, чтобы добавить ее в формулу.
-
Введите символ «звездочка» (*).
-
Щелкните ячейку C2, чтобы добавить ее в формулу.
org/ListItem»>
-
нажмите клавишу ВВОД.
Введите символ $ перед C и еще один перед 2: $C$2.
Совет: Вместо символа $ можно разместить точку вставки до или после ссылки на ячейку, которую вы хотите сделать «абсолютной», и нажать клавишу F4, которая добавляет символы $.
Теперь вернемся немного назад и рассмотрим простой способ скопировать формулу в последующие ячейки столбца после нажатия клавиши ВВОД в ячейке B2.
-
Выберите ячейку B2.
-
Дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки.

Формула автоматически копируется на последующие ячейки столбца до ячейки B6.
После копирования формулы в столбце B появляются правильные результаты.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е. 1,45 .
е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | Знак плюс | Сложение | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | Знак минус | Вычитание | 2 9/3904 91922 0005||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | знак умножения | умножение | 2/3 × | 13 3 | : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1
Решено
Помогите пожалуйста
Дан куб ABCDA1B1C1D1
Задание 1. Назовите:
а)пару параллельных прямых;
б) пару пересекающихся прямых;
в) пару скрещивающихся прямых;
г) пару
Назовите:
а)пару параллельных прямых;
б) пару пересекающихся прямых;
в) пару скрещивающихся прямых;
г) пару
Решено
Определи скалярное произведение данных векторов, если длина ребра куба равна 2 ед. изм 1. A1D1⋅BC 2. D1B1⋅BD 3. AD⋅AC 4.DA⋅B1D1
По шоссе в одном направлении с постоянной скоростью через равные интервалы времени идут без остановок автобусы. Один человек прошел по шоссе 4 км,
Боря купил 4 книги. Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Пользуйтесь нашим приложением
Кубический корень из 27 — Как найти кубический корень из 27? [Решено]
Значение кубического корня из 27 равно 3. Это действительное решение уравнения x 3 = 27. Кубический корень из 27 выражается как ∛27 в радикальной форме и как (27 ) ⅓ или (27) 0,33 в экспоненциальной форме. Поскольку кубический корень из 27 — целое число, 27 — совершенный куб.
Поскольку кубический корень из 27 — целое число, 27 — совершенный куб.
- Кубический корень из 27: 3
- Кубический корень из 27 в экспоненциальной форме: (27) ⅓
- Кубический корень из 27 в подкоренной форме: ∛27
| 1. | Что такое кубический корень из 27? |
| 2. | Как вычислить кубический корень из 27? |
| 3. | Является ли кубический корень из 27 иррациональным? |
| 4. | Часто задаваемые вопросы о кубическом корне из 27 |
Что такое кубический корень из 27?
Кубический корень из 27 — это число, которое при трехкратном умножении само на себя дает произведение 27. Поскольку 27 можно выразить как 3 × 3 × 3. Следовательно, кубический корень из 27 = ∛(3 × 3 × 3 ) = 3.
Как вычислить значение кубического корня из 27?
Кубический корень из 27 с помощью простой факторизации
- Простая факторизация из 27 равна 3 × 3 × 3
- Упрощение приведенного выше выражения: 3 3
Таким образом, кубический корень из 27 по простой факторизации равен (3 × 3 × 3) 1/3 = 3.
Является ли кубический корень из 27 иррациональным?
Нет, потому что ∛27 = ∛(3 × 3 × 3) можно выразить в виде p/q, т.е. 3/1. Следовательно, значение кубического корня из 27 является целым числом (рациональным).
☛ Также проверьте:
- Кубический корень из 8000
- Кубический корень из 68
- Кубический корень из 144
- Кубический корень из 57
- Кубический корень из 10000
- Кубический корень из 529
- Кубический корень из 243
Кубический корень из 27 решенных примеров
Пример 1.
 Чему равно ∛27 + ∛(-27)?
Чему равно ∛27 + ∛(-27)? Решение:
Кубический корень из -27 равен минусу кубического корня из 27.
т. е. ∛-27 = -∛27Следовательно, ∛27 + ∛(-27) = ∛27 — ∛27 = 0
Пример 2: Объем сферического шара равен 27π в 3 . Каков радиус этого шара?
Решение:
Объем сферического шара = 27π в 3
= 4/3 × π × R 3
⇒ Р 3 = 3/4 × 27
⇒ R = ∛(3/4 × 27) = ∛(3/4) × ∛27 = 0,90856 × 3 (∵ ∛(3/4) = 0,90856 и ∛27 = 3)
⇒ R = 2,72568 в 3Пример 3: Дан объем куба 27 в 3 . Найдите длину стороны куба.
Решение:
Объем куба = 27 дюймов 3 = 3
⇒ а 3 = 27
Укоренение куба с обеих сторон,
⇒ а = ∛27 в
Поскольку кубический корень из 27 равен 3, следовательно, длина стороны куба равна 3 дюймам.
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о кубическом корне из 27
Каково значение кубического корня из 27?
Мы можем выразить 27 как 3 × 3 × 3, т. е. ∛27 = ∛(3 × 3 × 3) = 3. Следовательно, значение кубического корня из 27 равно 3.
Если кубический корень из 27 равен 3 , Найдите значение ∛0,027.
Представим ∛0,027 в форме p/q, т. е. ∛(27/1000) = 3/10 = 0,3. Следовательно, значение ∛0,027 = 0,3.
Почему значение кубического корня из 27 рационально?
Значение кубического корня из 27 можно выразить в виде p/q, т.е. = 3/1, где q ≠ 0. Следовательно, ∛27 рационально.
Является ли число 27 идеальным кубом?
Число 27 при разложении на простые множители дает 3 × 3 × 3. При объединении простых делителей в группы по 3 дает 3. Итак, кубический корень из 27 = ∛(3 × 3 × 3) = 3 (совершенный куб).
При объединении простых делителей в группы по 3 дает 3. Итак, кубический корень из 27 = ∛(3 × 3 × 3) = 3 (совершенный куб).
Каково значение 2 плюс 8 кубический корень 27?
Значение ∛27 равно 3. Итак, 2 + 8 × ∛27 = 2 + 8 × 3 = 26. Следовательно, значение 2 плюс 8 кубический корень 27 равно 26,
Что такое куб кубического корня из 27?
Куб кубического корня из 27 — это само число 27, т.е. (∛27) 3 = (27 1/3 ) 3 = 27.
Калькулятор дробей
9012 Калькулятор дробей и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т.е. 1,45 .
Математические символы
| Символ | Имя символа | Символ Значение | Пример | |||
|---|---|---|---|---|---|---|
| + | знак плюс | сложение | 1/2 + 1/3 | |||
| — | знак минус | вычитание | 2 2/3 2/3/2/3/2/3/2/3/2/3 2/390 1 0034 | |||
| * | звездочка | умножение | 2/3 * 3/4 | |||
| × | знак умножения | умножение | 2/3 × 9037 9037 9034 2 | : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
|


 «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.
«Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа.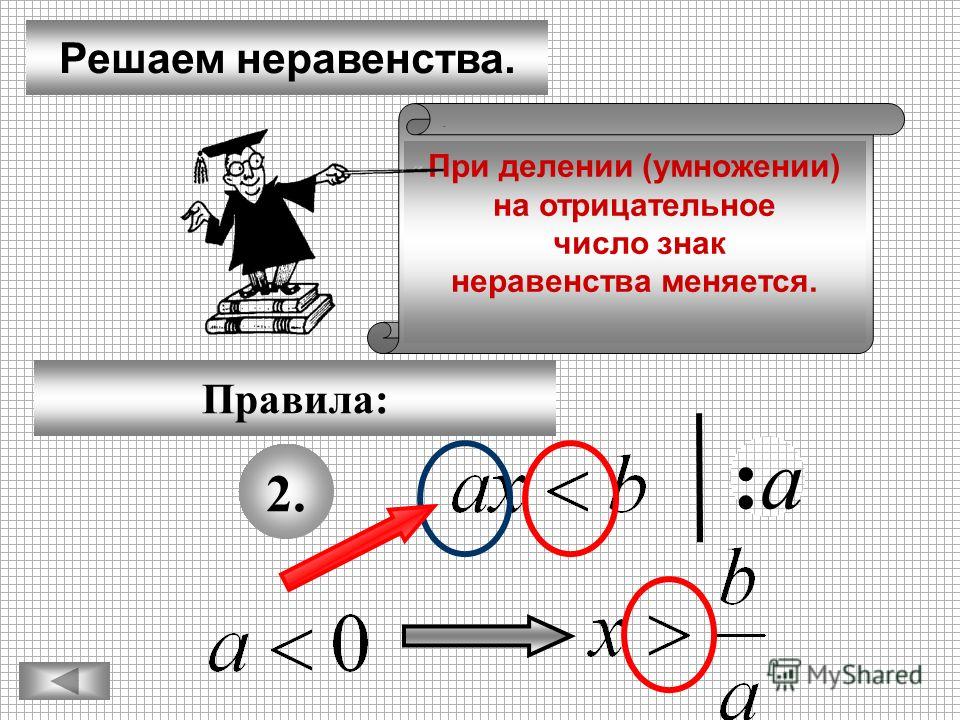 «Отбрасывая» логарифмы, делаем это грамотно.
«Отбрасывая» логарифмы, делаем это грамотно.
 Если вы получите ответ, что решение неравенства – все числа, от минус до плюс бесконечности, то это значит, что неравенство выполняется при любых значениях p
Решим неравенство
Перенесем все в левую часть.
Раскрываем скобки.
Приводим подобные члены.
Раскрываем скобки.
Приводим подобные члены.
Изменим знаки выражений на противоположные.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: p-любое.
Это значит, что оно истинно при любых значениях p.
Решим еще одно неравенство, в которой в качестве переменно будет не p, а у
Перенесем все в левую часть.
Раскрываем скобки, используя распределительный закон умножения
Раскрываем скобки, помня, что при раскрытии скобок знаки выражений меняются на противоположные
Приводим подобные члены.
Если вы получите ответ, что решение неравенства – все числа, от минус до плюс бесконечности, то это значит, что неравенство выполняется при любых значениях p
Решим неравенство
Перенесем все в левую часть.
Раскрываем скобки.
Приводим подобные члены.
Раскрываем скобки.
Приводим подобные члены.
Изменим знаки выражений на противоположные.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: p-любое.
Это значит, что оно истинно при любых значениях p.
Решим еще одно неравенство, в которой в качестве переменно будет не p, а у
Перенесем все в левую часть.
Раскрываем скобки, используя распределительный закон умножения
Раскрываем скобки, помня, что при раскрытии скобок знаки выражений меняются на противоположные
Приводим подобные члены. Изменяем порядок действий. Ставим слагаемые так, чтобы нам было удобно применять формулу корней квадратного уравнения в дальнейшем
Решаем вспомогательное уравнение.
Решаем это квадратное уравнение через дискриминант.
Находим дискриминант по стандартной формуле
Дискриминант равен нулю, значит, уравнение имеет один корень.
Старший коэффициент положителен.
Квадратичная функция принимает только неотрицательные значения.
Следующее неравенство равносильно предыдущему.
Окончательный ответ: y — любое.
При решении неравенства мы по показали, что его решениями являются все действительные числа. А это значит, что при любых у выполняется неравенство, что и требовалось доказати.
Решим еще одно неравенство, в котором неизвестной будет переменная x
Для начала перенесем все в левую часть.
Теперь умножаем друг на другу, пользуясь стандартным правилом.
Изменяем порядок действий. Ставим слагаемые так, чтобы нам было удобно применять формулу корней квадратного уравнения в дальнейшем
Решаем вспомогательное уравнение.
Решаем это квадратное уравнение через дискриминант.
Находим дискриминант по стандартной формуле
Дискриминант равен нулю, значит, уравнение имеет один корень.
Старший коэффициент положителен.
Квадратичная функция принимает только неотрицательные значения.
Следующее неравенство равносильно предыдущему.
Окончательный ответ: y — любое.
При решении неравенства мы по показали, что его решениями являются все действительные числа. А это значит, что при любых у выполняется неравенство, что и требовалось доказати.
Решим еще одно неравенство, в котором неизвестной будет переменная x
Для начала перенесем все в левую часть.
Теперь умножаем друг на другу, пользуясь стандартным правилом. Приводим подобные члены в скобках
Раскрываем скобки, меняя знаки выражений на противоположные
Приводим подобные члены и изменяем порядок действий.
Изменим знаки выражений на противоположные. При этом x в квадрате окажется без знака минуса, а
— 2 изменится +2
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: x –любое, так выражение x в квадрате +2 в любом случаем принимает положительное значение
Таким мы доказали то, что нам требовалось.
Приводим подобные члены в скобках
Раскрываем скобки, меняя знаки выражений на противоположные
Приводим подобные члены и изменяем порядок действий.
Изменим знаки выражений на противоположные. При этом x в квадрате окажется без знака минуса, а
— 2 изменится +2
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Окончательный ответ: x –любое, так выражение x в квадрате +2 в любом случаем принимает положительное значение
Таким мы доказали то, что нам требовалось. Здесь, как вы увидите, в этом нет необходимости, поэтому вы можете решить это так же, как уравнение. Сначала умножьте обе части на 2, чтобы исключить знаменатель:
Здесь, как вы увидите, в этом нет необходимости, поэтому вы можете решить это так же, как уравнение. Сначала умножьте обе части на 2, чтобы исключить знаменатель: Если бы вы выбрали , то увидели бы, что данное неравенство принимает вид: , что работает, потому что
Если бы вы выбрали , то увидели бы, что данное неравенство принимает вид: , что работает, потому что  Однако что, если это отрицательное число? Помните, что когда вы умножаете или делите на отрицательное число в неравенстве, вы должны перевернуть знак. Но здесь вы не знаете, означает ли умножение на умножение на положительное или отрицательное число, поэтому вы не знаете, в каком направлении должен указывать знак. Важным соображением при работе с неравенствами является то, что вы никогда не сможете умножать или делить на переменную, если не знаете знак переменной. В результате возможны и I, и II, но ни один из них не гарантирован:
Однако что, если это отрицательное число? Помните, что когда вы умножаете или делите на отрицательное число в неравенстве, вы должны перевернуть знак. Но здесь вы не знаете, означает ли умножение на умножение на положительное или отрицательное число, поэтому вы не знаете, в каком направлении должен указывать знак. Важным соображением при работе с неравенствами является то, что вы никогда не сможете умножать или делить на переменную, если не знаете знак переменной. В результате возможны и I, и II, но ни один из них не гарантирован: Таким образом, вы можете решить эту проблему, проделав одно и то же с обеими сторонами неравенства. Начиная с , вы можете:
Таким образом, вы можете решить эту проблему, проделав одно и то же с обеими сторонами неравенства. Начиная с , вы можете: Если вы вычтете 6 из обеих сторон, вы получите:
Если вы вычтете 6 из обеих сторон, вы получите: В этой задаче вам не нужно делать этот шаг.
В этой задаче вам не нужно делать этот шаг. Здесь это означает, что если вы сделаете (логический) первый шаг деления обеих частей на , вам нужно изменить знак неравенства с больше на меньше, чтобы получить:
Здесь это означает, что если вы сделаете (логический) первый шаг деления обеих частей на , вам нужно изменить знак неравенства с больше на меньше, чтобы получить: Если вы умножаете или делите на отрицательное число, вы должны изменить знак неравенства. Этой ситуации (как вы увидите здесь) обычно легко избежать.
Если вы умножаете или делите на отрицательное число, вы должны изменить знак неравенства. Этой ситуации (как вы увидите здесь) обычно легко избежать. Когда мы умножаем или делим на отрицательное число, мы должны перевернуть знак неравенства, поскольку мы в основном «переворачиваем» отношение над 0 на числовой прямой. (Число, которое больше, когда оно положительное, становится «более отрицательным» и, следовательно, меньше, когда оно отрицательное, и наоборот).
Когда мы умножаем или делим на отрицательное число, мы должны перевернуть знак неравенства, поскольку мы в основном «переворачиваем» отношение над 0 на числовой прямой. (Число, которое больше, когда оно положительное, становится «более отрицательным» и, следовательно, меньше, когда оно отрицательное, и наоборот).
 Для этого отнимите 6 с обеих сторон.
Для этого отнимите 6 с обеих сторон.

 49
49
_hrom_images/lekciya_15_(himiya)_hrom_2.jpg)
 Он достаточно ломкий, но при этом имеет несравненный плюс по сравнению со многими другими металлами – устойчивость к заражению коррозией; именно поэтому он является важным компонентом при производстве нержавеющей стали, а также используется для нанесения на поверхность других металлов, более склонных к коррозии. Хром обладает плохой тепло- и электропроводностью.
Он достаточно ломкий, но при этом имеет несравненный плюс по сравнению со многими другими металлами – устойчивость к заражению коррозией; именно поэтому он является важным компонентом при производстве нержавеющей стали, а также используется для нанесения на поверхность других металлов, более склонных к коррозии. Хром обладает плохой тепло- и электропроводностью. Если раскалить Cr, то способен вступить в реакцию с водяными парами.
Если раскалить Cr, то способен вступить в реакцию с водяными парами.
 Мысленно отделяем последний элемент (с уже определённой степенью окисления) от двух других элементов. Нам требуется, чтобы СО двух первых и последнего элементов в сумме была равна нулю.
Мысленно отделяем последний элемент (с уже определённой степенью окисления) от двух других элементов. Нам требуется, чтобы СО двух первых и последнего элементов в сумме была равна нулю.



 1993; Мерц, 1993].
1993; Мерц, 1993]. Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности.
Включение в базу данных NLM не означает одобрения или согласия с
содержание NLM или Национальных институтов здравоохранения.
Узнайте больше о нашем отказе от ответственности. Термодинамически наиболее стабильными состояниями являются +3 и +2, тогда как степени окисления +3 и +6 наиболее распространены в водном растворе. Кинетически хром +3 инертен замещению: для водообмена k(сек-1) = 2,5 х 10(-6) из-за наличия полузаполненного состояния d(t2g)3,4A2g. С другой стороны, протонирование/депротонирование происходит довольно быстро. Полимеризация протекает очень медленно, но ускоряется при более высоких значениях pH; кислотное расщепление протонированных олигомеров также происходит довольно медленно. Хром +6 как ион хромата сильно окисляется при низких значениях pH и в меньшей степени в щелочном растворе. Ион хромата действительно образует некоторые поликислоты и полианионы. Эти факторы необходимо учитывать при анализе образцов на содержание общего хрома и количество каждой степени окисления.
Термодинамически наиболее стабильными состояниями являются +3 и +2, тогда как степени окисления +3 и +6 наиболее распространены в водном растворе. Кинетически хром +3 инертен замещению: для водообмена k(сек-1) = 2,5 х 10(-6) из-за наличия полузаполненного состояния d(t2g)3,4A2g. С другой стороны, протонирование/депротонирование происходит довольно быстро. Полимеризация протекает очень медленно, но ускоряется при более высоких значениях pH; кислотное расщепление протонированных олигомеров также происходит довольно медленно. Хром +6 как ион хромата сильно окисляется при низких значениях pH и в меньшей степени в щелочном растворе. Ион хромата действительно образует некоторые поликислоты и полианионы. Эти факторы необходимо учитывать при анализе образцов на содержание общего хрома и количество каждой степени окисления.
 В. Ященко, 2020. Вариант 8, задача 15
В. Ященко, 2020. Вариант 8, задача 15 Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?
Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили? Лучше всего оформлять решение неравенства именно так.
Лучше всего оформлять решение неравенства именно так. Такое, что не решается обычными способами.
Такое, что не решается обычными способами.
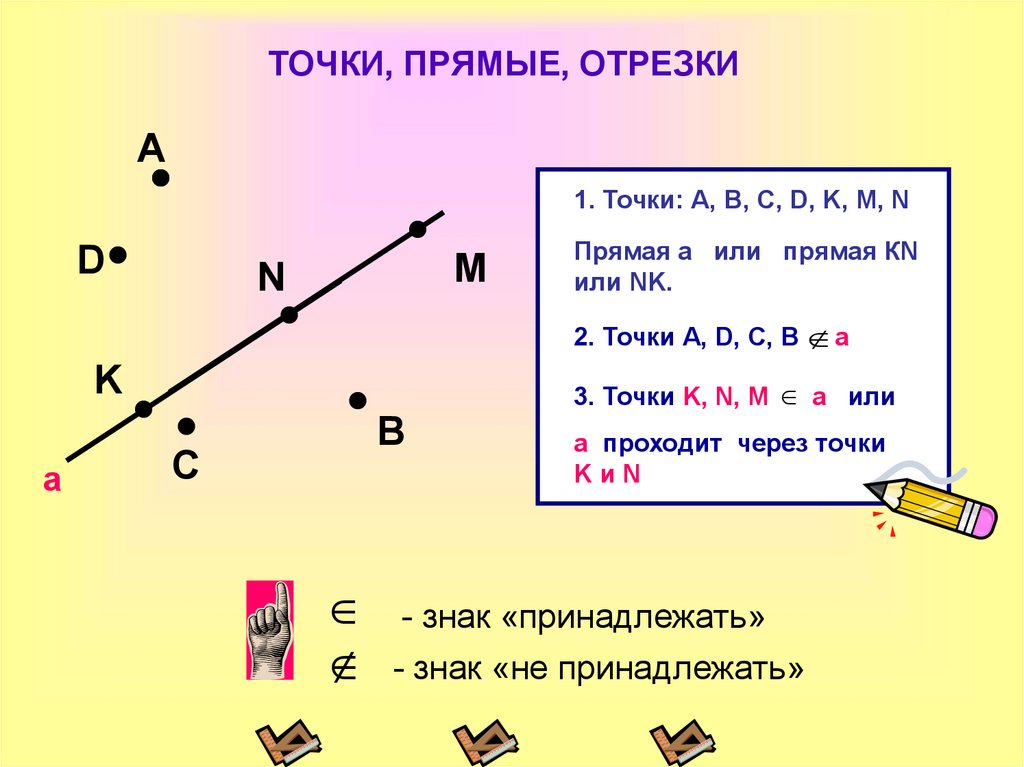 Точки обозначаются большими латинскими буквами, прямые обозначаются малыми латинскими буквами.
Точки обозначаются большими латинскими буквами, прямые обозначаются малыми латинскими буквами.
 Урок 3
Урок 3
 Вторым обязательным аргументом является цвет. Цвет задается в формате RGB, используется трехэлементный целочисленный кортеж. Например, (255, 0, 0) определяет красный цвет.
Вторым обязательным аргументом является цвет. Цвет задается в формате RGB, используется трехэлементный целочисленный кортеж. Например, (255, 0, 0) определяет красный цвет. rect() и некоторые другие третьим аргументом можно передавать не кортеж, а заранее созданный экземпляр Rect. В примере ниже показан такой вариант.
rect() и некоторые другие третьим аргументом можно передавать не кортеж, а заранее созданный экземпляр Rect. В примере ниже показан такой вариант.

 Например, пиксель с координатами (10, 10) светится синим цветом, в следующем кадре синим загорается пиксель (11, 11), в то время как (10, 10) становится таким же как фон. В следующем кадре синей будет только точка (12, 12) и так далее. При этом человеку будет казаться, что синяя точка движется по экрану по диагонали.
Например, пиксель с координатами (10, 10) светится синим цветом, в следующем кадре синим загорается пиксель (11, 11), в то время как (10, 10) становится таким же как фон. В следующем кадре синей будет только точка (12, 12) и так далее. При этом человеку будет казаться, что синяя точка движется по экрану по диагонали. После этого возвращается назад – от правой границы к левой, касается ее, опять двигается вправо. Циклы движения квадрата повторяются до завершения программы.
После этого возвращается назад – от правой границы к левой, касается ее, опять двигается вправо. Циклы движения квадрата повторяются до завершения программы. tick(FPS)
tick(FPS)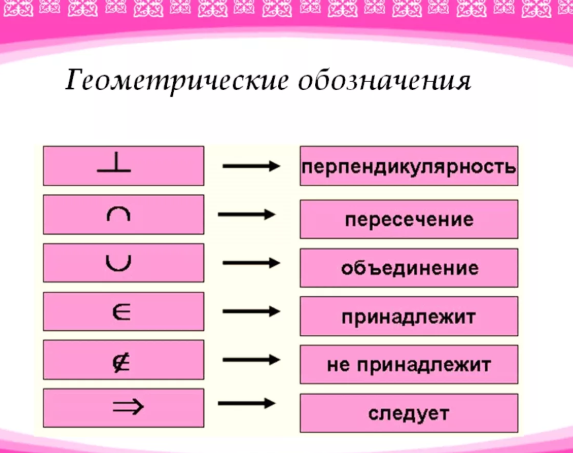


 Какова будет величина центрального угла в этом случае?
Какова будет величина центрального угла в этом случае?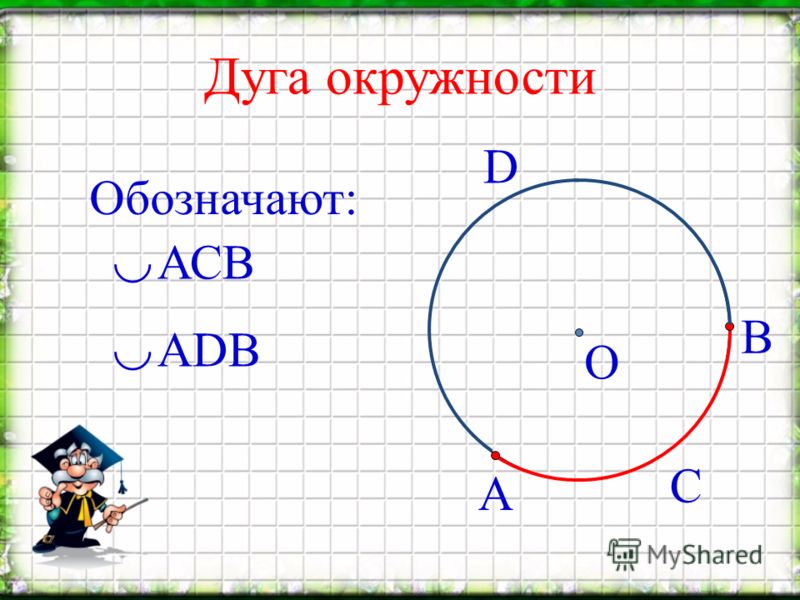

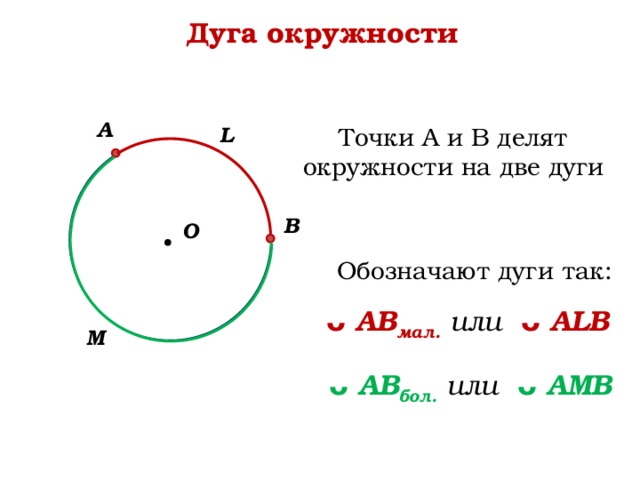 Здесь у нас есть главная дуга FUN :
Здесь у нас есть главная дуга FUN :


 в математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней.
в математике довольно редко бывает так, чтобы введенный термин не имел, образно выражаясь, житейской подоплеки. Возьмем новое понятие — дискриминант. Вспомните слово «дискриминация». Что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к различным людям. Оба слова (и дискриминант, и дискриминация) происходят от латинского discriminans — «различающий». Дискриминант различает квадратные уравнения по числу корней. 9 класс — презентация онлайн
9 класс — презентация онлайн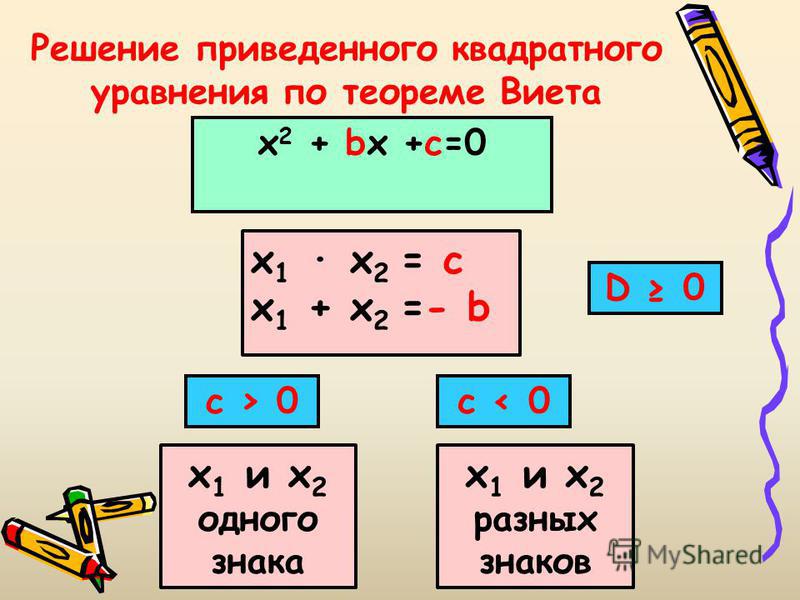
 ах² + bх + с = 0,
ах² + bх + с = 0, В любом квадратном уравнении есть два значения переменной.
В любом квадратном уравнении есть два значения переменной.
 Опять же, два линейных фактора также решаются, чтобы получить решение уравнения. корни, полученные из уравнения, должны удовлетворять заданному квадратному уравнению. 92-4ac}}{2a}\) и найти два корня данного квадратного уравнения.
Опять же, два линейных фактора также решаются, чтобы получить решение уравнения. корни, полученные из уравнения, должны удовлетворять заданному квадратному уравнению. 92-4ac}}{2a}\) и найти два корня данного квадратного уравнения.
 H.S. = x 2 — 8x + 12
H.S. = x 2 — 8x + 12 H.S. = х 2 — 8х + 12
H.S. = х 2 — 8х + 12 Х.С. = x 2 — 5x + 6
Х.С. = x 2 — 5x + 6 ……………(i)
……………(i) H.S. x = 3x 2 — 5x — 2
H.S. x = 3x 2 — 5x — 2
 H .S доказано, что верно
H .S доказано, что верно С. доказано, что верно
С. доказано, что верно ………..(i)
………..(i) IF.C.8.A
— Используйте процесс факторизации и завершения квадрата квадратичной функции, чтобы показать нули, экстремальные значения и симметрию графика, и интерпретируйте их с точки зрения контекста.
IF.C.8.A
— Используйте процесс факторизации и завершения квадрата квадратичной функции, чтобы показать нули, экстремальные значения и симметрию графика, и интерпретируйте их с точки зрения контекста. 


 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
 В любом треугольнике можно провести три средних линии.
В любом треугольнике можно провести три средних линии.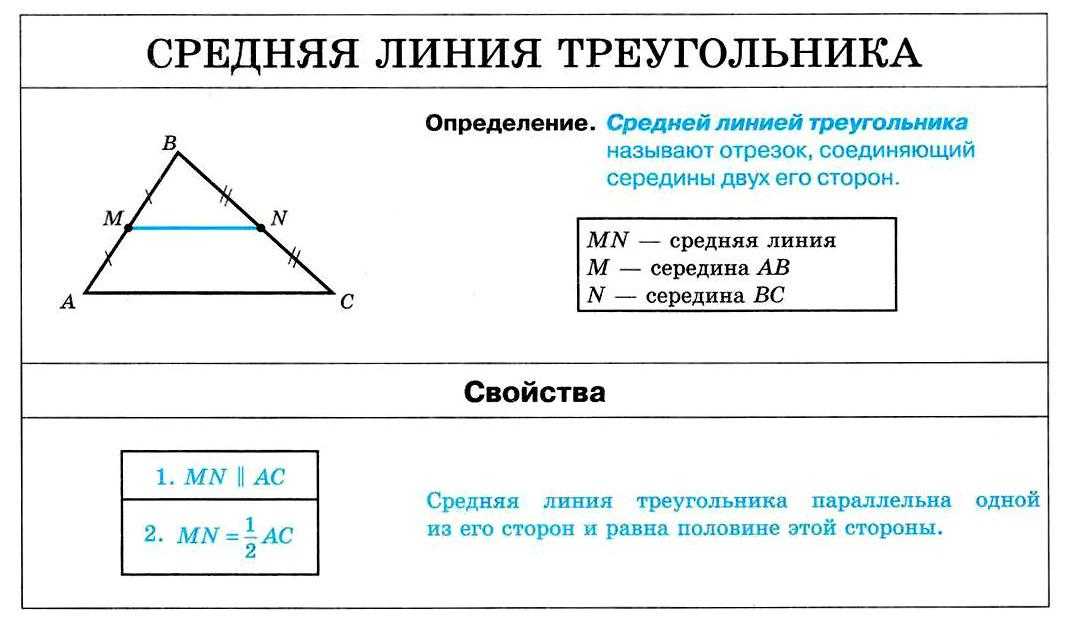
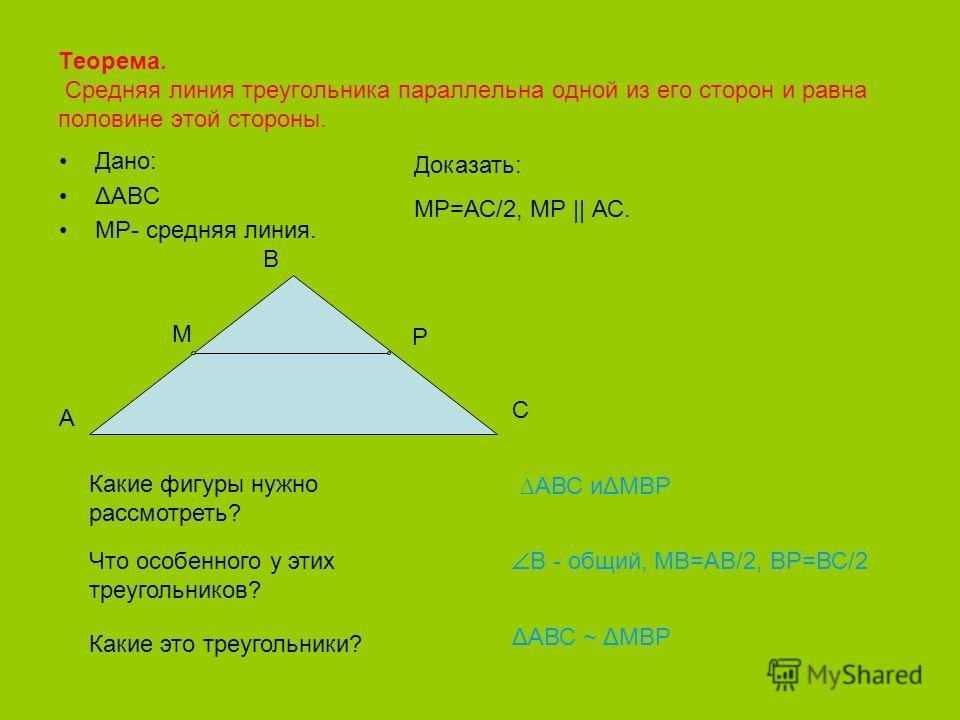
 Значит, доказано, что средняя линия равна половине основания.
Значит, доказано, что средняя линия равна половине основания. Найти площадь большого прямоугольного треугольника.
Найти площадь большого прямоугольного треугольника.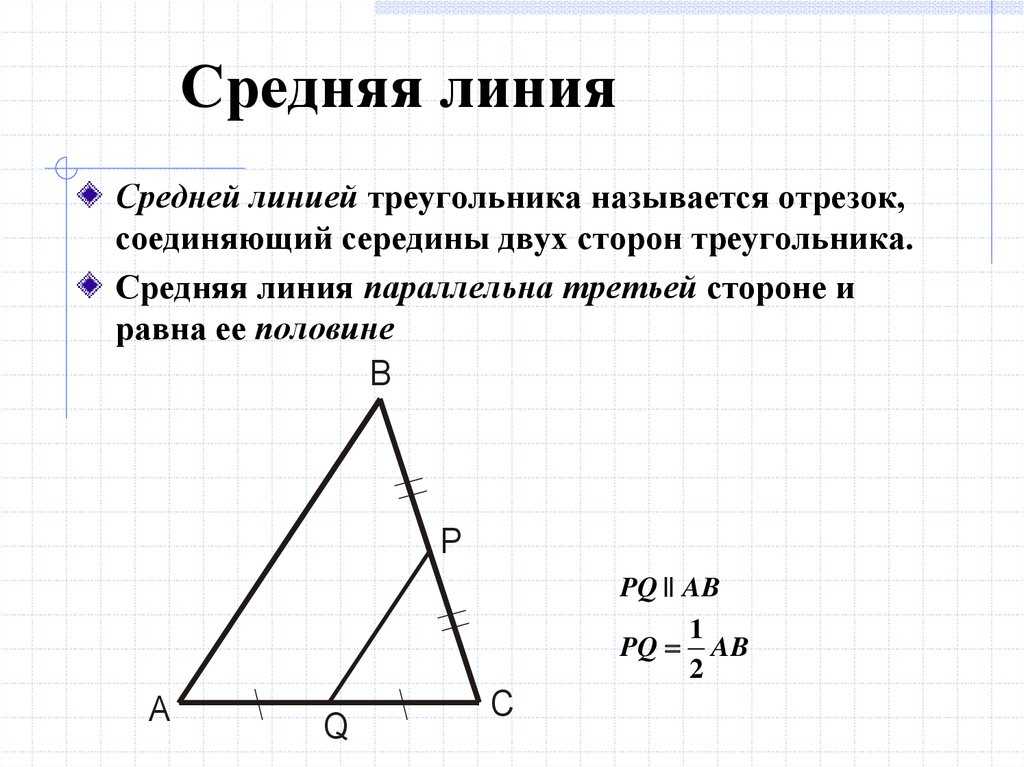
 Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…
Здравствуйте, друзья! Сегодня теоретический материал, связан он с треугольником. В составе экзамена имеется группа заданий, в которых используется свойство его средней линии. Причём не только в задачах с треугольниками, но и с трапециями. Была на блоге статья, в которой сии факты я предлагал просто запомнить, теперь подробнее…
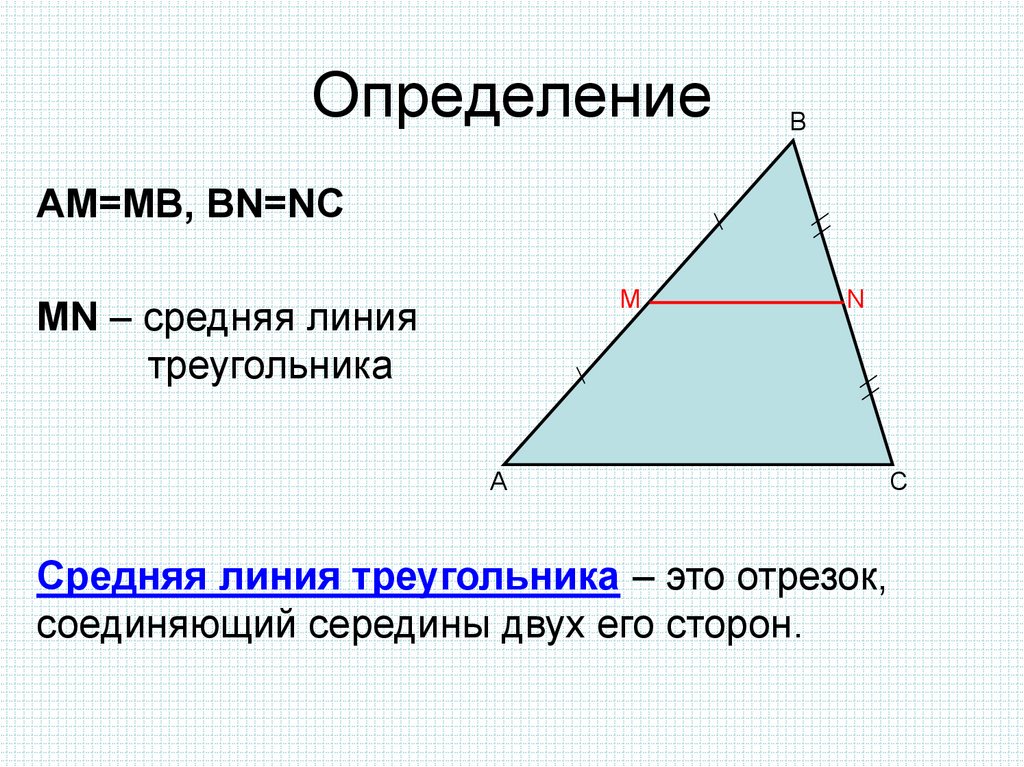
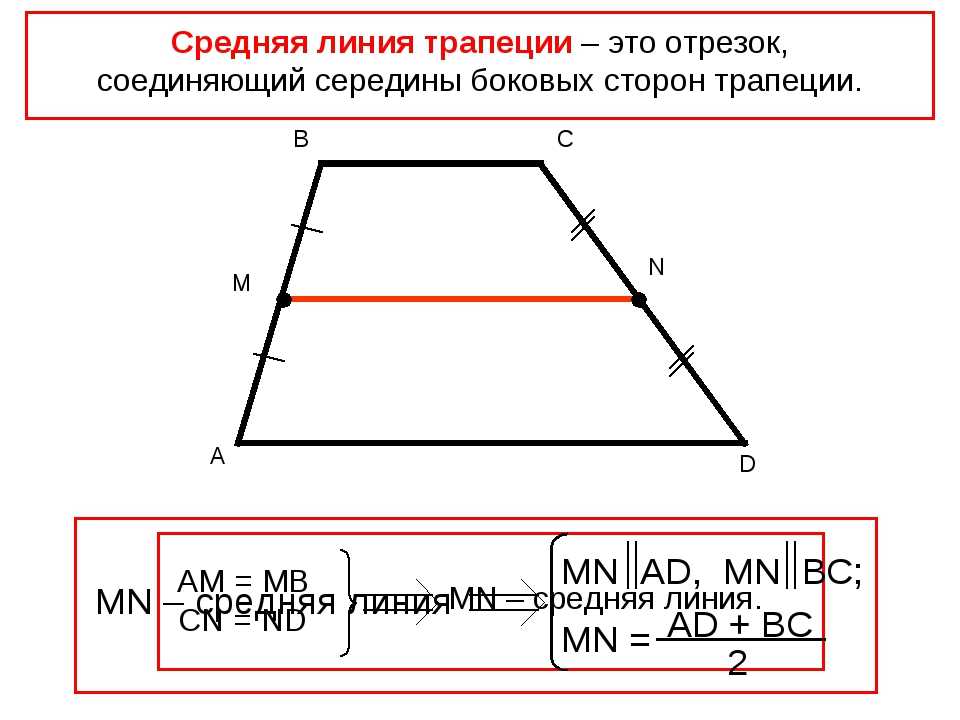
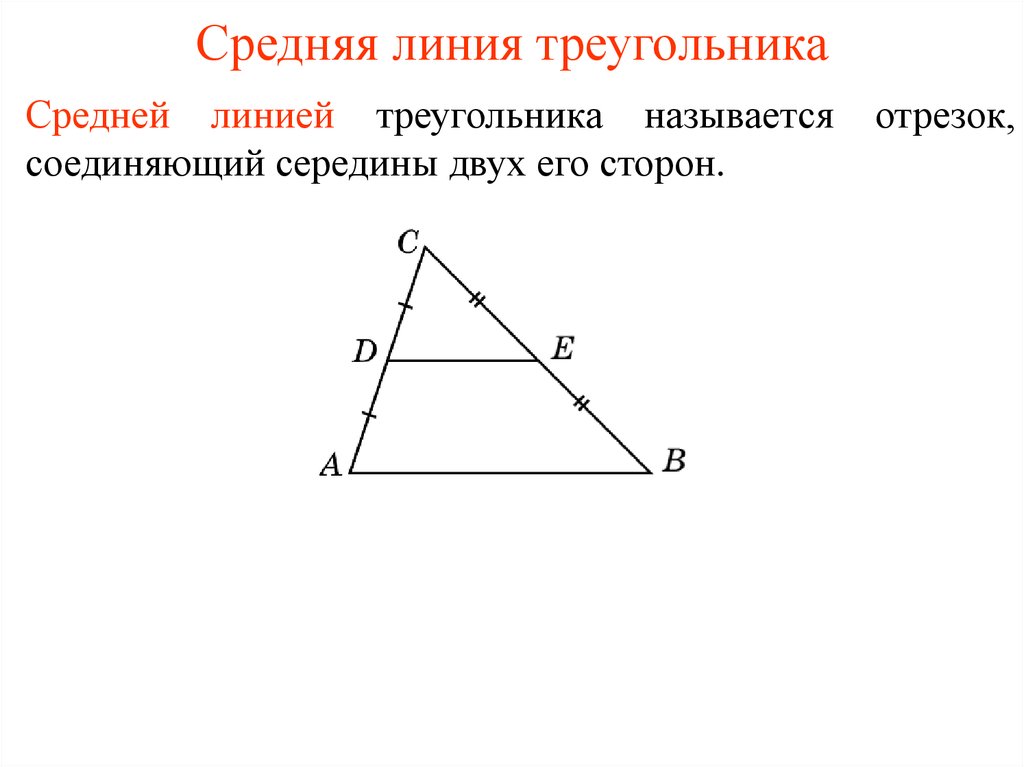 Поскольку мы знаем длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см с любого конца. Точка R на AH точно равна 18 см с любого конца.
Поскольку мы знаем длины сторон, мы знаем, что точка C , середина стороны AS , точно равна 12 см с любого конца. Точка R на AH точно равна 18 см с любого конца.

 Сторона 9{2}482,5 дюйма2.
Сторона 9{2}482,5 дюйма2. Шаги просты, а результаты визуально приятны:
Шаги просты, а результаты визуально приятны: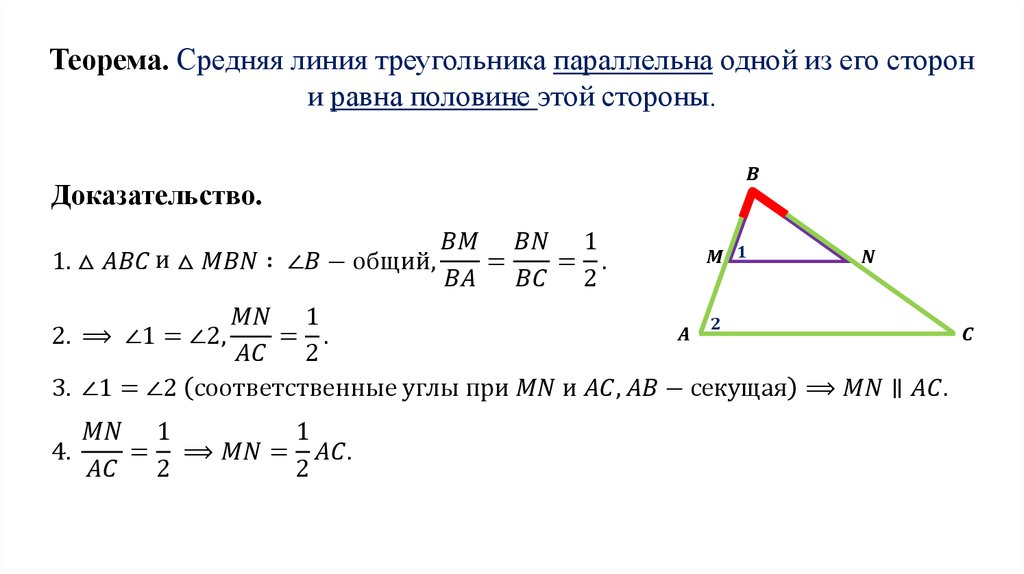 Даже если это не так, вы все равно найдете этот инструмент полезным.
Даже если это не так, вы все равно найдете этот инструмент полезным.


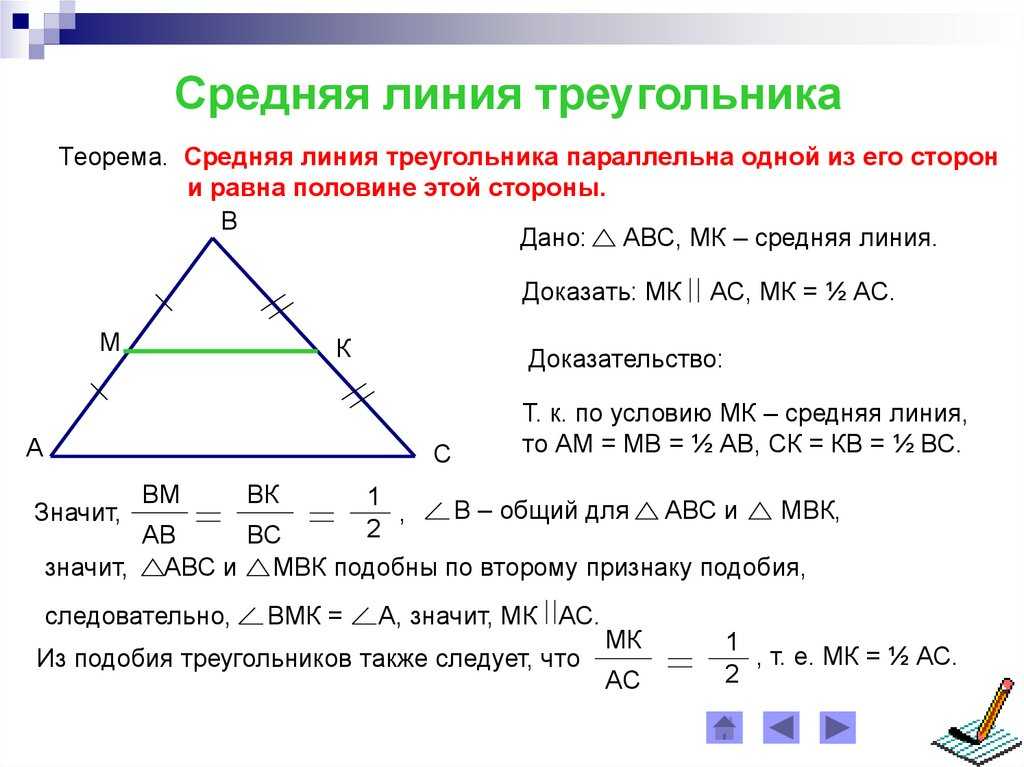

 Таким же образом они руками своими доставляли все это царям Хеттейским и царям Арамейским.
Таким же образом они руками своими доставляли все это царям Хеттейским и царям Арамейским.



 5
5 7112185277
7112185277 11, GOST R 34.11-94, GOST(7369657)
11, GOST R 34.11-94, GOST(7369657) 112.115.185
112.115.185 Записанная в Bell Sound в Нью-Йорке в 1964 и 1965 годах и выпущенная прямо в разгар британского вторжения, эта музыка показывает влияние британских групп того периода без ущерба для собственного звучания Шеннона — его оригиналы, в основном перегруженные хуками, болезненно красивые и бодрящие, в том числе «Почему бы тебе не сказать ей», «Незнакомец в городе», «Я разваливаюсь», «Продолжай искать (Мы будем следовать за солнцем)» и «Над тобой». хорошо сочетаются с каверами на песни «Do You Wanna Dance», «Needles and Pins», «Rag Doll», «I’m Gonna Be Strong» и «Running Scared». «Needles and Pins» показывает, что Шеннон перенимает подход Searchers к песне, а также адаптирует ее к своему стилю, в то время как «Running Scared», помимо того, что это отличный трек сам по себе, интригует, поскольку он вписывается в понятие , плавал ненадолго в конце 1980-х годов, что Шеннон должен был стать преемником Роя Орбисона в Traveling Wilburys. Поскольку Гарри Балк продюсирует в манере, похожей на Фила Спектора, на протяжении всего альбома много реверберации, но в его основе был мощный гитарный звук (любезно предоставленный Шенноном), Деннисом Коффи и Биллом Найтом, а также выразительный бас — есть Муситрон используется нечасто, если не считать таких чисел, как «Продолжай искать».
Записанная в Bell Sound в Нью-Йорке в 1964 и 1965 годах и выпущенная прямо в разгар британского вторжения, эта музыка показывает влияние британских групп того периода без ущерба для собственного звучания Шеннона — его оригиналы, в основном перегруженные хуками, болезненно красивые и бодрящие, в том числе «Почему бы тебе не сказать ей», «Незнакомец в городе», «Я разваливаюсь», «Продолжай искать (Мы будем следовать за солнцем)» и «Над тобой». хорошо сочетаются с каверами на песни «Do You Wanna Dance», «Needles and Pins», «Rag Doll», «I’m Gonna Be Strong» и «Running Scared». «Needles and Pins» показывает, что Шеннон перенимает подход Searchers к песне, а также адаптирует ее к своему стилю, в то время как «Running Scared», помимо того, что это отличный трек сам по себе, интригует, поскольку он вписывается в понятие , плавал ненадолго в конце 1980-х годов, что Шеннон должен был стать преемником Роя Орбисона в Traveling Wilburys. Поскольку Гарри Балк продюсирует в манере, похожей на Фила Спектора, на протяжении всего альбома много реверберации, но в его основе был мощный гитарный звук (любезно предоставленный Шенноном), Деннисом Коффи и Биллом Найтом, а также выразительный бас — есть Муситрон используется нечасто, если не считать таких чисел, как «Продолжай искать». Даже «Rag Doll», один из самых ненужных треков здесь с точки зрения оригинальности, который имитирует аранжировку и ритм оригинала Four Seasons, имеет более пробивную ритм-секцию, благодаря которой вокал звучит еще более страстно. One Thousand Six-Hundred Sixty-One Seconds with Del Shannon длится менее 30 минут, что делает этот альбом аккуратного размера, который очень легко воспринимается даже сегодня, с не меньшей музыкальной ценностью, чем типичный материал British Invasion того же альбома. период.
Даже «Rag Doll», один из самых ненужных треков здесь с точки зрения оригинальности, который имитирует аранжировку и ритм оригинала Four Seasons, имеет более пробивную ритм-секцию, благодаря которой вокал звучит еще более страстно. One Thousand Six-Hundred Sixty-One Seconds with Del Shannon длится менее 30 минут, что делает этот альбом аккуратного размера, который очень легко воспринимается даже сегодня, с не меньшей музыкальной ценностью, чем типичный материал British Invasion того же альбома. период. Как написать 45 965 657 прописью? а. Сорок пятьсот миллионов девятьсот шестьдесят пять тысяч шестьсот б. Сорок пять миллионов девятьсот шестьдесят пять тысяч шесть пятьдесят семь c. Сорок пять миллионов девятьсот шестьдесят пять тысяч шестьсот пятьдесят семь д. Сорок пятьсот девятьсот шестьдесят пять тысяч шестьсот пятьдесят семь
Как написать 45 965 657 прописью? а. Сорок пятьсот миллионов девятьсот шестьдесят пять тысяч шестьсот б. Сорок пять миллионов девятьсот шестьдесят пять тысяч шесть пятьдесят семь c. Сорок пять миллионов девятьсот шестьдесят пять тысяч шестьсот пятьдесят семь д. Сорок пятьсот девятьсот шестьдесят пять тысяч шестьсот пятьдесят семь двадцать девять тысяч шестьсот сорок девять = 4. девяносто девять тысяч девятьсот девяносто девять = 5. сорок пять тысяч сто два символа мичино и
двадцать девять тысяч шестьсот сорок девять = 4. девяносто девять тысяч девятьсот девяносто девять = 5. сорок пять тысяч сто два символа мичино и ) 9 , 3 2 1 , 7 902 81 0 2
) 9 , 3 2 1 , 7 902 81 0 2  Запишите следующие числовые слова цифрами.
восемь и семьдесят четыре сотых1.____
пять и девятьсот сорок три тысячи шестьсот семьдесят одна миллионная2.____
сорок шесть триста тридцать три тысячных3._____
двадцать четыре восемьдесят четыре тысячи пятьсот тысяч4.____
пятьдесят шесть и девятьсот пятьдесят три тысячных5.____
две и шесть тысяч семьсот сорок три десятитысячных6.__
Запишите следующие числовые слова цифрами.
восемь и семьдесят четыре сотых1.____
пять и девятьсот сорок три тысячи шестьсот семьдесят одна миллионная2.____
сорок шесть триста тридцать три тысячных3._____
двадцать четыре восемьдесят четыре тысячи пятьсот тысяч4.____
пятьдесят шесть и девятьсот пятьдесят три тысячных5.____
две и шесть тысяч семьсот сорок три десятитысячных6.__ 6. Как читать и писать 0.2941a. Две тысячи девятьсот сорок одна десятая. Две тысячи девятьсот сорок одна сотая. Две тысячи девятьсот сорок одна тысячная. Две тысячи девятьсот сорок одна десятитысячная7. Как три и четыре десятитысячных в стандарте fo
6. Как читать и писать 0.2941a. Две тысячи девятьсот сорок одна десятая. Две тысячи девятьсот сорок одна сотая. Две тысячи девятьсот сорок одна тысячная. Две тысячи девятьсот сорок одна десятитысячная7. Как три и четыре десятитысячных в стандарте fo Wha — разрядное значение цифры 9 в шестидесяти девяти тысячах пятистах сорок восьми
Wha — разрядное значение цифры 9 в шестидесяти девяти тысячах пятистах сорок восьми )270000.0675.00000164 9 0005
)270000.0675.00000164 9 0005 Напишите следующее в десятичных дробях.1. Сорок две тысячи пятьсот тридцать двести тысячных2. пять тысяч семьдесят одна миллионная3. двести восемьдесят шесть тысяч четыреста пятьдесят пять миллионных4. две тысячи семьсот девять миллионов шестьсот семьдесят пять тысяч сто шестьдесят четыре десятимиллионные5. десятимиллионные, девять и девять миллиардных долей
Напишите следующее в десятичных дробях.1. Сорок две тысячи пятьсот тридцать двести тысячных2. пять тысяч семьдесят одна миллионная3. двести восемьдесят шесть тысяч четыреста пятьдесят пять миллионных4. две тысячи семьсот девять миллионов шестьсот семьдесят пять тысяч сто шестьдесят четыре десятимиллионные5. десятимиллионные, девять и девять миллиардных долей Сорок пять тысяч одиннадцать 9000 5
Сорок пять тысяч одиннадцать 9000 5 1. Одна тысяча триста сорок девять -2. Тридцать три тысячи шестьсот двенадцать -3. Семьсот пятьдесят восемь -4. Шестьдесят семь тысяч сто двадцать пять -5. Девять тысяч двести восемьдесят три -6. Пятнадцать тысяч триста двадцать один -7. Двести шестьдесят три-8. Восемь тысяч пятьсот сорок четыре -9. Одиннадцать тысяч четыреста семьдесят пять -10. Девятнадцать тысяч семьсот девяносто девять -
1. Одна тысяча триста сорок девять -2. Тридцать три тысячи шестьсот двенадцать -3. Семьсот пятьдесят восемь -4. Шестьдесят семь тысяч сто двадцать пять -5. Девять тысяч двести восемьдесят три -6. Пятнадцать тысяч триста двадцать один -7. Двести шестьдесят три-8. Восемь тысяч пятьсот сорок четыре -9. Одиннадцать тысяч четыреста семьдесят пять -10. Девятнадцать тысяч семьсот девяносто девять - триста сорок девять миллионов девятьсот восемьдесят четыре тысячи пятьсот шесть Ответ:
триста сорок девять миллионов девятьсот восемьдесят четыре тысячи пятьсот шесть Ответ:  Напишите следующее в десятичных дробях.1. Сорок две тысячи пятьсот тридцать двести тысячных2. пять тысяч семьдесят одна миллионная3. двести восемьдесят шесть тысяч четыреста пятьдесят пять миллионных4. две тысячи семьсот девять миллионов шестьсот семьдесят пять тысяч сто шестьдесят четыре десятимиллионные5. десятимиллионные, девять и девять миллиардных частей
Напишите следующее в десятичных дробях.1. Сорок две тысячи пятьсот тридцать двести тысячных2. пять тысяч семьдесят одна миллионная3. двести восемьдесят шесть тысяч четыреста пятьдесят пять миллионных4. две тысячи семьсот девять миллионов шестьсот семьдесят пять тысяч сто шестьдесят четыре десятимиллионные5. десятимиллионные, девять и девять миллиардных частей Тысяча
Тысяча Дко сюр
Дко сюр 5 , 5 3 3 , 7 0 5
5 , 5 3 3 , 7 0 5 
 Чему равно ∛27 + ∛(-27)?
Чему равно ∛27 + ∛(-27)? 
 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
