Чему равно значение корня 3, деленного на 3? – Обзоры Вики
Таким образом, это означает, что квадратный корень из $3$ никогда не даст нам натурального числа. $\поэтому $ Квадратный корень $3$, разделенный на $3$, равен $\dfrac{1}{\sqrt{3}}$, который в десятичной форме равен $ $ 0.577.
Можно ли упростить root 3 3? Поскольку u221a3u221a3 равно 1 , вы просто переставили так, как было написано. Значение упрощенной дроби остается прежним.
Кроме того, квадратный корень из 3 равен 3? Квадратный корень из 3 выражается как u221a3 в радикальной форме и как (3) ½ или (3) 0.5 в экспоненциальной форме. Квадратный корень из 3, округленный до 7 знаков после запятой, составляет 1.7320508.
…
Квадратный корень из 3 в радикальной форме: u221a3.
1. | Что такое квадратный корень из 3? |
|---|---|
| 4. | Важные замечания |
| 5. | Часто задаваемые вопросы о квадратном корне из 3 |
| 6. | Сложные вопросы |
Чему равен кубический корень из корня 3? Следовательно, кубический корень из 8 равен 2, а из 27 равен 3. Кубический корень любого числа n — это число x, например x 3 = н. Следовательно, чтобы найти кубический корень из 3, мы должны определить число, которое при трехкратном умножении дает число 3, например x 3 = 3 или х = 3 √3.
…
Списки кубических корней.
| Число | Кубический корень ∛a |
|---|---|
| 3 | 1.442 |
| 4 | 1.587 |
| 5 | 1.710 |
| 6 | 1.817 |
Что отвечает корень 3?
Значение √3 примерно равно 1. 732.
732.
Что такое куб 3 3? Кубический корень из 3 выражается как ∛3 в радикальной форме и как (3) ⅓ или (3) 0 . 33 в экспоненциальной форме.
…
Кубический корень из 3 в радикальной форме: ∛3.
| 1. | Что такое кубический корень из 3? |
|---|---|
| 2. | Как вычислить кубический корень из 3? |
| 3. | Является ли кубический корень из 3 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 3 |
Что такое куб из 3 ответов? Таким образом, для 3 в кубе вы бы умножили это в 3 раза. 3³ = 3x3x3; 3×3 равно 9, а 9×3 равно 27. Следовательно, 3 в кубе равно 27.
Является ли квадратный корень 3 иррациональным?
Квадратный корень из 3 равен иррациональное число. Она также известна как константа Феодора в честь Феодора из Кирены, доказавшего ее иррациональность.
Также Как найти корень 3? Значение корня 3 является положительным действительным числом, когда оно умножается само на себя; это дает число 3. Это не натуральное число, а дробь. Квадратный корень из 3 обозначается √3.
…
Таблица квадратного корня.
| Число | Квадратный корень (√) |
|---|---|
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
• 4 июня 2020 г.
Как решить корни?
Каковы 3 кубических корня из 8?
Кубический корень из 8 выражается как 8 в радикальной форме и как (8) ⅓ или (8) 0 . 33 в экспоненциальной форме.
33 в экспоненциальной форме.
…
Кубический корень из 8 в радикальной форме: ∛8.
| 1. | Что такое кубический корень из 8? |
|---|---|
| 3. | Является ли кубический корень из 8 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 8 |
Как найти три корня числа?
Что такое куб 3? Другой пример кубического числа: 27 потому что это 33 (3х3х3, или «три в кубе»). Кубическое число также можно назвать числом в кубе. 2³ = 2 × 2 × 2 = 8.
3 √ 3 — рациональное или иррациональное число? Выпуск 3
Таким образом, 3 + √3 это иррациональное число. (ii) Поскольку мы знаем, что вычитание рационального и иррационального числа иррационально, то √7 – 2 иррационально. Таким образом, это рациональное число.
Таким образом, это рациональное число.
3.14 — рациональное число?
3.14 можно записать в виде дроби двух целых чисел: 314100 и поэтому рационально. π нельзя записать в виде дроби от двух целых чисел.
Какой квадрат равен 3? Квадратный корень из 3 обозначается √3. Квадратный корень в основном дает значение, которое при умножении на себя дает исходное число. Следовательно, это корень исходного числа.
…
Таблица квадратного корня.
| Число | Квадратный корень (√) |
|---|---|
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
• 4 июня 2020 г.
Как найти квадратный корень без калькулятора?
Чтобы найти квадратный корень числа без калькулятора, см. если вы можете получить это целое число, возведя в квадрат меньшие числа или умножив меньшее число само на себя. Если число представляет собой идеальный квадрат, вы получите целое число как квадратный корень.
Если число представляет собой идеальный квадрат, вы получите целое число как квадратный корень.
Как проще всего найти значение корня?
Вот шаги к методу длинного деления:
- Разделите основание квадратного корня на пары. …
- Найдите самый большой квадрат, который делится на первое число или пару. …
- Вычтите квадрат из первого числа или пары. …
- Отбросьте следующую пару. …
- Умножьте первую цифру квадрата на два. …
- Составьте следующее факторное уравнение.
Является ли v3 реальным числом? Что такое действительные числа в математике? Действительные числа включают в себя рациональные числа, такие как положительные и отрицательные целые числа, дроби и иррациональные числа. Другими словами, любое число, которое мы можем придумать, кроме комплексных чисел, это реальное число. Например, 3, 0, 1.5, 3/2, √5 и так далее — действительные числа.
Например, 3, 0, 1.5, 3/2, √5 и так далее — действительные числа.
Как найти квадратный корень?
Как извлечь квадратный корень из квадратного корня?
Как проще всего найти кубический корень методом деления?
Нахождение корня куба с помощью метода деления
MAKE пара трехзначных чисел сзади наперед. Следующий шаг — найти число, кубический корень которого меньше или равен заданному числу. Теперь вычтите полученное число из данного числа и запишите второе число.
Чему равен кубический корень из 125*? Значение кубического корня из 125 равно 5.
Как быстро найти кубический корень?
3 умножить корень из 2 деленное на 2,срочно!!!! — Знания.site
Ответы 1
Это будет 3. Простой пример же)
Автор:
barkley
Оценить ответ:
0
Знаешь ответ? Добавь его сюда!
Последние вопросы
Французский язык
8 часов назад
Помогите пожалуйста с французским упр 4🙏🙏🙏
Математика
12 часов назад
24.
Ділянку прямокутної форми що має розміри 250м на 80м, засіяли кукурудзою. Скільки зерна було використано для цього, якщо на 10000м потрібно 18 кг? 02.2022?
02.2022?Математика
13 часов назад
32) найдите область определение функции z = (1/x) + (1/y)Математика
14 часов назад
33) найдите область определение функции z = (y — 1) / (x² + y²)Математика
14 часов назад
31) найдите область определение функции z = 1 / (x-y)Геометрия
16 часов назад
100 баллов таму кто поможетАнглийский язык
16 часов назад
Subjunctive Mood
Test
I.
 Choose the right form:
Choose the right form:1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (worked/ had worked) harder he wouldn’t (fail/ have failed) at his exams. 5. The weather is too cold today. If it (were/ had been) a little warmer, we would (go/ have gone) for a walk. 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.

II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.
- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.

Английский язык
16 часов назад
Subjunctive Mood
Test
I. Choose the right form:
1. Jack doesn’t speak English. If he (spoke/ had spoken) English, he would (get/ have got) a good job at a travel agency. 2. I was in Rome on business. If I (had/ had had) more free time, I would (go/ have gone) sightseeing. 3. It is unlikely that he will repair his car soon. He would (give/ have given) us a ride to the train station if he (repaired/ had repaired) his car soon enough. 4. Bob failed at his exams. If he (worked/ had worked) harder he wouldn’t (fail/ have failed) at his exams. 5. The weather is too cold today. If it (were/ had been) a little warmer, we would (go/ have gone) for a walk.
 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.II. Describe these situations in a different way. Use the Subjunctive Mood.
- The problems of the company were very serious. As a result Tom worked hard all the weekends.
- The alarm clock was broken. And John was late for his first lesson.
- My mother was in Italy. I had to cook everything on my own.
- She lost her mobile phone. That’s why I gave her mine.
- She was late for their wedding. Her fiancé got angry.
III. Translation.
- Если бы Майк сдал отчет вовремя, его бы не уволили.
- Жаль, что арбуз оказался гнилой.
- Если бы она не вмешивалась в его дела, он бы не дерзил ей.

- Если бы не твоя помощь, я бы не смог закрепить эти шторы.
- Если бы Джонни был хорошим студентом, он бы не использовал так много шпаргалок на экзамене.
- Мне бы хотелось, чтобы ты заботился о своем здоровье!
- Если бы тебе было все равно, ты бы не ревновал ее к другим мужчинам.
Литература
22 часов назад
А где почему это напряжоный момент
Биология
1 день назад
У голонасінних рослин уперше з’являєтся:
Математика
1 день назад
Математика третий класс запиши все возможные значения длины и ширины по известному периметру прямоугольника периметр 98 м 120 м 140
Алгебра
1 день назад
Решите графически системы уравнений (выражая у через х) 1 система {х+2у=6 х-4у=0} 2 система{3у-х=3 х-4у=1}
Физика
1 день назад
Електричний нагрівник за 7 хв доводить до кипіння 10 кг води, початкова температура якої дорівнює 20 °С.
 Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.Физика
2 дня назад
Тело движется вдоль оси Ох. График зависимости проекции его скорости Vх от времени t изображён на рисунке. Найди путь S, пройденный телом за рассмотренный промежуток времени. Результат вырази в метрах, округлив до целого числа.
Українська мова
2 дня назад
Допоможіть будь ласка! Написати твір — роздум за алгоритмом.
GMAT Math: Как разделить на квадратный корень
By Mike MᶜGarry on 8 марта 2017 г. в GMAT Math Basics
Многие студенты, готовящиеся к GMAT Quant, особенно те, кто давно не занимался математикой, теряются, пытаясь разделить на квадратный корень. Однако деление на квадратные корни не должно вас пугать. Пройдя короткий курс повышения квалификации, вы сможете быстро делить на квадратные корни.
Однако деление на квадратные корни не должно вас пугать. Пройдя короткий курс повышения квалификации, вы сможете быстро делить на квадратные корни.
Практические вопросы: Как разделить на квадратный корень
Во-первых, рассмотрите эти три практических вопроса.
1. В приведенном выше уравнении x =
2. Треугольник ABC является равносторонним треугольником с высотой 6. Какова его площадь?
3. В приведенном выше уравнении x =
Второй добавляет немного геометрии. Вы можете просмотреть свойства треугольника 30-60-90 и равностороннего треугольника, если они вам незнакомы. Первый — это простая арифметика. Третий довольно тяжелый. Для любого из них вполне может случиться так, что, даже если вы выполнили все ваши умножения и деления правильно, вы получили ответы в форме — что-то, разделенное на квадратный корень из чего-то — и вы остались недоумевать: почему не Этот ответ вообще не появляется среди вариантов ответов? Если это вас сбило с толку, вы нашли именно тот пост.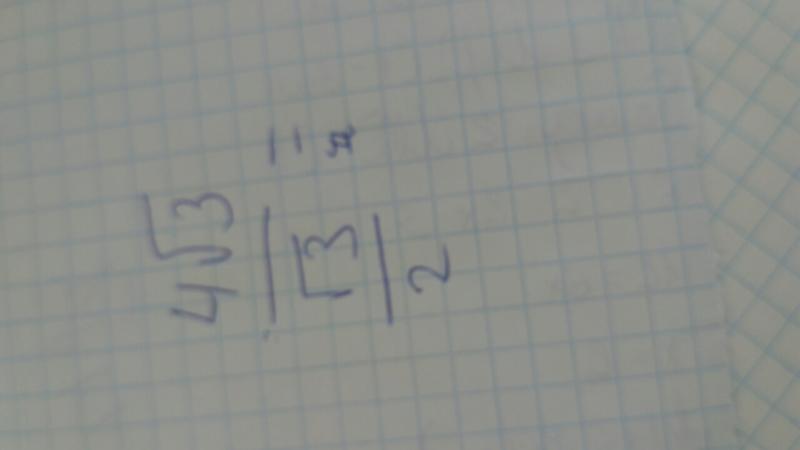
Дроби и радикалы
Когда мы впервые познакомились с дробями, в нашем нежном предпубертатном возрасте, и числители, и знаменатели были простыми положительными целыми числами. Как мы теперь понимаем, в числителе или знаменателе дроби может стоять любое действительное число, любое число на всей числовой прямой. Помимо прочего, радикалы, то есть выражения с квадратным корнем, могут появляться как в числителе, так и в знаменателе. Нет особой проблемы, если у нас есть квадратный корень в числителе. Например,
— отличная дробь. Фактически, те из вас, кто когда-либо занимался тригонометрией, могли бы даже узнать эту особую дробь. Предположим, однако, что у нас есть квадратный корень в знаменателе: что тогда? Возьмем обратное значение этой дроби.
Это уже не идеально хорошая фракция. Математически это дробь «без вкуса», потому что мы делим на квадратный корень. Эта фракция взывает к какому-то упрощению. Как нам это упростить?
Работа с квадратными корнями в знаменателе
Согласно стандартному математическому соглашению, которому следует GMAT, мы не оставляем квадратные корни в знаменателе дроби. Если в знаменателе дроби появляется квадратный корень, мы следуем процедуре, называемой , рационализации знаменателя .
Если в знаменателе дроби появляется квадратный корень, мы следуем процедуре, называемой , рационализации знаменателя .
Мы знаем, что любой квадратный корень, умноженный на самого себя, равен положительному целому числу. Таким образом, если бы мы умножили знаменатель квадратного корня из 3 сам по себе, это было бы 3, а не радикал. Проблема в том, что мы не можем умножать знаменатель дроби на что-то, оставляя числитель в покое, и ожидать, что дробь сохранит свое значение. НО, помните проверенный временем трюк с дробью — мы всегда можем умножить дробь на A/A, на что-то сверх себя, потому что новая дробь будет равна 1, а умножение на 1 ничего не меняет.
Таким образом, чтобы упростить дробь с квадратным корнем из 3 в знаменателе, мы умножаем квадратный корень из 3 на квадратный корень из 3!
Это последнее выражение численно равно первому выражению, но в отличие от первого, оно теперь соответствует математическому «хорошему вкусу», потому что в знаменателе нет квадратного корня. Знаменатель был рационализирован (то есть дробь теперь является рациональным числом).
Знаменатель был рационализирован (то есть дробь теперь является рациональным числом).
Иногда происходит некоторое сокращение между числом в исходном числителе и целым числом, полученным в результате рационализации знаменателя. Рассмотрим следующий пример:
Эта модель отмены в процессе упрощения может дать вам некоторое представление о практической проблеме № 1, описанной выше.
Квадратные корни и сложение в знаменателе
Это следующий уровень сложности деления на квадратные корни. Предположим, мы делим число на выражение, которое включает прибавление или вычитание квадратного корня. Например, рассмотрим эту дробь:
Это фракция нуждается в рационализации. НО, если мы просто умножим знаменатель сам на себя, это НЕ устранит квадратный корень — скорее, это просто создаст более сложное выражение, включающее квадратный корень. Вместо этого мы используем формулу разности двух квадратов = (a + b) (a – b). Факторы вида (a + b) и (a – b) называются конъюгирует друг друга. Когда у нас есть (число + квадратный корень) в знаменателе, мы создаем сопряжение знаменателя, изменяя знак сложения на знак вычитания, а затем умножаем и числитель, и знаменатель на сопряжение знаменателя . В приведенном выше примере знаменатель равен трем минус квадратный корень из двух. Сопряженным знаменателем будет три плюс квадратный корень из двух. Чтобы рационализировать знаменатель, мы умножаем и числитель, и знаменатель на это сопряженное.
Когда у нас есть (число + квадратный корень) в знаменателе, мы создаем сопряжение знаменателя, изменяя знак сложения на знак вычитания, а затем умножаем и числитель, и знаменатель на сопряжение знаменателя . В приведенном выше примере знаменатель равен трем минус квадратный корень из двух. Сопряженным знаменателем будет три плюс квадратный корень из двух. Чтобы рационализировать знаменатель, мы умножаем и числитель, и знаменатель на это сопряженное.
Обратите внимание, что умножение в знаменателе привело к упрощению «разности двух квадратов», которое очистило квадратные корни от знаменателя. Этот последний термин является полностью рационализированной и полностью упрощенной версией оригинала.
Резюме
Прочитав эти сообщения о делении на квадратные корни, вы можете еще раз попробовать ответить на три практических вопроса в начале этой статьи, прежде чем читать пояснения ниже. Если у вас есть какие-либо вопросы о делении на квадратные корни или объяснениях ниже, задавайте их в разделах комментариев! И удачи в их преодолении во время GMAT!
Объяснение практических вопросов
1) Чтобы найти x, мы начнем с перекрестного умножения. Обратите внимание, что
Обратите внимание, что
, потому что, вообще говоря, мы можем умножать и делить через радикалы.
Перемножая, получаем
Возможно, вы нашли это и задались вопросом, почему его нет в списке ответов. Это численно равно правильному ответу, но, конечно, как объясняется в этом посте, эта форма не рационализирована. Нам нужно рационализировать знаменатель.
Ответ = (Д)
2) Мы знаем высоту ABC и нам нужно найти основание. Итак, высота BD делит треугольник ABC на два треугольника 30-60-90. Из пропорций в треугольнике 30-60-90 мы знаем:
Я предпочитаю сразу рационализировать знаменатель.
Теперь AB упрощен. Мы знаем, что AB = AC, потому что ABC равносторонний, поэтому у нас есть основание.
Ответ = (К)
3) Начнем с деления на выражение в скобках, чтобы выделить x.
Разумеется, эта форма не фигурирует среди вариантов ответа. Опять же, нам нужно рационализировать знаменатель, и этот случай немного сложнее, потому что у нас есть сложение в знаменателе вместе с квадратным корнем. Здесь нам нужно найти сопряжение знаменателя, поменяв знак плюс на знак минус, а затем умножить числитель и знаменатель на это сопряжение. Это приведет к:
Опять же, нам нужно рационализировать знаменатель, и этот случай немного сложнее, потому что у нас есть сложение в знаменателе вместе с квадратным корнем. Здесь нам нужно найти сопряжение знаменателя, поменяв знак плюс на знак минус, а затем умножить числитель и знаменатель на это сопряжение. Это приведет к:
Ответ = (А)
Автор
← Предыдущий
Следующий →
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс | сложение | 1/2 + 1/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | минус | вычитание | 90 051 1 1/2 — 2/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | знак умножения | умножение | 2/3 × 5/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | знак деления | деление 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
| равно | 4,5 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 460 сантиметров | равно | 4,6 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 470 сантиметров | равно 0,8 | 4,6 метра 0026 | 480 сантиметров | равно | 4,8 метра | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 490 сантиметров | равно | 4,9 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 500 сантиметров | равно | 5 метров | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 510 сантиметров | равно | 5,1 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 520 сантиметров | равно | 5,2 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9038 сантиметров | 8 | 8 1 5,3 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 540 сантиметров | равно | 5,4 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 550 сантиметров | равно | 5,5 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 560 сантиметров | равно | 5,6 метра | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Примечание. Значения округлены до 4 значащих цифр. Дроби округляются до ближайшей восьмой дроби.
Значения округлены до 4 значащих цифр. Дроби округляются до ближайшей восьмой дроби.
Преобразование образцов
Отказ от ответственности
Несмотря на усилия по предоставлению точной информации на этом веб-сайте, ее точность не гарантируется. Поэтому контент не должен использоваться для принятия решений, касающихся здоровья, финансов или собственности.
О нас | Свяжитесь с нами | КонфиденциальностьCopyright © 2016 — 2023 HowMany.wiki
Перевести 500 сантиметров в метры
Какова длина 500 сантиметров? Сколько будет 500 сантиметров в метрах? Преобразование 500 см в м.
От АнгстремыСантиметрыГаземыНогиФурлонгиДюймыКилометрыМетрМикроныМилиМиллиметрыНанометрыМорские милиПикометрыЯрды
До Ангстремы Сантиметры Морские сажени Ноги Фурлонги Дюймы Километры Метры Микроны Мили Миллиметры Нанометры Морские мили Пикометры Ярды 500 сантиметров =
5 метров
(точный результат)
Показать результат как NumberFraction (точное значение)
Сантиметр или сантиметр — это единица длины, равная одной сотой метра. В дюйме 2,54 сантиметра.
В дюйме 2,54 сантиметра.
Метр или метр — это основная единица длины в метрической системе, на которой основаны все другие единицы длины. Он равен 100 сантиметрам, 1/1000 километра или примерно 39,37 дюйма.
Перевод сантиметров в метры
(некоторые результаты округлены)
| см | м |
|---|---|
| 500,00 | 5 |
| 500,05 | 5.0005 |
| 500.10 | 5.001 |
| 500.15 | 5.0015 |
| 500.20 | 5.002 |
| 500.25 | 5,0025 |
| 500,30 | 5.003 |
| 500,35 | 5.0035 |
| 500.40 | 5.004 |
| 500.45 | 5,0045 |
| 500,50 | 5,005 |
| 500,55 | 5,0055 |
| 500,60 | 5,006 |
| 500,65 | 5,0065 |
| 500,70 | 5,007 |
| 500,75 | 5. 0075 0075 |
| 500.80 | 5,008 |
| 500,85 | 5,0085 |
| 500,90 | 5,009 |
| 500,95 | 5,0095 |
| 501,00 | 5.01 |
| 501.05 | 5.0105 |
| 501.10 | 5.011 |
| 501.15 | 5.0115 |
| 501.20 | 5.012 |
| см | м |
|---|---|
| 501,25 | 5,0125 |
| 501,30 | 5,013 |
| 501,35 | 5,0135 |
| 501,40 | 5,014 |
| 501,45 | 5,0145 |
| 501,50 | 5,015 |
| 501,55 | 5,0155 |
| 501,60 | 5,016 |
| 501,65 | 5,0165 |
| 501,70 | 5,017 |
| 501,75 | 5,0175 |
| 501,80 | 5,018 |
| 501,85 | 5,0185 |
| 501,90 | 5,019 |
| 501,95 | 5. 0195 0195 |
| 502.00 | 5,02 |
| 502,05 | 5.0205 |
| 502.10 | 5.021 |
| 502.15 | 5.0215 |
| 502.20 | 5,022 |
| 502,25 | 5,0225 |
| 502,30 | 5,023 |
| 502,35 | 5,0235 |
| 502,40 | 5,024 |
| 502,45 | 5.0245 |
| см | м |
|---|---|
| 502,50 | 5,025 |
| 502,55 | 5,0255 |
| 502,60 | 5,026 |
| 502,65 | 5,0265 |
| 502,70 | 5,027 |
| 502,75 | 5,0275 |
| 502,80 | 5,028 |
| 502,85 | 5.0285 |
| 502.90 | 5,029 |
| 502,95 | 5. 0295 0295 |
| 503.00 | 5,03 |
| 503,05 | 5.0305 |
| 503.10 | 5.031 |
| 503.15 | 5.0315 |
| 503.20 | 5,032 |
| 503,25 | 5,0325 |
| 503,30 | 5,033 |
| 503,35 | 5,0335 |
| 503,40 | 5,034 |
| 503,45 | 5,0345 |
| 503,50 | 5,035 |
| 503,55 | 5,0355 |
| 503,60 | 5,036 |
| 503,65 | 5,0365 |
| 503,70 | 5.037 |
| см | м | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 503,75 | 5,0375 | ||||||||||||||||||
| 503,80 | 5,038 | ||||||||||||||||||
| 503,85 | 5,0385 | ||||||||||||||||||
| 503,90 | 5,039 | ||||||||||||||||||
| 503,95 | 5. Распечатать таблица сложения и вычитания до 20 распечатать 1 класс распечатать: Таблица сложения — распечатать для 1 классаТаблица сложения 1 2. Табличное сложение и вычитание натуральных чиселТаблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу Таблица сложения до 20 распечатать и скачатьТаблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11. Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием. Таблица вычитания до 20 распечатать и скачатьВ качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ. Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах. Таблица вычитания без ответов распечатать и скачатьНа данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. Тема: Знакомство с основными понятиями в математике Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20 С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток. Каким способом можно сложить 9 и 7? (рис. 1) Рис. 1 На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как 9 + 1 = 10, значит 7 = 1 + 6. (рис. 2) Рис. 2 Выполним сложение по частям: 9 + 7 = (9 + 1) + 6 = 10 + 6 = 16 Ответ: 9 + 7 = 16. Можно сложить эти числа по-другому. (рис. 3) Рис. 3 Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6. Рис. 4 Выполним сложение по частям: 7 + 9 = (7 + 3) + 6 = 10 + 6 = 16 Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы. 9 + 5 = 9 + (1 + 4) = 14 Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы. 6 + 6 = 6 + (4 + 2) = 12 Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы. 4 + 8 = 4 + (6 + 2) = 12 В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы. 15 — 7 = 15 — (5 + 2) = 8 В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. 16 — 9 = 16 — (6 + 3) = 7 В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2. 12 — 4 = 12 — (2 + 2) = 8 Ответ: 12 — 4 = 8. Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть. На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7) Рис. 7 В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм. 9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8) Рис. 8 В каждой строке записаны суммы с одинаковыми ответами. Список литературы
Домашнее задание 1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд. 2. Помогите лягушке решить примеры. 3. Решите примеры и раскрасьте рисунок. На данном уроке вы научитесь складывать и вычитать однозначные числа с переходом через разряд. Решая интересные задания, вы изучите алгоритм сложения и вычитания чисел с переходом через десяток и познакомитесь с таблицей сложения однозначных чисел до 20. Тема: Знакомство с основными понятиями в математике Урок: Сложение и вычитание однозначных чисел с переходом через разряд. Таблица сложения до 20 С помощью графической модели можно объяснить сложение однозначных чисел с переходом через десяток. Каким способом можно сложить 9 и 7? (рис. 1) Рис. 1 На графической модели видно, что первое слагаемое 9 надо дополнить до 10. Для этого разобьем второе слагаемое на две части, одна из которых равна числу 1, так как 9 + 1 = 10, значит 7 = 1 + 6. (рис. 2) Рис. 2 Выполним сложение по частям: 9 + 7 = (9 + 1) + 6 = 10 + 6 = 16 Ответ: 9 + 7 = 16. Можно сложить эти числа по-другому. (рис. 3) Рис. 3 Второе слагаемое 7 можно дополнить до 10. Для этого первое слагаемое разобьем на две части, одна из которых равна числу 3. Следовательно, 9 = 3 + 6. Рис. 4 Выполним сложение по частям: 7 + 9 = (7 + 3) + 6 = 10 + 6 = 16 Первое слагаемое — 9, ему недостаёт до 10 одной единицы, поэтому второе слагаемое разбиваем на части. 5 — это 1 и 4. Добавляем к 9 сначала одну единицу, а потом оставшиеся четыре единицы. 9 + 5 = 9 + (1 + 4) = 14 Первое слагаемое — 6, ему недостаёт до 10 четырёх единиц, поэтому второе слагаемое разбиваем на части: 4 и 2. Добавляем к 6 сначала 4 и получаем десять единиц, а потом оставшиеся две единицы. 6 + 6 = 6 + (4 + 2) = 12 Первое слагаемое — 4, ему недостаёт до 10 шести, поэтому второе слагаемое 8 разбиваем на части: 6 и 2. Добавляем к 4 сначала шесть единиц и получаем десять единиц, а потом оставшиеся две единицы. 4 + 8 = 4 + (6 + 2) = 12 В уменьшаемом 15 — пять единиц, поэтому вычитаемое 7 разбиваем на части: 5 и 2. Вычитаем из 15 сначала пять единиц, получится 10. Потом из десяти вычитаем оставшиеся две единицы. 15 — 7 = 15 — (5 + 2) = 8 В уменьшаемом 16 — шесть единиц, поэтому вычитаемое 9 разбиваем на части: 6 и 3. 16 — 9 = 16 — (6 + 3) = 7 В уменьшаемом 12 — две единицы, поэтому вычитаемое 4 разбиваем на части: 2 и 2. Из 12 вычитаем 2, получится 10. И от 10 отнимаем 2. 12 — 4 = 12 — (2 + 2) = 8 Ответ: 12 — 4 = 8. Использовать прием сложения и вычитания по частям с переходом через десяток не всегда удобно, поэтому необходимо выучить таблицу сложения однозначных чисел до 20 наизусть. На рисунке изображена таблица, с помощью которой вам будет легче выучить случаи сложения однозначных чисел до 20. (рис. 7) Рис. 7 В каждом столбике первое слагаемое — одинаковое, а второе — увеличивается на один, значит сумма тоже будет увеличиваться на один. Найдём значение данных сумм. 9 + 2 = 11, следовательно: 9 + 3 = 12, рассуждая так, заполняем всю таблицу. (рис. 8) Рис. 8 В каждой строке записаны суммы с одинаковыми ответами. Список литературы
Домашнее задание 1. Вспомните как правильно складывать и вычитать однозначные числа с переходом через разряд. 2. Помогите лягушке решить примеры. 3. Решите примеры и раскрасьте рисунок. Таблица сложения и вычитания натуральных чисел приведена для сложения чисел первого десятка и вычитания чисел от 1 до 18. Таблицей удобно пользоваться при сложении или вычитании по разрядам для натуральных многозначных чисел, устный счет построен на сложении по разрядам, т. Работа с таблицей предполагает такой результат: таблицу вы запомните, выучите наизусть в процессе вычислений, что значительно сократит время нахождения результата при сложении и вычитании натуральных чисел. Правила пользования таблицейКрайний левый столбец и верхняя строка — числа первого десятка — слагаемые при сложении и разность при вычитании. Чтобы сложить два числа, нужно первое слагаемое взять в крайнем левом столбце, а второе — в верхней строке. На пересечении столбца и строки в поле таблицы считывается результат сложения — сумма. Чтобы вычесть одно число из другого, в поле таблицы нужно найти уменьшаемое и, двигаясь по этому числу по диагонали поля, выбрать строку, в которой в левом крайнем столбце помещено число вычитаемого. По месту строки и числу уменьшаемого расположен столбец, в верхней строке которого считывается разность (результат вычитания). Примеры пользования таблицейСложение . 3 + 5 = 8 Вычитание . 8 — 3 = 5. Таблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу Таблица сложения до 20 распечатать и скачатьТаблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11. Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Таблица вычитания до 20 распечатать и скачатьВ качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ. Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах. Таблица вычитания без ответов распечатать и скачатьНа основе макета таблицы вычитания с ответами в формате Excel при необходимости можно сделать и другие таблицы вычитания, например больших значений, до 20, до 30 и т. Таблица сложения для первоклассников. Как научить ребенка считать? Советуют педагогиТаблицы сложения и вычитания используются для обучения детей счету или для проверки их навыков в сложении и вычитании. Для двух этих задач используются разные таблицы. Оба варианта таблиц можно скачать распечатать на этой страницу Таблица сложения до 20 распечатать и скачатьТаблица сложения используется для обучения детей. Вертикальный крайний левый столбец и горизонтальная верхняя строка представляют собой слагаемые. Для того что бы сложить два числа, нужно найти их в вертикальном столбце и в горизонтальной строке. Пересечение образует сумму этих двух слагаемых. Например, как показано на рисунке ниже, 6 + 5 = 11. Вы можете распечатать таблицу сложения до 20 в формате Word или PDF. Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием. Таблица вычитания до 20 распечатать и скачатьВ качестве таблицы вычитания используется та же таблица сложения, которую можно распечатать выше. Предположим нам нужно решить пример 14 — 8 = 6. Используя, таблицу вычитания, находим в поле таблицы диагональ с уменьшаемым 14. На рисунке ниже эта диагональ выделена светло-зеленым цветом. Выбираем на этой диагонали число 14, которое находится напротив вычитаемого 8. Получившееся в верхнем ряду число 6 и есть ответ. Как вы можете увидеть, для сложения и вычитания используется одна и та же таблица сложения и вычитания, распечатать или скачать которую вы можете по ссылкам выше в разных форматах. Таблица вычитания без ответов распечатать и скачатьНа основе макета таблицы вычитания с ответами в формате Excel при необходимости можно сделать и другие таблицы вычитания, например больших значений, до 20, до 30 и т.д. Самые первые примеры, с которыми знакомится ребенок еще до школы — это сложение и вычитание. Если ваш ребенок первоклашка или только идет в первый класс — начните с повторения состава числа по домикам. А теперь можно браться и за примеры. Фактически сложение и вычитание в пределах десяти — это и есть первое практическое применение ребенком знания состава числа. Кликайте по картинкам и открывайте тренажер в максимальном увеличении, далее можно скачать изображение себе на компьютер и распечатать в хорошем качестве. Есть возможность разрезать А4 пополам и получить 2 листа с заданиями, если хотите уменьшить нагрузку на ребенка, или давать решать по столбику в день, если решили позаниматься летом.
Сложение и вычитание в пределах 10А теперь вразброс! И с пропусками (окошками): Примеры на сложение и вычитание в пределах 20К моменту, когда ребенок приступит к изучению этой темы математики, он должен очень хорошо, на зубок знать состав чисел первого десятка. Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток . Примеры для печати без перехода через десяток вперемешку: Сложение и вычитание в пределах 20 с переходом через десяток основаны на приемах добавления до 10 или убавления до 10 соответственно, то есть на теме «состав числа 10», поэтому ответственно подойдите к изучению с ребенком этой темы. Примеры с переходом через десяток (половина листа сложение, половина вычитание, лист также можно распечатать в формате А4 и разрезать пополам на 2 задания): Учим таблицу сложения и вычитания в пределах 10 Одной из важных задач курса математики за 1 класс является прочное усвоение детьми таблицы сложения и вычитания в пределах десяти. При изучении состава чисел важным моментом является опора на наглядность и игровую деятельность. Работа над изучением таблицы сложения и вычитания должна проводиться систематически, формы работы должны быть разнообразны. Только при таких условиях можно избежать скуки и монотонности, гарантировано прочное запоминание детьми состава чисел. Конечно, это бумажные тренажёры по составу чисел. Но больше всего детям нравятся интерактивные или онлайн игры! Игра является одним из важных средств в усвоении знаний, развитии и воспитании детей. Она может быть применена в рамках разных методов обучения. Очень важный момент в игре – преодоление препятствий, достижение целей, самостоятельный поиск. Все эти элементы игры развивают умственные способности школьника. Именно с помощью различных компьютерных игр и тренажёров, заданий для интерактивного стола современный учитель может разнообразить виды работы, направленные на усвоение детьми таблицы сложения и вычитания. Они помогут ученикам не только довести до автоматизма навык устного счёта, но и дадут возможность закрепить правила работы в группе. Состав числа 5 Состав числа 6 Состав числа 7 Состав числа 8 Состав числа 9 Состав числа 10 Далее представлены онлайн игр, направленные на закрепление и автоматизацию состава числа — это математические тренажеры, которые включают примеры и уравнения, помогут довести знание состава числа до автоматизма. Однако, не забывайте и о других способах заучивания состава числа, так как долгое время находиться перед экраном компьютера ребенку вредно. Первый этап. Не используем запись числа Первостепенная задача — научить считать до 10, н е используя соответствующие цифры. На первый план выходят действия с предметами. Например, была одна ложка, положили еще одну — стало две ложки. Потом можно увеличивать количество ложек, говоря название числа. Помогут в решении этой задачи практические задания. Например, чаще спрашивать у ребенка о количестве чего-нибудь: сколько тарелок, сколько тапочек, сколько птиц на той ветке. Считать можно что угодно, даже ступеньки лестницы. Второй этап. Знакомство с самими цифрами. В первом классе сначала изучается цифра 1, 2, 0, а потом уже 3, 4, 5, 6, 7, 8, 9. Обусловлено положение нуля тем, что ученику на первых порах сложно понять, почему пустота обозначается цифрой. И тогда, когда уже практикуются действия с цифрами, становится понятно, зачем нужен нуль. Еще вариант: Показываются эти рисунки, и спрашивает учитель у детей: «Что изменилось?». Они отметят: «Ничего». На втором образце показано, что если в одном квадрате три точки убрать совсем, то будет пустой квадрат и точек вообще не останется. Главное правило, которые должны понять дети при счете до десяти: каждая цифра меньше последующей на один и больше прошлой цифры на один. Приемы обучения счету до десяти:
Стихотворения-запоминалки для изучения счетаЯгодный счет По опушке шла лисичка: Раз — рука, два — рука — Пошли пальчики гулять,
Как выучить таблицу сложения и вычитания в пределах десяти?После того как ребенок знает порядок числительных, полезно применять задания на состав числа. Например: В одной тарелке было 4 апельсина, а в другой — 2. Сколько всего апельсинов? (Задача на нахождение суммы) Всего 6 яблок, а друзей — трое. Разделите каждому поровну, одинаково. Сочетать с простыми задачами можно и маленькие схемы, которые легко применять на уроке и дома. На переместительный закон сложения не сложно привести такой пример: одна тарелка с двумя яблоками лежит на столе, а другая тарелка с четырьмя яблоками — лежит рядышком, если поменять их местами, то все равно общее количество яблок останется неизменным. Как научить ребенка складывать и вычитать с переходом через десяток?В приведенном ниже примере, чтобы сложить числа 8 и 5, второе слагаемое раскладывается так, чтобы дополнить первое слагаемое до десяти, а потом остаток прибавляется к десяти. Что касается вычитания, то тут раскладывается уменьшаемое по разрядному составу. Просмотр дополнительных рабочих листов для печати | Education.comСсылки для быстрого добавления:Двузначное сложение, Упражнения на сложение, Факты сложения, Сложение с переносом, Сложение с перегруппировкой, Сложение словесных задач, Сложение числовой строкиРабочие тетради для печатиНаучные проектыПесня Видео 1 188 отфильтрованных результатов 1 188 отфильтрованных результатов Добавление Сортировать поПопулярностьПоследниеЗаголовокРелевантность
Поиск дополнительных рабочих листов для печати9 0002 Есть причина, по которой математический поезд делает первую остановку на сложении: это фундаментальный арифметический навык, который должен быть доведен до совершенства, прежде чем локомотив продолжит путь к таким направлениям, как умножение, дроби, геометрия и алгебра. Вот почему родители должны получить доступ к нашим рабочим листам для сложения, которые обеспечивают повторную практику, необходимую детям, когда они начинают гонку к математическому мастерству. Мы предлагаем множество методов, которые помогут детям овладеть этим важным навыком, от рабочих листов для сложения однозначных чисел до карточек и задач со словами. Вот почему родители должны получить доступ к нашим рабочим листам для сложения, которые обеспечивают повторную практику, необходимую детям, когда они начинают гонку к математическому мастерству. Мы предлагаем множество методов, которые помогут детям овладеть этим важным навыком, от рабочих листов для сложения однозначных чисел до карточек и задач со словами.Дом, милый дом: дополнительные способы практиковать сложение у вас под крышейПомимо нашей обширной базы рабочих листов на сложение, есть множество предметов домашнего обихода, которые родители могут использовать, чтобы добавить немного дополнительной практики в распорядок дня своих детей (и в то же время чтобы было весело). Рассмотрим эти идеи:
20 печатных листов для сложения и вычитанияEtsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии. Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript. Нажмите, чтобы увеличить Цена: €1,69 Погрузка С учетом НДС 90 продаж | 5 из 5 звездВы можете сделать предложение только при покупке одного товара Внесен в список 8 мая 2023 г. 35 избранных Сообщить об этом элементе в Etsy Выберите причину… С моим заказом возникла проблемаОн использует мою интеллектуальную собственность без разрешенияЯ не думаю, что это соответствует политике EtsyВыберите причину… Первое, что вы должны сделать, это связаться с продавцом напрямую. Если вы уже сделали это, ваш товар не прибыл или не соответствует описанию, вы можете сообщить об этом Etsy, открыв кейс. Сообщить о проблеме с заказом Мы очень серьезно относимся к вопросам интеллектуальной собственности, но многие из этих проблем могут быть решены непосредственно заинтересованными сторонами. Мы рекомендуем связаться с продавцом напрямую, чтобы уважительно поделиться своими проблемами. Если вы хотите подать заявление о нарушении авторских прав, вам необходимо выполнить процедуру, описанную в нашей Политике в отношении авторских прав и интеллектуальной собственности. Посмотрите, как мы определяем ручную работу, винтаж и расходные материалы Посмотреть список запрещенных предметов и материалов Ознакомьтесь с нашей политикой в отношении контента для взрослых Товар на продажу…не ручная работа не винтаж (20+ лет) не ремесленные принадлежности запрещены или используют запрещенные материалы неправильно помечен как содержимое для взрослых Пожалуйста, выберите причину Расскажите нам больше о том, как этот элемент нарушает наши правила. Расскажите нам больше о том, как этот элемент нарушает наши правила. Решение неравенств дробно линейных: Дробные неравенства и их решениеМатематика: Справ. материалыМатематика: Справ. материалы
Дробно-рациональные неравенства: примерыСоответствие между решениями целых рациональных неравенств и дробно-рациональных неравенствДля решения целых рациональных неравенств следует раскладывать соответствующие многочлены на линейные множители, и затем использовать метод интервалов (см. §7 данного справочника). Дробно-рациональное выражение можно представить в виде частного двух многочленов $(P_n (x))/(Q_m (x))$, каждый из которых также можно раскладывать на линейные множители, знак которых будет влиять на общий знак частного. Поэтому для решения дробно-рациональных неравенств применяются те же алгоритмы, что и для решения целых рациональных неравенств. Это – парабола ветками вверх. Точки пересечения с осью OX:(0;0)и (1;0) Ось симметрии:$ x_0 = \frac{x_1+x_2}{2} = \frac{0+1}{2} = \frac{1}{2}$ Вершина: $f(x_0 ) = f \left(\frac{1}{2}\right) = \frac{1}{4}- \frac{1}{2} =- \frac{1}{4}$ В этой же системе координат строим уровни: y = -3, y = -1, y = 0, y = 2 и отмечаем области: $y \le -3,-1 \lt y \le 0, y \gt 2$ Записываем решение – те x, для которых точки параболы попадают в заштрихованные области: $x \lt -1 \cup 0 \le x \le 1 \cup x \gt 2 $ Ответ: $x \in (-\infty;-1) \cup [0;1] \cup (2;+\infty)$ ORCCA Линейные уравнения и неравенства с дробямиВ этом разделе мы научимся решать линейные уравнения и неравенства с дробями. Подраздел 3.3.1 ВведениеДо сих пор на последнем шаге решения для переменной мы разделили каждую часть уравнения на константу, например: \begin{align*} 2x\ампер=10\\ \divideunder{2x}{2} \amp= \divideunder{10}{2}\\ х\ампер=5 \end{align*} Если у нас есть коэффициент, который является дробью, мы мог бы действовать точно так же: \begin{align*} \frac{1}{2}x\amp=10\\ \divideunder{\frac{1}{2}x}{\frac{1}{2}} \amp= \divideunder{10}{\frac{1}{2}}\\ х\amp=10\cdot \frac{2}{1}=20 \конец{выравнивание*} Что, если бы наше уравнение или неравенство были более сложными, например, \(\frac{1}{4}x+\frac{2}{3}=\frac{1}{6}\text{?}\) Мы пришлось бы сначала выполнить много арифметических операций с дробями, чтобы затем разделить каждую сторону на коэффициент \(x\text{. \начать{выровнять*} \frac{1}{2}x\amp=10\\ \multiplyleft{2}\left(\frac{1}{2}x\right)\amp=\multiplyleft{2}10\\ х\ампер=20 \конец{выравнивание*} Для более сложных уравнений мы умножим каждую часть уравнения на наименьший общий знаменатель (НОД) всех дробей, содержащихся в уравнении. Подраздел 3.3.2 Исключение знаменателейПример 3.3.1.Дешон посадил у себя во дворе деревце высотой \(4\) фута. Дерево будет расти на \(\frac{2}{3}\) фута каждый год. Через сколько лет его дерево вырастет \(10\) футов в высоту? Поскольку дерево растет на \(\frac{2}{3}\) фута каждый год, мы можем использовать таблицу, чтобы написать формулу, моделирующую рост дерева:
Исходя из этого, мы определили, что через \(y\) лет с момента посадки дерева высота дерева будет \(4+\frac{2}{3}y\) футов. Чтобы найти, когда дерево Дешона будет \(10\) футов в высоту, мы напишем и решим это уравнение: \begin{выравнивание*} 4+\frac{2}{3}y\amp=10\\ \multiplyleft{3}\left(4+\frac{2}{3}y\right)\amp=\multiplyleft{3}10\\ 3\cdot4+3\cdot\frac{2}{3}y\amp=30\\ 12+2г\ампер=30\\ 2г\ампер=18\\ у\ампер=9 \end{align*} Теперь проверим решение \(9\) в уравнении \(4+\frac{2}{3}y=10\text{:}\) \begin{align *} 4+\frac{2}{3}y\amp=10\\ 4+\frac{2}{3}(\substitute{9})\amp\stackrel{?}{=}10\\ 4+6\amp\stackrel{\checkmark}{=}10 \конец{выравнивание*} Таким образом, дереву Дешона потребуется \(9\) лет, чтобы достичь \(10\) футов в высоту. Давайте рассмотрим еще несколько примеров. Пример 3.3.2.Найдите \(x\) в \(\frac{1}{4}x+\frac{2}{3}=\frac{1}{6}\text{.}\) Объяснение Чтобы решить это уравнение, нам сначала нужно определить LCD всех дробей в уравнении. С левой стороны у нас есть \(\frac{1}{4}\) и \(\frac{2}{3}\text{. \begin{align*} \frac{1}{4}x+\frac{2}{3}\amp=\frac{1}{6}\\ \multiplyleft{12}\left(\frac{1}{4}x+\frac{2}{3}\right)\amp=\multiplyleft{12}\frac{1}{6}\\ 12\cdot\left(\frac{1}{4}x\right)+12\cdot\left(\frac{2}{3}\right)\amp=12\cdot\frac{1}{6} \\ 3x+8\усилитель=2\\ 3x\ампер=-6\\ \divideunder{3x}{3}\amp=\divideunder{-6}{3}\\ х\ампер=-2 \end{align*} Проверка решения \(-2\text{:}\) \begin{align*} \frac{1}{4}x+\frac{2}{3}\amp=\frac{1}{6}\\ \frac{1}{4}(\substitute{-2})+\frac{2}{3}\amp\stackrel{?}{=}\frac{1}{6}\\ -\frac{2}{4}+\frac{2}{3}\amp\stackrel{?}{=}\frac{1}{6}\\ -\frac{6}{12}+\frac{8}{12}\amp\stackrel{?}{=}\frac{1}{6}\\ \frac{2}{12}\amp\stackrel{\checkmark}{=}\frac{1}{6} \end{выравнивание*} Следовательно, решение равно \(-2\), а набор решений равен \(\{-2\}\text{. Пример 3.3.3.Найдите \(z\) в \(-\frac{2}{5}z-\frac{3}{2}=-\frac{1}{2}z+\frac{4}{5}\ текст{.}\) Объяснение Первое, что нам нужно сделать, это определить LCD всех знаменателей в этом уравнении. Поскольку знаменатели равны \(2\) и \(5\text{,}\), ЖК-дисплей равен \(10\text{.}\). Итак, в качестве нашего первого шага мы умножим каждую часть уравнения на \( 10\), чтобы исключить все знаменатели: \begin{выравнивание*} -\frac{2}{5}z-\frac{3}{2}\amp=-\frac{1}{2}z+\frac{4}{5}\\ \multiplyleft{10}\left(-\frac{2}{5}z-\frac{3}{2}\right)\amp=\multiplyleft{10}\left(-\frac{1}{2} z+\frac{4}{5}\right)\\ 10\left(-\frac{2}{5}z\right)-10\left(\frac{3}{2}\right)\amp=10\left(-\frac{1}{2}z \вправо)+10\влево(\фракция{4}{5}\вправо)\\ -4z-15\amp=-5z+8\\ z-15\ампер=8\\ г\ампер=23 \end{align*} Проверка решения \(23\text{:}\) \begin{align*} -\frac{2}{5}z-\frac{3}{2}\amp=-\frac{1}{2}z+\frac{4}{5}\\ -\frac{2}{5}(\substitute{23})-\frac{3}{2}\amp\stackrel{?}{=}-\frac{1}{2}(\substitute{23} )+\фракция{4}{5}\\ -\frac{46}{5}-\frac{3}{2}\amp\stackrel{?}{=}-\frac{23}{2}+\frac{4}{5}\\ -\frac{46}{5}\cdot\frac{2}{2}-\frac{3}{2}\cdot\frac{5}{5}\amp\stackrel{?}{=}-\ frac{23}{2}\cdot\frac{5}{5}+\frac{4}{5}\cdot\frac{2}{2}\\ -\ гидроразрыв{92}{10}-\frac{15}{10}\amp\stackrel{?}{=}-\frac{115}{10}+\frac{8}{10}\\ -\frac{107}{10}\amp\stackrel{\checkmark}{=}-\frac{107}{10} \end{align*} Таким образом, решение равно \(23\), поэтому множество решений равно \(\{23\}\text{. Пример 3.3.4.Найдите \(a\) в уравнении \(\frac{2}{3}(a+1)+5=\frac{1}{3}\text{.}\) Объяснение \begin{align*} \frac{2}{3}(a+1)+5\amp=\frac{1}{3}\\ \multiplyleft{3}\left(\frac{2}{3}(a+1)+5\right)\amp=\multiplyleft{3}\frac{1}{3}\\ 3\cdot\frac{2}{3}(a+1)+3\cdot5\amp=1\\ 2(а+1)+15\амп=1\\ 2а+2+15\амп=1\\ 2а+17\амп=1\\ 2а\ампер=-16\\ а\ампер=-8 \end{выравнивание*} Проверяем решение \(-8\) в уравнении \(\frac{2}{3}(a+1)+5=\frac{1}{3}\text{,}\) мы находим, что : \begin{выравнивание*} \frac{2}{3}(a+1)+5\amp=\frac{1}{3}\\ \frac{2}{3}(\substitute{-8}+1)+5\amp\stackrel{?}{=}\frac{1}{3}\\ \frac{2}{3}(-7)+5\amp\stackrel{?}{=}\frac{1}{3}\\ -\frac{14}{3}+\frac{15}{3}\amp\stackrel{\checkmark}{=}\frac{1}{3} \end{align*} Следовательно, решение равно \(-8\), а набор решений равен \(\{-8\}\text{.}\) Пример 3.3.5.Найдите \(b\) в уравнении \(\frac{2b+1}{3}=\frac{2}{5}\text{.}\) Объяснение \begin{align*} \frac{2b+1}{3}\amp=\frac{2}{5}\\ \multiplyleft{15}\frac{2b+1}{3}\amp=\multiplyleft{15}\frac{2}{5}\\ 5(2b+1)\amp=6\\ 10b+5\amp=6\\ 10б\ампер=1\\ b\amp=\frac{1}{10} \end{align*} Проверка решения \(\frac{1}{10}\text{:}\) \begin{align*} \frac{2b+1}{3}\amp=\frac{2}{5}\\ \frac{2\left(\substitute{\frac{1}{10}}\right)+1}{3}\amp\stackrel{?}{=}\frac{2}{5}\\ \frac{\frac{1}{5}+1}{3}\amp\stackrel{?}{=}\frac{2}{5}\\ \ frac {\ frac {1} {5} + \ frac {5} {5} {3} \ amp \ stackrel {?} {=} \ frac {2} {5} \\ \ frac {\ frac {6} {5} {3} \ amp \ stackrel {?} {=} \ frac {2} {5} \\ \frac{6}{5}\cdot \frac{1}{3}\amp\stackrel{\checkmark}{=}\frac{2}{5} \end{выравнивание*} Решение: \(\frac{1}{10}\), а набор решений: \(\left\{\frac{1}{10}\right\}\text{. Пример 3.3.7.В научной лаборатории в 9:00 утра в контейнере было \(21\) унций воды. Вода испарялась со скоростью \(3\) унций каждые \(5\) минут. Когда останется \(8\) унций воды? Объяснение Поскольку контейнер теряет \(3\) унций воды каждые \(5\) минут, он теряет \(\frac{3}{5}\) унций каждую минуту. Через \(м\) минут с 9:00 утра контейнер потеряет \(\frac{3}{5}m\) унций воды. Поскольку вначале в контейнере было \(21\) унций воды, количество воды в контейнере можно смоделировать как \(21-\frac{3}{5}м\) (в унциях). Чтобы определить, когда останется \(8\) унций воды, запишем и решим это уравнение: \begin{align*} 21-\frac{3}{5}m\amp=8\\ \multiplyleft{5}\left(21-\frac{3}{5}x\right)\amp=\multiplyleft{5}8\\ 5\cdot21-5\cdot\frac{3}{5}x\amp=40\\ 105-3м\ампер=40\\ 105–3 м\вычитание вправо{105}\amp=40\вычитание вправо{105}\\ -3м\ампер=-65\\ \divideunder{-3m}{-3}\amp=\divideunder{-65}{-3}\\ m\amp=\frac{65}{3} \end{выравнивание*} Проверка решения \(\frac{65}{3}\text{:}\) \begin{align*} 21-\frac{3}{5}m\amp=8\\ 21-\frac{3}{5}\left(\substitute{\frac{65}{3}}\right)\amp\stackrel{?}{=}8\\ 21-13\amp\stackrel{\checkmark}{=}8 \end{align*} Следовательно, решение равно \(\frac{65}{3}\text{. КПП 3.3.8.Подраздел 3.3.3 Решение неравенств с дробямиМы также можем решать линейные неравенства с дробями, умножая каждую часть неравенства на НЛД всех дробей в неравенстве. Помните, что с линейными неравенствами все работает точно так же, как и с решением линейных уравнений, за исключением того, что знак неравенства меняет направление всякий раз, когда мы умножаем каждую часть неравенства на отрицательное число. Давайте рассмотрим несколько примеров, чтобы увидеть, как решить линейное неравенство, сначала очистив дроби. Пример 3.3.9.Найдите \(x\) в неравенстве \(\frac{3}{4}x-2\gt\frac{4}{5}x\text{.}\) Запишите набор решений в обоих множествах- нотация построителя и нотация интервала. Объяснение \begin{align*} \frac{3}{4}x-2\amp\gt\frac{4}{5}x\\ \multiplyleft{20}\left(\frac{3}{4}x-2\right)\amp\gt\multiplyleft{20}\frac{4}{5}x\\ 20\cdot\frac{3}{4}x-20\cdot2\amp\gt16x\\ 15x-40\ампер\gt16x\\ 15x-40\subtractright{15x}\amp\gt16x\subtractright{15x}\\ -40\ампер\гт х\\ х\усилитель\лт-40 \end{выравнивание*} Набор решений в нотации построителя наборов имеет вид \(\{x\mid x\lt-40\}\text{. Набор решений в интервальной нотации: \((-\infty,-40)\text{.}\) Пример 3.3.10.Найдите \(y\) в неравенстве \(\frac{4}{7}-\frac{4}{3}y\le\frac{2}{3}\text{.}\) Запишите набор решений как в нотации построителя наборов, так и в нотации интервала. Объяснение \begin{align*} \frac{4}{7}-\frac{4}{3}y\amp\le\frac{2}{3}\\ \multiplyleft{21}\left(\frac{4}{7}-\frac{4}{3}y\right)\amp\le\multiplyleft{21}\left(\frac{2}{3}\ верно)\\ 21\влево(\frac{4}{7}\вправо)-21\влево(\frac{4}{3}y\вправо)\amp\le21\влево(\frac{2}{3}\вправо) \\ 12-28лет\ампер\ле14\\ -28г\ампер\ле2\\ \divideunder{-28y}{-28}\amp\ge\divideunder{2}{-28}\\ y\amp\ge-\frac{1}{14} \end{align*} Обратите внимание, что когда мы разделили каждую часть неравенства на \(-28\text{,}\), символ неравенства изменил направление. Набор решений в нотации построителя наборов: \(\left\{y\mid y\ge-\frac{1}{14}\right\}\text{.}\) Набор решений в интервале обозначение \(\left[-\frac{1}{14},\infty\right)\text{.}\) Пример 3.3.11.В определенном классе оценка учащегося рассчитывается по среднему баллу за 3 теста. Эйдан набрал \(78\%\) и \(54\%\) в первых двух тестах. Если он хочет получить хотя бы оценку C \((70\%)\text{,}\), какой самый низкий балл ему нужно получить на третьем экзамене? Объяснение Предположим, Эйдан наберет \(x\%\) на третьем тесте. Чтобы его средний балл за тест был больше или равен \(70\%\text{,}\), запишем и решим это неравенство: \begin{align*} \frac{78+54+x}{3}\amp\ge70\\ \frac{132+x}{3}\amp\ge70\\ \multiplyleft{3}\frac{132+x}{3}\amp\ge\multiplyleft{3}70\\ 132+х\усилитель\ge210\\ х\amp\ge78 \end{align*} Чтобы получить хотя бы оценку C, Эйдан должен набрать не менее \(78\%\) в третьем тесте. Упражнения 3. 3.4 Упражнения 3.4 УпражненияОбзор и прогрев1.Умножить: \(\displaystyle{8\cdot \frac{2}{3} }\) 2.Умножить: \(\displaystyle{3\cdot \frac{3}{8} }\) 3.Умножить: \(\displaystyle{4\cdot\left( -{\frac{5}{2}} \right)}\) 4.Умножить: \(\displaystyle{28\cdot\left( -{\frac{6}{7}} \right)}\) 5.Выполните следующие умножения.
6.Выполните следующие умножения.
Решение линейных уравнений с дробями7.Решите уравнение. \(\displaystyle{{\frac{q}{7}+120}={3q}}\) 8.Решите уравнение. \(\displaystyle{{\frac{y}{4}+57}={5y}}\) 9. Решите уравнение. \(\displaystyle{{\frac{t}{10}+8}={13}}\) 10.Решите уравнение. \(\displaystyle{{\frac{a}{7}+5}={7}}\) 11.Решите уравнение. \(\displaystyle{ {3-\frac{c}{7}} = {1} }\) 12.Решите уравнение. \(\displaystyle{ {9-\frac{A}{2}} = {3} }\) 13.Решите уравнение. \(\displaystyle{{-42} = {6-\frac{8C}{5}} }\) 14.Решите уравнение. \(\displaystyle{ {-22} = {2-\frac{4m}{9}} }\) 15.Решите уравнение. \(\displaystyle{{5p} = {\frac{3p}{10}+282}}\) 16.Решите уравнение. \(\displaystyle{{5q} = {\frac{7q}{6}+115}}\) 17.Решите уравнение. \(\displaystyle{{64} = {{\frac{10}{3}}y+2y}}\) 18.Решите уравнение. \(\displaystyle{{195} = {{\frac{4}{7}}r+5r}}\) 19. Решите уравнение. \(\displaystyle{{74-{\frac{7}{6}}a} = {5a}}\) 20.Решите уравнение. \(\displaystyle{{65-{\frac{5}{2}}c} = {4c}}\) 21.Решите уравнение. \(\displaystyle{ {5A} = {{\frac{4}{9}}}A+8} }\) 22.Решите уравнение. \(\displaystyle{{3C} = {{\frac{2}{3}}C+4}}\) 23.Решите уравнение. \(\displaystyle{{{\frac{7}{2}}-9m}={8}}\) 24.Решите уравнение. \(\displaystyle{{{\frac{3}{8}}-7p}={8}}\) 25.Решите уравнение. \(\displaystyle{{{\frac{5}{4}}-{\frac{1}{4}}q}={3}}\) 26.Решите уравнение. \(\displaystyle{{{\frac{9}{2}}-{\frac{1}{2}}y}={1}}\) 27.Решите уравнение. \(\displaystyle{{\frac{4r}{7}-8}={-{\frac{40}{7}}}}\) 28.Решите уравнение. \(\displaystyle{{\frac{6a}{5}-6}={-{\frac{6}{5}}}}\) 29. Решите уравнение. \(\displaystyle{{{\frac{2}{9}}+{\frac{8}{9}}c}={7c}}\) 30.Решите уравнение. \(\displaystyle{{{\frac{6}{7}}+{\frac{10}{7}}A}={7A}}\) 31.Решите уравнение. \(\ displaystyle { {\ frac {3C} {7} — {\ frac {32} {7}}} = {- {\ frac {5} {7}} C}} \) 32.Решите уравнение. \(\ displaystyle { {\ frac {5m} {11} — {\ frac {21} {11}}} = {- {\ frac {2} {11}} m}} \) 33.Решите уравнение. \(\ displaystyle { {\ frac {6p} {7} + {\ frac {7} {2}}} = {p}} \) 34.Решите уравнение. \(\ displaystyle { {\ frac {2q} {3} + {\ frac {5} {8}}} = {q}} \) 35.Решите уравнение. \(\ displaystyle { {\ frac {4y} {7} -111} = {- {\ frac {3} {4}} y}} \) 36.Решите уравнение. \(\displaystyle{{\frac{2r}{5}-19}={-{\frac{3}{2}}r}}\) 37.Решите уравнение. \(\displaystyle{ {-{\frac{5}{8}}a+39}={\frac{3a}{16}}}\) 38. Решите уравнение. \(\displaystyle{{-{\frac{7}{10}}b+51}={\frac{3b}{20}}}\) 39.Решите уравнение. \(\displaystyle{{\frac{5A}{6}-8A}={{\frac{5}{12}}}}\) 40.Решите уравнение. \(\displaystyle{{\frac{7C}{2}-8C}={{\frac{3}{4}}}}\) 41.Решите уравнение. \(\displaystyle{{\frac{7m}{6}+{\frac{8}{9}}}={{\frac{3}{4}}m}}\) 42.Решите уравнение. \(\ displaystyle { {\ frac {7p} {4} + {\ frac {4} {7}}} = {{\ frac {3} {8}} p}} \) 43.Решите уравнение. \(\displaystyle{{{\frac{3}{2}}q}={{\frac{4}{7}}+\frac{5q}{3}}}\) 44.Решите уравнение. \(\displaystyle{{{\frac{5}{6}}y}={{\frac{5}{7}}+\frac{3y}{5}}}\) 45.Решите уравнение. \(\displaystyle{{{\frac{7}{6}}}={\frac{r}{24}}}\) 46.Решите уравнение. \(\displaystyle{{{\frac{3}{2}}}={\frac{a}{8}}}\) 47. Решите уравнение. \(\displaystyle{{-\frac{b}{14}}={{\frac{8}{7}}}}\) 48.Решите уравнение. \(\displaystyle{{-\frac{A}{30}}={{\frac{2}{5}}}}\) 49.Решите уравнение. \(\displaystyle{{-\frac{C}{10}}={-{\frac{5}{2}}}}\) 50.Решите уравнение. \(\displaystyle{{-\frac{m}{24}}={-{\frac{9}{8}}}}\) 51.Решите уравнение. \(\displaystyle{{-{\frac{3}{4}}}={\frac{7p}{5}}}\) 52.Решите уравнение. \(\displaystyle{ {-{\frac{7}{10}}}={\frac{5q}{9}}}\) 53.Решите уравнение. \(\displaystyle{{{\frac{3}{8}}}={\frac{y+6}{24}}}\) 54.Решите уравнение. \(\displaystyle{{{\frac{7}{4}}}={\frac{r+3}{12}}}\) 55.Решите уравнение. \(\displaystyle{ \frac{9}{10} = \frac{a-4}{9} }\) 56.Решите уравнение. \(\displaystyle{ \frac{5}{6} = \frac{b-4}{7} }\) 57. Решите уравнение. \(\ displaystyle { {\ frac {A-8} {2}} = {\ frac {A + 5} {4}}} \) 58.Решите уравнение. \(\ displaystyle { {\ frac {B-2} {6}} = {\ frac {B + 2} {8}}} \) 59.Решите уравнение. \(\ displaystyle { {\ frac {m + 7} {4} — \ frac {m-9{8}}={{\frac{9}{4}}} }\) 60.Решите уравнение. \(\displaystyle{{\frac{p+1}{2}-\frac{p-6}{4}}={{\frac{3}{4}}}}\) 61.Решите уравнение. \(\ displaystyle { {\ frac {q} {7} -2} = {\ frac {q} {9}}} \) 62.Решите уравнение. \(\ displaystyle { {\ frac {y} {5} -1} = {\ frac {y} {10}}} \) 63.Решите уравнение. \(\displaystyle{{\frac{r}{2}-3}={\frac{r}{5}+6}}\) 64.Решите уравнение. \(\ displaystyle { {\ frac {a} {6} -2} = {\ frac {a} {9} +1}} \) 65.Решите уравнение. \(\displaystyle{{{\frac{5}{2}}b+{\frac{7}{4}}}={{\frac{1}{2}}b+{\frac{5}{2} }}} }\) 66. Решите уравнение. \(\displaystyle{{1A+3}={5A+{\frac{3}{2}}}}\) 67.Решите уравнение. \(\ displaystyle { {\ frac {7B+6} {4} — \ frac {4-B} {8}} = {{\ frac {1} {9}}}} }\) 68.Решите уравнение. \(\displaystyle{{\frac{5m+6}{2}-\frac{1-m}{4}}={{\frac{1}{5}}}}\) 69.Решите уравнение. \(\displaystyle{{11}={\frac{p}{3}+\frac{p}{8}}}\) 70.Решите уравнение. \(\displaystyle{{27}={\frac{q}{7}+\frac{q}{2}}}\) 71.Решите уравнение. \(\ displaystyle { {{\ frac {5} {9}}y — {\ frac {6} {7}}} = {- {\ frac {7} {2}} y + {\ frac {1} {2}}} }\) 72.Решите уравнение. \(\displaystyle{{-{\frac{1}{2}}r-1}={-r-{\frac{7}{5}}}}\) 73.Решите уравнение. \(\ displaystyle { {-{\ frac {7} {8}} a — {\ frac {10} {9}}} = {{\ frac {7} {2}} a — {\ frac {5 {2}}} }\) 74. Решите уравнение. \(\displaystyle{{-{\frac{5}{9}}b+{\frac{5}{7}}}={{\frac{5}{3}}b-1}}\) 75.Решите уравнение.
76.Решите уравнение.
Приложения77.Линдси бежит по прямой. У нее была фора в \(10\) метрах от стартовой линии, и она пробегала \(2\) метра каждые \(7\) секунд. Через сколько секунд Линдсей окажется в \(18\) метрах от линии старта? Линдси будет в \(18\) метрах от линии старта секунд с момента начала бега. 78.Эмбер бежит по прямой. Она стартовала в месте \(30\) метров от линии старта и бежала к линии старта со скоростью \(2\) метров каждые \(3\) секунды. Через сколько секунд Эмбер окажется в \(26\) метрах от линии старта? Эмбер будет в \(26\) метрах от стартовой линии секунд с тех пор, как начала бежать. 79.В копилке Джозефа было всего \({\$10.00}\), и он решил начать откладывать больше. Он сохраняет \({\$5.00}\) каждые \(8\) дней. Через сколько дней у него будет \({\$25.00}\) в копилке? Джозеф будет откладывать \({\$25.00}\) в свою копилку спустя несколько дней. 80.Росс накопил в своей копилке \({\$50.00}\) и решил начать их тратить. Он тратит \({\$3.00}\) каждые \(4\) дней. Через сколько дней у него останется \({\$44.00}\) в копилке? Через несколько дней в копилке Росса останется \({\$44.00}\). Решение неравенств с дробями Для каждой задачи, приведенной ниже, решите неравенство и, в дополнение к написанию построителя наборов и обозначений интервалов для каждого набора решений, нарисуйте график каждого набора решений на числовой прямой. 81.\({\frac{x}{3}+84}\geq{5x}\) ; 82.\({\frac{x}{4}+28}\geq{2x}\) ; 83.\({{\frac{3}{4}}-5y} \lt{3}\) ; 84.\({{\frac{5}{4}}-2y} \lt{6}\) ; 85.\({-{\frac{3}{4}}t} > {{\frac{4}{5}}t-93}\) ; 86.\({-{\frac{5}{6}}t} > {{\frac{2}{7}}t-47}\) ; 87.\(\) ; 88.\(\) ; 89.\({-\frac{z}{4}} \lt {-\frac{3}{2}}\) ; 90.\({-\frac{z}{8}} \lt {-\frac{9}{2}}\) ; 91.\({\ frac {x} {7}-12} \leq {\ frac {x} {3}} \) ; 92.\({\ frac {x} {7}-4} \leq {\ frac {x} {5}} \) ; 93.\({\frac{y-8}{6}} \geq {\frac{y+8}{4}}\) ; 94.\({\frac{y-4}{6}} \geq {\frac{y+3}{4}}\) ; 95.\({{\frac{17}{12}}} \lt {\frac{x+1}{6}-\frac{x-7}{12}}\) ; 96. \({{\frac{17}{12}}} \lt {\frac{x+7}{6}-\frac{x-1}{12}}\) ; Приложения97.Ваша оценка в классе определяется средним баллом по трем тестам. Вы набрали \(75\) и \(86\) в первых двух тестах. Чтобы заработать не менее \(80\) за этот курс, сколько вам нужно набрать на третьем тесте? Пусть \(x\) будет баллом, который вы заработаете на третьем тесте.
98. Ваша оценка в классе определяется средним баллом по трем тестам. Вы набрали \(70\) и \(90\) на первых двух тестах.
2.4 Линейные уравнения дробного порядка – Алгебра среднего уровняПерейти к содержимому Глава 2: Линейные уравнения При работе с дробями, встроенными в линейные уравнения, часто проще всего удалить дробь на самом первом шаге. Обычно это означает нахождение LCD дроби, а затем умножение каждого члена во всем уравнении на LCD. Найдите [латекс]x[/латекс] в уравнении [латекс]\dfrac{3}{4}x — \dfrac{7}{2} = \dfrac{5}{6}.[/latex] Для этого уравнения LCD равно 12, поэтому каждый член этого уравнения будет умножен на 12. [латекс]\dfrac{3}{4}x(12) — \dfrac{7}{2}( 12) = \dfrac{5}{6}(12)[/latex] Сокращение знаменателя дает: [latex]3x(3) — 7(6) = 5(2)[/latex] Результат умножения: [латекс]\begin{array}{rrrrr} 9x&-&42&=&10 \\ &+&42&&+42 \\ \hline &&\dfrac{9x}{9}&=&\dfrac{52 {9} \\ \\ &&x&=&\dfrac{52}{9} \end{массив}[/латекс] Найдите [латекс]x[/латекс] в уравнении [латекс]\dfrac{3\left(\dfrac{5}{9}x+\dfrac{4}{27}\right)}{2}=3 .[/latex] Сначала удалите внешний знаменатель 2, умножив обе части на 2: [латекс]\left(2\right)\dfrac{3\left(\dfrac{5}{9}x+\ dfrac{4}{27}\right)}{2}=3(2)[/latex] [latex]3\left(\dfrac{5}{9}x+\dfrac{4}{27}\ right)=6[/latex] Теперь разделите обе части на 3, что даст: [latex]\dfrac{5}{9}x + \dfrac{4}{27} = 2[/latex] Чтобы удалить 9 и 27, умножьте обе стороны на ЖК-дисплей, 27: [латекс]\dfrac{5}{9}x\left(27\right) + \dfrac{4}{27}\left (27\right) = 2(27)[/latex] Это оставляет: [latex]\begin{array}{rrrrl} 5x(3)&+&4&=&54 \\ &-&4&&-4 \\ \hline &&15x&=&50 \\ \\ &&x&=&\dfrac{50}{15}\text{ или }\dfrac{10}{3} \end{массив}[/latex] В вопросах с 1 по 18 решите каждое линейное уравнение. Y 2 x 3 1: Mathway | Популярные задачи 2 |
| 1 | Оценка с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценка с использованием заданного значения | квадратный корень из 45 | |
| 3 | Оценить | 5+5 | |
| 4 | Оценить | 7*7 | |
| 5 | Найти простую факторизацию | 24 | |
| 6 | Преобразование в смешанный номер | 52/6 | |
| 7 | Преобразование в смешанный номер | 93/8 | |
| 8 | Преобразование в смешанный номер | 34/5 | |
| 9 | График | у=х+1 | |
| 10 | Оценка с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найдите площадь поверхности | сфера (3) | |
| 12 | Оценить | 54-6÷2+6 | |
| 13 | График | г=-2x | |
| 14 | Оценить | 8*8 | |
| 15 | Преобразование в десятичное число | 5/9 | |
| 16 | Оценка с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | у=2 | |
| 18 | Преобразование в смешанный номер | 7/8 | |
| 19 | Оценить | 9*9 | |
| 20 | Решите для C | С=5/9*(Ф-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | у=х+4 | |
| 23 | График | г=-3 | |
| 24 | График | х+у=3 | |
| 25 | График | х=5 | |
| 26 | Оценить | 6*6 | |
| 27 | Оценить | 2*2 | |
| 28 | Оценить | 4*4 | |
| 29 | Оценить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Оценить | 1/3+13/12 | |
| 31 | Оценка | 5*5 | |
| 32 | Решить для d | 2д=5в(о)-вр | |
| 33 | Преобразование в смешанный номер | 3/7 | |
| 34 | График | г=-2 | |
| 35 | Найдите склон | у=6 | |
| 36 | Преобразование в проценты | 9 | |
| 37 | График | у=2х+2 | |
| 38 | 92+5х+6=0|||
| 41 | Преобразование в смешанный номер | 1/6 | |
| 42 | Преобразование в десятичное число | 9% | |
| 43 | Найти n | 12н-24=14н+28 | |
| 44 | Оценить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразование в упрощенную дробь | 43% | |
| 47 | График | х=1 | |
| 48 | График | у=6 | |
| 49 | График | г=-7 | |
| 50 | График | у=4х+2 | |
| 51 | Найдите склон | у=7 | |
| 52 | График | у=3х+4 | |
| 53 | График | у=х+5 | |
| 54 | График | 92-9=0||
| 58 | Оценка с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценка с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Найти простую факторизацию | 14 | |
| 61 | Преобразование в смешанный номер | 7/10 | |
| 62 | Решите для | (-5а)/2=75 | |
| 63 | Упростить | х | |
| 64 | Оценить | 6*4 | |
| 65 | Оценить | 6+6 | |
| 66 | Оценить | -3-5 | |
| 67 | Оценить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найди обратное | 1/3 | |
| 71 | Преобразование в смешанный номер | 20. 11. 11. | |
| 72 | Преобразование в смешанный номер | 7/9 | |
| 73 | Найти LCM | 11, 13, 5, 15, 14 | , , , , |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | у=-х-2 | |
| 79 | График | у=3х+7 | |
| 80 | Определить, является ли многочлен | 2x+2 | |
| 81 | График | у=2х-6 | |
| 82 | График | у=2х-7 | |
| 83 | График | у=2х-2 | |
| 84 | График | у=-2х+1 | |
| 85 | График | у=-3х+4 | |
| 86 | График | у=-3х+2 | |
| 87 | График | у=х-4 | |
| 88 | Оценить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | х+2у=4 | |
| 91 | График | х=7 | |
| 92 | График | х-у=5 | |
| 93 | Решение с использованием свойства квадратного корня 92-2x-3=0 | ||
| 95 | Найдите площадь поверхности | конус (12)(9) | |
| 96 | Преобразование в смешанный номер | 3/10 | |
| 97 | Преобразование в смешанный номер | 7/20 | 9{b}-1$$, где $a,b \in \mathbb{Z}$ и $(a,b)=1$ и $a < b$.
План решения любого линейного уравнения. Алгебра 7 класс смотреть онлайн видео от Математика от Баканчиковой в хорошем качестве.
12+7 месяцев назад
Проголосовать за видео
Математика от Баканчиковой316 подписчиков
Алгебра 7 класс. Как решить линейное уравнение? Cегодня мы дадим Вам универсальный план решения ЛЮБОГО линейного уравнения. Придерживаясь этого плана и помня действия с одночленами, многочленами и формулы сокращенного умножения многочленов, у Вас никогда не будет проблем с решением линейных уравнений. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:30 1-й пункт плана
03:39 2-й пункт плана.
04:21 3-й пункт плана.
05:21 4-й пункт плана.
05:50 5-й пункт плана.
Если Вы впервые на нашем канале, и у Вас остались вопросы или Вы хотите освежить в памяти некоторые действия над числами или арифметическими выражениями, то рекомендуем Вам посмотреть следующие видео:
Уравнение. Определение. Компоненты. Корень уравнения и его проверка. https://rutube.ru/video/4f580720c801f4e208850eb6dbe0bc55/
Виды уравнений. Свойства уравнений. Перенос слагаемых из одной части уравнения в другую. Алгебра 7 класс. https://rutube.ru/video/a9f6b5235eef52f2ad92643e66cb8d9d/
Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Примеры решения уравнений. Алгебра 7 класс. https://rutube.ru/video/dac5537908ebbf1c3b8f3ae7a36bfc20/
Линейное уравнение и его разновидности. Алгебра 7 класс. https://rutube.ru/video/f0e3f219d18c4bbc28bb6ad5cd5f2c6e/
Решение линейного уравнения ax=b. Сколько корней может быть у линейного уравнения. Алгебра 7 класс. https://rutube.ru/video/c3e27eee3b1ebcd05e4ba6764e72a84f/
Алгебра 7 класс. Формулы сокращенного умножения. Квадраты суммы и разности. Примеры упражнений. Урок 1 из 5. https://rutube.ru/video/a020561e2096a53c4c5e640f17d82eac/
Алгебра 7 класс. Формулы сокращенного умножения. Разность квадратов двух выражений. Примеры упражнений.
Определение. Компоненты. Корень уравнения и его проверка. https://rutube.ru/video/4f580720c801f4e208850eb6dbe0bc55/
Виды уравнений. Свойства уравнений. Перенос слагаемых из одной части уравнения в другую. Алгебра 7 класс. https://rutube.ru/video/a9f6b5235eef52f2ad92643e66cb8d9d/
Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Примеры решения уравнений. Алгебра 7 класс. https://rutube.ru/video/dac5537908ebbf1c3b8f3ae7a36bfc20/
Линейное уравнение и его разновидности. Алгебра 7 класс. https://rutube.ru/video/f0e3f219d18c4bbc28bb6ad5cd5f2c6e/
Решение линейного уравнения ax=b. Сколько корней может быть у линейного уравнения. Алгебра 7 класс. https://rutube.ru/video/c3e27eee3b1ebcd05e4ba6764e72a84f/
Алгебра 7 класс. Формулы сокращенного умножения. Квадраты суммы и разности. Примеры упражнений. Урок 1 из 5. https://rutube.ru/video/a020561e2096a53c4c5e640f17d82eac/
Алгебра 7 класс. Формулы сокращенного умножения. Разность квадратов двух выражений. Примеры упражнений. Урок 2 из 5. https://youtu.be/nEcHKGozPkQ
Алгебра 7 класс. Правила и примеры умножения многочлена на многочлен. Характерные ошибки и как их избежать. https://rutube.ru/video/69bde5d2cce83606f0ed9ba3a806bd49/
Алгебра 7 класс. Возведение одночленов в степень. Свойство возведения степени в степень. Свойства степеней с одинаковым основанием. Примеры упражнений. https://rutube.ru/video/39301474c85fdc5819ab506f78e25814/
Алгебра 7 класс. Умножение одночленов. Упрощение выражений с одночленами. https://rutube.ru/video/e153c4b44f74200f7c4baf8da9861672/
Алгебра 7 класс. Сложение и вычитание одночленов. Упрощение выражений с одночленами. https://rutube.ru/video/a4a08f8bbd0fccd15a051aeb19135269/
Алгебра 7 класс. Одночлен и его компоненты — коэффициент, буквенная часть и степень одночлена. Определения. https://rutube.ru/video/65308be4cfbadb19bcb5d307cac94113/
#ЛинейныеУравнения #РешениеУравненийВ7классе #МатематикаОтБаканчиковой
Алгебра 7 класс, линейные уравнения, решение линейного уравнения, решение уравнений в 7 классе, план решения линейного уравнения, как решать линейные уравнения
Урок 2 из 5. https://youtu.be/nEcHKGozPkQ
Алгебра 7 класс. Правила и примеры умножения многочлена на многочлен. Характерные ошибки и как их избежать. https://rutube.ru/video/69bde5d2cce83606f0ed9ba3a806bd49/
Алгебра 7 класс. Возведение одночленов в степень. Свойство возведения степени в степень. Свойства степеней с одинаковым основанием. Примеры упражнений. https://rutube.ru/video/39301474c85fdc5819ab506f78e25814/
Алгебра 7 класс. Умножение одночленов. Упрощение выражений с одночленами. https://rutube.ru/video/e153c4b44f74200f7c4baf8da9861672/
Алгебра 7 класс. Сложение и вычитание одночленов. Упрощение выражений с одночленами. https://rutube.ru/video/a4a08f8bbd0fccd15a051aeb19135269/
Алгебра 7 класс. Одночлен и его компоненты — коэффициент, буквенная часть и степень одночлена. Определения. https://rutube.ru/video/65308be4cfbadb19bcb5d307cac94113/
#ЛинейныеУравнения #РешениеУравненийВ7классе #МатематикаОтБаканчиковой
Алгебра 7 класс, линейные уравнения, решение линейного уравнения, решение уравнений в 7 классе, план решения линейного уравнения, как решать линейные уравнения
Мистер Нуссбаум Занятия по математическим уравнениям
09. 05 — MrNussbaum.com исполнилось 20 лет. Отпразднуйте наш день рождения с подарком со скидкой 60 % при регистрации на MrN 365 – подписной версии MrNussbaum.com с расширенными функциями, без рекламы, со всем содержимым, курируемой преподавателями. Используйте код
05 — MrNussbaum.com исполнилось 20 лет. Отпразднуйте наш день рождения с подарком со скидкой 60 % при регистрации на MrN 365 – подписной версии MrNussbaum.com с расширенными функциями, без рекламы, со всем содержимым, курируемой преподавателями. Используйте код
Главная > Математика > Уравнения
Этот раздел содержит действия и ресурсы, связанные с уравнениями.
Причудливые окна — Онлайн игра
Описание: Добро пожаловать в причудливую Windows. Именно здесь, за одним из 15 окон, вы можете найти давно потерянного черного жеребца-единорога. Однако каждое окно заблокировано, и открыть его может только специальное уравнение. Чтобы найти уравнение, вам нужно посмотреть на отношения между упорядоченными парами, выгравированными в каждом окне. Одно уравнение управляет каждой из упорядоченных пар. Такая связь называется функцией. Нажмите на окно и найдите уравнение. Если вы правы, окно откроется, и вы обнаружите одного из сорока возможных анимированных животных. Вы можете найти тигра, жирафа, гигантскую панду, коалу или других, таких как саблезубый тигр, полностью мамонт, кракен, белый единорог и, конечно же, мифический и таинственный черный жеребец-единорог. Игра заканчивается, и все окна открываются, когда вы решаете уравнение для окна, которое открывается для черного жеребца-единорога.
Чтобы найти уравнение, вам нужно посмотреть на отношения между упорядоченными парами, выгравированными в каждом окне. Одно уравнение управляет каждой из упорядоченных пар. Такая связь называется функцией. Нажмите на окно и найдите уравнение. Если вы правы, окно откроется, и вы обнаружите одного из сорока возможных анимированных животных. Вы можете найти тигра, жирафа, гигантскую панду, коалу или других, таких как саблезубый тигр, полностью мамонт, кракен, белый единорог и, конечно же, мифический и таинственный черный жеребец-единорог. Игра заканчивается, и все окна открываются, когда вы решаете уравнение для окна, которое открывается для черного жеребца-единорога.
Тип: Математическая игра
Формат: онлайн-активность
Уровни оценок: 5, 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
Очередь за обедом — Онлайн игра
Описание: Очередь за обедом — это забавная (и забавная) игра, в которой учащиеся тренируются в упорядочивании дробей, десятичных знаков и процентов. Студенты должны расположить знаменитостей и исторических деятелей в очереди за обедом, основываясь на значениях, плавающих в их головах, от наименьшего к наибольшему. Если учащиеся расставят все десять правильно, очередь за обедом плавно переместится в столовую по прямой линии, и они смогут распечатать справку с указанием лидера очереди. При неправильном расположении фигур обеденная очередь будет криво и неэффективно шататься к столовой, тем самым разозлив учителя.
При неправильном расположении фигур обеденная очередь будет криво и неэффективно шататься к столовой, тем самым разозлив учителя.
Тип: Математическая игра — Фокус на десятичных дробях
Формат: игра
Уровни оценок: 5, 6
Стандарты СС:
Ланг.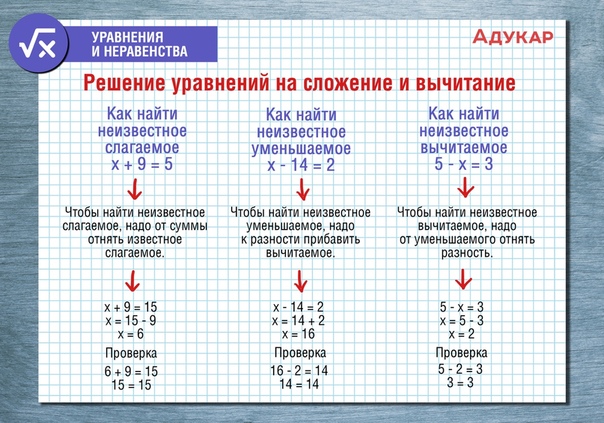 Стандарты искусства:
Стандарты искусства:
Slope Man — Использование склона для восхождения на высокие пики
Описание: Добро пожаловать, Человек со склона. Вы один из самых предприимчивых альпинистов в мире. Ваша задача состоит в том, чтобы взобраться на десять самых высоких вершин мира, рассчитав уклон в различных точках вашего восхождения. Поднимитесь на гору Фудзи, Мауна-Лоа, Монблан и даже на Эверест и другие, но будьте осторожны — неверные расчеты приведут к ледяным катастрофам.
Тип: Математическая игра
Формат: игра
Уровни оценок: 6
Стандарты СС:
Ланг. Стандарты искусства:
Стандарты искусства:
ОБНОВИТЬ ДО MRN365.COM
ПодробнееНе хотите обновляться?
Вы по-прежнему можете купить этот ресурс по отдельности на
Учителя платят учителям за .
ОБНОВЛЕНИЕ ДО MRN365.COM
Обновите до MrN 365, чтобы получить доступ ко всей нашей библиотеке невероятных образовательных ресурсов и инструментов для учителей в среде без рекламы. Если вам нравится MrNussbaum.com, вы ПОЛЮБИТЕ MrN 365!
Узнать большеПлитки алгебры
Оценка: С 6 по 8, средняя школа
Используйте плитки для представления переменных и констант, научитесь представлять и решить задачу по алгебре. Решить уравнения, подставив в переменную выражения, а также расширение и множитель. Перевернуть плитки, удалить нулевые пары, скопировать и организовать, и сделать свой путь к лучшему пониманию алгебры.
Этот интерактив оптимизирован для настольных компьютеров и планшетов.
Примечание: в режиме «Факторы» все коэффициенты необходимо вводить в скобках. x(x + 1) будет помечен неправильно. (x)(x + 1) будет принято.
Режимы
Имеется 4 режима: Решить , Подставить , Расширить или Фактор .
- В Решите и Замените , вертикальные линии означают «равно» (=).
- В Expand и Factor большая площадь является произведением верхней и левой площадей, как в стандартной таблице умножения.
Добавьте плитки в рабочую область из нижнего левого банка. Значение каждой плитки указано. При перемещении в рабочую область значение быть стерты.
- Flip переворачивает плитки, получая обратное значение. Например, если перевернуть зеленую плитку размером 90 124 x 90 125, она станет красной – 90 124 x 90 125. Если перевернуть красную плитку размером 90 124 x 90 125, получится инверсная зеленая плитка размером 90 124 x 90 125.
плитка. Вы можете нажать кнопку, чтобы перевернуть все плитки в банке или переместить
плитки в рабочее пространство, а затем щелкните, чтобы перевернуть эти плитки.

- Поворот поворачивает зеленую x и красную плитку x на 90°. Это наиболее полезно в действиях Expand и Factor .
Инструменты можно использовать на отдельных плитках, выбрав их или группу плитки, выбрав несколько или перетащив прямоугольник вокруг группы плитка. Инструмент может быть выбран перед плиткой для одного действия или после, чтобы разрешить повторное действие.
- Указатель выбирает и перемещает плитки. Это инструмент по умолчанию. Когда пусто выбрана рабочая область или тайл из банка, этот инструмент выбран автоматически. Примечание: В зависимости от активности некоторые плитки могут не удаляться.
- Ластик удаляет плитки из рабочей области. Примечание: В зависимости от активности некоторые плитки могут не удаляться.
- Удалить нулевые пары позволяет удалять из рабочей области только нулевые пары.
 Это наиболее полезно при решении Решите и Расширьте проблемы или в любое время в Фактор проблем, чтобы обеспечить правильное удаление плиток. Пара нулей — это пара плиток, сумма которых равна 0, например желтая плитка 1 и красная плитка -1.
Это наиболее полезно при решении Решите и Расширьте проблемы или в любое время в Фактор проблем, чтобы обеспечить правильное удаление плиток. Пара нулей — это пара плиток, сумма которых равна 0, например желтая плитка 1 и красная плитка -1. - Копировать копирует выбранные плитки. Переместите плитку(и), чтобы увидеть копировать. Это особенно полезно, когда необходимо разместить большое количество плиток. в рабочей области, например, для x 2 – 16.
Все задачи необходимо решать в два этапа:
- Построить модель
Разместите правильные части в рабочей области. После того, как вы построите модель данной проблемы, проверьте свой ответ, чтобы перейти к следующему шагу. Только тип плитки, количество плитки, и рабочая область проверяются, а не так, как плитки согласованный.
Если вы хотите начать заново, Сбросьте , чтобы очистить рабочее пространство.

- Решить проблему
После решения проблемы Проверьте свой ответ. Там, где это применимо, ответы должны быть даны в упрощенном виде. форма. Введенный ответ и рабочее пространство должны быть правильными. Если один или оба неверны, будет указана неправильная часть. Примечание: в режиме Фактор , все коэффициенты должны быть введены в круглых скобках. x(x + 1) будет помечен неправильно. (x)(x + 1) будет принято.
Если вы хотите начать заново, Сбросьте , чтобы вернуться к исходной модели.
- Когда вы закончите свою задачу или в любой другой момент, вы можете начать Новая проблема .
Поместите плитки, равные выражению, слева от знака = слева
Рабочее пространство. Поместите плитки, равные выражению, справа от = в
правильное рабочее пространство. Например, если выражение равно 3 90 124 x 90 125 – 2, поместите 3 зеленые плитки размером 90 124 x 90 125 и 2 красные плитки размером 90 124 1 90 125.

 02.2022?
02.2022? Choose the right form:
Choose the right form: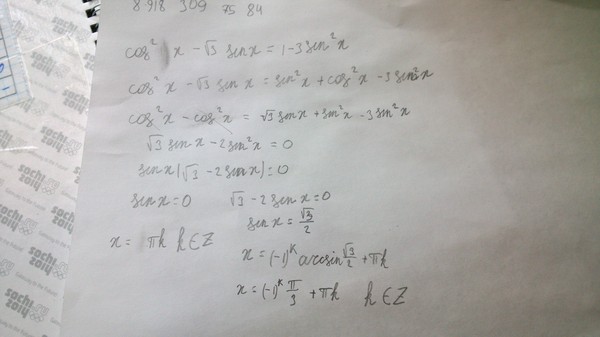

 6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
6. Jill lost her ticket. If she (didn’t lose/ hadn’t lost) her ticket, she would (arrive/ have arrived) in London yesterday. 7. He didn’t have much money at that moment. If he (had/ had had) more money, he would (buy/ have bought) new toys for his children.
 Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %.
Якою є сила струму в його нагрівальному елементі, якщо напруга в мережі становить 220 В? ККД нагрівника 90 %. Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  Какая часть носков Макса коричневого или черного цвета?
Какая часть носков Макса коричневого или черного цвета?
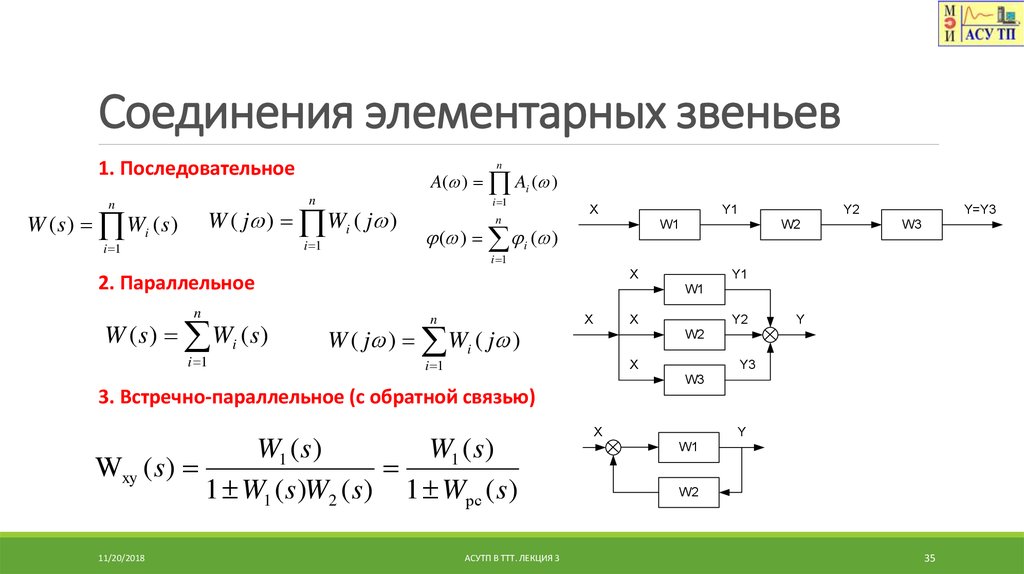
 Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
Ошибки бывают у всех, мы готовы дорабатывать бесплатно и в сжатые сроки, а если у вас появятся вопросы, готовы на них ответить.
 На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант.
На цену влияют: сложность, количество заданий и срок выполнения. Поэтому для оценки стоимости заказа максимально качественно сфотографируйте или пришлите файл задания, при необходимости загружайте поясняющие фотографии лекций, файлы методичек, указывайте свой вариант. Присланное качественное задание моментально изучается и оценивается.
Присланное качественное задание моментально изучается и оценивается.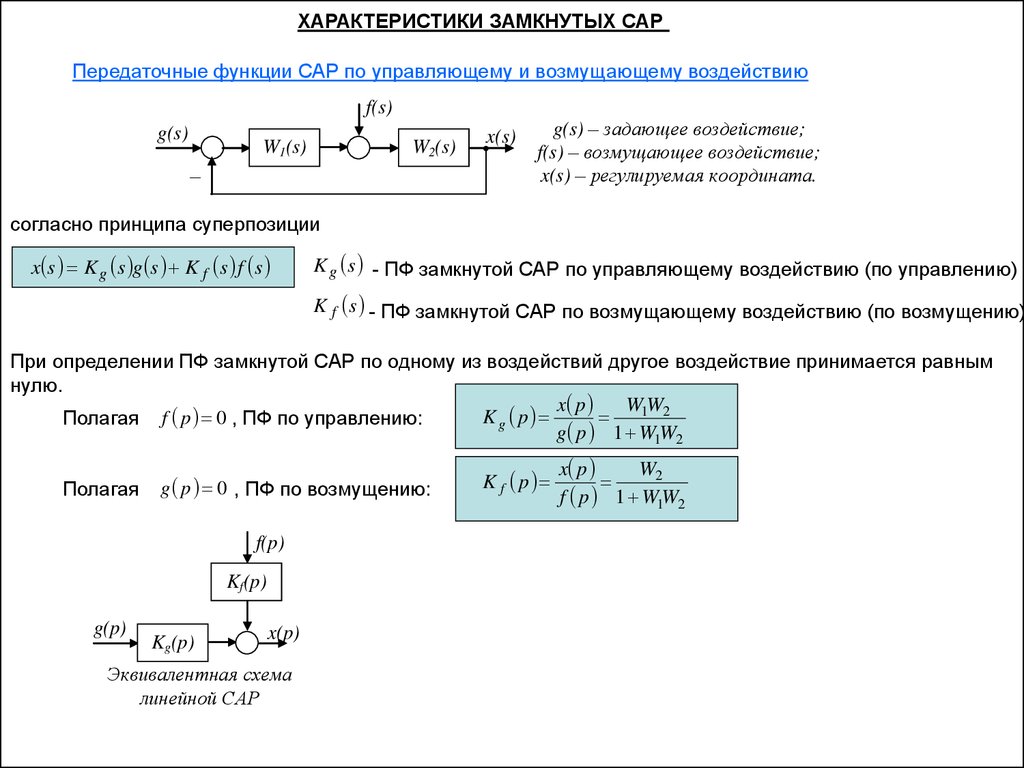 Мы изучим много теорем геометрии и будем работать над всеми видами доказательств. Мы будем изучать объем, площадь поверхности и площадь сложных фигур. Самое главное, что на этом занятии мы не остаемся на уровне доказательства, мы решаем сложные задачи по геометрии, применяя изученные теоремы. У SAT и математических соревнований нет доказательств, у них есть проблемы!
Мы изучим много теорем геометрии и будем работать над всеми видами доказательств. Мы будем изучать объем, площадь поверхности и площадь сложных фигур. Самое главное, что на этом занятии мы не остаемся на уровне доказательства, мы решаем сложные задачи по геометрии, применяя изученные теоремы. У SAT и математических соревнований нет доказательств, у них есть проблемы!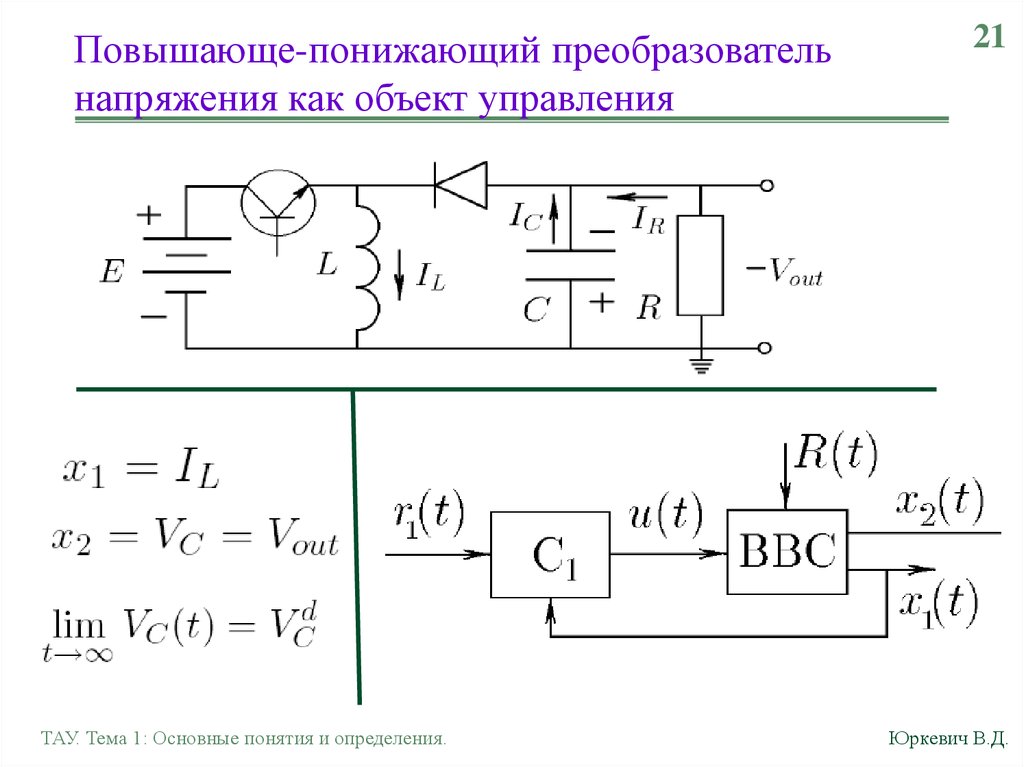

 Он состоит из явного добавления тау слагаемых в УЧП, которые вводят степени свободы, которые позволяют решать задачу точно над полиномами.
Определение оптимальных тау-членов для добавления к данному УЧП является открытой проблемой, и хотя мы надеемся в конечном итоге автоматизировать этот процесс в Dedalus, в настоящее время эти члены необходимо добавлять вручную при задании уравнений в Dedalus v3.
Он состоит из явного добавления тау слагаемых в УЧП, которые вводят степени свободы, которые позволяют решать задачу точно над полиномами.
Определение оптимальных тау-членов для добавления к данному УЧП является открытой проблемой, и хотя мы надеемся в конечном итоге автоматизировать этот процесс в Dedalus, в настоящее время эти члены необходимо добавлять вручную при задании уравнений в Dedalus v3.
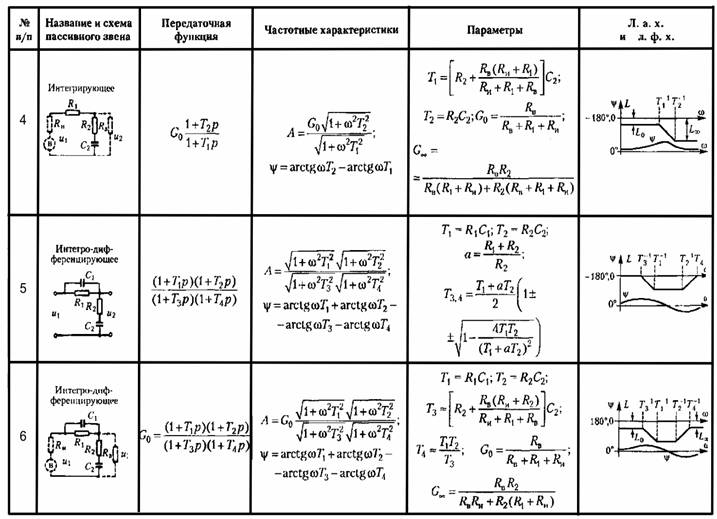 Если члены RHS усечены в степени \(N\) по \(y\), а тау-многочлен \(P(y)\) имеет степень \(N\) по \(y\), то система будет имеют точные полиномиальные решения для \(u\), \(v\), \(p\), \(u_y\) и \(v_y\) также степени \(N\) по \(y\).
Если члены RHS усечены в степени \(N\) по \(y\), а тау-многочлен \(P(y)\) имеет степень \(N\) по \(y\), то система будет имеют точные полиномиальные решения для \(u\), \(v\), \(p\), \(u_y\) и \(v_y\) также степени \(N\) по \(y\). Для чебышевских размеров, а также колец и сферических оболочек мы рекомендуем добавлять в уравнения тау-члены в соответствии с формулировками первого порядка, обсуждавшимися выше.
Например, после добавления вышеприведенных тау-членов мы можем исключить редукционные переменные первого порядка, чтобы восстановить исходные уравнения второго порядка, но содержащие те же тау-поправки: 92 v) + \partial_y p + \tau_4(x) P(y) — \nu \tau_2(x) \partial_y P(y) = g
\конец{собрано}\конец{разделено}\]
Для чебышевских размеров, а также колец и сферических оболочек мы рекомендуем добавлять в уравнения тау-члены в соответствии с формулировками первого порядка, обсуждавшимися выше.
Например, после добавления вышеприведенных тау-членов мы можем исключить редукционные переменные первого порядка, чтобы восстановить исходные уравнения второго порядка, но содержащие те же тау-поправки: 92 v) + \partial_y p + \tau_4(x) P(y) — \nu \tau_2(x) \partial_y P(y) = g
\конец{собрано}\конец{разделено}\]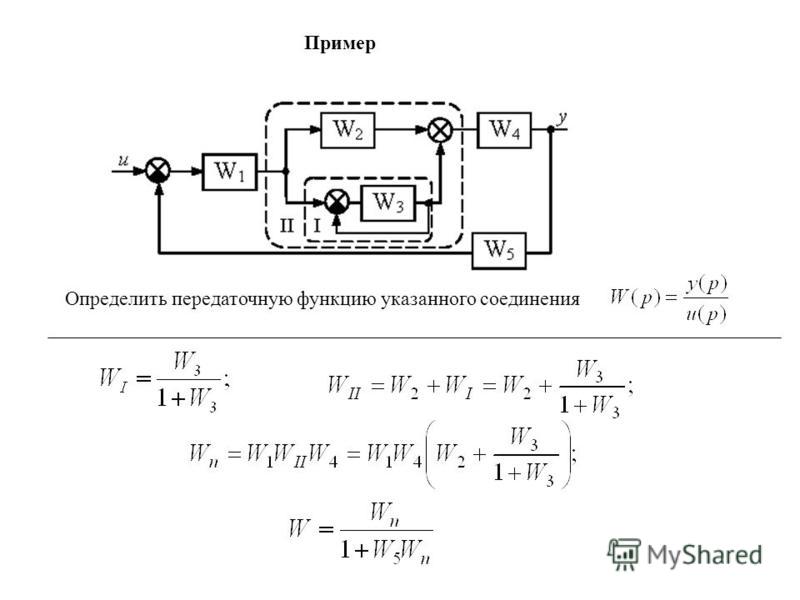 Определяя \(G = \nabla \vec{u} — \vec{e}_y \vec{\tau}_1(x) P(y)\), приведенные выше уравнения можно записать в векторной форме как: 92 \vec{u} — \vec{\tau}_1(x) \partial_y P(y)\]
Определяя \(G = \nabla \vec{u} — \vec{e}_y \vec{\tau}_1(x) P(y)\), приведенные выше уравнения можно записать в векторной форме как: 92 \vec{u} — \vec{\tau}_1(x) \partial_y P(y)\] Здесь мы возьмем \(P(y)\) за высшую моду в базисе Чебышева-U в соответствии с описанным выше ультрасферическим методом первого порядка:
Здесь мы возьмем \(P(y)\) за высшую моду в базисе Чебышева-U в соответствии с описанным выше ультрасферическим методом первого порядка: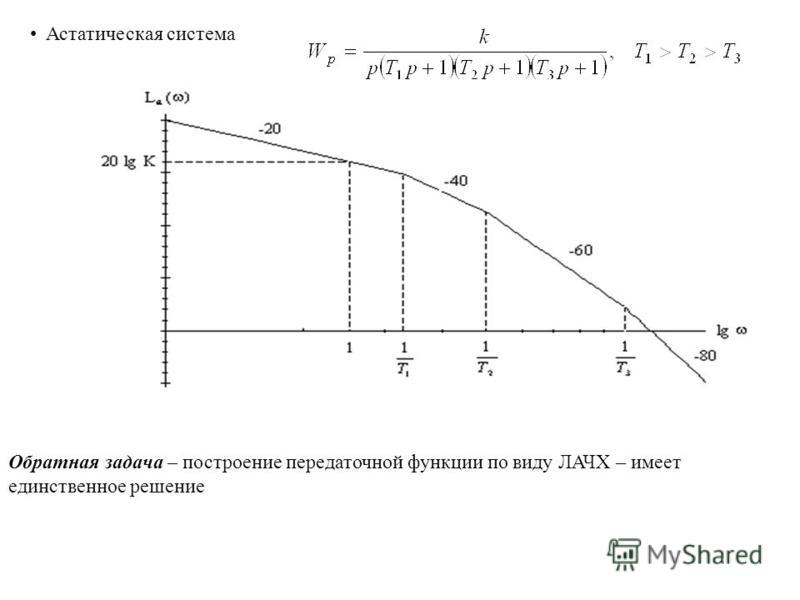 add_equation("u(y=-1) = 0")
проблема.add_equation ("и (у = + 1) = 0")
проблема.add_equation ("целое число (p) = 0")
add_equation("u(y=-1) = 0")
проблема.add_equation ("и (у = + 1) = 0")
проблема.add_equation ("целое число (p) = 0")
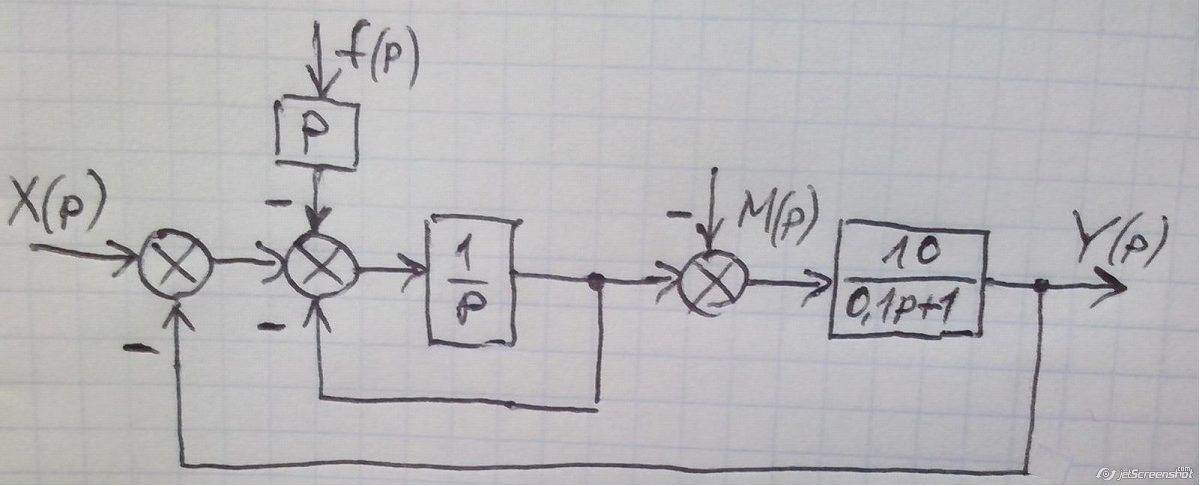 Field (имя = 'p', bases = disk_basis)
u = dist.VectorField (координаты, имя = 'u', базы = disk_basis)
tau_u = dist.VectorField (координаты, имя = 'tau_u', основания = фи_базис)
tau_p = расстояние. Поле (имя = 'tau_p')
Field (имя = 'p', bases = disk_basis)
u = dist.VectorField (координаты, имя = 'u', базы = disk_basis)
tau_u = dist.VectorField (координаты, имя = 'tau_u', основания = фи_базис)
tau_p = расстояние. Поле (имя = 'tau_p')
 IVP([p, u, tau_u, tau_p], namespace=locals())
проблема.add_equation("div(u) + tau_p = 0")
problem.add_equation("dt(u) - nu*lap(u) + grad(p) + lift(tau_u) = f")
проблема.add_equation("u(r=1) = 0")
проблема.add_equation ("целое число (p) = 0")
IVP([p, u, tau_u, tau_p], namespace=locals())
проблема.add_equation("div(u) + tau_p = 0")
problem.add_equation("dt(u) - nu*lap(u) + grad(p) + lift(tau_u) = f")
проблема.add_equation("u(r=1) = 0")
проблема.add_equation ("целое число (p) = 0")


 Например, 32 читается как «три в квадрате» или квадрат числа три.
Например, 32 читается как «три в квадрате» или квадрат числа три.
 когда графически. Это самая высокая экспоненциальная степень в полиномиальном уравнении. Давайте узнаем подробно об этом понятии и о том, как найти степень многочлена.
когда графически. Это самая высокая экспоненциальная степень в полиномиальном уравнении. Давайте узнаем подробно об этом понятии и о том, как найти степень многочлена.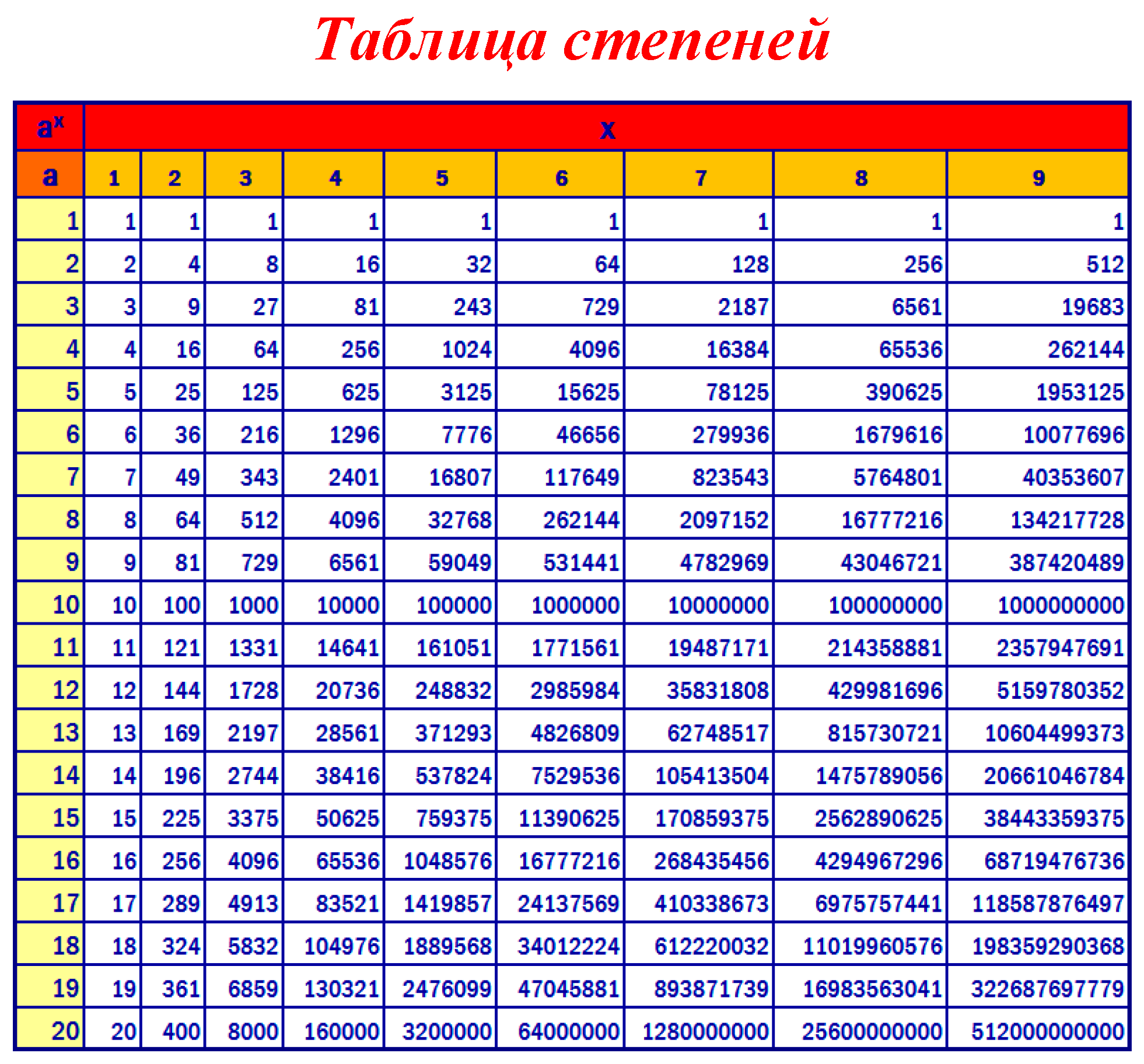 .. + a 1 x 1 + a 0 в стандартной форме обозначается как «n».
.. + a 1 x 1 + a 0 в стандартной форме обозначается как «n». Мы можем представить степень многочлена как Deg(p(x)). Ниже приведены некоторые примеры:
Мы можем представить степень многочлена как Deg(p(x)). Ниже приведены некоторые примеры:
 Давайте классифицировать многочлены на основе степени многочлена с примерами.
Давайте классифицировать многочлены на основе степени многочлена с примерами.
 Это и будет считаться степенью многочлена.
Это и будет считаться степенью многочлена.

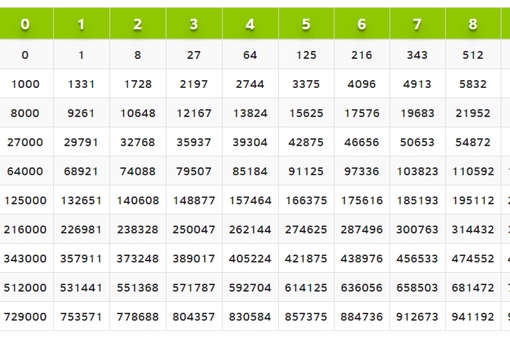
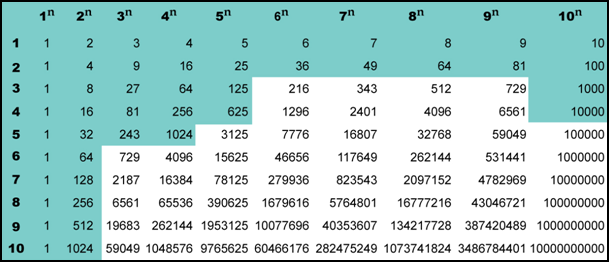

 Так что, если бы я знал, как узнать корни, это могло бы наградить меня большим количеством баллов.
Так что, если бы я знал, как узнать корни, это могло бы наградить меня большим количеством баллов. Остальные сложные, но различные ли они?
Остальные сложные, но различные ли они?
 n.
n. 06.1922
06.1922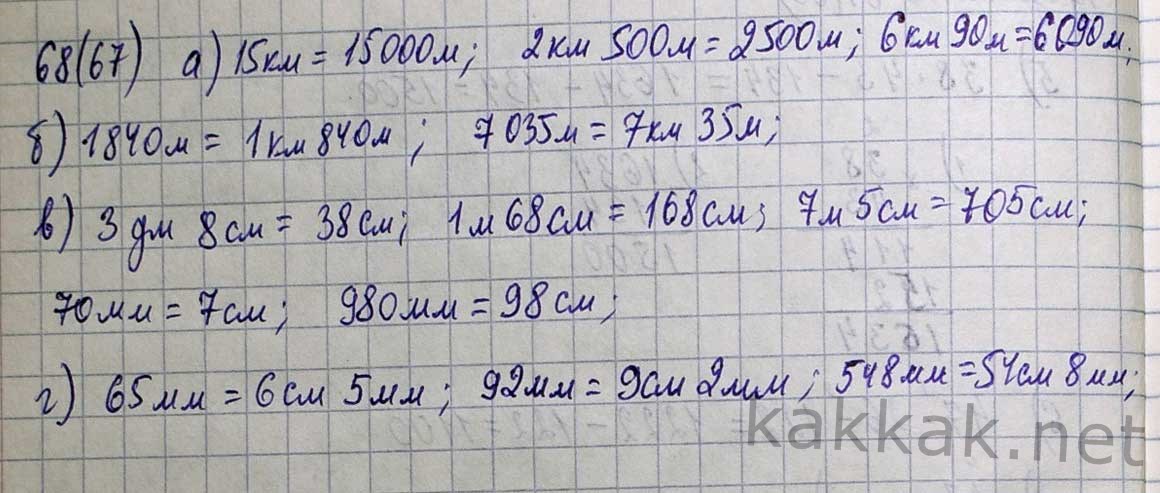 ..ЧастотаЭквивалентная дозаЭкспозиционная дозаЭлектрическая эластичностьЭлектрический дипольный моментЭлектрический зарядЭлектрический токЭлектрическое напряжениеЭлектрическое сопротивлениеЭлектрической проводимостиЭнергияЯркостьFuel consumption
..ЧастотаЭквивалентная дозаЭкспозиционная дозаЭлектрическая эластичностьЭлектрический дипольный моментЭлектрический зарядЭлектрический токЭлектрическое напряжениеЭлектрическое сопротивлениеЭлектрической проводимостиЭнергияЯркостьFuel consumption  С помощью этих измерений могут быть рассчитаны расстояния. И это далеко не все возможные измерения, а лишь наиболее распространенные из них.
В случаях измерений площади (квадратный метр, квадратный километр, ар, гектар, морган, акр и другие), температуры
(в градусах по Цельсию, по Кельвину, по Фаренгейту), скорости (м/с, км/час, миль/ч, узлы, мах), веса
(центнер, килограмм, метрическая тонна, американская тонна, стандартная тонна, фунт и другие) и объема
(кубический метр, гектолитр, английский галлон жидкости, американский жидкий галлон, американский сухой галлон, баррель и другие)
ситуация не намного лучше. А если всего этого вам показалось мало — большинство из этих единиц также имеют подразделения и высшие единицы
(например, милли-, санти-, деци-). Короче говоря, хаос, в котором так трудно разобраться без помощи справочника или других средств.
Данный калькулятор единиц измерения идеально подходит для перевода данных единиц.
С помощью этих измерений могут быть рассчитаны расстояния. И это далеко не все возможные измерения, а лишь наиболее распространенные из них.
В случаях измерений площади (квадратный метр, квадратный километр, ар, гектар, морган, акр и другие), температуры
(в градусах по Цельсию, по Кельвину, по Фаренгейту), скорости (м/с, км/час, миль/ч, узлы, мах), веса
(центнер, килограмм, метрическая тонна, американская тонна, стандартная тонна, фунт и другие) и объема
(кубический метр, гектолитр, английский галлон жидкости, американский жидкий галлон, американский сухой галлон, баррель и другие)
ситуация не намного лучше. А если всего этого вам показалось мало — большинство из этих единиц также имеют подразделения и высшие единицы
(например, милли-, санти-, деци-). Короче говоря, хаос, в котором так трудно разобраться без помощи справочника или других средств.
Данный калькулятор единиц измерения идеально подходит для перевода данных единиц.
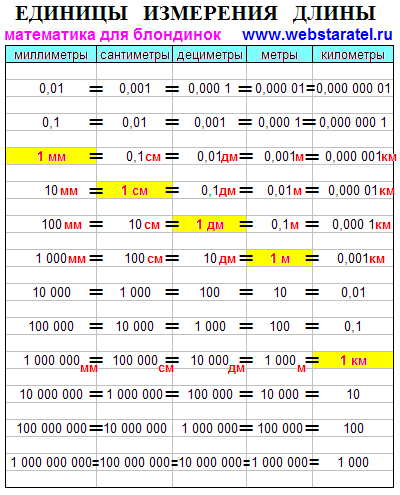 Сантиметр (см) — единица длины, которая ранее была базовой единицей длины в системе единиц сантиметр-грамм-секунда (СГС). Хотя технические специалисты предпочитают префиксы SI для коэффициентов 10 3 , сантиметр остается практической единицей длины для повседневных измерений. Ширина ногтя среднего взрослого человека примерно равна одному сантиметру, что делает его удобным для измерения небольших предметов или расстояний. Узнайте больше о сантиметре и его использовании в повседневной жизни.
Сантиметр (см) — единица длины, которая ранее была базовой единицей длины в системе единиц сантиметр-грамм-секунда (СГС). Хотя технические специалисты предпочитают префиксы SI для коэффициентов 10 3 , сантиметр остается практической единицей длины для повседневных измерений. Ширина ногтя среднего взрослого человека примерно равна одному сантиметру, что делает его удобным для измерения небольших предметов или расстояний. Узнайте больше о сантиметре и его использовании в повседневной жизни. Один метр примерно на 3 3/8 дюйма длиннее ярда, то есть примерно 39 3/8 дюйма.
Один метр примерно на 3 3/8 дюйма длиннее ярда, то есть примерно 39 3/8 дюйма.
 У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
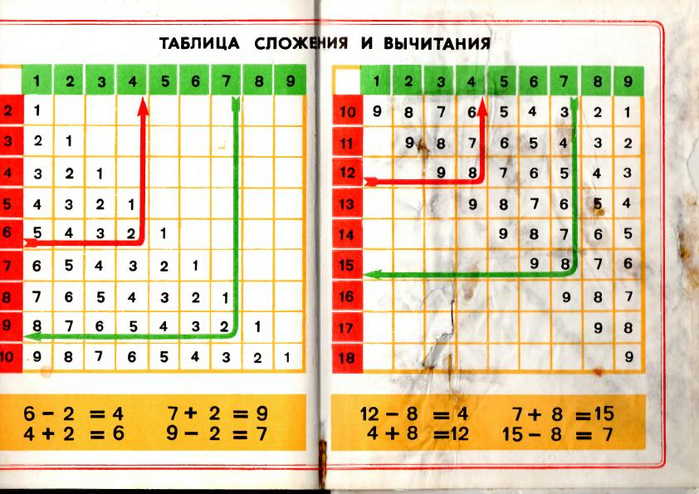 Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.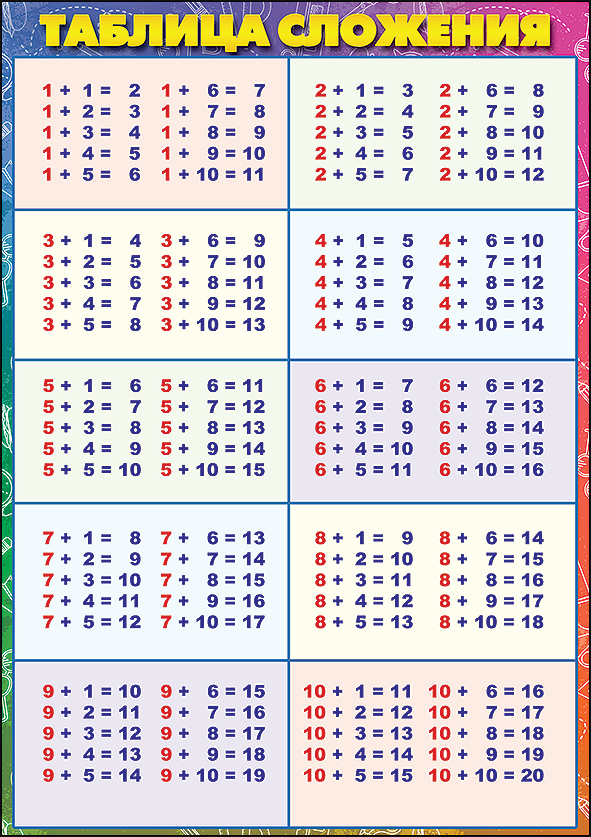 Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20. У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.
У вас будет возможность попрактиковать изученный ранее материал на интересных примерах.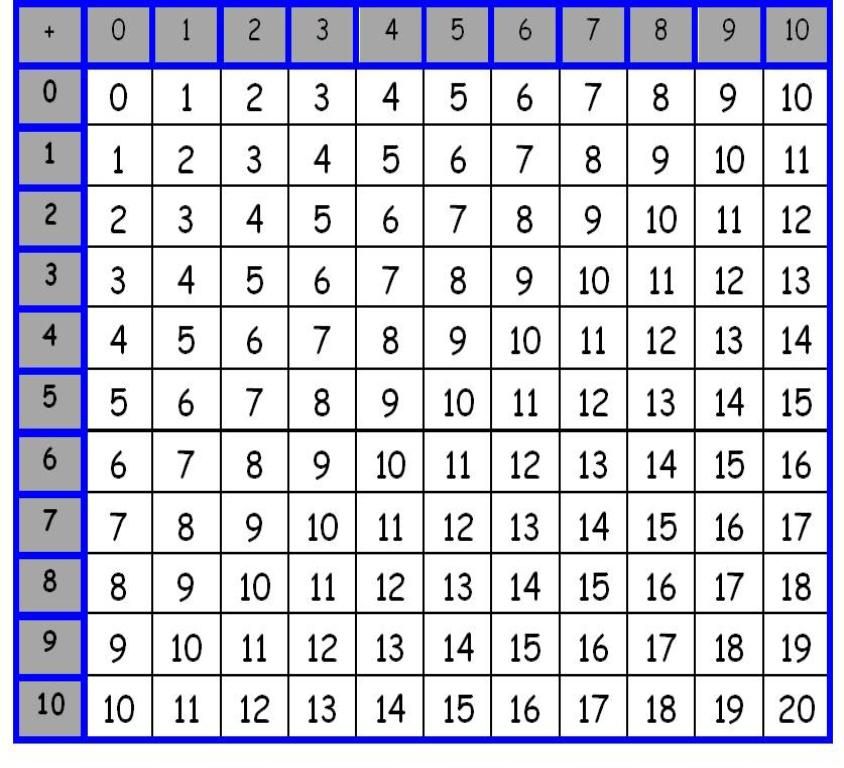
 Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы.
Вычитаем сначала из 16 шесть единиц, получится 10. А потом из 10 вычитаем оставшиеся три единицы. Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20.
Выберите способ, как вам легче будет запомнить ответы: по столбикам или по строкам. Если вы хорошо выучите таблицу сложения однозначных чисел до 20, то вам будет нетрудно выполнять и вычитание однозначных чисел в пределах 20. е. на сложении по этой таблице.
е. на сложении по этой таблице. На пересечении столбца и строки — сумма (8).
На пересечении столбца и строки — сумма (8). Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием.
Если вам нужна таблица сложения до 10, её можно легко сделать, удалив ненужные ячейки в формате Word. Если вам нужна таблица сложения больше, чем до 20, то вы можете скачать таблицу сложения в формате Excel и добавить нужные столбцы и строки копированием. д.
д.
 Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.
Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.



 Например, было пять яблок на столе, пять съели. Осталось — ничего, то есть ноль.
Например, было пять яблок на столе, пять съели. Осталось — ничего, то есть ноль. Это устаревший метод, основанный на механическом запоминании и наглядном доказательстве порядка чисел.
Это устаревший метод, основанный на механическом запоминании и наглядном доказательстве порядка чисел.
 Можно, конечно, зазубрить состав числа 5, например, но лучше использовать игровые действия с предметами с параллельной установкой на запоминание.
Можно, конечно, зазубрить состав числа 5, например, но лучше использовать игровые действия с предметами с параллельной установкой на запоминание. На примере 15 минус 8 мы видим, что число 15 раскладывается до своих разрядных единиц. В итоге всегда получается 10 и разрядные единички — 5. Теперь: вычитаемое надо разложить на слагаемые. Первым слагаемым будут разрядные единицы от 15-ти, а второе слагаемое подбирается (дети знают состав числа 8). Теперь остается от 10-ти отнять второе слагаемое от восьмерки. И ответ готов. Немного потренировавшись, можно будет легко решать подобные примеры в уме.
На примере 15 минус 8 мы видим, что число 15 раскладывается до своих разрядных единиц. В итоге всегда получается 10 и разрядные единички — 5. Теперь: вычитаемое надо разложить на слагаемые. Первым слагаемым будут разрядные единицы от 15-ти, а второе слагаемое подбирается (дети знают состав числа 8). Теперь остается от 10-ти отнять второе слагаемое от восьмерки. И ответ готов. Немного потренировавшись, можно будет легко решать подобные примеры в уме. Если она получает правильный ответ в течение определенного периода времени (скажем, 10 секунд), она оставляет карточки себе. Если нет, вы добираетесь до сохранения карт.
Если она получает правильный ответ в течение определенного периода времени (скажем, 10 секунд), она оставляет карточки себе. Если нет, вы добираетесь до сохранения карт.

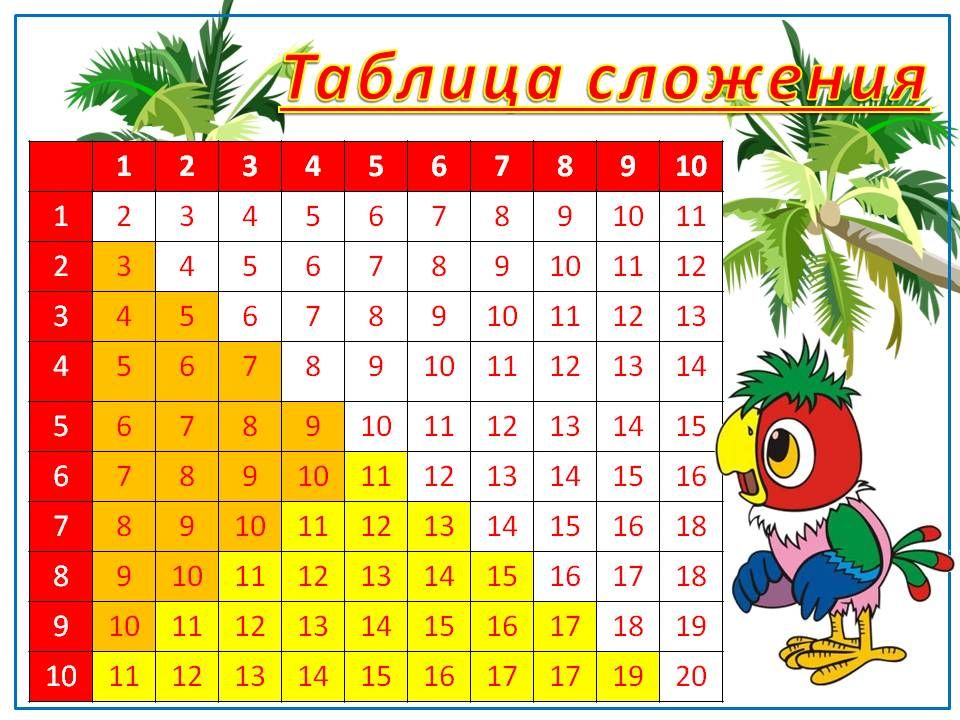

 3.
3.


 Неравенства и системы неравенств с двумя переменными.
Неравенства и системы неравенств с двумя переменными. Производная и ее применения
Производная и ее применения Правила вычисления первообразных.
Правила вычисления первообразных. Простейшие задачи на построение.
Простейшие задачи на построение.
 Понятие движения.
Понятие движения. 2-x = x(x-1)$.
2-x = x(x-1)$. }\). Альтернативный подход состоит в том, чтобы вместо этого умножить с каждой стороны уравнения на выбранную константу, исключающую знаменатель. В уравнении \(\frac{1}{2}x=10\text{,}\) мы могли бы просто умножить каждую часть уравнения на \(2\text{,}\), что исключило бы знаменатель \ (2\текст{:}\)
}\). Альтернативный подход состоит в том, чтобы вместо этого умножить с каждой стороны уравнения на выбранную константу, исключающую знаменатель. В уравнении \(\frac{1}{2}x=10\text{,}\) мы могли бы просто умножить каждую часть уравнения на \(2\text{,}\), что исключило бы знаменатель \ (2\текст{:}\)
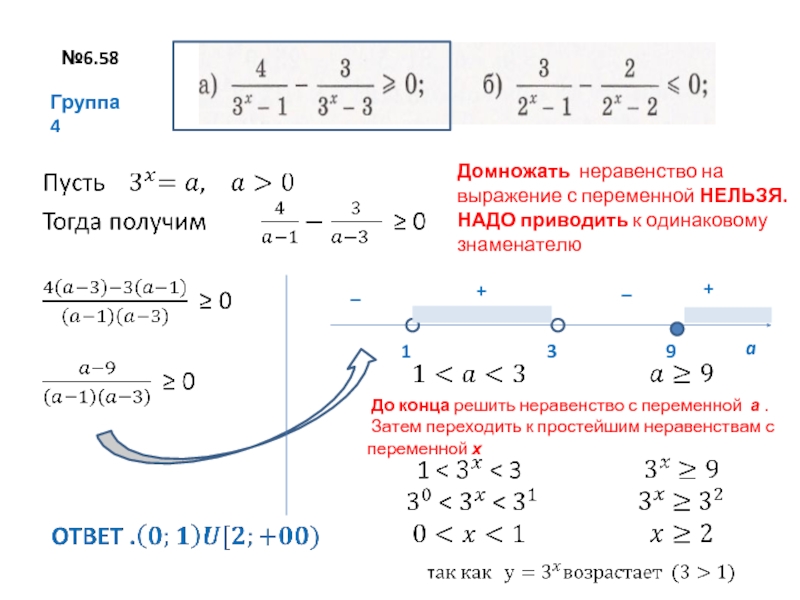 }\) С правой стороны у нас есть \(\frac{1}{ 6}\text{.}\) ЖК-дисплей \(3, 4\text{,}\) и \(6\) равен \(12\text{,}\), поэтому мы умножим каждую часть уравнения на \(12\), чтобы исключить все знаменателей:
}\) С правой стороны у нас есть \(\frac{1}{ 6}\text{.}\) ЖК-дисплей \(3, 4\text{,}\) и \(6\) равен \(12\text{,}\), поэтому мы умножим каждую часть уравнения на \(12\), чтобы исключить все знаменателей: }\)
}\) }\)
}\) }\)
}\) }\) В качестве смешанного числа это \(21\frac{2}{3}\text {.}\) В контексте это означает, что \(21\) минут и \(40\) секунд после 9:00 в 9:21:40 в контейнере будет \(8\) унций воды. левый.
}\) В качестве смешанного числа это \(21\frac{2}{3}\text {.}\) В контексте это означает, что \(21\) минут и \(40\) секунд после 9:00 в 9:21:40 в контейнере будет \(8\) унций воды. левый. }\) Обратите внимание, что это эквивалентно записи \(\{x\mid-40\gt x \}\text{,}\), но это легче понять, если мы сначала напишем \(x\) в неравенстве.
}\) Обратите внимание, что это эквивалентно записи \(\{x\mid-40\gt x \}\text{,}\), но это легче понять, если мы сначала напишем \(x\) в неравенстве.


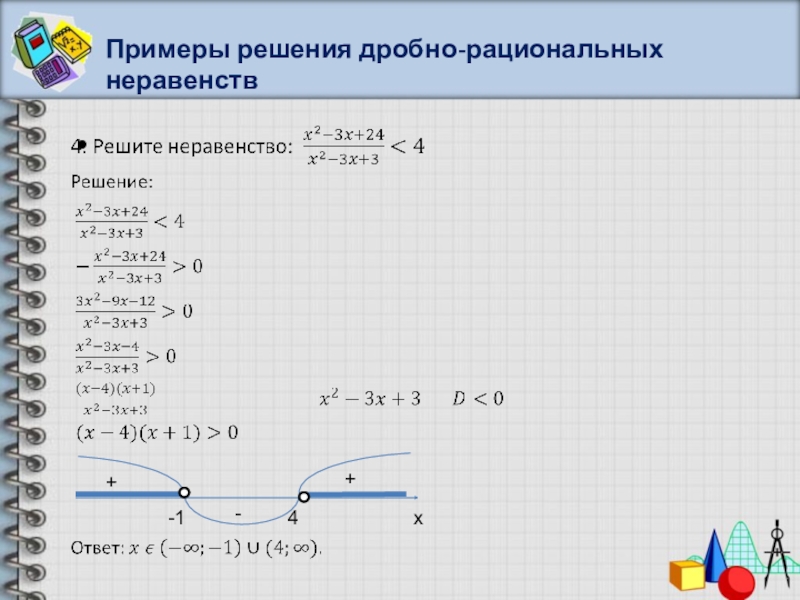


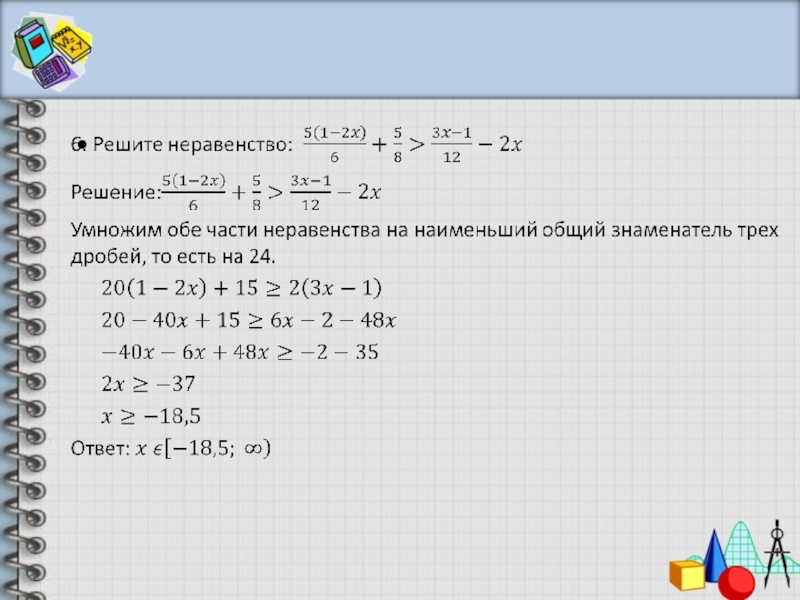 Чтобы заработать не менее \(83\) за этот курс, сколько вам нужно набрать на третьем тесте? Пусть \(x\) будет баллом, который вы заработаете на третьем тесте.
Чтобы заработать не менее \(83\) за этот курс, сколько вам нужно набрать на третьем тесте? Пусть \(x\) будет баллом, который вы заработаете на третьем тесте.

 Тогда есть ли какой-либо результат, который говорит о природе решения этого уравнения.
Тогда есть ли какой-либо результат, который говорит о природе решения этого уравнения.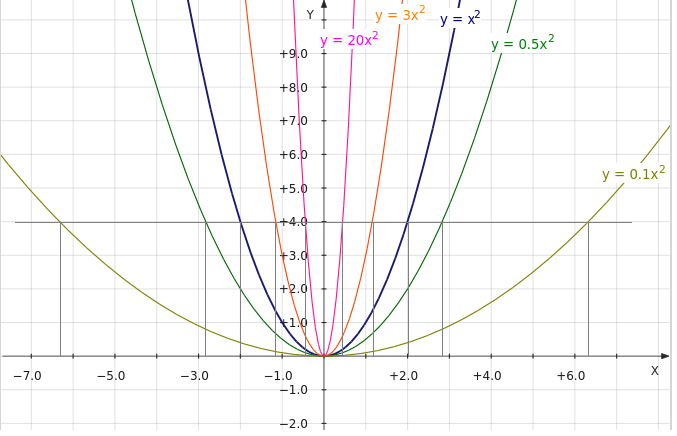

 Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Дмитрий Письменный
«Сборник задач по высшей математике с контрольными работами1 курс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы.
Если вы находитесь в Москве, Санкт-Петербурге, Нижнем Новгороде, Казани, Екатеринбурге, Ростове-на-Дону или любом
другом регионе России, вы можете оформить заказ на книгу
Дмитрий Письменный
«Сборник задач по высшей математике с контрольными работами1 курс» и выбрать удобный способ его получения: самовывоз, доставка курьером или отправка
почтой. Чтобы покупать книги вам было ещё приятнее, мы регулярно проводим акции и конкурсы. А., Гольдберг В.В. «Тензорное исчисление»
А., Гольдберг В.В. «Тензорное исчисление»
 В. «Лекции по математическому анализу»
В. «Лекции по математическому анализу»
 С., Михайлов В.П., Михайлова Т.В., Шабунин М.И. «Сборник задач по уравнениям математической физики»
С., Михайлов В.П., Михайлова Т.В., Шабунин М.И. «Сборник задач по уравнениям математической физики»
 С., Потемкин А.В., Эйсымонт И.М. «Теория вероятностей и математическая статистика» Под ред. П. С. Геворкяна
С., Потемкин А.В., Эйсымонт И.М. «Теория вероятностей и математическая статистика» Под ред. П. С. Геворкяна
 С. «Колебания и волны»
С. «Колебания и волны»
 Б. «Высшая математика для начинающих и ее приложения к физике» Под общ. ред. С.С. Герштейна
Б. «Высшая математика для начинающих и ее приложения к физике» Под общ. ред. С.С. Герштейна
 В.А. Ильина
В.А. Ильина
 Б., Гасанов Э.Э., Долотова О.А., Погосян Г.Р. «Теория тестирования логических устройств» Под ред. В.А. Садовничего
Б., Гасанов Э.Э., Долотова О.А., Погосян Г.Р. «Теория тестирования логических устройств» Под ред. В.А. Садовничего
 С., Розанова С.А., Сирота А.И. и др. «Высшая математика» Под ред. С. А. Розановой
С., Розанова С.А., Сирота А.И. и др. «Высшая математика» Под ред. С. А. Розановой
 Руководство к решению задач»
Руководство к решению задач»
 Д. «Прикладная математика для инженеров. Специальные курсы»
Д. «Прикладная математика для инженеров. Специальные курсы»
 П. «Дискретная математика»
П. «Дискретная математика»
 В. «Математические задачи»
В. «Математические задачи»
 Е. «Основы алгебры»
Е. «Основы алгебры»

 Элемент кислорода имеет 3 атома.
Элемент кислорода имеет 3 атома. AgNO3 раствор добавляют в колбу Эрленмейера.
AgNO3 раствор добавляют в колбу Эрленмейера.
 61 кДж/моль.
61 кДж/моль.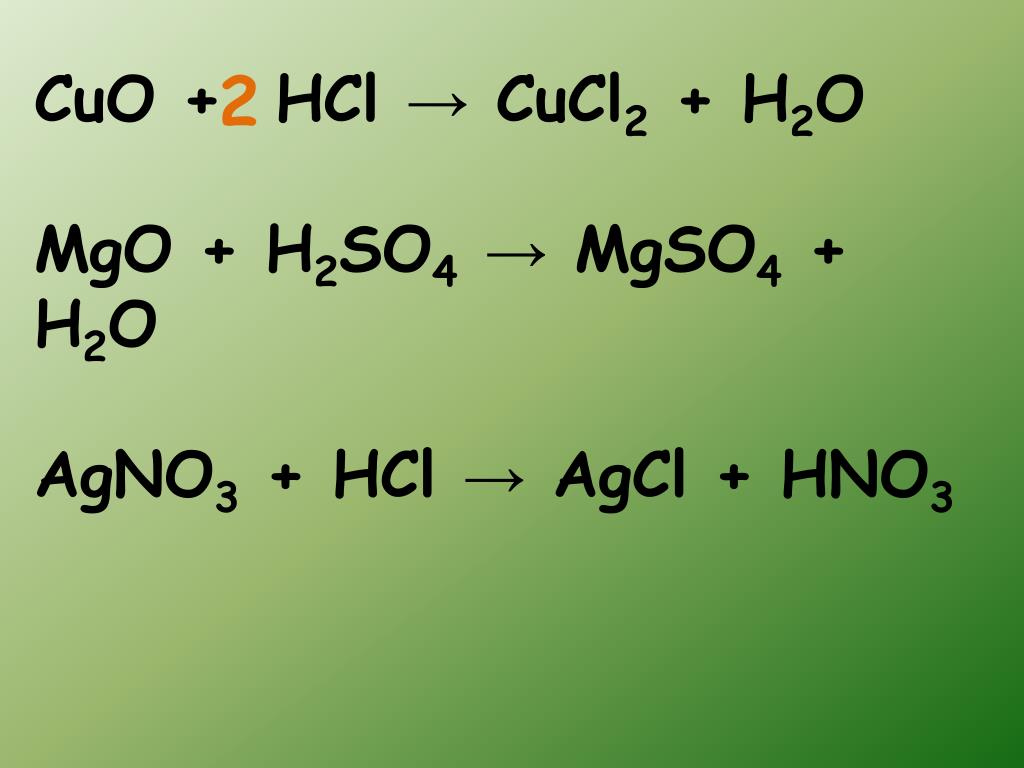
 И уравнять количество атомов с обеих сторон.
И уравнять количество атомов с обеих сторон. Таким образом, уравнение уравновешивается.
Таким образом, уравнение уравновешивается. Поскольку значение энтальпии положительно, это эндотермическая реакция, необратимая, так как это реакция осаждения.
Поскольку значение энтальпии положительно, это эндотермическая реакция, необратимая, так как это реакция осаждения.






 Обчислюємо кількість речовини BaCl2 масою 41,6 г за формулою n=m/M, де M=Mrг/моль
Обчислюємо кількість речовини BaCl2 масою 41,6 г за формулою n=m/M, де M=Mrг/моль
 Обчислюємо кількість речовини MgCO3 масою 126 г за формулою n=m/M, де
Обчислюємо кількість речовини MgCO3 масою 126 г за формулою n=m/M, де Ее также можно назвать реакцией нейтрализации, поскольку HCl действует как кислота, а AgNO 3 действует как основание.
Ее также можно назвать реакцией нейтрализации, поскольку HCl действует как кислота, а AgNO 3 действует как основание. 

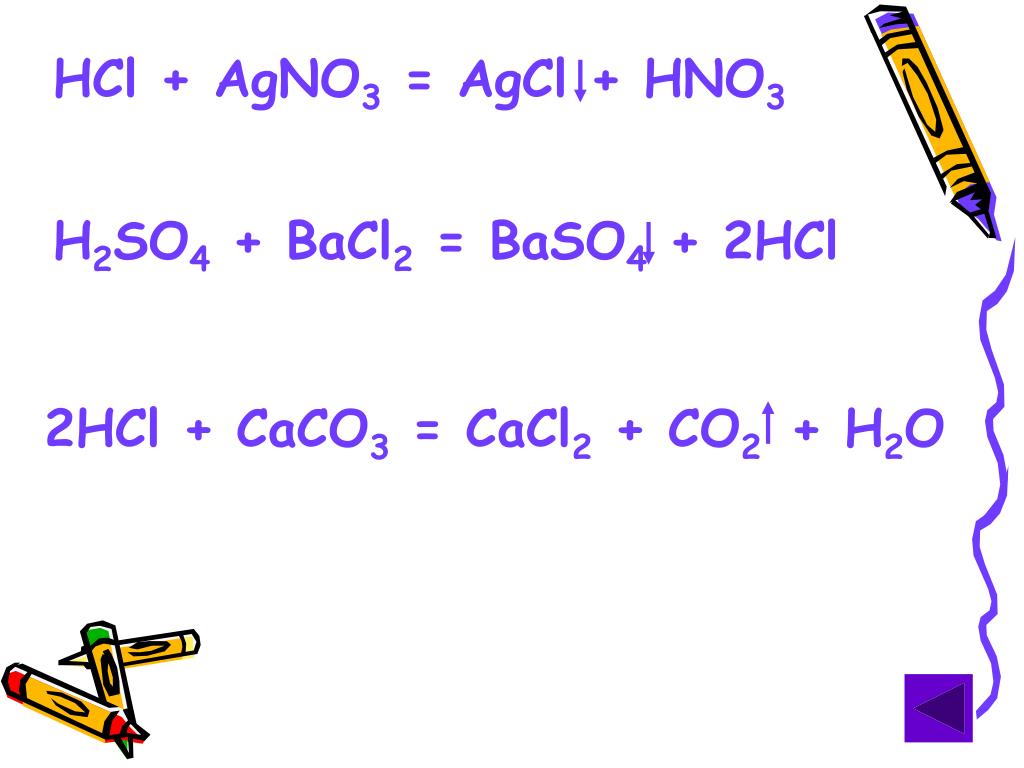 Обратите внимание на следующую реакцию.
Обратите внимание на следующую реакцию. 
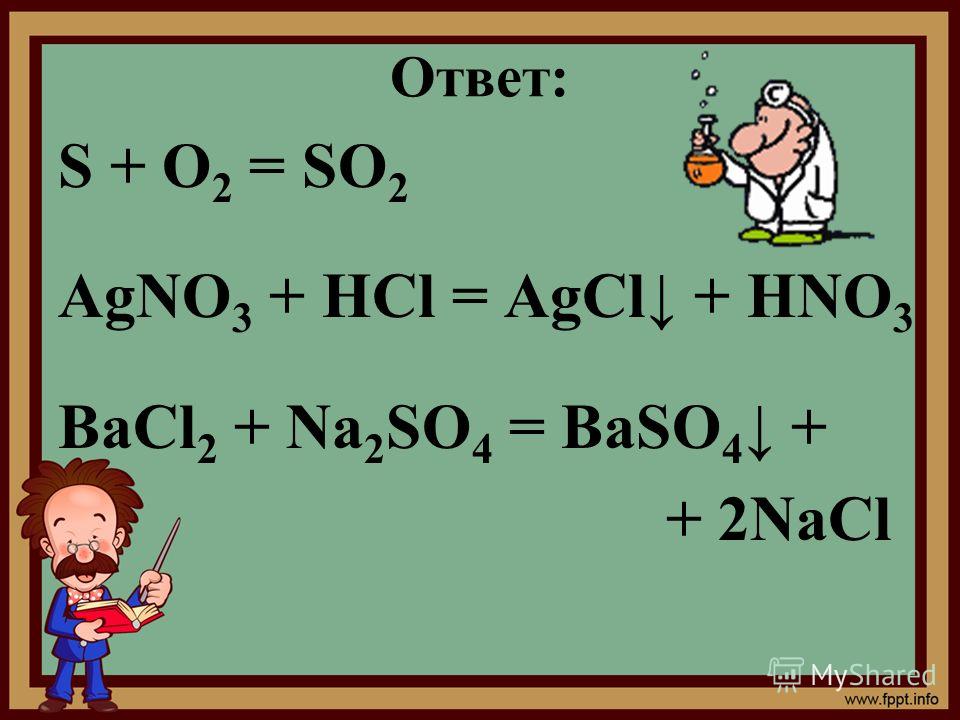 (Со стороны реагента и продукта степень окисления остается одинаковой). Это подтверждает, что это не окислительно-восстановительная реакция.
(Со стороны реагента и продукта степень окисления остается одинаковой). Это подтверждает, что это не окислительно-восстановительная реакция.  И уравнять количество атомов с обеих сторон.
И уравнять количество атомов с обеих сторон. 
 Поскольку значение энтальпии положительно, это эндотермическая реакция, необратимая, так как это реакция осаждения.
Поскольку значение энтальпии положительно, это эндотермическая реакция, необратимая, так как это реакция осаждения.



 {3}$$
{3}$$

 Это наиболее полезно при решении Решите и Расширьте проблемы или в любое время в Фактор проблем, чтобы обеспечить правильное удаление плиток. Пара нулей — это пара плиток, сумма которых равна 0, например желтая плитка 1 и красная плитка -1.
Это наиболее полезно при решении Решите и Расширьте проблемы или в любое время в Фактор проблем, чтобы обеспечить правильное удаление плиток. Пара нулей — это пара плиток, сумма которых равна 0, например желтая плитка 1 и красная плитка -1.