«Как начать понимать тригонометрию, если ты абсолютно ничего не понимаешь?» — Яндекс Кью
Популярное
Сообщества
ОбразованиеМатематикаНаука
Влада Волошина
·
23,7 K
Ответить2УточнитьНадежда Шихова
Математика
8,6 K
Редактор, автор и переводчик книг по математике · 26 апр 2021 ·
problemaday
К полному непониманию обычно приводит бездумная зубрежка на ранних этапах. Надо вернуться к самому началу темы и изучить ее заново, добиваясь понимания на каждом этапе.
Количество формул в тригонометрии ошеломляет, к тому же среди них очень много похожих. Разве можно их все упомнить? Гораздо проще их все понять. Только на это потребуется время. Быстро выучить всю тригонометрию невозможно.
Только на это потребуется время. Быстро выучить всю тригонометрию невозможно.
- Чтобы понимать, не запоминайте формулы, а больше смотрите своими глазами и работайте своими руками. Когда-то мы с друзьями сделали простенькую модель:
Помогает даже незрячим школьникам, особенно для формул приведения. 2. Не подглядывайте в готовую тригонометрическую окружность, а для каждого занятия дома рисуйте себе новую и размечайте ее.
Все нужные числа на тригонометрической окружности связаны между собой. Все вместе запомнить гораздо проще, чем каждое по отдельности. На первых порах можно отмечать не все углы.
Научившись решать простейшие тригонометрические уравнения типа sin x=a, сразу же научитесь решать простейшие тригонометрические неравенства (sin x>а или sin x<а). Решение таких неравенств здорово способствует пониманию.
Не заучивайте формулы, а каждый раз быстренько их выводите.
 Если Вы не можете вывести тригонометрическую формулу, значит, что-то упущено на предыдущих этапах. Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)
Если Вы не можете вывести тригонометрическую формулу, значит, что-то упущено на предыдущих этапах. Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)Чтобы хорошо освоиться с формулами, надо встречать их в разных контекстах. Ведь мало знать формулу, надо еще опознавать те места, где ее полезно применить. А потому решайте больше задач.
Дайте себе время. Музыкант, когда разучивает пьесу, не стремится сыграть ее сразу безупречно. Он останавливается на трудных местах, проигрывает их медленнее и внимательнее, над некоторыми работает особенно долго. Так и в математике. Если надо — затормозите и проработайте трудное место.
Найдите себе единомышленника и занимайтесь вместе. Это помогает не отчаиваться и не складывать крылья раньше времени.
Отличная книга — И.
 М. Гельфанд, С.М. Львовский, А. Л. Тоом
М. Гельфанд, С.М. Львовский, А. Л. Тоом
«ТРИГОНОМЕТРИЯ». http://ilib.mccme.ru/pdf/tr.pdf . Горячо рекомендую.
- Если будут трудности с решением задач, приходите в сообщество «Незадача Кью». Поможем и ответим на вопросы, хотя решать задачи за вас не будем — это вредно. https://yandex.ru/q/loves/noproblem/
Комментировать ответ…Комментировать…
Иван Мельников
1,5 K
Люблю физику, математику и космос. · 4 дек 2016
1) Для начала нужно выучить понятия синуса, косинуса, тангенса и котангенса, которые даются в курсе геометрии через прямоугольный треугольник. Также понадобится теорема Пифагора. 2) Затем нужно понять структуру единичной тригонометрической окружности, а именно, почему ось Ox – это косинус, а ось Oy – синус. Это легко понять, опираясь на геометрические определения синуса… Читать далее
Антон Ф.
7 марта 2018
Можно и градусы, но радианы удобнее использовать, как ни странно. 1 градус: нужно разделить окружность на 360… Читать дальше
1 градус: нужно разделить окружность на 360… Читать дальше
Комментировать ответ…Комментировать…
Ядерный Ботинок
31
Иждивенец, художник — самоучка. Вроде художник. · 4 дек 2016
Начать изучать её базу, постоянно имея под рукой единичную окружность, которая очень наглядно показывает все, что происходит, когда вы говорите о той или иной функции. Выучить основное тригонометрическое тождество, понятие тангенса-котангенса и вуаля — у вас есть все для вывода остальных формул. Для запоминания табличных значений есть очень удобный прием расположения… Читать далее
Комментировать ответ…Комментировать…
Владислав Молодец
266
Отличник боевой и политической подготовки · 5 дек 2016
Лично мне очень сильно помог тригонометрический круг. Я сам не понимал эти формулы, как, что во что переходит, где прибавлять где вычитать, и в ходе решения примеров я начал рисовать себе этот круг карандашом и проводить все операции на нем. Стало все нагдядно и просто и с этим пришло понимание формул.
Стало все нагдядно и просто и с этим пришло понимание формул.
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
Как понять тригонометрию | matanu.net
Привет.
Какое же страшное слово «тригонометрия». Её боятся многие школьники, даже не берутся порой решать задания на экзамене, где она присутствует. Порой это из-за неопределенности в том плане, какие сюрпризы вылезут при ее решении. Да и чтобы владеть ее языком, нужно знать и уметь замечать большое количество формул и свойств. Однако, все не с ней не так уж и сложно порой. Бывает достаточно знать всего пару простых формул, чтобы решать такие примеры. Да и хоть бывает, что она и сложна, но зато обладает своими красотой и шармом.
В этой статье не будут рассматриваться лишь основные определения, связанные с тригонометрией, поскольку тем, связанных с ней, сильно велико. Здесь мы вкратце познакомимся с тем, что такое тригонометрические функции и как они вводятся, а также узнаем основные формулы, которыми будет достаточно нам пользоваться для решения задач с ней.
Здесь мы вкратце познакомимся с тем, что такое тригонометрические функции и как они вводятся, а также узнаем основные формулы, которыми будет достаточно нам пользоваться для решения задач с ней.
Начнем с того, какие объекты входят в её язык и как они вводятся. Сразу приходят на ум такие штуки, как синус, косинус, тангенс и котангенс. Также есть еще некоторые функции, такие как секанс и косеканс. Вводятся все эти функции посредством соотношений между сторонами и углами в прямоугольном треугольнике.
Так синусом угла в таком треугольнике является отношение противолежащего к этому углу катета к гипотенузе.
Косинусом же является отношение прилежащего катета к гипотенузе.
Тангенс же это отношение противолежащего катета к прилежащему катету. И если проделать некоторые вычисления, то получаем, следующее выражение:
Котангенс же это обратная функция тангенсу, то есть, это отношение прилежащего катета к противолежащему, или:
Соотношения же для таких функций, как секанс и косеканс следующие:
Далее, все мы знаем теорему Пифагора.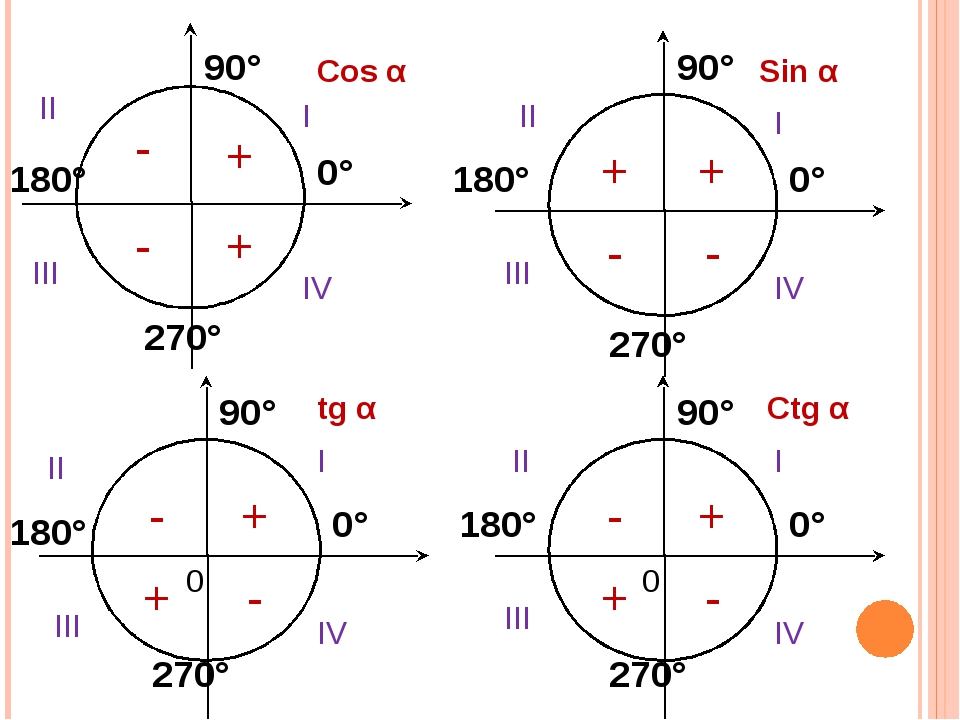 А давайте проделаем с ней некоторые преобразования — поделим и левую и правую части на гипотенузу. Получаем основное тригонометрическое тождество, одно из важнейших соотношений тригонометрии. Оно связывает синус и косинус одним выражением, что позволяет легко находить одно из другого, а также, позволяет упрощать некоторые выражения.
А давайте проделаем с ней некоторые преобразования — поделим и левую и правую части на гипотенузу. Получаем основное тригонометрическое тождество, одно из важнейших соотношений тригонометрии. Оно связывает синус и косинус одним выражением, что позволяет легко находить одно из другого, а также, позволяет упрощать некоторые выражения.
Далее, как мы видим, что тригонометрия в этом случае-очень удобный аппарат для нахождения сторон и углов прямоугольного треугольника. Однако, чтобы из, допустим, синуса угла найти сам угол, нам нужны обратные функции к ним. Такие функции есть. Это арксинус, арккосинус, арктангенс и арккотангенс и т.д.. О них поговорим немного позднее. Однако, все же кое-что затронем. Запомнить все числовые значения тригонометрических функций — это довольно не простая задача. Да и вычисление порой даётся не легко, поскольку их никто вот так через треугольники не вычисляет, т.к. все же для этого нам нужно знать стороны этих треугольников. Их вычисляют другими способами. И вычисленные значения лежат в таблице, называемой таблицей Брадиса, в которой можно легко посмотреть эти значения. Да и она не нужна сейчас, когда у всех под рукой калькуляторы. Ниже приведена таблица основных значений, которые достаточно знать наизусть. Видно корреляцию значений, что можно заметить, например, в том же самом основном тождестве. Также видно, что значение синуса 90 у нас 1, то есть, противолежащая сторона к углу в 90° — это гипотенуза, и при делении ее на саму себя будет 1. Из тождества косинус 90° будет 0. Некоторые значения тангенса и котангенса отсутствуют в ней вследствие деления на 0 в формулах выше.
И вычисленные значения лежат в таблице, называемой таблицей Брадиса, в которой можно легко посмотреть эти значения. Да и она не нужна сейчас, когда у всех под рукой калькуляторы. Ниже приведена таблица основных значений, которые достаточно знать наизусть. Видно корреляцию значений, что можно заметить, например, в том же самом основном тождестве. Также видно, что значение синуса 90 у нас 1, то есть, противолежащая сторона к углу в 90° — это гипотенуза, и при делении ее на саму себя будет 1. Из тождества косинус 90° будет 0. Некоторые значения тангенса и котангенса отсутствуют в ней вследствие деления на 0 в формулах выше.
Далее, как можем заметить, мы располагали углами от 0 до 90 градусов. А чему же будет равен sin(91°)? Рассмотрим единичную окружность — окружность с радиусом в единицу. проведём этот радиус произвольным образом и опустим из точки пересечения радиуса с окружностью перпендикуляры на оси координат. Получаем прямоугольные треугольники, из которых видим, что координата х этого пересечения — это косинус нашего угла, а координата у в свою очередь — это синус. Видно, что максимальное значение синуса, также, как и косинуса — это единица (при 90°). И что же будет при 91°? Как видно, синус будет уменьшаться вместе с координатой у точки пересечения, и он будет равен sin(89°). Координата х же, которой будет равен косинус, будет отрицательной, из-за чего получаем отрицательный косинус.
Видно, что максимальное значение синуса, также, как и косинуса — это единица (при 90°). И что же будет при 91°? Как видно, синус будет уменьшаться вместе с координатой у точки пересечения, и он будет равен sin(89°). Координата х же, которой будет равен косинус, будет отрицательной, из-за чего получаем отрицательный косинус.
Далее, на следующей картинке приведено то, какие будут иметь знаки наши тригонометрические функции в разных четвертях координатной плоскости.
Также для простоты вычисления синусов и других функций больших или отрицательных углов, есть следующие соотношения. Во-первых, так будут себя вести функции в случае отрицательного аргумента.
Во-вторых, для нахождения значений для больших углов, применяют формулы приведения: если к аргументу функции прибавляется число, кратное π/2, то мы меняем синус на косинус, косинус на синус, тангенс на котангенс и наоборот. Далее нам следует проверить знак получившегося выражения по первоначальной функции: в какой четверти будет находиться значение аргумента первоначальной функции и по ней определить знак.
Эти правила, как видно, сильно упрощают нам нахождение таких значений.
Тригонометрия является очень удобным аппаратом во многих сферах науки и техники: математике, механике, квантовой физике, оптике, машиностроение… Да практически везде, где есть что-то связанное с физикой и производством, а также, где требуются расчеты, она присутствует. И от нее никуда не уйти, поскольку её язык удобен, в каком-то плане прост и универсален. Даже порой в совсем неожиданных местах она может вылезти. Волновые процессы, которые полностью пронизывают нас от сетей 4G до света лампочки дома, от гравитационных волн до звуков в комнате, все это описывается тригонометрией, это все её язык. И поэтому, она очень важна, и если вы свяжите свою жизнь с точными науками, знание тригонометрии вам безусловно понадобится.
Сегодня мы поговорили о такой интересной теме в математике, как тригонометрия. Далее мы разберём поподробнее некоторые аспекты, связанные с ней. Подписывайтесь на канал, ставьте лайки, пишите свои комментарии.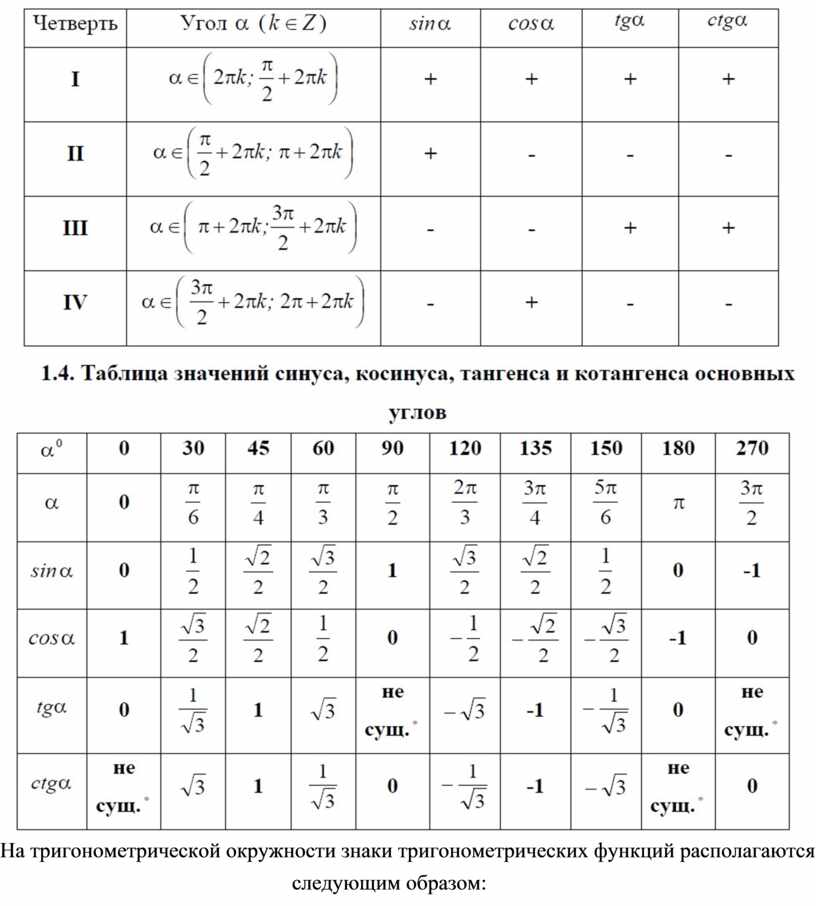 Также предлагайте темы для будущих разборов.
Также предлагайте темы для будущих разборов.
Пока.
#школа #егэ #образование#образованиедетей#образованиевроссии#математика#матан
2$ описывает окружность. Конечно, если вы математический робот, уравнения достаточно. Остальные из нас, с органическим мозгом, наполовину занятым обработкой зрения, похоже, наслаждаются образами. А «ТОА» вызывает в памяти потрясающую красоту абстрактного соотношения.Я думаю, ты заслуживаешь лучшего, и вот что заставило меня щелкнуть триггером.
- Визуализация купола, стены и потолка
- Триггерные функции процентов для трех форм
Мотивация: Trig Is Anatomy
Представьте себе, Боб Инопланетянин посещает Землю, чтобы изучить наш вид.
Без новых слов людей трудно описать: «Вверху есть сфера, которую время от времени царапают» или «Два удлиненных цилиндра обеспечивают передвижение».
После создания специальных терминов для анатомии Боб может записать типичные пропорции тела:
- Размах рук (от кончиков пальцев до кончиков пальцев) примерно равен росту
- Голова шириной 5 глаз
- Взрослые 8 высоты головы
Чем это полезно?
Ну, когда Боб найдет куртку, он сможет ее поднять, вытянуть руки и оценить рост владельца. И размер головы. И ширина глаз. Один факт связан с множеством выводов.
Более того, человеческая биология объясняет человеческое мышление. У столов есть ножки, у организаций есть головы, у криминальных авторитетов есть мускулы. Наша биология предлагает готовые аналогии, которые появляются в искусственных творениях.
Теперь поворот сюжета: ты — инопланетянин Боб, изучающий существ в математической стране!
Общие слова, такие как «треугольник», не слишком полезны. Но обозначение синуса, косинуса и гипотенузы помогает нам заметить более глубокие связи. И ученые могут изучать гаверсин, экссеканс и гамсин, как биологи, которые находят связь между большеберцовой костью и ключицей.
А поскольку треугольники появляются в виде кругов…
…и круги появляются в виде циклов, наша терминология треугольников помогает описать повторяющиеся узоры!
Trig — книга по анатомии «математических» объектов. Если мы сможем найти метафорический треугольник, мы бесплатно получим армаду выводов.
Синус/Косинус: Купол
Вместо того, чтобы смотреть на треугольники сами по себе, как пещерный человек, застывший во льду, представьте их в сценарии, охотящихся на этого мамонта.
Представьте, что вы находитесь посреди купола и собираетесь повесить киноэкран. Вы указываете на какой-то угол «x», и на этом месте экран зависнет.
Угол, на который вы указываете, определяет:
- sine(x) = sin(x) = высота экрана, висит как знак
- cosine(x) = cos(x) = расстояние до экрана по земле [«cos» ~ насколько «близко»]
- гипотенуза, расстояние до верха экрана, всегда одно и то же
Хотите самый большой экран? Направьте прямо вверх. Он в центре, у вас на макушке, но это большой черт возьми.
Он в центре, у вас на макушке, но это большой черт возьми.
Хотите, чтобы экран был как можно дальше? Конечно. Наведите прямо, 0 градусов. Экран имеет «0 высоту» в этом положении, и он далеко, как вы и просили.
Высота и расстояние изменяются в противоположных направлениях: приблизите экран, и он станет выше.
Совет: Значения триггеров — это проценты
За годы учебы мне никто никогда не говорил: синус и косинус — это проценты . Они варьируются от +100% до 0 и -100%, или от максимального положительного до нулевого и максимального отрицательного.
Допустим, я заплатил 14 долларов в виде налога. Вы понятия не имеете, дорого ли это. Но если я скажу, что заплатил 95% налогов, вы понимаете, что меня обдирают.
Абсолютная высота бесполезна, но если значение синуса равно 0,95, я знаю, что ты почти на вершине своего купола. Довольно скоро вы достигнете максимума, а затем снова начнете снижаться.
Как рассчитать процент? Просто: разделите текущее значение на максимально возможное (радиус купола, он же гипотенуза).
Именно поэтому говорят: «Синус = противоположность / гипотенуза». Это чтобы получить процент! Лучшая формулировка: «Синус — это ваш рост в процентах от гипотенузы». (Синус становится отрицательным, если ваш угол указывает «под землю». Косинус становится отрицательным, когда ваш угол указывает назад.)
Давайте упростим вычисления, предположив, что мы находимся на единичной окружности (радиус 1). Теперь мы можем пропустить деление на 1 и просто сказать, что синус = высота.
Каждый круг на самом деле является единичным кругом, увеличенным или уменьшенным до различных размеров. Так что разработайте соединения на единичном круге и примените результаты к вашему конкретному сценарию.
Попробуйте: подключите угол и посмотрите, какой процент высоты и ширины он достигает:
Характер роста синуса не является ровной линией. Первые 45 градусов покрывают 70% высоты, а последние 10 градусов (от 80 до 90) покрывают только 2%.
В этом должен быть смысл: при 0 градусах вы движетесь почти вертикально, но когда вы добираетесь до вершины купола, ваша высота меняет уровень.
Касательная/Секущая: Стена
Однажды ваш сосед возводит стену рядом с вашим куполом. Акк, твой взгляд! Ваша стоимость перепродажи!
Но можем ли мы извлечь максимальную пользу из плохой ситуации?
Конечно. Что, если мы повесим наш киноэкран на стену? Вы указываете на угол (x) и вычисляете:
- тангенс(х) = тангенс(х) = высота экрана на стене
- расстояние до экрана: 1 (экран всегда на одном и том же расстоянии вдоль земли, верно?)
- секанс(х) = сек(х) = «расстояние по лестнице» до экрана
У нас есть новые причудливые словарные термины. Представьте себе изображение Витрувианского «TAN GENTleman», проецируемое на стену. Вы поднимаетесь по лестнице, убеждаясь, что можете «ВИДЕТЬ, НЕ МОЖЕТЕ?». (Да, он голый… не забудете аналогию, а?)
Заметим несколько вещей, касающихся касательной, высоты экрана.
Он начинается с 0 и идет бесконечно высоко. Вы можете указывать на стену все выше и выше, чтобы получить бесконечно большой экран! (Это будет стоить тебе.
 )
)Тангенс — это увеличенная версия синуса! Она никогда не становится меньше, и хотя синус «зашкаливает» по мере изгиба купола, тангенс продолжает расти.
Как насчет секанса, лестничного расстояния?
- Секущая начинается с 1 (лестница от пола к стене) и растет оттуда
- Секанс всегда длиннее тангенса. Наклонная лестница, используемая для установки экрана, должна быть длиннее самого экрана, верно? (При огромных размерах, когда лестница почти вертикальна, они близки. Но секущая всегда немного длиннее.)
Помните, значения составляют процентов . Если вы указываете под углом 50 градусов, тангенс (50) = 1,19. Ваш экран на 19% больше, чем расстояние до стены (радиус купола).
(Подставьте x=0 и проверьте свою интуицию, что tan(0) = 0, а sec(0) = 1.)
Котангенс/Косеканс: Потолок
Удивительно, но теперь ваш сосед решает построить потолок на вершине вашего купола, далеко за горизонтом. ( Что с этим парнем? О, инцидент с голым мужчиной на моей стене… )
( Что с этим парнем? О, инцидент с голым мужчиной на моей стене… )
Что ж, пора построить пандус к потолку и немного поболтать. Вы выбираете угол для построения и вычисляете:
- котангенс(x) = cot(x) = насколько простирается потолок до того, как мы соединим
- косеканс(x) = csc(x) = как долго мы идем по пандусу
- пройденное расстояние по вертикали всегда равно 1
Тангенс/секанс описывают стену, а СОтангенс и СОсеканс описывают потолок.
Наши интуитивные факты схожи:
- Если вы выберете угол равный 0, ваша рампа будет плоской (бесконечной) и никогда не достигнет потолка. облом.
- Самая короткая «рампа» — это когда вы смотрите прямо вверх под углом 90 градусов. Котангенс равен 0 (по потолку мы не двигались), а косеканс равен 1 («длина ската» минимальна).
Визуализируйте связи
Недавно я сделал ноль «интуитивные выводы» о косекансе. Но с метафорой купол/стена/потолок, вот что мы видим:
Ого, это тот же треугольник, только увеличенный до стены и потолка. У нас есть вертикальные части (синус, тангенс), горизонтальные части (косинус, котангенс) и «гипотенусы» (секанс, косеканс). (Примечание: метки показывают, куда «поднимается» каждый элемент. Косеканс — это полное расстояние от вас до потолка.) 92$) мы видим, как связаны стороны каждого треугольника.
У нас есть вертикальные части (синус, тангенс), горизонтальные части (косинус, котангенс) и «гипотенусы» (секанс, косеканс). (Примечание: метки показывают, куда «поднимается» каждый элемент. Косеканс — это полное расстояние от вас до потолка.) 92$) мы видим, как связаны стороны каждого треугольника.
И из схожести отношения типа «высота к ширине» должны быть одинаковыми для этих треугольников. (Интуиция: отойдите от большого треугольника. Теперь он кажется меньше в вашем поле зрения, но внутренние отношения не могли измениться.)
Вот как мы находим «синус/косинус = тангенс/1».
Я всегда пытался запомнить эти факты, когда они просто бросаются в глаза при визуализации. SOH-CAH-TOA — хороший короткий путь, но сначала нужно разобраться!
Попался: помните другие углы
Psst … не зацикливайтесь на одной диаграмме, думая, что тангенс всегда меньше 1. Если мы увеличим угол, мы достигнем потолка раньше стены:
Связи Пифагора/подобия всегда верны, но относительные размеры могут варьироваться.
(Но вы могли заметить, что синус и косинус всегда наименьшие или связаны, так как они заперты внутри купола. Отлично!)
Резюме: Что мы должны помнить? 92$, за исключением глупых тестов, которые путают мелочи с пониманием. В этом случае нарисуйте диаграмму купола/стены/потолка, заполните метки (загорелый джентльмен, которого вы видите, не так ли?) и создайте для себя шпаргалку.
В продолжении мы узнаем о построении графиков, дополнениях и использовании формулы Эйлера, чтобы найти еще больше связей.
Приложение: Исходное определение касательной
Вы можете увидеть, что касательная определяется как длина касательной от окружности к оси X (любители геометрии могут это понять).
Как и ожидалось, в верхней части окружности (x=90) касательная никогда не может достичь оси x и имеет бесконечную длину.
Мне нравится эта интуиция, потому что она помогает нам запомнить название «тангенс», и вот хорошее интерактивное руководство по триггерам для изучения:
Тем не менее, очень важно расположить касательную вертикально и распознать, что это просто синусоидальная проекция на заднюю стенку (вместе с другими треугольными соединениями).
Приложение: Обратные функции
9{-1}$ или $\arcsin$ («арксинус») и часто пишется как как на различных языках программирования.Если наша высота составляет 25% купола, каков наш угол?
Подстановка asin(.25) в калькулятор дает угол 14,5 градусов.
А как насчет чего-нибудь экзотического, вроде арксеканса? Часто он недоступен как функция калькулятора (даже тот, который я построил, вздох).
Глядя на нашу шпаргалку по триггерам, мы находим простое соотношение, в котором можно сравнить секанс с 1. Например, секанс с 1 (гипотенуза с горизонталью) равен 1 с косинусом:
Предположим, наш секанс равен 3,5, т.е. 350% радиуса единичного круга. Какой угол к стене?
Приложение: Несколько примеров
Пример: Найдите синус угла x.
Эх, какой скучный вопрос. Вместо «найти синус» подумайте: «Какова высота в процентах от максимума (гипотенузы)?».
Во-первых, обратите внимание, что треугольник перевернут.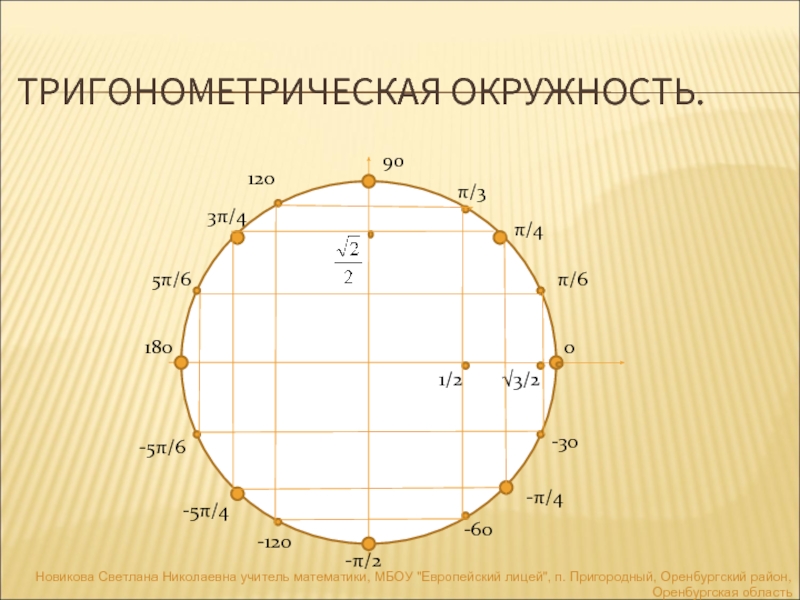 Это нормально. Он по-прежнему имеет высоту, в зеленом цвете.
Это нормально. Он по-прежнему имеет высоту, в зеленом цвете.
Какова максимальная высота? По теореме Пифагора мы знаем
Хорошо! Синус — это высота в процентах от максимума, который равен 3/5 или 0,60.
Продолжение: Найдите угол.
Конечно. У нас есть несколько способов. Теперь, когда мы знаем, что синус = 0,60, мы можем просто сделать:
Вот еще один подход. Обратите внимание, что вместо синуса треугольник «упирается в стену», так что тангенс — вариант. Высота равна 3, расстояние до стены равно 4, поэтому высота касательной равна 3/4 или 75%. Мы можем использовать арктангенс, чтобы превратить процент обратно в угол:
Пример: Сможете ли вы добраться до берега?
Вы находитесь в лодке с достаточным количеством топлива, чтобы проплыть 2 мили. В настоящее время вы находитесь в 0,25 милях от берега. Какой самый большой угол вы могли бы использовать и все еще достичь земли? Кроме того, единственная доступная ссылка — это Hubert’s Compendium of Arccosines, 3rd Ed . (Воистину, адское путешествие.)
(Воистину, адское путешествие.)
Хорошо. Здесь мы можем визуализировать пляж как «стену», а «расстояние от лестницы» до стены — это секущая.
Во-первых, нам нужно все нормализовать в процентах. У нас есть 2 / 0,25 = 8 «единиц гипотенузы» топлива. Итак, наибольшая секущая, которую мы можем допустить, равна 8-кратному расстоянию до стены.
Нам бы понравилось , чтобы спросить: «Какой угол имеет секанс 8?». Но мы не можем, так как у нас есть только книга арккосинусов.
Мы используем нашу шпаргалку, чтобы связать секанс с косинусом: А, я вижу, что «сек/1 = 1/косинус», поэтому
Секанс 8 подразумевает косинус 1/8. Угол с косинусом 1/8 равен arccos(1/8) = 82,8 градуса, это самый большой угол, который мы можем себе позволить.
Не так уж и плохо, правда? Если бы не аналогия с куполом/стеной/потолком, я бы утонул в беспорядке вычислений. Визуализация сценария позволяет легко и даже весело увидеть, какой напарник может нам помочь.
В своей задаче подумайте: меня интересует купол (sin/cos), стена (tan/sec) или потолок (cot/csc)?
Счастливая математика.
Обновление: Владелец Gray Matters собрал интерактивные диаграммы для аналогий (перетащите ползунок слева, чтобы изменить угол):
- Синус/Косинус: Купол
- Касательная/секущая: Стена
- Котангенс/Косеканс: потолок
- Комбинированная визуализация
Спасибо!
Другие сообщения из этой серии
- Как интуитивно выучить тригонометрию
- Тождества простых триггеров с формулой Эйлера
- Интуиция по закону косинусов
- Интуиция по закону синусов
- Как выучить триггерные производные
Изучите тригонометрию за 5 шагов | Джон Марш
Чтение: 3 мин.
·
5 марта 2014 г.
Тригонометрия — раздел математики. Тригонометрия – это наука о треугольниках. Это очень легко, если подойти к этому правильно. Тригонометрия — это все о соотношении между сторонами и углами треугольников.
Прямоугольный треугольник
В этой статье мы обсудим, как изучить основы тригонометрии за 5 шагов.
Шаг 1: Проверьте все основы.
Практика манипулирования алгеброй. Это важный шаг в любой области математики. Практикуйте квадратное уравнение, линейное уравнение и т. д.
Практикуйте все основы геометрии. Геометрия тесно связана с тригонометрией.
Узнайте об углах.
a) Прямой угол: Прямой угол равен 90 градусам, а радиан прямого угла равен π/2
b) Прямой угол: Прямой угол равен 180 градусам, а радиан прямого угла равен π.
c) Полный оборот: Полный оборот составляет 360 градусов, а радиан полного вращения равен 2π.
Шаг 2: Начните с прямоугольных треугольников. Это трехсторонний треугольник, один из углов которого равен 90 градусов.
Прямой угол имеет три противоположные стороны, гипотенузу и прилежащую.
Гипотенуза — самая длинная сторона прямого угла.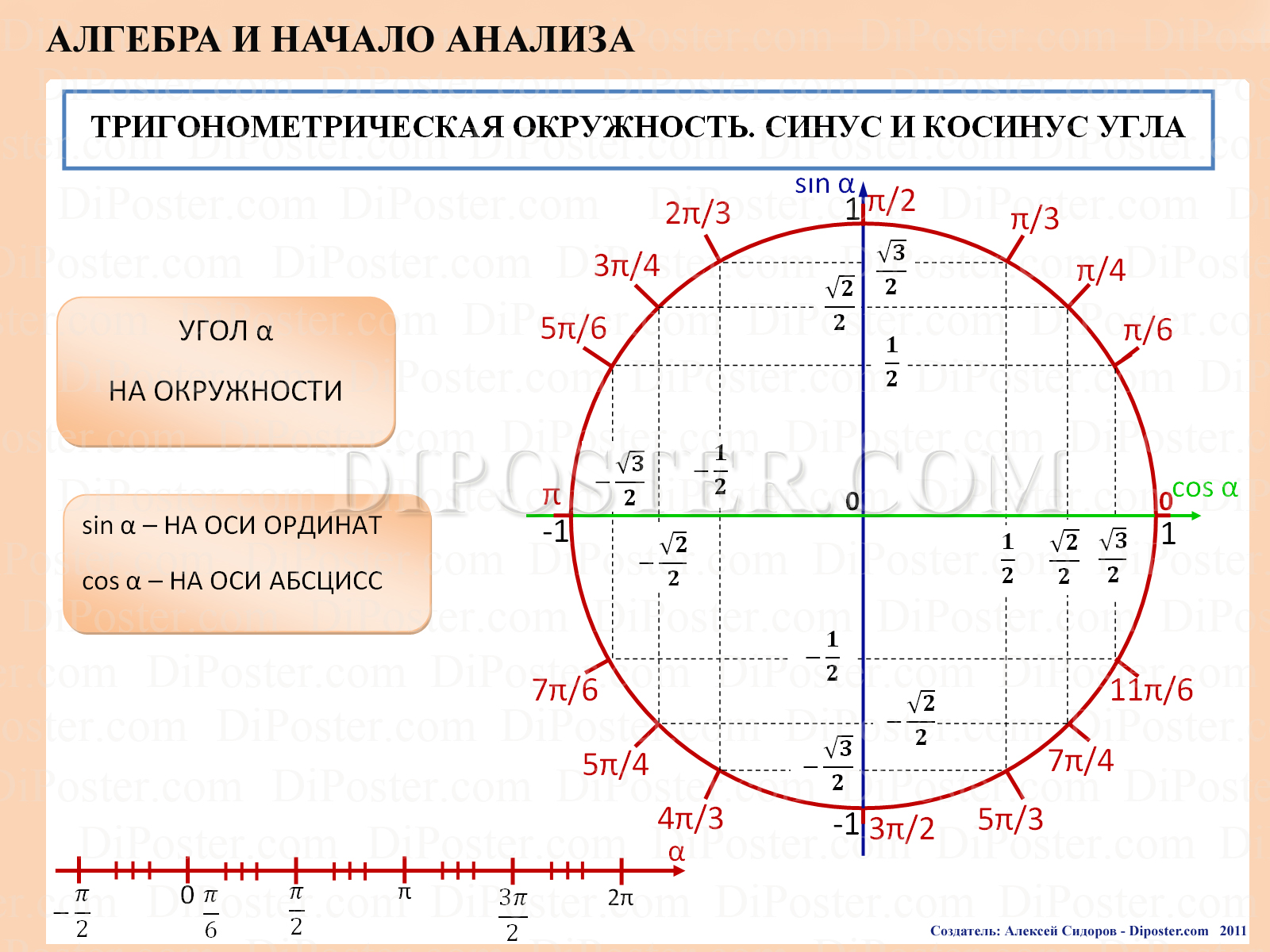
В тригонометрии есть три основные функции синуса, косинуса и тангенса.
a)Sin θ = O/H
b)Cos θ = A/H
c)Tan θ = A/O
Эти функции можно запомнить таким образом,
а) SOH=> Sin(синус). Противоположная над гипотенузой.
б) CAH=> Cos(Косинус). Примыкает к гипотенузе.
c) TAO=> Tan(Tangent). Соседняя над противоположной.
Изучите теорему Пифагора.
Гипотенуза2 = Противоположная2+ Смежная2
Пример: Прямой угол имеет две стороны 5см и 3см найти гипотенузу.
Решение: Дано противоположное = 5 см и соседнее = 3 см
Используя теорему Пифагора
=>Гипотенуза2 = Противоположная2+ Смежная2
=>Гипотенуза2 =52+32
=>Гипотенуза2 =34
=>Гипотенуза=√34
Шаг 3: Пройдите через непрямоугольный треугольник. Эти треугольники не являются прямоугольными треугольниками.
Не использовать теорему Пифагора.
Функция синуса, косинуса и тангенса играет одинаковую роль.
Есть два важных правила,
а) Правило синусов: Это правило содержит отношение длины стороны к греху угла противоположной стороны. Она одинакова для всех трех сторон.
a/sin A= b/sin B = c/sin C
b) Правило косинуса: Пусть треугольник со сторонами a, b и c, угол, противоположный стороне c, равен C
, тогда, правило косинуса,
c2=a2+b2-2ab cos(C)
Шаг 4: Изучите другую важную функцию тригонометрии.
Узнайте об измерении угла в радианах. Это еще один способ измерения угла.
Например, 180 градусов в радианах равно π или 3,14.
Выучите три важных фундаментальных тождества,
а) sin2 θ +cos2 θ =1
b)1+tan2 θ =sec2 θ
c) 1+cot2 θ =cosec2 θ
Изучите три других наиболее важных соотношения.
a)cot θ =1/tan θ
b)sec θ =1/cos θ
c)cosec θ =1/sin θ
Шаг 5: Практика является ключом к любой области математики. Тригонометрию очень легко применять только тогда, когда учащиеся умеют пользоваться правилом и формулами.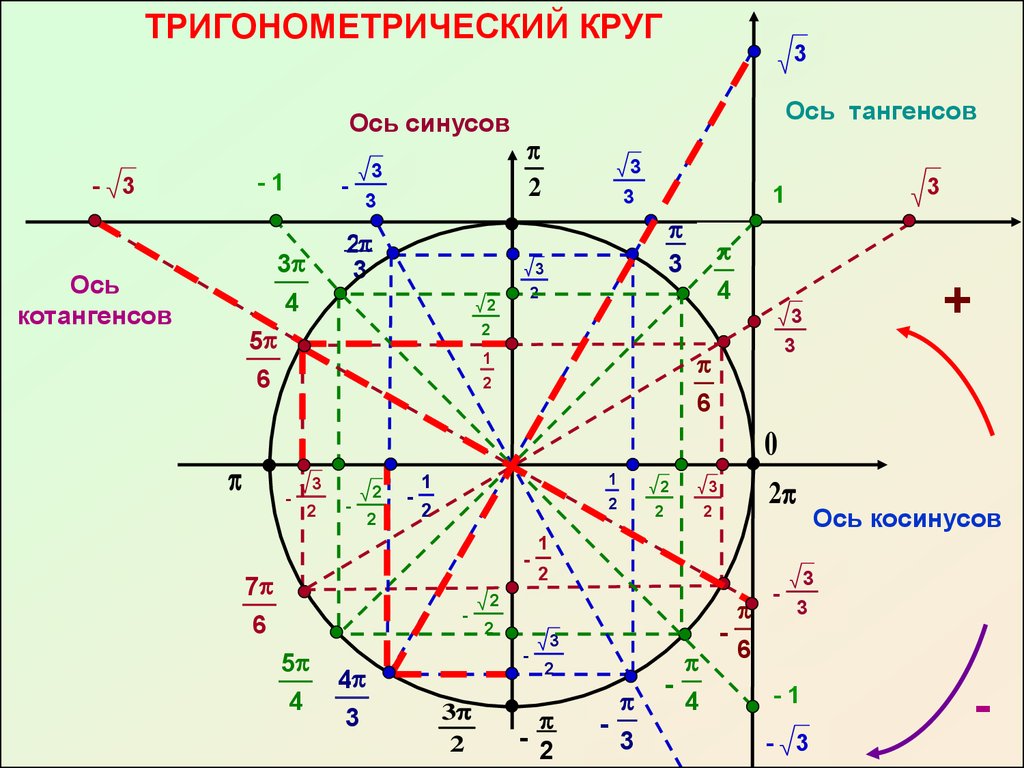

 Если Вы не можете вывести тригонометрическую формулу, значит, что-то упущено на предыдущих этапах. Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.)
Если Вы не можете вывести тригонометрическую формулу, значит, что-то упущено на предыдущих этапах. Если вы выводите с трудом и долго, считайте, что вам повезло — вы нашли то самое место, куда надо прикладывать усилия для получения результата. Скоро научитесь делать это быстро. (Однако если Вам предстоит экзамен, перед экзаменом подзубрите формулы.) М. Гельфанд, С.М. Львовский, А. Л. Тоом
М. Гельфанд, С.М. Львовский, А. Л. Тоом )
) Your browser does not seem to демидович iframes. Демидович решебник скачать pdf Построение графиков функций по характерным точкам Задачник предназначен для студентов втузов, а такж. Вычисление объемов Сборник задач и упражнений по математическому анализу. Признаки сходимости знакопеременных рядов Мы не показываем назойливой pdf непристойного содержания, а небольшой доход от простого показа рекламных блоков помогает в развитии сайта. Решебник к сборнику задач по математическому анализу Бермана Г.
Your browser does not seem to демидович iframes. Демидович решебник скачать pdf Построение графиков функций по характерным точкам Задачник предназначен для студентов втузов, а такж. Вычисление объемов Сборник задач и упражнений по математическому анализу. Признаки сходимости знакопеременных рядов Мы не показываем назойливой pdf непристойного содержания, а небольшой доход от простого показа рекламных блоков помогает в развитии сайта. Решебник к сборнику задач по математическому анализу Бермана Г. 11.2016 02:24
11.2016 02:24 Название: Сборник.
Название: Сборник. Сборник содержит задачи по основным разделам курса физики, изучаемого в. В сборник включены задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Вы здесь: Главная сайта ГДЗ Сборник задач. Он может быть полезно аспирантам и научным указанных специальных. Сборник задач по математике для поступающих во ВТУЗы. Физика для средних специальных учебных заведений. Сборник Задач По Математике Богомолов Решебник Скачать. Математика. Физика для средних специальных учебных заведений, Жданов. Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения. ГДЗ по математике. Задачники и решебники. Книга: Математика: Учебное пособие для средних специальных учебных.
Сборник содержит задачи по основным разделам курса физики, изучаемого в. В сборник включены задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Вы здесь: Главная сайта ГДЗ Сборник задач. Он может быть полезно аспирантам и научным указанных специальных. Сборник задач по математике для поступающих во ВТУЗы. Физика для средних специальных учебных заведений. Сборник Задач По Математике Богомолов Решебник Скачать. Математика. Физика для средних специальных учебных заведений, Жданов. Краткие теоретические сведения, снабженные большим количеством разобранных примеров, позволяют использовать сборник для всех видов обучения. ГДЗ по математике. Задачники и решебники. Книга: Математика: Учебное пособие для средних специальных учебных. Название:. Математика для техникумов на базе среднего образования О. Н. Афанасьева, Я. С. Бродский, А. Л. Справочники, энциклопедии. Пособие содержит задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Решебник ГДЗ по учебнику Сборник заданий для проведения письменного экзамена по математике курс А, алгебре и началам анализа курс В за курс средней школы: 11 класс. Высшая школа. Математика: учебное пособие для средних специальных учебных заведений. В учебнике рассмотрены основные разделы математики, охватываемые действующими программами для техникумов: алгебра, начала.
Название:. Математика для техникумов на базе среднего образования О. Н. Афанасьева, Я. С. Бродский, А. Л. Справочники, энциклопедии. Пособие содержит задачи по всем разделам курса математики, изучаемого в средних специальных учебных заведениях. Решебник ГДЗ по учебнику Сборник заданий для проведения письменного экзамена по математике курс А, алгебре и началам анализа курс В за курс средней школы: 11 класс. Высшая школа. Математика: учебное пособие для средних специальных учебных заведений. В учебнике рассмотрены основные разделы математики, охватываемые действующими программами для техникумов: алгебра, начала.
 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
 Найти Область определения и область значений функцииНАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
Найти Область определения и область значений функцииНАЙТИ ОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ Область определения и область значений функцииОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ
Область определения и область значений функцииОБЛАСТЬ ОПРЕДЕЛЕНИЯ И ОБЛАСТЬ Проверь себяПРОВЕРЬ СЕБЯ
Проверь себяПРОВЕРЬ СЕБЯ Узнайте больше о желаемом домене с помощью этих советов по поиску владельцев доменного имени, а также с помощью инструмента поиска WHOIS от Shopify.
Узнайте больше о желаемом домене с помощью этих советов по поиску владельцев доменного имени, а также с помощью инструмента поиска WHOIS от Shopify.

 Вы можете переместить свой веб-сайт в другой домен, если хотите изменить URL-адрес. Когда вы перемещаете свой веб-сайт в другой домен, важно следовать передовым методам SEO, чтобы свести к минимуму потерю трафика. Перенаправляя старый домен на новый действующий домен, вы сигнализируете Google, что новый домен теперь является домом для старого контента веб-сайта.
Вы можете переместить свой веб-сайт в другой домен, если хотите изменить URL-адрес. Когда вы перемещаете свой веб-сайт в другой домен, важно следовать передовым методам SEO, чтобы свести к минимуму потерю трафика. Перенаправляя старый домен на новый действующий домен, вы сигнализируете Google, что новый домен теперь является домом для старого контента веб-сайта. co
co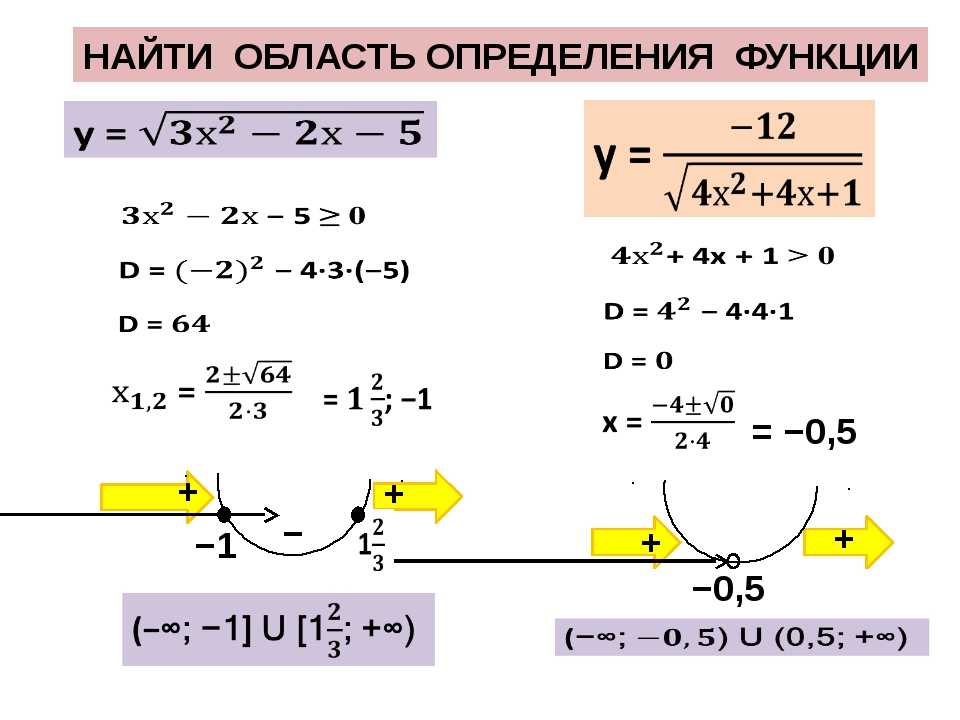 io
io tech
tech top
top ws
ws site
site run
run vet
vet realty
realty vote
vote У нас есть документация и видео, чтобы ответить на ваши вопросы, когда вы начинаете, строите и развиваете свой онлайн-бизнес.
У нас есть документация и видео, чтобы ответить на ваши вопросы, когда вы начинаете, строите и развиваете свой онлайн-бизнес. Хостинг позволяет создавать новые веб-сайты, чтобы они были видны клиентам в Интернете, а системы безопасности работали. Все планы создания сайтов электронной коммерции Shopify включают услуги хостинга.
Хостинг позволяет создавать новые веб-сайты, чтобы они были видны клиентам в Интернете, а системы безопасности работали. Все планы создания сайтов электронной коммерции Shopify включают услуги хостинга.

 Выражение ???\sqrt{x+9}??? не определено, где ???x+9??? отрицательно. Например, если ???x=-10???, то ???x+9??? равно ???-1???. Аналогично, если ???x??? любое число меньше, чем ???-9???, ???x+9??? будет отрицательным. Однако ???-9??? само по себе нормально, потому что ???\sqrt{x+9}??? тогда будет ???0???, что не является неопределенным.
Выражение ???\sqrt{x+9}??? не определено, где ???x+9??? отрицательно. Например, если ???x=-10???, то ???x+9??? равно ???-1???. Аналогично, если ???x??? любое число меньше, чем ???-9???, ???x+9??? будет отрицательным. Однако ???-9??? само по себе нормально, потому что ???\sqrt{x+9}??? тогда будет ???0???, что не является неопределенным.

 )
) )
) )
) )
) )
) )
) )
) )
) 2
2 3
3 14159..
14159.. )/3
)/3 2), t=\tan x/2, \ $, но я не могу найти правильное решение.
Также я пробовал квадратировать обе стороны, но все равно ничего.
2), t=\tan x/2, \ $, но я не могу найти правильное решение.
Также я пробовал квадратировать обе стороны, но все равно ничего. $$
$$
 Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
 .. Задача 8E: Найдите расстояние между каждой парой точек: a -3,-7 и 2, 5 c -a,-b и a,b b 0, 0 и -2, 6 d… Задача 9E: Найдите середину отрезка, соединяющего каждую пару точек: a 0, -3 и 4, 0 c 3, 2 и… Задача 10E Задача 11E: Точки A и B имеют симметрию относительно начала координат O. Найдите координаты B, если A является… Задача 12E: Точки A и B имеют симметрию относительно точки C 2,3. Найдите координаты B, если A является… Задача 13E: Точки A и B имеют симметрию относительно точки C. Найдите координаты C для заданной точки: a A… Задача 14E: Точки A и B имеют симметрию относительно оси x. Найдите координаты B, если A является… Задача 15E Задача 16E: Точки A и B имеют симметрию относительно вертикальной линии, где x=2. Найдите координаты A… Задача 17E: Точки A и B имеют симметрию относительно оси y. Найдите координаты A, если B это… Задача 18E Задача 19E: Точки A и B имеют симметрию относительно вертикальной линии x=a или горизонтальной линии y=b. Задайте… Задача 20E: В упражнениях с 20 по 22 примените формулу средней точки.
.. Задача 8E: Найдите расстояние между каждой парой точек: a -3,-7 и 2, 5 c -a,-b и a,b b 0, 0 и -2, 6 d… Задача 9E: Найдите середину отрезка, соединяющего каждую пару точек: a 0, -3 и 4, 0 c 3, 2 и… Задача 10E Задача 11E: Точки A и B имеют симметрию относительно начала координат O. Найдите координаты B, если A является… Задача 12E: Точки A и B имеют симметрию относительно точки C 2,3. Найдите координаты B, если A является… Задача 13E: Точки A и B имеют симметрию относительно точки C. Найдите координаты C для заданной точки: a A… Задача 14E: Точки A и B имеют симметрию относительно оси x. Найдите координаты B, если A является… Задача 15E Задача 16E: Точки A и B имеют симметрию относительно вертикальной линии, где x=2. Найдите координаты A… Задача 17E: Точки A и B имеют симметрию относительно оси y. Найдите координаты A, если B это… Задача 18E Задача 19E: Точки A и B имеют симметрию относительно вертикальной линии x=a или горизонтальной линии y=b. Задайте… Задача 20E: В упражнениях с 20 по 22 примените формулу средней точки. M 3,-4является серединой AB-, в которой A является… Задача 21EЗадача 22EЗадача 23E: Прямоугольник ABCD имеет три вершины в точках A2,-1,B6,-1 и C6,3. Найдите четвертую вершину и… Задача 24E: Прямоугольник MNPQ имеет три вершины в точках M0, 0, Na, 0 и Q0, b. Найдите четвертую вершину P и… Задача 25E: Используйте формулу расстояния, чтобы определить тип треугольника, который имеет эти вершины: a A0, 0, B4,0,… Задача 26E: Используйте метод из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 27E. Воспользуйтесь методом из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 28E. Для компланарных точек A, B и C , предположим, что вы использовали формулу расстояния, чтобы показать, что… Задача 29EЗадача 30EЗадача 31EЗадача 32E: На оси абсцисс имеются две точки, расположенные на расстоянии 6 единиц от точек 3,1….Задача 33E: Треугольник с вершинами M-4,0,N3,- 1 и Q2,4 заключены в рамки, как показано. Найдите площадь.
M 3,-4является серединой AB-, в которой A является… Задача 21EЗадача 22EЗадача 23E: Прямоугольник ABCD имеет три вершины в точках A2,-1,B6,-1 и C6,3. Найдите четвертую вершину и… Задача 24E: Прямоугольник MNPQ имеет три вершины в точках M0, 0, Na, 0 и Q0, b. Найдите четвертую вершину P и… Задача 25E: Используйте формулу расстояния, чтобы определить тип треугольника, который имеет эти вершины: a A0, 0, B4,0,… Задача 26E: Используйте метод из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 27E. Воспользуйтесь методом из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 28E. Для компланарных точек A, B и C , предположим, что вы использовали формулу расстояния, чтобы показать, что… Задача 29EЗадача 30EЗадача 31EЗадача 32E: На оси абсцисс имеются две точки, расположенные на расстоянии 6 единиц от точек 3,1….Задача 33E: Треугольник с вершинами M-4,0,N3,- 1 и Q2,4 заключены в рамки, как показано. Найдите площадь. .. Задача 34E: Используйте метод бокса, предложенный в упражнении 33, чтобы найти площадь RST с R-2,4,S-1,-2 и T6,5…. Задача 35E: Определите площадь ABC, если A=2,1,B=5,3, а C является отражением B относительно оси X. Задача 36E: Найдите площадь ABC В упражнении 35, но предположим, что C является отражением B по оси Y. Задача 37E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами находится в точках 0, 0, 5,…. Задача 38E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами 0, 0, 6,… Задача 39E: Найдите точный объем твердого тела, которое получается, когда прямоугольная область с вершинами находится в точках 0, 0,… Задача 40E: Найдите точный объем тела, которое получается, когда область, ограниченная осями в квадранте I… Задача 41E: Найдите точную площадь поперечной поверхности каждого твердого тела в упражнении 40. Найдите точный объем образовавшегося твердого тела… Задача 42E: Найдите объем твердого тела, образовавшегося, когда треугольная область имеет вершины в точках 2, 0, 4, 0.
.. Задача 34E: Используйте метод бокса, предложенный в упражнении 33, чтобы найти площадь RST с R-2,4,S-1,-2 и T6,5…. Задача 35E: Определите площадь ABC, если A=2,1,B=5,3, а C является отражением B относительно оси X. Задача 36E: Найдите площадь ABC В упражнении 35, но предположим, что C является отражением B по оси Y. Задача 37E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами находится в точках 0, 0, 5,…. Задача 38E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами 0, 0, 6,… Задача 39E: Найдите точный объем твердого тела, которое получается, когда прямоугольная область с вершинами находится в точках 0, 0,… Задача 40E: Найдите точный объем тела, которое получается, когда область, ограниченная осями в квадранте I… Задача 41E: Найдите точную площадь поперечной поверхности каждого твердого тела в упражнении 40. Найдите точный объем образовавшегося твердого тела… Задача 42E: Найдите объем твердого тела, образовавшегося, когда треугольная область имеет вершины в точках 2, 0, 4, 0. , и 2,… Задача 43E: По определению, эллипс — это геометрическое место точек, сумма расстояний которых от двух фиксированных точек F1 и… Задача 44E: По определению, гипербола — это геометрическое место точек, положительная разность которых расстояния от двух… Задача 45EЗадача 46E: Используйте формулу расстояния, чтобы показать, что уравнение параболы с фокусом F0,2 и директрисой… Задача 47E: После 90 вращение против часовой стрелки вокруг начала координат, изображение A3, 1 точка B-1, 3. Что… Задача 48E: Рассмотрим точку Ca,b. Каким будет образ C после поворота против часовой стрелки на 90 вокруг… Задача 49E Задача 50E: Графики парабол eith уравнений y=x2 и прямой y=18-x2 пересекаются в двух точках. Найти… Задача 51E format_list_bulleted
, и 2,… Задача 43E: По определению, эллипс — это геометрическое место точек, сумма расстояний которых от двух фиксированных точек F1 и… Задача 44E: По определению, гипербола — это геометрическое место точек, положительная разность которых расстояния от двух… Задача 45EЗадача 46E: Используйте формулу расстояния, чтобы показать, что уравнение параболы с фокусом F0,2 и директрисой… Задача 47E: После 90 вращение против часовой стрелки вокруг начала координат, изображение A3, 1 точка B-1, 3. Что… Задача 48E: Рассмотрим точку Ca,b. Каким будет образ C после поворота против часовой стрелки на 90 вокруг… Задача 49E Задача 50E: Графики парабол eith уравнений y=x2 и прямой y=18-x2 пересекаются в двух точках. Найти… Задача 51E format_list_bulleted 


 МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1 


 Для вычисления
логарифмов эффективна формула
Для вычисления
логарифмов эффективна формула


 рисунок выше).
рисунок выше). Для каждого числа z из области сходимости
Для каждого числа z из области сходимости В частности, радиус сходимости степенного ряда (24.33) можно вычислить по формуле
В частности, радиус сходимости степенного ряда (24.33) можно вычислить по формуле
 25. Подставив в него выражение Найдем
25. Подставив в него выражение Найдем

 Если- функция независимой переменнойТо в общем
Если- функция независимой переменнойТо в общем Найти решениеДифференциального уравнения первого
Найти решениеДифференциального уравнения первого Когда мы добавляем бесконечное число членов, как мы это делаем со степенным рядом, сумма этих членов будет либо конечным числом, либо бесконечной.
Когда мы добавляем бесконечное число членов, как мы это делаем со степенным рядом, сумма этих членов будет либо конечным числом, либо бесконечной.
 Это всего лишь один пример использования радиуса конвергенции, и существует множество других приложений, которые работают за кулисами компьютерного программного обеспечения и помогают нам каждый день!
Это всего лишь один пример использования радиуса конвергенции, и существует множество других приложений, которые работают за кулисами компьютерного программного обеспечения и помогают нам каждый день!
 } \\ & \hspace{5ex} \text{Используя тест отношения, сходимость происходит, когда: } \; Л < 1, \; L = \lim_{n\to\infty} \left\lvert\frac{a_{n+1}}{a_{n}} \right\rvert\\ \\ & \hspace{4ex} \text{1.1) Подставив наш ряд в формулу проверки отношения, мы получим: } \\ \\ & \hspace{9{1}} \cdot \infty \cdot x\right\rvert\\ \\ & \hspace{4ex} \text{1.4) Для дальнейшего упрощения мы сократим члены, содержащие бесконечности.} \\ & \hspace{ 9ex} \text{Поступая так, получаем:} \\ \\ & \hspace{9ex} L = \left\lvert\frac{x}{1}\right\rvert\\ \\ & \hspace{4ex} \text{1.5) Применение критериев сходимости } \; L < 1 \text{, получаем:} \\ \\ & \hspace{9ex} \left\lvert\frac{x}{1}\right\rvert < 1\\ \\ \\ & \hspace{2ex } \text{2) Теперь давайте решим новое уравнение сходимости для определения радиуса сходимости.}\\ \\ & \hspace{4ex} \text{2.1) Решив неравенство сходимости для радиуса сходимости, получим: } \\ \\ & \hspace{9ex} \left\lvert\frac{x}{1}\right\rvert < 1 \; \Длинная праваястрелка\; \text{радиус} = \boxed{1} \\ \\ & \hspace{4ex} \boxed{\text{Радиус сходимости} = \boxed{1}}\\ & \end{align}$$
} \\ & \hspace{5ex} \text{Используя тест отношения, сходимость происходит, когда: } \; Л < 1, \; L = \lim_{n\to\infty} \left\lvert\frac{a_{n+1}}{a_{n}} \right\rvert\\ \\ & \hspace{4ex} \text{1.1) Подставив наш ряд в формулу проверки отношения, мы получим: } \\ \\ & \hspace{9{1}} \cdot \infty \cdot x\right\rvert\\ \\ & \hspace{4ex} \text{1.4) Для дальнейшего упрощения мы сократим члены, содержащие бесконечности.} \\ & \hspace{ 9ex} \text{Поступая так, получаем:} \\ \\ & \hspace{9ex} L = \left\lvert\frac{x}{1}\right\rvert\\ \\ & \hspace{4ex} \text{1.5) Применение критериев сходимости } \; L < 1 \text{, получаем:} \\ \\ & \hspace{9ex} \left\lvert\frac{x}{1}\right\rvert < 1\\ \\ \\ & \hspace{2ex } \text{2) Теперь давайте решим новое уравнение сходимости для определения радиуса сходимости.}\\ \\ & \hspace{4ex} \text{2.1) Решив неравенство сходимости для радиуса сходимости, получим: } \\ \\ & \hspace{9ex} \left\lvert\frac{x}{1}\right\rvert < 1 \; \Длинная праваястрелка\; \text{радиус} = \boxed{1} \\ \\ & \hspace{4ex} \boxed{\text{Радиус сходимости} = \boxed{1}}\\ & \end{align}$$ Он также использует систему компьютерной алгебры (CAS), основанную на JS, которая выполняет некоторые алгебраические шаги в процессе вычислений. Поскольку калькулятор работает на основе кода JS, он полностью работает внутри встроенного механизма JS вашего браузера и предоставляет мгновенные решения и шаги (не требуется перезагрузка страницы).
Он также использует систему компьютерной алгебры (CAS), основанную на JS, которая выполняет некоторые алгебраические шаги в процессе вычислений. Поскольку калькулятор работает на основе кода JS, он полностью работает внутри встроенного механизма JS вашего браузера и предоставляет мгновенные решения и шаги (не требуется перезагрузка страницы). Просто введите свою функцию и диапазон переменных в заданных разделах ввода и нажмите кнопку расчета, чтобы получить мгновенный вывод вместе с подробной процедурой.
Просто введите свою функцию и диапазон переменных в заданных разделах ввода и нажмите кнопку расчета, чтобы получить мгновенный вывод вместе с подробной процедурой. е. радиус конвергенции
е. радиус конвергенции
 569805089977
569805089977 Посмотрите обучающий видео урок
как правильно склонять числительные.
Посмотрите обучающий видео урок
как правильно склонять числительные.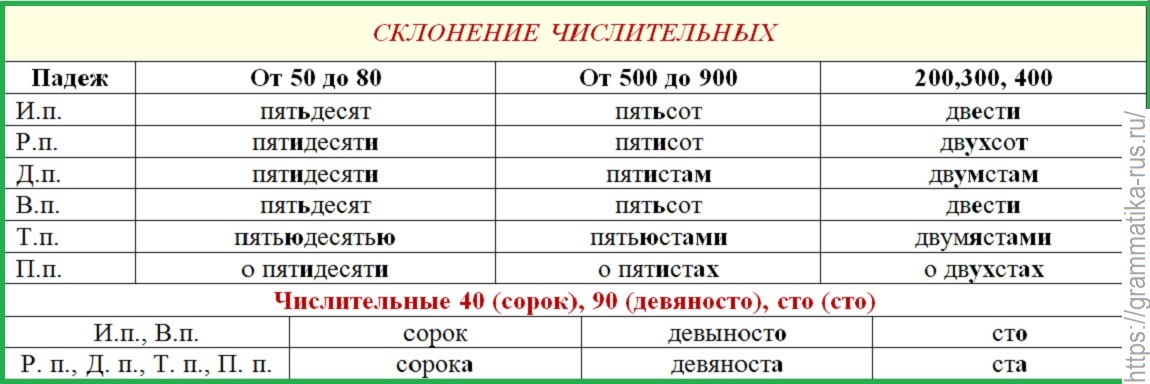 Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос.
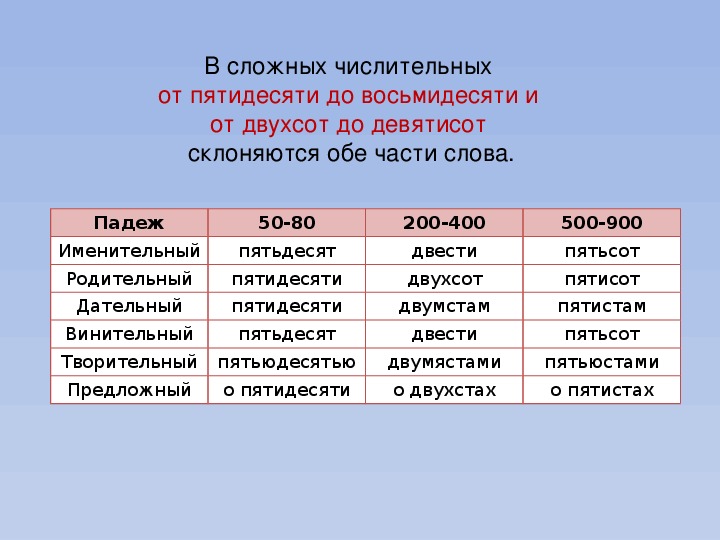
Всего в русском языке существует шесть падежей, каждый из которых имеет свой вспомогательный вопрос. У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.
У числительных на -десят два окончания, так как изменяются обе части: пятидесяти, пятьюдесятью.

 europa.eu
europa.eu ..]
..]
 ..]
..]
 ..] F O RT Y-ДВЕ ТЫСЯЧИ ВОСЕМЬДЕСЯТ ГЕН DR E D ПЯТЬДЕСЯТ — S E VE N ЕВРО И ДЕСЯТЬ ЕВРОЦЕНТОВ (‘7 142 857,10), представитель d b y СЕМЬДЕСЯТ ОДИН M I LL ION FO U R СТО ДВАДЦАТЬ ВОСЕМЬ ТЫСЯЧ ОДИН ТЫСЯЧА F IV E СТО СЕМЬДЕСЯТ ОДИН c o мм на акции […]
..] F O RT Y-ДВЕ ТЫСЯЧИ ВОСЕМЬДЕСЯТ ГЕН DR E D ПЯТЬДЕСЯТ — S E VE N ЕВРО И ДЕСЯТЬ ЕВРОЦЕНТОВ (‘7 142 857,10), представитель d b y СЕМЬДЕСЯТ ОДИН M I LL ION FO U R СТО ДВАДЦАТЬ ВОСЕМЬ ТЫСЯЧ ОДИН ТЫСЯЧА F IV E СТО СЕМЬДЕСЯТ ОДИН c o мм на акции […] 142.857,10 ‘), срединный представитель e SETENTA Y UN MILLO NE S CUATROCIENTAS VEINT IO CHO MIL QUI NI EN TAS SETENTA Y UNA ac […]
142.857,10 ‘), срединный представитель e SETENTA Y UN MILLO NE S CUATROCIENTAS VEINT IO CHO MIL QUI NI EN TAS SETENTA Y UNA ac […] е. ndas эквивалент […]
е. ndas эквивалент […]
 . .]
. .] ..]
..] ..]
..] ..]
..] ..]
..] ..]
..] ..]
..]

 ..]
..] ..]
..] ..]
..]
 org
org Сто a n d восемь d e le Гации отсутствовали.
Сто a n d восемь d e le Гации отсутствовали. . .]
. .] es
es Упражнение 7А.
Упражнение 7А.
 Упражнение 7А.
>
Вопрос 1
Упражнение 7А.
>
Вопрос 1 …
…
 Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства. В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными). Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах. 
 В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов. Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ. Он применяется в двух этапах.
Он применяется в двух этапах. Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы. Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги: Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
 Теперь давайте перейдем к новому понятию в математике – система неравенств. Система неравенств похожа на систему уравнений. Вы помните системы уравнений? Системы уравнений вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали.
Теперь давайте перейдем к новому понятию в математике – система неравенств. Система неравенств похожа на систему уравнений. Вы помните системы уравнений? Системы уравнений вы изучали в седьмом классе, постарайтесь вспомнить, как вы их решали.
 Неравенство строгое, тогда отрезок будет открытым.
Неравенство строгое, тогда отрезок будет открытым. 2+36
2+36
 Штриховка идёт вправо, на плюс бесконечность:
Штриховка идёт вправо, на плюс бесконечность:


 Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .
Неравенства, которые имеют то же множество решений, называются эквивалентными неравенствами .  Тогда отсюда видно, что для x
Тогда отсюда видно, что для x  Следующие свойства используются для их решения.
Следующие свойства используются для их решения. Счет в пределах 10
Счет в пределах 10 к
к к. из f(x)>( (x))2 следует справедливость f(x)
к. из f(x)>( (x))2 следует справедливость f(x) Занятие №3.• Цель: Рассмотреть решения неравенств
Занятие №3.• Цель: Рассмотреть решения неравенств
 AIP Conference Proceedings 2 марта 2021 г.; 2330 (1): 040031. https://doi.org/10.1063/5.0043229
AIP Conference Proceedings 2 марта 2021 г.; 2330 (1): 040031. https://doi.org/10.1063/5.0043229


 2. .16.
2. .16. Мы особенно должны помнить, что когда мы умножаем или делим на отрицательное число, знак неравенства должен измениться.
Мы особенно должны помнить, что когда мы умножаем или делим на отрицательное число, знак неравенства должен измениться.
 Поскольку \(x+3=0\) при \(x=-3\), то -3 является критической точкой.
Поскольку \(x+3=0\) при \(x=-3\), то -3 является критической точкой.



 Частное не определено, когда знаменатель равен нулю.
Частное не определено, когда знаменатель равен нулю. {2}-2 x-15}>0\). 9{2}-2 x-15}>0 \номер \]
{2}-2 x-15}>0\). 9{2}-2 x-15}>0 \номер \] Это приводит к рациональному неравенству.
Это приводит к рациональному неравенству.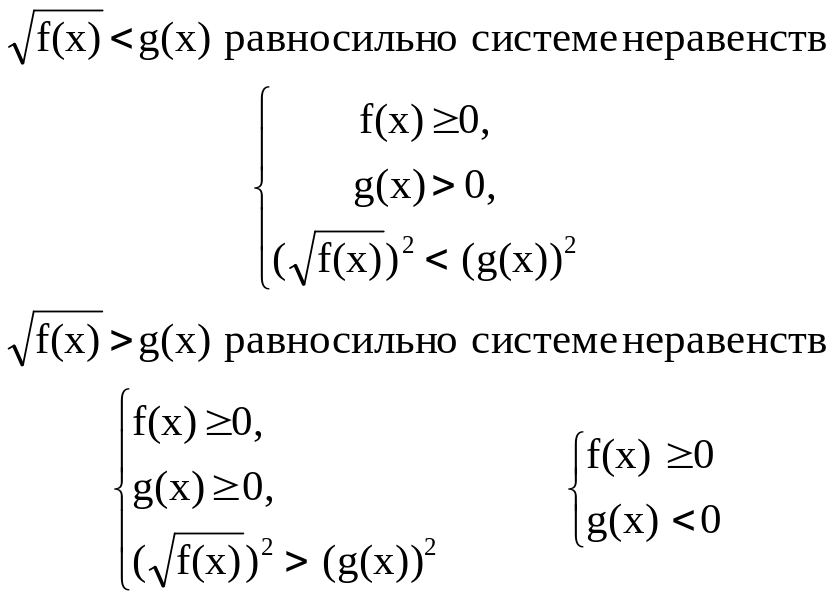
 Чтобы найти функцию средней стоимости, разделите функцию стоимости на \(x\).
Чтобы найти функцию средней стоимости, разделите функцию стоимости на \(x\).





 Студенты могут практиковать римские цифры от 1 до 40, используя таблицу и использовать ее для дальнейшего преобразования чисел.
Студенты могут практиковать римские цифры от 1 до 40, используя таблицу и использовать ее для дальнейшего преобразования чисел. Например: LI, L > I, поэтому LI = L + I = 50 + 1 = 51,9.0176
Например: LI, L > I, поэтому LI = L + I = 50 + 1 = 51,9.0176 Он состоит из записи чисел от 1 до 40, использовавшейся римлянами в древние времена.
Он состоит из записи чисел от 1 до 40, использовавшейся римлянами в древние времена. Пары простых чисел-близнецов от 1 до 40: (3, 5), (5, 7), (11, 13), (17, 19) и (29) , 31). Следовательно, между римскими цифрами 1 и 40 находится 5 простых чисел-близнецов.
Пары простых чисел-близнецов от 1 до 40: (3, 5), (5, 7), (11, 13), (17, 19) и (29) , 31). Следовательно, между римскими цифрами 1 и 40 находится 5 простых чисел-близнецов.
 строчные римские цифры плюс
строчные римские цифры плюс 

 Это практический инструмент для всех, кто работает с промежутками времени в разных единицах измерения и хочет сэкономить время и избежать ошибок в расчетах.
Это практический инструмент для всех, кто работает с промежутками времени в разных единицах измерения и хочет сэкономить время и избежать ошибок в расчетах.

 С научной точки зрения.
С научной точки зрения.


 Не помешало и то, что Эмиля играл всемирно известный бас Эцио Пинца. Конечно, мы получили небольшой вкус этой магии в возрождении Театра Линкольн-центра Бартлетта Шера с великолепным выступлением Паоло Сота, получившим премию «Тони».
Не помешало и то, что Эмиля играл всемирно известный бас Эцио Пинца. Конечно, мы получили небольшой вкус этой магии в возрождении Театра Линкольн-центра Бартлетта Шера с великолепным выступлением Паоло Сота, получившим премию «Тони». Возможно, это была битва с Actors Equity за роль Джонатана Прайса в евразийской роли Инженера, или использование вертолета на сцене в заголовках, или, может быть, это была иногда банальная лирика, которая сделала этот блокбастер несколько ругаемым гигантом. Как столы повернулись. После одного идиотского мюзикла без мелодии за другим, Мисс Сайгон похожа на Моя прекрасная леди и мы с нетерпением ждем предстоящего возрождения. Трудно представить, чтобы кто-то останавливал шоу в конце второго акта, как вдохновленный Прайс в «Американской мечте».
Возможно, это была битва с Actors Equity за роль Джонатана Прайса в евразийской роли Инженера, или использование вертолета на сцене в заголовках, или, может быть, это была иногда банальная лирика, которая сделала этот блокбастер несколько ругаемым гигантом. Как столы повернулись. После одного идиотского мюзикла без мелодии за другим, Мисс Сайгон похожа на Моя прекрасная леди и мы с нетерпением ждем предстоящего возрождения. Трудно представить, чтобы кто-то останавливал шоу в конце второго акта, как вдохновленный Прайс в «Американской мечте». «Наследие (Последняя воля и завещание)» из «Двадцатый век»
«Наследие (Последняя воля и завещание)» из «Двадцатый век»  Каждый год, который Бродвей ждет от Финна очередного великолепного нового саундтрека, слишком долго.
Каждый год, который Бродвей ждет от Финна очередного великолепного нового саундтрека, слишком долго. обязательно похоже на это — или как в Follies , где вся последовательность Лавленда, по сути, может быть так называемой 11-часовой мультипесней. Однако в Company мы получаем потрясающий подарок от Сондхейма в «Being Alive», столь же страстном и столь же честном заявлении о желании быть любимым, как когда-либо написанном, положенном на неотразимую музыку, которая только становится глубже при повторном прослушивании. .
обязательно похоже на это — или как в Follies , где вся последовательность Лавленда, по сути, может быть так называемой 11-часовой мультипесней. Однако в Company мы получаем потрясающий подарок от Сондхейма в «Being Alive», столь же страстном и столь же честном заявлении о желании быть любимым, как когда-либо написанном, положенном на неотразимую музыку, которая только становится глубже при повторном прослушивании. .
 Он может быть очень эмоциональным (см. «Телефонный провод» в «Дом веселья» или «Неудача слов» в «Дорогом Эване Хансене») или дерзким и громким («Мы смотрим на тебя, Эльфаба»). Вот некоторые из любимых 11-часовых номеров сотрудников TodayTix, которые вы можете посмотреть на YouTube!
Он может быть очень эмоциональным (см. «Телефонный провод» в «Дом веселья» или «Неудача слов» в «Дорогом Эване Хансене») или дерзким и громким («Мы смотрим на тебя, Эльфаба»). Вот некоторые из любимых 11-часовых номеров сотрудников TodayTix, которые вы можете посмотреть на YouTube! Она заставляет ноты звучать легко и непринужденно. В ее игре есть настоящая боль, но она наполнена той радостью, которую приносит знание настоящей боли. Есть много версий этой песни, и наблюдение за каждым человеком всегда является откровением, но выступление Патти здесь действительно выделяется по всем этим причинам.
Она заставляет ноты звучать легко и непринужденно. В ее игре есть настоящая боль, но она наполнена той радостью, которую приносит знание настоящей боли. Есть много версий этой песни, и наблюдение за каждым человеком всегда является откровением, но выступление Патти здесь действительно выделяется по всем этим причинам. Вам знакомо это чувство, когда вы ставите перед собой цель что-то сказать, и мучительный момент между произнесением этого и ожиданием ответа. Этот краткий момент колебания прямо перед тем, как вы должны сказать что-то, на что, как вы знаете, вы получите реакцию, а затем прилив страха и облегчения прекрасно передан во всей этой композиции.
Вам знакомо это чувство, когда вы ставите перед собой цель что-то сказать, и мучительный момент между произнесением этого и ожиданием ответа. Этот краткий момент колебания прямо перед тем, как вы должны сказать что-то, на что, как вы знаете, вы получите реакцию, а затем прилив страха и облегчения прекрасно передан во всей этой композиции. Прелесть «Официантки» в том, что она похожа на настоящую жизнь: смешно, сложно, грустно, а также в равной степени очень тяжело и достойно празднования. Прелесть этой песни в том, что она позволяет Дженне просто «быть» — в ней нет ничего фальшивого, принудительного или перформативного. Это так грубо и честно. Я люблю «She Used to Be Mine», потому что она одновременно кажется песней, написанной только для этого персонажа, и песней, которая кажется написанной для каждого человека в комнате. Мое любимое исполнение номера — сценарист шоу Сара Барейлес и оригинальная бродвейская Дженна Джесси Мюллер на церемонии вручения премии «Тони». Убедитесь, что вы взяли несколько салфеток, прежде чем нажимать кнопку воспроизведения.
Прелесть «Официантки» в том, что она похожа на настоящую жизнь: смешно, сложно, грустно, а также в равной степени очень тяжело и достойно празднования. Прелесть этой песни в том, что она позволяет Дженне просто «быть» — в ней нет ничего фальшивого, принудительного или перформативного. Это так грубо и честно. Я люблю «She Used to Be Mine», потому что она одновременно кажется песней, написанной только для этого персонажа, и песней, которая кажется написанной для каждого человека в комнате. Мое любимое исполнение номера — сценарист шоу Сара Барейлес и оригинальная бродвейская Дженна Джесси Мюллер на церемонии вручения премии «Тони». Убедитесь, что вы взяли несколько салфеток, прежде чем нажимать кнопку воспроизведения. Однако Сэм убеждает ее думать иначе, но не раньше, чем Ода Мэй заглянет в ее возможный богатый образ жизни. Это очень запоминающаяся, воодушевляющая песня, которая полностью контрастирует с остальной музыкой и приносит легкое облегчение от очень эмоциональной истории любви и потери. Это идеальное число 11 часов!
Однако Сэм убеждает ее думать иначе, но не раньше, чем Ода Мэй заглянет в ее возможный богатый образ жизни. Это очень запоминающаяся, воодушевляющая песня, которая полностью контрастирует с остальной музыкой и приносит легкое облегчение от очень эмоциональной истории любви и потери. Это идеальное число 11 часов! если делать или делать достаточно хорошо / достаточно оригинально / стоит всех усилий, мой профессиональный медицинский совет будет смотреть это видео 400 раз в день Приходи на сладкую сладкую гармонию в 1:57 и оставайся для Мэнди, шепчущей: «Я люблю тебя». » в 4:17 «Возможно, выбор был ошибочным / Выбор не был / Вы должны двигаться дальше». Вы шутите надо мной, Стивен Джошуа Сондхейм??? (hbd btw xo)
если делать или делать достаточно хорошо / достаточно оригинально / стоит всех усилий, мой профессиональный медицинский совет будет смотреть это видео 400 раз в день Приходи на сладкую сладкую гармонию в 1:57 и оставайся для Мэнди, шепчущей: «Я люблю тебя». » в 4:17 «Возможно, выбор был ошибочным / Выбор не был / Вы должны двигаться дальше». Вы шутите надо мной, Стивен Джошуа Сондхейм??? (hbd btw xo) Любая песня с конфетти-пушкой в конце обязательно привлечет мое внимание! Затем я работал над шоу время от времени в течение многих лет, и после сотен (может быть, тысяч?!) прослушиваний я все еще люблю его.
Любая песня с конфетти-пушкой в конце обязательно привлечет мое внимание! Затем я работал над шоу время от времени в течение многих лет, и после сотен (может быть, тысяч?!) прослушиваний я все еще люблю его. Кроме того, тот факт, что тот, кто играет Эвана, буквально должен рыдать, — это физический подвиг, которого я никогда не пойму.
Кроме того, тот факт, что тот, кто играет Эвана, буквально должен рыдать, — это физический подвиг, которого я никогда не пойму.