Смежные и вертикальные углы. Перпендикулярные прямые. Какие углы называются смежными? Чему равна сумма двух смежных углов
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2. 1 следует, что если два угла равны, то смежные с ними углы равны.
1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2. 3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять?
Смежные углы – определение понятия
Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Смежные углы – основные свойства
1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°:
- Если μ и η являются смежными углами, то μ + η = 180°.
- Зная величину одного из смежных углов (например, μ), можно легко вычислить градусную меру второго угла (η), используя выражение η = 180° – μ.
2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым.
3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее:
- sinη = sin(180° – μ) = sinμ,
- cosη = cos(180° – μ) = -cosμ,
- tgη = tg(180° – μ) = -tgμ,
- ctgη = ctg(180° – μ) = -ctgμ.
Смежные углы – примеры
Пример 1
Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
- Продлим каждую из сторон треугольника прямой.
- Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:
смежным для угла ∠QMP будет ∠LMP,
смежным для угла ∠MPQ будет ∠SPQ,
смежным для угла ∠PQM будет ∠HQP.
Пример 2
Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?
- Два смежных угла в сумме образуют 180°.
- Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.
Пример 3
Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.
- Обозначим величину одного (меньшего) угла через – ∠μ = λ.
- Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
- Исходя из основного свойства смежных углов, μ + η = 180° следует
λ + 3λ = μ + η = 180°,
λ = 180°/4 = 45°.
Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.
Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.
Г Л А В А I.
ОСНОВНЫЕ ПОНЯТИЯ.
§11. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (черт. 72): / А ВС и / СВD, у которых одна сторона ВС общая, а две другие АВи ВD составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, / АDF и / FDВ — углы смежные (черт. 73).
Смежные углы могут иметь самые разнообразные положения (черт. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 2d.
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 3 / 5 d , то второй угол будет равен:
2d — 3 / 5 d = l 2 / 5 d .
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На чертеже 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть / 1 = 7 / 8 d (черт. 76). Смежный с ним / 2 будет равен 2d — 7 / 8 d , т. е. 1 1 / 8 d .
Таким же образом можно вычислить, чему равны / 3 и / 4.
/ 3 = 2d — 1 1 / 8 d = 7 / 8 d ; / 4 = 2d — 7 / 8 d = 1 1 / 8 d (черт. 77).
77).
Мы видим, что / 1 = / 3 и / 2 = / 4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём рассуждения, путём доказательства.
Доказательство можно провести следующим образом (черт. 78):
/ a + / c = 2d ;
/ b + / c = 2d ;
(так как сумма смежных углов равна 2d ).
/ a + / c = / b + / c
(так как и левая часть этого равенства равна 2d , и правая его часть тоже равна 2d ).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: / a = / b , т. е. вертикальные углы равны между собой.
При рассмотрении вопроса о вертикальных углах мы сначала объяснили, какие углы называются вертикальными, т. е. дали определение вертикальных углов.
Затем мы высказали суждение (утверждение) о равенстве вертикальных углов и в справедливости этого суждения убедились путём доказательства. Такие суждения, справедливость которых надо доказывать, называются теоремами . Таким образом, в данном параграфе мы дали определение вертикальных углов, а также высказали и доказали теорему об их свойстве.
В дальнейшем при изучении геометрии нам постоянно придётся встречаться с определениями и доказательствами теорем.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 / 1, / 2, / 3 и / 4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
В сумме эти углы составляют развёрнутый угол, т. е.
/ 1+ / 2+/ 3+ / 4 = 2d .
На чертеже 80 / 1, / 2, / 3, / 4 и / 5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. / 1 + / 2 + / 3 + / 4 + / 5 = 4d .
Упражнения.
1. Один из смежных углов равен 0,72 d. Вычислить угол, составленный биссектрисами этих смежных углов.
2. Доказать, что биссектрисы двух смежных углов образуют прямой угол.
3. Доказать, что если два угла равны, то равны и их смежные углы.
4. Сколько пар смежных углов на чертеже 81?
5. Может ли пара смежных углов состоять из двух острых углов? из двух тупых углов? из прямого и тупого угла? из прямого и острого угла?
6. Если один из смежных углов прямой, то что можно сказать о величине смежного с ним угла?
7. Если при пересечении двух прямых линий один угол прямой, то что можно сказать о величине остальных трёх углов?
Как найти смежный угол?
Математика — древнейшая точная наука, которую в обязательном порядке изучают в школах, колледжах, институтах и университетах. Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Однако, базовые знания всегда закладываются еще в школе. Порой, ребенку задают достаточно сложные задания, а родители не в силах помочь, потому что просто забыли некоторые вещи из математики. Например, как найти смежный угол по величине основного угла и т.п. Задача проста, но может вызвать затруднения при решении из-за незнания того, какие углы называются смежными и как их найти.
Рассмотрим подробнее определение и свойства смежных углов, а также как их вычислить по данным в задаче.
Определение и свойства смежных углов
Два луча, исходящие из одной точки образуют фигуру под названием «плоский угол». При этом эта точка именуется вершиной угла, а лучи являются его сторонами. Если продолжить один из лучей дальше начальной точки по прямой, то образуется еще один угол, который и называется смежным. У каждого угла в этом случае есть два смежных угла, так как стороны угла равнозначны. То есть всегда присутствует еще смежный угол в 180 градусов.
К основным свойствам смежных углов относят
- Смежные углы имеют общую вершину и одну сторону;
- Сумма смежных углов равна всегда 180 градусам или числу Пи, если вычисление ведется в радианах;
- Синусы смежных углов всегда равны;
- Косинусы и тангенсы смежных углов равны, но имеют противоположные знаки.

Как найти смежные углы
Обычно даются три вариации задач на нахождение величины смежных углов
- Дана величина основного угла;
- Дано соотношение основного и смежного угла;
- Дана величина вертикального угла.
Каждый вариант задачи имеет свое решение. Рассмотрим их.
Дана величина основного угла
Если в задаче указана величина основного угла, то найти смежный угол очень просто. Для этого достаточно из 180 градусов вычесть величину основного угла, и вы получите величину смежного угла. Данное решение исходит из свойства смежного угла — сумма смежных углов равна всегда 180 градусам.
Если же величина основного угла дана в радианах и в задаче требуется найти смежный угол в радианах, то необходимо вычесть из числа Пи величину основного угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Дано соотношение основного и смежного угла
В задаче может быть дано соотношение основного и смежного угла вместо градусов и радиан величины основного угла. В этом случае решение будет выглядеть, как уравнение пропорции:
В этом случае решение будет выглядеть, как уравнение пропорции:
- Обозначаем долю пропорции основного угла, как переменную «Y».
- Долю относящуюся к смежному углу обозначаем, как переменную «Х».
- Количество градусов, которые приходятся на каждую пропорцию, обозначим, например, «a».
- Общая формула будет выглядеть так — a*X+a*Y=180 или a*(X+Y)=180.
- Находим общий множитель уравнения «a» по формуле a=180/(X+Y).
- Затем полученное значение общего множителя «а» умножаем на долю угла, который необходимо определить.
Таким образом мы можем найти величину смежного угла в градусах. Однако, если необходимо найти величину в радианах, то нужно просто перевести градусы в радианы. Для этого умножаем угол в градусах на число Пи и делим все на 180 градусов. Полученное значение будет в радианах.
Дана величина вертикального угла
Если в задаче не дана величина основного угла, но дана величина вертикального угла, то вычислить смежный угол можно по такой же формуле, что и в первом пункте, где дана величина основного угла.
Вертикальный угол — это угол, который исходит из той же точки, что и основной, но при этом он направлен в строго противоположном направлении. Тем самым получается зеркальное отражение. Это значит, что вертикальный угол по величине равен основному. В свою очередь, смежный угол вертикального угла равен смежному углу основного угла. Благодаря этому можно вычислить смежный угол основного угла. Для этого просто вычитаем из 180 градусов величину вертикального и получаем значение смежного угла основного угла в градусах.
Если же величина дана в радианах, то необходимо вычесть из числа Пи величину вертикального угла, так как величина полного развернутого угла в 180 градусов равна числу Пи.
Также вы можете прочесть наши полезные статьи и .
угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.
Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.
Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.
Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.
Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).
Источники:
- Большой Энциклопедический Словарь — Смежные углы
- угол 180 градусов
Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.
Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.
Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно.
В качестве единицы измерения углов принят – 1/180
Что таоке смежные углы. Смежные и вертикальные углы
Что таоке смежные углы. Смежные и вертикальные углы
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами. На рисунке 20 углы АОВ и ВОС смежные.
Сумма смежных углов равна 180°
Теорема 1. Сумма смежных углов равна 180°.
Доказательство. Луч ОВ (см. рис.1) проходит между сторонами развернутого угла. Поэтому ∠ АОВ + ∠ ВОС = 180° .
Поэтому ∠ АОВ + ∠ ВОС = 180° .
Из теоремы 1 следует, что если два угла равны, то смежные с ними углы равны.
Вертикальные углы равны
Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого. Углы АОВ и COD, BOD и АОС, образованные при пересечении двух прямых, являются вертикальными (рис. 2).
Теорема 2. Вертикальные углы равны.
Доказательство. Рассмотрим вертикальные углы АОВ и COD (см. рис. 2). Угол BOD является смежным для каждого из углов АОВ и COD. По теореме 1 ∠ АОВ + ∠ BOD = 180°, ∠ COD + ∠ BOD = 180°.
Отсюда заключаем, что ∠ АОВ = ∠ COD.
Следствие 1. Угол, смежный с прямым углом, есть прямой угол.
Рассмотрим две пересекающиеся прямые АС и BD (рис.3). Они образуют четыре угла. Если один из них прямой (угол 1 на рис.3), то остальные углы также прямые (углы 1 и 2, 1 и 4 — смежные, углы 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Перпендикулярность прямых АС и BD обозначается так: AC ⊥ BD.
Серединным перпендикуляром к отрезку называется прямая, перпендикулярная к этому отрезку и проходящая через его середину.
АН — перпендикуляр к прямой
Рассмотрим прямую а и точку А, не лежащую на ней (рис.4). Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.
Чертежный угольник
Справедлива следующая теорема.
Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).
Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы.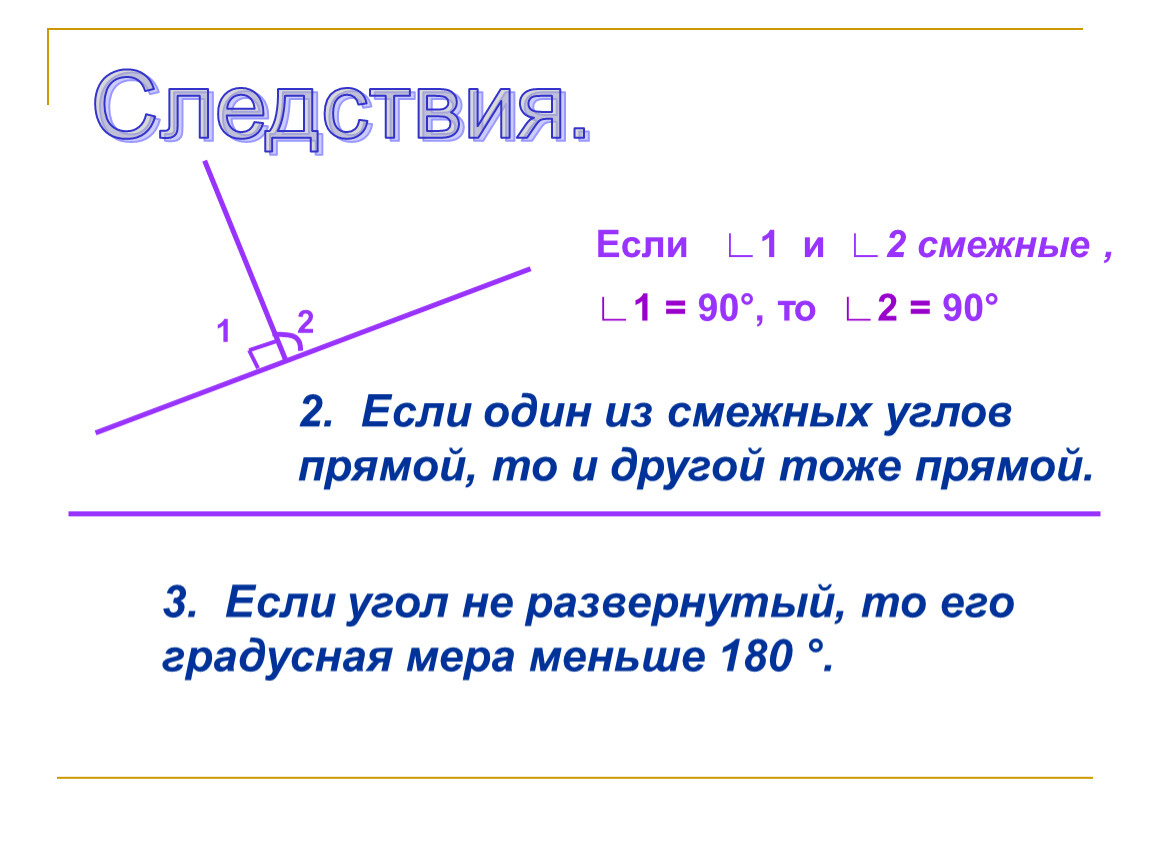 Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.
Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».
Пример 1. Один из смежных углов равен 44°. Чему равен другой?
Решение. Обозначим градусную меру другого угла через x , тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.
Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?
Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.
∠ АОС = 180° — ∠ COD = 180° — 45° = 135°.
Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.
Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.
Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.
Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол
АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.
В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять?
Смежные углы – определение понятия
Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Смежные углы – основные свойства
1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°:
- Если μ и η являются смежными углами, то μ + η = 180°.
- Зная величину одного из смежных углов (например, μ), можно легко вычислить градусную меру второго угла (η), используя выражение η = 180° – μ.
2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым.
3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее:
- sinη = sin(180° – μ) = sinμ,
- cosη = cos(180° – μ) = -cosμ,
- tgη = tg(180° – μ) = -tgμ,
- ctgη = ctg(180° – μ) = -ctgμ.
Смежные углы – примеры
Пример 1
Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
- Продлим каждую из сторон треугольника прямой.
- Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:
смежным для угла ∠QMP будет ∠LMP,
смежным для угла ∠MPQ будет ∠SPQ,
смежным для угла ∠PQM будет ∠HQP.
Пример 2
Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?
- Два смежных угла в сумме образуют 180°.
- Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.
Пример 3
Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.
- Обозначим величину одного (меньшего) угла через – ∠μ = λ.
- Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
- Исходя из основного свойства смежных углов, μ + η = 180° следует
λ + 3λ = μ + η = 180°,
λ = 180°/4 = 45°.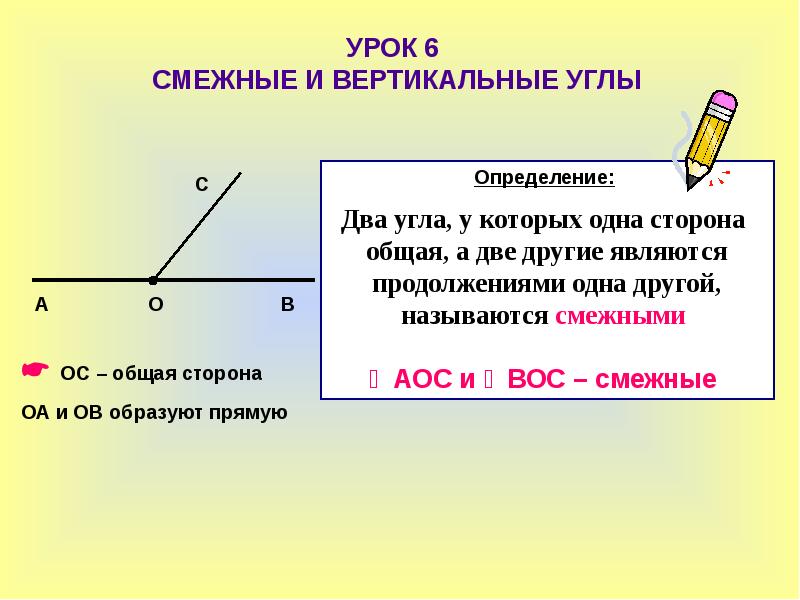
Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.
Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.
Вопрос 1. Какие углы называются смежными?
Ответ. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 31 углы (a 1 b) и (a 2 b) смежные. У них сторона b общая, а стороны a 1 и a 2 являются дополнительными полупрямыми.
Вопрос 2. Докажите, что сумма смежных углов равна 180°.
Ответ. Теорема 2.1. Сумма смежных углов равна 180°.
Доказательство. Пусть угол (a 1 b) и угол (a 2 b) — данные смежные углы (см. рис.31). Луч b проходит между сторонами a 1 и a 2 развёрнутого угла. Поэтому сумма углов (a 1 b) и (a 2 b) равна развёрнутому углу, т. е. 180°. Что и требовалось доказать.
Вопрос 3. Докажите, что если два угла равны, то смежные с ними углы также равны.
Ответ.
Из теоремы 2.1 следует, что если два угла равны, то смежные с ними углы равны.
Допустим, углы (a 1 b) и (c 1 d) равны. Нам нужно доказать, что углы (a 2 b) и (c 2 d) тоже равны.
Сумма смежных углов равна 180°. Из этого следует, что a 1 b + a 2 b = 180° и c 1 d + c 2 d = 180°. Отсюда, a 2 b = 180° — a 1 b и c 2 d = 180° — c 1 d. Так как углы (a 1 b) и (c 1 d) равны, то мы получаем, что a 2 b = 180° — a 1 b = c 2 d. По свойству транзитивности знака равенства следует, что a 2 b = c 2 d. Что и требовалось доказать.
Вопрос 4. Какой угол называется прямым (острым, тупым)?
Ответ. Угол, равный 90°, называется прямым углом.
Угол, меньший 90°, называется острым углом.
Угол, больший 90° и меньший 180°, называется тупым.
Вопрос 5. Докажите, что угол, смежный с прямым, есть прямой угол.
Ответ. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом, есть прямой угол: x + 90° = 180°, x= 180° — 90°, x = 90°.
Вопрос 6. Какие углы называются вертикальными?
Ответ. Два угла называются вертикальными, если стороны одного угла являются дополнительными полупрямыми сторон другого.
Вопрос 7. Докажите, что вертикальные углы равны.
Ответ. Теорема 2.2. Вертикальные углы равны.
Доказательство. Пусть (a 1 b 1) и (a 2 b 2)- данные вертикальные углы (рис. 34). Угол (a 1 b 2) является смежным с углом (a 1 b 1) и с углом (a 2 b 2). Отсюда по теореме о сумме смежных углов заключаем, что каждый из углов (a 1 b 1) и (a 2 b 2) дополняет угол (a 1 b 2) до 180°, т.е. углы (a 1 b 1) и (a 2 b 2) равны. Что и требовалось доказать.
Вопрос 8. Докажите, что если при пересечении двух прямых один из углов прямой, то остальные три угла тоже прямые.
Ответ. Предположим, что прямые AB и CD пересекают друг друга в точке O. Предположим, что угол AOD равен 90°. Так как сумма смежных углов равна 180°, то получаем, что AOC = 180°-AOD = 180°- 90°=90°. Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Угол COB вертикален углу AOD, поэтому они равны. То есть угол COB = 90°. Угол COA вертикален углу BOD, поэтому они равны. То есть угол BOD = 90°. Таким образом, все углы равны 90°, то есть они все – прямые. Что и требовалось доказать.
Вопрос 9. Какие прямые называются перпендикулярными? Какой знак используется для обозначения перпендикулярности прямых?
Ответ. Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Перпендикулярность прямых обозначается знаком \(\perp\). Запись \(a\perp b\) читается: «Прямая a перпендикулярна прямой b».
Вопрос 10. Докажите, что через любую точку прямой можно провести перпендикулярную ей прямую, и только одну.
Ответ. Теорема 2.3. Через каждую прямую можно провести перпендикулярную ей прямую, и только одну.
Доказательство. Пусть a — данная прямая и A — данная точка на ней. Обозначим через a 1 одну из полупрямых прямой a с начальной точкой A (рис. 38). Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Отложим от полупрямой a 1 угол (a 1 b 1), равный 90°. Тогда прямая, содержащая луч b 1 , будет перпендикулярна прямой a.
Допустим, что существует другая прямая, тоже проходящая через точку A и перпендикулярная прямой a. Обозначим через c 1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b 1 .
Углы (a 1 b 1) и (a 1 c 1), равные каждый 90°, отложены в одну полуплоскость от полупрямой a 1 . Но от полупрямой a 1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не быть другой прямой, проходящей через точку A и перпендикулярной прямой a. Теорема доказана.
Вопрос 11. Что такое перпендикуляр к прямой?
Ответ. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра.
Вопрос 12. Объясните, в чём состоит доказательство от противного.
Ответ. Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Способ доказательства, который мы применили в теореме 2.3, называется доказательством от противного. Этот способ доказательства состоит в том, что мы cначала делаем предположение, противоположное тому, что утверждается теоремой. Затем путем рассуждений, опираясь на аксиомы и доказанные теоремы, приходим к выводу, противоречащему либо условию теоремы, либо одной из аксиом, либо доказанной ранее теореме. На этом основании заключаем, что наше предположение было неверным, а значит, верно утверждение теоремы.
Вопрос 13. Что называется биссектрисой угла?
Ответ. Биссектрисой угла называется луч, который исходит из вершины угла, проходит между его сторонами и делит угол пополам.
Углы, у которых одна сторона общая, а другие стороны лежат на одной прямой (на рис. углы 1 и 2 смежные). Рис. к ст. Смежные углы … Большая советская энциклопедия
СМЕЖНЫЕ УГЛЫ — углы, имеющие общую вершину и одну общую сторону, а две др. их стороны лежат на одной прямой … Большая политехническая энциклопедия
См. Угол … Большой Энциклопедический словарь
Угол … Большой Энциклопедический словарь
СМЕЖНЫЕ УГЛЫ, два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла … Научно-технический энциклопедический словарь
См. Угол. * * * СМЕЖНЫЕ УГЛЫ СМЕЖНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь
— (Angles adjacents) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие С. углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через вершину … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
См. Угол … Естествознание. Энциклопедический словарь
Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия
Пара комплементарных углов, дополняющих друг друга до 90 градусов Комплементарные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия
Если два комплементарных угла являются соседними (т.е. имеют общую вершину и разделяются только… … Википедия
Пара дополнительных углов, дополняющих друг друга до 90 градусов Дополнительные углы это пара углов, которые дополняют друг друга до 90 градусов. Если два дополнительных угла являются с … Википедия
Книги
- О доказательстве в геометрии , Фетисов А.И.. Эта книга будет изготовлена в соответствии с Вашим заказом по технологии Print-on-Demand. Однажды, в самом начале учебного года, мне пришлось услышать разговор двух девочек. Старшая из них…
- Комплексная тетрадь для контроля знаний. Геометрия. 7 класс. ФГОС , Бабенко Светлана Павловна, Маркова Ирина Сергеевна. В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия…
Что такое смежный угол
Угол – это геометрическая фигура (рис.1), образованная двумя лучами OA и OB (стороны угла), исходящими из одной точки O (вершина угла).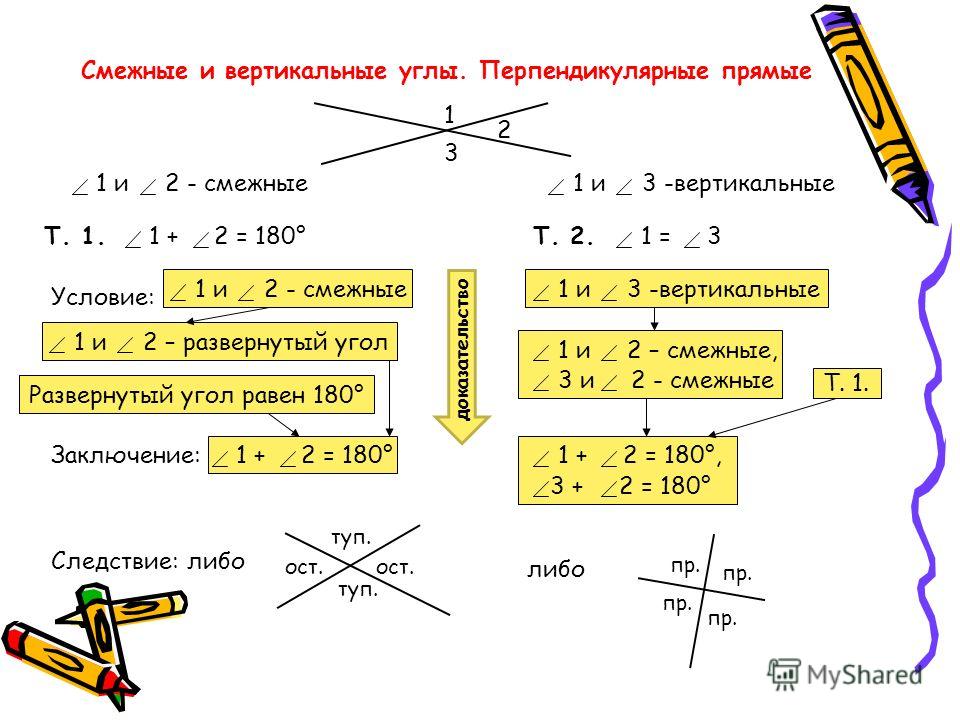
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
рис. 2
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
рис. 3
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки — вершины угла — и двух различных полупрямых, исходящих из этой точки, — сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол — это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.
рис. 4
Связь математики с музыкой
«Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства.»
Г. Нейгауз
Казалось бы, искусство — весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика — самая абстрактная из наук, а музыка — наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых — Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т. е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a: l ,
где а — коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились.
Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
Задание 1.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Задание 2.
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
Задание 3.
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.
Решение задач
1) Даны два угла, относящиеся друг к другу как 1: 2, а смежные с ними — как 7: 5. Нужно найти эти углы.
2) Известно, что один из смежных углов больше другого в 4 раза. Чему равны смежные углы?
Чему равны смежные углы?
3) Необходимо найти смежные углы, при условии, что один из них на 10 градусов больше от второго.
Математический диктант на повторение ранее выученного материала
1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а — через а1 и а2, а прямой b — через b1 i b2.
2) Пользуясь выполненным рисунком, впишите нужные значения и объяснения в места пропусков в тексте:
а) угол 1 и угол …. смежные, поскольку…
б) угол 1 и угол …. вертикальные, поскольку…
в) если угол 1 = 60°, то угол 2 = …, потому что…
г) если угол 1 = 60°, то угол 3 = …, потому что…
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
Назовите эти углы.
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1: 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Вопросы:
- Что такое угол?
- Какие бывают типы углов?
- Какая особенность смежных углов?
Предмети > Математика > Математика 7 класс
Что такое смежный?, значение, смежные углы, решенные примеры, часто задаваемые вопросы в геометрии относится к соседним (бок о бок) элементам друг к другу по форме. Обычно применяется к линиям, дугам или углам. В тригонометрии прилежащей стороной прямоугольного треугольника называется сторона, следующая за углом.
| 1. | Значение соседнего |
2. | Смежные углы |
| 3. | Что такое смежный угол, а что нет? |
| 4. | Решенные примеры |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы о соседнем |
Значение слова «прилегающий»
Значение слова «прилегающий» означает «рядом» или «рядом с». Примером смежности являются два соседних дома. Мы обычно считаем людей на нашей улице своими соседями. Кто тогда наш ближайший сосед? Человек, который живет в доме или квартире рядом с нами. Соседний может относиться к двум вещам, соприкасающимся друг с другом или разделяющим одну и ту же стену или границу. А как насчет двух линий, которые пересекаются в вершине многоугольника? Можно ли считать их смежными сторонами? В треугольниках и других многоугольниках две стороны, которые встречаются в вершине многоугольника, являются смежными.
Смежные углы
В математике соседними могут быть разные вещи, но смежные в основном применяются к отрезкам прямых и углам.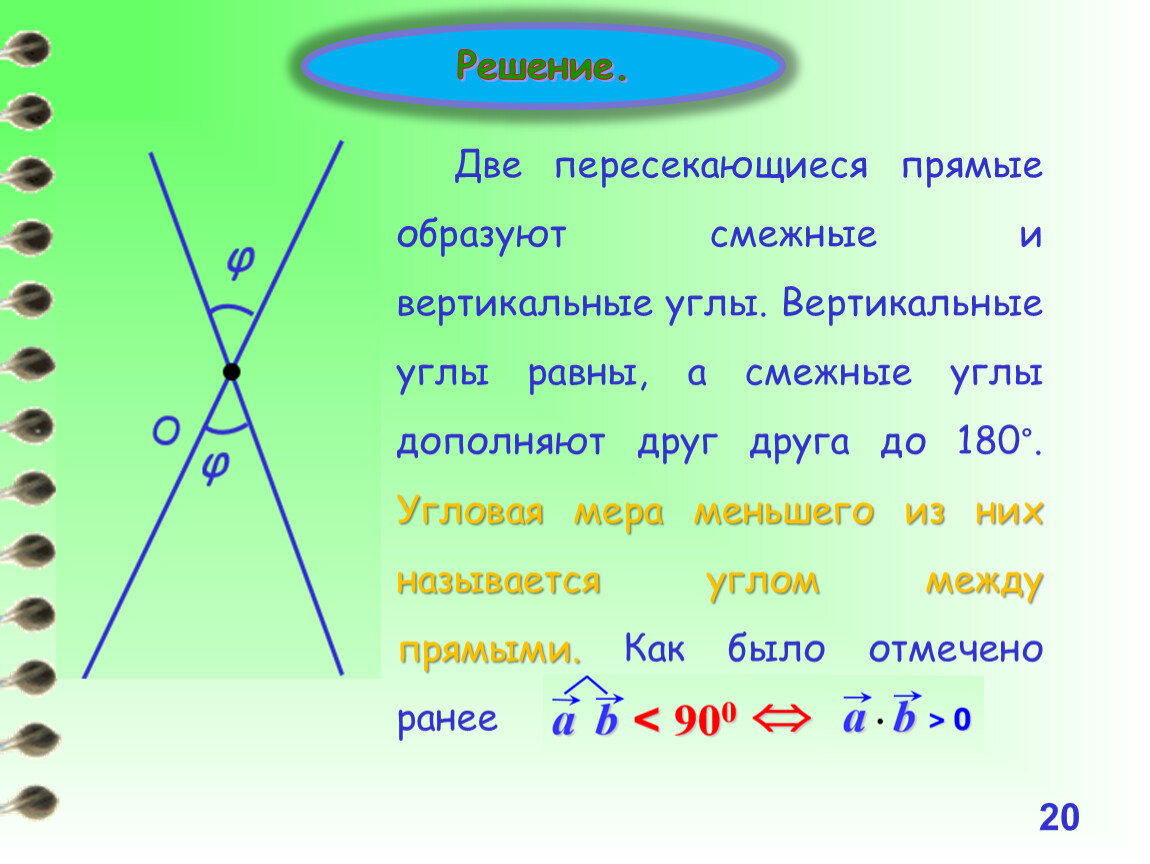 Любые два угла, имеющие общий луч или сторону, общую вершину и внутренние части которых не пересекаются, называются смежными углами. Например, посмотрите на изображение ниже: внутренности ∠ABD и ∠CBD не перекрываются и, следовательно, являются смежными углами.
Любые два угла, имеющие общий луч или сторону, общую вершину и внутренние части которых не пересекаются, называются смежными углами. Например, посмотрите на изображение ниже: внутренности ∠ABD и ∠CBD не перекрываются и, следовательно, являются смежными углами.
Что такое смежный угол, а что нет?
Ниже перечислены несколько важных моментов, касающихся того, что можно считать смежным углом, а что нельзя считать смежным углом, даже если у него одна и та же вершина и сторона.
- Смежные углы имеют общую вершину и сторону, как показано на рисунке ниже
- Углы не считаются смежными, если они имеют только общую вершину, а не сторону
- Углы не считаются смежными углами, если они имеют общую сторону, а не вершину
- Углы не считаются смежными, если углы a и b перекрываются, как показано на рисунке ниже
Статьи по теме на сайте Adjacent
Ознакомьтесь с этими интересными статьями на сайте Adjacent. Нажмите, чтобы узнать больше!
Нажмите, чтобы узнать больше!
- Симметрия
- Уголки
- Дополнительные углы
- Вертикальные углы
- Равные углы
- Дополнительные уголки
Пример 1: Посмотрите на стрелки часов. Образуют ли они пару смежных углов?
Решение:
В данных часах часовая стрелка образует угол с секундной стрелкой, а секундная стрелка образует другой угол с минутной стрелкой. Обе эти пары углов лежат рядом друг с другом и образуют пару смежных углов. Следовательно, стрелки часов образуют пары смежных углов.
Пример 2 : Смежны ли углы, отмеченные цифрами 1 и 2 на следующих рисунках? Обоснуйте свои ответы.
Решение
На данном рисунке
Ясно, что ∠1 и ∠2 имеют общую вершину O и общее плечо OB. У них есть необщие плечи OA и OC по обе стороны от общего плеча OB.
 Итак, ∠1 и ∠2 – смежные углы.
Итак, ∠1 и ∠2 – смежные углы.Да, ∠1 и ∠2 — смежные углы.
Пример 3. Перечислите 5 пар смежных углов на следующем рисунке.
Решение:
Ниже приведены пять пар смежных углов.
Старший № Пары смежных углов 1. ∠AOE, ∠EOC 2. ∠EOC, ∠COB 3. ∠AOC, ∠COB 4. ∠COB, ∠BOD 5. ∠ЕОБ, ∠БПК
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика — это жизненный навык. Помогите своему ребенку усовершенствовать это с помощью реального приложения с Cuemath.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы на соседнем сайте
Что такое определение смежности?
Смежный означает, что две вещи находятся рядом или рядом друг с другом. В классе каждая скамья, на которой сидят 2 ученика, считается смежной. Когда состояния имеют общую границу, мы можем называть их соседними состояниями, поскольку они имеют общую границу и находятся рядом друг с другом. В математике смежный используется для обозначения двух сторон или углов, которые лежат рядом друг с другом, и мы называем их смежными сторонами и смежными углами.
В классе каждая скамья, на которой сидят 2 ученика, считается смежной. Когда состояния имеют общую границу, мы можем называть их соседними состояниями, поскольку они имеют общую границу и находятся рядом друг с другом. В математике смежный используется для обозначения двух сторон или углов, которые лежат рядом друг с другом, и мы называем их смежными сторонами и смежными углами.
Что такое определение смежных углов?
Углы считаются смежными, если два угла имеют общую сторону и вершину и не пересекаются. Смежные углы не обязательно должны быть равными или дополнительными. Между двумя углами не должно быть зазоров или перекрытий, чтобы их можно было рассматривать как смежные углы.
Что такое смежные стороны?
Смежные стороны — это стороны многоугольника, имеющие общую вершину. Например, в треугольнике PQR соседними сторонами являются PQ и QR, поскольку между обеими сторонами лежит общая вершина (то есть Q).
Смежные углы равны?
Смежные углы не всегда должны быть равны. Два различных угла также могут считаться смежными, если они удовлетворяют всем условиям, относящимся к смежным углам. В случае квадрата или прямоугольника смежные углы равны, так как все углы равны 90º.
Два различных угла также могут считаться смежными, если они удовлетворяют всем условиям, относящимся к смежным углам. В случае квадрата или прямоугольника смежные углы равны, так как все углы равны 90º.
Вертикальные углы не являются смежными?
Нет, вертикальные углы всегда несмежные. При пересечении двух прямых образуются вертикальные углы, не являющиеся смежными углами. Эти углы имеют общую вершину, но никогда не имеют общей стороны.
Соседний означает Бок о бок?
Да, смежные означает рядом расположенные, т. е. когда углы расположены рядом друг с другом, имеют одну и ту же вершину и одну и ту же сторону. Прилегающая сторона треугольника — это сторона, ближайшая к углу, а противоположная сторона — это сторона, расположенная напротив угла.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по углам
Рабочие листы по математике и
наглядный учебный план
Что такое перпендикулярные линии? Определение, свойства, примеры 9{\circ})$.
 Термин «перпендикуляр» произошел от латинского слова «perpendicularis», что означает отвес.
Термин «перпендикуляр» произошел от латинского слова «perpendicularis», что означает отвес.Если две прямые AB и CD перпендикулярны, то их можно записать как AB $\bot$ CD. Символ $\bot$ используется для обозначения того, что линии перпендикулярны.
Некоторые примеры: стороны квадрата, стрелки часов, углы доски, окна и символ Красного Креста.
Перпендикулярные линии представлены символом ‘$\bot$’. Предположим, m и n две прямые, пересекающиеся под углом 90 градусов, тогда они перпендикулярны друг другу и представляются как m $\bot$ n . Точка пересечения перпендикулярных прямых называется основанием перпендикуляра.
Шаг 2: Поместите транспортир на линию м так, чтобы его базовая линия совпадала с м , а его центр приходился на точку A. , Возьмите соответствующий радиус и нарисуйте дугу по обе стороны от данной точки.
Шаг 2: Растяните компас шире. Поместите кончик компаса на новые точки и сделайте небольшую дугу над заданной линией. Две новые дуги пересекутся.
Поместите кончик компаса на новые точки и сделайте небольшую дугу над заданной линией. Две новые дуги пересекутся.
Шаг 3 : Используйте линейку, чтобы соединить заданную точку A и точку B, где пересекаются дуги.
Дайте детям возможность наблюдать перпендикулярные линии в объектах или местах вокруг них, например, высокое дерево на земле, электрический столб на тротуаре, железнодорожный перекресток, угол двух соседних стен и высокие здания.
Пример 2: Напишите отношение между сегментами линии, обозначенными стрелкой в каждой фигуре.
Пример 3: Диагонали ромба перпендикулярны друг другу. Сколько прямых углов образовано при пересечении?
Поскольку прямые AC и BD пересекают друг друга под углом 90 градусов, в точке пересечения имеется 4 прямых угла.
$\angle \text{AED} = \angle \text{DEC} = \angle \text{CEB} = \angle \text{BEA} = 90$ градусов
Пример 5: Если AB $\left|\right|$ CD и CD $\left|\right|$ EF. Что вы можете сказать об AB и EF?
Что вы можете сказать об AB и EF?
Если две прямые перпендикулярны одной и той же прямой, то эти две прямые параллельны друг другу.
Нет, эти линии не перпендикулярны, потому что они не пересекаются под прямым углом.
Практические задачи на перпендикулярных прямых
1
Определите пару перпендикулярных отрезков заданной формы.
AG и AB
FE и ED
FE и CD
CB и AB
Правильный ответ: FE и ED
FE и ED являются перпендикулярными отрезками.
2
Каждый объект имеет выделенную пару линий. Какой из выделенных парой линий этого объекта не показывает перпендикулярных линий?
A
B
C
D
Правильный ответ: A
Свеча. Его выделенная пара линий показывает параллельные линии.
3
В какое время стрелки часов будут перпендикулярны друг другу?
12 часов
6 часов
3 часа
5 часов
Правильный ответ: 3 часа
В 3 часа стрелки часов находятся под углом 90 градусов к друг друга. Значит, они перпендикулярны друг другу.
4
Сколько прямых перпендикулярно прямой CD на данном рисунке?
1
2
3
4
Правильный ответ: 3
Линия PQ, линия RS и линия TU перпендикулярны CD. Итак, на данном рисунке перпендикулярны прямой CD 3 прямые.
5
В какое время стрелки часов будут перпендикулярны?
15:40
16:00
09:00
10:10
Правильный ответ: 09:00
Стрелки часов пересекаются под прямым углом, когда время 9: 00 утра.
6
Перпендикулярные линии пересекаются друг с другом под углом _____.
 9{\circ}$ углы известны как прямые углы.
9{\circ}$ углы известны как прямые углы.7
В каком из следующих объектов мы можем найти перпендикулярные линии?
Мяч
Шляпа на день рождения
Банан
Ноутбук
Правильный ответ: Ноутбук
Края ноутбука пересекаются под прямым углом. Все остальные изображения не имеют линий, пересекающихся под прямым углом.
Часто задаваемые вопросы о перпендикулярных линиях
Что такое перпендикулярные линии?
9{\circ}$ угол друг с другом. Перпендикулярные прямые – это те прямые, которые пересекают друг друга под углом 90 градусов.Должны ли пересекаться перпендикулярные линии?
Эти линии всегда пересекаются под прямым углом.
Что такое перпендикулярный символ?
Символ перпендикуляра $\left|\right|$. Он используется между двумя линиями, чтобы показать, что они перпендикулярны друг другу.
В чем разница между перпендикулярными линиями и параллельными линиями? 9{\circ}$ .


 Итак, ∠1 и ∠2 – смежные углы.
Итак, ∠1 и ∠2 – смежные углы.

 Но аналогично нашему разумному тренеру
поступит и любой другой рационально
мыслящий экономический агент. Сначала
мы включаем в производство самые лучшие
ресурсы, затем — лучшие из оставшихся,
итд.
Но аналогично нашему разумному тренеру
поступит и любой другой рационально
мыслящий экономический агент. Сначала
мы включаем в производство самые лучшие
ресурсы, затем — лучшие из оставшихся,
итд. 4.2.
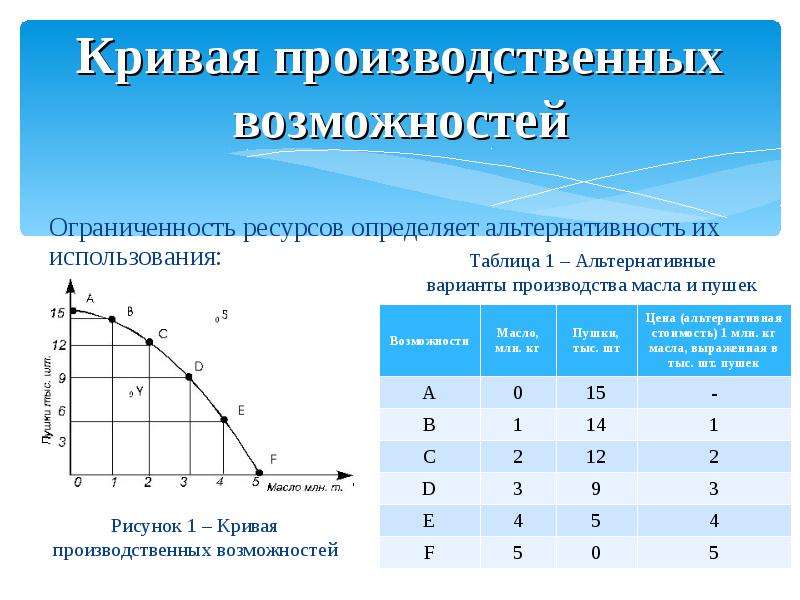
КПВ – убывающая линейная функция
4.2.
КПВ – убывающая линейная функция
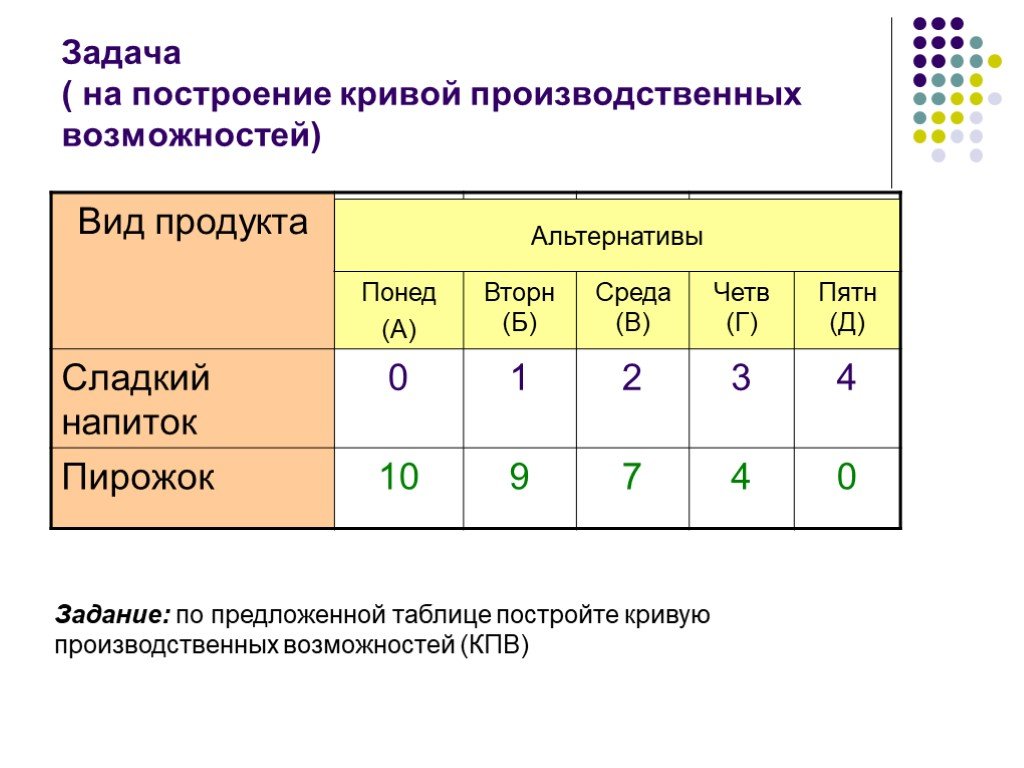 Эссе можно писать, сидя по двое
за партой, тест – строго по одному за
партой;
Эссе можно писать, сидя по двое
за партой, тест – строго по одному за
партой; Итого «производственные» возможности
класса составляют 10 эссе за час.
Итого «производственные» возможности
класса составляют 10 эссе за час. Нерационально? Естественно.
Следовательно – в экономической тео-
Нерационально? Естественно.
Следовательно – в экономической тео- Еще на двух грядках по прихоти
тетушки Марфы можно выращивать только
укроп, а на двух оставшихся участках –
петрушку (вот такая она капризная, ваша
тетушка). Предположим, что на каждой
грядке может вырасти 1 килограмм укропа
или 2 килограмма петрушки. Построим КПВ
для всего участка. Обратите внимание,
что тетушка Марфа не заставляет вас
становиться «счастливым фермером» и
засаживать все грядки, а лишь разрешает выращивать урожай, то есть на КПВ мы
показываем не результат, а возможности
производства на этом участке.
Еще на двух грядках по прихоти
тетушки Марфы можно выращивать только
укроп, а на двух оставшихся участках –
петрушку (вот такая она капризная, ваша
тетушка). Предположим, что на каждой
грядке может вырасти 1 килограмм укропа
или 2 килограмма петрушки. Построим КПВ
для всего участка. Обратите внимание,
что тетушка Марфа не заставляет вас
становиться «счастливым фермером» и
засаживать все грядки, а лишь разрешает выращивать урожай, то есть на КПВ мы
показываем не результат, а возможности
производства на этом участке.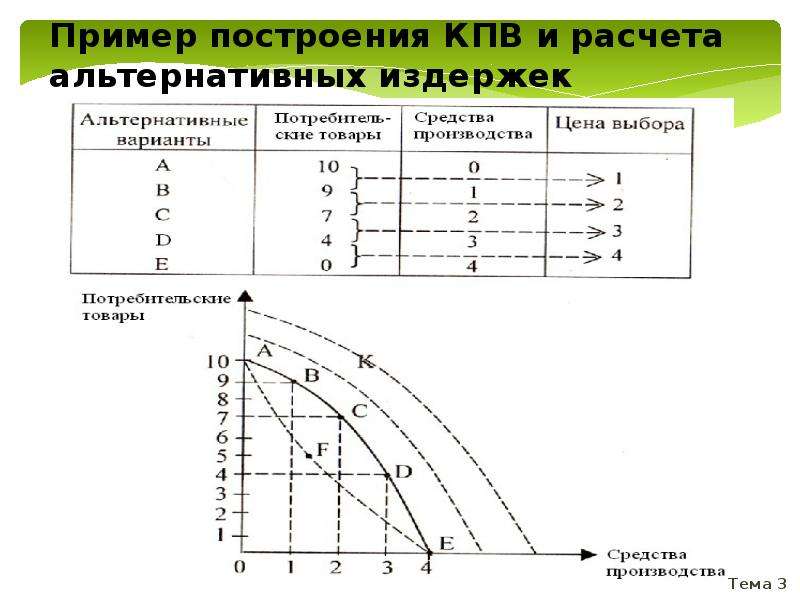 Если
мы не будем делать этого, укропа будет
меньше, но петрушки от этого
Если
мы не будем делать этого, укропа будет
меньше, но петрушки от этого


 Необходимо следовать вооружению по научной теории марксизма, крепко придерживать этого мощного политического преимущества, углублять обмены и взаимообучение, строить прочную идеологическую защиту и объединить усилия для продвижения дела социализма. Необходимо придерживаться подхода, ориентированного на народ, совершенствовать стратегии развития и объединение проектов, содействовать связыванию объектов инфраструктуры и связи между народами, укреплять традиционное дружественное обучение, чтобы укрепить фундамент общественного мнения для долгосрочного развития отношений между двумя странами. Необходимо сделать все возможное для укрепления безопасности правящей партии, поддержания национальной стабильности и развития, твердо придерживаться благородных идеалов приверженности делу мира и прогресса, укреплять сотрудничество в международных делах, решительно противостоять гегемонизму и лагерной конфронтации, сохранять результаты поддержания регионального мира и развития, объединить усилия для продвижения строительства сообщества единой судьбы человечества.
Необходимо следовать вооружению по научной теории марксизма, крепко придерживать этого мощного политического преимущества, углублять обмены и взаимообучение, строить прочную идеологическую защиту и объединить усилия для продвижения дела социализма. Необходимо придерживаться подхода, ориентированного на народ, совершенствовать стратегии развития и объединение проектов, содействовать связыванию объектов инфраструктуры и связи между народами, укреплять традиционное дружественное обучение, чтобы укрепить фундамент общественного мнения для долгосрочного развития отношений между двумя странами. Необходимо сделать все возможное для укрепления безопасности правящей партии, поддержания национальной стабильности и развития, твердо придерживаться благородных идеалов приверженности делу мира и прогресса, укреплять сотрудничество в международных делах, решительно противостоять гегемонизму и лагерной конфронтации, сохранять результаты поддержания регионального мира и развития, объединить усилия для продвижения строительства сообщества единой судьбы человечества.
 Вьетнам всегда ставит в приоритет развитие дружественного сотрудничества с Китаем, твердо придерживается принципа одного Китая и поддерживает процесс воссоединения Китая. Вьетнамская сторона готова сотрудничать с Китаем для реализации важных консенсусов между высшими руководителями двух партий, придерживаться политики «курса 16 иероглифов» и духа «четырех хороших отношений», тесных контактов на высоком уровне между двумя партиями, продвигать «Два коридора и один круг» и совместное строительство «Одного пояса, одного пути», а также содействовать постоянному развитию отношений между двумя партиями и дела социализма. Вьетнамская сторона решительно поддерживает важные глобальные инициативы, выдвинутые генеральным секретарем Си Цзиньпином, поддерживает проведение в Китае третьего Форума международного сотрудничества в рамках «Одного пояса, одного пути» и надеется на укрепление регионального и международного сотрудничества с Китаем в целях содействия миру и развитию в регионе и во всем мире.
Вьетнам всегда ставит в приоритет развитие дружественного сотрудничества с Китаем, твердо придерживается принципа одного Китая и поддерживает процесс воссоединения Китая. Вьетнамская сторона готова сотрудничать с Китаем для реализации важных консенсусов между высшими руководителями двух партий, придерживаться политики «курса 16 иероглифов» и духа «четырех хороших отношений», тесных контактов на высоком уровне между двумя партиями, продвигать «Два коридора и один круг» и совместное строительство «Одного пояса, одного пути», а также содействовать постоянному развитию отношений между двумя партиями и дела социализма. Вьетнамская сторона решительно поддерживает важные глобальные инициативы, выдвинутые генеральным секретарем Си Цзиньпином, поддерживает проведение в Китае третьего Форума международного сотрудничества в рамках «Одного пояса, одного пути» и надеется на укрепление регионального и международного сотрудничества с Китаем в целях содействия миру и развитию в регионе и во всем мире.

 «Мы очень рады, что компания Competitive Power Ventures выбрала округ Доддридж для реализации этого инновационного проекта, и надеемся на продолжение сотрудничества с этой дальновидной компанией».
«Мы очень рады, что компания Competitive Power Ventures выбрала округ Доддридж для реализации этого инновационного проекта, и надеемся на продолжение сотрудничества с этой дальновидной компанией». Мы ценим тяжелую работу всех участников и с нетерпением ждем продолжения работы с округом Доддридж и штатом, чтобы продвинуть этот монументальный проект в процессы получения разрешений и регулирования».
Мы ценим тяжелую работу всех участников и с нетерпением ждем продолжения работы с округом Доддридж и штатом, чтобы продвинуть этот монументальный проект в процессы получения разрешений и регулирования».
 использовать улавливание и хранение углерода, чтобы воспользоваться государственной налоговой льготой.
использовать улавливание и хранение углерода, чтобы воспользоваться государственной налоговой льготой.
 Джастис сказал, что электростанция поддержит существующие производственные и промышленные компании штата, а также принесет будущие инвестиции.
Джастис сказал, что электростанция поддержит существующие производственные и промышленные компании штата, а также принесет будущие инвестиции.

 Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ): В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего. е.
е. е.
е.
 е. P = 2 n), можно произвести по более простым алгоритмам. Получим эти правила.
е. P = 2 n), можно произвести по более простым алгоритмам. Получим эти правила.
 10101111
10101111
 Это преобразование выполняется с использованием показателей степени; формат преобразованного значения будет следующим: a.bcdef…×10 n , где a, b, c, d, e, f и т. д. – цифры, а n – положительное или отрицательное целое число.
Это преобразование выполняется с использованием показателей степени; формат преобразованного значения будет следующим: a.bcdef…×10 n , где a, b, c, d, e, f и т. д. – цифры, а n – положительное или отрицательное целое число. . Научная нотация упрощает работу.
. Научная нотация упрощает работу.
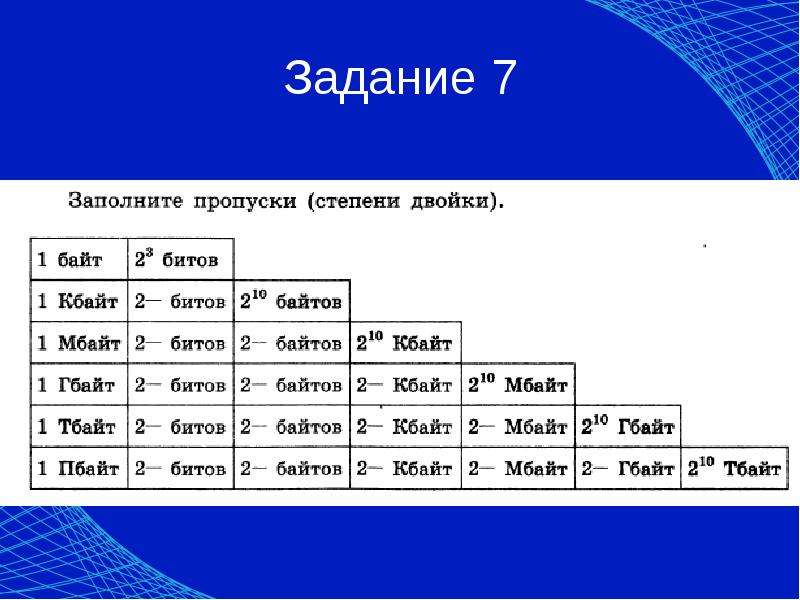
 И 100 = 10 2 .
И 100 = 10 2 . Поскольку показатель степени 10 равен 12, мне нужно переместить десятичную точку на двенадцать разрядов.
Поскольку показатель степени 10 равен 12, мне нужно переместить десятичную точку на двенадцать разрядов. е. числовая часть, а не десятичная часть в степени) будет равен «4,36». Итак, я посчитаю, на сколько знаков десятичная точка должна переместиться, чтобы попасть из того места, где она сейчас, туда, где она должна быть:
е. числовая часть, а не десятичная часть в степени) будет равен «4,36». Итак, я посчитаю, на сколько знаков десятичная точка должна переместиться, чтобы попасть из того места, где она сейчас, туда, где она должна быть:
 Если у вас небольшой число в десятичной форме (меньше 1 по модулю), тогда степень отрицательна для научной записи; если это большое десятичное число (больше 1 по абсолютной величине), то показатель степени положителен для научного представления.
Если у вас небольшой число в десятичной форме (меньше 1 по модулю), тогда степень отрицательна для научной записи; если это большое десятичное число (больше 1 по абсолютной величине), то показатель степени положителен для научного представления.
 Теперь мне нужно иметь дело с 2,6 умножить на 9,2, не забывая перевести произведение в экспоненциальное представление:
Теперь мне нужно иметь дело с 2,6 умножить на 9,2, не забывая перевести произведение в экспоненциальное представление: 3) (10 −1 ) (10 −1 )
3) (10 −1 ) (10 −1 )  {-3}\hfill \end{array}[/latex]
{-3}\hfill \end{array}[/latex] Трудно понять, насколько велики миллиард или триллион. Вот способ, который поможет вам подумать об этом.
Трудно понять, насколько велики миллиард или триллион. Вот способ, который поможет вам подумать об этом.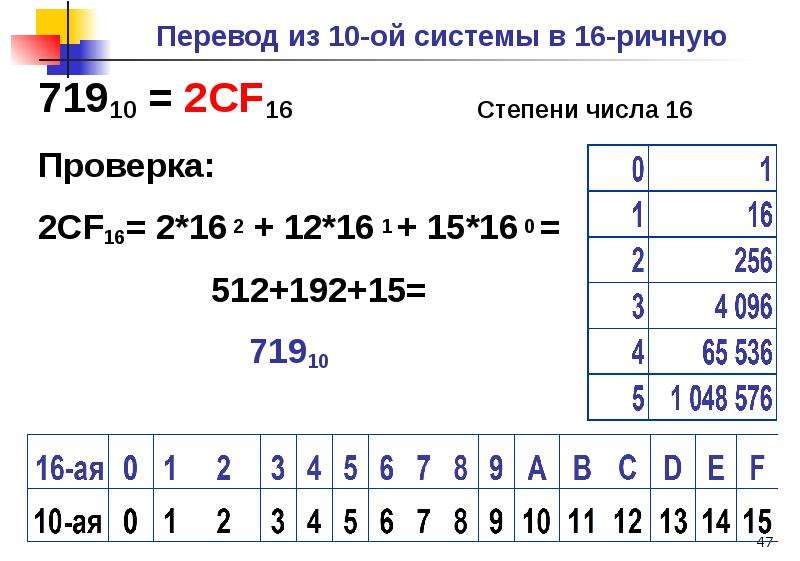 Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.
Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.

 000000000000000793[/латекс]
000000000000000793[/латекс] Когда показатель степени был положительным, десятичная дробь сдвигалась вправо. Когда показатель степени был отрицательным, десятичная точка перемещалась влево. 9{-8}=\underset{\longleftarrow}{0.00000005.}=0.00000005\end{массив}[/latex]
Когда показатель степени был положительным, десятичная дробь сдвигалась вправо. Когда показатель степени был отрицательным, десятичная точка перемещалась влево. 9{-8}=\underset{\longleftarrow}{0.00000005.}=0.00000005\end{массив}[/latex]
 Квадратный корень из 675, округленный до 9 знаков после запятой, равен 25,980762114. Это положительное решение уравнения x 2 = 675. Мы можем выразить квадратный корень из 675 в его низшей радикальной форме как 15 √3.
Квадратный корень из 675, округленный до 9 знаков после запятой, равен 25,980762114. Это положительное решение уравнения x 2 = 675. Мы можем выразить квадратный корень из 675 в его низшей радикальной форме как 15 √3. Таким образом, квадратный корень из 675 = √675 = 15 √3 = 25,98076211353316.
Таким образом, квадратный корень из 675 = √675 = 15 √3 = 25,98076211353316.
 е.
х = ±√675
е.
х = ±√675 
 Мы знаем, что квадратный корень из 675 равен 25,981. Следовательно, 10 + 17 √675 = 10 + 17 × 25,981 = 10 + 441,673 = 451,673
Мы знаем, что квадратный корень из 675 равен 25,981. Следовательно, 10 + 17 √675 = 10 + 17 × 25,981 = 10 + 441,673 = 451,673
 1*)
1*)
 А вот матрицы и равны, согласно определению 5.
А вот матрицы и равны, согласно определению 5. Элементы матрицы заключаются
в круглые и квадратные скобки, обозначаются
они строчными буквами с индексом ij,
где i
– строка, j
– столбец. Элемент матрицы находится
на пересечении i-строки
и j-столбца.
Элементы матрицы заключаются
в круглые и квадратные скобки, обозначаются
они строчными буквами с индексом ij,
где i
– строка, j
– столбец. Элемент матрицы находится
на пересечении i-строки
и j-столбца.
 Матрица А называется согласованной
с матрицей В, если число столбцов матрицы
А равно числу строк матрицы В. Если
матрица А и В квадратные, то они всегда
взаимно-согласованы.
Матрица А называется согласованной
с матрицей В, если число столбцов матрицы
А равно числу строк матрицы В. Если
матрица А и В квадратные, то они всегда
взаимно-согласованы. (А*В)т = Ат*Вт,
если матрицы согласованы между собой.
(А*В)т = Ат*Вт,
если матрицы согласованы между собой. пункт 2, смысл 3 штампа) или штамп
пункт 2, смысл 3 штампа) или штамп одновременный смысл 2) линейных уравнений), которые можно комбинировать для образования сумм и произведений. с аналогичными массивами, имеющими соответствующее количество строк и столбцов
одновременный смысл 2) линейных уравнений), которые можно комбинировать для образования сумм и произведений. с аналогичными массивами, имеющими соответствующее количество строк и столбцов И матрица был хорошим выбором в качестве названия реальности, в которой живут все люди, в известной серии научно-фантастических фильмов.
И матрица был хорошим выбором в качестве названия реальности, в которой живут все люди, в известной серии научно-фантастических фильмов. Чтобы понять почему, рассмотрим конкретный набор из 12 чисел в матрице из трех строк и четырех столбцов.
— Джон Маккормик, , Fortune , 9 мая 2023 г.
Заставляя лучи света смешиваться и мешать друг другу, чип способен выполнять матричных умножений на и, таким образом, реализовывать фотонную нейронную сеть.
— IEEE Spectrum , 5 мая 2023 г.
Продолжая традицию обновления решетки радиатора, Flying Spur Speed и S заменяют вертикальную решетку радиатора классической матрицей Bentley .
— Джек Фицджеральд, Автомобиль и водитель , 28 апреля 2023 г.
Эта задача, известная как прогрессивные матрицы Равена , представляет изображения геометрических объектов, скажем, в сетке 3 на 3.
— Анил Анантасвами, 9 лет.
Чтобы понять почему, рассмотрим конкретный набор из 12 чисел в матрице из трех строк и четырех столбцов.
— Джон Маккормик, , Fortune , 9 мая 2023 г.
Заставляя лучи света смешиваться и мешать друг другу, чип способен выполнять матричных умножений на и, таким образом, реализовывать фотонную нейронную сеть.
— IEEE Spectrum , 5 мая 2023 г.
Продолжая традицию обновления решетки радиатора, Flying Spur Speed и S заменяют вертикальную решетку радиатора классической матрицей Bentley .
— Джек Фицджеральд, Автомобиль и водитель , 28 апреля 2023 г.
Эта задача, известная как прогрессивные матрицы Равена , представляет изображения геометрических объектов, скажем, в сетке 3 на 3.
— Анил Анантасвами, 9 лет. 0095 Журнал Quanta , 13 апреля 2023 г.
Показатели вербального рассуждения, матричных рассуждений, рассуждений и рядов букв и чисел снизились, но, что интересно, баллы по пространственному мышлению выросли.
— Тим Ньюкомб, Popular Mechanics , 9 апреля 2023 г.
Лидерство требует установления четкого набора этических норм и стандартов для построения матрицы принятия решений, которой можно следовать на любой ступени корпоративной лестницы.
— Крис Кардинал, 9 лет0095 Кварц , 27 марта 2023 г.
Сплитерс говорит, что осколочная матрица в Шахед-131 не была сделана по тому же стандарту, что и остальная часть устройства.
— Дэвид Хэмблинг, Popular Mechanics , 24 февраля 2023 г.
Узнать больше
0095 Журнал Quanta , 13 апреля 2023 г.
Показатели вербального рассуждения, матричных рассуждений, рассуждений и рядов букв и чисел снизились, но, что интересно, баллы по пространственному мышлению выросли.
— Тим Ньюкомб, Popular Mechanics , 9 апреля 2023 г.
Лидерство требует установления четкого набора этических норм и стандартов для построения матрицы принятия решений, которой можно следовать на любой ступени корпоративной лестницы.
— Крис Кардинал, 9 лет0095 Кварц , 27 марта 2023 г.
Сплитерс говорит, что осколочная матрица в Шахед-131 не была сделана по тому же стандарту, что и остальная часть устройства.
— Дэвид Хэмблинг, Popular Mechanics , 24 февраля 2023 г.
Узнать больше Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.
Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах. Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/matrix. По состоянию на 2 июня 2023 г. Ссылка на копию
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/matrix. По состоянию на 2 июня 2023 г. Ссылка на копию com: Энциклопедическая статья о матрице
com: Энциклопедическая статья о матрице 

 t \cdot y \]
t \cdot y \]
 Конечно, альтернативным выражением для него является
Конечно, альтернативным выражением для него является


 Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить скалярное произведение, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычислить онлайн скалярное произведение векторов».
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить скалярное произведение, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вычислить онлайн скалярное произведение векторов». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить онлайн скалярное произведение векторов. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить скалярное произведение векторов).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить онлайн скалярное произведение векторов. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить скалярное произведение векторов).
 2`.
2`. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.

 Эти компоненты соответствуют измерениям x, y и z в трехмерном евклидовом пространстве (второй вектор).
Эти компоненты соответствуют измерениям x, y и z в трехмерном евклидовом пространстве (второй вектор).
 Калькулятор
Калькулятор
 На сайте представлено много математических онлайн калькуляторов, которые в режиме реального времени (онлайн) решают задачи + работает форум, на котором всегда можно задать вопрос. Наша помощь дистанционна и онлайн, то есть ответ на вопрос или помощь в решении задачи Вы получите очень быстро!
На сайте представлено много математических онлайн калькуляторов, которые в режиме реального времени (онлайн) решают задачи + работает форум, на котором всегда можно задать вопрос. Наша помощь дистанционна и онлайн, то есть ответ на вопрос или помощь в решении задачи Вы получите очень быстро! На них предложены одни и те же решения уравнений, найдены одинаковые интегралы, производные, рассчитаны похожие треугольники. Зачем нам 15 одинаковых сайтов?
На них предложены одни и те же решения уравнений, найдены одинаковые интегралы, производные, рассчитаны похожие треугольники. Зачем нам 15 одинаковых сайтов?

 Модули можно изучать по порядку или выбирать только те, что вам нужны.
Модули можно изучать по порядку или выбирать только те, что вам нужны.
 Но сейчас есть стимул подтянуть знания. Нравится подача материала с историями и элементами игры. Лично у меня сложность в том, что я тороплюсь всегда, хотя никто в шею не гонит, не внимательно читаю условия и потому даю неверные ответы. Буду дополнительно тренировать внимательность.
Но сейчас есть стимул подтянуть знания. Нравится подача материала с историями и элементами игры. Лично у меня сложность в том, что я тороплюсь всегда, хотя никто в шею не гонит, не внимательно читаю условия и потому даю неверные ответы. Буду дополнительно тренировать внимательность. Еще мне очень нравятся задачи на настоящих примерах не только из практики (аналитиков, маркетологов и проч.), но и из жизни, про размеры планет, про разные места и города, очень познавательно! Ценю и этот материал. Часто хожу по ссылкам на доп курсы. Например, прошла тест по английскому (не знала, что у ЯП есть такие курсы…). Присмотрела себе курс Python-разработчика, позже пройду пробный. Сложностей у меня нет. Прохожу курс в своем темпе, мозг доволен! Рекомендовала этот курс знакомым, планирую купить уже платный вариант. В том числе, интересно как пойдёт развиваться история героев. Отличная идея в курсе с этой историей. Спасибо!
Еще мне очень нравятся задачи на настоящих примерах не только из практики (аналитиков, маркетологов и проч.), но и из жизни, про размеры планет, про разные места и города, очень познавательно! Ценю и этот материал. Часто хожу по ссылкам на доп курсы. Например, прошла тест по английскому (не знала, что у ЯП есть такие курсы…). Присмотрела себе курс Python-разработчика, позже пройду пробный. Сложностей у меня нет. Прохожу курс в своем темпе, мозг доволен! Рекомендовала этот курс знакомым, планирую купить уже платный вариант. В том числе, интересно как пойдёт развиваться история героев. Отличная идея в курсе с этой историей. Спасибо! Модули «Числа», «Дроби» и «Алгебра» построены по нарастанию сложности.
Модули «Числа», «Дроби» и «Алгебра» построены по нарастанию сложности.

 Но есть сообщество студентов, в котором можно задать вопрос по теории или задаче.
Но есть сообщество студентов, в котором можно задать вопрос по теории или задаче. Это не все. После решения вашей проблемы Math Solver предлагает множество вариантов продолжения обучения с помощью дополнительных материалов, таких как викторины, рабочие листы и видеоуроки.
Это не все. После решения вашей проблемы Math Solver предлагает множество вариантов продолжения обучения с помощью дополнительных материалов, таких как викторины, рабочие листы и видеоуроки.
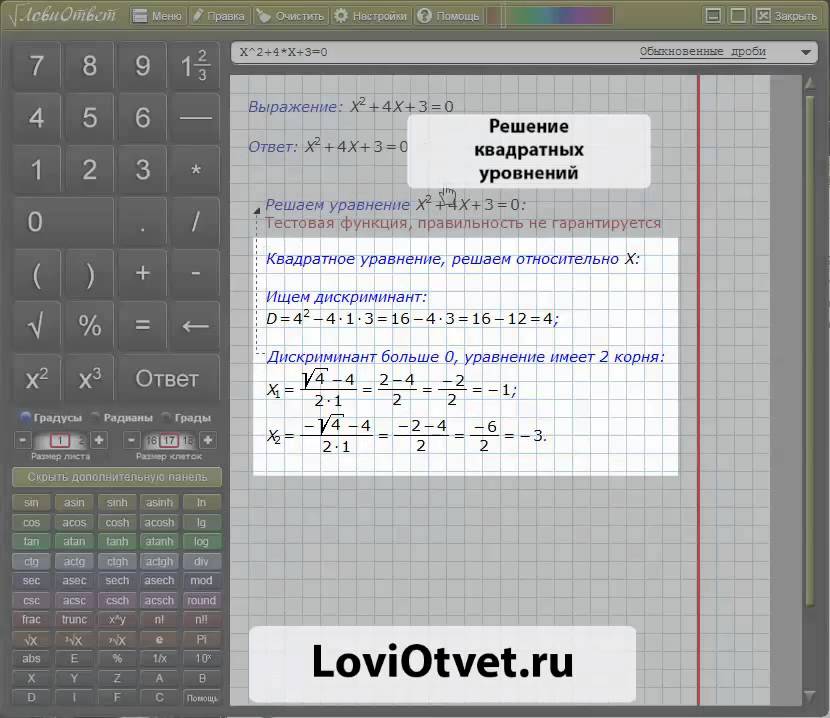 Пожалуйста, отправьте нам отзыв, если что-то работает не так или есть что-то, что вы хотели бы добавить. Мы слушаем! Вы можете оставить нам сообщение в Твиттере, используя #EdgeEDU, #EdgeMathSolver или в Edge, выбрав меню «…» > «Справка и отзывы» > «Отправить отзыв », чтобы оставить отзыв.
Пожалуйста, отправьте нам отзыв, если что-то работает не так или есть что-то, что вы хотели бы добавить. Мы слушаем! Вы можете оставить нам сообщение в Твиттере, используя #EdgeEDU, #EdgeMathSolver или в Edge, выбрав меню «…» > «Справка и отзывы» > «Отправить отзыв », чтобы оставить отзыв. 
 )
)  Photomath также предоставляет пошаговое руководство по решению каждой проблемы». — Huffington Post
Photomath также предоставляет пошаговое руководство по решению каждой проблемы». — Huffington Post com
com Photomath позволяет навести камеру на проблему, и на экране мгновенно появится пошаговое объяснение (и ответ!) Трехзначное умножение? Фотомат получил это. Линейные и квадратные неравенства? Без проблем.
Photomath позволяет навести камеру на проблему, и на экране мгновенно появится пошаговое объяснение (и ответ!) Трехзначное умножение? Фотомат получил это. Линейные и квадратные неравенства? Без проблем. Это полезно, если вы поняли, что написали уравнение неправильно, потому что вы можете просто перейти прямо к части калькулятора и исправить его, так как все части уравнения, которые приложение увидело на фотографии, сразу же помещаются в калькулятор. Лучшая часть, на мой взгляд, — это последняя функция, где она точно сообщает вам, как она решила уравнение, и даже позволяет вам просматривать каждый шаг и дает вам краткое, но хорошее объяснение того, что происходит на шаге. Если вы также прокрутите вниз, находясь в той же функции, если вы сфотографировали уравнение, которое нужно изобразить в виде графика, вы действительно сможете увидеть уравнение, построенное для вас. Это очень хорошее приложение, и я НАСТОЯТЕЛЬНО рекомендую.
Это полезно, если вы поняли, что написали уравнение неправильно, потому что вы можете просто перейти прямо к части калькулятора и исправить его, так как все части уравнения, которые приложение увидело на фотографии, сразу же помещаются в калькулятор. Лучшая часть, на мой взгляд, — это последняя функция, где она точно сообщает вам, как она решила уравнение, и даже позволяет вам просматривать каждый шаг и дает вам краткое, но хорошее объяснение того, что происходит на шаге. Если вы также прокрутите вниз, находясь в той же функции, если вы сфотографировали уравнение, которое нужно изобразить в виде графика, вы действительно сможете увидеть уравнение, построенное для вас. Это очень хорошее приложение, и я НАСТОЯТЕЛЬНО рекомендую.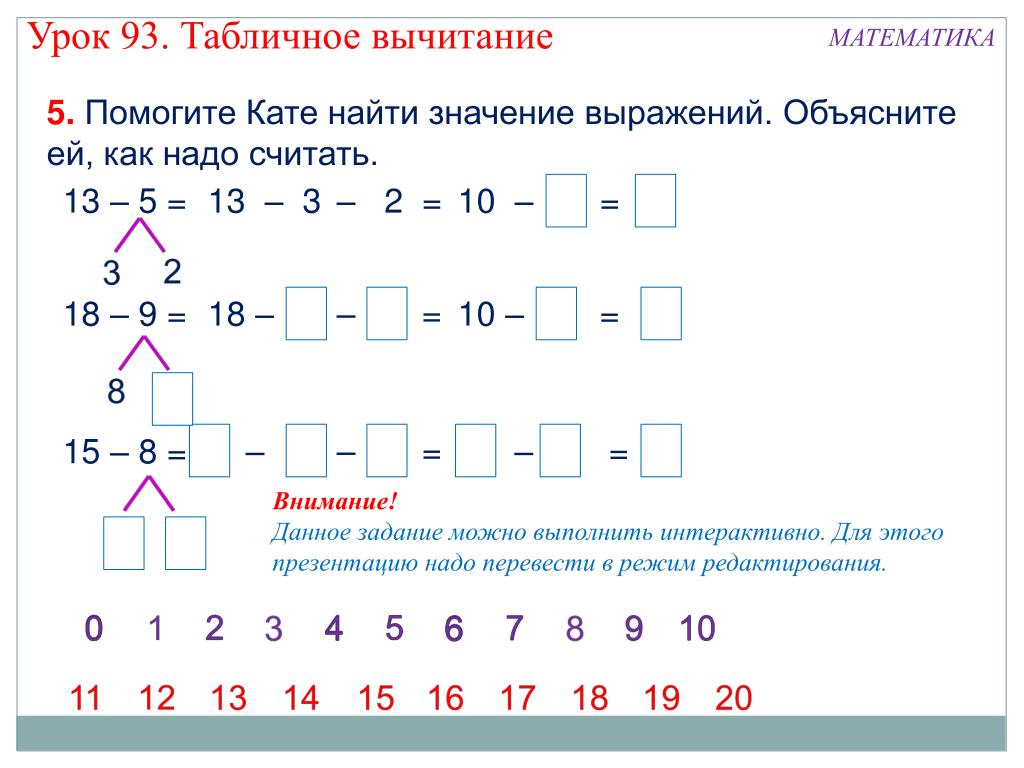 Хотели бы вы присоединиться к этому пулу и в конечном итоге получить шанс дать показания для прессы? Напишите нам по адресу
Хотели бы вы присоединиться к этому пулу и в конечном итоге получить шанс дать показания для прессы? Напишите нам по адресу  Я мог видеть, правильно или неправильно я понял это, и если я ошибался, Photo Math разложил задачу для меня, чтобы я мог лучше понять ее. Это приложение помогло мне лучше понять математику и помогает выполнять сложные домашние задания. (Это приложение прекрасно, если вы уже решили задачу и не жульничаете.) Не устанавливайте это приложение только для того, чтобы получить ответы на все свои математические задачи. В целом у приложения не так много проблем, оно не глючит и не зависает. В целом, мне нравится это приложение, и я рекомендую его многим ученикам на уроках математики! Они тоже это любят!
Я мог видеть, правильно или неправильно я понял это, и если я ошибался, Photo Math разложил задачу для меня, чтобы я мог лучше понять ее. Это приложение помогло мне лучше понять математику и помогает выполнять сложные домашние задания. (Это приложение прекрасно, если вы уже решили задачу и не жульничаете.) Не устанавливайте это приложение только для того, чтобы получить ответы на все свои математические задачи. В целом у приложения не так много проблем, оно не глючит и не зависает. В целом, мне нравится это приложение, и я рекомендую его многим ученикам на уроках математики! Они тоже это любят!
 Ибо его подстановка даёт бессмыслицу. Его мы просто отбрасываем. Окончательный корень один.
Ибо его подстановка даёт бессмыслицу. Его мы просто отбрасываем. Окончательный корень один. Или которые разрешены для данного примера.
Или которые разрешены для данного примера. В нашей теме такое действие всего одно — деление. Нельзя делить на ноль. Есть ещё запреты в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках.
В нашей теме такое действие всего одно — деление. Нельзя делить на ноль. Есть ещё запреты в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках. Осмотрев, мы сразу замечаем операцию деления на х+1.
Осмотрев, мы сразу замечаем операцию деления на х+1. «
«

 До упора. Переписать уравнение с учётом этого факта.
До упора. Переписать уравнение с учётом этого факта. До упора. Переписать пример с учётом этого факта.
До упора. Переписать пример с учётом этого факта.
 Нужно ещё найти иксы, которые обеспечивают эти железные требования. ОДЗ ведь к иксам относится, а не к кусочкам примера…
Нужно ещё найти иксы, которые обеспечивают эти железные требования. ОДЗ ведь к иксам относится, а не к кусочкам примера…
 )
) Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Получить решения (кандидаты в ответ).
Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Получить решения (кандидаты в ответ). Самое время вспомнить про ОДЗ. Про самый последний пункт:
Самое время вспомнить про ОДЗ. Про самый последний пункт: Понимание всегда побеждает механическую память.)
Понимание всегда побеждает механическую память.) И всё получится. Я в вас верю!)
И всё получится. Я в вас верю!) В частности, решением уравнения 0/g(x)=0 является любое число из ОДЗ для этого уравнения, а уравнение C/g(x)=0, где С – отличное от нуля число, не имеет решений.
В частности, решением уравнения 0/g(x)=0 является любое число из ОДЗ для этого уравнения, а уравнение C/g(x)=0, где С – отличное от нуля число, не имеет решений.
 Очевидно, что равенство 0/g(x0)=0 имеет смысл тогда и только тогда, когда x0 принадлежит ОДЗ для уравнения 0/g(x)=0. Значит, решение уравнения 0/g(x)=0 есть ОДЗ для этого уравнения.
Очевидно, что равенство 0/g(x0)=0 имеет смысл тогда и только тогда, когда x0 принадлежит ОДЗ для уравнения 0/g(x)=0. Значит, решение уравнения 0/g(x)=0 есть ОДЗ для этого уравнения.

 А это равенство означает, что x0 – корень уравнения f(x)/g(x)=0.
А это равенство означает, что x0 – корень уравнения f(x)/g(x)=0.

 Ими мы закроем все три типичные ситуации.
Ими мы закроем все три типичные ситуации.
 Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.
Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер. — М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.

 У вас есть решение, когда вы получаете уравнение x = некоторое значение.
У вас есть решение, когда вы получаете уравнение x = некоторое значение. Помните, что дроби подразумевают деление, поэтому вы можете думать о [latex]\frac{k}{10}[/latex] как о переменной k делится на 10. Чтобы «отменить» деление, вы можете использовать умножение, чтобы изолировать k . Наконец, обратите внимание, что в уравнении есть отрицательный член, поэтому будет важно подумать о знаке каждого члена, когда вы будете решать задачу. Останавливайтесь после каждого шага, чтобы убедиться, что все термины имеют правильный знак.
Помните, что дроби подразумевают деление, поэтому вы можете думать о [latex]\frac{k}{10}[/latex] как о переменной k делится на 10. Чтобы «отменить» деление, вы можете использовать умножение, чтобы изолировать k . Наконец, обратите внимание, что в уравнении есть отрицательный член, поэтому будет важно подумать о знаке каждого члена, когда вы будете решать задачу. Останавливайтесь после каждого шага, чтобы убедиться, что все термины имеют правильный знак.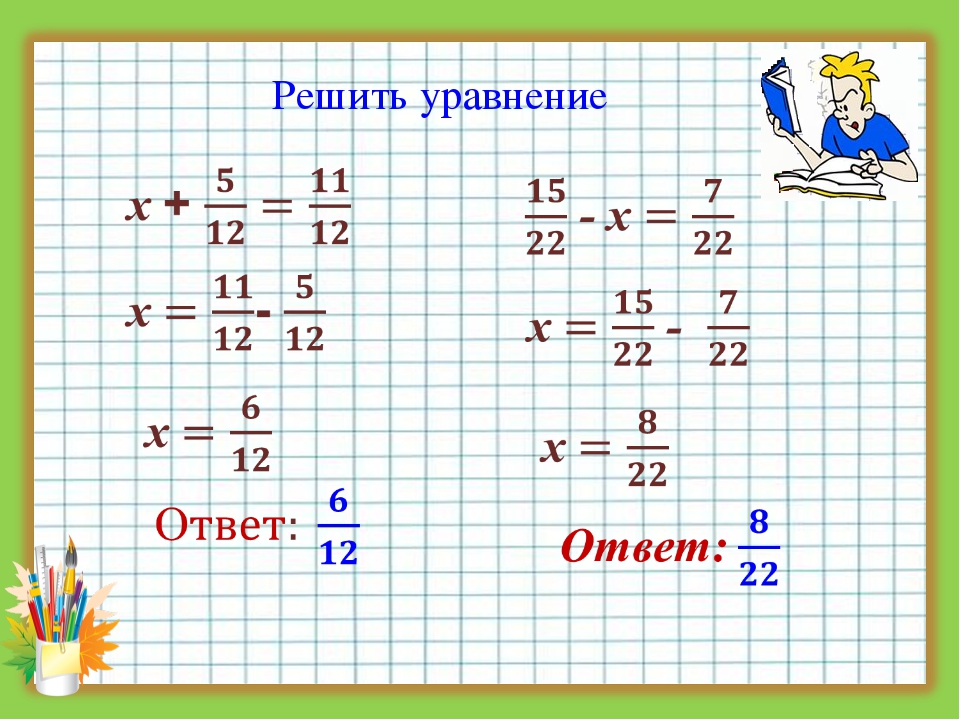 Это удалит все дроби из уравнения.
Это удалит все дроби из уравнения. В следующем видео мы покажем пример.
В следующем видео мы покажем пример. Например, [латекс] \frac{2x+1}{4}=\frac{x}{3}[/latex] является рациональным уравнением. Рациональные уравнения могут быть полезны для представления ситуаций из реальной жизни и для поиска ответов на реальные проблемы. В частности, они неплохо подходят для описания различных пропорциональных отношений.
Например, [латекс] \frac{2x+1}{4}=\frac{x}{3}[/latex] является рациональным уравнением. Рациональные уравнения могут быть полезны для представления ситуаций из реальной жизни и для поиска ответов на реальные проблемы. В частности, они неплохо подходят для описания различных пропорциональных отношений.









 д.
д. При сложении и вычитании вам необходимо найти наименьший/наименьший общий знаменатель (иногда называемый наименьшим общим кратным или НОК). При решении уравнений с дробями умножьте обе части уравнения на знаменатель дроби.
При сложении и вычитании вам необходимо найти наименьший/наименьший общий знаменатель (иногда называемый наименьшим общим кратным или НОК). При решении уравнений с дробями умножьте обе части уравнения на знаменатель дроби.


 {3}}{8}=\frac{2 \cdot 8+1 \cdot 3}{24}=\frac{16+3}{24}=\frac{19}{24}$
{3}}{8}=\frac{2 \cdot 8+1 \cdot 3}{24}=\frac{16+3}{24}=\frac{19}{24}$ $3 \frac{2}{5}+4 \frac{7}{10}=8 \frac{1}{10}$
$3 \frac{2}{5}+4 \frac{7}{10}=8 \frac{1}{10}$
 Например, в задаче:
Например, в задаче: Чтобы найти числитель, нам нужно разделить:
Чтобы найти числитель, нам нужно разделить:



 Итак, вам понадобится 4/5 стакана масла всего , чтобы приготовить торт.
Итак, вам понадобится 4/5 стакана масла всего , чтобы приготовить торт.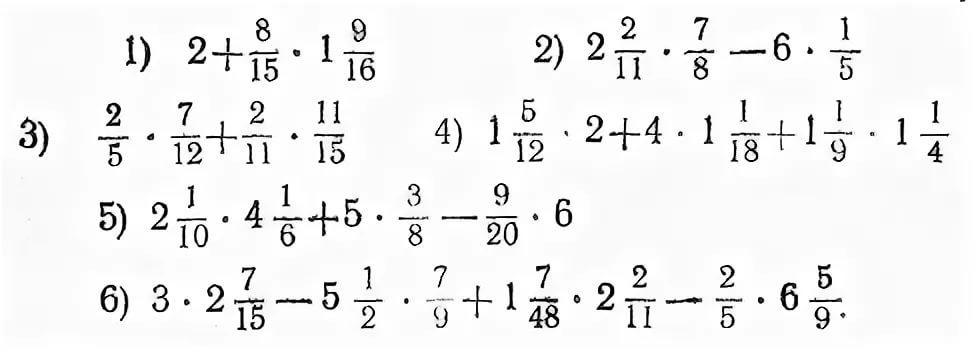
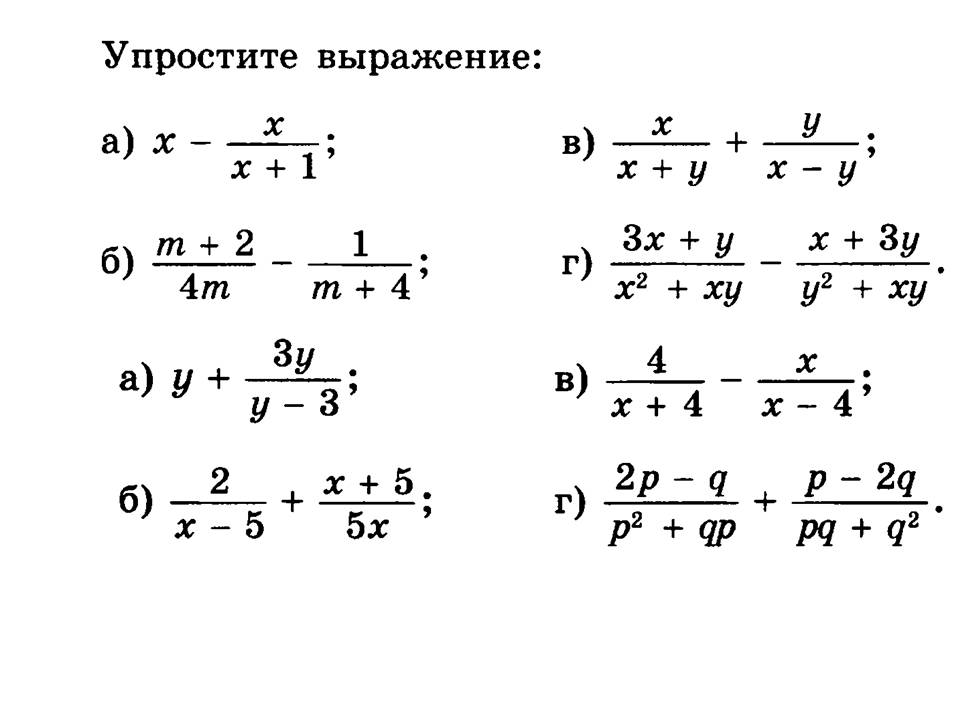 Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.
Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.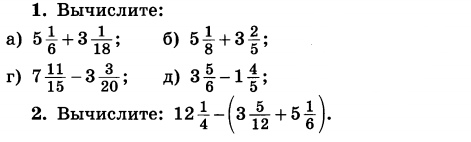 Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.
Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.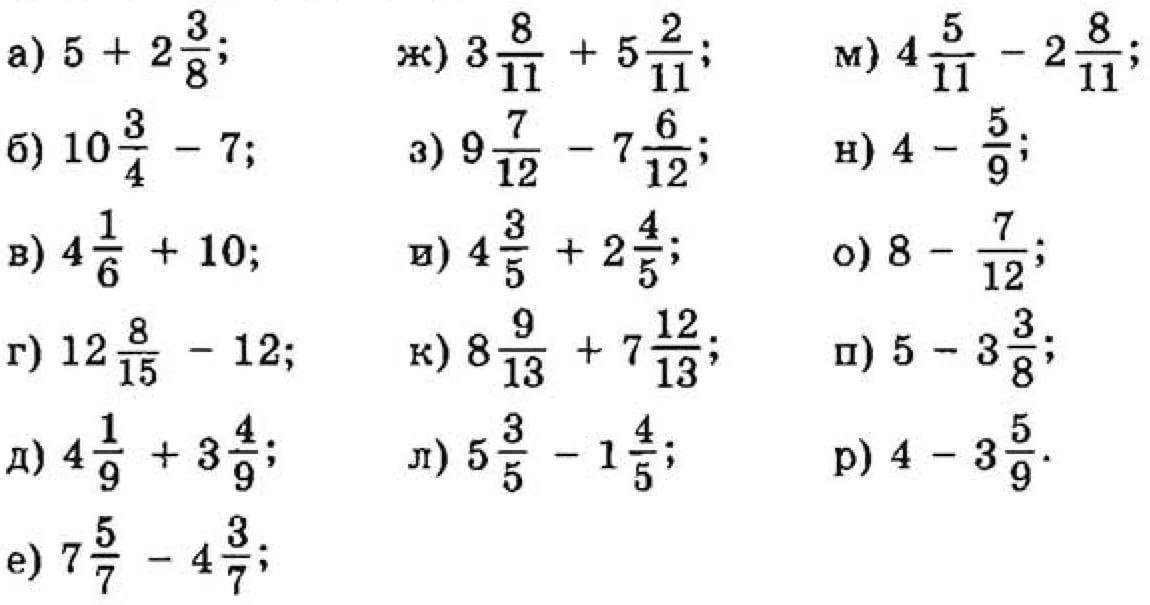




 Первые 3 часа они шли по лесу со скоростью 6 км/ч. Остальную часть пути отряд туристов прошел по горам за 6 часов. С какой скоростью отряд туристов прошёл остальную часть пути?
Первые 3 часа они шли по лесу со скоростью 6 км/ч. Остальную часть пути отряд туристов прошел по горам за 6 часов. С какой скоростью отряд туристов прошёл остальную часть пути?
 Решите задачу.
Решите задачу. Решите примеры столбиком.
Решите примеры столбиком.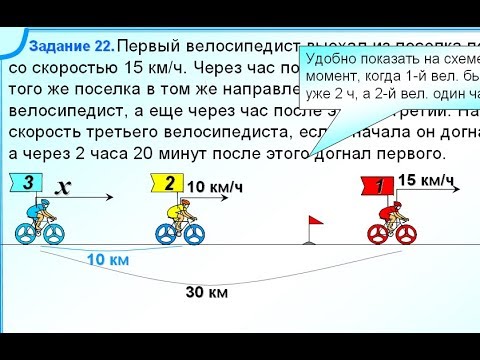 {2}–22x+120}=\frac{2}{1}
{2}–22x+120}=\frac{2}{1} Поставь оценку первым.
Поставь оценку первым. Спасибо!
Спасибо! После позвоночного они прошли то же расстояние на 6 минут дольше. С какой средней скоростью они ехали на позвоночном?
После позвоночного они прошли то же расстояние на 6 минут дольше. С какой средней скоростью они ехали на позвоночном? Средняя скорость менее способных составляет 20 км/ч. Они оба отправились по одному и тому же маршруту в одно и то же время. Хороший велосипедист проехал его на 2 часа раньше. Какой длины был маршрут?
Средняя скорость менее способных составляет 20 км/ч. Они оба отправились по одному и тому же маршруту в одно и то же время. Хороший велосипедист проехал его на 2 часа раньше. Какой длины был маршрут? Через 1 час 10 минут из того же города и в том же направлении выехал велосипедист со скоростью 18 км/ч. Через сколько минут велосипедист догонит пешехода и на каком расстоянии от города S?
Через 1 час 10 минут из того же города и в том же направлении выехал велосипедист со скоростью 18 км/ч. Через сколько минут велосипедист догонит пешехода и на каком расстоянии от города S? Определит ли он, какое расстояние проехал Марек, прежде чем Джон его догнал, и с какой скоростью ехал Марек?
Определит ли он, какое расстояние проехал Марек, прежде чем Джон его догнал, и с какой скоростью ехал Марек? час За какое время и на каком расстоянии легковой автомобиль догонит велосипедистов?
час За какое время и на каком расстоянии легковой автомобиль догонит велосипедистов? В 9 часов утра к нему подъехала машина, двигавшаяся со средней скоростью 60 км/ч. Во сколько грузовик догонит?
В 9 часов утра к нему подъехала машина, двигавшаяся со средней скоростью 60 км/ч. Во сколько грузовик догонит? Пешеход шел со средней скоростью 4 км/ч и встретил велосипедиста через 90 минут ходьбы. Какова была средняя скорость велосипедиста?
Пешеход шел со средней скоростью 4 км/ч и встретил велосипедиста через 90 минут ходьбы. Какова была средняя скорость велосипедиста?