Соотношение между величиной некоего элемента, обеспечивающего производство, и объемом или стоимостью соответствующей продукции, 6 (шесть) букв
Вопрос с кроссворда
Ответ на вопрос «Соотношение между величиной некоего элемента, обеспечивающего производство, и объемом или стоимостью соответствующей продукции «, 6 (шесть) букв:
отдача
Альтернативные вопросы в кроссвордах для слова отдача
Как назвать одним словом действие силы давления пороховых газов на дно канала ствола огнестрельного оружия?
Огнестрельный возврат
И удар приклада в плечо, и вхождение путаны в «творческий процесс»
«Подарок» ружья при выстреле
Максимальная польза
КПД
максим. польза от вложенного
«месть» ружья за выстрел
Максимальная эффективность
Определение слова отдача в словарях
Толковый словарь русского языка. Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
Д.Н. Ушаков Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
отдачи, ж. только ед. Действие по глаг. отдать-отдавать (книжн.). Отдача под суд. Отдача повода (ослабление). Ответный удар, отбрасывание мяча в игре (спорт.). Движение назад, толчок орудия, огнестрельного оружия после выстрела (воен.). Отношение полезной …
Примеры употребления слова отдача в литературе.
Сильнейшая отдача взрыва заставила авианосец беспорядочно, хотя и весьма медленно, вращаться.
Пленум ЦК КПСС указал, что для выполнения Продовольственной программы работникам агропромышленного комплекса нужно изо дня в день наращивать усилия, трудиться так, чтобы огромные средства, направляемые на решение этой задачи, давали отдачу уже сегодня и еще большую — завтра.
Как пишет Баграмян в своих воспоминаниях, ему казалось, что маршал Тимошенко, говоря эти слова, внутренне все-таки еще не был готов на отдачу более категоричного приказа об отходе войск, но уже в ходе этого распоряжения он, понимая всю сложность положения и предстоящие неминуемые колоссальные потери, вроде бы решился и уже твердо сказал: — Доложите, товарищ Баграмян, генералу Кирпоносу, что в создавшейся обстановке Военный совет Юго-Западного направления единственно целесообразным решением для войск Юго-Западного фронта считает организованный отход.
Эта винтовка, вследствие повышения требований по уменьшении силы отдачи, вибрации и нагрева, имела вес 6,5 килограммов со схемным восьмикратным оптическим прицелом.
Естественно, что участники Всеармейского собрания обвинили генерала Грачева в измене Родине, потребовали его отдачи под суд по подрасстрельной, 64-й статье уголовного кодекса, а на его место постановили назначить генерал-полковника Ачалова.
Виражи на малой высоте, вблизи склонов, среди высоченных деревьев, в дыму, постоянная смена высоты и скорости, строгое выдерживание боевого курса, частая работа рычагами газа — все это требует отдачи всех сил.
Источник: библиотека Максима Мошкова
Соотношение между величиной запасов природных ресурсов и размерами их добычи называется:
а) хозяйственная оценка б) ресурсообеспеченность в) экономическая эффективность освоения ресурсов.
Большая часть запасов нефти и газа сосредоточена в:
а) Мексиканском и Бенгальском заливах б) Гвинейском заливе и Карском море
в)
Персидском заливе и Северном море
г) Бискайском заливе и Баренцевом
море.
Наиболее обеспечены лесными ресурсами страны: а) США, Египет б) Россия, Китай в) Канада, Финляндия
Главным потребителем пресной воды является:
а) промышленность б) С/Х в) транспорт г) коммунально-бытовое хозяйство
Выберите страны с наиболее высоким гидроэнергетическим потенциалом:
а) Китай, Россия, США б) Конго, Египет, Мали в) ФРГ, Бразилия, Великобритания
К исчерпаемым невозобновимым природным ресурсам относятся:
а) земельные б) климатические в) минеральные г) биологические
Страной Западной Европы, обладающей мировыми запасами железной руды, является:
а) Великобритания б) Франция в) Швеция г) Германия
Наиболее обеспеченным биологическими ресурсами морем является:
а) Азовское море б) море Лаптевых в) Норвежское море г) Чёрное море
Укажите долю пашни в мировом земельном фонде: а) 0,8 %; б) 10,3 %; в) 26,0 %; г) 31,7 %.

Выделите страну, в структуре земельного которой преобладают пастбища: а) Канада б) Конго в) Монголия г) Франция
ПР / 10 класс / 15 ФИ: __________________________________
В Северный лесной пояс входят страны:
а) Швеция и Канада б) Россия и Австралия в) Бразилия и США г) Афганистан и Индия
Величина площади пашни в расчете на душу населения в мире: а) увеличивается б) не изменяется в) уменьшается
Соотношение между величиной запасов природных ресурсов и размером их использования называется: ____________________________
Наиболее обеспечена водными ресурсами: а) Бразилия б) Алжир в) Ливия г) Монголия
Наиболее благоприятными климатическими ресурсами обладает:
а) Франция и Испания б) Норвегия и Швеция в) Египет и Марокко г) Афганистан и Исландия
Укажите долю земель сельскохозяйственного назначения в мировом земельном фонде:
а)
11 %; б) 25 %; в) 35%; г) 41%.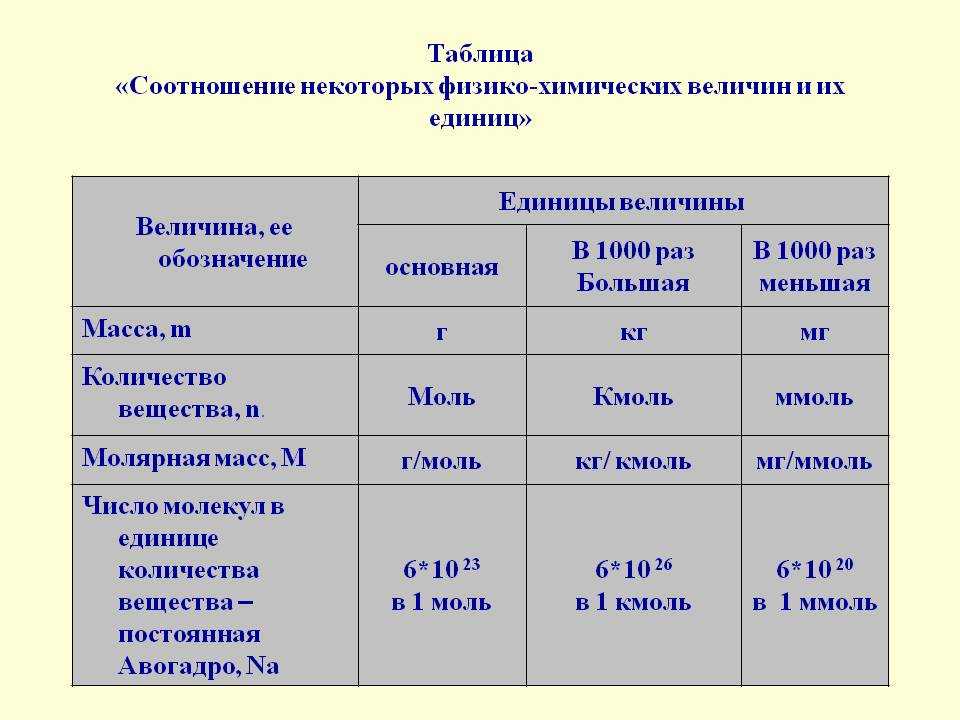
Укажите три страны — мировые лидеры по размерам экономического гидроэнергетического потенциала:
а) Китай б) Россия в) США г) Япония д) Индия.
К неисчерпаемым ресурсам относятся:
а) биологические б) минеральные в) энергия приливов и отливов г) земельные.
Какими природными ресурсами особенно хорошо обеспечены Бразилия и Венесуэла:
а) водными б) почвенными в) графитом г) ураном
Страны-лидеры по разведанным запасам урана: а) Австрия б) Канада в) Австралия г) Габон д) Казахстан е) Польша
ПР / 10 класс / 16 ФИ: __________________________________
Совокупность всех земных оболочек (литосферы, гидросферы, атмосферы и биосферы) называется:
а) географической оболочкой б) географическим пространством в) географической средой г) ноосферой
К исчерпаемым возобновимым ресурсам относятся: а) лесные и почвенные б) минеральные и геотермальные
в) рекреационные и биологические г) климатические и водные
В Южный лесной пояс входят: а) Швеция и Финляндия б) Россия и Австралия
в) Бразилия и Заир(Конго) г) Афганистан и Индия
Укажите примерную площадь мирового земельного фонда (без учета Антарктиды и Гренландии):
а) 11 млрд га б) 13 млрд га в) 15 млрд га г) 17 млрд га
Назовите государство, занимающее первое место в мире по размерам пашни на душу населения:
а)
Индия б) Китай в) Россия
г) США.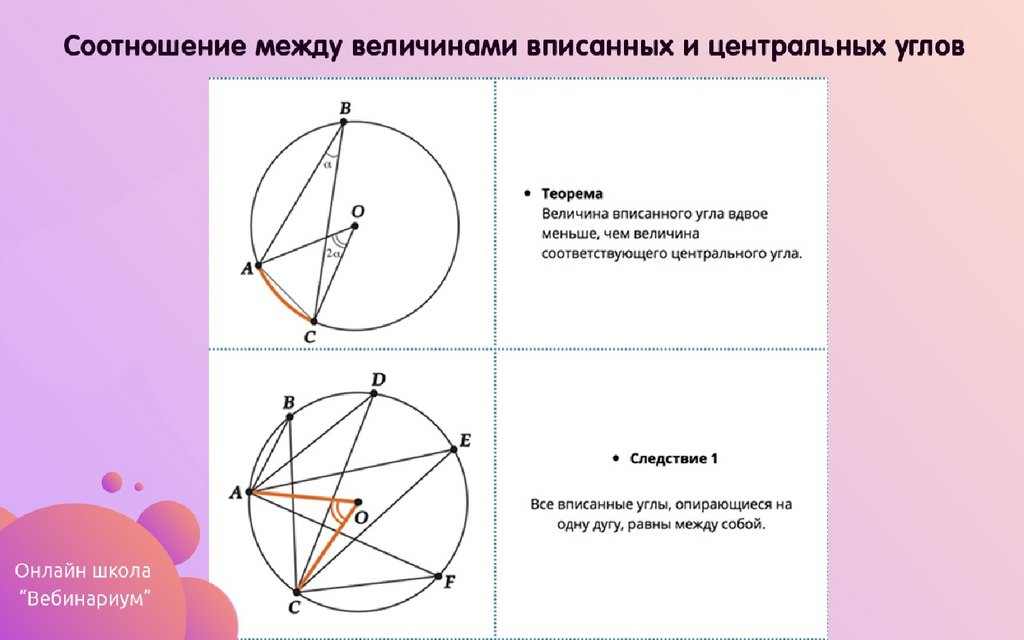
Назовите государство, занимающее первое место в мире по размерам ресурсов пресных вод:
а) Китай б) Канада в) Россия г) Бразилия
Главным потребителем пресной воды является:
а) промышленность б) сельское хозяйство в) транспорт г) коммунально-бытовое хозяйство
Выберите страны, являющиеся лидерами по уровню лесистости:
а) Австралия и Индонезия б) Бразилия и Канада в) Гвиана и Суринам г) Россия и США
Самыми крупными запасами медных руд облают страны: а) Чили б )Вьетнам в)Италия г) США д)Канада е) Перу
Крупнейший производитель опресненной воды: а) ОАЭ б) Катар в) Кувейт г) Ливия
ПР / 10 класс / 17 ФИ: __________________________________
Сырье и ресурсы, вовлеченные в производство и многократно в нем преобразованные — _______________________
Леса Северного пояса наиболее богаты ……….
 .породами деревьев и расположены
в зоне:
.породами деревьев и расположены
в зоне:
а) экваториальных лесов б) тайги в) саванн г) степей
Укажите страну с самым высоким показателем подушевой обеспеченности земельными ресурсами:
а) Австралия б) Россия в) Бразилия г) США.
Укажите основную причину деградации почв в мире: а) оскудение и вымирание лесных массивов
б) чрезмерное пастбищное животноводство в) сельскохозяйственная деятельность.
Укажите примерный размер (по большинству оценок) мирового экономического гидроэнергетического потенциала (в трлн кВт/ч в год): а) 5 б)10 в) 20 г) 40.
Укажите вариант, в котором перечислены страны южного лесного пояса с самой высокой лесистостью:
а) Конго, Индия, Перу, Венесуэла, Габон;
б) Суринам, Гайана, Габон, Демократическая Республика Конго, Папуа — Новая Гвинея;
в) Австралия, Папуа — Новая Гвинея, Габон, Бразилия, Суринам;
г)
Гайана, Демократическая Республика
Конго, Китай, Индия, Перу.
Наиболее обеспечены водными ресурсами страны:
а) экваториального пояса б) тропического пояса в) субтропического пояса г) субарктического пояса
Большая часть запасов нефти и газа сосредоточена в:
а) Персидском заливе и Северном море б) Карибском и Беринговом морях
в) Аравийском и Балтийском морях г) Баренцевом и Охотском морях.
Страна-лидер по запасам газа — ________________
Выделите страну, испытывающую наибольший дефицит водных ресурсов: а) Алжир б) Перу в) Финляндия г) Япония
ПР / 10 класс / 18 ФИ: __________________________________
Как рассчитать коэффициенты — онлайн-руководство и советы 2023
Обновлено 10 марта 2023 г.
Что такое коэффициенты?
Соотношение — это математический термин, используемый для описания того, сколько одного предмета по сравнению с другим.
Соотношения обычно записываются в следующих форматах:
- 2:1
- от 2 до 1
- 2/1
Используемые в математике и повседневной жизни, вы, возможно, сталкивались с соотношениями, не зная об этом, например, в масштабных чертежах или моделях, в выпечке и кулинарии и даже при конвертации валюты для отдыха за границей.
Соотношения полезны, когда вам нужно знать, сколько одной вещи должно быть по сравнению с другой вещью.
Знать, как найти соотношение, легче, если вы знаете, как они работают и как соотношение может быть представлено в различных сценариях.
Пример 1:
В пакете из 20 конфет соотношение синего к розовому может быть 2:3
Использование отношения в этом примере сообщит нам, что будет 8 синих конфет и 12 розовые сладости. (Этот вопрос и способ его решения подробно описаны ниже).
Пример 2:
Если вы делаете торт, и вам нужно 3 стакана муки и 2 стакана сахара, чтобы накормить 10 человек, то вы можете выразить это соотношением 3:2.
Подготовка к любому экзамену по оценке работы с помощью JobTestPrep
Чтобы увеличить количество ингредиентов, чтобы накормить 20 человек (чтобы удвоить размер рецепта), вам нужно удвоить количество ингредиентов, поэтому вам потребуется 6 чашек муки и 4 чашки сахара (или 6:4).
Понимание того, как рассчитать коэффициент, облегчит вам работу с этими повседневными сценариями.
Факты о ключевом соотношении
Изучая, как найти соотношение, помните, что отношения могут описывать количество, измерения или масштаб .
При описании соотношения первое число известно как « предшествующее », а второе — как « последующее ». Итак, в отношении 3:1 антецедент равен 3, а консеквент равен 1.
Соотношения всегда должны быть представлены в их упрощенной форме . Когда вы пытаетесь понять, как рассчитать отношение, убедитесь, что вы упрощаете отношение, разделив обе части на наибольший общий множитель.
 Например, упрощенное соотношение 12:4 будет равно 3:1 — обе части соотношения, разделенные на 4.
Например, упрощенное соотношение 12:4 будет равно 3:1 — обе части соотношения, разделенные на 4.Эквивалентные отношения можно разделить и/или умножить на одно и то же число с обеих сторон, так что, как указано выше, 12:4 является эквивалентным отношением к 3:1.
Соотношения могут информировать вас о прямой пропорциональности каждого числа по сравнению с другим. Например, когда пара чисел увеличивается или уменьшается в одном и том же отношении, они прямо пропорциональны.
При выражении соотношений нужно следить, чтобы и антецедент, и консеквент были одними и теми же единицами – будь то см, мм, км. Это облегчает обучение решению задачи на соотношение.
Соотношения используются на картах для обеспечения масштаба . Обычно выражаемый как 1:10 000 или аналогичный, это говорит вам, что для каждого 1 юнита на карте реальное расстояние составляет 10 000 юнитов.
 Если вы измерите 1 см на карте, реальное расстояние будет 10 000 см (или 100 м).
Если вы измерите 1 см на карте, реальное расстояние будет 10 000 см (или 100 м).Соотношения также используются в чертежах, таких как архитектурные проекты, чтобы показать перспективу и относительный размер в меньшем масштабе, а также в моделях. Например, модель автомобиля может иметь соотношение 1:20, поэтому 1 см на модели будет 20 см на реальном автомобиле. Вот почему изучение того, как вычислять пропорции, может помочь вам не только в математических задачах или в выпечке.
Примеры вопросов и их решения
Понимание того, как вычислять отношения, является важным навыком и может быть особенно полезным при приеме на работу, где требуется хорошее понимание математики.
Перед прохождением математических расчетов или других математических тестов на способности рекомендуется проверить подобные навыки.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
Вот основные навыки, которыми вам необходимо овладеть. См. приведенное объяснение для полной разбивки о том, как найти ответ:
См. приведенное объяснение для полной разбивки о том, как найти ответ:
1. Как рассчитать отношение
Пример вопроса
У Алана и Альберта 30 конфет. Они собираются делить сладости, но Альберт заплатил за них больше, чем Алан, поэтому они решили разделить их в пропорции 1:2.
Сколько конфет получил Альберт?
2. Как найти соотношение двух вещей
Пример вопроса
В мешочке с 20 конфетами 8 синих и 12 розовых конфет. Каково соотношение голубых и розовых конфет?
Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .
Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
3.
 Как преобразовать соотношения в различных единицах измерения
Как преобразовать соотношения в различных единицах измеренияПример вопроса
Как масштабный коэффициент 3 см : 15 м должен быть выражен в виде упрощенного соотношения?
4. Работа с десятичными дробями
Пример вопроса
Упрощение 10:2.5
5. Использование пропорций для расчета прямых пропорций количества
Пример вопроса
Если вы пойдете в магазин и купи 4 яблока за 0,64 фунта стерлингов, сколько будут стоить 11 яблок?
6. Как разделить число на отношение
Пример вопроса
У Эндрю и Джеймса 400 конфет, и они должны разделить их в соотношении 5:3. Сколько конфет получит каждый из них?
7. Как использовать коэффициенты для поиска неизвестного числа
Пример вопроса
Компания по производству сладостей любит класть в пакеты нечетное количество конфет. В настоящее время они создают пакет из голубых и розовых конфет в соотношении 4:6.
Если вы получите пакет с 12 синими конфетами, сколько их будет всего?
8.
 Как найти соотношение
Как найти соотношениеПример вопроса
В вазе с фруктами лежат яблоки, апельсины и бананы.
Если есть 4 яблока, 6 апельсинов и 12 бананов, каково соотношение фруктов?
Подготовьтесь к любому тесту по оценке работы с помощью JobTestPrep
Важность коэффициентов в бизнесе
Коэффициенты являются полезным инструментом в бизнесе, оказывающим большое влияние на стратегию, поскольку они используются как часть аналитического инструментария, который помогает компании понять свои прогресс до сих пор, и предоставляет данные, чтобы помочь создать улучшения на будущее.
Научившись правильно рассчитывать коэффициенты, предприятия могут применять их по-разному.
Прибыльность
Это один из важнейших ориентиров для бизнеса, и для эффективного роста бизнес должен стать более прибыльным.
Некоторые коэффициенты, которые могут использоваться для оценки прибыльности, включают:
- Маржа чистой прибыли: Чистая прибыль после налогообложения по сравнению с чистыми продажами.

- Прибыль от продукта: Разница между себестоимостью производства и продажной ценой
- Расходы на персонал: Доля бюджета на персонал, которая используется для найма
Денежные потоки и ликвидность
Хотя некоторые предприятия могут быть богаты активами и бедны денежными средствами, они должны иметь возможность покрывать немедленные расходы, и именно здесь полезен анализ ликвидности и денежных потоков.
Некоторые коэффициенты, которые могут быть использованы, включают:
- Оборотный капитал: Сравнение текущих активов с текущими обязательствами
- Денежные средства: Сравнение ликвидных активов с текущими обязательствами
Финансовый риск и доходность
Это может быть измерением того, насколько здоровы инвестиции, сделанные бизнесом, что можно использовать в качестве показателя рентабельности инвестиций при расчете будущей прибыли.
Оборачиваемость запасов
Достаточно ли запасов, чтобы удовлетворить спрос, или слишком много запасов удерживается, а не продается?
Сравнение количества товаров на складе с количеством продаж — это один коэффициент, а другим может быть стоимость проданных товаров по отношению к среднему запасу.
Отслеживание персонала
Насколько эффективен персонал? Это можно измерить, сравнив количество отработанных часов с объемом продаж или другими показателями.
Возврат товара
Довольны ли в целом покупатели тем, что они приобрели? Если отношение продаж продукта к возврату меняется, это может указывать, например, на проблему с контролем качества.
Распространенные ошибки, которых следует избегать при обучении вычислению дробей
- Не ошибитесь в информации. Иногда формулировка вопроса может затруднить получение правильного отношения, а смещенные числа сделают весь ваш расчет неверным.
- Убедитесь, что вы знаете, о чем идет речь.
 Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей.
Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей. - Соотношения всегда представляют собой целые числа, а не десятичные дроби или дроби.
- Всегда представляйте свои коэффициенты полностью упрощенными.
Часто задаваемые вопросы
Для расчета коэффициентов используется формула 9.0025 a:b = a/b
Например, отношение к и b к равно 3:5.
Вы знаете, что a = 86 и вам нужно найти b .
Чтобы рассчитать соотношение, выполните следующие действия:
a:b = 3:5
a/b = 3/5
86/b = 3/5
b = (5/3) x 86
b = 143,3
В зависимости от имеющейся у вас информации, самый простой способ рассчитать соотношение:
Сценарий A: Сколько будет 3:5 от 30 долларов?
- Найдите общее количество частей – если соотношение 3:2, то всего 5
- Разделите цифру на количество частей, чтобы найти сумму одной части – 30 долларов разделить на 5 = 6.
 Одна часть равна 6
Одна часть равна 6 - Умножьте каждое число в пропорции на значение одной части – 3 x 6 и 2 x 6. Если вы найдете 3:2 от 30 долларов, ваш ответ будет 18:12
Сценарий B: Каково соотношение яблок и лимонов на поле из 100 яблок и 80 лимонов?
- Найдите две стартовые фигуры. Например, если вы искали соотношение яблок и лимонов на поле со 100 орхидеями и 80 тюльпанами. 100 и 80 — ваши исходные цифры.
- В этом сценарии вы пытаетесь найти простейшее соотношение. Вы делаете это, находя наибольшее число, на которое делятся обе цифры. В данном случае 20 – это максимальное значение.
- Затем вы делите каждую цифру на это число: 100/20 = 5 и 80/20 = 4
- Ответы дают вам соотношение 5:4
Анализ коэффициентов — это аналитический метод, который объединяет несколько финансовых коэффициентов для оценки финансового положения компании.
В зависимости от цифр, которые вам нужно найти, вы можете использовать одно, несколько или все эти отношения:
Ликвидность
- Коэффициент текущей ликвидности = Текущие активы / Текущие обязательства
- Соотношение денежных средств = Денежные средства и их эквиваленты / Текущие обязательства
- Коэффициент быстрой ликвидности = (Денежные средства и их эквиваленты + Дебиторская задолженность) / Текущие обязательства
Платежеспособность
- Отношение долга к собственному капиталу = общий долг / общий капитал
- Коэффициент долга = общий долг / общие активы
- Коэффициент покрытия процентов = EBITDA / Процентные расходы
Эффективность
- Коэффициент оборачиваемости дебиторской задолженности = Продажи / Дебиторская задолженность
- Коэффициент оборачиваемости запасов = Себестоимость / Запасы
- Коэффициент оборачиваемости кредиторской задолженности = Себестоимость / Кредиторская задолженность
- Коэффициент оборачиваемости активов = Продажи / Общие активы
- Чистый коэффициент оборачиваемости основных средств = Продажи / Чистые основные средства
- Коэффициент оборачиваемости капитала = Продажи / Общий капитал
Прибыль
- Валовая прибыль = (Продажи – Себестоимость) / Продажи
- Маржа операционной прибыли = EBIT / Продажи
- Чистая маржа = Чистая прибыль / Продажи
- Рентабельность общих активов (ROA) = EBIT / общие активы
- Рентабельность общего капитала (ROE) = чистая прибыль / общий капитал
Чтобы рассчитать эти отношения, вам просто нужно ввести правильные цифры или ввести эти формулы в программу, такую как Microsoft Excel.
Простейшую форму пропорции можно найти, найдя число, общее для обеих частей пропорции, и разделив их.
Например, соотношение 20:60.
Обе стороны кратны 10.
20/10 = 2
60/10 = 6
Тогда отношение становится 2:6
Или, если хотите упростить, и 2, и 6 кратны 2.
2/2 = 1
6/2 = 3
Окончательное соотношение 1:3.
Для расчета коэффициента анализа есть несколько программ и приложений, которые вы можете использовать.
К ним относятся:
- Готовые пропорции
- Microsoft Excel
- Google Таблицы
- Приложение «Калькулятор финансового коэффициента»
Если вы хотите найти отношение двух чисел онлайн, вы должны использовать калькулятор отношений, такой как Calculator Soup.
Существуют специальные онлайн-калькуляторы для соотношений, но можно также использовать физический калькулятор для расчета ваших соотношений.
Метод, который вы используете для нахождения соотношений на калькуляторе, зависит от имеющейся у вас информации. Тем не менее, вы будете следовать тем же простым шагам, которые вы бы использовали, если бы вычисляли в уме:
Тем не менее, вы будете следовать тем же простым шагам, которые вы бы использовали, если бы вычисляли в уме:
- Найдите две стартовые фигуры. Например, если вы искали соотношение орхидей и тюльпанов в саду, где 150 орхидей и 70 тюльпанов. 150 и 70 — ваши исходные цифры.
- В этом сценарии вы пытаетесь найти простейшее соотношение. Вы делаете это, находя наибольшее число, на которое делятся обе цифры. В данном случае 10 является самым высоким.
- С помощью калькулятора введите первое число и разделите на полученное число: 150/10 = 15 и 70/10 = 7
- Ответом на оба вопроса является ваше соотношение: 15:7
В качестве альтернативы, если вы хотите узнать соотношение числа, скажем, 6:2 к 70 долларам, вы должны:
- Определить общее количество частей: если соотношение равно 6:2, сумма равна 8
- Разделите цифру на количество частей, чтобы найти сумму одной части: 70 долларов разделить на 8 = 8,75. Итак, одна часть равна 8,75.

- Умножьте каждое число в соотношении на значение одной части: 6 x 8,75 и 2 x 8,75
Следовательно, 6:2 от 70 долларов равно 52,5:17,5
Резюме
Соотношения — это математическое выражение для сравнения единиц измерения.
Их можно использовать в качестве эквивалентных соотношений, чтобы помочь вам масштабировать числа — например, количество ингредиентов для выпечки торта.
С математической точки зрения их можно использовать для решения задач, связанных с прямой пропорцией, когда увеличение или уменьшение единиц происходит в одном и том же отношении.
Соотношения можно упростить, и в большинстве случаев предпочтительнее давать в качестве ответа упрощенное соотношение. Как и дроби, вы можете упростить отношение, разделив его на наибольший общий делитель.
При использовании масштабов на чертежах или моделях соотношения помогают описать взаимосвязь между реальным и созданным предметом, обеспечивая точные измерения, а также представление о пропорциях.
При попытке понять отношения проще всего работать с одними и теми же единицами измерения.
Помните, что для полного изучения пропорции вам нужно использовать целое число, поэтому старайтесь избегать десятичных дробей при преобразовании единиц для соответствия.
Практика решения задач на соотношение значительно облегчит их понимание.
Вполне вероятно, что вы будете использовать коэффициенты на протяжении всей своей жизни и, возможно, сдадите тест на математические навыки при приеме на работу в технических отраслях.
Как рассчитать коэффициенты — онлайн-руководство и советы 2023
Обновлено 10 марта 2023 г.
Что такое коэффициенты?
Соотношение — это математический термин, используемый для описания того, сколько одного предмета по сравнению с другим.
Соотношения обычно записываются в следующих форматах:
- 2:1
- от 2 до 1
- 2/1
Используемые в математике и повседневной жизни, вы, возможно, сталкивались с соотношениями, не зная об этом, например, в масштабных чертежах или моделях, в выпечке и кулинарии и даже при конвертации валюты для отдыха за границей.
Соотношения полезны, когда вам нужно знать, сколько одной вещи должно быть по сравнению с другой вещью.
Знать, как найти соотношение, легче, если вы знаете, как они работают и как соотношение может быть представлено в различных сценариях.
Пример 1:
В пакете из 20 конфет соотношение синего к розовому может быть 2:3
Использование соотношения в этом примере сообщит нам, что будет 8 синих конфет и 12 розовые сладости. (Этот вопрос и способ его решения подробно описаны ниже).
Пример 2:
Если вы делаете торт, и вам нужно 3 стакана муки и 2 стакана сахара, чтобы накормить 10 человек, то вы можете выразить это соотношением 3:2.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
Чтобы увеличить количество ингредиентов, чтобы накормить 20 человек (чтобы удвоить размер рецепта), вам нужно удвоить количество ингредиентов, поэтому вам потребуется 6 чашек муки и 4 чашки сахара (или 6:4).
Понимание того, как рассчитать коэффициент, облегчит вам работу с этими повседневными сценариями.
Факты о ключевых соотношениях
Изучая, как найти соотношение, помните, что отношения могут описывать количество, размеры или масштаб .
При описании соотношения первое число известно как « предшествующее », а второе — как « последующее ». Итак, в отношении 3:1 антецедент равен 3, а консеквент равен 1.
Соотношения всегда должны быть представлены в их упрощенной форме . Когда вы пытаетесь понять, как рассчитать отношение, убедитесь, что вы упрощаете отношение, разделив обе части на наибольший общий множитель. Например, упрощенное соотношение 12:4 будет равно 3:1 — обе части соотношения, разделенные на 4.
Эквивалентные отношения можно разделить и/или умножить на одно и то же число с обеих сторон, так что, как указано выше, 12:4 является эквивалентным отношением к 3:1.

Соотношения могут информировать вас о прямой пропорции каждого числа по сравнению с другим. Например, когда пара чисел увеличивается или уменьшается в одном и том же отношении, они прямо пропорциональны.
При выражении соотношений необходимо убедиться, что и антецедент, и консеквент равны те же единицы – будь то см, мм, км. Это облегчает обучение решению задачи на соотношение.
Соотношения используются на картах для обеспечения масштаба . Обычно выражаемый как 1:10 000 или аналогичный, это говорит вам, что для каждого 1 юнита на карте реальное расстояние составляет 10 000 юнитов. Если вы измерите 1 см на карте, реальное расстояние будет 10 000 см (или 100 м).
Соотношения также используются в чертежах, таких как архитектурные проекты, чтобы показать перспектива и относительный размер в меньшем масштабе и в моделях. Например, модель автомобиля может иметь соотношение 1:20, поэтому 1 см на модели будет 20 см на реальном автомобиле.
 Вот почему изучение того, как вычислять пропорции, может помочь вам не только в математических задачах или в выпечке.
Вот почему изучение того, как вычислять пропорции, может помочь вам не только в математических задачах или в выпечке.
Примеры вопросов и их решения
Понимание того, как вычислять отношения, является важным навыком и может быть особенно полезным при приеме на работу, где требуется хорошее понимание математики.
Перед прохождением математических расчетов или других математических тестов на способности рекомендуется проверить подобные навыки.
Подготовьтесь к любому экзамену по оценке работы с помощью JobTestPrep
Вот основные навыки, которыми вам необходимо овладеть. См. приведенное объяснение для полной разбивки о том, как найти ответ:
1. Как рассчитать отношение
Пример вопроса
У Алана и Альберта 30 конфет. Они собираются делить сладости, но Альберт заплатил за них больше, чем Алан, поэтому они решили разделить их в пропорции 1:2.
Сколько конфет получил Альберт?
2. Как найти соотношение двух вещей
Пример вопроса
В мешочке с 20 конфетами 8 синих и 12 розовых конфет. Каково соотношение голубых и розовых конфет?
Каково соотношение голубых и розовых конфет?
Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .
Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.
Подготовьтесь к любому аттестационному тесту с помощью JobTestPrep
3. Как преобразовать соотношения в различных единицах измерения
Пример вопроса
Как масштабный коэффициент 3 см : 15 м должен быть выражен в виде упрощенного соотношения?
4. Работа с десятичными дробями
Пример вопроса
Упрощение 10:2.5
5. Использование пропорций для расчета прямых пропорций количества
Пример вопроса
Если вы пойдете в магазин и купи 4 яблока за 0,64 фунта стерлингов, сколько будут стоить 11 яблок?
6.
 Как разделить число на отношение
Как разделить число на отношениеПример вопроса
У Эндрю и Джеймса 400 конфет, и они должны разделить их в соотношении 5:3. Сколько конфет получит каждый из них?
7. Как использовать коэффициенты для поиска неизвестного числа
Пример вопроса
Компания по производству сладостей любит класть в пакеты нечетное количество конфет. В настоящее время они создают пакет из голубых и розовых конфет в соотношении 4:6.
Если вы получите пакет с 12 синими конфетами, сколько их будет всего?
8. Как найти соотношение
Пример вопроса
В вазе с фруктами лежат яблоки, апельсины и бананы.
Если есть 4 яблока, 6 апельсинов и 12 бананов, каково соотношение фруктов?
Подготовьтесь к любому тесту по оценке работы с помощью JobTestPrep
Важность коэффициентов в бизнесе
Коэффициенты являются полезным инструментом в бизнесе, оказывающим большое влияние на стратегию, поскольку они используются как часть аналитического инструментария, который помогает компании понять свои прогресс до сих пор, и предоставляет данные, чтобы помочь создать улучшения на будущее.
Научившись правильно рассчитывать коэффициенты, предприятия могут применять их по-разному.
Прибыльность
Это один из важнейших ориентиров для бизнеса, и для эффективного роста бизнес должен стать более прибыльным.
Некоторые коэффициенты, которые могут использоваться для оценки прибыльности, включают:
- Маржа чистой прибыли: Чистая прибыль после налогообложения по сравнению с чистыми продажами.
- Прибыль от продукта: Разница между себестоимостью производства и продажной ценой
- Расходы на персонал: Доля бюджета на персонал, которая используется для найма
Денежные потоки и ликвидность
Хотя некоторые предприятия могут быть богаты активами и бедны денежными средствами, они должны иметь возможность покрывать немедленные расходы, и именно здесь полезен анализ ликвидности и денежных потоков.
Некоторые коэффициенты, которые могут быть использованы, включают:
- Оборотный капитал: Сравнение текущих активов с текущими обязательствами
- Денежные средства: Сравнение ликвидных активов с текущими обязательствами
Финансовый риск и доходность
Это может быть измерением того, насколько здоровы инвестиции, сделанные бизнесом, что можно использовать в качестве показателя рентабельности инвестиций при расчете будущей прибыли.
Оборачиваемость запасов
Достаточно ли запасов, чтобы удовлетворить спрос, или слишком много запасов удерживается, а не продается?
Сравнение количества товаров на складе с количеством продаж — это один коэффициент, а другим может быть стоимость проданных товаров по отношению к среднему запасу.
Отслеживание персонала
Насколько эффективен персонал? Это можно измерить, сравнив количество отработанных часов с объемом продаж или другими показателями.
Возврат товара
Довольны ли в целом покупатели тем, что они приобрели? Если отношение продаж продукта к возврату меняется, это может указывать, например, на проблему с контролем качества.
Распространенные ошибки, которых следует избегать при обучении вычислению дробей
- Не ошибитесь в информации. Иногда формулировка вопроса может затруднить получение правильного отношения, а смещенные числа сделают весь ваш расчет неверным.
- Убедитесь, что вы знаете, о чем идет речь.
 Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей.
Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей. - Соотношения всегда представляют собой целые числа, а не десятичные дроби или дроби.
- Всегда представляйте свои коэффициенты полностью упрощенными.
Часто задаваемые вопросы
Для расчета коэффициентов используется формула 9.0025 a:b = a/b
Например, отношение к и b к равно 3:5.
Вы знаете, что a = 86 и вам нужно найти b .
Чтобы рассчитать соотношение, выполните следующие действия:
a:b = 3:5
a/b = 3/5
86/b = 3/5
b = (5/3) x 86
b = 143,3
В зависимости от имеющейся у вас информации, самый простой способ рассчитать соотношение:
Сценарий A: Сколько будет 3:5 от 30 долларов?
- Найдите общее количество частей – если соотношение 3:2, то всего 5
- Разделите цифру на количество частей, чтобы найти сумму одной части – 30 долларов разделить на 5 = 6.
 Одна часть равна 6
Одна часть равна 6 - Умножьте каждое число в пропорции на значение одной части – 3 x 6 и 2 x 6. Если вы найдете 3:2 от 30 долларов, ваш ответ будет 18:12
Сценарий B: Каково соотношение яблок и лимонов на поле из 100 яблок и 80 лимонов?
- Найдите две стартовые фигуры. Например, если вы искали соотношение яблок и лимонов на поле со 100 орхидеями и 80 тюльпанами. 100 и 80 — ваши исходные цифры.
- В этом сценарии вы пытаетесь найти простейшее соотношение. Вы делаете это, находя наибольшее число, на которое делятся обе цифры. В данном случае 20 – это максимальное значение.
- Затем вы делите каждую цифру на это число: 100/20 = 5 и 80/20 = 4
- Ответы дают вам соотношение 5:4
Анализ коэффициентов — это аналитический метод, который объединяет несколько финансовых коэффициентов для оценки финансового положения компании.
В зависимости от цифр, которые вам нужно найти, вы можете использовать одно, несколько или все эти отношения:
Ликвидность
- Коэффициент текущей ликвидности = Текущие активы / Текущие обязательства
- Соотношение денежных средств = Денежные средства и их эквиваленты / Текущие обязательства
- Коэффициент быстрой ликвидности = (Денежные средства и их эквиваленты + Дебиторская задолженность) / Текущие обязательства
Платежеспособность
- Отношение долга к собственному капиталу = общий долг / общий капитал
- Коэффициент долга = общий долг / общие активы
- Коэффициент покрытия процентов = EBITDA / Процентные расходы
Эффективность
- Коэффициент оборачиваемости дебиторской задолженности = Продажи / Дебиторская задолженность
- Коэффициент оборачиваемости запасов = Себестоимость / Запасы
- Коэффициент оборачиваемости кредиторской задолженности = Себестоимость / Кредиторская задолженность
- Коэффициент оборачиваемости активов = Продажи / Общие активы
- Чистый коэффициент оборачиваемости основных средств = Продажи / Чистые основные средства
- Коэффициент оборачиваемости капитала = Продажи / Общий капитал
Прибыль
- Валовая прибыль = (Продажи – Себестоимость) / Продажи
- Маржа операционной прибыли = EBIT / Продажи
- Чистая маржа = Чистая прибыль / Продажи
- Рентабельность общих активов (ROA) = EBIT / общие активы
- Рентабельность общего капитала (ROE) = чистая прибыль / общий капитал
Чтобы рассчитать эти отношения, вам просто нужно ввести правильные цифры или ввести эти формулы в программу, такую как Microsoft Excel.
Простейшую форму пропорции можно найти, найдя число, общее для обеих частей пропорции, и разделив их.
Например, соотношение 20:60.
Обе стороны кратны 10.
20/10 = 2
60/10 = 6
Тогда отношение становится 2:6
Или, если хотите упростить, и 2, и 6 кратны 2.
2/2 = 1
6/2 = 3
Окончательное соотношение 1:3.
Для расчета коэффициента анализа есть несколько программ и приложений, которые вы можете использовать.
К ним относятся:
- Готовые пропорции
- Microsoft Excel
- Google Таблицы
- Приложение «Калькулятор финансового коэффициента»
Если вы хотите найти отношение двух чисел онлайн, вы должны использовать калькулятор отношений, такой как Calculator Soup.
Существуют специальные онлайн-калькуляторы для соотношений, но можно также использовать физический калькулятор для расчета ваших соотношений.
Метод, который вы используете для нахождения соотношений на калькуляторе, зависит от имеющейся у вас информации. Тем не менее, вы будете следовать тем же простым шагам, которые вы бы использовали, если бы вычисляли в уме:
Тем не менее, вы будете следовать тем же простым шагам, которые вы бы использовали, если бы вычисляли в уме:
- Найдите две стартовые фигуры. Например, если вы искали соотношение орхидей и тюльпанов в саду, где 150 орхидей и 70 тюльпанов. 150 и 70 — ваши исходные цифры.
- В этом сценарии вы пытаетесь найти простейшее соотношение. Вы делаете это, находя наибольшее число, на которое делятся обе цифры. В данном случае 10 является самым высоким.
- С помощью калькулятора введите первое число и разделите на полученное число: 150/10 = 15 и 70/10 = 7
- Ответом на оба вопроса является ваше соотношение: 15:7
В качестве альтернативы, если вы хотите узнать соотношение числа, скажем, 6:2 к 70 долларам, вы должны:
- Определить общее количество частей: если соотношение равно 6:2, сумма равна 8
- Разделите цифру на количество частей, чтобы найти сумму одной части: 70 долларов разделить на 8 = 8,75. Итак, одна часть равна 8,75.

- Умножьте каждое число в соотношении на значение одной части: 6 x 8,75 и 2 x 8,75
Следовательно, 6:2 от 70 долларов равно 52,5:17,5
Резюме
Соотношения — это математическое выражение для сравнения единиц измерения.
Их можно использовать в качестве эквивалентных соотношений, чтобы помочь вам масштабировать числа — например, количество ингредиентов для выпечки торта.
С математической точки зрения их можно использовать для решения задач, связанных с прямой пропорцией, когда увеличение или уменьшение единиц происходит в одном и том же отношении.
Соотношения можно упростить, и в большинстве случаев предпочтительнее давать в качестве ответа упрощенное соотношение. Как и дроби, вы можете упростить отношение, разделив его на наибольший общий делитель.
При использовании масштабов на чертежах или моделях соотношения помогают описать взаимосвязь между реальным и созданным предметом, обеспечивая точные измерения, а также представление о пропорциях.


 .породами деревьев и расположены
в зоне:
.породами деревьев и расположены
в зоне: Например, упрощенное соотношение 12:4 будет равно 3:1 — обе части соотношения, разделенные на 4.
Например, упрощенное соотношение 12:4 будет равно 3:1 — обе части соотношения, разделенные на 4. Если вы измерите 1 см на карте, реальное расстояние будет 10 000 см (или 100 м).
Если вы измерите 1 см на карте, реальное расстояние будет 10 000 см (или 100 м).
 Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей.
Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей. Одна часть равна 6
Одна часть равна 6

 Вот почему изучение того, как вычислять пропорции, может помочь вам не только в математических задачах или в выпечке.
Вот почему изучение того, как вычислять пропорции, может помочь вам не только в математических задачах или в выпечке. Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей.
Иногда может показаться, что нужно произвести расчет по частям, когда на самом деле нужно использовать все числа. Например, вопрос может заключаться в нахождении пропорции одной вещи к общему количеству вещей. Одна часть равна 6
Одна часть равна 6
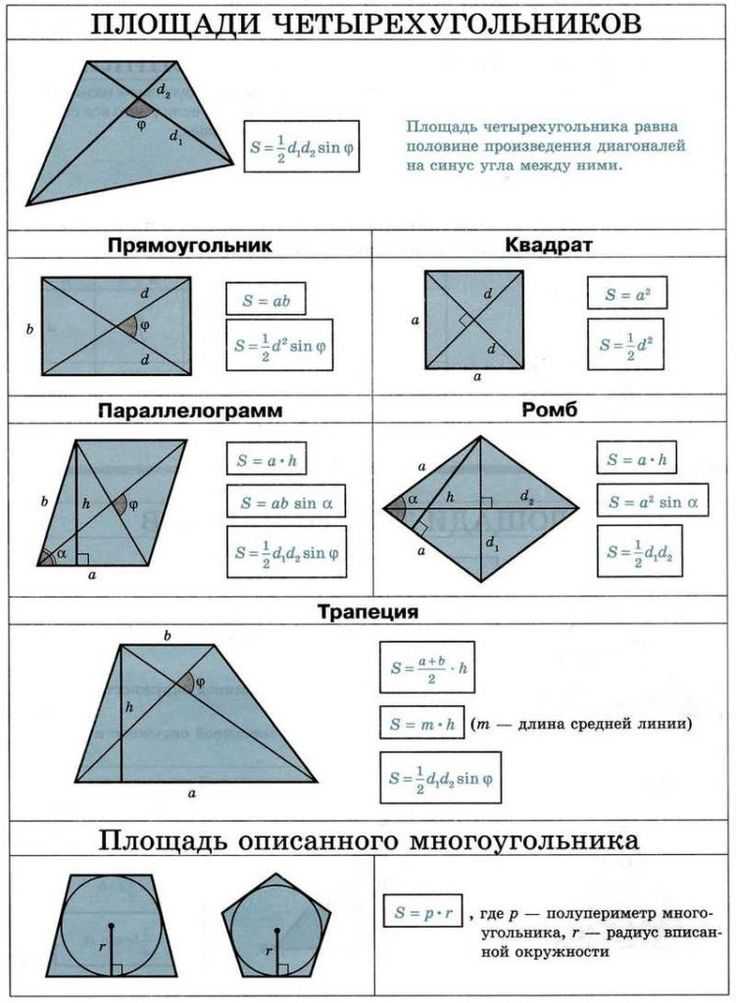
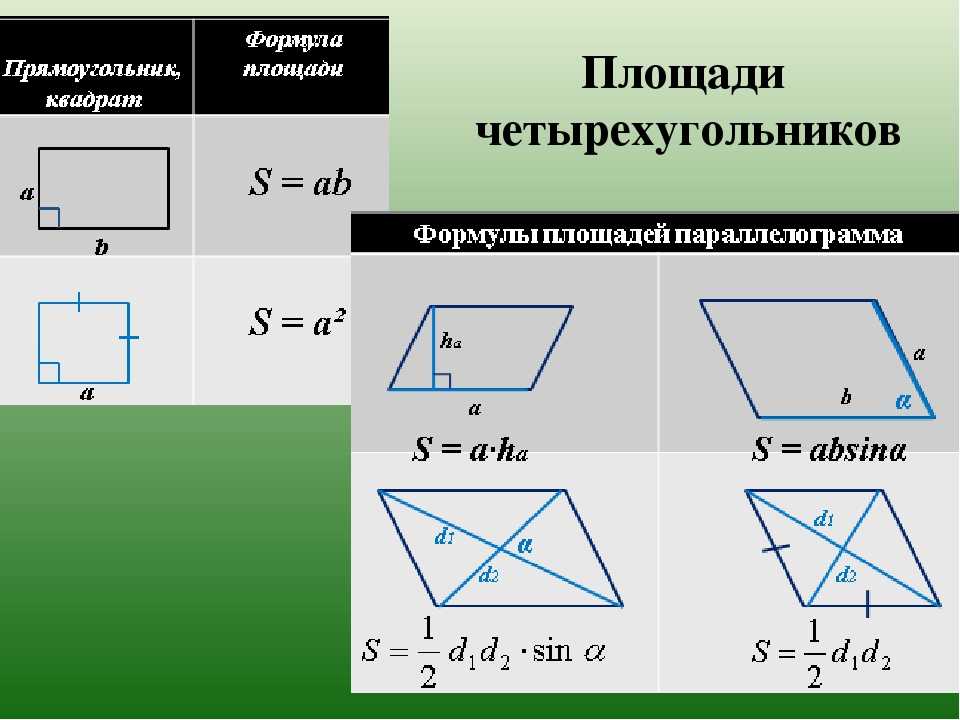 Площади четырехугольников
Площади четырехугольников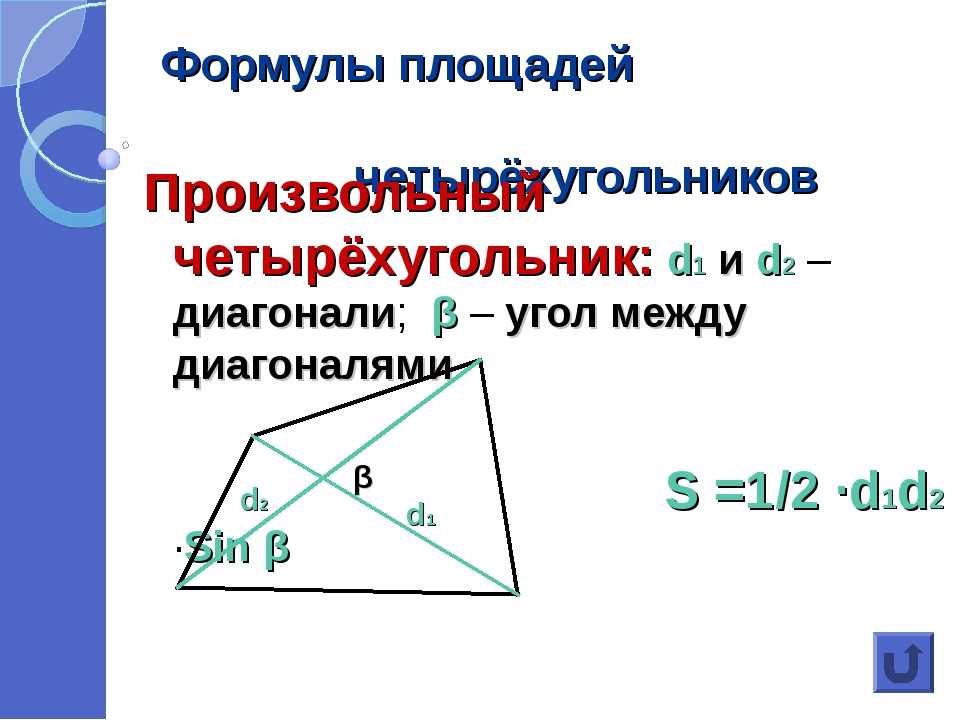
 Разделим обе части равенства на – 2. В
результате получим,
Разделим обе части равенства на – 2. В
результате получим, Пусть – некоторый параллелограмм. – высота .
Докажем, что площадь параллелограмма равна .
Пусть – некоторый параллелограмм. – высота .
Докажем, что площадь параллелограмма равна .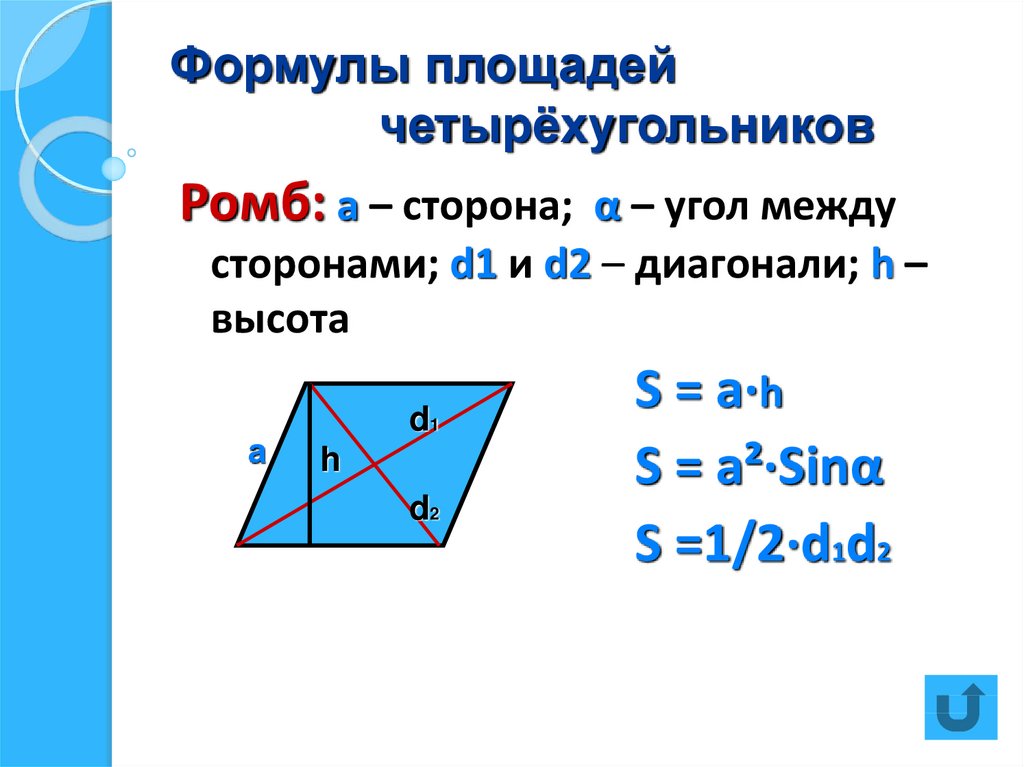 То есть площадь параллелограмма равна произведению длины стороны на высоту,
проведённую к ней.
То есть площадь параллелограмма равна произведению длины стороны на высоту,
проведённую к ней. и – основания, –
высота .
и – основания, –
высота . Он прямоугольный, так как высота
по построению. в
по условию. (см).
Тогда по теореме Пифагора можем выразить сторону .
Он прямоугольный, так как высота
по построению. в
по условию. (см).
Тогда по теореме Пифагора можем выразить сторону .

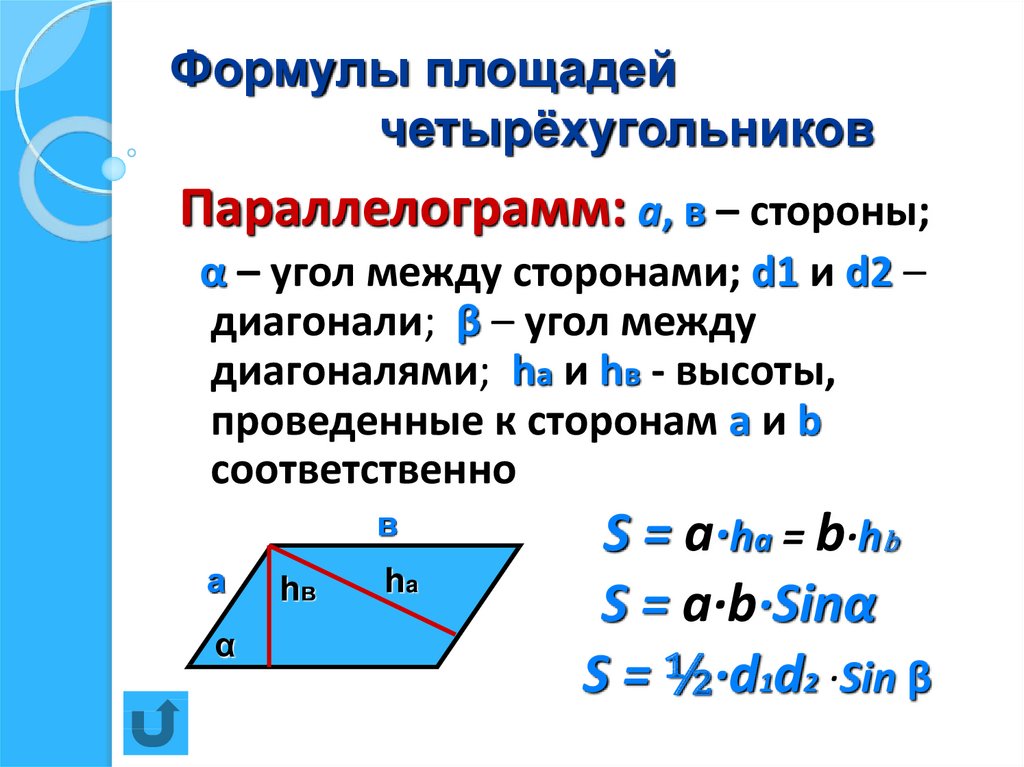 ;white-space:pre-wrap;»>Четырехугольником называется четырехсторонняя двумерная геометрическая фигура, сумма всех четырех внутренних углов которой равна 360 o . Также он имеет 4 ребра (стороны) и четыре вершины ( Четырехугольники бывают двух разных типов, а именно правильные четырехугольники и неправильные четырехугольники. Несколько известных примеров четырехугольников: квадрат, прямоугольник, трапеция, ромб, воздушный змей и параллелограмм.0003
;white-space:pre-wrap;»>Четырехугольником называется четырехсторонняя двумерная геометрическая фигура, сумма всех четырех внутренних углов которой равна 360 o . Также он имеет 4 ребра (стороны) и четыре вершины ( Четырехугольники бывают двух разных типов, а именно правильные четырехугольники и неправильные четырехугольники. Несколько известных примеров четырехугольников: квадрат, прямоугольник, трапеция, ромб, воздушный змей и параллелограмм.0003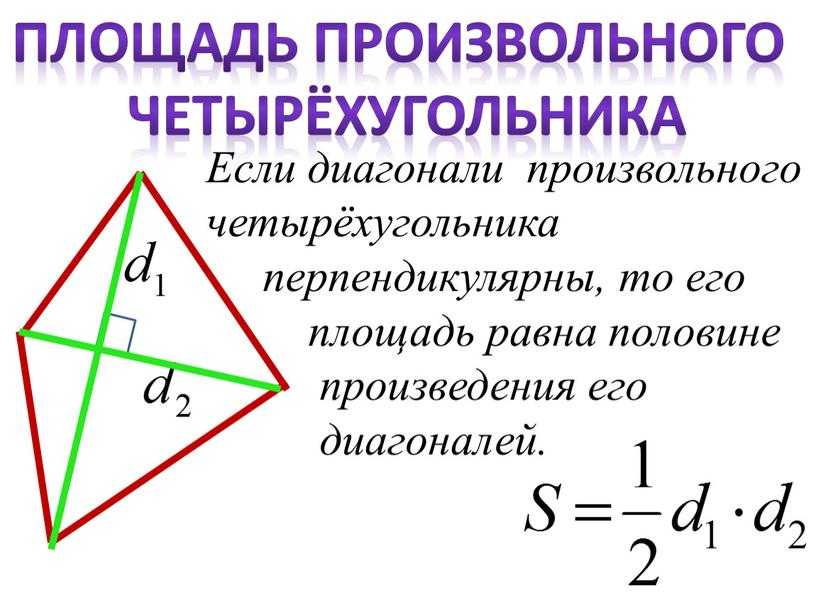
 unit
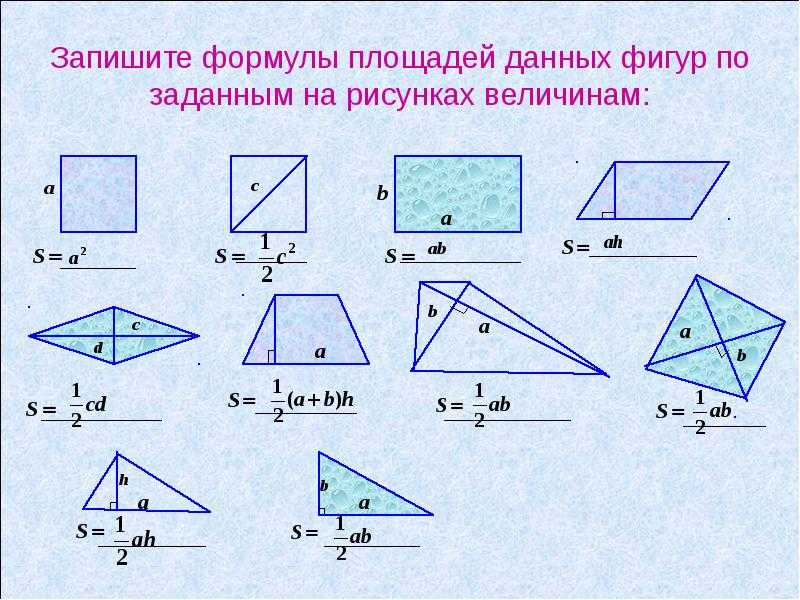
unit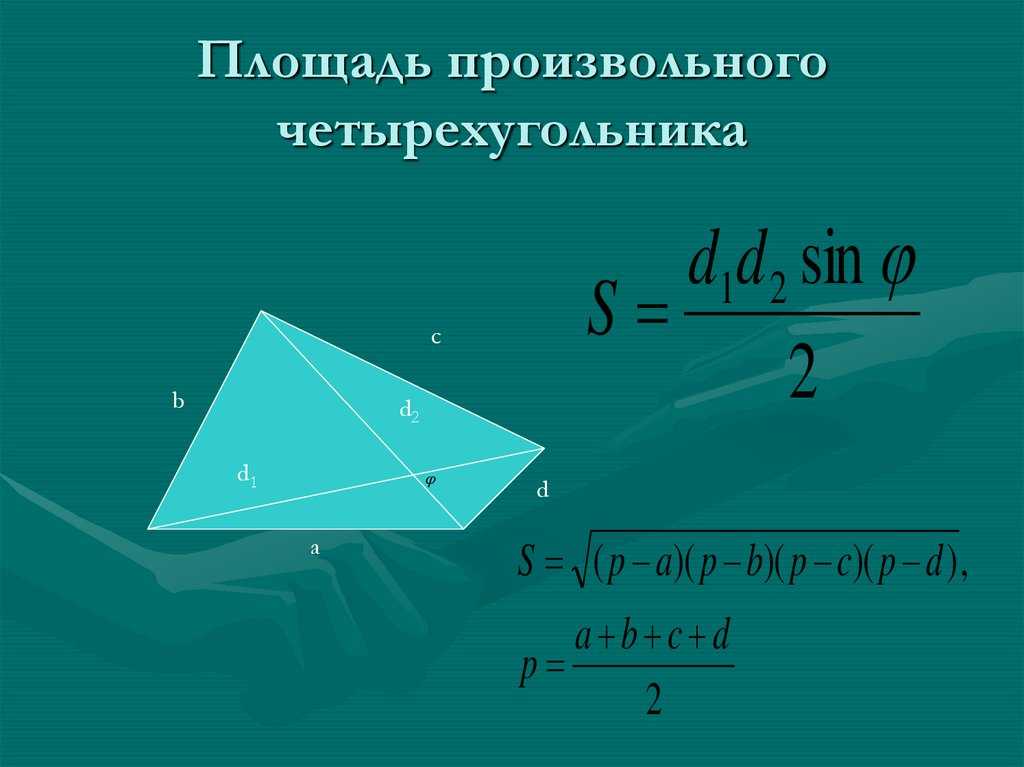 Эти формулы четырехугольника помогут вам вычислить площадь квадрата, прямоугольника, параллелограмма, воздушного змея, ромба и трапеции. Мы также обсудили площадь четырехугольника с формулой координатной геометрии, которая получается путем деления четырехугольника на два треугольника, вычисления площади каждого треугольника с учетом его вершин и сложения этих значений для получения общей площади четырехугольника.
Эти формулы четырехугольника помогут вам вычислить площадь квадрата, прямоугольника, параллелограмма, воздушного змея, ромба и трапеции. Мы также обсудили площадь четырехугольника с формулой координатной геометрии, которая получается путем деления четырехугольника на два треугольника, вычисления площади каждого треугольника с учетом его вершин и сложения этих значений для получения общей площади четырехугольника.

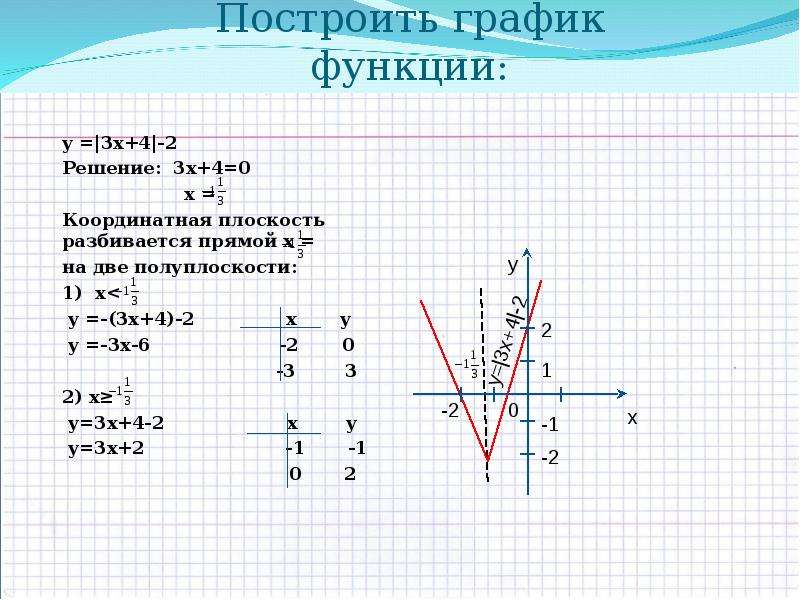

 КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. (1/3)
(1/3) 04.17
04.17 2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные



 е. 42.
е. 42. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле (а > 0, n ≥ 2).
Степень с дробным показателем можно представить в виде корня некоторой степени по формуле (а > 0, n ≥ 2). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂
Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂 3 = 8. Пояснение: 2 в 3-й степени можно записать как 23 = 2 × 2 × 2, так как 2 умножается на себя 3 раза. Здесь 2 называется «основанием», а 3 — «показателем» или «степенью».
3 = 8. Пояснение: 2 в 3-й степени можно записать как 23 = 2 × 2 × 2, так как 2 умножается на себя 3 раза. Здесь 2 называется «основанием», а 3 — «показателем» или «степенью». th мощность т.е. 28 is 256.
th мощность т.е. 28 is 256. …
…
 Чтобы вставить знак в квадрат, просто нажмите и удерживайте цифру 2, и он вставьте верхний индекс².
Чтобы вставить знак в квадрат, просто нажмите и удерживайте цифру 2, и он вставьте верхний индекс². Хотя это невообразимо большое число, существует еще бесконечное количество больших чисел. Одним из таких чисел является гуголплекс, который равен 10 в степени гугола, или 1, за которой следует гугол нулей.
Хотя это невообразимо большое число, существует еще бесконечное количество больших чисел. Одним из таких чисел является гуголплекс, который равен 10 в степени гугола, или 1, за которой следует гугол нулей.


 ..
..
 Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому:
Это интервал от 270 до 360 градусов (четвёртая четверть). Как переводить радианы в градусы можно посмотреть здесь. Значение синуса в этой четверти отрицательное, поэтому: Угол принадлежит интервалу (3Пи/2;2Пи).
Угол принадлежит интервалу (3Пи/2;2Пи). Разделим обе части уравнения на cos2 α, получим:
Разделим обе части уравнения на cos2 α, получим: Найдите tg α, если
Найдите tg α, если
 Докажем основное тригонометрическое тождество. Подробно рассмотрим примеры, в которых надо найти синусы, косинусы и тангенсы острых углов прямоугольного треугольника.
Докажем основное тригонометрическое тождество. Подробно рассмотрим примеры, в которых надо найти синусы, косинусы и тангенсы острых углов прямоугольного треугольника.
 Острые углы этих
треугольников равны по 45º. Находя для них такие же отношения, получим,
что и в этом случае эти отношения для обоих треугольников равны.
Острые углы этих
треугольников равны по 45º. Находя для них такие же отношения, получим,
что и в этом случае эти отношения для обоих треугольников равны.

 А раз равны синусы и косинусы, то из формулы ,
получим, что .
Таким образом, наше утверждение доказано.
А раз равны синусы и косинусы, то из формулы ,
получим, что .
Таким образом, наше утверждение доказано.

 Если вы возьмете другой треугольник с тем же отношением, например, треугольник со сторонами 6, 8 и 10, то синус, косинус и тангенс угла будет таким же, как в треугольнике 3, 4, 5. Проще говоря, синус угла, отношение между двумя сторонами треугольника, которые определяют угол.
Если вы возьмете другой треугольник с тем же отношением, например, треугольник со сторонами 6, 8 и 10, то синус, косинус и тангенс угла будет таким же, как в треугольнике 3, 4, 5. Проще говоря, синус угла, отношение между двумя сторонами треугольника, которые определяют угол.
 Если вы сейчас введете тангенс угла, калькулятор рассчитает градус этого угла.
Если вы сейчас введете тангенс угла, калькулятор рассчитает градус этого угла. Вычисление сторон с касательной
Вычисление сторон с касательной 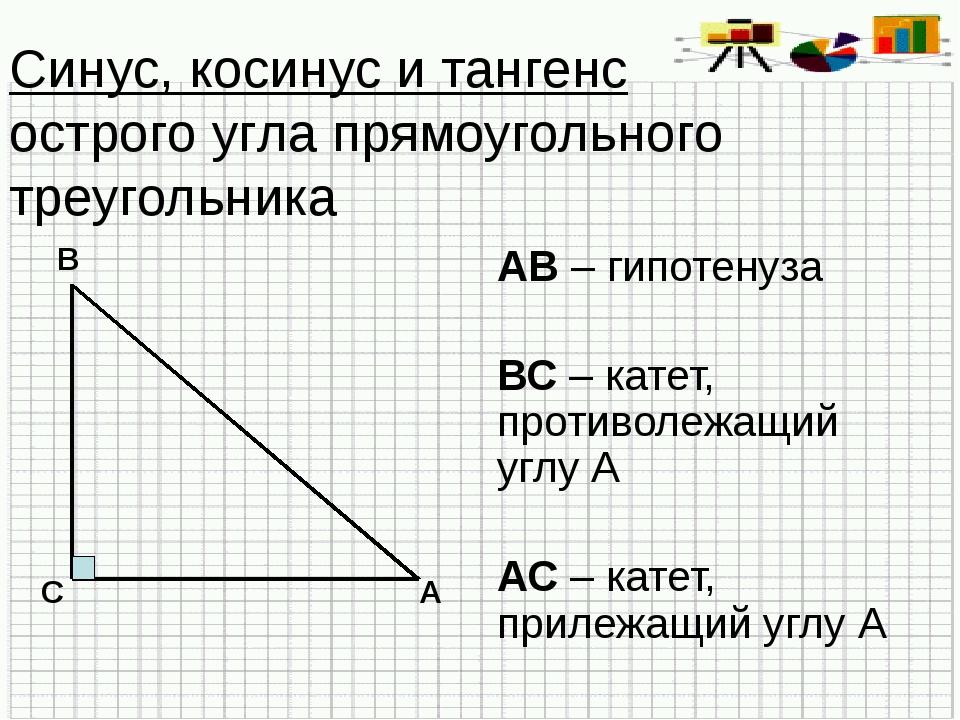 Формулы
Формулы  Je kunt dit aanpassen door op de «mode» button op je rekenmachine te drukken totdat je «Deg» of «Rad» ziet staan. Selecteer de optie die je nodig hebt.
Je kunt dit aanpassen door op de «mode» button op je rekenmachine te drukken totdat je «Deg» of «Rad» ziet staan. Selecteer de optie die je nodig hebt.  Zullen de sinus, cosinus en tangens van een bepaalde hoek in beide drie Хекен Хетцельфде зейн. De sinus ван een hoek является kortgezegd де verhouding tussen twee zijdes die een hoek bepalen.
Zullen de sinus, cosinus en tangens van een bepaalde hoek in beide drie Хекен Хетцельфде зейн. De sinus ван een hoek является kortgezegd де verhouding tussen twee zijdes die een hoek bepalen. Это ook de enigste zijde die niet langs de gevraagde hoek ligt.
Это ook de enigste zijde die niet langs de gevraagde hoek ligt. Это мы делаем дверь в машине rekenmachine *shift* en *tan* in te toetsen. Je ziet dat je rekenmachine nu «tan-1» laat zien. Als je nu де тангенс ван een hoek invult berekent де rekenmachine он aantal град ван де хука.
Это мы делаем дверь в машине rekenmachine *shift* en *tan* in te toetsen. Je ziet dat je rekenmachine nu «tan-1» laat zien. Als je nu де тангенс ван een hoek invult berekent де rekenmachine он aantal град ван де хука. Совет
Совет  В het voorbeeld hieronder kunnen мы één van de zijden en de tangens van de hoek invullen. De vraag in dit geval: Wat moeten we delen door de aanliggende zijde, om een tangens van 0.75 te krijgen.
В het voorbeeld hieronder kunnen мы één van de zijden en de tangens van de hoek invullen. De vraag in dit geval: Wat moeten we delen door de aanliggende zijde, om een tangens van 0.75 te krijgen.
 Два других угла в прямоугольном треугольнике — острые углы (с мерой менее [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления.
Два других угла в прямоугольном треугольнике — острые углы (с мерой менее [латекс]90[/латекс] градусов). Один из этих углов мы называем опорным углом и используем [латекс]θ[/латекс] (тета) для его представления. 5.3
5.3
 5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс].
5.2 опорными углами могут быть угол [латекс]Е[/латекс] или угол [латекс]F[/латекс]. Используя определение тригонометрических отношений, мы можем написать [latex]sin(E)=\frac{e}{d}[/latex], [latex]cos(E)=\frac{f}{d}[/latex ] и [латекс]тан(Е)=\фрак{е}{е}[/латекс]. При необходимости округлить до четырех знаков после запятой.
При необходимости округлить до четырех знаков после запятой.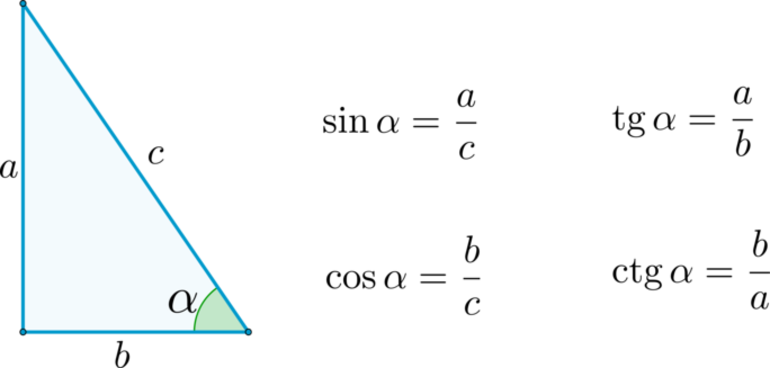 Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.
Мы адаптируем нашу стратегию решения задач для приложений тригонометрии. Кроме того, поскольку в этих задачах будет задействован прямоугольный треугольник, полезно нарисовать его (если рисунок не предоставлен) и пометить его с помощью данной информации. Мы включим это в первый шаг стратегии решения проблем для тригонометрических приложений.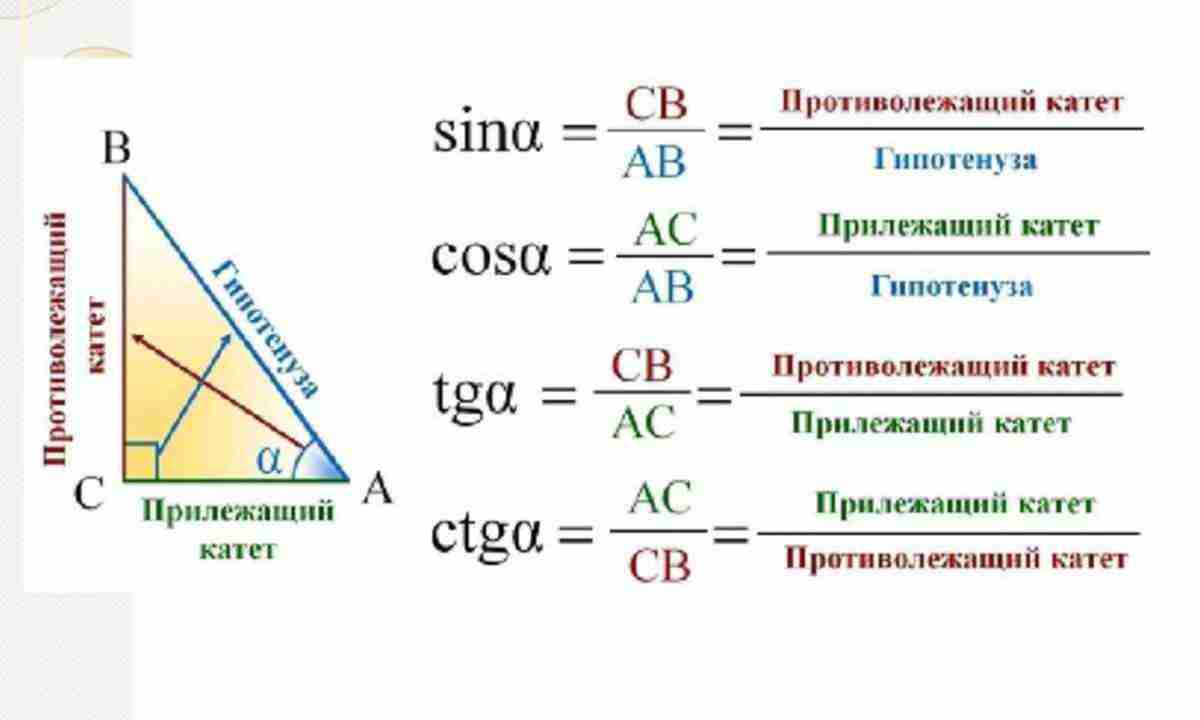
 }\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
}\;0,57&\overset?=8,03 \div14\\ 0,57&=0,57\checkmark\\[3ex] \text{b.}\;0,82& \overset?=11,47 \div14\\ 0,82&=0,82 \checkmark \end{align*}[/latex]
 {-1}[/latex] находятся на вашем научном калькуляторе. . 9\циркуляр[/латекс]
{-1}[/latex] находятся на вашем научном калькуляторе. . 9\циркуляр[/латекс]





 Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события элементарны, но событие не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).
Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события элементарны, но событие не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов). Например:
Например:

 То есть можно записать согласно теореме сложения:
То есть можно записать согласно теореме сложения: Определив таким образом события, получаем запись:
Определив таким образом события, получаем запись: Допустим есть два ящика. В одном из них находится 1 шар белого цвета и 5 шаров чёрного цвета. В другой положили белых — 8 штук, а чёрных — 4 штуки. Теперь вынимаем из ящиков по шару из каждого. Необходимо найти вероятность, что шары окажутся разных цветов.
Допустим есть два ящика. В одном из них находится 1 шар белого цвета и 5 шаров чёрного цвета. В другой положили белых — 8 штук, а чёрных — 4 штуки. Теперь вынимаем из ящиков по шару из каждого. Необходимо найти вероятность, что шары окажутся разных цветов. Второе — из первого появился шар чёрного цвета, а из второго шар белого. Записать эти события можно как $А\overline{В}$ и $\overline{A}В$. Вероятность каждого из них составит:
Второе — из первого появился шар чёрного цвета, а из второго шар белого. Записать эти события можно как $А\overline{В}$ и $\overline{A}В$. Вероятность каждого из них составит:  Совместная вероятность – это вероятность того, что событие Y произойдет одновременно с событием X.
Совместная вероятность – это вероятность того, что событие Y произойдет одновременно с событием X.
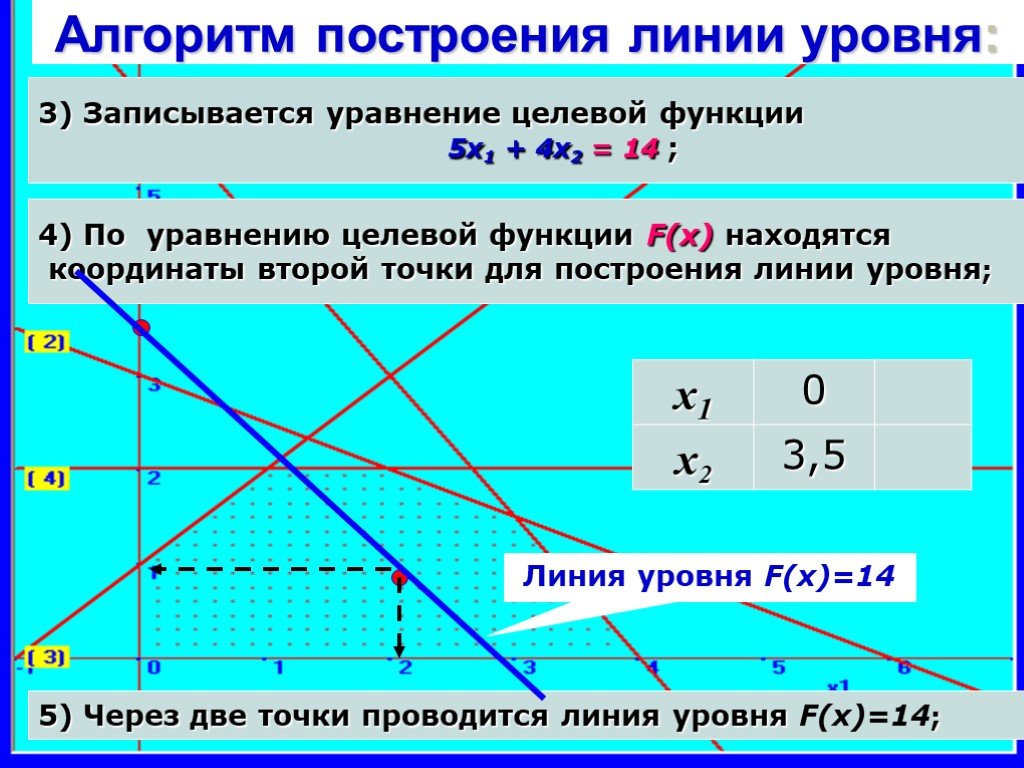
 Вероятность события X и события Y — это то же самое, что и точка пересечения X и Y. Поэтому совместную вероятность также называют пересечением двух или более событий. Диаграмма Венна, пожалуй, лучший визуальный инструмент для объяснения пересечения:
Вероятность события X и события Y — это то же самое, что и точка пересечения X и Y. Поэтому совместную вероятность также называют пересечением двух или более событий. Диаграмма Венна, пожалуй, лучший визуальный инструмент для объяснения пересечения: Например, из колоды карт вероятность того, что вы вытащите шестерку, при условии, что вы вытащили красную карту, равна P(6│красная) = 2/26 = 1/13, так как из 26 красных карточек две шестерки. .
Например, из колоды карт вероятность того, что вы вытащите шестерку, при условии, что вы вытащили красную карту, равна P(6│красная) = 2/26 = 1/13, так как из 26 красных карточек две шестерки. . Например, совместную вероятность можно использовать для оценки вероятности падения промышленного индекса Доу-Джонса (DJIA), сопровождаемого падением цены акций Microsoft, или вероятности того, что стоимость нефти вырастет одновременно с ослаблением доллара США. .
Например, совместную вероятность можно использовать для оценки вероятности падения промышленного индекса Доу-Джонса (DJIA), сопровождаемого падением цены акций Microsoft, или вероятности того, что стоимость нефти вырастет одновременно с ослаблением доллара США. . Пример: Подбрасывание монеты два раза. Исход подбрасывания монеты в первый раз не повлияет на исход второго события.
Пример: Подбрасывание монеты два раза. Исход подбрасывания монеты в первый раз не повлияет на исход второго события.  Вероятность того, что событие А и событие В произойдут вместе. Это вероятность пересечения двух или более событий, записанная как p(A ∩ B) .
Вероятность того, что событие А и событие В произойдут вместе. Это вероятность пересечения двух или более событий, записанная как p(A ∩ B) . Все знают, что дождь идет из туч. Так что дождь может идти только тогда, когда на небе есть облака. Это означает, что наличие облаков будет влиять на вероятность дождя, а это означает, что эти два события НЕ независимы!
Все знают, что дождь идет из туч. Так что дождь может идти только тогда, когда на небе есть облака. Это означает, что наличие облаков будет влиять на вероятность дождя, а это означает, что эти два события НЕ независимы! 
 Фактор, который связывает два, P(E|H) / P(E) , называется отношением правдоподобия .
Фактор, который связывает два, P(E|H) / P(E) , называется отношением правдоподобия .


 Если вы решите сделать это вручную, вам нужно знать, что данный подход требует преамбулы, которая будет зависеть от типа предоставляемой информации.
Если вы решите сделать это вручную, вам нужно знать, что данный подход требует преамбулы, которая будет зависеть от типа предоставляемой информации.

 Получаем:
Получаем:

 Во время загрузки и создания может происходить замедление работы браузера.
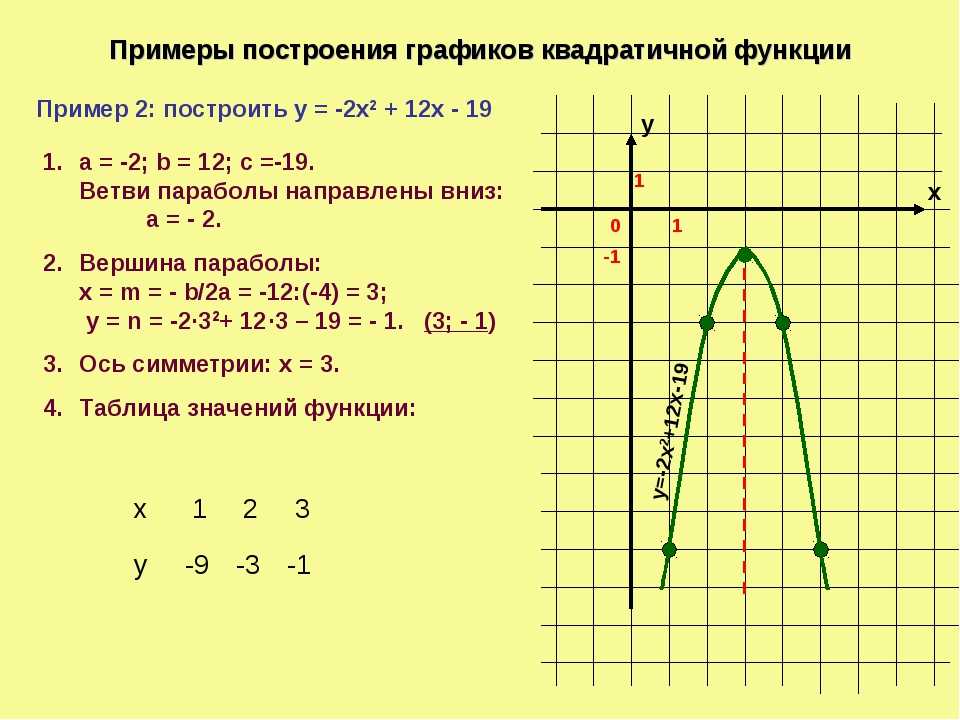
Во время загрузки и создания может происходить замедление работы браузера. На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.
На практике тип функции определяют путем визуального сравнения точек таблицы с графиками известных функций.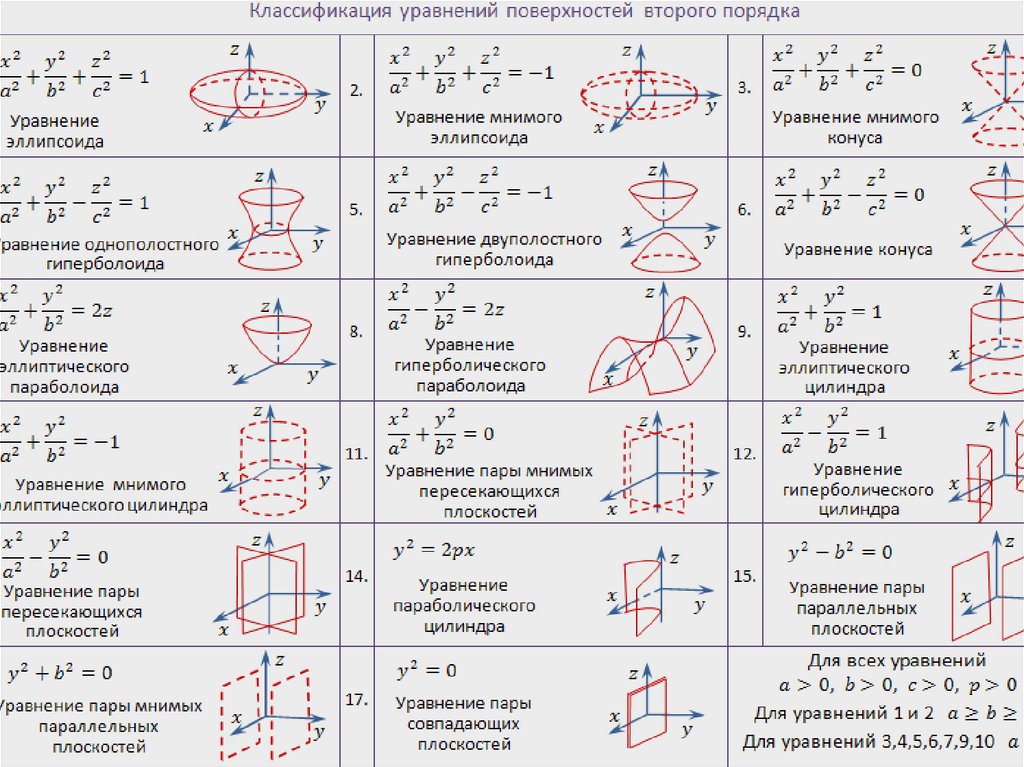 Для нахождения минимума найдем точки экстремума, в которых частные производные равны нулю.
Для нахождения минимума найдем точки экстремума, в которых частные производные равны нулю. Секреты торговли и практические правила для базовой математики:
Секреты торговли и практические правила для базовой математики: Имеются специальные калькуляторы для сложения футов, дюймов и долей дюймов.
доступны, но они всегда казались мне трудными в использовании. Таким образом, добавление
строка размеров в футах, дюймах и долях дюйма получает много
легче, если мы можем просто преобразовать в десятичные футы.
Имеются специальные калькуляторы для сложения футов, дюймов и долей дюймов.
доступны, но они всегда казались мне трудными в использовании. Таким образом, добавление
строка размеров в футах, дюймах и долях дюйма получает много
легче, если мы можем просто преобразовать в десятичные футы.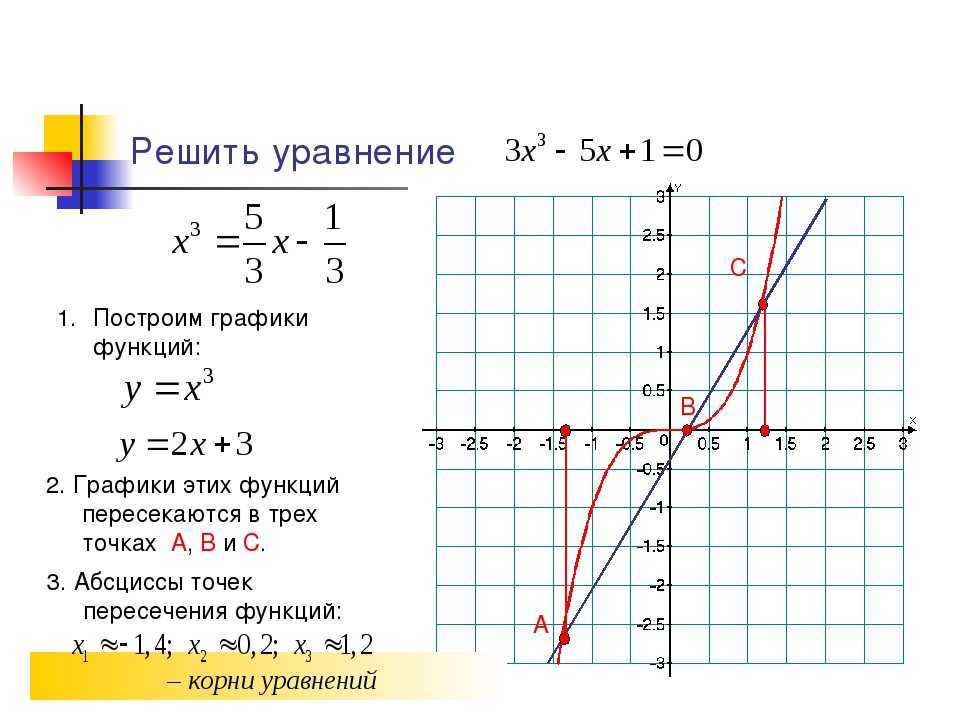 Итак, 401′ —
6 1/4 дюйма преобразуется в 401,52. Затем вычтите 400,14, чтобы найти изменение уклона.
1,38′. Чтобы найти уклон, разделите изменение уклона на 1,38 фута на
расстояние 30 футов, чтобы получить наклон 0,046 или 4,6%, что меньше, чем
максимум 5% разрешено кодом. Так что это работает.
Итак, 401′ —
6 1/4 дюйма преобразуется в 401,52. Затем вычтите 400,14, чтобы найти изменение уклона.
1,38′. Чтобы найти уклон, разделите изменение уклона на 1,38 фута на
расстояние 30 футов, чтобы получить наклон 0,046 или 4,6%, что меньше, чем
максимум 5% разрешено кодом. Так что это работает. Этот курс дает много базовых и более продвинутых
Информация для понимания математики.
Этот курс дает много базовых и более продвинутых
Информация для понимания математики. Я использовал этот навык с тех пор, и это помогло мне
решить много проблем (и избежать множества ошибок). Процесс
преобразование единиц является простым и мощным. Секрет постоянного
получение правильных ответов заключается в том, чтобы всегда перечислять единицы измерения и
время отмены единиц по мере прохождения процесса. Немного
примеры, показанные ниже в разделе «Преобразование
Единицы — примеры», которая наглядно иллюстрирует процесс.
Я использовал этот навык с тех пор, и это помогло мне
решить много проблем (и избежать множества ошибок). Процесс
преобразование единиц является простым и мощным. Секрет постоянного
получение правильных ответов заключается в том, чтобы всегда перечислять единицы измерения и
время отмены единиц по мере прохождения процесса. Немного
примеры, показанные ниже в разделе «Преобразование
Единицы — примеры», которая наглядно иллюстрирует процесс.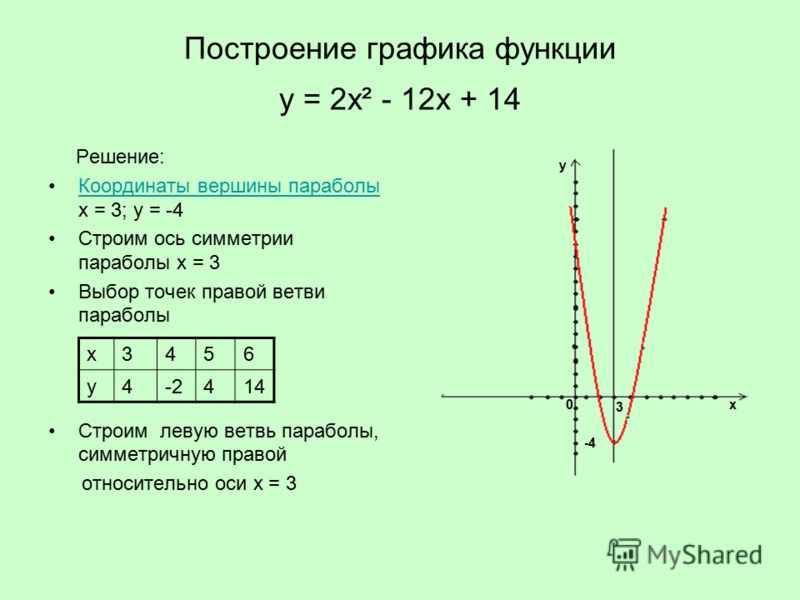
 Чем яснее вы
понять основные строительные блоки математики, тем лучше вы научитесь
и сохранить более продвинутые концепции. Недостаток работы через
весь курс — это время, которое он займет, и что вы, вероятно,
узнать много вещей, которые напрямую не применимы к строительству.
Чем яснее вы
понять основные строительные блоки математики, тем лучше вы научитесь
и сохранить более продвинутые концепции. Недостаток работы через
весь курс — это время, которое он займет, и что вы, вероятно,
узнать много вещей, которые напрямую не применимы к строительству.  Мы используем статистику, чтобы принимать обоснованные решения. А
строительная компания, например, может быть заинтересована в улучшении
производительность для своих профессий. Поскольку различные биты информации
проанализировав, возможно, они обнаружат, что прогулы по пятницам
значительно выше, чем в любой другой день. Статистика может помочь
понять, какая часть этого отсутствия случайна или это
значительная находка. Скажем, статистика указывает на существенно более высокий
прогулов по пятницам, то компания ищет причины. Работники
получают зарплату по четвергам во второй половине дня. Так что теперь есть руководство
выбор, который нужно сделать.
Мы используем статистику, чтобы принимать обоснованные решения. А
строительная компания, например, может быть заинтересована в улучшении
производительность для своих профессий. Поскольку различные биты информации
проанализировав, возможно, они обнаружат, что прогулы по пятницам
значительно выше, чем в любой другой день. Статистика может помочь
понять, какая часть этого отсутствия случайна или это
значительная находка. Скажем, статистика указывает на существенно более высокий
прогулов по пятницам, то компания ищет причины. Работники
получают зарплату по четвергам во второй половине дня. Так что теперь есть руководство
выбор, который нужно сделать. Некоторое хорошее преподавание статистики может
найти в
Курс «Введение в статистику ВМС США».
Некоторое хорошее преподавание статистики может
найти в
Курс «Введение в статистику ВМС США». 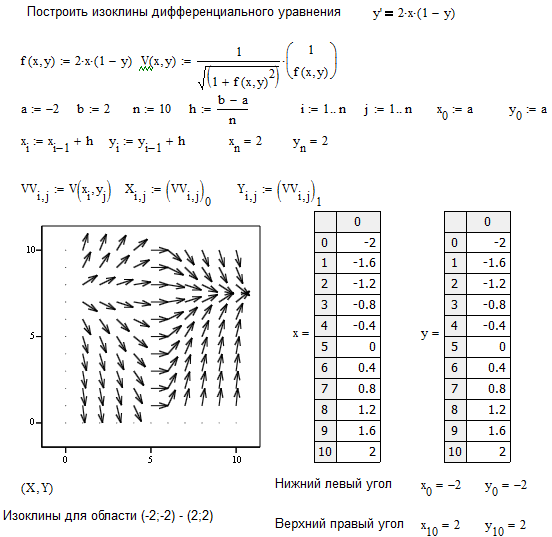
 При этом символы
всех величин, входящих в определяющее
уравнение, должны рассматриваться не
как сами величины, а как их именованные
числовые значения;
При этом символы
всех величин, входящих в определяющее
уравнение, должны рассматриваться не
как сами величины, а как их именованные
числовые значения; Подстановка вместо
L
и t
их единиц в системе СИ дает v
= 1м/c.
Следовательно, единица скорости является
когерентной.
Подстановка вместо
L
и t
их единиц в системе СИ дает v
= 1м/c.
Следовательно, единица скорости является
когерентной. д.;
д.; Например, исчисление может быть разработано почти полностью как абстрактный набор идей, сосредоточенных на свойствах функций. В то же время, если мы рассмотрим функции, представляющие значимые процессы, исчисление может описать наш опыт физической реальности. Мы уже видели, что для функции положения \(y = s(t)\) мяча, подброшенного вертикально вверх, производная функции положения \(v(t) = s'(t)\ text{,}\) дает скорость мяча в момент времени \(t\text{.}\)
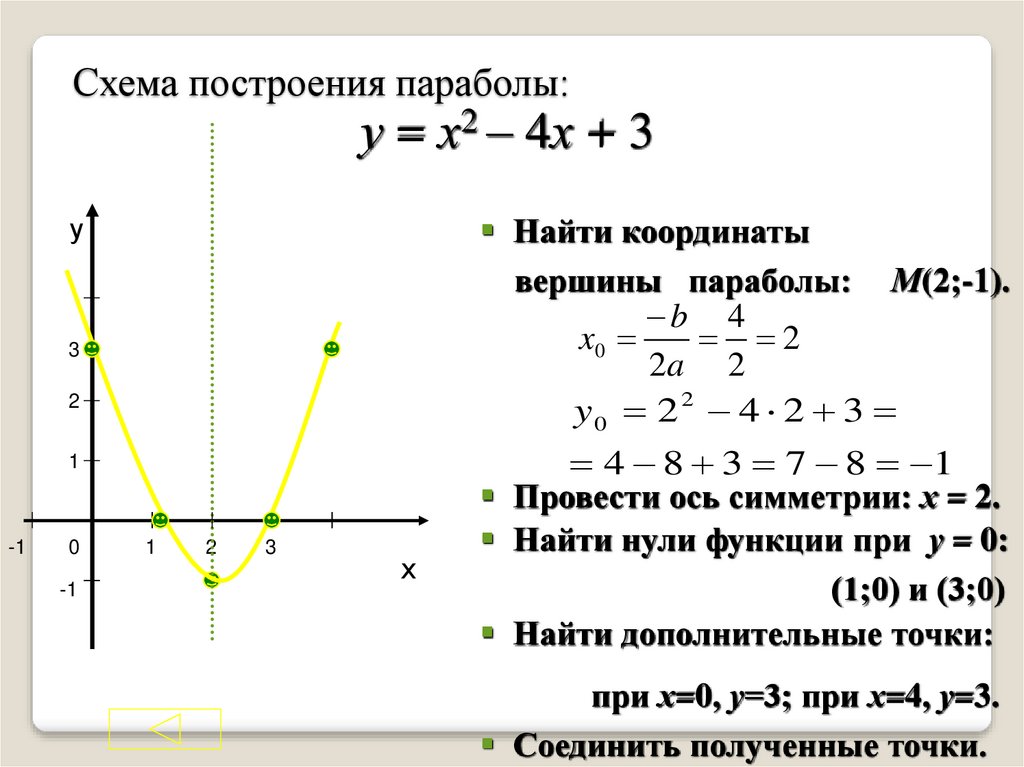
Например, исчисление может быть разработано почти полностью как абстрактный набор идей, сосредоточенных на свойствах функций. В то же время, если мы рассмотрим функции, представляющие значимые процессы, исчисление может описать наш опыт физической реальности. Мы уже видели, что для функции положения \(y = s(t)\) мяча, подброшенного вертикально вверх, производная функции положения \(v(t) = s'(t)\ text{,}\) дает скорость мяча в момент времени \(t\text{.}\) 4 и проходит через город Гакл. Автомобиль выезжает из города (в момент времени \(t = 0\)) и направляется на восток по шоссе 46; его положение в милях от Гакла в момент времени \(t\) в минутах определяется графиком функции на рисунке 1.5.1. На графике отмечены три важные точки; где кривая выглядит линейной, предположим, что это действительно прямая линия.
4 и проходит через город Гакл. Автомобиль выезжает из города (в момент времени \(t = 0\)) и направляется на восток по шоссе 46; его положение в милях от Гакла в момент времени \(t\) в минутах определяется графиком функции на рисунке 1.5.1. На графике отмечены три важные точки; где кривая выглядит линейной, предположим, что это действительно прямая линия.
 }\) Полезно помнить, что единицами измерения производной функции являются «единицы вывода на единицу ввода» для переменных исходной функции.
}\) Полезно помнить, что единицами измерения производной функции являются «единицы вывода на единицу ввода» для переменных исходной функции. С этой целью введем понятие центральной разности и его роль в оценке деривативов.
С этой целью введем понятие центральной разности и его роль в оценке деривативов. }
\end{equation*}
}
\end{equation*} }\) Обратите внимание, как первый наклон переоценивает наклон касательной в точке \((2 ,f(2))\text{,}\), а второй наклон занижает \(f'(2)\text{.}\) Справа мы видим секущую, наклон которой определяется центральная разность
}\) Обратите внимание, как первый наклон переоценивает наклон касательной в точке \((2 ,f(2))\text{,}\), а второй наклон занижает \(f'(2)\text{.}\) Справа мы видим секущую, наклон которой определяется центральная разность  }\)
}\)

 }\) Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ.
}\) Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ. }
\end{уравнение*}
}
\end{уравнение*}
 )
)  )
)  )
) 




 Умение работать с рациональными показателями — полезный навык, так как он очень применим в исчислении.
Умение работать с рациональными показателями — полезный навык, так как он очень применим в исчислении.
 6=1$.
6=1$. ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
ru: главная страница / / Техническая информация/ / Математический справочник / / Таблицы логарифмов и основные формулы. Десятичные и натуральные логарифмы. Степени, корни. / / Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).  Но ряд:
Но ряд: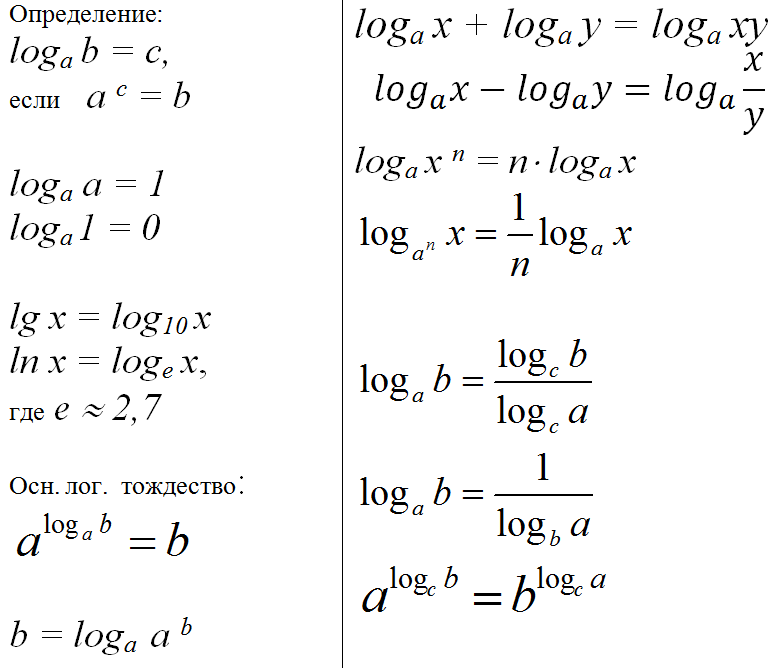 Введите свой запрос:
Введите свой запрос: Free xml sitemap generator
Free xml sitemap generator

 Его также называют логарифмом по основанию e. Здесь константа e обозначает число, которое является трансцендентным числом и иррациональным числом, приблизительно равным значению 2,71828182845. Натуральный логарифм (ln) может быть представлен как ln x или \[\log_{e}x\].
Его также называют логарифмом по основанию e. Здесь константа e обозначает число, которое является трансцендентным числом и иррациональным числом, приблизительно равным значению 2,71828182845. Натуральный логарифм (ln) может быть представлен как ln x или \[\log_{e}x\].
 302585
302585
 Поскольку мы знаем, что число 98 не является степенью числа 10 (в отличие от 100), поэтому мы можем найти значение, подключив его к калькулятору, не забывая использовать клавишу «LOG» (а не клавишу «LN» ), и мы получаем log(98) = 1,99122607569… или log(98) = 1,99, округленное до двух знаков после запятой.
Поскольку мы знаем, что число 98 не является степенью числа 10 (в отличие от 100), поэтому мы можем найти значение, подключив его к калькулятору, не забывая использовать клавишу «LOG» (а не клавишу «LN» ), и мы получаем log(98) = 1,99122607569… или log(98) = 1,99, округленное до двух знаков после запятой. 3
(стр. 341) текста.
3
(стр. 341) текста. Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень.
Проверьте это, оценив log 4 7, а затем возведя 4 в эту степень. Конденсация — это обратная сторона этого
процесс.
Конденсация — это обратная сторона этого
процесс.