Как найти площадь сектора круга: формулы, примеры задач
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение площади сектора круга
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь сектора круга, а также разберем примеры решения задач для демонстрации их практического применения.
- Определение сектора круга
- Формулы нахождения площади сектора круга
- Через длину дуги и радиус круга
- Через угол сектора (в градусах) и радиус круга
- Через угол сектора (в радианах) и радиус круга
- Примеры задач
Определение сектора круга
Сектор круга – это часть круга, образованная двумя его радиусами и дугой между ними. На рисунке ниже сектор закрашен зеленым цветом.
На рисунке ниже сектор закрашен зеленым цветом.
- AB – дуга сектора;
- R (или r) – радиус круга;
- α – это угол сектора, т.е. угол между двумя радиусами. Также его иногда называют центральным углом.
Формулы нахождения площади сектора круга
Через длину дуги и радиус круга
Площадь (S) сектора круга равняется одной второй произведения длины дуги сектора (L) и радиуса круга (r).
Через угол сектора (в градусах) и радиус круга
Площадь (S) сектора круга равняется площади круга, умноженной на угол сектора в градусах (α°) и деленной на 360°.
Через угол сектора (в радианах) и радиус круга
Площадь (S) сектора круга равняется половине произведения угла сектора в радианах (aрад) и квадрата радиуса круга.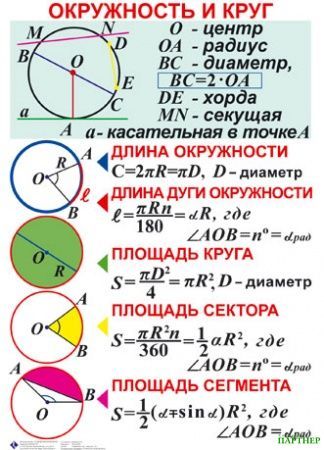
Примеры задач
Задание 1
Дан круг радиусом 6 см. Найдите площадь сектора, если известно, что длина его дуги составляет 15 см.
Решение
Воспользуемся первой формулой, подставив в нее заданные значения:
Задание 2
Найдите угол сектора, если известно, что его площадь равна 78 см2, а радиус круга – 8 см.
Решение
Выведем формулу для нахождения центрального угла из второй формулы, рассмотренной выше:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
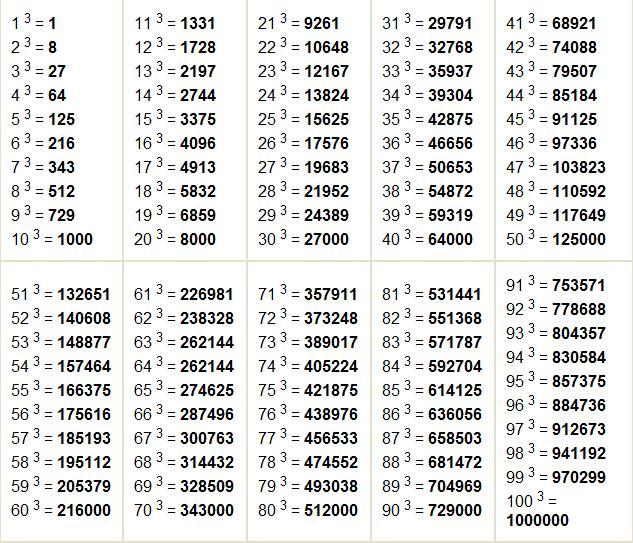
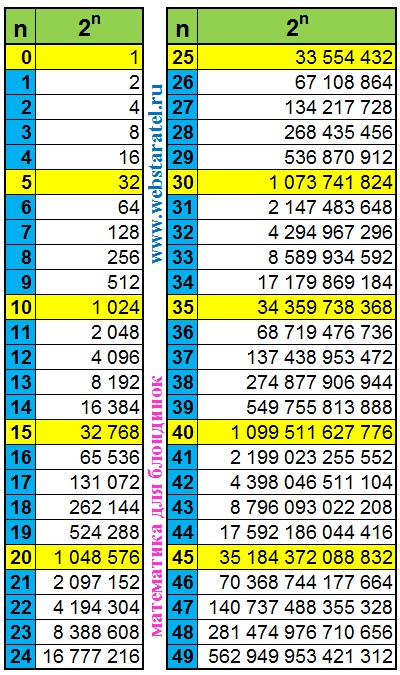
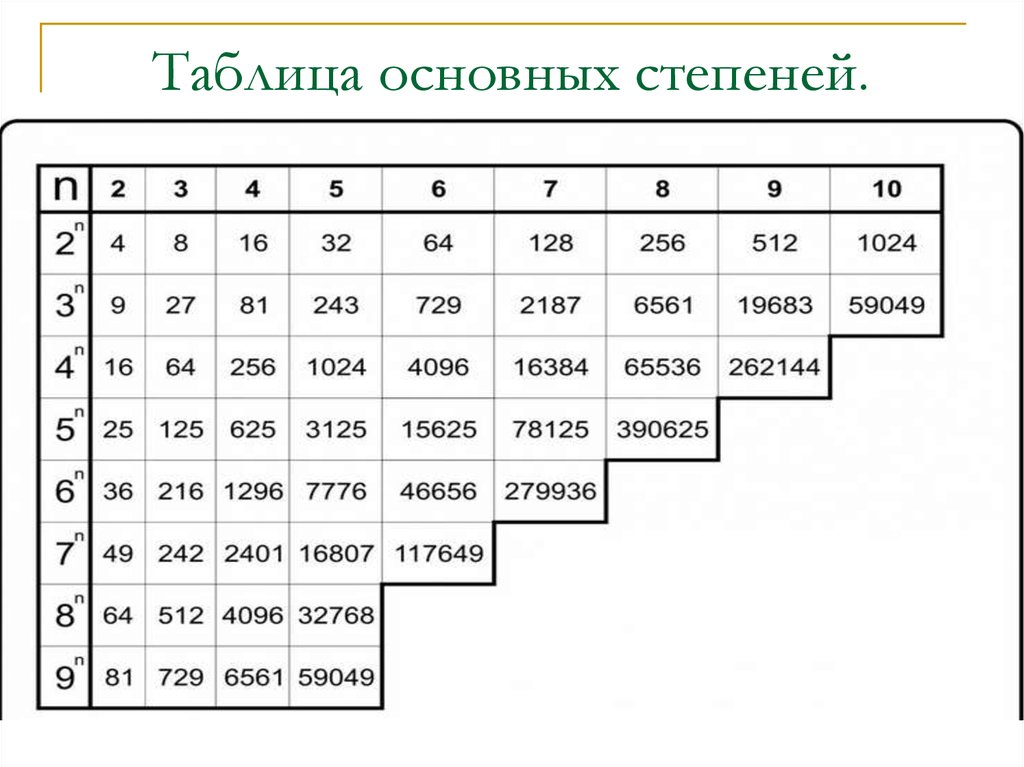
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Площадь сектора круга
Бизнес с Oriflame — рост и РАЗВИТИЕ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-01-17
Площадь сектора круга и площадь сегмента учить не нужно! Дорогие друзья! Вы, наверное, не раз просматривали справочник с математическими формулами, и, наверняка, возникала мысль: «Да разве возможно их все выучить?». Скажу вам, что возможно, но зачем? Зачем забивать голову массой формул, постоянно повторять их, ужасаться тому, что какую-то забыл и снова повторять? Не надо!
Скажу вам, что возможно, но зачем? Зачем забивать голову массой формул, постоянно повторять их, ужасаться тому, что какую-то забыл и снова повторять? Не надо!
На самом деле достаточно запомнить треть всех формул, базовых формул или ещё меньше. Далее вы поймёте о чём идёт речь. Все остальные формулы можно быстро вывести, зная основу, применяя логику, и запомнив принципы, которым нужно следовать.
Приведу пример, существует 32 формулы приведения, учить их – это бессмысленное занятие. Как быстро вспомнить любую из них — изложено в статье «Формулы приведения», посмотрите.
В этой статье мы рассмотрим, как быстро восстановить в памяти формулы площади сектора круга, площади его сегмента, длину дуги окружности. Именно эти формулы понадобятся для решения ряда по планиметрии, которые разберем в следующей статье. Итак, «базовые» формулы, их нужно выучить и знать!
Площади круга (формула):
Формула длины окружности:
Изобразим сектор, соответствующий определённому центральному углу n:
Рассуждаем логически: если площадь круга равна S=ПR2, то площадь соответствующая сектору в один градус будет равна 1/360 от площади круга (мы знаем, что вся окружность — это угол в 360 градусов), то есть
Далее понятно, что площадь сектора, соответствующая центральному углу в n градусов равна произведению одной тристашестидесятой площади круга и центрального угла n (соответствующего сектору), то есть
Вот вам и формула площади сектора.
Или можно выстроить рассуждение следующим образом:
Сектор в 1 градус — это 1/360 часть круга, соответственно сектор в n градусов — это n/360 часть круга. То есть площадь сектора будет равна произведению площади круга и этой части:
Далее найдём площадь сегмента.
Всё просто. Необходимо из площади сектора вычесть площадь треугольника (он обозначен жёлтым цветом). Площадь треугольника, как мы знаем, равна половине произведения соседних сторон на синус угла между ними (эту формулу нужно знать, она не сложная). В данном случае это:
Значит,
Вот вам и площадь сегмента!
Площадь сегмента, где центральный угол больше 180 градусов находится просто:
Из площади круга вычитаем площадь полученного нами сегмента:
Угол 360 – n градусов это угол, который соответствует изображённому сектору (жёлтый цвет):
То есть, другими словами, к его площади мы прибавляем площадь треугольника и получаем площадь оговоренного сегмента.
Аналогичным образом определяем длину дуги окружности. Как уже сказано, длина окружности равна:
Значит, длина дуги окружности соответствующая одному градусу будет равна одной тристашестидесятой от 2πR, то есть
Далее понятно, что длина дуги, соответствующая центральному углу в n градусов равна произведению одной тристашестидесятой длины окружности и соответствующему углу, то есть
Получили длину дуги окружности. Конечно, данную информацию учителя дают ученикам, и ничего такого секретного вы не узнали. Но, уверен, статья принесёт вам пользу.
Повторюсь, что самое главное — знать формулы площади круга и длины окружности, а далее работает только логика.
Предлагаю посмотреть дополнительный урок Дмирия Тарасова на эту тему. Рассматриваются формулы длины дуги окружности и площади сектора, где центральный угол задан в радианной мере.
На этом всё. Успехов Вам!!
Успехов Вам!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | Как запомнитьОкружность КругФормулы
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Калькулятор площади сектора
Автор: Hanna Pamuła, PhD
Отзыв от Bogna Szyk и Jack Bowater
Последнее обновление: 14 февраля 2023 г.
Содержание:- Что такое сектор круга? Определение сектора
- Формула площади сектора
- Особые случаи: площадь полукруга, площадь квадранта
- Калькулятор площади сектора – когда он может быть полезен?
- Часто задаваемые вопросы
С помощью этого калькулятора площади сектора вы быстро найдете любую площадь сектора круга , например, площадь полукруга или квадранта. В этой короткой статье мы будем:
В этой короткой статье мы будем:
Дайте определение сектора и объясните, что такое сектор круга.
Покажите формулу площади сектора и объясните, как самостоятельно вывести уравнение без особых усилий.
Назовите несколько примеров из реальной жизни, где калькулятор площади сектора может пригодиться.
Что такое сектор круга? Определение сектора
Итак, давайте начнем с определения сектора — что такое сектор в геометрии?
Сектор — геометрическая фигура, ограниченная двумя радиусами и дугой окружности .
Секторы круга чаще всего визуализируются на круговых диаграммах, где круг разделен на несколько секторов, чтобы показать вес каждого сегмента. На рисунках ниже показано несколько примеров секторов круга — это не обязательно означает, что они будут выглядеть как кусок пирога, но иногда он выглядит как остальная часть пирога после того, как вы взяли кусочек:
Очень редко можно услышать о секторе эллипса, но формулы way , way более сложны в использовании, чем уравнения площади сектора круга.
🙋 Прежде чем продолжить чтение, вы уже должны быть знакомы с кругами и эллипсами. Прочитайте наш калькулятор круга: найдите c, d, a, r и наш калькулятор эллипса, чтобы убедиться, что вы хорошо разбираетесь в этих предметах.
Формула площади сектора
Формула площади сектора проста – умножьте центральный угол на квадрат радиуса и разделите на 2:
-
Площадь сектора = r² × α / 2
Но откуда он взялся? Его можно найти, используя пропорции. Все, что вам нужно запомнить, это формулу площади круга (и мы уверены!):
- .
Площадь круга рассчитывается как
A = πr². Это отличная отправная точка. Полный угол равен 2π в радианах или 360° в градусах, последнее из которых является более распространенной единицей измерения угла.
Затем мы хотим вычислить площадь части круга, выраженную центральным углом.
Для углов 2π (полный круг) площадь равна πr²:
2π → πr²Итак, какова площадь сектора круга:
α → Площадь сектора
Из пропорции мы можем легко найти окончательную формулу площади сектора:
Площадь сектора = α × πr² / 2π = α × r² / 2
Тот же метод можно использовать для определения длины дуги – вам нужно только запомнить формулу длины окружности. Подробнее об этом читайте в нашем калькуляторе длины окружности и калькуляторе длины дуги .
Подробнее об этом читайте в нашем калькуляторе длины окружности и калькуляторе длины дуги .
💡 Обратите внимание, что Теперь найти площадь полукруга или квадранта не составит труда. Только подумайте, какой частью круга они являются! 1. Площадь полукруга: Зная, что это половина круга, разделить площадь на 2: Конечно, вы получите тот же результат, используя формулу площади сектора. 2. Площадь квадранта: Так как квадрант — это четверть круга, мы можем записать формулу как: — прямой угол (π/2 или 90°), так что вы быстро придёте к тому же уравнению: Мы знаем, мы знаем: « зачем нам это учить? Мы никогда не будем использовать это «. Что ж, мы хотели бы показать вам, что геометрия окружает нас повсюду: Если вам интересно, какой большой торт вы должны заказать на свою потрясающую вечеринку по случаю дня рождения — бинго, вот оно! Используйте формулу площади сектора, чтобы оценить размер кусочка 🍰 для ваших гостей, чтобы никто не умер с голоду. Та же история и с пиццей — вы заметили, что каждый кусочек — это сектор круга 🍕? Например, если вы не большой поклонник корочки, вы можете рассчитать, какой размер пиццы даст вам лучшее предложение (не забудьте потом о чаевых). Есть здесь энтузиасты шитья?👗 Расчет площади сектора может быть полезен при изготовлении юбки-солнце (поскольку это не всегда полный круг, а сектор круга). Помимо этих простых примеров из реальной жизни, формула площади сектора может быть полезна в геометрии, например, для нахождения площади поверхности конуса. Сектор круга представляет собой срез окружности, ограниченной двумя радиусами и дугой окружности . Мы идентифицируем сектора круга, используя их центральный угол . Центральный угол — это угол между двумя радиусами. Сектора с центральным углом, равным 90°, называются квадрантами . Для вычисления площади сектора круга можно использовать два метода. Если вы знаете радиус: Преобразование центрального угла в радиан : Умножьте радиус на угол в радианах. Разделить результат на 2. Если известна площадь круга: Вычислите отношение между полным углом и центральным углом . Умножьте результат на площадь круга. Площадь сектора с центральным углом подставляя: Таким образом: Обратите внимание, что это также четверть площади всего круга. Чтобы найти центральный угол сектора круга, можно инвертировать формулу его площади : где: Тогда формула для Чтобы найти угол в градусах, умножьте результат на Hanna Pamula, PhD Центральный угол Радиус Диаметр Площадь сектора (A) Длина дуги (L) α должно быть в радианах при использовании данной формулы. Если вы знаете центральный угол вашего сектора в градусов , умножьте его сначала на π/180° , чтобы найти его эквивалентное значение в радианах. Или вместо этого вы можете использовать эту формулу, где θ — центральный угол в градусах квадрант πr² / 2 Площадь полукруга = Площадь круга / 2 = πr² / 2  Просто помните, что прямой угол равен π (180°):
Просто помните, что прямой угол равен π (180°): Площадь полукруга = α × r² / 2 = πr² / 2 πr² / 4 Площадь квадранта = Площадь круга / 4 = πr² / 4 Площадь квадранта = α × r² / 2 = πr² / 4 Калькулятор площади сектора – когда он может быть полезен?

Часто задаваемые вопросы
Что такое сектор круга?

Как вычислить площадь сектора круга?
α [рад] = α [град] · π/180° Какова площадь 90° сектора круга с r = 1?
α = 90° круга с радиусом r = 1 равна π/4 . Чтобы вычислить этот результат, вы можете использовать следующую формулу: A = r² · α/2 , r = 1 ; и α = 90° · π/180° = π/2 .
A = (1² · π/2)/2 = π/4 . Как найти центральный угол сектора?
A = r² · α/2 , р — радиус ; и α — Центральный угол в радианах . α будет следующей: α = 2 · A/r² 180°/π .
Посмотреть 11 подобных калькуляторов окружностей ⭕
Длина дугиПлощадь кругаРассчитать окружность: найти c, d, a, r… Еще 8
Площадь сектора — Формула
Площадь сектора круга – это пространство, заключенное в пределах границы сектора. Сектор всегда начинается из центра круга. Давайте узнаем больше о площади сектора по формуле и о том, как найти площадь сектора в радианах и градусах.
Сектор всегда начинается из центра круга. Давайте узнаем больше о площади сектора по формуле и о том, как найти площадь сектора в радианах и градусах.
| 1. | Что такое площадь сектора круга? |
| 2. | Площадь сектора Формула |
| 3. | Площадь сектора в радианах |
| 4. | Часто задаваемые вопросы о районе сектора |
Что такое площадь сектора круга?
Пространство, ограниченное сектором круга, называется площадью сектора. Например, кусок пиццы является примером сектора, представляющего часть пиццы. Существует два типа секторов: второстепенные и крупные секторы. Малый сектор — это сектор, который меньше полукруга, тогда как большой сектор — это сектор, который больше полукруга.
На приведенном ниже рисунке показаны сектора в круге. Заштрихованная область показывает площадь сектора OAPB. Здесь ∠AOB — угол сектора. Следует отметить, что незаштрихованная область также является сектором круга. Таким образом, заштрихованная область — это область меньшего сектора , а незаштрихованная область — область большого сектора .
Заштрихованная область показывает площадь сектора OAPB. Здесь ∠AOB — угол сектора. Следует отметить, что незаштрихованная область также является сектором круга. Таким образом, заштрихованная область — это область меньшего сектора , а незаштрихованная область — область большого сектора .
Теперь давайте узнаем о формуле площади сектора и ее выводе после изучения определения сектора.
Определение сектора
Сектор круга определяется как часть круга, заключенная между двумя его радиусами и дугой, примыкающей к ним. Он рассматривается как часть окружности с двумя радиусами и дугой. Круг разделен на два сектора: меньший сектор и большой сектор, где меньший сектор является меньшей частью круга, а больший сектор является основной частью. Полукруг — наиболее распространенный сектор круга, представляющий половину круга.
Площадь сектора Формула
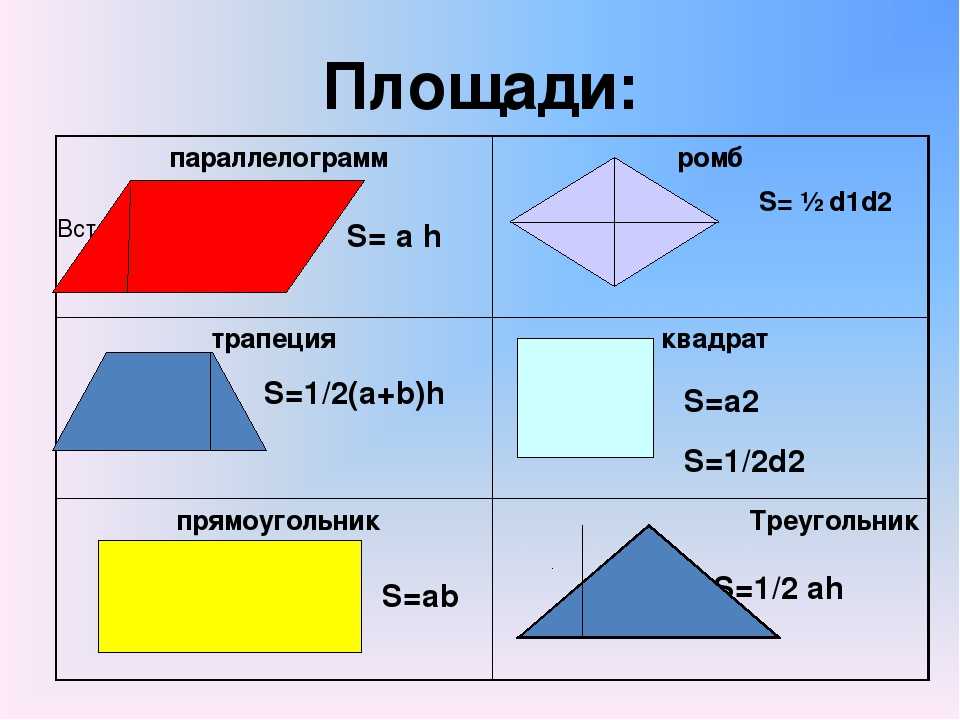
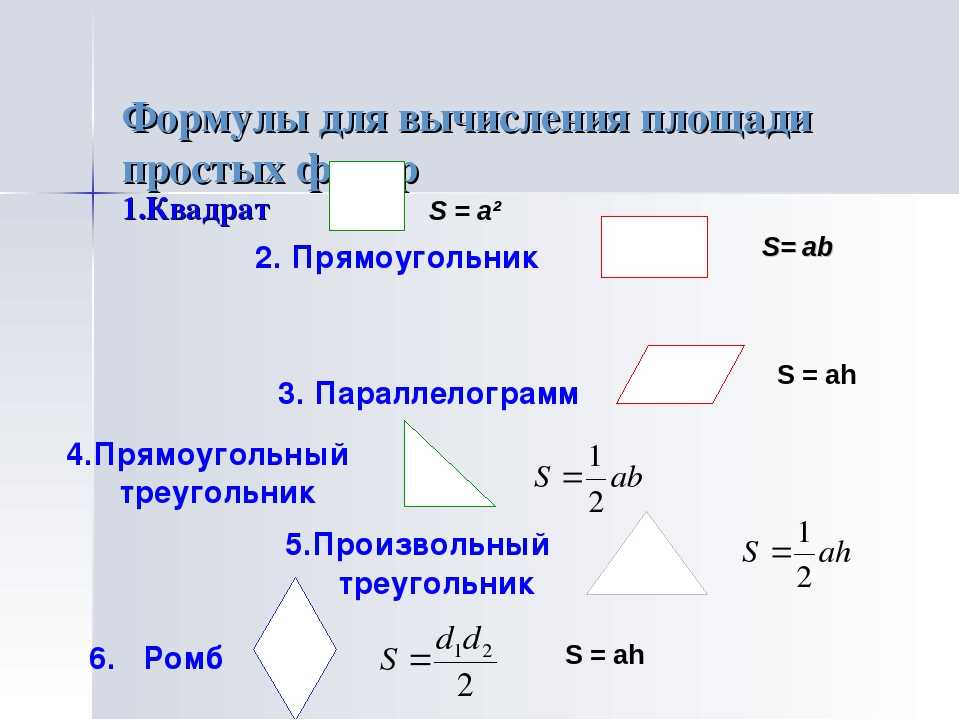
Чтобы найти общее пространство, заключенное в секторе, мы используем площадь сектора формулы. Площадь сектора можно рассчитать по следующей формуле:
Площадь сектора можно рассчитать по следующей формуле:
- Площадь сектора круга = (θ/360º) × πr 2 , где θ — угол сектора, образуемый дугой в центре, в градусов, а «r» — радиус окружности.
- Площадь сектора круга = 1/2 × r 2 θ, где θ — угол сектора, образуемый дугой в центре, в радианах, а r — радиус окружности.
Вывод формулы площади сектора
Применим унитарный метод для вывода формулы площади сектора круга. Мы знаем, что полный круг имеет длину 360º. Площадь круга с углом, измеряющим 360º в центре, равна πr 2 , где «r» — радиус круга.
Если угол в центре круга равен 1º, площадь сектора равна πr 2 /360º. Итак, если угол в центре равен θ, площадь сектора равна площади сектора круга = (θ/360º) × πr 2 , где
- θ — угол, стягиваемый в центре, дается в градусах.
- r — радиус окружности.
Другими словами, πr 2 представляет площадь полного круга, а θ/360º говорит нам, какая часть круга покрыта сектором.
Если угол в центре равен θ в радианах, то формула площади сектора круга = (1/2) × r 2 θ, где
- θ — угол, стягиваемый в центре, выраженный в радианах.
- r — радиус окружности.
Следует отметить, что полуокружности и квадранты являются особыми видами секторов окружности с углами 180° и 90° соответственно.
Площадь сектора в градусах
Воспользуемся этими формулами и на примере научимся вычислять площадь сектора круга, когда стягиваемый угол задан в градусах.
Пример: Окружность разделена на 3 сектора, а центральные углы, образуемые радиусом, составляют 160°, 100° и 100° соответственно. Найдите площади всех трех секторов.
Решение:
Угол, образуемый первым сектором, равен θ = 160°. Следовательно, площадь первого сектора = (θ/360°) × πr 2 = (160°/360°) × (22/7) × 6 2 = 4/9 × 22/7 × 36 = 352/7 = 50,28 квадратных единиц.
Угол, образуемый вторым сектором, равен θ = 100°. Следовательно, площадь второго сектора = (θ/360°) × πr 2 = (100°/360°) × (22/7) × 6 2 = 5/18 × 22/7 × 36 = 220/7 = 31,43 кв.
Угол, образуемый третьим сектором, такой же, как угол второго сектора (θ = 100°). Таким образом, площадь второго сектора равна площади третьего сектора. Следовательно, площадь третьего сектора = 31,43 кв.
Площадь сектора в радианах
Если нам нужно найти площадь сектора, когда угол задан в радианах, мы используем формулу Площадь сектора = (1/2) × r 2 θ; где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности. Итак, давайте разберемся, откуда берется формула. Мы знаем, что формула площади сектора (в градусах) = (θ/360º) × πr 2 , потому что это часть круга. Та же концепция применяется к формуле, когда мы хотим выразить ее в радианах, но нам просто нужно заменить 360° на 2π, потому что 2π (в радианах) = 360°. Это означает, что площадь сектора в радианах = (θ/2π) × πr 2 . При дальнейшем упрощении формулы площади сектора получаем площадь сектора = (θ/2) × r 2 или (1/2) × r 2 θ. Давайте разберемся, как найти площадь сектора в радианах на примере.
Это означает, что площадь сектора в радианах = (θ/2π) × πr 2 . При дальнейшем упрощении формулы площади сектора получаем площадь сектора = (θ/2) × r 2 или (1/2) × r 2 θ. Давайте разберемся, как найти площадь сектора в радианах на примере.
Пример: Найдите площадь сектора, если радиус окружности равен 6 единицам, а угол, образуемый в центре = 2π/3
Решение: Дано, радиус = 6 единиц; Угловая мера (θ)= 2π/3
Площадь данного сектора можно рассчитать по формуле Площадь сектора (в радианах) = (θ/2) × r 2 . Подставляя значения в формулу, получаем Площадь сектора (в радианах) = [2π/(3×2)] × 6 2 = (π/3) × 36 = 12π.
Следовательно, площадь данного сектора в радианах выражается как 12π квадратных единиц.
Реальный пример площади сектора круга
Одним из наиболее распространенных реальных примеров площади сектора является кусок пиццы. Форма ломтиков круглой пиццы похожа на сектор. Обратите внимание на приведенный ниже рисунок, на котором показана пицца, разделенная на 6 равных ломтиков, где каждый ломтик представляет собой сектор, а радиус пиццы составляет 7 дюймов. Теперь давайте найдем площадь сектора, образованного каждым срезом, используя формулу площади сектора. Следует отметить, что поскольку пицца разделена на 6 равных ломтиков, угол сектора равен 60°. Площадь ломтика пиццы = (θ/360°) × πr 2 = (60°/360°) × (22/7) × 7 2 = 1/6 × 22 × 7 = 77/3 = 25,67 квадратных единиц.
Обратите внимание на приведенный ниже рисунок, на котором показана пицца, разделенная на 6 равных ломтиков, где каждый ломтик представляет собой сектор, а радиус пиццы составляет 7 дюймов. Теперь давайте найдем площадь сектора, образованного каждым срезом, используя формулу площади сектора. Следует отметить, что поскольку пицца разделена на 6 равных ломтиков, угол сектора равен 60°. Площадь ломтика пиццы = (θ/360°) × πr 2 = (60°/360°) × (22/7) × 7 2 = 1/6 × 22 × 7 = 77/3 = 25,67 квадратных единиц.
Советы по области сектора
Вот список нескольких важных моментов, которые помогут решить проблемы области сектора.
- Площадь сектора круга — это дробная часть площади круга.
- Площадь сектора круга с радиусом r рассчитывается по формуле Площадь сектора = (θ/360º) × π r 2
- Длина дуги сектора радиуса r может быть рассчитана по формуле Длина дуги сектора = r × θ
☛ Похожие статьи
- Площадь круга
- Дуги и вытянутые углы
- Сегмент круга
- Что такое число Пи?
- Калькулятор площади сектора
Площадь сектора Примеры
Пример 1: Если угол сектора круга равен 60°, а радиус круга равен 7 дюймам, какова площадь сектора этого круга?
Решение:
Радиус круга 7 дюймов, угол 60°.
 Итак, воспользуемся формулой площади сектора. Площадь сектора = (θ/360°) × π r 2 = (60°/360°) × (22/7) × 7 2 = 77/3 = 25,67 квадратных единиц. Следовательно, площадь малого сектора равна 25,67 кв.
Итак, воспользуемся формулой площади сектора. Площадь сектора = (θ/360°) × π r 2 = (60°/360°) × (22/7) × 7 2 = 77/3 = 25,67 квадратных единиц. Следовательно, площадь малого сектора равна 25,67 кв.Пример 2: Зонт имеет 8 ребер, расположенных на одинаковом расстоянии друг от друга. Если рассматривать его как плоский круг радиусом 7 единиц, какова будет площадь между двумя последовательными ребрами зонта? (Подсказка: площадь между двумя последовательными ребрами образует сектор круга)
Решение:
Радиус плоского зонта = 7 единиц. В зонтике 8 ребер. Так как полный угол круга = 360°, угол каждого сектора зонта = 360/8 = 45°, потому что круг разделен на 8 равных секторов. Таким образом, площадь сектора = (θ/360°) × π r 2 = (45°/360°) × 22/7 × 7 2 = 77/4 = 19,25 квадратных единиц. Следовательно, площадь между двумя последовательными ребрами зонта равна 19,25 кв.
Пример 3: Круг диаметром 2 единицы разделен на 10 равных секторов.
 Сможете ли вы найти площадь каждого сектора круга?
Сможете ли вы найти площадь каждого сектора круга?Решение:
Диаметр окружности равен 2 единицам, следовательно, радиус окружности равен 1 единице. Поскольку полный угол окружности = 360°, угол каждого сектора окружности равен 360/10 = 36°, потому что полный угол делится на 10 равных частей. Площадь сектора = (θ/360°) × πr 2 = 36°/360° × 22/7 × 1 = 11/35 = 0,314 квадратных единиц. Следовательно, площадь каждого сектора круга составляет 0,314 квадратных единиц.
перейти к слайду перейти к слайду перейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Запись на бесплатное пробное занятие
Практические вопросы по сектору
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади сектора круга
Какова площадь сектора круга?
Пространство, ограниченное сектором круга, называется площадью сектора круга.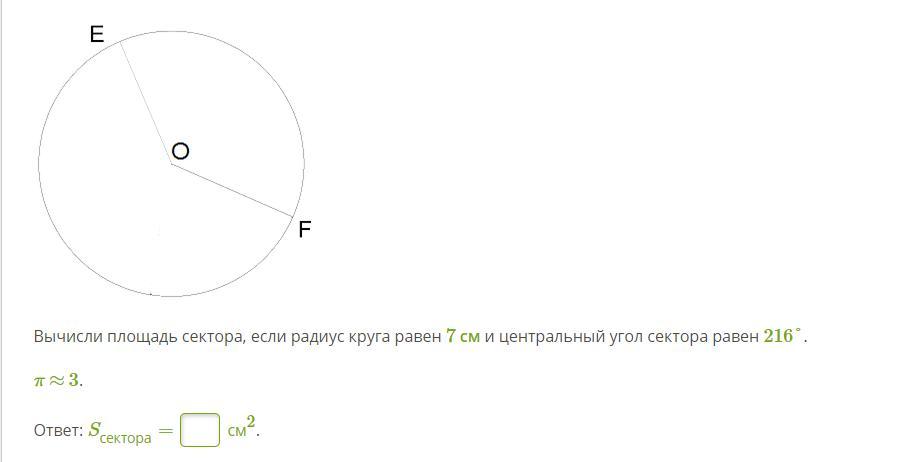 Часть окружности, ограниченная двумя радиусами и соответствующей дугой, называется сектором окружности.
Часть окружности, ограниченная двумя радиусами и соответствующей дугой, называется сектором окружности.
Какая формула площади сектора круга?
Две основные формулы, используемые для нахождения Площадь сектора :
- Площадь сектора круга = (θ/360º) × πr 2 , где θ — угол, стягиваемый в центре, указанный в градусах, а r — угол радиус окружности.
- Площадь сектора круга = 1/2 × r 2 θ, где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности.
Как рассчитать площадь сектора с помощью градусов?
Если угол, образуемый в центре, указан в градусах, площадь сектора можно рассчитать по следующей формуле: площадь сектора круга = (θ/360º) × πr 2 , где θ — угол, образуемый в центре, в градусах, а r — радиус окружности.
Что вы подразумеваете под сектором круга?
Сектор определяется как часть круга, заключенная между двумя его радиусами и дугой, примыкающей к ним. Полукруг — наиболее распространенный сектор круга, представляющий собой половину круга.
Полукруг — наиболее распространенный сектор круга, представляющий собой половину круга.
Что вы подразумеваете под дугой окружности?
Часть кривой или часть окружности окружности называется дугой. Многие объекты имеют кривую форму. Изогнутая часть этих объектов математически называется дугой.
Как выводится формула площади сектора круга?
Площадь сектора показывает площадь части площади круга. Мы знаем, что площадь круга рассчитывается по формуле πr 2 . Формула площади сектора круга выводится следующим образом:
- Применим унитарный метод для вывода формулы площади сектора круга.
- Мы знаем, что полный круг имеет длину 360º. Площадь круга с углом, измеряющим 360º в центре, равна πr 2 , где r — радиус окружности.
- Если угол в центре круга равен 1º, площадь сектора равна πr 2 /360º. Итак, если угол в центре равен θ, площадь сектора равна площади сектора круга = (θ/360º) × πr 2 , где θ — угол, стягиваемый в центре, указанный в градусов, а r — радиус окружности.

- Другими словами, πr 2 представляет площадь полного круга, а θ/360º говорит нам, какая часть круга покрыта сектором.
Как найти площадь сектора с длиной дуги и радиусом?
Площадь сектора можно рассчитать, если известны длина и радиус дуги. Сначала мы вычисляем угол (θ), образуемый дугой, по формуле Длина дуги = (θ/360) × 2πr. Теперь мы уже знаем радиус, а когда известен угол, площадь сектора можно рассчитать по формуле Площадь сектора круга = (θ/360º) × πr 2
Как найти радиус от площади сектора?
Если известна площадь сектора и известен угол (θ), образуемый дугой, радиус можно рассчитать, подставив данные значения в формулу Площадь сектора круга = (θ/360º ) × πr 2 . Например, найдем радиус, если площадь сектора равна 36π, а угол сектора равен 90°. Подставим данные значения в формулу Площадь сектора круга = (θ/360º) × πr 2 , то есть 36π = (90/360) × πr 2 . Итак, значение r 2 = 144, значит r = 12 единиц.
Как найти площадь сектора с точки зрения числа Пи?
Площадь сектора также может быть выражена через пи (π). Например, если радиус окружности равен 4 единицам, а угол, образуемый дугой сектора, равен 90°, найдем площадь сектора в единицах пи. Площадь сектора = (θ/360º) × πr 2 . Подставляя значения в формулу Площадь сектора = (90/360) × π × 4 2 . Решив это, мы получим площадь как 4π.
Как найти площадь сектора в радианах?
Чтобы найти площадь сектора с центральным углом в радианах, мы используем формулу Площадь сектора = (θ/2) × r 2 ; где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности. Например, если радиус окружности равен 12 единицам, а угол сектора, образуемый дугой в центре, = 4π/3, найдем площадь сектора. Площадь сектора (в радианах) = (θ/2) × r 2 . Подставляя значения в формулу, получаем Площадь сектора (в радианах) = [4π/(3×2)] × 12 2 = (2π/3) × 144 = 96π. Следовательно, площадь сектора в радианах выражается как 96π квадратных единиц.
Следовательно, площадь сектора в радианах выражается как 96π квадратных единиц.
Как найти площадь сектора без угла?
Если угол сектора не задан, но известны длина дуги и радиус, можно вычислить площадь сектора. Сначала мы находим секторный угол, подставляя заданные значения длины и радиуса дуги в формулу Длина дуги = (θ/360) × 2πr. После вычисления угла мы можем легко найти площадь сектора по формуле Площадь сектора круга = (θ/360º) × πr 2 .
Как найти длину дуги сектора?
Длина дуги — это расстояние вдоль части окружности окружности. Длину дуги окружности можно рассчитать по следующим формулам:
- Длина дуги = θ × r; где θ = центральный угол, опирающийся на дугу, а r = радиус окружности. Эта формула используется, когда θ выражено в радианах.
- Длина дуги = θ × (π/180) × r; где θ = центральный угол, опирающийся на дугу, а r = радиус окружности. Эта формула используется, когда θ выражается в градусах.
Как найти площадь малого сектора?
Площадь малого сектора – это площадь сектора, который меньше половины данного круга. Мы знаем, что малый сектор — это сектор, который меньше полукруга, тогда как большой сектор — это сектор, который больше полукруга. Формула, используемая для нахождения малого сектора, такая же, как и для нахождения площади любого сектора круга. Это означает, что площадь малого сектора может быть рассчитана по следующим формулам:
Мы знаем, что малый сектор — это сектор, который меньше полукруга, тогда как большой сектор — это сектор, который больше полукруга. Формула, используемая для нахождения малого сектора, такая же, как и для нахождения площади любого сектора круга. Это означает, что площадь малого сектора может быть рассчитана по следующим формулам:
- Площадь сектора круга = (θ/360º) × πr 2 , где θ — угол, стягиваемый в центре, в градусах, а «r» — радиус круга.
- Площадь сектора круга = 1/2 × r 2 θ, где θ — угол, стягиваемый в центре, в радианах, а r — радиус окружности.
Как найти радиус по длине дуги и площади сектора?
- Радиус окружности можно рассчитать, если известны длина дуги и площадь сектора. Простой способ — подставить данные значения в формулу Площадь сектора = (длина дуги × радиус)/2. Давайте разберемся в этом на примере. Например, если длина дуги окружности равна 15 см, а площадь сектора равна 225 см 2 .


 Итак, воспользуемся формулой площади сектора. Площадь сектора = (θ/360°) × π r 2 = (60°/360°) × (22/7) × 7 2 = 77/3 = 25,67 квадратных единиц. Следовательно, площадь малого сектора равна 25,67 кв.
Итак, воспользуемся формулой площади сектора. Площадь сектора = (θ/360°) × π r 2 = (60°/360°) × (22/7) × 7 2 = 77/3 = 25,67 квадратных единиц. Следовательно, площадь малого сектора равна 25,67 кв.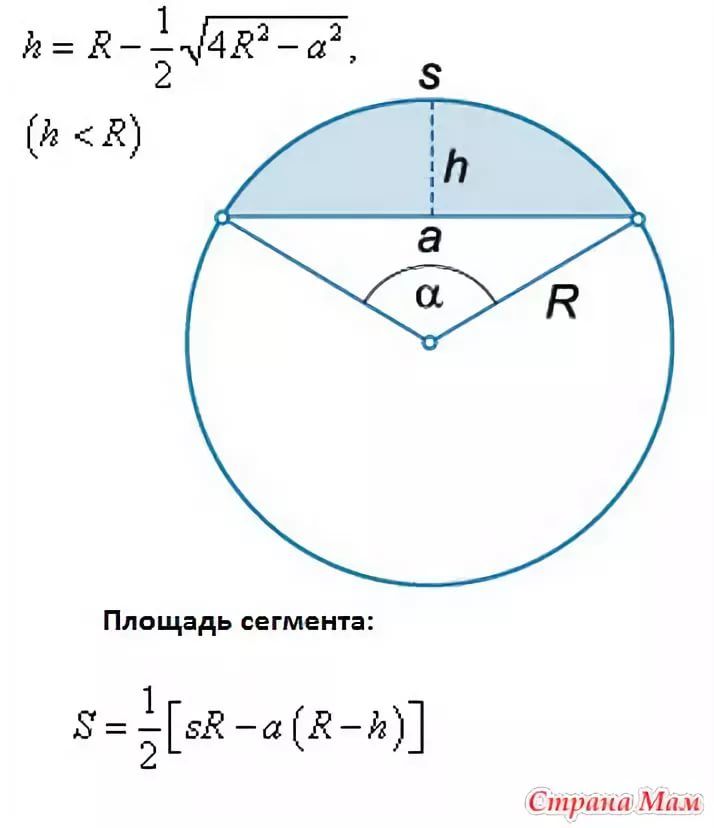 Сможете ли вы найти площадь каждого сектора круга?
Сможете ли вы найти площадь каждого сектора круга?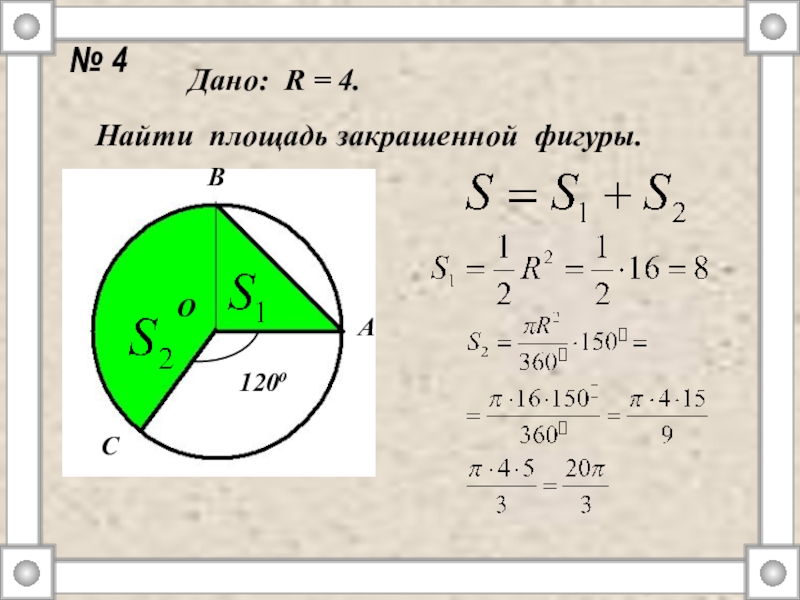

 {2m}.$$
{2m}.$$ Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений.
Такой способ задания Ф. часто применяется в тех случаях, когда область определения состоит из конечного числа значений. корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат.
корень, изображается верхней половиной шаровой поверхности радиуса 1 с центром в начале координат. 2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$.
2}$ отображает отрезок $–1 ⩽ x ⩽ 1$ на отрезок $0 ⩽ y ⩽ 1$. Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф.
Ферма «Введение и изучение плоских и телесных мест» (1636, опубл. в 1679). Изучение линий по их уравнениям в «Геометрии» Р. Декарта (1637) также указывает на ясное представление о взаимной зависимости двух переменных величин. У англ. математика И. Барроу («Лекции по геометрии», 1670) в геометрич. форме устанавливается взаимная обратность действий дифференцирования и интегрирования (разумеется, без употребления самих этих терминов). Это свидетельствует о совершенно отчётливом владении понятием Ф. В геометрич. и механич. виде это понятие можно найти и у И. Ньютона. Однако термин «Ф.» впервые появляется лишь в 1692 у Г. Лейбница, и притом не совсем в современном его понимании. Лейбниц называет Ф. разл. отрезки, связанные с к.-л. кривой, напр. абсциссы её точек. В первом печатном курсе «Анализа бесконечно малых» франц. математика Г. Лопиталя (1696) термин «Ф. » не употребляется.
» не употребляется. Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.
Так сложилось совр. понятие Ф., свободное от упоминания о её аналитич. задании.



 n, вычисленное эффективно.
n, вычисленное эффективно.


 Например, вместо того, чтобы ось X считала вверх на 1, первая отметка справа от 0 может быть помечена как 2, последующая — как 4, а следующая — как 6. В этом случае расстояние между каждой отметкой представляет собой 2. единицы измерения. Ось Y в этом же примере может даже иметь деления, представляющие 3 единицы; ось X и ось Y не должны иметь одинаковый интервал между метками. Поэтому важно обращать внимание на маркировку осей, поскольку различия в выбранных интервалах осей могут существенно повлиять на форму данного графика.
Например, вместо того, чтобы ось X считала вверх на 1, первая отметка справа от 0 может быть помечена как 2, последующая — как 4, а следующая — как 6. В этом случае расстояние между каждой отметкой представляет собой 2. единицы измерения. Ось Y в этом же примере может даже иметь деления, представляющие 3 единицы; ось X и ось Y не должны иметь одинаковый интервал между метками. Поэтому важно обращать внимание на маркировку осей, поскольку различия в выбранных интервалах осей могут существенно повлиять на форму данного графика. Другими словами, (x, y) не то же самое, что (y, x). Рассмотрим точки A, B и C, нанесенные на координатную плоскость ниже.
Другими словами, (x, y) не то же самое, что (y, x). Рассмотрим точки A, B и C, нанесенные на координатную плоскость ниже. Как только мы научились рисовать точки на координатной плоскости, мы можем перейти к графическому изображению более сложных объектов, поскольку график прямой или какой-либо другой функции — это просто визуальное представление всех точек или упорядоченных пар, составляющих функцию.
Как только мы научились рисовать точки на координатной плоскости, мы можем перейти к графическому изображению более сложных объектов, поскольку график прямой или какой-либо другой функции — это просто визуальное представление всех точек или упорядоченных пар, составляющих функцию.
 Оси X и Y — это оси, используемые в системах координат, образующих координатную плоскость. Горизонтальная ось представлена осью x, а вертикальная ось представлена осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости. Ось x также известна как абсцисса или график x, тогда как ось y также известна как график ординат или график y. На изображении ниже показано соответствующее представление.
Оси X и Y — это оси, используемые в системах координат, образующих координатную плоскость. Горизонтальная ось представлена осью x, а вертикальная ось представлена осью y. Точка пересечения осей x и y называется началом координат и используется в качестве опорной точки для плоскости. Ось x также известна как абсцисса или график x, тогда как ось y также известна как график ординат или график y. На изображении ниже показано соответствующее представление. ось x или перпендикулярное расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найти точку. Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как:
ось x или перпендикулярное расстояние от оси y, а координата y представляет собой точку на оси y или перпендикулярное расстояние от оси x, поэтому сверху ясно, что ось x идет первой при записи упорядоченной пары в найти точку. Здесь мы видим, что расположение каждой точки на графике отмечено как упорядоченная пара, где ось x или координата x опережает ось y или координату y. Затем представить эти точки на диаграмме x и y, используя годы на оси x и соответствующее население на оси y как: Затем соедините точки прямой линией, чтобы нарисовать график уравнения.
Затем соедините точки прямой линией, чтобы нарисовать график уравнения.
 С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.


 Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры).
Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры). Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.
Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.
 Если пять микроволновых печей выбрали случайно для поставки в отель, сколько бракованных печей может попасться?
Если пять микроволновых печей выбрали случайно для поставки в отель, сколько бракованных печей может попасться? Испытания Бернулли.
Испытания Бернулли.
 Вы можете найти пример использования под калькулятором.
Вы можете найти пример использования под калькулятором. В наборе 10 неисправных микроволновых печей. Если 5 печей выбраны случайным образом для отправки в гостиницу, сколько дефектных печей они могут ожидать?
В наборе 10 неисправных микроволновых печей. Если 5 печей выбраны случайным образом для отправки в гостиницу, сколько дефектных печей они могут ожидать?

 dll»
dll»

 Дополнительные сведения о синтаксисе, доступных для использования типах переменных и поведении при подключении инструмента Калькулятор растра в ModelBuilder см. в справке по инструменту Калькулятор растра.
Дополнительные сведения о синтаксисе, доступных для использования типах переменных и поведении при подключении инструмента Калькулятор растра в ModelBuilder см. в справке по инструменту Калькулятор растра.


 Смит
Смит 

 Новый NOC изменит право на участие в некоторых иммиграционных программах Канады, включая Express Entry.
Новый NOC изменит право на участие в некоторых иммиграционных программах Канады, включая Express Entry.





 Стандартизированные результаты необходимы для документирования в электронных записях, для использования в клинических информационных системах, для развития сестринских знаний и обучения профессиональных медсестер и студентов. Исход определяется как измеримое состояние, поведение или восприятие отдельного человека, семьи или сообщества, которые измеряются в континууме в ответ на сестринское вмешательство. Результаты разработаны для использования во всех клинических условиях и со всеми группами пациентов. Результаты NOC можно использовать на протяжении всего периода оказания медицинской помощи, чтобы отслеживать результаты лечения пациентов на протяжении всего эпизода болезни или в течение длительного периода времени. Медсестры в больницах третичного уровня, общественных больницах, общественных учреждениях, центрах престарелых и домах престарелых оценили использование результатов NOC в своей практике в рамках гранта NIH, финансируемого из федерального бюджета. Поскольку результаты описывают статус пациента, семьи или сообщества, другие дисциплины могут найти их полезными для оценки вмешательств, которые они оказывают пациентам.
Стандартизированные результаты необходимы для документирования в электронных записях, для использования в клинических информационных системах, для развития сестринских знаний и обучения профессиональных медсестер и студентов. Исход определяется как измеримое состояние, поведение или восприятие отдельного человека, семьи или сообщества, которые измеряются в континууме в ответ на сестринское вмешательство. Результаты разработаны для использования во всех клинических условиях и со всеми группами пациентов. Результаты NOC можно использовать на протяжении всего периода оказания медицинской помощи, чтобы отслеживать результаты лечения пациентов на протяжении всего эпизода болезни или в течение длительного периода времени. Медсестры в больницах третичного уровня, общественных больницах, общественных учреждениях, центрах престарелых и домах престарелых оценили использование результатов NOC в своей практике в рамках гранта NIH, финансируемого из федерального бюджета. Поскольку результаты описывают статус пациента, семьи или сообщества, другие дисциплины могут найти их полезными для оценки вмешательств, которые они оказывают пациентам.
 Результаты сгруппированы по тридцати четырем классам и семи доменам для простоты использования. Семь доменов: функциональное здоровье, физиологическое здоровье, психосоциальное здоровье, знания о здоровье и поведение, воспринимаемое здоровье, здоровье семьи и здоровье сообщества. Каждый результат имеет уникальный кодовый номер, который облегчает его использование в компьютеризированных клинических информационных системах и позволяет манипулировать данными для ответа на вопросы о качестве и эффективности сестринского ухода. Классификация постоянно обновляется, чтобы включать новые результаты и пересматривать результаты на основе новых исследований или отзывов пользователей.
Результаты сгруппированы по тридцати четырем классам и семи доменам для простоты использования. Семь доменов: функциональное здоровье, физиологическое здоровье, психосоциальное здоровье, знания о здоровье и поведение, воспринимаемое здоровье, здоровье семьи и здоровье сообщества. Каждый результат имеет уникальный кодовый номер, который облегчает его использование в компьютеризированных клинических информационных системах и позволяет манипулировать данными для ответа на вопросы о качестве и эффективности сестринского ухода. Классификация постоянно обновляется, чтобы включать новые результаты и пересматривать результаты на основе новых исследований или отзывов пользователей. Кроме того, были установлены связи между Международной классификацией функционирования, инвалидности и здоровья (МКФ) и НОК в попытке изучить компоненты МКФ и ее международное и междисциплинарное использование. Более подробный обзор связи между NOC, NIC и NANDA-I доступен в отдельной книге 9.0205 Связь NOC и NIC с NANDA-I и клиническими состояниями: поддержка критического мышления и качественного ухода .
Кроме того, были установлены связи между Международной классификацией функционирования, инвалидности и здоровья (МКФ) и НОК в попытке изучить компоненты МКФ и ее международное и междисциплинарное использование. Более подробный обзор связи между NOC, NIC и NANDA-I доступен в отдельной книге 9.0205 Связь NOC и NIC с NANDA-I и клиническими состояниями: поддержка критического мышления и качественного ухода .
 2
2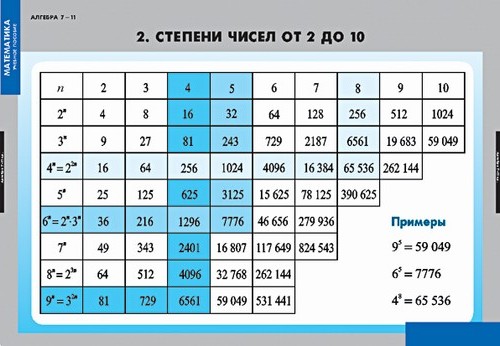 ee
ee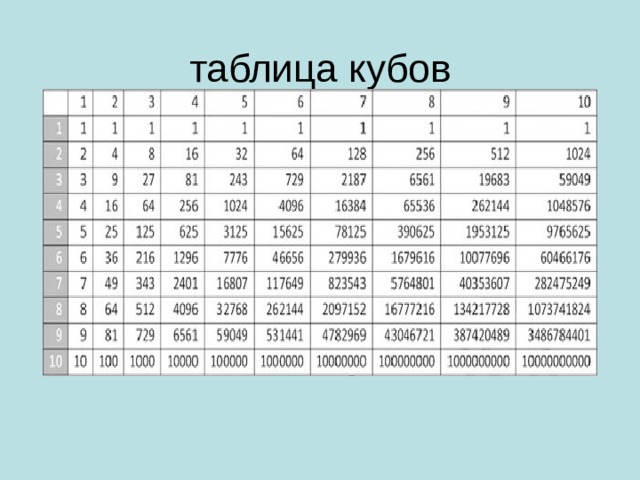 Промилле показывает массу алкоголя в 1000 мл крови. Например, 0,5-процентное опьянение означает, что в 1000 мл циркулирующей в организме крови содержится 0,5 г чистого алкоголя.
Промилле показывает массу алкоголя в 1000 мл крови. Например, 0,5-процентное опьянение означает, что в 1000 мл циркулирующей в организме крови содержится 0,5 г чистого алкоголя.
 Усиливаются эмоции – хорошее настроение становится еще лучше и точно так же усиливаются отрицательные эмоции. Вы можете ощущать легкую эйфорию. Мыслительные способности и память могут слегка нарушиться, делая вас неосмотрительным.
Усиливаются эмоции – хорошее настроение становится еще лучше и точно так же усиливаются отрицательные эмоции. Вы можете ощущать легкую эйфорию. Мыслительные способности и память могут слегка нарушиться, делая вас неосмотрительным.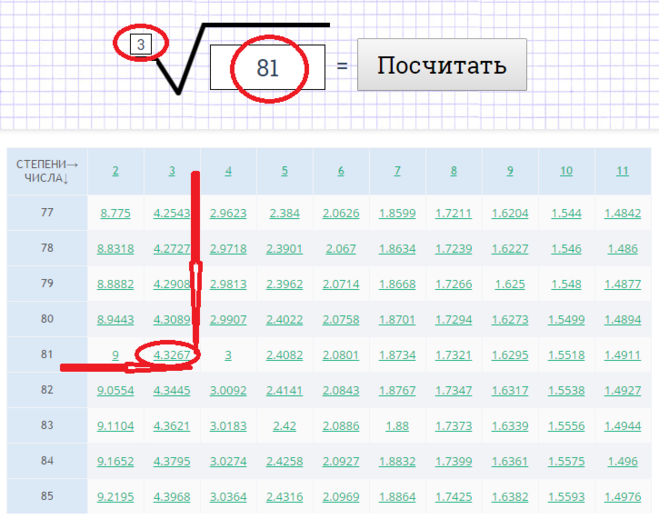 Мышление, восприятие и способность к принятию решений сильно нарушены. Эйфория понемногу проходит и сменяется неприятными чувствами, такими как тревожность, беспокойство, гнев и подавленность.
Мышление, восприятие и способность к принятию решений сильно нарушены. Эйфория понемногу проходит и сменяется неприятными чувствами, такими как тревожность, беспокойство, гнев и подавленность.
 Проверяйте трезвость алкометром!
Проверяйте трезвость алкометром!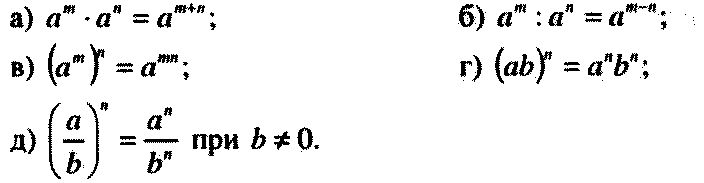 Небольшое количество выделяется с выдыхаемым воздухом, с мочой и через кожу. Единственный способ протрезветь – выждать время.
Небольшое количество выделяется с выдыхаемым воздухом, с мочой и через кожу. Единственный способ протрезветь – выждать время. Аналогично кофе действует и душ: процесс сжигания алкоголя происходит прежде всего в печени, и его скорость изменить невозможно. Совместное употребление алкоголя и энергетических напитков повышает вероятность алкогольного отравления. Оно также может вызвать обезвоживание, сопровождающееся диареей, тошнотой или рвотой, мышечными судорогами, усталостью и головной болью.
Аналогично кофе действует и душ: процесс сжигания алкоголя происходит прежде всего в печени, и его скорость изменить невозможно. Совместное употребление алкоголя и энергетических напитков повышает вероятность алкогольного отравления. Оно также может вызвать обезвоживание, сопровождающееся диареей, тошнотой или рвотой, мышечными судорогами, усталостью и головной болью.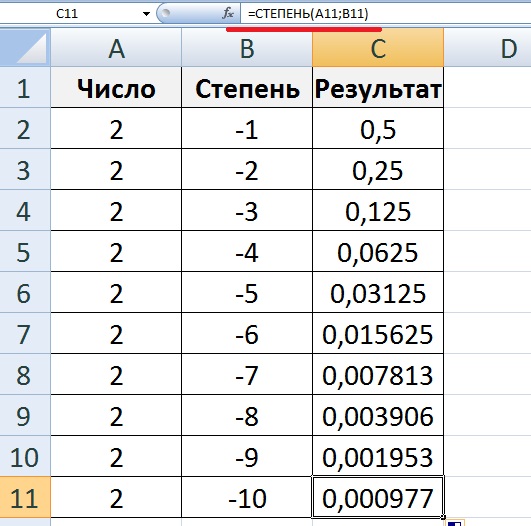
 Число 5 называется основанием, а число 2 – показателем степени.
Число 5 называется основанием, а число 2 – показателем степени.  775. Затем значение корня 5 умножается на 2 согласно вопросу. Значение корня 2 из 5 равно 4,47 .
775. Затем значение корня 5 умножается на 2 согласно вопросу. Значение корня 2 из 5 равно 4,47 .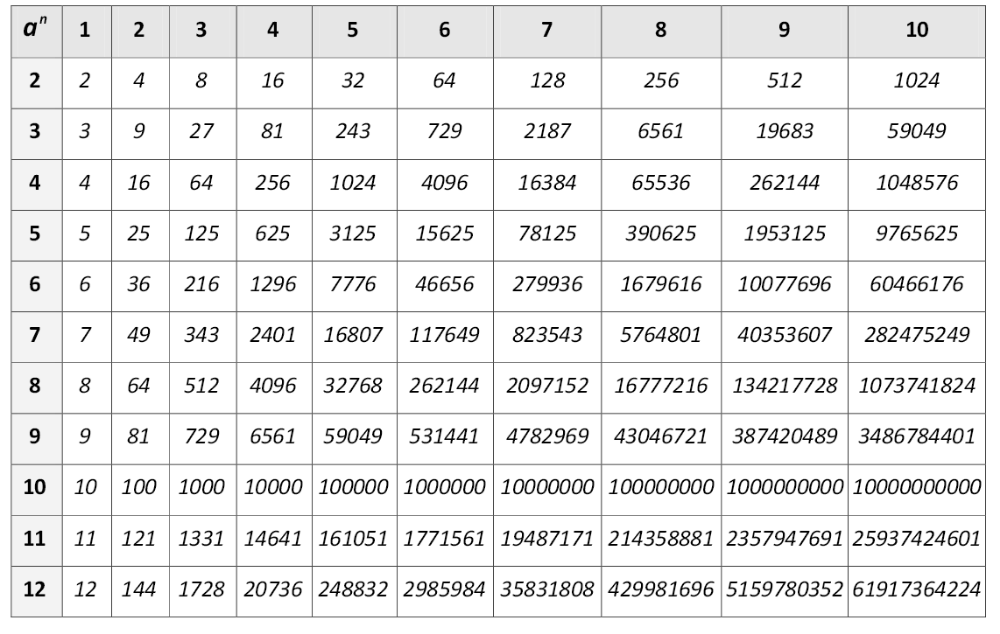 Пятые степени также образуются путем умножения числа на его четвертую степень или квадрата числа на его куб.
Пятые степени также образуются путем умножения числа на его четвертую степень или квадрата числа на его куб.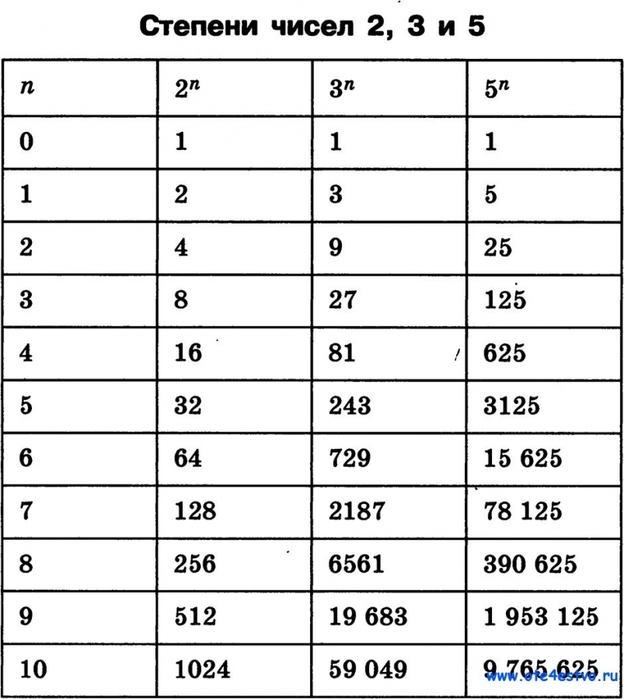

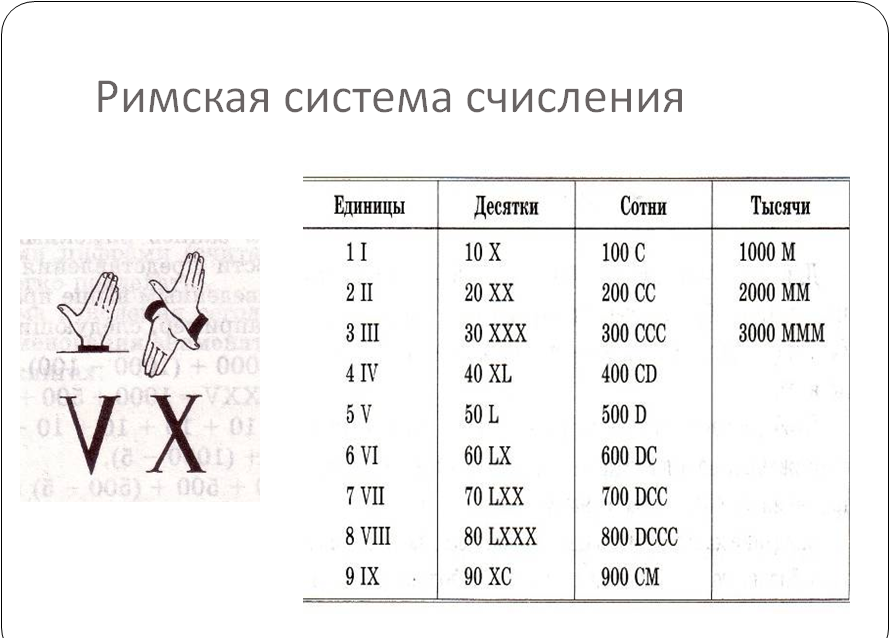
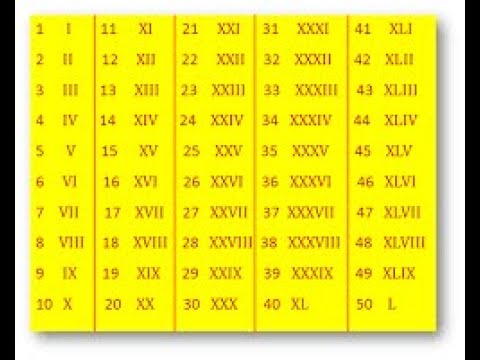
 Две палочки II означают два, III — три. Однако, для большего числа количество становиться очень большим и абсолютно не читаемым….
Две палочки II означают два, III — три. Однако, для большего числа количество становиться очень большим и абсолютно не читаемым….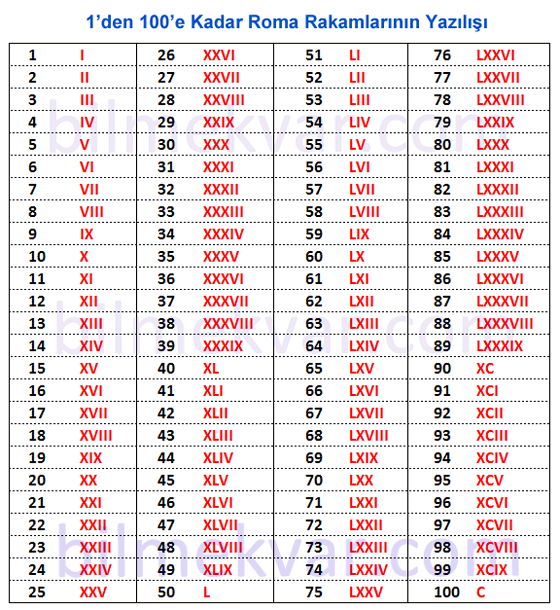 Расположение перед ним единички: IV — или расположение любого другого меньшего числа, чем последующий (в нашем случае символ пять) — означает вычитание. Таким образом, IV означает 4. После V можно указать меньшие цифры, тогда это будет означать складывание — VI означает 6, VII означает 7, VIII равно 8.
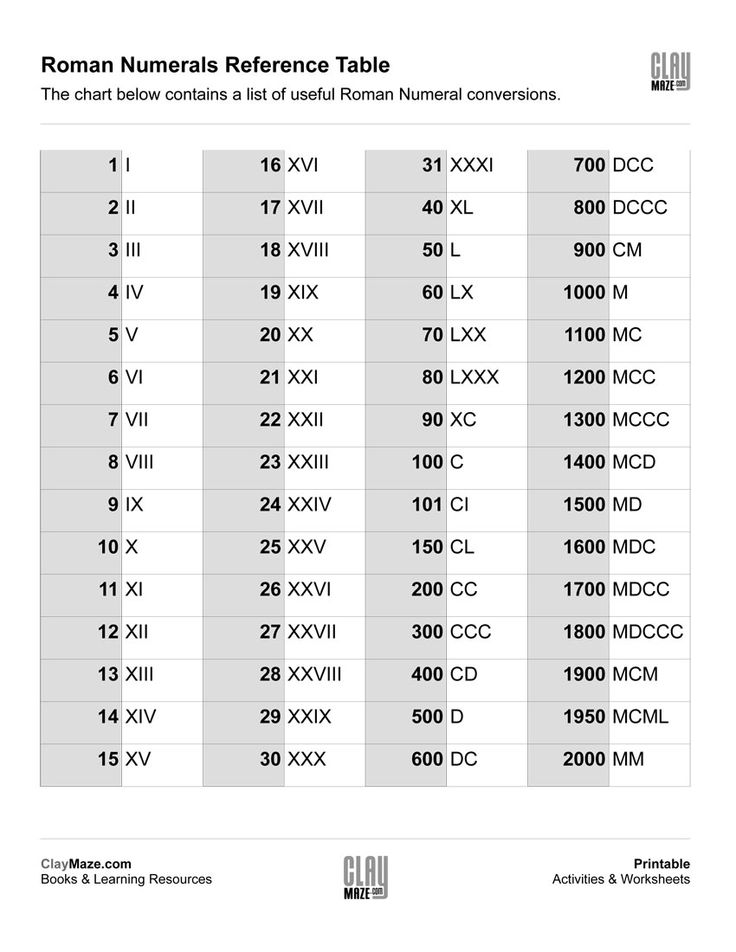
Расположение перед ним единички: IV — или расположение любого другого меньшего числа, чем последующий (в нашем случае символ пять) — означает вычитание. Таким образом, IV означает 4. После V можно указать меньшие цифры, тогда это будет означать складывание — VI означает 6, VII означает 7, VIII равно 8. centurion означает 100 людей. Мы по-прежнему используем такие слова, как «century» (столетие) и «cent» (цент). Как и с L, вычитание десятка означает понижение основной последующей цифры: 90 будет записано, как 100 минус 10 = XC. Несколько подряд цифр C будет означать соответствующее количество сотен: CCCLXIX равно 369.
centurion означает 100 людей. Мы по-прежнему используем такие слова, как «century» (столетие) и «cent» (цент). Как и с L, вычитание десятка означает понижение основной последующей цифры: 90 будет записано, как 100 минус 10 = XC. Несколько подряд цифр C будет означать соответствующее количество сотен: CCCLXIX равно 369. Таблица
Таблица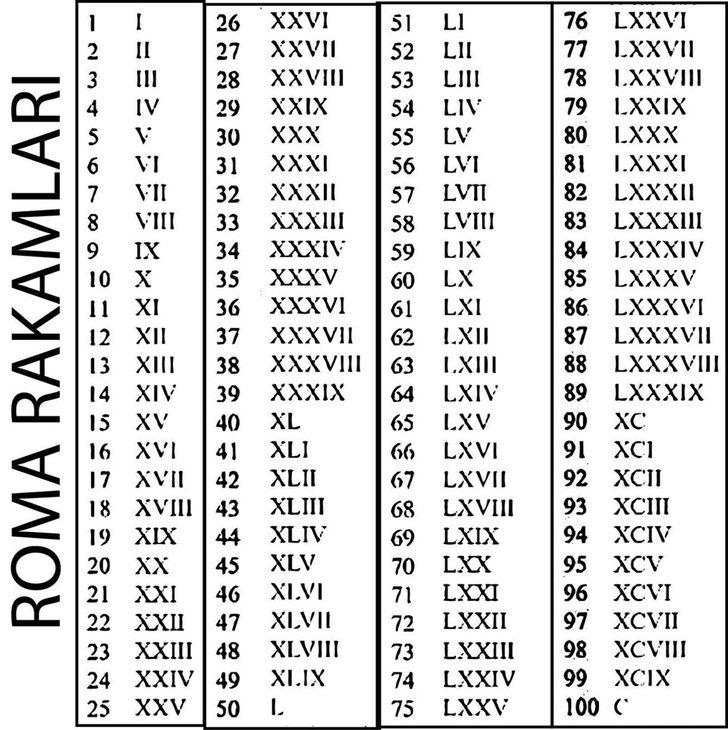
 Таблица
Таблица Таблица
Таблица е. MCMXIV = M + (M — C) + X + V — I = 1000 + (1000 — 100) + 10 + 5 — 1 = 1914. Старшие римские цифры предшествуют младшим цифрам, что обеспечивает правильный перевод римских цифр MCMXIV. В этой статье мы объясним, как преобразовать римские цифры MCMXIV в правильный перевод числа.
е. MCMXIV = M + (M — C) + X + V — I = 1000 + (1000 — 100) + 10 + 5 — 1 = 1914. Старшие римские цифры предшествуют младшим цифрам, что обеспечивает правильный перевод римских цифр MCMXIV. В этой статье мы объясним, как преобразовать римские цифры MCMXIV в правильный перевод числа.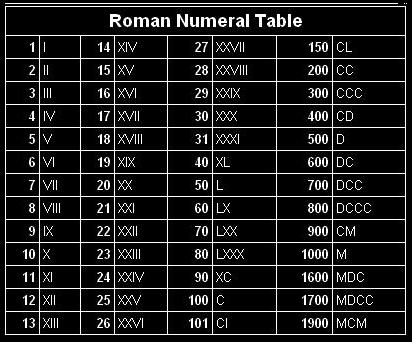

 Теперь 3 = III. Следовательно, когда MCMXIV делится на XIII, остаток равен III.
Теперь 3 = III. Следовательно, когда MCMXIV делится на XIII, остаток равен III.
 Ключ состоит в том, чтобы обрабатывать по одной арабской цифре за раз и переводить ее в правильное римское число, где нули становятся пустыми. Используйте конвертер и наблюдайте, как таблица показывает решение в реальном времени!
Ключ состоит в том, чтобы обрабатывать по одной арабской цифре за раз и переводить ее в правильное римское число, где нули становятся пустыми. Используйте конвертер и наблюдайте, как таблица показывает решение в реальном времени!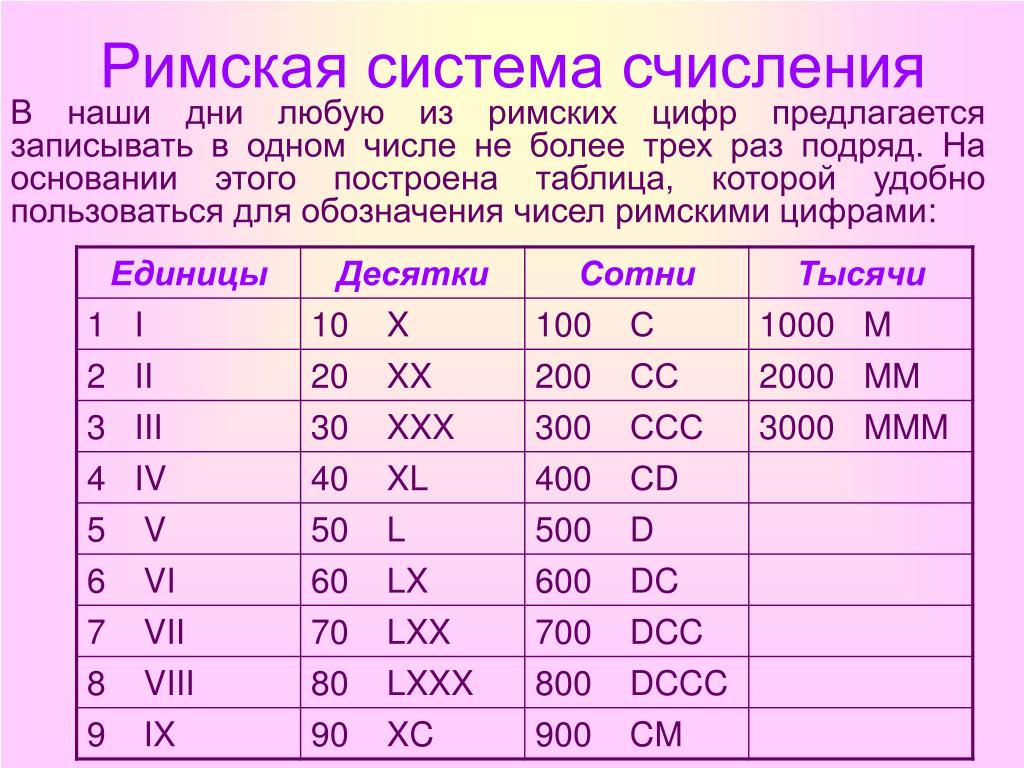
 В отличие от нашей позиционной системы с основанием 10, римская система основана на сложении (а иногда и вычитании) семи различных значений. Это символы, используемые для представления этих значений:
В отличие от нашей позиционной системы с основанием 10, римская система основана на сложении (а иногда и вычитании) семи различных значений. Это символы, используемые для представления этих значений: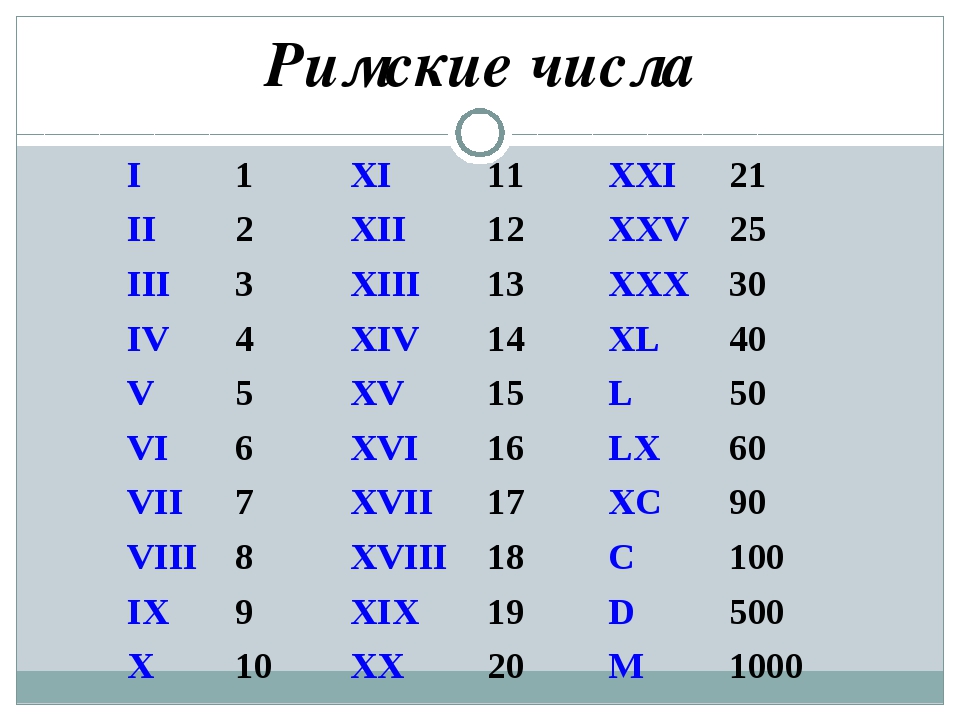
 )
) )
) )
) )
) )
) )
) )
) )
) 2
2 3
3 14159..
14159.. )/3
)/3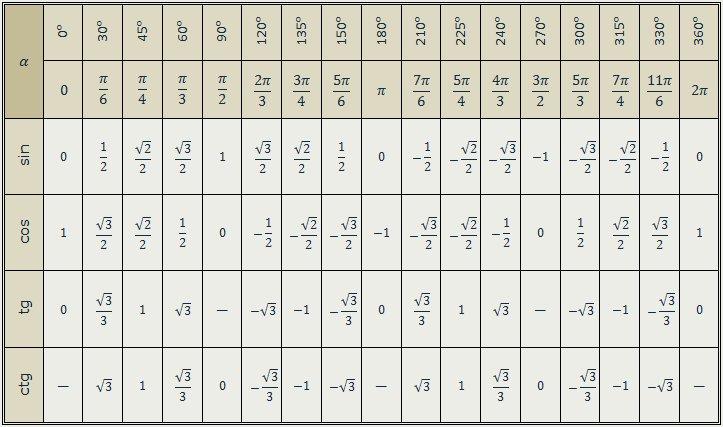
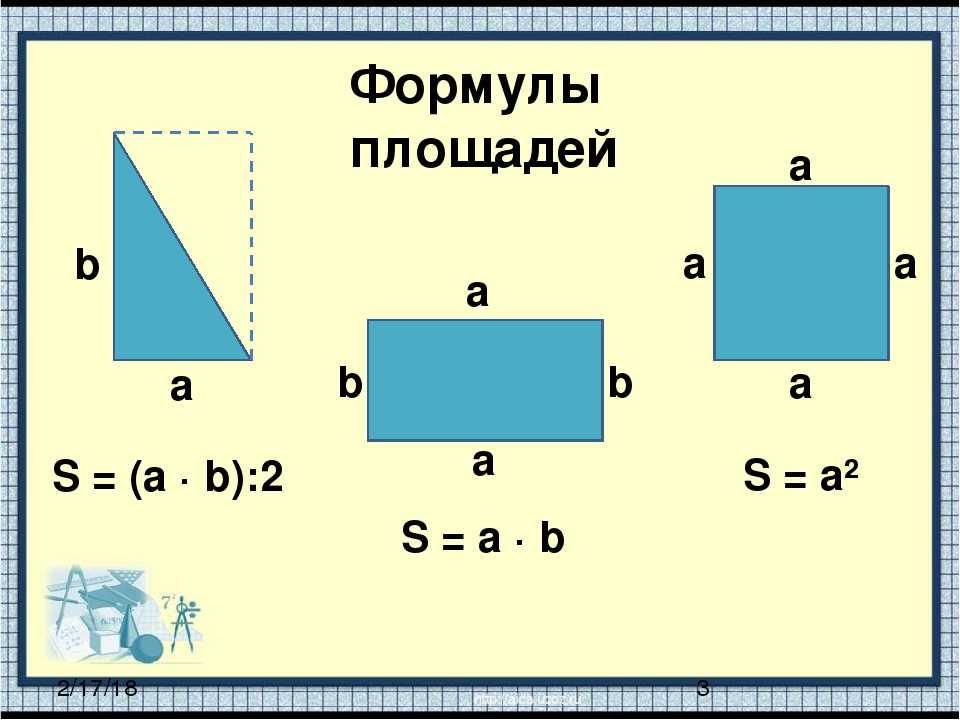


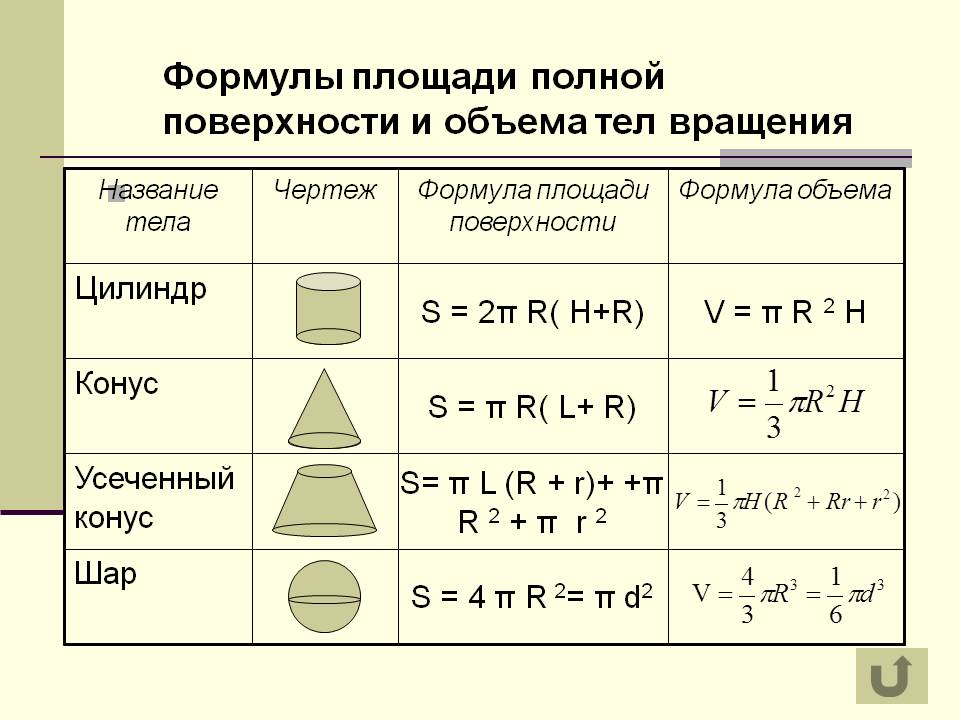
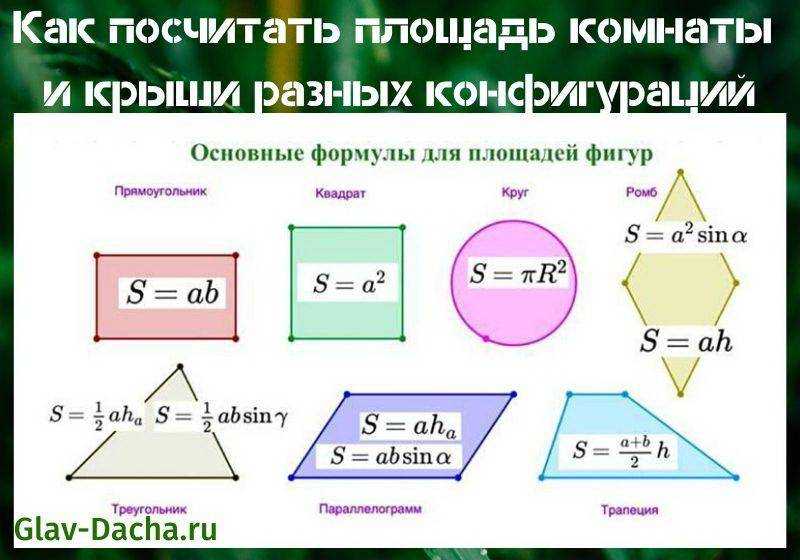
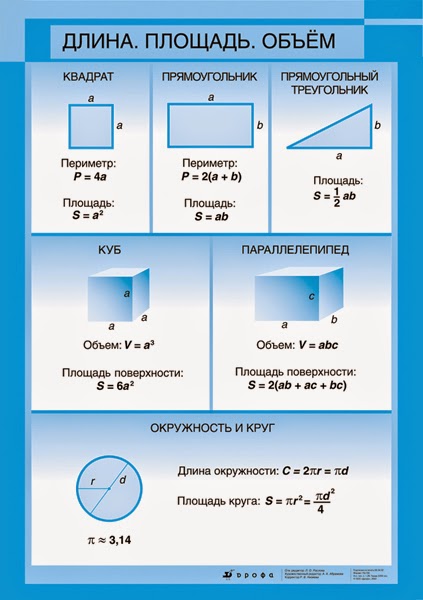 Величина площади выражается числом заключающихся в него квадратных единиц.
Величина площади выражается числом заключающихся в него квадратных единиц. также: Программа для расчета площади треугольника.
также: Программа для расчета площади треугольника. также: Программа для расчета площади параллелограмма.
также: Программа для расчета площади параллелограмма.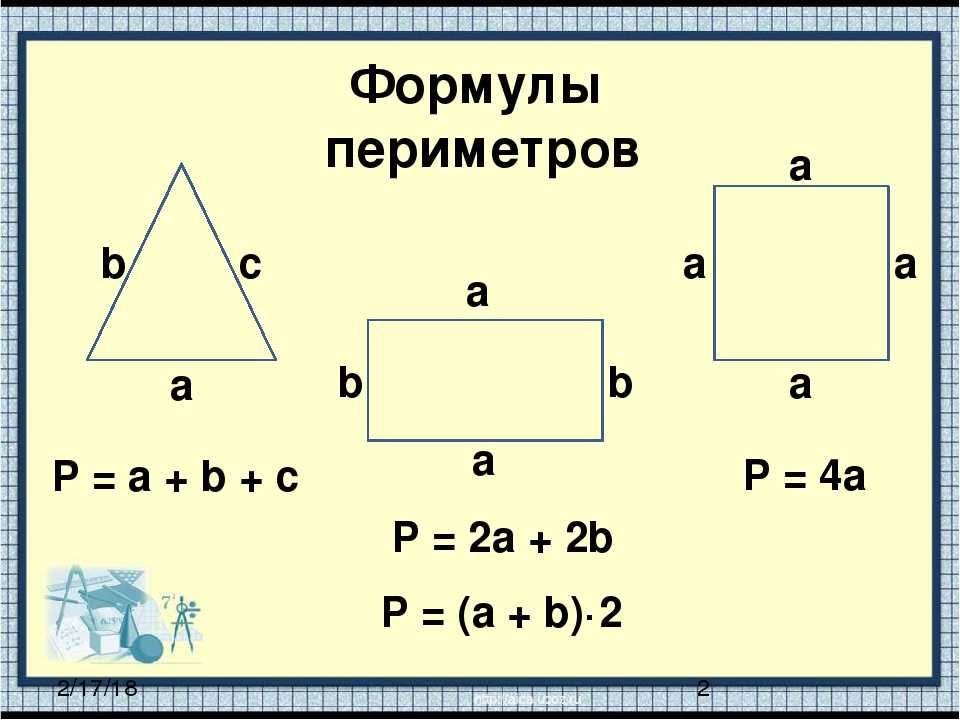 1415).
1415). 141592…)
141592…)  Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол.
Площадь фигуры
количество квадратов, необходимых для его полного покрытия, как плитки на
пол. Формула полной вероятности.
Формула полной вероятности. У второго рабочего
брак составляет 4%.У третьего рабочего
брак составляет 2%. Случайно выбранная
для контроля деталь оказалась бракованной.
Найти, чей брак вероятнее всего.
У второго рабочего
брак составляет 4%.У третьего рабочего
брак составляет 2%. Случайно выбранная
для контроля деталь оказалась бракованной.
Найти, чей брак вероятнее всего. Телевизоры от первого, второго и третьего
поставщиков не потребуют ремонта в
течение гарантийного срока, в следующих
98%, 88% и 92% случаях.
Телевизоры от первого, второго и третьего
поставщиков не потребуют ремонта в
течение гарантийного срока, в следующих
98%, 88% и 92% случаях.
 (n) = f(x)
(n) = f(x) Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки
Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки Момент инерции и координаты центра масс тела
Момент инерции и координаты центра масс тела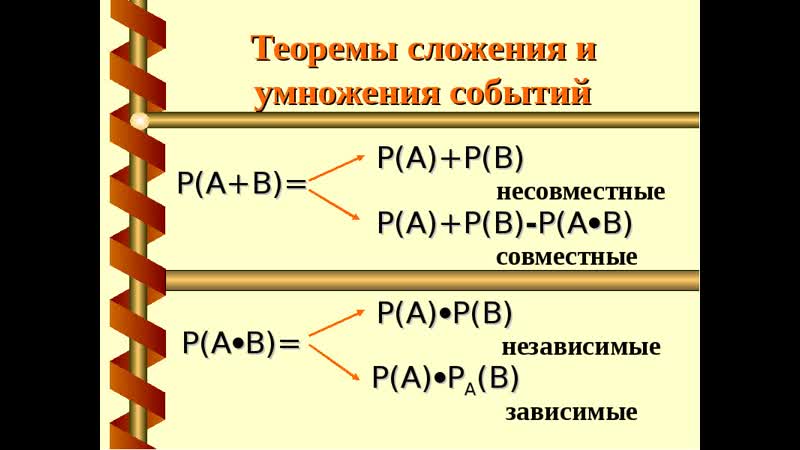 Степенные ряды. Интервал сходимости
Степенные ряды. Интервал сходимости Ряды Фурье для четных и нечетных функций
Ряды Фурье для четных и нечетных функций Уравнение распространения тепла в стержне. Формулировка краевой задачи
Уравнение распространения тепла в стержне. Формулировка краевой задачи Дифференцирование изображения
Дифференцирование изображения Классическое определение вероятности и непосредственный подсчет вероятностей
Классическое определение вероятности и непосредственный подсчет вероятностей Нормальный закон распределения. Математическое ожидание нормального распределения
Нормальный закон распределения. Математическое ожидание нормального распределения Задачи математической статистики. Статистический материал
Задачи математической статистики. Статистический материал Преобразование матрицы линейного преобразования при переходе от одного базиса к другому
Преобразование матрицы линейного преобразования при переходе от одного базиса к другому

 Чтобы найти вероятность инклюзивного события, мы сначала складываем вероятности отдельных событий, а затем вычитаем вероятность того, что два события произойдут одновременно.
Чтобы найти вероятность инклюзивного события, мы сначала складываем вероятности отдельных событий, а затем вычитаем вероятность того, что два события произойдут одновременно.






 Найдите вероятность того, что карта либо красная, либо королевская.
Найдите вероятность того, что карта либо красная, либо королевская. Во время своего трюка он случайно роняет мяч и не поднимает его. Пока он продолжает, еще один мяч падает. Какова вероятность того, что первый выпавший шар будет синим, а второй зеленым?
Во время своего трюка он случайно роняет мяч и не поднимает его. Пока он продолжает, еще один мяч падает. Какова вероятность того, что первый выпавший шар будет синим, а второй зеленым? Какова вероятность того, что оба ученика девочки?
Какова вероятность того, что оба ученика девочки?

 Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.
Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.