Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
| Справочник по математике | Алгебра | Уравнения, сводящиеся к квадратным уравнениям |
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
| Трёхчленные уравнения | |
| Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии | |
| Возвратные (симметричные) уравнения 3-ей степени | |
| Возвратные (симметричные) уравнения 4-ой степени | |
| Обобщенные возвратные уравнения 4-ой степени |
Замечание. Уравнения, носящие название «Биквадратные уравнения», относятся к типу «Трехчленные уравнения».
Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| ax3 + bx2 + bx + a = 0, | (1) |
где a, b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
ax2 + (b – a) x + a = 0.
Пример 1. Решить уравнение
| 2x3 + 7x2 + 7x + 2 = 0. | (2) |
Решение. Разложим левую часть уравнения (2) на множители:
Разложим левую часть уравнения (2) на множители:
Ответ:.
Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| ax4 + bx3 + cx2 + + bx + a = 0, | (3) |
а также уравнения вида
| ax4 + bx3 + cx2– – bx + a = 0, | (4) |
где a, b, c – заданные числа.
Для того, чтобы решить возвратное уравнение (3), разделим его на x2. В результате получится уравнение
| (5) |
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
| (6) |
Если теперь обозначить
| (7) |
то уравнение (6) станет квадратным уравнением:
ay2 + by + c – 2a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x2. В результате получится уравнение
| (9) |
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
| (10) |
Если теперь обозначить
| (11) |
то уравнение (10) станет квадратным уравнением:
| ay2 + by + c + 2a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (4) завершено.
Пример 2. Решить уравнение
| 2x4 – 3x3 – x2 – – 3x + 2 = 0. | (13) |
Решение. Уравнение (13) является возвратным и относится к виду (3). Разделим его на x2. В результате получится уравнение
| (14) |
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
| (15) |
Если теперь обозначить
| (16) |
то уравнение (15) станет квадратным уравнением:
2y2 – 3y – 5 = 0. | (17) |
Решим уравнение (17):
| (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ:
Пример 3. Решить уравнение
| 6x4 – 25x3 + 12x2 + + 25x + 6 = 0. | (19) |
Решение. Уравнение (19) является возвратным и относится к виду (4). Разделим его на x2. В результате получится уравнение
| (20) |
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
| (21) |
Если теперь обозначить
| (22) |
то уравнение (21) станет квадратным уравнением:
6y2 – 25y + 24 = 0. | (23) |
Решим уравнение (23):
| (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ:
Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
| (25) |
где a, b, c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x2. В результате получится уравнение
| (26) |
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
| (28) |
то уравнение (27) станет квадратным уравнением:
| (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x.
Описание метода решения уравнений вида (25) завершено.
Пример 4. Решить уравнение
| 2x4 – 15x3 + 35x2 – – 30 x + 8 = 0. | (30) |
Решение. Введем для коэффициентов уравнения (30) следующие обозначения
a = 2 , b =– 15,
c = 35, d = – 30,
и найдем значение выражения
Поскольку
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x2. В результате получится уравнение
| (31) |
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
| (32) |
Если теперь обозначить
| (33) |
то уравнение (32) станет квадратным уравнением:
2y2 – 15y + 27 = 0. 2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения. 2 + b*x + c = 0,где x- переменная, a,b,c – константы; a<>0. Задача состоит в отыскании корней уравнения.Геометрический смысл квадратного уравненияГрафиком функции, которая представлена квадратным уравнением является парабола. Решения (корни) квадратного уравнения — это точки пересечения параболы с осью абсцисс (х). Из этого следует, что есть три возможных случая: 2) парабола имеет одну точку пересечения с осью Ох. Такую точку называют вершиной параболы, а квадратное уравнение в ней приобретает свое минимальное или максимальное значение. В этом случае квадратное уравнение имеет один действительный корень (или два одинаковых корня). 3) Последний случай на практике интересный больше — существует две точки пересечения параболы с осью абсцисс. Отсюда находим Формула дискриминанта и корней квадратного уравненияДискриминантом называют значение подкоренного выраженияЕсли он положительный то уравнение имеет два действительных корня, вычисляемые по формулеПри нулевом дискриминант квадратное уравнение имеет одно решение (два совпадающих корня), которые легко получить из приведенной выше формулы при D=0При отрицательном дискриминант уравнения действительных корней нет. Однако исують решения квадратного уравнения в комплексной плоскости, и их значение вычисляют по формуле Теорема ВиетаРассмотрим два корня квадратного уравнения и построим на их основе квадратное уравнение.С записи легко следует сама теорема Виета: если имеем квадратное уравнение видато сумма его корней равна коэффициенту p, взятому с противоположным знаком, а произведение корней уравнения равен свободному слагаемому q. Формульная запись вышесказанного будет иметь видЕсли в классическом уравнении константа а отлична от нуля, то нужно разделить на нее все уравнение, а затем применять теорему Виета. Решение: В случаях когда есть малые коэффициенты при х целесообразно применять теорему Виета. По ее условию получаем два уравнения
Задача 5. Найти длины сторон прямоугольника, если его периметр 18 см, а площадь 77 см2. Решение: Половина периметра прямоугольника равна сумме соседних сторон. Обозначим х – большую сторону, тогда 18-x меньшая его сторона. Площадь прямоугольника равна произведению этих длин:
Задача 6. Разложить квадратное 10x2-11x+3=0 уравнения на множители. Решение: Вычислим корни уравнения, для этого находим дискриминант Квадратное уравнение с параметромПример 1. При каких значениях параметра а, уравнение (а-3)х2+(3-а)х-1/4=0 имеет один корень? Решение: Прямой подстановкой значения а=3 видим, что оно не имеет решения. Далее воспользуемся тем, что при нулевом дискриминанте уравнение имеет один корень кратности 2. Выпишем дискриминант Решение:Рассмотрим сначала особые точки, ими будут значения а=0 и а=-3. При а=0 уравнение упростится до вида 6х-9=0; х=3/2 и будет один корень. При а= -3 получим тождество 0=0. уравнений с бесконечными решениями (6 примеров и пояснений) — JDM EducationalРешая уравнение, мы можем обнаружить, что решения нет, есть одно решение, несколько решений или бесконечное количество решений (мы также можем сказать «бесконечно много решений») . Полезно знать, как выглядят некоторые из них, чтобы вы могли узнать их в случае, если вы столкнетесь с ними. Итак, какие есть уравнения с бесконечными решениями? Некоторые уравнения с тригонометрическими функциями (например, sin(x) = 0) имеют бесконечно много решений. Есть некоторые уравнения с одной переменной (типа (x+1) 2 = х 2 + 2х + 1), которые имеют бесконечно много решений. Существуют также уравнения с двумя или более переменными (например, x = y), которые имеют бесконечно много решений. Конечно, существует множество уравнений с бесконечными решениями — приведенные выше лишь несколько примеров. В этой статье мы поговорим о том, что означает, что уравнение имеет бесконечные решения. Начнем. Уравнения с бесконечными решениямиСуществуют некоторые общие признаки того, что уравнение может иметь бесконечные решения. Например:
*Примечание: когда мы говорим, что уравнение имеет бесконечные решения (или бесконечно много решений), мы не имеем в виду, что ∞ является решением уравнения. Мы имеем в виду, что существует неограниченное число решений уравнения (каждое решение — конечное число). Теперь давайте рассмотрим несколько примеров уравнений с бесконечными решениями, а также объяснение каждого из них. Использование квадратных корней Пожалуйста, включите JavaScript Использование квадратных корней Пример 1. Уравнение с одной переменной с бесконечным числом решенийРассмотрим следующее уравнение с одной переменной:
Нам нужно будет выполнить некоторую работу (используя FOIL и комбинируя подобные термины), чтобы увидеть, существуют ли бесконечные решения:
Это последнее утверждение всегда истинно, независимо от того, какое значение x мы выбираем. Пример 2. Уравнение с двумя переменными и бесконечным числом решенийРассмотрим следующее уравнение с двумя переменными:
У этого уравнения бесконечно много решений. . В этом случае мы можем выбрать любое реальное значение x и найти y, подставив выбранное значение x в уравнение. Например:
График ниже показано множество решений (парабола, которая является графиком квадратного). График квадратного уравнения y = 2x 2 – 5x + 1, имеющего бесконечно много решений. Пример 3. Уравнение с тремя переменными с бесконечным числом решенийРассмотрим следующее уравнение с двумя переменными:
У этого уравнения бесконечно много решений. В этом случае мы можем выбрать любое действительное значение для x и любое действительное значение для y и найти z, подставив выбранные нами значения x и y в уравнение. Например:
График уравнения z = x + y будет представлять собой целую плоскость при отображении в 3D космос. Плоскость (например, z = x + y) отображается в трехмерном пространстве. У уравнения z = x + y есть бесконечные решения.Пример 4. Уравнение с тригонометрическими функциями с бесконечным числом решенийРассмотрим следующее уравнение с тригонометрической функцией:
Поскольку k может быть любым целым числом, существуют бесконечно много решений уравнения. Обратите внимание, что шаблон того же типа будет иметь место для любой периодической функции (синуса, косинуса и т. д.) Пример 5. Уравнение с триггерными функциями с бесконечным числом решенийРассмотрим следующее уравнение с тригонометрической функцией:
Поскольку k может быть любым целым числом, у уравнения существует бесконечно много решений. Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = cos(x) и y = 1. Здесь показаны некоторые решения уравнения cos(x) = 1. Синяя кривая — часть графика y = cos(x), а красная линия — горизонтальная линия y = 1. Существует бесконечное количество решений уравнения уравнение cos(x) = 1. Существует бесконечное количество решений уравнения уравнение cos(x) = 1.Пример 6. Уравнение с тригонометрическими функциями с бесконечным числом решенийРассмотрим следующее уравнение с тригонометрической функцией:
Это происходит, когда x = (8k+1)π/4 и x = (8k+5)π/4 для каждого целого числа k. *Примечание: поскольку мы делили на cos(x), мы должны проверить случай, когда cos(x) = 0, что имеет место, когда x = kπ/2 для каждого k. В этом случае sin(x) равен 1, что не равно 0. Поскольку k может быть любым целым числом, у уравнения существует бесконечно много решений. Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = cos(x) и y = 1. Здесь показаны некоторые решения уравнения sin(x) = cos(x). Синяя кривая является частью графика y = sin(x), а красная линия является частью графика y = cos(x). У уравнения sin(x) = cos(x) есть бесконечные решения. У уравнения sin(x) = cos(x) есть бесконечные решения.ЗаключениеТеперь вы знаете о некоторых уравнениях, имеющих бесконечные решения, и о том, как они выглядят. Чтобы узнать больше о системах линейных уравнений с бесконечными решениями, ознакомьтесь с этой статьей. Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию. Не забудьте подписаться на наш канал YouTube и получать обновления о новых математических видео! Подпишитесь на наш канал на YouTube! Решения линейного уравнения | Калькулятор Решения линейного уравнения относятся к набору значений переменных в линейных уравнениях, дающих все возможные решения. Линейные уравнения включают неизвестные величины в виде одной или нескольких переменных для представления реальных задач. Это помогает легко узнать стоимость, пробег, скорость, расстояние и т. Д. Мы все используем линейные уравнения в нашей повседневной жизни, не зная об этом. В этом уроке мы подробно узнаем о решениях линейных уравнений, типах решений, способах их нахождения и т. д.
Каковы решения линейного уравнения? Решениями линейных уравнений являются точки, в которых линии или плоскости, представляющие линейные уравнения, пересекаются или встречаются друг с другом. Множество решений системы линейных уравнений — это множество значений переменных всех возможных решений. Например, при решении линейных уравнений можно визуализировать решение системы одновременных линейных уравнений, нарисовав 2 линейных графика и найдя точку их пересечения. Красная линия представляет все решения уравнения 1, а синяя линия — решения уравнения 2. Пересечение в единственной точке (2,4) — это решение, удовлетворяющее обоим уравнениям. Типы решений линейных уравненийСистема линейных уравнений может иметь 3 типа решений. Единственное решение системы линейных уравненийЕдинственное решение системы линейных уравнений означает, что существует только одна точка, при подстановке которой левая и правая стороны уравнения становятся равными. Линейное уравнение с одной переменной всегда имеет единственное решение. Например, 3m = 6 имеет единственное решение m = 2, для которого L.H.S = R.H.S. Точно так же для одновременных линейных уравнений с двумя переменными единственным решением является упорядоченная пара (x, y), которая удовлетворяет обоим уравнениям. Нет решения Система линейных уравнений не имеет решения, если не существует точки, в которой прямые пересекаются друг с другом, или графики линейных уравнений параллельны. Бесконечное множество решенийСистема линейных уравнений имеет бесконечное множество решений, если существует множество решений, состоящее из бесконечных точек, для которых левая и правая стороны уравнения становятся равными или на графике прямые линии перекрывают друг друга. Как найти решение линейного уравнения?Решения для линейных уравнений с одной переменнойРассмотрим уравнение 2x + 4 = 8
Следовательно, решение уравнения 2x + 4 = 8 равно x=2. Решения линейных уравнений с двумя переменнымиДля нахождения решений линейных уравнений с двумя переменными можно использовать следующие методы. Метод подстановки Рассмотрим следующую пару линейных уравнений, давайте решим следующие линейные уравнения. x + y = 4 и x — y = 2
Должно быть понятно, почему этот процесс называется замещением. Мы выражаем одну переменную через другую, используя одно из двух уравнений, и подставляем это выражение во второе уравнение. Метод исключения Рассмотрим следующую пару линейных уравнений: 2x + 3y — 11 = 0, 3x + 2y — 9 = 0 Коэффициенты x в двух уравнениях равны 2 и 3 соответственно. Умножим первое уравнение на 3, а второе уравнение на 2, чтобы коэффициенты при x в двух уравнениях стали равными:
Теперь вычтем два уравнения, это значит, что мы вычтем левые части двух уравнений, а правые части двух уравнений и равенство все равно сохранится. 6x + 9y — 33 = 0 ,6x + 4y — 18 = 0 0 + 5y — 15 = 0, 5y = 15, y = 3 . Получив значение y, мы действуем, как и раньше, — подставляем его в любое из двух уравнений. Подставим это в первое уравнение: 2х + 3у — 11 = 0, 2х + 3 (3) — 11 = 0, 2х + 9 — 11 = 0\, 2х = 2, х = 1 Таким образом, нетривиальное решение: x = 1, y = 3 Графический метод В качестве примера решим следующее линейное уравнение: x — y + 2 = 0, 2x + y — 5 = 0. Рисуем соответствующие линии на тех же осях: Точка пересечения (1,3), что означает, что x = 1, y = 3 является решением пары линейных уравнений, заданной (2). Фактически, это единственное решение пары , так как две непараллельные прямые не могут пересекаться более чем в одной точке. Важные примечания Вы можете напрямую проверить типы решений, используя следующие условия:
Часто задаваемые вопросы о решениях линейных уравненийКак решить систему линейных уравнений?У нас есть разные методы решения системы линейных уравнений:
Что такое уникальное решение линейного уравнения? Единственным решением системы линейных уравнений является упорядоченная пара или точка, которая делает равенство истинным в уравнении. Что произойдет, если пара линейных уравнений непротиворечива?Если пара линейных уравнений непротиворечива, то линии либо пересекаются, либо совпадают (накладываются) друг на друга. Каковы 3 решения линейных уравнений?Существует три способа решения систем линейных уравнений: замена, исключение и построение графика Как найти решение линейной системы?
Линии пересекаются в нулевых точках. Как найти решение двух линейных уравнений?Решение систем уравнений путем замены
Как решать линейные уравнения с одной переменной?
Сколько существует решений линейного уравнения 2x-5y=7?В данном уравнении 2x – 5y = 7 для каждого значения x мы получаем соответствующее значение y и наоборот. Следовательно, линейное уравнение имеет бесконечно много решений. Как найти упорядоченные парные решения линейных уравнений? Чтобы выяснить, является ли упорядоченная пара решением уравнения, вы можете выполнить тест. Определите значение x в упорядоченной паре и подставьте его в уравнение. При упрощении, если полученное вами значение y совпадает со значением y в упорядоченной паре, то эта упорядоченная пара действительно является решением уравнения. Упражнение: 1 Выберите сильное основание: а) NH3 • H2O; б) Cu(OH)2; в) KOH; Сильное основание КОН – щелочь α → 1 Упражнение: 2 Дайте характеристику гидроксида бария, используя различные признаки классификации оснований. Упражнение: 3 Закончите молекулярные уравнения возможных реакций, запишите соответствующие им ионные уравнения: а) P2O5 + KOH(изб) → б) Fe(OH)2 + 2HNO3(изб) = Fe(NO3)2 + 2H2O в) (NH4)2SO4 + 2NaOH(изб) = Na2SO4 + 2NH3↑ + 2H2O г) Ca(OH)2(изб) + CO2 = CaCO2↓ H2O д) 3Ba(OH)2 + 2Fe(NO3)3 = 3Ba(NO3)2 + 2 Fe(OH)3↓ е) KOH + NaNO3 = KNO3 + NaOH ж) Mg(OH)2 + FeO ≠ Реакция не идет так как гидроксиды металлов не взаимодействуют с оксидами металлов з) 2CuOH = Cu2O + H2O Упражнение: 4 Вычислите объем аммиака (н.у.), который выделиться при взаимодействии 890 г нитрата аммония, содержащего 20% примесей, с раствором гидроксида натрия. Солько граммов 20%-го раствора щелочи потребуется для реакции? 712 : 80 = х : 22,4; х = 199,36 л аммиака 712 : 80 = х : 40 х = 356 г (NaOH) 100 : х = 20 : 356; х = 1780 г или 1,789кг раствора Упражнение: 5 Запишите формулы оксидов, которые будут соответствовать следующим гидроксидам: Cu(OH)2, CuOH, Fe(OH)3, Fe(OH)2. NaOH. Расписание Электронный журнал Поступающим Олимпиады, турниры, конкурсы Планы работы Подготовительные курсы 07.05.2023 Лицеисты заняли I и II места в Школе практического программирования. 06.05.2023 В СУНЦ стартует регистрация на поэтический вечер, который пройдёт 15 мая в 15:30 в актовом зале. 05.05.2023 Наши лицеисты достойно выступили на заключительном этапе Всероссийской олимпиады школьников. 04.05.2023 Лицеисты привезли из солнечного Кыргызстана золотую и бронзовую медали международного форума «Мы — интеллектуалы XXI века!». 04.05.2023 Лицеисты СУНЦ с успехом выступили на всероссийском конкурсе научно-исследовательских работ и проектов. 25.04.2023 Соцэки СУНЦ совершенствуют свои практические навыки.
Больше новостей
Мужчины СУНЦ о 8 Марта (2023) Концерт к 8 Марта (2023) Поздравление с Днем защитника Отечества (2023)
Больше видео
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ). В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей. Иногородние обучающиеся проживают в уютном общежитии. Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы. Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝ Проезд: . дои: 10.3390/nano12101774. Мехрдад Ростами Осанлу 1 , Коладе А Оекан 2 , Уильям Дж. Ванденберге 2 Принадлежности Бесплатная статья ЧВК Мехрдад Ростами Осанлу и др.
Наноматериалы (Базель). . Бесплатная статья ЧВК . 2022 23 мая; 12 (10): 1774. дои: 10.3390/nano12101774. Мехрдад Ростами Осанлу 1 , Коладе А Оекан 2 , Уильям Дж. Ванденберге 2 Мы выполняем первопринципные расчеты для изучения электронных, термодинамических и диэлектрических свойств двумерных (2D) слоистых гидроксидов щелочноземельных металлов Ca(OH)2 и Mg(OH)2. Мы рассчитываем параметры решетки, энергии расслоения и фононные спектры монослоев, а также исследуем тепловые свойства этих монослоев, такие как свободная энергия Гельмгольца, теплоемкость при постоянном объеме и энтропия как функция температуры. Ключевые слова: гетеробислой (OH)2/HfS2; двумерные диэлектрические материалы; 2D-диэлектрики с TMD-каналами; двумерные гетероструктуры для полевых транзисторов; двумерные ван-дер-ваальсовые диэлектрики; Гетеробислой Mg(OH)2/W2. Авторы заявляют об отсутствии конфликта интересов. Рисунок 1 Схематический вид… Рисунок 1 Схематическое изображение полевого транзистора из монослойного диэлектрика M(OH) 2… Схематическое изображение полевого транзистора, изготовленного из монослойного диэлектрика M(OH)2 и монослойного TMD-канала. Рисунок 2 Структуры гидроксидов щелочноземельных металлов… Рисунок 2 Структуры гидроксидов щелочноземельных металлов. Вид сбоку ( и ) и сверху… Структуры гидроксидов щелочноземельных металлов. Вид сбоку ( a ) и вид сверху монослоя ( d ) в дополнение к виду бислоя сбоку ( c ). ( b ) демонстрирует длину связи Ca-O/Mg-O (l1) и O-H (l2), а также углы между связями (α и β). Толщина монослоя ( t ) указана на двухслойных конструкциях. Рисунок 3 M(OH) 2 фононная дисперсия… Рисунок 3 M(OH) 2 Дисперсионные кривые фононов. M(OH)2. ( a ) Фононный дисперсионный спектр Ca(OH)2. ( b ) Фононный дисперсионный спектр Mg(OH)2. Моды Eg (синий), A1g (красный), Eg(OH) (оранжевый) и A1g(OH) (зеленый) соответственно представляют собой поступательное движение и возвратно-поступательное движение связей O-H. На вставках визуализируются плоские и внеплоскостные колебательные моды OH. Ломаная ось показывает, что между 9 и 9 фононными ветвями нет.0 и 450 мэВ. Плоские энергетические кривые на высокоэнергетических модах (∼470 мэВ) связаны с внеплоскостными смещениями водорода и кислорода. Рисунок 4 Термодинамические свойства Ca(OH) 2… Рисунок 4 Термодинамические свойства Ca(OH) 2 и Mg(OH) 2 . Термодинамические свойства Ca(OH)2 и Mg(OH)2. Энтропия (Sv(T)), теплоемкость при постоянном объеме (Cv), внутренняя энергия ( U ( T )) и свободная энергия Гельмгольца ( A ( T )) Mg(OH)2 (Ca (OH)2) показаны сплошными (пунктирными) синими, зелеными, голубыми и красными линиями соответственно. Меньшая свободная энергия Гельмгольца означает, что с термодинамической точки зрения монослой Ca(OH)2 является лучшим материалом по сравнению с монослоем Mg(OH)2. Рисунок 5 Структура полосы и общий DOS… Рисунок 5 Полосная структура и суммарная ПЭС монослоя ( a ) Ca(OH) 2 и… Зонная структура и суммарная ПЭС монослоя ( a ) Ca(OH)2 и ( b ) Mg(OH)2. Рисунок 6 Выравнивание полос Ca(OH) 2… Рисунок 6 Выравнивание полос Ca(OH) 2 и Mg(OH) 2 . ( и ) В… Выравнивание полос Ca(OH)2 и Mg(OH)2. ( a ) Смещение полос HfS2 и WS2 с Ca(OH)2, Mg(OH)2. Уровень вакуума установлен на ноль, и для сравнения включен монослой h-BN. ( b ) Средний потенциал гетероструктур (Ca(OH)2/HfS2 и Mg(OH)2/WS2) показан относительно направления z, перпендикулярного плоскости листов. Максимум зоны проводимости (CBM) и минимум валентной зоны (VBM) каждого материала показаны цветными сплошными и пунктирными линиями. См. это изображение и информацию об авторских правах в PMC Нитрид-галогенидные диэлектрики переходных металлов для дихалькогенидных транзисторов переходных металлов. Ростами Осанлу М., Саадат А., Ван де Пут М.Л., Латурия А., Ванденберге В.Г.
Ростами Осанлу М. и др.
Наномасштаб. 2021 23 декабря; 14 (1): 157-165. дои: 10.1039/d1nr05250k.
Наномасштаб. 2021.
PMID: 348 Идентификация двумерных слоистых диэлектриков из первых принципов. Осанлоо М. Сверхвысокое внеплоскостное пьезоэлектричество, низкая теплопроводность и фотокаталитическая способность в сверхтонких двумерных ван-дер-ваальсовых гетероструктурах монофосфида бора и нитрида галлия. Моханта М.К., Рават А., Димпл, Джена Н., Ахамед Р., Де Саркар А.
Моханта М.К. и др.
Наномасштаб. 21 ноября 2019 г .; 11 (45): 21880-21890. дои: 10.1039/c9nr07586k.
Наномасштаб. 2019.
PMID: 31697290 Структуры и характеристики атомарно тонкого ZrO 2 от монослоя к бислою и двумерного гетероперехода ZrO 2 -MoS 2 . Венг Дж., Гао С.П.
Венг Дж. и соавт.
RSC Adv. 2019 16 октября; 9 (57): 32984-32994. дои: 10.1039/c9ra06074j. Электронная коллекция 2019 15 октября.
RSC Adv. 2019.
PMID: 35529155
Бесплатная статья ЧВК. Сотовый монослой HfO 2 и расчет статической диэлектрической проницаемости, исключающий влияние вакуумного зазора. Венг Дж., Гао С.П.
Венг Дж. и соавт.
Phys Chem Chem Phys. 2018 7 ноября; 20 (41): 26453-26462. дои: 10.1039/c8cp04743j. Epub 2018 11 октября.
Phys Chem Chem Phys. 2018.
PMID: 30306170 Посмотреть все похожие статьи На этой странице обсуждается растворимость гидроксидов, сульфатов и карбонатов элементов 2-й группы — бериллия, магния, кальция, стронция и бария — в воде Основность оксида металла группы II и растворимость гидроксида в воде увеличиваются по мере продвижения вниз по колонке. Оксиды металлов группы II становятся более щелочными по мере продвижения вниз по колонке. Эту тенденцию легко увидеть, если сравнить электроотрицательность металла II группы с электроотрицательностью кислорода. Как вы можете видеть, электроотрицательность металлов уменьшается вниз по столбцу, в результате чего изменение электроотрицательности увеличивается вниз по группе. Гидроксиды металлов группы II становятся более растворимыми в воде по мере продвижения вниз по колонке. Эту тенденцию можно объяснить уменьшением энергии решетки гидроксида соли и увеличением координационного числа иона металла по мере спуска по колонке. Чем больше энергия решетки, тем больше энергии требуется для ее разрушения на ионы металла и гидроксида. Следующие примеры иллюстрируют эту тенденцию: Эта простая тенденция верна при условии, что рассматривается гидратированный сульфат бериллия, а не безводный сульфат бериллия. Два распространенных примера иллюстрируют эту тенденцию: Решение простых уравнений 5 класс
Решение сложных (составных) уравнений Под сложными (составными) уравнениями мы понимаем уравнения, которые содержат
два или более арифметических действия. Решение таких уравнений выполняется по тем же правилам, которые мы рассмотрели
на странице «Решение простых уравнений 5 класс» в этой же теме. Но решение составных уравнений производится в определённой последовательности. Рассмотрим уравнение: Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. Чтобы найти неизвестный множитель, надо произведение разделить
на известный множитель. Всё верно. Значит уравнение решено правильно. Некоторые сложные (составные уравнения) можно решать другим способом. Зная и умея применять свойства сложения
и вычитания, а также свойства умножения и деления, уравнения решаются следующем образом. Рассмотрим уравнение. (x + 54) − 28 = 38 Чтобы из суммы отнять число, нужно это число вычесть из одного слагаемого и прибавить результат вычитания
к другому слагаемому. x = 38 − 26 x = 12 (12 + 54) − 28 = 38 66 − 28 = 38 38 = 38 Запомните! Если в уравнении встречается выражения, которые можно упростить, то вначале упрощаем выражения, и только
после этого решаем уравнение. Решить уравнение. 5x + 2x = 49 Левую часть уравнения можно упростить. Сделаем это. 7x = 49 Теперь решим простое уравнение по правилу нахождения неизвестного множителя. x = 49 : 7 x = 7 Завершив пример, выполним проверку. Решение простых уравнений 5 класс
Решение сложных (составных) уравнений Важно! Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте». Оставить комментарий: Все рациональные числа, которые мы можем себе представить, можно разделить на положительные и отрицательные. Изучается данная тема в 5-6 классах. Начиная с этих классов, учащиеся решают примеры, уравнения и задачи, в которых могут быть как положительные, так и отрицательные числа. Решение примеров с отрицательными числами без ошибок — очень важный математический навык. То же самое касается и решения уравнений с отрицательными числами. В этом контексте в школьном курсе рассматривается и понятие модуля числа. Давайте сегодня разберем эти вопросы. Чтобы отличить положительное число от отрицательного, перед отрицательным числом ставят знак минус. Например: «5» – положительное число «-5» — отрицательное число Если рассматривать числа на координатной прямой, то все числа, находящиеся слева от нуля, будут называться отрицательными, а числа, находящиеся справа от нуля – будут, соответственно, положительными. Правила сложения, вычитания, умножения и деления отрицательных чисел имеют свои особенности. Например, если нам необходимо выполнить действие: «7 + 5» Т.е. сложить два положительных числа, мы механически складываем их величины и получаем результат: 7 + 5 = 12 Если даже у нас будет длинный и трудоемкий пример, принцип его решения будет точно такой же, если числа положительные, то мы механически складываем их: 7 + 5 + 21 + 17 + 19 + 25 = 94 Операция вычитания может быть уже не такой простой. Если выражение: 7 – 5 = 2 Мы вычисляем легко, то выражение: 5 – 7 = — 2 Это уже серьезная проверка наших знаний в области отрицательных чисел. Здесь важно в ответе правильно поставить знаки «плюс» и «минус». Здесь перед числом «7» стоит знак «минус». Получается из меньшего числа «5» нужно вычесть большее число «7». Есть несколько способов. Один из которых вот какой: Необходимо вспомнить понятие модуля числа. Модуль числа – это число, записанное в вертикальных скобках: |5| или |-7| Когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем: |5| = 5 |-7| = 7 Записываем наше выражение для модулей этих чисел: |5| – |7| Такая запись позволяет нам определить, какое число большее «по модулю», т.е. по своему абсолютному значению, без учета знака «минус» перед числом и стоит правее на числовой оси. В нашем случае, это число «7». Поэтому мы из большего «по модулю» числа вычитаем меньшее «по модулю» число и в ответе ставим тот знак (плюс или минус), который стоял в выражении перед большим «по модулю» числом: |5| – |7| = — |7 — 5| = — |2| = -2 Запишем: 5 + (– 7) Представим каждое слагаемое как выражение двух чисел, с умножением на «-1», получим: 5 = — 1 · (- 5) — 7 = — 1 · 7 Теперь сложим эти выражения, как в нашем примере, получим: 5 + (– 7) = (- 1 · (- 5)) + (- 1 · 7) Вынесем за скобки «-1»: -1·(- 5 + 7) = -1·(7 – 5) = -1· 2 = — 2 Когда мы выносим за скобку «-1», мы получаем возможность вычитать из большего числа меньшее, что гораздо удобнее. Теперь мы знаем, как решать примеры с отрицательными числами. Умножение на «-1» помогает нам вспомнить правила умножения и деления, в выражениях с положительными и отрицательными числами. Вот эти правила: «Если умножать «минус» на «плюс», то получается в ответе «минус».» «А если умножать «минус» на «минус», то получается в ответе «плюс».» Проиллюстрируем все возможные варианты применения этих правил: 5 · 7 = 35 5 · (– 7) = — 35 (- 5) · 7 = — 35 (- 5) · (– 7) = 35 Возьмем более сложный случай, вычислим: 7 · (- 5) · 21 · (- 17) Чтобы было проще, выполним вычисления по действиям: 1) 7 · (- 5) = — 35 2) 21 · (- 17) = — 357 3) (- 35) · (-357) = 12495 Таким образом: 7· (- 5) · 21 · (- 17) = 12495 Теперь рассмотрим, как решать уравнения с отрицательными числами и переменными. Возьмем пример с уравнением: 3 + 4(5 – х) = 15 Сначала раскроем скобки: 3 + 4 · 5 + 4 · (- х) = 15 Обязательно обращаем внимание на минусы, стоящие перед числами и переменной «х», помним о приведенном выше правиле, получаем: 3 + 20 – 4х = 15 Приведем подобные (3 + 20 = 23) и запишем: 23 – 4х = 15 Переносим слагаемое без переменной «х» из левой части в правую, меняя при этом перед ним знак на противоположный — 4х = 15 – 23 После приведения подобных в правой части уравнения (15 – 23 = — 8), получим: — 4х = — 8 Деление отрицательных чисел проводим по тем же правилам, что и умножение: х = — 8 : (- 4) «Минус» делим на «минус», получаем «плюс»: х = 2 Напомню, что, когда мы выводим число из модуля, мы оставляем только его значение, а минус убираем. Например: |5| + |-7| = 5 + 7 = 12 |5| — |-7| = 5 — 7 = — 2 |5| · |-7| = 5 · 7 = 35 |-35| : |-7| = 35 : 7 = 5 Как видите, в примерах, где числа стоят под знаком модуля, необходимо следовать правилу: «Сначала раскрываем скобки модуля, а потом проводим операции сложения, вычитания, умножения или деления». Конечно, существуют и более сложные примеры с отрицательными числами и модулями. Чтобы познакомиться с правилами их решения, а также вспомнить все, что необходимо, связанное с модулями — следите за нашими уроками или обратитесь к репетитору на нашем сайте. Алгебра 1 Практика навыков Произошла ошибка при загрузке этого видео. Попробуйте обновить страницу или обратитесь в службу поддержки. Вы студент или преподаватель? Попробуйте Study. Как участник вы также получите неограниченный доступ к более чем 88 000
уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспевать. Получите неограниченный доступ к более чем 88 000 уроков. Попробуйте без риска Настройка занимает всего несколько минут, и вы можете отменить ее в любое время. Это займет всего лишь несколько минут. Отменить в любое время. Назад Что учителя говорят об Study.com Попробуйте без риска в течение 30 дней Уже зарегистрирован? Войдите здесь для доступа Перейти к конкретному примеру Скорость Скорость Дэниел Джибсон, ЭМИ МЕЙЕРС Дэниел преподает физику и инженерию с 2011 года. Эми преподает математику и алгебру в средней школе более семи лет. Она имеет степень бакалавра математических наук Университета Хьюстона и степень магистра учебных программ и инструкций Университета Сент-Томас. Она является сертифицированным учителем математики в Техасе для 4-12 классов. Примеры решений Практические вопросы Порядок, в котором мы выполняем математические шаги, известен как порядок операций и является важной частью правильного решения уравнений. Одно общее правило состоит в том, чтобы разрешать любые операторы в скобках перед выполнением операций за пределами скобок. Линейное уравнение : Линейное уравнение представляет собой полином первого порядка, что означает, что единственный показатель степени, применяемый к неизвестной переменной, равен 1. Коэффициент : Коэффициент неизвестной переменной или выражение в скобках, указывающее на умножение между коэффициентом и выражением или термином, который он модифицирует. Распределительное свойство умножения : Распределительное свойство умножения утверждает, что умножение числа на сумму двух слагаемых равносильно умножению каждого слагаемого по отдельности на это число: {eq}a(b+c) = ab + ак {/экв}. Аддитивное свойство равенства : Аддитивное свойство равенства гласит, что когда одна и та же операция выполняется с обеих сторон уравнения, равенство остается неизменным. Следующие две задачи демонстрируют, как решать многоступенчатые линейные уравнения, содержащие скобки. Решите уравнение {eq}5(2x-3) = 2(3x + 2) {/eq} для x . Поскольку в скобках нет одинаковых членов для объединения, мы сначала воспользуемся распределительным свойством умножения, чтобы распределить 5 слева в операторе в скобках: $$5(2x-3) = 5\times 2x — 5\times 3 = 10x — 15 $$ Теперь мы распределим 2 в правой части: $$2(3x+2) = 2\ умножить на 3x + 2\times 2 = 6x + 4 $$ Переписав уравнение с распределенными коэффициентами, получим: $$10x-15 = 6x + 4 $$ Теперь мы должны объединить все константы и все условия, содержащие x . Используя аддитивное свойство равенства, мы можем вычесть 6x из обеих частей уравнения без изменения равенства: $$10x — 6x — 15 = 6x — 6x + 4 $$ Поскольку {eq}6x — 6x = 0 {/eq}, эти члены сокращаются в правой части. $$4x — 15 = 4 $$ Чтобы изолировать термин x , мы добавим 15 к обеим сторонам. : $$4x-15+15 = 4 + 15 $$ Опять же, поскольку {eq}-15 + 15 = 0 {/eq}, эти члены сокращаются в левой части. Правую часть можно упростить, добавив: $$4x = 19 $$ Теперь мы можем разделить обе стороны на 4, чтобы выделить x : $$\dfrac{4x}{4} = \dfrac{19}{4} $$ Одна с левой стороны, {eq}\dfrac{4}{4} = 1 {/eq}, поэтому 4 с этой стороны сокращается. В правой части мы выполним деление и представим решение уравнения в виде десятичной дроби: $$x = 4,75 $$ Решите уравнение {eq}- 2(6t — 4) = 3(2t + 1 + t) {/экв}. Округлите ответ до двух знаков после запятой. Сначала отметим, что мы можем объединить два члена, содержащие t , в скобках в правой части уравнения. $$-2(6t — 4) = 3(3t + 1) $$ Теперь распределим коэффициенты в выражениях в скобках с обеих сторон: $$-12t + 8 = 9t + 3 $$ Обратите внимание, что в левой части мы распределили отрицательных 2, поэтому первый член в распределении отрицательный. Второй член в распределении положительный, потому что коэффициент умножен на отрицательное значение в скобках. Прибавим {eq}12t {/eq} к обеим сторонам: $$8 = 21t + 3 $$ Затем вычтем 3 с обеих сторон: $$5 = 21t $$ Деление обе части на 21 дает нам решение: $$t = \dfrac{5}{21} \ приблизительно 0,24 $$ Станьте участником, чтобы разблокировать остальную часть этого учебного ресурса и тысячи подобных. Создать аккаунт Мастерство вождения студента. Разблокируйте практические навыки и учебные материалы. Соответствует ГОСТам. Завести аккаунт Если уравнение, которое вам нужно решить, содержит скобки, упростите скобки (чаще всего с помощью распределения) и затем решите, как обычно. Решение уравнений Максимально упростите обе части уравнения, используя порядок операций (распределение, объединение одинаковых членов и т. д.). Если переменная (буква), которую вы пытаетесь найти, появляется в обеих частях уравнения, переместите ее на другую сторону. Перенесите все свои «???x???» в Техас или отправьте все ???x??? в одну сторону уравнения. Решите, работая в обратном порядке от порядка операций. Используйте обратные операции до тех пор, пока переменная не станет единственной, и не забывайте делать то же самое с обеими частями уравнения, чтобы оно оставалось сбалансированным. Привет! Я Криста. Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. Узнать больше Пример Решите для переменной. ???-(3x+4)=6(2x-7)+8??? Начните с упрощения обеих частей уравнения. Вам нужно будет распределить коэффициенты перед скобками. ???-3x-4=12x-42+8??? Упростите правую часть уравнения, объединив одинаковые члены. ???-3x-4=12x-34??? Переместить все ???x??? члены к одной стороне уравнения, добавляя ???3x??? в обе стороны. ???-3x+3x-4=12x+3x-34??? ???-4=15x-34??? Отменить ???-34??? добавив ???34??? в обе стороны. ???-4+34=15x-34+34??? ???30=15x??? Отменить умножение ???15??? разделив обе части на ???15???. ???\frac{30}{15}=\frac{15x}{15}??? ???2=х??? Чтобы решить уравнение, в котором есть круглые скобки, распределите, чтобы избавиться от круглых скобок, затем следуйте порядку операций, чтобы упростить остальную часть уравнения 90-4)-4(б+8)??? Начните с упрощения всего, что возведено в степень ???0???. Найти решение системы методом Крамера: Запишем систему в виде: A = 10 1 4 1 -2 -7 2 1 5 1 1 4 -3 -2 -7 0 1 5 10 1 4 1 -3 -7 2 0 5 10 1 1 1 -2 -3 2 1 0 Решить систему линейных уравнений (метод Крамера или метод Гаусса ) Запишем систему в виде: A = 2 3 1 1 -1 -1 5 2 4 BT = (6,1,11) 6 3 1 1 -1 -1 11 2 4 Найдем определитель полученной матрицы. 2 6 1 1 1 -1 5 11 4 Найдем определитель полученной матрицы. 2 3 6 1 -1 1 5 2 11 Решить систему линейных уравнений по формулам Крамера и методом Гаусса. Решить систему линейных уравнений по правилу Крамера: Решить систему уравнений с помощью формул Крамера. Решить систему линейных уравнений с помощью формул Крамера: Находим определитель матрицы системы: В определителе матрицы системы последовательно меняем 1-й, 2-й, 3-й столбцы на столбец свободных членов и находим полученные определители: Решение системы: Ответ: (6; 2; — 4). Решить систему линейных уравнений (метод Крамера или метод Гаусса ) Запишем систему в виде: 7 -1 4 3 3 -1 4 -2 -3 2 7 4 7 3 -1 5 4 -3 2 -1 7 7 3 3 5 -2 4 Ответ: а) Ответ:X=1 Y=1 Z=1 б) Из вышеизложенной таблицы следует: X=1 Y=1 Z=1 Решить систему линейных уравнений по правилу Крамера: Решить систему трех линейных уравнений с тремя неизвестными методом Гаусса и методом Крамера. Решить сиситему методом Крамера и сдеать проверку: Запишем систему в виде: A = 1 5 1 -2 3 -1 3 1 1 3 5 1 -2 3 -1 1 1 1 1 3 1 -2 -2 -1 3 1 1 1 5 3 -2 3 -2 3 1 1 Вопрос Обновлено: 26/04/2023 Рекомендуемые вопросы РЕКЛАМА Ab Padhai каро бина объявления ке Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке! Похожие видео Решите следующую систему линейных уравнений по правилу Крамера 3x+y+z=2,2x−4y+3z=−1and4x+y−3z=−11 Свойства определителей|Правило Крамера#!#Однородная система уравнений 642676223 44:35 Система линейных уравнений с 2 или 3 переменными (правило Крамера) 643440933 58:06 Теория правила Крамера (Решение системы уравнений) 643443859 01:05:22 645362781 02:54 Проверьте, является ли следующая система линейных уравнений непротиворечивой. Если непротиворечиво, решите систему, используя правило Крамера: 6x−2y+3=0,−9.x+3y=0 645362782 02:37 Проверьте, непротиворечива ли следующая система линейных уравнений. Если непротиворечиво, решите систему, используя правило Крамера: 2x−3y=0,−8x+12y=0 645362783 02:26 Детерминанты#!#Правило Крамерса для решения системы линейных уравнений 64539 6913 37 :37 РЕКЛАМА Рекомендуемые вопросы Правило Крамера для системы трех линейных уравнений 07:53 Решите следующую систему линейных уравнений по правилу Крамера 3x… 04:54 Правило Крамера для системы двух линейных уравнений Правило Крамера для системы трех линейных уравнений 07:53 Используя свойства определителей, вычислить |[18, 40, 89] , [40, 89, 19. Из предыдущей статьи мы узнали о таких показателях, как размах вариации, межквартильный размах и среднее линейное отклонение. В этой статье изучим дисперсию, среднеквадратичное отклонение и коэффициент вариации. Дисперсия случайной величины – это один из основных показателей в статистике. Он отражает меру разброса данных вокруг средней арифметической. Сейчас небольшой экскурс в теорию вероятностей, которая лежит в основе математической статистики. Как и матожидание, дисперсия является важной характеристикой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра. Формула дисперсии в теории вероятностей имеет вид: То есть дисперсия — это математическое ожидание отклонений от математического ожидания. На практике при анализе выборок математическое ожидание, как правило, не известно. где s2 – выборочная дисперсия, рассчитанная по данным наблюдений, X – отдельные значения, X̅– среднее арифметическое по выборке. Стоит отметить, что у такого расчета дисперсии есть недостаток – она получается смещенной, т.е. ее математическое ожидание не равно истинному значению дисперсии. Подробней об этом здесь. Однако при увеличении объема выборки она все-таки приближается к своему теоретическому аналогу, т.е. является асимптотически не смещенной. Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Генеральную и выборочную дисперсии легко рассчитать в Excel. Есть специальные функции: ДИСП.Г и ДИСП.В соответственно. В чистом виде дисперсия не используется. Это вспомогательный показатель, который нужен в других расчетах. Например, в проверке статистических гипотез или расчете коэффициентов корреляции. Отсюда неплохо бы знать математические свойства дисперсии. Свойство 1. Дисперсия постоянной величины A равна 0 (нулю). D(A) = 0 Свойство 2. Если случайную величину умножить на постоянную А, то дисперсия этой случайной величины увеличится в А2 раз. Другими словами, постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат. D(AX) = А2 D(X) Свойство 3. Если к случайной величине добавить (или отнять) постоянную А, то дисперсия останется неизменной. D(A + X) = D(X) Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий. D(X+Y) = D(X) + D(Y) Свойство 5. Если случайные величины X и Y независимы, то дисперсия их разницы также равна сумме дисперсий. D(X-Y) = D(X) + D(Y) Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (стандартное) отклонение (сокращенно СКО). Встречается название среднее квадратичное отклонение и сигма (от названия греческой буквы). Общая формула стандартного отклонения в математике следующая: На практике формула стандартного отклонения следующая: Как и с дисперсией, есть и немного другой вариант расчета. Для расчета стандартного отклонения достаточно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупности соответственно). Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, поэтому является сопоставимым с исходными данными. Значение стандартного отклонения зависит от масштаба самих данных, что не позволяет сравнивать вариабельность разных выборках. Чтобы устранить влияние масштаба, необходимо рассчитать коэффициент вариации по формуле: По нему можно сравнивать однородность явлений даже с разным масштабом данных. В статистике принято, что, если значение коэффициента вариации менее 33%, то совокупность считается однородной, если больше 33%, то – неоднородной. Расчет коэффициента вариации в Excel также производится делением стандартного отклонения на среднее арифметическое: =СТАНДОТКЛОН.В()/СРЗНАЧ() Коэффициент вариации обычно выражается в процентах, поэтому ячейке с формулой можно присвоить процентный формат: Еще один показатель разброса данных на сегодня – коэффициент осцилляции. Это соотношение размаха вариации (разницы между максимальным и минимальным значением) к средней. Готовой формулы Excel нет, поэтому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ. Коэффициент осцилляции показывает степень размаха вариации относительно средней, что также можно использовать для сравнения различных наборов данных. Таким образом, в статистическом анализе существует система показателей, отражающих разброс или однородность данных. Ниже видео о том, как посчитать коэффициент вариации, дисперсию, стандартное (среднеквадратичное) отклонение и другие показатели вариации в Excel. Поделиться в социальных сетях: Дисперсия в статистике находится как среднее квадратическое отклонение индивидуальных значений признака в квадрате от средней арифметической. В зависимости от исходных данных она определяется по формулам простой и взвешенной дисперсий: 1. Простая дисперсия (для несгруппированных данных) вычисляется по формуле: 2. где n — частота (повторяемость фактора Х) На данной странице описан стандартный пример нахождения дисперсии, также Вы можете посмотреть другие задачи на её нахождение Пример 1. Имеются следующие данные по группе из 20 студентов заочного отделения. Нужно построить интервальный ряд распределения признака, рассчитать среднее значение признака и изучить его дисперсию Построим интервальную группировку. Определим размах интервала по формуле: где X max– максимальное значение группировочного признака; Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6 Составим интервальную группировку Для дальнейших расчетов построим вспомогательную таблицу: X’i– середина интервала. Среднюю величину роста студентов определим по формуле средней арифметической взвешенной: Определим дисперсию по формуле: Пример 2. Определение групповой, средней из групповой, межгрупповой и общей дисперсии Пример 3. Нахождение дисперсии и коэффициента вариации в группировочной таблице Пример 4. Нахождение дисперсии в дискретном ряду Формулу дисперсии можно преобразовать так: Из этой формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней. Дисперсия в вариационных рядах с равными интервалами по способу моментов может быть рассчитана следующим способом при использовании второго свойства дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по следующей формуле менее трудоемок: где i — величина интервала; Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле: Подставляя в данную формулу дисперсии q =1- р, получаем: Общая дисперсия измеряет вариацию признака по всей совокупности в целом под влиянием всех факторов, обуславливающих эту вариацию. Внутригрупповая дисперсия характеризует случайную вариацию, т.е. часть вариации, которая обусловлена влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Такая дисперсия равна среднему квадрату отклонений отдельных значений признака внутри группы X от средней арифметической группы и может быть вычислена как простая дисперсия или как взвешенная дисперсия. Таким образом, внутригрупповая дисперсия измеряет вариацию признака внутри группы и определяется по формуле: где хi — групповая средняя; Например, внутригрупповые дисперсии, которые надо определить в задаче изучения влияния квалификации рабочих на уровень производительности труда в цехе показывают вариации выработки в каждой группе, вызванные всеми возможными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т. Средняя из внутри групповых дисперсий отражает случайную вариацию, т. е. ту часть вариации, которая происходила под влиянием всех прочих факторов, за исключением фактора группировки. Она рассчитывается по формуле: Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, которая обусловлена влиянием признака-фактора, положенного в основание группировки. Она равняется среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле: Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий: Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки. Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с. Оглавление Содержание Что такое дисперсия? Понимание дисперсии Преимущества и недостатки Пример Часто задаваемые вопросы Часто задаваемые вопросы о различиях К Адам Хейс Полная биография Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. Узнайте о нашем
редакционная политика Обновлено 14 марта 2023 г. Рассмотрено Майкл Дж. Бойл Рассмотрено
Майкл Дж. Бойл Полная биография Майкл Бойл — опытный специалист в области финансов, более 10 лет занимающийся финансовым планированием, деривативами, акциями, фиксированным доходом, управлением проектами и аналитикой. Узнайте о нашем
Совет финансового контроля Факт проверен Викки Веласкес Факт проверен
Викки Веласкес Полная биография Викки Веласкес — исследователь и писатель, которая руководила, координировала и руководила различными общественными и некоммерческими организациями. Узнайте о нашем
редакционная политика Инвестопедия / Алекс Дос Диас Термин дисперсия относится к статистическому измерению разброса между числами в наборе данных. В частности, дисперсия измеряет, насколько далеко каждое число в наборе от среднего (среднего) и, следовательно, от любого другого числа в наборе. Дисперсия часто обозначается этим символом: σ 2 . Он используется как аналитиками, так и трейдерами для определения волатильности и безопасности рынка. Квадратный корень из дисперсии представляет собой стандартное отклонение (SD или σ), которое помогает определить постоянство доходности инвестиций в течение определенного периода времени. В статистике дисперсия измеряет отклонение от среднего или среднего значения. Он рассчитывается путем взятия разностей между каждым числом в наборе данных и средним значением, затем возведения в квадрат разностей, чтобы сделать их положительными, и, наконец, деления суммы квадратов на количество значений в наборе данных. Дисперсия рассчитывается по следующей формуле: о 2 «=» ∑ я «=» 1 н ( Икс я − Икс ‾ ) 2 Н где: Икс я «=» Каждое значение в наборе данных Икс ‾ «=» Среднее значение всех значений в наборе данных Н «=» Количество значений в наборе данных \begin{align}&\sigma^2 = \frac { \sum_{i = 1} ^ { n } \big (x_i — \overline { x } \big ) ^ 2 }{ N } \\&\textbf{ где:} \\&x_i = \text{Каждое значение в наборе данных} \\&\overline { x } = \text{Среднее значение всех значений в наборе данных} \\&N = \text{Количество значений в наборе данных набор данных} \\\end{выровнено}
σ2=N∑i=1n(xi−x)2где:xi=Каждое значение в наборе данныхx=Среднее значение всех значений в наборе данныхN=Количество значений в наборе данных Вы также можете использовать приведенную выше формулу для расчета дисперсии в других областях, кроме инвестиций и торговли, с некоторыми небольшими изменениями. Статистики используют дисперсию, чтобы увидеть, как отдельные числа соотносятся друг с другом в наборе данных, а не используют более широкие математические методы, такие как распределение чисел по квартилям. Преимущество дисперсии в том, что она рассматривает все отклонения от среднего значения как одинаковые, независимо от их направления. Квадраты отклонений не могут в сумме равняться нулю и вообще не создают видимость изменчивости данных. Однако одним из недостатков дисперсии является то, что она придает дополнительный вес выбросам. Это цифры, далекие от среднего. Возведение этих чисел в квадрат может исказить данные. Еще одна ловушка использования дисперсии заключается в том, что ее нелегко интерпретировать. Пользователи часто используют его в первую очередь для извлечения квадратного корня из его значения, которое указывает на стандартное отклонение данных. В некоторых случаях риск или волатильность могут быть выражены в виде стандартного отклонения, а не дисперсии, поскольку первое часто легче интерпретировать. Вот гипотетический пример, демонстрирующий, как работает дисперсия. Допустим, доходность акций компании ABC составляет 10 % в первый год, 20 % в год 2 и −15 % в год 3. Среднее значение этих трех доходностей составляет 5 %. Различия между каждой доходностью и средним значением составляют 5%, 15% и -20% за каждый последующий год. Возведение этих отклонений в квадрат дает 0,25%, 2,25% и 4,00% соответственно. Если мы сложим эти квадраты отклонений, то получим в сумме 6,5%. Когда вы делите сумму 6,5% на единицу меньше количества возвратов в наборе данных, поскольку это выборка (2 = 3-1), это дает нам дисперсию 3,25% (0,0325). Чтобы вычислить дисперсию, выполните следующие действия: Дисперсия — это, по сути, степень разброса в наборе данных относительно среднего значения этих данных. Он показывает количество вариаций, существующих между точками данных. Визуально, чем больше дисперсия, тем «жирнее» будет распределение вероятностей. В финансах, если что-то вроде инвестиций имеет большую дисперсию, это может быть интерпретировано как более рискованное или волатильное. Стандартное отклонение — это квадратный корень из дисперсии. Иногда это более полезно, так как при извлечении квадратного корня единицы измерения удаляются из анализа. Это позволяет проводить прямое сравнение между разными вещами, которые могут иметь разные единицы измерения или разные величины. Например, если сказать, что увеличение X на одну единицу увеличивает Y на два стандартных отклонения, это позволяет понять взаимосвязь между X и Y независимо от того, в каких единицах они выражены. Опубликован в
18 января 2023 г.
к
Прита Бхандари. Дисперсия является мерой изменчивости. Он рассчитывается путем взятия среднего квадрата отклонений от среднего. Дисперсия говорит вам о степени разброса в вашем наборе данных. Стандартное отклонение выводится из дисперсии и показывает, в среднем, насколько далеко каждое значение отстоит от среднего. Это квадратный корень из дисперсии. Обе меры отражают изменчивость распределения, но их единицы различаются: Поскольку единицы дисперсии намного больше, чем единицы типичного значения набора данных, сложнее интуитивно интерпретировать число дисперсии. Однако дисперсия более информативна в отношении изменчивости, чем стандартное отклонение, и она используется для статистических выводов. Для расчета дисперсии используются разные формулы в зависимости от того, есть ли у вас данные из всей совокупности или из выборки. Когда вы соберете данные о каждом члене интересующей вас совокупности, вы сможете получить точное значение дисперсии совокупности. Формула дисперсии населения выглядит следующим образом: При сборе данных из выборки выборочная дисперсия используется для оценок или выводов о дисперсии генеральной совокупности. Формула выборочной дисперсии выглядит следующим образом: Для выборок мы используем n – 1 в формуле, потому что использование n дало бы нам смещенную оценку, которая последовательно занижает изменчивость. Выборочная дисперсия, как правило, ниже, чем реальная дисперсия генеральной совокупности. Уменьшение выборки n до n – 1 делает дисперсию искусственно большой, давая вам объективную оценку изменчивости: лучше переоценить, чем недооценить изменчивость в выборках. Важно отметить, что выполнение того же действия с формулами стандартного отклонения не приводит к полностью объективным оценкам. Профессиональные редакторы вычитывают и редактируют вашу статью, уделяя особое внимание: См. пример Вы можете рассчитать дисперсию вручную или с помощью нашего калькулятора дисперсии ниже. Дисперсия обычно рассчитывается автоматически любым программным обеспечением, которое вы используете для статистического анализа. Но вы также можете рассчитать его вручную, чтобы лучше понять, как работает формула. Существует пять основных шагов для нахождения дисперсии вручную. Чтобы найти среднее значение, сложите все баллы, а затем разделите их на количество баллов. Вычтите среднее из каждой оценки, чтобы получить отклонения от среднего. Поскольку x̅ = 50, отнимите 50 от каждого результата. Умножить каждое отклонение от среднего само на себя. Сложите все квадраты отклонений. Это называется сумма квадратов. Разделить сумму квадратов на n – 1 (для выборки) или N (для генеральной совокупности). Так как мы работаем с образцом, мы будем использовать n – 1, где n = 6. Разница имеет значение по двум основным причинам: Важно учитывать дисперсию перед выполнением параметрических тестов. Эти тесты требуют равных или близких дисперсий, также называемых однородностью дисперсии или гомоскедастичностью, при сравнении разных выборок. Неравномерная дисперсия между образцами приводит к смещенным и искаженным результатам теста. Если у вас неравномерная дисперсия по выборкам, более подходящими являются непараметрические тесты. Статистические тесты, такие как дисперсионные тесты или дисперсионный анализ (ANOVA), используют выборочную дисперсию для оценки групповых различий. Они используют дисперсии выборок, чтобы оценить, отличаются ли друг от друга совокупности, из которых они взяты. Чтобы оценить групповые различия, вы выполняете дисперсионный анализ. Основная идея дисперсионного анализа состоит в том, чтобы сравнить дисперсии между группами и дисперсии внутри групп, чтобы увидеть, лучше ли результаты объясняются групповыми различиями или индивидуальными различиями. Если дисперсия между группами выше, чем внутригрупповая дисперсия, то группы, вероятно, будут отличаться в результате вашего лечения. Если нет, то вместо этого результаты могут быть получены из индивидуальных различий членов выборки. Для этого вы получаете соотношение межгрупповой дисперсии окончательных оценок и внутригрупповой дисперсии окончательных оценок — это F-статистика. При большой F-статистике вы найдете соответствующее значение p и сделаете вывод, что группы значительно отличаются друг от друга. Дисперсия — это среднеквадратичное отклонение от среднего значения, а стандартное отклонение — это квадратный корень из этого числа. Обе меры отражают изменчивость распределения, но их единицы различаются: Хотя единицы дисперсии сложнее интуитивно понять, дисперсия важна в статистических тестах. Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования. Бхандари, П.
(2023, 18 января). Как рассчитать дисперсию | Калькулятор, анализ и примеры. 1)
Посмотреть всех экспертов из раздела Учеба и наука > Математика Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . В двузначном натуральном числе сумма цифр равна 13.Число десятков на 3 больше числа единиц. Найдите это число. 1 класс. Тема: От первого до двадцатого и наоборот. 1. Мальчик стоит на первой ступени лестницы, в которой 20 ступеней. 1) Сколько ступеней нужно… отрезок BD -диаметр окружности с центром О.Хорда AC делит пополам радиус OB и перпендикулярна у нему.Найдите углы четырехугольника ABCD И ГРАДУСНЫЕ МЕРЫ ДУГ AB BC CD AD. Пользуйтесь нашим приложением Интересные вопросы Школа Подскажите, как бороться с грубым отношением одноклассников к моему ребенку? Новости Поделитесь, сколько вы потратили на подготовку ребенка к учебному году? Школа Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе? Школа Когда в 2018 году намечено проведение основного периода ЕГЭ? Новости Будет ли как-то улучшаться система проверки и организации итоговых сочинений? Вузы Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»? Привет, помогите решить уравнение. ответы Лови, ток не реви)) ваш ответ Можно ввести 4000 cимволов отправить дежурный Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения похожие темы ЕГЭ 9 класс 11 класс Химия похожие вопросы 5 В какой момент времени ускорение движения будет наименьшим? Колмогоров Алгебра 10-11 класс Упр 309 Привет! Поможете с решением?) ГДЗ11 классКолмогоров А.Н.10 классАлгебра Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ГДЗ11 классКолмогоров А.Н.Алгебра Почему сейчас школьники такие агрессивные ? Читали новость про 10 классника который растрелял ? как вы к этому относитесь Новости10 классБезопасность Это правда, что будут сокращать иностранные языки в школах? Хочется узнать, когда собираются сократить иностранные языки в школе? Какой в итоге оставят? (Подробнее…) ШколаНовостиИностранные языки ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… 18. ГДЗЕГЭРусский языкЦыбулько И.П. В уравнении $x$ представляет собой угол с косинусом $\frac{1}{\sqrt{2}}$. НО! Мы могли бы повторять единичный круг снова и снова, и каждый раз находить новые решения. Поскольку каждый раз это соответствует добавлению (или вычитанию) $2\pi$ радиан, мы получаем новое решение уравнения каждый раз, когда добавляем некоторое целое число, кратное $2\pi$, к любому решению, которое у нас уже есть.
Поэтому множество решений есть множество
$$ \left\{ \pm\frac{\pi}{4} + 2k\pi : k\in\mathbb{Z} \right\}. Теперь мы ищем решения между (включая ) $\frac{\pi}{11}$ и $7\pi$. Есть немного более элегантные способы решения проблемы, но пока, почему бы нам просто не применить грубую силу? Начнем с того, что заметим, что $-\frac{\pi}{4}$ слишком мало, чтобы попасть в интервал. Однако обратите внимание, что
$$ \frac{\pi}{11} < \frac{\pi}{4} < 7\pi, $$
так что работает. Далее мы можем взять наши два решения и добавить к ним $2\pi$. Это дает нам
$$ -\frac{\pi}{4} + 2\pi = \frac{7\pi}{4}
\qquad\text{и}\qquad
\ гидроразрыва {\ пи} {4} + 2 \ пи = \ гидроразрыва {9 \ пи} {4}.
$$
Оба они больше, чем $\frac{\pi}{11}$, и, заметив, что $7\pi = \frac{28\pi}{4}$, мы можем видеть, что оба меньше, чем $7\pi$ . Следовательно, у нас есть еще два значения, которые работают. Снова ходим по кругу, получаем решения
$$ \frac{7\pi}{4} + 2\pi = \frac{15\pi}{4}
\qquad\text{и}\qquad
\фракция{9\pi}{4} + 2\pi = \frac{17\pi}{4}.
$$
Опять же, эти решения работают. Итак, повторите еще раз:
$$ \frac{15\pi}{4} + 2\pi = \frac{23\pi}{4}
\qquad\text{и}\qquad
\frac{17\pi}{4} + 2\pi = \frac{25\pi}{4}. Поможем понять и полюбить математику Начать учиться 315.4K В 5 классе ученики знакомятся с объемными фигурами. Оглянитесь вокруг — мир состоит из параллелепипедов. Так что в любой непонятной ситуации просто ищите их объём. Давай научимся это делать. В статье найдете все необходимые формулы и правила. Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями. Объём — это количественная характеристика пространства, занимаемого телом или веществом. Другими словами, это то, сколько места занимает предмет. Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см3), кубический миллиметр (1 мм3), кубический метр (1 м3). Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе. Два свойства объёма Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно. Реши домашку по математике на 5. Подробные решения помогут разобраться в самой сложной теме. Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом. Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками. Формула объема прямоугольного параллелепипеда Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты: V = a × b × h Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями. a длина параллелепипеда b ширина параллелепипеда h высота параллелепипеда P (осн) периметр основания S (осн) площадь основания S (бок) площадь боковой поверхности S (п. площадь полной поверхности V объем Пример 1. Чему равен объем параллелепипеда со сторонами 9 см, 6 см, 3 см. a = 9 см b = 6 см h = 3 см V = a × b × h V = 9 × 6 × 3 = 162 см3. Ответ: объем прямоугольного параллелепипеда равен 162 см3. Следствие Объем параллелепипеда равен произведению площади основания на высоту. V = Sосн × h Из этого следствия выведем формулу нахождения площади основания параллелепипеда. Sосн = V : h Пример 2. Найдите площадь основания параллелепипеда, если его объем равен 96 см3, а высота 8 см. V = 96 см3 h = 8 см V = Sосн × h Sосн = V : h Sосн = 82 см3 : 8 см = 12 см2. Ответ: площадь основания параллелепипеда равна 12 см2. Обучение на курсах по математике в онлайн-школе Skysmart поможет быстрее разобраться в теме и правильно решать задачки! Как вы уже поняли, вычисление объёма параллелепипеда напрямую зависит от вычисления его площади. Давайте разберемся, сколько всего площадей можно найти в параллелепипеде. Чтобы найти площадь боковой поверхности параллелепипеда, вычислите по отдельности площадь каждой боковой грани, а затем найдите сумму получившихся значений. Так как противолежащие грани прямоугольного параллелепипеда одинаковые, то получим формулу: Чтобы вычислить площадь полной поверхности параллелепипеда, сложите площадь боковой поверхности и две площади основания. Так как площади оснований у прямоугольного параллелепипеда одинаковые, то получим формулу: Пример 3. Найдем площадь поверхности параллелепипеда, если длина основания равна 6 сантиметров, ширина — 4 см соответственно, а высота — 3 см. Sп. п. = 2 (ab + ac + bc) Sп. п. = 2 (6 × 4 + 6 × 3 + 4 × 3) = 2 × (24 + 18 + 12) = 2 × 54 = 108 см2. Ответ: площадь поверхности параллелепипеда — 108 см2. Как видите, вычислить объём и найти площадь параллелепипеда совсем не трудно. Пользоваться онлайн-калькуляторами можно, когда вы уже натренировались в решении задачек и с закрытыми глазами можете вычислить объем любого параллелепипеда. Давайте разберем еще несколько примеров. Задачка 1. Найдите объём параллелепипеда со сторонами 18 см, 10 см, 7 см. Как решаем: a = 18 см b = 10 см h = 7 см Формула нахождения объема параллелепипеда: V = a × b × h Подставляем наши числа: V = 18 × 10 × 7 = 1260 см3. Ответ: объём параллелепипеда равен 1260 см3. Задачка 2. Найдите площадь основания параллелепипеда, если его объём равен 120 см3, а высота — 15 см. Как решаем: V = 120 см h = 15 см V = Sосн × h Sосн = V : h Sосн = 120 см3: 15 см = 8 см2. Ответ: площадь основания параллелепипеда равна 8 см2. Задачка 3. Найдите площадь полной поверхности прямоугольного параллелепипеда, если длина основания равна 30 сантиметров, ширина равна 12 см, а высота равна 5 см. Как решаем: Sп. п. = 2 (ab + ac + bc) Sп. п. = 2 (30 × 12 + 30 × 5 + 12 × 5) = 2 × (360 + 150 + 60) = 2 × 570 = 1140 см2. Ответ: площадь полной поверхности параллелепипеда равна 1140 см2. Пусть все необходимые формулы будут под рукой в нужный момент. Сохраняйте табличку-шпаргалку на гаджет или распечатайте ее и храните в учебнике. V параллелепипеда V = a × b × h V = Sосн × h S боковой поверхности Sб. п. = 2 (ac + bc) S полной поверхности Sп. п. = 2 (ab + ac + bc) Шпаргалки для родителей по математике Все формулы по математике под рукой Анастасия Белова К предыдущей статье 412.3K Время, скорость, расстояние К следующей статье 500. Порядок действий в математике Выявим пробелы в знаниях и дадим советы по обучению Расскажем, как проходят занятия Подберём курс
{S_{полн} = 2(ab+bc+ac)}
Найти площадь
полной поверхностибоковой поверхности Длина a
ммсмдммкмдюймы (in)футы (ft) Ширина b
ммсмдммкмдюймы (in)футы (ft) Высота c
ммсмдммкмдюймы (in)футы (ft) Результат в
мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)
Виджет
Ссылка на расчет
Сообщить об ошибке
Сохранить расчет
Печатать
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. В дополнение на сайте можно найти объем параллелепипеда. Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники. Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.
{S_{полн} = 2(ab+bc+ac)}
a — длина прямоугольного параллелепипеда b — ширина прямоугольного параллелепипеда c — высота прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a — длина прямоугольного параллелепипеда b — ширина прямоугольного параллелепипеда c — высота прямоугольного параллелепипеда Задача 1 Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5. Ответ: 126 см² Как всегда ответ можно проверить с помощью калькулятора . Параллелепипед – это трехмерная фигура, образованная шестью параллелограммами. Слово «параллелепипед» происходит от греческого слова parallelepdon , что означает «тело, имеющее параллельные тела». Можно сказать, что параллелепипед относится к параллелограмму так же, как куб относится к квадрату. Параллелепипед имеет 6 граней в форме параллелограмма, 8 вершин и 12 ребер. Давайте разберемся со свойствами и различными формулами, связанными с площадью поверхности и объемом параллелепипеда, в следующих разделах. Параллелепипед представляет собой трехмерную фигуру с шестью гранями, каждая из которых имеет форму параллелограмма. У него 6 граней, 8 вершин и 12 ребер. Куб, прямоугольный параллелепипед и ромбовидный — все это частные случаи параллелепипеда. Куб – это параллелепипед, все стороны которого имеют форму квадрата. Точно так же кубоид и ромбоид являются параллелепипедами с прямоугольной и ромбовидной гранями соответственно. На приведенном ниже рисунке мы можем наблюдать параллелепипед с длинами сторон «a», «b» и «c», а «h» — высотой параллелепипеда. Существуют определенные свойства параллелепипеда, которые помогают нам отличить его от других трехмерных фигур. Эти свойства перечислены ниже: Площадь поверхности параллелепипеда определяется как общая площадь, занимаемая всеми поверхностями параллелепипеда. Площадь поверхности параллелепипеда выражается в квадратных единицах, например 9.0087 2 , см 2 , м 2 , фут 2 , ярд 2 и т. д. Площадь поверхности параллелепипеда может быть двух типов: Площадь боковой поверхности параллелепипеда определяется как площадь боковых или боковых граней параллелепипеда. Общая площадь поверхности параллелепипеда определяется как площадь всех граней параллелепипеда. Чтобы вычислить TSA параллелепипеда, нам нужно найти сумму площадей, покрытых 6 гранями. Формула для расчета площади боковой поверхности и общей площади поверхности параллелепипеда: TSA параллелепипеда = LSA + 2 × B = (P × H) + (2 × B) где, Объем параллелепипеда определяется как пространство, занимаемое фигурой в трехмерной плоскости. Объем параллелепипеда выражается в кубических единицах, например, 3 , см 3 , м 3 , фут 3 , ярд 3 и т. Объем параллелепипеда можно рассчитать, используя площадь основания и высоту. Формула для расчета объема параллелепипеда дается как, Пример 1: Если базовая грань параллелепипеда имеет противоположные стороны размером 6 дюймов и 10 дюймов, а его высота равна 7 дюймам, найдите площадь боковой поверхности параллелепипеда. Решение: Используя формулу площади боковой поверхности параллелепипеда, Ответ: Площадь боковой стороны данного параллелепипеда = 224 в 3. Пример 2: Подарок упакован в прямоугольную коробку размером 10, 7 и 8 дюймов и должен быть обернут подарочной бумагой. Решение: Размеры данной подарочной коробки, Чтобы найти необходимое количество подарочной бумаги, нам нужно найти общую площадь поверхности коробки. Поскольку форму коробки можно сравнить с прямоугольным параллелепипедом, ВПС = 2 (дв + вх + вл) = 2 (10 × 7 + 7 × 8 + 8 × 10) = 2 (70 + 56 + 80) = 412 в 2 . Ответ: Площадь необходимой подарочной бумаги = 412 в 2 . перейти к слайдуперейти к слайду Отличное обучение в старшей школе с использованием простых подсказок Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами. Забронировать бесплатный пробный урок перейти к слайдуперейти к слайду Параллелепипед представляет собой трехмерную фигуру с 6 гранями в форме параллелограмма, 12 ребрами и 8 вершинами. Объем параллелепипеда – это емкость, форма или общее пространство, занимаемое в трехмерной плоскости. Объем параллелепипеда в кубических единицах, например, 3 , см 3 , фут 3 , 3 и т. д. Полная площадь поверхности параллелепипеда – это площадь, покрытая всеми гранями параллелепипеда. Выражается в квадратных единицах, например, в 2 , м 2 , см 2 , фут 2 и т. д. Площадь боковой поверхности параллелепипеда – это площадь или область, покрываемая всеми боковыми или боковыми гранями параллелепипеда. Формулы, связанные с параллелепипедом, даны как, где B — площадь основания, H — высота параллелепипеда, P — периметр основания. Прямоугольный параллелепипед — тип параллелепипеда, все шесть граней которого имеют прямоугольную форму, а длины параллельных ребер равны. Параллелепипед — это трехмерная фигура, все стороны которой имеют форму параллелограмма. Противоположные грани параллелепипеда являются зеркальным отражением друг друга. Скачать БЕСПЛАТНЫЕ учебные материалы Рабочие листы для фигур Параллелепипед — это трехмерная фигура или призма с основанием в виде параллелограмма, состоящим из шести сторон параллелограмма. Параллелепипед представляет собой трехмерную фигуру, образованную шестью параллелограммами, и его можно определить как многогранник с шестью гранями, также называемый шестигранником, каждая грань которого представляет собой параллелограмм. Параллелепипед также называют ромбом. По аналогии с 2D Shapes, он соотносится с параллелограммом так же, как куб соотносится с квадратом. Прямоугольный кубоид с шестью прямоугольными гранями, куб с шестью квадратными гранями и ромбоэдр с шестью ромбовидными гранями — все это частные случаи параллелепипеда. Объем параллелепипеда — это количество пространства, которое содержит параллелепипед. Объем параллелепипеда равен произведению площади основания на высоту. Из геометрического определения перекрестного произведения мы знаем, что его величина, ∥a×b∥, представляет собой площадь основания параллелограмма и что направление вектора a×b перпендикулярно основанию. Для описания параллелепипеда нам нужны три его смежные стороны и мера углов между ними, или три смежных вектора. Формула объема параллелепипеда: Формула объема параллелепипеда, образованного векторами \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) с той же начальной точкой задается их скалярным тройным произведением: \(V=∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\). V – Объем параллелепипеда, образованного тремя векторами; \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) Первый шаг вычисления объема параллелепипеда включает в себя нахождение векторного произведения или векторного произведения \((\vec{a}\times\vec{b})\). Последующее скалярное произведение между \((\vec{a}\times\vec{b})\) и \(\vec{c}\) обозначает проекцию \(\vec{a}\times\vec {b}\) на \(\vec{c}\). Другими словами, он перемещает базовый параллелограмм вдоль \(\vec{c}\), аналогично умножению базовой площади на высоту. Формулу можно упростить и свести к одному определителю: \(\begin{matrix} Это дает нам объем параллелепипеда, когда векторы \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) известны. Если мы знаем вершины параллелепипеда, мы можем найти его векторы, используя простую формулу расстояния. Если \(A < x_1, y_1, z_ 1 >, B < x_2, y_2, z_ 2 >\), \(C < x_3, y_3, z_ 3 >\) и \(D < x_4, y_4, z_ 4 > \) тогда мы можем найти векторы AB =a, AC=b и AD=c, имеющие одну и ту же начальную точку, и использовать их в качестве наших базисных векторов, образующих параллелепипед. AB будет задан как \( a = Получив векторы a, b и c, выполните следующие простые шаги: Найдите векторное произведение между векторами \(\vec{a}\) и \(\vec{b}\), чтобы получить \(\ vec{a}\times\vec{b}\). Вычислите скалярное произведение между векторами \(\vec{a}\times\vec{b}\) и \(\vec{c}\), чтобы получить скалярное значение \((\vec{a}\ раз\vec{b})\cdot\vec{c}\). Определите объем параллелепипеда как абсолютное значение этого скаляра, заданного как \(∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\). Где, \(\alpha\) — угол между сторонами b и c; \(\beta\) – Угол между сторонами а и с; и \(\gamma\) – угол между сторонами a и b. Площадь параллелепипеда равна сумме площадей всех его поверхностей. Это называется полной площадью поверхности параллелепипеда. Когда дело доходит до площади 3D-объектов, есть две важные площади поверхности: Узнайте о площади четырехугольника. Площадь боковой поверхности параллелепипеда Площадь боковой поверхности параллелепипеда определяется как сумма площадей поверхностей его граней без учета основания и вершины. Площадь боковой поверхности (LSA) параллелепипеда равна произведению периметра основания на высоту параллелепипеда. Площадь боковой поверхности параллелепипеда Формула: \(LSA= 2(a+b){\times}c\) Общая площадь поверхности параллелепипеда Полная площадь поверхности параллелепипеда определяется как общая область, покрытая всеми гранями формы. Общая площадь поверхности параллелепипеда Формула: \(TSA=2(ab+bc+ac)\) В векторной форме мы можем записать это как \(A = 2{\times}( ∣\vec{a}{\times}\vec{b}∣ + ∣\vec{b}{\times}\vec{c}∣ + ∣\vec{a}{\times}\vec{c}∣ )\) Где, \(∣\vec{a}{\times}\vec{b}|: Величина \; из \; \; перекрестное произведение \; между \; \vec{a}\) и \(\vec{a}\) \(∣\vec{b}{\times}\vec{c}|: Величина \; of \; \; перекрестное произведение \; между \; \vec{ b}\) и \(\vec{c}\) \(∣\vec{c}{\times}\vec{a}|: Величина \; of \; \; перекрестное произведение \; между \; \vec{c}\) и \(\vec{b}\) Существует альтернативный способ расчета площади параллелепипеда с использованием длин его сторон \ (a\), \(b\) и углы. \(A = 2\times(a{\cdot}b{\cdot}sin(\gamma) + b{\cdot}c{\cdot}sin(\alpha) + a{\cdot}c{\ cdot}sin(\beta))\), где: \(\alpha\) – угол между b и c; \(\beta\) – Угол между а и с; и \(\gamma\) – Угол между a и b. Прямоугольный параллелепипед представляет собой многогранник с шестью гранями, также известный как шестигранник. Это трехмерная структура в виде параллелепипеда, все шесть граней которой имеют прямоугольную форму, а длины параллельных ребер равны. Это частный случай параллелепипеда. Прямоугольный параллелепипед аналогичен двумерному прямоугольнику. Узнайте о прямоугольниках. Формула прямоугольного параллелепипеда включает формулу площади поверхности, объема и диагоналей. Площадь поверхности прямоугольного параллелепипеда На фигуре прямоугольного параллелепипеда шесть прямоугольников. Площадь поверхности \(= 2(l{\times}h) + 2(l{\times}w) + 2(h{\times}w)\) \(S = 2[(l{\ times}h) + (l{\times}w) + (h{\times}w)]\) , где \(l\), \(w\), \(h\) — длина, ширина, высота прямоугольного параллелепипеда соответственно. Площадь боковой поверхности прямоугольного параллелепипеда Произведение периметра основания и высоты называется площадью боковой поверхности. Каждая грань прямоугольного параллелепипеда представляет собой прямоугольник, поэтому периметр основания равен периметру прямоугольника. Ниже приведена формула для LSA (площадь боковой поверхности): LSA = периметр основания × высота Поскольку периметр основания равен 2 (длина + ширина) = 2 (длина + ширина) × высота \(LSA = 2lh + 2wh\) где \(l\), \(w\), \(h\) — длина, ширина и высота прямоугольного параллелепипеда соответственно. Площадь основания, умноженная на высоту, дает объем прямоугольного параллелепипеда. Основание прямоугольного параллелепипеда — прямоугольник, как и каждая его грань, а его площадь равна произведению его длины на ширину. Формула объема следующая: 92}\) Некоторые важные решенные примеры на параллелепипеде приведены ниже: Пример 1: Найдите общую площадь поверхности данного параллелепипеда, если длина 13 см, ширина 12 см и высота 10 см. Решение: Мы знаем, что Общая площадь поверхности (TSA) = 2(ab + bc + ac), здесь a = 13 см, b = 12 см, c = 10 см = 2(13 × 12 + 12 × 10 + 10 × 13 ) = 812 кв.см Пример 2: Рассмотрим параллелепипед ABCDEFGH с длинами ребер a = 7, b = 5 и c = 3. Если ∠DAE=45°, ∠BAD=63° и ∠BAE=50°, то что площадь поверхности параллелепипеда? Решение: Здесь \(\alpha=∠BAD=63°\) – угол между b и c; \(\beta=∠DAE=45°\) – Угол между а и с; и \(\gamma=∠BAE=50°\) – угол между a и b. Площадь поверхности будет равна, будет равна \(A = 2\times(a{\cdot}b{\cdot}sin(\gamma) + b{\cdot}c{\cdot}sin(\alpha) + a{\cdot}c{\ cdot} sin (\ beta)) \) \ (A = 2 \ times (7 {\ cdot} 5 {\ cdot} sin (50) + 5 {\ cdot} 3 {\ cdot} sin (63) + 7 {\ cdot} 3 {\ cdot} sin (45)) \) \ (A = 2 \ times (35 {\ cdot} sin (50) + 15 {\ cdot} sin (63) + 21 {\ cdot}sin(45))\) \(A = 110,05\) квадратных единиц Пример 3: Найти объем параллелепипеда с векторами a = (1, 1, 2), b = (2 , 1, 3) и с = (3, 1, 2). Решение: Объем параллелепипеда определяется определителем матрицы: \( V= Подставляя значения получаем \( V= Находим определитель, получаем, \(V = |3(1\times3 – 2\times1) – 1(1\times3 – 2\times2) + 2( 1\раз1 – 1\раз2)|\) \(V = |3\times1 – 1\times(-1) + 2\times(-1)|\) \(V = 2 \) единиц куба. Надеюсь, эта статья о параллелепипеде была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас! В.1 Что такое параллелепипед? Ответ 1 Параллелепипед — это трехмерная фигура или призма с основанием в виде параллелограмма, состоящим из шести сторон параллелограмма. Q.2 Что такое объем формулы параллелепипеда? Ответ 2 Формула объема параллелепипеда, образованного векторами \(\vec{a}\), \(\vec{b}\) и \(\vec{c}\) с одна и та же начальная точка задается их скалярным тройным произведением: \(V=∣(\vec{a}\times\vec{b})\cdot\vec{c}∣\) Q.3 Что площадь параллелепипеда? Ответ 3 Площадь параллелепипеда равна сумме площадей всех его поверхностей. Это называется полной площадью поверхности параллелепипеда. В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами. Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке. Запись предела: Таким образом, финальная запись предела выглядит выглядит так (в нашем случае): Читается как “предел функции при икс, стремящемся к единице”. x→1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут). Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x→1): Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу). В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например: Если x→∞, то заданная функция стремится к минус бесконечности (-∞), т. Другой более сложный пример Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом. Таким образом при “икс”, стремящемся к бесконечности, функция x2 + 3x – 6 неограниченно растет. В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности. Пример: давайте вычислим предел ниже. Решение Выражения и в числителе, и а знаменателе стремятся к бесконечности. Однако не все так просто. Чтобы решить предел нам нужно сделать следующее: 1. Находим x в старшей степени для числителя (в нашем случае – это два). 2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум). 3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень. 4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2. И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности. В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль. Пример: Найдем предел функции ниже. Решение 1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида. 2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение. В нашем случаем корнями выражения в числителе (2x2 – 5x + 3 = 0) являются числа 1 и 1,5. Следовательно его можно представить в виде: 2(x-1)(x-1,5). Знаменатель (x – 1) изначально является простым. 3. Получаем вот такой видоизмененный предел: 4. Дробь можно сократить на (x – 1): 5. Остается только подставить число 1 в выражение, получившееся под пределом: При вычисление пределов вида в случае если числи- Тель или знаменатель содержит выражение , стремящееся к нулю при часто бывает полезным избавиться от иррациональности в числителе или в знаменателе путём домножения числителя и знаменателя на соответствующий сопряжённый множитель . Для разности таким множителем является , для выражения таким множителем является . В самом деле , где , , Где . В общем случае для разности сопряжённое выражение . В результате умножения получаем , т. е. . Для сокращения записи можно вычислить отдельно и если он конечен и не равен нулю, вынести за знак предела. Пример 1 A = Решение: Т. к. х8, то х-80. Выделим множитель в числителе и знаменателе. Умножим числитель и знаменатель дроби на множитель . Тогда в числителе мы получим В знаменателе множитель будет стремиться к конечному пределу, не равному 0, а именно к 10 при х8, поэтому по теореме о пределе Произведения множитель можно вынести за знак предела. Знаменатель представим в виде произведения х2 – 6х – 16 = (х – 8)(х + 2). Таким образом, вычисление данного предела сводиться к следующим действиям: A = Пример 2. Вычислить Решение: Выделим в числителе и знаменателе множитель, стремящийся к нулю, т. Числитель: Знаменатель: . Таким образом, предел приобретает вид A = Пример 3. A = Решение: Выделим в числителе и знаменателе множитель, стремящийся к 0, т. е. (х – 2) Числитель: Знаменатель: . Тогда A = . Пример 3. A = Решение: Как и в предыдущем случае выделим множитель, стремящийся к 0, т. е. (х+1) в числителе и знаменателе. Тогда Числитель: . Знаменатель: Таким образом A = При раскрытии неопределенностей вида нужно выполнить тождественные преобразования, позволяющие свести такую неопределенность к виду или . Например, в случае, если выражение содержит иррациональности с невысоким показателем корня, этого можно добиться путем умножения и деления данного выражения на «сопряженное». Пример 5. Пример 6. (Сумма двух бесконечно больших одного знака есть величина бесконечно большая) Пример 7. Решение. Данный предел содержит корень с высоким показателем, поэтому умножение и деление на сопряженное выражение нецелесообразно. Преобразуем данное выражение следующим образом: При выражение , т. е. является бесконечно малой величиной. Если воспользоваться следствием из 2-го замечательного предела , то выражение, стоящее в скобках, можно заменить эквивалентной величиной . Так как величина является бесконечно малой более высокого порядка, чем , то ее можно отбросить, поэтому данная дробь будет эквивалентна выражению . Следовательно, Пример 8. Решение. Выделим Главную часть в каждом из слагаемых. Очевидно, что при ; . Таким образом, оба радикала имеют одинаковую часть . Вычтем ее из каждого радикала. Тогда получим = . Пример 9. Решение. 1 Способ: Выделим главную часть числителя и знаменателя. Т. к. то главная часть числителя будет совпадать с Аналогично, поэтому главная часть знаменателя совпадает с Тогда 2 способ: Вынесем из-под каждого корня старшую степень переменной. При раскрытии неопределенностей вида можно также выделить главную часть числителя и знаменателя. Пример 10. Решение. 1 способ:Этот пример можно решить, воспользовавшись для выделения главной части эквивалентными бесконечно большими величинами, а именно: Значит 2 способ: Этот же предел можно вычислить и непосредственно, а именно вынести за скобки старшую степень переменной в числителе и знаменателе. Пример 11. Решение: 1 способ: Как и в предыдущем примере, выделим главную часть числителя и знаменателя. , Тогда 2 способ: Вынесем в числителе и знаменателе за скобки старшую степень х. Ограничения Пример Рассмотрим функцию х 2 — 1 Если мы подставим 1, мы получим 0/0
который не определен. Мы можем построить следующую таблицу: Мы можем видеть, что эта функция приближается к 0,5, когда x приближается к
1. Ниже приведен график этой функции. Этот пример приводит нас к следующему определению Определение предела Если
f(x) становится сколь угодно близким к одному числу
L по мере приближения x
c с обеих сторон, затем Мы можем думать об определении предела как x -> c как о двух туристах, один
идущий справа, а другой идущий слева. Свойства пределов Предположим, что и что а является константой. затем А) Б) С) Д) Е) Пример Предположим, что , затем Алгебра и пределы При нахождении предела всегда сначала подставляйте число. Если вы получите
определенное значение, то это и есть ответ. В противном случае вам, возможно, придется сделать
алгебра, чтобы найти предел. Пример: lim как х -> 1 (х 2 — 1)/(х 2 +2x — 3) = lim as x -> 1 (x — 1)(x + 1)/(x + 3)(x — 1) = lim как х -> 1 (х + 1)/(х + 3) = 2/4 = 0,5 Найдите предел Решение Во-первых, обратите внимание: если мы подставим 1 вместо x, мы получим 0/0. Теперь подключите 1, чтобы получить 2/4
= 1/2 Пример Найдите предел Решение Опять же, если мы подключаемся, мы получаем 0/0. Какая алгебра подойдет для этого
проблема? Вспомните из основ алгебры, как рационализировать знаменатель.
Наша стратегия будет заключаться в рационализации числителя. Мы умножаем
числитель и знаменатель на сопряженный корень. Теперь мы можем подставить 9 вместо х
получить 1
1 Односторонние ограничения Определим левый предел как координата y кривой при движении точки слева. Аналогично определим правый предел как координата y кривой, когда точка движется слева. Пример Находить Решение График функции изображен ниже. Прогуливаясь с левой стороны, значение y приближается к -1. Следовательно
предел -1. Обратите внимание, что без знака «-» предел
не существовало бы. Мы говорим, что предел существует, если левый и правый пределы равны. Неограниченные пределы Пример Находить Решение Подставив 2, мы получим 6/0, что не определено. Если мы подставим число
слева от 2, например 1,99999, мы получаем очень большое отрицательное число. Мы
говорят, что предел отрицательная бесконечность. Назад
на главную страницу исчисления Назад к математике
домашняя страница отдела электронная почта
Вопросы и предложения Пределы оказались очень полезными в области исчисления, они стали прочной основой для определения многих понятий, таких как непрерывность, дифференцируемость, интегралы и производные. Рассмотрим функцию f(x) и точку x = c, предел в этой точке определяется как значение, которое функция, по-видимому, принимает при приближении к этому значению x = c либо слева- ручная или правая сторона. Предел функции в конкретной точке определяется как Большинство пределов можно вычислить простой подстановкой точки x = a в функцию. Это называется методом прямой замены. Иногда при вычислении пределов мы можем столкнуться с некоторыми выражениями, которые не определены. Это неопределенные формы предела. Например, рассмотрим функцию f(x) =. Обратите внимание, что при прямой подстановке этот предел принимает вид 0/0. Это неопределенная форма, и она называется неопределенной формой. Точно так же ∞/∞, 1 ∞ также называются неопределенными формами. Для решения таких форм используется ряд стратегий. Существует несколько стратегий и методов, используемых для нахождения пределов функции. Какой метод будет использоваться для какой функции, зависит от нескольких факторов. Например, тип функции (тригонометрическая, экспоненциальная, полиномиальная и т. д.), встречающаяся неопределенная форма (∞/∞, 1 ∞ , 0/0 и так далее). Для этих вещей нет установленных правил, нужно практиковаться, и это приходит с опытом, когда человек находит ограничения для различных видов функций. Давайте рассмотрим некоторые стратегии для преодоления ограничений. Прямая замена Многие пределы можно оценить, просто подставив значение точки в функцию. Пример. Рассмотрим функцию f(x) = x 2 + 4x + 13. Найдите Решение: ⇒ ⇒ ⇒ 1 +4 + 13 ⇒ 18 Факторинг и отмена Иногда в некоторых функциях при использовании метода подстановки предел принимает вид 0/0. Часто в этих случаях в числителе и знаменателе есть некоторые общие множители, которые можно разложить на множители и сократить. Пример. Рассмотрим функцию f(x) = . Найти Решение: ⇒ Используя метод подстановки, ⇒ Теперь используется метод факторинга и отмены. ⇒ ⇒ ⇒ Особый случай с функцией синуса Иногда при оценке формы 0/0, если функция синуса присутствует. Пример: Рассмотрим функцию f(x) = . Найдите Решение: Этот предел имеет вид 0/0. ⇒ ⇒ ⇒ Используя упомянутое выше тождество, ⇒ Умножить В случае формы ∞/∞ в пределах и полиномиальных функций . Этот метод может быть использован для решения предела. В этом случае и числитель, и знаменатель делятся на наибольшую степень числа x, входящего в функцию. Пример: Рассмотрим функцию f(x) = . Найдите Решение: Этот предел имеет вид ∞/∞. ⇒ ⇒ ⇒ ⇒ ⇒ Госпиталь Правило Это правило полезно для неопределенных форм, таких как 0/0 или ∞/∞. Нет ограничений на класс функций, к которым он может применяться. Пример: упомянутая выше функция f(x) = . Найдите , используя правило Лопиталя. Решение: Дифференцирование числителя и знаменателя. Теперь этот предел не в неопределенной форме, ⇒ Давайте рассмотрим еще несколько примеров этих методов. Вопрос 1. Рассмотрим функцию f(x) = x 3 + 4x 2 + 1. Найти Решение: ⇒ ⇒ ⇒ 1 + 4 + 1 ⇒ 6 Вопрос 2. Рассмотрим функцию f(x) = . Решение: ⇒ Используя метод подстановки, ⇒ Теперь используется метод факторинга и отмены. ⇒ ⇒ ⇒ -1 Вопрос 3: Рассмотрим функцию f(x) = . Найдите Решение: Этот предел имеет вид ∞/∞. ⇒ ⇒ ⇒ ⇒ 4 Вопрос 4. Функция, упомянутая выше, f(x) = . Найдите , используя правило Лопиталя. Решение: Дифференцирование числителя и знаменателя. Теперь этот предел не в неопределенной форме, ⇒ Вопрос 5: Рассмотрим функцию f(x) = 9 0298 . Найдите Решение: Этот предел имеет вид ∞/∞. Если числа обозначены различными буквами, то можно лишь обозначить из произведение; пусть, напр., надо число a умножить на число b, – мы можем это обозначить или a ∙ b или ab, но не может быть и речи о том, чтобы как-нибудь выполнить это умножение. Однако, когда имеем дело с одночленами, то, благодаря 1) присутствию коэффициентов и 2) тому обстоятельству, что в состав этих одночленов могут входить множители, обозначенные одинаковыми буквами, является возможность говорить о выполнении умножения одночленов; еще шире такая возможность при многочленах. Разберем ряд случаев, где возможно выполнять умножение, начиная с простейшего. 1. Умножение степеней с одинаковыми основаниями. Пусть, напр., требуется a3 ∙ a5. Напишем, зная смысл возведения в степень, то же самое подробнее: a ∙ a ∙ a ∙ a ∙ a ∙ a ∙ a ∙ a Рассматривая эту подробную запись, мы видим, что у нас написано a множителем 8 раз, или, короче, a8. Пусть требуется b42 ∙ b28. Пришлось бы написать сначала множитель b 42 раза, а затем опять множитель b 28 раз – в общем, получили бы, что b берется множителем 70 раз. т. е. b70. Итак, b42 ∙ b28 = b70. Отсюда уже ясно, что при умножении степеней с одинаковыми основаниями основание степени остается без перемены, а показатели степеней складываются. Если имеем a8 ∙ a, то придется иметь в виду, что у множителя a подразумевается показатель степени 1 («a в первой степени»), – следовательно, a8 ∙ a = a9. Примеры: x ∙ x3 ∙ x5 = x9; a11 ∙ a22 ∙ a33 = a66; 35 ∙ 36 ∙ 3 = 312; (a + b)3 ∙ (a + b)4 = (a + b)7; (3x – 1)4 ∙ (3x – 1) = (3x – 1)5 и т. д. Иногда приходится иметь дело со степенями, показатели которых обозначены буквами, напр. Поясним некоторые из этих примеров: bn – 3 ∙ b5 надо основание b оставить без перемены, а показатели сложить, т. е. (n – 3) + (+5) = n – 3 + 5 = n + 2. Конечно, подобные сложения должно научиться выполнять быстро в уме. Еще пример: xn + 2 ∙ xn – 2, – основание x надо оставить без перемены, а показатель сложить, т. е. (n + 2) + (n – 2) = n + 2 + n – 2 = 2n. Можно выше найденный порядок, как выполнять умножение степеней с одинаковыми основаниями, выразить теперь равенством: am ∙ an = am + n 2. Умножение одночлена на одночлен. Пусть, напр., требуется 3a²b³c ∙ 4ab²d². Мы видим, что здесь обозначено точкою одно умножение, но мы знаем, что этот же знак умножения подразумевается между 3 и a², между a² и b³, между b³ и c, между 4 и a, между a и b², между b² и d². Поэтому мы можем здесь видеть произведение 8 множителей и можем перемножить их любыми группами в любом порядке. 3 ∙ 4 ∙ a² ∙ a ∙ b³ ∙ b² ∙ c ∙ d². Тогда мы сможем перемножить 1) коэффициенты и 2) степени с одинаковыми основаниями и получим 12a³b5cd². Итак, при умножении одночлена на одночлен мы можем перемножить коэффициенты и степени с одинаковыми основаниями, а остальные множители приходится переписывать без изменения. Еще примеры: 3. Умножение многочлена на одночлен. Пусть надо сначала какой-нибудь многочлен, напр., a – b – c + d умножить на положительное целое число, напр., +3. Так как положительные числа считаются совпадающими с арифметическими, то это все равно, что (a – b – c + d) ∙ 3, т. е. a – b – c + d взять 3 раза слагаемым, или (a – b – c + d) ∙ (+3) = a – b – c + d + a – b – c + d + a – b – c + d = 3a – 3b – 3c + 3d, т. е. в результате пришлось каждый член многочлена умножить на 3 (или на +3). Отсюда вытекает: (a – b – c + d) ÷ (+3) = a – b – c + d, т. и т. п. Пусть теперь надо (a – b – c + d) умножить на положительную дробь, напр., на +. Это все равно, что умножить на арифметическую дробь , что значит взять части от (a – b – c + d). Взять одну пятую часть от этого многочлена легко: надо (a – b – c + d) разделить на 5, а это уже умеем делать, – получим . Остается повторить полученный результат 3 раза или умножить на 3, т. е. В результате мы видим, что пришлось каждый член многочлена умножить на или на +. Пусть теперь надо (a – b – c + d) умножить на отрицательное число, целое или дробное, т. е. и в этом случае пришлось каждый член многочлена умножить на –. Таким образом, какое бы ни было число m, всегда (a – b – c + d) ∙ m = am – bm – cm + dm. Так как каждый одночлен представляет собою число, то здесь мы видим указание, как умножать многочлен на одночлен – надо каждый член многочлена умножить на этот одночлен. 4. Умножение многочлена на многочлен. Пусть надо (a + b + c) ∙ (d + e). Так как d и e означают числа, то и (d + e) выражает какое-либо одно число. Поэтому (a + b + c) ∙ (d + e) = a(d + e) + b(d + e) + c(d + e) (мы можем объяснить это и так: мы вправе d + e временно принять за одночлен). Далее, выполняя ряд полученных умножений (одночлена на многочлен), получим: = ad + ae + bd + be + cd + ce В этом результате можно изменить порядок членов. Получим: (a + b + c) ∙ (d + e) = ad + bd + ed + ae + be + ce, т. е. для умножения многочлена на многочлен приходится каждый член одного многочлена умножать на каждый член другого. Удобно (для этого и был выше изменен порядок полученных членов) умножить каждый член первого многочлена сперва на первый член второго (на +d), затем на второй член второго (на +e), затем, если бы он был, на третий и т. д.; после этого следует сделать приведение подобных членов. В этих примерах двучлен умножается на двучлен; в каждом двучлене члены расположены по нисходящим степеням буквы, общей для обоих двучленов. Напр.: От умножения старшего члена первого двучлена на старший член второго, т. е. 4x² на 3x, получим 12x³ старший член произведения – ему подобных, очевидно, не будет. Далее мы ищем, от перемножения каких членов получатся члены с меньшею на 1 степенью буквы x, т. е. с x². Легко видим, что такие члены получатся от умножения 2-го члена первого множителя на 1-й член второго и от умножения 1-го члена первого множителя на 2-ой член второго (скобки внизу примера это указывают). Выполнить эти умножения в уме и выполнить также приведение этих двух подобных членов (после чего получим член –19x²) – дело нетрудное. Затем замечаем, что следующий член, содержащий букву x в степени еще на 1 меньшей, т. е. x в 1-ой степени, получится только от умножения второго члена на второй, и ему подобных не будет. Еще пример: (x² + 3x)(2x – 7) = 2x³ – x² – 21x. Также в уме легко выполнять примеры, вроде следующего: Старший член получается от умножения старшего члена на старший, ему подобных членов не будет, и он = 2a³. Еще пример: (4a3 + 3a2 – 2a) ∙ (3a2 – 5a) = 12a5 – 11a4 – 21a3 + 10a2. Из всех предыдущих примеров мы также получим общий результат: старший член произведения получается всегда от перемножения старших членов множителей, и подобных ему членов быть не может; также младший член произведения получается от перемножения младших членов множителей, и подобных ему членов также быть не может. Остальным членам, получаемым при умножении многочлена на многочлен, могут быть подобные, и может даже случиться, что все эти члены взаимно уничтожатся, а останутся лишь старший и младший. Вот примеры: (a² + ab + b²) (a – b) = a³ + a²b + ab² – a²b – ab² – b³ = a³ – b³ Эти результаты достойны внимания и их полезно запомнить. Особенно важен следующий случай умножения: (a + b) (a – b) = a² + ab – ab – b² = a² – b² Во всех этих примерах, применяясь к арифметике, мы имеем произведение суммы двух чисел на их разность, а в результате получается разность квадратов этих чисел. Если мы увидим подобный случай, то уже нет нужды выполнять умножение подробно, как это делалось выше, а можно сразу написать результат. Напр., (3a + 1) ∙ (3a – 1). Здесь первый множитель, с точки зрения арифметики, есть сумма двух чисел: первое число есть 3a и второе 1, а второй множитель есть разность тех же чисел; потому в результате должно получиться: квадрат первого числа (т. е. 3a ∙ 3a = 9a²) минус квадрат второго числа (1 ∙ 1 = 1), т. е. (3a + 1) ∙ (3a – 1) = 9a² – 1. Также (ab – 5) ∙ (ab + 5) = a²b² – 25 и т. п. Итак, запомним (a + b) (a – b) = a² – b² т. е. произведение суммы из двух чисел на их разность равно разности квадратов этих чисел. Платон считал, что в идеальном городе должно быть 5040 граждан. Никто не знает, почему их должно быть именно столько. Одна из причин может заключаться в том, что число 5040 является произведением первых семи натуральных чисел: 1 ? 2 ? 3 ? 4 ? 5 ? 6 ? 7 = 5040. Вторая причина может заключаться в том, что произведение чисел от 7 до 10 — Пифагор, между прочим, называл число десять «числом совершенства» — в точности равно 5040. В любом случае древние греки умели перемножать сомножители числом более двух. Если же эти сомножители представляют собой одно и то же число, то говорят о степени этого числа. Рассмотрим, например, число 7. Вот его степени, не считая самого числа 7: 7 ? 7 = 49, 7 ? 7 ? 7 = 343, 7 ? 7 ? 7 ? 7 = 2401, 7 ? 7 ? 7 ? 7 ? 7 = 16 807… Очевидно, что величины степеней числа, большего единицы, растут очень быстро. Кроме того, с первого взгляда очень трудно определить, сколько раз было умножено какое-либо число само на себя после того, как число умножений переваливает за четыре. Поэтому математики приняли изобретенный еще в XIV в. английским кардиналом, богословом и философом Томасом Брадвардином способ написания: справа над числом пишут индекс, показатель степени, каковой сообщает нам, сколько раз умножается число само на себя. То есть мы можем записать: 71 = 7, 7? = 49, 7? = 343, 74 = 2401, 75 = 16 807… С числом 10 мы использовали такую форму записи уже много раз: миллион, число, представляющее собой единицу с шестью нулями, выглядит при записи в виде степени числа 10 как 106, то есть шесть перемноженных чисел 10. Но вот степени единицы — вещи довольно скучные и однообразные, любая степень единицы равна в точности единице. Если же к единице прибавить небольшую ее долю, то картина меняется. Степени такого числа сначала увеличиваются весьма незначительно, но затем значения степеней резко взмывают ввысь. Знание этой особенности может уберечь от финансовой катастрофы. Об этом рассказывает печальная, но, слава богу, вымышленная история, действие которой происходит в Тоскане во времена Возрождения. Некий крестьянин по имени Симпличио хочет приобрести близ Сиены участок земли и для этой цели занимает в банке «Монте ди Пьета» сто флоринов. Каждая из этой сотни чудесных монет содержит три с половиной грамма чистейшего золота; сто флоринов — это нешуточное состояние. — Мы с радостью одолжим тебе эти деньги, — деликатно сообщает банковский служащий, глядя, как Симпличио укладывает монеты в мешок, — но все же подумай: каждый год твой долг будет увеличиваться на десять процентов. — Что значит «десять процентов»? — интересуется Симпличио, и служащий пускается в объяснения: — Если ты берешь у нас сто флоринов, то сейчас ты должен нам только эти деньги. Ты можешь отдать их нам обратно. Если же нам придется ждать год, прежде чем ты вернешь нам долг, то мы захотим получить не только те сто флоринов, что дали тебе сегодня, но и десять процентов суммы. Десять процентов — это буквально означает «десять из ста», то есть десять сотых твоего долга. Это десятая часть тех денег, которые ты берешь у нас сегодня. — Но я не хочу платить больше, чем беру, — возмущается Симпличио. — Мне очень жаль, но в таком случае я не смогу дать тебе деньги, — сокрушенно говорит банковский служащий и протягивает руку к мешку с деньгами. — Но спроси у кого хочешь в Сиене, и ты узнаешь, что ни один заимодавец не дает деньги в долг просто так. Все хотят иметь свой процент. Большинство берет пятнадцать процентов, но есть и такие наглые ростовщики, что берут и двадцать. Симпличио соглашается. Он берет деньги, ставит крестик под долговой распиской, где сказано о десяти процентах, покупает землю и надеется на скорое обогащение. Но скоро сказка сказывается, да нескоро дело делается. Сиену поражает засуха, неурожай повторяется из года в год целых семь лет. Почти всем, даже самым богатым крестьянам едва хватает средств, чтобы просто сводить концы с концами. Ни о каких накоплениях не может быть и речи. Не слишком тучными оказываются и следующие семь лет. Каждый месяц Симпличио туже затягивает пояс, чтобы отложить на уплату долга один-два флорина. Симпличио понимает, что рано или поздно долг придется возвращать. Через четырнадцать лет Симпличио наконец набирает требуемую сумму. Крестьянин посчитал, что за каждый год он должен уплатить сверх ста флоринов еще десять. В банке Симпличио отвели к молодому, надменному служащему, на стол которого Симпличио выложил свои 240 флоринов. Нахальный банкир положил перед собой расписку Симпличио и бумажку с какими-то расчетами, с недовольной миной пересчитал принесенные деньги и сказал ледяным тоном: — Этого очень мало. — Почему мало? — искренне удивился Симпличио. — Я занял у вас сто флоринов и каждый год прибавлял по десять флоринов. За четырнадцать лет получилось сто сорок флоринов, которые я и принес вместе с прежней сотней. — Ваш долг составляет 380 флоринов. Я возьму сейчас двести сорок флоринов, но вы останетесь нам должны еще сто сорок. Между прочим, за эти сто сорок флоринов вы будете впредь выплачивать по 12 процентов в год… Симпличио не стал выслушивать эту фразу до конца. В бешенстве он выскакивает из банка, бежит по улицам Сиены, пока не оказывается в кабаке, где собираются недовольные режимом новески(11) — разбойники, периодически наводящие страх на бюргеров Сиены. Судьба бедного Симпличио была решена уже в тот момент, когда он решил, что при расчете процентов их величины складываются. Это самая страшная ошибка, которую совершают при начислении процентов, и совершил ее не только выдуманный нами Симпличио — ее совершают очень многие и в наши дни. На самом деле при расчете процентов надо не складывать, а умножать. Симпличио подсчитал, сколько флоринов составят десять процентов от долга, а потом каждый год откладывал по десять флоринов в течение четырнадцати лет, считая по 10 процентов от первоначальной суммы. Счетоводы «Монте ди Пьета» считали несколько по-иному: ставка в десять процентов означает, что в течение года одолженный капитал увеличивается на коэффициент 1 + 10 % = 1 + 10/100, то есть первоначальную сумму надо умножить на величину 1,1. В первый год расчет банка не отличается от расчета, произведенного Симпличио. 100 ? (1 + 10/100) = 100 ? 1,1 = 110 = 100 + 10 флоринов. Далее Симпличио думает, что через два года он должен вернуть банку 100 + 20, то есть 120 флоринов. Банк, однако, отсчитывает увеличение выплаты от 110 флоринов, умножая на этот раз уже эту сумму на 1,1 и получая долг, равный 121 флорину. Разница между 120 и 121 флорином кажется совершенно безобидной — но через семь лет становится ясно, что долг стал уже достаточно тягостным для Симпличио. Сам крестьянин думает, что по истечении семи лет он должен вернуть банку 100 + 7 ? 10, то есть 170 флоринов. Банк же семь раз увеличивает долг на 10 процентов, то есть семь раз умножает исходную сумму в сто флоринов на 1,1. Это в результате дает: 100 ? 1,1 ? 1,1 ? 1,1 ? 1,1 ? 1,1 ? 1,1 ? 1,1 = 100 ? 1,17 = 100 ? 1,9487171, или, округляя, 195 флоринов. Именно такой расчет лежал на столе молодого банковского служащего: он рассчитал величину 1,1, возведенную в четырнадцатую степень — 1,114, — и получил число, приблизительно равное 3,7975. Если умножить это число на сто флоринов, одолженных Симпличио у банка, то округленно мы и получим 380 флоринов, которые банковский служащий и потребовал у простодушного крестьянина. Почему же служащий банка не растолковал Симпличио то, как он подсчитал сумму 380 флоринов? Это объясняется само собой: Симпличио — неграмотный крестьянин XV в. Он умел с грехом пополам складывать числа, но об умножении не имел ни малейшего понятия и именно поэтому попал в беду. Умножение: Чтобы умножить числа в экспоненциальном представлении, умножьте десятичные числа. Раздел: Чтобы разделить числа в экспоненциальном представлении, сначала разделите десятичные числа. Затем вычтите показатели вашей степени 10. Поместите новую степень 10 с десятичной дробью в научной форме записи. Если полученное десятичное число меньше 1, переместите десятичную точку вправо и уменьшите показатель степени на количество знаков, на которые переместилась десятичная точка. 97$$ Он используется во многих местах, где необходимо измерить очень большие или очень маленькие величины. Например: Количество атомов в моле (химия). Расстояния между планетами или звездами во Вселенной, измеряемые в милях. И в другой крайности, для очень крошечных чисел, таких как размер или вес атома или молекулы. Смотреть видео Академии Хана » Экспоненциальная запись » Умножение и деление экспоненциальной записи » A Переменная — это символ числа, которое мы еще не знаем.
Обычно это буква типа x или y. Показатель степени (например, 2 в x 2 ) указывает, сколько раз
использовать переменную в умножении. ( yy означает y , умноженное на y , потому что в алгебре поставить две буквы рядом означает умножить их) Аналогично z 3 = zzz и x 5 = xxxxx Когда показатель степени равен 1, у нас есть только сама переменная (пример x 1 = x ) Обычно мы не пишем «1», но иногда полезно помнить, что x также x 1 Когда показатель степени равен 0, мы ни на что не умножаем, и ответ равен «1» Итак, как нам умножить это: (y 2 )(y 3 ) Мы знаем, что y 2 = yy и y 9 0083 3 = гггг поэтому давайте напишем из всех умножает: y 2 y 3 = yy yyy Это 5 «y», умноженных вместе, поэтому новый показатель степени должен быть 5: y 2 y 3 900 84 = у 5 Но почему считают «y», когда показатели степени уже говорят нам, сколько? Показатель степени говорит нам, что есть два «y», умноженные на 3 «y», всего 5 «y»: y 2 y 3 = y 2+3 = y 5 Итак, самый простой способ — всего добавить показатели степени ! (Примечание: это один из законов экспоненты) Когда у нас есть смесь переменных, просто сложите показатели степени для каждой, например (нажмите кнопку воспроизведения): (Помните: переменная без экспоненты действительно имеет экспоненту 1, например: y is y 1 ) Часто также будут смешаны константы (числа вроде 3, 2. Никогда не бойся! Просто перемножьте константы по отдельности и подставьте результат в ответ: (Примечание: «·» означает умножение, которое мы используем, когда «×» можно спутать с буквой «x») Вот более сложный пример с константами и показателями степени: Отрицательные показатели означают деление! Ознакомьтесь с этой идеей, это очень важно и полезно! Итак, как мы это делаем? y 3 y 2 Выпишем все множители: yyy yy Теперь удалите все совпадающие символы «y», равные И у нас осталось: y Таким образом, 3 «y» над линией уменьшаются на 2 «y» под линией, оставляя только 1 «y»: y 3 y 2 = yyy yy = y 3-2 = y 1 900 84 = y ИЛИ мы могли бы сделать это так: у 3 у 2 = у 3 у -2 = у 3-2 = y 1 = y Итак. x=\frac{-\left(-24\right)±\sqrt{576-4\left(-3\right)\left(-y-42\right)}}{2\left(-3\right)} Возведите -24 в квадрат. x=\frac{-\left(-24\right)±\sqrt{576+12\left(-y-42\right)}}{2\left(-3\right)} Умножьте -4 на -3. x=\frac{-\left(-24\right)±\sqrt{576-12y-504}}{2\left(-3\right)} Умножьте 12 на -42-y. x=\frac{-\left(-24\right)±\sqrt{72-12y}}{2\left(-3\right)} Прибавьте 576 к -504-12y. x=\frac{-\left(-24\right)±2\sqrt{18-3y}}{2\left(-3\right)} Извлеките квадратный корень из 72-12y. x=\frac{24±2\sqrt{18-3y}}{2\left(-3\right)} Число, противоположное -24, равно 24. x=\frac{24±2\sqrt{18-3y}}{-6} Умножьте 2 на -3. x=\frac{2\sqrt{18-3y}+24}{-6} Решите уравнение x=\frac{24±2\sqrt{18-3y}}{-6} при условии, что ± — плюс. Прибавьте 24 к 2\sqrt{18-3y}. x=-\frac{\sqrt{18-3y}}{3}-4 Разделите 24+2\sqrt{18-3y} на -6. x=\frac{-2\sqrt{18-3y}+24}{-6} Решите уравнение x=\frac{24±2\sqrt{18-3y}}{-6} при условии, что ± — минус. Кусочная функция – это функция, части которой заданы на определенном промежутке. Например, рассмотрим две функции: \(y = 3x\ –\ 5\ \)и\(\ y = \frac{x}{2}\) Данные функции не являются кусочными. Это две линейные функции. Построим их на одной координатной плоскости: Можем сделать из двух функций одну, для этого зададим для каждой функции промежуток. Пример №1: \(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x \geq 2 \\ \frac{x}{2},\ если\ x < 2 \\ \end{matrix} \right.\ \) Получим новую функцию, которая задается кусочками двух линейных. Она и будет являться кусочной. Чтобы её построить, рассмотрим таблицу точек для этих функции по отдельности. 1. y = 3x – 5, если x ≥ 2. Из условия мы видим, что минимальный x равен 2. Точка x = 2 будет закрашенной, так как знак нестрогий. Меньше это точки мы брать не будем: 2. Для данной функции x = 2 – будет максимальным значением, при этом x ≠ 2, так как знак неравенства строгий. Возьмем эту точку. На графике для этой функции она будет выколотой. Видим, что закрашенная точка x = 2 у первого графика перекрывает пустую точку второго графика, значит у этой кусочной функции нет разрывов и она называется неразрывна. Пример №2: Если задать другие промежутки для кусочной функции, она поменяет свой вид: \(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x \leq 2 \\ \frac{x}{2},\ если\ x > 2 \\ \end{matrix} \right.\ \) 1. y = 3x – 5, если x ≤ 2. Теперь у этой функции x = 2 – максимально возможная абсцисса: 2. y = 0,5x, если x > 2. А для этой функции, наоборот, x = 2 – минимальная абсцисса. Аналогично первому примеру эта точка будет выколота, но перекроется точкой первого графика: Кусочные функции, представленные выше, называются непрерывными, так как одна линейная функция заканчивается там, где начинается вторая, т. Пример №3: Примером кусочной разрывной функции может служить следующая функция: \(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x > 2 \\ \frac{x}{2},\ если\ x < 2 \\ \end{matrix} \right.\ \) Этот график будет выглядеть так же, как график в примере №1, но с одним отличием. Точка x = 2 не принадлежит ни одной из функций, поэтому в этой точке как раз находится разрыв. 1. y = 3x – 5, если x > 2. 2. y = 0,5x, если x < 2. Пример №4: Или, например, такая функция тоже является разрывной и кусочной: \(y = \left\{ \begin{matrix} 3x\ –\ 5,\ если\ x > 3 \\ \frac{x}{2},\ если\ x < \ –2 \\ \end{matrix} \right.\ \) 1. y = 3x – 5, если x > 3. Здесь будем брать все значения x больше 3. Сама точка x = 3 будет выколотой: 2. Значение x = –2 – максимальное. А сама эта точка тоже выколотая: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Оценить | квадратный корень из 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Оценить | квадратный корень из 20 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Оценить | квадратный корень из 50 | 94 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Оценить | квадратный корень из 45 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Оценить | квадратный корень из 32 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Оценить | квадратный корень из 18 | 92 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Графические линейные уравнения: больше примеров
T-Chartsplotting & BlakeExamples
Purplemath
Во всех предыдущих упражнениях, которые мы выполняли, уравнения были даны для одного из переменных, обычно y . .
.
Иногда, однако, нам дают уравнения, которые не решены.
Содержание продолжается ниже
MathHelp.com
Графики линейных уравнений
В таком случае обычно проще сначала заняться алгеброй, чтобы решить уравнение (обычно для » y =»), чтобы упростить нашу жизнь. (Возможно, вы слышали, что это называется «решением буквальных уравнений».)
Не обязательно сначала выполнять алгебраические вычисления, но мы можем сначала решить уравнение, а затем просто «подключи и пыхни», или мы можем подключиться к уравнение, как указано, а затем решить для каждого значения плагина. Первое обычно значительно экономит время по сравнению со вторым.
- График 4 x — 3 y = 12
Я считаю, что для такого рода уравнений проще всего сначала найти » y =». Это особенно верно, если я использую графический калькулятор для заполнения своей T-диаграммы, потому что графические калькуляторы могут обрабатывать линейные уравнения только в том случае, если они имеют форму » y =». Итак, чтобы облегчить себе жизнь, я сначала решу это уравнение алгебраически.
Итак, чтобы облегчить себе жизнь, я сначала решу это уравнение алгебраически.
Для этого я вычту 12 из левой части и прибавлю −3 и на правую сторону. Тогда я разделю на 3 и упрощу. Наконец, я перестрою уравнение (поменяв местами стороны), чтобы получить и в левой части, где я привык. Вот эти шаги:
4 x — 12 = 3 y
4 х — 12 = 3 у
(4 х )/3 — (12)/3 = (3 у )/3
(4/3) х — 4 = у
y = (4/3) x − 4
Итак, я на самом деле нарисовал это уравнение:
дробь, знаменатель которой равно 3, проще всего выбрать x значений, кратных 3, чтобы знаменатель уравновешивался.
Вот моя Т-диаграмма…
…и вот мой график:
Они попросили график; Я дал им график, так что я сделал.
График −3
x = 6 y − 2
Сначала я решу уравнение для » y =»
Итак, после того, как я поменял местами стороны, чтобы привести значения в обычный формат, мое уравнение будет таким:
y = −(1/ 2) x + 1/3
Итак, вычисление точек сюжета для этого будет запутанным из-за всех дробей.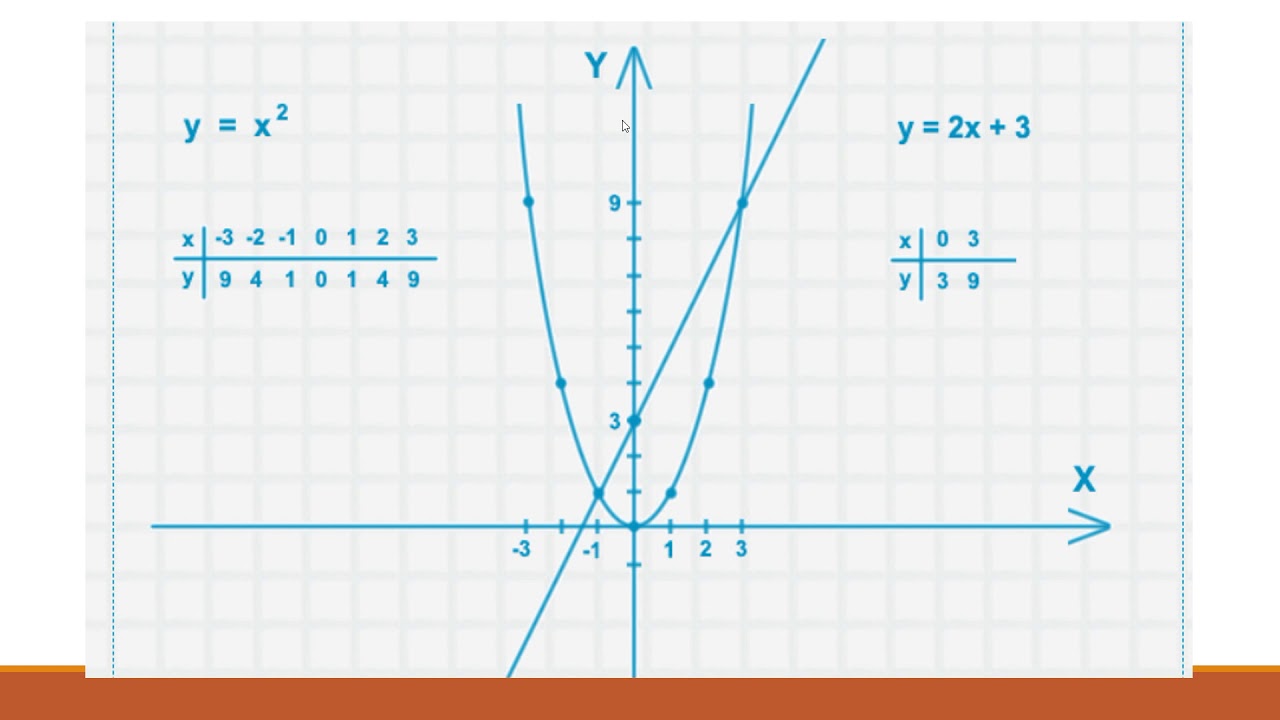 Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я буду делать все, что в моих силах, когда буду строить свои точки:
Я сделаю все, что в моих силах, для Т-диаграммы, помня, что я буду делать все, что в моих силах, когда буду строить свои точки:
Из этих точек я строю свой график:
Обратите внимание, что этот график должен быть больше (с точки зрения минимального и максимального значений осей), чем тот, который я нарисовал раньше. Это потому, что точки были «беспорядочными», поэтому мне нужно было больше точек, и мне нужно было, чтобы эти точки были дальше друг от друга, чтобы убедиться, что моя линия верна. Это пример графика, для которого стоит потратить дополнительное время и быть осторожным!
Редко вы увидите графическое упражнение, в котором используются десятичные дроби. Преобразование в дроби может быть полезным, так как вы сможете увидеть, какие виды x — значения могут быть более полезными.
График
y = 0,4 x − 4
Десятичная дробь 0,4 аналогична дроби 4/10 = 2/5. Таким образом, я могу рассматривать это уравнение как:
Таким образом, я могу рассматривать это уравнение как:
y = (2/5) x − 4
мне приятные, аккуратные моменты сюжета. Вот моя Т-диаграмма:
| х | г |
| −10 | (2/5)(-10) — 4 = -4 — 4 = -8 |
| −5 | (2/5)(-5) — 4 = -2 — 4 = -6 |
| 0 | (2/5)(0) — 4 = 0 — 4 = -4 |
| 5 | (2/5)(5) — 4 = 2 — 4 = -2 |
| 10 | (2/5)(10) — 4 = 4 — 4 = 0 |
| 15 | (2/5)(15) — 4 = 6 — 4 = 2 |
| 20 | (2/5)(20) — 4 = 8 — 4 = 4 |
Даже если я пропущу несколько точек на концах (что, я думаю, так и сделаю), это будет широкий график, по крайней мере, с точки зрения масштаба.
Взгляните еще раз на этот график выше; в частности, посмотрите на шкалы по двум осям. Весы помечены неодинаково, поэтому мне нужно было нанести на весы цифры. В противном случае можно было бы предположить, что шкалы равны -1, 0, 1, 2, 3 и так далее.
Вместо этого я нарисовал область графика, чтобы он соответствовал моему вкусу. (То есть я подгонял вещи так, чтобы они выглядели лучше, по моему личному мнению.) В результате мне нужно было пометить шкалы осей, чтобы избежать путаницы.
Не думайте, что вам нужно ограничивать каждую область графика значениями от −10 до 10. Если вы считаете, что ваш график становится слишком высоким или слишком широким, отрегулируйте масштаб соответствующим образом. Пока вы маркируете четко, вы можете нарисовать область графика в любом удобном для вас масштабе.
Какие существуют четыре способа графического отображения линейных уравнений?
Вместе с методом, показанным в этом уроке, существует четыре метода построения графика прямых линий.
- построение графика с помощью T-диаграммы (которая всегда работает и может быть полезна при принятии решения о том, как нарисовать область графика)
- построение графика по перехватам (что дает вам только две точки, так что это может быть немного сомнительно)
- график из у -перехват и наклон (если вы правильно поймете перехват, то наклон даст вам столько очков, сколько захотите)
- построение графиков с помощью переводов (что включает в себя каким-то образом определение правильного «эталонного» графика, а затем каким-то образом определение того, как перемещать этот график «правильным» образом)
Я бы использовал точки пересечения только в том случае, когда уравнение не было решено для y =; в этом случае вы должны подставить ноль для каждой из переменных по очереди и найти соответствующее значение другой переменной.
Я бы *никогда* не использовал переводы, особенно для таких простых вещей, как построение графиков линейных уравнений.

 2 и осуществим преобразование
2 и осуществим преобразование 2+x-6=0.
2+x-6=0.
 2+(2а+6)х-3а-9=0 имеет более одного корня?
2+(2а+6)х-3а-9=0 имеет более одного корня?
 Мы также рассмотрим несколько примеров и объясним, почему в этих случаях существует бесконечное число решений.
Мы также рассмотрим несколько примеров и объясним, почему в этих случаях существует бесконечное число решений. Например, sin(x) = 0 имеет бесконечно много решений, поскольку каждое целое число, кратное π радианам, является решением (таким образом, π, 2π, 3π, 4π,… все являются решениями).
Например, sin(x) = 0 имеет бесконечно много решений, поскольку каждое целое число, кратное π радианам, является решением (таким образом, π, 2π, 3π, 4π,… все являются решениями). Итак, исходное уравнение имеет бесконечное число решений — подойдет любое реальное значение x!
Итак, исходное уравнение имеет бесконечное число решений — подойдет любое реальное значение x! Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = 2sin(x) и y = 1.
Ниже вы можете увидеть график, показывающий некоторые точки пересечения y = 2sin(x) и y = 1.







 аммиака, 1780г 20% раствора щелочи потребуется для реакции.
аммиака, 1780г 20% раствора щелочи потребуется для реакции. narod.ru/
narod.ru/ 

 2022 23 мая; 12 (10): 1774.
2022 23 мая; 12 (10): 1774. 3390/нано12101774
3390/нано12101774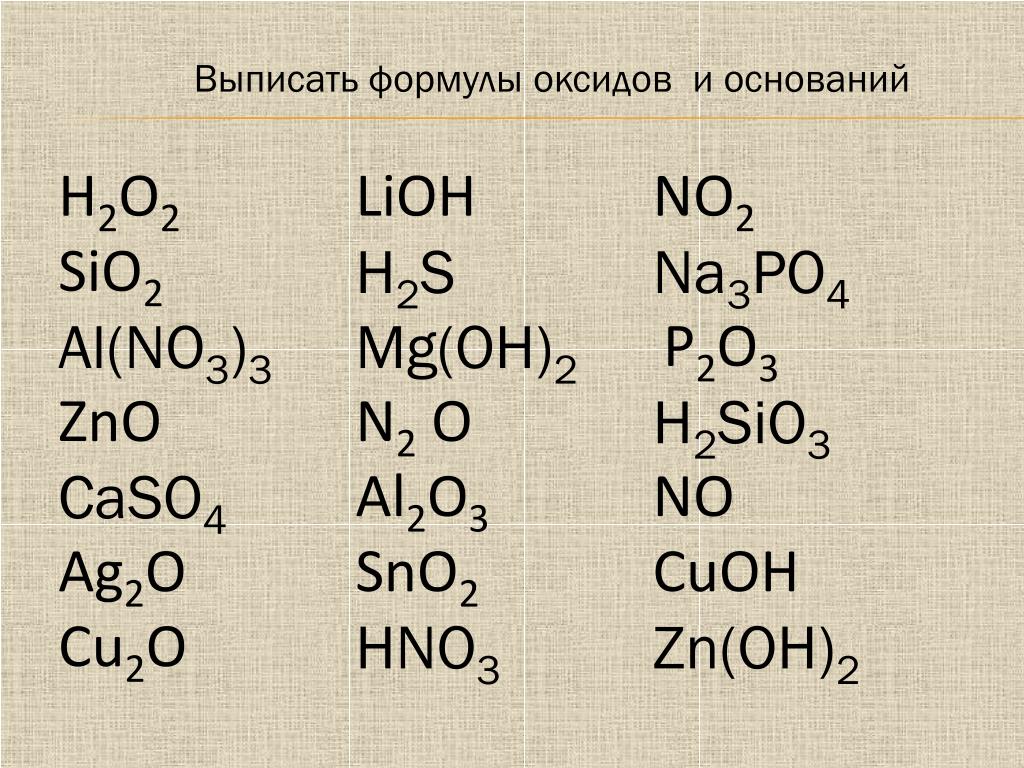
 Мы используем теорию возмущений функционала плотности (DFPT) для расчета статической диэлектрической проницаемости в плоскости и вне плоскости объемных и монослойных образцов. Мы вычисляем значения ширины запрещенной зоны и сродства к электрону с помощью функционала HSE06 и оцениваем плотность тока утечки транзисторов с монослоями Ca(OH)2 и Mg(OH)2 в качестве диэлектриков в сочетании с HfS2 и WS2 соответственно. Наши результаты показывают, что бислой Mg(OH)2 (EOT∼0,60 нм) с более низкой растворимостью в воде обеспечивает более высокие диэлектрические проницаемости вне плоскости и более низкие токи утечки, чем бислой Ca(OH)2 (EOT∼0,56 нм). Кроме того, внеплоскостная диэлектрическая проницаемость, ток утечки и EOT Mg(OH)2 превосходят двухслойный h-BN. Мы проверяем применимость правила Андерсона и делаем вывод, что бислои Ca(OH)2 и Mg(OH)2, соответственно, в паре с согласованными по решетке монослоями HfS2 и WS2 являются эффективными структурными комбинациями, которые могут привести к развитию инновационных многослойных структур.
Мы используем теорию возмущений функционала плотности (DFPT) для расчета статической диэлектрической проницаемости в плоскости и вне плоскости объемных и монослойных образцов. Мы вычисляем значения ширины запрещенной зоны и сродства к электрону с помощью функционала HSE06 и оцениваем плотность тока утечки транзисторов с монослоями Ca(OH)2 и Mg(OH)2 в качестве диэлектриков в сочетании с HfS2 и WS2 соответственно. Наши результаты показывают, что бислой Mg(OH)2 (EOT∼0,60 нм) с более низкой растворимостью в воде обеспечивает более высокие диэлектрические проницаемости вне плоскости и более низкие токи утечки, чем бислой Ca(OH)2 (EOT∼0,56 нм). Кроме того, внеплоскостная диэлектрическая проницаемость, ток утечки и EOT Mg(OH)2 превосходят двухслойный h-BN. Мы проверяем применимость правила Андерсона и делаем вывод, что бислои Ca(OH)2 и Mg(OH)2, соответственно, в паре с согласованными по решетке монослоями HfS2 и WS2 являются эффективными структурными комбинациями, которые могут привести к развитию инновационных многослойных структур. функциональные полевые транзисторы (FET).
функциональные полевые транзисторы (FET).
 ( a ) Фононный дисперсионный спектр…
( a ) Фононный дисперсионный спектр… Энтропия( S v (…
Энтропия( S v (… Гибридные функционалы HSE06 используются для коррекции обычной недооценки ширины запрещенной зоны. Оба материала имеют прямую запрещенную зону с шириной запрещенной зоны Ca(OH)2 (5,19эВ) немного больше ширины запрещенной зоны Mg(OH)2 (4,93 эВ).
Гибридные функционалы HSE06 используются для коррекции обычной недооценки ширины запрещенной зоны. Оба материала имеют прямую запрещенную зону с шириной запрещенной зоны Ca(OH)2 (5,19эВ) немного больше ширины запрещенной зоны Mg(OH)2 (4,93 эВ).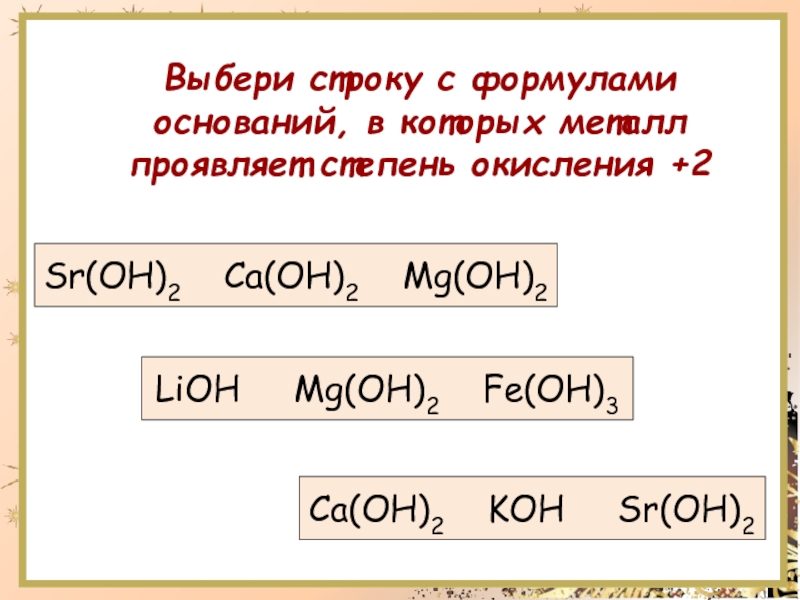 CBM и VBM каждой гетероструктуры показаны длинными сплошными горизонтальными линиями. Правило Андерсона используется для расчета ширины запрещенной зоны и сродства к электрону каждой гетероструктуры.
CBM и VBM каждой гетероструктуры показаны длинными сплошными горизонтальными линиями. Правило Андерсона используется для расчета ширины запрещенной зоны и сродства к электрону каждой гетероструктуры. Р., Ван де Пут М.Л., Саадат А., Ванденберге В.Г.
Осанлу М.Р. и соавт.
Нац коммун. 2021 19 августа; 12 (1): 5051. doi: 10.1038/s41467-021-25310-2.
Нац коммун. 2021.
PMID: 34413289
Бесплатная статья ЧВК.
Р., Ван де Пут М.Л., Саадат А., Ванденберге В.Г.
Осанлу М.Р. и соавт.
Нац коммун. 2021 19 августа; 12 (1): 5051. doi: 10.1038/s41467-021-25310-2.
Нац коммун. 2021.
PMID: 34413289
Бесплатная статья ЧВК.
 Всемирный научный; Сингапур: 2010 г. Расцвет графена; стр. 11–19.
Всемирный научный; Сингапур: 2010 г. Расцвет графена; стр. 11–19. Г. Определение электронных, структурных, диэлектрических, магнитных и транспортных свойств в новых электронных материалах: использование методов первых принципов. IEEE Нанотехнологии. Маг. 2021;15:68-C3. дои: 10.1109/МНАНО.2021.3113223.
—
DOI
Г. Определение электронных, структурных, диэлектрических, магнитных и транспортных свойств в новых электронных материалах: использование методов первых принципов. IEEE Нанотехнологии. Маг. 2021;15:68-C3. дои: 10.1109/МНАНО.2021.3113223.
—
DOI BeO и Be(OH)2 амфотерны и реагируют с кислотами и сильными основаниями, такими как NaOH. MgO является основным, а Mg(OH)2 является слабоосновным и не растворяется в растворе NaOH. Оксиды кальция, стронция и бария являются основными, а гидроксиды — сильноосновными. Растворимость гидроксидов в воде следует в следующем порядке: Be(OH)2 < Mg(OH)2 < Ca(OH)2 < Sr(OH)2 < Ba(OH)2.
BeO и Be(OH)2 амфотерны и реагируют с кислотами и сильными основаниями, такими как NaOH. MgO является основным, а Mg(OH)2 является слабоосновным и не растворяется в растворе NaOH. Оксиды кальция, стронция и бария являются основными, а гидроксиды — сильноосновными. Растворимость гидроксидов в воде следует в следующем порядке: Be(OH)2 < Mg(OH)2 < Ca(OH)2 < Sr(OH)2 < Ba(OH)2. Чем больше разница в электроотрицательности, тем более ионной становится связь металл-кислород. Чем более ионна связь металл-кислород, тем более основным является оксид.0003
Чем больше разница в электроотрицательности, тем более ионной становится связь металл-кислород. Чем более ионна связь металл-кислород, тем более основным является оксид.0003 Поскольку атомные радиусы увеличиваются вниз по группе, имеет смысл, что координационные числа также увеличиваются, потому что чем больше ион металла, тем больше места для координации с ним молекул воды.
Поскольку атомные радиусы увеличиваются вниз по группе, имеет смысл, что координационные числа также увеличиваются, потому что чем больше ион металла, тем больше места для координации с ним молекул воды. В книге данных Наффилда любой водный сульфат бериллия BeSO 4 указан как нерастворимый, тогда как гидратированная форма BeSO 4 .4H 2 O растворим, с растворимостью около 39 г BeSO 4 на 100 г воды при комнатной температуре. Показатели растворимости сульфата магния и сульфата кальция также варьируются в зависимости от того, гидратирована ли соль или нет, но изменения менее значительны.
В книге данных Наффилда любой водный сульфат бериллия BeSO 4 указан как нерастворимый, тогда как гидратированная форма BeSO 4 .4H 2 O растворим, с растворимостью около 39 г BeSO 4 на 100 г воды при комнатной температуре. Показатели растворимости сульфата магния и сульфата кальция также варьируются в зависимости от того, гидратирована ли соль или нет, но изменения менее значительны.






 com, без риска
com, без риска Он имеет степень бакалавра физико-астрономических наук Университета Бригама Янга и степень магистра естественных наук Бостонского университета. В настоящее время он имеет лицензию преподавателя естественных наук для 8-12 классов.
Он имеет степень бакалавра физико-астрономических наук Университета Бригама Янга и степень магистра естественных наук Бостонского университета. В настоящее время он имеет лицензию преподавателя естественных наук для 8-12 классов. Вот несколько шагов для решения уравнений, содержащих скобки для неизвестной переменной.
Вот несколько шагов для решения уравнений, содержащих скобки для неизвестной переменной.
 В левой части мы можем объединить термины, содержащие x , в один термин, используя вычитание:
В левой части мы можем объединить термины, содержащие x , в один термин, используя вычитание: Мы можем переписать это уравнение как:
Мы можем переписать это уравнение как:
 🙂
🙂




 Сравнить полученные результаты.
Сравнить полученные результаты.





 Если система непротиворечива, решите систему, используя правило Крамера: 4x+y=2,12x+3y=6
Если система непротиворечива, решите систему, используя правило Крамера: 4x+y=2,12x+3y=6
 Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
Затем, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отклонения возводятся в квадрат, и считается средняя. Теперь вы знаете, как найти дисперсию.
 Но с ростом выборки разница исчезает.
Но с ростом выборки разница исчезает. В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
В реальности, если коэффициент вариации превышает 33%, то специально ничего делать по этому поводу не нужно. Это информация для общего представления. В общем коэффициент вариации используют для оценки относительного разброса данных в выборке.
 Взвешенная дисперсия (для вариационного ряда):
Взвешенная дисперсия (для вариационного ряда): (например середина интервала 159 – 165,6 = 162,3)
(например середина интервала 159 – 165,6 = 162,3) Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия.
Она равняется среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и может быть определена как простая дисперсия или взвешенная дисперсия. д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию).
д.), кроме отличий в квалификационном разряде (внутри группы все рабочие имеют одну и ту же квалификацию). 2 раз.
2 раз. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме. Она провела углубленное исследование социальных и экономических вопросов, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.
Она провела углубленное исследование социальных и экономических вопросов, а также пересмотрела и отредактировала учебные материалы для района Большого Ричмонда.
 Например, при расчете выборочной дисперсии для оценки дисперсии совокупности знаменатель уравнения дисперсии становится равным N — 1, так что оценка является несмещенной и не занижает дисперсию совокупности.
Например, при расчете выборочной дисперсии для оценки дисперсии совокупности знаменатель уравнения дисперсии становится равным N — 1, так что оценка является несмещенной и не занижает дисперсию совокупности. Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько постоянна доходность с течением времени.
Как отмечалось выше, инвесторы могут использовать стандартное отклонение, чтобы оценить, насколько постоянна доходность с течением времени. Извлечение квадратного корня из дисперсии дает стандартное отклонение 18% (√0,0325 = 0,180) для доходности.
Извлечение квадратного корня из дисперсии дает стандартное отклонение 18% (√0,0325 = 0,180) для доходности.
 Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению.
Чем более разбросаны данные, тем больше дисперсия по отношению к среднему значению. Вот почему стандартное отклонение часто предпочитают в качестве основной меры изменчивости.
Вот почему стандартное отклонение часто предпочитают в качестве основной меры изменчивости.
 Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.
Поскольку квадратный корень не является линейной операцией, такой как сложение или вычитание, беспристрастность формулы выборочной дисперсии не распространяется на формулу выборочного стандартного отклонения.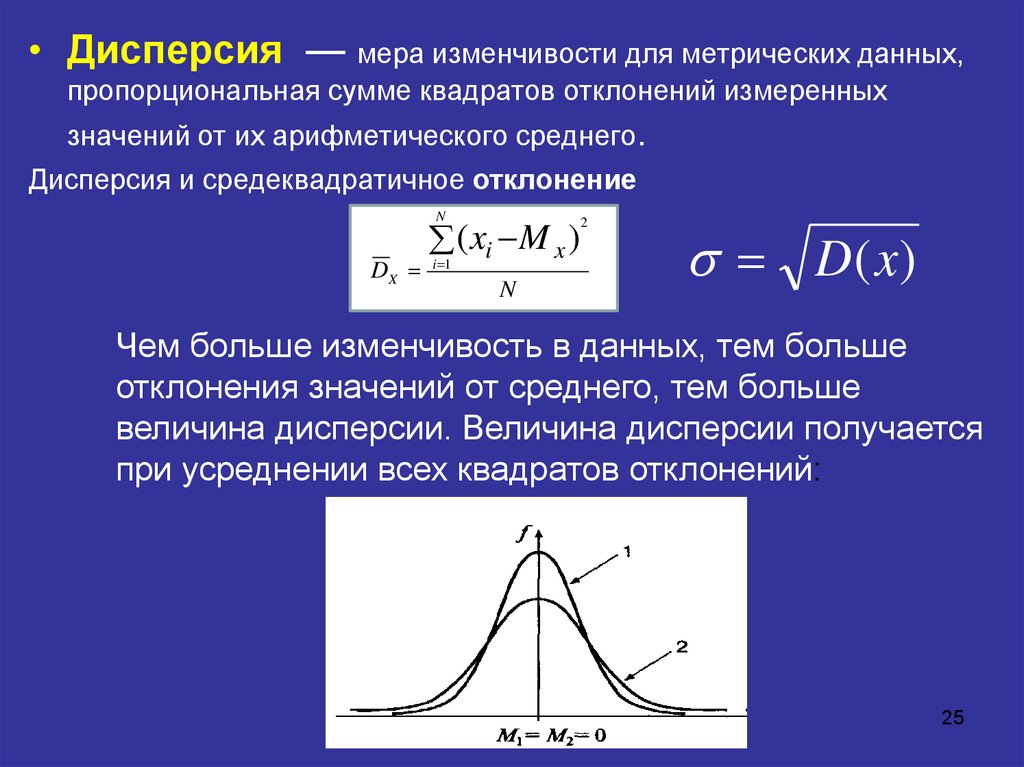 Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам.
Мы будем использовать небольшой набор данных из 6 баллов, чтобы пройти по шагам. Это приведет к положительным числам.
Это приведет к положительным числам.



 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение… Спс
Спс ..)
..) )/3
)/3 То есть $x$ — это угол, который пересекает единичную окружность в точке с горизонтальной координатой, равной $\frac{1}{\sqrt{2}}$ (не буду называть ее $x$-координатой , потому что мы уже используем $x$ для представления угла — это то, что я бы назвал плохой педагогикой). Нетрудно заметить, что таких углов два:
$$ x = \frac{\pi}{4} \qquad\text{and}\qquad x = -\frac{\pi}{4}; $$
угол $\pi/4$ пересекает единичную окружность в точке $\big(\frac{1}{\sqrt{2}}, \frac{\sqrt{3}}{2}\big)$, и угол $-\pi/4$ пересекается в точке $\big(\frac{1}{\sqrt{2}}, -\frac{\sqrt{3}}{2}\big)$.
То есть $x$ — это угол, который пересекает единичную окружность в точке с горизонтальной координатой, равной $\frac{1}{\sqrt{2}}$ (не буду называть ее $x$-координатой , потому что мы уже используем $x$ для представления угла — это то, что я бы назвал плохой педагогикой). Нетрудно заметить, что таких углов два:
$$ x = \frac{\pi}{4} \qquad\text{and}\qquad x = -\frac{\pi}{4}; $$
угол $\pi/4$ пересекает единичную окружность в точке $\big(\frac{1}{\sqrt{2}}, \frac{\sqrt{3}}{2}\big)$, и угол $-\pi/4$ пересекается в точке $\big(\frac{1}{\sqrt{2}}, -\frac{\sqrt{3}}{2}\big)$. $$
$$
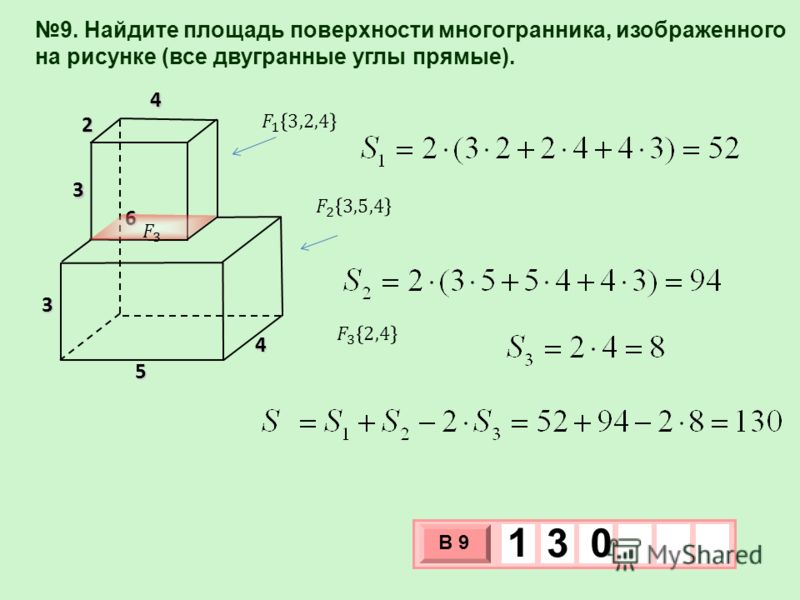
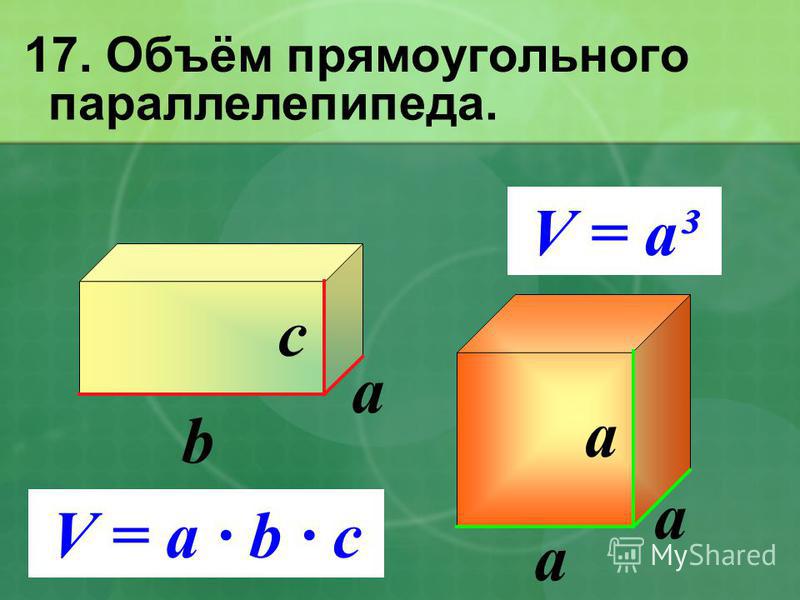 п.)
п.)

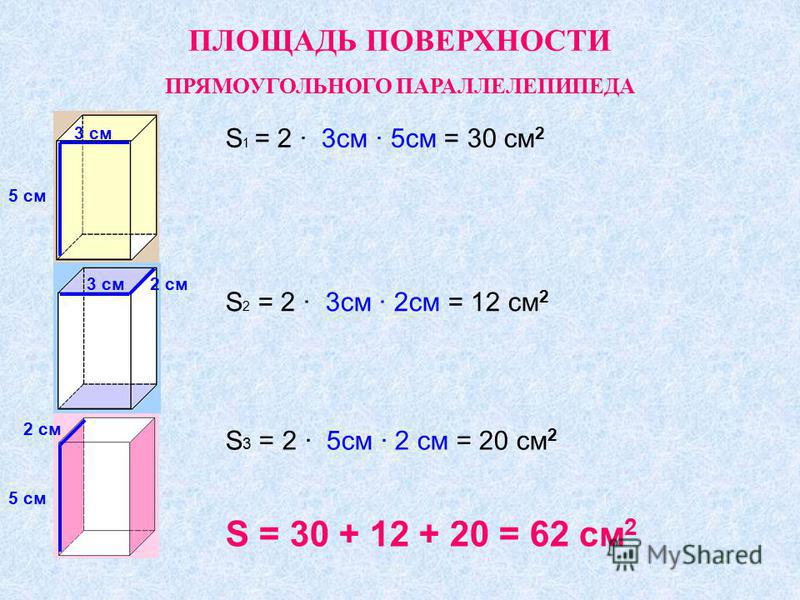

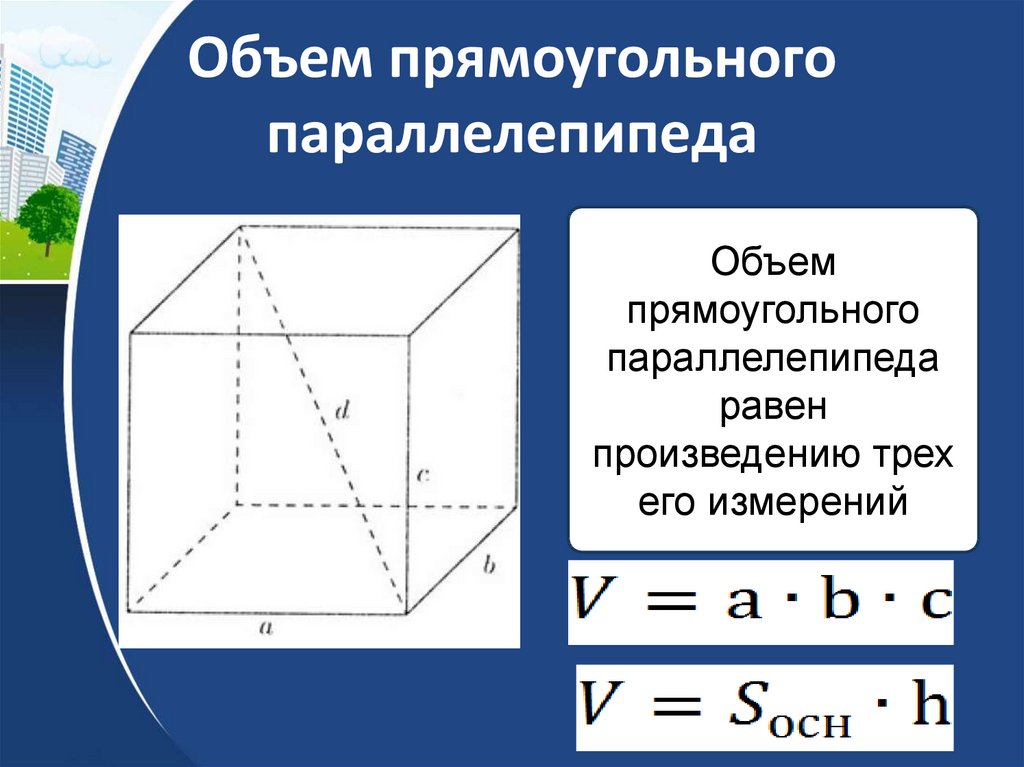 9K
9K Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.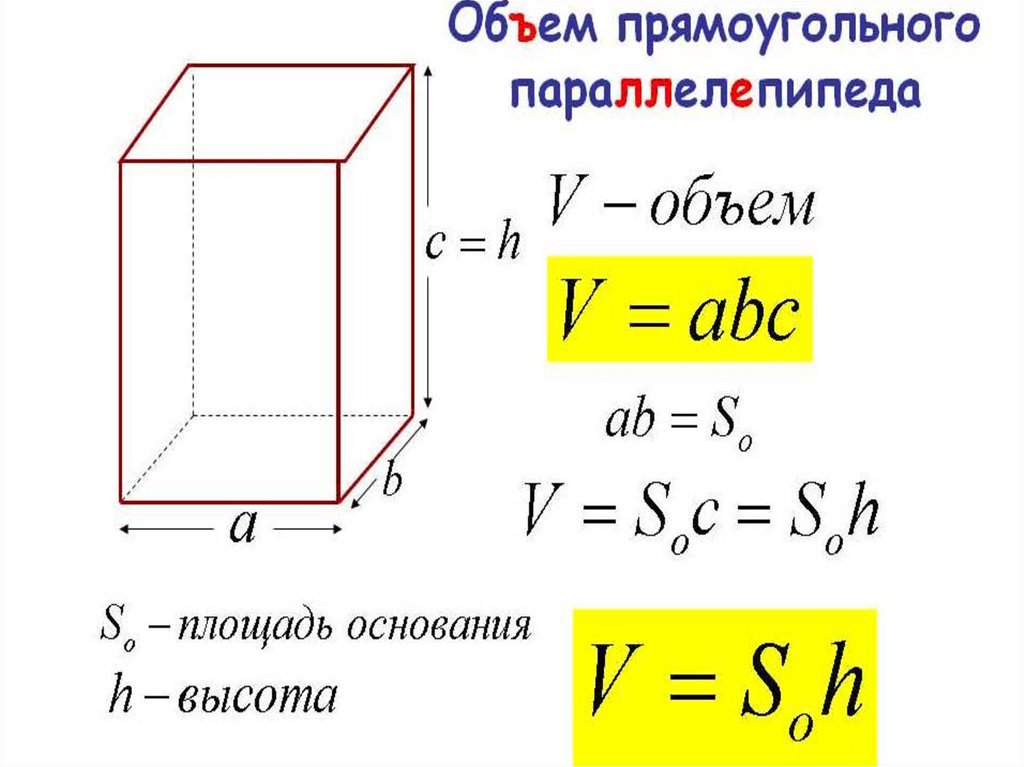 2
2

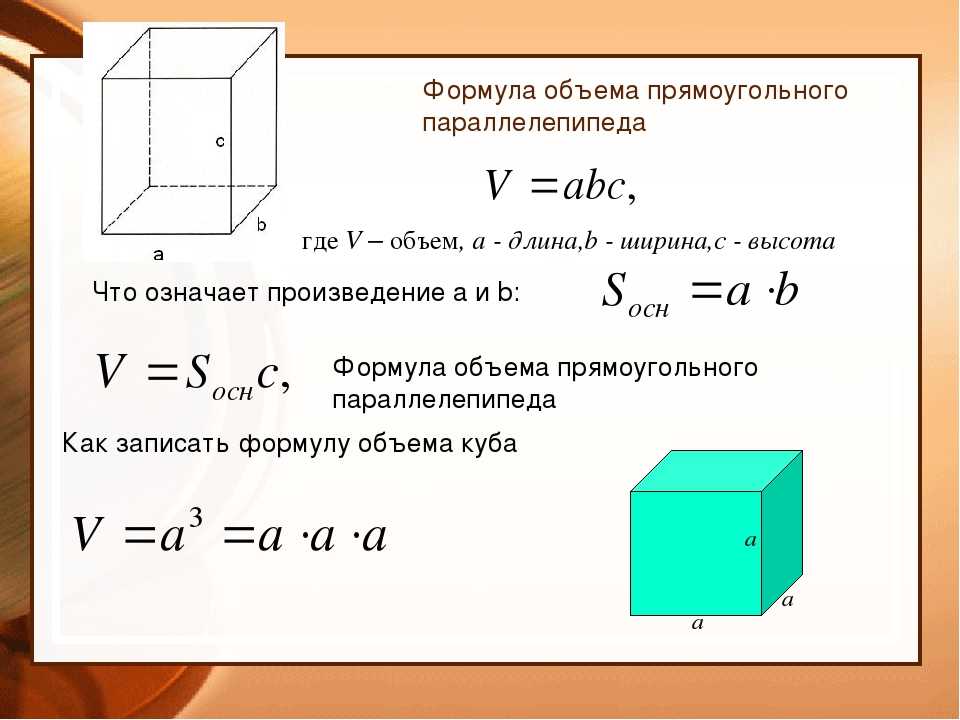
 Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.
Чтобы вычислить LSA параллелепипеда, нам нужно найти сумму площадей, занимаемых 4 боковыми гранями.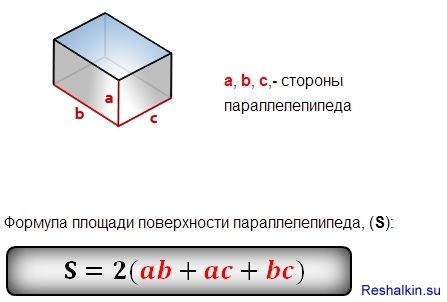 д.
д. Сколько подарочной бумаги требуется для упаковки подарочной коробки?
Сколько подарочной бумаги требуется для упаковки подарочной коробки? Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно.
Параллелепипед часто называют призмой с основанием в виде параллелограмма. Куб, прямоугольный параллелепипед и ромб — все это частные случаи параллелепипеда с гранями в форме квадрата, прямоугольника и ромба соответственно. Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д.
Он выражается в квадратных единицах с использованием таких единиц, как квадратные дюймы, квадратные метры, квадратные футы и т. д. Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. Мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами.
Трехмерные фигуры — это твердые формы или объекты, имеющие три измерения. Они измеряются по трем параметрам: длина, ширина и высота. Мы узнаем о конкретной трехмерной форме, называемой параллелепипедом, ее свойствах, формулах для общей площади, площади поверхности и объема, а также об уравнении прямоугольного параллелепипеда с решенными примерами. Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда.
Чтобы понять это, рассмотрим параллелепипед, наполненный водой. Объем воды, который помещается в параллелепипеде, является объемом параллелепипеда. Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.
Вектор произведения перпендикулярен как \(\vec{a}\), так и \(\vec{b}\). Обратите внимание, что величина результирующего вектора \(\lvert\vec{a}\times\vec{b}\rvert\) равна площади параллелограмма, описываемого этими двумя векторами.


 Он находится по формуле
Он находится по формуле Мы должны вычислить площади шести прямоугольников, чтобы определить площадь их поверхностей (граней). Формула площади поверхности:
Мы должны вычислить площади шести прямоугольников, чтобы определить площадь их поверхностей (граней). Формула площади поверхности:
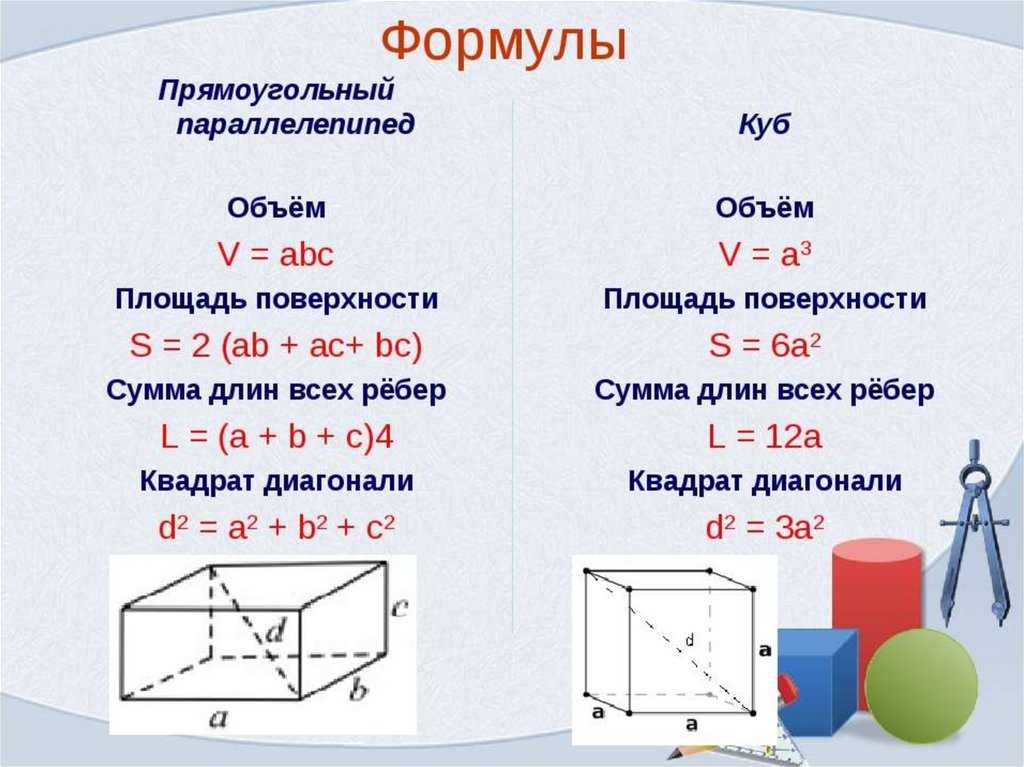
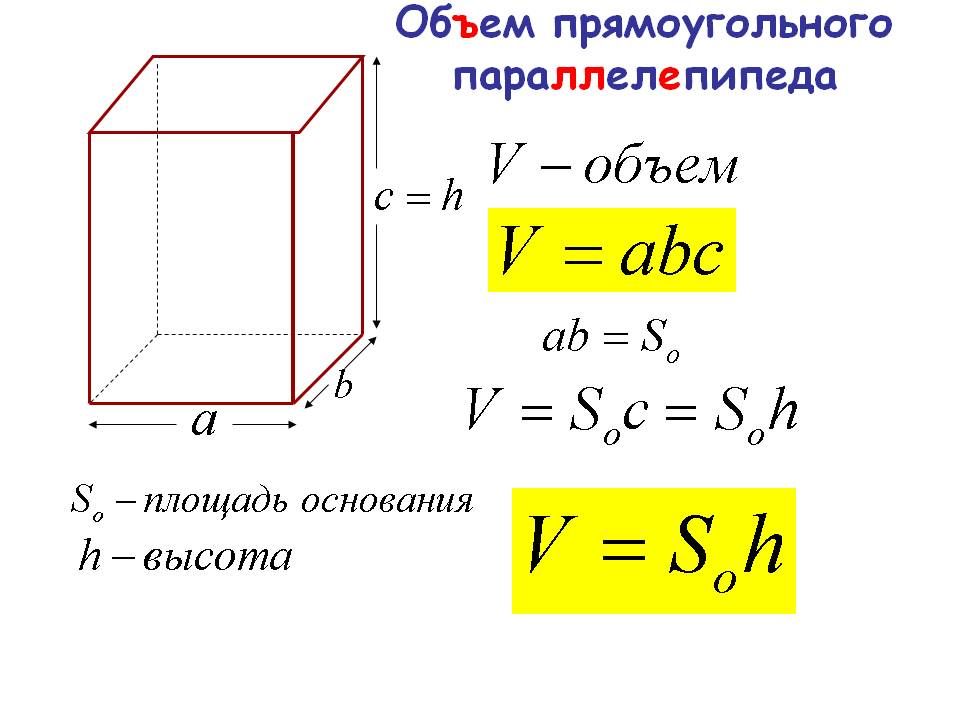
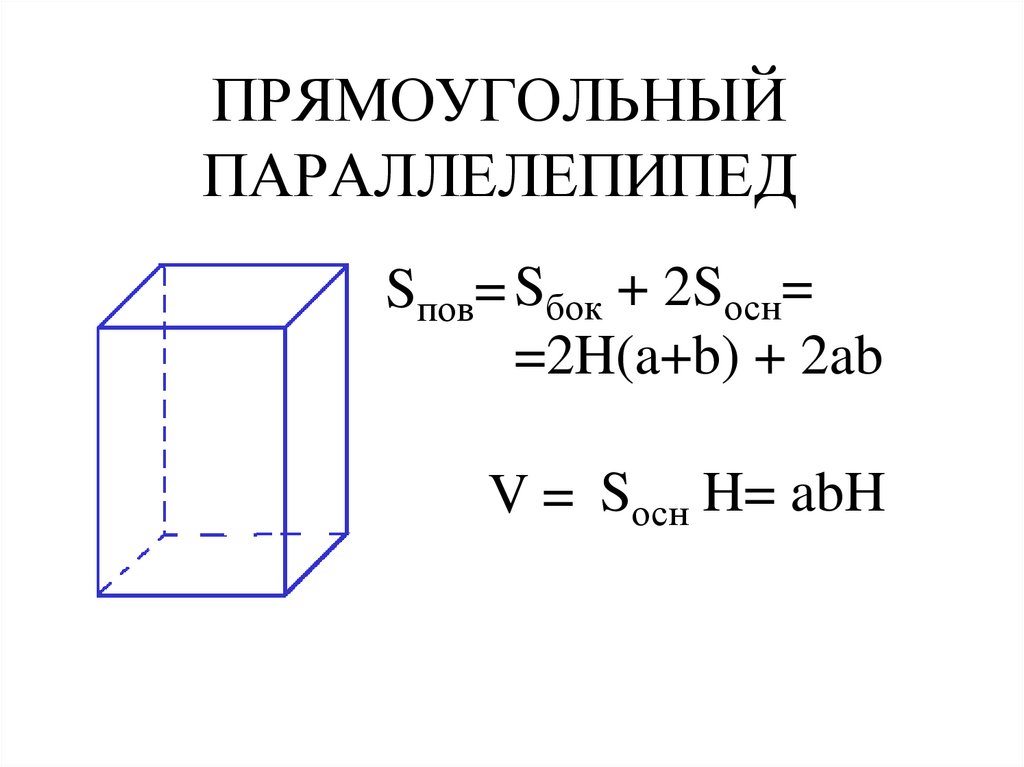
 к.:
к.: Можно предположить, что в таком случае решение будет таким:
Можно предположить, что в таком случае решение будет таким:

 е. х.
е. х.

 Как выглядит эта функция
около х = 1?
Как выглядит эта функция
около х = 1? Если
они будут идти к одному и тому же месту, тогда это место называется пределом.
Если
они будут идти к одному и тому же месту, тогда это место называется пределом. Алгебра, которая будет
работа факторинговая.
Алгебра, которая будет
работа факторинговая.
 Эти концепции также помогают нам анализировать множество функций и их поведение в исчислении. Пределы были основой почти для всех концепций исчисления. Таким образом, становится необходимым научиться вычислять пределы для различных типов функций и как обращаться с неопределенными формами пределов. Давайте посмотрим на различные методы, которые помогают нам вычислять пределы для сложных функций и выражений.
Эти концепции также помогают нам анализировать множество функций и их поведение в исчислении. Пределы были основой почти для всех концепций исчисления. Таким образом, становится необходимым научиться вычислять пределы для различных типов функций и как обращаться с неопределенными формами пределов. Давайте посмотрим на различные методы, которые помогают нам вычислять пределы для сложных функций и выражений. Цель состоит в том, чтобы найти предел этой функции при x = 2.
Цель состоит в том, чтобы найти предел этой функции при x = 2.  Необходимым условием использования этого подхода является то, что функция должна быть непрерывной, а предел не должен давать на выходе какой-либо неопределенной формы.
Необходимым условием использования этого подхода является то, что функция должна быть непрерывной, а предел не должен давать на выходе какой-либо неопределенной формы. Это удостоверение пригодится.
Это удостоверение пригодится. Его можно применять для любого типа функций, которые оцениваются в неопределенных формах с помощью метода подстановки. В этом правиле числитель и знаменатель дифференцируются до тех пор, пока предел не придет в детерминированную форму.
Его можно применять для любого типа функций, которые оцениваются в неопределенных формах с помощью метода подстановки. В этом правиле числитель и знаменатель дифференцируются до тех пор, пока предел не придет в детерминированную форму. Найти
Найти 
 , xn (x в степени n). С такими выражениями надо привыкнуть обращаться. Вот примеры:
, xn (x в степени n). С такими выражениями надо привыкнуть обращаться. Вот примеры: Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями оказались рядом, т. е.
Переставим их так, чтобы коэффициенты и степени с одинаковыми основаниями оказались рядом, т. е. е. пришлось каждый член многочлена разделить на (+3). Также, обобщая, получим:
е. пришлось каждый член многочлена разделить на (+3). Также, обобщая, получим:
 Подобные умножения легко выполнять в уме и сразу писать окончательный результат.
Подобные умножения легко выполнять в уме и сразу писать окончательный результат. Затем ищем, от каких умножений получатся члены с a² – от умножения 1-го члена (a²) на 2-ой (–5) и от умножения второго члена (–3a) на 1-ый (2a) – это указано внизу скобками; выполнив эти умножения и соединив полученные члены в один, получим –11a². Затем ищем, от каких умножений получатся члены с a в первой степени – эти умножения отмечены скобками сверху. Выполнив их и соединив полученные члены в один, получим +11a. Наконец, замечаем, что младший член произведения (+10), вовсе не содержащий a, получается от перемножения младшего члена (–2) одного многочлена на младший член (–5) другого.
Затем ищем, от каких умножений получатся члены с a² – от умножения 1-го члена (a²) на 2-ой (–5) и от умножения второго члена (–3a) на 1-ый (2a) – это указано внизу скобками; выполнив эти умножения и соединив полученные члены в один, получим –11a². Затем ищем, от каких умножений получатся члены с a в первой степени – эти умножения отмечены скобками сверху. Выполнив их и соединив полученные члены в один, получим +11a. Наконец, замечаем, что младший член произведения (+10), вовсе не содержащий a, получается от перемножения младшего члена (–2) одного многочлена на младший член (–5) другого.

 То есть 7 ? 8 ? 9 ? 10 = 5040.
То есть 7 ? 8 ? 9 ? 10 = 5040.

 Ты сам подумай: если ты купишь землю и засеешь ее, то через год ты наверняка будешь богаче, чем сейчас, и сможешь легко отдать долг вместе с процентами.
Ты сам подумай: если ты купишь землю и засеешь ее, то через год ты наверняка будешь богаче, чем сейчас, и сможешь легко отдать долг вместе с процентами. Он сложил сто сорок флоринов и сто, получил 240 флоринов и решил, что сможет рассчитаться с банком.
Он сложил сто сорок флоринов и сто, получил 240 флоринов и решил, что сможет рассчитаться с банком. Во время очередного восстания Симпличио оказывается в первых рядах с обнаженной саблей. Дальше следы его теряются.
Во время очередного восстания Симпличио оказывается в первых рядах с обнаженной саблей. Дальше следы его теряются. По истечении одного года он должен вернуть банку
По истечении одного года он должен вернуть банку
 Затем добавьте показатели степени числа 10. Поместите новую степень числа 10 с десятичной дробью в экспоненциальной форме. Если ваше десятичное число больше 10, подсчитайте, сколько раз десятичная дробь перемещается влево, и добавьте это число к показателю степени.
Затем добавьте показатели степени числа 10. Поместите новую степень числа 10 с десятичной дробью в экспоненциальной форме. Если ваше десятичное число больше 10, подсчитайте, сколько раз десятичная дробь перемещается влево, и добавьте это число к показателю степени.
 9, ½ и т. д.).
9, ½ и т. д.).
 y = 0,5x, если x < 2.
y = 0,5x, если x < 2. е. между кусочками функции нет разрыва.
е. между кусочками функции нет разрыва. y = 0,5x, при x < –2.
y = 0,5x, при x < –2.