Расчет значения экспоненциальной функции: онлайн калькулятор
Экспонента (число e) — иррациональное число, приблизительно равное 2,71828. Число e играет большую роль в дифференциальном и интегральном исчислениях и используется практически во всех научных сферах. Столь сухое математическое определение совершенно не раскрывает сути о физическом смысле экспоненты. Рассмотрим подробнее.
Смысл числа e
Число Пи представляет собой не просто иррациональное число, равное 3,1415, а одинаковое для всех случаев соотношение длины окружности к диаметру. Точно так же и число e имеет свой собственный смысл.
Экспонента — это базовое соотношение роста для всех растущих процессов. Любое число можно рассматривать как увеличенную единицу, любой квадрат — как масштабированный единичный квадрат, любой равносторонний треугольник — как увеличенный или уменьшенный правильный треугольник, ну а любой коэффициент роста можно представить в виде масштабированного коэффициента е.
Именно операции с числом e дадут вам возможность определить темпы роста в таких ситуациях, как прирост населения, начисление процентов по депозиту или объем полураспада радиоактивного вещества.
Дискретный рост
В качестве базового примера системы непрерывного удвоения можно привести размножение бактерий, которые удваиваются каждые сутки. Если удвоение происходит один раз, то математически мы получаем 2 в первой степени, то есть просто 2. Если удвоений x раз, то в итоге мы получаем 2 в степени x бактерий, денег или любого другого добра.
Однако система может изменяться не в 2 раза, а например на 20% или 120%. В этом случае мы можем представить удвоение не как двойку, а как 1+1 или 1+100%. В такой записи мы можем подставить любой коэффициент прироста и получить формулу роста как:
Рост = (1 + прирост)x,
где x — это количество циклов прироста.
Благодаря этой формуле мы можем узнать, сколько бактерий мы получим из одной клетки через 30 дней. Однако бактерии делятся дискретно, то есть пока новая клетка не сформируется в течение суток, она не сможет производить новые организмы. Применяя эту формулу к деньгам, мы получим совсем другой результат.
Непрерывный рост
При начислении процентов на деньги происходит не дискретный, а непрерывный рост. Как только по депозиту начисляется прибыль в размере пары пенни, эти деньги начинают приносить уже свою прибыль. Нет нужды ждать, пока «родится» целый доллар, который начнет делиться по подобию бактерий. Достаточно сформироваться центу, который начнет генерировать свою микроприбыль.
Представим, что мы вложили $1 в бизнес, который обещает нам 100% прибыли через год. Это значит, что мы получим прирост:
Доход = (1 + 1)1 = 2
Всего $2 — негусто. Однако если мы разобьем год на два полугодия, то мы получим по 50 центов за каждые полгода. Полученные центы уже могут самостоятельно генерировать прибыль, и тогда формула изменится.
Доход = (1 + 0,5)2 = 2,25
Так как у нас теперь два периода удвоения, мы возвели прирост в квадрат и получили дополнительные 25 центов дохода. Если разбить нашу прибыль на 5 частей по 20 центов, то получится еще привлекательнее:
Доход = (1 + 0,2)5 = 2,4883
Может быть, мы сможем разделить прибыль на бесконечно большое количество мелких частей и получим бесконечную прибыль? Увы, нет.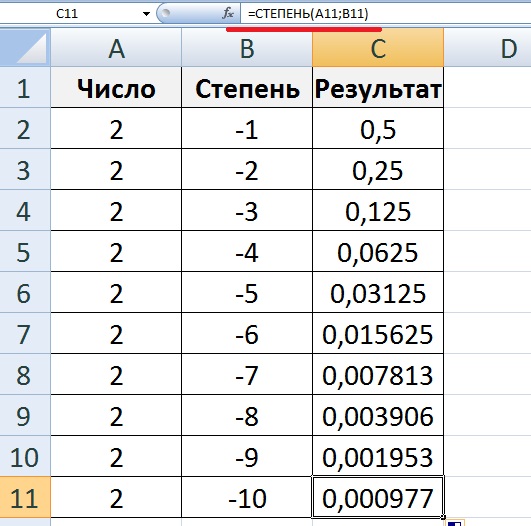 Даже если мы разделим наш доллар на 100 000 частей, доход составит:
Даже если мы разделим наш доллар на 100 000 частей, доход составит:
Доход= (1 + 0,00001)100 000 = 2,71826
При бесконечном дроблении доллара прибыль будет увеличиваться на стотысячные знаки после запятой. Наши 2,71826 доллара прибыли будут стремиться к значению 2,718281828, что есть ничто иное как число Е.
И что все это значит
Экспонента — это наибольший возможный результат стопроцентного непрерывного роста за конкретный период времени. Да, изначально нам обещают 100% прибыли, то есть всего $2, но каждый цент приносит свои дивиденды и по итогам у нас оказывается ровно $2,71828 прибыли. Число е – это максимум, который мы можем получить при разбиении прибыли на суммы бесконечно малых величин.
Это означает, что если при потенциальной стопроцентной прибыли мы вложим в бизнес $1, то получим $2,718 чистой прибыли. Если $2, то мы получим 2е чистой прибыли, а если $100, то наш профит составит 100е. Таким образом, e — это предельная константа, которая ограничивает процессы роста точно так же, как скорость света ограничивает передвижение информации в пространстве.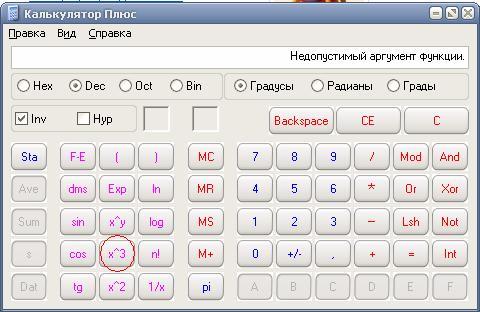 Число е – это максимально возможный результат, труднодостижимый на практике, поэтому в реальности многие процессы описываются с использованием частей экспоненты.
Число е – это максимально возможный результат, труднодостижимый на практике, поэтому в реальности многие процессы описываются с использованием частей экспоненты.
Использование экспоненты на практике
На первый взгляд рост изображается в виде прибавления 1%, однако, математически такая прибавка выражается как умножение на 1,01. Таким образом, при операциях с числом e мы используем степени или корни. Или натуральные логарифмы, если нам необходима обратная операция. Какой бы коэффициент прироста мы не взяли, он будет означать степень для числа е. К примеру, если мы знаем, что в течение 3 лет получим прибыль в размере 200%, то мы просто умножаем прирост (e 2) на 3 периода и получаем:
Рост = (е3)2 = e6
Для лучшего понимания рассмотрим примеры.
Депозит в банке
Допустим, мы положили на депозит в банке $100 под годовую ставку в размере 8%. Выбранный банк предлагает нам полную капитализацию процентов, какую же прибыль мы получим через 5 лет? Так как банк обеспечивает нам непрерывный рост денег, через 5 лет на нашем счету уже будет:
Прибыль = 100 × е(0,08 × 5) = 149,1
Потрясающе, правда? К сожалению, реальные банки редко используют сложные проценты, а если и рассчитывают капитализацию, то по своим формулам, которые несколько отличаются от классической экспоненты.
Период полураспада
Представьте, что у вас есть 5 кг радиоактивного урана, который распадается со скоростью 100% в год. Сколько урана у вас останется через 2 года? По идее, весь уран должен распасться за первый же год, однако это не так. Через 6 месяцев у вас останется только 2,5 кг урана, который в свою очередь начнет распадаться со скоростью всего 2,5 кг в год. Еще через пару месяцев в вашем хранилище останется 1 кг урана, но и он будет распадаться с еще меньшей скоростью на уровне 1 кг в год. С течением времени вы теряете радиоактивное топливо, при этом снижается и скорость распада. Таким образом, через 2 года у вас останется:
Радиоактивный остаток = 5 × e−2 = 0,676
Заключение
Экспонента находит широкое применение в ситуациях, где что-либо непрерывно или дискретно растет. Вы можете использовать калькулятор возведения числа e в степень для подсчета результатов роста любых непрерывных процессов.
Экспонента на калькуляторе
Автор Admin На чтение 5 мин Просмотров 2 Опубликовано
Что такое экспонента и с чем её едят, мы разберемся в следующий раз. Сейчас мы разберемся, как где находится экспонента на калькуляторе и как её на калькуляторе считать. Нажимайте на ссылку, калькулятор откроется в новом окне. Приступим к практическим занятиям. Нажимайте на те же кнопочки, что нажимал я и смотрите на результат.
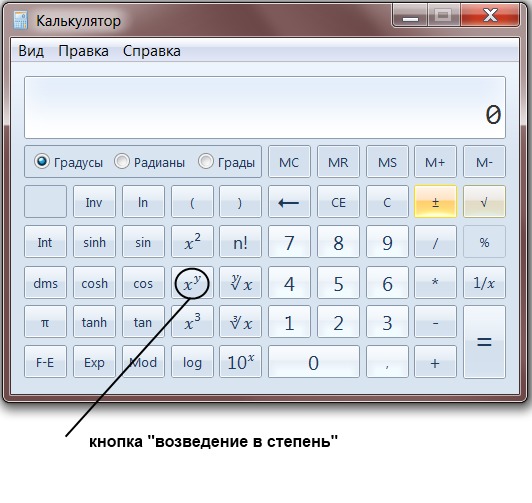
Для начала возведем число е в степень 4. В начале нужно набрать показатель степени. Нажимаем на кнопочку 4. Результат нашего вмешательства в беззаботную жизнь калькулятора можете посмотреть на картинке.
После этого нажимаем на специальную кнопочку экспоненты, обозначенную на калькуляторе е в степени х. Как видно из рисунка, калькулятор нас правильно понял и отреагировал именно так, как нам нужно.
Для вычисления заданного нами примера экспоненты необходимо нажать кнопочку равно.
Всё, мы получили требуемое значение.
е4=54,598
Общий порядок нахождения экспоненты на калькуляторе такой: набираете показатель степени, потом нажимаете специальную кнопку ех и кнопку =, результат готов.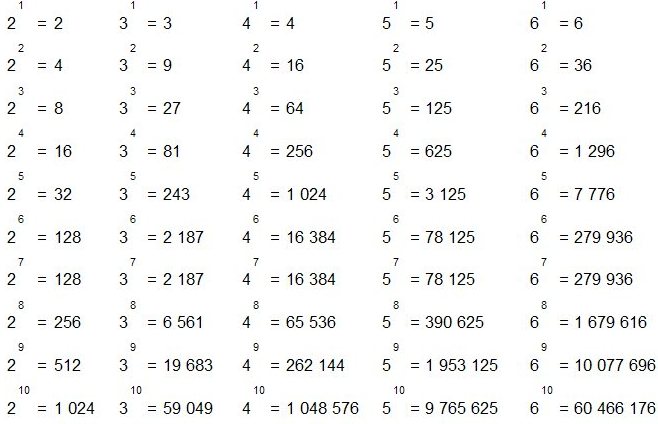 Можно поступить наоборот — сперва нажать кнопочку экспоненты ех, после этого ввести значение показателя степени и нажать кнопку равно. Для показателей степени в виде целях чисел или десятичных дробей оба варианта одинаковы. Если же показатель степени задан обыкновенной дробью, то лучше пользоваться вторым способом. Сперва нажимаете кнопку экспоненты, потом вводите числитель дроби, нажимаете кнопку деления, вводите знаменатель дроби и нажимаете кнопку равно. На этой странице мы рассмотрим первый способ.
Можно поступить наоборот — сперва нажать кнопочку экспоненты ех, после этого ввести значение показателя степени и нажать кнопку равно. Для показателей степени в виде целях чисел или десятичных дробей оба варианта одинаковы. Если же показатель степени задан обыкновенной дробью, то лучше пользоваться вторым способом. Сперва нажимаете кнопку экспоненты, потом вводите числитель дроби, нажимаете кнопку деления, вводите знаменатель дроби и нажимаете кнопку равно. На этой странице мы рассмотрим первый способ.
Для начала вычислим е в первой степени. Собственно, это и будет значение числа е. Напомню, что любое число в первой степени равно самому себе. Порядок нажимания кнопочек пронумерован на картинке красными цифрами.
Мы получили округленное до 14 знаков после запятой значение числа е:
е1=е=2,71828182845905≈2,718
Число е подчиняется всем свойствам степени, как и любое другое число. Результаты возведения его в степень такие же, как у чисел больших единицы. При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке.
При возведении в степень больше единицы результат будет больше первоначального. Для примера, возведем число е в не целую степень 9,876. Порядок нажимания кнопочек показан красными цифрами, результат виден на картинке.
Если показатель степени меньше единицы но больше нуля, то результат получится меньше первоначального но больше единицы. Это соответствует извлечению корня из числа е. Если на калькуляторе ввести показатель степени 0,5 (что равнозначно 1/2) то мы найдем квадратный корень числа е. Мы для примера возьмем экспоненту в степени 0,123
По логике, дальше следует показатель степени 0. Число е, как и любое другое число в нулевой степени, равняется единице. Это мы знаем и без калькулятора.
е0=1
Теперь переходим к отрицательным показателям степени экспоненты. Знак минус возле степени означает обратное число, то есть единицу, деленную на число е в указанной степени, но уже без знака минус. Умный калькулятор это понимает и без наших подсказок — он отлично справляется с отрицательной степенью. Для начала вычислим е в минус первой степени. Смотрим на картинку.
Умный калькулятор это понимает и без наших подсказок — он отлично справляется с отрицательной степенью. Для начала вычислим е в минус первой степени. Смотрим на картинку.
Мы получили число, обратное числу е:
е-1=1/е1=1/e=0,36787944117144≈0,368
Дальше пробуем добыть экспоненту со степенью меньше минус единицы.
Здесь полученный результат нужно преобразовать в удобоваримый для математиков вид. Делается это так:
е-9,876=1/е9,876=1/e=0,00005139344103≈5,139*10-5
Если после полученного на калькуляторе результата нажать ещё раз на знак равенства, десятичная дробь преобразуется в обычную дробь. Результат этой хитрой операции виден на картинке.
Но этот результат мне не нравится. Одна тысячная почти в два раза больше пяти десятитысячных. Если бы программа с калькулятором была русской, я бы подумал, что эту функцию писал бывший госслужащий, привыкший всё увеличивать в два раза (нужно же откуда-то себе воровать). Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.
Остается только предупредить, что и калькулятору полностью доверять нельзя, нужно самому анализировать результат, который он выдает.
В заключение найдем экспоненту с показателем степени больше минус единицы, но меньше нуля.
Теперь попробуем преобразовать результат в обычную дробь.
На этот раз калькулятор выдал более красивый результат. Но я уже ему не верю. Проверим результат преобразования, разделив на калькуляторе числитель на знаменатель. Результат деления записан ниже экспоненты.
Вот теперь можно поверить калькулятору, поскольку погрешность преобразования совсем незначительная. Округление даже до пяти знаков после запятой дает одинаковый результат.
Что делать, если вы пользуетесь виндосовским калькулятором и даже в инженерном варианте нет заветной кнопочки «е в степени икс»? Найдите кнопочку «Inv», рядом с ней есть кнопочка натурального логарифма «ln». Смело нажимайте кнопочку «Inv».
| Экспонента на калькуляторе Виндовс картинка 1 |
После нажатия этой кнопочки, расположенная рядом кнопочка натурального логарифма волшебным образом превратится в кнопочку «число е в степени икс».
| Экспонента на калькуляторе Виндовс картинка 2 |
По замыслу создателей калькулятора, такие превращения натурального логарифма и ежу понятны. Но…
Во-первых. Ёжик должен быть трезвым.
Во-вторых. Ёжик должен быть сообразительным.
В третьих. В памяти ежа на первом месте должны бить свойства натуральных логарифмов, а не какая-то ерунда типа любви, смысла жизни или завтрашнего урока по математике.
Что касается меня. Я редко бываю трезвым — это раз. Иногда я ужасно туплю — это два. Для меня смысл математики гораздо важнее свойств каких-то там логарифмов — это три.
e Калькулятор (e в степени x)
Введите число или выражение (базовое)
Введите число или выражение (степень)
Оглавление:
- Что такое экспоненты?
- Типы показателей степени
- Как решать показатели степени вручную?
- Правила экспоненты:
- Ссылки:
Этот потрясающий электронный калькулятор поможет вам найти решение экспоненциальной формы выражения. Вы можете найти как положительные, так и отрицательные показатели степени, используя наш калькулятор, возведенный в степень. Ниже мы обсудим, что такое экспоненты и калькуляторы экспонент? Как вы рассчитываете показатели степени/мощности основания вручную, а также с помощью нашего экспоненциального калькулятора?
Вы можете найти как положительные, так и отрицательные показатели степени, используя наш калькулятор, возведенный в степень. Ниже мы обсудим, что такое экспоненты и калькуляторы экспонент? Как вы рассчитываете показатели степени/мощности основания вручную, а также с помощью нашего экспоненциального калькулятора?
Что такое экспоненты?
Показатель степени — это степень, возводимая в верхнем углу справа от основания показателя степени. Они представляют количество операций умножения или деления, необходимых для упрощения выражения. Экспоненты бывают разных типов. Они могут быть дробными, комплексными, иррациональными или целыми положительными числами.
Типы экспонентов
Экспоненты делятся на два типа в зависимости от их природы.
Положительный:
Когда степень выражения — положительные числа, говорят, что это положительный показатель степени. Он говорит, сколько раз основание должно быть умножено само на себя.
например 2 4 = 2 x 2 x 2 x 2
Отрицательное число:
Когда степень выражения имеет отрицательный характер, его часто называют отрицательным показателем степени.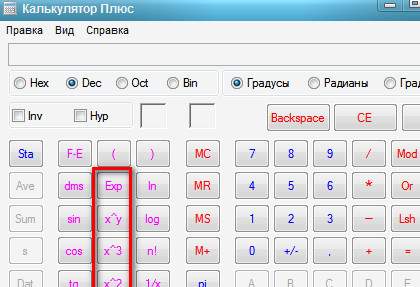 Он указывает количество обратных оснований, которые необходимо умножить на себя. Упростите такие дроби с помощью нашего калькулятора степени.
Он указывает количество обратных оснований, которые необходимо умножить на себя. Упростите такие дроби с помощью нашего калькулятора степени.
например 2 -4 = 12 x 12 x 12 x 12
Как решить Экспоненты вручную?
Когда показатели степени представляют собой небольшие целые числа, их можно легко вычислить вручную.
Пример:1
Вычислите значение выражения 5 в степени 4. (5 в степени 4)
Решение:
Это означает 5 4 .
5 * 5 * 5 * 5 = 625
5 в степени 4 = 625
Следовательно, показатель степени равен 625.
Пример:2
Найдите решенное значение экспоненциального выражения 3 -3 .
Решение:
Это показывает 13 х 13 х 13.
13 х 13 х 13 = 127.
127 = 0,037037037.
Следовательно, показатель степени равен 0,037037037
Ниже приведены некоторые решения часто используемых экспоненциальных выражений.
| 0,5 в степени 2 | 0,25 |
| 1,05 в степени 10 | 1,628894 | 9 0096
| 0,4 в степени 2 | 0,160000 |
| 0,5 в степени 4 | 0,0625 |
| 1,05 в степени 5 | 1,276281 | 1,5 в степени 1 | 0,5 |
| 1,4 в степени 2 | 1,959999 |
| 0,2 в степени 2 | 0,040000 |
| 0,5 в степени 1 | 0,5 9 0093 |
| 0,6 в степени 10 | 0,006046 |
| 0,2 в степени 3 | 0,008000 |
| 2 в степени 4 | 16 |
| 16384 | |
| 0,5 в степени 3 | 0,125 |
| 1,4 в степени 10 | 28,92546 |
| 1,5 в степени -10 | 0,017341 |
| -2,5 в степени -2 | 0,16 |
| 22 в степени 15 | 13688006 |
| 1,03 в степени 10 | 1,343916 | 0,4 в степени 4 | 0,025600 |
| 1,06 в степени 10 | 0,006046 |
| -11 в степени 7 | -1948717 |
| -2,5 в степени -2 | 0,16 90 093 |
| 0,2 в степени 5 | 0,000320 |
| 1,5 в степени 2 | 2,25 |
| 0,5 в степени -16 | 65536 |
| 0,4 в степени 10 | 0,000104 |
| 1,06 в степени 5 | 1,338225 |
| -200 в степени -200 | 0 |
| 21 в степени 2 | 441 9 0093 |
| 2,5 в степени 3 | 15,625 |
| 0,4 в степени -8 | 1525,878 |
| 11 в степени 2 | 121 |
| 1,5 в степени -10 | 0,017341 |
| 1,05 в степени 4 | 1.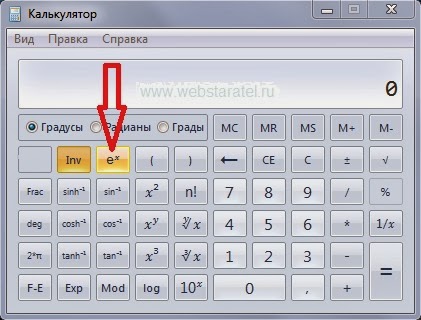 215506 215506 |
| 5 в степени 8 | 390625 |
Правила показателей: есть некоторые правила, применимые к экспонентам.
- Отрицательное свойство:
b -n = 1b
Пример:
Решить 24 -2 .Решение:
24 -2 = 2 x 14 -2= 2 x 4 4
= 2 x 16
= 32
Ссылки:
- https://www.mathsisfun.com/exponent.html, что такое показатели степени?
- https://www.rapidtables.com/math/number/exponent.html, Законы показателей.
Online e power x Calculator
Создано : Bhagya
Отзыв от : Rajashekhar Valipishetty
Последнее обновление в : 15 апреля 2023 г.
Используете ли вы число Эйлера для решения уравнения? Наш онлайн-калькулятор вам в помощь! Вы можете использовать наш
инструмент для вычисления e в степени любого числа. Если вы все еще не уверены, что такое число Эйлера, что означает e на
калькулятор, или как вычислить е в х, продолжайте читать.
Если вы все еще не уверены, что такое число Эйлера, что означает e на
калькулятор, или как вычислить е в х, продолжайте читать.
Введите x
Одна из самых важных констант в математике — это e в степени x. Мы не можем записать e в виде дроби, и это как и его знаменитый двоюродный брат пи (π), имеет бесконечное количество десятичных знаков. В математике буква е известны под разными именами. Оно также известно как натуральное число или число Эйлера. Его значение 2,7182818284590452353602… и это еще продолжается! (Округление и аппроксимация имеют решающее значение в этом пункт.)
Применение числа Эйлера e?
Теперь, когда мы знаем, что такое e и каково его приблизительное значение, мы можем приступить к рассмотрению его приложений.
- Шаг 1: Основание натурального логарифма равно e.
- Шаг 2: В естественной экспоненциальной функции мы используем e (eˣ = e степень x),
- Шаг 3: Наклон касательной к любой точке на графике равен ее координате Y в этой точке
в экс функции.
 (1 + 1/н)
(1 + 1/н) - Шаг 4: Последовательность, которую мы используем для оценки значения e, называется n. Чем больше n, тем ближе последовательность доходит до е; однако, даже если n = бесконечность, значение последовательности не равно числу Эйлера. В соединении расчет процентов, мы используем это уравнение.
- Шаг 5: Результат следующего уравнения факториала равен e:
- 1/0! + 1/1! 1/2!+ 1/3! + 1/4! + 1/5!………
- {iπ} + 1 = 0
Соберите коллекцию арифметических калькуляторов в одном месте на Arithmeticcalculator.com и избавьтесь от сомнений в кратчайшие сроки.
Как ввести число e в калькулятор?
Мы можем просто ввести значение e в любой калькулятор, потому что мы вынуждены использовать приблизительное значение e. Если
Ваш калькулятор не поддерживает символы, просто введите 2,718281828 (или любую округленную версию этого числа) в поле
поле значения выбора.

 (1 + 1/н)
(1 + 1/н)


 Все то же повторяют снизу-вверх, получая диагональную матрицу. Эти действия называются обратным ходом преобразования матрицы.
Все то же повторяют снизу-вверх, получая диагональную матрицу. Эти действия называются обратным ходом преобразования матрицы.


 .. — и съел! Тогда все закричали: «Но как же мы теперь узнаем, что было написано на той бумажке, которую ты съел?». А юноша улыбнулся и ответил: «Но ведь осталась вторая бумажка! Можно посмотреть, что написано на ней!» Посмотрели — а на ней написано «смерть». Значит, на той, что вытащил юноша, должно было быть написано «жизнь». Королю было стыдно признаваться в своём коварстве — и юноша был спасён!
.. — и съел! Тогда все закричали: «Но как же мы теперь узнаем, что было написано на той бумажке, которую ты съел?». А юноша улыбнулся и ответил: «Но ведь осталась вторая бумажка! Можно посмотреть, что написано на ней!» Посмотрели — а на ней написано «смерть». Значит, на той, что вытащил юноша, должно было быть написано «жизнь». Королю было стыдно признаваться в своём коварстве — и юноша был спасён! В этом был убеждён известный советский математик, профессор Алексей Иванович Маркушевич.
В этом был убеждён известный советский математик, профессор Алексей Иванович Маркушевич. (Треугольник)
(Треугольник) .. Стоял без слов…
.. Стоял без слов…

 (по 1 баллу)
(по 1 баллу) Кто старше?(Серёжа)
Кто старше?(Серёжа)


 А С такой игрой это делать удобно, интересно! Спасибо Большое❤️
А С такой игрой это делать удобно, интересно! Спасибо Большое❤️
 Подробнее
Подробнее Список ниже, от самодельных манипуляторов до веселых игр, поможет вашим ученикам практиковать эти основные математические навыки в игровой и увлекательной форме! Большинство занятий легко настраиваются в соответствии с потребностями вашего класса.
Список ниже, от самодельных манипуляторов до веселых игр, поможет вашим ученикам практиковать эти основные математические навыки в игровой и увлекательной форме! Большинство занятий легко настраиваются в соответствии с потребностями вашего класса.
 Домино Tally Mark
Домино Tally Mark  Адаптируйте это к потребностям ваших учеников начальной школы, используя их для практики пропущенного счета!
Адаптируйте это к потребностям ваших учеников начальной школы, используя их для практики пропущенного счета! Домино Дополнение
Домино Дополнение  Используйте их снова и снова, чтобы сортировать, создавать фигуры, строить числа и многое другое!
Используйте их снова и снова, чтобы сортировать, создавать фигуры, строить числа и многое другое! Усложняйте задачу, рисуя более сложные узоры, чтобы попробовать!
Усложняйте задачу, рисуя более сложные узоры, чтобы попробовать!
 Они создают полезную визуализацию для учащихся, которые только начинают понимать дроби!
Они создают полезную визуализацию для учащихся, которые только начинают понимать дроби!
 Игра неудержимо человечна, и мы можем играть, чтобы учиться. Игра и мышление не противоречат друг другу. Хотя игра обычно связана с отключением мышления и отдачей себя приятной деятельности, работа над интересными задачами может стать триггером потока. Есть благоприятный момент, часто около 30 минут работы над интересной проблемой, когда идеи начинают становиться решениями.
Игра неудержимо человечна, и мы можем играть, чтобы учиться. Игра и мышление не противоречат друг другу. Хотя игра обычно связана с отключением мышления и отдачей себя приятной деятельности, работа над интересными задачами может стать триггером потока. Есть благоприятный момент, часто около 30 минут работы над интересной проблемой, когда идеи начинают становиться решениями. Такие сайты, как Visual Patterns, Fraction Talks или Estimation180, предлагают простые и быстрые способы сделать математические концепции интересными.
Такие сайты, как Visual Patterns, Fraction Talks или Estimation180, предлагают простые и быстрые способы сделать математические концепции интересными. Решения важны, но не менее важен и процесс. Слушая и разговаривая со своими учениками во время их работы, вы можете давать хорошие отзывы и получать данные об оценках.
Решения важны, но не менее важен и процесс. Слушая и разговаривая со своими учениками во время их работы, вы можете давать хорошие отзывы и получать данные об оценках.
 10 = 9,765,625 (это будет кол-во комбинаций для строки из 10 символов с пятью вариациями).
10 = 9,765,625 (это будет кол-во комбинаций для строки из 10 символов с пятью вариациями).
 12*999)12*12 = 1 726 272 вариантов номеров.
12*999)12*12 = 1 726 272 вариантов номеров. Для каждого первого сколькими можно выбрать второй? 36. Итого — 36*36. Для каждых первых двух… — ну, и так далее.
Для каждого первого сколькими можно выбрать второй? 36. Итого — 36*36. Для каждых первых двух… — ну, и так далее.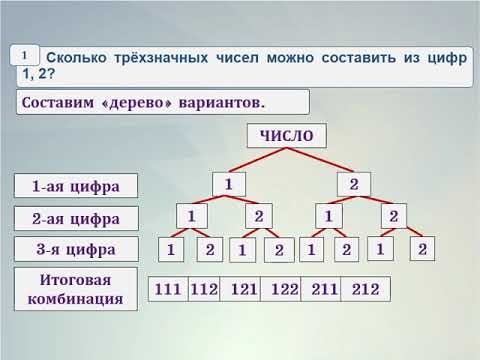
 С/без повторения, с/без порядка.
С/без повторения, с/без порядка.
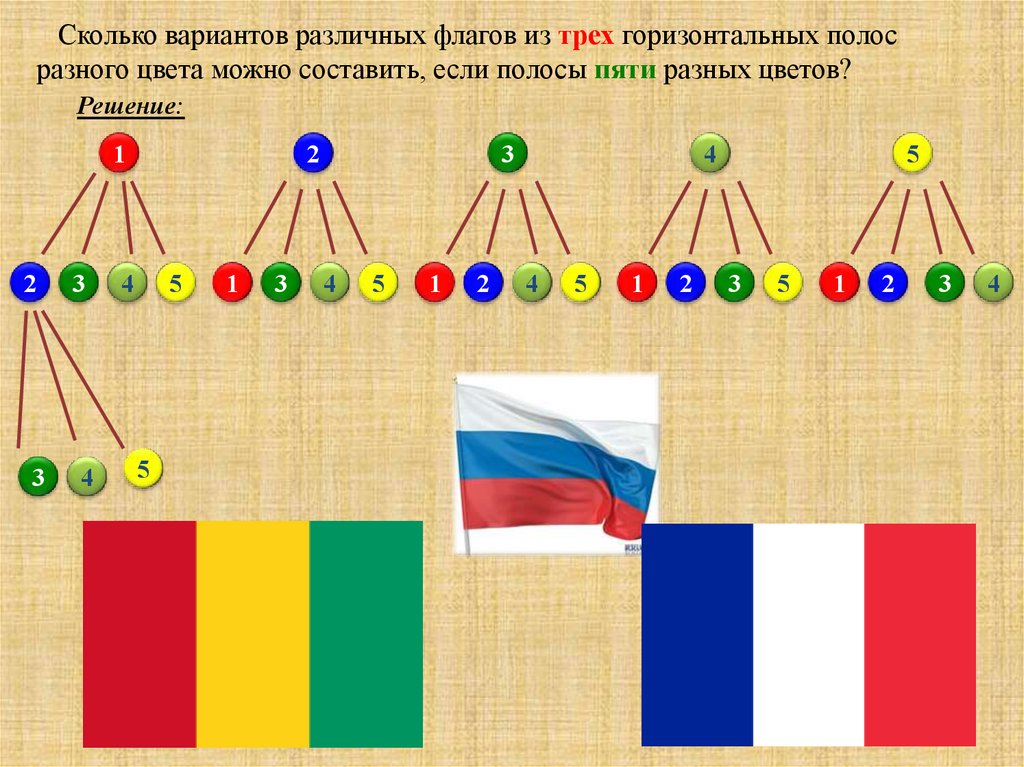 Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.
Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.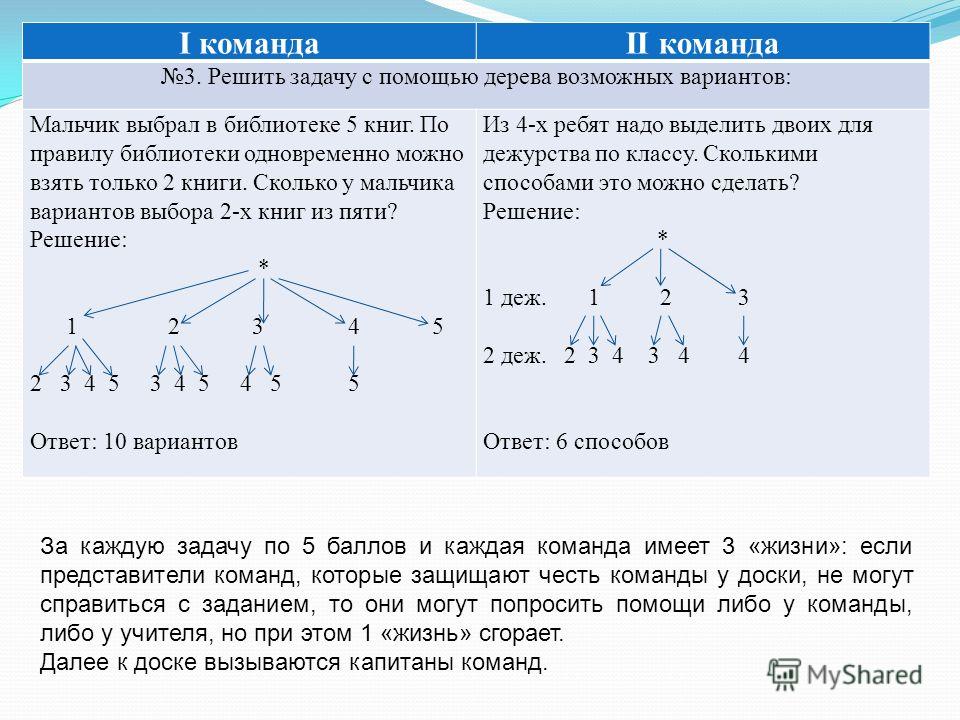 k логически больше n (иначе мы получили бы обычные комбинации).
Их счет:
k логически больше n (иначе мы получили бы обычные комбинации).
Их счет: Исследователь случайным образом выбирает двух взрослых. Вероятность (округленная до трех знаков после запятой) того, что у первого взрослого есть кредитная карта, а у второго взрослого нет кредитной карты, равна
Исследователь случайным образом выбирает двух взрослых. Вероятность (округленная до трех знаков после запятой) того, что у первого взрослого есть кредитная карта, а у второго взрослого нет кредитной карты, равна
 Верхний «нейтронный предел» установлен только для первых восьми элементов: от водорода до кислорода.
Верхний «нейтронный предел» установлен только для первых восьми элементов: от водорода до кислорода.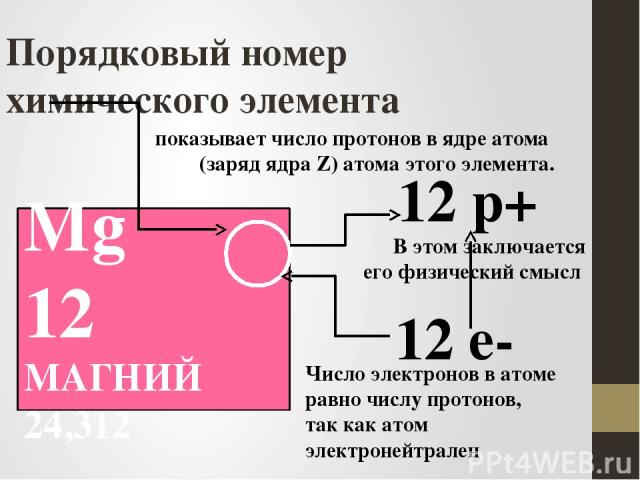 Детекторы, однако, зафиксировали более 20 ядер странного изотопа, практически не оставляя сомнений в его существовании.
Детекторы, однако, зафиксировали более 20 ядер странного изотопа, практически не оставляя сомнений в его существовании.


 Исследователи объединили мощность трех циклотронов — типа ускорителя частиц, впервые разработанного основателем лаборатории Беркли Эрнестом Лоуренсом в 19 году.31 — для создания пучков частиц очень высокой энергии, движущихся со скоростью около 60 процентов от скорости света.
Исследователи объединили мощность трех циклотронов — типа ускорителя частиц, впервые разработанного основателем лаборатории Беркли Эрнестом Лоуренсом в 19 году.31 — для создания пучков частиц очень высокой энергии, движущихся со скоростью около 60 процентов от скорости света.
 форма, которую демонстрируют соседние изотопы магния.
форма, которую демонстрируют соседние изотопы магния. Гельмгольца GSI в Германии также участвовали в исследовании.
Гельмгольца GSI в Германии также участвовали в исследовании. Для получения дополнительной информации посетите веб-сайт science.energy.gov .
Для получения дополнительной информации посетите веб-сайт science.energy.gov . «Это чрезвычайно экзотический вид».
«Это чрезвычайно экзотический вид». Это один из самых тяжелых изотопов, который в настоящее время можно экспериментально получить вблизи линии капельного полива».
Это один из самых тяжелых изотопов, который в настоящее время можно экспериментально получить вблизи линии капельного полива». Исследователи объединили мощность трех циклотронов — типа ускорителя частиц, впервые разработанного основателем лаборатории Беркли Эрнестом Лоуренсом в 1919 году.31 — для создания пучков частиц очень высокой энергии, движущихся со скоростью около 60 процентов от скорости света.
Исследователи объединили мощность трех циклотронов — типа ускорителя частиц, впервые разработанного основателем лаборатории Беркли Эрнестом Лоуренсом в 1919 году.31 — для создания пучков частиц очень высокой энергии, движущихся со скоростью около 60 процентов от скорости света.

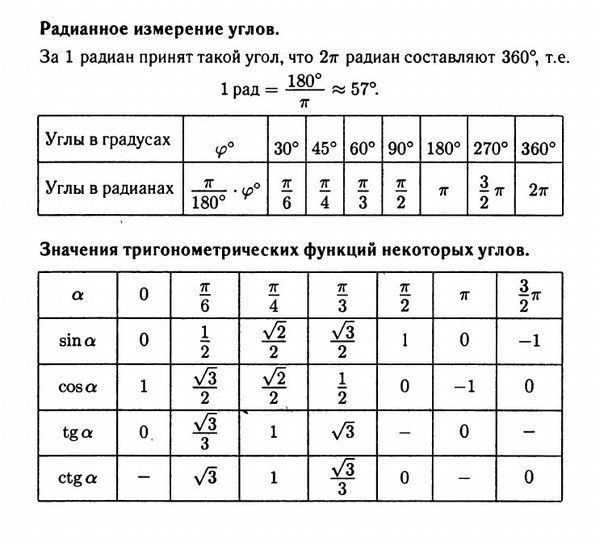 )
) )
) )
) )
)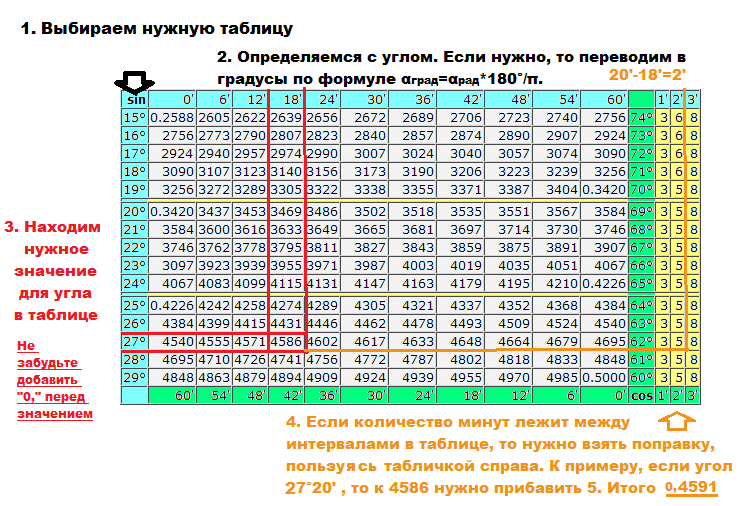 )
)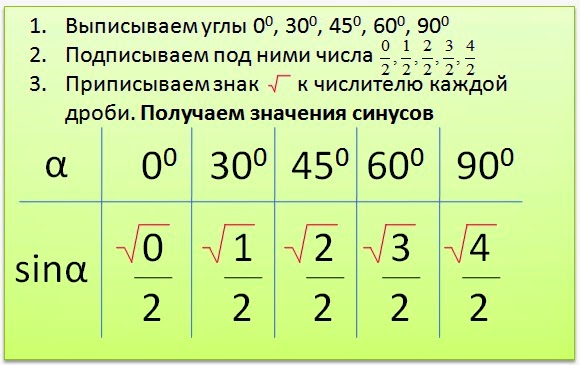 )
) )
)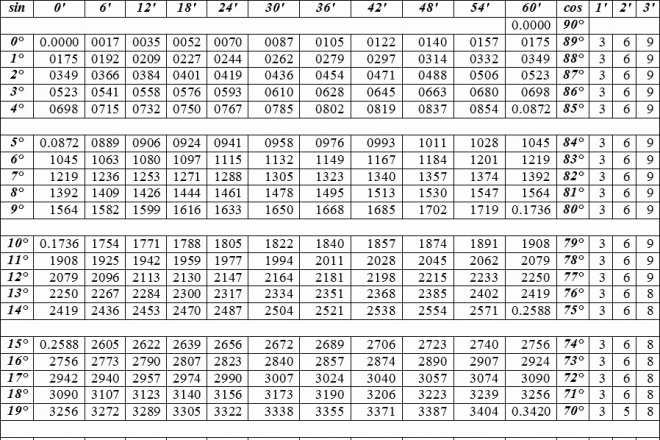 )
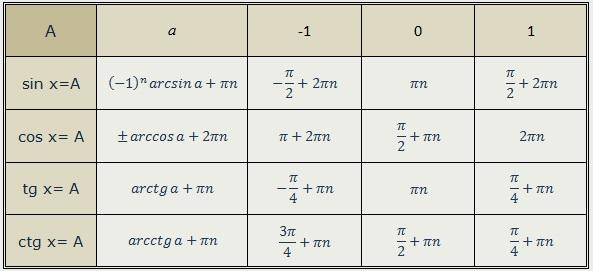
) Эти формулы позволяют от суммы или разности синусов и косинусов углов
и
перейти к произведению синусов и/или косинусов углов
и
. В этой статье мы сначала перечислим эти формулы, дальше покажем их вывод, а в заключение рассмотрим несколько примеров их применения.
Эти формулы позволяют от суммы или разности синусов и косинусов углов
и
перейти к произведению синусов и/или косинусов углов
и
. В этой статье мы сначала перечислим эти формулы, дальше покажем их вывод, а в заключение рассмотрим несколько примеров их применения. Такое представление правомерно, так как и для любых углов и .
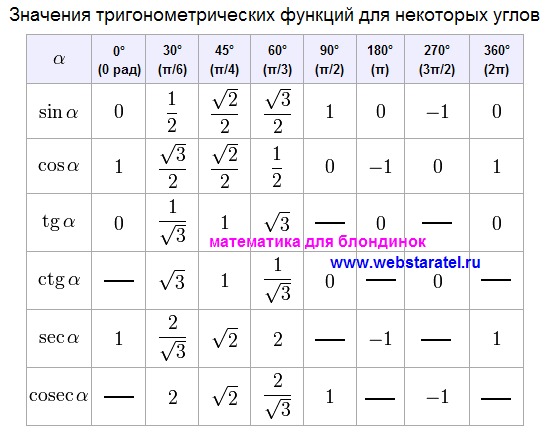
Такое представление правомерно, так как и для любых углов и .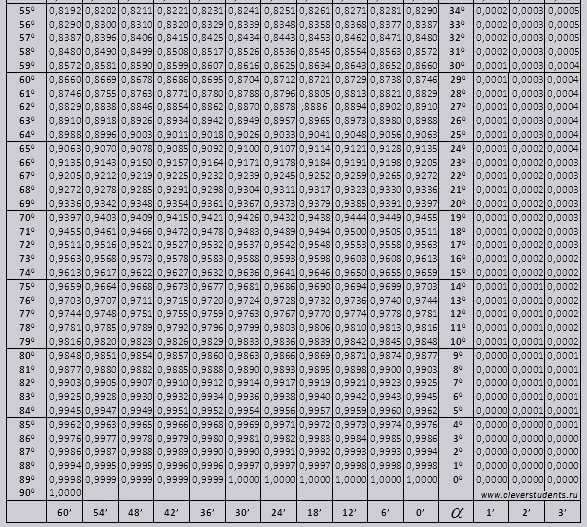 Чтобы это сделать, вычислим значения левой и правой частей формулы для данных углов. Так как и (при необходимости смотрите таблицу основных значений синусов и косинусов), то . При и имеем и , тогда . Таким образом, значения левой и правой частей формулы суммы синусов для и совпадают, что подтверждает справедливость этой формулы.
Чтобы это сделать, вычислим значения левой и правой частей формулы для данных углов. Так как и (при необходимости смотрите таблицу основных значений синусов и косинусов), то . При и имеем и , тогда . Таким образом, значения левой и правой частей формулы суммы синусов для и совпадают, что подтверждает справедливость этой формулы.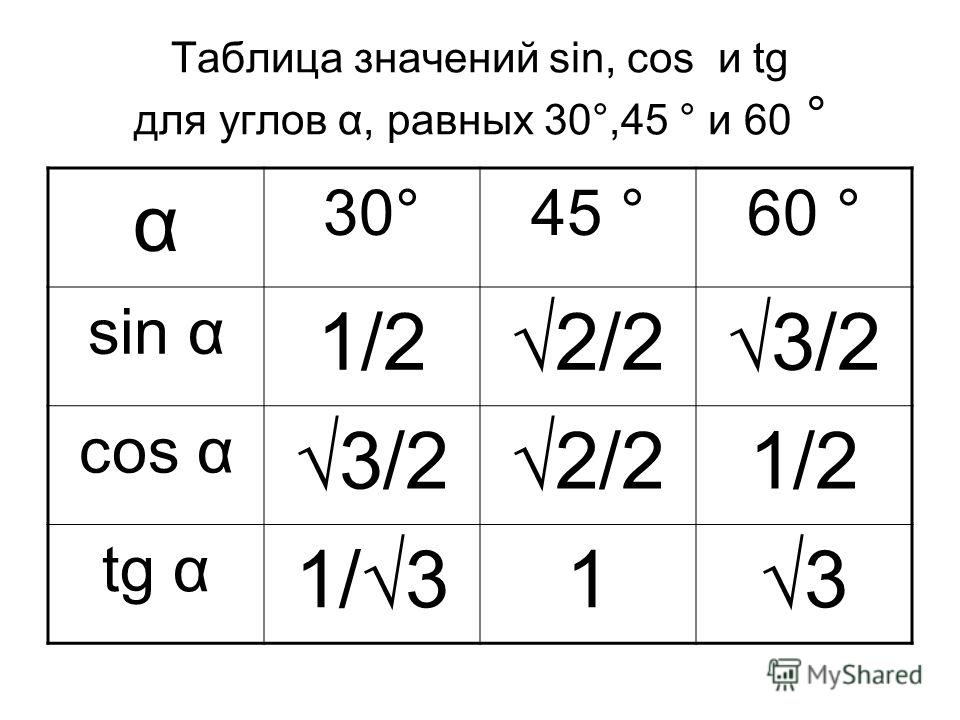
 для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.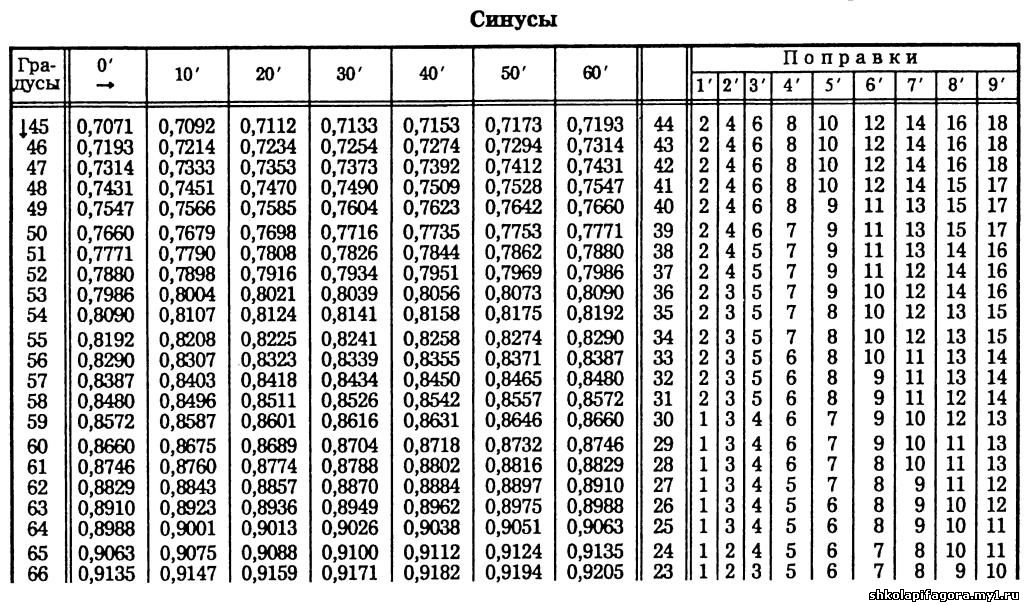
 Многие формулы уже изучены, но оказывается, не все. Поэтому девизом этого урока станет изречение Пифагора «Дорогу осилит идущий, а математику – мыслящий». Давайте мыслить!
Многие формулы уже изучены, но оказывается, не все. Поэтому девизом этого урока станет изречение Пифагора «Дорогу осилит идущий, а математику – мыслящий». Давайте мыслить!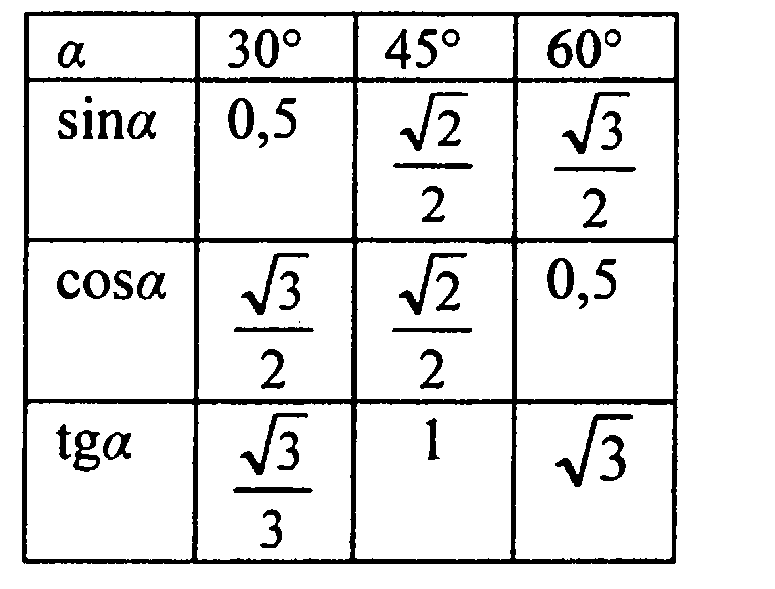 Сумма и разность косинусов. – запись в тетради
Сумма и разность косинусов. – запись в тетради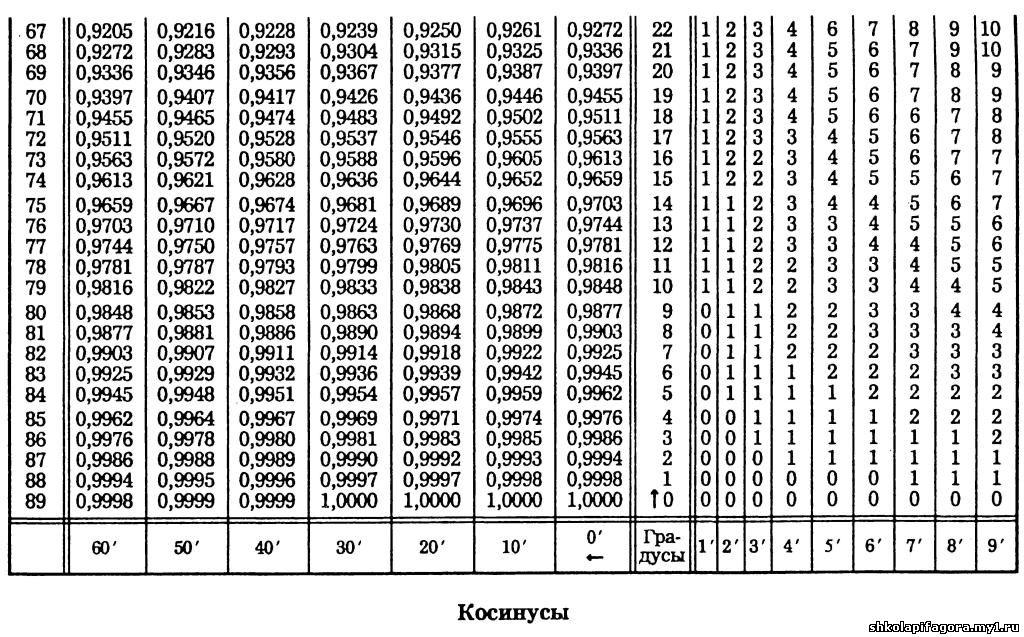 Домашнее задание: выучить формулы, индивидуальные задания на карточках.
Домашнее задание: выучить формулы, индивидуальные задания на карточках. \circ -\left(A+B\right)$.
\circ -\left(A+B\right)$. Дадим формулировку для каждой формулы.
Дадим формулировку для каждой формулы.

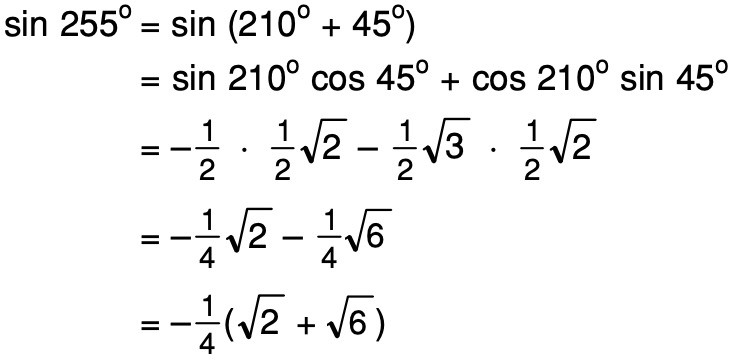 Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
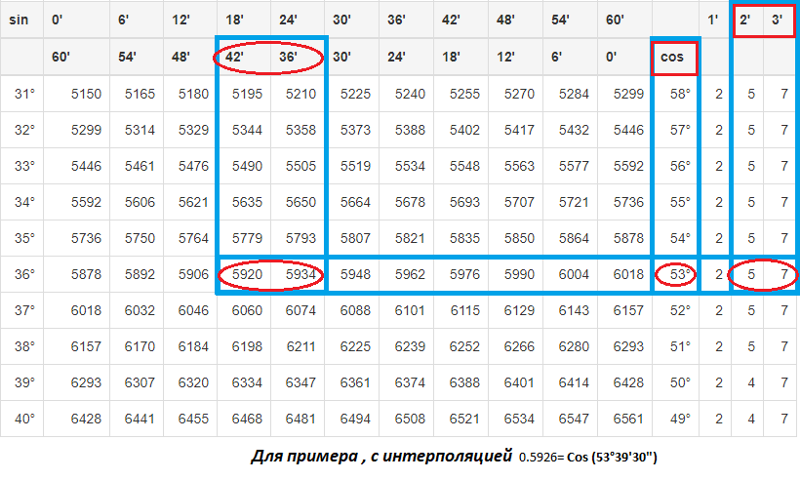
 . .
. .  Поскольку 75° лежит в 1-м квадранте, конечное значение sin 75° будет положительным.
Поскольку 75° лежит в 1-м квадранте, конечное значение sin 75° будет положительным.
 Значение sin 75° равно (√6 + √2)/4 или 0,9659 (приблизительно).
Значение sin 75° равно (√6 + √2)/4 или 0,9659 (приблизительно). 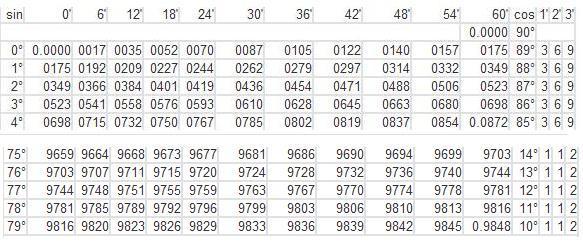 )/3
)/3
 2
2 Особенности владения, пользования и распоряжения объектом культурного наследия, включенным в реестр, и выявленным объектом культурного наследия \ КонсультантПлюс
Особенности владения, пользования и распоряжения объектом культурного наследия, включенным в реестр, и выявленным объектом культурного наследия \ КонсультантПлюс

 6 настоящего Федерального закона или пунктом 8 настоящей статьи, лицо, у которого на основании указанных договоров возникает право собственности на объект культурного наследия, включенный в реестр, земельный участок, в границах которого располагается объект археологического наследия, либо права владения и (или) пользования таким имуществом, обязано выполнять требования в отношении объекта культурного наследия, включенного в реестр, предусмотренные пунктами 1 — 3 статьи 47.3 настоящего Федерального закона, соблюдать установленный статьей 5.1 настоящего Федерального закона особый режим использования земельного участка, в границах которого располагается объект археологического наследия, до момента вручения такому лицу охранного обязательства, предусмотренного статьей 47.6 настоящего Федерального закона.
6 настоящего Федерального закона или пунктом 8 настоящей статьи, лицо, у которого на основании указанных договоров возникает право собственности на объект культурного наследия, включенный в реестр, земельный участок, в границах которого располагается объект археологического наследия, либо права владения и (или) пользования таким имуществом, обязано выполнять требования в отношении объекта культурного наследия, включенного в реестр, предусмотренные пунктами 1 — 3 статьи 47.3 настоящего Федерального закона, соблюдать установленный статьей 5.1 настоящего Федерального закона особый режим использования земельного участка, в границах которого располагается объект археологического наследия, до момента вручения такому лицу охранного обязательства, предусмотренного статьей 47.6 настоящего Федерального закона.
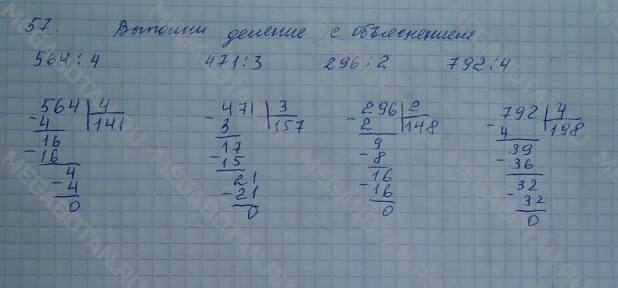



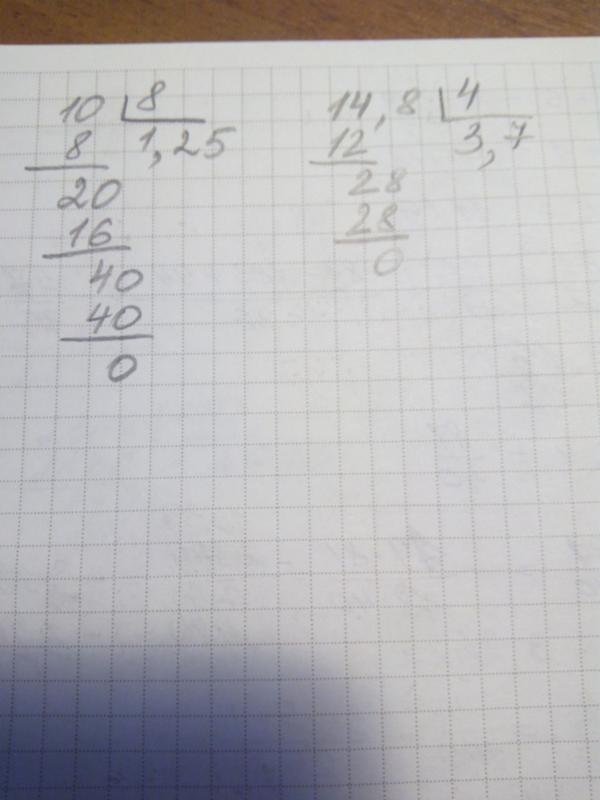 com , http://visualfractions.com/calculator/long-division/what-is-48-divided-by-8-using-long-division/. По состоянию на 21 апреля 2023 г.
com , http://visualfractions.com/calculator/long-division/what-is-48-divided-by-8-using-long-division/. По состоянию на 21 апреля 2023 г. Вот следующая задача, которую вам нужно решить:
Вот следующая задача, которую вам нужно решить:
 {\circ}\)
{\circ}\) В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен. По определению контангенса:
По определению контангенса: По определению контангенса:
По определению контангенса: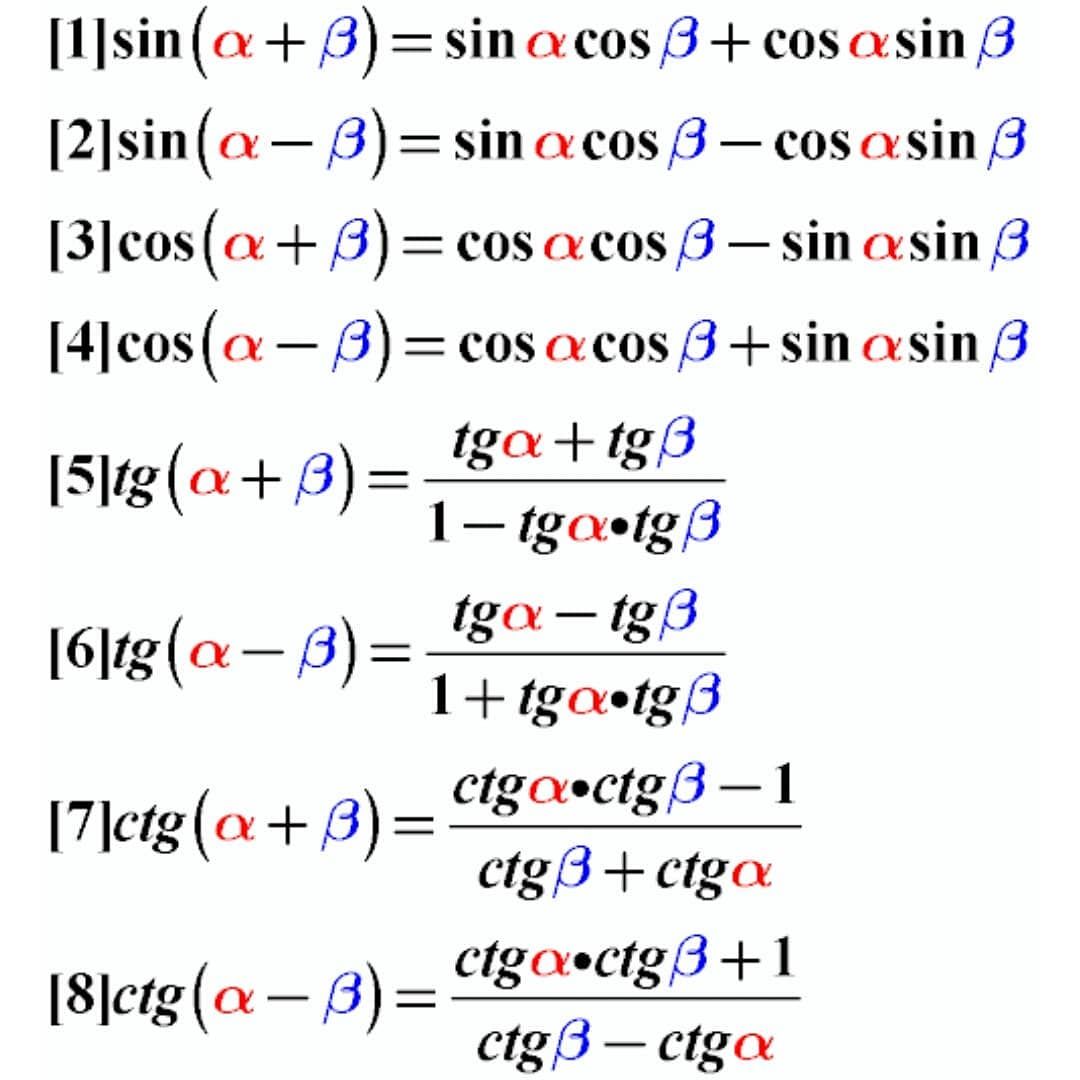 По определению тангенса:
По определению тангенса: По определению тангенса:
По определению тангенса: \]
\] \]
\]
 \]
\] \]
\] Отсчитываем против часовой стрелки от точки $P$, пусть
$Q$ — точка, длина дуги которой равна $A$, пусть $R$ —
точка, длина дуги которой равна $A+B$, и пусть $S$ будет точкой, длина дуги которой равна
$-B$. Тогда $(\cos A,\sin A)$
— координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$ — координаты точки $S$. 92
\end{уравнение*}
Отсчитываем против часовой стрелки от точки $P$, пусть
$Q$ — точка, длина дуги которой равна $A$, пусть $R$ —
точка, длина дуги которой равна $A+B$, и пусть $S$ будет точкой, длина дуги которой равна
$-B$. Тогда $(\cos A,\sin A)$
— координаты точки $Q$, $(\cos(A+B),\sin(A+B))$ — координаты точки $R$, $(\cos(-B),\sin( -B))$ — координаты точки $S$. 92
\end{уравнение*} ♦
♦ Тождества разности углов могут быть получены непосредственно
с того же рисунка, отождествив угол $A$ с углом $TPS$,
и
угол $B$ с углом $TPU$.♦
Тождества разности углов могут быть получены непосредственно
с того же рисунка, отождествив угол $A$ с углом $TPS$,
и
угол $B$ с углом $TPU$.♦ Доказательства степенных формул для остальных пяти функций
похожи.♦
Доказательства степенных формул для остальных пяти функций
похожи.♦
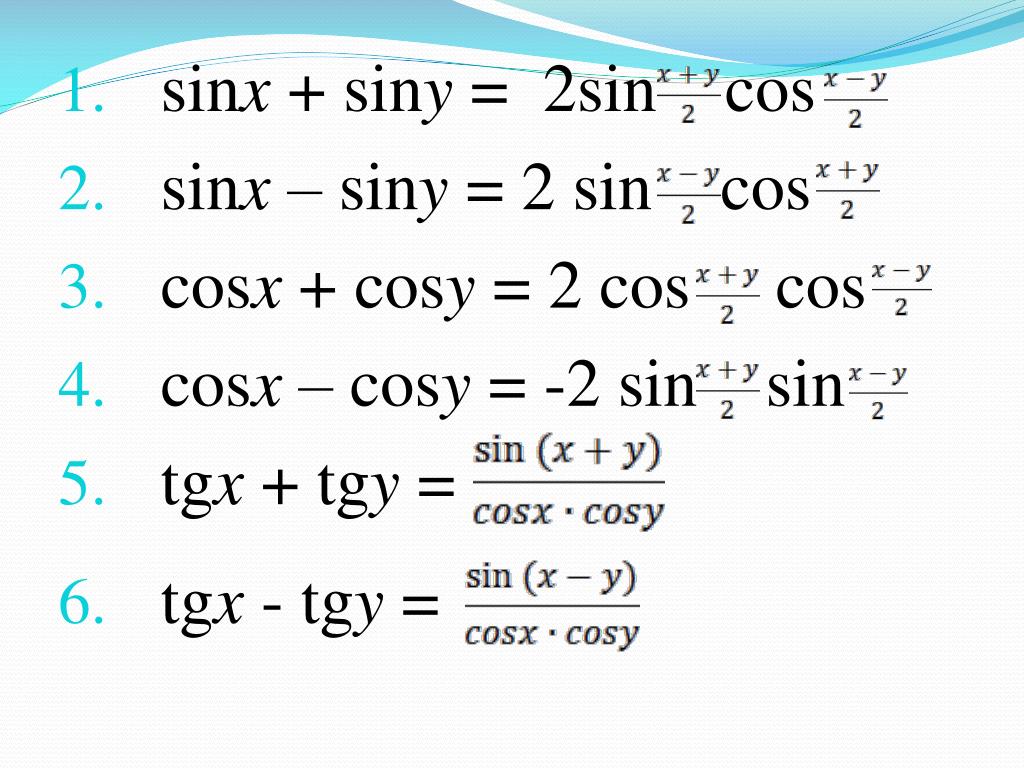 )
)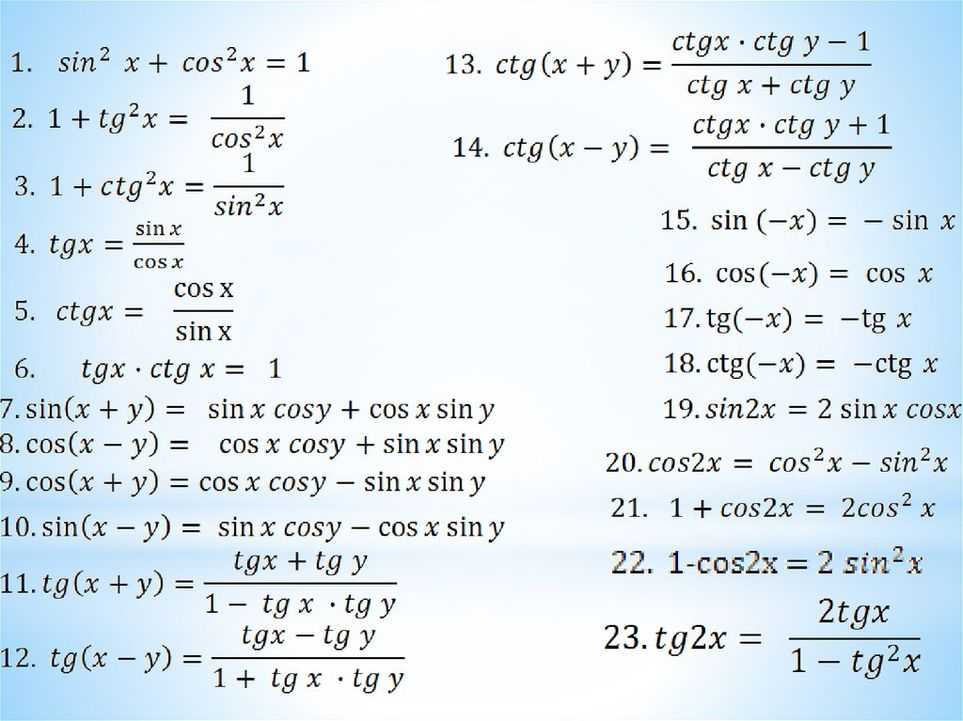 )
) )
) )
) )
) )
) )
) )
) ..МАТЕМАТИКА Выпуск 1, 2ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 1. Тождественные преобразованияСодержаниеМАТЕМАТИКА Выпуск 3,4ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 2. Алгебраические уравнения и неравенстваСодержание МАТЕМАТИКА Выпуск 5, 6Задачи и упражнения Выпуск 4 Пропорции, проценты, задачи на составление уравнений. ПрогрессииСодержаниеМАТЕМАТИКА Выпуск 7ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 3 Логарифмы Показательные и логарифмические уравнения и неравенстваСодержаниеЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 5 Тригонометрия СодержаниеМАТЕМАТИКА Выпуск 9ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 6 ПланиметрияСодержаниеМАТЕМАТИКА Выпуск 10, 11Задачи и упражнения Выпуск 7 Стереометрия. ВекторыСодержаниеМАТЕМАТИКА Выпуск 12Задачи и упражнения Выпуск 8 Элементы математического анализаСодерханиеМатематика контрольные работы для абитуриентов целевого набора.Вариант тестирования 1Вариант тестирования 2Вариант тестирования 3
..МАТЕМАТИКА Выпуск 1, 2ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 1. Тождественные преобразованияСодержаниеМАТЕМАТИКА Выпуск 3,4ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 2. Алгебраические уравнения и неравенстваСодержание МАТЕМАТИКА Выпуск 5, 6Задачи и упражнения Выпуск 4 Пропорции, проценты, задачи на составление уравнений. ПрогрессииСодержаниеМАТЕМАТИКА Выпуск 7ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 3 Логарифмы Показательные и логарифмические уравнения и неравенстваСодержаниеЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 5 Тригонометрия СодержаниеМАТЕМАТИКА Выпуск 9ЗАДАЧИ И УПРАЖНЕНИЯ Выпуск 6 ПланиметрияСодержаниеМАТЕМАТИКА Выпуск 10, 11Задачи и упражнения Выпуск 7 Стереометрия. ВекторыСодержаниеМАТЕМАТИКА Выпуск 12Задачи и упражнения Выпуск 8 Элементы математического анализаСодерханиеМатематика контрольные работы для абитуриентов целевого набора.Вариант тестирования 1Вариант тестирования 2Вариант тестирования 3 ..
.. ..
..

 Найдите корень уравнения (7-х)(х+7) + х(х-14)=49. (Выбрать один из вариантов ответа.)А) 0
Найдите корень уравнения (7-х)(х+7) + х(х-14)=49. (Выбрать один из вариантов ответа.)А) 0 Решение:
Решение: Прививая понятие смыла, мы учим ребенка думать и совершать простые логические действия самостоятельно, ограждая его тем самым от «тупого» тестового ответа. Важно, чтобы дети с первых лет в школе научились этому и далее получали бы радость не только от результата, но и от процесса обучения. Ученик должен быть знаком с правилами нахождения неизвестного, знать и понимать, что такое слагаемое, уменьшаемое, вычитаемое, разность и сумма. Также, для самоконтроля он может и должен уметь проверить правильность решения своего уравнения. Кроме того, в тесте неизвестное представлено не только в классическом виде «х», но есть и вариант «b», что позволяет ученику привыкнуть к многообразию данной позиции. Сам тест – это своего рода проверочная, итоговая работа, поэтому необходимо обладать определенными навыками решения такого рода уравнений. Время в тесте неограниченно, но тестируемый не должен засыпать над заданием или долго вспоминать, как это делается. В процессе прохождения теста необходимо следить за психологическим состоянием ребенка, объясняя ему, что ошибки – это не всегда так уж и плохо, Приступая к заданию можно предложить тестируемому ручку и бумагу для более успешного прохождения теста, но выбор, по-прежнему, остается за учеником.
Прививая понятие смыла, мы учим ребенка думать и совершать простые логические действия самостоятельно, ограждая его тем самым от «тупого» тестового ответа. Важно, чтобы дети с первых лет в школе научились этому и далее получали бы радость не только от результата, но и от процесса обучения. Ученик должен быть знаком с правилами нахождения неизвестного, знать и понимать, что такое слагаемое, уменьшаемое, вычитаемое, разность и сумма. Также, для самоконтроля он может и должен уметь проверить правильность решения своего уравнения. Кроме того, в тесте неизвестное представлено не только в классическом виде «х», но есть и вариант «b», что позволяет ученику привыкнуть к многообразию данной позиции. Сам тест – это своего рода проверочная, итоговая работа, поэтому необходимо обладать определенными навыками решения такого рода уравнений. Время в тесте неограниченно, но тестируемый не должен засыпать над заданием или долго вспоминать, как это делается. В процессе прохождения теста необходимо следить за психологическим состоянием ребенка, объясняя ему, что ошибки – это не всегда так уж и плохо, Приступая к заданию можно предложить тестируемому ручку и бумагу для более успешного прохождения теста, но выбор, по-прежнему, остается за учеником.
 Решите уравнение 6 + а = 12
Решите уравнение 6 + а = 12 Решить уравнение – значит найти такое число. При котором получается верное …
Решить уравнение – значит найти такое число. При котором получается верное … Где уравнение решено не верно?
Где уравнение решено не верно?
 193-195 №3, 5, 6, 8-13, 16, 18, 20
193-195 №3, 5, 6, 8-13, 16, 18, 20 208-210 #3бд, 4бд, 11, 12,
208-210 #3бд, 4бд, 11, 12, 4 Решения
4 Решения Узнать больше
Узнать больше Множественный выбор
Множественный выбор n — (-2) = -14
n — (-2) = -14 Множественный выбор
Множественный выбор