Помогите найти предел функции двух переменных : Анализ-I
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| MaxMelnikov |
| ||
28/03/09 |
| ||
| |||
| Brukvalub |
| |||
01/03/06 |
| |||
| ||||
| MaxMelnikov |
| ||
28/03/09 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| ASA |
| ||
30/01/09 |
| ||
| |||
| Atata379 |
| ||
09/02/12 |
| ||
| |||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| Atata379 |
| ||
09/02/12 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| AKM |
| |||
18/05/09 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| kw_artem |
| ||
17/01/12 |
| ||
| |||
| AKM |
| |||
18/05/09 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 15 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Предел функции двух переменных.
 Тема
ТемаПредел функции двух переменных. Тема
Что такое предел функции двух переменных, и почему при вычислении пределов функций двух переменных следует учитывать траекторию, по которой переменная точка приближается к своему предельному значению.
Когда мы вычисляем пределы в обычном понимании, то есть, пределы функций одной переменной, мы говорим, что переменная приближается (или стремится) к своему предельному значению, при этом функция ведет себя так-то (стремится к конечному значению, бесконечно растет и так далее).
То же самое происходит и в случае предела функции двух переменных, только в этом случае переменная точка может приближаться к предельному положению разными способами.
Действительно, у переменного числа есть только два направления: слева направо (в сторону убывания) и справа налево (в сторону возрастания). А у переменной точки таких направлений бесконечно много: слева направо, справа налево, по диагонали, по криволинейной траектории — как угодно.
А у переменной точки таких направлений бесконечно много: слева направо, справа налево, по диагонали, по криволинейной траектории — как угодно.
Так вот, предел функции двух переменных существует, если предельное значение функции двух переменных не зависит от траектории, по которой переменная точка приближается к своему предельному значению.
В остальном вычисление пределов функций двух переменных мало отличается от вычисления пределов функций одной переменной: точно так же нужно раскрывать неопределенности, использовать эквивалентность бесконечно малых и так далее.
Просмотрите видео по теме «Предел функции двух переменных», затем перейдите к вопросам по теме «Предел функции двух переменных» и попробуйте самостоятельно вычислит предложенные вам пределы функций двух переменных, и, наконец, проверьте себя, просмотрев ответы на вопросы по теме «Предел функции двух переменных».
Тема «Предел функции двух переменных»
Вопросы по теме «Предел функции двух переменных»
Ответы на вопросы по теме «Предел функции двух переменных»
Для того чтобы лучше разобраться с темой «Предел функции двух переменных», обязательно решите все задания.
Все лекции здесь.
Популярные сообщения из этого блога
Двойной интеграл в полярных координатах. Вопросы
Даны два двойных интеграла. Требуется вычислить их путем перехода к полярным координатам.
Замена переменных в двойном интеграле. Вопросы
Даны два двойных интеграла. Требуется подобрать замены так, чтобы области интегрирования перешли в прямоугольники со сторонами, параллельными осям, и вычислить интегралы в новых координатах.
Репетиторство и консультации по Skype
$ Общее время занятий включает в себя, помимо онлайн-занятия, несколько часов видео для предварительного изучения (которые не оплачиваются). Таким образом, занимаясь фактически 3, 4, 5 и более часов, вы оплачиваете только 2 академических часа. Это выгодно. Ознакомиться с условиями занятий
Это выгодно. Ознакомиться с условиями занятий
Исчисление III — Пределы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 13.1: Ограничения
В этом разделе мы рассмотрим ограничения, включающие функции более чем одной переменной. На самом деле мы сконцентрируемся в основном на пределах функций двух переменных, но идеи можно распространить и на функции с более чем двумя переменными. 9- }} f\влево( х \вправо)\]
На самом деле мы сконцентрируемся в основном на пределах функций двух переменных, но идеи можно распространить и на функции с более чем двумя переменными. 9- }} f\влево( х \вправо)\]
— это левосторонний предел, который требует, чтобы мы рассматривали только те значения \(x\), которые меньше \(a\).
Другими словами, мы будем иметь \(\mathop {\lim }\limits_{x \to a} f\left( x \right) = L\) при условии \(f\left( x \right)\) приближается к \(L\), когда мы приближаемся к \(x = a\) (не пропуская \(x = a\)) с обеих сторон.
Теперь обратите внимание, что в этом случае есть только два пути, по которым мы можем двигаться по направлению к \(x = a\). Мы можем двигаться либо слева, либо справа. Тогда для существования предела функции одной переменной функция должна приближаться к одному и тому же значению по мере того, как мы идем по каждому из этих путей в направлении \(x = a\).
С функциями двух переменных нам придется сделать что-то подобное, за исключением того, что на этот раз (потенциально) потребуется гораздо больше работы.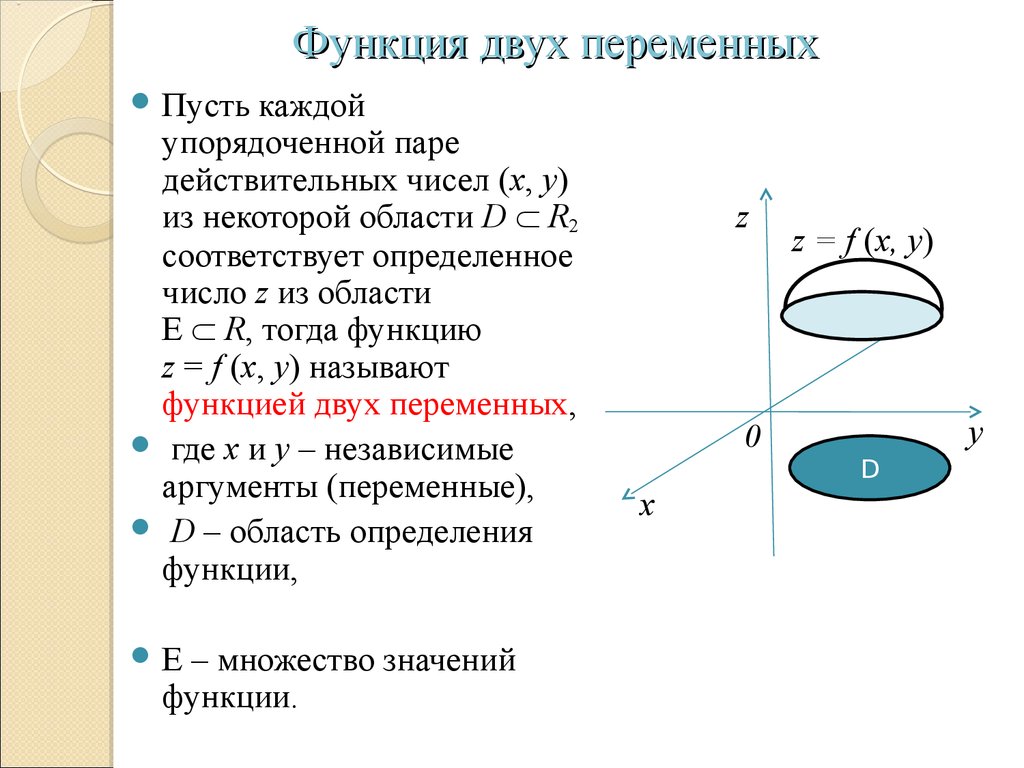 Давайте сначала обратимся к обозначениям и почувствуем, что мы собираемся просить в таких ограничениях.
Давайте сначала обратимся к обозначениям и почувствуем, что мы собираемся просить в таких ограничениях.
Мы попросим взять предел функции \(f\left( {x,y} \right)\) при приближении \(x\) к \(a\) и при приближении \(y\) к \ (б\). Это можно записать несколькими способами. Вот пара более стандартных обозначений.
\[\ mathop {\lim }\limits_{x \to a\top y\to b} f\left({x,y} \right)\hspace{0.5in}\mathop {\lim }\limits_{\ влево( {x,y} \right) \to \left( {a,b} \right)} f\left( {x,y} \right)\]
В этом курсе мы чаще будем использовать второе обозначение. Второе обозначение также немного более полезно для иллюстрации того, что мы на самом деле делаем здесь, когда берем предел. Беря предел функции двух переменных, мы на самом деле спрашиваем, что делает значение \(f\left( {x,y} \right)\) при перемещении точки \(\left( {x,y } \right)\) все ближе и ближе к точке \(\left( {a,b} \right)\) фактически не позволяя ей быть \(\left( {a,b} \right)\).
Как и в случае с пределами функций одной переменной, для того, чтобы этот предел существовал, функция должна приближаться к одному и тому же значению независимо от пути, по которому мы движемся по направлению к \(\left( {a,b} \верно)\). Проблема, с которой мы сразу сталкиваемся, заключается в том, что существует буквально бесконечное количество путей, по которым мы можем двигаться по направлению к \(\left( {a,b} \right)\). Вот несколько примеров путей, по которым мы могли бы пойти.
Мы добавили пару прямых путей, а также пару «странных» путей, которые не являются прямыми путями. Кроме того, мы включили здесь только 6 путей, и, как вы можете видеть, просто изменяя наклон прямых путей, их бесконечное количество, и тогда нам нужно будет рассмотреть пути, которые не являются прямыми путями.
Другими словами, чтобы показать, что предел существует, нам технически нужно проверить бесконечное количество путей и убедиться, что функция приближается к одному и тому же значению независимо от пути, который мы используем для приближения к точке.
К счастью для нас, мы можем использовать одну из основных идей из пределов Исчисления I, чтобы помочь нам установить пределы здесь.
Определение
Функция \(f\left( {x,y} \right)\) является непрерывной в точке \(\left( {a,b} \right)\), если
\[\ mathop {\lim }\limits_{\left({x,y} \right) \to \left({a,b} \right)} f\left({x,y} \right) = f \влево( {а,б} \вправо)\]
С графической точки зрения это определение означает то же самое, что и когда мы впервые увидели непрерывность в исчислении I. Функция будет непрерывной в точке, если в этой точке на графике нет дыр или разрывов.
Как это может помочь нам установить ограничения? Что ж, как и в исчислении I, если вы знаете, что функция непрерывна в точке \(\left( {a,b} \right)\), то вы также знаете, что
\[\ mathop {\lim }\limits_{\left({x,y} \right) \to \left({a,b} \right)} f\left({x,y} \right) = f \влево( {а,б} \вправо)\]
должно быть правдой. Итак, если мы знаем, что функция непрерывна в точке, то все, что нам нужно сделать, чтобы получить предел функции в этой точке, — это подставить точку в функцию.
Итак, если мы знаем, что функция непрерывна в точке, то все, что нам нужно сделать, чтобы получить предел функции в этой точке, — это подставить точку в функцию.
Все стандартные функции, которые, как мы знаем, являются непрерывными, остаются непрерывными, даже если мы сейчас подставляем более одной переменной. Нам просто нужно следить за делением на ноль, квадратными корнями из отрицательных чисел, логарифмами нуля или отрицательных чисел, и т. д.
Обратите внимание, что идея о путях — это то, что мы не должны забывать, поскольку это хороший способ определить, не существует ли предел. Если мы сможем найти два пути, на которых функция приближается к разным значениям по мере приближения к точке, мы будем знать, что предела не существует.
Давайте рассмотрим пару примеров.
Пример 1. Определите, существуют ли следующие ограничения. Если они существуют, укажите значение предела. 92}\left( { — 1} \right) + \left( 1 \right)\left( 2 \right)\cos \left( {2\pi + \pi } \right) = — 14\]
б \(\displaystyle \mathop {\lim}\limits_{\left({x,y} \right) \to \left({5,1} \right)} \frac{{xy}}{{x + y}}\) Показать решение
В этом случае функция не будет непрерывной вдоль прямой \(y = — x\), так как при этом мы получим деление на ноль. Однако для этой проблемы нам не о чем беспокоиться, поскольку точка, в которой мы берем предел, не находится на этой линии.
Однако для этой проблемы нам не о чем беспокоиться, поскольку точка, в которой мы берем предел, не находится на этой линии.
Следовательно, все, что нам нужно сделать, это подставить точку, так как функция в этой точке непрерывна.
\[\ mathop {\lim }\limits_{\left({x,y} \right) \to \left({5,1} \right)} \frac{{xy}}{{x + y}} = \фракция{5}{6}\]
В предыдущем примере не было никаких пределов. Функции были непрерывны в рассматриваемой точке, поэтому все, что нам нужно было сделать, это подключить точку. Это, конечно, не всегда так, поэтому давайте рассмотрим несколько примеров, более типичных для тех, что вы здесь увидите. 92}}}\]
Показать решение
В этом случае функция не является непрерывной в рассматриваемой точке (явное деление на ноль). Однако это не означает, что ограничение невозможно. Мы видели много примеров этого в исчислении I, где функция не была непрерывной в точке, на которую мы смотрели, и все же предел существовал.
В случае этого предела обратите внимание, что мы можем разложить как числитель, так и знаменатель функции следующим образом: 92}}} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left({1,1} \right)} \frac{{\left({2x + y } \right)\left( {x — y} \right)}}{{\left( {x — y} \right)\left( {x + y} \right)}} = \mathop {\lim } \limits_{\left( {x,y} \right) \to \left({1,1} \right)} \frac{{2x + y}}{{x + y}}\]
Итак, как мы видели во многих примерах из Исчисления I, после разложения на множители и сокращения общих множителей мы приходим к функции, для которой фактически можно взять предел. Итак, чтобы закончить этот пример, все, что нам нужно сделать, это взять предел. 92}}} = \mathop {\lim }\limits_{\left( {x,y} \right) \to \left({1,1} \right)} \frac{{2x + y}}{{ х + у}} = \ гидроразрыва {3} {2} \]
Прежде чем мы перейдем к следующему набору примеров, мы должны отметить, что ситуация в предыдущем примере — это то, что обычно происходит во многих предельных примерах/задачах в исчислении I. Однако в исчислении III это, как правило, исключение в примерах /problems, как будет показано в следующем наборе примеров. Другими словами, не ожидайте, что большинство этих типов ограничений будут просто факторизованы, а затем будут существовать, как в исчислении I. 94}}}\) Показать решение
Однако в исчислении III это, как правило, исключение в примерах /problems, как будет показано в следующем наборе примеров. Другими словами, не ожидайте, что большинство этих типов ограничений будут просто факторизованы, а затем будут существовать, как в исчислении I. 94}}}\) Показать решение
В этом случае функция не является непрерывной в рассматриваемой точке, поэтому мы не можем просто подключить точку. Также обратите внимание, что, в отличие от предыдущего примера, мы не можем факторизовать эту функцию и сделать некоторую отмену, чтобы можно было взять предел.
Следовательно, поскольку функция не является непрерывной в этой точке и поскольку мы не можем произвести факторинг, есть по крайней мере шанс, что предела не существует. Если бы мы могли найти два разных пути к точке, дающей разные значения предела, мы бы знали, что предела не существует. Двумя наиболее распространенными путями для проверки являются оси \(x\) и \(y\), так что давайте попробуем их.
Перед тем, как сделать это, нам нужно выяснить, что именно мы имеем в виду, когда говорим, что собираемся приблизиться к точке на пути. Когда мы приближаемся к точке на пути, мы будем делать это, либо фиксируя \(x\) или \(y\), либо связывая \(x\) и \(y\) через некоторую функцию. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из исчисления I.
Когда мы приближаемся к точке на пути, мы будем делать это, либо фиксируя \(x\) или \(y\), либо связывая \(x\) и \(y\) через некоторую функцию. Таким образом, мы можем уменьшить предел до предела, включающего одну переменную, что мы знаем, как это сделать из исчисления I.
Итак, давайте посмотрим, что происходит вдоль оси \(x\). Если мы собираемся приблизиться к \(\left( {0,0} \right)\) по оси \(x\), мы можем воспользоваться тем фактом, что вдоль оси \(x\) мы знаем что \(y = 0\). Это означает, что по оси \(x\) мы подставим \(y = 0\) в функцию, а затем возьмем предел, когда \(x\) приблизится к нулю. 94}}} = \mathop {\lim }\limits_{\left({0,y}\right) \to \left({0,0}\right)} 0 = 0\]
Итак, одинаковый лимит по двум путям. Не поймите это неправильно. Это НЕ говорит о том, что предел существует и имеет нулевое значение. Это означает только то, что предел имеет одинаковое значение на двух путях.
Давайте рассмотрим третий довольно распространенный путь. 2}}}\) Показать решение
93}} \right) \to \left( {0,0} \right)} \frac{1}{2} = \frac{1}{2}\]
2}}}\) Показать решение
93}} \right) \to \left( {0,0} \right)} \frac{1}{2} = \frac{1}{2}\]
Теперь у нас есть два пути, которые дают разные значения предела, поэтому предела не существует.
Как показало нам это ограничение, мы можем и часто должны использовать пути, отличные от линий, как мы это делали в первой части этого примера.
Итак, как мы видели в предыдущем примере, пределы здесь немного отличаются от тех, которые мы видели в исчислении I. Ограничения по нескольким переменным довольно сложно оценить, и мы показали несколько примеров, где это потребовало небольшой работы. просто чтобы показать, что предела не существует.
14.2: Пределы и непрерывность — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4537
Цели обучения
- Вычислить предел функции двух переменных.

- Узнайте, как функция двух переменных может приближаться к разным значениям в граничной точке в зависимости от пути приближения.
- Укажите условия непрерывности функции двух переменных.
- Проверить непрерывность функции двух переменных в точке.
- Вычислить предел функции трех и более переменных и проверить непрерывность функции в точке.
Теперь мы рассмотрели функции более чем одной переменной и увидели, как их изобразить. В этом разделе мы увидим, как взять предел функции более чем одной переменной и что означает непрерывность функции более чем одной переменной в точке ее области определения. Оказывается, у этих концепций есть аспекты, которые просто не встречаются с функциями одной переменной.
Предел функции двух переменных
Напомним из раздела 2.5, что определение предела функции одной переменной:
Пусть \(f(x)\) определено для всех \(x≠a\) в открытом интервале, содержащем \(a\). Пусть \(L\) — действительное число. Тогда
Тогда
\[\lim_{x→a}f(x)=L \nonumber \]
, если для любого \(ε>0,\) существует такое \(δ>0\), что если \ (0<|x−a|<δ\) для всех \(x\) в области определения \(f\), тогда
\[|f(x)−L|<ε. \номер\] 92\} \nonumber \]
, как показано на рисунке \(\PageIndex{1}\).
Рисунок \(\PageIndex{1}\): диск \(δ\) с центром вокруг точки \((2,1)\).Идея круга \(δ\) появляется в определении предела функции двух переменных. Если \(δ\) мало, то все точки \((x,y)\) в круге \(δ\) близки к \((a,b)\). Это совершенно аналогично тому, как х близко к а в определении предела функции одной переменной. В одном измерении мы выражаем это ограничение как
\[a−δ В более чем одном измерении мы используем диск \(δ\). Пусть \(f\) — функция двух переменных, \(x\) и \(y\). Предел \(f(x,y)\) при приближении \((x,y)\) к \((a,b)\) равен \(L\), записанному \[\lim_{(x ,y)→(a,b)}f(x,y)=L \nonumber \] , если для каждого \(ε>0\) существует достаточно малое \(δ>0\) такое, что для всех точек \((x,y)\) в диске \(δ\) вокруг \((a,b)\), за исключением, возможно, самого \((a,b)\), значение \(f( x,y)\) не более чем на \(ε\) от \(L\) (рисунок \(\PageIndex{2}\)). Доказательство существования предела с использованием определения предела функции двух переменных может быть сложной задачей. Вместо этого мы воспользуемся следующей теоремой, которая поможет нам найти пределы. Формулы этой теоремы являются расширением формул теоремы о предельных законах из книги «Предельные законы». Пусть \(f(x,y)\) и \(g(x,y)\) определены для всех \((x,y)≠(a,b) \) в окрестности \((a,b)\), и предположим, что эта окрестность полностью содержится внутри области определения \(f\). Предположим, что \(L\) и \(M\) — действительные числа такие, что \[\lim_{(x,y)→(a,b)}f(x,y)=L \nonumber \] и \[\lim_{(x,y)→(a,b)}g(x,y)=M, \nonumber \] и пусть \(c\) — константа. Постоянный закон: \[\lim_{(x,y)→(a,b)}c=c \nonumber \] Законы тождества: \[\lim_{(x, y)→(a,b)}x=a \nonumber \] \[\lim_{(x,y)→(a,b)}y=b \nonumber \] Закон суммы: \[\lim_{(x,y)→(a,b)}(f(x,y)+g(x,y))=L+M \nonumber \] Разностный закон: \[\lim_{(x,y)→(a,b)}(f(x,y)−g(x,y))=L−M \nonumber \] Постоянный кратный закон: Определение: предел функции двух переменных
 92}<δ. \nonumber \]
92}<δ. \nonumber \] Предельные законы для функций двух переменных
 Тогда верно каждое из следующих утверждений:
Тогда верно каждое из следующих утверждений:
для любого положительного целого числа \(n\).
Корневой закон:
\[\lim_{(x,y)→(a,b)}\sqrt[n]{f(x,y)}=\sqrt[n]{L} \nonumber \]
для всех \(L\), если \(n\) нечетно и положительно, и для \(L≥0\), если n четно и положительно.
Доказательства этих свойств аналогичны доказательствам для пределов функций одной переменной. Мы можем применить эти законы для нахождения пределов различных функций.
Пример \(\PageIndex{1}\): нахождение предела функции двух переменных 92−4(2)+3(−1)−6 \\[4pt] =−6. \end{выравнивание*}\]
б. Перед применением частного закона нам нужно убедиться, что предел знаменателя отличен от нуля. Используя разностный закон, постоянный множественный закон и закон тождества,
\[\begin{align*} \lim_{(x,y)→(2,−1)}(4x−3y) =\lim_{(x ,y)→(2,−1)}4x−\lim_{(x,y)→(2,−1)}3y \\[4pt] =4(\lim_{(x,y)→(2, −1)}x)−3(\lim_{(x,y)→(2,−1)}y) \\[4pt] =4(2)−3(−1)=11. \end{align*}\]
Поскольку предел знаменателя не равен нулю, применяется закон частного. Теперь вычислим предел числителя, используя разностный закон, закон констант-множителей и закон тождества:
\[\begin{align*} \lim_{(x,y)→(2,−1)}(2x+3y) =\lim_{(x,y)→(2,−1)}2x+\ lim_{(x,y)→(2,−1)}3y \\[4pt] =2(\lim_{(x,y)→(2,−1)}x)+3(\lim_{(x ,y)→(2,−1)}y) \\[4pt] =2(2)+3(−1)=1. \end{align*}\]
Следовательно, согласно закону о частных имеем
\[\begin{align*} \lim_{(x,y)→(2,−1)}\dfrac{2x+ 3y}{4x−3y} =\dfrac{\displaystyle \lim_{(x,y)→(2,−1)}(2x+3y)}{\displaystyle \lim_{(x,y)→(2, −1)}(4x−3y)} \\[4pt] =\dfrac{1}{11}. 2}=0 \номер\] 92}=\tfrac{1}{2}. \nonumber \]
2}=0 \номер\] 92}=\tfrac{1}{2}. \nonumber \]
Это верно для любой точки на прямой \(y=x\). Если мы позволим \(x\) приблизиться к нулю, оставаясь на этой линии, значение функции останется фиксированным на \(\tfrac{1}{2}\), независимо от того, насколько мал \(x\).
Выберите значение ε меньше \(1/2\) — скажем, \(1/4\). Тогда, независимо от того, насколько маленький диск \(δ\) мы нарисуем вокруг \((0,0)\), значения \(f(x,y)\) для точек внутри этого диска \(δ\) будут включают как \(0\), так и \(\tfrac{1}{2}\). Следовательно, определение предела в точке никогда не выполняется, и предел не существует. 92}.\) Вдоль прямой \(y=0\) функция равна нулю; вдоль линии \(y=x\) функция равна \(\tfrac{1}{2}\).
б. Подобно а., мы можем приблизиться к началу координат по любой прямой, проходящей через начало координат. Если мы попытаемся использовать ось \(x\) (т. е. \(y=0\)), то функция останется фиксированной на нуле. То же верно и для оси \(y\). Предположим, мы приближаемся к началу координат по прямой линии наклона \(k\). Уравнение этой линии \(y=kx\). Тогда предел становится
Уравнение этой линии \(y=kx\). Тогда предел становится
- Точка \(P_0\) называется внутренней точкой \(S\), если существует диск \(δ\) с центром вокруг \(P_0\), полностью содержащийся в \(S\).
- Точка \(P_0\) называется граничной точкой \(S\), если каждый \(δ\) круг с центром в \(P_0\) содержит точки как внутри, так и вне \(S\).
- \(S\) называется открытым множеством , если каждая точка \(S\) является внутренней точкой.
- \(S\) называется замкнутым множеством , если оно содержит все свои граничные точки.
Примером открытого множества является диск \(δ\). Если мы включим границу диска, то он станет замкнутым множеством. Множество, которое содержит некоторые, но не все, его граничные точки, не является ни открытым, ни закрытым. Например, если мы включаем половину границы круга \(δ\), но не другую половину, то множество не является ни открытым, ни закрытым. 92\) (Рисунок \(\PageIndex{4}\)).
Например, если мы включаем половину границы круга \(δ\), но не другую половину, то множество не является ни открытым, ни закрытым. 92\) (Рисунок \(\PageIndex{4}\)).
- Открытое множество \(S\) является связным множеством , если оно не может быть представлено как объединение двух или более непересекающихся, непустых открытых подмножеств.
- Множество \(S\) является областью , если оно открыто, связно и непусто.
Определение предела функции двух переменных требует, чтобы диск \(δ\) содержался внутри области определения функции. Однако если мы хотим найти предел функции в граничной точке области, \(δ\) диск не содержится внутри домена. По определению некоторые точки диска \(δ\) находятся внутри области, а некоторые — снаружи. Поэтому нам нужно рассматривать только точки, которые находятся как внутри круга \(δ\), так и внутри области определения функции. Это приводит к определению предела функции в граничной точке. 2}<δ. \номер\] 92} \номер \]
2}<δ. \номер\] 92} \номер \]
Непрерывность функций двух переменных
В разделе Непрерывность мы определили непрерывность функции одной переменной и увидели, как она зависит от предела функции одной переменной. В частности, необходимы три условия для непрерывности \(f(x)\) в точке \(x=a\)
- \(f(a)\).
- \(\displaystyle \lim_{x→a}f(x)\) существует.
- \(\displaystyle \lim_{x→a}f(x)=f(a).\)
Эти три условия необходимы и для непрерывности функции двух переменных.
Определение: непрерывные функции
Функция \(f(x,y)\) непрерывна в точке \((a,b)\) своей области определения, если выполняются следующие условия:
- \(f (а,б)\) существует.
- \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\) существует.
- \(\ displaystyle \ lim_ {(x, y) → (a, b)} f (x, y) = f (a, b). \)
Пример \(\PageIndex{4}\): демонстрация непрерывности функции двух переменных
Показать, что функция
\[f(x,y)=\dfrac{3x+2y}{x+y+1} \nonumber \]
непрерывна в точке \((5,−3). \)
\)
Решение
Согласно определению непрерывности должны быть выполнены три условия. В этом примере \(a=5\) и \(b=−3.\)
1. \(f(a,b)\) существует. Это верно, потому что область определения функции f состоит из тех упорядоченных пар, для которых знаменатель не равен нулю (т. Е. \ (x + y + 1 ≠ 0 \)). Точка \((5,−3)\) удовлетворяет этому условию. Кроме того,
\[f(a,b)=f(5,−3)=\dfrac{3(5)+2(−3)}{5+(−3)+1}=\dfrac{15−6 {2+1}=3. \nonumber \]
2. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)\) существует. Это также верно:
\[\begin{align*} \lim_{(x,y)→(a,b)}f(x,y) =\lim_{(x,y)→(5,− 3)} \ dfrac {3x + 2y} {x + y + 1} \\ = \ dfrac {\ displaystyle \ lim_ {(x, y) → (5, −3)} (3x + 2y)} {\ displaystyle \lim_{(x,y)→(5,−3)}(x+y+1)} \\ = \dfrac{15−6}{5−3+1} \\ = 3. \end{align *}\]
3. \(\displaystyle \lim_{(x,y)→(a,b)}f(x,y)=f(a,b).\) Это верно, потому что мы только что показано, что обе части этого уравнения равны трем. 92}<δ\) верно, \(|f(x,y)−f(a,b)|<ε. \) Это определение можно комбинировать с формальным определением (то есть эпсилон–дельта определение ) непрерывности функции одной переменной для доказательства следующих теорем:
\) Это определение можно комбинировать с формальным определением (то есть эпсилон–дельта определение ) непрерывности функции одной переменной для доказательства следующих теорем:
Сумма непрерывных функций непрерывна
Если \(f(x,y)\) непрерывна в \((x_0,y_0)\ ), и \(g(x,y)\) непрерывна в \((x_0,y_0)\), то \(f(x,y)+g(x,y)\) непрерывна в \(( х_0,у_0)\).
Произведение непрерывных функций непрерывно 92\) в диапазон \(R⊆R.\) Предположим, что \(g\) непрерывна в некоторой точке \((x_0,y_0)∈D\) и определим \(z_0=g(x_0,y_0)\) . Пусть f будет функцией, которая отображает \(R\) в \(R\), так что \(z_0\) находится в области определения \(f\). Наконец, предположим, что \(f\) непрерывно в \(z_0\). Тогда \(f∘g\) непрерывен в \((x_0,y_0)\), как показано на рисунке \(\PageIndex{7}\).
Рисунок \(\PageIndex{7}\): Композиция двух непрерывных функций непрерывна. Теперь воспользуемся предыдущими теоремами, чтобы показать непрерывность функций в следующих примерах. 3\)? Что значит быть непрерывным в точке в четырех измерениях? 92}<δ\большой\}. \nonumber \]
3\)? Что значит быть непрерывным в точке в четырех измерениях? 92}<δ\большой\}. \nonumber \]
Чтобы показать, что предел функции трех переменных существует в точке \((x_0,y_0,z_0)\), достаточно показать, что для любой точки шара \(δ\) с центром в \((x_0,y_0,z_0)\) значение функции в этой точке сколь угодно близко к фиксированному значению (предельное значение). Все предельные законы для функций двух переменных справедливы и для функций более чем двух переменных.
Пример \(\PageIndex{6}\): нахождение предела функции трех переменных 92y−3z}{2x+5y−z}. \nonumber \]
Решение
Прежде чем мы сможем применить закон о частных, нам нужно проверить, что предел знаменателя не равен нулю. Используя разностный закон, закон тождества и постоянный закон,
\[\begin{align*}\lim_{(x,y,z)→(4,1,−3)}(2x+5y−z ) =2(\lim_{(x,y,z)→(4,1,−3)}x)+5(\lim_{(x,y,z)→(4,1,−3)}y )−(\lim_{(x,y,z)→(4,1,−3)}z) \\ = 2(4)+5(1)−(−3) \\ = 16. \end{ align*}\]
Так как это не ноль, мы затем находим предел числителя. Используя закон произведения, степенной закон, разностный закон, постоянный множественный закон и закон тождества, 92}=2 \номер\]
Используя закон произведения, степенной закон, разностный закон, постоянный множественный закон и закон тождества, 92}=2 \номер\]
Основные понятия
- Для изучения пределов и непрерывности функций двух переменных мы используем диск \(δ\) с центром в заданной точке.
- Функция многих переменных имеет предел, если для любой точки шара \(δ\) с центром в точке \(P\) значение функции в этой точке сколь угодно близко к фиксированному значению (предельное значение ).
- Предельные законы, установленные для функции одной переменной, имеют естественное распространение на функции более чем одной переменной.
- Функция двух переменных непрерывна в точке, если в этой точке существует предел, функция существует в этой точке и предел и функция в этой точке равны.
Глоссарий
- граничная точка
- точка \(P_0\) в \(R\) является граничной точкой, если каждый \(δ\) круг с центром в \(P_0\) содержит точки как внутри, так и вне \(R\)
- закрытый набор
- множество \(S\), содержащее все его граничные точки 93\), лежащие на расстоянии менее \(δ\) от \((x_0,y_0,z_0)\)
- внутренняя точка
- точка \(P_0\) множества \(\mathbb{R}\) является граничной точкой, если существует диск \(δ\) с центром в \(P_0\), полностью содержащийся в \(\mathbb{R}\ )
- открытый набор
- множество \(S\), не содержащее ни одной из своих граничных точек
- регион
- открытое связное непустое подмножество \(\mathbb{R}^2\)
14.

 03.2009, 18:17
03.2009, 18:17  03.2009, 19:04
03.2009, 19:04  03.2009, 00:58
03.2009, 00:58  03.2009, 01:11
03.2009, 01:11 
 По-моему нужно так:
По-моему нужно так:  ..
.. 02.2012, 00:31
02.2012, 00:31 
 .. хочу найти о них какую-нибудь информацию. Спасибо за ответ.
.. хочу найти о них какую-нибудь информацию. Спасибо за ответ. Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует:
Решал только с одной переменной, и те давались тяжело. Помогите найти предел или же доказать что его не существует:  е. предел зависит от пути, т.е. предела по двум переменным нет.
е. предел зависит от пути, т.е. предела по двум переменным нет. е. предел зависит от пути, т.е. предела по двум переменным нет.
е. предел зависит от пути, т.е. предела по двум переменным нет. 07.2012, 00:22
07.2012, 00:22  07.2012, 12:13
07.2012, 12:13 
 07.2012, 19:02
07.2012, 19:02  Следовательно если есть хотя бы в одном направлении значит просто — есть. Значит по аналогии и в пространстве — если есть хотя бы в одном направлении значит просто — есть.
Следовательно если есть хотя бы в одном направлении значит просто — есть. Значит по аналогии и в пространстве — если есть хотя бы в одном направлении значит просто — есть.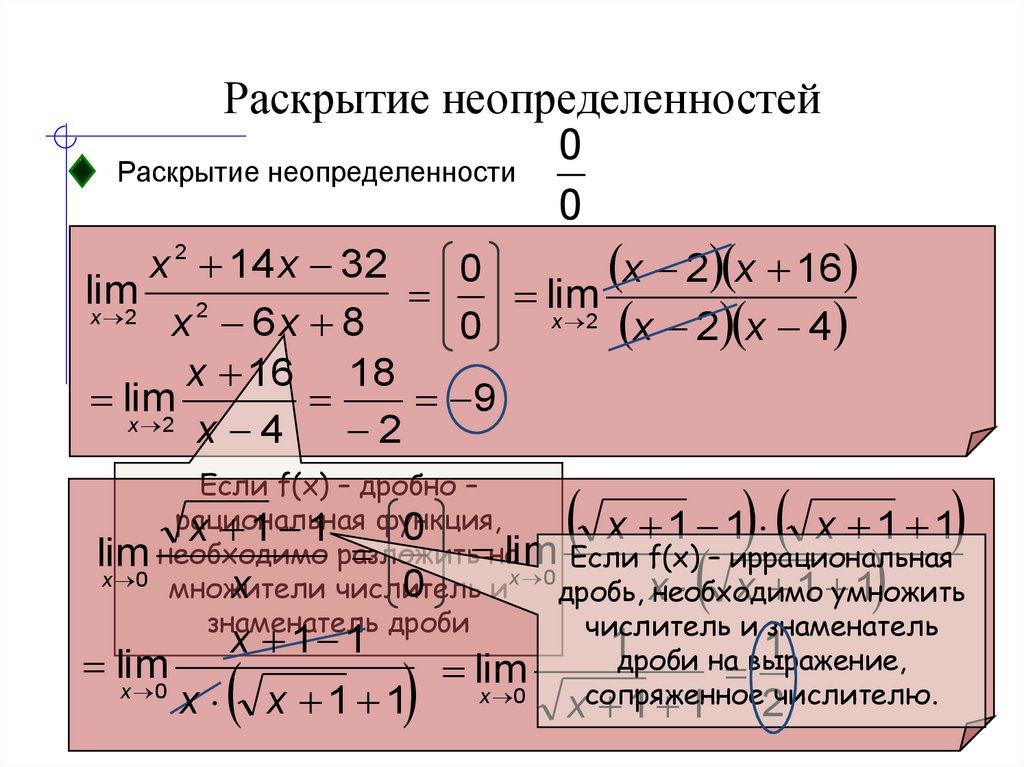 А мне один раз уже закрыли мою тему, мотивировав, что таких тем уже полно и дескать не надо плодить — пишите в уже созданных.
А мне один раз уже закрыли мою тему, мотивировав, что таких тем уже полно и дескать не надо плодить — пишите в уже созданных. Соответственно, у функции типа предела в бесконечности нет, поскольку упомянутая kw_artem
Соответственно, у функции типа предела в бесконечности нет, поскольку упомянутая kw_artem
 Получаем картину: диаграммы и графики
Получаем картину: диаграммы и графики  Эксперименты: открытия в медицине или результаты, вводящие в заблуждение?
Эксперименты: открытия в медицине или результаты, вводящие в заблуждение? Материал предназначен для студентов-заочников и других читателей, которые хотят в самые короткие сроки освоить практику.
Материал предназначен для студентов-заочников и других читателей, которые хотят в самые короткие сроки освоить практику.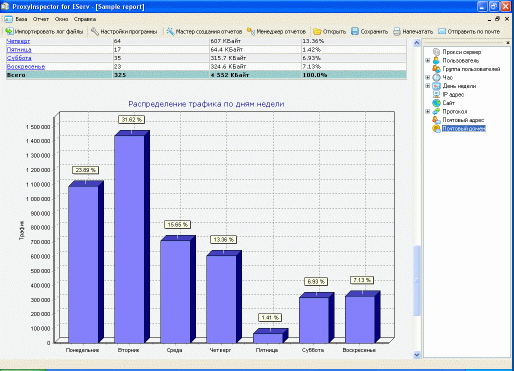 2.4. Исправленная выборочная дисперсия
2.4. Исправленная выборочная дисперсия 5.1. Если генеральная дисперсия известна
5.1. Если генеральная дисперсия известна 4. Корреляционная зависимость и причинно-следственная связь и итоги по главе
4. Корреляционная зависимость и причинно-следственная связь и итоги по главе Но область статистики касается не только данных. Статистика — это весь процесс, связанный со сбором данных для ответов на вопросы о мире, в тех случаях, когда эти данные представляют собой числовые данные. Статистика для чайников предназначен для всех, кто хочет разобраться и оценить невероятное количество статистической информации, которая поступает к ним ежедневно. (Вы знаете, что это такое: диаграммы, графики, таблицы, а также заголовки, рассказывающие о результатах последнего опроса, опроса, эксперимента или другого научного исследования.) Эта книга вооружает вас способностью расшифровывать и принимать важные решения относительно статистические результаты, всегда осознавая, как люди могут ввести вас в заблуждение статистикой. Получите внутреннюю информацию о нюансах обработки чисел, а также о том, как вы можете
Но область статистики касается не только данных. Статистика — это весь процесс, связанный со сбором данных для ответов на вопросы о мире, в тех случаях, когда эти данные представляют собой числовые данные. Статистика для чайников предназначен для всех, кто хочет разобраться и оценить невероятное количество статистической информации, которая поступает к ним ежедневно. (Вы знаете, что это такое: диаграммы, графики, таблицы, а также заголовки, рассказывающие о результатах последнего опроса, опроса, эксперимента или другого научного исследования.) Эта книга вооружает вас способностью расшифровывать и принимать важные решения относительно статистические результаты, всегда осознавая, как люди могут ввести вас в заблуждение статистикой. Получите внутреннюю информацию о нюансах обработки чисел, а также о том, как вы можете Статистика для чайников отличается от традиционных статистических текстов, справочников, дополнительных книг и учебных пособий следующим образом:
Статистика для чайников отличается от традиционных статистических текстов, справочников, дополнительных книг и учебных пособий следующим образом: Wat cijfertjes над mijn leesgedrag:
Wat cijfertjes над mijn leesgedrag:
 Все действительно начинает обретать смысл, когда я читаю эту книгу.
Все действительно начинает обретать смысл, когда я читаю эту книгу. Статистика требует времени!
Статистика требует времени!  Se trata де уна recopilacion де концепции, формулы у ejemplos sobre estadística descriptiva e inferencia estadística básicas. Adaptando аль currículo escolar español, cubre todas las materias de la educación secundaria (ESO y Bach) и incluso parte de algunas materias universitarias de introducción.
Se trata де уна recopilacion де концепции, формулы у ejemplos sobre estadística descriptiva e inferencia estadística básicas. Adaptando аль currículo escolar español, cubre todas las materias de la educación secundaria (ESO y Bach) и incluso parte de algunas materias universitarias de introducción. Включите повторение ejemplos. Eso Hace Que Si Lees Solo Capítulos sueltos, о salteados, не pierdas nada de información, pero Hace Que leerlo todo seguido acabe resultante cargante hasta el extremo.
Включите повторение ejemplos. Eso Hace Que Si Lees Solo Capítulos sueltos, о salteados, не pierdas nada de información, pero Hace Que leerlo todo seguido acabe resultante cargante hasta el extremo. Para ello, parte casi de cero, y puede ser leído por quien no tenga casi experiencia anterior con la estadística más allá de esa información diaria con la que se nos bombardea.
Para ello, parte casi de cero, y puede ser leído por quien no tenga casi experiencia anterior con la estadística más allá de esa información diaria con la que se nos bombardea. Stellenweise ein wenig zu viel Повторение, während an andren Orten ein wenig detaillierter auf die Konzepte eingegangen werden könnte. Alles in allem gut geeignet für alle die eine Auffrischung in Sachen Statistik oder eine erste Einführung benötigen.
Stellenweise ein wenig zu viel Повторение, während an andren Orten ein wenig detaillierter auf die Konzepte eingegangen werden könnte. Alles in allem gut geeignet für alle die eine Auffrischung in Sachen Statistik oder eine erste Einführung benötigen.
 Muy recomendable para aquellos Que necesitan «masticar» más las definiciones.
Muy recomendable para aquellos Que necesitan «masticar» más las definiciones.





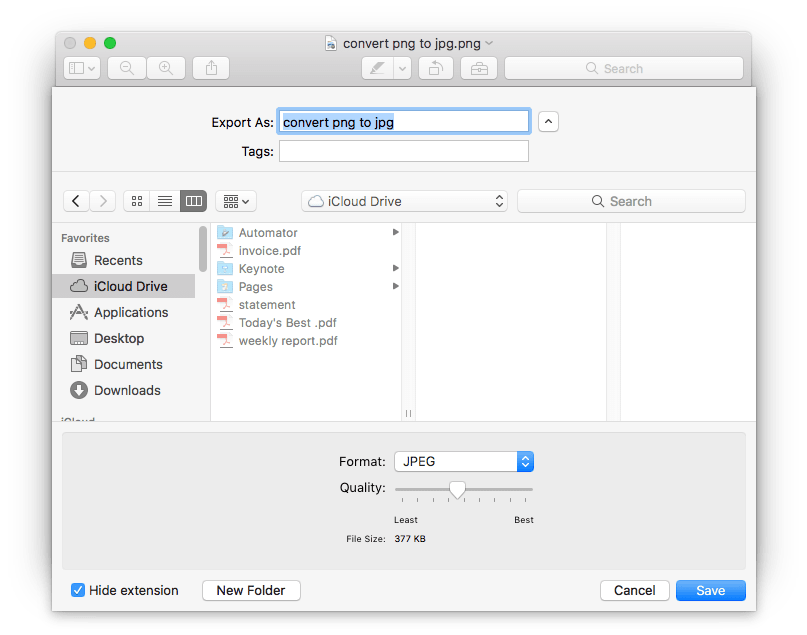
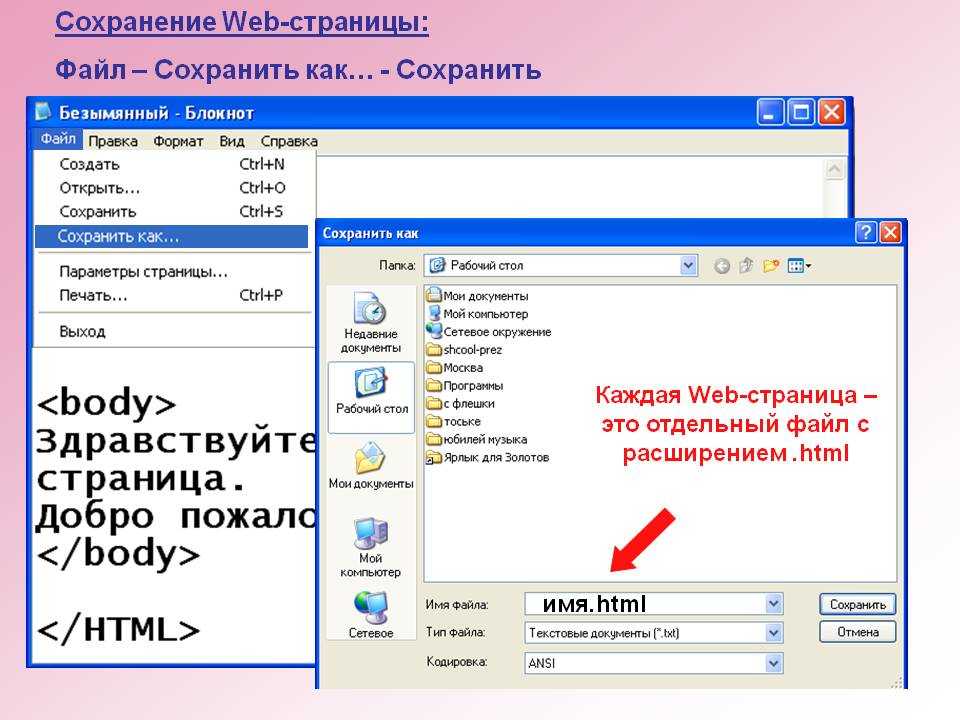
 Вы получите выходные файлы Джипег одним кликом мыши.
Вы получите выходные файлы Джипег одним кликом мыши.





 Именно это обозначение позволяет нам правильно обращаться с ними и использовать их. Можете ли вы представить, что произойдет, если вы получите PDF-файл от своего друга, но не сможете его открыть, потому что ваш читатель не распознал его? Вы бы сразу пришли к выводу, что на самом деле это не PDF-документ. Потому что программа для чтения PDF-файлов может открыть любой PDF-файл. В этом случае, даже если бы это был настоящий PDF-файл, вы все равно не смогли бы его открыть, если бы он не был помечен должным образом. И это то, что делает формат файла. Это обеспечивает плавный переход файлов и обработку между двумя сторонами.
Именно это обозначение позволяет нам правильно обращаться с ними и использовать их. Можете ли вы представить, что произойдет, если вы получите PDF-файл от своего друга, но не сможете его открыть, потому что ваш читатель не распознал его? Вы бы сразу пришли к выводу, что на самом деле это не PDF-документ. Потому что программа для чтения PDF-файлов может открыть любой PDF-файл. В этом случае, даже если бы это был настоящий PDF-файл, вы все равно не смогли бы его открыть, если бы он не был помечен должным образом. И это то, что делает формат файла. Это обеспечивает плавный переход файлов и обработку между двумя сторонами.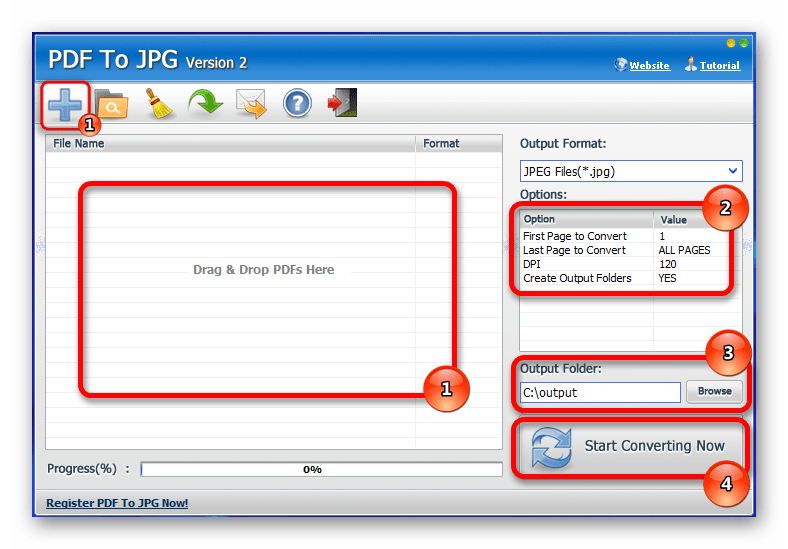 Эти файлы хранятся в легком и удобном для перемещения формате, поскольку они обычно содержат важную информацию. Вы никогда не захотите, чтобы файл с ценной информацией застрял во время загрузки или скачивания.
Эти файлы хранятся в легком и удобном для перемещения формате, поскольку они обычно содержат важную информацию. Вы никогда не захотите, чтобы файл с ценной информацией застрял во время загрузки или скачивания.
 Разные веб-сайты требуют разной информации и, следовательно, разных форматов изображений. Вы хотите иметь возможность конвертировать PNG в JPG бесплатно, чтобы ваши изображения могли соответствовать любым вещам, которые вам нужно делать в Интернете.
Разные веб-сайты требуют разной информации и, следовательно, разных форматов изображений. Вы хотите иметь возможность конвертировать PNG в JPG бесплатно, чтобы ваши изображения могли соответствовать любым вещам, которые вам нужно делать в Интернете.  Прежде всего, вам больше никогда не придется беспокоиться о том, что ваши изображения будут иметь какие-либо проблемы с совместимостью в Интернете. Вы можете просто перейти на веб-страницу инструмента и преобразовать свое изображение. См. пошаговое руководство ниже, чтобы узнать, как использовать инструмент
Прежде всего, вам больше никогда не придется беспокоиться о том, что ваши изображения будут иметь какие-либо проблемы с совместимостью в Интернете. Вы можете просто перейти на веб-страницу инструмента и преобразовать свое изображение. См. пошаговое руководство ниже, чтобы узнать, как использовать инструмент Здесь у вас есть три варианта. Либо загрузите из хранилища вашего устройства, либо загрузите с Google Диска, либо загрузите из Dropbox. Чтобы загрузить из своего хранилища, нажмите «Загрузить» и перейдите к файлу. Процедуры загрузки с Google Диска и Dropbox очень похожи.
Здесь у вас есть три варианта. Либо загрузите из хранилища вашего устройства, либо загрузите с Google Диска, либо загрузите из Dropbox. Чтобы загрузить из своего хранилища, нажмите «Загрузить» и перейдите к файлу. Процедуры загрузки с Google Диска и Dropbox очень похожи.






 Правильные ответы для сверки с учащимися отражаются на проекторе.
Правильные ответы для сверки с учащимися отражаются на проекторе. Итог урока
Итог урока Для этого первую дробь переписываем без изменений и умножаем на перевернутую вторую. Сокращаем 18 и 36 на 18, 35 и 7 — на 7. В результате — неправильная дробь. Выделяем из нее целую часть.
Для этого первую дробь переписываем без изменений и умножаем на перевернутую вторую. Сокращаем 18 и 36 на 18, 35 и 7 — на 7. В результате — неправильная дробь. Выделяем из нее целую часть.
 Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Если получится сократить дробь, то вам легче будет дальше производить расчеты.
 Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.




 Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].
Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].

 Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:
Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:


 Все преобразования html в pdf происходят в облаке и не используют какие-либо ресурсы вашего компьютера.
Все преобразования html в pdf происходят в облаке и не используют какие-либо ресурсы вашего компьютера. Поэтому может возникнуть необходимость конвертировать HTML в PDF, чтобы вы могли собирать информацию для будущих ссылок. Это связано с тем, что формат PDF позволяет вам организовать весь контент, который вы собираете, что упрощает организацию информации в исследовательской статье или проекте компании.
Поэтому может возникнуть необходимость конвертировать HTML в PDF, чтобы вы могли собирать информацию для будущих ссылок. Это связано с тем, что формат PDF позволяет вам организовать весь контент, который вы собираете, что упрощает организацию информации в исследовательской статье или проекте компании. 


 Преобразование HTML в PDF позволяет предприятиям автоматически генерировать множество пользовательских сообщений. В этом нуждаются все, кто предлагает услуги через веб-порталы. Преобразование создает аккуратные копии страниц веб-браузера в формате PDF для удобного просмотра или загрузки.
Преобразование HTML в PDF позволяет предприятиям автоматически генерировать множество пользовательских сообщений. В этом нуждаются все, кто предлагает услуги через веб-порталы. Преобразование создает аккуратные копии страниц веб-браузера в формате PDF для удобного просмотра или загрузки. 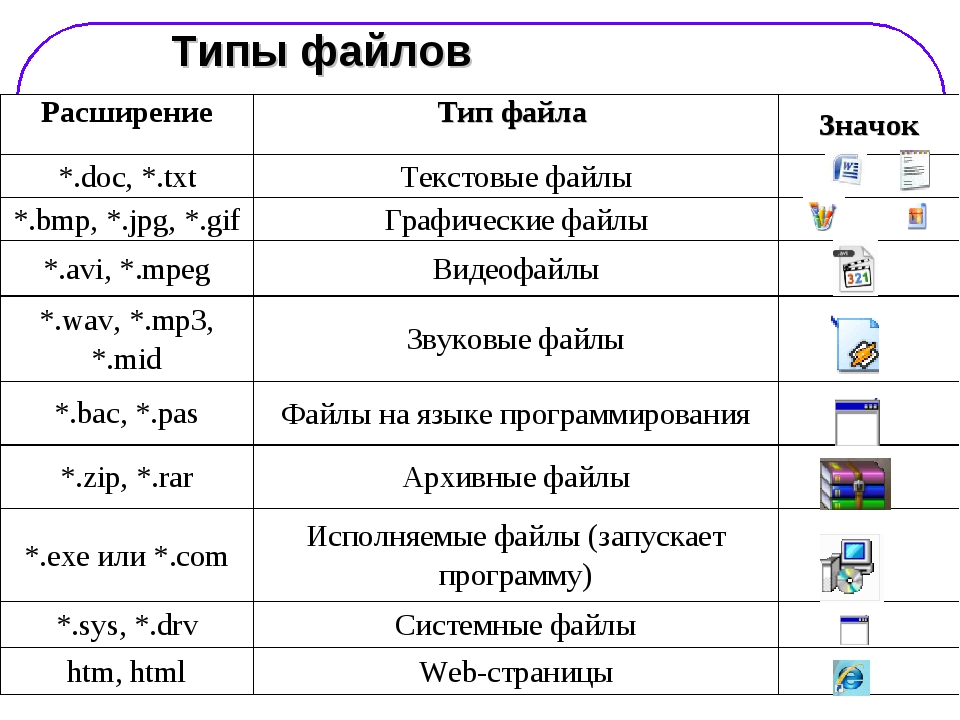 Они должны сохранять PDF как файлы HTML, преобразовывать таблицы HTML в CSV, преобразовывать Word в PDF и выполнять множество других преобразований. Эти преобразования позволяют компаниям унифицировать собранную информацию и передавать данные между программами.
Они должны сохранять PDF как файлы HTML, преобразовывать таблицы HTML в CSV, преобразовывать Word в PDF и выполнять множество других преобразований. Эти преобразования позволяют компаниям унифицировать собранную информацию и передавать данные между программами.  Тем не менее, если вам нужно автоматически отображать тонны файлов, вам нужно будет настроить автоматическую визуализацию и подготовить исходный код HTML. Узнайте больше о том, как это сделать ниже.
Тем не менее, если вам нужно автоматически отображать тонны файлов, вам нужно будет настроить автоматическую визуализацию и подготовить исходный код HTML. Узнайте больше о том, как это сделать ниже. 
 Эти советы должны помочь вам провести конвертацию гладко.
Эти советы должны помочь вам провести конвертацию гладко.  Поэтому, прежде чем запускать конвертацию, просмотрите HTML-теги. Это сводит к минимуму вероятность ошибок в конечном файле.
Поэтому, прежде чем запускать конвертацию, просмотрите HTML-теги. Это сводит к минимуму вероятность ошибок в конечном файле.
 Он позволяет сделать преобразование HTML в PDF частью сложных программных операций, таких как создание и хранение счетов. Веб-решения, основанные на API, автоматически обрабатывают тысячи счетов с максимальной легкостью.
Он позволяет сделать преобразование HTML в PDF частью сложных программных операций, таких как создание и хранение счетов. Веб-решения, основанные на API, автоматически обрабатывают тысячи счетов с максимальной легкостью. 
 Программы таких быдлокодеров никогда не бывают кроссплатформенными и редко бывают стабильными, а любимыми высокоуровневыми языками являются те, которые и позволяют писать нечитаемый код. Их девиз: «Пишу как хочу, преобразовываю во что хочу, вызываю как мне нравится, имею право на запуск ошибочного кода и только тот язык мне друг, чья парадигма это позволяет». Это породило в начале 70-х феномен жопоязыка, код на котором, даже написанный прыганием жопой по клавиатуре, компилируется и запускается. И этот феномен к несчастью становится стандартом де-факто в сегодняшнем программировании из-за превалирования быдлокодеров, у которых на хоть что-то математическое (читайте структурированное, строгое, однозначное, чёткое, наглядное, лаконичное и логичное) начинается приступ тошноты. И это неудивительно. У класса быдла, наследником которого является класс быдлокодеров, всё, что построено по чётким правилам, что предъявляет строгие требования к чему-либо, что сковывает свободу во имя порядка и правильного функционирования чего-либо, что учит хорошим манерам (стилю), является неприемлемым, недопустимым и уродливым, и только их хаос и анархия есть гармония.
Программы таких быдлокодеров никогда не бывают кроссплатформенными и редко бывают стабильными, а любимыми высокоуровневыми языками являются те, которые и позволяют писать нечитаемый код. Их девиз: «Пишу как хочу, преобразовываю во что хочу, вызываю как мне нравится, имею право на запуск ошибочного кода и только тот язык мне друг, чья парадигма это позволяет». Это породило в начале 70-х феномен жопоязыка, код на котором, даже написанный прыганием жопой по клавиатуре, компилируется и запускается. И этот феномен к несчастью становится стандартом де-факто в сегодняшнем программировании из-за превалирования быдлокодеров, у которых на хоть что-то математическое (читайте структурированное, строгое, однозначное, чёткое, наглядное, лаконичное и логичное) начинается приступ тошноты. И это неудивительно. У класса быдла, наследником которого является класс быдлокодеров, всё, что построено по чётким правилам, что предъявляет строгие требования к чему-либо, что сковывает свободу во имя порядка и правильного функционирования чего-либо, что учит хорошим манерам (стилю), является неприемлемым, недопустимым и уродливым, и только их хаос и анархия есть гармония. Стоит обратить внимание, что (чуть меньше, чем все) быдлокодеры избегают использования форматирования кода (что, к примеру, вынудило компанию Microsoft разработать средства принудительного форматирования Visual Basic-кода).
Стоит обратить внимание, что (чуть меньше, чем все) быдлокодеры избегают использования форматирования кода (что, к примеру, вынудило компанию Microsoft разработать средства принудительного форматирования Visual Basic-кода). В доказательство демонстрирует всем вакансию с какого-нибудь хедхантерского сайта, абсолютно не соответствующую его компетенциям и навыкам;
В доказательство демонстрирует всем вакансию с какого-нибудь хедхантерского сайта, абсолютно не соответствующую его компетенциям и навыкам; Схватки быдлокодеров по весне представляют собой интересное зрелище.
Схватки быдлокодеров по весне представляют собой интересное зрелище. .. Но проблема в факте, что официальная наука априори приняла закон не рассматривать вечные двигатели потому, что они «невозможны потому что невозможны»..
.. Но проблема в факте, что официальная наука априори приняла закон не рассматривать вечные двигатели потому, что они «невозможны потому что невозможны».. В то же самое время, когда другие грызут SQL и многопоточность, эти обсуждают «заработок в интернете» и прочую «коммерцию».
В то же самое время, когда другие грызут SQL и многопоточность, эти обсуждают «заработок в интернете» и прочую «коммерцию». Быдлоскрипты могут выдавать аццкие глюки, по дизайну чаще напоминают merde, иногда всплывает ощущение, что быдлокодер здорово нажрался, когда писал этот скрипт.
Быдлоскрипты могут выдавать аццкие глюки, по дизайну чаще напоминают merde, иногда всплывает ощущение, что быдлокодер здорово нажрался, когда писал этот скрипт.
 моделирования и теории графов. А если ты, школьник, хочешь написать свой Фоллавут онлине в полном Тридэ, то тебе совершенно точно понадобятся знания матричной (и векторной, как частный случай) алгебры и аналитической геометрии (для трехмерного движка — даже если ты берешь уже готовый, все равно оперировать с векторами и матрицами придется чуть реже, чем всегда), теоретической механики и дифференциальной геометрии (это если ты планируешь, чтобы твои болванчики перемещались поразнообразнее, чем по прямой). А ты думал, что преподавателям скучно дома, и они решили тебя помучить бесполезными науками за государственный счет?
моделирования и теории графов. А если ты, школьник, хочешь написать свой Фоллавут онлине в полном Тридэ, то тебе совершенно точно понадобятся знания матричной (и векторной, как частный случай) алгебры и аналитической геометрии (для трехмерного движка — даже если ты берешь уже готовый, все равно оперировать с векторами и матрицами придется чуть реже, чем всегда), теоретической механики и дифференциальной геометрии (это если ты планируешь, чтобы твои болванчики перемещались поразнообразнее, чем по прямой). А ты думал, что преподавателям скучно дома, и они решили тебя помучить бесполезными науками за государственный счет? Но примеры обратного достаточно редки. В любом случае, если нет соответствующего раздела в мозге, абстрактное мышление не разовьёт даже матан. Правда, он позволяет произвести начальный отсев и отправить несостоявшегося быдлокодера учить другие подходящие вещи или более гуманитарные науки.
Но примеры обратного достаточно редки. В любом случае, если нет соответствующего раздела в мозге, абстрактное мышление не разовьёт даже матан. Правда, он позволяет произвести начальный отсев и отправить несостоявшегося быдлокодера учить другие подходящие вещи или более гуманитарные науки.
 С течением времени это ваше фидо постепенно самовыпиливалось, а интернеты прогрессировали — быдло набигало. И срач приобрел более современную форму: Delphi vs. C++. Причём основная масса дерьма (если не вся), генерируемая срачем Delphi vs. C++, обрушивается на Delphi. Исходя из этого, а также того, что дерьмо в процессе подобных срачев способны генерировать только быдлокодеры, можно понять, во что воплотился идеал быдлокодерского языка.
С течением времени это ваше фидо постепенно самовыпиливалось, а интернеты прогрессировали — быдло набигало. И срач приобрел более современную форму: Delphi vs. C++. Причём основная масса дерьма (если не вся), генерируемая срачем Delphi vs. C++, обрушивается на Delphi. Исходя из этого, а также того, что дерьмо в процессе подобных срачев способны генерировать только быдлокодеры, можно понять, во что воплотился идеал быдлокодерского языка. 0 и Турбо Паскаль 6.0 четырьмя разными языками или их всего 2 (или 3). Быдлокодеры считают, что добавление объектов создаёт принципиально новый язык. Другие быдлокодеры возражают, что нет. С и С++ всё-таки отличаются (правда полутора операторами) даже без использования объектов. Однако чуть менее, чем все быдлокодеры, говоря о прелестях «чистого С», имеют ввиду, естественно, не эти различия, а именно использование объектов.
0 и Турбо Паскаль 6.0 четырьмя разными языками или их всего 2 (или 3). Быдлокодеры считают, что добавление объектов создаёт принципиально новый язык. Другие быдлокодеры возражают, что нет. С и С++ всё-таки отличаются (правда полутора операторами) даже без использования объектов. Однако чуть менее, чем все быдлокодеры, говоря о прелестях «чистого С», имеют ввиду, естественно, не эти различия, а именно использование объектов.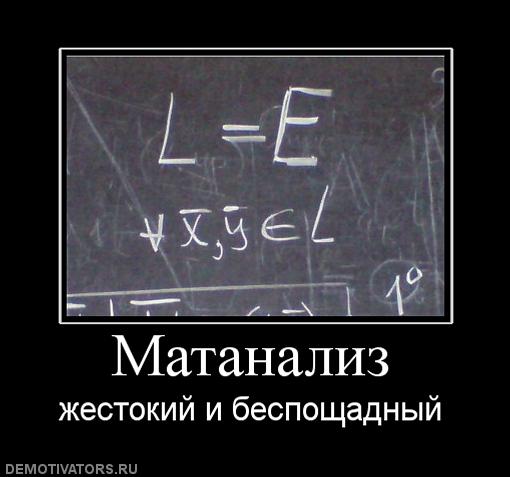 Причём к примеру boost.regex я прикрутил к одному Билдеровскому проекту. Ещё раз насчёт недоученности, у меня универ был лажовый, группа 17 человек, из них я один программист, остальные и рядом не валялись. Я вообще программирую не благодаря, а вопреки университету. Никаким из своих навыков программирования, я универу не обязан. Разве что может основы UML там узнал. Всё остальное самообучение. Результаты неплохие, но есть к чему стремиться. НО МЛЯ НА ЭТОМ ФОРУМЕ ЗАКОЛЕБАЛИ УЖЕ ВСЯКИЕ ОНАНИЗМУСЫ МЕНЯ ОСКОРБЛЯТЬ!!! Чем я показал какую-то недоученность и ущербность? Я справляюсь с работой, и дома программирую из личного желания, в чём я не прав то опять? Короче, смотался отсюда, му**ло, ты запарил уже!
Причём к примеру boost.regex я прикрутил к одному Билдеровскому проекту. Ещё раз насчёт недоученности, у меня универ был лажовый, группа 17 человек, из них я один программист, остальные и рядом не валялись. Я вообще программирую не благодаря, а вопреки университету. Никаким из своих навыков программирования, я универу не обязан. Разве что может основы UML там узнал. Всё остальное самообучение. Результаты неплохие, но есть к чему стремиться. НО МЛЯ НА ЭТОМ ФОРУМЕ ЗАКОЛЕБАЛИ УЖЕ ВСЯКИЕ ОНАНИЗМУСЫ МЕНЯ ОСКОРБЛЯТЬ!!! Чем я показал какую-то недоученность и ущербность? Я справляюсь с работой, и дома программирую из личного желания, в чём я не прав то опять? Короче, смотался отсюда, му**ло, ты запарил уже! Тем более когда под рукой интернетов йок, за каждой хреновиной чеши в библиотеку, а там очередь и чтоб сдать книгу обратно до восхода солнца. иначе линчуют такие же ушлепки как ты. Быдлокодерство, к сожалению, это не цель а средство. Как только писание строчечек когда исчисляется не количеством и не качеством, а потраченным временеи и соответствующей оплатой последнего, фигушки позадрачиваешься. Помню дали заданьице — до конца НЕДЕЛИ — был вторник — отсканировать, внести в базу и написать часть поиска (по заглавию хотя бы) триста газетных статей из газетных же архивов. То есть на все про все — включая OCR и физическое перетаскивание хреновин с газетными вырезками из подвала наверх — меньше чем пять дней. нормально. Хорошо хоть уже инет был и интерфейсы можно было делать в дельфи, правда в самой первой версии со всякими тараканами и без поддержки локального алфавита (самой пришлось писать коробочки с праволевной ориентацией и поддержку иврита мать их). Да-да, там вдобавок на иврите все было.
Тем более когда под рукой интернетов йок, за каждой хреновиной чеши в библиотеку, а там очередь и чтоб сдать книгу обратно до восхода солнца. иначе линчуют такие же ушлепки как ты. Быдлокодерство, к сожалению, это не цель а средство. Как только писание строчечек когда исчисляется не количеством и не качеством, а потраченным временеи и соответствующей оплатой последнего, фигушки позадрачиваешься. Помню дали заданьице — до конца НЕДЕЛИ — был вторник — отсканировать, внести в базу и написать часть поиска (по заглавию хотя бы) триста газетных статей из газетных же архивов. То есть на все про все — включая OCR и физическое перетаскивание хреновин с газетными вырезками из подвала наверх — меньше чем пять дней. нормально. Хорошо хоть уже инет был и интерфейсы можно было делать в дельфи, правда в самой первой версии со всякими тараканами и без поддержки локального алфавита (самой пришлось писать коробочки с праволевной ориентацией и поддержку иврита мать их). Да-да, там вдобавок на иврите все было. Ну так вот пять дней. С ограниченным доступом в инет — два часа за рабочий день, пока выделенку не дали нам. Тут уже не нашлифуешься, работает — и хрен с ней, а память пусть сами докупают если такие нетерпеливые. Вот так и появляется быдлокод, даже в такой херне как базы данных. Хотя знание определенных правил очень помогает, все равно наизобретаешь велосипедов. А им боссам тоже похуй, лишь бы своему можно было отчитаться — мол дедлайн вытянули, на отладку время не дают, сразу новый проект. Это хорошо когда бородатые дяти пишут. но бородатые дяди и берут хорошо, а сопляков можно за копейки гонять. Такая философия и рождает быдлокодеров. Гораздо быстрее чем просто глупость и амбиции тех кто программировать толком не научился. Как-то так.
Ну так вот пять дней. С ограниченным доступом в инет — два часа за рабочий день, пока выделенку не дали нам. Тут уже не нашлифуешься, работает — и хрен с ней, а память пусть сами докупают если такие нетерпеливые. Вот так и появляется быдлокод, даже в такой херне как базы данных. Хотя знание определенных правил очень помогает, все равно наизобретаешь велосипедов. А им боссам тоже похуй, лишь бы своему можно было отчитаться — мол дедлайн вытянули, на отладку время не дают, сразу новый проект. Это хорошо когда бородатые дяти пишут. но бородатые дяди и берут хорошо, а сопляков можно за копейки гонять. Такая философия и рождает быдлокодеров. Гораздо быстрее чем просто глупость и амбиции тех кто программировать толком не научился. Как-то так.
 Не взлетел из-за закрытия самого Бурана-Энергии (спойлер: да и Шаттлов тоже).
Не взлетел из-за закрытия самого Бурана-Энергии (спойлер: да и Шаттлов тоже). ru/%D5%E0%F1%F2%EB
ru/%D5%E0%F1%F2%EB В отличие от спортиков, социальщик практически никогда не принимает участие в конкурсах, мотивируя это тем, что «времени нет», «мне это не нужно», «Конкурсы — херня» и тому подобные отговорки, хотя на самом деле,
В отличие от спортиков, социальщик практически никогда не принимает участие в конкурсах, мотивируя это тем, что «времени нет», «мне это не нужно», «Конкурсы — херня» и тому подобные отговорки, хотя на самом деле, Спортсмены вмешиваются в спор, если социальщик пишет откровенную хуиту. Почти всегда остаются неуслышанными, несмотря на то, что в сабже разбираются гораздо лучше.
Спортсмены вмешиваются в спор, если социальщик пишет откровенную хуиту. Почти всегда остаются неуслышанными, несмотря на то, что в сабже разбираются гораздо лучше. Своего партнера, с которым занимается в студии, считает долбоебом и танцевальным импотентом, в силу чего на дискотеках с чужими партнерами танцует чаще, чем со своим. Может не подозревать, что более профессиональные танцоры танцуют с ней только из-за того, что у нее длинные ноги, подтянутая жопа и смазливое личико, и им просто не с кем танцевать.
Своего партнера, с которым занимается в студии, считает долбоебом и танцевальным импотентом, в силу чего на дискотеках с чужими партнерами танцует чаще, чем со своим. Может не подозревать, что более профессиональные танцоры танцуют с ней только из-за того, что у нее длинные ноги, подтянутая жопа и смазливое личико, и им просто не с кем танцевать. ..
.. Эта фраза часто используется как уничижительный эвфемизм для информирования пользователей о том, что они не нужны/не приветствуются, но также может использоваться в качестве законного совета для новых пользователей. Раньше для передачи того же сообщения использовалась аббревиатура RTFM.
Эта фраза часто используется как уничижительный эвфемизм для информирования пользователей о том, что они не нужны/не приветствуются, но также может использоваться в качестве законного совета для новых пользователей. Раньше для передачи того же сообщения использовалась аббревиатура RTFM. Чтобы помочь пользователям справиться с противоречивым контентом, таким как троллинг, 4chan советует им «спрятаться» перед публикацией. Когда кому-то не удавалось выполнить это требование, его замечания и мнения часто встречались с командой: «Спрячьтесь, Моар, ньюфаг».
Чтобы помочь пользователям справиться с противоречивым контентом, таким как троллинг, 4chan советует им «спрятаться» перед публикацией. Когда кому-то не удавалось выполнить это требование, его замечания и мнения часто встречались с командой: «Спрячьтесь, Моар, ньюфаг».




 Реформа просто расширит эту структуру и позволит большему количеству компаний выдавать сертификаты кошерности.
Реформа просто расширит эту структуру и позволит большему количеству компаний выдавать сертификаты кошерности.


 Таким образом, реформы Каханы складываются к современной православной контратаке в борьбе за власть и войне идей, которые бушуют уже более 120 лет.
Таким образом, реформы Каханы складываются к современной православной контратаке в борьбе за власть и войне идей, которые бушуют уже более 120 лет.
 Профессионально-общественная аккредитация
Профессионально-общественная аккредитация Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав 1 «Два набора данных» и графическое представление каждого из них, называемое точечным графиком , на рисунке 2.10 «Точечные графики наборов данных».
1 «Два набора данных» и графическое представление каждого из них, называемое точечным графиком , на рисунке 2.10 «Точечные графики наборов данных». набора данных — это число R , определенное по формуле
набора данных — это число R , определенное по формуле  , перепись).
, перепись). 1 «Два набора данных».
1 «Два набора данных». 12 «Пример 3» в разделе 2.2 «Показатели центрального местоположения».
12 «Пример 3» в разделе 2.2 «Показатели центрального местоположения».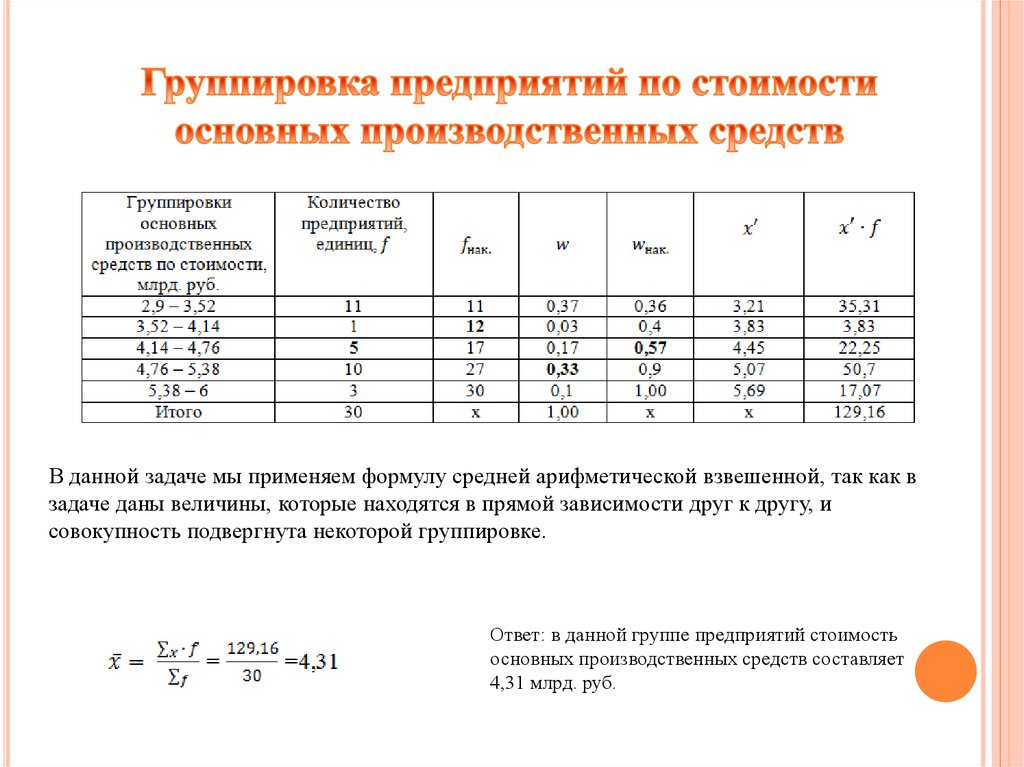



 Данные сгруппированы на показанной диаграмме стебля и листа. (Стебли стоят тысячи долларов, листья — сотни, так что, например, самое большое наблюдение — 3800.)
Данные сгруппированы на показанной диаграмме стебля и листа. (Стебли стоят тысячи долларов, листья — сотни, так что, например, самое большое наблюдение — 3800.)






 Кроме того, мы предоставим вам практические задачи, чтобы вы могли усовершенствовать или освежить свои знания по этим 9 упражнениям.0055 мощные меры изменчивости. В других разделах этого руководства по описательной статистике вы узнаете, как эти меры применяются на более сложном уровне, например, как интерпретировать каждую меру и в каких ситуациях следует использовать дисперсию вместо стандартного отклонения.
Кроме того, мы предоставим вам практические задачи, чтобы вы могли усовершенствовать или освежить свои знания по этим 9 упражнениям.0055 мощные меры изменчивости. В других разделах этого руководства по описательной статистике вы узнаете, как эти меры применяются на более сложном уровне, например, как интерпретировать каждую меру и в каких ситуациях следует использовать дисперсию вместо стандартного отклонения.

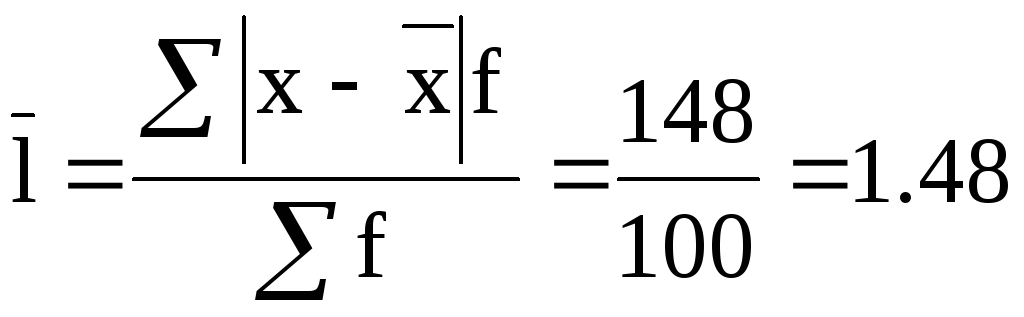
 Эта разница возводится в квадрат для работы с отрицательными значениями. Если бы мы оставили эти отрицательные значения, сумма разницы была бы недооценена. Например, предположим, что у вас есть среднее значение 50 и точка данных 4, что даст разностное значение -46. Здесь важна величина этой разницы, а не положительная она или отрицательная. Однако, если мы сохраняем отрицательный знак, это искусственно занижает сумму. Возведение в квадрат — это простой способ работы с отрицательными числами в целом.
Эта разница возводится в квадрат для работы с отрицательными значениями. Если бы мы оставили эти отрицательные значения, сумма разницы была бы недооценена. Например, предположим, что у вас есть среднее значение 50 и точка данных 4, что даст разностное значение -46. Здесь важна величина этой разницы, а не положительная она или отрицательная. Однако, если мы сохраняем отрицательный знак, это искусственно занижает сумму. Возведение в квадрат — это простой способ работы с отрицательными числами в целом.
 Хотя полезно думать о вариации как о среднем расстоянии каждой точки данных от среднего, вы должны помнить, что вы не только делите сумму разностей на n — 1, а не только на n, но также и то, что сумма разностей равна в квадратных единицах. Это означает, что дисперсия также выражается в квадратах. В буквальном переводе из приведенного выше примера дисперсия сигнализирует о приблизительной квадратичной разнице в 118,7 на точку данных.
Хотя полезно думать о вариации как о среднем расстоянии каждой точки данных от среднего, вы должны помнить, что вы не только делите сумму разностей на n — 1, а не только на n, но также и то, что сумма разностей равна в квадратных единицах. Это означает, что дисперсия также выражается в квадратах. В буквальном переводе из приведенного выше примера дисперсия сигнализирует о приблизительной квадратичной разнице в 118,7 на точку данных.

 Найдите периметр правильного шестиугольника описанного около той же окружности.
Найдите периметр правильного шестиугольника описанного около той же окружности. Поэтому важно знать угол между ними.
Поэтому важно знать угол между ними.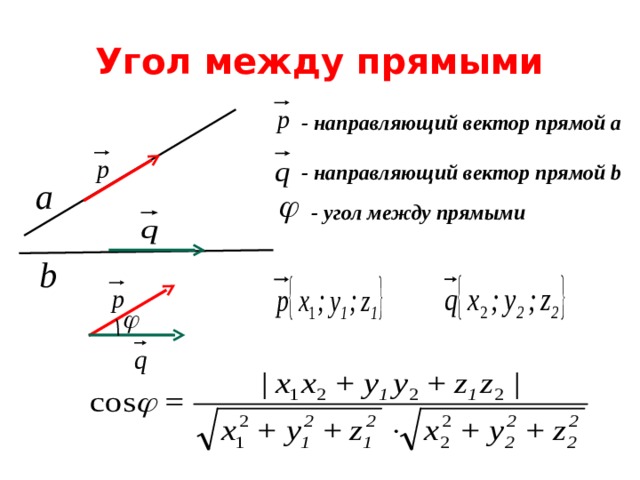

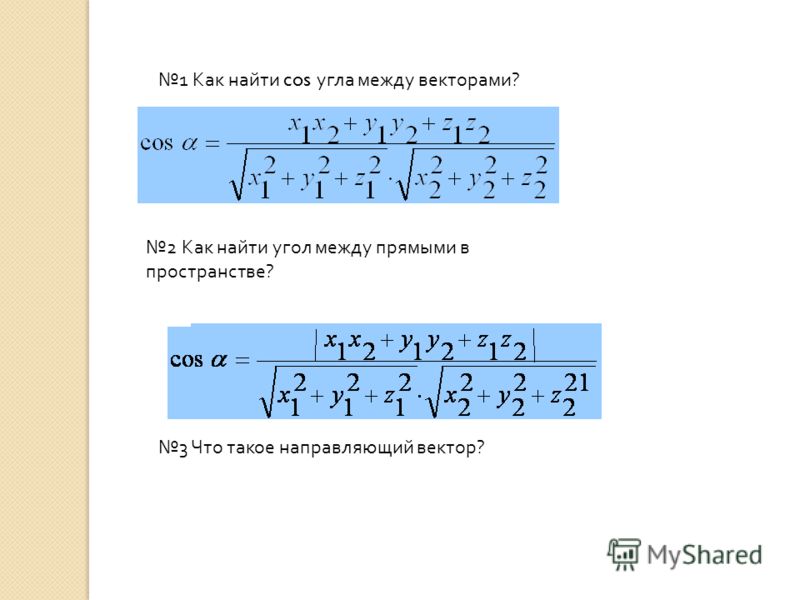



 Найдите скалярное произведение двух векторов
Найдите скалярное произведение двух векторов 
 Величина вектора |a|=√ ( a x 2 + a y 2
Величина вектора |a|=√ ( a x 2 + a y 2 

 Если значение cosθ отрицательно, угол между векторами тупой.
Если значение cosθ отрицательно, угол между векторами тупой. 
 Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби.
Принято только указывать дополнительный множитель за скобочкой чуть правее и выше исходной дроби. е. найти для каждой дроби дополнительный множитель.
е. найти для каждой дроби дополнительный множитель.  Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Выпишем разложение числа 60 и добавим недостающие множители 2 и 7 из второго разложения. Умножим 60 на 14 и получим общий знаменатель 840. Дополнительный множитель для первой дроби — это 14. Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840. 1.2. данного урока.
1.2. данного урока.
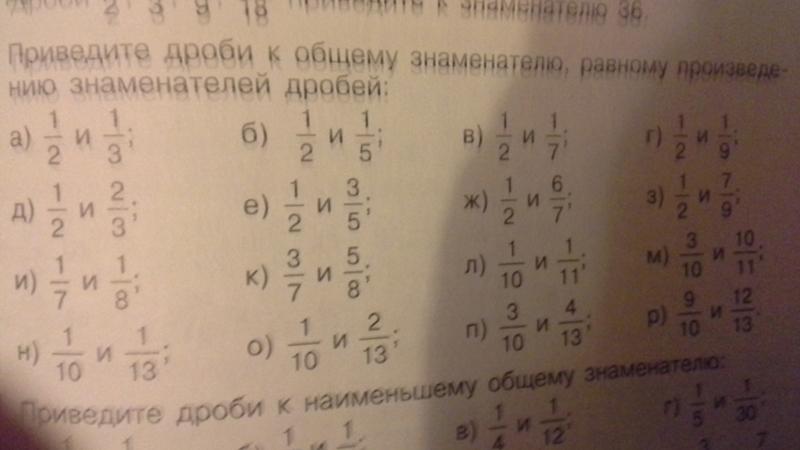 Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.


 Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
Дадим определение понятию наименьший общий знаменатель (НОЗ) и решим ряд задач на его нахождение.
 Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
Для простоты дроби приводят к наименьшему общему знаменателю. Он равен наименьшему общему кратному знаменателей данных дробей.
 Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840.
Дополнительный множитель для второй дроби — 5. Приведем дроби к общему знаменателю 840. 1.2)
1.2)

 После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач.
После этого сформулируем основное правило приведения дробей к новым знаменателям и проиллюстрируем его примерами задач. Считаем: 11 · 4 = 44 и 25 · 4 = 100 . В итоге получилась дробь 44 100 .
Считаем: 11 · 4 = 44 и 25 · 4 = 100 . В итоге получилась дробь 44 100 .


 Маршрут 80 отправляется каждые 30 минут, маршрут 81 — каждые 20 минут, а маршрут 82 — каждые 40 минут. Во сколько они снова уйдут?
Маршрут 80 отправляется каждые 30 минут, маршрут 81 — каждые 20 минут, а маршрут 82 — каждые 40 минут. Во сколько они снова уйдут? Сколько раз автобус встречается в 18:00 по местному времени?
Сколько раз автобус встречается в 18:00 по местному времени?