Уравнения с модулями 6 класс :: mymalama
17.12.2021 02:59
Автор: Голованов А. С. Упорядочивание по возрастанию убыванию. Уравнения, задачи и примеры с модулями. Система линейных уравнений с. Математика 1 класс.13 3 Модуль Уравнения и неравенства с модулем: 9:. Тип урока: Урок обобщения понятия модуль с элементами самостоятельной работы. Целевая аудитория: для 6 класса. Уравнения с модулем в 6 классе сводятся к простейшим уравнениям, решение которых опирается на определение модуля. Решение неравенств с модулями. ИЗУЧЕНИЕ.
МОДУЛЯ РАЦИОНАЛЬНОГО ЧИСЛА В 6 КЛАССЕ НА. Модуль и. Математика 1 класс. Математичний калькулятор. Решение уравнений с модулем 6 й класс. Как решать уравнения с модулем. Противоположные числа и модуль. Задачи в 6 классе. Третий интервал дает два корня, которые удовлетворяют исходное уравнение с модулями. Занятия по математике, русскому языку и литературе. Положительные и отрицательные числа. Сразу рассмотрим на примере решение уравнений. Уравнения с модулями. Модуль числа. Правила. Задания.
Решение уравнений с модулем 6 й класс. Как решать уравнения с модулем. Противоположные числа и модуль. Задачи в 6 классе. Третий интервал дает два корня, которые удовлетворяют исходное уравнение с модулями. Занятия по математике, русскому языку и литературе. Положительные и отрицательные числа. Сразу рассмотрим на примере решение уравнений. Уравнения с модулями. Модуль числа. Правила. Задания.
С проверкой ответов. Материалы предыдущего фестиваля. Система линейных уравнений с модулями. Квадратные уравнения и системы уравнений. Получили простейшее уравнение с модулем. Квадратные уравнения с параметрами.6 часов Целью данного курса является формирование целостной системы решения упражнений с модулями и параметрами, формированию навыков организации учащимися самостоятельных микроисследований. При изучении данной темы мы опираемся на общепринятое определение модуля числа: Решение уравнений с модулем в 6 классе. Уравнением.
С модулем абсолютной. Онлайн уроки для школьников с дистанционным репетитором через интернет. Решение уравнений с модулем. Математика 5 класса, повторение. Урок по математике для 6 класса. Определение модуля числа, примеры на модуль числа. Решить уравнение. Подготовка к контрольным, ЕГЭ. Форма заявки на участие. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен. Категория: Презентации по математике.
Решение уравнений с модулем. Математика 5 класса, повторение. Урок по математике для 6 класса. Определение модуля числа, примеры на модуль числа. Решить уравнение. Подготовка к контрольным, ЕГЭ. Форма заявки на участие. Понятно, что в этом случае уравнение не имеет решений, так как по определению модуль всегда неотрицателен. Категория: Презентации по математике.
Вместе с Уравнения с модулями 6 класс часто ищут
уравнения с модулем 7 класс
модульные уравнения 6 класс
решить уравнение с модулем онлайн калькулятор
модуль числа 6 класс виленкин
модуль числа 6 класс презентация
неравенства с модулем примеры
решение уравнений с модулем онлайн
квадратные уравнения с модулем
Читайте также:
Скачать тесты по окружающему миру о. т поглазова 3 класс
т поглазова 3 класс
Решебник гдз по учебнику обшествоведенье 11 класс
Задание по русскому языку на сегодня 3 класс 45 школа
Графический способ решения уравнений с модулем
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тема урока
Графический способрешения уравнений с модулем
Тема урока
2.
 Задай функцию формулой
Задай функцию формулой3. Задай функцию формулой
4. Задай функцию формулой
5. Задай функцию формулой
6. Задай функцию формулой
7. Задай функцию формулой
8. Задай функцию формулой
9. Задай функцию формулой
10. Задай функцию формулой
Выполнила ученица 10 «А»Засыпалова Анна
17. Правило построения графика функции y=f(|x|). :
1. Построим график функции y=f(x), для х≥02. Достроим левую часть графика, симметричную
построенной правой части относительно оси
ординат
18. 1.Построить график функции y=|x|
1.Построить график функцииПостроение:
1).
х
у
0
0
2
2
Строим график функции
y=x, х ≥0
2)Симметрично
отображаем
построенную часть
графика относительно
оси оу.
.
y=|x|
Y
y=|x|
X
20. 2. Построить график функции Y=|x|²-4|x|+3
2. Построить график функции+3
1)Строим
Y=|x|²-4|x|
Построение.

y=x²-4x+3,
х≥0
Y
Y=|x|²-4|x|+3
а)Хверш= -в/2а=-4/2=2
Уверш=2²-4·2+3=-1
(2;-1)-вершина параболы
б)Нули функции (точки пересечения с ох)
x²-4x+3=0
х1=1
х2=3
(1;0) (3;0) — точки пересечения графика с осью ох
в)Если х=0, то у=3
(0;3)
2).Симметрично отображаем построенную часть
графика относительно оси оу
X
21. 3. Построить график функции у = sin|x|
Y
•X
22. 4. Построить график функции y=cos|x|
YX
23. 5. Построить график функции y= cos|x|+2
5. Построить график функции y= cos|x|+2
Y
X
24. 6. Построить график функции у=3|х|+2
Построение.1)Cтроим график функции
у=3х+2, х≥0
х
у
0
2
Y
1
5
X
2).Симметрично
отобразим построенную
часть графика
относительно оси ох.
Y
у=3|х|+2
X
Выполнила: Кузьмина Валерия
ученица 10 «а» класса
27. Правило Построения графика функции y=|f(x)|
1. Построить график y=f(x)
Построить график y=f(x)2.Сохранить без изменения части графика
y=f(x), расположенные выше оси OX.
3.Отобразить симметрично оси OX части
графика y=f(x), расположенные ниже
оси OX.
y
2
-1
0
x
30. 2) Построить график функции Y=|X²-4x+3|. Построение.
y0
1
3
x
31. 3) Построить график функции y=|cosx| Построение.
3) Построить график функции y=|cosx|
Построение.
y
1
0
-1
x
32. 4)Построить график функции y=|sinx|-4 Построение.
y1
0
-1
-4
x
33. Решение уравнений, содержащих модуль
Решениеуравнений,
содержащих
Способы решения уравнений,
содержащих модуль
Использование
определения модуля
Графический способ
Метод введения
новой переменной
35. Графический способ
|х-2|=у
х
1. у =|х-2|
2. у =
0
1 2
4
х
Ответ: 1; 4.
х
36. Задания командам
Реши уравнение графическим способома) |x-1|=2;
б) x2 = |x|;
в)sin|x| = — х2;
г) |x-1|= |x|-1;
д) 3|x|=4 — х2 (МФТИ, 2000г)
е)|x2-3x|=2x-4 (МГУ, 2000г)
№/
Команда
1
команда
2
команда
1
2
3
4
5
6
Устная
работа
итог
Слово «модуль» произошло от латинского слова «modulus», что в переводе
означает «мера».
 Это многозначное слово(омоним), которое имеет множество
Это многозначное слово(омоним), которое имеет множествозначений и применяется не только в математике, но и в архитектуре, физике,
технике, программировании и других точных науках.
В архитектуре — это исходная единица измерения, устанавливаемая для данного
архитектурного сооружения и служащая для выражения кратных соотношений его
составных элементов.
В технике — это термин, применяемый в различных областях техники, не имеющий
универсального значения и служащий для обозначения различных коэффициентов
и величин, например модуль зацепления, модуль упругости и .т.п.
Модуль объемного сжатия( в физике)-отношение нормального напряжения в
материале к относительному удлинению.
44. Модуль числа
Абсолютная величина или модуль,обозначается |x|, |x-1| , |a|
45. Знак модуля
Считают, что термин предложилиспользовать
Котс, ученик Ньютона. Лейбниц тоже
использовал
эту функцию, которую называл модулем и
обозначал: mol x.

Общепринятое обозначение
абсолютной величины введено в 1841
году Вейерштрассом.
Для комплексных чисел это понятие ввели
Коши и Арган в начале XIX века.
Математики шутят.
Трехмерная кубическая линейка
Калькулятор для умных
English Русский Правила
Модуль в линейных уравнениях с двумя переменными
- Выражение
- Уравнение
- Неравенство
- Свяжитесь с нами
- Упрощение
- Факт или
- Expand
- GCF
- LCM
- Решить
- График
- Система
- Решение
- График
- Система
- Математический решатель на вашем сайте
Наших пользователей:
Если у вас нет денег, чтобы платить домашнему репетитору, тогда Алгебратор — это то, что вам нужно, и поверьте мне, он делает все, что репетитор сделал бы, и, возможно, даже больше.
Дэниел Коттон, Невада
Я действительно боролся со старой версией. .. настолько сильно, что просто отказался от нее. Эта новая версия выглядит лучше и кажется более удобной для навигации. Думаю будет здорово! Спасибо!
.. настолько сильно, что просто отказался от нее. Эта новая версия выглядит лучше и кажется более удобной для навигации. Думаю будет здорово! Спасибо!
Том Сэнди, NE
Я использовал вашу программу для подготовки к экзамену по алгебре. Мне очень нравится пошаговый процесс решения и пояснения.
Ричард Уильямс, Лос-Анджелес
Нет проблем, эта новая программа очень проста в использовании и понимании. Это хорошая программа, я желаю вам всего наилучшего. Спасибо!
Мэри Браун, Северная Дакота
Я работаю учителем математики в старшей школе более шестнадцати лет, и, к счастью, со времен Apple II у меня были компьютеры, которые помогали мне в классе. Но ничто еще не дало результатов и не помогло моим ученикам понять столько сложных уравнений и понятий, как Алгебратор! Вот почему в настоящее время я слежу за тем, чтобы каждая школьная система (даже ноутбуки) работала на ней! По крайней мере, это делает нашу работу намного проще!
Адам Боттс, Флорида
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь.
 Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные 04.11.2009:
- Калькулятор стандартной формы онлайн
- задания 3 класс чтение 2007 рабочие листы
- «разложить следующие выражения методом общих множителей»
- ПРОЦЕНТНЫЕ ФОРМУЛЫ
- обучение алгебре онлайн
- онлайн-рабочих листа + поиск тома
- образец бумаги 7 класса
- решить онлайн частное рациональных выражений
- Однородные непостоянные коэффициенты 2-го порядка
- Калькулятор умножения и упрощения рациональных выражений
- Рабочие листы переменных деления дробей
- три фута на четыре фута равно количеству дюймов Таблица формул GED
- онлайн калькулятор для решения неравенств
- математический лист для комбинаций и перестановок
- прентис холл математика алгебра 1 онлайн книга
- рабочие листы по наибольшему общему делителю
- ответ по алгебре 1
- практика перестановки
- факторные уравнения онлайн
- алгебраизатор
- калькулятор упрощающих подкоренных выражений
- как разложить трехчлен куба на множители
- завершить квадратный калькулятор
- квадратный корень с использованием коэффициентов
- алгебра пицца
- решение задач и пропорции с рациональными выражениями рабочие листы
- как решить ряд по математике
- классная математика для детей.
 com
com - Вычисление квадрата и умножения
- Рабочие листы пересечения уклонов
- проверить приведенное уравнение -3-4(t-5)=2(t+3)+11
- упорядочивание дробей от наибольшего к наименьшему листу
- excel полином 3-го порядка
- практика Пирсона 12-4 ответы алгебра 1 помощь
- Бесплатное домашнее задание по первому курсу дифференциальных уравнений с приложениями для моделирования
- листа ответов для Макдугала Литтелла
- бесплатные учебные листы по математике для 9-го класса для квадратных корней
- листы деления целых чисел
- Пример мировой задачи на показатели с решением или ответами
- слабое решение уравнения в частных производных первого порядка
- как возвести в квадрат многочлен в знаменателе
- prentice hall сложение экспонент
- математические углы
- учебник по математике для 1 класса (Онтарио)
- математика для чайников
- абсолютные значения и радикалы
- программирование Ti-83 плюс делать sin cos tan
- планы уроков по уравнениям с двумя переменными
- рабочих листа по математике, которые вы можете сделать онлайн
- логарифм домашнее задание ответы
- вычитание в слове
- распечатки по математике практика
- Нахождение общего знаменателя в полиномиальных уравнениях
- Образец вступительного экзамена по математике для 9-го класса
- целая сумма Java
- как решить мнимые числа в ti 84
- Программа решения кубических уравнений TI-83
- математических анкеты для второго года обучения
- Курс математики 1 ответы
- базовая алгебра для четвероклассников
- онлайн-решатель факторинга
- Поиск слов по истории Техаса 7-го класса
- Урок PowerPoint о сложении и вычитании
- Как сделать элементарную алгебру
- калькулятор решения алгебраических выражений бесплатно
- вероятности на ti 83
- написание программ калькулятора факторинга
- «Распределительное свойство алгебры»
- Алгебра Гленко 1 ответы
- бесплатных математических листа для ged
- алгебра 2 с pizazz
- Дифференциальные уравнения цепей первого порядка
- алгебра 1 онлайн для чайников
- ПРОСТАЯ ЗАДАЧА С ИНТЕРЕСОМ + решатель
- решение квадратных уравнений, представляющих собой последовательные целые числа
- f(x) квадратный корень из дроби
- математический в Visual Basic
- google элементарная математика нечетная дробь
- бесплатный калькулятор квадратного корня, где я могу ввести свои ответы в
- Алгебра с ключом ответов Pizzazz
- решение уравнений с несколькими корнями с помощью Excel
- уроки дроби в четвертом классе
- график уравнения лайнера
- как обучать детей технической алгебре
- калькулятор упрощения произведения суммы
- бесплатные оценки для восьмиклассников
- Рабочий лист графика наклона/пересечения
- Алгебра 1/ Тригонометрия регентов
- факторинг трехчленов 9 класс математика
| Предыдущий | Далее |
Квадратное уравнение Python — javatpoint
следующий → ← предыдущая Квадратное уравнение: Квадратное уравнение образовано от латинского термина «quadrates», что означает квадрат. топор 2 +bx+c=0 Здесь «x» неизвестен, который нужно найти, а «a», «b», «c» задает такие числа, что «a» не равно 0. Если a = 0, то уравнение становится линейным, а не квадратичным больше. В уравнении a, b и c называются коэффициентами. Возьмем пример решения квадратного уравнения 8x 2 + 16x + 8 = 0 См. этот пример: # импортировать сложный математический модуль импортировать cmath a = float(input(‘Введите a:’)) b = float(input(‘Введите b:’)) c = float(input(‘Введите c:’)) # вычисляем дискриминант д = (б**2) — (4*а*в) # найти два решения sol1 = (-b-cmath.sqrt(d))/(2*a) sol2 = (-b+cmath.sqrt(d))/(2*a) print(‘Решение: {0} и {1}’.format(sol1,sol2)) Вывод: Введите: 8 Введите б: 5 Введите с: 9 Решение: (-0,3125-1,0135796712641785j) и (-0,3125+1,0135796712641785j) Пояснение — В первой строке мы импортировали модуль cmath и определили три переменные с именами a, b и c, которые принимают ввод от пользователя. Второй методМы можем получить решение квадратного уравнения, используя прямую формулу. Давайте разберем следующий пример. Вышеприведенная формула состоит из следующих случаев.
Пример — # Программа Python для поиска корней квадратного уравнения
импортировать математику # функция поиска корней
def findRoots(a, b, c): dis_form = б * б — 4 * а * с
sqrt_val = math. Вывод: Введите a:7 Введите б:5 Введите c:2 Сложные корни -0,35714285714285715 + i 5,5677643628300215 -0,35714285714285715 - я 5,5677643628300215 Пояснение — В приведенном выше коде мы импортировали математический модуль и определили формулу для вычисления дискриминанта. К главной странице Тема: множества.
Задача. Докажите, что множество $A$ тогда и только тогда является подмножеством множества $B$, когда каждый элемент, не принадлежащий $B$, не принадлежит $A$.
Решение. Оборот «тогда и только тогда» означает два утверждения:
1) $(A \subset B) \Rightarrow {}$(для любого $x$, не принадлежащего $B$, $x$ не принадлежит $A$),
2) (для любого $x$, не принадлежащего $B$, $x$ не принадлежит $A$)${} \Rightarrow (A \subset B)$.
Продемонстрируем на примере этой задачи, как применяется метод доказательства «от противного». Чтобы доказать некоторое утверждение, мы предполагаем, что оно не выполняется и приходим к противоречию
Докажем здесь только утверждение 1). Предположим противное, то есть что $A \subset B$, но существует некоторый элемент $x$, не принадлежащий $B$, но принадлежащий $A$. По определению того, что $A \subset B$ мы знаем, что каждый элемент, принадлежащий $A$, должен принадлежать $B$. Тема: множества.
Задача. Может ли у множества быть ровно: 1) 0; 2) 7; 3) 16 подмножеств?
Решение. Во-первых, заметим, что число подмножеств пустого множества равно 1, число подмножеств множества, состоящего из одного элемента, равно 2, из двух – 4, из трех – 8, из четырех – 16. Второе важное наблюдение – монотонность: если у одного множества больше элементов, чем у другого, то и подмножеств у него больше. Тема: Комбинаторика.
Задача. Сколько существует «cлов» из двух букв английского языка?
Комментарий. Во-первых, в этой задаче, конечно, имеются в виду не те слова, которые можно встретить в словаре, а произвольные сочетания букв английского языка. Теперь перейдем к главным идеям решений подобных комбинаторных задач. Когда требуется посчитать кол-во каких-то специальных объектов, часто работает следующая схема: 1. перечисление всех вариантов в разумном порядке; 2. понимание того, какие «записи» соответствуют одному и тому же объекту. В этой задаче нам понадобится только 1. Второй пункт будет проиллюстрирован в следующем примере. Другая полезная (отнюдь не только в комбинаторике) идея состоит в том, что, прежде чем решать задачу для произвольного (или очень большого) $n$, полезно сначала разобраться со случаем небольших $n$. Замеченные при этом закономерности (даже если они не доказаны) часто существенно упрощают решение задачи. Тема: комбинатрика.
Задача. Сколькими способами можно выбрать из десяти человек двух дежурных и одного старшего дежурного?
Решение. Полезным упражнением является честное выписывание троек дежурных, выбираемых из, скажем, четырех человек (Вася, Коля, Леша, Петя).
При этом первым будем писать старшего дежурного, а остальных дежурных записывать в алфавитном порядке. Удобно при этом сначала выбирать старшим дежурным первого по алфавиту, потом второго по алфавиту и т.д. Если
каждый элемент множества В является в
то же время элементом множества А, то
говорят, что В – подмножество в А, и пишут
.
Каждое непустое множество имеет по
крайней мере два подмножества: пустое
множество Ø и само множество А.
Таким образом, пустое множество является
подмножеством любого множества. Приведем примеры
подмножеств: числовой
отрезок [–1, 3] есть подмножество
числового отрезка
[–4; 5]; множество
всех квадратов есть подмножество
множества всех прямоугольников; множество
Z
всех целых чисел есть подмножество
множества Q
всех рациональных чисел; множество
точек треугольника, вписанного в круг,
есть подмножество множества точек
этого круга; множество точек
круга является подмножеством множества
точек описанного вокруг него квадрата; множество
звезд нашей Галактики является
подмножеством множества всех звезд
Вселенной; множество
учеников восьмого класса данной школы
есть подмножество множества всех
учеников этой школы. множество
жителей Москвы является подмножеством
множества всех жителей России; множество
граждан г. Минск является подмножеством
множества всех людей на земном шаре. Н
а
рисунке 6 прямые MN и PQ пересекаются в точке R. Эта
точка принадлежит как прямой MN,
так и прямой PQ,
т.е. является общим элементом двух
множеств – множества точек прямой MN и множества точек прямой PQ.
Точно так же множество точек прямой MN
и множество точек окружности Г (рис. 7) имеют два общих элемента – точку А и точку B.
Прямая и окружность пересекаются в
двух точках. Введем
теперь общее понятие пересечения
нескольких множеств. Пересечение
множеств А и В обозначают
или AB.
Например, если А – множество мальчиков, обучающихся в
данной школе, а В – множество всех учеников из 8 класса,
то
– множество мальчиков, которые учатся
в 8 классе. С
понятием пересечения множеств приходится
иметь дело и в арифметике. Пусть А – множество натуральных делителей
числа 72: A
={1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72}, а В – множество натуральных делителей
числа 54: B ={1, 2, 3, 6, 9, 18, 27,
54}. Тогда
множество
состоит из чисел 1, 2, 3, 6, 9, 18: ={1,
2, 3, 6, 9, 18}. Эти
числа являются общими делителями для
72 и 54. С
= {72, 144, 216, … , 72n, …}. Бесконечно и
множество кратных числа 54: D = {54, 108, 162, 216, … ,
54m, …}. Пересечением
этих множеств является множество общих
кратных для чисел 72 и 54: =
{216, 432, …}. Наименьшее
число в
,
т.е. 216, называется наименьшим
общим кратным для 72 и 54. Иногда
приходится пересекать множества
геометрических фигур. Например, множество
всех квадратов является пересечением
множества всех прямоугольников с
множеством всех ромбов, т.к. квадрат –
это фигура, являющаяся одновременно и
прямоугольником, и ромбом. Пересечением
множества всех треугольников с множеством
всех правильных многоугольников
является множество правильных
треугольников. В сегодняшней статье мы рассмотрим небольшое введение в множества и подмножества: какие существуют типы, как они выражаются… Все с некоторыми примерами, которые очень легко понять. Для этого вместо чисел мы будем использовать такие элементы, как фрукты, животные, дети… Первое, что мы должны знать, это , что такое множество. Мы можем определить его как набор объектов, который мы называем элементами , которые имеют некоторые общие характеристики. Наборы могут содержать элементы любого типа: цифры, буквы, предметы, люди… Например, этот набор содержит фрукты: Набор можно классифицировать по в количество элементов, которые он имеет. Это: С точки зрения отношения между ними множества могут быть: Например, множества фруктов и животных не пересекаются, потому что нет ни плода, который мог бы быть животным, ни животного, которое могло бы быть плодом: Например, набор красных фруктов и набор желтых фруктов являются равными наборами фруктов, поскольку все красные фрукты являются фруктами, и все желтые фрукты также являются фруктами. Множество живых существ очень велико: оно имеет множество подмножеств. Например: Пересечение подмножеств: иногда разные наборы отличаются друг от друга, но имеют некоторые общие элементы. Затем определяется область пересечения, содержащая все общие элементы. Например, у нас есть группа девушек и группа людей, которые носят очки. Поскольку есть девушки, которые носят очки, они составляют часть пересечения двух наборов: Что вы думаете об этом посте? Помогло ли это вам лучше понять множества и подмножества? Если вы хотите попрактиковаться в этих наборах упражнений и многом другом, зарегистрируйтесь и попробуйте бесплатную пробную версию Smartick. Подробнее: Smartick Команда создания контента. Последние сообщения Smartick (посмотреть все) Поиск Пример 1: Учитывая A = {1, 2, 4} и B = {1, 2, 3, 4, 5}, какова связь между этими множествами? Мы говорим, что A является подмножеством B , так как каждый элемент A также находится в B . Это обозначается: Диаграмма Венна для отношения между этими множествами показана справа. Ответ: A является подмножеством B . Другой способ определения подмножества: A является подмножеством B если каждый элемент A содержится в Б . Пример 2: Учитывая X = {a, r, e} и Y = {r, e, a, d}, какова связь между этими множествами? Мы говорим, что X является подмножеством Y , поскольку каждый элемент X также находится в Y. Обозначается: Диаграмма Венна для связь между этими наборами показана справа. Ответ: X является подмножеством Y . Пример 3: Учитывая P = {1, 3, 4} и Q = {2, 3, 4, 5, 6}, какова связь между этими множествами? Мы говорим, что P не является подмножеством Q s , поскольку не каждый элемент P не содержится в 90 008 Q. Например, мы можем видеть, что 1 Q . Утверждение «P не является подмножеством Q» обозначается: Обратите внимание, что эти множества имеют некоторые общие элементы. Ответ: P не является подмножеством Q . Обозначения для подмножеств показаны ниже. Пример 4: Даны A = {1, 2, 3, 4, 5} и B = {3, 1, 2, 5, 4}, какая связь между A и B ? Анализ: Напомним, что порядок, в котором элементы появляются в наборе, не важен. Глядя на элементы этих наборов, становится ясно, что: Ответ: A и B эквивалентны. Определение: Для любых двух наборов, если A B и B A, , то 9 0008 A = B. Таким образом, A и B эквивалентны. Пример 5: Список всех подмножеств набора C = {1, 2, 3}. Ответ: Глядя на пример 5, вы можете удивиться, почему нулевой набор указан как подмножество C. В нулевом наборе нет элементов, поэтому в нулевом наборе не может быть элементов, которые не являются содержится в комплекте. Следовательно, нулевой набор является подмножеством каждого набора. Вам также может быть интересно: является ли множество подмножеством самого себя? Ответ положительный: любое множество содержит себя как подмножество. Это обозначается как: A A. Подмножество, которое меньше полного набора, называется правильным подмножеством . Таким образом, набор {1, 2} является правильным подмножеством набора {1, 2, 3}, поскольку элемент 3 не входит в первый набор. В примере 5 видно, что G является правильным подмножеством C . На самом деле каждое подмножество, указанное в примере 5, является правильным подмножеством C, , кроме P . If A B и A ≠ B , тогда A называется собственным подмножеством B и обозначается A B . Несмотря на то, что указанная выше информация важна, она может немного запутать. Итак, давайте подумаем о подмножествах и надлежащих подмножествах следующим образом: Видите ли вы закономерность в приведенных ниже примерах? Пример 6: Список всех подмножеств набора R = {x, y, z}. Сколько их там? Ответ: Существует восемь подмножеств множества R = {x, y, z}. Пример 7: Список всех подмножеств набора C = {1, 2, 3, 4}. Сколько их там? Ответ: Существует 16 подмножеств множества C = {1, 2, 3, 4}. В примере 6 набор R состоит из трех (3) элементов и восьми (8) подмножеств. В примере 7 набор C состоит из четырех (4) элементов и 16 подмножеств. Чтобы найти количество подмножеств множества из n элементов, возведите 2 в n-ю степень: То есть: Количество подмножеств в наборе A равно 2 n , где n — количество элементов в наборе A. Итоги урока 9000 3 Подмножество: A есть подмножество B: , если каждый элемент A содержится в B . Обозначается A B. Эквивалентные наборы: Для любых двух наборов, если A B и B A, , затем A = B. Нулевой набор: Нулевой набор является подмножеством каждого набора . Наборы и подмножества: Любой набор содержит себя как подмножество. Правильные подмножества: If A B и A 9000 8 ≠ B , тогда A называется правильным подмножеством Б и обозначается A B . Количество подмножеств: Количество подмножеств в наборе A равно 2 n , где n — количество элементов в наборе A. Указания: Прочитайте каждый вопрос ниже. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку. G = {d, a, r, e} ОКНО РЕЗУЛЬТАТОВ: ОКНО РЕЗУЛЬТАТОВ: А = {2, 3, 5, 7, 11} ОКНО РЕЗУЛЬТАТОВ: Под понятие 3D-графики можно отнести двухмерные изображения с элементами объема, который придается за счет работы с освещением и другими элементами, создающими на экране визуальную иллюзию. Еще к 3D-графике относятся полноценные трехмерные модели, создаваемые в специальных программах и применяемые в играх, кинематографе и мультипликации. Далее я предлагаю детальнее остановиться на этом типе графики, разобраться во всех ее тонкостях, характеристиках и принципах создания при помощи современных технологий. Для начала остановимся на 3D-изображениях и поймем, что вообще делает их трехмерными и какие типы картинок можно отнести к этой категории. Если при просмотре изображения вы можете описать ширину и высоту, но не наблюдаете глубины, значит, это двухмерная графика. Значки на рабочем столе и указатели на улицах – все это относится к 2D-графике (за некоторым исключением, когда художник использует тень или другие приемы, чтобы сделать картинку объемной). Если нарисовать квадрат, представив только основные его четыре линии, это будет двухмерная модель. Но если немного повернуть квадрат, дорисовать грани и вершины, получится куб, являющийся объемным элементом, а значит, к нему относится характеристика 3D-модели. Комьюнити теперь в Телеграм Подпишитесь и будьте в курсе последних IT-новостей Подписаться Полноценное представление 3D-элементов на экране мир увидел в короткометражном фильме «A Computer Animated Hand», вышедшем в 1972 году. На скриншоте ниже вы видите то, как аниматоры смогли спроектировать человеческую руку и анимировать ее на экране. Это дало сильный толчок в развитии анимационных технологий и применении подобных эффектов в кинематографе. Одним из первых фильмов, в котором зритель мог увидеть анимацию человеческого лица, считается «Futureworld», вышедший в 1976 году. Как же работает трехмерная графика на компьютерах и на какие этапы делится ее создание? 3D-моделирование. На компьютере создается модель, в точности передающая форму объекта, который нужно представить. Это может быть любой предмет, животное или человек. В общем, все, что нас окружает. Существует несколько видов трехмерного моделирования, каждый из которых имеет свои особенности и принципы, но сейчас не будем вдаваться в эту тему. Если хотите, можете ознакомиться с такими программами, как Blender или 3Ds Max, чтобы узнать, как трехмерные объекты рисуются при помощи программ. Сценарий и анимация. Модели всегда размещены на сцене и необходимы для выполнения определенного действия: перемещения, разрушения или передачи любого другого эффекта. Для расположения объектов на сцене и их анимирования может использоваться та же программа, которая применялась и для моделирования, но иногда разработчики обращаются к другому софту. Анимации тоже бывают разными, например, сейчас особо популярен захват движения (когда программа считывает движения человека и передает их на трехмерную фигуру). Рендеринг. Завершающий процесс работы над проектом. Подразумевает обработку цветов, типов поверхности, освещения и всех других параметров сцены. Для обработки необходим мощный компьютер, способный быстро считывать кадры и выдавать на экран необходимый результат. В рамках этой статьи остановимся только на 3D-моделировании, поскольку именно этот процесс и является основной трехмерной графики. Изначально модель имеет серый цвет, поэтому обязательным этапом является наложение текстур и материалов. В крупных компаниях этим занимается специально обученный человек, получивший заготовку от 3D-моделировщика. Он по эскизам или специальным шаблонам накладывает на модель различные элементы, имитирующие волосы, ткань или типы поверхностей. Это и делает 3D-модель похожей на настоящую. Тему можно развивать бесконечно, поскольку 3D-графика обладает огромным множеством интересных особенностей, которые делают индустрию такой сложной и высокооплачиваемой. Кинокомпании тратят миллионы долларов на создание моделей и эффектов, которые в реальной жизни повторить проблематично и еще более затратно. Каждый из нас при работе за компьютером взаимодействует с трехмерной графикой. Обычно мы просто не обращаем на это внимания: идеальные элементы оформления, анимированные изображения и 3D-модели – это уже привычные составляющие рекламы и Интернет-приложений. Прежде чем построить дом или разработать дизайн интерьера – необходимо создать проект. Когда-то это было трудным и кропотливым делом, а сегодня благодаря 3D-графике это делают быстрее и качественнее. 3D моделирование крепко вошло в современную жизнь и уже применяется в рекламе, архитектуре, индустрии. После появления 3D-печати, трехмерное моделирование перешло на новый уровень и стало еще более популярным. Соответственно, появилась новая профессия: 3D-дизайнер, имеющий множество специализаций. ONLINE курс польского языка Регистрируйся на авторский курс от UniverPL Забронировать место Где сейчас используется 3D-графика: Быстрое развитие 3D моделирования предполагает возникновение множества направлений, в которых можно развиваться. Основными являются: К тому же, каждое направление имеет еще массу специализаций. Сегодня на основе трехмерной графики создают точные копии объекта, воплощают в жизнь некогда нереальные дизайнерские задумки. 3D технологии приносят пользу человечеству и большую прибыль специалистам сферы. Начать изучение 3D-моделирования в университете – это сделать старт в профессии. На момент выпуска из института вы будете на достаточном уровне, чтобы стать необходимым для рынка молодым специалистом. В Польше есть два университета, которые предоставляют качественные и актуальные знания по 3D-графике, особенно по разработке компьютерных игр. Это Польско-Японская Академия Компьютерных Технологий в Варшаве и Нижнесилезский Университет во Вроцлаве. Специальность 3D-графика для тех, кто интересуется индустрией игровых разработок. Студенты получают теоретические и практические знания, связанные как с технологической ИТ-подготовкой, так и в сфере дизайна и креативных индустрий. Занятия проводят эксперты, работающие над лучшими польскими мобильными играми. На эти вопросы нам ответил Oleksii Havrysh, имеющий 6 лет опыта в GameDev, он работал на таких проектах как “Halo Infinite” и “World of Tanks”, а сейчас занимает должность Level/Environment Artist. Я начинал с архитектурной визуализации, разрабатывал интерьеры. Однако с детства любил играть в компьютерные игры и стал интересоваться тем, как их создают. 6 лет назад обучение GameDev вообще не было развито, информацию искал сам: посещал всевозможные курсы, изучал все, что было в Интернете. Делал много тестовых заданий в разные компании, в одну из которых меня и приняли. Когда ты начинаешь знакомиться с 3D-графикой, то понимаешь, насколько она обширна, насколько много специализаций. Здесь себя может обрести каждый, ведь работы очень много. Поступить в университет Польши Гарантия поступления в рейтинговые университеты Узнать больше Если 10 лет назад этому не учили в университетах, и диплом не был важным — сейчас все изменилось. В Европе многие вузы имеют это направление, постепенно оно появляется и в Украине. Я бы выделил несколько моментов важности образования по 3D-графике. Структурированные знания. Университет выступает более как условная сторона, которая дает фундаментальную подготовку, но параллельно – нужно самому дополнительно учиться, посещать курсы, делать первые разработки. Работа в международных компаниях. Сейчас, если программист хочет переехать в США или Германию на работу, образование является важнейшим фактором. К тому же профильное образование. Если человек мега-крутой специалист, как исключение, могут простить отсутствие диплома, но это бывает редко. Приоритеты сейчас на дипломированных специалистах. Также, университет – это знакомства, рекомендации и практика в компаниях. В Польше, например, есть известная компания CD Projekt RED — компания разработчик компьютерных игр, выпустившая легендарные: “The Witcher”, “Cyberpunk 20772. Еще во время обучения нужно ставить себе цель попасть туда на работу. Что касается Украины, здесь тоже множество крутых работодателей и здоровая конкуренция на рынке труда. Дисциплина. Самое главное, что дает университет – это дисциплина. Быстро учиться, овладевать материалом, структурировано изучать все — база, которую предоставит ВУЗы. Главное не думать, что вуз дает все и больше не нужно учиться. Это ошибочное видение. Не каждый художник, работающий в компьютерной графике, умеет классно рисовать от руки. Это умение нужно для 2Д-графики, для концепт-художника. Для специалиста по 3D-графике необходимы навыки понимания пропорций, материала, креативность. Скажу больше, рисование – не закон успеха. Также стоит еще обладать техническими знаниями. К примеру, есть комната, ты творчески в ней расставляешь все предметы, делаешь атмосферу, но есть и техническая сторона: правильное расположение стен, длины и высоты дверей. Поэтому сочетание творческого видения и технических знаний – лучшее для качественного результата. Часто в ИТ или 3D-сферу идут ради больших зарплат. В начале, когда ты джуниор, заработные платы невысокие, и чтобы они росли – стоит самому развиваться и много работать. Если ожидаешь просто финансовых наград – результата не будет. Надо целиться на развитие, на желание делать крутой продукт – тогда тебя заметят и начнется карьерный (и финансовый) рост. 3D-художники и 2D-художники – необходимы компаниям одинаково. Так как 2D-художник (именно в GameDev) – это человек, рисующий концепции. Например: в одной из программ (используемой при создании 2D-графики (Photoshop) создают персонажа, рисуют его — и это 2D-изображение. Но затем его передают к художнику персонажей, и по этому концепту создадут 3D-модель. Они взаимосвязанные, и потому одинаково популярные на рынке. Game Development – разработка компьютерных игр. Здесь необходимы специалисты всех направлений, даже тестировщики. Также, сейчас активно развивается сфера VR (Виртуальной реальности) и игры в VR приобретают большую популярность. Такой скорости развития информации, как в ИТ технологиях — нет ни в одной сфере. Это касается и 3D-графики. Ты работаешь в коллективе, где все ежедневно развиваются, проходят обучение, и если ты не успеваешь – то знания просто устареют. Это не та профессия, где выучился, пошел работать – и этого достаточно. Факт: 35% того, что я использовал в работе 6 лет назад – уже не актуально. На данный момент рынок не перегрет. Очень круто искать те ниши, на которых высок спрос, но низкая популярность среди исполнителей. Например, заходишь на Artstation и видишь, сколько художников создают обычные объекты окружения, такие как – шкаф, дом, авто и другие. А если искать художника по растениям – таких специалистов очень мало. Так что можно выбрать не слишком популярную нишу и чувствовать себя в ней комфортно. Когда поступаешь в университет – не всегда знаешь, что именно там будешь изучать. Поэтому нужно заранее себе определить то, какие направления наиболее интересны, в чем хочется развиваться. Ведь после прохождения специализированных курсов будет и сертификат, и знания которые можно добавлять в резюме. Сейчас часто есть реклама курсов, по типу «Изучи за 30 дней программу и работай!». Нет, никто за 30 дней не сделает из вас полноценного специалиста, разве что познакомит с основами работы и программами и все. Учитывайте, кто ведет обучение и как его рекламируют. В общем можно выделить 3 критерия выбора курсов: Больше склоняюсь к тому, чтобы быть узкоспециализированным. Когда начинаешь работать по узкой специализации, становишься в ней профессионалом – потом уже можно пополнять багаж знаний и по другим дисциплинам. Таким образом расширяется объем наших знаний. Если же изучать всего понемногу сразу – специалистом стать не получится. К тому же очень просто менять специализации, ведь сферы связаны между собой. Принцип разработки оружия и объекта окружения схож: использование техники, иногда и одинакового софта, работа с геометрией. К примеру, работаешь художником по уровням, но захотел пойти в Light Art – обеспечивать освещение в игре. Таких случаев много, и это нормально. Обычно люди не увольняются из компании, а в ней же идут на новую должность и руководство это только поддерживает. Безусловный плюс, что тебе не нужно учиться снова 3 года и всегда можно вернуться к предыдущей работе. Сначала рекомендую посвятить себя обучению в университете, «проникнуться» основами, которые дает вуз. И при изучении – выбирать сферы, в которых есть желание работать. Если вы уже изучаете графику в университете, то начинайте создавать свое портфолио. Заходите на сайт компании, где хотите работать, находите вакансии, читаете требования и навыки, которые необходимо иметь и начинаете развивать их. Понимать, что именно нужно учить – это лучший вариант для будущего трудоустройства. На сайтах корпораций всегда есть информация, какие кандидаты им необходимы. Создание, отображение и манипулирование объектами на компьютере в трех измерениях. Программы 3D CAD и 3D-графики позволяют создавать объекты в масштабе X-Y-Z (ширина, высота, глубина). Как 3D-объекты, их можно вращать и просматривать под любым углом, а также увеличивать или уменьшать масштаб. Они также позволяют автоматически применять освещение на этапе рендеринга. 3D-сцена В 3D-графике объекты создаются на трехмерной сцене, где текущий вид определяется углом камеры и источниками света, как в реальном мире. (Изображение предоставлено Intergraph Computer Systems.) Реклама {X-html заменен} Выбор редакции Информационные бюллетени PCMag Информационные бюллетени PCMag Наши лучшие истории в вашем почтовом ящике Подпишитесь на PCMag PCMag. Как мы тестируем Редакционные принципы (Открывается в новом окне) PCMag поддерживает Group Black и ее миссию по увеличению разнообразия голосов в СМИ и прав собственности на СМИ. © 1996-2023 Ziff Davis, LLC., компания Ziff Davis. Все права защищены. PCMag, PCMag.com и PC Magazine входят в число зарегистрированных на федеральном уровне товарных знаков Ziff Davis и не могут использоваться третьими лицами без явного разрешения. Отображение сторонних товарных знаков и торговых наименований на этом сайте не обязательно указывает на какую-либо принадлежность или поддержку PCMag. Если вы нажмете на партнерскую ссылку и купите продукт или услугу, этот продавец может заплатить нам комиссию. следующий →
← предыдущая Трехмерные преобразования являются расширениями двумерного преобразования. Для трехмерных изображений и объектов необходимы трехмерные преобразования. Это переводы, масштабирование и вращение. Они также называются базовыми преобразованиями, представленными с помощью матрицы. Более сложные преобразования выполняются с использованием матрицы в 3D. 2D может отображать двумерные объекты. Например, линейчатая диаграмма, круговая диаграмма, графики. Но некоторые природные объекты можно представить с помощью 3D. Используя 3D, мы можем видеть разные формы объекта в разных сечениях. В 3D, когда выполняется перемещение, нам также нужны три фактора для вращения, это компонент трех вращений. Каждая из них может быть выполнена вдоль любых трех декартовых осей. В 3D мы также можем представить последовательность преобразований в виде одной матрицы. Компьютерная графика использует САПР. CAD позволяет манипулировать компонентами машин, которые являются трехмерными. Трехмерная система имеет три оси x, y, z. Ориентация трехмерной системы координат бывает двух типов. Правосторонняя система и левосторонняя система. В правосторонней системе большой палец правой руки указывает на положительное направление z, а в левой системе большой палец указывает на два отрицательных направления. На следующем рисунке показана правосторонняя ориентация куба. Использование правой системы координат углов А, В, С, D куба Точка A x, y, z Создание реализма в 3D: Трехмерные объекты выполнены с использованием компьютерной графики. Техника, используемая для двухмерного отображения трехмерных объектов, называется проекцией. 1. Параллельная проекция: В этой проекции точка на экране определяется в пределах точки трехмерного объекта линией, перпендикулярной экрану дисплея. Архитектор
Чертеж, т. е. план, вид спереди, вид сбоку, фасад есть не что иное, как линии параллельных проекций. 2. Перспективная проекция: Эта проекция обладает тем свойством, что дает представление о глубине. Чем дальше объект от зрителя, тем меньше он будет казаться. Все линии в перспективной проекции сходятся в центральной точке, называемой центром проекции. 3. Орфографическая проекция: Самый простой вид проекции. При этом мы берем вид сверху, снизу и сбоку на объект, извлекая параллельные линии из объекта. Методы создания различных изображений твердого объекта зависят от типа объекта. Продолжаем изучать модуль числа. Сегодня мы научимся решать неравенства с модулем. Чтобы решать неравенства с модулем, нужно прежде всего уметь решать простейшие линейные неравенства, а также знать что такое модуль и как его раскрывать. Независимо от того, решаем мы уравнение или неравенство, нужно уметь раскрывать модуль. Рассмотрим к примеру простейшее неравенство с модулем: |x| > 2 Чтобы решить данное неравенство раскроем его модуль. Если подмодульное выражение больше или равно нулю, то исходное неравенство примет вид: x > 2 Решением этого неравенства является множество всех чисел, бóльших 2. Отметим их на координатной прямой: А если подмодульное выражение меньше нуля, то исходное неравенство примет вид: −x > 2 Умнóжим обе части этого неравенства на −1. Тогда полýчим неравенство x < −2. Решением этого неравенства является множество всех чисел, мéньших −2. Забавно, но получившиеся промежутки x < −2 и x > 2 являются ответом к нашей задаче. Если в исходное неравенство |x| > 2 подставить какое-нибудь значение x, удовлетворяющее данному неравенству, то это значение будет принадлежать промежутку (−∞ ; −2) или промежутку (2 ; +∞). То есть решением исходного неравенства является совокупность из x < −2 и x > 2 Совокупностью неравенств мы будем называть несколько неравенств, объединённых квадратной скобкой, и которые имеют множество решений, удовлетворяющих хотя бы одному из неравенств, входящих в данную совокупность. Чтобы записать окончательный ответ, промежутки x < −2 и x > 2 следует объединить. В математике знаком объединения служит ∪. Тогда: x ∈ (−∞ ; −2) ∪ (2 ; +∞) Знак объединения ∪ читается как «или». Значение переменной x принадлежит промежутку (−∞ ; −2) или промежутку (2 ; +∞) Действительно, если подставить какое-нибудь значение x, являющееся решением исходного неравенства, то это значение будет принадлежать промежутку (−∞ ; −2) или промежутку (2 ; +∞). Например, число 3, является решением исходного неравенства |x| > 2 |3| > 2 ⇔ 3 > 2 Значение 3 принадлежит промежутку (2 ; +∞). Также оно удовлетворяет хотя бы одному из неравенств совокупности , а именно неравенству x>2. Значение −4 тоже является решением исходного неравенства |x| > 2. Это значение принадлежит промежутку (−∞ ; −2) |−4| > 2 ⇔ 4 > 2 Также значение −4 удовлетворяет хотя бы одному из неравенств совокупности , а именно неравенству x < −2. Согласно определению, модуль числа x есть расстояние от начала координат до точки x. Действительно, от начала координат (точка 0) любое расстояние бóльшее двух, будет решением неравенства |x| > 2 Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞) Обратите внимание, что границы −2 и 2 не включены в соответствующие промежутки. Это потому, что при подстановке этих чисел в исходное неравенство, получается неверное неравенство. Теперь немного поменяем наш пример. В неравенстве|x| > 2 поменяем знак > на знак < |x| < 2 Решим это неравенство. Как и раньше для начала раскрываем модуль. Если подмодульное выражение больше или равно нулю, то получим неравенство x < 2. Решениями этого неравенства являются все числа, мéньшие двух. Отметим их: А если подмодульное выражение меньше нуля, то получим неравенство −x < 2. Умнóжим обе части этого неравенства на −1. Тогда получим неравенство x > −2. Для наглядности, решения неравенства x > −2 отметим красным цветом: Если выражение |x| это расстояние от начала координат до точки x, то неравенство |x| < 2 говорит, что это расстояние меньше чем 2. На рисунке видно, что от начала координат расстояния, мéньшие двух, лежат в промежутках от −2 до 0 и от 0 до 2 А эти расстояния одновременно будут принадлежать промежуткам x < 2 и x > −2 Обратите внимание, что в этот раз промежутки обрамлены знáком системы, а не знáком совокупности как в прошлом примере. Это означает, что значения x одновременно удовлетворяют обоим неравенствам (промежуткам x < 2 и x > −2) То есть решением неравенства |x| < 2 является пересечение промежутков x < 2 и x > −2. x ∈ (−2 ; 0) ∩ (0 ; 2) Знак пересечения ∩ читается как «и». Тогда запись x ∈ (−∞ ; 2) ∩ (−2 ; +∞) можно прочитать так: Значение переменной x одновременно принадлежит промежутку (−∞ ; 2) и промежутку (−2 ; +∞) Действительно, если подставить какое-нибудь значение x, являющееся решением неравенства |x| < 2, то это значение будет принадлежать одновременно промежутку (−∞ ; 2) и (−2 ; +∞). Например, число 1 является решением исходного неравенства |x| < 2 |1| < 2 ⇔ 1 < 2 Значение 1 одновременно принадлежит промежутку (−∞ ; 2) и промежутку (−2 ; +∞) Также, значение 1 удовлетворяет обоим неравенствам системы А если к примеру подставить значение, не являющееся решением неравенства |x| < 2, то это значение не будет одновременно принадлежать промежуткам (−∞ ; 2) и (−2 ; +∞). |7| < 2 ⇔ 7 < 2 Несмотря на то, что значение 7 принадлежит одному из промежутков, а именно промежутку (−2 ; +∞), данное значение не является решением исходного неравенства, поскольку оно не удовлетворяет ему. Также, данное значение не принадлежит одновременно обоим промежуткам: (−∞ ; 2) и (−2 ; +∞). Для неравенства |x| < 2 ответ можно записать покороче: x ∈ (−2 ; 2) Из рассмотренных примеров видно, что решением неравенства с модулем может быть либо объединение промежутков либо их пересечение. В первом примере мы решили неравенство |x| > 2, то есть неравенство вида |x| > a. Это неравенство при котором модуль больше какого-нибудь числа или буквенного выражения. Решением такого неравенства является объединение решений неравенств, получающихся после раскрытия модуля исходного неравенства. Неравенства, получающиеся после раскрытия модуля, следует записывать в виде совокупности: Совокупность свóдится потому, что итоговые решения будут удовлетворять хотя бы одному из неравенств, полученных после раскрытия модуля исходного неравенства. Во втором примере мы решили неравенство |x| < 2, то есть неравенство вида |x| < a. От предыдущего неравенства оно отличается только знáком. Но это неравенство при котором модуль меньше какого-нибудь числа или буквенного выражения. Решением такого неравенства является пересечение решений неравенств, получающихся после раскрытия модуля исходного неравенства. Неравенства, получающиеся после раскрытия модуля, следует записывать в виде системы: Система записывается потому, что итоговые решения будут удовлетворять обоим неравенствам, полученным после раскрытия модуля исходного неравенства. Эти же правила сохраняются и для неравенств, содержащих знаки ≥ и ≤ Например, решим неравенство |x| ≥ 1. Модуль больше или равен числу. Поэтому решением будет объединение решений неравенств, которые получатся после раскрытия модуля. После раскрытия модуля и выполнения необходимых тождественных преобразований, получим совокупность неравенств x ≥ 1 и x ≤ −1 Решением служит объединение промежутков x ≤ −1 и x ≥ 1 x ∈ (−∞ ; −1] ∪ [1 ; +∞) Обратите внимание, что границы −1 и 1 включены в соответствующие промежутки. Решим теперь к примеру неравенство |x| ≤ 1. Модуль меньше или равен числу. Поэтому решением будет пересечение решений неравенств, которые получатся после раскрытия модуля. После раскрытия модуля и выполнения необходимых тождественных преобразований, получим систему неравенства: x ≤ 1 и x ≥ −1 Решением служит пересечение промежутков x ≤ 1 и x ≥ −1 x ∈ (−∞ ; 1] ∩ [−1 ; +∞) или покороче: x ∈ [−1 ; 1] Обратите внимание, что границы −1 и 1 включены в соответствующие промежутки. Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство. Аналогично решаются неравенства, в левой части которого модуль, а справа не просто число, а буквенное выражение. Пример 4. Решить неравенство |7x − 6| < x + 12 Решение Для начала раскроем модуль. Вспоминаем, что если неравенство содержит знак < или ≤, то неравенства получившиеся после раскрытия модуля, следует записать в виде системы. Это будет означать, что итоговые решения будут удовлетворять обоим неравенствам. Итак, после раскрытия модуля получим следующую систему: В данном случае система содержит не совсем элементарные неравенства как в прошлых примерах. Данные неравенства следует упростить, используя известные тождественные преобразования. Раскроем скобки во втором неравенстве. Тогда получим следующую систему: В обоих неравенствах выражения, содержащие неизвестные, перенесём в левую часть, а числовые выражения — в правую. Затем приведём подобные слагаемые. Тогда получим систему: В первом неравенстве разделим обе части на 6. Во втором неравенстве разделим обе части на −8. Изобразим решения на координатной прямой: Решением является пересечение промежутков (−∞ ; 3) и , то есть промежуток Ответ: Пример 5. Решить неравенство |1 − 2x| ≥ 4 − 5x Решение Для начала раскроем модуль. Вспоминаем, что если неравенство содержит знак > или ≥, то неравенства получившиеся после раскрытия модуля, следует записать в виде совокупности: После раскрытия модуля получим следующую совокупность: Выполним необходимые тождественные преобразования в обоих неравенствах. В результате получим: Изобразим решения на координатной прямой: Решением является объединение промежутков и [1 ; +∞), то есть промежуток Ответ: . Задание 1. Решить неравенство: Решение: Ответ: x ∈ (−36 ; 36). Показать решение Задание 2. Решение: Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞). Показать решение Задание 3. Решить неравенство: Решение: Ответ: Показать решение Задание 4. Решить неравенство: Решение: Ответ: x ∈ [−5 ; 2] Показать решение Задание 5. Решить неравенство: Решение: Ответ: x ∈ (−∞ ; 0) Показать решение Задание 6. Решить неравенство: Решение: Ответ: Показать решение Понравился урок?
Возникло желание поддержать проект? I тип: Неравенство содержит некоторое выражение под модулем и число вне модуля: где (3.27) Решение зависит от знака числа А. 1. Если то неравенство (3.27) не имеет решений. 2. Если то неравенство (3.27) равносильно системе неравенств где (3.28) 1. Если то неравенство (3.28) не имеет решений. 2. Если то неравенство (3.28) равносильно уравнению 3. Если , то неравенство (3.28) равносильно системе неравенств где (3.29) 1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения 2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что 3. Если то неравенство (3.29) равносильно совокупности где (3.30) 1. Если то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения 2. Если то неравенство (3. II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его: (3.31) Где – некоторые выражения с переменной Х. Для решения неравенств типа (3.31) можно использовать следующие способы. 1-й способ: используя определение модуля, получаем равносильную совокупность систем: 2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения 1. Если (3.32) То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32). 2. Если То решением является множество всех значений Х, которые удовлетворяют системе 3. Если решение определяется системой Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3. 3-й способ: метод интервалов. Для решения необходимо: 1) найти значения Х, для которых 2) найденные значения Х нанести на числовую ось; 3) определить знак выражения на всех полученных промежутках; 4) нарисовать кривую знаков; 5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку; 6) в ответе неравенства указать совокупность полученных решений. III тип: Неравенство содержит несколько модулей и решается двумя способами: 1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным. 2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений. IV тип: Неравенство вида где (3.33) Решается двумя способами: 1-й способ: метод интервалов. 2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат: Решение неравенства (3.33) сводится к решению неравенства Аналогично решают неравенства IV типа (3. V тип: Неравенства, решаемые заменой переменной. В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа. Пример 1. Решить неравенства: 1) 2) 3) 4) 5) 6) Решение. 1) Решаем как неравенство I типа: Получаем ответ: 2) Решаем как неравенство I типа: Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду Его решение: это и есть ответ. 3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему: Получаем ответ: 4) Заданное неравенство может быть записано в виде Заменим переменную Решаем неравенство Его решение Возвращаемся к переменной Х и решаем совокупность Получаем Т. 5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10). ОДЗ: Рис. 3.10 А) рассмотрим неравенство на 1-м промежутке. Получаем систему (3.34) Решаем неравенство Получаем Система (3.34) сводится к системе На данном промежутке решений нет. Б) Если , то С учетом рассматриваемого промежутка имеем: Получаем В) Решением является промежуток: Объединим полученные решения и приходим к ответу: 6) ОДЗ: Введем новую переменную: тогда и приходим к неравенству вида Решаем его Используем метод интервалов (рис. 3.11). Рис. Запишем полученное решение в виде совокупности: Вернемся к переменной Х: (3.35) – выполняется при любых С учетом ОДЗ второе неравенство системы (3.35) равносильно системе Получаем ответ: спросил Изменено
10 лет, 6 месяцев назад Просмотрено
2к раз $\begingroup$ Может кто-нибудь объяснить мне (или дать ссылку на сайт, который делает), как решить эту проблему?
$$
||х+1| -1| \geq 3
$$
Я понятия не имею, как вычислить этот знак двойного абсолютного значения. $\endgroup$ 1 $\begingroup$ Работа снаружи внутрь. Для начала у вас есть неравенство $|u-1|\ge 3$, где $u=|x+1|$. Это эквивалентно $$u-1\le -3\quad\mathbf{or}\quad u-1\ge 3\;.$$ Решая их, мы находим, что $$u\le-2\quad\mathbf {или}\quad u\ge 4\;,$$, что в терминах исходной переменной $x$ равно $$|x+1|\le -2\quad\mathbf{or}\quad|x+1|\ge 4\;.\tag{1}$$ Абсолютное значение невозможно отрицательно, поэтому $(1)$ сводится к $|x+1|\ge 4$. Как и в самом первом шаге, это эквивалентно $$x+1\le-4\quad\mathbf{or}\quad x+1\ge 4\;,$$, решение которого равно $$x \le-5\quad\mathbf{or}\quad x\ge 3\;.$$ $\endgroup$ 4 $\begingroup$ Так как у тебя уже есть раствор снаружи, я открою тебе изнанку. Сначала возьмем случай $x+1\geq 0$. Таким образом, $||x+1|-1|=|x+1-1|=|x|$. $|x|\geq3$ имеет решение $x\leq-3$ или $x\geq3$. Зная, что $x\geq-1$, первое невозможно. Теперь рассмотрим $x+1\leq0$. Таким образом, $||x+1|-1|=|-(x+1)-1|=|-x-2|=|x+2|$.
$|x+2|\geq3$ имеет решение $x\leq-5$ или $x\geq1$. Зная, что $x\leq-1$, второе невозможно. $\endgroup$ $\begingroup$ Если бы я был перед классом, который столкнулся с этой проблемой, я бы изобразил ее на графике, проанализировав ее изнутри. Во-первых, $|x+1|$ имеет V-образный граф с вершиной в $(-1,0)$. Тогда $|x+1|-1$ также имеет V-образный граф с вершиной в $(-1,-1)$. Обратите внимание, что этот график пересекает ось $x$ в точке $(-2,0)$ и начале координат. $\endgroup$ Как решать неравенства с модулем : В этом разделе мы узнаем, как решить неравенство с модулем. Если задан вопрос в любой из следующих форм, мы должны следовать данным методам для решения x. Вопросы в форме Первый шаг, который нужно сделать Решение |х — а| < r -г < х - а < г (-р + а, г + а) |х — а| ≤ г -r ≤ x — a ≤ r [а- г, а + г] |х — а| > r х — а < -r и х — а > r (∞,a-r)U(a+r,∞) |х — а| ≥ р х — а ≤ -r и х — а ≥ r (∞,а-р]U[а+r,∞) и выразить решение в виде интервалов. Решение: -2 < x - 9 < 2 Добавьте 9 к уравнению -2 + 9 < x - 9 + 9 < 2 + 9 7 < x < 11 неравенство (7, 11). Пример 2 : Решите абсолютное неравенство, приведенное ниже |2/ (x — 4)| > 1 , x ≠ 4 и выразить решение в виде интервалов. Решение: Из данного неравенства получаем, что 2 > (x — 4) -2 < x - 4 < 2 Добавьте 4 по всему неравенству -2 + 4 < x - 4 + 4 < 2 + 4 2 < x < 6 Мы не можем выразить решение в виде (2 , 6). Потому что в середине 2 и 6 у нас есть значение 4. Итак, мы должны разбить его на два интервала. (2, 4) U (4, 6) Пример 3 : Решите абсолютное неравенство, приведенное ниже |3 — (3x/4)| ≤ 1/4 и выразить решение в виде интервалов. Решение: (-1/4) ≤ 3 — (3x/4) ≤ (1/4) (-1/4) ≤ (12 — 3x)/4 ≤ (1/4) Умножить на 4 во всем уравнении -1 ≤ (12 — 3x) ≤ 1 Вычесть 12 во всем уравнении -1 — 12 ≤ 12 — 3x — 12 ≤ 1 -12 -13 ≤ — ≤ -11 Делится на (-3) во всем уравнении -13/(-3) ≤ — 3x ≤ -11 13/3 ≤ x ≤ 11/3 11/3 ≤ x ≤ 13/ 3 Следовательно, набор решений приведенного выше абсолютного неравенства равен [11/3, 13/3]. Стандарт IEEE754 определяет несколько типов представления действительных чисел,
основными из которых являются числа одинарной точности (для их хранения требуется 4 байта),
двойной точности (8 байт) и расширенной точности (10 байт). Точность Размер (байт) C, C++ Pascal Python Мантисса (бит) Точность, Максимальное Минимальное одинарная 4 float single — 23 \(\approx 7{,}2\) \(3{,}4\cdot10^{38}\) \(1{,}4\cdot10^{-45}\) двойная 8 double double float 52 \(\approx 15{,}9\) \(1{,}7\cdot10^{308}\) \(5{,}0\cdot10^{-324}\) расширенная 10 long double extended — 63 \(\approx 19{,}2\) \(1{,}1\cdot10^{4932}\) \(1{,}9\cdot10^{-4951}\) Рациональные числа, которые не могут быть представлены в виде дроби со знаменателем,
являющимся степенью двойки, не могут быть точно представлены в виде конечной двоичной дроби,
а, значит, не могут быть в точности представлены в памяти компьютера. Таким образом, сравнивать действительные числа в компьютерных программах
на точное равенство нельзя. Вместо этого если нужно сравнить два числа
\(a\) и \(b\) на равенство, правильным будет проверка условия, что эти два
числа не сильно различаются, то есть что модуль их разности не превосходит некоторого
небольшого значения \(\varepsilon\), то есть что \(|a-b|<\varepsilon\).
Значение \(\varepsilon\) как правило определяется для каждой задачи исходя из той точности, с которой необходимо получить результат. В следующей таблице указано, как нужно проверять различные сравнения действительных чисел с использованием \(\varepsilon\). Условие Как нужно проверять \(a=b\) \(|a-b|\lt\varepsilon\) \(a\ne b\) \(|a-b|\ge \varepsilon\) \(a\lt b\) \(a \le b — \varepsilon\) \(a \le b\) \(a \lt b + \varepsilon\) \(a\gt b\) \(a \ge b + \varepsilon\) \(a\ge b\) \(a \gt b — \varepsilon\) При работе с действительными числами, как правило, в результате алгоритмических ошибок,
возникают некоторые специальные значения, например, Значение Значение Также есть отрицательное значение При ряде операций со значением В заголовочном файле Введение Перевод чисел Дробные числа Отрицательные числа Двоичная арифметика Двоичная
система счисления является основной системой представления информации
в памяти компьютера. В этой системе
счисления используются две цифры: 0 и 1.
Двоичную цифру называют
битом. Первое
опубликованное обсуждение двоичной системы счисления принадлежит испанскому
священнику Хуану Карамюэлю Лобковицу (
1670 г
.). Всеобщее внимание к этой системе привлекла статья немецкого математика
Готфрида Вильгельма Лейбница, опубликованная в
1703 г
. В ней пояснялись двоичные операции сложения, вычитания, умножения
и деления. Лейбниц не рекомендовал использовать эту систему для практических
вычислений, но подчёркивал её важность для теоретических исследований.
Со временем двоичная система счисления становится хорошо известной
и получает развитие. Ей было тысяча сто лет. Но станет всё совсем обычным, ——————— С
помощью двоичной системы кодирования можно зафиксировать любые данные
и знания. Это легко понять, если вспомнить принцип кодирования и
передачи информации с помощью азбуки Морзе.
Телеграфист,
используя только два символа этой азбуки — точки и тире, может
передать практически любой текст.
Объём памяти компьютера измеряется в байтах.
Каждый байт может выражать букву, число, пробел, знак препинания
или какой-либо другой символ. Количество символов, которые компьютер
может хранить в оперативной памяти, меняется в широких пределах
от вида компьютера и его модели. Объём памяти, хотя он и измеряется в байтах,
обычно выражается в килобайтах. Слово «килобайт», вообще говоря, означает «1000 байт».
(Напомним, что приставка «кило» означает «тысяча».) Фактически же килобайт равен 1024 байтам:
1 Кбайт = 1024 байт. Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов. Объём памяти первых микрокомпьютеров
составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128,
256, 512, 1024 Мб и более Объём памяти новейших компьютеров так велик,
что она выражается в гигабайтах, т. е. в миллиардах байтов. 1 Мбайт = 1024 Кбайт = 1 048 576 байт.
Итак, каждый символ алфавитно-цифровой информации
представляется в компьютере кодом из восьми двоичных цифр. имеет
в двоичной форме объём 25 байт: 23 буквы и 2 символа «пробел» по
1 байту.
Пример. Измерим
в байтах объём текстовой информации в книге из 258 страниц, если
на одной странице размещается в среднем 45 строк по 60 символов
(включая пробелы).
Один символ в двоичной форме содержит 1 байт. Строка будет содержать
61 байт, учитывая и служебный символ окончания строки. Тогда
61
байт * 45 строк = 2745 байт. Так
как в книге 258 страниц текста и на каждой странице в среднем по
2745 байт информации, то объём алфавитно-цифровой информации в книге 2745
байт * 258 страниц = 708210 байт » 692 Кбайт Таким
образом, текст книги имеет объём около 692 Кбайт. Перевод чисел Для перевода десятичного числа в двоичное надо разделить
его на 2 и собрать остатки, начиная с последнего частного. 7310 = 10010012
А вот как происходит перевод двоичного числа в десятичное: В любой системе счисления нужно уметь представлять не только целые
числа, но и дробные. С математической точки зрения это ординарная задача,
которая давно решена. Однако с точки зрения компьютерной техники это
далеко не тривиальная проблема, во многом связанная с архитектурой
компьютера. Запишем формулу представления дробного числа в позиционной системе
счисления:
Ap = an-1·pn-1+an-2·pn-2 +
… + a1·p1+a0·p0 +a-1·p-1+a-2·p-2 +
. В случае десятичной системы счисления получим: 24,7310 = (2·101+4·100+7·10-1+3·10-2)10 Перевод дробного числа из двоичной системы счисления в десятичную
производится по следующей схеме: 101101,1012 = (1·25+0·24+1·23+1·22+0·21+1·20+1·2-1+0·2-2+1·2-3)10=45,62510 Перевод дробного числа из десятичной системы счисления в двоичную
осуществляется по следующему алгоритму: · Вначале переводится целая часть десятичной
дроби в двоичную систему счисления; · Затем дробная часть десятичной дроби умножается
на основание двоичной системы счисления; · В полученном произведении выделяется целая
часть, которая принимается в качестве значения первого после запятой
разряда числа в двоичной системе счисления; · Алгоритм завершается, если дробная часть полученного
произведения равна нулю или если достигнута требуемая точность вычислений. Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число. Перевод целой части дает 20610=110011102 по
ранее описанным алгоритмам; дробную часть умножаем на основание 2,
занося целые части произведения в разряды после запятой искомого дробного
двоичного числа:
.116 • 2 = 0.232 .232 • 2 = 0.464 .464 • 2 = 0.928 .928 • 2 = 1.856 .856 • 2 = 1.612 . .224 • 2 = 0.448 .448 • 2 = 0.896 .896 • 2 =1.792 .792 • 2 = 1.584 и т.д. Получим: 206,11610=11001110,00011100112 Таблицу степеней первых восьми отрицательных степеней двойки Степень
основания
2
8
16
0 1 1 1 1 2 8 16 2 4 64 256 3 8 512 4096 4 16 4096 65536 5 32 32768 1048576 6 64 262144 16777216 7 128 2097152 268435456 8 256 16777216 4294967296 9 512 134217728 68719476736 10 1024 1073741824 1099511627776 11 2048 8589934552 17592186044416 12 4096 68719476736 281474976710656 13 8192 549755813888 4503599627370496 14 16384 4398046511104 72057594037927936 15 32768 35184372088832 1152921504606846976 16 65536 281474976710756 18446744073709551616 Отрицательные числа Перейдем теперь к вопросу представления отрицательных чисел. Ясно, что на месте символов Итак, число — 1 должно кодироваться как Отрицательные числа всегда имеют в своем двоичном представлении
единицу в самом старшем разряде, который поэтому называют знаковым, а
абсолютная величина кодируемого числа получается как двоичное дополнение
остальных бит (нули нужно заменить на единицы и наоборот), увеличенное на один.
Легко видеть, что при этом самым маленьким отрицательным числом,
которое принадлежит типу Интересным является следующее
наблюдение: если число 127 + 1 = — 128 !!!
Итак, множество элементов типа То, что для элементов множества
, являющегося машинным аналогом
Z, нарушено фундаментальное свойство целых
чисел X + 1 > X, способно привести к различным невероятным на первый взгляд
результатам, однако гораздо более странные вещи происходят при работе с
вещественными числами. Двоичная арифметика Над
числами в двоичной системе счисления можно выполнять арифметические
действия. При этом используются следующие таблицы:
Сложение
Вычитание
Умножение
0+0=0
0-0=0
0*0=0
1+0=1
1-0=1
1*0=0
0+1=1
1-1=0
0*1=0
1+1=10
10-1=1
1*1=1
Рассмотрим примеры: Для
деления в двоичной системе счисления нужно уметь сравнивать числа
(определять, какое больше) и хорошо вычитать. Пример:
Еще
несколько примеров:
Если вы поищете в Интернете «Как преобразовать десятичные числа в двоичные», вы найдете четыре простых алгоритма: два для целых чисел и два для дробей. Они представлены на примерах ниже в первой части статьи. Но хотя почти всегда достаточно просто знать алгоритмы, я решил попытаться понять, почему они работают. Чтобы преобразовать целое число в двоичное, начните с рассматриваемого целого числа и разделите его на 2, обращая внимание на частное и остаток. Продолжайте делить частное на 2, пока не получите частное, равное нулю. Затем просто выпишите остатки в обратном порядке. Вот пример такого преобразования с использованием целого числа 12. Теперь осталось просто выписать остаток в обратном порядке — 1100 . Итак, 12 в десятичной системе представляется как 1100 в двоичной. Чтобы преобразовать дробь в двоичную, начните с рассматриваемой дроби и умножьте ее на 2 , обращая внимание на полученную целую и дробную части. Продолжайте умножать на 2, пока не получите в результате дробную часть, равную нулю. Затем просто выпишите целые части из результатов каждого умножения. Вот пример такого преобразования с использованием дроби 0,375 . Теперь просто выпишем полученную целую часть на каждом шаге — 0,011 . Итак, 0,375 в десятичной системе представляется как 0,011 в двоичной. Чтобы преобразовать двоичное целое число в десятичное, начните слева. Возьмите текущую сумму, умножьте ее на два и добавьте текущую цифру. Продолжайте до тех пор, пока не останется цифр. Вот пример такого преобразования с использованием дроби 1011 . Чтобы преобразовать двоичную дробь в десятичную, начните справа с суммы 0. Возьмите текущую сумму, добавьте текущую цифру и разделите результат на 2. Вот вам 4 простых алгоритма, которые позволят вам преобразовывать двоичные числа в десятичные и обратно. Ключом к пониманию того, почему эти алгоритмы работают, является расширение числа где Аналогично дробное число в любой системе счисления может быть представлено в следующем виде: где, 4 Для номера 2 14 в десятичной и двоичной системах представления выглядит следующим образом: Как оказалось, мы можем использовать эту форму расширения base-q для преобразования числа из десятичной системы в двоичную. Давайте сделаем это для того же числа 12 . Наша задача — найти все x . Давайте посмотрим, что мы можем сделать здесь. Первое, на что мы должны обратить внимание, это то, что все слагаемые, кроме последнего, будут четными числами, потому что все они кратны двум. Теперь, используя эту информацию, мы можем вывести цифру для 9.0080 x0 — если преобразуемое целое четное, то x0 Далее нам нужно найти значение для x1 . Также легко увидеть, что сумма значений в скобках равна 6 . Итак, мы можем записать наш первый шаг как: Продолжим поиск оставшихся x . Мы можем записать многочлен в скобках как отдельное утверждение: Здесь, применяя ту же логику, что и выше, мы видим, что x1 равно 0 . Давайте перепишем его и снова вынесем 2: Итак, наш второй шаг: Теперь мы можем увидеть закономерность. Мы можем продолжить факторинг 2 , пока частное не станет равным нулю. Давайте последуем этой схеме и посмотрим, что у нас получится. Поскольку частное равно 1, осталось только одно слагаемое, поэтому давайте перепишем предыдущее выражение: Итак, наш третий шаг: Итак, мы получаем следующее: Понятно, что x3 равно 1 . Но, так как для нашего алгоритма нам нужно частное, перепишем предыдущее выражение так, чтобы оно имело частное: Поскольку мы получили частное 0 , больше не с чем работать, и это был наш последний шаг. Запишем: Итак, мы закончили преобразование. Вот как выглядит наше преобразование по шагам: Теперь понятно, что остаток на каждом шаге соответствует значению x на соответствующих позициях: первый остаток соответствует первому x, второй остаток второму х и так далее. Итак, число 12 в двоичном виде с использованием описанного выше алгоритма представляется как 1100 . Помните, что мы начали с идеи показать, почему алгоритм, который включает погружение на 2 , работает. Давайте выполним шаги, описанные выше, и переместим 2 в левую часть выражений: Таким образом, вы можете увидеть, как мы пришли к алгоритму, описанному в начале. Мы также можем поместить вычисления для этих четырех шагов в одно представление, подобное этому 9.0003 Убедитесь, что вы понимаете, как мы пришли к этому представлению, так как оно понадобится нам при изучении того, как работает алгоритм преобразования из двоичного в десятичный. Чтобы показать, почему мы умножаем на 2 и берем целую часть при преобразовании дробей в двоичную, я также буду использовать base-q форму расширения для дробей. Я буду использовать дробное число 0,375 из первой части статьи. Аналогично целой части, давайте представим, что мы не знаем, как это число представлено в двоичном виде, и запишем его, заменив неизвестные цифры на 9. Как и в случае с целыми числами, наша задача состоит в том, чтобы найти все x , выделив x . Давайте посмотрим, как мы можем это сделать. Первое, на что следует обратить внимание, это то, что отрицательные степени числа 2 дают нам дроби со знаменателем числа 2 с положительными степенями. Давайте перепишем приведенное выше выражение: Сразу видно, что мы можем просто вынести 1/2 в правой части выражения. Сделаем так: и тогда мы можем переместить 1/2 в левую часть Хорошо, здесь мы выделили x1 2 1 либо 2 , и мы знаем, что это может быть 90 или 0 . Чтобы определить, какая у него цифра, давайте посмотрим на оставшиеся слагаемые: Давайте подумаем, насколько большой может быть сумма этих чисел. Ну, это геометрический ряд дробей, и сумма такого ряда лежит в границах [0 < сумма < 1], поэтому максимальное количество таких сумма может дать нам 1. Давайте теперь снова посмотрим на наше выражение: Теперь здесь должно быть ясно, что если правая часть меньше 1, то x1 не может быть равно 1 и, следовательно, равно 0 , а оставшаяся часть равна 0,75 . Именно так выглядит первый шаг алгоритма, представленного в начале: Отнимем дробную часть от 0,75 и выделим еще 1/2 , чтобы выделить x2 и переместить 1/2 влево: Теперь, если x2 равно 0 , то сумма левой части выражения не может быть больше 1 , но левая часть равна 1,5 2 , поэтому х 2 должно быть 1 а оставшаяся часть 0. Опять же, это следует схеме в алгоритме, представленном в начале: Повторим те же действия для оставшейся дробной части 0,5 . Используя ту же логику, что и выше, мы можем видеть, что x3 равно 1 и нет оставшейся дробной части: вот как выглядит наш последний шаг: Итак, давайте еще раз выпишем все шаги: Это именно тот алгоритм, который я представил в начале. Точно так же, как мы делали с целыми числами, мы также можем поместить вычисления для этих трех шагов в одно представление, например: Опять же, важно, чтобы вы полностью усвоили это представление, так как оно понадобится нам при изучении двоичного преобразования в десятичное. Тот факт, что некоторые дроби, представленные конечно в десятичной системе, не могут быть представлены конечно в двоичной системе, является неожиданностью для многих разработчиков. и не может конечно представлять 1/3: То же самое касается системы с основанием 2: Но если мы проверим 0,1, знаменатель будет равен 10, и это не степень 2, поэтому 0,1 будет бесконечная дробь в двоичной системе. Давайте посмотрим на это, используя алгоритм, который мы изучили выше: Мы можем продолжать делать это бесконечно, но давайте запишем это в виде периодической цепной дроби: Я собираюсь использовать то же самое двоичное целое число 1011 из первого раздела, чтобы показать вам, почему работает алгоритм умножения на 2. Поскольку все слагаемые кратны 2 , мы можем продолжать выносить на множители 2 , пока частное не станет равным нулю. Давайте сделаем так: Теперь, если вы просто будете следовать порядку математических операций, вы получите точно такие же шаги, как я показал в начале, а именно: Таким образом, 1011 в двоичном виде равно 11 в десятичном виде. Вот мы и подошли к последнему алгоритму. Наверное, вы уже сами разобрались с механикой, стоящей за этим. Если нет, давайте посмотрим, почему это работает. Расширение числа base-q от числа также является ключевым здесь. Число 0,1011 возьмем из первого раздела. Опять же, поскольку все слагаемые кратны 1/2 , мы можем продолжать разлагать 1/2 до тех пор, пока не останется дробной части. Сделаем так: Следуя порядку математических операций, получается алгоритм, описанный в начале: Таким образом, 0,1011 в двоичном виде равно 0,6875 в десятичном. Число, представляющее значение, может состоять из двух частей: целой и дробной части. Разделение между этими двумя частями представлено точкой (точкой). Дробная часть представляет собой значение между двумя целыми числами для выражения точности. Число также может быть представлено только целым числом без дроби, что просто зависит от степени точности, необходимой для представления значения. Число с дробной частью может принадлежать любой системе счисления, т. Давайте сначала рассмотрим дроби в широко используемой десятичной системе счисления, которая является системой счисления с основанием 10. Будучи числом с основанием 10, он может выбрать любое из десяти (10) возможных чисел для представления значения цифры. Десять (10) возможных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Кроме того, каждая десятичная цифра имеет позиционный вес, который она несет, который увеличивается на десять (10) раз для каждого позиционного шага справа налево. И наоборот, позиционный вес каждой десятичной цифры уменьшается в десять (10) раз с каждым позиционным шагом слева направо. В выражении это может быть представлено как (10 n ), где «n» представляет позицию десятичной цифры. При движении слева направо позиции за пределами «n = 0» представлены отрицательными значениями, т. е. -1, -2, -3, … и т. д., и поэтому их позиционный вес уменьшается на десять (10) с каждым шаг. Эти отрицательные позиционные веса вместе с соответствующими цифровыми значениями составляют дробное число . Из предыдущих статей известно, что данное число является взвешенной суммой значений его цифр и относительных позиционных весов. Это можно выразить следующим образом: Рассмотрим пример (123,456 10 ) , который представляет собой десятичное число, состоящее из целой и дробной частей, разделенных десятичной точкой. Числа слева и справа от десятичной точки (.) составляют целое число и дробных частей соответственно. В соответствии с этим 123 10 является целой частью, тогда как 456 10 составляет дробную часть данного (123,456 10 ) числа. Позиционный вес каждой цифры зависит от ее относительного положения относительно десятичной точки. Это показано ниже: Позиционные веса цифр 1, 2 и 3 слева от десятичной точки:0650 0 (1) соответственно. Состав числа (123,456 10 ) с использованием относительных позиционных весов цифр объясняется следующим образом: Концепция позиционной записи для представления относительного веса каждой десятичной цифры может быть применена к другим системам счисления. Однако каждая система нумерации использует другую базу или 9.0012 множитель значение. Например, Octal использует систему счисления по основанию 8, и каждый позиционный шаг увеличивает или уменьшает вес в восемь (8) раз в зависимости от направления шага. Аналогично, в двоичных числах каждая двоичная цифра или бит имеет весовую разницу в два (2) раза по сравнению с соседним битом. Двоичное число использует систему счисления с основанием 2 , и каждая двоичная цифра (бит) имеет два варианта представления своего значения: «0» и «1». Относительные позиционные веса двоичных цифр поясняются ниже: Учитывая двоичную дробь 0,1101 2 , считается, что позиционный вес каждой двоичной цифры или бита, составляющих двоичную дробь, составляет ее десятичный эквивалент. Двоичная дробь 0,1101 2 дает эквивалентную десятичную дробь 0,8125 10 . Следующие двоичные дроби преобразуются в эквивалентные им десятичные дроби с помощью описанного выше метода. Сверху видно, что биты двоичной дроби имеют вес, уменьшающийся в два (2) раза с каждым позиционным шагом вправо или, наоборот, вес становится вдвое (1/2 раза) в пересчете на десятичный эквивалент. Для преобразования десятичной дроби в ее двоичный эквивалент применяется метод, использованный ранее для преобразования десятичной дроби в двоичную. Однако вместо многократного деления на два (2) применяется умножение дробной части. Десятичное число, состоящее из целой и дробной части, требует преобразования каждой части отдельно. Для целочисленной части требуется метод повторного деления на 2, тогда как для дробной части требуется повторное умножение на 2. Обсуждавшийся ранее метод преобразования десятичной дроби в двоичную применяется только к целой части, составляющей положительные веса. Целая часть десятичного числа многократно делится на два (2), отмечая остаток в обратном порядке (от LSB к MSB), пока разделенное десятичное значение не станет «0». Это показано ниже путем преобразования 238 10 в его двоичный эквивалент. Следовательно, двоичный эквивалент числа 238 10 , состоящий только из целой части, равен 11101110 2 . Аналогично, двоичный эквивалент дробной части десятичного числа находится повторным умножением на 2 и отметкой переносов вниз в порядке пересылки, пока дробная часть не станет равной «0». Данную десятичную дробь, которая будет заведомо меньше 1, умножают на два (2), в результате чего получается значение, которое будет либо больше, либо меньше единицы (1). Если в результате умножения получается значение меньше единицы (1), перенос вперед не выполняется, т. В некоторых случаях может показаться, что повторное умножение не сходится к решению, т. е. дает точную единицу или результирующую дробь, равную «0». В таких случаях дробные числа имеют бесконечную длину, а умножения или числовые биты ограничены для получения желаемой степени точности. Следующие примеры преобразования десятичной дроби в двоичную объясняют вышеупомянутый метод. Двоичный эквивалент 0,625 10 равно 0,101 2 . Таким образом, двоичный эквивалент смешанного десятичного числа (43,375 10 2) 101011.011 2. Алгебраическое выражение — это запись, составленная со смыслом, в которой числа могут быть обозначены и буквами, и цифрами. Также она может содержать знаки арифметических действий и скобки. Любую букву, обозначающую число, и любое число, изображённое с помощью цифр, принято считать в алгебре также алгебраическим выражением. Алгебраические выражения, входящие в состав формул, могут применяться к решению частных арифметических задач, если в них заменить буквы данными числами и произвести указанные действия. Число, которое получится, если взять вместо букв какие-либо числа и произвести над ними указанные действия, называется численной величиной алгебраического выражения. Из этого легко сделать вывод, что одно и то же алгебраическое выражение при различных значениях входящих в него букв может иметь различные числовые величины. Примеры: 1) Выражение am + bn, при a = 2, m = 5, b = 1, n = 4 вычисляется: 2 · 5 + 1 · 4 = 14, а при a = 3, m = 4, b = 5, n = 1 вычисляется: 3 · 4 + 5 · 1 = 17 и т. д. 2) Выражение abс, при a = 1, b = 2, c = 3 равно: 1 · 2 · 3 = 6, а при a = 2, b = 3, c = 4 равно: 2 · 3 · 4 = 24 и т. д. Коэффициент — это числовой множитель алгебраического выражения, представляющего собой произведение нескольких сомножителей. Коэффициент в выражении ставится перед всеми остальными буквенными множителями. Таким образом, произведение чисел a, b, c, d, 4 записывается так: 4abcd; произведение чисел m, n, , p записывается так: . Числа 4 и — это коэффициенты. 4abcd = abcd + abcd + abcd + abcd и точно также . Итак, коэффициент показывает, сколько раз целое алгебраическое выражение или известная его часть берется слагаемым. Если в алгебраическом выражении нет числового множителя, то подразумевается, что коэффициент равен единице, так как a = 1 · a; bc = 1 · bc и так далее. Алгебраическое выражение, в которое не входят буквенные делители, называется целым, в противном случае дробным или алгебраической дробью. Пример. Целые алгебраические выражения: Дробные алгебраические выражения: Выражения, не содержащие корней, называются рациональными, а содержащие корни — иррациональными или радикальными. Например, все выражения, приведённые выше, являющиеся целыми или дробными, так же можно назвать и рациональными. √a , 53√c + a√mn — иррациональные или радикальные выражения. Алгебраическое выражение – это выражение, которое состоит из чисел, переменных и математических знаков. Выражение может содержать скобки, рациональную степень переменной (с целым или дробным показателем), знак модуля. Например, алгебраические выражения – это: . Область допустимых значений (ОДЗ) алгебраического выражения – это такие значения переменных, при которых это выражение имеет смысл. Пример 3. Найдите ОДЗ алгебраического выражения: . Решение. Если , то выражение не имеет смысла. Ответ. ОДЗ: . Пример 4. Найдите ОДЗ выражения: . Решение. Из условия имеем:. Это значит, что если или , то выражение не имеет смысла. Ответ. ОДЗ: . Рассмотрим рисунок 3.1 подробнее, для этого дадим характеристику каждому компоненту рисунка. Алгебраические выражения могут быть рациональными и иррациональными. Рациональное выражение – это выражение, в котором содержатся действия сложения, вычитания, умножения, деления, возведения в степень (здесь показатель степени – это натуральное число). Например, ; ; – это рациональные выражения. Рациональные выражения могут быть Целыми и Дробными. Целое рациональное выражение не содержит деления на буквенное выражение. Например, ; – это целые рациональные выражения. Целые рациональные выражения подразделяются на одночлены и многочлены. Одночлен – это произведение числового коэффициента на натуральную степень переменных. Например, ; ; – это одночлены, где ; ; – это числовые коэффициенты; ; ; – это буквенные выражения. Степень одночлена – это сумма показателей степеней всех переменных одночлена. Например, одночлен – это одночлен шестой степени одночлен – это одночлен четвертой степени 7 – это одночлен нулевой степени. Одночлен имеет Стандартный вид, если числовой коэффициент стоит на первом месте (перед буквенным выражением), а неизвестные множители записаны в алфавитном порядке. Одночлены называются Подобными, если они имеют одинаковые буквенные выражения. Привести подобные одночлены (члены) – это значит найти их сумму или разность. Например, ; ; – это подобные одночлены. Пример 5. Приведите подобные члены: . Решение. ; ; . Ответ. . Многочлен – это алгебраическая сумма одночленов (их сумма или разность). Например, – это многочлен. Степень многочлена – это степень его старшего члена. Например, многочлен – это многочлен четвертой степени; многочлен – это многочлен пятой степени. Дробное рациональное выражение содержит деление на выражение с переменными. Дробное рациональное выражение называют алгебраической дробью. Например, ; – это алгебраические дроби. Используют и другое определение алгебраической дроби. Выражение вида , где и – это многочлены или одночлены, называется Алгебраической дробью. Область допустимых значений (ОДЗ) Алгебраической дроби это множество значений переменной, при которых ее знаменатель не равен нулю (). Алгебраическая дробь равна нулю, если ее числитель равен нулю, т. е. . Если в алгебраическом выражении используется возведение переменных в дробную степень (извлечение корня из переменных), то такое алгебраическое выражение называется Иррациональным. Например, ; – это иррациональные выражения. Алгебраические выражения могут быть рациональными и иррациональными. Рациональные выражения разделяются на целые и дробные. Целые рациональные выражения состоят из одночленов и многочленов. Дробные рациональные выражения включают в себя алгебраические дроби. Буквенные уравнения , проще говоря, представляют собой уравнения, содержащие две или более переменных. Ваша цель состоит в том, чтобы решить только одну переменную по отношению к другим. Если вы знаете, как решать регулярные уравнения, то я гарантирую вам, что решение буквальных уравнений будет легкой задачей. Буквенное уравнение — это уравнение, включающее более одной переменной. Более того, переменная или «литерал» — это математический символ, представляющий произвольное значение или число. «Суть» решения буквального уравнения в том, чтобы изолировать или оставить отдельно определенную переменную с одной стороны уравнения (слева или справа), а остальные – с противоположной стороны. Если вы знаете, как решать обычные одношаговые уравнения, двухшаговые уравнения и многошаговые уравнения, процесс решения буквенных уравнений очень похож. Поэтому вас не должны пугать буквальные уравнения, потому что у вас уже могут быть навыки для их решения. Это просто вопрос практики и знакомства. Итак, ключевая идея выглядит так. Обратите внимание, что переменная, которую вы хотите решить, изолирована на одной стороне уравнения. В данном случае она находится на левой стороне. Обратите внимание, что переменная \color{red}\Large{x} сама по себе находится на одной стороне уравнения, а остальные — на противоположной. Давайте рассмотрим несколько примеров! Пример 1 : Найдите s в буквальном уравнении P = 4s. Помните эту формулу? Это периметр квадрата, где P означает периметр, а s – размер одной стороны квадрата. Таким образом, чтобы получить периметр квадрата, мы имеем P = s + s + s + s = 4s. Чтобы найти s, нам нужно избавиться от коэффициента 4, который умножает s. Обратное умножение — это деление, поэтому мы должны делить обе части на 4! Пример 2 : Найдите L в буквальном уравнении P = 2L + 2W. Буквенное уравнение, упомянутое выше, также является формулой для определения периметра прямоугольника, где: P = периметр, L = длина и W = ширина. Пусть вас не пугает внешний вид. Просто сосредоточьтесь на вещах, которые вы хотите сделать, то есть на решении для L, а остальные шаги последуют за вами. Пример 3 : Найдите x в приведенном ниже буквальном уравнении. Что делает это буквальное уравнение интересным, так это то, что мы собираемся изолировать переменную, которая является частью числителя дроби. Я не уверен, помните ли вы, что всякий раз, когда вы видите что-то подобное, постарайтесь сначала избавиться от знаменателя. Поскольку знаменатель 3 делит выражение «x − y», противоположная операция, которая может его отменить, — умножение. Имеет смысл сначала умножить обе части на 3, а затем добавить на «y», чтобы оставить x отдельно. Не так уж плохо, верно? Пример 4 : Решите для C в буквальном уравнении ниже. Это формула, используемая для преобразования меры температуры в единицах Цельсия в шкалу Фаренгейта. Обратите внимание: чтобы найти значение F (по Фаренгейту), нам нужно подставить некоторое значение C (по Цельсию). Однако можем ли мы также использовать данную формулу для нахождения градусов Цельсия всякий раз, когда задано значение Фаренгейта? Абсолютно да! В конце концов, это буквальное уравнение, поэтому можно выразить C через F. Это то, что мы собираемся сделать сейчас… Пример 5 : Найдите h в буквальном уравнении 3h + g = 5h − hg. Это действительно интересно! Некоторые из вас могут подумать, что невозможно изолировать переменную h, поскольку она находится почти в трех местах: одно h слева и два справа. Используйте метод факторинга, чтобы выбрать эту переменную h из группы. Но прежде чем вы сможете разложить h, убедитесь, что вы переместили все h на одну сторону уравнения. Поскольку у нас есть два члена h в правой части, мы могли бы также переместить член 3h слева на другую сторону. Вау, это здорово! Всего одиночных ч с правой стороны. Разделите обе части на (2 − g). Пример 6 : Найдите x в приведенном ниже буквальном уравнении. Самый простой способ решить это буквальное уравнение — выполнить перекрестное умножение . При этом знаменатели в обеих частях уравнения должны исчезнуть. С этого момента мы можем применить ту же стратегию из примера 5, чтобы найти x , которая включает в себя сбор всех членов x на одной стороне уравнения, а затем, как мы надеемся, факторизацию x. Начните с , избавьтесь от -5x справа, добавив 5x с обеих сторон. Викторина по буквальным уравнениям Вам может быть интересно: Решение одношаговых уравнений Решение двухэтапных уравнений Решение многошаговых уравнений Смотри, ты идешь! Теперь вы научились решать одношаговые уравнения, двухшаговые уравнения и многошаговые уравнения. Теперь пришло время обсудить решение буквальных уравнений . На этом уроке мы дадим определение буквенным уравнениям, рассмотрим примеры буквенных уравнений, а также научимся решать буквальные уравнения. Давайте буквально взволнован, чтобы начать! Что мы рассматриваем Напомним из нашего предыдущего исследования, что уравнение — это математическое предложение, в котором используется знак равенства = , чтобы показать, что два выражения равны. В отличие от других уравнений, с которыми вы уже работали, буквальные уравнения состоят в основном из букв и переменных. Многие из буквальных уравнений, с которыми вы работали в своей жизни, были формулы. Хотя эти уравнения будут выглядеть иначе, чем наши обычные уравнения, они по-прежнему подчиняются тем же правилам решения. Вернуться к оглавлению Хотя идея уравнений, состоящих в основном из букв, может показаться чуждой, вы много раз использовали буквальные уравнения в своей жизни. Площадь прямоугольника A = b \cdot h Длина окружности C = \pi \cdot D Формула простых процентов I = p \cdot r \cdot t Каждая буква (или переменная) в буквальном уравнении имеет особое значение и изменяется от задачи к задаче. Вернуться к оглавлению Решение буквенных уравнений следует тем же правилам, что и решение одношагового или двухэтапного уравнения. Идея «решения» буквального уравнения, по сути, означает, что мы переставляем буквы (или переменные), чтобы изолировать новую переменную. Буквальное уравнение «решено», когда интересующая переменная находится одна на одной стороне уравнения. Ознакомьтесь с лицензиями школы Альберта ! Подобно решению уравнений, мы будем использовать обратные операции, чтобы изолировать переменную саму по себе. \text{Сложение} \leftrightarrow \text{Вычитание} \text{Умножение} \leftrightarrow \text{Деление} Вот несколько примеров решения буквенных уравнений: Найдите h в следующем буквальном уравнении: А = b \cdot h Помните эту формулу? Как сказано выше, это площадь прямоугольника. Как отмечалось ранее, в буквенных уравнениях в основном используются буквы и переменные. Если бы это было простое уравнение, такое как 10 = 2x, мы бы просто разделили обе части на 2, чтобы получить мой окончательный ответ. При «решении» буквенных уравнений мы следуем тем же правилам, что и простые уравнения. Следовательно, чтобы найти h в этом уравнении, нам нужно выделить его отдельно. Поэтому мы разделим обе части на b . \dfrac{A}{b} = \dfrac{b \cdot h}{b} Это изолирует h , что даст нам ответ: h = \dfrac{A}{b} Хотя формулы являются распространенным примером буквенных уравнений, не все буквальные уравнения являются формулами. Найдите m в следующем уравнении: Несмотря на то, что в уравнении не было чисел, мы «решили» буквальное уравнение для m . Вернуться к оглавлению Не все буквальные уравнения решаются только за один шаг. Вот пример использования нескольких шагов для решения буквенных уравнений. 92} Теперь у нас есть r, изолированный сам по себе, что дает нам новое буквальное уравнение: r = \sqrt{\dfrac{V}{\pi h}} Вот пример буквального уравнения, которое не является формулой, но которое мы можем решить для переменной. Найдите x в следующем уравнении: 4(x + y) = P Есть два способа решить эту проблему. Первый метод состоит в том, чтобы рассматривать его как уравнение и распределять 4 , а затем решать: 4x + 4y = Р Затем мы можем вычесть 4y с каждой стороны: 4x + 4y \textcolor{red}{- 4y} = P \textcolor{red}{ — 4y} Затем нам нужно разделить каждую сторону на 4 : \dfrac{4x}{4} = \dfrac{P — 4y}{4} Наконец, нам нужно упростить наше уравнение: x = \dfrac{P}{4} — \dfrac{4y}{4} х = \dfrac{P}{4} — у Теперь мы, наконец, нашли x в буквальном уравнении. Давайте посмотрим, как можно решить уравнение, не упрощая в конце. В другом методе мы можем просто разделить на 4 в начале, чтобы избежать использования свойства распределения. Например: \dfrac{4(x + y)}{4} = \dfrac{P}{4} Тогда нам просто нужно вычесть y с каждой стороны: x + y \textcolor{red}{- y} = \dfrac{P}{4} \textcolor{red}{ — y} Таким образом, мы получаем: x = \dfrac{P}{4}- y Обратите внимание, что уравнение уже упрощено, и никаких других шагов не требуется. Вернуться к оглавлению Вот короткое видео, демонстрирующее, как решать буквенные уравнения: Давайте поработаем над некоторыми примерами буквенных уравнений с дробями! Ознакомьтесь с лицензиями школы Альберта ! Многие буквенные уравнения и формулы в той или иной степени содержат дроби. Например, вот формула объема сферы: Теперь, когда r изолировано, мы успешно нашли r . Что произойдет, если мы просто захотим изменить уравнение для другой переменной? Например, решите следующее уравнение для x : y = \dfrac{x}{4} — \dfrac{1}{8} Обратите внимание, что в уравнении две переменные, и наша конечная цель по-прежнему состоит в том, чтобы изолировать x . В этом буквальном уравнении наименьший общий знаменатель равен 8 . Следовательно, мы умножим каждое слагаемое на 8. 8 \cdot y = 8 \cdot \dfrac{x}{4} — 8 \cdot \dfrac{1}{8} Это даст нам уравнение, в котором больше нет дробей: 8y = 2x — 1 Затем продолжайте решать, как обычное уравнение: Теперь, когда мы изолировали x отдельно, мы правильно «решил» буквальное уравнение. Классическая модульная коляска Роан Марита — это настоящая классика проверенная временем. Коляска выпускается уже более 17 лет и за всё время она претерпела только небольшие доработки для более комфортного использования. Роан Марита по праву считается одной из лучших колясок в мире. Она выполнена из качественных экологически чистых материалов, которые готовы служить не один десяток лет. Рама данной коляски уникальна, регулировка высоты ручки и сложения происходит при помощи кнопки на ручке. О мягкости укачивания можно писать долго, но лучше один раз попробовать. В основе системы амортизации установлены 4 пружины, за счёт них коляска легко укачивается в 3 плоскостях, а на дороге подвеска «съедает» все неровности. За многие годы выпуска у коляски накопилось огромное количество расцветок, но многие из них сейчас не доступны. Люлька коляски Марита выполнена из прочного пластика, который защитит ребенка от любых внешних воздействий. Внутри люльки вложен ортопедический двухсторонний фирменный матрасик, его можно перевернуть для использования в разные времена года. Внутренняя обшивка люльки и чехол матрасика выполнены из 100% хлопка и снимаются для стирки. Размер матрасика 76 х 36 см толщина 2 см. Внутри люльки установлен подъёмный механизм, с его помощью ребенка можно посадить или приподнять, всего 6 положений. На дне вырезаны специальные отверстия для проветривания, они помогают избежать появлению конденсата в люльке. Специальные полозья на дне люльке позволяют использовать её для укачивания, а для кормления можно вытащить специальные ножки. В стильных кармашка люльки прячутся специальные ремни для переноски. Капюшон съёмный, единый для люльки и прогулочного блока. В новых версиях Мариты он удобно крепится и снимается с люльки с помощью специальный кнопок. Капор имеет 5 положений закрывания. В новых версиях колясок Марита изменена система крепления на люльку, она стала более удобная и понятная. Люльку можно установить в любом направление. Прогулочный блок устанавливает ниже уровня люльки, благодаря этому Вам не надо высоко поднимать ребенка для того, что бы посадить его в прогулочный блок, а ребенок постарше сам сможет забраться в коляску. Ширина сидячего места 35 см, высота спинки 45 см, глубина сиденья 25 см, длина подножки 20 см. т.е. общее спальное место 90 на 35 см. Вес прогулочного блока 5 кг. Спинка прогулочного блока откидывается и имеет 3 положения от полностью лежачего до сидячего. На подноже есть ламинация для защиты от грязи. За безопасность ребенка отвечают пятиточечные ремни безопасности с удобными фастексами. Бампер на новых моделях легко снимается путём нажатия на специальные кнопки. Большой тёплый чехол идёт в комплекте. Рама имеет следующие размеры в разложенном виде без колес: 90 х 60 х 99 см. На пластиковой ручке есть специальная кнопка, с помощью её можно регулировать высоту ручки, она имее 2 положения 102 и 110 см от пола, третье положение используется для заходу в короткий лифт или полного сложения рамы. Специальный предохранитель защитит коляску от случайного сложения. Тормоз активируется нажитием специальной клавиши на задней оси коляски, тормоз стояночный очень недежный приего активации задние колёса провернуть невозможно. Корзина для покупок открытая и выполнена из стали. Колёса на классической Марите надувные, диски металлические хромированные, диаметр 12 дюймов или 30 см. Возможен заказ Модели Элеганс, она отличается хромированной рамой и увеличенными колёсами 14 дюймов или 36 см, которые могут быть с разными видами покрышек (черный надувные, белые надувные и белые имитация надувных). Сумка для мамы на молнии, она имеет одно большое отделение, 2 кармашка и держатель бутылочки. За дополнительную плату коляску можно заказать, как модель 3 в 1, в этом случае в комплекте будет итальянская автолюлька группы +0 Roan Kite, которая устанавливается на раму. Сборка коляски Roan Marita 1 в 1 цвет E73. Сравнение колясок Роан Эмма, Марита и Кортина у нас на канале Tutis Zippy New 2 в 1(Тутис Зиппи Нью 2 в 1) это универсальная и очень мобильная коляска для молодых и активных родителей живущих в мегаполисе. В комплект коляски входит полноценная люлька для новорожденного малыша, основной прогулочный блок, и универсальное шасси на которое устанавливаются эти два модуля. Первое время, а именно с рождения и до 6-8 месяцев (до 9 кг) вы будете пользоваться полноценной люлькой переноской. Сама люлька невероятно функциональна, она с легкостью фиксируется, и так же легко снимается с шасси коляски, довольно просторная и глубокая-легко вместит даже самый объемный меховой конверт. Люлька коляски Tutis Zippy New имеет глубокий козырек от солнца с дополнительной встроенной в его основание силиконовой защитой, которой при необходимости можно воспользоваться в солнечный или ненастный день. Для проветривания люльки в основание также встроена москитная сетка, а для поднятия спинки вашего малыша в дно люльки вмонтирован специальный регулирующийся механизм. Основная ваша коляска это сочетание полноценного прогулочного блока, и универсального шасси. Почему именно так? Потому, что используется такой дуэт примерно с 6-8 месяцев и до 3-х лет (до 20 кг). Прогулочный блок имеет возможность установки на раму коляски Tutis Zippy в два направления: против и по ходу движения коляски. Таким образам во время прогулки вы легко сможете расположить вашего ребенка лицом к себе. При помощи теплого качественного чехла на ножки вы всегда защитите вашего малыша в холодную погоду, а при помощи глубокого козырька всегда возможно, создать уют и дополнительную защиту от ветра и яркого солнца. Шасси коляски Tutis Zippy New, выполнено и высококачественного алюминия, складывается буквально одной рукой и фиксируется, в таком положении коляска войдет даже в самый маленький багажник. Благодаря передним надувным поворотным колесам, коляска обладает высокой маневренностью и проходимостью. Основные характеристики люльки Tutis Zippy New: Основные характеристики прогулочного блока Tutis Zippy New: Основные характеристики рамы и колес коляски Tutis Zippy New: Технические характеристики: Комплектация: Скрыть текст Показать полностью Справка См. интерпретации этого варианта в сочетании с другими вариантами Справка Справка Справка См. Документы Федеральной службы государственной регистрации, кадастра и картографии ФЕДЕРАЛЬНАЯ СЛУЖБА ГОСУДАРСТВЕННОЙ РЕГИСТРАЦИИ, ПИСЬМО О РАССМОТРЕНИИ ОБРАЩЕНИЯ Управление нормативно-правового регулирования в сферах регистрации недвижимости, геодезии и картографии Росреестра (далее — Управление), рассмотрев обращение, сообщает следующее. В соответствии с Положением о Федеральной службе государственной регистрации, кадастра и картографии, утвержденным постановлением Правительства Российской Федерации от 01.06.2009 N 457, Росреестр не наделен полномочиями по разъяснению законодательства. Вместе с тем полагаем возможным обратить внимание на следующие положения действующего законодательства. Особенности государственной регистрации прав и (или) государственного кадастрового учета при изъятии недвижимого имущества для государственных или муниципальных нужд определены статьей 60 Федерального закона от 13. Согласно части 1 статьи 60 Закона N 218-ФЗ основанием для государственной регистрации прав на изъятые для государственных или муниципальных нужд земельный участок и (или) расположенные на таком земельном участке объекты недвижимости является заключенное в порядке, установленном земельным законодательством, соглашение об изъятии недвижимости для государственных или муниципальных нужд (далее — соглашение об изъятии недвижимости) или вступившее в силу решение суда об изъятии недвижимости для государственных или муниципальных нужд. Подготовка соглашения об изъятии недвижимости регулируется нормами Земельного кодекса Российской Федерации (далее — ЗК РФ). Согласно положениям ЗК РФ, составлению соглашения об изъятии недвижимости предшествует принятие решения об изъятии земельных участков для государственных или муниципальных нужд (статьи 56.6, 56.7, 56.9 ЗК РФ). Подпунктом 4 пункта 1 статьи 56. Согласно части 3 статьи 60 Закона N 218-ФЗ государственная регистрация прав на объекты недвижимости, изъятые для государственных или муниципальных нужд, осуществляется на основании заявления органа государственной власти, органа местного самоуправления или лица, на основании ходатайства которого принято решение об изъятии объектов недвижимости для государственных или муниципальных нужд. С заявлением о государственном кадастровом учете от имени лиц, права на недвижимое имущество которых подлежат прекращению в соответствии с решением об изъятии недвижимого имущества для государственных или муниципальных нужд, вправе обратиться орган исполнительной власти или орган местного самоуправления, принявшие данное решение, или организация, на основании ходатайства которой принято данное решение (часть 7 статьи 60 Закона N 218-ФЗ). Частью 10 статьи 60 Закона N 218-ФЗ установлено, что снятие с государственного кадастрового учета и прекращение государственной регистрации прав на исходные земельные участки, права на которые прекращаются в связи с их изъятием для государственных или муниципальных нужд, осуществляются только одновременно с осуществлением государственной регистрации прав на земельные участки, образованные на основании решения об изъятии недвижимого имущества для государственных или муниципальных нужд, в том числе на земельные участки, права на которые у граждан или юридических лиц возникают на основании соглашения об изъятии недвижимого имущества для государственных или муниципальных нужд или решения суда о таком изъятии. При этом частью 12 статьи 60 Закона N 218-ФЗ предусмотрена возможность государственной регистрации прав на образованные в связи с изъятием земельные участки (включая остающиеся в собственности правообладателя исходного земельного участка) только на основании заявления органа, принявшего решение об изъятии земельного участка, без заявления правообладателя исходного земельного участка. Таким образом, по мнению Управления, положения пункта 8 части 5 статьи 14 Закона N 218-ФЗ не противоречат положениям статьи 60 Закона N 218-ФЗ. Дополнительно информируем, что письма Управления не содержат правовых норм или общих правил, конкретизирующих нормативные предписания, не являются нормативными правовыми актами, имеют информационный характер и не препятствуют руководствоваться непосредственно нормами законодательства. Начальник Управления Задайте вопрос юристу: +7 (499) 703-46-71 — для жителей Москвы и Московской области BeneVision N1 Monitor/Modulelaura2023-03-14T16:23:25-04:00 BeneVision N1 — это компактное решение «3 в 1», разработанное для адаптации к потребностям пациента в мониторинге в больнице. Являясь базовым модулем серии N, N1 включает в себя все ваши стандартные параметры. В сочетании со многими расширенными модулями параметров в мониторе N-серии это решение гибко адаптируется для поддержки самых тяжелых пациентов. Включая полную запись пациента, N1 помогает обеспечить безопасность ваших пациентов при транспортировке, а также упрощает логистику передвижения. Просто сдвиньте N1 с прикроватного монитора, и все готово; N1 мгновенно превращается в беспроводной транспортный монитор, обеспечивая непрерывность данных с помощью BeneVision DMS/EMR. При подключении к 22-дюймовому сенсорному дисплею Mindray N1 имеет все возможности мониторинга у постели больного, а также такие функции, как несколько макетов экрана и настраиваемые клавиши быстрого доступа, обеспечивающие универсальность для удовлетворения потребностей многих больничных отделений. Оценка ECRI аппаратов BeneVision серии N и BeneVision DMS в качестве системы физиологического мониторинга в отделении интенсивной терапии s System, предоставлена в ознакомительных целях только. Содержание, содержащееся здесь, защищено законами об авторском праве и не может — полностью, частично или путем ссылки — использоваться в рекламе или рекламных материалах. Вставьте N1 со стойкой для транспортных модулей (TMR) в прикроватную док-станцию, чтобы мгновенно расширить возможности просмотра и мониторинга с помощью 22-дюймового сенсорного дисплея Mindray. Комплексные возможности мониторинга N1 расширены за счет добавления нескольких экранов и параметров конфигурации, что позволяет подробно просматривать важные данные о пациентах. Широкий набор параметров N1 позволяет выполнять мониторинг на транспорте того же уровня, что и у постели больного. Варианты параметров, такие как CO 2 и в общей сложности четыре инвазивных давления при транспортировке, N1 — ваш мобильный партнер для интенсивной терапии. Используя N1, просто «бери и работай» — никаких кабелей или регулировок настроек не требуется. В основе платформы серии N лежит многопараметрический модуль N1. N1 аккуратно размещается в модульном отсеке любого монитора N-серии, обеспечивая комплексный мониторинг у постели больного. Клиницисты уверены, что все собранные данные о пациентах безопасны, доступны и не содержат пробелов. При транспортировке или у постели больного N1 выдерживает самые сложные больничные условия, увеличивая срок службы изделия и окупаемость ваших инвестиций. Брошюра по семейству N-Series Руководство по решениям для жизненного цикла N-Series N1 3-in-1 Brochure N1 Product Sheet Физические характеристики N1 Серия N/Epiphany 12 -Lead ECG Data Management Partnership Гарантийный талон BeneVision серии N Очистка и дезинфекция продуктов Mindray Monitoring Каталог расходных материалов и принадлежностей Приобретение в Mindray включает комплексное клиническое обучение, проводимое специалистами Mindray. Наша специализированная группа выездного обслуживания и собственная служба технической поддержки представляют собой одну из крупнейших команд прямого обслуживания в отрасли. Индивидуально и коллективно они стремятся улучшить уход за пациентами, защищая ваши инвестиции. Отличные бургеры. Наши огромные сочные бургеры ОБЯЗАТЕЛЬНО ПОПРОБУЙТЕ! Посмотреть наше меню Отличные бургеры. Наши большие сочные бургеры ОБЯЗАТЕЛЬНО ПОПРОБУЙТЕ! Отличные бутерброды. Мы известны своими потрясающими бутербродами. Который твой любимый? Посмотреть наше меню Отличные бутерброды. Крафтовое пиво — У нас есть отличный выбор крафтового пива! Приходи и узнай, что сегодня в моде! Посмотреть наше меню Крафтовое пиво — У нас есть отличный выбор крафтового пива! Приходи и узнай, что сегодня в моде! Комфортная еда. Нам сказали, что у нас лучшая домашняя еда и комфортная еда в городе! Посмотреть наше меню Комфортная еда — Нам сказали, что у нас лучшая домашняя кухня и комфортная еда в городе! Большой выбор вин. У нас есть удивительный и обширный выбор вин. Мы поможем подобрать идеальную пару! Посмотреть наше меню Большой выбор вин — У нас есть удивительный и обширный выбор вин. Мы поможем подобрать идеальную пару! Семейный ресторан — семейный ресторан с вежливым обслуживанием и вкусной едой! Посмотреть наше меню Семейный ресторан — семейный ресторан, дружелюбное обслуживание и вкусная еда! Офисные функции — Планируете офисное мероприятие / счастливый час? Мы вас прикрыли! Позвоните, чтобы узнать Офисные функции — Планируете офисное мероприятие / счастливый час? Мы вас прикрыли! Выпускные вечера. Звоните, чтобы узнать Выпускные вечеринки. Позвольте нам помочь вам сделать этот выпускной сезон особенным, если вы чествуете новых выпускников. Плей-офф НБА — Смотри вместе с нами плей-офф НБА! Ближайшие события Плей-офф НБА — Приходите посмотреть плей-офф НБА вместе с нами! Крафтовые коктейли. У нас есть убийственное меню крафтовых коктейлей. Приходи и попробуй что-то новое! Посмотреть наше меню Крафтовые коктейли. У нас есть потрясающее меню крафтовых коктейлей. Приходи и попробуй что-то новое! Мы надеемся, что вы придете и насладитесь нашими 18 сортами разливного пива. Наша гостиная (21 год и старше) представляет собой сигарную зону площадью 1000 кв. футов с фильтрующей системой вентиляции, шезлонгами и столами для игры в нарды или шахматы. Узнайте больше о нас В нашем меню много отличных блюд и закусок. Существует большой выбор вин на выбор. Мы надеемся, что вы скоро приедете к нам в гости. Меню Алоха Пятница 19:00 — 22:00 ВСЕ СПЕЦИАЛЬНЫЕ ПРЕДЛОЖЕНИЯ Много раз был на 3N1. Всегда отличный опыт. Это единственный пойти в спорт-бар к востоку от 805! Рик и его команда всегда принимают своих гостей. Для обедов на улице были приобретены обогреватели, столы, кострища и удобные стулья. У них тоже есть проектор и показывают лучшие игры/драки! Профессионализм, вкусная еда и напитки на высоте! Я не курю сигары, но салон и хьюмидор приятны. Есть кондиционер!.. Работая в сфере продуктов питания и напитков, мы с женой всегда любим пробовать новые места. Большой выбор напитков, множество телевизоров, где можно посмотреть любой вид спорта. Они даже вытащили огромный наружный телевизор для футбольного матча. Мне сказали, что он отлично подходит для боев UFC. Отличная атмосфера. Скрытый драгоценный камень. Обязательно вернусь. Бургеры и картофель фри здесь просто огонь! Удивительный сервис. Автор: Адам Гроден Используйте наш практический тест SAT по математике ниже, чтобы подготовиться к экзамену. Мы включили несколько практических экзаменов для вас. Наши вопросы касаются тем, по которым вы будете тестироваться. Используйте пояснения к ответам, чтобы лучше понять эти сложные темы. Резюме: Используйте приведенные ниже математические вопросы SAT для изучения. Если вам нужна дополнительная помощь, воспользуйтесь курсом подготовки к SAT. Ниже мы перечислили 6 различных практических тестов. Каждый экзамен включает объяснения ответов в конце. Объяснения ответов помогут вам научиться решать проблемы и решать их быстрее. Если вам нужны пробные экзамены по другим предметам, посетите наш сайт пробных экзаменов SAT. Вы также можете воспользоваться нашими советами по изучению SAT для получения дополнительной помощи. Математический раздел SAT включает 2 раздела: (нажмите на картинку, чтобы увеличить) У вас будет 5-минутный перерыв между разделом без калькулятора и разделом с калькулятором. Важно использовать подготовку к SAT по математике для подготовки к разделу без калькулятора, так как многие учащиеся испытывают трудности с этим разделом. Просмотрите даты SAT, чтобы убедиться, что вы уделяете себе достаточно времени на учебу. Большинство вопросов представляют собой вопросы с несколькими вариантами ответов, но 22% вопросов будут представлять собой ответы учащихся (также известные как вставки). На математическом разделе SAT будут тестироваться 4 основные темы: Сердце алгебры включает такие подтемы, как: Решение проблем и анализ данных включает такие подтемы, как: Паспорт высшей математики включает такие подтемы как: Дополнительные темы по математике включают такие подтемы, как: Хотите потренироваться для другого раздела SAT? Посетите наш бесплатный тестовый дом SAT, чтобы найти больше экзаменов. Есть один раздел, в котором вы можете использовать калькулятор, и один раздел, в котором вы не можете использовать калькулятор. Эти 2 раздела являются отдельными, и у вас будет 5-минутный перерыв между ними. Да, у вас будет 5-минутный перерыв между калькулятором и разделом без калькулятора. Нет, не все вопросы имеют формат множественного выбора. 22% вопросов будут «сетчатыми» вопросами. Это вопросы, на которые студент должен дать ответ. Test-Guide.com был основан группой преподавателей, стремящихся подготовить учащихся к успешной сдаче экзаменов. [О нас] Рекомендуемые подготовительные курсы Заявление об отказе от ответственности: Не связано и не одобрено The College Board. Вы также можете конвертировать DJVU во многие другие форматы файлов. Пожалуйста, смотрите полный список ниже. DJVU TO EPUB Конвертер (Формат файла цифровой электронной книги) DJVU TO MOBI Конвертер (Электронная книга Mobipocket) DJVU TO AZW3 Конвертер (Kindle eBook format) DJVU TO SVG Конвертер (Файл масштабируемой векторной графики) DJVU TO PPT Конвертер (Презентация PowerPoint) DJVU TO PPS Конвертер (Слайд-шоу Microsoft PowerPoint) DJVU TO PPTX Конвертер (Презентация PowerPoint Open XML) DJVU TO PPSX Конвертер (Слайд-шоу PowerPoint Open XML) DJVU TO ODP Конвертер (Формат файла презентации OpenDocument) DJVU TO OTP Конвертер (Шаблон графика происхождения) DJVU TO POTX Конвертер (Открытый XML-шаблон Microsoft PowerPoint) DJVU TO POT Конвертер (Шаблон PowerPoint) DJVU TO POTM Конвертер (Шаблон Microsoft PowerPoint) DJVU TO PPTM Конвертер (Презентация Microsoft PowerPoint) DJVU TO PPSM Конвертер (Слайд-шоу Microsoft PowerPoint) DJVU TO FODP Конвертер (Плоская XML-презентация OpenDocument) DJVU TO TIFF Конвертер (Формат файла изображения с тегами) DJVU TO TIF Конвертер (Формат файла изображения с тегами) DJVU TO JPEG Конвертер (Изображение в формате JPEG) DJVU TO PNG Конвертер (Портативная сетевая графика) DJVU TO GIF Конвертер (Графический файл формата обмена) DJVU TO BMP Конвертер (Формат растрового файла) Преобразовать DJVU TO ICO (Файл значка Майкрософт) Преобразовать DJVU TO PSD (Документ Adobe Photoshop) Преобразовать DJVU TO WMF (Метафайл Windows) Преобразовать DJVU TO EMF (Расширенный формат метафайла) Преобразовать DJVU TO DCM (DICOM-изображение) Преобразовать DJVU TO DICOM (Цифровая визуализация и коммуникации в медицине) Преобразовать DJVU TO WEBP (Формат файла растрового веб-изображения) Преобразовать DJVU TO JP2 (Основной файл изображения JPEG 2000) Преобразовать DJVU TO EMZ (Расширенный сжатый метафайл Windows) Преобразовать DJVU TO WMZ (Метафайл Windows сжат) Преобразовать DJVU TO SVGZ (Сжатый файл масштабируемой векторной графики) Преобразовать DJVU TO TGA (Тарга Графика) Преобразовать DJVU TO PSB (Файл изображения Adobe Photoshop) Преобразовать DJVU TO DOC (Документ Microsoft Word) Преобразовать DJVU TO DOCM (Документ Microsoft Word с поддержкой макросов) Преобразовать DJVU TO DOCX (Документ Microsoft Word с открытым XML) Преобразовать DJVU TO DOT (Шаблон документа Microsoft Word) Преобразовать DJVU TO DOTM (Шаблон Microsoft Word с поддержкой макросов) Преобразовать DJVU TO DOTX (Шаблон документа Word Open XML) Преобразовать DJVU TO RTF (Расширенный текстовый формат файла) Преобразовать DJVU TO ODT (Открыть текст документа) Преобразовать DJVU TO OTT (Открыть шаблон документа) DJVU TO TXT Преобразование (Формат обычного текстового файла) DJVU TO MD Преобразование (Уценка) DJVU TO PDF Преобразование (Портативный документ) DJVU TO HTM Преобразование (Файл языка гипертекстовой разметки) DJVU TO HTML Преобразование (Язык гипертекстовой разметки) DJVU TO MHTML Преобразование (MIME-инкапсуляция совокупного HTML) DJVU TO MHT Преобразование (MIME-инкапсуляция совокупного HTML) DJVU TO XLS Преобразование (Формат двоичного файла Microsoft Excel) DJVU TO XLSX Преобразование (Электронная таблица Microsoft Excel Open XML) DJVU TO XLSM Преобразование (Электронная таблица Microsoft Excel с поддержкой макросов) DJVU TO XLSB Преобразование (Двоичный файл электронной таблицы Microsoft Excel) DJVU TO ODS Преобразование (Открыть электронную таблицу документов) DJVU TO XLTX Преобразование (Открытый XML-шаблон Microsoft Excel) DJVU TO XLT Преобразование (Шаблон Microsoft Excel) DJVU TO XLTM Преобразование (Шаблон Microsoft Excel с поддержкой макросов) DJVU TO TSV Преобразование (Файл значений, разделенных табуляцией) DJVU TO XLAM Преобразование (Надстройка Microsoft Excel с поддержкой макросов) DJVU TO CSV Преобразование (Файл значений, разделенных запятыми) DJVU TO FODS Преобразование (Плоская XML-таблица OpenDocument) DJVU TO SXC Преобразование (Электронная таблица StarOffice Calc) DJVU TO XPS Преобразование (Спецификация документа Open XML) DJVU TO TEX Преобразование (Исходный документ LaTeX) Шаг
1 Загрузить файл: Можете добавить до 5 файлов Перетащите файлы сюда ИЛИ Выберите файл Ввести URL файла: Файл не выбран Исходный формат:CSV — Comma Separated ValuesDOC — Microsoft Word DocumentDOCX — Microsoft Word 2007 DocumentDJVU — DjVu DocumentODP — OpenDocument PresentationODS — OpenDocument SpreadsheetODT — OpenDocument Text DocumentPPS — PowerPoint Slide ShowPPSX — PowerPoint Slide Show 2007PPT — PowerPoint PresentationPPTX — PowerPoint Presentation 2007PDF — Portable Document FormatPS — PostScriptEPS — Encapsulated PostScriptRTF — Rich Text FormatTXT — Text documentWKS — Microsoft Works SpreadsheetWPS — Microsoft Works DocumentXLS — Microsoft Excel SpreadsheetXLSX — Microsoft Excel 2007 SpreadsheetXPS — XML Paper Specification3GP — 3GP Multimedia FileAVI — Audio Video Interleave FileFLV — Flash Video FileM4V — MPEG-4 Video FileMKV — Matroska Video FileMOV — Apple QuickTime Movie FileMP4 — MPEG-4 Video FileMPEG — Moving Picture Experts Group FileOGV — Ogg Vorbis Video FileWMV — Windows Media Video FileWEBM — HTML5 Video FileAAC — Advanced Audio Coding FileAC3 — AC3 Audio FileAIFF — Audio Interchange File FormatAMR — Adaptive Multi-Rate Audio FileAPE — Monkey’s Lossless Audio FormatAU — Sun’s Audio File FormatFLAC — Free Lossless Audio CodecM4A — MPEG-4 Audio FileMKA — Matroska Audio FileMP3 — MPEG-1 Audio Layer 3 FileMPC — MusePack Audio FileOGG — Ogg Vorbis Audio FileRA — RealMedia Streaming MediaWAV — Waveform Audio File FormatWMA — Windows Media Audio FileBMP — Windows BitmapEXR — OpenEXR File FormatGIF — Graphics Interchange FormatICO — ICO File FormatJP2 — JPEG 2000 compliant imageJPEG — Joint Photographic Experts GroupPBM — Netpbm Portable Bitmap formatPCX — Paintbrush image formatPGM — Netpbm Portable Graymap formatPNG — Portable Network GraphicsPPM — Netpbm Portable Pixmap formatPSD — Photoshop DocumentTIFF — Tagged Image File FormatTGA — Truevision Graphics AdapterCHM — Microsoft Compiled HTML HelpEPUB — Electronic PublicationFB2 — Fiction Book 2. Конвертировать в:CSV — Comma Separated ValuesDOC — Microsoft Word DocumentDOCX — Microsoft Word 2007 DocumentDJVU — DjVu DocumentHTML — HTML 5HTML — HTMLODP — OpenDocument PresentationODS — OpenDocument SpreadsheetODT — OpenDocument Text DocumentPPS — PowerPoint Slide ShowPPSX — PowerPoint Slide Show 2007PPT — PowerPoint PresentationPPTX — PowerPoint Presentation 2007PDF — Portable Document FormatPS — PostScriptEPS — Encapsulated PostScriptRTF — Rich Text FormatTXT — Text documentXLS — Microsoft Excel SpreadsheetXLSX — Microsoft Excel 2007 SpreadsheetXPS — XML Paper Specification3GP — 3GP Multimedia FileAVI — Audio Video Interleave FileFLV — Flash Video FileM4V — MPEG-4 Video FileMKV — Matroska Video FileMOV — Apple QuickTime Movie FileMP4 — MPEG-4 Video FileMPEG — Moving Picture Experts Group FileWMV — Windows Media Video FileApple iPhone / iPod / iPad / TVBlackBerryCommon Mobile Phones VideoAndroid DevicesMicrosoft XboxSony PS3 / PSP / WalkmanAAC — Advanced Audio Coding FileAC3 — AC3 Audio FileFLAC — Free Lossless Audio CodecMKA — Matroska Audio FileMP3 — MPEG-1 Audio Layer 3 FileOGG — Ogg Vorbis Audio FileWAV — Waveform Audio File FormatWMA — Windows Media Audio FileBMP — Windows BitmapGIF — Graphics Interchange FormatICO — ICO File FormatJP2 — JPEG 2000 compliant imageJPEG — Joint Photographic Experts GroupPBM — Netpbm Portable Bitmap formatPCX — Paintbrush image formatPGM — Netpbm Portable Graymap formatPNG — Portable Network GraphicsPPM — Netpbm Portable Pixmap formatTIFF — Tagged Image File FormatTGA — Truevision Graphics AdapterEPUB — Electronic PublicationFB2 — Fiction Book 2. Получить емейл с ссылкой на скачивание файла (необязательно): Конвертер файлов / Изображения / Книги / Конвертировать в DJVU / Конвертер JPG / DJVU в JPG Выберите файл для конвертации Перетащите файлы сюда. Максимальный размер файла 100 МБ или Зарегистрироваться Наш бесплатный онлайн-конвертер позволяет конвертировать файлы djvu в jpg, а также во множество других форматов. Вы можете легко преобразовать файл jpg в djvu, выполнив следующие действия. Шаг 1 Вы можете выбрать djvu-файл, который хотите конвертировать, со своего компьютера, Google Диска, Dropbox или просто перетащив его на страницу. Шаг 2 Выберите jpg или любой другой из 200+ поддерживаемых форматов, в который вы хотите конвертировать. Шаг 3 Дождитесь завершения преобразования, затем нажмите кнопку загрузки, чтобы получить преобразованный файл в формате jpg. Быстро и просто Просто перетащите файлы djvu на веб-страницу, и вы сможете конвертировать их в jpg или более чем в 250 различных форматов без регистрации, предоставьте адрес электронной почты или добавить водяной знак. Вам не нужно беспокоиться о безопасности. Как только вы загрузите файлы djvu, мы моментально их удалим. Затем преобразованные файлы удаляются через 24 часа. Кроме того, мы гарантируем, что все передачи файлов безопасны благодаря расширенному шифрованию SSL. Все хранится в облаке. Вам не нужно утруждать себя установкой какого-либо программного обеспечения. djvu to bmpdjvu to gifdjvu to jpegdjvu to tiffdjvu to htmldjvu to pdfdjvu to docdjvu to docxdjvu to rtfdjvu to txtdjvu to lrfdjvu to fb2djvu to jpgdjvu to epubdjvu to mobidjvu в azw3 art в jpgarw в jpgbmp в jpgcgm в jpgcr2 в jpgcrw в jpgcur в jpgdcm в jpgdcr в jpgdjvu в jpgdng в jpgemf в jpgfax в jpggif в jpghdr в jpgico в jpgjpeg в pjpgxmf в jpgor в jpgpes в jpgpgm в jpgpict в jpgpng в jpgpnm в jpgppm в jpgpsd в jpgpwp в jpgraf в jpgsfw в jpgsvg в jpgtga в jpgtiff в jpgtim в jpgttf в jpgwpg в jpgxcf в jpgxwd в jpghtml в jpgpdf в jpgdoc в jpgdocx в jpgxls в jpgxlsx в jpgxlsx в jpgodt в jpgwps в jpgdot в jpgrtf в jpgtxt в jpgpages в jpgods в jpgcsv в jpgodp в jpgodg в jpgpps в jpgdxf в jpgeps в jpgpcd в jpgpct в jpgwmf в jpgppsx в jpgppt в jpgdotx в jpgpdb в jpgepub в jpgmobi в jpgmpai в jpg в jpgmp4 в jpgxps в jpgoxps в jpgcbr в jpgcbz в jpgavi в jpgmov в jpgswf в jpgwebm в jpgwmv в jpgmpg в jpgtif в jpghtm в jpgdst в jpgkey в jpgdds в jpgdwg в jpgraw в jpgwebp в jpgpub в jpgcdr в jpgheic в jpgps в jpgmsg в jpgnrw в jpgplt в jpgjfif в jpgotf в jpgheif в jpgavif в jpgvideo в jpgword в jpgall в jpgpsp в jpgfig в jpgpat в jpgmovie в jpgexp в jpgals в jpgsid в jpgsite в jpgmax в jpgmix в jpgdex в jpgjpe в jpgjp2 в jpgrgb в jpgjps в jpgexr в jpgwbmp в jpgmap в jpgbin в jpgjif в jpgxpm в jpgyuv в jpgkdc в jpgpef в jpgrw2 в jpgsr2 в jpgwmz в jpg DjVu — это популярный формат файлов, созданный в основном для хранения отсканированных отчетов, особенно тех, которые содержат смесь текста, штриховых рисунков, индексированных цветных изображений. На этой странице: Часть 1: Бесплатно скачать инструмент для конвертации DjVu в JPG Часть 2: Как преобразовать файл DjVu в формат JPG? Часть 3: Выдающиеся функции программного обеспечения DJVU в JPEG по преобразованию Часть 4: Расширить точки знаний Часть 5: FAQS Весь процесс включает всего несколько щелчков мышью. Если вы являетесь обычным пользователем и хотите протестировать его бесплатно, попробуйте DEMO VERSION . Для расширенного использования и экспорта файлов DjVu в JPG без ограничений обновите лицензионные ключи. Чтобы преобразовать DjVu в формат JPG, выполните следующие действия: Связанная запись в блоге: Преобразование DjVu в Word Шаг 1. Запустите конвертер DjVu в JPG После успешной загрузки и установки запустите инструмент преобразования DjVu в JPG на компьютере с Windows. Шаг 2. Загрузите файлы DjVu Теперь вы увидите опцию Select Folders… и Select Files… в середине интерфейса программы. Обе эти вкладки позволят вам выбрать файлы DjVu. Выберите любой из них, а затем выберите документы DjVu, которые необходимо преобразовать в JPG. Шаг 3. Выберите необходимые документы DjVu Здесь вы можете прочитать информацию о количестве страниц в папках DjVu. Итак, включите требуемые папки DjVu , которые нужны для миграции. Шаг 4. Выберите формат JPG После этого перейдите к . Выберите параметр сохранения и выберите параметр «JPG» в раскрывающемся меню. Шаг 5. Настройте параметр расширенного режима Конвертер DjVu в JPG предлагает расширенные функции, которые вы можете выбрать в соответствии с вашими потребностями. Шаг 6. Сохранение выходных данных в место назначения Последний шаг — выбрать место назначения и сохранить преобразованные файлы DjVu в JPG. Чтобы выбрать новое местоположение, щелкните значок папки . Шаг 7. Нажмите на кнопку «Конвертировать» Наконец, нажмите на кнопку « Конвертировать », расположенную в правом нижнем углу экрана. Это автоматически запустит процесс преобразования файла DjVu в JPG. Шаг 8. Open Output Перейти к результирующему месту назначения для просмотра преобразованных файлов DjVu . Читайте также: Преобразование DjVu в формат PDF Помимо этого, есть несколько причин, по которым вы, несомненно, оцените свой выбор. Универсальность: Когда дело доходит до инструментов преобразования DjVu в JPG, вы вряд ли найдете более универсальную альтернативу, чем наш продукт. Опять же, вы можете воспользоваться бесплатной демо-версией и конвертировать несколько файлов DjVu в соответствующие форматы. Высокая гибкость и дополнительные параметры: С помощью этой утилиты преобразование DjVu в JPG происходит со значительной скоростью. Вы можете выбрать любой из параметров «Расширенного режима», например «Все страницы», «Выбрать диапазон страниц (необходимо ввести начальную и конечную страницы)», «Выбрать несколько несмежных страниц (например, 12,2 ,36)». Пакетное преобразование: Преобразователь файла DjVu в JPG является одним из таких приложений, которое предоставляет возможность пакетного преобразования DjVu в формат JPG. За одну попытку пользователи могут выполнять массовые преобразования без изменения целостности данных. Прочитать информацию о количестве страниц: После того, как вы выбрали файлы DjVu для задачи переноса, после этого инструмент показывает все данные в виде древовидной структуры предварительного просмотра. Вы можете прочитать информацию о количестве страниц в этой иерархической структуре и перепроверить все данные для эффективного процесса миграции DjVu в JPG. Любое место сохранения: Пользователи имеют полную свободу выбора места назначения для вывода. Совместимость с Windows: Наш инструмент экспорта DjVu в jpeg поддерживает все последние и предыдущие версии операционных систем Microsoft Windows. Вы можете запустить программу в таких версиях, как Windows 10, Windows 8.1, Windows 8, Windows 7, Windows XP, Windows Vista, Windows Server 2019, Windows Server 2016 и т. д. Сохраняет неизменное качество данных: На протяжении всего процесса конвертировать DjVu в JPG, программа сохраняет качество исходных данных. Он сохраняет форматирование текста, цветовые эффекты документа, разрешение изображения, гиперссылки, фон и т. д. ВОПРОС: Что такое файл DjVu? Формат DjVu — это формат сжатых файлов, созданный AT&T. Он представляет собой отсканированный документ, который может включать содержимое, изображения или рисунки. ВОПРОС: Каково происхождение формата файла DjVu? Технология DjVu изначально была разработана Яном Лекуном, Леоном Ботту, Патриком Хаффнером, Полом Г. Ховардом, Патрисом Симаром и Йошуа Бенжио в AT&T Labs с 1996 по 2001 год. ВОПРОС: Почему файлы JPG особенные? Файлы JPG имеют строго контролируемый уровень сжатия. Пользователь самостоятельно выбирает соотношение качество/размер документа. Он совместим и эффективно отображается в любом веб-браузере, текстовых и иллюстративных программах, на всех ПК, планшетах и мобильных телефонах. Формат подходит для реалистичных изображений с множеством изменений цвета и контраста. Кроме того, качество изображения JPG высокое. ⭐ Как уменьшить размер изображения для преобразования DjVu в JPG? Если вы хотите уменьшить размер изображения, выберите целевой файл DjVu (количество файлов не ограничено) и перейдите в «Расширенный режим»>> «Качество изображения». ⭐ Приведет ли изменение качества изображения к снижению качества моих выходных изображений JPG? Нет, наш продукт идеально подходит для оптимизации файлов DjVu для преобразования в формат jpeg. ⭐ Какой максимальный размер файла позволяет конвертировать файл DjVu в JPG? Размер файла не ограничен. Вы можете конвертировать большие файлы DjVu в формат JPG. ⭐ Где открыть сконвертированные файлы? Вы можете выбрать любое место для сохранения по своему усмотрению. По умолчанию программа сохраняет его на рабочем столе. Однако вы можете открывать преобразованные файлы в любом месте. ⭐ Безопасно ли использовать бесплатный конвертер DjVu в JPG? Да, преобразование файлов DjVu в JPG абсолютно безопасно. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 com
com Это особый тип уравнения, имеющий форму:
Это особый тип уравнения, имеющий форму: Затем вычисляем дискриминант по формуле. Используя метод cmath.sqrt() , мы вычислили два решения и распечатали результат.
Затем вычисляем дискриминант по формуле. Используя метод cmath.sqrt() , мы вычислили два решения и распечатали результат. sqrt (abs (dis_form)) если dis_form > 0:
print(«настоящие и разные корни»)
print((-b + sqrt_val) / (2 * a))
print((-b — sqrt_val) / (2 * a)) Элиф dis_form == 0:
print(» действительные и одинаковые корни»)
напечатать (-b / (2 * а)) еще:
print(«Сложные корни»)
print(- b / (2 * a), » + i», sqrt_val)
print(- b / (2 * a), «- i», sqrt_val) a = int(input(‘Введите a:’))
b = int(input(‘Введите b:’))
c = int(input(‘Введите c:’)) # Если a равно 0, то неверное уравнение
если а == 0:
print(«Введите правильное квадратное уравнение») еще:
найтиКорни (а, б, в)
sqrt (abs (dis_form)) если dis_form > 0:
print(«настоящие и разные корни»)
print((-b + sqrt_val) / (2 * a))
print((-b — sqrt_val) / (2 * a)) Элиф dis_form == 0:
print(» действительные и одинаковые корни»)
напечатать (-b / (2 * а)) еще:
print(«Сложные корни»)
print(- b / (2 * a), » + i», sqrt_val)
print(- b / (2 * a), «- i», sqrt_val) a = int(input(‘Введите a:’))
b = int(input(‘Введите b:’))
c = int(input(‘Введите c:’)) # Если a равно 0, то неверное уравнение
если а == 0:
print(«Введите правильное квадратное уравнение») еще:
найтиКорни (а, б, в)
 {-1}[B_1\cup B_2]$.
{-1}[B_1\cup B_2]$. Решение. Попробуем для начала решить ту же задачу, но с алфавитом, состоящим всего из трех букв – а, b, c. Здесь мы можем явно выписать все слова, состоящие из двух букв: аа, аb, аc, bа, bb, bc, cа, cb, cc. Получили $9=3\cdot3$.
В общем случае подсчет числа таких слов будем вести следующим образом: сначала посчитаем число слов, которые начинаются с буквы «а», затем – число слов, начинающихся с буквы «b» и так далее. Совершенно очевидно, что таким образом мы посчитаем каждое «слово» по разу.
Заметим, что двухбуквенных слов, начинающихся на букву «а», будет ровно столько же, сколько есть букв в алфавите. Слов, начинающихся на букву «б», будет столько же. И так со всеми буквами.
В нашей задаче слов, начинающихся с буквы «а», будет 26. Столько же будет слов, начинающихся с буквы «b», и так далее. Значит, всего слов, состоящих из двух букв, будет $26\cdot 26=676$.
Комментарий. На самом деле тут речь идет о прямом (или декартовом) произведении множеств.
Решение. Попробуем для начала решить ту же задачу, но с алфавитом, состоящим всего из трех букв – а, b, c. Здесь мы можем явно выписать все слова, состоящие из двух букв: аа, аb, аc, bа, bb, bc, cа, cb, cc. Получили $9=3\cdot3$.
В общем случае подсчет числа таких слов будем вести следующим образом: сначала посчитаем число слов, которые начинаются с буквы «а», затем – число слов, начинающихся с буквы «b» и так далее. Совершенно очевидно, что таким образом мы посчитаем каждое «слово» по разу.
Заметим, что двухбуквенных слов, начинающихся на букву «а», будет ровно столько же, сколько есть букв в алфавите. Слов, начинающихся на букву «б», будет столько же. И так со всеми буквами.
В нашей задаче слов, начинающихся с буквы «а», будет 26. Столько же будет слов, начинающихся с буквы «b», и так далее. Значит, всего слов, состоящих из двух букв, будет $26\cdot 26=676$.
Комментарий. На самом деле тут речь идет о прямом (или декартовом) произведении множеств.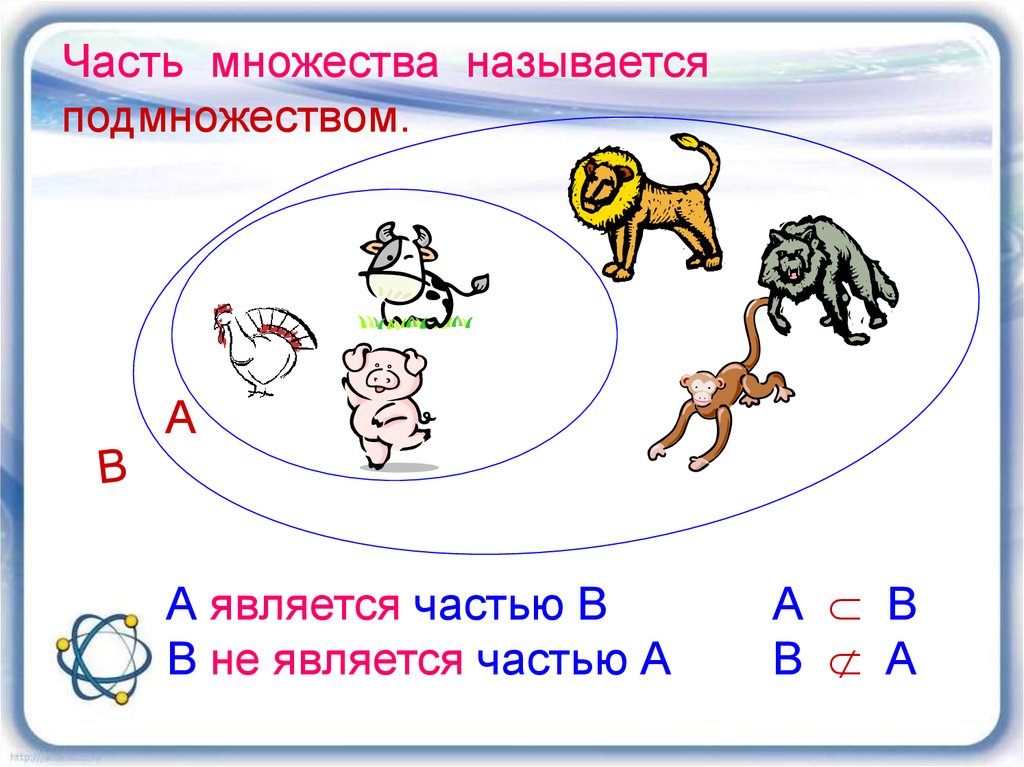 Произведением множеств называют множество из упорядоченных пар. Число элементов в произведении множеств равно произведению числа элементов исходных множеств (правило умножения). В нашем случае множество всех слов из 2 букв на английском языке – это как раз множество неупорядоченных пар английских букв, а значит равно произведению множества букв английского алфавита (их 26 штук) с самим собой, а значит в нем 26*26=676 элементов.
Произведением множеств называют множество из упорядоченных пар. Число элементов в произведении множеств равно произведению числа элементов исходных множеств (правило умножения). В нашем случае множество всех слов из 2 букв на английском языке – это как раз множество неупорядоченных пар английских букв, а значит равно произведению множества букв английского алфавита (их 26 штук) с самим собой, а значит в нем 26*26=676 элементов.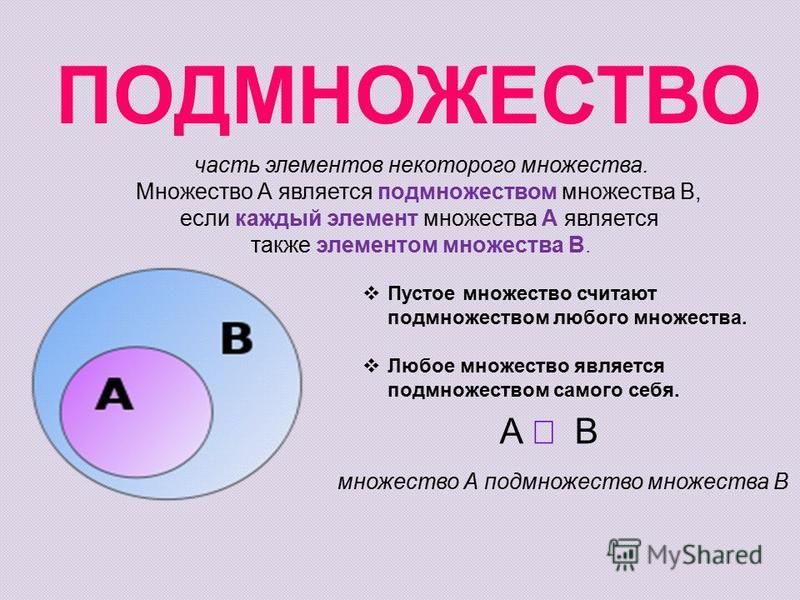 Так как порядок «обычных» дежурных не важен, выписывая их по алфавиту, мы никакой случай не забудем и не повторим дважды.
(Вася, Коля, Леша), (Вася, Коля, Петя),& (Вася, Леша, Петя),
(Коля, Вася, Леша), (Коля, Вася, Петя),& (Коля, Леша, Петя),
(Леша, Вася, Коля), (Леша, Вася, Петя),& (Леша, Коля, Петя),
(Петя, Вася, Коля), (Петя, Вася, Леша),& (Петя, Коля, Леша).
Итого $12$ вариантов.
Теперь перейдем к решению исходной задачи. Старшего дежурного можно выбрать десятью способами. Когда мы уже выбрали старшего, мы можем выбрать первого дежурного девятью (потому что одного человека мы уже назначили старшим дежурным) способами. После того, как мы выбрали старшего дежурного и еще одного дежурного, второго дежурного мы можем выбрать восемью способами. Итого, вроде бы, по «правилу умножения» должно получаться $10\cdot9\cdot8=720$.
Однако если мы внимательно посмотрим на наше решение, то увидим, что каждую тройку дежурных мы посчитали по два раза.
Так как порядок «обычных» дежурных не важен, выписывая их по алфавиту, мы никакой случай не забудем и не повторим дважды.
(Вася, Коля, Леша), (Вася, Коля, Петя),& (Вася, Леша, Петя),
(Коля, Вася, Леша), (Коля, Вася, Петя),& (Коля, Леша, Петя),
(Леша, Вася, Коля), (Леша, Вася, Петя),& (Леша, Коля, Петя),
(Петя, Вася, Коля), (Петя, Вася, Леша),& (Петя, Коля, Леша).
Итого $12$ вариантов.
Теперь перейдем к решению исходной задачи. Старшего дежурного можно выбрать десятью способами. Когда мы уже выбрали старшего, мы можем выбрать первого дежурного девятью (потому что одного человека мы уже назначили старшим дежурным) способами. После того, как мы выбрали старшего дежурного и еще одного дежурного, второго дежурного мы можем выбрать восемью способами. Итого, вроде бы, по «правилу умножения» должно получаться $10\cdot9\cdot8=720$.
Однако если мы внимательно посмотрим на наше решение, то увидим, что каждую тройку дежурных мы посчитали по два раза.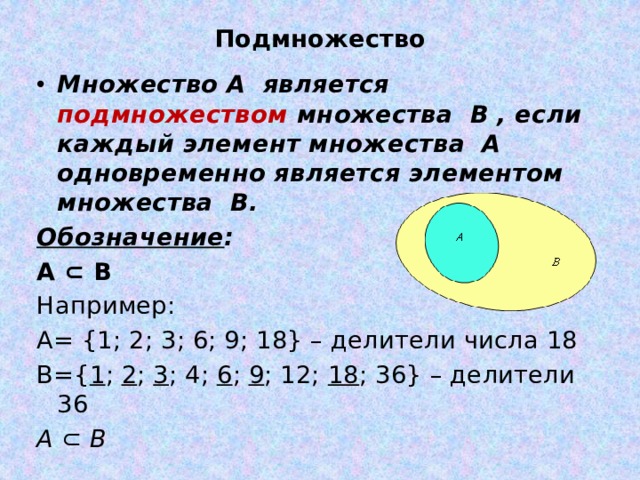 Например, тройку дежурных (Вася – старший дежурный, Леша, Петя) мы посчитали два раза: как тройку (Вася, Петя, Леша) и как тройку (Вася, Леша, Петя). Поэтому правильный ответ в два раза меньше – 360.
Например, тройку дежурных (Вася – старший дежурный, Леша, Петя) мы посчитали два раза: как тройку (Вася, Петя, Леша) и как тройку (Вася, Леша, Петя). Поэтому правильный ответ в два раза меньше – 360. В свою очередь
множество учеников этой школы является
подмножеством множества всех школьников
в Республики Беларусь;
В свою очередь
множество учеников этой школы является
подмножеством множества всех школьников
в Республики Беларусь; Пересечением множеств А и В называют новое множество Х,
содержащее те и только те элементы,
которые входят и в множество А и в множество В.
Пересечением множеств А и В называют новое множество Х,
содержащее те и только те элементы,
которые входят и в множество А и в множество В. Наибольший элемент множества
равен 18. Это – наибольший
общий делитель чисел 54 и 72. Множество делителей числа
72 конечно. А множество кратных этого
числа бесконечно:
Наибольший элемент множества
равен 18. Это – наибольший
общий делитель чисел 54 и 72. Множество делителей числа
72 конечно. А множество кратных этого
числа бесконечно:
 Несмотря на то, что это может быть трудно, можно сосчитать все виды фруктов в мире, поэтому оно конечно.
Несмотря на то, что это может быть трудно, можно сосчитать все виды фруктов в мире, поэтому оно конечно.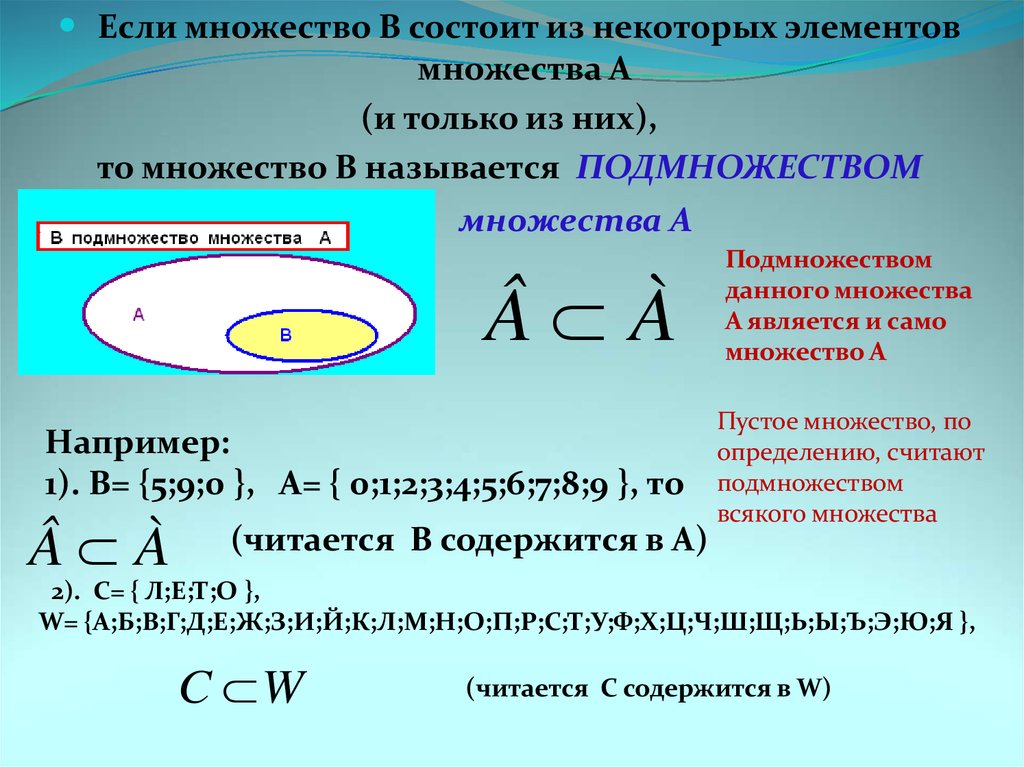

 Оба определения показаны на приведенной выше диаграмме Венна.
Оба определения показаны на приведенной выше диаграмме Венна.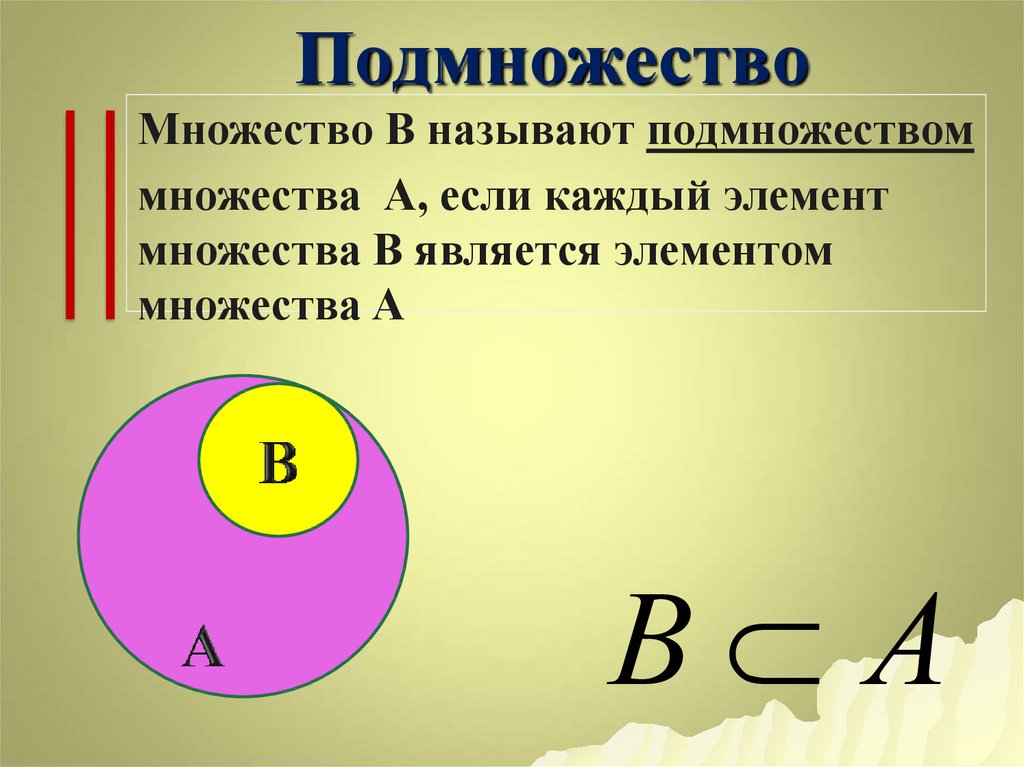 Пересечение этих множеств показано на диаграмме Венна ниже.
Пересечение этих множеств показано на диаграмме Венна ниже.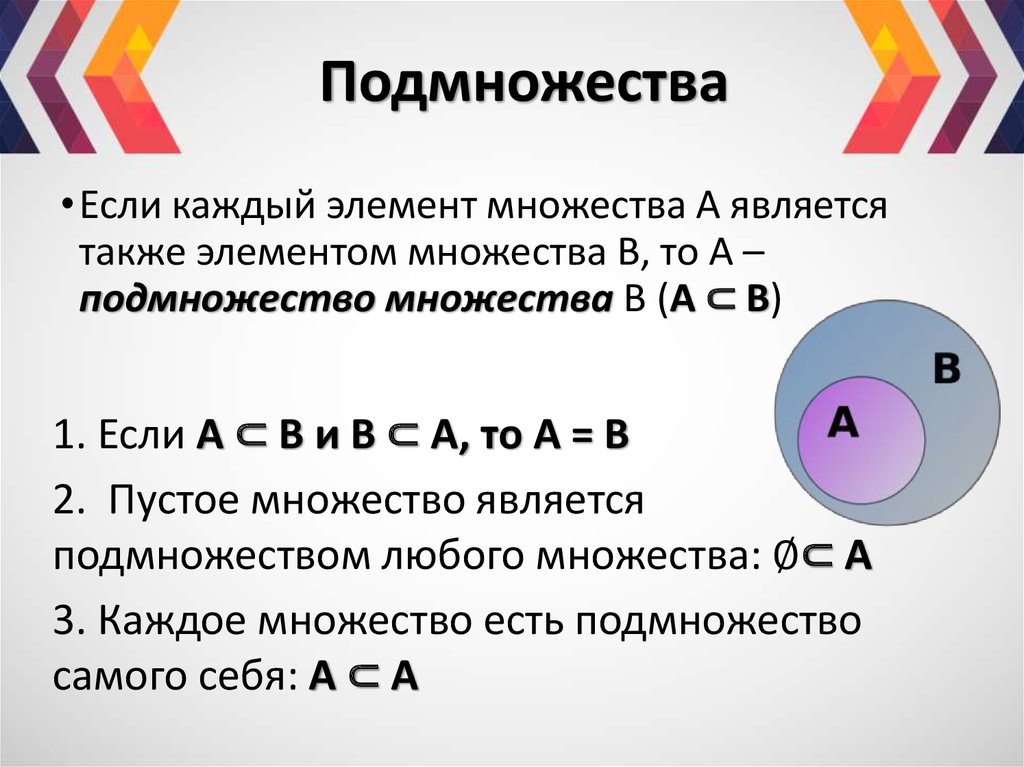

 Это связано с тем, что P и C являются эквивалентными множествами ( P = C ) . Некоторые математики используют символ для обозначения подмножества и символ для обозначения правильного подмножества, с определением для правильных подмножеств следующим образом:
Это связано с тем, что P и C являются эквивалентными множествами ( P = C ) . Некоторые математики используют символ для обозначения подмножества и символ для обозначения правильного подмножества, с определением для правильных подмножеств следующим образом:

 Это обозначается A A.
Это обозначается A A. 

 Сразу после этого трехмерная графика начала прогрессировать очень быстро. Появились специальные программы, кинокомпании стали набирать сотрудников соответствующих должностей и реализовывали самые разные эффекты в своих проектах. Обладатели персональных компьютеров уже в начале 80-х годов могли скачать программу под названием 3D Art Graphics, которая включала в себя набор различных трехмерных объектов и эффектов.
Сразу после этого трехмерная графика начала прогрессировать очень быстро. Появились специальные программы, кинокомпании стали набирать сотрудников соответствующих должностей и реализовывали самые разные эффекты в своих проектах. Обладатели персональных компьютеров уже в начале 80-х годов могли скачать программу под названием 3D Art Graphics, которая включала в себя набор различных трехмерных объектов и эффектов. 
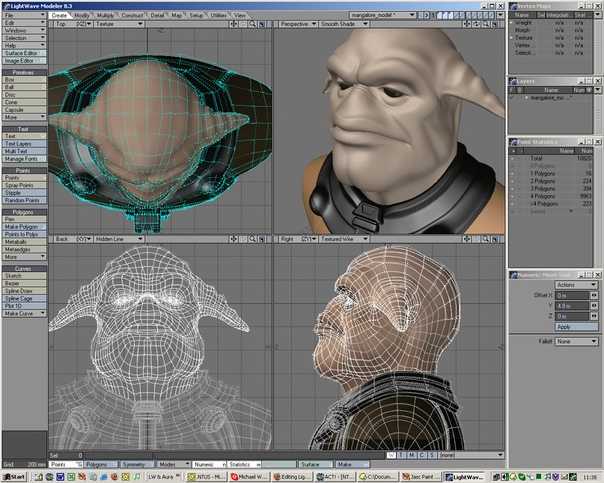 Вы уже знаете, что для выполнения данной операции используется специальный софт. Аниматор может взаимодействовать как с отдельными геометрическими фигурами и точками, преобразовывая их в необходимый объект, так и с одной болванкой, доводя ее до необходимой формы (как скульптор в реальной жизни).
Вы уже знаете, что для выполнения данной операции используется специальный софт. Аниматор может взаимодействовать как с отдельными геометрическими фигурами и точками, преобразовывая их в необходимый объект, так и с одной болванкой, доводя ее до необходимой формы (как скульптор в реальной жизни). Сейчас при помощи 3D-графики создаются практически все современные игры и мультфильмы.
Сейчас при помощи 3D-графики создаются практически все современные игры и мультфильмы.

 Стоит отметить, что в Польше расположены такие компании как 11 bit studios S.A., CD Projekt RED, которые выпускают известные миру компьютерные игры. Поэтому проблем с трудоустройством после успешного окончания университета у выпускников нет.
Стоит отметить, что в Польше расположены такие компании как 11 bit studios S.A., CD Projekt RED, которые выпускают известные миру компьютерные игры. Поэтому проблем с трудоустройством после успешного окончания университета у выпускников нет. Во время их выполнения я смог собрать своё портфолио и узнать о требованиях, которые нужны при разработке объектов для игр. Так начался мой путь. Поначалу я занимался тем, что окружает персонажа в игре, а сейчас уже работаю над разработкой уровней для игр.
Во время их выполнения я смог собрать своё портфолио и узнать о требованиях, которые нужны при разработке объектов для игр. Так начался мой путь. Поначалу я занимался тем, что окружает персонажа в игре, а сейчас уже работаю над разработкой уровней для игр. Есть классный сайт Artstation, на котором художники разных стилей выставляют свои работы. Это и определенная социальная сеть, помогающая компаниям находить специалистов со всего мира. Но помните, заказчики из другого уголка планеты не знают украинский, поэтому английский стоит учить.
Есть классный сайт Artstation, на котором художники разных стилей выставляют свои работы. Это и определенная социальная сеть, помогающая компаниям находить специалистов со всего мира. Но помните, заказчики из другого уголка планеты не знают украинский, поэтому английский стоит учить. Разница между европейскими и украинскими компаниями в 3D-графике уже не сильно ощутима.
Разница между европейскими и украинскими компаниями в 3D-графике уже не сильно ощутима.




 См. графику, графический конвейер, затенение Гуро, затенение Фонга и 2D-графику. См. также 3D-визуализация.
См. графику, графический конвейер, затенение Гуро, затенение Фонга и 2D-графику. См. также 3D-визуализация. com является ведущим авторитетом в области технологий, предоставляющим независимые лабораторные обзоры новейших продуктов и услуг. Наш экспертный отраслевой анализ и практические решения помогут вам принимать более обоснованные решения о покупке и получать больше от технологий.
com является ведущим авторитетом в области технологий, предоставляющим независимые лабораторные обзоры новейших продуктов и услуг. Наш экспертный отраслевой анализ и практические решения помогут вам принимать более обоснованные решения о покупке и получать больше от технологий.
 В 2D используются две координаты, то есть x и y, тогда как в 3D используются три координаты x, y и z.
В 2D используются две координаты, то есть x и y, тогда как в 3D используются три координаты x, y и z. Он также обеспечивает изучение кузовов автомобилей, деталей самолетов. Все эти действия требуют реализма. Для реалистичности требуется 3D. В производстве реалистичной 3D-сцены из 2D сложно. Для этого требуется трехмерность, то есть глубина.
Он также обеспечивает изучение кузовов автомобилей, деталей самолетов. Все эти действия требуют реализма. Для реалистичности требуется 3D. В производстве реалистичной 3D-сцены из 2D сложно. Для этого требуется трехмерность, то есть глубина. Доступны несколько типов проекции, например,
Доступны несколько типов проекции, например,
 Тогда запись x ∈ (−∞ ; −2) ∪ (2 ; +∞) можно прочитать так:
Тогда запись x ∈ (−∞ ; −2) ∪ (2 ; +∞) можно прочитать так: В неравенстве |x| > 2 это расстояние больше чем 2.
В неравенстве |x| > 2 это расстояние больше чем 2. Решениями этого неравенства являются все числа, бóльшие −2. Отметим эти решения на том же рисунке, где мы отметили решения для неравенства x < 2.
Решениями этого неравенства являются все числа, бóльшие −2. Отметим эти решения на том же рисунке, где мы отметили решения для неравенства x < 2. Напомним, что пересечением двух промежутков является промежуток, состоящий из чисел, которые принадлежат как первому промежутку так и второму:
Напомним, что пересечением двух промежутков является промежуток, состоящий из чисел, которые принадлежат как первому промежутку так и второму: Например, значение 7
Например, значение 7
 Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
 Тогда получим окончательную систему:
Тогда получим окончательную систему: Решить неравенство:
Решить неравенство: Неравенства с модулем
Неравенства с модулем 30) равносильно совокупности
30) равносильно совокупности
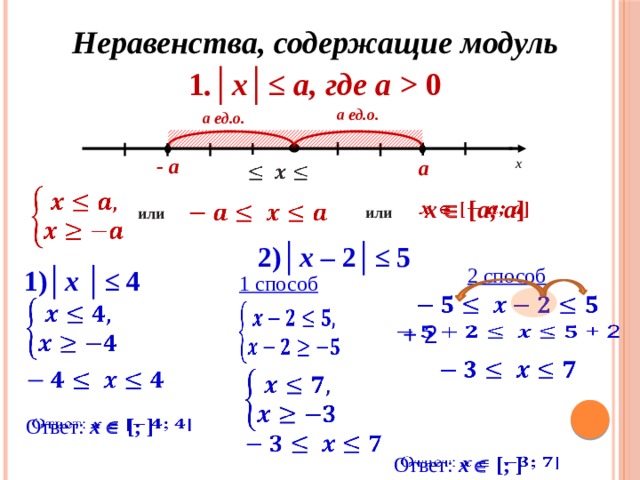 33), если они заданы со знаками
33), если они заданы со знаками 3.11
3.11

 Когда вы берете абсолютное значение функции $|x+1|-1$, часть графика, расположенная ниже оси $x$, отражается выше. Результат теперь W -образный график с левым углом в $(-2,0)$, средним углом в $(-1,1)$ и прямым углом в начале координат. Слева от $(-2,0)$ график поднимается (по мере удаления от начала координат) с наклоном $-1$, т.е. имеет уравнение $y=-x-2$, а справа от начала координат, график поднимается с наклоном $1$, т.е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.
Когда вы берете абсолютное значение функции $|x+1|-1$, часть графика, расположенная ниже оси $x$, отражается выше. Результат теперь W -образный график с левым углом в $(-2,0)$, средним углом в $(-1,1)$ и прямым углом в начале координат. Слева от $(-2,0)$ график поднимается (по мере удаления от начала координат) с наклоном $-1$, т.е. имеет уравнение $y=-x-2$, а справа от начала координат, график поднимается с наклоном $1$, т.е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.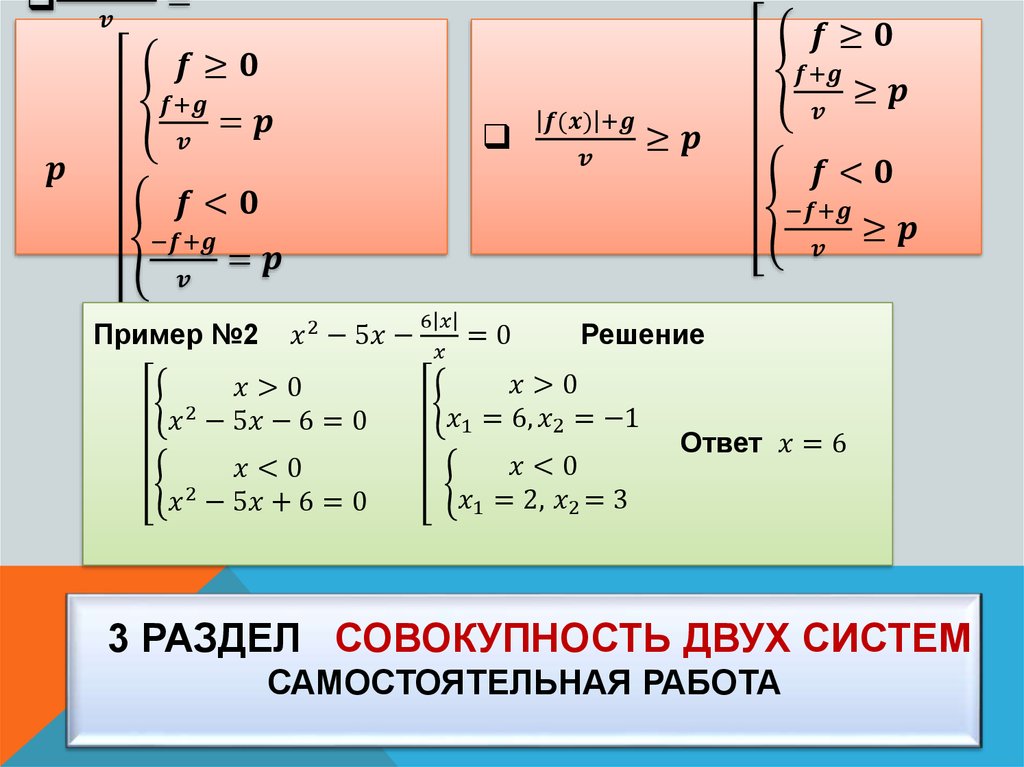

 1 + 0.2 \ne 0.3\).
Эту проблему (неточное представление действительных чисел и выполнение
арифметических операций с действительными числами) всегда следует иметь в виду.
1 + 0.2 \ne 0.3\).
Эту проблему (неточное представление действительных чисел и выполнение
арифметических операций с действительными числами) всегда следует иметь в виду.
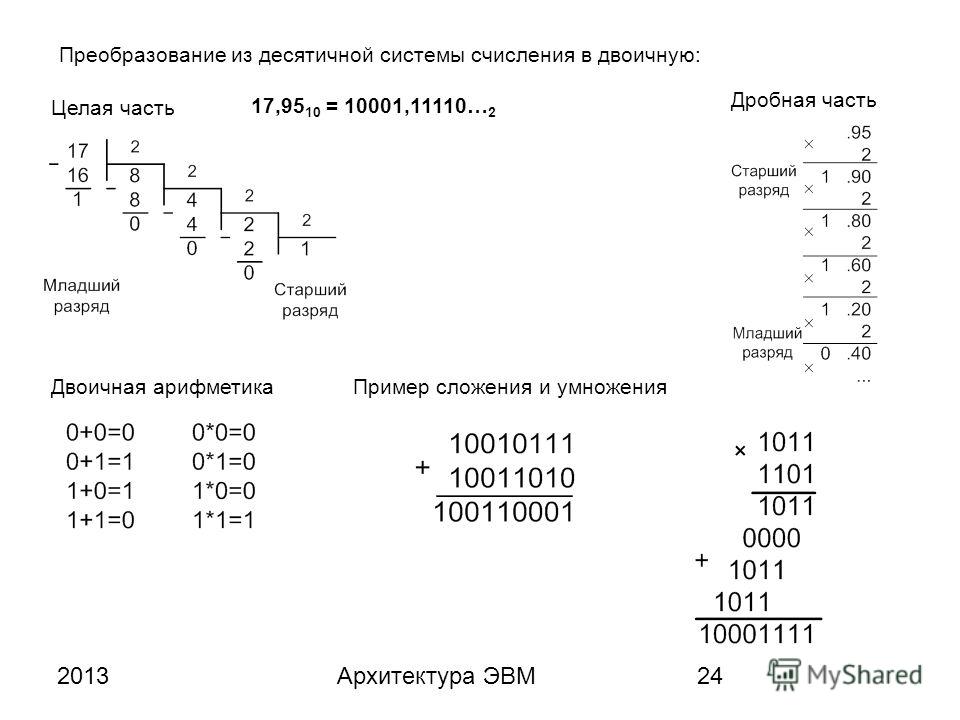
 И даже если значения двух переменных
И даже если значения двух переменных 
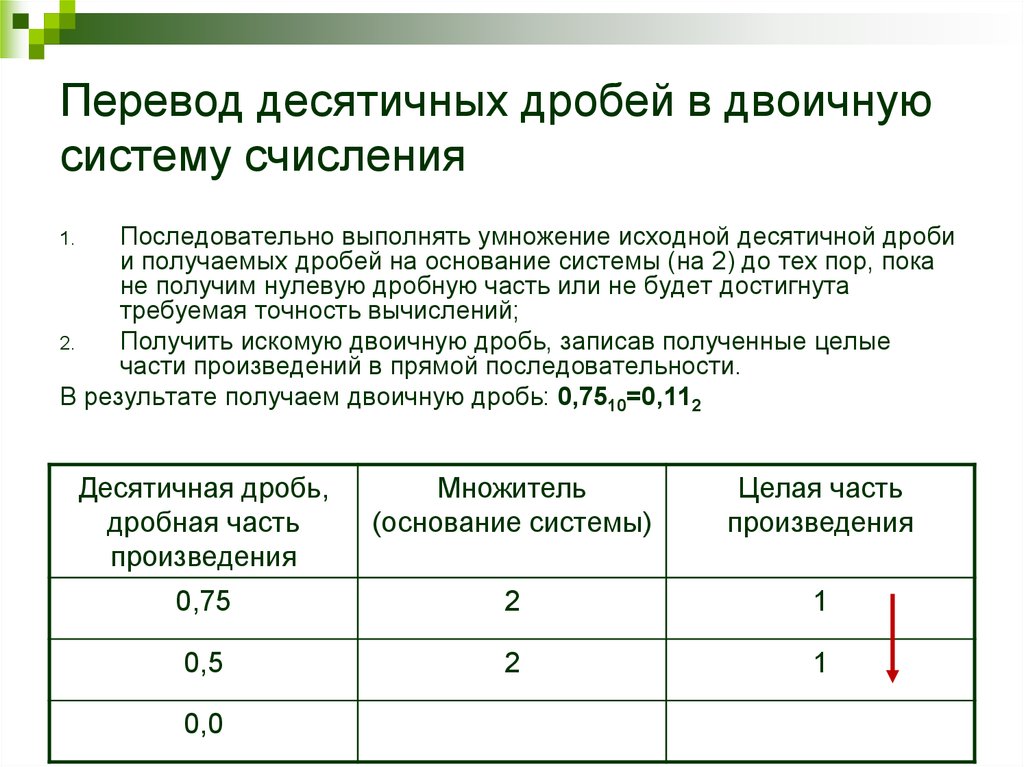 Большинство современных электронно-вычислительных
машин используют в своей работе именно эту систему чисел.
Большинство современных электронно-вычислительных
машин используют в своей работе именно эту систему чисел.


 Следовательно,
каждый символ в компьютере имеет код объёмом 1 байт.
Следовательно,
каждый символ в компьютере имеет код объёмом 1 байт.

 Ресурсы компьютеров не бесконечны, и основной трудностью
является представление периодических и непериодических дробей. Следовательно,
такие дроби следует округлять, задавать класс точности участвующих
(и могущих появиться в результате вычислений!) чисел без потери точности
вычислений, а также следить за тем, чтобы потеря точности не произошла
при переводе чисел из одной системы счисления в другую. Особенно важно
аккуратно производить вычисления при операциях с плавающей точкой.
Ресурсы компьютеров не бесконечны, и основной трудностью
является представление периодических и непериодических дробей. Следовательно,
такие дроби следует округлять, задавать класс точности участвующих
(и могущих появиться в результате вычислений!) чисел без потери точности
вычислений, а также следить за тем, чтобы потеря точности не произошла
при переводе чисел из одной системы счисления в другую. Особенно важно
аккуратно производить вычисления при операциях с плавающей точкой.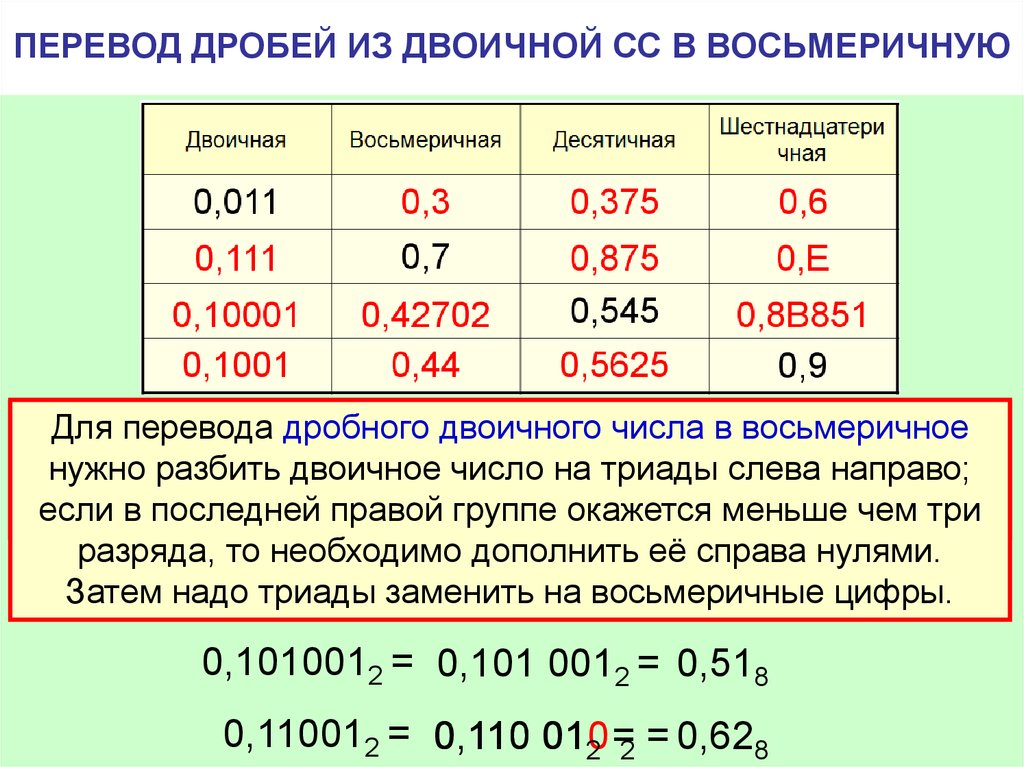 .. + a-m·p-m,
.. + a-m·p-m,
 В противном случае вычисления продолжаются с предыдущего шага.
В противном случае вычисления продолжаются с предыдущего шага.  612 • 2 = 1.224
612 • 2 = 1.224 Для
определенности рассмотрим тип
Для
определенности рассмотрим тип  д.
д.

 Посмотри деление на анимированном примере
Посмотри деление на анимированном примере Во второй части этой статьи объясняется самая основная математика, стоящая за каждым из них. Знание этого может помочь вам вспомнить любой из алгоритмов, если вы вдруг забудете их. Я настоятельно рекомендую вам взять блокнот и ручку и выполнять операции вместе со мной, чтобы лучше запомнить математику. Вот четыре алгоритма с примерами, которые вы можете найти в Интернете.
Во второй части этой статьи объясняется самая основная математика, стоящая за каждым из них. Знание этого может помочь вам вспомнить любой из алгоритмов, если вы вдруг забудете их. Я настоятельно рекомендую вам взять блокнот и ручку и выполнять операции вместе со мной, чтобы лучше запомнить математику. Вот четыре алгоритма с примерами, которые вы можете найти в Интернете.
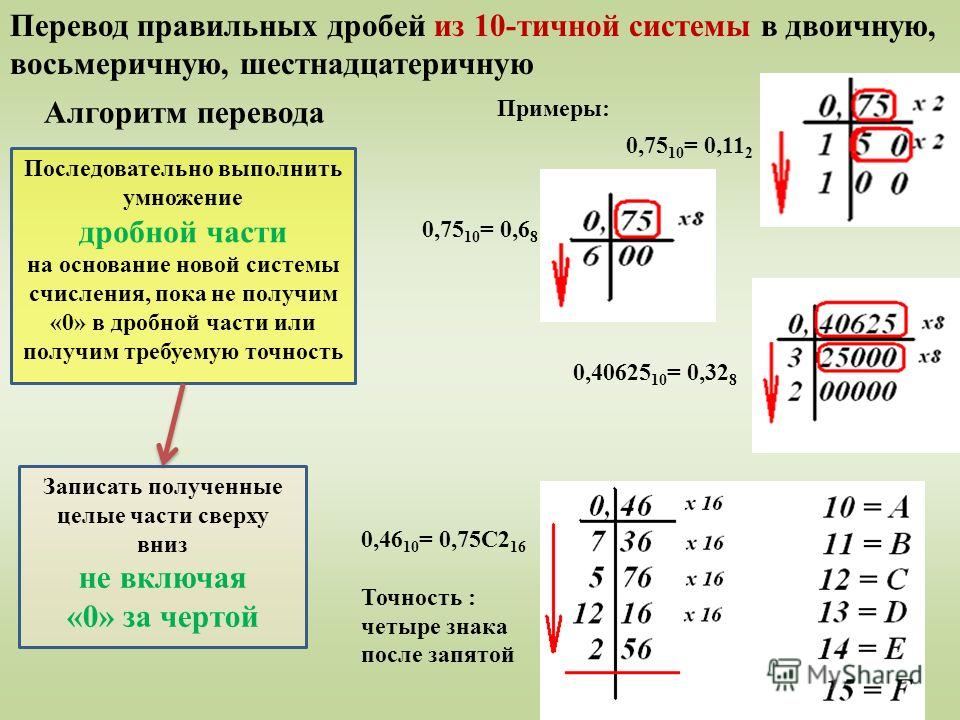 Чтобы сохранить их как числа с плавающей запятой IEEE-754, их необходимо округлить до количества доступных битов для мантиссы — 10 бит для половинной точности, 23 бита для одинарной точности или 52 бита для двойной точности. В зависимости от того, сколько битов точности доступно, приближения с плавающей запятой 0,1 и 0,2 могут быть немного меньше или больше, чем соответствующие десятичные представления, но никогда не равны. Из-за этого у вас никогда не будет 0,1+0,2 == 0,3.
Чтобы сохранить их как числа с плавающей запятой IEEE-754, их необходимо округлить до количества доступных битов для мантиссы — 10 бит для половинной точности, 23 бита для одинарной точности или 52 бита для двойной точности. В зависимости от того, сколько битов точности доступно, приближения с плавающей запятой 0,1 и 0,2 могут быть немного меньше или больше, чем соответствующие десятичные представления, но никогда не равны. Из-за этого у вас никогда не будет 0,1+0,2 == 0,3. Продолжайте, пока не останется цифр. . Вот пример такого преобразования с использованием дроби 0,1011 . Я просто заменил деление на 2 умножением на 1/2 .
Продолжайте, пока не останется цифр. . Вот пример такого преобразования с использованием дроби 0,1011 . Я просто заменил деление на 2 умножением на 1/2 . Посмотрим, как выглядит число 12 в десятичной и двоичной системах счисления:
Посмотрим, как выглядит число 12 в десятичной и двоичной системах счисления: Во-первых, давайте притворимся, что мы не знаем, как оно представлено в двоичном формате, и запишем его, заменив неизвестные цифры на x :
Во-первых, давайте притворимся, что мы не знаем, как оно представлено в двоичном формате, и запишем его, заменив неизвестные цифры на x : Поскольку все слагаемые от x1 до xN кратны двум, мы можем выделить 9014 . выделить x1 . Сделаем так:
Поскольку все слагаемые от x1 до xN кратны двум, мы можем выделить 9014 . выделить x1 . Сделаем так: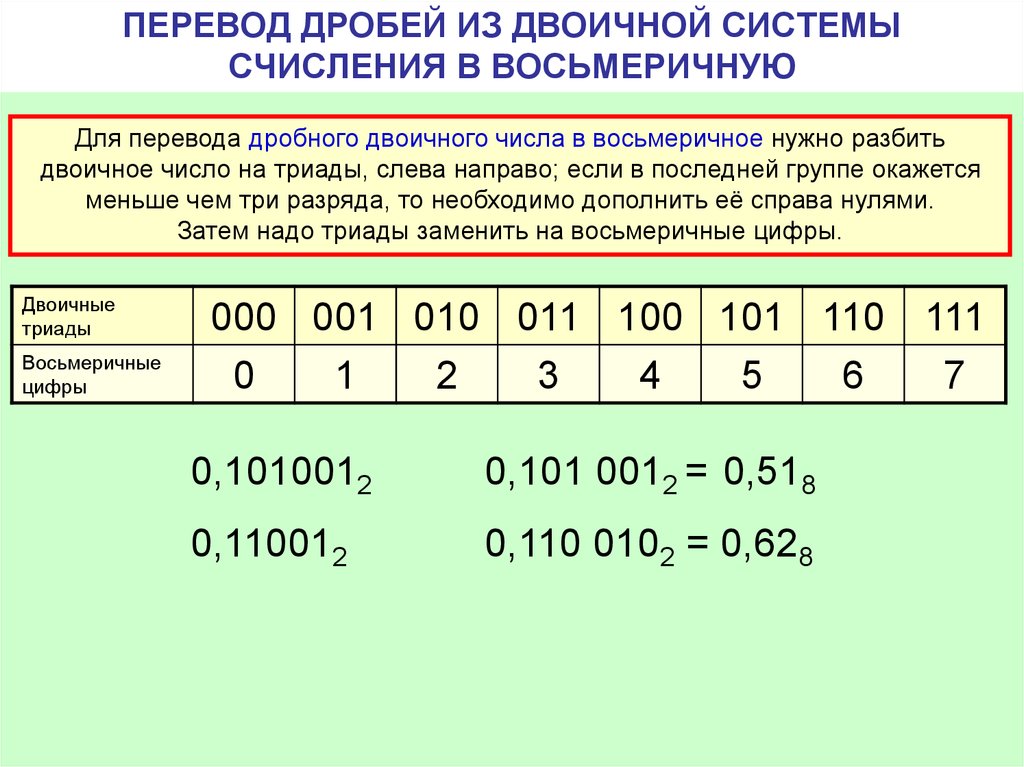

 0080 x :
0080 x : Если максимальное количество цифр x равно 1, то мы можем просто заменить x с единицами и запишите сумму в виде:
Если максимальное количество цифр x равно 1, то мы можем просто заменить x с единицами и запишите сумму в виде: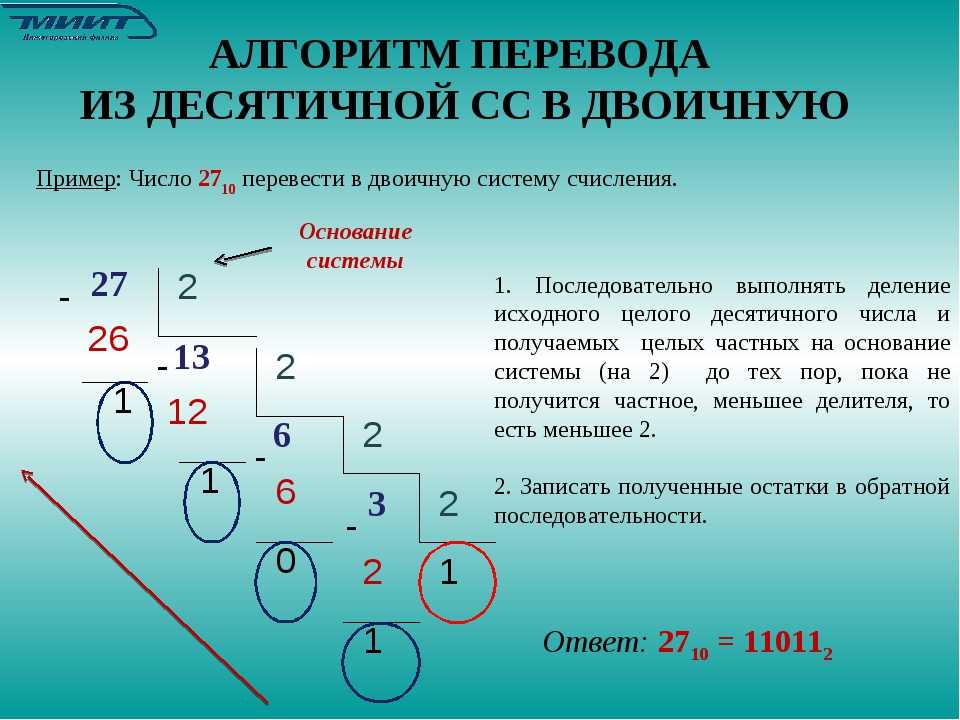 5 . Давайте запишем это:
5 . Давайте запишем это: Но именно эта путаница лежит в основе кажущегося странным результата прибавления 0,1 к 0,2. Так что же определяет, может ли дробь быть конечно представлена в системе счисления? Это довольно сложно. Но базовая версия такова — для конечного представления числа знаменатель в дроби должен быть степенью основания системы. Например, для системы с основанием 10 знаменатель должен быть степенью 10, поэтому мы можем конечно представить 0,625 в десятичном виде:
Но именно эта путаница лежит в основе кажущегося странным результата прибавления 0,1 к 0,2. Так что же определяет, может ли дробь быть конечно представлена в системе счисления? Это довольно сложно. Но базовая версия такова — для конечного представления числа знаменатель в дроби должен быть степенью основания системы. Например, для системы с основанием 10 знаменатель должен быть степенью 10, поэтому мы можем конечно представить 0,625 в десятичном виде: Запишем в развернутом виде:
Запишем в развернутом виде: е. десятичной, двоичной, шестнадцатеричной и т. д.
е. десятичной, двоичной, шестнадцатеричной и т. д. Разделение между положительными («n=0») и отрицательными позиционными («n=-1») значениями представлено десятичной точкой .
Разделение между положительными («n=0») и отрицательными позиционными («n=-1») значениями представлено десятичной точкой . Точно так же цифры 4, 5 и 6 справа от запятой имеют позиционные веса 10 -1 (0,1), 10 -2 (0,01) и 10 -3 (0,001) соответственно. .
Точно так же цифры 4, 5 и 6 справа от запятой имеют позиционные веса 10 -1 (0,1), 10 -2 (0,01) и 10 -3 (0,001) соответственно. . Как и десятичная цифра, каждая двоичная цифра (бит) имеет связанный с ней позиционный вес относительно двоичной точки (десятичной точки в случае десятичной цифры). Вес двоичных разрядов увеличивается в два (2) раза на каждый шаг разряда при движении справа налево. Более того, двоичные числа без знака также могут иметь дробные числа, т.е. прямо до двоичной точки. Вес двоичных цифр, представляющих дробные числа, уменьшается в два раза на каждом шаге при движении вправо от двоичной точки. Это означает, что двоичные цифры имеют позиционный вес 9.0012 2 0 , 2 1 , 2 2 , и т. д. , начиная с левого двоичного числа, т. е. номера позиций 0, 1, 2 и т. д. соответственно. Точно так же двоичные цифры имеют позиционный вес 2 -1 , 2 -2 , 2 -3 и т. д. , начиная непосредственно справа от двоичной точки.
Как и десятичная цифра, каждая двоичная цифра (бит) имеет связанный с ней позиционный вес относительно двоичной точки (десятичной точки в случае десятичной цифры). Вес двоичных разрядов увеличивается в два (2) раза на каждый шаг разряда при движении справа налево. Более того, двоичные числа без знака также могут иметь дробные числа, т.е. прямо до двоичной точки. Вес двоичных цифр, представляющих дробные числа, уменьшается в два раза на каждом шаге при движении вправо от двоичной точки. Это означает, что двоичные цифры имеют позиционный вес 9.0012 2 0 , 2 1 , 2 2 , и т. д. , начиная с левого двоичного числа, т. е. номера позиций 0, 1, 2 и т. д. соответственно. Точно так же двоичные цифры имеют позиционный вес 2 -1 , 2 -2 , 2 -3 и т. д. , начиная непосредственно справа от двоичной точки. Это показано ниже:
Это показано ниже:
 е. «0», и процесс умножения повторяется с отметкой «0», пока результат не станет равным или больше единицы. Умножение, в результате которого получается значение, большее или равное единице (1), производит перенос вперед, т. е. «1», и процесс умножения повторяется только для его дробной части (для случаев, когда умножение приводит только к значению больше единицы). В случае, если значение становится равным единице (1), дальнейшее умножение не применяется.
е. «0», и процесс умножения повторяется с отметкой «0», пока результат не станет равным или больше единицы. Умножение, в результате которого получается значение, большее или равное единице (1), производит перенос вперед, т. е. «1», и процесс умножения повторяется только для его дробной части (для случаев, когда умножение приводит только к значению больше единицы). В случае, если значение становится равным единице (1), дальнейшее умножение не применяется. Точно так же смешанное десятичное число (43,375 10 ) можно преобразовать в его двоичный эквивалент, как показано ниже:
Точно так же смешанное десятичное число (43,375 10 ) можно преобразовать в его двоичный эквивалент, как показано ниже:
 Очевидно, что
Очевидно, что




 Буквы в алфавите обычно используются для обозначения таких переменных, как a, b, c, x, y и z. Решить буквальное уравнение означает выразить одну переменную по отношению к другим переменным в уравнении.
Буквы в алфавите обычно используются для обозначения таких переменных, как a, b, c, x, y и z. Решить буквальное уравнение означает выразить одну переменную по отношению к другим переменным в уравнении.
 Можно изолировать переменную L в правой части. Однако почему бы не перевернуть уравнение, чтобы мы могли оставить только переменную L слева? Что ж, звучит как план!
Можно изолировать переменную L в правой части. Однако почему бы не перевернуть уравнение, чтобы мы могли оставить только переменную L слева? Что ж, звучит как план! Это значительно упрощает весь процесс решения.
Это значительно упрощает весь процесс решения.
 Ну не сдавайся еще! Открою вам небольшой «секрет».
Ну не сдавайся еще! Открою вам небольшой «секрет».


 Вот несколько примеров буквальных уравнений, с которыми вы уже работали в своей жизни:
Вот несколько примеров буквальных уравнений, с которыми вы уже работали в своей жизни: Вот примеры обратных операций:
Вот примеры обратных операций: Мы также можем изменить и «решить» буквальное уравнение для любой переменной. Например:
Мы также можем изменить и «решить» буквальное уравнение для любой переменной. Например: 

 Помните, мы можем убрать все дроби за один ход, умножив все члены на 9.0003 Наименьший общий знаменатель .
Помните, мы можем убрать все дроби за один ход, умножив все члены на 9.0003 Наименьший общий знаменатель .

 Размеры рамы в сложенном виде без колес: 30 х 60 х 89 см. На раме под пластиковыми наличниками спрятаны надежные пружины, благодаря им коляска имеет очень мягкое укачивание, как при продольном качание, так и поперечном.
Размеры рамы в сложенном виде без колес: 30 х 60 х 89 см. На раме под пластиковыми наличниками спрятаны надежные пружины, благодаря им коляска имеет очень мягкое укачивание, как при продольном качание, так и поперечном.
 Прежде всего хочется сказать о ее главном плюсе, это вес (всего 12 кг) за счет этого коляска становится более транспортабельна и подходит для путешествий.
Прежде всего хочется сказать о ее главном плюсе, это вес (всего 12 кг) за счет этого коляска становится более транспортабельна и подходит для путешествий. Внутренняя ткань выполнена из 100% хлопка, ее легко можно снять для стирки, внешняя ткань со специальной пропиткой против дождя.
Внутренняя ткань выполнена из 100% хлопка, ее легко можно снять для стирки, внешняя ткань со специальной пропиткой против дождя. В задние стойки встроены мягкие амортизаторы, благодаря которым перед препятствием коляска буквально пружинит.
В задние стойки встроены мягкие амортизаторы, благодаря которым перед препятствием коляска буквально пружинит. 02+17.19
02+17.19 27 — ClinVar — NCBI
27 — ClinVar — NCBI
 4(BRCA1):c.594-2A>C
4(BRCA1):c.594-2A>C .. больше HGVS
… меньше HGVS
.. больше HGVS
… меньше HGVS
 7 ЗК РФ установлено, что уполномоченный орган исполнительной власти или орган местного самоуправления, принявшие решение об изъятии, либо в случае, если решение об изъятии принято на основании ходатайства об изъятии, организация, подавшая такое ходатайство, обращаются от имени правообладателя изымаемой недвижимости без доверенности с заявлением о кадастровом учете земельных участков, подлежащих изъятию, земельных участков, предоставляемых взамен изымаемых земельных участков, или земельных участков, границы которых подлежат уточнению в связи с изъятием, если необходимо проведение государственного кадастрового учета таких земельных участков.
7 ЗК РФ установлено, что уполномоченный орган исполнительной власти или орган местного самоуправления, принявшие решение об изъятии, либо в случае, если решение об изъятии принято на основании ходатайства об изъятии, организация, подавшая такое ходатайство, обращаются от имени правообладателя изымаемой недвижимости без доверенности с заявлением о кадастровом учете земельных участков, подлежащих изъятию, земельных участков, предоставляемых взамен изымаемых земельных участков, или земельных участков, границы которых подлежат уточнению в связи с изъятием, если необходимо проведение государственного кадастрового учета таких земельных участков.

 Являясь частью ведущей платформы мониторинга пациентов серии N, N1 оснащен интуитивно понятным дисплеем в стиле смартфона и основными параметрами, обеспечивающими высококачественную помощь, ориентированную на пациента. N1 служит комплексным многопараметрическим модулем, мощным транспортным монитором и универсальным прикроватным монитором — все в одном.
Являясь частью ведущей платформы мониторинга пациентов серии N, N1 оснащен интуитивно понятным дисплеем в стиле смартфона и основными параметрами, обеспечивающими высококачественную помощь, ориентированную на пациента. N1 служит комплексным многопараметрическим модулем, мощным транспортным монитором и универсальным прикроватным монитором — все в одном.
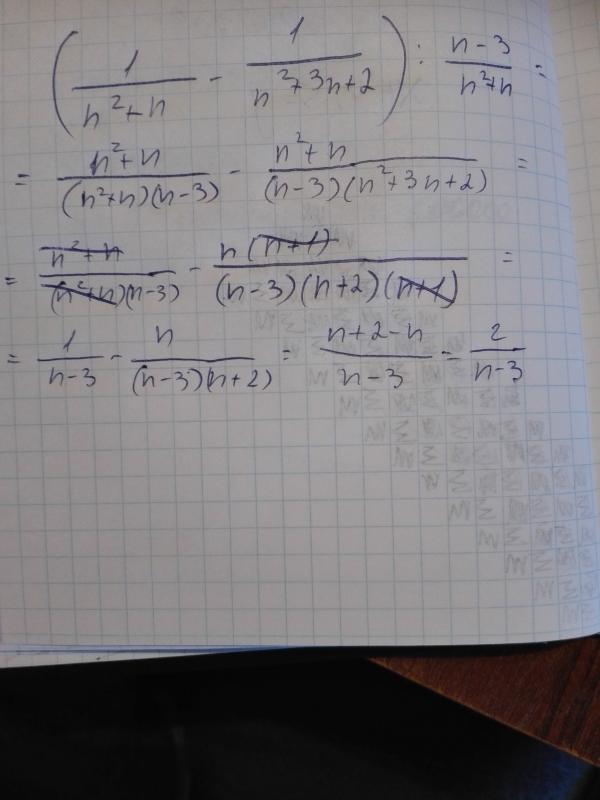 Дополнительный анализ ST и мониторинг интервала QT/QTc.
Дополнительный анализ ST и мониторинг интервала QT/QTc.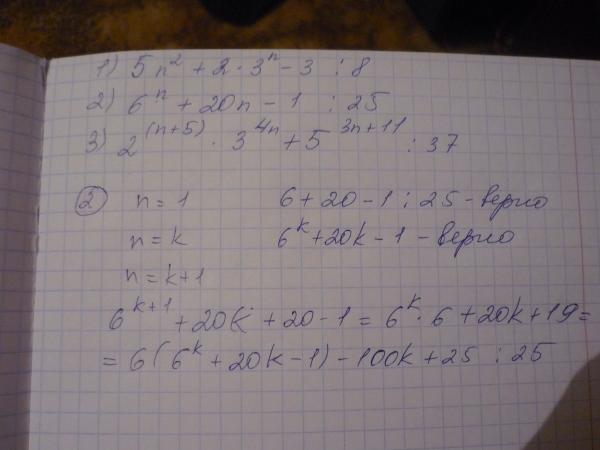
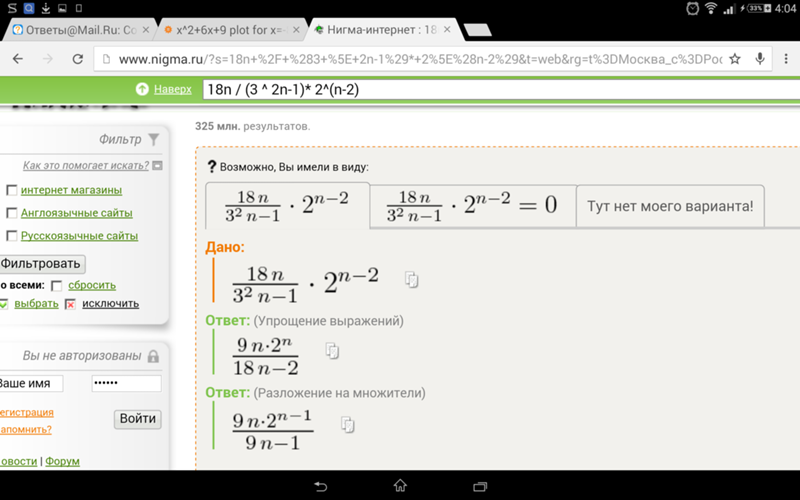
 Кроме того, техническая удаленная поддержка доступна 24 часа в сутки, 7 дней в неделю бесплатно.
Кроме того, техническая удаленная поддержка доступна 24 часа в сутки, 7 дней в неделю бесплатно.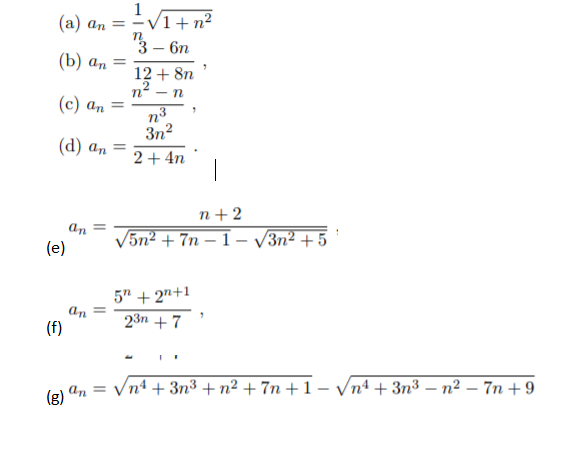 Мы известны своими потрясающими бутербродами. Который твой любимый?
Мы известны своими потрясающими бутербродами. Который твой любимый? Позвольте нам помочь вам сделать этот выпускной сезон особенным, если вы чествуете новых выпускников.
Позвольте нам помочь вам сделать этот выпускной сезон особенным, если вы чествуете новых выпускников.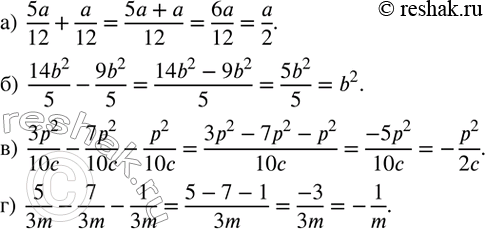
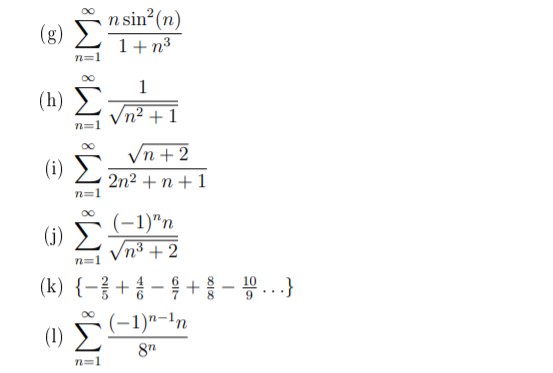 3N1 был очень приятным сюрпризом. У нас был сэндвич с пастрами и сэндвич с курицей Баха. Оба были вкусными. Отличный сервис и очень уютная атмосфера. Вы должны попробовать это место.
3N1 был очень приятным сюрпризом. У нас был сэндвич с пастрами и сэндвич с курицей Баха. Оба были вкусными. Отличный сервис и очень уютная атмосфера. Вы должны попробовать это место.



 0LIT — Microsoft LiteratureLRF — Sony Portable ReaderMOBI — Mobipocket eBookPDB — Palm Media eBookRB — RocketEdition eBookTCR — Psion eBook7Z — 7-ZipZIP — ZipRAR — Roshal ArchiveJAR — Java ArchiveTAR — TarballTAR.GZ — TAR GZippedCAB — Cabinet
0LIT — Microsoft LiteratureLRF — Sony Portable ReaderMOBI — Mobipocket eBookPDB — Palm Media eBookRB — RocketEdition eBookTCR — Psion eBook7Z — 7-ZipZIP — ZipRAR — Roshal ArchiveJAR — Java ArchiveTAR — TarballTAR.GZ — TAR GZippedCAB — Cabinet
 Мы обрабатываем все преобразования djvu в jpg в облаке, что означает, что никакие ресурсы вашего компьютера не будут использоваться в процессе.
Мы обрабатываем все преобразования djvu в jpg в облаке, что означает, что никакие ресурсы вашего компьютера не будут использоваться в процессе. и фотографии. Хотя этот формат становится все более распространенным, просмотр файлов DjVu может быть опасным, и для их открытия и расшифровки потребуются подключаемые модули или программы просмотра. Чтобы сделать файлы DjVu доступными, конвертируйте DjVu в JPEG, используя BitRecover Конвертер файлов DjVu в JPG. JPEG сделает документы DjVu подходящими для Интернета, электронной почты и многого другого.
и фотографии. Хотя этот формат становится все более распространенным, просмотр файлов DjVu может быть опасным, и для их открытия и расшифровки потребуются подключаемые модули или программы просмотра. Чтобы сделать файлы DjVu доступными, конвертируйте DjVu в JPEG, используя BitRecover Конвертер файлов DjVu в JPG. JPEG сделает документы DjVu подходящими для Интернета, электронной почты и многого другого. Это одно автономное приложение, которое совместимо с большим преобразованием документов DjVu в широкий спектр форматов файлов, таких как JPG, PDF, DOC, DOCX, XLS, HTML, GIF, JPG, PNG, TIFF, PSD .
Это одно автономное приложение, которое совместимо с большим преобразованием документов DjVu в широкий спектр форматов файлов, таких как JPG, PDF, DOC, DOCX, XLS, HTML, GIF, JPG, PNG, TIFF, PSD . Как преобразовать файл DjVu в формат JPG?
Как преобразовать файл DjVu в формат JPG?
 Отзывы показывают, что это программное обеспечение совместимо для преобразования больших файлов DjVu в формат JPEG. С ним вам никогда не придется ставить конфиденциальность и конфиденциальность данных .
Отзывы показывают, что это программное обеспечение совместимо для преобразования больших файлов DjVu в формат JPEG. С ним вам никогда не придется ставить конфиденциальность и конфиденциальность данных . Кроме того, вы можете установить «Параметры качества изображения», чтобы включить коэффициент сжатия изображения, значение по умолчанию — 25, а также вы можете ввести допустимые значения от 25 до 150.
Кроме того, вы можете установить «Параметры качества изображения», чтобы включить коэффициент сжатия изображения, значение по умолчанию — 25, а также вы можете ввести допустимые значения от 25 до 150. Либо вы можете создать новую папку, либо оставить целевой путь сохранения без изменений.
Либо вы можете создать новую папку, либо оставить целевой путь сохранения без изменений. Документы DJVU предназначены для того, чтобы дизайнеры контента могли просматривать цветные страницы книг, журналов и т. д. с высоким разрешением и распространять их в Интернете.
Документы DJVU предназначены для того, чтобы дизайнеры контента могли просматривать цветные страницы книг, журналов и т. д. с высоким разрешением и распространять их в Интернете. Размер по умолчанию, который предоставляет конвертер DjVu в JPG, составляет 25, но вы можете изменить его от 25 до 150 в соответствии с вашими потребностями.
Размер по умолчанию, который предоставляет конвертер DjVu в JPG, составляет 25, но вы можете изменить его от 25 до 150 в соответствии с вашими потребностями.