детерминант матрицы 3 на 3
Вы искали детерминант матрицы 3 на 3? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как в матрице найти определитель, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «детерминант матрицы 3 на 3».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как детерминант матрицы 3 на 3,как в матрице найти определитель,как вычислить определитель в матрице,как вычислить определитель матрицы 3 на 3,как вычислять матрицы,как искать определитель матрицы,как найти в матрице определитель,как найти детерминант матрицы 3 на 3,как находить определитель матрицы,как посчитать определитель матрицы 3 на 3,как решать матрицу 3 на 3,как решать матрицы 3х3,как решить матрицу 3 на 3,как считать определитель матрицы 3 на 3,матрица 3 на 3 пример,матрицы 3 на 3,матрицы определитель формула,нахождение определителя матрицы формула,определители,определитель в матрице как найти,определитель как решать,определитель матрицы 2х2,определитель матрицы как вычислить,определитель матрицы как найти,определитель матрицы примеры,правило треугольника матрица,формула нахождение определителя матрицы,формула определитель матрицы,формула определителя матрицы. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и детерминант матрицы 3 на 3. Просто введите задачу в окошко и нажмите «решить» здесь (например, как вычислить определитель в матрице).
Где можно решить любую задачу по математике, а так же детерминант матрицы 3 на 3 Онлайн?
Решить задачу детерминант матрицы 3 на 3 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Matrices & Linear Algebra | Mathematica & Wolfram Language for Math Students—Fast Intro
В Языке Wolfram матрицы представляются как списки списков:
| In[1]:= | ⨯{{1, 2}, {3, 4}} |
Их можно вводить в табличном виде, используя CTRL+ ENTER для добавления строк и CTRL+ , для добавления столбцов:
| In[2]:= | ⨯{
{a, b},
{c, d}
} |
| Out[2]= |
Функция MatrixForm позволяет отобразить матрицу в классическом виде:
| In[3]:= | ⨯MatrixForm[{{a, b}, {c, d}}] |
| Out[3]= |
Матрицы можно создавать с помощью итерационных функций:
| In[1]:= | ⨯Table[x + y, {x, 1, 3}, {y, 0, 2}] |
| Out[1]= |
Или импортировать данные, которые представляют собой матрицу:
| In[2]:= | ⨯Import["data.csv"] |
| Out[2]= |
IdentityMatrix, DiagonalMatrix и другие встроенные функции используются для создания матриц специального вида.
Стандартные матричные операции работают поэлементно:
| In[1]:= | ⨯{1, 2, 3} {a, b, c} |
| Out[1]= |
Вычисление произведения двух матриц:
| In[2]:= | ⨯{{1, 2}, {3, 4}}.{{a, b}, {c, d}} |
| Out[2]= |
Вычисление детерминанта:
| In[3]:= | ⨯Det[{{a, b}, {c, d}}] |
| Out[3]= |
Поиск обратной матрицы:
| In[4]:= | ⨯Inverse[{{1, 1}, {0, 1}}] |
| Out[4]= |
Функция LinearSolve используется для решения систем линейных уравнений:
| In[1]:= | ⨯LinearSolve[{{1, 1}, {0, 1}}, {x, y}] |
| Out[1]= |
Реализованы также функции для минимизации и декомпозиции матриц.
Справочная информация: Матрицы и линейная алгебра »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
Вычисление определителей 2-го и 3-го порядков.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$
Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$
— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число
$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}.2+5x+4=0:$
$D=25-16=9$
$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$
Ответ: $x_1=-4;\,\,\, x_2=-1.$
{jumi[*4]}
3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$
Решение.
$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$
$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$
Ответ: $0.$
3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$
Решение.
$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$
$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$
$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).T=\det A.$
2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.
3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.
4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.
6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).
Примеры:
3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
Доказательство.
$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$
$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$
$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$
$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$
$=8a+15b+12c-19d.$
Ответ: $8a+15b+12c-19d.$
{jumi[*4]}
3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью приведения определителя к треугольному виду:
$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два
$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394.2.$
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$
Ответ: $-14.$
3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$
Ответ: $4.$
3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$
Ответ: $2a-8b+c+5d.$
3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$
Ответ: $665.$
{jumi[*4]}
1.3.4. Примеры решения задач по теме «Обратная матрица»
Задача 1.
Найти обратную матрицу для матрицы
И проверить выполнение условий А А-1 = А-1А = Е.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Убедимся, что матрица А – невырожденная. ΔА = 1·4 — 2·(-1) ≠ 0, следовательно, А-1 существует.
Вычислим алгебраические дополнения к элементам А:
Применим способ вычисления обратной матрицы:
.
Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы! |
Найдем произведения А А-1 и А-1А:
Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.
Ответ: .
Задача 2.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Следовательно, матрица А невырожденная, и обратная матрица существует.
Вычислим алгебраические дополнения к элементам матрицы А:
Обратная матрица имеет вид:
Ответ: .
Задача 3.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
Вычислим определитель матрицы А разложением по первому столбцу:
.
Следовательно, обратная матрица для матрицы А существует.
Найдем алгебраические дополнения к элементам матрицы А:
Значит,
.
Ответ: .
Задача 4.
Найти обратную матрицу для матрицы
.
Указание
Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.
Решение
.
Ответ:
Задача 5.
При каких X, Y, Z матрица
Является обратной к матрице
Указание
Необходимым условием того, что В = А-1, является требование АВ = Е.
Решение
Проверим невырожденность матрицы А:
Необходимым условием того, что В = А-1, является требование АВ = Е.
Найдем АВ:
Для того, чтобы выполнялось условие АВ = Е, X, Y, Z должны быть решением системы уравнений
Проверим, будет ли равно единичной матрице произведение ВА:
Значит, при найденных значениях X, Y, Z В = А-1.
Ответ: X = -3, Y = -3, Z = 4.
| < Предыдущая | Следующая > |
|---|
Определитель матрицы: алгоритм, примеры вычисления, правила
Определение 1Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.
|А|, ∆, det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Пример 1Определитель матрицы 2-го порядка вычисляют по формуле:
А=1-231.
Решение:
det A=1-231=1×1-3×(-2)=1+6=7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
Пример 2А=13402115-1
Решение:
det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 3А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.
Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Пример 4Разложение матрицы по элементам строки:
det A=ai1×Ai1+ai2×Ai2+…+аin×Аin
Разложение матрицы по элементам столбца:
det A=а1i×А1i+а2i×А2i+…+аni×Аni
ЗамечаниеЕсли раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
Пример 5А=01-132100-24513210
Решение:
- раскладываем по 2-ой строке:
А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310
- раскладываем по 4-му столбцу:
А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321
Свойства определителя
Свойства определителя:
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
А=134021005
Решение:
det А=134021005=1×5×2=10
ЗамечаниеОпределитель матрицы, который содержит нулевой столбец, равняется нулю.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Линейная алгебра на Python. [Урок 4]. Определитель матрицы
Четвертый урок из цикла “Линейная алгебра на Python“, посвящен понятию определителя матрицы и его свойствам.
Определитель матрицыОпределитель матрицы размера (n-го порядка) является одной из ее численных характеристик. Определитель матрицы A обозначается как |A| или det(A), его также называют детерминантом. Рассмотрим квадратную матрицу 2×2 в общем виде:
Определитель такой матрицы вычисляется следующим образом:
➣ Численный пример
Перед тем, как привести методику расчета определителя в общем виде, введем понятие минора элемента определителя. Минор элемента определителя – это определитель, полученный из данного, путем вычеркивания всех элементов строки и столбца, на пересечении которых стоит данный элемент. Для матрицы 3×3 следующего вида:
Минор M23 будет выглядеть так:
Введем еще одно понятие – алгебраическое дополнение элемента определителя – это минор этого элемента, взятый со знаком плюс или минус:
В общем виде вычислить определитель матрицы можно через разложение определителя по элементам строки или столбца. Суть в том, что определитель равен сумме произведений элементов любой строки или столбца на их алгебраические дополнения. Для матрицы 3×3 это правило будет выполняться следующим образом:
Это правило распространяется на матрицы любой размерности.
➣ Численный пример
➤ Пример на Python
На Python определитель посчитать очень просто. Создадим матрицу A размера 3×3 из приведенного выше численного примера:
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
Для вычисления определителя этой матрицы воспользуемся функцией det() из пакета linalg.
>>> np.linalg.det(A) -14.000000000000009
Мы уже говорили про особенность работы Python с числами с плавающей точкой, поэтому можете полученное значение округлить до -14.
Свойства определителя матрицы.
Свойство 1. Определитель матрицы остается неизменным при ее транспонировании:
➤Пример на Python
Для округления чисел будем использовать функцию round().
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(A.T)
[[-4 10 8]
[-1 4 3]
[ 2 -1 1]]
>>> det_A = round(np.linalg.det(A), 3)
>>> det_A_t = round(np.linalg.det(A.T), 3)
>>> print(det_A)
-14.0
>>> print(det_A_t)
-14.0
Свойство 2. Если у матрицы есть строка или столбец, состоящие из нулей, то определитель такой матрицы равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 0 0 0; 8 3 1')
>>> print(A)
[[-4 -1 2]
[ 0 0 0]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0
Свойство 3. При перестановке строк матрицы знак ее определителя меняется на противоположный:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> B = np.matrix('10 4 -1; -4 -1 2; 8 3 1')
>>> print(B)
[[10 4 -1]
[-4 -1 2]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
14.0
Свойство 4. Если у матрицы есть две одинаковые строки, то ее определитель равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> np.linalg.det(A)
0.0
Свойство 5. Если все элементы строки или столбца матрицы умножить на какое-то число, то и определитель будет умножен на это число:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> B = A.copy()
>>> B[2, :] = k * B[2, :]
>>> print(B)
[[-4 -1 2]
[10 4 -1]
[16 6 2]]
>>> det_A = round(np.linalg.det(A), 3)
>>> det_B = round(np.linalg.det(B), 3)
>>> det_A * k
-28.0
>>> det_B
-28.0
Свойство 6. Если все элементы строки или столбца можно представить как сумму двух слагаемых, то определитель такой матрицы равен сумме определителей двух соответствующих матриц:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; -4 -1 2; 8 3 1')
>>> B = np.matrix('-4 -1 2; 8 3 2; 8 3 1')
>>> C = A.copy()
>>> C[1, :] += B[1, :]
>>> print(C)
[[-4 -1 2]
[ 4 2 4]
[ 8 3 1]]
>>> print(A)
[[-4 -1 2]
[-4 -1 2]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 8 3 2]
[ 8 3 1]]
>>> round(np.linalg.det(C), 3)
4.0
>>> round(np.linalg.det(A), 3) + round(np.linalg.det(B), 3)
4.0
Свойство 7. Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и тоже число, то определитель матрицы не изменится:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> k = 2
>>> B = A.copy()
>>> B[1, :] = B[1, :] + k * B[0, :]
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> print(B)
[[-4 -1 2]
[ 2 2 3]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
-14.0
>>> round(np.linalg.det(B), 3)
-14.0
Свойство 8. Если строка или столбец матрицы является линейной комбинацией других строк (столбцов), то определитель такой матрицы равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = A[0, :] + k * A[2, :]
>>> round(np.linalg.det(A), 3)
0.0
Свойство 9. Если матрица содержит пропорциональные строки, то ее определитель равен нулю:
➤ Пример на Python
>>> A = np.matrix('-4 -1 2; 10 4 -1; 8 3 1')
>>> print(A)
[[-4 -1 2]
[10 4 -1]
[ 8 3 1]]
>>> k = 2
>>> A[1, :] = k * A[0, :]
>>> print(A)
[[-4 -1 2]
[-8 -2 4]
[ 8 3 1]]
>>> round(np.linalg.det(A), 3)
0.0P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Действия с матрицами
Матрицы и действия с ними, определителиСложение матриц
Сложение определено для матриц одного типа, т.е. для матриц, у которых число строк и столбцов совпадает. Сумма матриц \(A=\{A_{ik}\}\) и \(B=\{B_{ik}\}\), матрица \(A+B\), определяется следующим образом: \((A+B)_{ik}=A_{ik}+B_{ik}\), \(1 \leq i \leq m, 1 \leq k \leq n\). Иными словами: складываются элементы матриц \(A\) и \(B\), стоящие на одинаковом месте (т.е. на пересечении одинаковых строк и столбцов) и записываются в то же место.
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , \] \[ B=\left( \begin{array}{ccc} 2 &1 & 0 \\ 1 & 3 & 4 \end{array} \right) , \] тогда \[ A+B=\left( \begin{array}{ccc} 3 & 5 & -1 \\ 4 & -3 & 11 \end{array} \right) . \]
Умножение матрицы на число
Пусть \(A=\{a_{ik}\}\) — матрица типа \((m,n)\), \(\lambda\) — произвольное число. Тогда матрица \(\{\lambda a_{ik}\}\) называется произведением числа \(\lambda \) на матрицу \(A\) и обозначается \(\lambda \cdot A\).
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 7 & 5 & 2 \\ 3 & -6 & 7 \end{array} \right) , \] тогда \[ 5A=\left( \begin{array}{ccc} 5 &20 & -5 \\ 35 & 25 & 10 \\ 15 & -30 & 35 \end{array} \right) .T\) (это выражение занимает меньше места).
Элементарные свойства операций с матрицами
Введенные операции обладают многими естественными арифметическими свойствами. Перечислим ряд из них.
1. Для любых матриц \(A,B,C\) одного типа \((A+B)+C=A+(B+C)\)(ассоциативность сложения).
2. Для любых матриц \(A,B\) одного типа \(A+B=B+A\) (коммутативность сложения).
3. Пусть \((m,n)\)-матрица \(O\) состоит из нулей. Такая матрица играет роль нуля при сложении матриц типа \((m,n)\), \(A+O=A\), \(0\cdot A=O\) для любой матрицы \(A\) того же типа.
4. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1+c_2)A=c_1A+c_2A\).
5. Для любых матриц \(A,B\) одного типа и любого числа \(c\) верно \(c(A+B)=cA+cB\).
6. Для любых чисел \(c_1,c_2\) и любой матрицы \(A\) верно \((c_1c_2)A=c_1(c_2A)\).
7. Для любой матрицы \(A\) верно \(1\cdot A=A\).
8. Для любых матриц \(A,B\) одного типа \((A+B)^T=A^T+B^T\).na_{im}b_{mk}. \] Таким образом следует вычислить все \(mp\) элементов матрицы \(C\). Еще раз подчеркнем, что для того, чтобы можно было перемножать матрицы \(A\) и \(B\), их типы должны быть согласованы!
Пример. Пусть \[ A=\left( \begin{array}{ccc} 1 &4 & -1 \\ 3 & -6 & 7 \end{array} \right) , B=\left( \begin{array}{cc} 2 &1 \\ 1 & 3 \\ -3 &5 \end{array} \right) . \]
В данном случае матрица \(A\) имеет тип (2,3), матрица \(B\) имеет тип (3,2), так что типы матриц согласнованы и в результате умножения \(A\) на \(B\) получим матрицу типа \((2,2)\). Получаем: \[ AB=\left ( \begin{array}{cc} 1\cdot 2 +4 \cdot 1+(-1)\cdot (-3) & 1\cdot 1 +4 \cdot 3+(-1)\cdot 5\\ 3\cdot 2 +(-6) \cdot 1+7\cdot (-3) &3\cdot 1 +(-6) \cdot 3+7\cdot 5 \end{array} \right )= \left( \begin{array}{cc} 9 & 8\\ -21 & 20 \end{array} \right).T\).
6. Для квадратных матриц \(A,B\) одного типа \(det(AB)=detA \cdot detB\).
7. Рассмотрим квадратную матрицу порядка \(n\), \(E=diag\{1,1,1,…,1\}\). Такая матрица играет выделенную роль в умножении матриц: для любых матриц \(A,B\) имеем \(EA=A\), \(BE=B\). Матрица \(E\) называется единичной матрицей порядка \(n\). Согласно описанным выше результатам, \(detE=1\).
1. Умножить матрицы:
а) \[ \left( \begin{array}{cc} 2 & 1 \\ 3 & 4 \end{array} \right)\cdot \left( \begin{array}{cc} 1 & -1 \\ 2 & 1 \end{array} \right). \]
б) \[ \left( \begin{array}{ccc} 3 & 1 & 1 \\ 2 & 1 & 2 \\ 1 & 2 & 1 \end{array} \right)\cdot \left( \begin{array}{ccc} 1 &1 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & 1 \end{array} \right). \]
2. Вычислить \[ \left( \begin{array}{cc} 3 & 2 \\ -4 & -2 \end{array} \right)^5.{-1}=\frac{1}{ad-bc}\left( \begin{array}{cc} d & -b \\ -c & a \end{array} \right). \]
Таким образом, для матрицы порядка 2 формулы для обратной матрицы достаточно простые. Для больших порядков формулы становятся существенно более громоздкими.
Найти обратную матрицу для матрицы
1. \[ A=\left( \begin{array}{ccc} 2 &2 & 3 \\ 1 & -1 & 0 \\ -1 & 2 & 1 \end{array} \right). \]
2. \[ A=\left( \begin{array}{ccc} 2 &-1 & 0 \\ 0 & 2 & -1 \\ -1 & -1 & 1 \end{array} \right). \]
3. \[ A=\left( \begin{array}{ccc} 1 &1 & 1 \\ 1 & 2 & 2 \\ 2 & 3 & 4 \end{array} \right). \]
Матричные уравнения
Матричными уравнениями называются уравнения вида \[ AX=G, \quad \quad(12)\] \[ XB=G, \quad \quad(13)\] \[ AXB=G, \quad \quad(14)\] где матрицы \(A,B,G\) заданы и требуется построить матрицу \(X\).{-1}. \]
1. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 2 & 6 \\ -9 & 3 \end{array} \right) , G=\left( \begin{array}{cc} -26 & -50 \\ 27 & -15 \end{array} \right) . \]
2. Найти решение матричного уравнения (12), если \[ A=\left( \begin{array}{cc} 8 & -7 \\ -5 & 4 \end{array} \right) , G=\left( \begin{array}{cc} 25 & -34 \\ -16 & 22 \end{array} \right) . \]
3. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} -8 & -5 \\ -9 & 5 \end{array} \right) , G=\left( \begin{array}{cc} -20 & 30 \\ -19 & 20 \end{array} \right) . \]
4. Найти решение матричного уравнения (13), если \[ B=\left( \begin{array}{cc} 9 & 8 \\ -3 & 7 \end{array} \right) , G=\left( \begin{array}{cc} -72 & 23 \\ 0 & 58 \end{array} \right) . \]
5. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} 4 & 2 \\ 3 & -4 \end{array} \right) , B=\left( \begin{array}{cc} -1 & 2 \\ -2 & -1 \end{array} \right) , G=\left( \begin{array}{cc} 20 & -50 \\ 26 & 23 \end{array} \right) . \]
6. Найти решение матричного уравнения (14), если \[ A=\left( \begin{array}{cc} -4 & -2 \\ -3 & 3 \end{array} \right) , B=\left( \begin{array}{cc} 3 & 4 \\ 4 & 3 \end{array} \right) , G=\left( \begin{array}{cc} 132 & 134 \\ 18 & 24 \end{array} \right) . \]
Определитель матрицы 3×3 — ChiliMath
Стандартная формула для определения определителя матрицы 3 × 3 представляет собой разбиение меньших задач определителя 2 × 2 , с которыми очень легко справиться. Если вам нужно напомнить что-то новое, посмотрите мой другой урок о том, как найти определитель 2 × 2. Предположим, нам дана квадратная матрица A, где,
Определитель матрицы A вычисляется как
Вот ключевые моменты:
- Обратите внимание, что элементы верхней строки, а именно a, b и c, служат скалярными умножителями для соответствующей матрицы 2 на 2.
- Скаляр a умножается на матрицу 2 × 2 оставшихся элементов, созданную, когда сегменты вертикальной и горизонтальной линии проходят через a.
- Тот же процесс применяется для построения матриц 2 × 2 для скалярных множителей b и c.
Определитель матрицы 3 x 3 (анимированный)
Примеры определения определителя матрицы 3 × 3
Пример 1: Найдите определитель матрицы 3 × 3 ниже.
Приведенная ниже настройка поможет вам найти соответствие между общими элементами формулы и элементами реальной проблемы.
Применяя формулу,
Пример 2: Вычислите определитель матрицы 3 × 3 ниже.
Будьте очень осторожны при замене значений в правильные места в формуле. Распространенные ошибки возникают, когда ученики становятся небрежными на начальном этапе подстановки значений.
Вдобавок убедитесь, что ваша арифметика верна.В противном случае одна ошибка в вычислении приведет к неверному ответу.
С,
наше вычисление определителя становится…
Пример 3: Найдите определитель матрицы 3 × 3 ниже.
Наличие нуля (0) в первой строке должно значительно упростить наши вычисления. Помните, что эти элементы в первой строке действуют как скалярные множители. Следовательно, умножение нуля на что-либо приведет к исчезновению всего выражения.
Вот снова настройка, показывающая соответствующее числовое значение каждой переменной в формуле.
По формуле имеем…
Практика с рабочими листами
Вас также может заинтересовать:
Детерминанты матрицы 2 × 2
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее.Один из способов — увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведения записей на по каждой из трех диагоналей (от нижнего левого угла к верхнему правому). Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
[латекс] A = \ left [\ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \\ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} \ right] [/ латекс]
- Дополните [латекс] A [/ латекс] первыми двумя столбцами.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} {a} _ {1} & {b} _ {1} & {c} _ {1} \ \ {a} _ {2} & {b} _ {2} & {c} _ {2} \\ {a} _ {3} & {b} _ {3} & {c} _ {3} \ end {array} | \ begin {array} {c} {a} _ {1} \\ {a} _ {2} \\ {a} _ {3} \ end {array} \ begin {array} {c } {b} _ {1} \\ {b} _ {2} \\ {b} _ {3} \ end {array} | [/ latex]
- С верхнего левого угла в нижний правый: умножение значений по первой диагонали. Добавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
- От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали. Из этого результата вычтите произведение входов вверх по второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Рисунок 2
Алгебра выглядит следующим образом:
[латекс] | A | = {a} _ {1} {b} _ {2} {c} _ {3} + {b} _ {1} {c} _ {2} {a} _ {3 } + {c} _ {1} {a} _ {2} {b} _ {3} — {a} _ {3} {b} _ {2} {c} _ {1} — {b} _ {3} {c} _ {2} {a} _ {1} — {c} _ {3} {a} _ {2} {b} _ {1} [/ latex]
Пример 3: Нахождение определителя матрицы 3 × 3
Найдите определитель матрицы 3 × 3 для данного
[латекс] A = \ left [\ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} \ right] [/ latex]
Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
[латекс] \ begin {array} {l} | A | = | \ begin {array} {ccc} 0 & 2 & 1 \\ 3 & -1 & 1 \\ 4 & 0 & 1 \ end {array} | \ begin {array} {c} 0 \\ 3 \\ 4 \ end {array} \ begin {array} {c} 2 \\ -1 \\ 0 \ end {array} | \ hfill \\ = 0 \ left (-1 \ right ) \ влево (1 \ вправо) +2 \ влево (1 \ вправо) \ влево (4 \ вправо) +1 \ влево (3 \ вправо) \ влево (0 \ вправо) -4 \ влево (-1 \ вправо) \ left (1 \ right) -0 \ left (1 \ right) \ left (0 \ right) -1 \ left (3 \ right) \ left (2 \ right) \ hfill \\ = 0 + 8 + 0 + 4 — 0-6 \ hfill \\ = 6 \ hfill \ end {array} [/ latex]
Попробуй 2
Найдите определитель матрицы 3 × 3.
[латекс] \ mathrm {det} \ left (A \ right) = | \ begin {array} {ccc} 1 & -3 & 7 \\ 1 & 1 & 1 \\ 1 & -2 & 3 \ end {array} | [/ latex ]
Вопросы и ответы
Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для [latex] 2 \ text {} \ times \ text {} 2 [/ latex] и [latex] \ text {3} \ text {} \ times \ text {} 3 [/ латексные] матрицы. Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы 3 × 3, мы можем применить Правило Крамера для решения системы трех уравнений с тремя переменными .Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц 2 × 2. Однако по мере увеличения порядка матрицы до 3 × 3 требуется гораздо больше вычислений.
Когда мы вычисляем, что определитель равен нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или есть бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений 3 × 3.
Рисунок 3
[латекс] x = \ frac {{D} _ {x}} {D}, y = \ frac {{D} _ {y}} {D}, z = \ frac {{D} _ {z} } {D}, D \ ne 0 [/ латекс]
где
Рисунок 4
Если мы записываем определитель [latex] {D} _ {x} [/ latex], мы заменяем столбец [latex] x [/ latex] на столбец констант.Если мы пишем определитель [latex] {D} _ {y} [/ latex], мы заменяем столбец [latex] y [/ latex] постоянным столбцом. Если мы пишем определитель [latex] {D} _ {z} [/ latex], мы заменяем столбец [latex] z [/ latex] постоянным столбцом. Всегда проверяйте ответ.
Пример 4: Решение системы 3 × 3 с использованием правила Крамера
Найдите решение данной системы 3 × 3, используя правило Крамера.
[латекс] \ begin {array} {c} x + y-z = 6 \\ 3x — 2y + z = -5 \\ x + 3y — 2z = 14 \ end {array} [/ latex]
Решение
Используйте правило Крамера.
[латекс] D = | \ begin {array} {ccc} 1 & 1 & -1 \\ 3 & -2 & 1 \\ 1 & 3 & -2 \ end {array} |, {D} _ {x} = | \ begin { array} {ccc} 6 & 1 & -1 \\ -5 & -2 & 1 \\ 14 & 3 & -2 \ end {array} |, {D} _ {y} = | \ begin {array} {ccc} 1 & 6 & -1 \\ 3 & -5 & 1 \\ 1 & 14 & -2 \ end {array} |, {D} _ {z} = | \ begin {array} {ccc} 1 & 1 & 6 \\ 3 & -2 & -5 \\ 1 & 3 & 14 \ end {array} | [/ latex]
Затем,
[латекс] \ begin {array} {l} x = \ frac {{D} _ {x}} {D} = \ frac {-3} {- 3} = 1 \ hfill \\ y = \ frac { {D} _ {y}} {D} = \ frac {-9} {- 3} = 3 \ hfill \\ z = \ frac {{D} _ {z}} {D} = \ frac {6} {-3} = — 2 \ hfill \ end {array} [/ latex]
Решение [латекс] \ left (1,3, -2 \ right) [/ latex].
Попробовать 3
Используйте правило Крамера, чтобы решить матрицу 3 × 3.
[латекс] \ begin {array} {r} \ hfill x — 3y + 7z = 13 \\ \ hfill x + y + z = 1 \\ \ hfill x — 2y + 3z = 4 \ end {array} [/ латекс]
Пример 5: Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
[латекс] \ begin {array} {l} 3x — 2y = 4 \ text {} \ left (1 \ right) \\ 6x — 4y = 0 \ text {} \ left (2 \ right) \ end {массив } [/ latex]
Решение
Начнем с нахождения определителей [латекс] D, {D} _ {x}, \ text {и} {D} _ {y} [/ latex].
[латекс] D = | \ begin {array} {cc} 3 & -2 \\ 6 & -4 \ end {array} | = 3 \ left (-4 \ right) -6 \ left (-2 \ right) = 0 [/ латекс]
Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс].
- Добавьте результат в уравнение [латекс] \ left (2 \ right) [/ latex].
[латекс] \ begin {array} \ text {} \ hfill − 6x + 4y = −8 \\ \ hfill6x − 4y = 0 \\ \ hfill \ text {_____________} \\ \ hfill 0 = 8 \ end { array} [/ latex]
Получаем уравнение [латекс] 0 = -8 [/ латекс], которое неверно.Следовательно, у системы нет решения. График системы показывает две параллельные линии.
Рисунок 5
Пример 6. Использование правила Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
[латекс] \ begin {array} {rr} \ hfill x — 2y + 3z = 0 & \ hfill \ left (1 \ right) \\ \ hfill 3x + y — 2z = 0 & \ hfill \ left (2 \ right) \\ \ hfill 2x — 4y + 6z = 0 & \ hfill \ left (3 \ right) \ end {array} [/ latex]
Решение
Давайте сначала найдем определитель.Создайте матрицу, дополненную первыми двумя столбцами.
[латекс] | \ begin {array} {rrr} \ hfill 1 & \ hfill -2 & \ hfill 3 \\ \ hfill 3 & \ hfill 1 & \ hfill -2 \\ \ hfill 2 & \ hfill -4 & \ hfill 6 \ end { array} \ text {} | \ text {} \ begin {array} {rr} \ hfill 1 & \ hfill -2 \\ \ hfill 3 & \ hfill 1 \\ \ hfill 2 & \ hfill -4 \ end {array} | [ / латекс]
Затем,
[латекс] 1 \ влево (1 \ вправо) \ влево (6 \ вправо) + \ влево (-2 \ вправо) \ влево (-2 \ вправо) \ влево (2 \ вправо) +3 \ влево (3 \ вправо) \ влево (-4 \ вправо) -2 \ влево (1 \ вправо) \ влево (3 \ вправо) — \ влево (-4 \ вправо) \ влево (-2 \ вправо) \ влево (1 \ вправо) -6 \ влево (3 \ вправо) \ влево (-2 \ вправо) = 0 [/ латекс]
Поскольку определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.
- Умножьте уравнение (1) на [латекс] -2 [/ латекс] и добавьте результат к уравнению (3):
[латекс] \ frac {\ begin {array} {r} \ hfill -2x + 4y — 6x = 0 \\ \ hfill 2x — 4y + 6z = 0 \ end {array}} {0 = 0} [/ latex ]
- Получение ответа [latex] 0 = 0 [/ latex], утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы видим, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.
Рисунок 6
Матрица, обратная 3 на 3 — решенные примеры
Найти обратную матрицу 3 на 3 онлайн
Обратная матрица 3 на 3 — немного сложная задача, но ее можно оценить, выполнив шаги, указанные ниже. Матрица 3 на 3 включает 3 строки и 3 столбца. Элементами матрицы являются числа, образующие матрицу. Единственная матрица — это матрица, определитель которой не эквивалентен нулю. Для каждой квадратной матрицы x x x существует обратная матрица.Матрица, обратная x * x, представлена как X. Матрицу, обратную матрице, нелегко вычислить с помощью калькулятора и метода быстрого доступа.
XX-1 = X-1 X = I2
В приведенном выше свойстве I2 указывает матрицу x * x. Например, возьмем матрицу 2 * 2 как
\ [\ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix} \]
Любая квадратная матрица X x * x, которая всегда имеет нулевой определитель. включает инверсию X-1.
Это подходит почти для всех квадратных матриц и определяется как XX-1 = X-1 X = I2
Как найти обратную матрицу 3 на 3?
Здесь вы можете увидеть обратные шаги матрицы 3 на 3, чтобы найти в Интернете обратную матрицу 3 на 3
Оценить определитель данной матрицы
Найти транспонирование данной матрицы
Вычислить определитель матрицы 2 x 2.
Подготовьте матрицу сомножителей
Наконец, разделите каждый член сопряженной матрицы на определитель
Формула обратной матрицы
Первым шагом является вычисление определителя матрицы 3 * 3 и затем найдите его сомножители, миноры и присоединенный элемент, а затем включите результаты в формулу обратной матрицы, приведенную ниже.
A-1 = 1 / | A | Adj (A)
Пример, обратный матрице 3 X3
Давайте решим матрицу 3 X 3
\ [\ begin {bmatrix} a & b & c \\ d & e & f \\ g & h & i \ end {bmatrix} \]
Изучите данную матрицу 3 X 3
A = \ [\ begin {bmatrix} 1 & 2 & 3 \\ 0 & 1 & 4 \\ 5 & 6 & 0 \ end {bmatrix} \]
Давайте узнаем, как найти обратную матрицу 3 X 3 онлайн.
Проверим, является ли данная матрица обратимой.
Это можно доказать, если ее определитель не равен нулю.Если определитель данной матрицы равен нулю, то обратной данной матрице не будет.
det (A) = 1 (0-24) — 2 (0-20) + 3 (0-5)
det (A) = -24 + 40-15
det (A) = 1
Поскольку определитель значения равен 1, мы можем сказать, что данная матрица имеет обратную матрицу.
Нахождение транспонирования данной матрицы
Чтобы найти транспонирование заданной матрицы 3 X 3
Следовательно, A-1 = \ [\ begin {bmatrix} 1 & 0 & 5 \\ 2 & 1 & 6 \ \ 3 & 4 & 0 \ end {bmatrix} \]
Определение определителей младших матриц 2 X 2.
Теперь мы определим определитель каждой без исключения второстепенных матриц 2 X 2.
Для элементов первой строки
\ [\ begin {bmatrix} 1 & 6 \\ 4 & 0 \ end {bmatrix} \] = -24
\ [\ begin {bmatrix} 12 & 6 \\ 3 & 0 \ end {bmatrix} \] = -18
\ [\ begin {bmatrix} 2 & 1 \\ 3 & 4 \ end {bmatrix} \] = 5
Для элементов второй строки
\ [\ begin {bmatrix } 0 & 5 \\ 4 & 0 \ end {bmatrix} \] = -20
\ [\ begin {bmatrix} 1 & 5 \\ 3 & 0 \ end {bmatrix} \] = -15
\ [ \ begin {bmatrix} 1 & 0 \\ 3 & 4 \ end {bmatrix} \] = 4
Для элемента третьей строки
\ [\ begin {bmatrix} 10 & 65 \\ 14 & 60 \ end {bmatrix} \] = -5
\ [\ begin {bmatrix} 1 & 5 \\ 2 & 6 \ end {bmatrix} \] = -4
\ [\ begin {bmatrix} 1 & 0 \\ 2 & 1 \ end {bmatrix} \] = 1
Теперь новая матрица —
\ [\ begin {bmatrix} -24 & -18 & 5 \\ -20 & -15 & 4 \\ -5 & 14 & 1 \ end {bmatrix} \]
Создание матрицы сомножителей
Чтобы сформулировать сопряженную или сопряженную матрицу, поменяйте знак чередующихся членов, как показано ниже:
Мы получаем новую матрицу как
A = \ [\ begin {bmatrix} -24 & -18 & 5 \\ -20 & -15 & 4 \\ -5 & 14 & 1 \ end {bmatrix} \]
Adj (A) = новая матрица
A = \ [\ begin {bmatrix} -24 & -18 & 5 \\ -20 & -15 & 4 \\ -5 & 14 & 1 \ end {bmatrix} \] X \ [\ begin {bmatrix} + & — & + \\ — & + & + \\ + & — & + \ end {bmatrix} \]
Adj (A) = \ [\ begin {bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \ end {bmatrix} \]
Нахождение обратной матрицы 3 x 3
Теперь, если мы заменим значение из det (A) и adj (A) в формуле:
A-1 = [1 / det (A)] Adj (A)
A-1 = (1/1) = \ [\ begin { bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \ end {bmatrix} \]
Следовательно, обратная матрица для данной матрицы равна
A-1 = ( 1/1) = \ [\ begin {bmatrix} -24 & 18 & 5 \\ 20 & -15 & -4 \\ -5 & 4 & 1 \ end {bmatrix} \]
Решенные примеры
1.Найдите матрицу, обратную следующей
1 \ [\ begin {bmatrix} 2 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & -1 & 2 \ end {bmatrix} \]
Решение:
-2 \ [\ begin {bmatrix} 1 & 1 \\ -1 & 2 \ end {bmatrix} \] -1 \ [\ begin {bmatrix} 1 & 1 \\ 1 & 2 \ end {bmatrix} \] + 1 \ [\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix} \]
| A | = 2 [2 — (- 1)] -1 [2-1] +1 [-1-1]
= 2 [2 + 1] -1 [1] +1 [-2]
= 2 [ 3] -1-2
= 6 — 3
= 3
| A | = 3
As, A — невырожденная матрица.Существует -1
Младший и кофакторы строки 1
Младший из 2
\ [\ begin {bmatrix} 1 & 1 \\ -1 & 2 \ end {bmatrix} \]
= [2 — (- 1)]
= [2 + 1]
= (3)
= 3
Кофактор 2 = + (3)
= 3
Младший из 1
\ [\ begin {bmatrix} 1 & 1 \\ 1 & 2 \ end {bmatrix} \]
= [2-1]
= (2)
= 2
Кофактор 1 = (-1)
= -1
Незначительный из 1
\ [\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix} \]
= [- 1-1]
= (-2)
= -2
Кофактор 1 = + (-2)
= -2
Минор и кофакторы строки 2
Минор 1
\ [\ begin {bmatrix} 1 & 1 \\ 1 & -2 \ end {bmatrix} \]
= [-2-1]
= -3
Кофактор 1 = — (-3)
= -3
Незначительное число 1
\ [\ begin {bmatrix} 2 & 1 \ \ 1 & 2 \ end {bmatrix} \]
= [4-1] 90 007
= (3)
= 3
Кофактор 1 = — (-3)
= -3
Незначительное число 1
\ [\ begin {bmatrix} 2 & 1 \\ 1 & -1 \ end {bmatrix} \]
[-2-1]
= (-3)
= -3
Кофактор 1 = — (-3)
= 3
Второстепенные и сомножители строки 3
Незначительное число из 1
\ [\ begin {bmatrix} 1 & 1 \\ 1 & 1 \ end {bmatrix} \]
= [1-1]
= 0
Кофактор 1 = + (0)
= 0
Незначительное число -1
\ [\ begin {bmatrix} 2 & 1 \\ 1 & 1 \ end {bmatrix} \]
= [2-1]
= 1
Кофактор -1 = — (1)
= -1
Младший из 2
\ [\ begin {bmatrix} 2 & 1 \\ 1 & 1 \ end {bmatrix} \]
= [2-1]
= 1
Кофактор 2 = + (1)
= 1
Матрица кофакторов
\ [\ begin {bmatrix} 3 & -1 & -2 \\ -3 & 3 & 3 \\ 0 & — 1 & 1 \ end {bmatrix} \]
Сопряженная матрица 90 007
\ [\ begin {bmatrix} 3 & -3 & 0 \\ -1 & 3 & -1 \\ -2 & 3 & 1 \ end {bmatrix} \]
Следовательно, матрица, обратная данной матрице
A-1 = ⅓ \ [\ begin {bmatrix} -3 & 3 & 0 \\ 1 & -3 & 1 \\ 2 & -3 & -1 \ end {bmatrix} \]
1.Найдите матрицу, обратную следующей
\ [\ begin {bmatrix} 6 & 2 & 3 \\ 3 & 1 & 1 \\ 10 & 3 & 4 \ end {bmatrix} \]
Решение:
-6 \ [\ begin {bmatrix} 1 & 1 \\ 3 & 4 \ end {bmatrix} \] -2 \ [\ begin {bmatrix} 3 & 1 \\ 10 & 4 \ end {bmatrix} \] +3 \ [ \ begin {bmatrix} 13 & 1 \\ 10 & 3 \ end {bmatrix} \]
| A | = 2 [2 — (- 1)] -1 [2-1] +1 [-1-1]
= 2 [2 + 1] -1 [1] +1 [-2]
= 2 [ 3] -1-2
= 6 — 3
= 3
| A | = 3
As, A — невырожденная матрица.A -1 существует
| A | = 6 [4-3] — 2 [12-10] + 3 [9-10]
= 6 [1] — 2 [2] + 3 [-1]
= 6 — 4 — 3
= 6-7
= -1
| A | = -1 ≠ 0
Младший и сомножители строки 1
Младший из 6
\ [\ begin {bmatrix} 1 & 1 \\ 3 & 4 \ end {bmatrix} \]
= [4-3]
= (1)
= 1
Кофактор 6 = + (1)
= 1
Незначительный из 2
\ [\ begin {bmatrix} 3 & 1 \\ 10 & 4 \ end {bmatrix } \]
= [12-10]
= (2)
= 2
Кофактор 2 = (-2)
= -2
Младший из 3
\ [\ begin {bmatrix} 3 & 1 \\ 10 & 3 \ end {bmatrix} \]
[9-10]
= (-1)
= -1
Кофактор 3 = + (-1)
= -1
Младший и сомножители строки 2
Младший из 3
\ [\ begin {bmatrix} 2 & 3 \\ 3 & 4 \ end {bmatrix} \]
= [8-9]
= (- 1)
= -1
Кофактор 3 = — (-1)
= 1
Младший из 1
\ [\ begin {bmatrix} 6 & 3 \\ 10 & 4 \ end {bmatrix} \ ]
= [24-30]
9025 0 = (-6)= -6
Кофактор 1 = + (-6)
= -6
Незначительное число 1
\ [\ begin {bmatrix} 6 & 2 \\ 10 & 3 \ end {bmatrix} \]
[18-20]
= (-2)
-2
Кофактор 1 = — (-2)
= 2
Минор и кофакторы строки 3
Второстепенный из 10
\ [\ begin {bmatrix} 2 & 3 \\ 1 & 1 \ end {bmatrix} \]
= [2-3]
= -1
Кофактор 1 = + (-1)
= (-1)
= -1
Незначительное число из 3
\ [\ begin {bmatrix} 6 & 3 \\ 3 & 1 \ end {bmatrix} \]
= [6-9]
= (-3)
= -3
Кофактор 3 = — (-3)
= 3
Незначительный из 4
\ [\ begin {bmatrix} 6 & 2 \\ 3 & 1 \ end {bmatrix} \]
= [6-6]
= (0)
= 0
Кофактор 4 = + (0)
= 0
Матрица кофакторов
\ [\ begin {bmatrix} 1 & -2 & -1 \\ -1 & -6 & 2 \\ -1 & 3 & 0 \ end {bmatrix} \]
Присоединенный к матрице
= \ [\ begin {bmatrix} 1 & 1 & -1 \\ -2 & -6 & 3 \\ -1 & 2 & 0 \ конец {bmatrix} \]
A-1 = 1/1 = \ [\ begin {bmatrix} -1 & -1 & 1 \\ 2 & 6 & -3 \\ 1 & -2 & 0 \ end {bmatrix } \]
Обратная матрица 3 на 3
Обратная матрица 3 на 3Как вы знаете, каждая матрица A 2 на 2, которая не является сингулярной (то есть чей определитель не равен нулю), имеет обратную матрицу A ^ {- 1} со свойством, которое
A \, A ^ {- 1} = A ^ {- 1} A \, = \, I_ {2},
где I_ {2} — это единичная матрица 2 на 2, \ left (\ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right).{-1} A \, = \, I_ {n}.
Если мы знаем это обратное, это в целом очень полезно. Например, оказывается, что обратная матрица
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right)
является
\ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right),
как можно быстро проверить:
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) \ left (\ begin {array} {ccc} 4 & — 5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right) = \ left (\ begin {array} {ccc} 0-15 + 16 & 0 + 18-18 & 0 + 6-6 \\ 4 -20 + 16 & -5 + 24-18 & -2 + 8-6 \\ — 12 + 20-8 & 15-24 + 9 & 6-8 + 3 \ end {array} \ right) = \ left (\ begin {array} { ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right).
Теперь рассмотрим систему уравнений
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) \ left (\ begin {array} {c} x \ \ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right). {- 1} \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left ( \ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right) \ left (\ begin {array} {c} 2 \\ 5 \\ — 9 \ end {array} \ right) = \ left (\ begin {array} {c} 1 \\ — 2 \\ 2 \ end {array} \ right).
К сожалению, для больших квадратных матриц не существует четкой формулы для обратного. Действительно, поиск обратных чисел настолько трудоемок, что обычно не стоит усилий, и мы используем альтернативные методы для решения систем уравнений (см. Исключение Гаусса).
Однако иногда оно того стоит. Например, мы можем обнаружить, что хотим многократно решать
\ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) \ left (\ begin {array} {c} x \ \ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} v_ {1} \\ v_ {2} \\ v_ {3} \ end {array} \ right)
для множества различных значений v_ {1}, v_ {2} и v_ {3}, и в этом случае зная, что обратное
\ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right)
очень пригодится.
Есть три основных метода поиска инверсий. Первый метод, который называется методом кофакторов, подробно описан здесь. Второй называется исключением Гаусса-Жордана и рассматривается в другом месте. В третьем используется так называемая теорема Кэли-Гамильтона: на одних курсах она рассматривается, а на других — нет.
Мы не будем здесь доказывать, что метод кофакторов работает; вместо этого мы представляем его просто как пошаговый рецепт.
Шаг 1: замените каждую запись ее второстепенной
Для данной записи в матрице 3 на 3 вычеркните всю ее строку и столбец и возьмите определитель оставшейся матрицы 2 на 2 (это называется второстепенным).
В нашем примере это дает нам
\ left (\ begin {array} {ccc} \ left (-4 \ right) \ times 1- \ left (-2 \ right) \ times 4 & 1 \ times 1- \ left (-2 \ right) \ times \ left (-3 \ right) & 1 \ times 4- \ left (-4 \ right) \ times \ left (-3 \ right) \\\ left (-3 \ right) \ times 1- \ left (-2 \ вправо) \ раз 4 и 0 \ раз 1- \ влево (-2 \ вправо) \ раз \ влево (-3 \ вправо) и 0 \ раз 4- \ влево (-3 \ вправо) \ раз \ влево (-3 \ вправо ) \\\ влево (-3 \ вправо) \ раз \ влево (-2 \ вправо) — \ влево (-2 \ вправо) \ раз \ влево (-4 \ вправо) & 0 \ раз \ влево (-2 \ вправо ) — \ left (-2 \ right) \ times 1 & 0 \ times \ left (-4 \ right) — \ left (-3 \ right) \ times 1 \ end {array} \ right) = \ left (\ begin { array} {ccc} 4 & -5 & -8 \\ 5 & -6 & -9 \\ — 2 & 2 & 3 \ end {array} \ right).
Шаг 2: измените некоторые знаки
Теперь меняем приметы некоторых несовершеннолетних по схеме
\ left (\ begin {array} {ccc} + & — & + \\ — & + & — \\ + & — & + \ end {array} \ right),
таким образом создавая так называемую матрицу кофакторов. В нашем случае это
\ left (\ begin {array} {ccc} 4 & 5 & -8 \\ — 5 & -6 & 9 \\ — 2 & -2 & 3 \ end {array} \ right).
Шаг 3: транспонировать
Теперь транспонируем матрицу сомножителей.В нашем случае мы получаем
\ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right).
Шаг 4: разделите на определитель
Наконец, делим на определитель исходной матрицы. В нашем случае определитель
\ text {det} \ left (\ begin {array} {ccc} 0 & -3 & -2 \\ 1 & -4 & -2 \\ — 3 & 4 & 1 \ end {array} \ right) = 0 \ times \ text {det } \ left (\ begin {array} {cc} -4 & -2 \\ 4 & 1 \ end {array} \ right) +3 \ times \ text {det} \ left (\ begin {array} {cc} 1 & -2 \\ — 3 & 1 \ end {array} \ right) -2 \ times \ text {det} \ left (\ begin {array} {cc} 1 & -4 \\ — 3 & 4 \ end {array} \ right) = 1,
так что обратное просто
A ^ {- 1} = \ left (\ begin {array} {ccc} 4 & -5 & -2 \\ 5 & -6 & -2 \\ — 8 & 9 & 3 \ end {array} \ right).
Умножение матриц — примеры
М. Борна
На этой странице вы можете увидеть множество примеров умножения матриц.
Вы можете повторно загружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел и матриц. Вы также можете выбрать матрицы разного размера (внизу страницы).
(Если вам сначала нужна справочная информация о матрицах, вернитесь к «Введение в матрицы» и «4. Умножение матриц»).
Пример
Умножение матриц A и B .
|
Ответ
Для экономии работы мы сначала проверяем, можно ли их умножить.
У нас есть (3 × 2) × (2 × 4), и поскольку количество столбцов в A совпадает с количеством строк в B (в данном случае два средних числа равны 2), мы можем перемножить эти матрицы. Нашим результатом будет матрица (3 × 4).
Первый шаг — записать две матрицы рядом, как показано ниже:
|
Мы умножаем отдельные элементы вдоль первой строки матрицы A на соответствующие элементы в первом столбце матрицы B и складываем результаты.Это дает нам число, которое нам нужно поместить в первую строку, первую позицию столбца в матрице ответов.
-3 × -4 + 6 × 2 = 24
После этого мы умножаем элементы в первой строке матрицы A, на соответствующие элементы во втором столбце матрицы B , затем складываем результаты. Это дает нам ответ, который нам нужно будет поместить в первую строку, второй столбец матрицы ответов.
-3 × 0 + 6 × -3 = -18
Продолжаем по строкам и столбцам следующим образом:
| = | -3 × -4 + 6 × 2 | -3 × 0 + 6 × -3 | -3 × 1 + 6 × -2 | -3 × 5 + 6 × 3 | ||
| 4 × -4 + -2 × 2 | 4 × 0 + -2 × -3 | 4 × 1 + -2 × -2 | 4 × 5 + -2 × 3 | |||
| 7 × -4 + -1 × 2 | 7 × 0 + -1 × -3 | 7 × 1 + -1 × -2 | 7 × 5 + -1 × 3 |
| = | 24 | -18 | -15 | 3 | ||
| -20 | 6 | 8 | 14 | |||
| -30 | 3 | 9 | 32 |
Посмотреть другой пример?
Вы можете обновить эту страницу, чтобы увидеть другой пример с матрицами другого размера и другими числами; ИЛИ
Выберите нужные вам размеры матрицы и нажмите кнопку.
Нахождение определителя матрицы 3×3
Постановка задачи
Мы собираемся рассмотреть, как найти определитель для матрицы 3×3, но сначала нам нужно знать, что такое определитель. Определитель — это одно конкретное число, связанное с определенной квадратной матрицей. Следует отметить, что определители определены только для квадратных матриц. Давайте посмотрим на процесс, используемый для поиска определителя для конкретной матрицы.
- Шаг 1 — Запишите матрицу
Мы должны знать, над чем мы работаем, верно? Итак, вот матрица 3 x 3, которую мы будем использовать в этом упражнении.
3 x 3 обозначает количество строк и столбцов в нашей матрице. Поскольку он состоит из трех строк и трех столбцов, мы называем его матрицей 3 x 3. Поскольку количество столбцов и строк равно, это квадратная матрица, что означает, что у нее будет определитель.
- Шаг 2 — Запишите матрицу с определителями символов
На этом изображении и на последнем есть небольшая разница: скобки превратились в прямые линии.С математической точки зрения, однако, это указывает на очень большую разницу. Матрица представляет собой целую серию отношений между числами, в то время как определитель — это всего лишь одно число.
- Шаг 3 — Запишите матрицу без скобок и определяющих символов
Теперь, когда мы знаем матрицу, над которой работаем, что такое определитель и как он записан, мы можем начать процесс поиска определителя. Этот шаг включает просто запись столбцов и чисел без каких-либо других символов.
Просто, правда? Теперь перейдем к следующему шагу.
- Шаг 4. Добавьте первые два столбца справа
Теперь справа от наших трех столбцов мы добавим еще два столбца. Но не только какие-либо столбцы — мы просто собираемся повторить первые два столбца из нашей матрицы.
Пунктирная линия на этом рисунке предназначена только для демонстрационных целей — нет необходимости вставлять ее, когда вы работаете над другими определяющими проблемами.Хотя, если это поможет вам отслеживать, на каком этапе процесса вы находитесь, вы, безусловно, сможете его сохранить.
- Шаг 5 — Сложите произведение первой диагонали вниз
Посмотрите на изображение ниже, прежде чем мы продолжим говорить об этом шаге.
Начните с числа в первой строке и первом столбце и умножьте вместе три числа по диагонали вниз и вправо.На изображении выше эти три числа обведены. Мы собираемся сложить числа по диагонали вниз.
- Шаг 6 — Сложите произведение второй и третьей диагоналей вниз
Повторите шаг 5 для второй и третьей диагоналей вниз. Опять же, мы выбираем три числа из нашей расширенной матрицы, которые расположены по диагонали, идущей вниз и вправо. Получив эти числа, мы собираемся их умножить и добавить к нашему растущему выражению.Не умножайте числа на этом этапе — мы сделаем это позже.
- Шаг 7 — Вычтите произведение диагоналей вверх
Теперь проделаем аналогичный процесс с диагоналями вверх. Для каждой диагонали мы по-прежнему будем выбирать три числа для умножения, но для диагоналей вверх мы будем вычитать члены умножения вместо сложения.
Вы заметили, что у нас есть большой знак вычитания перед каждым членом по диагонали вверх? На этом этапе очень легко получить неправильный знак, поэтому убедитесь, что вы знаете, почему он там.
Теперь, когда у нас есть все условия для вычисления детерминанта, мы можем приступить к выполнению операций. Помните, что отрицательное значение, умноженное на отрицательное, является положительным, и если какой-либо из множителей равен 0, то этот член будет равен 0.
Что мы имеем после всех вышеперечисленных шагов:
Определитель A
= + (1) (3) (2) + (-4) (- 1) (2) + (0) (0) (0) — (2) (3) (0) — (0) (- 1) (1) — (2) (0) (- 4)
Когда мы вычисляем каждый из членов умножения, мы получаем:
Вычислить определитель матрицы Пошаговое решение математических задач
Мы знаем, что не каждая система линейных уравнений имеет единственное решение. Иногда система из n уравнений от n переменных не имеет решения или бесконечное множество решений.В этом разделе мы вводим определитель матрица. В следующем разделе мы увидим, что определитель можно использовать чтобы определить, имеет ли система уравнений единственное решение.
Каждой квадратной матрице A соответствует действительное число, называемое определителем A, написано | A |.
Определитель матрицы 2 x 2 A,
определяется как
ПРИМЕЧАНИЕ Обратите внимание, что матрицы заключены в квадратные скобки, а определители обозначаются вертикальными полосами.Кроме того, матрица представляет собой массив чисел, но ее определитель — это одно число.
ОЦЕНКА A 2 X 2
ДЕТЕРМИНАНТ
Если
, затем
ОПРЕДЕЛИТЕЛЬ А МАТРИЦА 3 X 3
Определитель матрицы 3 x 3 A,
определяется как
Простой метод вычисления определителей 3 X 3 находится путем перестановки и факторинг условий, приведенных выше, чтобы получить
Каждая из величин в скобках представляет определитель 2 X 2 матрица, которая является частью матрицы 3 x 3, остающейся, когда строка и столбец множитель исключается, как показано ниже.
Эти определители матриц 2 X 2 называются минорами элемента в матрица 3 x 3. Обозначение M ij представляет определитель матрица, которая получается при удалении строки i и столбца j. Следующий список дает некоторые из миноров из приведенной выше матрицы.
В матрице 4 x 4 миноры являются определителями матриц 3 X 3, а n x
Матрица n имеет миноры, которые являются определителями (n — 1) X (n — 1) матрицы.
Чтобы найти определитель матрицы 3 X 3 или больше, сначала выберите любую строку или
столбец. Затем необходимо умножить минор каждого элемента в этой строке или столбце.
на + l или — 1, в зависимости от того, сумма номеров строк и столбцов
числа четные или нечетные. Произведение младшего и числа +1 или — l равно
называется кофактором .
КОФАКТОР Пусть M ij будет второстепенным для элемента au в матрице n x n . Кофактор ij , написано A ij , это:
Наконец, определитель матрицы n x n находится следующим образом.
ПОИСК ОПРЕДЕЛЕНИЯ МАТРИЦЫ
Умножьте каждый элемент в любой строке или столбце матрицы на его кофактор. В
сумма этих продуктов дает значение определителя.
эта сумма продуктов называется расширением по данной строке или столбцу.
НАЙТИ
КОФАКТОР ЭЛЕМЕНТА
Для матрицы
найдите сомножитель каждого из следующих элементов.
(a) 6
Поскольку 6 находится в первой строке и первом столбце матрицы, i = 1 и j = 1.
Кофактор: (-1) 1 + 1 * (-6) = 1 * (-6) = -6.
(b) 3
Здесь i = 2 и j = 3.
Кофактор (-1) 2 + 3 * 10 = (-1) * 10 = -10.
(c) 8
Мы имеем i = 2 и j = l.
Кофактор: (-1) 2 + 1 * (-8) = (-1) * (-8) = 8.
ОЦЕНКА ДЕТЕРМИНАНТА 3 X 3
Оценить
во втором столбце.
Чтобы найти этот определитель, сначала получите миноры каждого элемента во втором
столбец.
Теперь найдите сомножитель каждого из этих младших.
Определитель находится путем умножения каждого сомножителя на его соответствующий элемент матрицы и нахождение суммы этих произведений.
ВНИМАНИЕ: Будьте очень осторожны, чтобы отслеживать все отрицательные знаки, когда оценка детерминант. Работайте осторожно, записывая каждый шаг, как в Примеры.Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Точно такой же ответ можно найти, используя любую строку или столбец матрицы.
Одна из причин использования столбца 2 в примере 3 заключается в том, что он содержит элемент 0,
так что рассчитывать M 32 и A 32 толком не пришлось
выше. Быстро понять, что нули могут быть очень полезны при работе с
детерминанты.
Вместо вычисления (-1) i + j для данного элемента следующие
можно использовать доски для проверки знаков:
Знаки чередуются для каждой строки и столбца, начиная с + в первом строка, позиция первого столбца.Таким образом, эти массивы знаков можно воспроизвести как нужный. Если мы развернем матрицу 3 X 3 около строки 3, например, первый второстепенный будет иметь знак +, связанный с ним, второй второстепенный знак — и третий минор а + знак. Эти массивы знаков могут быть расширены таким образом для определителей матриц 5 × 5, 6 × 6 и более крупных.
ОЦЕНКА ДЕТЕРМИНАНТА 4 X 4
Оценить
Расширение на несовершеннолетние около четвертой строки дает
Каждый из четырех определяющих факторов в примере 4 должен быть оценен путем раскрытия три несовершеннолетних, требующих большой работы, чтобы получить окончательное значение.Всегда ищите строка или столбец с наибольшим количеством нулей для упрощения работы. В следующем разделе мы ввести несколько свойств, упрощающих вычисление определителей. К счастью, детерминанты больших матриц можно оценить быстро и легко с помощью компьютера или некоторых калькуляторов.
.

 5
5 8076615359
8076615359 11, GOST R 34.11-94, GOST(3425489)
11, GOST R 34.11-94, GOST(3425489) 52.68.209
52.68.209 02.2022
02.2022 02.2022 00:00
02.2022 00:00 04.2022 00:00
04.2022 00:00 80
80 08.2022 00:00
08.2022 00:00 Иркутск, к/с 30101810900000000607 БИК 042520607. Суммы внесенных заявителями задатков возвращаются всем заявителям, за исключением победителя торгов, в течение пяти рабочих дней со дня подписания протокола о результатах проведения торгов.
Иркутск, к/с 30101810900000000607 БИК 042520607. Суммы внесенных заявителями задатков возвращаются всем заявителям, за исключением победителя торгов, в течение пяти рабочих дней со дня подписания протокола о результатах проведения торгов. 80 KZT
80 KZT
 При расчете используются официальные курсы национального банка Казахстана на сегодня. Для проведения вычисления выберите валюту, в которую хотите конвертировать и укажите сумму. В результате вы получите сумму, эквивалентную указанной сумме, только в целевой валюте.
При расчете используются официальные курсы национального банка Казахстана на сегодня. Для проведения вычисления выберите валюту, в которую хотите конвертировать и укажите сумму. В результате вы получите сумму, эквивалентную указанной сумме, только в целевой валюте.

 32
32 68
68 32
32 12
12

 ru/data/moduleImages/QRCodes/425/e6d0cb31f42d3fe95e9c387a8cd58cc5.png
ru/data/moduleImages/QRCodes/425/e6d0cb31f42d3fe95e9c387a8cd58cc5.png 615528128088
615528128088 Деньги так не читаются.
Деньги так не читаются. Новые века читаются как целые числа сотен. Мы не используем слово «тысяча», по крайней мере, не для чтения лет за последние 1000 лет.
Новые века читаются как целые числа сотен. Мы не используем слово «тысяча», по крайней мере, не для чтения лет за последние 1000 лет.
 Те, кто следует британским правилам письма, обычно используют «и». Например:
Те, кто следует британским правилам письма, обычно используют «и». Например: Постарайтесь помочь своим читателям.)
Постарайтесь помочь своим читателям.) Упражнение 1.5.
Упражнение 1.5. 1
1 ….
….



 д.
д. Один миллион…
Один миллион…  Файлы cookie
используется только для регистрации статистики анонимных посетителей и управления определенными
Основные функции страницы. Чтобы удалить это уведомление, нажмите;
в противном случае
нажмите для получения дополнительной информации о блокировке
печенье
Файлы cookie
используется только для регистрации статистики анонимных посетителей и управления определенными
Основные функции страницы. Чтобы удалить это уведомление, нажмите;
в противном случае
нажмите для получения дополнительной информации о блокировке
печенье 2, строка 3, вычеркнуть «семь
тысяча пятьсот шестьдесят» вставка «десять тысяч двадцать»
2, строка 3, вычеркнуть «семь
тысяча пятьсот шестьдесят» вставка «десять тысяч двадцать» 6, черты с 12 по 45
6, черты с 12 по 45 Государственный секретарь должен
внести сумму в фонд.
Государственный секретарь должен
внести сумму в фонд. В противном случае секретарь
Штат направляет факсимиле всех бланков регистраторам округов для
проверки, и регистраторы округа проверяют все бланки в соответствии с
процесс выше. Регистратор округа не должен проверять уже проверенные бланки. Регистратор округа должен
ежедневно сообщать о проверенных итогах государственному секретарю до тех пор, пока не будет принято решение
сделал, что было представлено достаточное количество проверенных квитанций. Если
достаточное количество подтвержденных квитанций было отправлено в один или несколько округов
регистраторы, регистраторы округа могут остановить процесс проверки.
В противном случае секретарь
Штат направляет факсимиле всех бланков регистраторам округов для
проверки, и регистраторы округа проверяют все бланки в соответствии с
процесс выше. Регистратор округа не должен проверять уже проверенные бланки. Регистратор округа должен
ежедневно сообщать о проверенных итогах государственному секретарю до тех пор, пока не будет принято решение
сделал, что было представлено достаточное количество проверенных квитанций. Если
достаточное количество подтвержденных квитанций было отправлено в один или несколько округов
регистраторы, регистраторы округа могут остановить процесс проверки.
 6. Тема
требованиям статьи IV, часть 1, раздел 1, Конституции штата Аризона,
раздел 16-953, Пересмотренный Устав штата Аризона, изменен следующим образом:
6. Тема
требованиям статьи IV, часть 1, раздел 1, Конституции штата Аризона,
раздел 16-953, Пересмотренный Устав штата Аризона, изменен следующим образом: А
кандидат-участник должен ежемесячно отчитываться перед комиссией о
статус спора по оспариваемым векселям. Любые деньги в
Предвыборный счет кандидатов после оплаты счетов должен быть возвращен незамедлительно
в фонд.
А
кандидат-участник должен ежемесячно отчитываться перед комиссией о
статус спора по оспариваемым векселям. Любые деньги в
Предвыборный счет кандидатов после оплаты счетов должен быть возвращен незамедлительно
в фонд. возвратить в фонд все денежные средства в
предвыборный счет кандидатов сверх суммы, достаточной для оплаты любых невыплаченных
счета за расходы, сделанные до даты, когда кандидат не прошел квалификацию
первичное голосование.
возвратить в фонд все денежные средства в
предвыборный счет кандидатов сверх суммы, достаточной для оплаты любых невыплаченных
счета за расходы, сделанные до даты, когда кандидат не прошел квалификацию
первичное голосование. END_STATUTE
END_STATUTE
 Неисключаемость
Неисключаемость




 Базовые
математические способности развивают в школе.
Базовые
математические способности развивают в школе.

 Родителям важно не упустить этот момент и
объяснить ребёнку, зачем вообще заниматься
математикой и учиться решать задачи.
Родителям важно не упустить этот момент и
объяснить ребёнку, зачем вообще заниматься
математикой и учиться решать задачи.
 Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических
способностей.
Это поможет комплексному развитию логики у ребенка, познавательных, творческих и математических
способностей.
 Мы знаем, как увлечь ребёнка математикой!
Мы знаем, как увлечь ребёнка математикой!
 Попробуйте
«Закономерности», «Логические задачи», «Умный счёт» и другие.
Попробуйте
«Закономерности», «Логические задачи», «Умный счёт» и другие.
 Чтобы помочь родителям и учителям, команда опытных методистов и педагогов
«ЛогикЛайк» регулярно создает новые уроки, упражнения и тесты.
Чтобы помочь родителям и учителям, команда опытных методистов и педагогов
«ЛогикЛайк» регулярно создает новые уроки, упражнения и тесты.
 Постепенно сложность нарастает, открываются новые
интересные задания.
Постепенно сложность нарастает, открываются новые
интересные задания.


 Составная на вычитание
или деление
Составная на вычитание
или деление









 Значит,
площадь четырёхугольника самая маленькая.
Значит,
площадь четырёхугольника самая маленькая.
 Проходит первая
четверть и способный ребёнок начинает скучать от однообразных или слишком простых для него
заданий.
Проходит первая
четверть и способный ребёнок начинает скучать от однообразных или слишком простых для него
заданий.
 В курсе мы чередуем
математические и логические задачи, закономерности, фигуры в пространстве и другие типы
заданий.
В курсе мы чередуем
математические и логические задачи, закономерности, фигуры в пространстве и другие типы
заданий.







 Кролик легче щенка, значит, правая более легкая
чаша с кроликом поднимется вверх.
Кролик легче щенка, значит, правая более легкая
чаша с кроликом поднимется вверх. Видеоуроки, советы и
подсказки помогут школьнику самостоятельно разобраться даже с очень сложными задачами.
Видеоуроки, советы и
подсказки помогут школьнику самостоятельно разобраться даже с очень сложными задачами.




 Миллиметр
Миллиметр Можно сказать, что её возраст не сильно отличается от возраста человечества. Математика помогает, с одной стороны, развивать абстрактное мышление, с другой — решать прикладные задачи в повседневной жизни.
Можно сказать, что её возраст не сильно отличается от возраста человечества. Математика помогает, с одной стороны, развивать абстрактное мышление, с другой — решать прикладные задачи в повседневной жизни. Детское любопытство и азарт позволяют вовлечься в мир абстрактных подсчётов и пройти путь от развлекательных задачек к настоящей сложной математике.
Детское любопытство и азарт позволяют вовлечься в мир абстрактных подсчётов и пройти путь от развлекательных задачек к настоящей сложной математике. Не обязательно использовать развёрнутое решение задачек по математике; можно проходит лабиринты, вырезать узоры, собирать по схемам различные поделки. Творческий подход приветствуется, ведь математика — это не всегда про сухие цифры.
Не обязательно использовать развёрнутое решение задачек по математике; можно проходит лабиринты, вырезать узоры, собирать по схемам различные поделки. Творческий подход приветствуется, ведь математика — это не всегда про сухие цифры. При правильном выполнении заданий дети получают кубки, медали и именные дипломы.
Наградами можно поделиться в социальных сетях, а диплом – распечатать.
При правильном выполнении заданий дети получают кубки, медали и именные дипломы.
Наградами можно поделиться в социальных сетях, а диплом – распечатать. Идёт запись
Идёт запись
 При верном составлении у вас
должно поучится слово. (Слайд 6)
При верном составлении у вас
должно поучится слово. (Слайд 6) Постановка учебной задачи
Постановка учебной задачи


 = (9 + 27) * 2 = 72 м
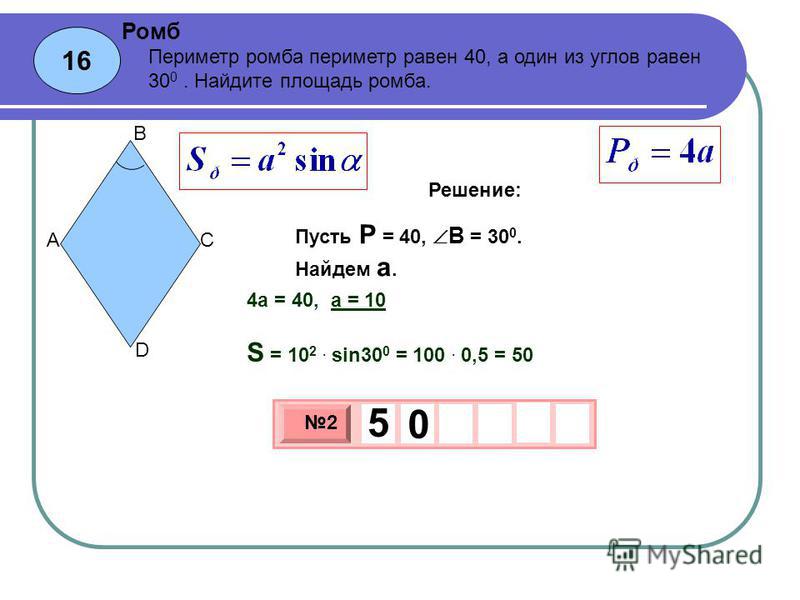
= (9 + 27) * 2 = 72 м Лучшая бригада награждается
путевкой в зимний пришкольный лагерь. (Слайд 12)
Лучшая бригада награждается
путевкой в зимний пришкольный лагерь. (Слайд 12)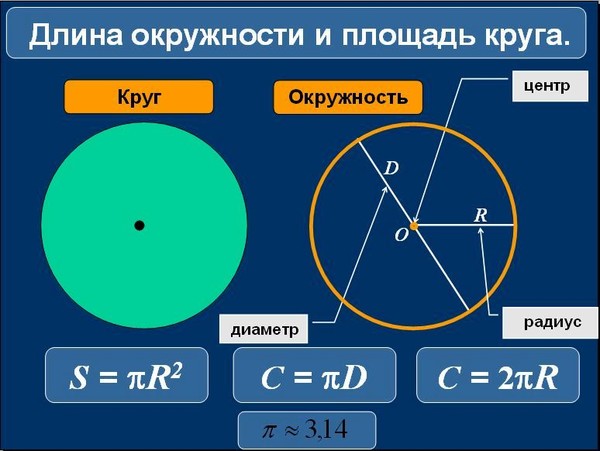 Вычислите, сколько
материала уйдет на каждый участок?
Вычислите, сколько
материала уйдет на каждый участок?

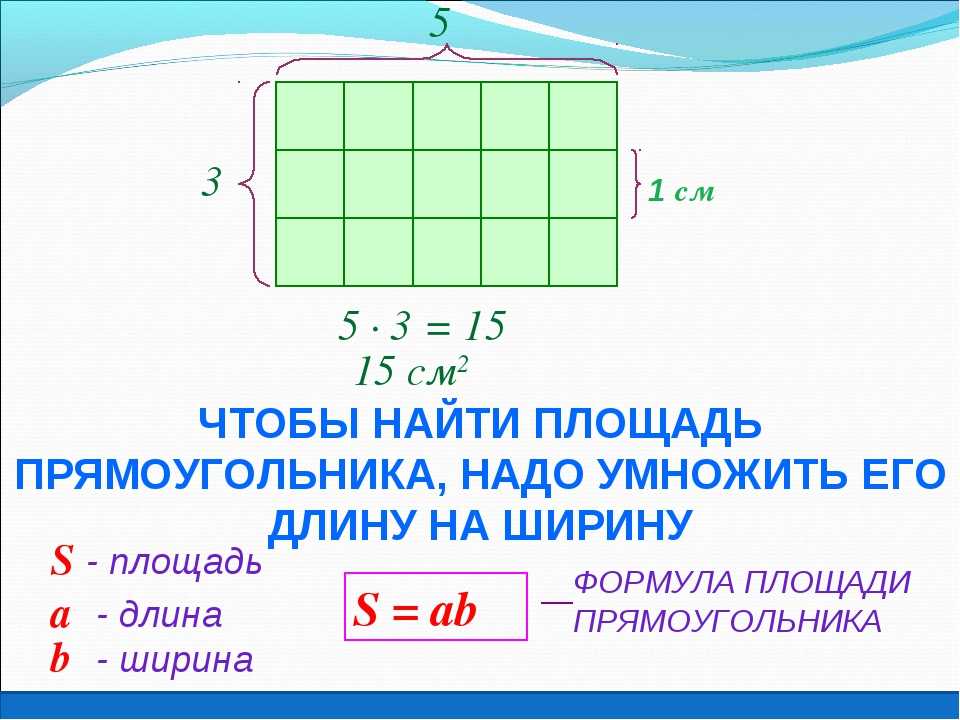
 В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.
В нашей жизни многие фигуры имеют форму прямоугольника. Например, поверхность стола, тетрадь и другие.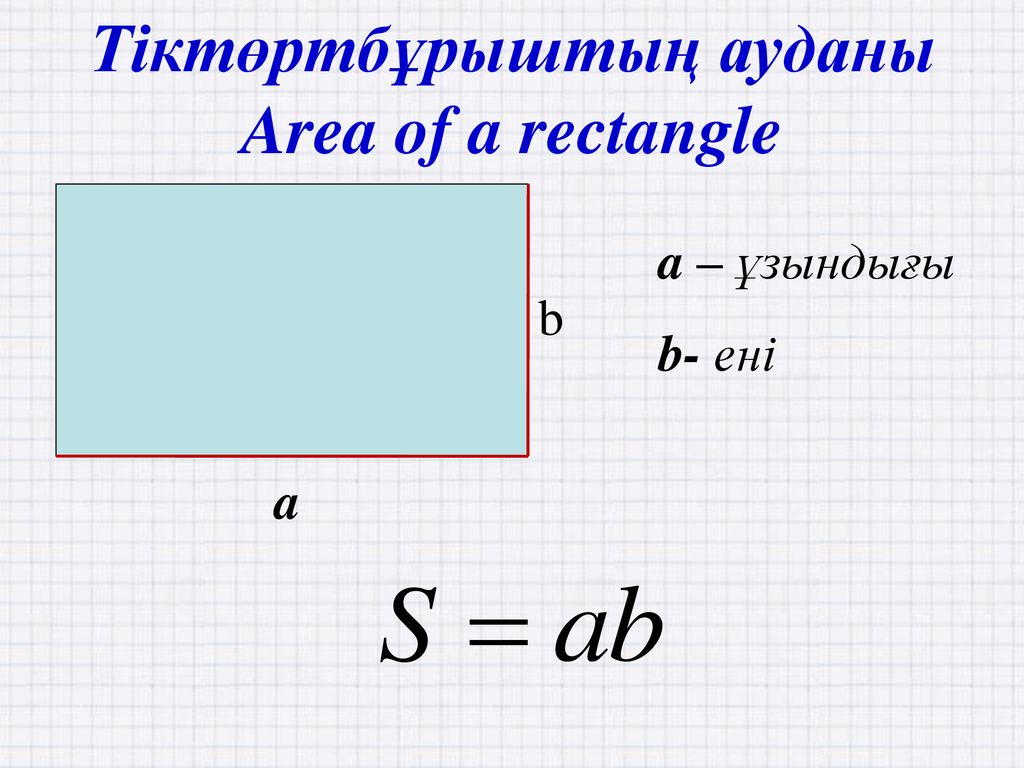
 Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.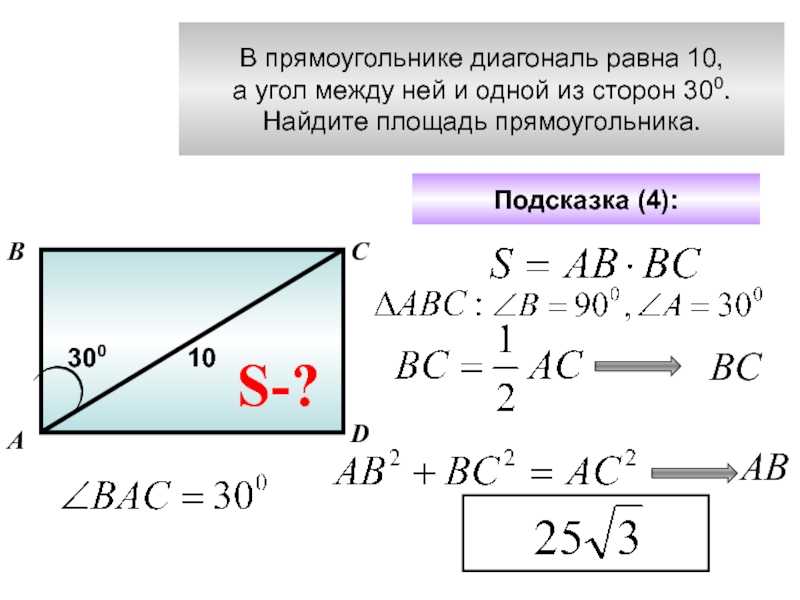 Найдем его периметр.
Найдем его периметр. А уже после периметр вычисляется по стандартной формуле.
А уже после периметр вычисляется по стандартной формуле.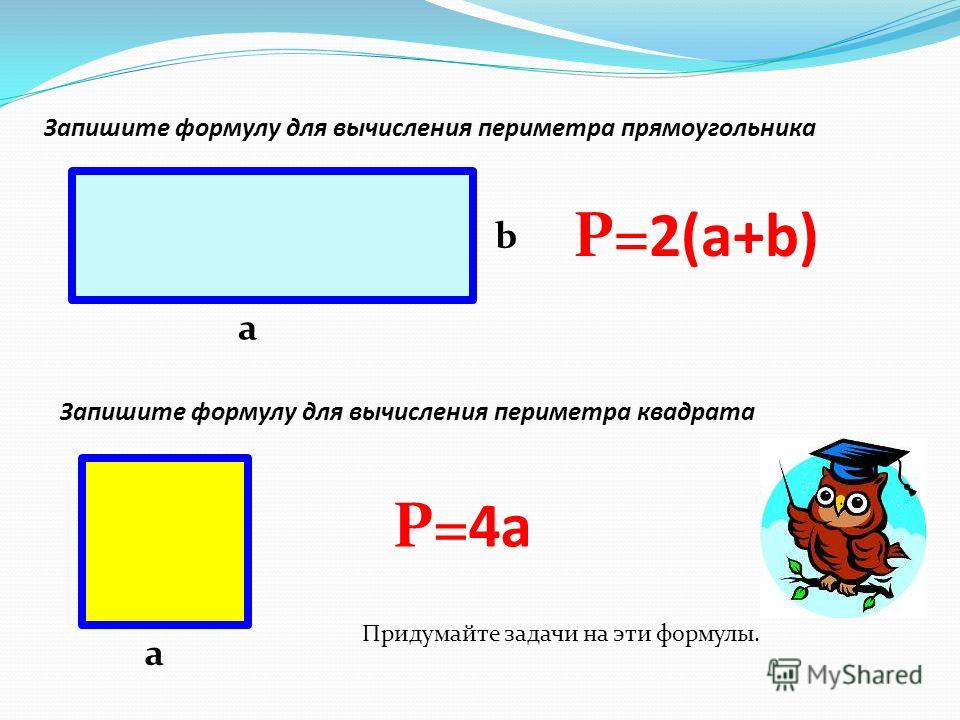 2})}, где d — диагональ прямоугольника, a — сторона прямоугольника.
2})}, где d — диагональ прямоугольника, a — сторона прямоугольника. Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон (MN=a-b).
Если соединить центры всех возможных вписанных окружностей то получим отрезок MN длина которого равна разности сторон (MN=a-b). 2) или
2) или
 ru/voprosy-i-otvety/ploshchad-pryamougolnika-najti-formule-diagonal-perimetr.html
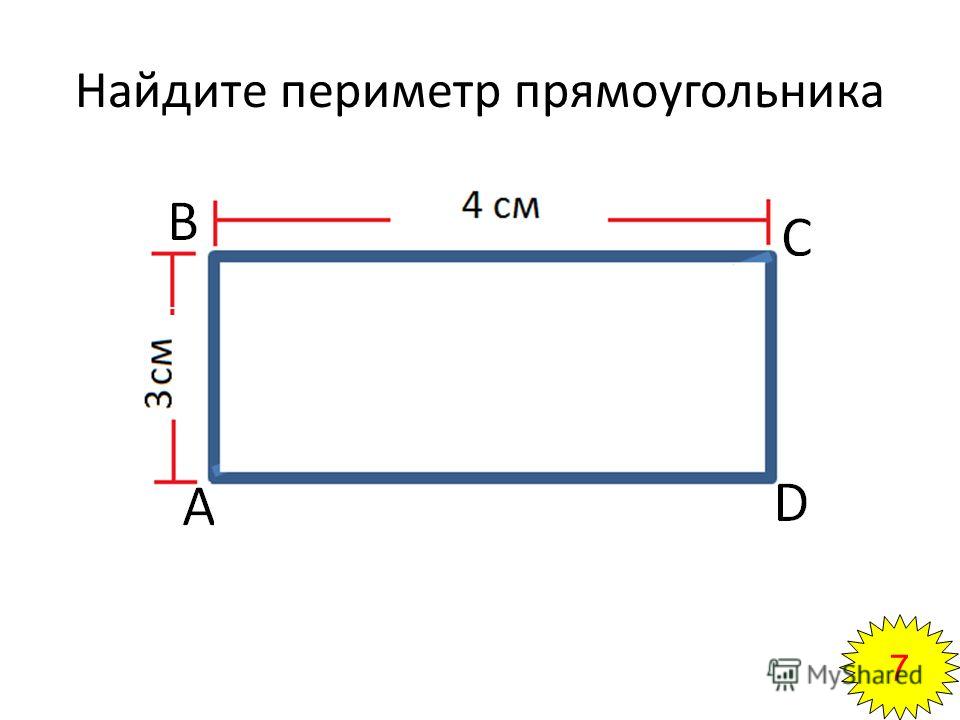
ru/voprosy-i-otvety/ploshchad-pryamougolnika-najti-formule-diagonal-perimetr.html Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
 Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
 Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).
Для их вычисления применяют одни и те же параметры, но смысл конечных величин имеет принципиальные различия. На упаковке многих товаров указывается площадь или размеры сторон в виде A х B (если речь идет о товаре, одна из сторон которого имеет форму прямоугольника).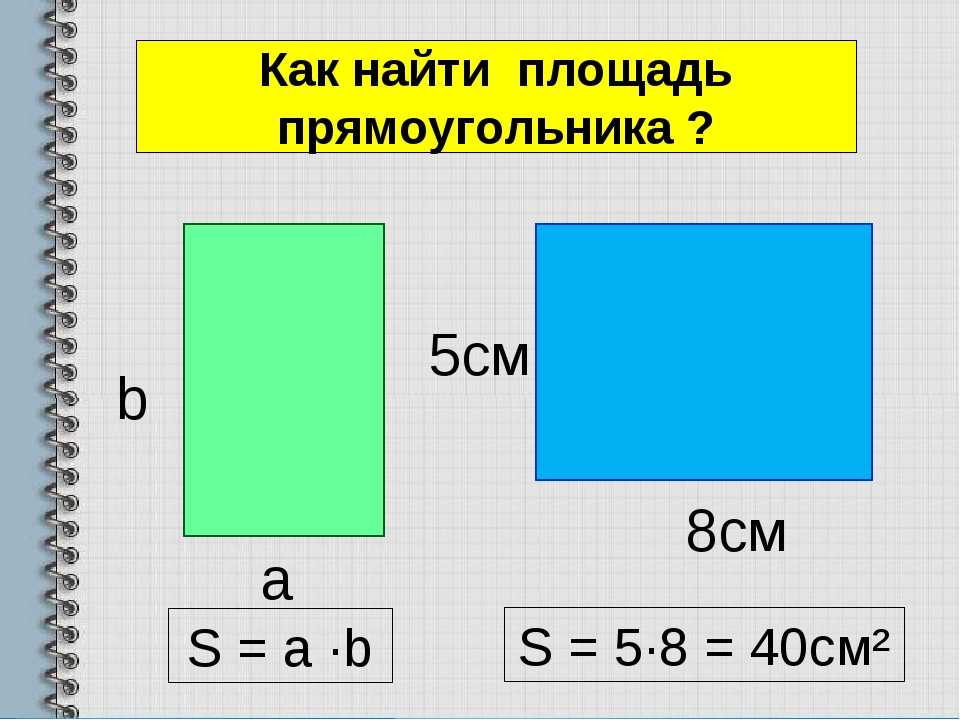 Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.
Понятие «квадратура» частично отражает смысл площади, в основе которой положено измерение квадрата поверхности.


 (39)
(39)  )
) 
 Поставили точку. Начинаем
движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4
– вправо вверх. Какая фигура? Преврати её в
прямоугольник. Дострой. Найди Р разными
способами.
Поставили точку. Начинаем
движение. 2 – вправо, 4 – вправо вниз, 10 – влево, 4
– вправо вверх. Какая фигура? Преврати её в
прямоугольник. Дострой. Найди Р разными
способами.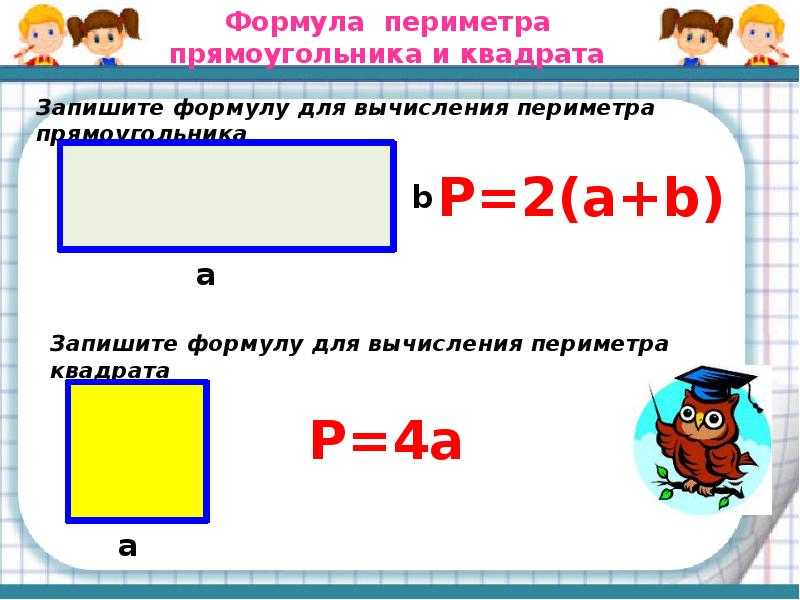 Самостоятельная работа
Самостоятельная работа 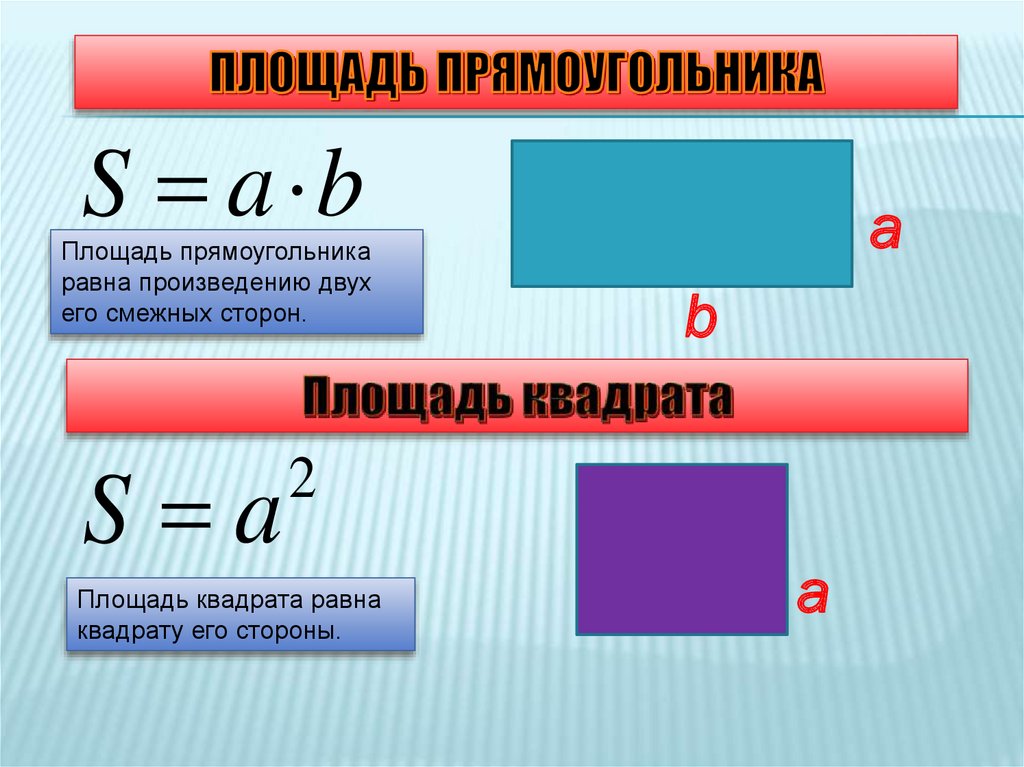
 Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.
Формула для подсчета периметра прямоугольника : , здесь a — длина прямоугольника, а b — ширина прямоугольника. Сумма длины и ширины называется полупериметром . Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.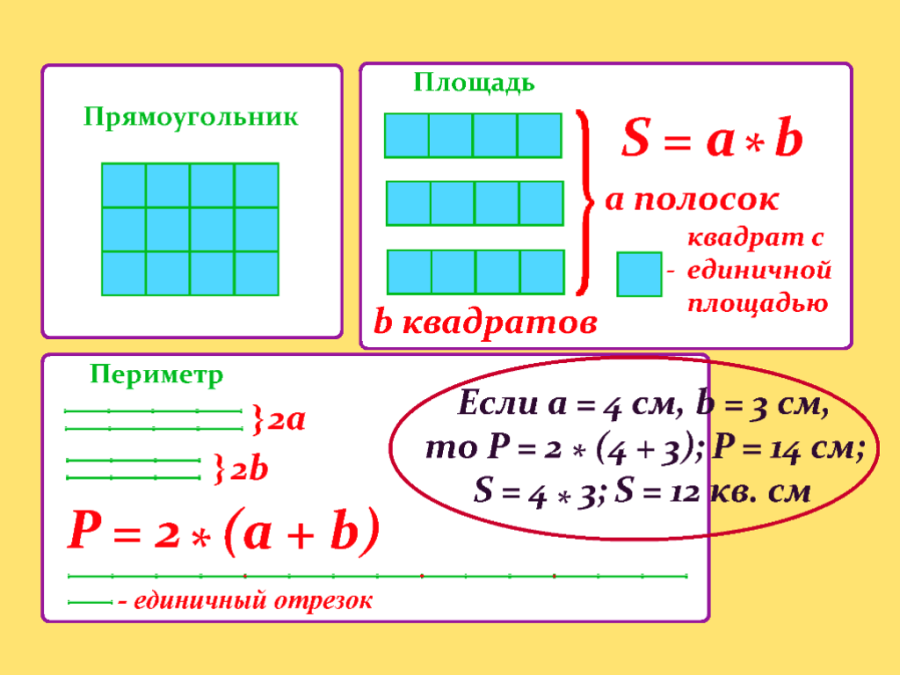 — М.: Дрофа, 2004.
— М.: Дрофа, 2004. Вспомним, какие отличительные особенности прямоугольника мы знаем.
Вспомним, какие отличительные особенности прямоугольника мы знаем.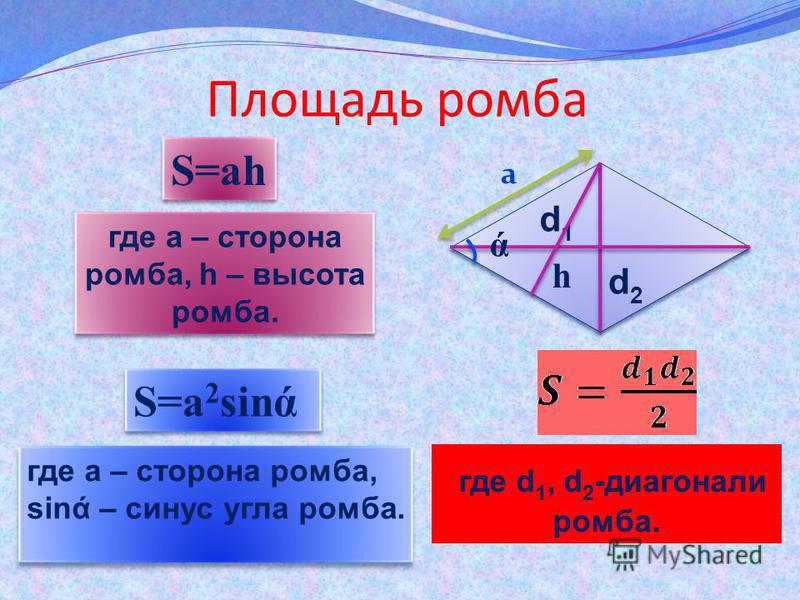 Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.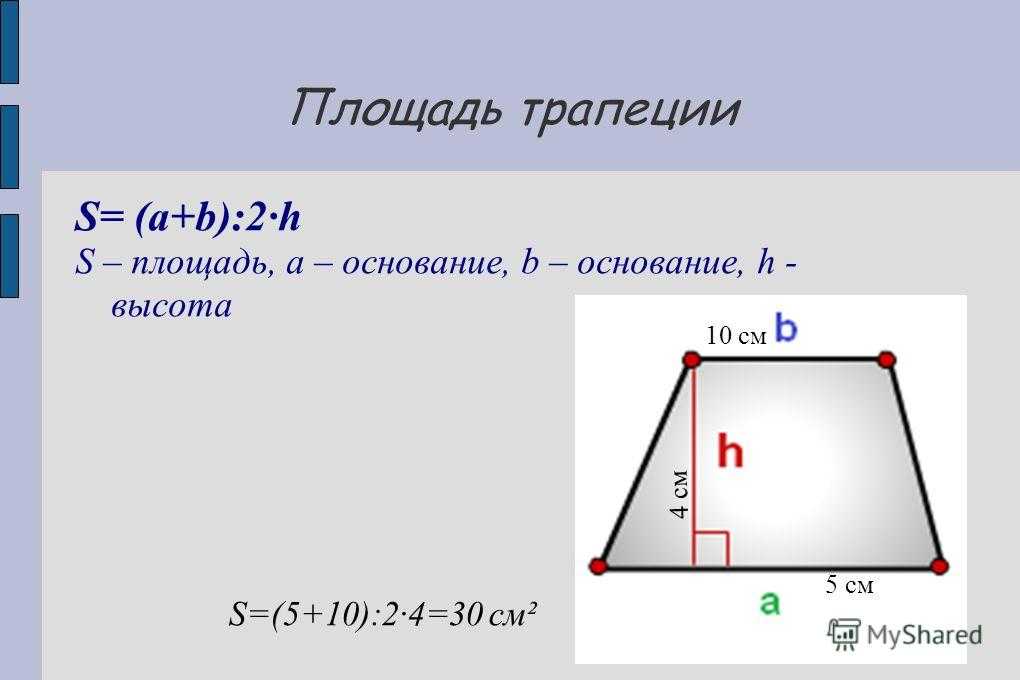 Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках — (a+b)).
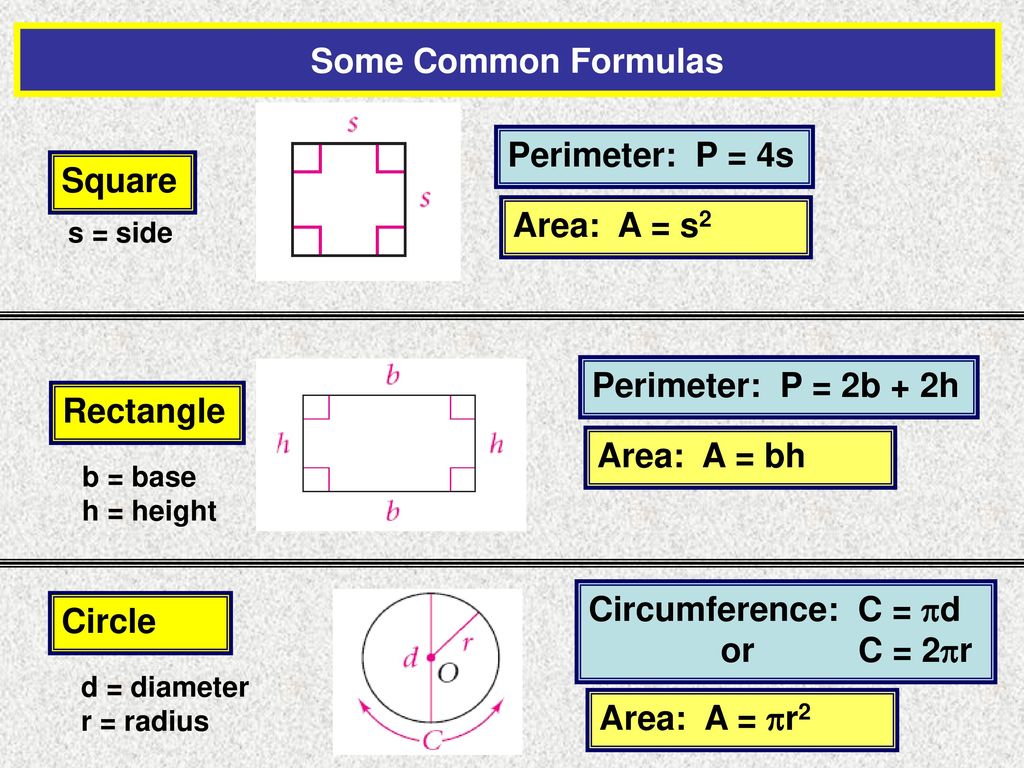
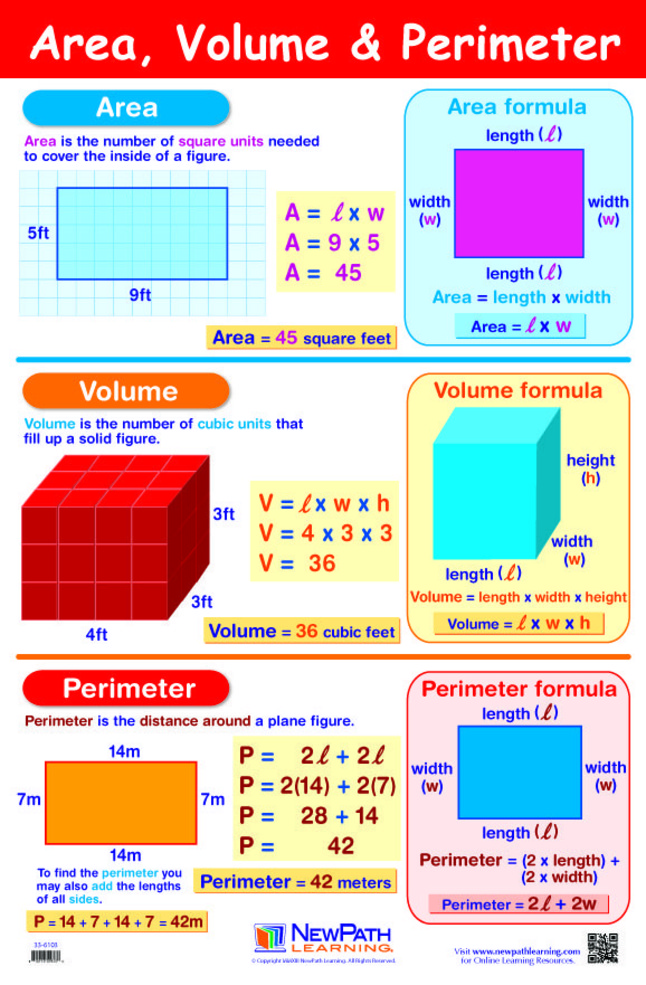 Найдите периметр прямоугольника ABCD».
Найдите периметр прямоугольника ABCD».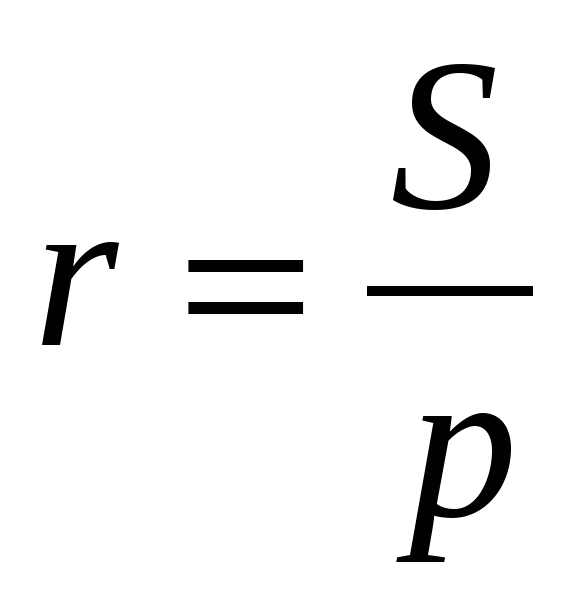 Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.
Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.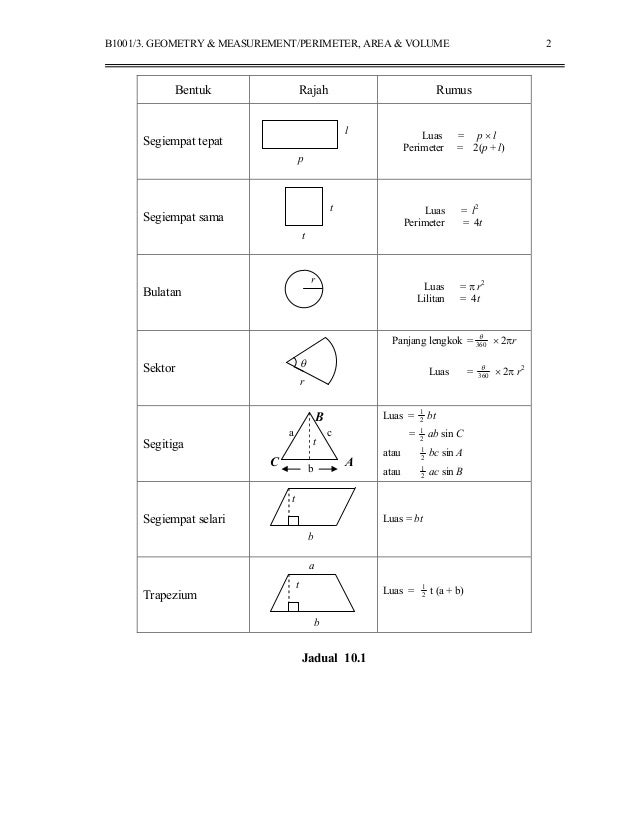 После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.
После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».
Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?». Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
/918870b1bc4a305.s.siteapi.org/img/fa91516c043aa701896b5ea126baf73168f97729.jpg) Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.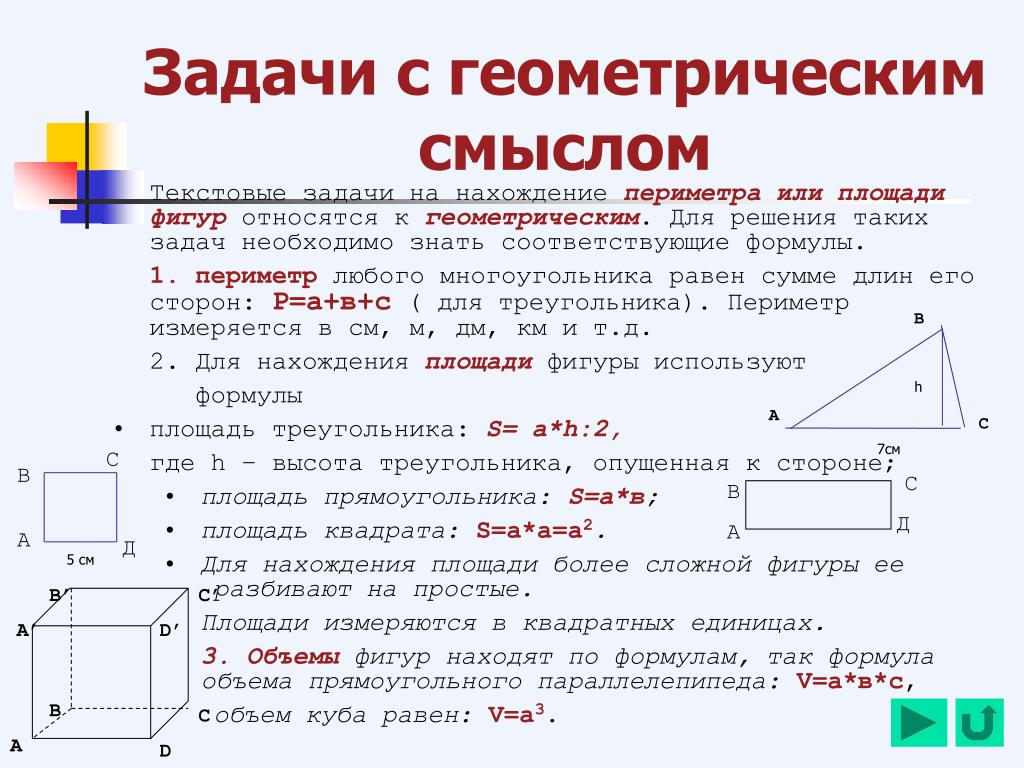 В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах: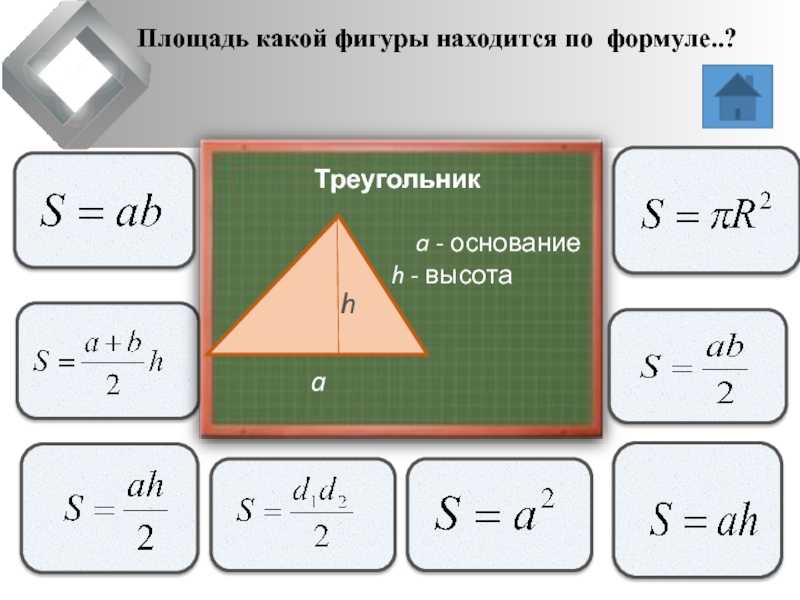
 Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз: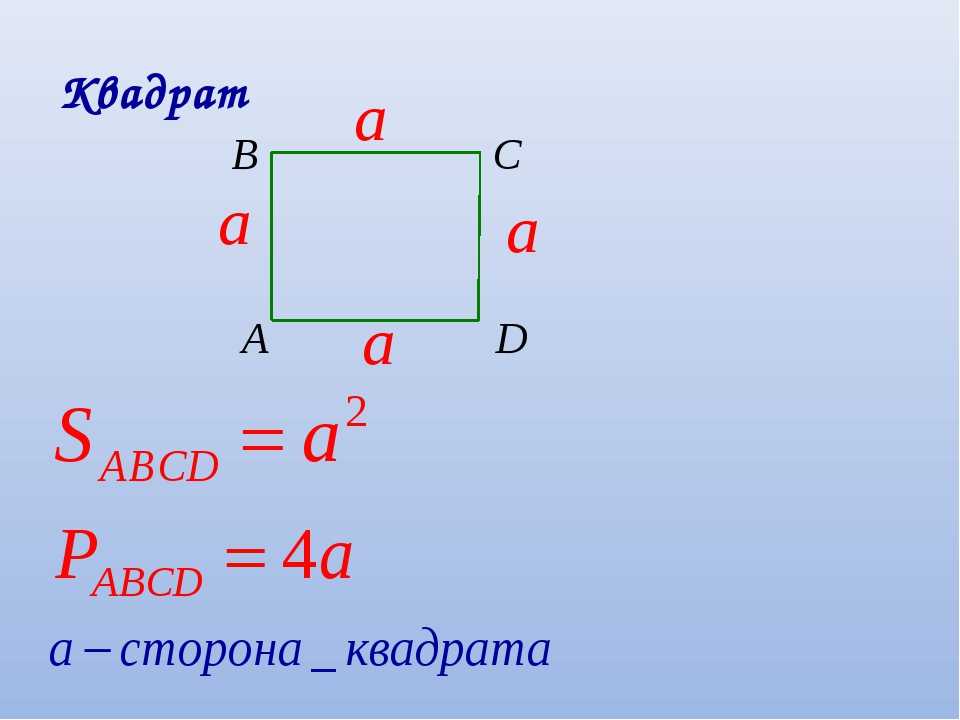 Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:

 Выразить 5 м2 13 см2 в квадратных сантиметрах.
Выразить 5 м2 13 см2 в квадратных сантиметрах.
 На рисунке показан прямоугольный параллелепипед:
На рисунке показан прямоугольный параллелепипед: Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3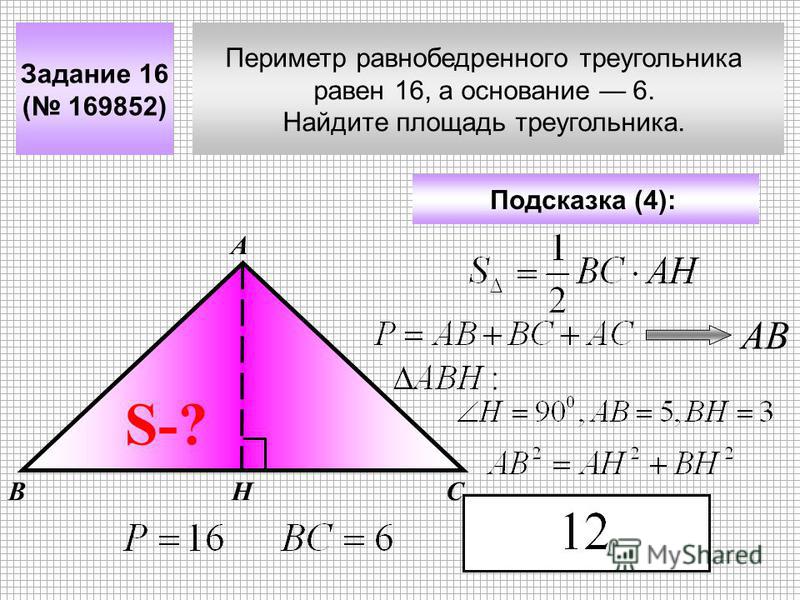 Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
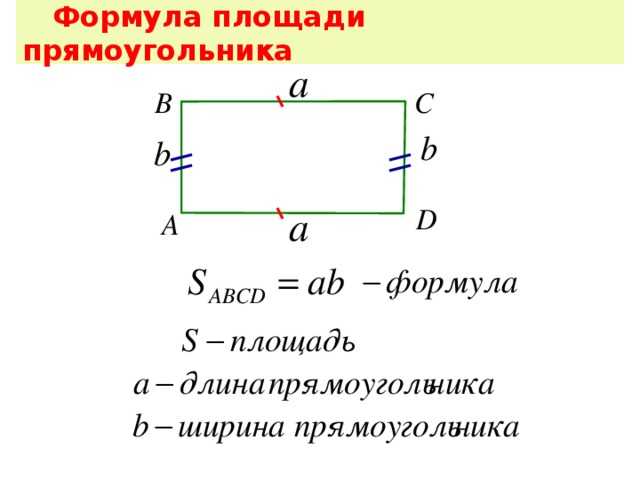 Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3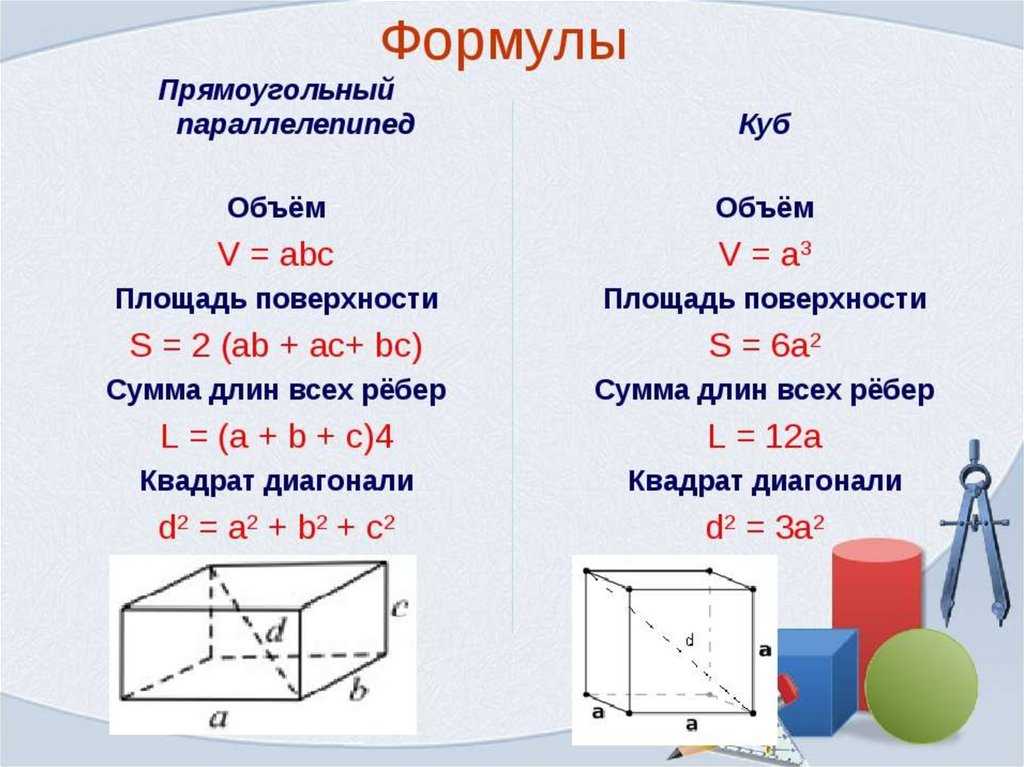
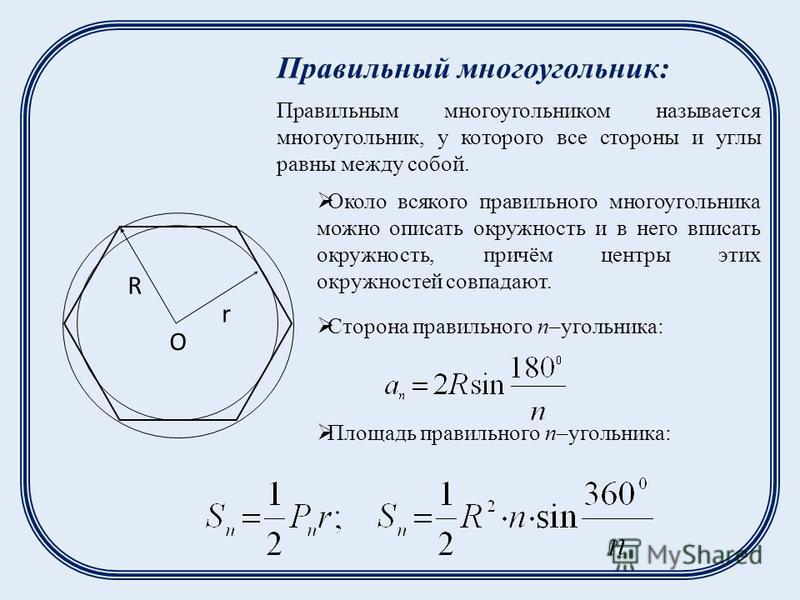
 В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
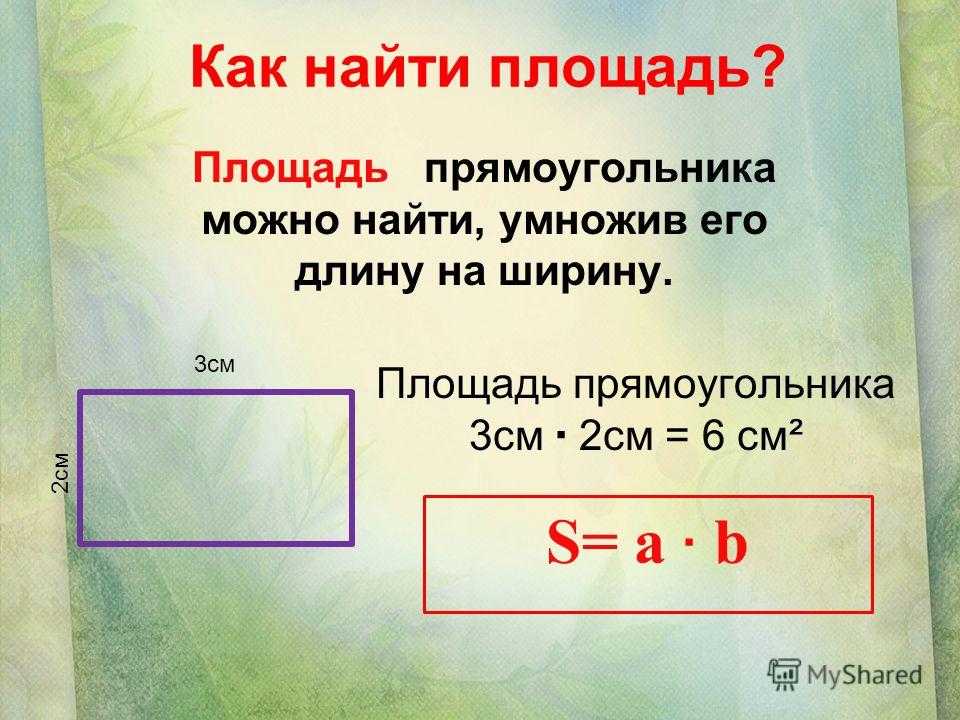

 Это позволит вычислит объем бассейна:
Это позволит вычислит объем бассейна: д.:
д.:

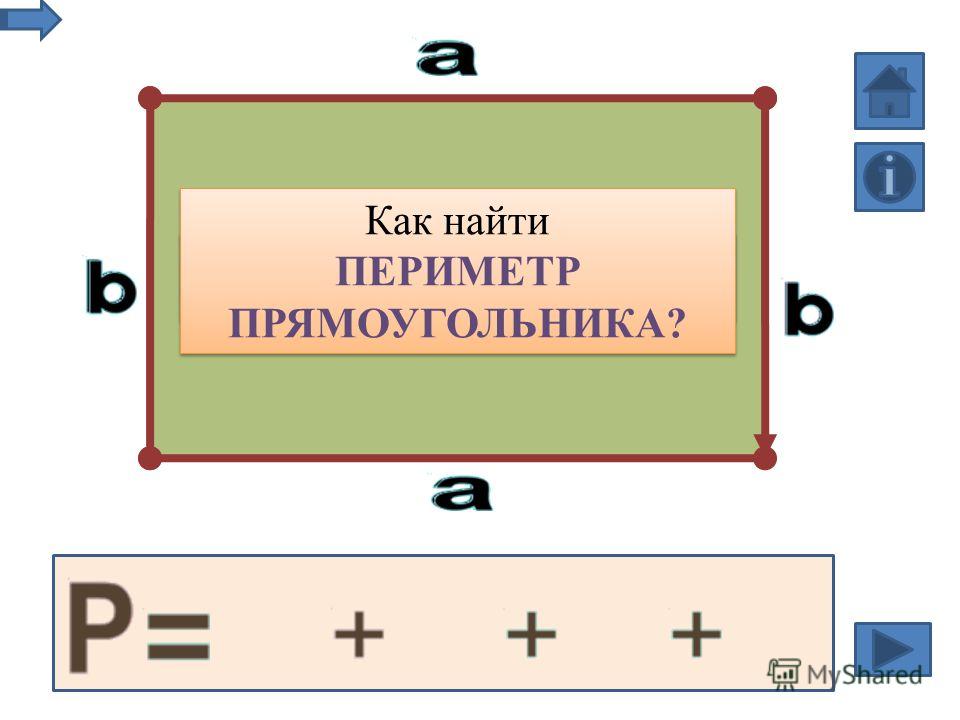 Прямоугольник замкнут четырьмя перпендикулярными сторонами, две из которых единственные. Периметр уравнения прямоугольника равен
Прямоугольник замкнут четырьмя перпендикулярными сторонами, две из которых единственные. Периметр уравнения прямоугольника равен 
 2, а длина 4 м? 9 по длине
2, а длина 4 м? 9 по длине 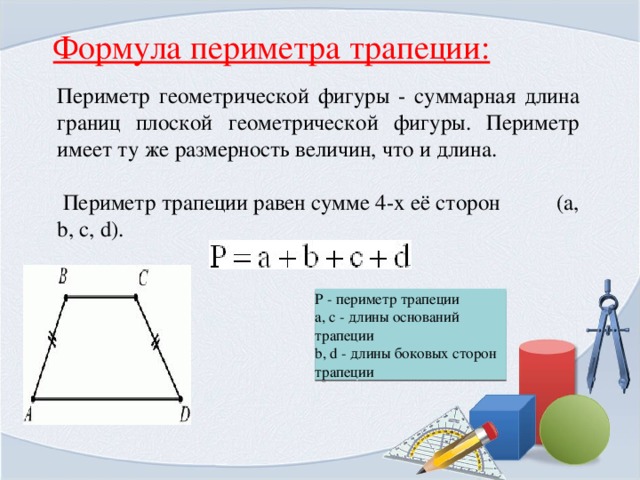 Зная длину и ширину, можно вычислить периметр как 9.0021 Р=2×(11+5)=32 .
Зная длину и ширину, можно вычислить периметр как 9.0021 Р=2×(11+5)=32 . Поскольку две длинные стороны равны 12 см, а две более короткие стороны равны 7 см, периметр можно найти по формуле:
Поскольку две длинные стороны равны 12 см, а две более короткие стороны равны 7 см, периметр можно найти по формуле:
 Таким образом, периметр этой фермы равен
Таким образом, периметр этой фермы равен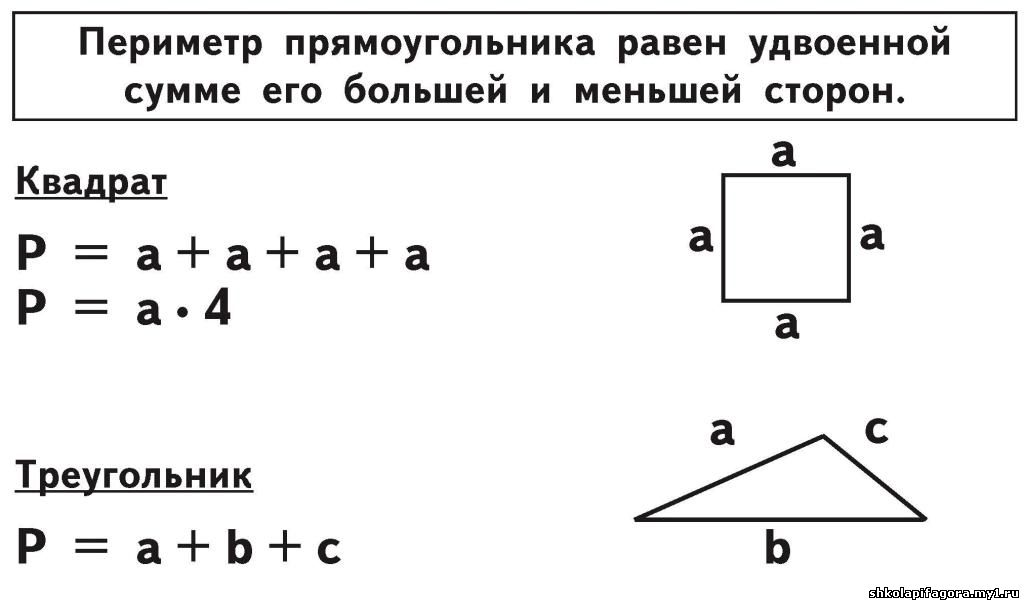
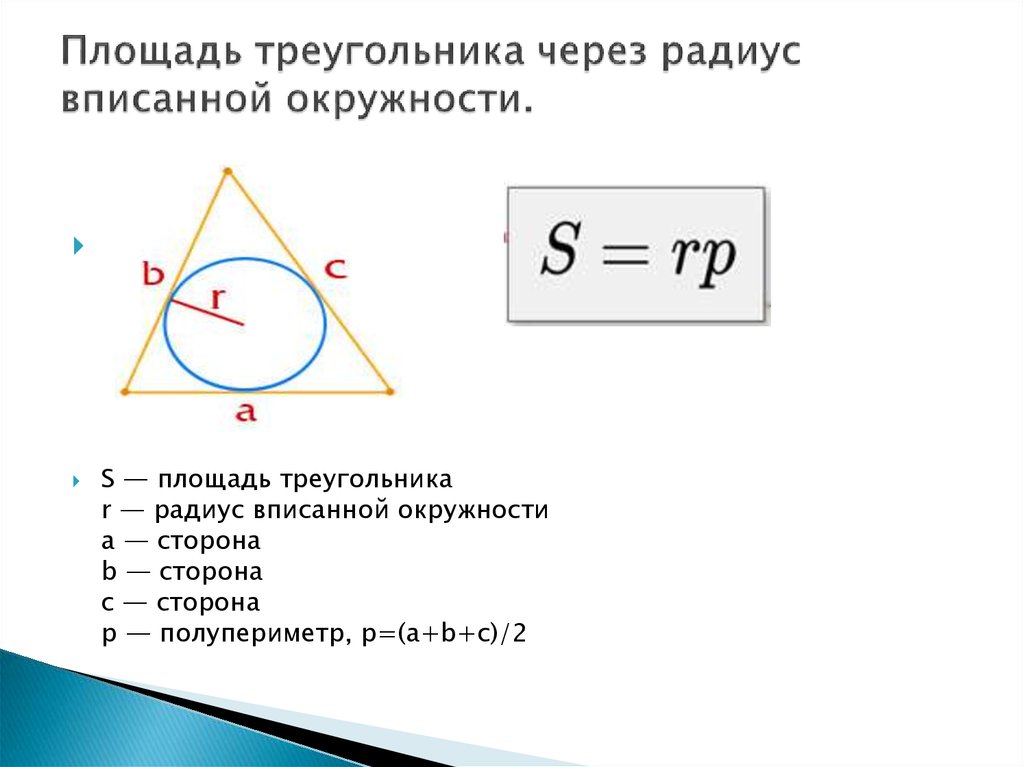
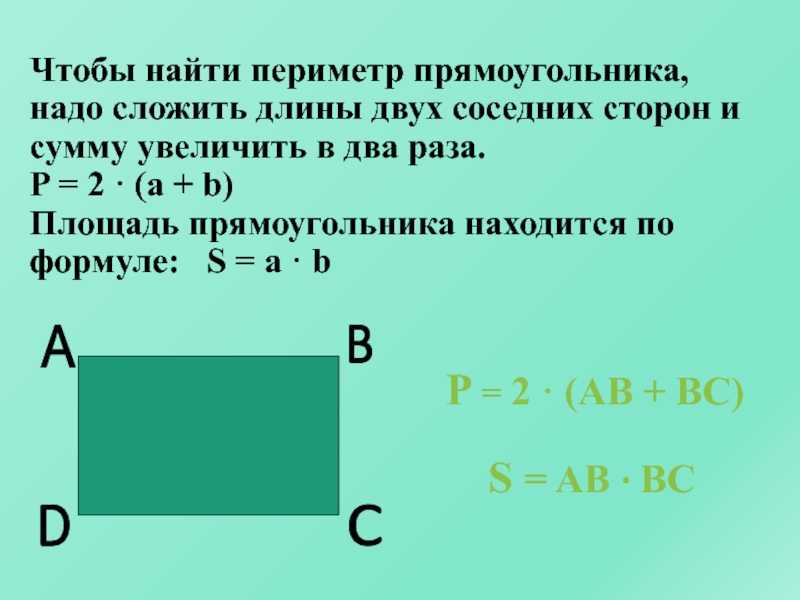
 Например, мы можем использовать расчеты периметра для таких ситуаций, как требования к ограждению вокруг игрового поля, размеры рамы картины, расстояния вокруг пешеходной дорожки или размеры большого окна. Вычисление периметра прямоугольников — полезный навык, потому что он часто используется в нашей повседневной жизни.
Например, мы можем использовать расчеты периметра для таких ситуаций, как требования к ограждению вокруг игрового поля, размеры рамы картины, расстояния вокруг пешеходной дорожки или размеры большого окна. Вычисление периметра прямоугольников — полезный навык, потому что он часто используется в нашей повседневной жизни. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр. Например, если прямоугольник ниже представляет собой сад, который нуждается в кирпичной рамке, мы можем использовать формулу периметра, чтобы определить, сколько футов кирпичной бордюры нам нужно всего.
Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр. Например, если прямоугольник ниже представляет собой сад, который нуждается в кирпичной рамке, мы можем использовать формулу периметра, чтобы определить, сколько футов кирпичной бордюры нам нужно всего. Чтобы решить такую проблему периметра, нам нужно пересмотреть наше понимание площади. Помните, чтобы вычислить площадь прямоугольника, мы просто умножаем длину на ширину. Прямоугольник размером 3,5 см на 4 см будет иметь площадь 14 см 2 , потому что 3,5 × 4 = 14. Давайте воспользуемся этим знанием площади и применим его к задаче периметра.
Чтобы решить такую проблему периметра, нам нужно пересмотреть наше понимание площади. Помните, чтобы вычислить площадь прямоугольника, мы просто умножаем длину на ширину. Прямоугольник размером 3,5 см на 4 см будет иметь площадь 14 см 2 , потому что 3,5 × 4 = 14. Давайте воспользуемся этим знанием площади и применим его к задаче периметра. Есть ли у прямоугольника площадью 20 квадратных футов более одного возможного варианта периметра? Если вы сказали да, то вы правы. Прямоугольники с ограниченной площадью, например 20 квадратных футов, могут иметь различные периметры. Например, прямоугольник площадью 20 квадратных футов может иметь размеры 1 фут × 20 футов, 2 фута × 10 футов или 4 фута × 5 футов. Все эти варианты будут давать разные периметры, хотя все они имеют одинаковую площадь. . Давайте докажем эту концепцию, рассчитав периметр трех только что упомянутых возможных прямоугольников: 1 фут × 20 футов, 2 фута × 10 футов и 4 фута × 5 футов.
Есть ли у прямоугольника площадью 20 квадратных футов более одного возможного варианта периметра? Если вы сказали да, то вы правы. Прямоугольники с ограниченной площадью, например 20 квадратных футов, могут иметь различные периметры. Например, прямоугольник площадью 20 квадратных футов может иметь размеры 1 фут × 20 футов, 2 фута × 10 футов или 4 фута × 5 футов. Все эти варианты будут давать разные периметры, хотя все они имеют одинаковую площадь. . Давайте докажем эту концепцию, рассчитав периметр трех только что упомянутых возможных прямоугольников: 1 фут × 20 футов, 2 фута × 10 футов и 4 фута × 5 футов.

 Площадь прямоугольника вычисляется путем умножения \(длина×ширина\), поэтому мы можем использовать следующее уравнение, чтобы найти недостающее значение (w).
Площадь прямоугольника вычисляется путем умножения \(длина×ширина\), поэтому мы можем использовать следующее уравнение, чтобы найти недостающее значение (w).

 Различные фигуры в геометрии имеют формулу периметра в зависимости от формы и размера. Давайте посмотрим на формулы периметра этих фигур.
Различные фигуры в геометрии имеют формулу периметра в зависимости от формы и размера. Давайте посмотрим на формулы периметра этих фигур. Для разных типов треугольников используются разные формулы периметра. Но общая формула, используемая для нахождения периметра треугольника, такова:
Для разных типов треугольников используются разные формулы периметра. Но общая формула, используемая для нахождения периметра треугольника, такова: Однако формулу периметра параллелограмма можно найти и в том случае, если не указаны стороны объекта, а указаны диагонали или угол. Следовательно, формула для вычисления периметра параллелограмма:
Однако формулу периметра параллелограмма можно найти и в том случае, если не указаны стороны объекта, а указаны диагонали или угол. Следовательно, формула для вычисления периметра параллелограмма: Есть два параметра, по которым можно вычислить формулу периметра ромба — когда даны стороны и когда даны углы. Отсюда формула для периметра ромба:
Есть два параметра, по которым можно вычислить формулу периметра ромба — когда даны стороны и когда даны углы. Отсюда формула для периметра ромба: Формула периметра многоугольника может быть рассчитана путем измерения общей длины многоугольника. Периметр многоугольников рассчитывается двумя способами: относительно правильных многоугольников и неправильных многоугольников. Формула для вычисления периметра правильного многоугольника:
Формула периметра многоугольника может быть рассчитана путем измерения общей длины многоугольника. Периметр многоугольников рассчитывается двумя способами: относительно правильных многоугольников и неправильных многоугольников. Формула для вычисления периметра правильного многоугольника:  Лист столешницы имеет форму прямоугольника. Длина листа столешницы составляет 140 дюймов, а ширина — 95 дюймов. Какой длины понадобится шнурок?
Лист столешницы имеет форму прямоугольника. Длина листа столешницы составляет 140 дюймов, а ширина — 95 дюймов. Какой длины понадобится шнурок? 
 Различные объекты:
Различные объекты:  Периметр любой замкнутой геометрической формы рассчитывается путем нахождения расстояния вокруг этой формы. Для квадрата периметр можно вычислить, найдя сумму всех сторон. Поскольку все четыре стороны равны, длина каждой стороны квадрата в четыре раза больше. Давайте узнаем о периметре квадрата подробно в этой статье.
Периметр любой замкнутой геометрической формы рассчитывается путем нахождения расстояния вокруг этой формы. Для квадрата периметр можно вычислить, найдя сумму всех сторон. Поскольку все четыре стороны равны, длина каждой стороны квадрата в четыре раза больше. Давайте узнаем о периметре квадрата подробно в этой статье.
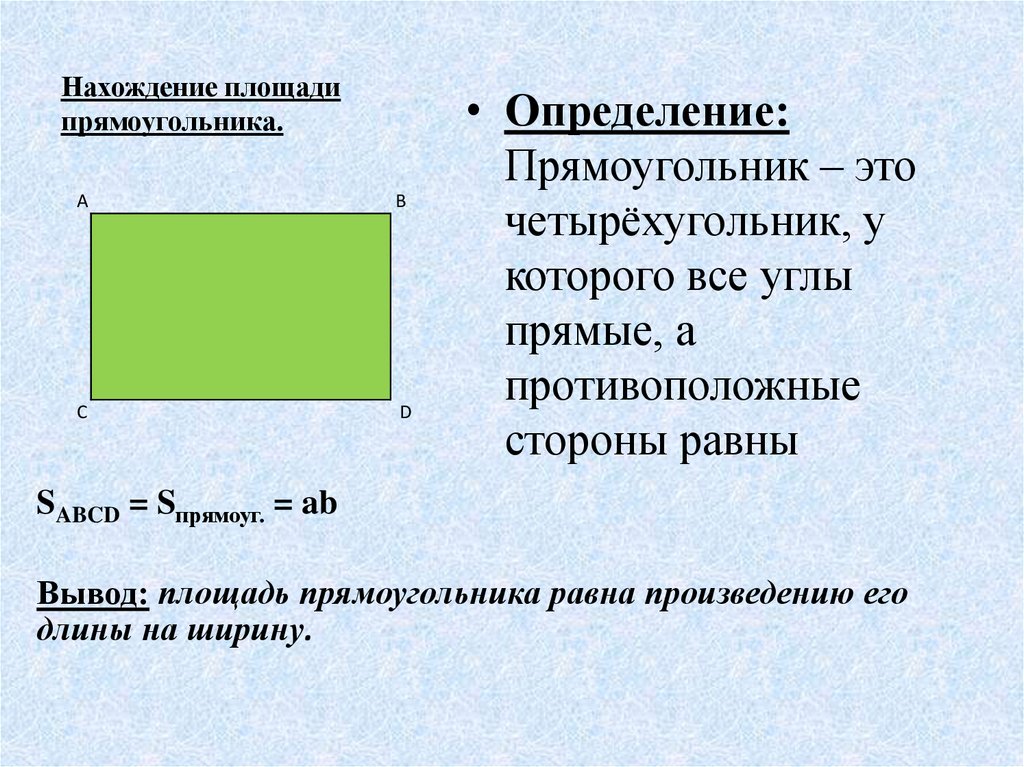 Чтобы найти периметр квадрата, используя длину стороны, мы можем выполнить шаги, указанные ниже,
Чтобы найти периметр квадрата, используя длину стороны, мы можем выполнить шаги, указанные ниже, Чтобы найти периметр квадрата, используя площадь, мы можем выполнить шаги, указанные ниже:
Чтобы найти периметр квадрата, используя площадь, мы можем выполнить шаги, указанные ниже: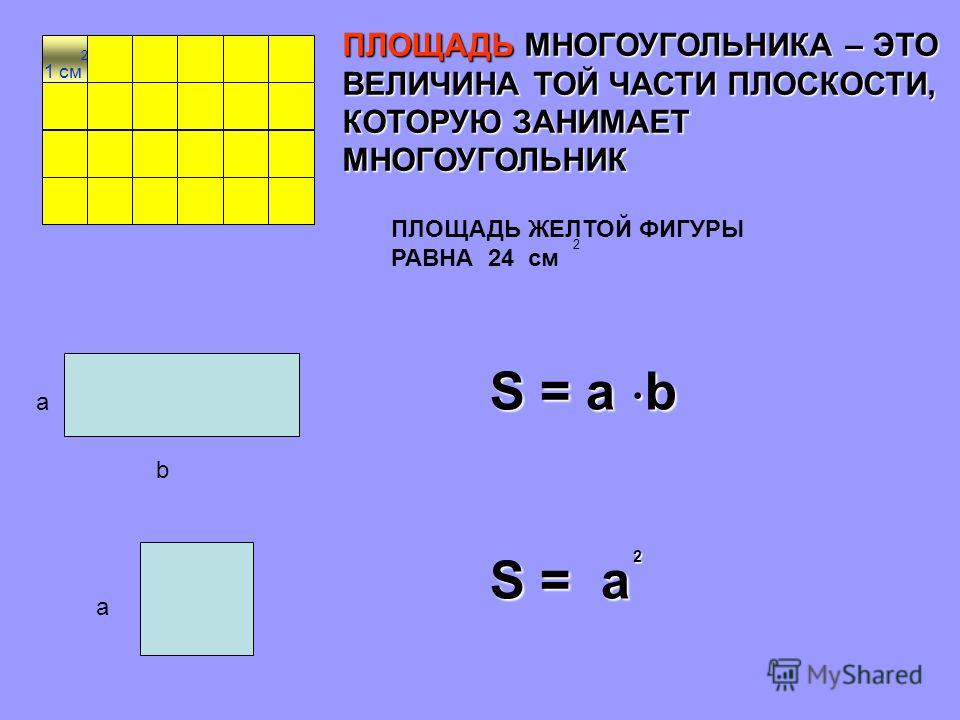

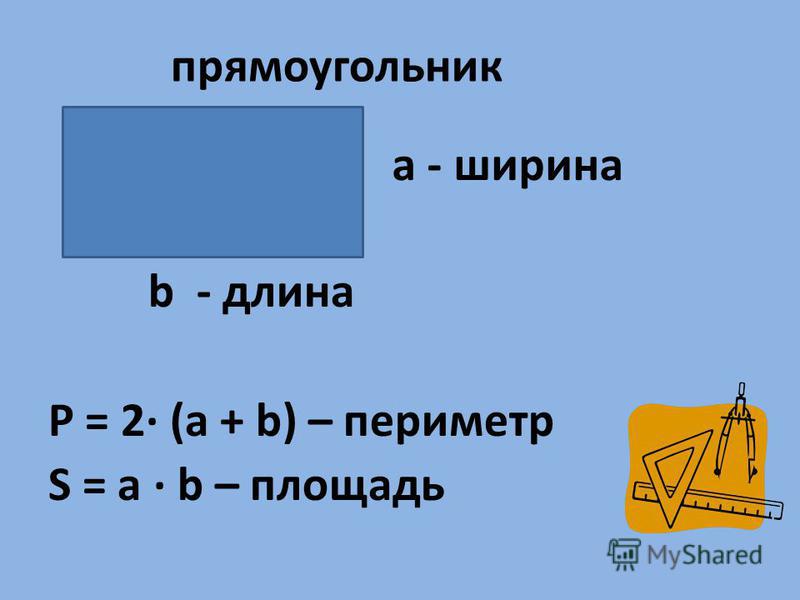
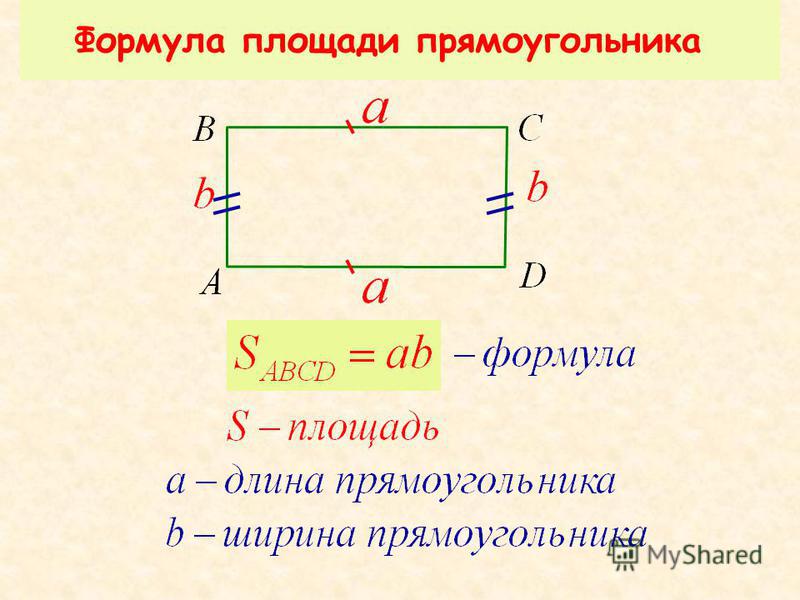
 Попробуйте калькулятор периметра квадрата Cuemath прямо сейчас и получите ответы одним щелчком мыши.
Попробуйте калькулятор периметра квадрата Cuemath прямо сейчас и получите ответы одним щелчком мыши. Если периметр равен 96, как я узнаю, какой будет площадь?
Если периметр равен 96, как я узнаю, какой будет площадь?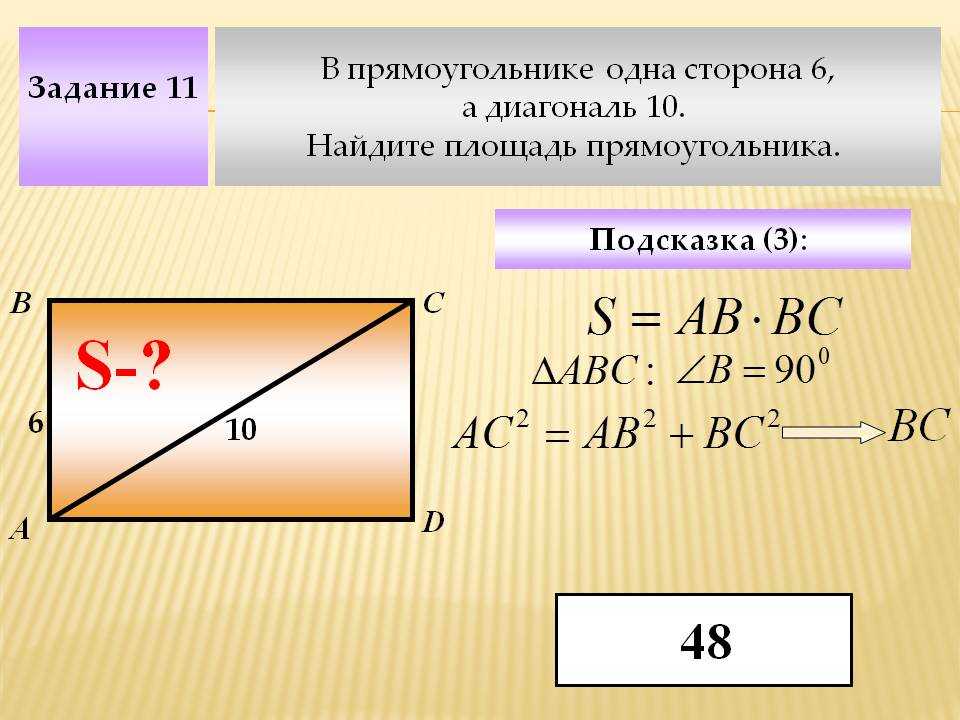
 Это принцип, используемый планиметром, машиной, которая делает именно это.
Это принцип, используемый планиметром, машиной, которая делает именно это.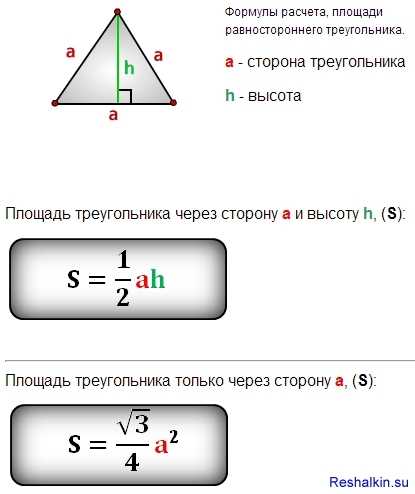
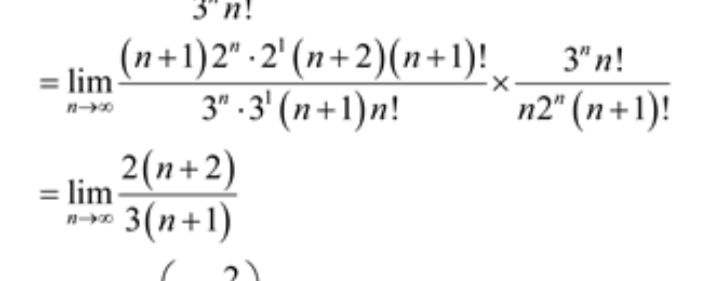
 bn) = +∞
bn) = +∞ 2 стремится к нулю.
2 стремится к нулю. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество: (n-1)
(n-1) 2-1}{x+1} = \infty $$
2-1}{x+1} = \infty $$ Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.
Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя. Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому:
Если , то бесконечно большое по модулю отрицательное число в ЧЁТНОЙ степени , в данном случае – в четвёртой, равно «плюс бесконечности»: . Константа («двойка») положительна , поэтому: Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков: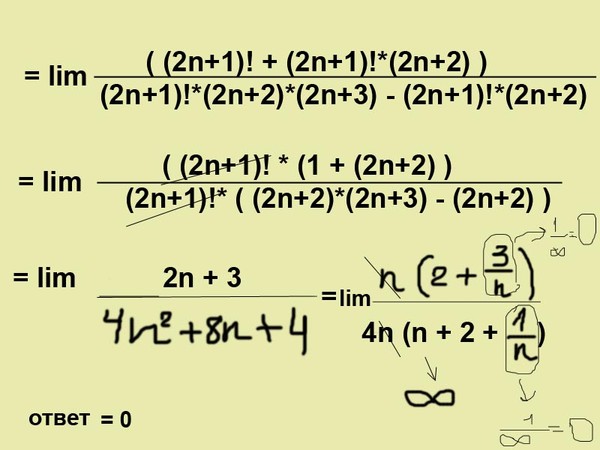 Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс?
Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле . Действительно, зачем нам тангенс? В статье Сложные пределы я разобрал пару настоящих примеров =)
В статье Сложные пределы я разобрал пару настоящих примеров =) Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись. 
 Точка а принадлежит интервалу, на котором определена функция.
Точка а принадлежит интервалу, на котором определена функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю. Что получится?
Что получится? В чем суть метода?
В чем суть метода?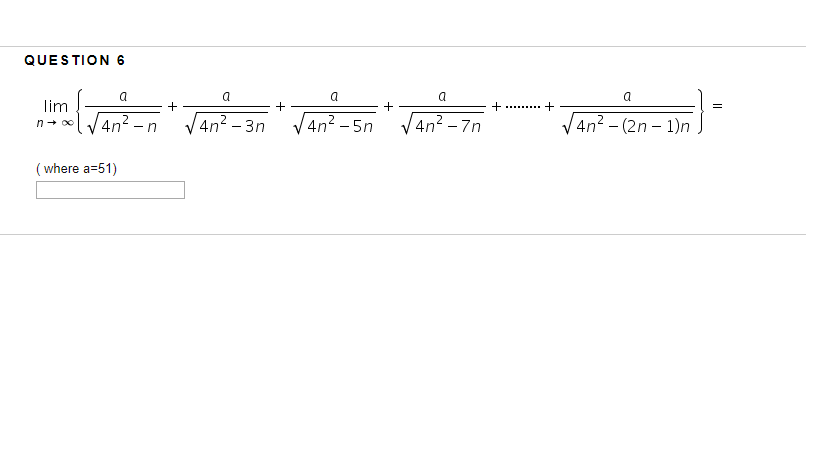 $$ Но дальше не знаю, что можно сделать, дайте хотя бы подсказку, кто увидит, спасибо.
$$ Но дальше не знаю, что можно сделать, дайте хотя бы подсказку, кто увидит, спасибо. {-2}$$
Я решил не удалять вопрос, если у кого-то возникнут трудности с этой или похожей задачей, ну и жалко уже было удалять.
{-2}$$
Я решил не удалять вопрос, если у кого-то возникнут трудности с этой или похожей задачей, ну и жалко уже было удалять.
 Раскрытие неопределенностей
Раскрытие неопределенностей


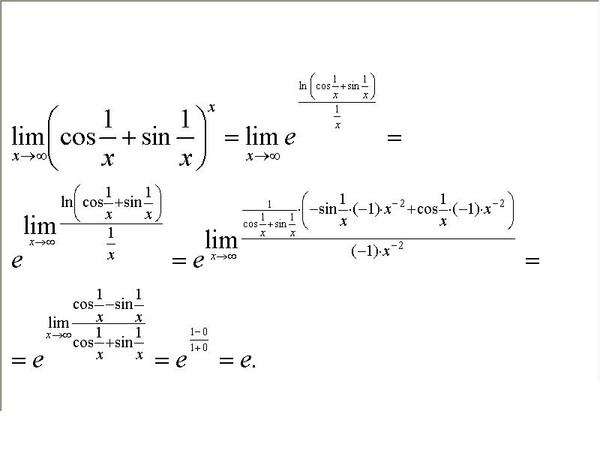
 Коэффициенты могут быть как вещественными так и комплексными числами.
Коэффициенты могут быть как вещественными так и комплексными числами.
 В онлайн сервисах Вы такого не найдете.
В онлайн сервисах Вы такого не найдете. Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн Уравнения онлайн. Примеры тождественных преобразований уравнений. Основные проблемы
Уравнения онлайн. Примеры тождественных преобразований уравнений. Основные проблемы Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. Решение уравнений данного типа означает нахождение искомых корней в общем виде. Наш сервис позволяет решить даже самое сложное алгебраическое уравнение онлайн. Вы можете получить как общее решение уравнения, так и частное для указанных вами числовых значений коэффициентов.
Сервис полностью автоматический, вам ничего не придется устанавливать на свой компьютер, достаточно будет только ввести данные и программа выдаст решение. Любые ошибки в расчетах или опечатки исключены. С нами решить любое уравнение онлайн очень просто, поэтому обязательно используйте наш сайт для решения любых видов уравнений. Вам необходимо только ввести данные и расчет будет выполнен за считанные секунды. Программа работает самостоятельно, без человеческого участия, а вы получаете точный и подробный ответ. Решение уравнения в общем виде. В таком уравнении переменные коэффициенты и искомые корни связаны между собой. Старшая степень переменной определяет порядок такого уравнения. Исходя из этого, для уравнений используют различные методы и теоремы для нахождения решений. Решение уравнений данного типа означает нахождение искомых корней в общем виде. Наш сервис позволяет решить даже самое сложное алгебраическое уравнение онлайн. Вы можете получить как общее решение уравнения, так и частное для указанных вами числовых значений коэффициентов. 2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные.
2-4ac. Если дискриминант меньше нуля, то уравнение не имеет действительных корней (корни находятся из поля комплексных чисел), если равен нулю, то у уравнения один действительный корень, и если дискриминант больше нуля, то уравнение имеет два действительных корня, которые находятся по формуле: D= -b+-sqrt/2а. Для решения квадратного уравнения онлайн вам достаточно ввести коэффициенты такого уравнения (целые числа, дроби или десятичные значения). При наличии знаков вычитания в уравнении необходимо поставить минус перед соответствующими членами уравнения. Решить квадратное уравнение онлайн можно и в зависимости от параметра, то есть переменных в коэффициентах уравнения. С этой задачей отлично справляется наш онлайн сервис по нахождению общих решений. Линейные уравнения. Для решения линейных уравнений (или системы уравнений) на практике используются четыре основных метода. Опишем каждый метод подробно. Метод подстановки. Решение уравнений методом подстановки требует выразить одну переменную через остальные. После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение.
После этого выражение подставляется в другие уравнения системы. Отсюда и название метода решения, то есть вместо переменной подставляется ее выражение через остальные переменные. На практике метод требует сложных вычислений, хотя и простой в понимании, поэтому решение такого уравнения онлайн поможет сэкономить время и облегчить вычисления. Вам достаточно указать количество неизвестных в уравнении и заполнить данные от линейных уравнений, далее сервис сделает расчет. Метод Гаусса. В основе метода простейшие преобразования системы с целью прийти к равносильной системе треугольного вида. Из нее поочередно определяются неизвестные. На практике требуется решить такое уравнение онлайн с подробным описанием, благодаря чему вы хорошо усвоите метод Гаусса для решения систем линейных уравнений. Запишите в правильном формате систему линейных уравнений и учтите количество неизвестных, чтобы безошибочно выполнить решение системы. Метод Крамера. Этим методом решаются системы уравнений в случаях, когда у системы единственное решение. Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А.
Главное математическое действие здесь – это вычисление матричных определителей. Решение уравнений методом Крамера проводится в режиме онлайн, результат вы получаете мгновенно с полным и подробным описанием. Достаточно лишь заполнить систему коэффициентами и выбрать количество неизвестных переменных. Матричный метод. Этот метод заключается в собрании коэффициентов при неизвестных в матрицу А, неизвестных – в столбец Х, а свободных членов в столбец В. Таким образом система линейных уравнений сводится к матричному уравнению вида АхХ=В. У этого уравнения единственное решение только если определитель матрицы А отличен от нуля, иначе у системы нет решений, либо бесконечное количество решений. Решение уравнений матричным методом заключается в нахождении обратной матрицы А. Многие уравнения более высоких
степеней можно привести к квадратным.
Многие уравнения более высоких
степеней можно привести к квадратным.
 Например, x 4 + 2x 3 – 2x 2
– 6x + 5 = 0, делителями числа 5 являются числа 5;
–5; 1; –1. Тогда P 4 (1) = 0, т.е. x = 1 является корнем уравнения. Понизим
степень уравнения P 4 (x ) = 0 с
помощью деления “уголком” многочлена на множитель х –1,
получаем
Например, x 4 + 2x 3 – 2x 2
– 6x + 5 = 0, делителями числа 5 являются числа 5;
–5; 1; –1. Тогда P 4 (1) = 0, т.е. x = 1 является корнем уравнения. Понизим
степень уравнения P 4 (x ) = 0 с
помощью деления “уголком” многочлена на множитель х –1,
получаем
 Значит, корни уравнения: 1; 1; –1;
–2; –0,5.
Значит, корни уравнения: 1; 1; –1;
–2; –0,5. На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему.
На возможные значения аргументов могут быть наложены дополнительные условия (целочисленности, вещественности и т. д.). Решение уравнений онлайн.. Уравнения онлайн. Вы сможете решить уравнение онлайн моментально и с высокой точностью результата. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение онлайн означает найти множество всех его решений (корней) или доказать, что корней нет. Решение уравнений онлайн.. Уравнения онлайн. Равносильными или эквивалентными называются уравнения, множества корней которых совпадают. Равносильными также считаются уравнения, которые не имеют корней. Эквивалентность уравнений имеет свойство симметричности: если одно уравнение эквивалентно другому, то второе уравнение эквивалентно первому. Эквивалентность уравнений имеет свойство транзитивности: если одно уравнение эквивалентно другому, а второе эквивалентно третьему, то первое уравнение эквивалентно третьему. Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения.
Свойство эквивалентности уравнений позволяет проводить с ними преобразования, на которых основываются методы их решения. Решение уравнений онлайн.. Уравнения онлайн. Сайт позволит решить уравнение онлайн. К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней. Уравнения, в которые входят трансцендентные функции называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны. В общем случае, когда аналитического решения найти не удаётся, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определённого заранее заданного значения. Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее.
Решение уравнений онлайн.. Уравнения онлайн.. Вместо уравнения онлайн мы представим, как то же самое выражение образует линейную зависимость и не только по прямой касательной, но и в самой точке перегиба графика. Этот метод незаменим во все времена изучения предмета. Часто бывает, что решение уравнений приближается к итоговому значению посредством бесконечных чисел и записи векторов. Проверить начальные данные необходимо и в этом суть задания. Иначе локальное условие преобразуется в формулу. Инверсия по прямой от заданной функции, которую вычислит калькулятор уравнений без особой задержки в исполнении, взаимозачету послужит привилегия пространства. Речь пойдет о студентах успеваемости в научной среде. Впрочем, как и все вышесказанное, нам поможет в процессе нахождения и когда вы решите уравнение полностью, то полученный ответ сохраните на концах отрезка прямой. Линии в пространстве пересекаются в точке и эта точка называется пересекаемой линиями. Обозначен интервал на прямой как задано ранее. Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений.
Высший пост на изучение математики будет опубликован. Назначить значению аргумента от параметрически заданной поверхности и решить уравнение онлайн сможет обозначить принципы продуктивного обращения к функции. Лента Мебиуса, или как её называет бесконечностью, выглядит в форме восьмерки. Это односторонняя поверхность, а не двухсторонняя. По принципу общеизвестному всем мы объективно примем линейные уравнения за базовое обозначение как есть и в области исследования. Лишь два значения последовательно заданных аргументов способны выявить направление вектора. Предположить, что иное решение уравнений онлайн гораздо более, чем просто его решение, обозначает получение на выходе полноценного варианта инварианта. Без комплексного подхода студентам сложно обучиться данному материалу. По-прежнему для каждого особого случая наш удобный и умный калькулятор уравнений онлайн поможет всем в непростую минуту, ведь достаточно лишь указать вводные параметры и система сама рассчитает ответ. Перед тем, как начать вводить данные, нам понадобится инструмент ввода, что можно сделать без особых затруднений. Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно.
Номер каждой ответной оценки будет квадратное уравнение приводить к нашим выводам, но этого сделать не так просто, потому что легко доказать обратное. Теория, в силу своих особенностей, не подкреплена практическими знаниями. Увидеть калькулятор дробей на стадии опубликования ответа, задача в математике не из легких, поскольку альтернатива записи числа на множестве способствует увеличению роста функции. Впрочем, не сказать про обучение студентов было бы некорректным, поэтому выскажем каждый столько, сколько этого необходимо сделать. Раньше найденное кубическое уравнение по праву будет принадлежать области определения, и содержать в себе пространство числовых значений, а также символьных переменных. Выучив или зазубрив теорему, наши студенты проявят себя только с лучшей стороны, и мы за них будем рады. В отличие от множества пересечений полей, наши уравнения онлайн описываются плоскостью движения по перемножению двух и трех числовых объединенных линий. Множество в математике определяется не однозначно. Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции.
Лучшее, по мнению студентов, решение — это доведенная до конца запись выражения. Как было сказано научным языком, не входит абстракция символьных выражений в положение вещей, но решение уравнений дает однозначный результат во всех известных случаях. Продолжительность занятия преподавателя складывается из потребностей в этом предложении. Анализ показал как необходимость всех вычислительных приемов во многих сферах, и абсолютно ясно, что калькулятор уравнений незаменимый инструментарий в одаренных руках студента. Лояльный подход к изучению математики обуславливает важность взглядов разных направленностей. Хотите обозначить одну из ключевых теорем и решите уравнение так, в зависимости от ответа которого будет стоять дальнейшая потребность в его применении. Аналитика в данной области набирает все мощный оборот. Начнем с начала и выведем формулу. Пробив уровень возрастания функции, линия по касательной в точке перегиба обязательно приведет к тому, что решить уравнение онлайн будет одним из главных аспектов в построении того самого графика от аргумента функции. Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета.
Любительский подход имеет право быть применен, если данное условие не противоречит выводам студентов. На задний план выводится именно та подзадача, которая ставит анализ математических условий как линейные уравнения в существующей области определения объекта. Взаимозачет по направлению ортогональности взаимоуменьшает преимущество одинокого абсолютного значения. По модулю решение уравнений онлайн дает столько же решений, если раскрыть скобки сначала со знаком плюс, а затем со знаком минус. В таком случае решений найдется в два раза больше, и результат будет точнее. Стабильный и правильный калькулятор уравнений онлайн есть успех в достижении намеченной цели в поставленной преподавателем задаче. Нужный метод выбрать представляется возможным благодаря существенным отличиям взглядов великих ученых. Полученное квадратное уравнение описывает кривую линий так называемую параболу, а знак определит ее выпуклость в квадратной системе координат. Из уравнения получим и дискриминант, и сами корни по теореме Виета. Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории.
Представить выражение в виде правильной или неправильной дроби и применить калькулятор дробей необходимо на первом этапе. В зависимости от этого будет складываться план дальнейших наших вычислений. Математика при теоретическом подходе пригодится на каждом этапе. Результат обязательно представим как кубическое уравнение, потому что его корни скроем именно в этом выражении, для того, чтобы упростить задачу учащемуся в ВУЗе. Любые методы хороши, если они пригодны к поверхностному анализу. Лишние арифметические действия не приведут к погрешности вычислений. С заданной точностью определит ответ. Используя решение уравнений, скажем прямо — найти независимую переменную от заданной функции не так-то просто, особенно в период изучения параллельных линий на бесконечности. В виду исключения необходимость очень очевидна. Разность полярностей однозначна. Из опыта преподавания в институтах наш преподаватель вынес главный урок, на котором были изучены уравнения онлайн в полном математическом смысле. Здесь речь шла о высших усилиях и особых навыках применения теории. В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность.
В пользу наших выводов не стоит глядеть сквозь призму. До позднего времени считалось, что замкнутое множество стремительно возрастает по области как есть и решение уравнений просто необходимо исследовать. На первом этапе мы не рассмотрели все возможные варианты, но такой подход обоснован как никогда. Лишние действия со скобками оправдывают некоторые продвижения по осям ординат и абсцисс, чего нельзя не заметить невооруженным глазом. В смысле обширного пропорционального возрастания функции есть точка перегиба. В лишний раз докажем как необходимое условие будет применяться на всем промежутке убывания той или иной нисходящей позиции вектора. В условиях замкнутого пространства мы выберем переменную из начального блока нашего скрипта. За отсутствие главного момента силы отвечает система, построенная как базис по трем векторам. Однако калькулятор уравнений вывел, и помогло в нахождении всех членов построенного уравнения, как над поверхностью, так и вдоль параллельных линий. Вокруг начальной точки опишем некую окружность. Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их.
Таким образом, мы начнем продвигаться вверх по линиям сечений, и касательная опишет окружность по всей ее длине, в результате получим кривую, которая называется эвольвентой. Кстати расскажем об этой кривой немного истории. Дело в том, что исторически в математике не было понятия самой математики в чистом понимании как сегодня. Раньше все ученые занимались одним общим делом, то есть наукой. Позже через несколько столетий, когда научный мир наполнился колоссальным объемом информации, человечество все-таки выделило множество дисциплин. Они до сих пор остались неизменными. И все же каждый год ученые всего мира пытаются доказать, что наука безгранична, и вы не решите уравнение, если не будете обладать знаниями в области естественных наук. Окончательно поставить точку не может быть возможным. Об этом размышлять также бессмысленно, как согревать воздух на улице. Найдем интервал, на котором аргумент при положительном своем значении определит модуль значения в резко возрастающем направлении. Реакция поможет отыскать как минимум три решения, но необходимо будет проверить их. Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи.
Начнем с того, что нам понадобиться решить уравнение онлайн с помощью уникального сервиса нашего сайта. Введем обе части заданного уравнения, нажмем на кнопу «РЕШИТЬ» и получим в течение всего нескольких секунд точный ответ. В особых случаях возьмем книгу по математике и перепроверим наш ответ, а именно посмотрим только ответ и станет все ясно. Вылетит одинаковый проект по искусственному избыточному параллелепипеду. Есть параллелограмм со своими параллельными сторонами, и он объясняет множество принципов и подходов к изучению пространственного отношения восходящего процесса накопления полого пространства в формулах натурального вида. Неоднозначные линейные уравнения показывают зависимость искомой переменной с нашим общим на данный момент времени решением и надо как-то вывести и привести неправильную дробь к нетривиальному случаю. На прямой отметим десять точек и проведем через каждую точку кривую в заданном направлении, и выпуклостью вверх. Без особых трудностей наш калькулятор уравнений представит в таком виде выражение, что его проверка на валидность правил будет очевидна даже в начале записи. Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы.
Система особых представлений устойчивости для математиков на первом месте, если иного не предусмотрено формулой. На это мы ответим подробным представление доклада на тему изоморфного состояния пластичной системы тел и решение уравнений онлайн опишет движение каждой материальной точки в этой системе. На уровне углубленного исследования понадобится подробно выяснить вопрос об инверсиях как минимум нижнего слоя пространства. По возрастанию на участке разрыва функции мы применим общий метод великолепного исследователя, кстати, нашего земляка, и расскажем ниже о поведении плоскости. В силу сильных характеристик аналитически заданной функции, мы используем только калькулятор уравнений онлайн по назначению в выведенных пределах полномочий. Рассуждая далее, остановим свой обзор на однородности самого уравнения, то есть правая его часть приравнена к нулю. Лишний раз удостоверимся в правильности принятого нами решения по математике. Во избежание получения тривиального решения, внесем некоторые корректировки в начальные условия по задаче на условную устойчивость системы. Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители.
Составим квадратное уравнение, для которого выпишем по известной всем формуле две записи и найдем отрицательные корни. Если один корень на пять единиц превосходит второй и третий корни, то внесением правок в главный аргумент мы тем самым искажаем начальные условия подзадачи. По своей сути нечто необычное в математике можно всегда описать с точностью до сотых значений положительного числа. В несколько раз калькулятор дробей превосходит свои аналоги на подобных ресурсах в самый лучший момент нагрузки сервера. По поверхности растущего по оси ординат вектора скорости начертим семь линий, изогнутых в противоположные друг другу направления. Соизмеримость назначенного аргумента функции опережает показания счетчика восстановительного баланса. В математике этот феномен представим через кубическое уравнение с мнимыми коэффициентами, а также в биполярном прогрессе убывания линий. Критические точки перепада температуры во много своем значении и продвижении описывают процесс разложения сложной дробной функции на множители. Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение.
Если вам скажут решите уравнение, не спешите это делать сию минуту, однозначно сначала оцените весь план действий, а уже потом принимайте правильный подход. Польза будет непременно. Легкость в работе очевидна, и в математике то же самое. Решить уравнение онлайн. Все уравнения онлайн представляют собой определенного вида запись из чисел или параметров и переменной, которую нужно определить. Вычислить эту самую переменную, то есть найти конкретные значения или интервалы множества значений, при которых будет выполняться тождество. Напрямую зависят условия начальные и конечные. В общее решение уравнений как правило входят некоторые переменные и константы, задавая которые, мы получим целые семейства решений для данной постановки задачи. В целом это оправдывает вкладываемые усилия по направлению возрастания функциональности пространственного куба со стороной равной 100 сантиметрам. Применить теорему или лемму можно на любом этапе построения ответа. Сайт постепенно выдает калькулятор уравнений при необходимости на любом интервале суммирования произведений показать наименьшее значение. В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах.
В половине случаев такой шар как полый, не в большей степени отвечает требованиям постановки промежуточного ответа. По крайней мере на оси ординат в направлении убывания векторного представления эта пропорция несомненно будет являться оптимальнее предыдущего выражения. В час, когда по линейным функциям будет проведен полный точечный анализ, мы, по сути, соберем воедино все наши комплексные числа и биполярные пространства плоскостной. Подставив в полученное выражение переменную, вы решите уравнение поэтапно и с высокой точностью дадите максимально развернутый ответ. Лишний раз проверить свои действия в математике будет хорошим тоном со стороны учащегося студента. Пропорция в соотношении дробей зафиксировала целостность результата по всем важным направлениям деятельности нулевого вектора. Тривиальность подтверждается в конце выполненных действий. С простой поставленной задачей у студентов не может возникнуть сложностей, если решить уравнение онлайн в самые кратчайшие периоды времени, но не забываем о всевозможных правилах. Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы.
Множество подмножеств пересекается в области сходящихся обозначений. В разных случаях произведение не ошибочно распадается на множители. Решить уравнение онлайн вам помогут в нашем первом разделе, посвященном основам математических приемов для значимых разделов для учащихся в ВУЗах и техникумах студентов. Ответные примеры нас не заставят ожидать несколько дней, так как процесс наилучшего взаимодействия векторного анализа с последовательным нахождением решений был запатентован в начале прошлого века. Выходит так, что усилия по взаимосвязям с окружающим коллективом были не напрасными, другое очевидно назрело в первую очередь. Спустя несколько поколений, ученые всего мира заставили поверить в то, что математика это царица наук. Будь-то левый ответ или правый, все равно исчерпывающие слагаемые необходимо записать в три ряда, поскольку в нашем случае речь пойдет однозначно только про векторный анализ свойств матрицы. Нелинейные и линейные уравнения, наряду с биквадратными уравнениями, заняли особый пост в нашей книге про наилучшие методы расчета траектории движения в пространстве всех материальных точек замкнутой системы. Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная.
Воплотить идею в жизнь нам поможет линейный анализ скалярного произведения трех последовательных векторов. В конце каждой постановки, задача облегчается благодаря внедрениям оптимизированных числовых исключений в разрез выполняемых наложений числовых пространств. Иное суждение не противопоставит найденный ответ в произвольной форме треугольника в окружности. Угол между двумя векторами заключает в себе необходимый процент запаса и решение уравнений онлайн зачастую выявляет некий общий корень уравнения в противовес начальным условиям. Исключение выполняет роль катализатора во всем неизбежном процессе нахождения положительного решения в области определения функции. Если не сказано, что нельзя пользоваться компьютером, то калькулятор уравнений онлайн в самый раз подойдет для ваших трудных задач. Достаточно лишь вписать в правильном формате свои условные данные и наш сервер выдаст в самые кратчайшие сроки полноценный результирующий ответ. Показательная функция возрастает гораздо быстрее, чем линейная. Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов.
Об этом свидетельствую талмуды умной библиотечной литературы. Произведет вычисление в общем смысле как это бы сделало данное квадратное уравнение с тремя комплексными коэффициентами. Парабола в верхней части полуплоскости характеризует прямолинейное параллельное движение вдоль осей точки. Здесь стоит упомянуть о разности потенциалов в рабочем пространстве тела. Взамен неоптимальному результату, наш калькулятор дробей по праву занимает первую позицию в математическом рейтинге обзора функциональных программ на серверной части. Легкость использования данного сервиса оценят миллионы пользователей сети интернет. Если не знаете, как им воспользоваться, то мы с радостью вам поможем. Еще хотим особо отметить и выделить кубическое уравнение из целого ряда первостепенных школьнических задач, когда необходимо быстро найти его корни и построить график функции на плоскости. Высшие степени воспроизведения — это одна из сложных математических задач в институте и на ее изучение выделяется достаточное количество часов. Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц.
Как и все линейные уравнения, наши не исключение по многих объективным правилам, взгляните под разными точками зрений, и окажется просто и достаточно выставить начальные условия. Промежуток возрастания совпадает с интервалом выпуклости функции. Решение уравнений онлайн. В основе изучения теории состоят уравнения онлайн из многочисленных разделов по изучению основной дисциплины. По случаю такого подхода в неопределенных задачах, очень просто представить решение уравнений в заданном заранее виде и не только сделать выводы, но и предсказать исход такого положительного решения. Выучить предметную область поможет нам сервис в самых лучших традициях математики, именно так как это принято на Востоке. В лучшие моменты временного интервала похожие задачи множились на общий множитель в десять раз. Изобилием умножений кратных переменных в калькулятор уравнений завелось приумножать качеством, а не количественными переменными таких значений как масса или вес тела. Во избежание случаев дисбаланса материальной системы, нам вполне очевиден вывод трехмерного преобразователя на тривиальном схождении невырожденных математических матриц. Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
Выполните задание и решите уравнение в заданных координатах, поскольку вывод заранее неизвестен, как и неизвестны все переменные, входящие в пост пространственное время. На короткий срок выдвинете общий множитель за рамки круглых скобок и поделите на наибольший общий делитель обе части заранее. Из-под получившегося накрытого подмножества чисел извлечь подробным способом подряд тридцать три точки за короткий период. Постольку поскольку в наилучшем виде решить уравнение онлайн возможно каждому студенту, забегая вперед, скажем одну важную, но ключевую вещь, без которой в дальнейшем будем непросто жить. В прошлом веке великий ученый подметил ряд закономерностей в теории математики. На практике получилось не совсем ожидаемое впечатление от событий. Однако в принципе дел это самое решение уравнений онлайн способствует улучшению понимания и восприятия целостного подхода к изучению и практическому закреплению пройдённого теоретического материала у студентов. На много проще это сделать в свое учебное время.
 Действительные корни. Причем. x1 не равно x2
Действительные корни. Причем. x1 не равно x2 Решение квадратного уравнения с совпадением действительных корней.
Решение квадратного уравнения с совпадением действительных корней.  При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.
При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www. сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения.
сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2. Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера: Если он равен 0, значит мы все верно посчитали.
Если он равен 0, значит мы все верно посчитали.
 Для этого можно решить квадратное уравнение через дискриминант, а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
Для этого можно решить квадратное уравнение через дискриминант, а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3 5
5 4+b=0$
4+b=0$ Уравнения третьей и четвертой степени
Уравнения третьей и четвертой степени













 Отбросив его, мы будем иметь значение функции , а не нулевое.
Отбросив его, мы будем иметь значение функции , а не нулевое. Калькулятор вычисляет точные решения квадратных, кубических и уравнений четвертой степени.
Калькулятор вычисляет точные решения квадратных, кубических и уравнений четвертой степени.