Авторская программа по математике для одаренных детей по теме избранные вопросы математики “ Уравнения высших степеней” 9 класс Выполнена: учителем математики МБОУ СОШ №3 п.Редкино Конаковского района Тверской области Алешиной М.В. Авторская программа по математике для одаренных детей по теме избранные вопросы математики “ Уравнения высших степеней” 9 класс Решение алгебраических уравнений высших степеней — одна из сложных тем в курсе математики. Знание способов решения различных уравнений высших степеней и умение применять их являются необходимым для успешной учебы в старших классах по профилю “Математика”. Цель:
Задачи:
Планируемые результаты:
Программа курса для учащихся 9-ого класса. Уравнения высших степеней. Пояснительная записка. Данная программа для учащихся 9-ого класса посвящен одной из важнейших тем алгебры — решению уравнений высших степеней. В основной школе этой теме не уделяется достаточного внимания. Важные приемы, необходимые для решения уравнений, вообще отсутствуют, и в итоге все сводится к решению уравнений одного вида (биквадратные уравнения). Предполагаемая программа является развитием системы ранее приобретенных знаний. Задания данного курса часто не просты в решении, что позволяет повысить учебную мотивацию учащихся. Ознакомление с методами и приемами решения уравнений высших степеней необходимо для успешного обучения в старшей школе, а также для сдачи ОГЭ. Есть много уравнений, которые считаются для школьников задачами повышенной трудности. Содержание данной программы ориентировано на достижение следующих целей: — выработать навыки преобразования многочленов и решения различных алгебраических уравнений, — создать целостное представление о данной теме, значительно расширить спектр задач, посильных учащимся. Задачи: — познакомить школьников с различными методами решения, позволяющих расширить программу школьного курса. — привить школьникам навыки использования нестандартных методов рассуждения при решении задач, способствующих развитию познавательного интереса и творческих наклонностей учащихся. Освоение данного курса позволит развить интеллект, интерес к познавательной деятельности, будет способствовать приобретению опыта поиска информации, позволит осуществить сознательный выбор учащимися их будущего профиля.
Планирование курса. Содержание курса 1.
2.
3.
а) решение симметричных и обобщенных возвратных уравнений, б) решение однородных уравнений, в) решение уравнений вида (х + а)(х + b)(х + с)(х + d) = А, если а+d = с+b. 4.
Содержание программы:
Рn(х) = •+ • + • + … +•x+ — многочлен с одной переменной, n N N (если ≠ 0 — степень многочлена (старшая степень Х). Замечание: а) любое действительное число, отличное от нуля — многочлен нулевой степени б) 0 — многочлен, степень которого не определена (нулевой многочлен) х0 — корень многочлена Р (х0) = 0. №1 Какова степень многочлена: а) Рn(х) = х б) Рn(х) = (х2— З)3 +1 в) Рn(х) = -2 n=1 n=6 n = 0 №2 1) Проверить, что х0 — корень многочлена Рn(х), если а) Р4 (х) = 2х4 + 7х3 — 2х2 -13х + 6, х0 = 1 Р4(х) = 2•1 + 7•1 -2•1 — 13•1 + 6 = 2 + 7- 2 — 13 + 6= 15-15 =0 Т. Р4(-2) = (4 — 2)2 + 4(4 + 1) -12 = 22 + 4-5 — 12 = 4 + 20 -12 = 24-12 = 12 Т.к. Р4 (-2) ≠ 0, то х0 = -2 — не является корнем данного многочлена.
Правило деления многочлена на многочлен аналогично правилу деления чисел углом. Разделить многочлен Рп(х) на Gm(х) — это значит найти многочлен Qk(х) и Rр(х) такие, что имеет место равенство: Рn(х) = Gm(х) • Qk(х) + Rр(х), где Рп(х) — делимое Gm(х) — делитель Qk(х) — частное Rр(х) — остаток n ≥ m > 0, k + m= n, р m, рN,mN,kN. Пример 1. Разделить многочлен Р4 (х) = + +1 на многочлен (х) = — + 1 + +1 — + 1 — + + + + 1 + — — + — — + 1 Rр (х) = 0 + +1 = + + 1) ( — + 1) + 0 Замечание: В данном примере остаток от деления равен нулю. В этом случае говорят, что многочлен Рn(х) делится на многочлен Оm(х). Разделить многочлен (х) = Зх5 — 2х4 + х3 — 4х2 + 2х — 1 на многочлен (х) = х3 — х2 + 2х + 3. — Зх5 — Зх4 + 6х3 + 9х2 + — 4 х4— 5х3 — 13х2 + 2х -1 — х4— х3 + 2х2 + Зх — 4х3 — 15х2 — х — 1 — 4х3 + 4х2 — 8х — 12 _ 19х2 + 7х +11 Зх5 — 2х4 + х3 — 4х2 + 2х — 1 = (Зх2 + х — 4)( х3 — х2 + 2х + 3) — 19х2 + 7х2 + 11 (х) = Зх2 + х — 4 R2(х) = — 19х2 +7х2+ 11 Разделить многочлен (х) = х5 — 6х4 + 16х3 — 32х2 + 48х — 32 на (х) = х3 — 6х4 + 12х — 8 х5 — 6х4+ 16х3 — 32х2 + 48х – 32 х3 — 6х4 + 12х — 8 — х5— 6х4 + 12х3 — 8х2 х2 + 4 4х3 — 24х2 + 48х – 32 — 4х3 — 24х2 + 48х — 32 0 Rр(х) = 0 (х) = х2 + 4 | ||||||||||||||
| Программа элективного курса «Избранные вопросы математики» для обучающихся 9-ых классов .  .. .. | Методическая разработка урока математики по теме «Линейные уравнения с одной переменной» Место выполнения работы: гоу спо «Мариинский аграрный техникум» г. Мариинска Кемеровской области | |||||||||||||
| Самостоятельная работа №2 Конкретизация целей обучения математике… Карта темы «Квадратные уравнения» | Программы естественно-научной направленности По математике «математика +» Ленинградском областном центре развития творчества одаренных детей и юношества «Интеллект» | |||||||||||||
| Учебный проект по математике по теме Формировать понимание межпредметных связей, значимости математики в общественной жизни | Учебной сессии в Мурманской областной очно-заочной школе для одарённых детей «а-элита» В период с 27 по 29 сентября 2016 года состоялась осенняя сессия в Мурманской областной очно-заочной школе дополнительного образования… | |||||||||||||
Решение головоломок с одинаковыми цифрами издавна любимое развлечение. .. ..Избранные занимательные задания из книги И. Г. Сухина «Весёлая математика: 1500 головоломок для математических олимпиад, уроков,… | Рабочая программа по алгебре для 10 класса При изучении курса математики… «Алгебра», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики»,… | |||||||||||||
| Исследовательская работа по математике: «Решение приведенных квадратных уравнений» … | Урок по математике в 5 г классе по теме: «В царстве математических сказок» Цель: раскрыть волшебную роль математики в сказках, показать как в форме сказок, стихов можно запоминать разные математические понятия,… |
1. Задачи элементарной математики.
Упростить алгебраическое выражение.
№ | Алгебраическое выражение |
1 | х4 — х3 — 11х2 + 9x +18 x3 — 9x2 + 26x — 24 |
x4 — 3x3 — 7x2 + 27x -18 x3 — 8x2 +19x -12 | |
2 | 2 — x 3x4 — 24x3 — 3x2 + 204x — 252 |
x +1 220x — 70x2 -168 — 15x3 + 10x4 — x5 | |
3 | x3 + 2x2 + 4x + 8 2x4 +10x3 -16x — 80 |
x5 + 5x4 -16x — 80 x2 + 2x + 4 | |
4 | 2 x4 +10 x3 — 2 x -10 x3 + x2 + x +1 |
x2 + x +1 x5 + 5 x4 — x — 5 | |
5 | 4x4 + x5 — 81x — 324 3x3 + 19x2 + 57x + 90 |
3x4 +10x3 — 81x — 270 x4 + 7x3 + 21x2 + 63x +108 | |
6 | 4x5 + 40x4 +100x3 — 80x2 — 320x + 256 3x3 — 3x2 |
x4 + x3 — 9x2 + 11x — 4 x2 + 8x +16 | |
7 | 5x4 +10x3 -100x2 — 330x — 225 x2 — 2x -15 |
x4 + x3 — 7x2 — x + 6 x2 — 3x + 2 | |
8 | x3 + 3x2 — 9x — 27 x4 — 8x3 — 27x + 216 |
x3 — 5x2 — 15x — 72 49x4 — 882x2 + 3969 | |
9 | 7x4 -126x2 + 567 (x3 — 5x2 -15x — 72) |
(x5 — 8x4 — 27x2 + 216x) (x3 + 3x2 — 9x — 27) | |
10 | x3 + 6 x2 +12 x + 8 x4 + x3 — 9 x2 + 11x — 4 |
x2 + 3x — 4 9x5 + 36x4 + 9x3 — 90x2 — 36x + 72 | |
11 | (x3 — x2 — 4x + 4) 3x — 3 (x3 — 3x + 2) 2x — 4 |
12 | (x4 + 2x3 — 72x2 — 416x — 640) ( x -10 J |
(9x3 -144x2 +180x + 3600) tx2 + 8x +16J | |
13 | (x4 + x3 — 3x2 — 5x — 2) tx2 — 40x + 400^ |
(9x3351x2 + 3240x + 3600) [ x3 -3x-2 J | |
14 | (2x4 + 4x3 — 4x — 2) f x4 — 7 ^ |
(x3 + x2 — x -1) ^ 2 x + 2 J | |
15 | (4x4 + 4x3 — 48x2 -112x — 64) f x + 4 ^ |
(2x3 + 4x2 — 32x — 64) tx2 + 3x + 2 J | |
16 | (4x4 — 45x2 + 35x3 — 315x + 81) f x + 9 ^ |
8x4 +166x3 + 1038x2 +1674x — 486) t x2 — 6x + 9 J |
17 | х4 + х3 — 7 х2 — х + 6 х3 — 2 х2 -15 х |
(5х4 +10х3 -100х2 — 330х — 225) х2 — 3х + 2 | |
18 | (220х — 70х2 -168 — 15х3 +10х4 — х5) 3х2 — 6х2 +12 |
(3х4 — 24х3 — 3х2 + 204х — 252) х — 2 | |
19 | (х2 + 3х + 2) (2х3 + 4х2 — 32х — 64) |
(х2 -16) (4х4 + 4х3 — 48х2 -112х — 64) | |
20 | х2 — 9 (8х4 +166х3 +1038х2 +1674х- 486) |
х2 +12х + 27 (4х4 — 45х2 + 35х3 — 315х + 81) | |
21 | х2 + 8х +16 (9х3 -144х2 +180х + 3600) |
х -10 (х4 + 2х3 — 72х2 — 416х — 640) | |
22 | 2(х +1) (х3 + х2 — х -1) |
х3 + 2х (2х4 + 4х3 — 4х — 2) | |
23 | 2х — 4 (х3 — 3х + 2) |
х -1 (х3 — х2 — 4 х + 4) | |
24 | х3 — 3х — 2 (9х3 — 351х2 + 3240х + 3600) |
(х2 — 40х + 400) (х4 + х3 — 3х2 — 5х — 2) | |
25 | х2 — 3х + 2 (5х4 +10х3 -100х2 — 330х — 225) |
х2 — 2 х -15 х4 + х3 — 7 х2 — х + 6 | |
26 | 9х5 + 36х4 + 9х3 — 90х2 — 36х + 72 х3 + 3х2 — 4х |
х4 + х3 — 9 х2 + 11х — 4 х3 + 6 х2 +12 х + 8 | |
27 | х2 + 8 х +16 х4 + х3 — 9 х2 + 11х — 4 |
х2 — х 4х5 + 40х4 +100х3 — 80х2 — 320х + 256 | |
28 | х3 + 2х2 + 4х х5 + 5х4 -16х — 80 |
2х4 +10х3 -16х — 80 х3 + 2х2 + 4х + 8 | |
29 | х3 + 2х2 + 4х + 8 2х4 +10х3 -16х — 80 |
х5 + 5х4 -16х — 80 х2 + 2х + 4 | |
30 | 3х5 +10х4 — 81х2 — 270х х4 + 7х3 + 21х2 + 63х +108 |
4х4 + х5 — 81х — 324 3х3 +19х2 + 57х + 90 |
Раскройте скобки
и приведите подобные слагаемые.
№ | Алгебраическое выражение |
1 | (х -1)4( х + 2)( х + 4)2(3х + 8) |
2 | (3х + 2)3(х2 + 2)4(х — 3)2(0.5 — х) |
3 | ((х2 -1)(2х — 3))2(3х + 2)3 |
4 | (х2 + 4х — 6)((х3 -1)(2 — 4х))2 (2х + 4)2 |
5 | (7х3 + 4х)((х2 — 9)(3 + х)(2х + 4))2 |
6 | х(х3 — 3х2 + 4)((х2 — 9)(3 + х)(2х + 4))2 |
7 | ((х3 -1)(2х2 + 2х — 3))3 (3х + 2)2 |
8 | (6 х — 9)5 (2 — 7 х)( х4 + 4 х)2 (3х + 8) |
9 | (х -3х2 + 7)2(х2 + 3х -1)(9х4 -1)3 |
10 | (7 х + 5х2 )((7 х — 4)( х 4 + 3)(8 х + 4))3 |
11 | (х3 — 3х2 + 4)((х4 — 81)(3х4 + х)(2х + 4))3 х |
12 | ((х3 — 3)(х6 -11))2 ((3х4 + 2х + 4)(2х + 4))3 |
13 | (х — 54)4 (12 х + 4)(2 х + 4)2( х — 8 х6) |
14 | (5х2 — 2х3 + 5х)2 (3 — х2 + х)(7х4 — х)3 |
15 | ((9х2 — 3х
+1)(х2 + х
— 2))2 (1. |
16 | (х3 — 3х2 + 4)((х4 — 81)(3х4 + х)(2х + 4))3 х |
17 | ((3х + х2)(х3 — 3))2((6х3 + 2х2 + 4)(4 — 2х))3 |
18 | (2 х + 27)5(12 + 6 х)(2 х — 9)2( х2 + 6 х3) |
19 | (х2 + 3х3 — 2)((х2 -16)(2х2 + 5))3(2х + 4)2 |
20 | (10 х — 2)4 (13х — 4)(5х + 3)3 (х — 8 х2) |
21 | ((х3 — 1)(5х — 2))3 (7х + 3)3 |
22 | (3х2 + 89х -16)((х4 -1)(7 + 9х))2(6х +1)2 |
23 | (4х
+ 3)3(х2 + 2)2(х
— 3)4(2. |
24 | ((2х3 — 3)(5х2 +12х — 33))3 (2х + 0.5)2 |
25 | (3х — 7)5 (1 — 5х)(2 х3 + 4 х)2 (3 + 8х) |
26 | ((5х2 -125)(х — 3))6(3х + 2)2 |
27 | х(2х3 — 3х2 + 2)((х2 -1)(4 + 3х)(х + 5))2 |
28 | (4 х — 2х3 + 7)2 (х2 -1)(9 х 4 — х + 8)3 |
29 | (3х — 5х2 )((2 х -1)( х3 + 5)(7 х + 6))3 |
30 | (5х3 + 3х)((х2 — 4)(6 + х)(8х + 4))2 |
Разложите
алгебраическое выражение на множители.
№ | Алгебраическое выражение |
1 | х3 + 2 х2 + 4 х + 8 |
2 | 6 х3 + 55х2 +129 х + 90 |
3 | х4 + 2х3 — 72х2 — 416х — 640 |
4 | 2 х 4 + 4 х3 — 4 х — 2 |
5 | 9х5 + 36х4 + 9х3 — 90х2 — 36х + 72 |
6 | х4 + х3 — 9 х2 + 11х — 4 |
7 | 6 х3 + 62 х2 +184 х +168 |
8 | х4 + 7 х3 + 21х2 + 63х +10 |
9 | 3х5 +10х4 — 81х2 — 270х |
10 | 4х4 + х5 — 81х — 324 |
11 | 3х3 +19 х2 + 57 х + 90 |
12 | 2х4 +10х3 -16х — 80 |
13 | х5 + 5х4 -16х — 80 |
14 | х5 + х4 — 21х3 — 45х2 |
15 | х4 + 6х3 + 4х2 — 30х — 45 |
16 | 4 х 4 +14 х3 + 22 х2 + 35х + 30 |
17 | х4 + 2х3 — 143х2 -144х + 5164 |
18 | х6 + 4х3 + х5 + 4х2 — 48х -12х4 |
19 | 2х5 + 8х2 + х4 + 4х — 6х3 — 24 |
20 | 4х4 — 31х3 + 33х2 — 93х + 63 |
21 | 2х3 — 25х2 + 93х — 90 |
22 | 14х4 — 82х2 — 46х3 + 138х +120 |
23 | 3х4 + х3 — 22х2 — 4х + 40 |
24 | 6х4 + 23х3 — 9х2 — 92х — 60 |
25 | 16х4 + 76х3 + 68х2 — 76х — 84 |
26 | — х4 — 5х +12х3 + 60 — х5 — 5х2 |
27 | — 6 х2 + 58х +120 — 4 х3 |
28 | х4 + 7 х2 + 9 х3 + 63х |
29 | 16х3 — 67х2 + 64х — х4 — 252 |
30 | 5 х3 + 56 х2 +112 х -128 |
Разложите
рациональную дробь на простейшие дроби.
№ | Алгебраическое выражение | ||
1 | 5 х 4 + 7 х3 + 5 х — 4 | 16 | х4 + х3 — 5 х — 7 |
(х2 + 4)(х — 2)2(х2 -1) | (х2 + 4х +1)(х — 2)2(х2 -1) | ||
2 | 3х5 + 6 х3 + 5х -1 | 17 | х6 + 2 х -1 |
(х2 — 4х + 3)(х — 2)2(х2 -16) | (х2 — х + 5)(х — 3)3(х2 -1) | ||
3 | х3 + 2 х2 + 3х + 4 | 18 | х4 + х3 — 5 х — 7 |
(х2 — х)(3 — х)3 (х2 — 81) | (х2 + 4х +1)(х — 2)2(х2 -1) | ||
4 | х5 — 7 х 4 + 2 х — 8 | 19 | 2х6 — 3х4 + 9 |
(х3 — 4х2 + 5х)(х — 3)2(х2 -1) | (х2 — 2х -15)(4х +1)3 х | ||
5 | х5 + 2х3 + 9х2 — 7 | 20 | х5 + 2 х3 + 9 х2 — 7 |
(4х2 — 6х — 10)(5х + 3)2 х | (2х2 — 6х +1)(4х + 2)х3 | ||
6 | 6 х6 + 4 х2 + 9 х | 21 | 3х5 + х2 + 4х |
(х2 — 4)(2 — 3х)3(х2 — 4) | (3х2 — 6х)(х + 2)4 х2 | ||
7 | 2 х7 + 4 х2 +1 | 22 | 5х6 + 9 х3 +10 х +15 |
(25х2 — 30х — 5)(3х2 + х)2 | (5х2 -125)(6х2 + 2х)2 | ||
8 | х6 + 3х3 + 4 х +12 | 23 | 7х5 — 5х6 +1 |
(х2 — 25)(3х2 + 9х)3 | (х2 + 8х)х3(х2 — 9)2 | ||
9 | х7 + 2 х5 + 15х +14 | 24 | х7 + 2 х6 + 5х + 51 |
(х2 + 5 х + 13)(3х — 6)4 | (х2 + 3х +1)х2(х2 — 4)3 | ||
10 | 3х4 + 3х + 4 | 25 | 4 х4 + 5х3 + 2 х -1 |
(х2 -1)(2 — х)3 (х2 — 9) | (х2 — 4х + 5)(х -1)2(х2 — 9) | ||
11 | 3х5 + х2 + 4х | 26 | 6 х5 + 3х3 + 4 х +1 |
(5 х2 + 6 х -1)( х + 2)3( х — 3) | (5х2 + 6х -1)(х + 4)3(х2 — 4) |
12 | 7x5 — 3x3 + 7x + 77 | 27 | 4 x7 + 9 x6 + x + 5 |
(x2 +10x + 25)(x2 — 9)2 | (x2 + 3x)x2(x2 — 25)3 | ||
13 | 8x5 -14x3 + 34 | 28 | 5x6 + x5 — 4x + 21 |
x(x2 — x)(7 — x)3 | (2 x2 + x +14)(3 — 6 x)4 | ||
14 | x6 + 4x3 -14x2 + 35 | 29 | x6 — 3x3 + 6x +11 |
x(2 x2 + x)(5 — 2 x)4 | (x2 -10x + 25)(3x2 + 9)3 | ||
15 | 4x2 — 3x3 — x | 30 | x5 — 2 x3 + 9 x2 + 4 |
(x2 — 2x +1)(4x +1)2(x2 — 64) | (x2 — 6x +1)(x + 2)x4 |
Построить графики
предложенных многочленов y = fn (x) и найти все корни
уравнения fn (x) = 0 .
№ | Уравнение для многочленов y = fn (x) |
1 | 12x5 + 108x4 + 315x3 + 360x2 + 303x + 252 |
2 | x5 — 15x4 + 85x3 — 225x2 + 274x -120 |
3 | x5 — 87x3 + 82x2 +1032x -1728 |
4 | x5 — 4x4 — 36x3 + 226x2 — 397x + 210 |
5 | x5 — 2x4 — 45x3 + 230x2 — 376x +192 |
6 | 7x5 — 99x4 + 511x3 -1149x2 + 994x -120 |
7 | 2x5 — 9x4 — 34x3 + 231x2 — 346x +120 |
8 | 3x5 — 50x4 + 299x3 — 760x2 + 748x — 240 |
9 | 4x5 — 79x4 + 533x3 — 1481x2 + 1563x — 540 |
10 | 2x5 — 47x4 + 423x3 -1822x2 + 3736x — 2880 |
11 | 7x5 — 25x4 — 37x3 + 217x2 — 234x + 72 |
12 | 2x5 — 11x4 — 41x3 + 404x2 — 948x + 720 |
13 | x5 + 5x4 + 7x3 — x2 — 8x — 4 |
14 | 6x5 — 65x4 + 195x3 + 5x2 — 561x +180 |
15 | 6x5 + 15x4 — 372x3 + 771x2 -120x — 300 |
16 | 3x5 + 7x4 — 115x3 — 63x2 + 412x +140 |
17 | 4x5 — 61x3 — 28x2 + 57x + 28 |
18 | 16x5 + 76x4 — 588x3 -1272x2 +1112x + 2240 |
19 | 4x5 + 39x4 — 44x3 — 687x2 — 320x +1008 |
20 | 6x5 — 5x4 — 73x3 + 40x2 + 200x |
21 | x5 — 15x4 + 85x3 — 225x2 + 274x -120 |
22 | 8x5 + 36x4 — 158x3 — 81x2 + 315x |
23 | 24x5 +172x4 -186x3 -1507x2 + 297x + 2520 |
24 | 12x5 + 40x4 — 547x3 — 778x2 +136x +192 |
25 | 81x5 +675x4 — 846x3 — 3144x2 +1248x + 3456 |
26 | 64x5 + 64x4 — 564x3 -4x2 + 35x |
27 | 2x5 + 8x2 + x4 + 4x — 6x3 — 24 |
28 | x5 + 5x4 -16x — 80 |
29 | 3x5 +10x4 — 81x3 — 270x |
30 | 9x5 + 36x4 + 9x3 — 90x2 — 36x + 72 |
Графически
исследовать решение нелинейных уравнений
и для каждого корня получить решение.
№ | Уравнение | № | Уравнение |
1 | ln2( x -1) = 3cos2 x +1 | 16 | л/25 — x2 = arctg2x |
2 | 3П 01x 2 cos x = е • arcctg2x | 17 | sin x^ л/81 — x2 = 5 xarctgx |
3 | 10e «x = V 2nx + sin x | 18 | arctg 2 x
—
0. |
10 | X —4x = Vx3 + 4ecos3x x2 — 4 x + 8 | 25 | 2x —1 = Vx4 + 4esin2x x2 — 2x + 2 |
11 | 10 x — 2 „ „ 4/ — = 2cos2 x + 4 x 3 + x2 | 26 | x 2— 9 \ * =v X2 + 1ex cos x x2 + 4 |
12 | V64 — x2 log2 x = sin 3x | 27 | x2— 4 л ^ 1 ^„X sin X 2 = V xe X2 + 1 |
13 | 10е ~азx2 = V 2nx + x2 + 3sin x | 28 | 4xtg(0. |
14 | 5 • 3—x2 +1 = V3X + sin 2x | 29 | arctg2x — (x — 0.1)4 + sin2 x = 0 |
15 | 5n _ _01x2 rs cos 2 x = 3 • arcctg 2 x | 30 | sin2 x • V81 — x2 = 5e—x2 |
Решить уравнение y 0.
 Решение квадратных уравнений
Решение квадратных уравнений2x 4 + 5x 3 — 11x 2 — 20x + 12 = 0
Для начала нужно методом подбора найти один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 12 являются ±1, ±2, ±3, ±4, ±6, ±12. Начнем их подставлять по-очереди:
1: 2 + 5 — 11 — 20 + 12 = -12 ⇒ число 1
-1: 2 — 5 — 11 + 20 + 12 = 18 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 16 + 5 ∙ 8 — 11 ∙ 4 — 20 ∙ 2 + 12 = 0 ⇒ число 2 является корнем многочлена
Мы нашли 1 из корней многочлена. Корнем многочлена является 2, а значит исходный многочлен должен делиться на x — 2 . Для того, чтобы выполнить деление многочленов, воспользуемся схемой Горнера:
| 2 | 5 | -11 | -20 | 12 | |
| 2 |
В верхней строке выставляются коэффициенты исходного многочлена. В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
В первой ячейке второй строки ставится найденный нами корень 2. Во второй строке пишутся коэффициенты многочлена, который получится в результате деления. Они считаются так:
| Во вторую ячейку второй строки запишем число 2, просто перенеся его из соответствующей ячейки первой строки. | ||||||||||||
| 2 ∙ 2 + 5 = 9 | ||||||||||||
| 2 ∙ 9 — 11 = 7 | ||||||||||||
| 2 ∙ 7 — 20 = -6 | ||||||||||||
| 2 ∙ (-6) + 12 = 0 |
Последнее число — это остаток от деления. Если он равен 0, значит мы все верно посчитали.
Если он равен 0, значит мы все верно посчитали.
2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(2x 3 + 9x 2 + 7x — 6)
Но это еще не конец. Можно попробовать разложить таким же способом многочлен 2x 3 + 9x 2 + 7x — 6.
Опять ищем корень среди делителей свободного члена. Делителями числа -6 являются ±1, ±2, ±3, ±6.
1: 2 + 9 + 7 — 6 = 12 ⇒ число 1 не является корнем многочлена
-1: -2 + 9 — 7 — 6 = -6 ⇒ число -1 не является корнем многочлена
2: 2 ∙ 8 + 9 ∙ 4 + 7 ∙ 2 — 6 = 60 ⇒ число 2 не является корнем многочлена
-2: 2 ∙ (-8) + 9 ∙ 4 + 7 ∙ (-2) — 6 = 0 ⇒ число -2 является корнем многочлена
Напишем найденный корень в нашу схему Горнера и начнем заполнять пустые ячейки:
| Во вторую ячейку третьей строки запишем число 2, просто перенеся его из соответствующей ячейки второй строки. | ||||||||||||||||||
| -2 ∙ 2 + 9 = 5 | ||||||||||||||||||
| -2 ∙ 5 + 7 = -3 | ||||||||||||||||||
| -2 ∙ (-3) — 6 = 0 |
Таким образом мы исходный многочлен разложили на множители:
2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(2x 2 + 5x — 3)
Многочлен 2x 2 + 5x — 3 тоже можно разложить на множители. Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
Для этого можно решить квадратное уравнение через дискриминант , а можно поискать корень среди делителей числа -3. Так или иначе, мы придем к выводу, что корнем этого многочлена является число -3
| Во вторую ячейку четвертой строки запишем число 2, просто перенеся его из соответствующей ячейки третьей строки. | ||||||||||||||||||||||||
| -3 ∙ 2 + 5 = -1 | ||||||||||||||||||||||||
| -3 ∙ (-1) — 3 = 0 |
Таким образом мы исходный многочлен разложили на линейные множители:
2x 4 + 5x 3 — 11x 2 — 20x + 12 = (x — 2)(x + 2)(x + 3)(2x — 1)
А корнями уравнения являются.
I. Линейные уравнения
II. Квадратные уравнения
ax 2 + bx + c = 0, a ≠ 0, иначе уравнение становится линейным
Корни квадратного уравнения можно вычислять различными способами, например:
Мы хорошо умеем решать квадратные уравнения. Многие уравнения более высоких степеней можно привести к квадратным.
III. Уравнения, приводимые к квадратным.
замена переменной: а) биквадратное уравнение ax 2n + bx n + c = 0, a ≠ 0, n ≥ 2
2) симметрическое уравнение 3 степени – уравнение вида
3) симметрическое уравнение 4 степени – уравнение вида
ax 4 + bx 3 + cx 2 + bx + a = 0, a ≠ 0, коэффициенты a b c b a или
ax 4 + bx 3 + cx 2 – bx + a = 0, a ≠ 0, коэффициенты a b c (–b) a
Т.к. x = 0 не
является корнем уравнения, то возможно деление обеих частей уравнения на x 2 , тогда получаем:
.
Произведя замену решаем квадратное уравнение a (t 2 – 2) + bt + c = 0
Например, решим уравнение x 4 – 2x 3 – x 2 – 2x + 1 = 0, делим обе части на x 2 ,
, после замены получаем уравнение t 2 – 2t – 3 = 0
– уравнение не имеет корней.
4) Уравнение вида (x – a )(x – b )(x – c )(x – d ) = Ax 2 , коэффициенты ab = cd
Например, (x + 2 )(x +3 )(x + 8 )(x + 12 ) = 4x 2 . Перемножив 1–4 и 2–3 скобки, получим (x 2 + 14x + 24)(x 2 +11x + 24) = 4x 2 , разделим обе части уравнения на x 2 , получим:
Имеем (t + 14)(t + 11) = 4.
5) Однородное уравнение 2 степени – уравнение вида Р(х,у) = 0, где Р(х,у) – многочлен, каждое слагаемое которого имеет степень 2.
Ответ: -2; -0,5; 0
IV. Все приведенные уравнения узнаваемы и типичны, а как быть с уравнениями произвольного вида?
Пусть дан многочлен P n (x ) = a n x n
+ a n-1 x n-1 + . ..+a 1 x + a 0 , где a n
≠
0
..+a 1 x + a 0 , где a n
≠
0
Рассмотрим метод понижения степени уравнения.
Известно, что, если коэффициенты a являются целыми числами и a n = 1 , то целые корни уравнения P n (x ) = 0 находятся среди делителей свободного члена a 0 . Например, x 4 + 2x 3 – 2x 2 – 6x + 5 = 0, делителями числа 5 являются числа 5; –5; 1; –1. Тогда P 4 (1) = 0, т.е. x = 1 является корнем уравнения. Понизим степень уравнения P 4 (x ) = 0 с помощью деления “уголком” многочлена на множитель х –1, получаем
P 4 (x ) = (x – 1)(x 3 + 3x 2 + x – 5).
Аналогично, P 3 (1) = 0, тогда P 4 (x ) = (x – 1)(x –
1)(x 2 + 4x +5), т.е. уравнение P 4 (x) = 0 имеет корни x 1 = x 2 = 1.
Покажем более короткое решение этого уравнения (с помощью схемы Горнера).
| 1 | 2 | –2 | –6 | 5 | |
| 1 | 1 | 3 | 1 | –5 | 0 |
| 1 | 1 | 4 | 5 | 0 |
значит, x 1 = 1 значит, x 2 = 1.
Итак, (x – 1) 2 (x 2 + 4x + 5) = 0
Что мы делали? Понижали степень уравнения.
V. Рассмотрим симметрические уравнения 3 и 5 степени.
а) ax 3 + bx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.
б) ax 5 + bx 4 + cx 3
+ cx 2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень
уравнения до двух.
Например, покажем решение уравнения 2x 5 + 3x 4 – 5x 3 – 5x 2 + 3x + = 0
| 2 | 3 | –5 | –5 | 3 | 2 | |
| –1 | 2 | 1 | –6 | 1 | 2 | 0 |
| 1 | 2 | 3 | –3 | –2 | 0 | |
| 1 | 2 | 5 | 2 | 0 |
x = –1
Получаем (x – 1) 2 (x + 1)(2x 2
+ 5x + 2) = 0. Значит, корни уравнения: 1; 1; –1;
–2; –0,5.
Значит, корни уравнения: 1; 1; –1;
–2; –0,5.
VI. Приведем список различных уравнений для решения в классе и дома.
Предлагаю читателю самому решить уравнения 1–7 и получить ответы…
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0.
Тогда дискриминант — это просто число D = b 2 − 4ac .
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Основная формула корней квадратного уравнения
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод:
Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c /a )
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Вынесение общего множителя за скобку
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Цели:
- Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
- Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
- Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.
Тип урока : комбинированный.
Оборудование: графопроектор.
Наглядность: таблица «Теорема Виета».
Ход урока
1. Устный счет
а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а?
б) Сколько корней может иметь кубическое уравнение?
в) С помощью чего мы решаем уравнение третьей и четвертой степени?
г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2
2. Самостоятельная работа (в группах)
Самостоятельная работа (в группах)
Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»
1 группа
Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6
Составить уравнение:
B=1 -2-3+6=2; b=-2
с=-2-3+6+6-12-18= -23; с= -23
d=6-12+36-18=12; d= -12
е=1(-2)(-3)6=36
х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)
Решение . Целые корни ищем среди делителей числа 36.
р = ±1;±2;±3;±4;±6…
р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера
р 3 (x) = х 3 -х 2 -24x -36
р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2
р 2 (x) = х 2 -3х -18=0
х 3 =-3, х 4 =6
Ответ: 1;-2;-3;6 сумма корней 2 (П)
2 группа
Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5
Составить уравнение:
B=-1+2+2+5-8; b= -8
с=2(-1)+4+10-2-5+10=15; с=15
D=-4-10+20-10= -4; d=4
е=2(-1)2*5=-20;е=-20
8+15+4х-20=0 (это уравнение решает на доске 3 группа)
р = ±1;±2;±4;±5;±10;±20.
р 4 (1)=1-8+15+4-20=-8
р 4 (-1)=1+8+15-4-20=0
р 3 (x) = х 3 -9х 2 +24x -20
р 3 (2) = 8 -36+48 -20=0
р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5
Ответ: -1;2;2;5 сумма корней 8(Р)
3 группа
Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3
Составить уравнение:
В=-1+1-2+3=1;в=-1
с=-1+2-3-2+3-6=-7;с=-7
D=2+6-3-6=-1; d=1
е=-1*1*(-2)*3=6
х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)
Решение. Целые корни ищем среди делителей числа 6.
р = ±1;±2;±3;±6
р 4 (1)=1-1-7+1+6=0
р 3 (x) = х 3 — 7x -6
р 3 (-1) = -1+7-6=0
р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3
Ответ:-1;1;-2;3 Сумма корней 1(О)
4 группа
Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3
Составить уравнение:
B=-2-2-3+3=-4; b=4
с=4+6-6+6-6-9=-5; с=-5
D=-12+12+18+18=36; d=-36
е=-2*(-2)*(-3)*3=-36;е=-36
х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)
Решение. Целые корни ищем среди делителей числа -36
Целые корни ищем среди делителей числа -36
р = ±1;±2;±3…
р(1)= 1 + 4-5-36-36 = -72
р 4 (-2) = 16 -32 -20 + 72 -36 = 0
р 3 (х) = х 3 +2х 2 -9х-18 = 0
р 3 (-2)= -8 + 8 + 18-18 = 0
р 2 (х) = х 2 -9 = 0; x=±3
Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)
5 группа
Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4
Составить уравнение
х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)
Решение . Целые корни ищем среди делителей числа 24.
р = ±1;±2;±3
р 4 (-1) = 1 -10 + 35 -50 + 24 = 0
р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0
p 3 (-2) = -8 + 36-52 + 24 = О
р 2 (х) = x 2 + 7x+ 12 = 0
Ответ:-1;-2;-3;-4 сумма-10 (И)
6 группа
Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8
Составить уравнение
B=1+1-3+8=7;b=-7
с=1 -3+8-3+8-24= -13
D=-3-24+8-24= -43; d=43
х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске)
Решение . Целые корни ищем среди делителей числа -24.
Целые корни ищем среди делителей числа -24.
р 4 (1)=1-7-13+43-24=0
р 3 (1)=1-6-19+24=0
р 2 (x)= х 2 -5x — 24 = 0
х 3 =-3, х 4 =8
Ответ: 1;1;-3;8 сумма 7 (Л)
3. Решение уравнений с параметром
1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1)
Ответ записать в порядке возрастания
R=Р 3 (-1)=-1+3-m-15=0
х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0
По условию х 1 = — 1; Д=1+15=16
Р 2 (х) = х 2 +2х-15 = 0
х 2 =-1-4 = -5;
х 3 =-1 + 4 = 3;
Ответ:- 1;-5; 3
В порядке возрастания: -5;-1;3. (Ь Н Ы)
2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.
Решение: R=Р 3 (1) = Р 3 (-2)
Р 3 (1) = 1-3 + а- 2а + 6 = 4-а
Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а
x 3 -Зх 2 -6х + 12 + 6 = х 3 -Зх 2 -6х + 18
x 2 (x-3)-6(x-3) = 0
(х-3)(х 2 -6) = 0
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю, а другой при этом имеет смысл.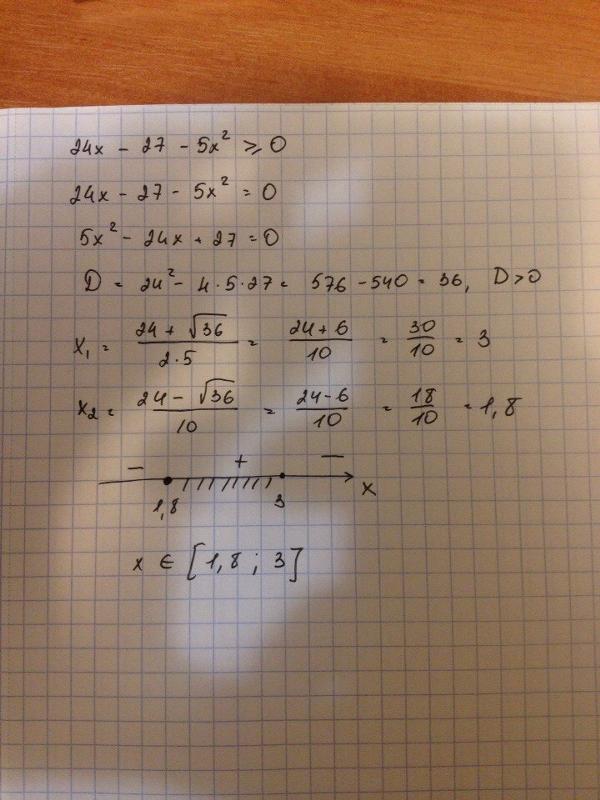
2 группа . Корни: -3; -2; 1; 2;
3 группа . Корни: -1; 2; 6; 10;
4 группа . Корни: -3; 2; 2; 5;
5 группа . Корни: -5; -2; 2; 4;
6 группа . Корни: -8; -2; 6; 7.
Презентация «Способы решения квадратных уравнений»
Слайд 1
Муниципальное бюджетное общеобразовательное учреждение «Макуловская средняя общеобразовательная школа» Верхнеуслонского муниципального района Республики Татарстан Исследовательская работа Выполнила ученица 9 класса Хабибулина Алия Руководитель : учитель математики Маханова Т.А. Россия, с.Макулово, 2013 год Способы решения квадратных уравнений
Слайд 2
Квадратные уравнения Когда уравнение решаешь, дружок, Ты должен найти у него корешок, Значение буквы проверить не сложно, Поставь в уравненье его осторожно. Коль верное равенство выйдет у вас, То корнем значенье зовите тот час. О.Севастьянова. Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Они находят широкое применение при решении огромного количества задач. Каждый уважающий себя человек должен научиться их решать.
Они находят широкое применение при решении огромного количества задач. Каждый уважающий себя человек должен научиться их решать.
Слайд 3
В школьном курсе математики изучаются некоторые способы решения квадратных уравнений. Однако, существуют и другие, которые позволяют очень быстро и рационально найти корни уравнения и получить ответ. Напомним уже известные способы и разберём несколько новых.
Слайд 4
1. Разложение на множители левой части уравнения Решим уравнение х 2 + 10х – 24 = 0 . Разложим на множители левую часть: х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х(х + 12) – 2(х + 12) = (х + 12)(х – 2). Уравнение примет вид : (х + 12)(х – 2) = 0 ; х + 12 = 0 или х – 2 = 0 х = -12. х = 2. Ответ: -12 ; 2. Решите уравнения: х 2 — х = 0 ; х 2 + 2х = 0 ; х 2 — 81 = 0 ; х 2 + 4х + 3 = 0 ; х 2 + 2х – 3 = 0 .
Слайд 5
2. Метод выделения полного квадрата (1 случай) Решим уравнение х 2 – 1 0х + 25 = 0 . Заметим, что левая часть уравнения представляет собой полный квадрат двучлена. Запишем уравнение в виде : (х – 5) 2 = 0 ; х – 5 = 0 ; х = 5. Ответ: 5. Решите уравнения: x 2 + 4 x + 4 = 0; x 2 – 2 x + 1 = 0; 36 x 2 + 12 x + 1 = 0; x 2 – 6 x + 9 = 0 .
Запишем уравнение в виде : (х – 5) 2 = 0 ; х – 5 = 0 ; х = 5. Ответ: 5. Решите уравнения: x 2 + 4 x + 4 = 0; x 2 – 2 x + 1 = 0; 36 x 2 + 12 x + 1 = 0; x 2 – 6 x + 9 = 0 .
Слайд 6
3. Метод выделения полного квадрата (2 случай) Решим уравнение х 2 + 6х – 7 = 0. Выделим квадрат двучлена в левой части уравнения. х 2 + 6х – 7 = х 2 + 6х + 3 2 – 3 2 – 7 = (х + 3) 2 – 9 – 7 = (х + 3) 2 – 16. Уравнение примет вид : (х + 3) 2 – 16 = 0 ; (х + 3) 2 = 16 ; х + 3 = 4 или х + 3 = — 4 х = 1. х = -7. Ответ: 1 ; — 7. Решите уравнения: х 2 – 8х +15 = 0 ; х 2 +12х +20 = 0 ; х 2 + 4х + 3 = 0 ; х 2 + 2х – 2 = 0 ;
Слайд 7
4. Решение квадратных уравнений по формуле I D 0 Решите уравнения: 2х 2 — 5х + 2 = 0 ; 6х 2 + 5х + 1 = 0 ; 4х 2 — 5х + 2 = 0 ; 2х 2 + 3х + 1 =0.
Слайд 8
5 . Решение квадратных уравнений по формуле II b = 2k ( четное число) Решите уравнения: 2х 2 — 6х + 4=0 ; х 2 — 18х +17=0 ; 3х 2 – 14х + 16 = 0 ; х 2 + 2х – 80 = 0.
Слайд 9
6. Решение уравнений с помощью теоремы, обратной теореме Виета Решим уравнение х 2 +10х – 24 = 0. а = 1, это приведённое квадратное уравнение. Заметим, что D>0 и х 1 х 2 = — 24, х 1 + х 2 = -10, значит х 1 = — 12, х 2 = 2. Ответ: — 12 ; 2 . Решите уравнения: х 2 — 7х — 30 = 0 ; х 2 +2х — 15 = 0 ; х 2 — 7х + 6 = 0 .
а = 1, это приведённое квадратное уравнение. Заметим, что D>0 и х 1 х 2 = — 24, х 1 + х 2 = -10, значит х 1 = — 12, х 2 = 2. Ответ: — 12 ; 2 . Решите уравнения: х 2 — 7х — 30 = 0 ; х 2 +2х — 15 = 0 ; х 2 — 7х + 6 = 0 .
Слайд 10
7. Свойства коэффициентов квадратного уравнения (1 случай) Если a + b + c = 0, то х 1 = 1, х 2 = с /a . Решим уравнение х 2 + 6х – 7 = 0, где а = 1, b = 6, с = — 7. Заметим, что D>0 и 1 + 6 – 7 = 0, значит х 1 = 1, х 2 = — 7 /1 = — 7 . Ответ: — 7 ; 1. Решите уравнения: х 2 – 2013х + 2012 = 0 ; 345 х 2 -137х -208 = 0 ; 3 х 2 +5х – 8 = 0 ; 5 х 2 + 4х – 9 = 0 ; 5 х 2 — 7х +2 = 0 .
Слайд 11
8 . Свойства коэффициентов квадратного уравнения ( 2 случай) Если a – b + c = 0, то х 1 = — 1 , х 2 = -с / а . Решим уравнение 3 х 2 +5х +2 = 0, где а = 3, b = 5, с = 2. Заметим, что D>0 и 3 — 5 + 2 = 0, значит х 1 = — 1, х 2 = — 2 / 3. Ответ: — 1 ; — 2/ 3. Решите уравнения: х 2 + 2013х + 2012 = 0 ; 11 х 2 +25х +14=0 ; 5 х 2 + 4х — 1=0 ; х 2 + 4х +3=0 ; 5 х 2 — 7х -12 =0 .
Слайд 12
9. Графическое решение квадратного уравнения Решим уравнение х 2 + 2х – 3 = 0. Запишем уравнение в виде х 2 = 3-2х. В одной и той же системе координат построим графики функций у = х 2 и у = 3-2х. Найдём абсциссы точек пересечения графиков : х 1 = 1, х 2 = -3. Ответ: — 3; 1. Решите уравнение: х 2 -х — 6=0 ; х 2 — 4х + 4=0 ; х 2 +4х +6=0 ; х 2 -2х — 3=0 ; х 2 +2х — 3=0 .
Слайд 13
10. Решение уравнений способом переброски Дано уравнение а х 2 + b х + с = 0. Умножим обе части уравнения на а, получим а 2 х 2 + а b х + ас = 0. Пусть ах = у, откуда х = у/а. Тогда у 2 + b у + ас = 0. Его корни у 1 и у 2 . Окончательно х 1 = у 1 /а, х 1 = у 2 /а. Решим уравнение 2 х 2 — 11х + 15 = 0. Перебросим коэффициент 2 к свободному члену: у 2 — 11у + 30 = 0. Согласно теореме, обратной теореме Виета у 1 = 5 и у 2 = 6. Значит х 1 = 5/2 и х 2 = 6/2 или х 1 = 2,5 и х 2 = 3. Ответ: 2,5 ; 3. Решите уравнение: 2 х 2 — 9х + 9 = 0 ; 10 х 2 — 11х + 3 = 0 ; 3 х 2 + 11х + 6 = 0 ; 6 х 2 + 5х – 6 = 0 .
Слайд 14
11. Решение уравнений с помощью циркуля и линейки Решим уравнение a х 2 + b х + c = 0 : Отметим на координатной плоскости точку S (- b :2 a; ( a + c ):2 a ) — центр окружности и точку А(0 ; 1). Построим окружность радиуса SA . Абсциссы точек пересечения окружности с осью Ох и есть корни исходного уравнения.
Слайд 15
Рассмотрим примеры : 1. Решим уравнение х 2 — 2х + 1= 0. S(1; 1), А(0 ; 1). Ответ: 1. 2. Решим уравнение х 2 + 4х — 5 = 0. S(- 2; — 2), A(0;1). Ответ: -5; 1. 3. Решите уравнение х 2 — 4х + 5 = 0. S(2; 3), A(0;1). Ответ: нет корней.
Слайд 16
12. Решение квадратных уравнений с помощью номограммы Номограмма для решения уравнения z 2 + px + q = 0 даёт значения положительных корней. Если уравнение имеет корни разных знаков или оба корня отрицательны, то необходимо воспользоваться специальной методикой их вычисления, также, как и в случае, когда коэффициенты p и q выходят за пределы шкал.
Слайд 17
13. Геометрический способ решения уравнения Решим уравнение у 2 — 6у – 16 = 0. Представим уравнение в виде у 2 — 6у = 16. На рисунке «изображено» выражение у 2 — 6у , т.е. из площади квадрата со стороной у дважды вычитается площадь квадрата со стороной 3. Значит у 2 – 6у + 9 есть площадь квадрата со стороной у-3. Выполнив замену у 2 — 6у = 16, получим (у-3) 2 = 16 + 9 ; у-3 = 5 или у-3 = — 5 у = 8 у = -2 Ответ: — 2; 8. Решить уравнение у 2 + 6у – 16 = 0.
Представим уравнение в виде у 2 — 6у = 16. На рисунке «изображено» выражение у 2 — 6у , т.е. из площади квадрата со стороной у дважды вычитается площадь квадрата со стороной 3. Значит у 2 – 6у + 9 есть площадь квадрата со стороной у-3. Выполнив замену у 2 — 6у = 16, получим (у-3) 2 = 16 + 9 ; у-3 = 5 или у-3 = — 5 у = 8 у = -2 Ответ: — 2; 8. Решить уравнение у 2 + 6у – 16 = 0.
Слайд 18
Заключение В ходе данной исследовательской работы мною были изучены способы решения полных квадратных уравнений ; Считаю, что работа помогла мне лучше подготовиться к ГИА по математике ; Данная презентация была предложена на школьной предметной конференции старшеклассников ; Я работала под девизом : «Научился сам – научи другого!».
Слайд 19
УЧИТЬСЯ НЕЛЕГКО, НО ИНТЕРЕСНО! Ян Амос Коменский (1592-1670), чешский педагог, писатель.
Слайд 20
Литература и источники Макарычев Ю.Н., Миндюк Н.Г., Нешков К. И., Суворова С.Б. Алгебра 8. – М. : Просвещение, 2005. Приложение «Математика» к газете «Первое сентября», №40 – 2000г. 2/x-2=16/x-2 найдите корень уравнения (если он единственный)
2/x-2=16/x-2 найдите корень уравнения (если он единственный)
Ответ
Ответ разместил: lizas7777
(2х² — х -7)² — (5х + 1)² = 0
Применим формулу разности квадратов
(2х² — х — 7 + 5х + 1) * (2х² — х — 7 — 5х — 1) = 0
(2х² +4х — 6) * (2х² — 6х — 8) = 0
Приравняв каждую скобку к 0, получим два уравнения
2х² +4х — 6 = 0 и 2х² — 6х — 8 = 0
Решим первое
2х² + 4х — 6 = 0
D = 4² — 4 * 2 * 6 = 16 — 48 = — 32 отрицательный, корней нет
Решим второе
2х² — 6х — 8 = 0
Сократив на 2, получим уравнение
х² — 3х — 4 = 0
D = 9 — 4 * 1 * (-4) = 9 + 16 = 25
√D = √25 = 5
х₁ = (3 + 5)/2 = 8/2 = 4 — наибольший корень
х₂ = (3 — 5)/2 = -2/2 = — 1 — наименьший корень
|x₁ — x₂| = |4 — (-1)| = |4+1| =5
ответ: 5
Ответ
Ответ разместил: nightlovell15
(3x²-7)/(x-3)=(6-2x²)/(x-3)
x≠3
3x²-7=6-2x²
5x²=13
x²=2,6
x1=-√2,6
x2=√2,6
x2-x1=2√2,6
Ответ
Ответ разместил: Андртян
1 пример: -10х²+9=0 Пусть х²=а, где а >=0, тогда а²-10а+9=0 а1=9, а2=9 (теорема виета) Если а1=9, то х²=9 х1=3 х2=-3 (посторонний корень, так как а больше или равен нуля) Если а2=1, то х²=1 х1=1 х2=-1 (посторонний корень) 2 пример: -5х²+2=0 Пусть х²=а, где а>=0, тогда 3а²-5а+2=0 D=b²-4ac, D=(-5)²-4*3*2=1. 2=4
2=4
x3=-2
x4=2
Разность наибольшего и наименьшего корней уравнения равна 3-(-3)=6
Ответ
Ответ разместил: denkarlay
Корни уравнения :-3, -1 , 1 , 3
разность равна=3-(-3)=6
Другие вопросы по: Алгебра
Вкакой из фраз () слово походил употребленно неправильно? (а)щенок походил на медвежонка, и его назвали умкой. (б)коля походил по комнате и успокоился. (в)гроссмейстер походил пешк…
01.03.2019 04:30
Ответов: 3
Переведите текст на . «я люблю глянцевые журналы такие как glamour, cosmopolitan и другие. так же мне нравятся местные газеты «из рук в руки», «всякая всячина» и др. я расскажу про…
01.03.2019 14:00
Ответов: 3
Написать сочинение к стихотворению «неохотно и не смело» или «листья» автор фёдор иванович тючев. (по плану) план. 1. какую картину природы создаёт поэт? 2.какие изобразительные ср…
01.03.2019 18:40
Ответов: 1
Сарай имеющий форму прямугольного сеном. 2/x-2=16/x-2 найдите корень уравнения (если он единственный) или разность наибол…
2/x-2=16/x-2 найдите корень уравнения (если он единственный) или разность наибол…
Популярные вопросы
Чтобы переправить туристов на другой берег реки, надо их рассадить в каждую лодку по 3 человека или по 5 человек. в этом случае свободных мест в лодках не будет. какое наименьшее к…
01.03.2019 02:20
Ответов: 1
Определите кокое количество теплоты потребуется для плавления 200г олова имеющего температуру 232 градусов цельсия….
01.03.2019 22:00
Ответов: 2
Катеты прям. треуг. =40 и 42см. на сколько радиус описанной окружности больше радиуса вписанной?…
02.03.2019 23:40
Ответов: 1
Вмагазин 11 пакетов с орехами массой по 1,5 кг и массой по 1,8 кг. масса орехов в пакетах по 1,5 кг равна массе орехов в пакетах по 1,8 кг. сколько пакетов с орехами по 1,5 кг заве…
03.03.2019 00:30
Ответов: 1
6. в каких парах слов представлены антонимы? а) тихий – странный; б) кричать – смеяться; в) ругать – хвалить; г) найти – потерять; д) обрести – утратить; е) узнать – забыть; ж) утр. ..
..
03.03.2019 03:40
Ответов: 1
Как ты считаешь, в чем польза добрых дел?…
03.03.2019 15:40
Ответов: 1
Маленький заряженный шарик массой m, подвешенный на лёгкой нерастяжимой непроводящей нити, помещают в горизонтальное однородное электрическое поле. нить отклоняется от вертикали на…
04.03.2019 12:40
Ответов: 2
Решить дробное уравнение 2третих х + 4 девятых х =3,2…
06.03.2019 21:10
Ответов: 3
Диагонали выпуклого четырехугольника abcd взаимно перпендикулярны и длины их равны 12,4см и 15см. найдите его площадь….
07.03.2019 14:10
Ответов: 2
Fe(no3)3 = fe2o3+ no2+o2 agno3 = ag + no2 +o2 ag(no3)3 = ag + no2 +o2 уровняйте…
07.03.2019 14:30
Ответов: 1
Больше вопросов по предмету: Алгебра Случайные вопросы
3-8 Чтобы найти a и b, составим решаемую систему.
Чтобы найти a и b, составим решаемую систему.1,-16 2,-8 4,-4
Поскольку ab отрицательно, a и b имеют противоположные знаки. Поскольку a+b отрицательно, отрицательное число имеет большее абсолютное значение, чем положительное. Перечислите все такие пары целых чисел, которые дают произведение -16.
1-16=-15 2-8=-6 4-4=0
Подсчитайте сумму для каждой пары.
a=-8 b=2
Решением является пара, которая дает сумму -6. 9{2}-4ac}}{2a}.
x=\frac{-\left(-6\right)±\sqrt{36-4\left(-16\right)}}{2}
Square -6.
x=\frac{-\left(-6\right)±\sqrt{36+64}}{2}
Умножьте -4 на -16.
x=\frac{-\left(-6\right)±\sqrt{100}}{2}
Прибавь 36 к 64.
x=\frac{-\left(-6\right)± 10}{2}
Извлеките квадратный корень из 100.
x=\frac{6±10}{2}
Противоположность -6 равна 6.
x=\frac{16}{2}
Теперь решите уравнение x=\frac{6±10}{2}, если ± равно плюсу. Добавьте 6 к 10. 92+6x=16 Решите для X, заполнив квадрат. .. Показать работу шаг за шагом
.. Показать работу шаг за шагом
Алгебра 2
Тэ М.
спросил 18.02.21ТААААААААААААААААААА… У меня сейчас очень большие проблемы с математикой, и у меня нет денег, чтобы платить за репетитора, так что я ценю это невероятное.
Подписаться І 3
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Эшли П. ответил 18.02.21
Репетитор
5,0 (33)
Успешный первокурсник колледжа с результатом 1500 баллов SAT
См. таких репетиторов
Смотрите таких репетиторов
Привет, Тэ!
Завершить квадрат может быть сложно, я помню, что мне тоже было нелегко его выучить.
Одна фраза, которая мне помогла, звучит так: «Половина, возведение в квадрат, добавление к обеим сторонам».
Что такое «Оно»?
Давайте сначала посмотрим на основную формулу вашего уравнения:
ax 2 +bx+c
Эта фраза относится к коэффициенту «В».
Давайте посмотрим на ваше уравнение:
x 2 +6x=16
B в этом уравнении будет 6, потому что это средний множитель.
Итак, вернемся к фразе: «Пополам, возведи в квадрат, прибавь к обеим сторонам»
6/2=3
3 2 =9
x 2 +6x+9=16+9
Это важно: теперь левая часть может быть приведена к факторизованной форме!
(x+3) 2 = 25
*Три — это число, которое получится, если вы разделите средний член пополам.
Теперь, чтобы решить, вы можете извлечь квадратный корень из обеих частей!
x+3=±√25
x+3=±5
Теперь изолируйте x
x=-3±5
-3+5=2
-3-5=-8
x=2 и -8
Надеюсь, это помогло!
Если у вас все еще есть проблемы, но вы не можете найти репетитора с финансовой точки зрения, я могу провести для вас бесплатный сеанс
Голосовать за 1 Понизить
Подробнее
Отчет
Джон Л. ответил 18.02.21
ответил 18.02.21
Репетитор
Новое в Византе
Выпускник Военно-морской академии с более чем 10-летним опытом преподавания
Об этом репетиторе ›
Об этом репетиторе ›
Сначала подумайте о примерах идеального квадрата и их механике. Например, если бы у вас было (x+1) 2 и вы должны были расширить его, вы бы получили x 2 + 2x +1. Точно так же, если бы у вас было (x+5) 2 , расширение было бы x 2 + 10х +25. Обратите внимание на возникающую здесь закономерность. Второй коэффициент – это удвоенный квадратный корень из последнего. Другими словами, в обоих случаях, если вы возьмете последнее число, извлечете из него квадратный корень и удвоите этот ответ, вы получите второй коэффициент. Это ключ к пониманию завершения квадрата.
Для этой задачи попросите посмотреть на первые два члена только x 2 + 6x. Каким должно быть третье число с учетом только что описанного шаблона. Это должно быть 9разложить на (x+3) 2 . Так что просто добавьте 9, но подождите — вы не можете просто добавить 9, если не сделаете это с обеими частями уравнения. Вот так:
Каким должно быть третье число с учетом только что описанного шаблона. Это должно быть 9разложить на (x+3) 2 . Так что просто добавьте 9, но подождите — вы не можете просто добавить 9, если не сделаете это с обеими частями уравнения. Вот так:
x 2 + 6x = 16 (исходное) — теперь добавьте 9 к обеим сторонам:
x 2 + 6x + 9 = 16 +9 или
x 2 + 6x +9 = 25 или
(x 2 + 6x +9 — 25 = 0 или
(x+3) 2 .- 25 = 0
Графически, путем преобразования, это сдвинутая кривая x 2 влево на 3 и вверх на 25.
Голосовать за 0 Понизить
Подробнее
Отчет
Юрий О. ответил 18.02.21
Репетитор
Новое в Византе
16 лет онлайн, 464 бывших проблемы SAT подробно изучены
См. таких репетиторов
таких репетиторов
Смотрите таких репетиторов
Завершение квадрата:
x 2 + 6x = 16
x 2 + 6x — 16 = 0
x 2 + 2 • 7 (90 = 906) • 906 х 2 ) + 2 • (3) • (х) + (3 2 ) — 3 2 — 16 = 0
(х 2 + 2 • 3 • х + 3 2 ) — 3 2 — 16 = 0
(х + 3) 2 — 9 — 16 = 0
(х + 3) 2 — 25 = 0
6 (113 913 9) (113 913 9)2 = 25Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас
Выберите эксперта и встретьтесь онлайн. Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Уравнения и неравенства
Принцип сложения
Изучив этот раздел, вы сможете:
1. Решать уравнения вида x + b = c, используя принцип сложения.
2. Использование принципа сложения
Когда мы используем знак равенства (=), мы указываем, что два выражения равны по значению. Это называется уравнением . Например, x + 5 = 23 — это уравнение. Выбирая определенные процедуры, можно шаг за шагом перейти от заданного уравнения к уравнению x = некоторому числу. Число является решением уравнения.
Одна из первых процедур, используемых при решении уравнений, нашла применение в нашем повседневном мире. Предположим, мы поместили 10-килограммовый ящик с одной стороны качелей и 10-килограммовый камень с другой стороны. Если центр ящика находится на таком же расстоянии от точки баланса, как и центр камня, мы ожидаем, что качели будут балансировать. Коробка и камень не выглядят одинаково, но имеют одинаковую ценность по весу. Если мы добавим 2-килограммовый свинцовый груз к центру веса каждого объекта одновременно, качели все равно должны балансировать. Результаты равны.
Предположим, мы поместили 10-килограммовый ящик с одной стороны качелей и 10-килограммовый камень с другой стороны. Если центр ящика находится на таком же расстоянии от точки баланса, как и центр камня, мы ожидаем, что качели будут балансировать. Коробка и камень не выглядят одинаково, но имеют одинаковую ценность по весу. Если мы добавим 2-килограммовый свинцовый груз к центру веса каждого объекта одновременно, качели все равно должны балансировать. Результаты равны.
Похожий принцип есть и в математике. Мы можем выразить это такими словами.
Принцип сложения
Если к обеим частям уравнения прибавить одно и то же число, результаты каждой стороны будут равны по значению.
Мы можем переформулировать это в символах таким образом.
Для действительных чисел a, b, c, если a=b thenat+tc=b+ec
Вот пример.
Если 3=6/2, то 3+5=6/2+5
Поскольку мы добавили одинаковое количество 5 к обеим сторонам, каждая сторона имеет одинаковую ценность.
3+5=6/2+5
8 =6/2+10/2
8 = 16/2
8=8
Мы можем использовать принцип сложения для решения уравнения.
ПРИМЕР 1 Найдите x. x + 16 = 20
x + 16 + (-16) = 20 + (-16) Используйте принцип сложения, чтобы добавить -16 к обеим частям.
x+0=4 Упростить.
x=4 Значение x равно 4.
Мы только что нашли решение уравнения. Решение — это значение переменной, которая делает уравнение верным. Затем мы говорим, что значение 4 в нашем примере удовлетворяет уравнению. Мы можем легко проверить, что 4 является решением, подставив это значение в исходное уравнение. Этот шаг называется проверка решения.
Чек . x + 16 = 20
4 + 16 ≟ 20
20 = 20 ✔
Когда одно и то же значение появляется с обеих сторон знака равных, мы называем уравнение Identity . Поскольку две части уравнения в нашей проверке имеют одинаковое значение, мы знаем, что исходное уравнение было решено правильно. Мы нашли решение.
Мы нашли решение.
Когда вы пытаетесь решить эти типы уравнений, вы замечаете, что вы должны добавить определенное число к обеим частям уравнения. Какой номер выбрать? Посмотрите на число, которое находится на той же стороне уравнения, что и х, то есть на число, прибавленное к х. Затем подумайте о числе, которое равно напротив знака . Это называется добавкой , обратной числа. Аддитивное значение, обратное 16, равно -16. Аддитивное обратное значение -3 равно 3. Число, которое нужно добавить к обеим частям уравнения, и есть это аддитивное обратное.
Неважно, в какой части уравнения стоит переменная. Термин x может быть справа или слева. В следующем примере член x будет справа.
ПРИМЕР 2 Решите для x. 14 =x- 3
14+3=x-3 +3 Добавьте 3 к обеим частям, так как 3 является аддитивной инверсией к -3. Это устранит -3 справа и изолирует x.
17 =x+0 Упростить.
17=x Значение x равно 17.
Проверить . 14 = x-3
14 ≟ 17-3 Замените x на 17.
14 =14 ✔ Упрощение. Это проверяет. Решение x = 17.
Прежде чем прибавлять число к обеим частям, всегда следует упростить уравнение. В следующем примере показано, как объединение чисел путем сложения по отдельности в обеих частях уравнения упрощает уравнение.
ПРИМЕР 3 Найдите х. 15 +2=3+x+2
17=x+5 Упростите, добавив.
17+ (-5) =x+5+(-5) Добавьте значение -5 к обеим частям, так как -5 является аддитивной величиной, обратной 5.
12=x Упростите. Значение x равно 12.
Чек . 15+2 = 3+x+2
15+2 ≟ 3+12+2 Замените x на 12 в исходном уравнении.
17=17 ✔ Проверено.
В примере 3 мы добавили -5 к каждой стороне. Вы можете вычесть по 5 с каждой стороны и получить тот же результат. В предыдущем уроке мы обсуждали, что вычитание 5 равносильно прибавлению минус 5. Понимаете, почему?
Понимаете, почему?
Мы можем определить, является ли значение решением уравнения, выполнив те же шаги, что и для проверки ответа. Подставьте проверяемое значение переменной в исходное уравнение. Мы получим тождество, если значение является решением.
ПРИМЕР 4 Является ли x = 10 решением уравнения -15 + 2 = x-3? Если это не так, найдите решение.
Подставим 10 вместо x в уравнение и посмотрим, получится ли тождество.
-15+2=х-3
-15+2=10-3
-13 ≠ 7 Это неправда. Это не личность.
Таким образом, x = 10 не является решением. Теперь возьмем исходное уравнение и решим, чтобы найти решение.
-15+2=x-3
-13=x-3 Упростите, добавив.
-13+3=x-3+3 Прибавьте 3 к обеим сторонам. 3 является аддитивной инверсией -3.
-10=x
Проверить, является ли решение x = -10. Значение x = 10 было неверным из-за ошибки знака. Мы должны быть особенно внимательны, чтобы писать правильный знак для каждого числа при решении уравнений.
ПРИМЕР 5 Найдите значение x, удовлетворяющее уравнению 1/5+x = -1/10+1/2
Чтобы объединить дроби, дроби должны иметь общие знаменатели. Наименьший общий знаменатель (LCD) дробей равен 10.
(1*2)/(5*2)+x = −1/10+(1*5)/(2*5) Замените каждую дробь на эквивалентная дробь со знаменателем 10.
2/10 + x = −1/10+5/10 Это эквивалентное уравнение.
2/10+x = 4/10 Упростите, добавив.
2/10+(-2/10)+x = 4/10+(-2/10) Добавить добавку, обратную 2/10, к каждой стороне
x=2/10 Сложите дроби.
x= 1/5 Упростите ответ.
Чек . Подставим 1/5 вместо x в исходное уравнение и посмотрим, получим ли мы тождество.
1/5+x = −1/10+1/2
1/5+1/5 ≟ −1/10+1/2 Подставьте 1/5 вместо x
2/5 ≟ −1/10 +1/2
2/5 = 4/10
2/5 = 2/5 ✔ Проверено.
Принцип умножения
Изучив этот раздел, вы сможете:
1. Решать уравнения вида 1/ax=b.
2. Решить уравнения вида ax = b.
Решить уравнения вида ax = b.
Решение уравнений вида 1/ax=b
Принцип сложения позволяет нам добавлять одно и то же число к обеим частям уравнения. Что произойдет, если мы умножим каждую часть уравнения на одно и то же число? Например, что произойдет, если мы умножим каждую часть уравнения на 3?
Чтобы ответить на этот вопрос, вернемся к нашему простому примеру с коробкой и камнем на сбалансированных качелях. Если мы утроим количество грузов с каждой стороны (мы умножаем каждую сторону на 3), качели все равно должны балансировать. «Значение веса» каждой стороны остается равным.
На словах мы можем сформулировать этот принцип так.
Принцип умножения
Если обе части уравнения умножить на одно и то же число, результаты каждой стороны
будут равны по значению.
В символах мы можем переформулировать принцип умножения таким образом.
|
Для действительных чисел a,b,c с #0 ifa@=b thenca=cb |
Давайте посмотрим на уравнение, в котором было бы полезно умножить каждую часть уравнения на 3.
ПРИМЕР 1 Найдите х. 1/3x=-15
Мы знаем, что (3)(1/3) = 1. Мы умножим каждую часть уравнения на 3, потому что мы хотим изолировать переменную x.
(3)(1/3x)=3(-15) Умножьте каждую часть уравнения на 3, так как (3)(1/3) = 1.
(3/1)(1/3)(x )=-45
1x=-45 Упрощение.
x= -45
Проверить . 1/3(-45) ≟ -15 Замените x на -45 в исходном уравнении.
-15=-15 ✔ Проверяет.
Обратите внимание, что 1/5x можно записать как x/5. Чтобы решить уравнение x/5=3, мы могли бы умножить каждую часть уравнения на 5. Попробуйте. Затем проверьте свое решение.
Решение уравнений вида ax = b
Мы можем видеть, что использование принципа умножения для умножения каждой стороны уравнения на 1/2 равносильно делению каждой стороны уравнения на 2. Таким образом, было бы кажется, что принцип умножения позволил бы нам разделить каждую часть уравнения на любое ненулевое действительное число. Есть ли реальный пример этой идеи?
Есть ли реальный пример этой идеи?
Вернемся к нашему простому примеру с коробкой и камнем на сбалансированных качелях. Предположим, что мы должны были разрезать два объекта пополам (так, чтобы количество веса каждого было разделено на 2). Затем мы возвращаем предметы на те же места на качелях. Качели все равно будут балансировать. «Значение веса» каждой стороны остается равным.
На словах мы можем сформулировать этот принцип так:
Принцип деления
Если обе части уравнения разделить на одно и то же ненулевое число, результаты
с каждой стороны равны по значению.
Примечание : Мы накладываем ограничение на число, на которое мы делим. Мы не можем разделить на ноль. Мы говорим, что такие выражения, как 2/0, не определены. Таким образом, мы ограничиваем наш делитель ненулевыми числами. Мы можем переформулировать принцип деления таким образом.
a b
Для действительных чисел a, b, c, где c ~ 0, если a=b, то — = —
coc
ПРИМЕР 2 Найдите x. 5x = 125
5x = 125
(5x)/5=125/5 Поделите обе части на 5.
x = 25 Упростите. Решение 25.
Чек . 5x = 125
5(25) ≟ 125 Замените x на 25.
125 = 125 ✔ Это проверяет.
Для уравнений вида ax = b (число, умноженное на x, равно другому числу), мы решаем уравнение, разделив обе части на определенное число. Какой номер выбрать? Смотрим на ту часть уравнения, которая содержит х. Мы замечаем число, которое умножается на х. Делим на это число. Принцип деления говорит нам, что у нас все еще может быть истинное уравнение, если мы разделим на это число 9.1612 с обеих сторон уравнения.
Решением уравнения может быть правильная или неправильная дробь.
ПРИМЕР 3 Решите для x. 4x = 38
(4x)/4= 38/4 Поделите обе части на 4.
x=19/2 Упростите. Решение 19/2.
Если оставить решение в виде дроби, будет легче проверить это решение в исходном уравнении.
Проверить : 4x = 38 Заменить x на 19/2.
4(19/2) ≟ 38
38 = 38 ✔ Проверяет.
В примерах 2 и 3 мы делили на число, умноженное на х (коэффициент при х). Эта процедура выполняется независимо от того, положительный или отрицательный знак этого числа.
ПРИМЕР 4 Найдите x. -3x = 48
(-3x)/-3=48/-3 Поделите обе части на -3.
x=-16 Решение равно -16.
Коэффициент x может быть 1 или -1. Возможно, вам придется переписать уравнение так, чтобы коэффициент 1 или -1 был очевиден. С практикой вы сможете «увидеть» коэффициент, фактически не переписывая уравнение.
ПРИМЕР 5 Найдите x. -x = -24
-1x = -24 Перепишите уравнение. -1x совпадает с -x. Теперь коэффициент -1 очевиден.
(-1x)/-1=-24/-1 Поделите обе части на -1
x= 24 Решение будет 24.
Используйте вместе принципы сложения и умножения
умеет:
1. Решать уравнения вида ax + b =c.
2. Решите уравнения, в которых переменная присутствует в обеих частях уравнения.
3. Решите уравнения со скобками.
Решение уравнений вида ax +b=c
Для решения многих уравнений мы должны использовать как принцип сложения, так и принцип умножения.
ПРИМЕР 1 Найдите x и проверьте свое решение. 5x +3 = 18
5x + 3 + (-3)= 18+ (-3) Добавьте -3 к обеим частям, используя принцип сложения.
5x = 15 Упростить.
(5x)/5=15/5 Поделите обе части на 5, используя принцип деления.
x=3 Решение 3.
Проверить . 5(3)+3 ≟ 18
Чек . 15+3 ≟ 18
Чек . 18=18 ✔ Проверил.
Переменная в обеих частях уравнения
В некоторых случаях переменная появляется в обеих частях уравнения. Мы хотели бы переписать уравнение так, чтобы все члены, содержащие переменную, оказались с одной стороны. Для этого применим принцип сложения к переменному члену.
ПРИМЕР 2 Решите для x. 9x = 6x + 15
9x = 6x + 15
9x + (-6x) = 6x + (-6x) + 15 Добавьте -6x к обеим сторонам. Обратите внимание, что 6x + (-6x) исключает переменную с правой стороны.
3x = 15 Соберите одинаковые члены.
(3x)/3=15/3 Поделите обе части на 3.
x=5 Решение равно 5.
Многие задачи имеют переменные и постоянные члены в обеих частях уравнения. Вы захотите получить все переменные члены с одной стороны и все постоянные члены с другой стороны.
ПРИМЕР 3 Найдите x и проверьте свое решение. 9х + 3 = 7х -2.
9x + (-7x) + 3 = 7x + (-7x) — 2 Добавьте -7x к обеим частям уравнения.
2x+3=-2 Комбинируйте одинаковые термины.
2x + 3+ (-3) = -2 + (-3) Добавьте -3 к обеим сторонам.
2x = -5 Упростить.
(2x)/2=-5/2 Поделите обе части на 2.
x = -5/2 Решение равно −5/2.
Чек . 9x + 3 = 7x -2
Чек . 9(-5/2)+3 ≟ 7(-5/2)-2 Замените x на −5/2.
Чек . −45/2+3 ≟ −35/2-2 Упростить.
Чек . −45/2+6/2 ≟ −35/2-4/2 Переведите в эквивалентные дроби с общим знаменателем.
Чек . −39/2 = −39/2 ✔ Это проверка. x = −5/2 является решением.
В следующем примере мы изучим уравнения, которые необходимо упростить, прежде чем предпринимать какие-либо другие шаги. Там, где это возможно, вы должны сначала собрать одинаковые члены в одной или обеих частях уравнения. Переменные члены могут быть собраны на правой или левой стороне. В этом примере мы соберем все термины x с правой стороны.
ПРИМЕР 4 Решите для x. 5x + 26 -6 = 9x + 12x
5x + 20 = 21x Соедините подобные термины.
5x + (-5x) + 20 = 21x + (-5x) Добавьте -5x к обеим сторонам.
20 = 16x Объедините одинаковые члены.
20/16 =(16x)/16 Разделите обе части на 16
5/4=x (Не забудьте уменьшить полученную дробь.)
Все уравнения, которые мы изучали до сих пор, называются первыми уравнения степени. 2, попытайтесь собрать их на одной стороне уравнения. Если квадратный член выпадает, вы можете решить его как уравнение первой степени, используя методы, обсуждаемые в этом разделе. 92 = 0.
2, попытайтесь собрать их на одной стороне уравнения. Если квадратный член выпадает, вы можете решить его как уравнение первой степени, используя методы, обсуждаемые в этом разделе. 92 = 0.
6y+y-2=-y+y+12 Добавьте y к каждой стороне.
7y-2= 12 Упростить.
7y-2+2=12+2 Добавьте по 2 с каждой стороны.
7y=14 Упрощение.
(7y)/7 = 14/7 Разделите каждую сторону на 7.
y=2 Упростите. Решение 2.
Решение уравнений со скобками
Уравнения, которые вы только что решили, представляют собой более простые версии уравнений, которые мы сейчас обсудим. Эти уравнения содержат круглые скобки. Если скобки сначала удалить, проблемы становятся такими же, как те, с которыми мы сталкивались ранее. Мы используем распределительное свойство, чтобы удалить круглые скобки.
ПРИМЕР 6 Найдите x и проверьте свое решение. 4(x + 1)- 3(x-3) = 25
4(x + 1)- 3(x-3) = 25
4x +4-3x+9 = 25 Умножьте на 4 и -3, чтобы убрать скобки. Будьте осторожны со знаками. Помните, что (-3)(-3) = 9.
Будьте осторожны со знаками. Помните, что (-3)(-3) = 9.
После удаления скобок важно собрать одинаковые члены с каждой стороны уравнения. Сделайте это, прежде чем переходить к изоляции переменной.
x + 13 = 25 Соберите одинаковые термины.
x+ 13-13 = 25-13 Добавьте -13 к обеим сторонам, чтобы изолировать переменную.
x = 12 Решение 12.
Проверить . 4(12+1)-3(12-3) ≟ 25 Замените x на 12.
4(13)-3(9) ≟ 25 Объедините числа в скобках.
52-27 ≟ 25 Умножить.
25=25 ✔ Упрощение. Это проверяет.
В задачах с десятичными дробями следует проявлять большую осторожность. На некоторых шагах вы будете умножать десятичные числа, а на других шагах вы будете их складывать.
ПРИМЕР 7 Найдите x. 0,3(1,2x-3,6) = 4,2x-16,44
0,36x-1,08 = 4,2x -16,44 Удалите скобки.
0,36x-0,36x-1,08 = 4,2x-0,36x-16,44 Вычтите 0,36x с обеих сторон.
-1,08 = 3,84x -16,44 Соберите одинаковые термины.
-1,08 + 16,44 = 3,84x-16,44 + 16,44 Прибавьте 16,44 к обеим сторонам.
15,36 = 3,84x Упростить.
15,36/3,84=(3,84x)/3,84 Поделите обе стороны на 3,84.
4=x Решение: x = 4.
ПРИМЕР 8 Найдите z и проверьте. 2(3z-5) + 2 = 4z -3(2z + 8)
6z-10 + 2 = 4z-6z-24 Удалите скобки.
6z- 8 = -2z-24 Соберите одинаковые термины.
6z-8 + 2z = -2z + 2z-24 Добавьте по 2z с каждой стороны.
8z-8 = -24 Упростить.
8z-8 +8 = -24+ 8 Добавьте 8 с каждой стороны.
8z =-16 Упрощение.
(8z)/8=-16/8 Разделите каждую сторону на 8.
z=-2 Упростите. Решение -2.
Чек . 2[3(-2)-5] +2 ≟ 4(-2)-3[2(-2) + 8] Замените z на -2.
2[-6-5] +2 ≟ -8 -3[-4 + 8] Умножить.
2[-11] +2 ≟ -8 -3[4] Упрощение.
-22 +2 ≟ -8 -12
-20 = -20 ✔ Проверяет.
Уравнения с дробями
Изучив этот раздел, вы сможете:
1. Решать уравнения с дробями.
Решение уравнений с дробями
Уравнения с дробями решить довольно сложно. Эта трудность просто из-за особой осторожности, которую мы обычно должны проявлять при вычислениях с дробями. Фактические процедуры решения уравнений одинаковы, с дробями или без них. Чтобы избежать лишней работы, преобразуем данное уравнение с дробями в эквивалентное уравнение, не содержащее дробей. как нам это сделать? Умножаем каждую часть уравнения на наименьший общий знаменатель всех дробей, содержащихся в уравнении. Затем мы используем распределительное свойство, так что LCD умножается на каждый член уравнения.
ПРИМЕР 1 Решите для x. 1/4x-2/3=5/12x
Сначала находим, что LCD = 12.
12(1/4x-2/3)=12(5/12x) Умножаем каждую сторону на 12
(12 /1)(1/4)(x)-(12/1)(2/3)=(12/1)(5/12)(x) Используйте распределительное свойство.
3x-8 = 5x Упростить.
3x + (-3x)-8 = 5x + (-3x) Добавьте -3x к каждой стороне.
-8 = 2x Упростить.
-8/2=(2x)/2 Поделить каждую сторону на 2.
-4= x Упростить.
Проверка . 1/4(-4)-2/3 ≟ 5/12(-4)
-1-2/3 ≟ -5/3
-3/3-2/3 ≟ -5/3
− 5/3 = -5/3 ✔ Проверяет.В примере 1 мы умножили каждую часть уравнения на LCD. Обычной практикой является немедленно перейти ко второму шагу и умножить каждое слагаемое на LCD, а не
ПРИМЕР 2 Решить x. (x+5)/7=x/4+1/2
x/7+5/7=x/4+1/2 Сначала запишем отдельными дробями
(28)(x/7)+( 28)(5/7)=(28)(x/4)+(28)(1/2) Мы видим, что LCD равно 28, поэтому мы умножаем каждое слагаемое на 28.
4x + 20 = 7x + 14 Упрощение.
4x-4x + 20 = 7x-4x + 14 Добавьте -4x к обеим сторонам.
20 = 3x + 14 Соберите одинаковые члены.
20-14=3x + 14- 14 Добавьте -14 к обеим сторонам.
6 = 3x Соберите одинаковые термины.
6/3=(3x)/3 Разделите обе части на 3.
2=x Решение: x = 2.
Если в задаче есть и скобки, и дроби, лучше сначала убрать скобки. Многие студенты считают полезным иметь письменную процедуру решения этих более сложных уравнений.
Процедура решения линейных уравнений
1. Удалите все скобки.
2. Если существуют дроби, умножьте все члены с обеих сторон на наименьший общий знаменатель всех дробей.
3. Соберите одинаковые термины, если это возможно. Если возможно, упростите числовую работу.
4. Добавьте или вычтите члены с обеих сторон уравнения, чтобы получить все члены с переменной на одной стороне уравнения.
5. Добавьте или вычтите значение в обеих частях уравнения, чтобы получить все члены, не содержащие переменную в другой части уравнения.
6. Разделите обе части уравнения на коэффициент при переменной.
7. Упростите решение (если возможно).
8. Проверьте свое решение.
Давайте используем каждый шаг в решении этого примера.
ПРИМЕР 3 Найдите x и проверьте свое решение. 1/3(x-2)= 1/5(x+4)+2
Шаг 1 x/3-2/3=x/5+4/5+2 Удалите скобки.
Шаг 2 15(x/3)-15(2/3) = 15(x/5) +15(4/5) +15(2) Умножить на ЖК-дисплей, 15.
Шаг 3 5x-10 = 3x + 12 + 30 Упростить.
5x-10 = 3x + 42 Упростить.
Шаг 4 5x-3x-10 = 3x-3x + 42 Добавьте -3x к обеим сторонам.
2x-10 = 42 Упростить.
Шаг 5 2x-10+ 10 = 42+ 10 Прибавьте 10 к обеим сторонам.
2x = 52 Упростить.
Шаг 6 (2x)/2=52/2 Разделите обе части на 2.
Шаг 7 x = 26 Упростите решение.
Шаг 8 Проверка . 1/3(26-2) ≟ 1/5(26 +4)+2 Замените x на 26.
1/3(24) ≟ 1/5(30)+2 Объедините значения в скобках.
8 ≟ 6+2 Упростить.
8 = 8 ✔ x=26 — это решение.
Следует помнить, что не каждый шаг будет необходим в каждой задаче. Вы также можете комбинировать некоторые шаги, если вы постоянно получаете правильное решение. Тем не менее, вам рекомендуется записывать каждый шаг, чтобы избежать ошибок по невнимательности.
Важно помнить, что когда мы пишем десятичные дроби, эти числа на самом деле представляют собой дроби, записанные особым образом. Таким образом, 0,3 = 7 и 0,07 = 745. Можно взять линейное уравнение, содержащее десятичные дроби, и умножить каждый член на соответствующее значение, чтобы получить целые коэффициенты.
Формулы
Изучив этот раздел, вы сможете:
1. Решать формулы для заданной переменной.
Решение указанной переменной в формуле
Формулы — это уравнения с одной или несколькими переменными, которые используются для описания реальных ситуаций. Формула описывает отношения, существующие между переменными. Например, в формуле d = rt расстояние (d) связано с показателем скорости (r) и временем (t). Мы можем использовать эту формулу, чтобы найти расстояние, если мы знаем скорость и время. Иногда, однако, нам дают расстояние и скорость, и нас просят найти время.
Например, в формуле d = rt расстояние (d) связано с показателем скорости (r) и временем (t). Мы можем использовать эту формулу, чтобы найти расстояние, если мы знаем скорость и время. Иногда, однако, нам дают расстояние и скорость, и нас просят найти время.
ПРИМЕР 1 Джозеф проехал 156 миль со средней скоростью 52 мили в час. Сколько времени понадобилось Иосифу, чтобы совершить путешествие?
d= rt Используйте формулу расстояния.
156 = 52t Подставьте известные значения переменных.
156/52=52/52t Поделите обе части уравнения на 52, чтобы найти t.
3=t Мы нашли t.
Джозефу потребовалось 3 часа, чтобы проехать 156 миль со скоростью 52 мили в час.
Если у нас есть много задач, требующих нахождения времени по расстоянию и скорости, может оказаться целесообразным переписать формулу с точки зрения времени.
ПРИМЕР 2 Решите для t. d=rt
d/r=(rt)/r Мы хотим изолировать t. Поэтому мы делим обе части уравнения на коэффициент при t, который равен r.
d/r=t Вы решили для указанной переменной.
Простое уравнение первой степени с двумя переменными можно рассматривать как уравнение прямой. Часто полезно найти у, чтобы упростить построение графика.
ПРИМЕР 3 Решите для y. 3x-2y = 6
-2y = 6-3x Мы хотим изолировать член, содержащий y, поэтому мы вычитаем 3x с обеих сторон.
(-2y)/(-2)= (6-3x)/(-2) Поделите обе части на коэффициент y.
y=6/-2+(-3x)/-2 Перепишите дробь.
y= 3/2x-3 Упростите и перегруппируйте.
Это известно как форма уравнения прямой с пересечением наклона.
Наша процедура решения уравнения первой степени может быть переписана так, чтобы получить процедуру решения формулы для заданной переменной.
Процедура решения формулы для указанной переменной
1. Удалите все скобки.
2. Если существуют дроби, умножьте все члены с обеих сторон на ЖКИ всех дробей.
3. Соберите одинаковые термины или упростите, если возможно.
4. Добавьте или вычтите члены с обеих сторон уравнения, чтобы получить все члены с нужной переменной на одной стороне уравнения.
5. Прибавьте или вычтите соответствующую величину, чтобы получить все члены, в которых нет нужной переменной на другой стороне уравнения.
6. Разделите обе части уравнения на коэффициент при нужной переменной.
7. Если возможно, упростите.
ПРИМЕР 4 Трапеция – четырехсторонняя фигура с двумя параллельными сторонами. Если параллельные стороны равны a и b, а высота равна h, площадь определяется как
A=h/2(a+b)
Решите это уравнение для a.
A=h/2(a+b)
A=(ha)/2+(hb)/2 Удалите скобки.
2(A) = 2((га)/2)+2((hb)/2) Умножьте все члены на 2.
2A = га + hb Упростите.
2A-hb = ha Мы хотим выделить термин, содержащий a. Поэтому мы вычитаем hb с обеих сторон.
(2A-hb)/h= (га)/h Поделите обе части на h (коэффициент при а).
(2A-hb)/h=a Решение получено.
Примечание : Хотя решение представлено в простой форме, его можно записать другим способом. Поскольку
(2A-hb)/h=(2A)/h-(hb)/h=(2A)/h-b
, мы могли бы иметь (2A)/h-b = a в качестве альтернативного способа записи ответа.
Написание и графическое отображение неравенств
Изучив этот раздел, вы сможете:
1. Интерпретировать утверждение о неравенстве.
2. Нарисуйте неравенство на числовой прямой.
Заявления о неравенстве
Мы часто говорим, что одно значение больше или меньше другого значения. Мы говорим, что «5 меньше 7» или «9 больше 4». Эти соотношения называются неравенствами . Мы можем записать неравенства в математике, используя символы. Мы используем символ < для представления слов «меньше чем». Мы используем символ > для представления слов «больше чем».
Заявление в словах в алгебре
5 меньше 7. 5 <7
9 больше 4. 9> 4
Примечание . «5 меньше 7» и «7 больше 5» имеют одинаковый смысл. Точно так же 5 < 7 и 7 > 5 имеют одинаковый смысл. Они представляют собой два эквивалентных способа описания одной и той же связи между двумя числами 5 и 7.
«5 меньше 7» и «7 больше 5» имеют одинаковый смысл. Точно так же 5 < 7 и 7 > 5 имеют одинаковый смысл. Они представляют собой два эквивалентных способа описания одной и той же связи между двумя числами 5 и 7.
Мы можем проиллюстрировать концепцию неравенства графически, если рассмотрим числовую прямую.
+++ +—_ +++ +_+_+—_—_+_¢_ _ +>
-5 -4 -3 -—2 -] 0 I 2 3 4 5 6 7 8
Мы говорим, что одно число больше другого, если оно находится справа от другого на числовой прямой. Таким образом, 7 > 5, так как 7 правее 5.
А как насчет отрицательных чисел? Мы можем сказать: «-1 больше, чем -3» и записать это символами -1 > -3, потому что мы знаем, что -1 лежит справа от -3 на числовой прямой.
ПРИМЕР 1 Замените вопросительный знак символом < или > в каждом утверждении.
(а) 3 ? -1 (б) -2 ? 1 (в) -3 ? -4 (г) 0 ? 3
(a) 3>-1 Используйте >, так как 3 находится справа от -1.
(b) -2< 1 Use <, поскольку -2 находится слева от 1. (Или, что то же самое, мы могли бы сказать, что 1 находится справа от -2.)
(Или, что то же самое, мы могли бы сказать, что 1 находится справа от -2.)
(c) -3 > -4 Так как -3 справа от -4.
(d) 0<3
Построение графика неравенства на числовой прямой
Иногда мы будем использовать неравенство, чтобы выразить связь между переменной и числом. x > 3 означает, что x может иметь значение любого числа больше 3. Это можно изобразить на числовой прямой на графике следующим образом:
-5 -4 -3 -2 -1 0 l 2 3 4 5
Обратите внимание, что незаштрихованный кружок на цифре 3 означает, что мы не включаем точку для числа 3.
-2 следующим образом:
$$ —} fj —_ + —_;_+_+_+_ + > x
-5 -4 -3 -2 -l 0 I 2 3 #4 = =# §
Иногда переменная больше или равна определенному числу. В утверждении «x больше или равно 3» мы подразумеваем, что x может иметь значение 3 или любое число больше 3. Мы запишем это как x >= 3. Мы представим это графически следующим образом:
—+—. >! 4H_{_AH_ ee ee et
—2 -1 0 l 2 3 4 5 6 7
Обратите внимание, что замкнутый кружок у 3 означает, что мы делаем включаем точку для числа 3.
x <= -2 следующим образом:
—— t+. et Ht HH HH
-5 -4 -3 -2 -1 0 1 2 3 4 5
ПРИМЕР 2 Назовите каждое математическое соотношение словами, а затем проиллюстрируйте его графически.
(а) x< -2 (б) -3 (a) Мы утверждаем, что «x меньше -2». x<-20 ——+-+—O—_1+—_+—_+—_++— (б) Мы можем утверждать, что -3 меньше x» или, эквивалентное утверждение, »x больше -3». Убедитесь, что вы видите, что -3 < x эквивалентно x > -3. Хотя оба способа верны, мы обычно записываем сначала переменную в простом линейном неравенстве, содержащем переменную и числовое значение. (c) Мы утверждаем, что «x меньше или равно -6». _-—od—_tH¥!_t—_t*—_+—_ +t + значение и неравенство. Мы можем перевести эти ситуации в алгебраические утверждения. Это первый шаг в решении текстовых задач с использованием неравенств. ПРИМЕР 3 Переведите каждое английское выражение в алгебраическое выражение. (a) Прибывшая на место полиция сообщила, что автомобиль двигался со скоростью более 80 миль в час (используйте переменную s для скорости). (b) Владелец автотранспортной компании сказал, что полезная нагрузка грузовика никогда не должна превышать 4500 фунтов (используйте переменную p для полезной нагрузки). (a) Поскольку скорость должна быть больше 80, мы имеем s > 80. (b) Если полезная нагрузка грузовика никогда не может превышать 4500 фунтов, то полезная нагрузка всегда должна быть меньше или равна 4500 фунтов. Таким образом, мы пишем p <= 4500. Изучив этот раздел, вы сможете: 1. Решить неравенство. Решение неравенств Возможные значения, которые делают неравенство верным, называются его решениями . Таким образом, когда мы решим неравенство , мы найдем все значения, которые делают его верным. Чтобы решить неравенство, мы упрощаем его до такой степени, что можем ясно видеть возможные значения переменной. Сначала мы рассмотрим закономерность, возникающую при выполнении данной операции с обеих сторон неравенства. Пример 1 Оригинальное неравенство Новое неравенство (a) 3 <5 → Умножение обеих сторон на 2 → 6 <10 (b) -2 -1 → ard-3 → 6 <10 (b) -1 ° °. стороны. → -5<-4 (c) 0>-4 → Поделить обе части на 2. → 0>-2 (d) 8 >4 → Вычтите 6 с обеих сторон. → 2>-2 Обратите внимание, что мы избегали умножения или деления на отрицательное число ! Теперь посмотрим, что произойдет, если мы умножим или разделим на отрицательное число. Оригинальное неравенство Новое неравенство 3 <5 → Умножение на -2. → 6 ? -10 Какой правильный знак неравенства? Поскольку -6 находится справа от -10, мы знаем, что новое неравенство должно быть -6 > -10, если мы хотим, чтобы утверждение оставалось верным. Обратите внимание, как мы меняем направление неравенства с < (меньше) на > (больше). Таким образом, мы получили бы новое неравенство -6 > -10. Таким образом, 3<5 → Умножить на -2. → -6>-10 Знак <, с которого мы начали (3 < 5), меняется на > (-6 > -10). Аналогичное обращение имеет место в следующем примере. Пример 2 Оригинальное неравенство Новое неравенство (a) -2 <-1 → Умножение на -3. → 6>3 (b) 0>-4 → Поделите обе части на -2. → 0<2 (c) 8 >4 → Поделите обе части на -4. Обратите внимание, что мы выполняем арифметические действия с числами со знаком так же, как всегда. Но новое неравенство имеет обратный знак неравенства (по сравнению с исходным неравенством). Всякий раз, когда обе части неравенства умножаются или делятся на отрицательное число, направление неравенства меняется на противоположное. Порядок решения неравенств ПРИМЕР 3 Решите и нарисуйте 3x + 7 >= 13. 3x +7-7>=13-7 Вычтите 7 с обеих сторон. 3x>= 6 Упростить. (3x)/3>=6/3 Обе части разделить на 3. x>=2 Упростить. Обратите внимание, что направление неравенства не изменилось, так как мы разделили на положительное число. Графическое представление en ee ПРИМЕР 4 Решите и начертите 5-3x > 7. 5-5-3x>7-5 Вычтите 5 с обеих сторон. -3x>2 Упрощение. (-3x)/-3<2/-3 Разделите на -3 и измените неравенство, так как обе части делятся на минус 3. x< -2/3 Обратите внимание на направление неравенства. Графическое представление Ht Ht Как и уравнения, некоторые неравенства содержат круглые скобки и дроби. Начальные шаги для решения этих неравенств будут такими же, как и для решения уравнений со скобками и дробями. Когда переменная появляется в обеих частях неравенства, целесообразно собрать члены x в левой части символа неравенства. 9ПРИМЕР 5 )(15/8) Умножьте все члены на LCD = 8. Мы делаем , а не , меняем направление символа неравенства на противоположное, поскольку мы умножаем на положительное число, 8. -52x <= 4x-5 Упростить. -52x-4x <= 4x-15-4x Добавьте -4x к обеим сторонам. -56x <= -15 Объедините одинаковые термины. (-56x)/56>= -15/-56 Поделите обе части на -56. x>=15/56 Графическое представление: 0 15 28 l Наиболее распространенная ошибка, которую учащиеся допускают при решении неравенств, — это забывание изменить направление символа неравенства на противоположное при умножении или делении на отрицательное число. Пример 1. Факторизация квадратного выражения: x 2 -8x -9 Перепишем это выражение как: x 2 -8x -9 x 2 — 9x + 1x -9 = x(x — 9) + 1 (x — 9) = (x — 9) (x + 1) Перепишем это выражение как: x 2 +13x -168 x 2 + 21x — 8x -168 = x(x + 21) — 8 (x + 21) = (x + 21) (x — 8) Перепишем это выражение следующим образом: x 2 +3x -40 x 2 + 8x — 5x -40 = x(x + 8) — 5 (x + 8) = (x + 8) (x — 5)
-4 -3 -2 -!1 0 ] 2
-7 -6 -5 -4 -3 -2 -1 0 л 2
Решать неравенства
 Мы решали уравнения путем сложения, вычитания, умножения и деления определенного значения в обеих частях уравнения. Здесь мы проделываем аналогичные операции с неравенствами, за одним важным исключением. Мы покажем несколько примеров, чтобы вы могли увидеть операции, которые мы можем выполнять с неравенствами так же, как и с уравнениями.
Мы решали уравнения путем сложения, вычитания, умножения и деления определенного значения в обеих частях уравнения. Здесь мы проделываем аналогичные операции с неравенствами, за одним важным исключением. Мы покажем несколько примеров, чтобы вы могли увидеть операции, которые мы можем выполнять с неравенствами так же, как и с уравнениями. Начнем с исходного, истинного неравенства. Мы хотим получить новое, тоже истинное неравенство.
Начнем с исходного, истинного неравенства. Мы хотим получить новое, тоже истинное неравенство. → -2<-1
→ -2<-1
| Вы можете использовать те же процедуры для решения неравенств, что и для решения уравнений, за исключением того, что направление неравенства меняется на противоположное, если вы умножаете или делите
обе части на отрицательное число.
—2 -Il 0 I 2 3 4
-1_2_1 0 l
3 3 мы изменить направление неравенства, если мы разделим обе части на отрицательное число.
мы изменить направление неравенства, если мы разделим обе части на отрицательное число.
56 56
. ] Факторизация квадратных выражений путем разделения средних членов
Средний член нужно разделить на два члена, произведение которых равно -9x 2 , а сумма остается -8x Пример 2. Факторизация квадратного выражения: x
2 +13x -168
Средний член нужно разделить на два члена, произведение которых равно -168x 2 а сумма остается +13x Пример 3.
 Факторизация квадратного выражения: x 2 +3x -40
Факторизация квадратного выражения: x 2 +3x -40
Средний член необходимо разделить на два члена, произведение которых равно — 40x 2 а сумма остается +3x перепишите это выражение как: x
2 +5x -300
Средний член необходимо разделить на два члена, произведение которых равно -300x 2 , а сумма остается +5x
x 2 — 15x + 20x -300
= x(x — 15) + 20 (x — 15)
= (x — 15) (x + 20)
Пример 5. Факторизация квадратного выражения: x
2 +32x +240 Перепишем это выражение как: x 2 +32x +240
Средний член нужно разделить на два члена, произведение которых равно +240x 2 , а сумма останется +32x
x 2 + 20x + 12x +240
= x(x + 20) + 12 (x + 20)
= (x + 20) (x + 12)
Пример 6.
 Факторизация квадратного выражения: x 2 -15x -216
Факторизация квадратного выражения: x 2 -15x -216 Перепишем это выражение как: x 2 -15x -216
Средний член необходимо разделить на два слагаемых, произведение которых равно -216x 2 , а сумма остается -15x
x 2 — 24x + 9x -216
= x(x — 24) + 9 (x — 24)
= (x — 24) (x + 9)
Пример 7. Факторизация квадратного выражения: x
2 -39x +380 Перепишем это выражение как: x 2 + -39 380
Средний член нужно разделить на два члена, произведение которых равно +380x 2 , а сумма остается -39x
x 2 — 20x — 19x +380
= x(x — 20) — 19 (x — 20)
= (x — 20) (x — 19)
91:367 квадратное выражение: x 2 +22x +85
Перепишем это выражение как: x 2 +22x +85
Средний член нужно разделить на два члена, произведение которых равно +85x 2 , а сумма остается +22x
x 2 + 5x + 17x +85
= x(x + 5) + 17 (x + 5)
= (x + 5) (x + 17)
Пример 9.
 Факторизация квадратного выражения: x 2 -13x -230
Факторизация квадратного выражения: x 2 -13x -230Перепишем это выражение как: x 2 -13x -4060 средний член необходимо разделить на два члена, произведение которых равно -230x 2 , а сумма остается -13x
x 2 — 23x + 10x -230
= x(x — 23) + 10 (x — 23 )
= (x — 23) (x + 10)
Пример 10: Факторизация квадратного выражения: x
2 -15x -76 Перепишем это выражение как: x 2 -15x -76
Средний член нужно разделить на два члена, произведение которых равно -76x 2 , а сумма остается -15x
x 2 — 19x + 4x -76
= x(x — 19) + 4 (x — 19)
= (x — 19) (x + 4)
Пример 11. Факторизация квадратного выражения: x
2 -17x +16 Перепишем это выражение как: x 2 -17x +16
Средний член необходимо разделить на два члена, произведение которых равно +16x 2 , а сумма остается -17x
x 2 — 16x — 1x +16
= x(x — 16) — 1 (x — 16)
= (x — 16) (x — 1)
Пример 12.
 Факторизация квадратного выражения: x 2 -21x +90
Факторизация квадратного выражения: x 2 -21x +90 Перепишем это выражение как: x 2 + -21150 90
Средний член необходимо разделить на два члена, произведение которых равно +90x 2 , а сумма остается -21x
x 2 — 15x — 6x +90
= x(x — 15) — 6 (x — 15)
= (x — 15) (x — 6)
Пример 13. Факторизация квадратичного уравнения выражение: x
2 -7x -170 Перепишем это выражение как: x 2 -7x -170
Средний член нужно разделить на два члена, произведение которых равно -170x 2 , а сумма остается — 7x
x 2 + 10x — 17x -170
= x(x + 10) — 17 (x + 10)
= (x + 10) (x — 17)
Пример 14. Факторизация квадратного выражения: x
2 +7x -78 Перепишем это выражение как: x 2 +7x -78
Середина член должен быть разделен на два члена, произведение которых равно -78x 2 , а сумма остается +7x
x 2 + 13x — 6x -78
= x(x + 13) — 6 (x + 13)
= (x + 13) (x — 6)
Пример 15: Факторизация квадратного выражения: x
2 -44x +483 Перепишем это выражение как: x 2 -44x +483
Средний член нужно разделить на два члена, произведение которых равно +483x 2 , а сумма остается -44x
x 2 — 21x — 23x +483
= x(x — 21) — 23 (x — 21)
= (x — 21) (x — 23)
Пример 16.
 Факторизация квадратного выражения: x 2 -6x -247
Факторизация квадратного выражения: x 2 -6x -247 Перепишем это выражение как: x 2 -6x -247
Средний член необходимо разделить на два члена, произведение которых равно -247x 2 , а сумма остается -6x
x 2 — 19x + 13x -247
= x(x — 19) + 13 (x — 19)
= (x — 19) (x + 13)
Пример 17. Факторизация квадратного выражения: x
2 -14x -32 Перепишем это выражение как: x 2 9114x — -1 32
Средний член нужно разделить на два члена, произведение которых равно -32x 2 , а сумма остается -14x
x 2 + 2x — 16x -32
= x(x + 2) — 16 (x + 2)
= (x + 2) (x — 16)
Пример 18. Факторизация квадратичного уравнения выражение: x
2 -8x -384 Перепишем это выражение как: x 2 -8x -384
Средний член нужно разделить на два члена, произведение которых равно -384x 2 , а сумма остается — 8x
x 2 + 16x — 24x -384
= x(x + 16) — 24 (x + 16)
= (x + 16) (x — 24)
Пример 19.
 Факторизация квадратного выражения: x 2 -10x -119
Факторизация квадратного выражения: x 2 -10x -119Перепишем это выражение как: x 2 -10x -116 Середина 6 необходимо разделить на два слагаемых, произведение которых равно -119x 2 , а сумма остается -10x
x 2 + 7x — 17x -119
= x(x + 7) — 17 (x + 7)
= (x + 7) (x — 17)
Пример 20: Факторизация квадратного выражения: x
2 -9x -10 Перепишем это выражение как: x 2 -9x -10
Средний член нужно разделить на два члена, произведение которых равно -10x 2 , а сумма останется -9x
x 2 + 1x — 10x -10
= x(x + 1) — 10 (x + 1)
= (x + 1) (x — 10)
Пример 21. Факторизация квадратного выражения: x
2 -25x +66 Перепишем это выражение как: x 2 -25x +66
Средний член нужно разделить на два члена, произведение которых равно +66x 2 пока остается сумма -25x
x 2 — 22x — 3x +66
= x(x — 22) — 3 (x — 22)
= (x — 22) (x — 3)
Пример 22.
 Факторизация квадратного выражения: x 2 +27x +140
Факторизация квадратного выражения: x 2 +27x +140 Перепишем это выражение следующим образом: x 2 +27x +140
Средний член нужно разделить на два члена, произведение которых равно + 140x 2 а сумма остается +27x
x 2 + 7x + 20x +140
= x(x + 7) + 20 (x + 7)
= (x + 7) (x + 20)
Перепишем это выражение как: x
2 -6x -72Средний член нужно разделить на два члена, произведение которых равно -72x 2 , а сумма останется -6x
x 2 + 6x — 12x — 72
= x(x + 6) — 12 (x + 6)
= (x + 6) (x — 12)
Пример 24. Факторизация квадратного выражения: x
2 -7x -30 Перепишем это выражение как: x 2 -7x -30
Средний член нужно разделить на два члена, произведение которых равно -30x 2 , а сумма останется -7x
x 2 — 10x + 3x -30
= x(x — 10) + 3 (x — 10)
= (x — 10) (x + 3)
Пример 25.
 Факторизация квадратного выражения: x 2 +13x -198
Факторизация квадратного выражения: x 2 +13x -198 Перепишем это выражение как: x 2 +13x -198
Средний член необходимо разделить на два слагаемых, произведение которых равно -198x 2 , а сумма остается +13x
x 2 + 22x — 9x -198
= x(x + 22) — 9 (x + 22)
= (x + 22) (x — 9)
Пример 26. Факторизация квадратного выражения: x
2 +32x +252 Перепишем это выражение в виде: 252
Средний член нужно разделить на два члена, произведение которых равно +252x 2 , а сумма остается +32x
x 2 + 18x + 14x +252
= x(x + 18) + 14 (x + 18)
= (x + 18) (x + 14)
выражение: x
2 +17x -38 Перепишем это выражение как: x 2 +17x -38
Средний член нужно разделить на два члена, произведение которых равно -38x 2 , а сумма остается + 17x
x 2 + 19x — 2x -38
= x(x + 19) — 2 (x + 19)
= (x + 19) (x — 2)
Пример 28.
 Факторизация квадратного выражения: x 2 +2x -48
Факторизация квадратного выражения: x 2 +2x -48 Перепишем это выражение как: x 2 +2x -48
Середина член необходимо разделить на два члена, произведение которых равно -48x 2 , а сумма остается +2x
x 2 — 6x + 8x -48
= x(x — 6) + 8 (x — 6)
= (x — 6) (x + 8)
Пример 29. Факторизация квадратного выражения: x
2 -20x -21 Перепишем это выражение как: x 2 -20x -21
Средний член нужно разделить на два члена, произведение которых равно -21x 2 , а сумма остается -20x
x 2 — 21x + 1x -21
= x(x — 21) + 1 (x — 21)
= (x — 21) (x + 1)
Пример 30. Факторизация квадратного выражения: x
2 +28x +195 Перепишем это выражение как: x 2 +28x +195
Средний член необходимо разделить на два члена, произведение которых равно +195x 2 , а сумма остается +28x
x 2 + 13x + 15x +195
= x(x + 13) + 15 (x + 13)
= (x + 13) (x + 15)
Пример 31.
 Факторизация квадратного выражения: x 2 -21x -22
Факторизация квадратного выражения: x 2 -21x -22 Перепишем это выражение как: x 2 911x — -2 22
Средний член нужно разделить на два члена, произведение которых равно -22x 2 , а сумма остается -21x
x 2 — 22x + 1x -22
= x(x — 22) + 1 (x — 22)
= (x — 22) (x + 1)
выражение: x
2 +24x +63 Перепишем это выражение как: x 2 +24x +63
Средний член нужно разделить на два члена, произведение которых равно +63x 2 , а сумма остается + 24x
x 2 + 3x + 21x +63
= x(x + 3) + 21 (x + 3)
= (x + 3) (x + 21)
Пример 33. Факторизация квадратного выражения: x
2 -10x -11 Перепишем это выражение как: x 2 -10x -11
Середина необходимо разделить на два слагаемых, произведение которых равно -11x 2 , а сумма остается -10x
x 2 + 1x — 11x -11
= x(x + 1) — 11 (x + 1)
= (x + 1) (x — 11)
Пример 34.
 Факторизация квадратного выражения: x 2 -29x +204
Факторизация квадратного выражения: x 2 -29x +204 Перепишем это выражение как: x 2 -29x +204
Средний член нужно разделить на два члена, произведение которых равно +204x 2 , а сумма остается -29x
x 2 — 12x — 17x +204
= x(x — 12) — 17 (x — 12)
= (x — 12) (x — 17)
Пример 35. Факторизация квадратного выражения: x
2 -6x -391 Перепишем это выражение как: x 2 -6x -391
Средний член нужно разделить на два члена, произведение которых равно -391x 2 , а сумма остается -6x
x 2 + 17x — 23x -391
= x(x + 17) — 23 ( x + 17)
= (x + 17) (x — 23)
Пример 36. Факторизация квадратного выражения: x
2 -28x +96 Перепишем это выражение как: x 2 — +96
Средний член необходимо разделить на два члена, произведение которых равно +96x 2 , а сумма остается -28x
x 2 — 24x — 4x +96
= x(x — 24) — 4 (x — 24)
= (x — 24) (x — 4)
выражение: x
2 +20x +19 Перепишем это выражение как: x 2 +20x +19
Средний член нужно разделить на два члена, произведение которых равно +19x 2 , а сумма останется + 20x
x 2 + 19x + 1x +19
= x(x + 19) + 1 (x + 19)
= (x + 19) (x + 1)
Пример 38.
 Факторизация квадратного выражения: x 2 -32x +240
Факторизация квадратного выражения: x 2 -32x +240 Перепишем это выражение как: x 2 -32x +240
Середина член должен быть разделен на два члена, произведение которых равно +240x 2 , а сумма остается -32x
x 2 — 20x — 12x +240
= x(x — 20) — 12 (x — 20)
= (x — 20) (x — 12)
Пример 39. Факторизация квадратного выражения: x
2 +13x -30 Перепишем это выражение как: x 2 +13x -30
Средний член нужно разделить на два члена, произведение которых равно -30x 2 , а сумма останется +13x
x 2 + 15x — 2x -30
= x(x + 15) — 2 (x + 15)
= (x + 15) (x — 2)
Пример 40. Факторизация квадратного выражения: x
2 +3x -504 Перепишем это выражение как: x 2 +3x -504
Средний член необходимо разделить на два члена, произведение которых равно -504x 2 , а сумма остается +3x
x 2 — 21x + 24x -504
= x(x — 21) + 24 (x — 21)
= (x — 21) (x + 24)
Пример 41.
 Факторизация квадратного выражения: x 2 -11x -276
Факторизация квадратного выражения: x 2 -11x -276Перепишем это выражение как: x 2
0 — — 276Средний член нужно разделить на два члена, произведение которых равно -276x 2 , а сумма остается -11x
x 2 + 12x — 23x -276
= x(x + 12) — 23 (x + 12)
= (x + 12) (x — 23)
выражение: x
2 +7x -18 Перепишем это выражение как: x 2 +7x -18
Средний член нужно разделить на два члена, произведение которых равно -18x 2 , а сумма остается + 7x
x 2 + 9x — 2x -18
= x(x + 9) — 2 (x + 9)
= (x + 9) (x — 2)
Пример 43. Факторизация квадратного выражения: x
2 -29x +168 Перепишем это выражение как: x 2 -29x +168
Середина необходимо разделить на два слагаемых, произведение которых равно +168x 2 , а сумма остается -29x
x 2 — 21x — 8x +168
= x(x — 21) — 8 (x — 21)
= (x — 21) (x — 8)
Пример 44.
 Факторизация квадратного выражения: x 2 -22x +72
Факторизация квадратного выражения: x 2 -22x +72 Перепишем это выражение как: x 2 -22x +72
Средний член нужно разделить на два члена, произведение которых равно +72x 2 , а сумма остается -22x
x 2 — 4x — 18x +72
= x(x — 4) — 18 (x — 4)
= (x — 4) (x — 18)
Пример 45. Факторизация квадратного выражения: x
2 -9x +8 Перепишем это выражение в следующем виде: x 2 -9x +8
Средний член нужно разделить на два члена, произведение которых равно +8x 2 пока остается сумма -9x
x 2 — 8x — 1x +8
= x(x — 8) — 1 (x — 8)
= (x — 8) (x — 1)
Пример 46. Факторизация квадратного выражения: x
2 +4x +4 Перепишем это выражение следующим образом: x 2 +4x +4
Средний член нужно разделить на два члена, произведение которых равно + 4x 2 , пока сумма остается +4x
x 2 + 2x + 2x +4
= x(x + 2) + 2 (x + 2)
= (x + 2) (x + 2)
Пример 47.
 Факторизация квадратного выражения: x 2 -15x -216
Факторизация квадратного выражения: x 2 -15x -216Перепишем это выражение как: x 2 -15x -4016 средний член необходимо разделить на два слагаемых, произведение которых равно -216x 2 , а сумма остается -15x
x 2 — 24x + 9x -216
= x(x — 24) + 9 (x — 24 )
= (x — 24) (x + 9)
Пример 48. Факторизация квадратного выражения: x
2 +32x +240 Перепишем это выражение как: x 2 +32x +240
Средний член нужно разделить на два члена, произведение которых равно +240x 2 , а сумма останется +32x
x 2 + 20x + 12x +240
= x(x + 20) + 12 (x + 20)
= (x + 20) (x + 12)
Пример 49. Факторизация квадратного выражения: x
2 -20x +64 Перепишем это выражение как: x 2 -20x +64
Средний член необходимо разделить на два члена, произведение которых равно +64x 2 , а сумма остается -20x
x 2 — 4x — 16x +64
= x(x — 4) — 16 (x — 4)
= (x — 4) (x — 16)
Пример 50.
 Факторизация квадратного выражения: x 2 -49x +600
Факторизация квадратного выражения: x 2 -49x +600 Перепишем это выражение как: x 2 + -49x 600
Средний член нужно разделить на два члена, произведение которых равно +600x 2 , а сумма остается -49x
x 2 — 24x — 25x +600
= x(x — 24) — 25 (x — 24)
= (x — 24) (x — 25)
91:367 квадратное выражение: x 2 -12x -13
Перепишем это выражение как: x 2 -12x -13
Средний член нужно разделить на два члена, произведение которых равно -13x 2 , а сумма остается -12x
x 2 — 13x + 1x -13
= x(x — 13) + 1 (x — 13)
= (x — 13) (x + 1)
Пример 52. Факторизация квадратного выражения: x
2 +23x +42Перепишем это выражение как: x 2 +22×4062 средний член необходимо разделить на два слагаемых, произведение которых равно +42x 2 , а сумма остается +23x
x 2 + 2x + 21x +42
= x(x + 2) + 21 (x + 2 )
= (x + 2) (x + 21)
Пример 53: Факторизация квадратного выражения: x
2 +11x -42 Перепишем это выражение как: x 2 +11x -42
Средний член нужно разделить на два члена, произведение которых равно -42x 2 , а сумма остается +11x
x 2 + 14x — 3x -42
= x(x + 14) — 3 (x + 14)
= (x + 14) (x — 3)
Пример 54.
 Факторизация квадратного выражения: x 2 -23x +120
Факторизация квадратного выражения: x 2 -23x +120 Перепишем это выражение как: x 2 -23x +120
Средний член необходимо разделить на два члена, произведение которых равно +120x 2 , а сумма остается -23x
x 2 — 15x — 8x +120
= x(x — 15) — 8 (x — 15)
= (x — 15) (x — 8)
Пример 55. Факторизация квадратного выражения: x
2 +16x +63 Перепишем это выражение как: x 2 + +16x 63
Средний член нужно разделить на два члена, произведение которых равно +63x 2 , а сумма остается +16x
x 2 + 9x + 7x +63
= x(x + 9) + 7 (x + 9)
= (x + 9) (x + 7)
выражение: x
2 +17x +60 Перепишем это выражение как: x 2 +17x +60
Средний член нужно разделить на два члена, произведение которых равно +60x 2 , а сумма остается + 17x
x 2 + 5x + 12x +60
= x(x + 5) + 12 (x + 5)
= (x + 5) (x + 12)
Пример 57.
 Факторизация квадратного выражения: x 2 -27x +180
Факторизация квадратного выражения: x 2 -27x +180 Перепишем это выражение следующим образом: x 2 -27x +180
Средний член нужно разделить на два члена, произведение которых равно + 180x 2 а сумма остается -27x
x 2 — 12x — 15x +180
= x(x — 12) — 15 (x — 12)
= (x — 12) )
Пример 58. Факторизация квадратного выражения: x
2 +17x +66 Перепишем это выражение как: x 2 +17x +66
Средний член нужно разделить на два члена, произведение которых равно +66x 2 , а сумма останется +17x
x 2 + 6x + 11x +66
= x(x + 6) + 11 (x + 6)
= (x + 6) (x + 11)
Пример 59. Факторизация квадратного выражения: x
2 -2x — 3 Перепишем это выражение как: x 2 -2x -3
Средний член нужно разделить на два члена, произведение которых равно -3x 2 пока остается сумма -2x
x 2 + 1x — 3x -3
= x(x + 1) — 3 (x + 1)
= (x + 1) (x — 3)
Пример 60.
 Факторизация квадратного выражения: x 2 +10x -336
Факторизация квадратного выражения: x 2 +10x -336 Перепишем это выражение следующим образом: x 2 +10x -336
Средний член необходимо разделить на два члена, произведение которых равно — 336x 2 а сумма остается +10x
x 2 + 24x — 14x -336
= x(x + 24) — 14 (x + 24)
= (x + 24) (x — 14)
перепишите это выражение как: x
2 -25x +114Средний член необходимо разделить на два члена, произведение которых равно +114x 2 , а сумма останется -25x
x 2 — 19x — 6x +114
= x(x — 19) — 6 (x — 19)
= (x — 19) (x — 6)
Пример 62. Факторизация квадратного выражения: x
2 +12x -189 Перепишем это выражение как: x 2 +12x -189
Средний член нужно разделить на два члена, произведение которых равно -189x 2 , а сумма остается +12x
x 2 + 21x — 9x -189
= x(x + 21) — 9 (x + 21)
= (x + 21) (x — 9)
Пример 63.
 Факторизация квадратного выражения: x 2 -8x -128
Факторизация квадратного выражения: x 2 -8x -128 Перепишем это выражение как: x 2 -8x -128
Средний член необходимо разделить на два члена, произведение которых равно -128x 2 , а сумма остается -8x
x 2 + 8x — 16x -128
= x(x + 8) — 16 (x + 8)
= (x + 8) (x — 16)
Пример 64. Факторизация квадратного выражения: x
2 -12x -325 Перепишем это выражение как: x 2 — -12 325
Средний член необходимо разделить на два члена, произведение которых равно -325x 2 , а сумма остается -12x
x 2 — 25x + 13x -325
= x(x — 25) + 13 (x — 25)
= (x — 25) (x + 13)
выражение: x
2 +10x +9 Перепишем это выражение как: x 2 +10x +9
Средний член нужно разделить на два члена, произведение которых равно +9x 2 , а сумма остается + 10x
x 2 + 9x + 1x +9
= x(x + 9) + 1 (x + 9)
= (x + 9)) (x + 1)
Пример 66.
 Факторизация квадратного выражения: x 2 -3x -40
Факторизация квадратного выражения: x 2 -3x -40 Перепишем это выражение следующим образом: x 2 -3x -40
Средний член необходимо разбить на два слагаемых, произведение которых равно -40x 2 , а сумма остается -3x
x 2 — 8x + 5x -40
= x(x — 8) + 5 (x — 8)
= (x — 8) (x + 5)
Пример 67. Факторизация квадратного выражения: x
2 +40x +391 Перепишем это выражение как: x 2 +40x +391
Средний член нужно разделить на два члена, произведение которых равно +391x 2 , а сумма останется +40x
x 2 91×150 + 23x + 17x +391
= x(x + 23) + 17 (x + 23)
= (x + 23) (x + 17)
Пример 68. Факторизация квадратного выражения: x
2 -18x +45 Перепишем это выражение как: x 2 -18x +45
Средний член нужно разделить на два члена, произведение которых равно +45x 2 пока остается сумма -18x
x 2 — 3x — 15x +45
= x(x — 3) — 15 (x — 3)
= (x — 3) (x — 15)
Пример 69.
 Факторизация квадратного выражения: x 2 +3x -238
Факторизация квадратного выражения: x 2 +3x -238 Перепишем это выражение следующим образом: x 2 +3x -238
Средний член необходимо разделить на два члена, произведение которых равно — 238x 2 , а сумма остается +3x
x 2 + 17x — 14x -238
= x(x + 17) — 14 (x + 17)
= (x + 17) (x — 14)
Пример 70. Факторизация квадратного выражения: x
2 +6x -315 перепишите это выражение как: x 2 +6x -315
Средний член необходимо разделить на два члена, произведение которых равно -315x 2 , а сумма остается +6x
x 2 — 15x + 21x -315
= x(x — 15) + 21 (x — 15)
= (x — 15) (x + 21)
Пример 71. Факторизация квадратного выражения: x
2 -8x -308 Перепишем это выражение как: x 2 -8x -308
Средний член нужно разделить на два члена, произведение которых равно -308x 2 , а сумма остается -8x
x 2 — 22x + 14x -308
= x(x — 22) + 14 (x — 22)
= (x — 22) (x + 14)
Пример 72.
 Факторизация квадратного выражения: x 2 +9x -190
Факторизация квадратного выражения: x 2 +9x -190 Перепишем это выражение как: x 2 +9x -190
Средний член нужно разделить на два члена, произведение которых равно -190x 2 , а сумма остается +9x
x 2 — 10x + 19x -190
= x(x — 10) + 19 ( x — 10)
= (x — 10) (x + 19)
Пример 73. Факторизация квадратного выражения: x
2 -11x -60 Перепишем это выражение в виде: -60
Средний член нужно разделить на два члена, произведение которых равно -60x 2 , а сумма остается -11x
x 2 + 4x — 15x -60
= x(x + 4) — 15 (x + 4)
= (x + 4) (x — 15)
выражение: x
2 +0x -25 Перепишем это выражение как: x 2 +0x -25
Средний член нужно разделить на два члена, произведение которых равно -25x 2 , а сумма остается + 0x
x 2 + 5x — 5x -25
= x(x + 5) — 5 (x + 5)
= (x + 5) (x — 5)
Пример 75.
 Факторизация квадратного выражения: x 2 +45x +504
Факторизация квадратного выражения: x 2 +45x +504 Перепишем это выражение следующим образом: x 2 +45x +504
Средний член нужно разделить на два члена, произведение которых равно + 504x 2 а сумма остается +45x
x 2 + 24x + 21x +504
= x(x + 24) + 21 (x + 24)
= (x + 24) )
Пример 76. Факторизация квадратного выражения: x
2 +0x -289 Перепишем это выражение как: x 2 +0x -289
Средний член нужно разделить на два члена, произведение которых равно -289x 2 , а сумма останется +0x
x 2 — 17x + 17x -289
= x(x — 17) + 17 (x — 17)
= (x — 17) (x + 17)
Пример 77. Факторизация квадратного выражения: x
2 -28x + 196 Перепишем это выражение как: x 2 -28x +196
Средний член нужно разделить на два члена, произведение которых равно +19.6x 2 а сумма остается -28x
x 2 — 14x — 14x +196
= x(x — 14) — 14 (x — 14)
= (x — 14) (x — 14) (x — 14) )
Пример 78.
 Факторизация квадратного выражения: x 2 -17x -18
Факторизация квадратного выражения: x 2 -17x -18 Перепишем это выражение следующим образом: x 2 -17x -18
Средний член нужно разделить на два члена, произведение которых -18x 2 , а сумма остается -17x
x 2 — 18x + 1x -18
= x(x — 18) + 1 (x — 18)
= (x — 18) (x + 1)
Перепишем это выражение как: x
2 -20x -96Средний член нужно разделить на два члена, произведение которых равно -96x 2 , а сумма останется -20x
x 2 — 24x + 4x — 96
= x(x — 24) + 4 (x — 24)
= (x — 24) (x + 4)
Пример 80. Факторизация квадратного выражения: x
2 +22x +117 Перепишем это выражение как: x 2 +22x +117
Средний член нужно разделить на два члена, произведение которых равно +117x 2 , а сумма останется +22x
x 2 + 9x + 13x +117
= x(x + 9) + 13 (x + 9)
= (x + 9) (x + 13)
Пример 81.
 Факторизация квадратного выражения: x 2 -11x -42
Факторизация квадратного выражения: x 2 -11x -42 Перепишем это выражение как: x 2 -11x -42
Средний член необходимо разделить на два слагаемых, произведение которых равно -42x 2 , а сумма остается -11x
x 2 + 3x — 14x -42
= x(x + 3) — 14 (x + 3)
= (x + 3) (x — 14)
Пример 82. Факторизация квадратного выражения: x
2 -19x +18 Перепишем это выражение как: x 2 + -19x 18
Средний член нужно разделить на два члена, произведение которых равно +18x 2 , а сумма остается -19x
x 2 — 18x — 1x +18
= x(x — 18) — 1 (x — 18)
= (x — 18) (x — 1)
Пример 83. Факторизация квадратное выражение: x
2 -8x -384 Перепишем это выражение как: x 2 -8x -384
Средний член нужно разделить на два члена, произведение которых равно -384x 2 , а сумма остается -8x
x 2 — 24x + 16x -384
= x(x — 24) + 16 (x — 24)
= (x — 24) (x + 16)
Пример 84.
 Факторизация квадратного выражения: x 2 +18x -63
Факторизация квадратного выражения: x 2 +18x -63Перепишем это выражение как: x 2 +18x -63 92x средний член необходимо разделить на два слагаемых, произведение которых равно -63x 2 , а сумма остается +18x
x 2 — 3x + 21x -63
= x(x — 3) + 21 (x — 3 )
= (x — 3) (x + 21)
Пример 85: Факторизация квадратного выражения: x
2 -30x +221 Перепишем это выражение как: x 2 -30x +221
Средний член нужно разделить на два члена, произведение которых равно +221x 2 , а сумма остается -30x
x 2 — 13x — 17x +221
= x(x — 13) — 17 (x — 13)
= (x — 13) (x — 17)
Пример 86. Факторизация квадратного выражения: x
2 +5x -456 Перепишем это выражение как: x 2 +5x -456
Средний член необходимо разделить на два члена, произведение которых равно -456x 2 , а сумма остается +5x
x 2 — 19x + 24x -456
= x(x — 19) + 24 (x — 19)
= (x — 19) (x + 24)
Пример 87.
 Факторизация квадратного выражения: x 2 -21x +80
Факторизация квадратного выражения: x 2 -21x +80 Перепишем это выражение как: x 2 911x + -2 80
Средний член нужно разделить на два члена, произведение которых равно +80x 2 , а сумма остается -21x
x 2 — 16x — 5x +80
= x(x — 16) — 5 (x — 16)
= (x — 16) (x — 5)
выражение: x
2 -32x +207 Перепишем это выражение как: x 2 -32x +207
Средний член нужно разделить на два члена, произведение которых равно +207x 2 , а сумма остается — 32x
x 2 — 9x — 23x +207
= x(x — 9) — 23 (x — 9)
= (x — 9) (x — 23)
Пример 89. Факторизация квадратного выражения: x
2 +32x +240 Перепишем это выражение как: x 2 +32x +240
Середина нужно разделить на два слагаемых, произведение которых равно +240x 2 , а сумма остается +32x
x 2 + 20x + 12x +240
= x(x + 20) + 12 (x + 20)
= (x + 20) (x + 12)
Пример 90: Факторизация квадратного выражения: x
2 -2x -15 Перепишем это выражение как: x 2 -2x -15
Средний член нужно разделить на два члена, произведение которых равно -15x 2 , а сумма остается -2x
x 2 — 5x + 3x -15
= x(x — 5) + 3 (x — 5)
= (x — 5) (x + 3)
Пример 91.
 Факторизация квадратного выражения: x 2 -37x +300
Факторизация квадратного выражения: x 2 -37x +300 Перепишем это выражение как: x 2 -37x +300
Средний член нужно разделить на два члена, произведение которых равно +300x 2 пока остается сумма -37x
x 2 — 25x — 12x +300
= x(x — 25) — 12 (x — 25)
= (x — 25) (x — 12)
Пример 92. Факторизация квадратного выражения: x
2 -21x +54 Перепишем это выражение следующим образом: x 2 -21x +54
Средний член нужно разделить на два члена, произведение которых равно + 54x 2 а сумма остается -21x
x 2 — 18x — 3x +54
= x(x — 18) — 3 (x — 18)
= (x — 18) (x — 3)
Пример 93. Факторизация квадратного выражения: x
2 +26x +88 Перепишем это выражение как: x 2 +26x +88
Средний член нужно разделить на два члена, произведение которых равно +88x 2 , а сумма останется +26x
x 2 + 4x + 22x + 88
= х(х + 4) + 22 (х + 4)
= (х + 4) (х + 22)
Пример 94.
 Разложите на множители квадратное выражение: x 2 -27x +72
Разложите на множители квадратное выражение: x 2 -27x +72. Перепишем это выражение следующим образом: x 2 -27x +72
Средний член нужно разделить на два члена, произведение которых равно +72x 2 а сумма остается -27x
x 2 — 3x — 24x +72
= x(x — 3) — 24 (x — 3)
= (x — 3) (x — 24)
Пример 95. Факторизация квадратного выражения: x
2 -5x -6 Перепишем это выражение как: x 2 -5x -6
Средний член нужно разделить на два члена, произведение которых равно -6x 2 , а сумма остается -5x
x 2 + 1x — 6x -6
= x(x + 1) — 6 (x + 1)
= (x + 1) (x — 6)
Пример 96. Факторизация квадратного выражения: x
2 +10x -56 Перепишем это выражение как: x 2 +10x -56
Средний член необходимо разделить на два члена, произведение которых равно -56x 2 пока сумма остается +10x
x 2 — 4x + 14x -56
= x(x — 4) + 14 (x — 4)
= (x — 4) (x + 14)
Пример 97.
 Факторизация квадратного выражения: x 2 +12x +20
Факторизация квадратного выражения: x 2 +12x +20 Перепишем это выражение следующим образом: x 2 +12x +20
Средний член нужно разделить на два члена, произведение которых равно +20x 2 пока остается сумма +12x
x 2 + 10x + 2x +20
= x(x + 10) + 2 (x + 10)
= (x + 10) (x + 2)
перепишите это выражение как: x
2 -36x +323Средний член необходимо разделить на два члена, произведение которых равно +323x 2 , а сумма останется -36x
x 2 — 17x — 19x +323
= х(х — 17) — 19 (х — 17)
= (х — 17) (х — 19)
Пример 99. Разложите на множители квадратное выражение: x
2 +3x +2. Перепишем это выражение следующим образом: x 2 +3x +2
Средний член нужно разделить на два члена, произведение которых равно +2x 2 а сумма остается +3x
x 2 + 2x + 1x +2
= x(x + 2) + 1 (x + 2)
= (x + 2) (x + 1)
Пример 100.
 {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le.
X2+6x+8, то это (x+4)(x+2) при факторизации.
4, 5, 1 и 5.
Найдите пару целых чисел, произведение которых равно c c, а сумма равна b b.
9{\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le.
Система оценивания присваивает баллы качества буквенным оценкам следующим образом:
Установите первый множитель равным и решите.
{\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le.
X2+6x+8, то это (x+4)(x+2) при факторизации.
4, 5, 1 и 5.
Найдите пару целых чисел, произведение которых равно c c, а сумма равна b b.
9{\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le.
Система оценивания присваивает баллы качества буквенным оценкам следующим образом:
Установите первый множитель равным и решите.Показать изображение
= (х + 6) (х + 2) Коэффициент. 1. х 2 +8х + 12 2. х 2 +16х + 48
Но моя книга говорит, что это не так. Я сделал это, используя метод переменного тока. Чтобы решить уравнение, размножьте x 2 − 6 x − 1 6, используя формулу x 2. 92 + bx + c учиться с помощью карточек, игр и многого другого — бесплатно. Система завершите предложения, чтобы объяснить, какие шаги были предприняты для получения системы уравнений ниже.
Показать изображение
= (х + 6) (х + 2) Коэффициент.
 1. х 2 +8х + 12 2. х 2 +16х + 48
1. х 2 +8х + 12 2. х 2 +16х + 48Я рассчитал это так: Возврат до 2,56 долларов США, что является факторизованной формой x2 6x 16. У этих курсов было соответствующее количество кредитных часов: 925x+6 с коэффициентом
Возврат до 2,56 долларов США, что является факторизованной формой x2 6x 16. A = 4, b = 3, c = 2, d = 1 и f = 0. Система оценивания присваивает баллы качества буквенным оценкам следующим образом:
Показать изображение
Ответил A. Направления Сопоставьте следующее… bartleby
Вычислите средний балл успеваемости (gpa) и округлите результат до двух знаков после запятой. Запишите факторизованную форму, используя эти целые числа. 4, 5, 1 и 5. 9{\msquare} \log_ {\msquare} \sqrt {\square} \nthroot [\msquare] {\square} \le. Что из следующего является факторизованной формой (формой пересечения) функции f(x)?
Показать изображение
👍 правильный ответ на вопрос вопрос 2 из 9 введите правильный ответ в поле. Вы искали дробный калькулятор с корнями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор дробей с корнями, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «дробный калькулятор с корнями». Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как дробный калькулятор с корнями,калькулятор дробей с корнями,калькулятор дробей со степенями и корнями,калькулятор дробей со степенями онлайн с решением,калькулятор квадратов чисел,калькулятор корень уравнения,калькулятор онлайн корней уравнений,калькулятор онлайн с дробями и корнями онлайн калькулятор,калькулятор онлайн с дробями и с корнями калькулятор,калькулятор онлайн с корнями и дробями онлайн калькулятор,калькулятор радикалов,калькулятор с дробями и корнями и степенями,калькулятор с корнями дробный,калькулятор с корнями и дробями,калькулятор с корнями и дробями и степенями,калькулятор с корнями и дробями онлайн,калькулятор с корнями и степенями и дробями,калькулятор с корнями с решением,калькулятор с кубами и квадратами,калькулятор сокращения дробей с буквами и степенями онлайн,калькулятор степеней с дробями онлайн,калькулятор уравнений с корнями,найти значение выражения с дробями и степенями онлайн,онлайн калькулятор квадратов,онлайн калькулятор корней с решением,онлайн калькулятор корней уравнений,онлайн решение выражений с корнями,онлайн решение примеров с корнями,онлайн решить пример с корнями,решение выражений с корнями онлайн,решение примеров онлайн с корнями,решение примеров с корнями онлайн,решение примеров с корнями онлайн калькулятор с решением,решить выражение онлайн с корнями,решить выражение с корнями онлайн,решить онлайн пример с корнями,решить пример онлайн с корнями,сложение корней калькулятор,сократить дробь с корнями онлайн калькулятор. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и дробный калькулятор с корнями. Просто введите задачу в окошко и нажмите
«решить» здесь (например, калькулятор дробей со степенями и корнями). Решить задачу дробный калькулятор с корнями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора. В зависимости от возможностей и сферы применения калькуляторы бывают простые, бухгалтерские, финансовые, инженерные. Отдельно выделяются: Простейший калькулятор предназначен выполнять ординарные арифметические расчеты (сложение, вычитание и т.п.), вычислять процент, извлекать квадратный корень, возводить число в степень. Помимо простых расчетов, строителям и архитекторам, инженерно-техническим и научным работникам, математикам и геодезистам, старшеклассникам и студентам технических специальностей очень часто приходится решать важнейшие инженерные задачи, осуществлять сложные математические расчеты. Представленный на сайте тригонометрический калькулятор выполняет расчет: А также обратных тригонометрических функций: Все тригонометрические расчеты с углами выполняются в радианах, градах и градусах. На нашем сайте вы сможете пользоваться инженерным онлайн калькулятором, предназначенным для инженерных и научных расчетов разного уровня сложности. Инженерный калькулятор позволяет: Онлайн калькулятор прост и понятен в обращении, применять его не составит труда тем, кто пользуется настольным инженерным калькулятором, принципы работы функций и программ аналогичны. По своему виду инженерный калькулятор онлайн имитирует настоящий калькулятор, поэтому для ознакомления с ним вам не понадобится много времени. Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы? В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений. Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы? В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений. С его помощью вы сможете вводить данные, при этом используя интерфейсные визуальные кнопки либо непосредственно клавиатуру. Кроме этого предоставленный калькулятор онлайн позволить осуществить расчеты сложных выражений, к примеру:(21-45)/(1.52)(8+2*2)=-96. Наверняка в повседневной жизни вы сталкивались с такой ситуацией, что вам требовалось решить простое уравнение или выполнить несколько иных математических действий, чтобы произвести финансовые расчеты, например, при расчете выгодности вклада в банк или насколько подходит ипотечный кредит по условиям, а под рукой на тот момент не оказалось обыкновенного электронного калькулятора или специальной программы. В таком случае для вас незаменимым станет этот удобный и простой в применении онлайн калькулятор уравнений. 2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним: 1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения). 2. Если , то (правило извлечения корня из дроби). 3. Если , то (правило извлечения корня из корня). 4. Если , то (правило возведения корня в степень). 5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число. 6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня. 7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например: (правило умножения корней), (правило деления корней), 8. Правило вынесения множителя из-под знака корня. При . 9. Обратная задача — внесение множителя под знак корня. Например, 10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним. Выполнить действия со степенями самостоятельно, а затем посмотреть решения. Калькулятор предназначен для решения показательных уравнений онлайн. Калькулятор предназначен для решения показательных уравнений онлайн. Для того чтобы найти решение показательного уравнения, необходимо ввести это уравнение в ячейку. В ответе получаем корни уравнения, а также график показательной функции. Решения показательных уравнений. Показательная функция всегда монотонна и она принимает только положительные значения. https://okcalc.com/ru/equation/ https://www.function-x.ru/powers_and_radicals.html https://allcalc.ru/node/667 Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней. В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении. Степенное выражение – это выражение, которое содержит степени. Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем. Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22. Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5. В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx. С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием. В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями. Вычислите значение степенного выражения 23·(42−12). Решение Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4. Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ. Ответ: 23·(42−12)=32. Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7. Решение Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1. Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1. Представьте выражение со степенями 9-b3·π-12 в виде произведения. Решение Представим число 9 как степень 32 и применим формулу сокращенного умножения: 9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1 Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1. А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений. Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением. Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному. Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1). Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа: В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0. Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение. При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней». Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a. Решение Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием: a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2. Ответ: a2,5·(a2)−3:a−5,5=a2. Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении. Найти значение степенного выражения 313·713·2123. Решение Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21. Есть еще один способ провести преобразования: 313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21 Ответ: 313·713·2123=31·71=21 Нужна помощь преподавателя? Опиши задание — и наши эксперты тебе помогут! Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5. Решение Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6. Ответ: t3−t−6. Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами. Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2. Решение Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе: 3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2 Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2 Ответ: 3·523·513-5-231+2·x2-3-3·x2=-122+x2 Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения. Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12. Решение а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль. Выполним умножение числителя и знаменателя дроби на a0,3: a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a б) Обратим внимание на знаменатель: x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162 Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т.е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь. Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби: Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12. Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12. Решение а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53. Получаем: 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1) б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов: a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14 Ответ: а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14. К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей. Выполните действия x12+1×12-1-x12-1×12+1·1×12. Решение Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю: x12-1·x12+1 Вычтем числители: x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12 Теперь умножаем дроби: 4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12 Произведем сокращение на степень x12, получим 4×12-1·x12+1. Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1. Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1 Упростите степенное выражение x34·x2,7+12x-58·x2,7+13. Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1. Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1. Переходим от последнего произведения к дроби x138x2,7+1. Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1. Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить на x3·(x+1)0,2. В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков. Представьте выражение x19·x·x36 в виде степени. Решение Область допустимых значений переменной x определяется двумя неравенствами x≥0 и x·x3≥0 , которые задают множество [0, +∞). На этом множестве мы имеем право перейти от корней к степеням: x19·x·x36=x19·x·x1316 Используя свойства степеней, упростим полученное степенное выражение. x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13 Ответ: x19·x·x36=x13. Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0. Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения: 52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0. Теперь поделим обе части равенства на 72·x. Это выражение на ОДЗ переменной x принимает только положительные значения: 5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0 Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0. Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0. Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0. Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Этот онлайн калькулятор рассчитывает любые степени действительных или комплексных чисел.
Поможет Вам рассчитать корень комплексного числа, возвести в степень действительное или комплексное выражение.
Рассчитывает степень любого числа
Хотелось бы заметить, что возведение любого действительного числа в дробную степень, не так сложно как может показаться на первый взгляд.
то есть, если мы хотим возвести число 3 в степень
то решение такое
Итого
Если речь идет о комплексных числах, то возведение степень и извлечени корня осуществляется по уравнению Муавра.
Формулы следующие:
Для возведения в степень
— модуль комплексного числа
— аргумент комплексного числа
Для извлечения корня
где p = 0, 1, …, k—1.
Есть еще третий возможный вариант, когда не только основание является комплексным числом, но и степень этого числа также число комплексное.
Конечно возникает желание использовать формулу Муавра и преобразовать её, для наших нужд, но мы воспользуемся первым вариантом вычисления степеней.
то есть вот этой формулой
Формула расчета логарифа комплексного числа известна
здесь k — может принимать любые целые значения, поэтому говорят, что логарифм комплексного числа многозначен.
Для практических целей используется главное значение(k=0)
Формула расчета экспоненты комплексного числа тоже
Таким образом у нас есть всё, что бы рассчитать на практике комплексную степень комплексного числа.
Если используете XMPP клиент: step_i <запрос>
Если используете этот сайт: <запрос>
где запрос — состоит из двух чисел. Сначала идет основание потом в другом окне степень.
Основание может быть как действительным числом так и комплексным, положительным или отрицательным
Комплексное значение пишется как x:y где х- действительная часть числа, а y- мнимая часть, но можно написать и в нормальном виде через символ i
Степень может быть быть целым числом,как положительным так и отрицательным.
Степень может быть выражена также степенью двух целых чисел например 1/2 или -5/7. В таком случае альтернативный вывод покажет Вам, все 2 или все 7 корней соответственно.
Степень может быть комплексным числом записанным как в нормальной форме через символ i, так и через сокращенную запись x:y, где x- действительная часть числа, y — мнимая часть числа
Замечание: В поле можно вводить только числа и никак не выражение, если у Вас есть желание посчитать вот такое выражение
то эта страница вам не поможет, Вам надо использовать универсальный калькулятор комплексных чисел
где x- это основание, а y-степень
Например: взять степень 2/5 от комплексного числа 1-2.5i
Пишем 1:-2.5 2/5 или если делаете запрос через Jabber step_i 1:-2.5 2/5
Ответ получим
Комплексное число 1:-2.5 в степени 2/5 равно Действительная часть: 1.3209 Комплексная часть: -0.6812
Интересно, а чему будет равна мнимая единица в степени мнимой единицы?
пишем i i
и получаем что
возведем еще одно число в комплексную степень.
число 1+i в комплексную степень 1-i
результат вот такой Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве
сооружений и даже спорте.{nm}:\] Прибавляем к исходному уравнению: Вынесем за скобки \ Выразим \ Поскольку степени одинаковые, отбрасываем их: Ответ: \ Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель
позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию
и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам. для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами. Инструкция
. Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц. Пример №1
. Задание . Найти решение матричного уравнения Обратная матрица A -1: Пример №2
. Задание. Решить матричное уравнение Пример №3
. Задание. Найти решение матричного уравнения Удобный и простой онлайн калькулятор дробей с подробным решением может: Результат решения дробей будет тут… 0
1
2
3
4
5
6
7
8
9 Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную. Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю. Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ. Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо. Квадратное уравнение — это уравнение вида ax
2 + bx
+ c
= 0, где коэффициенты a
, b
и c
— произвольные числа, причем a ≠ 0. Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса: В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант . Пусть дано квадратное уравнение ax
2 + bx
+ c
= 0. Тогда дискриминант — это просто число D
= b
2 − 4ac
. Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно: Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете: Задача. Сколько корней имеют квадратные уравнения: Выпишем коэффициенты для первого уравнения и найдем дискриминант: Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение: Дискриминант отрицательный, корней нет. Осталось последнее уравнение: Дискриминант равен нулю — корень будет один. Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество. Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много. Теперь перейдем, собственно, к решению. Если дискриминант D
> 0, корни можно найти по формулам: Основная формула корней квадратного уравнения Когда D
= 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D Первое уравнение: D
> 0 ⇒ уравнение имеет два корня. Найдем их: Второе уравнение: D
> 0 ⇒ уравнение снова имеет два корня. Найдем их \[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\] Наконец, третье уравнение: D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую: Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок. Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например: Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие: Уравнение ax
2 + bx
+ c
= 0 называется неполным квадратным уравнением, если b
= 0 или c
= 0, т.е. коэффициент при переменной x
или свободный элемент равен нулю. Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b
= c
= 0. В этом случае уравнение принимает вид ax
2 = 0. Очевидно, такое уравнение имеет единственный корень: x
= 0. Рассмотрим остальные случаи. Пусть b
= 0, тогда получим неполное квадратное уравнение вида ax
2 + c
= 0. Немного преобразуем его: Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c
/a
) ≥ 0. Вывод: Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c
/a
) ≥ 0. Достаточно выразить величину x
2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще. Теперь разберемся с уравнениями вида ax
2 + bx
= 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители: Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений: Задача. Решить квадратные уравнения: x
2 − 7x
= 0 ⇒ x
· (x
− 7) = 0 ⇒ x
1 = 0; x
2 = −(−7)/1 = 7. 5x
2 + 30 = 0 ⇒ 5x
2 = −30 ⇒ x
2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу. 4x
2 − 9 = 0 ⇒ 4x
2 = 9 ⇒ x
2 = 9/4 ⇒ x
1 = 3/2 = 1,5; x
2 = −1,5. калькулятор корней онлайн корня поможет вам найти квадратный корень n-й степени любого положительного числа, которое вы хотите. Кроме того, этот калькулятор sqrt сообщает вам, что введенное вами число является точным квадратом или не является идеальным квадратом. Например; 4, 9 и 16 – это идеальные квадраты 2, 3 и 4 соответственно. Квадратный корень из числа – это число, которое при умножении на себя равно исходному числу. Например, квадрат 9 и 16 равен 3 и 4 соответственно. Если вы беспокоитесь о простом ручном вычислении, продолжайте читать, чтобы узнать формулу квадратного корня, вычисление дроби, отрицательные числа и многое другое! Кроме того, вы можете попробовать наш онлайн калькулятор корней, который поможет вам вычислить значение любого числа, возведенного в любую степень. Но давайте перейдем к основам! Проведите по! Чтобы подготовиться к вычислению квадратного корня, вам следует запомнить основной идеальный квадратный корень. Поскольку квадрат 1, 4, 9, 16, 25, 100 равен 1, 2, 3, 4, 5 и 10. Чтобы найти квадрат √25, давайте посмотрим! √25 = √5 * 5 √25 = √52 √25 = 5 Это простейшие квадратные корни, потому что они всегда дают целое число, но что, если у числа нет точного квадратного корня? Например, вы должны оценить квадрат в 54? Где a / b – любая дробь. Приведем еще один пример: Пример: Что такое квадратный корень из 9/25? Решение: √9 / 25 = √9 / √25 √9 / √25 = 3/5 = 0,6 В школе нас учили, что квадратный корень из отрицательных чисел не может существовать. Но математики вводят общий набор чисел (Комплексные числа). В виде, х = а + би Где a – действительное число, а b – мнимая часть. Йота (i) – это комплексное число со значением: я = √-1. Приведем несколько примеров: Квадрат -4 = √-4 = √-1 * 9 = √ (-1) √9 = 3i Чему равен квадратный корень из -17 = √-17 = √-1 * 17 = √ (-1) √17 = 17i С помощью этого калькулятор корней онлайн квадратный корень стало очень просто. Для точных расчетов вам просто нужно выполнить указанные шаги. Читать дальше! Входы: Выходы: Как только вы закончите, калькулятор покажет: Заметка: Независимо от того, какой параметр ввода, онлайн-калькулятор с корнями корня покажет вам точные результаты в соответствии с выбранным вводом. Да, положительные числа имеют более одного sqrt, одно положительное, а другое отрицательное. Нет, это иррациональное число. Причина: Квадратный корень из 2 не может быть выражен как частное двух чисел. Некоторые корни рациональны, а другие иррациональны. Квадратные корни часто встречаются в математических формулах, включая квадратную формулу, дискриминант, а также во многих законах физики. Кроме того, он используется во многих местах повседневной жизни, используется инженерами, плотниками, менеджерами по строительству, фельдшерами и многими другими. Когда дело доходит до вычислений для большого количества, это очень сложно и сложно. Просто попробуйте калькулятор корней онлайн, который поможет вам определить квадратный корень в соответствии с вашими потребностями. Other languages: Square Root Calculator, Karekök Hesaplama, Kalkulator Akar Kuadrat, Kalkulator Pierwiastków, Wurzel Ziehen Rechner, 平方根 計算, 제곱근 계산, Kalkulačka Odmocniny, Calculadora De Raiz Quadrada, Calculatrice Racine Carré, Calculadora Raiz Cuadrada, Calcolo Radice Quadrata, حاسبة الجذر التربيعي, Neliöjuuri Laskin, Kvadratrot Kalkulator, Kvadratni Koren Kalkulator. Я чувствую себя прекрасно, что больше не нужно выполнять домашние задания, задания и тесты. Я закончила школу. Наконец-то получил свой B.S. в телекоммуникациях. Ура! Спасибо за помощь и новую версию. Желаю тебе всего наилучшего. Я хочу поблагодарить вас за вашу помощь. Ваша помощь в решении того, как решить проблему, помогла мне понять, как решать проблемы, и на самом деле получить правильный результат.Спасибо. Это хорошая новость для любой школы, учителя или студента, когда такая фантастическая программа разработана специально для алгебры. Отличная работа! При работе с дробными показателями есть несколько условий.Вы можете увидеть их все и узнать, как решать дробные показатели с разными условиями. Они следующие Дробные экспоненты с числителем 1 Дробные экспоненты — это способ выражения степеней вместе с корнями в одной нотации. Давайте посмотрим на несколько примеров, числитель которых равен 1, и узнаем, как они называются. 36 1/2 = √36 27 3 = 27 Первый показатель степени 1/2 называется квадратным корнем, а следующий показатель степени 1/3 называется кубическим корнем. Если мы продолжим так же. Показатель 1 / k называется k-м корнем. x 1 / k = k √x Дробные экспоненты с числителем, отличным от 1 (любые дроби) В случаях, когда числитель не равен 1 (n 1) a = x н / д Вам просто нужно возвести число в степень n и вынуть из него корень d.Вам не нужно беспокоиться о порядке, так как вы можете разделить его на две части. x n / d = x ( n.1 / d ) = (x n ) 1 / d = (x 1 / d ) n x n / d = d√x n = (d√x) n Вы можете выбрать любой из удобных для вас методов и провести вычисления. Пример: вычислить дробную экспоненту 16 3/2 ? Раствор: Дан дробный показатель степени 16 3/2 16 3/2 = 16 (3. 1/2) = (16 3 ) 1/2 = √16 3 = √4096 = 64 Сделайте все свои математические задачи проще и быстрее с нашим онлайн-калькулятором.Сайт гуру предоставил бесплатные онлайн-калькуляторы для различных математических и статистических концепций. Этот калькулятор дробной степени поможет вам — сюрприз, сюрприз — дробные показатели. Вы боретесь с концепцией дробных показателей? Отрицательные и дробные показатели — это для вас закрытая книга? Что ж, больше не о чем беспокоиться, прокрутите вниз, чтобы найти полезные объяснения. Дробные показатели — это способ выражения степеней, а также корней в одном представлении . Что именно это означает? Давайте сначала рассмотрим несколько простых примеров, где наш числитель равен 1 : Из приведенных выше уравнений мы можем вывести, что: Давайте воспользуемся законом экспонент, который гласит, что мы можем складывать показатели при умножении двух степеней с одинаковым основанием: x a + b = x a * x b так, например, если n = 2 x² = x¹⁺¹ = x¹ * x¹ = x * x Попробуйте это с любым числом, которое вам нравится, это всегда правда! Затем давайте посмотрим на дробные показатели x: x = x¹ = x (1/2 + 1/2) = x (1/2) * x (1/2) Как позвонить по номеру, умножение которого само на себя дает другой номер? Конечно, это квадратный корень из ! Итак, мы выяснили, что: x (1/2) = √x Если хотите, вы можете аналогичным образом проверить другие корни, например.г. кубический корень: x = x (1/3 + 1/3 + 1/3) = x (1/3) * x (1/3) * x (1/3) = ³√x * ³√x * ³√x т. x (1/3) = ³√x Теперь мы знаем, что x в степени одной трети равен кубическому корню из x. Итак, что произойдет, если наш числитель не равен 1 (n 1)? Все, что вам нужно сделать, это возвести это число в степень n и взять корень d-th .Порядок не имеет значения, дробь n / d может быть разделена на две части: Давайте посмотрим на пример, где дробная экспонента = 3/2 и x = 16: Или, как вариант, можно написать, что И результат действительно тот же.Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени! Положительные показатели говорят нам, сколько раз мы используем число при умножении: Но что произойдет, если наша экспонента будет отрицательным числом, вы можете догадаться? Да, он говорит вам, сколько раз вам нужно разделить на это число: Кроме того, вы можете просто вычислить положительную экспоненту (например, x 4 ), а затем взять обратную величину (в нашем случае 1 / x 4 ).Конечно, аналогично, если у нас есть отрицательная И дробная экспонента. Мы считаем, что этот инструмент настолько интуитивно понятен и прост, что никаких дополнительных пояснений не требуется, но для записи мы быстро объясним, как вычислить дробные показатели: Надо ли говорить о гибкости нашего инструмента? Вам не нужно переходить калькулятор сверху вниз — вычислите любое неизвестное, какое захотите! Введите любые три значения, и четвертое появится в мгновение ока. Еще одна полезная функция калькулятора — дробью может быть не только показатель степени, но и основание ! Например, если вы хотите вычислить (1/16) 1/2 , просто введите 1/16 в базовое поле. Отлично! ‘Cuemath’s Fractions with Exponents Calculator’ — это онлайн-инструмент, который помогает найти значение заданного показателя степени. Cuemath поможет вам найти значение данного показателя дроби в течение нескольких секунд. Пожалуйста, выполните следующие шаги, чтобы найти значение заданной дробной экспоненты: Показатель степени определяется как количество раз умножения основного числа на себя. Проще говоря, сколько раз конкретное число умножается само на себя, показано с помощью экспонент. Показатель степени выражается в форме: x a / b , где x — это базовое число, a / b представляет дробь, a — числитель, а b — знаменатель Хотите найти сложные математические решения за секунды? Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов.С Cuemath находите решения простым и легким способом. Забронируйте бесплатную пробную версию Класс Решить 4 -1/2 ? = 4 -1/2 = 1/4 1/2 = 1 / √4 = 1/2 Аналогично, вы можете попробовать калькулятор, чтобы найти дроби с показателями для 1) 10 -3/2 2) 9 3/2 Попробуйте бесплатную программу для решения математических задач или прокрутите вниз до учебных пособий! Я никогда ничего подобного не видел! Постепенно я изучаю сложную алгебру вместе со своими детьми! Пока все отлично! Переезжать из города в город сложно, особенно когда нужно понимать, как преподает каждый учитель. С Алгебратором кажется, что есть только один учитель, и тоже хороший. Теперь мне не нужно беспокоиться о том, чтобы справиться с алгеброй. Я ищу помощи и в других областях. Чтобы вычислить квадратный корень, воспользуйтесь кнопкой квадратного корня на вашем научном калькуляторе.Чтобы использовать эту кнопку, вам необходимо знать, как работает ваш калькулятор. В некоторых калькуляторах сначала нужно ввести число, а затем нажать кнопку извлечения квадратного корня. В других случаях вы сначала нажимаете кнопку извлечения квадратного корня, а затем свое число. Так, например, чтобы найти квадратный корень из 5, вы нажмете эти кнопки, если в вашем калькуляторе вы сначала вводите число. Квадратный корень из 5 должен быть около 2,236. Чтобы найти другие корни, вы воспользуетесь специальной кнопкой, которая позволит вам выбрать корень.Если вы не видите такой кнопки, возможно, она находится в меню одной из функциональных клавиш. Вы можете использовать настраиваемую корневую кнопку , чтобы найти кубический, четвертый и пятый корни или любой положительный целочисленный корень. Чтобы использовать эту кнопку, вам нужно посмотреть руководство к вашему калькулятору. В некоторых калькуляторах вы сначала вводите число, затем кнопку корня, а затем желаемый корень. В других случаях вы выполняете эти операции в обратном порядке, начиная с желаемого корня, затем кнопки корня и числа. Чтобы найти кубический корень из 5 с помощью калькулятора, в который вы вводите желаемый корень последним, вы нажимаете следующие кнопки: Кубический корень из 5 должен быть около 1,7. Если в вашем калькуляторе нет настраиваемой кнопки корня, вы можете использовать кнопку настраиваемой степени, чтобы найти корень. Чтобы использовать кнопку настраиваемой экспоненты , преобразуйте желаемый корень в показатель степени, инвертируя его или используя 1 в качестве числителя и корня в качестве знаменателя дроби.Таким образом, кубический корень становится показателем 1/3, квадратный корень становится показателем или степенью 1/2, а корень пятой степени становится 1/5 и так далее. После преобразования желаемого корня используйте кнопки в круглых скобках, чтобы сообщить калькулятору, что у вас есть дробная экспонента. Итак, чтобы ввести квадратный корень из 9, нажмите эти кнопки: Помните, что в зависимости от вашего калькулятора вам может потребоваться сначала ввести дробную экспоненту, прежде чем нажимать кнопку настраиваемой экспоненты.символ). Если у вас есть, вы можете использовать его вместо кнопки настраиваемой экспоненты. Обе кнопки означают, что базовое число взято в степень. Давайте попробуем вычислить седьмой корень из 24. Если в вашем калькуляторе вы выбираете корень последним, вы нажимаете на кнопки, как это. Вы должны получить ответ около 1,5746. На этом уроке вы узнали, как использовать научный калькулятор для вычисления корней.Корень в математике относится к этому символу: Например, когда вы извлекаете квадратный корень из числа, вы ищете число, которое при умножении само на себя дает заданное число. Например, квадратный корень из 9 равен 3, потому что 3 умножения на себя равно 9. Кубический корень числа — это число, которое при трехкратном умножении на себя дает данное число. Кроме того, любое положительное целое число может иметь корень. При использовании научного калькулятора для нахождения корня вам необходимо следовать его руководству и посмотреть, вводите ли вы сначала число, а затем нажимаете кнопку корня, или наоборот. Пользовательская кнопка корня может использоваться для вычисления кубического, четвертого и пятого корней или любого положительного целочисленного корня.), которую можно использовать вместо кнопки настраиваемой экспоненты. Версия для Windows Версия для Mac OSX Просмотреть больше загрузок Поддержка кнопок и клавиш Стек Поддон Intro Дополнение Вычитание Умножение Дивизион Знак Площадь Квадратный корень Повышение мощности Естественная экспонента Логарифм Натуральный логарифм Обратный Показатель Факториал PI Синус Обратный синус Косинус Обратный косинус Касательная Обратный тангенс Косеканс Обратный косеканс Секант Обратный секанс Котангенс Обратный котангенс Гиперболический синус Гиперболический косинус Гиперболический тангенс Гиперболический косеканс Гиперболический секанс Гиперболический котангенс Обратный гиперболический синус Обратный гиперболический косинус Обратный гиперболический тангенс Обратный гиперболический косеканс Обратный гиперболический секанс Обратный гиперболический котангенс Формат Уголок Система координат Режимы онлайн-калькулятора Система координат eCalc — это бесплатный и простой в использовании научный калькулятор, который поддерживает множество расширенных функций, включая преобразование единиц измерения, решение уравнений и даже математику с комплексными числами.eCalc предлагается как бесплатный онлайн-калькулятор, так и в виде калькулятора для загрузки. Онлайн-калькулятор работает либо с алгебраическим вводом (режим по умолчанию), либо с вводом RPN. Режим калькулятора устанавливается щелчком по символу «ALG / RPN» в строке состояния или путем изменения режима в диалоговом окне меню. Онлайн-калькулятор поддерживает ввод данных с помощью графической кнопки или традиционных клавиш компьютерной клавиатуры. Пользователю предоставляется возможность использовать любой метод ввода, и оба они одинаково действительны; тем не менее, существуют некоторые тригонометрические функции (как указано ниже), которые ограничены вводом с клавиатуры компьютера, поскольку для размещения графических кнопок доступно ограниченное пространство. Стек — это функция калькулятора, которая позволяет просматривать историю результатов. В стеке одновременно отображаются только 4 элемента, но можно прокручивать вверх и вниз по стеку, щелкая стрелки вверх и вниз над стопкой. Значения в стеке также можно «вытолкнуть» вниз в поле ввода калькулятора, щелкнув стрелки вниз слева от строки в стеке. Калькулятор разделен на две части: интерфейс научного калькулятора слева и панель калькулятора справа.Поддон обеспечивает область отображения для специальных функций. Некоторые из этих функций включают в себя: преобразователь единиц, библиотеку констант, решатель уравнений, полиномиальный решатель, базовое преобразование и преобразование десятичного числа в дробное. Сложение (функция суммы) используется при нажатии кнопки «+» или с помощью клавиатуры. Функция дает a + b. Вычитание (функция минуса) используется при нажатии кнопки «-» или с помощью клавиатуры.Функция приводит к a-b. Умножение (функция умножения) используется нажатием кнопки «x» или клавишей «*» на клавиатуре. Функция возвращает a * b. -1 или делению 1 на число.Икс. Числа автоматически отображаются в формате, когда число слишком велико или слишком мало для отображения. Чтобы ввести число в этом формате, используйте кнопку экспоненты «EEX». Для этого введите мантиссу (не экспоненциальную часть), затем нажмите «EEX» или введите «e», а затем введите показатель степени. Факториальная функция используется при нажатии «!» кнопку или введите «!». PI — математическая константа отношения длины окружности к ее диаметру. Функция Sine (SIN) используется при нажатии кнопки «SIN» или вводе «SIN ()». Результат — отношение длины противоположной стороны к длине гипотенузы прямоугольного треугольника. Для использования функции обратного синуса (ASIN или ARCSIN) нажмите кнопку «ASIN» или введите «ASIN ()». Результат действителен только от -pi / 2 до pi / 2. Функция косинуса (COS) используется при нажатии кнопки «COS» или вводе «COS ()».В результате получается отношение длины соседней стороны к длине гипотенузы прямоугольного треугольника. Функция обратного косинуса (ACOS или ARCCOS) используется нажатием кнопки «ACOS» или вводом «ACOS ()». Результат действителен только от 0 до пи. Функция тангенса (TAN) используется при нажатии кнопки «TAN» или типа «TAN ()». Результат — отношение длины противоположной стороны к длине смежной стороны прямоугольного треугольника. Функция обратной тангенсации (ATAN или ARCTAN) используется при нажатии кнопки «ATAN» или при вводе «ATAN ()». Результат действителен только от -pi / 2 до pi / 2. Функция косеканса (CSC) используется при вводе «CSC ()». Косеканс — это мультипликативная обратная функция синусоиды. Функция обратного косеканса (ACSC) используется при вводе «ACSC ()». Результат действителен только от -pi / 2 до pi / 2, исключая 0. Функция секанса (SEC) используется при вводе «SEC ()». Секанс — это мультипликативная величина, обратная функции косинуса. Функция обратного секанса (ASEC) используется при вводе «ASEC ()». Результат действителен только от 0 до pi, исключая pi / 2. Функция котангенса (COT) используется при вводе «COT ()». Котангенс — это мультипликативная обратная функция касательной. Функция обратного котангенса (ACOT) используется при вводе «ACOT ()». Результат действителен только от 0 до пи. Функция гиперболического синуса (SINH) используется при вводе «SINH ()». Функция гиперболического косинуса (COSH) используется при вводе «COSH ()». Функция гиперболического тангенса (TANH) используется при вводе «TANH ()». Функция гиперболического косеканса (CSCH) используется при вводе «CSCH ()». Функция гиперболического секанса (SECH) используется при вводе «SECH ()». Функция гиперболического котангенса (COTH) используется при вводе «COTH ()». Функция обратного гиперболического синуса (ASINH) используется при вводе «ASINH ()». Функция обратного гиперболического косинуса (ACOSH) используется при вводе «ACOSH ()». Функция обратного гиперболического тангенса (ATANH) Используется при вводе «ATANH ()». Функция обратного гиперболического косеканса (ACSCH) используется путем ввода «ACSCH ()». Функция обратного гиперболического секанса (ASECH) используется путем ввода «ASECH ()». Функция обратного гиперболического котангенса (ACOTH) используется при вводе «ACOTH ()». Доступно 4 типа числовых форматов, и формат можно изменить, нажав кнопку «Меню». Доступные типы чисел: стандартные, фиксированные, научные и инженерные. В инженерии можно выбрать количество цифр для отображения в поле ввода в строке формата.Используемый числовой формат можно увидеть над стеком, это третий статус меню слева. Это место можно щелкнуть, чтобы изменить числовой формат. Доступно 3 типа представления углов, и эти типы углов можно изменить, нажав кнопку «Меню». Форматы углов: радианы, градусы и градиенты. Формат угла отображается над стеком и является первым статусом меню. На это место можно щелкнуть, чтобы изменить формат угла. Для представления комплексных чисел доступны две системы координат. Системы координат бывают прямоугольными и полярными. Систему координат можно выбрать, нажав кнопку «Меню». Выбранная система координат отображается над стеком и является вторым статусом меню. Чтобы ввести число в прямоугольном формате, его необходимо ввести в формате «(3,4)». Чтобы ввести число в полярном формате, его необходимо ввести в формате «(3 @ 75)».Вместо символа «@» можно использовать символ угла клавиатуры калькулятора. Есть два режима онлайн-калькулятора: Алгебраический и RPN. Режим выбирается нажатием на кнопку «Меню». Режим калькулятора отображается в четвертом индикаторе состояния меню, при нажатии на это место режим изменяется. Нижняя зеленая кнопка «возврат» или «=» изменяется в зависимости от режима. Функция преобразования десятичной дроби в дробь этого калькулятора позволяет представить десятичное число в дробных оценках, а также в точном эквиваленте дроби.Функция преобразования десятичной дроби в дробь активируется нажатием кнопки «d> f» (десятичная дробь в дробную) на клавиатуре калькулятора. Откроется дисплей в боковом поддоне с полем ввода вверху. Десятичное значение можно ввести непосредственно в поле ввода, или, щелкнув стрелку ввода, будет введено значение из поля ввода калькулятора. Онлайн-калькулятор полностью поддерживает комплексные числа. Комплексные числа являются расширением системы действительных чисел и включают второе число, которое является воображаемым, создавая плоскость комплексных чисел.Числовой формат для комплексных чисел — «a + bi», где a — действительное число, а b — мнимое число. Эти числа также могут быть представлены как величина и угол, когда система координат калькулятора находится в полярном режиме. Онлайн-конвертер единиц отображается на поддоне, и его можно выбрать, нажав кнопку «Единицы». Конвертер единиц имеет 11 категорий: масса, скорость, время, мощность, объем, площадь, длина, энергия, температура, сила и давление. Библиотека констант — это функция поддона, доступ к которой можно получить, щелкнув кнопку «CONST». Чтобы поместить константу в поле ввода калькулятора, просто нажмите на константу. Эта библиотека содержит множество популярных констант, которые используются регулярно. Библиотека констант включает в себя следующее: скорость света, кулоновская постоянная, ускорение гравитации, гравитационная постоянная, постоянная Планка, постоянная Больцмана, постоянная Фарадея, масса покоя электрона, масса покоя нейтрона, масса покоя протона, число Авогадро, заряд электронов, радиус Бора. , Молярная газовая постоянная, постоянная Ридберга, молярный объем, диэлектрическая проницаемость вакуума, постоянная Стефана-Больцмана, квант магнитного потока, проницаемость вакуума, магнетон Бора, постоянная Джозефсона, импеданс вакуума и квант проводимости. В онлайн-калькуляторе есть два часто используемых решателя. Доступ к этим решателям можно получить, щелкнув кнопку палитры «РЕШИТЬ». Доступные решатели: Линейный решатель и Корневой решатель. Базовый преобразователь — это функция, которая включена в поддон, и к ней можно получить доступ, нажав кнопку «BASE». Рациональная функция — это дробь вида ,
числитель и знаменатель которой — многочлены или произведения многочленов. Из урока «Интегрирование некоторых
рациональных дробей и иррациональностей» известно, что рациональные дроби
бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в
знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в
знаменателе. В том же уроке говорилось о том, как представить неправильную дробь в виде суммы её
целой части и некоторой правильной дроби. На этом уроке будем учиться интегрировать такие рациональные функции, которые
представлены в виде правильных дробей. Приведённый ниже алгоритм интегирования рациональных функций будет пошагово
проиллюстрирован в примерах. Переходим к первому шагу алгоритма Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида
, в которой
каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых
коэффициентов будет следующим: Пример 1. Шаг 1. Дан интеграл от рациональной функции
. От нас требуется разложить подынтегральное выражение — правильную дробь
на простые дроби. Решение. Дискриминант уравнения положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение
исходной дроби на сумму простых дробей: . Пример 2. Шаг 1.Дан интеграл от рациональной функции . Решение. . Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение: Получаем разложение знаменателя на множители в подынтегральном выражении: . Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело
со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби
подынтегрального выражения будет следующим: . Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название — метод неопределённых коэффициентов. Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида
,
то есть один из многочленов в степени 2 и больше. Пример 3. Шаг 1. Дан интеграл от рациональной функции
. Решение. Представляем разность квадратов
в виде произведения суммы и разности . Тогда подынтегральное выражение запишется в виде , все уравнения с многочленами которого имеют действительные корни. Это случай кратных
действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее
разложение исходной дроби на простые дроби: Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой
и записывать простую дробь с каждой из этих степеней в знаменатель. Пример 4. Шаг 1. Дан интеграл от рациональной функции
. Решение. . Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения
, присутствующего в
цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в
числителе нужно записывать линейное выражение с переменной x (это выражение — последнее в следующей записи): Пример 5. Шаг 1. Дан интеграл от рациональной функции
. Решение. Уравнение в скобках имеет комплексные корни,
а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее
разложение исходной дроби на простые дроби: . Пример 6. Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего
произведения сомножителей: . Решение. Уравнение с последним сомножителем имеет комплексные корни,
а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее
разложение исходной дроби на простые дроби: Многочлен в знаменателе имеет кратные комплексные корни:
дискриминант квадратного уравнения
, присутствующего в
цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим: То есть в сумме простых дробей число простых дробей с линейным выражением
в числителе должно быть равно степени сомножителя, имеющего комплексные корни. Пример 7. Шаг 1. Дан интеграл от рациональной функции
. Решение. Квадратный трёхчлен имеет
комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения: . Пример 8. Шаг 1. Дан интеграл от рациональной функции
. Решение. Квадратный трёхчлен в знаменателе имеет
комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения: . На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными
коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю.
После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет
в данной отдельной дроби, но которые есть в других полученных дробях. Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем
составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся
неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются методом подстановки и методом сложения. Нет времени вникать в решение? Можно заказать работу! Пример 1. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: . Умножаем неопределённые коэффициенты на многочлены, которых нет
в данной отдельной дроби, но которые есть в других полученных дробях: . Раскрываем скобки и приравниваем полученое к полученному выражению числитель
исходной подынтегральной дроби: . В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и
составляем из них систему уравнений: . Сокращаем все иксы и получаем эквивалентную систему уравнений: . Решая систему, получаем следующие значения неопределённых коэффициентов: . Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей: . Пример 2. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: . Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю
выражения, полученного после приведения суммы дробей к общему знаменателю: Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения: Решаем полученную систему: Итак, , отсюда
получаем окончательное разложение подынтегральной дроби на сумму простых дробей: . Пример 3. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю
выражения, полученного после приведения суммы дробей к общему знаменателю: Как и в предыдущих примерах составляем систему уравнений: Сокращаем иксы и получаем эквивалентную систему уравнений: Решая систему, получаем следующие значения неопределённых коэффициентов: . Получаем окончательное разложение подынтегральной дроби на сумму простых дробей: . Пример 4. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: . Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби
на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров.
Поэтому лишь для контроля приведём получившуюся систему уравнений: Решая систему, получаем следующие значения неопределённых коэффициентов: . Получаем окончательное разложение подынтегральной дроби на сумму простых дробей: Пример 5. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: . Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель
этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений: Решая систему, получаем следующие значения неопределённых коэффициентов: . Получаем окончательное разложение подынтегральной дроби на сумму простых дробей: . Пример 6. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: Производим с этой суммой те же действия, что и в предыдущих примерах.
В результате должна получиться следующая система уравнений: Решая систему, получаем следующие значения неопределённых коэффициентов: . Получаем окончательное разложение подынтегральной дроби на сумму простых дробей: . Пример 7. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: . После известных действий с полученной суммой должна получиться следующая система уравнений: Решая систему, получаем следующие значения неопределённых коэффициентов: . Получаем окончательное разложение подынтегральной дроби на сумму простых дробей: . Пример 8. Шаг 2. На шаге 1 получили следующее разложение
исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях: . Внесём некоторые изменения в уже доведённые до автоматизма действия для получения
системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних
вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения
к числителю исходной дроби, получаем: Можно заметить, что если принять за значение икса единицу, то второе и третье
слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем,
что .
Далее по уже отработанной схеме получаем систему уравнений: Решая систему, получаем следующие значения неопределённых коэффициентов: . Получаем окончательное разложение подынтегральной дроби на сумму простых дробей: . Полученные простые дроби и интегировать проще. К исходной сумме дробей применяется
правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы.
Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу. Пример 1. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: . Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный
интеграл 10, приводящий к натуральному логарифму: Последнее действие с натуральным логарифмом — приведение к единому выражению под
логарифмом — может требоваться при выполнении работ,
но требуется не всегда. Пример 2. . Вновь применяем табличный интеграл, приводящий к натуральному логарифму: Пример 3. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: . В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби,
на случай, если требуется преобразование к единому логарифму, делаем и это: Пример 4. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: В результате интегрирования получаем сумму натуральных логарифмов и одной дроби,
на случай, если требуется преобразование к единому логарифму, делаем и это: Пример 5. . Интегрируем и получаем сумму натурального логарифма и арктангенса: Пример 6. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: . Опять получаем сумму натурального логарифма и арктангенса: Пример 7. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: . Интегрируя, получаем натуральные логарифмы и дробь: Приведение к единому логарифму попробуйте выполнить самостоятельно. Пример 8. Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: . Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби: К началу страницы Пройти тест по теме Интеграл Начало темы «Интеграл» Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов Найти неопределённый интеграл: начала начал, примеры решений Метод замены переменной в неопределённом интеграле Интегрирование подведением под знак дифференциала Метод интегрирования по частям Интегрирование дробей Интегрирование некоторых иррациональных функций Продолжение темы «Интеграл» Интегрирование тригонометрических функций Определённый интеграл Несобственные интегралы Площадь плоской фигуры с помощью интеграла Объём тела вращения с помощью интеграла Вычисление двойных интегралов Длина дуги кривой с помощью интеграла Площадь поверхности вращения с помощью интеграла Определение работы силы с помощью интеграла
Инструкция. Введите числитель и знаменатель дроби. Нажмите кнопку Решить.
Пусть подынтегральное выражение есть рациональная дробь , где и — полиномы (многочлены) степеней k и n соответственно. Не умаляя общности, можем считать, что k < n, так как в противном случае всегда можно представить числитель в виде Примеры
Также рекомендуется ознакомиться с возможностью решения интегралов онлайн.
Пример. Найти .
Здесь мы приводим подробные решения трех примеров интегрирования следующих рациональных дробей: Вычислить интеграл: Решение Здесь под знаком интеграла стоит рациональная функция, поскольку подынтегральное выражение является дробью из многочленов. Степень многочлена знаменателя (3) меньше степени многочлена числителя (4). Поэтому, вначале необходимо выделить целую часть дроби. 1. Выделим целую часть дроби. Делим x 4 на x 3 – 6x 2 + 11x – 6: 2. Разложим знаменатель дроби на множители. Для этого нужно решить кубическое уравнение: Итак, мы нашли один корень x = 1. Делим на x – 1: Отсюда 3. Разложим дробь на простейшие. . Итак, мы нашли: Ответ . Вычислить интеграл: Решение Здесь в числителе дроби – многочлен нулевой степени (1 = x 0). В знаменателе – многочлен третьей степени. Поскольку 0 < 3, то дробь правильная. Разложим ее на простейшие дроби. 1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение третьей степени: Итак, мы нашли один корень x = 1. Делим x 3 + 2x – 3 на x – 1: Итак, Решаем квадратное уравнение: 2. Разложим дробь на простейшие. Ищем разложение в виде: Подставим в (2.1) x = 0: Приравняем в (2.1) коэффициенты при x 2: Итак, мы нашли разложение на простейшие дроби: 3. Интегрируем. ; Вычисляем I2. . Поставляем в (2.2): Ответ . Вычислить интеграл: Решение Здесь под знаком интеграла стоит дробь из многочленов. 1. Разложим знаменатель дроби на множители. Для этого нужно решить уравнение четвертой степени: Итак, мы нашли один корень x = –1. Делим на x – (–1) = x + 1: Теперь нужно решить уравнение третьей степени: Итак, мы нашли еще один корень x = –1. Поскольку уравнение x 2 + 2 = 0 не имеет действительных корней, то мы получили разложение знаменателя на множители: 2. Разложим дробь на простейшие. Ищем разложение в виде: Продифференцируем (3.1): ; . Подставим в (3.1) x = 0: Приравняем в (3.1) коэффициенты при x 3: Итак, мы нашли разложение на простейшие дроби: 3. Интегрируем. . Ответ . Содержание: Согласно (2. многочлена и правильной рациональной дроби. В свою очередь, в силу (2.25) эту дробь можно разложить на простейшие. Многочлен определен на всей числовой прямой и его интегрирование не представляет трудностей. Неопределенные интегралы от простейших рациональных дробей, рассмотренные в 2.2, могут быть выражены через дробно-рациональные функции, логарифмическую и обратную тригонометрическую, а именно через арктангенс, т.е. неопределенный интеграл от любой рациональной дроби представим элементарными функциями. По этой ссылке вы найдёте полный курс лекций по высшей математике: Итак, интегрирование любой дробно-рациональной функции состоит из следующих этапов: Рассмотрим эти этапы подробнее на нескольких характерных примерах. Возможно вам будут полезны данные страницы: Комбинаторика Формулы комбинаторики Метод Лагранжа Метод вариации постоянных Найдем интеграл от неправильной рациональной дроби Преобразуем ее числитель так, чтобы в нем можно было выделить слагаемое, кратное знаменателю и включающее старшую степень аргумента Многочлен в знаменателе выделенной правильной рациональной дроби можно представить как разность кубов: Он имеет простой действительный нуль и пару комплексно сопряженных нулей-Поэтому разложение правильной рациональной дроби в (2.31) простейшие, согласно (2.25), примет вид После приведения правой части данного равенства к общему знаменателю получим Это равенство верно при любых значениях Полагая в нем находим т. Таким образом, Первые два интеграла в правой части нетрудно найти при помощи табличных интегралов 1 и 2 в знаменателе подынтегральной функции в третьем интеграле выделим полный квадрат: и обозначим Тогда, используя линейность неопределенного интеграла и применяя интегрирование подведением под знак дифференциала, получаем с учетом табличных интегралов 2 и 13 Возвращаясь к исходному переменному находим или окончательно Функция является правильной рациональной дробью. Разложим ее знаменатель на множители: т.е. знаменатель имеет двукратные действительные нули и и простой действительный нуль Следовательно, согласно (2.25), разложение функции на простейшие рациональные дроби имеет вид Из этого равенства после приведения его правой части к общему знаменателю следует равенство многочленов Последовательно полагая в (2. Продифференцировав (2.32) по выпишем справа лишь те слагаемые, которые не обращаются в нуль при Отсюда соответственно имеем или с учетом значений получим Таким образом, заданная функция принимает вид Неопределенный интеграл от этой функции находим при помощи табличных интегралов 1 и 2: Функция является неправильной рациональной дробью. Выделив из нее многочлен и правильную рациональную дробь, запишем Нули многочлена в знаменателе являются корнями биквадратно уравнения Обозначив получим квадратное уравнение имеющее простые корни Следовательно, знаменатель можно представить в виде Тогда для правильной рациональной дроби, согласно (2.25), имеем разложение Приводя правую часть этого равенства к общему знаменателю, приходим к равенству многочленов Приравнивая коэффициенты при одинаковых степенях получаем систему линейных алгебраических уравнений Из первого и третьего уравнений находим а из второго и четвертого — В итоге заданную функцию запишем в виде Тогда с учетом табличного интеграла 13 получим Найдем неопределенный интеграл от функции представив его суммой интегралов Первый интеграл в правой части (2. разложим правильную рациональную дробь на простейшие: Затем, приводя правую часть к общему знаменателю, получаем Отсюда, полагая, что находим т.е. При запишем откуда а из равенства нулю коэффициента при следует, что Таким образом, Подынтегральная функция во втором интеграле справа является простейшей рациональной дробью третьего типа (см. 2.2). Поэтому Следовательно, Возвращаясь к аргументу вместо (2.33) в итоге получаем Замечание 2.5. При интегрировании дробно-рациональной функции этап ее разложения на простейшие рациональные дроби не всегда является обязательным. В некоторых случаях удается найти интеграл более простым путем. Ясно, что разложение правильной рациональной дроби на простейшие будет весьма громоздким. В данном случае проще обозначить и вычислить Возвратившись к переменному получим Дробной — рациональной функцией называется функция, равная частному от деления двух многочленов: R(x) = . Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, в противном случае — неправильной. Отметим, что всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби: , где r(x) — многочлен, степени меньше степени знаменателя Q(x). Таким образом, интегрирование рациональной функции сводится к интегрированию правильной рациональной дроби. А интегрирование правильной рациональной дроби сводится к интегрированию простейших дробей типа: 1. ; 2. ; 3. ; 4. . (x2 +рх + q — не имеет действительных корней.) Интегрирование простейших рациональных дробей: 1. . 2. . 3. Основной способ нахождения интеграла состоит в предварительном выделении полного квадратного трехчлена: Рассмотрим этот способ на примере. Пример 53. Вычислить интеграл Решение. Выделим полный квадрат в знаменателе и преобразуем дробь: х2 +2х -1 = х2 +2х +1-1-1 = (х+1)2 -2. Тогда = = — = = — +С. 4. Если введем новую переменную t, положив t = х + и х2 + рх + q = t2 + a2, где a2 = q — , то интеграл =In можно вычислить с помощью реккурентной формулы In = . 9.5. Интегрирование рациональных дробей с помощью разложения на простейшие дроби Случай 1.Знаменатель имеет только действительные различные корни, т.е. разлагается на неповторяющиеся множители первой степени. Пример 54. Найти интеграл Решение. Так как каждый из двухчленов входит в знаменатель в первой степени, то данная правильная рациональная дробь может быть представлена в виде Освобождаясь от знаменателей, получим При х = 1 6 = 3А, А = 2; при х = 2 11 = -2В, В= — ; при х = 4 27 = 6С, С = . Итак, разложение рациональной дроби на простейшие имеет вид Таким образом, Случай 2. Знаменатель имеет лишь действительные корни, причем некоторые из них кратные, т.е. знаменатель разлагается на множители первой степени и некоторые из них повторяются. Пример 55. Найти интеграл Решение. Множителю соответствует сумма трех простейших дробей , а множителю — простейшая дробь Итак, Освободимся от знаменателя: Откуда В = , С = . Окончательное разложение данной дроби на простейшие имеет вид Таким образом, получим = Случай 3. Пример 56. Найти интеграл Решение. Разлагаем дробь на простейшие дроби Освобождаемся от знаменателя: . Выпишем коэффициенты при одинаковых степенях: Откуда найдем А = 1, В = -1, С = -1. Итак, Следовательно, = ln|x|- — — = ln|x| — — — +C. Случай 4. Среди корней знаменателя имеются кратные комплексные корни, т.е. разложение знаменателя содержит повторяющиеся квадратичные множители. Пример 57. Решение. Так как есть двукратный множитель, то Освобождаясь от знаменателей, получим Приравняем коэффициенты при одинаковых степенях : Следовательно, = = 9.5. Интегрирование иррациональных функций Неопределенный интеграл вида интегрируется путем введения новой переменной . Интегралы вида интегрируются путем выделения полного квадрата из квадратного трехчлена. Пример 58. Вычислить интеграл . Решение: = = , где Пример 59. Вычислить интеграл . Решение: = Интеграл вида , где n Î Z, интегрируются путем введения новой переменной t n = ax + b. Пример 60. Вычислить интеграл . Решение: = = -2t-2 = -2 +С. Интегралы вида , где Pn (x) — многочлен степени n, вычисляются с помощью реккурентной формулы = , (21) где Q n— 1 (x) — многочлен степени (n — 1) с неопределенными коэффициентами и l — число. Коэффициенты многочлена и число l находятся при помощи дифференцирования тождества (21). Пример 61. Вычислить интеграл . Решение. Применяем формулу (21): = (Ах+В) . Дифференцируем это тождество: . Откуда х2 = А(х2 + 4) + х(Ах+В) + l. Выпишем коэффициенты при одинаковых степенях: х2: 1 = А +А х: 0 = Вх х0: 0 = 4A + l. Итак, А = , В = 0, l = -2. Следовательно, = = +С. Интеграл от дифференциального бинома , где m, n, p — рациональные числа: 1) если р — целое число, то делаем замену х = t s, где s — общий знаменатель дробей m и n; 2) если — целое число, то делаем замену а+bх n = t s, где s — знаменатель дроби р; 3) если +р — целое число, то делаем замену ах – n+b = t s, где s — знаменатель дроби р. Пример 62. Вычислить интеграл Решение: = = 9.7. Интегрирование тригонометрических функций 1.Интегралы вида где R — рациональная функция, приводятся к интегралам от рациональных функций с помощью так называемой универсальной тригонометрической подстановки В результате этой подстановки имеем: ; Пример 63. Найти интеграл Решение. = = = arctg + +C = +C. Универсальная подстановка во многих случаях приводит к сложным вычислениям, так как при ее применении и выражаются через в виде рациональных дробей, содержащих . В некоторых частных случаях нахождение интеграла вида может быть упрощено: 1. Если — нечетная функция относительно , т.е., если , то интеграл рационализируется подстановкой 2. Если — нечетная функция относительно , т.е., если , то интеграл рационализируется с помощью подстановки 3. Если — четная функция и относительно и относительно , т.е., если , то к цели приводит подстановка Пример 64. Найти интеграл Решение. Так как подынтегральная функция нечетна относительно синуса, то полагаем = 2. Интегралы вида Выделим здесь два случая, имеющие особенно важное значение. Случай 1. По крайней мере один из показателей m или n – нечетное положительное число. Если n – нечетное положительное число, то применяется подстановка Если же m — нечетное положительное число, подстановка Пример 65. Найти интеграл Решение. Полагая получим Случай 2. Оба показателя степени m и n — четные положительные числа. Здесь следует преобразовать подынтегральную функцию с помощью следующих формул: (22) (23) (24) Пример 66. Найти интеграл Решение. Из формулы (22) следует, что Применив теперь формулу (23), получаем Итак, 3. Интегралы вида Тригонометрические формулы дают возможность произведение тригонометрических функций представить в виде суммы. Дата добавления: 2020-07-18; просмотров: 261; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ Лекция 3. Интегрирование рациональных функций. Рациональная функция – это отношение двух целых функций – многочленов (полиномов). Если порядок полинома – числителя ниже порядка полинома – знаменателя, то такая рациональная функция называется рациональной дробью. Лемма 1. Если рациональная функция не является рациональной дробью, то ее можно привести к сумме целой части – полинома и рациональной дроби. Доказательство основано на правиле деления многочленов с остатком, например, на алгоритме деления многочленов «уголком » . Пример. . Отсюда следует, что . Поэтому интегрирование рациональной функции сводится к интегрированию многочлена и интегрированию рациональной дроби. Интеграл от многочлена равен по свойствам линейности интеграла сумме произведений интегралов от степенных функций на постоянные коэффициенты. Разложение рациональной дроби на элементарные. Полином – знаменатель рациональной дроби может иметь действительный корень некоторой — ой кратности. Тогда , где многочлен уже не имеет корня . В этом случае из рациональной дроби можно выделить элементарную рациональную дробь вида . Лемма 2. Пусть — действительный корень — ой кратности полинома – знаменателя рациональной дроби. Тогда = , где многочлен уже не имеет корня . Доказательство. Приведем дроби к общему знаменателю и приравняем числители полученных дробей. . Тогда выражение должно делиться на , т.е. . Этого можно добиться, выбрав . Следствие 1. В условиях леммы 2 рациональную дробь можно представить в виде где не имеет корня . Доказательство. Применим лемму 2 раз и получим указанное разложение. Полином – знаменатель рациональной дроби может иметь пару комплексно сопряженных корней — ой кратности. Лемма 3. Пусть – знаменатель рациональной дроби имеет пару комплексно сопряженных корней — ой кратности. Тогда рациональную дробь можно представить в виде = , где уже не являются корнями полинома . Доказательство. Приведем дроби к общему знаменателю и приравняем числители полученных дробей. =. должно делиться как на , так и на . Поэтому , где =, = Отсюда имеем систему уравнений для определения констант . Определитель этой системы равен , так как корни комплексные и . Поэтому система имеет единственное решение. Следствие 2. В условиях леммы 2 рациональную дробь можно представить в виде = ++ …++ , где уже не являются корнями полинома . Доказательство. Применяем лемму 3 нужное число раз и получаем искомое разложение. Теорема. Рациональная функция может быть представлена в виде =++…+ +…+++ …++ …+, где — простой действительный корень , — действительный корень кратности , — пара комплексно сопряженных корней кратности (комплексно сопряженные корни ), — простая пара комплексно сопряженных корней (корни ). Доказательство. Применяем к рациональной функции лемму 1, выделяем полином – целую часть , затем по лемме 2, выделяем члены разложения, соответствующие простым и кратным действительным корням. Затем по лемме 3 выделяем члены разложения, соответствующие простым и кратным парам комплексно сопряженных корней. Так как многочлен может иметь корни лишь перечисленных типов, то разложение этим и исчерпывается. Следствие 3. Задача интегрирования рациональной функции сводится к задачам интегрирования элементарных рациональных дробей четырех типов 1) , 2) , 3) , 4). Способы вычисления коэффициентов при разложении рациональной дроби на элементарные. Пример. Теперь надо приравнивать многочлены в числителях дробей и определять неизвестные коэффициенты A, B, M, N, P, Q. Это можно сделать двумя способами. 1 способ – приравнивать коэффициенты при одинаковых степенях переменной, составлять и решать систему уравнений. X5| 3=A+B+M X4| 1=A-B+N X3| 7=2A+2B+P X2| 2=2A-2B+Q Решение системы A=2, B=1, M=N=Q=0, P=1. X |2=A+B-N-P 1 |1=A-B-N-Q 2 способ – задавать значения неизвестной, вычислять значения числителей и составлять систему уравнений. X=1 | 16=8A X= -1| -8=-8B X=0 | 1=A-B-N-P X=2 | 181=75A-25B+30M+15N+6P+3Q X=-2 | -96= -25A-75B-30M+15N-6P+3Q X=-3 | -824= -200A –400B-240M –80N –24P+8Q Решая эту систему уравнений, получим то же решение A=2, B=1, M=N=Q=0, P=1. Какой способ применять – зависит от того, где получается более простая и удобная для решения система уравнений. В данном примере вторая система сложнее первой. Интегрирование элементарных рациональных дробей четырех типов. 1) , 2) 3) = (пример рассмотрен во второй лекции). Для того, чтобы вычислить интеграл от дроби в п.3, достаточно в соответствующем примере второй лекции обозначить коэффициенты другими буквами. 4) == , где . Вычислим интеграл . .= -= По этой рекуррентной формуле можно последовательно вычислять интегралы при различных , предварительно вычислив . Таким образом, показано, что все четыре типа элементарных рациональных дробей интегрируемы. Следовательно, класс рациональных функций представляет собой класс интегрируемых функций. При интегрировании конкретных рациональных функций выделяют целую часть и раскладывают рациональную дробь на элементарные. Затем интегрируют элементарные рациональные дроби. Пример. Составляем и решаем систему уравнений относительно неопределенных коэффициентов (первый способ определения коэффициентов) Получим Можно воспользоваться и вторым способом определения коэффициентов. X=0 | -1 = B-A-C X=1 | 4 = A+B+2B+C+B-A-C= 4B X=-1| -2 = A+B-2B-C+B-A-C= -2C. Отсюда C=1, B=1, A=1. Ещё посмотрите лекцию «Критерии качества интерфейса (продолжение)» по этой теме. Вторая система проще, чем первая. Теперь интегрируем сумму элементарных дробей. Метод Остроградского. Если знаменатель рациональной дроби содержит пары комплексно сопряженных корней большой кратности, то удобно применять метод Остроградского. Он состоит в следующем: вычисляют . Затем интеграл представляют в виде , где степень на единицу меньше степени , а степень на единицу меньше степени . Коэффициенты полиномов , определяются при дифференцировании левой и правой частей и приравнивания коэффициентов при равных степенях x. Напомним, что рациональная функция представляет собой отношение двух многочленов P ( x )/ Q ( x ). Будем считать, что у нас есть правильная рациональная функция, в которой степень числителя меньше степени знаменателя. Чтобы преобразовать неправильную рациональную функцию в правильную, мы можем использовать длинное деление: \[\frac{{P\left( x \right)}}{{Q\left( x \right)}} = F\left( x \right) + \frac{{R\left( x \right) )}}{{Q\влево( x \вправо)}},\] , где F ( x ) — многочлен, P ( x )/ Q ( x ) — правильная рациональная функция. Чтобы проинтегрировать правильную рациональную функцию, мы можем применить метод частичных дробей. Этот метод позволяет превратить интеграл сложной рациональной функции в сумму интегралов более простых функций. Знаменатели неполных дробей могут содержать неповторяющиеся линейные множители, повторяющиеся линейные множители, неповторяющиеся неприводимые квадратичные множители и повторяющиеся неприводимые квадратичные множители. 92} + 2x + 1}}}.\] Найдите интеграл \[\int {\frac{{x + 2}}{{x — 1}} dx}.\] Раствор. Поскольку рациональная дробь в подынтегральном выражении неправильная, мы выполняем деление в большую сторону, чтобы получить \[\frac{{x + 2}}{{x — 1}} = 1 + \frac{3}{{x — 1}}. Теперь мы можем легко вычислить интеграл: \[\int {\frac{{x + 2}}{{x — 1}}dx} = \int {\left( {1 + \frac{3}{{x — 1}}} \right) dx} = \ int {dx} + 3 \ int {\ frac {{dx}} {{x — 1}}} = x + 3 \ ln \ left | {х — 1} \право| + С.\] 92} — 9}} = \frac{{2x + 3}}{{\left( {x — 3} \right)\left( {x + 3} \right)}} = \frac{A}{{ х — 3}} + \frac{B}{{х + 3}}.\] Приравнять коэффициенты: \[А\влево( {х + 3} \вправо) + В\влево( {х — 3} \вправо) = 2х + 3,\;\; \Стрелка вправо Ax + 3A + Bx — 3B = 2x + 3,\;\; \стрелка вправо \влево( {A + B} \вправо)x + 3A — 3B = 2x + 3.\] Следовательно, \[
\left\{ \begin{массив}{l}
А + В = 2\\
3А — 3В = 3
\end{массив} \right.,\;\; \Правая стрелка
\left\{ \begin{массив}{l}
А = \ гидроразрыва {3} {2} \\
B = \ гидроразрыва {1} {2}
\end{массив} \right..\] 92}}}{2} — x — \ln \left| {х + 1} \право| + С.\] Найдите интеграл \[\int {\frac{{dx}}{{\left( {2x — 1} \right)\left( {x + 3} \right)}}}.\ ] Раствор. Сначала разложим подынтегральную функцию: \[\frac{1}{{\left( {2x — 1} \right)\left( {x + 3} \right)}} = \frac{A}{{2x — 1}} + \frac {В}{{х + 3}}.\] Определить коэффициенты \(A\) и \(B:\) \[1 = A\влево( {x + 3} \вправо) + B\влево( {2x — 1} \вправо),\] \[1 = Ах + 3А + 2Вх — В,\] \[1 = \влево( {A + 2B} \вправо)x + \влево( {3A — B} \вправо).\] Получаем следующую систему: \[\left\{ \begin{массив}{l}
А + 2В = 0\\
3А — В = 1
\end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l}
А + 2\влево({3А — 1}\вправо) = 0\\
В = 3А — 1
\end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l}
7А — 2 = 0\\
В = 3А — 1
\end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l}
А = \ гидроразрыва {2} {7} \\
В = — \фракция{1}{7}
\end{массив} \right..\] Таким образом, разложение на неполные дроби имеет вид \[\frac{1}{{\left( {2x — 1} \right)\left( {x + 3} \right)}} = \frac{2}{{7\left( {2x — 1 } \right)}} — \frac{1}{{7\left( {x + 3} \right)}}. Исходный интеграл записывается в виде суммы двух более простых интегралов: \[I = \int {\frac{{dx}}{{\left({2x — 1} \right)\left({x + 3} \right)}}} = \frac{2}{7 }\int {\frac{{dx}}{{2x — 1}}} — \frac{1}{7}\int {\frac{{dx}}{{x + 3}}} .\] Интеграция выходов: 92} — 9}} = \ frac {x} {{\ left ( {x — 3} \ right) \ left ( {x + 3} \ right)}} = \ frac {A} {{x — 3} } + \frac{B}{{x + 3}}.\] Рассчитать неизвестные коэффициенты: \[x = A\left( {x + 3} \right) + B\left( {x — 3} \right),\] \[х = Ах + 3А + Вх — 3В,\] \[x = \left( {A + B} \right)x + \left( {3A — 3B} \right).\] Отсюда \[\left\{ \begin{массив}{l}
А + В = 1\\
3А — 3В = 0
\end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l}
А + В = 1\\
А — В = 0
\end{массив} \right.,\;\; \стрелка вправо \влево\{ \begin{массив}{l}
А = \ гидроразрыва {1} {2} \\
B = \ гидроразрыва {1} {2}
\end{массив} \right..\] 92}}}} = \ln \left| {х + 1} \право| + \frac{1}{{x + 1}} + C. Дополнительные проблемы см. на стр. 2. Мы рассмотрели несколько методов, позволяющих интегрировать определенные рациональные функции. Например, мы знаем, что 92−x−2}\nonumber \] в виде выражения, такого как \[ \dfrac{1}{x+1}+\dfrac{2}{x−2}. Ключом к методу разложения на неполные дроби является возможность предвидеть форму, которую примет разложение рациональной функции. Как мы увидим, эта форма предсказуема и сильно зависит от факторизации знаменателя рациональной функции. Также чрезвычайно важно иметь в виду, что разложение на неполные дроби может быть применено к рациональной функции \( \dfrac{P(x)}{Q(x)}\) только в том случае, если \( deg(P(x))< град(Q(x))\). В случае, когда \( deg(P(x))≥deg(Q(x))\), мы должны сначала выполнить деление в длину, чтобы переписать частное \( \dfrac{P(x)}{Q(x)} \) в виде \( A(x)+\dfrac{R(x)}{Q(x)}\), где \( deg(R(x)) Посетите этот веб-сайт для ознакомления с делением многочленов в длину. Оценка \[ \int \dfrac{x−3}{x+2}\,dx. \номер\] Используйте длинное деление, чтобы получить \( \dfrac{x−3}{x+2}=1−\dfrac{5}{x+2}. \nonumber \) \[ x−5\ln |x+2|+C \не число \] Для интегрирования \(\displaystyle \int \dfrac{P(x)}{Q(x)}\,dx\), где \( deg(P(x)) Если \( Q(x)\) можно разложить на множители как \( (a_1x+b_1)(a_2x+b_2)…(a_nx+b_n)\), где каждый линейный множитель различен, то можно найти константы \( A_1,A_2,…A_n\), удовлетворяющие \[ \dfrac{P(x)}{Q(x)}=\dfrac{A_1}{a_1x+b_1}+\dfrac{A_2 }{a_2x+b_2}+⋯+\dfrac{A_n}{a_nx+b_n}. \label{eq:7.4.1} \] 92−2x=x(x−2)(x+1)\). Таким образом, существуют константы \(A\), \(B\) и \(C\), удовлетворяющие уравнению \ref{eq:7. \[ \dfrac{3x+2}{x( x−2)(x+1)}=\dfrac{A}{x}+\dfrac{B}{x-2}+\dfrac{C}{x+1}. \nonumber \] Теперь мы должны найти эти константы. Для этого начнем с получения общего знаменателя справа. Таким образом, \[ \dfrac{3x+2}{x(x−2)(x+1)}=\dfrac{A(x−2)(x+1)+Bx(x+1)+Cx (х-2)}{х(х-2)(х+1)}. \nonumber \] Теперь приравняем числители друг к другу, получив 92+(-А+В-2С)х+(-2А). \nonumber \] Приравнивание коэффициентов дает систему уравнений \[\begin{align*} A+B+C &=0 \\[4pt] −A+B−2C &= 3 \\[4pt] −2А &=2. \end{align*}\] Чтобы решить эту систему, мы сначала заметим, что \( −2A=2⇒A=−1.\) Подстановка этого значения в первые два уравнения дает нам систему \( B +C=1\) \(B−2C=2\). Умножение второго уравнения на \( −1\) и добавление полученного уравнения к первому дает \(−3C=1,\) , что, в свою очередь, означает, что \(C=−\dfrac{1}{3}\). Подстановка этого значения в уравнение \(B+C=1\) дает \(B=\dfrac{4}{3}\). Важно отметить, что система, полученная этим методом, непротиворечива тогда и только тогда, когда мы правильно установили декомпозицию. Если система противоречива, в нашей декомпозиции есть ошибка. Вторая стратегия: метод стратегического замещения Метод стратегической замены основан на предположении, что мы правильно настроили декомпозицию. Если разложение настроено правильно, то должны быть значения \(A, B,\) и \(C\), которые удовлетворяют уравнению \(\ref{Ex2Numerator}\) для всех значений \(x\). То есть это уравнение должно быть истинным для любого значения \(х\), которое мы хотим подставить в него. Следовательно, тщательно выбирая значения \(x\) и подставляя их в уравнение, мы можем легко найти \(A, B\) и \(C\). Например, если мы подставим \(x=0\), уравнение сведется к \(2=A(−2)(1)\). Решение для \(A\) дает \(A=−1\). Затем, подставив \(x=2\), уравнение сводится к \(8=B(2)(3)\) или, что то же самое, \(B=4/3\). Вычислить \(\displaystyle \int \dfrac{x+1}{(x+3)(x−2)}\,dx.\) \[ \dfrac{x+1}{(x+3)(x−2)}=\dfrac{A}{x+3}+\dfrac{B}{x−2} \nonumber \] \[ \dfrac{2}{5}\ln |x+3|+\dfrac{3}{5}\ln |x−2|+C \nonumber \] Приравнивание коэффициентов дает \( 2A+4C=0\), \(−3A+B−4C=1\) и \(A−B+C=−2\). Решение этой системы дает \(A=2, B=3,\) и \(C=−1.\) В качестве альтернативы мы можем использовать метод стратегической замены. В этом случае подстановка \(x=1\) и \(x=1/2\) в уравнение \(\ref{Ex5Numerator}\) легко дает значения \(B=3\) и \(C=- 1\). На данный момент может показаться, что у нас закончились хорошие варианты для \(x\), однако, поскольку у нас уже есть значения для \(B\) и \(C\), мы можем подставить эти значения и выбрать любое значение для \(x\), которое ранее не использовалось. Теперь, когда мы начинаем понимать, как работает метод разложения на неполные дроби, давайте наметим основной метод в следующей стратегии решения задач. Чтобы разложить рациональную функцию \( P(x)/Q(x)\), выполните следующие действия: Решение Начнем с наброска области вращения (см. рисунок \(\PageIndex{1}\)). Из скетча мы видим, что метод оболочки — хороший выбор для решения этой задачи. Объем дается 92} \номер \] Этот подход предполагает, что вы можете разложить знаменатель на линейные и квадратичные члены с действительными коэффициентами. Следовательно, он не будет работать в случаях, когда факторизация неизвестна. Обратитесь к разделу «Частичные дроби», если вы не знакомы с этим процессом. Сначала мы выполняем частичные дроби над f(x)g(x) \frac{f(x)} {g(x)} g(x)f(x), чтобы преобразовать его в многочлен остатка, а также линейный и квадратичный знаменатели. Тип 1: полином остатка r(x) r(x) r(x) Тип 2a: 1x−a \frac{1}{ x -a } x−a1, линейный член в первой степени Наилучший способ чтобы понять, как это работает, нужно проработать несколько примеров, чтобы увидеть, как работать с каждым из этих типов. Мы начнем с нескольких основных примеров, в которых используется только один тип дробей. 2x(x−1)(x+1)=1x+1+1x−1. \frac{2x}{ (x-1)(x+1) } = \frac{ 1}{x+1} + \frac{1}{x-1} . (x−1)(x+1)2x=x+11+x−11. Мы интегрируем каждый термин отдельно как тип 2а, чтобы получить ∫2x(x−1)(x+1) dx=∫1x+1 dx+∫1x−1 dx=ln∣x+1∣+ln∣x−1∣+C. □ \begin{выровнено}
\int \frac{2x}{ (x-1)(x+1) } \, \mathrm dx
& = \int \frac{ 1}{x+1} \, \mathrm dx + \int \frac{1}{x-1} \, \mathrm dx \\
& = \ln \влево|x+1\вправо| + \ln \влево|x-1\вправо| + С.\ _\квадрат
\end{выровнено} ∫(x−1)(x+1)2xdx=∫x+11dx+∫x-11dx=ln∣x+1∣+ln∣x-1∣+C. □ 93 + 1}x3+11 непрерывно от 000 до ∞\infty∞, поэтому мы можем использовать основную теорему исчисления. Чтобы вычислить определенный интеграл, мы вычислим неопределенный интеграл при x=0x = 0x=0 и ∞\infty∞. При x=0x = 0 x=0 первые два члена становятся ln1,\ln 1,ln1, что равно нулю. Третий член равен 13arctan−13=13⋅−π6=−π63\frac{1}{\sqrt{3}} \arctan\frac{-1}{\sqrt{3}} =\frac{1}{ \sqrt{3}} \cdot \frac{ — \pi} {6} = — \frac{\pi}{6 \sqrt{3}}31arctan3−1=31⋅6 −π=−63π. (А), (В) и (С)
(А), (В), (С) и (D)
(А), (В) и (Г)
(А) и (С)
(А), (С) и (D)
(А) и (Г)
(Б) и (С)
(Б), (С) и (Г) 9{ 2 }+2x+2) } } dx Y=∫01(x+1)(x2+2x+2)2×2+3x+3dx Какие из следующих вариантов равны Y?Y?Y ? (A) π4+2log2−arctan2\ \frac { \pi }{ 4 } +2\log2-\arctan { 2 } 4π+2log2−arctan2 (B) π4+2log2 −arctan13\ \frac { \pi }{4} +2\log2-\arctan {\frac{1}{3}} 4π+2log2−arctan31 (C) 2log2−arccot 3\ 2 \log 2 — \text{arccot 3} 2log2−arccot 3 (D) −π4+log4+arccot 2\ -\frac{\pi}{4}+\log4+\text{arccot 2} − 4π+log4+arccot 2 Метод частичной дроби сильно зависит от предположения, что мы можем разложить знаменатель на линейные и квадратичные члены. Напомним, что мы используем uuu-подстановку, когда интеграл имеет следующий вид: ∫g(f(x))⋅f′(x) dx,\int g\big(f(x)\big) \ cdot f'(x) \, dx,∫g(f(x))⋅f'(x)dx, , где ggg легко интегрируется. Подставим u=f(x)u = f(x)u=f(x) и получим du=f′(x) dx du = f'(x) \, dxdu=f′(x)dx. Интегрирование упрощается до ∫g(u) du\int g(u) \, du∫g(u)du, что легко вычислить. Давайте рассмотрим несколько примеров, которые сложно решить с помощью метода неполных дробей, но которые очень легко решить с помощью uuu-подстановки. 9c}∫(x7+x2+1)37×13+5×15dx=a1⋅(x7+x2+1)cxb Учитывая, что приведенный выше неопределенный интеграл верен, каково значение a+b+c, a +b+c, a+b+c, где a,b, и ca,b,\text{ и }ca,b, и c – положительные целые числа? Процитировать как: Интеграция рациональных функций. Brilliant.org .
Извлекаются из
https://brilliant. Шаблон:Стратегия интеграции конкретного функционального класса Для получения дополнительной информации см. Преобразование рациональной функции из неправильной дроби в форму смешанной дроби Чтобы получить ситуацию, когда числитель имеет меньшую степень, чем знаменатель, мы выполняем евклидово деление и, следовательно, переписываем рациональную функцию как сумму многочлена и рациональной функции, которая находится в правильная дробь формы, т. е. числитель имеет меньшую степень, чем знаменатель. Полиномиальное слагаемое интегрируется почленно с использованием правила интегрирования степенных функций. Таким образом, мы вынуждены обращаться с правильной дробью. Если старший коэффициент (т. е. коэффициент при высшей степени) в знаменателе не равен 1, старший коэффициент может быть вынесен как постоянный множитель из знаменателя и, следовательно, из интеграция. Таким образом, мы можем выполнить интегрирование со старшим коэффициентом 1 для многочлена знаменателя (такой многочлен называется моническим многочленом). Но не забудьте сохранить эту константу снаружи и умножить ее, чтобы получить окончательный ответ! Мы предполагаем, что мы выполнили описанные выше сокращения. Таким образом, рассмотрим интегрирование вида: Обратите внимание, что это произвольные константы. Они могут быть нулевыми или ненулевыми. Формула интегрирования: Обратите внимание, что и можно определить из квадратичной формулы для корней квадратного многочлена. В частности, если многочлен в знаменателе равен , мы имеем: Вот подробности получения формулы: [ПОКАЗАТЬ БОЛЬШЕ] Формула интегрирования: Если знаменатель имеет вид , то этот случай возникает тогда и только тогда, когда мы имеем . Вот как получается формула: [ПОКАЗАТЬ БОЛЬШЕ] У нас есть: Учитывая знаменатель в форме , его можно переписать как где: Вот как получается формула: [ПОКАЗАТЬ БОЛЬШЕ] Здесь мы обсуждаем только редуцированный случай неопределенного интегрирования. Используя те же обозначения, что и для неопределенного интегрирования, мы имеем интегрирование в форме: Первообразная: где, если квадратное число в знаменателе изначально равно: Подынтегральная функция не определена в точках . Фактически область определения функции представляет собой объединение трех отдельных открытых интервалов: , , и . Общая первообразная для функции на всех интервалах может иметь разные значения константы на каждом интервале. Кроме того, мы можем опустить знаки абсолютного значения и уточнить входные данные для s в каждом интервале: Интеграл может быть вычислен, чтобы дать конечное числовое значение на любом интервале правильно содержал полностью внутри одного из этих интервалов. Ответ следующий: Используя те же обозначения, что и для неопределенного интегрирования, мы пытаемся выполнить интегрирование: Первообразная: где — произвольная константа. Далее, если знаменатель изначально был , то и . Областью определения подынтегральной функции являются все действительные числа, кроме . Таким образом, это объединение открытых интервалов и . На каждом из интервалов можно однозначно определить знак , поэтому первообразную можно записать более однозначно: Таким образом, для любого интервала, полностью содержащегося в одной из двух частей, мы можем вычислить определенный интеграл, используя приведенное выше. Мы пытаемся выполнить интегрирование: Первообразная: Учитывая знаменатель в форме, его можно переписать как где: Подынтегральная функция, а также ее первообразная определены для всех действительных чисел. В частности, имеет смысл взять определенный интеграл по любому конечному интервалу и получить конечный ответ. В частности, если , мы можем проинтегрировать функцию по всей прямой и получить конечный ответ. Это ответ. Рассмотрим задачу интегрирования: Вот как мы могли бы сделать это непосредственно с точки зрения формулы: [ПОКАЗАТЬ БОЛЬШЕ] В качестве альтернативы, вместо непосредственного использования формулы, мы можем проследить этапы ее вывода, чтобы получить первообразную: [ПОКАЗАТЬ БОЛЬШЕ] Заполните это позже — что-то Здесь речь идет о выборе базисных функций для частичных функций, соответствующих первообразных, имеющих дело с двумерным векторным пространством во всех трех случаях, но выбор базисных функций, которые мы используем, различается в разных случаях. Заполните это позже — что-то о том, что ответ является многочленом + что-то для случая сокращенной формы. Приведенные выше стратегии можно применять для вычисления старших первообразных рациональных функций с квадратичным знаменателем. Ключевая идея, используемая для доказательства более общего наблюдения о том, что рациональные функции могут многократно интегрироваться внутри элементарно выразимых функций, состоит в следующем следствии интегрирования по частям, полученном путем взятия 1 в качестве части для интегрирования в левостороннем внешнем интегрировании: Здесь важно отметить, что поскольку имеет квадратичный знаменатель, то и . Особенно: Двойное интегрирование Интегрирование обоих и , которые являются рациональными функциями с квадратичным знаменателем. Аналогично, Время интегрирования Интегрирование рациональных функций В частности, это означает, что общее выражение для первообразной представляет собой полином плюс линейную комбинацию двух базисных функций первообразной, которые зависят от только в знаменателе. Теперь рассмотрим следующую простую алгебру дробей:
$$
{A\над xr}+{B\над xs}={A(xs)+B(xr)\over (xr)(xs)}=
{(A+B)x-As-Br\over (x-r)(x-s)}.
$$
То есть сложение двух дробей с постоянными числителем и знаменателем
$(x-r)$ и $(x-s)$ дают дробь со знаменателем $(x-r)(x-s)$
и многочлен степени меньше 2 для числителя. Мы хотим
обратить этот процесс вспять: начиная с одной дроби, мы хотим
запишите его в виде суммы двух простых дробей. Пример должен сделать это
понятно как поступить.
93\over (x-2)(x+3)}\,dx$. Мы начинаем с
записав $\ds{7x-6\over (x-2)(x+3)}$ как сумму двух дробей. Мы
хочу закончить с
$${7x-6\over (x-2)(x+3)}={A\over x-2}+{B\over x+3}.$$
Если мы продолжим и добавим дроби в правой части, мы получим
$${7x-6\over (x-2)(x+3)}={(A+B)x+3A-2B\over (x-2)(x+3)}.$$
Итак, все, что нам нужно сделать, это найти $A$ и $B$ так, чтобы $7x-6=(A+B)x+3A-2B$,
то есть нам нужно $7=A+B$ и $-6=3A-2B$. Показать мобильное уведомление Показать все примечания Скрыть все примечания Уведомление для мобильных устройств Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Этот процесс взятия рационального выражения и разложения его на более простые рациональные выражения, которые мы можем складывать или вычитать, чтобы получить исходное рациональное выражение, называется разложением на частичные дроби . Итак, давайте проведем краткий обзор частичных дробей. Мы начнем с рационального выражения в форме .
\[f\left( x \right) = \frac{{P\left( x \right)}}{{Q\left( x \right)}}\] , где оба \(P\left( x \right)\) и \(Q\left( x \right)\) являются полиномами, а степень \(P\left( x \right)\) меньше, чем степень \(Q\left( x \right)\). Напомним, что степень многочлена — это наибольший показатель степени многочлена. Частичные дроби можно делать только в том случае, если степень числителя строго меньше степени знаменателя. Это важно помнить. Итак, как только мы определили, что частичные дроби можно делать, мы максимально полно разложим знаменатель. Затем для каждого фактора в знаменателе мы можем использовать следующую таблицу, чтобы определить члены, которые мы выбираем при разложении частичной дроби. Показать решение Первый шаг — максимально разложить знаменатель на множители и получить форму разложения на неполные дроби. Выполнение этого дает, \[\ frac{{3x + 11}}{{\left( {x — 3} \right)\left( {x + 2} \right)}}\, = \ frac{A}{{x — 3 }} + \frac{B}{{x + 2}}\] Следующим шагом будет добавление правой стороны. \[\ frac{{3x + 11}}{{\left( {x — 3} \right)\left( {x + 2} \right)}}\, = \ frac{{A\left( {x + 2} \right) + B\left( {x — 3} \right)}}{{\left( {x — 3} \right)\left( {x + 2} \right)}}\] Теперь нам нужно выбрать \(A\) и \(B\) так, чтобы числители этих двух были равны для каждого \(x\). Для этого нам нужно установить равные числители. \[3x + 11 = A\влево( {x + 2} \вправо) + B\влево({x — 3} \вправо)\] Обратите внимание, что в большинстве задач мы сразу переходим от общей формы декомпозиции к этому шагу и не утруждаем себя фактическим добавлением членов обратно. На данный момент у нас есть один из двух способов продолжить. Один способ всегда будет работать, но часто больше работы. Другой, хотя и не всегда будет работать, часто работает быстрее, когда работает. В этом случае оба будут работать, поэтому мы будем использовать более быстрый способ для этого примера. Мы рассмотрим другой метод в следующем примере. Здесь мы собираемся заметить, что числители должны быть равны для любого x , которое мы решили использовать. В частности, числители должны быть равны для \(x = — 2\) и \(x = 3\). Итак, давайте подключим их и посмотрим, что мы получим. \[\begin{align*}x & = — 2 : & \hspace{0.5in}5 & = A\left( 0 \right) + B\left( { — 5} \right) & \hspace{0.25in } & \Rightarrow & \hspace{0.25in}B & = — 1\\ x & = 3 \,\,\,\,: & \hspace{0. Таким образом, тщательно подобрав \(x\), мы получили быстрое выпадение неизвестных констант. Обратите внимание, что это значения, которые, как мы утверждали, будут выше. 92} — x — 6}}\,dx}} & = \int{{\frac{4}{{x — 3}}\, — \frac{1}{{x + 2}}dx}}\ \ & = \int{{\frac{4}{{x — 3}}\,dx}} — \int{{\frac{1}{{x + 2}}dx}}\\ & = 4\ пер \ влево | {х — 3} \право| — \лн\влево| {х + 2} \право| + с\конец{выравнивание*}\] Напомним, что для составления этого интеграла мы сначала разбили его на два интеграла, а затем использовали подстановки \[u = x — 3\hspace{0.5in}v = x + 2\] по интегралам, чтобы получить окончательный ответ. 92} + 4 = A\left( {x + 2} \right)\left( {3x — 2} \ right) + Bx\left( {3x — 2} \ right) + Cx\left( {x + 2 } \Правильно)\] Как и в предыдущем примере, похоже, что мы можем просто выбрать несколько значений \(x\) и найти константы, так что давайте сделаем это. \[\begin{align*}x & = 0 \,\,\,\,\, : & \hspace{0.5in}4 & = A\left( 2 \right)\left( { — 2} \right ) & \hspace{0.5in} & \Rightarrow & \hspace{0.25in}A & = — 1\\ x & = — 2 : & \hspace{0.5in}8 & = B\left( { — 2} \ вправо)\влево( { — 8} \вправо) & \hspace{0.25in}&\Rightarrow & \hspace{0.25in}B & = \frac{1}{2}\\ x & = \frac{2} {3}\,\, : & \hspace{0,5 дюйма}\frac{{40}}{92} — 4x}}\,dx}} & = \int{{ — \frac{1}{x} + \frac{{\frac{1}{2}}}{{x + 2}} + \ frac{{\frac{5}{2}}}{{3x — 2}}\,dx}}\\ & = — \ln \left| х \ справа | + \frac{1}{2}\ln \left| {х + 2} \право| + \frac{5}{6}\ln \left| {3x — 2} \право| + с\конец{выравнивание*}\] Опять же, как отмечалось выше, интегралы, которые генерируют натуральные логарифмы, очень распространены в этих задачах, поэтому убедитесь, что вы можете их решить. Кроме того, вы смогли правильно сделать последний интеграл, верно? Коэффициент при \(\frac{5}{6}\) правильный. Убедитесь, что вы делаете замену, необходимую для термина правильно. Теперь есть вариант метода, который мы использовали в первых двух примерах, который будет работать здесь. Есть пара значений \(x\), которые позволят нам быстро получить две из трех констант, но нет значения \(x\), которое просто даст нам третью. В этом примере мы выберем \(x\), чтобы получить две константы, которые мы можем легко получить, а затем мы просто выберем другое значение \(x\), с которым будет легко работать с ( т.е. он нигде не даст больших/запутанных чисел), а затем мы воспользуемся тем, что мы также знаем две другие константы, чтобы найти третью. \[\begin{align*}x & = 0 : & \hspace{0.25in} 18 & = B\left( { — 3} \right) & \hspace{0.15in}\Rightarrow \hspace{0.25in}B & = — 6\\ x & = 3 : & \hspace{0.25in} 18 & = C\left( 9 \right) & \hspace{0.15in} \Rightarrow \hspace{0.25in}C & = 2\\ x & = 1 : & 18 & = A\left( { — 2} \right) + B\left( { — 2} \right) + C = — 2A + 14 & \hspace{0. К оглавлению… Путь при равномерном движении: Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей): Средняя скорость пути: Средняя скорость перемещения: Определение ускорения при равноускоренном движении: Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении: Средняя скорость при равноускоренном движении: Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам: Координата при равноускоренном движении изменяется по закону: Проекция скорости при равноускоренном движении изменяется по такому закону: Скорость, с которой упадет тело падающее с высоты h без начальной скорости: Время падения тела с высоты h без начальной скорости: Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку): Формула для тормозного пути тела: Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле: Дальность полета тела при горизонтальном броске с высоты H: Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту: Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня): Время подъема до максимальной высоты при броске под углом к горизонту: Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю): Определение периода вращения при равномерном движении по окружности: Определение частоты вращения при равномерном движении по окружности: Связь периода и частоты: Линейная скорость при равномерном движении по окружности может быть найдена по формулам: Угловая скорость вращения при равномерном движении по окружности: Связь линейной и скорости и угловой скорости выражается формулой: Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии): Центростремительное ускорение находится по одной из формул: К оглавлению… Второй закон Ньютона: Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело: Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике): Третий закон Ньютона (сила действия равна силе противодействия): Сила упругости: Общий коэффициент жесткости параллельно соединённых пружин: Общий коэффициент жесткости последовательно соединённых пружин: Сила трения скольжения (или максимальное значение силы трения покоя): Закон всемирного тяготения: Если рассмотреть тело на поверхности планеты и ввести следующее обозначение: Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести: Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой: Скорость спутника на круговой орбите: Первая космическая скорость: Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра: К оглавлению… Момент силы определяется с помощью следующей формулы: Условие при котором тело не будет вращаться: Координата центра тяжести системы тел (аналогичные уравнения для остальных осей): К оглавлению… Определение давления задаётся следующей формулой: Давление, которое создает столб жидкости находится по формуле: Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид: Идеальный гидравлический пресс: Любой гидравлический пресс: КПД для неидеального гидравлического пресса: Сила Архимеда (выталкивающая сила, V — объем погруженной части тела): К оглавлению… Импульс тела находится по следующей формуле: Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная): Общий импульс системы тел (важно то, что сумма векторная): Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы: Закон сохранения импульса. Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется: Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например: К оглавлению… Механическая работа рассчитывается по следующей формуле: Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность): Мгновенная механическая мощность: Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы: Формула для кинетической энергии: Потенциальная энергия тела поднятого на высоту: Потенциальная энергия растянутой (или сжатой) пружины: Полная механическая энергия: Связь полной механической энергии тела или системы тел и работы внешних сил: Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот): К оглавлению… Химическое количество вещества находится по одной из формул: Масса одной молекулы вещества может быть найдена по следующей формуле: Связь массы, плотности и объёма: Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа: Определение концентрации задаётся следующей формулой: Для средней квадратичной скорости молекул имеется две формулы: Средняя кинетическая энергия поступательного движения одной молекулы: Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом: Следствия из основного уравнения МКТ: Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева): Газовые законы. Закон Бойля-Мариотта: Закон Гей-Люссака: Закон Шарля: Универсальный газовый закон (Клапейрона): Давление смеси газов (закон Дальтона): Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону: Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела: К оглавлению… Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле: Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле: Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом: Фазовые превращения. При парообразовании поглощается, а при конденсации выделяется количество теплоты равное: При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное: При сгорании топлива выделяется количество теплоты равное: Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных): Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде: Работа идеального газа: Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа: Изменение внутренней энергии рассчитывается по формуле: Первый закон (первое начало) термодинамики (ЗСЭ): Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const): Изобарный процесс (p = const): Изотермический процесс (T = const): Адиабатный процесс (Q = 0): КПД тепловой машины может быть рассчитан по формуле: Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл: Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен: Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула): Относительная влажность воздуха может быть рассчитана по следующим формулам: Потенциальная энергия поверхности жидкости площадью S: Сила поверхностного натяжения, действующая на участок границы жидкости длиной L: Высота столба жидкости в капилляре: При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной: При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр. К оглавлению… Электрический заряд может быть найден по формуле: Линейная плотность заряда: Поверхностная плотность заряда: Объёмная плотность заряда: Закон Кулона (сила электростатического взаимодействия двух электрических зарядов): Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом: Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле): Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его): Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра: Напряженность электрического поля, которую создает заряженная плоскость: Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой: Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой: В однородном электрическом поле существует связь между напряженностью поля и напряжением: Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов: Работа электрического поля в общем случае может быть вычислена также и по одной из формул: В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле: Определение потенциала задаётся выражением: Потенциал, который создает точечный заряд или заряженная сфера: Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле): Для диэлектрической проницаемости вещества верно следующее: Определение электрической ёмкости задаётся формулой: Ёмкость плоского конденсатора: Заряд конденсатора: Напряжённость электрического поля внутри плоского конденсатора: Сила притяжения пластин плоского конденсатора: Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора): Объёмная плотность энергии электрического поля: К оглавлению… Сила тока может быть найдена с помощью формулы: Плотность тока: Сопротивление проводника: Зависимость сопротивления проводника от температуры задаётся следующей формулой: Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления): Закономерности последовательного соединения: Закономерности параллельного соединения: Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы: Закон Ома для полной цепи: Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника): Сила тока короткого замыкания: Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике: Мощность электрического тока: Полезная мощность или мощность, выделяемая во внешней цепи: Максимально возможная полезная мощность источника достигается, если R = r и равна: Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле: Мощность потерь или мощность внутри источника тока: Полная мощность, развиваемая источником тока: КПД источника тока: Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит: Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле: Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея: К оглавлению… Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле: Момент сил действующих на рамку с током: Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле: Радиус траектории полета заряженной частицы в магнитном поле: Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением: Индукция поля в центре витка с током радиусом R: Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией: Магнитная проницаемость вещества выражается следующим образом: Магнитным потоком Φ через площадь S контура называют величину заданную формулой: ЭДС индукции рассчитывается по формуле: При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе): Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В: Индуктивность катушки: Где: n — концентрация витков на единицу длины катушки: Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой: ЭДС самоиндукции возникающая в катушке: Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки): Объемная плотность энергии магнитного поля: К оглавлению… Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0: Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид: Период колебаний вычисляется по формуле: Частота колебаний: Циклическая частота колебаний: Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой: Максимальное значение скорости при гармонических механических колебаниях: Зависимость ускорения от времени при гармонических механических колебаниях: Максимальное значение ускорения при механических гармонических колебаниях: Циклическая частота колебаний математического маятника рассчитывается по формуле: Период колебаний математического маятника: Циклическая частота колебаний пружинного маятника: Период колебаний пружинного маятника: Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой: Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника: Взаимосвязь энергетических характеристик механического колебательного процесса: Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре: Период гармонических колебаний в электрическом колебательном контуре определяется по формуле: Циклическая частота колебаний в электрическом колебательном контуре: Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом: Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре: Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре: Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле: Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре: Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока: Действующее значение напряжения: Мощность в цепи переменного тока: Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение: Коэффициент трансформации вычисляется по формуле: Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны): В неидеальном трансформаторе вводится понятие КПД: Длина волны может быть рассчитана по формуле: Разность фаз колебаний двух точек волны, расстояние между которыми l: Скорость электромагнитной волны (в т.ч. света) в некоторой среде: Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле: Скорости электромагнитной волны (в т.ч. света) в среде и в вакууме также связаны между собой формулой: При этом показатель преломления некоторого вещества можно рассчитать используя формулу: К оглавлению… Оптическая длина пути определяется формулой: Оптическая разность хода двух лучей: Условие интерференционного максимума: Условие интерференционного минимума: Формула дифракционной решетки: Закон преломления света на границе двух прозрачных сред: Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом: Формула тонкой линзы: Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета: К оглавлению… Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле: Импульс фотона: Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ): Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е: Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением: Второй постулат Бора или правило частот (ЗСЭ): В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах: На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами: Общее число нуклонов в ядре равно сумме числа протонов и нейтронов: Дефект массы: Энергия связи ядра выраженная в единицах СИ: Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах): Формула альфа-распада: Формула бета-распада: Закон радиоактивного распада: Для произвольной ядерной реакции описывающейся формулой вида: Выполняются следующие условия: Энергетический выход такой ядерной реакции при этом равен: К оглавлению… Релятивистское сокращение длины: Релятивистское удлинение времени события: Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения: Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость: Энергия покоя тела: Любое изменение энергии тела означает изменение массы тела и наоборот: Полная энергия тела: Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения: Релятивистское увеличение массы: Кинетическая энергия тела, движущегося с релятивистской скоростью: Между полной энергией тела, энергией покоя и импульсом существует зависимость: К оглавлению… В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время): К оглавлению… На этой странице представлен исчерпывающий список формул по физике и важнейших физических свойств для успешной подготовки к ЦТ или ЕГЭ. Список составлен в формате «вопрос-ответ» на основе многолетнего опыта, и является самым полным на этом сайте. Успешное изучение всех формул по физике и физических свойств из этого файла позволит абитуриентам, не просто очень уверенно чувствовать себя на ЦТ или ЕГЭ, но и с легкостью, чуть ли не автоматически, решить большую часть экзаменационных заданий. Знание всех этих формул позволит Вам набрать очень солидный балл на экзамене, даже если у Вас нет феноменальных способностей в физике. А если Вы хотите набрать максимальный балл на ЦТ или ЕГЭ, то выучив эти формулы, Вы с легкостью и очень быстро прорешаете основную часть теста, и у Вас останется много времени на решение самых сложных задач теста, в которых Вам, к слову, также понадобится знание этих формул. Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия: Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны. Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка. Знание формул по физике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по физике. Формулы по физике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении физических задач. На этой странице сайта представлены основные формулы по школьной физике в двух частях. В первой части Вы найдете самые важные физические формулы, а во второй — дополнительный набор полезных формул по физике. К оглавлению… К оглавлению… Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия: Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны. Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка. Доброго дня уважаемые радиолюбители! Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем. Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить. В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки. Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице: В этой таблице используются следующие общепринятые обозначения физических величин: U — напряжение (В), I — ток (А), Р — мощность (Вт), R — сопротивление (Ом), Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца. А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен: I = U / R Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник. Что же в этой формуле есть что? Рассмотрим переменные подробнее. > U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В. > I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А. > R: искомое сопротивление токоограничивающего резистора, в омах. В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R: R = U/I = 8,5 В / 0,050 А= 170 Ом Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее. Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин. > Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно. > Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи. Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления: Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов) В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина. Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм. Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид: R общ = R1 * R2 / (R1 + R2) где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим 776,47 = 2640000 / 3400 Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула: Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина. Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи. Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы: Собщ = CI + С2 + СЗ + … В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина. Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула: Собщ = С1 * С2 /( С1+С2) где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи: И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина. Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники. Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова: ватт-часы = Р х Т В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600. В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка). Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов. Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами. T = RC В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах. Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс. Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу: Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах. Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны: Частота = 300000 / длина волны Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах. Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота: Длина волны = 300000 / Частота Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах. Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим: 6000 миллиметров = 300000 / 50 МГц Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно! Исполнительный директор и президент Формулы 1 Стефано Доменикали рассказал о развитии спорта и заявил,… Руководитель McLaren Андреас Зайдль доволен итогами Гран При Великобритании и надеется так же успешно… Технический директор команды Mercedes Джеймс Эллисон рассказал о стратегии команды в Гран При Великобритании,… После Гран При Великобритании директор гонок FIA Майкл Маси в основном отвечал на вопросы журналистов,… Медицинский делегат FIA доктор Иан Робертс рассказал, в каком состоянии был Макс Ферстаппен после столкновения… Росс Браун, спортивный директор Формулы 1, считает, что первый эксперимент с квалификационным спринтом… Карлос Сайнс стартовал девятым в спринте Гран При Великобритании и рассчитывал отыграть позиции, но получилось… Кристиан Хорнер, руководитель Red Bull Racing, рад, что Макс Ферстаппен стал победителем первого в истории… Субботний спринт помог Кими Райкконену отыграть четыре позиции – и в гонке он надеется закрепить успех… В этом сезоне Ландо Норрис регулярно проходил в финал квалификации и заработал очки во всех гонках. Он… Макс Ферстаппен поделился ожиданиями, связанными с британским гоночным уик-эндом, а также напомнил, что… Перед началом уик-энда в Сильверстоуне мексиканский гонщик Red Bull Racing рассказал о своих ожиданиях… В первую очередь необходимо рассмотреть формулы по экономике, которые касаются спроса и предложения. Уравнение функции спроса можно представить в виде следующей формулы: Сама функция спроса выглядит следующим образом: Функция предложения: Если рассмотреть показатели эластичности, то можно выделить формулы по экономике, определяющие эластичность спроса по цене: Вторая формула представляет собой расчет средней точки, здесь значение P1 – цена продукции до изменения, P2 – цена продукции после изменения, Q1 – спрос до изменения цены, Q2 –спрос после изменения цены. Формула коэффициента эластичности спроса в общем виде: Формулы по экономике включают в себя формулы по микроэкономике (спрос и предложение, издержки фирмы и др.), а также формулы по макроэкономике. Важной формулой по макро экономике является формула расчета необходимого в обращении количества денег: КД — количество денег в обращении, ЦТ — сумма цен на товары; К — товары, продаваемые в кредит; СП — срочные платежи; ВП — взаимно погашаемые платежи по бартерным сделкам; СО — годовая скорость оборота денежной единицы. Для того чтобы определить денежную массу в обращении необходимо воспользоваться следующей формулой: Здесь M — денежная масса, которая находится в обращении; V — скорость обращения денег; Р — средние цены на продукцию; Q — количество выпущенной продукции в постоянных ценах. Уравнение обмена может быть представлено следующим равенством:
Это уравнение отражает, равенство совокупных расходов в денежном выражении и стоимости всех товаров и услуг, которые выпущены в государстве. Рассмотрим еще несколько формул по экономике, среди которых важное место занимает формула вычисления реального дохода: Здесь РД – реальный доход, НД – номинальный доход, ИПЦ – показатель индекса потребительских цен. Формула для вычисления индекса потребительских цен представлена следующим выражением: СТТГ – стоимость потребительской корзины в текущем году, СТБГ – в базовом году. В соответствии с показателем индексов цен можно определить темп инфляции по соответствующей формуле: В соответствии с темпами инфляции можно выделить несколько видов: 1. Ползучая инфляция с ростом цен до 5 % годовых, 2. Умеренная инфляция до 10 % годовых, 3. Галопирующая инфляция с ростом цен 20-200% годовых, 4. Гиперинфляция с катастрофическим ростом цен более 200 % в год. Экономические расчеты часто требуют расчета процентов. Формулы по экономике включают расчет, как сложного, так и простого процента. Формула расчета простого процента представлена следующим образом: Здесь P — сумма долга, включая проценты; С — общая сумма кредита; n – количество дней; i — годовой процент в долях. Формула для вычисления сложного процента выглядит так: K – количество лет. Формула для расчёта сложного процента, который вычисляется за несколько лет: Формулы по экономике также помогают рассчитать уровень безработицы: Здесь ЧРС – численность рабочей силы.
Формула для вычисления уровня занятости выглядит следующим образом:
Формула для вычисления валового национального продукта вычисляется так:
Здесь Тр – корпорации, Кнал – косвенные налоги, ЧС – чистые субсидии, Р – рента, Ам – сумма амортизации, ДС – доходы от собственности. Формула расчёта ВНП в соответствии с расходами: Формулы по экономике при расчете выручки и прибыли: Прибыль = TR — TC
Формула для вычисления средних общих издержек выглядит так: Для того чтобы рассчитать общие издержки необходимо применить следующую формулу: Формула для вычисления средних постоянных издержек: При расчете средних переменных издержек можно воспользоваться следующей формулой: Обычно электрический ток сравнивают с течением жидкости по трубке, а напряжение или разность потенциалов — с разностью уровней жидкости. В этом случае поток воды, падающий сверху вниз, несет с собой определенное количество энергии. В условиях свободного падения эта энергия растрачивается бесполезно для человека. Если же направить падающий поток воды на лопасти турбины, то последняя начнет вращаться и сможет производить полезную работу. Работа, производимая потоком воды в течение определенного промежутка времени, например, в течение одной секунды, будет тем больше, чем с большей высоты падает поток и чем больше масса падающей воды. Точно так же и электрический ток, протекая по цепи от высшего потенциала к низшему, совершает работу. В каждую данную секунду времени будет совершаться тем больше работы, чем больше разность потенциалов и чем большее количество электричества ежесекундно проходит через поперечное сечение цепи. Мощность электрического тока это количество работы, совершаемой за одну секунду времени, или скорость совершения работы. Количество электричества, проходящего через поперечное сечение цепи в течение одной секунды, есть не что иное, как сила тока в цепи. Следовательно, мощность электрического тока будет прямо пропорциональна разности потенциалов (напряжению) и силе тока в цепи. Для измерения мощности электрического тока принята единица, называемая ватт (Вт). Мощностью в 1 Вт обладает ток силой в 1 А при разности потенциалов, равной 1 В. Для вычисления мощности постоянного тока в ваттах нужно силу тока в амперах умножить на напряжение в вольтах. Если обозначить мощность электрического тока буквой P, то приведенное выше правило можно записать в виде формулы P = I*U. (1) Воспользуемся этой формулой для решения числового примера. Требуется определить, какая мощность электрического тока необходима для накала нити радиолампы, если напряжение накала равно 4 в, а ток накала 75 мА Определим мощность электрического тока, поглощаемую нитью лампы: Р= 0,075 А*4 В = 0,3 Вт. Мощность электрического тока можно вычислить и другим путем. Предположим, что нам известны сила тока в цепи и сопротивление цепи, а напряжение неизвестно. В этом случае мы воспользуемся знакомым нам соотношением из закона Ома: U=IR и подставим правую часть этого равенства (IR) в формулу (1) вместо напряжения U. Тогда формула (1) примет вид: P = I*U =I*IR или Р = I2*R. (2) Например, требуется узнать, какая мощность теряется в реостате сопротивлением в 5 Ом, если через него проходит ток, силой 0,5 А. Пользуясь формулой (2), найдем: P= I2*R = (0,5)2*5 =0,25*5 = 1,25 Вт. Наконец, мощность электрического тока может быть вычислена и в том случае, когда известны напряжение и сопротивление, а сила тока неизвестна. Для этого вместо силы тока I в формулу (1) подставляется известное из закона Ома отношение U/R и тогда формула (1) приобретает следующий вид: Р = I*U=U2/R (3) Например, при 2,5 В падения напряжения на реостате сопротивлением в 5 Ом поглощаемая реостатом мощность будет равна: Р = U2/R=(2,5)2/5=1,25 Вт Таким образом, для вычисления мощности требуется знать любые две из величин, входящих в формулу закона Ома. Мощность электрического тока равна работе электрического тока, производимой в течение одной секунды. P = A/t ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ! P — это статистическая мера, которая помогает исследователям определить, верна ли их гипотеза. Это помогает определить значимость результатов. Нулевая гипотеза Нулевая гипотеза предполагает, что выборочные данные и данные о совокупности не имеют разницы или, говоря простыми словами, она предполагает, что утверждение, сделанное человеком относительно данных или совокупности, является абсолютной истиной и всегда верно.Таким образом, даже если образец взят из совокупности, результат, полученный при изучении выборки, будет таким же, как и предположение. Читать дальше — это позиция по умолчанию, согласно которой нет никакой связи между двумя измеряемыми явлениями. Она обозначается как H 0. Альтернативная гипотеза — это гипотеза, в которую вы поверили бы, если бы пришел к выводу, что нулевая гипотеза неверна. Его символ — H 1 или H a. P-значение в Excel — это число от 0 до 1. Существуют таблицы, программы для работы с электронными таблицами и статистическое программное обеспечение, помогающее рассчитать p-значение.Уровень значимости (α) — это заранее определенный порог, установленный исследователем. Обычно это 0,05. Очень маленькое p-значение, которое меньше уровня значимости, указывает на то, что вы отвергаете нулевую гипотезу. P-значение, превышающее уровень значимости, указывает на то, что мы не можем отвергнуть нулевую гипотезу. Формулу для вычисления p-значения можно получить, выполнив следующие шаги: Шаг 1: Нам нужно узнать статистику теста z Z = (p̂ — p0) / √ [p0 (1-p0) / n] Вы можете свободно использовать это изображение на своем веб-сайте, в шаблонах и т. Д. Пожалуйста, предоставьте нам ссылку с указанием авторства Ссылка на статью, которая будет гиперссылкой Где Шаг 2: Нам нужно найти соответствующий уровень p из полученного значения z. Для этого нам нужно взглянуть на таблицу z. Источник: www.dummies.com Например, найдем значение p, соответствующее z ≥ 2,81. Поскольку нормальное распределение симметрично, отрицательные значения z равны его положительным значениям.2,81 — это сумма 2,80 и 0,01. Посмотрите на 2,8 в столбце z и соответствующее значение 0,01. Получаем p = 0,0025. Давайте рассмотрим несколько простых и сложных примеров уравнения P-Value, чтобы лучше понять его. a) Значение P составляет 0,3015. Если уровень значимости составляет 5%, выясните, можем ли мы отклонить нулевую гипотезу. б) P-значение 0,0129.Если уровень значимости составляет 5%, выясните, можем ли мы отклонить нулевую гипотезу. Решение: Используйте следующие данные для расчета P-Value. P-Value будет — a) Поскольку p-значение 0,3015 превышает уровень значимости 0,05 (5%), мы не можем отвергнуть нулевую гипотезу. б) Поскольку p-значение 0,0129 меньше уровня значимости 0,05, мы отклоняем нулевую гипотезу. Согласно исследованию, 27% людей в Индии говорят на хинди. Исследователю интересно, выше ли эта цифра в его деревне. Следовательно, основывается на нулевой и альтернативной гипотезах. Он проверяет H 0: p = 0,27. H a: p> 0,27. Здесь p — доля жителей деревни, говорящих на хинди. Он заказывает опрос в своей деревне, чтобы выяснить, сколько людей может говорить на хинди. Он обнаружил, что 80 из 240 опрошенных людей могут говорить на хинди.Найдите приблизительное значение p для теста исследователя, если бы мы предположили, что необходимые условия выполняются, а уровень значимости составляет 5%. Решение: Используйте следующие данные для расчета P-Value. Здесь объем выборки n = 240, p 0 — доля населения. Нам нужно будет найти образец пропорции Z Статистика Расчет статистики Z = 0.33 — 0,27 / √ 0,27 * (1 — 0,27) / 240 Z Статистика будет — Z = 2,093696 P-Value будет — Значение P = P (z ≥ 2,09) Мы должны посмотреть на значение 2,09 в таблице z. Итак, нам нужно посмотреть на -2,0 в столбце z и значение в столбце 0,09. Поскольку нормальное распределение симметрично, площадь справа от кривой равна площади слева. Мы получаем значение p 0,0183. P Значение = 0.0183 Поскольку значение p меньше значимого уровня 0,05 (5%), мы отклоняем нулевую гипотезу. Примечание: В Excel значение p равно 0,0181 Исследования показывают, что мужчины покупают больше авиабилетов, чем женщины. Их покупают самцы и самки в соотношении 2: 1. Исследование проводилось в конкретном аэропорту Индии, чтобы выяснить, как распределяются авиабилеты среди мужчин и женщин.Из 150 билетов 88 билетов купили мужчины, 62 — женщины. Нам нужно выяснить, вызывает ли экспериментальная манипуляция изменение результатов или мы наблюдаем случайную вариацию. Рассчитайте p-значение, предполагая, что степень значимости равна 0,05. Решение: Используйте следующие данные для расчета P-Value. Шаг 1: Наблюдаемое значение составляет 88 для мужчин и 62 для женщин. Шаг 2: Найдите хи-квадрат = ((88-100) 2 ) / 100 + (62-50) 2 /50 = 1.2) = 4,32 Шаг 3: Найдите степени свободы Поскольку есть 2 переменные — мужчины и женщины, n = 2 Степени свободы = n-1 = 2-1 = 1 Шаг 4: Из таблицы значений p мы смотрим на первую строку в таблице, поскольку степень свободы равна 1. Мы видим, что значение p находится между 0,025 и 0,05. Поскольку значение p меньше степени значимости 0,05, мы отклоняем нулевую гипотезу. P-Value будет — P Значение = 0,037666922 Примечание: Excel напрямую дает p-значение по формуле: ЧИТЕСТ (фактический диапазон, ожидаемый диапазон) Известно, что 60% людей, заходящих в магазины одежды в городе, что-то покупают. Владелец магазина одежды хотел выяснить, больше ли число для магазина одежды, принадлежащего ему. У него уже были результаты исследования, проведенного для его магазина.128 из 200 человек, зашедших в его магазин, что-то купили. Владелец магазина обозначил долю людей, которые вошли в его магазин одежды и что-то купили. Нулевая гипотеза, сформулированная им, была p = 0,60, а альтернативная гипотеза была p> 0,60. Найдите значение p для исследования с уровнем значимости 5%. Решение: Используйте следующие данные для расчета P-Value. Здесь размер выборки n = 200. Нам нужно будет найти долю выборки = 128/200 Z Статистика Расчет статистики Z = 0,64 — 0,60 / √ 0,60 * (1 — 0,60) / 200 Z Статистика будет — Статистика Z = 1,1547 Значение P = P (z ≥ 1,1547) Функция НОРМСТРАСП в Excel НОРМСТРАСП будет — НОРМСТРАСП = 0,875893461 В Excel есть встроенная функция для вычисления p-значения из z-статистики.Это известно как функция НОРМСТРАСП. Функция НОРМСТРАСП Excel вычисляет стандартную нормальную кумулятивную функцию распределения на основе предоставленного значения. Его формат — НОРМСТРАСП (z). Так как статистическое значение z находится в ячейке B2, используется функция = НОРМСТРАСП (B2). P Значение будет — P Значение = 0,12410654 Так как нам нужно найти площадь справа от кривой, p-значение = 1 — 0,875893 = 0,124107 Поскольку p-значение равно 0.124107 больше, чем значимый уровень 0,05, мы не можем отвергнуть нулевую гипотезу. P-Value имеет широкое применение в статистической проверке гипотез. Проверка гипотез — это статистический инструмент, который помогает измерить вероятность правильности результата гипотезы, полученного после выполнения гипотезы на выборочных данных. Он подтверждает правильность полученных результатов первичной гипотезы. Подробнее, в частности, при проверке нулевой гипотезы.Например, управляющий фондом управляет паевым инвестиционным фондом. Он утверждает, что доход от конкретной схемы взаимного фонда эквивалентен Nifty, который является эталонным индексом фондового рынка. Он бы выдвинул нулевую гипотезу о том, что доходность схемы взаимных фондов эквивалентна доходности Nifty. Альтернативная гипотеза заключалась бы в том, что доходность Scheme и доходность Nifty не эквивалентны. Затем он вычислял p-значение. Это руководство по формуле P-Value.Здесь мы обсудим, как рассчитать p-value, z-статистику с практическими примерами и загружаемым шаблоном Excel. Вы можете узнать больше о моделировании в Excel из следующих статей — Формула P-значения является сокращением от значения вероятности. P-значение определяет вероятность получения такого же или более экстремального результата, чем другие фактические наблюдения. P-значение представляет собой вероятность наступления данного события.Формула P-значения используется в качестве альтернативы точке отклонения, чтобы обеспечить наименьшее значение, при котором нулевая гипотеза будет отклонена. Чем меньше P-значение, тем сильнее доказательства в пользу альтернативной гипотезы, учитывая наблюдаемую частоту и ожидаемую частоту. Р-значение — важный статистический показатель, который помогает определить, верна ли гипотеза или нет. Значение P всегда находится между 0 и 1.Уровень значимости (α) — это заранее определенный порог, который должен быть установлен исследователем. Обычно он равен 0,05. Формула для расчета P-значения: Шаг 1. Выясните, что статический тест Z равен \ (Z = \ frac {\ hat {p} -p 0} {\ sqrt {\ frac {p 0 (1-p 0)} {n}}} \) Где, Шаг 2: Посмотрите в Z-таблицу, чтобы найти соответствующий уровень P из полученного значения z. Формула для расчета P-значения: \ (Z = \ frac {\ hat {p} -p 0} {\ sqrt {\ frac {p 0 (1-p 0)} {n}}} \) Где, \ (\ hat {p} = \) Пропорция образца Приведенная ниже таблица P-значения помогает в определении гипотезы в соответствии с p-значением. Есть вопросы по основным математическим понятиям? Станьте чемпионом в решении проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами Забронируйте бесплатную пробную версию Class Пример 1: Статистик проверяет гипотезу H0: μ = 120, используя подход альтернативной гипотезы Hα: μ> 120 и предполагая, что α = 0.05. Выборочные значения, которые он взял, следующие: n = 40, σ = 32,17 и x̄ = 105,37. Каков вывод этой гипотезы? Раствор: Мы это знаем, По статической формуле теста получаем т = (105,37 — 120) / 5,0865 Следовательно, t = -2,8762 Используя таблицу Z-Score, найдите значение P (t> -2.8762) получаем, P (t <-2,8762) = P (t> 2,8762) = 0,003 Следовательно, Если P (t> -2,8762) = 1 — 0,003 = 0,997 Значение P = 0,997> 0,05 При значении p> 0,05 принимается нулевая гипотеза. Следовательно, принимается нулевая гипотеза. Пример 2: P-значение 0,3105. Если уровень значимости составляет 5%, выясните, можем ли мы отклонить нулевую гипотезу. Решение: Если посмотреть на таблицу значений P, то значение p равно 0.3105 больше, чем уровень значимости 0,05 (5%), мы не можем отвергнуть нулевую гипотезу. Пример 3: P-значение 0,0219. Если уровень значимости составляет 5%, выясните, можем ли мы отклонить нулевую гипотезу. Решение: Глядя на таблицу значений P, , значение p 0,0219 меньше уровня значимости 0,05, мы отвергаем нулевую гипотезу. Формула P-значения является сокращением от значения вероятности.P-значение определяет вероятность получения такого же или более экстремального результата, чем другие фактические наблюдения. P-значение представляет собой вероятность наступления данного события. Формула для вычисления p-значения: \ (Z = \ frac {\ hat {p} -p 0} {\ sqrt {\ frac {p 0 (1-p 0)} {n}}} \) Формула для расчета P-значения: \ (Z = \ frac {\ hat {p} -p 0} {\ sqrt {\ frac {p 0 (1-p 0)} {n}}} \) Где, Таблица формулы P-значения: Глядя на таблицу, значение p 0,354 превышает уровень значимости 0,05 (5%), мы не можем отвергнуть нулевую гипотезу. Добро пожаловать в наш калькулятор p-value! Вам больше никогда не придется задаваться вопросом, как найти p-значение, так как здесь вы можете определить односторонние и двусторонние p-значения из тестовой статистики, следуя всем наиболее популярным распределениям: нормальному, t-Студенту, хи-квадрат и F. Р-значения встречаются повсюду в науке, но многие люди находят эту концепцию немного пугающей. Не волнуйтесь — в этой статье мы объясняем не только, что такое p-значение, но и , как правильно интерпретировать p-значения . Вам когда-нибудь было интересно, как вычислить p-value вручную? Мы также предоставим вам все необходимые формулы! Формально, p-значение — это вероятность того, что тестовая статистика даст значения, по крайней мере, такие же экстремальные, как значение, полученное для вашей выборки .Крайне важно помнить, что эта вероятность рассчитана в предположении, что нулевая гипотеза верна ! Более интуитивно понятно, что значение p отвечает на вопрос: Предполагая, что я живу в мире, где выполняется нулевая гипотеза, насколько вероятно, что для другого образца тест, который я выполняю, сгенерирует значение, по крайней мере такое же экстремальное, как то, которое я наблюдал для образца, который у меня уже есть? Это альтернативная гипотеза , которая определяет, что на самом деле означает «крайний» , поэтому значение p зависит от альтернативной гипотезы, которую вы формулируете: левосторонняя, правосторонняя или двусторонняя.В формулах ниже Левосторонний тест: Правосторонний тест: Двусторонний тест: ( Если распределение тестовой статистики при H 0 является симметричным относительно 0 , то или, что то же самое, Так как картинка стоит тысячи слов, давайте проиллюстрируем эти определения. Здесь мы используем тот факт, что вероятность может быть аккуратно изображена как площадь под кривой плотности для данного распределения.Мы даем два набора изображений: один для симметричного распределения, а другой для асимметричного (несимметричного) распределения. На последнем изображении (двустороннее значение p для асимметричного распределения) площадь левой части равна площади правой части. Чтобы определить p-значение, вам необходимо знать распределение вашей тестовой статистики в предположении, что нулевая гипотеза верна .Затем, с помощью кумулятивной функции распределения ( Левосторонний тест: Правосторонний тест: Двусторонний тест: Если распределение тестовой статистики согласно H 0 является симметричным относительно 0 , то двустороннее p-значение можно упростить как Распределения вероятностей, которые наиболее распространены при проверке гипотез, как правило, имеют сложные формулы cdf, и найти значение p вручную может быть невозможно.Скорее всего, вам придется прибегнуть к компьютеру или к статистической таблице, где люди собрали приблизительные значения cdf. Что ж, теперь вы знаете, как вычислить p-значение, но … зачем вам вообще нужно вычислять это число? При проверке гипотез подход p-значения является альтернативой подходу критического значения. Напомним, что последнее требует от исследователей предварительно установить уровень значимости α, который представляет собой вероятность отклонения нулевой гипотезы, если она верна (например, для ошибки типа I ).Как только у вас есть p-значение, вам просто нужно сравнить его с любым заданным α, чтобы быстро решить, следует ли отклонять нулевую гипотезу на этом уровне значимости α. Подробнее читайте в следующем разделе, где мы объясняем, как интерпретировать p-значения. Как мы уже упоминали выше, p-значение является ответом на следующий вопрос: Предполагая, что я живу в мире, где выполняется нулевая гипотеза, насколько вероятно, что для другого образца тест, который я выполняю, сгенерирует значение, по крайней мере такое же экстремальное, как то, которое я наблюдал для образца, который у меня уже есть ? Что это значит для вас? Что ж, у вас есть два варианта: Однако может случиться так, что нулевая гипотеза верна, но ваша выборка очень необычна! Например, представьте, что мы изучали действие нового препарата и получили значение p На вопрос «что такое p-значение» также можно ответить следующим образом: p-значение — это наименьший уровень значимости, при котором нулевая гипотеза будет отклонена. Итак, если теперь вы хотите, чтобы принял решение о нулевой гипотезе на некотором уровне значимости Очевидно, судьба нулевой гипотезы зависит от Также имейте в виду, что знание предметной области (и общая причина) имеет решающее значение. В противном случае, бездумно применяя статистические принципы, вы легко можете прийти к статистически значимому, несмотря на то, что вывод на 100% неверен. Поскольку наш калькулятор p-значения здесь к вашим услугам, вам больше не нужно думать, как найти p-значение из всей этой сложной статистики тестов! Вот шаги, которые вам необходимо выполнить: Выберите альтернативную гипотезу : двусторонняя, правосторонняя или левосторонняя. Сообщите нам распределение вашей тестовой статистики при нулевой гипотезе: это N (0,1), t-Стьюдента, хи-квадрат или F Снедекора? Если вы не уверены, проверьте разделы ниже, так как они посвящены этим дистрибутивам. При необходимости укажите степень свободы распределения тестовой статистики. Введите значение тестовой статистики , вычисленной для вашей выборки данных. Наш калькулятор определяет значение p на основе статистики теста и предоставляет решение, которое необходимо принять о нулевой гипотезе.Стандартный уровень значимости по умолчанию составляет 0,05. Перейдите в расширенный режим В терминах кумулятивной функции распределения (cdf) стандартного нормального распределения, которое традиционно обозначается как Левосторонний z-тест: Правосторонний z-тест: Двусторонний z-тест: Мы используем Z-оценку , если статистика теста приблизительно соответствует стандартному нормальному распределению N (0,1) .Благодаря центральной предельной теореме вы можете рассчитывать на приближение, если у вас большая выборка (скажем, не менее 50 точек данных), и рассматривать свое распределение как нормальное. Z-тест чаще всего относится к проверке среднего для генеральной совокупности или разницы между двумя средними значениями для генеральной совокупности, в частности между двумя пропорциями. Вы также можете найти Z-тесты в оценках максимального правдоподобия. Значение p из t-оценки задается следующими формулами, в которых Левосторонний t-критерий: Правосторонний t-критерий: Двусторонний t-тест: или Используйте вариант Наиболее распространены t-тесты для популяции означает с неизвестным стандартным отклонением совокупности или для разницы между средними значениями двух популяций с равными или неравными, но неизвестными стандартными отклонениями совокупности. Также существует t-тест для парных (зависимых) образцов . Используйте опцию Как найти p-значение из показателя хи-квадрат ? Это можно сделать с помощью следующих формул, в которых Левосторонний χ²-тест: Правосторонний χ²-тест: Помните, что χ²-тесты на соответствие и независимость — это тесты с правым хвостом! (см. ниже) Двусторонний χ²-тест: (Под Самыми популярными тестами, которые дают оценку χ², являются следующие: Проверка того, имеет ли отклонение нормально распределенных данных некоторое заранее определенное значение. В этом случае статистика теста имеет χ²-распределение с Тест согласия проверяет, согласуется ли эмпирическое (выборочное) распределение с некоторым ожидаемым распределением вероятностей.В этом случае статистика теста следует χ²-распределению с Тест на независимость используется для определения наличия статистически значимой связи между двумя переменными. В этом случае его тестовая статистика основана на таблице непредвиденных обстоятельств и следует χ²-распределению с Наконец, параметр Чтобы увидеть, откуда берутся эти степени свободы, рассмотрим независимые случайные величины Значение p из F-оценки определяется по следующим формулам, где мы позволяем Левосторонний F-тест: Правосторонний F-тест: Двусторонний F-тест: (Под Ниже мы перечисляем наиболее важные тесты, которые дают F-баллы. Все это правосторонние тесты . Тест на равенство отклонений в двух нормально распределенных совокупностях . Его тестовая статистика соответствует F-распределению с ANOVA используется для проверки равенства средних в трех или более группах, которые происходят из нормально распределенных популяций с равной дисперсией.Мы приходим к F-распределению с Тест на общую значимость регрессионного анализа . Статистика теста имеет F-распределение с При наличии линейной зависимости , установленной в вашей выборке данных с помощью вышеуказанного теста, вы можете рассчитать коэффициент детерминации R², который указывает на силу этой связи . Тест с сравнивает две вложенные регрессионные модели . Статистика теста соответствует F-распределению с Вы можете заметить, что F-тест общей значимости — это особая форма F-теста для сравнения двух вложенных моделей: он проверяет, работает ли наша модель значительно лучше, чем модель без предикторов (т. Е. Модель только с перехватом ). Нет, p-значение не может быть отрицательным, поскольку p-значение — это вероятность того, что тестовая статистика удовлетворяет определенным условиям, поскольку, как мы все знаем, вероятности не могут быть отрицательными. Высокое значение p означает, что при нулевой гипотезе существует высокая вероятность того, что для другой выборки тестовая статистика сгенерирует значение, по крайней мере такое же экстремальное, как то, которое наблюдалось для уже имеющейся у вас выборки. Высокое значение p не позволяет отвергнуть нулевую гипотезу. Низкое p-значение означает, что при нулевой гипотезе существует небольшая вероятность того, что для другой выборки тестовая статистика сгенерирует значение, по крайней мере такое же экстремальное, как то, которое наблюдалось для уже имеющейся у вас выборки.Низкое значение p свидетельствует в пользу альтернативной гипотезы — оно позволяет отклонить нулевую гипотезу. В нашем примере, касающемся среднего среднего балла, предположим, что наша случайная выборка из n = 15 студентов, специализирующихся на математике, дает статистику теста t *, равную 2,5. Поскольку n = 15, наша тестовая статистика t * имеет n — 1 = 14 степеней свободы. Также предположим, что мы установили наш уровень значимости α равным 0.05, так что вероятность ошибки I типа составляет всего 5%. P -значение для проведения правостороннего теста H 0 : μ = 3 по сравнению с H A : μ > 3 — вероятность того, что мы увидим тест статистика больше t * = 2,5, если среднее значение \ (\ mu \) действительно было 3. Напомним, что вероятность равна площади под кривой вероятности.Таким образом, значение P — это область под кривой t n — 1 = t 14 и до правого тестовой статистики t * = 2,5. С помощью статистического программного обеспечения можно показать, что значение P равно 0,0127. График это изображает визуально. Значение P , 0,0127, говорит нам, что «маловероятно», чтобы мы наблюдали такую экстремальную статистику теста t * в направлении H A , если бы нулевая гипотеза была верна.Следовательно, наше первоначальное предположение о том, что нулевая гипотеза верна, должно быть неверным. То есть, поскольку значение P , 0,0127, меньше \ (\ alpha \) = 0,05, мы отклоняем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : мкм > 3. Обратите внимание, что мы не отклонили бы H 0 : μ = 3 в пользу H A : μ > 3, если бы мы снизили нашу готовность делать ошибку типа I до \ (\ alpha \) = 0.01 вместо этого, поскольку значение P , 0,0127, тогда больше, чем \ (\ alpha \) = 0,01. В нашем примере, касающемся среднего среднего балла, предположим, что наша случайная выборка из n = 15 студентов, специализирующихся на математике, дает тестовую статистику t * вместо -2,5. P -значение для проведения левостороннего теста H 0 : μ = 3 по сравнению с H A : μ <3 - это вероятность того, что мы увидим статистику теста менее т * = -2.5, если среднее значение по совокупности μ, действительно было 3. Таким образом, значение P является областью ниже t n — 1 = t 14 кривой и до слева статистика теста t * = -2,5. С помощью статистического программного обеспечения можно показать, что значение P равно 0,0127. График это изображает визуально. Значение P , 0,0127, говорит нам, что «маловероятно», чтобы мы наблюдали такую экстремальную статистику теста t * в направлении H A , если бы нулевая гипотеза была верна.Следовательно, наше первоначальное предположение о том, что нулевая гипотеза верна, должно быть неверным. То есть, поскольку значение P , 0,0127, меньше α = 0,05, мы отклоняем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : мкм <3. Обратите внимание, что мы не отклонили бы H 0 : μ = 3 в пользу H A : μ <3, если бы мы снизили нашу готовность делать ошибку I типа до α = 0.01 вместо этого, поскольку значение P , 0,0127, тогда больше, чем \ (\ alpha \) = 0,01. В нашем примере, касающемся среднего среднего балла, предположим снова, что наша случайная выборка из n = 15 студентов, специализирующихся на математике, дает тестовую статистику t * вместо -2,5. Значение P для проведения двустороннего теста H 0 : μ = 3 по сравнению с H A : μ ≠ 3 — вероятность того, что мы увидим статистику теста менее -2.5 или больше 2,5, если среднее значение совокупности μ действительно было 3. То есть двусторонний тест требует учета возможности того, что тестовая статистика может попасть в любой из хвостов (отсюда и название «двусторонний» тест ). Таким образом, значение P — это область под кривой t n — 1 = t 14 до слева от -2,5 и до справа от 2,5. С помощью статистического программного обеспечения можно показать, что значение P равно 0.0127 + 0,0127 или 0,0254. График это изображает визуально. Обратите внимание, что значение P для двустороннего теста всегда в два раза больше значения P для любого из односторонних тестов. Значение P , 0,0254, говорит нам, что «маловероятно», чтобы мы наблюдали такую экстремальную статистику теста t * в направлении H A , если бы нулевая гипотеза была верна. Следовательно, наше первоначальное предположение о том, что нулевая гипотеза верна, должно быть неверным.То есть, поскольку значение P , 0,0254, меньше α = 0,05, мы отклоняем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : мкм ≠ 3. Обратите внимание, что мы не отклонили бы H 0 : μ = 3 в пользу H A : μ ≠ 3, если бы мы снизили нашу готовность делать ошибку типа I до α = 0,01. , как значение P , 0.0254, тогда больше, чем \ (\ alpha \) = 0,01. Теперь, когда мы рассмотрели процедуры подхода к критическому значению и P -значению для каждой из трех возможных гипотез, давайте рассмотрим три новых примера — один из теста с правым хвостом, один из теста с левым хвостом и один из двусторонний тест. Хорошая новость заключается в том, что, когда это возможно, мы будем использовать статистику тестов и значения P , полученные в статистическом программном обеспечении, таком как Minitab, для проведения тестов гипотез в этом курсе. Ковариационная функция Excel относится к категории Статистических функций. ФункцииСписок наиболее важных функций Excel для финансовых аналитиков. Эта шпаргалка охватывает сотни функций, которые критически важно знать аналитику Excel. Он вычисляет совместную изменчивость двух случайных величин по двум наборам данных. Предположим, что вы являетесь финансовым аналитиком Описание работы финансового аналитика В описании должности финансового аналитика ниже приводится типичный пример всех навыков, образования и опыта, необходимых для работы аналитиком в банке, учреждении или корпорации.Выполняйте финансовое прогнозирование, отчетность и отслеживание операционных показателей, анализируйте финансовые данные, создавайте финансовые модели, которые мы хотим определить, сопровождает ли больший доход более высокий уровень образования населения или нет. В таком сценарии мы можем использовать функцию COVARIANCE.P. Он был введен в MS Excel 2010 для замены COVAR с улучшенной точностью по сравнению с его предшественником. = COVARIANCE.P (array1, array2) Ковариация.Функция P использует следующие аргументы: Несколько вещей, которые следует помнить об аргументах: Чтобы понять использование функции, давайте рассмотрим несколько примеров: Предположим, нам даны ежемесячные доходы от двух активов , золото и биткойн, как показано ниже: Мы хотим выяснить ковариацию в Excel, то есть определить, существует ли какая-либо связь между ними.Связь между значениями в столбцах C и D можно рассчитать по формуле = COVARIANCE.P (C5: C16, D5: D16). x и y — это средние значения выборки для двух наборов значений Формула дает результат 0.0008, что указывает на отрицательную корреляцию между двумя активами. Щелкните здесь, чтобы загрузить образец файла Excel Спасибо за то, что прочитали руководство CFI по важным функциям Excel! Потратив время на изучение и освоение этих функций, вы значительно ускорите свой финансовый анализ. Чтобы узнать больше, ознакомьтесь с этими дополнительными ресурсами CFI: Mobil Super ™ 3000 является синтетической и разработана для обеспечения исключительной защиты. Mobil Super 3000 Formula P 5W-30 — высокоэффективное малозольное моторное масло, разработанное для продления срока службы двигателя и поддержания эффективности систем снижения выбросов выхлопных газов в легковых автомобилях, легких коммерческих транспортных средствах и фургонах с дизельным и бензиновым двигателем. Этот продукт рекомендуется для использования в автомобилях Peugeot, Citroen и в широком спектре европейских автомобилей и легких коммерческих автомобилей, которые должны соответствовать или превосходить требования ACEA C2 или A5 / B5. Mobil Super 3000 Formula P 5W-30 обеспечивает превосходную защиту от износа при высоких и низких температурах и улучшенную чистоту двигателя. Основные характеристики и преимущества: • Состав с низким содержанием золы, фосфора и серы, помогающий продлить срок службы и поддерживать эффективность систем снижения выбросов как в дизельных, так и в бензиновых двигателях. • Совместимость с дизельными сажевыми фильтрами и каталитическими преобразователями. • Помогает достичь экономии топлива (согласно ACEA C2, A5 / B5). • Превосходные низкотемпературные характеристики для надежного запуска в холодную погоду, обеспечивающие быструю защиту двигателя и электрической системы. • Высокоэффективная защита от износа. • Активные чистящие средства, уменьшающие образование отложений и шлама, что обеспечивает долгий и чистый срок службы двигателя. Mobil Super 3000 Formula P 5W-30 рекомендуется для различных современных автомобильных двигателей, особенно для высокоэффективных бензиновых, турбодизельных двигателей с системой впрыска Common Rail и других дизельных двигателей, используемых в новейших легковых автомобилях, внедорожниках и легких фургонах. • Легковые и легкие коммерческие автомобили Peugeot-Citroen или фургоны • Легковые и легкие коммерческие автомобили или фургоны, требующие ACEA A5 / B5 или C2, такие как фургоны Iveco и Fiat • Бензин и дизельное топливо с дизельными сажевыми фильтрами (DPF) и каталитическими преобразователями • Нормальные и иногда тяжелые условия эксплуатации (включая условия движения по городу) Всегда обращайтесь к руководству пользователя, чтобы проверить рекомендуемый класс вязкости и технические характеристики для вашего конкретного автомобиля.Не рекомендуется для двухтактных или авиационных двигателей, если иное не одобрено производителем. Данный продукт имеет следующие одобрения производителей оборудования: Автомобиль Peugeot / Citroën B71 2290 Этот продукт рекомендуется для приложений, требующих: API CF Этот продукт превосходит следующие требования или соответствует им: API SN ACEA C2 Имущество Оценка SAE 5W-30 Плотность при 15 ° C, г / мл, ASTM D4052 0.85 Температура вспышки, ° C, ASTM D92 226 Кинематическая вязкость при 100 C, мм2 / с, ASTM D445 10,5 Кинематическая вязкость при 40 C, мм2 / с, ASTM D445 60 Фосфор, мас.%, ASTM D4951 0.08 Температура застывания, ° C, ASTM D97 -39 Зола сульфатная,% масс., ASTM D874 0,7 Рекомендации по охране здоровья и безопасности для этого продукта можно найти в Паспорте безопасности материала (MSDS) @ http: // www.msds.exxonmobil.com/psims/psims.aspx В комплекте: Биномиальное распределение можно рассматривать как просто вероятность УСПЕХА или НЕУДАЧИ в эксперименте или опросе, который повторяется несколько раз.Биномиальное распределение — это тип распределения, который имеет два возможных результата (префикс «би» означает два или два). Например, подбрасывание монеты имеет только два возможных результата: орел или решка, а сдача теста может иметь два возможных результата: сдан или не пройден. Биномиальное распределение показывает либо (S) успех, либо (F) недостаток. Например, предположим, что вы хотите узнать вероятность получения 1 при броске кубика. если вы бросили кубик 20 раз, вероятность выпадения кубика при любом броске равна 1/6. Бросьте двадцать раз, и вы получите биномиальное распределение (n = 20, p = 1/6). УСПЕХ будет означать «выбросить один», а НЕИСПРАВНОСТЬ — это «выбросить что-нибудь еще». Если бы рассматриваемый результат представлял собой вероятность того, что кубик выпадет на четное число, тогда биномиальное распределение будет иметь вид (n = 20, p = 1/2). Это потому, что ваша вероятность выпадения четного числа равна половине. Биномиальные распределения также должны соответствовать следующим трем критериям: Посмотрите видео для примера: Нужна помощь с формулой? Chegg.com подберет для вас живого репетитора, и ваши первые 30 минут будут бесплатными! Биномиальное распределение тесно связано с распределением Бернулли. Согласно Вашингтонскому государственному университету: «Если каждое испытание Бернулли является независимым, то количество успехов в следах Бернулли имеет биномиальное распределение. С другой стороны, распределение Бернулли — это биномиальное распределение с n = 1 ». Распределение Бернулли — это набор испытаний Бернулли.Каждое испытание Бернулли имеет один возможный исход, выбираемый из S — успех или F — неудача. В каждом испытании вероятность успеха P (S) = p одинакова. Вероятность неудачи составляет всего 1 минус вероятность успеха: P (F) = 1 — p. (Помните, что «1» — это полная вероятность возникновения события… вероятность всегда находится между нулем и 1). Наконец, все испытания Бернулли независимы друг от друга, и вероятность успеха не меняется от испытания к испытанию, даже если у вас есть информация о результатах других испытаний. В реальной жизни можно найти множество примеров биномиальных распределений. Например, если новое лекарство вводится для лечения болезни, оно либо лечит болезнь (это успешно), либо не лечит болезнь (это неудача). Если вы покупаете лотерейный билет, вы либо выиграете, либо нет. По сути, все, что вы можете придумать, может быть только успехом или неудачей, может быть представлено биномиальным распределением. Биномиальное распределение показывает либо (S) успех, либо (F) недостаток. Посмотрите видео для примера: Формула биномиального распределения: b (x; n, P) = n C x * P x * (1 — P) n — x Где: Примечание: Формулу биномиального распределения также можно записать немного иначе, потому что n C x = n! / х! (п — х)! (в этой формуле биномиального распределения используются факториалы (что такое факториал?).«Q» в этой формуле — это просто вероятность неудачи (вычтите вероятность успеха из 1). Формула биномиального распределения может вычислить вероятность успеха для биномиальных распределений. Часто вам говорят «вставить» числа в формулу и вычислить . Это легко сказать, но не так-то просто сделать — если вы не очень осторожны с порядком операций, вы не получите правильный ответ. Если у вас есть Ti-83 или Ti-89, калькулятор может сделать большую часть работы за вас.Если нет, вот как разбить проблему на простые шаги, чтобы каждый раз получать правильный ответ. В. Монета подбрасывается 10 раз. Какова вероятность выпадения ровно 6 голов? Я собираюсь использовать эту формулу: b (x; n, P) — n C x * P x * (1 — P) n — x P (x = 6) = 10 C 6 * 0.4 = 210 * 0,015625 * 0,0625 = 0,205078125 Совет: Вы можете использовать калькулятор комбинаций , чтобы вычислить значение для n C x . 80% людей, приобретающих страховку для домашних животных, составляют женщины. Если случайным образом выбраны 9 владельцев страховки для домашних животных, найдите с вероятностью, что именно 6 из них — женщины. Шаг 1: Определите «n» из проблемы.В нашем примере вопроса n (количество случайно выбранных элементов) равно 9. Шаг 2: Определите «X» из проблемы. X (число, которое вас просят найти вероятность) равно 6. Шаг 3: Обработайте первую часть формулы. Первая часть формулы — н! / (п — Х)! ИКС! Подставьте свои переменные: 9! / ((9-6)! × 6!) Что равняется 84. Отложите это число на мгновение. Шаг 4: Найдите p и q.p — вероятность успеха, q — вероятность неудачи. Нам дан p = 80%, или 0,8. Таким образом, вероятность отказа составляет 1 — 0,8 = 0,2 (20%). Шаг 5: Обработайте вторую часть формулы. p X Отложите это число на мгновение. Шаг 6: Обработайте третью часть формулы. q (n — X) Шаг 7: Умножьте ответ из шагов 3, 5 и 6 вместе. 60% покупателей спорткаров — мужчины. Если случайным образом выбрано 10 владельцев спортивных автомобилей, найдите с вероятностью, что именно 7 из них — мужчины. Шаг 1: : Определите «n» и «X» из проблемы. Используя наш примерный вопрос, n (количество случайно выбранных элементов — в данном случае случайным образом выбираются владельцы спортивных автомобилей) равно 10, а X (число, которое вам предлагается «найти вероятность») равно 7. Шаг 2: Определите первую часть формулы, а именно: н! / (п — Х)! ИКС! Подставляем переменные: 10! / ((10-7)! × 7!) Что равно 120. Отложите это число на мгновение. Шаг 3: Найдите «p» — вероятность успеха и «q» — вероятность неудачи. Нам дан p = 60%, или 0,6. следовательно, вероятность отказа составляет 1 — 0,6 = 0,4 (40%). Шаг 4: Выполните следующую часть формулы. p X Отложите это число, пока вы работаете с третьей частью формулы. Шаг 5: Обработайте третью часть формулы. q (0,4-7) Шаг 6: Умножьте три ответа из шагов 2, 4 и 5 вместе. Вот и все! Бейер, В.H. Стандартные математические таблицы CRC, 28-е изд. Бока-Ратон, Флорида: CRC Press, стр. 531, 1987. вперед от:http://math001.com/inverse_trigonometric_functions/ вТригонометрическая функцияДобавить передarc, Означает ихОбратная функция f-1 (x). То есть текущий угол можно получить из тригонометрической функции. Скомпилируйте ffmpeg — это болезненная вещь, которая обычно используется напрямуюZeranoe FFmpeg Builds。 Если вы используете эту версию, вам нужно обратить внимание на абзац о помощи FFMPEG: То есть фа… Используйте идею + Maven + Springboot Создание новых проектов (1) Интегрированный MVC 1. Создайте новый файл проекта -> Новый -> Проект maven —> next 2. Заполните идентификатор организации и… Redis использует два — инструкции Окружающая среда: Redis-5. основная концепция Что такое цепь Цепь представляет собой коллекцию узлов. Каждый узел цепи может быть разделен и реорганизован. Режим цепочки обязанностей Сделайте несколько объектов иметь возможност… Easynts, как Gateway Video Cloud, имеет такие функции, как сети видеопотоков, удаленная работа и техническое обслуживание. До запуска он будет протестирован отделом департамента исследований и разрабо… Сегодня я столкнулся с ошибкой: VM4735:2 Uncaught TypeError: Cannot read property ‘0’ of undefined После долгих поисков было обнаружено, что тринокулярный расчет был неправильным. Градуированная бедная собака использовала paperYY для проверки дубликатов. Контент проверки дубликатов отображается в формате html. Чтобы облегчить изменение повторяющихся мест в документе, содержание… … В последние месяцы я выполнял различные работы по техническому обслуживанию, и блог не обновляется часто. В мгновение ока наступит 2011 год, и я надеюсь, что в наступающем году я найду свою страсть. З… Контент поступает из само переведенных и организованных учебных пособий OpenCV-Python. цели: Мы объединим сопоставление характерных точек и поиск гомографии, а также будем использовать модуль calib3d … © 2020-2022 All rights reserved by russianblogs.com Алгебра и начала математического анализа, 11 класс Урок №6. Обратные тригонометрические функции. Перечень вопросов, рассматриваемых в теме Глоссарий по теме Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений . Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений Основная литература: Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с. Дополнительная литература: Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с. Открытые электронные ресурсы: Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/ Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/ Теоретический материал для самостоятельного изучения Актуализация знаний Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Объяснение нового материала Рассмотрим свойства функции y=arcsin x и построим ее график. Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Свойства Функции y=arcsin х E(f) D(f) Чётность Нечётная, т.к. arcsin(-x)= — arcsin x Промежутки монотонности Возрастающая Рис. Рассмотрим свойства функции y=arcos x и построим ее график. Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Свойства Функции y=arccos х E(f) D(f) Чётность Ни чётная, ни нечётная Промежутки монотонности Убывающая Рис.2 График функции y=arccos х Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики. Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Свойства y=arctg х y=arcctg х E(f) R R D(f) Чётность Нечётная Нечётная Промежутки монотонности Возрастающая Убывающая Рис. Рис.4 График функции y=arcсtgx Примеры и разборы решения заданий тренировочного модуля: Пример 1. Найдите значение выражения Обозначим , по определения арктангенса получаем х=60°, т.е. нам нужно найти Ответ: Пример 2. Решите неравенство ; ; ; ; Накладываем ограничения по свойствам арксинуса: ; Ответ: Обратные тригонометрические функции Вернемся к определению функции, данному в § 2.2.1. Отметим, что в этом определении функция f не обязана разным элементам x1
и x2
множества X ставить в соответствие разные элементы множества Y.
Если Y – множество значений функции f (x) и для любого элемента y∈Y
существует единственный элемент x∈X
такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Рассмотрим функцию f (x) = sin x для x∈[-π2; π2].
Тогда D (f)=[-π2; π2], E (f)=[-1; 1].
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения D (f-1)=[-1; 1]
и областью значений E (f-1)=[-π2; π2].
Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке. Аналогично, на промежутке D (f–1) = E (f) = [–1; 1] можно определить функцию, обратную cos x, c областью значений E (f–1) = D (f) = [0; π]
Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке. Рассмотрим функцию f (x) = tg x для x∈(-π2; π2).
Тогда D (f)=(-π2; π2), E (f)=R.
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения D (f-1)=R
и областью значений E (f-1)=(-π2; π2).
Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке. Для построения арккотангенса выберем промежуток x ∈ (0; π). Тогда D (f)=(0; π), E (f)=R.
Построим обратную функцию с областью определения D (f-1)=E (f)=R
и областью значений E (f-1)=D (f)=(0; π).
Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке. Итак, запись b = arcsin a обозначает, что b∈[-π2; π2]
и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций. Докажите тождество arcsinx+arccosx=π2. Пусть y=arcsinx⇔{-π2≤y≤π2, sin y=x;
пусть также z=arccosx⇔{0≤z≤π, cos z=x.
Следовательно, требуется доказать неравенство y+z=π2.
Перенесём z в правую часть и возьмём синус от обеих частей получившегося равенства:
y=π2-z⇒sin y=sin(π2-z)=cos z. Но sin y = x и cos z = x, значит, наше равенство принимает вид x = x. Однако для того, чтобы доказать нужное нам тождество, мы должны обосновать возможность перехода от верного равенства x = x к исходному. В самом деле, переход от равенства sin y = cos z к равенству y=π2-z,
вообще говоря, не является равносильным преобразованием. Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)). Обозначим через y переменную, для которой выполняется равенство: y=arcsinx⇔{-π2≤y≤π2, sin y=x,
тогда cos y = cos (arcsin x). Значит,
cos y=+1-sin2 (arcsin x)=+1-x2.
Здесь поставлен знак «+», поскольку y − угол первой или четвёртой четверти, в которых косинус положителен. Равенство sin (arcsin x) = x справедливо по определению функции арксинус. Значит, cos(arcsinx)=1-x2. Вычислим sin (arccos x) = sin z, где z=arccosx⇔{0≤z≤π,cos z=x.
Значит,
sin z=+1-cos2 (arccos x)=+1-x2.
Здесь поставлен знак плюс, поскольку z − угол первой или второй четверти, в которых синус положителен. Итак, A (x)=arcsin1-x2
и B (x)=arccos1-x2.
В предыдущем примере мы установили, что сумма арксинуса и арккосинуса одного и того же аргумента равна π2.
Окончательно, A (x)+B (x)=π2. Ответ. A (x)+B (x)=π2.
Посмотреть всех экспертов из раздела Учеба и наука > Математика Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов». Решено В прямоугольной трапеции диагональ является биссектрисой острого угла. Найдите. площадь трапеции, если боковые стороны равны 8 см и 10 см Решено Начертите треугольник АВС. Постройте вектор:
1) АС+СВ 2)ВА-ВС 3)АС+АВ Периметр правильного треугольника, вписанного в окружность, равен 6√3 дм. Найдите периметр правильного шестиугольника описанного около той же окружности. Решено В лесу на разных кустах висят 100 шнурков. Сова утверж-дает, что в среднем три шнурка из четырёх, которые мож-но найти в лесу, ей не подходят, Пользуйтесь нашим приложением Похожие презентации: Элементы комбинаторики ( 9-11 классы) Применение производной в науке и в жизни Проект по математике «Математика вокруг нас. Знакомство детей с математическими знаками и монетами Тренажёр по математике «Собираем урожай». Счет в пределах 10 Методы обработки экспериментальных данных Лекция 6. Корреляционный и регрессионный анализ Решение задач обязательной части ОГЭ по геометрии Дифференциальные уравнения Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи y English
Русский
Правила Практическая работа № 14 Вычисление производных сложных функций Цель урока. Задания 2. 2.1. 2.2. 2.3. 2.4. 2.5. 2.6. 2.7. 2.8. 2.9. 2.10. 2.11. 2.12. 2.13. 2.14. 2.15. 2.16. 2.17. 2.18. 2.19. 2.20. 2.21. 2.22. 2.23. 2.24. 2.25. 2.26. 2.27. 2.28. 2.29. 2.30. 3.
3. 3.19. у = cos5x * arccos4x. 3.20. у = sin37x * arcctg5x2. 3.21. y = sin23x * arcctg3x5. 3.22. у = cos * arctg x4 3.23. y = tg62x * cos7x2. 3.24. y = ctg34x * arcsin . 3.25. y = ctg1/x * arccos x4 3.26. у = tg * arcctg 3x5. 3.27. у = tg32x * arccos2x3. 3.28. y = 2tg x * arctg5 3x. 3.29. y = sin53x * arctg . 3.30. у = cos43x * arcsin3x2. 4. 4.1. y = arcctg25x * ln(x — 4). 4.2. у = аrctg32x * ln(x + 5). 4.3. у = arccos4x * ln(x2 + x — 1). 4.4. 4.5. y = tg43x * arctg7x2. 4.6. у = 5-x2 * arcsin3x3. 4. 4.9. у = е-x * arcsin25x. 4.10. у = log4(x — 1) * arcsin4 x. 4.11. у = (x — 4)5 * arcctg 3x2. 4.12. y = ctg34x * arctg 2x3. 4.13. y = e-cos x * arctg7x5. 4.14. y = (x + l) * arccos3x4 4.15. у = 2 sinx * arcctg x4. 4.16. y = 3-x3 * arctg 2x5. 4.17. у = 3cos x * arcsin2 3x. 4.18. y = ln(x — 10) * arccos24x. 4.19. у = lg(x — 2) * arcsin5 x. 4.20. у = log3(x + 1) * arctg5 7x. 4.21. y = ln(x + 9) * arcctg32x. 4.22. у = lg(x + 2) * arcsin2 3x. 4.23. y = 4-sin x * arctg 3x. 4.24. у = 2cos x * arcctg3 x 4. 4.27. y = 2-x * arctg3 4x. 4.28. y = ln(x — 4) * arcctg4 3x. 4.29. y = lg(x + 3) * arcctg2 5x. 4.30. у = log5(x + 1) * arctg2 x3. 5. 5.1. у = tg43x * arcsin 2x3. 5.2. y = (x — 2)4 * arcsin 5x4. 5.3. у = 2—x3 * arctg 7x4. 5.4. у = (x + 6)5 * arcctg 3x5. 5.5. у = 3cos x * ln(x2 — 3x + 7). 5.6. y = log2(x -7) * arctg 5.7. y = arccos35x * tgx4. 5.8. y = (x — 5)7 * arcctg 7x3 5.9. у = arccos x2 * ctg 7x3. 5.10. у = 5-x2 * arccos 5x4. 5.11. y = arctg4x * cos 7x4. 5.13. у = (x + 5)2 arccos3 5x. 5.14. y = 2-sin x * arcsin32x 5.15. у = (x + 2)7 * arccos 5.16. у = (x — 7)5 * arcsin 7x4 5.17. y = ln(x — 3) * arccos 3x4 5.18. у = log2(x — 4) * arctg3 4x. 5.19. y = (x — 7)4 * arcctg2 7x 5.20. 5.21. 5.22. y = (x – 3)5arccos 3x6 5.23. 5.24. 5.25. y = tg3 x * arcctg 3x 5.26. 5.27. 5.28. y = arcsin3 4x * ctg 3x 5.29. y = e-cos x arcsin 2x 5.30. 6. 6.1. у = (х — 3)4 * arccos 5x3. 6.2. у = (3х — 4)3 * arccos 3x2. 6.3. у = sh3 4x * аrссоs . 6.4. у = th2 * arcctg3x2. 6.5. y = cth3 5x * arcsin 3x2. 6.6. y = ch2/x * arctg(7x + 2). 6.7. у = ch3 4x * arccos 4x2. 6.8. y = sh33x * arcctg5x2. 6.9. у = th5 Зx * arcsin . 6.10. у = сth2(x + 1) * arccos1/x. 6.11. у = sh4 2x * arccos x2. 6.12. y = ch3(3x + 2) * arctg3x. 6.13. у = th34x * аrссtg3x4 6.14. у = cth4 7x * arcsin . 6.15. у = sh3 2x * arcsin 7x2. 6.16. у = th5 4x * arccos 3x4. 6.17. у = ch2 5x * arctg . 6.18. y = cth42x * arctg x3. 6.19. y = sh4 5x * arccos 3x2. 6.20. у = ch3 9x * arctg(5x — 1). 6.21. y = th4x * arcctg 1/x. 6.22. у = cth3 4x * arcsin (3x + 1). 6.23. y = ch25x * arctgx4. 6.25. у = cth 4х5 * arccos 2x. 6.26. у = cth 3х * arcsin4 2x. 6.27. у = th5 3х * arcctg 6.28. у = sh4 3х * arccos 5x4. 6.29. у = cth2 4x * arcsin x3. 6.30. у = th3 5x * arcctg(2x — 5). 7. 7.1. 7.2. 7.3. 7.4. 7.5. 7.6. 7.7. 7.8. 7.9. 7.10. 7.11. 7.12. 7.13. 7.14. 7.15. 7.16. 7.17. 7.18. 7.19. 7.20. 7.21. 7.22. 7.23. 7.24. 7.25. 7.26. 7.27. 7.28. 7.29. 7.30. 8. 8.1. 8.2. 8.3. 8.4. 8.5. 8.6. 8.7. 8.8. 8.9. 8.10. 8.11. 8.12. 8. 8.15. 8.16. 8.17. 8.18. 8.19. 8.20. 8.21. 8.22. 8.23. 8.24. 8.25. 8.26. 8.27. 8.28. 8.29. 8.30. 9. 9.1. 9.2. 9.3. 9.4. 9.5. 9.6. 9.7. 9.8. 9.9. 9.10. 9.11. 9.12. 9.13. 9.14. 9.15. 9.16. 9.17. 9.18. 9.19. 9.20. 9.21. 9.22. 9.23. 9.24. 9.25. 9.26. 9.27. 9.28. 9.29. 9.30. 10. 10.1. 10.2. 10.3. 10.4. 10.5. 10.6. 10.7. 10.8. 10.9. 10.10. 10.11. 10.12. 10.13. 10.14. 10.15. 10.16. 10.17. 10.18. 10.19. 10.20. 10. 10.23. 10.24. 10.25. 10.26. 10.27. 10.28. 10.29. 10.30. 11. 11.1. 11.2. 11.3. 11.4. 11.5. 11.6. 11.7. 11.8. 11.9. 11.10. 11.11. 11.12. 11.13. 11.14. 11.15. 11.16. 11.17. 11.18. 11.19. 11.20. 11.21. 11.22. 11.23. 11.24. 11.25. 11.26. 11.27. 11.28. 11.29. 11.30. 12. 12.1. y = (cth 3x)arcsin x 12.2. y = (cos (x+2))ln x 12.3. y = (sin 3x)arccos x 12.4. y = (th 5x)arcsin (x+1) 12.5. y = (sh (x+2))arcsin 2x 12.6. 12.7. 12.8. 12.9. y = (log2(x+4))ctg7x 12. 12.11. y = (ch 3x)ctg 1/x 12.12. 12.13. y = (arccos 5x)ln x 12.14. y = (arctg 2x)sin x 12.15. y = (ln (x+7))ctg 2x 12.16. 12.17. 12.18. y = (cth 1/x)arcsin 7x 12.19. y = (cos (x+5))arcsin 3x 12.20. 12.21. y = (sin 4x)arctg 1/x 12.22. 12.23. 12.24. 12.25. 12.26. y = (ctg 7x)sh(x+3) 12.27. y = (sh 5x)arctg(x+2) 12.28. y = (arctg x)th(3x+1) 12.29. 12.30. y = (sh 3x)arcctg 2x Решние типового варианта Продифференцировать данные функции. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. Прологарифмируем данную функцию: тогда Отсюда выразим y`: Дата добавления: 2015-08-27; просмотров: 590 | Нарушение авторских прав Арккосинус, записывается как arccos или cos-1 (не путать с ), является функцией арккосинуса. Домен должен быть ограничен, поскольку для того, чтобы у функции была обратная функция, она должна быть взаимно однозначной, то есть никакая горизонтальная линия не может пересекать график функции более одного раза. Поскольку косинус является периодической функцией, без ограничения области определения горизонтальная линия будет периодически пересекать функцию бесконечно много раз. Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, то точка (b, a) находится на графике обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через прямую y = x. График y = arccos(x) показан ниже. Как видно из рисунка, y = arccos(x) является отражением cos(x) для ограниченной области 0≤x≤π через прямую y = x. Ниже приведен калькулятор для определения либо значения arccos числа от -1 до 1, либо значения косинуса угла. Хотя мы можем найти значение арккосинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0°, 30°, 45°, 60°, 90° и их кратные и эквиваленты в радианах), значения косинуса и арккосинуса которых стоит запомнить. Ниже приведена таблица, показывающая эти углы (θ) в градусах и их соответствующие значения косинуса, cos(θ). Один из методов, который может помочь в запоминании этих значений, заключается в выражении всех значений cos(θ) в виде дробей с квадратным корнем. От 90° до 180° вместо этого мы увеличиваем число под радикалом на 1, но также должны учитывать квадрант, в котором находится угол. Косинус отрицателен в квадрантах II и III, поэтому значения будут равны но отрицательный. В квадрантах I и IV значения будут положительными. Этот шаблон периодически повторяется для соответствующих угловых измерений. После того, как мы запомнили значения или если у нас есть какая-то ссылка, становится относительно просто распознавать и определять значения косинуса или арккосинуса для специальных углов. Пример: Найти arccos() , arccos() и arccos(2) в радианах. , . , . arccos(2) не определен, так как 2 не находится в интервале -1≤arccos(θ)≤1, домене arccos(x). Как правило, функции и их обратные свойства демонстрируют отношение f(f -1 (x)) = x и f -1 (f(x)) = x при условии, что x находится в области определения функции. То же самое верно для cos(x) и arccos(x) в пределах их соответствующих ограниченных доменов: cos(arccos(x)) = x для всех x в [-1, 1] и arccos(cos (x)) = x, для всех x в [0, π] Эти свойства позволяют нам оценить композицию тригонометрических функций. Если x находится в области определения, вычисление композиции арккосинуса и косинуса относительно просто. Примеры: 1. 2. Если x не входит в область значений, нам необходимо определить опорный угол, а также соответствующий квадрант. 3. В приведенном выше примере опорный угол равен , а cos() равен , но поскольку он лежит в квадранте III, его косинус отрицательный, и единственный угол, косинус которого равен , который лежит в области определения arccos(x), равен . Мы также можем составить композиции, используя все другие тригонометрические функции: синус, тангенс, косеканс, секанс и котангенс. Пример: Найти sin(arccos()). Так как не является одним из отношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции. Учитывая arccos() = θ, мы можем найти, что cos(θ) = . Прямоугольный треугольник ниже показывает θ и отношение его смежной стороны к гипотенузе треугольника. Чтобы найти синус, нам нужно найти противоположную сторону, так как sin(θ)=. Пусть а — длина противоположной стороны. Используя теорему Pythagorean, A 2 + 12 2 = 13 2 A 2 + 144 = 169 A 2 = 25907 = 169 A 2 = 25907 = 169 A 2 = 94907 A 2 = 94 = 169 A 2 = 144 = 169 A 2 = 144 = 169 A 2 . (arccos()) = sin(θ) = Тот же процесс можно использовать с переменным выражением. Пример: Найдите tan(arccos(4x)). Учитывая arccos(4x) = θ, мы можем найти, что cos(θ)= и построить следующий прямоугольный треугольник: Чтобы найти касательную, нам нужно найти противоположную сторону, так как tan(θ)=. Пусть b — длина противоположной стороны. Using the Pythagorean theorem, (4x) 2 + b 2 = 1 2 16x 2 + b 2 = 1 b 2 = 1 — 16x 2 b = и tan(arccos(4x)) = tan(θ) = , где — Арккосинус также можно использовать для решения тригонометрических уравнений, включающих функцию косинуса. Пример: Решите следующие тригонометрические уравнения относительно x, где 0≤x<2π. 1. 2cos(x) = 2cos(x) = cos(x) = x = arccos() Косинус отрицателен в квадрантах II и III, поэтому есть два решения: x= и х=. Это единственные два угла в пределах 0≤x<2π, значение косинуса которых равно . 2. 6cos 2 (x) + 9cos(x) — 36 = 0 6cos 2 (x) + 9sin(x) — 6 = 0 (6cos(x) — 3)(cos (x) + 2) = 0 6cos(x) — 3 = 0 или cos(x) + 2 = 0 cos(x) = или cos(x) = -2 x = arccos() или x = arccos(-2) Решение для x = arccos(), x = или Мы не можем решить для x = arccos(-2), потому что оно не определено, поэтому x= или являются единственными решениями. спросил Изменено
6 лет, 9 месяцев назад Просмотрено
8к раз $\begingroup$ Я вроде как могу понять основное направление (наклон) $y$ на разных интервалах $x$, но я не могу понять, почему значения $y$ принимают форму прямых линий, а не кривых, выглядящих больше похоже на греховные, потому что. РЕДАКТИРОВАТЬ : Я понимаю, что производная от Arccos(Sin(x)) дает 1 или -1 в зависимости от интервала x, но это не дает мне интуитивно понять, почему это так. тригонометрия обратная композиция функций и отношений $\endgroup$ 3 $\begingroup$ Что ж, чтобы подумать об уравнении $$y=\arccos(\sin(x))$$, давайте сначала рассмотрим более простое уравнение, полученное путем наложения косинуса обеих сторон (отметив, что $\cos(\arccos( x))=x$ — то есть $\arccos$ является правой инверсией $\cos$):
$$\cos(y)=\sin(x).$$
Если мы построим это, мы получим следующий график: $\hskip1.5in$ который представляет собой просто набор диагональных линий, идущих в двух направлениях. Эта тайна раскрывается, когда мы переписываем
$$\cos(y)=\cos\left(x+\frac{\pi}2\right)$$
и обратите внимание, что из симметрии и периодичности мы имеем, что $\cos(u)=\cos(v)$ всякий раз, когда $u=2\pi k \pm v$ для некоторого целого числа $k$. Однако определение $\arccos$, которое вы используете, кажется, требует, чтобы его выходные данные попадали в интервал $[0,\pi]$, следовательно, $y$ должен быть там. Если мы выделим подходящий диапазон $y$ серым цветом и обведем линии, которые он покрывает красным, мы восстановим наблюдаемую вами закономерность: $\hskip1.5in$ , из чего становится ясно, что чередование является лишь небольшой частью более крупного шаблона, чем невозможно полностью представить из-за того, что диапазон $\arccos$ ограничен. $\endgroup$ 1 $\begingroup$ Инверсия косинуса определена на $[-1, 1]$ и отображается в $[0, \pi]$. $$
\арккос(\грех(х)) =
\begin{случаи}
-x + \pi/2 + 2\pi k & \text{for } x \in [-\pi+2\pi k, \pi/2 + 2\pi k] \\
x — \pi/2 + 2\pi k & \text{for} x \in [\pi/2+2\pi k, \pi/2 + \pi + 2\pi k] \\
\end{случаи}
$$
где $k \in \mathbb{Z}$. $\endgroup$ $\begingroup$ Обратите внимание, что $$cos(x-\pi)=sin(x)$$ $$x-\pi=arccos(sin(x))$$ $$and$$ $$cos(x)=cos( x\pm 2n\pi), n=0,1,2,3,…$$ Вы получаете решения между $\pi$ и $0$ из-за $arccos$. Это объясняет, почему ваше решение является линейным с наклоном, равным единице. ТАКЖЕ:
$$cos(x)=cos(-x)$$ Это означает, что ваше решение является положительным и отрицательным. Объединение всех этих результатов дает $$arccos(sin(x))=\pm(x-\pi\pm2n\pi)$$ $$=x\pm(2n-1)\pi,-x\pm(2n -1)\pi$$ $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Обязательно, но не отображается Электронная почта Требуется, но не отображается Я даже проверил это с помощью wolfram alpha и понял правильно, но проблема с $\cos$ заключается в том, что когда я пытаюсь решить его так же, как я сделал с $\tan$, и получаю интервал, в котором $n$ лежит, крайние точки интервала отличаются на $0,5$, из-за чего для некоторых значений их нижний и верхний предел совпадают, но для некоторых значений в этом интервале нет целочисленного значения, как это :- из wolfram alpha поэтому что делать в таком случае и что означает отсутствие значения $n$, лежащего в интервале? 9{-1}$. (Читатель может проверить $\overset{2}{=}$ и $\overset{3}{=}$, используя формулы вычитания для косинуса.) $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Обязательно, но не отображается Электронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie Арккосинус является одной из обратных тригонометрических функций и также записывается как cos -1 . Поскольку cos -1 (x) является обратной функцией cos(x), арккосинус (x) является обратной функцией cos x. У нас есть 6 обратных тригонометрических функций, таких как Здесь мы подробно изучим обратную функцию косинуса (арккосинус), а также ее график, область значений, диапазон, формулы, производную и интеграл, а также несколько решенных примеров. Арккосинус — это функция, обратная косинусу и, следовательно, одна из обратных тригонометрических функций. Арккосинус произносится как «арккосинус». Арккосинус x также может быть записан как «acosx» (или) «cos -1 x» или «arccos». Если f и f -1 являются обратными функциями друг друга, то f(x) = y ⇒ x = f -1 (y). Итак, y = cos x ⇒ x = cos -1 (y) . В этом смысл арккосинуса. Давайте рассмотрим несколько примеров, чтобы увидеть, как работает функция арккосинуса. В прямоугольном треугольнике косинус угла (θ) представляет собой отношение прилежащего катета к гипотенузе. Таким образом, функция арккосинуса используется для нахождения неизвестных углов в прямоугольном треугольнике. Кроме того, его можно использовать для нахождения неизвестных углов в любом треугольнике, используя закон косинусов. Например, в треугольнике ABC, если AB = c, BC = a и CA = b, то по закону косинусов a 2 = b 2 + c 2 — 2bc cos A Используя это, cos A = (b 2 + c 2 — a 2 ) / (2bc) A = cos -1 [(b 2 + c 2 — a 2 ) / (2bc)] ([или (2bc) арксинус)] б 2 + с 2 — а 2 ) / (2bc)]. Точно так же мы можем найти другие углы треугольника, зная длины его сторон. В этом разделе мы посмотрим, как можно найти домен и диапазон функции арккосинуса. Мы знаем, что функция косинуса является функцией из R → [-1, 1]. Но функция косинуса НЕ является биекцией (поскольку она НЕ является однозначной) в области R. Следовательно, она не может иметь обратную, если ее областью определения является R. Чтобы функция косинуса была однозначной, ее область определения может быть ограничена единицей. интервалов [-π, 0], [0, π], [π, 2π] и т. д. Каждому из этих интервалов соответствует ветвь арккосинуса. Ветвь арккосинуса с диапазоном [0, π] называется главной ветвью. Таким образом, область определения косинуса обычно ограничивается значением [0, π], а его диапазон — [-1, 1]. Мы знаем, что область определения и область значений функции будут соответственно областью значений и областью значений обратной функции. Следовательно, область обратного косинуса, который является арккосинусом, равна [-1, 1], а его диапазон равен [0, π] . arccos x (или) cos -1 x : [-1, 1] → [0, π] График функции арккосинуса с диапазоном значений главной ветви [0, π] можно нарисовать с помощью следующей таблицы. Здесь мы выбрали случайные значения для x в области арккосинуса, которая равна [-1, 1]. Нанеся эти точки на график, мы получим график arccos. Вот некоторые свойства/формулы арккосинуса. Найдем производную от y = cos -1 x. По определению арккосинуса y = cos -1 x можно записать как cos y = x. Дифференцируя это с обеих сторон по x с использованием цепного правила, — sin y (dy/dx) = 1 dy/dx = -1/sin y . Теперь у нас есть sin 2 y + cos 2 y = 1 ⇒ sin 2 y = 1 — cos 2 y ⇒ sin y = √(1 — cos²y) = √1 — x². Подставив это в (1), dy/dx = -1/√1 — x² Таким образом, производная арккосинуса (или) производная от cos -1 x равна -1/√(1 — x² ). ∫cos -1 x dx найдем с помощью интегрирования по частям. Для этого запишем приведенный выше интеграл в виде ∫cos -1 x · 1 dx Используя LIATE, f(x) = cos -1 x и g(x) = 1. Интегрируя по части, ∫f(x) . g(x) dx = f(x) ∫g(x) dx − ∫(f′(x) ∫g(x) dx) dx + C ∫cos -1 x · 1 dx = cos — 1 x ∫1 dx — ∫ [d/dx(cos -1 x) ∫x dx] + C ∫cos -1 x dx = cos -1 x (x) — ∫ [- 1/√1 — x²] x dx + C Мы вычислим этот интеграл с помощью u-подстановки. Для этого пусть 1-х 2 = u. ∫cos -1 x dx = x cos -1 x — ∫(-1/√u) (-1/2) du + C = x cos -1 x — 1/2 ∫u -1/2 du + C = x cos -1 x — (1/2) (u 1/2 /( 1/2)) + C = x cos -1 x — √u + C = x cos -1 x — √1 — x² + C Следовательно, ∫cos -1 x dx = x cos -1 x — √(1 — x²) + C. Важные примечания по арккосинусу: Вот несколько важных замечаний, связанных с функцией арккосинуса. ☛ Связанные темы: Вот некоторые темы, которые могут вас заинтересовать при чтении об арккосинусе. Часто задаваемые вопросы по арккосинусу Арккосинус является обратной функцией тригонометрической функции cos x и, следовательно, является обратной тригонометрической функцией. По определению обратной функции y = cos x ⇒ x = cos -1 (y). В прямоугольном треугольнике, если θ — один из острых углов, то cos θ = (прилежащий)/(гипотенуза). Тогда θ = arccos((соседний)/(гипотенуза). Арккосинус является обратным cos x, поэтому да, арккосинус x равен cos⁻¹x. Нет. Арккосинус является обратной функцией косинуса, т. е. arccos x = cos -1 x. Но оно НЕ равно (cos x) -1 , поскольку (cos x) -1 = 1/ cos x = sec x. «Арккосинус» является одной из обратных тригонометрических функций и может произноситься как «арккосинус» или «арккосинус». Область определения арккосинуса (или) арккосинуса x равна [-1, 1], так как диапазон его обратной функции (которая является функцией косинуса) равен [-1, 1]. Диапазон значений arccos x (или) cos -1 x равен [0, π], поскольку ограниченная область значений обратной функции (которая является функцией косинуса) равна [0, π], чтобы сделать функцию косинуса однократной. Арккосинус cos x равен x (или) cos -1 (cos x) = x, если x ∈ [0, π]. Если x ∉ [0, π], то либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π], а затем примените cos -1 (cos x) = x . Косинус арккосинуса числа x равен x (или) cos(cos -1 x) = x, если x ∈ [-1, 1]. Если x ∉ [-1, 1], то cos(cos -1 x) НЕ определен. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. arccos online Функция арккосинуса является обратной функцией
функция косинуса,
это вычисляет арккосинус числа онлайн . Число, к которому вы хотите применить функцию функции арккосинуса, должно принадлежать диапазону [-1,1]. Чтобы вычислить арккосинус числа , просто введите число и примените функция arccos .
Таким образом, для , вычисляющего , арккосинус числа, следующего за 0,4,
вы должны ввести
arccos(`0.4`) или сразу 0.4, если кнопка arccos уже есть,
результат 1.1592)`.
Онлайн калькулятор с корнями и дробями и степенями: Калькулятор онлайн со степенями процентами корнями математический
дробный калькулятор с корнями
Где можно решить любую задачу по математике, а так же дробный калькулятор с корнями Онлайн?
Калькулятор онлайн для расчетов процентов, дробей, степеней
Калькулятор давно и прочно вошел в нашу жизнь. Мы часто пользуемся им в повседневной жизни подбивая свои расходы за день, неделю, рассчитывая выплату коммунальных за месяц и т.д. С помощью онлайн калькулятора осуществляют простые арифметические расчеты студенты и школьники, продавцы в магазинах, торговцы на рынках, работники коммунальных служб, что позволяет сэкономить время, получить точные расчеты, избежать досадных ошибок.Клавиша Символ Операция pi pi Постоянная pi е е Число Эйлера % % Процент ( ) ( ) Открыть/Закрыть скобки , , Запятая sin sin (α) Синус угла cos cos (β) Косинус tan tan (y) Тангенс sinh sinh () Гиперболический синус cosh cosh () Гиперболический косинус tanh tanh () Гиперболический тангенс sin-1 asin () Обратный синус cos-1 acos () Обратный косинус tan-1 atan () Обратный тангенс sinh-1 asinh () Обратный гиперболический синус cosh-1 acosh () Обратный гиперболический косинус tanh-1 atanh () Обратный гиперболический тангенс x2 ^2 Возведение в квадрат х3 ^3 Возведение в куб xy ^ Возведение в степень 10x 10^() Возведение в степень по основанию 10 ex exp () Возведение в степень числа Эйлера vx sqrt (x) Квадратный корень 3vx sqrt3 (x) Корень 3-ей степени yvx sqrt (x,y) Извлечение корня log2x log2 (x) Двоичный логарифм log log (x) Десятичный логарифм ln ln (x) Натуральный логарифм logyx log (x,y) Логарифм I / II Сворачивание/Вызов дополнительных функций Unit Конвертер величин Matrix Матрицы Solve Уравнения и системы уравнений Построение графиков Дополнительные функции (вызов клавишей II) mod mod Деление с остатком ! ! Факториал i / j i / j Мнимая единица Re Re () Выделение целой действительной части Im Im () Исключение действительной части |x| abs () Модуль числа Arg arg () Аргумент функции nCr ncr () Биноминальный коэффициент gcd gcd () НОД lcm lcm () НОК sum sum () Суммарное значение всех решений fac factorize () Разложение на простые множители diff diff () Дифференцирование Deg Градусы Rad Радианы Виды калькуляторов
решение уравнений онлайн со степенями
Показательные уравнения – это уравнения, в которых переменная величина входит в аргумент показательной функции. Показательная функция это математическая функция вида f(x) = ax, где a является основанием степени, а x – показателем степени. Показательная функция всегда монотонна и она принимает только положительные значения.
Показательные уравнения – это уравнения, в которых переменная величина входит в аргумент показательной функции. Показательная функция это математическая функция вида f(x) = ax, где a является основанием степени, а x – показателем степени. Показательная функция всегда монотонна и она принимает только положительные значения.
Калькулятор решает любые показательные уравнения онлайн.
Для получения полного хода решения нажимаем в ответе Step-by-step и Approximate form.Степенные выражения (выражения со степенями) и их преобразование
Что представляют собой степенные выражения?
Основные виды преобразований степенных выражений
Работа с основанием и показателем степени
Использование свойств степеней
Преобразование дробей, содержащих степени
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12
РешениеПреобразование выражений с корнями и степенями
Преобразование степеней с переменными в показателе
Преобразование выражений со степенями и логарифмами
Комплексные корни и степени чисел онлайн
Вы ввели следующее выражение Результат вычисления степени Результат выражения (альтернативный вывод) со всеми корнями
Синтаксис
Примеры
Действительная часть: 1.0560 Комплексная часть: 1.0457
Действительная часть: -0.6682 Комплексная часть: 1.3275
Действительная часть: -1.4690 Комплексная часть: -0.2253
Действительная часть: -0.2396 Комплексная часть: -1.4667Решить уравнение со степенями онлайн калькулятор. Решение показательных уравнений по математике
Где можно решить показательное уравнение онлайн решателем?
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >
Знак дроби «/»
+
—
*
:
_cтереть
Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби «.
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .Знаки используемые для записи в калькуляторе
Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.Возможности онлайн калькулятора дробей
Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.
Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.Дискриминант
a
= 1, b
= −8, c
= 12;
D
= (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
a
= 5; b
= 3; c
= 7;
D
= 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
a
= 1; b
= −6; c
= 9;
D
= (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.Корни квадратного уравнения
x
2 − 2x
− 3 = 0 ⇒ a
= 1; b
= −2; c
= −3;
D
= (−2) 2 − 4 · 1 · (−3) = 16.
15 − 2x
− x
2 = 0 ⇒ a
= −1; b
= −2; c
= 15;
D
= (−2) 2 − 4 · (−1) · 15 = 64.
x
2 + 12x
+ 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.Неполные квадратные уравнения
Калькулятор Корней — Найдите квадратный корень
Онлайн-калькулятор предалгебры
Наших пользователей:
S.D., Орегон
до н.э., Флорида
Джеймс Мур, Мичиган Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 25.02.2012:
Калькулятор дробных показателей | Как упростить рациональные экспоненты?
Калькулятор дробной степени
Дробные показатели с числителем 1
Но почему это так? Постараемся это доказать: Дробные показатели с числителем, отличным от 1 (любая дробь)
Отрицательный и дробный показатель степени
Калькулятор степени дроби — как использовать
Калькулятор дробей с показателями — Онлайн-калькулятор дробей с показателями
Что такое калькулятор дробей с показателями?
Онлайн-калькулятор дробей с показателями Как использовать дроби с калькулятором показателей?
Как найти дроби с показателями?
Калькулятор экспонент
Введите выражение, например.2-1 Пример задачи Ничья Количество решаемых уравнений: 23456789 Пример задачи Решить Введите неравенство в график, например.г. y Пример задачи Ничья Количество решаемых неравенств: 23456789 Пример задачи 908 Решить Наших пользователей:
Лиза Шустер, Нью-Йорк
М.Б., Иллинойс
Питер Гудман, TN Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2010-04-15:
Как оценить корни с помощью научного калькулятора — видео и стенограмма урока
Квадратный корень
Пользовательская кнопка корня
Кнопка экспоненты
Практическая задача
Резюме урока
Интернет-научный калькулятор — инструмент
Скачать научный калькулятор eCalc
Онлайн-калькулятор и справка по математике
Основные функции
Тригонометрические функции онлайн
Онлайн-гиперболические тригонометрические функции
Меню
от десятичной дроби к дроби
Комплексные числа
Онлайн-конвертер единиц
Библиотека констант
Онлайн-решатель
Базовый преобразователь
Онлайн-калькулятор и справка по математике
Режим ввода (алгебраический или RPN)
Алгебраический режим
Алгебраический режим ввода обычно называют «инфиксной записью» и широко используется в большинстве портативных калькуляторов.Выражения, вводимые в режиме алгебраического ввода, выполняются способом, который очень похож на естественную форму выражения, а порядок операций определяется приоритетом операторов и скобками. Режим RPN
RPN, что означает обратную польскую нотацию, представляет собой нотацию на основе стека, в которой операторы должны следовать за своими операндами. Например, чтобы оценить выражение «1 + 2» в RPN, пользователь должен ввести «1 2 +», и выражение вычисляется сразу после оператора.Выражения, содержащие круглые скобки, такие как «(1 + 2) * 3», оцениваются, отмечая порядок приоритета и вводя форму как «1 2 + 3 *». Поддержка графических кнопок и клавиатуры
Стек
Поддон Введение
Основные функции
Дополнение
Вычитание
Умножение
Факториал
PI
Тригонометрические функции онлайн
синус
Обратный синус
Косинус
Обратный косинус
Касательная
Обратная касательная
Косеканс
Обратный косеканс
Секант
Обратная секущая
Котангенс
Обратный котангенс
Онлайн-гиперболические тригонометрические функции
Гиперболический синус
Гиперболический косинус
Гиперболический тангенс
Гиперболический косеканс
Гиперболический секанс
Гиперболический котангенс
Обратный гиперболический синус
Обратный гиперболический косинус
Обратный гиперболический тангенс
Обратный гиперболический косеканс
Обратный гиперболический секанс
Обратный гиперболический котангенс
Меню
Формат
Угол
Система координат
Режимы онлайн-калькулятора
от десятичной дроби к дроби
Комплексные числа
Онлайн-конвертер единиц
Библиотека констант
Онлайн-решатель
Линейный решатель
Линейный решатель выбирается одним из 4 вариантов. Этот решатель позволяет решать для переменных, когда существует равное количество уравнений, уникальных для каждой неизвестной переменной.Решатель требует, чтобы были введены коэффициенты уравнений. При вводе номеров переменных убедитесь, что каждая запись в столбце используется для одной и той же переменной. Коэффициенты комплексных чисел могут быть введены, как только все значения введены, щелкнув по кнопке «Решить». Результаты помечены как x1 … xn. X1 соответствует переменной, используемой в столбце 1 и x2, столбце 2 и так далее. Решатель полиномов
Решатель полиномов (решатель корня) выбирается щелчком по соответствующему порядку уравнения.Коэффициенты вводятся в поля ввода ниже. Затем нажмите «Решить», и результаты станут корнями уравнения.
Базовый преобразователь
Интегралы от рациональных функций: Интегрирование рациональных функций
Интегрирование рациональных функций
 Для этого существует метод неопределённых коэффициентов, основанный
на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.
Для этого существует метод неопределённых коэффициентов, основанный
на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.Алгоритм интегрирования рациональных функций

 Разложим знаменатель подынтегрального выражения на множители. Сначала
можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:
Разложим знаменатель подынтегрального выражения на множители. Сначала
можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь: В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:
В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим: Уравнения с многочленами в знаменателе имеют действительные корни,
а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее
разложение исходной дроби на простые дроби:
Уравнения с многочленами в знаменателе имеют действительные корни,
а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее
разложение исходной дроби на простые дроби: Шаг 1. Дан интеграл от рациональной функции
.
Шаг 1. Дан интеграл от рациональной функции
.







 Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей: Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
Шаг 3. На шаге 2 получили окончательное разложение
подынтегральной дроби на сумму простых дробей:
Назад Листать Вперёд>>> Интегрирование рациональных дробей
Данный онлайн калькулятор служит для вычисления интегралов рациональных дробей вида .
P(x) = Q(x)R(x) + S(x), где R(x) и S(x) — полиномы, называемые обычно, как и в случае действительных чисел, частным и остатком, причем степень полинома S(x) меньше n. Тогда
, (1.1)
а интеграл от полинома R(x) мы вычислять умеем. Покажем на примере, как можно получить разложение (1.1). Пусть P(x)=x7+3x6+3x5–3x3+4x2+x-2, Q(x)=x3+3x2+x-2. Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор
Разделим полином P(x) на полином Q(x) так же, как мы делим вещественные числа (решение получаем через калькулятор деления столбиком
). Имеем
R(x) = x4+2x2–4x+7 и остаток S(x) = 9x2–14x+12 от этого деления.
По основной теореме алгебры любой полином может быть разложен на простейшие множители, то есть представлен в виде , где xl – корни полинома Q(x) повторенные столько раз, какова их кратность.
Пусть полином Q(x) имеет n различных корней x1, x2,…, xn. Тогда правильная рациональная дробь может быть представлена в виде , где A1, A2,…,An — числа подлежащие определению. Если xi — корень кратности α, то ему в разложении на простейшие дроби соответствует α слагаемых . Если xj — комплексный корень кратности α полинома с действительными коэффициентами, то комплексно сопряженное число xj — тоже корень кратности α этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида , если xj, xj – корни кратности один. Если xj, xj – корни кратности α, то им соответствует α слагаемых и соответствующее разложение имеет вид
Если xj — комплексный корень кратности α полинома с действительными коэффициентами, то комплексно сопряженное число xj — тоже корень кратности α этого полинома. Чтобы не иметь дело с комплексными числами при интегрировании рациональных дробей, слагаемые в разложении правильной рациональной дроби, соответствующие парам комплексно сопряженных корней, объединяют и записывают одним слагаемым вида , если xj, xj – корни кратности один. Если xj, xj – корни кратности α, то им соответствует α слагаемых и соответствующее разложение имеет вид
Таким образом, интегрирование правильных рациональных дробей свелось к интегрированию простейших дробей, из которых , , являются табличными, может быть найден по рекуррентной формуле, которая получается интегрированием по частям. Интегралы , в случае, когда знаменатель имеет комплексные корни (дискриминант D=p2-4q<0), сводятся, с помощью выделения полного квадрата, к интегралам , заменой .
Одним из способов нахождения коэффициентов Aj, Mj, Nj в разложении правильной рациональной дроби является следующий. Правую часть полученного разложения с неопределенными коэффициентами Aj, Mj, Nj приводят к общему знаменателю. Так как знаменатели правой и левой частей равны, то должны быть равны и числители, которые являются полиномами. Приравнивая коэффициенты при одинаковых степенях x (так как полиномы равны, если равны коэффициенты при одинаковых степенях x), получаем систему линейных уравнений для определения этих коэффициентов.
1. Найти .
Корни знаменателя – x1 = -2 кратности 1 и x2=1 кратности 2. Поэтому x3 – 3x + 2 = (x+2)(x-1)2 и подынтегральная функция может быть представлена в виде
Приводя к общему знаменателю, получаем
Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем
Решая эту систему, находим A1=7/9, A2=2/9, A3=1/3.
Таким образом,
2. Найти .
Корни знаменателя – x1=2 кратности 1 и два комплексных корня x2,3, = -1±i. Поэтому x3 – 2x – 4 = (x-2)(x2 + 2x+2) и подынтегральная функция может быть представлена в виде
Приводя к общему знаменателю, получаем
Приравнивая коэффициенты при одинаковых степенях x в числителях правой и левой частей последнего соотношения, получаем
Решая эту систему, находим A=1, M=1, N=2.
Таким образом,
=ln|x-2|+1/2ln(x2+2x+2)+arctg(x+1)+C
Решение. Используем метод разложения на простейшие. Знаменатель имеет действительные корни, причем корень —1 имеет кратность два. Разложим подынтегральную функцию на простейшие слагаемые
2x+1 = A(x-1)2+Bx(x-1) + Dx = (A+B)x2+(-2A-B+D)x+A
→ A=1, B=-1, D=3
Следовательно
Примеры интегрирования рациональных функций (дробей)
, , .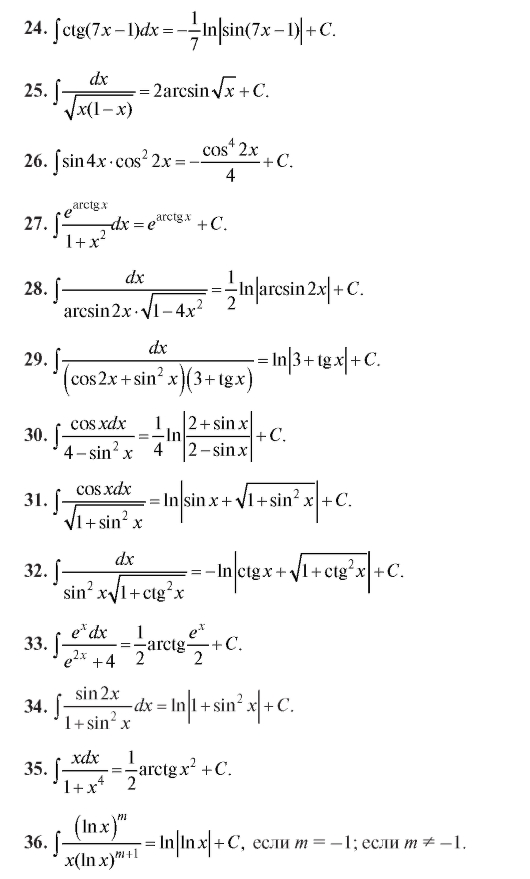
Пример 1
.
Отсюда
.
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 6 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, 3, 6, –1, –2, –3, –6.
Подставим x = 1:
.
.
Решаем квадратное уравнение .
.
Корни уравнения: , .
Тогда
.
.
Интегрируем.Пример 2
.
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 3 (члена без x). То есть целый корень может быть одним из чисел:
1, 3, –1, –3.
Подставим x = 1:
.
.
x 2 + x + 3 = 0.
Находим дискриминант: D = 1 2 – 4·3 = –11. Поскольку D < 0, то уравнение не имеет действительных корней. Таким образом, мы получили разложение знаменателя на множители:
.
.
Освобождаемся от знаменателя дроби, умножаем на (x – 1)(x 2 + x + 3):
(2.1) .
Подставим x = 1. Тогда x – 1 = 0,
.
1 = 3A – C;
.
;
0 = A + B;
.
.
(2.2) .
Для вычисления второго интеграла, выделим в числителе производную знаменателя и приведем знаменатель к сумме квадратов.
;
.
Поскольку уравнение x 2 + x + 3 = 0 не имеет действительных корней, то x 2 + x + 3 > 0. Поэтому знак модуля можно опустить.
.Пример 3
. Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
Поэтому подынтегральное выражение является рациональной функцией. Степень многочлена в числителе равна 3. Степень многочлена знаменателя дроби равна 4. Поскольку 3 < 4, то дробь правильная. Поэтому ее можно раскладывать на простейшие дроби. Но для этого нужно разложить знаменатель на множители.
.
Предположим, что оно имеет хотя бы один целый корень. Тогда он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
.
Итак,
.
.
Если предположить, что это уравнение имеет целый корень, то он является делителем числа 2 (члена без x). То есть целый корень может быть одним из чисел:
1, 2, –1, –2.
Подставим x = –1:
. Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
Можно было бы, как и в предыдущем случае, разделить многочлен на , но мы сгруппируем члены:
.
.
.
Освобождаемся от знаменателя дроби, умножаем на (x + 1) 2(x 2 + 2):
(3.1) .
Подставим x = –1. Тогда x + 1 = 0,
.
Подставим x = –1 и учтем, что x + 1 = 0:
;
; .
0 = 2A + 2B + D;
.
;
1 = B + C;
.
.Интегрирование рациональных дробей с примерами решения
Интегрирование дробно-рациональных функций 2), любую дробно-рациональную функцию — многочлены с действительными коэффициентами степени и соответственно, в общем случае можно представить суммой некоторого
2), любую дробно-рациональную функцию — многочлены с действительными коэффициентами степени и соответственно, в общем случае можно представить суммой некоторогоВысшая математика: лекции, формулы, теоремы, примеры задач с решением 
Пример с решением 1:
 е. При имеем откуда Наконец, приравнивая коэффициенты при получаем или Итак, вместо (2.31) запишем
е. При имеем откуда Наконец, приравнивая коэффициенты при получаем или Итак, вместо (2.31) запишемПример с решением 2:
 32) получаем откуда
32) получаем откудаПример с решением 3:
Пример с решением 4:
 33) подстановкой к табличному интегралу 13, а второй подстановкой — к интегралу
33) подстановкой к табличному интегралу 13, а второй подстановкой — к интегралуПример с решением 5:
Интегрирование рациональных функций
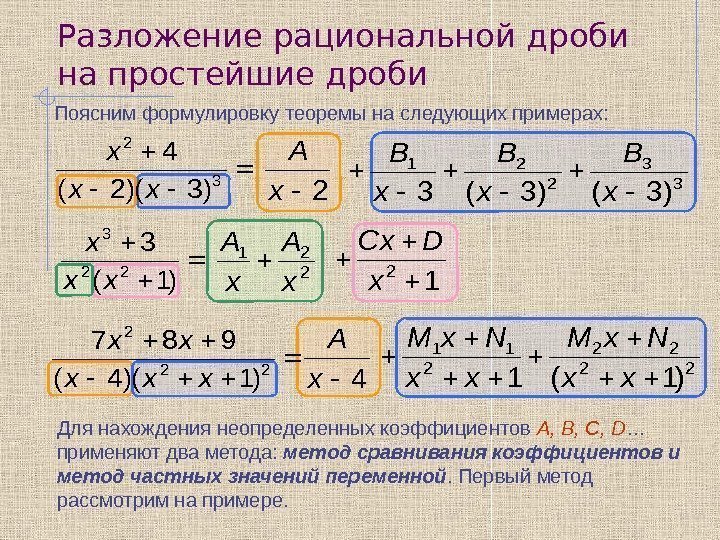


х = 1
2 = 4А; A = x = -3
10 = -64D; D = — x = 0
1= -3B + 3C + x = -1
2 = 1- 4B + 8C +  Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители.
Среди корней знаменателя имеются простые комплексные корни, т.е. разложение знаменателя содержит квадратичные неповторяющиеся множители. при х2:
0 = А+В
x:
0 = A+C
x0:
1 = A
 Найти интеграл
Найти интеграл

 Введем новую переменную tg . Тогда = =
Введем новую переменную tg . Тогда = =

Интегрирование рациональных функций — Интегралы и дифференциальные уравнения (Математика)
 Интеграл от степенной функции легко вычислить по таблице интегралов.
Интеграл от степенной функции легко вычислить по таблице интегралов. Тогда Причем уже не являются корнями полинома . В этом случае из рациональной дроби тоже можно выделить некоторую элементарную рациональную дробь вида .
Тогда Причем уже не являются корнями полинома . В этом случае из рациональной дроби тоже можно выделить некоторую элементарную рациональную дробь вида .



Интеграция рациональных функций

Пример 1.
 \]
\] Пример 5.

 \]
\] \]
\] 7.4: Интегрирование рациональных функций с помощью дробей
Цели обучения
 \nonumber \]
\nonumber \]
Упражнение \(\PageIndex{1}\)
Неповторяющиеся линейные множители
 4.1} такие, что
4.1} такие, что Таким образом, решение этих уравнений дает \(A=-1, B=\dfrac{4}{3}\) и \(C=-\dfrac{1}{3}\).
Таким образом, решение этих уравнений дает \(A=-1, B=\dfrac{4}{3}\) и \(C=-\dfrac{1}{3}\). 2−2x}\,dx=\int \left(−\dfrac{1}{x}+\dfrac{4}{3}⋅\dfrac{1}{x−2}−\dfrac{1}{3 }⋅\dfrac{1}{x+1}\right)\,dx. \номер\] 92x−\sin x}\,dx=−\ln |u|+\ln |u−1|+C=−\ln |\sin x|+\ln |\sin x−1|+C. \nonumber \]
2−2x}\,dx=\int \left(−\dfrac{1}{x}+\dfrac{4}{3}⋅\dfrac{1}{x−2}−\dfrac{1}{3 }⋅\dfrac{1}{x+1}\right)\,dx. \номер\] 92x−\sin x}\,dx=−\ln |u|+\ln |u−1|+C=−\ln |\sin x|+\ln |\sin x−1|+C. \nonumber \] Упражнение \(\PageIndex{2}\)
 2\) или, что то же самое, \(A=2 .\) 92} \номер \]
2\) или, что то же самое, \(A=2 .\) 92} \номер \] Общий метод
Стратегия решения задач: разложение дробей
 \номер\] 92}\) и оси x на интервале \([0,1]\) относительно оси y .
\номер\] 92}\) и оси x на интервале \([0,1]\) относительно оси y . Ключевые понятия
 Типы факторов включают неповторяющиеся линейные факторы, повторяющиеся линейные факторы, неповторяющиеся неприводимые квадратичные факторы и повторяющиеся неприводимые квадратичные факторы.
Типы факторов включают неповторяющиеся линейные факторы, повторяющиеся линейные факторы, неповторяющиеся неприводимые квадратичные факторы и повторяющиеся неприводимые квадратичные факторы. Глоссарий
На этой странице нет тегов.

Интеграция рациональных функций | Brilliant Math & Science Wiki
Содержание
 У нас есть 9{n_j} } \right). g(x)f(x)=r(x)+∑((x−ai)niki)+∑(((x−bj)2+cj2)njljx+ мж).
У нас есть 9{n_j} } \right). g(x)f(x)=r(x)+∑((x−ai)niki)+∑(((x−bj)2+cj2)njljx+ мж). Их относительно легко решить.
Их относительно легко решить. 92 -1 = (x-1)(x+1) x2-1=(x-1)(x+1) и частичные дроби дают

 Иногда это нехорошо или не дает хорошего результата. В таких случаях мы должны попробовать uuu-подстановку.
Иногда это нехорошо или не дает хорошего результата. В таких случаях мы должны попробовать uuu-подстановку. org/wiki/integration-of-rational-functions-easy/
org/wiki/integration-of-rational-functions-easy/ Интегрирование рациональной функции с квадратичным знаменателем
Содержимое
 1 Примеры уменьшенного корпуса
1 Примеры уменьшенного корпуса Приведение
Приведение к случаю, когда числитель имеет меньшую степень, чем знаменатель
 Но не забудьте добавить первообразную для многочлена к вашему окончательному ответу!
Но не забудьте добавить первообразную для многочлена к вашему окончательному ответу! Приведение к случаю унитарного знаменателя
Неопределенная интеграция для правильной дроби с единым знаменателем
Резюме случаев
Знак дискриминанта Качественное описание случая Первообразная (мы опускаем +C для экономии места) Функции, линейная комбинация которых дает первообразную (зависит от только в знаменателе) Описание новых констант в терминах положительный Знаменатель имеет различные корни
множителей как ноль Знаменатель повторяет корень
множителей как отрицательный знаменатель имеет вид
с Случай, когда знаменатель имеет различные линейные множители
UPSHOT : Первообразная в этом случае выражается как линейная комбинация с постоянными коэффициентами натуральных логарифмов абсолютных значений линейных множителей.

Это относится к общему случаю интегрирования рациональной функции, знаменатель которой имеет различные линейные множители
Случай, когда знаменатель повторяет линейные множители
UPSHOT : Первообразная в этом случае представляет собой константу, деленную на линейный множитель плюс константу, умноженную на натуральный логарифм линейного множителя.
Случай, когда знаменатель имеет отрицательный дискриминант
UPSHOT : Первообразная в этом случае представляет собой константу, умноженную на функцию арктангенса, плюс константу, умноженную на натуральный логарифм абсолютного значения.
 квадратичного.
квадратичного. Определенное интегрирование
Случай, когда знаменатель имеет различные линейные множители
Интервал Первообразная на интервале  Обратимся теперь к вопросу, можем ли мы вычислить несобственных интегралов, т. е. интегралов, у которых одним из пределов является одно из значений .
Обратимся теперь к вопросу, можем ли мы вычислить несобственных интегралов, т. е. интегралов, у которых одним из пределов является одно из значений . Это согласуется с тестом разницы градусов. Для приведенной выше первообразной предельное значение at равно 0,
Это согласуется с тестом разницы градусов. Для приведенной выше первообразной предельное значение at равно 0, Случай, когда знаменатель повторяет линейные множители
Интервал Первообразная на интервале  Рассмотрим теперь вопрос о несобственных интегралах, т. е. интегралах, у которых один из концов интегрирования входит в число:
Рассмотрим теперь вопрос о несобственных интегралах, т. е. интегралах, у которых один из концов интегрирования входит в число: Случай, когда знаменатель имеет отрицательный дискриминант
 Теперь рассмотрим несобственные интегралы:
Теперь рассмотрим несобственные интегралы: Примеры
Примеры сокращенного случая
Частные дроби и интерпретация линейной алгебры
Случай сокращенной формы

Общий случай
Повторное антидифференцирование
 2+bx+c$.
93\over (x-2)(x+3)}\,dx=\int x-1\,dx +\int {7x-6\over
(х-2)(х+3)}\,дх.
$$
Первый интеграл прост, поэтому только второй требует некоторой работы.
$\квадрат$
2+bx+c$.
93\over (x-2)(x+3)}\,dx=\int x-1\,dx +\int {7x-6\over
(х-2)(х+3)}\,дх.
$$
Первый интеграл прост, поэтому только второй требует некоторой работы.
$\квадрат$ 2\over 2}-x+{8\over5}\ln |x-2|+{27\over5}\ln|x+3|+C.\cr
}$$
$\квадрат$
92+3x}\,dx$
(отвечать)
2\over 2}-x+{8\over5}\ln |x-2|+{27\over5}\ln|x+3|+C.\cr
}$$
$\квадрат$
92+3x}\,dx$
(отвечать) Исчисление II. Частичные дроби
Раздел 1-4: Частичные дроби 92} — x — 6}}\,dx}} & = \int{{\frac{4}{{x — 3}}\, — \frac{1}{{x + 2}}dx}}\ \ & = 4\ln \влево| {х — 3} \право| — \лн\влево| {х + 2} \право| + с\конец{выравнивание*}\]
 Многие интегралы, включающие рациональные выражения, могут быть получены, если мы сначала возьмем частичные дроби под интегралом.
Многие интегралы, включающие рациональные выражения, могут быть получены, если мы сначала возьмем частичные дроби под интегралом. 2} — x — 6}}\,dx}}\]
2} — x — 6}}\,dx}}\] Единственный смысл сложения членов состоит в том, чтобы получить числитель, и мы можем получить его, фактически не записывая результаты сложения.
Единственный смысл сложения членов состоит в том, чтобы получить числитель, и мы можем получить его, фактически не записывая результаты сложения. 5in}20 & = A\left( 5 \right) + B\left( 0 \right) & \hspace{0.25in} & \Rightarrow & \hspace{0.25in}A & = 4\end{align*}\]
5in}20 & = A\left( 5 \right) + B\left( 0 \right) & \hspace{0.25in} & \Rightarrow & \hspace{0.25in}A & = 4\end{align*}\]
 92}\]
92}\]
Р формула: Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
Кинематика
Динамика
Статика
Гидростатика
Импульс
Работа, мощность, энергия
Молекулярная физика
Термодинамика
Электростатика
Электрический ток
Энергобаланс замкнутой цепи
Электролиз
Магнетизм
Колебания
Трансформатор
Волны
Оптика
Атомная и ядерная физика
Ядерные реакции
Основы специальной теории относительности (СТО)
Равномерное движение по окружности
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
Еще больше физических формул и свойств — Физика — Теория, тесты, формулы и задачи
Изучать еще больше формул по физике и физических свойств онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Нашли ошибку?
Основные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные формулы по школьной физике (Часть I)
Основные формулы по школьной физике (Часть II)
Как успешно подготовиться к ЦТ по физике и математике?
Нашли ошибку?
10 формул по физике
Приветствую вас на сайте “Радиолюбитель“Искомая величина Формула Напряжение, В U=I*R Ток, А I=U/R Сопротивление, Ом R=U/I Мощность, Вт P=U*I
Расчёты частоты и длины волныЗначение емкости конденсатора, мкФ Емкость конденсатора для расчета 10 0,000 01 1 0,000 001 0,1 0,000 000 1 0,01 0,000 000 01 Формула 1 на F1News.ru — все новости Формулы 1 2021
Формулы по экономике
Формулы спроса и эластичности
y= к*x+b
QD= к*P+b
Qs= к*P+b
EDP= Δ QD (%) : Δ P (%)
EDP= (Q2 –Q1)/(Q2 + Q1) : (P2 –P1)/(P2 + P1)
EDI= (Q2 –Q1)/ Q1 : (Р2 –Р1)/ Р1
Формулы макроэкономики
КД = ∑ ЦТ – К + СП – ВП / СО
М = Р * Q / V
M*V = P*Q
Другие формулы макроэкономики
РД = НД / ИПЦ * 100 %
ИПЦ = СТТГ / СТБГ
ТИ =(ИПЦ1 – ИПЦ0) / ИПЦ0 * 100 %
Формулы для расчета процентов
С = Р * (1 + in/360)
С = Р (1 + in/360)k
С = Р (1+i)k
Формула безработицы, занятости и ВНП
УБ = Число безработных/ЧРС * 100%
УЗ = Число занятых / ЧРС * 100 %
ВНП = % + ЗП + Тр + КНал – ЧС + Р + Ам + ДС
ВНП = ЛПР + ГЗ + ВЧВИ – ЧИ
Расчет выручки, прибыли и издержек
TR = P*Q
АС = AFC + AVC или
АС = TC / Q
ТС = TFC + TVC
AFC = TFC / Q
AVC = TVC / Q
Примеры решения задач
Мощность электрического тока — Основы электроники
Похожие материалы:
Добавить комментарий
Формула значения P | Пошаговые примеры расчета P-значения
Что такое формула P-Value?
Объяснение формулы P-Value
Расчет P-значения по статистике Z
Например:
Источник: Формула значения P (wallstreetmojo.com) Примеры формулы P-значения (с шаблоном Excel)
Пример # 1
Пример # 2
, пример # 3
, пример # 4
Актуальность и использование
Рекомендуемые статьи
Формула P-значения — Что такое формула P-значения? Примеры
Что такое формула P-значения?
Формула P-значения
\ (\ mathrm {P0} = \) предполагаемая доля населения в нулевой гипотезе Таблица значений P
P-значение Описание Интерпретация гипотез Значение P ≤ 0.05 Это указывает на то, что нулевая гипотеза очень маловероятна. Отклонено Значение P> 0,05 Указывает, что нулевая гипотеза очень вероятна. Принято или «не отклонено». Значение P> 0.05 Значение P близко к пороговому значению. Считается маргинальным номером Гипотеза требует большего внимания. Примеры использования формулы P-значения
\ (\ sigma _ {\ bar {x}} = \ dfrac {\ sigma} {\ sqrt {n}} \)
Теперь подставляем заданные значения
\ (\ sigma _ {\ bar {x}} = \ dfrac {32.17} {\ sqrt {40}} = 5.0865 \) Часто задаваемые вопросы по формуле P-value
Что означает формула P-value?
Какова формула для расчета P-значения?
Что такое таблица формул P-значения?
P-значение Описание Интерпретация гипотез Значение P ≤ 0.05 Это указывает на то, что нулевая гипотеза очень маловероятна. Отклонено Значение P> 0,05 Указывает, что нулевая гипотеза очень вероятна. Принято или «не отклонено». Значение P> 0.05 Значение P близко к пороговому значению. Считается маргинальным номером Гипотеза требует большего внимания. Используя таблицу формул P-значения, проверьте, отклонена ли гипотеза или нет, когда P-значение составляет 0,354 с 5% уровнем значимости.
| Формула | Интерпретация
Что такое p-значение?
S обозначает тестовую статистику, x — значение, полученное для данной выборки, а Pr (событие | H 0 ) — вероятность события, рассчитанная в предположении, что H 0 верно: p-значение = Pr (S ≤ x | H 0 ) p-значение = Pr (S ≥ x | H 0 ) p-значение = 2 * min {Pr (S ≤ x | H 0 ), Pr (S ≥ x | H 0 )} min {a, b} мы обозначаем меньшее число из a и b .) p-значение = 2 * Pr (S ≥ | x | | H 0 ) p-значение = 2 * Pr (S ≤ - | x | | H 0 ) Как рассчитать p-значение из тестовой статистики?
cdf ) этого распределения, мы можем выразить вероятность того, что тестовая статистика будет такими же экстремальными значениями, как ее значение x для выборки: p-значение = cdf (x) p-значение = 1 - cdf (x) p-значение = 2 * min {cdf (x), 1 - cdf (x)} p-value = 2 * cdf (- | x |) , или, эквивалентно, поскольку p-значение = 2–2 * cdf (| x |) Как интерпретировать значение p?
0,03 . Это означает, что в 3% подобных исследованиях только случайный случай все равно мог бы дать значение статистических данных теста, которое мы получили, или даже более экстремальное значение, даже если бы лекарство не оказало никакого эффекта! α , просто сравните свое значение p с α : p-значение ≤ α , то вы, , отклоняете нулевую гипотезу и принимаете альтернативную гипотезу; и ≥ α , то у вас недостаточно доказательств, чтобы отклонить нулевую гипотезу. α .Например, если значение p было 0,03 , мы бы отклонили нулевую гипотезу на уровне значимости 0,05 , но не на уровне 0,01 . Вот почему уровень значимости следует указывать заранее, а не адаптировать удобно после того, как установлено значение p! Уровень значимости 0,05 является наиболее распространенным значением, но в этом нет ничего волшебного. Здесь вы можете увидеть, к чему может привести слишком сильная вера в порог 0,05 .Всегда лучше сообщать p-значение и позволять читателю сделать свои собственные выводы. Как использовать калькулятор p-значения, чтобы найти p-значение из тестовой статистики?
, если вам нужно увеличить точность , с которой выполняются вычисления, или измените уровень значимости . Как найти p-значение из z-значения?
Как найти p-значение из Z-значения?
Φ , значение p определяется по следующим формулам: p-значение = Φ (Z оценка ) p-значение = 1 - Φ (Z оценка ) p-значение = 2 * Φ (- | Z оценка |) или p-значение = 2 - 2 * Φ (| Z оценка |)
Стефан Поль / CC0
Викимедиа.org Как найти p-значение из t?
cdf t, d обозначает кумулятивную функцию распределения t-распределения Стьюдента с d степенями свободы: p-значение = cdf t, d (t оценка ) p-значение = 1 - cdf t, d (t оценка ) p-значение = 2 * cdf t, d (- | t оценка |) p-значение = 2 - 2 * cdf t, d (| t оценка |) t-score , если ваша статистика теста соответствует распределению t-Стьюдента .Это распределение имеет форму , аналогичную N (0,1) (колоколообразная и симметричная), но имеет на более тяжелые хвосты. — точная форма зависит от параметра, называемого степенями свободы . Если количество степеней свободы велико (> 30), что обычно происходит для больших выборок, t-распределение Стьюдента практически неотличимо от нормального распределения N (0,1).
Skbkekas / CC BY
Викимедиа.org Значение p по шкале хи-квадрат (оценка χ2)
χ²-score при выполнении теста, в котором статистика теста соответствует χ²-распределению .Это распределение возникает, если, например, вы берете сумму квадратов переменных, каждая из которых соответствует нормальному распределению N (0,1). Не забудьте проверить количество степеней свободы χ²-распределения вашей тестовой статистики!
Geek3 / CC BY
wikimedia.org cdf χ², d обозначает кумулятивную функцию распределения χ²-распределения с d степенями свободы: p-значение = cdf χ², d (χ² , оценка ) p-значение = 1 - cdf χ², d (χ² , оценка ) p-значение = 2 * мин. {Cdf χ², d (χ² , оценка ), 1 - cdf χ², d (χ² , оценка )} min {a, b} мы обозначаем меньшее из чисел a и b .) n - 1 степенями свободы, где n — размер выборки. Это может быть односторонний или двусторонний тест . k - 1 степенями свободы, где k — это количество классов, на которые разделена выборка. Это правосторонний тест . (r - 1) (c - 1) степенями свободы, где r — количество строк, а c — число строк. количество столбцов в этой таблице непредвиденных обстоятельств.Это также правосторонний тест . p-значение из F-оценки
F-score следует использовать при выполнении теста, в котором статистика теста соответствует F-распределению , также известному как распределение Фишера – Снедекора. Точная форма F-распределения зависит от двух степеней свободы .
IkamusumeFan / CC BY-SA
Викимедиа.org X и Y , которые подчиняются χ²-распределениям с d 1 и d 2 степеней свободы соответственно . В этом случае соотношение (X / d 1 ) / (Y / d 2 ) следует F-распределению с (d 1 , d 2 ) -градусами свободы. По этой причине два параметра d 1 и d 2 также называются числителем и степенями свободы знаменателя . cdf F, d 1 , d 2 обозначают кумулятивную функцию распределения F-распределения, с (d 1 , d 2 ) -градусов свободы: p-значение = cdf F, d 1 , d 2 (оценка F ) p-значение = 1 - cdf F, d 1 , d 2 (оценка F ) p-значение = 2 * мин {cdf F, d 1 , d 2 (F оценка ), 1 - cdf F, d 1 , d 2 (F оценка )} min {a, b} мы обозначаем меньшее из чисел a и b .) (n - 1, m - 1) -градусами свободы, где n и m — размеры выборки соответственно. (k - 1, n - k) -градусами свободы, где k — количество групп, а n — общий размер выборки (во всех группах вместе). (k - 1, n - k) -градусами свободы, где n — размер выборки, а k — количество переменных (включая точку пересечения). (k 2 - k 1 , n - k 2 ) -градусами свободы, где k 1 и k 2 — это количество переменных в меньшей и большей моделях, соответственно, и n — размер выборки. FAQ
Может ли p-значение быть отрицательным?
Что означает высокое значение p?
Что означает низкое значение p?
S.3.2 Проверка гипотез (подход P-значения)
Правый хвост
Левосторонний
Двусторонний
, примеры, функция Excel ковариации
Что такое функция Excel ковариации?
Формула ковариации в Excel
Как использовать функцию Covariance Excel
Пример 1 — Ковариация Excel
Примечания о функции Covariance Excel
Дополнительные ресурсы
Mobil Super ™ 3000 Formula P 5W-30
Описание продукта
Серия моторных масел Особенности и преимущества
Приложения
Технические характеристики и разрешения
Свойства и характеристики
Здоровье и безопасность
, что это такое и как ее использовать в простых шагах
Критерии
Как только вы узнаете, что ваше распределение биномиально, вы можете применить формулу биномиального распределения для вычисления вероятности.
Не можете посмотреть видео? Кликните сюда. Что такое биномиальное распределение? Примеры из реальной жизни
Не можете посмотреть видео? Кликните сюда.
b = биномиальная вероятность
x = общее количество «успехов» (прошел или не прошел, орел или решка и т. Д.)
P = вероятность успеха в отдельном испытании
n = количество испытаний Пример 1
Количество испытаний (n) составляет 10
Вероятность успеха («подбрасывание орла») составляет 0,5 (Итак, 1-p = 0,5)
x = 6 Как работать с формулой биномиального распределения: пример 2
= 0,8 6
= 0,262144
= 0,2 (9-6)
= 0,2 3
=.008
84 × 0,262144 × 0,008 = 0,176. Пример 3
= 0,6 7
= 0,0279936
= 0,4 (10-7)
= 0,4 3
= 0,064
120 × 0,0279936 × 0,064 = 0,215. Список литературы
Папулис, А. Вероятность, случайные величины и случайные процессы, 2-е изд. Нью-Йорк: Макгроу-Хилл, стр. 102-103, 1984.
Шпигель М. Р. Теория и проблемы вероятности и статистики. Нью-Йорк: McGraw-Hill, стр. 108-109, 1992.
Steinhaus, H. Mathematical Snapshots, 3-е изд. Нью-Йорк: Довер, 1999.
WSU. Получено 15 февраля 2016 г. с сайта: www.stat.washington.edu/peter/341/Hypergeometric%20and%20binomial.График arccos cosx: Элементарная математика
Тригонометрическая функция и график обратной тригонометрической функции
1. Синус-функция sin x, арксинус-функция arcsin x
2. Функция косинуса cos x, функция обратного косинуса arccos x
3.
 Функция обратного синуса arcsin x, функция обратного косинуса arccos x
Функция обратного синуса arcsin x, функция обратного косинуса arccos x4. Функция тангенса tan x, функция котангенса cot x
5. Функция обратного тангенса arctan x, обратного котангенса arccot x
6.
 Функция косеканса csc x
Функция косеканса csc x7. Секущая функция sec x
Интеллектуальная рекомендация
FFMPEG и VS2010
Встроенная идея + Maven + Sprilboot Project Project Prience Integration MVC
Redis Обзор и общие инструкции
 0.3, Centos605 Обзор Redis — это высокоскоростная база данных памяти NoSQL, которая является системой хранения структуры данных в памяти, а …
0.3, Centos605 Обзор Redis — это высокоскоростная база данных памяти NoSQL, которая является системой хранения структуры данных в памяти, а … Режим цепочки режима дизайна режима
Проникновение в сеть/динамическое сетевые сети/видео Shangyun Gateway Easynts Network Platform Номер учетной записи и пароль нельзя войти в систему, как решить
Вам также может понравиться
Аплет WeChat сообщил об ошибке: не удалось прочитать свойство 0 из undefined
 Такую низкоуровневую …
Такую низкоуровневую … beaurifulsoup считывает данные локальной веб-страницы и сохраняет их в csv
【CCF】201609-1
Два элемента управления JS — список и пейджер
Начало работы с сопоставлением точек функций python opencv + цель поиска по гомографии (39)
Урок 6.
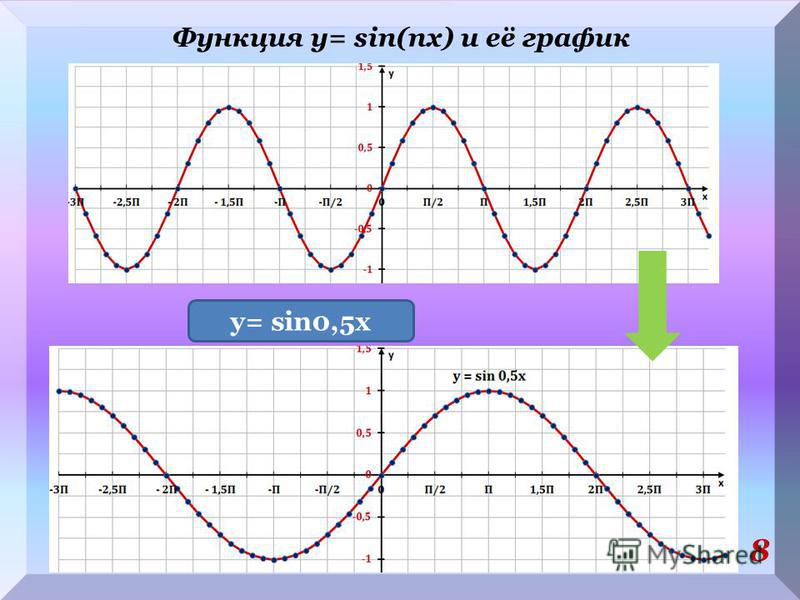 обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс
обратные тригонометрические функции — Алгебра и начала математического анализа — 11 класс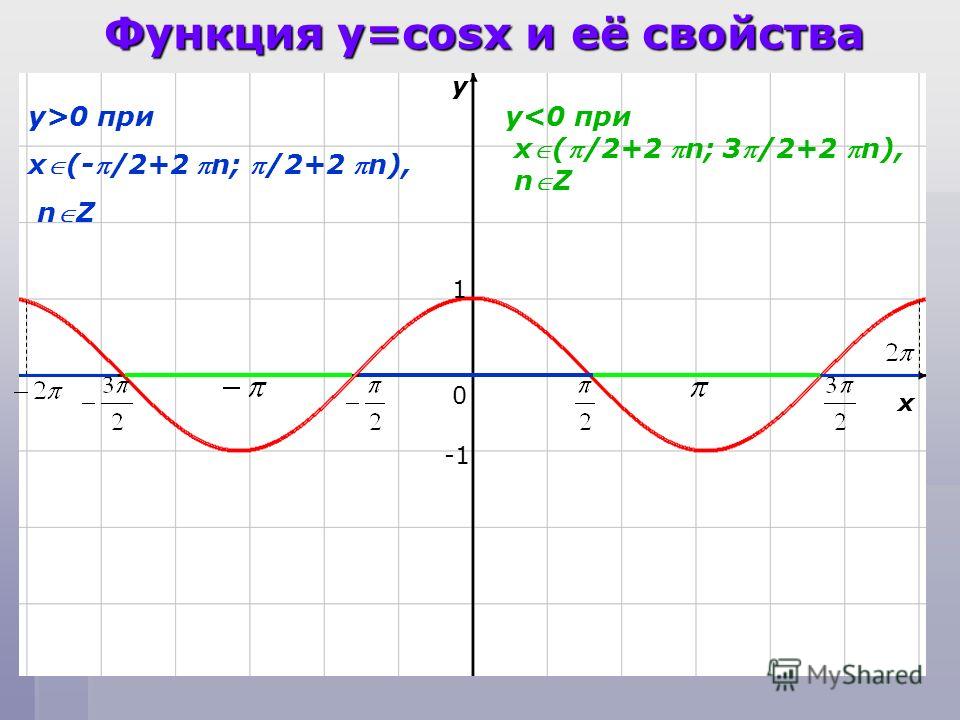 Он имеет область определения и множество значений .
Он имеет область определения и множество значений .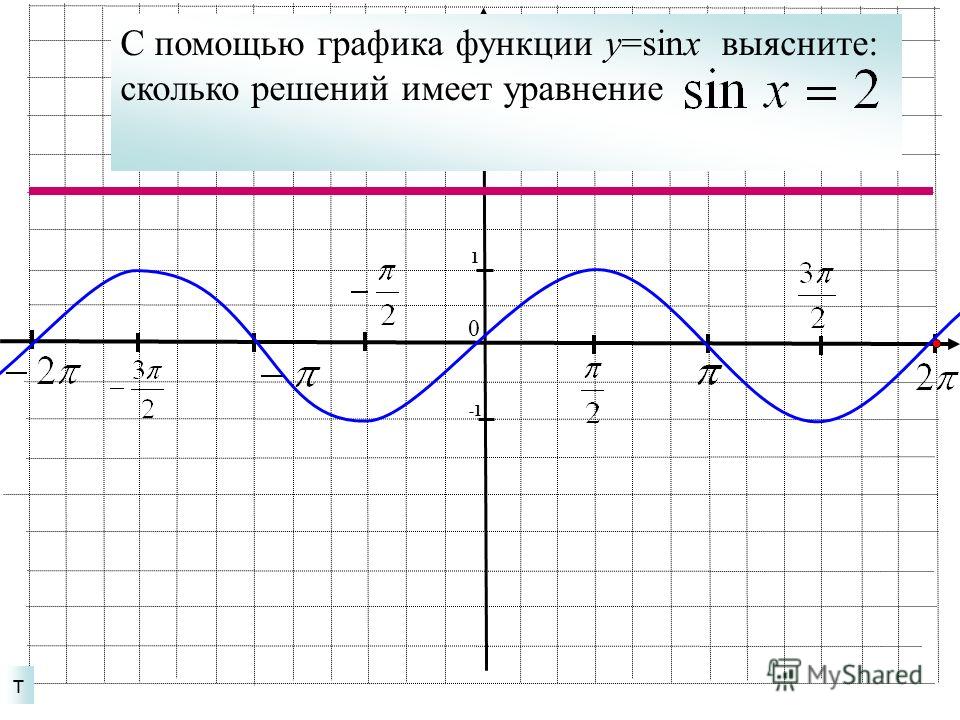 Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.
Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.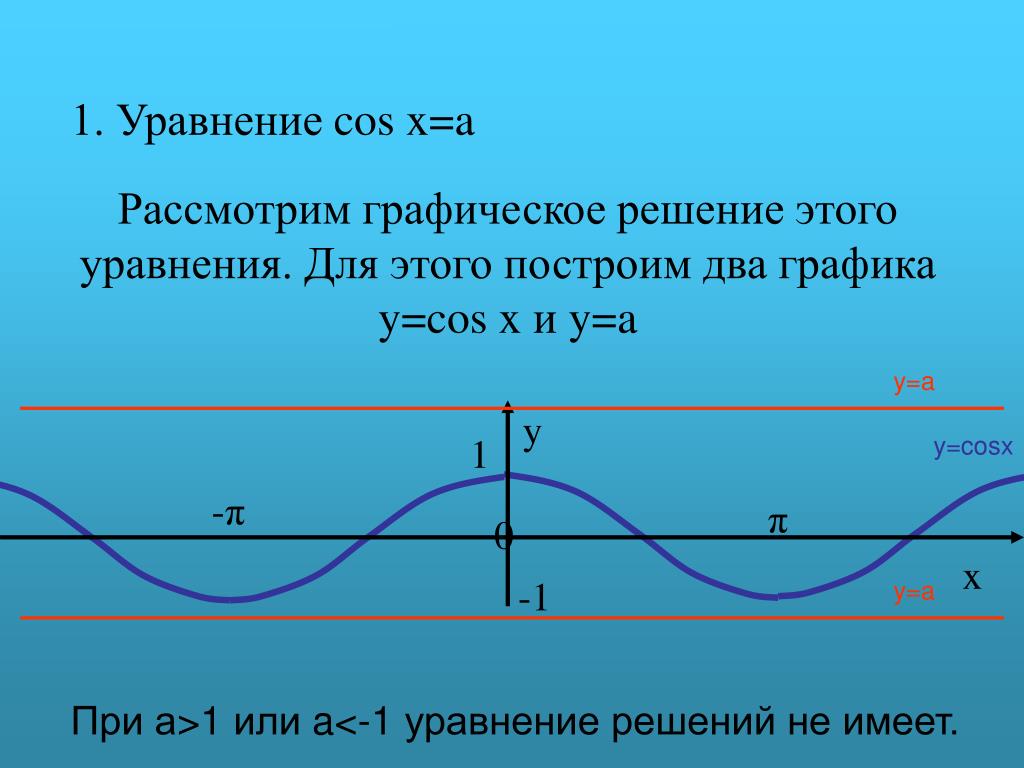 1 График функции y=arcsin х
1 График функции y=arcsin х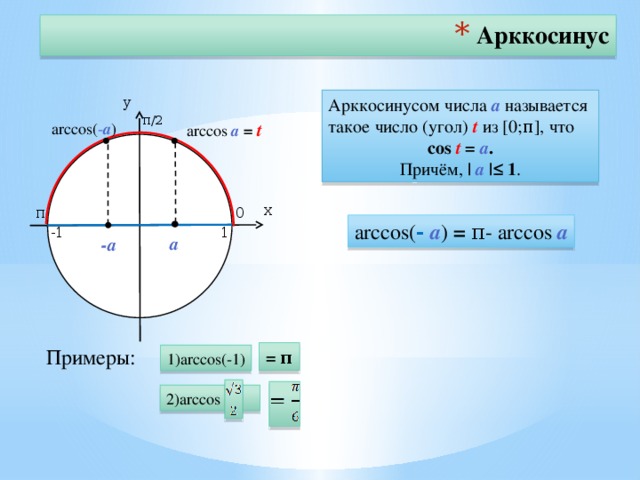 3 График функции y=arctgx
3 График функции y=arctgxОткрытая Математика. Алгебра. Обратные тригонометрические функции
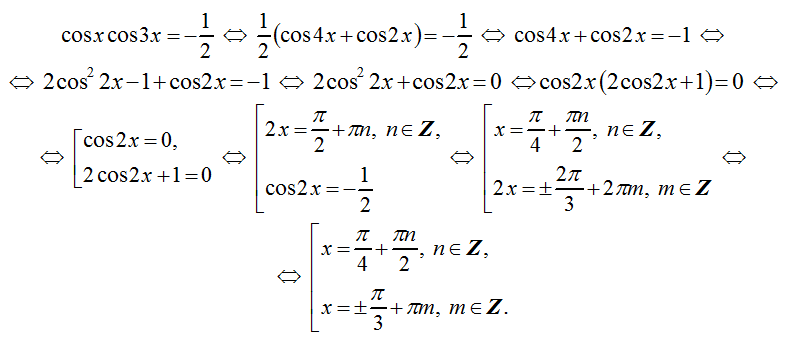 Другими словами, соответствие называется взаимнооднозначным, если каждому элементу x∈X соответствует единственный элемент y∈Y
и наоборот, каждому элементу y∈Y
соответствует единственный элемент x∈X. Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается f-1
и каждому элементу y∈Y
ставит в соответствие такой элемент x∈X,
что f (x) = y; этот факт записывают так: x=f-1 (y).
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных x↔y,
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что y=f-1 (x)
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции: D (f-1)=E (f)=Y.
Другими словами, соответствие называется взаимнооднозначным, если каждому элементу x∈X соответствует единственный элемент y∈Y
и наоборот, каждому элементу y∈Y
соответствует единственный элемент x∈X. Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается f-1
и каждому элементу y∈Y
ставит в соответствие такой элемент x∈X,
что f (x) = y; этот факт записывают так: x=f-1 (y).
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных x↔y,
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что y=f-1 (x)
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции: D (f-1)=E (f)=Y. Область значений обратной функции совпадает с множеством определения самой функции: E (f-1)=D (f)=X.
Область значений обратной функции совпадает с множеством определения самой функции: E (f-1)=D (f)=X.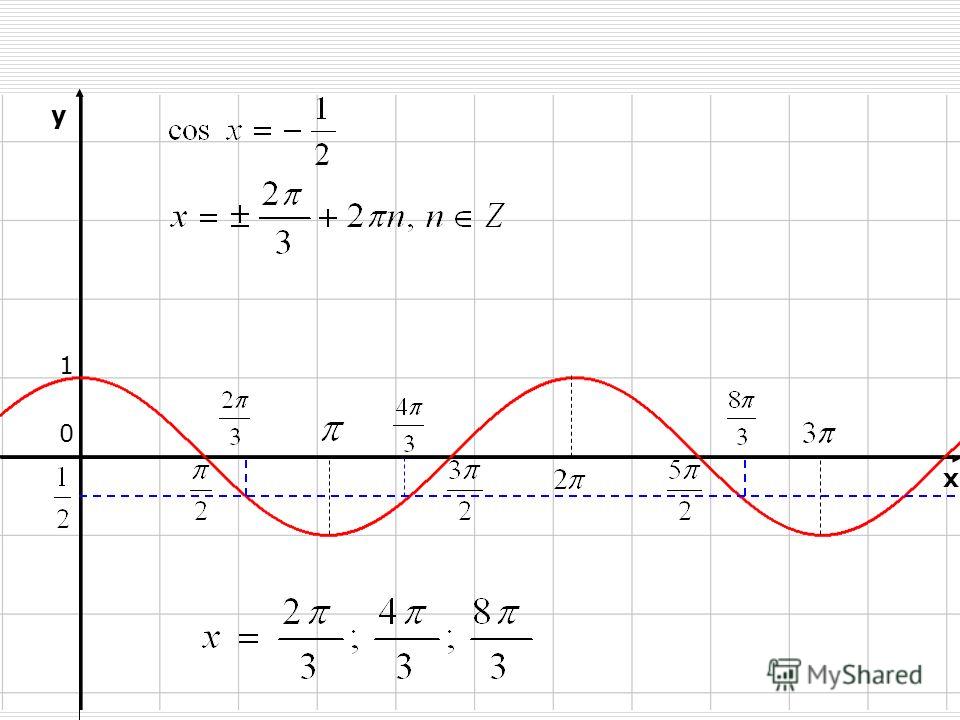

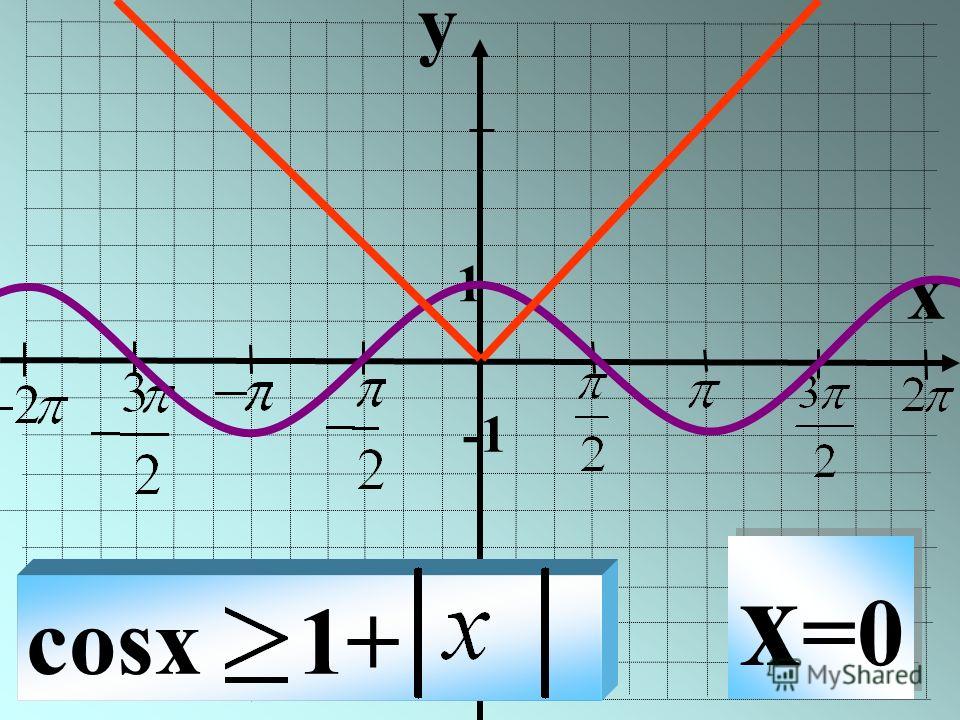 Но у нас есть ограничения на y и z в виде неравенств -π2≤y≤π2, 0≤z≤π,
а для таких y и z равенство sin y = cos z возможно только при y=π2-z.
Следовательно, y+z=π2
и наконец arcsinx+arccosx=π2,
что и требовалось доказать.
Но у нас есть ограничения на y и z в виде неравенств -π2≤y≤π2, 0≤z≤π,
а для таких y и z равенство sin y = cos z возможно только при y=π2-z.
Следовательно, y+z=π2
и наконец arcsinx+arccosx=π2,
что и требовалось доказать.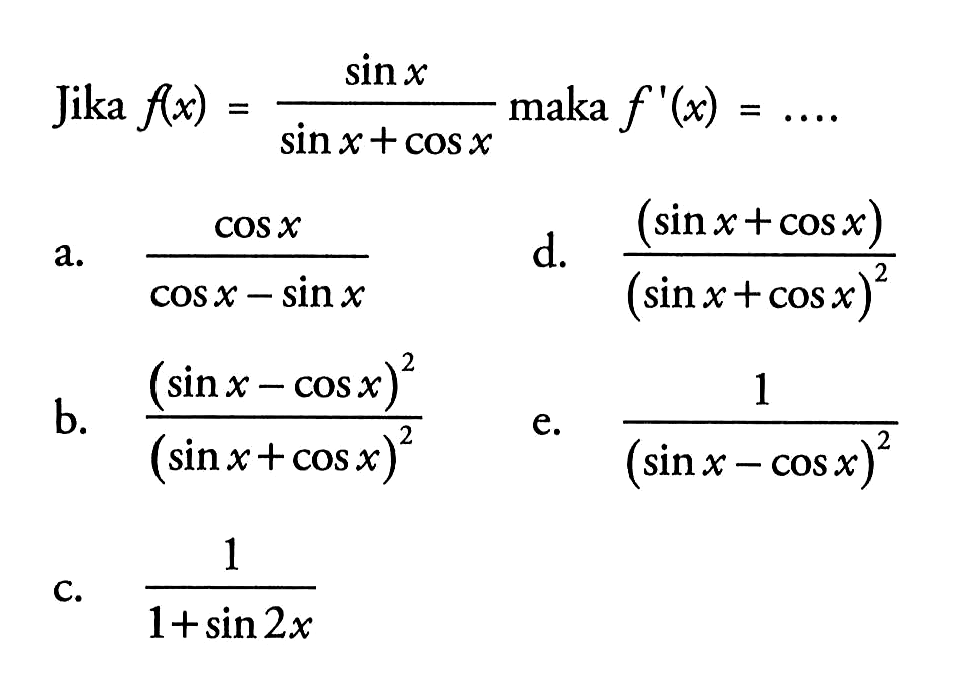 Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда sin(arccosx)=1-x2.
Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда sin(arccosx)=1-x2.
Функция, производная которой равна y ‘ = — cos x, имеет вид …. Выбери… — Учеба и наука
Ответы
02. 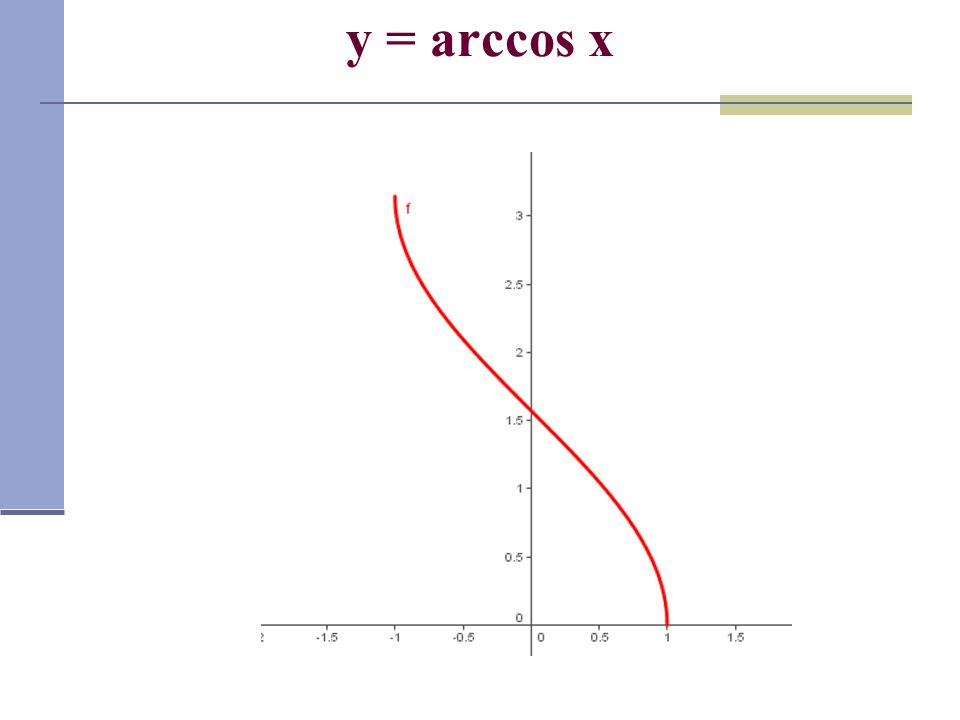 03.21
03.21
Екатерина
Читать ответы
Михаил Александров
Читать ответы
Андрей Андреевич
Читать ответы
Похожие вопросы  Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше
Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея большеФункция у=arccos x — презентация онлайн
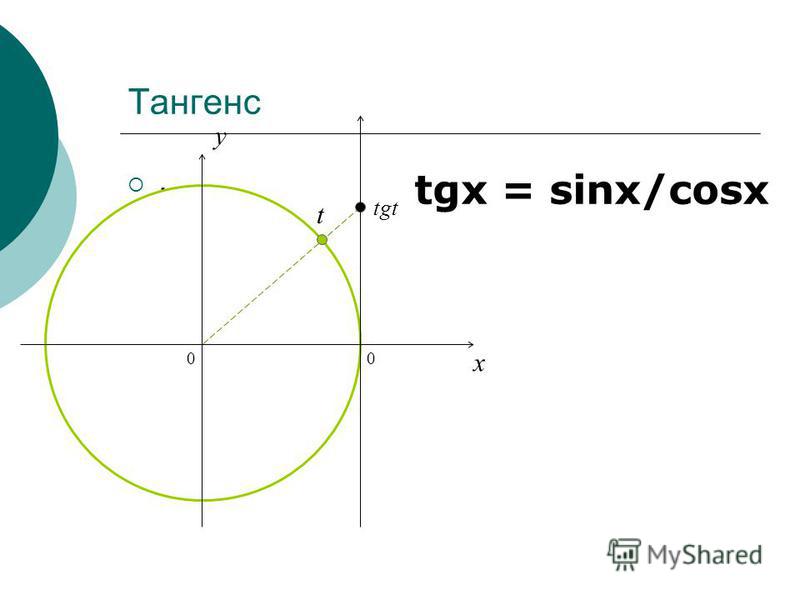 Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
y = cos x
2
3
2
2
1
0
-1
Функция y=cosx, взятая на
всей области определения, не
имеет обратной, т.к. одно и
тоже её значение достигается
при разных значениях
аргумента.
2
x
3
2
Кривая симметричная
косинусоиде относительно
прямой у=х не является
функцией (функциональная
зависимость предполагает
соответствие каждому
значению аргумента
единственное значение
функции).
2
y
Рассмотрим функцию
y=cosx только на отрезке
[0; ]
2
2
3
2
y = cos x
-1
1
0
1
-1
2
D
E( y) : yx 1;1
; 1
0
0;;1
2
x
3
2
Обратная
функция
y = arccos
x
D
E( у) : yх 0;
101;;;0
2
2
y = arccosx
y
D( y) : x 1;1
E( у) : y 0;
-1
0
1
x
Функция ни четная ни нечетная
Функция убывает
Функция непрерывна
Повторим
y = f(x)
y
y = f(x)
y = — f(x)
-1
x
1
y = — f(x)
y
y = — arccosx
D( y) : x 1;1
2
Найдем E(y) методом оценки
0 arccos x
(-1)
0 arccos x
arccos x 0
E( у) : y ; 0
1
-1
2
x
Повторим
y = f(x)
y = f(-x)
y
y = f(x)
y = f(-x)
-1
1
x
y
y = arccos(-x)
Найдем D(y) методом оценки
1 x 1
(-1)
2
1 x 1
1 x 1
D( y) : x 1;1
E( у) : у 0;
1
-1
2
x
y
y = 2arccos x
2
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
2
0 2 arccos x 2
0 y 2
2
E( у) : у 0; 2
-1
1
x
y
1
=
y — 2 arccos x
D( y) : х 1;1
2
Найдем E(y) методом оценки
0 arccos x
0 0,5 arccos x
2
(–0,5)
0,5 arccos x 0
E ( у ) : у ; 0
2
1
-1
2
2
x
y
y = arccos 12 x
Найдем D(y) методом оценки
1
1 x 1
2
2 x 2
2
2
D( y) : х 2; 2
E( у) : у 0;
-2
1
-1
2
2
x
y
y = arccos 2x
Найдем D(y) методом оценки
1 2x 1 : 2
1
1
x
2
2
2
1 1
D( y ) : х ;
2 2
E( у) : у 0;
-1– 1
2
1 1
2
2
x
y
y = 1,5arccosx +
2
2
3
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
* 1,5
0 1,5 arccos x 1,5 + 2
3
2
13
1,5 arccos x
3
6
2 13
E ( у ) : у
;
3
6
2
-1
1
x
Повторим
y = f(x)
y = f(x)
y
y = f(x)
1
x
y
Повторим
1
y = f(x)
y= f x
Функция четная
(график симметричен
относительно оси Оу)
x
y
y = arccosx
2
1
-1
2
График y =arccosx не изменится.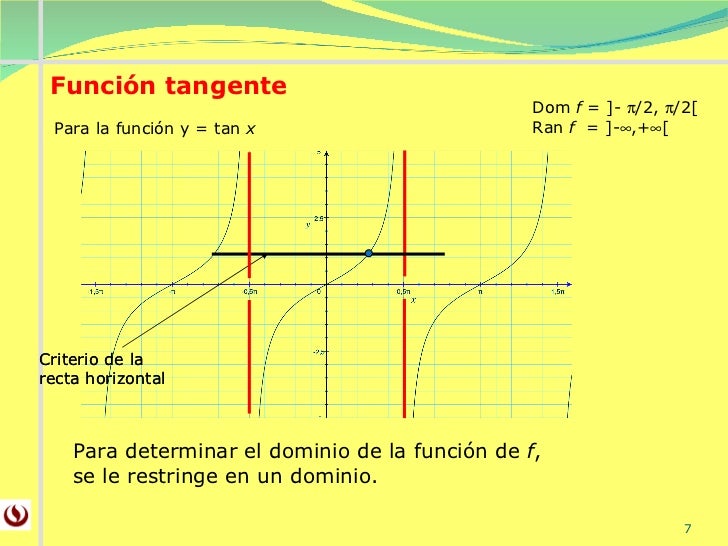
Почему?
x
y = arccos x –
D( y) : х 1;1
Найдем E(y) методом оценки
0 arccos x
0 arccos x
–6
2
arccos x
6 3
6
0
E ( у ) : у 0;
3
y
6
g ( x) = x
При x [ 1; 1]
x [0; 1]
-1
0
1
x
1
x
y
y( x) = arccos x
При x [0; 1]
arccos x [0;
2
]
-1
0
y = arccos x –
y
6
D( y) : х 1;1
E ( у ) : у 0;
3
Функция четная
(график симметричен
относительно оси Оу)
2
-1
1
2
x
y 3
Найдем область определения и
множество значений, затем
построим график.
2
y = -1,5arccos (x–2)
3
1 x 2 1 +2
1 x 3
D( y ) : x 1; 3
[ 1; 1]
0 arccos( x 2)
(-1,5)
1,5 2 arccos( x 2) 0
1,5 y 0
E ( y ) : y 1,5 ; 0
4
2
1
-1
3
4
3
2
3
x
3
y = arccos( x – )
4
D( y )
3
1 х 1
4
+3
4
1
3
х 1
4
4
3
х 1
4
3
3
1 х 1
4
4
3 3
D ( y ) : х 1 ;1
4 4
y( x) = arccos g ( x)
3
При g ( x) [ ; 1]
4
E ( y)
3
y = arccos( x – )
4
y
3
g ( x) = x
4
x 0
3
arccos
4
–3
4
3
3
x
4
4
3
1 х 1
4
3
3
х 1
4
4
-1– 3 0
1
x
4
3
E ( у ) : у 0; arccos
4
y
3
y = arccos( x – )
4
3 3
D ( y ) : х 1 ;1
4 4
2
3
–1
3 4
E ( у ) : у 0; arccos
4
Функция четная
(график симметричен
относительно оси Оу)
3
arccos
4
-1
1
2
1
3
4
xВычисление производных сложных функций
Вычисление производных сложных функцийАрхитектура Биология География Другое Иностранные языки Информатика История Культура Литература Математика Медицина Механика Образование Охрана труда Педагогика Политика Право Программирование Психология Религия Социология Спорт Строительство Физика Философия Финансы Химия Экология Экономика Электроника 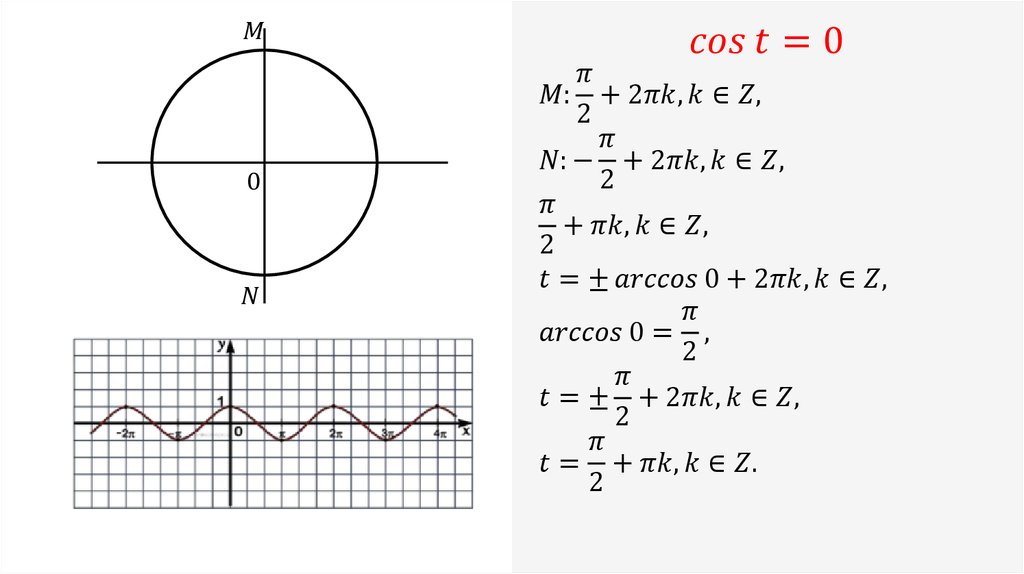 Проверить навыки и умения студентов по вычислению производных простейших функций.
Проверить навыки и умения студентов по вычислению производных простейших функций.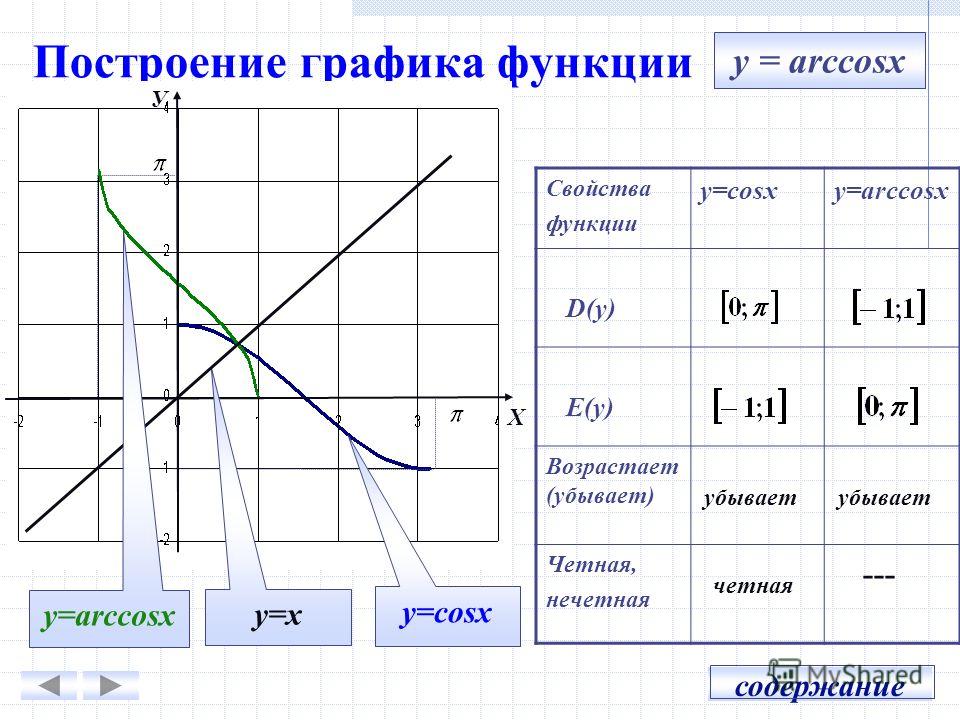 18. y = ecos x * ctg8x3.
18. y = ecos x * ctg8x3.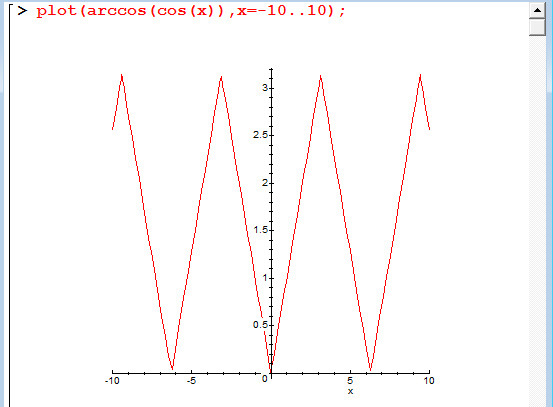 7. у = arctg5x * log2(x — 3). 4.8. у = log3(x + 5) * arccos 3x.
7. у = arctg5x * log2(x — 3). 4.8. у = log3(x + 5) * arccos 3x.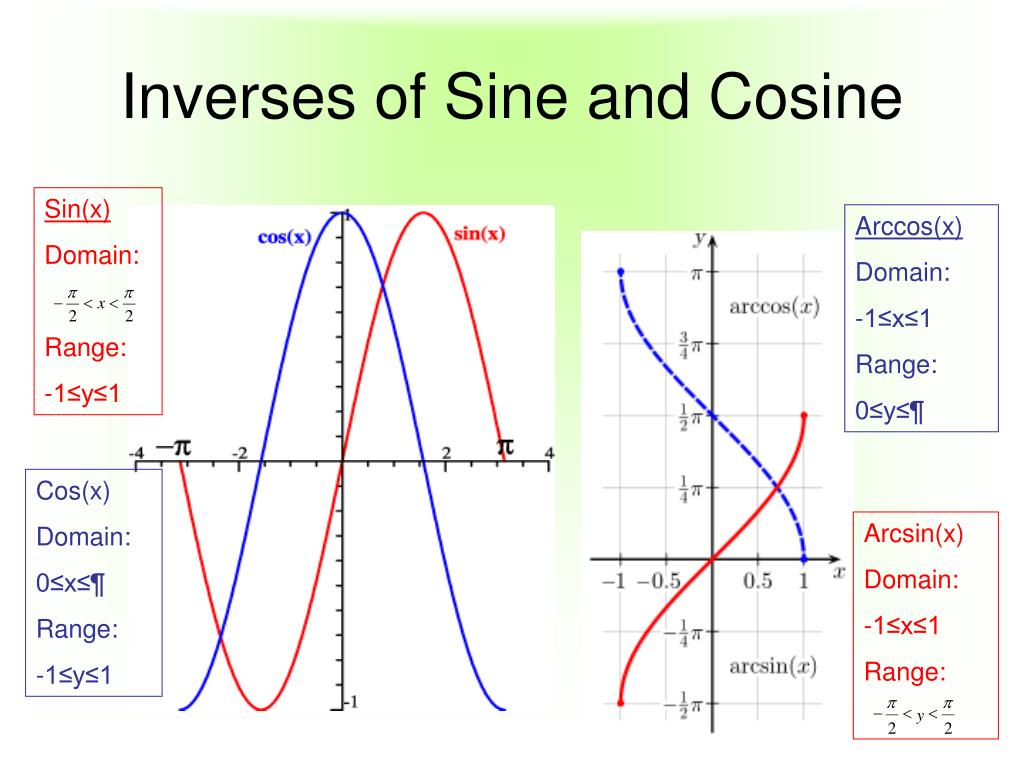 25. у = lg(x — 3) * arcsin2 5x. 4.26. y = log2(x + 3) * arccos2x.
25. у = lg(x — 3) * arcsin2 5x. 4.26. y = log2(x + 3) * arccos2x. 5.12. у = 4(x — 7)6 * arcsin 3x5.
5.12. у = 4(x — 7)6 * arcsin 3x5.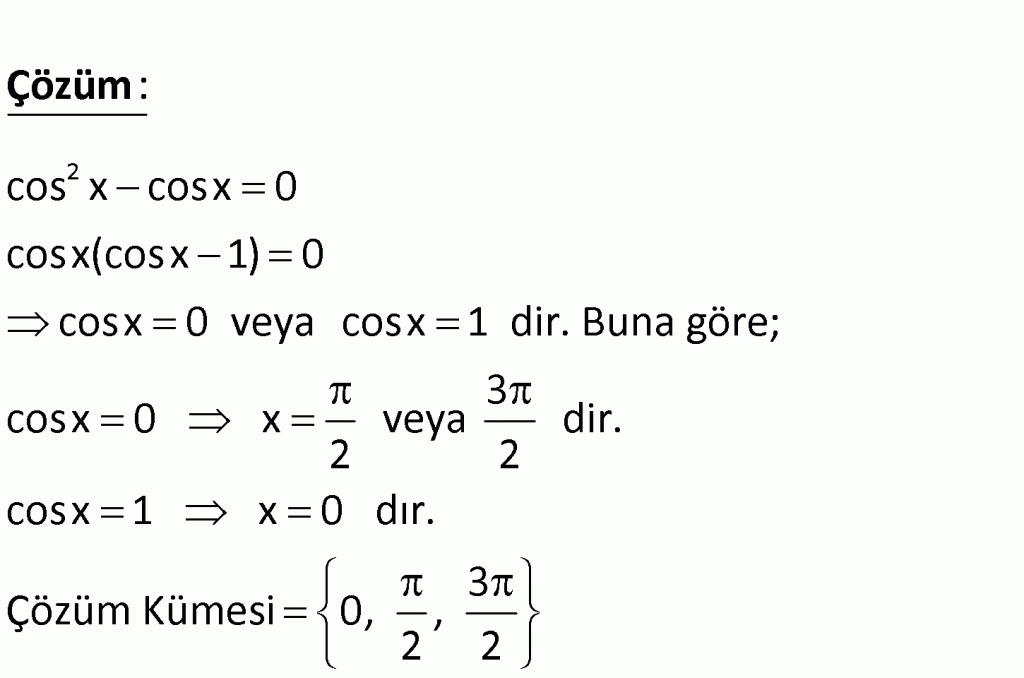
 6.24. у = th4 7x * arccos x3.
6.24. у = th4 7x * arccos x3. 13. 8.14.
13. 8.14.
 21. 10.22.
21. 10.22. 10. y = (sh 3x)arctg (x+2)
10. y = (sh 3x)arctg (x+2)
| следующая лекция ==> Министерство образования и науки Российской Федерации | Правила общения с ГАИ (Украина)  su — 2015-2022 год. (0.105 сек.)
su — 2015-2022 год. (0.105 сек.) Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение cos(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 92 35 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктан(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт.  )/3
)/3 42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение тан(пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найти точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение соз(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найти точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение загар((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 пи)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение КСК(45) 83 Упростить арктан( квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение загар((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение грех(пи/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразование градусов в радианы 88 градусов Arccos
 Косинус имеет обратный только в ограниченной области, 0≤x≤π. На рисунке ниже часть графика, выделенная красным цветом, показывает часть графика cos(x), которая имеет обратную.
Косинус имеет обратный только в ограниченной области, 0≤x≤π. На рисунке ниже часть графика, выделенная красным цветом, показывает часть графика cos(x), которая имеет обратную. Домен arccos(x), -1≤x≤1, является диапазоном cos(x), а его диапазон, 0≤x≤π, является доменом cos(x).
Домен arccos(x), -1≤x≤1, является диапазоном cos(x), а его диапазон, 0≤x≤π, является доменом cos(x). Калькулятор Arccos
арккос = деградировать Использование специальных углов для нахождения арккосинуса
θ 0° 30° 45° 60° 90° 120° 135° 150° 180° соз(θ) 1 0 -1  Начиная с 0° и увеличивая до 90°, cos(0°)=1=. Последующие значения cos(30°), cos(45°), cos(60°) и cos(90°) следуют шаблону, так что используя значение cos(0°) в качестве эталона, чтобы найти значения косинуса для последующих углов, мы просто уменьшаем число под знаком радикала в числителе на 1, как показано ниже:
Начиная с 0° и увеличивая до 90°, cos(0°)=1=. Последующие значения cos(30°), cos(45°), cos(60°) и cos(90°) следуют шаблону, так что используя значение cos(0°) в качестве эталона, чтобы найти значения косинуса для последующих углов, мы просто уменьшаем число под знаком радикала в числителе на 1, как показано ниже: θ 0° 30° 45° 60° 90° соз(θ) 0 
Обратные свойства
Композиция арккосинуса и косинуса
 Учитывая arccos(cos()), мы не можем оценить это, как мы сделали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть . Чтобы оценить это, нам нужно сначала определить cos() перед использованием arccos:
Учитывая arccos(cos()), мы не можем оценить это, как мы сделали выше, потому что x не находится в пределах [0, π], поэтому решение не может быть . Чтобы оценить это, нам нужно сначала определить cos() перед использованием arccos: Композиция других тригонометрических функций

Использование арккосинуса для решения тригонометрических уравнений

тригонометрия — Почему Arccos(Sin(x)) выглядит так??
 ..
.. Это дает нам, что есть линия $y=x+\frac{\pi}2$, а также линия $y=x-\frac{\pi}2$ и любой их сдвиг по горизонтали (или вертикали) на $2\pi$, что приводит к решетчатому узору.
Это дает нам, что есть линия $y=x+\frac{\pi}2$, а также линия $y=x-\frac{\pi}2$ и любой их сдвиг по горизонтали (или вертикали) на $2\pi$, что приводит к решетчатому узору.
Функция синуса на $[-\pi/2, \pi/2]$ отображается в $[-1,1]$. $$
\арккос(\грех(х))
= \arccos(\cos(\pi/2 — x))
= -х + \пи/2
$$
Функция синуса на $[\pi/2, \pi/2 + \pi]$ равна
$$
\sin(x) = -\sin(x-\pi) = \sin(\pi — x)
$$
и отображается в $[-1,1]$. Мы получаем
$$
\arccos(\sin(x)) = \arccos(\cos(\pi/2 — (\pi -x)) = x — \pi/2
$$
В обоих случаях мы можем добавить целое число, кратное $2\pi$, к аргументу функции косинуса. Это дает
$$
\арккос(\грех(х))
= \arccos(\cos(\pi/2 — x))
= -х + \пи/2
$$
Функция синуса на $[\pi/2, \pi/2 + \pi]$ равна
$$
\sin(x) = -\sin(x-\pi) = \sin(\pi — x)
$$
и отображается в $[-1,1]$. Мы получаем
$$
\arccos(\sin(x)) = \arccos(\cos(\pi/2 — (\pi -x)) = x — \pi/2
$$
В обоих случаях мы можем добавить целое число, кратное $2\pi$, к аргументу функции косинуса. Это дает
Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
 По определению,
$$\arccos(\cos y)=y\qquad(0\leq y\leq\pi)\ .$$
Для произвольного $x\in{\mathbb R}$ определим
$$d(x):=\min\bigl\{|x-2k\pi|\,\bigm|\,k\in{\mathbb Z}\bigr\}$$
быть расстоянием $x$ от ближайшего целого числа, кратного $2\pi$. затем
$$0\leq d(x)\leq\pi,\quad \cos x=\cos\bigl(d(x)\bigr)\qquad\forall x\in{\mathbb R}\ .$$
Это следует из того
$$\arccos(\cos x)=\arccos\bigl(\cos\bigr(d(x)\bigr)\bigr)=d(x)\qquad(x\in{\mathbb R})\ ,$ $
что показывает, что $\arccos\circ\cos$ является пилообразной функцией. 9{-1}\left[\cos\left(\left(k+1\right)\pi-x\right)\right]\overset{1}{=}\left(k+1\right)\pi -Икс. \tag*{∎}$$
По определению,
$$\arccos(\cos y)=y\qquad(0\leq y\leq\pi)\ .$$
Для произвольного $x\in{\mathbb R}$ определим
$$d(x):=\min\bigl\{|x-2k\pi|\,\bigm|\,k\in{\mathbb Z}\bigr\}$$
быть расстоянием $x$ от ближайшего целого числа, кратного $2\pi$. затем
$$0\leq d(x)\leq\pi,\quad \cos x=\cos\bigl(d(x)\bigr)\qquad\forall x\in{\mathbb R}\ .$$
Это следует из того
$$\arccos(\cos x)=\arccos\bigl(\cos\bigr(d(x)\bigr)\bigr)=d(x)\qquad(x\in{\mathbb R})\ ,$ $
что показывает, что $\arccos\circ\cos$ является пилообразной функцией. 9{-1}\left[\cos\left(\left(k+1\right)\pi-x\right)\right]\overset{1}{=}\left(k+1\right)\pi -Икс. \tag*{∎}$$ Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость

Арккосинус (Arccos) — определение, примеры, график
1. 
Что такое арккосинус? 2. Домен, диапазон и график арккосинуса 3. Свойства арккосинуса 4. Производная Arccos x 5. Интеграл Arccos x 6. Часто задаваемые вопросы по Arccosine Что такое арккосинус?
Примеры арккосинуса
Арккосинус Определение
 т. е. cos θ = (прилежащая сторона) / (гипотенуза). Тогда по определению арккосинуса θ = cos -1 [(прилежащая сторона)/(гипотенуза)] .
т. е. cos θ = (прилежащая сторона) / (гипотенуза). Тогда по определению арккосинуса θ = cos -1 [(прилежащая сторона)/(гипотенуза)] . Домен, диапазон и график арккосинуса
 Кроме того, мы увидим, как изобразить его в его основной области.
Кроме того, мы увидим, как изобразить его в его основной области. Домен и диапазон арккосинуса
 т. е.,
т. е., График арккосинуса
х y = cos -1 x (или) arccos x -1 потому что -1 (-1) = π — 0 = π -0,5 потому что -1 (-0,5) = π — π/3 = 2π/3 0 потому что -1 (0) = π/2 0,5 , потому что -1 (0,5) = π/3 1 , потому что -1 (1) = 0 Свойства арккосинуса
 Они очень полезны при решении задач, связанных с обратными косами в тригонометрии.
Они очень полезны при решении задач, связанных с обратными косами в тригонометрии.
([Когда x ∉ [-1, 1], cos(cos -1 х) НЕ определено)
(Когда x ∉ [0, π], либо найдите котерминальный угол x, либо примените тригонометрические тождества, чтобы найти эквивалентный угол x, лежащий в [0, π] ) Производная Arccos x
 .. (1)
.. (1) Интеграл Arccos x
 Тогда -2x dx = du (или) x dx = -1/2 du.
Тогда -2x dx = du (или) x dx = -1/2 du. cos(cos -1 x) = x только тогда, когда x ∈ [-1, 1].
cos(cos -1 x) = x только тогда, когда x ∈ [-1, 1]. Что такое арккосинус?
Что такое формула арккосинуса?
 Это формула арккосинуса (или arccos).
Это формула арккосинуса (или arccos). Является ли арккосинус x таким же, как cos⁻¹x?
Является ли арккосинус таким же, как (cos x)⁻¹?
Что такое произношение арккосинуса?
Что такое домен Arccos x?
Каков ассортимент Arccos x?
 один.
один. Что такое арккосинус Cos x?
Что такое косинус арккосинуса x?
Калькулятор — arccos(cos(x)) — Solumaths
Arccos, расчет онлайн
Резюме:
Описание:

arccos(`-1`) `pi` arccos(`-sqrt(3)/2`) `5*pi/6` arccos(sqrt`-4 2)/2`) `3*pi/4` arccos(`-1/2`) `2*pi/3` arccos(`0`) ` `2*pi/3` pi/2` arccos(`1/2`) `pi/3` arccos(`sqrt(2)/2`) `pi/4` Arccos (` sqrt (3)/2`) `pi/6` Arccos (` 1`) `0` 888888888894 `0`
88888888888888888888888888888 :
arccos(x), где x — число.
Иногда используются другие обозначения: acos
Примеры:
arccos(`1`) возвращает 0
Производная арккосинуса :
Чтобы дифференцировать функцию арккосинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции арккосинуса 92)`
Предел арккосинуса :
Калькулятор предела позволяет вычислить пределы функции арккосинуса.
предел arccos(x) is limit(`»arccos»(x)`)
Обратная функция арккосинуса :
обратная функция арккосинуса — это функция косинуса, отмеченная как cos.
Графический арккосинус :
Графический калькулятор может отображать функцию арккосинуса в заданном интервале.
Расчет онлайн с арккосинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos.
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.



 Для решения таких задач применяются нетрадиционные методы и приемы. При направляющей роли учителя школьники могут самостоятельно найти различные приемы решений уравнений, а также комбинируя данные.
Для решения таких задач применяются нетрадиционные методы и приемы. При направляющей роли учителя школьники могут самостоятельно найти различные приемы решений уравнений, а также комбинируя данные. При изучении предполагается использование таких форм и методов работы, как семинарские занятия, самостоятельная работа, работа в парах и группах сменного состава, метод учебного проекта и озвучивание проектов решения уравнений. Применяемые формы и методы работы должны располагать к самостоятельному поиску решений.
При изучении предполагается использование таких форм и методов работы, как семинарские занятия, самостоятельная работа, работа в парах и группах сменного состава, метод учебного проекта и озвучивание проектов решения уравнений. Применяемые формы и методы работы должны располагать к самостоятельному поиску решений.

 к. Р4(1) = 0, то х0 = 1 — корень данного многочлена.
к. Р4(1) = 0, то х0 = 1 — корень данного многочлена.
 5
— 4х)4
5
— 4х)4 5
— х)
5
— х) 9
— x2)
=
10sin3x
9
— x2)
=
10sin3x 9
— X2)
=
10sin3x
9
— X2)
=
10sin3x Тогда дискриминант — это просто число D
= b
2 − 4ac
.
Тогда дискриминант — это просто число D
= b
2 − 4ac
.

 Для студентов и преподавателей вузов экономических и других специальностей, требующих изучения вероятностно-статистических методов, слушателей послевузовского образования.
Для студентов и преподавателей вузов экономических и других специальностей, требующих изучения вероятностно-статистических методов, слушателей послевузовского образования.


 Планируем за некоторое время собрать хорошую библиотеку классических и популярных книг и статей.
Планируем за некоторое время собрать хорошую библиотеку классических и популярных книг и статей.
 Весьма продуктивный и общий подход, который встречается не очень часто. Книга рассчитана на школьников старших классов.
Весьма продуктивный и общий подход, который встречается не очень часто. Книга рассчитана на школьников старших классов.  Ориентирована на студентов экономических вузов. Будет понятна и полезна заинтересованным школьникам, учителям, преподавателям вузов.
Ориентирована на студентов экономических вузов. Будет понятна и полезна заинтересованным школьникам, учителям, преподавателям вузов. Книга рассчитана на читателя, пожелавшего на элементарном уровне ознакомиться с теорией вероятностей и составить себе некоторое впечатление о ее применениях. Доступна школьникам старших классов. От себя добавим, что книга написана сжато, емко и не изобилует комбинаторными упражнениями, так характерными для современных российских курсов вероятности в вузах.
Книга рассчитана на читателя, пожелавшего на элементарном уровне ознакомиться с теорией вероятностей и составить себе некоторое впечатление о ее применениях. Доступна школьникам старших классов. От себя добавим, что книга написана сжато, емко и не изобилует комбинаторными упражнениями, так характерными для современных российских курсов вероятности в вузах. ..
.. Его лаконичная, написанная с юмором книга полна поучительных парадоксов и примеров, которые объединяет главная тема: рассказ о том, как теория игр влияет на наш…
Его лаконичная, написанная с юмором книга полна поучительных парадоксов и примеров, которые объединяет главная тема: рассказ о том, как теория игр влияет на наш… ..
.. ..
.. 448 с.
448 с. Для научных работников и инженеров. 640 с.
Для научных работников и инженеров. 640 с. Изложены элементы теории вероятностей в том виде, в каком они должны в первую очередь находить применение в астрономии и физике. 264 с.
Изложены элементы теории вероятностей в том виде, в каком они должны в первую очередь находить применение в астрономии и физике. 264 с. Книга будет полезной для студентов, для специалистов математиков, физиков и инженеров, занимающихся приложениями теории вероятностей. 156 с.
Книга будет полезной для студентов, для специалистов математиков, физиков и инженеров, занимающихся приложениями теории вероятностей. 156 с. 112 с.
112 с. 752 с.
752 с. Включено много полезных дополнений и упражнений. Книга может служить хорошим учебником для студентов и аспирантов, желающих серьезно изучить теорию случайных процессов, и отличным справочником для специалистов. 310 с.
Включено много полезных дополнений и упражнений. Книга может служить хорошим учебником для студентов и аспирантов, желающих серьезно изучить теорию случайных процессов, и отличным справочником для специалистов. 310 с. Для студентов математических специальностей, а также инженерных и научных работников, которые интересуются теорией вероятностей и ее применениями. 112 с.
Для студентов математических специальностей, а также инженерных и научных работников, которые интересуются теорией вероятностей и ее применениями. 112 с. Из путешествия читатель возвратится обогащенный понятиями и методами теории вероятностей, знанием областей ее применения. 90 с.
Из путешествия читатель возвратится обогащенный понятиями и методами теории вероятностей, знанием областей ее применения. 90 с. .. (1949, djvu, 6,26 Mb)
.. (1949, djvu, 6,26 Mb) Эта книга — одно из наиболее замечательных достижений математики ХХ века. 264 с.
Эта книга — одно из наиболее замечательных достижений математики ХХ века. 264 с. От других учебников, предназначенных для той же категории читателей, книга отличается большим вниманием к важным для приложений новым ветвям теории вероятностей (теории случайных процессов, теории информации, теории массового обслуживания и др.). 576 с.
От других учебников, предназначенных для той же категории читателей, книга отличается большим вниманием к важным для приложений новым ветвям теории вероятностей (теории случайных процессов, теории информации, теории массового обслуживания и др.). 576 с. В этих главах введены понятия вероятности, математического ожидания, независимости, случайной величины. Распространение этих понятий на общий случай дано в главах 6-12. Главы 13-16 посвящены некоторым задачам математической статистики. Каждая глава сопровождается небольшим количеством задач.
В этих главах введены понятия вероятности, математического ожидания, независимости, случайной величины. Распространение этих понятий на общий случай дано в главах 6-12. Главы 13-16 посвящены некоторым задачам математической статистики. Каждая глава сопровождается небольшим количеством задач. 
 На этой основе находятся различные характеристики случайных полей, возникающих в предлагаемой общей теоретико-вероятностной модели, изучается их вероятностное поведение (например, устанавливается марковское свойство), рассматриваются различные задачи прогнозирования, задачи идентификации и оценки параметров самой модели по статистическим данным и др. От читателя предполагается знание основ функционального анализа и теории вероятностей. 254 с.
На этой основе находятся различные характеристики случайных полей, возникающих в предлагаемой общей теоретико-вероятностной модели, изучается их вероятностное поведение (например, устанавливается марковское свойство), рассматриваются различные задачи прогнозирования, задачи идентификации и оценки параметров самой модели по статистическим данным и др. От читателя предполагается знание основ функционального анализа и теории вероятностей. 254 с. 224 с.
224 с. Книга ориентируется на умеренные аппетиты к строгости и детализации. Помимо классических разделов теории вероятностей в книге освещается ряд новых направлений: нелинейный закон больших чисел, асимптотическое агрегирование. Изложение сопровождается большим количеством примеров им парадоксов, способствующих рельефному восприятию материала. Затрагиваются многие прикладные области: управление запасами, биржевые игры, массовое обслуживание, страховое дело, стохастическая аппроксимация, обработка статистики. Несмотря на краткость, достаточно полно излагается теория информации с ответвлениями «энтропийно термодинамического» характера. Изложение построено так, что можно ограничиться любым желаемым срезом содержания. Для студентов, преподавателей, инженеров и научных работников. 216 с.
Книга ориентируется на умеренные аппетиты к строгости и детализации. Помимо классических разделов теории вероятностей в книге освещается ряд новых направлений: нелинейный закон больших чисел, асимптотическое агрегирование. Изложение сопровождается большим количеством примеров им парадоксов, способствующих рельефному восприятию материала. Затрагиваются многие прикладные области: управление запасами, биржевые игры, массовое обслуживание, страховое дело, стохастическая аппроксимация, обработка статистики. Несмотря на краткость, достаточно полно излагается теория информации с ответвлениями «энтропийно термодинамического» характера. Изложение построено так, что можно ограничиться любым желаемым срезом содержания. Для студентов, преподавателей, инженеров и научных работников. 216 с. Первый уровень рассчитан на студентов общетехнических специальностей, второй – на студентов специальностей, требующих повышенной математической подготовки. 592 с.
Первый уровень рассчитан на студентов общетехнических специальностей, второй – на студентов специальностей, требующих повышенной математической подготовки. 592 с. 160 с.
160 с. Теория вероятностей в примерах и задачах (2001, pdf,
Теория вероятностей в примерах и задачах (2001, pdf,  476 с.
476 с. Данное пособие предназначено для студентов и аспирантов естественно-научных и экономических факультетов. 119 с.
Данное пособие предназначено для студентов и аспирантов естественно-научных и экономических факультетов. 119 с. Может быть использован преподавателями, аспирантами и студентами высших учебных заведений. 295 c.
Может быть использован преподавателями, аспирантами и студентами высших учебных заведений. 295 c. Хобби. Досуг
Хобби. Досуг
 Виноделие
Виноделие
 Зарубежная
Зарубежная
 Ш.
Ш.
 С. Статистика. Вероятность. Комбинаторика
С. Статистика. Вероятность. Комбинаторика  (Школьное образование) ISBN 957-5-89415-561-0
(Школьное образование) ISBN 957-5-89415-561-0 
 В центре внимания автора — усвоение детьми 10—14 лет математических понятий в ходе занимательных игр.
В центре внимания автора — усвоение детьми 10—14 лет математических понятий в ходе занимательных игр.
 Р., Ященко И. В. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь
Р., Ященко И. В. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь
 Пособие для учащихся. М., «Просвещение», 1975. -223 с ил. (Мир знаний).
Пособие для учащихся. М., «Просвещение», 1975. -223 с ил. (Мир знаний).  17 Мб, 600dpi+OCR) ifolder или onlinedisk
17 Мб, 600dpi+OCR) ifolder или onlinedisk 23 Мб) ifolder.ru || onlinedisk
23 Мб) ifolder.ru || onlinedisk На большом количестве примеров изложены начальные понятия, идеи и методы комбинаторики, теории вероятностей и статистики. Даны задачи с решениями н ответами, а также упражнения с возрастающей степенью сложности для самостоятельной работы школьников (включая ответы). Содержатся рекомендации по примерному поурочному планированию учебного материала.
На большом количестве примеров изложены начальные понятия, идеи и методы комбинаторики, теории вероятностей и статистики. Даны задачи с решениями н ответами, а также упражнения с возрастающей степенью сложности для самостоятельной работы школьников (включая ответы). Содержатся рекомендации по примерному поурочному планированию учебного материала.
 В. Гнеденко.
В. Гнеденко.  В. Ященко. — М: МЦНМО: АО «Московские учебники», 2004.— 256 с: ил. ISBN 5-94057-161-1
В. Ященко. — М: МЦНМО: АО «Московские учебники», 2004.— 256 с: ил. ISBN 5-94057-161-1 ru || rghost.ru
ru || rghost.ru
 — 90 с.
— 90 с.
 38 Мб) ifolder.ru || onlinedisk
38 Мб) ifolder.ru || onlinedisk Для чтения файлов данного формата скачатьWinDjView-1.0 (885Кб) или страница с последней версией WinDjView
Для чтения файлов данного формата скачатьWinDjView-1.0 (885Кб) или страница с последней версией WinDjView д., а также, возможно, примеры «реальных» ситуаций, в которых они будут использоваться.0005
д., а также, возможно, примеры «реальных» ситуаций, в которых они будут использоваться.0005
 Красивое произведение на мой взгляд.
Красивое произведение на мой взгляд.
 1, 3-е издание
1, 3-е издание https://www.springer.com/gp/book/9783540438717
https://www.springer.com/gp/book/9783540438717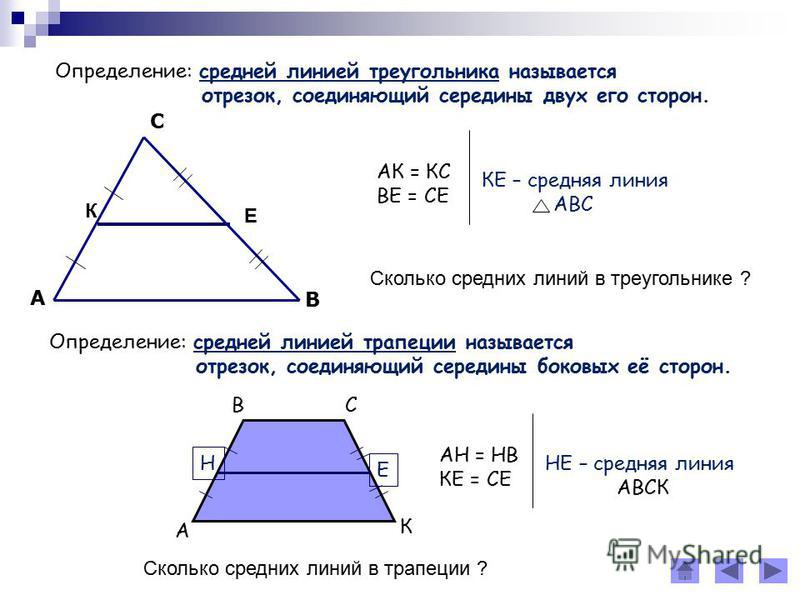 Расчетные геометрические характеристики рассматриваемых сечений.
Расчетные геометрические характеристики рассматриваемых сечений.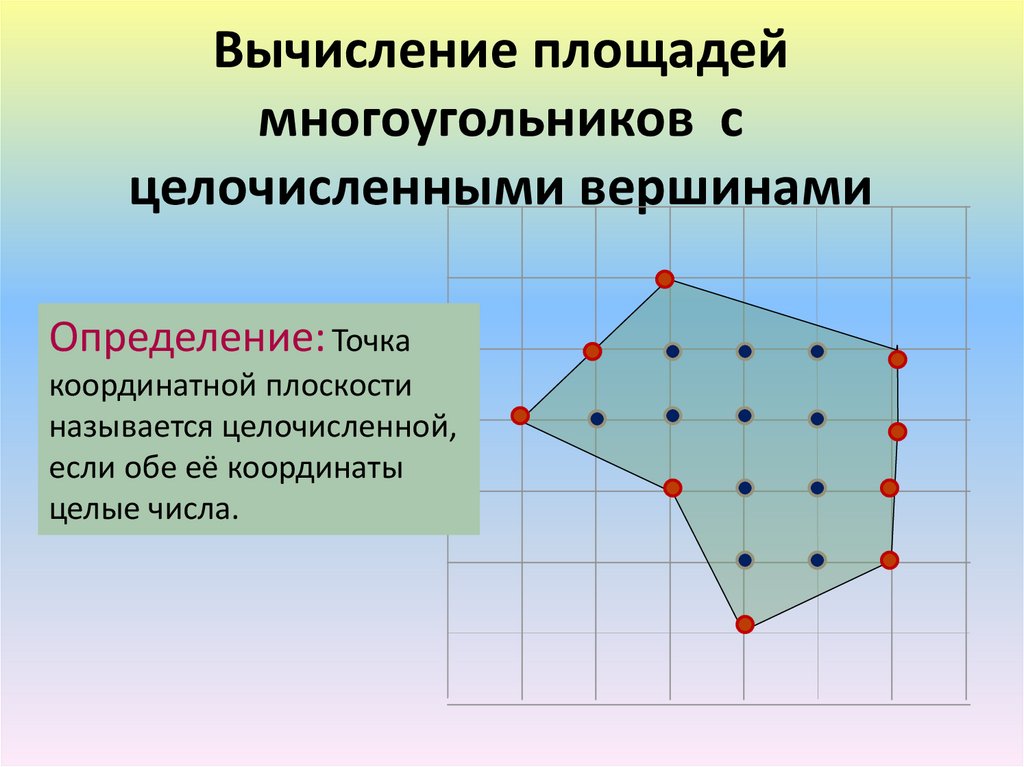
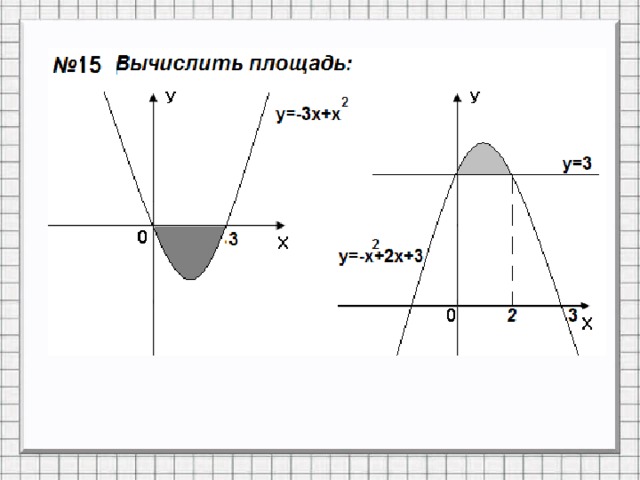 09.2022
09.2022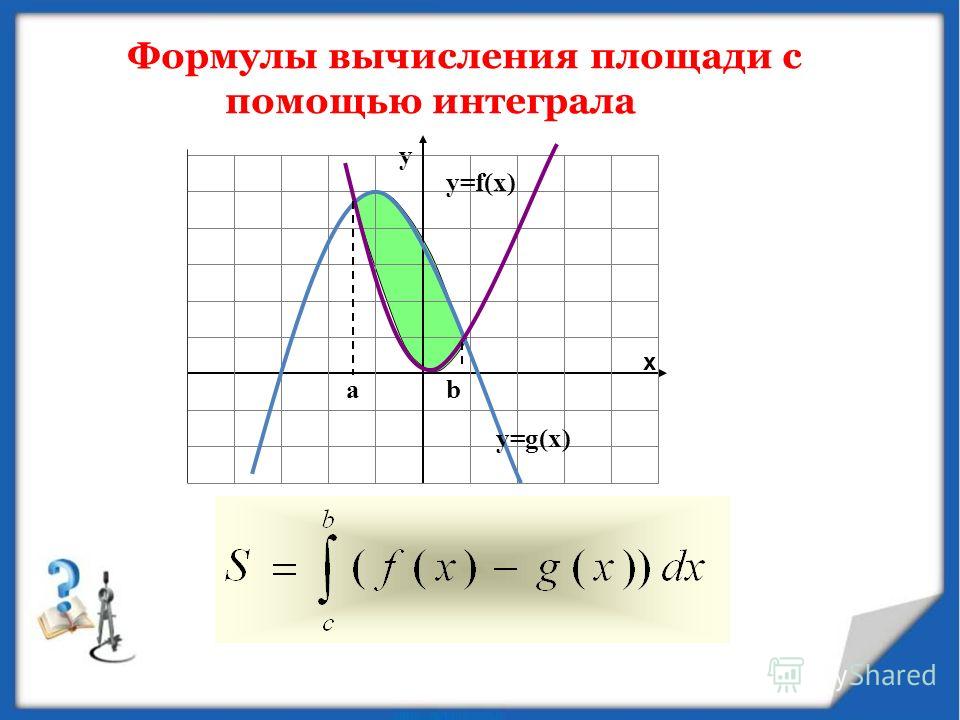 )
) Восстания)
Восстания) )
) Типанова, к Авиационной ул.)
Типанова, к Авиационной ул.) )
) )
) Добролюбова)
Добролюбова)
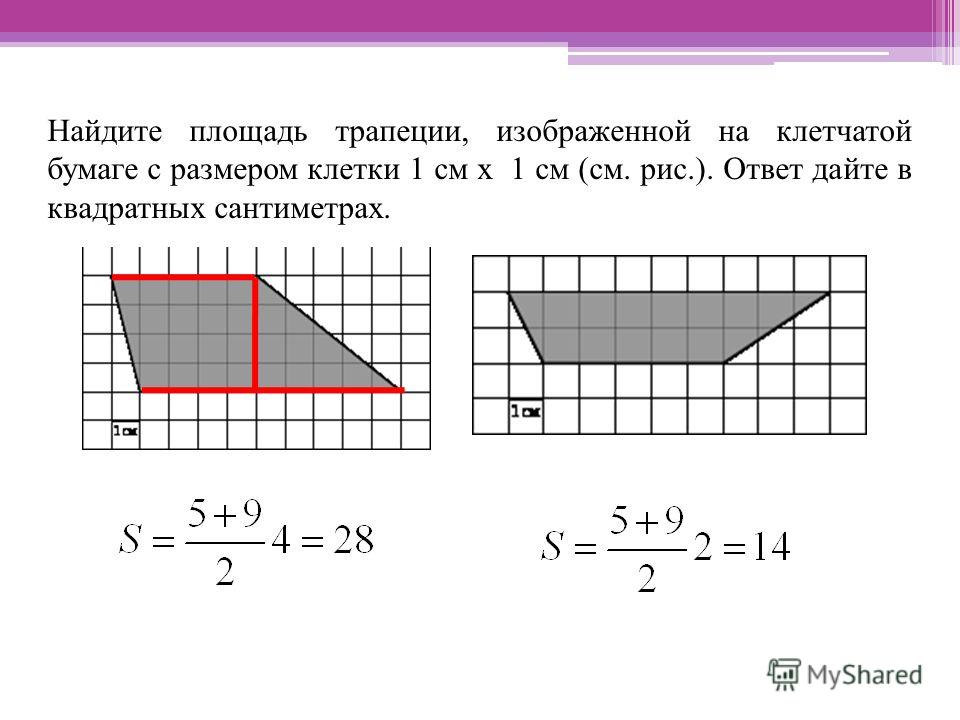 — пр. Металлистов — Кондратьевский пр. — Арсенальная ул. — ул. Комсомола — ул. Академика Лебедева — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала
— пр. Металлистов — Кондратьевский пр. — Арсенальная ул. — ул. Комсомола — ул. Академика Лебедева — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала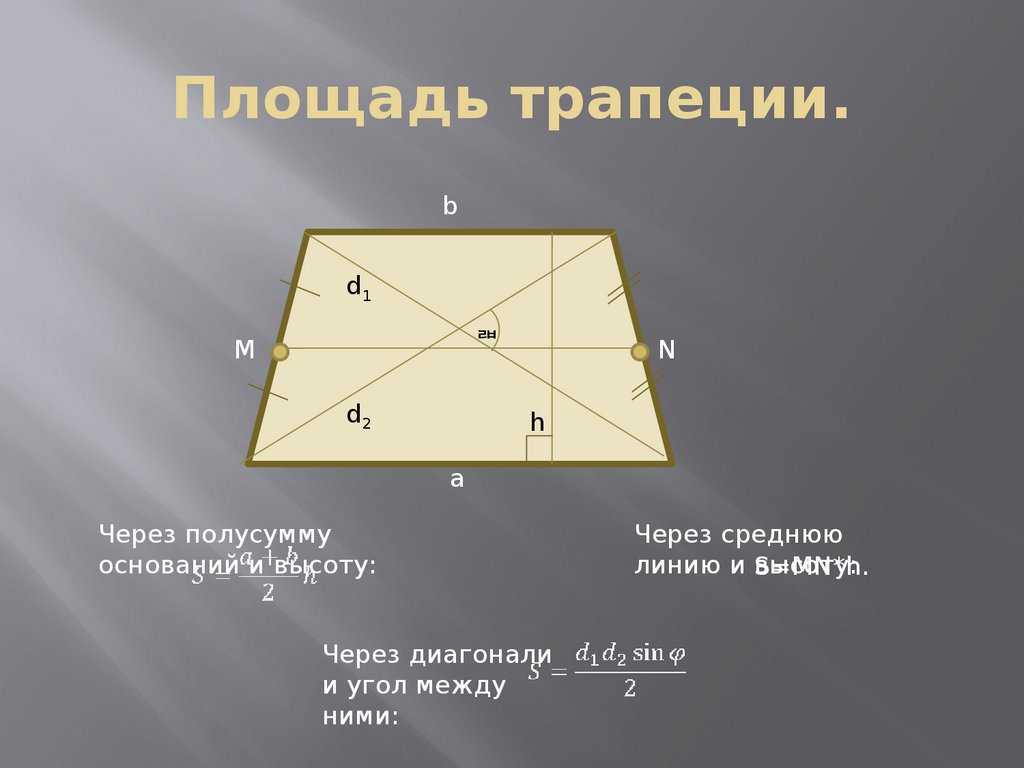 — станция метро «Чёрная речка»
— станция метро «Чёрная речка»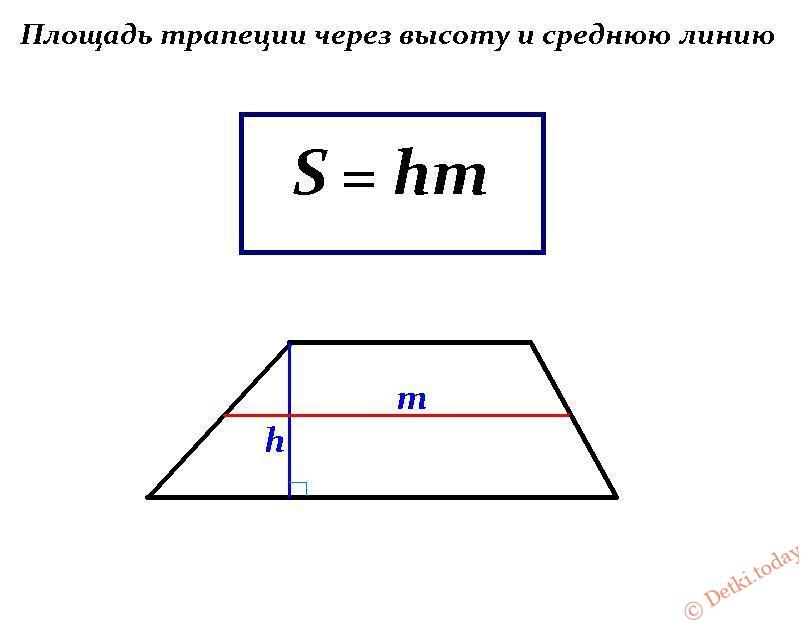 — ул. Комсомола — ул. Академика Лебедева — Литейный мост — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала
— ул. Комсомола — ул. Академика Лебедева — Литейный мост — Литейный пр. — Владимирский пр. — Загородный пр. — Московский пр. — 1-я Красноармейская ул. — Троицкий пр. — Лермонтовский пр. — площадь у Балтийского вокзала Кораблестроителей — Тульская ул.
Кораблестроителей — Тульская ул. Обуховской Обороны)
Обуховской Обороны)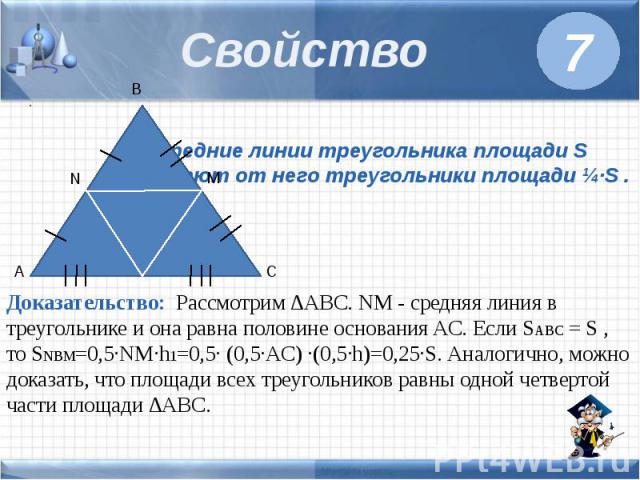 Костюшко
Костюшко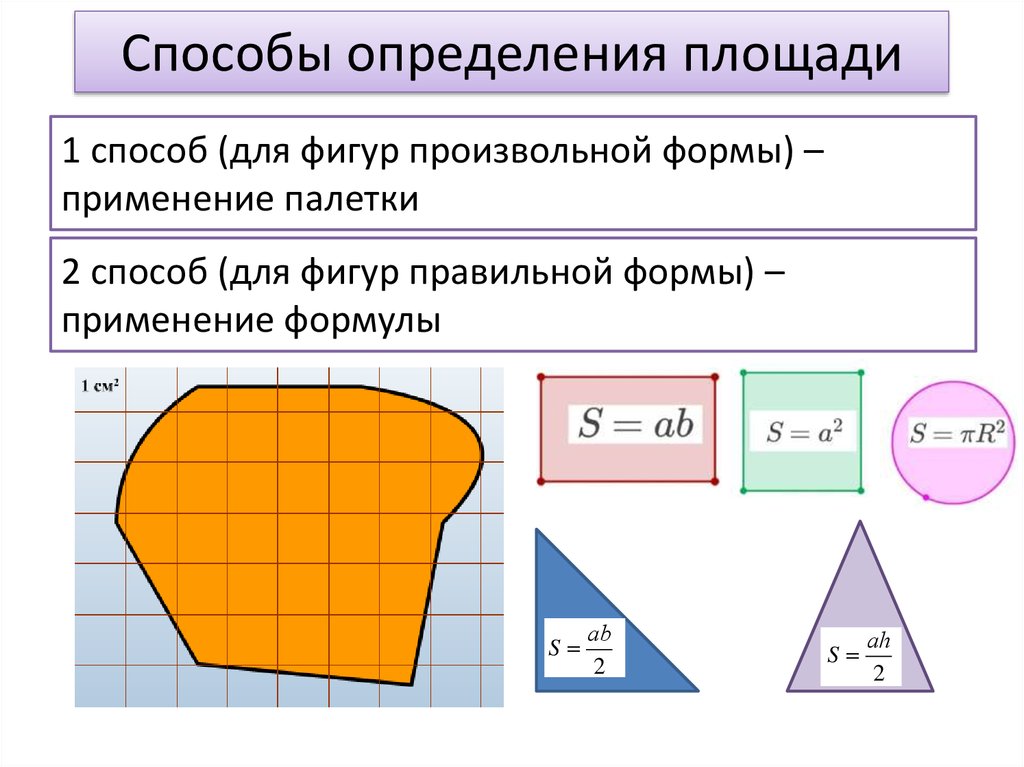 Композиторов — пр. Просвещения — пр. Художников — пр. Луначарского — пр. Культуры — Тихорецкий пр. — Политехническая ул. — пл. Мужества
Композиторов — пр. Просвещения — пр. Художников — пр. Луначарского — пр. Культуры — Тихорецкий пр. — Политехническая ул. — пл. Мужества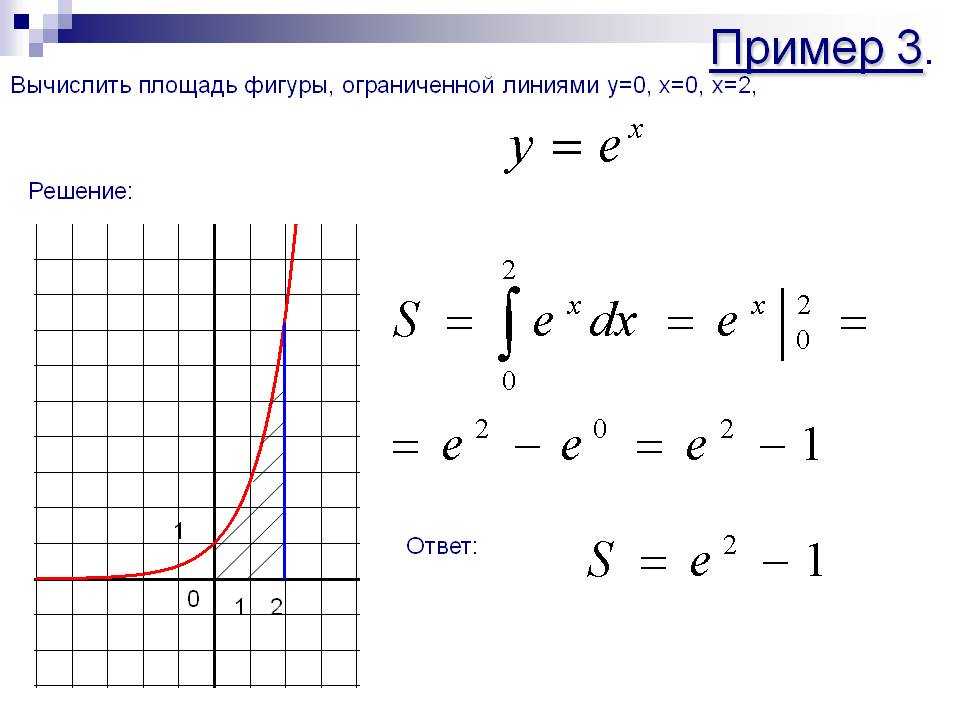 — Арцеуловская аллея.
— Арцеуловская аллея. Конституции
Конституции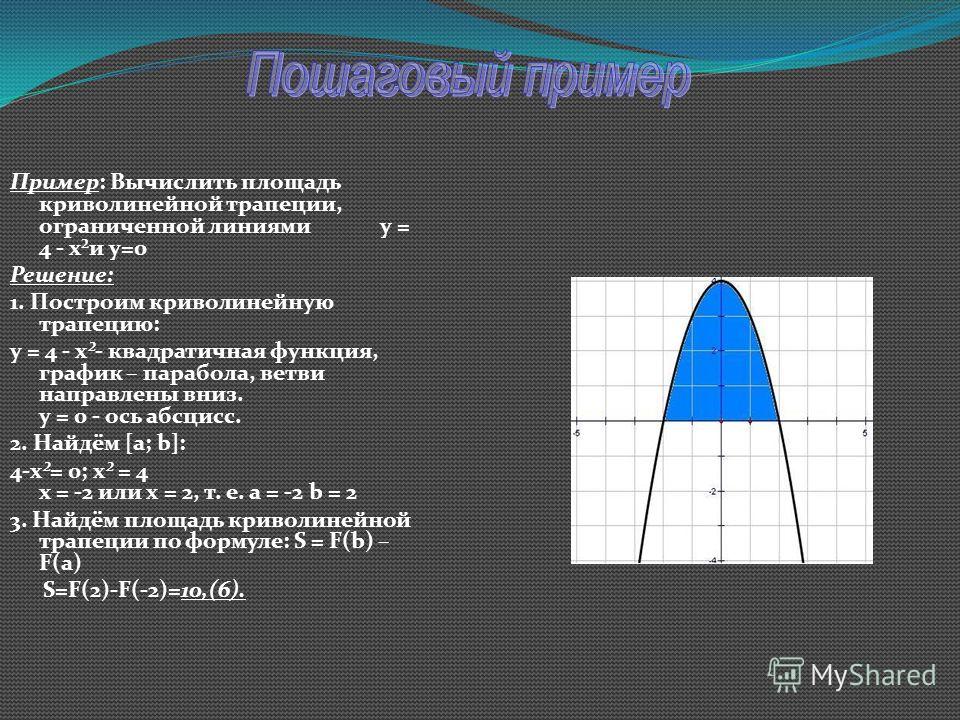 — пр. Добролюбова
— пр. Добролюбова — Суворовский пр.)
— Суворовский пр.) -д. станции Сортировочная — пр. Славы — Пражская ул. — ул. Белы Куна — Будапештская ул. — ул. Фучика — Белградская ул. — ул. Салова — Благодатная ул. — Московский пр. (обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.)
-д. станции Сортировочная — пр. Славы — Пражская ул. — ул. Белы Куна — Будапештская ул. — ул. Фучика — Белградская ул. — ул. Салова — Благодатная ул. — Московский пр. (обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.)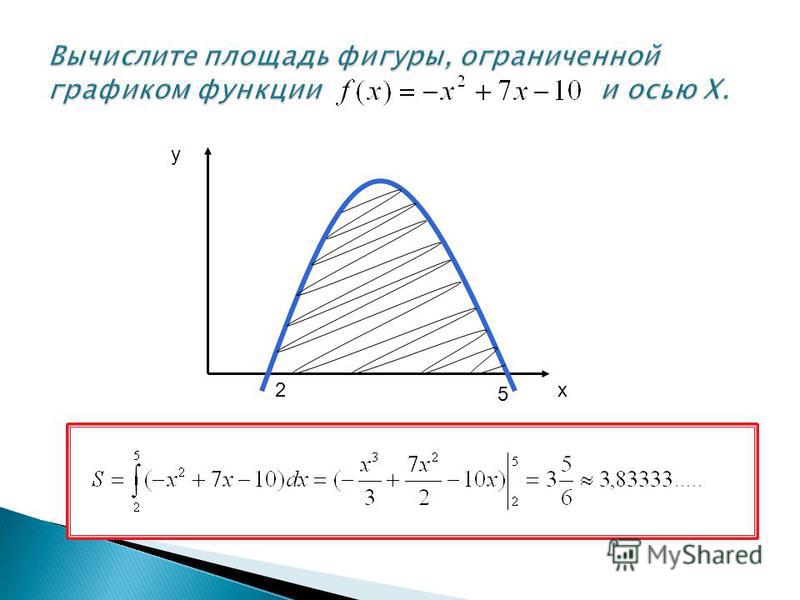 — ул. Салова — Благодатная ул. — Московский пр.(обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.)
— ул. Салова — Благодатная ул. — Московский пр.(обратно: ул. Решетникова — Сызранская ул. — Благодатная ул.) (обратно: Камчатская ул. — Касимовская ул. — Бухарестская ул.)
(обратно: Камчатская ул. — Касимовская ул. — Бухарестская ул.) — пр. Героев
— пр. Героев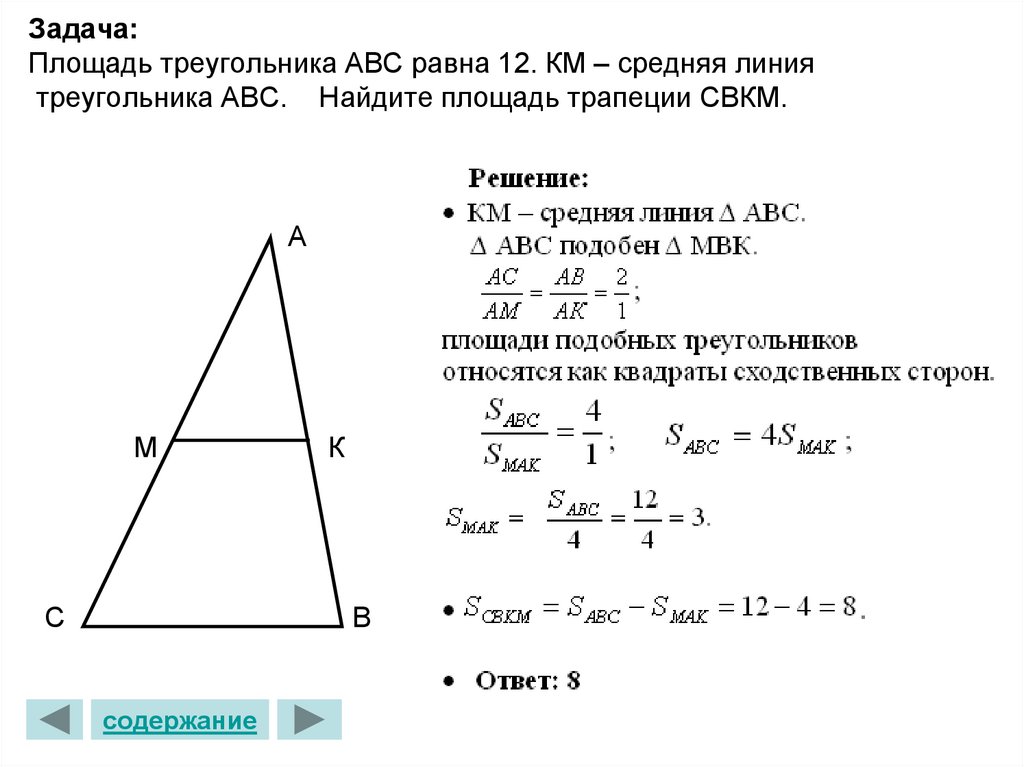 Партизана Германа — ул.Доблести — Ленинский пр.
Партизана Германа — ул.Доблести — Ленинский пр.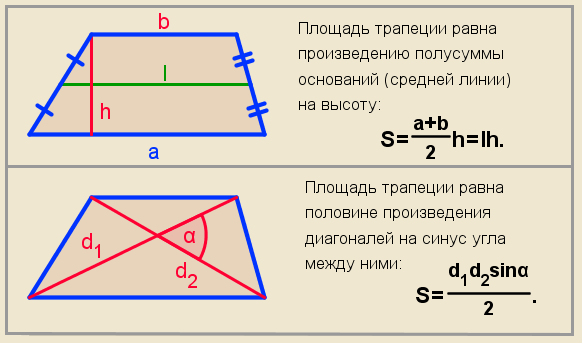
 Его можно обойти с любой стороны. Если Вы обойдете музей справа, то окажетесь ближе к кремлевской стене и мавзолею Ленина. Если обойдете музей с левой стороны, то путь Ваш будет идти через Воскресенские ворота, перед которыми установлен символический памятник Нулевой километр Автодорог России. Здесь можно бросить монетку и загадать желание.
Его можно обойти с любой стороны. Если Вы обойдете музей справа, то окажетесь ближе к кремлевской стене и мавзолею Ленина. Если обойдете музей с левой стороны, то путь Ваш будет идти через Воскресенские ворота, перед которыми установлен символический памятник Нулевой километр Автодорог России. Здесь можно бросить монетку и загадать желание.
 Поэтому те кто никогда не был в нашей столице часто спрашивают «Как добраться до Красной площади».
Поэтому те кто никогда не был в нашей столице часто спрашивают «Как добраться до Красной площади».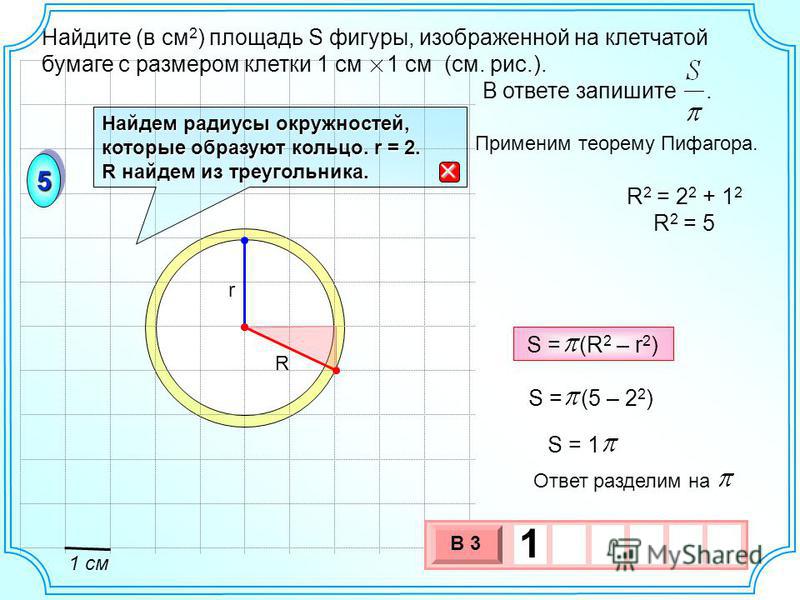
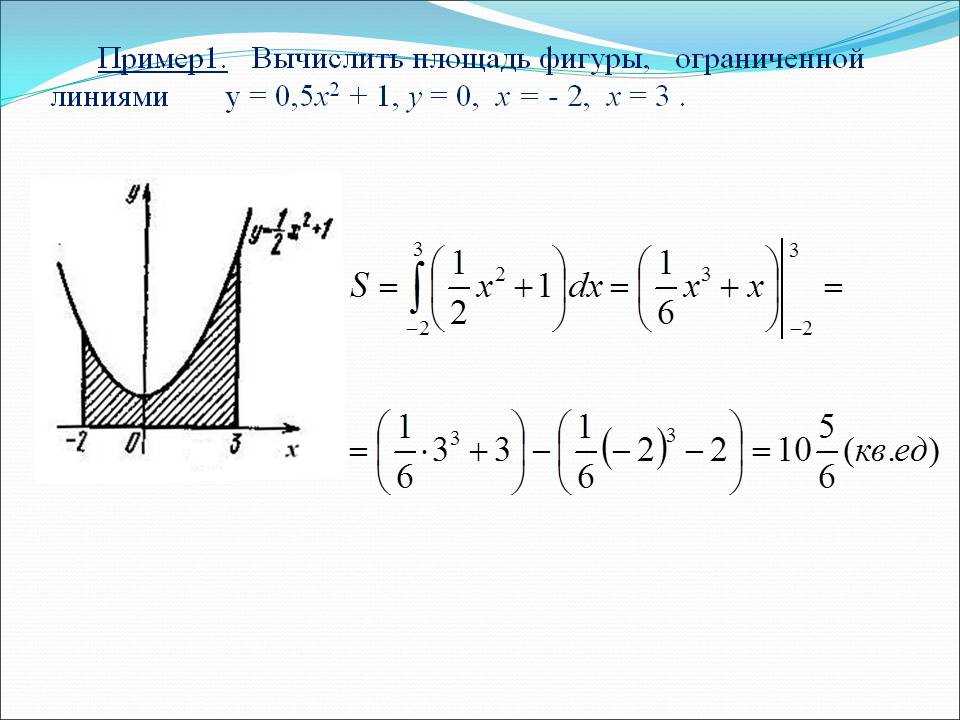 Реестры должны быть размещены в открытом доступе на официальных сайтах муниципалитетов, а если у органа местного самоуправления таковых нет, то – на порталах субъектов РФ.
Реестры должны быть размещены в открытом доступе на официальных сайтах муниципалитетов, а если у органа местного самоуправления таковых нет, то – на порталах субъектов РФ.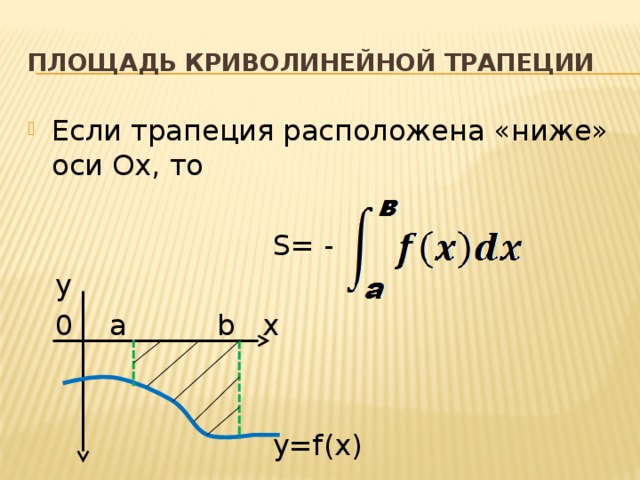 Для получения компенсации необходимо обратиться в отдел социальной защиты населения по месту жительства.
Для получения компенсации необходимо обратиться в отдел социальной защиты населения по месту жительства.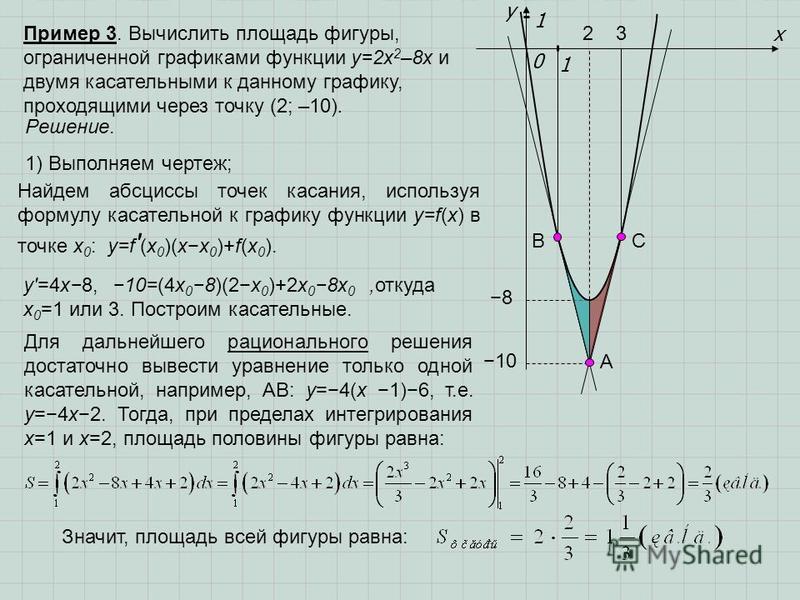

 При заключении договора с регоператором по обращению с ТКО нужно предоставить документ, подтверждающий, что зарегистрированный в доме или квартире человек проживает в другом месте. Это может быть документ о регистрации по факту временного пребывания, справка из учебного заведения. Полный перечень таких документов – в постановлении Правительства РФ № 354.
При заключении договора с регоператором по обращению с ТКО нужно предоставить документ, подтверждающий, что зарегистрированный в доме или квартире человек проживает в другом месте. Это может быть документ о регистрации по факту временного пребывания, справка из учебного заведения. Полный перечень таких документов – в постановлении Правительства РФ № 354.
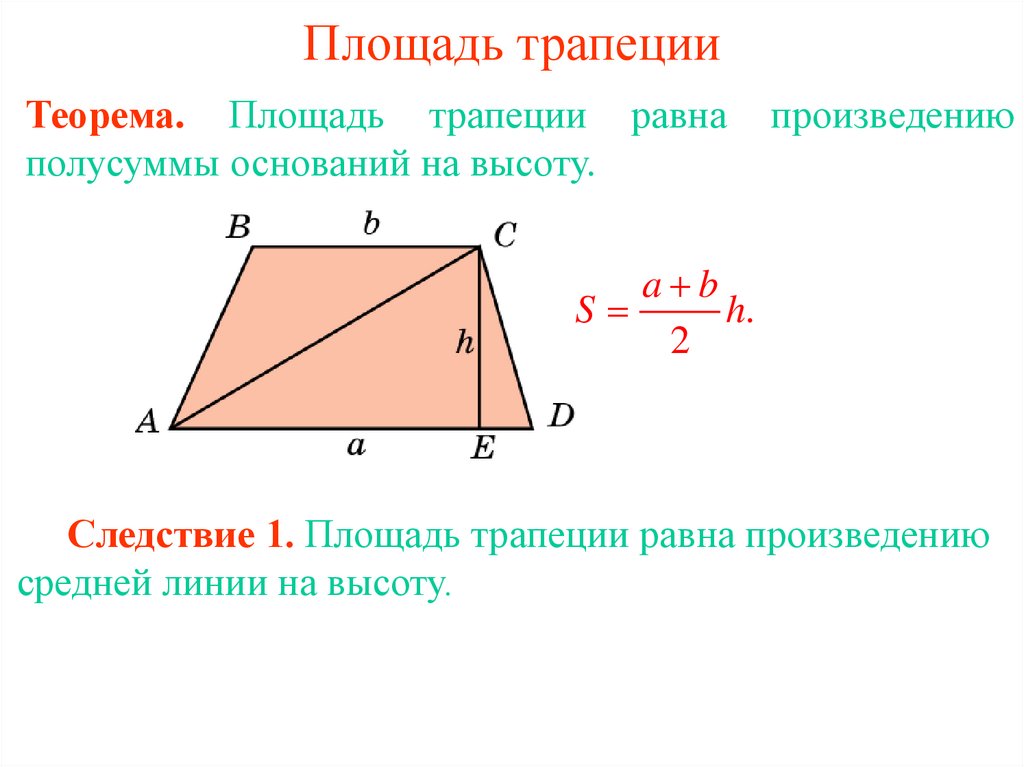
 6–24.13 Закона № 89-ФЗ.
6–24.13 Закона № 89-ФЗ.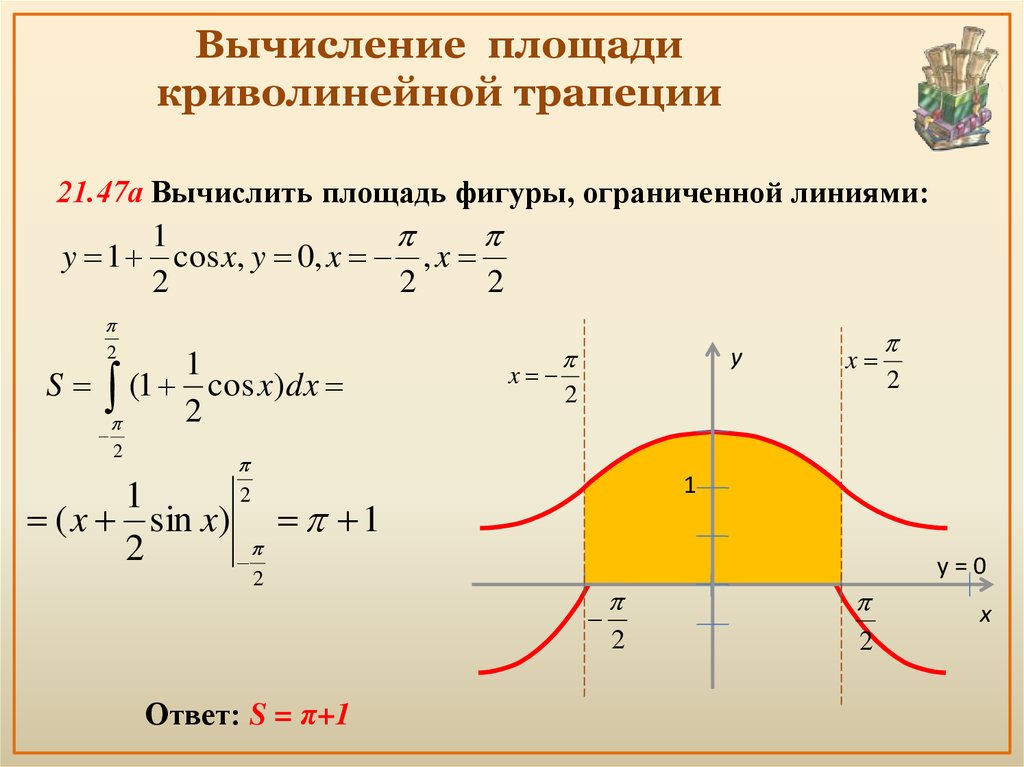 Условия образования ТКО обуславливают также особенность их удаления, которое осуществляется в настоящее время, в основном, путем захоронения, в ряде случаев с предварительной сортировкой. Виды отходов, отнесенные к ТКО, относятся к IV или V классу опасности в силу того, что в составе присутствуют в основном отходы материалов и изделий, отнесенных к IV и/или V классу опасности.
Условия образования ТКО обуславливают также особенность их удаления, которое осуществляется в настоящее время, в основном, путем захоронения, в ряде случаев с предварительной сортировкой. Виды отходов, отнесенные к ТКО, относятся к IV или V классу опасности в силу того, что в составе присутствуют в основном отходы материалов и изделий, отнесенных к IV и/или V классу опасности.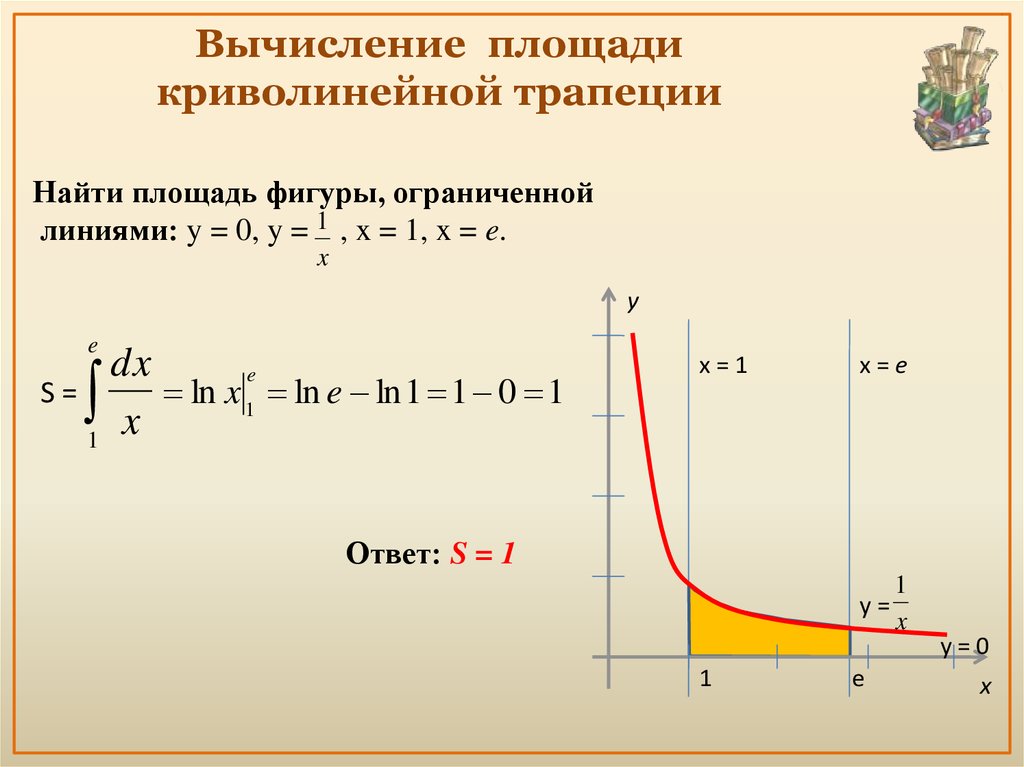
 Указанный договор заключается в порядке и в соответствии с требованиями, установленными гражданским законодательством Российской Федерации и законодательством Российской Федерации в области обращения с отходами производства и потребления.
Указанный договор заключается в порядке и в соответствии с требованиями, установленными гражданским законодательством Российской Федерации и законодательством Российской Федерации в области обращения с отходами производства и потребления.


 Кроме того, в некоторых субъектах РФ нормы накопления установлены для всей территории субъекта, а в некоторых – устанавливаются отдельно для каждого из городов, вплоть до самого небольшого муниципального района. Есть случаи, когда нормативы накопления в разных субъектах РФ указаны в различных единицах измерения. Аналогичная ситуация выявлена в случае анализа единых тарифов на услуги региональных операторов по обращению с ТКО. Нормативы накопления ТКО устанавливаются в м3 или кг на расчетную единицу. Расчетнойединицей является один проживающий или 1 кв. м общей площади.
Кроме того, в некоторых субъектах РФ нормы накопления установлены для всей территории субъекта, а в некоторых – устанавливаются отдельно для каждого из городов, вплоть до самого небольшого муниципального района. Есть случаи, когда нормативы накопления в разных субъектах РФ указаны в различных единицах измерения. Аналогичная ситуация выявлена в случае анализа единых тарифов на услуги региональных операторов по обращению с ТКО. Нормативы накопления ТКО устанавливаются в м3 или кг на расчетную единицу. Расчетнойединицей является один проживающий или 1 кв. м общей площади. 06.2016 № 505 (далее – Правила № 505), в целях сопоставления объема и массы ТКО определяется средняя плотность ТКО, рассчитываемая как отношение объема ТКО, принятых от собственников ТКО (без учета ТКО, коммерческий учет которых осуществляется исходя из их массы), к массе таких отходов, переданных на объекты обработки, утилизации, обезвреживания и захоронения отходов за последний истекший календарный год, а при отсутствии таких данных – как отношение установленного годового норматива накопления в объемных показателях к годовому нормативу накопления по массе (далее – средняя плотность ТКО).
06.2016 № 505 (далее – Правила № 505), в целях сопоставления объема и массы ТКО определяется средняя плотность ТКО, рассчитываемая как отношение объема ТКО, принятых от собственников ТКО (без учета ТКО, коммерческий учет которых осуществляется исходя из их массы), к массе таких отходов, переданных на объекты обработки, утилизации, обезвреживания и захоронения отходов за последний истекший календарный год, а при отсутствии таких данных – как отношение установленного годового норматива накопления в объемных показателях к годовому нормативу накопления по массе (далее – средняя плотность ТКО).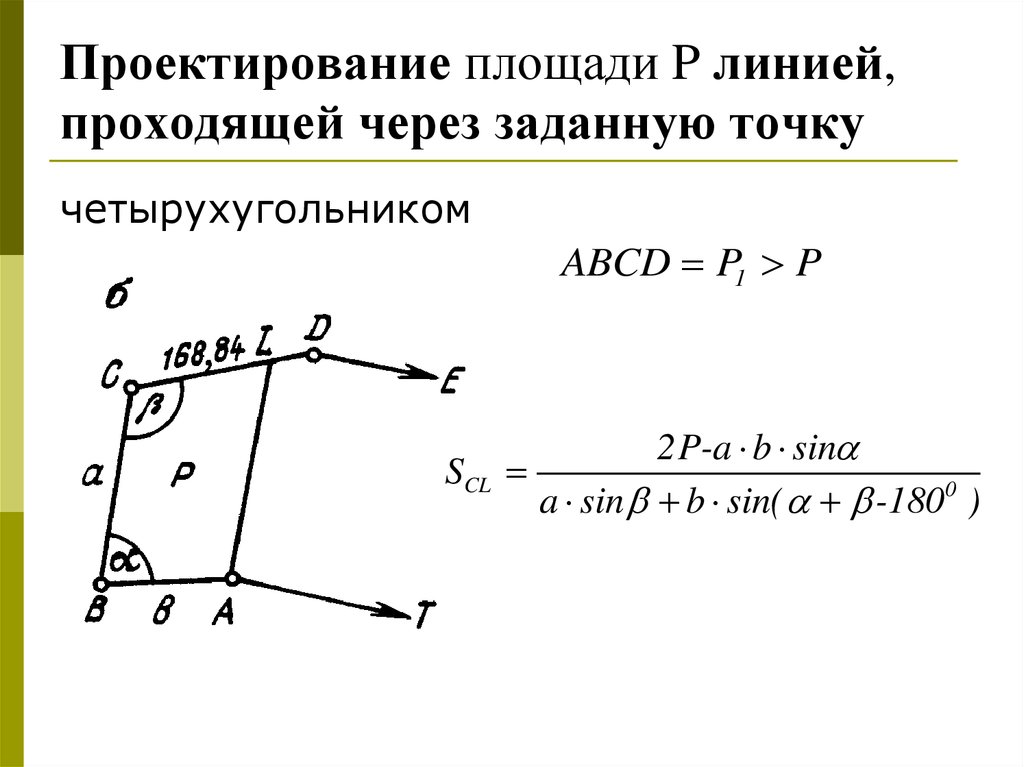

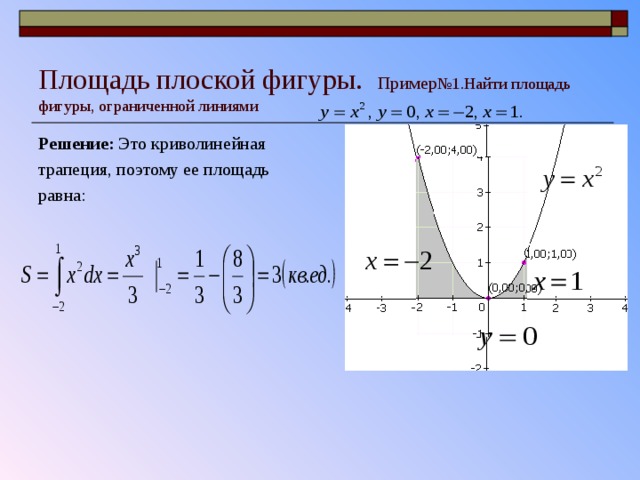
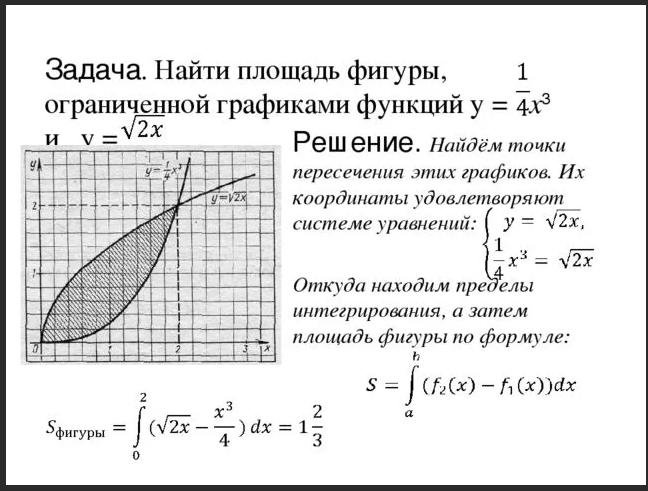

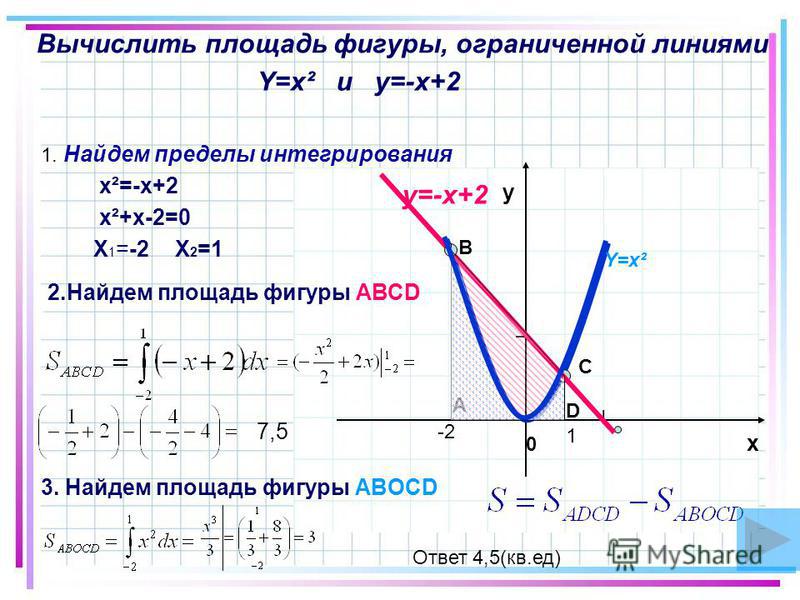
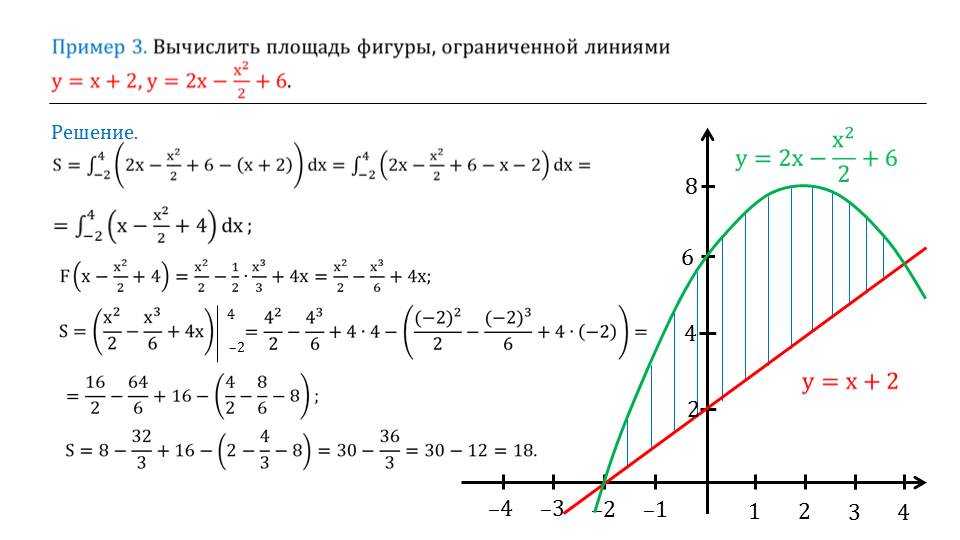 Одним из важнейших его событий традиционно остается программа «Музейная линия», где свои издательские проекты представляют различные музеи и галереи
Одним из важнейших его событий традиционно остается программа «Музейная линия», где свои издательские проекты представляют различные музеи и галереи Патронами события выступают Министерство цифрового развития, связи и массовых коммуникаций РФ и Российский книжный союз, поддерживают его федеральные министерства культуры и просвещения, а также правительство Москвы.
Патронами события выступают Министерство цифрового развития, связи и массовых коммуникаций РФ и Российский книжный союз, поддерживают его федеральные министерства культуры и просвещения, а также правительство Москвы.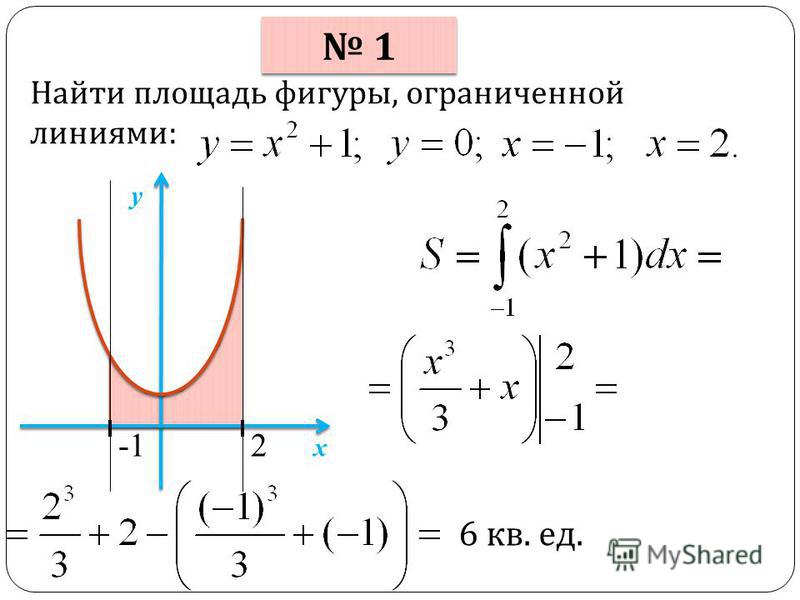 И.Харджиева. Русский авангард: материалы и документы из собрания РГАЛИ», каталог к проходившей в In artibus выставке «Французский рисунок из собрания Инны Баженовой» и другие.
И.Харджиева. Русский авангард: материалы и документы из собрания РГАЛИ», каталог к проходившей в In artibus выставке «Французский рисунок из собрания Инны Баженовой» и другие.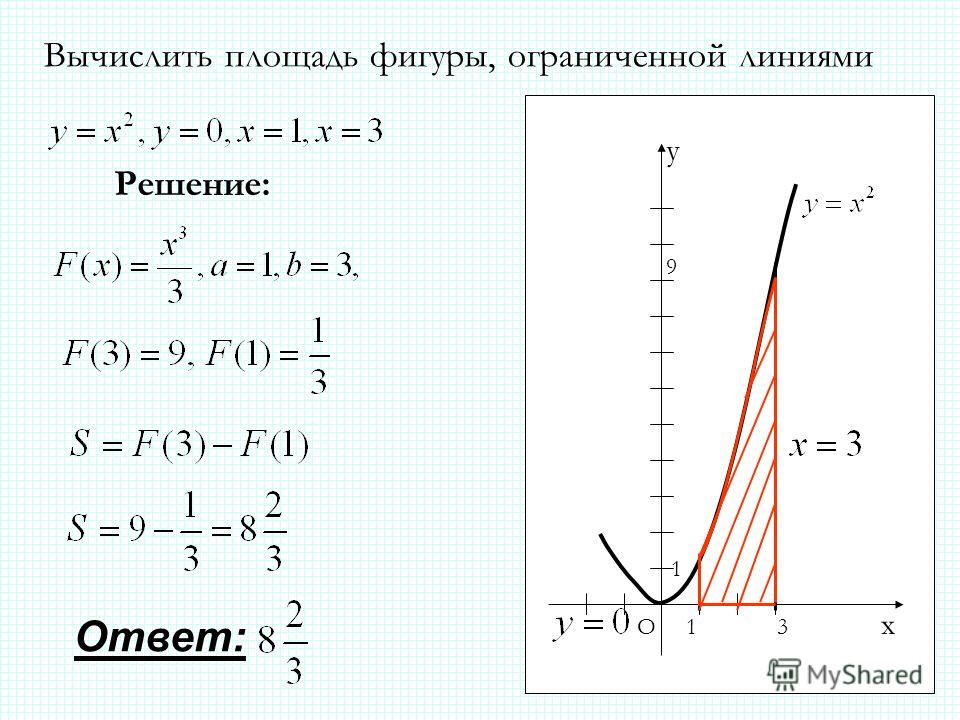
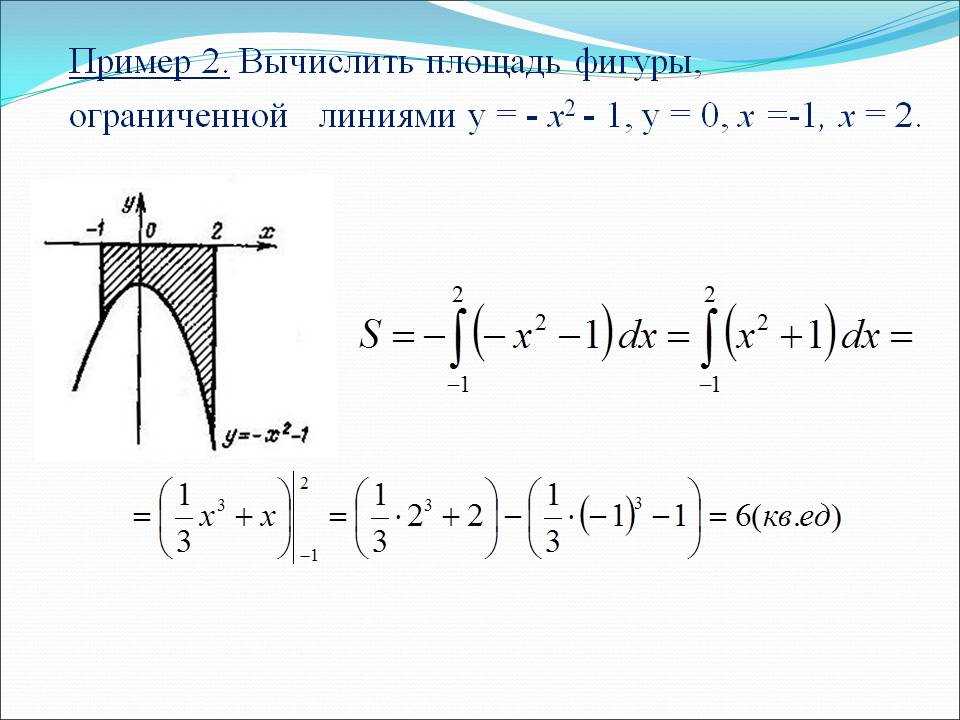 Numbered. Человек под номером» — это собрание портретов сотен людей, выживших в холокосте. Инициатива, возникшая в 2018 году, нашла отклик у 300 фотографов из 30 стран.
Numbered. Человек под номером» — это собрание портретов сотен людей, выживших в холокосте. Инициатива, возникшая в 2018 году, нашла отклик у 300 фотографов из 30 стран.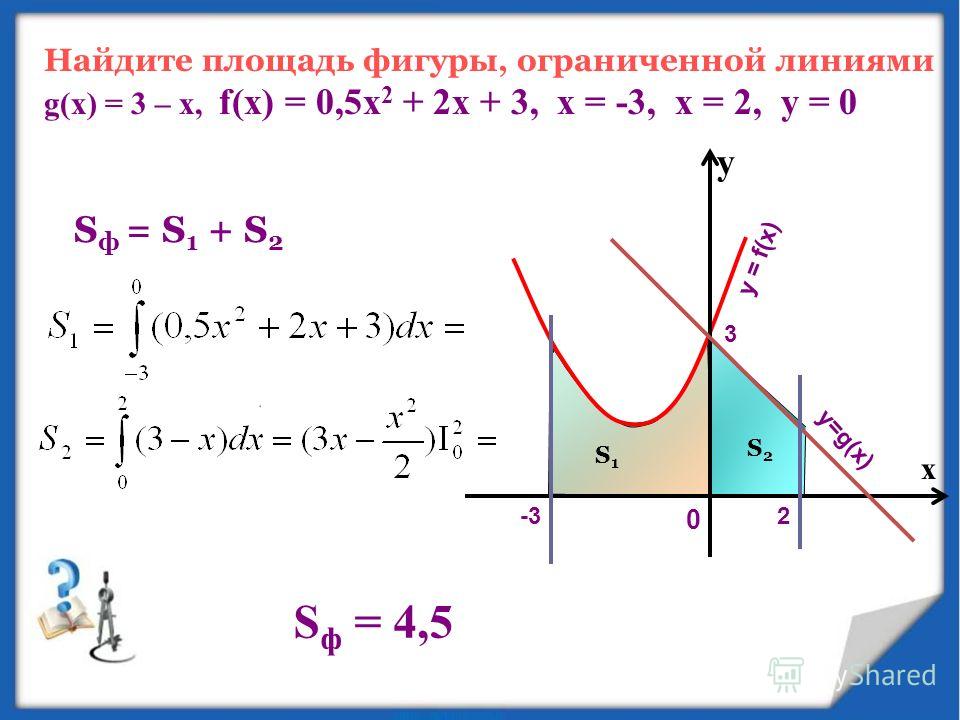 08.2022
08.2022 09.2022
09.2022 разделить на составные части. Это приводит к двум различным типам диаграмм с областями, по одному для каждого варианта использования.
разделить на составные части. Это приводит к двум различным типам диаграмм с областями, по одному для каждого варианта использования.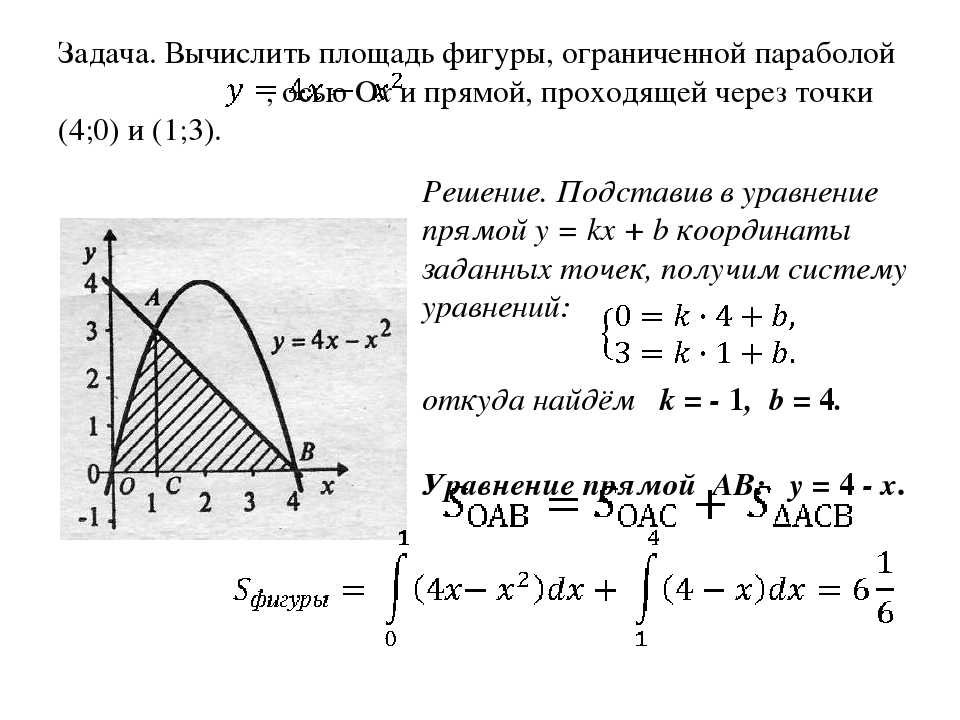 В этих случаях лучшим выбором будет просто придерживаться стандартной линейной диаграммы.
В этих случаях лучшим выбором будет просто придерживаться стандартной линейной диаграммы.
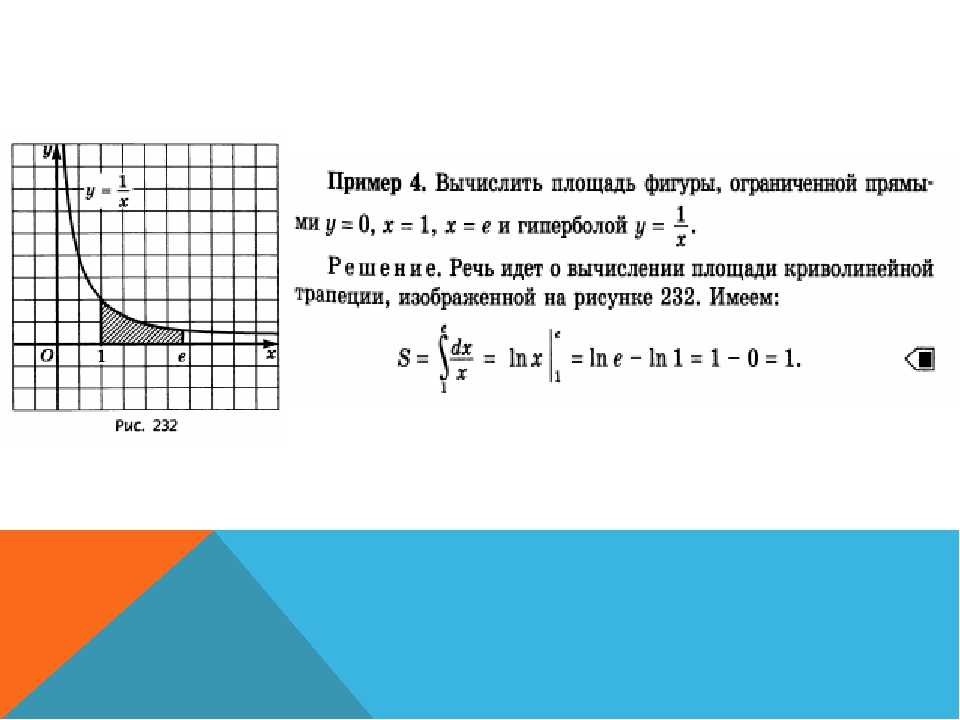 В каждом последующем столбце будет указан вертикальный вклад для каждой точки, по одному столбцу на серию, которую необходимо нанести на график. Этот формат применим как для перекрывающихся, так и для составных диаграмм с областями, при этом основное различие между диаграммами заключается в способе интерпретации значений для визуализации.
В каждом последующем столбце будет указан вертикальный вклад для каждой точки, по одному столбцу на серию, которую необходимо нанести на график. Этот формат применим как для перекрывающихся, так и для составных диаграмм с областями, при этом основное различие между диаграммами заключается в способе интерпретации значений для визуализации.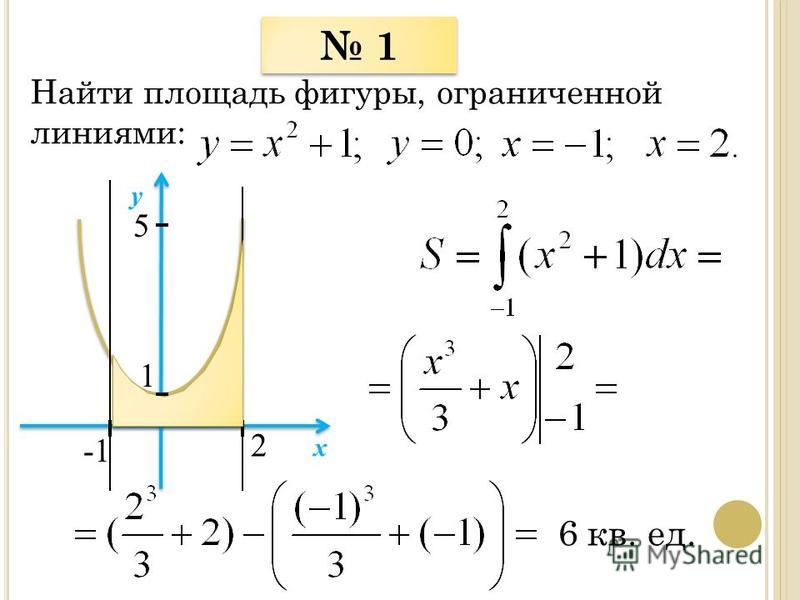 Таким образом, как и в гистограмме, обязательно наличие нулевой базовой линии, относительно которой должно выполняться затенение. Сокращение оси приведет к тому, что фактическое соотношение в значениях группы не будет соответствовать тому, что подразумевается на сгенерированном графике.
Таким образом, как и в гистограмме, обязательно наличие нулевой базовой линии, относительно которой должно выполняться затенение. Сокращение оси приведет к тому, что фактическое соотношение в значениях группы не будет соответствовать тому, что подразумевается на сгенерированном графике. Даже при наличии всего трех серий иногда бывает слишком много для отслеживания: три отдельных цвета, три попарных перекрытия и один цвет для всех трех перекрывающихся групп, всего семь цветов.
Даже при наличии всего трех серий иногда бывает слишком много для отслеживания: три отдельных цвета, три попарных перекрытия и один цвет для всех трех перекрывающихся групп, всего семь цветов.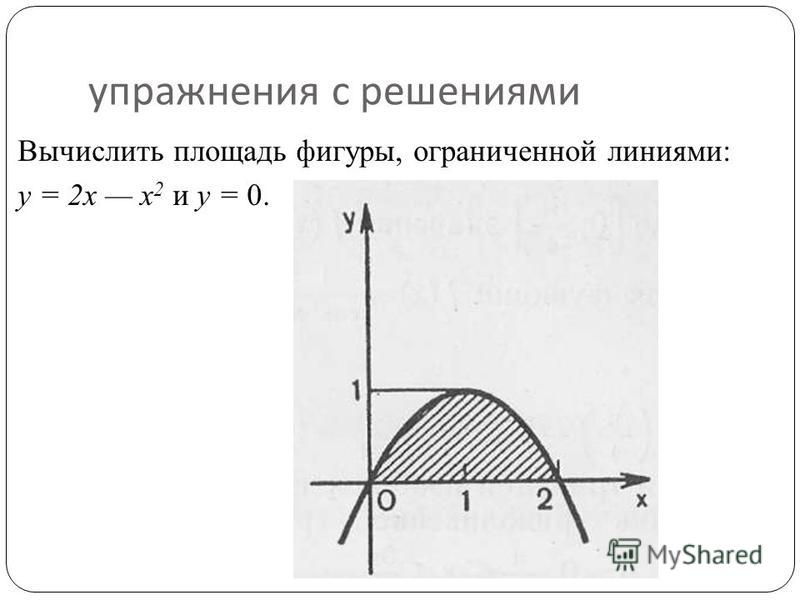 Как будет упомянуто в следующем разделе, чтение значений для любой отдельной группы, за исключением самой нижней, требует работы, поэтому рекомендуется сделать ее самой важной.
Как будет упомянуто в следующем разделе, чтение значений для любой отдельной группы, за исключением самой нижней, требует работы, поэтому рекомендуется сделать ее самой важной. Кроме того, когда у нас много значений, нас, вероятно, больше интересуют направление и наклон трендов, а не точные значения, когда линейные диаграммы работают лучше.
Кроме того, когда у нас много значений, нас, вероятно, больше интересуют направление и наклон трендов, а не точные значения, когда линейные диаграммы работают лучше.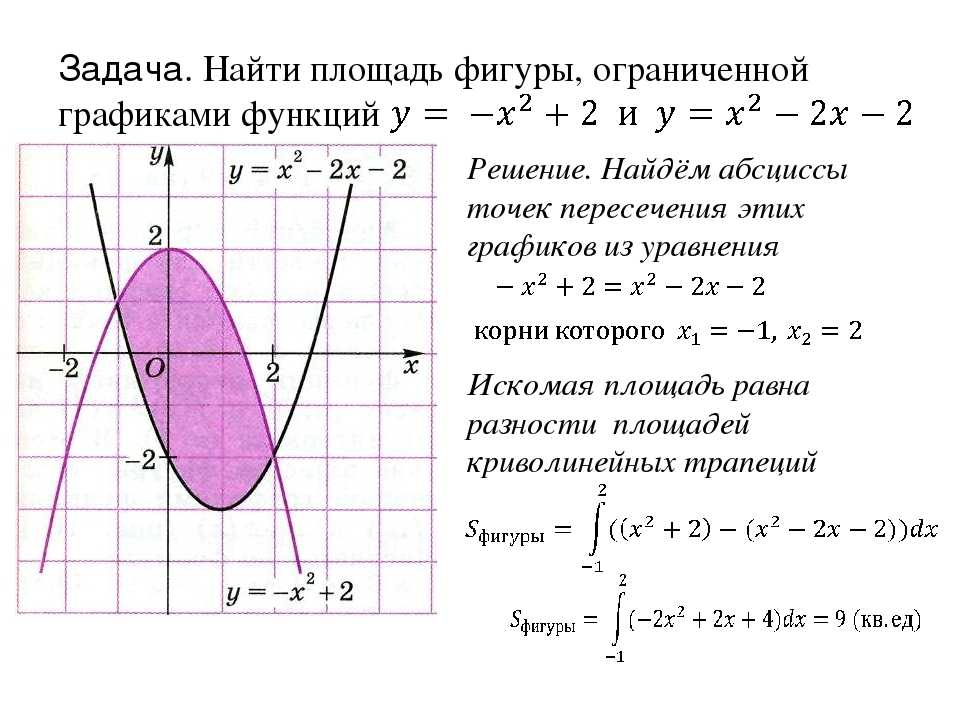
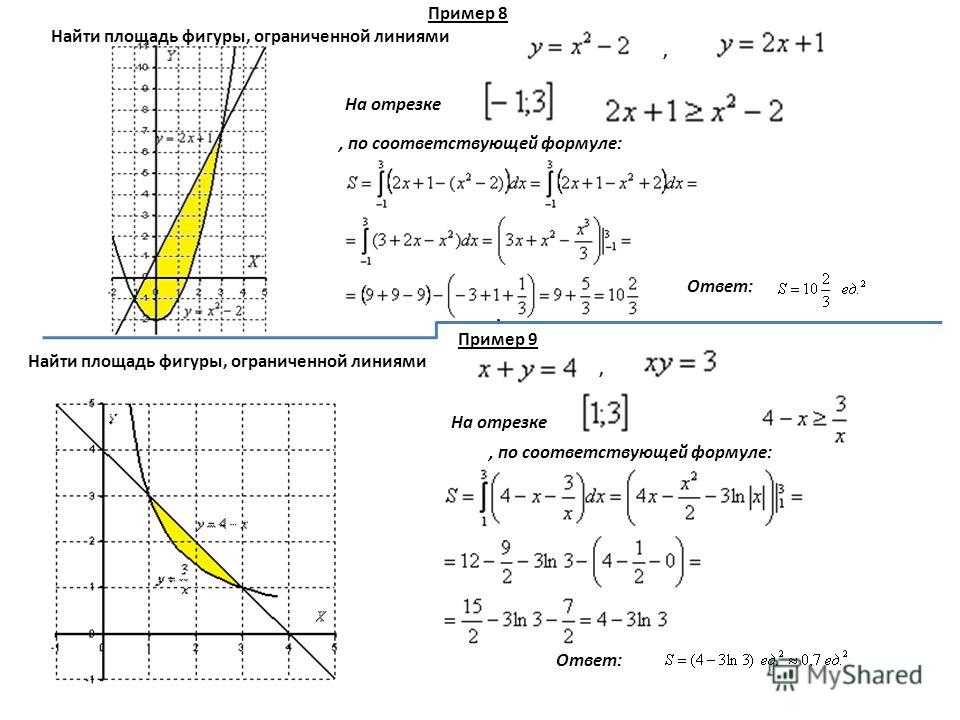 Если вы не уверены, что вас интересует диаграмма с областями, использование линейной диаграммы вряд ли приведет вас к неверному пути. Это особенно верно для диаграммы с перекрывающимися областями, где перекрывающиеся области могут быстро выйти из-под контроля. В качестве еще одного соображения, всегда можно просто создать больше графиков, если вы заинтересованы в проведении нескольких сравнений в своих данных, а не просто чувствуете необходимость выбрать только один тип диаграммы, чтобы нести как можно больше.
Если вы не уверены, что вас интересует диаграмма с областями, использование линейной диаграммы вряд ли приведет вас к неверному пути. Это особенно верно для диаграммы с перекрывающимися областями, где перекрывающиеся области могут быстро выйти из-под контроля. В качестве еще одного соображения, всегда можно просто создать больше графиков, если вы заинтересованы в проведении нескольких сравнений в своих данных, а не просто чувствуете необходимость выбрать только один тип диаграммы, чтобы нести как можно больше.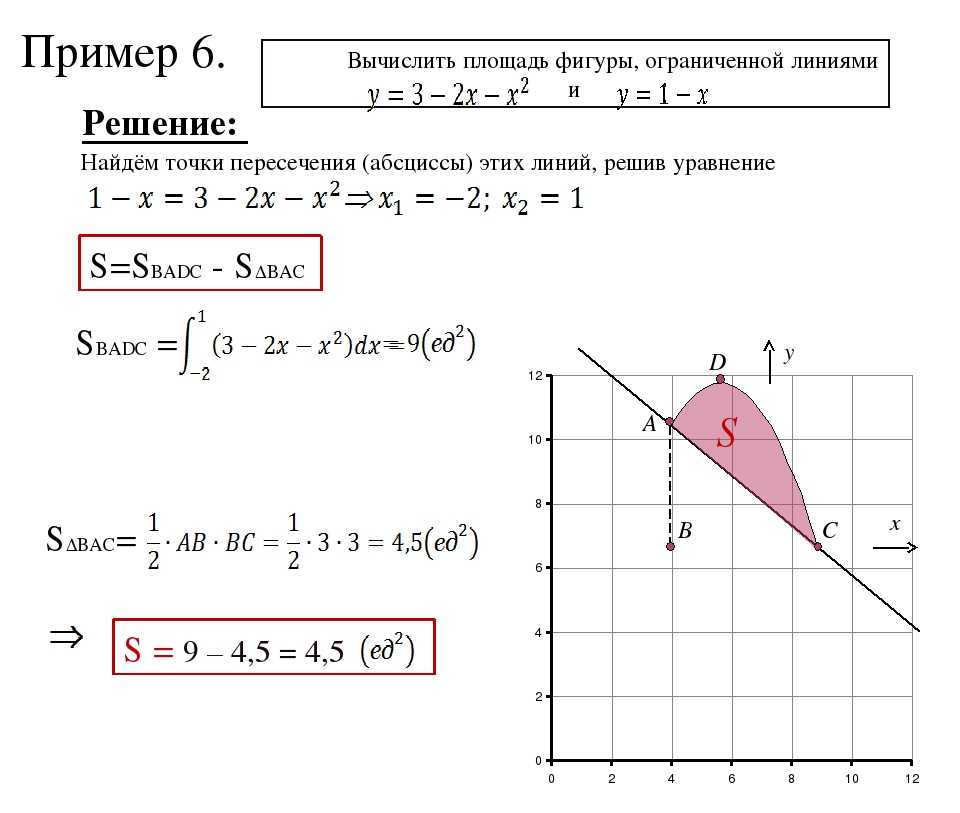 Таким образом, многие ограничения диаграммы с областями с накоплением также применимы к линейчатой диаграмме с накоплением. Однако одним из преимуществ столбцов, расположенных друг над другом, является то, что гораздо проще сделать последовательное суждение о стоимости в пределах каждого интервала горизонтальной оси. Заштрихованные области на диаграмме с областями могут искажаться, как показано выше, особенно когда линия меняет направление. Поскольку каждая область на линейчатой диаграмме с накоплением имеет прямоугольную форму, такого рода искажений можно избежать.
Таким образом, многие ограничения диаграммы с областями с накоплением также применимы к линейчатой диаграмме с накоплением. Однако одним из преимуществ столбцов, расположенных друг над другом, является то, что гораздо проще сделать последовательное суждение о стоимости в пределах каждого интервала горизонтальной оси. Заштрихованные области на диаграмме с областями могут искажаться, как показано выше, особенно когда линия меняет направление. Поскольку каждая область на линейчатой диаграмме с накоплением имеет прямоугольную форму, такого рода искажений можно избежать.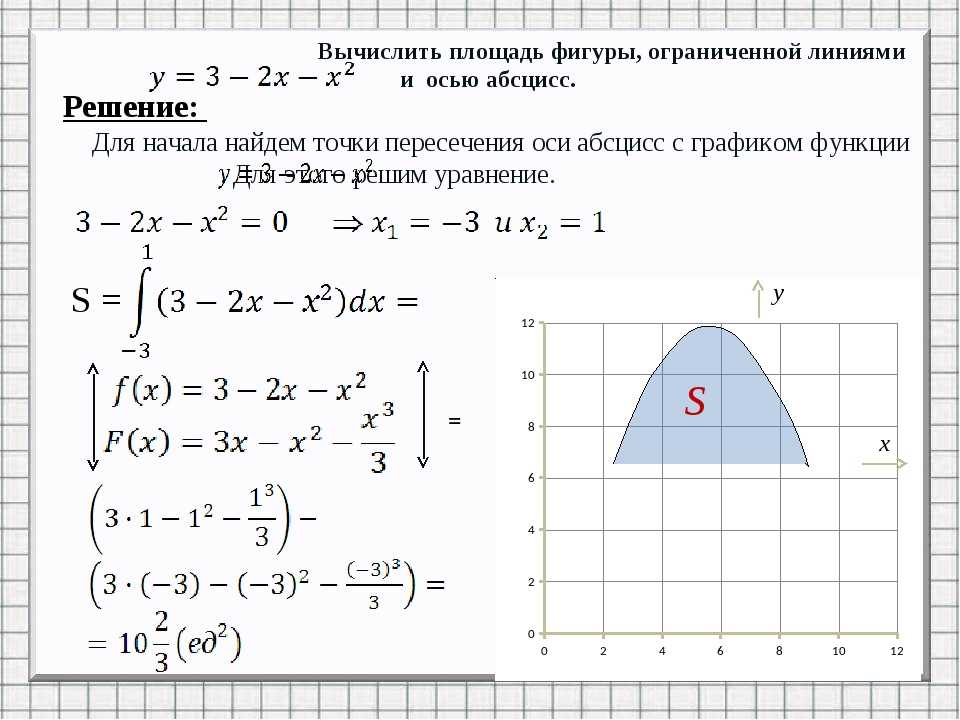
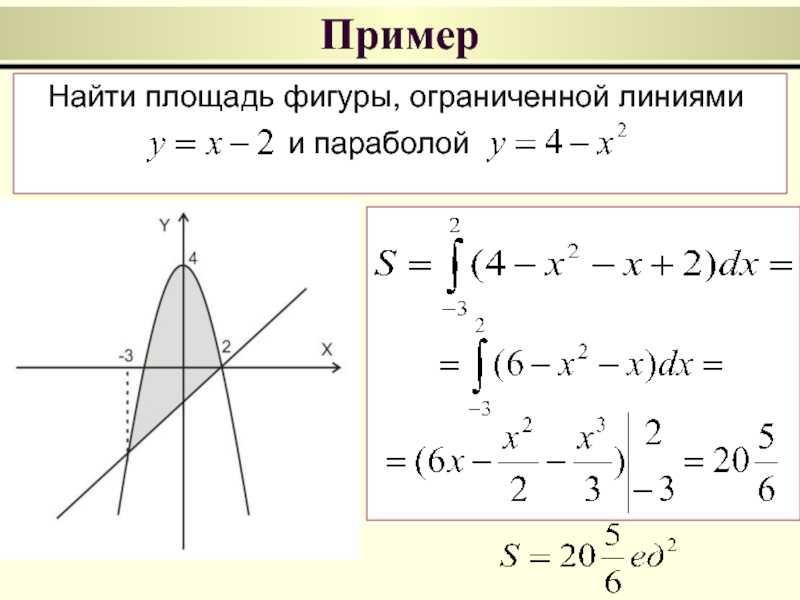
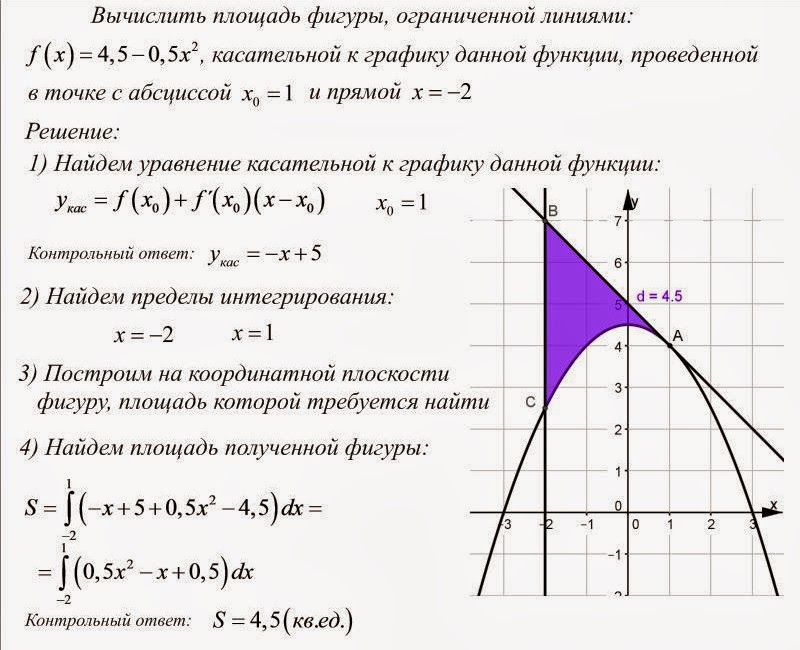
 Затем эти точки данных соединяются прямыми линиями, чтобы визуально показать тенденцию.
Затем эти точки данных соединяются прямыми линиями, чтобы визуально показать тенденцию. Когда этот год завершится, вы можете использовать существующую линейную диаграмму, чтобы показать, как на самом деле работала команда. Вы получите параллельное сравнение прогнозируемого роста и фактического роста.
Когда этот год завершится, вы можете использовать существующую линейную диаграмму, чтобы показать, как на самом деле работала команда. Вы получите параллельное сравнение прогнозируемого роста и фактического роста.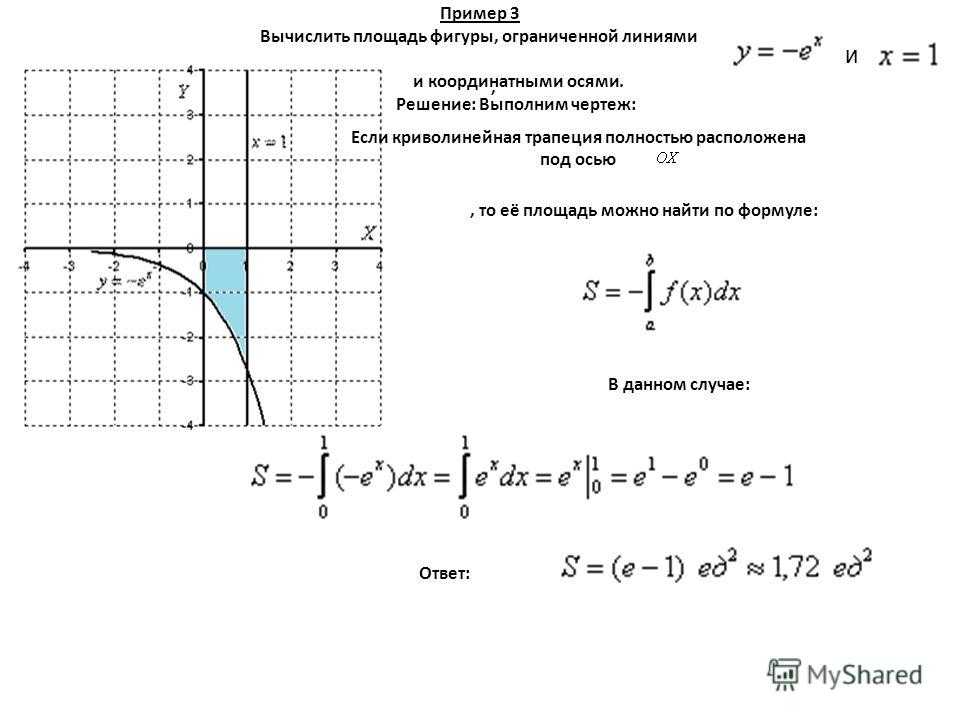 Точки данных отмечаются на сетке XY, а затем соединяются в линию. Оттуда область между построенной линией и осью X заштрихована цветами или текстурами.
Точки данных отмечаются на сетке XY, а затем соединяются в линию. Оттуда область между построенной линией и осью X заштрихована цветами или текстурами. 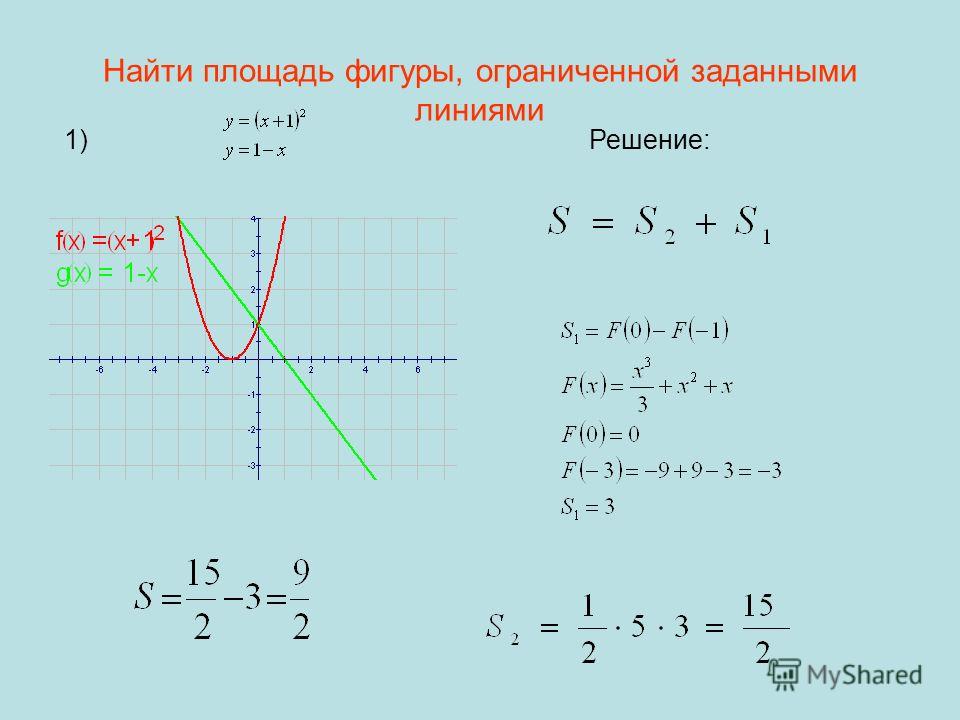 Диаграмма с областями, на которой сравниваются разные наборы данных, называется диаграммой с перекрывающимися областями. Например, если вы хотите узнать, сколько предметов женской и мужской одежды продала ваша компания по производству одежды в прошлом квартале, вы должны нанести точки данных для каждой категории и заполнить эти области другим цветом. Вы можете сразу увидеть, какая линия одежды показала лучшие результаты в квартальных продажах.
Диаграмма с областями, на которой сравниваются разные наборы данных, называется диаграммой с перекрывающимися областями. Например, если вы хотите узнать, сколько предметов женской и мужской одежды продала ваша компания по производству одежды в прошлом квартале, вы должны нанести точки данных для каждой категории и заполнить эти области другим цветом. Вы можете сразу увидеть, какая линия одежды показала лучшие результаты в квартальных продажах. 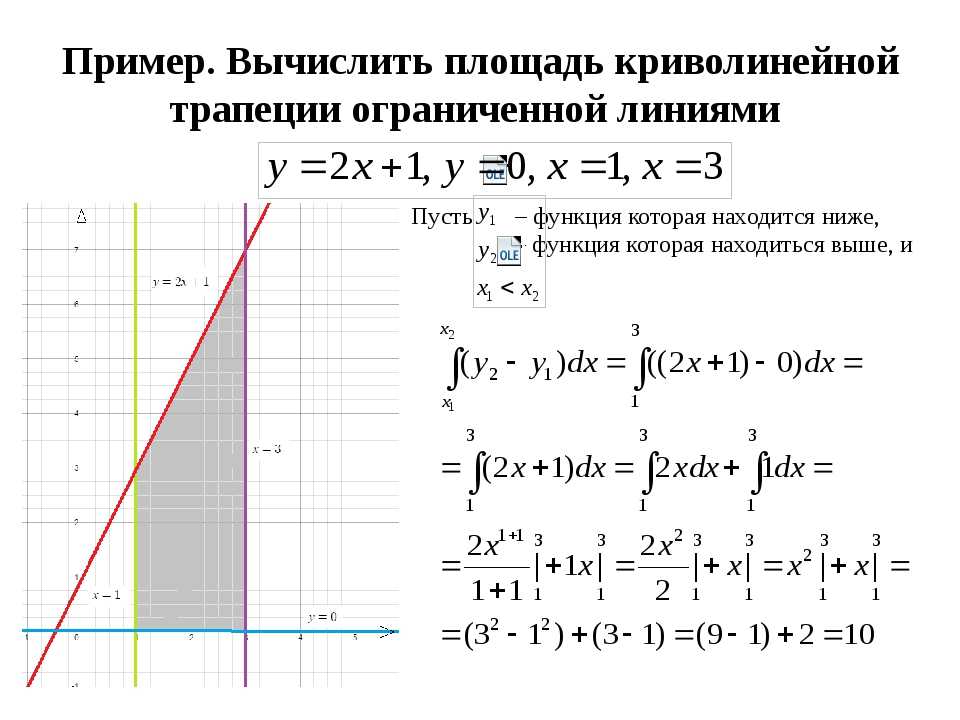 Они могут превратить скучные данные в профессиональные и легко читаемые диаграммы в вашей презентации. Линейные диаграммы хорошо отображают краткосрочные данные и точные точки данных, а диаграммы с областями отлично подходят для отображения долгосрочных данных и нескольких наборов данных.
Они могут превратить скучные данные в профессиональные и легко читаемые диаграммы в вашей презентации. Линейные диаграммы хорошо отображают краткосрочные данные и точные точки данных, а диаграммы с областями отлично подходят для отображения долгосрочных данных и нескольких наборов данных.  В диаграммах с областями
пространство под сегментами линий заполнено цветом, тогда как в
на линейных диаграммах визуализируются только линейные сегменты без дополнительных
окрашивание или затенение. Эти диаграммы облегчают визуализацию данных в течение
период времени (с использованием данных временных рядов) и выявление тенденций и
закономерности во всем диапазоне данных. Поддержка линейных и площадных диаграмм
визуализации как дискретных, так и непрерывных данных.
В диаграммах с областями
пространство под сегментами линий заполнено цветом, тогда как в
на линейных диаграммах визуализируются только линейные сегменты без дополнительных
окрашивание или затенение. Эти диаграммы облегчают визуализацию данных в течение
период времени (с использованием данных временных рядов) и выявление тенденций и
закономерности во всем диапазоне данных. Поддержка линейных и площадных диаграмм
визуализации как дискретных, так и непрерывных данных.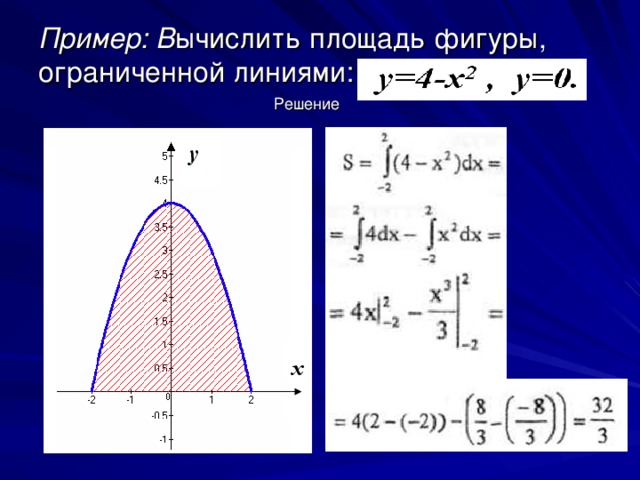
 сопоставляется с агрегацией оси Y
канал кодирования.
сопоставляется с агрегацией оси Y
канал кодирования.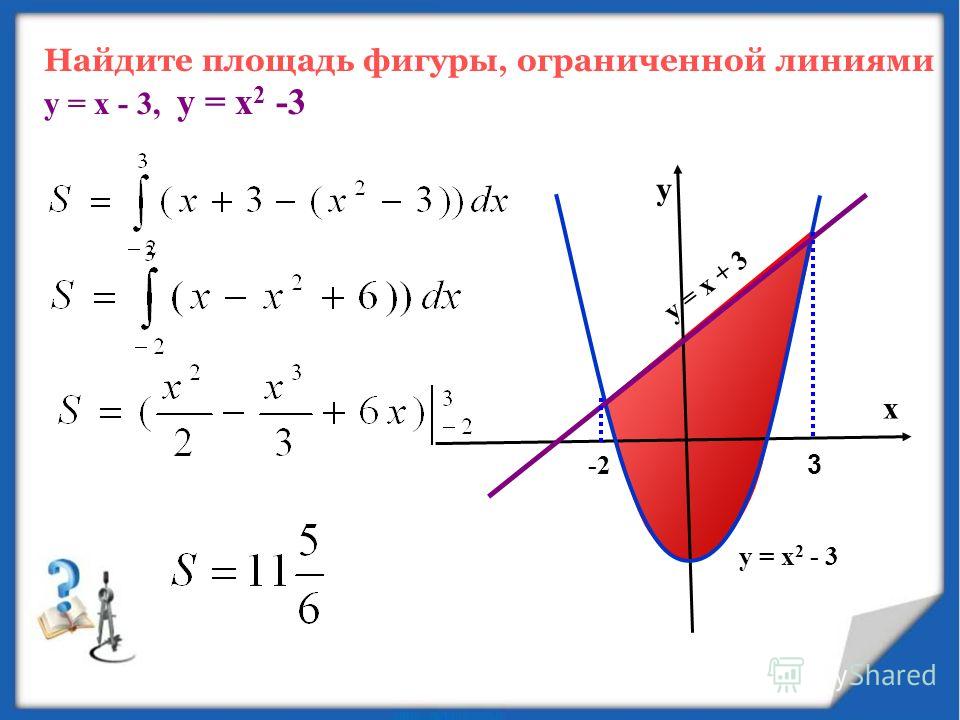 Непрерывные диаграммы не поддерживают агрегацию или группировку. непрерывный
график был бы полезен для визуализации цен закрытия акций с течением времени,
если предположить, что каждая цена закрытия исходит из отдельного документа в
набор данных.
Непрерывные диаграммы не поддерживают агрегацию или группировку. непрерывный
график был бы полезен для визуализации цен закрытия акций с течением времени,
если предположить, что каждая цена закрытия исходит из отдельного документа в
набор данных.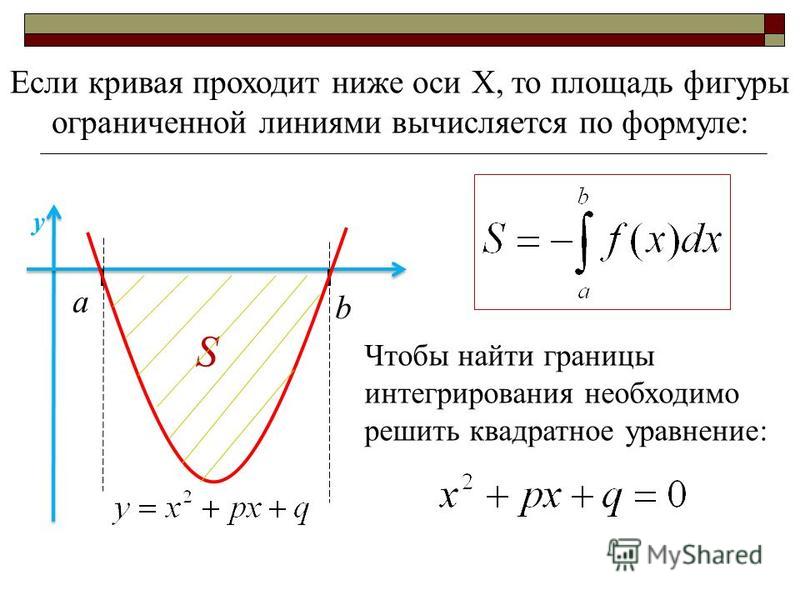

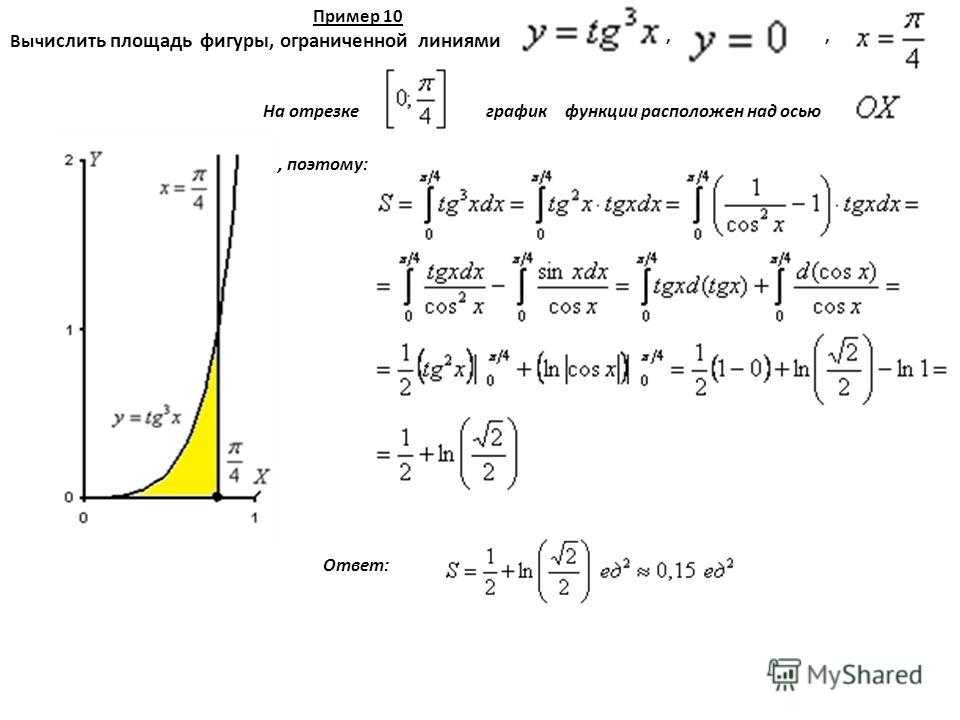
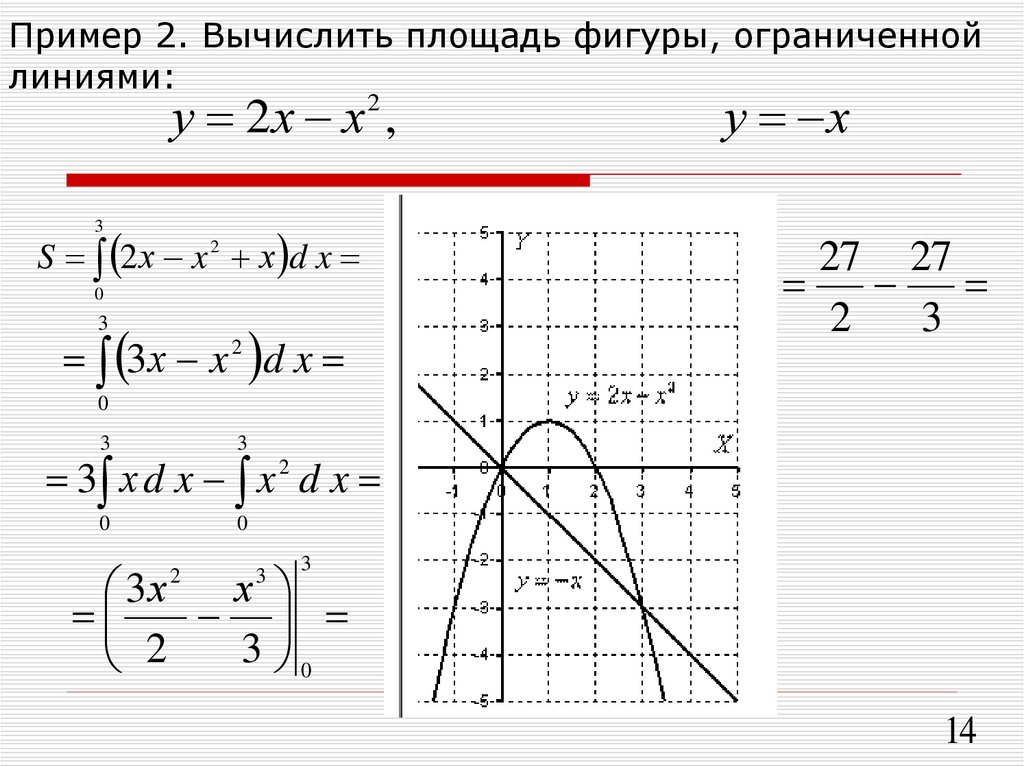
 Чтобы просмотреть все доступные параметры настройки, см.
Настроить диаграммы.
Чтобы просмотреть все доступные параметры настройки, см.
Настроить диаграммы.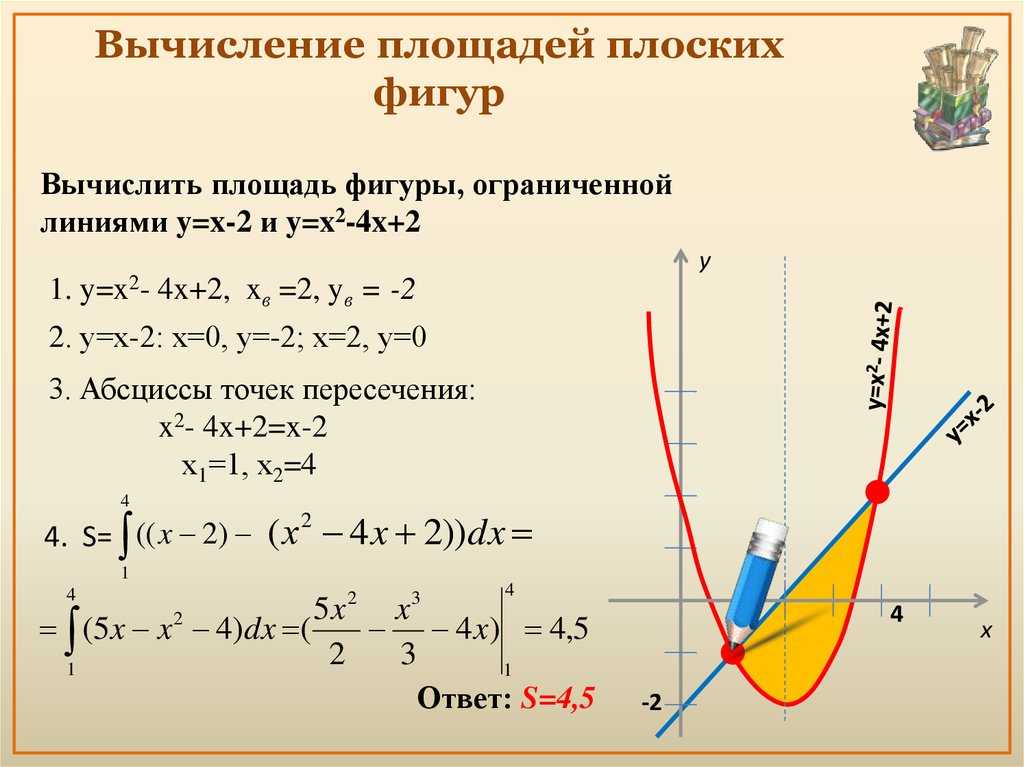

 параметр.
параметр.