интерполяционный полином лагранжа, ньютона, формула трапеций, формула Симпсона, формула левых прямоугольников, формула правых прямоугольнико
ЗАДАЧИ:
Дана табличная функция
x | 0.1 | 0.4 | 0.7 |
y | 5.7 | 8.9 | 9.3 |
Построить для нее интерполяционный полином
а) Ньютона;
б) Лагранжа.
Решение:
а) 
b)
Дан интеграл . Для вычисления этого интеграла записать формулу
а) левых прямоугольников,
б) правых прямоугольников,
в) трапеций,
г) Симпсона.
Решение:
Разобьем отрезок интегрирования на 10 частей с длиной .
Составим таблицу значений подынтегральной функции в полученных точках:
i | x | |
0 | 1 | 0,95634 |
1 | 1,2 | 0,67227 |
2 | 1,4 | 0,21264 |
3 | 1,6 | -0,37011 |
4 | 1,8 | -0,99990 |
5 | 2 | -1,58346 |
6 | 2,2 | -2,01935 |
7 | 2,4 | -2,21042 |
8 | 2,6 | -2,07991 |
9 | 2,8 | -1,58951 |
10 | 3 | -0,75582 |
Формулы для вычисления интеграла и их результат:
а) Формула левых прямоугольников:
b) Формула правых прямоугольников:
с) Формула трапеций:
d) Формула Симпсона:
4,688 просмотров всего, 2 просмотров сегодня
otvet-prost.ru
Интерполяционным многочленом Лагранжа называется многочлен
(31.1)
Этот многочлен удовлетворяет условиямГде—
Узлы (или полюсы) интерполяции,— заданные числа.
Интерполяционной формулой Лагранжа называется формула
(31.2)
Формулы (31.1) и (31.2) можно записать так:
Где
(31.3)
Производя интерполирование функцииПо формуле Лагранжа (31.2), заменяют эту функцию полиномом, совпадающим с ней вДанных точках отрезка, В остальных точках этого отрезка разность
Отлична от нуля и представляет собой погрешность метода. Эта разность, называемая остаточным членом интерполяции, определяется формулой
В которойВыражается равенством (31.3),- точка промежутка
Зависящая от
Пример 31.1. Найти интерполяционный многочлен Лагранжа, который в точкахПринимает соответственно значения
ПриФормула (31.1) имеет вид
Подставляя в эту формулу заданные значения, находим Итак,
Пример 31.2. Найти интерполяционный многочлен Лагранжа, для которого
В данном случае
ПриФормула (31.1) принимает вид
Подставляя в эту формулу данные значения, получаем 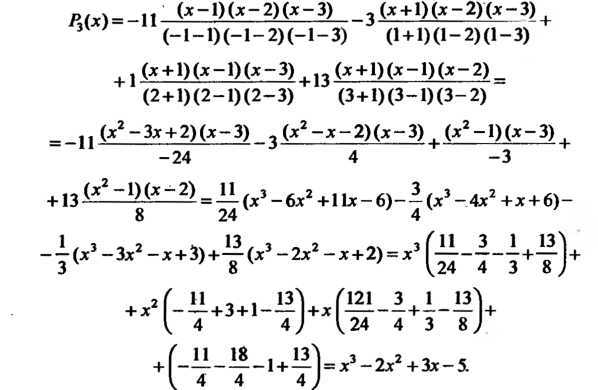 Следовательно,
Следовательно,
Термин «интерполяция» впервые употребил Д. Валлис (1656) при составлении астрономических и математических таблиц.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Моделирование в электроэнергетике — Интерполяционный многочлен в форме Лагранжа
Выборка экспериментальных данных представляет собой массив данных, который характеризует процесс изменения измеряемого сигнала в течение заданного времени (либо относительно другой переменной). Для выполнения теоретического анализа измеряемого сигнала необходимо найти аппроксимирующую функцию, которая свяжет дискретный набор экспериментальных данных с непрерывной функцией — интерполяционным полиномом n-степени. Одним из способов представления данного интерполяционного полинома n-степени может быть использован многочлен в форме Лагранжа.
Интерполяционный многочлен в форме Лагранжа – это математическая функция позволяющая записать полином n-степени, который будет соединять все заданные точки из набора значений, полученных опытным путём или методом случайной выборки в различные моменты времени с непостоянным временным шагом измерений.
1. Интерполяционная формула Лагранжа
В общем виде интерполяционный многочленв форме Лагранжа записывается в следующем виде:
где ˗ степень полинома ;
˗ значение значения интерполирующей функции в точке ;
˗ базисные полиномы (множитель Лагранжа), которые определяются по формуле:
Так, например, интерполяционный многочленв форме Лагранжа, проходящий через три заданных точки , будет записываться в следующем виде:
Многочлен в форме Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что при построении полинома степени n+1 полностью теряется информация о предыдущем полиноме степени n, т.е. с изменением числа узлов приходится все вычисление выполнить заново.
2. Погрешность интерполяционного полинома в форме Лагранжа
Рассмотрим функцию f(x), которая непрерывна и дифференцируема на рассматриваемом отрезке [a, b]. Интерполяционный полином L(x) в форме Лагранжа принимает в точках заданные значения функции . В остальных точках интерполяционный полином L(x) отличается от значения функции f(x) на величину остаточного члена, который определяет абсолютную погрешность интерполяционной формулы Лагранжа:
Абсолютную погрешность интерполяционной формулы Лагранжа определяют следующим образом:
где n˗ степень полинома
Переменная представляет собой верхнюю границу значения модуля (n +1)-й производной функции f(x) на заданном интервале [a, b]
Погрешность интерполяции методом Лагранжа зависит от свойств функцииf(x), а также от расположения узлов интерполяции и точки x. В случае если погрешность не достигает нужной точности, то нужно разбить отрезок на части и интерполировать каждую часть в отдельности – кусочная интерполяция.
Выбор узлов интерполяции
С помощью корректного выбора узлов можно минимизировать значение в оценке погрешности, тем самым повысить точность интерполяции. Данная задача может быть решена с помощью многочлена Чебышева:
В качестве узлов следует взять корни этого многочлена, то есть точки:
3. Методика вычисления полинома в форме Лагранжа
Алгоритм вычисления полинома в форме Лагранжа позволяет разделить задачи определения коэффициентов и вычисления значений полинома при различных значениях аргумента:
1. В качестве исходных данных задается выборка из n-точек, которая включает в себя значения функции и значения аргумента функции.
2. Выполняется вычисление полинома n-степени в форме Лагранжа по следующей формуле:
Алгоритм вычисления полинома в форме Лагранжа представлен на рисунке 1.
Методика вычисления полинома в форме Лагранжа

Рис.1. Методика вычисления полинома в форме Лагранжа
В качестве примера рассмотрим следующую практическую задачу. В рамках задачи известен набор шести значений, которые получены методом случайной выборки для различных моментов времени. Следует отметить, что данная выборка значений описывает функция на интервале [0, 10]. Необходимо построить многочлен в форме Лагранжа для представленного набора значений. С помощью интерполяционной формулывычислить приближенное значение функции в точке , а также определить оценку погрешности результата вычислений.
Многочлен в форме Лагранжа, который строится на основании шести значений, представляет собой полином 5 степени. Результат построения полинома в форме Лагранжа показан в графическом виде.
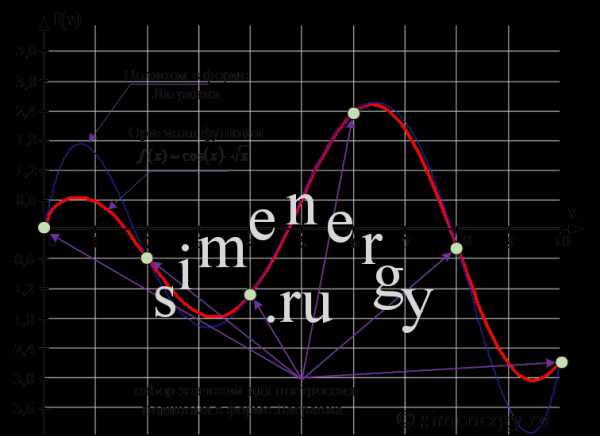
Рис.2. Исходная функция и полином в форме Лагранжа, построенный по шести заданным точкам
С помощью найденного полинома можно определить значение функции в любой точке заданного интервала. Определение промежуточных значений величины по имеющемуся дискретному набору известных значений называется «интерполяцией». В соответствии с условиями задачи полином в форме Лагранжа в точке x=9,5 принимает следующее значение: L(9,5)= – 4,121. Из графика видно, что полученное значение не совпадает cо значением функции f(x) на величину абсолютной погрешности интерполяционной формулы Лагранжа.
Интерполяционный полином в форме Лагранжа часто оказывается удобным для проведения различных теоретических исследований в области вычислительной математики. Так, например, полином в форме Лагранжа используются для интерполяции, а также для численного интегрирования таблично-заданной функцией.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
simenergy.ru
Интерполяция полиномом Лагранжа | Компьютерная графика
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
namespace Newton_Interpolate
{
public partial class Form1 : Form
{
public struct point //Структура точки
{
public float X, Y; //Машинные координаты
public float x, y; //Реальные координаты
}
//Координаты исходных точек. Значение x и y должны быть по модулю не больше 30.
public float[,] Pts = { { -27f, 24.5f },
{ -22f, 12.8f },
{ -18.4f, 10.2f },
{ 8.6f, -4f },
{ 0f, -4.5f},
{4f, 2.8f},
{14.2f, 12.6f},
{17f, 24.5f},
{21f, 26f}
};
public point[] Points = new point[100]; //Массив точек
public Font drawFont = new Font("Arial", 8); //Стиль шрифта и его размер, для отрисовки координат точек на плоскости
public int xc=300, yc=300; //Координаты центра координатных осей
public Form1()
{
InitializeComponent();
}
//Отрисовка плоскости, с точками и координатными осями
public void drawPlain()
{
Graphics g = Graphics.FromHwnd(picturebox1.Handle);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
g.Clear(Color.White);
Pen Axis = new Pen(Color.Black, 1);
g.DrawLine(Axis, 0, 300, 600, 300);
g.DrawLine(Axis, 300, 0, 300, 600);
for (int i = 0; i <= 600; i += 10)
{
g.DrawLine(Axis, i, 298, i, 302);
g.DrawLine(Axis, 298, i, 302, i);
}
for (int i = 0; i < (Pts.Length / 2); i++)
{
Points[i].x = Pts[i, 0];
Points[i].y = Pts[i, 1];
Points[i].X = xc + Points[i].x * 10;
Points[i].Y = yc - Points[i].y * 10;
}
DrawPoints();//Отрисовка точек
}
public int ChangeCoordinates(float a, int isY) //Перевод координат из реальных в машинные
{
if (isY == 1) return (int)(yc - a * 10);
return (int)(xc + a * 10);
}
//Высчитывание полинома Лагранжа в заданном отрезка, с заданными точками.
public float Lagrange(float x)
{
float res = 0f, s = 0f, s1 = 1f, s2 = 1f;
for (int i = 0; i < (Pts.Length / 2); i++)
{
s1 = 1f; s2 = 1f;
for (int j = 0; j < (Pts.Length / 2); j++)
{
if (i != j)
{
s1 = s1 * (x - Points[j].x);
s2 = s2 * (Points[i].x - Points[j].x);
}
}
s = Points[i].y * (s1 / s2);
res = res + s;
}
return res;
}
//Отрисовка точек и их координат на плоскости
public void DrawPoints()
{
Graphics g = Graphics.FromHwnd(picturebox1.Handle);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
SolidBrush pointBrush = new SolidBrush(Color.Red);
SolidBrush drawPointBrush = new SolidBrush(Color.Black);
for (int i = 0; i < (Pts.Length / 2); i++)
{
g.FillEllipse(pointBrush, Points[i].X-2, Points[i].Y-2, 4, 4);
String drawString = "[" + Points[i].x + "; " + Points[i].y + "]";
PointF drawPoint = new PointF(Points[i].X, Points[i].Y);
g.DrawString(drawString, drawFont, drawPointBrush, drawPoint);
}
}
//Отрисовка интерполированной функции по нажатию на кнопку "Нарисовать"
private void Draw_Button_Click(object sender, EventArgs e)
{
Graphics g = Graphics.FromHwnd(picturebox1.Handle);
g.SmoothingMode = System.Drawing.Drawing2D.SmoothingMode.AntiAlias;
SolidBrush drawLineNewton = new SolidBrush(Color.Blue);
drawPlain();
for (float i = -30.0f; i <= 30.0f; i += 0.0005f)
{
g.FillRectangle(drawLineNewton, ChangeCoordinates(i, 0), ChangeCoordinates(Lagrange(i), 1), 1, 1);
}
}
}
}grafika.me
Интерполяция, полином Лагранжа
Общие положения
В
вычислительной практике часто приходится
иметь дело с функциями 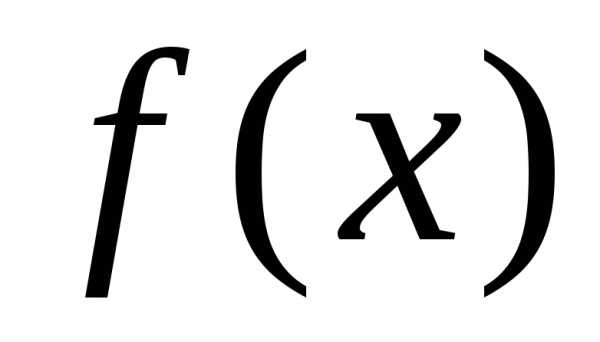 ,
заданными таблицами их значений для
некоторого конечного множества значенийх: .
,
заданными таблицами их значений для
некоторого конечного множества значенийх: .
В
процессе же решения задачи необходимо
использовать значения 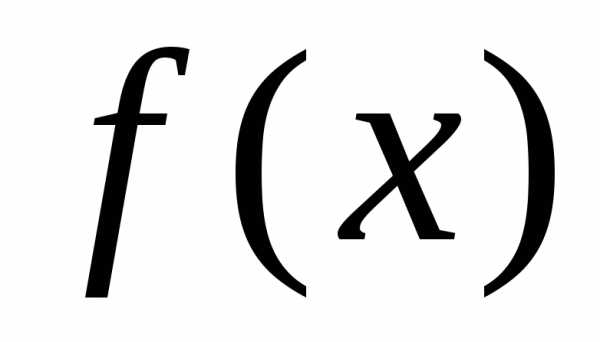 для промежуточных значений аргумента.
В этом случае строят функцию Ф(x),
достаточно простую для вычислений,
которая в заданных точкахx0,
x1,…,xn,называемых узлами интерполяции, принимает
значения ,
а в остальных точках отрезка (x0,xn),
принадлежащего области определения
для промежуточных значений аргумента.
В этом случае строят функцию Ф(x),
достаточно простую для вычислений,
которая в заданных точкахx0,
x1,…,xn,называемых узлами интерполяции, принимает
значения ,
а в остальных точках отрезка (x0,xn),
принадлежащего области определения 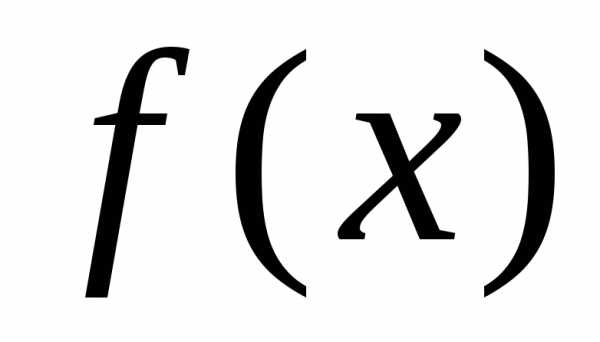 ,
приближенно представляет функцию
,
приближенно представляет функцию 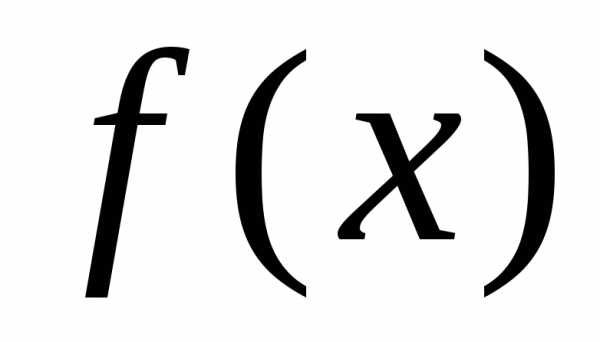 с той или иной степенью точности.
с той или иной степенью точности.
При
решении задачи в этом случае вместо
функции 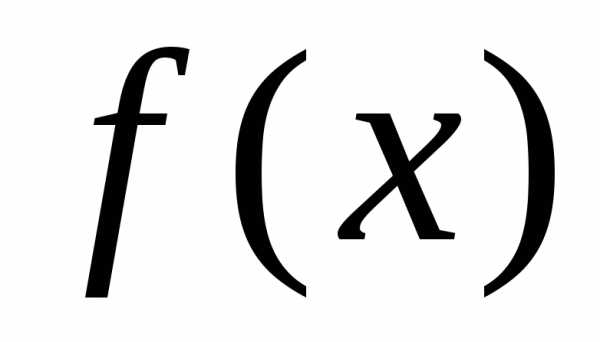 оперируют с функцией Ф(x). Задача построения
такой функции Ф(x) называется задачей
интерполирования. Чаще всего интерполирующую
функцию Ф(x) отыскивают в виде алгебраического
полинома.
оперируют с функцией Ф(x). Задача построения
такой функции Ф(x) называется задачей
интерполирования. Чаще всего интерполирующую
функцию Ф(x) отыскивают в виде алгебраического
полинома.
Интерполяционный полином
Для каждой функции 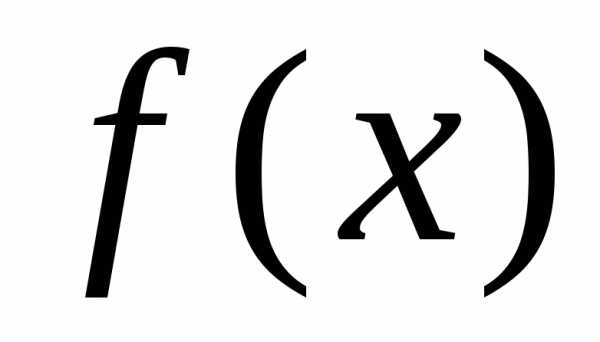 ,
определенной на [a,b],
и любого набора узлов x0,
x1,….,xn( xi
,
определенной на [a,b],
и любого набора узлов x0,
x1,….,xn( xi [a,b], xi
[a,b], xi xj при i
xj при i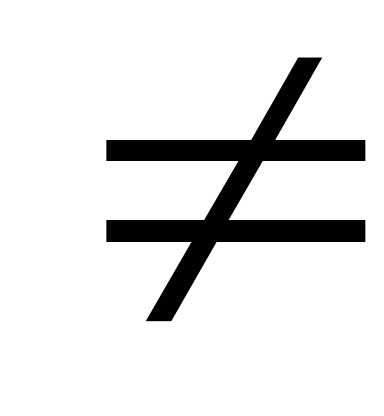
 j
) среди алгебраических многочленов
степени не выше n существует единственный
интерполяционный многочлен Ф(x), который
может быть записан в форме:
j
) среди алгебраических многочленов
степени не выше n существует единственный
интерполяционный многочлен Ф(x), который
может быть записан в форме:
, (3.1)
где 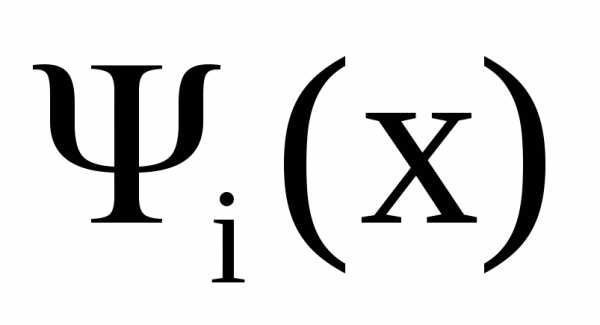 — многочлен n-ой степени, обладающий
следующим свойством:
— многочлен n-ой степени, обладающий
следующим свойством:
(3.2)
Для
интерполяционного полинома многочлен 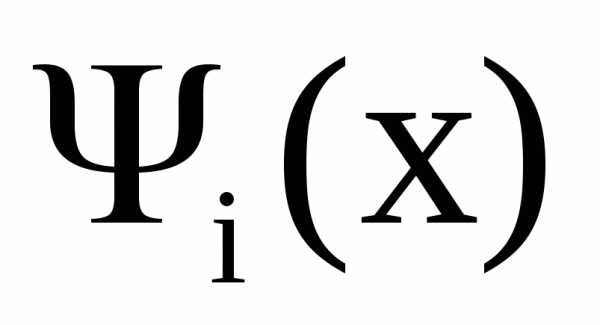 имеет вид:
имеет вид:
(3.3)
Этот многочлен (3.1) и решает задачу интерполирования и называется интерполяционным полиномом Лагранжа.
Пример
В
качестве примера рассмотрим функцию
вида 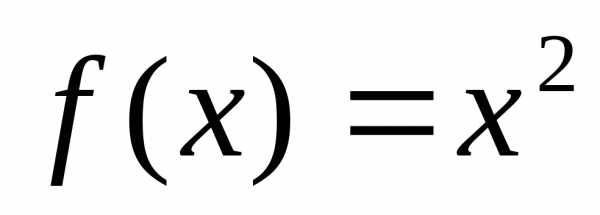 на интервале
на интервале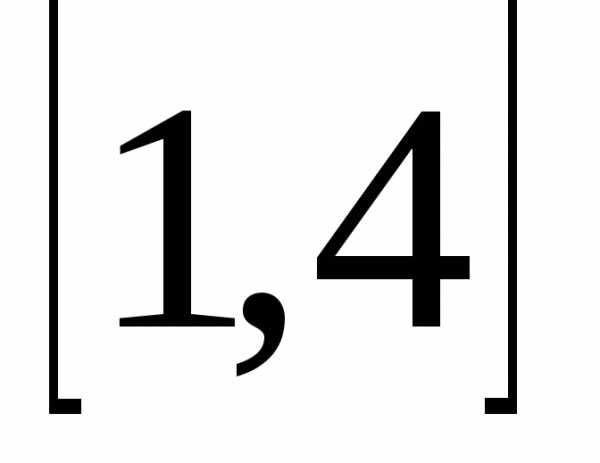 заданную табличным способом.
заданную табличным способом.
Необходимо определить значение функции в точке x-2.5. Воспользуемся для этого полином Лагранжа. Исходя из формул (3.1 и 3.3) запишем этот полином в явном виде:
(3.4).
Тогда подставляя в формулу (3.4) исходные значения из нашей таблицы получим
Полученный результат соответствует теории т.е. .
Интерполяционная формула Лагранжа
Интерполяционный полином Лагранжа может быть записан в другой форме:
(3.5)
Запись полинома в виде (3.5) более удобна для программирования.
При
решении задачи интерполяции величина n называется порядком интерполирующего
полинома. При этом, как видно из формул
(3.1) и (3.5), число узлов интерполирования
всегда будет равно n+1 и значение x, для которого
определяется величина 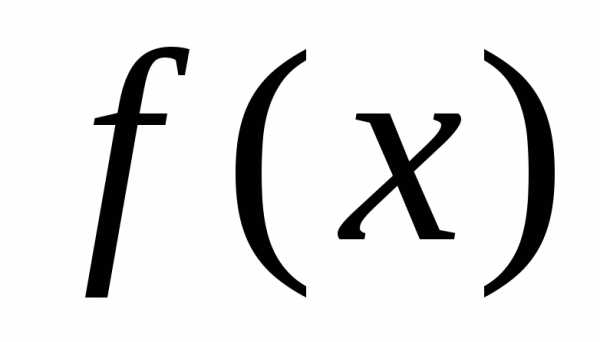 , должно
лежать внутри области определения узлов
интерполяции т.е.
, должно
лежать внутри области определения узлов
интерполяции т.е.
. (3.6)
В некоторых практических случаях общее известное число узлов интерполяции m может быть больше, чем порядок интерполирующего полинома n.
В этом случае, прежде чем реализовывать процедуру интерполяции согласно формуле (3.5), необходимо определить те узлы интерполяции, для которых справедливо условие (3.6). При этом следует помнить, что наименьшая погрешность достигается при нахождении значения x в центре области интерполяции. Для обеспечения этого предлагается следующая процедура:
После ввода в программу значения величины х необходимо проверить условие x0 x xm, где x0 и xm – начальное и конечное значение узловых точек интерполяции.
При выполнения предыдущего условия начинается поиск области интерполяции, для чего находим первое xi такое, для которого выполняется условие xi > x, при этом номер i будет соответствовать середине интервала интерполяции. Для определения области интерполяции ее левая граница будет начинаться с номера , а заканчиваться узлом с номером.
После выполнения пунктов 1 и 2 программируется формула (3.5).
Основное назначение интерполяции – это вычисление значений табулированной функции для не узловых (промежуточных) значений аргумента, поэтому интерполяцию часто называют «искусством чтения таблиц между строками».
studfiles.net
Интерполяционный полином Лагранжа
45
ИНТЕРПОЛИРОВАНИЕ
При исследовании явлений природы с помощью математического аппарата используются различные функции.
Функции могут задаваться различными способами. Простейший из них – задание аналитического выражения, которое дает возможность по любым допустимым значениям аргумента вычислить значение функции. На практике такие случаи бывают весьма редко.
Часто функции определяются бесконечными рядами. Вычисление значений функции с помощью бесконечного ряда – довольно громоздкая операция, требующая сходимости и достаточного количества членов ряда.
Функция может быть представлена неопределенным интегралом или дифференциальным уравнением.
Во всех
случаях, когда значения функции либо
невозможно точно вычислить, либо
вычисление слишком громоздко, прибегают
к составлению таблиц функции, если эта
функция встречается в различных задачах.
Таким образом, мы приходим к табличному
заданию функции, то есть такому, когда
функция 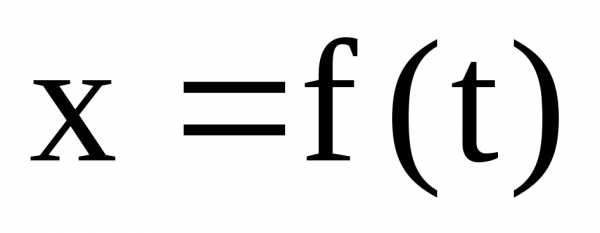 определяется таблицей своих значений
определяется таблицей своих значений 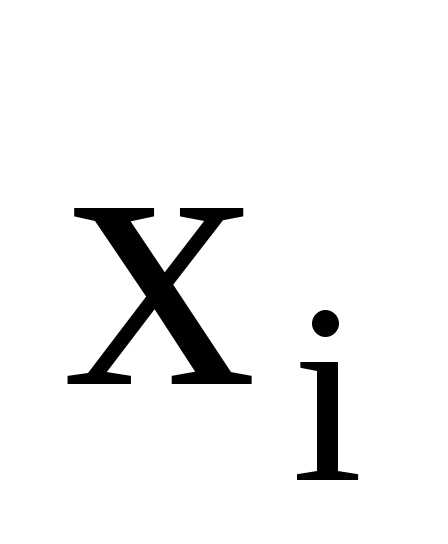 при заданных значениях аргументов
при заданных значениях аргументов  ,
i=1,2,…n:
,
i=1,2,…n:
t1 | x1 |
t2 | x2 |
… | … |
ti | xi |
… | … |
tn | xn |
Табличные значения функции и аргумента называют узлами таблицы.
Разность двух соседних значений аргумента называется шагом таблицы . Если эта разность изменяется, то таблица называется таблицей с переменным шагом, если разность неизменна, то это таблица с постоянным шагом. Стараются строить таблицы с постоянным шагом. Шаг, вообще говоря, не может быть очень малым, иначе сильно возрастает объем таблицы.
Обычно таблица располагается так, что аргумент (например, время) возрастает.
При решении задач естествознания, как правило, приходится иметь дело со случаями, когда нужны значения функции не только для табличных значений аргумента (узлов). Так, например, часто требуется знать координаты Солнца относительно Земли, но почти всегда не в 0h Всемирного времени, как дается в Астрономическом ежегоднике, а в определенные промежуточные моменты.
Поэтому имеет большое практическое значение следующая задача: дана табличная функция; необходимо найти способ приближенного определения значений функции для произвольных значений аргумента, не совпадающих с узлами таблицы.
Если значение аргумента задано внутри области табличных значений аргумента, то указанную задачу называют задачей интерполяции; если же значение аргумента задано вне табличной области, то говорят об экстраполяции.
Интерполирование по табличной функции сводится к приближению табличной функции другой, легко вычисляемой функцией. Выражение для этой легко вычисляемой функции используется для интерполяции: заданное значение аргумента подставляется в нее и производятся вычисления.
Построение приближения табличной функции представляет неопределенную задачу и требует дополнительных соглашений.
Во-первых, надо условиться относительно класса функций, используемых для приближения. Очевидно, желательна возможность легкого вычисления функции по заданному значению аргумента. Этому условию удовлетворяют алгебраические полиномы, которые чаще всего и используются для приближения.
Если табличная функция периодическая и приближение нужно в области, охватывающей весь период, то используют тригонометрические полиномы. Когда периодическую функцию нужно приблизить только на небольшой части периода, то обычно используют алгебраические полиномы.
Во-вторых, надо потребовать, чтобы приближение было возможно лучшим. Что значит «лучшим»? На практике употребляют различные критерии наилучшего приближения. Мы примем такой: приближающий полином, который должен точно представлять узлы таблицы. То есть интерполяционный полином должен на графике пройти через все точки (узлы) табличной функции. По этой причине интерполяция с указанным условием называется точечной интерполяцией.
Если какая-либо величина изменяется пропорционально времени, то разность значений через равные промежутки времени постоянна. В этом случае, можно применить простейшее линейное интерполирование.
Если за 24 часа величина Х изменяется равномерно на , то ее значение для момента t часов, прошедших после момента t0 равно
 .
.
Но такого практически никогда не бывает, разность соседних значений в таблице изменяется, и иногда сложным образом. Можно допустить линейное интерполирование, если не требуется большой точности. Но если надо получить значение табличной функции с той же точностью, что и в узлах, то, согласно принятым соглашениям, надо строить интерполяционный полином.
Предположим,
имеется таблица из двух столбцов 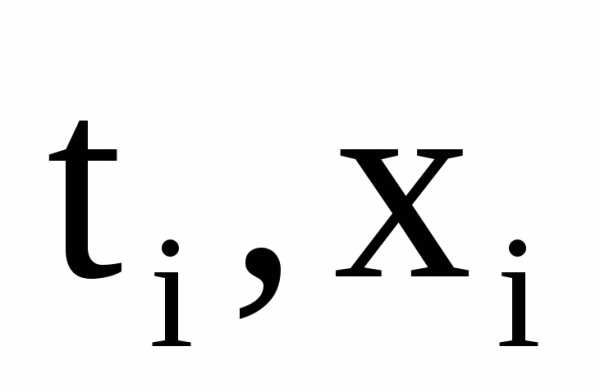 ,
,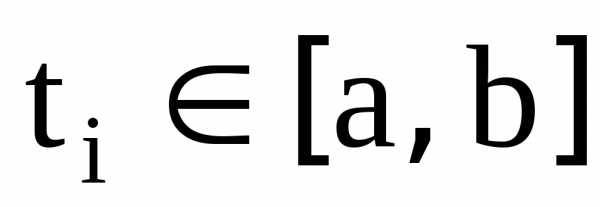 ,
,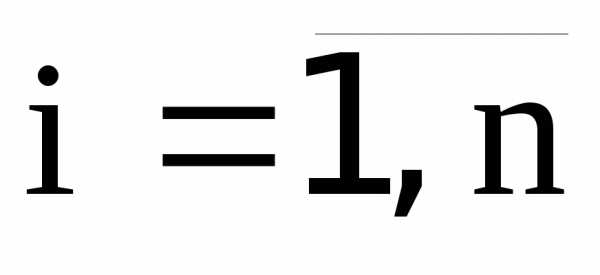 .
Требуется найти полином низшей степени,
который принимает значения
.
Требуется найти полином низшей степени,
который принимает значения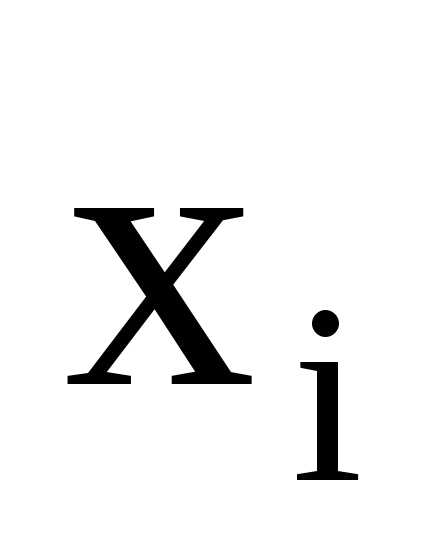 для каждого аргумента
для каждого аргумента :
: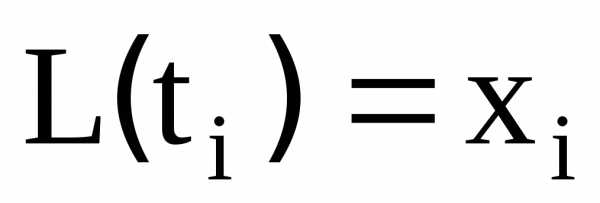 ,
то есть совпадающий со значениями
табличной функции в узлах. Приближенно
будем считать, что для любого значения
аргументаt
,
,
то есть совпадающий со значениями
табличной функции в узлах. Приближенно
будем считать, что для любого значения
аргументаt
,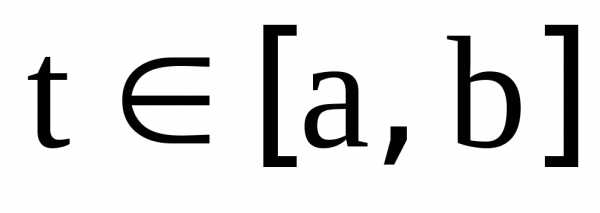 .
Подобное приближенное равенство называют
интерполяционной формулой. Итак, надо
найти интерполяционную формулу, а затем
оценить ее погрешность.
.
Подобное приближенное равенство называют
интерполяционной формулой. Итак, надо
найти интерполяционную формулу, а затем
оценить ее погрешность.
Найдем, прежде всего, полином (многочлен), который принимает значение 1 в одной узловой точке и 0 во всех других. Очевидно несложная функция
, [7]
где
штрих у знака произведения означает 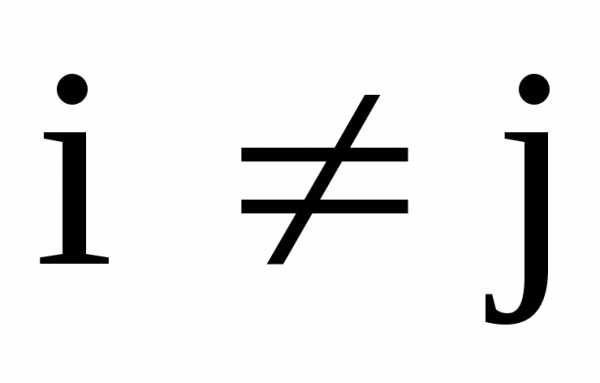 ,
является требуемым полиномом степениn-1.
,
является требуемым полиномом степениn-1.
Заметим, что через n точек однозначно можно провести полином степени не выше n-1, например, через 2 точки можно однозначно провести прямую (кривую 1-го порядка), через 3 точки – параболу (кривую 2-го порядка) и т.д.
Легко
проверить, что 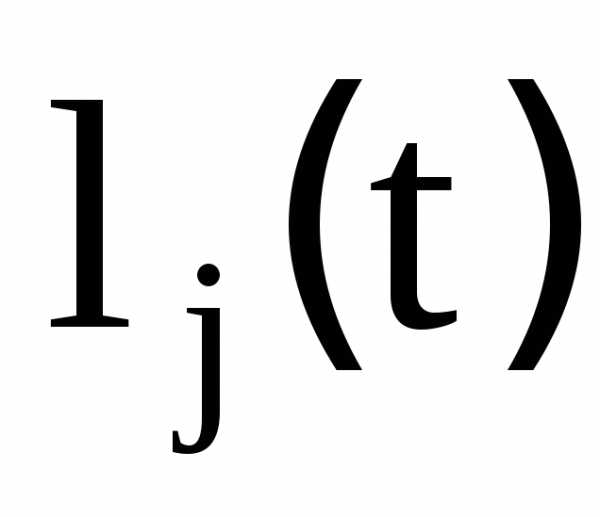 равен 1, если
равен 1, если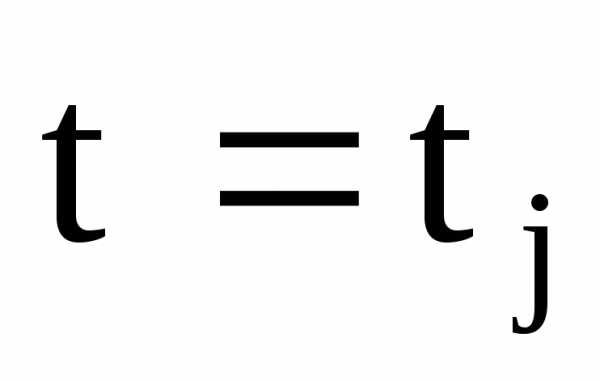 ;
и 0, когда.
Домножим
;
и 0, когда.
Домножим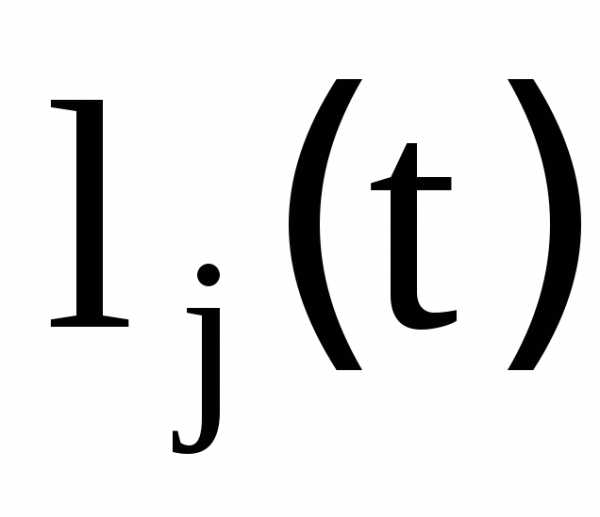 на
на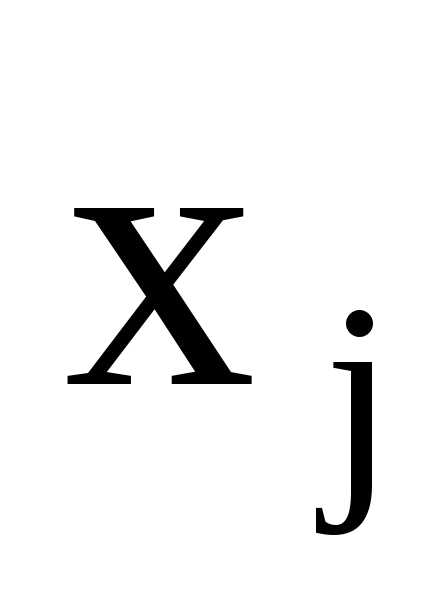 ,
полученный полином
,
полученный полином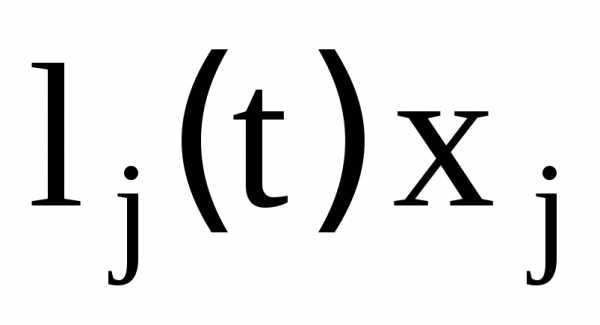 принимает значение
принимает значение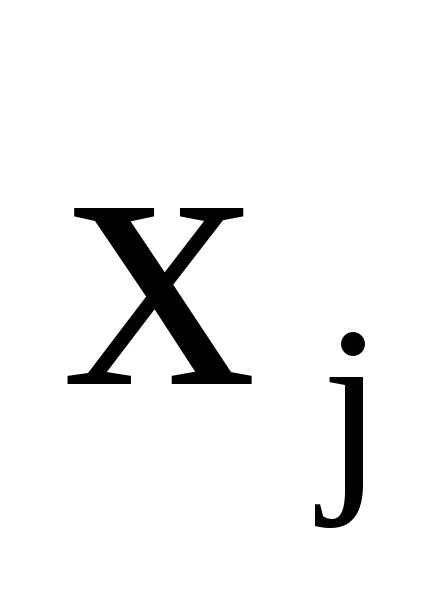 в j-й узловой точке и равен нулю во всех
других узлах. Поэтому сумма таких
полиномов будет принимать значения
в j-й узловой точке и равен нулю во всех
других узлах. Поэтому сумма таких
полиномов будет принимать значения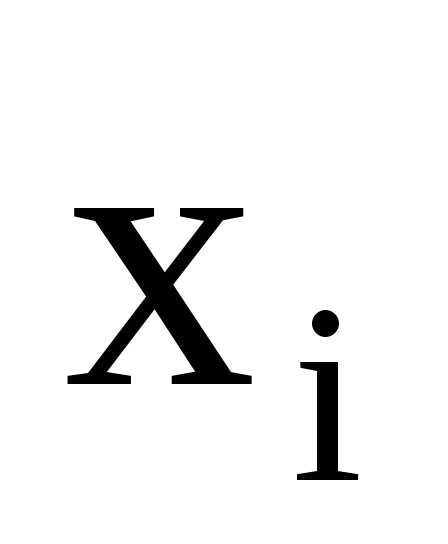 для аргумента
для аргумента :
:
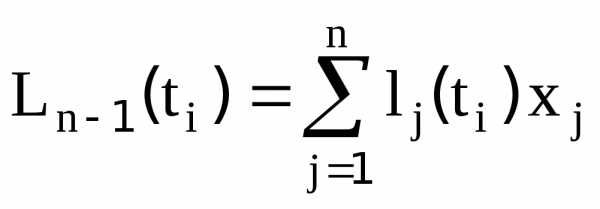 ,
,
Отметим:
j
– порядковый номер промежуточного
полинома 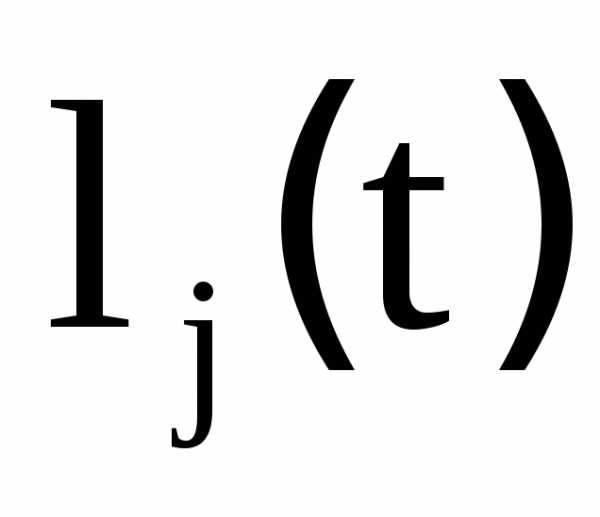 в сумме, строящей полином Лагранжа;i
– номер любого узла таблицы.
в сумме, строящей полином Лагранжа;i
– номер любого узла таблицы.
В общем случае
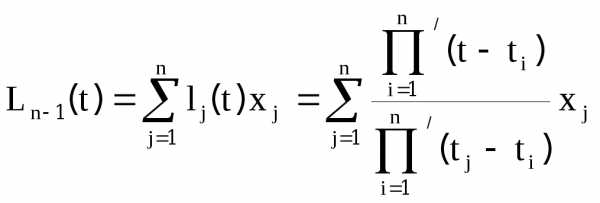 [8]
[8]
Это
и есть искомый полином степени n-1,
проходящий через все n
узлов таблицы 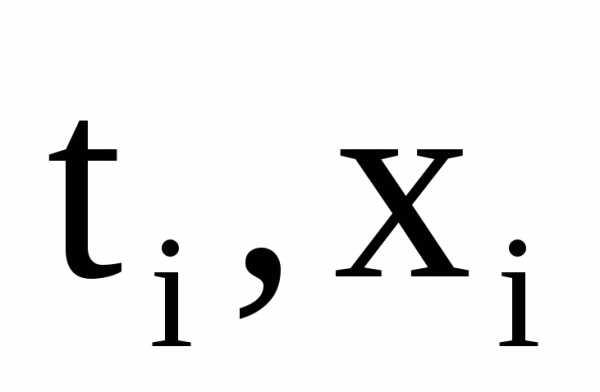 :,
:,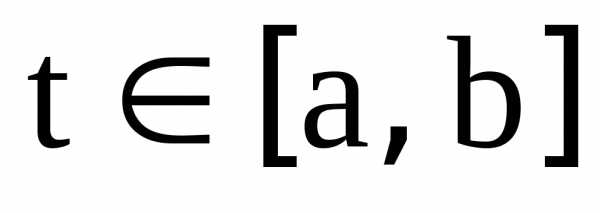 .
.
Впервые интерполяционный полином Лагранжа был опубликован в 1795 году.
Подчеркнем: если дано n узловых точек, то соответствующий полином степени n-1, проходящий через эти точки, однозначно (в пределах ошибок округления) определен, независимо от способа построения и системы обозначений. Если используются разные узловые точки, то, конечно, полиномы могут быть различными, но одинаковые узловые точки должны приводить к одинаковым полиномам (в пределах ошибок округления).
Потребовав,
чтобы полином принимал значения 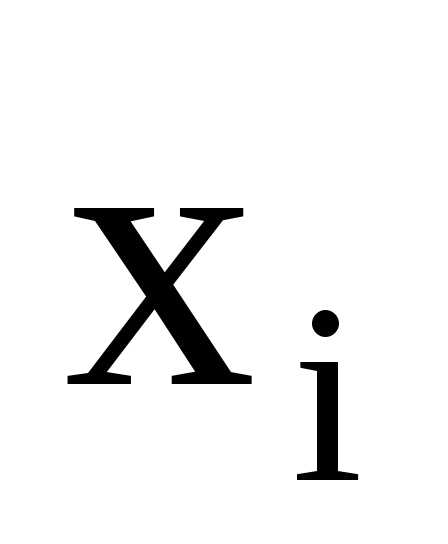 для каждого аргумента
для каждого аргумента ,
мы построили полином Лагранжа. Если
потребовать, чтобы полином принимал не
только значения табличной функции в
узлах, но и первая производная от полинома
была равна первой производной табличной
функции в узлах, то мы построим полином
Эрмита.
,
мы построили полином Лагранжа. Если
потребовать, чтобы полином принимал не
только значения табличной функции в
узлах, но и первая производная от полинома
была равна первой производной табличной
функции в узлах, то мы построим полином
Эрмита.
Пример. Дана таблица
Построить интерполяционный полином Лагранжа и найти значение L(2).
n=2. Согласно [8] ;
Согласно [7] ;.
Или ,
. Подставляя числа
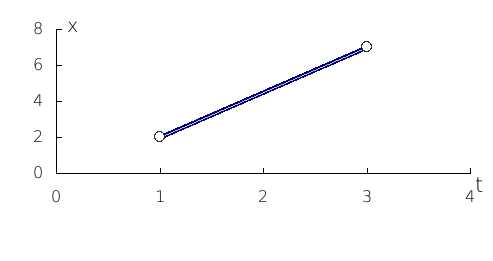 .
.
Это интерполяционный полином 1-го порядка – прямая.
Для t=2, L=4.5.
Пример. Дана таблица
Построить интерполяционный полином Лагранжа и найти значение L(2).
n=3. Согласно [8] ;
Согласно [7]
;
,
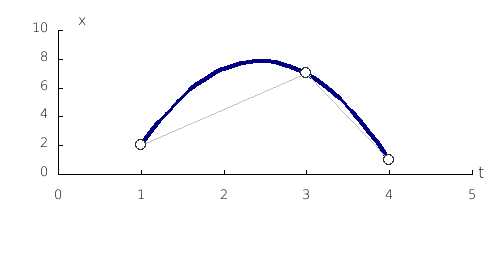 .
.
Это интерполяционный полином 2-го порядка – парабола.
Для t=2, L=7.33.
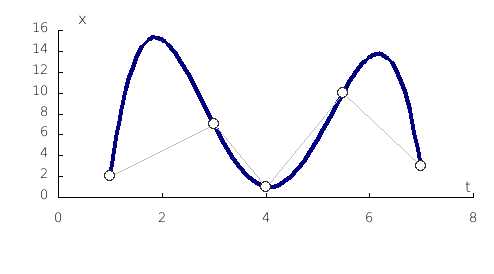
На этом рисунке показан график полинома Лагранжа, построенного по 5-ти узлам – полином 4-го порядка.
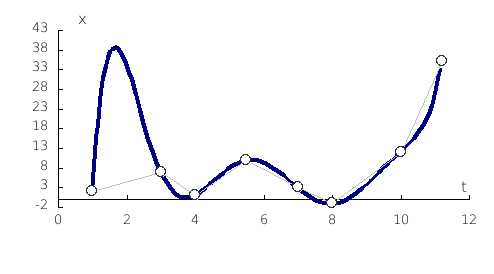
На этом рисунке показан график полинома Лагранжа, построенного по 8-ти узлам – полином 7-го порядка.
Из рисунков видно, что значения табличной функции между узлами полиномом Лагранжа представляются неудовлетворительно. Кроме того, полином Лагранжа неудобен для практического использования. На практике обычно известна требуемая точность результата, а множество используемых узлов можно выбирать.
studfiles.net
2. Интерполяционный многочлен лагранжа
Интерполяционная формула Лагранжа используется для произвольно заданных узлов интерполирования.
Пусть в точках x0, x1, …, xn таких, что a x0<…< xnb, известны значения функции y=f(x), т.е. на отрезке [a, b] задана табличная (сеточная) функция
x | x0 | x1 | … | xn |
y | y0 | y1 | … | yn |
Требуется построить полиномLn(x) степени не выше n, имеющий в заданных узлах x0, x1, …, xn те же значения, что и функция f(x), т.е. такой, что
Ln(xi)=yi (i=0, 1, 2,…, n).
Будем
строить многочлен n-ой
степени Ln(x) в виде линейной комбинации 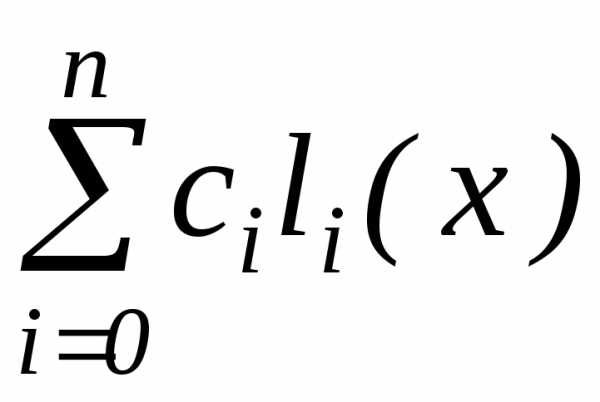 многочленов n-й
же степени li(x) (i=0,
1, 2,…, n).
Индекс i показывает номер многочлена. Для того
чтобы этот многочлен был интерполяционным
для функции f(x),
достаточно зафиксировать в качестве
коэффициентов ci этой линейной комбинации заданные в
табл. (2.1) значения yi=f(xi),
а от базисных многочленов li(x)
потребовать выполнения условия
многочленов n-й
же степени li(x) (i=0,
1, 2,…, n).
Индекс i показывает номер многочлена. Для того
чтобы этот многочлен был интерполяционным
для функции f(x),
достаточно зафиксировать в качестве
коэффициентов ci этой линейной комбинации заданные в
табл. (2.1) значения yi=f(xi),
а от базисных многочленов li(x)
потребовать выполнения условия
 (2.2)
(2.2)
где ij – символ Кронекера.
В этом случае для многочлена
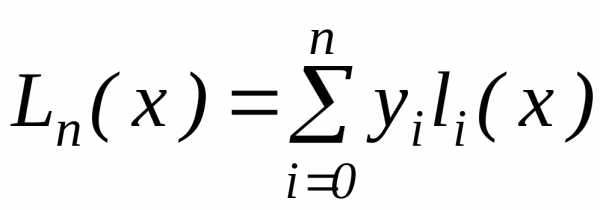 в каждом узлеxj (j{0,
1,…,n}),
в силу (2.2), справедливо
в каждом узлеxj (j{0,
1,…,n}),
в силу (2.2), справедливо
Ln(xj)=l0(xj)y0+…+lj-1(xj)yj-1+lj(xj)yj+lj+1(xj)yj+1+…+ln(xj)yn=0+…+0+yj+0+…+0=yj
Чтобы конкретизировать базисные многочлены li(X), учтем, что они должны удовлетворять условиям (2.2). Равенство нулюi-го многочлена во всех узлах, кромеi-го, означает, чтоli(X)можно записать в виде
li(x)=Ai(x-x0)…(x-xi-1)(x-xi+1)…(x-xn),
а коэффициент Ai этого представления легко получается из содержащегося в (2.2) требования li(xi)=1. Подставляя в выражение li(xi) значение x=xi и приравнивая результат единице, получаем:
Таким образом, базисные многочлены Лагранжа имеют вид:
,
а искомый интерполяционный многочлен Лагранжа:
(2.3)
Пример. Построить интерполяционный полином для функции y=sin x.
Возьмем
сетку, состоящую из трех точек: x0=0; x1=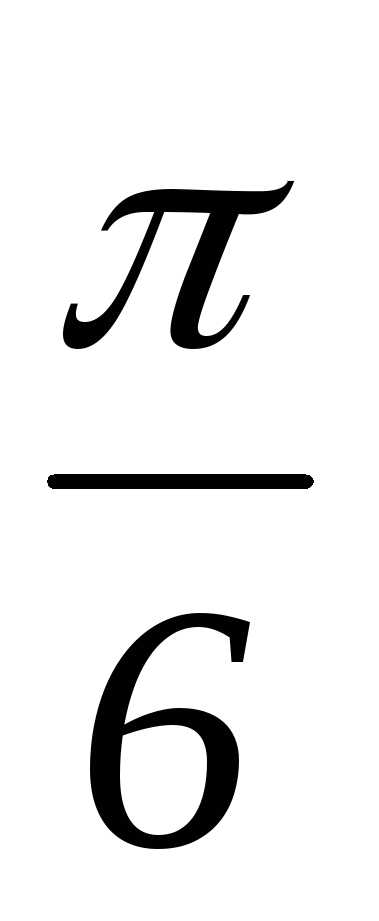 ; x2=
; x2=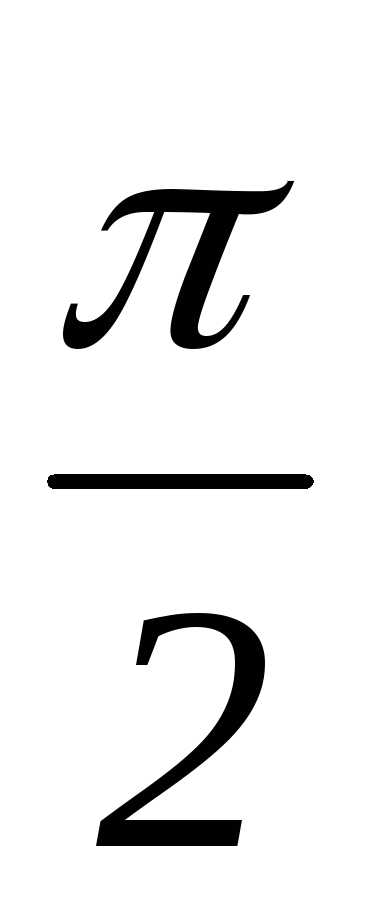 ,
выпишем соответствующие этим аргументам
значения функции sin x: y0=0; y1=
,
выпишем соответствующие этим аргументам
значения функции sin x: y0=0; y1=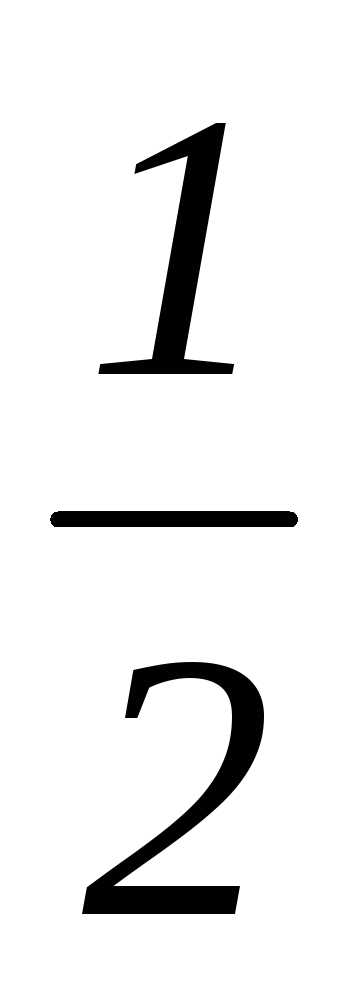 ; y2=1.
; y2=1.
Построим по этой таблице интерполяционный полином второй степени. По формуле Лагранжа (2.3):
.
Легко
проверить, что в точках сетки этот
полином принимает нужные значения.
Чтобы получить представление о погрешности
интерполирования, сравнивая значения sin x и интерполяционного полинома в точке х=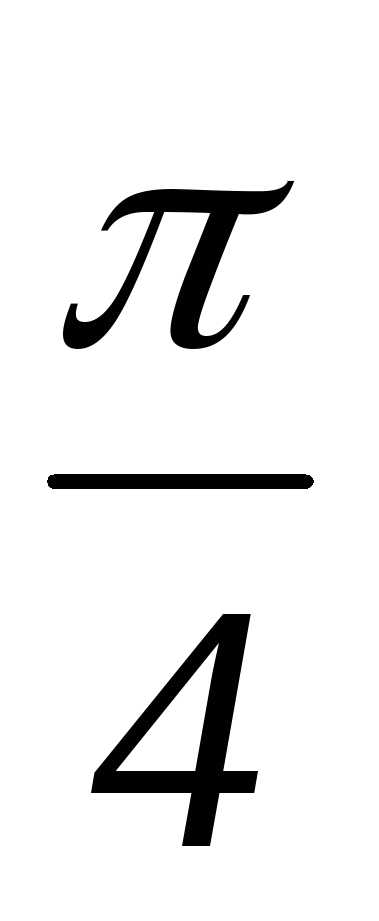 .
.
.
Значительная
величина погрешности определяется тем,
что на отрезке длиной 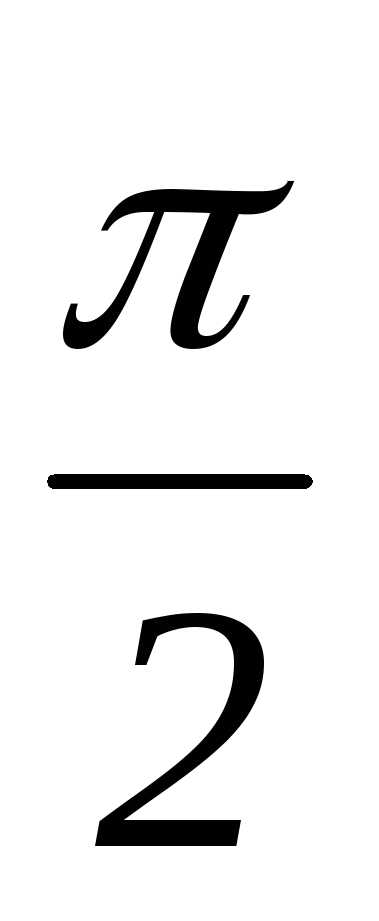 мы взяли грубую сетку, состоящую всего
из трех точек. Чтобы улучшить точность
интерполирования, нужно либо увеличить
число точекn
и повысить соответственно степень
интерполяционного полинома Ln(x),
либо уменьшить длину исходного отрезка.
мы взяли грубую сетку, состоящую всего
из трех точек. Чтобы улучшить точность
интерполирования, нужно либо увеличить
число точекn
и повысить соответственно степень
интерполяционного полинома Ln(x),
либо уменьшить длину исходного отрезка.
3. Интерполяционная схема эйткена
Пусть функция f(x) и расположение узлов x0, x1, …, xn на отрезке интерполяции [a, b] таковы, что имеет место сходимость процесса интерполяции, т.е. Rn(x)0 при n. Пусть требуется найти не общее выражение Ln(x), а лишь его значения при конкретных x, т.е. решается частная задача вычисления отдельных приближенных значений функции f(x) с помощью вычисления соответствующих им значений интерполяционного многочлена Лагранжа Ln(x). Для построения эффективного способа решения такой частной задачи интерполяции учтем следующее:
использование многочлена Лагранжа в виде (2.3) неудобно из-за его громоздкости, что ведет к большим вычислительным затратам;
заранее не известно, многочлены какой степени нужно использовать для интерполирования данной функции с требуемой точностью. А постепенное улучшение точности за счет вычислений Ln(x) с большим показателем степени n невыгодно, т.к. Ln-1(x) плохо перестраивается в Ln(x);
функция f(x) задается таблицей своих приближенных значений. Процесс сходимости Ln(x) к f(x) при больших значениях n будет нарушен влиянием на результат исходных ошибок.
Построим
вычислительную схему для получения
приближенного значения сеточной функции f(x) в заданной точке 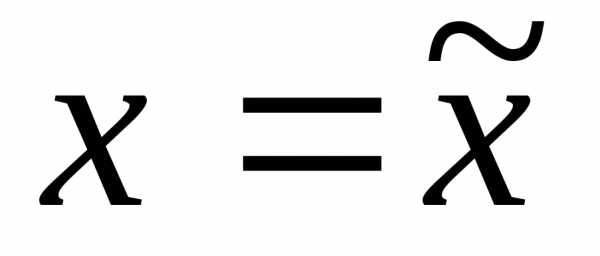 ,
в основу которой будет положена
интерполяция Лагранжа на сетке узловx0, x1, …, xn.
Организация вычислений по этой схеме
будет иметь итерационный характер.
Каждый шаг заключается в вычислении
некоторого определителя второго порядка.
,
в основу которой будет положена
интерполяция Лагранжа на сетке узловx0, x1, …, xn.
Организация вычислений по этой схеме
будет иметь итерационный характер.
Каждый шаг заключается в вычислении
некоторого определителя второго порядка.
Пусть даны две точки на кривой y=f(x): (x0, y0) и (x1, y1). Построим функцию P0,1(x):
.
.
Т.е. P0,1(x) совпадает с интерполяционным многочленом Лагранжа первой степени, построенным по двум данным точкам (сравните с 2.3).
Построим через определитель функцию P1,2(x) для точек (x1, y1), (x2, y2):
.
.
Она тоже является многочленом Лагранжа первой степени, построенным по двум точкам (x1, y1) и (x2, y2).
Если на кривой y=f(x) заданы три точки (x0, y0), (x1, y1), (x2, y2), то, используя введенные линейные функции P0,1(x) и P1,2(x) образуем новую функцию:
.
Покажем, что эта функция есть многочлен второй степени. Учитывая, что
P0,1(x0)=P1,2(x1)=y0,
P0,1(x1)=y1, P1,2(x2)=y2,
подставляя в P0,1,2(x) поочередно значения x=x0, x1, x2, получим:
P0,1,2(x0)=y0; P0,1,2(x1)=y1; P0,1,2(x2)=y2.
Т.о., функция P0,1,2(x) – это многочлен второй степени, решающий задачу параболической интерполяции по трем точкам (x0, y0), (x1, y1), (x2, y2). Но такой многочлен единственный, следовательно, P0,1,2(x)=L2(x), где L2(x) – многочлен Лагранжа.
Продолжая процесс рассуждения, получим рекуррентное задание последовательности интерполяционных многочленов Лагранжа, которое составляет суть интерполяционной схемы Эйткена:
, (3.1)
где i=1, 2, …, n и по определению P0(x)=y0, P1(x)=y1.
Схема Эйткена легко реализуется на ЭВМ. Организация вычислений по формуле (3.1) должна быть такова, что если заранее неизвестна степень интерполяционного многочлена, который нужно использовать для вычисления y(x), то должно происходить постепенное повышение степени k интерполирующих ее многочленов за счет подключения новых узлов. Счет ведется до тех пор, пока идет уточнение приближенного значения y(x).
Об этом можно судить по уменьшению величины |Pi, i+k-1(x)-Pi, i+k(x)| при увеличении k и подходящем фиксировании i.
Пример. Пусть некоторая функция y=y(x) задана таблицей своих значений, округленных до двух знаков после запятой:
xi | 0.0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
yi | 1.00 | 1.02 | 1.08 | 1.12 | 1.34 | 1.54 | 1.81 | 2.15 |
Рассмотрим
процесс вычисления двух значений этой
функции по схеме Эйткена в точках: а) 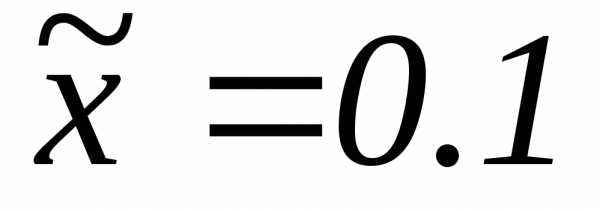 ;
б).
Результаты промежуточных вычислений
(в которых один знак запасной) сведем в
табл. 3.1, 3.2. Числа в столбцах, помеченных
посредством
;
б).
Результаты промежуточных вычислений
(в которых один знак запасной) сведем в
табл. 3.1, 3.2. Числа в столбцах, помеченных
посредством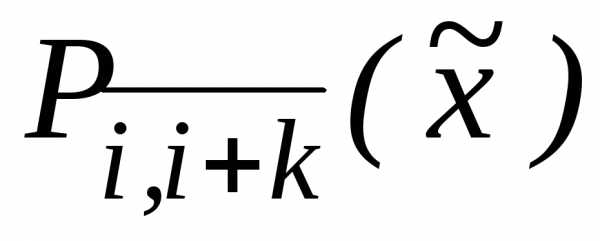 ,
представляют собой значения многочленов
Лагранжаk-ой степени,
построенных по узлам отi-го
до(i+k)-го
рекуррентно по формуле:
,
представляют собой значения многочленов
Лагранжаk-ой степени,
построенных по узлам отi-го
до(i+k)-го
рекуррентно по формуле:
, (3.2)
где k=1, 2, …,  ,
в соответствии с интерполяционной
схемой Эйткена. Порядок получения этих
значений показан проставленными в
каждой клетке номерами.
,
в соответствии с интерполяционной
схемой Эйткена. Порядок получения этих
значений показан проставленными в
каждой клетке номерами.
Таблица 3.1.
Вычисление по схеме Эйткена значения y(0.1)
|
|
|
|
|
|
| ||||
0 | 0 | 1.00 | 1 | 1.01 | 3 | 1.005 | 6 | 1.001 | 10 | 0.991 |
1 | 0.2 | 1.02 | 2 | 0.99 | 5 | 0.983 | 9 | 0.920 | ||
2 | 0.4 | 1.08 | 4 | 1.02 | 8 | 1.358 | ||||
3 | 0.6 | 1.12 | 7 | 0.57 | ||||||
4 | 0.8 | 1.34 | ||||||||
5 | 1.0 | 1.54 | ||||||||
6 | 1.2 | 1.81 | ||||||||
7 | 1.4 | 2.15 | ||||||||
Таблица 3.2
Вычисление по схеме Эйткена значения y(0.25)
|
|
|
|
|
|
| |||
0 | 0 | 1.00 | |||||||
1 | 0.2 | 1.02 | 1 | 1.035 | 3 | 1.038 | 6 | 1.048 | |
2 | 0.4 | 1.08 | 2 | 1.050 | 5 | 1.169 | |||
3 | 0.6 | 1.12 | 4 | 0.735 | |||||
4 | 0.8 | 1.34 | |||||||
5 | 1.0 | 1.54 | |||||||
6 | 1.2 | 1.81 | |||||||
7 | 1.4 | 2.15 | |||||||
Процесс вычисления
значений многочленов Лагранжа ведется
до тех пор, пока идет уточнение
приближенного значения  ,
т.е. уменьшается величинапри увеличенииkи
подходящем фиксированииi.
,
т.е. уменьшается величинапри увеличенииkи
подходящем фиксированииi.
Например, для
подсчета приближенного значения данной
функции в точке 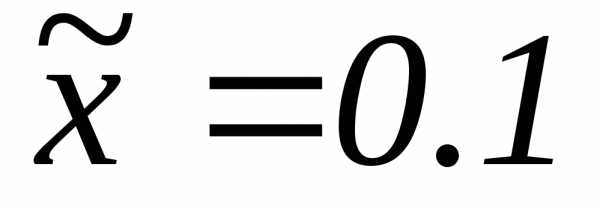 ,
расположенной между узламиx0=0.0иx1=0.2,
целесообразно в качестве основной
последовательности значений многочленов
Лагранжа брать строку таблицы 3.1,
соответствующую значениюi=0,
т.е. числа,и т.д.
,
расположенной между узламиx0=0.0иx1=0.2,
целесообразно в качестве основной
последовательности значений многочленов
Лагранжа брать строку таблицы 3.1,
соответствующую значениюi=0,
т.е. числа,и т.д.
Вычислив разности между последующими и предыдущими числами этой строки, а именно:
0.005 0.004 0.010,
видим, что дальнейший счет бессмыслен; разность перестала уменьшаться. Т.е. по данной информации о функции y(x)более точное значениеy(0.1), чемy(0.1)=1.001, получаемое с помощьюL3(0.1), найти не удастся.
В случае б) вычисление по схеме Эйткена дает следующий результат: y(0.25)1.038, полученный с помощьюL3(0.25).
studfiles.net

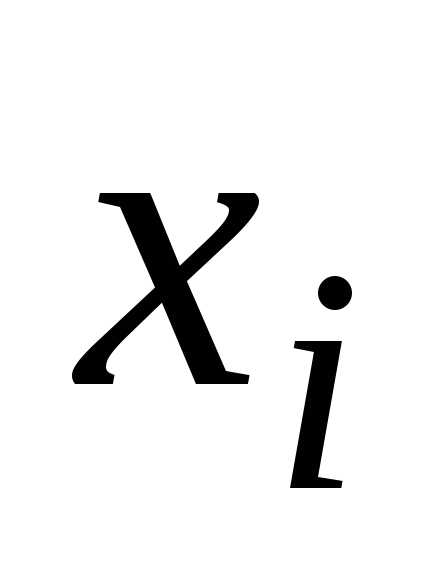
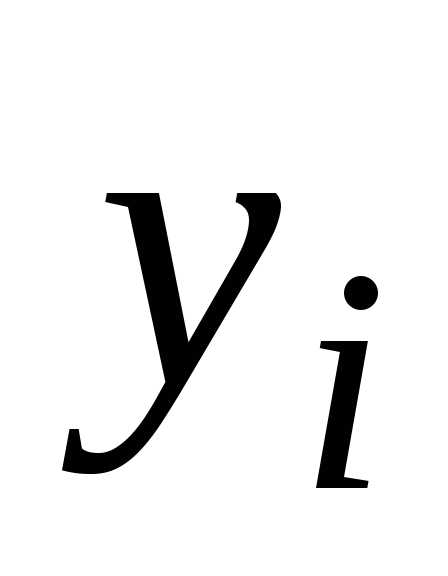

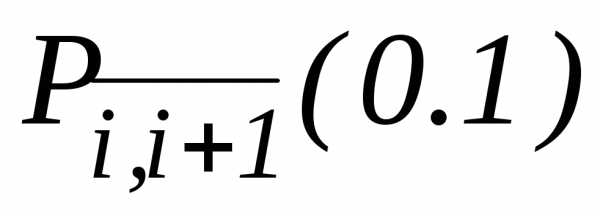

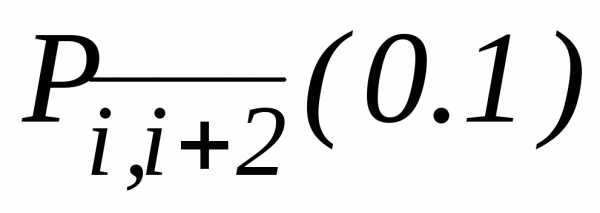



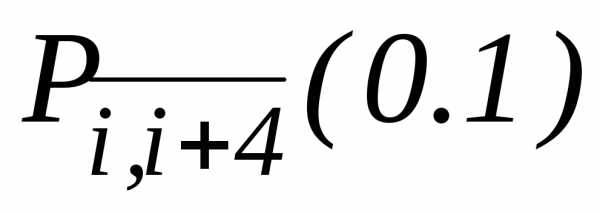
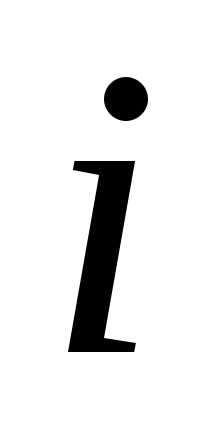
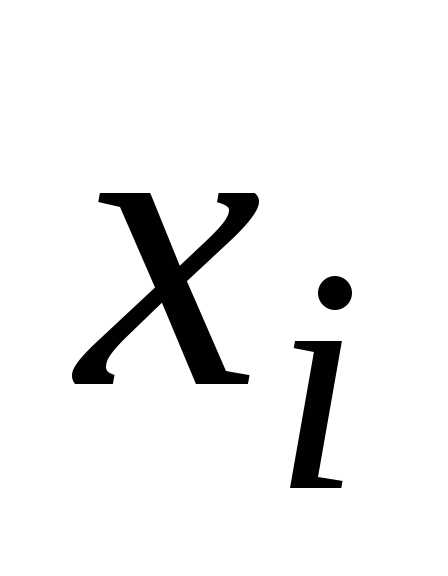
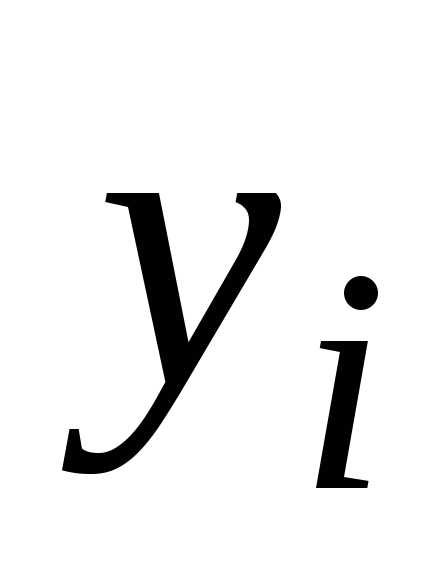






 Муниципальное бюджетное общеобразовательное учреждение
Муниципальное бюджетное общеобразовательное учреждение

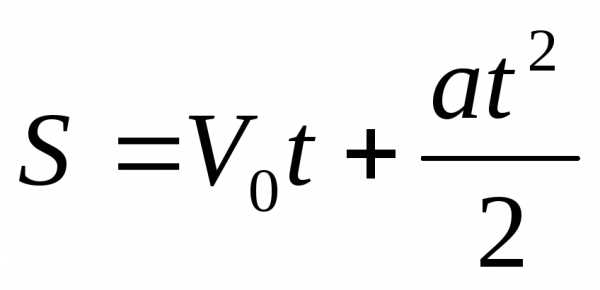
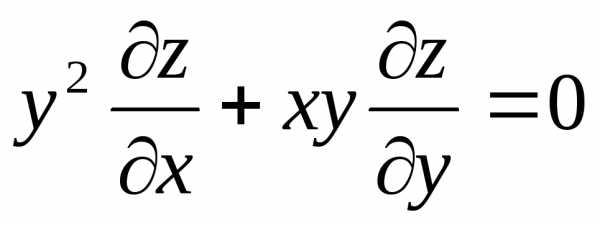 —
дифференциальное уравнение в частных
производных первого порядка.
—
дифференциальное уравнение в частных
производных первого порядка. уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
уравнения,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
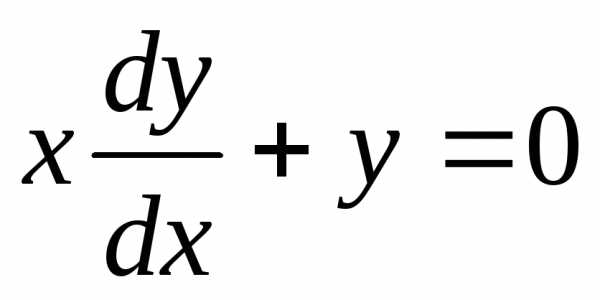

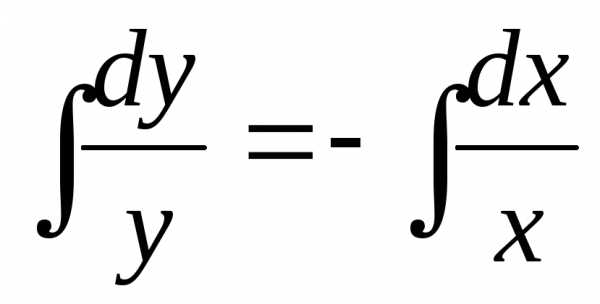

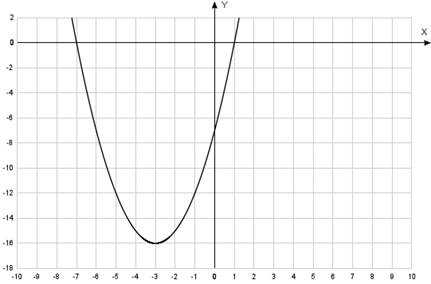
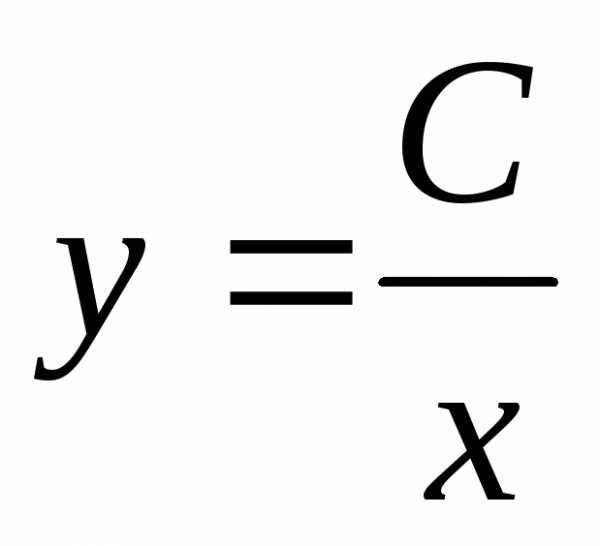 —
это общее решение исходного дифференциального
уравнения.
—
это общее решение исходного дифференциального
уравнения.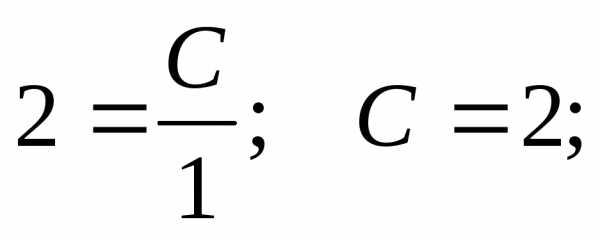
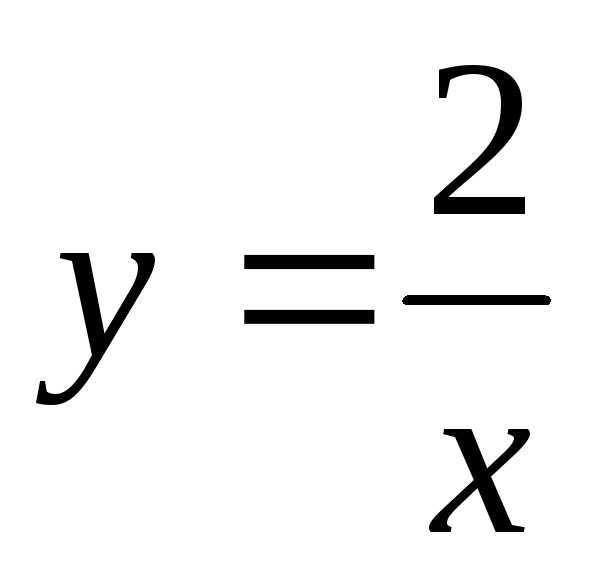

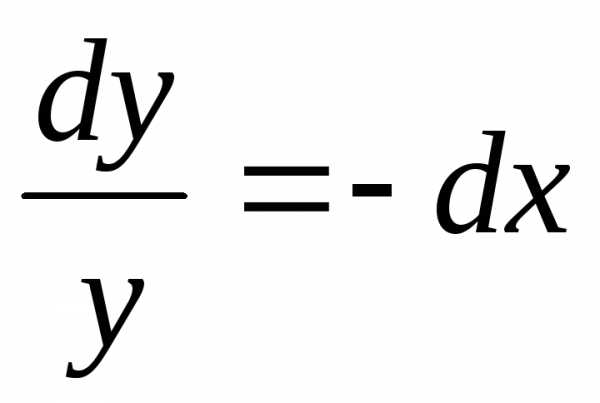
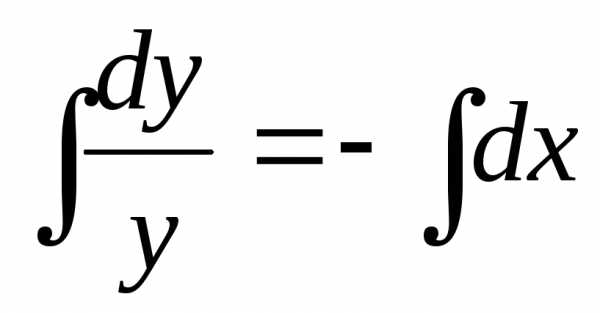
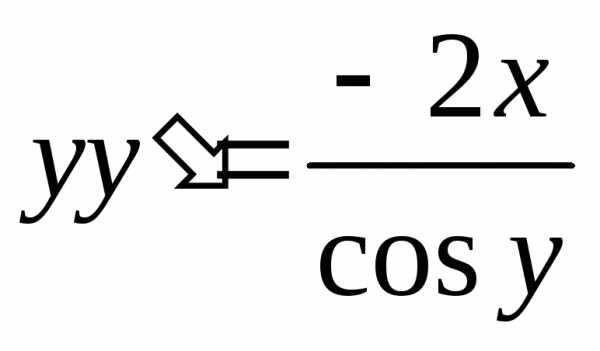
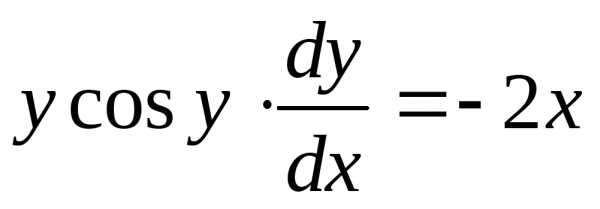

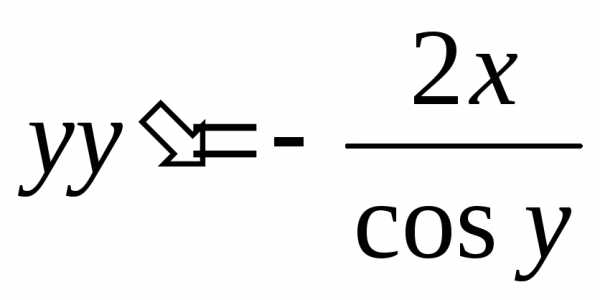 —
верно
—
верно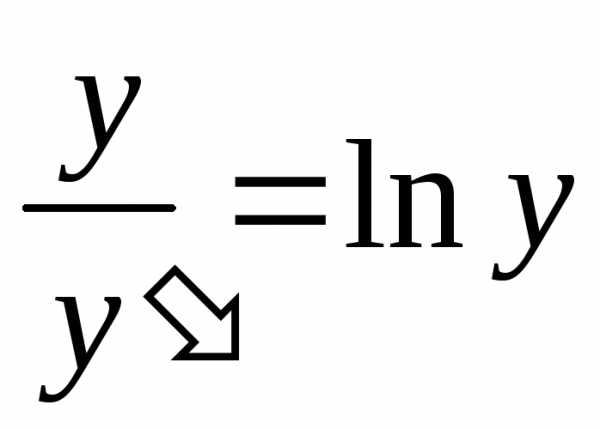 при условии у(2) = 1.
при условии у(2) = 1.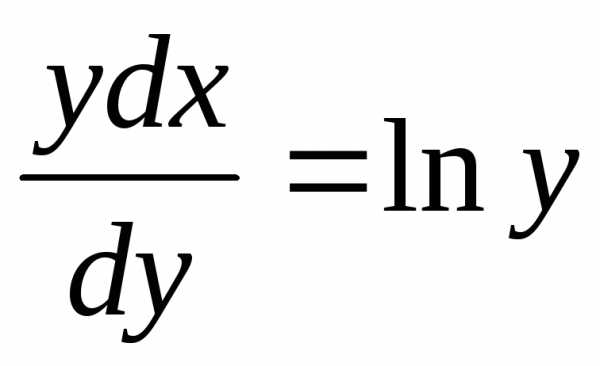
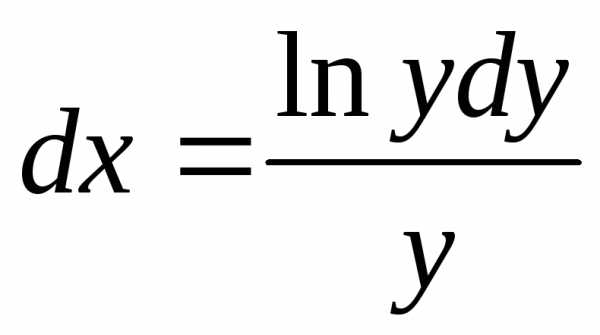
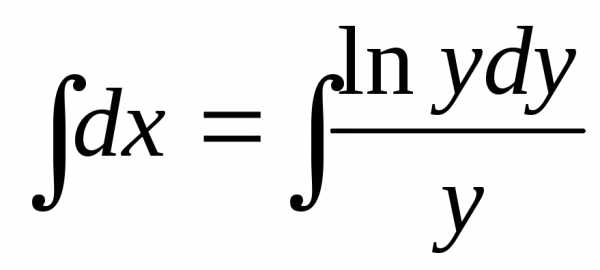
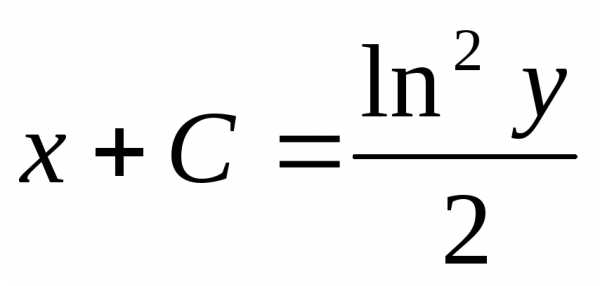
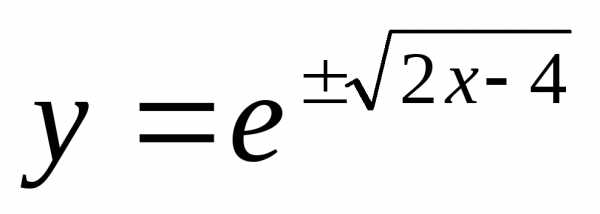 — частное решение;
— частное решение;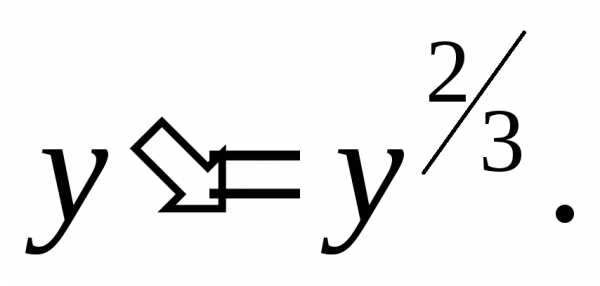
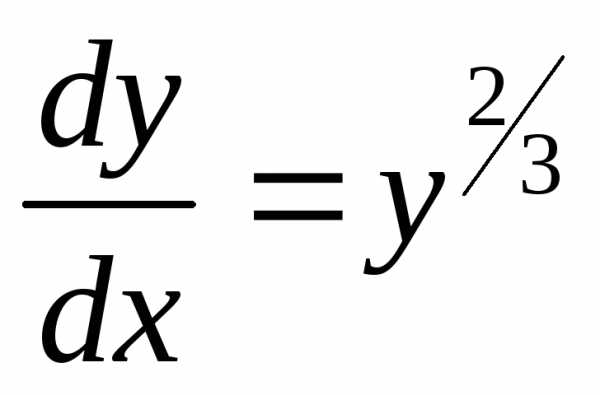
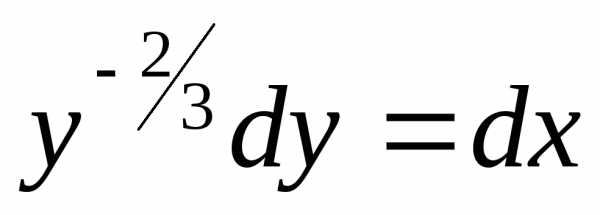
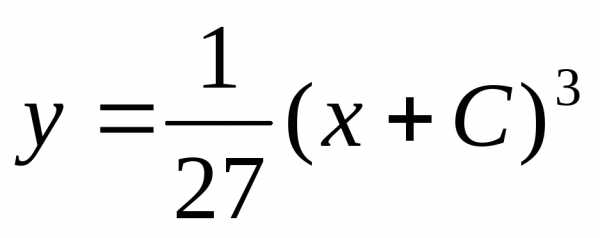 —
общее решение
—
общее решение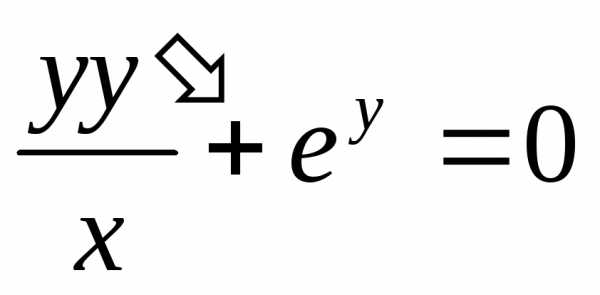 при
условии у(1) = 0.
при
условии у(1) = 0.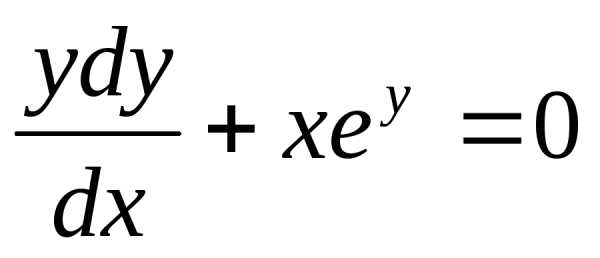
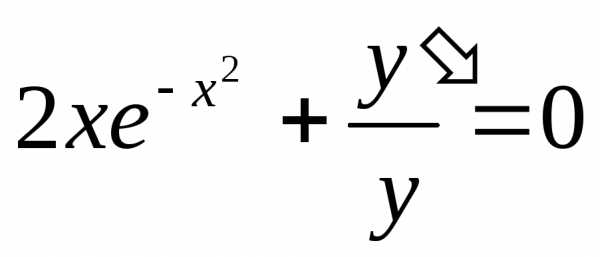
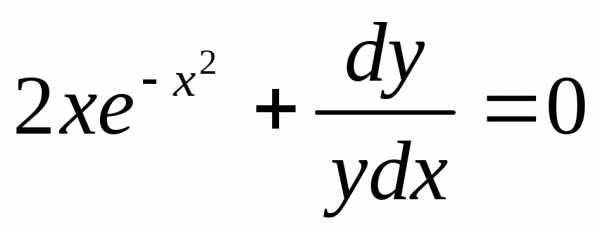
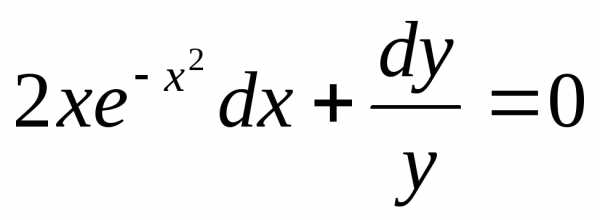
 Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.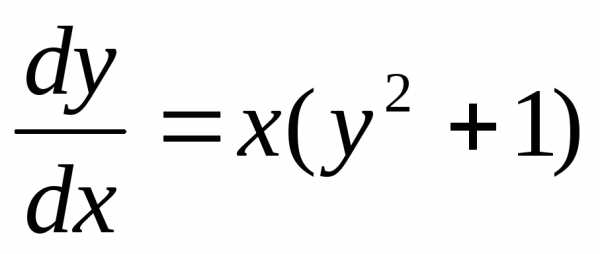
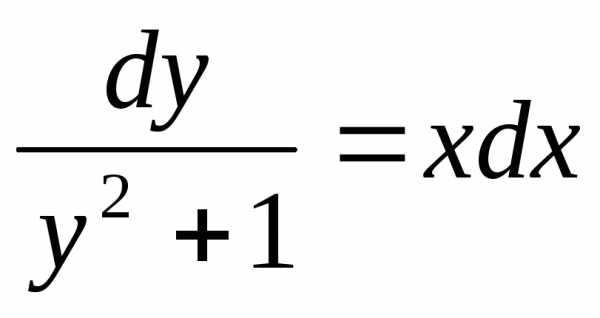
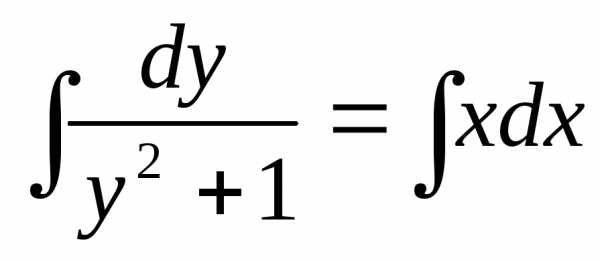 ;
; 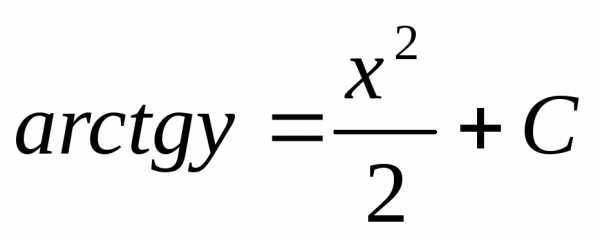 ;
;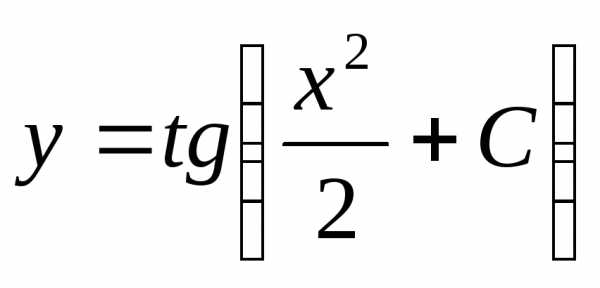
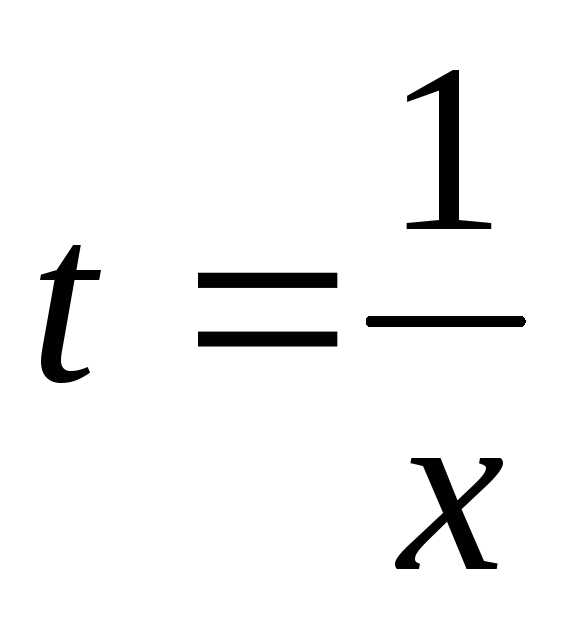 .
Получаем:
.
Получаем: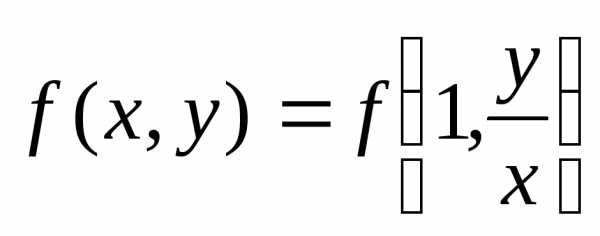
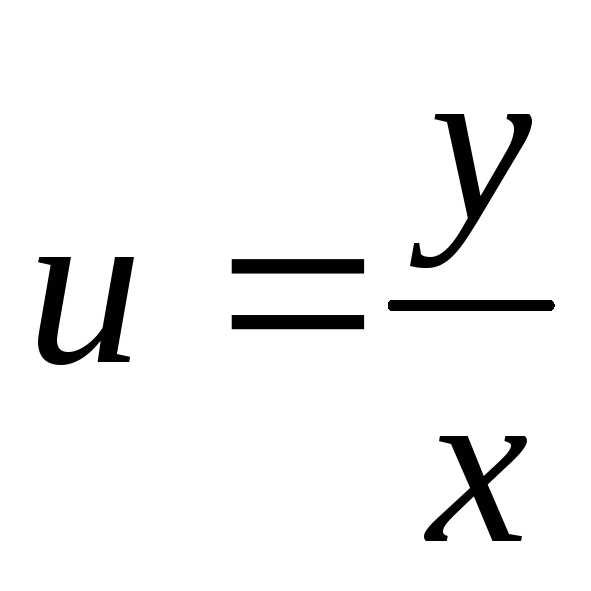 ,
т.е.
,
т.е. .
.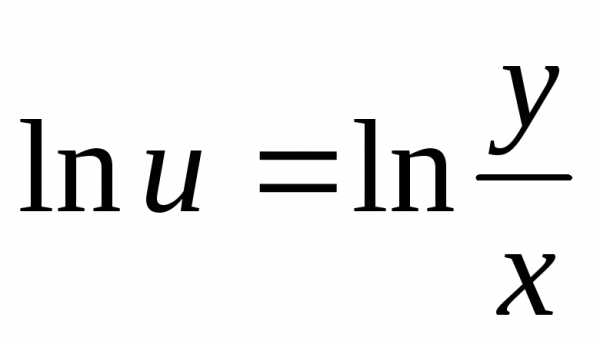 .
.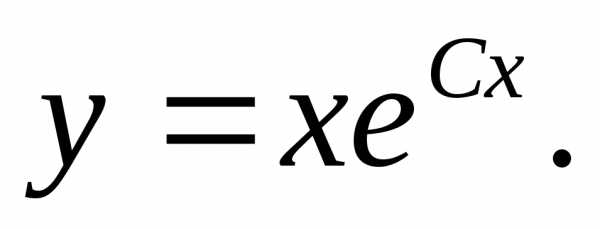
 .
. то переменные могут быть разделены
подстановкой
то переменные могут быть разделены
подстановкой