| Урок 1. Информатика — сфера деятельности человека |
| Урок 1. Операционные системы ПК и мобильных устройств |
| Урок 2. Информационная безопасность и каналы утечка информации |
| Урок 2. Пользовательский интерфейс Windows 7 |
| Урок 3. Пользовательский интерфейс Windows |
| Урок 4. Windows 7. Системные требования и восстановление системы |
| Урок 4. Аудиосистема компьютера |
| Урок 5. Windows 7. Защита данных на съёмных устройствах |
| Урок 5. Браузеры сети Интернет |
| Урок 6. Windows 7. Стандартные программы. Часть 1 |
| Урок 6. Выбираем клавиатуру и мышь |
| Урок 6. Поиск информации в сети Интернет |
| Урок 9. Источник бесперебойного питания и сетевой фильтр |
| Информатика 10- 11 класс. Кодирование информации в ЦЭВМ |
| Информатика 10- 11 классы. Алгоритмы повторения |
| Информатика 10-11 класс. АЯ Паскаль |
| Информатика 10-11 класс. Записной тип данных |
| Информатика 10-11 класс. Линейные и ветвящиеся алгоритмы |
| Информатика 10-11 класс. Многомерные массивы |
| Информатика 10-11 класс. Множественный тип данных |
| Информатика 10-11 класс. Основы алгебры и логики |
| Информатика 10-11 класс. Параметры. Стек и очередь |
| Информатика 10-11 класс. Подпрограммы |
| Информатика 10-11 класс. Понятие типов данных |
| Информатика 10-11 класс. Ссылочные и процедурные типы данных |
| Информатика 10-11 класс. Строковый и текстовый типы данных |
| Информатика 10-11 класс. Файловый тип данных |
| Информатика 10-11 класс.Подключение к интернету. Электронная почта |
| Информатика 10-11 классы |
| Информатика 10-11 классы. Введение в алгоритмику |
| Информатика от EduLibNet |
| Информатика. 10-11 класс. Основы структурного программирования |
| Информатика. 10, 11 класс. Информация и информационные процессы |
| Информатика. Выпуск 1. Системы счисления. |
| Информатика. Выпуск 10. Операционные системы и архитектура компьютерных сетей. |
| Информатика. Выпуск 11. Языки программирования и типы данных. |
| Информатика. Выпуск 12. Операторы ветвления и логические операции. |
| Информатика. Выпуск 13. Операторы цикла. |
| Информатика. Выпуск 2. Информация и ее кодирование. |
| Информатика. Выпуск 3. Технологии обработки и хранения информации. Часть 1. |
| Информатика. Выпуск 4. Технологии обработки и хранения информации. Часть 2. |
| Информатика. Выпуск 5. Комбинаторика и теория информации. |
| Информатика. Выпуск 6. Алгебра логики. Основные логические операции. |
| Информатика. Выпуск 7. Алгебра логики. Основные законы алгебры логики. |
| Информатика. Выпуск 8. Математические модели. |
| Информатика. Выпуск 9. Электронные таблицы и базы данных. |
| Лабораторная работа. Microsoft Office Access 2007. Часть 1 |
| Лабораторная работа. Microsoft Office Access 2007. Часть 2 |
| Лабораторная работа. Microsoft Office Access 2007. Часть 3 |
| Лабораторная работа. Microsoft Office Access 2007. Часть 4 |
| Лабораторная работа. Microsoft Office Access 2007. Часть 6 |
| Лабораторная работа. Microsoft Office Excel 2007. Часть 1 |
| Лабораторная работа. Microsoft Office Excel 2007. Часть 2 |
| Лабораторная работа. Microsoft Office Word 2007. Часть 1 |
| Лабораторная работа. Microsoft Office Word 2007. Часть 2 |
| Лабораторная работа. Mirosoft Office Access 2007 Часть 5 |
| Урок 1. История сети Интернет |
| Урок 1. Поисковые системы |
| Урок 1. Системный подход при формировании системы защиты информации |
| Урок 10. Microsoft и облачные вычисления |
| Урок 10. Операционные системы для мобильных устройств. Часть 2 |
| Урок 10. Профилактика неисправностей персонального компьютера |
| Урок 10. Сервисы сети Интернет: потоковое мультимедиа |
| Урок 10. Средства и способы перехвата акустических сигналов |
| Урок 11. Характеристики и виды средств акустической разведки |
| Урок 12. Средства радиотехнической и радиоразведки и их характеристики |
| Урок 13. Способы предотвращения утечки обрабатываемой информации за счёт электромагнитных излучений |
| Урок 14. Безопасность оптоволоконных кабельных систем |
| Урок 15. Защита от утечки информации по цепям заземления |
| Урок 16. Способы защиты информации при эксплуатации слаботочного оборудования |
| Урок 17. Системы пространственного зашумления объектов ЭВТ |
| Урок 18. Применение экранирующих конструкций |
| Урок 19. Основные организационно-технические мероприятия по защите информации |
| Урок 2. Подключение к сети Интернет |
| Урок 2. Сервисы и инструменты Google |
| Урок 2. Состав персонального компьютера |
| Урок 3. Защита информации в сети Интернет |
| Урок 3. Информационная безопасность и кадровая политика на предприятии |
| Урок 3. Монитор и видеосистема компьютера |
| Урок 3. Услуги сети Интернет: web-формы, блоги |
| Урок 4. Википроекты |
| Урок 4. Защита информации в сети Интернет. Продолжение |
| Урок 4. Каналы утечки информации в здании, служебных помещениях и инженерных системах здания |
| Урок 5. Внешняя память компьютера |
| Урок 5. Интернет-магазины, интернет-аукционы, электронные платёжные системы |
| Урок 5. Электромагнитные каналы утечки информации, причины возникновения утечки информации |
| Урок 6. Каналы утечки информации: силовая сеть предприятия |
| Урок 6. Социальные сети, файлообменные сети |
| Урок 7. Windows 7. Стандартные программы. Часть 2 |
| Урок 7. Защита информации: силовая сеть информационной системы в условиях периодических токов |
| Урок 7. Интернет-радио, интернет-телевидение, IP-телефония, мессенджеры |
| Урок 7. Принтеры |
| Урок 7. Сервисы сети Интернет: World Wide Web |
| Урок 8. Каналы утечки информации: структурированная кабельная система |
| Урок 8. Модем или сетевой адаптер? |
| Урок 8. Облачные технологии сети Интернет |
| Урок 8. Операционная система Linux |
| Урок 8. Сервисы сети Интернет: электронная почта |
| Урок 9. Документы Google |
| Урок 9. Каналы утечки информации: рабочие места пользователей и персонала ИС |
forkettle.ru
Уроки информатики
В современном мире изучение данного предмета в школе является уже необходимостью, ведь компьютеризация проникла уже практически во все сферы жизнедеятельности человека. Вот почему знание хотя бы основ компьютерной грамотности позволит детям чувствовать себя уверенно в наше время.
Изучать информатику онлайн вы можете, зайдя на наш сайт, который содержит практически все темы по информатике, составляющих школьную программу, в видеоформате. Поэтому, располагая достаточным временем, компьютером и доступом в Сеть, вы можете обратиться к видеоурокам и разобрать нужную тему.
Дисциплина строится на принципах и методах обработки, хранения и передачи информации при помощи компьютера и компьютерных сетей. Одним из приоритетных направлений в современном преподавании информатики в школе является направление «Глобальная сеть Интернет». Данный факт обуславливается популяризацией интернет-коммуникаций и общей информатизацией общества.
Программа по информатике
Уроки информатики в формате видео, представленные на нашем портале, помогут ребенку в освоении школьного курса по данному предмету. Во всех школах изучение начал информатики начинается в 5 классе, где рассказывается, как устроен компьютер, как им пользоваться, ребенок также знакомится с наиболее распространенными компьютерными программами. В разделе информатики 5 класса вы сможете найти интересные видеоуроки по всем этим темам. Информатика 6 класса знакомит школьников с основами программирования, что способствует развитию логического мышления у ребенка, этому также помогает изучение теоретических вопросов о формах мышления. Изучение программирования, в частности, на языке Basic, продолжается также и в следующем классе. На нашем сайте в доступной форме объясняются все нюансы этих непростых вопросов, которые изложены в видеоуроках по информатике 7 класса. В 8 классе школьники узнают о таких понятиях, как информационные модели, изучают архитектуру компьютера, узнают, что такое алгоритмы, знакомятся с их свойствами. Все это вы тоже можете найти на нашем портале в разделе информатике 8 класса.
Далее на уроках информатики начинается детальное изучение компьютерной графики, компьютерной анимации, средств и технологий обработки числовой информации, а также трехмерного моделирования и технологий хранения информации, в том числе баз данных. Эти сложные темы могут быть непонятны школьнику с первого раза, именно поэтому на сайте InternetUrok.ru представлены видеоуроки по информатике 9 класса в простой и наглядной форме изложения. С каждым классом курс становится все сложнее: на уроках по информатике 10 класса школьники будут осваивать понятия моделирования живой и неживой природы, логико-математические модели, а также информационную деятельность человека с использованием в ней компьютерных технологий. На уроках информатики 11 класса школьники продолжают изучение вопросов информационной деятельности человека, а еще повторяют и углубляют свои познания, касающиеся особенностей операционных систем и программного обеспечения. Эти и многие другие темы по информатике ждут вас на страницах портала InternetUrok.ru.
ГИА по информатике является необязательным экзаменом для учеников 9 класса. Экзамен состоит из трёх частей: части А (подразумевает выбор правильного ответа), части B(подразумевает краткий ответ на вопрос) и части С (подразумевает развёрнутое решение). При сдаче экзамена по данной дисциплине ученик должен сообщить, на каком языке программирования он будет выполнять задание С. Эта часть выполняется при помощи компьютера. Чтобы успешно сдать ГИА по информатике, нужно готовиться систематически и подойти к процессу изучения материала серьёзно, используя учебники, лекции и конспекты, а также проверочные материалы по всем темам курса, решать диагностические и тренировочные контрольные.
В процессе изучения тем в рамках программы по информатике важна не только теоритическая составляющая, но и практический компонент. Потому что информационные технологии и процессы невозможно полностью осмыслить и понять, изучив лишь только теорию – как правило, навык приобретается на практике. Грамотное использование компьютера способно превратить невероятно сложную задачу в простейший алгоритм действий и тем самым упростить имеющуюся задачу.
Курс начальной информатики призван расширить кругозор младшеклассников, развить мыслительный процесс и познакомить с базовыми понятиями предмета.
При преподавании информатики в школе в старших классах должны достигаться следующие цели:
1. Приобретение навыков работы со средствами информационно-коммуникационных технологий.
2. Знакомство с различными видами информации и умение работать с ними при помощи ПК.
3. Выполнение и разработка проектов разной сложности.
4. Получение основополагающих теоретических знаний.
5. Развитие творческих способностей.
Роль компьютерных технологий в жизни человека растет с каждым днем. И на данный момент ПК применяется практически во всех сферах нашей повседневности. XXI век – эпоха глобальной информатизации общества, поэтому залогом успешной профессиональной деятельности любого человека является компьютерная грамотность. Следовательно, важно, чтобы школьник, изучая информатику в школе, в полной мере овладел основами компьютерной грамотности.
Изучать материал и повторять знания вы сможете с помощью нашего ресурса. Здесь содержится большое количество материалов, которые помогут изучить самостоятельно информатику онлайн.
interneturok.ru
Подготовка к ЕГЭ по Информатике с нуля от А до Я
Лада Есакова
Когда учащийся 11 класса начинает готовиться к ЕГЭ по информатике – как правило, он готовится с нуля. В этом одно из отличий ЕГЭ по информатике от экзаменов по другим предметам.
По математике у старшеклассника знания точно не нулевые. По русскому языку – тем более.
А с информатикой ситуация намного сложнее. То, что изучается в школе на уроках, никак не связано с программой подготовки к ЕГЭ по информатике.
Что такое ЕГЭ по информатике?
Контрольный тест ЕГЭ по информатике содержит 27 заданий, который относятся к самым разным темам. Это системы счисления, это булева алгебра, алгоритмика, это программирование, моделирование, элементы теории графов.
ЕГЭ по информатике охватывает очень большой спектр информации. Конечно, на экзамене понадобятся только азы, но это основы важных и современных тем.
Подготовка к ЕГЭ по информатике с нуля подразумевает, что ни одну из этих тем ученик не проходил в школе. Обычно это так и есть!
Например, такая тема, как булева алгебра, или алгебра логики, включена в ЕГЭ по информатике. Но она не изучается в школах, даже в специализированных. Ее нет ни в курсе школьной информатики, ни в курсе математики. Школьник о ней понятия не имеет!
И поэтому знаменитую задачу на системы логических уравнений не решает практически никто из учеников. Эта задача в ЕГЭ по информатике идет под номером 23. Скажем больше — преподаватели часто рекомендуют старшеклассникам вообще не пытаться решить эту задачу, и даже не смотреть на нее, чтобы не тратить время.
Означает ли это, что задача 23 из ЕГЭ по информатике не решается вообще? Нет, конечно! Наши ученики регулярно решают ее каждый год. На нашем курсе подготовки к ЕГЭ по информатике из многих тем мы берем только то, что потребуется на экзамене. И уделяем этим задачам максимальное внимание.
Почему же школа не готовит к ЕГЭ по информатике?
Связано это с тем, что информатика – предмет не обязательный. Каких-либо стандартов и программ Министерство образования не дает. Поэтому учителя на уроках информатики дают школьникам совершенно разный материал – кто что может. Более того — в некоторых школах вообще нет уроков информатики.
— Чем же обычно занимаются старшеклассники на уроках по информатике? Неужели играют в стрелялки?
К счастью, в школе на уроках информатики все-таки школьники занимаются не ерундой, а вполне полезными вещами. Например, изучают Word и Escel. В жизни это пригодится, но, к сожалению, для сдачи ЕГЭ – абсолютно бесполезно.
Причем Word ребята изучают на серьезном уровне, и некоторые даже сдают экзамены по компьютерной верстке и получают свидетельство верстальщика. В каких-то школах изучают 3D-моделирование. Очень многие школы дают веб-дизайн. Это прекрасная, полезная в будущем тема, но к ЕГЭ она совсем никак не относится! И приходя к нам на курсы, ученик действительно готовится к ЕГЭ по информатике с нуля.
Похожая ситуация – у старшеклассников профильных лицеев. Сильные профильные лицеи честно дают на уроках информатике программирование. Ребята выходят оттуда хорошими программистами. Но ведь в ЕГЭ по информатике всего 5 заданий хоть как-то связаны с программированием, и из них ровно одна задача в варианте ЕГЭ посвящена написанию программы! Результат – максимум 6 задач на ЕГЭ по информатике.
Сколько же нужно времени, чтобы подготовиться к ЕГЭ по информатике с нуля?
Есть хорошая новость! Подготовиться к ЕГЭ по информатике с нуля можно за один год. Это не легко, но можно, и наши ученики каждый год это доказывают. Курс подготовки к ЕГЭ по информатике не очень большой. Заниматься на курсах можно 1 раз в неделю по 2 часа. Конечно, надо активно выполнять домашние задания.
Но есть одна поправка. Если ученик никогда до 11 класса не занимался программированием, за год вряд ли возможно освоить программирование в полной мере. Поэтому нерешенной останется задача №27 варианта ЕГЭ по информатике. Она самая сложная.
Особенно трудно готовиться к ЕГЭ по информатике с нуля тем ученикам, кто вообще никогда не был знаком с программированием и не знает, что это такое. Это область достаточно специфичная, поэтому подготовке по программированию нужно уделять много времени и нарешивать огромное количество задач.
На наших курсах мы обязательно разбираем все типовые задания по программированию. И ни разу на экзамене задача по программированию не оказалась для наших учеников сюрпризом –все они были на курсах разобраны. И только задача 27 остается за бортом для тех, кто вообще до 11 класса программированием не занимался.
Приходя к нам на курсы по информатике, ученики и родители иногда удивляются, не видя в учебном классе компьютеров. Они думают, что раз пришли готовиться к ЕГЭ по информатике, то на столах должны быть компьютеры. Но их нет! Насколько необходимо при подготовке к ЕГЭ по информатики наличие ноутбуков и компьютеров?
Это особенность ЕГЭ по информатике. На экзамене компьютера не будет! И да, надо будет решать задания ручкой на листе бумаги, потому что именно в таком формате сейчас проходит ЕГЭ по информатике. Это реальная проблема для тех, кто его сдает.

Даже старшеклассники из специализированных лицеев, хорошо умеющие программировать, могут оказаться беспомощны на ЕГЭ по информатике. Они, разумеются, программируют на компьютерах, то есть в специальной среде. Но что будет, когда компьютера нет? И не только школьники – даже профессиональные программисты с очень большим трудом могут написать программу на бумаге. Поэтому мы готовимся к такому сложному формату сразу. Мы осознанно не используем при подготовке к ЕГЭ по информатике компьютеры и ноутбуки – согласно правилу «Тяжело в учении, легко в бою».
Уже несколько лет ходят слухи, что ЕГЭ по информатике переведут в компьютерную форму. Это обещали сделать в 2017 году, но не сделали. Сделают ли в 2018 году? Пока не знаем. Если введут такой формат экзамена – готовиться к ЕГЭ по информатике с нуля будет намного проще.
Итак, год активной подготовки к ЕГЭ по информатике с нуля, и ваш результат — 26 задач из 27 возможных. А если вы хоть немного знакомы с программированием – то и все 27 из 27. Мы желаем вам достичь на экзамене такого результата!
И еще раз рекомендую для подготовки теоретический материал и свою книгу «Информатика. Авторский курс подготовки к ЕГЭ», где дается практика решения задач.
Расскажи друзьям!
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Изучение Информатики с Нуля.

Если спросить молодого человека, желающего изучать информатику: зачем ему это нужно? – в половине случаев ответ будет одинаковым: чтобы сдать тесты и поступить в ВУЗ. Не будем задаваться вопросом, что в таком случае он делал в школе, поскольку внятного ответа все равно не будет.
Зайдем с другой стороны – в какой ВУЗ требуется поступить? На какую специальность и почему? Хочется стать программистом и зарабатывать много денег? Это причина уважительная. Только вот хорошими программистами за день не становятся, и никакой ВУЗ не поможет, если нет огромного желания, терпения и трудолюбия. Вы готовы?
Тогда добро пожаловать в информатику для начинающих.
Базовые понятия и основы информатики преподают в любой школе. Если вам не повезло, и уроки не принесли пользы, займитесь самообразованием. Да-да, все традиционно: книжка, видеоурок в интернете “Информатика с нуля”, и, конечно, английский язык. Так уж сложилось, что большинство полезной информации, литературы и обучающих программ написаны на английском. Впрочем, существуют русскоязычные образовательные сайты с изложением базовых основ информатики.
Не нужно бояться. На самом деле с информатикой, а точнее, с информационно – коммуникационными технологиями, мы знакомимся с удовольствием и без всякой школы. Компьютером пользуетесь? По просторам Интернета гуляете? Составляете документы, отчеты, таблички, рисунки? Значит, базовый уровень вами освоен.
На следующей ступени можно приступать к освоению какого-либо языка программирования. Специалисты утверждают, что одним из самых простых и доступных для самостоятельного изучения является “Python” – язык для новичков.
Самостоятельное изучение любой науки – дело не простое. Поэтому обратите внимание на курсы информатики и программирования в вашем городе или дистанционные. К примеру, в Алматы существуют школы для разного уровня подготовки, с программами обучения для детей и взрослых. Это SummIT, “Жаңа Жол”, “Пифагор”, “Algorithm”. Здесь можно получить уроки информатики для начинающих.
Современный и удобный вариант – это дистанционное обучение.
Профессиональные курсы программирования и Школа программирования “Method” – один из возможных путей освоения информатики и программирования.
Вот мы и подошли к цели изучения информатики с нуля – поступлению в ВУЗ на специальность, связанную с информационными технологиями.
Выбор университетов велик: только в Алматы десять ВУЗов готовят IT – специалистов.
В их числе: Международный Университет Информационных Технологий, Казахский Национальный Университет им. аль Фараби, UIB, Алматинский Университет техники и связи, AlmaU, Казахстанско – Британский Технический Университет, КазНАУ и другие.
Профессионалы в сфере информационных технологий – это самые востребованные специалисты на рынке труда. Программисты, веб – дизайнеры, проектировщики информационных систем, специалисты в области кибер – безопасности – всех не перечислить. Изучая информатику, вы приблизитесь к пониманию того, чем хотели бы заниматься, и сможете уверенно смотреть в будущее.
informatik.kz
Обучение информатике
Также смотрите разделы связанные с разделом Обучение информатике, презентации по информатике:
- Книги, задачники и учебники по информатике
- Книги и учебники по программированию
- Обучение пользованию Интернет
- Полезные сайты, ссылки, утилиты, программы
- Уроки и советы по PHP, HTML, CSS, JavaScript, Java, JSP, Servlet
- Уроки и советы по CSS
- Обучение компьютерным программам
- Решебники и ГДЗ по Информатике
- ГИА, экзаменационные билеты по Информатике
- Словари по информатике и компьютерам
- Книги по Веб-дизайну, CSS, HTML, создание сайтов и верстка
- ЕГЭ по информатике
- Все книги по информатике
Ниже Вы можете бесплатно скачать электронные книги и учебники и читать статьи и уроки к разделу Обучение информатике:
- Информатика и ИКТ, 3 класс, Методическое пособие, Бененсон Е.П., Паутова А.Г., 2013
- Информатика, 5-6 класс, 7-9 класс, Программа для основной школы, Босова Л.Л., Босова А.Ю., 2013
- Учебно-методический журнал, Информатика, №1, 2013
- Учебно-методический журнал, Информатика, №2, 2013
- Информатика и ИКТ, 2 класс, Методическое пособие, Бененсон Е.П., Паутова А.Г., 2012
- Информатика и ИКТ, 4 класс, Методическое пособие, Бененсон Е.П., Паутова А.Г., 2012
- Информатика и ИКТ, 5 класс, Поурочные разработки, Босова Л.Л., 2012
- Информатика и ИКТ, 5 класс, Поурочные разработки, Методическое пособие, Босова Л.Л., Босова А.Ю., 2012
- Информатика и ИКТ, 8-9 класс, Учебная программа и поурочное планирование, Босова Л.Л., 2012
- Информатика, 7-9 класс, Программа для основной школы, Угринович Н.Д., 2012
- Информатика, 9 класс, Поурочные планы по учебникам Семакина И.Г., Угриновича Н.Д., 2012
- Информатика, методическое пособие, 4 Класс, Бененсон Е.П., Паутова А.Г., 2012
- Учебно-методическая газета, Информатика, №11, 2012
- Информатика и ИКТ, 4 класс, Методическое пособие, Бененсон Е.П., 2011
- Информатика и ИКТ, 5-7 класс, Методическое пособие, Босова Л.Л., 2011
- Информатика, 11 класс, Поурочное планирование, 136 часов, Поляков К.Ю., Шестаков А.П., Еремин Е.А., 2011
- Тематический план по информатике — 10 класс — 2010 — 2011 учебный год
- Журнал, ПРОграммист, № 1, 2010
- Журнал, ПРОграммист, № 2, 2010
- Журнал, ПРОграммист, № 3, 2010
- Журнал, ПРОграммист, № 4, 2010
- Журнал, ПРОграммист, № 5, 2010
- Журнал, ПРОграммист, № 6, 2010
- Журнал, ПРОграммист, № 7, 2010
- Журнал, ПРОграммист, № 8, 2010
- Журнал, ПРОграммист, № 9, 2010
- Информатика, 10 класс, Поурочное планирование, 140 часов, Поляков К.Ю., Шестаков А.П., Еремин Е.А., 2010
- Информатика, 2-11 класс, Программы для общеобразовательных учреждений, Бородин М.Н., 2010
- Реестр Windows Vista
- Тематический план по информатике — 10 класс — 2010 — 2011 учебный год
- Учебно-методическая газета, Информатика, №21, 2010
- CGI — модуль, реализующий функции Common Gateway Interface — описание версии 2.56
- Internet Explorer 9 — включение строки меню
- Microsoft Word — Контрольная работа — Практическое задание — Текстовый процессор Word — Вариант 1
- Microsoft Word — Контрольная работа — Практическое задание — Текстовый процессор Word — Вариант 2
- Microsoft Word — Рисование, сноски — Практическое задание
- Microsoft Word — Создание рекламного листа брошюр издательства — Практическое задание
- Microsoft Word — Таблицы, колонки, назначение клавиш символам — Практическое задание
- Microsoft Word — Форматирование текста — Практическое задание
- Microsoft Word — Формулы, таблицы, нижние индексы — Практическое задание
- Paket Excel 2008
- Photoshop
- Photoshop Tutorials — Уроки Фотошопа
- В чем заключается ошибка — 404 Not found?
- Видеокарта и Видеоускоритель
- Виды операционных систем
- Внеклассное мероприятие — Спаси компьютер от вирусов
- Внеклассное мероприятие по информатике — Игра «1001»
- Внеклассное мероприятие по информатике — Игра «Весёлая информатика»
- Внеклассное мероприятие по информатике — Игра Счастливый случай
- Внеклассное мероприятие по информатике — Интелектуальная игра — Брей-ринг
- Гигиенические и санитарные требования в кабинете информатики
- Горячие комбинации и клавиши WORD
- Графическая информация и её представление — урок по информатике
- Жесткий диск
- Зачем нужна операция безопасного извлечения USB-накопителя данных?
- Информатика — Microsoft Excel — Поиск данных — Практическое задание
- Информатика — Microsoft Excel — Построение графика — Практическое задание
- Информатика — Microsoft Excel — Построение таблицы истинности — Практическое задание
- Информатика — Microsoft Excel — Создание диаграммы — Практическое задание
- Информатика — Microsoft Excel — Сортировка данных — Практическое задание
- Информатика — Microsoft Excel — Суммирование значений диапазона ячеек. Составление таблицы значений функции , с использованием Мастера функций — Практическое задание
- Информатика — Microsoft Excel — Установка надстроек. Подбор параметра — Практическое задание
- Информатика — Microsoft Word — Выбор формата данных. Копирование формул, содержащих относительные и абсолютные ссылки — Практическое задание
- Информатика — Microsoft Word — Гипертекст — Практическое задание
- Информатика — Microsoft Word — Параметры страницы — Практическое задание
- Информатика — Microsoft Word — Свойства документа. Редактирование и печать документа. Вставка объектов — Практическое задание
- Информатика — Microsoft Word — Сохранение и открытие документа в определенном формате — Практическое задание
- Информатика — Microsoft Word — Списки — Практическое задание
- Информатика — Microsoft Word — Таблицы — Практическое задание
- Информатика — Microsoft Word — Форматирование абзацев — Практическое задание
- Информатика — Microsoft Word — Шрифт — Практическое задание
- Информатика — Интернет — Броузер Internet Explorer 5.5. Настройка обозревателя — Практическое задание — Лабораторная работа
- Информатика — Интернет — Навигация в WWW — Практическое задание — Лабораторная работа
- Информатика — Интернет — Настройка окна броузера. Поиск в Интернет — Практическое задание — Лабораторная работа
- Информатика — Интернет — Работа с объектами Веб-страниц — Практическое задание — Лабораторная работа
- Информатика — Интернет — Электронная почта Web-Mail — Практическое задание — Лабораторная работа
- Информатика — Лабораторная работа — Практическое задание — Вставка рисунков, графических примитивов, выбор дизайна презентации
- Информатика — Лабораторная работа — Практическое задание — Преобразование растрового изображения
- Информатика — Лабораторная работа — Практическое задание — Редактирование растрового изображения
- Информатика — Лабораторная работа — Практическое задание — Создание векторного изображения
- Информатика — Лабораторная работа — Практическое задание — Создание презентации с помощью PowerPoint
- Информатика — Лабораторная работа — Практическое задание — Создание прямых переходов между слайдами в презентации
- Информатика — Операционная система (ОС) — Основные задачи ОС — Интерфейс пользователя — Хараткеристики, оболочки
- Информатика — Проверочная работа — Системы счисления — Двоичная, десятичная, восьмеричная, шестнадцатеричная
- Информатика — Программирование — html — Графика
- Информатика — Программирование — html — Настройки цвета
- Информатика — Программирование — html — Основные понятия
- Информатика — Программирование — html — Списки
- Информатика — Программирование — html — Ссылки
- Информатика — Программирование — html — Таблицы
- Информатика — Программирование — html — Форматирование
- Информатика и ИКТ, 10-11 класс, Программа курса, Фиошин М.Е., Ресин А.А., Юнусов С.М.
- Информатика и ИКТ, 8 класс, Поурочные разработки, Методическое пособие, Босова Л.Л.
- Информатика и ИКТ, 9 класс, Поурочные разработки, Методическое пособие, Босова Л.Л.
- Информатика, 2 класс, Рабочая программа, Горячев А.В.
- Информатика, Практическая работа по созданию презентации, Тарасов Д.
- Информатика, Решение задач с использованием цикла, Утенков С.А.
- Информатика, Создание и форматирование таблиц, Тарасов Д.
- Как в Windows создать несколько рабочих столов?
- Как в Windows удалить программы из автозагрузки?
- Как восстановить в системном трее пропавшую иконку ?
- Как восстановить значок Корзины на рабочем столе в операционной системе Windows XP?
- Как вызвать командную строку (консоль) в Windows?
- Как изменить оформление и внешний вид Windows?
- Как настроить локальную сеть?
- Как отобразить скрытые файлы и папки в ОС Windows XP?
- Как поставить пароль на папку и (или) на файл?
- Как почистить Windows?
- Как появился первый компьютерный вирус?
- Как расшифровать коды ошибок Windows?
- Как сделать снимок экрана в Windows?
- Как скопировать защищённый диск?
- Как узнать сетевые настройки (IP-адрес, MAC-адрес модема и IP-адрес шлюза провайдера)?
- Как форматировать жесткий диск в Windows?
- Какие бывают языки программирования?
- Компьютерный вирус 666
- Компьютерный корпус
- Кулер
- Лекция по Информатике — Информатика — Вводное занятие
- Локальные вычислительные сети
- Материнская плата
- Методы определения параметров компьютера, определения температуры процессора, материнской платы, жесткого диска
- Оперативная память
- Оптический привод
- Оптическое волокно
- Организация и работа VGA адаптера — Разработка для урока.
- Основные составляющие компьютера
- Открытый урок по информатике — Поиск информации в Интернете
- Отладка приложений
- Паскаль — типы данных — разработка урока
- Полезный совет — Восстановление ярлыка Свернуть все окна
- Поурочные планы — Информатика — 11 класс — По учебнику Макарова Н.В. — 2 часть
- Поурочные планы — Информатика — 8 класс — По учебнику Угриновича Н.Д.
- Поурочные планы — Информатика — Макаров Н.В. — 9 класс
- Поурочные планы по информатике, Анимация движения нескольких объектов, Анимация движения по траектории
- Поурочные планы по информатике, создание и редактирование векторных изображений
- Поурочные планы по информатике, среда программирования, структура программы
- Поурочные планы по информатике, типы данных, арифметические операции и выражения, стандартные функции
- Поурочный план — Информатика — Автоматический ввод документов — Системы распознавания текста
- Поурочный план — Информатика — Автоматический перевод документов — Программы переводчики
- Поурочный план — Информатика — Информационные технологии — Компьютерная графика — Компьютерная графика и анимация
- Поурочный план — Информатика — Информационные технологии — Системы управления базами данных — СУБД
- Поурочный план — Информатика — Информационные технологии — Табличный процессор
- Поурочный план — Информатика — Компьютерные коммуникации — Средства работы в сети Интернет
- Поурочный план — Информатика — Математические и статистические системы
- Поурочный план — Информатика — Персональный компьютер
- Поурочный план — Информатика — Развитие и совершенствование навыков работы с компьютером
- Поурочный план — Информатика — Сжатые папки — Архивация — Программы для архивации
- Поурочный план — Информатика — Системы создания презентаций
- Поурочный план — Информатика — Системы создания презентаций — Информационно-поисковые системы
- Поурочный план — Информатика — Создание Web-страниц
- Поурочный план по информатике — . Использование элементов анимации и встроенной графики.
- Поурочный план по информатике — . Понятие о файловой системе. Файловый менеджер.
- Поурочный план по информатике — : Компьютерные презентации. Понятие презентации. Структура презентации.
- Поурочный план по информатике — : Конструирование из графических объектов.
- Поурочный план по информатике — Анимация движения нескольких объектов. Анимация движения по траектории.
- Поурочный план по информатике — Анимация движения.
- Поурочный план по информатике — Архивация данных. Создание архивных файлов.
- Поурочный план по информатике — Виды вредоносного ПО и способы защиты от него.
- Поурочный план по информатике — Виды графики
- Поурочный план по информатике — Вставка символов и формул.
- Поурочный план по информатике — Графический растровый редактор Paint.
- Поурочный план по информатике — Запуск программ с помощью ярлыков и меню.
- Поурочный план по информатике — Изучение программы Microsoft PowerPoint
- Поурочный план по информатике — Инструменты Графического растрового редактора Paint.
- Поурочный план по информатике — Информационные процессы.
- Поурочный план по информатике — Информация. Виды информации. Информационные процессы
- Поурочный план по информатике — Команда присваивания. Ввод и вывод данных.
- Поурочный план по информатике — Компьютерные презентации.
- Поурочный план по информатике — Контрольная работа.
- Поурочный план по информатике — Назначение электронной почты.
- Поурочный план по информатике — Нумерация страниц. Параметры страницы документа.
- Поурочный план по информатике — Оператор ветвления
- Поурочный план по информатике — Оператор присваивания.
- Поурочный план по информатике — Операции над векторными графическими изображениями.
- Поурочный план по информатике — Операции с объектами файловой системы.
- Поурочный план по информатике — Основные работы в локальной компьютерной сети
- Поурочный план по информатике — Подготовка презентаций к демонстрации. Демонстрация презентаций.
- Поурочный план по информатике — Поиск и замена в тексте. Проверка правописания.
- Поурочный план по информатике — Понятие алгоритма. Способы записи алгоритмов.
- Поурочный план по информатике — Понятие векторного изображения. Элементы интерфейса векторного изображения.
- Поурочный план по информатике — Понятие об операционной системе.
- Поурочный план по информатике — Понятие презентации. Структура презентации.
- Поурочный план по информатике — Практическая работа на компьютере по теме «Компьютерные сети».
- Поурочный план по информатике — Практическая работа по созданию презентации. Разработка отдельных слайдов презентации.
- Поурочный план по информатике — Практическая работа по созданию презентации. Разработка сюжета презентации.
- Поурочный план по информатике — Практическая работа.
- Поурочный план по информатике — Практические задания
- Поурочный план по информатике — Практические задания (Информационно-коммуникационные технологии)
- Поурочный план по информатике — Простые и составные условия. Алгоритмическая конструкция «ветвление».
- Поурочный план по информатике — Работа с объектами операционной системы.
- Поурочный план по информатике — Работа с текстом
- Поурочный план по информатике — Реализация алгоритмов с использованием ветвления.
- Поурочный план по информатике — Решение задач на составление алгоритмов.
- Поурочный план по информатике — Рисование в документе
- Поурочный план по информатике — Рисование в редакторе Flash. Практическая работа.
- Поурочный план по информатике — Роль компьютера в жизни человека. Функциональные блоки компьютера.
- Поурочный план по информатике — Самостоятельная работа
- Поурочный план по информатике — Самостоятельная работа на компьютере
- Поурочный план по информатике — Создание анимации. Практическая работа (продолжение).
- Поурочный план по информатике — Создание и использование слоев.
- Поурочный план по информатике — Создание и редактирование векторных изображений.
- Поурочный план по информатике — Создание и форматирование таблиц.
- Поурочный план по информатике — Среда программирования. Структура программы.
- Поурочный план по информатике — Текст как форма представления информации.
- Поурочный план по информатике — Типы данных. Арифметические операции и выражения, стандартные функции.
- Поурочный план по информатике — Фотомонтаж
- Появление и развитие информатики
- Правильная чистка клавиатуры
- Презентация — Microsoft Office FrontPage — Программа создания Веб-сайтов и управления ими
- Презентация — Адресация в Интернет
- Презентация — Алгоритм
- Презентация — Алгоритм, свойства алгоритма, исполнители алгоритмов
- Презентация — Алгоритм, свойства алгоритма, исполнители алгоритмов — Компьютер как формальный исполнитель алгоритмов
- Презентация — Архивация файлов
- Презентация — Введение в TURBO PASCAL
- Презентация — Введение в WINDOWS — Файл, каталог, работа с объектами
- Презентация — Введение в информатику — Зарождение информатики — Человек и компьютер
- Презентация — Внутренние устройства ПК — Знакомство с компьютером
- Презентация — Графический интерфейс Windows
- Презентация — Двоичное кодирование графической информации — Информация и информационные процессы
- Презентация — Двоичное кодирование звука — Представление видеоинформации
- Презентация — Двоичное кодирование текстовой информации
- Презентация — Двоичное чисел — Представление, кодирование чисел
- Презентация — Другие сервисы Интернет
- Презентация — Единицы измерения информации
- Презентация — Знакомство с компьютером — Устройства памяти компьютера
- Презентация — Знакомство с компьютером — Устройство компьютера
- Презентация — Измерение информации — алфавитный подход
- Презентация — Измерение информации — Алфавитный подход — Содержательный подход
- Презентация — Измерение информации — содержательный подход
- Презентация — Изобретение компьютера
- Презентация — Инструкция присваивания — Вывод информации на экран
- Презентация — Интернет — Всемирная паутина
- Презентация — Интернет — Коммуникационные технологии
- Презентация — Интернет — Телекоммуникация
- Презентация — Информация — Свойства информации
- Презентация — Кодирование информации
- Презентация — Компьютерная графика
- Презентация — Компьютерная преступность и безопасность — Компьютерные преступления в Уголовном кодексе РФ
- Презентация — Компьютерные вирусы — методы распространения, профилактика заражения
- Презентация — Компьютерные презентации — Мультимедийные технологии
- Презентация — Компьютерные презентации — Урок информатики — 10 класс
- Презентация — Компьютерные сети — Коммуникационные технологии
- Презентация — Компьютерные сети — Компьютерные телекоммуникации
- Презентация — Компьютерные сети — Локальная сеть
- Презентация — Магистрально-модульный принцип построения компьютера
- Презентация — Методы представления графических изображений
- Презентация — Моделирование — Модель процесса управления
- Презентация — Оператор присваивания — Язык ТУРБО ПАСКАЛЬ
- Презентация — Операторы ветвления
- Презентация — Операционная система
- Презентация — Основные информационные процессы
- Презентация — Основные понятия в Интернете
- Презентация — Основные понятия компьютерной графики
- Презентация — Основные этапы разработки и исследования моделей на компьютере
- Презентация — Передача информации — Локальные и глобальные компьютерные сети
- Презентация — Поиск информации в Интернет — web
- Презентация — Поисковые системы Интернет
- Презентация — Понятие компьютерной технологиии
- Презентация — Понятие об информации
- Презентация — Представление информации
- Презентация — Представление о Power Point
- Презентация — Программирование на языке Паскаль
- Презентация — Программирование на языке Паскаль — Часть 2
- Презентация — Программное обеспечение — Файлы и файловая система
- Презентация — Прямоугольный треугольник
- Презентация — Работа протоколов стека TCP/IP
- Презентация — Работа с основными ресурсами Internet
- Презентация — Работа с основными ресурсами Интернет — Internet
- Презентация — Растровое кодирование графической информации
- Презентация — Сервис Интернет — Коммуникационные и информационные службы
- Презентация — Средства обмена информацией в internet
- Презентация — Структура данных на магнитных дисках
- Презентация — Структура программы — Объявление переменных — Pascal
- Презентация — Таблицы в документах Word
- Презентация — Тесты по информатике — Adobe Photoshop
- Презентация — Тесты по информатике — Компьютерная графика
- Презентация — Форматирование текста — выравнивание, отступы и интервалы
- Презентация — Форматы графических файлов
- Презентация — Цвета в компьютерной графике
- Презентация — Что такое пиксель
- Презентация — Электронная почта
- Презентация — Электронная почта — Коммуникационные технологии
- Презентация по информатике — Биоинформатика
- Презентация по информатике — Графика в Pascal
- Презентация по информатике — Звуковые карты
- Презентация по Информатике — История развития ЭВМ
- Презентация по информатике — Компьютерная графика
- Презентация по информатике — Поисковые системы
- Презентация по информатике — Растровый графический редактор — Corel Paint Shop Pro X
- Презентация по информатике — Форматы графических файлов
- Презентация по информатике на тему История ЭВМ, Коротич Е.
- Презентация по информатике на тему Линейные алгоритмы, 9 класс
- Презентация по информатике на тему Поисковые системы интернета, Корпачева Л.
- Презентация по информатике на тему Разветвляющиеся алгоритмы
- Презентация по информатике, Электронная почта
- Презентация Электронная почта в сети Интернет
- Презентация, понятие и свойства информации
- Процессор
- Роль информации в современном обществе.
- Строение и назначение компьютеров
- Структура информатики
- Тест по информатике — Базы данных
- Технические средства информатики
- Урок по информатике — Объем текстовой информации в ЭВМ и её представление.
- Урок по информатике — Программирование — Basic
- Урок-игра для проведения урока информатики — Морские пираты — 6 класс
- Устройства хранения информации — лекция по информатике
- Флоппи-дисковод
- Чем открывать и как смотреть файлы формата mkv?
- Что такое ждущий режим Windows?
- Что такое патч?
- Что такое программа?
- Что такое процессор?
- Что такое ЭВМ?
- Что такое ярлык?
- Языки программирования
Описание раздела «Обучение информатике»
В данном разделе Вашему вниманию предоставляются обучающие материалы по информатике. Здесь собраны презентации, поурочные планы, статьи, журналы по информатике. Все это безусловно пригодится как учителям информатики, так и учащимся самых различных учебных заведений.Как известно, информатика – это наука о способах получения, накопления, хранения, преобразования, передачи, защиты и использования информации. А обучение информатике становится одной из важнейших составляющих человеческого существования. В нашем мире тот, кто владеет информацией, тот и владеет преимуществом перед остальными.
В современном мире трудно представить жизнь без компьютера и Интернета. Это уже стало какой-то обыденностью. И найти какую угодно информацию не составляет труда. Дети уже с малых лет знают, что такое мышка и клавиатура. Трудно представить, что будет лет через 10!
Изучая материалы данного раздела, Вы без проблем изучите компьютер на уровне пользователя. Очень хорошо описываются принципы работы с компьютером, работа с базовыми компьютерными программами. Как установить и качественно настроить Windows? Как поставить Office? Как работать в программах Word, Excel, PowerPoint? Какой лучше использовать Антивирус? На эти и многие другие вопросы в интересной манере преподнесены исчерпывающие ответы.
Для творческих людей, любящих рисовать и работать с изображениями, специально выложены уроки Photoshop.
Также много статей посвящено различным языкам программирования. Вы узнаете в какой области использовать тот или иной язык программирования, его возможности, синтаксис, плюсы и минусы.
Просмотрев обучающую литературу данной категории, обязательно загляните в раздел «Книги по информатике». Подготовиться к экзамену Вам помогут «Экзаменационные билеты по информатике». А выполнить домашнюю работу не составит труда благодаря «ГДЗ по информатике».
nashol.com
Как выучить программирование с нуля
Как учить программирование с нуля
1. Самостоятельно
Если вы обладаете железной силой воли и горите желанием стать программистом, то можете добиться своей цели с помощью самообразования. Это не самый простой и короткий путь: вам придётся самому разбираться в информационном хаосе и бороться с прокрастинацией. Зато вы можете учиться в удобное время за относительно небольшие деньги или же совсем бесплатно.
Начинать проще всего с интерактивных онлайн-курсов. В Сети есть множество площадок, материалы которых доступно объясняют основы программирования и задают направление для дальнейшего развития. Особое внимание уделяйте тем курсам, которые обучают на примерах реальных проектов, то есть поэтапно рассказывают, как создавать конкретную программу или сайт.
 Платформа с бесплатными курсами по веб-разработке freeCodeCamp
Платформа с бесплатными курсами по веб-разработке freeCodeCampЗапомните, что у вас ничего не получится без практики. Учитесь по проектно-ориентированным курсам и пытайтесь сами писать разобранные в них программы и сайты. Ищите лекции на YouTube с разбором проектов, которые вы бы хотели разрабатывать. Сначала копируйте работу других людей и анализируйте её. Затем пробуйте отходить от оригинала, экспериментируйте, изменяйте отдельные элементы, пока не сможете создавать что-то уникальное.
Помимо курсов и видеолекций, к вашим услугам официальная документация, доступная на сайтах языков, и книги. Когда разберётесь в основах, поищите свежие издания с подзаголовком Best Practices по выбранному языку программирования. Такие книги содержат лучшие приёмы разработки.
Обязательно поставьте перед собой цель создать свой проект и постоянно работайте над ним.
Это поможет закрепить полученные знания и понять, какой информации вам ещё не хватает. Ваши навыки будут развиваться вместе с проектом. Когда закончите его, работайте над новым — более сложным.
Если у вас возникнут трудности в процессе обучения или разработки, вы всегда сможете обратиться по любому вопросу к сообществам программистов вроде «Тостер» и Stack Overflow. Вам, например, помогут решить какую-нибудь задачу, выбрать хороший курс или укажут на ошибки в коде.
 Сервис вопросов и ответов на технологические темы «Тостер»
Сервис вопросов и ответов на технологические темы «Тостер»Оттачивать навыки удобно на специальных площадках, где можно посоревноваться с другими программистами, решая с помощью кода различные практические задачи. В числе таких сервисов — Codewars, TopCoder и HackerRank.
Если почувствуете, что ваше развитие зашло в тупик, или захотите ускорить обучение, попробуйте следующие варианты.
13 советов тем, кто изучает программирование самостоятельно →
2. С помощью ментора
Ментор — персональный наставник, который указывает на ошибки, предупреждает о подводных камнях, помогает прокладывать курс обучения. Полезная рекомендация, полученная в нужный момент, может избавить вас от многих проблем и сэкономить массу времени. Поэтому ментор никому не помешает.
Узнайте, есть ли среди ваших знакомых разработчики. Возможно, кто-нибудь из них захочет вам помогать. Если таких людей вы не знаете, можете поискать их в сообществах программистов. К примеру, на том же «Тостере». Только услуги менторства стоят недёшево, а за просто так тратить много времени на незнакомых людей никто не желает.
3. У преподавателей «живых» курсов
Дистанционные и очные курсы с преподавателями, которые обучают программистов с нуля, стали невероятно популярными за последние годы. В рамках этого формата вам также предстоит очень много работать самостоятельно. Зато вы будете заниматься по профессионально подготовленной программе, а решения задач будет проверять живой человек. К недостаткам курсов можно отнести высокую стоимость обучения.
Популярные русскоязычные онлайн-площадки, которые занимаются системной подготовкой программистов: «Нетология», GeekBrains и Loftschool.
Если предпочитаете заниматься очно, можете поискать образовательные центры, которые обучают программированию в вашем населённом пункте. К сожалению, такие заведения чаще всего присутствуют только в больших городах. В качестве примера можно привести компьютерную академию «ШАГ», у которой есть филиалы в нескольких странах.
4. В университете
Если у вас много времени в запасе и вы уверены, что хотите связать жизнь с программированием, можете изучать компьютерные науки в университете. Но имейте в виду, что традиционные учебные заведения отстают от прогресса, так что современные языки программирования и прочие технологии вам придётся осваивать самостоятельно.
С другой стороны, университет даст фундаментальные знания математики, алгоритмов и других областей, которые помогут вам стать высококлассным программистом. За годы усердной учёбы вы сформируете правильный тип мышления, благодаря которому будете схватывать всё на лету в профессиональной сфере.
Как выбрать направление и язык
В ИТ-индустрии можно выделить несколько направлений, в каждом из которых используют свой набор языков. Перечислим основные направления в порядке возрастания сложности:
- Веб-разработка. Популярные языки: JavaScript, PHP, Python, Ruby.
- Мобильная разработка. Популярные языки: Java, Swift.
- Разработка игр и программ для настольных компьютеров. Популярные языки: C++, C#, C.
- Big Data, машинное обучение. Популярные языки: Python, R, Scala.
На что обратить внимание при выборе
Чтобы сделать правильный выбор направления и, в частности, языка, учитывайте следующие факторы: сложность освоения и количество обучающих материалов в Сети, ваши личные предпочтения (что именно хотите разрабатывать) и востребованность языка на рынке труда.
 График востребованности языков на международном рынке труда / research.hackerrank.com
График востребованности языков на международном рынке труда / research.hackerrank.comВостребованность языка в вашем регионе легко проверить на сайтах для поиска работы. Просто откройте раздел для разработчиков ПО и посмотрите количество доступных вакансий.
ИНФОГРАФИКА: Какой язык программирования учить первым →
Если не можете определиться
Если вы в замешательстве, присмотритесь к JavaScript — языку, на котором написан почти весь веб. Многие организации и программисты советуют новичкам выбирать именно этот язык в качестве первого.
Например, основатель образовательного ресурса freeCodeCamp Квинси Ларсон рекомендует JavaScript всем начинающим. Ларсон приводит очень простые аргументы:
- JavaScript относительно легко освоить. А чтобы написать что-то и запустить на этом языке, достаточно иметь редактор кода и браузер.
- JavaScript — самый востребованный язык на международном рынке труда и у него большие перспективы. В экосистему JavaScript инвестируют крупные компании вроде Google, Microsoft и Facebook.
- У JavaScript очень широкая сфера применения: от сайтов и браузерных игр до мобильных приложений.
Кроме того, вокруг этого языка сформировалось крупное сообщество разработчиков. Высокий интерес к JavaScript обеспечивает огромное количество курсов, книг и другого образовательного контента.
Что ещё должен знать программист: математика и английский?
Любому программисту не помешает глубокое понимание математики. Для таких направлений, как разработка игровой графики или большие данные, математический ум — это необходимость. Но что касается веб-разработки и создания несложных программ, то в большинстве случаев без математики можно обойтись. Хотя среди профессионалов на этот счёт нет единого мнения.
А вот понимание английского, хотя бы на уровне беглого чтения документации, обязательно для всех программистов. Официальные документы и большая часть образовательных материалов появляются в первую очередь на английском языке. Книги часто устаревают ещё до того, как выходит перевод. Кроме того, знание английского открывает перспективы для работы со всем миром.
Как выучить английский язык: всё самое интересное и полезное →
Как получить первый опыт и первую работу
Чтобы найти первую работу в качестве программиста, вы должны иметь портфолио. Это созданный вами проект, а лучше несколько, которые демонстрируют все ваши умения разработчика. В программу большинства курсов входит разработка проектов, которые могут войти в ваше портфолио.
Очень ценным пунктом в резюме будет наличие опыта работы, особенно командной разработки. Но где его взять, если вы ищете первую работу?
- Выполните несколько заказов на биржах фриланса. Это могут быть «Фрилансим» или Upwork. Предлагайте свои услуги бесплатно, тогда к вам придут первые заказчики.
- Найдите единомышленников и создайте с ними общий проект. Люди объединяются для таких целей почти на каждой образовательной площадке, где есть курсы по программированию.
- Выберите курсы, организатор которых помогает с трудоустройством. Например, в GeekBrains после обучения открывается доступ к стажировкам от разных компаний, в том числе — оплачиваемым. GeekUniversity и «ШАГ» гарантируют трудоустройство своим выпускникам.
Перед собеседованием не забудьте поискать в Сети списки задач и вопросов, которые часто задают соискателям.
lifehacker.ru
875 бесплатных онлайн-курсов от топовых университетов
Вы можете пройти онлайн-курсы от самых известных университетов мира — Stanford, Yale, MIT, Harvard, Berkeley, Oxford и других, и не заплатить за них ни копейки. Эта коллекция, созданная сообществом Open Culture включает в себя 875 бесплатных курсов по свободным наукам и искусству. Вы можете загрузить аудио- и видео-курсы (часто с iTunes, Youtube или сайта университета) на свой компьютер и просматривать в свободное время.
Если вы хорошо владеете английским, огромная база информации полностью в вашем распоряжении. Онлайн курсы распределены по наукам и дисциплинам — ищите интересующие вас области и получайте знания абсолютно бесплатно, в любое удобное время.
Гуманитарные и социальные науки
Археология
- Ганнибал — Free iTunes Audio – Patrick Hunt, Stanford
- Ближневосточные искусства и археология – Free Online Video – Free iTunes Video — Dana D. DePietro, Margaret Larkin, UC Berkeley
- Из прошлого – Free Online Video – David Webster and William T. Sanders, Penn State
Архитектура
Искусство и история искусства
- Эстетика и философия искусства – Free iTunes Audio — Free Online Video — James Grant, Oxford University
- Искусство сквозь время: глобальный взгляд – Free Online Video — Annenberg Media
- Демонстрация цифровой фотографии – Free iTunes Video — Free Online Video & Course Materials — Dan Armendariz, Harvard
- Основы американской кибер-культуры – Free Online Video – UC Berkeley
- Введение в визуальные исследования – Free iTunes iOS App — Anna Divinsky, Penn State
- Введение в визуальный образ мыслей – Free Online Video – Free iTunes Video – John McNamara, UC Berkeley
- Пусть это будет уроком: герои, героини и повествование в картинках Йельского университета – Free Online Video – John Walsh, Yale
- Основы освещения – Free iTunes Video — Free Online Video — Simon McIntyre, The University of New South Wales
- Фотография – Free Online Video — Free iTunes App — Jonathan Worth & Matt Johnston at Coventry University
- Видео лекции по истории искусств – Free Online Video/Audio — Beth Harris, MoMA & Steven Zucker, Pratt Institute
- Элементы рисования – Free iTunes Video — Free Online Video —Stephen Farthing, Oxford University
Мир классики
- Древняя и средневековая философия (Syllabus) — Free iTunes Video— Free Online Video — David O’Connor, Notre Dame
- История Древней Греции — Free Online Video — Free iTunes Audio— iTunes Video — Free Video & Course Materials — Donald Kagan, Yale
- Древний Израиль— Free Online Video & Course Info — Free Online Video –Daniel Fleming, NYU
- Античная философия — Free iTunes Audio — Free Online Audio — David Ebrey, UC Berkeley
- Древняя мудрость и современная любовь (Syllabus) — Free iTunes Video— Free Online Video – David O’Connor, Notre Dame
- Ганнибал- Free iTunes Audio — Patrick Hunt, Stanford
- Римская архитектура— Free Online Video — Free iTunes Audio — Free iTunes Video — Course Materials — Diana E. E. Kleiner, Yale
- Рим – Free iTunes Video – Rhiannon Evans, La Trobe University
- Герои и анти-герои в классической греческой цивилизации – Multiple Formats – Gregory Nagy, Harvard
- Вергилиева Энеида: разбор произведения — Free iTunes Audio — Suanna Braund, Stanford University
Демография
Дизайн
Экономика
- Расширенная политическая экономика — Free Online Video — Steven Keen, University of Western Sydney
- Несмотря ни на что: в статистике— Free Online Video — Pardis Sabeti, Harvard
- Американский капитализм: история – Free iTunes Video — Louis Hyman & Edward Baptist, Cornell
- История американской экономики (Syllabus) – Free Online Video — Free iTunes Video – Free iTunes Audio — Martha Olney, UC Berkeley
- История американской экономики (Syllabus)- Free Online Video — Gerald Friedman, UMass-Amherst
- Австрийская экономика: введение — Free Online Audio — Murray N. Rothbard — New York Polytechnic University
- Поведенческие финансы – Free Online Video – Steven Keen, University of Western Sydney
- Капитализм: успех, кризис и реформы — Free iTunes Video — Free iTunes Audio — Free Online Video — Course Materials — Douglas W. Rae, Yale
- Кризис, глобализация и экономика – Free Online Video — Roberto Mangabeira Unger, Harvard
- Экономика развития — Free Online Video — Tyler Cowan and Alex Tabarrok, George Mason
- Экономика развития: макроэкономика – Free Online Video & Course Info – Robert Townsend, MIT
- Анализ в микроэкономике – Free iTunes Audio — Steven Wood, UC Berkeley
- Экономическая география индустриального мира – Free iTunes Audio — Richard Walker, UC Berkeley.
- Экономическая статистика и эконометрика — Free Online Video –Free iTunes Video – Free iTunes Audio – Glenn Woroch, UC Berkeley
- Экономика СМИ — Free Online Video — Tyler Cowan and Alex Tabarrok, George Mason
- Финансовая теория 1 — Free iTunes Video — Free Online Video & Course Info — Andrew Lo, MIT
- Финансовые рынки – Free Online Video — Free iTunes Audio – Free iTunes Video — Course Materials — Robert Shiller, Yale
- Финансовые рынки 2011 — Free Online Video — Free iTunes Audio — Course Materials — Robert Shiller, Yale
- Финансовая теория – Free Online Video — Free iTunes Video — Free iTunes Audio — Course Materials — John Geanakoplos, Yale
- Теория игр– Free Online Video – Free iTunes Audio — Free iTunes Video — Course Materials — Ben Polak, Yale
- Теория игр в социальных науках — Free iTunes Video – Yves Zenou, UC Berkeley
- Теория игр и экономика — Free Online Video – Free Video Download — Debarshi Das, IIT Guwahati
- Глобальная бедность и оценки влияния – Free Online Video — Free iTunes Video — Edward Miguel, UC Berkeley
- Великие идеи — Free Online Video — Steven Pinker, Larry Summers, Michio Kaku, etc, Floating University
- Великие экономисты: классическая экономика и её предшественники —Free Online Video — Tyler Cowan & Alex Tabarrok, George Mason
- История экономической теории – Free Online Video – Free Video Download — Dr. Shivakumar, IIT Madras
- Международные финансы — Free Online Video — Free Video Download — Arun K. Misra, IIT Kharagpur
- Международная политическая экономия — Free iTunes Audio — James Morrison, Middlebury College
- Международная торговля — Free Online Video — Free iTunes Video – Steven Wood, UC Berkeley
- Международная торговля – Free Online Video — Tyler Cowan and Alex Tabarrok, George Mason
- Введение в экономику – Free Online Video – Free iTunes Video — Syllabus – Martha Olney, UC Berkeley
- Введение в экономику и политику окружающей среды — Free Online Video — Free Online Video 2 — Peter Berck, UC Berkeley
- Законы и экономика I — Free iTunes Audio — Robert Cooter, UC Berkeley
- Лекции по капиталу — Free Online Video – Gary Becker, U Chicago
- Марксистская экономика – Free Online Video — Stephen Resnick, UMass – Amherst
- Экономика Мексики: история и перспективы — Free Online Video — Robin Grier, U. of Oklahoma
- Деньги и банковское дело (Syllabus) – Free Online Video – Gerald Epstein, UMass-Amherst
- Деньги и банковское дело — Free Online Video — Free iTunes Video — Thomas Wyrick, Missouri State
- Политическая экономика после кризиса– Free Online Video — Roberto Mangabeira Unger, Harvard
- Принципы микроэкономики— Free iTunes Video — Free Video –Jonathan Gruber, MIT
- Принципы макроэкономики– Free iTunes Video – Free Online Video — Thomas Wyrick, Missouri State
- Психология и экономика – Free Online Video – Free iTunes Video– Daniel Acland, UC Berkeley
- Экономика общественного сектора — Free Online Video – Free Video & Related Materials — Raj Chetty, Harvard
- Общественная экономика и финансы – Free Video & Course Info — Free Online Video – Nirupama Rao, NYU
- Чтения «Капитал» Маркса — Free iTunes Video – Free Online Video — Free Video & Related Materials — David Harvey, City University of New York
- Кризис Еврозоны — Free Online Video — Tyler Cowan and Alex Tabarrok, George Mason
- Федеральный резерв и финансовый кризис — Free Online Video —Ben Bernanke at George Washington University
- Австрийская школа экономики: введение – Free Online Audio: 1, 2, 3, 4 — Friedrich A. Hayek & colleagues – Recorded at University of Colorado
- Проблема мировой бедности — Free iTunes Video – Free Online Video — Related Materials — Esther Duflo & Abhijit Banerjee, MIT
- Элементы экономического анализа – Free Online Video — Glen Weyl, U Chicago
- История мировой экономики до индустриальной революции —Free Online Video & Syllabus — Free iTunes Video — Gregory Clark, UC Davis
- Мировая экономика в 20 веке – Free Online Video – Free iTunes Video – Calanit Kamala, UC Berkeley
Кинематограф
Еда
География
История
- Африканская история Америки: эмансипация до наших дней – Free Online Video — Course Materials — Jonathan Holloway, Yale
- Афроамериканская история: современная борьба за свободу – Free Online Video – Free iTunes Video — Clay Carson, Stanford
- История американской экономики (Syllabus) — Free Online Video — Free iTunes Video — Free iTunes Audio — Martha Olney, UC Berkeley
- История американской экономики (Syllabus) – Free Online Video — Gerald Friedman, UMass-Amherst
- История античной Греции — Free Online Video — Free iTunes Audio — Free iTunes Video — Course Materials — Donald Kagan, Yale
- Древний Израиль— Free Online Video & Resources — Free Online Video — Daniel Fleming, NYU
- Современная Азия: изображения и представления – Free Online Video & Course Info — John Dower, MIT
- Бенжамин Франклин и мир просвещения– Free iTunes Audio — Bruce Thompson, Stanford/UC Santa Cruz
- Китай: традиции и изменения– Free Course in Multiple Formats – Peter K. Bol & William Kirby, Harvard
- Колониальная и революционная Америка – Free iTunes Audio — Jack Rakove, Stanford
- Ранняя современная Англии: политика, религии и общество во времена Тюдоров и Стюартов – Free Online Video — Free iTunes Video — Free iTunes Audio — Course Materials — Keith E. Wrightson, Yale
- Ранняя современная Германия— Free iTunes Audio – David Wetzel, UC Berkeley
- Эпидемии в западном обществе с 1600 годов — Free iTunes Video— Free iTunes Audio — Free Online Video — Course Materials — Frank Snowden, Yale
- Европа в 19 веке – Free iTunes Audio – David Wetzel, UC Berkeley
- Европа и мир: войны, империи, нации 1648-1914 –Free iTunes Audio — David Wetzel, UC Berkeley
- Европейская цивилизация, 1648-1945 — Free Online Video – Free iTunes Audio – Free iTunes Video — Course Materials — John Merriman, Yale
- Европейская цивилизация от эпохи Возрождения до наших дней – Free iTunes Audio — Carla Hesse, UC Berkeley
- Европейская цивилизация от эпохи Возрождения до наших дней —Free Online Video — Free iTunes Video – Free Online Audio — Thomas Laqueur, UC Berkeley
- История европейской культуры, 1500-1815 — Free Online Audio — George Mosse, University of Wisconsin- Madison
- История европейской культуры, 1660-1870 — Free Online Audio —George Mosse, University of Wisconsin- Madison
- История европейской культуры, 1880-1920 — Free Online Audio —George Mosse, University of Wisconsin- Madison
- Франция с 1871 — Free Online Video – Free iTunes Video — Free iTunes Audio — Course Materials — John Merriman, Yale
- Ганнибал — Free iTunes Audio — Patrick Hunt, Stanford
- Лекции Харви Голберга (1975-1983) – Free Online Audio — Harvey Goldberg, University of Wisconsin
- Иисус в истории – Free iTunes Audio – Thomas Sheehan, Stanford University
- История антропологической мысли – Free iTunes Audio —Rosemary Joyce, UC Berkeley
- История и практика прав человека – Free Online Video – Free Video 2 — Free iTunes Video – Free iTunes Audio – Thomas Laqueur
- История информации – Free Online Video – Free iTunes Video –Free Online Video 2 — Geoffrey D. Nunberg, Paul Duguid, UC Berkeley
- История Ирана в период Сефевидов – Free iTunes Audio — Richard Bulliet, Columbia University
- История чайной культуры Китая и Японии — Free iTunes Audio — John Wallace, UC Berkeley
- История международной системы – Free iTunes Audio — James Sheehan, Stanford University
- История Массачусетского технического университета– Web — David Mindell and Merritt Roe Smith, MIT
- История современного Ближнего Востока – Free iTunes Audio — Richard Bulliet, Columbia University
- История Нью-Йорка: современная история (Syllabus) — Free Online Video & Course Info — Free iTunes Video — Free Online Video —Daniel Walkowitz, NYU
- История Соединенных Штатов с 1945 – Free iTunes Audio —Daniel Sargent, UC Berkeley
- История Соединенных Штатов с 1877 – Free iTunes Video — Dominic Capeci
- История мира до 1500 – Free Online Video — Free iTunes Video – Richard Bulliet, Columbia University
- История мира с 1500 — Free Online Video — Free iTunes Video – Richard Bulliet, Columbia University
- Интеллектуальная история США с 1865 — Free iTunes Video — Free Online Video — Richard Candida Smith, UC Berkeley
- Международная и глобальная история с 1945 – Free iTunes Audio — Daniel Sargent, UC Berkeley
- Введение в афро-американские исследования– Real Player Video— Abdul Alkalimat, University of Illinois
- Введение в историю Древней Греции — Free Online Video – Free iTunes Video — Free iTunes Audio — Course Materials — Donald Kagan, Yale
- Введение в американские исследования — Free Online Video – Free iTunes Video — Free iTunes Audio – Michael Cohen, UC Berkeley
- Создатель современного мира? Британская империя с 1714 до наших дней — (Syllabus) – Free Online Video – Free iTunes Video – James Vernon, UC Berkeley
- Медицина и здравоохранение в американской истории — Free Online Audio — Chris Hamlin, Notre Dame
- Современная цивилизация: с 1975 до наших дней — Free Online Video – Lynn Hunt, UCLA
- Современная еврейская история – Free Online Audio — George Mosse, University of Wisconsin – Madison
- Переосмысления освободительного движения афро-американцев — Free Online Video — Abdul Alkalimat, University of Illinois
- Переосмысление теории в афро-американских исследованиях— Free Online Video — Abdul Alkalimat, University of Illinois
- Наука, магия и религия — Free iTunes Video — Free Online Video– Courtenay Raia, UCLA
- Американские отцы-основатели и их мир– Free iTunes Audio —Jack Rakove, Gordon Wood, etc. Stanford
- Американская революция – Free Online Video — Free iTunes Video— Free iTunes Audio — Course Materials— Joanne B. Freeman, Yale
- Средиземноморье в древности– Free Online Audio — Isabelle Pafford, UC Berkeley
- Гражданская война и эра реконструкции, 1845-1877 — Free Online Video – Free iTunes Audio – Free iTunes Video — Course Materials —David Blight, Yale
- Раннее Средневековье, 284-1000 — Free Online Video — Free iTunes Video & Audio — Course Materials — Paul H. Freedman, Yale
- История общественного здравоохранения – Free iTunes Audio — Free Online Audio & Course Materials — Graham Mooney, Johns Hopkins
- Полвека Кеннеди – Free iTunes Video – Larry Sabato, University of Virginia
- Современный мир: глобальная история с 1760 – Free iTunesU iOS Course – Philip Zelikow, UVA
- Специфическая современность Великобритании, 1848-2000 – Free iTunes Audio — Free Online Video – Free Online Video — James Vernon, UC Berkeley
- Взлет и падение Второго Рейха – Free iTunes Audio –Margaret Anderson, UC Berkeley
- Мир Рима — Free iTunes Video — Rhiannon Evans, La Trobe University
- История свободы в Америке — Free iTunes Video – Rufus Fears, University of Oklahoma
- США и мир с 1945 — Free iTunes Audio– Daniel Sargent, UC Berkeley
- История США с раннего XIX века до кануна Второй мировой войны – Free Online Video – Free iTunes Video – Free iTunes Audio –Richard Candida Smith, UC Berkeley
- История США от Гражданской войны до наших дней — Free iTunes Audio — Free Online Audio — Jennifer Burns, UC Berkeley
- Восточные традиции (видео) — Free Online Video — Course Outline– Eugen Weber, UCLA
- Война и мир: международные отношения с 1914 – Free iTunes Audio — David Wetzel, UC Berkeley
- Мировая война и общество в XX веке: Вторая мировая война –Free Course in Multiple Formats – Charles S. Maier, Harvard
Журналистика
- Британские СМИ– Free iTunes Video – Joe Foote, University of Oklahoma
- Журналистская этика – Free Online Video – Jim Newton, UCLA
Языки
- Арабский для начинающих 1 – Free Online Video — Darlarna University
- Древние языки (греческий, латинский, санскрит, старый английский и другие) – Free Web Site – UT-Austin Linguistics Research Center
- Основы немецкого языка — Free Application — Cambridge University
- Китайский для начинающих — Free iTunes Audio — Open University
- Китайский курс — Сэтон Хол
- Базовый китайский — Free iTunes Audio — Seton Hall
- Чтение для базового китайского — Free iTunes Audio — Seton Hall
- Средний уровень китайского — Free iTunes Audio — Seton Hall
- Чтение для среднего уровня китайского — Free iTunes Audio — Seton Hall
- Продвинутый уровень китайского — Free iTunes Audio — Seton Hall
- Чтение для продвинутого уровня китайского — Free iTunes Audio — Seton Hall
- Произношение в бразильском и португальском — Free iTunes Audio — Emory University
- Основы китайского языка — Free Application — Cambridge University
- Интерактивный французский — Free iTunes Audio — Free Video & Audio — University of Texas
- Низкий уровень французского 1 – Free Web Course — Carnegie Mellon
- Низкий уровень французского 2 – Free Web Course — Carnegie Mellon
- Французский в действии Free Online Video — Yale University
- Французский 1 и французский 2 — Free Web Course — Carnegie Mellon
- Исландский онлайн — Web Site — University of Iceland
- Средний уровень китайского – Free Application — Cambridge University
- Введение в алфавит урду — Free iTunes Audio — Emory University
- Японский язык, кана, хирагана – Free iTunes Video — Emory
- Знаки кандзи — Free iTunes Video — Emory University
- Мандаринский китайский язык — Free iTunes Video — Emory University
- Числа и радикалы — Free iTunes Video — Emory University
- Средний уровень корейского онлайн — Free Online Audio — University of California Press, 2002
- Путь к корейскому языку: разговорный корейский с нуля — Web Site — The Ohio State University
- Основы русского языка — Free Application — Cambridge University
- Русский для начинающих 1 – Free Online Video – Dalarna University
- Разговаривать по-итальянски и набитым ртом — Free Online Video & Course Info — Free Online Video — Free iTunes Video — MIT, Dr. Paola Rebusco
- Тайский алфавит — Free iTunes Video — Emory University
Чтобы начать изучение более 40 иностранных языков, вы можете посмотреть обширную коллекцию Бесплатного изучения языков. Вы можете скачать или просмотреть бесплатные уроки французского, испанского, английского, немецкого, мандаринского, итальянского и других.
Закон
- Цели и пределы уголовного права — Free iTunes Audio — Tamara Lave, UC Berkeley
- Изменение климата: закон и политика — Free Online Video – Free iTunes Audio – Free iTunes Video – Cymie Payne, Daniel Farber, UC Berkeley
- Экологическая справедливость и права человека в последствиях урагана Катрина — Free Online Audio – Cynthia Toms Smedley, Notre Dame
- Экологические законы и политика — Free Online Video – Bob Infelise, UC Berkeley
- Экологические законы и политика — Free Online Video — Free iTunes Video — Free iTunes Audio — Course Materials — John P. Wargo, Yale
- Свобода слова и прессы — Free Online Video – Free iTunes Video – William Turner, UC Berkeley
- Международные экологические законы — Free Online Video – Free iTunes Video – Free iTunes Audio – Cymie Payne, UC Berkeley
- Введение в законы об авторском праве — Free iTunes Video — Free Online Video — Free Online Video & Course Info — Keith Winstein, MIT
- Трудовое законодательство и дискриминация при найме на работу — Free Online Video– Greggory Groves, Missouri State
- Закон и экономика I — Free iTunes Audio – Robert Cooter, UC Berkeley
- Закон и справедливость — Free iTunesU iOS App – Kyle Harper, University of Oklahoma
- Законная и правовая теории в XXI веке — Free Online Video — Roberto Mangabeira Unger, Harvard
- Закон СМИ и этика — Free iTunes iOS App — Nicole Kraft, Ohio State
- Политика и свобода СМИ — Free Online Video — Richard Barbrook, University of Westminster
- Прогрессивные альтернативы: институциональная реконструкция сегодня — Free Online Video — Roberto Mangabeira Unger, Harvard
- Возобновляемые источники энергии и альтернативное топливо (закон и политика) – Free Online Video – Steven Weissman, UC Berkeley
- Личность, спокойствие и уязвимость — Free Online Video — Roberto Mangabeira Unger, Harvard
- Теория закона и общества — Free Online Audio — Free iTunes Audio — David Lieberman, UC Berkeley
- Закон о видео играх — Free Online Video — Jon Festinger, University of British Columbia/Centre for Digital Media
Лингвистика
Литература
- Американская литература I: начало Гражданской войны — Free Online Video & Course Info — Free iTunes Video – Free Online Video — Cyrus Patell, NYU
- Американские пассажи: литературный обзор — Free Online Video — Multiple profs, Annenberg Learner
- Приближение к Шекспиру — Free iTunes Audio — Free Online Audio —Emma Smith, Oxford
- Британская и Американская поэзия: с 1900 года до наших дней — Free iTunes Audio – Charles Altieri, UC Berkeley
- «Дон Кихот» Сервантеса — Free Online Video — Free iTunes Video— Free iTunes Audio — Course Materials — Roberto González Echevarría, Yale
- Современная литература — Free Online Video – Free Video Download — Aysha Iqbal Viswamohan, IIT Madras
- Творческое чтение — Free Online Audio — William S. Burroughs, Naropa University
- Творческое чтение: мастер-класс — Free iTunes Video – Alison Ersheid
- Культурология — Free Online Video – Free Video Download — Liza Das, IIT Guwahati
- Данте в переводе — Free Online Video — Free iTunes Audio — Free iTunes Video — Course Materials — Giuseppe Mazzotta, Yale
- Дарвин и дизайн — Free Online Video & Course Info — James Paradis, MIT
- Д.Х. Лоуренс — Free Online Video & Audio — Catherine Brown, Oxford
- Экзистенциализм в литературе и фильмах — Free iTunes Audio — Free Online Audio — Hubert Dreyfus, UC Berkeley
- Экспансивная поэтика — Free Online Audio — Allen Ginsberg, Naropa University
- Волшебство и фэнтази — Free Online Video & Audio — Corey Olsen, Washington College
- От богов и обратно — Free Online Audio — Hubert Dreyfus, UC Berkeley
- Джордж Элиот — Free Online Audio — Catherine Brown, Oxford
- Хемингуэй, Фицджеральд, Фолкнер — Free Online Video — Free iTunes Audio — Course Materials — Wai Chee Dimock, Yale
- Холокост в фильмах и литературе — Free Online Video – Todd Presner, UCLA
- Литература и окружающая среда: введение — Free Online Video — Free iTunes Video – Ken Hiltner, Princeton
- Поэзия: введение — Free iTunes Video – Lanette Cadle, Missouri State
- Предсовременная японская культура и литература: введение — Free iTunes Audio – John Wallace, UC Berkeley
- Введение в теорию литературы — Free Online Video — Free iTunes Audio – Free iTunes Video — Course Materials — Paul H. Fry, Yale
- Приглашение в мировую литературу — Free Online Video — David Damrosch, Harvard
- Джек Керуак — Free Online Audio Part 1 and Part 2 – Allen Ginsberg, Naropa University
- Литература и форма — Free Online Video & Audio — Free iTunes Video– Free iTunes Audio – Catherine Brown, Oxford
- Литература и психоанализ — Free Online Audio — John Fletcher, University of Warwick
- Английская литература с начала XVII века до середины XIX века — Free iTunes Audio — Charles Altieri, UC Berkeley
- Милтон — Free Online Video – Free iTunes Audio — Free iTunes Video— Course Materials — John Rogers, Yale
- Властелин колец I: Дорога вдаль и вдаль спешит — Free iTunes Video & Audio — Corey Olsen, Washington College
- Властелин колец II: Две башни — Free Tunes Video & Audio — Free Online Video & Audio — Corey Olsen, Washington College
- Властелин колец III: Возвращение короля — Free iTunes Video & Audio — Free Online Video & Audio — Corey Olsen, Washington College
- Современная поэзия — Free Online Video — Course Materials — Langdon Hammer, Yale
- Не Шекспир: Елизаветинский и Якобинский театры — Free iTunes Audio — Free Online Audio — Multiple profs, Oxford
- Старый английский язык в контексте — Free Online Audio — Stuart Lee, Oxford University
- Оскар Уайлд — Free Online Audio — Sos Eltis, Oxford
- Восстановление и поэзия XVIII века: от Драйдена до Вордсворта — Free Online Audio – William Flesch, Brandeis
- Научная фантастика и политика — Free iTunes Audio — Free Online Audio — Courtney Brown, Emory University
- Шекспир — Free iTunes Audio — Free Online Audio — Charles Altieri, UC Berkeley
- Шекспир: поздние пьесы — Free Course in Multiple Formats – Marjorie Garber, Harvard
- Основные пьесы Шекспира — Free iTunes Audio – Free Online Audio — Ralph Williams, University of Michigan
- Спенсер и Мильтон — Free Online Audio — William Flesch, Brandeis
- Обзор американской литературы II — Free iTunes Video — Clark Closser, Missouri State
- Обзор пьес Шекспира — Free Online Audio – William Flesch, Brandeis
- Американские романы с 1945 года — Free Online Video – Free iTunes Audio – Free iTunes Video — Download Course – Amy Hungerford, Yale
- Искусство жить — Free Online Video (More info) – Team taught, Stanford
- Эпопея — Free iTunes Audio — UC Berkeley — Maura Bridget Nolan &Charles Altieri
- Хоббит — Free iTunes Video — Free Online Audio — More – Corey Olsen, Washington College
- Литература в период кризиса — Free iTunes Audio — Marsh McCall & Martin Evans, Stanford
- Семинар по Сильмариллиону — Free Online Video & Audio — Corey Olsen, Washington College
- Западный канон: от Гомера до Мильтона — Free Online Audio– William Flesch, Brandeis
- Искусство стихов: лекции Чарльза Элиота Нортона — Free Online Audio – Jorge Luis Borges, Harvard
- Базовый обзор произведений Толкина — Free Online Video & Audio — Corey Olsen, Washington College
- Энеида Вергилия: анатомия классики — Free iTunes Audio —Susanna Braund, Stanford
- Голоса и видения: жизнь и работа 13 американских поэтов — Free Online Video — Annenberg Media
- Источники написания — Free Online Audio — William S. Burroughs, Naropa University
Вы можете найти другие онлайн курсы в этой бесплатной коллекции.
Исследования СМИ
Музыка и исполнительское искусство
Философия
- Легкий старт этики для начинающих — Free iTunes Video – Free Online Video – Free Online Audio – Marianne Talbot, Oxford University
- Легкий старт по философии сознания — Free iTunes Audio —Free Online Audio — Marianne Talbot, Oxford
- Эстетика и философия искусства — Free iTunes Audio — Free Online Audio — James Grant, Oxford University
- Аналитическая философия: Уилфрид Селларс — Free Online Audio — Robert Brandom, University of Pittsburgh
- Древняя и Средневековая философия — Free iTunes Video — Free Online Video – David O’Connor, Notre Dame
- Древняя философия — Free iTunes Audio — David Ebrey, UC Berkeley
- Древняя мудрость и современная любовь — Free iTunes Video — Free Online Video – David O’Connor, Notre Dame
- Диаграммы аргумента — Free Web Course — Carnegie Mellon
- Аристотель: этика — Free Online Audio — Leo Strauss, U Chicago
- Аристотель: риторика — Free Online Audio — Leo Strauss, U Chicago
- Аристотель: политика — Free Online Audio — Leo Strauss, U Chicago
- Власть и индивидуальность: шесть лекций BBC — Free Online Audio — Bertrand Russell, Cambridge
- Биоэтика: введение — Free Online Video & Audio — Free iTunes Video – Free iTunes Audio — Marianne Talbot, Oxford
- Современные проблемы в философии сознания и познания — Free Online Video — Multiple Profs, IIT Bombay
- Критические рассуждения для начинающих —Free iTunes Video – Free iTunes Audio – Free Online Video & Audio — Marianne Talbot, Oxford
- Смерть — Free Online Video – Free iTunes Audio – Free iTunes Video— Course Materials — Shelly Kagan, Yale
- Основные принципы Дэвида Юма — Free iTunes Video – Free iTunes Audio — Free Online Video & Audio — Peter Millican, Oxford
- Восемь курсов философии Жиля Делёза — Free Online Video —Gilles Deleuze, Université Paris-VIII
- Экологическая философия — Free iTunes Video — Free Online Video– Kenneth Sayre, Notre Dame
- Экзистенциализм в литературе и кинематографе — Free iTunes Audio — Free Online Audio — Hubert Dreyfus, UC Berkeley
- Экзистенциализм в литературе и кинематографе — RSS Feed — Sean Dorrance Kelly, Harvard University
- От богов и обратно — Free Online Audio — Hubert Dreyfus, UC Berkeley
- Общая философия — Free iTunes Video — Free Online Audio — Peter Millican, Oxford University
- Гёдель, Эшер, Бах: Космическая одиссея психики — Free Online Video — Justin Curry & Curran Kelleher, MIT
- Большие великие идеи — Free Online Video — Steven Pinker, Larry Summers, Michio Kaku, etc, Floating University
- Гегель: философия истории — Free Online Audio — Leo Strauss, U Chicago
- «Феноменология духа» Гегеля — Free Online Audio — JM Bernstein, New School
- «Феноменология духа» Гегеля – Free Online Audio — Richard Dien Winfield, University of Georgia
- «Философия права» Гегеля — Free Online Audio — Richard Dien Winfield, University of Georgia
- «Наука логики» Гегеля — Free Online Audio — Richard Dien Winfield, University of Georgia
- Хайдеггер: Бытие и время — RSS Feed — Web Site — Sean Dorrance Kelly, Harvard
- «Бытие и время» Хайдеггера — Free iTunes Audio — Free Online Audio —Hubert Dreyfus, UC Berkeley
- «Бытие и время» Хайдеггера. Раздел II – Free iTunes Audio — Hubert Dreyfus, UC Berkeley
- История политической теории — Free iTunes Audio — Wendy Brown, UC Berkeley
- Гоббс: Левиафан и де Сив (1964) — Free iTunes Audio — Leo Strauss, U Chicago
- Введение в индийскую философию — Free Online Video – Free Video Download — Satya Sundar Sethy, IIT Madras
- Введение в философию —
lifehacker.ru

 Решение иррациональных уравнений.
Решение иррациональных уравнений. Адрес для вставки QR-кода числа 26, размер 500×500:
Адрес для вставки QR-кода числа 26, размер 500×500:


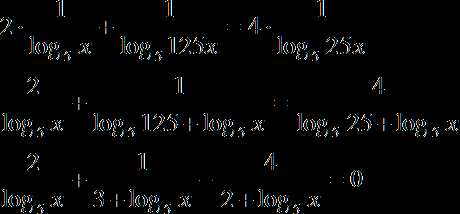 [Подпись к рисунку]
[Подпись к рисунку]


 Амплитуда и фаза факториала комплексного аргумента.
Амплитуда и фаза факториала комплексного аргумента. Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом. Амплитуда и фаза факториала комплексного аргумента.
Амплитуда и фаза факториала комплексного аргумента. Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.


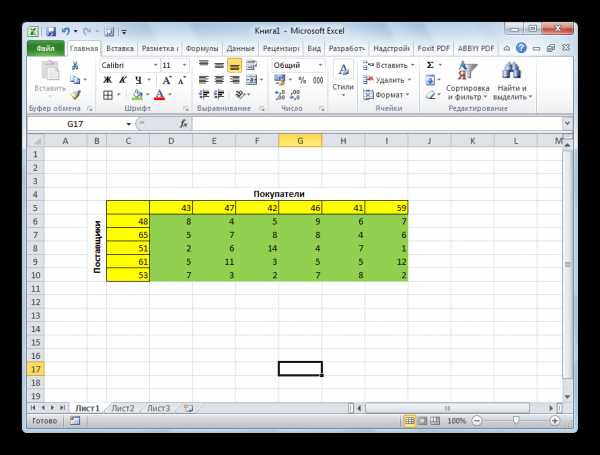
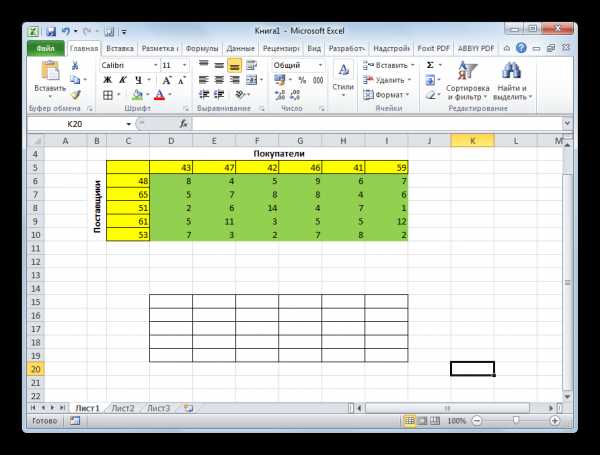
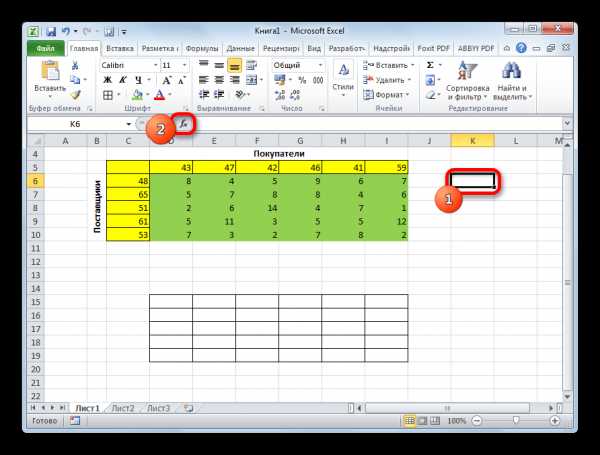

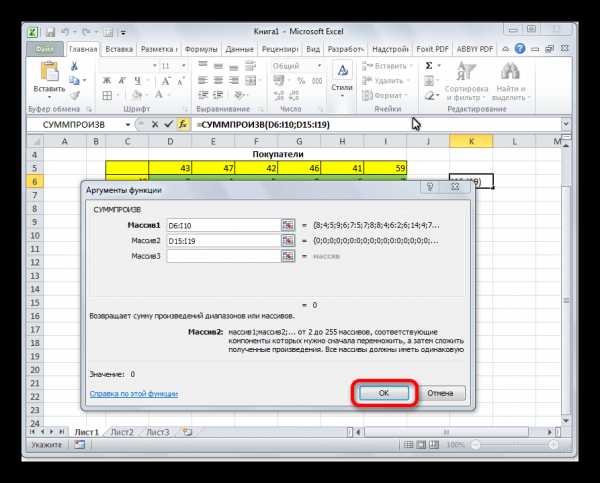
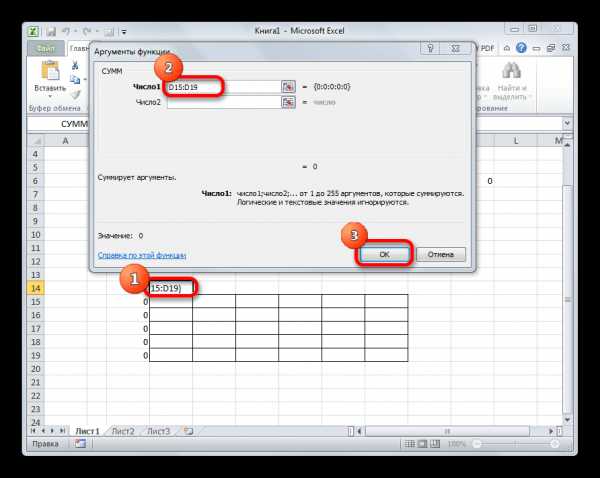
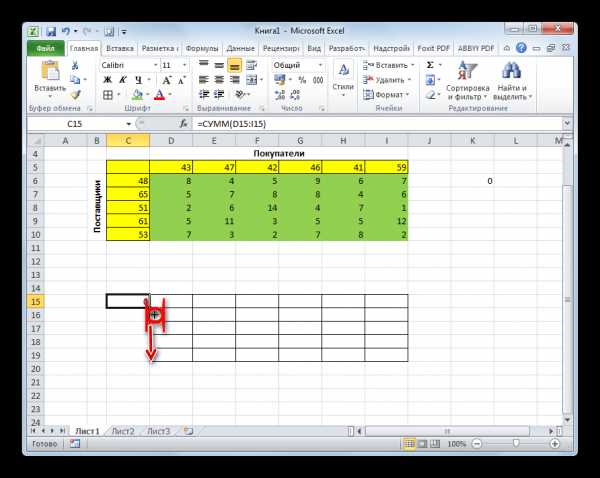

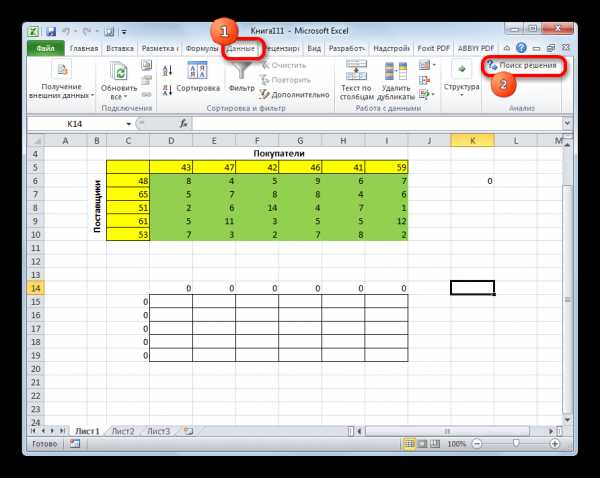
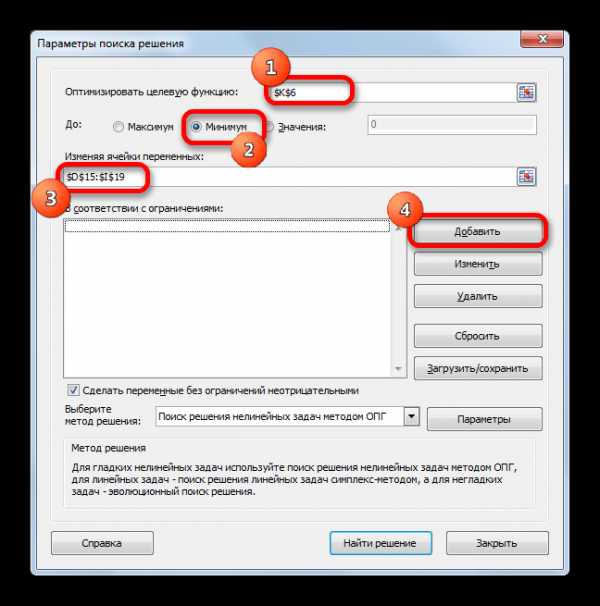
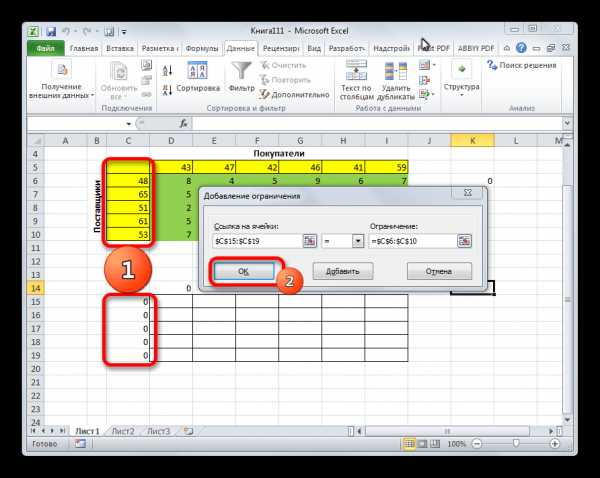
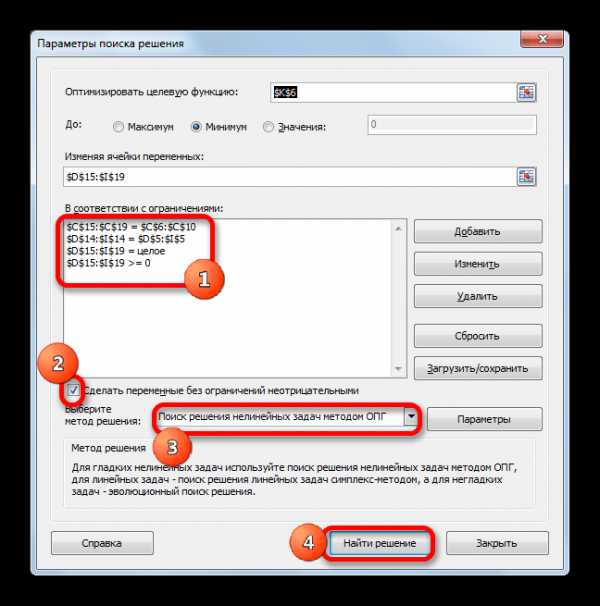



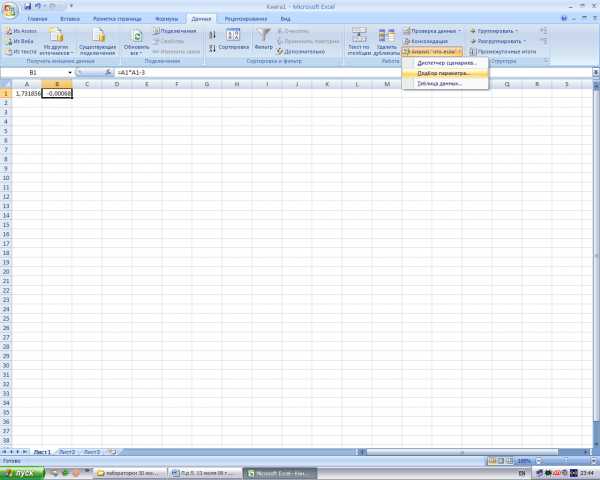
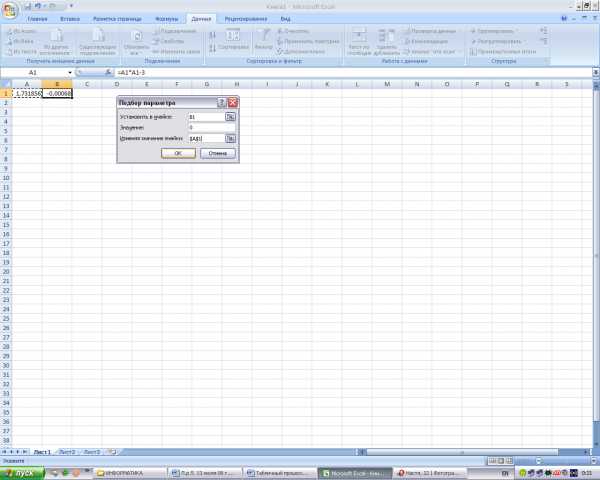

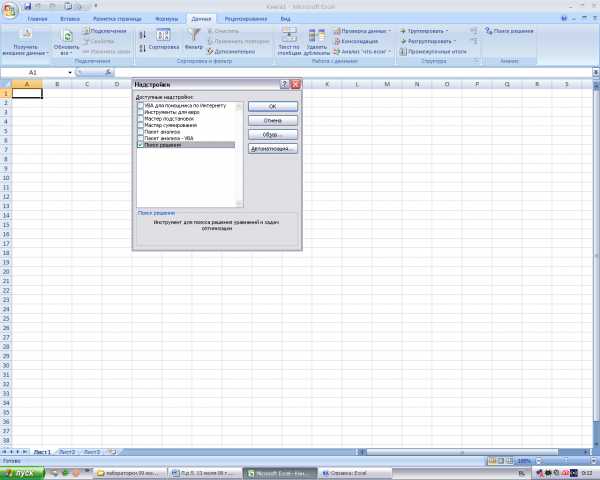

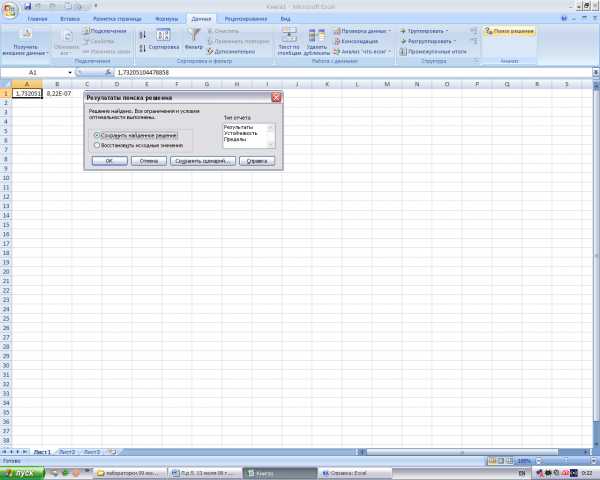


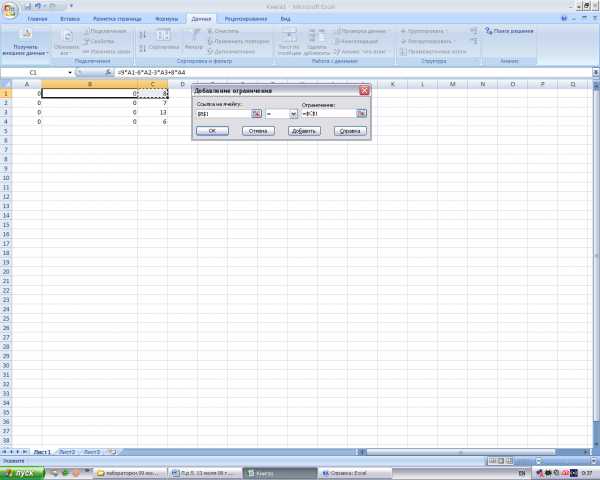
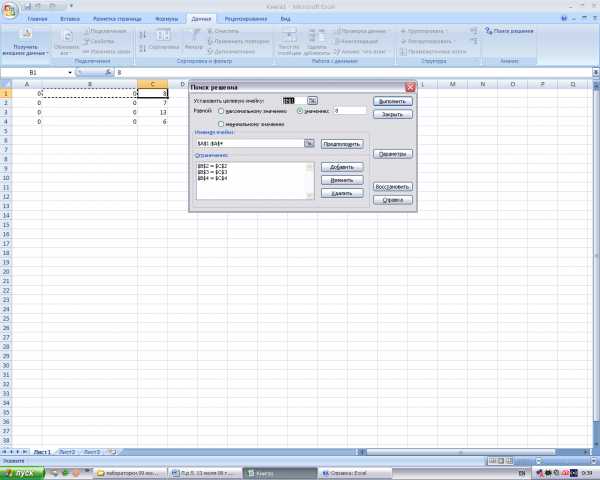
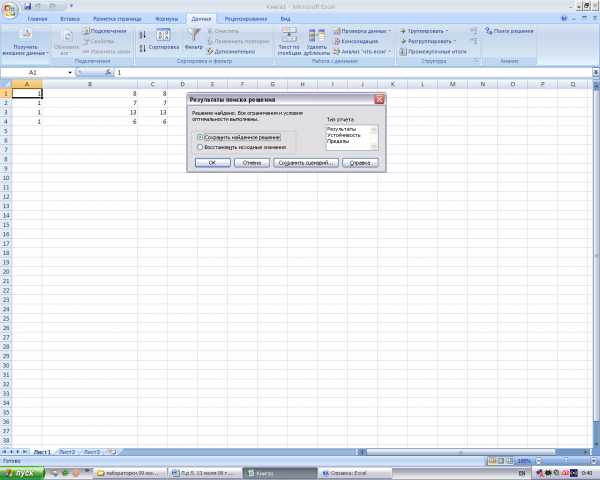



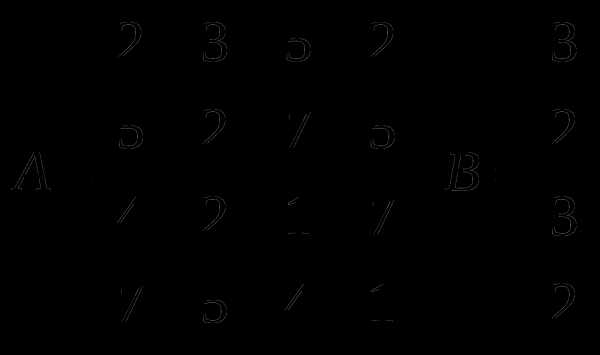
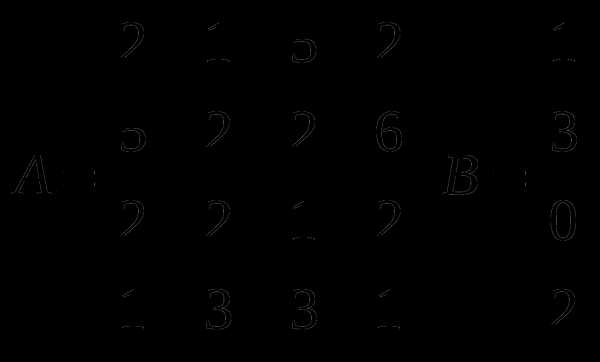
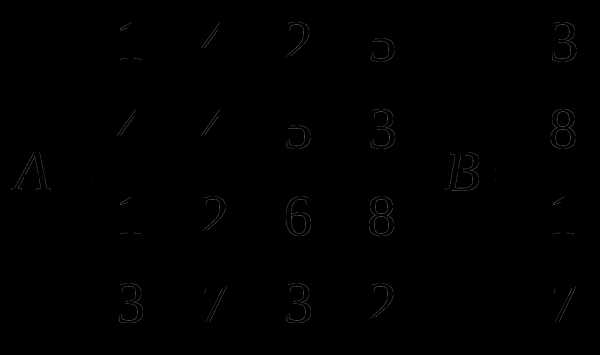








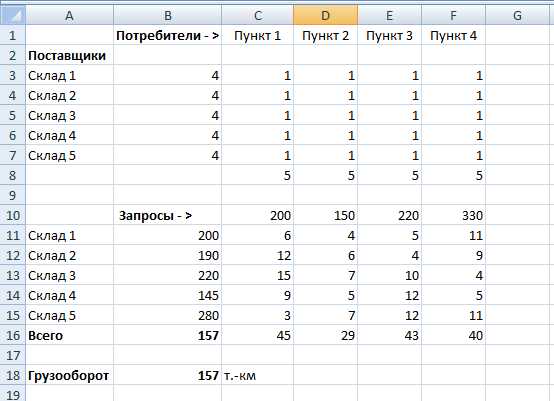 Рисунок 3. Рабочий лист, приготовленный для решения транспортной задачи.
Рисунок 3. Рабочий лист, приготовленный для решения транспортной задачи. Рисунок 4. Диалоговое окно Поиск решения.
Рисунок 4. Диалоговое окно Поиск решения.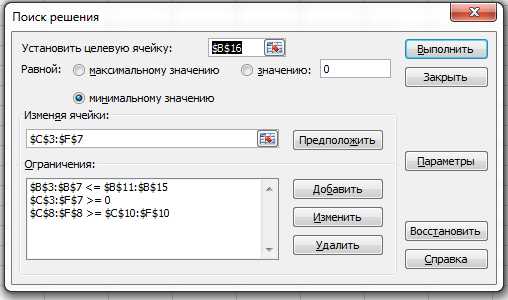 Рисунок 5. Условия для решения транспортной задачи.
Рисунок 5. Условия для решения транспортной задачи. Практическая работа 11 класс
Практическая работа 11 класс

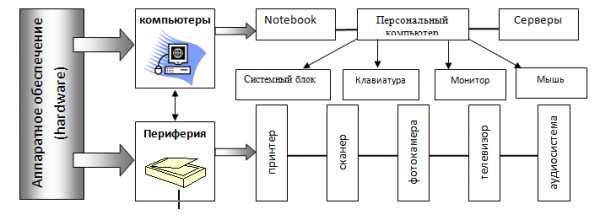

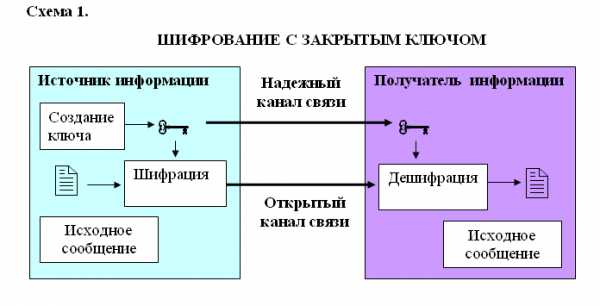
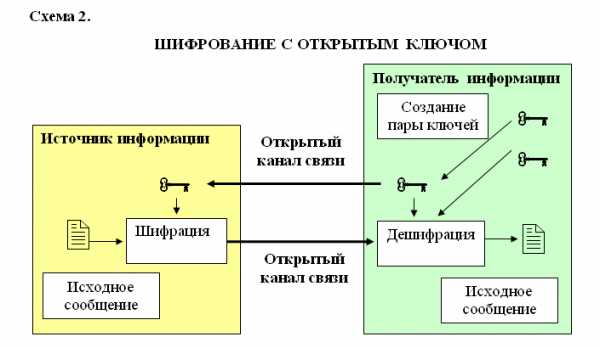
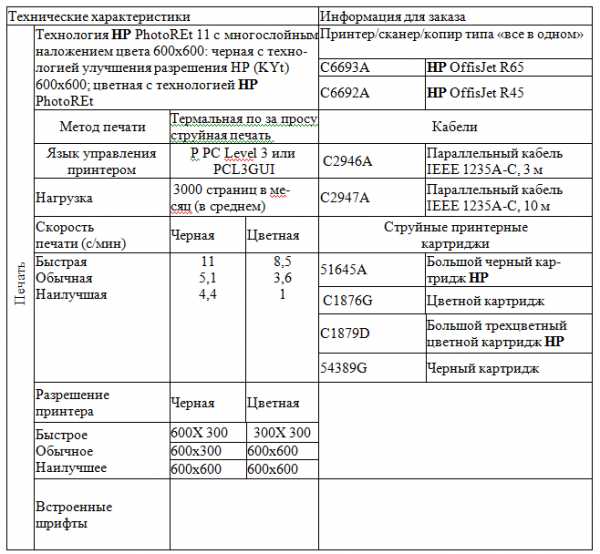











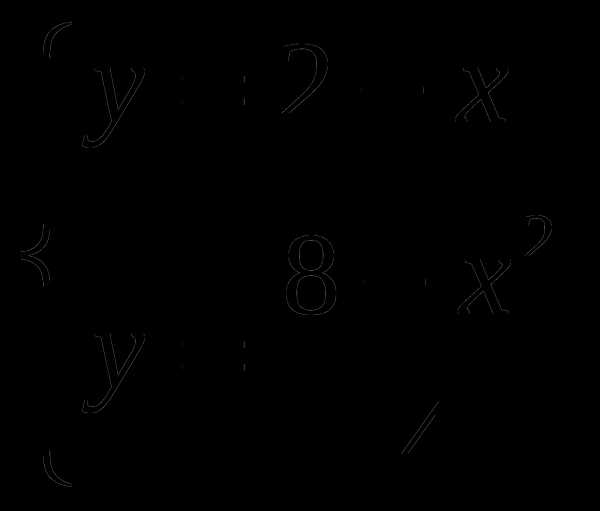
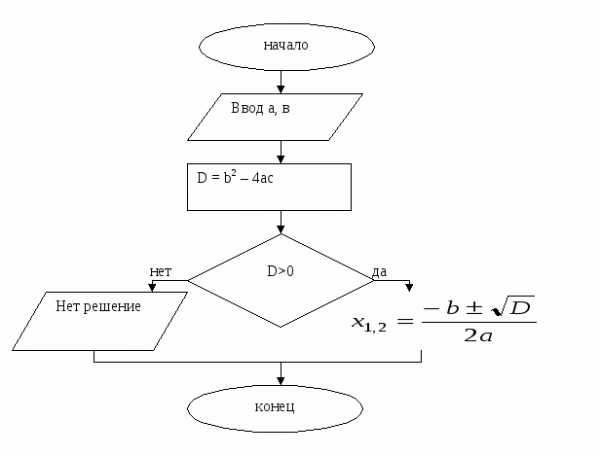
 нарисовать прямоугольник АВВ1А1
нарисовать прямоугольник АВВ1А1

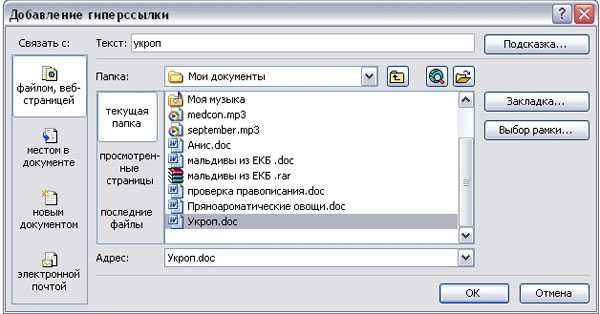
 . Установите выравнивание текста «По центру»
. Установите выравнивание текста «По центру»