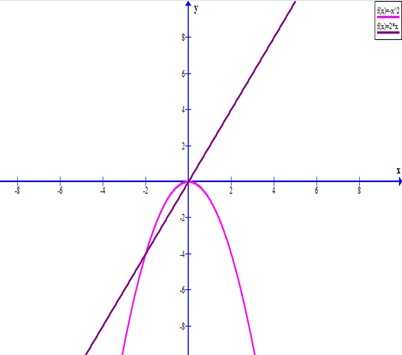
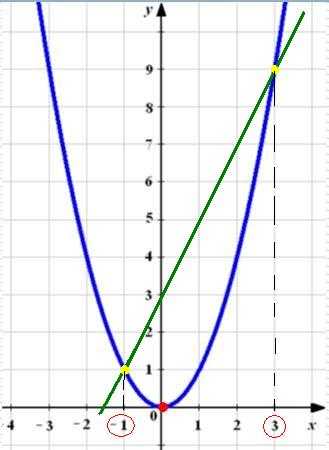
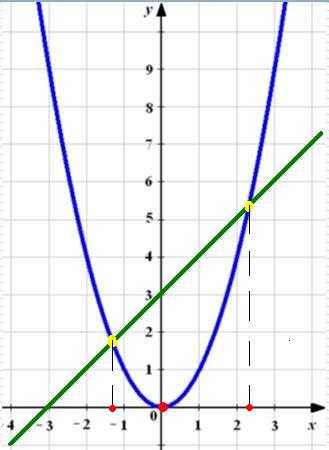
Окружность и круг. Части окружности и круга
Многие предметы вокруг нас имеют форму, похожую на геометрические фигуры. Чтобы разобраться, что такое окружность и чем она отличается от круга, необходимо иметь чёткое представление об этих фигурах. Если поставить круглый стакан на лист бумаги и обвести его карандашом, получится линия, изображающая окружность. Если рассмотреть эту линию под микроскопом, то мы увидим толстую неровную чету. Геометрическая окружность не имеет ширины. Все её точки одинаково удалены от центра. Кольцо, обруч напоминают своей формой окружность.
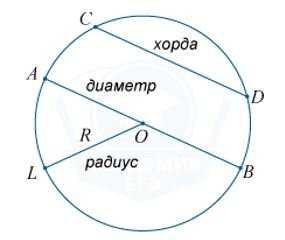
Окружностью называется фигура, которая состоит из всех точек плоскости, находящихся на данном расстоянии от данной точки. Эта точка называется центром окружности и обычно обозначается О.
Расстояние от точек окружности до её центра называется радиусом окружности и обычно обозначается R. Радиусом также называется любой отрезок, соединяющий точку окружности с её центром.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром.
Что же такое круг? Круг мы можем вырезать из бумаги. Арена цирка, дно стакана или тарелка имеют форму круга. Если окружность это «черта» (мы можем ниточкой выложить окружность), то круг это все, что находится внутри окружности.
Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние – радиусом круга. Границей круга является окружность с теми же центром и радиусом.
Окружность и круг состоят из разнообразных частей.
Две точки, взятые на окружности, разобьют эту окружность на две части – две дуги, концами которых будут взятые точки.
Отрезок, соединяющий две точки окружности, называется хордой окружности, и хордой круга, ограниченного этой окружностью.
Хорда, проходящая через центр окружности или круга, называется диаметром окружности или круга. Диаметр делит круг на два полукруга, а окружность – на две полуокружности.
Диаметр делится центром окружности пополам, и поэтому он равен двум радиусам.
Два радиуса разбивают круг на секторы.
Хорда разбивает круг на сегменты.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Круг. Окружность (центр, радиус, диаметр). Видеоурок. Математика 3 Класс
У круга есть одна подруга,
Знакома всем её наружность,
Она идет по краю круга
И называется окружность.
Если рассмотреть рисунки 1-6 в таблице 1 и определить те линии, которые являются незамкнутыми, увидим, что это рисунки 1 и 2. Из оставшихся фигур видно, что рисунки 3 и 6 – это ломаные замкнутые линии. А рисунки 4 – это овал, и 5 – это окружность.
Таблица 1. Линии
|
Рис. 1 |
Рис. 2 |
Рис. 3 |
|
Рис. 4 |
Рис. 5 |
Рис. 6 |
Давайте сравним между собой овал и окружность (рис. 7–8). А данные о сравнении занесём в таблицу 2.
Таблица 2. Сравнение овала и окружности
Окружность – это замкнутая кривая линия с точкой в середине, которая называется центром. Расстояния от центра до линии окружности одинаковые.
Если соединить центр окружности с линией окружности, получим радиус, например, на рисунке 8 и .
Радиус – длина отрезка, соединяющего центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра.
Если отрезок проходит через центр и соединяет две точки на окружности – это диаметр, например, на рисунке 8 отрезок .
Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего две точки на этой окружности.
Разгадаем загадку:
Мой циркач, циркач лихой
Чертит круг одной ногой,
А другой – проткнул бумагу,
Уцепился – и ни шагу.
В загадке речь идёт о циркуле – чертёжном инструменте (рис. 9), с помощью которого можно начертить окружности с разными радиусами.
Рис. 9. Циркуль (Источник)
Если заполнить пространство внутри окружности, например начертить окружность с помощью циркуля на бумаге или картоне и вырезать, то получим круг (рис. 10).
Рис. 10. Круг
Круг – это часть плоскости, ограниченная окружностью.
Условие: Витя Верхоглядкин начертил в своей окружности (рис. 11) 11 диаметров. А когда пересчитал радиусы, получил 21. Правильно ли он сосчитал?
Рис. 11. Иллюстрация к задаче
Решение: радиусов должно быть в два раза больше, чем диаметров, поэтому:
Витя сосчитал неправильно.
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012. – 112 с.: ил. – (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. – М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. – М.: Ювента.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Mypresentation.ru (Источник).
- Sernam.ru (Источник).
- School-assistant.ru (Источник).
Домашнее задание
1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] – 2-е изд. – М.: Просвещение, 2012., ст. 94 № 1, ст. 95 № 3.
2. Разгадайте загадку.
Мы живём с братишкой дружно,
Нам так весело вдвоём,
Мы на лист поставим кружку (рис. 12),
Обведём карандашом.
Получилось то, что нужно –
Называется …
Рис. 12. Кружка (Источник)
3. Необходимо определить диаметр окружности, если известно, что радиус равен 5 м.
4. * С помощью циркуля начертите две окружности с радиусами: а) 2 см и 5 см; б) 10 мм и 15 мм.
interneturok.ru
Определения: Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Расстояние (r) от точки окружности до ее центра называется радиусом окружности. Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром (d=2r).
Касательная — прямая (а), проходящая через точку (А) окружности перпендикулярно к радиусу, проведенному в эту точку, называется. При этом данная точка (А) окружности называется точкой касания.
Часть плоскости, ограниченная окружностью, называется кругом. |
|
Если две хорды АВ и CD пересекаются внутри круга в точке Е, то произведение отрезков одной хорды равно произведению отрезков другой хорды, т. е. AЕ·ЕВ = DE·EC
| |
AB·AC=АВ1·АС1.
|
|
Теорема о квадрате касательной
МC 2 = МВ·МА |
|
Диаметр окружности, перпендикулярный хорде, проходит через ее середину. Обратно: если диаметр проходит через середину хорды, то он ей перпендикулярен. |
|
Вписанный угол — угол, образованный двумя хордами СА и СВ, исходящими из одной точки на окружности (∠ACB). Описанный угол — угол, образованный двумя касательными DM и DN (∠MDN). Центральный угол имеет ту же градусную меру, что и дуга, на которую он опирается. Вписанный угол измеряется половиной дуги, на которую он опирается.
|
|
Угол, образованный двумя хордами и опирающийся на них центральный угол связаны соотношением |
|
Длина дуги, соответствующая центральному углу в n°
|
|
Площадь кругового сектора где α — градусная мера угла, R — радиус круга. Квадрант — сектор, отсекаемый радиусами, образующими угол 90°.
|
|
Площадь сегмента, не равного полукругу где α — градусная мера центрального угла, которая содержит дугу этого кругового сегмента, Знак «−» надо брать, когда αα>180°. Основание и высота сегмента | |
R, r — внешний и внутренний радиусы;
|
|
osiktakan.ru
5.1.4 Окружность и круг
Видеоурок: Окружность. Решение задач
Лекция: Окружность и круг
Окружность – это замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра.
В повседневной жизни Вы не раз встречали окружность. Именно её описывает часовая и секундная стрелка, именно форму окружности имеет гимнастический обруч.

А теперь представьте, что Вы нарисовали окружность на листке бумаги и захотели её разукрасить.

Так вот все разукрашенное пространство, ограниченное окружностью – это и есть круг.
И круг, и окружность имеют некоторые параметры:
Центр – это точка, которая равноудалена от всех точек окружности. Центр круга и окружности обозначается буквой О.
Радиус – это расстояние от центра до окружности (R).
Диаметр – это отрезок, проходящий через центр, который соединяет все точки окружности (d). Более того, диаметр равен двум радиусам: d = 2R.
Хорда – отрезок, который соединяет любые две точки на окружности. Диаметр является частным случаем хорды.
Чтобы найти длину окружности, необходимо воспользоваться формулой:
l=2πR
Обратите внимание, длина окружности, площадь зависят только от радиуса данной окружности.
Площадь круга можно найти по следующей формуле:
S=πR2.
Хотелось бы обратить Ваше внимание на число «Пи». Данное значение было найдено как раз с помощью окружности. Для этого её длину разделили на два радиуса, и таким образом получилось число «Пи».
Если круг разбить на некоторые части двумя радиусами, то такие части будут называться секторами. Каждый сектор имеет свою градусную меру – градусную меру той дуги, на которую опирается.
Чтобы найти длину дуги, необходимо воспользоваться формулой:
1. Используя градусную меру:
2. Используя радианную меру:
Если вершина некоторого угла опирается на центр окружности, а его лучи пересекают окружность, то такой угол называется центральным.
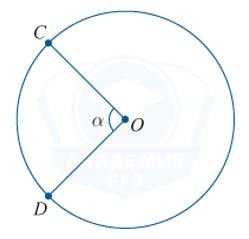
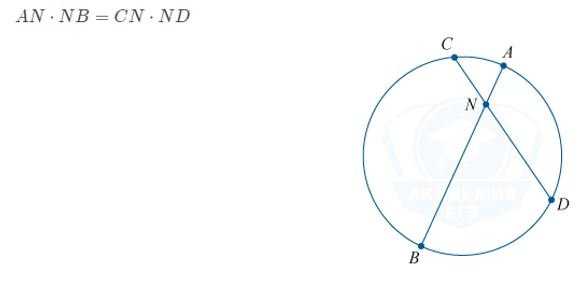
Если некоторые две хорды пересекаются в некоторой точке, то их отрезки пропорциональны:
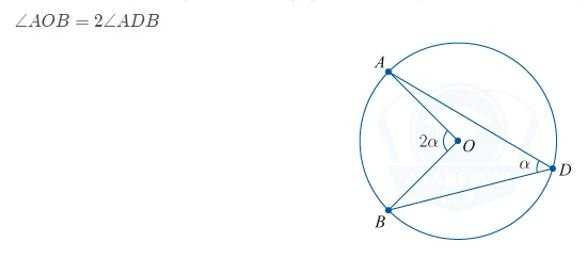
Угол, вершина которого опирается на окружность, называется вписанным углом. Если вписанный и центральный угол опирается на одну и ту же дугу, то градусные меры таких углов отличаются вдвое:
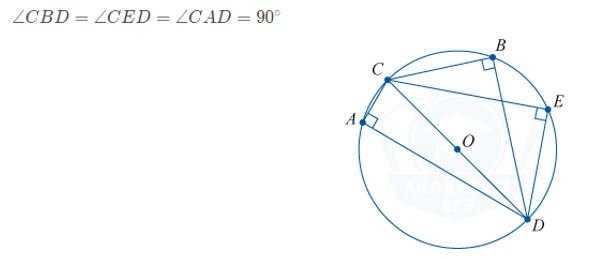
Если в некоторую окружность вписан треугольник, сторона которого является диаметром данной окружности, то этот треугольник обязательно прямоугольный:
cknow.ru
Окружность и круг | LAMPA
Круг — это множество точек, которые удалены от некоторой точки, называемой центром круга, на расстояние не более чем rrr. rrr называется радиусом круга. Граница круга называется окружностью.
Основные свойства:
- Длина любой не превосходит круга;
- Площадь круга равна S=πr2S=\pi r^2S=πr2;
- Длина окружности равна l=2πrl=2\pi rl=2πr.
Центральный угол
Центральный угол — это угол, вершина которого лежит в центре окружности.
Любые две точки AAA и BBB окружности разбивают ее на две части; каждая из этих частей называется дугой.
Градусная мера дуги — это градусная мера , который опирается на эту дугу.
Вписанный угол
Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Основные свойства:
- Если градусная мера дуги, на которую опирается вписанный угол, равна α\alphaα, то градусная мера вписанного угла равна α2\frac{\alpha }{2}2α, а градусная мера равна α\alphaα;
- Вписанные углы, опирающиеся на равные дуги, равны;
- Вписанный угол, опирающийся на окружности, равен 90∘90^{\circ}90∘.
Сектор
Сектор — это часть круга, ограниченная двумя радиусами.
Основные свойства:
- Площадь сектора с , имеющим градусную меру α\alphaα, и радиусом RRR равна S=πR2α360∘S=\pi R^2 \frac{\alpha }{360^{\circ}}S=πR2360∘α. Например, если α=90∘\alpha =90^{\circ}α=90∘, то площадь сектора равна 14πR2\frac{1}{4} \pi R^241πR2;
- Длина дуги сектора равна l=2πRα360∘l=2\pi R \frac{\alpha }{360^{\circ}}l=2πR360∘α.
lampa.io
Что такое окружность и круг, в чем их отличия и примеры данных фигур из жизни
Школьная пора для большинства взрослых людей ассоциируется с беззаботным детством. Конечно, многие неохотно посещают школу, но только там они могут получить базовые знания, которые впоследствии пригодятся им в жизни. Одним из таких является вопрос о том, что такое окружность и круг. Спутать данные понятия достаточно просто, ведь слова являются однокоренными. Но разница между ними не настолько большая, как может показаться неопытному ребенку. Дети данную тему любят по причине ее простоты.
Что такое окружность?

Окружность — это замкнутая линия, каждая точка которой равно удалена от центральной. Самым ярким примером окружности является обруч, который представляет собой замкнутое тело. Собственно, и говорить особо об окружности не приходится. В вопросе о том, что такое окружность и круг, значительно интереснее вторая его часть.
Что такое круг?

Представьте, что вы решили разукрасить нарисованную выше окружность. Для этого можно выбрать любые краски: синие, желтые или зеленые — кому что ближе по душе. И вот вы начали заполнять пустоту чем-то. После того как это было закончено, у нас получилась фигура, которая называется кругом. По сути, круг — это часть поверхности, очерченная окружностью.
У круга есть несколько важных параметров, часть из которых также характерна и для окружности. Первый — это радиус. Им называется расстояние между центральной точкой круга (ну или окружности) и самой окружностью, что создает границы кругу. Вторая важная характеристика, которая неоднократно используется в школьных задачах — это диаметр (то есть расстояние между противоположными точками окружности).
Ну и наконец, третья характеристика, присущая кругу — это площадь. Данное свойство специфичное только для него, окружность не имеет площади в силу того, что у нее нет ничего внутри, а центр, в отличие от круга, скорее воображаемый, чем настоящий. В самом же круге можно установить четкий центр, через который провести ряд линий, которые делят его на сектора.
Примеры круга в реальной жизни
На самом деле возможных предметов, которые можно назвать разновидностью круга, достаточно. Например, если посмотреть на колесо машины прямо, то вот вам пример готового круга. Да, он необязательно должен быть заполнен однотонно, вполне возможны различные узоры внутри него. Второй пример круга — это солнце. Конечно, на него посмотреть будет тяжело, но оно на небе выглядит, как маленький кружочек.
Да, сама звезда Солнце — это не круг, она имеет еще и объем. Но вот само солнце, которое мы видим над нашей головой в летнее время, является типичным кругом. Правда, площадь у него все равно высчитать не получится. Ведь сравнение его с кругом приводится только для наглядности, чтобы было проще понять, что такое окружность и круг.
Отличия окружности от круга
Значит, какой вывод мы можем сделать? Чем отличается окружность от круга, так это тем, что у последнего есть площадь, и в большинстве случаев окружность является границей круга. Хотя бывают и исключения на первый взгляд. Может показаться иногда, что нет окружности в круге, но это не так. В любом случае что-то да есть. Просто окружность может быть очень маленькой, и тогда ее не видно невооруженным глазом.
Также окружностью может быть то, что выделяет круг из фона. Например, на приведеном выше изображении синий круг находится на белом фоне. А вот та черта, по которой мы понимаем, что здесь начинается фигура, и называется в данном случае окружностью. Таким образом, окружность — это граница круга. Вот чем отличается окружность от круга.
Что такое сектор?
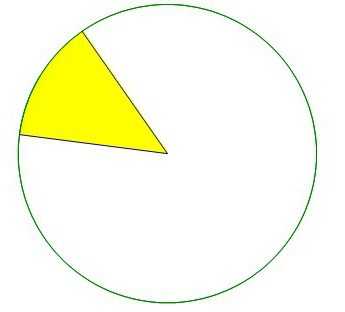
Сектор — это участок круга, который образуется двумя проведенными по нему радиусами. Чтобы понять это определение, нужно просто вспомнить пиццу. Когда ее разрезают на равные кусочки, все они и являются секторами круга, который представлен в виде такого вкусного блюда. При этом совершенно необязательно секторы должны быть равны. Они могут быть разной величины. Например, если отрезать половину пиццы, то она также будет сектором этого круга.
Предмет, отображаемый этим понятием, может иметь только круг. Окружность (радиус тоже можно провести, конечно, но после этого она станет кругом) не имеет площади, поэтому и сектор выделить не получится.
Выводы
Да, тема о круге и окружности (что это такое) очень проста для понимания. Но вообще все то, что касается этих геометрических фигур, является самым сложным для изучения. Школьнику нужно быть готовым к тому, что круг — фигура капризная. Но, как говорится, тяжело в учении — легко в бою. Да, геометрия — наука сложная. Зато успешное ее освоение позволяет сделать маленький шажок в сторону успеха. Потому что старания при обучении позволяют не только пополнять багаж собственных знаний, но и получать необходимые в жизни навыки. Собственно, на это и нацелена школа. А ответ на вопрос о том, что такое окружность и круг, является вторичным, хоть и важным.
fb.ru
Материал по математике «Окружность и круг»
Окружность и круг
Окружность и круг — геометрические фигуры, взаимосвязанные между собой. Окружность есть граничная ломаная линия (кривая) круга,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов, лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D).
Правило. Диаметр окружности равен двум ее радиусам.
d = 2r
D = 2R
Длина окружности вычисляется по формуле и зависит от радиуса (диаметра) окружности. В формуле присутствует число ¶, которое показывает во сколько раз длина окружности больше, чем ее диаметр. Число ¶ имеет бесконечное число знаков после запятой. Для вычислений принято ¶ = 3,14.
Длина окружности обозначается латинской большой буквой «цэ» (C). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
Примеры
Дано: d = 100 см.
Длина окружности: C = 3,14 * 100 см = 314 см
Дано: d = 25 мм.
Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой, уменьшается по мере удаления секущей от центра окружности.
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S) равна произведению квадрата радиуса ( r 2 ) на число ¶.
Примеры
Дано: r = 100 см
Площадь круга:
S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
Дано: d = 50 мм
Площадь круга:
S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами. Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности.
Определение. Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Площадь сектора составляет только часть площади круга, и ее величина пропорциональна длине дуги m или зависит от величины центрального угла a, образованного двумя радиусами с вершиной в центре круга.
Формула для вычисления площади сектора:
где S — площадь сектора; m — длина дуги; r — радиус круга; а — угловая величина дуги (и градусах).
videouroki.net

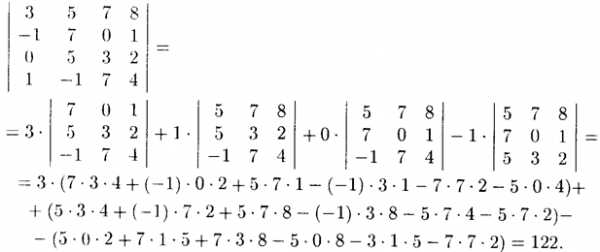
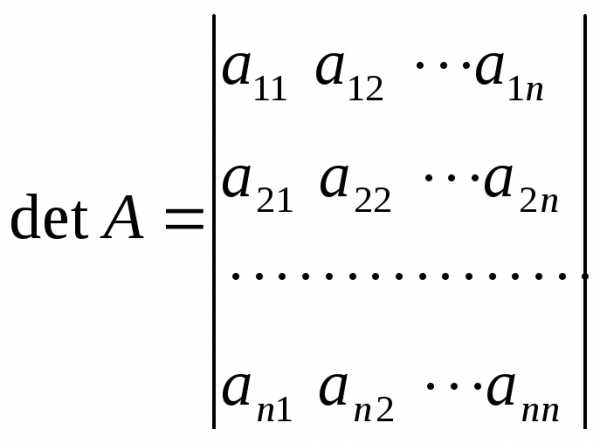 .
.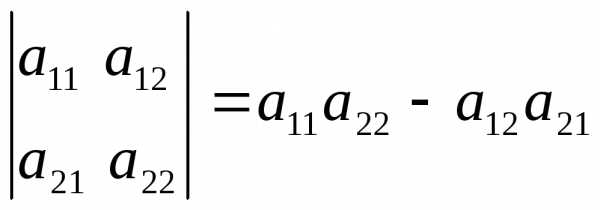 .
(1)
.
(1)
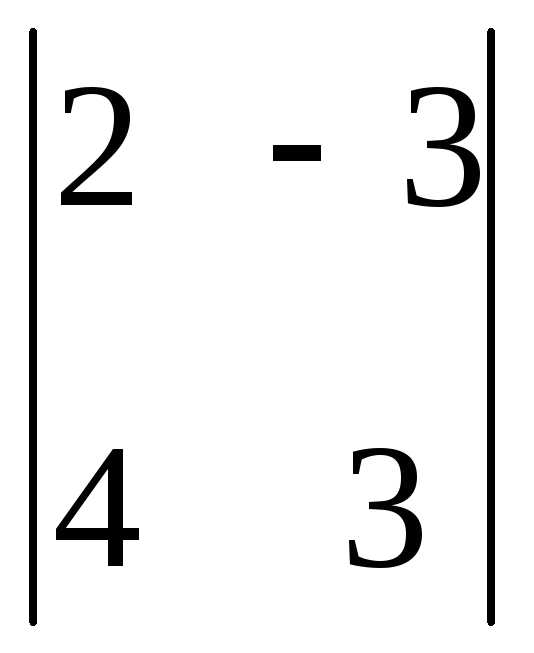 .
.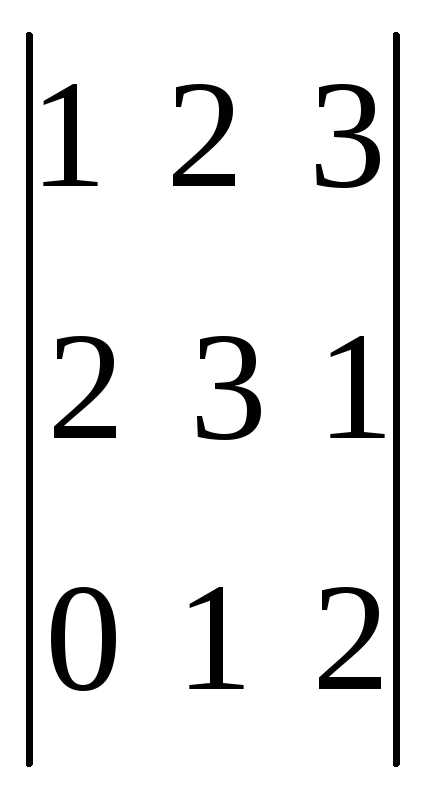 .
.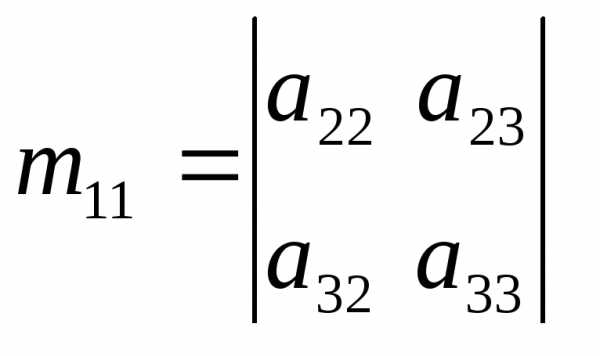 .
.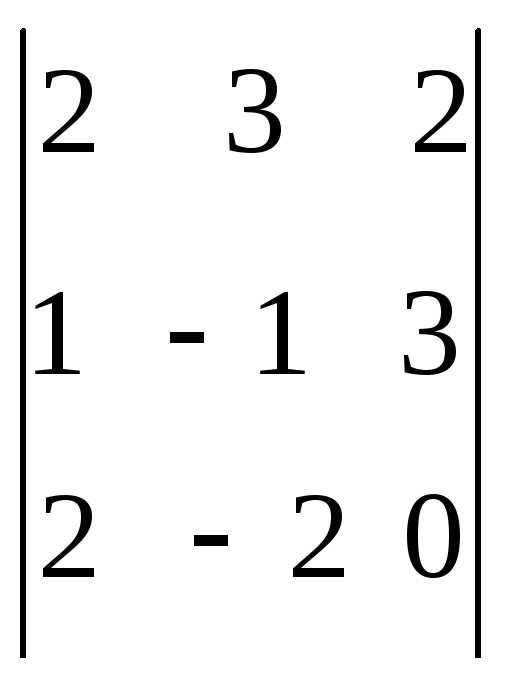 .
.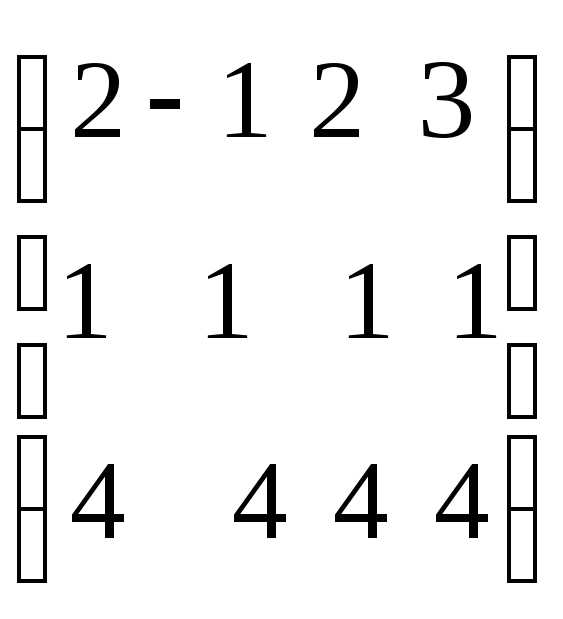 размерности3 4.
размерности3 4.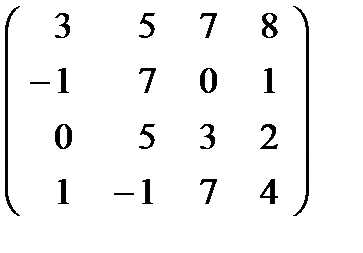 .
.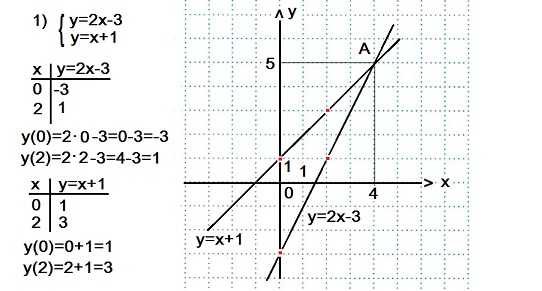 Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.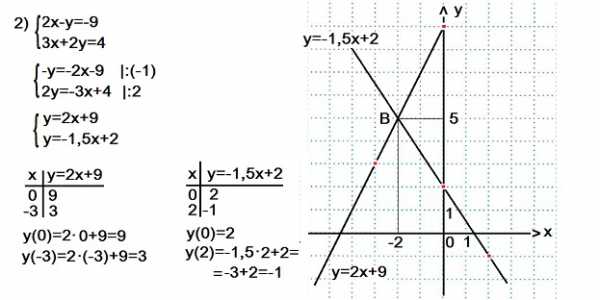 Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.