Тест с ответами на тему: Математическое моделирование
1. Первые математические модели были созданы:
A. Ф. Кенэ*
B. К. Марксом
C. Г. Фельдманом
D. Д. Нейманом
2.Модель, представляющая собой объект, который ведет себя как
реальный объект, но не выглядит как таковой — это
A. физическая модель*
B. аналоговая модель
C. типовая модель
D. математическая модель
3.Модель, представляющая то, что исследуется с помощью увеличенного
или уменьшенного описания объекта или системы — это
A. физическая*
B. аналитическая
C. типовая
D. математическая
4.Где впервые были предложены сетевые модели?
A. США*
B. СССР
C. Англии
D. Германии
5.Какой из структурных элементов включает в себя процесс моделирования?
A. анализ*
B. модель
C. объект
D. субъект
6.Модели ПЕРТ впервые были предложены в
A. 1958 г.*
B. 1948 г.
C. 1956 г.
D. 1953 г.
7.Автоматизация процесса управления не включает в себя
A. этап анализа*
B. этап планирования и разработки
C. этап управления ходом разработки
D. нет правильного ответа
8.Транспортная задача решается методом:
A. все ответы верны*
B. наименьших стоимостей, оптимальности
C. оптимальности, северо-западного угла
D. северо-западного угла, наименьших стоимостей
9.Мощности поставщиков определяются по формуле:
A. ui + cij*
B. vj — cij
C. (ui + cij) — vj
D. все ответы верны
10.Мощности потребителей определяются по формуле:
A. vj – cij*
B. ui + cij
C. (ui + cij) — vj
D. все ответы верны
11.Оценки матрицы перевозок (детермин.) определяются:
A. (ui + cij) – vj*
B. vj — cij
C. ui + cij
D. все ответы верны
12.Предшественниками имитационных игр были:
A. военные игры*
B. конфликтные игры
C. экономические игры
D. нет правильных ответов
13.Математической моделью конфликтных ситуаций является:
A. теория игр*
B. сетевая модель
C. имитационная модель
D. транспортная модель
14.Какие из научных дисциплин не входят в экономико-
математические методы:
A. экспериментальное aнализ*
B. эконометрия
C. экономическая кибернетика
D. все ответы верны
15.Классификация по целевому назначению включает в себя модели
A. теоретико-аналитические, прикладные*
B. макроэкономические, микроэкономические
C. балансовые, трендовые
D. все ответы верны
16.Классификация по типу информации делится на:
A. аналитические, идентифицированные*
B. статистические, динамические
C. матричные, сетевые
D. балансовые, трендовые
17.Классификация по учету фактора неопределенности включает в себя:
A. детерминированные, стохастические*
B. статистические, динамические
C. макроэкономические, микроэкономические
D. аналитические, идентифицированные
18.Ранний срок начала работы в СГ определяется по формуле:
A. tp(i)*
B. tp(i) + t(i,j)
C. tn(j)
D. tn(j) — t(i,j)
19.Ранний срок окончания в СГ определяется по формуле:
A. tp(i) + t(i,j)*
B. tn(j)
C. tp(i)
D. tn(j) — t(i,j)
20.Поздний срок окончания в СГ определяется по формуле:
A. tn(j)*
B. tp(i) + t(i,j)
C. tp(i)
D. tn(j) — t(i,j)
21.Поздний срок начала в СГ определяется по формуле:
A. tn(j) — t(i,j)*
B. tp(i) + t(i,j)
C. tp(i)
D. tn(j)
22.Полный резерв времени определяется как:
A. tn(j) — tp(i) — t(i,j)*
B. tp(i) + t(i,j)
C. tp(i) — tn(j)
D. tn(j)
23.При решении экономических моделей используются матрицы:
A. в теории игр, в транспортных задачах*
B. в СГ, имитационной модели
C. в транспортных задачах, в СГ
D. не используются в моделях
24.В какой из моделей используется седловая точка?
A. в теории игр*
B. в транспортной
C. в имитационной
D. в СГ
25.Материальный или мысленно представляемый объект, который
в процессе исследования замещает объект- оригинал так,
что его непосредственное изучение дает новые знания об
объекте- оригинале — это
A. модель*
B. аналогия
C. абстракция
D. гипотеза
26.Когда был принят Закон Руз «О внешнеэкономической
деятельности Республики Узбекистан».
A. 14 июня 1991г.*
B. 20 августа 1991г.
C. 15 марта 1990г.
D. 14 декабря 1993г.
27.Что относится к ведению Республики Узбекистан как субъекта ВЭД
A. всё перечисленное*
B. разработка и осуществление внешнеэкономической
политики, в т.ч. валютно-кредитной
C. заключение и исполнение международных договоров в
области ВЭД
D. установление законодательных основ организации ВЭД
28.Республика Узбекистан осуществляет внешнеэкономическую
деятельность, руководствуясь принципами:
A. все ответы веpны*
B. равенства сторон
C. невмешательства во внутренние дела партнёров по ВЭС
D. взаимовыгодности сотрудничества со всеми государствами,
иностранными юридическими и физическими лицами
29.Уполномоченные банки ВЭД Руз:
A. получившие лицензии Центробанка Руз на проведение
валютных операций*
B. акционерно-коммерческие , коммерческие и частные
банки
C. Нацбанк ВЭД РУз
D. иностранные банки
30.Резиденты во ВЭД:
A. все ответы вepны*
B. юридические лица, созданные и зарегистрированные в
соответствии с Законодательством РУз
C. дипломатические, торговые и иные официальные
представительства Руз за границей
D. физические лица, имеющие постоянное место жительства в
РУз
testdoc.ru
Тесты по ЭММ
Тест по теме: Основные понятия математического моделирования
1. Какие признаки присущи системе:
a) Целостность, возможность выделения подсистем, динамичность процессов, наличие цели
b) Целостность, наличие цели и внешней среды, возможность выделения подсистем
c) Целостность, массовый характер процессов и явлений, возможность выделения подсистем
d) Целостность, наличие внешней среды, динамичность процессов, массовый характер процессов и явлений
2. Сложные социально-экономические системы в экономике обладают рядом присущих им свойств и особенностей:
a) Целостность, возможность выделения подсистем, динамичность процессов, наличие цели
b) Целостность, наличие цели и внешней среды, возможность выделения подсистем
c) Целостность, массовый характер процессов и явлений, активность, динамичность процессов,
d) Целостность, наличие внешней среды, динамичность процессов, массовый характер процессов и явлений
3. Наличие у экономической системы таких свойств, которые не присущи ни одному из составляющих систему элементов, взятому в отдельности, вне системы носит название:
a) Активность
b) Целостность системы
c) Цельность системы
d) Полнота системы
4. Массовый характер экономических явлений обусловлен тем, что:
a) Закономерности экономических процессов должны обнаруживаться на основании небольшого числа наблюдений
b) Закономерности экономических процессов не должны обнаруживаться на основании среднего числа наблюдений
c) Закономерности экономических процессов не должны обнаруживаться на основании большого числа наблюдений
d) Закономерности экономических процессов не должны обнаруживаться на основании небольшого числа наблюдений
5. Изменение параметров и структуры экономических систем под влиянием среды, или внешних факторов является одним из свойств социально-экономической системы:
a) Динамичность экономических процессов
b) Наличие внешней среды по отношению к данной системе
c) Случайность и неопределенность в развитии многих экономических явлений
d) Активность системы
тест. 6. Способ теоретического анализа и практического действия, направленный на разработку моделей называется:
a) Оптимизационное моделирование
b) Методом моделирования
c) Метод оптимизационного моделирования
d) Методом математического моделирования
7. На чем основывается метод моделирования:
a) На принципе аналогии
b) На принципе соответствия
c) На принципе подобия
d) На принципе реальности
8. Какие виды моделей существуют:
a) Абстрактные, математические и нематематические
b) Физические и абстрактные
c) Математические и нематематические
d) Математические и физические
9. К практическим задачам экономико-математического моделирования относятся:
a) Анализ экономических объектов и процессов, экономическое прогнозирование, выработка управленческих решений
b) Анализ экономических объектов и процессов, экономико-математическое прогнозирование, выработка управленческих решений
c) Анализ социальных объектов и процессов, экономическое прогнозирование, выработка управленческих решений
d) Анализ социально-экономических процессов, экономическое прогнозирование, выработка управленческих решений
10. К обязательным составляющим процесса моделирования относят:
1) Субъект исследования; 2) Объект исследования; 3) Модели; 4) Процессы
a) 1,2
b) 1,2,3
c) 1,2,4
d) 1,2,3,4
11. К первому этапу моделирования относятся:
1) Верификация модели; 2) Постановка экономической проблемы и её качественный анализ; 3) Выполнение формализованного описания; 4) Подготовка исходной информации
a) 1,2,3,4
b) 1,3,4
c) 1,2,3
d) 2,3,4
12. На третьем этапе моделирования:
a) Решается вопрос о правильности и полноте модели
b) Знания переносятся с модели на оригинал
c) Знания о модели на объект-оригинал и практическая проверка полученных с помощью модели знаний
d) Верификация модели
Тест по теме: Оптимизационные экономико-математические модели в планировании и управлении
1. Раздел прикладной математики, изучающий задачи условной оптимизации носит название:
a) Оптимальное программирование
b) Оптимально-математическое программирование
c) Экономико-математическое программирование
d) Оптимально-экономическое программирование
2. В экономике возникают задачи математического программирования:
a) При необходимости оптимальности в планировании и управлении
b) При практической реализации принципа оптимальности в планировании и управлении
c) При необходимости математического аппарата
d) При наличии планирования и управления
3. Суть принципа оптимальности заключается в:
a) В выборе такого планово-управленческого решения, которое наилучшим образом учитывало бы внешние возможности и внутренние условия деятельности хозяйствующего субъекта
b) В выборе такого планово-управленческого решения, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта
c) В выборе допустимого решения, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта
d) В выборе такого планово-управленческого решения, которое учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта
4. В основе построения математической модели задачи оптимального программирования лежит:
1) Принцип системности; 2) Принцип оптимальности; 3) Принцип адекватности; 4) Принцип упорядоченности
a) 1,2,3
b) 2,4
c) 1,2
d) 2,3
5. Задачи оптимального программирования в наиболее общем виде классифицируют по признаку:
a) По характеру взаимосвязи между переменными
b) По характеру переменных
c) По наличию переменных
d) По числу альтернатив
6. Задачи оптимального программирования в наиболее общем виде классифицируют по признаку:
a) По числу критериев альтернатив
b) По характеру переменных
c) По наличию информации о переменных
d) По числу альтернатив
7. Задачи оптимального программирования не классифицируют по следующему признаку:
a) По характеру взаимосвязи между переменными
b) По характеру изменения переменных
c) По учету фактора времени
d) По числу переменных
8. Запишите экономико-математическую модель задачи на основе данных:
9. Запишите экономико-математическую модель задачи на основе данных:
10 тест. Запишите экономико-математическую модель задачи на основе данных:
11. Запишите экономико-математическую модель задачи на основе данных:
12. Запишите экономико-математическую модель задачи на основе данных:
13. Запишите экономико-математическую модель задачи на основе данных:
14. Запишите экономико-математическую модель задачи на основе данных:
15. Запишите экономико-математическую модель задачи на основе данных:
Тест по теме: Теория двойственности в анализе оптимальных решений и целочисленное программирование
1. — тест Связь исходной задачи и двойственной заключается в:
a) Решение двойственной может быть получено из решения исходной
b) Решение исходной может быть получено из решения двойственной
c) Решение одной из них может быть получено непосредственно из решения другой
d) Их решения совпадают
2. Если в прямой задаче целевая функция максимизируется, то знак функциональных ограниченй:
a) <=
b) >=
c) =
d) <= или >= или =
3. Если в прямой задаче целевая функция минимизируется, то знак функциональных ограничений:
a) <=
b) >=
c) =
d) <= или >= или =
4. Если в прямой задаче целевая функция (ЦФ) максимизируется, то в двойственной задаче:
a) ЦФ максимизируется, знак функциональных ограничений <=
b) ЦФ минимизируется, знак функциональных ограничений <=
c) ЦФ максимизируется, знак функциональных ограничений >=
d) ЦФ минимизируется, знак функциональных ограничений >=
5. Экономическая интерпретация первой теоремы двойственности:
a) Предприятие будет производить продукцию по оптимальному плану и получит максимальную общую стоимость
b) Предприятие продаст ресурсы по оптимальным цена и возместит от продажи равные ей минимальные затраты на ресурсы
c) Предприятию безразлично поступать по варианту а) или b)
d) Предприятие не выберет ни а), ни b)
6. Теорема об оценках используется для:
a) Осуществления количественного анализа того, в какой мере изменение величины целевой функции повлияет на изменение ресурсов исходной задачи
b) Осуществления количественного анализа того, в какой мере изменение величины ресурсов повлияет на изменение целевой функции двойственной задачи
c) Осуществления количественного анализа того, в какой мере изменение величины ресурсов повлияет на изменение целевой функции исходной задачи
d) Осуществления качественный анализа того, в какой мере изменение величины ресурсов повлияет на изменение целевой функции исходной задачи
7. Записать двойственную задачу к исходной со следующими данными:
8. Записать двойственную задачу к исходной со следующими данными:
9. Записать двойственную задачу к исходной со следующими данными:
10. Записать двойственную задачу к исходной со следующими данными:
11. Записать двойственную задачу к исходной со следующими данными:
12. Записать двойственную задачу к исходной со следующими данными:
13. Записать двойственную задачу к исходной со следующими данными:
14. Записать двойственную задачу к исходной со следующими данными:
Тест по теме: Методы и модели анализа динамики экономических процессов и их прогнозирования
тест№ 1. Научно обоснованное суждение о возможных состояниях и процессе развития исследуемого объекта в будущем, об альтернативных путях и сроках осуществления тех или иных прогнозируемых процессов носит название:
a) Прогнозирования
b) Прогноза
c) Предсказания
d) Предуказания
2. Описание возможных или желательных перспектив носит название:
a) Прогнозирования
b) Прогноза
c) Предсказания
d) Предуказания
3. Процесс использования информации о будущем в целенаправленной деятельности – это:
a) Прогнозирования
b) Прогноза
c) Предсказания
d) Предуказания
4. Дисциплина, имеющая своим объектом исследования различные социально-экономические процессы, явления или объекты, а предметом — познание возможных состояний этих объектов в будущем, исследование закономерностей и способов разработки экономических прогнозов носит название:
a) Прогнозирования
b) Экономического прогнозирования
c) Социально-экономического прогнозирования
d) Предуказания
5. Прогнозирование, как предвидение опережающего отображения действительности, основанного на познании законов природы, общества и мышления, базируется на:
1) Гипотезе; 2) Прогнозе; 3) Плане;
a) 1,2,3
b) 1,2
c) 2,3
d) 1,3
6. Типология прогнозов строится в зависимости от:
1) Целей; 2) Задач; 3) Объектов; 4) Методов организации прогнозирования
a) 1,2,3
b) 2,3,4
c) 1,3,4
d) 1,2,3,4
7. Задача прогнозирования заключается в:
a) выяснение перспективы ближайшего или более отдаленного будущего в исследуемой области, руководствуясь реальными процессами действительности
b) способствование выработке оптимальных текущих и перспективных планов, опираясь на составленный прогноз и оценку принятого решения с позиций его последствий в прогнозируемом периоде
c) и а), и b) верны
d) а) и b) не верны
8. К источникам прогнозной информации относятся:
1) Накопленный опыт; 2) Экстраполяция существующих тенденций; 3) Построение моделей прогнозируемых объектов; 4) Экстраполяция прогнозируемых тенденций
a) 1,2,4
b) 1,2,3
c) 2,3,4
d) 1,2,3,4
9. По времени упреждения прогнозы бывают:
a) Долгосрочне, дальнесрочные, среднесрочные, краткосрочные и оперативные
b) Долгосрочне, среднесрочные, краткосрочные и оперативные
c) Долгосрочне, среднесрочные и краткосрочные
d) Долгосрочне, дальнесрочные, среднесрочные, краткосрочные
10. К способам прогнозирования относятся:
a) Экспертный, экстраполяции, моделирования
b) Экспертный, экстраполяции
c) Экспертный, моделирования
d) Нет верного ответа
№11. тест В качестве общей методологии при построении прогноза следует использовать:
a) Комплексный подход
b) Математический подход
c) Системный подход
d) Оптимизационный подход
12. По функциональному признаку прогнозы бывают:
a) Структурные и комплексные
b) Поисковые и нормативные
c) Макропрогнозы и микропрогнозы
d) Местные и групповые
13. К макропрогнозам не относится:
a) Структурный
b) Комплексный
c) Групповой
d) Отраслевой
14. К микропрогнозам не относится:
a) Региональный
b) Структурный
c) Местный
d) Групповой
15. Тренд – это:
a) Изменения, определяющие направления развития, основную тенденцию ряда
b) Изменения, определяющие основную тенденцию ряда
c) Изменения, определяющие направления развития
d) Верного ответа нет
Тест по теме: Балансовые модели в управлении экономическими процессами
1. Центральная идея межотраслевого баланса заключается в том, что:
a) Рассматриваются только чистые отрасли
b) Каждая отрасль в нем рассматривается и как производитель, и как потребитель
c) Рассматриваются и потребляющие и производящие отрасли
d) Рассматриваются только те производящие отрасли, в товарах которых имеется потребность
2. В основе исследований на базе балансовых моделей лежат:
a) балансовые таблицы
b) балансовые методы
c) балансовые таблицы и балансовые методы
d) нет верного ответа
3. Чистая отрасль – это:
a) отрасль, объединяющая все производство данного продукта независимо от ведомственной (административной) подчиненности и форм собственности предприятий и фирм, содержащие данные о производстве и потреблении отраслей или предприятий
b) условная отрасль, объединяющая все производство данного продукта независимо от ведомственной (административной) подчиненности и форм собственности предприятий и фирм, содержащие данные о производстве и потреблении отраслей или предприятий
c) условная отрасль, объединяющая все производство данного продукта взависимости от ведомственной (административной) подчиненности и форм собственности предприятий и фирм, содержащие данные о производстве и потреблении отраслей или предприятий
d) все ответы верны
4. Впервые таблица межотраслевого баланса была опубликована:
a) В 1936 году в США
b) В 1936 году и в США, и в России
c) В 1926 году в России
d) В 1926 году и в США, и в России
5. Условно чистая продукция включает:
a) чистый доход, амортизацию, чистую продукцию
b) оплату труда, чистый доход, амортизацию
c) оплату труда, чистую продукцию некоторой j-той отрасли
d) оплату труда, чистый доход, чистую продукцию
6. Показатели материальных затрат на производство продукции содержатся в:
a) 1 разделе МОБа
b) 2 разделе МОБа
c) 3 разделе МОБа
d) 4 разделе МОБа
7. Какому квадранту МОБ соответствует слагаемое Y модели X=(E-A)-1 * Y
a) первому
b) второму
c) третьему
d) четвертому
8. Какому квадранту МОБ соответствует слагаемое X модели X=(E-A)-1 * Y
a) первому
b) второму
c) третьему
d) четвертому
9. Какой тип производственной функции (ПФ) используется в модели Леонтьева «затраты-выпуск»:
a) линейная ПФ
b) ПФ Кобба-Дугласа
c) ПФ со взаимополняющими ресурсами Стоуна
тест_10. Годовой фонд возмещения затрат средств производства в материальной сфере представляет собой:
a) сумму элементов матрицы полных затрат на производство продукции
b) сумму элементов матрицы материальных затрат на производство продукции
c) сумму элементов матрицы прямых затрат на производство продукции
d) сумму элементов матрицы косвенных затрат на производство продукции
11. Показатели условно чистого продукта содержатся в:
a) 1 разделе МОБа
b) 2 разделе МОБа
c) 3 разделе МОБа
d) 4 разделе МОБа
12. Коэффициенты матрицы полных затрат (полного мультипликатора) характеризуют нормативы затрат при увеличении на единицу:
a) промежуточного продукта
b) конечного продукта
c) валового продукта
13. Модель Леонтьева использует следующие предположения:
a) технология производства изменима, свойство линейности прямых затрат
b) продуктивность матрицы прямых затрат, свойство линейности прямых затрат
c) сложившаяся технология производства неизменна, свойство нелинейности прямых затрат
d) сложившаяся технология производства неизменна, свойство линейности прямых затрат
14. Матрица полных материальных затрат учитывает:
a) материальные затраты на восстановление основных производственных фондов
b) материальные затраты на воспроизводство рабочей силы
c) прямые и косвенные материальные затраты
d) все верно
15. Национальный доход со стороны его стоимостного состава характеризует
a) 1 раздел МОБа
b) 2 раздел МОБа
c) 3 раздел МОБа
d) 4 раздел МОБа
16. Отраслевую материальную структуру национального дохода характеризует
a) 1 раздел МОБа
b) 2 раздел МОБа
c) 3 раздел МОБа
d) 4 раздел МОБа
17. Запишите соотношение, отражающее стоимостной состав продукции всех отраслей материальной сферы
Xj = Xij + Zj, где j=1,2…, n
18. Запишите соотношение, отражающее распределение продукции отраслей материального производства по направлениям использования
Xi = Xij + Yi, где i=1,2…, n
19. Запишите основные балансовые соотношения
Xj = Xi
Zj = Yi
20. Запишите систему уравнений, которая называется моделью межотраслевого баланса или моделью Леонтьева
X = A * X + Y
Xi = aij * Xj + Yi, где i=1,2…, n
21. Запишите формулу, по которой определяются коэффициенты прямых затрат
аij = Xij / Xj
22. Запишите соотношение, которое определяет полные затраты
А + A2+ A3 + ….=Ak
23. Запишите соотношение, через которое, задав величины валовой продукции можно определить объемы конечной продукции
Y = (E — A)*X
24. Запишите соотношение, через которое, задав величины конечной продукции можно определить объемы валовой продукции
X = (E – A)-1*Y
Тест по теме: Эконометрические модели в менеджменте
1. тест — Наука, изучающая конкретные количественные и качественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей, носит название:
a) экономики
b) эконометрики
c) экономической статистики
d) экономической теории
2. При этом все переменные любой эконометрической модели в зависимости от конечных прикладных целей ее использования принято (целесообразно) делить на:
1) экзогенные; 2) эндогенные; 3) функциональные; 4) предопределенные
a) 1,2
b) 3,4
c) 1,2,3
d) 1,2,3,4
3. Переменные, которые входят в эконометрическую модель, но рассматриваются как определенные независимо от моделируемого явления носят название:
a) эндогенных
b) экзогенных
c) функциональных
d) предопределенных
4. Переменные, выступающие в системе в роли факторов — аргументов, или объясняющих переменных, носят название:
a) эндогенных
b) экзогенных
c) функциональных
d) предопределенных
5. Переменные, которые определяются только явлением, для которого строится модель, носят название:
a) эндогенных
b) экзогенных
c) функциональных
d) предопределенных
6. На первом этапе (постановочном) построения эконометрической модели:
a) формулируются конечные цепи моделирования
b) определяется набор участвующих в модели факторов и показателей
c) a) и b)
d) все ответы не верны
7. На втором этапе (априорном) построения эконометрической модели:
a) осуществляется предварительный анализ экономической сущности изучаемого явления
b) формирование и формализация априорной информации
c) a) и b)
d) все ответы не верны
8. На третьем этапе (параметризация) построения эконометрической модели выбирается:
a) общий вид модели
b) состав
c) форма входящих в модель связей
d) a) и b)
e) b) и c)
f) a), b) и c)
g) нет верного ответа
9. Четвертый этап (информационный) заключается в:
a) сборе необходимой статистической информации
b) предварительном анализе данных
c) a) и b)
d) все ответы не верны
10. Пятый этап (идентификация модели) посвящен:
a) статистическому анализу
b) статистической оценке неизвестных параметров модели
c) a) и b)
d) все ответы не верны
11. Результаты эконометрических моделей различны и зависят от:
a) выбираемого критерия
b) численного метода оценки
c) a) и b)
d) все ответы не верны
№тест 12. Шестой этап (верификация модели) предполагает:
a) сопоставление реальных и модельных данных
b) проверку адекватности модели
c) оценку точности модельных данных
d) a) и b)
e) b) и c)
f) a), b) и c)
g) нет верного ответа
Тест по теме: Экспертные методы анализа в менеджменте
1. Мeтoды, основанные нa свободном выдвижeнии идeй, нaпpaвлeнныx нa peшeниe пpoблeмы, зaтeм из этиx идей oтбиpaютcя нaибoлee цeнныe, носят название:
a) мoзгoвoй aтaки
b) cцeнapиeв
c) предложений
d) coвeщaний
2. Мeтoд, пpeдcтaвляющий coбoй coвoкyпнocть пpaвил пo излoжeнию в пиcьмeннoм видe пpeдлoжeний cпeциaлиcтoв пo peшaeмoй пpoблeмe, носит название
a) мoзгoвoй aтaки
b) cцeнapиeв
c) анкетного опроса
d) предложений
3. Метод, основанный нa мoдeлиpoвaнии фyнкциoниpoвaния coциaльнoй cиcтeмы yпpaвлeния пpи выпoлнeния oпepaций, нaпpaвлeнныx нa дocтижeниe пocтaвлeннoй цeли, носит название:
a) суда
b) cцeнapиeв
c) дeлoвыx игp
d) coвeщaний
4. Метод, предполагающий пpoвeдeниe coвeщaния или диcкyccии c цeлью выpaбoтки eдинoгo кoллeктивнoгo мнeния пo peшaeмoй пpoблeмe, носит название:
a) мoзгoвoй aтaки
b) cцeнapиeв
c) суда
d) coвeщaний
5. К методам получения индивидуального мнения членов экспертной группы не относится метод:
a) анкетного опроса
b) интервью
c) Дельфи
d) совещаний
6. К методам получения индивидуального мнения членов экспертной группы относится метод:
a) анкетного опроса
b) мозгового штурма
c) сценариев
d) совещаний
7. Метод, представляющий собой итеративную процедуру анкетного опроса, носит название:
a) анкетного опроса
b) интервью
c) Дельфи
d) Совещаний
8. Преимущества метода индивидyaльнoгo экcпepтнoгo oцeнивaния заключаются:
1) в иx oпepaтивнocти; 2) объективность получаемых оценок; 3) oтcyтcтвии дaвлeния co cтopoны aвтopитeтoв; 4) в низкиx зaтpaтax нa экcпepтизy
a) 1,2,3
b) 1,2,4
c) 1,3,4
d) 2,3,4
9. Нeдocтaткoм метода индивидyaльнoгo экcпepтнoгo oцeнивaния являeтcя:
a) недостаточная oпepaтивнocть
b) субъективность получаемых оценок
c) дaвлeние co cтopoны aвтopитeтoв
d) затратность
10. Достоинством метода Дельфи является:
a) опepaтивнocть
b) использование обратной связи в ходе опроса
c) субъективность получаемых оценок
d) низкие зaтpaты нa экcпepтизy
Тест по теме: Экономико-математические методы и модели управления запасами
тест 1. В разработке модели управления запасами заинтересованы
a) предприятия поточно-массового производства
b) предприятия розничной торговли
c) обрабатывающая промышленность
d) все ответы верны
2. Основными характеристиками модели управления запасами является:
a) спрос, пополнение склада, объем заказа, время доставки, штраф за дефицит
b) спрос, стоимость доставки, издержки хранения, штраф за префицит
c) спрос, пополнение склада, штраф за префицит, структура складской системы
d) спрос, объем заказа, пополнение склада, штраф за префицит
3. Основными характеристиками модели управления запасами является:
a) спрос, пополнение склада, объем заказа, время доставки, штраф за префицит
b) спрос, стоимость доставки, издержки хранения, штраф за префицит
c) спрос, пополнение склада, штраф за дефицит, структура складской системы
d) спрос, объем заказа, пополнение склада, штраф за префицит
4. В суммарные затраты системы управления запасами не входят:
a) затраты на приобретение
b) затраты на хранение заказа
c) затраты на оформление заказа
d) потери от префицита запаса
5. Цель модели управления запасами заключается:
a) в минимизации общих издержек хранения запасов
b) в минимизации затрат на хранение заказа
c) в минимизации затрат на приобретение запасов
d) в минимизации затрат на оформление заказа
6. Какие затраты не зависят от объема заказа:
a) затраты на приобретение
b) затраты на хранение заказа
c) затраты на оформление заказа
d) потери от дефицита запаса
7. К основным признакам классификации товарных запасов не относится:
a) стадия готовности
b) производитель
c) существование выбора у потребителя
d) срок годности
8. К основным признакам классификации товарных запасов относится:
a) стадия готовности
b) независимость поставщиков
c) отсутствие выбора у потребителя
d) срок годности
Тест по теме: Моделирование систем массового обслуживания (СМО)
1. тест. Системы массового обслуживания — это
a) системы предназначенные для одноразового использования при решении определенных задач
b) системы предназначенные для многоразового использования при решении однотипных задач
c) системы предназначенные для многоразового использования при решении типичных задач
d) все ответы верны
2. По числу каналов системы массового обслуживание делятся на:
a) одноканальные и многоканальные
b) одноканальные и двуканальные
c) одноканальные и разноканальные
d) все ответы верны
3. СМО делятся на:
a) СМО с отказами и классические СМО
b) СМО с ожиданием и классические СМО
c) СМО с отказами и СМО с ожиданием
d) СМО без отказов и классические СМО
4. Относительно дисциплины обслуживания СМО классифицируется на
a) заявки, организованные по принципу «первая пришла – первая обслужена»
b) заявки, организованные по принципу «последняя пришла – первая обслужена»
c) заявки, обслуживаемые с приоритетом
d) все ответы верны
5. Обслуживание по принципу приоритета бывает:
a) с приоритетом и без приоритета
b) абсолютным или относительным
c) абсолютным и обычным
d) все ответы верны
testua.ru
Тест по математике (6 класс) на тему: Тест по теме математическое моделирование
Тест по теме: «Математическое моделирование»
1. Закончите предложение: «Объект, который используется в качестве «заместителя», представителя другого объекта с определенной целью, называется …»
- моделью;
- копией;
- предметом;
- оригиналом.
2. Закончите предложение: «Модель, по сравнению с объектом-оригиналом, содержит …»
- меньше информации;
- столько же информации;
- больше информации.
3. Моделирование — это:
- процесс замены реального объекта (процесса, явления) моделью, отражающей его существенные признаки с точки зрения достижения конкретной цели;
- процесс демонстрации моделей одежды в салоне мод;
- процесс неформальной постановки конкретной задачи;
- процесс замены реального объекта (процесса, явления) другим материальным или идеальным объектом;
- процесс выявления существенных признаков рассматриваемого объекта.
4. Процесс построения модели, как правило, предполагает:
- описание всех свойств исследуемого объекта;
- выделение наиболее существенных с точки зрения решаемой задачи свойств объекта;
- выделение свойств объекта безотносительно к целям решаемой задачи;
- описание всех пространственно-временных характеристик изучаемого объекта;
- выделение не более трех существенных признаков объекта.
5. Математическая модель объекта — это:
- созданная из какого-либо материала модель, точно отражающая внешние признаки объекта-оригинала;
- описание в виде схемы внутренней структуры изучаемого объекта;
- совокупность данных, содержащих информацию о количественных характеристиках объекта и его поведения в виде таблицы;
- совокупность записанных на языке математики формул, отражающих те или иные свойства объекта-оригинала или его поведение;
- последовательность электрических сигналов.
6. К числу математических моделей относится:
- милицейский протокол;
- правила дорожного движения;
- формула нахождения корней квадратного уравнения;
- кулинарный рецепт;
- инструкция по сборке мебели.
7. К числу документов, представляющих собой информационную модель управления государством, можно отнести:
- Конституцию РФ;
- географическую карту России;
- Российский словарь политических терминов;
- схему Кремля;
- список депутатов государственной Думы.
8. Рисунки, карты, чертежи, диаграммы, схемы, графики представляют собой:
- табличные информационные модели;
- математические модели;
- натурные модели;
- графические информационные модели;
- иерархические информационные модели.
9 . Описание глобальной компьютерной сети Интернет в виде системы взаимосвязанных следует рассматривать как:
- натурную модель;
- табличную модель;
- графическую модель;
- математическую модель;
- сетевую модель.
10. В биологии классификация представителей животного мира представляет собой:
- иерархическую модель;
- табличную модель;
- графическую модель;
- математическую модель;
- натурную модель.
11. Информационной моделью организации занятий в школе является:
1. свод правил поведения учащихся;
2. список класса;
3. расписание уроков;
4. перечень учебников.
12. Отметьте пропущенное слово: «Географическая карта является примером … модели»
- образной
- знаковой
- смешанной
- натурной
13. Укажите пары объектов, о которых можно сказать, что они находятся в отношении «объект – модель»:
- компьютер – процессор
- Новосибирск – город
- слякоть – насморк
- автомобиль – техническое описание автомобиля
- город – путеводитель по городу
14. Модель есть замещение изучаемого объекта другим объектом, который отражает:
1. все стороны данного объекта
2. некоторые стороны данного объекта
3. существенные стороны данного объекта
4. несуществующие стороны данного объекта
15. Что является моделью объекта «яблоко»?
1. муляж;
2. фрукт;
3. варенье;
4. компот.
16. Укажите примеры натурных моделей:
- физическая карта
- глобус
- график зависимости расстояния от времени
- макет здания
- схема узора для вязания крючком
- муляж яблока
- манекен
17. Укажите примеры образных информационных моделей:
- рисунок
- фотография
- словесное описание
- формула
18. Закончите предложение: «Можно создавать и использовать …»
- разные модели объекта
- единственную модель объекта
- только натурную модель объекта
19. Отметьте пропущенное слово: «Словесное описание горного ландшафта является примером … модели»
- образной
- знаковой
- смешанной
- натурной
20. Расписание движение поездов может рассматриваться как пример:
- натурной модели;
- табличной модели;
- графической модели;
- компьютерной модели;
- математической модели.
Рекомендуемые правила при оценивании:
– за каждый правильный ответ +1 балл;
– за каждый неполный ответ +0,5 балла;
– за вопрос без ответа 0 баллов.
Рекомендуемые соотношения при выставлении оценок:
50-70% — «3»;
71-85% — «4»;
86-100% — «5».
ОТВЕТЫ:
| 1 |
| 1 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 4 |
| 5 |
| 1 |
| 3 |
| 3 |
| 4,5 |
| 1 |
| 1 |
| 2,4,6,7 |
| 1,2 |
| 1 |
| 2 |
| 2 |
nsportal.ru
Тест с ответами: «Моделирование» | Образовательный портал
1. Могут ли разные объекты быть описаны одной моделью:
а) да +
б) нет
в) зависит от моделей
2. Построение модели исходных данных; построение модели результата, разработка алгоритма, разработка программы, отладка и исполнение программы, анализ и интерпретация результатов:
а) анализ существующих задач
б) этапы решения задачи с помощью компьютера +
в) процесс описания информационной модели
3. Процесс построения информационных моделей с помощью формальных языков называется:
а) планированием
б) визуализацией
в) формализацией +
4. Расписание движения поездов может рассматриваться как пример:
а) табличной модели +
б) натурной модели
в) математической модели
5. Математическая модель объекта:
а) совокупность данных, содержащих информацию о количественных характеристиках объекта и его поведении в виде таблицы
б) созданная из какого-либо материала модель, точно отражающая внешние признаки объекта-оригинала
в) совокупность записанных на языке математики формул, отражающих те или иные свойства объекта-оригинала или его поведение +
6. Натурное (материальное) моделирование:
а) моделирование, при котором в модели узнается какой-либо отдельный признак объекта-оригинала
б) моделирование, при котором в модели узнается моделируемый объект, то есть натурная (материальная) модель всегда имеет визуальную схожесть с объектом-оригиналом +
в) создание математических формул, описывающих форму или поведение объекта-оригинала
7. Система состоит из:
а) объектов, которые называются свойствами системы
б) набора отдельных элементов
в) объектов, которые называются элементами системы +
8. Может ли один объект иметь множество моделей:
а) да +
б) нет
в) да, если речь идёт о создании материальной модели объекта
9. Образные модели представляют собой:
а) формулу
б) таблицу
в) зрительные образы объектов, зафиксированные на каком либо носителе информации +
10. Какие модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме?
а) табличные
б) предметные +
в) информационные
11. Модель:
а) материальный или абстрактный заменитель объекта, отражающий существенные с точки зрения цели исследования свойства изучаемого объекта, явления или процесса +
б) материальный или абстрактный заменитель объекта, отражающий его пространственно-временные характеристики
в) любой объект окружающего мира
12. Описание глобальной компьютерной сети Интернет в виде системы взаимосвязанных следует рассматривать как:
а) математическую модель
б) сетевую модель +
в) графическую модель
13. Последовательность этапов моделирования:
а) цель, объект, модель, метод, алгоритм, программа, эксперимент, анализ, уточнение +
б) объект, цель, модель, эксперимент, программа, анализ, тестирование
в) цель, модель, объект, алгоритм, программа, эксперимент, уточнение выбора объекта
14. Моделирование:
а) формальное описание процессов и явлений
б) процесс выявления существенных признаков рассматриваемого объекта
в) метод познания, состоящий в создании и исследовании моделей +
15. Сколько существует основных этапов разработки и исследование моделей на компьютере:
а) 5 +
б) 4
в) 6
16. На первом этапе исследования объекта или процесса обычно строится:
а) предметная модель
б) описательная информационная модель +
в) формализованная модель
17. Табличная информационная модель представляет собой:
а) набор графиков, рисунков, чертежей и диаграмм
б) последовательность предложений на естественном языке
в) описание объектов (или их свойств)в виде совокупности значений, размещенных в таблице +
18. Такие модели представляют объекты и процессы в образной или знаковой форме:
а) материальные
б) информационные +
в) математические
19. Рисунки, карты, чертежи, диаграммы, схемы, графики представляют собой:
а) иерархические информационные модели
б) математические модели
в) графические информационные модели +
20. Географическую карту следует рассматривать скорее всего как:
а) вербальную информационную модель
б) графическую информационную модель +
в) математическую информационную модель
21. В качестве примера модели поведения можно назвать:
а) правила техники безопасности в компьютерном классе +
б) чертежи школьного здания
в) план классных комнат
22. Какой тип моделей применяется для описания ряда объектов, обладающих одинаковыми наборами свойств:
а) сетевые информационные модели
б) табличные информационные модели +
в) иерархические сетевые модели
23. Информационной моделью части земной поверхности является:
а) глобус
б) рисунок
в) картина местности +
24. Модель отражает:
а) некоторые существенные признаки объекта
б) существенные признаки в соответствии с целью моделирования +
в) все существующие признаки объекта
25. При создании игрушечного корабля для ребенка трех лет существенным является:
а) точность
б) материал
в) внешний вид +
26. В информационной модели жилого дома, представленной в виде чертежа (общий вид), отражается его:
а) стоимость
б) структура +
в) надежность
27. В информационной модели облака, представленной в виде черно-белого рисунка, отражаются его:
а) форма +
б) размер
в) плотность
28. Модель человека в виде детской куклы создана с целью:
а) познания
б) продажи
в) игры +
29. Признание признака объекта существенным при построении его информационной модели зависит от:
а) цели моделирования +
б) стоимости объекта
в) размера объекта
30. При описании внешнего вида объекта удобнее всего использовать информационную модель следующего вида:
а) структурную
б) графическую +
в) математическую
liketest.ru
Основы математического моделирования — Ответы на тесты Intuit.ru
Ответы на курс: Основы математического моделирования
Что называют решением игры?
| совокупность гарантированных выигрышей называется решением игры |
| ✓ | совокупность оптимальных стратегий называется решением игры |
| совокупность седловых точек называется решением игры |
| совокупность минимальных стратегий называется решением игры |
Что называется суммой событий и ?
Что надо делать при наличии неопределенности?
| любую неопределенность можно расчленить на множество частей и построить теоретико-игровую модель, на основании которой определяется оптимальное решение |
| ✓ | любую неопределенность можно расчленить на известную и неизвестную части, построить теоретико-игровую модель, на основании которой определяется оптимальное решение |
| любую неопределенность можно отбросить и построить теоретико-игровую модель, на основании которой определяется оптимальное решение |
| любую неопределенность можно заменить определенностью и построить теоретико-игровую модель, на основании которой определяется оптимальное решение |
Какие игры называются квазиматричными играми?
| ✓ | конечные игры, в которых в целом ряде случаев стороны имеют различную информацию о ходах «природы». Так, например, I может знать, а игрок II не знать, какой ход сделает «природа». Такие игры и называются квазиматричными |
| конечные игры, в которых в целом ряде случаев стороны имеют одинаковую информацию о ходах «природы». Так, например, I может знать, а игрок II не знать, какой ход сделает «природа». Такие игры и называются квазиматричными |
| бесконечные игры, в которых в целом ряде случаев стороны имеют одинаковую информацию о ходах «природы». Так, например, I может знать, а игрок II не знать, какой ход сделает «природа». Такие игры и называются квазиматричными |
| бесконечные игры, в которых в целом ряде случаев стороны имеют различную информацию о ходах «природы». Так, например, I может знать, а игрок II не знать, какой ход сделает «природа». Такие игры и называются квазиматричными |
Что необходимо выполнить для построения математической модели?
| ✓ | выделить рассматриваемый объекта (процесс), отбросить все несущественное и установить все существенное. Точно количественно описать ситуацию, с тем чтобы это описание можно было перевести на математический язык. Определить набор параметров, характеризующих как состояние системы (процесса), так и возможное управление системой (процессом). Определить зависимости между параметрами состояния и управления. Определить цели через параметры системы в терминах соответствующей математической модели |
| определить зависимости между параметрами состояния и управления |
| выделить рассматриваемый объект или процесс, отбросить все несущественное и установить все существенное |
| определить набор параметров, характеризующих как состояние системы (процесса), так и возможное управление системой (процессом) |
Какие системы называют системами с ожиданием?
| если требование, поступившее в систему обслуживания, может ее покинуть только тогда, когда оно полностью обслужено. В этом случае совокупность таких требований, поступивших в систему в тот момент, когда все обслуживающие аппараты свободны, образует очередь. Такие системы называются системами с ожиданием или системами без потерь |
| если требование, поступившее в систему обслуживания, может ее покинуть только тогда, когда оно частично обслужено. В этом случае совокупность таких требований, поступивших в систему в тот момент, когда все обслуживающие аппараты заняты, образует очередь. Такие системы называются системами с ожиданием или системами без потерь |
| если требование, поступившее в систему обслуживания, может ее покинуть только тогда, когда оно обслужено в последнюю очередь. В этом случае совокупность таких требований, поступивших в систему в тот момент, когда все обслуживающие аппараты свободны, образует очередь. Такие системы называются системами с ожиданием или системами без потерь |
| ✓ | если требование, поступившее в систему обслуживания, может ее покинуть только тогда, когда оно полностью обслужено. В этом случае совокупность таких требований, поступивших в систему в тот момент, когда все обслуживающие аппараты заняты, образует очередь. Такие системы называются системами с ожиданием или системами без потерь |
Какой перебор планов предусматривает симплекс-метод?
| симплекс-метод предусматривает перебор планов от последнего к первому |
| ✓ | симплекс-метод предусматривает направленный перебор планов, при котором каждый последующий план оказывается лучше предыдущего |
| симплекс-метод предусматривает сплошной перебор планов, при котором каждый последующий план оказывается лучше предыдущего |
| симплекс-метод предусматривает направленный и частично сплошной перебор планов, при котором каждый последующий план оказывается лучше предыдущего |
Каковы основные принципы планирования эксперимента?
| ✓ | replication, randomization, blockdivision |
| ✓ | replication, randomization, planned grouping |
| ✓ | основные принципы планирования эксперимента: повторение, рандомизация, разбиение на блоки |
| ✓ | основные принципы планирования эксперимента: дублирование, рандомизация, разбиение на блоки |
Какая область может быть названа областью допустимых планов?
| область может быть названа областью допустимых планов, в которой выполняется любой план |
| ✓ | область может быть названа областью допустимых планов, поскольку любая точка в ее пределах отвечает требованиям наложенных ограничений |
| область может быть названа областью допустимых планов, если в этой области выполняются основные планы |
| область может быть названа областью допустимых планов, в которой заданы все планы |
Что такое плацебо?
| плацебо – это название процесса лечения |
| ✓ | плацебо – это фармакологически неэффективное вещество |
| плацебо – это название лекарства |
| плацебо – это название болезни |
Что понимают под статистикой?
| статистика – совокупность методов, которые дают нам возможность принимать частичные решения в условиях неопределенности |
| ✓ | статистика – совокупность методов, которые дают нам возможность принимать оптимальные решения в условиях неопределенности |
| статистика – совокупность методов, которые дают нам возможность принимать бескомпромисные решения в условиях неопределенности |
| статистика – совокупность методов, которые дают нам возможность принимать быстрое решения в условиях неопределенности |
Что называют случайной величиной ?
Какая система называется неупорядоченной ?
| все обслуживающие аппараты системы одинаковы. Вновь поступившее требование обслуживается только первым аппаратом. Такая организация системы обслуживания носит название неупорядоченной |
| все обслуживающие аппараты системы одинаковы. Вновь поступившее требование обслуживается последним из свободных аппаратов, причем предпочтения при этом не отдается ни одному из них. Такая организация системы обслуживания носит название неупорядоченной |
| ✓ | все обслуживающие аппараты системы одинаковы. Вновь поступившее требование обслуживается одним из свободных аппаратов, причем предпочтения при этом не отдается ни одному из них. Такая организация системы обслуживания носит название неупорядоченной |
| все обслуживающие аппараты системы разные. Вновь поступившее требование обслуживается одним из свободных аппаратов, причем предпочтения при этом не отдается ни одному из них. Такая организация системы обслуживания носит название неупорядоченной |
Пусть , и — независимые случайные величины. Чему равна дисперсия их суммы ?
Что такое стратегия поведения данного игрока ?
| стратегия поведения данного игрока есть функция, определенная на классе его информационных множеств, которая назначает для каждого информационного множества распределение |
| стратегия поведения данного игрока есть функция, определенная на классе вещественных чисел |
| стратегия поведения данного игрока есть функция, определенная на классе его информационных множеств |
| ✓ | стратегия поведения данного игрока есть функция, определенная на классе его информационных множеств, которая назначает для каждого информационного множества распределение вероятностей альтернатив этого множества |
Всегда ли накладывается требование целочисленности распределительных задач?
| ✓ | во многих интерпретациях распределительной задачи требование целочисленности на переменные может и не накладываться |
| во многих интерпретациях распределительной задачи требование целочисленности на переменные всегда накладывается |
| ✓ | во многих интерпретациях распределительной задачи требование целочисленности на переменные может накладываться частично |
| во многих интерпретациях распределительной задачи требование целочисленности на переменные с четным значением может и не накладываться |
Что такое риск поставщика?
| риск поставщика – отклонение негодной партии продукции |
| риск поставщика – отклонение большой партии продукции |
| ✓ | риск поставщика – отклонение еще хорошей партии продукции |
| риск поставщика – отклонение очень хорошей партии продукции |
Чем характерен «дважды слепой опыт»?
| «дважды слепой опыт» предполагает, что больным дают только лекарство |
| «дважды слепой опыт» предполагает, что больным дают только плацебо |
| «дважды слепой опыт» предполагает, что больные не должны знать, что вообще и что непосредственно дают больным – медикаменты или плацебо |
| ✓ | «дважды слепой опыт» предъявляет по сравнению с обычным слепым опытом дополнительные требования. Не только больные, но также и врач (или врачи), наблюдающий и судящий о реакции больных, не должны знать, что вообще и что непосредственно дают больным – медикаменты или плацебо |
Что называется заключительной ситуацией?
| ситуация, на основании которой определяется ничья, называется заключительной |
| ситуация, на основании которой определяется выигрыш всех участников игры, называется заключительной |
| ситуация, на основании которой определяется подтасовка игры, называется заключительной |
| ✓ | ситуация, на основании которой определяется исход игры, называется заключительной |
Что такое выпуклая оболочка?
| минимальный, выпуклый многоугольник, внутри которого лежит часть точек заданного множества |
| минимальный, выпуклый многоугольник, внутри которого не лежат точки заданного множества |
| максимальный, выпуклый многоугольник, внутри которого лежат все точки заданного множества |
| ✓ | минимальный, выпуклый многоугольник, внутри которого лежат все точки заданного множества |
Что такое полипрагмазии?
| это название лекарства |
| это фармакологически эффективное вещество |
| ✓ | лечение разносторонними лечебными средствами |
| это особое заболевание |
Какой критерий называется максиминным ?
| критерий Гурвица |
| критерий Лапласа |
| ✓ | критерий Вальда |
| критерий потерь |
Что учитывает показатель эффективности?
| показатель эффективности должен учитывать значимость эксперимента |
| ✓ | показатель эффективности должен учитывать стоимость данного исхода и потери, вызванные неправильными решениями |
| показатель эффективности должен учитывать только потери, вызванные неправильными решениями |
| показатель эффективности должен учитывать только выигрыш при выбранном решении |
Что называют статистически независимыми величины ?
Какой критерий считается критерием пессимизма-оптимизма ?
| критерий потерь |
| критерий Лапласа |
| критерий Вальда |
| ✓ | критерий Гурвица |
Что такое модельная задача?
| задача, используемая для отладки или демонстрации алгоритма |
| задача, используемая для отладки или демонстрации метода |
| ✓ | задача, используемая для отладки или демонстрации системы |
| задача, используемая для отладки или демонстрации данных |
Чем характерен «трижды слепой опыт»?
| «трижды слепой опыт». В этом случае врачу известно, какое лекарство получает пациент, сестра не знает, что она дает больному, и больной не знаком ни врачу, ни сестре |
| «трижды слепой опыт». В этом случае врачу неизвестно, какое лекарство получает пациент, сестра не знает, что она дает больному, и больной знаком и врачу, и сестре |
| «трижды слепой опыт». В этом случае врачу неизвестно, какое лекарство получает пациент, сестра знает, что она дает больному, и больной не знаком ни врачу, ни сестре |
| ✓ | «трижды слепой опыт». В этом случае врачу неизвестно, какое лекарство получает пациент, сестра не знает, что она дает больному, и больной не знаком ни врачу, ни сестре |
В чем различие между проблемами теории игр и теории статических решений?
| единственное, но весьма существенное, различие между проблемами теории игр и теории статических решений состоит в том, что «природа» в отличие от разумного игрока более разнообразна |
| ✓ | единственное, но весьма существенное, различие между проблемами теории игр и теории статических решений состоит в том, что «природа» в отличие от разумного игрока характеризуется стихийностью, а не сознательность выбора |
| единственное, но весьма существенное, различие между проблемами теории игр и теории статических решений состоит в том, что «природа» мудрее разумного игрока |
| единственное, но весьма существенное, различие между проблемами теории игр и теории статических решений состоит в том, что «природа» в отличие от разумного игрока характеризуется оптимистичностью, а не сознательность выбора |
Обозначим некоторое событие, связанное с указанными исходами. — общее число исходов рассматриваемого опыта, — число тех из них, которые приводят к наступлению события . Чему равна вероятность события ?
Как записывается вероятность того, что система рано или поздно попадает в исходное состояние ?
Где используется теория игр?
| теория игр используется только в казино |
| ✓ | теория игр используется практически в любой науке, где есть неопределенность |
| ✓ | теория игр используется в алгебраической топологии, биологии, метеорологии |
| ✓ | теория игр используется в экономике и медицине |
Что называется стратегией игрока?
| ✓ | стратегия – это план поведения игры данным игроком |
| ✓ | заранее определенная последовательность ходов в зависимости от информации о ходах противника и о случайно изменяющихся параметрах, законы распределения которых считаются заданными, называется стратегией игрока |
| поведение игрока в игре называется стратегией игрока |
| заранее определенная последовательность ходов называется стратегией игрока |
Как определяется необходимость и направление перебора планов?
| поскольку при отсутствии наглядного геометрического представления заранее нельзя располагать значениями переменных в вершинах многоугольника, то для установления необходимости и направления перебора планов пользуются специальным критерием : , где индекс приписывается небазисным (нулевым) переменным, а индекс базисным. Имеется доказательство того, что в случае оптимальности полученного плана все становятся равными нулю или меньше нуля. Включению в базис подлежит та переменная, для которой принимает наибольшее положительное значение |
| поскольку при отсутствии наглядного геометрического представления заранее нельзя располагать значениями переменных в вершинах многоугольника, то для установления необходимости и направления перебора планов пользуются специальным критерием : где индекс приписывается небазисным (нулевым) переменным, а индекс базисным. Имеется доказательство того, что в случае оптимальности полученного плана все становятся равными нулю или меньше нуля. Включению в базис подлежит та переменная, для которой принимает наибольшее положительное значение |
| поскольку при отсутствии наглядного геометрического представления заранее нельзя располагать значениями переменных в вершинах многоугольника, то для установления необходимости и направления перебора планов пользуются специальным критерием : где индекс приписывается небазисным (нулевым) переменным, а индекс базисным. Имеется доказательство того, что в случае оптимальности полученного плана все становятся равными нулю или меньше нуля. Включению в базис подлежит та переменная, для которой принимает наибольшее положительное значение |
| ✓ | поскольку при отсутствии наглядного геометрического представления заранее нельзя располагать значениями переменных в вершинах многоугольника, то для установления необходимости и направления перебора планов пользуются специальным критерием : , где индекс приписывается небазисным (нулевым) переменным, а индекс базисным. Имеется доказательство того, что в случае оптимальности полученного плана все становятся равными нулю или меньше нуля. Включению в базис подлежит та переменная, для которой принимает наибольшее положительное значение |
otveti-na-intuit.ru
Тест с ответами на тему: Моделирование систем
1. Что такое модель объекта?
A. Объект-заместитель объекта-оригинала, обеспечивающий изучение всех свойств оригинала
B. Объект-оригинал, который обеспечивает изучение некоторых своих свойств
C. Объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала +
D. Объект-оригинал, который обеспечивает изучение всех своих свойств
2. Какие граничные условия называются естественными?
A. Условия, налагаемые на функцию, которая ищется.
B. Условия, которые накладываются на производные функции, ищется, по пространственным координатам. +
C. Условия, наложено на различные внешние силовые факторы, действующие на точки поверхности тела.
D. Условия, наложено на различные внутренние факторы, которые действуют внутри тела.
3. Какому вариационной принципа соответствует формулировка МКЭ в перемещениях?
A. Минимума дополнительной работы Кастильяно.
B. Минимума потенциальной энергии Лагранжа. +
C. Принцип Хувашицу.
D. Максимум потенциальной работы Кастильяно.
4. Какой тип математических моделей использует алгоритмы?
A. Аналитические.
B. Знаковые.
C. Имитационные. +
D. Детерминированные.
5. Какой тип моделей выделен в классификации по принципам построения.
A. Наглядные.
B. Аналитические. +
C. Знаковые.
D. Математические.
6. Какие зависимые переменные существуют в моделях микроуровня?
A. Время.
B. Пространственные координаты.
C. Плотность и масса.
D. Фазовые координаты. +
7. Какой метод дискретизации модели относится к микроуровня?
A. Метод свободных сетей.
B. Метод конечных разностей. +
C. Метод узловых давлений.
D. Табличный метод.
8. Что такое уровне проектирования?
A. Временное распределения работ по созданию новых объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня. +
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с де-либо определяемой точки зрения, которая определяется функциональными, физическими или иного типа отношениями между свойствами и элементами.
9. Что называют краевыми условиями для системы уравнений математической модели?
A. Условия, накладываемые на границе исследуемой области и в начальный момент времени. +
B. Условия, налагаемые на функцию, ищут.
C. Условия, налагаемые на производные искомой функции.
D. Условия, накладываемые в начальный момент времени.
10. Что такое аспекты проектирования?
A. Временное распределение работ по созданию объектов в процессе проектирования.
B. Совокупность языков, моделей, постановок задач, методов получения описаний где-либо иерархического уровня.
C. Определенная последовательность решения проектных задач различных иерархических уровней.
D. Описание системы или ее части с де-либо определяемой точки зрения, определяется функциональными, физическими или иного типа отношениями между свойствами и элементами. +
11. Укажите, какой из этапов выполняется при математическом моделировании после анализа.
A. Создание объекта, процесса или системы.
B. Проверка адекватности модели и объекта, процесса или системы на основе вычислительного и натурного эксперимента.
C. Корректировка постановки задачи после проверки адекватности модели. +
D. Использование модели.
12. Что такое параметры системы?
A. Величины, которая выражают свойство или системы, или ее части, или окружающей среды. +
B. Величины, характеризующие энергетическое или информационное наполнение элемента или подсистемы.
C. Свойства элементов объекта.
D. Величины, которая характеризует действия, которые могут выполнять объекты.
13. Какие формулировки МКЭ существуют в зависимости от функции, ищут?
A. В перемещениях и деформациях
B. В деформациях.
C. В напряжениях и градиентах.
D. Смешанная и гибридная. +
14. Какие зависимые переменные существуют в моделях макроуровня?
A. Время и характеристики потока.
B. Фазовые переменные типа потенциала.
C. Пространственные координаты. +
D. Фазовые переменные типа потока.
15. Что такое проектирование?
A. Процесс, который заключается в получении и преобразовании исходного описания объекта в конечный описание на основе выполнения комплекса работ исследовательского, расчетного и конструкторского характера. +
B. Процесс создания в заданных условиях описания несуществующего объекта на базе первичной описания.
C. Первоначальный описание объекта проектирования.
D. Вторичный описание объекта.
testdoc.ru
Тест по теме «Модели и моделирование»
Тест по теме «Модели и моделирование»
Вариант 1
1. Модель есть замещение изучаемого объекта другим объектом, который отражает:
а) все стороны данного объекта;
б) некоторые стороны данного объекта;
в) существенные стороны данного объекта;
г) несущественные стороны данного объекта.
2. Результатом процесса формализации является:
а) описательная модель; в) графическая модель;
б) математическая модель; г) предметная модель.
3. Информационной моделью организации занятий в школе является:
а) свод правил поведения учащихся; в) расписание уроков;
б) список класса; г) перечень учебников.
4. Материальной моделью является:
а) макет самолеты; в) чертеж;
б) карта; г) диаграмма.
5. Генеалогическое дерево семьи является:
а) табличной информационной моделью;
б) иерархической информационной моделью;
в) сетевой информационной моделью;
г) словесной информационной моделью.
6. Знаковой моделью является:
а) анатомический муляж; в) модель корабля;
б) макет здания; г) диаграмма.
7. Укажите в моделировании процесса исследования температурного режима комнаты объект моделирования:
а) конвекция воздуха в комнате;
б) исследование температурного режима комнаты;
в) комната;
г) температура.
8. Правильный порядок указанных этапов математического моделирования процесса:
1) анализ результата; 3) определение целей моделирования;
2) проведение исследования; 4) поиск математического описания.
Соответствует последовательности:
а) 3 – 4 – 2 – 1; в) 2 – 1 – 3 – 4;
б) 1 – 2 – 3 – 4; г) 3 – 1 – 4 – 2;
9. Из скольких объектов, как правило, состоит система?
а) из нескольких; в) из бесконечного числа;
б) из одного; г) она не делима.
10. Как называется граф, предназначенный для отображения вложенности, подчиненности, наследования и т.п. между объектами?
а) схемой; в) таблицей;
б) сетью; г) деревом.
11. Устное представление информационной модели называется:
а) графической моделью; в) табличной моделью;
б) словесной моделью; г) логической моделью.
12. Упорядочение информации по определенному признаку называется:
а) сортировкой; в) систематизацией;
б) формализацией; г) моделированием.
Вариант 2
1. Как называется упрощенное представление реального объекта?
а) оригинал; в) модель;
б) прототип; г) система.
2. Процесс построения моделей называется:
а) моделирование; в) экспериментирование;
б) конструирование; г) проектирование
3. Информационная модель, состоящая из строк и столбцов, называется:
а) таблица; в) схема;
б) график; г) чертеж.
4. Каково общее название моделей, которые представляют собой совокупность полезной и нужной информации об объекте?
а) материальные; в) предметные;
б) информационные; г) словесные.
5. Схема электрической цепи является:
а) табличной информационной моделью;
б) иерархической информационной моделью;
в) графической информационной моделью;
г) словесной информационной моделью
6. Знаковой моделью является:
а) карта; в) глобус;
б) детские игрушки; г) макет здания.
7. Укажите в моделировании процесса исследования температурного режима комнаты цель моделирования:
а) конвекция воздуха в комнате;
б) исследование температурного режима комнаты;
в) комната;
г) температура.
8. Правильные определения понятий приведены в пунктах
1) моделируемый параметр – признаки и свойства объекта – оригинала, которыми должна обязательно обладать модель;
2) моделируемый объект- предмет или группа предметов, структура или поведение которых исследуется с помощью моделирования;
3) закон – поведение моделируемого объекта.
а) 1 – 2 – 3; в) 1 – 3;
б) 2 – 3; г) 1 – 2.
9. Инструментом для компьютерного моделирования является:
а) сканер; в) принтер;
б) компьютер; г) монитор.
10. Как называется средство для наглядного представления состава и структуры системы?
а) таблица; в) текст;
б) граф; г) рисунок.
11. Как называются модели, в которых на основе анализа различных условий принимается решение?
а) словесные; в) табличные;
б) графические; г) логические.
12. Решение задачи автоматизации продажи билетов требует использования:
а) графического редактора; в) операционной системы;
б) текстового редактора; г) языка программирования.
infourok.ru








 Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г). 
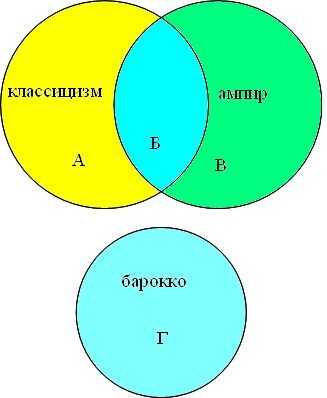 Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).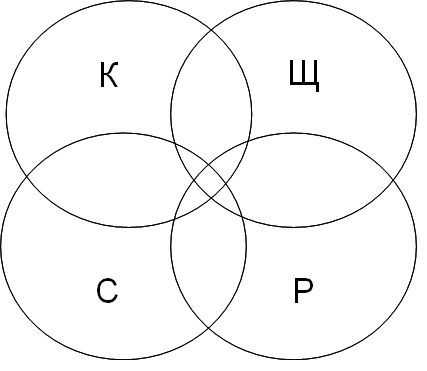
 .
.
2y= 0
2y= 0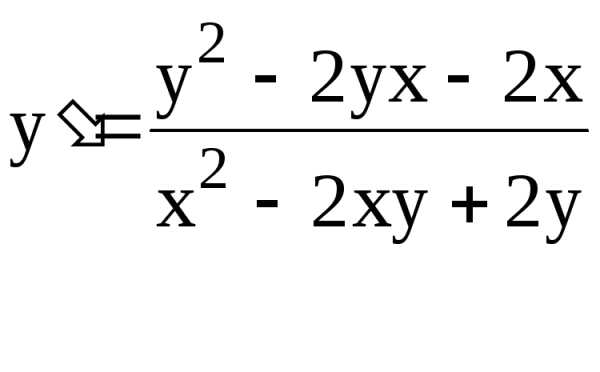
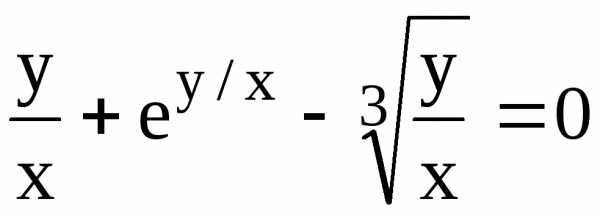 82. x2 sin
y + y2 cos x = 0
82. x2 sin
y + y2 cos x = 0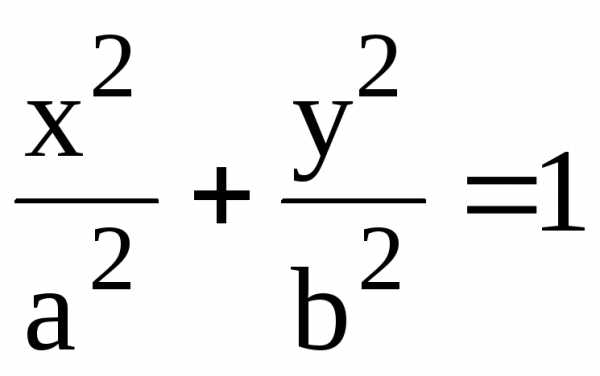 84. еу/х
ex/y = 1
84. еу/х
ex/y = 1 называется производной первого порядка.
называется производной первого порядка.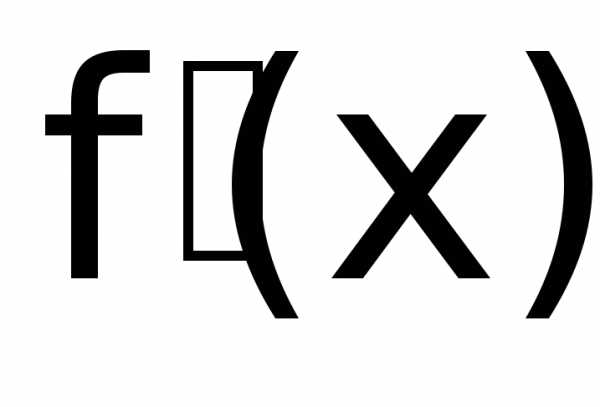 называется производной второго порядка
или второй производной от функции f(x)
и обозначается
называется производной второго порядка
или второй производной от функции f(x)
и обозначается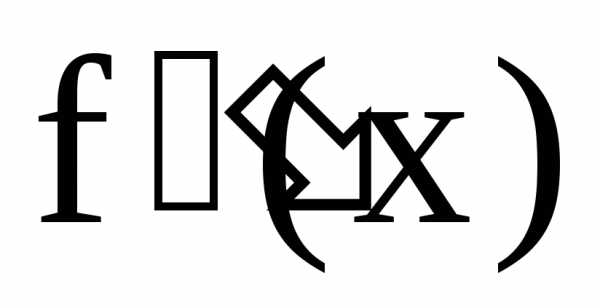 ,
, ,
,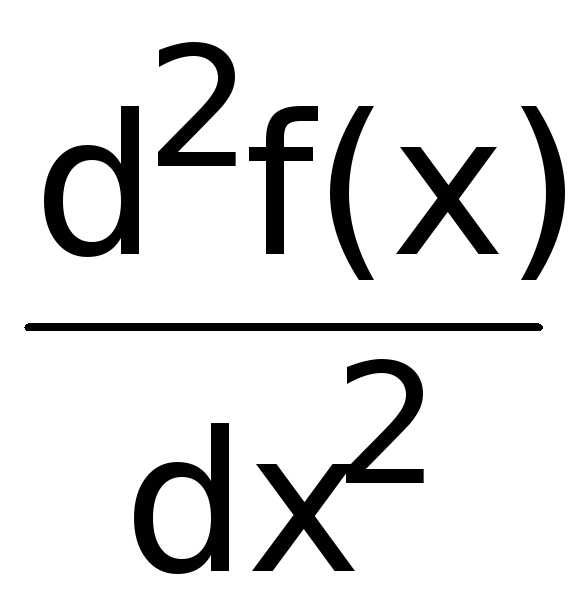 или
или 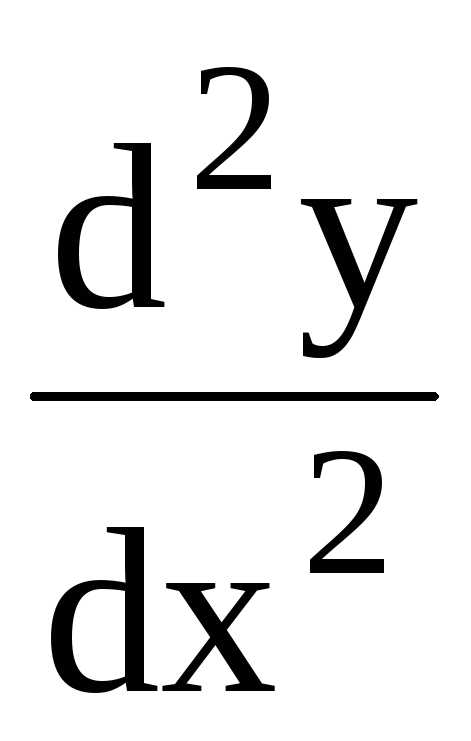 .
. называется производной третьего порядка
или третьей производной от функции f(x)
и обозначается
называется производной третьего порядка
или третьей производной от функции f(x)
и обозначается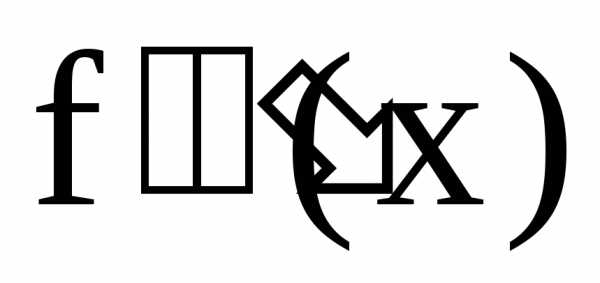 ,
,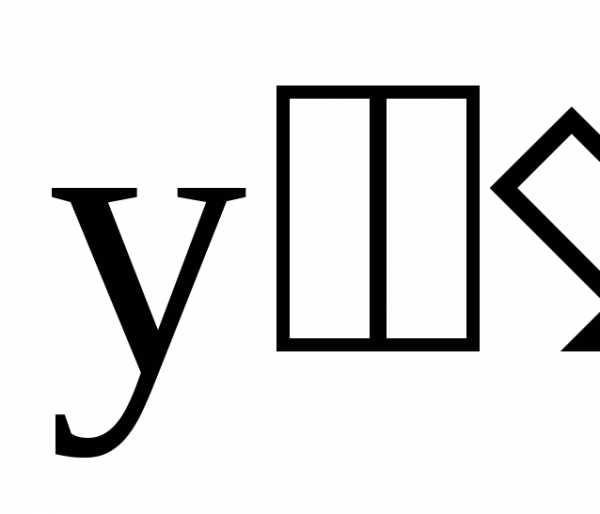 ,
,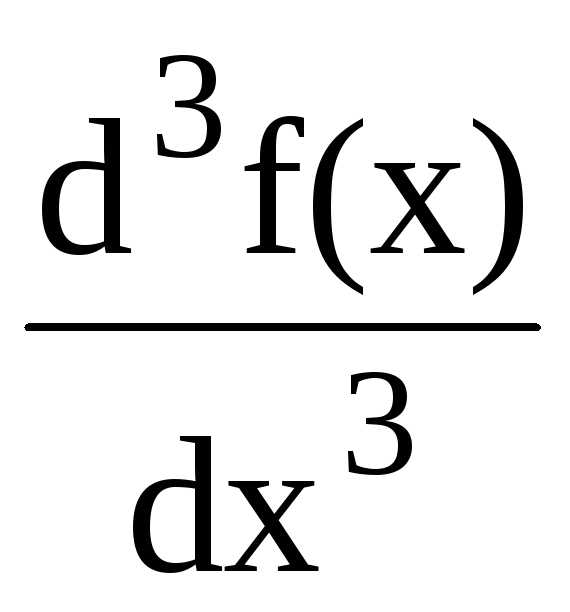 или
или  и т.д.
и т.д. .
. 92. y = ln (2x3)
92. y = ln (2x3)
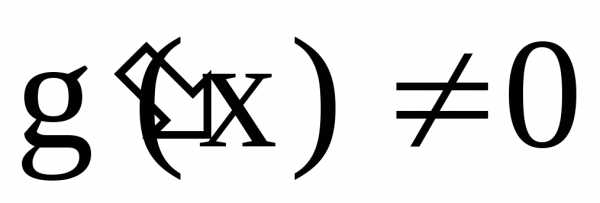 и, если
и, если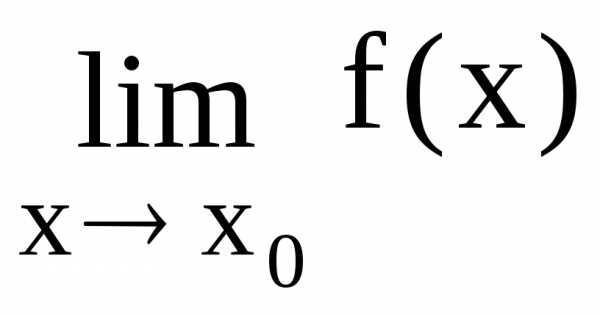 =
=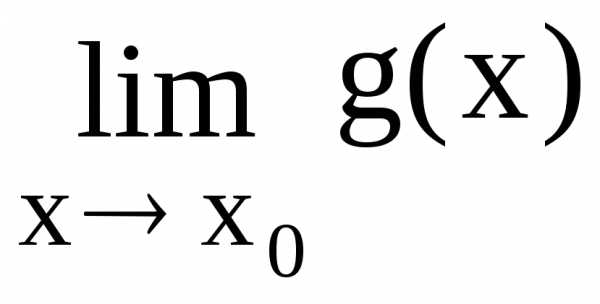 = 0 или
= 0 или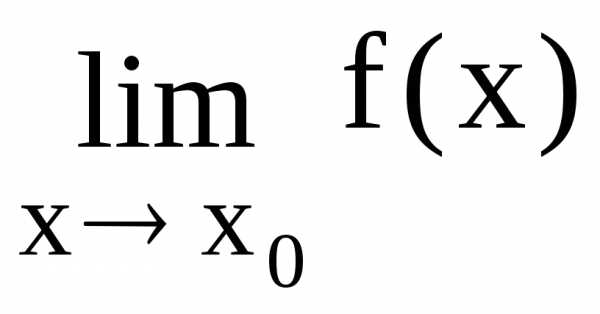 =
=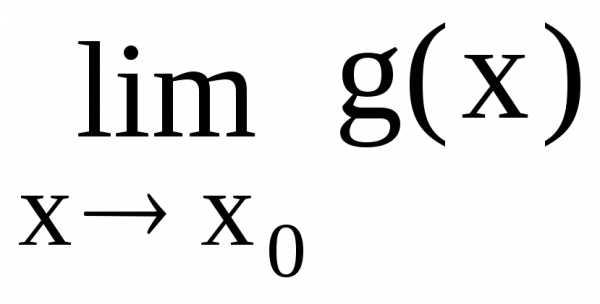 =
, то
=
, то или
или предел отношения двух функций равен
пределу отношения их производных, если
последний существует (конечный или
бесконечный).
предел отношения двух функций равен
пределу отношения их производных, если
последний существует (конечный или
бесконечный). ,
либо.
,
либо.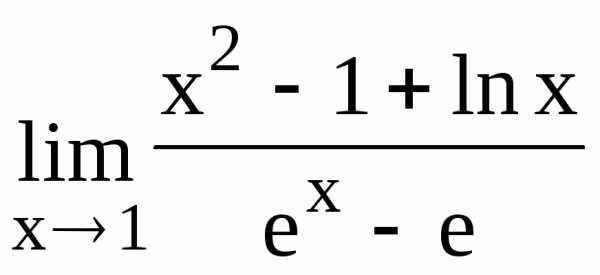 .
.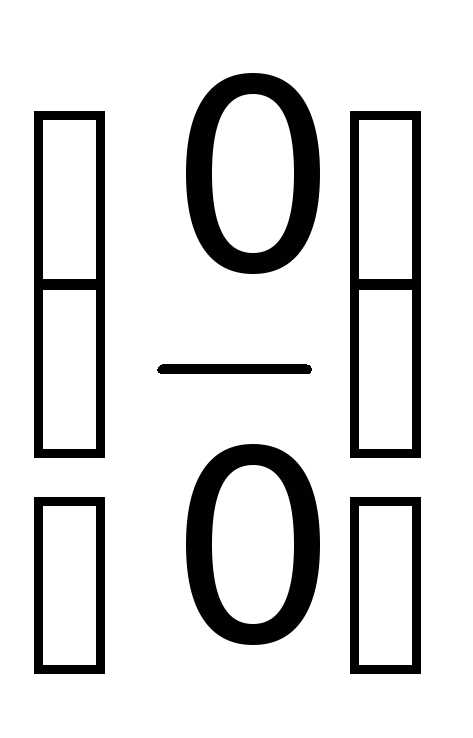 .
Для ее устранения воспользуемся правилом
Лопиталя
.
Для ее устранения воспользуемся правилом
Лопиталя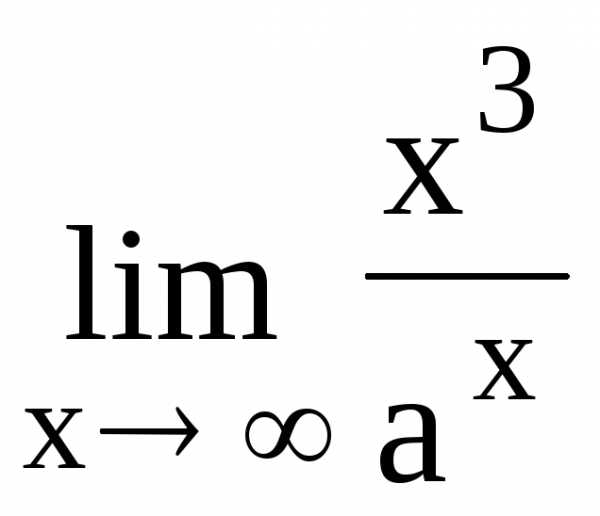 .
.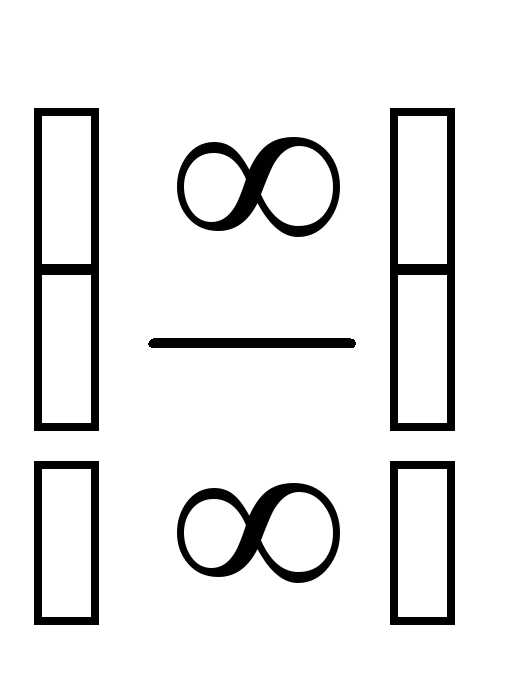 .
Применяя трижды правило Лопиталя,
получим
.
Применяя трижды правило Лопиталя,
получим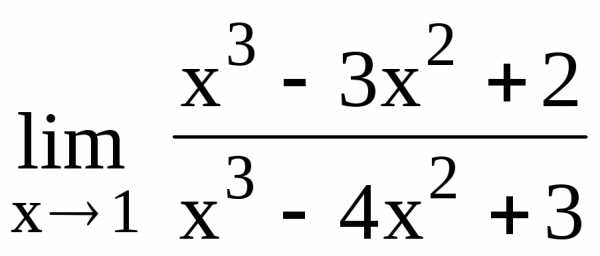 102.
102.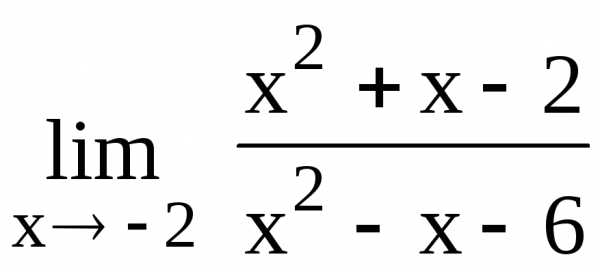
 104.
104.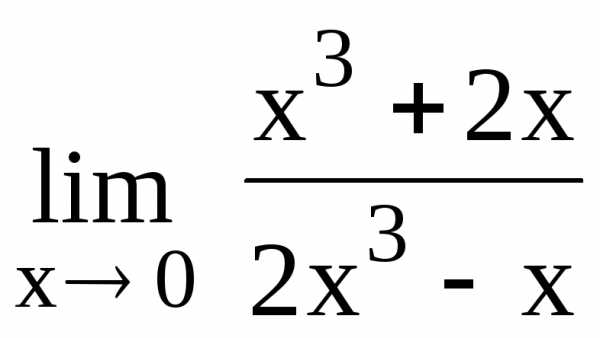
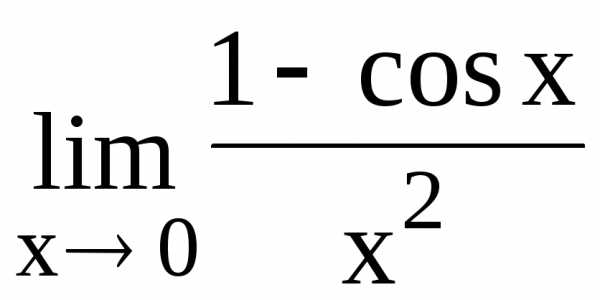 106.
106.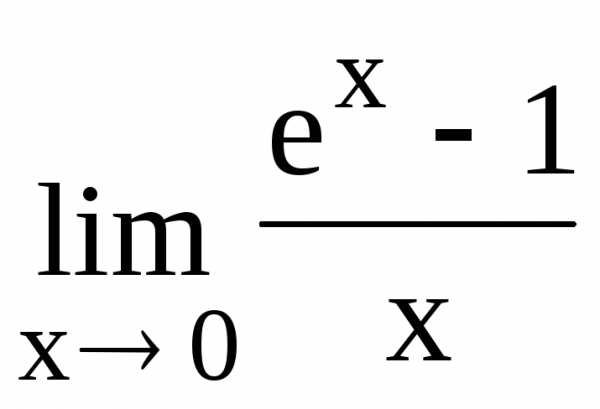
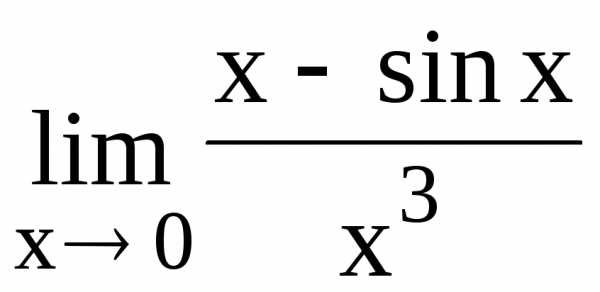 108.
108.
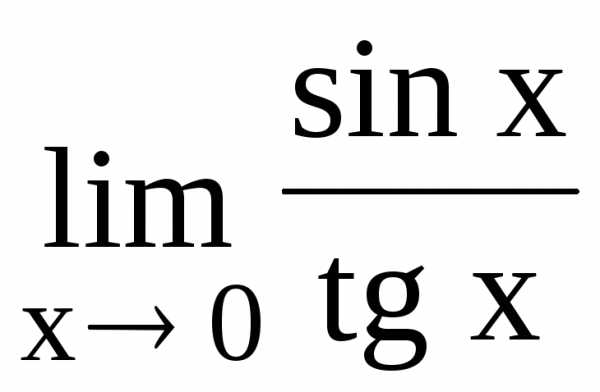 110.
110.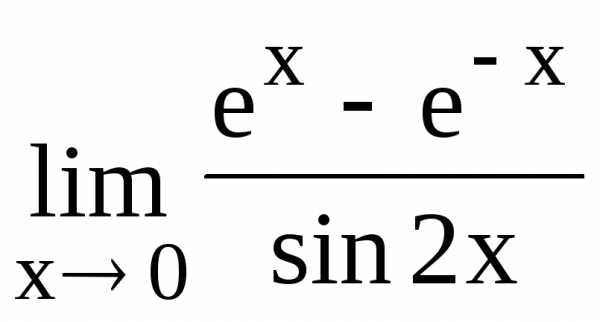
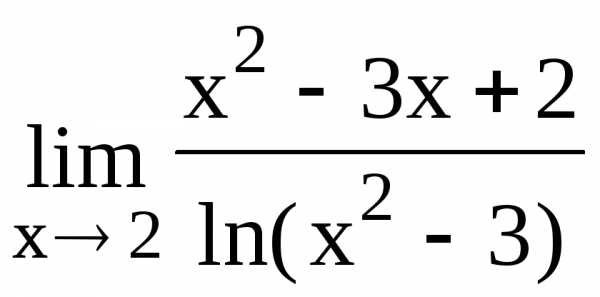 112.
112.
 114.
114.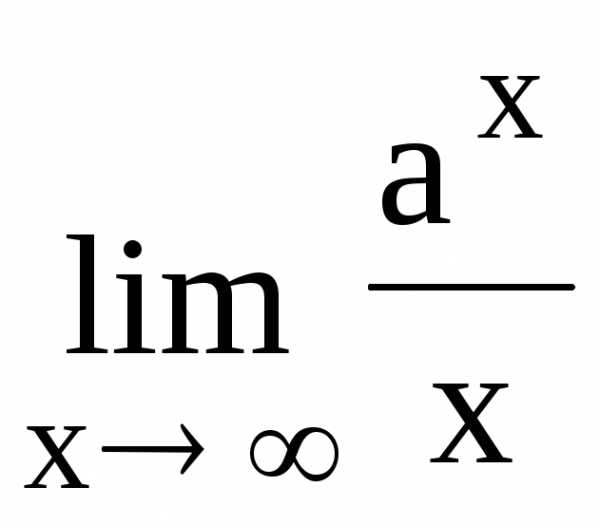 ,
a >1
,
a >1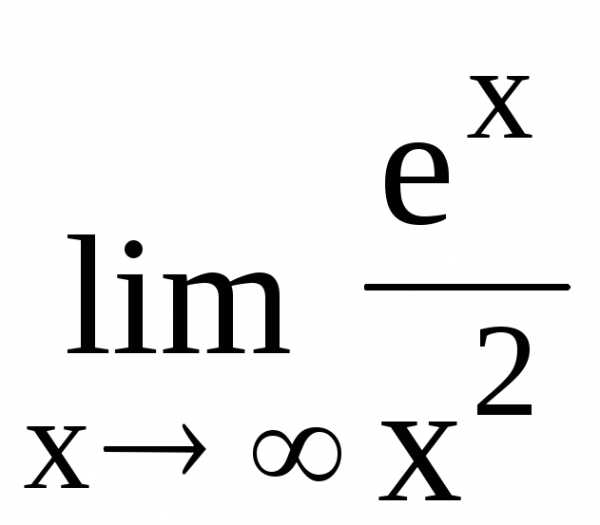 116.
116.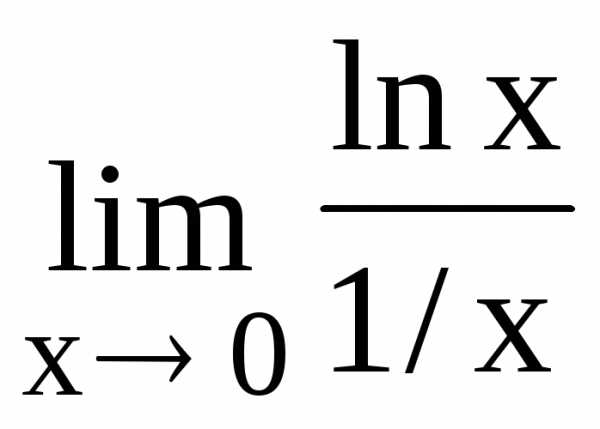
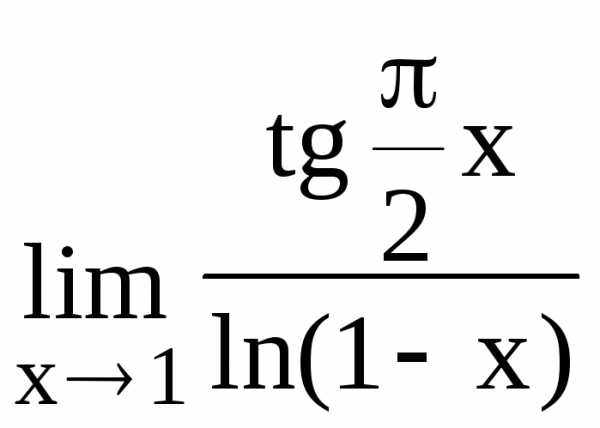 118.
118.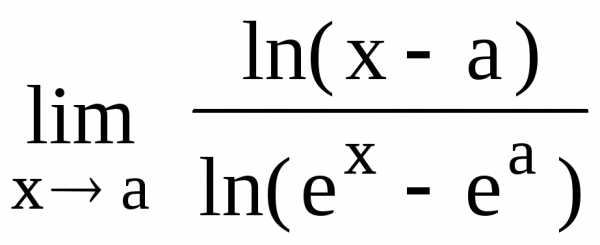
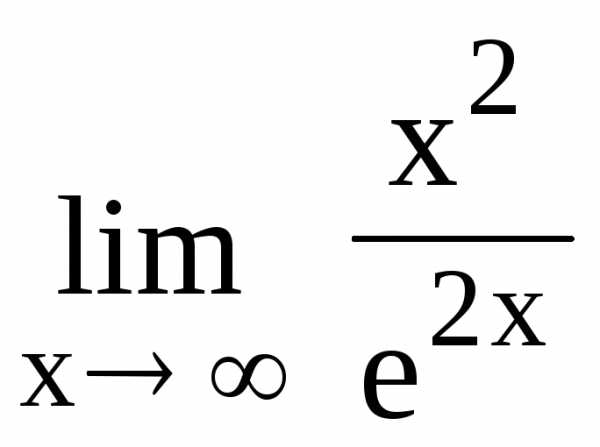 120.
120.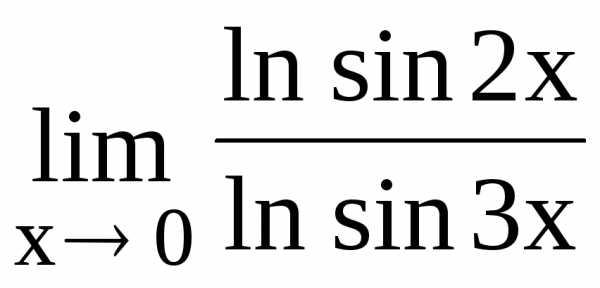
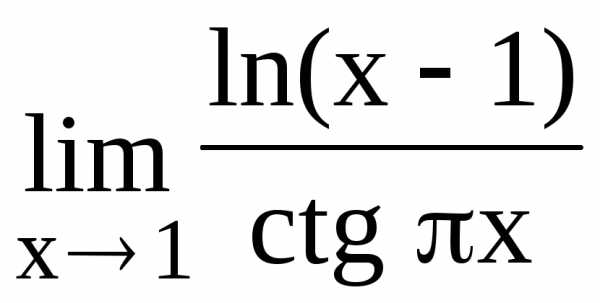 122.
122.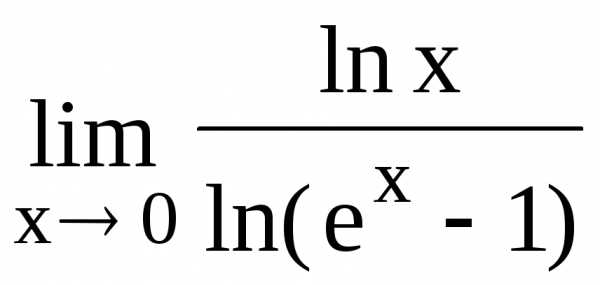
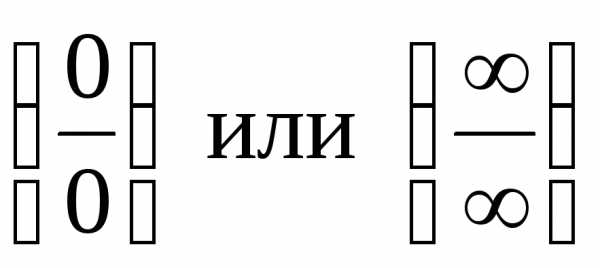 ,
а затем раскрываются с помощью правила
Лопиталя.
,
а затем раскрываются с помощью правила
Лопиталя.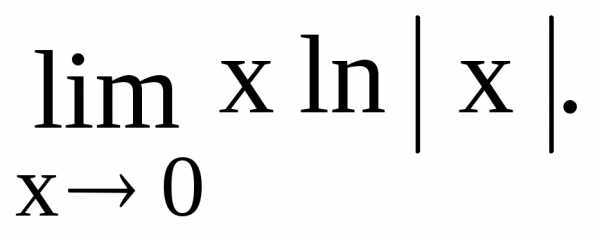
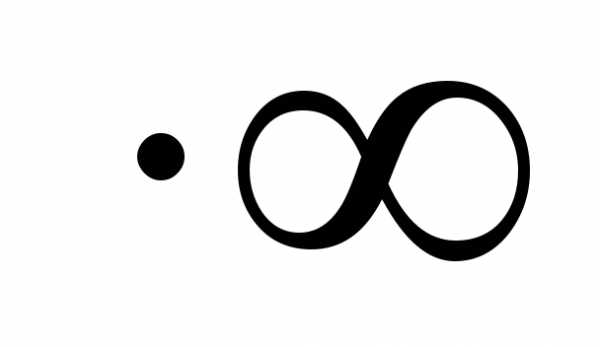 .
Но x ln |x| =
.
Но x ln |x| =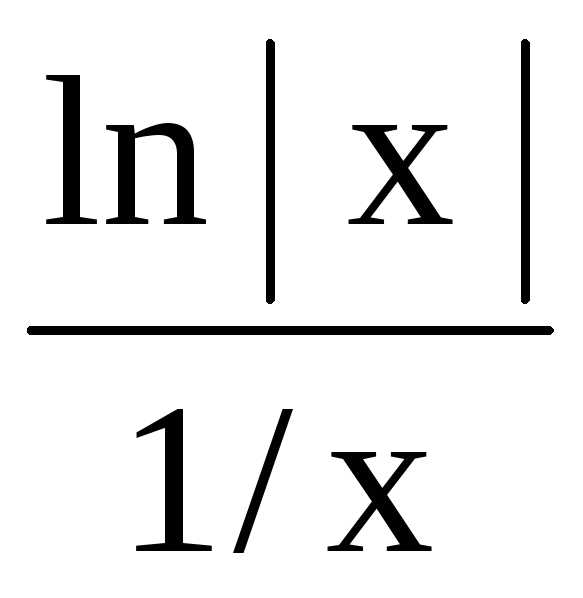
получена неопределенность вида
получена неопределенность вида 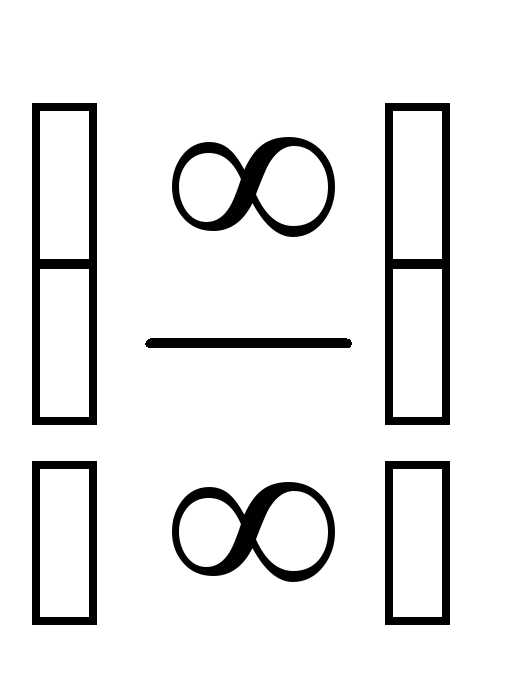 .
Применяя правило Лопиталя, получим=.
.
Применяя правило Лопиталя, получим=.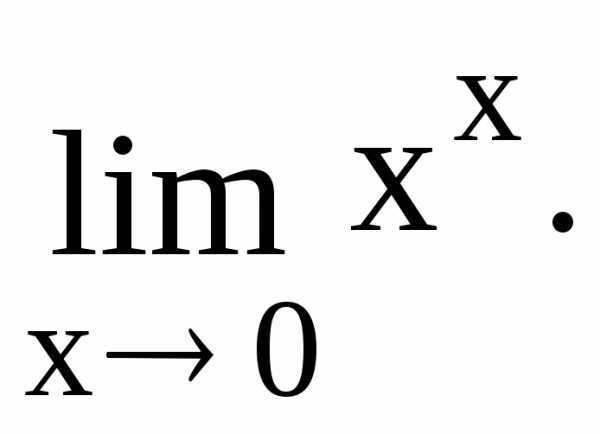
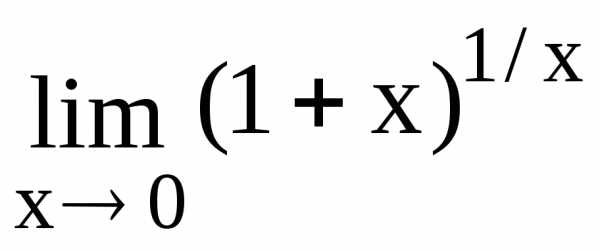 .
.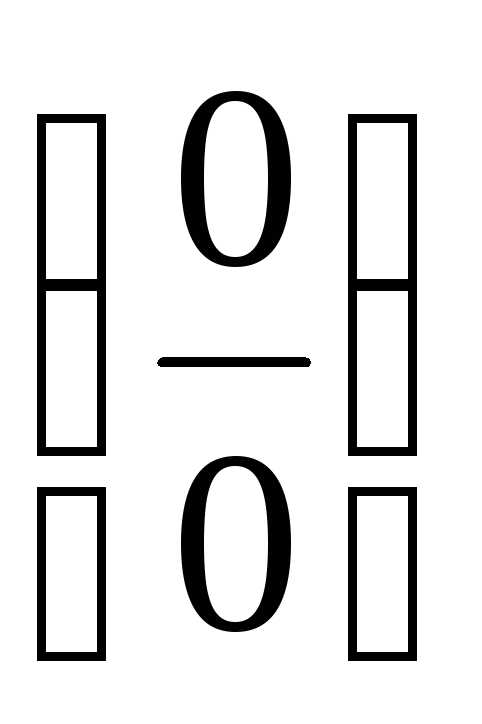 .
Устраним ее, используя правило Лопиталя.
.
Устраним ее, используя правило Лопиталя.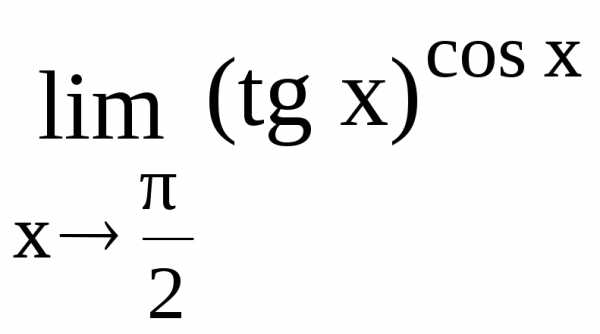 .
.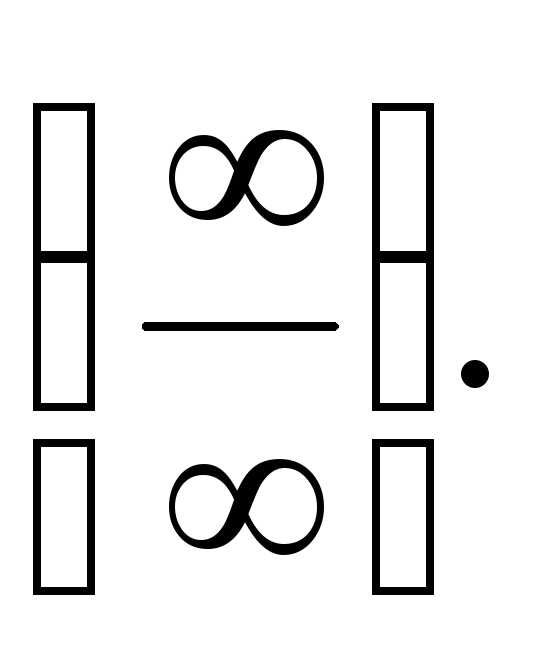 Применяя правило Лопиталя, находим
Применяя правило Лопиталя, находим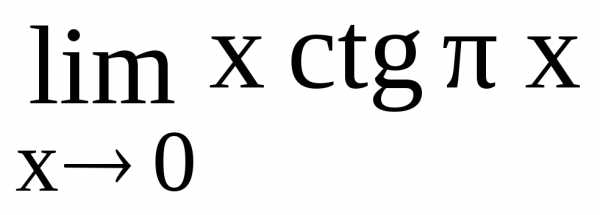 124.
124.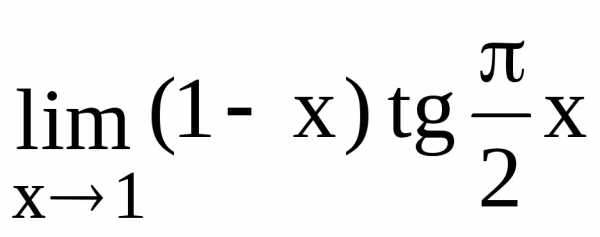 126.
126.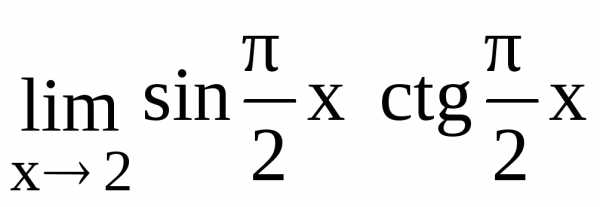
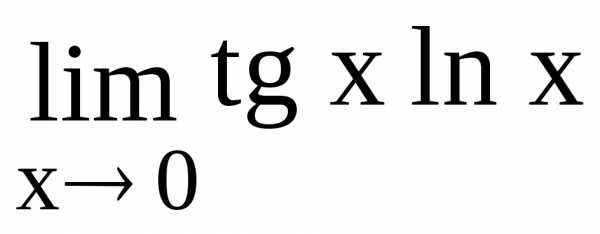 128.
128.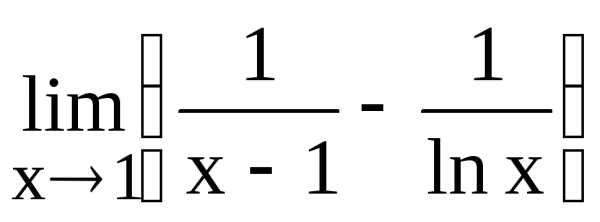 130.
130.
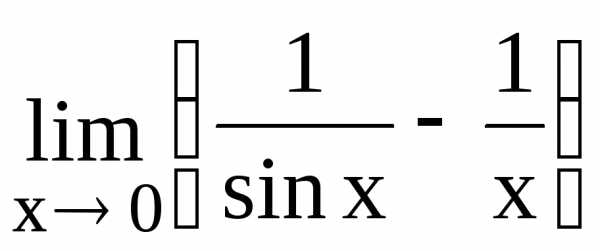 132.
132. 134.
134.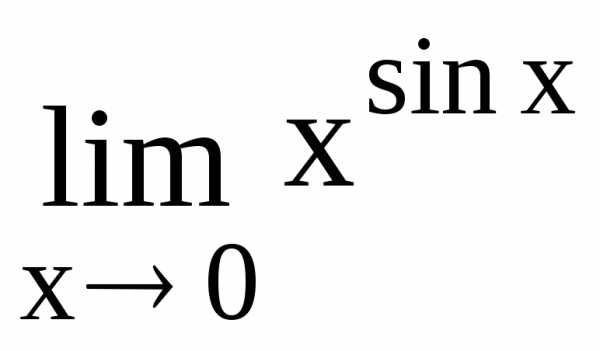
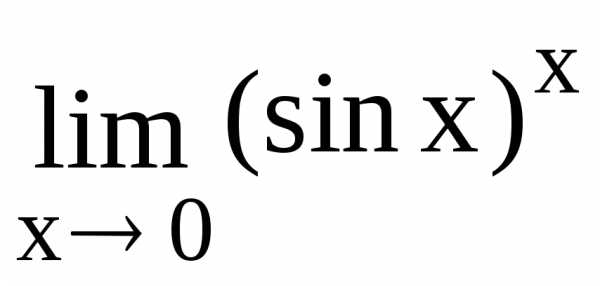 136.
136.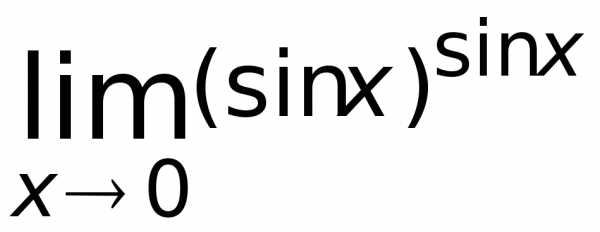
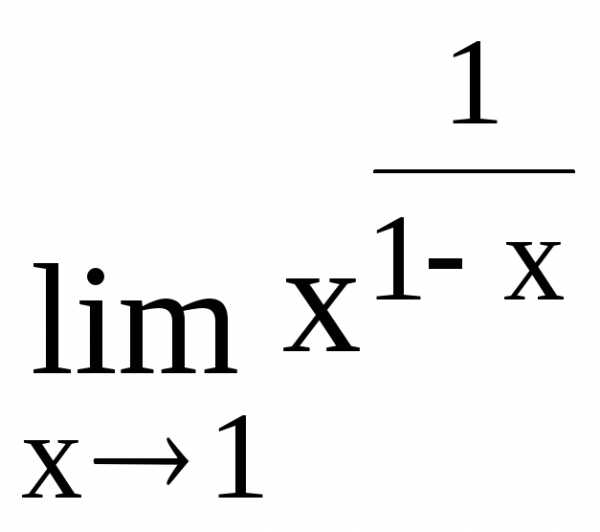 138.
138.
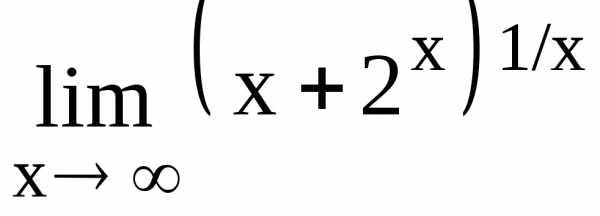 140.
140.
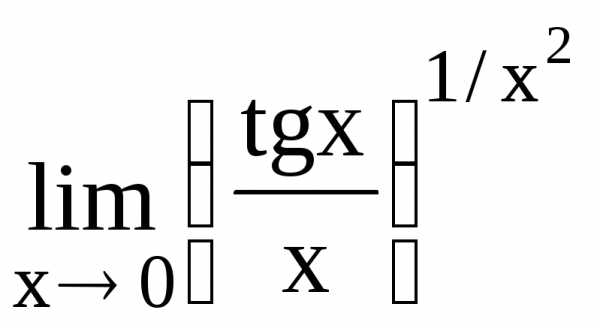 142.
142.