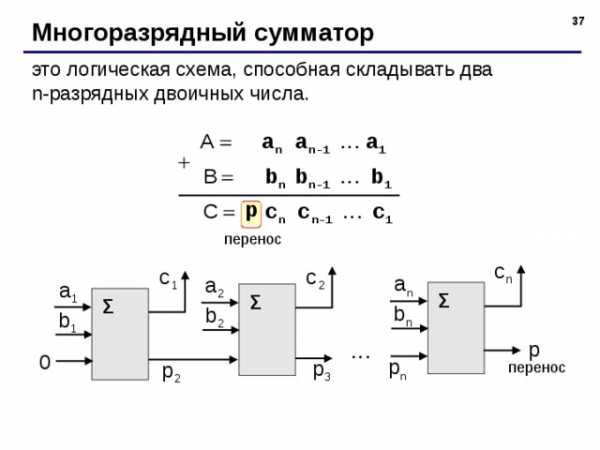
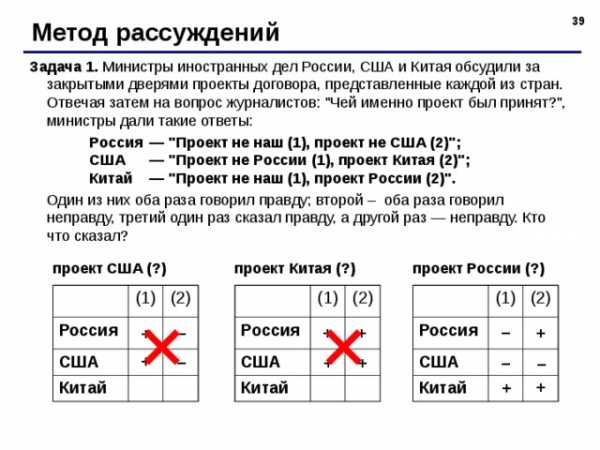
Линейное уравнение с одной переменной. 7-й класс
Разделы: Математика
Урок № 1.
Тип урока: закрепление пройденного материала.
Цели урока:
Образовательные:
- формирование навыка решения уравнения с одним неизвестным сведением его к линейному уравнению с помощью свойств равносильности.
Развивающие:
- формирование ясности и точности мысли, логического мышления, элементов алгоритмической культуры;
- развитие математической речи;
- развитие внимания, памяти;
- формирование навыков само и взаимопроверки.
Воспитательные:
- формирование волевые качества;
- формирование коммуникабельность;
- выработка объективной оценки своих достижений;
- формирование ответственности.
Оборудование: интерактивная доска, доска для фломастеров, карточки с заданиями для самостоятельной работы, карточки для коррекции знаний для слабоуспевающих учащихся, учебник, рабочая тетрадь, тетрадь для домашних работ, тетрадь для самостоятельных работ.
Ход урока
1. Организационный момент – 1мин.
Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.
2. Проверка домашнего задания – 4 мин.
Учащиеся проверяют домашнюю работу, решение которой выведено с обратной стороны доски одним из учащихся.
3. Устная работа– 6 мин.
(1) Пока идет устный счет, слабоуспевающие учащиеся получают карточку для коррекции знаний и выполняют 1), 2), 4) и 6) задания по образцу. (См. Приложение 1.)
Карточка для коррекции знаний.
(2) Для остальных учащихся задания проецируются на интерактивную доску: (См. Презентацию: Слайд 2)
- Вместо звездочки поставь знак “+” или “–”, а вместо точек – числа:
а) (*5)+(*7) = 2;
б) (*8) – (*8) = (*4)–12;
в) (*9) + (*4) = –5;
г) (–15) – (*…) = 0;
д) (*8) + (*…) = –12;
е) (*10) – (*…) = 12. - Составь уравнения, равносильные уравнению:
а) х – 7 = 5;
б) 2х – 4 = 0;
в) х –11 = х – 7;
г) 2(х –12) = 2х – 24.
3. Логическая задача: Вика, Наташа и Лена в магазине купили капусту, яблоки и морковь. Все купили разные продукты. Вика купила овощ, Наташа – яблоки или морковь, Лена купила не овощ. Кто что купил? (Один из учащихся, выполнивший задание выходит к доске и заполняет таблицу.) (Слайд 3)
| Вика | Наташа | Лена | |
| К | |||
| Я | |||
| М |
Заполнить таблицу
| Вика | Наташа | Лена | |
| К | + | – | – |
| Я | – | – | + |
| М | – | + | – |
Ответ
(Учащиеся используют пластиковые листы и фломастеры.)
4. Обобщение умения решать уравнения сведением их к линейному уравнению –9 мин.
Коллективная работа с классом. (Слайд 4)
Решим уравнение
12 – (4х – 18) = (36 + 5х) + (28 – 6х). (1)
для этого выполним следующие преобразования:
1. Раскроем скобки. Если перед скобками стоит знак “плюс”, то скобки можно опустить, сохранив знак каждого слагаемого, заключенного в скобки. Если перед скобками стоит знак “минус”, то скобки можно опустить, изменив знак каждого слагаемого, заключенного в скобки:
12 – 4х + 18 = 36 + 5х + 28 – 6х. (2)
Уравнения (2) и (1) равносильны:
2. Перенесем с противоположными знаками неизвестные члены так, чтобы они были только в одной части уравнения (или в левой, или в правой). Одновременно перенесем известные члены с противоположными знаками так, чтобы они были только в другой части уравнения.
Например, перенесем с противоположными знаками неизвестные члены в левую, а известные – в правую часть уравнения, тогда получим уравнение
– 4х – 5х + 6х = 36 + 28 – 18 — 12, (3)
равносильное уравнению (2), а следовательно, и уравнению (1).
3. Приведем подобные слагаемые:
–3х = 34. (4)
Уравнение (4) равносильно уравнению (3), а следовательно, и уравнению (1).
4. Разделим обе части уравнения (4) на коэффициент при неизвестном.
Полученное уравнение х = будет равносильно уравнению (4), а следовательно, и уравнениям (3), (2), (1)
Поэтому корнем уравнения (1) будет число
По этой схеме (алгоритму) решаем уравнения на сегодняшнем уроке:
- Раскрыть скобки.
- Собрать члены, содержащие неизвестные, в одной части уравнения, а остальные члены в другой.
- Привести подобные члены.
- Разделить обе части уравнения на коэффициент при неизвестном.
Примечание: следует отметить, что приведенная схема не является обязательной, так как часто встречаются уравнения, для решения которых некоторые из указанных этапов оказываются ненужными. При решении же других уравнений бывает проще отступить от этой схемы, как, например, в уравнении:
7(х – 2) = 42.
5. Тренировочные упражнения – 8 мин.
№ № 132(а, г), 135(а, г), 138(б, г) – с комментарием и записью на доске.
6. Самостоятельная работа – 14 мин. (выполняется в тетрадях для самостоятельных работ с последующей взаимопроверкой проверкой; ответы будут отображены на интерактивной доске)
Перед самостоятельной работой учащимся будет предложено задание на сообразительность – 2 мин.
Не отрывая карандаша от бумаги и не проходя дважды по одному и тому же участку линии, начертите распечатанное письмо. (Слайд 5)
(Учащиеся используют пластиковые листы и фломастеры.)
1. Решить уравнения (на карточках) (См. Приложение 2)
Дополнительное задание № 135 (б, в).
7. Подведение итогов урока – 1 мин.
Алгоритм сведения уравнения к линейному уравнению.
8. Сообщение домашнего задания – 2 мин.
п.6, № № 136 (а-г), 240 (а), 243(а, б), 224 (Разъяснить содержание домашнего задания).
Урок № 2.
Цели урока:
Образовательные:
- повторение правил, систематизация, углубление и расширение ЗУНов учащихся по решению линейных уравнений;
- формирование умения применять полученные знания при решении уравнений различными способами.
Развивающие:
- развитие интеллектуальных умений: анализа алгоритма решения уравнения, логического мышления при построении алгоритма решения уравнения, вариативности выбора способа решения, систематизации уравнений по способам решения;
- развитие математической речи;
- развитие зрительной памяти.
Воспитательные:
- воспитание познавательной активности;
- формирование навыков самоконтроля, взаимоконтроля и самооценки;
- воспитание чувства ответственности, взаимопомощи;
- привитие аккуратности, математической грамотности;
- воспитание чувства товарищества, вежливости, дисциплинированности, ответственности;
- Здоровьесбережение.
а) образовательная: повторение правил, систематизация, углубление и расширение ЗУНов учащихся по решению линейных уравнений;
б) развивающая: развитие гибкости мышления, памяти, внимания и сообразительности;
в) воспитательная: привитие интереса к предмету и к истории родного края.
Оборудование: интерактивная доска, сигнальные карточки (зеленая и красная), листы с тестовой работой, учебник, рабочая тетрадь, тетрадь для домашних работ, тетрадь для самостоятельных работ.
Форма работы: индивидуальная, коллективная.
Ход урока
1. Организационный момент – 1мин.
Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.
2. Устная работа – 10 мин.
(Задания для устного счета выводятся на интерактивную доску.) (Слайд 6)
1) Решите задачи:
а) Мама старше дочери на 22 года. Сколько лет маме, если им вместе 46 лет
б) В семье трое братьев и каждый следующий младше предыдущего в два раза. Вместе
всем братьям 21 год. Сколько лет каждому?
2) Решите уравнения: (Пояснить)
| ;
|
Какие из данных уравнений являются линейными?
(Во время устного счета учащиеся используют сигнальные карточки: зеленую и красную)
3) Проверьте, правильно ли решено уравнение, если нет, то найди ошибки. (Слайд 7)
| 4 · (х – 5) = 12 – х 4х – 5 = 12 – х 4х + х = 12 – 5 5х = 7 /:5 х = 1,4 |
Желающий выходит к интерактивной доске исправить ошибки
|
4) Пояснить задания из домашней работы, вызвавшие затруднение.
3. Выполнение упражнений – 10 мин. (Слайд 8)
(1) Какому неравенству удовлетворяет корень уравнения:
4 – 5х = 5
а) x > 1;
б) x < 0;
в) x > 0;
г) x < –1.
(2) При каком значении выражении у значение выражения 2у – 4 в 5 раз меньше значения выражения 5у – 10?
(3) При каком значении k уравнение kx – 9 = 0 имеет корень равный – 2?
Посмотри и запомни (7 секунд). (Слайд 9)
Через 30 секунд учащиеся воспроизводят рисунок на пластиковых листах.
4. Физкультминутка – 1,5 мин.
Упражнение для глаз и для рук
(Учащиеся смотрят и повторяют упражнения, которые проецируются на интерактивную доску.)
5. Самостоятельная тестовая работа – 15 мин.
(Учащиеся выполняют тестовую работу в тетрадях для самостоятельных работ, дублируя ответы в рабочих тетрадях. Сдав тесты, учащиеся сверяют ответы с ответами, отображенными на доске)
Учащиеся, справившиеся с работой раньше всех, помогают слабоуспевающим учащимся.
(См. Приложение 3)
6. Подведение итогов урока – 2 мин.
– Какое уравнение с одной переменной называется линейным?
– Что называется корнем уравнения?
– Что значит “решить уравнение”?
– Сколько корней может иметь уравнение?
7. Сообщение домашнего задания. – 1 мин.
п.6, № № 294(а, б),244, 241(а, в), 240(г) – Уровень А, В
п.6, № № 244, 241(б, в), 243(в),239, 237– Уровень С
(Разъяснить содержание домашнего задания.)
8. Рефлексия – 0,5 мин.
– Вы довольны своей работой на уроке?
– Какой вид деятельности вам понравился больше всего на уроке.
Литература:
- Алгебра 7. / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Пешков, С.В. Суворова. Под редакцией С.А. Теляковского. / М.: Просвещение, 1989 – 2006.
- Сборник тестовых заданий для тематического и итогового контроля. Алгебра 7 класс/ Гусева И.Л., Пушкин С.А., Рыбакова Н.В.. Общая ред.: Татур А.О. – М.: “Интеллект-Центр” 2009 – 160 с.
- Поурочное планирование по алгебре. / Т.Н.Ерина. Пособие для учителей /М: Изд. “Экзамен”, 2008. – 302,[2] с.
- Карточки для коррекции знаний по математике для 7 класса./ Левитас Г.Г. /М.: Илекса, 2000. – 56 с.
22.11.2010
xn--i1abbnckbmcl9fb.xn--p1ai
Линейное уравнение с одной переменной (В.А. Тарасов). Видеоурок. Алгебра 7 Класс
На данном уроке мы начнем изучение темы «Уравнения». Мы рассмотрим линейное уравнение с одной переменной в общем виде, а также на конкретных примерах. Кроме того, решим текстовые задачи.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»
Определение
Линейным уравнением с одной неизвестной называется уравнение вида:
.
Здесь – искомая неизвестная, и – коэффициенты, параметры.
Решить уравнение – значит найти все его корни или убедиться в том, что решений нет.
Определение
Корень уравнения – это такое значение , при котором уравнение превращается в верное числовое равенство.
Линейное уравнение описывает равномерное прямолинейное движение с постоянной скоростью:
– путь равен произведению скорости и времени.
Если перенести все слагаемые в одну сторону, получим:
.
Выполним переобозначение:
.
Получим изучаемое линейное уравнение.
Пример 1:
Прибавим три к обеим частям уравнения – при этом равенство не изменится:
.
Разделим обе части на два:
.
Ответ: .
Комментарий: наша главная цель – найти , для этого мы выполняем одинаковые преобразования над обеими частями уравнения.
Решим уравнение в общем виде:
.
Отнимем в обеих частях число :
.
Поскольку имеем право обе части поделить на :
.
Вывод: при линейное уравнение имеет единственный корень: .
Рассмотрим случай, когда :
.
Уравнение имеет бесчисленное множество решений, любое действительное удовлетворяет уравнению
.
Решений нет.
Так, в общем случае уравнение имеет решение:
При .
При – любое число, бесчисленное множество решений.
При решений нет.
В рассматриваемое линейное уравнение неизвестное входит в первой степени, поэтому такое уравнение носит название уравнения первой степени, к нему сводятся многие другие уравнения.
Пример 2:
.
Используя свойства уравнения, имеем право перенести слагаемое из правой части урвнения в левую с противоположным знаком или слагаемое из левой части — в правую тоже с противоположным знаком. Перенесем все члены с влево, а числа вправо:
.
Поделим обе части на два:
.
Ответ: .
Пример 3:
.
Раскроем скобки:
.
Прибавим пять к обеим частям уравнения:
.
Поделим обе части на два:
.
Очевидно, что решением данного уравнения может быть любое число.
Ответ: уравнение имеет бесчисленное множество решений.
Пример 4:
.
Раскроем скобки:
Перенесем все члены с влево, а числа вправо:
.
Получено неверное числовое равенство.
Ответ: решений нет.
Пример 5: решить задачу.
Папе и дедушке вместе 111 лет. Сколько лет каждому, если папа в два раза моложе дедушки?
Решение: пусть папе лет. Поскольку дедушка в два раза его старше, ему лет. Тогда имеем уравнение:
.
Поделим обе части на три:
.
Так, папе 37 лет. Тогда дедушке года.
Ответ: папе 37 лет, дедушке 74 года.
Пример 6
При каком значении значение выражения в три раза больше значения выражения ?
Решение
Если первое выражение в три раза больше второго, имеем право второе умножить на три и приравнять:
.
Раскроем скобки:
.
Перенесем все члены с влево, а числа вправо:
.
Поделим обе части на минус семь:
.
Ответ: при первое заданное выражение в три раза больше второго.
Вывод: на данном уроке мы рассмотрели линейное уравнение с одной переменной и выяснили его специфику. Такое уравнение может иметь одно решение, бесчисленное множество решений или вовсе не иметь решений.
Список литературы
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. – М.: Просвещение, 2010.
- Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. – М.: ВЕНТАНА-ГРАФ.
- Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 – М.: Просвещение, 2006.
Домашнее задание
- Решить уравнения:
а) ; б) ; в) ; г) . - Решить уравнения:
а) - в) ;
interneturok.ru
Линейное уравнение с одной переменной (Г.И. Вольфсон). Видеоурок. Алгебра 7 Класс
Решение различных текстовых задач часто сводится к решению уравнения с введенной нами переменной. На этом уроке мы познакомимся с определением одного типа таких уравнений, линейными, и методами решения уравнений этого типа. Также рассмотрим несколько примеров с решениями.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»
В каждом автобусе можно разместить 30 школьников. Сколько автобусов потребуется, чтобы перевезти 930 школьников (см. Рис. 1)?
Решение
Рис. 1. Иллюстрация к задаче
Решим данную задачу с помощью уравнения. Пусть – это искомое число автобусов. В каждый автобус помещается 30 учеников, следовательно, общее количество учеников, которые проедут в искомом числе автобусов, будет равно . Однако общее количество учеников нам известно – 930, поэтому получили уравнение:
Найдём , решив данное уравнение:
Ответ: 31 автобус.
В задаче 1 мы составили уравнение, которое называется линейным уравнением.
Уравнение вида , где – переменная, и – некоторые числа, называется линейным уравнением с одной переменной.
Число обычно называют коэффициентом, а число – свободным членом. Они могут быть положительными и отрицательными, целыми и нецелыми, и даже нулями. Например:
Рассмотрим 2 случая:
1. Коэффициент не равен 0 ()
В этом случае обе части линейного уравнения можно разделить на a:
При этом будет равен:
2. Коэффициент равен 0 ()
В этом случае линейное уравнение принимает вид . Из этого уравнения и свойства умножения чисел на ноль следует, что, какое бы число мы ни взяли в качестве , при его подстановке в уравнение получится числовое равенство . Это равенство верное, когда , а в остальных случаях при это равенство неверное.
Следовательно, при и любое число является корнем линейного уравнения, так как при этих условиях подстановка вместо любого числа дает верное числовое равенство . А при и линейное уравнение не имеет корней, так как при этих условиях подстановка вместо любого числа приводит к неверному числовому равенству (см. Рис. 2).
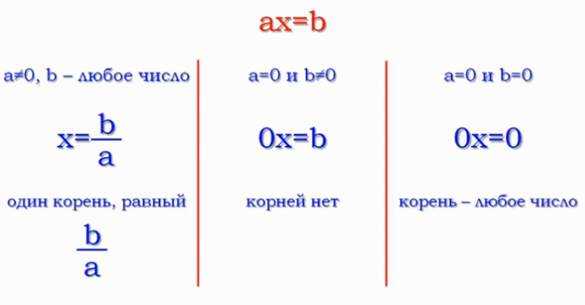
Рис. 2. Решение линейного уравнения с одной переменной
Решите уравнения:
1.
Коэффициент в данном уравнении не равен 0, поэтому корень данного уравнения будет равен:
2.
Коэффициент в данном уравнении равен 0, а свободный член не равен нулю, следовательно, у этого уравнения решений нет.
3.
можно представить, как . Поэтому будет равен:
4.
Коэффициент и свободный член в данном уравнении равны 0, поэтому – это любое число.
5.
Решите уравнения:
1.
Для удобства выполнения деления переведем и в неправильную дробь.
2.
представим в виде обыкновенной дроби.
При каких значениях выражение равно 0,1?
Решение
Формулировка данной задачи означа
interneturok.ru
| 1. |
Корень линейного уравнения
Сложность: лёгкое |
1 |
| 2. |
Решение линейного уравнения
Сложность: лёгкое |
1 |
| 3. |
Линейное уравнение, схема решения
Сложность: лёгкое |
1 |
| 4. |
Линейное уравнение (коэффициент при x дробный)
Сложность: лёгкое |
1 |
| 5. |
Составление и решение линейного уравнения
Сложность: лёгкое |
2 |
| 6. |
Линейное уравнение вида x + a = b
Сложность: лёгкое |
1 |
| 7. |
Линейное уравнение вида x + a = 0
Сложность: лёгкое |
1 |
| 8. |
Линейное уравнение вида ax + b = 0
Сложность: лёгкое |
1 |
| 9. |
Линейное уравнение (с дробями)
Сложность: среднее |
2 |
| 10. |
Линейное уравнение вида a — kx = c
Сложность: среднее |
3 |
| 11. |
Линейное уравнение вида a — b + kx = c + d — mx
Сложность: среднее |
4 |
| 12. |
Задача на движение
Сложность: среднее |
3 |
| 13. |
Задача на движение, скорость по течению и против течения
Сложность: среднее |
4 |
| 14. |
Задача на движение, две лодки
Сложность: среднее |
4 |
| 15. |
Задача на движение в одном направлении
Сложность: среднее |
4 |
| 16. |
Задача на движение, скорость течения реки
Сложность: сложное |
5 |
| 17. |
Решение уравнения, записанного в виде пропорции
Сложность: сложное |
3 |
| 18. |
Определение книг на полках
Сложность: сложное |
6 |
www.yaklass.ru
7 класс. Алгебра. Решение линейных уравнений с одной переменной. — Решение линейных уравнений с одной переменной.
Комментарии преподавателя
На данном уроке мы начнем изучение темы «Уравнения». Мы рассмотрим линейное уравнение с одной переменной в общем виде, а также на конкретных примерах. Кроме того, решим текстовые задачи.
Основные определения, истоки уравнения
Определение
Линейным уравнением с одной неизвестной называется уравнение вида:
.
Здесь – искомая неизвестная, и – коэффициенты, параметры.
Решить уравнение – значит найти все его корни или убедиться в том, что решений нет.
Определение
Корень уравнения – это такое значение , при котором уравнение превращается в верное числовое равенство.
Линейное уравнение описывает равномерное прямолинейное движение с постоянной скоростью:
– путь равен произведению скорости и времени.
Если перенести все слагаемые в одну сторону, получим:
.
Выполним переобозначение:
.
Получим изучаемое линейное уравнение.
Решение уравнений в общих и частном случаях
Пример 1:
Прибавим три к обеим частям уравнения – при этом равенство не изменится:
.
Разделим обе части на два:
.
Ответ: .
Комментарий: наша главная цель – найти , для этого мы выполняем одинаковые преобразования над обеими частями уравнения.
Решим уравнение в общем виде:
.
Отнимем в обеих частях число :
.
Поскольку имеем право обе части поделить на :
.
Вывод: при линейное уравнение имеет единственный корень: .
Рассмотрим случай, когда :
www.kursoteka.ru
Материал (алгебра, 7 класс) по теме: Линейное уравнение с одной переменной. Урок усвоения новых знаний. 7 класс
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа №1»
г.Воркуты
Конспект урока по математике
«Линейное уравнение с одной переменной»
подготовила
учитель математики
Морозова Раиса Аркадьевна
2015
Образовательные цели: (слайд 1, 2)
- познакомиться с определение линейного уравнения с одной переменной;
- выяснить сколько корней может иметь линейное уравнение;
- развивать умение решать и составлять уравнения;
Развивающие цели:
- развивать память, логическое мышление;
- умения работать в проблемной ситуации, развивать умение сравнивать, правильно излагать мысль;
Воспитательные цели:
- воспитывать интерес к предмету через содержание учебного материала;
- умения работать в парах.
Тип урока: Урок усвоения новых знаний.
Ход урока
I Организационный момент
Приветствие. (слайд 3)
«Лучший способ изучить что-либо – это открыть самому». Д.Пойа
«Математика уступает свои крепости лишь сильным и смелым». А.П.Конфорович
Сообщение учащимся цели урока.
II Актуализация опорных знаний
а) Фронтальная беседа
Ответить на вопросы: (слайд 4)
- Какое равенство называют уравнением?
- Какое значение переменной называют корнем уравнения?
- Что значит решить уравнение?
- Какие уравнения называют равносильными?
- Сформулируйте свойства уравнений
- Приведите примеры уравнения, равносильные уравнению 5х-4=6
б) Устная работа (задания написаны на слайде 5)
1. Вычислите:
2. Является ли корнем уравнения -1,5х=6 число: 2; 4; 0; -1; -4; -2.
3. Имеет ли корни уравнение:
4х=х; 3х=0; 2х+3=2х+8; 0х=0; 7х=2.
III Формирование знаний.
Задача на слайде 6.
— Бабушка, сколько лет твоему внуку?
— Моему внуку столько месяцев, сколько мне лет. А вместе нам 65 лет.
Сколько же лет бабушке и внуку?
Запишите в тетради тему урока. Из записанных на слайде уравнений выпишите в тетрадь только те уравнения, которые имеют вид ax=b, где x – переменная, a и b – числа. (слайд 7)
а) 6х+х2=4
б) 5х=-4
в) х2=144
г) -0,2х=0
д) –х=-6,5
е) х3=27
ж)
з) 4х=0
и) 0х=6
к) 0х=0
(Учащиеся должны записать: 5х=-4; -0,2х=0; –х=-6,5; ; 4х=0; 0х=6; 0х=0).
К доске выходит ученик, который справился первым с этим заданием. О должен записать уравнения на доске и назвать, чему равны числа a и b в каждом уравнении. Идет проверка выполнения задания и подведение итогов.
Уравнение вида ax=b, где x – переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной. (слайд 8)
Ребята, приведите свои примеры линейных уравнений с одной переменной. А теперь решим письменно на слайде. Один ученик работает у доски, остальные решают в тетрадях. (слайд 9)
б) г) д)
ж) з) и)
к)
Как вы думаете, ребята, линейное уравнение с одной переменной? От чего зависит количество корней этого уравнения? Давайте проведем небольшую исследовательскую работу.
Узнаем, сколько корней может иметь линейное уравнение в следующих случаях: 1) 2) и 3) и
На доске записаны схемы для каждого ряда. Необходимо переписать «свою» схему, заполнить пустые места «выкладками» и письменно сделать вывод. Дается указание: в случае затруднений, обратиться к учебнику, стр.27. В каждом ряду организуется работа в парах. (слайд 10)
I ряд
Уравнение:
Если , то …
Вывод: Если , то уравнение …
II ряд
Уравнение:
Если и , то …
Вывод: Если и , то уравнение …
III ряд
Уравнение:
Если и , то …
Вывод: Если и , то уравнение …
Учитель наблюдает за работой детей в парах. В тетрадях должны появиться записи: (слайд 11)
I Если , то | : a;
Вывод: Если , то уравнение имеет единственный корень.
II Если и , то не является верным равенством ни при каком x.
Вывод: Если и , то уравнение не имеет корней.
III Если и , то верное равенство при любом x.
Вывод: Если и , то уравнение имеет бесконечное множество решений.
Вызываю к доске по одному ученику от каждого ряды для восстановления записей в схемах. Класс слушает ответы и выводы записывает в тетрадь.
IV Закрепление изученного материала
Продолжим учиться решать уравнения.
По учебнику: №139 (а, в, д, ж, и, л).
Ребята решают на местах и сравнивают свои решения с решением, которое организуется у доски.
Самостоятельно: (слайд 12)
I вариант №141 (а, в)
II вариант №141 (б, г)
Слабым учащимся выдаются карточки с указанием. Рассмотри решение и реши по аналогии.
V Домашнее задание. (слайд 13)
Подготовка к зачету. п.8, №140, №142 (а, в)
Вопросы к зачету получает каждый ученик.
Вопросы теории: (слайд 14)
- Какое равенство называют уравнением?
- Какое значение переменной называют корнем?
- Что значит решить уравнение?
- Какие уравнения называются равносильными?
- Сформулируйте свойства уравнений.
- Дайте определение линейного уравнения с одной переменной.
- В каком случае уравнение имеет единственный корень?
- В каком случае уравнение не имеет корней, имеет множество корней.
VI Рефлексия
Поднимите руку (слайд 15)
nsportal.ru
Методическая разработка урока «Линейное уравнение с одной переменной» (7 класс)
Тема урока: Линейное уравнение с одной переменной ( 7 класс)
Тип урока: урок открытия новых знаний.
Цели урока: 1. Дать понятие о линейном уравнении и его решении.
2. Закрепить полученные знания решением практических примеров.
Ход урока:
1. Организационная часть.
2. Формулировка вместе с обучающимися темы и цели урока.
Учитель: В Британском музее хранится древний папирус Ринда ( его называют также папирусом Ахмета), относящийся к периоду 2000-1700гг. до н.э., на котором начертана задача: «Найти число, если известно, что от прибавления к нему 2/3 его и вычитания от полученной суммы ее трети получается число 11». А как бы мы, современные люди, решили эту задачу?
Один из возможных предложенных учащимися ответов: Решить задачу можно с помощью уравнения.
Учитель: Сколько в этом уравнении будет неизвестных? ( одно, неизвестное число). Обозначим это неизвестное число – буквой х. Тогда по условию задачи составим уравнение х + 2/3х -1/3*(х+2/3х)=10, решим его х = 9.
В ходе решения задачи мы составили уравнение, в котором одно неизвестное число (одна переменная). Итак, как вы думаете, что мы будем сегодня изучать на уроке? Сформулируйте тему урока и цели урока (учащиеся определяют тему урока, задачи и цели урока).
3. Изучение нового материала.
Линейным уравнением с одной переменной х называется уравнение вида aх + в=0, где
а и в – любые числа (коэффициенты).
Примеры: 3х = 7
2(3х – 5) = х-3
4(х + 3) + 2х = 2 (3х – 1)
Решить линейное уравнение – это значит найти все те значения переменной, при каждом из которых уравнение обращается в верное числовое равенство. Каждое такое значение переменной называется корнем уравнения.
Примеры:
1. 2х – 8 = 3х + 1, х = -9
2. 6х – 3 = 4х + 1, х = 2
3.3х + 5 = 2 (х + 1), х = -3
4. 1/5х + 2/15 = 0, х = -2/3
5. 2(3х-1) – 4(х + 3) = 2х, корней нет
6. 20(х-2) = 10(2х-4), х- любое число( уравнение имеет бесконечно много корней)
Рассмотрим общее решение линейного уравнения ах + в = 0.
ах = -в
х = -в/а, (а не равно 0)
Составим алгоритм (план)решения линейного уравнения ( Учащиеся предлагают свои варианты алгоритма). Вместе с учителем составляется:
Алгоритм решения линейного уравнения:
1.Преобразовать данное уравнение к виду ах = -в.
2.Записать корень уравнения х = (-в)/а ( а не равно 0).
4. Закрепление изученного материала.
Решение примеров № 4.1-4.10(а,б)
5. Контроль усвоения изученного материала. Самостоятельная работа.
УЧУСЬ РЕШАТЬ УРАВНЕНИЯ !
3х-8 = 1 4х + 7 = 3(х + 1) (5х + 2)/3 + (3х – 1)/5 = 5
(х = 3) ( х = -4) (х = 2)
6. Подведение итогов урока. Рефлексия ( технология «Острова», учащиеся рисуют кораблик у острова, название которого относится к восприятию изученной темы урока)
остров Неумения
остров
Неопределенности
остров Затруднений
остров Познания
остров Хорошего понимания
7. Домашнее задание П.4. № 4.1-4.10( в,г)
Литература:
1. А.Г.Мордкович « Алгебра7» Изд.»Мнемозина»,2015
2. А.П.Савин « Энциклопедический словарь юного математика» Изд. «Педагогика», 1990
3. А.Н.Рурукин « Поурочные разработки по алгебре», Изд. « ВАКО»,2007
infourok.ru

 (2)
(2) (3)
(3) (4)
(4) ¹ 0.
¹ 0. , Х = , В = .
, Х = , В = . ,
, ,
, ,
, .
.
 существует, то он единственный.
существует, то он единственный.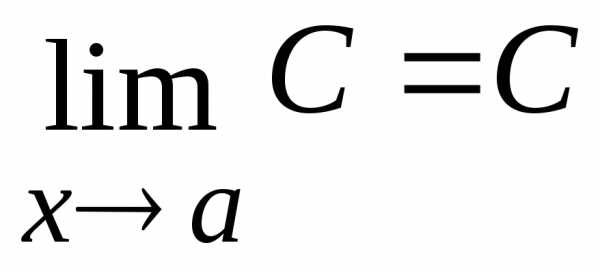 .
.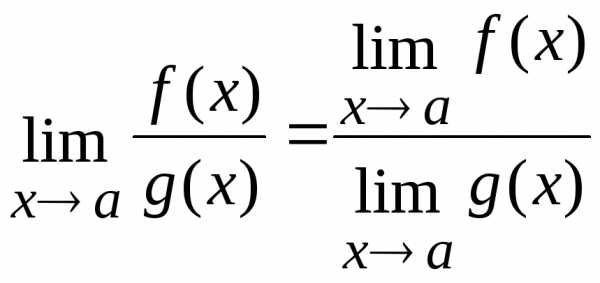 (при ).
(при ).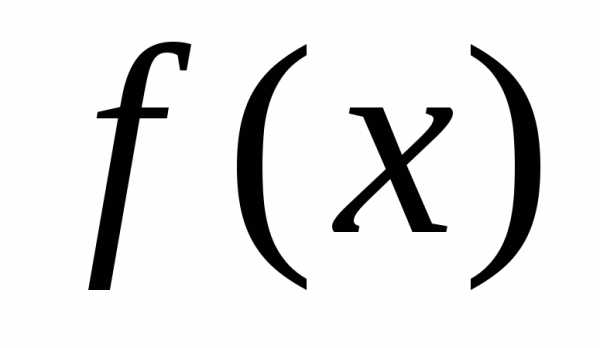 — элементарная функция,
то
.
Это означает, что если предельная точка
— элементарная функция,
то
.
Это означает, что если предельная точка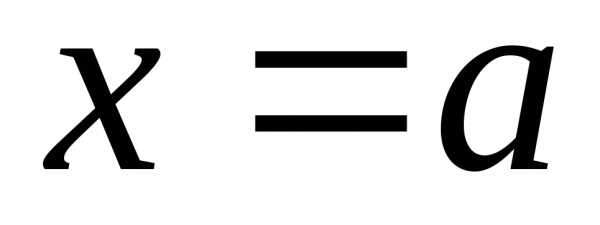 принадлежит области определения функции
принадлежит области определения функции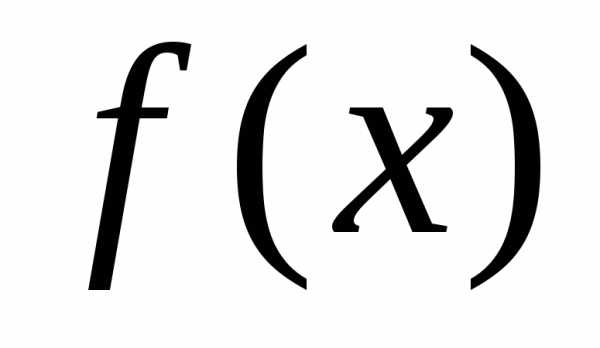 ,
то вычисление предела
,
то вычисление предела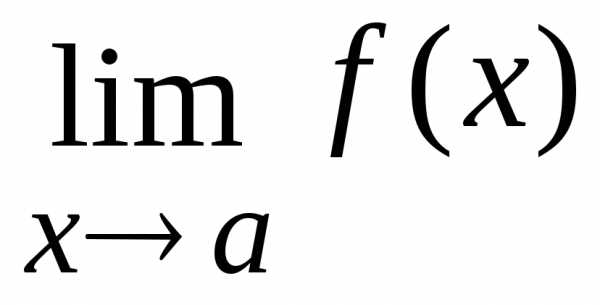 сводитсяк
подстановке в функцию
сводитсяк
подстановке в функцию 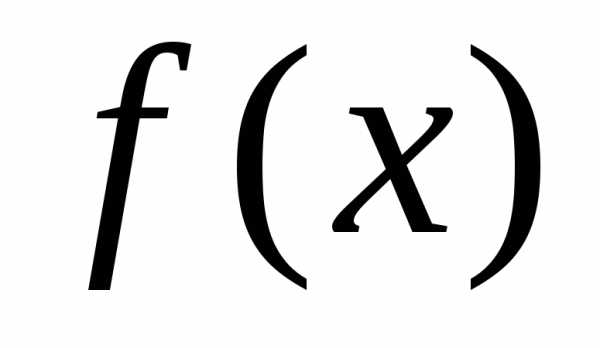 вместо
вместо 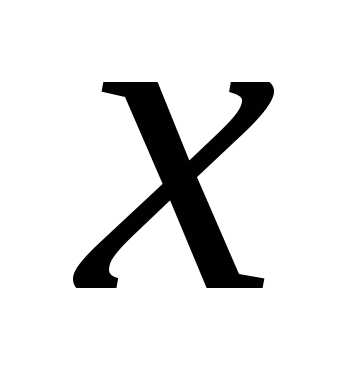 числа
числа  .
.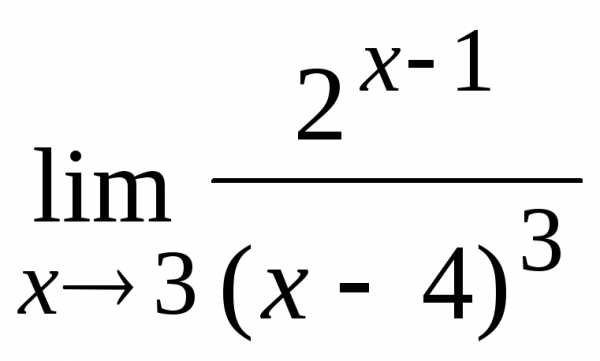 .
.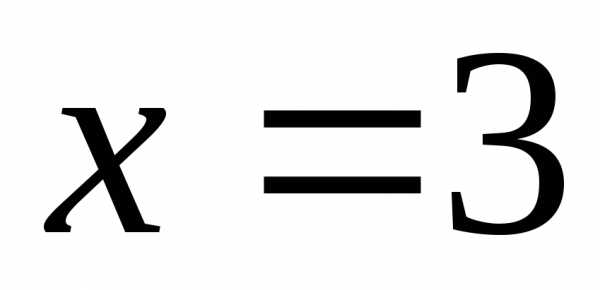 принадлежит области определения функции
принадлежит области определения функции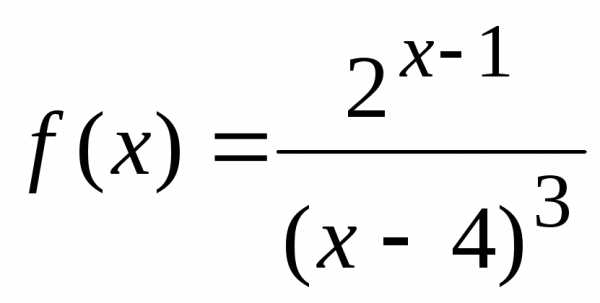 ,
значит,.
,
значит,.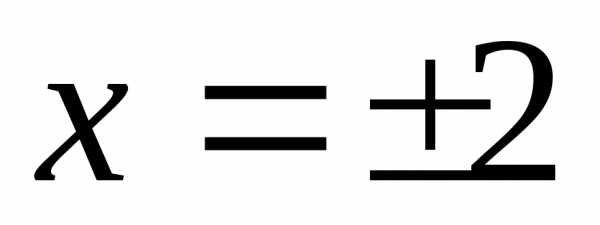 ,
т.к..
,
т.к..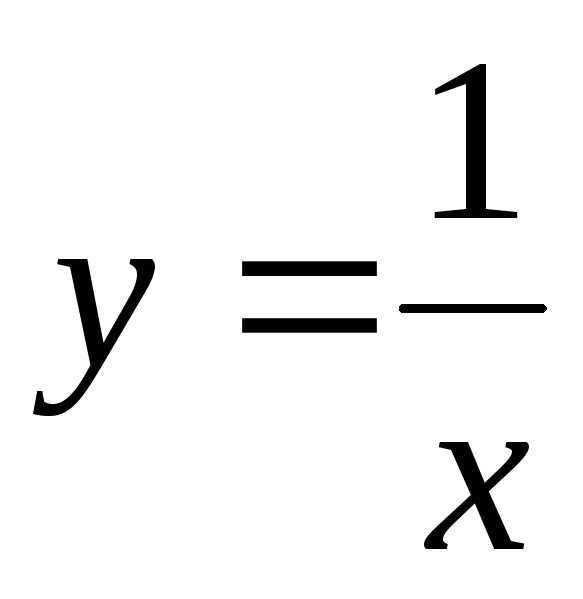 — б.м.ф. при,
т.к.
— б.м.ф. при,
т.к.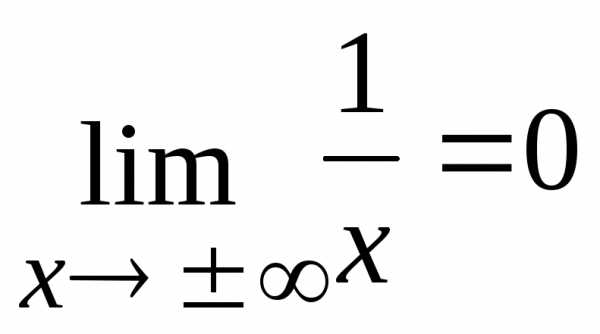 .
.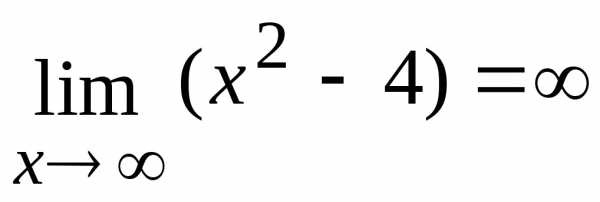 .
.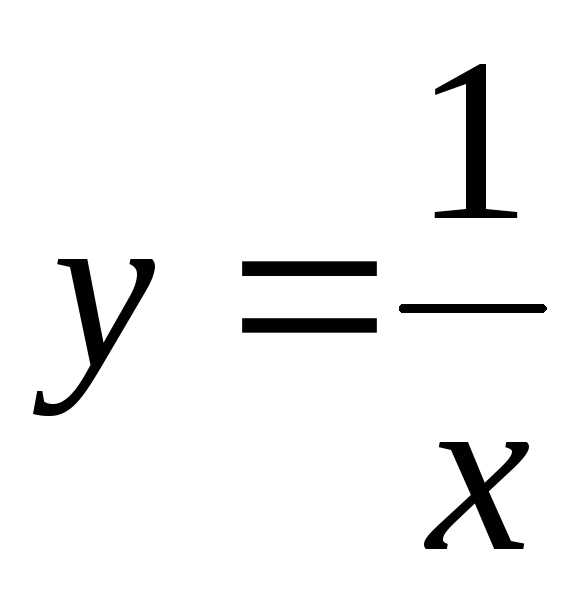 — б.б.ф. в точке
— б.б.ф. в точке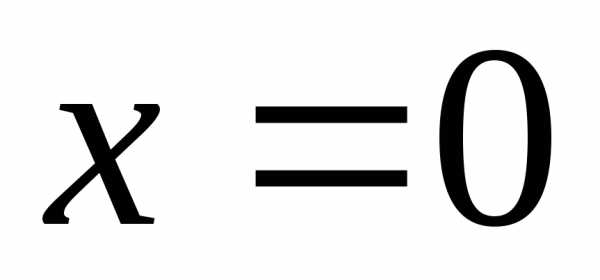 ,
т.к.
,
т.к. .
. ненулевой предел, есть б.м.ф.
ненулевой предел, есть б.м.ф.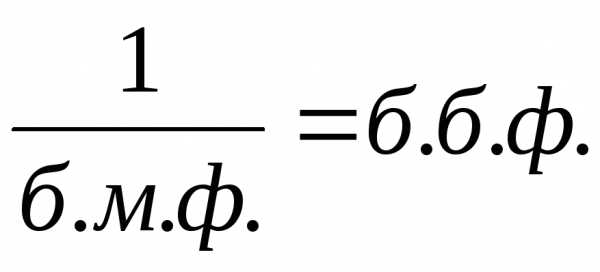
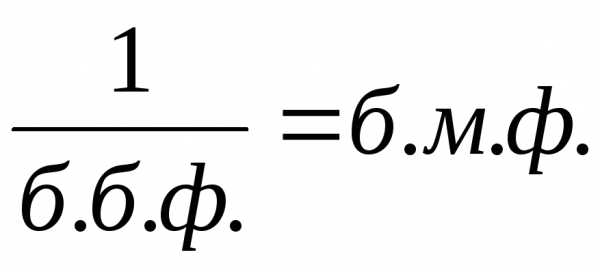
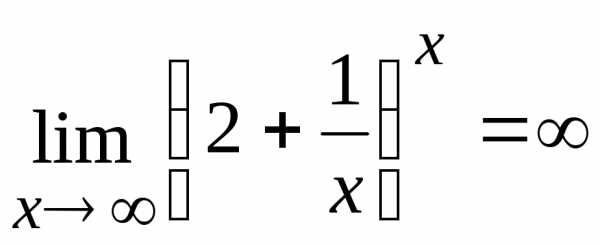 .
.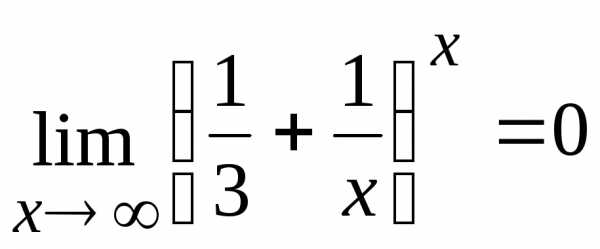 .
. ,
, ,
,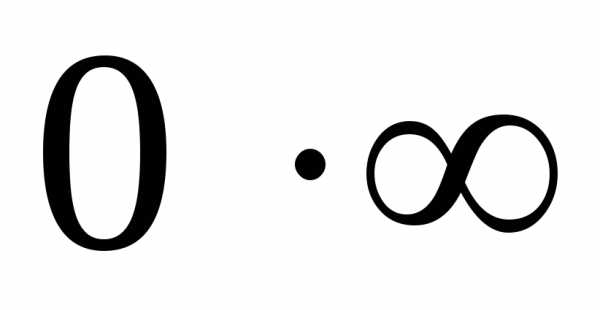 ,и так далее. В таких ситуациях при
вычислении предела нельзя применить
равенство,
ни свойства б.м.ф. и б.б.ф. Нахождение
предела в таких случаях называется
«раскрытием
неопределенности».
,и так далее. В таких ситуациях при
вычислении предела нельзя применить
равенство,
ни свойства б.м.ф. и б.б.ф. Нахождение
предела в таких случаях называется
«раскрытием
неопределенности». используют различные приемы.
используют различные приемы. .
Если функция
.
Если функция 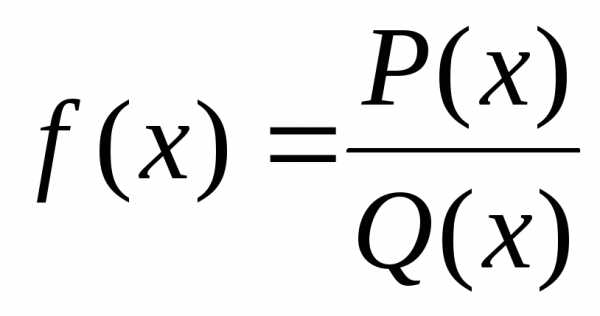 есть отношение многочленов, то для
раскрытия неопределенности
есть отношение многочленов, то для
раскрытия неопределенности  нужно числитель и знаменатель разделить
почленно на
нужно числитель и знаменатель разделить
почленно на 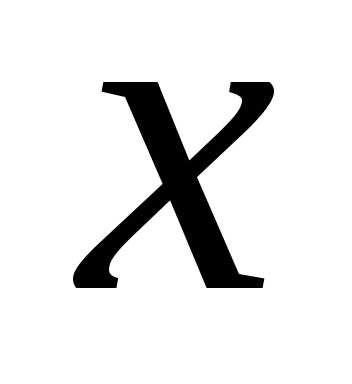 в наибольшей степени.
в наибольшей степени.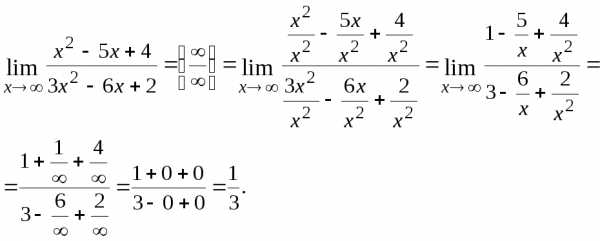
 .
.
 .
.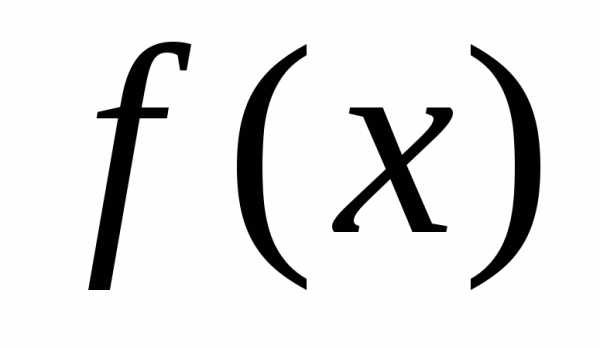 естьотношение
многочленов
естьотношение
многочленов 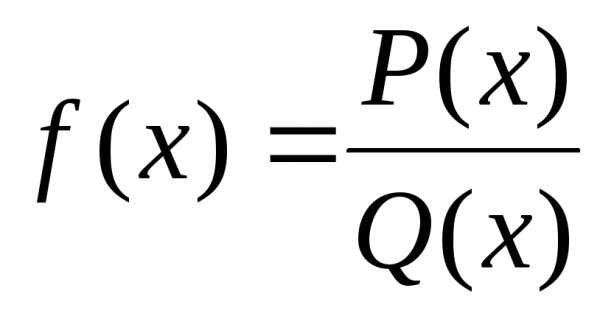 ,
то для раскрытия неопределенности
,
то для раскрытия неопределенности  нужно разложить многочлены
нужно разложить многочлены 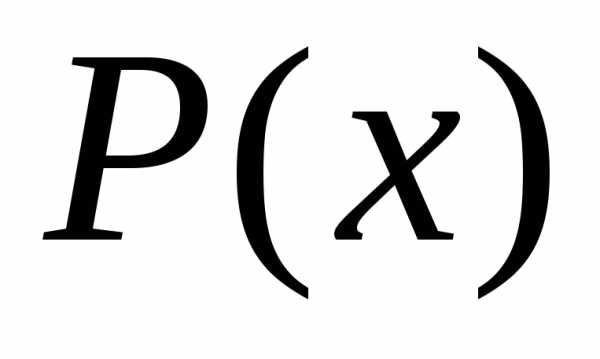 ина множители и сократить на множитель
ина множители и сократить на множитель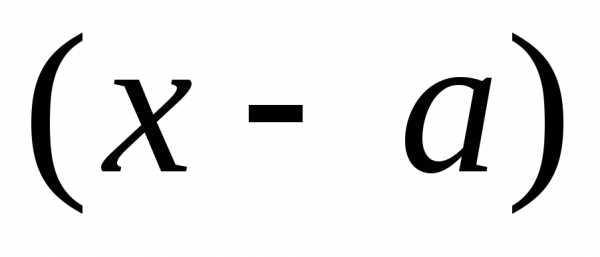 ,
стремящийся к нулю.
,
стремящийся к нулю.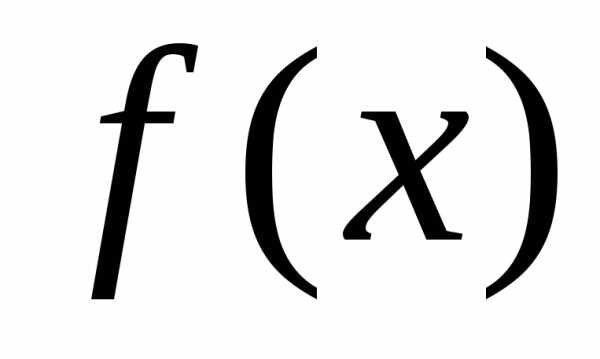 содержит
иррациональность,
то для раскрытия неопределенности
содержит
иррациональность,
то для раскрытия неопределенности  нужно избавиться от иррациональности
с помощью формул сокращенного умножения
и др.
нужно избавиться от иррациональности
с помощью формул сокращенного умножения
и др.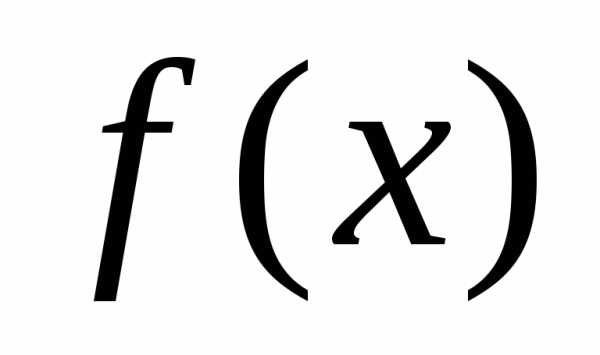 и
и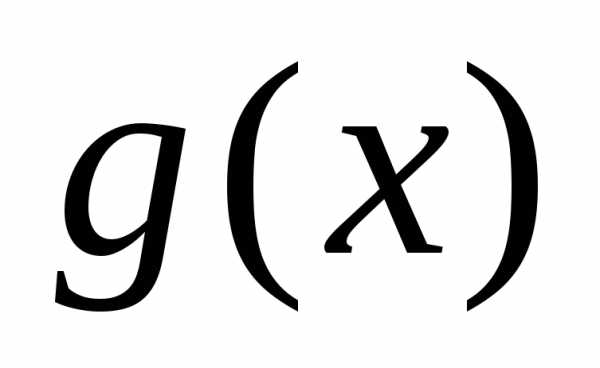 – функции, для которых существуют
пределы при
– функции, для которых существуют
пределы при (или при):,.
(или при):,.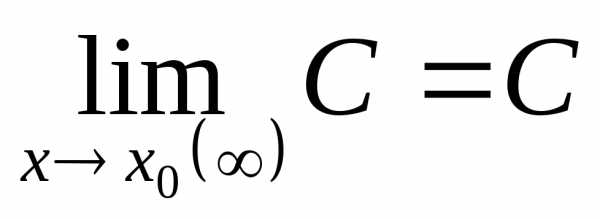 (4.16)
(4.16)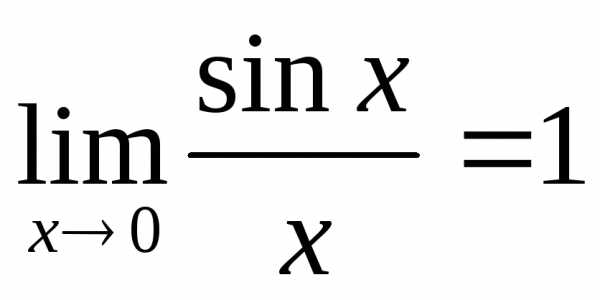 (4.19)
(4.19) (4.20)
(4.20)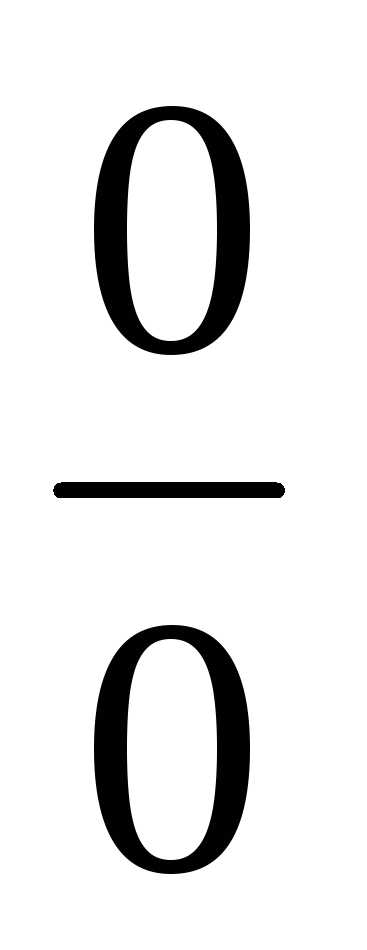 .
.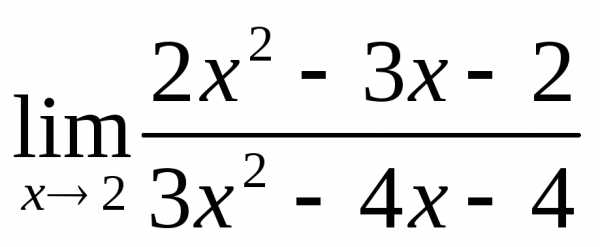 .
. число 2, то и в числителе и в знаменателе
получатся нулю, т.е. появится неопределенность
вида
число 2, то и в числителе и в знаменателе
получатся нулю, т.е. появится неопределенность
вида 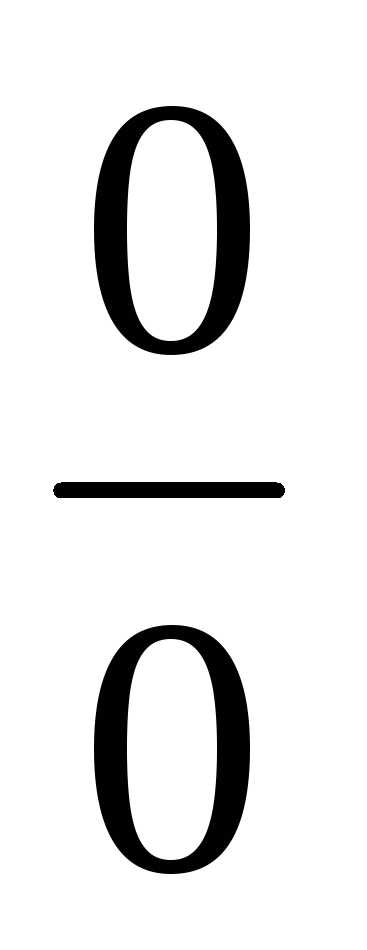 .
Чтобы вычислить предел необходимо
избавиться от данной неопределенности. Для этого надо представить числитель
и знаменатель в виде сомножителей:
.
Чтобы вычислить предел необходимо
избавиться от данной неопределенности. Для этого надо представить числитель
и знаменатель в виде сомножителей: и
и 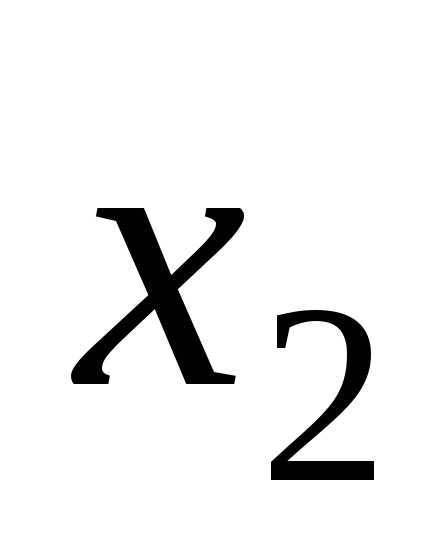 – корни квадратного трехчлена.
– корни квадратного трехчлена.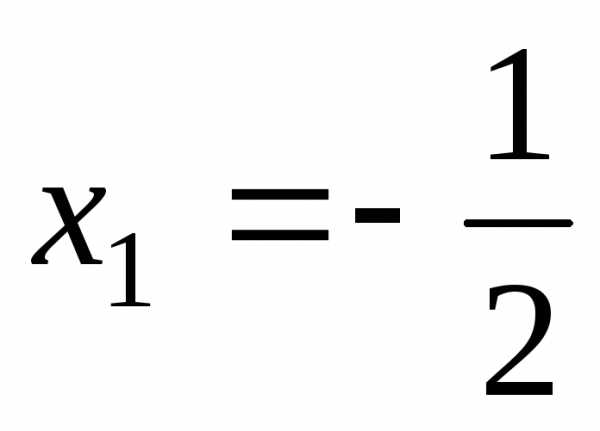 ;
;  ; .
; .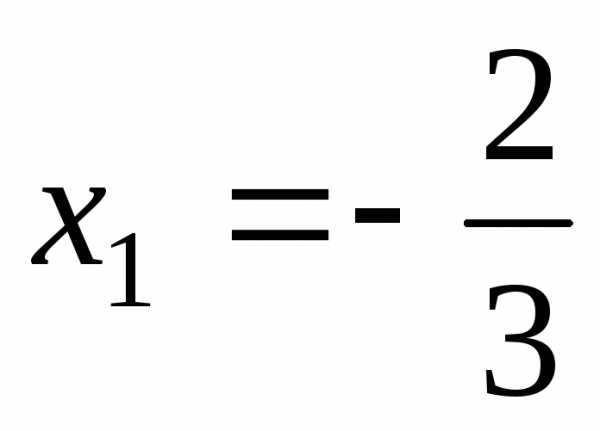 ;
; 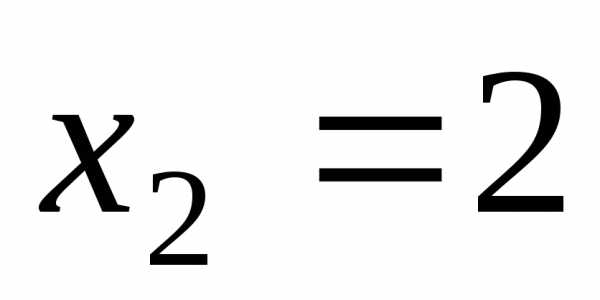 ; .
; . .
.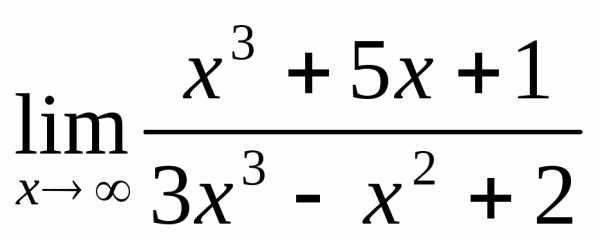 .
. ,
появляется неопределенность вида
,
появляется неопределенность вида .
Избавиться от нее можно следующим
образом:
.
Избавиться от нее можно следующим
образом: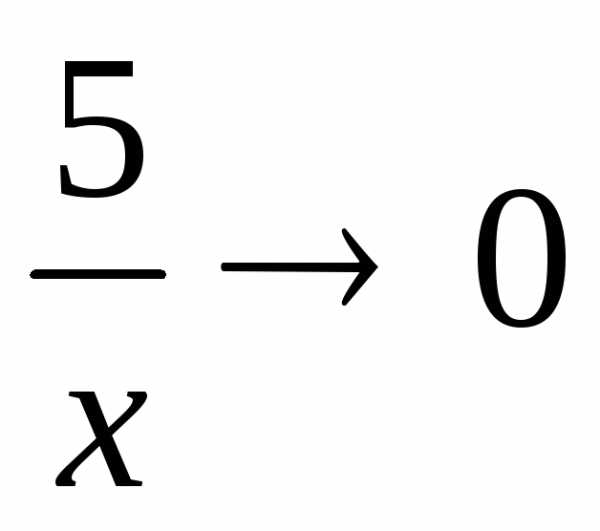 ;
; 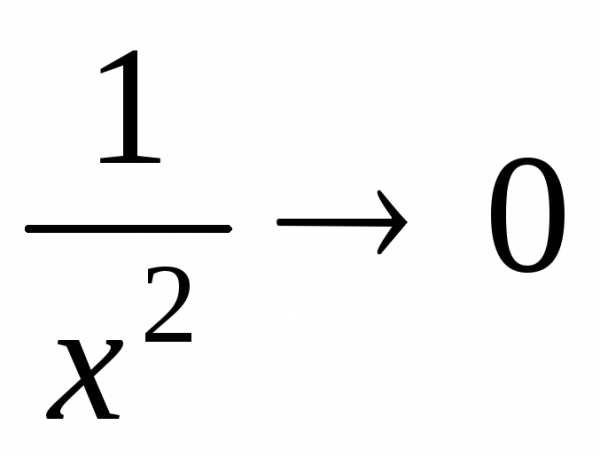 ;
; 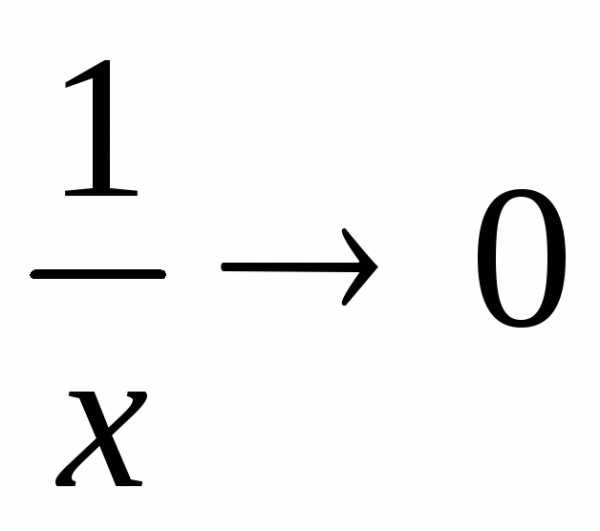 и
и 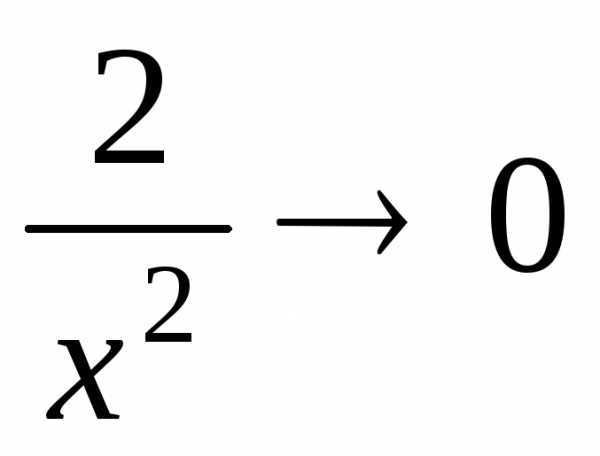 при .
при .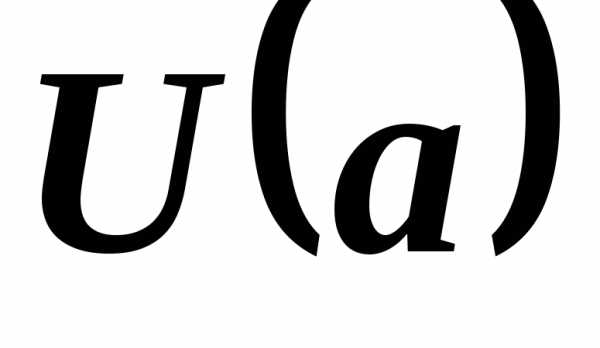 ,
,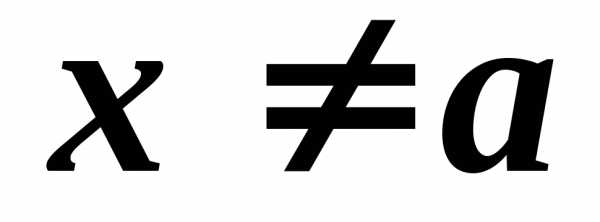 ,,
то
,,
то .
.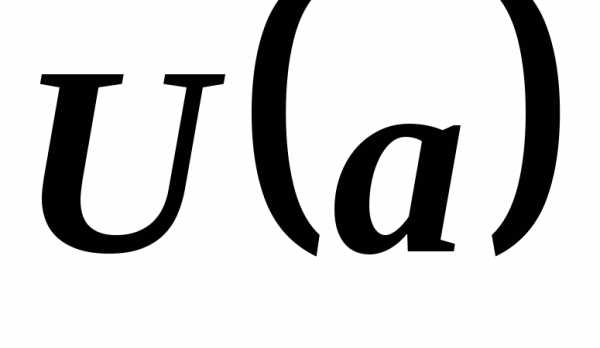 ,
,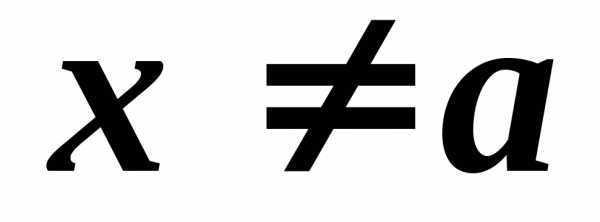 ,,
то.
,,
то. и
и — конечные числа. Тогда
— конечные числа. Тогда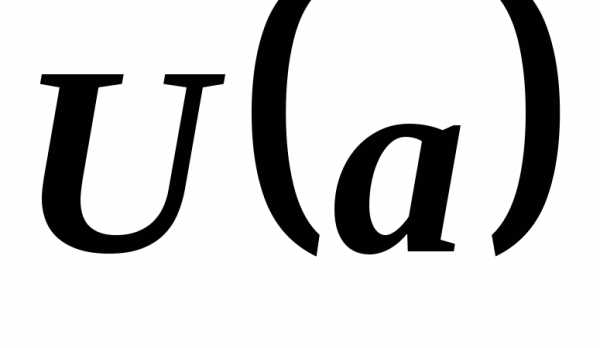 функция
функция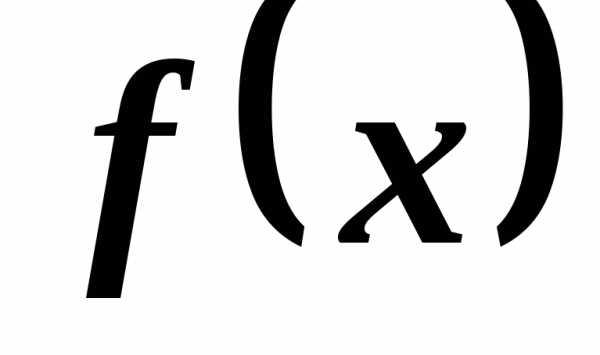 ограничена, т.е. существует положительное
числотакое, что
ограничена, т.е. существует положительное
числотакое, что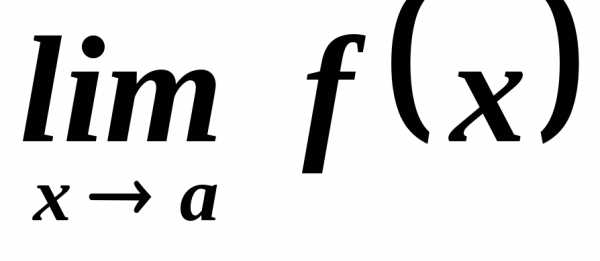 ,
необходимо и достаточно, чтобы функция
,
необходимо и достаточно, чтобы функция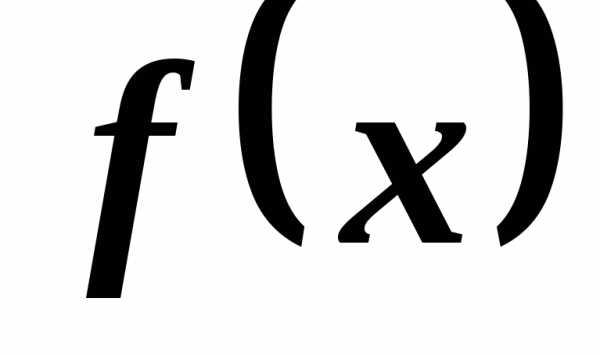 была определена в окрестности
была определена в окрестности ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки ,
и для всякого
,
и для всякого существовала такая окрестность
существовала такая окрестность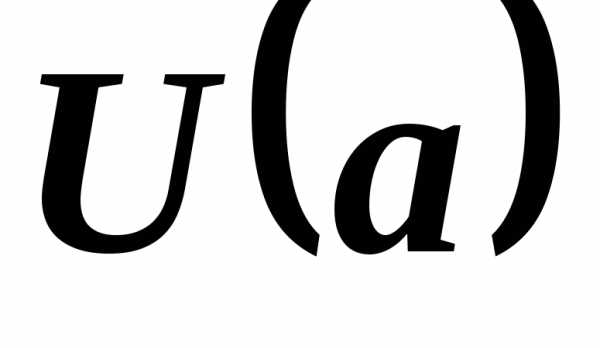 ,
что, каковы бы не были точки
,
что, каковы бы не были точки называется пределом функции
называется пределом функции в точке
в точке справа (слева), если она определена на
некотором полуинтервале
справа (слева), если она определена на
некотором полуинтервале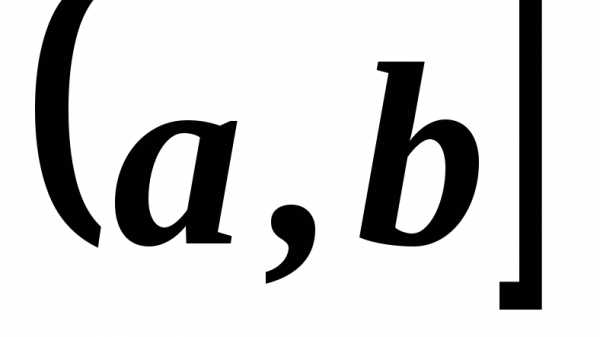 (
(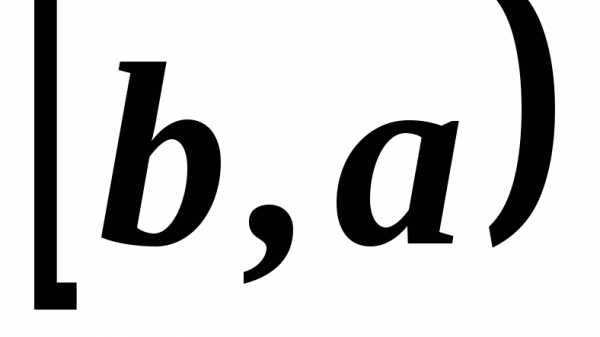 )
и для нее существует
)
и для нее существует .
. в точке
в точке принято обозначать так:
принято обозначать так: определена на интервале
определена на интервале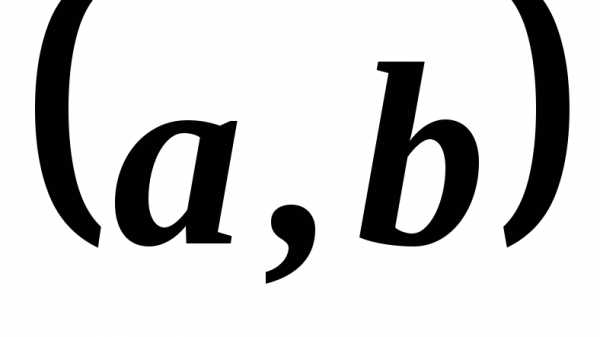 ,
то в точке
,
то в точке может иметь смысл только число
может иметь смысл только число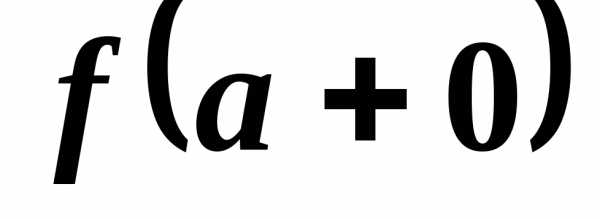 ,
а в точке
,
а в точке — только число
— только число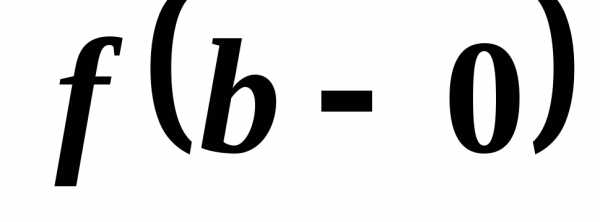 .
. .
. .
.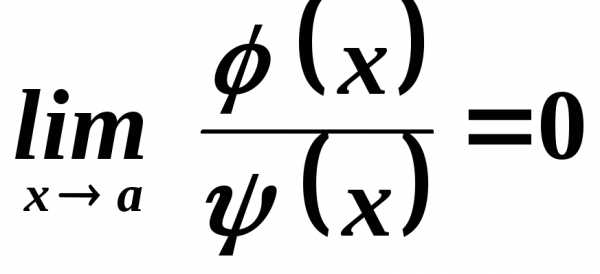 отражает тот факт, что функцию
отражает тот факт, что функцию можно записать в виде,
где
можно записать в виде,
где при
при .
. и
и сами бесконечно малые, то символ
сами бесконечно малые, то символ (по старинной терминологии) означает
бесконечно малую, более высокого порядка
.
(по старинной терминологии) означает
бесконечно малую, более высокого порядка
. и
и суть бесконечно большие, то символ
суть бесконечно большие, то символ (по старинной терминологии), означает
бесконечно большую более высокого
порядка .
(по старинной терминологии), означает
бесконечно большую более высокого
порядка .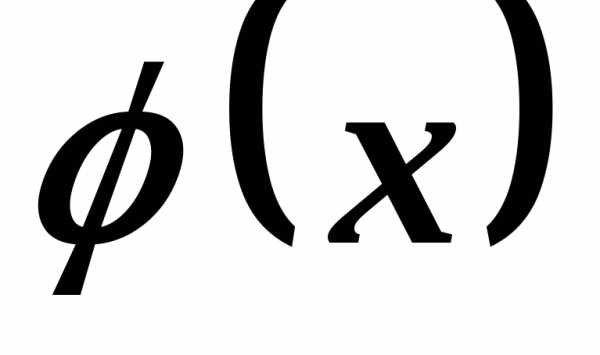 и
и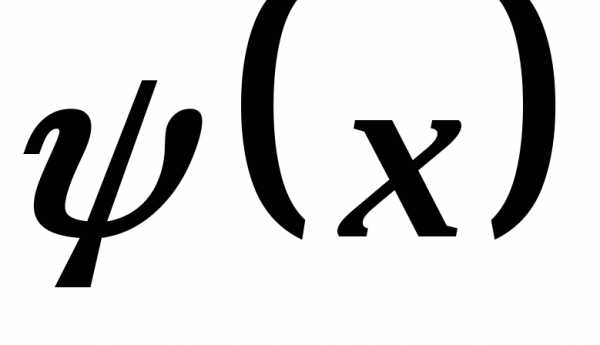 эквивалентными (асимптотически равными)
при
эквивалентными (асимптотически равными)
при ,
если выполняется свойство:
,
если выполняется свойство: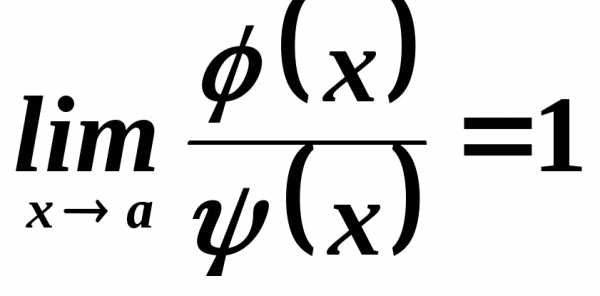
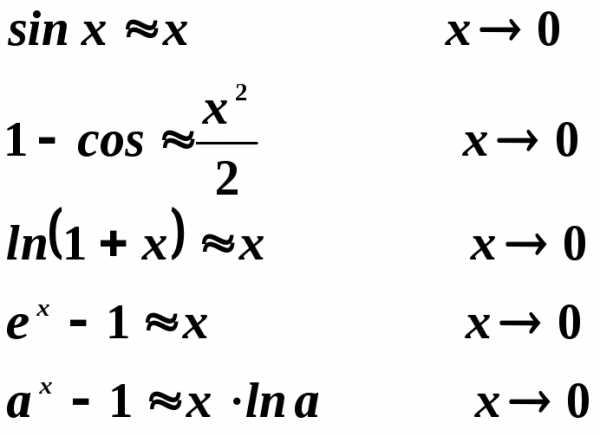
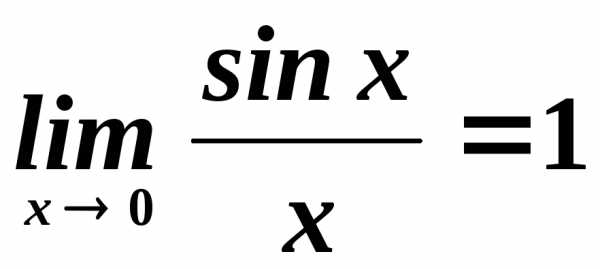
 .
Поэтому выражение
.
Поэтому выражение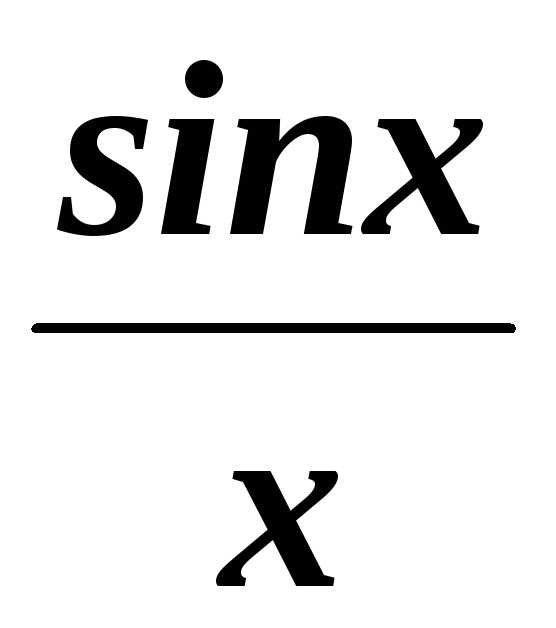 представляет собой неопределенность
типа
представляет собой неопределенность
типа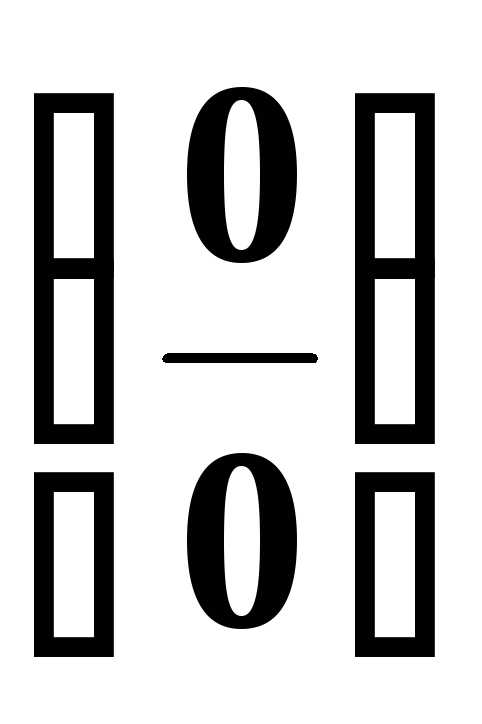 .
Предел раскрывает эту неопределенность.
.
Предел раскрывает эту неопределенность.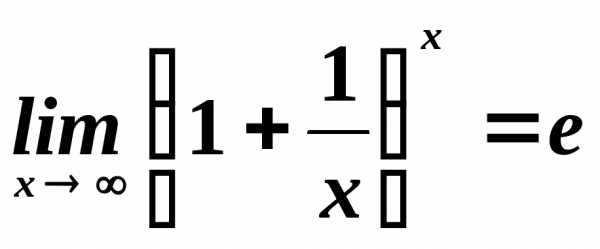
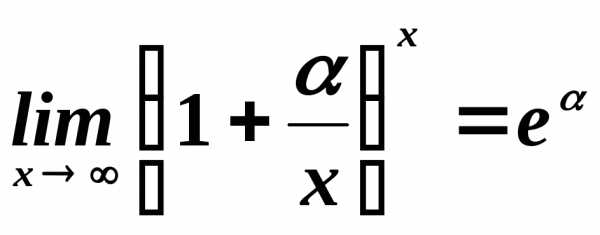
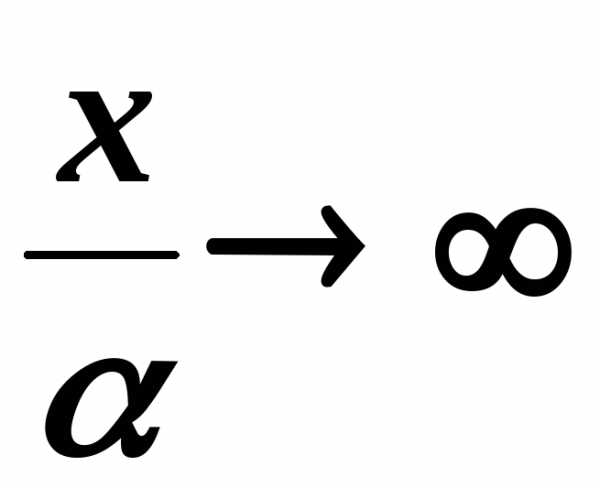 и
и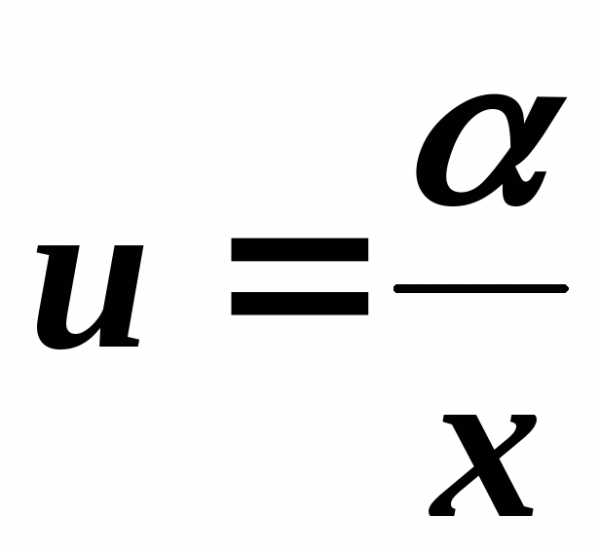
 ,.
,.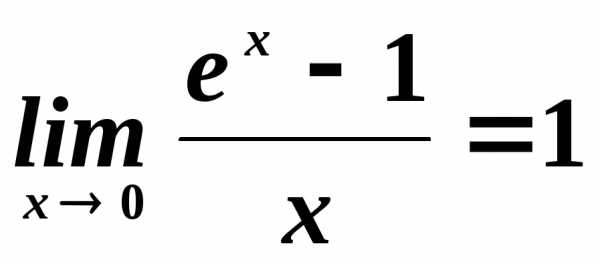 .
. .
Зададим точку.
Близкая ей точка,
где
.
Зададим точку.
Близкая ей точка,
где — приращение
— приращение .
Разность
.
Разность в точке
в точке ,
соответствующим приращению
,
соответствующим приращению .
На рисунке,.
.
На рисунке,. к нулю. Тогда для рассматриваемой функции
и
к нулю. Тогда для рассматриваемой функции
и будет стремиться к нулю
будет стремиться к нулю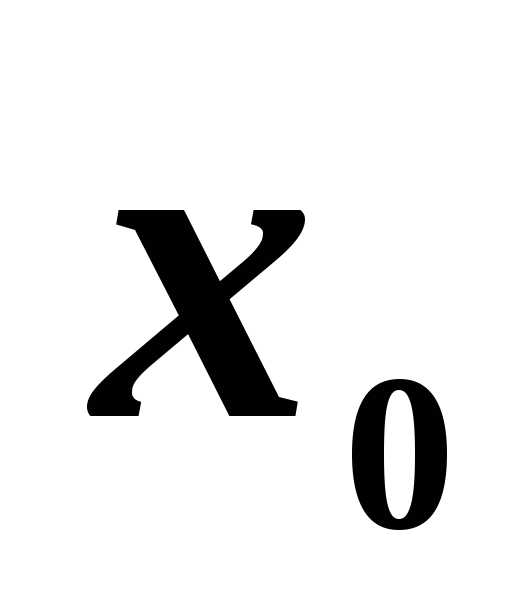 приращение
приращение и определим соответствующее приращение
функции
и определим соответствующее приращение
функции стремить к нулю, то теперь уже нельзя
сказать, что
стремить к нулю, то теперь уже нельзя
сказать, что стремится к нулю.
стремится к нулю. ,
заданную на отрезке
,
заданную на отрезке ,
называютнепрерывной в точке
,
называютнепрерывной в точке  этого отрезка, если приращение ее в этой
точке, соответствующее приращению
этого отрезка, если приращение ее в этой
точке, соответствующее приращению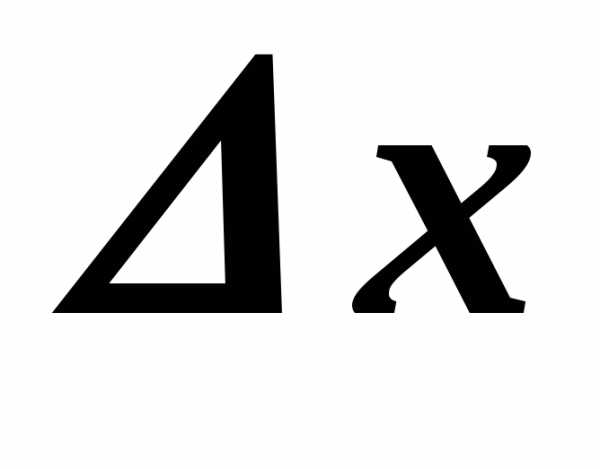 ,
стремится к нулю при любом способе
стремления
,
стремится к нулю при любом способе
стремления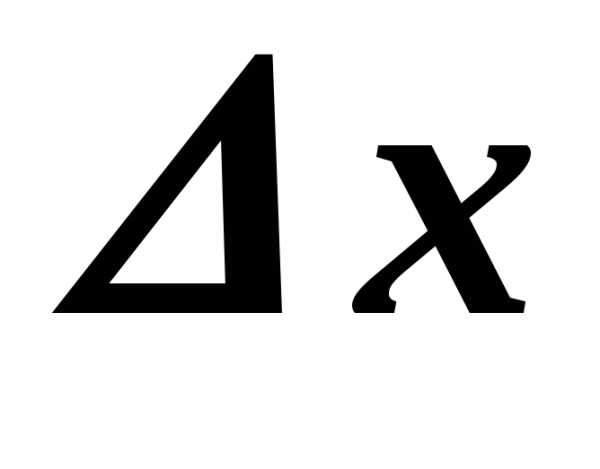 к нулю.
к нулю. в точке
в точке записывают в виде
записывают в виде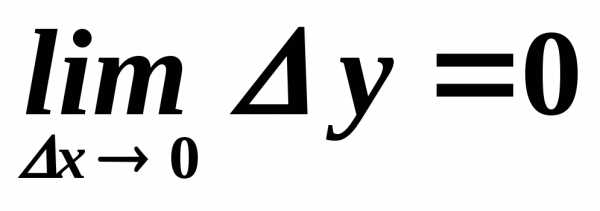
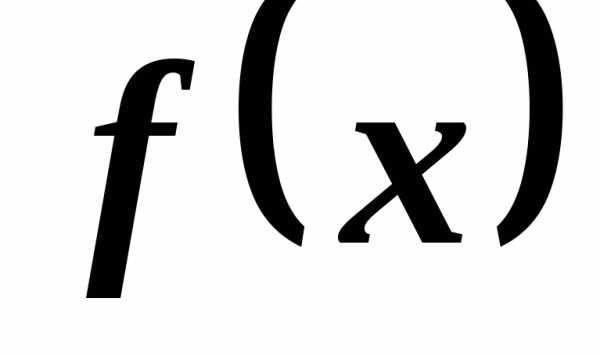 называется непрерывной в точке
называется непрерывной в точке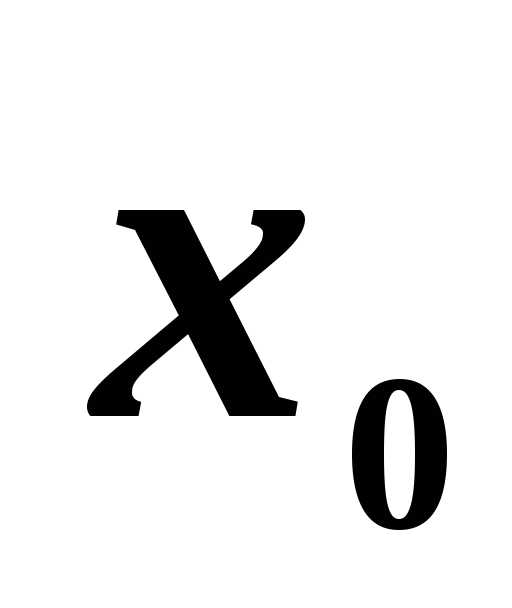 ,
если она определена в некоторой
окрестности этой точки, в том числе и в
самой точке
,
если она определена в некоторой
окрестности этой точки, в том числе и в
самой точке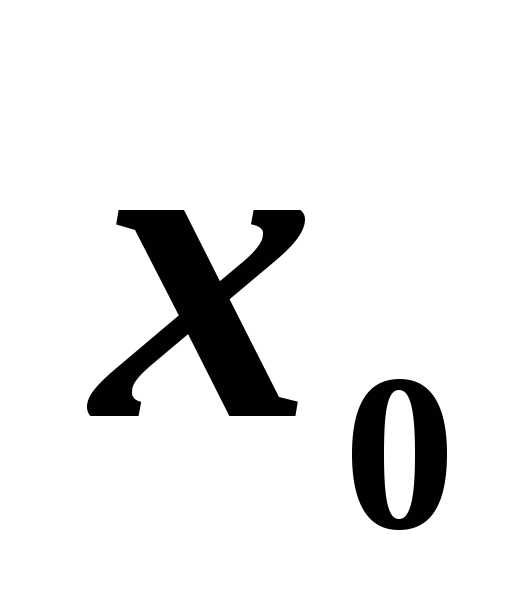 ,
и если ее приращение в этой точке,
соответствующее приращению аргумента
,
и если ее приращение в этой точке,
соответствующее приращению аргумента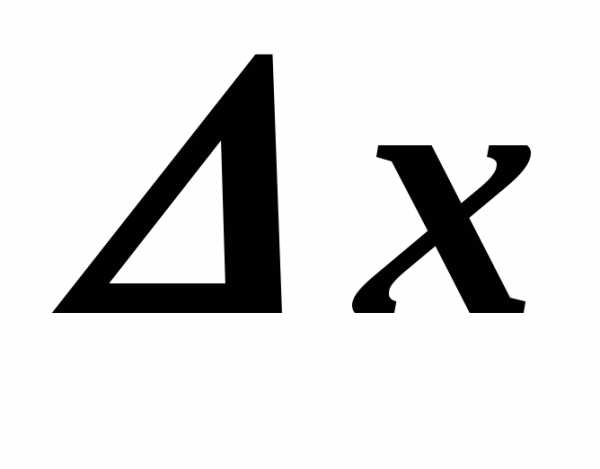 ,
стремится к нулю при
,
стремится к нулю при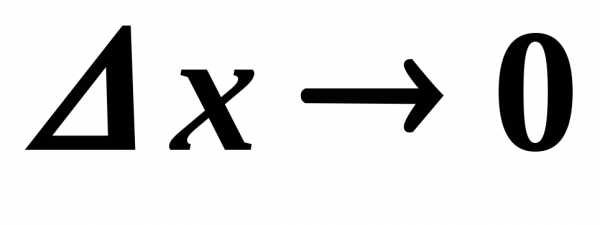
 .
В самом деле.
.
В самом деле. имеет место неравенство
имеет место неравенство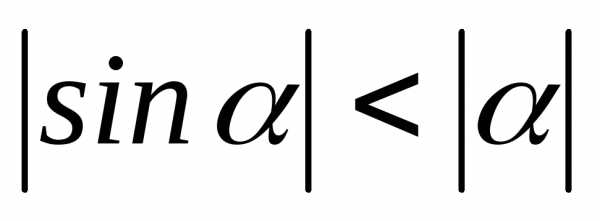 .
Если
.
Если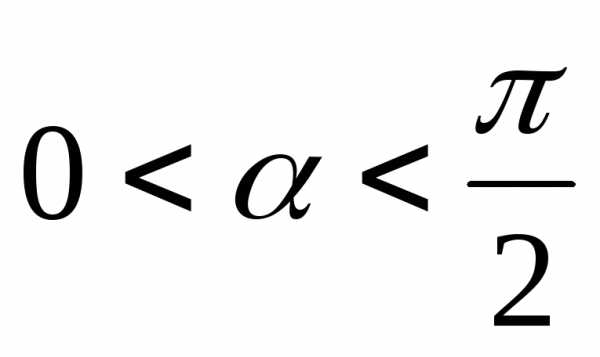 ,
то это следует из рисунка (длина дуги
больше стягивающей ее хорды). Отсюда
следует
,
то это следует из рисунка (длина дуги
больше стягивающей ее хорды). Отсюда
следует .
Что и требовалось доказать.
.
Что и требовалось доказать. и
и непрерывны в точке
непрерывны в точке ,
то непрерывны также в этой точке их
сумма, разность, произведение и частное
(при
,
то непрерывны также в этой точке их
сумма, разность, произведение и частное
(при ).
).













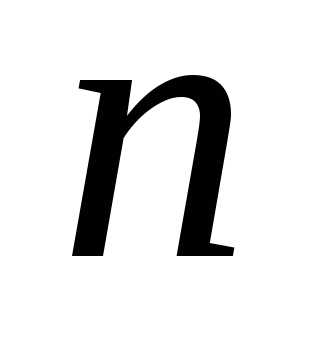 элементов по
элементов по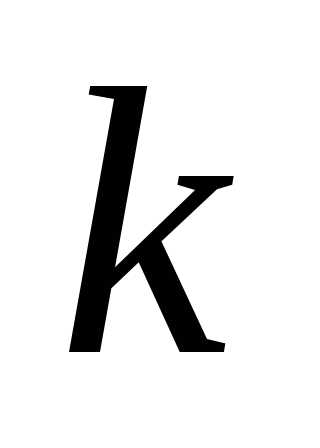 элементов (
элементов (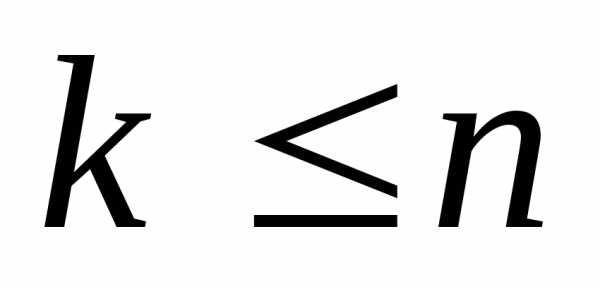 )
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают:
)
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают: 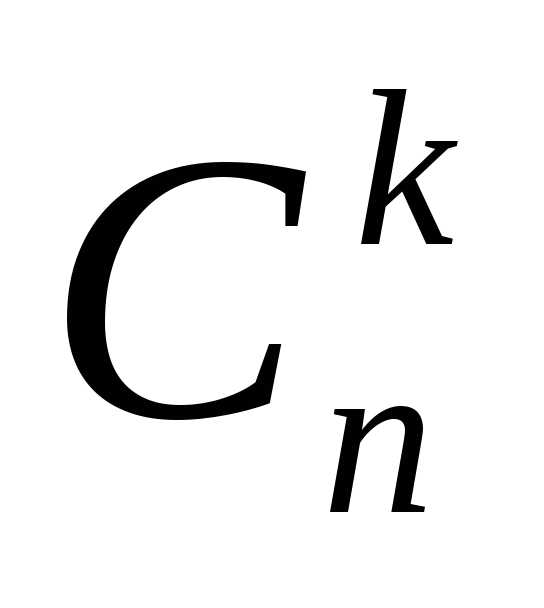 .
. .
.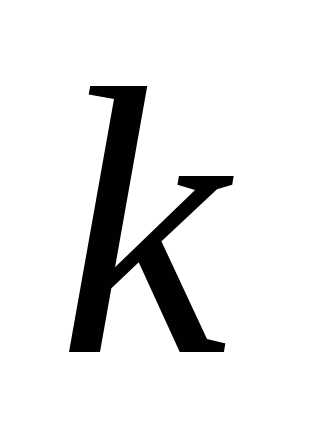 элементов одного типа и
элементов одного типа и элементов второго типа:
элементов второго типа: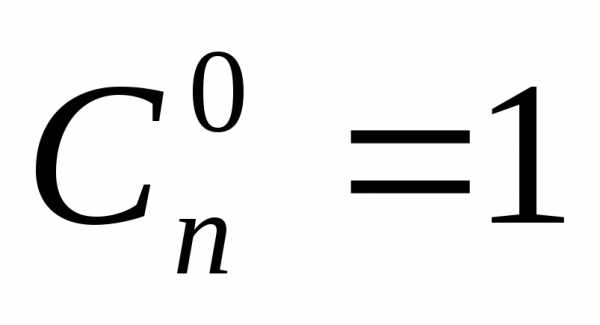 ,
, 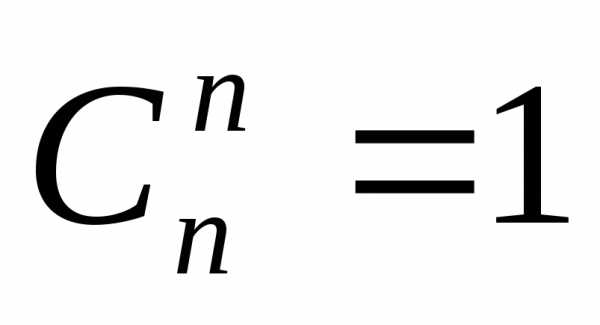 .
. различных типов. Сколько
различных типов. Сколько комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными. .
. .
. :.
:.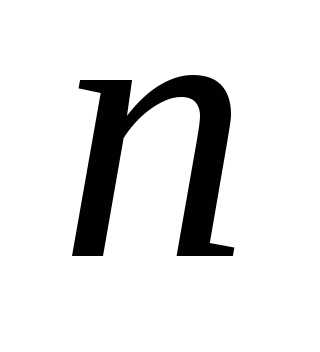 —
й степени:
—
й степени: бинома Ньютонаназываются
биномиальными коэффициентами.
бинома Ньютонаназываются
биномиальными коэффициентами.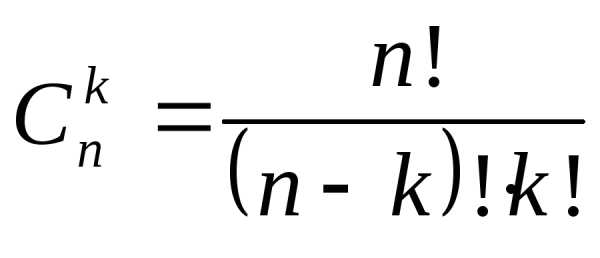 .
Готовые значения этих коэффициентов
располагаются в строкахтреугольника
Паскаля.
.
Готовые значения этих коэффициентов
располагаются в строкахтреугольника
Паскаля. и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы
и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы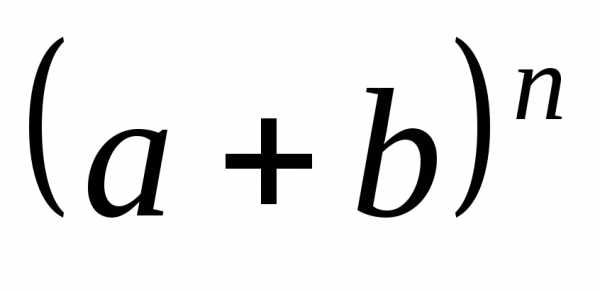 ,
нужно из треугольника Паскаля взять
строку, соответствующую данной степени
,
нужно из треугольника Паскаля взять
строку, соответствующую данной степени .
Эта строка будет содержать нужные
коэффициенты
.
Эта строка будет содержать нужные
коэффициенты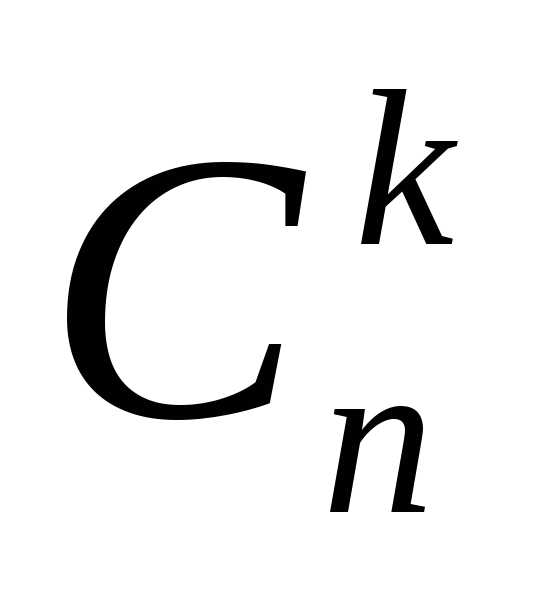 ,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.
,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент. на
на целых неотрицательных слагаемых,
при этом коэффициент находится по
формуле числа перестановок с повторениями:
целых неотрицательных слагаемых,
при этом коэффициент находится по
формуле числа перестановок с повторениями: получаются перестановкой из чисел,
то считается, что
получаются перестановкой из чисел,
то считается, что ,
, .
Значит, все коэффициенты можно для
каждого случая найти по формуле:
.
Значит, все коэффициенты можно для
каждого случая найти по формуле: ,
, ,
,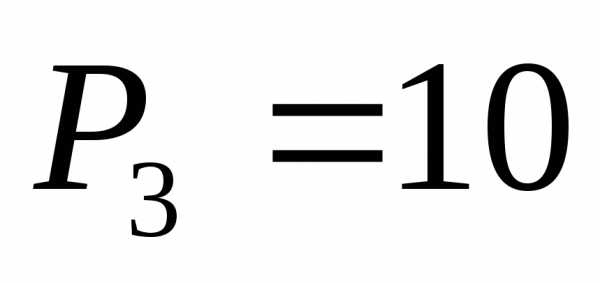 ,
,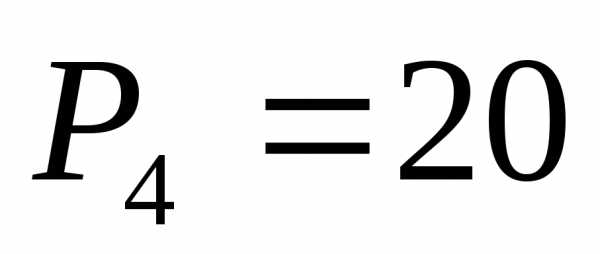 ,
,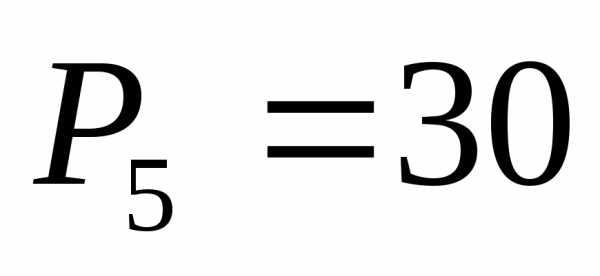 .
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
.
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше. —
сочетания с повторениями, составленные
из элементов
—
сочетания с повторениями, составленные
из элементов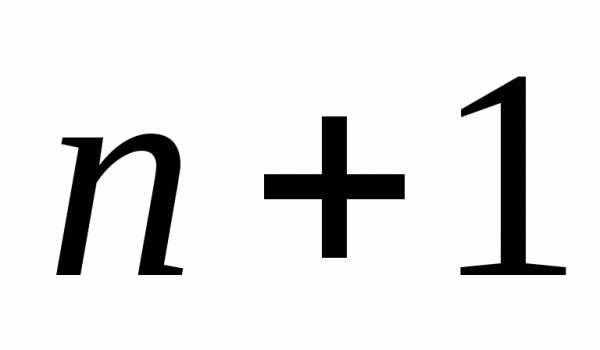 типа, например из
типа, например из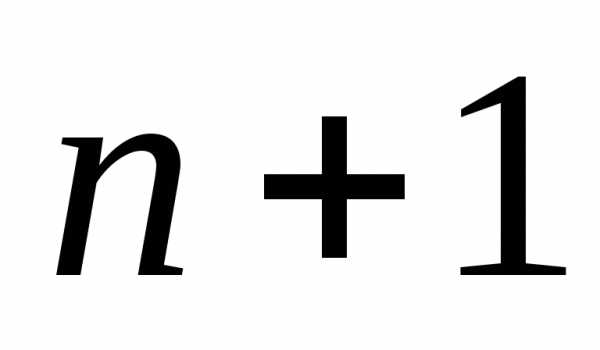 буквы.
Число таких сочетаний равно:
буквы.
Число таких сочетаний равно: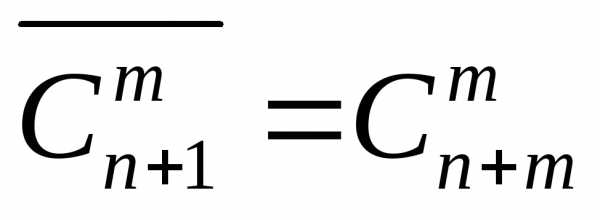 .
Разобьём все эти сочетания на классы,
отнеся к
.
Разобьём все эти сочетания на классы,
отнеся к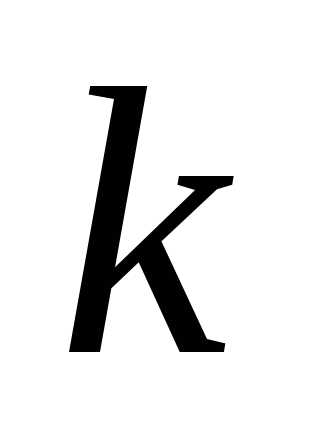 ‑
му классу сочетания, в которых
‑
му классу сочетания, в которых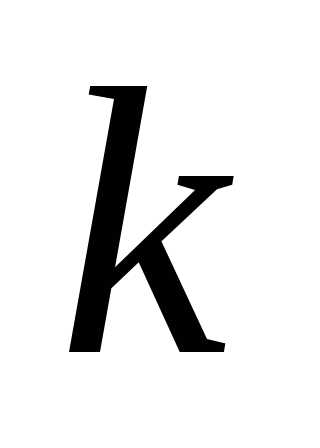 раз входит буква
раз входит буква .
Остальные
.
Остальные мест могут быть заняты оставшимися
буквами
мест могут быть заняты оставшимися
буквами ,
число которых равно
,
число которых равно .
Поэтому в
.
Поэтому в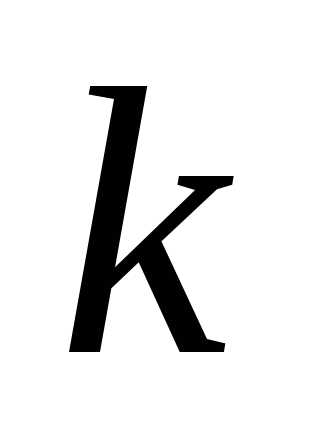 —
й класс входит столько сочетаний, сколько
можно составить
—
й класс входит столько сочетаний, сколько
можно составить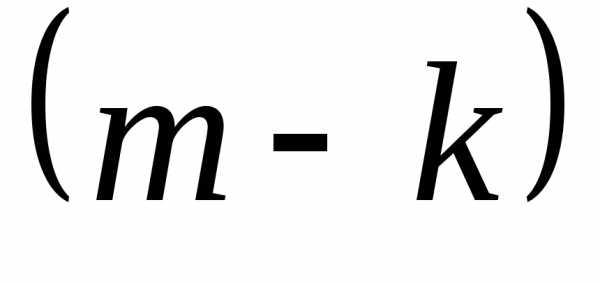 сочетаний с повторениями из элементов
сочетаний с повторениями из элементов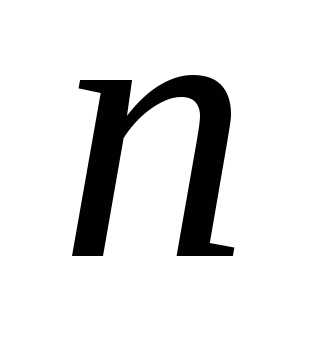 типов, т.е.
типов, т.е.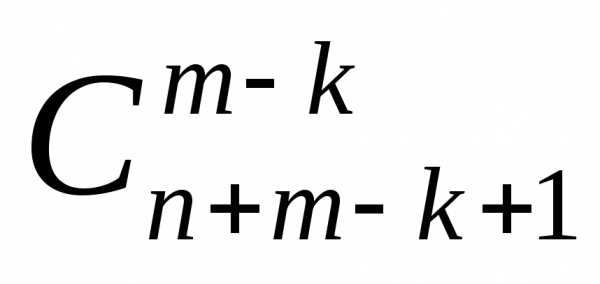 .
.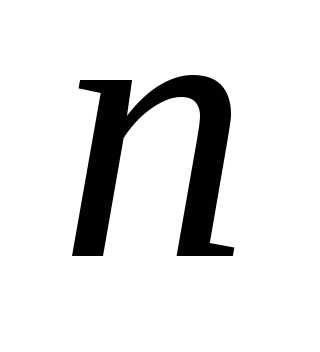 на
на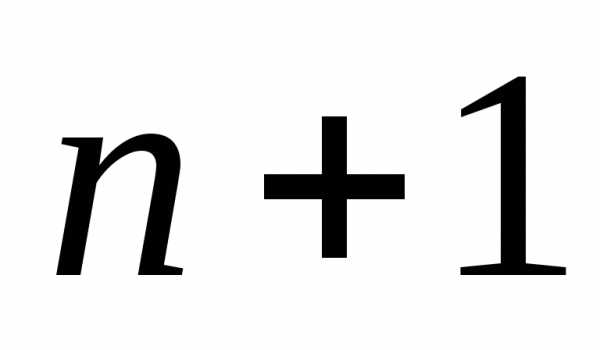 и
и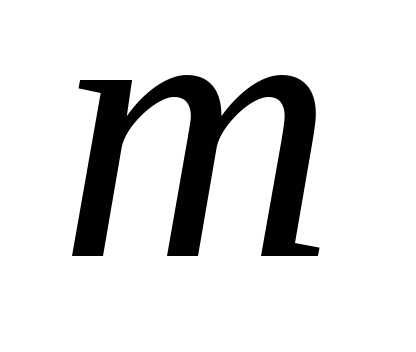 на
на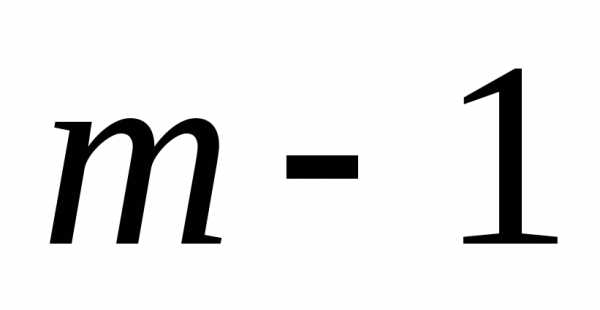 и используя равенство
и используя равенство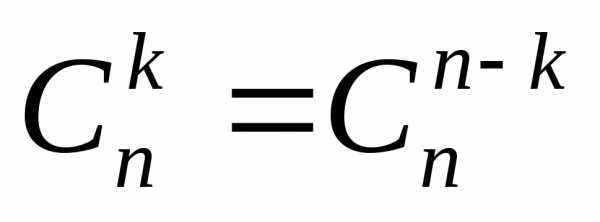 ,
получаем зависимость между биномиальными
коэффициентами:
,
получаем зависимость между биномиальными
коэффициентами: (при
(при ),
суммы квадратов натуральных чисел (при
),
суммы квадратов натуральных чисел (при ),
сумму кубов (при
),
сумму кубов (при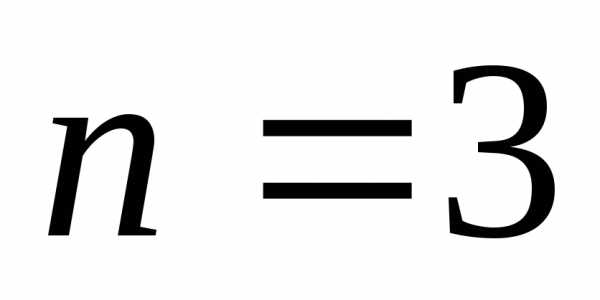 ).
).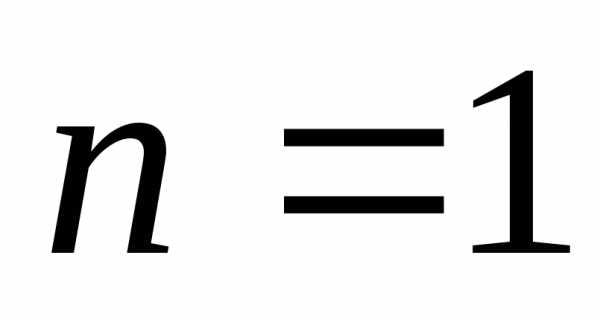 ,
то искомая зависимость имеет вид:
,
то искомая зависимость имеет вид: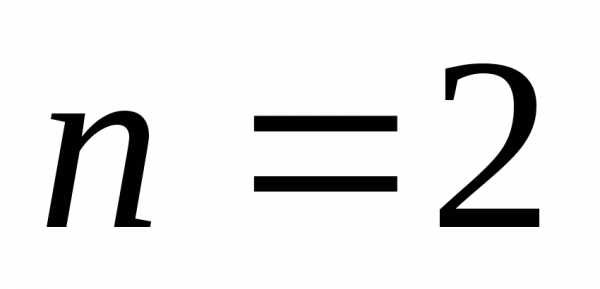 имеем:
имеем: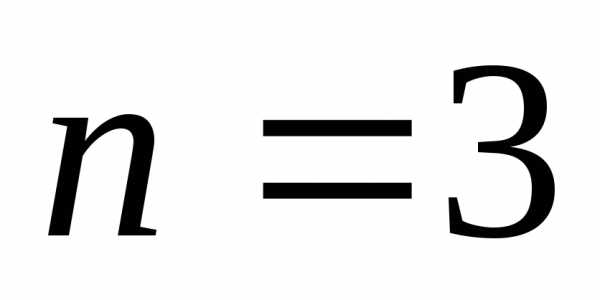 получаем:
получаем: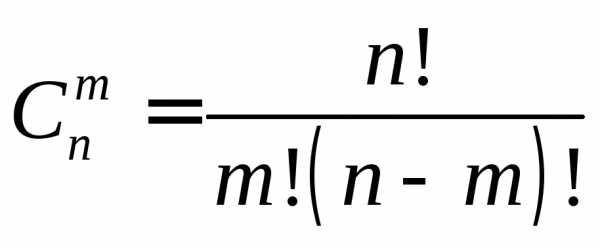 .
.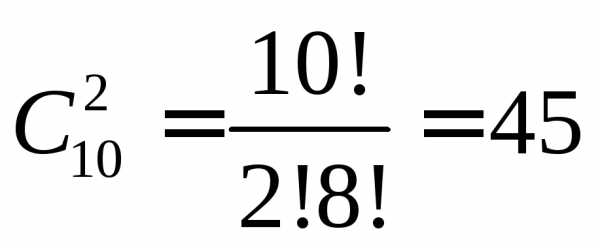 .
.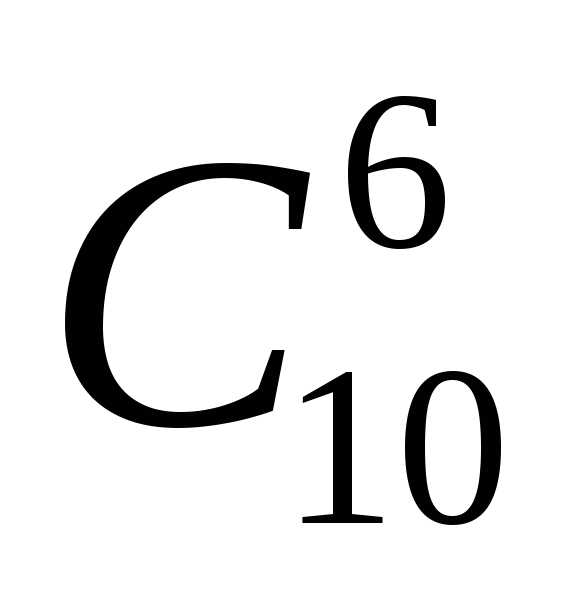 ).
). способами; при этом остальные 6 – 4 = 2
детали должны быть нестандартными;
взять же 2 нестандартные детали из 10 –
7 = 3 нестандартных деталей можно
способами; при этом остальные 6 – 4 = 2
детали должны быть нестандартными;
взять же 2 нестандартные детали из 10 –
7 = 3 нестандартных деталей можно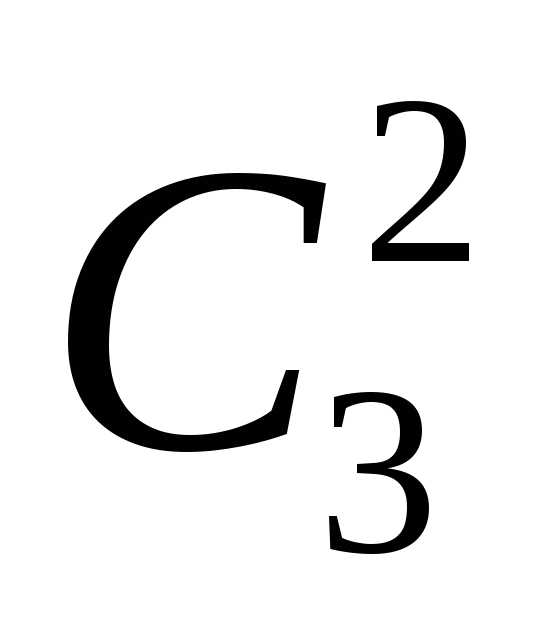 способами. Следовательно, число
благоприятствующих исходов равно
способами. Следовательно, число
благоприятствующих исходов равно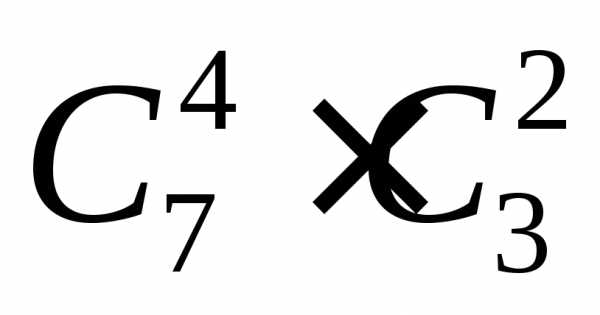 .
.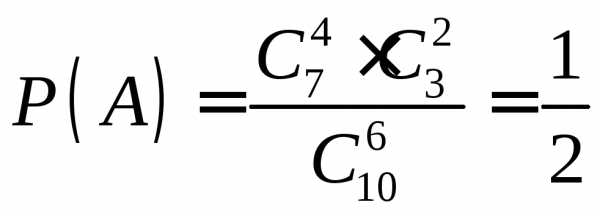











 ,
на котором значениеgравно 1, значениеfтакже
равно 1.
,
на котором значениеgравно 1, значениеfтакже
равно 1.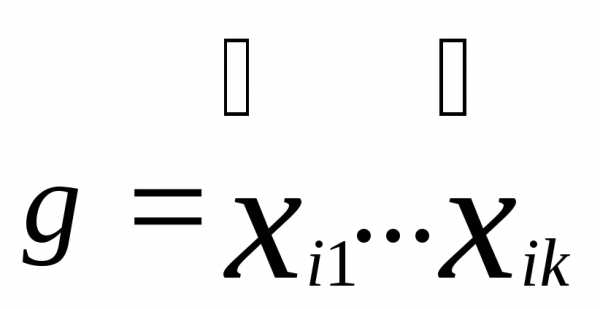 ,
являющееся импликантойfи такое, что никакая его собственная
часть (то есть произведение, получаемое
изgотбрасыванием одного
или нескольких компонент) уже не является
импликантой функцииf.
,
являющееся импликантойfи такое, что никакая его собственная
часть (то есть произведение, получаемое
изgотбрасыванием одного
или нескольких компонент) уже не является
импликантой функцииf.