Математика с нуля. Пошаговое изучение математики
Spacemath.xyz – это новый проект, предназначенный для людей, которые хотят изучить математику самостоятельно с нуля. Сразу скажем, здесь нет лёгких решений и подобных заявлений, таких как «Купи эту книгу и сдай математику на 5» или «Освой математику за 12 часов» вы тут не увидите. Математика довольно большая наука, которую следует осваивать последовательно и очень медленно.
Сайт представляет собой уроки по математике, которые упорядочены по принципу «от простого к сложному». Каждый урок затрагивает одну или несколько тем из математики. Уроки разбиты на шаги. Начинать изучение следует с первого шага, и так далее по возрастанию.
Каждый изученный урок должен быть понятным. Поэтому не поняв одного урока, нельзя переходить к следующему, поскольку каждый урок в математике основан на понимании предыдущего. Если вы с первого раза урок не поняли – не расстраивайтесь. Некоторые люди потратили месяцы и годы, чтобы понять хотя бы одну единственную тему. Отчаяние и уныние точно не ваш путь. Читайте, изучайте, пробуйте и снова пробуйте.
Математика хорошо усваивается, когда человек самостоятельно открыв учебник, учит самогó себя. При этом вырабатывается определенная дисциплина, которая очень помогает в будущем. Если вы будете придерживаться принципа «от простого к сложному», то с удивлением обнаружите, что математика не так уж и сложна. Возможно даже она покажется вам интересной и увлекательной.
Что даст вам знание математики? Во-первых, уверенность. Математику знает не каждый, поэтому осознание того, что вы знаете хоть какую-то часть этой серьёзной науки, делает вас особенным. Во-вторых, освоив математику, вы с лёгкостью освоите другие науки и сможете мыслить гораздо шире. Знание математики позволяет овладеть такими профессиями как программист, бухгалтер, экономист. Никто не станет спорить, что эти профессии сегодня очень востребованы.
В общем, дерзай друг!
Желаем тебе удачи в изучении математики!
Новые уроки будут скоро. Оставайся с нами!
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
spacemath.xyz
Как самому выучить математику? — Toster.ru
Изучать школьную математику, значит уметь решать задачи. Берешь любой задачник и решаешь. Сначала будет тяжко, но потом мозг включится. Начинай с самого начала. С первых классов. В математике знания накладываются одни на другие и буз базы ничего не получится. Хороший сайт: interneturok.ru, и подобные. Отличные сайты на английском. Здесь учебники www.alleng.ru/.Школьная математика, всего лишь запоминание правил и определений и потом их быстрое применение при решении задач. Ничего сложного. Но она основа, для всего остального. Вот здесь хорошо расписано: viripit.ru/index.htm . Купи старую книгу типа «Энциклопедия юного математика». Читай для удовольствия. Вообще процесс должен занять несколько месяцев, чтобы осилить школьную программу.
Натыкайся на те задачи которые не можешь решить и уделяй им время. Потом пойдет все быстрее и быстрее. Не слушай никого, кто говорит, что учить поздно. У каждого своя судьба, и свои стартовые условия. Но каждый в итоге получает то, что он действительно хочет. Осилить школьную математику, нармально любому человеку. Это общий культурный багаж, без понимания которого, человек будет ограничен. На самом деле все школьные предметы, развивают разные способности мышления. Потом неплохо повторить и физику — чтобы понимать, почему вокруг все так происходит.
Математика программисту в большинстве случаев не нужна. Но нужно знание основ, чтобы быстро разобраться в новом. Обязательно знание некоторых важных разделов:, типа логики и др. Без математики ты не сможешь зазкончить нормальное обучение по ComputerScience.
И самое главное, мозг должен уметь думать и решать задачи. Именно это и развивает в чистом виде — математика.
Но в реальности программисту, кроме умения думать, нужно и воображение, и абстрактное мышление, отличная память, знание английского, и умение общаться; еще умение постоянно учиться, хорошая общая эрудированность и вкус и тд. А так же крепкое здоровье. Так- что не циклись на математике, это всего лишь часть большого целого.
PS: Забудь про криптографию. Ты это не осилишь. Разберись, сейчас — как делить столбиком 🙂
toster.ru
Изучаем алгебру легко и просто
Алгебра — это важнейший предмет школьной программы, который изучается с начала средних классов и заканчивается сдачей ЕГЭ. Начиная с самых азов изучения алгебры школьнику очень важно хорошо разбираться и знать каждую тему. Поскольку этот предмет имеет эллиптический способ изучения, или «от простого — к сложному», какой-либо пробел даже в самой незначительной теме может сказаться отрицательно на результате сдачи ЕГЭ по алгебре. А ЕГЭ, как известно — это пропуск к получению высшего образования и освоению будущей специальности.
Изучение алгебры: особенности, варианты построения обучения
Далеко не всем легко дается алгебра, что вполне объяснимо. Это довольно сложный предмет, который не терпит условностей и предположений. И даже если в начальных классах преобладают неплохие результаты по математике, столкнувшись с сухим языком формул и функций, можно легко запутаться и алгебра станет «темным лесом», а обучаться тому предмету, который не понятен, очень тяжело.
Алгебра бесплатно сегодня предлагается для обучения многими интернет-ресурсами. Обучение может быть построено несколькими способами. Это может быть изучение всего школьного курса алгебры с нуля. Подобный подход интересен тем школьникам, которым особо тяжело даются точные науки. Например, если у человека гуманитарный склад ума и изучение алгебры ему нелегко даётся с самого начала. Также если непонятны некоторые конкретные темы, то можно дополнительно изучить их и прорешать все практические занятия по этим темам. Еще, для более успешной сдачи ЕГЭ по алгебре, можно решить задания ЕГЭ прошлого года. Это поможет понять смысл построения задач и подготовиться к экзамену. Готовясь к сдаче ЕГЭ важно осветить такие вопросы, как понятие линейной функции, решения неравенств, особенности геометрической прогрессии, интеграл и многие другие.
Бесплатные уроки алгебры, преподаваемые в средней школе, могут быть недостаточно понятны школьнику, элементарная нехватка времени и необходимость подготовки по другим дисциплинам делает невозможным более глубокое изучение некоторых тем и повторение пройденного материала. Конечно, можно обратиться к репетитору по алгебре, походить на платные факультативы, но это, опять же, займет время, нужно будет подстраиваться под график репетитора и посещать факультатив в строго определенные часы. Между тем, изучение алгебры невозможно без повторного осмысления и закрепления пройденного материала. Основным принципом составления обучения данного предмета должна являться доступность и научность в изложении материала.
Особое внимание стоит уделять решению практических заданий. ЕГЭ по алгебре имеет именно практическую направленность, поэтому важно, чтобы школьник умел решать задания по любой теме. Также важно, при изучении алгебры, заложить в сознании школьника основательные и крепкие знания по предмету. В современный век цифровых технологий алгебра — одна из наиболее важных и полезных наук. Если человек хочет избрать в будущем какую-либо техническую специальность, без более углублённого изучения алгебры не обойтись.
Альтернатива алгебры бесплатно — видеоуроки
Если вы не совсем хорошо разбираетесь в точных науках, а именно в алгебре, предлагаем прибегнуть к помощи нашего интернет ресурса. Это отличный способ повторить пройденный материал, понять особо сложные темы, позаниматься практически. Особенно важно изучение таких тем, как исследование функций, касательная, таблица производных и многие другие. В случае, когда школьник пропустил некоторые занятия, что усложнило понимание предмета, видеоуроки восполнят этот пробел в знаниях. Также это отличное решение проблемы временного отсутствия учителей. ЕГЭ по алгебре даст более высокий результат, если школьник будет постоянно практиковаться в решении задач по предмету. Поступив в институт и приступив к изучению Начала анализа, некогда будет возвращаться к пропущенным и недопонятым школьным темам, поэтому получать высшее образование нужно с уверенными и крепкими знаниями алгебры.
interneturok.ru
Школьная математика, онлайн-учебник: 1 класс и старше — бесплатно
Вопросы и комментарии
10 декабря, 2018 — 13:33
Гость
Ответить
22 августа, 2018 — 10:43
Иштван
14 июня, 2018 — 17:30
Абу
14 июня, 2018 — 17:28
Абу
Ответить
13 июня, 2018 — 03:06
Абу
19 апреля, 2018 — 17:57
VzlomT13
Ответить
19 апреля, 2018 — 17:56
VzlomT13
15 апреля, 2018 — 17:53
людмила
Ответить
14 апреля, 2018 — 13:24
Жасур
Ответить
9 октября, 2017 — 20:26
Даниэль
10 января, 2017 — 18:50
Евгений
Ответить
9 декабря, 2016 — 19:58
Гость
Ответить
24 ноября, 2016 — 03:06
Никита
17 ноября, 2016 — 12:21
tihiro
16 ноября, 2016 — 10:29
оксана
Ответить
30 сентября, 2016 — 23:54
Гость
13 сентября, 2016 — 13:43
А Мир
Ответить
14 апреля, 2016 — 17:57
Ваня
7 февраля, 2016 — 23:15
инесса
Ответить
29 октября, 2015 — 11:29
Елена
21 июля, 2015 — 00:27
Victor
21 июля, 2015 — 15:43
Леонид Некин
21 июля, 2015 — 20:01
Victor
27 июня, 2015 — 11:02
Сафия
5 февраля, 2015 — 07:12
таня короткова…
Ответить
27 января, 2015 — 13:45
Дмитрий
Ответить
23 ноября, 2014 — 15:59
мари)
Ответить
9 ноября, 2014 — 10:41
Елена
Ответить
30 октября, 2014 — 12:48
йогу тимати
29 апреля, 2014 — 00:04
ggg
Ответить
8 декабря, 2013 — 23:46
Саша
17 ноября, 2013 — 14:01
лера
15 октября, 2013 — 16:58
Orla Colgan
Ответить
22 марта, 2013 — 23:03
Akella
23 марта, 2013 — 01:15
Леонид Некин
Страницы: 1 2 > >>
www.nekin.info
ИНТЕНСИВНЫЙ КУРС . МАТЕМАТИКА С САМОГО НАЧАЛА . часть 01: galina6111
Я — Внук Яги
Год работы в маленькой сельской школе с выпускниками 9 класса и с классом 10 не прошёл даром.
Вывод простой , известный любому технарю — чем переделывать,проще с самого начала самому делать то что необходимо.
Вот и возникла необходимость написать курс обучения математике с самого начала.
Применяемые для обучения учебники имеют один принципиальный порок.
Они все написаны в расчёте на преподавателя — учителя.
А за что получет свою оплату учитель ? — За время.За часы.
Чем дольше учитель обучает — тем зарплата выше.
И никакой ответственности за результат этой учёбы.
Публикуемый материал ориентирован на ученика. Проверен на единичных учениках 5,6,7,8 классов.А также выпускниках 11 класса.Результаты испытания позволяют считать возможной эту публикацию. Для широкого применения.
Для обучения всяких гуманитариев, лиц женского пола и прочего контингента.Который считается ни на что не годным в плане обучения математике.
Редактор ЖЖ не позволяет постить статью полностью и с адекватным отображением мат. формул.Поэтому, пока идёт оформление материала,желающие могут скачать сразу и полностью,не дожидаясь публикации в ЖЖ.
Так же будет продолжена публикация цикла » Такая математика ! » ,отражающего мой личный взгляд на проблемы обучения и образования.Как в РФ ,так и в КР. Цикл имеет больше дискуссионную направленность.
Полностью скачать публикуемую часть курса математики ИНТЕНСИВНЫЙ КУРС. С САМОГО НАЧАЛА 01 :
ИНТЕНСИВНЫЙ КУРС. С САМОГО НАЧАЛА 01.docx https://cloud.mail.ru/public/LWKo/eexzhULQR
Математика с самого начала
Год работы в средней школе дал возможность оценить реальные знания выпускников. Очень часто средний выпускник 11 класса не знает простого. Например – сложения дробей.
Поэтому, для особо продвинутых и одарённых выпускников, — начнём с самого начала.
Внук Яги
Что такое – математика ?
Прежде всего – это просто ещё один язык.
И моя задача – научить на этом языке читать, понимать прочитанное. В идеале – ещё и суметь записать ответ на этом языке.
Учить думать школьников на этом языке – не есть задача учителя средней школы. Тем более, что сдав выпускные экзамены, нормальный человек этот язык нормально забывает .По экспоненте, иногда сразу после экзамена. Ввиду не востребованности этого языка в текущей реальности….
Что главное в любом языке ?
Это – не грамматика. И не умение читать написанное…
Это – Слово и умение на этом языке говорить. Используя слова языка.
Главное в любом языке – Взаимопонимание между людьми.
В языке Математика ,аналогично, главное – это Число. И умение выражать свои мысли.При помощи Чисел и для общения с другими людьми.
Говорить с Числами – производить некие действия, операции с ними.
1. Число́ — основное понятие математики[1],используемое для количественной
характеристики, сравнения, нумерации объектов и их частей.
2. ОПЕРАЦИЯ – это просто ДЕЙСТВИЕ. Действие над Числами.
В любом языке комбинацией слов можно выразить некую мысль.И эту мысль можно словами озвучить,произнести ,высказать. Её можно даже записать. При помощи иероглифов. Они же знаки, символы или буквы алфавита.
В языке Математика – всё точно так же. При помощи комбинации чисел и действий над этими числами можно выразить некую мысль. А при помощи иероглифов эту мысль можно записать. И прочитать.
Иероглифы в Математике то же самое – знаки, символы, буквы алфавита и цифры.
Что такое Число – посмотрите ещё раз выше. А цифра – это всего лишь знак или символ, при помощи которого записывается это число. Число – оно единственное в своём роде. Можно сказать – каждое число уникально. А вот знаков, которыми можно это число записать – бесконечное множество.
В отличии от большинства разговорных человеческих языков , которые считаются натуральными, язык Математика – язык искусственный. Примером искусственного человеческого языка является самый известный язык эсперанто.Как средство межнационального общения. Некоторые исследователи считают искусственными языки латынь и иврит. Дата создания языка иврит и его автор известны однозначно. Как и авторы и дата создания языка эсперанто.
Язык Математика предназначен решения ряда прикладных задач,круг которых постоянно расширяется.Соответственно , развивается и расширяется сам язык Математика.
Я вижу свою задачу,в рамках школьного курса языка Математика, научить всех желающий : читать и понимать мысли,записанные на языке Математика иероглифами этого языка.Поняв написанную мысль – решить поставленную этой мыслью задачу или принять своё решение.В идеале – сделать следующий шаг.То есть — записать решение и свой ответ иероглифами языка Математика.
ВСЁ !
В моих планах не стоит научить Вас думать на этом языке , делать из Вас Математика !
Только – читать, понимать написанное и записать решение и ответ.
Создатели языка Математика декларируют его однозначность.
То есть принцип, когда одному понятию или объекту соответствует один и только один иероглиф. И обратно – одному иероглифу соответствует одно и только одно понятие или объект.
В реальности этот принцип далеко не всегда соблюдается. И при изучении языка Математика на русском языке следует учитывать, что на других языках могут быть совершенно отличными как сами иероглифы, так и понятия , с которыми эти иероглифы связаны.
Начнём ?
Одночлены и многочлены
Числа можно записать разными иероглифами. Число, оно ведь — как ?
Число – это некая таки постоянная величина.
И мы можем записать его значение однозначно. При помощи цифр. Одной комбинации цифр соответствует одно число .И наоборот – одному числу соответствует одно число.
А можем записать число – в ОБЩЕМ ВИДЕ, при помощи других символов.Например, букв.В первую очередь – букв латинского алфавита. Причём, принято использовать буквы латинского алфавита начиная с НАЧАЛА этого алфавита для записи так называемых параметров , а латинские буквы ,начиная с КОНЦА алфавита – для записи переменных.
Что – такое параметр и что такое переменная – разберём при случае в следующий раз. Тема – достаточно ржачная….
Вот и получается, что так или иначе комбинируя иероглифы Математики, мы можем записывать различные смысловые или понятийные единицы :
1. Комбинацию из цифр, знаков операций ( не содержащая знаков операций сложения + и вычитания — ,а также операций сравнения ( = , >, < и их комбинаций), символов параметров или переменных – назовём Одночленом. Примеры :
3, c , 5a , 6by , cz3
это всё примеры — ОДНОЧЛЕНОВ
2. Знаки операций + и – отделяют одночлены друг от друга, превращая одночлен в МНОГОЧЛЕН.
Пример такого многочлена :
X2 + X – 2
Надеюсь, ничего непонятного в изложенном материале – нет.
Математические понятия ( слова)
Вы уже начали знакомиться с математическими словами (понятиями) : цифра, операция, параметр, переменная, знак, символ.
Продолжим знакомство с этим Матом.
И первое ,самое часто встречающееся матерное слово –
ВЫРАЖЕНИЕ
Оно же – алгебраическое выражение.
Это одночлен или многочлен, не содержащий знаки операций сравнения ( =, <, >другие ) Пример выражения :
X2 + X – 2
Вот встретилось выражение.Какое задание его обычно сопровождает ?
Упростить или найти значение. Потому как ничего другого с выражением сделать и нельзя.Упростить, если это возможно.
galina6111.livejournal.com
бесплатные онлайн курсы по математике для школьников
Домашнее обучение становится все более популярным. И сегодня не составляет труда найти полезные ресурсы для обучения онлайн. Поэма Жогло, мама хоумскулера, сделала поборку лучших сайтов по математике для школьников.
Основная идея – сделать ребёнка максимально самостоятельным, но при этом всё же контролируемым. Данные ресурсы больше подойдут для средних классов, хотя и для малышей тоже есть, что подобрать. Все сайты бесплатные или с бесплатной версией.
И так, программа №1 — это XtraMath. Это всего одна единственная программа, без которой у нас не обходится ни одного дня с математикой.
Суть этой программы — наработать скорость в простейших вычислениях: +,-,/,*. Для этого вы регистрируете вашего ребенка и себя, как родителя. Ребенок самостоятельно выполняет задания, а потом на почту родителям приходит подробнейший отчет об успехах. Отчёт можно смотреть и онлайн. Сайт на английском, но всё предельно понятно и просто. Можно выбирать разный режим — скорость, с которой будут подаваться примеры. Мы сначала прошли обычный, а сейчас делаем тоже самое, но быстрее. После прохождения блока ребенку выдается сертификат, который вы можете себе распечатать.
Алгоритм построения занятий
Далее, хочу рассказать об основном алгоритме, по которому строятся наши занятия дома. Здесь основной перечень сайтов, который подходит для ежедневных тренировок, связанных с освоением школьной программы по базовым темам. Мы не пользуемся ни учебниками, ни тетрадями, распечатками и пр., в равной степени, как и калькулятором.
- Новую тему мы смотрим, используя канал MathTutor на сайте Интерурок. Альтернативным вариантом (или дополнительным) подходит Академия Хана — с украинским или русским переводом. В русской версии роликов больше.
- Далее мы нарешиваем примеры для закрепления услышанного, используя тренажер на сайте Rastu. На этом же сайте найдёте и краткую информацию по теме (например формула или принцип расчета). Если пример сделан неправильно, то сверху над ним появится подсказка. Ребёнок занимается самостоятельно, так как на любом этапе видно сколько примеров решено и сколько сделано ошибок. По этому результату всегда понятно: или мы переходим к следующей подтеме, или стоит ещё порешать эту.
- Когда уже есть понимание темы, и она закреплена на тренажере, мы используем сайт ozenoknet. Этот сайт подходит именно для закрепления материала, а не для нарешивания в связи с тем, что примеров по каждому разделу не так много. Но зато там есть другие интересности: за выполненные задания ребёнок получает виртуальную коллекцию «призов» и «кубков». Они будут отражаться на его страничке в соответствующих разделах. Кроме этого здесь есть электронный журнал, где отражены все данные отдельно по каждой теме и присвоен уровень: «хорошо», «отлично» и «неплохо».
- Ну и напоследок самое приятное — это компьютерные игры на сайтах jmathpage.com и mathplayground.com. Игр необыкновенное множество и все они математические!
Перечень дополнительных ресурсов
1. Математические тренажёры
- www.mathgames.com/skills — это супер тренажёр, но требует минимальные знания английского. Мой сын от него в восторге! На личной страничке отображается вся статистика о проделанной работе: время затраченное на каждое задание, начало и конец занятий, результаты по каждой теме. Очень удобно использовать, так как выдаёт списки заданий либо по классу (наша программа немного не совпадает) либо по темам.
- www.ck12.org — ещё один тренажёр на английском. Отдельно для младшей школы, геометрия, алгебра, вычисления и пр.
- www.buzzmath.com — тренажёр на английском с очень интересной подачей заданий! Уверена вашим деткам он понравится!! На сайте указано, что задания рассчитаны на 6-9-й классы, но на мой взгляд, можно смело решать с 5-го. Сайт платный. Но если заходить как «визитор», то можно заниматься бесплатно. Единственный минус — ваши результаты сохраняться не будут.
- eu.ixl.com — это отличный сайт, тоже на английском. Этот сайт требует платной регистрации, но если не регистрироваться, то вы ежедневно можете проходить на нём ограниченное число заданий.
- www.splashmath.com — очень интересный тренажёр с мультяшной анимацией для 1-5 классов на английском языке. Уверена, что с ним математику полюбит любой ребёнок! Сайт платный, но есть и открытая версия, которая позволяет без оплаты решать по 20 вопросов ежедневно. Кроме этого, после каждого занятия вашего чада, с сайта на ваш электронный адрес будет приходить подробный отчёт о проделанной работе: с чем дитё отлично справилось, а по каким темам есть трудности.
- www.adaptedmind.com — очень весёленький тренажёр с «чудищами», участвующими в решении задачек. Сайт на английском языке для 1-6 классов.
- www.khanacademy.org/math — тренажёры от Академии Хана. На английском языке. Для того чтобы здесь заниматься, необходимо пройти небольшой тест, который определит, над какими темами стоит работать.
- www.tenmarks.com — тренажёр на английском языке с предварительным тестированием.
- www.yaklas.com.ua — отличный сайт, но только с 7-го класса. Можно выбрать как украинский язык, так и русский. Есть много разных предметов, кроме математики. Каждая тема делится на теоретическую часть и практическую. Бесплатно можно делать только несколько заданий.
- bitclass.ru/math — сайт на русском языке. Похож, в общем, на предыдущий, но охватывает темы начиная с 5-го.
- school-assistant.ru/?class=matematika — сайт на русском языке. Сначала идёт теория, а после — несколько задач на закрепление материала.
- www.knewton.com/learn — тренажёр на английском, интересная система, построенная на анализе индивидуальной успеваемости: в зависимости от допущенных ошибок — отсылает к тому или иному видео с теорией. К сожалению, большинство заданий рассчитаны на 7-й класс и старше.
- www.uchportal.ru/load/29-1-2 — тренажеры на русском языке (предварительно скачать по указанным ссылкам)
- www.kokch.kts.ru/math/index.html — тесты на русском языке
2. Генераторы случайных примеров
- egeurok.ru — на русском языке. Сначала формируете список заданий, потом ребёнок решает, а после нажимаете ответы и сверяете с ответами вашего чада. Можно распечатывать, а можно и не печатать — кому как удобно.
- www.math-aids.com — аналогичный вариант на английском языке.
- www.mathinenglish.com/menuWorksheets.php — примеры на сайте с английским языком.
- www.math-drills.com/ — отличный сайт на английском.
- www.worksheetworks.com/math.html — примеры формируете сами исходя из установленных вами ограничений.
- /www.bymath.net/ — сайт на русском языке. Много теории. По каждой теме есть задания.
3. Математические игры онлайн
На русском языке:
На английском языке:
4. Занимательная математика
Сайты на русском языке.
- www.problems.ru — сайт для продвинутых математиков — разобранные решения олимпиад и пр.
- domzadanie.ru — много интересных задачек.
- nazva.net/rubric/all — отличная копилка для тех, кто любит думать.
5. Программы помощники
- loviotvet.ru — помогает решать примеры и уравнения с отображением этапов решения, производит наглядно вычисления «в столбик». Сайт на русском языке.
- www.nigma.ru/index.php?t=math — поможет с уравнениями. Сайт на русском языке.
- math-prosto.ru — охватывает всего несколько тем как онлайн-решатель, но зато довольно доступно подаётся теория. Сайт на русском языке.
- www.mathway.com — проверит правильность составления уравнений. Англоязычный ресурс, но всё очень просто и понятно.
- znanija.com/predmet/matematika — русскоязычный сайт, на котором вы можете задать любой интересующий вас вопрос и получить ответ онлайн от помощника. Есть возможность и для других предметов.
6. Списки полезных ссылок на английском языке
Надеюсь, что ваши ежедневные занятия математикой теперь будут ещё увлекательнее!
Источник
ЧИТАЙ ТАКЖЕ: 10 украинских школ, в которых можно учиться дистанционно
ЧИТАЙ ТАКЖЕ: 10 сайтов для школьников, которые объяснят уроки лучше любого учителя
ЧИТАЙ ТАКЖЕ: Причины и следствия, или Год без лета: каким должно быть изучение истории в школе
Загрузка…
www.uaua.info
Как выучить математику с нуля самостоятельно?
Математика наравне с родным языком является одной из самых главных наук, и не только в школе. Зачастую без нее не обойтись ни в повседневной жизни, ни в карьере. Кроме того, математику необходимо сдавать в выпускных классах. Но как быть, если все упущено? Давайте разберемся, как выучить эту науку самостоятельно, да еще и с нуля, и подготовиться к экзаменам.

Эта статья будет полезна также тому, кто давно окончил школу, но есть желание поступить в колледж или вуз по технической специальности. В этом случае тоже нужно постигать математику с азов или же подтянуть знания в тех темах, которые были не понятны при учебе или попросту забыты.
Предлагаем воспользоваться приведенными ниже инструкциями. Но обращаем внимание: успех полностью зависит от самого учащегося.
Моральная подготовка
Прежде чем приступить к изучению математики, следует морально подготовиться. Особенно это касается тех, кому данный предмет в школе практически не давался. Ведь бывает так, что у человека не математический, а гуманитарный склад ума.
Ниже мы обсудим, что делать, если не получается разобраться в одной из тем. Но в любом случае нужно быть готовым к долгому изучению, ибо быстро выучить математику на самом деле практически невозможно.

Моральная подготовка заключается в том, чтобы:
- Постараться дать себе понять, что при желании можно изучить любую науку. Ведь как-то отличники и хорошисты разбираются в дисциплине. Тем более если учитель говорит, что это легкая тема, то стоит поверить.
- На время отложить развлечения, общение с друзьями и различные мероприятия, которые не столь важны, ради того чтобы подтянуть знания по царице всех наук. Пусть основная часть времени будет посвящена изучению непонятных тем.
- Перед началом занятий дать себе хорошенько отдохнуть. Например, погулять на свежем воздухе в парке, выполнить несколько физических упражнений или неотложных дел. Ибо очень важно, чтобы никакие заботы и просьбы со стороны не отвлекали.
- Настроиться на тренировку памяти с целью запомнить правила и формулы. Они на самом деле не такие сложные, как кажется.
- Понять, что математика по большей части требует от человека логического мышления и смекалки.
- Воспринимать науку не как что-то должное, а как игру в головоломку, в которой нужно пройти конкретные этапы и проверить «запасным вариантом» правильность решения задачи.
- Убедить себя в том, что тренировка на запоминание полезна для мозга.
- Понять, что решение многих задач и примеров, построение фигур и графиков, а также различные геометрические доказательства – это увлекательный процесс, который можно применить на практике.
Пусть подобные рекомендации станут для вас помощниками каждый раз, когда вам захочется оставить изучение сложных тем. Оказывается, не так уж и сложно выучить математику с нуля.
Оценка своих знаний
Очень важно уметь оценить свои знания. Например, вы являетесь учеником 9 класса, или же на данный момент лето, и стоит цель хорошо подучить пропущенные и непонятые ранее темы. В таком случае делаем так: открываем учебник 5-го класса, находим любую сложную задачу и решаем ее. Если ответ правильный, то с легкостью приступаем к задачам за 6-й класс и проверяем себя по ним. Желательно прорешать по паре заданий из каждой темы.
А теперь разберем, как быстро выучить правила математики.
Обязательно найдется такая задача, которую вы затруднитесь решить. Например, тема связана с квадратными уравнениями, но пример дан в виде двух произведений со скобками, которые нужно раскрыть. А вы забыли правила раскрытия скобок, вследствие чего ответ неправильный, проверочное решение не сходится. Стоит в таком случае отметить в отдельном листе-плане, что нужно разобраться, в каком случае ставится знак «+», а в каком «–» при раскрытии скобок. Также следует проработать и остальные темы.
Немного геометрии
Что касается геометрии, то ее тоже следует начинать изучать сначала, чтобы понять, что такое фигуры, теоремы, как вообще работать в данной дисциплине.
Но как выучить математику за короткий срок, если практически все темы непонятны или незнакомы, и возможно ли это? Вот несколько рекомендаций.
Если многое упущено
Стоит ли говорить о том, что математику с нуля лучше всего разбирать с репетитором или родственником, одноклассником? Самому изучить этот предмет довольно сложно, особенно по сравнению с историей или географией. Но тем не менее, если есть много свободного времени, можно пробовать решать примеры самостоятельно. Возможно, для этого придется детально изучить более простые темы, которые в основном входят в программу 5-го класса.
Теперь составим план наших действий:
- Приобретите учебники и решебники за все классы средней школы. Программа должна соответствовать тому, что вы изучаете в школе.
- Составьте список всех тем, которые имеются.
- Подготовьте чистую тетрадь для решения задач. Не рекомендуется решать примеры на клочках бумаги, пусть все проведенные действия будут перед глазами, даже если они с помарками и ошибками.
- Если у вас сохранились конспекты с пройденными уроками и решенными в классе примерами, обязательно проработайте их. Выпишите в тетрадь задачку, затем закройте конспект, начните решать самостоятельно. Как закончите, сверьтесь, что вы сделали правильно, а что не так.
- Выучите правило и формулы по текущей теме. Помните о том, что математика не «любит» зубрить, она «любит» понимать определение.
Такой подход поможет самостоятельно выучить математику. Как запомнить все и сразу? На самом деле этого делать не нужно.
Лучший способ запомнить
Как было сказано выше, обычное зазубривание не поможет. Нужно разобраться. Допустим, у вас тема связана с нахождением определения объема фигур в геометрии. Эти формулы довольно простые, их легко запомнить. Но чтобы лучше усвоить урок, желательно, следуя формуле, решить задачу. Заодно вы заметите последовательность: что от чего зависит и как выводится. Например, элементарное нахождение площади прямоугольника: умножаем длины двух сторон, не лежащих параллельно. И все, задача решена. Куда сложнее определить площадь круга или объем цилиндра, но если запомнить формулы, то и это не составит труда.

А как выучить математические правила, если они с формулами не связаны? Все довольно просто. Например, то же раскрытие скобок. Нужно лишь запомнить, что «умножение минуса на минус дает плюс, а умножение минуса на плюс (и наоборот) всегда дает минус». И все. В дальнейшем решить даже самые сложные задачи на раскрытие скобок будет получаться на раз-два!
Успешное освоение
Полученные знания всегда следует закреплять. Вы запомнили формулу дискриминанта или заучили последовательность нахождения неизвестной через построение графиков. Обязательно прорешайте различные примеры на эту тему еще и еще, чтобы отложилось все в памяти.
Учителя, да и репетиторы, рекомендуют время от времени возвращаться к пройденной теме, чтобы проверить себя. Это, на самом деле, отнимет несколько минут. Наверняка вы замечали, что те, кто успевает по математике, способны за 15-20 минут сдать работу, которая рассчитана на полчаса. Что здесь удивительного? Просто тема была освоена достаточно хорошо и не нужно долго ломать голову, вспоминать формулы или пытаться спросить у соседа.

Как выучить математику за 5 минут до контрольной, и возможно ли это? Разумеется, если предыдущие разделы освоены хорошо, а нынешний не изучен по каким-то причинам, то можно пробежаться по правилам и формулам. Но успех будет лишь в том случае, если тема логически продолжает ранее изученные.
Не дается и все тут
К сожалению, большинство учащихся не могут разобраться в науке ни в классе, ни самостоятельно. Нужно, чтобы тему объяснили отдельно. Зачастую приходится прибегать к помощи репетитора.
Но есть возможность выучить математику с нуля самостоятельно и бесплатно. Естественно, с помощью вездесущего интернета:
- видеоуроки на YouTube,
- ознакомительные курсы на математических сайтах,
- онлайн-репетитор.
Таким образом, можно найти способ без лишних затрат разобраться в теме. Существует множество видеоуроков на отдельно взятые темы, которые легко изучить, посмотрев, как правильно и в какой последовательности решаются задачи. Желательно повторить пройденный урок самостоятельно.
Если тема очень сложная
В математике сложных тем достаточно много, особенно в 9, 10 и 11 классах. Зачастую без помощи знающих людей не обойтись. Поэтому стоит внимательно слушать урок, чтобы не возникло проблем в будущем.

Ведь даже самая сложная тема поддается объяснению и пониманию. Только нужно тренировать в себе усидчивость, терпение и желание учиться. Ведь неспроста это слово означает «учи себя». Многие ученики ближе к выпускным экзаменам спрашивают, как выучить математику, чтобы балл был высокий. Все просто: готовиться следует заранее (прорабатывать все темы и решать предлагающиеся задачи).
Необходимые инструменты для работы
Многие учителя настоятельно требуют, чтобы ученики запоминали таблицу умножения, учились считать в уме и обходились без калькуляторов насколько это возможно. Действительно, существовала же как-то математика без электронно-вычислительной техники? Были счеты, но они только развивали мышление. А современные гаджеты, наоборот, ослабляют мыслительную деятельность и ухудшают запоминание. Поэтому современному школьнику лучше позаботиться заранее о том, как выучить математику, а точнее арифметику, чтобы в будущем было проще решать любые задачи без помощи калькулятора.
Как видите, математика – сложная наука, требующая усидчивости. Быстро выучить ее не удастся. Поэтому желательно изучать внимательно каждую тему начиная с младших классов.
fb.ru














 ) называется множество, состоящее из
всех тех элементов, которые принадлежат
хотя бы одному из множествA,B(рис. 2.2):
) называется множество, состоящее из
всех тех элементов, которые принадлежат
хотя бы одному из множествA,B(рис. 2.2): = {x:
= {x: или
или }.
}. ) называется множество, состоящее из
всех тех и только тех элементов, которые
принадлежат иА, иВ (рис.
2.3):
) называется множество, состоящее из
всех тех и только тех элементов, которые
принадлежат иА, иВ (рис.
2.3): = {x:
= {x: и
и }.
}. =
=
 )
называется множество всех элементов,
не принадлежащихA, но принадлежащихU (рис. 2.4):
)
называется множество всех элементов,
не принадлежащихA, но принадлежащихU (рис. 2.4): = U \ A.
= U \ A. и
и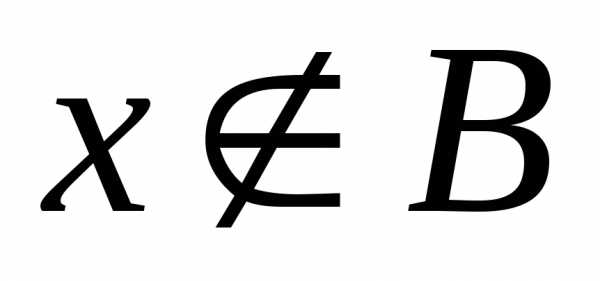 }.
}. В\А.
В\А. .
. B) называется множество всех тех элементовА или B, которые не содержатся вAиВ одновременно (рис. 2.6):
B) называется множество всех тех элементовА или B, которые не содержатся вAиВ одновременно (рис. 2.6): В= {x:
В= {x: или
или ,
но}.
,
но}. )|}.
)|}. )
называются кортежами (векторами,
наборами, словами). В произведении могут
участвовать более двух множеств.
Количество множеств, участвующих в
произведении, определяет длину кортежей.
)
называются кортежами (векторами,
наборами, словами). В произведении могут
участвовать более двух множеств.
Количество множеств, участвующих в
произведении, определяет длину кортежей. ; б); в); г)В \ С; д)С\B?
; б); в); г)В \ С; д)С\B? – множество сотрудников организации,
стаж работы которых не превышает 10 лет.
– множество сотрудников организации,
стаж работы которых не превышает 10 лет. ,
, ,
если:
,
если: – множество всех натуральных чисел,
больших 100.
– множество всех натуральных чисел,
больших 100. без указания универсального множестваU не ясна:
без указания универсального множестваU не ясна: = {a, b, c,d,e, f, g, h};
= {a, b, c,d,e, f, g, h};  = {c, d}.
= {c, d}. =U\А = {е, f, g,h},
=U\А = {е, f, g,h},  = U\B = {а, b}.
= U\B = {а, b}. 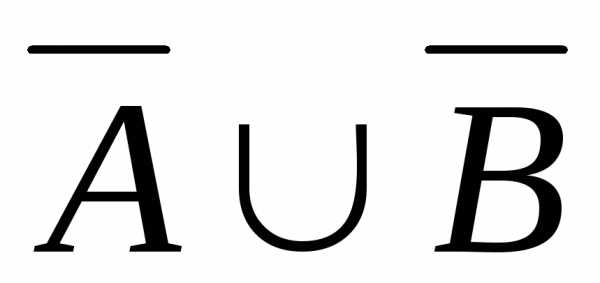 ; б)
; б)  ; в)
; в) ; г).
; г).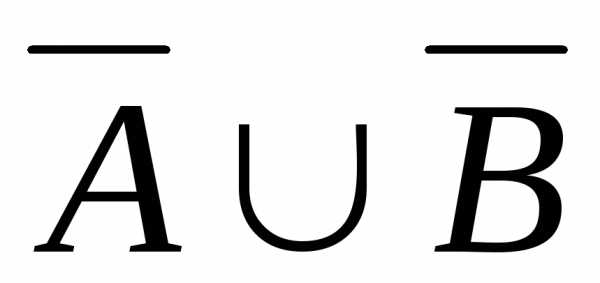 == ({1, 2, 3, 4} \ {1, 3, 4})
== ({1, 2, 3, 4} \ {1, 3, 4}) ({1,
2, 3, 4}\{2, 3}) =
({1,
2, 3, 4}\{2, 3}) = {1,
4} = {1, 2, 4}.
{1,
4} = {1, 2, 4}. = = {1, 2, 3, 4}\ ({1, 3, 4}
= = {1, 2, 3, 4}\ ({1, 3, 4} {2,
3}) = {1, 2, 3, 4}\{3} =
{2,
3}) = {1, 2, 3, 4}\{3} = =={l, 3, 4}
=={l, 3, 4} ({l,
2, 3, 4}\{2, 3}) ={1, 3, 4}
({l,
2, 3, 4}\{2, 3}) ={1, 3, 4} {1,
4} =
{1,
4} = ({1,
2, 3, 4}\{1, 4}) ={2}
({1,
2, 3, 4}\{1, 4}) ={2} {2,
3} =
{2,
3} = В = {(a, p),(a, q),(a, r),(b, p),(b, q),(b, r)}.
В = {(a, p),(a, q),(a, r),(b, p),(b, q),(b, r)}. и
и ,
расстояние между которыми равно,
и дано некоторое число
,
расстояние между которыми равно,
и дано некоторое число ,
которое удовлетворяет условиям:
,
которое удовлетворяет условиям: или
или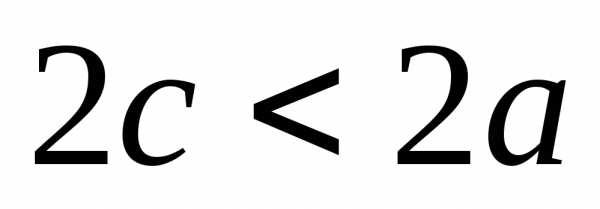 .
. и
и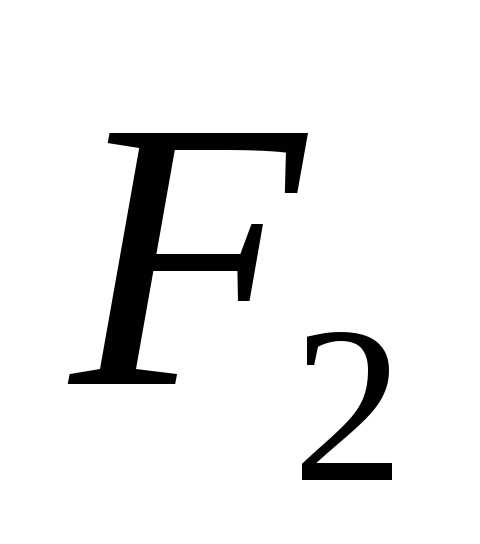 есть величина постоянная, равная
есть величина постоянная, равная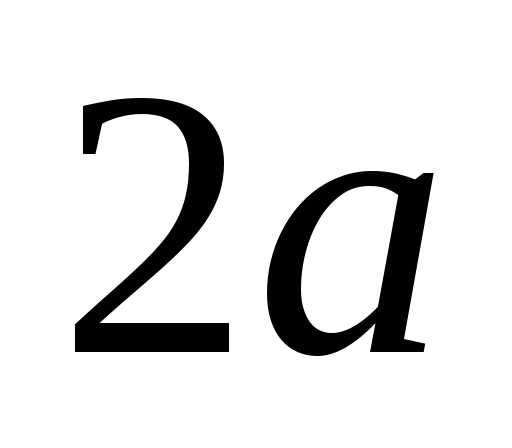
 и
и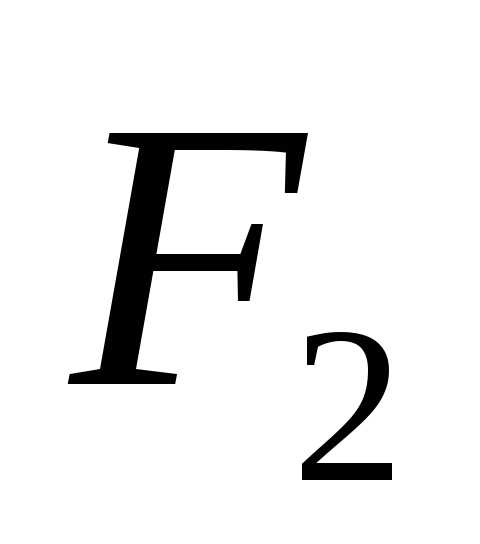 называются фокусами эллипса, расстояние
между ними обозначается через
называются фокусами эллипса, расстояние
между ними обозначается через  и называется фокусным расстоянием.
и называется фокусным расстоянием. пройдет через фокусы эллипса, ось
пройдет через фокусы эллипса, ось —
серединный перпендикуляр к отрезку
—
серединный перпендикуляр к отрезку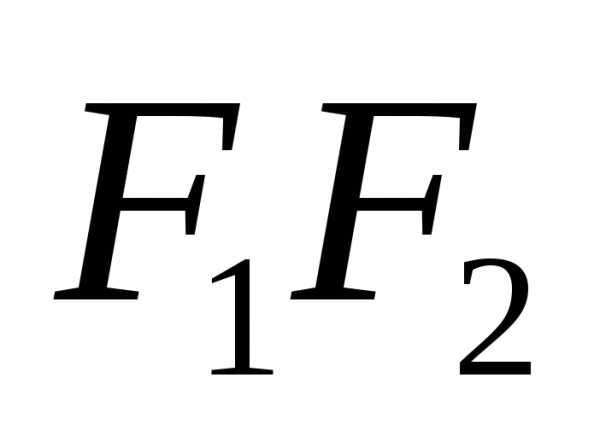 .
.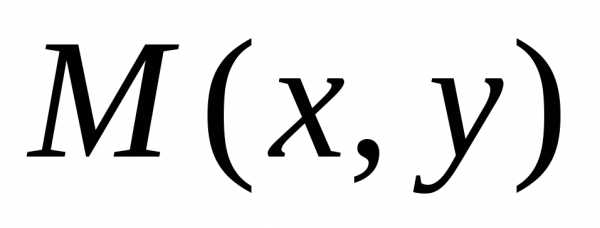 является
точкой эллипсатогда
и только тогда, когда
является
точкой эллипсатогда
и только тогда, когда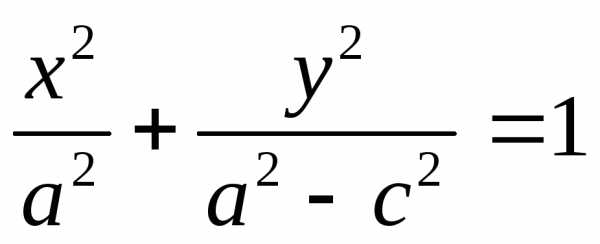
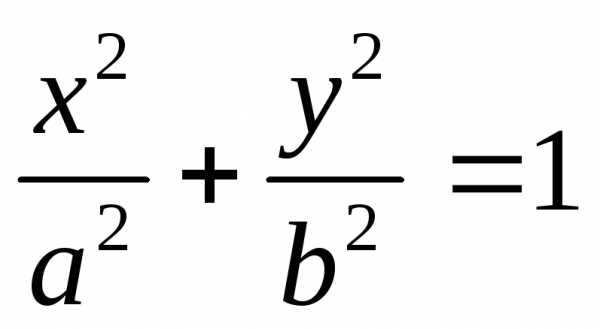 (2)
(2)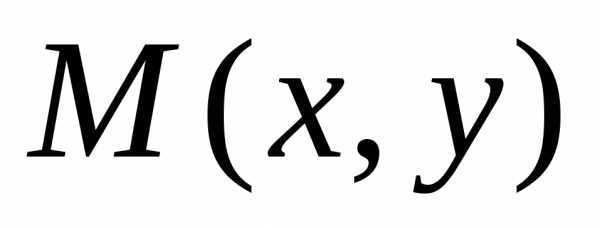 ,
удовлетворяющая уравнению (1) удовлетворяет
и уравнению (2). Докажем обратное
утверждение: каждая точка
,
удовлетворяющая уравнению (1) удовлетворяет
и уравнению (2). Докажем обратное
утверждение: каждая точка 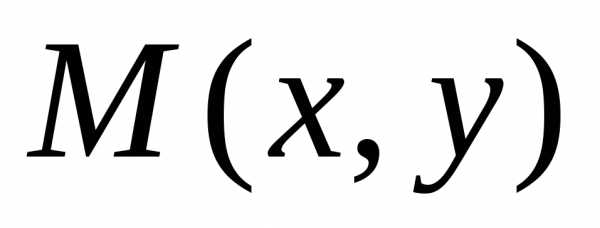 ,
удовлетворяющая уравнению (2), есть точка
эллипса, т.е. для нее выполняется условие
.
,
удовлетворяющая уравнению (2), есть точка
эллипса, т.е. для нее выполняется условие
.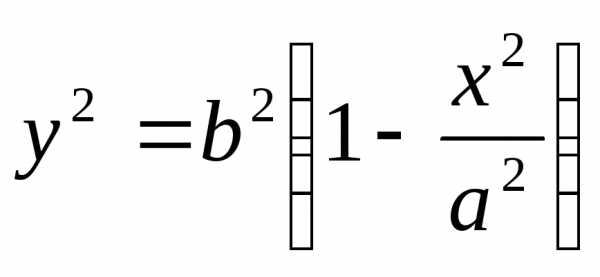 .
Так как,
имеем;
.
Так как,
имеем;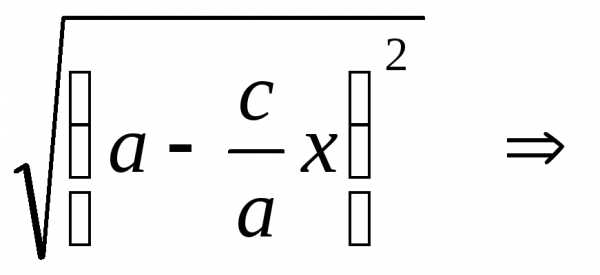
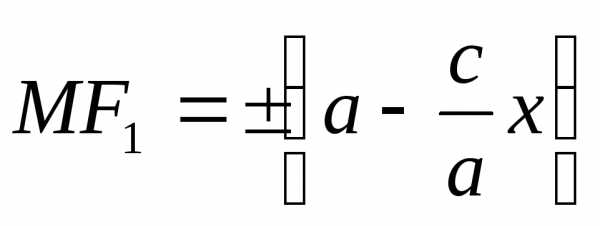 .
Так как,
то
.
Так как,
то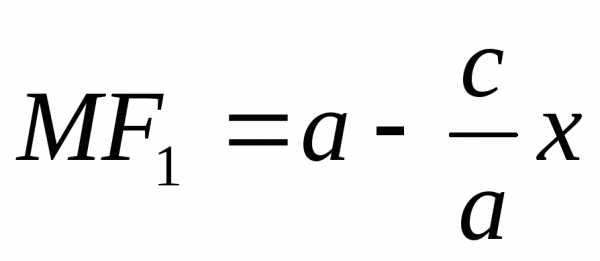 .
.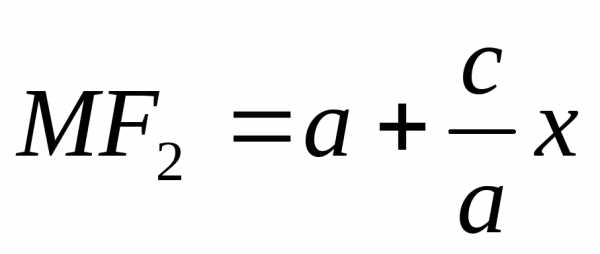
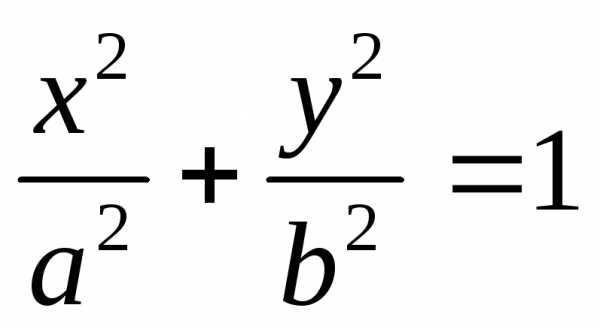 — каноническое уравнение эллипса
— каноническое уравнение эллипса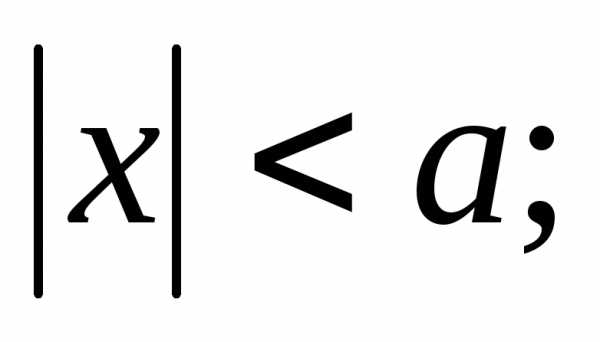
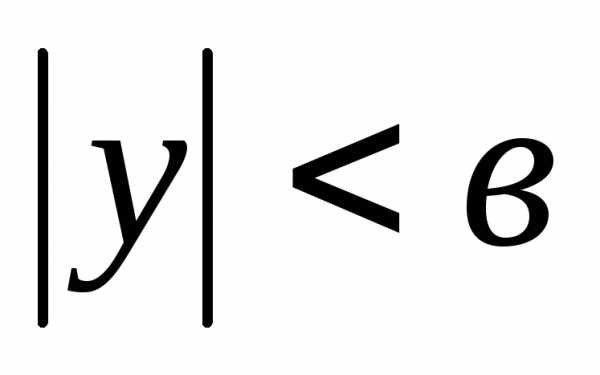 .
Это означает, что фигура эллипс есть
ограниченная фигура, не выходящая за
пределы прямоугольника со сторонами
.
Это означает, что фигура эллипс есть
ограниченная фигура, не выходящая за
пределы прямоугольника со сторонами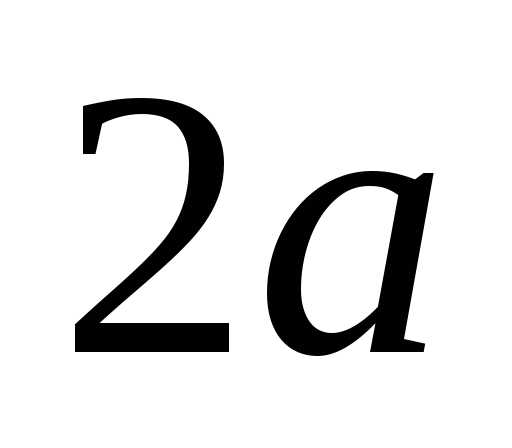 и
и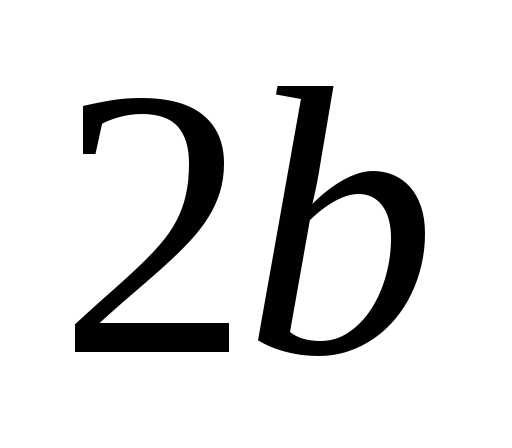 .
. ,
то она имеет координаты
,
то она имеет координаты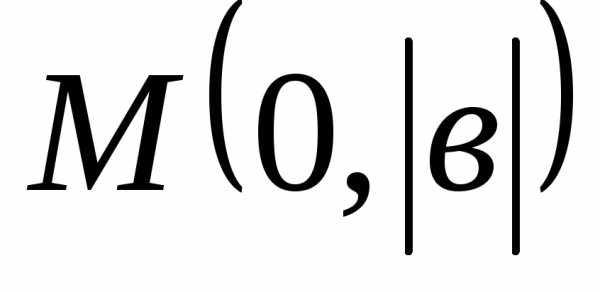 .
Если точка эллипса принадлежит оси
.
Если точка эллипса принадлежит оси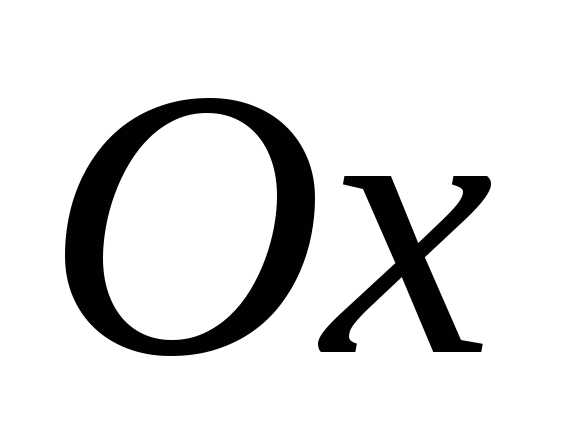 ,
то она имеет координаты
,
то она имеет координаты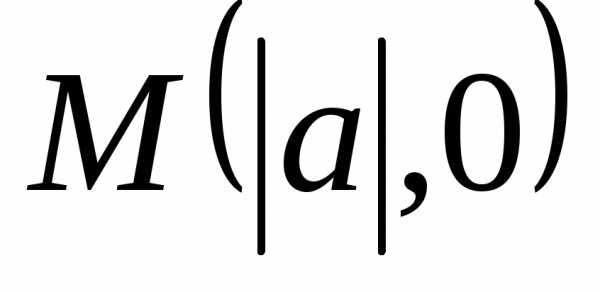 .
Значит, неравенства, определяющие
эллипс, имеют вид:
.
Значит, неравенства, определяющие
эллипс, имеют вид: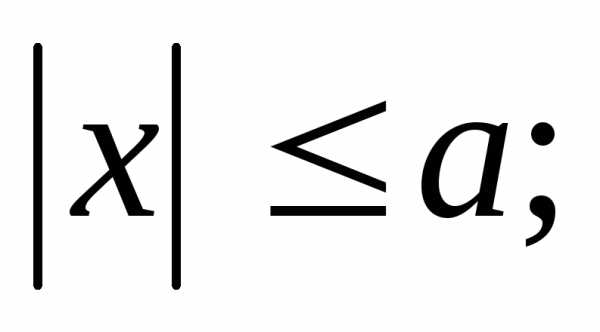
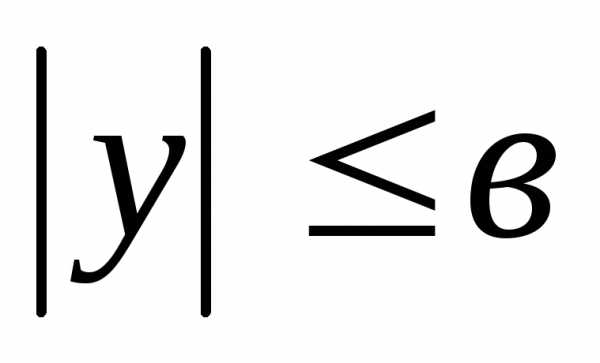 .
.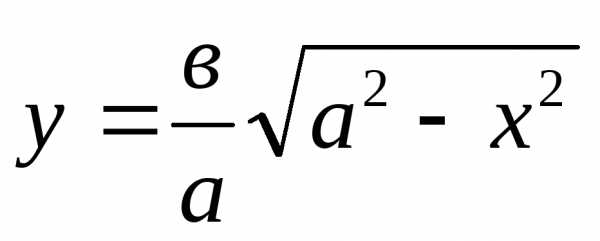 .
При возрастании
.
При возрастании от
от до
до ,
, монотонно убывает от
монотонно убывает от до
до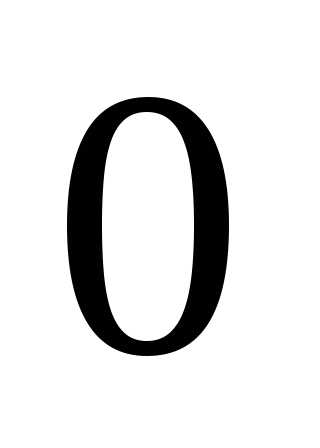 .
.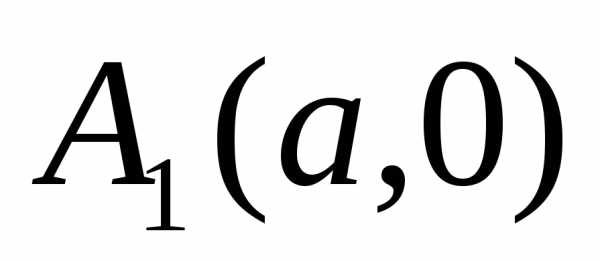 ,
,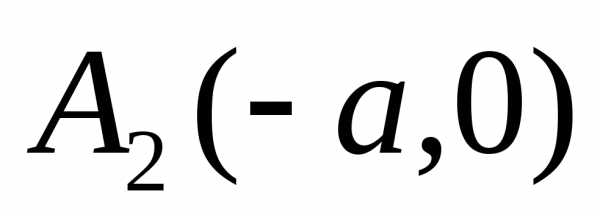 ,
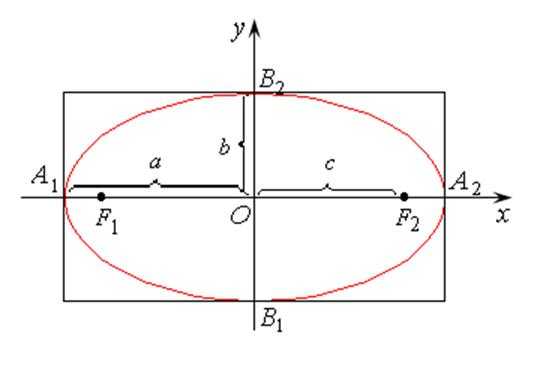
,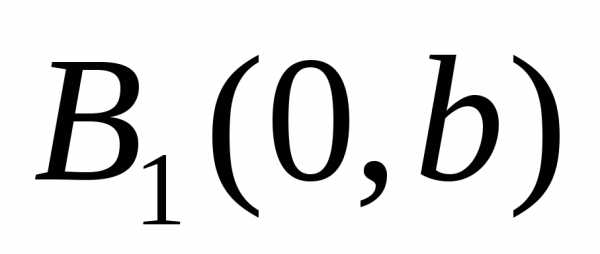 ,
,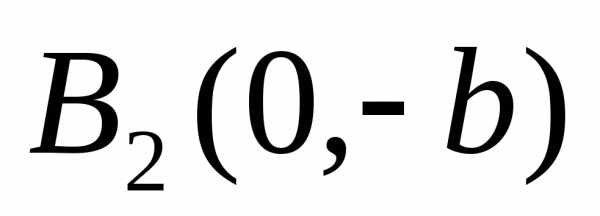 –вершины
эллипса.
Отрезки
–вершины
эллипса.
Отрезки  и
и называютсяосями
эллипса.
— большая ось,-
малая ось. Начало координат
называютсяосями
эллипса.
— большая ось,-
малая ось. Начало координат –центр
эллипса. Отрезки
–центр
эллипса. Отрезки  ,
, ,
, ,
, –полуоси
эллипса,
причём
–большие
полуоси;
–малые
полуоси.
–полуоси
эллипса,
причём
–большие
полуоси;
–малые
полуоси. ,
имеем, что.
Когда фокусы располагаются на оси
,
имеем, что.
Когда фокусы располагаются на оси ,
,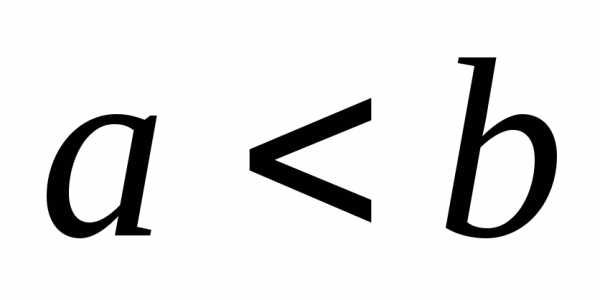 ,
тогда.
,
тогда.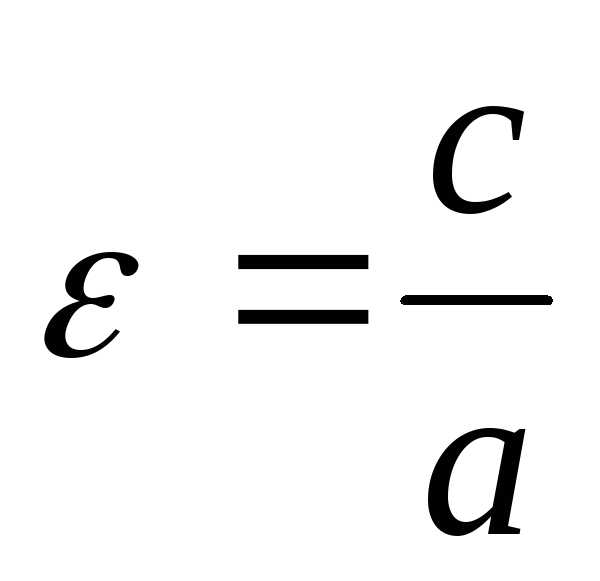 .
.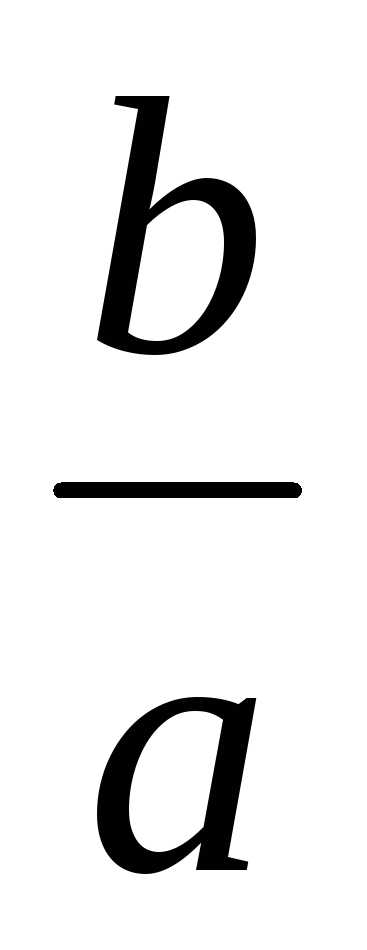 через эксцентриситет:.
Имеем, что
через эксцентриситет:.
Имеем, что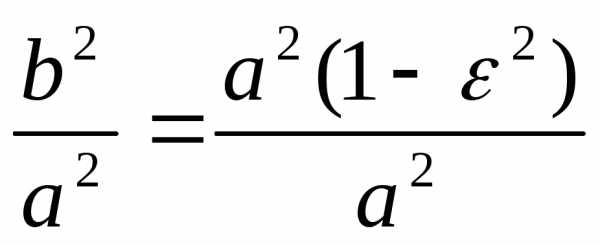

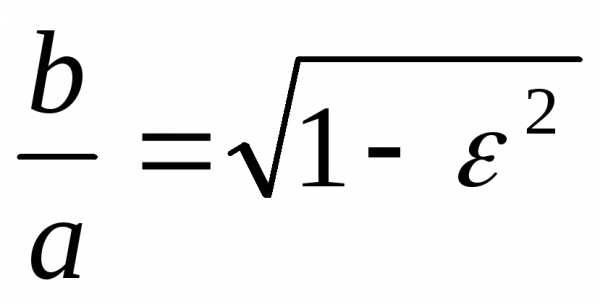 .
.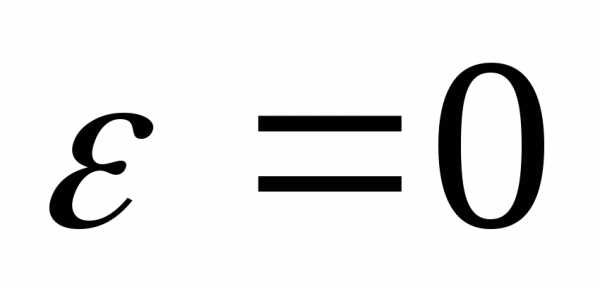
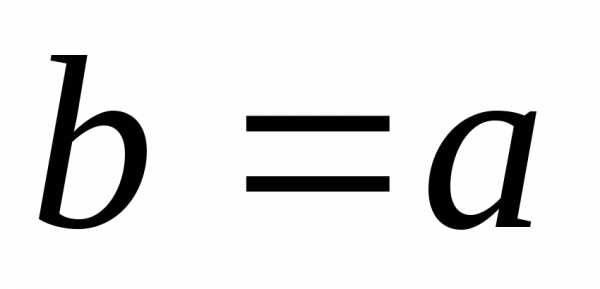 ,
эллипс похож на окружность. При увеличении
эксцентриситета эллипс вытягивается
вдоль оси
,
эллипс похож на окружность. При увеличении
эксцентриситета эллипс вытягивается
вдоль оси .
. ,
принадлежащей эллипсу, называются
отрезки, соединяющие эту точку с фокусами
,
принадлежащей эллипсу, называются
отрезки, соединяющие эту точку с фокусами и
и .
. ,
если он перпендикулярен оси
,
если он перпендикулярен оси и обозначается:
и обозначается: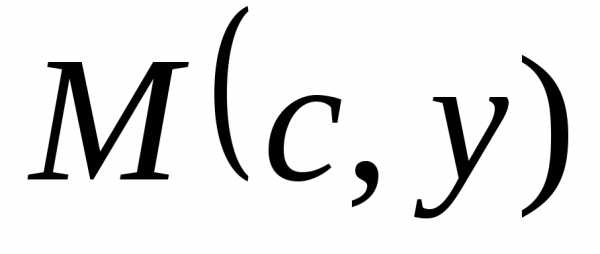 ,
то;
,
то;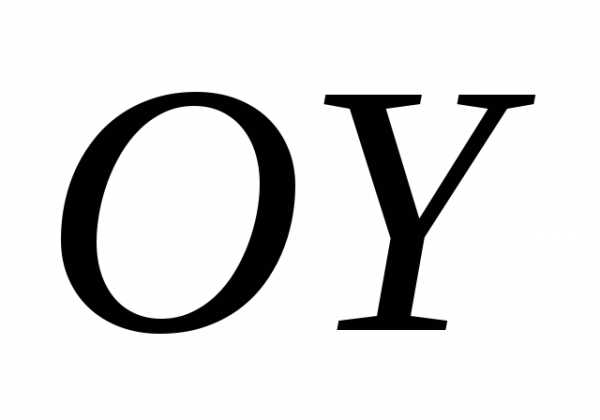 ,
находятся вне эллипса.
,
находятся вне эллипса.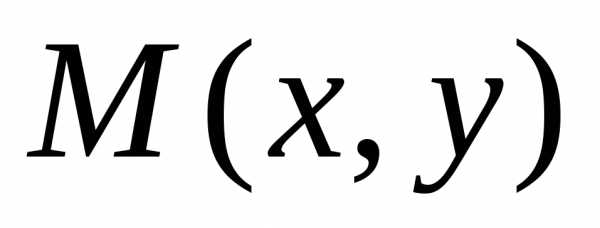 ,
принадлежащей эллипсу, до фокуса к
расстоянию от нее до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету.
,
принадлежащей эллипсу, до фокуса к
расстоянию от нее до соответствующей
директрисы есть величина постоянная,
равная эксцентриситету.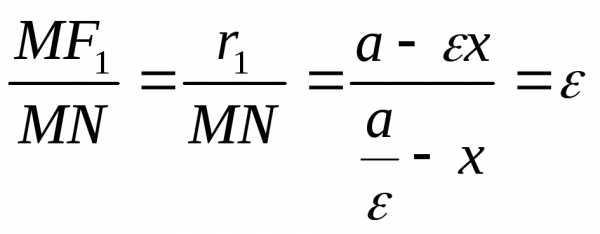
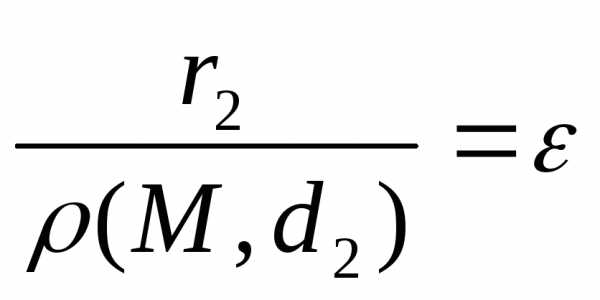
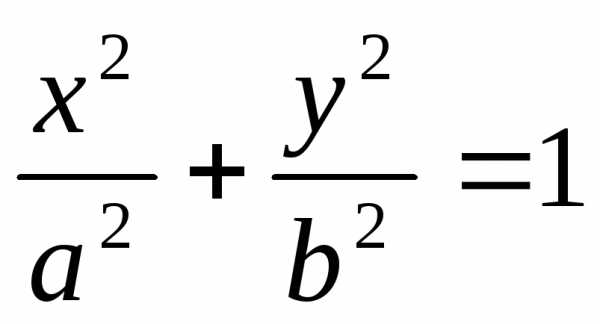 ,
причём
,
причём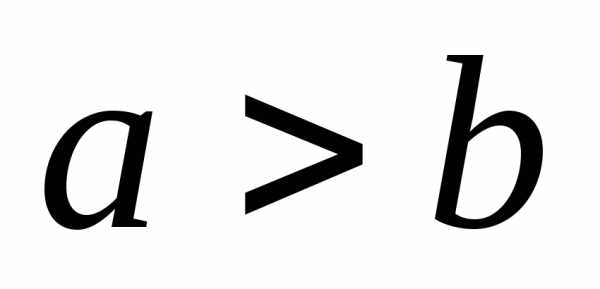 .
.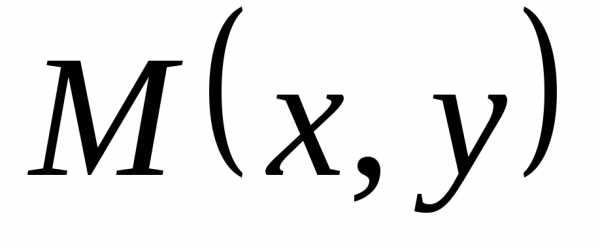 ,
принадлежащей
,
принадлежащей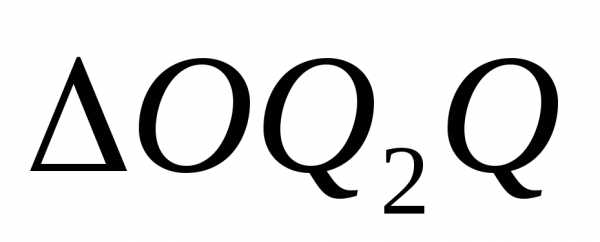 :
: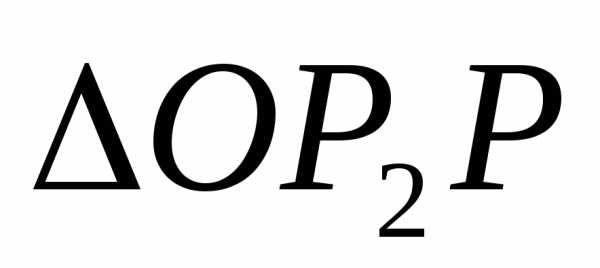 :
: .
.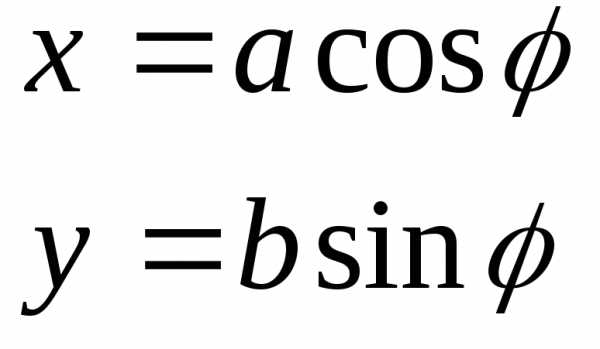 — параметрические
уравнения эллипса.
— параметрические
уравнения эллипса. и
и с расстоянием
с расстоянием .
В них фиксируются концы нити длиной
.
В них фиксируются концы нити длиной .
Натянув эту нить приложением к ней
острия карандаша, передвигают карандаш
так, чтобы нить все время была натянутой.
При этом карандаш вычертит эллипс, как
геометрическое место точек, сумма
расстояний каждой
из которых до двух данных
точек
.
Натянув эту нить приложением к ней
острия карандаша, передвигают карандаш
так, чтобы нить все время была натянутой.
При этом карандаш вычертит эллипс, как
геометрическое место точек, сумма
расстояний каждой
из которых до двух данных
точек  и
и есть величина постоянная, равная
есть величина постоянная, равная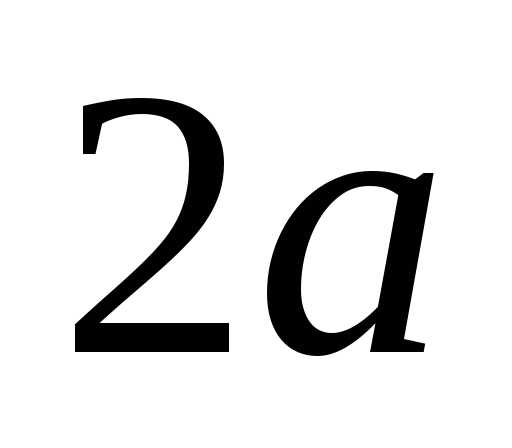
 .
.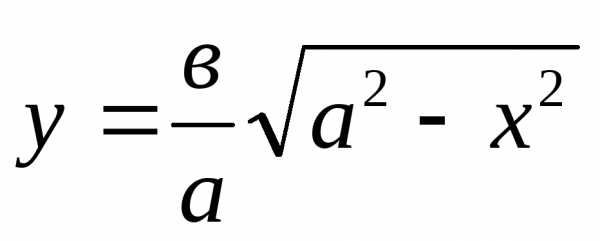 ,
а затем использовать симметричность
линии относительно осей координат и
начала координат.
,
а затем использовать симметричность
линии относительно осей координат и
начала координат. ,
,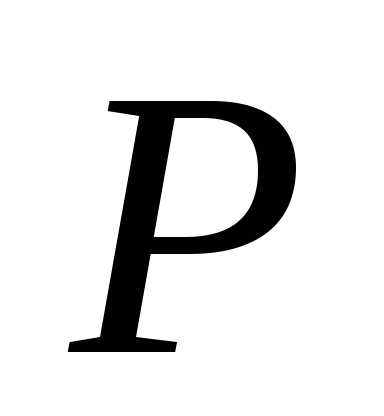 ;
; проведем прямую
проведем прямую ,
параллельно оси
,
параллельно оси ,
через точку
,
через точку — прямую
— прямую ,
параллельную оси
,
параллельную оси ;
; и
и –
точка эллипса
–
точка эллипса ;
; — произвольная точка эллипса, а
— произвольная точка эллипса, а есть
точка большой окружности, имеющая ту
же абсциссу, т.е. лежащая на той же
вертикальной прямой, что и
есть
точка большой окружности, имеющая ту
же абсциссу, т.е. лежащая на той же
вертикальной прямой, что и .
Тогда
.
Тогда ,.
,.
 большой окружности переходит в точку
большой окружности переходит в точку эллипса
с той же абсциссой, но с ординатой,
полученной из ординаты точки
эллипса
с той же абсциссой, но с ординатой,
полученной из ординаты точки умножением на число
умножением на число .
. .
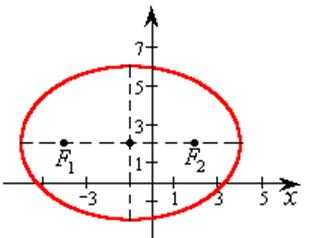
.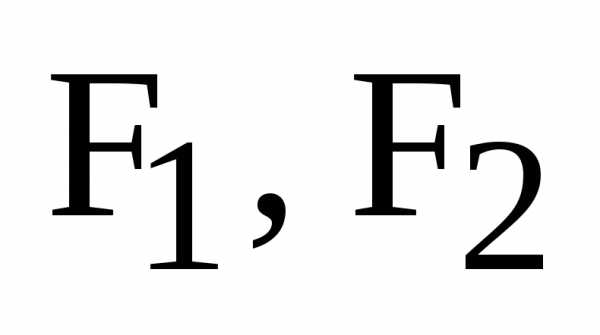 – фокусы эллипса,
– фокусы эллипса,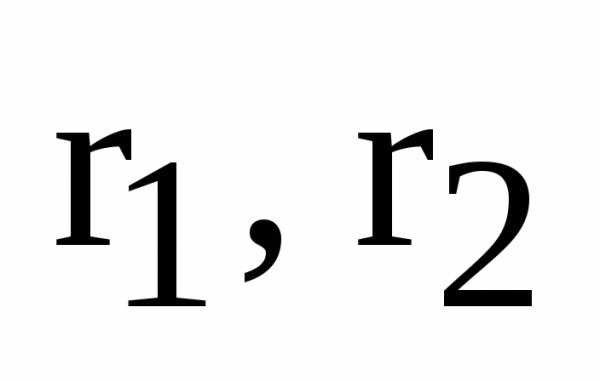 – фокальные радиусы точки М.
– фокальные радиусы точки М.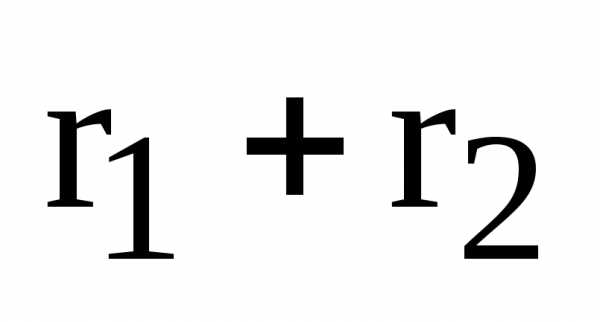 – постоянная величина. Эту постоянную
принято обозначать 2а:
– постоянная величина. Эту постоянную
принято обозначать 2а: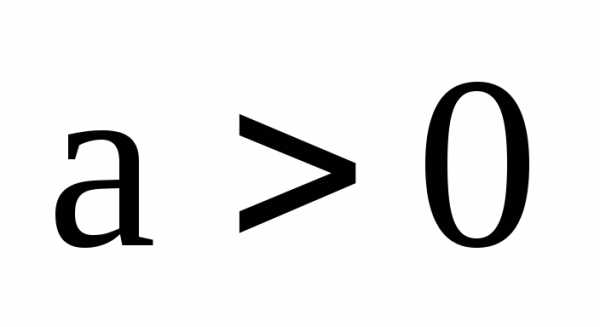 .
.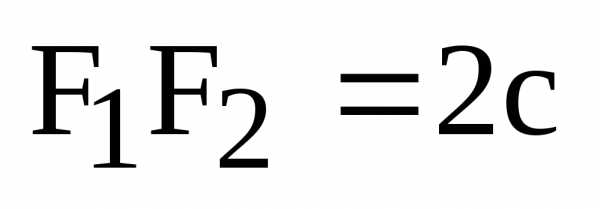 .
.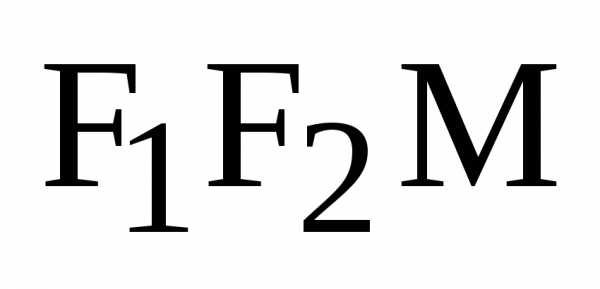 следует, что,
т.е.
следует, что,
т.е. .
.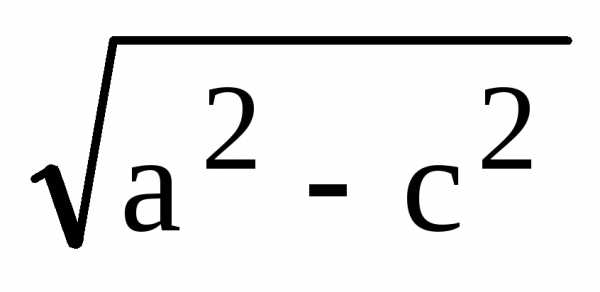 ,
т.е.
,
т.е.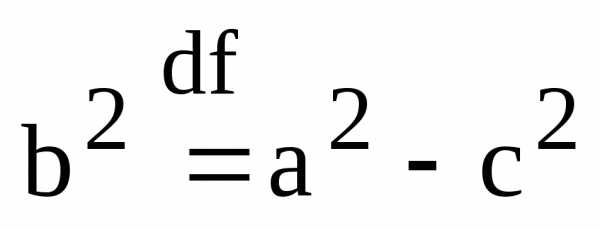 .
(2)
.
(2)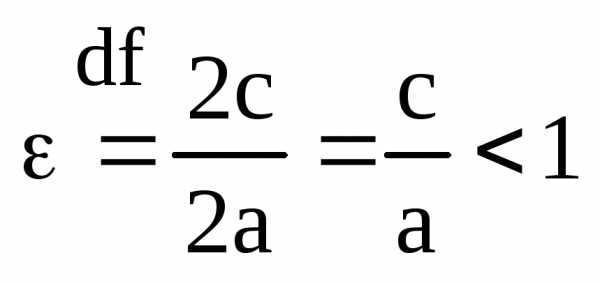 (3)
(3)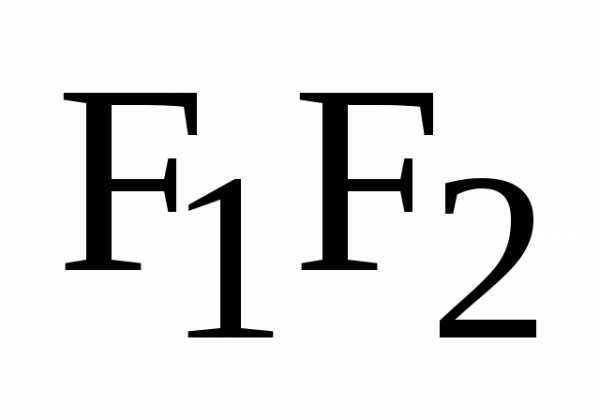 перпендикулярно фокальной оси.
перпендикулярно фокальной оси.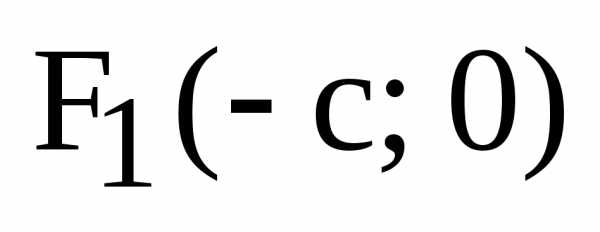 ,
,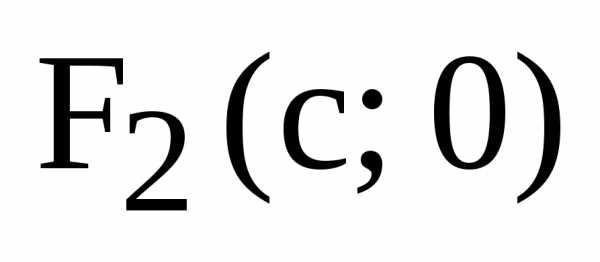 .
.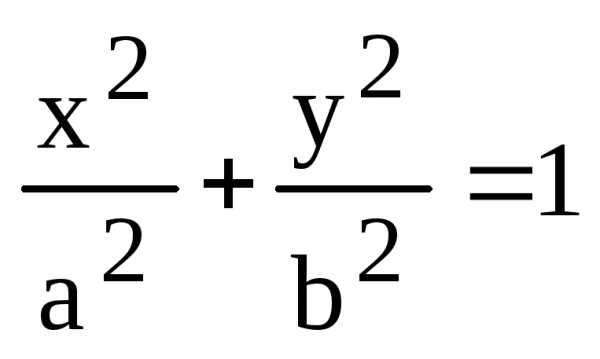 .
(4)
.
(4)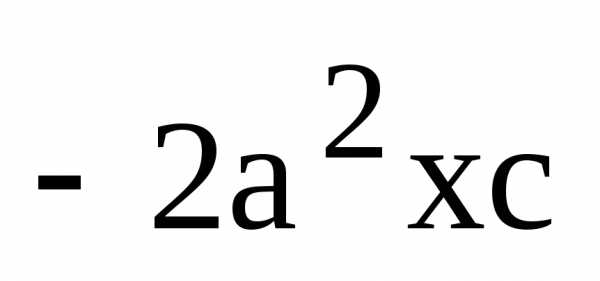 :
: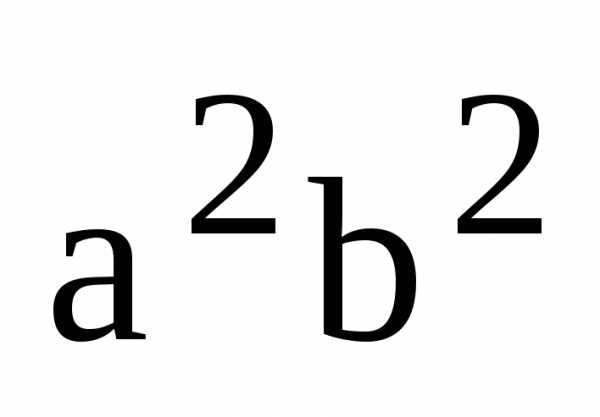 ,
получаем равенство (4), ч.т.д.
,
получаем равенство (4), ч.т.д.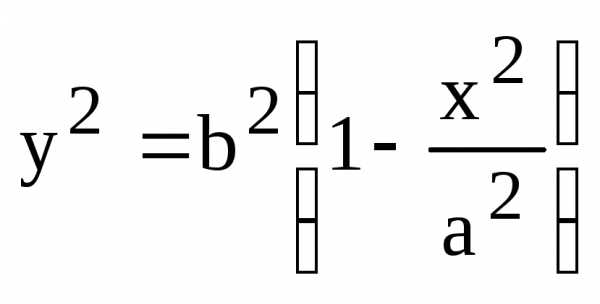 .
.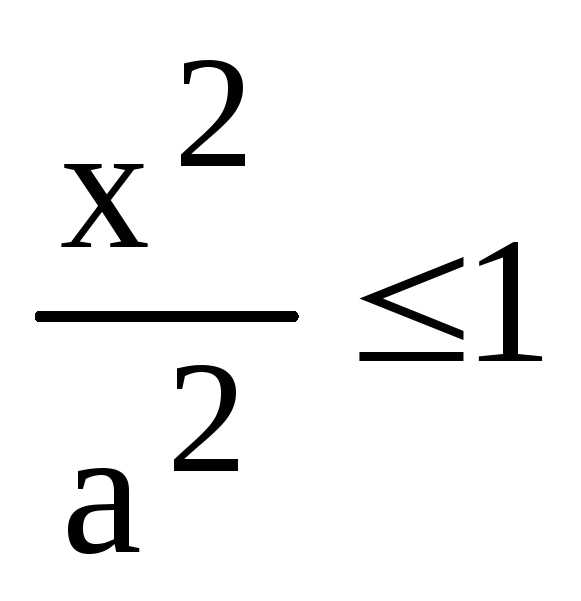 или
или 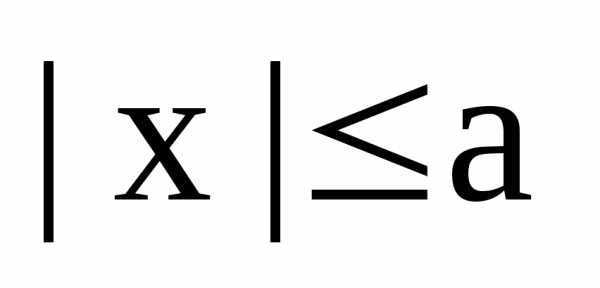 и т.к.
и т.к.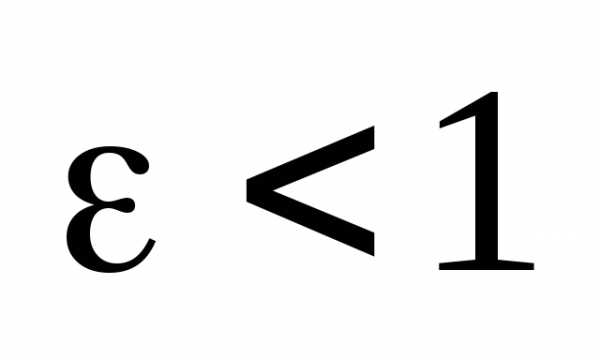 ,
то отсюда следует неравенство:
,
то отсюда следует неравенство: ,
.
(5)
,
.
(5) ,
,  .
. .
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.
.
Затем берем карандаш и с его помощью
натягиваем нить. Затем передвигаем
карандашный грифель по плоскости, следя
за тем, чтобы нить была в натянутом
состоянии.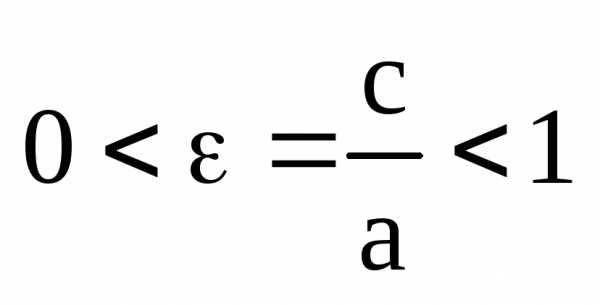
 ,
, и
и .
В пределе мы получаем
.
В пределе мы получаем или
– уравнение окружности.
или
– уравнение окружности. .
Тогда
.
Тогда ,
, и мы видим, что в пределе эллипс вырождается
в отрезок прямой
и мы видим, что в пределе эллипс вырождается
в отрезок прямой в обозначениях рисунка 3.
в обозначениях рисунка 3.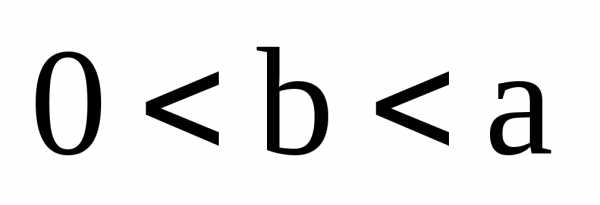 – произвольные действительные числа.
Тогда система уравнения
– произвольные действительные числа.
Тогда система уравнения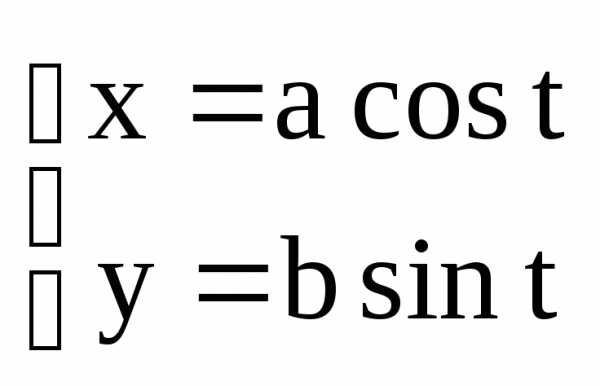 ,
, 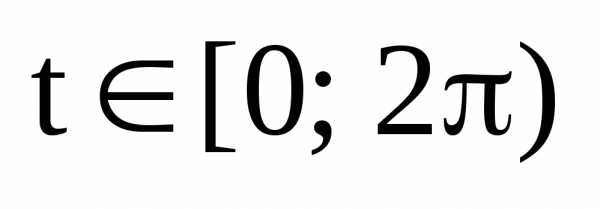 (6)
(6)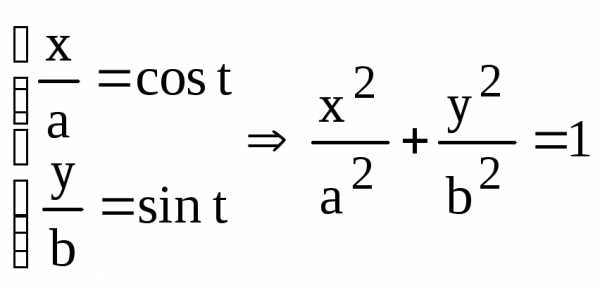 .
.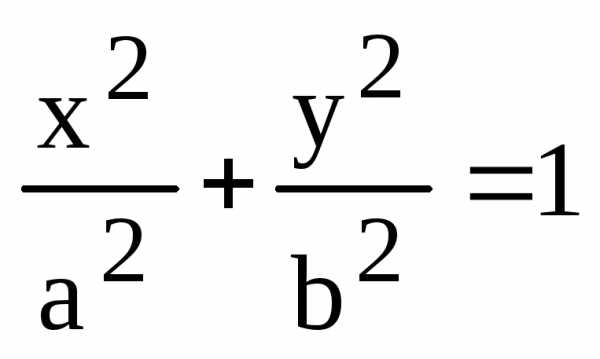 .
.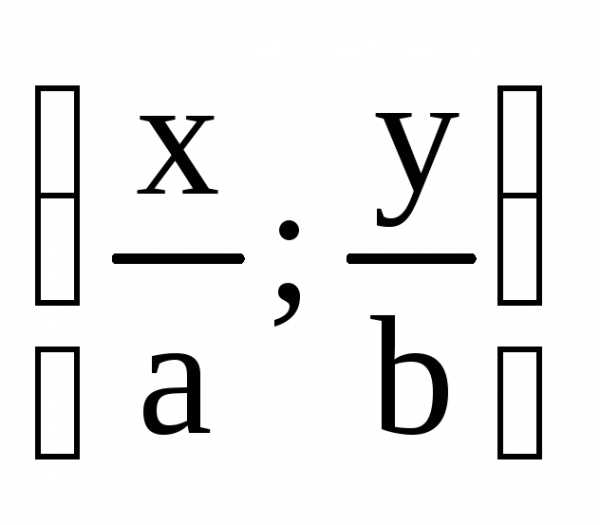 лежит на окружности единичного радиуса
с центром в начале координат, т.е. является
точкой тригонометрической окружности,
которой соответствует некоторый угол
лежит на окружности единичного радиуса
с центром в начале координат, т.е. является
точкой тригонометрической окружности,
которой соответствует некоторый угол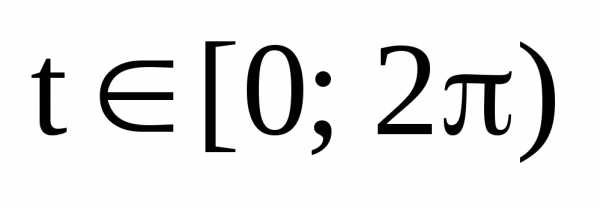 :
: ,
,  ,
где
,
где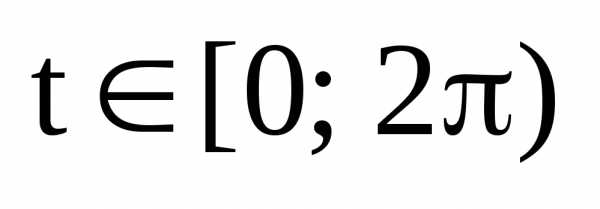 ,
откуда и следует, что пара (х, у) является
решением системы (6), ч.т.д.
,
откуда и следует, что пара (х, у) является
решением системы (6), ч.т.д.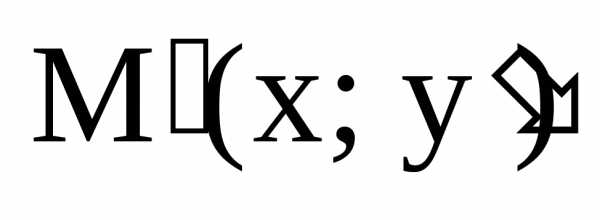 ,
где
,
где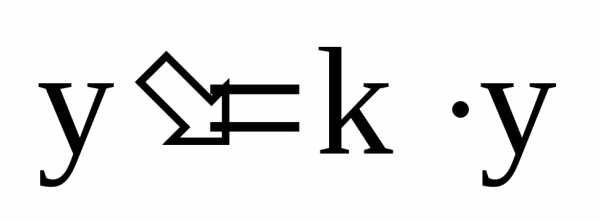 ,
,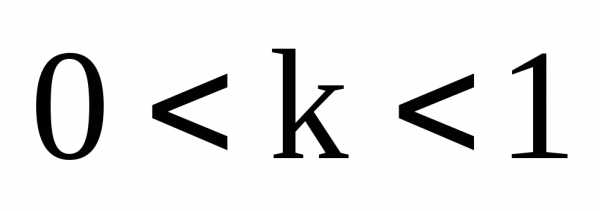 – коэффициент «сжатия».
– коэффициент «сжатия».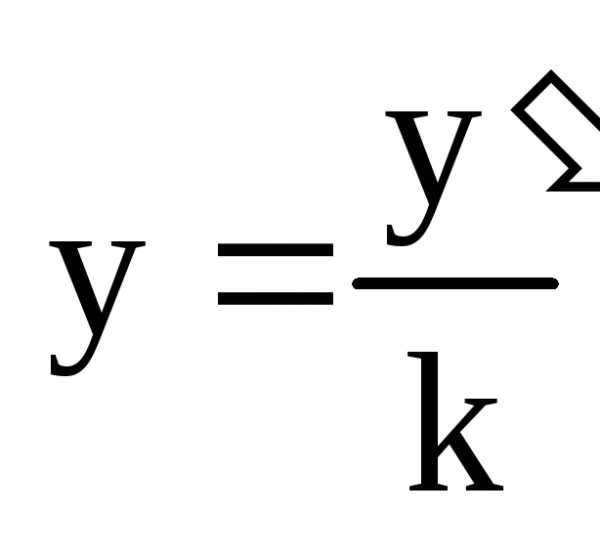
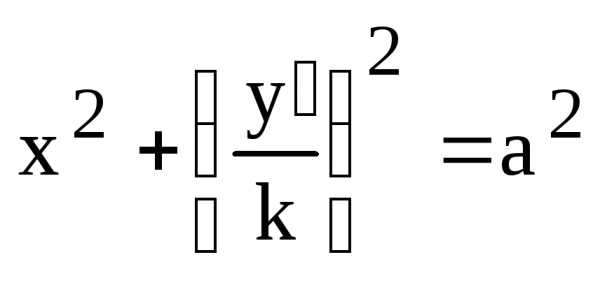 .
.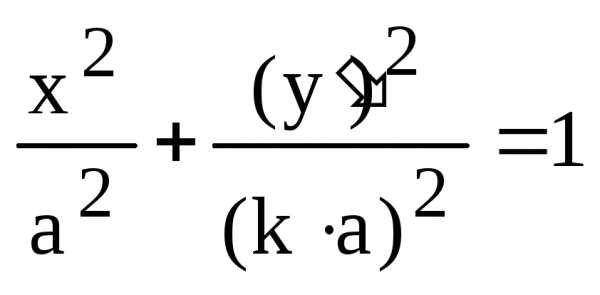 .
(7)
.
(7) ,
координаты которой удовлетворяют
уравнению эллипса (7). Если мы хотим
получить уравнение эллипса с малой
полуосьюb, то нужно взять
коэффициент сжатия
,
координаты которой удовлетворяют
уравнению эллипса (7). Если мы хотим
получить уравнение эллипса с малой
полуосьюb, то нужно взять
коэффициент сжатия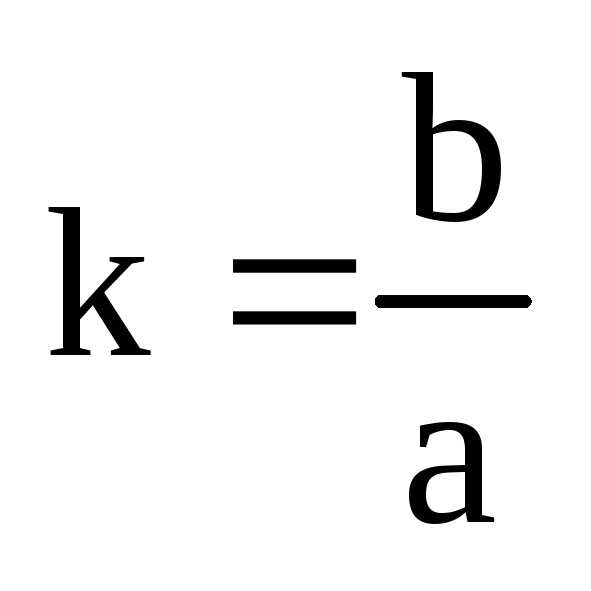 .
.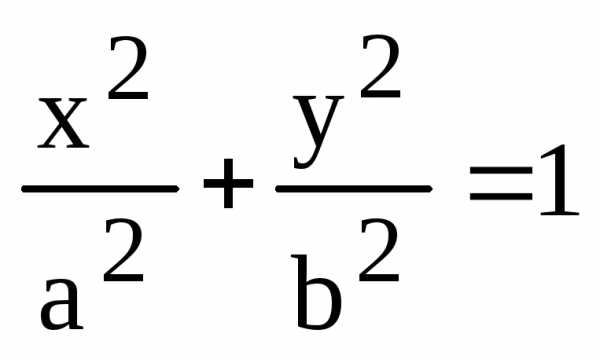 .
.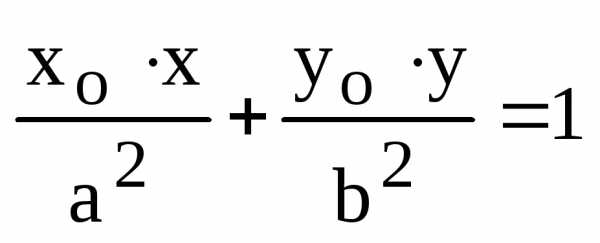 .
(8)
.
(8)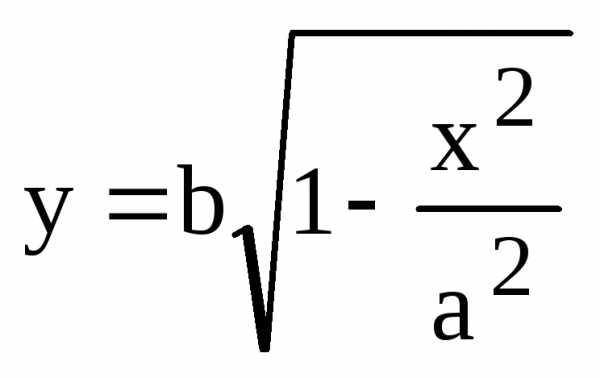 .
(9)
.
(9)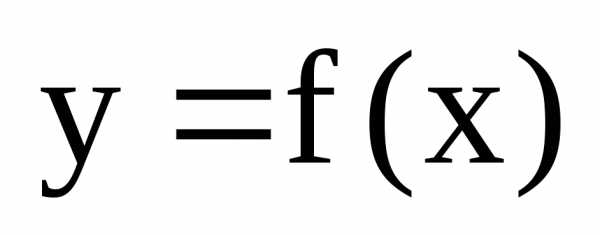 в точке:
в точке: – значение производной данной функции
в точке
– значение производной данной функции
в точке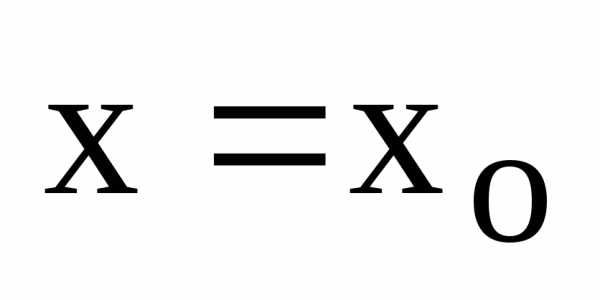 .
Эллипс в первой четверти можно
рассматривать как график функции (8).
Найдем ее производную и ее значение в
точке касания:
.
Эллипс в первой четверти можно
рассматривать как график функции (8).
Найдем ее производную и ее значение в
точке касания: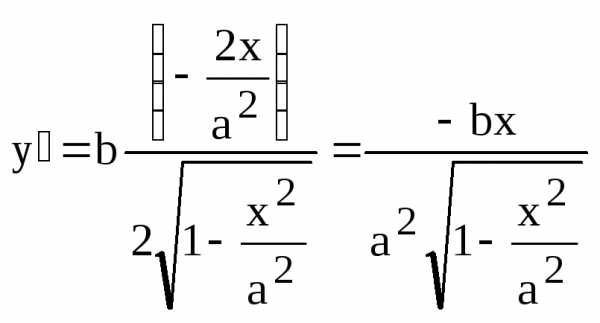 ,
,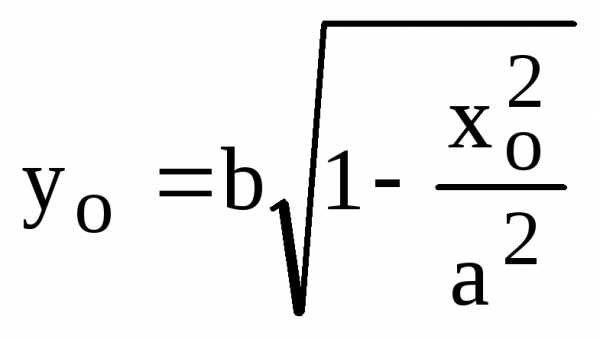 .
. :
: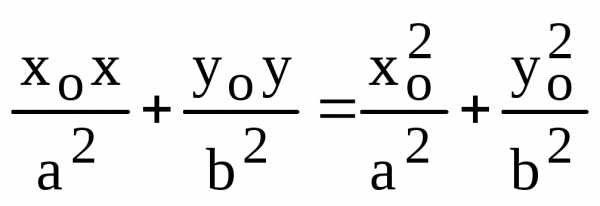 .
.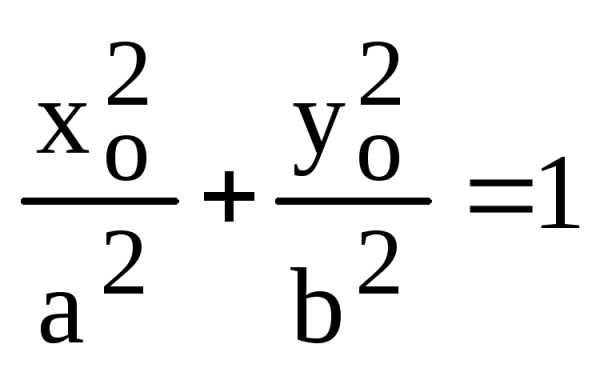 ,
т.к. точкапринадлежит эллипсу и ее координаты
удовлетворяют его уравнению.
,
т.к. точкапринадлежит эллипсу и ее координаты
удовлетворяют его уравнению.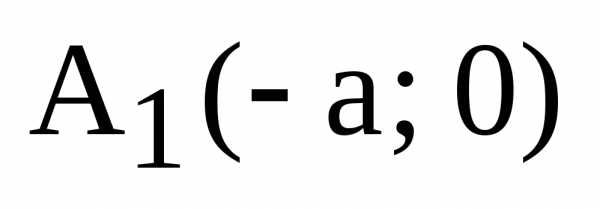 ,
,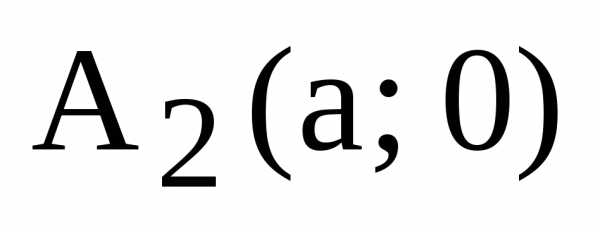 :
: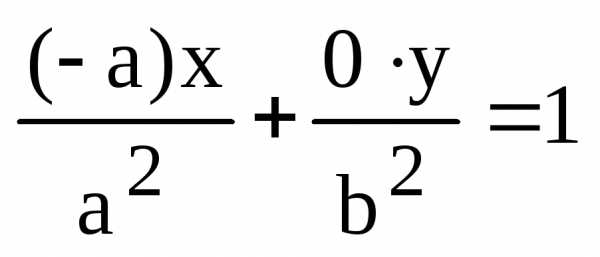 или
или 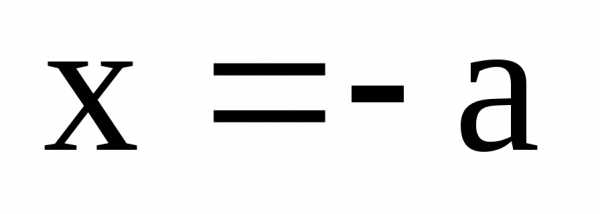 ,
и
,
и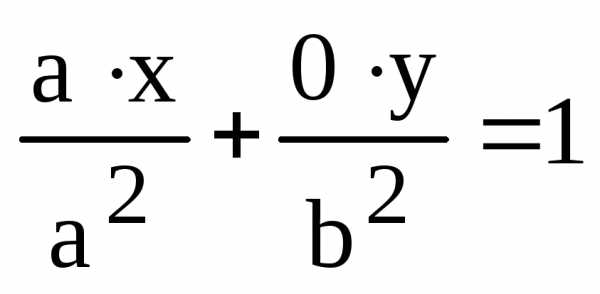 или
или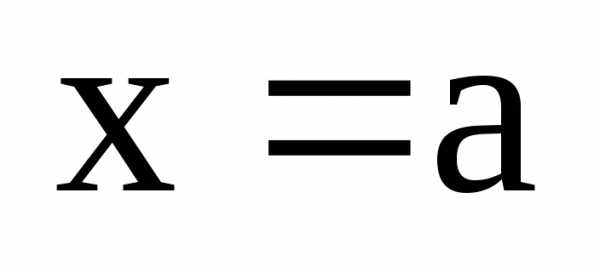 .
.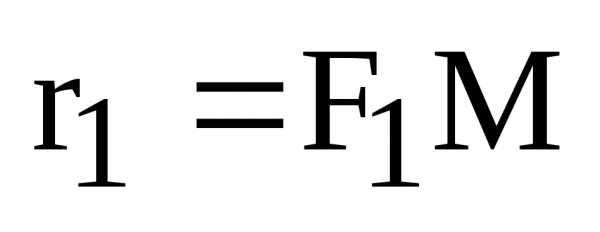 ,
,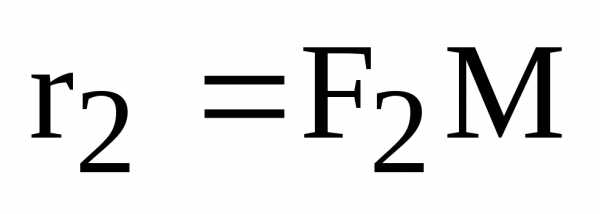 – фокальные радиусы точки касания, Р иQ– проекции фокусов на
касательную, проведенную к эллипсу в
точке.
– фокальные радиусы точки касания, Р иQ– проекции фокусов на
касательную, проведенную к эллипсу в
точке.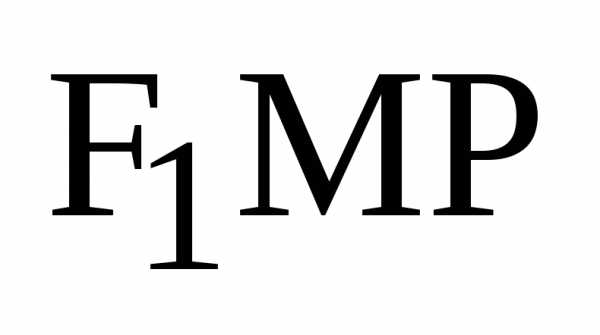 и
и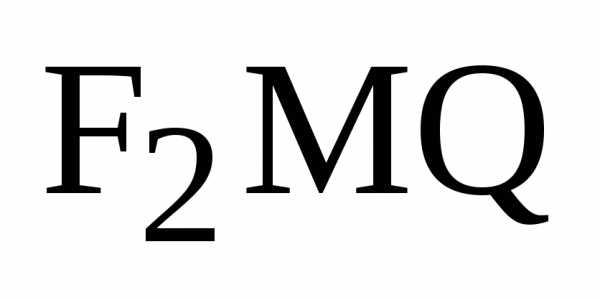 ,
в которых стороны
,
в которых стороны и
и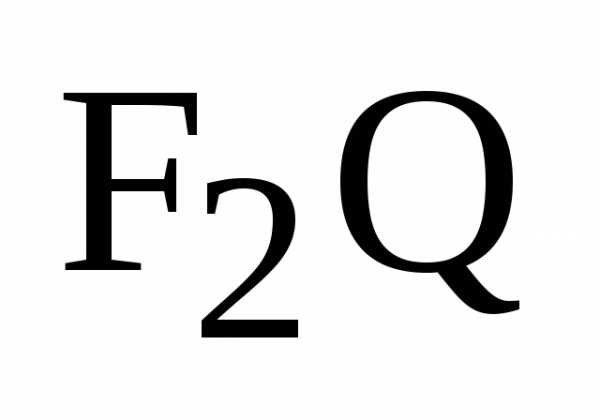 будут сходственными. Так как треугольники
прямоугольные, то достаточно доказать
равенство
будут сходственными. Так как треугольники
прямоугольные, то достаточно доказать
равенство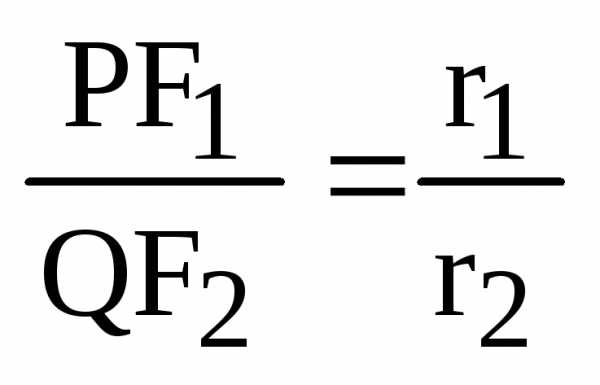 .
(12)
.
(12) до касательнойL(см.
рис.7),.
Воспользуемся формулой расстояния от
точки до прямой на плоскости:
до касательнойL(см.
рис.7),.
Воспользуемся формулой расстояния от
точки до прямой на плоскости: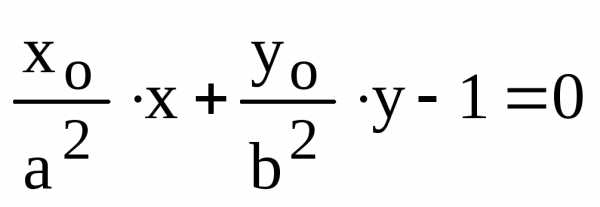 ,
,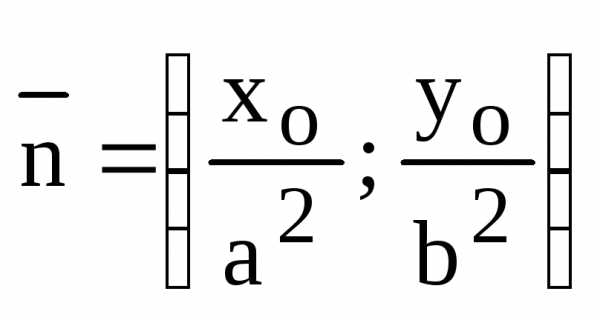 – нормальный вектор касательнойL.
– нормальный вектор касательнойL.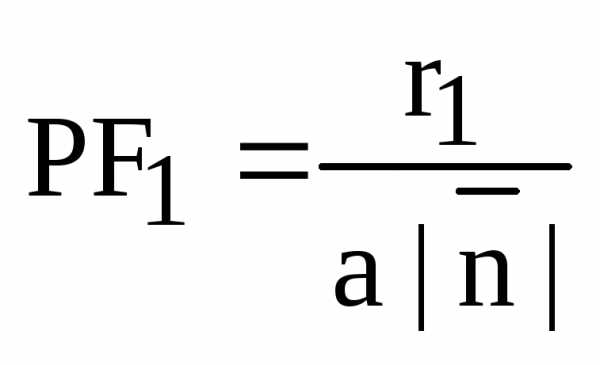 .
.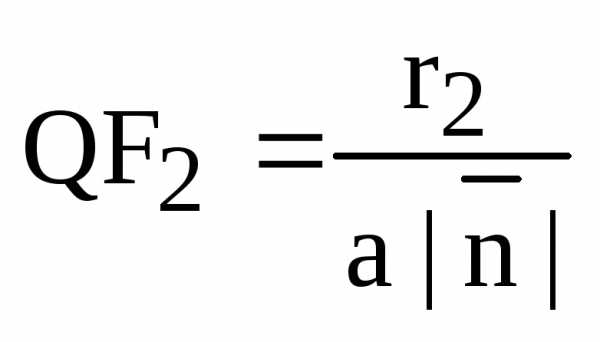 и
и ,
ч.т.д.
,
ч.т.д.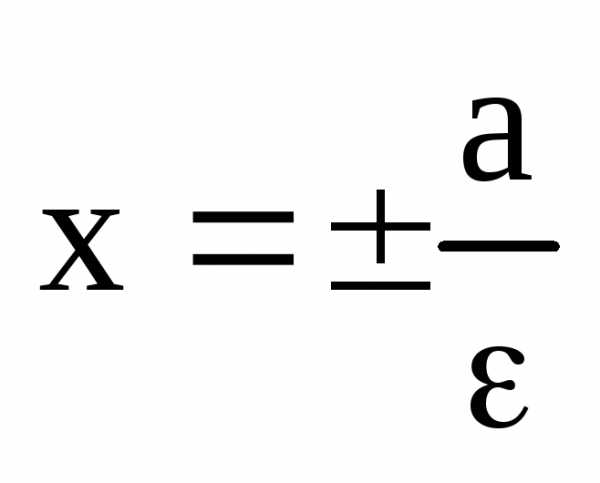 или
или  .
(13)
.
(13) ,
,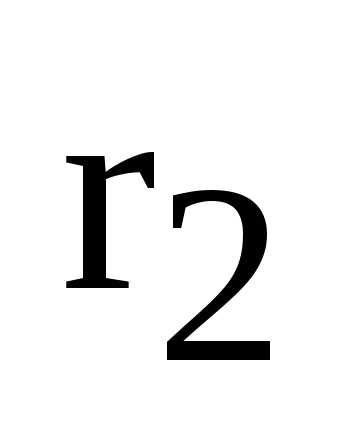 – ее фокальные радиусы,
– ее фокальные радиусы,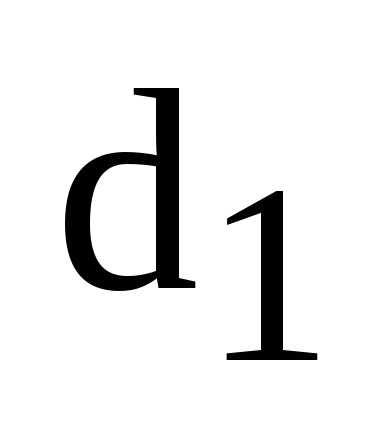 – расстояние от точки М до левой
директрисы,
– расстояние от точки М до левой
директрисы,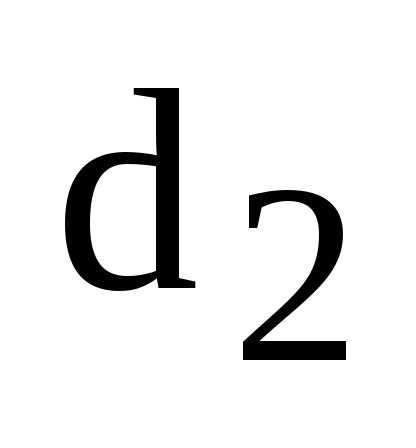 – до правой. Тогда
– до правой. Тогда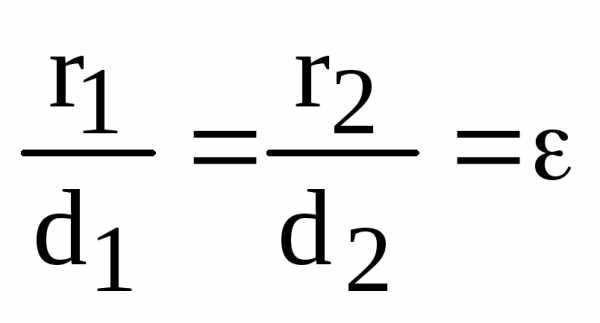 ,
(14)
,
(14) – эксцентриситет эллипса.
– эксцентриситет эллипса.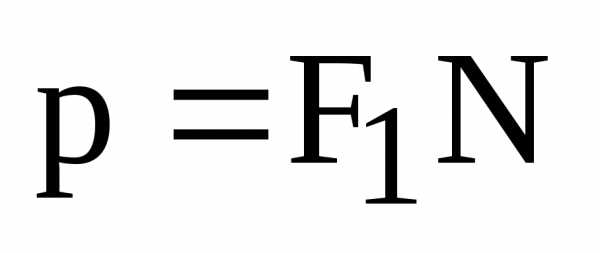 .
.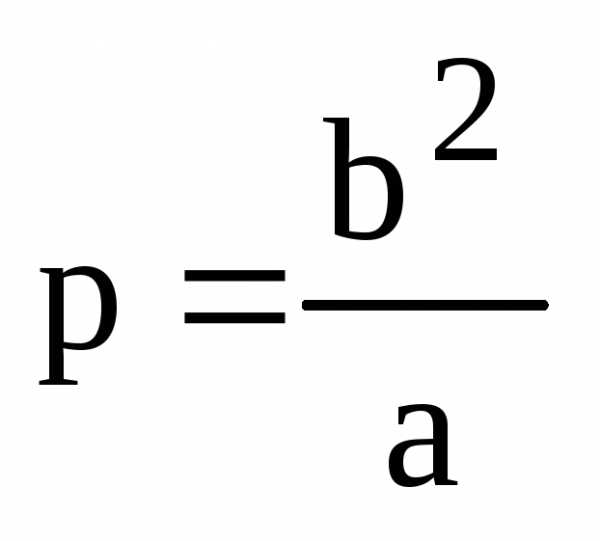 .
(15)
.
(15)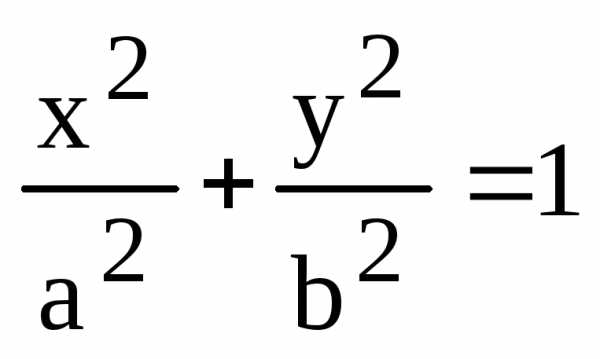 ,
то ее координаты удовлетворяют его
уравнению:
,
то ее координаты удовлетворяют его
уравнению: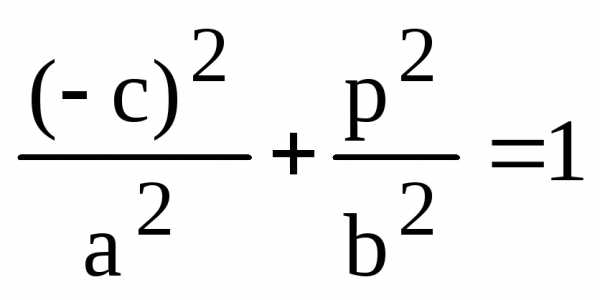 .
.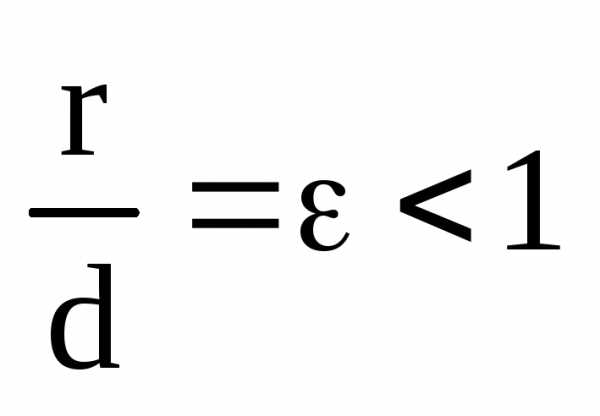 .
.
 Решение.
Сгруппируем слагаемые, содержащие x и y:
Решение.
Сгруппируем слагаемые, содержащие x и y: