Переход от одних способов выражения концентраций к другим — КиберПедия
1. Массовая доля (процентная концентрация) ω% ® молярная концентрация С(X):
или ,
где − плотность раствора; − молярная масса.
2. Массовая доля (процентная концентрация) ω% ® молярная концентрация эквивалента C[(1/z)X] (нормальная концентрация Cн):
или ,
где − плотность раствора; − молярная масса эквивалента.
3. Массовая доля (процентная концентрация) ω% ® моляльная концентрация B(X):
,
где − молярная масса.
4. Молярная концентрация С(X) − молярная концентрация эквивалента C[(1/z)X] (нормальная концентрация Cн):
, z – эквивалентное число.
Для растворов веществ с z = 1 молярная концентрация С(X) и молярная концентрация эквивалента C[(1/z)X] совпадают.
Решение задач
Приготовление растворов
Приготовить раствор заданной концентрации можно растворени-ем вещества в воде, разбавлением концентрированного раствора, смешиванием растворов разных концентраций. Как правило, задаются объем раствора и его концентрация. Необходимо рассчитать массу растворяемого вещества или объем концентрированного раствора, добавлением воды к которому до заданного объема получают раствор требуемой концентрации. Если концентрация раствора − массовая доля (ω%), то для расчета необходимо знать его плотность.
При решении задачи необходимо:
1. Рассчитать количество растворенного вещества, содержаще-гося в объеме раствора заданной концентрации. Это может быть масса (г), количество молей или эквивалентов, необходимое для приготовления раствора.
2. При растворении вещества определяют массу вещества, необ-ходимого для приготовления раствора (см. примеры 1, 2).
3. В случае приготовления раствора разбавлением рассчитывают объем концентрированного раствора, содержащий столько же веще-ства, сколько содержит заданный раствор (см. примеры 3, 4).
Пример 1. Приготовить 500 мл 10% раствора карбоната калия (K2CO3), плотность раствора . Рассчитать молярную концентрацию полученного раствора.
1. Масса раствора
.
2. Масса растворенного вещества
.
3. Молярная концентрация полученного раствора.
,
где М(K2CO3) = 39·2 + 12 + 16·3 = 138 г/моль.
Вывод. Для приготовления заданного раствора навеску карбоната калия m = 54,5 г растворить в воде и довести объем раствора до
500 мл. Молярная концентрация полученного раствора С(K2CO3) = = 0,79 моль/л.
Пример 2. Приготовить 1 л 0,1 н. раствора карбоната натрия (Na2CO3). Рассчитать процентную концентрацию полученного рас-твора. Плотность раствора .
Так как 0,1 н. раствор º молярная концентрация эквивалента C[(1/2)Na2CO3] = 0,1 моль/л, можно рассчитать массу растворенного вещества в 1 л раствора 0,1 н.
1. Расчет массы Na2CO3: 1 л раствора соли содержит 0,1 моль эквивалентов Na2CO3
n[(1/2)] = C[(1/2)Na2CO3]∙V = 0,1·1 = 0,1 моль.
М(Na2CO3) = 23·2 + 12 + 16·3 = 106 г/моль, z = 2,
,
m(Na2CO3) = M[(1/2)Na2CO3]·n[(1/2)Na2CO3] = 53·0,1 = 5,3 г.
2. Процентная концентрация полученного раствора
Вывод. Для приготовления заданного раствора навеску карбоната натрия m = 5,3 г растворить в воде и довести объем раствора до 1 л. Массовая доля Na2CO3 ω% = 0,5%.
Пример 3. Приготовить 200 мл 2 М раствора серной кислоты разбавлением 96% раствора с плотностью .
Так как 2М раствор ≡ молярная концентрация серной кислоты С(H2SO4) = 2 моль/л, следовательно, 1 л раствора кислоты содержит
2 моль H2SO4.
1. Масса растворенного вещества (H2SO4) в 200 мл 2 М раствора:
n(H2SO4) = С(H2SO4)·V = 2·0,2= 0,4 моль,
где V − объем раствора в литрах.
2. Масса серной кислоты:
m(H2SO4) = М(H2SO4)·n(H2SO4) = 98·0,4= 39,2 г,
где М(H2SO4) = 98 г/моль − молярная масса серной кислоты.
3. Масса раствора H2SO4 при ω% = 96%:
® .
Объем раствора H2SO4 при ω% = 96%:
см3.
Вывод. Для приготовления заданного раствора 22,2 мл H2SO4 ω% = 96 % растворить в воде и довести объем раствора до 200 мл.
Данную задачу можно решить другим способом. Если перейти
от массовой концентрации к молярной = , то можно воспользоваться условием равенства количества молей серной кислоты в концентрированном и заданном растворе:
n(H2SO4) = С(H2SO4)1∙V1 = С(H2SO4)2∙V2
.
Пример 4. Приготовить 500 мл 10% раствора соляной кислоты разбавлением концентрированного раствора ω% = = 35% с плотностью .
1. Масса раствора 10%
.
2. Масса растворенного вещества (HCl)
.
3. Масса раствора 35%
® .
Объем раствора HCl ω% = 35 %
см3.
Вывод. Для приготовления заданного раствора растворить 127,5 мл HCl с концентрацией ω% = 35 % в воде и довести объем раствора до 500 мл.
cyberpedia.su
Пересчет концентраций растворов из одних единиц в другие
В лабораторной практике часто приходится проводить пересчет концентрации имеющихся растворов из одних единиц в другие. При пересчете процентной концентрации в молярную и наоборот необходимо помнить, что процентная концентрация рассчитывается на определенную массу раствора, а молярная и нормальная — на объем, поэтому для пересчета необходимо знать плотность раствора.
Плотность раствора приводится в справочниках в соответствующих таблицах или измеряется ареометром. Если мы 0|бозначим: С — процентная концентрация; М — молярная концентрация; /V — нормальная концентрация; d — плотность раствора; Э — эквивалентная масса; m — мольная масса, то формулы для пересчета из процентной концентрации в молярную и нормальную будут следующими:
но пересчитать нормальную или молярную концентра-
цию на процентную. /
Пример 1. Какова молярная и нормальная концентрация 12% раствора серной кислоты, плотность которого d=l,08 г/см??
Решение. Мольная масса серной кислоты равна 98. Следовательно, oth2so4 =98 и 3h2so4 =98 : 2=49.
Подставляя необходимые значения в формулы, получим:
1) молярная концентрация 12% раствора серной кислоты равна
12-1,0810
М =——————— = 1,32 М;
2) нормальная концентрация 12% раствора серной кислоты равна
12-1,0810
N =———- ^——- = 2,64 н.
Пример 2. Какова процентная концентрация 1 н. раствора соляной кислоты, плотность которого 1,013?
Решение. Мольная масса НС1 равна 36,5, следовательно, Знс1 = = 36,5. Из приведенной выше формулы (2) получим:
9.N С~ 10 ‘
следовательно, процентная концентрация 1 н. раствора соляной кислоты равна
36,5-1 С= 1,013-10 =3‘6%—
Иногда в лабораторной практике приходится пересчитывать молярную концентрацию в нормальную и наоборот. Бели эквивалентная масса вещества равна мольной массе (например, для НО, КО, КОН), то нормальная концентрация равна молярной концентрации. Так, 1 н. раствор соляной кислоты будет одновременно 1 М раствором. Однако для большинства соединений эквивалентная масса не равна мольной и, следовательно, нормальная концентрация растворов этих веществ не равна молярной концентрации.
Для пересчета из одной концентрации в другую мы можем пользоваться формулами:
N9
М = (NЭ)/m ; N=M(m/Э)
Примеру 3. Нормальная концентрация 1 М раствора серной кислоты
\ /V=l^g- = 2H.
Пример 4, Молярная концентрация 0,5 н. раствора Na2C03
\ 53
M = 0,5^Qg- =0,25 М.
505days.com
Молярная и нормальная концентрации
Молярная концентрация (молярность) показывает, сколько моль вещества содержится в 1 л (1000мл) раствора. Молярность обозначается СМ — моль/л, (M), например, 1 моль/л, 0,5 М.
Нормальная концентрация (нормальность) показывает, сколько эквивалентов растворенного вещества содержится в 1л (1000мл) раствора. Нормальность раствора обозначают буквами СН – моль/л, (Н), например, 1 моль/л, 0,5 Н.
0,2 М раствора Na2SO4 — это означает, что в 1л (1000мл) содержится 0,2 моля Na2SO4 или 0,2∙106=21,2 г Na2SO4.
В 1 л 0,2 н раствора Na2SO4 содержится 0,2 моль эквивалентов соли или 0,2∙53=10,6 г Na2SO4.
Пример 6. Сколько граммов растворенного вещества содержится в 0,5 л 0,1 М раствора H2SO4?
Решение. 1 моль H2SO4 составляет 98 г
0,1 моль H2SO4 составляет Х г
1000 мл раствора содержат 9,8 г H2SO4
500 мл раствора содержат Х г H2SO4
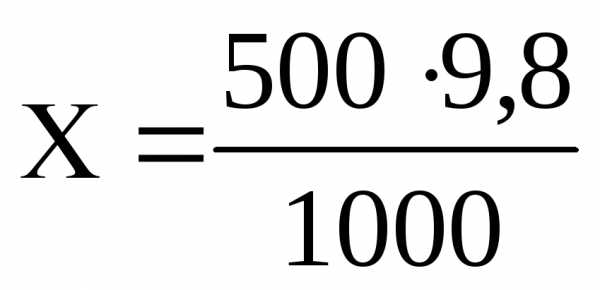 =
4,9 г H2SO4
=
4,9 г H2SO4
Пример 7. Определить молярную и нормальную концентрацию раствора Na2CO3 , в 2 л которого содержится 21,2 Na2CO3.
Решение. 2000 мл раствора содержат 21,2 г Na2CO3
1000 мл раствора содержат Х г Na2CO3
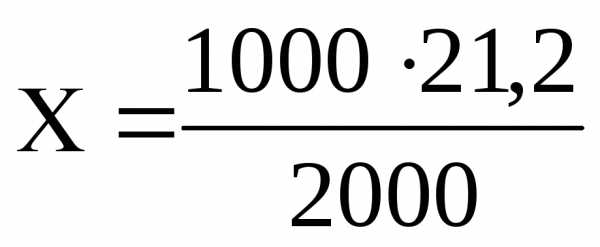 =
10,6 г Na2CO3
=
10,6 г Na2CO3
Молярная масса Na2CO3 равна 106 г/моль следовательно, моль.
Эквивалентная
масса
г/моль,
следовательно,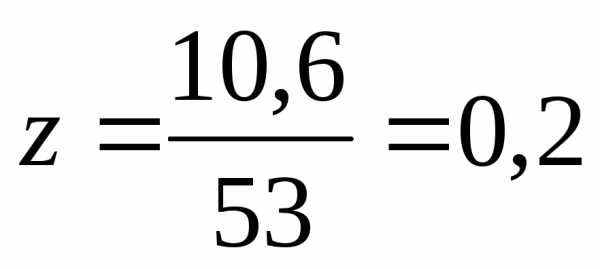 моль.
моль.
Ответ: 0,1 М, 0,2 н.
Пример 8. Определить молярность и нормальность 49 %-го раствора ортофосфорной кислоты (ρ =1,33) .
Решение. Известна процентная концентрация, т.е. содержание ортофосфорной кислоты 100 г раствора. Требуется определить, сколько грамм кислоты в 1000 мл раствора.
100 г раствора H3PO4 содержат 49 г H3PO4
1000 мл ∙1,33 —- Х г,
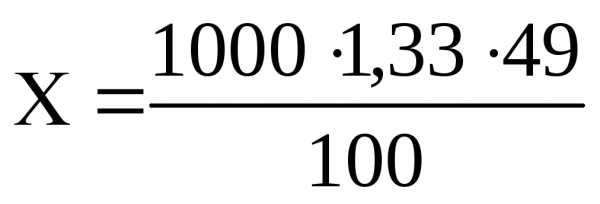 =
651,7 г.
=
651,7 г.
Масса одного моля H3PO4 составляет 98 г/моль.
Количество
моль ортофосфорной кислоты составляет 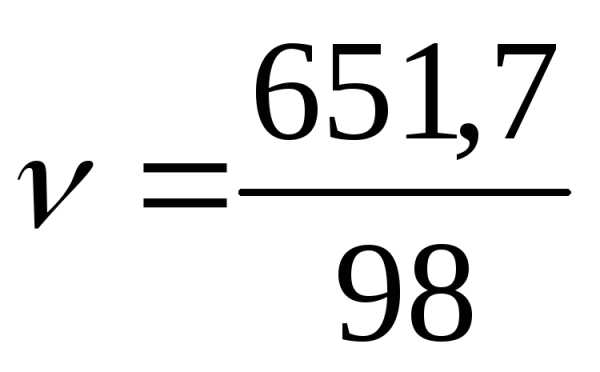 =6,65
моль.
=6,65
моль.
Количество
моль эквивалентов составляет 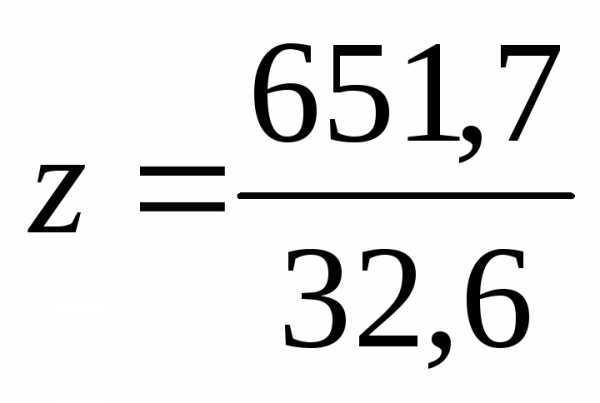 =19,95
моль, где 32,6 г/моль эквивалентная масса.
Таким образом, в 1 литре кислоты содержится
6,65 моль кислоты и 19,95 эквивалентов
кислоты. По определению это и есть
молярная и эквивалентная концентрации.
=19,95
моль, где 32,6 г/моль эквивалентная масса.
Таким образом, в 1 литре кислоты содержится
6,65 моль кислоты и 19,95 эквивалентов
кислоты. По определению это и есть
молярная и эквивалентная концентрации.
Ответ: 6,65 М, 19,95 н.
Пример 9. Для нейтрализации 30 мл 0,1 н раствора щелочи потребовалось 12 мл раствора кислоты. Определить нормальность кислоты.
Решение. Поскольку вещества взаимодействуют в эквивалентных количествах, то можно написать
Z кис. = Z осн.
Сн,к ∙Vк = Сн,щ ∙Vщ, где Сн,к , Сн,щ – нормальность кислоты и щелочи,
Vк, Vщ – соответствующие объемы.
моль/л.
Задание к разделу III
Провести необходимые вычисления
1. К 3л 10%-ного раствора HNO3 (ρ =1,054 г/мл) прибавили 5 л 2%-ного раствора той же кислоты (ρ =1,009 г/мл). Определить С % и См если считать, что объем полученного раствора равен 8 л.
2. Из 700г 60%-ного раствора H2SO4 выпариванием удалили 200г воды. Чему равна массовая доля полученного раствора?
3. Сколько воды необходимо прибавить к 200 мл 68 %-го раствора азотной кислоты (ρ =1,4 г/мл), чтобы получить 10 %-й раствор?
4. К 1л 10 %-го раствора KOH (ρ = 1,092 г/мл) прибавили 0,5 л 5% — го раствора (ρ =1,045 г/мл). Смесь разбавили до 5 л. Вычислить См, Сн.
5. Сколько мл 96 %-й серной кислоты (ρ=1,84 г/мл) необходимо взять для приготовления 2л 0,5Н раствора кислоты?
6. Какой объем 2Н раствора азотной кислоты можно приготовить из 50мл 100 %-й азотной кислоты (ρ = 1,51 г/мл)?
7. Сколько мл 38 %-й НСI (ρ =1,19 г/мл) необходимо для приготовления 1л 2Н раствора?
8. К 100мл 96 %-го раствора H2SO4 (ρ = 1,84 г/мл) прибавили 400 мл воды. Получился раствора плотностью 1.225 г/мл. Определить С %, См.
9. Какой объем 96 %-й H2SO4 (ρ = 1,84 г/мл) необходимо взять для приготовления 250 мл 0,1М раствора?
10. Какие объемы 60 % H2SO4 (ρ = 1,5 г/мл) и 14 % — й H2SO4 (ρ = 1,1 г/мл) нужно смешать, чтобы получить 10 л 27 % -го раствора (ρ = 1,2 г/мл)?
11. Смешали 100мл 10 %-го гидроксида калия (ρ=1,08 г/мл) и 200мл 20%-ного раствора гидроксида натрия (ρ =1,22 г/мл). Вычислить молярную и нормальную концентрации гидроксида в полученном растворе.
12. Вычислить нормальность раствора KOH, полученного при сливании 100мл 10 %-го раствора (ρ = 1,08 г/мл) и 200 мл 20%-ного раствора (ρ = 1,2 г/мл), изменением объема при смешении можно пренебречь.
13. К 1л 60 %-го раствора ортофосфорной кислоты (ρ = 1.43) добавили 2л воды. Определить С % полученного раствора.
14. В 1л воды растворили 660 г KOH. Плотность полученного раствора 1,395. Определить С %, См, Сн.
15. К 100 мл 80 %-ного раствора HNO3 (ρ =1,46 г/мл) прибавили 400 мл воды. Получился раствор с плотностью 1,128 г/мл. Определить С % и Сн полученного раствора.
16. Сколько воды надо прибавить к 100 мл 48 %-ного раствора азотной кислоты (ρ = 1.3 г/мл ), чтобы получить 20 %-й раствор?
17. Сколько мл 56 %-й серной кислоты (ρ = 1, 46 г/мл) потребуется для приготовления 3л 1Н раствора?
18. 3,5 г технического едкого калия растворили в воде и получили 500 мл 0,1М раствора КОН. Каково процентное содержание КОН в образце?
19. Образец технической каустической соды содержит 92 % -й NaOH. Сколько граммов такой соды надо взять для приготовления 10 л 2М раствора NaOH?
20. Смешали два раствора: 500 мл 0,2М раствора NaOH и 2 л 0,1М раствора NaCl. Какова молярная концентрация NaOH и NaCl в полученном растворе?
21. Сколько мл 70 %-го раствора нитрата калия (ρ = 1,6 г/мл) нужно взять, чтобы получить 0,5 л 0,2Н раствора?
22. Смешали 100 мл 96 % -го раствора серной кислоты (ρ = 1,4 г/мл) и 100 мл 10 % — го раствора H2SO4 (ρ = 1,04 г/мл). Смесь разбавили водой до 3 л. Определить молярную и эквивалентную концентрации, полученного раствора.
23. Определить процентную концентрацию раствора, полученного при испарении 500 мл. воды из 1 л 5 % -го раствора хлорида натрия (ρ = 1,02 г/мл).
24. Сколько воды надо взять для приготовления 0,5 л 1,5 молярного раствора хлорида натрия из 10 г NaCl (ρ = 1,1 г/мл).
25. Вычислить нормальность раствора КОН, полученного при сливании 100 мл 10 % -го раствора (ρ = 1,08 г/мл) и 200 мл 20 % -го раствора (ρ = 1,2 г/мл). Объем полученного раствора принять равным 300 мл.
26. К 1 л 60 % -го раствора ортофосфорной кислоты (ρ = 1,43 г/мл) добавили 2 л воды. Определить процентную концентрацию.
27. В 600 мл раствора содержится 11, 76 г ортофосфорной кислоты. Определить молярную, нормальную и процентную концентрации.
28. Сколько мл 30 % го раствора азотной кислоты (ρ = 1,2 г/мл) нужно взять для приготовления 0,5 л 1 н раствора?
29. Вычислить процентную и молярную концентрации раствора, полученного при добавлении к 70 мл 4 % -го раствора бромида натрия (ρ = 1,2 г/мл) 10,5 г кристаллического NaBr.
30. К 100 мл 80 % -го раствора азотной кислоты (ρ=1,46 г/мл) прибавили 400 мл воды. Получился раствор с плотностью 1,128 г/мл. Определить процентную и нормальную концентрации раствора.
31. Сколько воды надо прибавить к 100 мл 48% раствора азотной кислоты (ρ=1,3 г/мл), чтобы получить 20 % раствор?
32. Сколько мл 56%-й серной кислоты (ρ=1,46 г/мл) потребуется для приготовления 3 л 1н раствора?
33. Сколько нитрата меди (II) содержится в 50 мл 0,96 н раствора?
34. Какой объем воды при комнатной температуре надо добавить к 0,5 л 40%-го раствора едкого кали (ρ = 1,43 г/мл) для приготовления 10 % -го раствора?
35. Определить процентное содержание вещества в растворе, приготовленном смешиванием 100 мл 1 – молярного раствора уксусной кислоты (ρ = 1,007 г/мл) и 10 мл 60 % -го раствора той же кислоты (ρ = 1,064 г/мл).
36. 3,5 г технического едкого кали растворили в воде и получили 500 мл 0,1 М раствора KOH. Каково процентное содержание KOH в образце?
37. Образец технической каустической соды содержит 92 %-го NaOH. Сколько граммов такой соды надо взять для приготовления 10 л 2М раствора NaOH?
38. Смешали два раствора 500 мл 0,2 М раствора и 2 л 0,1 М раствора NaCl. Какова молярная концентрация NaOH и NaCl в полученном растворе?
39. Определить процентное содержание вещества в растворе, приготовленном смешиванием 200 мл 0,2 М BaCl2 (ρ=1,034 г/мл) и 50 мл 24 % раствора BaCl2 (ρ=1,06 г/мл).
40. Сколько мл 70 % -го раствора нитрата калия (ρ=1,6 г/мл) нужно взять, чтобы получить 0,5 л 0,2 Н раствора?
41. Имеется 40 %-й раствор гидроксида натрия (ρ = 1,43 г/мл). Какой объем этого раствора нужно взять для приготовления 10 л 15 % раствора (ρ = 1,16 г/мл)?
42. Найти массы воды и медного купороса CuSO4 ∙5H2O , необходимого для приготовления 3 л раствора, содержащего 10% безводной соли (ρ = 1,09 г/мл).
43. Сколько граммов глауберовой соли Na2SO4 ∙10H2O следует растворить в 500 г воды для получения 20 % -го раствора Na2SO4?
44. Сколько граммов Al2(SO4)3 ∙18H2O содержится в 1,5 кг 20 % — го раствора Al2(SO4)3?
45. Сколько граммов Na2НРO4 ∙12H2O требуется растворить в 1 л воды, чтобы получить 10 % -й раствор Na2НРO4?
46. Сколько граммов кристаллической соды Na2CO3 ∙ 10H2O необходимо взять для приготовления 100 г 0,5 % -го раствора Na2CO3?
47. Сколько молей MgSO4∙7H2O надо прибавить к 100 молям воды, чтобы получить 10 % -й раствор MgSO4?
48. Для борьбы с вредителями растений приготовлен раствор из 50 г BaCl2 ∙2H2O и 1 л воды, вычислить процентную концентрацию полученного раствора по безводной соли.
49. Сколько воды и буры Na2B4O7∙10H2O требуется для приготовления 1 кг 10% — го раствора Na2B4O7?
50. Сколько граммов кристаллогидрата СaCl2∙6H2O требуется для приготовления 7 л 0,25 н раствора СaCl2?
51. Сколько граммов NiCl2 ∙6H2O необходимо растворить в 1 л воды, чтобы получить 20 % раствор по безводной соли?
52. Сколько граммов FeSO4 ∙7H2O необходимо добавить к 400 мл 10 % раствора (ρ=1,1 г/мл) для получения 20 % -го раствора FeSO4?
53. Определить массу осадка BaCl2∙2H2O , который образуется из 5 л 1М раствора BaCl2.
54. Сколько граммов СuSO4 ∙5H2O и воды необходимо для приготовления 500 г 18 % -го раствора СuSO4 (ρ=1,2 г/мл)?
55. Сколько граммов щавелевой кислоты H2C2O4∙2H2O надо взять для приготовления 500 мл 0,02 н раствора H2C2O4 ?
56. Сколько мл 0,5 н раствора BaCl2 можно приготовить из 24,4 г BaCl2 ∙2H2O?
57. Сколько граммов медного купороса (CuSO4 ∙5H2O) образуется из 50 мл 0,2 н раствора CuSO4?
58. Определить молярную концентрацию FeSO4 полученного растворением в 0,5 л раствора 11,44 г FeSO4 ∙7H2O.
59. Определить процентную концентрацию раствора SrCl2 полученного растворением 84 г кристаллогидрата SrCl2∙6H2O в 100 г воды.
60. Сколько граммов глауберовой соли Na2SO4∙10H2O следует растворить в 500 г воды для получения 20 % -го раствора Na2SO4?
61. Определить молярную концентрацию CoCl2 полученного растворением в 1,2 л раствора 9,5 г CoCl2 ∙6H2O.
62. Определить молярную и эквивалентную концентрации растворенных веществ в следующих растворах
а) 16% раствора сульфата меди (ρ=1,18 г/мл).
б) 20% раствора хлорида цинка (ρ=1,17 г/мл).
в) 5% раствора ортофосфорной кислоты(ρ=1,2 г/мл).
г) 30,1% раствора азотной кислоты (ρ=1,185 г/мл).
д) 10% раствора сульфата натрия(ρ=1,1 г/мл).
е) 60% раствора уксусной кислоты (ρ=1,8 г/мл).
ж) 6% раствора ортоборной кислоты (ρ=1,2 г/мл).
з) 98% раствора серной кислоты (ρ=1,84 г/мл).
63. Определить молярную и процентную концентрации растворенных веществ в следующих растворах:
а)10 н раствора сульфата меди (ρ=1,18 г/мл).
б) 7,98 н раствора хлорида цинка (ρ=1,17 г/мл).
в) 5 н раствора ортофосфорной кислоты(ρ=1,27 г/мл).
г) 3,5 н раствора азотной кислоты (ρ=1.185 г/мл).
д) 1 н раствора сульфата натрия(ρ=1,1 г/мл).
е) 6 н раствора уксусной кислоты (ρ=1.068 г/мл).
ж) 4 н раствора ортоборной кислоты (ρ=1.2 г/мл).
з) 2 н раствора серной кислоты (ρ=1,84 г/мл).
64. Из 5 г карбоната натрия приготовлено 500 мл раствора. Какова нормальность и молярность этого раствора?
65. Какова процентная концентрация 5М раствора серной кислоты (ρ=1,29 г/мл), 2 н раствора сульфата никеля (II) (ρ=1,14 г/мл)?
66. К 100 мл 96 % раствора серной кислоты (ρ=1,84 г/мл) прибавили 400 мл воды. Определить ω и молярную концентрации полученного раствора (ρ=1,22 г/мл).
67. Сколько мл 5 %-го раствора серной кислоты (ρ=1,32 г/мл) пойдет на приготовление 2 л 0,5 н раствора серной кислоты?
68. 250 мл 96 %-го раствора серной кислоты (ρ=1,84 г/мл) разбавили водой до 1000 мл. Определить нормальную и молярную концентрации полученного раствора.
69. Сколько воды нужно прибавить к 200 мл 60 %-го раствора азотной кислоты (ρ=1,4 г/мл), чтобы получить 2 н раствор?
70. Сколько воды нужно выпарить из 2 л 1 М раствора гидроксида натрия, чтобы получить 10 %-го раствор (ρ=1,1 г/мл)?
71. До какого объема нужно разбавить 200 мл 20 %-го раствора хлорида меди (ρ=1,2 г/мл), чтобы получить 0,5 М раствор?
72. Сколько мл 2н раствора нитрата хрома (III) требуется для получения 0,2 молей гидроксида хрома (III)?
73. На нейтрализацию 250 мл 0,1 н раствора серной кислоты пошло 150 мл раствора гидроксида натрия. Какова нормальность раствора едкого натрия?
74. Сколько граммов серной кислоты содержится в 300 мл раствора, если на нейтрализацию его израсходовано 8 мл 1 н раствора гидроксида калия?
75. В 50 мл раствора содержится 0,5 г едкого натра. На нейтрализацию этого объема раствора потребовалось 25 мл раствора кислоты. Какова нормальность раствора?
76. Какова нормальная концентрация раствора нитрата серебра, если на реакцию с 0,924 г хлорида натрия израсходовано 16 мл раствора этой соли?
77. Сколько мл 20 %-го раствора серной кислоты (ρ=1,14 г/мл) вступило в реакцию с цинком, если при этом выделилось 56 л водорода? Сколько граммов цинка участвовало в реакции?
78. К раствору хлорида аммония добавили 100 мл 25 %-го раствора КОН (ρ=1,23г/мл). Вычислите объем выделившегося газа.
79. Какое количество моль сернистого газа необходимо пропустить через 200 мл 30% раствора NaOH (ρ=1,33 г/мл) для образования кислой соли?
80. Сколько требуется взять 2М раствора хлорноватистой кислоты, чтобы при взаимодействии его с карбонатом натрия получить 10 л СО2 у.н.?
81. Какой объем 20 %-го раствора гидроксида калия (ρ = 1,18 г/мл) необходимо взять для реакции с 200 мл 2 %-го раствора хлорида цинка (ρ = 1,02 г/мл), чтобы получить осадок гидроксида цинка?
82. Раствор, содержащий нитрат бария, смешан с 42 мл 26% раствора сульфата натрия (ρ = 1,3 г/мл). Сколько граммов сульфата бария образовалось?
83. Смешали 100 мл 4 %-го раствора хлороводородной кислоты (ρ=1,01 г/мл) и 50 мл 1М раствора гидроксида натрия. Сколько граммов соли образовалось? Какое вещество и в каком количестве взято в избытке?
84. Сколько мл 6,75 % -го раствора серной кислоты (ρ = 1,16 г/мл) требуется для реакции с раствором, содержащем 6,1 г BaCl2∙2H2O?
85. На 80 г цинка, содержащего 10% примесей, действуют 200 мл 20% -го раствора хлорноватистой кислоты (ρ=1,1 г/мл). Сколько хлорида цинка образовалось в результате реакции?
86. На 80 г цинка, содержащего 10 % примесей, действуют 200 мл 20 % -го раствора хлороводородной кислоты (ρ=1,1 г/мл). Сколько хлорида цинка образуется в результате реакции?
87. Сколько карбоната кальция получится при реакции 2,8 л СО2 и 200 г 5% — го раствора гидроксида кальция?
88. Какова нормальность раствора HCl, если на взаимодействие с 19,46 г карбоната натрия идет 2 л этого раствора?
89. При пропускании хлора через 500 мл раствора иодида калия вес выделившегося иода составил 75 г. Вычислить молярную концентрацию раствора иодида калия.
90. Для осаждения в виде BaSO4 всего бария, содержащегося в 500 мл раствора BaCl2 потребовалось 100 мл 0,3 н раствора H2SO4. Сколько граммов BaSO4 выпало в осадок? Чему равна нормальность раствора?
91.Какой объем 1 н раствора KOH потребуется для образования сульфида калия с сероводородом, полученным при взаимодействии сульфида железа (II) c 0,7 л 20 %-го раствора HCl (ρ=1,1 г/мл)?
92. Плотность раствора Na2CO3 равна 1,1 г/мл. Из 4 л этого раствора при действии соляной кислоты получено 60 л СО2 (н.у.). Вычислите процентную концентрацию Na2CO3 в этом растворе.
93. Какой объем 4 н раствора H2SO4 может взаимодействовать 0,65 л 20% раствора К2CO3 (ρ =1,19 г/мл)? Какой объем займет выделившийся газ при н.у.?
94. К 0,05 л 8 %-го раствора хлорида марганца (ρ=1,085 г/мл) прибавлено 0,2 л 10 %-го раствора гидроксида лития (ρ = 1,1 г/мл). Какое вещество взято в избытке и сколько его останется после реакции?
95. К 0,1 л 20% раствора хлорида бария (ρ=1,2 г/мл) прибавлен раствор сульфата хрома (III). Вычислить массу образовавшегося осадка BaSO4.
96. Какова масса Al(OH)3, если для его растворения потребовалось 0,2 л 30% раствора HNO3 (ρ=1,18)? Какой объем 2,5 н КОН необходимо затратить для растворения этого количества гидроксида алюминия?
97. Сколько миллилитров 8 % -го раствора NaOH (ρ=1,09 г/мл) требуется для нейтрализации 75 мл раствора H2SO4 , если известно, что из10 мл того же раствора можно получить 0,2334 г BaSO4.
98. Сколько молей хлорной кислоты необходимо для нейтрализации 1,5 л 0,25 М раствора гидроксида кальция?
99. Сколько миллилитров 8 %-го раствора едкого натра (ρ=1,1 г/мл) необходимо для растворения 8,1 г оксида цинка (II).
studfiles.net
Как связаны Нормальная и Молярная концентрация ? — 22 ответа
В разделе Естественные науки на вопрос Вопрос по химии: Как связаны Нормальная и Молярная концентрация ? заданный автором Александр Горелов лучший ответ это Формулой связаны: Cн=Cm*z,где z-число эквивалентности.
Ответ от 22 ответа[гуру]Привет! Вот подборка тем с ответами на Ваш вопрос: Вопрос по химии: Как связаны Нормальная и Молярная концентрация ?
Ответ от Невролог[гуру]
связаны очень жестко, подробности в учебнике по химии
Ответ от Мосол[гуру]
нормальная концентрация допустим NaCl берём 5г этой соли и кидаем у воду массой 43г. Вес раствора 43+5=48г концентрация соли в растворе 5/48*100%= 10,41%
Молярная концентрация это концентрация соли в растворе когда у растворе 1 литр находится соль массой 1 моль (колличество моль может меняться).
У таблице менделеева есть атомные массы хим элементов, Na 23 Cl 35,5 23+35,5=58,5 грамм на моль. концентрация раствора 1М NaCl значит что в 1 литре раствора есть 58,5 грамм этой соли.
Ответ от Впросак[гуру]
Молярная концентрация — число молей вещества в литре раствора.
Нормальность — число грамм-эквивалентов вещества в литре раствора, при этом
грамм-эквивалент — это молярная масса в-ва, делённая на валентность или число электронов, принимающих участие в реакции, к которой относится данный эквивалент. Вся фишка в том, что есть множество веществ, которые элементы, их образующие, могут проявлять различные степени окисления при реакциях. Например, марганцовка KMnO4, где Mn принимать 1, 3 или 5 электронов в зависимости от партнёра в реакции. Соответственно, при одинаковой молярной концентрации такого раствора, его нормальность по отношению к конкретной реакции будет различна…
Вообще, нормальность придумали для упрощения объёмных методов анализа (титрования), чтобы при одинаковых нормальностях реагентов взаимодействовали одинаковые их объёмы. А в остальных случаях работала пропорция: N1*V1 = N2*V2
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Ответить на вопрос:
22oa.ru
§ 1.3. Выражение концентрации растворов в единицах нормальности, молярности и моляльности. Взаимный переход от одних видов выражения концентрации к другим.
Молярная концентрация (молярность) – выражается числом молей растворенного вещества в 1 литре раствора.
См = υ/V (4),
где См – молярная концентрация (молярность) (моль/л),
υ – число молей (моль),
V – объём (мл).
Единицы измерения молярной концентрации моль/л.
Раствор, содержащий в 1 литре 1 моль растворенного вещества, называется молярным. Например, 1 молярный раствор NаOH – это такой раствор, 1литр которого содержит 1 моль растворенного вещества NaOH или 1·40 = 40 г NaOH.
Нормальная концентрация (нормальность) – выражается числом моль — эквивалентов растворенного вещества в 1 литре раствора.
Сн = υэ /V (5),
где Сн – нормальная концентрация (нормальность) моль-экв/л,
υэ – число моль — эквивалентов (моль — экв),
V – объём (л).
Раствор в 1 литре, которого содержится 1 моль-эквивалент, называется нормальным.
При нахождении моль эквивалентов вещества по его молекулярной массе необходимо знать, что молярная масса эквивалента данного вещества может быть различным при разных химических реакциях, в которых это вещество участвует. Поэтому один и тот же раствор в разных случаях может иметь различную нормальность.
Например, если при взаимодействии раствора серной кислоты, содержащей 9,8 г кислоты, с NaOH образуется кислая соль, то раствор серной кислоты будет 0,1 н., т.к. эта реакция сводится к замещению одного иона водорода в серной кислоте на ион натрия:
H2SO4 + NaOH = NaHSO4 + H2O
поэтому эквивалентная масса серной кислоты здесь равна её малярной массе 98 г/моль. Число моль — эквивалентов в1 литре (или нормальность) в этом случае равно 9,8/98 1= 0,1 н.
Если же образуется средняя соль, реакция сводится к замещению двух ионов водорода в серной кислоте на два иона натрия:
H2SO4 + 2NaOH = Na2SO4 + 2H2O
следовательно, молекула серной кислоты содержит два эквивалента. Значит, в данном случае эквивалентная масса будет равна ½ молярной массы 49г/моль. Число моль — эквивалентов в 1 литре (или нормальность) будет равно 9,8/49·1 = 0,2 н.
Для перехода от процентной концентрации к концентрациям, выраженным в единицах нормальности и молярности, и обратно необходимо учитывать плотность растворов.
Титром – называют число грамм растворенного вещества, содержащееся в 1 мл раствора. Единицы измерения титра г/мл.
ПРИМЕР 9: Рассчитать молярность, нормальность 36:-ного раствора серной кислоты (плотность раствора 1,268 г/см3).
РЕШЕНИЕ:
1) Рассчитаем массу 1л раствора 36%-ного раствора серной кислоты:
mр-ра = 1000·1,268 = 1268г
2) Рассчитаем массу серной кислоты, которая содержится в 1268г раствора. Зная, что исходный раствор 36%-ный, можно сделать вывод, что в 100г этого раствора содержится 36г серной кислоты. Тогда в 1268г 36%-ного раствора будет содержаться:
36·1268/100 = 456,48г серной кислоты.
3) Зная массу серной кислоты и молярную массу серной кислоты, можно найти число моей кислоты
υ = 456,48/98 = 4,65 моля
(98 г/моль –молярная масса серной кислоты).
Поскольку все расчеты мы вели на 1 литр, то мы нашли число молей растворенного вещества в 1 литре раствора, а значит, мы нашли молярность. Следовательно, См = 4,65 М.
4) Зная массу кислоты и эквивалентную массу серной кислоты, можем найти число моль — эквивалентов кислоты. Т.к. кислота двухосновная, то fэ=1/2, следовательно, Мэ = М·fэ = 98·1/2 = 49 г/моль. Отсюда:
υэ = 456,48/49 = 9,3 моль — эквивалента.
Т.к. найдено число моль — эквивалентов растворенного вещества в 1литре раствора, следовательно, найдена нормальная концентрация Сн = 9,3 н.
ОТВЕТ: См = 4,65 М, Сн = 9,3н.
ПРИМЕР10: Вычислите процентную концентрацию, молярность и титр 2 н. раствора КОН (ρ = 1,10 г/см3).
РЕШЕНИЕ:
1) Вычислим массу 1 литра раствора КОН
1000·1,10 = 1100 г
2) Определим массу растворенного вещества: нормальная концентрация показывает, сколько моль — эквивалентов растворенного вещества содержится в 1 литре раствора, т.к. наш раствор 2 н., то в 1 литре раствора содержится 2 моль — эквивалента КОН.
3) Зная число моль — эквивалентов и эквивалентную массу КОН рассчитаем массу КОН:
Мэ кон = М кон, т.к. fэ = 1.
m = υэ·Мэ = 2·56 = 112 г
4) Рассчитаем по формуле (1) процентную концентрацию:
ω = mраст. в-ва·100/ mр-ра = 112·100/1100 = 10,18 %.
5) Молярность и нормальность отличается друг от друга фактором эквивалентности: См =Сн·fэ или Сн = См/fэ
Для КОН fэ = 1, т.е. См=Сн, следовательно, См = 2 М.
6) Рассчитаем титр раствора
Т=mраств. в-ва /Vр-ра = 112/1000 = 0,112 г/мл.
ПРИМЕР11: Рассчитать объём 36:-ной кислоты НС1 (ρ = 1,179 г/см3) для приготовления а) 200 мл 0,1 н. раствора; б) 500 мл 0,5 М раствора.
РЕШЕНИЕ:
а)1) рассчитаем массу НС1, которая содержится в 200 мл 0,1 н. раствора:
mHCl = 0,1·200·36,5/1000 = 0,73 г
2)Рассчитаем массу 36%-ного раствора НС1, в которой содержится 0,73 г НС1
studfiles.net
Молярная концентрация Википедия
Концентра́ция или до́ля компонента смеси — величина, количественно характеризующая содержание компонента относительно всей смеси. Терминология ИЮПАК под концентрацией компонента понимает четыре величины: соотношение молярного, или численного количества компонента, его массы, или объёма исключительно к объёму раствора[1] (типичные единицы измерения — соответственно моль/л, л−1, г/л, и безразмерная величина). Долей компонента ИЮПАК называет безразмерное соотношение одной из трёх однотипных величин — массы, объёма или количества вещества.[2] Однако в обиходе термин «концентрация» могут применять и для долей, не являющихся объёмными долями, а также к соотношениям, не описанным ИЮПАК. Оба термина могут применяться к любым смесям, включая механические смеси, но наиболее часто применяются к растворам.
Массовая доля
Массовая доля компонента — отношение массы данного компонента к сумме масс всех компонентов. По рекомендациям ИЮПАК,[3] обозначается символом w{\displaystyle w}, в русскоязычной литературе чаще встречается обозначение ω{\displaystyle \omega }. Массовая доля — безразмерная величина, как правило выражается в долях единицы или в процентах (для выражения массовой доли в процентах следует умножить указанное выражение на 100 %):
- ωB=mBm{\displaystyle \omega _{\mathrm {B} }={\frac {m_{\mathrm {B} }}{m}}}
где:
- ωB — массовая доля компонента B
- mB — масса компонента B;
- m{\displaystyle m} — общая масса всех компонентов смеси.
В бинарных растворах часто существует однозначная (функциональная) зависимость между плотностью раствора и его концентрацией (при данной температуре). Это даёт возможность определять на практике концентрации важных растворов с помощью денсиметра (спиртометра, сахариметра, лактометра). Некоторые ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора (спирта, жира в молоке, сахара). Следует учитывать, что для некоторых веществ кривая плотности раствора имеет максимум, в этом случае проводят два измерения: непосредственное, и при небольшом разбавлении раствора.
Часто для выражения концентрации (например, серной кислоты в электролите аккумуляторных батарей) пользуются просто их плотностью. Распространены ареометры (денсиметры, плотномеры), предназначенные для определения концентрации растворов веществ.
| ω, % | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 95 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ H2SO4, г/мл | 1,032 | 1,066 | 1,102 | 1,139 | 1,219 | 1,303 | 1,395 | 1,498 | 1,611 | 1,727 | 1,814 | 1,834 |
Объёмная доля
Объёмная доля компонента — отношение объёма компонента к сумме объёмов компонентов до смешивания. Объёмная доля измеряется в долях единицы или в процентах.
- ϕB=VB∑Vi{\displaystyle \phi _{\mathrm {B} }={\frac {V_{\mathrm {B} }}{\sum V_{i}}}},
где:
- ϕB{\displaystyle \phi _{\mathrm {B} }} — объёмная доля компонента B,
- VB — объём компонента B;
- ∑Vi{\displaystyle \sum V_{i}} — сумма объёмов всех компонентов до смешивания.
При смешивании жидкостей их суммарный объём может уменьшаться, поэтому не следует заменять сумму объёмов компонентов на объём смеси.
Как было указано выше, существуют ареометры, предназначенные для определения концентрации растворов определённых веществ. Такие ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора. Для распространённых растворов этилового спирта, концентрация которых обычно выражается в объёмных процентах, такие ареометры получили название спиртомеров или андрометров.
Молярность (молярная объёмная концентрация)
Молярная концентрация (молярность, мольность[4]) — количество вещества (число молей) компонента в единице объёма смеси. Молярная концентрация в системе СИ измеряется в моль/м³, однако на практике её гораздо чаще выражают в моль/л или ммоль/л. Также используют выражение «в молярности». Возможно другое обозначение молярной концентрации, которое принято обозначать М. Так, раствор с концентрацией 0,5 моль/л называют 0,5-молярным, записывают «0,5 M».
По рекомендации ИЮПАК, обозначается буквой c{\displaystyle c} или [B]{\displaystyle [B]}, где B — вещество, концентрация которого указывается.[5]
Примечание: После числа пишут «моль», подобно тому, как после числа пишут «см», «кг» и т. п., не склоняя по падежам.
- cB=nBV{\displaystyle {c_{\mathrm {B} }}={\frac {n_{\mathrm {B} }}{V}}},
где:
Нормальная концентрация (молярная концентрация эквивалента, «нормальность»)
Нормальная концентрация — количество эквивалентов данного вещества в 1 литре смеси. Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов). Для записи концентрации таких растворов используют сокращения «н» или «N». Например, раствор, содержащий 0,1 моль-экв/л, называют децинормальным и записывают как 0,1 н.
- c(feq B)=c((1/z) B)=z⋅cB=z⋅nBV=1feq⋅nBV{\displaystyle c(f_{eq}~\mathrm {B} )=c{\big (}(1/z)~\mathrm {B} {\big )}=z\cdot c_{\mathrm {B} }=z\cdot {\frac {n_{\mathrm {B} }}{V}}={\frac {1}{f_{eq}}}\cdot {\frac {n_{\mathrm {B} }}{V}}},
где:
Нормальная концентрация может отличаться в зависимости от реакции, в которой участвует вещество. Например, одномолярный раствор H2SO4 будет однонормальным, если он предназначается для реакции со щёлочью с образованием гидросульфата калия KHSO4, и двухнормальным в реакции с образованием K2SO4.
Мольная (молярная) доля
Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов. Мольную долю выражают в долях единицы. ИЮПАК рекомендует обозначать мольную долю буквой x{\displaystyle x} (а для газов — y{\displaystyle y})[6], также в литературе встречаются обозначения χ{\displaystyle \chi }, X{\displaystyle X}.
- xB=nB∑ni{\displaystyle x_{\mathrm {B} }={\frac {n_{\mathrm {B} }}{\sum n_{i}}}},
где:
- xB{\displaystyle x_{\mathrm {B} }} — мольная доля компонента B;
- nB{\displaystyle n_{\mathrm {B} }} — количество компонента B, моль;
- ∑ni{\displaystyle \sum n_{i}} — сумма количеств всех компонентов.
Мольная доля может использоваться, например, для количественного описания уровня загрязнений в воздухе, при этом ее часто выражают в частях на миллион (ppm — от англ. parts per million). Однако, как и в случае с другими безразмерными величинами, во избежание путаницы, следует указывать величину, к которой относится указанное значение.
Моляльность (молярная весовая концентрация, моляльная концентрация)
Моляльная концентрация (моляльность,[4] молярная весовая концентрация) — количество растворённого вещества (число моль) в 1000 г растворителя. Измеряется в молях на кг, также распространено выражение в «моляльности». Так, раствор с концентрацией 0,5 моль/кг называют 0,5-мольным.
- mB=nBmA{\displaystyle {m_{\mathrm {B} }}={\frac {n_{\mathrm {B} }}{m_{\mathrm {A} }}}},
где:
Следует обратить особое внимание, что, несмотря на сходство названий, молярная концентрация и моляльность — величины различные. Прежде всего, в отличие от молярной концентрации, при выражении концентрации в моляльности расчёт ведут на массу растворителя, а не на объём раствора. Моляльность, в отличие от молярной концентрации, не зависит от температуры.
Массовая концентрация (Титр)
Массовая концентрация — отношение массы растворённого вещества к объёму раствора. По рекомендации ИЮПАК, обозначается символом γ{\displaystyle \gamma } или ρ{\displaystyle \rho }[7].
- ρB=mBV{\displaystyle \rho _{\mathrm {B} }={\frac {m_{\mathrm {B} }}{V}}}.
где:
- mB{\displaystyle m_{\mathrm {B} }} — масса растворённого вещества;
- V{\displaystyle V} — общий объём раствора;
В аналитической химии используется понятие титр по растворённому или по определяемому веществу (обозначается буквой T{\displaystyle T}).
Концентрация частиц
По рекомендациям ИЮПАК концентрация частиц обозначается буквой C{\displaystyle C}[8], однако также часто встречается обозначение n{\displaystyle n} (не путать с количеством вещества).
- CB=NBV=nB⋅NAV=cB⋅NA{\displaystyle C_{\mathrm {B} }={\frac {N_{\mathrm {B} }}{V}}={\frac {n_{\mathrm {B} }\cdot N_{\mathrm {A} }}{V}}=c_{\mathrm {B} }\cdot N_{\mathrm {A} }},
где:
Весообъёмные (массо-объёмные) проценты
Иногда встречается использование так называемых «весообъёмных процентов»[9], которые соответствуют массовой концентрации вещества, где единица измерения г/(100 мл) заменена на процент. Этот способ выражения используют, например, в спектрофотометрии, если неизвестна молярная масса вещества или если неизвестен состав смеси, а также по традиции в фармакопейном анализе.[10] Стоит отметить, что поскольку масса и объём имеют разные размерности, использование процентов для их соотношения формально некорректно. Также международное бюро мер и весов[11] и ИЮПАК[12] не рекомендуют добавлять дополнительные метки (например «% (m/m)» для обозначения массовой доли) к единицам измерения.
Другие способы выражения концентрации
Существуют и другие, распространённые в определённых областях знаний или технологиях, методы выражения концентрации. Например, при приготовлении растворов кислот в лабораторной практике часто указывают, сколько объёмных частей воды приходится на одну объёмную часть концентрированной кислоты (например, 1:3). Иногда используют также отношение масс (отношение массы растворённого вещества к массе растворителя) и отношение объёмов (аналогично, отношение объёма растворяемого вещества к объёму растворителя).
Применимость способов выражения концентрации растворов, их свойства
В связи с тем, что моляльность, массовая доля, мольная доля не включают в себя значения объёмов, концентрация таких растворов остаётся неизменной при изменении температуры. Молярность, объёмная доля, титр, нормальность изменяются при изменении температуры, так как при этом изменяется плотность растворов. Именно моляльность используется в формулах повышения температуры кипения и понижения температуры замерзания растворов.
Разные виды выражения концентрации растворов применяются в разных сферах деятельности, в соответствии с удобством применения и приготовления растворов заданных концентраций. Так, титр раствора удобен в аналитической химии для волюмометрии (титриметрического анализа) и т. п.
Формулы перехода от одних выражений концентраций к другим
В зависимости от выбранной формулы погрешность конвертации колеблется от нуля до некоторого знака после запятой.
От массовой доли к молярности
- cB=ρ⋅ωBM(B){\displaystyle c_{\mathrm {B} }={\frac {\rho \cdot \omega _{\mathrm {B} }}{M(\mathrm {B} )}}},
где:
- cB{\displaystyle c_{\mathrm {B} }} — молярная концентрация вещества B
- ρ{\displaystyle \rho } — плотность раствора;
- ωB{\displaystyle \omega _{\mathrm {B} }} — массовая доля вещества B;
- M(B){\displaystyle M(\mathrm {B} )} — молярная масса вещества B.
Если плотность раствора выражена в г/мл, а молярная масса в г/моль, то для выражения ответа в моль/л выражение следует домножить на 1000 мл/л. Если массовая доля выражена в процентах, то выражение следует также разделить на 100 %.
От молярной концентрации к нормальной
- c((1/z) B)=cB⋅z{\displaystyle {c((1/z)~\mathrm {B} )}={c_{\mathrm {B} }}\cdot {z}},
где:
От массовой доли к титру
- T=ρ⋅ω{\displaystyle {T}={\rho }\cdot {\omega }},
где:
- ρ{\displaystyle \rho } — плотность раствора, г/мл;
- ω{\displaystyle \omega } — массовая доля растворённого вещества, в долях от 1;
От молярности к титру
- T=cB⋅M{\displaystyle {T}={c_{\mathrm {B} }}\cdot {M}},
где:
- cB{\displaystyle {c_{\mathrm {B} }}} — молярная концентрация;
- M{\displaystyle M} — молярная масса растворённого вещества.
Если молярная концентрация выражена в моль/л, а молярная масса — в г/моль, то для выражения ответа в г/мл его следует разделить на 1000 мл/л.
От молярности к моляльности
- mB=cBρ{\displaystyle m_{\mathrm {B} }={\frac {c_{\mathrm {B} }}{\rho }}},
где:
- cB{\displaystyle {c_{\mathrm {B} }}} — молярная концентрация, моль/л;
- ρ{\displaystyle \rho } — плотность раствора, г/мл;
От моляльности к мольной доле
- xB=mBmB+1M(A){\displaystyle x_{\mathrm {B} }={\frac {m_{\mathrm {B} }}{m_{\mathrm {B} }+{\frac {1}{M(\mathrm {A} )}}}}},
где:
- mB{\displaystyle m_{\mathrm {B} }} — моляльность,
- M(A){\displaystyle M(\mathrm {A} )} — молярная масса растворителя.
Если моляльность выражена в моль/кг, а молярная масса растворителя в г/моль, то единицу в формуле следует представить как 1000 г/кг, чтобы слагаемые в знаменателе имели одинаковые единицы измерения.
Примечания
- ↑ International Union of Pure and Applied Chemistry. concentration (англ.) // IUPAC Compendium of Chemical Terminology. — Research Triagle Park, NC: IUPAC. — ISBN 0967855098. — DOI:10.1351/goldbook.C01222.
- ↑ International Union of Pure and Applied Chemistry. fraction (англ.) // IUPAC Compendium of Chemical Terminology. — Research Triagle Park, NC: IUPAC. — ISBN 0967855098. — DOI:10.1351/goldbook.F02494.
- ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — mass fraction, w (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
- ↑ 1 2 Z. Sobecka, W. Choiński, P. Majorek. Dictionary of Chemistry and Chemical Technology: In Six Languages: English / German / Spanish / French / Polish / Russian. — Elsevier, 2013-09-24. — С. 641. — 1334 с. — ISBN 9781483284439.
- ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — amount concentration, c (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
- ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — amount fraction, x ( y for gaseous mixtures) (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
- ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — mass concentration, γ, ρ (англ.). goldbook.iupac.org. Дата обращения 16 декабря 2018.
- ↑ International Union of Pure and Applied Chemistry. IUPAC Gold Book — number concentration, C,n (англ.). goldbook.iupac.org. Дата обращения 11 декабря 2018.
- ↑ Способы приготовления растворов на МедКурс. Ru
- ↑ Бернштейн И. Я., Каминский Ю. Л. Спектрофотометрический анализ в органической химии. — 2-е изд. — Ленинград: Химия, 1986. — с. 5
- ↑ The International System of Units (SI) (неопр.). www.bipm.org. Дата обращения 23 декабря 2018.
- ↑ Quantities, Units and Symbols in Physical Chemistry (неопр.). www.iupac.org. Дата обращения 23 декабря 2018.
wikiredia.ru
Концентрация растворов — Википедия
Концентрация — величина, характеризующая количественный состав раствора.
Согласно правилам ИЮПАК, концентрацией растворённого вещества (не раствора) называют отношение количества растворённого вещества или его массы к объёму раствора (моль/л, г/л), то есть это отношение неоднородных величин.
Те величины, которые являются отношением однотипных величин (отношение массы растворённого вещества к массе раствора, отношение объёма растворённого вещества к объёму раствора), правильно называть «долями». Однако на практике для обоих видов выражения состава применяют термин «концентрация» и говорят о концентрации растворов.
Существует много способов выражения концентрации растворов.
Массовая доля — отношение массы растворённого вещества к массе раствора. Массовая доля измеряется в долях единицы или в процентах:
где:
- ω — массовая доля растворённого вещества в долях
- ω(%) — массовая доля растворённого вещества в процентах
- m1 — масса растворённого вещества, г;
- m — общая масса раствора (масса растворённого вещества плюс масса растворителя) г.
В бинарных растворах часто существует однозначная (функциональная) зависимость между плотностью раствора и его концентрацией (при данной температуре). Это даёт возможность определять на практике концентрации важных растворов с помощью денсиметра (спиртометра, сахариметра, лактометра). Некоторые ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора (спирта, жира в молоке, сахара). Следует учитывать, что для некоторых веществ кривая плотности раствора имеет максимум, в этом случае проводят два измерения: непосредственное, и при небольшом разбавлении раствора.
Часто для выражения концентрации (например, серной кислоты в электролите аккумуляторных батарей) пользуются просто их плотностью. Распространены ареометры (денсиметры, плотномеры), предназначенные для определения концентрации растворов веществ.
| ω, % | 5 | 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 95 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ H2SO4, г/мл | 1,032 | 1,066 | 1,102 | 1,139 | 1,219 | 1,303 | 1,395 | 1,498 | 1,611 | 1,727 | 1,814 | 1,834 |
Объёмная доля — отношение объёма растворённого вещества к объёму раствора. Объёмная доля измеряется в долях единицы или в процентах.
- ,
где:
- V1 — объём растворённого вещества, л;
- V — общий объём раствора, л.
Как было указано выше, существуют ареометры, предназначенные для определения концентрации растворов определённых веществ. Такие ареометры проградуированы не в значениях плотности, а непосредственно концентрации раствора. Для распространённых растворов этилового спирта, концентрация которых обычно выражается в объёмных процентах, такие ареометры получили название спиртомеров или андрометров.
Молярность (молярная объёмная концентрация)[править]
Молярная концентрация — количество растворённого вещества (число молей) в единице объёма раствора. Молярная концентрация в системе СИ измеряется в моль/м³, однако на практике её гораздо чаще выражают в моль/л или ммоль/л. Также распространено выражение в «молярности». Возможно другое обозначение молярной концентрации , которое принято обозначать М. Так, раствор с концентрацией 0,5 моль/л называют 0,5-молярным.
Примечание: После числа пишут «моль», подобно тому, как после числа пишут «см», «кг» и т. п., не склоняя по падежам.
- ,
где:
Нормальная концентрация (мольная концентрация эквивалента, «нормальность»)[править]
Нормальная концентрация — количество эквивалентов данного вещества в 1 литре раствора. Нормальную концентрацию выражают в моль-экв/л или г-экв/л (имеется в виду моль эквивалентов). Для записи концентрации таких растворов используют сокращения «н» или «N». Например, раствор, содержащий 0,1 моль-экв/л, называют децинормальным и записывают как 0,1 н.
- ,
где:
Нормальная концентрация может отличаться в зависимости от реакции, в которой участвует вещество. Например, одномолярный раствор H2SO4 будет однонормальным, если он предназначается для реакции со щёлочью с образованием гидросульфата калия KHSO4, и двухнормальным в реакции с образованием K2SO4.
Мольная (молярная) доля[править]
Мольная доля — отношение количества молей данного компонента к общему количеству молей всех компонентов. Мольную долю выражают в долях единицы.
- ,
где:
- νi — количество i-го компонента, моль;
- n — число компонентов;
Моляльность (молярная весовая концентрация, моляльная концентрация)[править]
Моляльность — количество растворённого вещества (число моль) в 1000 г растворителя. Измеряется в молях на кг, также распространено выражение в «моляльности». Так, раствор с концентрацией 0,5 моль/кг называют 0,5-мольным.
- ,
где:
Следует обратить особое внимание, что, несмотря на сходство названий, молярная концентрация и моляльность — величины различные. Прежде всего, в отличие от молярной концентрации, при выражении концентрации в моляльности расчёт ведут на массу растворителя, а не на объём раствора. Моляльность, в отличие от молярной концентрации, не зависит от температуры.
Титр раствора — масса растворённого вещества в 1 мл раствора.
- ,
где:
- m1 — масса растворённого вещества, г;
- V — общий объём раствора, мл;
В аналитической химии обычно концентрацию титранта пересчитывают применительно к конкретной реакции титрования таким образом, чтобы объём использованного титранта непосредственного показывал массу определяемого вещества; то есть титр раствора показывает, какой массе определяемого вещества (в граммах) соответствует 1 мл титрованного раствора.
Весообъёмные (массо-объёмные) проценты[править]
Соответствуют отношению массы одной части вещества (например, 1 г) к 100 частям объёма раствора (например, к 100 мл).[1] Этот способ выражения используют, например, в спектрофотометрии, если неизвестна молярная масса вещества или если неизвестен состав смеси, а также по традиции в фармакопейном анализе.[2]
Другие способы выражения концентрации растворов[править]
Существуют и другие, распространённые в определённых областях знаний или технологиях, методы выражения концентрации. Например, в фотометрии часто используют массовую концентрацию, равную массе растворённого вещества в 1 л раствора. При приготовлении растворов кислот в лабораторной практике часто указывают, сколько объёмных частей воды приходится на одну объёмную часть концентрированной кислоты (например, 1:3). Концентрация загрязнений в воздухе может выражаться в частях на миллион (ppm — от англ. parts per million). Иногда используют также отношение масс (отношение массы растворённого вещества к массе растворителя) и отношение объёмов (аналогично, отношение объёма растворяемого вещества к объёму растворителя).
Применимость способов выражения концентрации растворов, их свойства[править]
В связи с тем, что моляльность, массовая доля, мольная доля не включают в себя значения объёмов, концентрация таких растворов остаётся неизменной при изменении температуры. Молярность, объёмная доля, титр, нормальность изменяются при изменении температуры, так как при этом изменяется плотность растворов. Именно моляльность используется в формулах повышения температуры кипения и понижения температуры замерзания растворов.
Разные виды выражения концентрации растворов применяются в разных сферах деятельности, в соответствии с удобством применения и приготовления растворов заданных концентраций. Так, титр раствора удобен в аналитической химии для волюмометрии (титриметрического анализа) и т. п.
Формулы перехода от одних выражений концентраций растворов к другим[править]
В зависимости от выбранной формулы погрешность конвертации колеблется от нуля до некоторого знака после запятой.
От массовой доли к молярности:
- ,
где:
- ρ — плотность раствора, г/мл;
- ω — массовая доля растворенного вещества, в долях от 1;
- M — молярная масса растворенного вещества, г/моль.
От молярности к нормальности:
- ,
где:
От массовой доли к титру:
- ,
где:
- ρ — плотность раствора, г/мл;
- ω — массовая доля растворенного вещества, в долях от 1;
От молярности к титру:
- ,
где:
- — молярность, моль/л;
- M — молярная масса растворенного вещества, г/моль.
От молярности к моляльности:
- ,
где:
- — молярность, моль/л;
- ρ — плотность раствора, г/мл;
От моляльности к мольной доле:
- ,
где:
- mi — моляльность, моль/1000г;
- M — молярная масса растворителя, г/моль.
Определение концентрации раствора методом добавок[править]
Точное количество стандарта исследуемого вещества вводят в исследуемый раствор, после чего измеряют поглощение вещества без добавки и раствора с добавкой . Увеличение поглощения в растворах с добавкой пропорционально разнице концентраций раствора с добавкой и раствора без добавки вещества , если при этом сохраняется подчинение закону Бугера-Ламберта-Бера. В таком случае справедлива пропорция:
Отсюда:
Наиболее распространённые единицы[править]
| Эта статья или раздел содержит незавершённый перевод с английского языка. Вы можете помочь проекту, закончив перевод. |
www.wikiznanie.ru

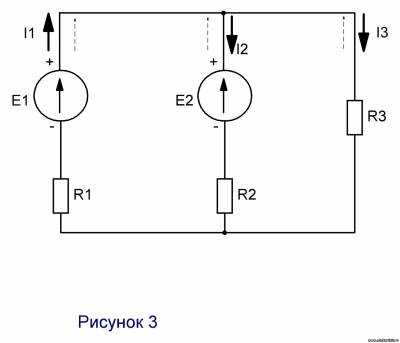
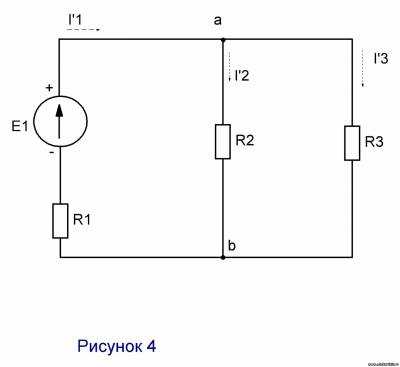
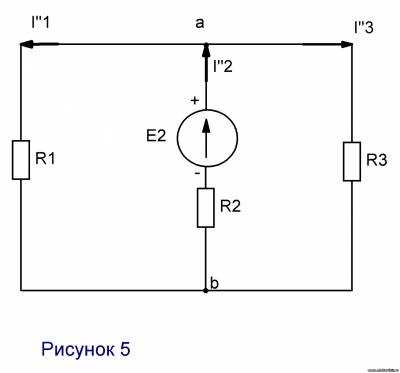
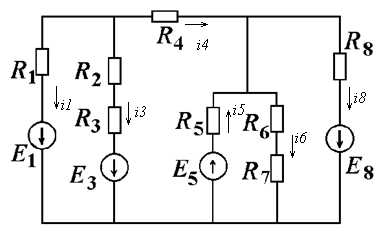
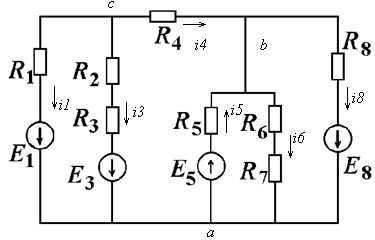
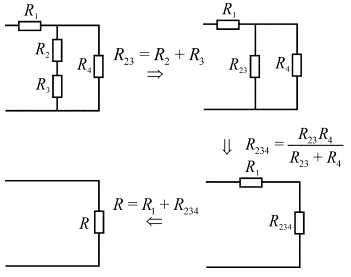
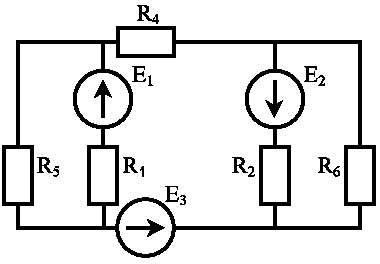
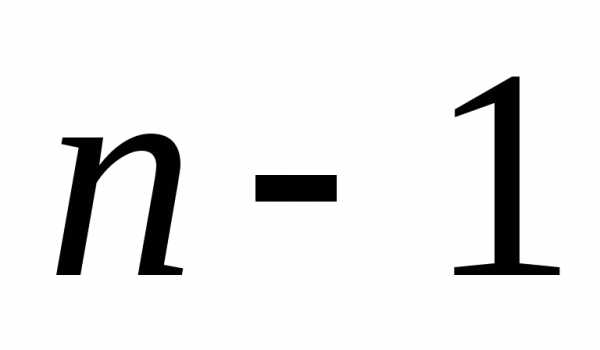 ,
где
,
где количество
узловых точек.
количество
узловых точек.
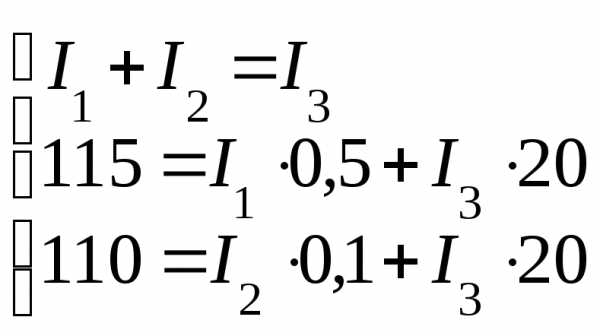
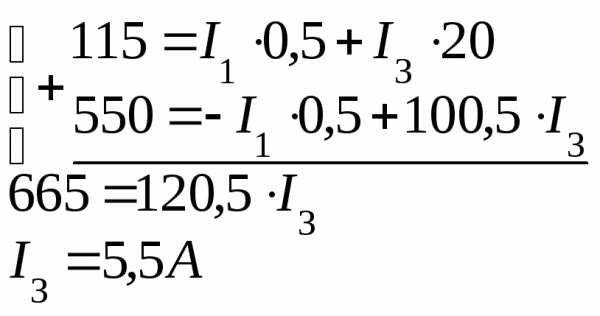
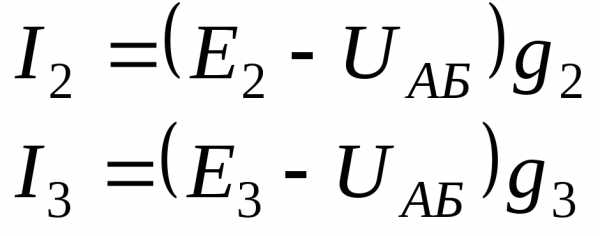
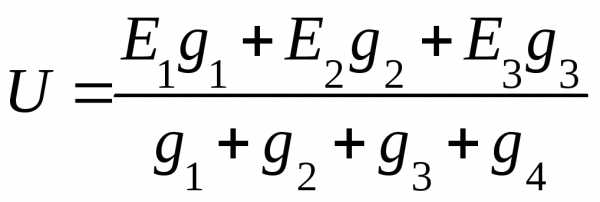
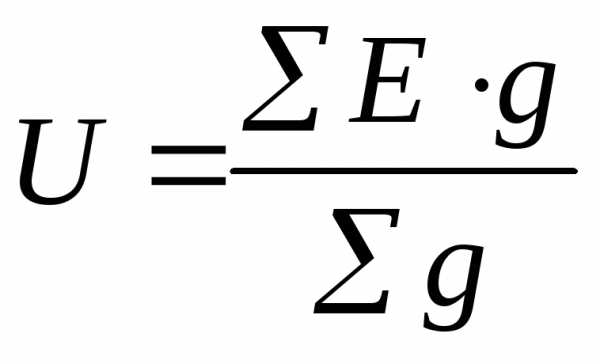
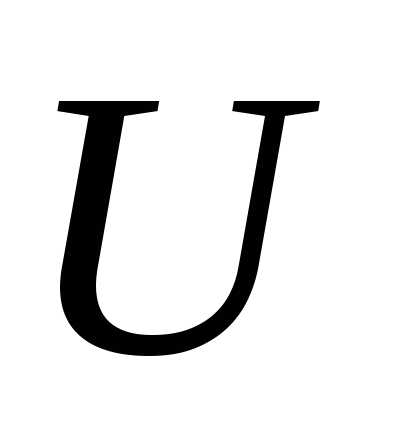 (напряжение
на шинах) практически мало отличается
от ЭДС, т.е. разность
(напряжение
на шинах) практически мало отличается
от ЭДС, т.е. разность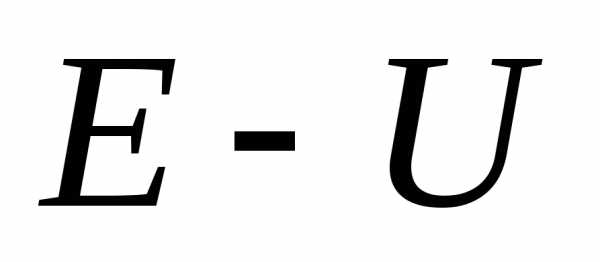 составляет несколько % от
составляет несколько % от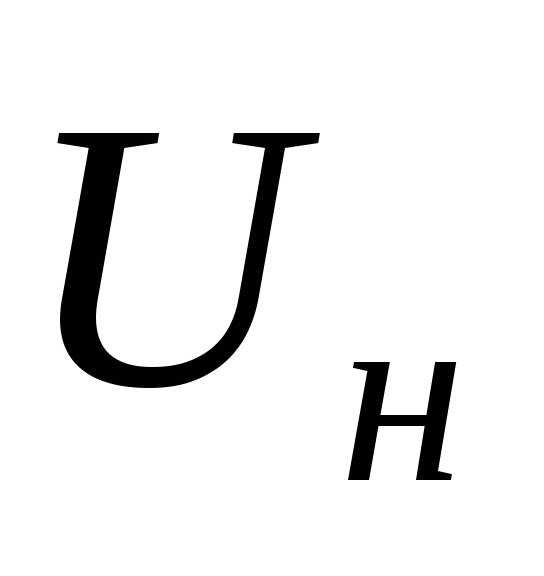 .
Поэтому, если ЭДС увеличить на 1%, то
разность увеличится на 40%. На столько
же увеличится ток нагрузки генератора,
т.к.
.
Поэтому, если ЭДС увеличить на 1%, то
разность увеличится на 40%. На столько
же увеличится ток нагрузки генератора,
т.к.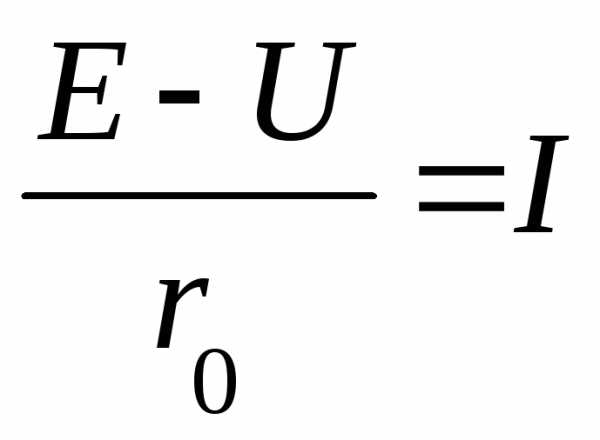 .
.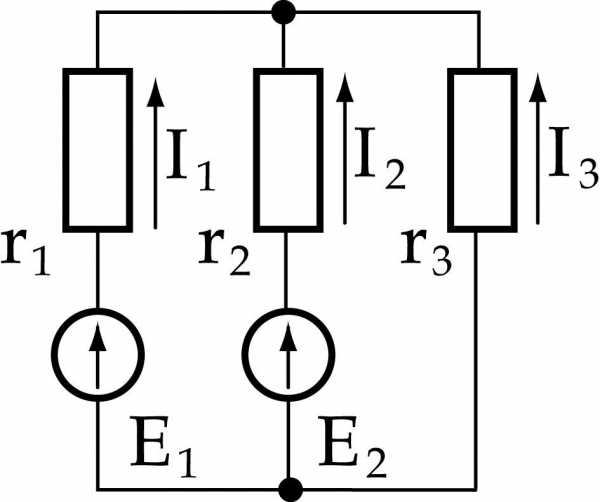
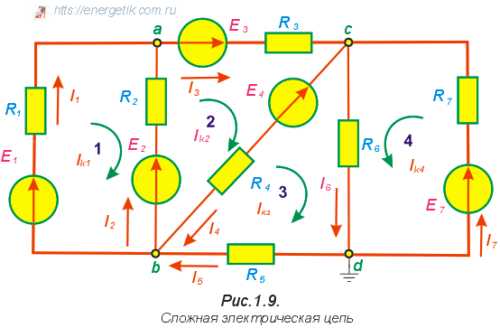
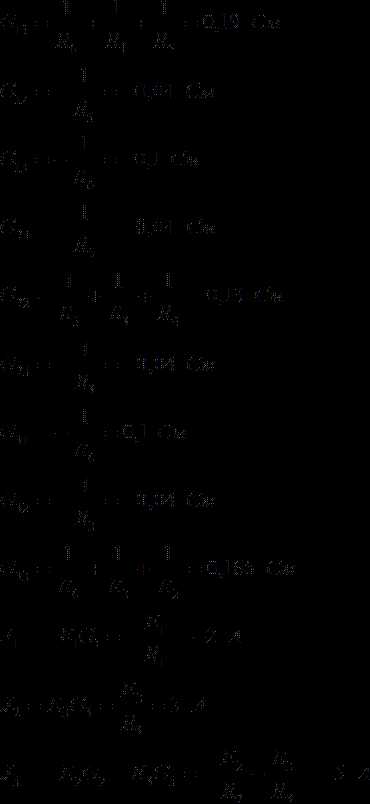
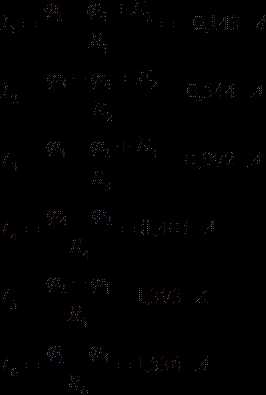

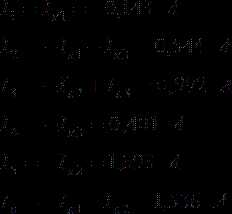
 Замена части электрической цепи эквивалентным генератором
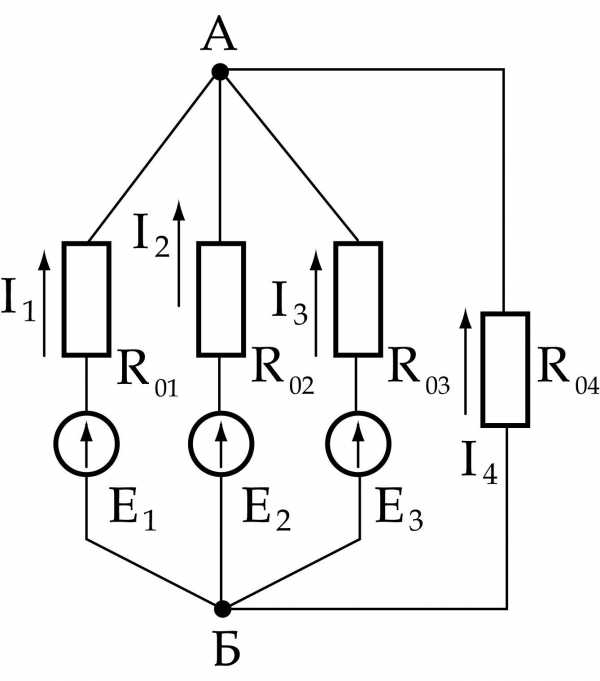
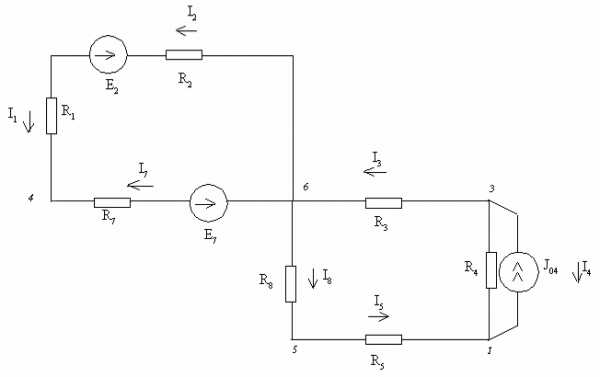
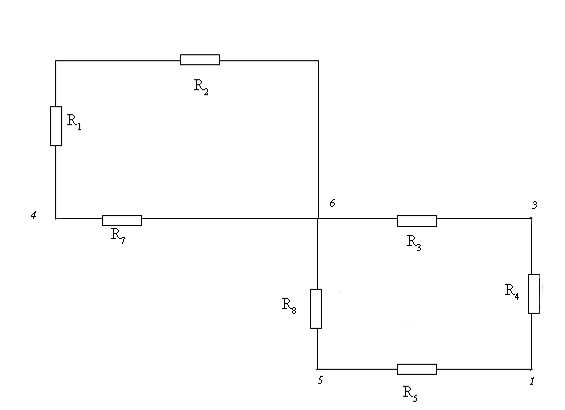
Замена части электрической цепи эквивалентным генератором Упрощенная схема
Упрощенная схема Определение
Определение 
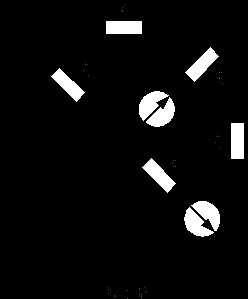
 Определение
Определение 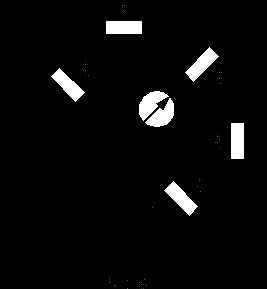 Упрощенная схема
Упрощенная схема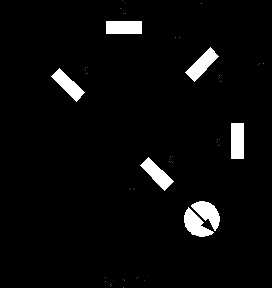 Упрощенная схема
Упрощенная схема ,331
,331
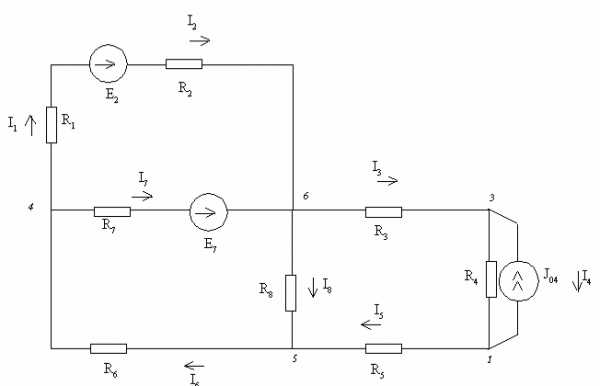
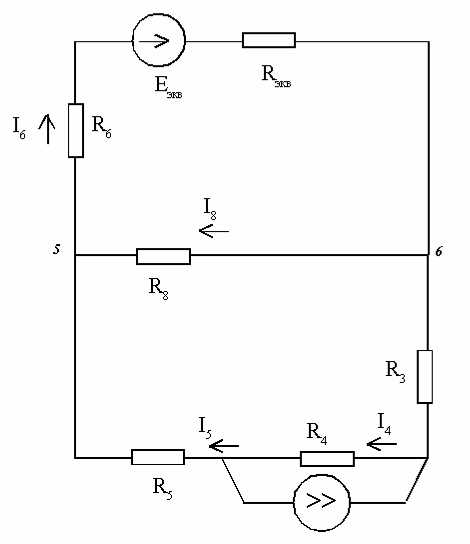
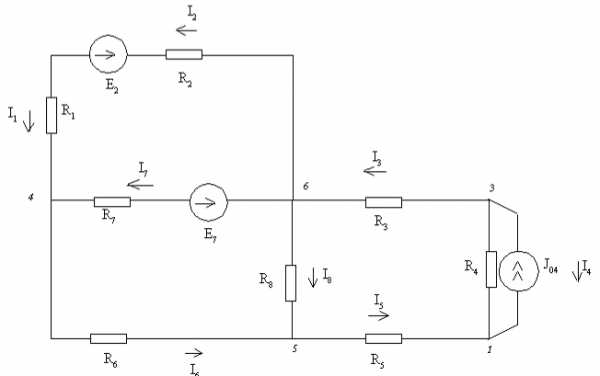
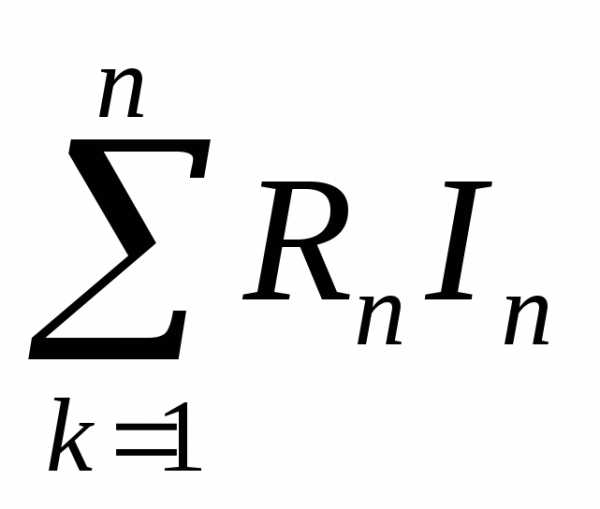 =250×0,3312 + 110×0,3312+ 310×3,4362+ 470×6,5642+ 320×3,4362+ 450×0,6472+ 410×0,3152+ 330×2,7892= 30524,099 (Вт)
=250×0,3312 + 110×0,3312+ 310×3,4362+ 470×6,5642+ 320×3,4362+ 450×0,6472+ 410×0,3152+ 330×2,7892= 30524,099 (Вт)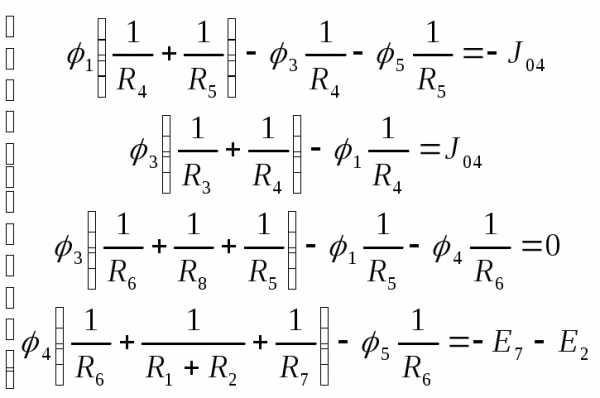
 .Суммой функцийfиg называется
функция,
значение которой в точке
.Суммой функцийfиg называется
функция,
значение которой в точке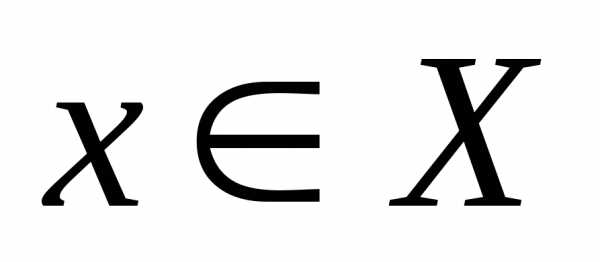 определяется как сумма значений функцийfиg в этой точке, то есть
определяется как сумма значений функцийfиg в этой точке, то есть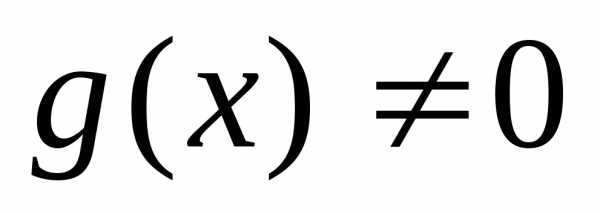 ,
,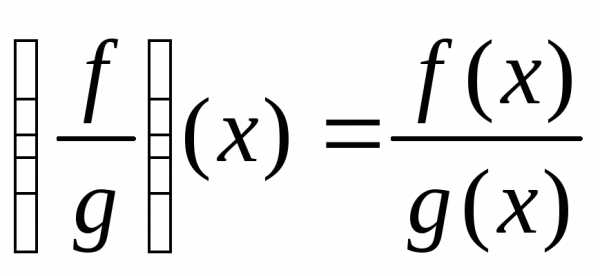 .
. — сложная функция, а тождественная ей
функция
— сложная функция, а тождественная ей
функция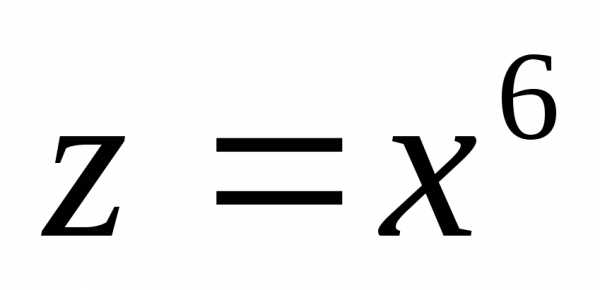 уже не является сложной.
уже не является сложной.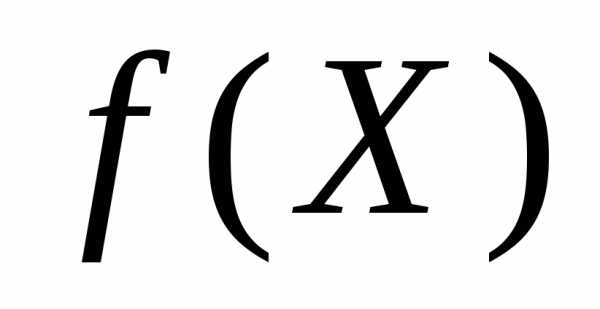 не является подмножеством множестваY. В этом случае сложная
функция определена лишь для техх,
для которых
не является подмножеством множестваY. В этом случае сложная
функция определена лишь для техх,
для которых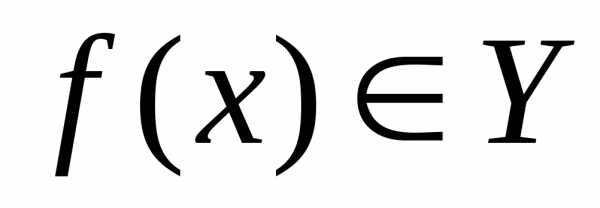 .
.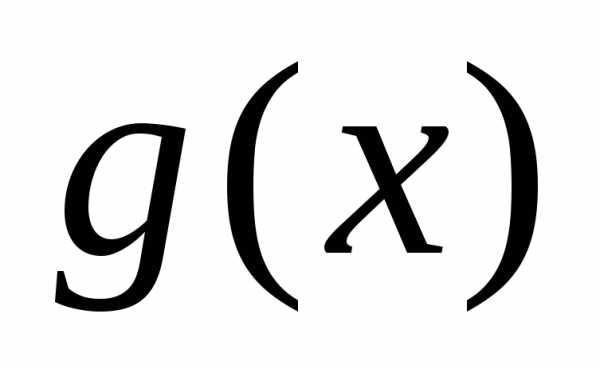 задана на множествезадана наи.
Сложная функция
задана на множествезадана наи.
Сложная функция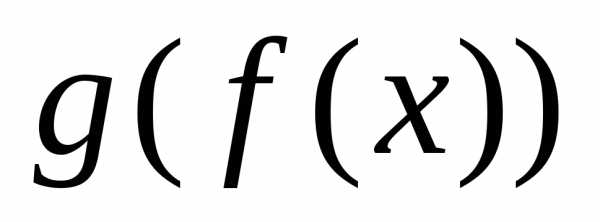 рассматривается
длях таких, что,
то есть.
рассматривается
длях таких, что,
то есть.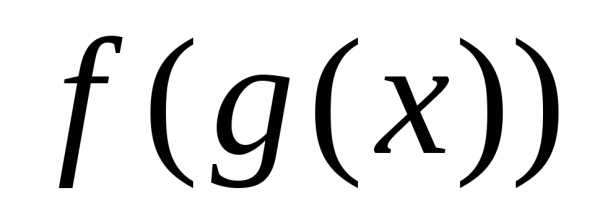 ,
так как
,
так как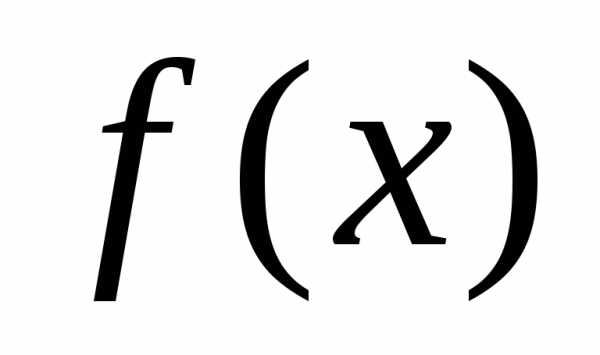 определена для
определена для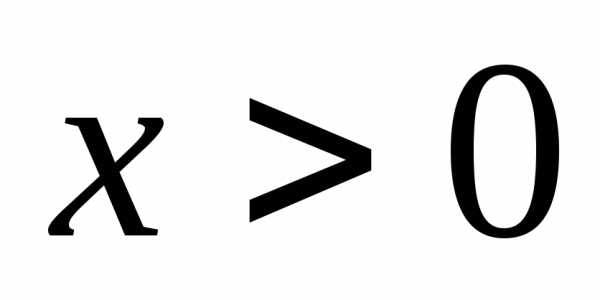 ,
а
,
а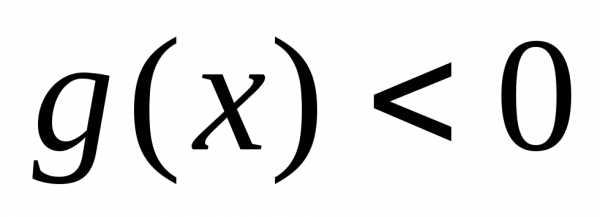 для всех
для всех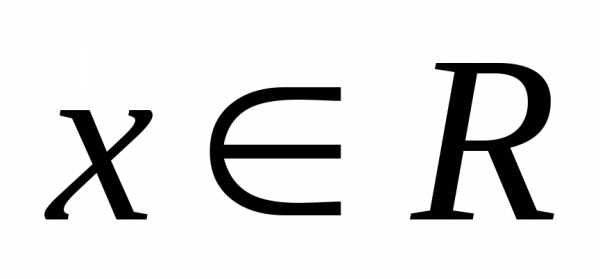 .
.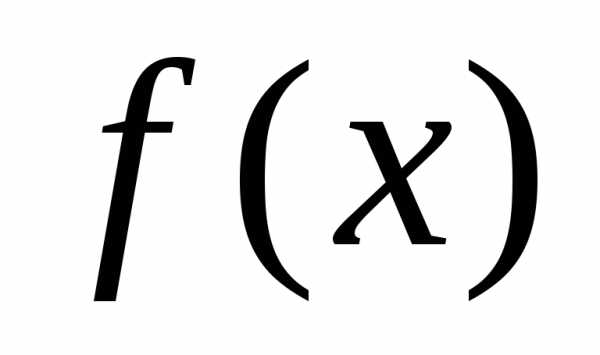 ,
заданная на множествеХ, называетсяограниченной сверху на этом
множестве, если существует числоМ,
такое, что.
Функция,
заданная на множествеХ, называетсяограниченной снизу на этом
множестве, если существует числоМ,
такое, что.
Функция
,
заданная на множествеХ, называетсяограниченной сверху на этом
множестве, если существует числоМ,
такое, что.
Функция,
заданная на множествеХ, называетсяограниченной снизу на этом
множестве, если существует числоМ,
такое, что.
Функция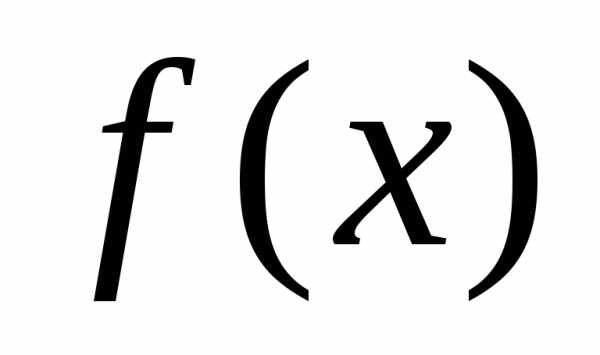 ,
заданная на множествеХ, называетсяограниченной на этом множестве,
если существуют числа
,
заданная на множествеХ, называетсяограниченной на этом множестве,
если существуют числа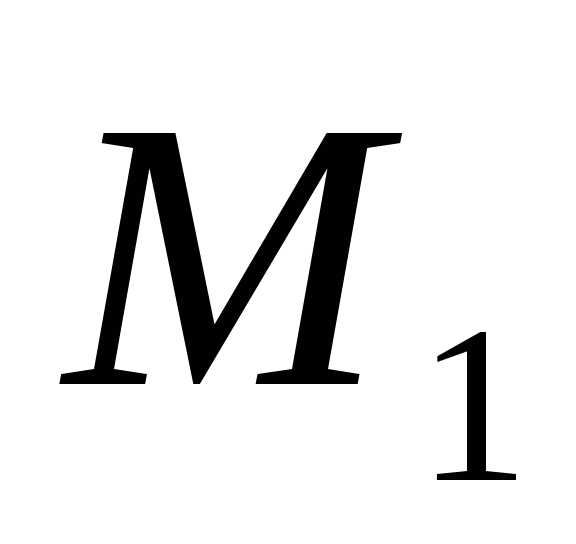 и
и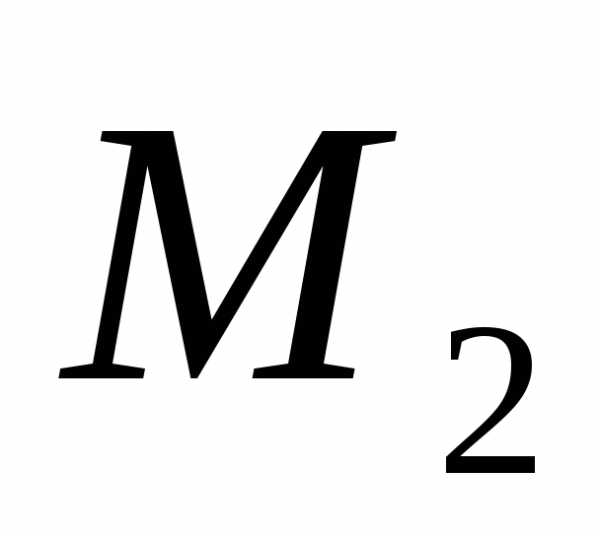 ,
такие, что.
,
такие, что. ограничена
на множествеХ, если на этом множестве
она ограничена и сверху, и снизу.
ограничена
на множествеХ, если на этом множестве
она ограничена и сверху, и снизу. ограничена снизу наR,
так как,
функция
ограничена снизу наR,
так как,
функция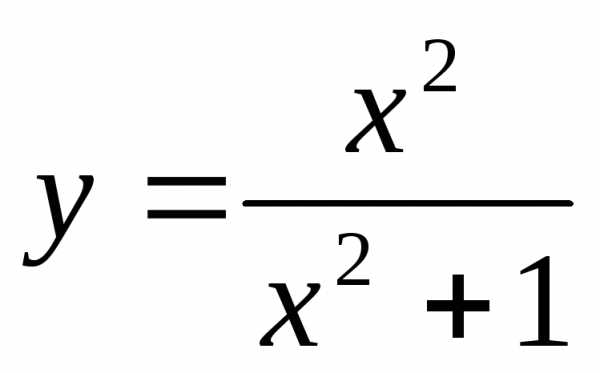 ограничена наR, так
как.
Ограниченными являются также функции
ограничена наR, так
как.
Ограниченными являются также функции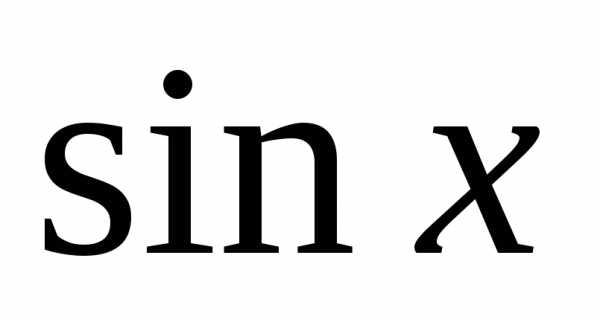 и
и ,
так как.
,
так как.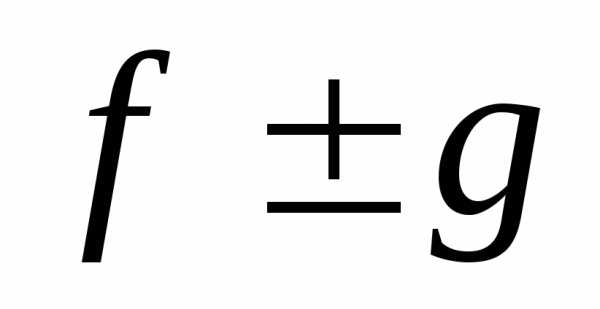 и
и тоже ограничены на множествеХ;
тоже ограничены на множествеХ;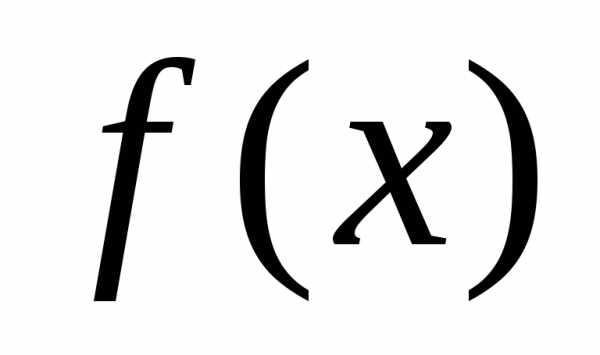 ограничена сверху, то функция
ограничена сверху, то функция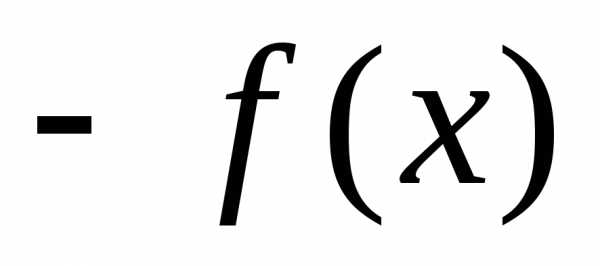 ограничена снизу;
ограничена снизу;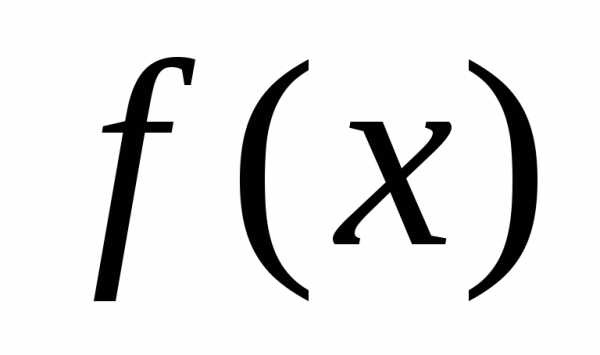 положительна
на множествеХи ограничена на нем
снизу положительным числом, то функция
положительна
на множествеХи ограничена на нем
снизу положительным числом, то функция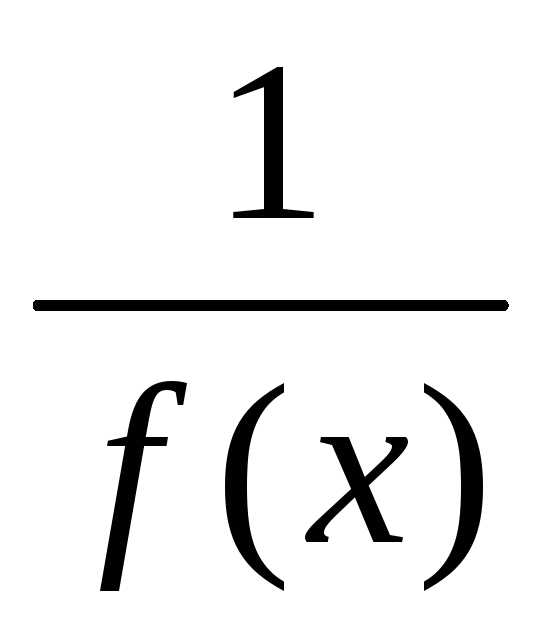 ограничена наХ.
ограничена наХ.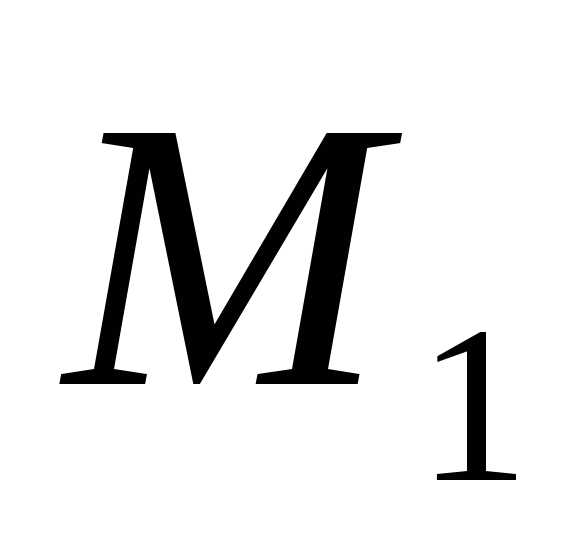 и
и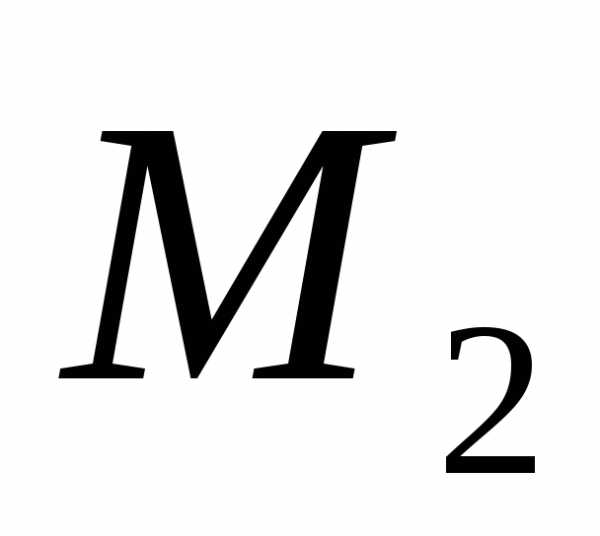 ,
,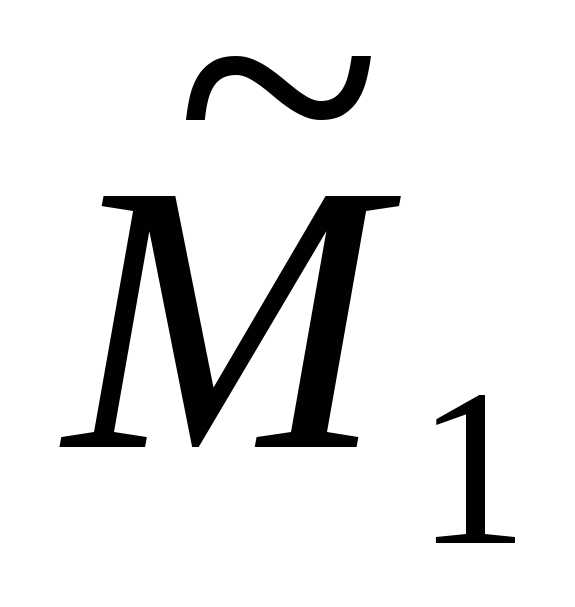 и
и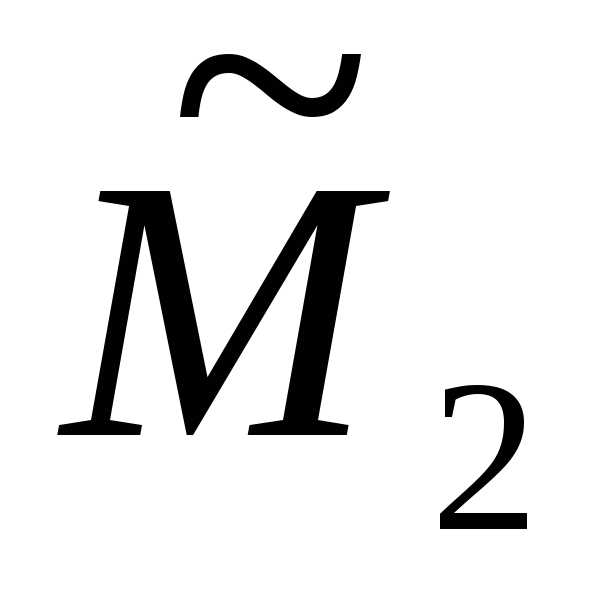 ,
такие, чтои.
А тогдаи
,
такие, чтои.
А тогдаи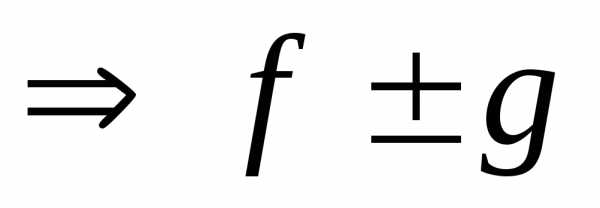 — ограниченные наХ функции. Чтобы
доказать ограниченность функции
— ограниченные наХ функции. Чтобы
доказать ограниченность функции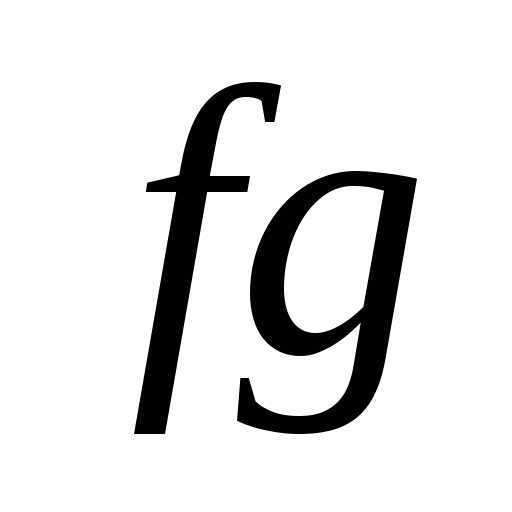 ,
положим.
Тогда имеют место неравенстваи,
из которых следует, что,
а это и означает ограниченность функции
,
положим.
Тогда имеют место неравенстваи,
из которых следует, что,
а это и означает ограниченность функции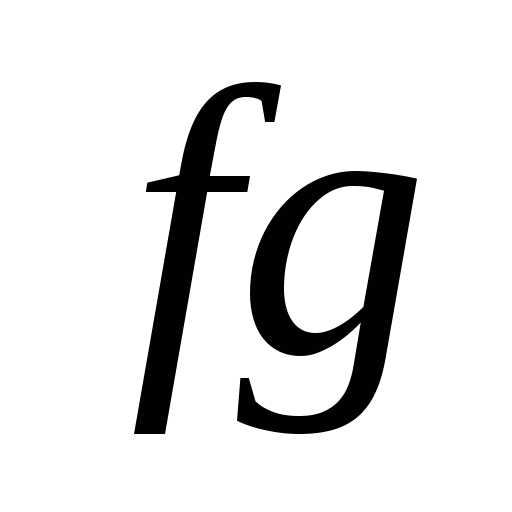 .
.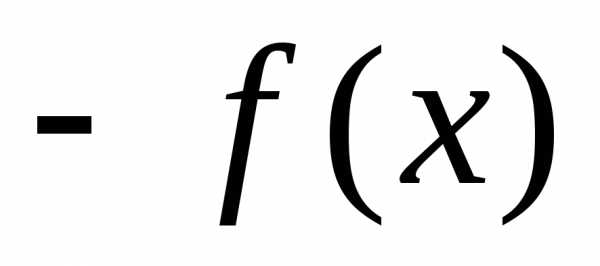 снизу.
снизу.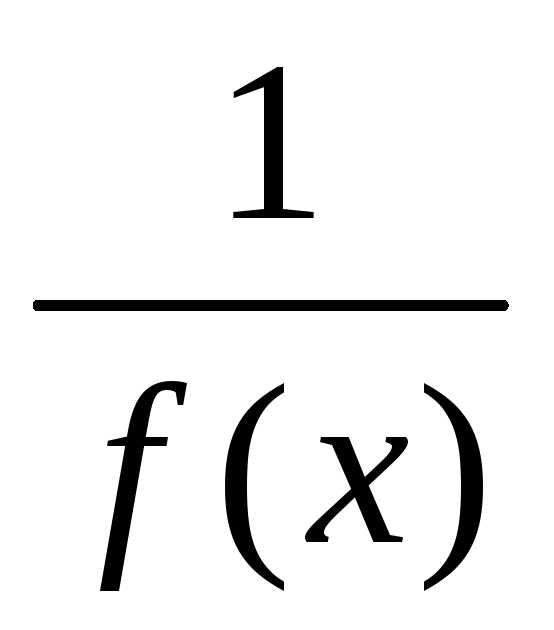 .
.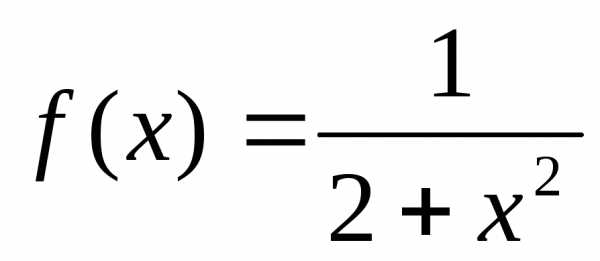 ограничена на множествеR действительных чисел, так как.
ограничена на множествеR действительных чисел, так как. называетсянеограниченной сверху на множествеХ, если не существует
числаМ, такого, чтодля любого
называетсянеограниченной сверху на множествеХ, если не существует
числаМ, такого, чтодля любого ,
то есть для любого числаМнайдется
число
,
то есть для любого числаМнайдется
число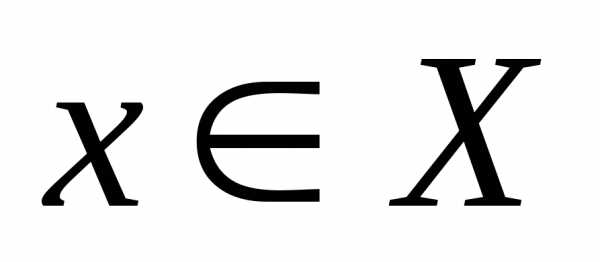 ,
такое, что.
,
такое, что. называетсянеограниченной снизу на
множествеХ, если для любого числаМнайдется число
называетсянеограниченной снизу на
множествеХ, если для любого числаМнайдется число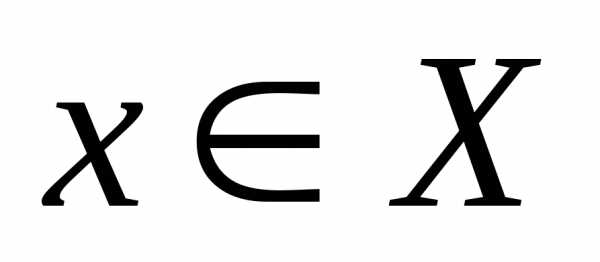 ,
такое, что.
,
такое, что. неограниченна на множестве
неограниченна на множестве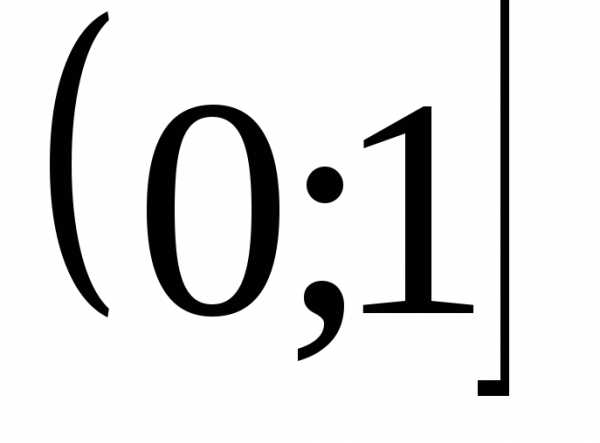 сверху. Возьмем произвольное число
сверху. Возьмем произвольное число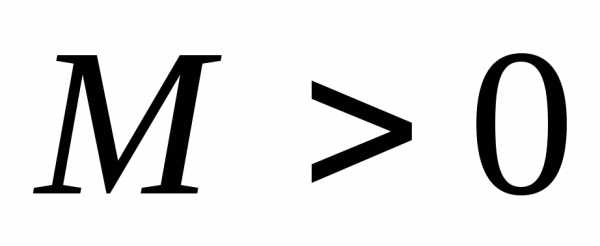 и покажем, что
и покажем, что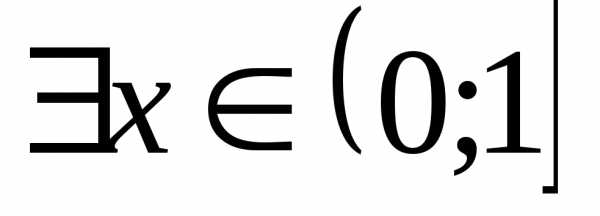 ,
такое, что
,
такое, что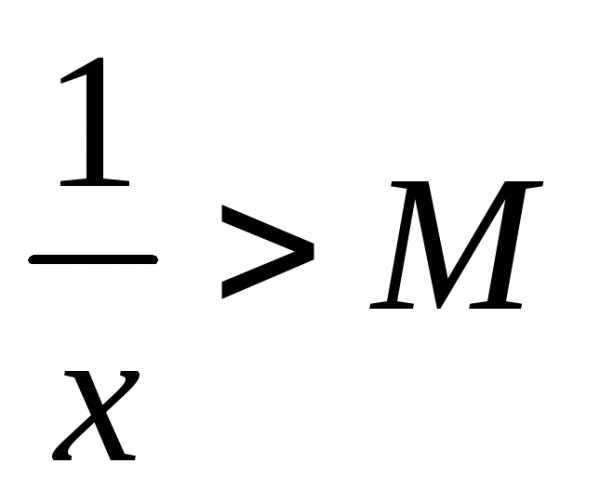 .
.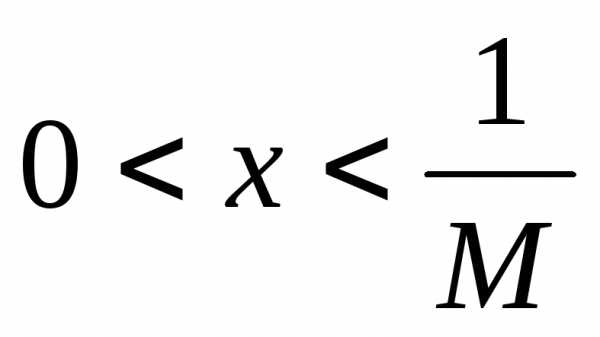 ,
например,
,
например,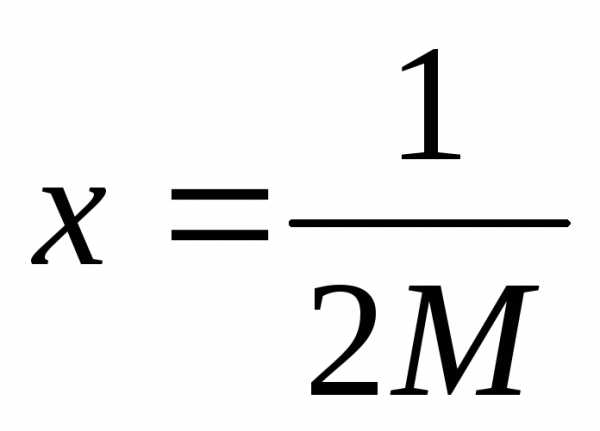 .
.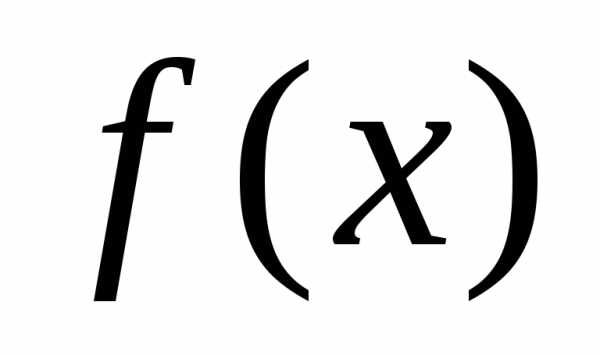 ограничена на множествеХ, то
множество
ограничена на множествеХ, то
множество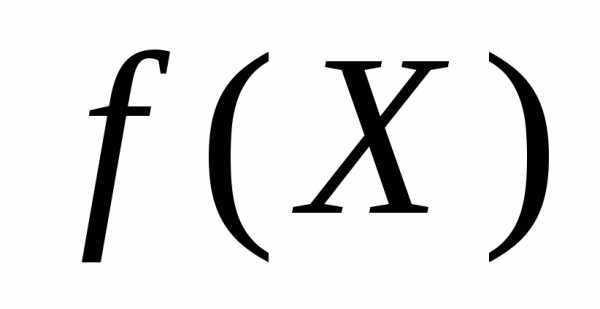 ограничено, поэтому имеет точную верхнюю
и точную нижнюю границы. Их обозначают
ограничено, поэтому имеет точную верхнюю
и точную нижнюю границы. Их обозначают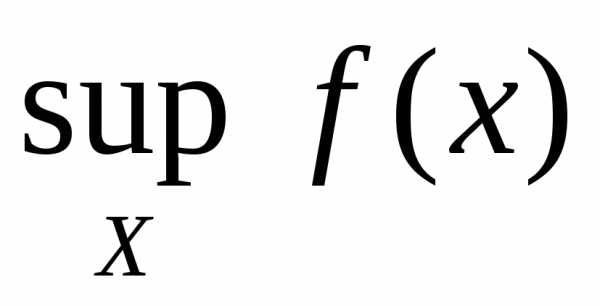 и
и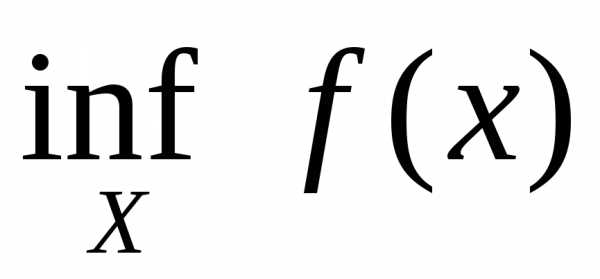 соответственно и называют точной
верхней границей и точной нижней границей
функции
соответственно и называют точной
верхней границей и точной нижней границей
функции на множествеХ.
на множествеХ. называетсявозрастающей на
множествеХ, если большему значению
аргумента соответствует большее значение
функции, т.е.,
таких, что
называетсявозрастающей на
множествеХ, если большему значению
аргумента соответствует большее значение
функции, т.е.,
таких, что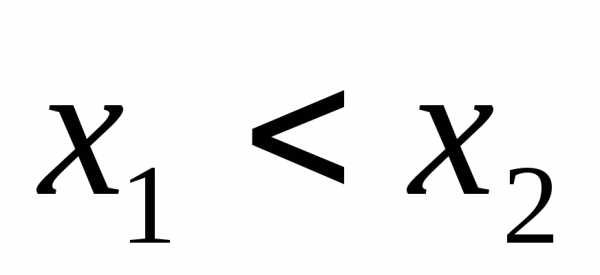 ,
имеем.
,
имеем. называетсяубывающей на множествеХ, если
называетсяубывающей на множествеХ, если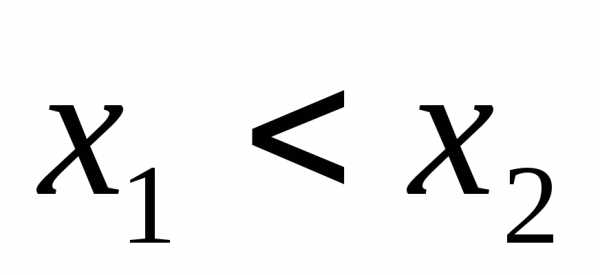
 .
. называетсянеубывающей на
множествеХ, если
называетсянеубывающей на
множествеХ, если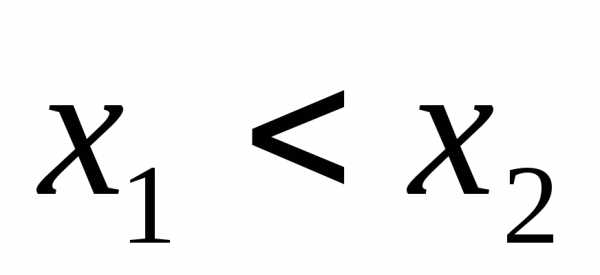
 .
.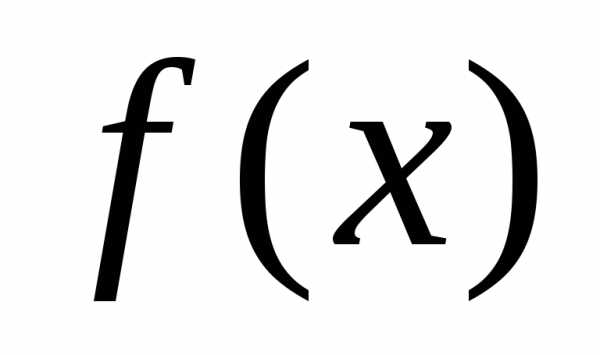 называетсяневозрастающей на
множествеХ, если
называетсяневозрастающей на
множествеХ, если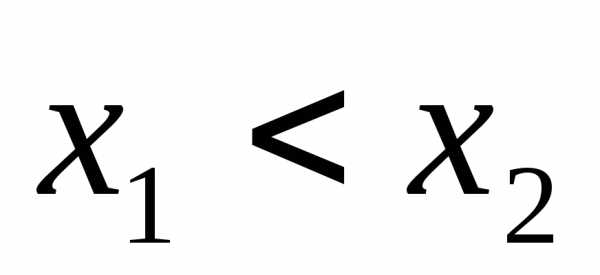
 .
.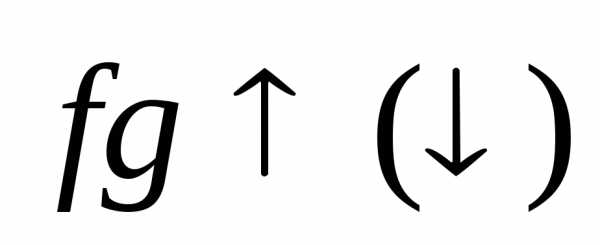 наХ.
наХ.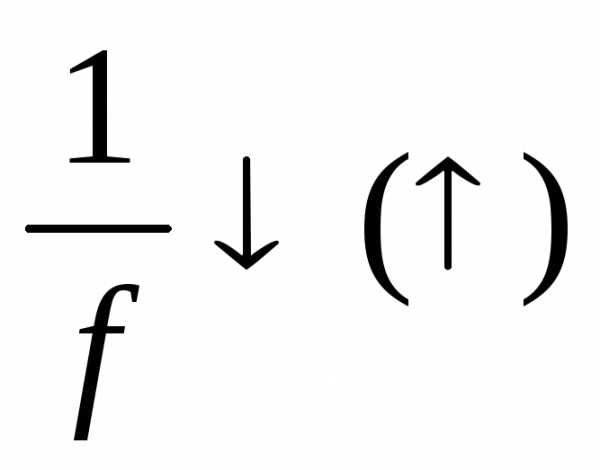 наХ.
наХ.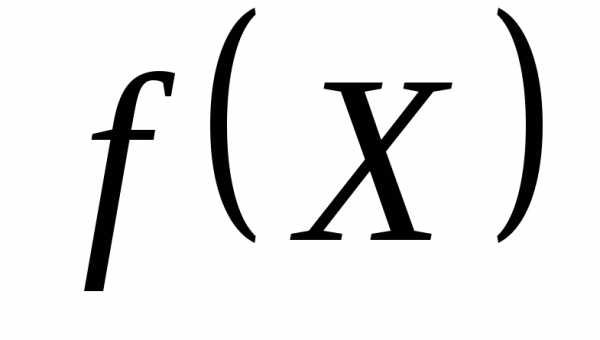 ,
то функция
,
то функция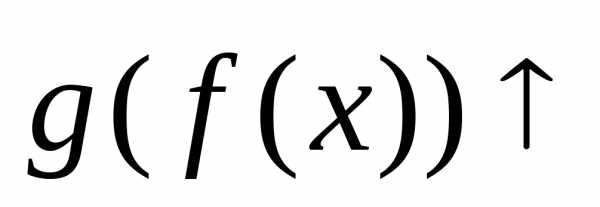 на множествеХ.
на множествеХ. .
Тогдаи поскольку неравенства одинакового
смысла можно складывать, то,
т.е. функцияf+g возрастает.
.
Тогдаи поскольку неравенства одинакового
смысла можно складывать, то,
т.е. функцияf+g возрастает.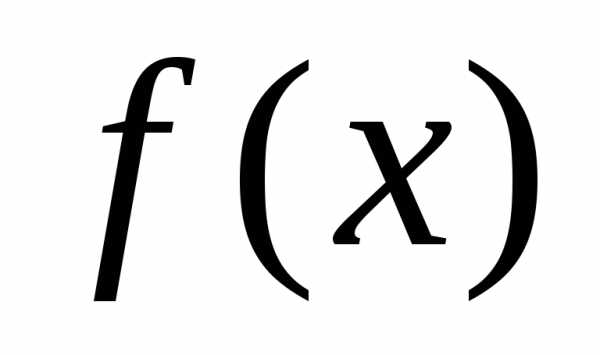 убывает на множествеХ, а функция
убывает на множествеХ, а функция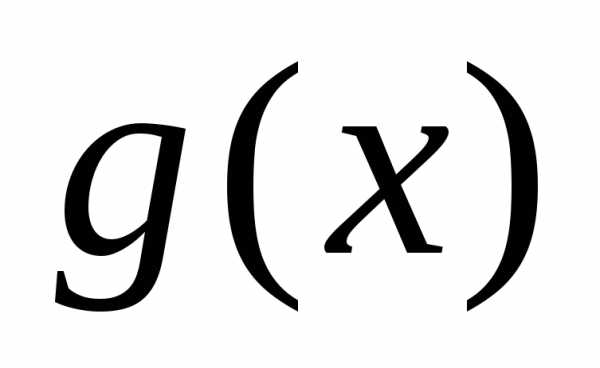 убывает на множестве
убывает на множестве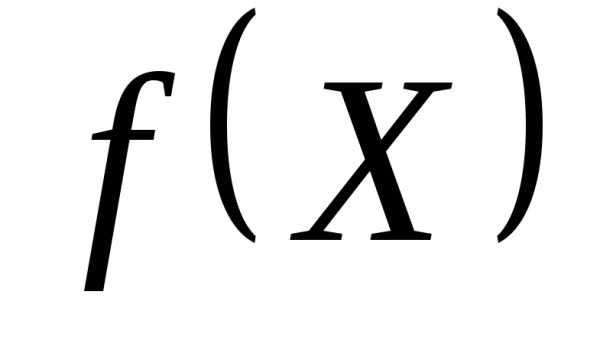 ,,
причем
,,
причем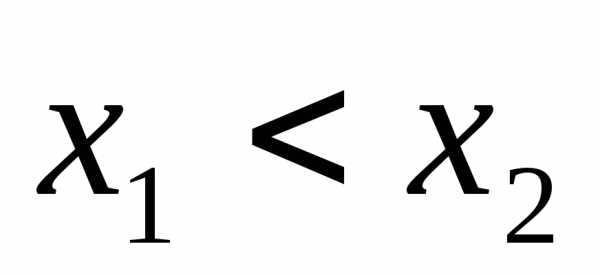 .
Тогдаи, так как,
т.е. функция
.
Тогдаи, так как,
т.е. функция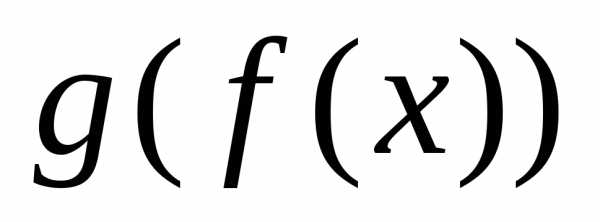 возрастает на множествеХ.
возрастает на множествеХ. возрастают на промежутке
возрастают на промежутке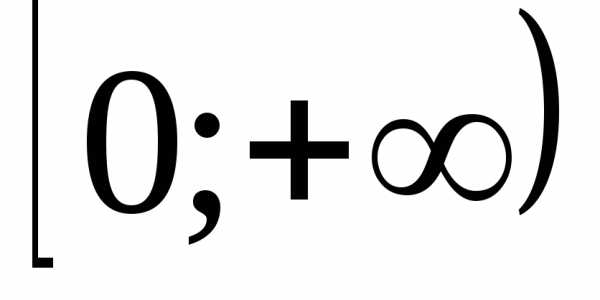 .
. возрастает
на промежутке
возрастает
на промежутке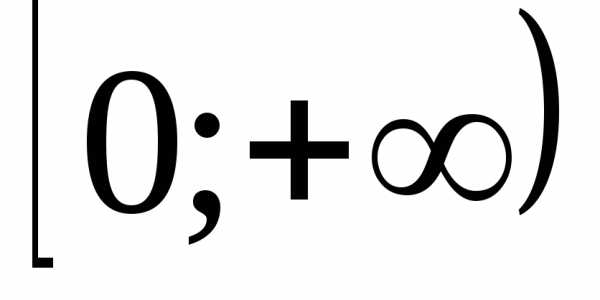 .
Тогда по свойству в)
.
Тогда по свойству в)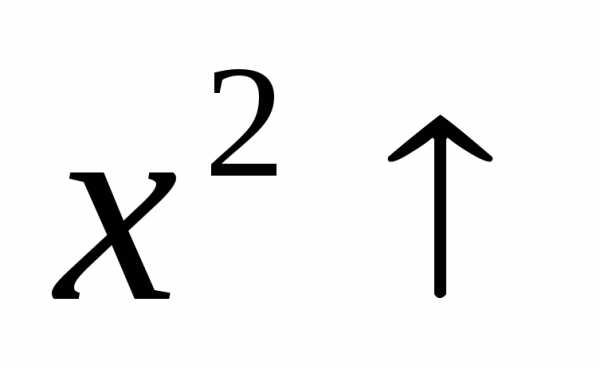 и
и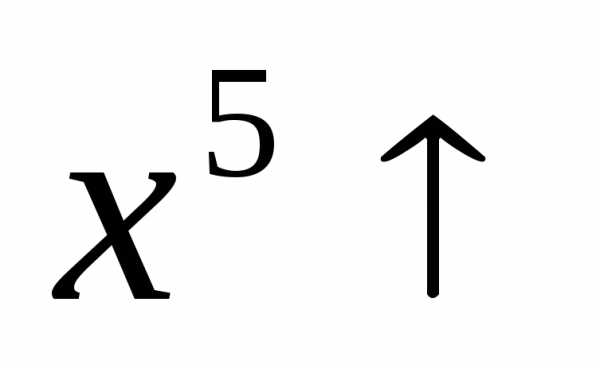 на
на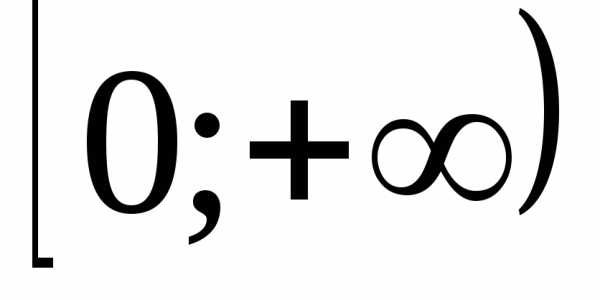 ,
,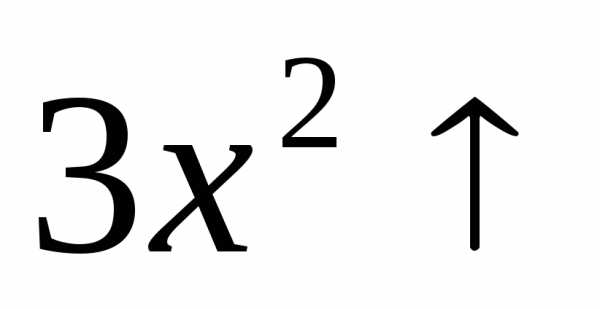 и
и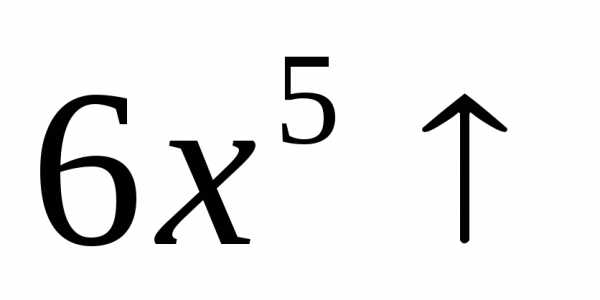 ,
поэтому по свойству а) возрастает и
функция
,
поэтому по свойству а) возрастает и
функция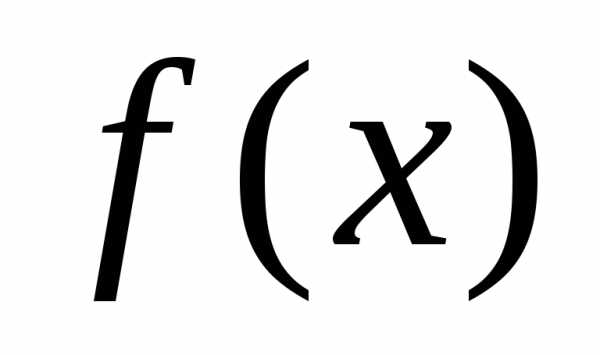 .
.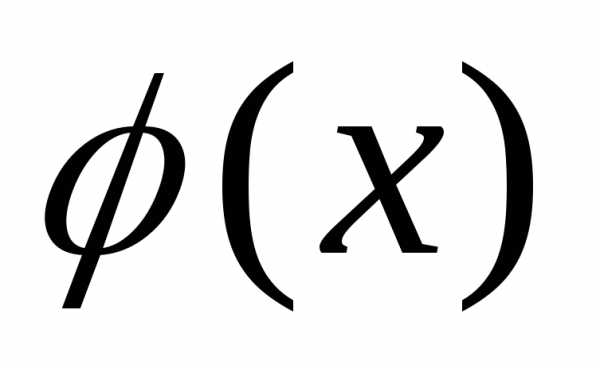 доказательство проведем методом от
противного. Пусть.
Предположим противное, т.е. что
доказательство проведем методом от
противного. Пусть.
Предположим противное, т.е. что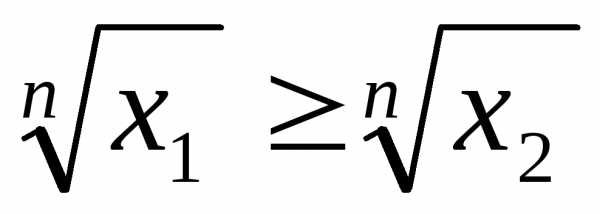 .
Тогда, в силу возрастания функции
.
Тогда, в силу возрастания функции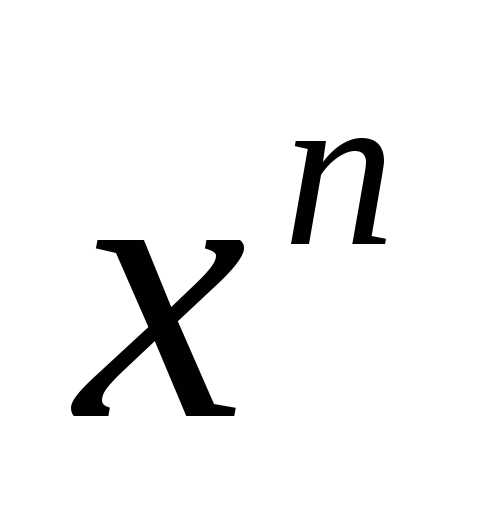 ,,
т.е.
,,
т.е.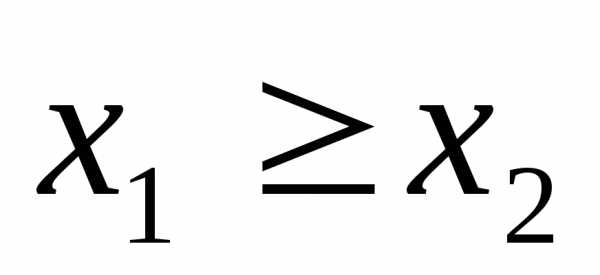 ,
что противоречит неравенству
,
что противоречит неравенству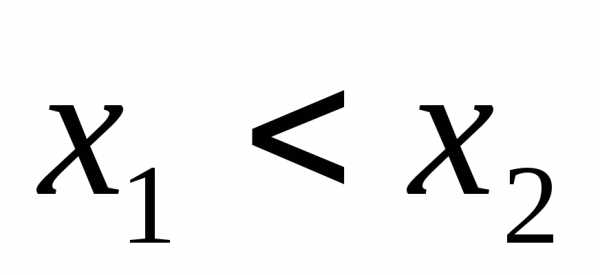 .
Из полученного противоречия следует,
что
.
Из полученного противоречия следует,
что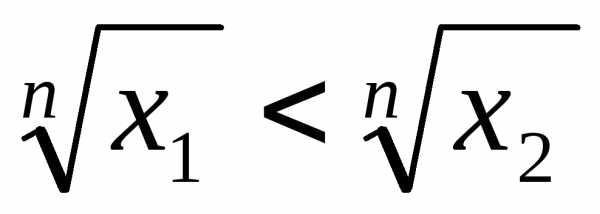 ,
т.е. функция
,
т.е. функция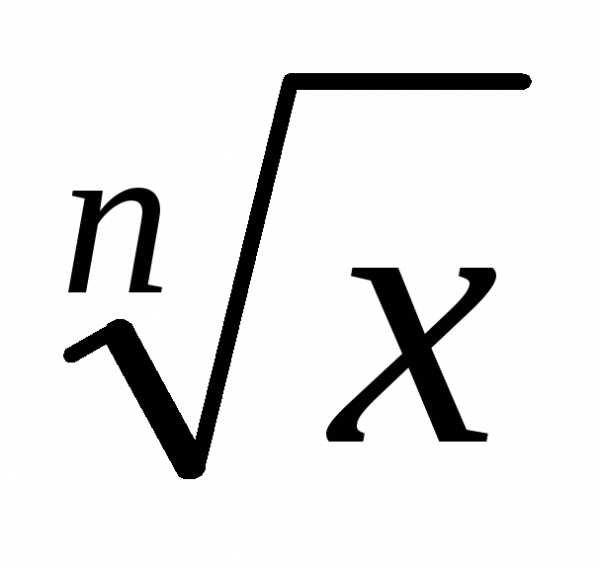 возрастает на промежутке
возрастает на промежутке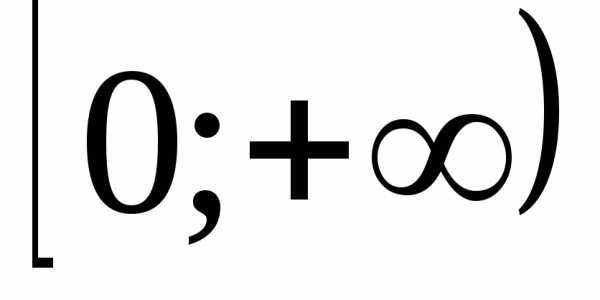 .
.








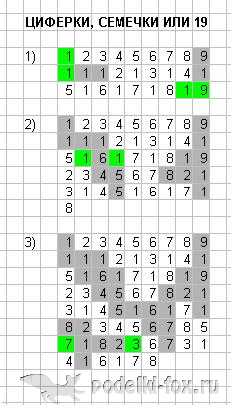 Краткое описание и количество игроков: игра на внимательность и состав числа для одного человека.
Краткое описание и количество игроков: игра на внимательность и состав числа для одного человека. Краткое описание и количество игроков: игра на внимательность и скорость, знание цифр до 100. Для двух человек. Подходит для дошкольников.
Краткое описание и количество игроков: игра на внимательность и скорость, знание цифр до 100. Для двух человек. Подходит для дошкольников.























 ,
,


 будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем

 для которого выполняются следующие
условия:
для которого выполняются следующие
условия: для которого выполняются следующие
условия:
для которого выполняются следующие
условия: ,
,


 будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем

 для которого выполняются следующие
условия:
для которого выполняются следующие
условия: для которого выполняются следующие
условия:
для которого выполняются следующие
условия: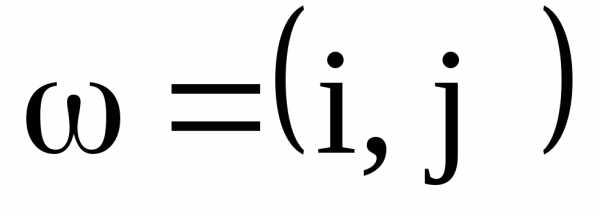 ,
,


 будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем

 для которого выполняются следующие
условия:
для которого выполняются следующие
условия: для которого выполняются следующие
условия:
для которого выполняются следующие
условия: