Тест статистика с ответами
1. К современным значениям термина «статистика» не относится:
отрасль практической деятельности людей, по сбору, обработки и анализу данных, характеризующих состояние экономики и культуры страны
общественная наука, разрабатывающая теоретические положения и методы, используемые статистической практикой
статистические данные, представляемые в отчетности предприятий
обследование нелегальных видов деятельности
2. К основным стадиям экономико-статис
планирование и организация
сбор информации методом массового статистического наблюдения
обработка информации методом статистических группировок
анализ статистической информации на основе расчета обобщающих статистических показателей абсолютных, относительных и средних величин
3. Статистической информаций является:
расчетный материал
первичный статистический материал о социально-эконом
ических явлениях, формирующийся в процессе статистического наблюдения, которые, затем подвергается систематизации, сводке, анализу и обобщению вариационный ряд распределения
обработанный материал
4. Основные свойства статистической информации:
постоянство и незаконность
периодичность динамичность
массовость и стабильность
единовременность
5 Статистическим наблюдением является:
научно организованный сбор информации о моментных процессах
научно организованный сбор информации о стабильных процессах
научно организованный сбор информации о массовых общественных явлениях и процессах общественной жизни
научно организованный сбор информации об единичных явлениях
6. Статистическое наблюдение не может проводиться:
органами государственной статистики
научно-исследова
тельскими институтами экономическими службами банков, бирж, фирм
частными лицами
7. Основные формы статистического наблюдения:
отчетность и специально организованные наблюдения
отчетность и атрибутивные ряды распределения
вариационные ряды распределения и специально организованные наблюдения
выборочные и специально организованные наблюдения
8. Специально организованное статистическое наблюдение это…
сбор сведений с помощью специально организованных переписей, единовременных учетов и обследований
сбор сведений с помощью опроса только менеджеров предприятий
сбор сведений о деятельности только строительных организаций
сбор сведений о деятельности только домашних хозяйств
9. Какая форма не является специально организованным наблюдением?
10. Какие отчетные документы деятельности предприятия представляются в органы государственной статистики?
декларация по страховым взносам на обязательное пенсионное страхование
расчетная ведомость по средствам фонда социального страхования
баланс и отчет о прибылях и убытках
сведения о затратах на производство и продажу продукции
11. Статистический ряд распределения это…
бессистемное распределение единиц изучаемой совокупности
упорядоченное распределение единиц изучаемой совокупности на группы по определенному варьирующему признаку
хаотичное распределение единиц изучаемой совокупности
упорядоченное распределение единиц изучаемой совокупности по баллам
12. Как называется ряд распределения, построенный по качественному признаку?
дискретный
атрибутивный
вариационный
интервальный
13. В чем отличие дискретного ряда распределения от интервального?
варианты имеют значения целых чисел
варианты имеют значения дробных чисел
варианты имеют значения отрицательных чисел
варианты имеют значения комплексных чисел
14. Какие показатели не входят в состав обобщающих показателей?
абсолютные показатели
относительные показатели
средние величины
атрибутивные показатели
15. К какому классу относятся средняя арифметическая, средняя гармоническая, средняя геометрическая?
к классу структурных средних
к классу порядковых средних
к классу степенных средних
к классу промежуточных средних.
16. Расположите средние величины в соответствии с правилом мажорантности (в порядке возрастания).
средняя квадратическая, средняя арифметическая, средняя геометрическая, средняя гармоническая
средняя арифметическая, средняя геометрическая, средняя квадратическая, средняя гармоническая
средняя гармоническая, средняя геометрическая, средняя арифметическая, средняя квадратическая
средняя геометрическая; средняя арифметическая; средняя квадратическая средняя гармоническая
17. Понятие средней величины.
обобщающий показатель, характеризующий структурные сдвиги
частный показатель, характеризующий индекс цен
частный показатель, характеризующий развитие явления
обобщающий показатель, характеризующий типичный уровень явления в конкретных условиях места и времени
18. Основное условие правильного расчета средних величин.
рассчитываются для качественно однородных совокупностей
рассчитываются для разнокачественны
х совокупностей рассчитываются для качественно не однородных совокупностей
рассчитываются для разнородных совокупностей по существенным признакам
refdocx.ru
Тесты статистика с ответами вопросы 187-250
187. Укажите, какой из индексов является общим индексом себестоимости:
4) I = ∑Z1Q1 / ∑Z0Q1;
188 Тест. Какое из приведенных ниже положений не дает характеристику несплошному наблюдению?
2) Сплошное;
189. В Законе «О государственной статистке» не включается следующий раздел…
4) Ежегодные статистические данные.
190. Чему равен нормальный момент четвёртого порядка, если за базу сравнения принимается нормальное распределение?
1) 3;
191. Общий индекс урожайности имеет вид:
1) I = ∑Y1*П1 / ∑у0*П1;
192. Какое из перечисленных правил построения статистических таблиц не отвечает требованиям?
3) при разных единицах измерения отводить отдельную графу нет смысла, а также не указывать единицы измерения по графам или строкам;
193. Как называется площадь, которая занята посевами к моменту окончания весеннего сева, и с которой в данном году предполагается получить продукцию?
2) весенняя продуктивная площадь;
194. .Каким термином можно определить количество продукции с гектара посева?
2) урожайность;
195. Как определяется показатель сохранности скота?
3) отношение поголовья скота в обороте к числу павших и погибших животных;
196. Если суммарную энергетическую мощность разделить на размер площади с/х угодий и умножить на 100, то получим:
2) Показатель энергообеспеченности;
197. Какой из перечисленных показателей рассчитывается делением общего объема выполненных тракторами работ в эталонных гектарах на среднегодовое кол-во условных эталонных тракторов?
3) Среднегодовая выработка;
198. Какой из ответов выходит за рамки вопроса о видах индекса производительности труда?
3) прямой, косвенный;
199. Как определить производство продукции всего по хозяйству на 100 га с/х угодий?
1) производство продукции (стоимость продукции) растениеводства и животноводства разделить на площадь с/х угодий и результат умножить на 100;
200. Какая себестоимость называется фактической?
1) себестоимость, отражающая фактические затраты и определяющаяся по данным бухгалтерского учета в конце года;
201. Что является объектом статистического наблюдения?
1) Совокупность общественных явлений и процессов, которые подлежат статистическому наблюдению;
202. Обследование бюджетов, доходов, расходов населения по охвату единиц совокупности является наблюдением:
3) обследованием основного массива;
203. Каким видом группировок решается задача по определению причинно-следственных связей между исследуемыми признаками?
3) Аналитическими;
Тест — 204. Расчленение однородной совокупности по величине варьирующего признака проводится в статистике при помощи группировок:
2) структурных;
205. Относительные величины структуры:
А) характеризуют состав явления и показывают, какой удельный вес в общем итоге составляет каждая его часть;
Б) характеризуют соотношение отдельных составных частей явления.
Относительные величины координации:
В) характеризуют состав явления и показывают, какой удельный вес в общем итоге составляет каждая его часть;
Г) характеризуют соотношение отдельных частей явления.
Ответы: 4) б, г.
206. Ряд динамики может состоять:
А) из абсолютных суммарных величин;
Б) из относительных и средних величин.
Ответы: 3) а, б;
207. За 2003 — 2005 гг. капитал коммерческого банка увеличился на 20%, абсолютное значение 1% прироста — 12 тыс. грн. Определите капитал банка в 2005 году (тыс. грн).
Ответы: 3) 2400;
208 Тест. Как называют способность выборочной совокупности возобновлять генеральную совокупность?
2) Репрезентативность;
209. Какую формулу необходимо выбрать, чтобы рассчитать среднюю гармоническую простую?
1) XСр = N / ∑1/X
210. Что понимается под статистической гипотезой?
3) Научное предположение о свойствах случайных величин, которое проверяется по результатам статистического наблюдения;
211. Какие существуют виды диаграмм?
2) Линейные, столбиковые, ленточные, прямоугольные, круговые, секторные, радиальные, фигурные;
212. Коэффициент вариации рассчитывается как:
1) процентное отношение среднего квадратического отклонения к средней арифметической;
Тест по статистике — 213. Сущность аналитического выравнивания заключается в:
1) применении тех или иных уравнений аналитического выравнивания;
214. Какова величина коэффициента корреляции, если связь слабая, не тесная?
1) 0 ≤ R ≤ 0,2;
215. 3емельныеучастки, покрытые естественной травянистой растительностью и используемые для сенокошения, называют:
3) сенокосы;
216. Среднее поголовье животных рассчитывается, как:
2) путем деления суммы кормо-дней за определенный период на число дней этого периода;
217. Что такое продуктивность животных?
3) это средний выход продукта в расчете на одно животное;
218. Показатель динамики средней заработной платы исчисляют формулой агрегатного индекса:
2) I = ∑X1T1 : ∑X0T;
219. Какая площадь называется весенней продуктивной?
2) площадь, которая сохранилась к окончанию весеннего сева;
220. Какая продукция называется товарной?
1) Часть валовой продукции, которая реализована;
221. Что является единицей статистического наблюдения?
1) Первичный элемент объекта исследования, который является носителем существенных признаков и особенноCmЕй, которые подлежат регистрации;
222. По полноте охвата единиц наблюдения — наблюдение бывает…
3) сплошное, несплошное;
223. Какая относительная величина характеризует изменение процессов и явлений во времени?
4) относительная величина динамики.
224 Тест по статистике. Относительные величины динамики получаются в результате сопоставления показателей каждого последующего периода:
А) с предыдущим;
Б) с первоначальным.
Ответы: 3) а, 6;
225. Ряд динамики характеризует:
А) структуру совокупности по какому-то признаку;
Б) изменение характеристики совокупности во времени.
Уровень ряда динамики это:
В) определенное значение варьирующего признака в совокyпности;
Г) величина показателя на определенную дату или за определенный период.
Ответы: 4) Б, Г;
226. Индивидуальный индекс представляет собой результат сравнения двух одноименных величин, относящихся к:
А) различным периодам времени;
Б) различным территориям.
Ответы: 1) а;
227. Дать определение показателю коэффициента корреляции…
3) измеритель тесноты связи при простой прямолинейной зависимости;
228. К какому виду средних относится варианта, которая приходится на середину вариационного ряда?
2) Медиана;
229. Какой способ отбора нуждается в предыдущей градации генеральной совокупности на качественно однородные группы?
2) Серийный;
230. При помощи какой формулы рассчитывается парный коэффициент корреляции?
1) R = Yx – Y*X / Gy*Gx;
231. Средняя арифметическая простая рассчитывается по формуле:
2) XСр = ∑Xi / N
232. Что называется темпом роста?
1) отношение каждого последующего уровня к предыдущему или к начальному уровню;
233. Какой имеет вид формула общего трудового индекса?
2) I = ∑T0Q1 : ∑T1Q1;
234 Тест. Что такое залежи?
1) это земли, которые раннее использовались под посевы с.-х. культур, но в течение нескольких лет не засевались;
235. Как называется показатель, который определяется отношением числа телят, полученных за год только от коров, к числу коров на начало года?
3) выход приплода на 100 коров;
236. Средняя яйценоскость кур рассчитывается…
2) путем деления валового сбора яиц (без яиц молодок) на среднюю численность кур-несушек за соответствующий период;
237. При помощи, каких средств предприятия возмещают стоимость износа основных фондов?
2) амортизационных отчислений;
238. Как рассчитать показатель среднедневной выработки?
1) общий объем выполненных тракторами работ в эталонных гектарах делим на количество отработанных тракторо-дней;
239. Какая площадь называется обсемененной?
1) площадь, на которую высеяли семена;
240. Какая продукция называется валовой?
2) продукция, полученная в хозяйстве;
241. Что является предметом статистики как общественной науки?
3) количественная сторона массовых общественных явлений в конкретных условиях места и времени;
242. Определить всхожесть зерна можно при помощи наблюдения…
2) выборочного;
243. Какая относительная величина характеризует отношение планового показателя к другой величине, принятой за базу сравнения?
3) относительная величина выполнения планового задания;
244. Ряды распределения бывают:
А) атрибутные;
Б) вариационные.
Ответы: 3) а, б;
245 Тест по статистике. Поголовье коров на фермах хозяйства на протяжении квартала изменялось следующим образом, (гол.) на:
1.01-614 1.02-588 1.03-610 1.04-620
Определить среднее поголовье коров за квартал.
Ответы: 3) 605;
246. За прошлый год объемы промышленного производства увеличились на 2,5%, А оптовые цены на промышленную продукцию уменьшились в среднем на 1,2%. Темп роста объема промышленного производства составил, % :
А) 102,5; б)97,5;
Оптовых цен:
В) 101,2; г) 98,8.
Ответы: 2) а, г;
Тест по статистике — 247. Каким ученым был открыт закон нормального распределения?
3) Гауссом;
248. Каким правилом пользуются на практике при исследовании совокупности на предмет её соответствия нормальному закону?
2) Правилом 3 сигм;
249. Какую из приведенных математических функций используют для выравнивания ряда динамики, если коэффициент роста (цепной) стабильный?
3) Yt = ао*а1T;
250 Тест. Формула среднего квадрата отклонения будет иметь такой вид…
2) G2 = ∑(Xi – XСр)2*Fi / ∑Fi
testua.ru
Тест с ответами по статистике
1. Что такое статистика?
а) вид научно-практической деятельности, направленной только на обработку информации
б) вид научно-практической деятельности, направленной только на получение информации, характеризующей количественные закономерности жизни общества
в) вид научно-практической деятельности, направленной на получение, обработку, анализ и хранение информации, характеризующей количественные закономерности жизни общества во всём ее многообразии в неразрывной связи с её качественным содержанием+
2. Продолжите фразу: «Статистика – это вид научно-практической деятельности, которая направлена на получение, обработку, анализ и хранение информации, характеризующей количественные закономерности жизни общества во всём ее многообразии в неразрывной связи с её…»
а) количественным содержанием
б) качественным содержанием+
в) объемом
г) формой существования
3.Индекс потребительских цен вырос за последние два года на 7,6 %. Каким образом произошло изменение покупательной способности денег?
а) увеличилась на 8,1 %
б) выросла на 7,1%
в) упала на 7,1 %+
4. Какой бывает статистическая совокупность?
а) первичной и вторичной
б) однородной и комбинированной
в) структурной и аналитической
г) однородной и разнородной+
5.Индекс потребительских цен в отчётном периоде по сравнению с базисным составил 112 %. Индекс покупательной способности рубля составляет:
а) 95,0 %
б) 89,2 %+
в) 110 %
6.Что такое индекс реальных денежных доходов?
а) как отношение индекса национального дохода и индекса цен+
б) как произведение индекса национального дохода и общего индекса потребления на душу населения
в) как отношение индекса национального дохода и индекса себестоимости
7. Какова особенность статистического исследования?
а) в нем изучаются только неварьирующие признаки
б) в нем изучаются как варьирующие, так и неварьирующие признаки
в) в нем изучаются только варьирующие признаки+
г) в нем изучаются не только варьирующие признаки
8. Какую закономерность можно назвать статистической?
а) выявленная на основе случайного наблюдения за объектами
б) выявленная на основе массового наблюдения, то есть проявляющаяся лишь в большой массе явлений через преодоление свойственной её единичным элементам случайности+
в) выявленная на основе единичного наблюдения и проявляющаяся лишь в большой массе явлений через преодоление несвойственной её элементам случайности
9. По данным 2% выборочного обследования (n=100) средний стаж работников = 6 годам при среднем квадратическом отклонении = 30%. Чему равна предельная ошибка выборки для среднего стажа работы с вероятностью 0,954?
а) 6%+
б) 0,3%
в) 5%
г) 3%
10. Коэффициент дожития это:
а) отношение средней численности доживших до возраста t и возраста t+1 в двух смежных возрастных периодах: t и t+1 к числу доживших до периода t+
б) отношение предстоящих лет жизни на среднюю численность доживших
в) отношение средней численности, живущих в двух смежных возрастных периодах: t и t+1 к числу живущих в период t
11. Какое из данных понятий отражает наиболее общие и существенные свойства, признаки, связи и отношения предметов и явлений объективного мира?
а) разряд
б) статистика
в) определение
г) вариант
д) категория+
12. Инфляция за пять лет составила 4,9 % , 5,7%, 6,3%,7,4%. Выясните, сколько составляет среднегодовая инфляция за пять лет?
а) 105,5%
б) 112,5%
в) 106,1 %+
13. Что такое «наблюдение основного массива»?
а) наблюдение за величинами «среднего» размера
б) наблюдение малозначительных величин
в) наблюдение за важнейшей единицей совокупности
г) наблюдение основной единицы совокупности
д) наблюдение за совокупностью за исключением малозначительных величин+
14. Торговое предприятие перевыполнило собственный план по товарообороту на 5%, при этом объем товарооборота снизился на 2%. Каков относительный показатель плана?
а) 103,0%
б) 107,1%
в) 102,9%
г) 93,3%+
15. Что за цель у «монографического наблюдения»?
а) изучение минимально-возможной единицы совокупности
б) изучение важнейшей для исследователя единицы совокупности+
в) изучение минимально допустимой единицы совокупности
г) изучение наибольшей единицы совокупности
д) изучение минимальной единицы совокупности
16. «Выборочное наблюдение» проводится:
а) заданным отбором единиц совокупности в необходимом количестве при ошибке репрезентативности
б) случайным отбором нескольких единиц совокупности в необходимом количестве при допустимой ошибке выборки+
в) случайным отбором нескольких единиц совокупности
г) случайным отбором нескольких единиц совокупности в необходимом количестве
д) заданным отбором нескольких единиц совокупности в необходимом количестве при допустимой ошибке выборки
17. Каким образом проводится организация «почтового способа» проведения наблюдения?
а) необходимые сведения тайно собираются непосредственно лицами-регистраторами
б) необходимые сведения запрашиваются и передаются через «почтовый ящик»
в) необходимые сведения по распоряжению руководящих органов собираются непосредственно лицами-регистраторами
г) необходимые сведения запрашиваются и передаются непосредственно из рук в руки
д) необходимые сведения запрашиваются и передаются при помощи соответствующих органов связи+
18. Как проходит организация «экспедиционного способа наблюдения»?
а) лица-регистраторы собирают по почте заполненные регистрируемыми лицами формуляры наблюдений
б) лица-регистраторы на месте проведения наблюдения собирают заполненные регистрируемыми лицами формуляры наблюдений
в) лица-регистраторы собирают в статистических органах заполненные регистрируемыми лицами формуляры наблюдений
г) регистрируемые лица самостоятельно заполняют формуляр и отправляют его в статистические органы
д) лица-регистраторы на месте проведения наблюдения сами получают необходимые сведения и заполняют формуляр наблюдений+
shooltest.ru
Статистика Тесты с ответами ИММиФ Тема 1-2
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
ТЕМА 1
Предметом статистики как науки является…
метод статистики
статистические показатели
+количественные закономерности массовых варьирующих общественных явлений
группировки и классификации
Статистическая наука начала оформляться…
+в XVII в.
в VII в.
в XIX в.
до начала современного летоисчисления
Укажите, что из перечисленного не является характерной особенностью статистики как науки
изучение количественной стороны массовых общественных явлений в неразрывной связи с качественной стороной
+изучение всех общественных и природных явлений
изучение явлений в конкретных условиях места и времени
выявление тенденций и закономерностей в массовых социально-экономических явлениях и процессах
Основным разделом статистической науки является…
+общая теория статистики
промышленная статистика
теория вероятностей
математическая статистика
Элементом какой отрасли статистической науки является статистика строительства
+экономической статистики
общей теории статистики
социальной статистики
математической статистики
«Социальной физикой» называл статистику представитель «статистико-математического» школы (кто?)…
Граунт, Галлей (Англия, 17 век)
Ахенваль (Германия, 18 век)
М.Ломоносов (Россия, 18 век)
+Кетле (Бельгия, 19 век)
Укажите неправильное суждение. Государственная статистика в России…
+издает 1 ежемесячный, 1 ежеквартальный журнал, 1 статистический ежегодник
разрабатывает и утверждает формы стат. отчетности, обязательные к исполнению юри-дическими лицами в РФ
имеет территориальные органы в регионах страны
представлена Госкомстатом РФ
Работник, для которого сбор статистических данных является профессиональной деятельностью, именуется…
сборщиком данных
статистом
переписчиком
+статистиком
Выберите наиболее точное определение: «Совокупность статистическая – это…»
множество элементов, обладающих общими признаками
множество элементов, обладающих одним общим и одним варьирующим признаками
любое предметное множество явлений природы и общества
+реально существующее множество однородных элементов, обладающих общими при-знаками и внутренней связью
Что является носителем информации в статистической совокупности?
+единица совокупности
элемент математического множества
атрибутивный варьирующий признак
признак совокупности
Статистическая совокупность отличается от математической…
тем, что преподается в статистике
существованием элементов в абстрактном представлении
количеством элементов
+существованием элементов в материальной действительности
Элемент статистической совокупности – это…
элемент таблицы Менделеева
элемент математического множества
признак совокупности
+носитель информации
Признак «площадь земельных участков для индивидуального строительства» является…
атрибутивным
+количественным
качественным
количественно-качественным
Признак «социальный слой в обществе» является…
+атрибутивным
+качественным
количественным
количественно-качественным
Вариация – это:
изменение состава совокупности
изменение массовых явлений во времени
изменение структуры статистической совокупности в пространстве
+изменение значений признака внутри наблюдаемой совокупности
Какой из перечисленных признаков является варьирующим?
скорость падения тела в пустоте
+курс доллара
+цена одного килограмма винограда
температура кипения воды
Тема 2
Чем отличается статистическое наблюдение от наблюдения писателя, художника
различием времени наблюдения
+различной целью наблюдения
+научной организованностью и планомерностью
различием объекта наблюдения
Перечень признаков (или вопросов), подлежащих регистрации в процессе наблюдения, называется
+программой наблюдения
инструментарием наблюдения
статистическим формуляром
инструкцией
Вопрос в формуляре статистического обследования «Сколько времени Вы посвящаете просмотру ТВ-передач (часов в неделю)?», — является по форме составления…
закрытым
+открытым
открыто-закрытым
смешанным
Вопрос в формуляре статистического обследования «Как часто Вы ходите в кинотеатры?»: « Почти каждую неделю», « Один раз вмесяц», «Реже, чем один раз в месяц», — является по форме составления…
косвенным
открыто-закрытым
+закрытым
открытым
Объект статистического наблюдения – это…
единица наблюдения
единица статистической совокупности
отчетная единица
+статистическая совокупность
Объект статистического наблюдения – это…
единицей наблюдения
единицей статистической совокупности
+отчетной единицей
учетной единицей
Единица наблюдения и отчетная единица – это понятия, которые…
никогда не совпадают
совпадают всегда
одно и то же
+иногда могут совпадать
Срок (период) наблюдения – это
критический момент (дата) наблюдения
+время, в течение которого происходит заполнение статистических формуляров
конкретный день года, час дня, по состоянию на который должна быть проведена регистрация признаков по каждой единице совокупности
Непрерывное статистическое наблюдение задолго временными процессами, имеющими фиксированное начало, стадию развития и фиксированный конец – это…
специально организованное статистическое наблюдение
+регистровая форма наблюдения
выборочное наблюдение основного массива
форма статистического наблюдения перепись населения России относится к…
единовременное, специально организованное наблюдение
периодическое, регистровое, выборочное наблюдение
+периодическое, специально организованное, сплошное наблюдение
Перепись населения России проводится…
один раз в 25 лет
один раз в 5 лет
+один раз в 10 лет
один раз в 15 лет
Перепись населения РФ проводилась в период с 9 по16 октября 2002 г.Критическим моментом было 00 часов ночи с 08 на 09 октября. Счетчик пришел в семью 16 октября. В семье 14 октября родился ребенок. Как должен поступить счетчик относительно этого ребенка?
проконсультироваться у руководства
пометить в блокноте
внести в переписной лист
+не вносить запись в переписной лист
Перепись населения РФ проводилась в период с 9 по 16 октября 2002 г.Критическим моментом было 00 часов ночи с 08 на 09 октября. Счетчик пришел всемью 11 октября. В семье 10 октября умер человек. Как должен поступить счетчик
пометить в блокноте
+внести с пометкой о смерти
не вносить сведения об умершем в переписной лист
внести без пометки о смерти
Перепись населения РФ проводилась в период с 9 по16 октября 2002 г.Критическим моментом было 0 часов ночи с 08 на 09 октября. Счетчик пришел всемью 15 октября и попал на свадьбу. Два часа назад молодожены возвратились из ЗАГСа после регистрации брака (до этого в браке они не состояли). Что должен записать счетчик в переписном листе в вопросе: «Состоите ли Вы в браке внастоящее время?» о каждом из супругов?
+не состоит в браке
состоит в браке
поставить прочерк, т.к. затруднительно определить
Почему переписи населения проводятся обычно в зимнее время?
меньшие транспортные расходы
достигается экономия ресурсов на подготовку персонала
не нужен критический момент наблюдения
+наименьшая подвижность опрашиваемых
В РФ существует такая форма статистического наблюдения, как регистр населения?
+только проектируется
+Нет
Да
test-for-you.ru
Тест с ответами по статистике
1. Что такое статистика?
а) вид научно-практической деятельности, направленной только на обработку информации
б) вид научно-практической деятельности, направленной только на получение информации, характеризующей количественные закономерности жизни общества
в) вид научно-практической деятельности, направленной на получение, обработку, анализ и хранение информации, характеризующей количественные закономерности жизни общества во всём ее многообразии в неразрывной связи с её качественным содержанием+
2. Пример: коэффициент младенческой смерти в регионе равен 15 %. Что это значит?
а) из каждой 1000 умерших 15 человек — это дети в возрасте до 1 года
б) из 1000 родившихся 15 детей умирают в возрасте до 1 года+
3.Какое из данных соотношений характерно для демографического старения населения?
а) К дет меньше К общ
б) К пож больше К общ+
в) К пож больше К дет
4. Что такое «объект наблюдения»?
а) совокупность единиц наблюдения, имеющая наименьший удельный вес в генеральной совокупности
б) определенная совокупность единиц наблюдения, выбранная согласно поставленной цели, для исследования+
в) определенная генеральная совокупность
г) определенная совокупность единиц наблюдения
д) совокупность единиц наблюдения, имеющая наибольший удельный вес в совокупности
5. Что подразумевает под собой понятие «место статистического наблюдения»?
а) адрес представителя статистического органа, проводящего сбор статистических данных
б) место обработки статистических данных
в) место сбора статистических данных+
г) адрес статистического органа
д) адрес местного органа власти, на территории которого проводится статистическое наблюдение
6.Определите, какой из данных методов определения показателя «валовой внутренний продукт» применяется, если он рассчитан как сумма валовой добавленной стоимости отраслей народного хозяйства?
а) производственный+
б) распределительный
в) конечного использования
7. ВВП методом конечного использования рассчитывается как:
а) сумма первичных доходов, получаемых институциональными единицами, участвовавшими в производстве
б) валовой выпуск – промежуточное потребление + чистые налоги на продукты и импорт
в) конечное потребление + валовое накопление + сальдо экспорта – импорта+
8.Что представляет собой наблюдение основного массива?
а) включение в состав совокупности малозначимых единиц
б) исключение из состава совокупности малозначимых единиц и исследование исключенной части
в) включение в состав совокупности малозначимых единиц и исследование всей совокупности
г) исключение из состава совокупности значимых единиц и исследование оставшейся части
д) исключение из состава совокупности малозначимых единиц и исследование основной ее части+
9.Каким образом изменится величина индекса –дефлятора если индекс стоимости ВВП равен 109,2 а, физический объём ВВП вырос на 4,1%?
а) вырос на 4.8 %+
б) сократился на 5,1 %
в) вырос на 5,1 %
10.Что такое «критический момент» при проведении статистического наблюдения?
а) определенное число статистических единиц наблюдения
б) определенная дата, на которую регистрируются все сведения+
в) календарные сроки проведения наблюдения
г) любое число статистических единиц наблюдения
д) срок статистического наблюдения
11. В 2004 году было изготовлено 850 мл.машин. По сравнению с 2001 годом темп прироста составил (-13,3%). Каков обьем производства в 2001 году?
а) 723,9
б) 748,3+
в) 963,0
12. Индекс цен фиксированного состава составил 95%, а индекс структурных сдвигов – 125%.Как изменилась средняя цена под влиянием изменения цен отдельных товаров и изменения ассортимента продаж?
а) Снизилась на 24%
б) Выросла на 19%+
в) Выросла на 32%
г) Выросла на 20%
13. Индекс средних затрат по совокупности компании составил 1,25. Произошли изменения в структуре производства каждой компании и индекс структурных сдвигов составил 0,98. Какие изменения произошли в затратах труда в среднем в каждой компании:
а) Снизились на 27,6%
б) Возросли на 22,5%
в) Снизились на 22,5%
г) Увеличились на 27,6%+
14. В отделении коммерческого банка обследовано 36% валютных счетов. В выборку попали 100 счетов, в том числе: пенсионеров – 60 человек, средний размер вклада х=200 дол., при дисперсии 4800; рабочих и служащих – 40 человек, средний размер вклада х=250 дол., при дисперсии 8800. Какова средняя ошибка типической выборки?
а) 10
б) 8,0
в) 6,4+
г) 4,8
15.Обследовано 36% продукции предприятия. На сколько меньше будет ошибка собственно – случайной бесповторной выборки,чем ошибка повторной выборки?
а) 64%
б) 20%
в) 36%
г) 25%+
answerstest.ru
Тест с ответами по правовой статистике
1. Дайте определение понятию «Средняя величина» – …
1. значение признака, находящееся в середине ряда распределения
2. обобщенная типическая характеристика признака в данной совокупности+
3. значение признака, встречающееся чаще других
2. Количественные характеристики преступности:
1. Уровень преступности+
2. Уголовно-правовая наказуемость
3. Территориальное распределение преступности
4. Латентность преступности.
3. Что такое отношение показателя уровня преступности к предшествующему значению того же показателя?
1. Коэффициент преступности
2. Индекс преступной активности
3. Темп роста преступности+
4. Темп прироста преступности.
4. Как называются таблицы, в которых статистическая совокупность расчленяется на отдельные группы по какому-либо одному признаку, причем каждая из групп может быть охарактеризована рядом показателей?
1. простыми таблицами
2. перечневыми таблицами
3. групповыми таблицами+
4. комбинационными таблицами.
5. Дайте определение понятию «Вариация»- …
1. изменение, некоторое уклонение от основного направления развития
2. изменчивость (отклонение) индивидуальных значений признака по единицам совокупности+
3. применение основного методического положения в разных видоизменениях
6. Что такое экспликация?
1. линия, на которую нанесены деления, отвечающие определенным числам.
2. условная величина отрезка шкалы, отвечающая определенной числовой единице.
3. словесное описание графика, включающее название, отражающее его содержание, цифровые данные, характеризующие масштабные шкалы и пояснения условных обозначений. +
4. совокупность линий, фигур, точек, которыми изображены статистические данные.
7. Что такое графики поверхностей распределения исследуемых объектов?
1. Точечные графики.
2. Линейные графики.
3. Объемные графики. +
4. Диаграммы.
8. Что такое величина, представляющая собой частное от деления суммы индивидуальных значений признаков на их количество?
1. Средняя гармоническая
2. Средняя арифметическая +
3. Средняя геометрическая
4. Средняя квадратическая.
9. НЕ относится к показателям вариации:
1. Показатели структуры
2. Показатели формы
3. Показатели качества+
4. Показатели размера
10. Сущность статистического анализа взаимосвязей заключается в следующем….
1. является необходимым этапом криминологических исследований
2. является важнейшим условием принятия обоснованных управленческих решений
3. имеет существенное теоретическое и практическое значение, поскольку дает возможность перейти от констатации социально-правовых фактов к их объяснению и воздействию на них+
11. Что полагает под собой отбор единиц наблюдения в случайном порядке методом жеребьевки?
1. Типическая выборка
2. Собственно случайная выборка +
3. Механическая выборка
4. Гнездовая выборка
12. Для оценки степени тесноты связи при линейной зависимости используется…
1. коэффициент парной корреляции
2. корреляционное отношение+
3. коэффициент корреляции рангов
13. Что из перечисленного является именованными числами?
1. средние обобщающие показатели
2. абсолютные обобщающие показатели+
3. относительные обобщающие показатели
4. все обобщающие показатели.
14. Дайте определение понятию «Статистический показатель» -…
1. то, по чему можно судить о развитии и ходе чего-нибудь
2. обобщающая характеристика какого-то свойства отдельных единиц, группы единиц или совокупности в целом+
3. количественное выражение результата какого-либо действия
15. Дайте определение понятию «Статистический анализ» – …
1. метод исследования путем разложения изучаемого предмета на составные части
2. третий этап статистического исследования, на котором исчисляются статистические показатели с целью 3. выявления сущности изучаемых явлений, установления взаимосвязей и закономерностей его развития+
4. разработка приемов вычислений и их применения к решению различных вопросов о величинах
shooltest.ru
Статистика Тесты с ответами Тема 3-4-5
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 3. Статистические графики
«Статистический график», это:
наглядного обобщение результатов произвольного исследования
изображения явления в пространстве в статике
изобразительная картина действительности
мысленное изображение закономерности
+это геометрические плоскостные (двухмерные) или объемные (трехмерные) изображения статистических данных, отражающие размеры статистических совокупностей, сложившуюся их структуру, размещение, выполнение плана, динамику и связь явлений
Что отражает столбиковая диаграмма?
статистические совокупности по составу
соотношения различных статистических совокупностей по какому-либо изменяющемуся в пространстве признаку
структуру совокупности по трем признакам
+единственную меру признака
Понятие «Экспликация графика» — это:
пространство размещения знаков, которое имеет определенные размеры и пропорции сторон
размещение знаков в поле графика
эталоны знака, отражающие величину геометрических знаков. Они изображаются в виде кругов, прямоугольников, квадратов и обычно выносятся с поля графика
+словесное объяснение содержания графика и значения каждого его геометрического знака
Масштабные ориентиры, это:
мысленное изображение закономерности
экспликация графика
символы понятий
пространство размещения знаков
+эталоны знака, отражающие величину геометрических знаков. Они изображаются в виде кругов, прямоугольников, квадратов и обычно выносятся с поля графика
Друзья, более 600 собак Воронежского приюта Дора https://vk.com/priyt_dora очень нуждаются в поддержке! Приют бедствует, не хватает средств на корм и лечение. Не откладывайте добрые дела, перечислите прямо сейчас любую сумму на «Голодный телефон» +7 960 111 77 23 или карту сбербанка 4276 8130 1703 0573. По всем вопросам обращаться +7 903 857 05 77 (Шамарин Юрий Иванович)
Центрограммы дают возможность:
выразить явление в пространстве
показать изменения явлений во времени
дать соотношения различных статистических совокупностей по какому-либо изменяющемуся в пространстве признаку
+составить целые статистико-географические описания
описать статистические совокупности по составу
Структурные диаграммы позволяют:
сопоставить статистические совокупности по времени
выразить явление в пространстве
разместить знаки в поле графика
+сопоставить статистические совокупности по составу
выразить символы понятий
Что положено в основу деления графиков на диаграммы и статистические карты
размещение знаков в поле графика
экспликация графика
символы понятий
+поле графика, в виде чистой бумаги, либо географической, либо контурной карты
эталоны знака, отражающие величину геометрических знаков
Картодиаграммы позволяют:
выразить явление в пространстве
отражают явления, периодически повторяющиеся во времени
составить целые статистико-географические описания
+показать географическое распределение отображаемого статистикой явления размещением на контурной географической карте специальных знаков-символов
показать структуру совокупности по трем признакам
Что выражает «Диаграммы сравнения»?
статистические совокупности по составу
+соотношения различных статистических совокупностей по какому-либо изменяющемуся в пространстве признаку
структуру совокупности по трем признакам
географическое распределение отображаемого статистикой явления
показывают изменения явлений во времени
Диаграмма «Знаки Варзара» относится к:
спиральным диаграммам
картодиаграммам
динамическим диаграммам
+структурным диаграммам
Центрограммам
Динамические диаграммы:
показывают географическое распределение отображаемого статистикой явления
статистические совокупности по составу
позволяют сопоставить статистические совокупности по составу
отражают явления, периодически повторяющиеся во времени
+показывают изменения явлений во времени
Тема 4. Сводка и группировка материалов статистических наблюдений
Назначение структурной группировки
выявить влияние фактора в основе группировки на результат
выявить влияние и взаимозависимость двух анализируемых факторов в генеральной совокупности
+определить удельный вес отдельных групп в генеральной совокупности
создать новую группировку
выявить возможность перегруппировки уже сгруппированных данных
Сущность аналитической группировки
создать новую группировку
выявить влияние фактора в основе группировки на результат
выявить возможность перегруппировки уже сгруппированных данных
+выявить влияние и взаимозависимость двух анализируемых факторов в генеральной совокупности
определить удельный вес отдельных групп в генеральной совокупности
С какой целью создаются комбинированные группировки
с целью учета различных признаков нескольких структурных группировок одновременно
с целью выявления одновременного влияния нескольких факторов на систему
с целью разделения генеральной совокупности по основным факторам
с целью выявления влияния нескольких факторов на систему
+с целью углубленного изучения генеральной совокупности по нескольким факторам
По каким направлениям проводятся вторичные группировки
по наименьшему удельному весу группы в общем итоге
по наибольшему удельному весу группы в общем итоге
+по величине интервалов первичной группировки
по величине наибольшей группы в первичной группировке
+по удельному весу отдельных групп в общем итоге
Назначение вторичной группировки
перегруппировка ранее сгруппированных материалов для выявления влияния факторов друг на друга
перегруппировка ранее сгруппированных материалов для обеспечения управляемости двумя или несколькими группировками
перегруппировка ранее сгруппированных материалов для обоснования полученных ранее выводов
перегруппировка ранее сгруппированных материалов для создания двух или нескольких группировок
+перегруппировка ранее сгруппированных материалов для обеспечения сопоставимости двух или нескольких группировок
Тема 5. Статистические показатели и система показателей. Абсолютные и относительные величины
Что выражают в статистике абсолютные величины
выражают количественные отношение новых значений явления к принятым за базу
выражают индексы исследуемого явления
выражают отношение новых значений явления к принятым за базу
выражают соотношение двух сопоставимых величин в единицах или процентах
+выражают конкретные значения исследуемого явления в натуральных единицах
Как определяется «относительная величина координации»
как соотношение аналогичных показателей за равный период времени
как отношение одноименных показателей, относящихся к различным объектам совокупности за один и тот же период
как соотношение различных показателей, приведенных к одной базе
как отношение заданной части совокупности ко всей совокупности
+как отношение заданной части совокупности к другой ее части, принятой за базу
Как определяется «относительная величина сравнения»
как соотношение различных показателей, приведенных к одной базе
как отношение одноименных показателей, относящихся к различным объектам совокупности за один и тот же период
как отношение заданной части совокупности ко всей совокупности
как отношение заданной части совокупности к другой ее части, принятой за базу
+как соотношение аналогичных показателей за равный период времени
В чем заключается сущность относительных величин
они выражают отношение новых значений явления к принятым за базу
они выражают количественные отношение новых значений явления к принятым за базу
они выражают индексы исследуемого явления
они выражают конкретные значения исследуемого явления в натуральных единицах
+они выражают соотношение двух сопоставимых величин в единицах или процентах
Как определяется «относительная величина структуры»
как соотношение различных показателей, приведенных к одной базе
как отношение одноименных показателей, относящихся к различным объектам совокупности за один и тот же период
изображения явления в пространстве в статике
+как отношение заданной части совокупности ко всей совокупности
как отношение заданной части совокупности к другой ее части, принятой за базу
как соотношение аналогичных показателей за равный период времени
изобразительная картина действительности
test-for-you.ru

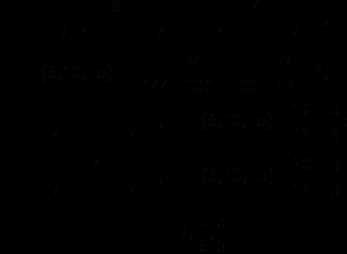
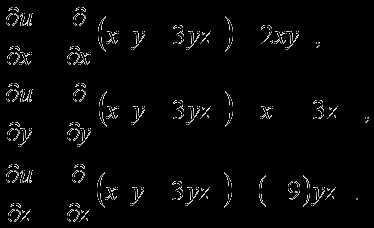
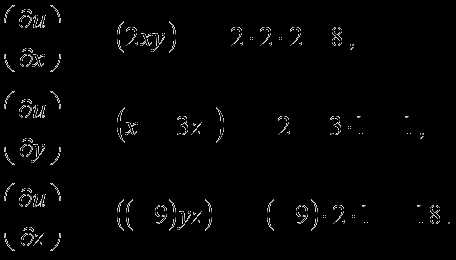
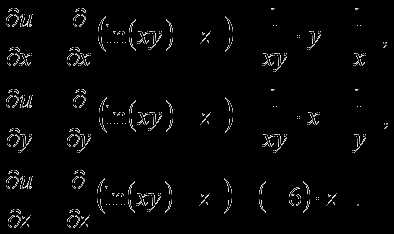
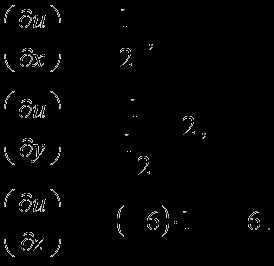
 ,
т. е. такой
величины, которая полностью характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом
,
т. е. такой
величины, которая полностью характеризуется
своим числовым значением. Например, это
может быть температура точек неравномерно
нагретого тела, плотность распределения
электрических зарядов, потенциал
электрического поля и т. д. При этом  называют скалярной функцией точки и
записывают.
называют скалярной функцией точки и
записывают.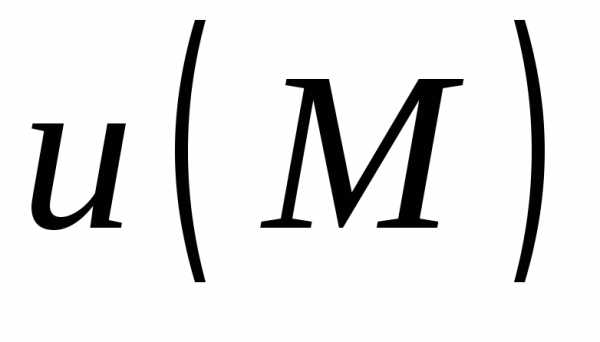 ,
то говорят, что в этой области задано
скалярное поле.
,
то говорят, что в этой области задано
скалярное поле.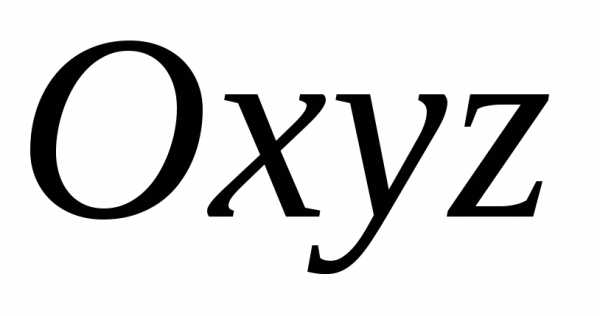 ,
то задание точкиМ равносильно
заданию ее координат
,
то задание точкиМ равносильно
заданию ее координат 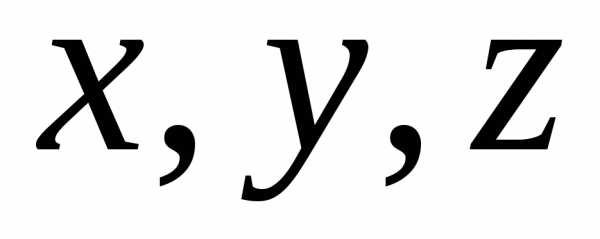 .
. принимает постоянное значение, т. е.,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.
принимает постоянное значение, т. е.,
в зависимости от физического смысла
поля они могут называться изотермическими,
изобарическими и т. п.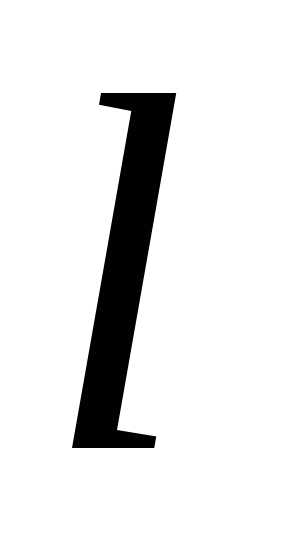 ,
определяемое направляющими косинусами.
При перемещении в данном направлении
точкив точкуфункцияполучает приращение
,
определяемое направляющими косинусами.
При перемещении в данном направлении
точкив точкуфункцияполучает приращение ,
тогда можно записать, что
,
тогда можно записать, что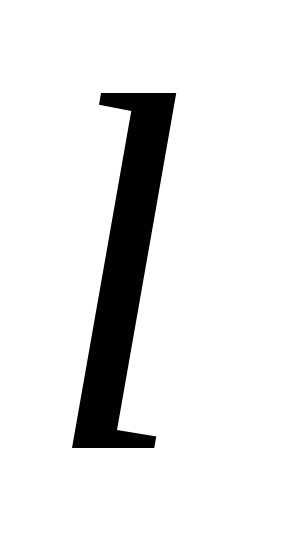 называют предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю
называют предел отношения приращения
функции в этом направлении к величине
перемещения при условии, что перемещение
стремится к нулю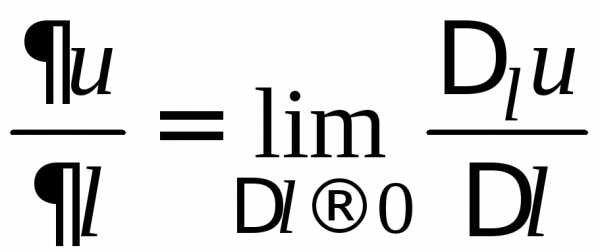 .
.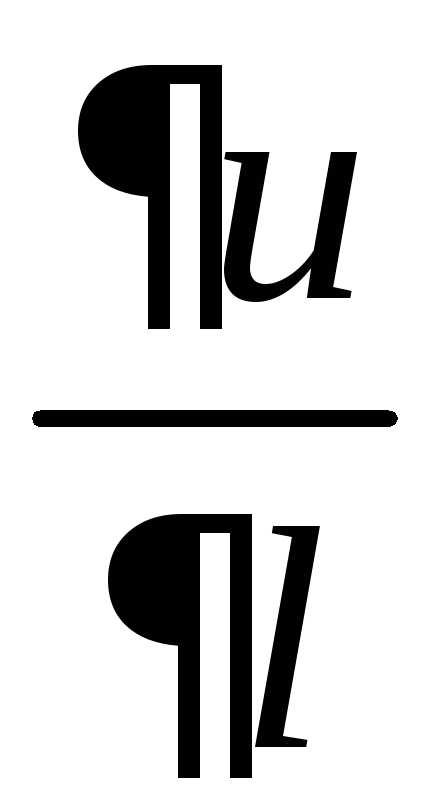 по любому направлению
по любому направлению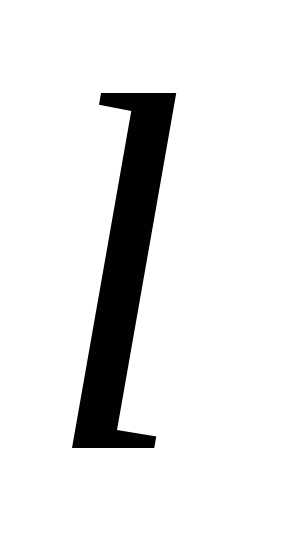 существует и равна
существует и равна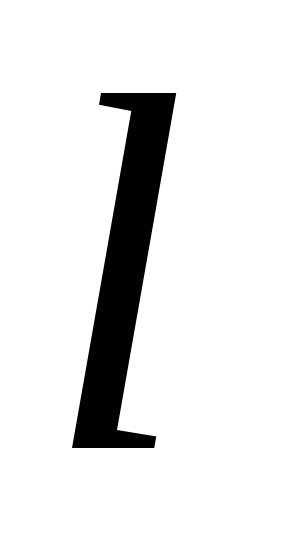 .
.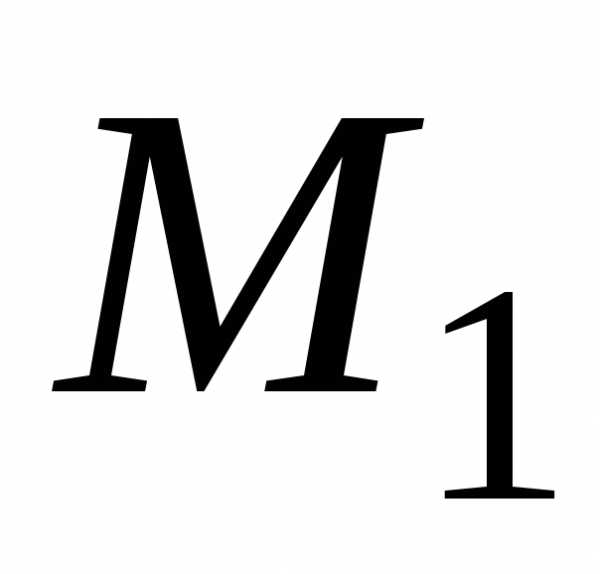 к точке.
к точке.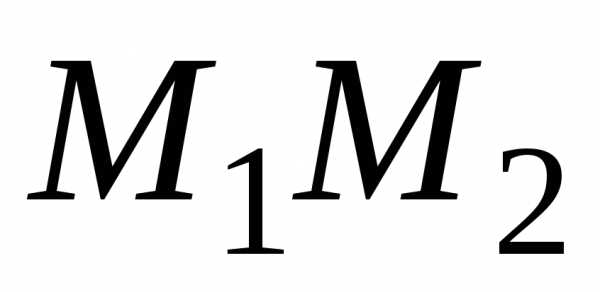 :
: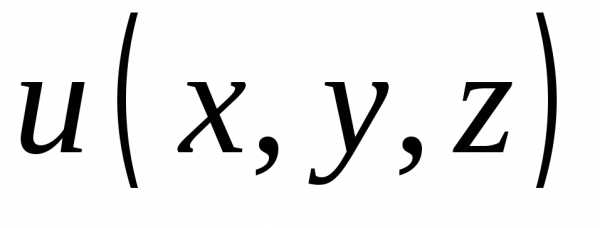 равны:
равны: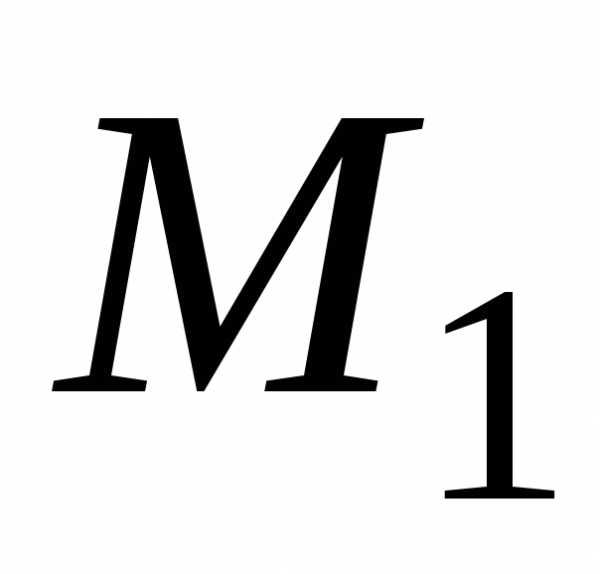 и найдем производную по направлению из
равенства
и найдем производную по направлению из
равенства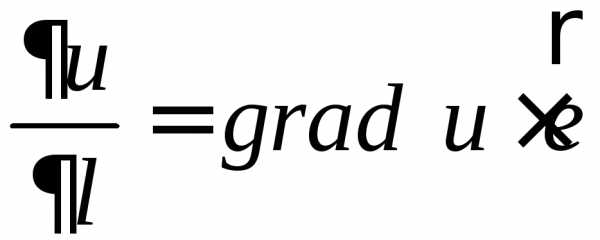 ,
,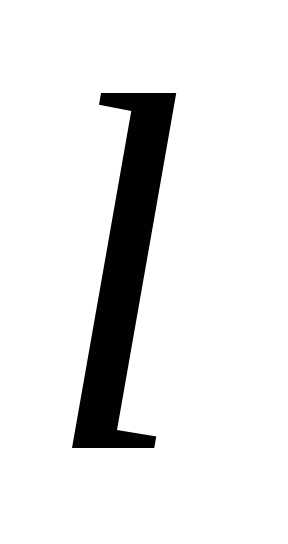 .
.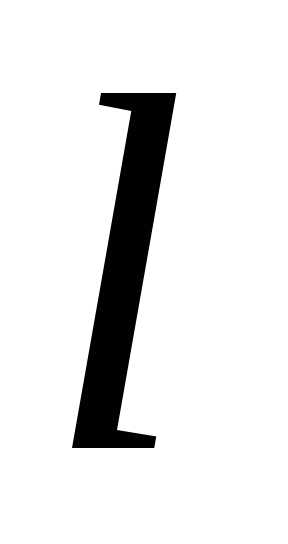 ,
мы будем получать различные значения
производной
,
мы будем получать различные значения
производной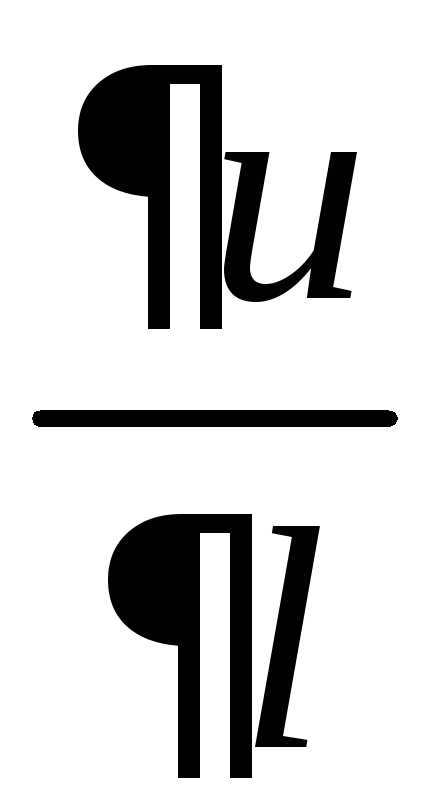 ,
причем наибольшее значение наблюдается,
когда направление
,
причем наибольшее значение наблюдается,
когда направление совпадает с вектором
совпадает с вектором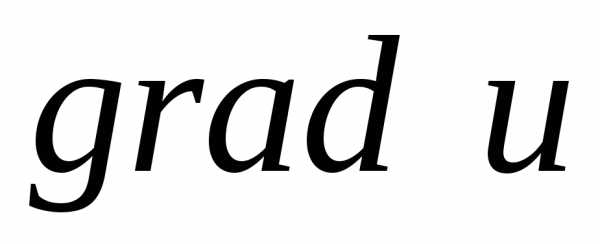 .
Таким образом,
.
Таким образом,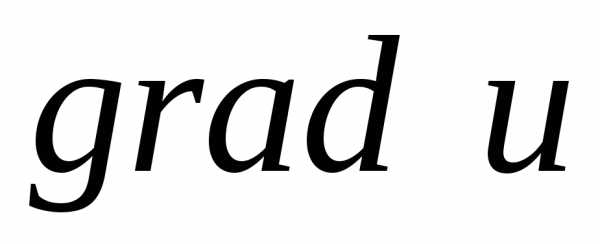 определяет направление, в котором
скорость возрастания функции является
наибольшей.
определяет направление, в котором
скорость возрастания функции является
наибольшей.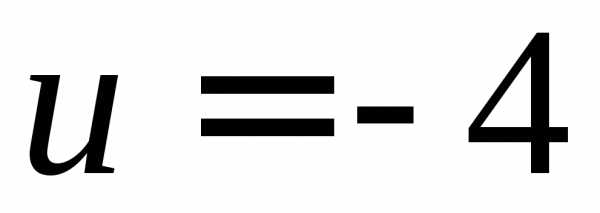 .
Вычислить с помощью градиента производную
скалярного поля в точке
.
Вычислить с помощью градиента производную
скалярного поля в точке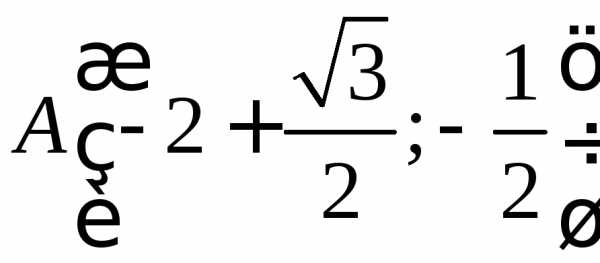 по направлению вектора
по направлению вектора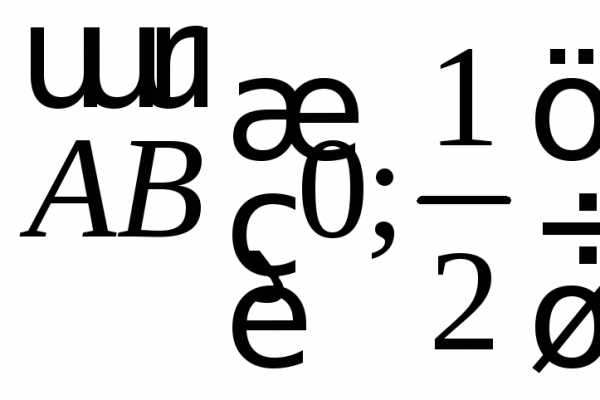 .
Найти наибольшую скорость изменения
скалярного поля в точке
.
Найти наибольшую скорость изменения
скалярного поля в точке .
.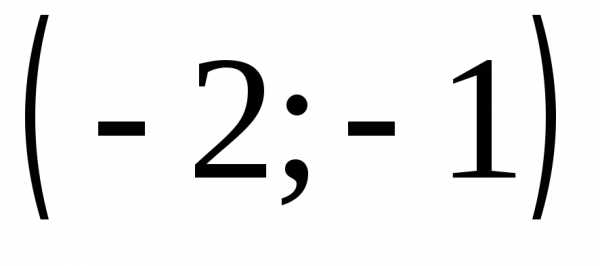 ,
радиуса 1:
,
радиуса 1: :
: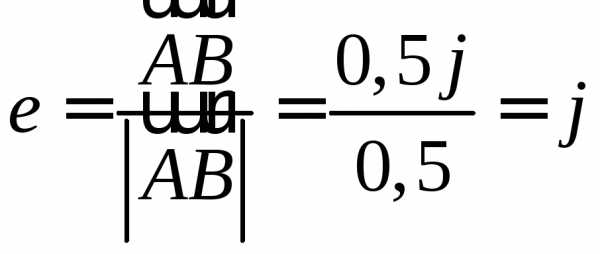 ,
а затем производную скалярного поля
,
а затем производную скалярного поля по направлению
по направлению в точке
в точке :
: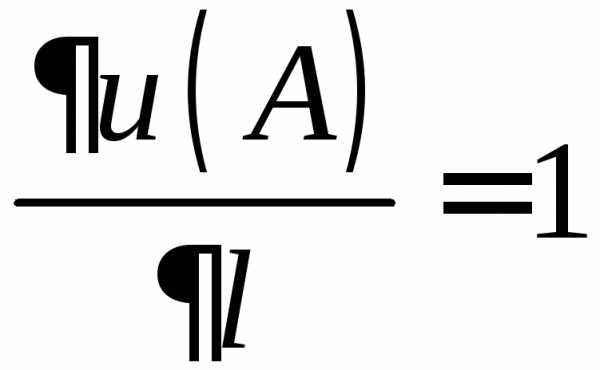 .
.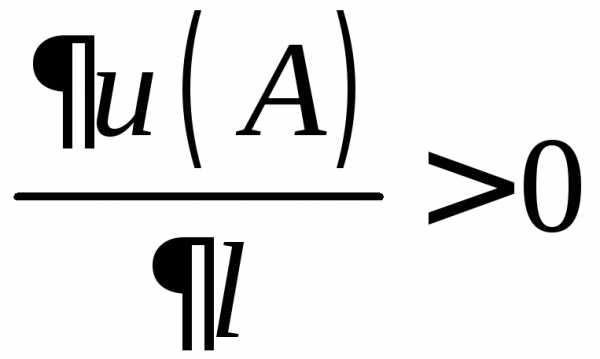 ,
то данное скалярное поле возрастает по
направлению вектора
,
то данное скалярное поле возрастает по
направлению вектора со скоростью равной 1.
со скоростью равной 1. :
: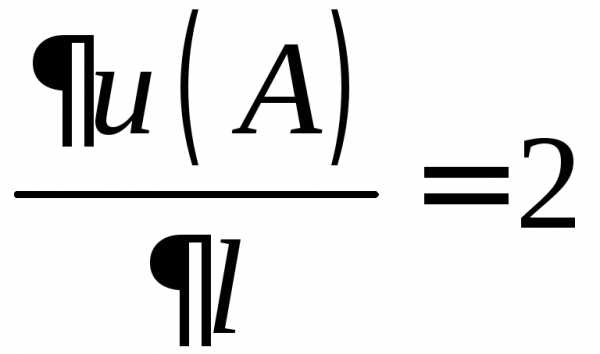 .
.
 равна 2.
равна 2. z
z
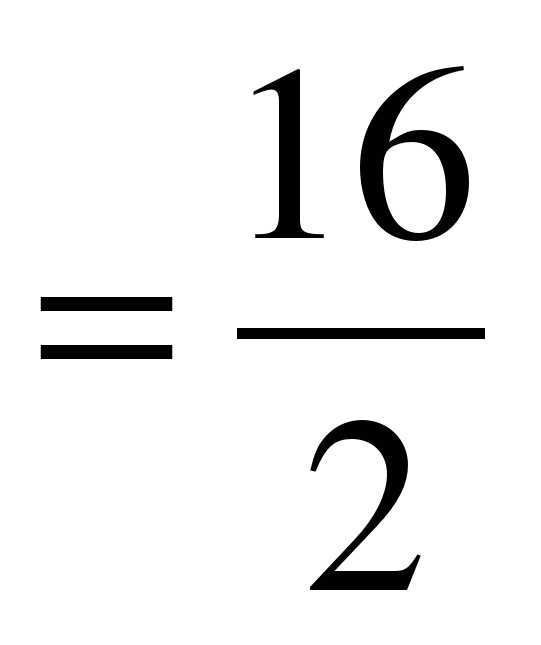
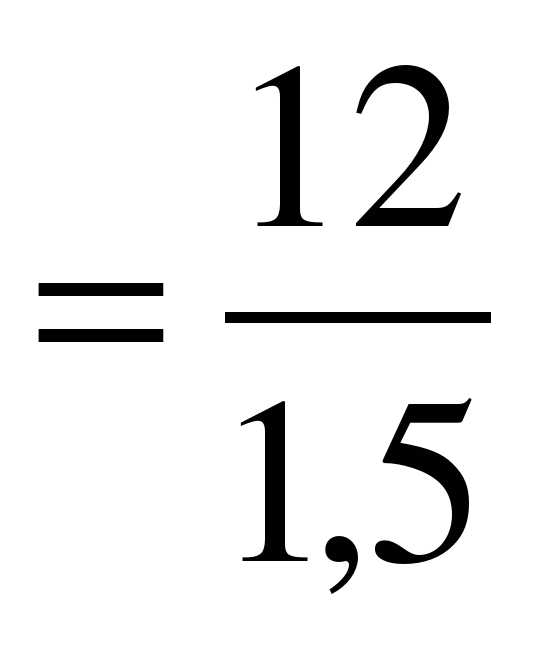
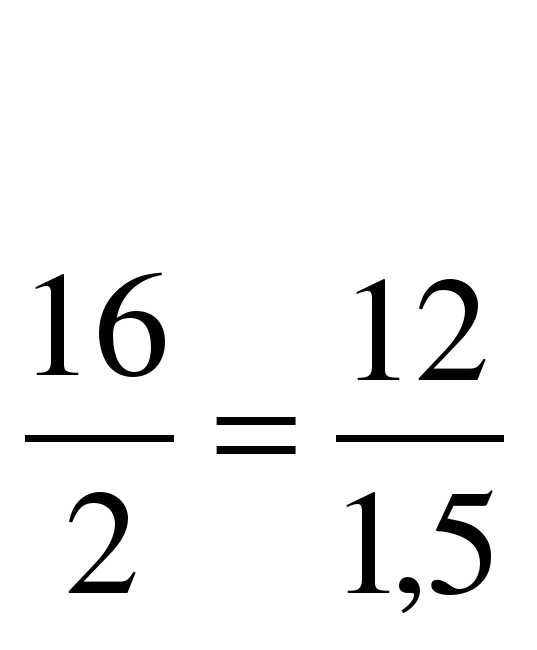 егодня на уроке продолжим работу над темой «Пропорция». Ребята, как вы думаете изученная нами тема «Пропорция» понадобится вам в жизни? Почему и где?
егодня на уроке продолжим работу над темой «Пропорция». Ребята, как вы думаете изученная нами тема «Пропорция» понадобится вам в жизни? Почему и где?

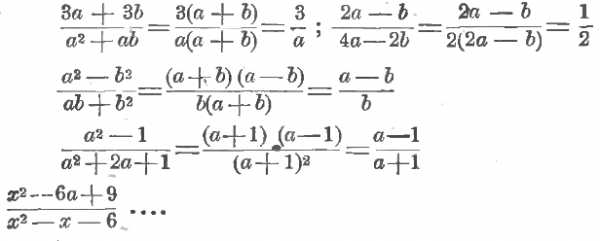


 2.
2. 
 4.
4.
 6.
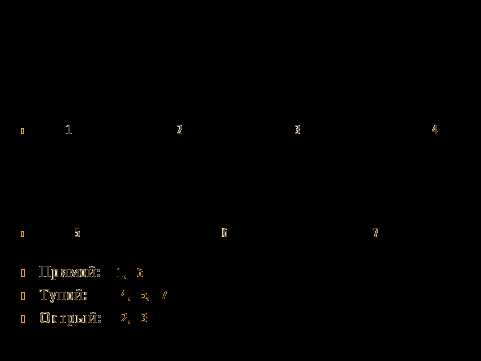
6.

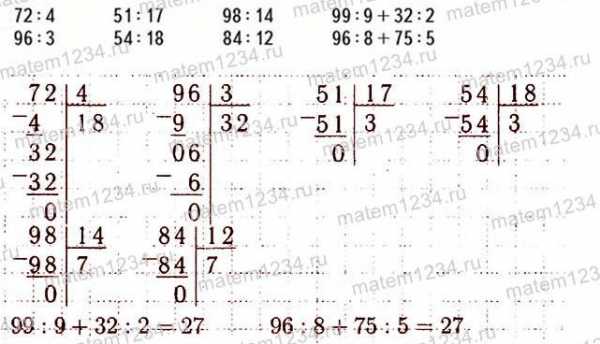
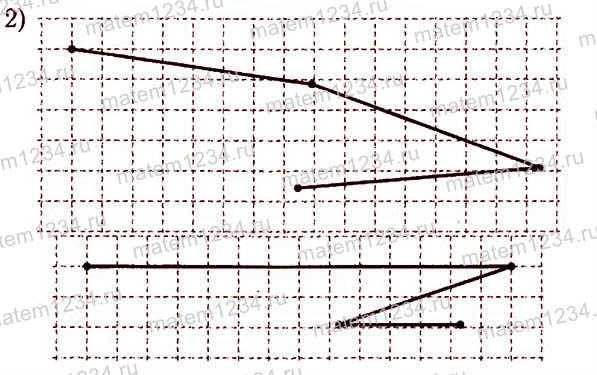
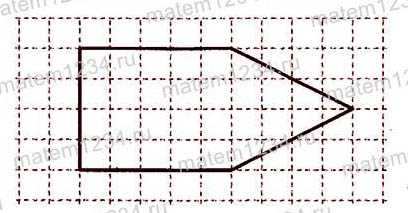




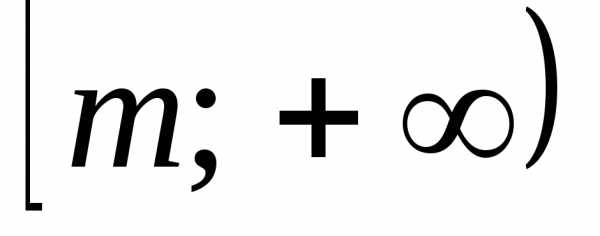 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.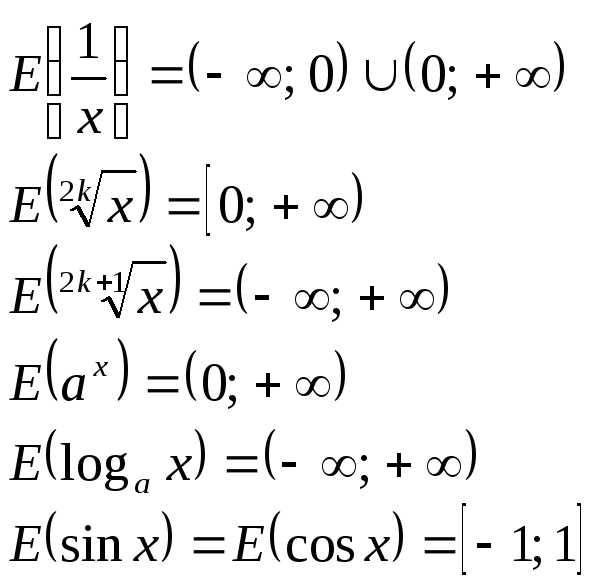
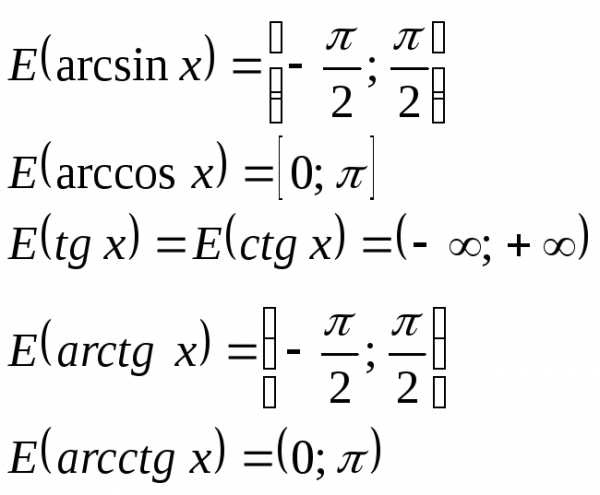
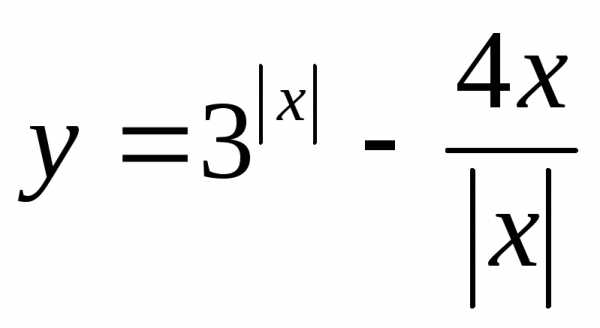 ,
еслиx≤1.
,
еслиx≤1. функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.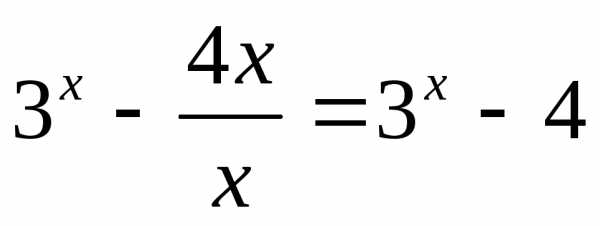 .
Так какдля
.
Так какдля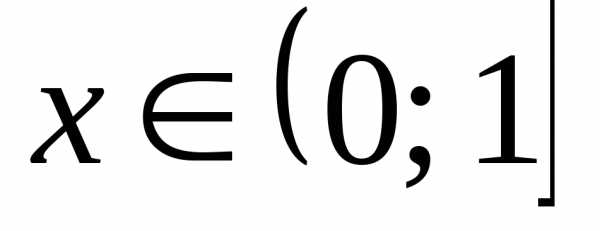 ,
то.
,
то.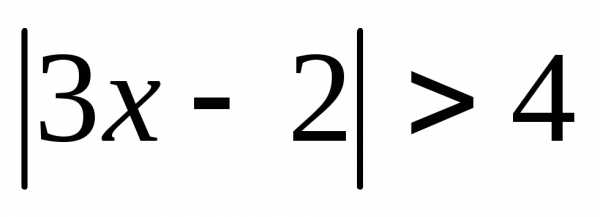 ; 2.
; 2.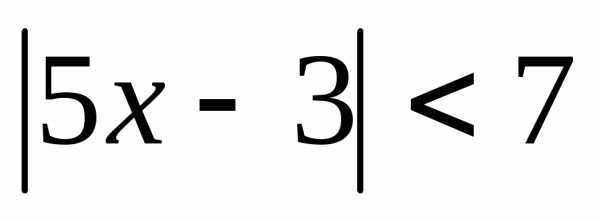 ; 3.;
; 3.;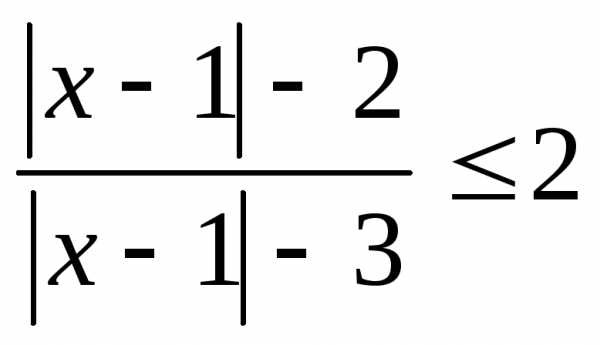 ; 11.
; 11.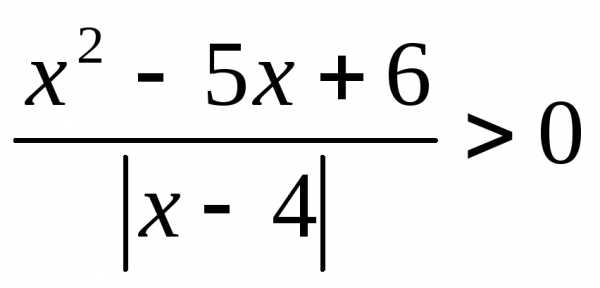 ; 12.
; 12.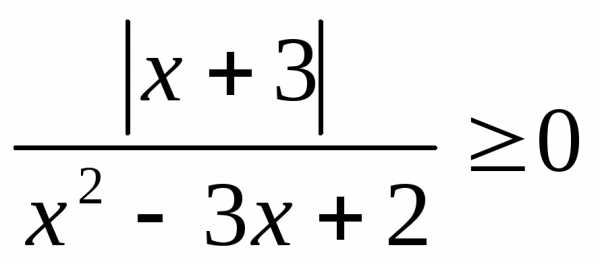 ;
;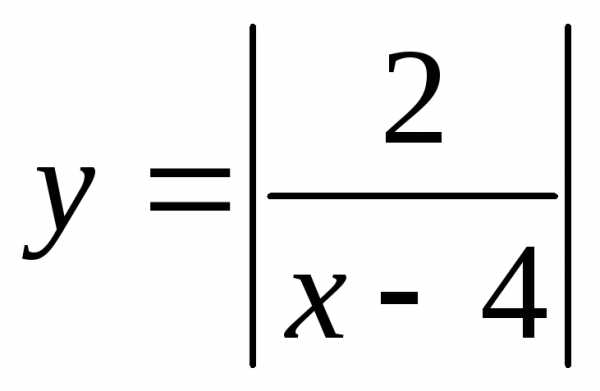 лежат
выше прямой
лежат
выше прямой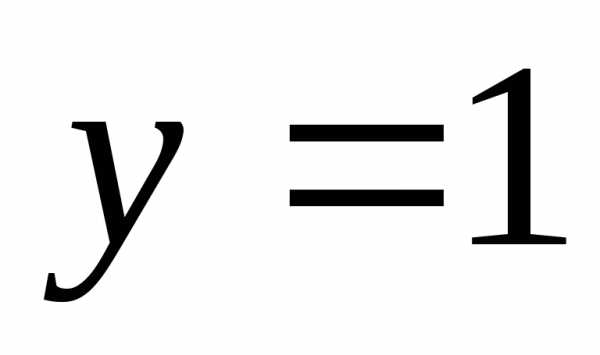 ?
?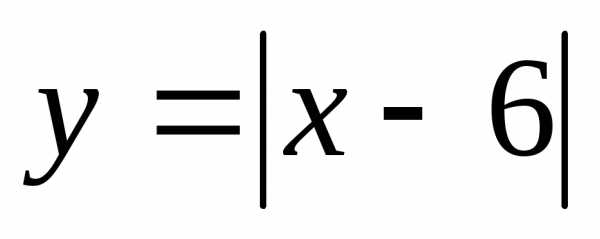 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?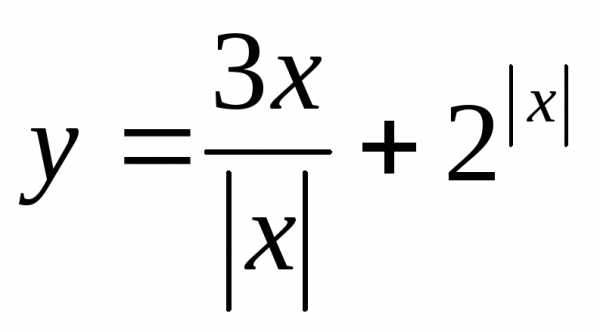 ,
если
,
если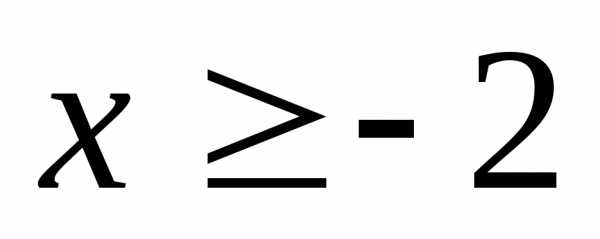 ; 22.
; 22.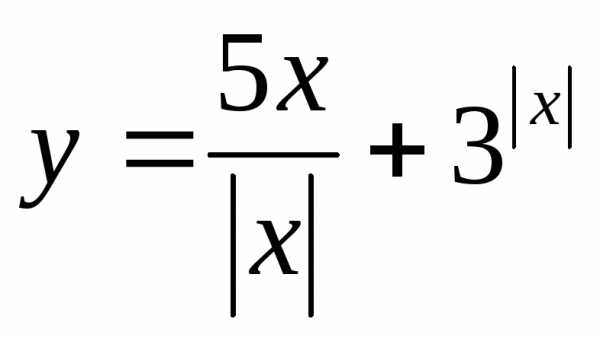 ,
если
,
если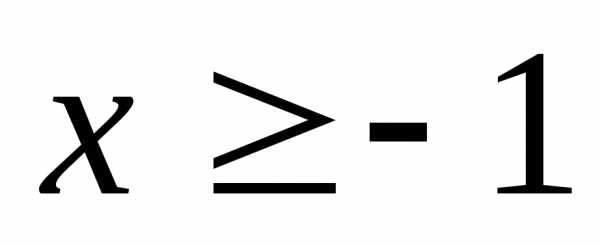 .
.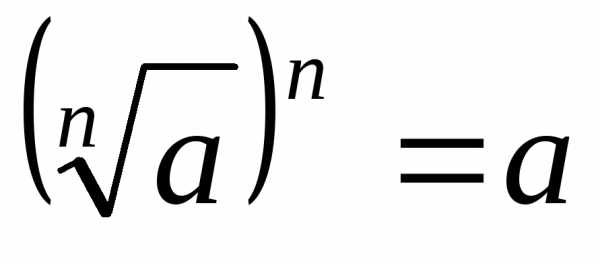 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.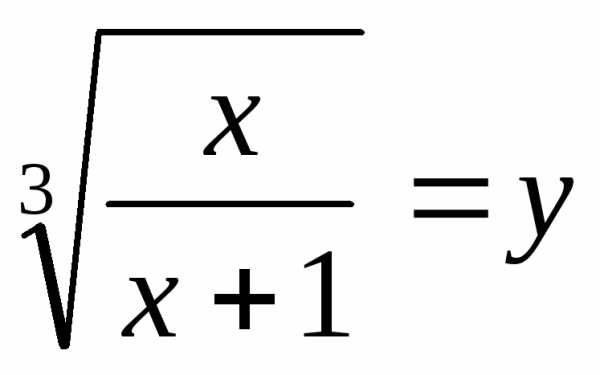 ,
тогда
,
тогда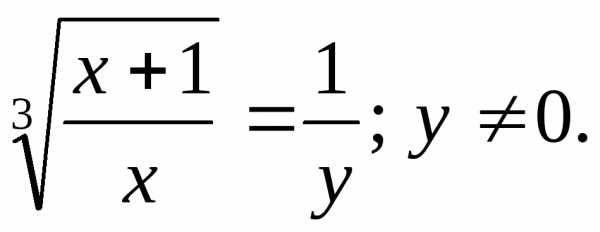 ПоэтомуОтсюда:
ПоэтомуОтсюда: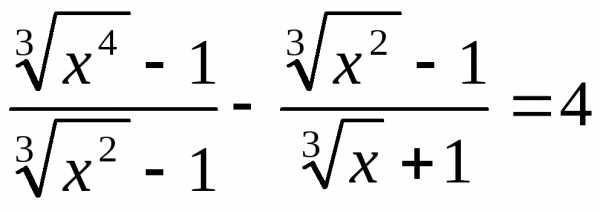 .
.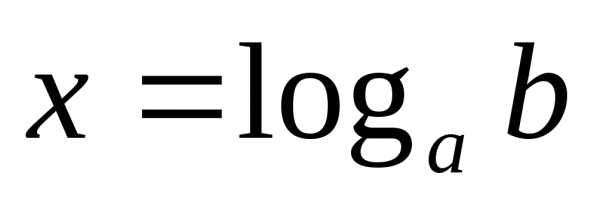 ;
;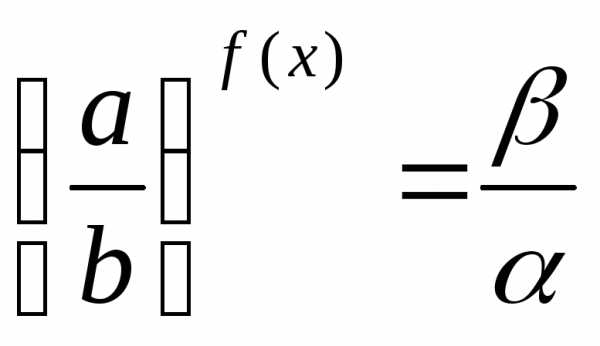 .
.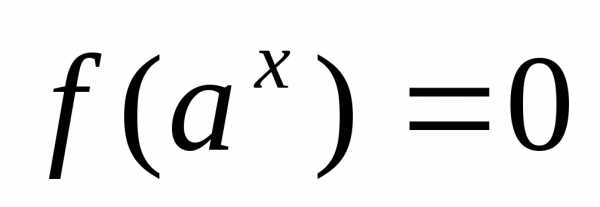 через замену
через замену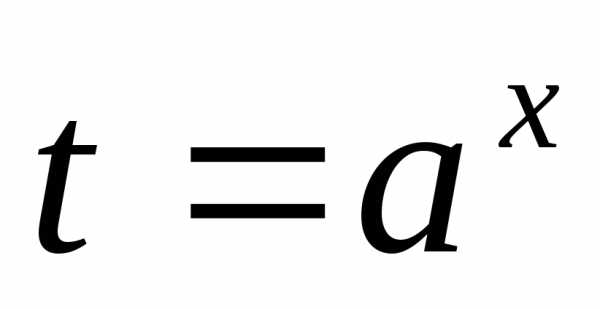 сводят к уравнению
сводят к уравнению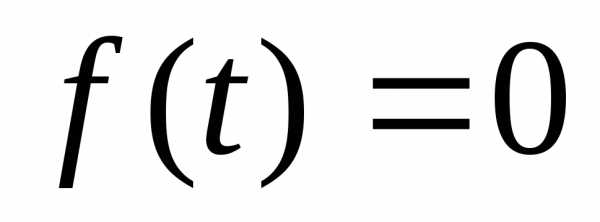 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений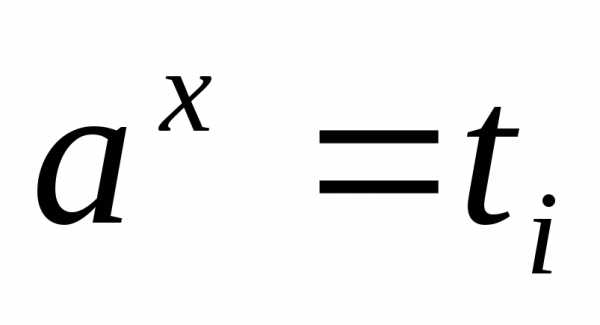 ;
;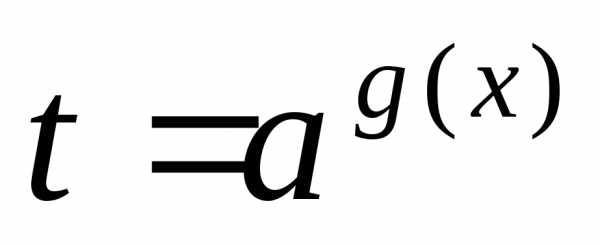 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений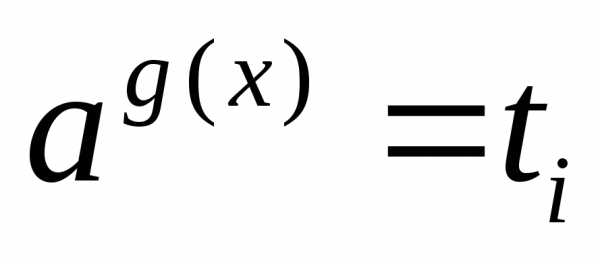 ;
;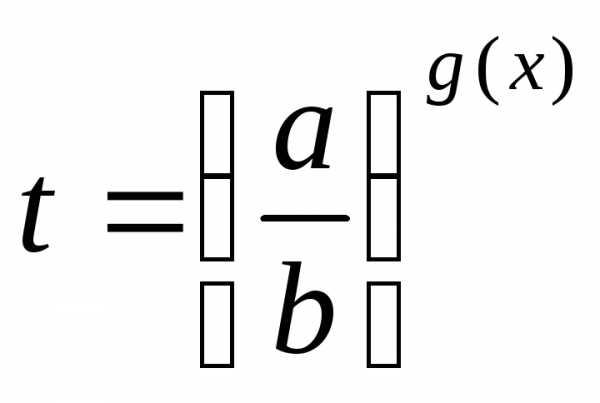 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений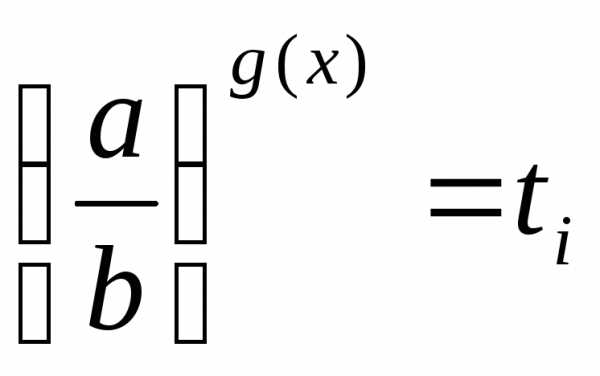 .
.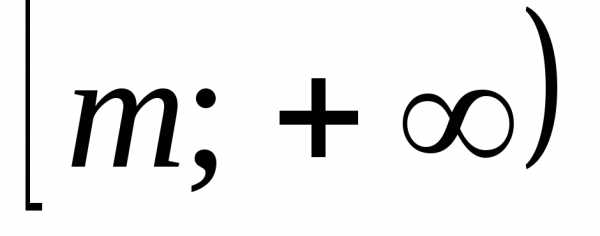 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.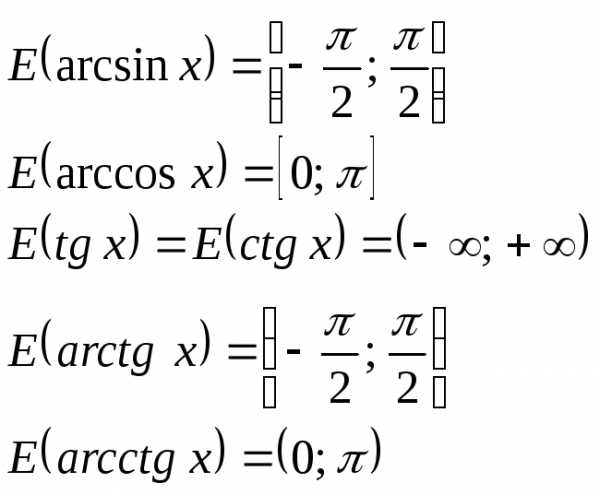
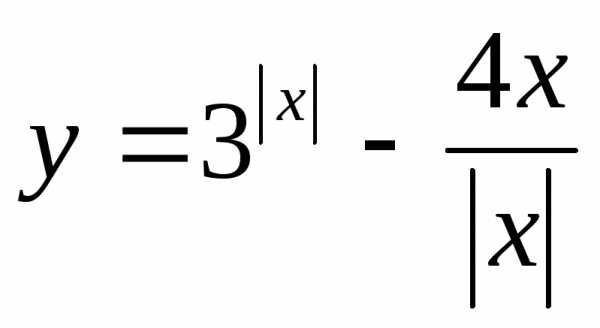 ,
еслиx≤1.
,
еслиx≤1. функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.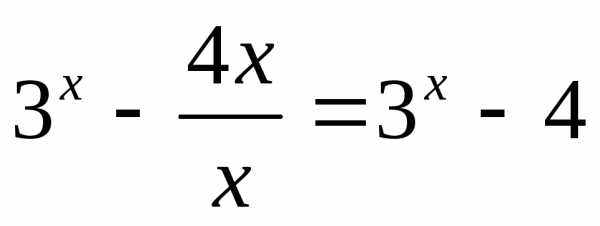 .
Так какдля
.
Так какдля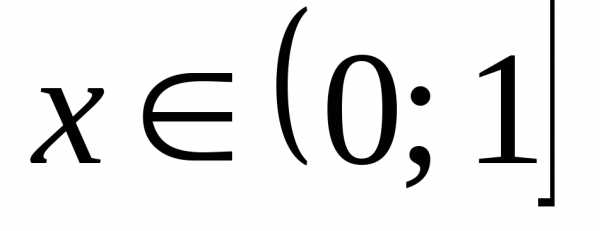 ,
то.
,
то.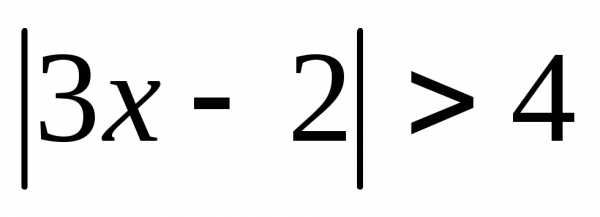 ; 2.
; 2.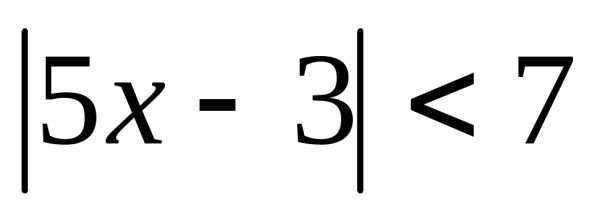 ; 3.;
; 3.;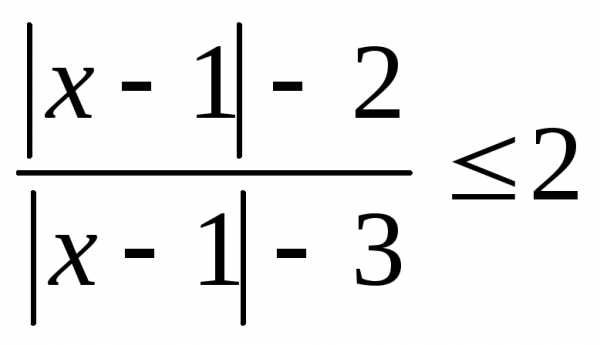 ; 11.
; 11.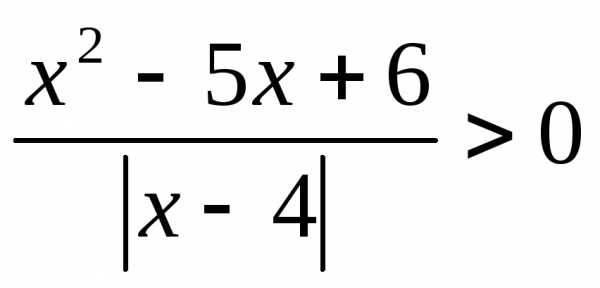 ; 12.
; 12.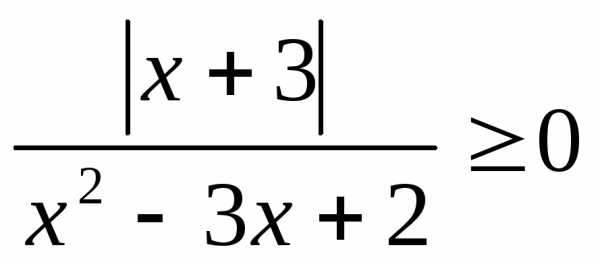 ;
;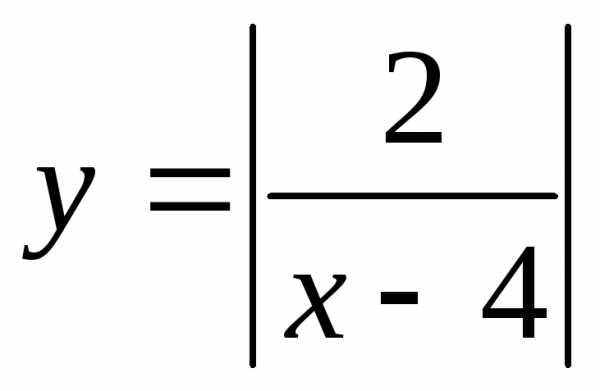 лежат
выше прямой
лежат
выше прямой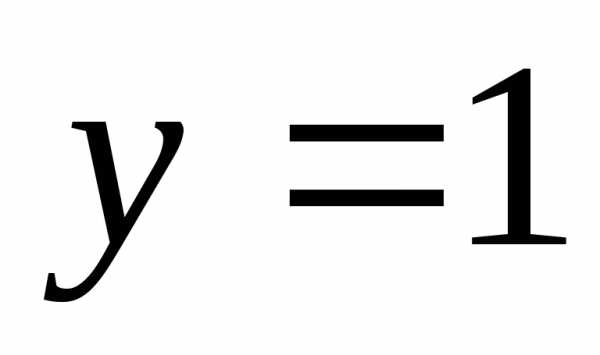 ?
?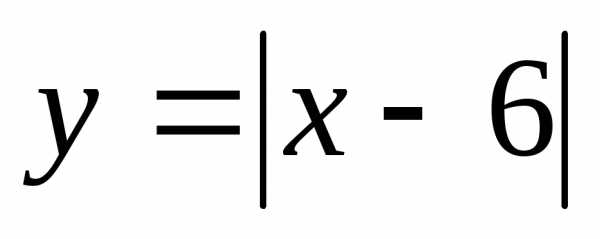 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?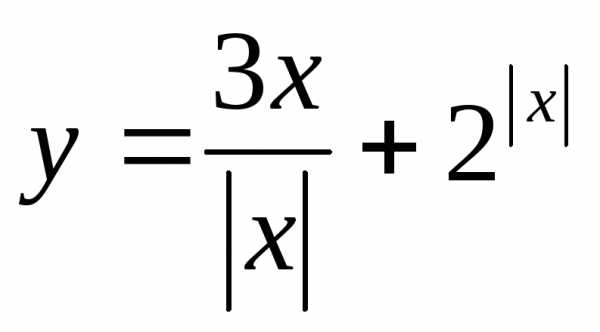 ,
если
,
если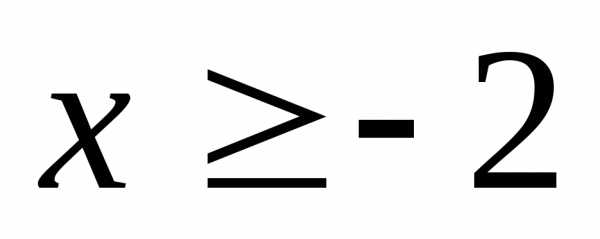 ; 22.
; 22.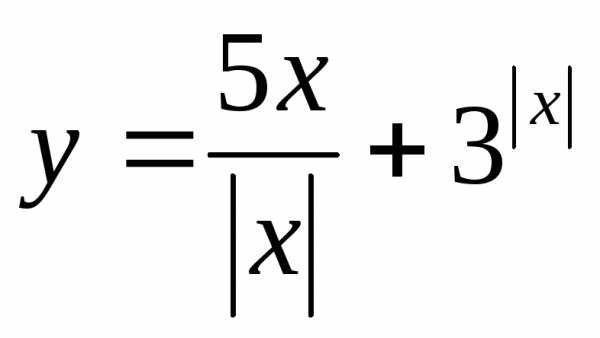 ,
если
,
если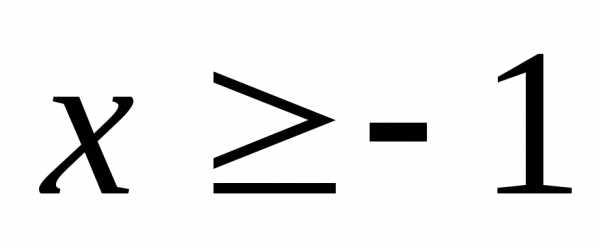 .
.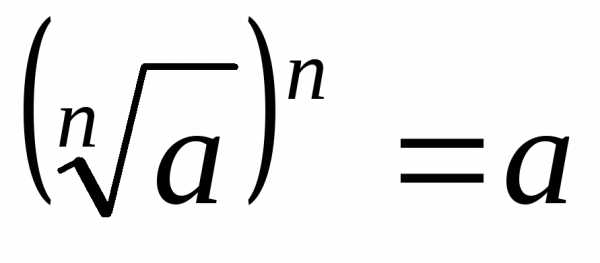 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.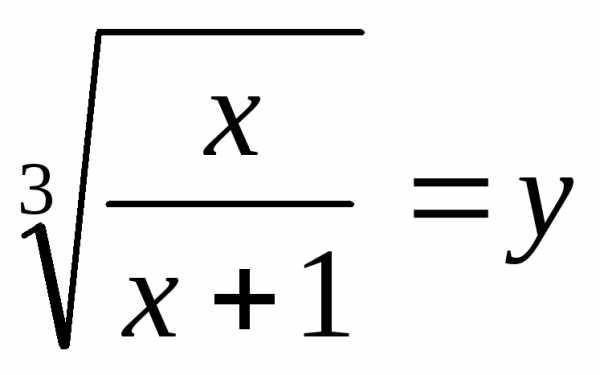 ,
тогда
,
тогда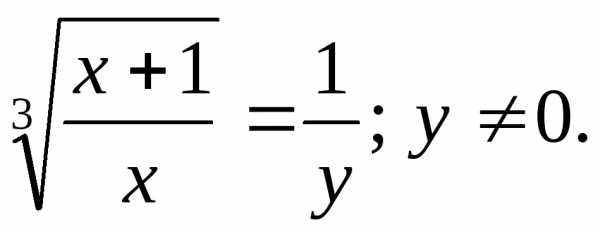 ПоэтомуОтсюда:
ПоэтомуОтсюда: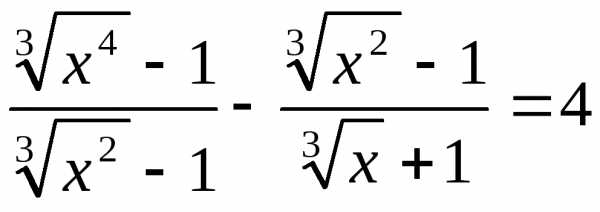 .
.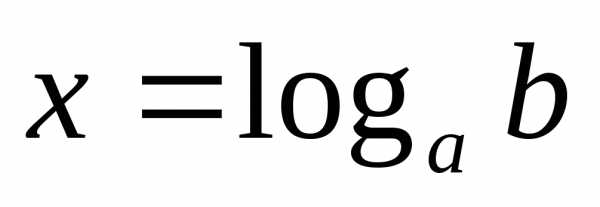 ;
;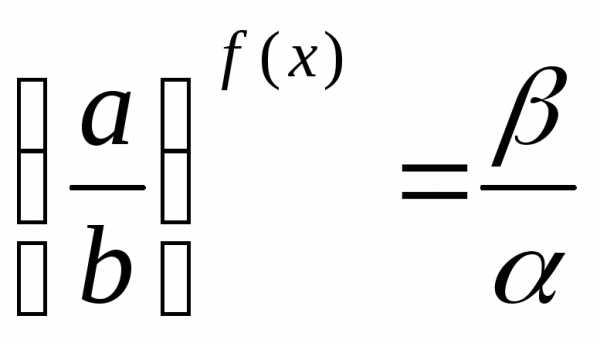 .
.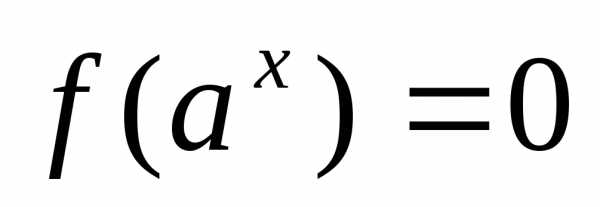 через замену
через замену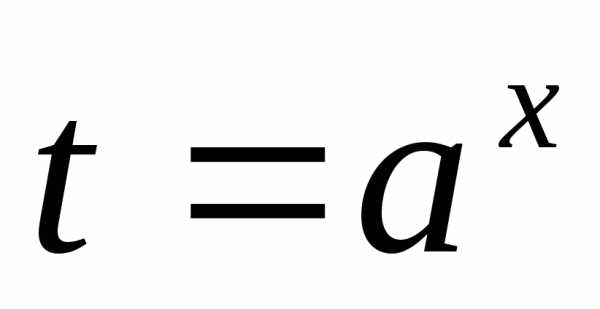 сводят к уравнению
сводят к уравнению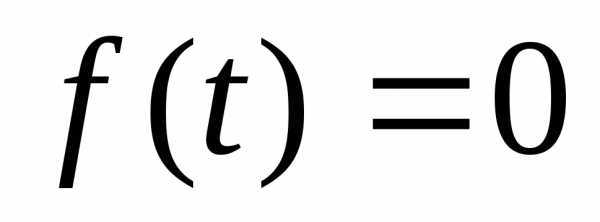 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений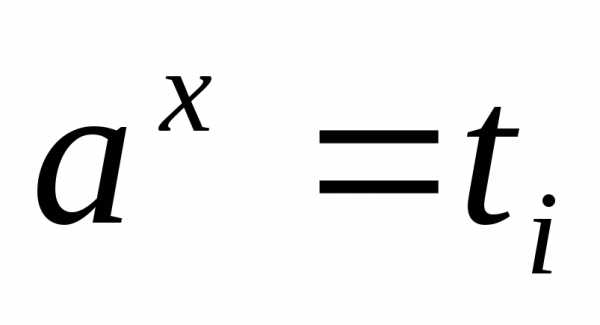 ;
;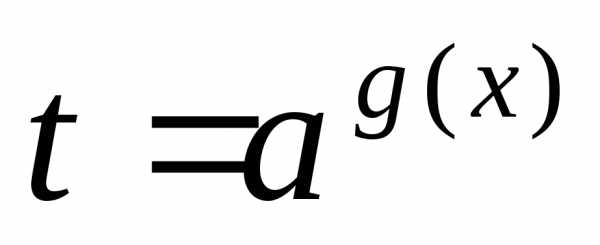 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений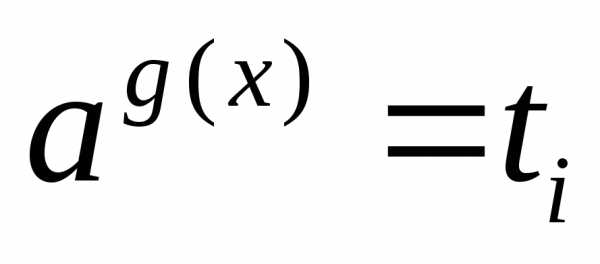 ;
;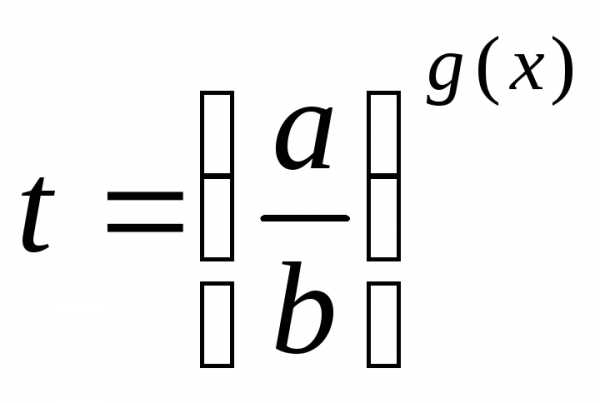 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений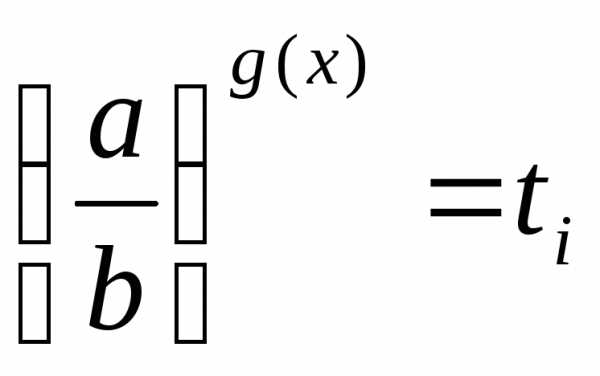 .
.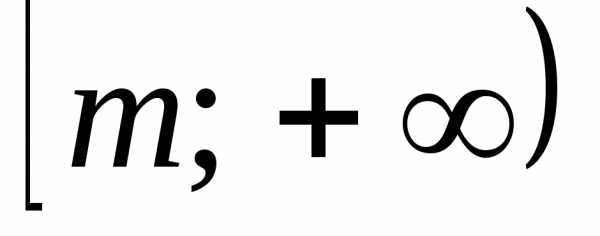 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.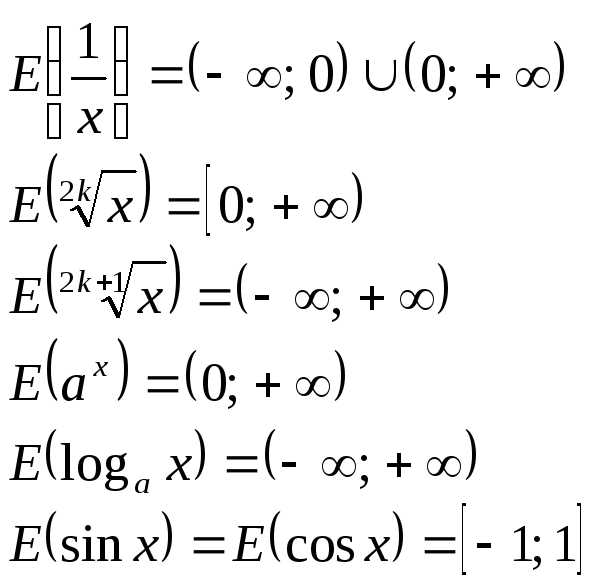
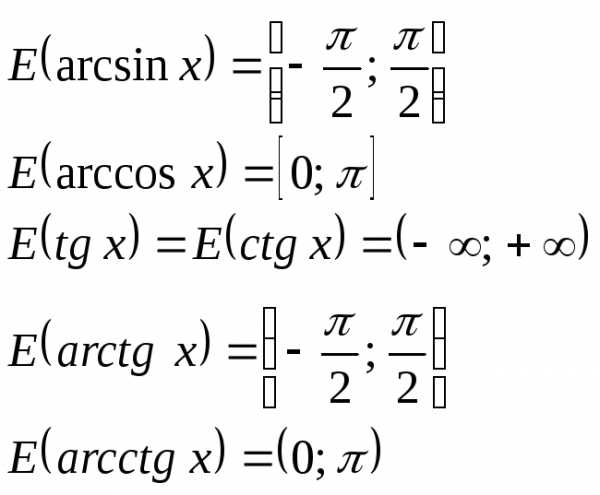
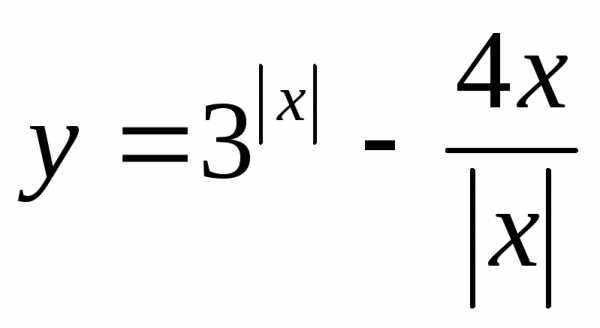 ,
еслиx≤1.
,
еслиx≤1. функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.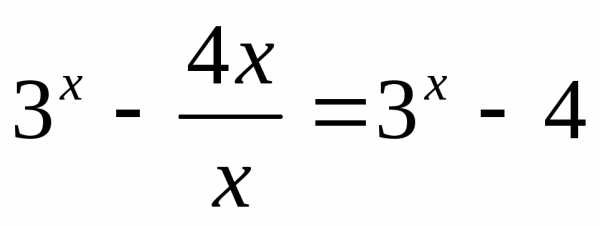 .
Так какдля
.
Так какдля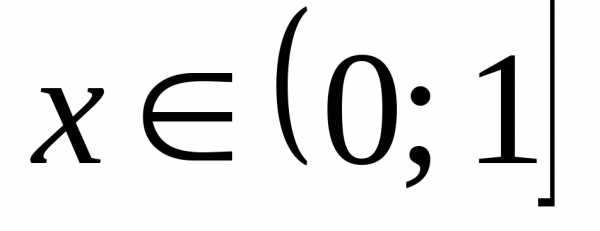 ,
то.
,
то.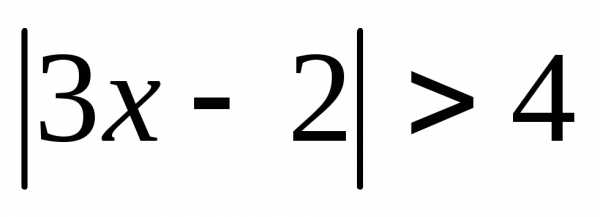 ; 2.
; 2.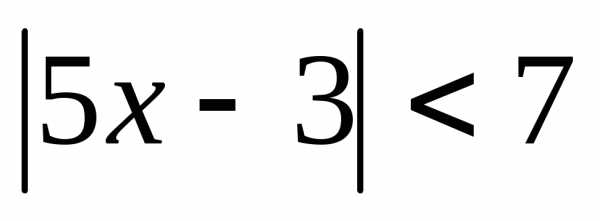 ; 3.;
; 3.;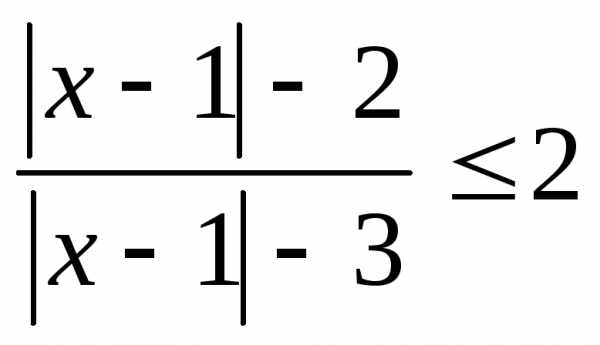 ; 11.
; 11.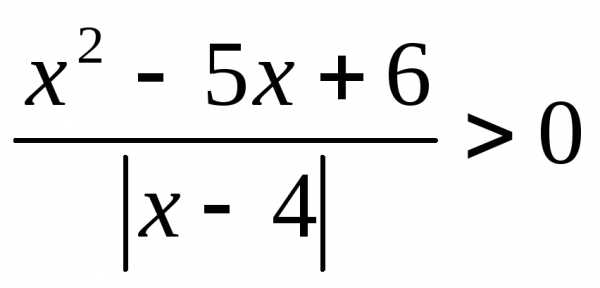 ; 12.
; 12.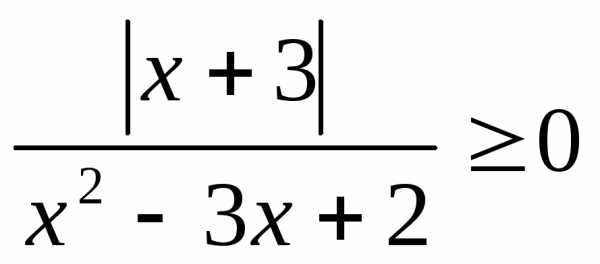 ;
;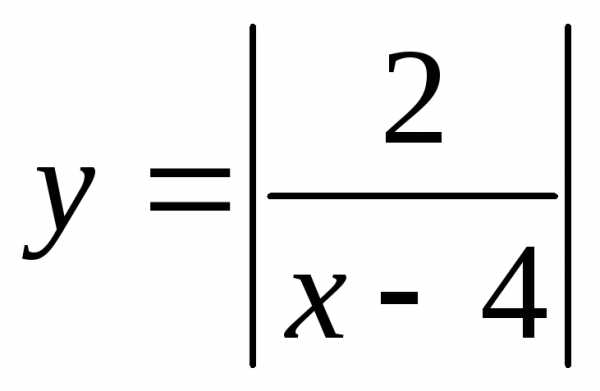 лежат
выше прямой
лежат
выше прямой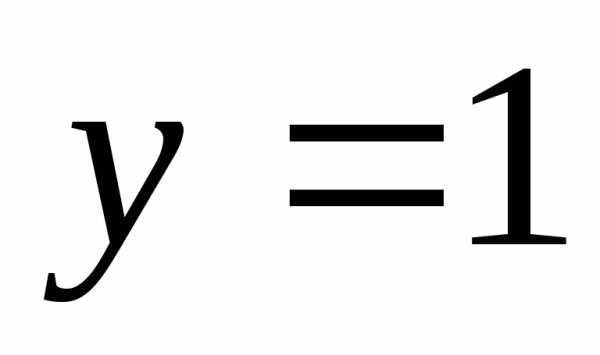 ?
?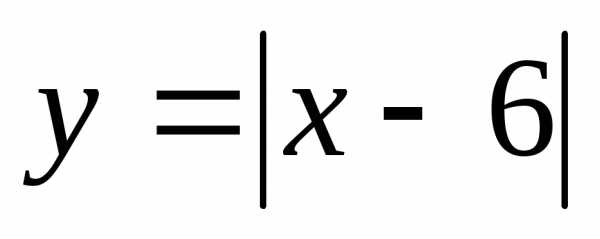 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?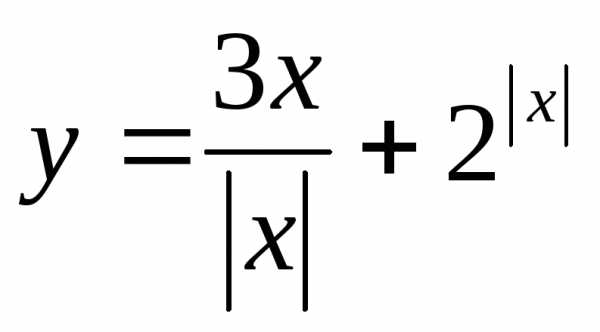 ,
если
,
если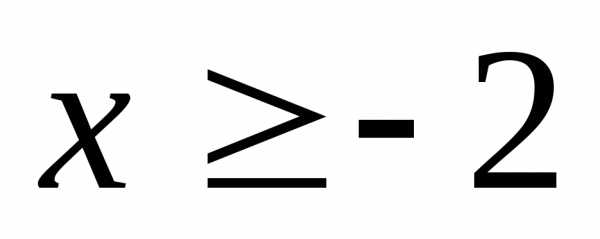 ; 22.
; 22.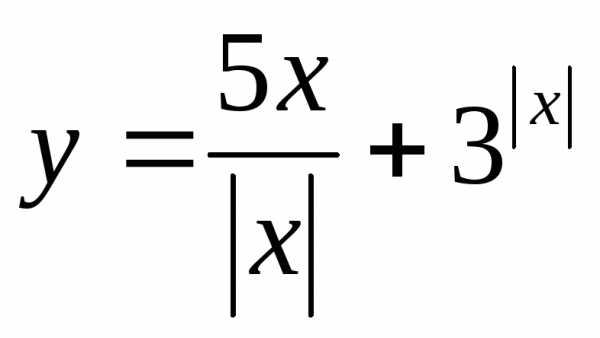 ,
если
,
если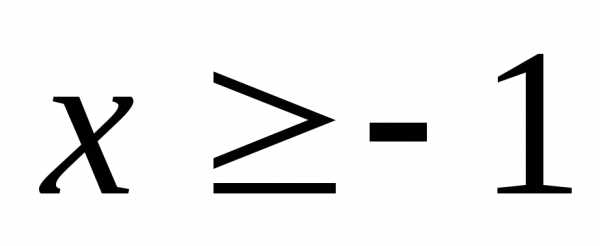 .
.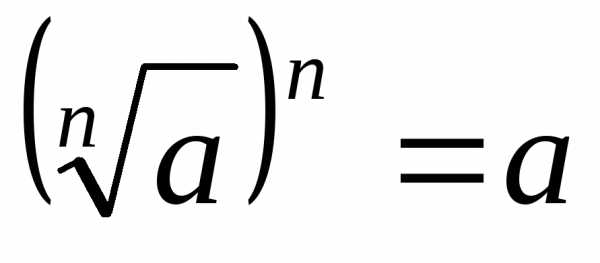 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.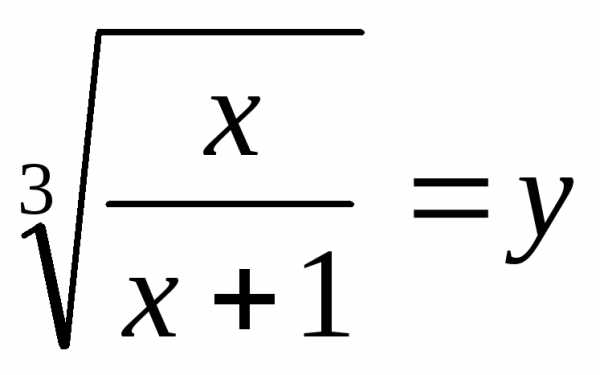 ,
тогда
,
тогда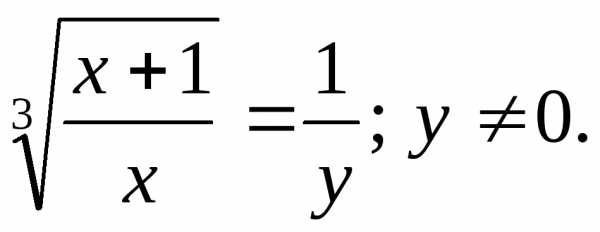 ПоэтомуОтсюда:
ПоэтомуОтсюда: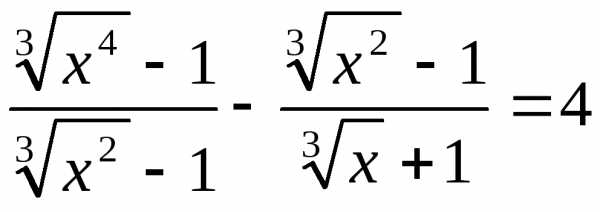 .
.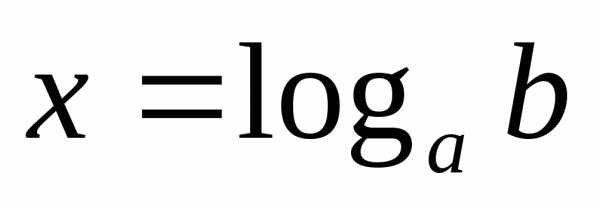 ;
;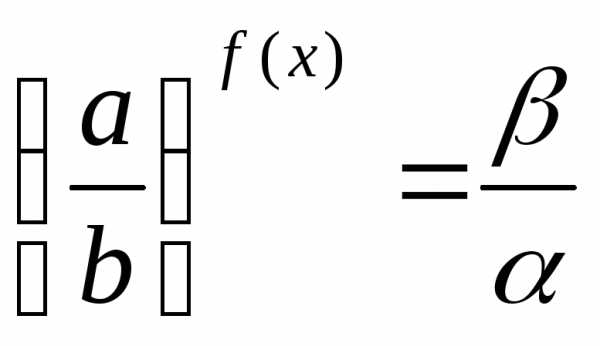 .
.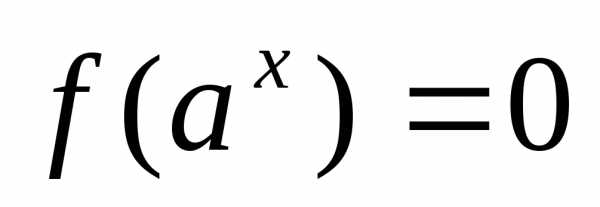 через замену
через замену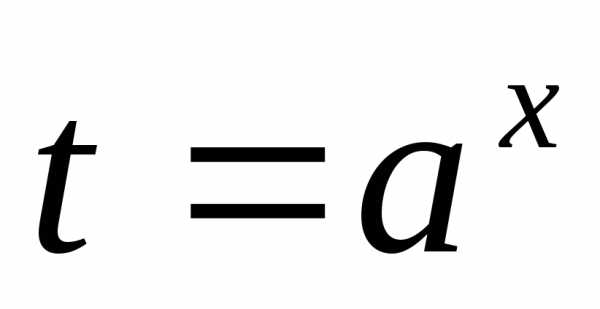 сводят к уравнению
сводят к уравнению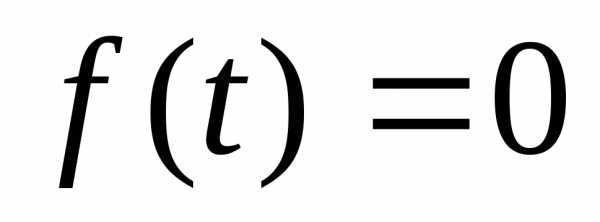 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений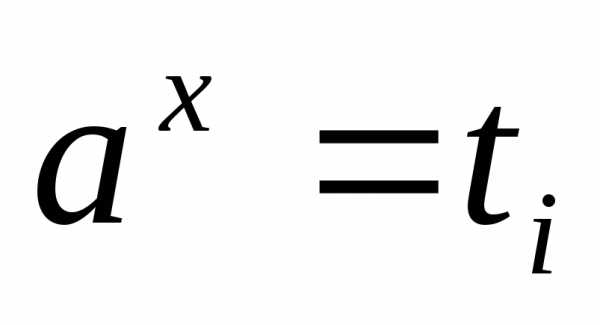 ;
;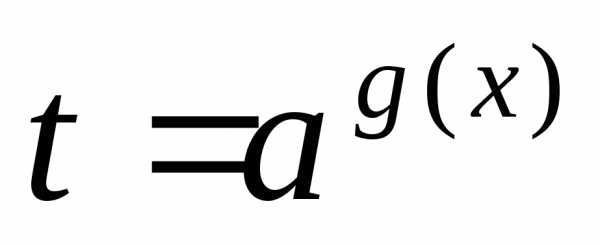 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений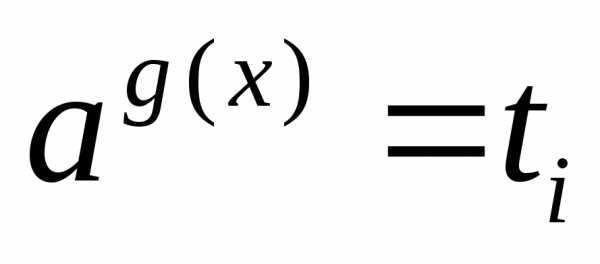 ;
;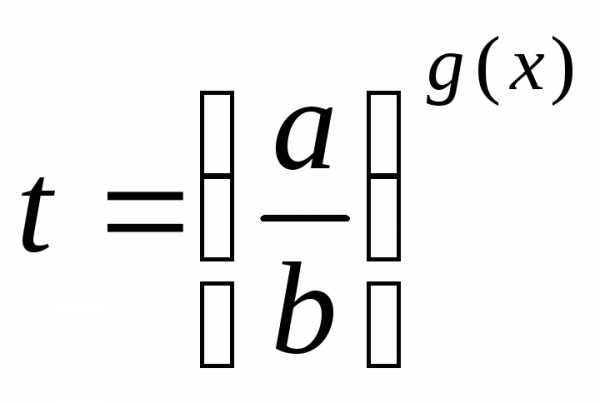 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений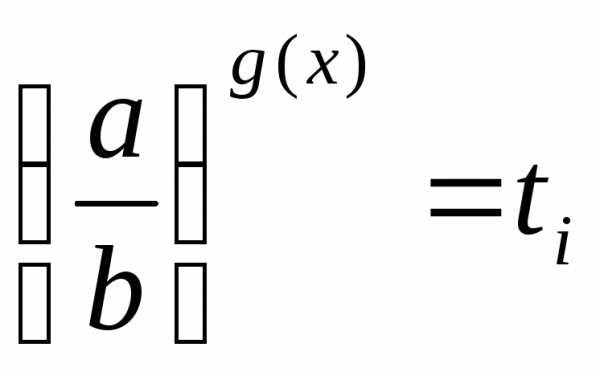 .
.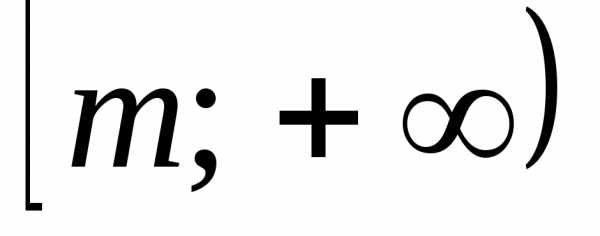 ,
гдеm– наименьшее
значение этого многочлена, либо промежуток
,
гдеm– наименьшее
значение этого многочлена, либо промежуток ,
гдеn– наибольшее
значение этого многочлена.
,
гдеn– наибольшее
значение этого многочлена.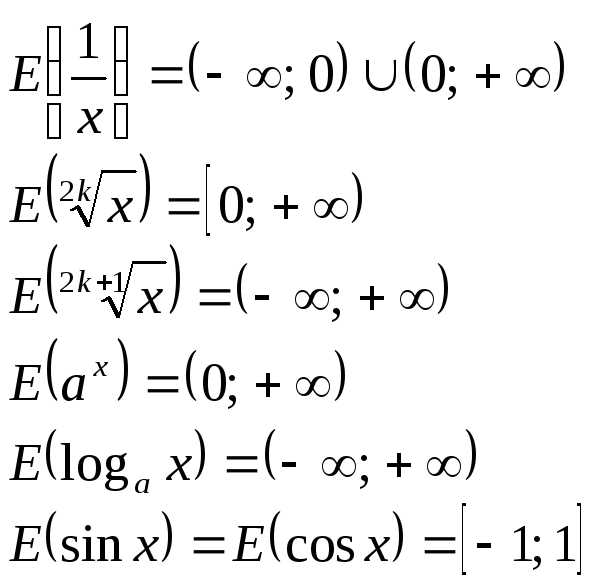
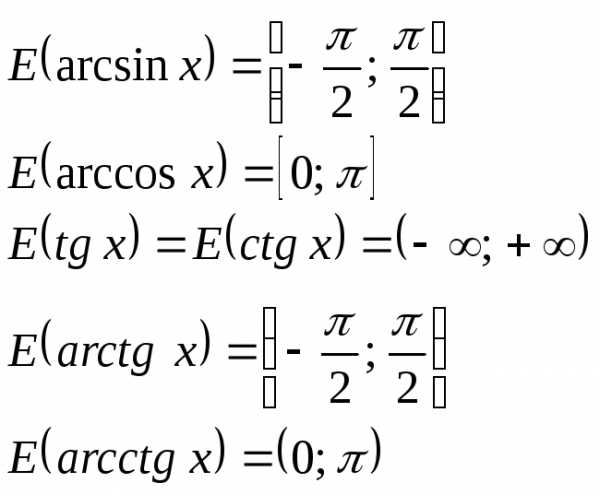
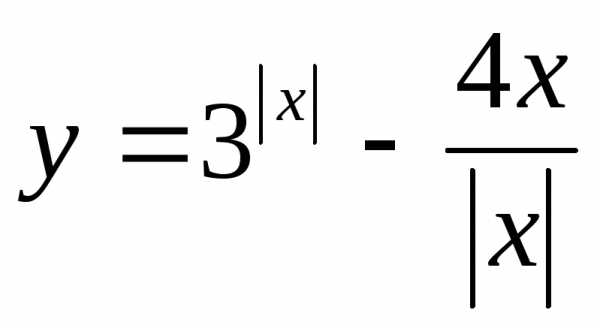 ,
еслиx≤1.
,
еслиx≤1. функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.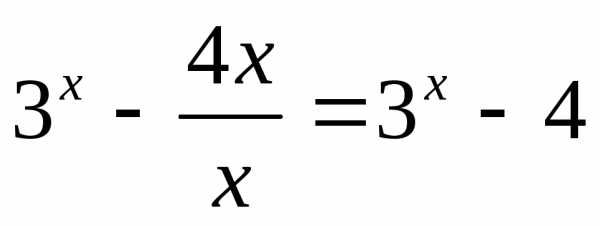 .
Так какдля
.
Так какдля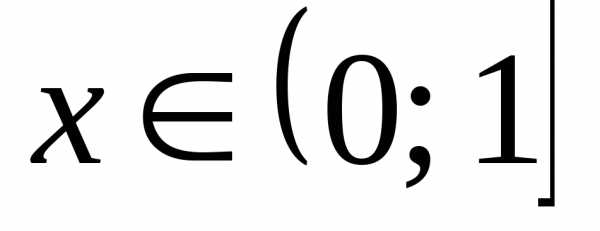 ,
то.
,
то.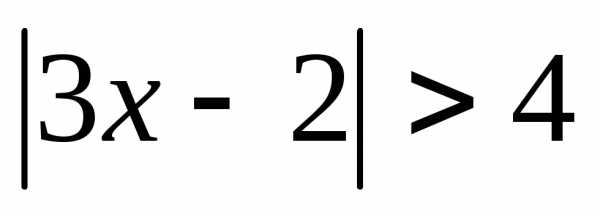 ; 2.
; 2.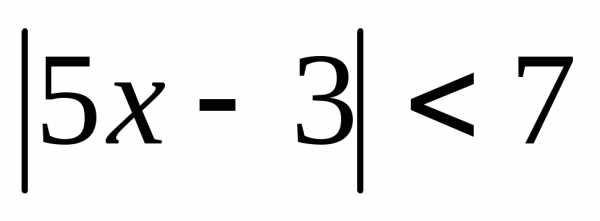 ; 3.;
; 3.;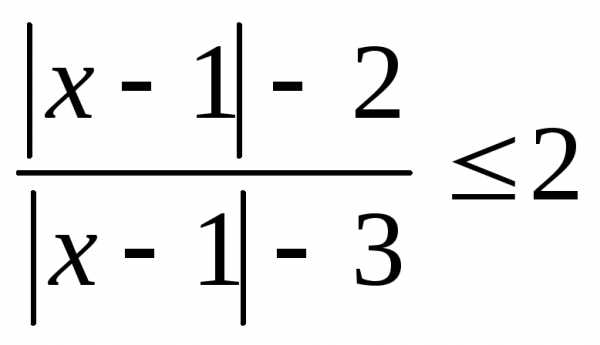 ; 11.
; 11.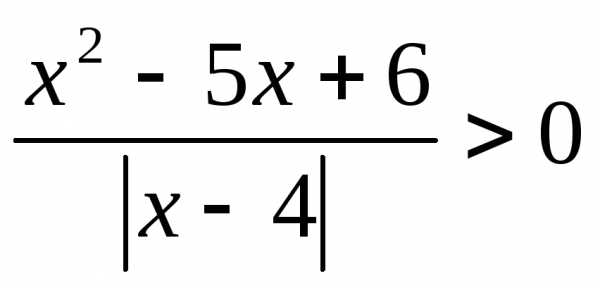 ; 12.
; 12.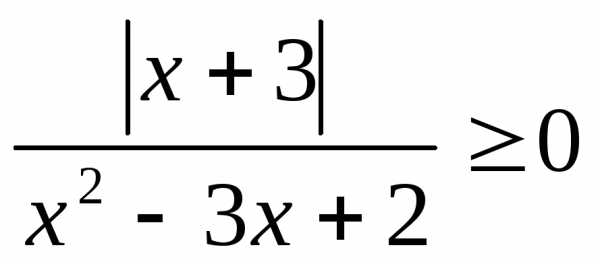 ;
;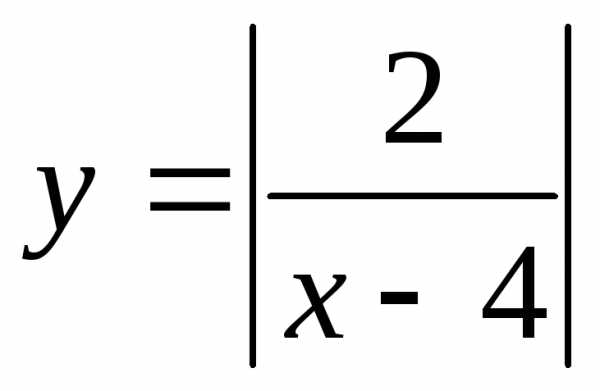 лежат
выше прямой
лежат
выше прямой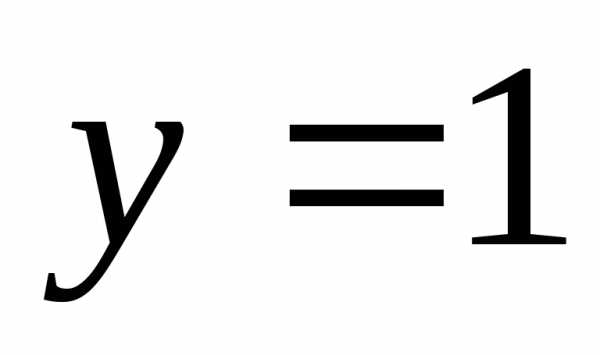 ?
?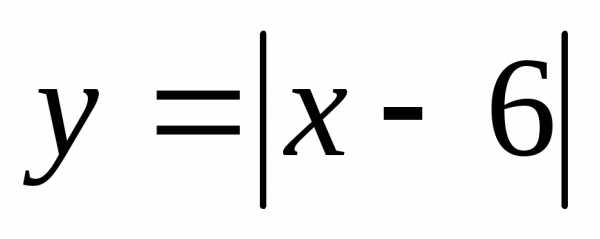 лежат не ниже точек графика функции?
лежат не ниже точек графика функции?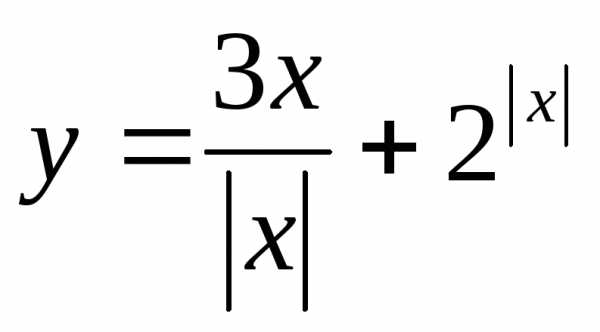 ,
если
,
если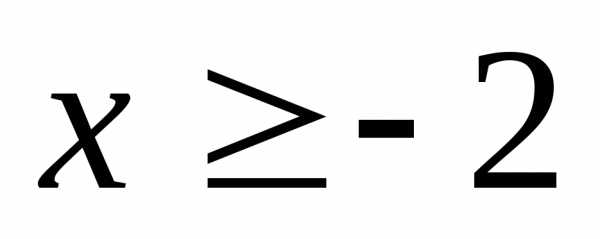 ; 22.
; 22.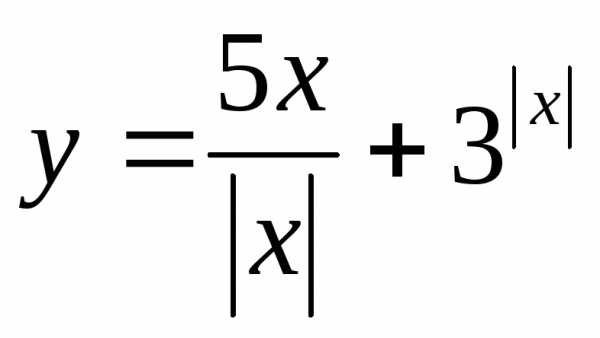 ,
если
,
если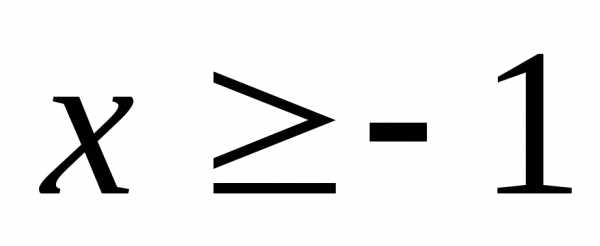 .
.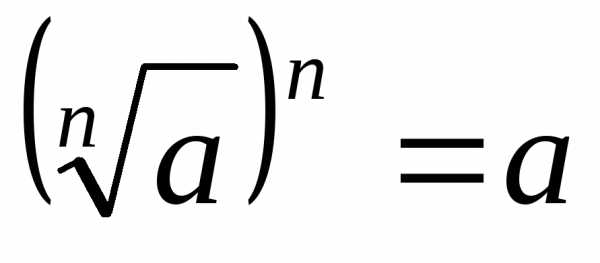 ,
получают уравнениеи решают его.
,
получают уравнениеи решают его.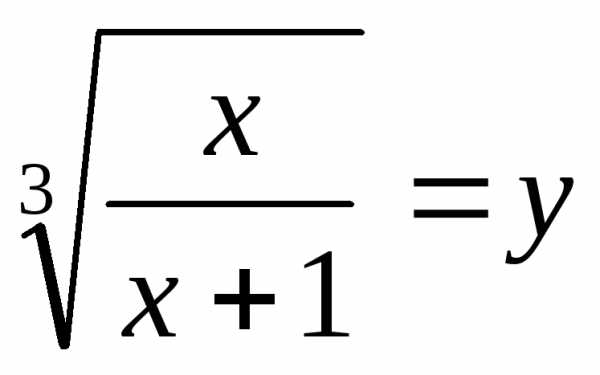 ,
тогда
,
тогда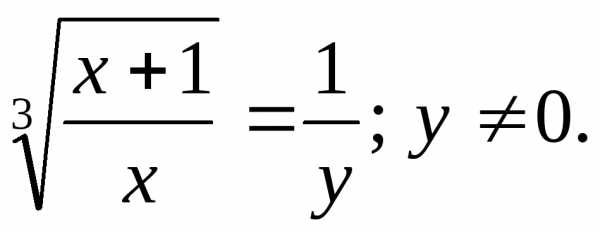 ПоэтомуОтсюда:
ПоэтомуОтсюда: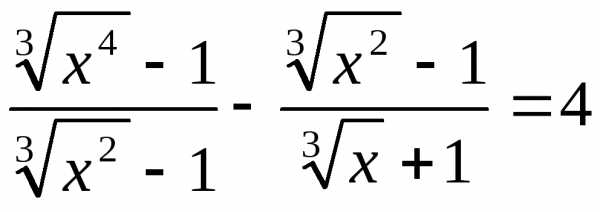 .
.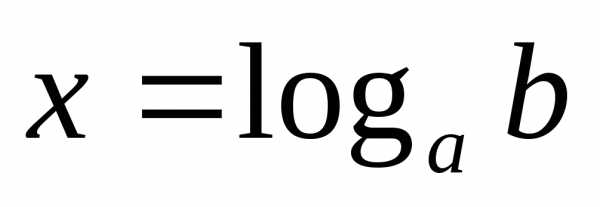 ;
;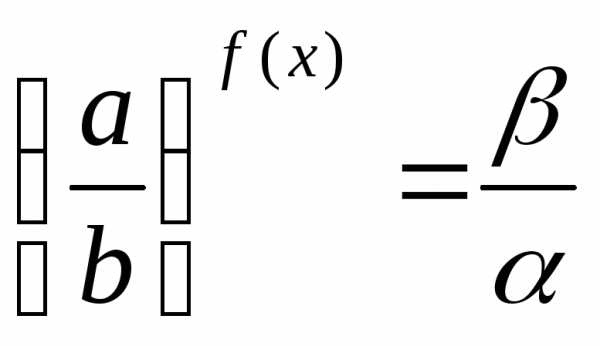 .
.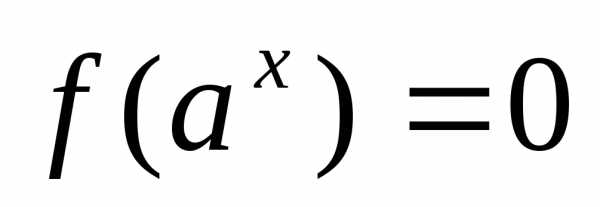 через замену
через замену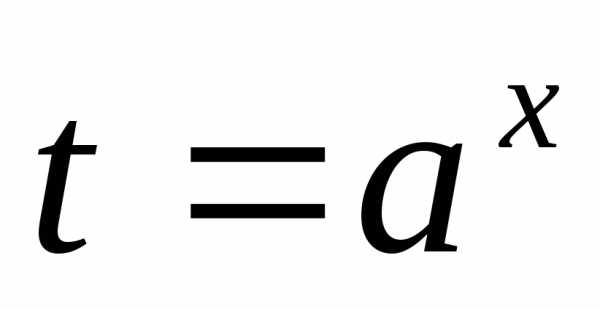 сводят к уравнению
сводят к уравнению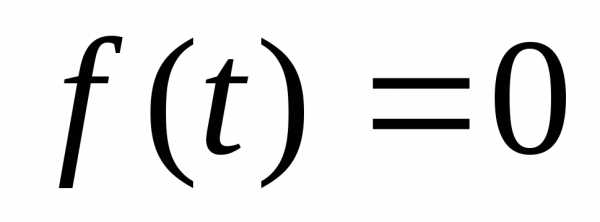 ,
а затем решают совокупность простейших
показательных уравнений
,
а затем решают совокупность простейших
показательных уравнений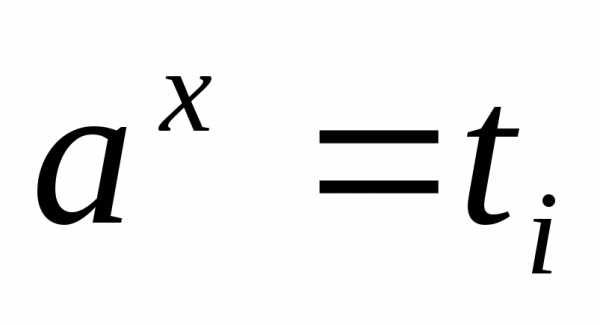 ;
;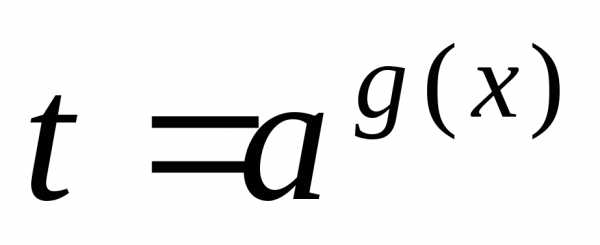 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений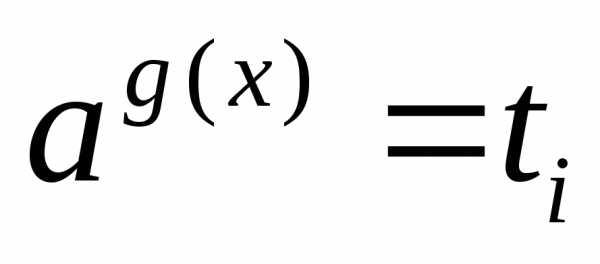 ;
;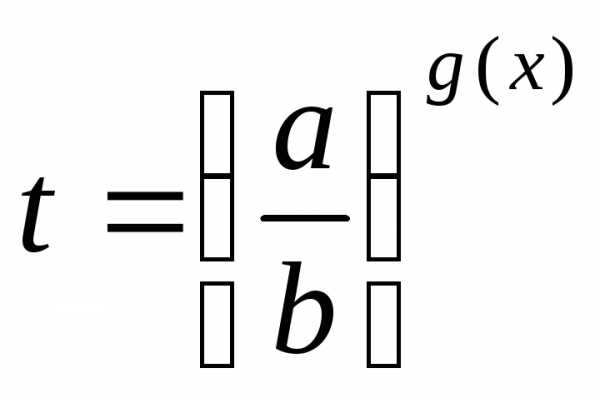 сводят к уравнению,
а затем решают совокупность уравнений
сводят к уравнению,
а затем решают совокупность уравнений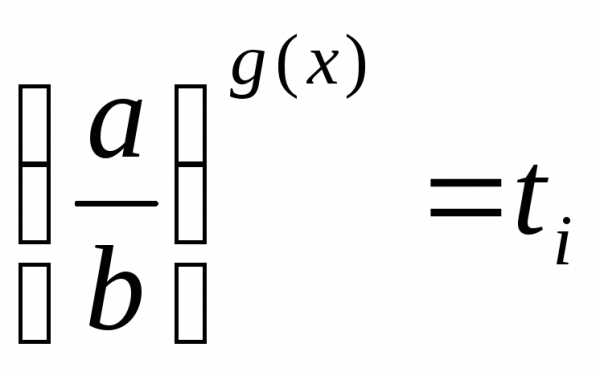 .
.
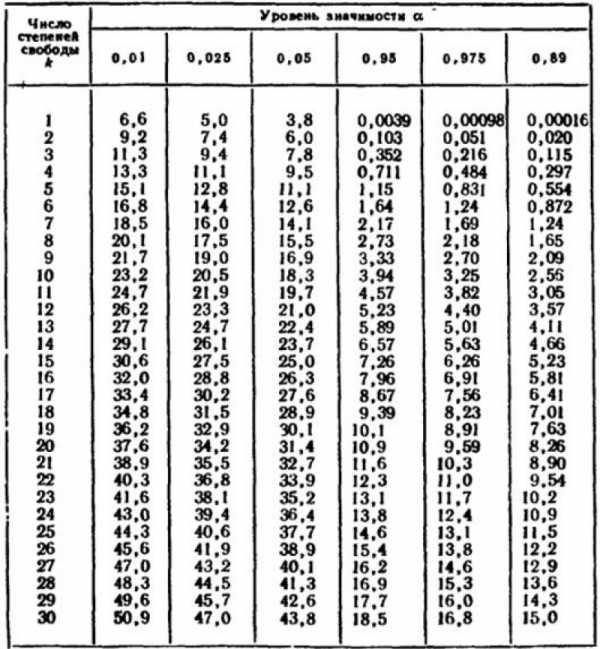
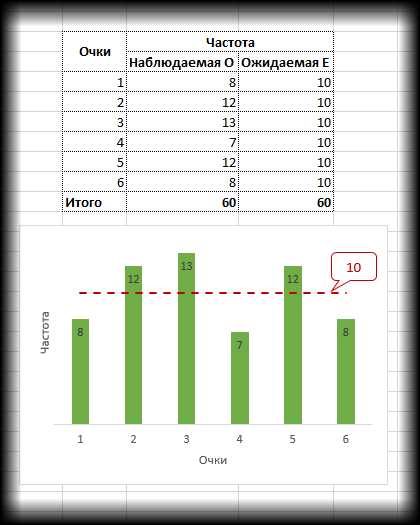
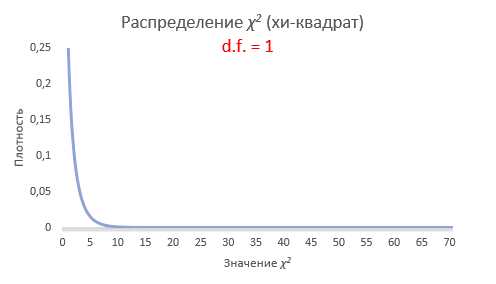
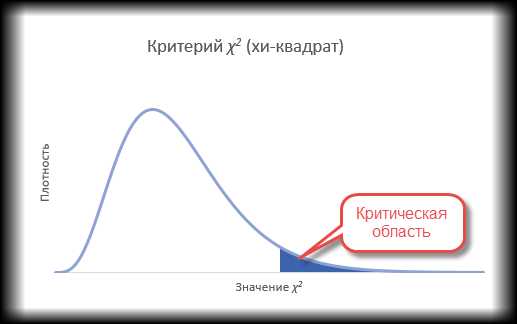
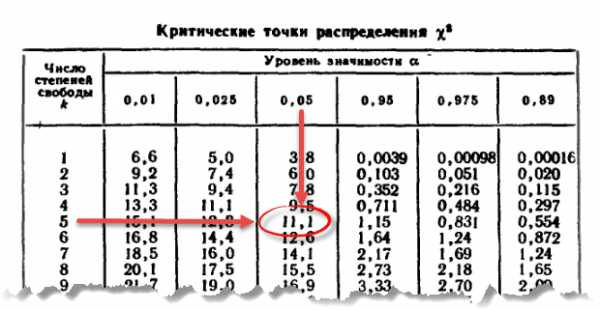
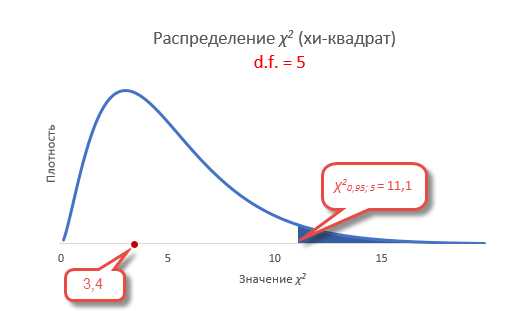
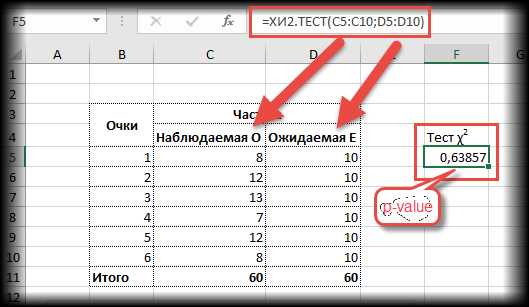 Проверка гипотезы с помощью функции эксель ХИ2.ТЕСТ
Проверка гипотезы с помощью функции эксель ХИ2.ТЕСТ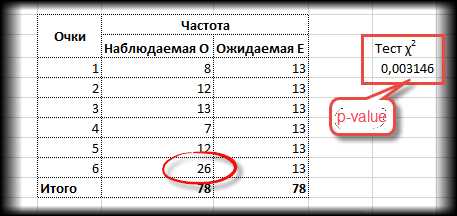
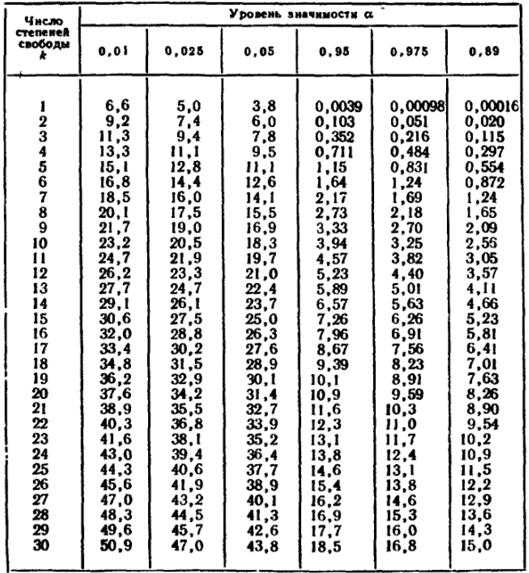

 строк.Построим
таблицу (табл. 3).
строк.Построим
таблицу (табл. 3).