Когда минус на минус не дает плюс. Немного об отрицательных остатках.
Когда-то очень давно, при моем первом опыте внедрения 1С:Управление торговлей 10.0 я не смогла защитить перед внутренним заказчиком регистр «Партии товаров организации», т.к. не являлась специалистом по финансовому учету. У заказчика был логичный вопрос: «Зачем один документ делает движения аж по трем регистрам остатков, тем самым съедая больше ресурсов памяти?». Мой недостаточно конкретный ответ на этот вопрос повлек то, что руководство этой организации до сих пор считает финансовый результат в Excel, т.к. без учета себестоимости в программе доходы/расходы не посчитаешь.
Речь шла, конечно, о регистрах «Товары на складах», «Товары организации» и «Партии товаров».
В этом посте я решила объяснить, зачем методически разделили эти 3 регистра, и за что каждый из них отвечает.
Товары на складах
Отвечают исключительно за количественный УПРАВЛЕНЧЕСКИЙ учет номенклатуры на складах исключительно с управленческой аналитикой: серии, характеристики, единицы измерения.
Почему этот регистр выделен? Потому, что есть документы, которые двигают исключительно его — это Складские ордера. Если на вашем предприятии есть сотрудники, которые осуществляют исключительно количественную приемку/отгрузку на складе и несут полную материальную ответственность (обычно, это Завскладом), однако не обладают компетенцией оформления первичной документации строгой отчетности (к примеру, ТОРГ-12) — ордерная схема складского учета для Вас! Кто готов доверить складскому работнику определение в документе Цен/Скидок/НДС и прочего?
Суть ордерной схемы в том, что регистрация первичных документов в системе фиксирует факты:
- перехода права собственности на товар
- возникновения взаиморасчетов
- возникновения налоговой базы
а регистрация складских ордеров — факты:
- движения товаров на складе
- изменения базы для материальной ответственности складских работников.
Товары организации
Отвечают за количественный РЕГЛАМЕНТИРОВАННЫЙ учет номенклатуры по юрлицам вашей организации в разрезе регламентированных аналитик и классификаторов: номеров ГТД, ТНВЭД и прочее…
Регистр двигают именно первичные документы и он фиксирует факт перехода права собственности.
Именно с этим регистром связан самый большой курьез конфигурации «1С:Управление производственным предприятием». Многие полагают, что раз в конфигурации доступна возможность устанавливать галки проведения по Управленческому и Регламентированному учету, то можно часть документов проводить только по Управленческому, а часть только по Бухгалтерскому и Налоговому учету. Но вот незадача: оба документа, проведенных с одними данными, но по разным учётам, двигают данный регистр. Следовательно, возникает задвоение количества и неправильные данные при закрытии месяца. Разделение галок проведения по учётам в документах позволяет не проводить некоторые документы по регламентированному учету, но не позволяет вести параллельно и независимо 2 учета в рамках одной базы.
Мой совет: если есть необходимость создавать 2 документа по разным учётам (очень часто Отчет производства за смену в управленческом и регламентированном учете создается по разным спецификациям) — создавайте их в 2-х разных базах с одной конфигурацией, обменивающихся между собой только частью документов.
Партии товаров
Отвечает за количественный и суммовой учет со всеми аналитиками.
Именно в него попадают данные о стоимости закупки, ТЗР (затрат на растаможку и доставку от поставщика), распределяемых на себестоимость поступившей партии, именно в него попадают данные о стоимости выпуска в производстве. Именно из этого регистра, при классическом партионном учете, берутся данные для оценки стоимости списания партий по принципу ФИФО или Средней и для получения Валовой прибыли.
Теперь об отрицательных остатках
Конечно, количественные значения всех этих регистров должны быть равны, а остатки по ним всегда положительны. Первое, что я настраиваю в отчетности для контроля корректности ведения учета, это отчеты по «-» остаткам.
Важно! Если Товары на складах и Товары организации при полных правах и неоперативном проведении документов могут уйти в минус, то Партии товаров в минус не двигаются. Такой документ вообще не будет иметь движение по данному регистру, следовательно даст некорректную погрешность в финансовом отчете.
Когда же допустимы отрицательные остатки? Есть ли исключения?
Да, исключения существуют, но касаются они только одного регистра из трех — Товары организации.
Современные конфигурации поддерживают систему Интеркампани. Она позволяет оформлять продажи с собственного юрлица компании на котором отсутствуют остатки товаров, при условии, что остаток есть на другой организации (другом собственном юрлице). В процедуру закрытия финансового месяца входит оформление документов Передачи товаров (купли-продажи между собственными юрлицами) по данным отрицательных остатков. Также, Передачу можно оформлять по отрицательным остаткам Товаров организации и оперативно.
saltsina.ru
В обычной розетеке есть ноль и фаза ,а плюс и минус когда постоянный ток
Честно сказать, не хотелось время терять на подобный вопрос, но прочел ответы предыдущих, и обнаружил, что полного ответа как такового НЕТ!! ! Наиболее близок к истине ответ Ивана Долинина, и я просто хочу его дополнить, расширить.. . К качестве питающей сети бытовых потребителей 220В, в России применяются трехфазные четырехпроводные электрические сети с глухо заземленной нейтралью 3х380/220В., используются нолевой и фазный проводники. Тоесть вторичные обмотки трансформатора на ТП, соединены в звезду, а их начала, точка нулевого потенциала заземлена, тоесть глухо соединена с контуром заземления на ТП. Получается, что ноль-это заземленный вывод фазной обмотки трансформатора, и он равнопотенциален с землей, поскольку заземлен. В вашей квартире, да и во всех остальных естесственно, нолевой проводник все-же имеет потенциал относительно земли, примерно 7-14 В, в зависимости от сопротивления линии, симметрии и величины токов нагрузки, но все равно, этот потенциал можно не учитывать. Указатель напряжения, не фиксирует такое напряжение, так как оно ниже порога зажигания неоновой лампы, а при проверке им, в качестве второго проводника выступает ваше тело, как правило заземленное через пол, обувь и т, д. Получается, что и вы, и нолевой проводник, имеете потенциалы, близкие, или равные потенциалу земли. А вот фазный проводник, имеет всегда полноценный потенциал относительно земли, тех-же 220+/- 5-10%… Именно поэтому мы его и обнаруживаем указателем напряжения. Именно он и представляет опасность поражения электрическим током. Думаю, что теперь понятно, чем «ноль», отличается от «фазы»
Про постоянный ток все видимо понятно. А переменный, если рассматривать пример относительно розетки, то там фаза меняеться с нулем с частотой 50 Гц (т. н. промышленная частота) . Фазный провод определяеться тестером (неонкой).
ну в двух словах не скажешь, по фазам ток течет, трехфазная обмотка транса соединяется звездой или треугольником, сумма токов в точке соединения равна 0,вот тебе и ноль. фазное напряжение-между фаз, у нас обычное 380,линейное-фаза с нулем, 220…в учебниках по электротехнике подробности….
Как сказал Андрей — вопрос не на 4000 знаков. Читайте здесь <a rel=»nofollow» href=»http://electricalschool.info/main/osnovy/424-chto-takoe-peremennyjj-tok-i-chem-on.html» target=»_blank»>http://electricalschool.info/main/osnovy/424-chto-takoe-peremennyjj-tok-i-chem-on.html</a> или школьный учебник физики.
нулем в электросети является провод связанный с землей. Если рассматривать два провода электросети отдельно от земли, то ни ноль ни фазу обнаружить не удасться. Плюс и минус это другое. Это направление движения зарядов, и объективно существует. В сети переменного тока, например в нашей электросети, полярность ( плюс и минус) меняется 50 раз в секунду (частота 50 гц)
Переменный ток меняет фаза-земля с частотой 50г, но если в простейшем случае к проводу подключить диод (проводник тока в одну сторону) то на выходе будем иметь «выпрямленный ток» , а значит плюс и минус.
Эх вы электрики, не можите обьяснить простых вещей. Лезите со своими мега знаниями. Вот есть 2 контакта, 1 — фаза, 2 — ноль. Суть переменного напряжения заключается в том, что на контакте 1 меняется потенциал по синусоидальному закону, тоесть сначала он положительный и повышается, потом доходит до максимума, потом оставаясь положительным понижается, становится равным нулю, потом меняет знак и опять повышается до максимума и опять понижается до нуля. Контакт 2 — на нём нет никакого потенциала, он вкопан в Землю. Суть постоянного тока в том, что на этой самой фазе потенциал не меняется. P S Петр Драгунов не прав, фаза с нулём ни когда не меняется.
touch.otvet.mail.ru
Когда зрение минус и плюс
Знак близорукости: плюс или минус
НАШИ ЧИТАТЕЛИ РЕКОМЕНДУЮТ!
Для лечения суставов наши читатели успешно используют Око-плюс. Видя, такую популярность этого средства мы решили предложить его и вашему вниманию.
Подробнее здесь…
Часто от людей в очках можно услышать фразу: «У меня очки минус (или плюс) столько-то». Что значит эта фраза, и какой знак зрения у людей с близорукостью? И, вообще, близорукость это плюс или минус?
Что значит плюс или минус в обозначении остроты зрения
После исследования остроты зрения всем пациентам с нарушением рефракции проводят пробную коррекцию зрения с помощью линз. Линзы имеются двух типов: рассеивающие, обозначаемые в офтальмологии знаком «–» (минус), и собирающие – обозначаются «+» (плюсом).
Очки для близорукости уменьшают предметы, но делают их более четкими.
Для коррекции близорукости применяю рассеивающие или «отрицательные» линзы. Поэтому, когда говорят об очках или линзах для коррекции близорукости, всегда имеется ввиду минус, а не плюс. Напротив, для коррекции дальнозоркости применяю «положительные» или собирающие линзы, поэтому дальнозоркость – это «плюс».
Сколько «минусов» нужно для коррекции близорукости и «плюсов» — для дальнозоркости
Итак, мы выяснили, что близорукость – это минус, а дальнозоркость – это плюс. А что значат цифры, например -2, -3,75, +0,75 или любые другие?
Цифры обозначают оптическую силу линз, необходимых пациенту с близорукостью, чтобы четко увидеть 10 строку в таблице Сивцева. Сила линз выражается в диоптриях и может иметь дробное значение. При выписке рецепта на очки или на линзы для каждого глаза указывается свое значение силы линз.
Теперь вы знаете, когда знакомый очкарик говорит, что у него зрение «минус столько-то», значит у него близорукость или, как говорят врачи, миопия. И еще один совет, как определить знак зрения: очки для близорукости зрительно уменьшают предметы при взгляде сквозь них, а для дальнозоркости – увеличивают.
Капли для улучшения зрения «Око-плюс» — хочу видеть!
Уникальные по своему воздействию капли для улучшения зрения Око-плюс помогают вылечить глазные заболевания и значительно улучшить зрение. В поисках лучшего средства для укрепления глаз тысячи наших соотечественников остановили свой выбор именно на каплях Око-Плюс.

Все больше современных людей проводят значительную часть времени возле экранов мониторов. Это создает дополнительную нагрузку на глаза, что постепенно приводит к снижению остроты зрения, чувству боли и жжения, красноте глаз. Статистика неумолима: те или иные отклонения в зрении отмечают у каждого второго человека нашей планеты.
Чтобы избежать серьезных нарушений глаз, необходимо позаботиться об их здоровье при первых же признаках нарушения их функции. Большую роль играют специальная гимнастика для глаз, правильное питание, употребление нужных витаминов, прогулки на природе. Но подобных профилактических мер явно недостаточно.
Когда вам нужен Око-Плюс?
Проблемы с глазами начинаются незаметно. Поначалу человек может решить, что неприятные ощущения связаны с долгой работой или усталостью. Но со временем снижение остроты зрения дает о себе знать в полную силу. Глазные капли для улучшения остроты зрения Око-Плюс точно нужны, если:
- тяжело четко различать предметы на близком расстоянии – текст книги, экран телефона;
- предметы на расстоянии выглядят размытыми и нечеткими;
- возникает боль в области глазниц;
- глаза слезятся или наоборот остаются излишне сухими, перед глазами появляются «мошки»;
- постоянно возникает желание прищуриться, часто мигать, тереть глаза;
- есть чувство дискомфорта от очков или линз.
Слабое зрение заставляет постоянно щуриться, что неминуемо ведет к появлению ранних морщин в уголках глаз. С плохим зрением опасно водить машину, неудобно делать покупки, дискомфортно смотреть фильм или телевизор.
 Избавься от очков
Избавься от очков
При отсутствии лечения глазницы будут получать дополнительную нагрузку, что еще больше ослабит орган зрения и может привести к необратимым последствиям. Заболевания глаз могут привести к частичной, а иногда и полной слепоте. Наиболее опасные болезни глаз:
- глаукома – патология зрительного нерва, приводит к слепоте;
- катаракта – помутнение глазного хрусталика, значительное снижение остроты зрения, возможна слепота;
- отслоение сетчатки – пелена на глазах, требуется хирургическое вмешательство;
- синдром сухого глаза – постоянный дискомфорт в глазах;
- близорукость – нечеткое восприятие предметов на расстоянии, значительные неудобства в повседневной жизни, необходимость коррекции очками или линзами;
- коньюктивит – гнойные выделения, зуд и боль, может быть заразен.
Преимущества капель для улучшения зрения Око-Плюс
В отличие от других глазных капель и корректирующих средств, Око-Плюс устраняет главные причины, вызвавшие нарушения зрения. Оно является абсолютно безвредным для всего организма, подходит как взрослым, так и детям, продается по доступной цене. Препарат прошел многоступенчатое тестирование ведущими российскими учеными из ОфтальмоЦентра.
Регулируемые очки для идеального зрения! Скидка 50%Теперь вы сами можете настроить диоптрии для своих глаз. Читать подробнее… |
 Упаковка каплей «Око-плюс»
Упаковка каплей «Око-плюс»
На разработку уникального средства было потрачено 8 лет. Почти 90% наших соотечественников успешно применили Око-Плюс в своем лечении и абсолютное большинство из них оставили лишь положительные отзывы о препарате.
Одним из секретов эффективности средства является его растительный состав. В него входят:
- Лютеолин и зеаксантин – оказывают положительное влияние на сетчатку;
- Млечный сок клевера – снимает воспаление, устраняет красноту, зуд и жжение;
- Кариозин – поддерживает зрение на необходимом уровне, замедляет процесс старения;
- Экстракт ячменя – борется с инфекциями, снимает воспаления.
Положительный результат после приема капель отмечается уже после двух применений. Проникая в слизистую глаза, растительные компоненты переходят вглубь клеток, нормализуют давление глазного дна, усиливают кровообращение, убивают возможные вирусы, защищают хрусталик от возрастных изменений.
Око-Плюс подарит вам острое зрение
Капли Око-Плюс – отличная альтернатива рискованному хирургическому вмешательству и дорогостоящей лазерной коррекции. Удачное сочетание компонентов комплексно борется с нарушениями глаз на любом этапе, даже при начинающейся слепоте. Препарат не вызывает побочных эффектов и не имеет противопоказаний к применению.
Как пользоваться каплями для глаз для улучшения зрения Око-Плюс?
Для устойчивого положительного эффекта очень большое значение имеет регулярное применение капель для улучшения зрения. Оптимальный курс лечения – 1 месяц. Достаточно капнуть по одной капле в каждый глаз всего лишь один раз в сутки в удобное для вас время. Для закрепления успеха и с согласия врача курс приема средства можно повторить.
Зачем натирать себе виски и переносицу неудобными очками? Нужны ли вам линзы, которые вырывают значительные суммы из бюджета и требуют много времени и сил по уходу? Всего лишь несколько капель Око-Плюс в день помогут вам восстановить остроту зрения и снизят риск серьезных заболеваний глаз. С каплями Око-Плюс вы посмотрите на окружающий мир другими глазами!
Заказать капли для улучшения остротыЙ зрения вы можете на официальном сайте, либо сделав заказ через специальную форму внизу статьи, после чего с вами свяжется консультант для уточнения деталей заказа.
Близорукость это плюс или минус
Под близорукостью (миопией) понимают дефект зрения, при котором изображение формируется перед сетчаткой, а не на ней. За последнее десятилетия число лиц, у которых имеется данное заболевание, значительно выросло.
Близорукость развивается в основном у людей молодого возраста, школьников и студентов. Часто при появлении первых признаков данного состояния у многих лиц возникает вопрос: «близорукость – это плюс или минус».
Причины заболевания
Миопия наиболее часто развивается в школьные годы. При этом наследственность здесь играет далеко не последнюю роль. Среди факторов, способствующих развитию данного заболевания, можно выделить длительную работу на близком расстоянии при плохих гигиенических условиях или неправильном освещении. Виду массового распространения компьютеров, данная проблема приобретает серьёзный характер.
Если вовремя не принимаются меры по устранению близорукости, то это состояние может привести к необратимым изменениям и значительной утрате зрительной функции. Это в свою очередь частично или полностью ограничит трудоспособность.
Ослабление глазных мышц также способствует развитию миопии. Для решения этой проблемы разработаны специальные комплексы физических упражнений, которые могут применяться как с лечебной, так и профилактической целью.
В результате процессы прогрессирования данного заболевания часто замедляются или приостанавливаются. Раньше рекомендовалось ограничивать физическую активность лицам, страдающим миопией. Однако в настоящее время рекомендуются умеренные нагрузки с рациональным режимом отдыха и сна.
В молодом возрасте близорукость может вызываться спазмом аккомодации, изменением формы роговицы (кератоконусом), смещением при травмах хрусталика (вывих, подвывих), склерозом хрусталика. Последнее патологическое состояние приводит к развитию миопии в пожилом возрасте.
Коррекция высокой близорукости затруднительна и требует индивидуального подхода в подборе линз для дали и близи. При развитии старческой миопии по причине склероза хрусталика, осуществляется его замена или имплантация факичных линз.
Методы лечения и коррекции

Исходя из вышеуказанных фактов, можно сделать вывод, что данное заболевание является минусом, поэтому требует незамедлительного лечения. Особенно это касается средней (3,26-6 диоптрий) и высокой (свыше шести диоптрий) степени заболевания.
Слабая (до трёх диоптрий), а иногда и средняя форма миопии устраняется при помощи оптической коррекции для дали с использованием слабых (на одну-две диоптрии) линз для работы на близких расстояниях.
Для коррекции близорукости используются минусовые (отрицательные) линзы. При этом перед глазом пациента ставят отрицательные линзы, затем смотрят на результат. Начинают со слабых линз, если зрение не улучшается, то используют более сильные стёкла. В результате добиваются максимального восстановления зрения с использованием определённой минусовой линзы.
В непосредственной зависимости от степени миопии человек может испытывать временную или постоянную необходимость в очках. Современным способом лечения данного заболевания является лазерная коррекция. Однако она позволяет компенсировать близорукость.
Что такое птеригиум, причины возникновения, современные методы лечения.
О том, какое лечение рекомендуется при блефароконъюнктивите, вы сможете узнать на этой странице.
Профилактические меры
Для того, чтобы избежать близорукости, необходимо осуществлять профилактические меры. К ним можно отнести правильное освещение при чтении и работе за компьютером, выполнение специальных упражнений для глаз, правильная осанка и др.
Витаминотерапия поможет укрепить не только иммунитет, но и повысить восприимчивость зрительного аппарата к нагрузкам. Физиотерапевтические процедуры стимулируют кровообращение в ткани глаза. С этими целями могут использоваться специальные медикаментозные средства.
Таким образом, на вопрос: «близорукость – это плюс или минус», можно дать однозначный ответ: «минус», так как данное заболевание склонно к постоянному прогрессированию, может привести к полной утрате зрения. Именно поэтому крайне важна его профилактика и адекватная коррекция.
НАШИ ЧИТАТЕЛИ РЕКОМЕНДУЮТ!
Для лечения суставов наши читатели успешно используют Око-плюс. Видя, такую популярность этого средства мы решили предложить его и вашему вниманию.
Подробнее здесь…
1ozrenii.ru
Когда минус – это плюс
Кажется, мир сошел с ума. Все вокруг только и говорят, как обрести былую стройность и/или не потерять ее. Дамочки 90-60-90 с экранов телевизоров пьют таблетки для похудения, соцсети заполонили бесконечные фото в стиле «до и после», а подруга то и дело отказывается от кусочка пиццы в кафе, потому что «безнадежно разжирела» (на деле это часто означает +200 г на ее весах). Бороться с лишним весом стало модно, только вот далеко не все объясняется эстетикой тела: лишние килограммы не приходят одни, они приводят проблемы со здоровьем. И, может быть, уже не стоит так иронизировать по поводу всеобщего помешательства на достижении идеального веса и перестать скрываться за словами типа «Хорошего человека должно быть много» или «Меня и так все устраивает»? Давайте разберем, когда похудеть действительно – стоит.

Лишний вес – это, в первую очередь, угроза Вашему здоровью. Вы можете быть обаятельной пышечкой, всеми любимой и счастливой, но все же складочки на талии могут влиять и на Ваше самочувствие, и на работу внутренних органов.
Во-первых, если Вы не следите за своим весом и забыли, как выглядят вещи размера M и ниже, страдает Ваша сердечно-сосудистая система. Часто это выливается в такие заболевания, как гипертония, сахарный диабет, ишемическая болезнь сердца. Про сердце вообще отдельный разговор – как только стрелка на весах движется вправо, нагрузка на него сильно возрастает. Из-за повышенного давления начинается поражение жизненно важных органов (почки, головной мозг). Самый страшный диагноз-последствие гипертонии – инсульт.

Во-вторых, тучность вызывает заболевания опорно-двигательного аппарата. Очень многие полные люди ощущают боли в коленях. Суставы – это второй очаг поражения при лишнем весе, поэтому иногда об артрите или артрозе можно позабыть, просто скинув с себя балласт в виде ненужного жира.
В-третьих, нарушается работа органов дыхания. Одышка и полный человек – это практически синонимы. Все потому, что жизненная емкость легких становится ниже нормы.
В-четвертых, полнота часто сопровождается деформацией позвоночника, не способного справиться с такой нагрузкой. Нередко врачи при ожирении диагностируют и деформацию грудной клетки.
В-пятых, лишний вес серьезно «бьет» по печени и другим органам пищеварительной системы. Чаще всего его причиной является переедание (в том числе, совсем не здоровой пищей), поэтому врачи-диетологи так много говорят об очищении организма, в частности, желудочно-кишечного тракта, на первом этапе похудения.

Список можно продолжить, но общая картина уже понятна. Не за модой нужно гнаться, не за новым платьем размера XS, а за диагнозом «Здоров», поставленным специалистом. Вам с Вашим телом еще жить и жить, подумайте о нем, а оно, в свою очередь, подарит Вам (помимо здоровья) цветущий вид и привлекательного человека в зеркале.
Рекомендуемые вам статьи:
www.of-md.com
Когда минус…. превращается в плюс?
о том, что это «минус» можно точно утверждать по прошествии определенного времени. . как правило УМНЫЙ человек из любого «минуса» сделает для себя «плюс»
Минус на минус дают плюс)))
Когда находишь его в себе .
когда встречается с минусом
Когда успокоишься и трезво посмотришь на ситуацию.
когда два минуса притягиваются а потом тесно друг к другу прижимаются
Когда погода меняется. Был заморозок и уши мерзли, а потом вдруг потеплело. Красота.
когда есть Понимание и желание..)
один из лучших радость в душе начинается!
когда МЫ ЭТОГО ЗАХОТИМ!
когда меняется угол зрения — на обратный
touch.otvet.mail.ru
Ответы@Mail.Ru: Когда… минус становится плюсом?
Когда любишь..
когда ты одна ))))
кагда встречается ещё один минус
Минус на минус = плюс. Это же школьная математика.
Когда появляется ещё один минус. ) Математика, однако.
когда не торопишься..
Плюс — это когда два минуса становятся друг другу поперек горла… (
когда его перечеркиваешь
когда меньше жрёшь (-), фигура исправляется (+).
Когда мы его перечеркиваем.
— Я слышала ты развелась… Как ты это пережила? ? — Ой, да щас хоть успокоилась, а сначала думала с ума от радости сойду..!) *
touch.otvet.mail.ru








 ;
;  ;
;  ;
; 
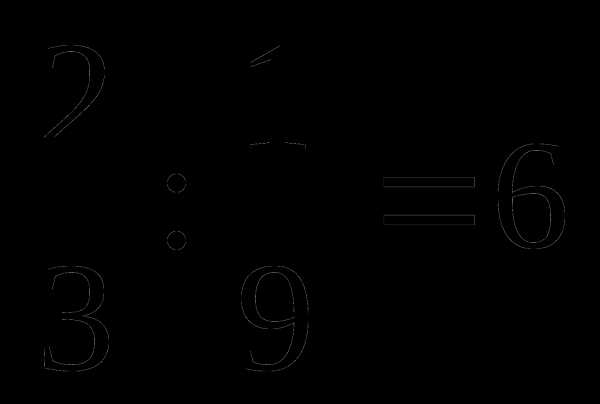 ;
; 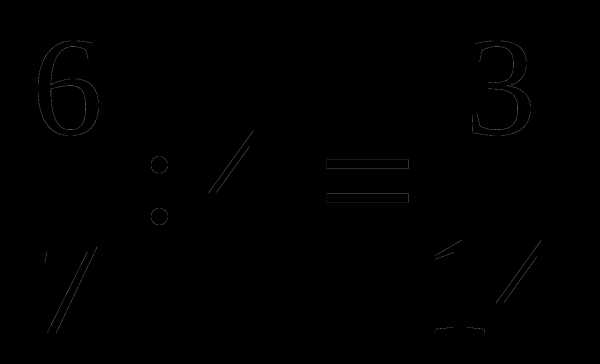 ;
;  ;
; 
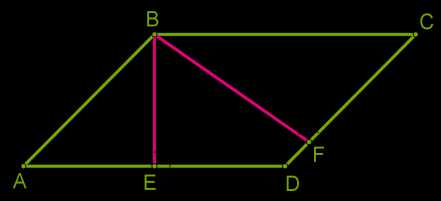
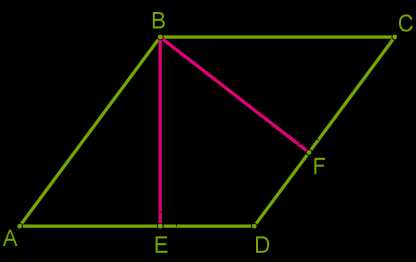





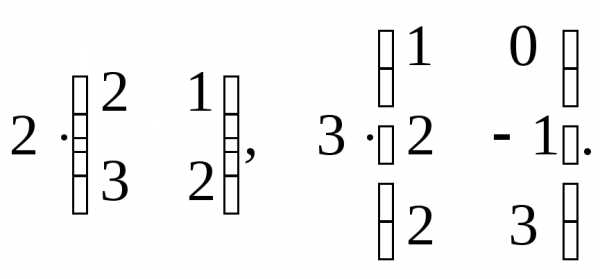
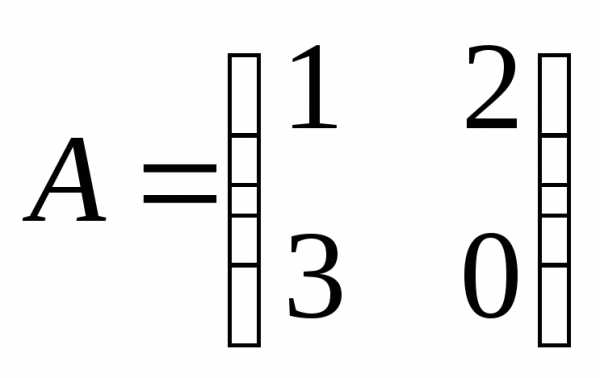 б)
б)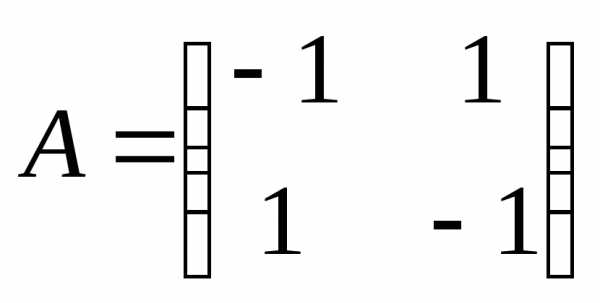 .
.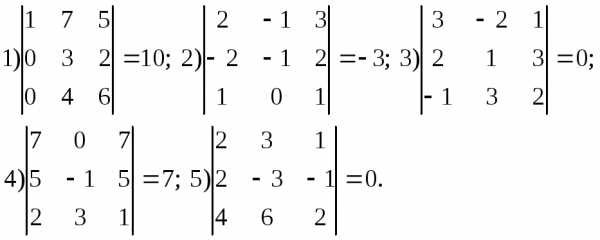
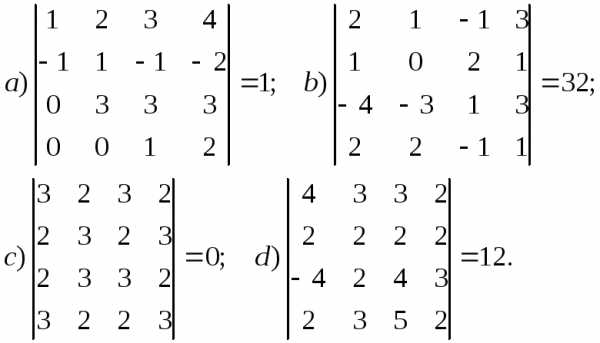
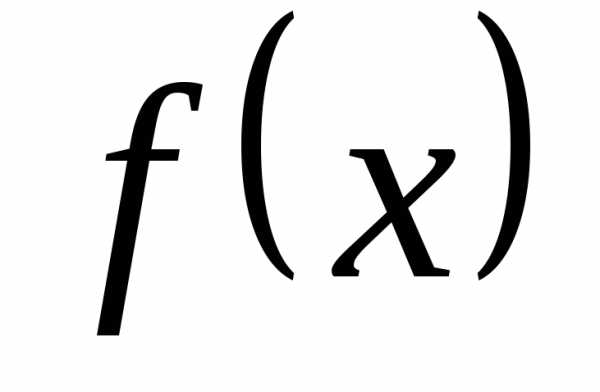 определена в (конечном или бесконечном)
промежутке .Функция
определена в (конечном или бесконечном)
промежутке .Функция 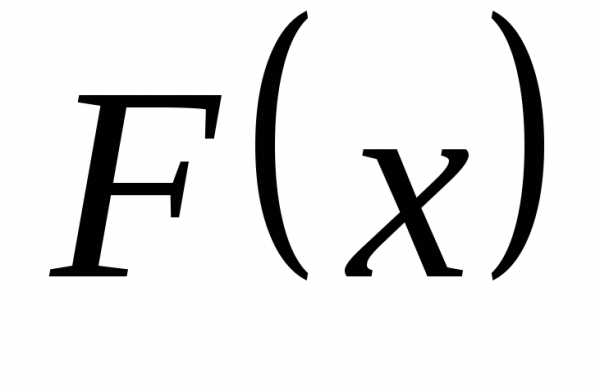 называетсяпервообразной
функцией для
называетсяпервообразной
функцией для 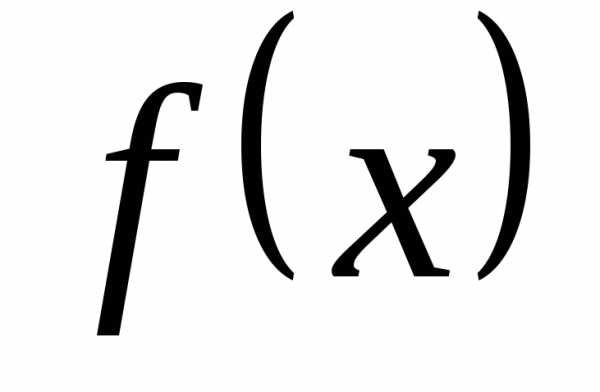 , если для любого
, если для любого 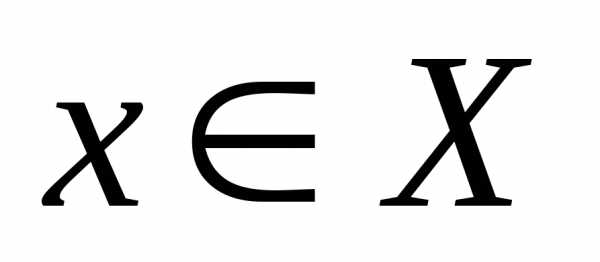 выполняется равенство:.
выполняется равенство:.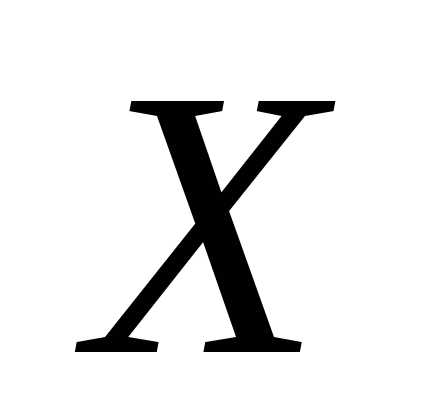 (конечном или бесконечном) функция
(конечном или бесконечном) функция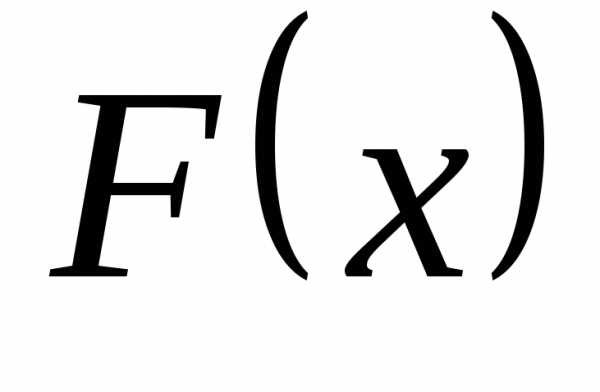 является первообразной для
является первообразной для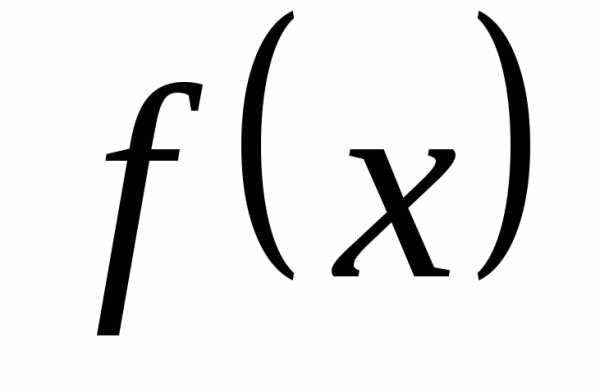 , то и
любая функция
, то и
любая функция 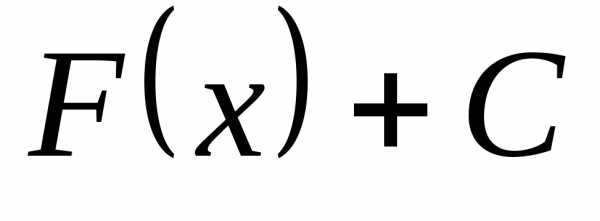 — тоже является первообразной для
— тоже является первообразной для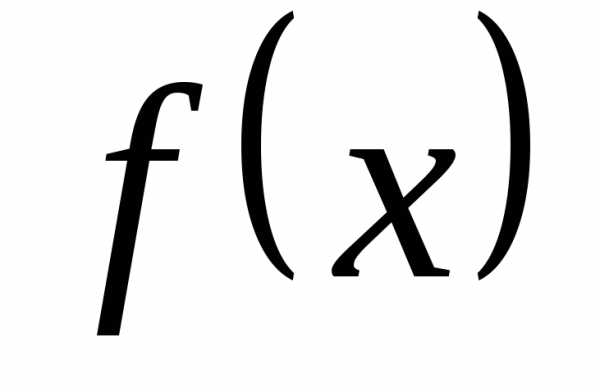 .
Обратно, для любой другой первообразной
функции
.
Обратно, для любой другой первообразной
функции 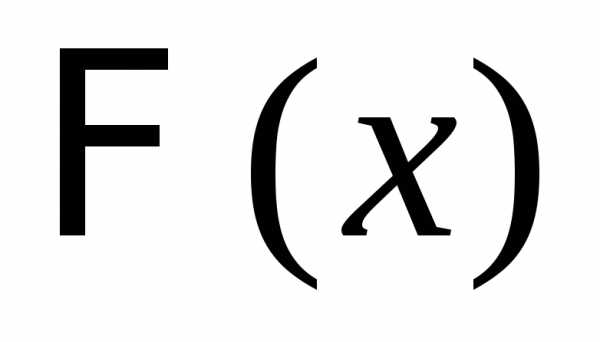 найдётся постоянная
найдётся постоянная  такая, что.
такая, что.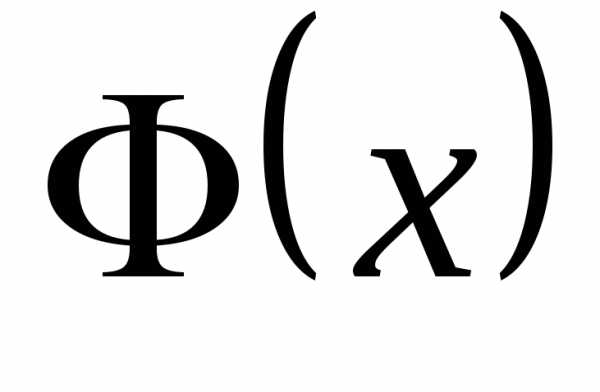 — какая-либо первообразная для
— какая-либо первообразная для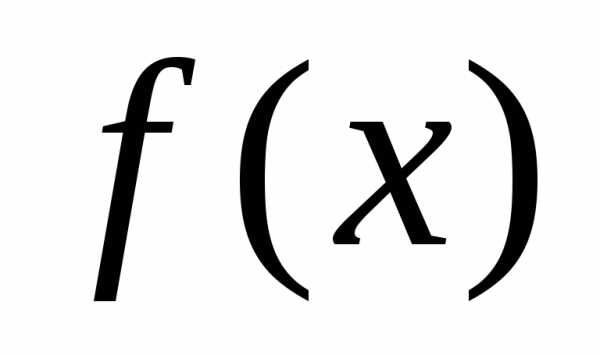 .
Рассмотрим разность.
Производная этой функции. По следствию
из теоремы 7.3. Лагранжа (критерию
постоянства функции на промежутке)
получим, что
,
что и требовалось доказать. ◄
.
Рассмотрим разность.
Производная этой функции. По следствию
из теоремы 7.3. Лагранжа (критерию
постоянства функции на промежутке)
получим, что
,
что и требовалось доказать. ◄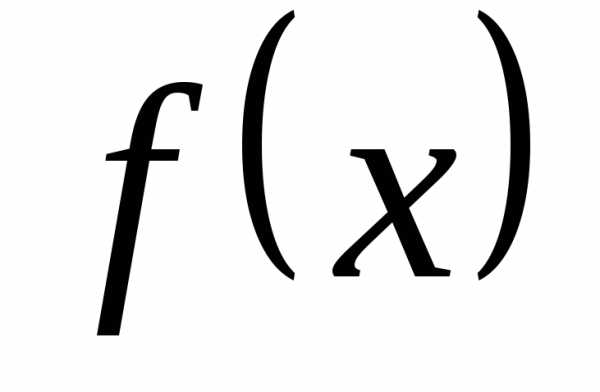 на заданном промежутке называется еёнеопределённым
интегралом и обозначается так:
на заданном промежутке называется еёнеопределённым
интегралом и обозначается так: 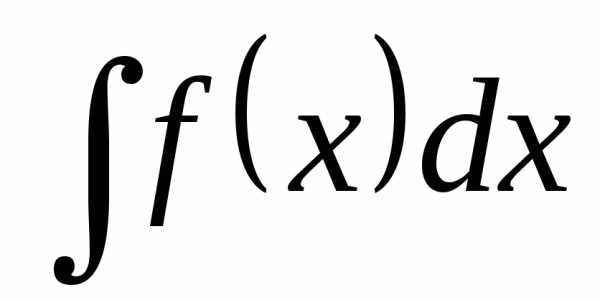 .
.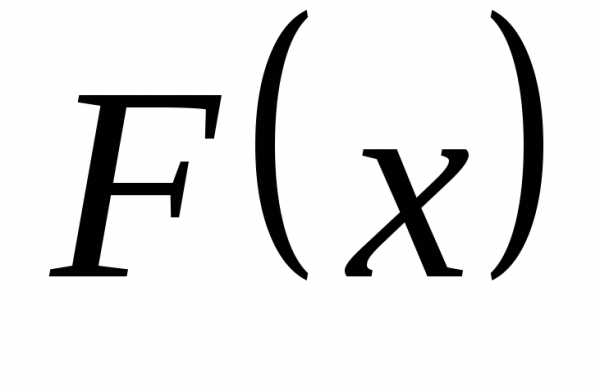 —
произвольная первообразная функция, а
—
произвольная первообразная функция, а —
произвольная постоянная. Обычно
используется обозначение,
в котором правая часть равенства
обозначает не одну из функций, а всё
семейство функций, образующих интеграл.
—
произвольная постоянная. Обычно
используется обозначение,
в котором правая часть равенства
обозначает не одну из функций, а всё
семейство функций, образующих интеграл.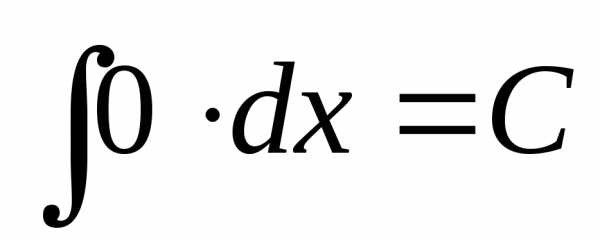
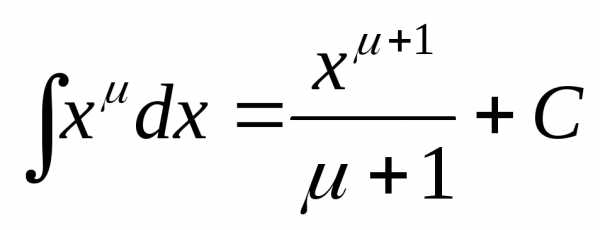 ,
,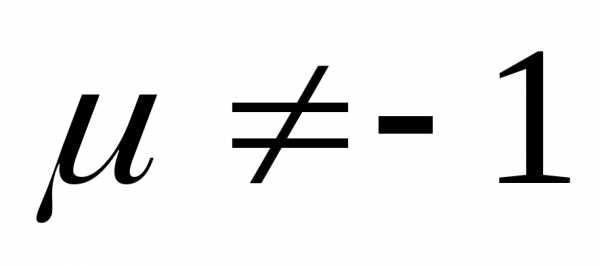 .
.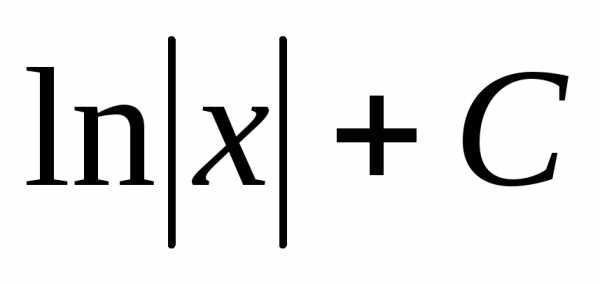 .
При этом следует иметь в виду, что
множество, на котором определена функция
.
При этом следует иметь в виду, что
множество, на котором определена функция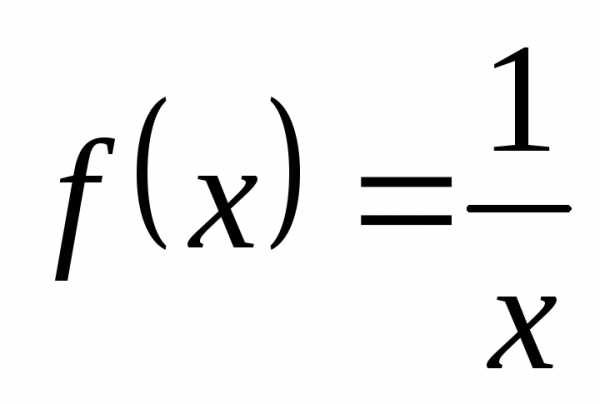 ,
состоит из двух промежутков, задаваемых
неравенствами
,
состоит из двух промежутков, задаваемых
неравенствами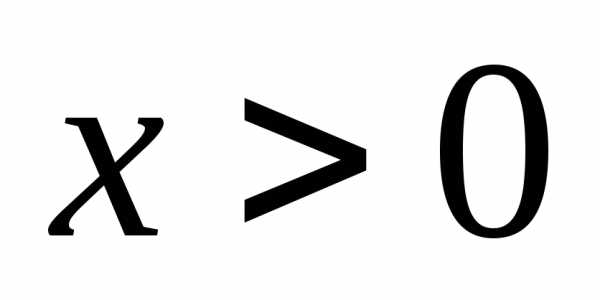 и,
соответственно. На каждом из этих
промежутков постоянную можно выбирать
независимо, что и отражено в формуле 4.
Так что формулу
и,
соответственно. На каждом из этих
промежутков постоянную можно выбирать
независимо, что и отражено в формуле 4.
Так что формулу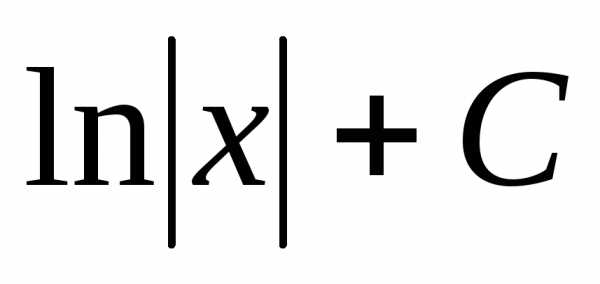 не следует понимать так, что к функции
не следует понимать так, что к функции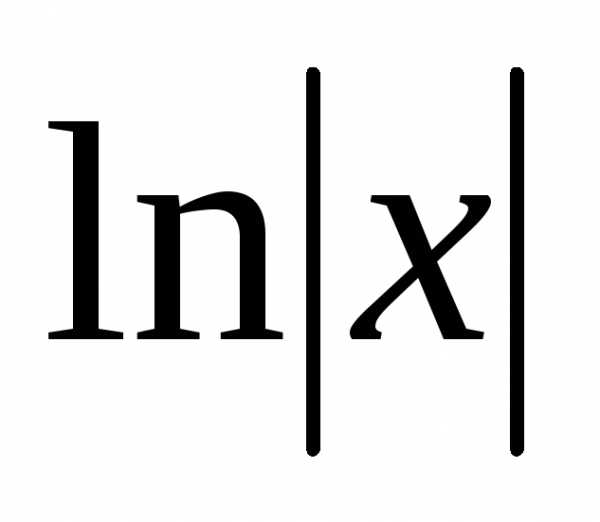 прибавляется одна и та же постоянная
прибавляется одна и та же постоянная как при
как при 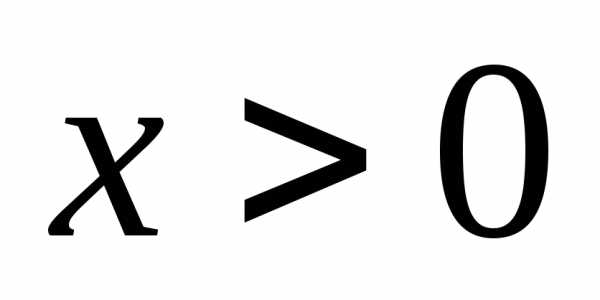 ,
так и при
,
так и при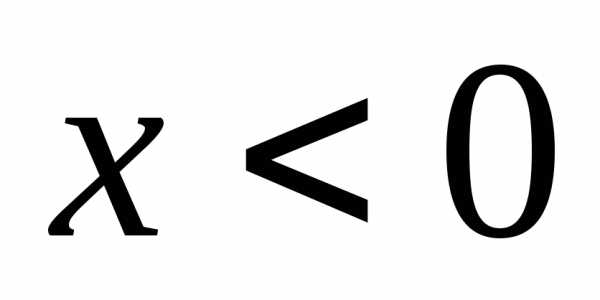 .
Еще раз повторим – точный смысл дан
равенством 4.
.
Еще раз повторим – точный смысл дан
равенством 4.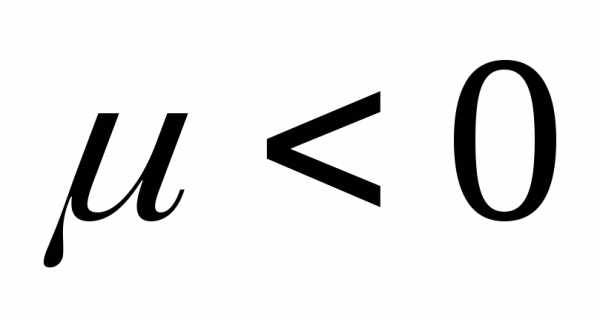 и таком, что
и таком, что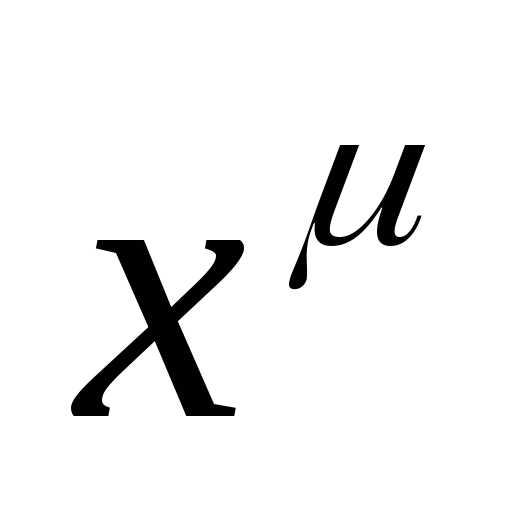 определена как при
определена как при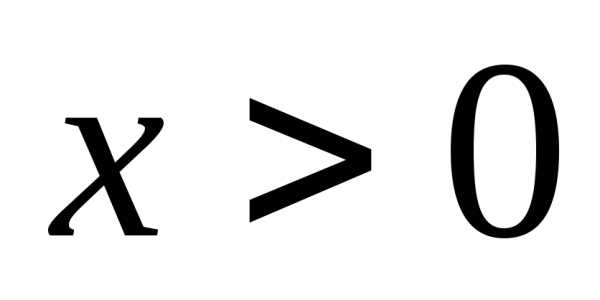 ,
так и при
,
так и при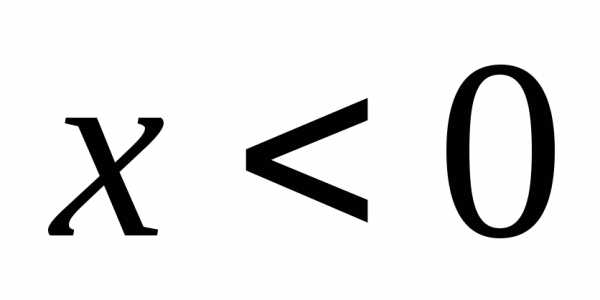 .
.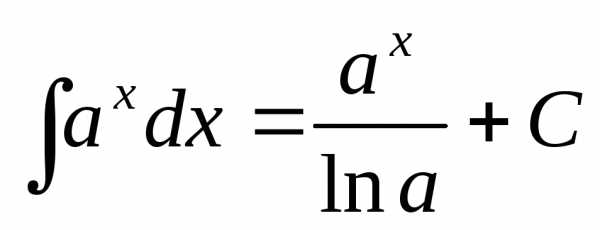 ,
в частности,
,
в частности,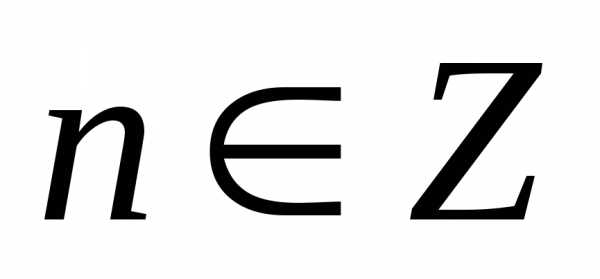 ,
для каждого
,
для каждого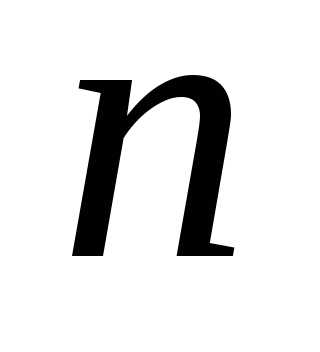 следует выбирать свою постоянную
следует выбирать свою постоянную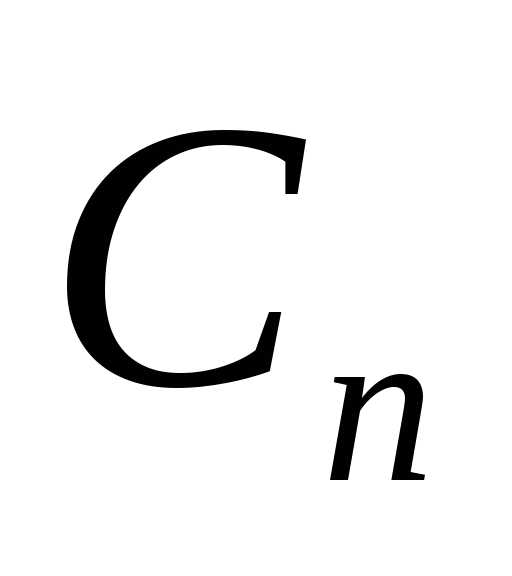 (так
же, как это было сделано в пункте 4).
(так
же, как это было сделано в пункте 4).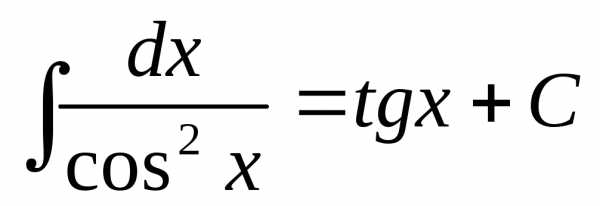 ,
,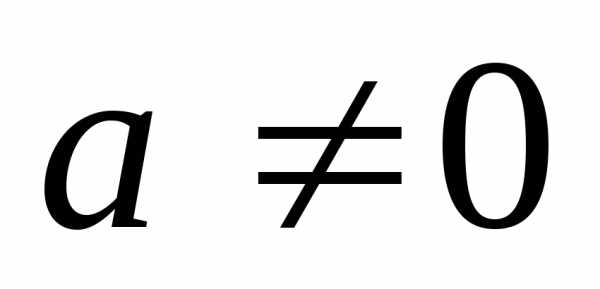 ,
то
,
то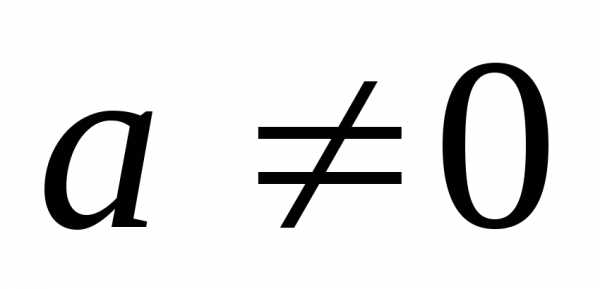 существенно
для справедливости этого равенства.
При
существенно
для справедливости этого равенства.
При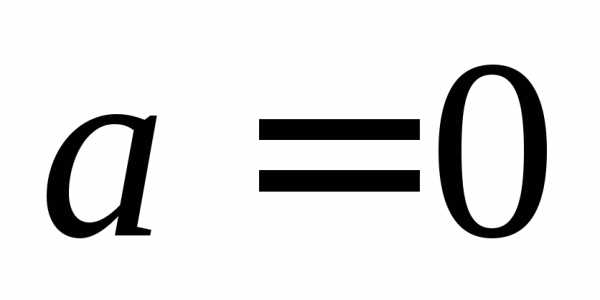 левая часть этого равенства представляет
собой множество постоянных функций, а
множество в правой части состоит только
из тождественно равной нулю функции,
притом при условии, что
левая часть этого равенства представляет
собой множество постоянных функций, а
множество в правой части состоит только
из тождественно равной нулю функции,
притом при условии, что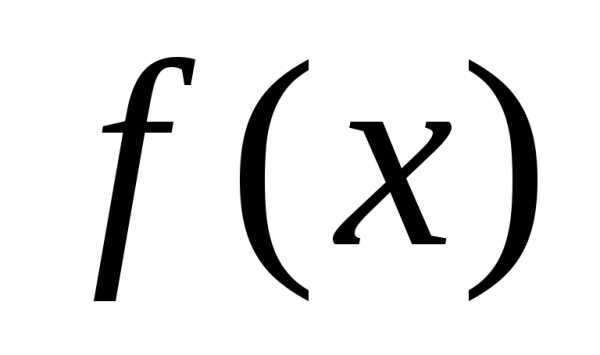 имеет первообразную функцию.
имеет первообразную функцию.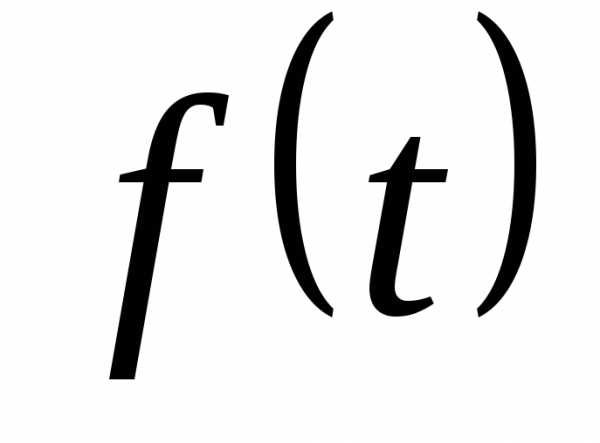 — непрерывная функция, то для любой
функции
— непрерывная функция, то для любой
функции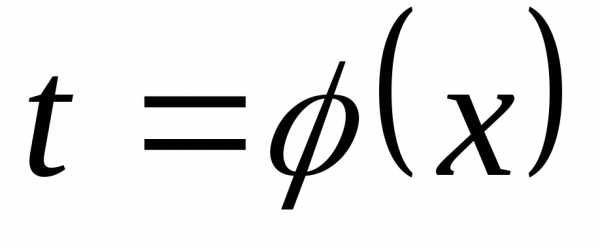 ,
такой, что
,
такой, что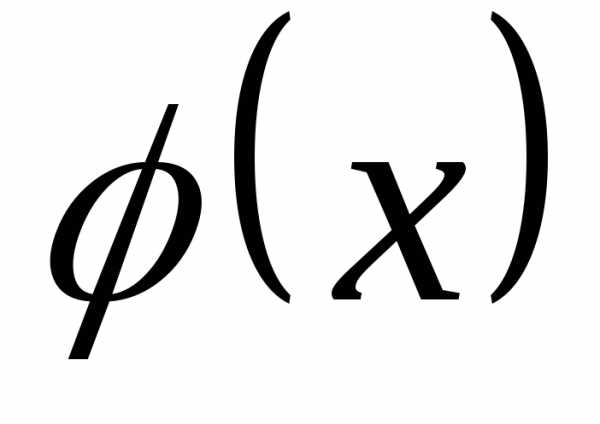 и
и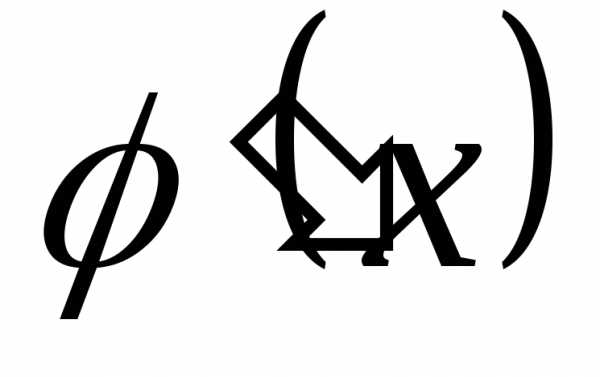 — непрерывные функции, и такой, что
— непрерывные функции, и такой, что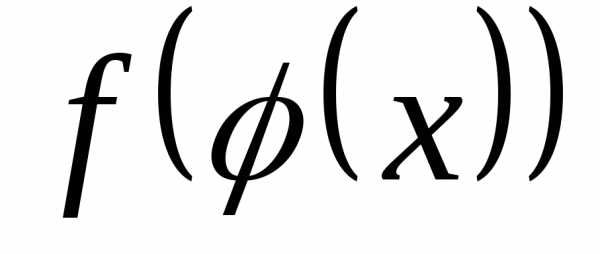 — определена, имеет место равенство
— определена, имеет место равенство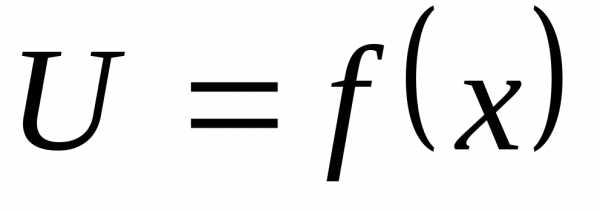 и
и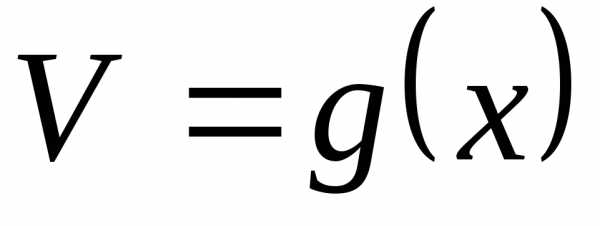 — непрерывные функции и пусть,
— непрерывные функции и пусть,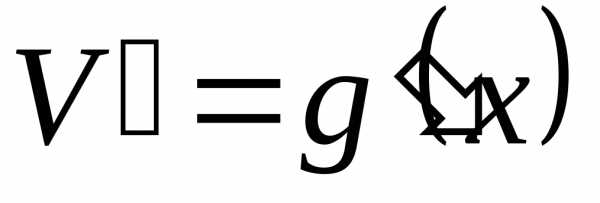 — тоже непрерывные функции. Тогда
— тоже непрерывные функции. Тогда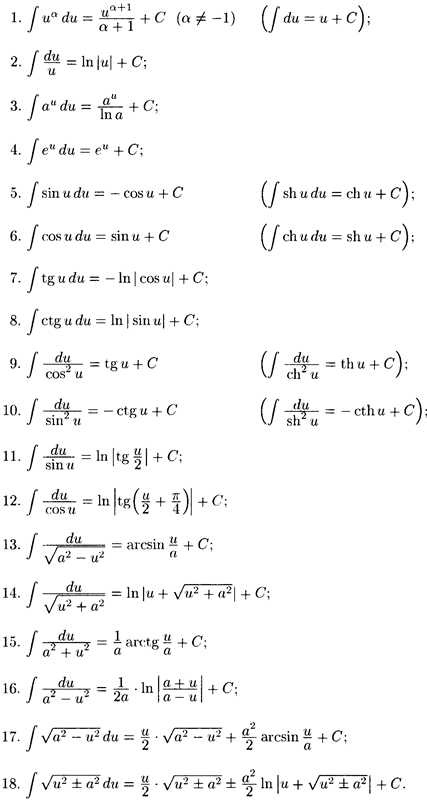

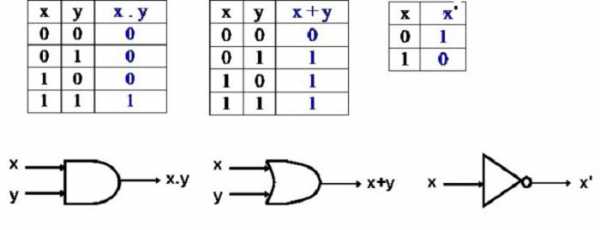
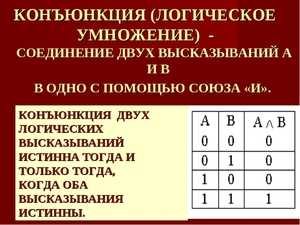
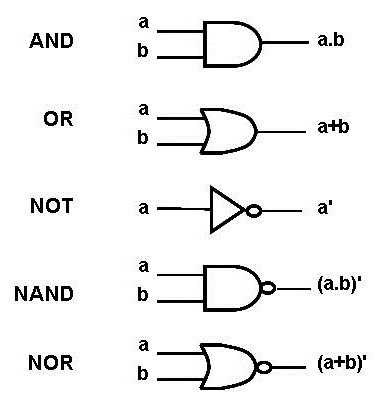 А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.
А, второе — В. Логические операции в информатике, обозначающие действие сложения (или дизъюнкция), при написании обозначаются либо словом «или», либо значком «v». Распишем возможные варианты данных и результаты вычислений.